We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that a form of the Erdӧs property (consistent with V = L[Hω2] and strictly weaker than the Weak Chang's Conjecture at ω1), together with Bounded Martin's Maximum implies that Woodin's principle ψAC holds, and therefore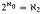 
. We also prove that ψAC implies that every function f: ω1 → ω1 is bounded by some canonical function on a club and use this to produce a model of the Bounded Semiproper Forcing Axiom in which Bounded Martin's Maximum fails.
