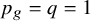1 Introduction
In order to distinguish smooth projective varieties varying in a family with continuous parameters, it is often useful to integrate the holomorphic forms over topological cycles. This idea wasused to great effect classically to distinguish smooth curves of a given genus
![]() $g>0$
. A modern reformulation of this problem in higher dimension asks whether the period mapping from a moduli space of varieties to an associated space of periodsis injective, either locally or globally on the source. We will show that while the local injectivity statement is true generically, the global statement fails for an important class of ellipticsurfaces.
$g>0$
. A modern reformulation of this problem in higher dimension asks whether the period mapping from a moduli space of varieties to an associated space of periodsis injective, either locally or globally on the source. We will show that while the local injectivity statement is true generically, the global statement fails for an important class of ellipticsurfaces.
An elliptic surface is a smooth, projective surface S equipped with a relatively minimal, genus one fibration
![]() $\pi \colon S\to C$
to a smooth curve and a distinguished section s. Moduli spaces
$\pi \colon S\to C$
to a smooth curve and a distinguished section s. Moduli spaces
![]() $F_{g,d}$
of elliptic surfaces are indexed by two nonnegative integers,
$F_{g,d}$
of elliptic surfaces are indexed by two nonnegative integers,
![]() $g=g(C)$
and
$g=g(C)$
and
![]() $d=\tfrac {1}{12}\chi _{\mathrm {top}}(S)$
. Counted with multiplicity, there are
$d=\tfrac {1}{12}\chi _{\mathrm {top}}(S)$
. Counted with multiplicity, there are
![]() $12d$
singular fibers. The canonical bundle of S is pulled back from a line bundle
$12d$
singular fibers. The canonical bundle of S is pulled back from a line bundle
![]() $L\otimes \omega _C$
of degree
$L\otimes \omega _C$
of degree
![]() $d+2g-2$
on C. We henceforth assume
$d+2g-2$
on C. We henceforth assume
![]() $d>0$
(that is, S has at least one singular fiber) so that
$d>0$
(that is, S has at least one singular fiber) so that
![]() $p_g(S):=h^0(K_S)=g+d-1$
.
$p_g(S):=h^0(K_S)=g+d-1$
.
In this paper, we focus on the moduli space
![]() $F:=F_{1,1}$
. Since
$F:=F_{1,1}$
. Since
![]() $g(C)=1$
,
$g(C)=1$
,
![]() $K_S=\pi ^*L$
for a degree
$K_S=\pi ^*L$
for a degree
![]() $1$
line bundle
$1$
line bundle
![]() $L={\mathcal O}_C(p)$
, and generically the fibration
$L={\mathcal O}_C(p)$
, and generically the fibration
![]() $\pi $
has
$\pi $
has
![]() $12$
singular fibers. There is a morphism
$12$
singular fibers. There is a morphism
![]() $S\to {\overline S}$
contracting ADE configurations in fibers not intersecting the section s. This contraction has a Weierstrass form [Reference KasKas77]
$S\to {\overline S}$
contracting ADE configurations in fibers not intersecting the section s. This contraction has a Weierstrass form [Reference KasKas77]
where
![]() $a\in H^0(C,L^4)$
and
$a\in H^0(C,L^4)$
and
![]() $b\in H^0(C,L^6)$
. A quick parameter count reveals that
$b\in H^0(C,L^6)$
. A quick parameter count reveals that
![]() $\dim F = 1 + 4 + 6 - 1=10$
where the parameters are, respectively, the j-invariant of
$\dim F = 1 + 4 + 6 - 1=10$
where the parameters are, respectively, the j-invariant of
![]() $(C,p)$
, the section a, the section b and the quotient by the action of
$(C,p)$
, the section a, the section b and the quotient by the action of
![]() $\lambda \in {\mathbb {C}}^*$
via
$\lambda \in {\mathbb {C}}^*$
via
![]() $(a,b)\mapsto (\lambda ^4a,\lambda ^6b)$
.
$(a,b)\mapsto (\lambda ^4a,\lambda ^6b)$
.
Noether’s formula implies that the Hodge numbers of S are
![]() $h^{2,0}(S)=h^{1,0}(S)=1$
and
$h^{2,0}(S)=h^{1,0}(S)=1$
and
![]() $h^{1,1}(S)=12$
. The Neron-Severi group
$h^{1,1}(S)=12$
. The Neron-Severi group
![]() $\mathrm {NS}(S)=H^{1,1}(S,{\mathbb {C}})\cap H^2(S,{\mathbb {Z}})$
always contains the classes of the fiber f and section s which have intersection numbers
$\mathrm {NS}(S)=H^{1,1}(S,{\mathbb {C}})\cap H^2(S,{\mathbb {Z}})$
always contains the classes of the fiber f and section s which have intersection numbers
![]() $s^2=-1$
,
$s^2=-1$
,
![]() $s\cdot f=1$
,
$s\cdot f=1$
,
![]() $f^2=0$
. Hence, there is a copy of the odd unimodular lattice
$f^2=0$
. Hence, there is a copy of the odd unimodular lattice
Its orthogonal complement
![]() $\{s,f\}^\perp \subset H^2(S,{\mathbb {Z}})$
is an even (since
$\{s,f\}^\perp \subset H^2(S,{\mathbb {Z}})$
is an even (since
![]() $[K_S]=f$
), unimodular lattice of signature
$[K_S]=f$
), unimodular lattice of signature
![]() $(2,10)$
, so it is isometric to
$(2,10)$
, so it is isometric to
![]() $I\!I_{2,10}=H\oplus H\oplus E_8$
.
$I\!I_{2,10}=H\oplus H\oplus E_8$
.
Let
![]() $\Gamma :=O(I\!I_{2,10})$
and define the period domain to be
$\Gamma :=O(I\!I_{2,10})$
and define the period domain to be
It is a ten-dimensional Type IV Hermitian symmetric domain. By general results of Griffiths [Reference GriffithsGri68], there is a holomorphic periodmap
![]() $P\colon F\to {\mathbb D}/\Gamma $
sending
$P\colon F\to {\mathbb D}/\Gamma $
sending
![]() $[S]\in F$
to the line
$[S]\in F$
to the line
![]() $H^{2,0}(S)\subset \{s,f\}^\perp \otimes {\mathbb {C}}$
. This map is only well-defined mod
$H^{2,0}(S)\subset \{s,f\}^\perp \otimes {\mathbb {C}}$
. This map is only well-defined mod
![]() $\Gamma $
since the isometry
$\Gamma $
since the isometry
![]() $\{s,f\}^\perp \to I\!I_{2,10}$
is ambiguous up to post-composition by an element of
$\{s,f\}^\perp \to I\!I_{2,10}$
is ambiguous up to post-composition by an element of
![]() $\Gamma $
. We may now state the first theorem of the paper:
$\Gamma $
. We may now state the first theorem of the paper:
Theorem 1.1. P is dominant.
Remark 1.2. For surfaces S with
![]() $h^{2,0}(S)\geq 2$
, the associated period map cannot be dominant due to Griffiths transversality. The general member
$h^{2,0}(S)\geq 2$
, the associated period map cannot be dominant due to Griffiths transversality. The general member
![]() $S\in F_{g,d}$
satisfies
$S\in F_{g,d}$
satisfies
![]() $h^{2,0}(S)= 1$
only when
$h^{2,0}(S)= 1$
only when
![]() $(g,d)=(1,1)$
or
$(g,d)=(1,1)$
or
![]() $(g,d)=(0,2)$
. In the latter case, the surfaces under consideration are elliptic K3 surfaces. By the Torelli theorem for K3 surfaces [Reference Pjateckiĭ-Shapiro and ShafarevičPSS71, Reference Looijenga and PetersLP81], the period mapping gives an isomorphism onto the corresponding period space.
$(g,d)=(0,2)$
. In the latter case, the surfaces under consideration are elliptic K3 surfaces. By the Torelli theorem for K3 surfaces [Reference Pjateckiĭ-Shapiro and ShafarevičPSS71, Reference Looijenga and PetersLP81], the period mapping gives an isomorphism onto the corresponding period space.
A local, respectively infinitesimal, Torelli theorem verifies the local injectivity of P, respectively injectivity of
![]() $dP$
, at some point. Such a result implies that P is generically finite onto its image. A generic Torelli theorem further proves thatP is generically one-to-one onto its image. Finally, a global Torelli theorem implies that P is an embedding, or an isomorphism if thedimensions are appropriate. We prove that, unlike for K3 surfaces,
$dP$
, at some point. Such a result implies that P is generically finite onto its image. A generic Torelli theorem further proves thatP is generically one-to-one onto its image. Finally, a global Torelli theorem implies that P is an embedding, or an isomorphism if thedimensions are appropriate. We prove that, unlike for K3 surfaces,
Theorem 1.3.
![]() $\deg P>1$
. Thus, generic Torelli is false for
$\deg P>1$
. Thus, generic Torelli is false for
![]() $P\colon F\to {\mathbb D}/\Gamma $
.
$P\colon F\to {\mathbb D}/\Gamma $
.
Remark 1.4. By a result of Lönne [Reference LönneLö2], the monodromy representation for the universal family over F is the subgroup of
![]() $O(I\!I_{2,10})$
preserving the connected component of
$O(I\!I_{2,10})$
preserving the connected component of
![]() ${\mathbb D}$
, so P does not factor through
${\mathbb D}$
, so P does not factor through
![]() ${\mathbb D} /\Gamma '$
for any subgroup
${\mathbb D} /\Gamma '$
for any subgroup
![]() $\Gamma '\subset \Gamma $
.
$\Gamma '\subset \Gamma $
.
To prove Theorem 1.1, we employ a degeneration argument, similar to Friedman’s proof [Reference FriedmanFri84] ofthe Torelli theorem for K3 surfaces. First degenerate the base curve C to a nodal curve
![]() $C_0$
formed from gluing two points on
$C_0$
formed from gluing two points on
![]() $\mathbb {P}^1$
. An elliptic fibration
$\mathbb {P}^1$
. An elliptic fibration
![]() $S\to C$
may be degenerated to an elliptic fibration
$S\to C$
may be degenerated to an elliptic fibration
![]() $S_0\to C_0$
, and the simplest case is when the fiber over the node of
$S_0\to C_0$
, and the simplest case is when the fiber over the node of
![]() $C_0$
is smooth. Normalizing,
$C_0$
is smooth. Normalizing,
is an elliptic fibration with
![]() $(g,d)=(0,1)$
– that is, a rational elliptic surface. To reconstruct
$(g,d)=(0,1)$
– that is, a rational elliptic surface. To reconstruct
![]() $S_0$
from X, we glue two smooth fibers
$S_0$
from X, we glue two smooth fibers
![]() $X_p$
and
$X_p$
and
![]() $X_q$
for
$X_q$
for
![]() $p,q\in \mathbb {P}^1$
in such a way that a section of
$p,q\in \mathbb {P}^1$
in such a way that a section of
![]() $X\to {\mathbb P}^1$
is glued to form a section of
$X\to {\mathbb P}^1$
is glued to form a section of
![]() $S_0 \to C_0$
.
$S_0 \to C_0$
.
The period map for such singular surfaces
![]() $S_0$
does not land in
$S_0$
does not land in
![]() ${\mathbb D}/\Gamma $
, but maps into the boundary divisor
${\mathbb D}/\Gamma $
, but maps into the boundary divisor
![]() $\Delta $
of a toroidal extension
$\Delta $
of a toroidal extension
![]() ${\mathbb D}/\Gamma \hookrightarrow ({\mathbb D}/\Gamma )^{\mathrm {II}}$
. It suffices to prove that the boundary period map
${\mathbb D}/\Gamma \hookrightarrow ({\mathbb D}/\Gamma )^{\mathrm {II}}$
. It suffices to prove that the boundary period map
![]() $P^{\mathrm {II}}\colon \{\textrm {moduli of }S_0\}\to \Delta $
is dominant. We find an explicit surface
$P^{\mathrm {II}}\colon \{\textrm {moduli of }S_0\}\to \Delta $
is dominant. We find an explicit surface
![]() $S_0$
for which any deformation of its period deforms its moduli. Thus,
$S_0$
for which any deformation of its period deforms its moduli. Thus,
![]() $P^{\mathrm {II}}$
has at least one fiber containing a
$P^{\mathrm {II}}$
has at least one fiber containing a
![]() $0$
-dimensional component, implying dominance of
$0$
-dimensional component, implying dominance of
![]() $P^{\mathrm {II}}$
, and in turn, P.
$P^{\mathrm {II}}$
, and in turn, P.
To prove Theorem 1.3, we describe a second type of degeneration of
![]() $S\to C$
, to a fibration
$S\to C$
, to a fibration
![]() $S_0\to C$
(here the base stays constant) whose generic fiber is a nodal curve. We analyze the limiting period mapping for these surfaces and prove that they too map dominantly into theboundary divisor
$S_0\to C$
(here the base stays constant) whose generic fiber is a nodal curve. We analyze the limiting period mapping for these surfaces and prove that they too map dominantly into theboundary divisor
![]() $\Delta $
. Since two different degenerations dominate the same divisor
$\Delta $
. Since two different degenerations dominate the same divisor
![]() $\Delta $
, we obtain that
$\Delta $
, we obtain that
![]() $\deg P>1$
.
$\deg P>1$
.
Our method of proof suggests an interesting conjecture. Each surface
![]() $S\in F$
contains two natural elliptic curves meeting at a point: the unique representative of the canonical class
$S\in F$
contains two natural elliptic curves meeting at a point: the unique representative of the canonical class
![]() $K_S$
and the marked section curve s. The degenerations we employ in the proof leave one of these curves fixed and degenerate the other to a nodal curve. Conjecture4.5 describes a birational involution of F, which commutes with the period mapping, and swaps the roles of the two naturalelliptic curves.
$K_S$
and the marked section curve s. The degenerations we employ in the proof leave one of these curves fixed and degenerate the other to a nodal curve. Conjecture4.5 describes a birational involution of F, which commutes with the period mapping, and swaps the roles of the two naturalelliptic curves.
History of the result
In 1983, M.-H. Saito [Reference SaitoSai83] claimed to prove the following infinitesimal Torelli theorem for elliptic surfaces: the differential
![]() $dP$
is injective if the j-invariant map
$dP$
is injective if the j-invariant map
![]() $j\colon C\to \mathbb {P}^1_j$
is non-constant, and
$j\colon C\to \mathbb {P}^1_j$
is non-constant, and
![]() $h^{2,0}(S) = g+d-1>0$
. However, in 2019, Ikeda [Reference IkedaIke19] found a four-dimensional family
$h^{2,0}(S) = g+d-1>0$
. However, in 2019, Ikeda [Reference IkedaIke19] found a four-dimensional family
![]() ${\mathcal B} \subset F_{1,1}$
for which
${\mathcal B} \subset F_{1,1}$
for which
![]() $P\big {|}_{\mathcal B}$
has three-dimensional image, despite the general member of
$P\big {|}_{\mathcal B}$
has three-dimensional image, despite the general member of
![]() ${\mathcal B}$
having non-constant j-map. Thus, [Reference SaitoSai83] has a gap, but the proof still works when
${\mathcal B}$
having non-constant j-map. Thus, [Reference SaitoSai83] has a gap, but the proof still works when
![]() $\omega _S$
is basepoint free. Observe that
$\omega _S$
is basepoint free. Observe that
![]() $\omega _S \simeq \pi ^*(L\otimes \omega _C)$
is basepoint free for all
$\omega _S \simeq \pi ^*(L\otimes \omega _C)$
is basepoint free for all
![]() $S\in F_{g,d}$
when
$S\in F_{g,d}$
when
![]() $g>0$
and
$g>0$
and
![]() $d>1$
, and
$d>1$
, and
![]() $\omega _S$
is basepoint free for generic
$\omega _S$
is basepoint free for generic
![]() $S\in F_{g,d}$
when
$S\in F_{g,d}$
when
![]() $g>1$
and
$g>1$
and
![]() $d=1$
. The only cases where
$d=1$
. The only cases where
![]() $\omega _S$
fails to be basepoint free for generic S are
$\omega _S$
fails to be basepoint free for generic S are
![]() $(g,d)=(1,1)$
and
$(g,d)=(1,1)$
and
![]() $(g,d)=(0,1)$
. The latter is the case of rational elliptic surfaces, where the period map is trivial.
$(g,d)=(0,1)$
. The latter is the case of rational elliptic surfaces, where the period map is trivial.
In 2020, R. Kloosterman [Reference KloostermanKlo22] independently proved that the infinitesimal Torelli theorem holds for elliptic surfaces with non-constantj-map when
![]() $d\neq 1$
, or when
$d\neq 1$
, or when
![]() $d=1$
and
$d=1$
and
![]() $h^0(C,L)=0$
. The techniques generalized those of Kiĭ [Reference KiĭKiĭ78] and Lieberman-Wilsker-Peters [Reference Lieberman, Wilsker and PetersLWP77] from the
$h^0(C,L)=0$
. The techniques generalized those of Kiĭ [Reference KiĭKiĭ78] and Lieberman-Wilsker-Peters [Reference Lieberman, Wilsker and PetersLWP77] from the
![]() $g=0$
case. Conversely, Kloosterman conjectured [Reference KloostermanKlo22, Conj. 6.1] that when
$g=0$
case. Conversely, Kloosterman conjectured [Reference KloostermanKlo22, Conj. 6.1] that when
![]() $d=h^0(C,L)=1$
, the infinitesimal Torelli theorem is false. But this condition holds at every point of
$d=h^0(C,L)=1$
, the infinitesimal Torelli theorem is false. But this condition holds at every point of
![]() $F_{1,1}$
, so our Theorem 1.1 proves that Kloosterman’s conjecture is, in fact, false.
$F_{1,1}$
, so our Theorem 1.1 proves that Kloosterman’s conjecture is, in fact, false.
Regarding a generic Torelli theorem, Chakiris [Reference ChakirisCha82] proved that generic Torelli holds in the
![]() $g=0$
,
$g=0$
,
![]() $d\geq 2$
case. Recently, Shepherd-Barron [Reference Shepherd-BarronSB20] has generalized these results to a higher genus base: elliptic surfaces
$d\geq 2$
case. Recently, Shepherd-Barron [Reference Shepherd-BarronSB20] has generalized these results to a higher genus base: elliptic surfaces
![]() $S\to C$
with
$S\to C$
with
![]() $q=h^{1,0}(S)$
and
$q=h^{1,0}(S)$
and
![]() $p_g=h^{2,0}(S)$
satisfying the bounds
$p_g=h^{2,0}(S)$
satisfying the bounds
![]() $4p_g>5(q-1)$
,
$4p_g>5(q-1)$
,
![]() $p_g\geq q+3$
also obey a generic Torelli theorem. By our Theorem 1.3, generic Torelli is false when
$p_g\geq q+3$
also obey a generic Torelli theorem. By our Theorem 1.3, generic Torelli is false when
![]() $p_g=q=1$
. Hence, the second linear inequality
$p_g=q=1$
. Hence, the second linear inequality
![]() $p_g\geq q+3$
appears to be necessary for Shepherd-Barron’s results to hold.
$p_g\geq q+3$
appears to be necessary for Shepherd-Barron’s results to hold.
2 Type II
 $_b$
degenerations
$_b$
degenerations
Let
![]() $\pi _0\colon S_0\to C_0$
be an elliptic fibration over an irreducible, nodal, arithmetic genus one curve
$\pi _0\colon S_0\to C_0$
be an elliptic fibration over an irreducible, nodal, arithmetic genus one curve
![]() $C_0$
with smooth fiber over the node, and
$C_0$
with smooth fiber over the node, and
![]() $\chi _{\mathrm {top}}(S_0)=12$
. Such a fibration has a Weierstrass form
$\chi _{\mathrm {top}}(S_0)=12$
. Such a fibration has a Weierstrass form
![]() $\{y^2=4x^3-a_0x-b_0\}$
with
$\{y^2=4x^3-a_0x-b_0\}$
with
![]() $a_0\in H^0(C_0,\mathcal {O}_{C_0}(4P_0))$
and
$a_0\in H^0(C_0,\mathcal {O}_{C_0}(4P_0))$
and
![]() $b_0\in H^0(C_0,\mathcal {O}_{C_0}(6P_0))$
for some point
$b_0\in H^0(C_0,\mathcal {O}_{C_0}(6P_0))$
for some point
![]() $P_0\in (C_0)_{\mathrm {sm}}$
. See Figure 1.
$P_0\in (C_0)_{\mathrm {sm}}$
. See Figure 1.

Figure 1 A Type II
![]() $_b$
surface
$_b$
surface
![]() $S_0$
with double locus D and section s.
$S_0$
with double locus D and section s.
Let
![]() $C_0\hookrightarrow {\mathcal C}$
be a smoothing over
$C_0\hookrightarrow {\mathcal C}$
be a smoothing over
![]() $(B,0)$
to a genus
$(B,0)$
to a genus
![]() $1$
curve, with smooth total space, and let
$1$
curve, with smooth total space, and let
![]() ${\mathcal P}$
be an extension of
${\mathcal P}$
be an extension of
![]() $P_0$
to a section of
$P_0$
to a section of
![]() $\rho \colon {\mathcal C}\to (B,0)$
. Then, for any
$\rho \colon {\mathcal C}\to (B,0)$
. Then, for any
![]() $k>0$
, Cohomology and Base Change [Reference HartshorneHar77, III.12.11] implies that
$k>0$
, Cohomology and Base Change [Reference HartshorneHar77, III.12.11] implies that
![]() $\rho _*{\mathcal O}_{{\mathcal C}}(k{\mathcal P})$
is a rank k vector bundle over B. In particular,
$\rho _*{\mathcal O}_{{\mathcal C}}(k{\mathcal P})$
is a rank k vector bundle over B. In particular,
![]() $a_0$
,
$a_0$
,
![]() $b_0$
extend locally to sections a, b of
$b_0$
extend locally to sections a, b of
![]() $\rho _*{\mathcal O}_{\mathcal C}(4{\mathcal P})$
,
$\rho _*{\mathcal O}_{\mathcal C}(4{\mathcal P})$
,
![]() $\rho _*{\mathcal O}_{\mathcal C}(6{\mathcal P})$
, and so we can smooth the elliptic fibration
$\rho _*{\mathcal O}_{\mathcal C}(6{\mathcal P})$
, and so we can smooth the elliptic fibration
![]() $S_0\hookrightarrow {\mathcal S}$
over
$S_0\hookrightarrow {\mathcal S}$
over
![]() $(B,0)$
. The resulting total space
$(B,0)$
. The resulting total space
![]() ${\mathcal S}$
is smooth with
${\mathcal S}$
is smooth with
![]() $S_0$
reduced normal crossings. The double locus D is the smooth elliptic curve fibering over the node of
$S_0$
reduced normal crossings. The double locus D is the smooth elliptic curve fibering over the node of
![]() $C_0$
.
$C_0$
.
Definition 2.1. We call such a degeneration
![]() ${\mathcal S}\to {\mathcal C}\to (B,0)$
a Type II
${\mathcal S}\to {\mathcal C}\to (B,0)$
a Type II
![]() $_b$
degeneration, and we call the central fiber
$_b$
degeneration, and we call the central fiber
![]() $S_0$
a Type II
$S_0$
a Type II
![]() $_b$
elliptic surface.
$_b$
elliptic surface.
The subscript b indicates that the base degenerates. The terminology is motivated by a similar terminology in the classification of one-parameter degenerations of K3 surfacesdue to Kulikov and Persson-Pinkham [Reference KulikovKul77, Reference Persson and PinkhamPP81]. They classify their
![]() $K_{\mathcal S}$
-trivial, reduced normal crossing degenerations into Types I, II, III depending on the depth of the singularity stratification of
$K_{\mathcal S}$
-trivial, reduced normal crossing degenerations into Types I, II, III depending on the depth of the singularity stratification of
![]() $S_0$
. Here, we instead have
$S_0$
. Here, we instead have
![]() $K_{\mathcal S}={\mathcal O}_{\mathcal S}({\mathcal F})$
for a relative fiber
$K_{\mathcal S}={\mathcal O}_{\mathcal S}({\mathcal F})$
for a relative fiber
![]() ${\mathcal F}\to (B,0)$
.
${\mathcal F}\to (B,0)$
.
As a reduced normal crossing degeneration, the Picard-Lefschetz transformation
![]() $T\colon H^2(S_t,{\mathbb {Z}})\to H^2(S_t,{\mathbb {Z}})$
is unipotent and has a logarithm
$T\colon H^2(S_t,{\mathbb {Z}})\to H^2(S_t,{\mathbb {Z}})$
is unipotent and has a logarithm
![]() $N:=\log T$
. Furthermore, there is a formula for N which can be deduced from the Picard-Lefschetz transformation for a nodal degeneration of curves, or from [Reference ClemensCle69, Thm. 5.6].
$N:=\log T$
. Furthermore, there is a formula for N which can be deduced from the Picard-Lefschetz transformation for a nodal degeneration of curves, or from [Reference ClemensCle69, Thm. 5.6].
Let
![]() $\gamma _t\subset C_t$
denote the vanishing
$\gamma _t\subset C_t$
denote the vanishing
![]() $1$
-cycle of the node of
$1$
-cycle of the node of
![]() $C_0$
. Since the fiber over the node of
$C_0$
. Since the fiber over the node of
![]() $C_0$
is smooth, the restriction of the elliptic fibration
$C_0$
is smooth, the restriction of the elliptic fibration
![]() $\pi _t\colon S_t\to C_t$
to the curve
$\pi _t\colon S_t\to C_t$
to the curve
![]() $\gamma _t$
is a topologically trivial
$\gamma _t$
is a topologically trivial
![]() $2$
-torus bundle. Trivialize it, and let
$2$
-torus bundle. Trivialize it, and let
![]() $\alpha , \beta $
be oriented generators of the homology of some fiber. Define
$\alpha , \beta $
be oriented generators of the homology of some fiber. Define
![]() $u:=[\gamma _t\times \alpha ]\in H^2(S_t,{\mathbb {Z}})$
,
$u:=[\gamma _t\times \alpha ]\in H^2(S_t,{\mathbb {Z}})$
,
![]() $v:=[\gamma _t\times \beta ]\in H^2(S_t,{\mathbb {Z}})$
. Then,
$v:=[\gamma _t\times \beta ]\in H^2(S_t,{\mathbb {Z}})$
. Then,
Proposition 2.2.
![]() $N(x) = (x\cdot u)v-(x\cdot v)u.$
$N(x) = (x\cdot u)v-(x\cdot v)u.$
Here
![]() $u,v\in \{s,f\}^\perp $
because
$u,v\in \{s,f\}^\perp $
because
![]() $s,f$
are classes of line bundles on the total space
$s,f$
are classes of line bundles on the total space
![]() ${\mathcal S}$
, and hence monodromy-invariant. So the classes
${\mathcal S}$
, and hence monodromy-invariant. So the classes
![]() $u,v$
determine a rank
$u,v$
determine a rank
![]() $2$
isotropic lattice
$2$
isotropic lattice
![]() $I:=({\mathbb {Z}} u\oplus {\mathbb {Z}} v)^{\mathrm {sat}}\subset I\!I_{2,10}$
.
$I:=({\mathbb {Z}} u\oplus {\mathbb {Z}} v)^{\mathrm {sat}}\subset I\!I_{2,10}$
.
Let
![]() $U_I$
be the unipotent subgroup of
$U_I$
be the unipotent subgroup of
![]() $\mathrm {Stab}_\Gamma (I)$
acting trivially on I and
$\mathrm {Stab}_\Gamma (I)$
acting trivially on I and
![]() $I^\perp /I$
. From the theory of toroidal compactifications [Reference Ash, Mumford, Rapoport and TaiAMRT75] (see also [Reference LooijengaLoo03, Sec. 1A], [Reference Alexeev and EngelAE23, Prop. 4.16] for the case of Type IV domains), the unipotent quotient
$I^\perp /I$
. From the theory of toroidal compactifications [Reference Ash, Mumford, Rapoport and TaiAMRT75] (see also [Reference LooijengaLoo03, Sec. 1A], [Reference Alexeev and EngelAE23, Prop. 4.16] for the case of Type IV domains), the unipotent quotient
embeds as a punctured disk bundle inside a
![]() ${\mathbb {C}}^*$
-bundle
${\mathbb {C}}^*$
-bundle
![]() $A_I\to I^\perp /I\otimes {\mathcal E}$
. Here
$A_I\to I^\perp /I\otimes {\mathcal E}$
. Here
![]() ${\mathcal E}$
is the universal elliptic curve over
${\mathcal E}$
is the universal elliptic curve over
![]() ${\mathbb {C}}\setminus \mathbb R$
whose fiber over
${\mathbb {C}}\setminus \mathbb R$
whose fiber over
![]() $\tau \in {\mathbb {C}}\setminus \mathbb R$
is the elliptic curve
$\tau \in {\mathbb {C}}\setminus \mathbb R$
is the elliptic curve
![]() ${\mathbb {C}}/{\mathbb {Z}}\oplus {\mathbb {Z}}\tau $
. Since
${\mathbb {C}}/{\mathbb {Z}}\oplus {\mathbb {Z}}\tau $
. Since
![]() $T\in U_I$
the period map P induces a holomorphic period map
$T\in U_I$
the period map P induces a holomorphic period map
![]() $B^*\to {\mathbb D}/U_I$
.
$B^*\to {\mathbb D}/U_I$
.
We enlarge
![]() $A_I\hookrightarrow {\overline A}_I$
to a line bundle and define
$A_I\hookrightarrow {\overline A}_I$
to a line bundle and define
![]() $({\mathbb D}/U_I)^{\mathrm {II}}$
as the closure of
$({\mathbb D}/U_I)^{\mathrm {II}}$
as the closure of
![]() ${\mathbb D}/U_I$
in
${\mathbb D}/U_I$
in
![]() ${\overline A}_I$
. This closure is a holomorphic disk bundle over
${\overline A}_I$
. This closure is a holomorphic disk bundle over
![]() $I^\perp /I\otimes {\mathcal E}$
. The nilpotent orbit theorem [Reference SchmidSch73, Thm. 4.9] (the case at hand follows as in [Reference FriedmanFri84, Thm. 4.2])implies that the period map from
$I^\perp /I\otimes {\mathcal E}$
. The nilpotent orbit theorem [Reference SchmidSch73, Thm. 4.9] (the case at hand follows as in [Reference FriedmanFri84, Thm. 4.2])implies that the period map from
![]() $B^*$
extends to a holomorphic map
$B^*$
extends to a holomorphic map
![]() $P\colon (B,0)\to ({\mathbb D}/U_I)^{\mathrm {II}}$
sending
$P\colon (B,0)\to ({\mathbb D}/U_I)^{\mathrm {II}}$
sending
![]() $0$
into the boundary divisor
$0$
into the boundary divisor
![]() $\Delta :={\overline A}_I\setminus A_I$
. As the zero-section of the line bundle, the boundary divisor is naturally isomorphic to
$\Delta :={\overline A}_I\setminus A_I$
. As the zero-section of the line bundle, the boundary divisor is naturally isomorphic to
Note that
![]() $I^\perp /I$
is an even, negative-definite, unimodular lattice of rank
$I^\perp /I$
is an even, negative-definite, unimodular lattice of rank
![]() $8$
, which uniquely determines it to be
$8$
, which uniquely determines it to be
![]() $I^\perp /I=E_8$
.
$I^\perp /I=E_8$
.
There is also a direct construction of the period point
![]() $P(0)\in E_8\otimes {\mathcal E}$
from the singular surface
$P(0)\in E_8\otimes {\mathcal E}$
from the singular surface
![]() $S_0$
described as follows. Let
$S_0$
described as follows. Let
![]() $X\to \mathbb {P}^1$
be the rational elliptic surface normalizing
$X\to \mathbb {P}^1$
be the rational elliptic surface normalizing
![]() $S_0\to C_0$
and denote the section and fiber classes again by s and f. Then
$S_0\to C_0$
and denote the section and fiber classes again by s and f. Then
![]() $\{s,f\}^\perp \subset H^2(X,{\mathbb {Z}})$
is isomorphic to
$\{s,f\}^\perp \subset H^2(X,{\mathbb {Z}})$
is isomorphic to
![]() $E_8$
. Let
$E_8$
. Let
![]() $X_p$
and
$X_p$
and
![]() $X_q$
be the two elliptic fibers glued to form the double locus D of
$X_q$
be the two elliptic fibers glued to form the double locus D of
![]() $S_0$
. A class
$S_0$
. A class
![]() $\gamma \in \{s,f\}^\perp $
defines a line bundle
$\gamma \in \{s,f\}^\perp $
defines a line bundle
![]() ${\mathcal L}_\gamma \in \mathrm {Pic}(X)$
, and we declare
${\mathcal L}_\gamma \in \mathrm {Pic}(X)$
, and we declare
where we have used the gluing isomorphism
![]() $X_p\to X_q$
to form the tensor product of these two restrictions.
$X_p\to X_q$
to form the tensor product of these two restrictions.
Then
![]() $\psi _{S_0}$
defines a homomorphism
$\psi _{S_0}$
defines a homomorphism
![]() $\psi _{S_0}\in \mathrm {Hom}(E_8,E)\simeq E_8\otimes E$
. Fixing an identification of
$\psi _{S_0}\in \mathrm {Hom}(E_8,E)\simeq E_8\otimes E$
. Fixing an identification of
![]() $\{s,f\}^\perp $
with a fixed copy of the
$\{s,f\}^\perp $
with a fixed copy of the
![]() $E_8$
lattice, then deforming
$E_8$
lattice, then deforming
![]() $S_0$
in moduli of Type II
$S_0$
in moduli of Type II
![]() $_b$
surfaces, we get a local holomorphic period map
$_b$
surfaces, we get a local holomorphic period map
which is identical to the extension of P coming from the nilpotent orbit theorem. The equivalence of these two definitions of the period map follows fromCarlson’s description [Reference CarlsonCar85] of the mixed Hodge structure on
![]() $S_0$
; see Section 6 and Proposition 6.6. From this description of the boundary periodmapping, we see the following:
$S_0$
; see Section 6 and Proposition 6.6. From this description of the boundary periodmapping, we see the following:
-
1. To prove that P is dominant, it suffices to show that
 $P^{\mathrm {II}}$
is dominant from the moduli of Type II
$P^{\mathrm {II}}$
is dominant from the moduli of Type II
 $_b$
elliptic surfaces to
$_b$
elliptic surfaces to
 $\mathrm {Hom}(E_8,{\mathcal E})$
.
$\mathrm {Hom}(E_8,{\mathcal E})$
. -
2. On Type II
 $_b$
surfaces, the period map
$_b$
surfaces, the period map
 $P^{\mathrm {II}}$
is constructed by comparing the restriction of a line bundle in
$P^{\mathrm {II}}$
is constructed by comparing the restriction of a line bundle in
 $\{s,f\}^\perp \subset \mathrm {Pic}(X)$
to the two glued fibers.
$\{s,f\}^\perp \subset \mathrm {Pic}(X)$
to the two glued fibers.
Observe that (1) follows from the observation at the beginning of this section that every Type II
![]() $_b$
elliptic surface is smoothable to the interior of F, so the Zariski closure of
$_b$
elliptic surface is smoothable to the interior of F, so the Zariski closure of
![]() $\mathrm {im}(P)\subset ({\mathbb D}/\Gamma )^{\mathrm {II}}$
must contain
$\mathrm {im}(P)\subset ({\mathbb D}/\Gamma )^{\mathrm {II}}$
must contain
![]() $\mathrm {im}(P^{\mathrm {II}})$
.
$\mathrm {im}(P^{\mathrm {II}})$
.
3 Dominance of the period map
Fix a smooth cubic
![]() $D\subset \mathbb {P}^2$
and let
$D\subset \mathbb {P}^2$
and let
![]() $\gamma \in PGL_3({\mathbb {C}})$
be generic. Then D and
$\gamma \in PGL_3({\mathbb {C}})$
be generic. Then D and
![]() $\gamma (D)$
generate a pencil of cubics with
$\gamma (D)$
generate a pencil of cubics with
![]() $9$
distinct base points. Blowing up at the nine base points
$9$
distinct base points. Blowing up at the nine base points
![]() $D\cap \gamma (D)=\{p_1,\dots ,p_9\}$
of this pencil, we get a rational elliptic surface
$D\cap \gamma (D)=\{p_1,\dots ,p_9\}$
of this pencil, we get a rational elliptic surface
![]() $X\to \mathbb {P}^1,$
together with an isomorphism
$X\to \mathbb {P}^1,$
together with an isomorphism
![]() $\gamma \colon D \to \gamma (D)$
between two of its fibers. The nine blow-ups give rise to nine exceptional sections
$\gamma \colon D \to \gamma (D)$
between two of its fibers. The nine blow-ups give rise to nine exceptional sections
![]() $F_1,\dots ,F_9$
of the resulting elliptic fibration. Let
$F_1,\dots ,F_9$
of the resulting elliptic fibration. Let
![]() $t\colon D\to D$
be an arbitrary translation and consider the surface
$t\colon D\to D$
be an arbitrary translation and consider the surface
![]() $S_0$
which results from gluing our two fibers of
$S_0$
which results from gluing our two fibers of
![]() $X\to \mathbb {P}^1$
by the isomorphism
$X\to \mathbb {P}^1$
by the isomorphism
This construction defines a family of singular surfaces
![]() ${\mathcal S}\to U$
over a Zariski open subset
${\mathcal S}\to U$
over a Zariski open subset
![]() $U\subset PGL_3({\mathbb {C}})\times E$
where
$U\subset PGL_3({\mathbb {C}})\times E$
where
![]() $E:=\mathrm {Pic}^0(D)$
.
$E:=\mathrm {Pic}^0(D)$
.
A very general surface over
![]() $(\gamma ,t)$
does not have a section, as there are only countably many sections of
$(\gamma ,t)$
does not have a section, as there are only countably many sections of
![]() $X\to \mathbb {P}^1$
; for a sufficiently general translation t, none of these will glue to a section of the singular surface. Still, for all such surfaces, there is a periodhomomorphism
$X\to \mathbb {P}^1$
; for a sufficiently general translation t, none of these will glue to a section of the singular surface. Still, for all such surfaces, there is a periodhomomorphism
![]() $\psi _{S_0}\colon H^2(X,{\mathbb {Z}})\to E$
defined by (2.1). It descends to the rank
$\psi _{S_0}\colon H^2(X,{\mathbb {Z}})\to E$
defined by (2.1). It descends to the rank
![]() $9$
quotient
$9$
quotient
![]() $L:=H^2(X,{\mathbb {Z}})/{\mathbb {Z}} f$
because
$L:=H^2(X,{\mathbb {Z}})/{\mathbb {Z}} f$
because
![]() $f|_D= \mathcal {O}_D$
and
$f|_D= \mathcal {O}_D$
and
![]() $f|_{\gamma (D)}= \mathcal {O}_{\gamma (D)}$
. There is a translation action of
$f|_{\gamma (D)}= \mathcal {O}_{\gamma (D)}$
. There is a translation action of
![]() $t\in E$
on U given by
$t\in E$
on U given by
![]() $ (\gamma _0,\,t_0)\mapsto (\gamma _0,\,t_0\circ t)=:(\gamma _0',t_0')$
. It acts on the period homomorphism as follows:
$ (\gamma _0,\,t_0)\mapsto (\gamma _0,\,t_0\circ t)=:(\gamma _0',t_0')$
. It acts on the period homomorphism as follows:
From this formula, we deduce that the dominance of the period map for Type II
![]() $_b$
elliptic surfaces is equivalent to dominance of the more general period map
$_b$
elliptic surfaces is equivalent to dominance of the more general period map
Consider the codimension one subtorus of
![]() $\mathrm {Hom}(L,E)$
for which
$\mathrm {Hom}(L,E)$
for which
![]() $\psi _{S_0}(h)=0\in E$
, where h is the pullback of the hyperplane class on
$\psi _{S_0}(h)=0\in E$
, where h is the pullback of the hyperplane class on
![]() $\mathbb {P}^2$
. The inverse image of this subtorus contains, as a component, the locus of
$\mathbb {P}^2$
. The inverse image of this subtorus contains, as a component, the locus of
![]() $(\gamma ,t)$
for which
$(\gamma ,t)$
for which
![]() $t=0$
, because under a projective linear identification
$t=0$
, because under a projective linear identification
![]() $\gamma $
, we have
$\gamma $
, we have
![]() $\gamma ^*{\mathcal O}_{\gamma (D)}(1)={\mathcal O}_D(1)$
. Thus, the dominance of (3.2) is implied by the dominance of
$\gamma ^*{\mathcal O}_{\gamma (D)}(1)={\mathcal O}_D(1)$
. Thus, the dominance of (3.2) is implied by the dominance of
This follows because the action of
![]() $t\in E$
on
$t\in E$
on
![]() $\mathrm {Hom}(L,E)$
described by (3.1) is translation by an elliptic subcurve transverse to the codimension
$\mathrm {Hom}(L,E)$
described by (3.1) is translation by an elliptic subcurve transverse to the codimension
![]() $1$
subtorus of
$1$
subtorus of
![]() $\mathrm {Hom}(L,E)$
appearing on the right-hand side of (3.3).
$\mathrm {Hom}(L,E)$
appearing on the right-hand side of (3.3).
Finally,
![]() ${\mathbb {Z}}^9 \simeq \textrm {span}\{F_i\,\big {|}\,i=1,\dots ,9\}=h^\perp $
surjects onto
${\mathbb {Z}}^9 \simeq \textrm {span}\{F_i\,\big {|}\,i=1,\dots ,9\}=h^\perp $
surjects onto
![]() $H^2(X,{\mathbb {Z}})/{\mathbb {Z}} f+{\mathbb {Z}} h$
. Pulling back the period map to this lattice, we get a map
$H^2(X,{\mathbb {Z}})/{\mathbb {Z}} f+{\mathbb {Z}} h$
. Pulling back the period map to this lattice, we get a map
 $$ \begin{align} \begin{aligned} PGL_3({\mathbb{C}})&\dashrightarrow \mathrm{Hom}({\mathbb{Z}}^9,E)/\mathfrak S_9 \\ \gamma&\mapsto\{\psi_{S_0}(F_1),\dots,\psi_{S_0}(F_9)\}.\end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} PGL_3({\mathbb{C}})&\dashrightarrow \mathrm{Hom}({\mathbb{Z}}^9,E)/\mathfrak S_9 \\ \gamma&\mapsto\{\psi_{S_0}(F_1),\dots,\psi_{S_0}(F_9)\}.\end{aligned} \end{align} $$
Here, the base points
![]() $D\cap \gamma (D)$
, and hence the exceptional curves
$D\cap \gamma (D)$
, and hence the exceptional curves
![]() $F_i$
, are not canonically ordered; they are permuted by the monodromy of the universal family. This is why we must quotient the target by the symmetric group
$F_i$
, are not canonically ordered; they are permuted by the monodromy of the universal family. This is why we must quotient the target by the symmetric group
![]() $\mathfrak S_9$
. Since
$\mathfrak S_9$
. Since
![]() $\sum _{i=1}^9 [F_i] = 3h-f$
in
$\sum _{i=1}^9 [F_i] = 3h-f$
in
![]() $H^2(X,{\mathbb {Z}})$
, the image of the period map (3.4) lands in
$H^2(X,{\mathbb {Z}})$
, the image of the period map (3.4) lands in
The last isomorphism follows from a well-known theorem of Looijenga [Reference LooijengaLoo76]. Applying the definition of
![]() $\psi _{S_0}$
gives a very explicit construction of (3.4):
$\psi _{S_0}$
gives a very explicit construction of (3.4):
Definition 3.1. Fix a smooth cubic
![]() $D\subset \mathbb {P}^2$
. Define
$D\subset \mathbb {P}^2$
. Define
![]() $E:=\mathrm {Pic}^0(D)$
and let
$E:=\mathrm {Pic}^0(D)$
and let
![]() $A\colon \mathrm {Sym}^9E\to E$
denote the addition map. For a generic
$A\colon \mathrm {Sym}^9E\to E$
denote the addition map. For a generic
![]() $\gamma \in PGL_3({\mathbb {C}})$
, set
$\gamma \in PGL_3({\mathbb {C}})$
, set
![]() $D\cap \gamma (D)=\{p_i\}_{i=1}^9$
and
$D\cap \gamma (D)=\{p_i\}_{i=1}^9$
and
![]() $q_i:=\gamma ^{-1}(p_i)\in D$
. We define
$q_i:=\gamma ^{-1}(p_i)\in D$
. We define
 $$ \begin{align} \begin{aligned} \Psi\colon PGL_3({\mathbb{C}}) & \dashrightarrow A^{-1}(0)\simeq \mathbb{P}^8 \\ \gamma &\mapsto \{{\mathcal O}_D(p_i-q_i)\}_{i=1}^9.\end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} \Psi\colon PGL_3({\mathbb{C}}) & \dashrightarrow A^{-1}(0)\simeq \mathbb{P}^8 \\ \gamma &\mapsto \{{\mathcal O}_D(p_i-q_i)\}_{i=1}^9.\end{aligned}\end{align} $$
Theorem 3.2. The rational map
![]() $\Psi $
from (3.5) is dominant. Thus, the period mapping for Type II
$\Psi $
from (3.5) is dominant. Thus, the period mapping for Type II
![]() $_b$
surfaces is dominant.
$_b$
surfaces is dominant.
Proof. Let
![]() $G\subset PGL_3({\mathbb {C}})$
be the finite subgroup for which
$G\subset PGL_3({\mathbb {C}})$
be the finite subgroup for which
![]() $g(D)=D$
. We claim that
$g(D)=D$
. We claim that
![]() $\Psi $
extends, as a morphism, from U to
$\Psi $
extends, as a morphism, from U to
![]() $PGL_3({\mathbb {C}})\setminus G$
. This is easy: the map
$PGL_3({\mathbb {C}})\setminus G$
. This is easy: the map
![]() $\Psi $
extends continuously because
$\Psi $
extends continuously because
![]() $D\cap \gamma (D)$
is still a finite set for all
$D\cap \gamma (D)$
is still a finite set for all
![]() $\gamma \in PGL_3({\mathbb {C}})\setminus G$
. Normality of
$\gamma \in PGL_3({\mathbb {C}})\setminus G$
. Normality of
![]() $PGL_3({\mathbb {C}})\setminus G$
implies that a continuous extension is algebraic.
$PGL_3({\mathbb {C}})\setminus G$
implies that a continuous extension is algebraic.
We choose D and
![]() $\gamma $
carefully so that the set
$\gamma $
carefully so that the set
![]() $D\cap \gamma (D)$
has only three elements. Concretely, consider the extremal cubic pencil
$D\cap \gamma (D)$
has only three elements. Concretely, consider the extremal cubic pencil
![]() $X_{9111}\to \mathbb {P}^1_{[\lambda :\mu ]}$
in the notation of [Reference Miranda and PerssonMP86], given by the equation
$X_{9111}\to \mathbb {P}^1_{[\lambda :\mu ]}$
in the notation of [Reference Miranda and PerssonMP86], given by the equation
See Figure 2. Let
![]() $D:=D_{[\lambda :\mu ]}$
be a generic fiber, and let
$D:=D_{[\lambda :\mu ]}$
be a generic fiber, and let
![]() $\gamma = \mathrm {diag}(1,\zeta _3,\zeta _3^2)$
where
$\gamma = \mathrm {diag}(1,\zeta _3,\zeta _3^2)$
where
![]() $\zeta _3$
is a primitive third root of unity. Then
$\zeta _3$
is a primitive third root of unity. Then
![]() $\gamma (D)=D_{[\zeta _3\lambda :\mu ]}$
, and so D and
$\gamma (D)=D_{[\zeta _3\lambda :\mu ]}$
, and so D and
![]() $\gamma (D)$
generate the pencil. The intersection multiset
$\gamma (D)$
generate the pencil. The intersection multiset
![]() $D\cap \gamma (D)$
is
$D\cap \gamma (D)$
is
![]() $\{3p_1,3p_2,3 p_3\}$
where
$\{3p_1,3p_2,3 p_3\}$
where
Since this
![]() $\gamma \in PGL_3({\mathbb {C}})$
fixes
$\gamma \in PGL_3({\mathbb {C}})$
fixes
![]() $p_1$
,
$p_1$
,
![]() $p_2$
,
$p_2$
,
![]() $p_3$
, the period
$p_3$
, the period
![]() $\Psi (\gamma )=\{0,\dots ,0\}\in \mathrm {Sym}^9E$
vanishes. To prove that
$\Psi (\gamma )=\{0,\dots ,0\}\in \mathrm {Sym}^9E$
vanishes. To prove that
![]() $\Psi $
is dominant, it suffices to show that there is no small deformation
$\Psi $
is dominant, it suffices to show that there is no small deformation
![]() $\gamma '\in PGL_3({\mathbb {C}})$
of
$\gamma '\in PGL_3({\mathbb {C}})$
of
![]() $\gamma $
for which
$\gamma $
for which
![]() $\Psi (\gamma ')=\{0,\dots ,0\}$
.
$\Psi (\gamma ')=\{0,\dots ,0\}$
.

Figure 2 The pencil generated by two cubics, shown in red and black, with set-theoretic base locus three blue points.
Suppose, to the contrary, that there were. Since
![]() $\Psi (\gamma ')=\{0,\dots ,0\}$
, every base point in
$\Psi (\gamma ')=\{0,\dots ,0\}$
, every base point in
![]() $D\cap \gamma '(D)$
is fixed by
$D\cap \gamma '(D)$
is fixed by
![]() $\gamma '$
. If
$\gamma '$
. If
![]() $|D\cap \gamma '(D)|\geq 4$
, then
$|D\cap \gamma '(D)|\geq 4$
, then
![]() $\gamma '$
must fix a line in
$\gamma '$
must fix a line in
![]() $\mathbb {P}^2$
. This is impossible for a small deformation of
$\mathbb {P}^2$
. This is impossible for a small deformation of
![]() $\gamma $
, which has isolated fixed points. Conversely,
$\gamma $
, which has isolated fixed points. Conversely,
![]() $|D\cap \gamma '(D)|\geq 3$
because each of
$|D\cap \gamma '(D)|\geq 3$
because each of
![]() $p_1$
,
$p_1$
,
![]() $p_2$
,
$p_2$
,
![]() $p_3$
deforms to some fixed point of
$p_3$
deforms to some fixed point of
![]() $\gamma '$
. Hence,
$\gamma '$
. Hence,
![]() $\gamma '$
fixes exactly three points
$\gamma '$
fixes exactly three points
![]() $p_1'$
,
$p_1'$
,
![]() $p_2'$
,
$p_2'$
,
![]() $p_3'$
. Furthermore,
$p_3'$
. Furthermore,
![]() $D\cap \gamma '(D)=\{3p_1',3p_2',3p_3'\}$
as a multiset, again because
$D\cap \gamma '(D)=\{3p_1',3p_2',3p_3'\}$
as a multiset, again because
![]() $\gamma '$
is near
$\gamma '$
is near
![]() $\gamma $
, and the map
$\gamma $
, and the map
sending
![]() $\gamma ' \mapsto D\cap \gamma '(D)$
with multiplicities is continuous.
$\gamma ' \mapsto D\cap \gamma '(D)$
with multiplicities is continuous.
Since
![]() ${\mathrm {mult}}_{p_i'}(D\cap \gamma '(D))\geq 2$
, we deduce that
${\mathrm {mult}}_{p_i'}(D\cap \gamma '(D))\geq 2$
, we deduce that
![]() $\gamma '$
preserves the tangent direction
$\gamma '$
preserves the tangent direction
![]() $T_{p_i'}D$
and the corresponding tangent line
$T_{p_i'}D$
and the corresponding tangent line
![]() $L_i'$
. Thus,
$L_i'$
. Thus,
![]() $\gamma '\in PGL_3({\mathbb {C}})$
fixes the point
$\gamma '\in PGL_3({\mathbb {C}})$
fixes the point
![]() $L_i'\cap L_j'\in \mathbb {P}^2$
. But, as we noted before,
$L_i'\cap L_j'\in \mathbb {P}^2$
. But, as we noted before,
![]() $\gamma '$
only fixes three points (this holds not just on D but in the ambient plane
$\gamma '$
only fixes three points (this holds not just on D but in the ambient plane
![]() $\mathbb {P}^2$
). Using that
$\mathbb {P}^2$
). Using that
![]() $\gamma '$
is a small deformation of
$\gamma '$
is a small deformation of
![]() $\gamma $
, we deduce that
$\gamma $
, we deduce that
Write
![]() $p_i'=p_i+t_i$
for a translation
$p_i'=p_i+t_i$
for a translation
![]() $t_i$
. By the addition law on a cubic, we have
$t_i$
. By the addition law on a cubic, we have
from which we can conclude that
![]() $t_1=(-2)^3t_1$
i.e.
$t_1=(-2)^3t_1$
i.e.
![]() $t_1$
is
$t_1$
is
![]() $9$
-torsion. But since
$9$
-torsion. But since
![]() $t_i$
are small, we conclude that
$t_i$
are small, we conclude that
![]() $t_1=t_2=t_3=0$
and so
$t_1=t_2=t_3=0$
and so
![]() $p_i'=p_i$
.
$p_i'=p_i$
.
Thus,
![]() $\gamma '$
fixes
$\gamma '$
fixes
![]() $(p_1,p_2,p_3)$
, implying that
$(p_1,p_2,p_3)$
, implying that
![]() $\gamma '\in ({\mathbb {C}}^*)^2\subset PGL_3( {\mathbb {C}})$
lies in the maximal torus associated to the coordinates
$\gamma '\in ({\mathbb {C}}^*)^2\subset PGL_3( {\mathbb {C}})$
lies in the maximal torus associated to the coordinates
![]() $[x:y:z]$
. Furthermore,
$[x:y:z]$
. Furthermore,
![]() $\gamma '$
preserves the base locus scheme
$\gamma '$
preserves the base locus scheme
![]() $D\cap \gamma '(D)$
, as this is the unique subscheme of D which has length
$D\cap \gamma '(D)$
, as this is the unique subscheme of D which has length
![]() $3$
at each of
$3$
at each of
![]() $p_1,p_2,p_3$
. So
$p_1,p_2,p_3$
. So
![]() $\gamma '$
induces an automorphism of the pencil generated by D and
$\gamma '$
induces an automorphism of the pencil generated by D and
![]() $\gamma '(D)$
. Since the automorphism group of a rational elliptic surface is discrete, and
$\gamma '(D)$
. Since the automorphism group of a rational elliptic surface is discrete, and
![]() $\gamma '$
is a small deformation of
$\gamma '$
is a small deformation of
![]() $\gamma $
, the automorphism
$\gamma $
, the automorphism
![]() $\gamma '$
must have order
$\gamma '$
must have order
![]() $3$
. But no nontrivial small deformation of
$3$
. But no nontrivial small deformation of
![]() $\gamma =\mathrm {diag}(1,\zeta _3,\zeta _3^2)$
within the torus
$\gamma =\mathrm {diag}(1,\zeta _3,\zeta _3^2)$
within the torus
![]() $({\mathbb {C}}^*)^2$
has order
$({\mathbb {C}}^*)^2$
has order
![]() $3$
. This is a contradiction.
$3$
. This is a contradiction.
Remark 3.3. Our original proof of Theorem 3.2 checked by computer that
![]() $d\Psi $
was nondegenerate for an explicitly chosen D and
$d\Psi $
was nondegenerate for an explicitly chosen D and
![]() $\gamma $
.
$\gamma $
.
4 Type II
 $_f$
degenerations
$_f$
degenerations
We consider in this section degenerations of
![]() $S\to C$
that keep the base C constant. These are never of Type II
$S\to C$
that keep the base C constant. These are never of Type II
![]() $_b$
because in all such degenerations,
$_b$
because in all such degenerations,
![]() $j(C)\to \infty $
.
$j(C)\to \infty $
.
Take a one-parameter deformation of
![]() $a,b\in H^0(C,{\mathcal O}_C(4p)), H^0(C,{\mathcal O}_C(6p))$
over
$a,b\in H^0(C,{\mathcal O}_C(4p)), H^0(C,{\mathcal O}_C(6p))$
over
![]() $(B,0)$
until the discriminant
$(B,0)$
until the discriminant
![]() $4a_0^3+27b_0^2=0\in H^0(C,{\mathcal O}_C(12p))$
vanishes identically. For instance, we can take the fiber over
$4a_0^3+27b_0^2=0\in H^0(C,{\mathcal O}_C(12p))$
vanishes identically. For instance, we can take the fiber over
![]() $0\in B$
to be
$0\in B$
to be
with
![]() $r\in H^0(C,{\mathcal O}_C(2p))$
. The degeneration
$r\in H^0(C,{\mathcal O}_C(2p))$
. The degeneration
of elliptic surfaces has a central fiber
![]() ${\overline S}_0\to C$
whose generic fiber is irreducible nodal, with two cuspidal fibers over the zeroes of r. In particular, the normalization
${\overline S}_0\to C$
whose generic fiber is irreducible nodal, with two cuspidal fibers over the zeroes of r. In particular, the normalization
![]() ${\overline S}^\nu _0:=X\to C$
is the smooth
${\overline S}^\nu _0:=X\to C$
is the smooth
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $X=\mathbb {P}_C({\mathcal O}\oplus L)$
, and
$X=\mathbb {P}_C({\mathcal O}\oplus L)$
, and
![]() ${\overline S}_0$
is reconstructed from gluing a bisection D of
${\overline S}_0$
is reconstructed from gluing a bisection D of
![]() $X\to C$
, branched over the two zeroes of r. This bisection D is glued along the involution switching the two sheets of
$X\to C$
, branched over the two zeroes of r. This bisection D is glued along the involution switching the two sheets of
![]() $\nu \colon D\to C$
.
$\nu \colon D\to C$
.
For future reference, note that
![]() $\mathrm {NS}(X)\simeq H^2(X,{\mathbb {Z}})$
is spanned by the
$\mathrm {NS}(X)\simeq H^2(X,{\mathbb {Z}})$
is spanned by the
![]() $\mathbb P^1$
-fiber class f and the class of the section
$\mathbb P^1$
-fiber class f and the class of the section
![]() $s_{\infty } = \mathbb P_C({\mathcal O}\oplus 0)$
, with intersection form
$s_{\infty } = \mathbb P_C({\mathcal O}\oplus 0)$
, with intersection form
and
![]() $K_X = -f-2s_\infty $
. The other natural section
$K_X = -f-2s_\infty $
. The other natural section
![]() $s_0 = \mathbb P_C(0\oplus L)$
has class
$s_0 = \mathbb P_C(0\oplus L)$
has class
![]() $f+s_\infty $
.
$f+s_\infty $
.
The bisection
![]() $D\subset X$
has genus 2, being a double cover of C branched over two points. Thus, its cohomology class is
$D\subset X$
has genus 2, being a double cover of C branched over two points. Thus, its cohomology class is
![]() $[D]=2f+2s_\infty = -K_X+f = 2s_0$
. Note that
$[D]=2f+2s_\infty = -K_X+f = 2s_0$
. Note that
![]() $[D]^2=4$
and
$[D]^2=4$
and
![]() $[D]\cdot K_X = -2$
. The section s that is present on the smooth surfaces in the family
$[D]\cdot K_X = -2$
. The section s that is present on the smooth surfaces in the family
![]() $\mathcal S$
limits to
$\mathcal S$
limits to
![]() $s_\infty $
, which is the unique section of X disjoint from D.
$s_\infty $
, which is the unique section of X disjoint from D.
Proposition 4.1. Generically, two singular fibers limit to each cuspidal fiber of
![]() ${\overline S}_0$
. The limits of the remaining eight singular fibers lie over a degree
${\overline S}_0$
. The limits of the remaining eight singular fibers lie over a degree
![]() $8$
divisor in C. The only restriction on this divisor is that it is linearly equivalent to
$8$
divisor in C. The only restriction on this divisor is that it is linearly equivalent to
![]() $8p$
.
$8p$
.
Proof. Consider a deformation of the Weierstrass equation
where
![]() $g_d\in H^0(C,{\mathcal O}_C(dp))$
has degree d. The discriminant
$g_d\in H^0(C,{\mathcal O}_C(dp))$
has degree d. The discriminant
![]() $\Delta = 4a^3+27b^2$
is
$\Delta = 4a^3+27b^2$
is
Thus, the Zariski closure of the discriminant divisor is
For fixed r, the sections
![]() $rg_6$
form a linear subspace
$rg_6$
form a linear subspace
![]() $\mathbb {P}^5\subset \mathbb {P}^7=\mathbb {P}H^0(C,{\mathcal O}(8p))$
of codimension
$\mathbb {P}^5\subset \mathbb {P}^7=\mathbb {P}H^0(C,{\mathcal O}(8p))$
of codimension
![]() $2$
. The sections
$2$
. The sections
![]() $g_4^2\in \mathbb {P}H^0(C,{\mathcal O}(8p))$
are the image of the degree
$g_4^2\in \mathbb {P}H^0(C,{\mathcal O}(8p))$
are the image of the degree
![]() $2$
Veronese embedding, followed by a linear projection
$2$
Veronese embedding, followed by a linear projection
The inverse image of
![]() $\{\mathrm {div}(rg_6)\}=\mathbb {P}^5\subset \mathbb {P}^7$
is a copy of
$\{\mathrm {div}(rg_6)\}=\mathbb {P}^5\subset \mathbb {P}^7$
is a copy of
![]() $\mathbb {P}^7\subset \mathbb {P}^9$
under the linear projection. Thus, the vanishing loci of linear combinations are represented geometrically as the join of the projective subvarieties
$\mathbb {P}^7\subset \mathbb {P}^9$
under the linear projection. Thus, the vanishing loci of linear combinations are represented geometrically as the join of the projective subvarieties
![]() $v_2(\mathbb {P}^3)$
,
$v_2(\mathbb {P}^3)$
,
![]() $\mathbb {P}^7\subset \mathbb {P}^9$
. This join is all of
$\mathbb {P}^7\subset \mathbb {P}^9$
. This join is all of
![]() $\mathbb {P}^9$
. Thus, we can realize any divisor in
$\mathbb {P}^9$
. Thus, we can realize any divisor in
![]() $|8p|$
as
$|8p|$
as
![]() $\lim _{\epsilon \to 0}\mathrm {div}(\Delta )-2\cdot \mathrm {div}(r)$
.
$\lim _{\epsilon \to 0}\mathrm {div}(\Delta )-2\cdot \mathrm {div}(r)$
.
For general
![]() $g_4$
and
$g_4$
and
![]() $g_6$
, the punctured family over
$g_6$
, the punctured family over
![]() $B\setminus 0$
has smooth total space. The threefold
$B\setminus 0$
has smooth total space. The threefold
![]() $\overline {{\mathcal S}}$
is a double cover branched over the vanishing locus of the cubic
$\overline {{\mathcal S}}$
is a double cover branched over the vanishing locus of the cubic
![]() $x^3-(3r^2+\epsilon g_4)x+(2r^3+\epsilon g_4r+\epsilon ^2g_6)$
, so it can only be singular where two of the roots of the cubic coincide. This shows that the singular locus
$x^3-(3r^2+\epsilon g_4)x+(2r^3+\epsilon g_4r+\epsilon ^2g_6)$
, so it can only be singular where two of the roots of the cubic coincide. This shows that the singular locus
![]() $\overline {{\mathcal S}}_{\mathrm {sing}}\subset V(y,x-r,\epsilon )$
is contained in the singularities of the fibers of
$\overline {{\mathcal S}}_{\mathrm {sing}}\subset V(y,x-r,\epsilon )$
is contained in the singularities of the fibers of
![]() ${\overline S}_0\to C$
.
${\overline S}_0\to C$
.
Since
![]() $\epsilon ^2\mid \mid \Delta $
, the local equation of the double cover is generically
$\epsilon ^2\mid \mid \Delta $
, the local equation of the double cover is generically
![]() $y^2=u^2+\epsilon ^2$
along the nodes of
$y^2=u^2+\epsilon ^2$
along the nodes of
![]() ${\overline S}_0\to C$
. So the nodes form a family of
${\overline S}_0\to C$
. So the nodes form a family of
![]() $A_1$
-singularities in
$A_1$
-singularities in
![]() $\overline {{\mathcal S}}$
. At the nodes on the fibers lying over
$\overline {{\mathcal S}}$
. At the nodes on the fibers lying over
![]() $\mathrm {div}(12rg_6-g_4^2)$
, the local equation is rather
$\mathrm {div}(12rg_6-g_4^2)$
, the local equation is rather
![]() $y^2=u^2+v\epsilon ^2$
. Thus, to find a semistable model
$y^2=u^2+v\epsilon ^2$
. Thus, to find a semistable model
![]() ${\mathcal S}\to (B,0)$
, we simply blow up the double locus of
${\mathcal S}\to (B,0)$
, we simply blow up the double locus of
![]() ${\overline S}_0$
in the total space
${\overline S}_0$
in the total space
![]() $\overline {{\mathcal S}}$
.
$\overline {{\mathcal S}}$
.
The resulting central fiber is
![]() $S_0=X\cup _DV$
for a ruled surface
$S_0=X\cup _DV$
for a ruled surface
![]() $V\to C$
, which contains D as a bisection and has
$V\to C$
, which contains D as a bisection and has
![]() $8$
reducible fibers over the points in
$8$
reducible fibers over the points in
![]() $\mathrm {div}(12rg_6-g_4^2)$
; see Figure 3. Thus,
$\mathrm {div}(12rg_6-g_4^2)$
; see Figure 3. Thus,
![]() $V\sim Bl_{p_1,\dots ,p_8}X$
is deformation-equivalent to the blow-up of X at
$V\sim Bl_{p_1,\dots ,p_8}X$
is deformation-equivalent to the blow-up of X at
![]() $8$
points on D, with the double locus on V identified with D via the strict transform. It is only deformation-equivalent because
$8$
points on D, with the double locus on V identified with D via the strict transform. It is only deformation-equivalent because
![]() $V\to C$
could be the projectivization of a non-split extension of L by
$V\to C$
could be the projectivization of a non-split extension of L by
![]() ${\mathcal O}$
. Regardless, we can identify
${\mathcal O}$
. Regardless, we can identify
and
![]() $[D] = 2s_0 - [E_1]-\cdots -[E_8]=-K_V+f$
.
$[D] = 2s_0 - [E_1]-\cdots -[E_8]=-K_V+f$
.
Definition 4.2. We call the degeneration
![]() ${\mathcal S}\to C\times B\to (B,0)$
a Type II
${\mathcal S}\to C\times B\to (B,0)$
a Type II
![]() $_f$
degeneration, and we call the central fiber
$_f$
degeneration, and we call the central fiber
![]() $S_0$
a Type II
$S_0$
a Type II
![]() $_f$
elliptic surface.
$_f$
elliptic surface.

Figure 3 A Type II
![]() $_f$
surface
$_f$
surface
![]() $S_0 = X\cup _D V$
with the genus
$S_0 = X\cup _D V$
with the genus
![]() $2$
double locus D shown in red, the section s in green, limits of
$2$
double locus D shown in red, the section s in green, limits of
![]() $8$
nodal fibers in blue, and limits of pairs of nodal fibers dashed.
$8$
nodal fibers in blue, and limits of pairs of nodal fibers dashed.
From Section 6 and Proposition 6.6, the mixed Hodge structure of a Type II
![]() $_f$
surface has a period map to
$_f$
surface has a period map to
![]() $E_8\otimes {\mathcal E}$
which can be described as follows. Consider the sublattice
$E_8\otimes {\mathcal E}$
which can be described as follows. Consider the sublattice
![]() $\{K_V,f\}^\perp \subset H^2(V,{\mathbb {Z}})$
. This is isometric to the root lattice
$\{K_V,f\}^\perp \subset H^2(V,{\mathbb {Z}})$
. This is isometric to the root lattice
via the map
![]() $(a_1,\dots ,a_8) \mapsto \sum _{i=1}^8 a_i[E_i] - \left (\frac {1}{2} \sum _{i=1}^8 a_i\right ) f$
. When this isometry is understood, we will refer to
$(a_1,\dots ,a_8) \mapsto \sum _{i=1}^8 a_i[E_i] - \left (\frac {1}{2} \sum _{i=1}^8 a_i\right ) f$
. When this isometry is understood, we will refer to
![]() $\{K_V,f\}^\perp $
simply as
$\{K_V,f\}^\perp $
simply as
![]() $D_8$
.
$D_8$
.
Let
![]() $E:=\mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)$
be the Prym variety of the double cover
$E:=\mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)$
be the Prym variety of the double cover
![]() $\nu \colon D\to C$
. We define a period homomorphism
$\nu \colon D\to C$
. We define a period homomorphism
 $$ \begin{align} \begin{aligned} \psi_{S_0}\colon D_8& \to E \\ \gamma & \mapsto \mathcal{L}_\gamma\big{|}_D\textrm{ mod }\mathrm{Pic}^0(C) \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} \psi_{S_0}\colon D_8& \to E \\ \gamma & \mapsto \mathcal{L}_\gamma\big{|}_D\textrm{ mod }\mathrm{Pic}^0(C) \end{aligned}\end{align} $$
by lifting an element
![]() $\gamma \in D_8$
to an element
$\gamma \in D_8$
to an element
![]() ${\mathcal L}_\gamma \in \mathrm {Pic}(V)$
. These lifts form a
${\mathcal L}_\gamma \in \mathrm {Pic}(V)$
. These lifts form a
![]() $\mathrm {Pic}^0(C)$
-torsor, and thus, the image of
$\mathrm {Pic}^0(C)$
-torsor, and thus, the image of
![]() ${\mathcal L}_\gamma \big {|}_D\in \mathrm {Pic}^0(D)$
under the map to E is well-defined.
${\mathcal L}_\gamma \big {|}_D\in \mathrm {Pic}^0(D)$
under the map to E is well-defined.
Remark 4.3. The period point
![]() $\psi _{S_0}\in \mathrm {Hom}(D_8,E)$
determines, up to a finite isogeny, the period point in
$\psi _{S_0}\in \mathrm {Hom}(D_8,E)$
determines, up to a finite isogeny, the period point in
![]() $E_8\otimes E$
. The extensions of an element of
$E_8\otimes E$
. The extensions of an element of
![]() $\mathrm {Hom}(D_8, E)$
to an element of
$\mathrm {Hom}(D_8, E)$
to an element of
![]() $\mathrm {Hom}(E_8, E)$
are a torsor over
$\mathrm {Hom}(E_8, E)$
are a torsor over
![]() $\mathrm {Hom}(E_8/D_8,E)=E[2]$
.
$\mathrm {Hom}(E_8/D_8,E)=E[2]$
.
Proof of Theorem 1.3.
To show
![]() $\deg P>1$
, it suffices to prove that the moduli of Type II
$\deg P>1$
, it suffices to prove that the moduli of Type II
![]() $_f$
surfaces (appearing as limits of elliptic surfaces in F) also dominate the boundary divisor
$_f$
surfaces (appearing as limits of elliptic surfaces in F) also dominate the boundary divisor
![]() $\Delta $
. This follows from Theorem 4.4 below.
$\Delta $
. This follows from Theorem 4.4 below.
Theorem 4.4. The period mapping for Type II
![]() $_f$
surfaces is dominant.
$_f$
surfaces is dominant.
Proof. The period point
![]() $\psi _{S_0}$
and limit mixed Hodge structure of
$\psi _{S_0}$
and limit mixed Hodge structure of
![]() ${\mathcal S}$
are encoded, up to a finite map, in the data
${\mathcal S}$
are encoded, up to a finite map, in the data
![]() $(\nu \colon D\to C,\{r_i\}_{i=1}^8)$
consisting of
$(\nu \colon D\to C,\{r_i\}_{i=1}^8)$
consisting of
-
1. a degree
 $2$
map
$2$
map
 $\nu \colon D\to C$
from a genus
$\nu \colon D\to C$
from a genus
 $2$
to a genus
$2$
to a genus
 $1$
curve, and
$1$
curve, and -
2. a multiset of
 $8$
points
$8$
points
 $\{r_1,\dots ,r_8\}\subset C$
.
$\{r_1,\dots ,r_8\}\subset C$
.
Let
![]() $\iota \colon D\to D$
be the involution switching the sheets of
$\iota \colon D\to D$
be the involution switching the sheets of
![]() $\nu $
and let
$\nu $
and let
![]() $\{p_i,q_i\}=\nu ^{-1}(r_i)$
. Then
$\{p_i,q_i\}=\nu ^{-1}(r_i)$
. Then
![]() ${\mathcal O}_D(p_i-q_i)\in \mathrm {Pic}^0(D)$
gives, upon quotienting by
${\mathcal O}_D(p_i-q_i)\in \mathrm {Pic}^0(D)$
gives, upon quotienting by
![]() $\mathrm {Pic}^0(C)$
, the period
$\mathrm {Pic}^0(C)$
, the period
where
![]() $F_i+F_i'$
is a reducible fiber of the ruling
$F_i+F_i'$
is a reducible fiber of the ruling
![]() $V\to C$
. Ranging over the eight reducible fibers, the tuple
$V\to C$
. Ranging over the eight reducible fibers, the tuple
encodes
![]() $\psi _{S_0}$
up to torsion because
$\psi _{S_0}$
up to torsion because
![]() $\bigoplus _{i=1}^8{\mathbb {Z}}(F_i-F_i')\subset D_8$
has finite index.
$\bigoplus _{i=1}^8{\mathbb {Z}}(F_i-F_i')\subset D_8$
has finite index.
Let
![]() $\{r_9, r_{10}\}\in C$
be the branch points of
$\{r_9, r_{10}\}\in C$
be the branch points of
![]() $\nu $
. Then
$\nu $
. Then
![]() $\nu $
is determined by the monodromy representation
$\nu $
is determined by the monodromy representation
![]() $\rho \colon \pi _1(C\setminus \{r_9,r_{10}\},*)\to {\mathbb {Z}}_2$
. Let
$\rho \colon \pi _1(C\setminus \{r_9,r_{10}\},*)\to {\mathbb {Z}}_2$
. Let
![]() $\mathrm {Prym}^2{\mathcal C}$
be the moduli space of Prym data
$\mathrm {Prym}^2{\mathcal C}$
be the moduli space of Prym data
![]() $(C,\{r_9,r_{10}\},\rho )$
over the universal genus
$(C,\{r_9,r_{10}\},\rho )$
over the universal genus
![]() $1$
curve
$1$
curve
![]() $\mathcal {C}\to \mathcal {M}_1$
. It is a Deligne-Mumford stack of dimension
$\mathcal {C}\to \mathcal {M}_1$
. It is a Deligne-Mumford stack of dimension
![]() $2$
, one dimension for
$2$
, one dimension for
![]() $j(C)$
and another for the element
$j(C)$
and another for the element
![]() $r_9-r_{10}\in \mathrm {Pic}^0(C)$
, well-defined up to sign. The data of
$r_9-r_{10}\in \mathrm {Pic}^0(C)$
, well-defined up to sign. The data of
![]() $\rho $
is finite.
$\rho $
is finite.
A point
![]() $r_i\in C$
determines
$r_i\in C$
determines
![]() $p_i$
up to switching
$p_i$
up to switching
![]() $p_i\leftrightarrow q_i$
which acts by negation on the image of
$p_i\leftrightarrow q_i$
which acts by negation on the image of
![]() ${\mathcal O}_D(p_i-q_i)$
in E. Thus, we globally get a well-defined map
${\mathcal O}_D(p_i-q_i)$
in E. Thus, we globally get a well-defined map
 $$ \begin{align}\begin{aligned} \Psi\colon \mathrm{Sym}^8{\mathcal C} \times_{\mathcal M_1} \mathrm{Prym}^2{\mathcal C} &\to {\mathbb{Z}}^8 \otimes {\mathcal{E}}/\mathfrak S_8^{\pm} \\ (C, \{r_1,\dots,r_8\} ,\{r_9,r_{10}\},\rho)& \mapsto \{{\mathcal O}_D(p_i-q_i)\textrm{ mod }\mathrm{Pic}^0(C)\}_{i=1}^8,\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \Psi\colon \mathrm{Sym}^8{\mathcal C} \times_{\mathcal M_1} \mathrm{Prym}^2{\mathcal C} &\to {\mathbb{Z}}^8 \otimes {\mathcal{E}}/\mathfrak S_8^{\pm} \\ (C, \{r_1,\dots,r_8\} ,\{r_9,r_{10}\},\rho)& \mapsto \{{\mathcal O}_D(p_i-q_i)\textrm{ mod }\mathrm{Pic}^0(C)\}_{i=1}^8,\end{aligned}\end{align} $$
where
![]() ${\mathcal E}$
is the universal elliptic curve. Since the image of each
${\mathcal E}$
is the universal elliptic curve. Since the image of each
![]() ${\mathcal O}_D(p_i-q_i)$
in E is only well-defined up to sign, and the reducible fibers of
${\mathcal O}_D(p_i-q_i)$
in E is only well-defined up to sign, and the reducible fibers of
![]() $V\to C$
are unordered, we must quotient the target by the signed permutation group
$V\to C$
are unordered, we must quotient the target by the signed permutation group
![]() $\mathfrak S_8^{\pm }$
.
$\mathfrak S_8^{\pm }$
.
Observe that
![]() $\mathrm {Sym}^8{\mathcal C} \times _{\mathcal M_1} \mathrm {Prym}^2{\mathcal C}$
is ten-dimensional. There is a single condition ensuring that a point in the domain of
$\mathrm {Sym}^8{\mathcal C} \times _{\mathcal M_1} \mathrm {Prym}^2{\mathcal C}$
is ten-dimensional. There is a single condition ensuring that a point in the domain of
![]() $\Psi $
arises from a degeneration of surfaces in F: If
$\Psi $
arises from a degeneration of surfaces in F: If
![]() $L\to C$
is the Hodge bundle, then
$L\to C$
is the Hodge bundle, then
![]() $r_9+r_{10}\in |2L|$
and so by Proposition 4.1,
$r_9+r_{10}\in |2L|$
and so by Proposition 4.1,
![]() $\{r_1,\dots ,r_8\},\{r_9,r_{10}\}$
can arise so long as
$\{r_1,\dots ,r_8\},\{r_9,r_{10}\}$
can arise so long as
![]() $r_1+\cdots +r_8\in |8L|$
(i.e., the relation
$r_1+\cdots +r_8\in |8L|$
(i.e., the relation
is satisfied). So the Type II
![]() $_f$
limits of degenerations from F are described by
$_f$
limits of degenerations from F are described by
Our goal is to prove the dominance of the map
![]() $\Psi \big {|}_Z\colon Z\to {\mathbb {Z}}^8 \otimes {\mathcal E}/\mathfrak S_8^{\pm }.$
$\Psi \big {|}_Z\colon Z\to {\mathbb {Z}}^8 \otimes {\mathcal E}/\mathfrak S_8^{\pm }.$
Fix an elliptic curve fiber E of
![]() $\mathcal {E}$
, consider the point
$\mathcal {E}$
, consider the point
![]() $\{0,\dots ,0\}\in \mathrm {Sym}^8E$
, and let
$\{0,\dots ,0\}\in \mathrm {Sym}^8E$
, and let
![]() $\ker _E(\Psi ):= \Psi ^{-1}(\{0,\dots ,0\})$
. It suffices to prove that
$\ker _E(\Psi ):= \Psi ^{-1}(\{0,\dots ,0\})$
. It suffices to prove that
![]() $Z\cap \ker _E(\Psi )$
contains, as a component, some zero-dimensional scheme. Let
$Z\cap \ker _E(\Psi )$
contains, as a component, some zero-dimensional scheme. Let
![]() $L_E\subset \mathrm {Prym}^2\mathcal {C}$
be the sublocus of Prym data whose Prym variety is E. It is a curve inside the surface
$L_E\subset \mathrm {Prym}^2\mathcal {C}$
be the sublocus of Prym data whose Prym variety is E. It is a curve inside the surface
![]() $\mathrm {Prym}^2{\mathcal C}$
. Then,
$\mathrm {Prym}^2{\mathcal C}$
. Then,
![]() $\mathrm {ker}_E(\Psi )$
contains, as a component, an unramified double cover
$\mathrm {ker}_E(\Psi )$
contains, as a component, an unramified double cover
![]() $M_E\to L_E$
on which
$M_E\to L_E$
on which
![]() $r=r_1=\cdots = r_8$
and
$r=r_1=\cdots = r_8$
and
![]() $r\in \{r_9,r_{10}\}$
because the morphism
$r\in \{r_9,r_{10}\}$
because the morphism
![]() $D\to E$
sending
$D\to E$
sending
![]() $p\mapsto {\mathcal O}_D(p-\iota (p))\textrm { mod }\mathrm {Pic}^0(C)$
is surjective.
$p\mapsto {\mathcal O}_D(p-\iota (p))\textrm { mod }\mathrm {Pic}^0(C)$
is surjective.
The defining equation (4.3) of Z restricts to
![]() $M_E$
to give the equation
$M_E$
to give the equation
(i.e.,
![]() $r_9-r_{10}\in \mathrm {Pic}^0(C)[4]).$
The locus in
$r_9-r_{10}\in \mathrm {Pic}^0(C)[4]).$
The locus in
![]() $L_E$
on which
$L_E$
on which
![]() $r_9-r_{10}$
is
$r_9-r_{10}$
is
![]() $4$
-torsion is finite and nonempty. So the theorem follows.
$4$
-torsion is finite and nonempty. So the theorem follows.
The proofs of Theorems 3.2 and 4.4 suggest a rather wild conjecture:
Conjecture 4.5.
![]() $F_{1,1}$
admits a period-preserving birational involution
$F_{1,1}$
admits a period-preserving birational involution
![]() $S\leftrightarrow S'$
for which
$S\leftrightarrow S'$
for which
![]() $j(C)=j(F')$
and
$j(C)=j(F')$
and
![]() $j(F)=j(C')$
. Here,
$j(F)=j(C')$
. Here,
![]() $C, C'$
are the bases and
$C, C'$
are the bases and
![]() $F, F'$
, are the canonical fibers. Furthermore, S and
$F, F'$
, are the canonical fibers. Furthermore, S and
![]() $S'$
are moduli spaces of stable vector bundles on each other of rank
$S'$
are moduli spaces of stable vector bundles on each other of rank
![]() $2$
, determinant
$2$
, determinant
![]() ${\mathcal O}(s)$
, and
${\mathcal O}(s)$
, and
![]() $c_2=\mathrm {pt}$
. A Fourier-Mukai transform induces an isomorphism of their integral Hodge structures.
$c_2=\mathrm {pt}$
. A Fourier-Mukai transform induces an isomorphism of their integral Hodge structures.
The existence of such a birational involution would give a geometric explanation for why degenerations of Type II
![]() $_b$
and II
$_b$
and II
![]() $_f$
can have the same periods, even though
$_f$
can have the same periods, even though
![]() $j(C)\to \infty $
in the former, while
$j(C)\to \infty $
in the former, while
![]() $j(F)\to \infty $
in the latter.
$j(F)\to \infty $
in the latter.
5 A family losing dimension
Let
![]() $F^{\mathrm {cusp}}\hookrightarrow F$
be the closure of the sublocus of elliptic fibrations
$F^{\mathrm {cusp}}\hookrightarrow F$
be the closure of the sublocus of elliptic fibrations
![]() $S\to C$
which have six cuspidal (Kodaira type II) fibers. These fibrations are isotrivial and have a Weierstrass form
$S\to C$
which have six cuspidal (Kodaira type II) fibers. These fibrations are isotrivial and have a Weierstrass form
![]() $y^2=x^3+b$
for some
$y^2=x^3+b$
for some
![]() $b\in H^0(C,{\mathcal O}_C(6p))$
. There is a fiber preserving automorphism
$b\in H^0(C,{\mathcal O}_C(6p))$
. There is a fiber preserving automorphism
![]() $\sigma \colon S\to S$
, given by
$\sigma \colon S\to S$
, given by
and
![]() $\sigma ^*\Omega _S=\zeta _6\Omega _S$
acts nontrivially on the holomorphic
$\sigma ^*\Omega _S=\zeta _6\Omega _S$
acts nontrivially on the holomorphic
![]() $2$
-form by a primitive sixth root of unity. Furthermore, since
$2$
-form by a primitive sixth root of unity. Furthermore, since
![]() $\sigma $
preserves s and f, it defines an element
$\sigma $
preserves s and f, it defines an element
![]() $\sigma ^*\in \Gamma =O(I\!I_{2,10})$
which is easily checked to fix only the origin of
$\sigma ^*\in \Gamma =O(I\!I_{2,10})$
which is easily checked to fix only the origin of
![]() $I\!I_{2,10}$
. So
$I\!I_{2,10}$
. So
![]() $\sigma ^*$
endows
$\sigma ^*$
endows
![]() $I\!I_{2,10}$
with the structure of a Hermitian lattice of hyperbolic signature
$I\!I_{2,10}$
with the structure of a Hermitian lattice of hyperbolic signature
![]() $(1,5)$
over the Eisenstein integers
$(1,5)$
over the Eisenstein integers
![]() ${\mathbb {Z}}[\zeta _6]$
, and
${\mathbb {Z}}[\zeta _6]$
, and
is a Type I Hermitian symmetric subdomain (a complex ball), of dimension
![]() $5$
. Letting
$5$
. Letting
![]() $\Gamma _0:=\{\gamma \in \Gamma \,\big {|}\,\gamma \circ \sigma ^* = \sigma ^*\circ \gamma \}$
be the group of Hermitian isometries, we get a period map to a
$\Gamma _0:=\{\gamma \in \Gamma \,\big {|}\,\gamma \circ \sigma ^* = \sigma ^*\circ \gamma \}$
be the group of Hermitian isometries, we get a period map to a
![]() $5$
-dimensional ball quotient
$5$
-dimensional ball quotient
But
![]() $\dim F^{\mathrm {cusp}}=1+5=6$
with parameters corresponding to
$\dim F^{\mathrm {cusp}}=1+5=6$
with parameters corresponding to
![]() $j(C)$
and the relative locations of the six cuspidal fibers. Thus,
$j(C)$
and the relative locations of the six cuspidal fibers. Thus,
![]() $P\big {|}_{F^{\mathrm {cusp}}}$
has positive fiber dimension.
$P\big {|}_{F^{\mathrm {cusp}}}$
has positive fiber dimension.
It seems likely that
![]() $P\big {|}_{F^{\mathrm {cusp}}}$
is surjective, with generic fiber dimension
$P\big {|}_{F^{\mathrm {cusp}}}$
is surjective, with generic fiber dimension
![]() $1$
. Regardless, this gives a second example, after Ikeda’s [Reference IkedaIke19], proving that P is not a finitemap, even though it is generically finite by Theorem 1.1:
$1$
. Regardless, this gives a second example, after Ikeda’s [Reference IkedaIke19], proving that P is not a finitemap, even though it is generically finite by Theorem 1.1:
Corollary 5.1. P is not finite.
6 Mixed Hodge Structures
MHS of a normal crossings surface
Let
![]() $S_0$
be a reduced normal crossings surface with smooth double locus and no triple points. Our goal in this section is to explicitly describe the mixed Hodge structure on
$S_0$
be a reduced normal crossings surface with smooth double locus and no triple points. Our goal in this section is to explicitly describe the mixed Hodge structure on
![]() $H^2(S_0)$
. Let
$H^2(S_0)$
. Let
![]() $S_0 = \bigcup _{i=1}^m S_i$
with the double curve
$S_0 = \bigcup _{i=1}^m S_i$
with the double curve
![]() $D_{ij} = S_i\cap S_j$
a smooth, possibly disconnected or empty curve for all
$D_{ij} = S_i\cap S_j$
a smooth, possibly disconnected or empty curve for all
![]() $i<j$
. Let
$i<j$
. Let
![]() $D:=\bigcup _{i<j} D_{ij}$
. The Mayer-Vietoris sequence associated to a covering of
$D:=\bigcup _{i<j} D_{ij}$
. The Mayer-Vietoris sequence associated to a covering of
![]() $S_0$
by neighborhoods of the irreducible components
$S_0$
by neighborhoods of the irreducible components
![]() $S_i$
reads
$S_i$
reads
 $$ \begin{align} \bigoplus_{i=1}^m H^1(S_i) \overset{\iota^*}\to \bigoplus_{i< j} H^1(D_{ij}) \to H^2(S_0) \to \bigoplus_{i=1}^m H^2(S_i)\overset{\mathrm{res}}\longrightarrow \bigoplus_{i< j} H^2(D_{ij}).\end{align} $$
$$ \begin{align} \bigoplus_{i=1}^m H^1(S_i) \overset{\iota^*}\to \bigoplus_{i< j} H^1(D_{ij}) \to H^2(S_0) \to \bigoplus_{i=1}^m H^2(S_i)\overset{\mathrm{res}}\longrightarrow \bigoplus_{i< j} H^2(D_{ij}).\end{align} $$
Here,
![]() $\iota ^*$
and
$\iota ^*$
and
![]() $\mathrm {res}$
are signed restriction maps. Let
$\mathrm {res}$
are signed restriction maps. Let
![]() $K\subset \bigoplus H^2(S_i)$
be the kernel of the morphism
$K\subset \bigoplus H^2(S_i)$
be the kernel of the morphism
![]() $\mathrm {res}$
– that is,
$\mathrm {res}$
– that is,
![]() $K=\{(\alpha _i\in H^2(S_i))\,\big {|}\,\alpha _i\cdot D_{ij} = \alpha _j\cdot D_{ij}\}$
. Define
$K=\{(\alpha _i\in H^2(S_i))\,\big {|}\,\alpha _i\cdot D_{ij} = \alpha _j\cdot D_{ij}\}$
. Define
By exactness of the sequence (6.1), we obtain a short exact sequence
In fact, it is a short exact sequence of mixed Hodge structures with left-hand term J pure of weight
![]() $1$
, and the right-hand term K pure of weight
$1$
, and the right-hand term K pure of weight
![]() $2$
.
$2$
.
Proposition 6.1. If
![]() $p_g(S_i)=0$
for all components
$p_g(S_i)=0$
for all components
![]() $S_i\subset S_0$
(equivalently, K is Hodge-Tate of weight
$S_i\subset S_0$
(equivalently, K is Hodge-Tate of weight
![]() $2$
), then the Carlson classifying map [Reference CarlsonCar85]
$2$
), then the Carlson classifying map [Reference CarlsonCar85]
of the extension coincides with the Abel-Jacobi map. More precisely, an element of K is a tuple
![]() $(\alpha _i\in H^2(S_i,{\mathbb {Z}}))$
represented by line bundles
$(\alpha _i\in H^2(S_i,{\mathbb {Z}}))$
represented by line bundles
![]() $\mathcal {L}_i$
such that for each
$\mathcal {L}_i$
such that for each
![]() $i<j$
, we have
$i<j$
, we have
![]() $c_1(\mathcal {L}_i|_{D_{ij}}) -c_1(\mathcal {L}_j|_{D_{ij}}) =0\in H^2(D_{ij})$
. Then
$c_1(\mathcal {L}_i|_{D_{ij}}) -c_1(\mathcal {L}_j|_{D_{ij}}) =0\in H^2(D_{ij})$
. Then
![]() $\phi = \pi \circ \mathrm {AJ} \circ \psi $
, where
$\phi = \pi \circ \mathrm {AJ} \circ \psi $
, where
![]() $\mathrm {AJ}\colon \mathrm {Pic}^0(D) \to \mathrm {Jac}(D)= \mathrm {Jac}(H^1(D))$
is the classical Abel-Jacobi isomorphism, and
$\mathrm {AJ}\colon \mathrm {Pic}^0(D) \to \mathrm {Jac}(D)= \mathrm {Jac}(H^1(D))$
is the classical Abel-Jacobi isomorphism, and
![]() $\pi \colon \mathrm {Jac}(D) \to \mathrm {Jac}(J)$
is the projection map.
$\pi \colon \mathrm {Jac}(D) \to \mathrm {Jac}(J)$
is the projection map.
Proof. Following Carlson’s construction, the classifying map
![]() $\phi $
for a weight separated extension of mixed Hodge structures is given by the composition of two splittings. First, choose a left-splitting
$\phi $
for a weight separated extension of mixed Hodge structures is given by the composition of two splittings. First, choose a left-splitting
![]() $a: H^2(S_0) \to J$
over
$a: H^2(S_0) \to J$
over
![]() ${\mathbb {Z}}$
. Next, choose a right-splitting
${\mathbb {Z}}$
. Next, choose a right-splitting
![]() $b:K \to F^1 H^2(S_0)_{\mathbb {C}}$
over
$b:K \to F^1 H^2(S_0)_{\mathbb {C}}$
over
![]() ${\mathbb {C}}$
, which respects the Hodge filtration. The composition
${\mathbb {C}}$
, which respects the Hodge filtration. The composition
![]() $a_{\mathbb {C}}\circ b: K \to J_{\mathbb {C}}$
gives the classifying map after passing to the Jacobian quotient:
$a_{\mathbb {C}}\circ b: K \to J_{\mathbb {C}}$
gives the classifying map after passing to the Jacobian quotient:
For a, it suffices to produce a morphism on homology
![]() $\ker (\iota _*) \to H_2(S_0)$
, and then use the universal coefficient theorem to give a map in the opposite direction:
$\ker (\iota _*) \to H_2(S_0)$
, and then use the universal coefficient theorem to give a map in the opposite direction:
To define the morphism
![]() $\ker (\iota _*) \to H_2(S_0)$
, choose a basis for
$\ker (\iota _*) \to H_2(S_0)$
, choose a basis for
![]() $\ker (\iota _*)$
at the singular chain level: tuples of 1-cycles
$\ker (\iota _*)$
at the singular chain level: tuples of 1-cycles
![]() $t_k=(\gamma ^k_{ij}\in \mathcal {Z}_1(D_{ij}))$
such that for each i,
$t_k=(\gamma ^k_{ij}\in \mathcal {Z}_1(D_{ij}))$
such that for each i,
We use the convention that
![]() $\gamma _{ij} = - \gamma _{ji}$
. Choosing such
$\gamma _{ij} = - \gamma _{ji}$
. Choosing such
![]() $\Gamma _i^k$
for each
$\Gamma _i^k$
for each
![]() $t_k$
in the basis of
$t_k$
in the basis of
![]() $\ker (i_*)$
, we construct a
$\ker (i_*)$
, we construct a
![]() $2$
-cycle (see Figure 4),
$2$
-cycle (see Figure 4),
We take the
![]() $1$
-cycles
$1$
-cycles
![]() $\gamma _{ij}^k$
to be
$\gamma _{ij}^k$
to be
![]() ${\mathbb {Z}}$
-linear combinations of some fixed
${\mathbb {Z}}$
-linear combinations of some fixed
![]() $2g(D_{ij})$
loops on each
$2g(D_{ij})$
loops on each
![]() $D_{ij}$
, whose union we call
$D_{ij}$
, whose union we call
![]() $\gamma $
, chosen so that their complement in
$\gamma $
, chosen so that their complement in
![]() $D_{ij}$
is a contractible
$D_{ij}$
is a contractible
![]() $4g$
-gon. The assignment
$4g$
-gon. The assignment
![]() $t_k \mapsto [T_k]\in H_2(S_0)$
then induces a splitting
$t_k \mapsto [T_k]\in H_2(S_0)$
then induces a splitting

Figure 4 Heuristic diagram of irreducible components
![]() $S_i$
in black, double curves
$S_i$
in black, double curves
![]() $D_{ij}$
in red,
$D_{ij}$
in red,
![]() $1$
-cycles
$1$
-cycles
![]() $\gamma _{ij}\subset D_{ij}$
in green, and
$\gamma _{ij}\subset D_{ij}$
in green, and
![]() $2$
-cycles
$2$
-cycles
![]() $\Gamma _i\subset S_i$
capping the
$\Gamma _i\subset S_i$
capping the
![]() $1$
-cycles in blue.
$1$
-cycles in blue.
To construct a splitting b, we use the Čech-de Rham model of
![]() $H^2(S_0,{\mathbb {C}})$
, and its Hodge filtration
$H^2(S_0,{\mathbb {C}})$
, and its Hodge filtration
![]() $F^1$
. An element of
$F^1$
. An element of
![]() $H^2(S_0,{\mathbb {C}})$
is represented by two tuples of differential forms:
$H^2(S_0,{\mathbb {C}})$
is represented by two tuples of differential forms:
such that for all
![]() $i<j$
, we have
$i<j$
, we have
![]() $\omega _i|_{D_{ij}} - \omega _j|_{D_{ij}} = d\theta _{ij}$
. If furthermore,
$\omega _i|_{D_{ij}} - \omega _j|_{D_{ij}} = d\theta _{ij}$
. If furthermore,
![]() $\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
for all
$\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
for all
![]() $i<j$
, then the element lies in
$i<j$
, then the element lies in
![]() $F^1H^2(S_0,{\mathbb {C}})$
.
$F^1H^2(S_0,{\mathbb {C}})$
.
Given
![]() $(\alpha _i)\in K = \ker (\mathrm {res})$
, we know that
$(\alpha _i)\in K = \ker (\mathrm {res})$
, we know that
![]() $\alpha _i|_{D_{ij}} - \alpha _j|_{D_{ij}}=0\in H^2(D_{ij})$
. To define
$\alpha _i|_{D_{ij}} - \alpha _j|_{D_{ij}}=0\in H^2(D_{ij})$
. To define
![]() $b:K \to F^1 H^2(S_0,{\mathbb {C}})$
, select a basis for K; for each basis element
$b:K \to F^1 H^2(S_0,{\mathbb {C}})$
, select a basis for K; for each basis element
![]() $(\alpha _i)\in K$
, there exists line bundles
$(\alpha _i)\in K$
, there exists line bundles
![]() $\mathcal {L}_i$
such that
$\mathcal {L}_i$
such that
![]() $c_1(\mathcal {L}_i)=\alpha _i$
. Since each
$c_1(\mathcal {L}_i)=\alpha _i$
. Since each
![]() $S_i$
is projective, we may assume that the
$S_i$
is projective, we may assume that the
![]() $\mathcal {L}_i \simeq \mathcal {O}_{S_i}(C_i - C^{\prime }_i)$
, where
$\mathcal {L}_i \simeq \mathcal {O}_{S_i}(C_i - C^{\prime }_i)$
, where
![]() $C_i$
and
$C_i$
and
![]() $C_i'$
are ample effective curves on
$C_i'$
are ample effective curves on
![]() $S_i$
meeting each
$S_i$
meeting each
![]() $D_{ij}$
transversely away from
$D_{ij}$
transversely away from
![]() $\gamma $
. We take
$\gamma $
. We take
![]() $\omega _i\in {\mathcal Z}^2(S_i)$
representing
$\omega _i\in {\mathcal Z}^2(S_i)$
representing
![]() $c_1(\mathcal {L}_i)$
and supported on a small neighborhood of
$c_1(\mathcal {L}_i)$
and supported on a small neighborhood of
![]() $C_i\cup C^{\prime }_i$
. Since
$C_i\cup C^{\prime }_i$
. Since
![]() $\omega _i|_{D_{ij}} - \omega _j|_{D_{ij}}\in {\mathcal Z}^2(D_{ij})$
integrates to 0, it has a
$\omega _i|_{D_{ij}} - \omega _j|_{D_{ij}}\in {\mathcal Z}^2(D_{ij})$
integrates to 0, it has a
![]() $\overline {\partial }$
-primitive
$\overline {\partial }$
-primitive
![]() $\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
, unique up to the addition of a holomorphic one-form.
$\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
, unique up to the addition of a holomorphic one-form.
To interpret the composition
![]() $\phi =a_{\mathbb {C}} \circ b:K \to J_{\mathbb {C}}$
, we will regard
$\phi =a_{\mathbb {C}} \circ b:K \to J_{\mathbb {C}}$
, we will regard
![]() $J_{\mathbb {C}}$
as
$J_{\mathbb {C}}$
as
![]() $\mathrm {Hom}(\ker (\iota _*),{\mathbb {C}})$
. Then
$\mathrm {Hom}(\ker (\iota _*),{\mathbb {C}})$
. Then
![]() $(a_{\mathbb {C}} \circ b)(\alpha _i)$
is the unique homomorphism
$(a_{\mathbb {C}} \circ b)(\alpha _i)$
is the unique homomorphism
![]() $\ker (\iota _*)\to {\mathbb {C}}$
which sends
$\ker (\iota _*)\to {\mathbb {C}}$
which sends
![]() $t_k$
to
$t_k$
to
 $$ \begin{align} \sum_{i=1}^m \int_{\Gamma_i^k} \omega_i + \sum_{i<j} \int_{\gamma_{ij}^k} \theta_{ij}. \end{align} $$
$$ \begin{align} \sum_{i=1}^m \int_{\Gamma_i^k} \omega_i + \sum_{i<j} \int_{\gamma_{ij}^k} \theta_{ij}. \end{align} $$
We henceforth drop the index k as we will consider a single basis vector
![]() $t=t_k$
.
$t=t_k$
.
We will make two simplifications in order to compare
![]() $\phi $
with the Abel-Jacobi map. First, the chains
$\phi $
with the Abel-Jacobi map. First, the chains
![]() $\Gamma _i$
can be replaced with
$\Gamma _i$
can be replaced with
![]() $\Gamma _i+x_i$
for any
$\Gamma _i+x_i$
for any
![]() $x_i\in \mathcal {Z}_2(S_i)$
such that the tuple of homology classes
$x_i\in \mathcal {Z}_2(S_i)$
such that the tuple of homology classes
![]() $(x_i)$
is Poincaré dual to an element of K. By Lefschetz duality, there is a perfect pairing associated to the 4-manifold with boundary
$(x_i)$
is Poincaré dual to an element of K. By Lefschetz duality, there is a perfect pairing associated to the 4-manifold with boundary
and we have
![]() $\int _{\Gamma _i} \omega _i = I(C_i - C_i', \Gamma _i) \in {\mathbb {Z}}$
. Since
$\int _{\Gamma _i} \omega _i = I(C_i - C_i', \Gamma _i) \in {\mathbb {Z}}$
. Since
![]() $(\alpha _i)$
is primitive in K, one can find
$(\alpha _i)$
is primitive in K, one can find
![]() $x\in K$
such that
$x\in K$
such that
So replacing
![]() $\Gamma _i$
with
$\Gamma _i$
with
![]() $\Gamma _i+x_i$
, we may assume that the first sum in (6.2) vanishes.
$\Gamma _i+x_i$
, we may assume that the first sum in (6.2) vanishes.
Second, the primitives
![]() $\theta _{ij}$
are not closed, so the second integral does not make sense on the homology classes
$\theta _{ij}$
are not closed, so the second integral does not make sense on the homology classes
![]() $[\gamma ^k_{ij}]$
. To remedy this, we construct smooth 1-forms
$[\gamma ^k_{ij}]$
. To remedy this, we construct smooth 1-forms
![]() $\lambda _{ij}\in {\mathcal Z}^1(D_{ij})$
supported away from
$\lambda _{ij}\in {\mathcal Z}^1(D_{ij})$
supported away from
![]() $\gamma $
such that
$\gamma $
such that
![]() $d(\theta _{ij}+\lambda _{ij})=0$
. Let
$d(\theta _{ij}+\lambda _{ij})=0$
. Let
![]() $\ell _{ij}$
be a smooth 1-chain on
$\ell _{ij}$
be a smooth 1-chain on
![]() $D_{ij}\setminus \gamma $
with boundary the signed intersection points:
$D_{ij}\setminus \gamma $
with boundary the signed intersection points:
By Lemma 6.2 below, we may produce a form
![]() $\lambda _{ij}$
supported in a neighborhood of
$\lambda _{ij}$
supported in a neighborhood of
![]() $\ell _{ij}$
. This allows us to write the Carlson map for our extension as
$\ell _{ij}$
. This allows us to write the Carlson map for our extension as
 $$ \begin{align*}\phi((\alpha_i)) = \left[ t \mapsto \sum_{i<j} \int_{\lambda_{ij}} (\theta_{ij}+\lambda_{ij}) \right] \in J_{\mathbb{C}} / (J_{\mathbb{Z}} + F^1J_{\mathbb{C}}).\end{align*} $$
$$ \begin{align*}\phi((\alpha_i)) = \left[ t \mapsto \sum_{i<j} \int_{\lambda_{ij}} (\theta_{ij}+\lambda_{ij}) \right] \in J_{\mathbb{C}} / (J_{\mathbb{Z}} + F^1J_{\mathbb{C}}).\end{align*} $$
But for any
![]() $\tau \in \Omega ^1(D_{ij})$
, since
$\tau \in \Omega ^1(D_{ij})$
, since
![]() $\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
we have, again by Lemma 6.2,
$\theta _{ij}\in \mathcal {A}^{1,0}(D_{ij})$
we have, again by Lemma 6.2,
 $$ \begin{align*}\int_{D_{ij}} (\theta_{ij}+\lambda_{ij})\wedge \tau = \int_{D_{ij}} \lambda_{ij}\wedge \tau = \int_{\ell_{ij}} \tau.\end{align*} $$
$$ \begin{align*}\int_{D_{ij}} (\theta_{ij}+\lambda_{ij})\wedge \tau = \int_{D_{ij}} \lambda_{ij}\wedge \tau = \int_{\ell_{ij}} \tau.\end{align*} $$
Observe that the classical Abel-Jacobi map
![]() $\mathrm {AJ}\colon \mathrm {Pic}^0(D)\to \mathrm {Jac}(D)$
indeed sends
$\mathrm {AJ}\colon \mathrm {Pic}^0(D)\to \mathrm {Jac}(D)$
indeed sends
![]() $[\partial \ell _{ij}] \mapsto \int _{\ell _{ij}}$
. The proposition follows.
$[\partial \ell _{ij}] \mapsto \int _{\ell _{ij}}$
. The proposition follows.
Now, we produce the one-form
![]() $\lambda _{ij}$
with the desired properties.
$\lambda _{ij}$
with the desired properties.
Lemma 6.2. Let C be a Riemann surface and let
![]() $\mathcal {L}=\mathcal {O}_C(q-p)$
. There is a hermitian metric h on
$\mathcal {L}=\mathcal {O}_C(q-p)$
. There is a hermitian metric h on
![]() $\mathcal {L}$
, a
$\mathcal {L}$
, a
![]() $(1,0)$
-form
$(1,0)$
-form
![]() $\theta \in \mathcal {A}^{1,0}(C)$
, and a smooth
$\theta \in \mathcal {A}^{1,0}(C)$
, and a smooth
![]() $1$
-form
$1$
-form
![]() $\lambda $
supported in a neighborhood of a path
$\lambda $
supported in a neighborhood of a path
![]() $\ell $
from p to q for which
$\ell $
from p to q for which
-
1.
 $\overline {\partial } \theta = \frac {i}{2\pi }\partial \overline {\partial }\log (h)$
,
$\overline {\partial } \theta = \frac {i}{2\pi }\partial \overline {\partial }\log (h)$
, -
2.
 $d\lambda = -\overline {\partial } \theta $
, and
$d\lambda = -\overline {\partial } \theta $
, and -
3.
 $\int \lambda \wedge \tau = \int _{\ell } \tau $
for any holomorphic one-form
$\int \lambda \wedge \tau = \int _{\ell } \tau $
for any holomorphic one-form
 $\tau $
.
$\tau $
.
Proof. Let z be a chart to
![]() ${\mathbb {C}}$
from a neighborhood of
${\mathbb {C}}$
from a neighborhood of
![]() $\ell $
. There exists a function
$\ell $
. There exists a function
![]() $f\colon C\setminus \{p,q\}\to {\mathbb {C}}^*$
of the following form:
$f\colon C\setminus \{p,q\}\to {\mathbb {C}}^*$
of the following form:

Such a smooth interpolation exists because
![]() $\frac {z-q}{z-p}$
has winding number zero along the boundary of
$\frac {z-q}{z-p}$
has winding number zero along the boundary of
![]() $N_{\epsilon /2}(\ell )$
. Let
$N_{\epsilon /2}(\ell )$
. Let
![]() $s\in \mathrm {Mero}(C, \mathcal {L})$
be a meromorphic section with a zero at q and a pole at p. Then, there is a hermitian metric h on
$s\in \mathrm {Mero}(C, \mathcal {L})$
be a meromorphic section with a zero at q and a pole at p. Then, there is a hermitian metric h on
![]() $\mathcal {L}$
for which
$\mathcal {L}$
for which
![]() $h(s,\overline {s})=|f|^2$
. The associated curvature form is
$h(s,\overline {s})=|f|^2$
. The associated curvature form is
![]() $\tfrac {i}{2\pi }\partial \overline {\partial } \log |f|^2$
, and since
$\tfrac {i}{2\pi }\partial \overline {\partial } \log |f|^2$
, and since
![]() $c_1(\mathcal {L})=0$
, we can find a
$c_1(\mathcal {L})=0$
, we can find a
![]() $(1,0)$
-form
$(1,0)$
-form
![]() $\theta $
satisfying (1). Furthermore,
$\theta $
satisfying (1). Furthermore,
![]() $\lambda = -\frac {i}{2\pi }(\overline {\partial } \log (f)-\partial \log (\overline {f}))$
is a
$\lambda = -\frac {i}{2\pi }(\overline {\partial } \log (f)-\partial \log (\overline {f}))$
is a
![]() $(0,1)$
-form, supported in
$(0,1)$
-form, supported in
![]() $A:=N_{\epsilon /2}(\ell )^c\cap N_\epsilon (\ell )$
and satisfying (2).
$A:=N_{\epsilon /2}(\ell )^c\cap N_\epsilon (\ell )$
and satisfying (2).
It remains to check (3). We may write
![]() $\tau = dg$
for some holomorphic function
$\tau = dg$
for some holomorphic function
![]() $g\colon N_\epsilon (\ell )\to {\mathbb {C}}$
. Applying Stokes’s formula and the residue formula, we have
$g\colon N_\epsilon (\ell )\to {\mathbb {C}}$
. Applying Stokes’s formula and the residue formula, we have
 $$ \begin{align*}\int_C \lambda\wedge \tau &=- \tfrac{i}{2\pi} \int_A\overline{\partial}\log(f) \wedge dg = \tfrac{i}{2\pi} \int_A d(ig\cdot d\log(f)) =\tfrac{i}{2\pi}\int_{\partial A} ig\cdot d\log(f) \\ &= -\tfrac{i}{2\pi}\int_{\partial N_{\epsilon/2}(\ell)}g \cdot d\log(\tfrac{z-q}{z-p}) = -\tfrac{i}{2\pi} (2\pi i)(g(q)-g(p)) = \int_\ell\tau. \end{align*} $$
$$ \begin{align*}\int_C \lambda\wedge \tau &=- \tfrac{i}{2\pi} \int_A\overline{\partial}\log(f) \wedge dg = \tfrac{i}{2\pi} \int_A d(ig\cdot d\log(f)) =\tfrac{i}{2\pi}\int_{\partial A} ig\cdot d\log(f) \\ &= -\tfrac{i}{2\pi}\int_{\partial N_{\epsilon/2}(\ell)}g \cdot d\log(\tfrac{z-q}{z-p}) = -\tfrac{i}{2\pi} (2\pi i)(g(q)-g(p)) = \int_\ell\tau. \end{align*} $$
More generally, the lemma holds for any degree zero line bundle
![]() $\mathcal {O}_C(\sum (q_i-p_i))$
, for a union of paths connecting each pair of points
$\mathcal {O}_C(\sum (q_i-p_i))$
, for a union of paths connecting each pair of points
![]() $p_i$
to
$p_i$
to
![]() $q_i$
by taking the product of the hermitian metrics, and sum of the corresponding
$q_i$
by taking the product of the hermitian metrics, and sum of the corresponding
![]() $\theta $
’s and
$\theta $
’s and
![]() $\lambda $
’s.
$\lambda $
’s.
Remark 6.3. To apply Lemma 6.2 to the proof of Proposition 6.1, our forms
![]() $\omega _i$
must be such that
$\omega _i$
must be such that
![]() $\omega _i|_{D_{ij}}-\omega _j|_{D_{ij}}$
is the two-form
$\omega _i|_{D_{ij}}-\omega _j|_{D_{ij}}$
is the two-form
![]() $\frac {i}{2\pi } \partial \overline {\partial }\log (h)$
supported in a neighborhood of
$\frac {i}{2\pi } \partial \overline {\partial }\log (h)$
supported in a neighborhood of
![]() $\ell _{ij}$
. This is achieved by choosing
$\ell _{ij}$
. This is achieved by choosing
![]() $\omega _i = \frac {i}{2\pi } \partial \overline {\partial } \log (h_i)$
for hermitian metrics on
$\omega _i = \frac {i}{2\pi } \partial \overline {\partial } \log (h_i)$
for hermitian metrics on
![]() $h_i$
on
$h_i$
on
![]() $\mathcal {L}_i$
(and similarly for j) so that
$\mathcal {L}_i$
(and similarly for j) so that
![]() $h=h_i/h_j$
is the desired hermitian metric on
$h=h_i/h_j$
is the desired hermitian metric on
![]() $\mathcal {L}_i|_{D_{ij}}\otimes \mathcal {L}_j|_{D_{ij}}^{-1}$
. Note though that we must allow the two-form
$\mathcal {L}_i|_{D_{ij}}\otimes \mathcal {L}_j|_{D_{ij}}^{-1}$
. Note though that we must allow the two-form
![]() $\omega _i$
to be supported in a tubular neighborhood of
$\omega _i$
to be supported in a tubular neighborhood of
![]() $C_i\cup C_i'\cup \ell _{ij}$
rather than just
$C_i\cup C_i'\cup \ell _{ij}$
rather than just
![]() $C_i\cup C_i'$
. Since
$C_i\cup C_i'$
. Since
![]() $\ell _{ij}$
is disjoint from
$\ell _{ij}$
is disjoint from
![]() $\gamma $
, the argument of Lemma 6.1 is unaffected.
$\gamma $
, the argument of Lemma 6.1 is unaffected.
Clemens-Schmid sequence
Let
![]() $\mathcal {S}\to (B,0)$
be a degeneration of projective surfaces with smooth total space and reduced normal crossings central fiber
$\mathcal {S}\to (B,0)$
be a degeneration of projective surfaces with smooth total space and reduced normal crossings central fiber
![]() $S_0=\bigcup _{i=1}^m S_i$
with smooth double locus. Assume, furthermore, that
$S_0=\bigcup _{i=1}^m S_i$
with smooth double locus. Assume, furthermore, that
![]() $p_g(S_i)=0$
for all i.
$p_g(S_i)=0$
for all i.
The monodromy is unipotent by Clemens [Reference ClemensCle69]. So let N be the nilpotent logarithm of the monodromy operator on
![]() $H^*(S_t)$
. We have the Clemens-Schmid sequence [Reference MorrisonMor84] relating the integral cohomology of
$H^*(S_t)$
. We have the Clemens-Schmid sequence [Reference MorrisonMor84] relating the integral cohomology of
![]() $S_0$
and
$S_0$
and
![]() $S_t$
:
$S_t$
:
Since the monodromy operator acts trivially on
![]() $H^0(S_t)$
, the first nilpotent operator in (6.3) is identically
$H^0(S_t)$
, the first nilpotent operator in (6.3) is identically
![]() $0$
. Using these two observations, the Clemens-Schmid sequence can be shortened to
$0$
. Using these two observations, the Clemens-Schmid sequence can be shortened to
The limit mixed Hodge structure
![]() $H^2(S_t)$
has a monodromy-weight filtration defined in terms of N:
$H^2(S_t)$
has a monodromy-weight filtration defined in terms of N:
![]() $\{0\} = W_0 \subset W_1 \subset W_2 \subset W_3 = H^2(S_t)$
.
$\{0\} = W_0 \subset W_1 \subset W_2 \subset W_3 = H^2(S_t)$
.
 $$ \begin{align*} W_1 H^2(S_t) &= \mathrm{im}(N) ;\\ W_2 H^2(S_t) &= \ker(N) ;\\ W_3 H^2(S_t) &= H^2(S_t). \end{align*} $$
$$ \begin{align*} W_1 H^2(S_t) &= \mathrm{im}(N) ;\\ W_2 H^2(S_t) &= \ker(N) ;\\ W_3 H^2(S_t) &= H^2(S_t). \end{align*} $$
We call
![]() $\ker (N)$
the 1-truncated mixed Hodge structure. To describe the 1-truncation explicitly, we combine (6.4) and (6.1) above at their common term
$\ker (N)$
the 1-truncated mixed Hodge structure. To describe the 1-truncation explicitly, we combine (6.4) and (6.1) above at their common term
![]() $H^2(S_0)$
, with Mayer-Vietoris written horizontally and Clemens-Schmid written vertically.
$H^2(S_0)$
, with Mayer-Vietoris written horizontally and Clemens-Schmid written vertically.

Here,
![]() $\xi _k:= \sum _j [D_{jk}]-[D_{kj}]$
, where
$\xi _k:= \sum _j [D_{jk}]-[D_{kj}]$
, where
![]() $[D_{jk}]\in H^2(S_j)$
and
$[D_{jk}]\in H^2(S_j)$
and
![]() $[D_{kj}]\in H^2(S_k)$
are the fundamental classes of the double loci, and
$[D_{kj}]\in H^2(S_k)$
are the fundamental classes of the double loci, and
![]() $\Lambda $
is the cokernel of
$\Lambda $
is the cokernel of
![]() $J\to \ker (N)$
. We have that
$J\to \ker (N)$
. We have that
![]() $\xi _k= c_1(\mathcal {O}_{\mathcal {S}}(S_k)|_{S_0})$
. By Proposition 6.1, we have
$\xi _k= c_1(\mathcal {O}_{\mathcal {S}}(S_k)|_{S_0})$
. By Proposition 6.1, we have
![]() $\xi _k\in \ker (\phi \colon K\to \mathrm {Jac}(J))$
because the line bundles
$\xi _k\in \ker (\phi \colon K\to \mathrm {Jac}(J))$
because the line bundles
![]() $\mathcal {O}_{\mathcal {S}}(S_k)\big {|}_{S_i}\simeq \mathcal {O}_{\mathcal {S}}(S_k)\big {|}_{S_j}$
agree on the double locus. Hence, the Carlson extension homomorphism
$\mathcal {O}_{\mathcal {S}}(S_k)\big {|}_{S_i}\simeq \mathcal {O}_{\mathcal {S}}(S_k)\big {|}_{S_j}$
agree on the double locus. Hence, the Carlson extension homomorphism
![]() $\phi $
descends to a homomorphism
$\phi $
descends to a homomorphism
encoding the 1-truncated mixed Hodge structure.
Application
In this section, we apply the general results above to the mixed Hodge structures associated to the degenerations of Type II
![]() $_b$
and II
$_b$
and II
![]() $_f$
, and relate their associated periods to the boundary of the toroidal extension
$_f$
, and relate their associated periods to the boundary of the toroidal extension
![]() $({\mathbb D}/\Gamma )^{\mathrm {II}}$
.
$({\mathbb D}/\Gamma )^{\mathrm {II}}$
.
It is convenient to make an order
![]() $2$
base change and resolution to the Type II
$2$
base change and resolution to the Type II
![]() $_b$
degenerations. The effect is to normalize the first component and insert a second component isomorphic to
$_b$
degenerations. The effect is to normalize the first component and insert a second component isomorphic to
![]() $\mathbb {P}^1\times E$
where E is the fiber over the node of
$\mathbb {P}^1\times E$
where E is the fiber over the node of
![]() $C_0$
. This second component is glued to the rational elliptic surface
$C_0$
. This second component is glued to the rational elliptic surface
![]() $X\to \mathbb {P}^1$
along the two fibers
$X\to \mathbb {P}^1$
along the two fibers
![]() $X_p, X_q$
.
$X_p, X_q$
.
After the base change and resolution, we have that in both II
![]() $_b$
and II
$_b$
and II
![]() $_f$
degenerations, the central fiber
$_f$
degenerations, the central fiber
![]() $S_0$
has two irreducible components and reduced normal crossings:
$S_0$
has two irreducible components and reduced normal crossings:
![]() $S_0 = S_1 \cup _D S_2$
. The double locus D is a disjoint union of two copies of the same elliptic curve E in Type II
$S_0 = S_1 \cup _D S_2$
. The double locus D is a disjoint union of two copies of the same elliptic curve E in Type II
![]() $_b$
and a connected, smooth genus
$_b$
and a connected, smooth genus
![]() $2$
curve in Type II
$2$
curve in Type II
![]() $_f$
. Let
$_f$
. Let
![]() $D_1\subset S_1$
and
$D_1\subset S_1$
and
![]() $D_2\subset S_2$
denote the double locus restricted to each component.
$D_2\subset S_2$
denote the double locus restricted to each component.
In both cases, the divisor D admits a natural involution
![]() $\iota $
, and the image of the first map
$\iota $
, and the image of the first map
![]() $\iota ^*$
in (6.1) is the
$\iota ^*$
in (6.1) is the
![]() $(+1)$
-eigenspace of this involution on
$(+1)$
-eigenspace of this involution on
![]() $H^1(D)$
. The image of the restriction map
$H^1(D)$
. The image of the restriction map
![]() $\mathrm {res}$
in (6.1) is a rank 1 subgroup of
$\mathrm {res}$
in (6.1) is a rank 1 subgroup of
![]() $H^2(D)\simeq H_0(D)$
, so the Mayer-Vietoris sequence takes the form
$H^2(D)\simeq H_0(D)$
, so the Mayer-Vietoris sequence takes the form
Case II
![]() $_{\mathbf {b}}$
. The component
$_{\mathbf {b}}$
. The component
![]() $S_1$
is a rational elliptic surface X, with
$S_1$
is a rational elliptic surface X, with
![]() $D_1 = X_p \cup X_q$
a pair of isomorphic elliptic curve fibers. The component
$D_1 = X_p \cup X_q$
a pair of isomorphic elliptic curve fibers. The component
![]() $S_2$
is simply
$S_2$
is simply
![]() ${\mathbb P}^1\times E$
with
${\mathbb P}^1\times E$
with
![]() $D_2=\{0,\infty \}\times E$
. The involution on D swaps the two isomorphic components. Note that since
$D_2=\{0,\infty \}\times E$
. The involution on D swaps the two isomorphic components. Note that since
![]() $[X_p] = [X_q]\in H^2(S_1)$
, and similarly for
$[X_p] = [X_q]\in H^2(S_1)$
, and similarly for
![]() $S_2$
, the two restriction maps
$S_2$
, the two restriction maps
![]() $H^2(S_i) \to H^2(D)\simeq H^2(E)^{\oplus 2}$
have the same image – namely, the diagonal.
$H^2(S_i) \to H^2(D)\simeq H^2(E)^{\oplus 2}$
have the same image – namely, the diagonal.
Case II
![]() $_{\mathbf {f}}$
. The component
$_{\mathbf {f}}$
. The component
![]() $S_1$
is an elliptic ruled surface
$S_1$
is an elliptic ruled surface
![]() $X\simeq {\mathbb P}_C({\mathcal O}\oplus L)$
, with
$X\simeq {\mathbb P}_C({\mathcal O}\oplus L)$
, with
![]() $D_1$
a genus 2 bisection of class
$D_1$
a genus 2 bisection of class
![]() $2s_0 = 2(s_\infty +f)$
. The component
$2s_0 = 2(s_\infty +f)$
. The component
![]() $S_2$
is the blow-up of (a deformation of)
$S_2$
is the blow-up of (a deformation of)
![]() $S_1$
at 8 points along
$S_1$
at 8 points along
![]() $D_1$
with
$D_1$
with
![]() $D_2$
the proper transform of
$D_2$
the proper transform of
![]() $D_1$
in the blow-up. The class of
$D_1$
in the blow-up. The class of
![]() $D_2$
is
$D_2$
is
![]() $2s_0 - \sum e_i$
. The involution on D is induced by the double cover map
$2s_0 - \sum e_i$
. The involution on D is induced by the double cover map
![]() $\nu \colon D \to C$
which comes from the ruling of X. Since D is irreducible,
$\nu \colon D \to C$
which comes from the ruling of X. Since D is irreducible,
![]() $H^2(D)\simeq {\mathbb {Z}}$
.
$H^2(D)\simeq {\mathbb {Z}}$
.
In both cases, the Jacobian
![]() $\mathrm {Jac}(H^1(D)^-)=E$
is an elliptic curve. In Type II
$\mathrm {Jac}(H^1(D)^-)=E$
is an elliptic curve. In Type II
![]() $_b$
, it is
$_b$
, it is
![]() $\mathrm {Jac}(E)$
, where E is either of the double curves, while in Type II
$\mathrm {Jac}(E)$
, where E is either of the double curves, while in Type II
![]() $_f$
, it is the Prym variety of the double cover map
$_f$
, it is the Prym variety of the double cover map
![]() $\nu \colon D\to C$
. Thus, the mixed Hodge structure on
$\nu \colon D\to C$
. Thus, the mixed Hodge structure on
![]() $H^2(S_0)$
is encoded by a Carlson extension map
$H^2(S_0)$
is encoded by a Carlson extension map
![]() $\phi \in \mathrm {Hom}(K,E)$
. By the previous subsection, this extension homomorphism descends to
$\phi \in \mathrm {Hom}(K,E)$
. By the previous subsection, this extension homomorphism descends to
![]() $\psi _{S_0}\in \mathrm {Hom}(\Lambda ,E)$
, where
$\psi _{S_0}\in \mathrm {Hom}(\Lambda ,E)$
, where
There is a symmetric bilinear form on
![]() $H^2(S_0)$
. Let
$H^2(S_0)$
. Let
be restriction, followed by the Poincaré duality, followed by inclusion. Then define
![]() $\alpha \cdot \beta := \langle \alpha , p(\beta )\rangle $
on
$\alpha \cdot \beta := \langle \alpha , p(\beta )\rangle $
on
![]() $H^2(S_0)$
. The map
$H^2(S_0)$
. The map
![]() $H^2(S_0)\to H^2(S_t)$
respects the bilinear forms on the source, and target and the bilinear form descends to
$H^2(S_0)\to H^2(S_t)$
respects the bilinear forms on the source, and target and the bilinear form descends to
![]() $K=\ker (\mathrm {res})$
.
$K=\ker (\mathrm {res})$
.
By Poincaré duality and the Hodge index theorem,
![]() $H^2(S_1)\oplus H^2(S_2)$
is a unimodular lattice of signature
$H^2(S_1)\oplus H^2(S_2)$
is a unimodular lattice of signature
![]() $(2,10)$
, and it is odd since at least one summand contains
$(2,10)$
, and it is odd since at least one summand contains
![]() $(-1)$
-curves. Since
$(-1)$
-curves. Since
![]() $D_1^2+D_2^2 =0$
, the lattice vector
$D_1^2+D_2^2 =0$
, the lattice vector
![]() $(D_1,-D_2)$
is isotropic, and its orthogonal complement is precisely
$(D_1,-D_2)$
is isotropic, and its orthogonal complement is precisely
![]() $\ker (\mathrm {res})$
. Hence, the lattice
$\ker (\mathrm {res})$
. Hence, the lattice
![]() $\Lambda $
is unimodular of signature
$\Lambda $
is unimodular of signature
![]() $(1,9)$
.
$(1,9)$
.
Our degenerating families are polarized by
![]() ${\mathbb {Z}} s\oplus {\mathbb {Z}}(s+f)\subset H^2(S_t)$
. The monodromy operator fixes these curve classes, and hence, we have a copy of
${\mathbb {Z}} s\oplus {\mathbb {Z}}(s+f)\subset H^2(S_t)$
. The monodromy operator fixes these curve classes, and hence, we have a copy of
![]() $I_{1,1}\subset \ker (N)$
. So s, f extend over the singular fiber by (6.3). They can be represented inK as follows:
$I_{1,1}\subset \ker (N)$
. So s, f extend over the singular fiber by (6.3). They can be represented inK as follows:
![]() $(s,s)$
,
$(s,s)$
,
![]() $(f,0)$
for Type II
$(f,0)$
for Type II
![]() $_b$
and
$_b$
and
![]() $(s_\infty , 0)$
,
$(s_\infty , 0)$
,
![]() $(f,f)$
for Type II
$(f,f)$
for Type II
![]() $_f$
, respectively. In both cases, they span a sublattice of
$_f$
, respectively. In both cases, they span a sublattice of
![]() $\Lambda $
isometric to
$\Lambda $
isometric to
![]() $I_{1,1}$
whose orthogonal complement we call
$I_{1,1}$
whose orthogonal complement we call
![]() $\Lambda _0\subset \Lambda $
. We also have
$\Lambda _0\subset \Lambda $
. We also have
![]() $\Lambda _0\simeq \Lambda /I_{1,1}$
canonically.
$\Lambda _0\simeq \Lambda /I_{1,1}$
canonically.
Proposition 6.4. The lattice
![]() $\Lambda _0$
is isometric to
$\Lambda _0$
is isometric to
![]() $E_8$
in both cases.
$E_8$
in both cases.
Proof. Note that
![]() $\Lambda _0$
is unimodular of signature
$\Lambda _0$
is unimodular of signature
![]() $(0,8)$
, so it suffices to check that it is even. The orthogonal complement of
$(0,8)$
, so it suffices to check that it is even. The orthogonal complement of
![]() $\{s,f\}$
in
$\{s,f\}$
in
![]() $\ker (N)$
is even because
$\ker (N)$
is even because
![]() $f=K_{S_t}$
and
$f=K_{S_t}$
and
![]() $x\cdot x\equiv x\cdot K_{S_t}\textrm { mod }2$
for any
$x\cdot x\equiv x\cdot K_{S_t}\textrm { mod }2$
for any
![]() $x\in H^2(S_t)$
. Hence, its image
$x\in H^2(S_t)$
. Hence, its image
![]() $\Lambda _0$
is even because
$\Lambda _0$
is even because
![]() $\ker (N)\to \Lambda $
preserves the intersection form.
$\ker (N)\to \Lambda $
preserves the intersection form.
Remark 6.5. The lattice
![]() $\Lambda _0$
can be described more directly using one irreducible component (only up to finite index in the Type II
$\Lambda _0$
can be described more directly using one irreducible component (only up to finite index in the Type II
![]() $_f$
case). For Type II
$_f$
case). For Type II
![]() $_b$
, the sublattice
$_b$
, the sublattice
![]() $\{s,f\}^\perp \subset H^2(S_1)$
lies in K and is even, unimodular of signature
$\{s,f\}^\perp \subset H^2(S_1)$
lies in K and is even, unimodular of signature
![]() $(0,8)$
. So it maps isometrically to
$(0,8)$
. So it maps isometrically to
![]() $\Lambda _0\simeq E_8$
. For II
$\Lambda _0\simeq E_8$
. For II
![]() $_f$
, the sublattice
$_f$
, the sublattice
![]() $\{D_2,f\}^\perp \subset H^2(S_2)$
lies in K and so maps isometrically to an index two sublattice
$\{D_2,f\}^\perp \subset H^2(S_2)$
lies in K and so maps isometrically to an index two sublattice
![]() $D_8\subset \Lambda _0\simeq E_8$
.
$D_8\subset \Lambda _0\simeq E_8$
.
We summarize the results of this section in the following proposition:
Proposition 6.6. Let
![]() $\mathcal {S}\to (B,0)$
be a degeneration of Type II
$\mathcal {S}\to (B,0)$
be a degeneration of Type II
![]() $_b$
or Type II
$_b$
or Type II
![]() $_f$
. Let
$_f$
. Let
![]() $K = \ker (H^2(S_1)\oplus H^2(S_2)\to H^2(D))$
be the kernel of signed restriction, and let
$K = \ker (H^2(S_1)\oplus H^2(S_2)\to H^2(D))$
be the kernel of signed restriction, and let
![]() $\Lambda :=K/{\mathbb {Z}}(D_1,-D_2)$
and
$\Lambda :=K/{\mathbb {Z}}(D_1,-D_2)$
and
![]() $\Lambda _0=\{s,f\}^\perp \subset \Lambda $
. Let E be
$\Lambda _0=\{s,f\}^\perp \subset \Lambda $
. Let E be
![]() $\mathrm {Pic}^0$
of either double curve in Type II
$\mathrm {Pic}^0$
of either double curve in Type II
![]() $_b$
and the Prym variety
$_b$
and the Prym variety
![]() $\mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)$
in Type II
$\mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)$
in Type II
![]() $_f$
.
$_f$
.
The Carlson extension class
![]() $\phi \in \mathrm {Hom}(K,E)$
describing the mixed Hodge structure on
$\phi \in \mathrm {Hom}(K,E)$
describing the mixed Hodge structure on
![]() $S_0$
descends to
$S_0$
descends to
![]() $\mathrm {Hom}(\Lambda ,E)$
, and so determines the
$\mathrm {Hom}(\Lambda ,E)$
, and so determines the
![]() $1$
-truncated limit mixed Hodge structure of the degeneration. This homomorphism further descends to a period point
$1$
-truncated limit mixed Hodge structure of the degeneration. This homomorphism further descends to a period point
![]() $\psi _{S_0}\in \mathrm {Hom}(\Lambda _0,E)$
where
$\psi _{S_0}\in \mathrm {Hom}(\Lambda _0,E)$
where
![]() $\Lambda _0\simeq E_8$
. Explicitly.
$\Lambda _0\simeq E_8$
. Explicitly.
-
(II b ) The period point
 $\psi _{S_0}$
given by the map sending
$\psi _{S_0}$
given by the map sending
 ${\mathcal L}\in \{s,f\}^\perp \subset \mathrm {Pic}(S_1)$
to
${\mathcal L}\in \{s,f\}^\perp \subset \mathrm {Pic}(S_1)$
to
 ${\mathcal L}\big {|}_{X_p}\otimes {\mathcal L}\big {|}_{X_q}^{-1}\in E$
.
${\mathcal L}\big {|}_{X_p}\otimes {\mathcal L}\big {|}_{X_q}^{-1}\in E$
. -
(II f ) The period point
 $\psi _{S_0}$
is determined up to
$\psi _{S_0}$
is determined up to
 $2$
-torsion by the map sending
$2$
-torsion by the map sending
 $c_1({\mathcal L})\in \{D,f\}^\perp \subset H^2(S_2)$
to
$c_1({\mathcal L})\in \{D,f\}^\perp \subset H^2(S_2)$
to
 ${\mathcal L}\big {|}_D \in \mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)=E$
.
${\mathcal L}\big {|}_D \in \mathrm {Pic}^0(D)/\mathrm {Pic}^0(C)=E$
.
A Appendix: Compact moduli
KSBA theory [Reference Kollár and Shepherd-BarronKSB88, Reference AlexeevAle96, Reference KollárKol23] gives a general method for constructingcompact moduli spaces of pairs
![]() $(X,B)$
, consisting of a projective variety X and a
$(X,B)$
, consisting of a projective variety X and a
![]() $\mathbb Q$
-Weil divisor B, which form a so-called stable slc pair:
$\mathbb Q$
-Weil divisor B, which form a so-called stable slc pair:
-
1. the pair
 $(X,B)$
has semi-log canonical singularities,
$(X,B)$
has semi-log canonical singularities, -
2.
 $K_X+B$
is
$K_X+B$
is
 $\mathbb Q$
-Cartier and ample.
$\mathbb Q$
-Cartier and ample.
In the case at hand, the pair
![]() $({\overline S},\epsilon s)$
satisfies these conditions, where
$({\overline S},\epsilon s)$
satisfies these conditions, where
![]() $S\to {\overline S}$
is the contraction to the Weierstrass form. The paper [Reference Ascher and BejleriAB21] of Ascher and Bejleri with an appendix by Inchiostro studies the correspondingcompactification by stable slc pairs
$S\to {\overline S}$
is the contraction to the Weierstrass form. The paper [Reference Ascher and BejleriAB21] of Ascher and Bejleri with an appendix by Inchiostro studies the correspondingcompactification by stable slc pairs
![]() $F\hookrightarrow {\overline F}^W.$
Every degeneration with generic fiber in F has a unique limit in
$F\hookrightarrow {\overline F}^W.$
Every degeneration with generic fiber in F has a unique limit in
![]() ${\overline F}^W$
called the stable model.
${\overline F}^W$
called the stable model.
No information is lost when considering Type II
![]() $_b$
degenerations because the stable model
$_b$
degenerations because the stable model
![]() ${\overline S}_0$
uniquely determines
${\overline S}_0$
uniquely determines
![]() $S_0$
: It is the resolution of ADE configurations in fibers. However, for Type II
$S_0$
: It is the resolution of ADE configurations in fibers. However, for Type II
![]() $_f$
degenerations, most period information is lost: the stable model
$_f$
degenerations, most period information is lost: the stable model
![]() ${\overline S}_0$
is the gluing of
${\overline S}_0$
is the gluing of
![]() ${\mathbb P}_C({\mathcal O}\oplus L)$
along the bisection D. Thus, the locus in
${\mathbb P}_C({\mathcal O}\oplus L)$
along the bisection D. Thus, the locus in
![]() ${\overline F}^W$
corresponding to Type II
${\overline F}^W$
corresponding to Type II
![]() $_f$
degenerations has dimension
$_f$
degenerations has dimension
![]() $2$
, remembering only the genus
$2$
, remembering only the genus
![]() $2$
double cover
$2$
double cover
![]() $\nu \colon D\to C$
.
$\nu \colon D\to C$
.
To record more period information, we can instead choose a different divisor on the general surface
![]() $S\in F$
. Let
$S\in F$
. Let
![]() $\textstyle R:=s+\sum _{i=1}^{12} f_i$
, where
$\textstyle R:=s+\sum _{i=1}^{12} f_i$
, where
![]() $f_i$
are the singular fibers of
$f_i$
are the singular fibers of
![]() $S\to C$
, counted with multiplicity. Because
$S\to C$
, counted with multiplicity. Because
![]() $({\overline S},\epsilon R)$
is a stable slc pair, we may again compactify the moduli space of such pairs using KSBA theory:
$({\overline S},\epsilon R)$
is a stable slc pair, we may again compactify the moduli space of such pairs using KSBA theory:
![]() $F\hookrightarrow {\overline F}^R$
, where
$F\hookrightarrow {\overline F}^R$
, where
![]() ${\overline F}^R$
is the closure of the pairs
${\overline F}^R$
is the closure of the pairs
![]() $\{({\overline S},\epsilon R)\,\big {|}\,S\in F\}$
in moduli of all stable slc pairs. Up to a finite map,
$\{({\overline S},\epsilon R)\,\big {|}\,S\in F\}$
in moduli of all stable slc pairs. Up to a finite map,
![]() ${\overline F}^R$
remembers the period information of a Type II
${\overline F}^R$
remembers the period information of a Type II
![]() $_f$
degeneration (and this is still so for Type II
$_f$
degeneration (and this is still so for Type II
![]() $_b$
surfaces).
$_b$
surfaces).
Thus, it is possible that the normalization of
![]() ${\overline F}^R$
actually dominates a toroidal compactification of
${\overline F}^R$
actually dominates a toroidal compactification of
![]() ${\mathbb D}/\Gamma $
. An analogous result for elliptic K3 surfaces
${\mathbb D}/\Gamma $
. An analogous result for elliptic K3 surfaces
![]() $(g,d)=(0,2)$
holds by [Reference Alexeev, Brunyate and EngelABE22]. We leave this as a conjecture:
$(g,d)=(0,2)$
holds by [Reference Alexeev, Brunyate and EngelABE22]. We leave this as a conjecture:
Conjecture A.1. There is a morphism
![]() $({\overline F}^R)^\nu \to \overline {{\mathbb D}/\Gamma }^{\mathfrak {F}}$
to some toroidal compactification, for an appropriately chosen fan
$({\overline F}^R)^\nu \to \overline {{\mathbb D}/\Gamma }^{\mathfrak {F}}$
to some toroidal compactification, for an appropriately chosen fan
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
Competing interest
The authors have no competing interest to declare.
Funding statement
The three authors were partially supported during this project by the NSF grants DMS-2201221, DMS-2302548 and DMS-2002183, respectively.