2. Design

We designed a linear SEA with high torque and power density based on a custom spring arrangement that enables a compression coil spring to work both in compression and extension. The custom spring arrangement is connected to a ball-screw and motor combination, as shown in Figure 1, which shows a photo of the actuator prototype and a sectioned view of the actuator model. The actuator uses a brushless DC motor (EC 4-Pole 30 200 W, Maxon Motors, Switzerland) which is connected to a helical drive gear (H2412R, Boston Gear, Charlotte, NC) using a flexible aluminum shaft coupling to eliminate radial forces due to shaft misalignments. The motor-drive gear mates with a larger helical gear (H2436L, Boston Gear, Charlotte, NC), creating a 3:1 gear ratio. The larger gear is mechanically connected using a key to a ball screw (SD 12X2R G7SHAFT-A, Ewellix, Sweden). The ball screw is supported by a double-row angular contact bearing (SRD 10300, Myonic, Chatsworth, CA).

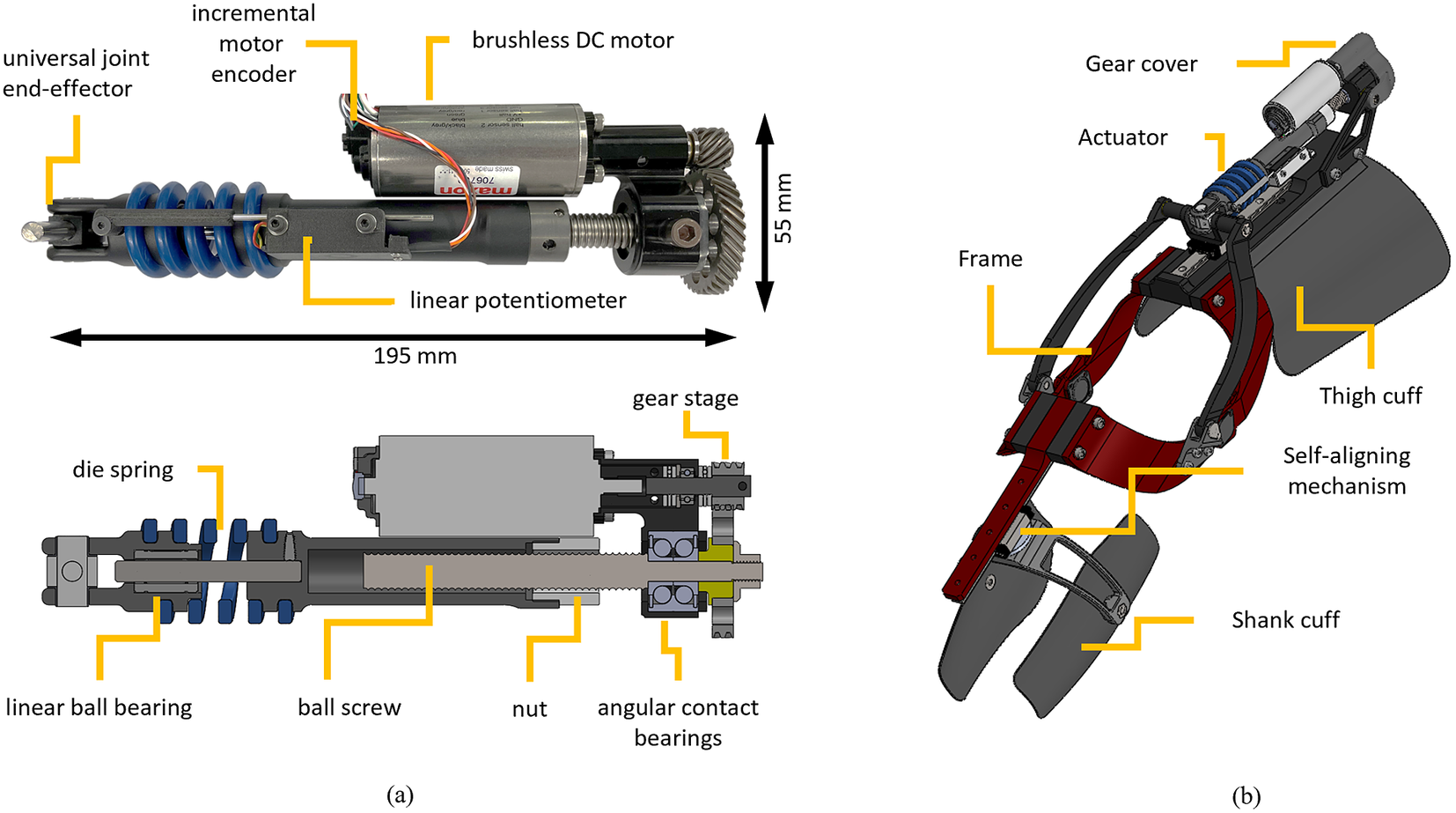
Figure 1. (a) The prototype of the series elastic actuator. The actuator uses a brushless DC motor, a 3:1 gear stage, a 2-mm lead ball screw system, and a die spring. The spring deflection is measured by a linear potentiometer combined with a custom ADC board. (b) Utah ExoKnee powered exoskeleton with the proposed actuator.

The nut of the ball screw system is threaded to a custom machined part that connects the nut to a coil spring (1.5″ OD X 0.75″ ID Chrome-Silicon Steel Die Spring, McMaster-Carr, Elmhurst, IL), which was modified to have open ends. The machined part connecting the ball-screw nut to the spring features a thread that matches the pitch and diameter of the coil spring and ensures a very tight press fit with no backlash. The other end of the spring is connected to the end-effector of the actuator using a similar custom part featuring a thread that matches the pitch and diameter of the coil spring. Due to this connection mechanism, the spring has a different number of active coils in compression and extension, resulting in different effective lengths. During compressive loading, the ends of the spring interact with the machined parts, effectively reducing the number of active coils by a quarter-coil on each side of the spring. In contrast, during tension loading, the inactive coils are pulled away from the machined parts increasing the effective length of the spring. Due to these differences in effective spring length, we expect the spring assembly to have higher stiffness in compression than extension. The end-effector of the actuator features a universal joint with low-friction polymer bushings (iglide Z, IGUS, Germany) to reduce undesired off-axis loading. A cylindrical linear ball bearing guide is used to ensure coaxiality of the machined parts interfacing with the coil spring regardless of the spring status.

An analog linear potentiometer (10 kΩ ±15%, LMC8–11, P3 America, Leander, TX) measures the spring deflection through a custom analog-to-digital converter (ADC) board. The ADC has an 18-bit resolution (ADS8887IDRCT, Texas Instruments, Dallas, TX) and is located close to the potentiometer to minimize noise. The custom ADC board is 30 mm long and 10 mm wide. The body of the potentiometer and the ADC board are attached to the nut side of the spring, and the shaft of the potentiometer is attached to the end effector side of the spring using a 3D-printed interface. An incremental magnetic rotary encoder measures the motor position and velocity (12-bit, RM08ID, RLS, Slovenia). The actuator is powered by a custom 10-cell Lithium–Ion battery pack (40 T 21700 4,000 mAh 35A battery cells, Samsung SDI, South Korea). The nominal battery voltage is 36 V.

The proposed SEA uses a custom electrical control system. The motherboard features a PIC32 microcontroller (PIC32MK0512MCF100, Microchip Technology Inc., Chandler, AZ) that reads all the sensors and communicates with the current motor driver (G-TWIR 80/80 SES, Elmo Motion Control Ltd., Israel) and the ADC board. The motherboard also features a Raspberry Pi (Compute Module 3+, Raspberry Pi Foundation, Cambridge, England, UK) running high-level code and communicating with the PIC32 using a serial peripheral interface (SPI). The control electronics and the battery pack are enclosed in a 3D-printed box that is worn by the subject at the waist. The box is 135 × 100 × 45 mm and weighs 312 g.

To test the performance of the proposed SEA, we modified the Utah ExoKnee (Figure 1b), a powered knee exoskeleton previously used for physical human–robot interaction studies (Sarkisian et al., Reference Sarkisian, Ishmael, Hunt and Lenzi2020, Reference Sarkisian, Ishmael and Lenzi2021) and stroke assistance (Sarkisian et al., Reference Sarkisian, Gunnell, Bo Foreman and Lenzi2022). The frame of the exoskeleton remained largely unchanged, aside from some machined parts to accommodate the specific dimensions of the proposed SEA.

3. Control

The low-level controller on the exoskeleton uses a PID algorithm to execute the desired torque received from the high-level controller. Designing a feedback controller that performs well in both set-point tracking and disturbance rejection can be challenging. Achieving fast load disturbance rejection usually requires a controller with high gains, which results in an oscillatory set-point step response. One way to address this issue is by implementing a 2DOF PID controller that combines feedforward and feedback control to improve tracking performance. This can be achieved by assigning weights to the reference signal for the proportional and derivative actions. The degree of freedom of the controller refers to the number of independently tunable transfer functions.

There are two PID algorithms implemented in this study – 1DOF PID (Figure 2a) and 2DOF PID (Figure 2b,c). Although the implementation of a 1DOF PID algorithm is very common, we show the algorithm here for clarity in comparison to the 2DOF PID algorithm. In the 1DOF PID torque controller (Figure 2a) C(s) is a PID compensator, P(s) is the plant, T _desired is the reference signal, T _measured is the measured output, T_disturb is the disturbance, K_P, K_I, and K_D are the proportional, integral, and derivative gains, respectively.

(1) $$ C(s)={K}_P+\frac{1}{s}{K}_I+{K}_Ds. $$

Figure 2. (a) Conventional 1DOF PID low-level controller block diagram. (b) The 2DOF PID low-level controller diagram. (c) The equivalent block diagram of the 2DOF PID controller.

Equation (1) then results in the following control law when combined with the reference r and measured output y.

(2) $$ {u}_{1\mathrm{DOF}}={K}_P\left({T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right)+{K}_I\frac{1}{s}\left({T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right)+{K}_Ds\left({T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right). $$

With a 2DOF PID controller, we introduce an additional compensator C_r(s) shown in (2), where the two additional gains b and c are introduced in association with the K_P and K_D gains.

(3) $$ {C}_r(s)=b\bullet {K}_P+\frac{1}{s}{K}_I+c\bullet {K}_Ds. $$

A control law can then be derived for the 2DOF PID system (Figure 2b) using C(s) and C_r(s).

(4) $$ {u}_{2\mathrm{DOF}}={K}_P\left(b\bullet {T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right)+{K}_I\frac{1}{s}\left({T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right)+{K}_Ds\left(c\bullet {T}_{\mathrm{desired}}-{T}_{\mathrm{measured}}\right). $$

The diagram shown in Figure 2b can be rearranged into an equivalent diagram, as shown in Figure 2c with unity feedback and a transfer function F(s) that is derived from C(s) and C_r(s).

(5) $$ F(s)=\frac{K_I+b\bullet {K}_Ps+c\bullet {K}_D{s}^2}{K_I+{K}_Ps+{K}_D{s}^2}. $$

Here, the gains b and c act as a filter of the change in the reference signal. The values of b and c can range between 0 and 1. The b and c gains of the 2DOF PID controller help reject disturbances that naturally occur due to human interaction. Unlike disturbance observers (Paine et al., Reference Paine, Oh and Sentis2014), a 2DOF PID controller can reject disturbances without requiring a plant model.

4. Benchtop experiments

We performed benchtop experiments with the SEA spring assembly to characterize the compression and extension stiffness. For this experiment, we used a custom benchtop setting (Figure 3a), which consisted of a four-bar linkage to convert rotary movement of the crank into linear motion of the slider. The crank had a 30 cm handle attached to it for manual backdriving. The slider, supported by a linear guide, was attached to the end-effector side of the spring assembly. The other end of the spring assembly was rigidly attached to a grounded 6-axis load cell (M3713D, Sunrise Instruments, China). The deformation of the spring was measured by the same linear potentiometer described in the previous section.

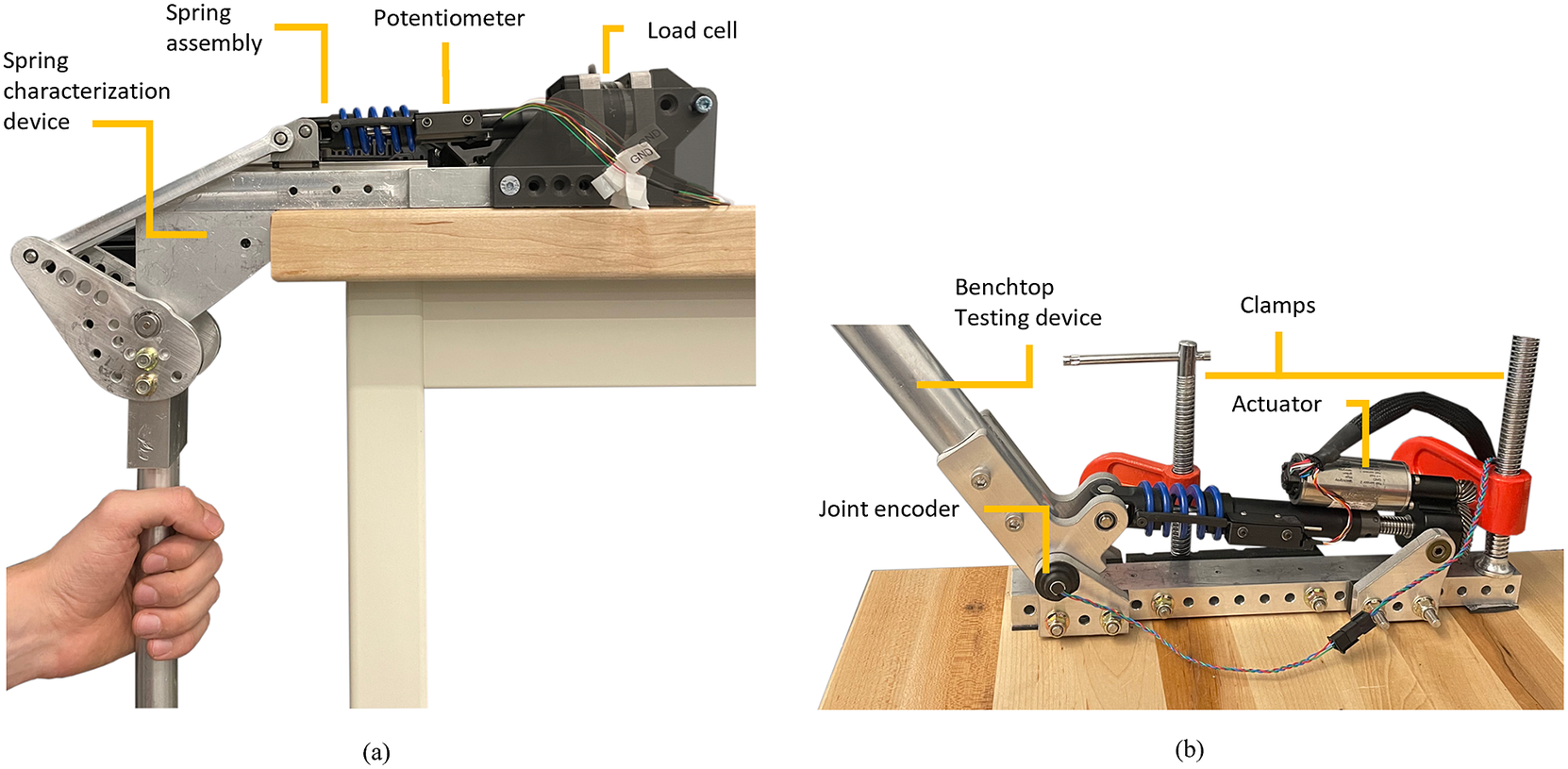
Figure 3. (a) Spring characterization setup. A benchtop device was used to manually drive the output and deform the spring. The spring was connected to a 6-axis load cell in series to measure the applied force. Additionally, a linear potentiometer was used to measure spring deformation. (b) Benchtop testing device used for benchtop actuator and controller characterization. In both cases, the testing devices were firmly clamped to a bench.

Using the handle, we slowly and progressively loaded and unloaded the SEA spring assembly while we recorded the spring deflection and the loadcell output. Separate trials were performed for tension and compression. We estimated the compression and extension stiffnesses offline by fitting the compression and extension load cell and deformation data separately with two first-order polynomial functions. The estimated spring stiffness values were 333 and 260 N/mm for compression and extension, respectively (Figure 4a). The fitting showed high linearity (R ² = 0.996 in compression, R ² = 0.989 in extension) and low error (root-mean-square [RMS] error = 1.07% in compression, RMS error = 2.05% in extension). Thus, the experiments show that the spring has linear behavior and that the stiffness is about 22% higher in compression than in extension, as expected from the design.

Figure 4. (a) Spring characterization data. The compression and extension stiffnesses were estimated by fitting a line to the load cell and deformation data and estimating the slope of the line. (b) Step response of the low-level controllers. A 5 Nm preload torque was used to eliminate backlash. The desired torque of 20 Nm was used. (c) Actuator backdriving torque during unpowered and controlled conditions (1DOF PID and 2DOF PID). (d) Estimated output impedance as a function of input frequency.

We characterized the performance of the closed-loop controller using a slightly different benchtop testing device (Figure 3b). This benchtop device worked as an inverted slider-crank four-bar linkage having a 90° range of motion, and sturdy mechanical end stops to ensure safety. The benchtop device used an absolute rotary encoder to measure the angular position of the joint (Linear voltage, RM08Vx, RLS, Slovenia). Similar to the previous test setup, this setup featured a 30 cm long handle attached to the crank of the four-bar linkage for manual backdriving.

Using this custom benchtop setup, we assessed the response of both the 1DOF PID and 2DOF PID controllers to a step change in set point. To this end, we rigidly constrained the output joint using a clamp. Then, we performed 10 repetitions of a 20-Nm torque step input with a pre-load of 5 Nm. We tuned the 2DOF PID and 1DOF PID controllers manually to achieve the same rise time and −3 dB bandwidth. For both PID controllers, we first set all the controller gains to zero. Then, we gradually increased the value of KP until sustained oscillations occur. We then increased the derivative gain KD to dampen the system and reduce the overshoot to below 40%, which is a relatively common value in the literature. Finally, we increased the integral gain KI to minimize steady-state error. For the 2DOF PID controller, we set b and c values together with KP and KD values, obtaining similar proportional and derivative actions to the 1DOF PID controller, which resulted in the same rise time and bandwidth. The gains of the 1DOF PID controller were selected as follows: P = 1.5, I = 20, D = 0.05. The gains of the 2DOF PID controller were selected as P = 2, I = 20, D = 0.0667, b = 0.75, and c = 0.75. The offline analysis of the 1DOF PID (Figure 4b) showed an average rise time of 11.9 ms, which corresponds to a −3 dB bandwidth of 29.4 Hz (first-order approximation). Moreover, the average overshoot was 39.5%, the settling time was 79.3 ms, and the steady-state error was 0.166 Nm. Similarly, the offline analysis of the 2DOF PID (Figure 4b) showed an average rise time of 11.9 ms, which corresponds to a −3 dB bandwidth of 29.4 Hz, the average overshoot was 36.5%, the settling time was 76.3 ms, and the steady-state error was 0.371 Nm. Except for some small but visible differences in settling time, the step responses for the 1DOF PID and 2DOF PID were almost identical.

We characterized the output impedance of the proposed SEA by backdriving the actuator manually. For consistency, the experimenter followed a sine sweep, which started at 0.25 Hz and ramped up to 2 Hz over a 150-second period, using both acoustic and visual cueing (Figure 4c). First, the backdriving test was performed while the actuator was unpowered. Then, we repeated the experiment with the actuator powered and set to transparent mode (i.e., zero desired torque) using the 1DOF PID and the 2DOF PID (Figure 4c).

We used the recorded data to estimate the maximum backdriving torque for all tested conditions. The minimum backdriving torque was 0.320 Nm for the unpowered system and 0.268 and 0.050 Nm with the 1DOF PID and 2DOF PID controllers, respectively. Thus, the 2DOF PID reduced the minimum backdriving torque by 81% compared to the 1DOF PID controller.

The measured exoskeleton joint torque and velocity data were processed offline with the System Identification Toolbox in MATLAB, using a two-pole one–zero model. For the unpowered system, the system identification resulted in an output impedance with equivalent inertia of 1.35 kg m² and equivalent damping of 0.509 Nms/rad (Figure 4d). For the controlled system using the 1DOF PID, the identification produced equivalent inertia of 0.817 kg m² and equivalent damping of 0.742 Nms/rad (Figure 4d). Finally, with the 2DOF PID controller, the equivalent inertia was 0.799 kg m^2, and the equivalent damping was 0.102 Nms/rad (Figure 4d). As expected, both PID controllers substantially reduced the output joint impedance compared to the unpowered case. However, the 2DOF PID controller provided substantial reductions of the output impedance by decreasing the equivalent damping by 86% compared to the 1DOF PID.

5. Human experiments

Three healthy subjects participated in the experiments (two males and one female, 28.0 ± 1.70 years old, 179 ± 7.50 cm tall, and 73.3 ± 5.77 kg). The experimental protocol was approved by the University of Utah Institutional Review Board. Written informed consent was provided by the subjects before the experiment took place. The subjects consented in writing to the publication of pictures and videos of the experiments.

The exoskeleton aids the user based on the algorithm shown in Figure 5. The high-level controller uses the activation of the Vastus Medialis on the exoskeleton side to define the desired extension knee torque during stair ascents (Figure 5; Sarkisian et al., Reference Sarkisian, Gunnell, Bo Foreman and Lenzi2022). We chose Vastus Medialis for high-level control because it is a monoarticular knee extensor, unlike Rectus Femoris, which is a biarticular muscle spanning both the knee and hip joints. We also chose the Vastus medialis because it is easy to visually locate to achieve a correct EMG sensor placement. During the push-up phase, the EMG signal coming from the Vastus Medialis is multiplied by a proportional gain (G = G _max) to define the desired knee extension torque. The EMG signals were rectified and filtered online by the commercially available sensor itself. The sensor provides the EMG envelope as an analog output, which is acquired by an on-board analog-digital converter within the embedded electronics at 2 kHz. The EMG signals were normalized by dividing the raw signal by the peak value of the EMG signal during the Transparent condition for each controller. The desired torque saturates at the maximum value ( $ {T}_{\mathrm{max}} $ ) which was set to 0.5 Nm/kg to account for the subject’s body mass. As the knee extends and the knee joint angle gets below a set threshold $ \left({\theta}_{\mathrm{threshold}}\right) $ , the proportional gain $ (G) $ ramps down to zero. The controller parameters $ \left({T}_{\mathrm{max}},{G}_{\mathrm{max}},{\theta}_{\mathrm{threshold}}\right) $ were adjusted by the experimenter through a graphical user interface. The proposed EMG controller was active during both the stance and the swing phases of the stair ascent.

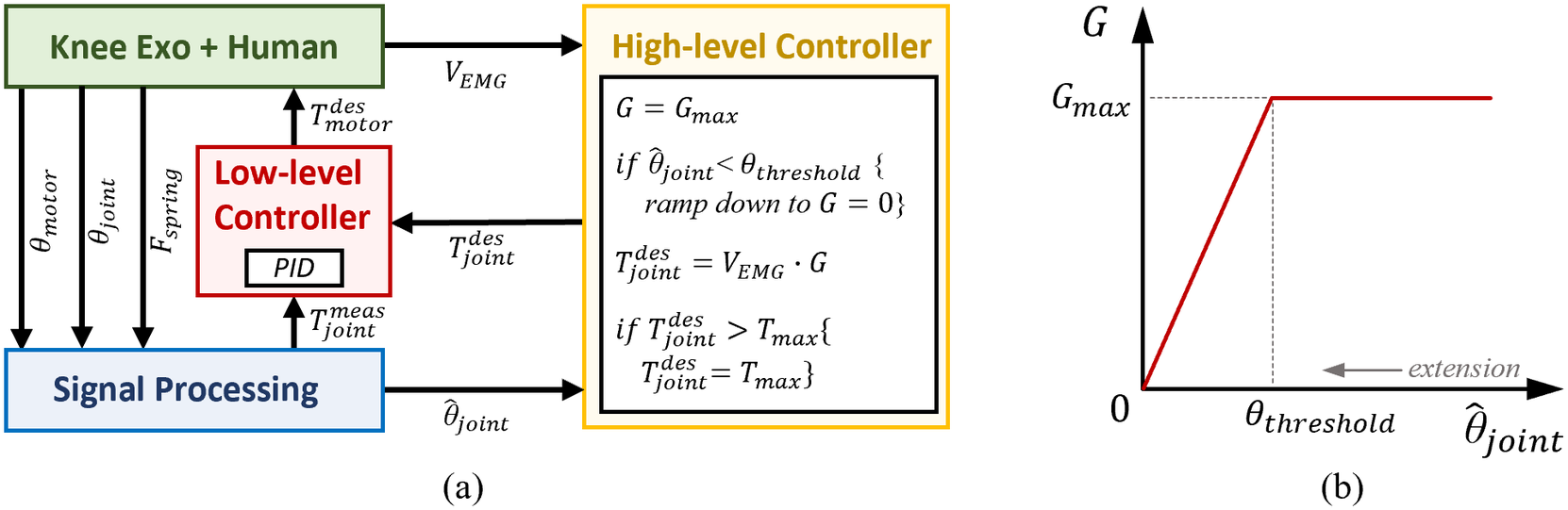
Figure 5. (a) Block diagram of the control and signal processing systems. At the high level, a proportional EMG controller defines the desired knee torque. At the low level, a closed-loop torque controller defines the desired motor current that is then imposed using a motor driver. (b) Relationship between the EMG gain $ G $ and $ {\hat{\theta}}_{\mathrm{joint}} $ , as well as $ {G}_{\mathrm{max}} $ and $ {\theta}_{\mathrm{threshold}} $ . In (b), the zero value of $ {\hat{\theta}}_{\mathrm{joint}} $ corresponds to full knee extension.

Before the subjects donned the exoskeleton, we placed a single EMG electrode (13E200, Ottobock, Duderstadt, Germany) on their Vastus Medialis muscle, following SENIAM guidelines (SENIAM, n.d.). After donning the exoskeleton, the subjects climbed stairs on a StairMaster machine (Figure 6, right) at the fixed pace of 54 steps/min in zero-torque mode (i.e., transparent mode) and in assistive mode using the proposed EMG controller (Figure 2) (see Supplementary Material). The StairMaster machine has steps with a height of 15 cm (about 6 inches) and depth of 23 cm (about 9 inches). Each subject completed the stair climbing task with the 1DOF PID low-level controller and then with the 2DOF PID low-level controller. For all assisted conditions and all subjects, the peak of the assistive torque was set to 0.5 Nm/kg. The values of G _max were chosen experimentally to reach the desired level of peak torque. During the familiarization period, the experimenter gradually increased the value of G _max until the peak exoskeleton joint torque was reached consistently. The resulting values of G _max were 15, 8, and 8 for S01, S02, and S03, respectively. The values of T _max were chosen based on subjects’ body mass and were 35, 40, and 35 Nm for S01, S02, and S03, respectively.

Figure 6. Experimental setup. The subject is wearing the exoskeleton and performing assisted stairs ascent. On the right, an enlarged view of the exoskeleton is shown.

We assessed the performance of the 1DOF PID and 2DOF PID controllers by quantifying the difference between the desired joint torque and the measured joint torque of the exoskeleton during the assisted stair-climbing experiments (Figure 7a). Specifically, we calculated the peak and the RMS error between the mass-normalized measured and mass-normalized desired torque (Figure 7b). The RMS error decreased from 0.0583 Nm/kg with the 1DOF PID controller to 0.0320 Nm/kg with the 2DOF PID controller. Additionally, the peak error decreased from 0.234 Nm/kg with the 1DOF PID to 0.118 Nm/kg with the 2DOF PID controllers. Thus, 2DOF PID reduced the RMS error and the peak error by 45.2 and 49.8%, respectively (Figure 7c). To statistically confirm these results, we conducted paired t-tests using the 1DOF and 2DOF controllers as independent variables and the RMS and peak errors as dependent variables, with correction for multiple comparisons. The results show statistical significance between the two low-level controller conditions (p < .00001).

Figure 7. (a) Desired versus measured exoskeleton joint torque during assisted stair ascent. The data were normalized by subjects’ respective body mass. (b) Torque tracking error. (c) The RMS error and the peak error of the torque tracking. All data were averaged between individual stair gait cycles. The solid lines represent the mean, and the shaded regions and error bars represent the standard error.

We assessed the performance of the proposed high-level controller by comparing the EMG signals during the stairs climbing in transparent mode and in assistive mode (Figure 8). With the 1DOF PID controller, the peak EMG signals were 0.836 and 0.689 during the transparent and assistive modes, respectively. Thus, there was a 17.5% reduction in the EMG peak. With the 2DOF PID controller, the peak EMG signals were 0.869 and 0.680 during the transparent and assistive modes, respectively. This difference corresponds to a 21.6% reduction. Thus, both the 1DOF PID and 2DOF PID controllers lead to EMG reductions, although there does not seem to be a significant difference between the 1DOF PID and the 2DOF PID.

Figure 8. Data recorded by the EMG sensor. The data were first normalized by the peak value of the Transparent mode data for each condition and then averaged across subjects. Solid lines represent the mean, and the shaded regions represent the standard error.