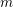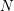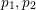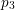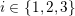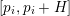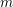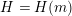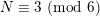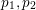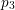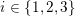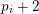1 Introduction
The Hardy–Littlewood prime tuples conjecture says that, for any admissible set of
![]() $k$
integers
$k$
integers
![]() ${\mathcal{H}}=\{h_{1},\ldots ,h_{k}\}$
, there are infinitely many values of
${\mathcal{H}}=\{h_{1},\ldots ,h_{k}\}$
, there are infinitely many values of
![]() $n$
such that
$n$
such that
![]() $n+h_{1},\ldots ,n+h_{k}$
are all prime. Here
$n+h_{1},\ldots ,n+h_{k}$
are all prime. Here
![]() ${\mathcal{H}}$
is said to be admissible if it misses at least one residue class modulo
${\mathcal{H}}$
is said to be admissible if it misses at least one residue class modulo
![]() $p$
for every prime
$p$
for every prime
![]() $p$
. In particular, the twin prime conjecture is the special case when
$p$
. In particular, the twin prime conjecture is the special case when
![]() ${\mathcal{H}}=\{0,2\}$
.
${\mathcal{H}}=\{0,2\}$
.
Using an elaboration of the linear sieve method, Chen [Reference ChenChe73] proved that there are infinitely many primes
![]() $p$
such that
$p$
such that
![]() $p+2$
is the product of at most two primes (this property is traditionally denoted by
$p+2$
is the product of at most two primes (this property is traditionally denoted by
![]() $p+2=P_{2}$
). If one insists on prime values, it is only recently that Zhang [Reference ZhangZha14], and subsequently Maynard [Reference MaynardMay15], made the breakthrough showing that there are infinitely many values of
$p+2=P_{2}$
). If one insists on prime values, it is only recently that Zhang [Reference ZhangZha14], and subsequently Maynard [Reference MaynardMay15], made the breakthrough showing that there are infinitely many values of
![]() $n$
for which at least two of
$n$
for which at least two of
![]() $n+h_{1},\ldots ,n+h_{k}$
are prime, provided that
$n+h_{1},\ldots ,n+h_{k}$
are prime, provided that
![]() $k$
is large enough but fixed. Indeed, Maynard’s argument shows that one can find
$k$
is large enough but fixed. Indeed, Maynard’s argument shows that one can find
![]() $m$
primes among
$m$
primes among
![]() $n+h_{1},\ldots ,n+h_{k}$
for any
$n+h_{1},\ldots ,n+h_{k}$
for any
![]() $m$
, provided that
$m$
, provided that
![]() $k$
is large enough in terms of
$k$
is large enough in terms of
![]() $m$
. This result was proved independently by Tao in an unpublished work. We refer the reader to the excellent survey article [Reference GranvilleGra15] for the main ideas behind these works.
$m$
. This result was proved independently by Tao in an unpublished work. We refer the reader to the excellent survey article [Reference GranvilleGra15] for the main ideas behind these works.
Since the introduction of the Hardy–Littlewood circle method, there have been a flurry of results about solving linear equations in prime variables, by analyzing exponential sums over primes. In 1937, Vinogradov showed that all sufficiently large odd positive integers can be written as a sum of three primes. This establishes the ternary version of the Goldbach conjecture. In this paper, we prove the analogous statement for the special types of almost twin primes mentioned above.
Theorem 1.1. For any positive integer
![]() $m$
, there exist positive constants
$m$
, there exist positive constants
![]() $H=H(m)$
and
$H=H(m)$
and
![]() $N_{0}=N_{0}(m)$
such that every odd integer
$N_{0}=N_{0}(m)$
such that every odd integer
![]() $N\geqslant N_{0}$
can be written in the form
$N\geqslant N_{0}$
can be written in the form
![]() $N=p_{1}+p_{2}+p_{3}$
, where, for
$N=p_{1}+p_{2}+p_{3}$
, where, for
![]() $i=1,2,3$
,
$i=1,2,3$
,
![]() $p_{i}$
are primes such that the interval
$p_{i}$
are primes such that the interval
![]() $[p_{i},p_{i}+H]$
contains at least
$[p_{i},p_{i}+H]$
contains at least
![]() $m$
primes.
$m$
primes.
In view of recent work of Helfgott [Reference HelfgottHel15], one can in fact take
![]() $N_{0}=7$
above (after possibly increasing
$N_{0}=7$
above (after possibly increasing
![]() $H$
).
$H$
).
Theorem 1.2. Every large enough integer
![]() $N\equiv 3~(\text{mod}~6)$
can be written in the form
$N\equiv 3~(\text{mod}~6)$
can be written in the form
![]() $N=p_{1}+p_{2}+p_{3}$
, where, for
$N=p_{1}+p_{2}+p_{3}$
, where, for
![]() $i=1,2,3$
,
$i=1,2,3$
,
![]() $p_{i}$
are primes such that
$p_{i}$
are primes such that
![]() $p_{i}+2$
is a product of at most two primes.
$p_{i}+2$
is a product of at most two primes.
Related problems have been considered before. Green and Tao [Reference Green and TaoGT06] showed that there are infinitely many three-term arithmetic progressions in the almost twin primes considered in Theorem 1.2, and this has been generalized in [Reference ZhouZho09] to handle
![]() $k$
-term progressions for any fixed
$k$
-term progressions for any fixed
![]() $k$
. See [Reference PintzPin15] for analogous results for the almost twin primes considered in Theorem 1.1. As we discuss in the next section, since the equation
$k$
. See [Reference PintzPin15] for analogous results for the almost twin primes considered in Theorem 1.1. As we discuss in the next section, since the equation
![]() $N=p_{1}+p_{2}+p_{3}$
is not translation-invariant, for subsets of the primes the ternary Goldbach problem involves additional complications compared to the problem of finding three-term arithmetic progressions. For the ternary Goldbach problem, Matomäki [Reference MatomäkiMat09] previously showed that
$N=p_{1}+p_{2}+p_{3}$
is not translation-invariant, for subsets of the primes the ternary Goldbach problem involves additional complications compared to the problem of finding three-term arithmetic progressions. For the ternary Goldbach problem, Matomäki [Reference MatomäkiMat09] previously showed that
![]() $N=p_{1}+p_{2}+p_{3}$
is solvable in primes with
$N=p_{1}+p_{2}+p_{3}$
is solvable in primes with
![]() $p_{1}+2=P_{2}$
,
$p_{1}+2=P_{2}$
,
![]() $p_{2}+2=P_{2}^{\prime }$
, and
$p_{2}+2=P_{2}^{\prime }$
, and
![]() $p_{3}+2=P_{7}$
.
$p_{3}+2=P_{7}$
.
It is worth mentioning that a vast generalization of Vinogradov’s theorem has been proved by Green and Tao [Reference Green and TaoGT10], with a crucial ingredient from the work of Green, Tao, and Ziegler [Reference Green, Tao and ZieglerGTZ12]. They introduced the concept of higher-order Fourier analysis, which allows one to handle all linear systems of finite complexity (that excludes the twin prime or the binary Goldbach case). We plan to return to a generalization of Theorem 1.1 in this direction in a future work.
2 Outline of proof
In this section we describe the main ingredients in the proofs of Theorems 1.1 and 1.2. The general strategy for proving both theorems follows closely the transference principle initiated in [Reference GreenGre05]. Let
![]() $f$
be the (weighted) indicator function of the considered subset of the primes, and let
$f$
be the (weighted) indicator function of the considered subset of the primes, and let
![]() $\unicode[STIX]{x1D708}$
be a sieve majorant so that
$\unicode[STIX]{x1D708}$
be a sieve majorant so that
![]() $f\leqslant \unicode[STIX]{x1D708}$
and that
$f\leqslant \unicode[STIX]{x1D708}$
and that
![]() $f$
has positive density in
$f$
has positive density in
![]() $\unicode[STIX]{x1D708}$
. The Fourier analytic transference principle in [Reference GreenGre05] produces a dense model
$\unicode[STIX]{x1D708}$
. The Fourier analytic transference principle in [Reference GreenGre05] produces a dense model
![]() $\widetilde{f}$
of
$\widetilde{f}$
of
![]() $f$
, such that
$f$
, such that
![]() $0\leqslant \widetilde{f}\leqslant 1$
and that
$0\leqslant \widetilde{f}\leqslant 1$
and that
![]() $\widetilde{f}$
has positive average. Moreover,
$\widetilde{f}$
has positive average. Moreover,
If we are instead looking for solutions of a homogeneous linear equation such as
![]() $n_{1}+n_{2}=2n_{3}$
, then the right-hand side above is bounded from below by Roth’s theorem. In this way one can find arithmetic progressions in subsets of primes [Reference Green and TaoGT06, Reference ZhouZho09, Reference PintzPin15]. In our current case, the right-hand side above could vanish if, for example,
$n_{1}+n_{2}=2n_{3}$
, then the right-hand side above is bounded from below by Roth’s theorem. In this way one can find arithmetic progressions in subsets of primes [Reference Green and TaoGT06, Reference ZhouZho09, Reference PintzPin15]. In our current case, the right-hand side above could vanish if, for example,
![]() $\widetilde{f}$
is supported on
$\widetilde{f}$
is supported on
![]() $[1,N/4]$
or if, writing
$[1,N/4]$
or if, writing
![]() $\Vert x\Vert$
for the distance from the nearest integer, we had
$\Vert x\Vert$
for the distance from the nearest integer, we had
![]() $\Vert \sqrt{2}N\Vert >3/10$
and
$\Vert \sqrt{2}N\Vert >3/10$
and
![]() $\widetilde{f}$
is supported on numbers
$\widetilde{f}$
is supported on numbers
![]() $n$
for which
$n$
for which
![]() $\Vert \sqrt{2}n\Vert <1/10$
.
$\Vert \sqrt{2}n\Vert <1/10$
.
To get around this issue, we need to know more about the structure of
![]() $\widetilde{f}$
. Examining the proof of the transference principle, one may observe that
$\widetilde{f}$
. Examining the proof of the transference principle, one may observe that
![]() $\widetilde{f}$
is the convolution of
$\widetilde{f}$
is the convolution of
![]() $f$
with a Bohr set. If we ensure that
$f$
with a Bohr set. If we ensure that
![]() $\widetilde{f}$
is bounded below pointwise, then the right-hand side of (2.1) is certainly bounded below as well. This pointwise lower bound translates to the requirement that primes from the considered subset can be found in Bohr sets.
$\widetilde{f}$
is bounded below pointwise, then the right-hand side of (2.1) is certainly bounded below as well. This pointwise lower bound translates to the requirement that primes from the considered subset can be found in Bohr sets.
2.1 Smooth Bohr cutoff
Given a cyclic group
![]() $G=\mathbb{Z}/N\mathbb{Z}$
, a subset
$G=\mathbb{Z}/N\mathbb{Z}$
, a subset
![]() $\unicode[STIX]{x1D6FA}\subseteq G$
and
$\unicode[STIX]{x1D6FA}\subseteq G$
and
![]() $\unicode[STIX]{x1D702}\in (0,1/2]$
, define the Bohr set
$\unicode[STIX]{x1D702}\in (0,1/2]$
, define the Bohr set
For technical reasons, it is more convenient to study a smooth version of
![]() $1_{B}$
, whose Fourier spectrum has bounded size.
$1_{B}$
, whose Fourier spectrum has bounded size.
For
![]() $\unicode[STIX]{x1D702}\in (0,1/2]$
and a positive integer
$\unicode[STIX]{x1D702}\in (0,1/2]$
and a positive integer
![]() $D$
, let
$D$
, let
![]() $S_{D,\unicode[STIX]{x1D702}}^{+}(x):\mathbb{R}/\mathbb{Z}\rightarrow [0,2]$
be the Selberg polynomial of degree
$S_{D,\unicode[STIX]{x1D702}}^{+}(x):\mathbb{R}/\mathbb{Z}\rightarrow [0,2]$
be the Selberg polynomial of degree
![]() $D$
that majorizes the interval
$D$
that majorizes the interval
![]() $[-\unicode[STIX]{x1D702},\unicode[STIX]{x1D702}]$
. The definition can be bound in [Reference MontgomeryMon94, ch. 1, formula
$[-\unicode[STIX]{x1D702},\unicode[STIX]{x1D702}]$
. The definition can be bound in [Reference MontgomeryMon94, ch. 1, formula
![]() $21^{+}$
] and is given in (3.1) below. The Selberg polynomial has a Fourier expansion
$21^{+}$
] and is given in (3.1) below. The Selberg polynomial has a Fourier expansion
with
![]() $|\widehat{S}_{D,\unicode[STIX]{x1D702}}^{+}(k)|\leqslant 1/(D+1)+\min \{2\unicode[STIX]{x1D702},1/|k|\}$
by [Reference MontgomeryMon94, ch. 1, formula (22)].
$|\widehat{S}_{D,\unicode[STIX]{x1D702}}^{+}(k)|\leqslant 1/(D+1)+\min \{2\unicode[STIX]{x1D702},1/|k|\}$
by [Reference MontgomeryMon94, ch. 1, formula (22)].
Definition 2.1 (Smooth Bohr cutoff).
Given a cyclic group
![]() $G=\mathbb{Z}/N\mathbb{Z}$
, a subset
$G=\mathbb{Z}/N\mathbb{Z}$
, a subset
![]() $\unicode[STIX]{x1D6FA}\subseteq G$
and
$\unicode[STIX]{x1D6FA}\subseteq G$
and
![]() $\unicode[STIX]{x1D702}\in (0,1/2]$
, let
$\unicode[STIX]{x1D702}\in (0,1/2]$
, let
![]() $D=\lceil 4/\unicode[STIX]{x1D702}\rceil ^{2|\unicode[STIX]{x1D6FA}|}$
and define the smooth Bohr cutoff
$D=\lceil 4/\unicode[STIX]{x1D702}\rceil ^{2|\unicode[STIX]{x1D6FA}|}$
and define the smooth Bohr cutoff
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
by
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
by
Note that since
![]() $S_{D,\unicode[STIX]{x1D702}}^{+}(x)$
is a majorant of
$S_{D,\unicode[STIX]{x1D702}}^{+}(x)$
is a majorant of
![]() $1_{\Vert x\Vert \leqslant \unicode[STIX]{x1D702}}(x)$
, we have the lower bound
$1_{\Vert x\Vert \leqslant \unicode[STIX]{x1D702}}(x)$
, we have the lower bound
![]() $\unicode[STIX]{x1D712}(n)\geqslant 1$
for
$\unicode[STIX]{x1D712}(n)\geqslant 1$
for
![]() $n\in \text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})$
.
$n\in \text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})$
.
Remark 2.2. Using the Selberg polynomials
![]() $S_{D,\unicode[STIX]{x1D702}}^{+}$
is not essential here, one could replace them for instance by the function
$S_{D,\unicode[STIX]{x1D702}}^{+}$
is not essential here, one could replace them for instance by the function
![]() $(\cos \unicode[STIX]{x1D70B}x)^{D}$
for some large even
$(\cos \unicode[STIX]{x1D70B}x)^{D}$
for some large even
![]() $D$
depending on
$D$
depending on
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $|\unicode[STIX]{x1D6FA}|$
. This way
$|\unicode[STIX]{x1D6FA}|$
. This way
![]() $\unicode[STIX]{x1D712}(n)$
would no longer be at least one in the Bohr set, but one could easily prove good enough variants of the lemmas we need.
$\unicode[STIX]{x1D712}(n)$
would no longer be at least one in the Bohr set, but one could easily prove good enough variants of the lemmas we need.
2.2 A transference type result
Let
![]() $G=\mathbb{Z}/N\mathbb{Z}$
. We use the standard notation
$G=\mathbb{Z}/N\mathbb{Z}$
. We use the standard notation
![]() $\mathbb{E}_{n\in G}$
to denote the average
$\mathbb{E}_{n\in G}$
to denote the average
![]() $N^{-1}\sum _{n\in G}$
. For a function
$N^{-1}\sum _{n\in G}$
. For a function
![]() $f:G\rightarrow \mathbb{C}$
, its Fourier transform is defined by
$f:G\rightarrow \mathbb{C}$
, its Fourier transform is defined by
and its
![]() $L^{1}$
-norm is defined by
$L^{1}$
-norm is defined by
For two functions
![]() $f,g:G\rightarrow \mathbb{C}$
, their convolution is defined by
$f,g:G\rightarrow \mathbb{C}$
, their convolution is defined by
In § 4 we prove the following transference type result. It says that we can handle a non-homogeneous linear equation if we have some additional hypotheses about averages in Bohr sets.
Theorem 2.3. Let
![]() $G=\mathbb{Z}/N\mathbb{Z}$
for some large
$G=\mathbb{Z}/N\mathbb{Z}$
for some large
![]() $N$
, and let
$N$
, and let
![]() $f_{1}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function. Let
$f_{1}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function. Let
![]() $K\geqslant 1$
and
$K\geqslant 1$
and
![]() $\unicode[STIX]{x1D6FF}>0$
be parameters. There exists a Bohr cutoff
$\unicode[STIX]{x1D6FF}>0$
be parameters. There exists a Bohr cutoff
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
(depending on
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
(depending on
![]() $f_{1}$
) with
$f_{1}$
) with
![]() $|\unicode[STIX]{x1D6FA}|\ll _{K,\unicode[STIX]{x1D6FF}}1$
,
$|\unicode[STIX]{x1D6FA}|\ll _{K,\unicode[STIX]{x1D6FF}}1$
,
![]() $1\in \unicode[STIX]{x1D6FA}$
, and
$1\in \unicode[STIX]{x1D6FA}$
, and
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(K,\unicode[STIX]{x1D6FF})\in (0,0.05)$
, such that the following statement holds. Let
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(K,\unicode[STIX]{x1D6FF})\in (0,0.05)$
, such that the following statement holds. Let
![]() $f_{2},f_{3}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be functions satisfying
$f_{2},f_{3}:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be functions satisfying
for every
![]() $t\in [N/4,N/2)$
and
$t\in [N/4,N/2)$
and
![]() $i\in \{2,3\}$
. Suppose that
$i\in \{2,3\}$
. Suppose that
and that
for every
![]() $i\in \{1,2,3\}$
. Then
$i\in \{1,2,3\}$
. Then
![]() $f_{1}\ast f_{2}\ast f_{3}(N)\geqslant \unicode[STIX]{x1D6FF}^{3}/200$
.
$f_{1}\ast f_{2}\ast f_{3}(N)\geqslant \unicode[STIX]{x1D6FF}^{3}/200$
.
The artificial requirement
![]() $1\in \unicode[STIX]{x1D6FA}$
and the assumption that (2.2) holds only for
$1\in \unicode[STIX]{x1D6FA}$
and the assumption that (2.2) holds only for
![]() $t\in [N/4,N/2)$
come from the way Theorem 2.3 will be applied. To avoid wrapping around issues, we will apply Theorem 2.3 with each
$t\in [N/4,N/2)$
come from the way Theorem 2.3 will be applied. To avoid wrapping around issues, we will apply Theorem 2.3 with each
![]() $f_{i}$
supported on
$f_{i}$
supported on
![]() $[N/4,N/2)$
. If
$[N/4,N/2)$
. If
![]() $1\in \unicode[STIX]{x1D6FA}$
and
$1\in \unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D702}<0.1$
, then
$\unicode[STIX]{x1D702}<0.1$
, then
![]() $B(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})\subset (-0.1N,0.1N)$
, so that (2.2) can be expected to hold when
$B(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})\subset (-0.1N,0.1N)$
, so that (2.2) can be expected to hold when
![]() $t\in [N/4,N/2)$
.
$t\in [N/4,N/2)$
.
We will see that the condition (2.4) for the types of almost twin primes we consider follows easily from the work of Green and Tao [Reference Green and TaoGT06].
2.3 Almost twin primes in Bohr sets
To apply Theorem 2.3 to prove Theorems 1.1 and 1.2 in § 5, we need to verify the hypothesis (2.2) for the indicator functions of the types of almost twin primes we consider. This is achieved in Theorems 2.5 and 2.6, in statements of which we use the following definition.
Definition 2.4. For a function
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{C}$
, we say that it has Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{C}$
, we say that it has Fourier complexity at most
![]() $M$
if
$M$
if
![]() $\unicode[STIX]{x1D712}$
can be written as a linear combination of at most
$\unicode[STIX]{x1D712}$
can be written as a linear combination of at most
![]() $M$
exponential phases:
$M$
exponential phases:
for some
![]() $|b_{i}|\leqslant M$
, and
$|b_{i}|\leqslant M$
, and
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
.
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
.
Note that since we do not request
![]() $b_{i}$
to be non-zero, if
$b_{i}$
to be non-zero, if
![]() $\unicode[STIX]{x1D712}$
is of Fourier complexity at most
$\unicode[STIX]{x1D712}$
is of Fourier complexity at most
![]() $M$
, then it is of Fourier complexity at most
$M$
, then it is of Fourier complexity at most
![]() $M^{\prime }$
for any
$M^{\prime }$
for any
![]() $M^{\prime }\geqslant M$
. Note also that the smooth Bohr cutoff
$M^{\prime }\geqslant M$
. Note also that the smooth Bohr cutoff
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
in Definition 2.1 (extended to
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
in Definition 2.1 (extended to
![]() $\mathbb{Z}$
in the obvious manner) has Fourier complexity at most
$\mathbb{Z}$
in the obvious manner) has Fourier complexity at most
![]() $O_{|\unicode[STIX]{x1D6FA}|,\unicode[STIX]{x1D702}}(1)$
.
$O_{|\unicode[STIX]{x1D6FA}|,\unicode[STIX]{x1D702}}(1)$
.
Theorem 2.5. For any positive integer
![]() $m$
, there exist a positive integer
$m$
, there exist a positive integer
![]() $k=k(m)$
and positive constants
$k=k(m)$
and positive constants
![]() $\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(m)$
and
$\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(m)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
such that the following holds. Let
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
such that the following holds. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
, and let
$M\geqslant 1$
, and let
![]() $\unicode[STIX]{x1D700}>0$
be given. Let
$\unicode[STIX]{x1D700}>0$
be given. Let
![]() $W=\prod _{p\leqslant w}p$
with
$W=\prod _{p\leqslant w}p$
with
![]() $w$
large enough in terms of
$w$
large enough in terms of
![]() $m,M$
and
$m,M$
and
![]() $\unicode[STIX]{x1D700}$
, and let
$\unicode[STIX]{x1D700}$
, and let
![]() $(b,W)=1$
. There exist non-zero distinct integers
$(b,W)=1$
. There exist non-zero distinct integers
![]() $h_{1},\ldots ,h_{k-1}=O_{m,M,\unicode[STIX]{x1D700}}(1)$
with
$h_{1},\ldots ,h_{k-1}=O_{m,M,\unicode[STIX]{x1D700}}(1)$
with
![]() $h_{j}$
positive for
$h_{j}$
positive for
![]() $j=1,\ldots ,m-1$
, and a positive integer
$j=1,\ldots ,m-1$
, and a positive integer
![]() $N_{0}=N_{0}(m,M,\unicode[STIX]{x1D700},w)$
such that, for every
$N_{0}=N_{0}(m,M,\unicode[STIX]{x1D700},w)$
such that, for every
![]() $N\geqslant N_{0}$
and
$N\geqslant N_{0}$
and
![]() $|t|\leqslant 5N$
,
$|t|\leqslant 5N$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ Wn+b\in \mathbb{P} \\ Wn+b+Wh_{i}\in \mathbb{P}\text{ for }i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn+b+Wh_{i})\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{w^{1/3}}+O_{m}(\unicode[STIX]{x1D700}N)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ Wn+b\in \mathbb{P} \\ Wn+b+Wh_{i}\in \mathbb{P}\text{ for }i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn+b+Wh_{i})\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{w^{1/3}}+O_{m}(\unicode[STIX]{x1D700}N)\biggr).\end{eqnarray}$$
Theorem 2.6. There exists a positive constant
![]() $\unicode[STIX]{x1D6FF}_{1}$
such that the following holds. Let
$\unicode[STIX]{x1D6FF}_{1}$
such that the following holds. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
. Let
$M\geqslant 1$
. Let
![]() $W=\prod _{p\leqslant w}p$
with
$W=\prod _{p\leqslant w}p$
with
![]() $w$
large enough in terms of
$w$
large enough in terms of
![]() $M$
, and let
$M$
, and let
![]() $(b,W)=1$
. There exists a positive constant
$(b,W)=1$
. There exists a positive constant
![]() $N_{0}=N_{0}(M,w)$
such that, for every
$N_{0}=N_{0}(M,w)$
such that, for every
![]() $N\geqslant N_{0}$
and
$N\geqslant N_{0}$
and
![]() $|t|\leqslant 5N$
,
$|t|\leqslant 5N$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ Wn+b\in \mathbb{P} \\ Wn+b+2=P_{2} \\ p\mid Wn+b+2\;\Longrightarrow \;p\geqslant N^{1/100}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{2}}\frac{W^{2}}{\unicode[STIX]{x1D711}(W)^{2}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{w^{1/3}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ Wn+b\in \mathbb{P} \\ Wn+b+2=P_{2} \\ p\mid Wn+b+2\;\Longrightarrow \;p\geqslant N^{1/100}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{2}}\frac{W^{2}}{\unicode[STIX]{x1D711}(W)^{2}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{w^{1/3}}\biggr).\end{eqnarray}$$
Let us briefly discuss the proofs of these results. In § 6 we shall state the results of Maynard and Chen saying that one can find almost twin primes in sets that are equidistributed in arithmetic progressions in certain precise senses. Bohr sets in general are not equidistributed but in § 7 we will show that it is enough to show variants of Theorems 2.5 and 2.6 that are more apt for applications of Maynard’s and Chen’s theorems. Then in §§ 9 and 10 we shall prove these variants using the Fourier expansion of the smooth Bohr cutoff discussed in § 3 as well as exponential sum estimates which we will state in § 8.
3 Smooth Bohr cutoff and its Fourier expansion
In this section we discuss a few basic properties of the Bohr cutoff
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
from Definition 2.1.
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
from Definition 2.1.
Lemma 3.1. Given a cyclic group
![]() $G=\mathbb{Z}/N\mathbb{Z}$
, a subset
$G=\mathbb{Z}/N\mathbb{Z}$
, a subset
![]() $\unicode[STIX]{x1D6FA}\subseteq G$
and
$\unicode[STIX]{x1D6FA}\subseteq G$
and
![]() $\unicode[STIX]{x1D702}\in (0,1/2]$
, the smooth Bohr cutoff
$\unicode[STIX]{x1D702}\in (0,1/2]$
, the smooth Bohr cutoff
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
has the following properties:
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
has the following properties:
-
(i) we have the lower bound
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D712}\Vert _{1}\geqslant (\unicode[STIX]{x1D702}/2)^{|\unicode[STIX]{x1D6FA}|};\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D712}\Vert _{1}\geqslant (\unicode[STIX]{x1D702}/2)^{|\unicode[STIX]{x1D6FA}|};\end{eqnarray}$$
-
(ii) if
 $n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then
$n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then  $$\begin{eqnarray}|\unicode[STIX]{x1D712}(n)|\leqslant (\unicode[STIX]{x1D702}^{2}/8)^{|\unicode[STIX]{x1D6FA}|}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D712}(n)|\leqslant (\unicode[STIX]{x1D702}^{2}/8)^{|\unicode[STIX]{x1D6FA}|}.\end{eqnarray}$$
Proof. Part (i) follows from the observation that
![]() $\unicode[STIX]{x1D712}(n)\geqslant 1$
when
$\unicode[STIX]{x1D712}(n)\geqslant 1$
when
![]() $n\in \text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})$
, together with the lower bound
$n\in \text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})$
, together with the lower bound
![]() $|\text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})|\geqslant (\unicode[STIX]{x1D702}/2)^{|\unicode[STIX]{x1D6FA}|}N$
from a standard pigeon-holing argument (see, e.g., [Reference Tao and VuTV10, Lemma 4.20]). For part (ii) we can clearly assume that
$|\text{Bohr}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702})|\geqslant (\unicode[STIX]{x1D702}/2)^{|\unicode[STIX]{x1D6FA}|}N$
from a standard pigeon-holing argument (see, e.g., [Reference Tao and VuTV10, Lemma 4.20]). For part (ii) we can clearly assume that
![]() $\unicode[STIX]{x1D702}\leqslant 1/4$
. Let us first give the precise definition of
$\unicode[STIX]{x1D702}\leqslant 1/4$
. Let us first give the precise definition of
![]() $S_{D,\unicode[STIX]{x1D702}}^{+}(x)$
. For an integer
$S_{D,\unicode[STIX]{x1D702}}^{+}(x)$
. For an integer
![]() $K\geqslant 1$
, write
$K\geqslant 1$
, write
![]() $\unicode[STIX]{x1D6E5}_{K}(x)$
for the Fejér kernel
$\unicode[STIX]{x1D6E5}_{K}(x)$
for the Fejér kernel
Then Vaaler’s polynomial
![]() $V_{D}(x)$
is defined as the trigonometric polynomial of degree
$V_{D}(x)$
is defined as the trigonometric polynomial of degree
![]() $D$
with
$D$
with
 $$\begin{eqnarray}\displaystyle V_{D}(x) & := & \displaystyle \frac{1}{D+1}\mathop{\sum }_{k=1}^{D}\biggl(\frac{k}{D+1}-\frac{1}{2}\biggr)\unicode[STIX]{x1D6E5}_{D+1}\biggl(x-\frac{k}{D+1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}(D+1)}\sin 2\unicode[STIX]{x1D70B}(D+1)x-\frac{1}{2\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6E5}_{D+1}(x)\sin 2\unicode[STIX]{x1D70B}x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{D}(x) & := & \displaystyle \frac{1}{D+1}\mathop{\sum }_{k=1}^{D}\biggl(\frac{k}{D+1}-\frac{1}{2}\biggr)\unicode[STIX]{x1D6E5}_{D+1}\biggl(x-\frac{k}{D+1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}(D+1)}\sin 2\unicode[STIX]{x1D70B}(D+1)x-\frac{1}{2\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6E5}_{D+1}(x)\sin 2\unicode[STIX]{x1D70B}x.\nonumber\end{eqnarray}$$
Finally,
Note that, writing
![]() $s(x)$
for the sawtooth function (so that
$s(x)$
for the sawtooth function (so that
![]() $s(x)=\{x\}-1/2$
if
$s(x)=\{x\}-1/2$
if
![]() $x\notin \mathbb{Z}$
and
$x\notin \mathbb{Z}$
and
![]() $s(x)=0$
if
$s(x)=0$
if
![]() $x\in \mathbb{Z}$
),
$x\in \mathbb{Z}$
),
except when
![]() $x=\unicode[STIX]{x1D702}$
or
$x=\unicode[STIX]{x1D702}$
or
![]() $x=-\unicode[STIX]{x1D702}$
. By a result of Vaaler [Reference VaalerVaa85, Theorem 18], we know that, for any
$x=-\unicode[STIX]{x1D702}$
. By a result of Vaaler [Reference VaalerVaa85, Theorem 18], we know that, for any
![]() $x$
,
$x$
,
Hence,
 $$\begin{eqnarray}\displaystyle |S_{D,\unicode[STIX]{x1D702}}^{+}(x)-1_{\Vert x\Vert \leqslant \unicode[STIX]{x1D702}}(x)| & {\leqslant} & \displaystyle \frac{2}{2D+2}(\unicode[STIX]{x1D6E5}_{D+1}(x-\unicode[STIX]{x1D702})+\unicode[STIX]{x1D6E5}_{D+1}(-x-\unicode[STIX]{x1D702}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{(D+1)^{2}}\biggl(\frac{1}{(\sin \unicode[STIX]{x1D70B}\Vert x-\unicode[STIX]{x1D702}\Vert )^{2}}+\frac{1}{(\sin \unicode[STIX]{x1D70B}\Vert \!-\!x-\unicode[STIX]{x1D702}\Vert )^{2}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |S_{D,\unicode[STIX]{x1D702}}^{+}(x)-1_{\Vert x\Vert \leqslant \unicode[STIX]{x1D702}}(x)| & {\leqslant} & \displaystyle \frac{2}{2D+2}(\unicode[STIX]{x1D6E5}_{D+1}(x-\unicode[STIX]{x1D702})+\unicode[STIX]{x1D6E5}_{D+1}(-x-\unicode[STIX]{x1D702}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{(D+1)^{2}}\biggl(\frac{1}{(\sin \unicode[STIX]{x1D70B}\Vert x-\unicode[STIX]{x1D702}\Vert )^{2}}+\frac{1}{(\sin \unicode[STIX]{x1D70B}\Vert \!-\!x-\unicode[STIX]{x1D702}\Vert )^{2}}\biggr).\nonumber\end{eqnarray}$$
If
![]() $\Vert x\Vert \geqslant 2\unicode[STIX]{x1D702}$
, then we get
$\Vert x\Vert \geqslant 2\unicode[STIX]{x1D702}$
, then we get
Now, if
![]() $n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then
$n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then
![]() $\Vert \unicode[STIX]{x1D709}_{0}n/N\Vert \geqslant 2\unicode[STIX]{x1D702}$
for some
$\Vert \unicode[STIX]{x1D709}_{0}n/N\Vert \geqslant 2\unicode[STIX]{x1D702}$
for some
![]() $\unicode[STIX]{x1D709}_{0}\in \unicode[STIX]{x1D6FA}$
. Thus,
$\unicode[STIX]{x1D709}_{0}\in \unicode[STIX]{x1D6FA}$
. Thus,
The conclusion then follows by our choice
![]() $D=\lceil 4/\unicode[STIX]{x1D702}\rceil ^{2|\unicode[STIX]{x1D6FA}|}$
.◻
$D=\lceil 4/\unicode[STIX]{x1D702}\rceil ^{2|\unicode[STIX]{x1D6FA}|}$
.◻
The following lemma gives the Fourier expansion of a function of bounded Fourier complexity in a convenient form. In particular, it allows us to separate the phases giving ‘major arc’ contribution from those giving ‘minor arc’ contribution.
Lemma 3.2. Let
![]() $A,M\geqslant 1$
, and let
$A,M\geqslant 1$
, and let
![]() $B=A(3M)^{M}$
. Let
$B=A(3M)^{M}$
. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{C}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{C}$
be a function with Fourier complexity at most
![]() $M$
, and let
$M$
, and let
![]() $W$
be a positive integer. Then for any large
$W$
be a positive integer. Then for any large
![]() $N$
, we may write
$N$
, we may write
for some
![]() $|b_{i}|\leqslant M$
,
$|b_{i}|\leqslant M$
,
![]() $0\leqslant a_{i}<q_{i}\leqslant N/(\log N)^{100B}$
,
$0\leqslant a_{i}<q_{i}\leqslant N/(\log N)^{100B}$
,
![]() $(a_{i},q_{i})=1$
, and
$(a_{i},q_{i})=1$
, and
![]() $|\unicode[STIX]{x1D6FD}_{i}|\leqslant W(\log N)^{100B}/(q_{i}N)$
. Moreover, there exists a positive integer
$|\unicode[STIX]{x1D6FD}_{i}|\leqslant W(\log N)^{100B}/(q_{i}N)$
. Moreover, there exists a positive integer
![]() $Q\leqslant (\log N)^{B}$
such that, for each
$Q\leqslant (\log N)^{B}$
such that, for each
![]() $1\leqslant i\leqslant M$
, either
$1\leqslant i\leqslant M$
, either
![]() $q_{i}\mid Q$
or
$q_{i}\mid Q$
or
![]() $q_{i}/(q_{i},Q^{2})>(\log N)^{A}$
.
$q_{i}/(q_{i},Q^{2})>(\log N)^{A}$
.
Proof. By the definition of Fourier complexity in Definition 2.4, we may write
for some
![]() $|b_{i}|\leqslant M$
and
$|b_{i}|\leqslant M$
and
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
. By the Dirichlet approximation theorem, for each
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
. By the Dirichlet approximation theorem, for each
![]() $1\leqslant i\leqslant M$
, there exist integers
$1\leqslant i\leqslant M$
, there exist integers
![]() $q_{i}\in [1,N/(\log N)^{100B}]$
and
$q_{i}\in [1,N/(\log N)^{100B}]$
and
![]() $a_{i}$
such that
$a_{i}$
such that
![]() $(a_{i},q_{i})=1$
and
$(a_{i},q_{i})=1$
and
This gives the desired Fourier expansion of
![]() $\unicode[STIX]{x1D712}$
, apart from the existence of
$\unicode[STIX]{x1D712}$
, apart from the existence of
![]() $Q$
mentioned in the last sentence of the statement.
$Q$
mentioned in the last sentence of the statement.
To define
![]() $Q$
, let
$Q$
, let
![]() ${\mathcal{Q}}=\{q_{1},\ldots ,q_{M}\}$
. Take
${\mathcal{Q}}=\{q_{1},\ldots ,q_{M}\}$
. Take
![]() $Q_{0}=1$
and for
$Q_{0}=1$
and for
![]() $i\geqslant 0$
define
$i\geqslant 0$
define
 $$\begin{eqnarray}Q_{i+1}=\mathop{\prod }_{\substack{ q\in {\mathcal{Q}} \\ q/(q,Q_{i}^{2})\leqslant (\log N)^{A}}}q.\end{eqnarray}$$
$$\begin{eqnarray}Q_{i+1}=\mathop{\prod }_{\substack{ q\in {\mathcal{Q}} \\ q/(q,Q_{i}^{2})\leqslant (\log N)^{A}}}q.\end{eqnarray}$$
There is some
![]() $I\leqslant |{\mathcal{Q}}|=M$
such that
$I\leqslant |{\mathcal{Q}}|=M$
such that
![]() $Q_{I+1}=Q_{I}$
. We claim that
$Q_{I+1}=Q_{I}$
. We claim that
![]() $Q=Q_{I}$
satisfies the desired properties. Indeed, for
$Q=Q_{I}$
satisfies the desired properties. Indeed, for
![]() $q\in {\mathcal{Q}}$
, if
$q\in {\mathcal{Q}}$
, if
![]() $q\nmid Q$
, then
$q\nmid Q$
, then
![]() $q\nmid Q_{I+1}$
so that
$q\nmid Q_{I+1}$
so that
![]() $q/(q,Q_{I}^{2})>(\log N)^{A}$
by the definition of
$q/(q,Q_{I}^{2})>(\log N)^{A}$
by the definition of
![]() $Q_{I+1}$
. Furthermore, it is easy to see from the construction that
$Q_{I+1}$
. Furthermore, it is easy to see from the construction that
Thus, a simple induction reveals that
![]() $Q_{i}\leqslant (\log N)^{A\cdot 3^{i}M^{i}}$
, so that
$Q_{i}\leqslant (\log N)^{A\cdot 3^{i}M^{i}}$
, so that
![]() $Q\leqslant (\log N)^{B}$
.◻
$Q\leqslant (\log N)^{B}$
.◻
This lemma can be thought of as a very special case of the general factorization theorem for nilsequences [Reference Green and TaoGT12, Theorem 1.19].
4 The transference-type result
In this section we prove Theorem 2.3. Let
![]() $\unicode[STIX]{x1D702},\unicode[STIX]{x1D700}>0$
be small enough depending on
$\unicode[STIX]{x1D702},\unicode[STIX]{x1D700}>0$
be small enough depending on
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6FF}$
, and take
$\unicode[STIX]{x1D6FF}$
, and take
By (2.4), we have
![]() $|\unicode[STIX]{x1D6FA}|\leqslant \unicode[STIX]{x1D700}^{-5/2}K+1$
. Let
$|\unicode[STIX]{x1D6FA}|\leqslant \unicode[STIX]{x1D700}^{-5/2}K+1$
. Let
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the smooth Bohr cutoff from Definition 2.1. For
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the smooth Bohr cutoff from Definition 2.1. For
![]() $i\in \{2,3\}$
, define
$i\in \{2,3\}$
, define
![]() $g_{i},h_{i}:G\rightarrow \mathbb{R}$
by setting
$g_{i},h_{i}:G\rightarrow \mathbb{R}$
by setting
Hence,
In particular, using the trivial bound
![]() $|\widehat{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D709})|\leqslant \Vert \unicode[STIX]{x1D712}\Vert _{1}$
we obtain
$|\widehat{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D709})|\leqslant \Vert \unicode[STIX]{x1D712}\Vert _{1}$
we obtain
We write
By the assumption (2.2) we have, for
![]() $i\in \{1,2\}$
the pointwise lower bound
$i\in \{1,2\}$
the pointwise lower bound
![]() $g_{i}(t)\geqslant \unicode[STIX]{x1D6FF}$
for all
$g_{i}(t)\geqslant \unicode[STIX]{x1D6FF}$
for all
![]() $t\in [N/4,N/2)$
. Thus,
$t\in [N/4,N/2)$
. Thus,
 $$\begin{eqnarray}f_{1}\ast g_{2}\ast g_{3}(N)\geqslant \frac{1}{N^{2}}\mathop{\sum }_{n_{1}}f_{1}(n_{1})\mathop{\sum }_{\substack{ N/4\leqslant n_{2},n_{3}<N/2 \\ n_{1}+n_{2}+n_{3}=N}}\unicode[STIX]{x1D6FF}^{2}\geqslant \frac{\unicode[STIX]{x1D6FF}^{2}}{100N}\mathop{\sum }_{0.1N\leqslant n_{1}\leqslant 0.4N}f_{1}(n_{1})\geqslant \frac{1}{100}\unicode[STIX]{x1D6FF}^{3}\end{eqnarray}$$
$$\begin{eqnarray}f_{1}\ast g_{2}\ast g_{3}(N)\geqslant \frac{1}{N^{2}}\mathop{\sum }_{n_{1}}f_{1}(n_{1})\mathop{\sum }_{\substack{ N/4\leqslant n_{2},n_{3}<N/2 \\ n_{1}+n_{2}+n_{3}=N}}\unicode[STIX]{x1D6FF}^{2}\geqslant \frac{\unicode[STIX]{x1D6FF}^{2}}{100N}\mathop{\sum }_{0.1N\leqslant n_{1}\leqslant 0.4N}f_{1}(n_{1})\geqslant \frac{1}{100}\unicode[STIX]{x1D6FF}^{3}\end{eqnarray}$$
by the assumption (2.3).
To conclude the proof, it remains to show that
and the same bound with either
![]() $h_{2}$
replaced by
$h_{2}$
replaced by
![]() $g_{2}$
or
$g_{2}$
or
![]() $h_{3}$
replaced by
$h_{3}$
replaced by
![]() $g_{3}$
. We have
$g_{3}$
. We have
First we bound the contribution of summands with
![]() $\unicode[STIX]{x1D709}\notin \unicode[STIX]{x1D6FA}$
. By the definition of
$\unicode[STIX]{x1D709}\notin \unicode[STIX]{x1D6FA}$
. By the definition of
![]() $\unicode[STIX]{x1D6FA}$
we have
$\unicode[STIX]{x1D6FA}$
we have
![]() $|\widehat{f_{1}}(\unicode[STIX]{x1D709})|<\unicode[STIX]{x1D700}$
for
$|\widehat{f_{1}}(\unicode[STIX]{x1D709})|<\unicode[STIX]{x1D700}$
for
![]() $\unicode[STIX]{x1D709}\notin \unicode[STIX]{x1D6FA}$
. Thus,
$\unicode[STIX]{x1D709}\notin \unicode[STIX]{x1D6FA}$
. Thus,
By Hölder’s inequality, this is bounded by
by (2.4) and (4.2). This is acceptable if
![]() $\unicode[STIX]{x1D700}$
is small enough. To bound the contribution to the right-hand side of (4.4) of summands with
$\unicode[STIX]{x1D700}$
is small enough. To bound the contribution to the right-hand side of (4.4) of summands with
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
, it suffices to show that
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
, it suffices to show that
![]() $|\widehat{h_{2}}(\unicode[STIX]{x1D709})|\leqslant 30\unicode[STIX]{x1D702}K^{2/5}$
for
$|\widehat{h_{2}}(\unicode[STIX]{x1D709})|\leqslant 30\unicode[STIX]{x1D702}K^{2/5}$
for
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
(the rest of the argument follows just as above). Since, by (2.4),
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
(the rest of the argument follows just as above). Since, by (2.4),
![]() $|\widehat{f_{2}}(\unicode[STIX]{x1D709})|\leqslant K^{2/5}$
, by (4.1) it suffices to show that
$|\widehat{f_{2}}(\unicode[STIX]{x1D709})|\leqslant K^{2/5}$
, by (4.1) it suffices to show that
for
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
. We may write
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6FA}$
. We may write
If
![]() $n\in \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then
$n\in \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then
![]() $|1-e(\unicode[STIX]{x1D709}n/N)|\leqslant 20\unicode[STIX]{x1D702}$
. If
$|1-e(\unicode[STIX]{x1D709}n/N)|\leqslant 20\unicode[STIX]{x1D702}$
. If
![]() $n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then by Lemma 3.1 we have
$n\notin \text{Bohr}(\unicode[STIX]{x1D6FA},2\unicode[STIX]{x1D702})$
, then by Lemma 3.1 we have
![]() $|\unicode[STIX]{x1D712}(n)|\leqslant \unicode[STIX]{x1D702}\Vert \unicode[STIX]{x1D712}\Vert _{1}$
. Combining these together we obtain
$|\unicode[STIX]{x1D712}(n)|\leqslant \unicode[STIX]{x1D702}\Vert \unicode[STIX]{x1D712}\Vert _{1}$
. Combining these together we obtain
as desired. This completes the proof of (4.3) and the cases where either
![]() $h_{2}$
is replaced by
$h_{2}$
is replaced by
![]() $g_{2}$
or
$g_{2}$
or
![]() $h_{3}$
is replaced by
$h_{3}$
is replaced by
![]() $g_{3}$
follow completely similarly. Hence, Theorem 2.3 follows.
$g_{3}$
follow completely similarly. Hence, Theorem 2.3 follows.
Remark 4.1. Theorem 2.3 in particular says that if, for a positive density subset of the primes, the ternary Goldbach does not hold for all large odd
![]() $N$
, then there must be some sort of Bohr set obstruction (including, as special cases, local obstructions modulo primes), since the condition (2.4) holds in this case by the work of Green and Tao [Reference Green and TaoGT06]. On the other hand, as mentioned in § 2, such obstructions may indeed prevent the ternary Goldbach from holding.
$N$
, then there must be some sort of Bohr set obstruction (including, as special cases, local obstructions modulo primes), since the condition (2.4) holds in this case by the work of Green and Tao [Reference Green and TaoGT06]. On the other hand, as mentioned in § 2, such obstructions may indeed prevent the ternary Goldbach from holding.
Remark 4.2. The condition (2.2) should be compared with the usual hypotheses needed in carrying out the circle method. In a traditional application of the circle method, one requires the set to be equidistributed in Bohr sets so that the minor arc contributions are negligible, leading to an asymptotic formula for the number of solutions. In Theorem 2.3, with a weaker assumption (2.2) about distribution in Bohr sets, we deduce a lower bound for the number of solutions (of the correct order of magnitude).
5 Proof of Theorems 1.1 and 1.2 assuming Theorems 2.5 and 2.6
In this section we deduce Theorems 1.1 and 1.2 from the transference principle, Theorems 2.5 and 2.6 and the work of Green and Tao [Reference Green and TaoGT06]. Let us first record the consequence of [Reference Green and TaoGT06] we shall need. Here and later, we call a set of linear forms
![]() ${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
admissible if they are distinct and
${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
admissible if they are distinct and
![]() $\prod _{i=1}^{k}L_{i}(n)$
has no fixed prime divisors. In this case, we define the singular series
$\prod _{i=1}^{k}L_{i}(n)$
has no fixed prime divisors. In this case, we define the singular series
Proposition 5.1. Let
![]() $\unicode[STIX]{x1D70C}\in (0,1/2)$
be real and let
$\unicode[STIX]{x1D70C}\in (0,1/2)$
be real and let
![]() $k\geqslant 1$
be an integer. Let
$k\geqslant 1$
be an integer. Let
![]() ${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
be an admissible set of
${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
be an admissible set of
![]() $k$
linear functions
$k$
linear functions
![]() $L_{i}(n)=a_{i}n+b_{i}$
with
$L_{i}(n)=a_{i}n+b_{i}$
with
![]() $|a_{i}|,|b_{i}|\leqslant N$
. Write
$|a_{i}|,|b_{i}|\leqslant N$
. Write
and let
![]() $\mathfrak{S}({\mathcal{L}})$
be defined as in (5.1). Let
$\mathfrak{S}({\mathcal{L}})$
be defined as in (5.1). Let
![]() $G=\mathbb{Z}/N\mathbb{Z}$
and let
$G=\mathbb{Z}/N\mathbb{Z}$
and let
![]() $f:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be such that
$f:G\rightarrow \mathbb{R}_{{\geqslant}0}$
be such that
Here we naturally identified
![]() $G$
with
$G$
with
![]() $\{1,2,\ldots ,N\}$
. Then
$\{1,2,\ldots ,N\}$
. Then
for some positive constant
![]() $K=K(k,\unicode[STIX]{x1D70C})$
.
$K=K(k,\unicode[STIX]{x1D70C})$
.
Proof. Let
![]() $F=L_{1}L_{2}\cdots L_{k}$
,
$F=L_{1}L_{2}\cdots L_{k}$
,
![]() $R=N^{\unicode[STIX]{x1D70C}/2}$
, and let
$R=N^{\unicode[STIX]{x1D70C}/2}$
, and let
![]() $\unicode[STIX]{x1D6FD}_{R}(n)$
be the enveloping sieve given by [Reference Green and TaoGT06, Proposition 3.1], so that
$\unicode[STIX]{x1D6FD}_{R}(n)$
be the enveloping sieve given by [Reference Green and TaoGT06, Proposition 3.1], so that
![]() $\unicode[STIX]{x1D6FD}_{R}(n)\,\gg _{k,\unicode[STIX]{x1D70C}}\,f(n)$
. Applying [Reference Green and TaoGT06, Proposition 4.2] with
$\unicode[STIX]{x1D6FD}_{R}(n)\,\gg _{k,\unicode[STIX]{x1D70C}}\,f(n)$
. Applying [Reference Green and TaoGT06, Proposition 4.2] with
![]() $a_{n}=f(n)/\unicode[STIX]{x1D6FD}_{R}(n)$
if
$a_{n}=f(n)/\unicode[STIX]{x1D6FD}_{R}(n)$
if
![]() $\unicode[STIX]{x1D6FD}_{R}(n)\neq 0$
and
$\unicode[STIX]{x1D6FD}_{R}(n)\neq 0$
and
![]() $a_{n}=0$
otherwise, we obtain that
$a_{n}=0$
otherwise, we obtain that
where the last inequality follows from [Reference Green and TaoGT06, Lemma 4.1]. ◻
Proof of Theorem 1.1.
Let
![]() $k=k(m)$
,
$k=k(m)$
,
![]() $\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(m)$
and
$\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(m)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
be as in Theorem 2.5, and let
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
be as in Theorem 2.5, and let
![]() $K=K(k,\unicode[STIX]{x1D70C}/2)$
, where
$K=K(k,\unicode[STIX]{x1D70C}/2)$
, where
![]() $K(k,\unicode[STIX]{x1D70C}/2)$
is as in Proposition 5.1. Let
$K(k,\unicode[STIX]{x1D70C}/2)$
is as in Proposition 5.1. Let
![]() $\unicode[STIX]{x1D700}>0$
be small enough depending on
$\unicode[STIX]{x1D700}>0$
be small enough depending on
![]() $m$
, let
$m$
, let
![]() $w$
be large enough depending on
$w$
be large enough depending on
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $m$
, and let
$m$
, and let
![]() $W=\prod _{p\leqslant w}p$
.
$W=\prod _{p\leqslant w}p$
.
Let
![]() $N^{\prime }$
be an odd positive integer, sufficiently large in terms of all the preceding quantities
$N^{\prime }$
be an odd positive integer, sufficiently large in terms of all the preceding quantities
![]() $m,k,\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D70C},K,\unicode[STIX]{x1D700},W$
. Our goal is to find a representation
$m,k,\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D70C},K,\unicode[STIX]{x1D700},W$
. Our goal is to find a representation
where, for
![]() $j=1,2,3$
,
$j=1,2,3$
,
![]() $p_{j}$
are primes such that the interval
$p_{j}$
are primes such that the interval
![]() $[p_{j},p_{j}+H]$
contains at least
$[p_{j},p_{j}+H]$
contains at least
![]() $m$
primes. For
$m$
primes. For
![]() $j=1,2,3$
, let
$j=1,2,3$
, let
![]() $b_{j}$
be integers such that
$b_{j}$
be integers such that
![]() $1\leqslant b_{j}\leqslant W$
,
$1\leqslant b_{j}\leqslant W$
,
![]() $(b_{j},W)=1$
, and
$(b_{j},W)=1$
, and
![]() $N^{\prime }\equiv b_{1}+b_{2}+b_{3}~(\text{mod}~W)$
. Let
$N^{\prime }\equiv b_{1}+b_{2}+b_{3}~(\text{mod}~W)$
. Let
Let
![]() $h_{1}^{(1)},\ldots ,h_{k-1}^{(1)}\,\ll _{m}\,1$
be as in Theorem 2.5 with
$h_{1}^{(1)},\ldots ,h_{k-1}^{(1)}\,\ll _{m}\,1$
be as in Theorem 2.5 with
![]() $\unicode[STIX]{x1D712}=1$
. We can assume that
$\unicode[STIX]{x1D712}=1$
. We can assume that
![]() $w$
is so large that
$w$
is so large that
![]() $|h_{i}^{(1)}|<w/2$
for each
$|h_{i}^{(1)}|<w/2$
for each
![]() $i$
.
$i$
.
With these choices
![]() $w,b_{1},h_{j}^{(1)}$
we define
$w,b_{1},h_{j}^{(1)}$
we define
 $$\begin{eqnarray}\displaystyle X_{1} & = & \displaystyle \biggl\{n\leqslant N:Wn+b_{1}\in \mathbb{P},Wn+b_{1}+Wh_{i}^{(1)}\in \mathbb{P}\;\text{for}\;i=1,\ldots ,m-1,\nonumber\\ \displaystyle & & \displaystyle \text{and}~p\biggm\vert\mathop{\prod }_{i=m}^{k-1}(Wn+b_{1}+Wh_{i}^{(1)})\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}/2}\biggr\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{1} & = & \displaystyle \biggl\{n\leqslant N:Wn+b_{1}\in \mathbb{P},Wn+b_{1}+Wh_{i}^{(1)}\in \mathbb{P}\;\text{for}\;i=1,\ldots ,m-1,\nonumber\\ \displaystyle & & \displaystyle \text{and}~p\biggm\vert\mathop{\prod }_{i=m}^{k-1}(Wn+b_{1}+Wh_{i}^{(1)})\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}/2}\biggr\},\end{eqnarray}$$
and let
![]() $f_{1}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be defined by
$f_{1}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be defined by
 $$\begin{eqnarray}f_{1}(n)=\left\{\begin{array}{@{}ll@{}}(\log N)^{k}{\displaystyle \frac{\unicode[STIX]{x1D711}(W)^{k}}{W^{k}}}\quad & \text{if}~n\in X_{1}\cap [0.2N,0.4N),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(n)=\left\{\begin{array}{@{}ll@{}}(\log N)^{k}{\displaystyle \frac{\unicode[STIX]{x1D711}(W)^{k}}{W^{k}}}\quad & \text{if}~n\in X_{1}\cap [0.2N,0.4N),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
Theorem 2.5 implies
whereas Proposition 5.1 applied with the linear forms
implies
since
![]() $|h_{j}^{(1)}|\leqslant |w|/2$
, so that
$|h_{j}^{(1)}|\leqslant |w|/2$
, so that
![]() $\mathfrak{S}({\mathcal{L}})\leqslant (W/\unicode[STIX]{x1D711}(W))^{k}$
.
$\mathfrak{S}({\mathcal{L}})\leqslant (W/\unicode[STIX]{x1D711}(W))^{k}$
.
Further, let
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the Bohr cutoff associated to
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the Bohr cutoff associated to
![]() $f_{1}$
with
$f_{1}$
with
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{0}/40$
from Theorem 2.3, with
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{0}/40$
from Theorem 2.3, with
![]() $|\unicode[STIX]{x1D6FA}|\,\ll _{m}\,1$
,
$|\unicode[STIX]{x1D6FA}|\,\ll _{m}\,1$
,
![]() $1\in \unicode[STIX]{x1D6FA}$
, and
$1\in \unicode[STIX]{x1D6FA}$
, and
![]() $1\,\ll _{m}\,\unicode[STIX]{x1D702}<0.05$
. For
$1\,\ll _{m}\,\unicode[STIX]{x1D702}<0.05$
. For
![]() $j=2,3$
, let
$j=2,3$
, let
![]() $h_{1}^{(j)},\ldots ,h_{k-1}^{(j)}\,\ll _{m}\,1$
be as in Theorem 2.5 with
$h_{1}^{(j)},\ldots ,h_{k-1}^{(j)}\,\ll _{m}\,1$
be as in Theorem 2.5 with
![]() $b=b_{j}$
and this choice of
$b=b_{j}$
and this choice of
![]() $\unicode[STIX]{x1D712}$
. We can assume that
$\unicode[STIX]{x1D712}$
. We can assume that
![]() $w$
is so large that
$w$
is so large that
![]() $|h_{i}^{(j)}|<w/2$
. With these choices
$|h_{i}^{(j)}|<w/2$
. With these choices
![]() $w,b_{j},h_{i}^{(j)}$
we define, for
$w,b_{j},h_{i}^{(j)}$
we define, for
![]() $j=2,3$
,
$j=2,3$
,
![]() $X_{j}$
and
$X_{j}$
and
![]() $f_{j}$
analogously to (5.2) and (5.3), but with
$f_{j}$
analogously to (5.2) and (5.3), but with
![]() $f_{j}$
now supported on
$f_{j}$
now supported on
![]() $[N/4,N/2)$
. For
$[N/4,N/2)$
. For
![]() $t\in [N/4,N/2)$
, Theorem 2.5 implies
$t\in [N/4,N/2)$
, Theorem 2.5 implies
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{N/4\leqslant n<N/2}f_{j}(n)\unicode[STIX]{x1D712}(t-n) & {\geqslant} & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{0}}{10}\biggl(\mathop{\sum }_{N/4\leqslant n<N/2}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{w^{1/3}}+\unicode[STIX]{x1D700}N\biggr)\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{0}}{30}\biggl(\mathop{\sum }_{n\in G}\unicode[STIX]{x1D712}(n)+O\biggl(\frac{N}{w^{1/3}}+\unicode[STIX]{x1D700}N\biggr)\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{N/4\leqslant n<N/2}f_{j}(n)\unicode[STIX]{x1D712}(t-n) & {\geqslant} & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{0}}{10}\biggl(\mathop{\sum }_{N/4\leqslant n<N/2}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{w^{1/3}}+\unicode[STIX]{x1D700}N\biggr)\biggr)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{0}}{30}\biggl(\mathop{\sum }_{n\in G}\unicode[STIX]{x1D712}(n)+O\biggl(\frac{N}{w^{1/3}}+\unicode[STIX]{x1D700}N\biggr)\biggr),\nonumber\end{eqnarray}$$
where the second inequality follows since
![]() $\unicode[STIX]{x1D712}$
is symmetric around zero and is essentially supported on
$\unicode[STIX]{x1D712}$
is symmetric around zero and is essentially supported on
![]() $|n|\leqslant 0.1N$
, in the sense that
$|n|\leqslant 0.1N$
, in the sense that
by Lemma 3.1. When
![]() $w$
is large enough and
$w$
is large enough and
![]() $\unicode[STIX]{x1D700}$
is small enough in terms of
$\unicode[STIX]{x1D700}$
is small enough in terms of
![]() $m,\unicode[STIX]{x1D702}$
and
$m,\unicode[STIX]{x1D702}$
and
![]() $|\unicode[STIX]{x1D6FA}|$
(the size of which depend only on
$|\unicode[STIX]{x1D6FA}|$
(the size of which depend only on
![]() $m$
), this together with Lemma 3.1 implies that
$m$
), this together with Lemma 3.1 implies that
Furthermore, Proposition 5.1 implies that, for
![]() $j=2,3$
,
$j=2,3$
,
Hence, all the assumptions of Theorem 2.3 are satisfied, and thus
![]() $f_{1}\ast f_{2}\ast f_{3}(N)\gg \unicode[STIX]{x1D6FF}^{3}$
. In particular, there exists
$f_{1}\ast f_{2}\ast f_{3}(N)\gg \unicode[STIX]{x1D6FF}^{3}$
. In particular, there exists
![]() $n_{1},n_{2},n_{3}$
lying in the support of
$n_{1},n_{2},n_{3}$
lying in the support of
![]() $f_{1},f_{2},f_{3}$
, respectively, such that
$f_{1},f_{2},f_{3}$
, respectively, such that
![]() $n_{1}+n_{2}+n_{3}\equiv 0~(\text{mod}~N)$
. By the definitions of
$n_{1}+n_{2}+n_{3}\equiv 0~(\text{mod}~N)$
. By the definitions of
![]() $f_{1},f_{2},f_{3}$
, we necessarily have
$f_{1},f_{2},f_{3}$
, we necessarily have
![]() $n_{1}+n_{2}+n_{3}=N$
, and moreover for
$n_{1}+n_{2}+n_{3}=N$
, and moreover for
![]() $i=1,2,3$
,
$i=1,2,3$
,
![]() $Wn_{i}+b_{i}$
are primes and so are
$Wn_{i}+b_{i}$
are primes and so are
![]() $Wn_{i}+b_{i}+Wh_{j}^{(i)}$
for
$Wn_{i}+b_{i}+Wh_{j}^{(i)}$
for
![]() $1\leqslant j\leqslant m-1$
. This gives the desired representation
$1\leqslant j\leqslant m-1$
. This gives the desired representation
once
![]() $H$
is large enough in terms of
$H$
is large enough in terms of
![]() $m$
.◻
$m$
.◻
Proof of Theorem 1.2.
Let
![]() $K=K(2,1/2000)$
, where
$K=K(2,1/2000)$
, where
![]() $K(k,\unicode[STIX]{x1D70C})$
is as in Proposition 5.1. Let
$K(k,\unicode[STIX]{x1D70C})$
is as in Proposition 5.1. Let
![]() $w$
be a large parameter, and let
$w$
be a large parameter, and let
![]() $W=\prod _{p\leqslant w}p$
.
$W=\prod _{p\leqslant w}p$
.
Let
![]() $N^{\prime }\equiv 3~(\text{mod}~6)$
be a positive integer, sufficiently large in terms of
$N^{\prime }\equiv 3~(\text{mod}~6)$
be a positive integer, sufficiently large in terms of
![]() $K,W$
. Our goal is to find a representation
$K,W$
. Our goal is to find a representation
where, for
![]() $j=1,2,3$
,
$j=1,2,3$
,
![]() $p_{j}+2$
has at most two prime factors. For
$p_{j}+2$
has at most two prime factors. For
![]() $j=1,2,3$
, let
$j=1,2,3$
, let
![]() $b_{j}$
be integers such that
$b_{j}$
be integers such that
![]() $1\leqslant b_{j}\leqslant W$
,
$1\leqslant b_{j}\leqslant W$
,
![]() $(b_{j},W)=(b_{j}+2,W)=1$
, and
$(b_{j},W)=(b_{j}+2,W)=1$
, and
![]() $N^{\prime }\equiv b_{1}+b_{2}+b_{3}~(\text{mod}~W)$
. Let
$N^{\prime }\equiv b_{1}+b_{2}+b_{3}~(\text{mod}~W)$
. Let
For
![]() $j=1,2,3$
, we define
$j=1,2,3$
, we define
and let
![]() $f_{1}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be defined by
$f_{1}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be defined by
 $$\begin{eqnarray}f_{1}(n)=\left\{\begin{array}{@{}ll@{}}(\log N)^{2}{\displaystyle \frac{\unicode[STIX]{x1D711}(W)^{2}}{W^{2}}}\quad & \text{if}~n\in X_{1}\cap [0.2N,0.4N),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(n)=\left\{\begin{array}{@{}ll@{}}(\log N)^{2}{\displaystyle \frac{\unicode[STIX]{x1D711}(W)^{2}}{W^{2}}}\quad & \text{if}~n\in X_{1}\cap [0.2N,0.4N),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
Now Theorem 2.6 with
![]() $\unicode[STIX]{x1D712}=1$
implies that
$\unicode[STIX]{x1D712}=1$
implies that
Further, let
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the Bohr cutoff associated to
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D702}}$
be the Bohr cutoff associated to
![]() $f_{1}$
with
$f_{1}$
with
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}/40$
from Theorem 2.3, with
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}/40$
from Theorem 2.3, with
![]() $|\unicode[STIX]{x1D6FA}|\ll 1$
,
$|\unicode[STIX]{x1D6FA}|\ll 1$
,
![]() $1\in \unicode[STIX]{x1D6FA}$
and
$1\in \unicode[STIX]{x1D6FA}$
and
![]() $1\ll \unicode[STIX]{x1D702}<0.05$
. We define
$1\ll \unicode[STIX]{x1D702}<0.05$
. We define
![]() $f_{j}$
for
$f_{j}$
for
![]() $j=2,3$
as
$j=2,3$
as
![]() $f_{1}$
but with support
$f_{1}$
but with support
![]() $[N/4,N/2)$
. Now Theorem 2.6 implies that, for
$[N/4,N/2)$
. Now Theorem 2.6 implies that, for
![]() $j=2,3$
, and
$j=2,3$
, and
![]() $t\in [N/4,N/2)$
,
$t\in [N/4,N/2)$
,
since
![]() $\unicode[STIX]{x1D712}(n)$
is essentially supported on
$\unicode[STIX]{x1D712}(n)$
is essentially supported on
![]() $|n|\leqslant 0.1N$
(see (5.4)) and is symmetric around zero. When
$|n|\leqslant 0.1N$
(see (5.4)) and is symmetric around zero. When
![]() $w$
is large enough in terms of
$w$
is large enough in terms of
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D6FA}$
(sizes of which depend only on
$\unicode[STIX]{x1D6FA}$
(sizes of which depend only on
![]() $m$
), this and Lemma 3.1 imply that
$m$
), this and Lemma 3.1 imply that
Furthermore Proposition 5.1 implies that, for
![]() $j=1,2,3$
,
$j=1,2,3$
,
Hence, all the assumptions of Theorem 2.3 are satisfied, and thus
![]() $f_{1}\ast f_{2}\ast f_{3}(N)\gg \unicode[STIX]{x1D6FF}^{3}$
. In particular, there exists
$f_{1}\ast f_{2}\ast f_{3}(N)\gg \unicode[STIX]{x1D6FF}^{3}$
. In particular, there exists
![]() $n_{1},n_{2},n_{3}$
lying in the support of
$n_{1},n_{2},n_{3}$
lying in the support of
![]() $f_{1},f_{2},f_{3}$
, respectively, such that
$f_{1},f_{2},f_{3}$
, respectively, such that
![]() $n_{1}+n_{2}+n_{3}\equiv 0~(\text{mod}~N)$
. By the definitions of
$n_{1}+n_{2}+n_{3}\equiv 0~(\text{mod}~N)$
. By the definitions of
![]() $f_{1},f_{2},f_{3}$
, we necessarily have
$f_{1},f_{2},f_{3}$
, we necessarily have
![]() $n_{1}+n_{2}+n_{3}=N$
, and moreover for each
$n_{1}+n_{2}+n_{3}=N$
, and moreover for each
![]() $i=1,2,3$
,
$i=1,2,3$
,
![]() $Wn_{i}+b_{i}$
is a prime and
$Wn_{i}+b_{i}$
is a prime and
![]() $Wn_{i}+b_{i}+2$
has at most two prime factors. This gives the desired representation
$Wn_{i}+b_{i}+2$
has at most two prime factors. This gives the desired representation
6 Weighted versions of Maynard’s theorem and Chen’s theorem
As discussed in the introduction, the celebrated result of Maynard [Reference MaynardMay15] (obtained independently by Tao in an unpublished work) states that, for each
![]() $m\geqslant 1$
, there exists a constant
$m\geqslant 1$
, there exists a constant
![]() $H=H(m)$
such that there exists infinitely many primes
$H=H(m)$
such that there exists infinitely many primes
![]() $p$
for which the interval
$p$
for which the interval
![]() $[p,p+H]$
contains at least
$[p,p+H]$
contains at least
![]() $m$
primes. In a subsequent paper [Reference MaynardMay16], Maynard generalized the result to show that any subset of the primes which is well-distributed in arithmetic progressions (in a certain precise sense) contains many primes with bounded gaps, and also made an extension to linear forms representing primes.
$m$
primes. In a subsequent paper [Reference MaynardMay16], Maynard generalized the result to show that any subset of the primes which is well-distributed in arithmetic progressions (in a certain precise sense) contains many primes with bounded gaps, and also made an extension to linear forms representing primes.
In this section we state a slight variant of the main result of [Reference MaynardMay16] in the case when the underlying set is weighted with weights
![]() $\unicode[STIX]{x1D714}_{n}\geqslant 0$
. We also carefully state the dependencies between different parameters.
$\unicode[STIX]{x1D714}_{n}\geqslant 0$
. We also carefully state the dependencies between different parameters.
For a linear function
![]() $L(n)=l_{1}n+l_{2}$
, we define
$L(n)=l_{1}n+l_{2}$
, we define
![]() $\unicode[STIX]{x1D711}_{L}(q)=\unicode[STIX]{x1D711}(|l_{1}|q)/\unicode[STIX]{x1D711}(|l_{1}|)$
. Let us first state the required hypotheses which correspond to [Reference MaynardMay16, Hypothesis 1].
$\unicode[STIX]{x1D711}_{L}(q)=\unicode[STIX]{x1D711}(|l_{1}|q)/\unicode[STIX]{x1D711}(|l_{1}|)$
. Let us first state the required hypotheses which correspond to [Reference MaynardMay16, Hypothesis 1].
Hypothesis 6.1. For a sequence
![]() $(\unicode[STIX]{x1D714}_{n})$
, a set of
$(\unicode[STIX]{x1D714}_{n})$
, a set of
![]() $k$
admissible linear forms
$k$
admissible linear forms
![]() ${\mathcal{L}}$
and real numbers
${\mathcal{L}}$
and real numbers
![]() $x\geqslant 2,~\unicode[STIX]{x1D703}\in (0,1)$
and
$x\geqslant 2,~\unicode[STIX]{x1D703}\in (0,1)$
and
![]() $C_{H}>0$
, we formulate the following hypothesis.
$C_{H}>0$
, we formulate the following hypothesis.
-
(i) The sequence
 $(\unicode[STIX]{x1D714}_{n})$
is well-distributed in arithmetic progressions: we have
$(\unicode[STIX]{x1D714}_{n})$
is well-distributed in arithmetic progressions: we have  $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{\unicode[STIX]{x1D703}}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}\biggr|\leqslant C_{H}\frac{\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}}{(\log x)^{101k^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{\unicode[STIX]{x1D703}}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}\biggr|\leqslant C_{H}\frac{\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}}{(\log x)^{101k^{2}}}.\end{eqnarray}$$
-
(ii) Primes represented by linear forms in
 ${\mathcal{L}}$
are well-distributed in arithmetic progressions: for any
${\mathcal{L}}$
are well-distributed in arithmetic progressions: for any
 $L\in {\mathcal{L}}$
, we have
$L\in {\mathcal{L}}$
, we have  $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{\unicode[STIX]{x1D703}}}\max _{(L(c),r)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r) \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{1}{\unicode[STIX]{x1D711}_{L}(r)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}\biggr|\leqslant C_{H}\frac{\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}}{(\log x)^{101k^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{\unicode[STIX]{x1D703}}}\max _{(L(c),r)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r) \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{1}{\unicode[STIX]{x1D711}_{L}(r)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}\biggr|\leqslant C_{H}\frac{\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}}{(\log x)^{101k^{2}}}.\end{eqnarray}$$
-
(iii) The sequence
 $(\unicode[STIX]{x1D714}_{n})$
is not too concentrated in any arithmetic progression: for any
$(\unicode[STIX]{x1D714}_{n})$
is not too concentrated in any arithmetic progression: for any
 $r\leqslant x^{\unicode[STIX]{x1D703}}$
and any
$r\leqslant x^{\unicode[STIX]{x1D703}}$
and any
 $c$
, we have
$c$
, we have  $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}\leqslant C_{H}\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}\leqslant C_{H}\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
The slight variant of Maynard’s main theorem [Reference MaynardMay16, Theorem 3.1] can now be stated as follows.
Theorem 6.2. Let
![]() $\unicode[STIX]{x1D6FC}>0,\unicode[STIX]{x1D703}\in (0,1)$
and
$\unicode[STIX]{x1D6FC}>0,\unicode[STIX]{x1D703}\in (0,1)$
and
![]() $C_{H}>0$
. There exist a constant
$C_{H}>0$
. There exist a constant
![]() $C=C(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
such that, for any
$C=C(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
such that, for any
![]() $k\geqslant C$
there exist positive constants
$k\geqslant C$
there exist positive constants
![]() $x_{0}=x_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k,C_{H}),\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k)$
and
$x_{0}=x_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k,C_{H}),\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k)$
such that the following holds.
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703},k)$
such that the following holds.
Let
![]() $(\unicode[STIX]{x1D714}_{n})$
be a sequence of non-negative real numbers, let
$(\unicode[STIX]{x1D714}_{n})$
be a sequence of non-negative real numbers, let
![]() ${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
be an admissible set of
${\mathcal{L}}=\{L_{1},\ldots ,L_{k}\}$
be an admissible set of
![]() $k$
linear functions and let
$k$
linear functions and let
![]() $x\geqslant x_{0}$
be an integer. Assume that the coefficients of
$x\geqslant x_{0}$
be an integer. Assume that the coefficients of
![]() $L_{i}(n)=a_{i}n+b_{i}$
satisfy
$L_{i}(n)=a_{i}n+b_{i}$
satisfy
![]() $1\leqslant a_{i},b_{i}\leqslant x^{\unicode[STIX]{x1D6FC}}$
for all
$1\leqslant a_{i},b_{i}\leqslant x^{\unicode[STIX]{x1D6FC}}$
for all
![]() $1\leqslant i\leqslant k$
, and assume that
$1\leqslant i\leqslant k$
, and assume that
![]() $k\leqslant (\log x)^{\unicode[STIX]{x1D6FC}}$
.
$k\leqslant (\log x)^{\unicode[STIX]{x1D6FC}}$
.
If Hypothesis 6.1 holds and
![]() $\unicode[STIX]{x1D6FF}>1/(\log k)$
is such that
$\unicode[STIX]{x1D6FF}>1/(\log k)$
is such that
 $$\begin{eqnarray}\frac{1}{k}\mathop{\sum }_{L\in {\mathcal{L}}}\frac{\unicode[STIX]{x1D711}(a_{i})}{a_{i}}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}\geqslant \frac{\unicode[STIX]{x1D6FF}}{\log x}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{k}\mathop{\sum }_{L\in {\mathcal{L}}}\frac{\unicode[STIX]{x1D711}(a_{i})}{a_{i}}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}\geqslant \frac{\unicode[STIX]{x1D6FF}}{\log x}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
then
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ \#(\{L_{1}(n),\ldots ,L_{k}(n)\}\cap \mathbb{P})\geqslant C^{-1}\unicode[STIX]{x1D6FF}\log k \\ p\mid L_{1}(n)\cdots L_{k}(n)\;\Longrightarrow \;p>x^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D714}_{n}\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{k}\exp (Ck)}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ \#(\{L_{1}(n),\ldots ,L_{k}(n)\}\cap \mathbb{P})\geqslant C^{-1}\unicode[STIX]{x1D6FF}\log k \\ p\mid L_{1}(n)\cdots L_{k}(n)\;\Longrightarrow \;p>x^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D714}_{n}\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{k}\exp (Ck)}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
where
![]() $\mathfrak{S}({\mathcal{L}})$
is defined as in (5.1).
$\mathfrak{S}({\mathcal{L}})$
is defined as in (5.1).
Proof. The proof is the same as Maynard’s [Reference MaynardMay16, Proof of Theorem 3.1]. Introducing the weights
![]() $\unicode[STIX]{x1D714}_{n}$
makes no difference once one replaces
$\unicode[STIX]{x1D714}_{n}$
makes no difference once one replaces
![]() $\#{\mathcal{A}}(x)$
in [Reference MaynardMay16] by the weighted version
$\#{\mathcal{A}}(x)$
in [Reference MaynardMay16] by the weighted version
![]() $\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}$
, etc. Furthermore, to see that the constants
$\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}$
, etc. Furthermore, to see that the constants
![]() $\unicode[STIX]{x1D6FF}_{0}$
and
$\unicode[STIX]{x1D6FF}_{0}$
and
![]() $\unicode[STIX]{x1D70C}$
do not depend on
$\unicode[STIX]{x1D70C}$
do not depend on
![]() $C_{H}$
, note that Hypothesis 6.1(1, 2) imply [Reference MaynardMay16, Hypothesis 1(1, 2)] with implied constant one once
$C_{H}$
, note that Hypothesis 6.1(1, 2) imply [Reference MaynardMay16, Hypothesis 1(1, 2)] with implied constant one once
![]() $x$
is large enough in terms of
$x$
is large enough in terms of
![]() $C_{H}$
. On the other hand, in [Reference MaynardMay16, Proof of Theorem 3.1], [Reference MaynardMay16, Hypothesis 1(3)] is only used together with [Reference MaynardMay16, Hypothesis 1(1) or (2)] to dispose of some divisor functions through the Cauchy–Schwarz inequality (see [Reference MaynardMay16, Formulas (9.2) and (9.3)] for a typical example). In these situations one also wins a power of
$C_{H}$
. On the other hand, in [Reference MaynardMay16, Proof of Theorem 3.1], [Reference MaynardMay16, Hypothesis 1(3)] is only used together with [Reference MaynardMay16, Hypothesis 1(1) or (2)] to dispose of some divisor functions through the Cauchy–Schwarz inequality (see [Reference MaynardMay16, Formulas (9.2) and (9.3)] for a typical example). In these situations one also wins a power of
![]() $\log x$
and thus can take the implied constant in the resulting bounds to be one once
$\log x$
and thus can take the implied constant in the resulting bounds to be one once
![]() $x$
is large enough in terms of
$x$
is large enough in terms of
![]() $C_{H}$
. Hence, none of the implied constants in the proof of Maynard’s theorem depend on
$C_{H}$
. Hence, none of the implied constants in the proof of Maynard’s theorem depend on
![]() $C_{H}$
once
$C_{H}$
once
![]() $x$
is large enough in terms of
$x$
is large enough in terms of
![]() $C_{H}$
.◻
$C_{H}$
.◻
Next we formulate a similar general version of Chen’s theorem. We will need the notion of a well-factorable function of level
![]() $R$
by which we mean a function
$R$
by which we mean a function
![]() $\unicode[STIX]{x1D706}:\mathbb{N}\cap [1,R]\rightarrow [-1,1]$
such that, for any
$\unicode[STIX]{x1D706}:\mathbb{N}\cap [1,R]\rightarrow [-1,1]$
such that, for any
![]() $S,T\geqslant 1$
with
$S,T\geqslant 1$
with
![]() $ST=R$
, we can write
$ST=R$
, we can write
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FE}\ast \unicode[STIX]{x1D6FF}$
with 1-bounded functions
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6FE}\ast \unicode[STIX]{x1D6FF}$
with 1-bounded functions
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
supported on
$\unicode[STIX]{x1D6FF}$
supported on
![]() $[1,S]$
and
$[1,S]$
and
![]() $[1,T]$
, respectively.
$[1,T]$
, respectively.
Hypothesis 6.3. For
![]() $\unicode[STIX]{x1D700}\in (0,0.1)$
, a sequence
$\unicode[STIX]{x1D700}\in (0,0.1)$
, a sequence
![]() $(\unicode[STIX]{x1D714}_{n})$
of non-negative real numbers, a set of two admissible linear forms
$(\unicode[STIX]{x1D714}_{n})$
of non-negative real numbers, a set of two admissible linear forms
![]() ${\mathcal{L}}=\{L_{1},L_{2}\}$
with
${\mathcal{L}}=\{L_{1},L_{2}\}$
with
![]() $L_{i}(n)=u_{i}n+v_{i}$
, and a real number
$L_{i}(n)=u_{i}n+v_{i}$
, and a real number
![]() $x\geqslant 2$
, we formulate the following hypotheses.
$x\geqslant 2$
, we formulate the following hypotheses.
-
(i) Primes represented by
 $L_{1}$
are well-distributed in arithmetic progressions: we have whenever
$L_{1}$
are well-distributed in arithmetic progressions: we have whenever $$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|L_{2}(n) \\ L_{1}(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{u_{1}}{\unicode[STIX]{x1D711}(ru_{1})}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log L_{1}(n)}\biggr)\leqslant \frac{\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}}{(\log x)^{10}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|L_{2}(n) \\ L_{1}(n)\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{u_{1}}{\unicode[STIX]{x1D711}(ru_{1})}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log L_{1}(n)}\biggr)\leqslant \frac{\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}}{(\log x)^{10}}\end{eqnarray}$$
 $\unicode[STIX]{x1D706}$
is a well-factorable function of level
$\unicode[STIX]{x1D706}$
is a well-factorable function of level
 $x^{1/2-\unicode[STIX]{x1D700}}$
or
$x^{1/2-\unicode[STIX]{x1D700}}$
or
 $\unicode[STIX]{x1D706}=1_{p\in [P,P^{\prime })}\ast \unicode[STIX]{x1D706}^{\prime }$
, where
$\unicode[STIX]{x1D706}=1_{p\in [P,P^{\prime })}\ast \unicode[STIX]{x1D706}^{\prime }$
, where
 $\unicode[STIX]{x1D706}^{\prime }$
is a well-factorable function of level
$\unicode[STIX]{x1D706}^{\prime }$
is a well-factorable function of level
 $x^{1/2-\unicode[STIX]{x1D700}}/P$
and
$x^{1/2-\unicode[STIX]{x1D700}}/P$
and
 $2P\geqslant P^{\prime }\geqslant P\in [x^{1/10},x^{1/3-\unicode[STIX]{x1D700}}]$
.
$2P\geqslant P^{\prime }\geqslant P\in [x^{1/10},x^{1/3-\unicode[STIX]{x1D700}}]$
.
-
(ii) Almost primes represented by
 $L_{2}$
are well-distributed in arithmetic progressions: we have, for
$L_{2}$
are well-distributed in arithmetic progressions: we have, for
 $j=1,2$
, whenever
$j=1,2$
, whenever $$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,u_{1}(u_{1}v_{2}-u_{2}v_{1}))=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|L_{1}(n) \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}-\frac{1}{\unicode[STIX]{x1D711}_{L_{2}}(r)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}\biggr)\leqslant \frac{\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}}{(\log x)^{10}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,u_{1}(u_{1}v_{2}-u_{2}v_{1}))=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|L_{1}(n) \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}-\frac{1}{\unicode[STIX]{x1D711}_{L_{2}}(r)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}\biggr)\leqslant \frac{\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}}{(\log x)^{10}}\end{eqnarray}$$
 $\unicode[STIX]{x1D706}$
is a well-factorable function of level
$\unicode[STIX]{x1D706}$
is a well-factorable function of level
 $x^{1/2-\unicode[STIX]{x1D700}}$
, where (6.2a)and
$x^{1/2-\unicode[STIX]{x1D700}}$
, where (6.2a)and $$\begin{eqnarray}B_{1}=\{n=p_{1}p_{2}p_{3}\mid x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}},x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2},p_{3}\geqslant x^{1/10}\}\end{eqnarray}$$
(6.2b)
$$\begin{eqnarray}B_{1}=\{n=p_{1}p_{2}p_{3}\mid x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}},x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2},p_{3}\geqslant x^{1/10}\}\end{eqnarray}$$
(6.2b) $$\begin{eqnarray}B_{2}=\{n=p_{1}p_{2}p_{3}\mid x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2},p_{3}\geqslant x^{1/10}\}.\end{eqnarray}$$
$$\begin{eqnarray}B_{2}=\{n=p_{1}p_{2}p_{3}\mid x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2},p_{3}\geqslant x^{1/10}\}.\end{eqnarray}$$
-
(iii) The sequence
 $(\unicode[STIX]{x1D714}_{n})$
is not concentrated in
$(\unicode[STIX]{x1D714}_{n})$
is not concentrated in
 $B_{j}$
: we have, for
$B_{j}$
: we have, for
 $j=1,2$
,
$j=1,2$
,  $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}\leqslant (1+o(1))\frac{|B_{j}\cap [L_{2}(x),L_{2}(2x))|}{\unicode[STIX]{x1D711}(u_{2})}\cdot \frac{1}{x}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{2}(n)\in B_{j}}}\unicode[STIX]{x1D714}_{n}\leqslant (1+o(1))\frac{|B_{j}\cap [L_{2}(x),L_{2}(2x))|}{\unicode[STIX]{x1D711}(u_{2})}\cdot \frac{1}{x}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n},\end{eqnarray}$$
Note that the factor
![]() $u_{1}/(\unicode[STIX]{x1D711}(ru_{1})\log L_{1}(n))$
in the first hypothesis is the probability that a randomly chosen
$u_{1}/(\unicode[STIX]{x1D711}(ru_{1})\log L_{1}(n))$
in the first hypothesis is the probability that a randomly chosen
![]() $n\in [x,2x)$
satisfies
$n\in [x,2x)$
satisfies
![]() $r\mid L_{2}(n)$
and
$r\mid L_{2}(n)$
and
![]() $L_{1}(n)\in \mathbb{P}$
. Note also that it is straightforward to find the density of
$L_{1}(n)\in \mathbb{P}$
. Note also that it is straightforward to find the density of
![]() $B_{j}$
: if
$B_{j}$
: if
![]() $u_{2},v_{2}\leqslant x^{o(1)}$
, then
$u_{2},v_{2}\leqslant x^{o(1)}$
, then
where
To see that the coprimality conditions
![]() $(r,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1$
and
$(r,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1$
and
![]() $(r,u_{1}(u_{1}v_{2}-u_{2}v_{1}))=1$
occur naturally, note that if
$(r,u_{1}(u_{1}v_{2}-u_{2}v_{1}))=1$
occur naturally, note that if
![]() $r$
and
$r$
and
![]() $u_{i}$
share a common prime divisor
$u_{i}$
share a common prime divisor
![]() $p$
, then
$p$
, then
![]() $p\nmid L_{i}(n)$
for all
$p\nmid L_{i}(n)$
for all
![]() $n$
by the admissibility of
$n$
by the admissibility of
![]() $L_{i}$
, and thus the sum over those
$L_{i}$
, and thus the sum over those
![]() $n$
satisfying
$n$
satisfying
![]() $r|L_{i}(n)$
is empty. Similarly, if
$r|L_{i}(n)$
is empty. Similarly, if
![]() $(r,u_{i})=1$
but
$(r,u_{i})=1$
but
![]() $r$
and
$r$
and
![]() $u_{2}v_{1}-u_{1}v_{2}$
share a common prime divisor
$u_{2}v_{1}-u_{1}v_{2}$
share a common prime divisor
![]() $p<x^{1/10}$
, then
$p<x^{1/10}$
, then
![]() $p|L_{i}(n)$
implies
$p|L_{i}(n)$
implies
![]() $p|L_{j}(n)$
(where
$p|L_{j}(n)$
(where
![]() $j=3-i$
), and thus the sum over those
$j=3-i$
), and thus the sum over those
![]() $n$
satisfying
$n$
satisfying
![]() $r|L_{i}(n)$
and
$r|L_{i}(n)$
and
![]() $L_{j}(n)\in B$
(or
$L_{j}(n)\in B$
(or
![]() $L_{j}(n)\in \mathbb{P}$
) is empty.
$L_{j}(n)\in \mathbb{P}$
) is empty.
Theorem 6.4. There exist positive constants
![]() $\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D6FF}_{0},\unicode[STIX]{x1D700}$
and
![]() $x_{0}$
such that the following holds. Let
$x_{0}$
such that the following holds. Let
![]() $(\unicode[STIX]{x1D714}_{n})$
be a sequence of non-negative real numbers,
$(\unicode[STIX]{x1D714}_{n})$
be a sequence of non-negative real numbers,
![]() ${\mathcal{L}}=\{L_{1},L_{2}\}$
be an admissible set of two linear functions and let
${\mathcal{L}}=\{L_{1},L_{2}\}$
be an admissible set of two linear functions and let
![]() $x\geqslant x_{0}$
. Assume that the coefficients of
$x\geqslant x_{0}$
. Assume that the coefficients of
![]() $L_{i}(n)=u_{i}n+v_{i}$
satisfy
$L_{i}(n)=u_{i}n+v_{i}$
satisfy
![]() $1\leqslant u_{i},v_{i}\leqslant x^{o(1)}$
, and that Hypothesis 6.3 holds. Then
$1\leqslant u_{i},v_{i}\leqslant x^{o(1)}$
, and that Hypothesis 6.3 holds. Then
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{1}(n)\in \mathbb{P} \\ L_{2}(n)=P_{2} \\ p\mid L_{2}(n)\;\Longrightarrow \;p\geqslant x^{1/10}}}\unicode[STIX]{x1D714}_{n}\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{2}}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}-O\Bigl(x^{0.9}\max _{n}\unicode[STIX]{x1D714}_{n}\Bigr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ L_{1}(n)\in \mathbb{P} \\ L_{2}(n)=P_{2} \\ p\mid L_{2}(n)\;\Longrightarrow \;p\geqslant x^{1/10}}}\unicode[STIX]{x1D714}_{n}\geqslant \unicode[STIX]{x1D6FF}_{0}\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{2}}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}-O\Bigl(x^{0.9}\max _{n}\unicode[STIX]{x1D714}_{n}\Bigr),\end{eqnarray}$$
where
![]() $\mathfrak{S}({\mathcal{L}})$
is as in (5.1).
$\mathfrak{S}({\mathcal{L}})$
is as in (5.1).
Since the proof is essentially Chen’s sieving device written in general terms, we postpone its proof to Appendix A.
7 Technical reductions
The conclusion of Maynard’s theorem does not quite correspond to the conclusion we want in Theorem 2.5. However, we can quickly deduce Theorem 2.5 from the following variant which is more apt for an application of Maynard’s theorem.
Proposition 7.1. For any positive integer
![]() $m$
, there exist a positive integer
$m$
, there exist a positive integer
![]() $k=k(m)$
and positive constants
$k=k(m)$
and positive constants
![]() $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
and
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
such that the following holds. Let
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
such that the following holds. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
, let
$M\geqslant 1$
, let
![]() $W=\prod _{p\leqslant w}p$
and let
$W=\prod _{p\leqslant w}p$
and let
![]() $(b,W)=1$
. There exists a positive constant
$(b,W)=1$
. There exists a positive constant
![]() $N_{0}=N_{0}(m,M,w)$
such that, for any distinct integers
$N_{0}=N_{0}(m,M,w)$
such that, for any distinct integers
![]() $h_{1},\ldots ,h_{k}$
with
$h_{1},\ldots ,h_{k}$
with
![]() $|h_{j}|<w/2$
, any
$|h_{j}|<w/2$
, any
![]() $N\geqslant N_{0}$
and
$N\geqslant N_{0}$
and
![]() $|t|\leqslant 5N$
,
$|t|\leqslant 5N$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ |\{W(n+h_{i})+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{M^{2}N}{w^{1/2}}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ |\{W(n+h_{i})+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{M^{2}N}{w^{1/2}}\biggr)\biggr).\end{eqnarray}$$
Proof that Proposition 7.1 implies Theorem 2.5.
Let
![]() $k=k(m)$
,
$k=k(m)$
,
![]() $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
and
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
and
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
be as in Proposition 7.1. Let
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
be as in Proposition 7.1. Let
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{M}$
be the phases appearing in the Fourier expansion of
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{M}$
be the phases appearing in the Fourier expansion of
![]() $\unicode[STIX]{x1D712}$
. By the simultaneous version of the Dirichlet approximation theorem, we can find
$\unicode[STIX]{x1D712}$
. By the simultaneous version of the Dirichlet approximation theorem, we can find
![]() $k$
distinct positive integers
$k$
distinct positive integers
![]() $h_{j}^{\prime }\,\ll _{M,\unicode[STIX]{x1D700},m}\,1$
such that
$h_{j}^{\prime }\,\ll _{M,\unicode[STIX]{x1D700},m}\,1$
such that
These choices ensure that, whenever
![]() $n-n^{\prime }\in \{h_{1}^{\prime },\ldots ,h_{k}^{\prime }\}$
, we have
$n-n^{\prime }\in \{h_{1}^{\prime },\ldots ,h_{k}^{\prime }\}$
, we have
We can assume that
![]() $w$
is so large in terms of
$w$
is so large in terms of
![]() $M,\unicode[STIX]{x1D700}$
and
$M,\unicode[STIX]{x1D700}$
and
![]() $m$
that
$m$
that
![]() $|h_{j}^{\prime }|<w/2$
for all
$|h_{j}^{\prime }|<w/2$
for all
![]() $j$
and
$j$
and
![]() $w^{1/6}$
is at least
$w^{1/6}$
is at least
![]() $2M^{2}$
times the implied constant in the conclusion of Proposition 7.1. By Proposition 7.1 we see that, for any
$2M^{2}$
times the implied constant in the conclusion of Proposition 7.1. By Proposition 7.1 we see that, for any
![]() $|t|\leqslant 5N$
,
$|t|\leqslant 5N$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ |\{W(n+h_{i}^{\prime })+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i}^{\prime })+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ |\{W(n+h_{i}^{\prime })+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i}^{\prime })+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
We get that, for some
![]() ${\mathcal{J}}\subseteq \{1,\ldots ,k\}$
with
${\mathcal{J}}\subseteq \{1,\ldots ,k\}$
with
![]() $\#{\mathcal{J}}=m$
,
$\#{\mathcal{J}}=m$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ W(n+h_{j}^{\prime })+b\in \mathbb{P}~\text{for each}~j\in {\mathcal{J}} \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i}^{\prime })+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ W(n+h_{j}^{\prime })+b\in \mathbb{P}~\text{for each}~j\in {\mathcal{J}} \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i}^{\prime })+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n)\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
Let
![]() $r\in {\mathcal{J}}$
be such that
$r\in {\mathcal{J}}$
be such that
![]() $h_{r}^{\prime }$
is the minimal among
$h_{r}^{\prime }$
is the minimal among
![]() $h_{j}^{\prime }$
with
$h_{j}^{\prime }$
with
![]() $j\in {\mathcal{J}}$
. We take
$j\in {\mathcal{J}}$
. We take
![]() $h_{1},\ldots ,h_{k-1}$
to be any choice (unique up to permutation) such that
$h_{1},\ldots ,h_{k-1}$
to be any choice (unique up to permutation) such that
and
Substituting
![]() $n^{\prime }=n+h_{r}^{\prime }$
, we see that
$n^{\prime }=n+h_{r}^{\prime }$
, we see that
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N+h_{r}^{\prime }\leqslant n^{\prime }<2N+h_{r}^{\prime } \\ Wn^{\prime }+b\in \mathbb{P} \\ Wn^{\prime }+Wh_{i}+b\in \mathbb{P}~\text{for}~i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn^{\prime }+Wh_{i}+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n^{\prime }+h_{r}^{\prime })\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N+h_{r}^{\prime }\leqslant n^{\prime }<2N+h_{r}^{\prime } \\ Wn^{\prime }+b\in \mathbb{P} \\ Wn^{\prime }+Wh_{i}+b\in \mathbb{P}~\text{for}~i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn^{\prime }+Wh_{i}+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n^{\prime }+h_{r}^{\prime })\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}\biggr).\end{eqnarray}$$
By (7.1) we may replace the summand
![]() $\unicode[STIX]{x1D712}(t-n^{\prime }+h_{r}^{\prime })$
above by
$\unicode[STIX]{x1D712}(t-n^{\prime }+h_{r}^{\prime })$
above by
![]() $\unicode[STIX]{x1D712}(t-n^{\prime })$
using a standard sieve bound for the number of elements counted on the left-hand side of (7.2), getting that
$\unicode[STIX]{x1D712}(t-n^{\prime })$
using a standard sieve bound for the number of elements counted on the left-hand side of (7.2), getting that
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N+h_{r}^{\prime }\leqslant n^{\prime }<2N+h_{r}^{\prime } \\ Wn^{\prime }+b\in \mathbb{P} \\ Wn^{\prime }+Wh_{i}+b\in \mathbb{P}~\text{for}~i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn^{\prime }+Wh_{i}+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n^{\prime })\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}+O(\unicode[STIX]{x1D700}N)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N+h_{r}^{\prime }\leqslant n^{\prime }<2N+h_{r}^{\prime } \\ Wn^{\prime }+b\in \mathbb{P} \\ Wn^{\prime }+Wh_{i}+b\in \mathbb{P}~\text{for}~i=1,\ldots ,m-1 \\ p\mid \mathop{\prod }_{i=m}^{k-1}(Wn^{\prime }+Wh_{i}+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D712}(t-n^{\prime })\geqslant \frac{\unicode[STIX]{x1D6FF}_{1}}{\binom{k}{m}}\cdot \frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\biggl(\mathop{\sum }_{N\leqslant n<2N}\unicode[STIX]{x1D712}(t-n)-\frac{N}{2w^{1/3}}+O(\unicode[STIX]{x1D700}N)\biggr)\end{eqnarray}$$
with the implied constant depending only on
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D70C}$
and thus only on
$\unicode[STIX]{x1D70C}$
and thus only on
![]() $m$
. Theorem 2.5 follows with
$m$
. Theorem 2.5 follows with
![]() $\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{1}/(2\binom{k}{m})$
through noting that the terms with
$\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{1}/(2\binom{k}{m})$
through noting that the terms with
![]() $n^{\prime }\in [2N,2N+h_{r}^{\prime })$
on the left-hand side contribute at most
$n^{\prime }\in [2N,2N+h_{r}^{\prime })$
on the left-hand side contribute at most
![]() $M^{2}h_{r}^{\prime }$
.◻
$M^{2}h_{r}^{\prime }$
.◻
Since Bohr sets (and, in general, functions with bounded Fourier complexity) are not equidistributed in arithmetic progressions, we cannot apply Maynard’s theorem to the situation in Proposition 7.1 directly, but we need to be careful with our choice of the sequence
![]() $\unicode[STIX]{x1D714}_{n}$
to which we apply Maynard’s theorem. In particular, the moduli
$\unicode[STIX]{x1D714}_{n}$
to which we apply Maynard’s theorem. In particular, the moduli
![]() $q_{i}\mid Q$
in the Fourier expansion of
$q_{i}\mid Q$
in the Fourier expansion of
![]() $\unicode[STIX]{x1D712}$
in Lemma 3.2 are problematic, and for this reason we will split into residue classes
$\unicode[STIX]{x1D712}$
in Lemma 3.2 are problematic, and for this reason we will split into residue classes
![]() $(\text{mod}~Q)$
.
$(\text{mod}~Q)$
.
In § 9 we shall use Maynard’s theorem (Theorem 6.2) and exponential sum estimates (which we will state in § 8) to prove the following proposition.
Proposition 7.2. For any positive integer
![]() $m$
, there exist a positive integer
$m$
, there exist a positive integer
![]() $k=k(m)$
and positive constants
$k=k(m)$
and positive constants
![]() $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
,
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{1}(m)$
,
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
and
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(m)$
and
![]() $A=A(m)$
such that the following holds. Let
$A=A(m)$
such that the following holds. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
. Let
$M\geqslant 1$
. Let
![]() $W=\prod _{p\leqslant w}p$
, let
$W=\prod _{p\leqslant w}p$
, let
![]() $(b,W)=1$
and let
$(b,W)=1$
and let
![]() $N\geqslant N_{0}(m,M,w)$
be large. Let
$N\geqslant N_{0}(m,M,w)$
be large. Let
![]() $Q$
be from Lemma 3.2 corresponding to
$Q$
be from Lemma 3.2 corresponding to
![]() $A$
. Then, for any distinct integers
$A$
. Then, for any distinct integers
![]() $h_{1},\ldots ,h_{k}$
with
$h_{1},\ldots ,h_{k}$
with
![]() $|h_{j}|<w/2$
, any
$|h_{j}|<w/2$
, any
![]() $|t|\leqslant 5N$
and
$|t|\leqslant 5N$
and
![]() $c_{0}\in {\mathcal{C}}_{M}$
,
$c_{0}\in {\mathcal{C}}_{M}$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ |\{W(n+h_{i})+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\!\!\!\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\frac{Q}{|{\mathcal{C}}_{M}|}\biggl(\!\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\!\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{Qw^{10}}\biggr)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ |\{W(n+h_{i})+b\}\cap \mathbb{P}|\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}}}}\!\!\!\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{k}}\frac{W^{k}}{\unicode[STIX]{x1D711}(W)^{k}}\frac{Q}{|{\mathcal{C}}_{M}|}\biggl(\!\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\!\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{Qw^{10}}\biggr)\biggr),\end{eqnarray}$$
where
Note that, since
![]() $|h_{i}|<w/2$
, by the Chinese reminder theorem
$|h_{i}|<w/2$
, by the Chinese reminder theorem
Let us next state a similar proposition that we shall prove using Chen’s theorem (Theorem 6.4).
Proposition 7.3. Let
![]() $\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
$\unicode[STIX]{x1D712}:\mathbb{Z}\rightarrow \mathbb{R}_{{\geqslant}0}$
be a function with Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
. Let
$M\geqslant 1$
. Let
![]() $W=\prod _{p\leqslant w}p$
, let
$W=\prod _{p\leqslant w}p$
, let
![]() $(b,W)=(b+2,W)=1$
and let
$(b,W)=(b+2,W)=1$
and let
![]() $N\geqslant N_{0}(M,w)$
be large. Let
$N\geqslant N_{0}(M,w)$
be large. Let
![]() $Q$
be from Lemma 3.2 corresponding to some large enough
$Q$
be from Lemma 3.2 corresponding to some large enough
![]() $A$
. Then, for any
$A$
. Then, for any
![]() $|t|\leqslant 5N$
, and
$|t|\leqslant 5N$
, and
![]() $c_{0}\in {\mathcal{C}}_{C}$
,
$c_{0}\in {\mathcal{C}}_{C}$
,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ Wn+b\in \mathbb{P} \\ Wn+b+2=P_{2} \\ p\mid Wn+b+2\;\Longrightarrow \;p\geqslant N^{1/100}}}\!\!\!\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{2}}\frac{W^{2}}{\unicode[STIX]{x1D711}(W)^{2}}\frac{Q}{|{\mathcal{C}}_{C}|}\biggl(\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{Q(\log N)^{100}}\biggr)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ Wn+b\in \mathbb{P} \\ Wn+b+2=P_{2} \\ p\mid Wn+b+2\;\Longrightarrow \;p\geqslant N^{1/100}}}\!\!\!\unicode[STIX]{x1D712}(t-n)\geqslant \unicode[STIX]{x1D6FF}_{1}\frac{1}{(\log N)^{2}}\frac{W^{2}}{\unicode[STIX]{x1D711}(W)^{2}}\frac{Q}{|{\mathcal{C}}_{C}|}\biggl(\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)+O\biggl(\frac{N}{Q(\log N)^{100}}\biggr)\biggr),\end{eqnarray}$$
for some absolute constant
![]() $\unicode[STIX]{x1D6FF}_{1}>0$
, where
$\unicode[STIX]{x1D6FF}_{1}>0$
, where
To show that Propositions 7.2 and 7.3 imply Proposition 7.1 and Theorem 2.6, we use the following lemma allowing us to sum over all the residue classes in
![]() ${\mathcal{C}}_{M}$
and
${\mathcal{C}}_{M}$
and
![]() ${\mathcal{C}}_{C}$
.
${\mathcal{C}}_{C}$
.
Lemma 7.4. Let
![]() $\unicode[STIX]{x1D712}$
be a function of Fourier complexity at most
$\unicode[STIX]{x1D712}$
be a function of Fourier complexity at most
![]() $M$
for some
$M$
for some
![]() $M\geqslant 1$
, and let
$M\geqslant 1$
, and let
![]() $N,Q$
be positive integers with
$N,Q$
be positive integers with
![]() $N\geqslant 2Q^{2}$
. Let also
$N\geqslant 2Q^{2}$
. Let also
![]() ${\mathcal{Q}}$
be a collection of residue classes modulo
${\mathcal{Q}}$
be a collection of residue classes modulo
![]() $Q$
such that, for all
$Q$
such that, for all
![]() $1\neq q\mid Q$
and
$1\neq q\mid Q$
and
![]() $(a,q)=1$
, one has
$(a,q)=1$
, one has
for some
![]() $\unicode[STIX]{x1D702}>0$
. Then
$\unicode[STIX]{x1D702}>0$
. Then
 $$\begin{eqnarray}\frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)\geqslant \mathop{\sum }_{\substack{ N\leqslant n<2N}}\unicode[STIX]{x1D712}(t-n)+O(\unicode[STIX]{x1D702}M^{2}N+QM^{2}N^{1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)\geqslant \mathop{\sum }_{\substack{ N\leqslant n<2N}}\unicode[STIX]{x1D712}(t-n)+O(\unicode[STIX]{x1D702}M^{2}N+QM^{2}N^{1/2}).\end{eqnarray}$$
Proof. By Definition 2.4, we have the Fourier expansion
for some
![]() $|b_{i}|\leqslant M$
and
$|b_{i}|\leqslant M$
and
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
. For each
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{R}/\mathbb{Z}$
. For each
![]() $1\leqslant i\leqslant M$
, we may find integers
$1\leqslant i\leqslant M$
, we may find integers
![]() $0\leqslant a_{i}<q_{i}\leqslant N^{1/2}$
with
$0\leqslant a_{i}<q_{i}\leqslant N^{1/2}$
with
![]() $(a_{i},q_{i})=1$
such that
$(a_{i},q_{i})=1$
such that
![]() $|\unicode[STIX]{x1D6FC}_{i}-a_{i}/q_{i}|\leqslant 1/(q_{i}N^{1/2})$
.
$|\unicode[STIX]{x1D6FC}_{i}-a_{i}/q_{i}|\leqslant 1/(q_{i}N^{1/2})$
.
Let us first consider the contribution of those
![]() $i$
with
$i$
with
![]() $q_{i}=1$
to the left-hand side of (7.5). This contribution is, using Lemma B.1,
$q_{i}=1$
to the left-hand side of (7.5). This contribution is, using Lemma B.1,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{1} & := & \displaystyle \frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))\nonumber\\ \displaystyle & = & \displaystyle \frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\biggl(\frac{1}{Q}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(N^{1/2})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(QM^{2}N^{1/2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{1} & := & \displaystyle \frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))\nonumber\\ \displaystyle & = & \displaystyle \frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\biggl(\frac{1}{Q}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(N^{1/2})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant i\leqslant M \\ q_{i}=1}}b_{i}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(QM^{2}N^{1/2}).\nonumber\end{eqnarray}$$
By Lemma B.2 we can extend the sum to go over all
![]() $1\leqslant i\leqslant M$
, at the cost of an error of size
$1\leqslant i\leqslant M$
, at the cost of an error of size
![]() $M^{2}\max _{i}q_{i}\ll M^{2}N^{1/2}$
, obtaining
$M^{2}\max _{i}q_{i}\ll M^{2}N^{1/2}$
, obtaining
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{1} & = & \displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N}}\mathop{\sum }_{1\leqslant i\leqslant M}b_{i}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(QM^{2}N^{1/2})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N}}\unicode[STIX]{x1D712}(t-n)+O(QM^{2}N^{1/2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{1} & = & \displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N}}\mathop{\sum }_{1\leqslant i\leqslant M}b_{i}e(\unicode[STIX]{x1D6FC}_{i}(t-n))+O(QM^{2}N^{1/2})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N}}\unicode[STIX]{x1D712}(t-n)+O(QM^{2}N^{1/2}).\nonumber\end{eqnarray}$$
Hence, we are finished if we can show that, for each
![]() $i$
such that with
$i$
such that with
![]() $q_{i}>1$
, we have
$q_{i}>1$
, we have
 $$\begin{eqnarray}\frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))=O(\unicode[STIX]{x1D702}N+QN^{1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{Q}{|{\mathcal{Q}}|}\mathop{\sum }_{\substack{ c_{0}\in {\mathcal{Q}}}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}_{i}(t-n))=O(\unicode[STIX]{x1D702}N+QN^{1/2}).\end{eqnarray}$$
In case
![]() $q_{i}\nmid Q$
, we have
$q_{i}\nmid Q$
, we have
![]() $q_{i}/(q_{i},Q)>1$
and, thus, by Lemma B.2, the left-hand side is
$q_{i}/(q_{i},Q)>1$
and, thus, by Lemma B.2, the left-hand side is
![]() $O(Qq_{i})=O(QN^{1/2})$
.
$O(Qq_{i})=O(QN^{1/2})$
.
In case
![]() $q_{i}\mid Q$
, writing
$q_{i}\mid Q$
, writing
![]() $\unicode[STIX]{x1D6FC}_{i}=a_{i}/q_{i}+\unicode[STIX]{x1D6FD}_{i}$
, the sum over
$\unicode[STIX]{x1D6FC}_{i}=a_{i}/q_{i}+\unicode[STIX]{x1D6FD}_{i}$
, the sum over
![]() $n$
on the left-hand side of (7.6) equals
$n$
on the left-hand side of (7.6) equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle e\biggl(\frac{a_{i}}{q_{i}}(t-c_{0})\biggr)\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}_{i}(t-n))\nonumber\\ \displaystyle & & \displaystyle \quad =e\biggl(\frac{a_{i}}{q_{i}}(t-c_{0})\biggr)\cdot \frac{1}{Q}\biggl(\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FD}_{i}(t-n))\biggr)+O(N^{1/2})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e\biggl(\frac{a_{i}}{q_{i}}(t-c_{0})\biggr)\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}_{i}(t-n))\nonumber\\ \displaystyle & & \displaystyle \quad =e\biggl(\frac{a_{i}}{q_{i}}(t-c_{0})\biggr)\cdot \frac{1}{Q}\biggl(\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FD}_{i}(t-n))\biggr)+O(N^{1/2})\nonumber\end{eqnarray}$$
by Lemma B.1. Hence, the left-hand side of (7.6) equals
To show that (7.4) holds for
![]() ${\mathcal{Q}}={\mathcal{C}}_{M}$
and for
${\mathcal{Q}}={\mathcal{C}}_{M}$
and for
![]() ${\mathcal{Q}}={\mathcal{C}}_{C}$
, we shall use the following elementary lemma related to a certain modification of Ramanujan sums.
${\mathcal{Q}}={\mathcal{C}}_{C}$
, we shall use the following elementary lemma related to a certain modification of Ramanujan sums.
Lemma 7.5. Let
![]() $q$
be a natural number,
$q$
be a natural number,
![]() $(a,q)=1$
and let
$(a,q)=1$
and let
![]() $P(n)$
be a polynomial with integer coefficients. Write
$P(n)$
be a polynomial with integer coefficients. Write
![]() $\unicode[STIX]{x1D70C}(n)=\#\{k~(\text{mod}~n):P(k)\equiv 0~(\text{mod}~n)\}$
. Then
$\unicode[STIX]{x1D70C}(n)=\#\{k~(\text{mod}~n):P(k)\equiv 0~(\text{mod}~n)\}$
. Then
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ (P(n),q)=1}}e\biggl(\frac{an}{q}\biggr)\biggr|\leqslant \unicode[STIX]{x1D70C}(q).\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ (P(n),q)=1}}e\biggl(\frac{an}{q}\biggr)\biggr|\leqslant \unicode[STIX]{x1D70C}(q).\end{eqnarray}$$
Proof. By Möbius inversion,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ (P(n),q)=1}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{\substack{ d\mid q}}\unicode[STIX]{x1D707}(d)\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ P(n)\equiv 0~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ (P(n),q)=1}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{\substack{ d\mid q}}\unicode[STIX]{x1D707}(d)\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ P(n)\equiv 0~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr).\end{eqnarray}$$
For a fixed
![]() $d\mid q$
, write
$d\mid q$
, write
![]() $x_{1},\ldots ,x_{\unicode[STIX]{x1D70C}(d)}$
for the roots of
$x_{1},\ldots ,x_{\unicode[STIX]{x1D70C}(d)}$
for the roots of
![]() $P(n)~(\text{mod}~d)$
. Then
$P(n)~(\text{mod}~d)$
. Then
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ P(n)\equiv 0~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D70C}(d)}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ n\equiv x_{i}~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D70C}(d)}e\biggl(\frac{ax_{i}}{q}\biggr)\mathop{\sum }_{\substack{ k~(\text{mod}~q/d)}}e\biggl(\frac{ak}{q/d}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ P(n)\equiv 0~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D70C}(d)}\mathop{\sum }_{\substack{ n~(\text{mod}~q) \\ n\equiv x_{i}~(\text{mod}~d)}}e\biggl(\frac{an}{q}\biggr)=\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D70C}(d)}e\biggl(\frac{ax_{i}}{q}\biggr)\mathop{\sum }_{\substack{ k~(\text{mod}~q/d)}}e\biggl(\frac{ak}{q/d}\biggr),\end{eqnarray}$$
where we have written
![]() $n=x_{i}+kd$
. The last sum vanishes unless
$n=x_{i}+kd$
. The last sum vanishes unless
![]() $d=q$
in which case (7.7) has absolute value at most
$d=q$
in which case (7.7) has absolute value at most
![]() $\unicode[STIX]{x1D70C}(q)$
, and the claim follows.◻
$\unicode[STIX]{x1D70C}(q)$
, and the claim follows.◻
Proof that Proposition 7.2 implies Proposition 7.1.
We may assume that
![]() $w$
is large enough in terms of
$w$
is large enough in terms of
![]() $m$
, since otherwise the error term dominates and the claim is trivial. By Lemma 7.4 it remains to show (7.4) for
$m$
, since otherwise the error term dominates and the claim is trivial. By Lemma 7.4 it remains to show (7.4) for
![]() ${\mathcal{Q}}={\mathcal{C}}_{M}$
and
${\mathcal{Q}}={\mathcal{C}}_{M}$
and
![]() $1\neq q\mid Q$
with
$1\neq q\mid Q$
with
![]() $\unicode[STIX]{x1D702}=w^{-1/2}$
. Writing
$\unicode[STIX]{x1D702}=w^{-1/2}$
. Writing
![]() $R(n)=\prod _{i=1}^{k}(Wn+Wh_{i}+b)$
, equation (7.4) reduces to
$R(n)=\prod _{i=1}^{k}(Wn+Wh_{i}+b)$
, equation (7.4) reduces to
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{0}~(\text{mod}~Q) \\ (R(c_{0}),Q)=1}}e\biggl(\frac{a}{q}c_{0}\biggr)=O\biggl(\frac{Q}{w^{1/2}}\mathop{\prod }_{\substack{ p\mid Q \\ p>w}}\biggl(1-\frac{k}{p}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{0}~(\text{mod}~Q) \\ (R(c_{0}),Q)=1}}e\biggl(\frac{a}{q}c_{0}\biggr)=O\biggl(\frac{Q}{w^{1/2}}\mathop{\prod }_{\substack{ p\mid Q \\ p>w}}\biggl(1-\frac{k}{p}\biggr)\biggr).\end{eqnarray}$$
We can uniquely decompose
![]() $Q=qq^{\prime }Q^{\prime }$
, where
$Q=qq^{\prime }Q^{\prime }$
, where
![]() $(Q^{\prime },q)=1$
and
$(Q^{\prime },q)=1$
and
![]() $p\mid q^{\prime }\;\Longrightarrow \;p\mid q$
. Then, when
$p\mid q^{\prime }\;\Longrightarrow \;p\mid q$
. Then, when
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
run through residue classes
$c_{2}$
run through residue classes
![]() $(\text{mod}~q^{\prime }Q^{\prime })$
and
$(\text{mod}~q^{\prime }Q^{\prime })$
and
![]() $(\text{mod}~q)$
, respectively,
$(\text{mod}~q)$
, respectively,
![]() $c_{1}q+c_{2}Q^{\prime }$
runs through residue classes
$c_{1}q+c_{2}Q^{\prime }$
runs through residue classes
![]() $(\text{mod}~Q)$
. Writing
$(\text{mod}~Q)$
. Writing
![]() $c_{0}$
in this form, the left-hand side of (7.8) becomes
$c_{0}$
in this form, the left-hand side of (7.8) becomes
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~q^{\prime }Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}\mathop{\sum }_{\substack{ c_{2}~(\text{mod}~q) \\ (R(c_{2}Q^{\prime }),q)=1}}e\biggl(\frac{aQ^{\prime }}{q}c_{2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~q^{\prime }Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}\mathop{\sum }_{\substack{ c_{2}~(\text{mod}~q) \\ (R(c_{2}Q^{\prime }),q)=1}}e\biggl(\frac{aQ^{\prime }}{q}c_{2}\biggr).\end{eqnarray}$$
Since
![]() $R(n)$
is always co-prime to
$R(n)$
is always co-prime to
![]() $W$
, Lemma 7.5 implies that the inner sum in (7.9) vanishes unless
$W$
, Lemma 7.5 implies that the inner sum in (7.9) vanishes unless
![]() $(q,W)=1$
. Furthermore, in this case it has absolute value at most
$(q,W)=1$
. Furthermore, in this case it has absolute value at most
since
![]() $p\mid q\;\Longrightarrow \;p>w$
and
$p\mid q\;\Longrightarrow \;p>w$
and
![]() $w$
is large enough. Hence, we obtain that the absolute value of (7.9) is at most
$w$
is large enough. Hence, we obtain that the absolute value of (7.9) is at most
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~q^{\prime }Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}q^{1/3}=q^{\prime }q^{1/3}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~q^{\prime }Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}q^{1/3}=q^{\prime }q^{1/3}\mathop{\sum }_{\substack{ c_{1}~(\text{mod}~Q^{\prime }) \\ (R(c_{1}q),Q^{\prime })=1}}1.\end{eqnarray}$$
By the definition of
![]() $R(n)$
,
$R(n)$
,
![]() $R(n)$
is always co-prime to
$R(n)$
is always co-prime to
![]() $W=\prod _{p\leqslant w}p$
, and for every
$W=\prod _{p\leqslant w}p$
, and for every
![]() $p>w$
,
$p>w$
,
![]() $R(n)\equiv 0~(\text{mod}~p)$
has
$R(n)\equiv 0~(\text{mod}~p)$
has
![]() $k$
incongruent solutions
$k$
incongruent solutions
![]() $(\text{mod}~p)$
(since
$(\text{mod}~p)$
(since
![]() $|h_{i}|<w/2$
for every
$|h_{i}|<w/2$
for every
![]() $i$
). Hence, the absolute value of (7.9) is at most
$i$
). Hence, the absolute value of (7.9) is at most
and (7.8) follows since
![]() $q>1$
and
$q>1$
and
![]() $(q,W)=1$
, so that
$(q,W)=1$
, so that
![]() $q>w$
.◻
$q>w$
.◻
8 Exponential sum estimates
In this section we state exponential sum estimates that we will use in the proofs of Propositions 7.2 and 7.3. Since the proofs closely follow previous works, we postpone them to Appendix B.
8.1 Major arc estimates
Lemma 8.1. Let
![]() $C_{1},C_{2}\geqslant 1$
and
$C_{1},C_{2}\geqslant 1$
and
![]() $\unicode[STIX]{x1D700}>0$
. There exists a constant
$\unicode[STIX]{x1D700}>0$
. There exists a constant
![]() $x_{0}=x_{0}(C_{1},C_{2},\unicode[STIX]{x1D700})$
such that the following holds. Let
$x_{0}=x_{0}(C_{1},C_{2},\unicode[STIX]{x1D700})$
such that the following holds. Let
![]() $Q\leqslant (\log x)^{C_{1}}$
and let
$Q\leqslant (\log x)^{C_{1}}$
and let
![]() $q\geqslant 1$
and
$q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $q\mid Q$
and
$q\mid Q$
and
![]() $(a,q)=1$
. Assume that
$(a,q)=1$
. Assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|\leqslant (\log x)^{C_{1}}/x$
. Then, for every
$|\unicode[STIX]{x1D6FC}-a/q|\leqslant (\log x)^{C_{1}}/x$
. Then, for every
![]() $x\geqslant x_{0}$
,
$x\geqslant x_{0}$
,
 $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}p)-\frac{Q}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~Q)}}\frac{e(\unicode[STIX]{x1D6FC}n)}{\log n}\biggr|\leqslant \frac{x}{Q(\log x)^{C_{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}p)-\frac{Q}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~Q)}}\frac{e(\unicode[STIX]{x1D6FC}n)}{\log n}\biggr|\leqslant \frac{x}{Q(\log x)^{C_{2}}}.\end{eqnarray}$$
Lemma 8.2. Let
![]() $C_{1},C_{2}\geqslant 1$
and
$C_{1},C_{2}\geqslant 1$
and
![]() $\unicode[STIX]{x1D700}>0$
. There exists a constant
$\unicode[STIX]{x1D700}>0$
. There exists a constant
![]() $x_{0}=x_{0}(C_{1},C_{2},\unicode[STIX]{x1D700})$
such that the following holds. Let
$x_{0}=x_{0}(C_{1},C_{2},\unicode[STIX]{x1D700})$
such that the following holds. Let
![]() $Q\leqslant (\log x)^{C_{1}}$
and let
$Q\leqslant (\log x)^{C_{1}}$
and let
![]() $q\geqslant 1$
and
$q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $q\mid Q$
and
$q\mid Q$
and
![]() $(a,q)=1$
. Assume that
$(a,q)=1$
. Assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|\leqslant (\log x)^{C_{1}}/x$
. Then, for every
$|\unicode[STIX]{x1D6FC}-a/q|\leqslant (\log x)^{C_{1}}/x$
. Then, for every
![]() $x\geqslant x_{0}$
, any bounded sequences
$x\geqslant x_{0}$
, any bounded sequences
![]() $\{a_{m}\}$
and
$\{a_{m}\}$
and
![]() $\{b_{n}\}$
, and any
$\{b_{n}\}$
, and any
![]() $x^{1/4}\leqslant M\leqslant x^{3/4}$
,
$x^{1/4}\leqslant M\leqslant x^{3/4}$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~rQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)-\frac{1}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ (mn,rQ)=1 \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q(\log x)^{C_{2}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~rQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)-\frac{1}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ (mn,rQ)=1 \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q(\log x)^{C_{2}}}.\nonumber\end{eqnarray}$$
8.2 Minor arc estimates
Our minor arc estimates are close variants of those proved in earlier papers. In particular, we follow [Reference MatomäkiMat09] which, in turn, is based on ideas developed in [Reference Balog and PerelliBP85, Reference MikawaMik00].
Lemma 8.3 (Type I estimate).
There exists
![]() $x_{0}$
such that the following holds. Let
$x_{0}$
such that the following holds. Let
![]() $Q,q\geqslant 1$
and
$Q,q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
. Let
$(a,q)=1$
. Let
![]() $|a_{m}|\leqslant 1$
. Write
$|a_{m}|\leqslant 1$
. Write
![]() $h=(q,Q)$
. Assume that
$h=(q,Q)$
. Assume that
![]() $\unicode[STIX]{x1D6FC}$
is such that
$\unicode[STIX]{x1D6FC}$
is such that
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/(Qq^{2})$
and that
$|\unicode[STIX]{x1D6FC}-a/q|<1/(Qq^{2})$
and that
![]() $Q\leqslant x^{1/2}$
. Then, for every
$Q\leqslant x^{1/2}$
. Then, for every
![]() $x\geqslant x_{0}$
and any
$x\geqslant x_{0}$
and any
![]() $M\geqslant 1$
,
$M\geqslant 1$
,
 $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/2}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~rQ) \\ M\leqslant m<2M}}a_{m}e(\unicode[STIX]{x1D6FC}mn)\biggr|\leqslant \frac{x}{Q}\biggl(\biggl(\frac{h}{q}\biggr)^{1/2}+\biggl(\frac{MQ}{x^{1/2}}\biggr)^{1/2}+\biggl(\frac{q}{x/Q}\biggr)^{1/2}\biggr)(\log x)^{4}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/2}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~rQ) \\ M\leqslant m<2M}}a_{m}e(\unicode[STIX]{x1D6FC}mn)\biggr|\leqslant \frac{x}{Q}\biggl(\biggl(\frac{h}{q}\biggr)^{1/2}+\biggl(\frac{MQ}{x^{1/2}}\biggr)^{1/2}+\biggl(\frac{q}{x/Q}\biggr)^{1/2}\biggr)(\log x)^{4}.\end{eqnarray}$$
Lemma 8.4 (Type II estimate).
Let
![]() $C\geqslant 1$
. There exists a constant
$C\geqslant 1$
. There exists a constant
![]() $x_{0}=x_{0}(C)$
such that the following holds. Let
$x_{0}=x_{0}(C)$
such that the following holds. Let
![]() $Q,q\geqslant 1$
and
$Q,q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
, write
$(a,q)=1$
, write
![]() $h=(q,Q^{2})$
, and assume that
$h=(q,Q^{2})$
, and assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Let
$|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Let
![]() $M\in [x^{1/2},x^{3/4}],Q\leqslant x^{3/2}/(2M^{2}(\log x)^{C})$
,
$M\in [x^{1/2},x^{3/4}],Q\leqslant x^{3/2}/(2M^{2}(\log x)^{C})$
,
![]() $D\leqslant x/(MQ(\log x)^{C})$
and
$D\leqslant x/(MQ(\log x)^{C})$
and
![]() $R\leqslant M/x^{1/2}$
, and let
$R\leqslant M/x^{1/2}$
, and let
![]() $c^{\prime }\in \mathbb{Z}$
.
$c^{\prime }\in \mathbb{Z}$
.
Then, for every
![]() $x\geqslant x_{0}$
and any
$x\geqslant x_{0}$
and any
![]() $|a_{k}|,|b_{k}|\leqslant \unicode[STIX]{x1D70F}(k)$
,
$|a_{k}|,|b_{k}|\leqslant \unicode[STIX]{x1D70F}(k)$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ D\leqslant d<2D}}\max _{(c,dQ)=1}\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{10}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ D\leqslant d<2D}}\max _{(c,dQ)=1}\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{10}.\nonumber\end{eqnarray}$$
Combining the type I and II estimates through Vaughan’s identity we will obtain the following minor arc estimates for exponential sums over primes.
Lemma 8.5. Let
![]() $C\geqslant 1$
. There exists a constant
$C\geqslant 1$
. There exists a constant
![]() $x_{0}=x_{0}(C)$
such that the following holds. Let
$x_{0}=x_{0}(C)$
such that the following holds. Let
![]() $Q,q\geqslant 1$
and
$Q,q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
, write
$(a,q)=1$
, write
![]() $h=(q,Q^{2})$
, and assume that
$h=(q,Q^{2})$
, and assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Then, for every
$|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Then, for every
![]() $x\geqslant x_{0}$
, and
$x\geqslant x_{0}$
, and
![]() $Q\leqslant x^{1/10}$
,
$Q\leqslant x^{1/10}$
,
 $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/8}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}p)\biggr|\leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{15}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/8}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}p)\biggr|\leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{15}.\end{eqnarray}$$
Lemma 8.6. Let
![]() $C\geqslant 1$
. There exists a constant
$C\geqslant 1$
. There exists a constant
![]() $x_{0}=x_{0}(C)$
such that the following holds. Let
$x_{0}=x_{0}(C)$
such that the following holds. Let
![]() $Q,q\geqslant 1$
and
$Q,q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
, write
$(a,q)=1$
, write
![]() $h=(q,Q^{2})$
, and assume that
$h=(q,Q^{2})$
, and assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Let
$|\unicode[STIX]{x1D6FC}-a/q|<1/(4q^{2}Q^{2}(\log x)^{2C})$
. Let
![]() $\unicode[STIX]{x1D706}_{r}$
be as in Hypothesis 6.3(i).
$\unicode[STIX]{x1D706}_{r}$
be as in Hypothesis 6.3(i).
Then, for every
![]() $x\geqslant x_{0}$
,
$x\geqslant x_{0}$
,
![]() $Q\leqslant x^{\unicode[STIX]{x1D700}/2}$
,
$Q\leqslant x^{\unicode[STIX]{x1D700}/2}$
,
![]() $(c,Q)=1$
and
$(c,Q)=1$
and
![]() $c^{\prime }\in \mathbb{Z}$
,
$c^{\prime }\in \mathbb{Z}$
,
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ r\leqslant x^{1/2-\unicode[STIX]{x1D700}} \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\!\!\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c^{\prime }~(\text{mod}~r) \\ p\equiv c~(\text{mod}~Q)}}\!\!e(\unicode[STIX]{x1D6FC}p)\biggr|\leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{15}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ r\leqslant x^{1/2-\unicode[STIX]{x1D700}} \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\!\!\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c^{\prime }~(\text{mod}~r) \\ p\equiv c~(\text{mod}~Q)}}\!\!e(\unicode[STIX]{x1D6FC}p)\biggr|\leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{15}.\end{eqnarray}$$
9 Proof of Proposition 7.2
In this section we prove Proposition 7.2 using Maynard’s theorem (Theorem 6.2). Let us start by choosing the sequence
![]() $\unicode[STIX]{x1D714}_{n}$
and other parameters to which we apply Theorem 6.2. Let
$\unicode[STIX]{x1D714}_{n}$
and other parameters to which we apply Theorem 6.2. Let
![]() $C=C(1/8,1/8)$
be as in Theorem 6.2,
$C=C(1/8,1/8)$
be as in Theorem 6.2,
![]() $k=\max \{C,e^{4Cm}\}$
, and let
$k=\max \{C,e^{4Cm}\}$
, and let
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(k,1/8,1/8)$
be as in Theorem 6.2. We take
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(k,1/8,1/8)$
be as in Theorem 6.2. We take
![]() $x=N/Q$
,
$x=N/Q$
,
We can assume that
![]() $\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}\geqslant x/w^{10}$
since otherwise Proposition 7.2 is trivial. With these choices, we shall show that, for any
$\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}\geqslant x/w^{10}$
since otherwise Proposition 7.2 is trivial. With these choices, we shall show that, for any
![]() $i=1,\ldots ,k$
,
$i=1,\ldots ,k$
,
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}\biggr|\,\ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}\biggr|\,\ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ c \\ (W(Qc+c_{0}+h_{i})+b,r)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r) \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ c \\ (W(Qc+c_{0}+h_{i})+b,r)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r) \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}},\end{eqnarray}$$
and that, for any
![]() $r\leqslant x^{1/8}$
and any
$r\leqslant x^{1/8}$
and any
![]() $c$
, we have
$c$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}\,\ll _{M,w}\,\frac{x}{rw^{10}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}\unicode[STIX]{x1D714}_{n}\,\ll _{M,w}\,\frac{x}{rw^{10}}.\end{eqnarray}$$
Now (9.1) implies Hypothesis 6.1(i) and (9.3) implies Hypothesis 6.1(iii). Furthermore, looking only at the
![]() $r=1$
summand, we see that (9.2) implies that
$r=1$
summand, we see that (9.2) implies that
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QW)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\,\ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QW)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\,\ll _{M,w}\,\frac{x}{(\log x)^{105k^{2}}},\end{eqnarray}$$
which implies (6.1) with
![]() $\unicode[STIX]{x1D6FF}=1/2$
(say). Furthermore, multiplying (9.4) by
$\unicode[STIX]{x1D6FF}=1/2$
(say). Furthermore, multiplying (9.4) by
![]() $\unicode[STIX]{x1D711}(QW)/\unicode[STIX]{x1D711}(QWr)$
and summing over
$\unicode[STIX]{x1D711}(QW)/\unicode[STIX]{x1D711}(QWr)$
and summing over
![]() $r\leqslant x^{1/8}$
, we see that
$r\leqslant x^{1/8}$
, we see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ c \\ (W(Qc+c_{0}+h_{i})+b,r)=1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl|\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{M,w}\,\frac{x}{(\log x)^{103k^{2}}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ c \\ (W(Qc+c_{0}+h_{i})+b,r)=1}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl|\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0}+h_{i})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0}+h_{i})+b)}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{M,w}\,\frac{x}{(\log x)^{103k^{2}}},\nonumber\end{eqnarray}$$
which together with (9.2) implies Hypothesis 6.1(ii) through the triangle inequality.
Hence, assuming we can prove (9.1)–(9.3), recalling our choice of
![]() $k$
, Maynard’s theorem with
$k$
, Maynard’s theorem with
![]() $\unicode[STIX]{x1D6FF}=1/2$
gives
$\unicode[STIX]{x1D6FF}=1/2$
gives
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ \#(\{L_{1}(n),\ldots ,L_{k}(n)\}\cap \mathbb{P})\geqslant m \\ p\mid L_{1}(n)\cdots L_{k}(n)\;\Longrightarrow \;p>x^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D714}_{n}\,\gg _{m}\,\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{k}}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ \#(\{L_{1}(n),\ldots ,L_{k}(n)\}\cap \mathbb{P})\geqslant m \\ p\mid L_{1}(n)\cdots L_{k}(n)\;\Longrightarrow \;p>x^{\unicode[STIX]{x1D70C}}}}\unicode[STIX]{x1D714}_{n}\,\gg _{m}\,\frac{\mathfrak{S}({\mathcal{L}})}{(\log x)^{k}}\mathop{\sum }_{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
Here
 $$\begin{eqnarray}\displaystyle \mathfrak{S}({\mathcal{L}}) & = & \displaystyle \mathop{\prod }_{p}\biggl(1-\frac{\#\{1\leqslant n\leqslant p:p\mid \mathop{\prod }_{i=1}^{k}(W(Qn+c_{0}+h_{i})+b)\}}{p}\biggr)\biggl(1-\frac{1}{p}\biggr)^{-k}\nonumber\\ \displaystyle & \gg & \displaystyle \frac{1}{\exp (O(k))}\cdot \biggl(\frac{QW}{\unicode[STIX]{x1D711}(QW)}\biggr)^{k}=\frac{1}{\exp (O(k))}\cdot \biggl(\frac{W}{\unicode[STIX]{x1D711}(W)}\biggr)^{k}\cdot \frac{Q}{|{\mathcal{C}}_{M}|}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{S}({\mathcal{L}}) & = & \displaystyle \mathop{\prod }_{p}\biggl(1-\frac{\#\{1\leqslant n\leqslant p:p\mid \mathop{\prod }_{i=1}^{k}(W(Qn+c_{0}+h_{i})+b)\}}{p}\biggr)\biggl(1-\frac{1}{p}\biggr)^{-k}\nonumber\\ \displaystyle & \gg & \displaystyle \frac{1}{\exp (O(k))}\cdot \biggl(\frac{QW}{\unicode[STIX]{x1D711}(QW)}\biggr)^{k}=\frac{1}{\exp (O(k))}\cdot \biggl(\frac{W}{\unicode[STIX]{x1D711}(W)}\biggr)^{k}\cdot \frac{Q}{|{\mathcal{C}}_{M}|}\nonumber\end{eqnarray}$$
by (7.3).
Recalling the definitions of
![]() $\unicode[STIX]{x1D714}_{n}$
and
$\unicode[STIX]{x1D714}_{n}$
and
![]() $L_{i}(n)$
, we obtain,
$L_{i}(n)$
, we obtain,
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ \#(\{W(n+h_{i})+b\}\cap \mathbb{P})\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}/2}}}\unicode[STIX]{x1D712}(t-n)\,\gg _{m}\,\biggl(\frac{W}{\unicode[STIX]{x1D711}(W)}\biggr)^{k}\cdot \frac{Q}{|{\mathcal{C}}_{M}|}\frac{1}{(\log x)^{k}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q) \\ \#(\{W(n+h_{i})+b\}\cap \mathbb{P})\geqslant m \\ p\mid \mathop{\prod }_{i=1}^{k}(W(n+h_{i})+b)\;\Longrightarrow \;p\geqslant N^{\unicode[STIX]{x1D70C}/2}}}\unicode[STIX]{x1D712}(t-n)\,\gg _{m}\,\biggl(\frac{W}{\unicode[STIX]{x1D711}(W)}\biggr)^{k}\cdot \frac{Q}{|{\mathcal{C}}_{M}|}\frac{1}{(\log x)^{k}}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}\unicode[STIX]{x1D712}(t-n)\end{eqnarray}$$
which was the claim.
Hence, it remains to show (9.1)–(9.3). By the Fourier expansion of
![]() $\unicode[STIX]{x1D712}(n)$
in Lemma 3.2, it is enough to show these with
$\unicode[STIX]{x1D712}(n)$
in Lemma 3.2, it is enough to show these with
where
![]() $0\leqslant a<q\leqslant N/(\log N)^{100B}$
,
$0\leqslant a<q\leqslant N/(\log N)^{100B}$
,
![]() $(a,q)=1$
,
$(a,q)=1$
,
![]() $|\unicode[STIX]{x1D6FD}|\leqslant W(\log N)^{100B}/(qN)$
, and, moreover, either
$|\unicode[STIX]{x1D6FD}|\leqslant W(\log N)^{100B}/(qN)$
, and, moreover, either
![]() $q\mid Q$
or
$q\mid Q$
or
![]() $q/(q,Q^{2})\geqslant (\log N)^{A}$
. In particular, (9.3) follows immediately from a trivial estimate.
$q/(q,Q^{2})\geqslant (\log N)^{A}$
. In particular, (9.3) follows immediately from a trivial estimate.
We also note that when considering (9.1)–(9.2) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (9.5), in case
$\unicode[STIX]{x1D714}_{n}$
as in (9.5), in case
![]() $|\unicode[STIX]{x1D6FD}|\leqslant 1/(Qx(\log x)^{111k^{2}})$
we can assume that
$|\unicode[STIX]{x1D6FD}|\leqslant 1/(Qx(\log x)^{111k^{2}})$
we can assume that
![]() $\unicode[STIX]{x1D6FD}=0$
since
$\unicode[STIX]{x1D6FD}=0$
since
![]() $|e(y+h)-e(y)|=O(h)$
. On the other hand, if
$|e(y+h)-e(y)|=O(h)$
. On the other hand, if
![]() $|\unicode[STIX]{x1D6FD}|>1/(Qx(\log x)^{111k^{2}})$
, then this combined with the upper bound for
$|\unicode[STIX]{x1D6FD}|>1/(Qx(\log x)^{111k^{2}})$
, then this combined with the upper bound for
![]() $|\unicode[STIX]{x1D6FD}|$
implies that
$|\unicode[STIX]{x1D6FD}|$
implies that
![]() $|\unicode[STIX]{x1D6FD}|<1/(4Q^{2}q^{2}(\log x)^{3200k^{2}})$
. Hence, we can in any case assume that
$|\unicode[STIX]{x1D6FD}|<1/(4Q^{2}q^{2}(\log x)^{3200k^{2}})$
. Hence, we can in any case assume that
9.1 Establishing (9.1)
For
![]() $q\mid Q$
, the left-hand side of (9.1) with
$q\mid Q$
, the left-hand side of (9.1) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (9.5) equals
$\unicode[STIX]{x1D714}_{n}$
as in (9.5) equals
 $$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}e(\unicode[STIX]{x1D6FD}Qn)-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}e(\unicode[STIX]{x1D6FD}Qn)\biggr|\ll \mathop{\sum }_{r\leqslant x^{1/8}}(|\unicode[STIX]{x1D6FD}|Qx+1)\ll x^{1/2}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}e(\unicode[STIX]{x1D6FD}Qn)-\frac{1}{r}\mathop{\sum }_{\substack{ x\leqslant n<2x}}e(\unicode[STIX]{x1D6FD}Qn)\biggr|\ll \mathop{\sum }_{r\leqslant x^{1/8}}(|\unicode[STIX]{x1D6FD}|Qx+1)\ll x^{1/2}\end{eqnarray}$$
by Lemma B.1.
For
![]() $q\nmid Q$
, the left-hand side of (9.1) with
$q\nmid Q$
, the left-hand side of (9.1) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (9.5) is by triangle inequality at most
$\unicode[STIX]{x1D714}_{n}$
as in (9.5) is by triangle inequality at most
 $$\begin{eqnarray}\log x\mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}e\biggl(\biggl(W\frac{a}{q}+\unicode[STIX]{x1D6FD}\biggr)Qn\biggr)\biggr|.\end{eqnarray}$$
$$\begin{eqnarray}\log x\mathop{\sum }_{r\leqslant x^{1/8}}\max _{c}\biggl|\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~r)}}e\biggl(\biggl(W\frac{a}{q}+\unicode[STIX]{x1D6FD}\biggr)Qn\biggr)\biggr|.\end{eqnarray}$$
Recall (9.6) and that
![]() $q/(q,WQ)\geqslant (\log N)^{A}/W$
, so that, by Lemma 8.3 with
$q/(q,WQ)\geqslant (\log N)^{A}/W$
, so that, by Lemma 8.3 with
![]() $M=Q=h=1$
and
$M=Q=h=1$
and
![]() $q/(q,QW)$
in place of
$q/(q,QW)$
in place of
![]() $q$
, we obtain that (9.7) is at most
$q$
, we obtain that (9.7) is at most
once
![]() $A$
is large enough in terms of
$A$
is large enough in terms of
![]() $k$
.
$k$
.
9.2 Establishing (9.2)
By changes of variables
![]() $p,n^{\prime }=W(Qn+c_{0}+h_{i})+b$
and
$p,n^{\prime }=W(Qn+c_{0}+h_{i})+b$
and
![]() $c^{\prime }=W(Qc+c_{0}+h_{i})+b$
, the left-hand side of (9.2) with
$c^{\prime }=W(Qc+c_{0}+h_{i})+b$
, the left-hand side of (9.2) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (9.5) is at most
$\unicode[STIX]{x1D714}_{n}$
as in (9.5) is at most
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ (c^{\prime },QWr)=1}}\biggl|\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv c^{\prime }~(\text{mod}~QWr)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv c^{\prime }~(\text{mod}~QW)}}(\log n^{\prime })^{-1}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)n\biggr)\biggr|+O(x^{1/2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ (c^{\prime },QWr)=1}}\biggl|\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv c^{\prime }~(\text{mod}~QWr)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv c^{\prime }~(\text{mod}~QW)}}(\log n^{\prime })^{-1}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)n\biggr)\biggr|+O(x^{1/2}).\nonumber\end{eqnarray}$$
In case
![]() $q\mid Q$
this is
$q\mid Q$
this is
![]() $O(x/(\log x)^{200k^{2}})$
by Lemma 8.1 recalling (9.6).
$O(x/(\log x)^{200k^{2}})$
by Lemma 8.1 recalling (9.6).
In case
![]() $q\nmid Q$
, note that
$q\nmid Q$
, note that
![]() $q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (9.6). We use the triangle inequality and estimate the two terms corresponding to the two sums inside the absolute values separately. The contribution corresponding to the sum over
$q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (9.6). We use the triangle inequality and estimate the two terms corresponding to the two sums inside the absolute values separately. The contribution corresponding to the sum over
![]() $n^{\prime }$
can be satisfactorily estimated by Lemma 8.3 with
$n^{\prime }$
can be satisfactorily estimated by Lemma 8.3 with
![]() $r=M=1$
after partial summation. Furthermore, Lemma 8.5 with
$r=M=1$
after partial summation. Furthermore, Lemma 8.5 with
![]() $C=1600k^{2}$
implies
$C=1600k^{2}$
implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ (c^{\prime },QWr)=1}}\biggl|\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv c^{\prime }~(\text{mod}~QWr)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant x\cdot \biggl(\frac{(\log x)^{800k^{2}}}{((\log N)^{A}/W^{2})^{1/8}}+(\log x)^{800k^{2}}Q^{1/2}W\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{200k^{2}}}\biggr)(\log x)^{15}\ll \frac{x}{(\log x)^{150k^{2}}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/8}}\max _{\substack{ (c^{\prime },QWr)=1}}\biggl|\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv c^{\prime }~(\text{mod}~QWr)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant x\cdot \biggl(\frac{(\log x)^{800k^{2}}}{((\log N)^{A}/W^{2})^{1/8}}+(\log x)^{800k^{2}}Q^{1/2}W\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{200k^{2}}}\biggr)(\log x)^{15}\ll \frac{x}{(\log x)^{150k^{2}}}\nonumber\end{eqnarray}$$
when
![]() $A$
is large enough in terms of
$A$
is large enough in terms of
![]() $k$
.
$k$
.
10 Proof of Proposition 7.3
In this section we prove Proposition 7.3 using Chen’s theorem (Theorem 6.4). Let
![]() ${\mathcal{L}}=\{L_{1},L_{2}\}$
be the collection of two linear forms
${\mathcal{L}}=\{L_{1},L_{2}\}$
be the collection of two linear forms
![]() $L_{1}(n)=W(Qn+c_{0})+b$
and
$L_{1}(n)=W(Qn+c_{0})+b$
and
![]() $L_{2}(n)=W(Qn+c_{0})+b+2$
, and note that
$L_{2}(n)=W(Qn+c_{0})+b+2$
, and note that
Let
![]() $x=N/Q$
. Define the sequence
$x=N/Q$
. Define the sequence
![]() $(\unicode[STIX]{x1D714}_{n})$
for
$(\unicode[STIX]{x1D714}_{n})$
for
![]() $x\leqslant n<2x$
by
$x\leqslant n<2x$
by
Since
![]() $\unicode[STIX]{x1D712}$
has Fourier complexity at most
$\unicode[STIX]{x1D712}$
has Fourier complexity at most
![]() $M$
, we have
$M$
, we have
![]() $\unicode[STIX]{x1D714}_{n}\leqslant M^{2}$
for every
$\unicode[STIX]{x1D714}_{n}\leqslant M^{2}$
for every
![]() $n$
. Thus, the conclusion follows from Chen’s theorem (Theorem 6.4), once we verify the hypotheses. We may assume that
$n$
. Thus, the conclusion follows from Chen’s theorem (Theorem 6.4), once we verify the hypotheses. We may assume that
![]() $\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}\geqslant x/(\log x)^{100}$
since otherwise the conclusion is trivial. Under this assumption, it suffices to show that, for
$\sum _{x\leqslant n<2x}\unicode[STIX]{x1D714}_{n}\geqslant x/(\log x)^{100}$
since otherwise the conclusion is trivial. Under this assumption, it suffices to show that, for
![]() $\unicode[STIX]{x1D706}_{r}$
as in Hypothesis 6.3(i),
$\unicode[STIX]{x1D706}_{r}$
as in Hypothesis 6.3(i),
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|W(Qn+c_{0})+b+2 \\ W(Qn+c_{0})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0})+b)}\biggr)\ll \frac{x}{(\log x)^{200}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|W(Qn+c_{0})+b+2 \\ W(Qn+c_{0})+b\in \mathbb{P}}}\unicode[STIX]{x1D714}_{n}-\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\frac{\unicode[STIX]{x1D714}_{n}}{\log (W(Qn+c_{0})+b)}\biggr)\ll \frac{x}{(\log x)^{200}}\end{eqnarray}$$
and that, for
![]() $B_{j}$
and
$B_{j}$
and
![]() $\unicode[STIX]{x1D706}_{r}$
as in Hypothesis 6.3(ii),
$\unicode[STIX]{x1D706}_{r}$
as in Hypothesis 6.3(ii),
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|W(Qn+c_{0})+b \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}-\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}\biggr)\ll \frac{x}{(\log x)^{200}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ x\leqslant n<2x \\ r|W(Qn+c_{0})+b \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}-\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}\biggr)\ll \frac{x}{(\log x)^{200}}\end{eqnarray}$$
and that, for
![]() $\unicode[STIX]{x1D6FF}(B_{j})$
as in (6.3),
$\unicode[STIX]{x1D6FF}(B_{j})$
as in (6.3),
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}=\frac{\unicode[STIX]{x1D6FF}(B_{j})+o(1)}{\log x}\cdot \frac{QW}{\unicode[STIX]{x1D711}(QW)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ W(Qn+c_{0})+b+2\in B_{j}}}\unicode[STIX]{x1D714}_{n}=\frac{\unicode[STIX]{x1D6FF}(B_{j})+o(1)}{\log x}\cdot \frac{QW}{\unicode[STIX]{x1D711}(QW)}\mathop{\sum }_{\substack{ x\leqslant n<2x}}\unicode[STIX]{x1D714}_{n}.\end{eqnarray}$$
By the Fourier expansion of
![]() $\unicode[STIX]{x1D712}(n)$
in Lemma 3.2, it is enough to show these with
$\unicode[STIX]{x1D712}(n)$
in Lemma 3.2, it is enough to show these with
where
![]() $0\leqslant a<q\leqslant N/(\log N)^{100B}$
,
$0\leqslant a<q\leqslant N/(\log N)^{100B}$
,
![]() $(a,q)=1$
,
$(a,q)=1$
,
![]() $|\unicode[STIX]{x1D6FD}|\leqslant W(\log N)^{100B}/(qN)$
and, moreover, either
$|\unicode[STIX]{x1D6FD}|\leqslant W(\log N)^{100B}/(qN)$
and, moreover, either
![]() $q\mid Q$
or
$q\mid Q$
or
![]() $q/(q,Q^{2})\geqslant (\log N)^{A}$
. Furthermore, arguing as before (cf. (9.6)), we can assume
$q/(q,Q^{2})\geqslant (\log N)^{A}$
. Furthermore, arguing as before (cf. (9.6)), we can assume
10.1 Establishing (10.1)
After changes of variables
![]() $p,n^{\prime }=W(Qn+c_{0})+b$
, we can rewrite the left-hand side of (10.1) with
$p,n^{\prime }=W(Qn+c_{0})+b$
, we can rewrite the left-hand side of (10.1) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (10.4) essentially as
$\unicode[STIX]{x1D714}_{n}$
as in (10.4) essentially as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv -2~(\text{mod}~r) \\ p\equiv Wc_{0}+b~(\text{mod}~QW)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv Wc_{0}+b~(\text{mod}~QW)}}(\log n^{\prime })^{-1}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)n^{\prime }\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ QWx\leqslant p<2QWx \\ p\equiv -2~(\text{mod}~r) \\ p\equiv Wc_{0}+b~(\text{mod}~QW)}}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)p\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{QW}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv Wc_{0}+b~(\text{mod}~QW)}}(\log n^{\prime })^{-1}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)n^{\prime }\biggr)\biggr).\nonumber\end{eqnarray}$$
In case
![]() $q\mid Q$
, this is
$q\mid Q$
, this is
![]() $O(x/(\log x)^{200})$
by Lemma 8.1 recalling (10.5). In case
$O(x/(\log x)^{200})$
by Lemma 8.1 recalling (10.5). In case
![]() $q\nmid Q$
, note that
$q\nmid Q$
, note that
![]() $q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (10.5). We estimate the two terms corresponding to the sums over
$q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (10.5). We estimate the two terms corresponding to the sums over
![]() $p$
and
$p$
and
![]() $n^{\prime }$
separately. The contribution from the term corresponding to the sum over
$n^{\prime }$
separately. The contribution from the term corresponding to the sum over
![]() $n^{\prime }$
can be satisfactorily estimated by Lemma 8.3 with
$n^{\prime }$
can be satisfactorily estimated by Lemma 8.3 with
![]() $r=M=1$
after partial summation. For the term corresponding the sum over
$r=M=1$
after partial summation. For the term corresponding the sum over
![]() $p$
, Lemma 8.6 with
$p$
, Lemma 8.6 with
![]() $C=20000$
implies the desired bound once
$C=20000$
implies the desired bound once
![]() $A$
and
$A$
and
![]() $B$
are large enough.
$B$
are large enough.
10.2 Establishing (10.2)
By the definition of
![]() $B_{1}$
in (6.2) we can write
$B_{1}$
in (6.2) we can write
 $$\begin{eqnarray}\mathbf{1}_{W(Qn+c_{0})+b+2\in B_{1}}=\mathop{\sum }_{\substack{ mp=W(Qn+c_{0})+b+2 \\ p\geqslant x^{1/10}}}a_{m},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}_{W(Qn+c_{0})+b+2\in B_{1}}=\mathop{\sum }_{\substack{ mp=W(Qn+c_{0})+b+2 \\ p\geqslant x^{1/10}}}a_{m},\end{eqnarray}$$
where
![]() $a_{m}=1$
if
$a_{m}=1$
if
![]() $m=p_{1}p_{2}$
for some
$m=p_{1}p_{2}$
for some
![]() $x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}}$
and
$x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}}$
and
![]() $x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}<(L_{2}(2x)/p_{1})^{1/2}$
, and
$x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}<(L_{2}(2x)/p_{1})^{1/2}$
, and
![]() $a_{m}=0$
otherwise. Note that
$a_{m}=0$
otherwise. Note that
![]() $a_{m}$
is supported on
$a_{m}$
is supported on
![]() $m\in [x^{1/3},x^{2/3}]$
. After a dyadic division and changes of variables
$m\in [x^{1/3},x^{2/3}]$
. After a dyadic division and changes of variables
![]() $mp=W(Qn+c_{0})+b+2$
, to prove (10.2) with
$mp=W(Qn+c_{0})+b+2$
, to prove (10.2) with
![]() $\unicode[STIX]{x1D714}_{n}$
as in (10.4) it suffices to show that for
$\unicode[STIX]{x1D714}_{n}$
as in (10.4) it suffices to show that for
![]() $M\in [x^{1/3},x^{2/3}]$
,
$M\in [x^{1/3},x^{2/3}]$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ QWx\leqslant mp<2QWx \\ mp\equiv 2~(\text{mod}~r) \\ mp\equiv Wc_{0}+b+2~(\text{mod}~QW) \\ M\leqslant m<2M}}a_{m}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)mp\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant mp<2QWx \\ mp\equiv Wc_{0}+b+2~(\text{mod}~QW) \\ M\leqslant m<2M}}a_{m}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)mp\biggr)\biggr)\ll \frac{x}{(\log x)^{210}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ r \\ (r,QW)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\biggl(\mathop{\sum }_{\substack{ QWx\leqslant mp<2QWx \\ mp\equiv 2~(\text{mod}~r) \\ mp\equiv Wc_{0}+b+2~(\text{mod}~QW) \\ M\leqslant m<2M}}a_{m}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)mp\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D711}(QW)}{\unicode[STIX]{x1D711}(QWr)}\mathop{\sum }_{\substack{ QWx\leqslant mp<2QWx \\ mp\equiv Wc_{0}+b+2~(\text{mod}~QW) \\ M\leqslant m<2M}}a_{m}e\biggl(\biggl(\frac{a}{q}+\frac{\unicode[STIX]{x1D6FD}}{W}\biggr)mp\biggr)\biggr)\ll \frac{x}{(\log x)^{210}}.\nonumber\end{eqnarray}$$
In case
![]() $q\mid Q$
, this follows from Lemma 8.2 applied twice (once with the
$q\mid Q$
, this follows from Lemma 8.2 applied twice (once with the
![]() $r=1$
term only), recalling (10.5) and noting that we may add the restriction
$r=1$
term only), recalling (10.5) and noting that we may add the restriction
![]() $(mp,QWr)=1$
in the second sum above at a negligible cost, since for each
$(mp,QWr)=1$
in the second sum above at a negligible cost, since for each
![]() $r$
there are
$r$
there are
![]() $O(x^{0.9})$
values of
$O(x^{0.9})$
values of
![]() $mp$
with
$mp$
with
![]() $(mp,QWr)>1$
. In case
$(mp,QWr)>1$
. In case
![]() $q\nmid Q$
, note that
$q\nmid Q$
, note that
![]() $q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (10.5). We estimate the two sums separately. The easier second sum can be estimated by Lemma 8.3 with
$q/(q,(QW)^{2})>(\log N)^{A}/W^{2}$
and recall (10.5). We estimate the two sums separately. The easier second sum can be estimated by Lemma 8.3 with
![]() $r=1$
. The first sum can be estimated by Lemma 8.4 (after factorizing
$r=1$
. The first sum can be estimated by Lemma 8.4 (after factorizing
![]() $\unicode[STIX]{x1D706}_{r}$
) with
$\unicode[STIX]{x1D706}_{r}$
) with
![]() $C=20000$
once
$C=20000$
once
![]() $A$
is large enough.
$A$
is large enough.
Hypothesis (10.2) for
![]() $B_{2}$
follows similarly noting that
$B_{2}$
follows similarly noting that
 $$\begin{eqnarray}\mathbf{1}_{W(Qn+c_{0})+b+2\in B_{2}}=\mathop{\sum }_{\substack{ mp=W(Qn+c_{0})+b+2 \\ p\geqslant x^{1/10}}}a_{m},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}_{W(Qn+c_{0})+b+2\in B_{2}}=\mathop{\sum }_{\substack{ mp=W(Qn+c_{0})+b+2 \\ p\geqslant x^{1/10}}}a_{m},\end{eqnarray}$$
where
![]() $a_{m}=1$
if
$a_{m}=1$
if
![]() $m=p_{1}p_{2}$
for some
$m=p_{1}p_{2}$
for some
![]() $x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2}$
and
$x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2}$
and
![]() $a_{m}=0$
otherwise; thus,
$a_{m}=0$
otherwise; thus,
![]() $a_{m}$
is supported on
$a_{m}$
is supported on
![]() $m\in [x^{2/3-2\unicode[STIX]{x1D700}},x^{2/3+o(1)}]$
, so that our type II results (Lemmas 8.2 and 8.4) are still applicable.
$m\in [x^{2/3-2\unicode[STIX]{x1D700}},x^{2/3+o(1)}]$
, so that our type II results (Lemmas 8.2 and 8.4) are still applicable.
10.3 Establishing (10.3)
In case
![]() $q\mid Q$
, by partial summation it is enough to prove (10.3) in case
$q\mid Q$
, by partial summation it is enough to prove (10.3) in case
![]() $\unicode[STIX]{x1D6FD}=0$
(strictly speaking one should consider the interval
$\unicode[STIX]{x1D6FD}=0$
(strictly speaking one should consider the interval
![]() $n\in [x,x^{\prime }]$
instead of
$n\in [x,x^{\prime }]$
instead of
![]() $n\in [x,2x)$
but this makes no difference). Since
$n\in [x,2x)$
but this makes no difference). Since
![]() $q\mid Q$
, we have
$q\mid Q$
, we have
![]() $\unicode[STIX]{x1D714}_{n}\equiv 1$
. By a change of variables
$\unicode[STIX]{x1D714}_{n}\equiv 1$
. By a change of variables
![]() $n^{\prime }=W(Qn+c_{0})+b+2$
, it suffices to show that
$n^{\prime }=W(Qn+c_{0})+b+2$
, it suffices to show that
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv Wc_{0}+b+2~(\text{mod}~QW)}}\mathbf{1}_{n^{\prime }\in B_{j}}=\frac{\unicode[STIX]{x1D6FF}(B_{j})+o(1)}{\unicode[STIX]{x1D711}(QW)}\cdot \frac{QWx}{\log x},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ QWx\leqslant n^{\prime }<2QWx \\ n^{\prime }\equiv Wc_{0}+b+2~(\text{mod}~QW)}}\mathbf{1}_{n^{\prime }\in B_{j}}=\frac{\unicode[STIX]{x1D6FF}(B_{j})+o(1)}{\unicode[STIX]{x1D711}(QW)}\cdot \frac{QWx}{\log x},\end{eqnarray}$$
which follows easily from the prime number theorem in arithmetic progressions. In case
![]() $q\nmid Q$
, both sides of (10.3) are easily shown to be small using the argument from the previous subsection: the left-hand side can be estimated by Lemma 8.3 and the right-hand side can be estimated by Lemma B.2.
$q\nmid Q$
, both sides of (10.3) are easily shown to be small using the argument from the previous subsection: the left-hand side can be estimated by Lemma 8.3 and the right-hand side can be estimated by Lemma B.2.
Acknowledgements
This work started when both authors were visiting CRM in Montreal during the analytic part of the thematic year in number theory in Fall 2014, whose hospitality is greatly appreciated. The authors are grateful to Joni Teräväinen for pointing out a few mistakes in an earlier draft, and to the anonymous referee for valuable suggestions.
Appendix A Proof of the generalized Chen’s theorem
In this section we prove Theorem 6.4.
A.1 The linear sieve
For a (finitely supported) sequence
![]() ${\mathcal{A}}=(a_{m})$
of non-negative numbers we write
${\mathcal{A}}=(a_{m})$
of non-negative numbers we write
![]() $|{\mathcal{A}}|=\sum _{m}a_{m}$
and
$|{\mathcal{A}}|=\sum _{m}a_{m}$
and
![]() ${\mathcal{A}}_{d}=(a_{dm})_{m}$
. We also define a sieving function
${\mathcal{A}}_{d}=(a_{dm})_{m}$
. We also define a sieving function
where
To bound
![]() $S({\mathcal{A}},z)$
we need some information about
$S({\mathcal{A}},z)$
we need some information about
![]() ${\mathcal{A}}$
. We will assume that, for all square-free integers
${\mathcal{A}}$
. We will assume that, for all square-free integers
![]() $d$
, we have
$d$
, we have
where
![]() $g(d)$
is multiplicative and
$g(d)$
is multiplicative and
![]() $X$
is independent of
$X$
is independent of
![]() $d$
. Further, let
$d$
. Further, let
We will use the linear sieve with a well-factorable error term due to Iwaniec [Reference IwaniecIwa80]. For the following statement, see [Reference Friedlander and IwaniecFI10, Theorems 12.19 and 12.20].
Lemma A.1. Let
![]() $2\leqslant z\leqslant D^{1/2}$
and
$2\leqslant z\leqslant D^{1/2}$
and
![]() $s=\log D/\!\log z$
. Let
$s=\log D/\!\log z$
. Let
![]() $\unicode[STIX]{x1D700}>0$
be small enough and let
$\unicode[STIX]{x1D700}>0$
be small enough and let
![]() $L(\unicode[STIX]{x1D700})=e^{1/\unicode[STIX]{x1D700}^{3}}$
. Assume that, for some absolute constant
$L(\unicode[STIX]{x1D700})=e^{1/\unicode[STIX]{x1D700}^{3}}$
. Assume that, for some absolute constant
![]() $K>1$
,
$K>1$
,
for all
![]() $z_{2}\geqslant z_{1}\geqslant 2$
. Then
$z_{2}\geqslant z_{1}\geqslant 2$
. Then
and
Here, for each
![]() $l$
,
$l$
,
![]() $\unicode[STIX]{x1D706}_{l}^{\pm }$
are well-factorable functions of level
$\unicode[STIX]{x1D706}_{l}^{\pm }$
are well-factorable functions of level
![]() $D$
, and
$D$
, and
![]() $F,f:[1,\infty )\rightarrow \mathbb{R}_{{\geqslant}0}$
are the continuous solutions to the system
$F,f:[1,\infty )\rightarrow \mathbb{R}_{{\geqslant}0}$
are the continuous solutions to the system
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}sF(s)=2e^{\unicode[STIX]{x1D6FE}}\quad & \text{if}~1\leqslant s\leqslant 3,\\ sf(s)=0\quad & \text{if}~1\leqslant s\leqslant 2,\\ (sF(s))^{\prime }=f(s-1)\quad & \text{if}~s>3,\\ (sf(s))^{\prime }=F(s-1)\quad & \text{if}~s>2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}sF(s)=2e^{\unicode[STIX]{x1D6FE}}\quad & \text{if}~1\leqslant s\leqslant 3,\\ sf(s)=0\quad & \text{if}~1\leqslant s\leqslant 2,\\ (sF(s))^{\prime }=f(s-1)\quad & \text{if}~s>3,\\ (sf(s))^{\prime }=F(s-1)\quad & \text{if}~s>2.\end{array}\right.\end{eqnarray}$$
A.2 Introducing Chen’s weights
Write
![]() ${\mathcal{A}}=(a_{m})$
for the sequence defined by
${\mathcal{A}}=(a_{m})$
for the sequence defined by
Note that
![]() ${\mathcal{A}}$
is supported on
${\mathcal{A}}$
is supported on
![]() $L_{2}(x)\leqslant m<L_{2}(2x)$
.
$L_{2}(x)\leqslant m<L_{2}(2x)$
.
Using a slight modification of the weighted sieve method of Chen, we consider
 $$\begin{eqnarray}\displaystyle S & = & \displaystyle \mathop{\sum }_{\substack{ m \\ (m,P(x^{1/10}))=1}}a_{m}\biggl(1-\frac{1}{2}\mathop{\sum }_{\substack{ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ p_{1}\mid m}}1\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{\substack{ m=p_{1}p_{2}p_{3} \\ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}1-\mathop{\sum }_{\substack{ m=p_{1}p_{2}p_{3} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}1\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & = & \displaystyle \mathop{\sum }_{\substack{ m \\ (m,P(x^{1/10}))=1}}a_{m}\biggl(1-\frac{1}{2}\mathop{\sum }_{\substack{ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ p_{1}\mid m}}1\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{\substack{ m=p_{1}p_{2}p_{3} \\ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}1-\mathop{\sum }_{\substack{ m=p_{1}p_{2}p_{3} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}1\biggr).\nonumber\end{eqnarray}$$
Observe that the quantity in the parenthesis above is positive only if
![]() $m=P_{2}$
or
$m=P_{2}$
or
![]() $p^{2}\mid m$
for some
$p^{2}\mid m$
for some
![]() $x^{1/10}\leqslant p<x^{1/3-\unicode[STIX]{x1D700}}$
. Since the number of those
$x^{1/10}\leqslant p<x^{1/3-\unicode[STIX]{x1D700}}$
. Since the number of those
![]() $m$
of the latter type is
$m$
of the latter type is
![]() $O(x^{0.9})$
, it suffices to show that
$O(x^{0.9})$
, it suffices to show that
Using the sieve notation, we can write
 $$\begin{eqnarray}\displaystyle S & = & \displaystyle S({\mathcal{A}},x^{1/10})-\frac{1}{2}\mathop{\sum }_{x^{1/10}\leqslant p<x^{1/3-\unicode[STIX]{x1D700}}}S({\mathcal{A}}_{p},x^{1/10})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{\substack{ p_{1},p_{2},p_{3} \\ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}a_{p_{1}p_{2}p_{3}}-\mathop{\sum }_{\substack{ p_{1},p_{2},p_{3} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}a_{p_{1}p_{2}p_{3}}\nonumber\\ \displaystyle & = & \displaystyle S_{1}-\frac{1}{2}S_{2}-\frac{1}{2}T_{1}-T_{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & = & \displaystyle S({\mathcal{A}},x^{1/10})-\frac{1}{2}\mathop{\sum }_{x^{1/10}\leqslant p<x^{1/3-\unicode[STIX]{x1D700}}}S({\mathcal{A}}_{p},x^{1/10})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\mathop{\sum }_{\substack{ p_{1},p_{2},p_{3} \\ x^{1/10}\leqslant p_{1}<x^{1/3-\unicode[STIX]{x1D700}} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}a_{p_{1}p_{2}p_{3}}-\mathop{\sum }_{\substack{ p_{1},p_{2},p_{3} \\ x^{1/3-\unicode[STIX]{x1D700}}\leqslant p_{1}\leqslant p_{2}\leqslant (L_{2}(2x)/p_{1})^{1/2} \\ p_{3}\geqslant x^{1/10}}}a_{p_{1}p_{2}p_{3}}\nonumber\\ \displaystyle & = & \displaystyle S_{1}-\frac{1}{2}S_{2}-\frac{1}{2}T_{1}-T_{2},\nonumber\end{eqnarray}$$
say.
A.3 Handling
 $S_{1}$
and
$S_{1}$
and
 $S_{2}$
$S_{2}$
Write
and let
![]() $g_{1}$
be the multiplicative function defined by
$g_{1}$
be the multiplicative function defined by
 $$\begin{eqnarray}g_{1}(d)=\left\{\begin{array}{@{}ll@{}}0\quad & (d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1,\\ {\displaystyle \frac{d\unicode[STIX]{x1D711}(u_{1})}{\unicode[STIX]{x1D711}(u_{1}d)}}\quad & (d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g_{1}(d)=\left\{\begin{array}{@{}ll@{}}0\quad & (d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1,\\ {\displaystyle \frac{d\unicode[STIX]{x1D711}(u_{1})}{\unicode[STIX]{x1D711}(u_{1}d)}}\quad & (d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))=1.\end{array}\right.\end{eqnarray}$$
Since
![]() $|{\mathcal{A}}_{d}|=0$
whenever
$|{\mathcal{A}}_{d}|=0$
whenever
![]() $(d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1$
, we have, by Hypothesis 6.3,
$(d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1$
, we have, by Hypothesis 6.3,
for any well-factorable function
![]() $\unicode[STIX]{x1D706}$
of level
$\unicode[STIX]{x1D706}$
of level
![]() $D=x^{1/2-\unicode[STIX]{x1D700}}$
.
$D=x^{1/2-\unicode[STIX]{x1D700}}$
.
Hence, by Lemma A.1 with
![]() $z=x^{1/10}$
,
$z=x^{1/10}$
,
where
 $$\begin{eqnarray}V_{1}(z)=\mathop{\prod }_{p\mid P(z)}\biggl(1-\frac{g_{1}(p)}{p}\biggr)=\mathop{\prod }_{\substack{ p<z \\ p|u_{1},p\nmid u_{2}}}\biggl(1-\frac{1}{p}\biggr)\mathop{\prod }_{\substack{ p<z \\ p\nmid u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}V_{1}(z)=\mathop{\prod }_{p\mid P(z)}\biggl(1-\frac{g_{1}(p)}{p}\biggr)=\mathop{\prod }_{\substack{ p<z \\ p|u_{1},p\nmid u_{2}}}\biggl(1-\frac{1}{p}\biggr)\mathop{\prod }_{\substack{ p<z \\ p\nmid u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
Similarly, for any
![]() $2P\geqslant P^{\prime }\geqslant P\in [x^{1/10},x^{1/3-\unicode[STIX]{x1D700}}]$
and any well-factorable bounded function
$2P\geqslant P^{\prime }\geqslant P\in [x^{1/10},x^{1/3-\unicode[STIX]{x1D700}}]$
and any well-factorable bounded function
![]() $\unicode[STIX]{x1D706}$
of level
$\unicode[STIX]{x1D706}$
of level
![]() $x^{1/2-\unicode[STIX]{x1D700}}/P$
we have, by Hypothesis 6.3,
$x^{1/2-\unicode[STIX]{x1D700}}/P$
we have, by Hypothesis 6.3,
since
![]() $|{\mathcal{A}}_{pd}|=0$
whenever
$|{\mathcal{A}}_{pd}|=0$
whenever
![]() $(d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1$
and also
$(d,u_{2}(u_{2}v_{1}-u_{1}v_{2}))>1$
and also
![]() $(p,d)=1$
whenever
$(p,d)=1$
whenever
![]() $d|P(x^{1/10})$
.
$d|P(x^{1/10})$
.
By Lemma A.1 with
![]() $s=\log (x^{1/2-\unicode[STIX]{x1D700}}/P)/\!\log x^{1/10}=5-10\unicode[STIX]{x1D700}-10\log P/\!\log x$
, we obtain
$s=\log (x^{1/2-\unicode[STIX]{x1D700}}/P)/\!\log x^{1/10}=5-10\unicode[STIX]{x1D700}-10\log P/\!\log x$
, we obtain
Using the fact that
since
![]() $\log L_{1}(n)=(1+o(1))\log L_{1}(x)=(1+o(1))\log x$
, we conclude that
$\log L_{1}(n)=(1+o(1))\log L_{1}(x)=(1+o(1))\log x$
, we conclude that
where
 $$\begin{eqnarray}V(z)=V_{1}(z)\frac{u_{1}}{\unicode[STIX]{x1D711}(u_{1})}=\mathop{\prod }_{p|(u_{1},u_{2})}\frac{p}{p-1}\mathop{\prod }_{\substack{ p\leqslant z \\ p\,\nmid \,u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}V(z)=V_{1}(z)\frac{u_{1}}{\unicode[STIX]{x1D711}(u_{1})}=\mathop{\prod }_{p|(u_{1},u_{2})}\frac{p}{p-1}\mathop{\prod }_{\substack{ p\leqslant z \\ p\,\nmid \,u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
A.4 Handling
 $T_{1}$
and
$T_{1}$
and
 $T_{2}$
$T_{2}$
Let
![]() $j\in \{1,2\}$
. For
$j\in \{1,2\}$
. For
![]() $B_{j}$
defined as in (6.2), we write
$B_{j}$
defined as in (6.2), we write
and let
![]() $g_{2}$
be the multiplicative function defined by
$g_{2}$
be the multiplicative function defined by
 $$\begin{eqnarray}g_{2}(d)=\left\{\begin{array}{@{}ll@{}}0\quad & (d,u_{1}(u_{2}v_{1}-u_{1}v_{2}))>1,\\ {\displaystyle \frac{d\unicode[STIX]{x1D711}(u_{2})}{\unicode[STIX]{x1D711}(u_{2}d)}}\quad & (d,u_{1}(u_{2}v_{1}-u_{1}v_{2}))=1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g_{2}(d)=\left\{\begin{array}{@{}ll@{}}0\quad & (d,u_{1}(u_{2}v_{1}-u_{1}v_{2}))>1,\\ {\displaystyle \frac{d\unicode[STIX]{x1D711}(u_{2})}{\unicode[STIX]{x1D711}(u_{2}d)}}\quad & (d,u_{1}(u_{2}v_{1}-u_{1}v_{2}))=1.\end{array}\right.\end{eqnarray}$$
We consider the sequence
![]() ${\mathcal{B}}^{(j)}=(b_{m}^{(j)})$
defined by
${\mathcal{B}}^{(j)}=(b_{m}^{(j)})$
defined by
Note that
![]() ${\mathcal{B}}^{(j)}$
is supported on
${\mathcal{B}}^{(j)}$
is supported on
![]() $L_{1}(x)\leqslant m<L_{1}(2x)$
, and that, for
$L_{1}(x)\leqslant m<L_{1}(2x)$
, and that, for
![]() $j=1,2$
,
$j=1,2$
,
Note also that, for
![]() $j=1,2$
,
$j=1,2$
,
We may apply Hypothesis 6.3(ii) to obtain that
for any well-factorable function
![]() $\unicode[STIX]{x1D706}_{d}$
of level
$\unicode[STIX]{x1D706}_{d}$
of level
![]() $D=x^{1/2-\unicode[STIX]{x1D700}}$
. Hence, by Lemma A.1 with
$D=x^{1/2-\unicode[STIX]{x1D700}}$
. Hence, by Lemma A.1 with
![]() $z=x^{1/6}$
, we have
$z=x^{1/6}$
, we have
where
 $$\begin{eqnarray}V_{2}(z)=\mathop{\prod }_{\substack{ p\leqslant z \\ p|u_{2},p\,\nmid \,u_{1}}}\biggl(1-\frac{1}{p}\biggr)\mathop{\prod }_{\substack{ p\leqslant z \\ p\,\nmid \,u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}V_{2}(z)=\mathop{\prod }_{\substack{ p\leqslant z \\ p|u_{2},p\,\nmid \,u_{1}}}\biggl(1-\frac{1}{p}\biggr)\mathop{\prod }_{\substack{ p\leqslant z \\ p\,\nmid \,u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\biggl(1-\frac{1}{p-1}\biggr).\end{eqnarray}$$
By Hypothesis 6.3(iii) and using (6.3), we have
Hence,
since
![]() $V(z)=V_{2}(z)(u_{2}/\unicode[STIX]{x1D711}(u_{2}))$
.
$V(z)=V_{2}(z)(u_{2}/\unicode[STIX]{x1D711}(u_{2}))$
.
A.5 Final numerical work
We may write
 $$\begin{eqnarray}V(z)=\biggl(\mathop{\prod }_{p|(u_{1},u_{2})}\frac{p}{p-1}\mathop{\prod }_{\substack{ p>2 \\ p|u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\frac{p-1}{p-2}\biggr)\mathop{\prod }_{2<p\leqslant z}\biggl(1-\frac{1}{p-1}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}V(z)=\biggl(\mathop{\prod }_{p|(u_{1},u_{2})}\frac{p}{p-1}\mathop{\prod }_{\substack{ p>2 \\ p|u_{1}u_{2}(u_{1}v_{2}-u_{2}v_{1})}}\frac{p-1}{p-2}\biggr)\mathop{\prod }_{2<p\leqslant z}\biggl(1-\frac{1}{p-1}\biggr),\end{eqnarray}$$
and note that the two products in the parenthesis contribute
![]() $\gg \mathfrak{S}({\mathcal{L}})$
by the definition of the singular series. Thus,
$\gg \mathfrak{S}({\mathcal{L}})$
by the definition of the singular series. Thus,
Since all the bounds we have obtained are continuous in
![]() $\unicode[STIX]{x1D700}$
and the double integral in
$\unicode[STIX]{x1D700}$
and the double integral in
![]() $\unicode[STIX]{x1D6FF}(B_{2})$
from (6.3) tends to zero when
$\unicode[STIX]{x1D6FF}(B_{2})$
from (6.3) tends to zero when
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
, it suffices to verify that
$\unicode[STIX]{x1D700}\rightarrow 0$
, it suffices to verify that
just like in Chen’s work. This is shown, for instance, in [Reference Halberstam and RichertHR74, ch. 11].
Appendix B Proof of the exponential sum estimates
In this appendix we prove a couple of very simple auxiliary lemmas as well as the exponential sum estimates stated in § 8.
Lemma B.1. Let
![]() $N\geqslant Q\geqslant 1$
and
$N\geqslant Q\geqslant 1$
and
![]() $c_{0}$
be integers, and let
$c_{0}$
be integers, and let
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{R}$
. Then
$\unicode[STIX]{x1D6FD}\in \mathbb{R}$
. Then
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}n)=\frac{1}{Q}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FD}n)+O(|\unicode[STIX]{x1D6FD}|N+1).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}n)=\frac{1}{Q}\mathop{\sum }_{\substack{ N\leqslant n<2N}}e(\unicode[STIX]{x1D6FD}n)+O(|\unicode[STIX]{x1D6FD}|N+1).\end{eqnarray}$$
Proof. We can clearly assume that
![]() $0\leqslant c_{0}<Q$
. Let us write
$0\leqslant c_{0}<Q$
. Let us write
![]() $n=c_{0}+kQ$
, obtaining that
$n=c_{0}+kQ$
, obtaining that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}n) & = & \displaystyle e(\unicode[STIX]{x1D6FD}c_{0})\mathop{\sum }_{\substack{ (N-c_{0})/Q\leqslant k<(2N-c_{0})/Q}}e(\unicode[STIX]{x1D6FD}kQ)\nonumber\\ \displaystyle & = & \displaystyle (1+O(\unicode[STIX]{x1D6FD}Q))\mathop{\sum }_{\substack{ N/Q\leqslant k<2N/Q}}e(\unicode[STIX]{x1D6FD}kQ)+O(1)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ N/Q\leqslant k<2N/Q}}e(\unicode[STIX]{x1D6FD}kQ)+O(|\unicode[STIX]{x1D6FD}|N+1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FD}n) & = & \displaystyle e(\unicode[STIX]{x1D6FD}c_{0})\mathop{\sum }_{\substack{ (N-c_{0})/Q\leqslant k<(2N-c_{0})/Q}}e(\unicode[STIX]{x1D6FD}kQ)\nonumber\\ \displaystyle & = & \displaystyle (1+O(\unicode[STIX]{x1D6FD}Q))\mathop{\sum }_{\substack{ N/Q\leqslant k<2N/Q}}e(\unicode[STIX]{x1D6FD}kQ)+O(1)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ N/Q\leqslant k<2N/Q}}e(\unicode[STIX]{x1D6FD}kQ)+O(|\unicode[STIX]{x1D6FD}|N+1).\nonumber\end{eqnarray}$$
Since the last expression is independent of
![]() $c_{0}$
, summing over
$c_{0}$
, summing over
![]() $0\leqslant c_{0}<Q$
, we see that
$0\leqslant c_{0}<Q$
, we see that
and the claim follows. ◻
Lemma B.2. Let
![]() $Q,q\geqslant 1$
and
$Q,q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
and
$(a,q)=1$
and
![]() $(Q,q)<q$
. Assume that
$(Q,q)<q$
. Assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|\leqslant 1/(2qQ)$
and let
$|\unicode[STIX]{x1D6FC}-a/q|\leqslant 1/(2qQ)$
and let
![]() $c_{0}\in \mathbb{Z}$
. Then
$c_{0}\in \mathbb{Z}$
. Then
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}n)\biggr|\ll \frac{q}{(Q,q)}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}n)\biggr|\ll \frac{q}{(Q,q)}.\end{eqnarray}$$
Proof. Let us write
![]() $n=c_{0}+kQ$
, obtaining that
$n=c_{0}+kQ$
, obtaining that
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}n)\biggr|=\biggl|\mathop{\sum }_{\substack{ (N-c_{0})/Q\leqslant k<(2N-c_{0})/Q}}e(\unicode[STIX]{x1D6FC}kQ)\biggr|\ll \frac{1}{\Vert \unicode[STIX]{x1D6FC}Q\Vert }\leqslant \frac{1}{1/(2q/(Q,q))}.\Box\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{\substack{ N\leqslant n<2N \\ n\equiv c_{0}~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}n)\biggr|=\biggl|\mathop{\sum }_{\substack{ (N-c_{0})/Q\leqslant k<(2N-c_{0})/Q}}e(\unicode[STIX]{x1D6FC}kQ)\biggr|\ll \frac{1}{\Vert \unicode[STIX]{x1D6FC}Q\Vert }\leqslant \frac{1}{1/(2q/(Q,q))}.\Box\end{eqnarray}$$
B.1 Major arc estimates
Proof of Lemma 8.1.
By partial summation, it is enough to prove the claim in case
![]() $\unicode[STIX]{x1D6FC}=a/q$
(strictly speaking one should consider intervals
$\unicode[STIX]{x1D6FC}=a/q$
(strictly speaking one should consider intervals
![]() $p,n\in [x,x^{\prime }]$
instead of
$p,n\in [x,x^{\prime }]$
instead of
![]() $[x,2x]$
but this makes no difference). Since
$[x,2x]$
but this makes no difference). Since
![]() $q\mid Q$
, the left-hand side of the claim equals
$q\mid Q$
, the left-hand side of the claim equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}1-\frac{Q}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~Q)}}\frac{1}{\log n}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}1-\frac{|\mathbb{P}\cap [x,2x)|}{\unicode[STIX]{x1D711}(rQ)}\biggr|+O(x(\log x)^{-C_{1}-C_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{d\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}}\max _{(c,d)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~d)}}1-\frac{|\mathbb{P}\cap [x,2x)|}{\unicode[STIX]{x1D711}(d)}\biggr|+O((\log x)^{-C_{1}-C_{2}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}1-\frac{Q}{\unicode[STIX]{x1D711}(rQ)}\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c~(\text{mod}~Q)}}\frac{1}{\log n}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{r\leqslant x^{1/2-\unicode[STIX]{x1D700}}}\max _{(c,rQ)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~rQ)}}1-\frac{|\mathbb{P}\cap [x,2x)|}{\unicode[STIX]{x1D711}(rQ)}\biggr|+O(x(\log x)^{-C_{1}-C_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{d\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}}\max _{(c,d)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c~(\text{mod}~d)}}1-\frac{|\mathbb{P}\cap [x,2x)|}{\unicode[STIX]{x1D711}(d)}\biggr|+O((\log x)^{-C_{1}-C_{2}}),\nonumber\end{eqnarray}$$
and the claim follows from the Bombieri–Vinogradov prime number theorem. ◻
Proof of Lemma 8.2.
Arguing similarly, Lemma 8.2 reduces to showing
 $$\begin{eqnarray}\mathop{\sum }_{d\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}}\max _{(c,d)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~d) \\ M\leqslant m<2M}}a_{m}b_{n}-\frac{1}{\unicode[STIX]{x1D711}(d)}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ (mn,d)=1 \\ M\leqslant m<2M}}a_{m}b_{n}\biggr|\ll \frac{x}{(\log x)^{2C_{1}+C_{2}+1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{d\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}}\max _{(c,d)=1}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c~(\text{mod}~d) \\ M\leqslant m<2M}}a_{m}b_{n}-\frac{1}{\unicode[STIX]{x1D711}(d)}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ (mn,d)=1 \\ M\leqslant m<2M}}a_{m}b_{n}\biggr|\ll \frac{x}{(\log x)^{2C_{1}+C_{2}+1}}\end{eqnarray}$$
which follows from type II information used in the proof of the Bombieri–Vinogradov prime number theorem (see, e.g., [Reference Iwaniec and KowalskiIK04, Theorem 17.4]). ◻
B.2 Minor arc estimates for type I sums
Note that all the minor arc estimates are trivial if
![]() $q>x$
, so that we can always assume that
$q>x$
, so that we can always assume that
![]() $q\leqslant x$
. Lemma 8.3 follows easily from the following slight variant of a lemma usually used in type I estimates.
$q\leqslant x$
. Lemma 8.3 follows easily from the following slight variant of a lemma usually used in type I estimates.
Lemma B.3. Let
![]() $q\geqslant 1$
and
$q\geqslant 1$
and
![]() $a$
be integers such that
$a$
be integers such that
![]() $(a,q)=1$
and assume that
$(a,q)=1$
and assume that
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/q^{2}$
. For any
$|\unicode[STIX]{x1D6FC}-a/q|<1/q^{2}$
. For any
![]() $x\geqslant M\geqslant 1$
and any integer
$x\geqslant M\geqslant 1$
and any integer
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
Proof. By the Cauchy–Schwarz inequality
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\mathop{\sum }_{M\leqslant m<2M}\unicode[STIX]{x1D70F}_{k}(m)\min \biggl\{\frac{x}{M},\frac{1}{\Vert \unicode[STIX]{x1D6FC}m\Vert }\biggr\}\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(\mathop{\sum }_{M\leqslant m<2M}\unicode[STIX]{x1D70F}_{k}(m)^{2}\frac{x}{M}\biggr)\cdot \biggl(\mathop{\sum }_{M\leqslant m<2M}\min \biggl\{\frac{x}{M},\frac{1}{\Vert \unicode[STIX]{x1D6FC}m\Vert }\biggr\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{k}x(\log 3x)^{k^{2}-1}\cdot \biggl(\frac{x}{q}+M+q\biggr)(\log 3x),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\mathop{\sum }_{M\leqslant m<2M}\unicode[STIX]{x1D70F}_{k}(m)\min \biggl\{\frac{x}{M},\frac{1}{\Vert \unicode[STIX]{x1D6FC}m\Vert }\biggr\}\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(\mathop{\sum }_{M\leqslant m<2M}\unicode[STIX]{x1D70F}_{k}(m)^{2}\frac{x}{M}\biggr)\cdot \biggl(\mathop{\sum }_{M\leqslant m<2M}\min \biggl\{\frac{x}{M},\frac{1}{\Vert \unicode[STIX]{x1D6FC}m\Vert }\biggr\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{k}x(\log 3x)^{k^{2}-1}\cdot \biggl(\frac{x}{q}+M+q\biggr)(\log 3x),\nonumber\end{eqnarray}$$
by a standard ingredient in type I estimates (see, e.g., [Reference Iwaniec and KowalskiIK04, Formula before Lemma 13.7]). ◻
Proof of Lemma 8.3.
We can clearly assume that
![]() $M\leqslant x^{1/2}/Q$
. Write
$M\leqslant x^{1/2}/Q$
. Write
![]() $S$
for the left-hand side of the claim, and write
$S$
for the left-hand side of the claim, and write
![]() $\overline{m}$
for the inverse of
$\overline{m}$
for the inverse of
![]() $m~(\text{mod}~rQ)$
. Then
$m~(\text{mod}~rQ)$
. Then
 $$\begin{eqnarray}S\leqslant \mathop{\sum }_{r\leqslant x^{1/2}}\max _{(c,rQ)=1}\mathop{\sum }_{\substack{ M\leqslant m<2M \\ (m,rQ)=1}}\biggl|\mathop{\sum }_{\substack{ x/m\leqslant n<2x/m \\ n\equiv c\overline{m}~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}mn)\biggr|.\end{eqnarray}$$
$$\begin{eqnarray}S\leqslant \mathop{\sum }_{r\leqslant x^{1/2}}\max _{(c,rQ)=1}\mathop{\sum }_{\substack{ M\leqslant m<2M \\ (m,rQ)=1}}\biggl|\mathop{\sum }_{\substack{ x/m\leqslant n<2x/m \\ n\equiv c\overline{m}~(\text{mod}~rQ)}}e(\unicode[STIX]{x1D6FC}mn)\biggr|.\end{eqnarray}$$
Writing
![]() $n=c\overline{m}+krQ$
, with
$n=c\overline{m}+krQ$
, with
![]() $k$
running over an interval with elements of size
$k$
running over an interval with elements of size
![]() $x/(mrQ)\gg 1$
, and summing the geometric series, we see that
$x/(mrQ)\gg 1$
, and summing the geometric series, we see that
By our assumption on
![]() $\unicode[STIX]{x1D6FC}$
, we have
$\unicode[STIX]{x1D6FC}$
, we have
![]() $|\unicode[STIX]{x1D6FC}Q-(Qa/h)/(q/h)|<1/q^{2}\leqslant 1/(q/h)^{2}$
. Hence, after a dyadic division on
$|\unicode[STIX]{x1D6FC}Q-(Qa/h)/(q/h)|<1/q^{2}\leqslant 1/(q/h)^{2}$
. Hence, after a dyadic division on
![]() $d$
, Lemma B.3 gives
$d$
, Lemma B.3 gives
B.3 Minor arc estimates for type II sums
In the proof of Lemma 8.4 we use the following auxiliary exponential sum estimate due to Mikawa [Reference MikawaMik00], in the proof of which one Fourier expands the
![]() $\min$
-function on the left-hand side and uses Weyl differencing.
$\min$
-function on the left-hand side and uses Weyl differencing.
Lemma B.4. Let
![]() $|\unicode[STIX]{x1D6FC}-a/q|<1/q^{2}$
for some
$|\unicode[STIX]{x1D6FC}-a/q|<1/q^{2}$
for some
![]() $(a,q)=1$
. For
$(a,q)=1$
. For
![]() $0<M,J\leqslant x$
, one has
$0<M,J\leqslant x$
, one has
Proof of Lemma 8.4.
Let us first note that in case
![]() $D\leqslant (\log x)^{C}$
, we can combine
$D\leqslant (\log x)^{C}$
, we can combine
![]() $dr=d^{\prime }\in [D^{\prime },4D^{\prime }]$
with
$dr=d^{\prime }\in [D^{\prime },4D^{\prime }]$
with
![]() $2D^{\prime }=2DR\leqslant 2(\log x)^{C}M/x^{1/2}\leqslant x/(MQ(\log x)^{C})$
which is still at most the upper bound for
$2D^{\prime }=2DR\leqslant 2(\log x)^{C}M/x^{1/2}\leqslant x/(MQ(\log x)^{C})$
which is still at most the upper bound for
![]() $D$
in Lemma 8.4. This allows us to assume that
$D$
in Lemma 8.4. This allows us to assume that
![]() $R=1$
in case
$R=1$
in case
![]() $D\leqslant (\log x)^{C}$
; combining
$D\leqslant (\log x)^{C}$
; combining
![]() $dr=d^{\prime }$
introduces at worst a divisor function
$dr=d^{\prime }$
introduces at worst a divisor function
![]() $\unicode[STIX]{x1D70F}(d^{\prime })$
, but the claim follows in any case if we can show the claimed upper bound for
$\unicode[STIX]{x1D70F}(d^{\prime })$
, but the claim follows in any case if we can show the claimed upper bound for
 $$\begin{eqnarray}I=\mathop{\sum }_{D\leqslant d<2D}\unicode[STIX]{x1D70F}(d)\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\unicode[STIX]{x1D703}(d,r)\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c_{d}~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn),\end{eqnarray}$$
$$\begin{eqnarray}I=\mathop{\sum }_{D\leqslant d<2D}\unicode[STIX]{x1D70F}(d)\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\unicode[STIX]{x1D703}(d,r)\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c_{d}~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn),\end{eqnarray}$$
for any choice of residue class
![]() $c_{d}~(\text{mod}~dQ)$
with
$c_{d}~(\text{mod}~dQ)$
with
![]() $(c_{d},dQ)=1$
and any choice of
$(c_{d},dQ)=1$
and any choice of
![]() $\unicode[STIX]{x1D703}(d,r)\in \mathbb{C}$
with
$\unicode[STIX]{x1D703}(d,r)\in \mathbb{C}$
with
![]() $|\unicode[STIX]{x1D703}(d,r)|=1$
. By the Cauchy–Schwarz inequality, we have
$|\unicode[STIX]{x1D703}(d,r)|=1$
. By the Cauchy–Schwarz inequality, we have
 $$\begin{eqnarray}|I|^{2}\ll DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{M\leqslant m<2M}\biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\unicode[STIX]{x1D703}(d,r)\mathop{\sum }_{\substack{ x/m\leqslant n<2x/m \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c_{d}~(\text{mod}~dQ)}}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}|I|^{2}\ll DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{M\leqslant m<2M}\biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }dQ)=1}}\unicode[STIX]{x1D703}(d,r)\mathop{\sum }_{\substack{ x/m\leqslant n<2x/m \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c_{d}~(\text{mod}~dQ)}}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|^{2}.\end{eqnarray}$$
Expanding out the square, moving the sum over
![]() $m$
inside, and noting that
$m$
inside, and noting that
![]() $|b_{n_{1}}b_{n_{2}}|\leqslant \,\,\unicode[STIX]{x1D70F}(n_{1})^{2}+\unicode[STIX]{x1D70F}(n_{2})^{2}$
, we obtain
$|b_{n_{1}}b_{n_{2}}|\leqslant \,\,\unicode[STIX]{x1D70F}(n_{1})^{2}+\unicode[STIX]{x1D70F}(n_{2})^{2}$
, we obtain
 $$\begin{eqnarray}\displaystyle |I|^{2} & \ll & \displaystyle DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{\substack{ R\leqslant r_{1},r_{2}<2R \\ (r_{1},c^{\prime }dQ)=(r_{2},c^{\prime }dQ)=1}}\mathop{\sum }_{x/2M\leqslant n_{1},n_{2}\leqslant 2x/M}\unicode[STIX]{x1D70F}(n_{1})^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl|\mathop{\sum }_{\substack{ M\leqslant m<2M \\ x/n_{j}\leqslant m<2x/n_{j} \\ mn_{1}\equiv c^{\prime }~(\text{mod}~r_{1}) \\ mn_{2}\equiv c^{\prime }~(\text{mod}~r_{2}) \\ mn_{1}\equiv mn_{2}\equiv c_{d}~(\text{mod}~dQ)}}e(\unicode[STIX]{x1D6FC}m(n_{1}-n_{2}))\biggr|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I|^{2} & \ll & \displaystyle DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{\substack{ R\leqslant r_{1},r_{2}<2R \\ (r_{1},c^{\prime }dQ)=(r_{2},c^{\prime }dQ)=1}}\mathop{\sum }_{x/2M\leqslant n_{1},n_{2}\leqslant 2x/M}\unicode[STIX]{x1D70F}(n_{1})^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl|\mathop{\sum }_{\substack{ M\leqslant m<2M \\ x/n_{j}\leqslant m<2x/n_{j} \\ mn_{1}\equiv c^{\prime }~(\text{mod}~r_{1}) \\ mn_{2}\equiv c^{\prime }~(\text{mod}~r_{2}) \\ mn_{1}\equiv mn_{2}\equiv c_{d}~(\text{mod}~dQ)}}e(\unicode[STIX]{x1D6FC}m(n_{1}-n_{2}))\biggr|.\nonumber\end{eqnarray}$$
The simultaneous congruences above are soluble if and only if
![]() $(n_{1},r_{1}dQ)=(n_{2},r_{2}dQ)=1$
and
$(n_{1},r_{1}dQ)=(n_{2},r_{2}dQ)=1$
and
![]() $n_{1}\equiv n_{2}~(\text{mod}~dQ(r_{1},r_{2}))$
, in which case they reduce to the single equation
$n_{1}\equiv n_{2}~(\text{mod}~dQ(r_{1},r_{2}))$
, in which case they reduce to the single equation
![]() $m\equiv b~(\text{mod}~dQ[r_{1},r_{2}])$
for some
$m\equiv b~(\text{mod}~dQ[r_{1},r_{2}])$
for some
![]() $b$
. Thus, substituting
$b$
. Thus, substituting
![]() $m=b+kdQ[r_{1},r_{2}]$
(and noticing
$m=b+kdQ[r_{1},r_{2}]$
(and noticing
![]() $DQR^{2}\leqslant M$
), we see that the inner sum over
$DQR^{2}\leqslant M$
), we see that the inner sum over
![]() $m$
is
$m$
is
Writing
![]() $n_{1}=n_{2}+\ell \cdot dQ(r_{1},r_{2})$
, we have
$n_{1}=n_{2}+\ell \cdot dQ(r_{1},r_{2})$
, we have
so that
 $$\begin{eqnarray}\displaystyle |I|^{2} & \ll & \displaystyle DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\,\mathop{\sum }_{R\leqslant r_{1},r_{2}<2R}\,\mathop{\sum }_{x/2M\leqslant n_{1}\leqslant 2x/M}\unicode[STIX]{x1D70F}(n_{1})^{2}\mathop{\sum }_{|\ell |\leqslant 2x/MdQ(r_{1},r_{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\min \biggl(\frac{M}{dQ[r_{1},r_{2}]},\frac{1}{\Vert \unicode[STIX]{x1D6FC}\ell (dQ)^{2}r_{1}r_{2}\Vert }\biggr)\nonumber\\ \displaystyle & \ll & \displaystyle Dx(\log x)^{9}\mathop{\sum }_{D\leqslant d<2D}\,\mathop{\sum }_{R\leqslant r_{1},r_{2}<2R}\,\mathop{\sum }_{|\ell |\leqslant 2x/MdQ(r_{1},r_{2})}\min \biggl(\frac{M}{dQ[r_{1},r_{2}]},\frac{1}{\Vert \unicode[STIX]{x1D6FC}\ell (dQ)^{2}r_{1}r_{2}\Vert }\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I|^{2} & \ll & \displaystyle DM(\log x)^{6}\mathop{\sum }_{D\leqslant d<2D}\,\mathop{\sum }_{R\leqslant r_{1},r_{2}<2R}\,\mathop{\sum }_{x/2M\leqslant n_{1}\leqslant 2x/M}\unicode[STIX]{x1D70F}(n_{1})^{2}\mathop{\sum }_{|\ell |\leqslant 2x/MdQ(r_{1},r_{2})}\nonumber\\ \displaystyle & & \displaystyle \times \,\min \biggl(\frac{M}{dQ[r_{1},r_{2}]},\frac{1}{\Vert \unicode[STIX]{x1D6FC}\ell (dQ)^{2}r_{1}r_{2}\Vert }\biggr)\nonumber\\ \displaystyle & \ll & \displaystyle Dx(\log x)^{9}\mathop{\sum }_{D\leqslant d<2D}\,\mathop{\sum }_{R\leqslant r_{1},r_{2}<2R}\,\mathop{\sum }_{|\ell |\leqslant 2x/MdQ(r_{1},r_{2})}\min \biggl(\frac{M}{dQ[r_{1},r_{2}]},\frac{1}{\Vert \unicode[STIX]{x1D6FC}\ell (dQ)^{2}r_{1}r_{2}\Vert }\biggr).\nonumber\end{eqnarray}$$
The terms with
![]() $\ell =0$
contribute to the right-hand side
$\ell =0$
contribute to the right-hand side
by the assumption on
![]() $D$
, which is acceptable. To treat the terms with
$D$
, which is acceptable. To treat the terms with
![]() $\ell \neq 0$
, write
$\ell \neq 0$
, write
![]() $j=\ell r_{1}r_{2}$
so that
$j=\ell r_{1}r_{2}$
so that
and that
It follows that
By a dyadic division, it suffices to show that
 $$\begin{eqnarray}\displaystyle & & \displaystyle D\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{J\leqslant j<2J}\unicode[STIX]{x1D70F}_{3}(j)\min \biggl(\frac{x/Q^{2}}{d^{2}j},\frac{1}{\Vert (\unicode[STIX]{x1D6FC}Q)^{2}d^{2}j\Vert }\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{x}{Q^{2}}\biggl(\frac{(\log x)^{C}}{(q/h)^{1/4}}+(\log x)^{C}Q\biggl(\frac{q}{x}\biggr)^{1/4}+\frac{1}{(\log x)^{C/4}}\biggr)(\log x)^{8}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D\mathop{\sum }_{D\leqslant d<2D}\mathop{\sum }_{J\leqslant j<2J}\unicode[STIX]{x1D70F}_{3}(j)\min \biggl(\frac{x/Q^{2}}{d^{2}j},\frac{1}{\Vert (\unicode[STIX]{x1D6FC}Q)^{2}d^{2}j\Vert }\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{x}{Q^{2}}\biggl(\frac{(\log x)^{C}}{(q/h)^{1/4}}+(\log x)^{C}Q\biggl(\frac{q}{x}\biggr)^{1/4}+\frac{1}{(\log x)^{C/4}}\biggr)(\log x)^{8}\end{eqnarray}$$
for
![]() $1\leqslant J\leqslant 4R^{2}x/(DMQ)$
. To prove this we divide into two cases depending on whether
$1\leqslant J\leqslant 4R^{2}x/(DMQ)$
. To prove this we divide into two cases depending on whether
![]() $D$
is large or small.
$D$
is large or small.
Case 1. First assume that
![]() $D>(\log x)^{C}$
. Note that, by assumption,
$D>(\log x)^{C}$
. Note that, by assumption,
It is also easy to see that
![]() $D,J\leqslant x/Q^{2}$
. We may thus apply Lemma B.4 to bound the left-hand side of (B.1) by
$D,J\leqslant x/Q^{2}$
. We may thus apply Lemma B.4 to bound the left-hand side of (B.1) by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \ll \biggl(D^{2}J+\biggl(\frac{x}{Q^{2}}\biggr)^{3/4}\biggl(\frac{x/Q^{2}}{q/h}+\frac{x/Q^{2}}{D}+q\biggr)^{1/4}\biggr)(\log x)^{8}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \ll \frac{x}{Q^{2}}\biggl(\frac{1}{(\log x)^{C}}+\frac{1}{(q/h)^{1/4}}+\frac{1}{(\log x)^{C/4}}+Q^{1/2}\biggl(\frac{q}{x}\biggr)^{1/4}\biggr)(\log x)^{8}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \ll \biggl(D^{2}J+\biggl(\frac{x}{Q^{2}}\biggr)^{3/4}\biggl(\frac{x/Q^{2}}{q/h}+\frac{x/Q^{2}}{D}+q\biggr)^{1/4}\biggr)(\log x)^{8}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \ll \frac{x}{Q^{2}}\biggl(\frac{1}{(\log x)^{C}}+\frac{1}{(q/h)^{1/4}}+\frac{1}{(\log x)^{C/4}}+Q^{1/2}\biggl(\frac{q}{x}\biggr)^{1/4}\biggr)(\log x)^{8}\nonumber\end{eqnarray}$$
by the upper bound on
![]() $J$
and the assumptions on
$J$
and the assumptions on
![]() $D$
and
$D$
and
![]() $R$
.
$R$
.
Case 2. Now assume that
![]() $D\leqslant (\log x)^{C}$
. Recall that in this case we can assume that
$D\leqslant (\log x)^{C}$
. Recall that in this case we can assume that
![]() $R=1$
. In this case, for each fixed
$R=1$
. In this case, for each fixed
![]() $D\leqslant d<2D$
we have, by assumption,
$D\leqslant d<2D$
we have, by assumption,
Moreover, the denominator of the fraction
![]() $a(dQ)^{2}/q$
is at least
$a(dQ)^{2}/q$
is at least
![]() $q/hD^{2}\geqslant q/(h(\log x)^{2C})$
after reducing it to the reduced form. Applying Lemma B.3 to the inner sum over
$q/hD^{2}\geqslant q/(h(\log x)^{2C})$
after reducing it to the reduced form. Applying Lemma B.3 to the inner sum over
![]() $j$
in (B.1) (noting that
$j$
in (B.1) (noting that
![]() $J\leqslant x/(D^{2}Q^{2})$
), we may bound the left-hand side of (B.1) by
$J\leqslant x/(D^{2}Q^{2})$
), we may bound the left-hand side of (B.1) by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \ll D^{2}\biggl(\frac{x/(Q^{2}D^{2})}{(q/(h(\log x)^{2C}))^{1/2}}+\biggl(\frac{x}{Q^{2}D^{2}}\biggr)^{1/2}\cdot \biggl(\frac{x}{DMQ}\biggr)^{1/2}+\biggl(\frac{x}{Q^{2}D^{2}}\biggr)^{1/2}q^{1/2}\biggr)(\log x)^{9/2}\nonumber\\ \displaystyle & & \displaystyle \ll \frac{x}{Q^{2}}\biggl(\frac{(\log x)^{C}}{(q/h)^{1/2}}+\frac{1}{(\log x)^{C/2}}+Q\biggl(\frac{q}{x}\biggr)^{1/2}(\log x)^{C}\biggr)(\log x)^{9/2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \ll D^{2}\biggl(\frac{x/(Q^{2}D^{2})}{(q/(h(\log x)^{2C}))^{1/2}}+\biggl(\frac{x}{Q^{2}D^{2}}\biggr)^{1/2}\cdot \biggl(\frac{x}{DMQ}\biggr)^{1/2}+\biggl(\frac{x}{Q^{2}D^{2}}\biggr)^{1/2}q^{1/2}\biggr)(\log x)^{9/2}\nonumber\\ \displaystyle & & \displaystyle \ll \frac{x}{Q^{2}}\biggl(\frac{(\log x)^{C}}{(q/h)^{1/2}}+\frac{1}{(\log x)^{C/2}}+Q\biggl(\frac{q}{x}\biggr)^{1/2}(\log x)^{C}\biggr)(\log x)^{9/2}\nonumber\end{eqnarray}$$
by our assumptions on
![]() $D$
and
$D$
and
![]() $M$
. ◻
$M$
. ◻
B.4 Minor arc estimates for sums over primes
Proof of Lemma 8.6.
By partial summation it is enough to consider the claim of Lemma 8.6 with
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c^{\prime }~(\text{mod}~r) \\ p\equiv c~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}p)\quad \text{replaced by}~\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c^{\prime }~(\text{mod}~r) \\ n\equiv c~(\text{mod}~Q)}}\unicode[STIX]{x1D6EC}(n)e(\unicode[STIX]{x1D6FC}n).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ x\leqslant p<2x \\ p\equiv c^{\prime }~(\text{mod}~r) \\ p\equiv c~(\text{mod}~Q)}}e(\unicode[STIX]{x1D6FC}p)\quad \text{replaced by}~\mathop{\sum }_{\substack{ x\leqslant n<2x \\ n\equiv c^{\prime }~(\text{mod}~r) \\ n\equiv c~(\text{mod}~Q)}}\unicode[STIX]{x1D6EC}(n)e(\unicode[STIX]{x1D6FC}n).\end{eqnarray}$$
Then, by a dyadic splitting on
![]() $r$
, Vaughan’s identity (see [Reference Iwaniec and KowalskiIK04, Proposition 13.4]) with
$r$
, Vaughan’s identity (see [Reference Iwaniec and KowalskiIK04, Proposition 13.4]) with
![]() $y=z=x^{2/3}$
, and further partial summation, it is then enough to show that, for any
$y=z=x^{2/3}$
, and further partial summation, it is then enough to show that, for any
![]() $M\leqslant x^{1/3}$
,
$M\leqslant x^{1/3}$
,
![]() $R\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}$
and any
$R\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}$
and any
![]() $|a_{m}|\leqslant 1$
, one has the type I estimate
$|a_{m}|\leqslant 1$
, one has the type I estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{12}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{12}.\end{eqnarray}$$
and that, for any
![]() $x^{1/3}\leqslant M\leqslant x^{2/3}$
,
$x^{1/3}\leqslant M\leqslant x^{2/3}$
,
![]() $R\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}$
and any
$R\leqslant x^{1/2-\unicode[STIX]{x1D700}/2}$
and any
![]() $|a_{k}|,|b_{k}|\leqslant \unicode[STIX]{x1D70F}(k)$
, one has the type II estimate
$|a_{k}|,|b_{k}|\leqslant \unicode[STIX]{x1D70F}(k)$
, one has the type II estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{12}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{\substack{ R\leqslant r<2R \\ (r,c^{\prime }Q)=1}}\unicode[STIX]{x1D707}(r)^{2}\unicode[STIX]{x1D706}_{r}\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{x}{Q}\cdot \biggl(\frac{(\log x)^{C/2}}{(q/h)^{1/8}}+(\log x)^{C/2}Q^{1/2}\frac{q^{1/8}}{x^{1/8}}+\frac{1}{(\log x)^{C/8}}\biggr)(\log x)^{12}.\end{eqnarray}$$
The estimate (B.2) follows directly from Lemma 8.3. On the other hand, to estimate (B.3), by symmetry we may assume that
![]() $M\geqslant x^{1/2}$
, and we take
$M\geqslant x^{1/2}$
, and we take
![]() $D=\min \{R,x/(MQ(\log x)^{C})\}$
and
$D=\min \{R,x/(MQ(\log x)^{C})\}$
and
![]() $R^{\prime }=R/D$
. Note that
$R^{\prime }=R/D$
. Note that
![]() $D\geqslant \min \{R,x^{1/3-\unicode[STIX]{x1D700}}\}$
and, thus, for either possibility of
$D\geqslant \min \{R,x^{1/3-\unicode[STIX]{x1D700}}\}$
and, thus, for either possibility of
![]() $\unicode[STIX]{x1D706}_{r}$
from Hypothesis 6.3(i), by the well-factorability property we always get for the left-hand side of (B.3) the upper bound
$\unicode[STIX]{x1D706}_{r}$
from Hypothesis 6.3(i), by the well-factorability property we always get for the left-hand side of (B.3) the upper bound
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ d\leqslant D \\ (d,c^{\prime }Q)=1}}\mathop{\sum }_{\substack{ r^{\prime }\leqslant R^{\prime } \\ (r^{\prime },c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~dr^{\prime }) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\substack{ d\leqslant D \\ (d,Q)=1}}\max _{(c_{0},dQ)=1}\mathop{\sum }_{\substack{ r^{\prime }\leqslant R^{\prime } \\ (r^{\prime },c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r^{\prime }) \\ mn\equiv c_{0}~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ d\leqslant D \\ (d,c^{\prime }Q)=1}}\mathop{\sum }_{\substack{ r^{\prime }\leqslant R^{\prime } \\ (r^{\prime },c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~dr^{\prime }) \\ mn\equiv c~(\text{mod}~Q) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\substack{ d\leqslant D \\ (d,Q)=1}}\max _{(c_{0},dQ)=1}\mathop{\sum }_{\substack{ r^{\prime }\leqslant R^{\prime } \\ (r^{\prime },c^{\prime }dQ)=1}}\biggl|\mathop{\sum }_{\substack{ x\leqslant mn<2x \\ mn\equiv c^{\prime }~(\text{mod}~r^{\prime }) \\ mn\equiv c_{0}~(\text{mod}~dQ) \\ M\leqslant m<2M}}a_{m}b_{n}e(\unicode[STIX]{x1D6FC}mn)\biggr|,\nonumber\end{eqnarray}$$
and the claim follows from Lemma 8.4 after dividing the variables
![]() $d$
and
$d$
and
![]() $r^{\prime }$
dyadically.◻
$r^{\prime }$
dyadically.◻
Let us note that, in the previous proof, in order to apply Lemma 8.4 when
![]() $M$
is close to
$M$
is close to
![]() $x^{2/3}$
, we needed to take
$x^{2/3}$
, we needed to take
![]() $D$
to be slightly smaller than
$D$
to be slightly smaller than
![]() $x^{1/3}$
. This is in contrast to what was claimed in [Reference MatomäkiMat09, Remark 10], but the caused mistake in the proof of [Reference MatomäkiMat09, Theorem 2] could be easily fixed by using a slight modification of Chen’s weights used here in Appendix A.
$x^{1/3}$
. This is in contrast to what was claimed in [Reference MatomäkiMat09, Remark 10], but the caused mistake in the proof of [Reference MatomäkiMat09, Theorem 2] could be easily fixed by using a slight modification of Chen’s weights used here in Appendix A.