1. Introduction
The presence of surface active agents (surfactants) can significantly alter the surface properties of a liquid and give rise to interesting phenomena, such as tip streaming from a highly deformed liquid droplet submerged in a shear or extensional flow (Eggers Reference Eggers1997; Anna Reference Anna2016; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020) and flower-like patterning of an evaporating liquid droplet spreading on a liquid substrate (Wodlei et al. Reference Wodlei, Sebilleau, Magnaudet and Pimienta2018). In a variety of applications including atomization, ink-jet printing, spinning, coating, emulsification, enhanced oil recovery, microfluidics, food industry and drug delivery, the addition of surfactant molecules can help to control actively and easily the motion, spread, transport, formation, deformation and breakup of films, jets, threads, drops, bubbles, colloids or biological molecules. Surfactants have been one of the most attractive and most studied factors in those liquid–air surface and liquid–liquid interfacial problems in the last three decades (Eggers & Villermaux Reference Eggers and Villermaux2008; Vlahovska Reference Vlahovska2019; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). Nevertheless, the underlying mechanisms have not yet been fully understood.
An insoluble surfactant monolayer at a liquid surface may affect the dynamics of the liquid in three ways (Kamat et al. Reference Kamat, Wagoner, Thete and Basaran2018; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020; Wee, Wagoner & Basaran Reference Wee, Wagoner and Basaran2022): it lowers the average capillary force by reducing the surface tension coefficient, i.e. the so-called soluto-capillarity effect; the non-uniform distribution of surfactant molecules at the surface causes a non-zero surface tension gradient and thereby the Marangoni stress that tends to eliminate the non-uniformity; it induces the surface rheological effects characterized by the surface shear and dilatational viscosities, and with shear and dilatational deformations of the surface, it yields the viscous stresses that participate in the force balance at the surface. The reduction in the surface tension, the surface tension gradient and the resulting Marangoni stress and the surface viscous stresses are all associated with the distribution of surfactant at the surface. The distribution of insoluble surfactant is basically determined by two mechanisms: surface convection and surface diffusion. The former gives rise to inhomogeneity and thereby surface tension gradients, whereas the latter tends to restore homogeneity (Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). The relative importance of surface convection and surface diffusion, represented by the surface Péclet number, may substantially influence the dynamics of a fluid system. In general, the multiple effects of a surfactant monolayer together with their complex mathematical descriptions make the related theoretical, numerical and experimental investigations challenging.
The situation can be more intricate when the surfactant is soluble. In such a case, surfactant molecules exist not only at the surface but also in the bulk. The solubility cannot be neglected when the adsorption/desorption characteristic time of the surfactant is comparable to or smaller than the other characteristic times of the system (e.g. the capillary time for a Newtonian jet or both the capillary time and the extensional relaxation time for a viscoelastic jet). If the bulk concentration of the surfactant is below the critical micellar concentration (CMC), it is presented as monomers in the bulk; if the bulk concentration is above the CMC, surfactant molecules partially aggregate into micelles spontaneously (Craster, Matar & Papageorgiou Reference Craster, Matar and Papageorgiou2009; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). The concentrations of monomers and micelles are governed by their respective conservation equations. There is a term describing the breakup or formation of micelles in each equation. Moreover, there is a term denoting the flux of surfactant from the bulk to the surface due to the adsorption/desorption process in the conservation equation at the surface. Surfactant solubility seems to affect fluid dynamics in an indirect way.
Studying how capillarity, bulk viscosity, inertia, Marangoni stress, surface viscosity and other possible factors compete with or cooperate with each other in a fluid system has both scientific and practical relevance. There have been many reports in the literature devoted to understanding the effects of insoluble or soluble surfactants on the linear and nonlinear dynamics of films, drops, bubbles, jets, threads and other similar configurations, e.g. Liao, Franses & Basaran (Reference Liao, Franses and Basaran2006), Hameed et al. (Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008), Craster et al. (Reference Craster, Matar and Papageorgiou2009), Young et al. (Reference Young, Booty, Siegel and Li2009), Ponce-Torres et al. (Reference Ponce-Torres, Herrada, Montanero and Vega2016), Martínez-Calvo & Sevilla (Reference Martínez-Calvo and Sevilla2018), Hu, Fu & Yang (Reference Hu, Fu and Yang2020), He & Wylie (Reference He and Wylie2021) and Wee et al. (Reference Wee, Wagoner, Garg, Kamat and Basaran2021). The mechanism in one geometric configuration may be extrapolated to another. It is also possible that different mechanisms play a major role in different configurations. In the following, we introduce the studies of cylindrical liquid jets and threads.
Linear theory has confirmed that the presence of surfactants has a stabilizing effect on the Rayleigh–Plateau instability of Newtonian viscous liquid jets (Craster, Matar & Papageorgiou Reference Craster, Matar and Papageorgiou2002; Timmermans & Lister Reference Timmermans and Lister2002; Ponce-Torres et al. Reference Ponce-Torres, Herrada, Montanero and Vega2016; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018). That is, surfactants reduce the growth rates of small disturbances. This effect is unsurprising, since the average capillary force is lowered and the Marangoni and surface viscous stresses are created in the presence of surfactants. Similarly, increasing surfactant activity or surface viscosity stabilizes liquid jets. Another finding is that the linear analysis based on the long wave approximation cannot accurately predict some instability features (such as the cutoff wavenumber) of surfactant-laden liquid jets and threads without the inclusion of the necessary high-order terms (Hansen, Peters & Meijer Reference Hansen, Peters and Meijer1999; Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018).
The nonlinear effects come into play, as disturbances grow with time. Linear theory fails to predict the late stages of jet or thread instability. The nonlinear dynamics of Newtonian jets and threads in the presence of surfactants has been studied via the asymptotic methods and numerical simulations, e.g. Anshus (Reference Anshus1973), Craster et al. (Reference Craster, Matar and Papageorgiou2002), Timmermans & Lister (Reference Timmermans and Lister2002), Dravid et al. (Reference Dravid, Songsermpong, Xue, Corvalan and Sojka2006), McGough & Basaran (Reference McGough and Basaran2006), Craster et al. (Reference Craster, Matar and Papageorgiou2009), Hameed & Maldarelli (Reference Hameed and Maldarelli2016), Martínez-Calvo et al. (Reference Martínez-Calvo, Rivero-Rodríguez, Scheid and Sevilla2020) and Wee et al. (Reference Wee, Wagoner, Garg, Kamat and Basaran2021). It was found that the pinch-off of Newtonian liquid threads can be delayed by surfactants (Anshus Reference Anshus1973; Craster et al. Reference Craster, Matar and Papageorgiou2002). The addition of surfactants to Newtonian viscous threads favours the formation of secondary droplets between primary droplets. The size of secondary droplets is increased or decreased by surfactants, depending on their strength and diffusivity (Dravid et al. Reference Dravid, Songsermpong, Xue, Corvalan and Sojka2006). Surface viscosities were found to be responsible for the accumulation of surfactant molecules in secondary droplets (Ponce-Torres et al. Reference Ponce-Torres, Herrada, Montanero and Vega2016, Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017). The detachment of primary droplets will never take place and the formation of secondary droplets will be impeded, as long as the Marangoni stress is sufficiently large (Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008). The experimental and numerical studies of McGough & Basaran (Reference McGough and Basaran2006) and Kamat et al. (Reference Kamat, Wagoner, Thete and Basaran2018) showed that the Marangoni stress near the pinching point of a thread induces the formation of microthread cascades. When the transport of an insoluble surfactant is dominated by surface convection (the surface Péclet number is large), surfactant molecules are swept away from the pinching point (Newtonian liquid threads pinch off at the neck where the primary droplet joins the ligament). As a result, surfactant-laden jets behave in a similar way to surfactant-free jets prior to pinch-off and exhibit the same similarity (Eggers Reference Eggers1993; Craster et al. Reference Craster, Matar and Papageorgiou2002; Timmermans & Lister Reference Timmermans and Lister2002; Liao et al. Reference Liao, Franses and Basaran2006; McGough & Basaran Reference McGough and Basaran2006; Eggers & Villermaux Reference Eggers and Villermaux2008). Remarkably, the surface viscous stresses can still play a role when most of surfactant molecules are swept away from the pinching point, because the surface-to-volume ratio at the pinching point becomes extremely large as the minimum radius of the jet tends to zero (Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020; Wee et al. Reference Wee, Wagoner, Kamat and Basaran2020, Reference Wee, Wagoner, Garg, Kamat and Basaran2021). However, surfactant molecules are not always evacuated from the pinching region, even for large surface Péclet numbers of the order of ![]() $10^5$, as detected by Ponce-Torres et al. (Reference Ponce-Torres, Rubio, Herrada, Eggers and Montanero2020). The one-dimensional (1-D) nonlinear analysis of surfactant-laden viscous threads in the Stokes limit showed that there exists a critical value of the surface Péclet number. Below this critical value, surface diffusion is dominant and the thread thins exponentially in time; above it, surface convection is dominant and the thinning of the thread exhibits a power-law dependence on time until pinch-off (Wee et al. Reference Wee, Wagoner and Basaran2022). In the Stokes limit, the surface viscous stresses enter the dominant force balance and tend to slow down the thinning of Newtonian threads (Ozan & Jakobsen Reference Ozan and Jakobsen2019; Wee et al. Reference Wee, Wagoner, Kamat and Basaran2020). The balance between the capillary force and the surface viscous stresses is established at sufficiently high surfactant surface concentrations, resulting in an asymptotic regime in which the filament thins exponentially in time at a rate only depending on the surface tension and the surface viscosities (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2020). When the inertia is taken into account, the inertial, capillary, bulk viscous and surface viscous forces establish the dominant force balance as the jet nears pinch-off, whereas the Marangoni stress plays a secondary role (Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021). For viscous threads laden with soluble surfactants at concentrations above the CMC, larger secondary droplets are formed due to the Marangoni stress (Craster et al. Reference Craster, Matar and Papageorgiou2009). The study of the surfactant effects has been extended to compound liquid jets (Craster, Matar & Papageorgiou Reference Craster, Matar and Papageorgiou2003; Yao, Yang & Fu Reference Yao, Yang and Fu2021).
$10^5$, as detected by Ponce-Torres et al. (Reference Ponce-Torres, Rubio, Herrada, Eggers and Montanero2020). The one-dimensional (1-D) nonlinear analysis of surfactant-laden viscous threads in the Stokes limit showed that there exists a critical value of the surface Péclet number. Below this critical value, surface diffusion is dominant and the thread thins exponentially in time; above it, surface convection is dominant and the thinning of the thread exhibits a power-law dependence on time until pinch-off (Wee et al. Reference Wee, Wagoner and Basaran2022). In the Stokes limit, the surface viscous stresses enter the dominant force balance and tend to slow down the thinning of Newtonian threads (Ozan & Jakobsen Reference Ozan and Jakobsen2019; Wee et al. Reference Wee, Wagoner, Kamat and Basaran2020). The balance between the capillary force and the surface viscous stresses is established at sufficiently high surfactant surface concentrations, resulting in an asymptotic regime in which the filament thins exponentially in time at a rate only depending on the surface tension and the surface viscosities (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2020). When the inertia is taken into account, the inertial, capillary, bulk viscous and surface viscous forces establish the dominant force balance as the jet nears pinch-off, whereas the Marangoni stress plays a secondary role (Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021). For viscous threads laden with soluble surfactants at concentrations above the CMC, larger secondary droplets are formed due to the Marangoni stress (Craster et al. Reference Craster, Matar and Papageorgiou2009). The study of the surfactant effects has been extended to compound liquid jets (Craster, Matar & Papageorgiou Reference Craster, Matar and Papageorgiou2003; Yao, Yang & Fu Reference Yao, Yang and Fu2021).
Polymer solutions are frequently encountered in applications. They belong to the family of non-Newtonian fluids, possessing rheological properties such as shear thinning and viscoelasticity. A dilute polymer solution can be approximately regarded as a viscoelastic liquid of constant viscosity (Tirtaatmadja, McKinley & Cooper-White Reference Tirtaatmadja, McKinley and Cooper-White2006; James Reference James2009). Thus the elastic effects are separated from the viscous effects, greatly facilitating the study of the viscoelastic liquid dynamics. The linear and nonlinear behaviour of viscoelastic liquid jets and threads has been studied analytically and numerically with the aid of simple viscoelastic models such as Oldroyd-B, Giesekus and finitely extensible nonlinear elastic (Goldin et al. Reference Goldin, Yerushalmi, Pfeffer and Shinnar1969; Goren & Gottlieb Reference Goren and Gottlieb1982; Entov & Hinch Reference Entov and Hinch1997; Chang, Demekhin & Kalaidin Reference Chang, Demekhin and Kalaidin1999; Brenn, Liu & Durst Reference Brenn, Liu and Durst2000; Fontelos & Li Reference Fontelos and Li2004; Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a; Liu & Liu Reference Liu and Liu2006; Eggers & Villermaux Reference Eggers and Villermaux2008; Ardekani, Sharma & Mckinley Reference Ardekani, Sharma and Mckinley2010; Bhat et al. Reference Bhat, Appathurai, Harris, Pasquali, Mckinley and Basaran2010; Ye, Yang & Fu Reference Ye, Yang and Fu2016; Turkoz et al. Reference Turkoz, Lopez-Herrera, Eggers, Arnold and Deike2018; Alsharif Reference Alsharif2019). In the linear regime, viscoelastic jets were found to be more unstable than their Newtonian counterparts when the axial viscoelastic stress in the base flow is relaxed sufficiently far away from the nozzle. In the nonlinear regime, phenomenally different from Newtonian jets, viscoelastic jets evolve into a quasistatic topological structure, i.e. the beads-on-a-string structure, which is characterized by primary droplets connected by a thin filament of almost uniform thickness (sometimes secondary droplets exist in the filament). The pinch-off of viscoelastic liquid threads, if it occurs in finite time, can be greatly delayed by viscoelasticity. Note that the aforementioned viscoelastic models possess a constant viscosity and a single relaxation time and cannot account for the concentration dependence or the conformation dependence of the viscosity or the relaxation time (Beck & Shaqfeh Reference Beck and Shaqfeh2006; Clasen et al. Reference Clasen, Plog, Kulicke, Macosko, Scriven, Verani and Mckinley2006b; Prabhakar, Prakash & Sridhar Reference Prabhakar, Prakash and Sridhar2006; Tirtaatmadja et al. Reference Tirtaatmadja, McKinley and Cooper-White2006; Dinic & Sharma Reference Dinic and Sharma2020; Kumar, Richter & Schroeder Reference Kumar, Richter and Schroeder2020). As a consequence, they may fail to capture accurately the capillary thinning or pinching dynamics of viscoelastic threads observed in experiments. Future theoretical and numerical studies are expected to consider more realistic models.
The addition of soluble surfactants to polymer solutions may introduce additional complexity and difficulty in mathematical formulation and experimental measurement (Martínez Narváez, Mazur & Sharma Reference Martínez Narváez, Mazur and Sharma2021). On the one hand, surfactants may influence the rheological properties of polymer solutions to a certain extent, for example, increasing bulk viscosity and lowering the critical shear rate for the onset of shear thinning.On the other hand, the interaction between polymer molecules and surfactant molecules may lead to the self-aggregation of the latter above the critical aggregation concentration when the bulk concentration of surfactant is sufficiently high. To date, the dynamics of polymer–surfactant association complexes has been rarely reported. An experimental investigation was executed by Dechelette et al. (Reference Dechelette, Campanella, Corvalan and Sojka2011) to examine the combined effect of polymer and soluble surfactant on the jet breakup and secondary droplet formation. It was found that the Marangoni stress may lead to an increase in secondary droplet size at sufficiently high surfactant concentrations.
If the surfactant has a negligible solubility or is insoluble, the interaction between polymer and surfactant molecules can be appropriately neglected. Even for this much simpler case, few studies can be found in the literature addressing the dynamics of surfactant-laden viscoelastic liquid jets or threads. An asymptotic approach based on the slenderness of the jet was used by Alhushaybari & Uddin (Reference Alhushaybari and Uddin2020) to study the absolute and convective instability of a viscoelastic liquid jet falling under the gravity in the presence of insoluble surfactants. They identified the convective/absolute instability boundaries for various parameter regimes. He & Wylie (Reference He and Wylie2021) studied the temporal linear instability of a viscoelastic thread surrounded by another immiscible viscoelastic fluid in the presence of insoluble surfactants. They carried out a detailed parametric study and concluded that the surfactant decreases the growth rates and increases the most unstable wavenumber corresponding to the maximum growth rate.
At the nonlinear stages, viscoelastic liquid jets and threads behave differently from Newtonian ones, particularly the delay of pinch-off and the formation of the beads-on-a-string structure. To our knowledge, the effect of surfactants on the nonlinear characteristics of viscoelastic liquid jets and threads has not yet been reported. In the present work, we build a 1-D model to describe the nonlinear dynamic behaviour of viscoelastic threads in the presence of insoluble surfactants, taking into account the surface rheological effects. A number of 1-D models based on the slender body theory have been developed for clean Newtonian viscous threads, surfactant-laden Newtonian viscous threads or clean viscoelastic threads (Eggers & Villermaux Reference Eggers and Villermaux2008; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). It has been shown that these simplified 1-D models provide reasonable results at a much lower computational cost than the two-dimensional (2-D) and three-dimensional (3-D) numerical simulations.
The paper is organized as follows: in § 2, the theoretical model is described; in § 3, the 1-D equations are derived; in § 4, the dispersion relation for the 1-D linear analysis is derived and a parametric study is performed to examine the effects of the surfactant on the linear and nonlinear behaviour of the viscoelastic thread; finally, in § 5, the main conclusion is drawn.
2. Theoretical description
Consider an infinitely long cylindrical liquid thread of radius ![]() $R$ surrounded by atmospheric air, as sketched in figure 1. The liquid, which is a polymer solution, is incompressible and viscoelastic. Before being perturbed, the thread is quiescent with no base flow, and moreover, the thread surface is covered uniformly with a monolayer of bulk-insoluble surfactant molecules of concentration
$R$ surrounded by atmospheric air, as sketched in figure 1. The liquid, which is a polymer solution, is incompressible and viscoelastic. Before being perturbed, the thread is quiescent with no base flow, and moreover, the thread surface is covered uniformly with a monolayer of bulk-insoluble surfactant molecules of concentration ![]() $\varGamma _0$. The rheological properties of the surfactant, characterized by the surface shear and dilatational viscosities, are taken into account. The hydrodynamic effect of the ambient air is neglected. The effect of the gravitational force, temperature and mass transfer is neglected as well. The cylindrical coordinate system
$\varGamma _0$. The rheological properties of the surfactant, characterized by the surface shear and dilatational viscosities, are taken into account. The hydrodynamic effect of the ambient air is neglected. The effect of the gravitational force, temperature and mass transfer is neglected as well. The cylindrical coordinate system ![]() $(z, r, \theta )$ with
$(z, r, \theta )$ with ![]() $z, r, \theta$ the axial, radial and azimuthal coordinates, respectively, is used to describe the problem. Upon a small-amplitude axisymmetric harmonic disturbance being imposed, the thread begins to deform, whose shape is denoted by
$z, r, \theta$ the axial, radial and azimuthal coordinates, respectively, is used to describe the problem. Upon a small-amplitude axisymmetric harmonic disturbance being imposed, the thread begins to deform, whose shape is denoted by ![]() $r=S(z,t)$. Simultaneously, the surfactant is redistributed along the thread surface, whose concentration is denoted by
$r=S(z,t)$. Simultaneously, the surfactant is redistributed along the thread surface, whose concentration is denoted by ![]() $\varGamma =\varGamma (z,t)$.
$\varGamma =\varGamma (z,t)$.

Figure 1. Schematic of a viscoelastic liquid thread covered with an insoluble surfactant.
The continuity and momentum equations governing the flow field are
 $$\begin{gather}\rho\left(\frac{\partial
v}{\partial t}+v\frac{\partial v}{\partial
r}+u\frac{\partial v}{\partial z}\right)={-}\frac{\partial
p}{\partial r}+\eta_s\left(\frac{\partial^2 v}{\partial
r^2}+\frac{1}{r}\frac{\partial v}{\partial
r}-\frac{v}{r^2}+\frac{\partial^2 v}{\partial
z^2}\right)\nonumber\\
\qquad \qquad \qquad\qquad +\frac{\partial \tau_{rr}}{\partial
r}+\frac{\partial \tau_{rz}}{\partial
z}+\frac{\tau_{rr}-\tau_{\theta\theta}}{r},
\end{gather}$$
$$\begin{gather}\rho\left(\frac{\partial
v}{\partial t}+v\frac{\partial v}{\partial
r}+u\frac{\partial v}{\partial z}\right)={-}\frac{\partial
p}{\partial r}+\eta_s\left(\frac{\partial^2 v}{\partial
r^2}+\frac{1}{r}\frac{\partial v}{\partial
r}-\frac{v}{r^2}+\frac{\partial^2 v}{\partial
z^2}\right)\nonumber\\
\qquad \qquad \qquad\qquad +\frac{\partial \tau_{rr}}{\partial
r}+\frac{\partial \tau_{rz}}{\partial
z}+\frac{\tau_{rr}-\tau_{\theta\theta}}{r},
\end{gather}$$
where ![]() $u$ and
$u$ and ![]() $v$ are the axial and radial components of the velocity vector
$v$ are the axial and radial components of the velocity vector ![]() $\boldsymbol {u}$, respectively,
$\boldsymbol {u}$, respectively, ![]() $\rho$ is the density of the polymer solution,
$\rho$ is the density of the polymer solution, ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $\eta _s$ is the contribution of the solvent to the viscosity and
$\eta _s$ is the contribution of the solvent to the viscosity and ![]() $\tau _{zz}, \tau _{rr}, \tau _{rz}$ and
$\tau _{zz}, \tau _{rr}, \tau _{rz}$ and ![]() $\tau _{\theta \theta }$ are the components of the polymer stress tensor
$\tau _{\theta \theta }$ are the components of the polymer stress tensor ![]() $\boldsymbol {\tau }_p$ which, in the form of a matrix, is
$\boldsymbol {\tau }_p$ which, in the form of a matrix, is
 \begin{equation} \boldsymbol{\tau}_p=\left( \begin{array}{@{}ccc@{}} \tau_{zz} & \tau_{rz} & 0 \\ \tau_{rz} & \tau_{rr} & 0 \\ 0 & 0 & \tau_{\theta\theta} \\ \end{array} \right). \end{equation}
\begin{equation} \boldsymbol{\tau}_p=\left( \begin{array}{@{}ccc@{}} \tau_{zz} & \tau_{rz} & 0 \\ \tau_{rz} & \tau_{rr} & 0 \\ 0 & 0 & \tau_{\theta\theta} \\ \end{array} \right). \end{equation}The viscoelasticity of the liquid is assumed to be described by the FENE-P (finitely extensible nonlinear elastic-Peterlin approximation) constitutive equation (Fontelos & Li Reference Fontelos and Li2004)
 \begin{equation} \boldsymbol{\tau}_p=\frac{\eta_p}{\lambda_c}\left( \frac{{{\boldsymbol{\mathsf{A}}}}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}- {{\boldsymbol{\mathsf{I}}}}\right),\end{equation}
\begin{equation} \boldsymbol{\tau}_p=\frac{\eta_p}{\lambda_c}\left( \frac{{{\boldsymbol{\mathsf{A}}}}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}- {{\boldsymbol{\mathsf{I}}}}\right),\end{equation}
where ![]() $\eta _p$ is the contribution of the polymer to the viscosity,
$\eta _p$ is the contribution of the polymer to the viscosity, ![]() $\lambda _c$ is the stress relaxation time,
$\lambda _c$ is the stress relaxation time, ![]() $L$ is the finite extensibility parameter,
$L$ is the finite extensibility parameter, ![]() ${{\boldsymbol{\mathsf{I}}}}$ is the identity tensor,
${{\boldsymbol{\mathsf{I}}}}$ is the identity tensor, ![]() ${{\boldsymbol{\mathsf{A}}}}$ is the conformation tensor whose components are
${{\boldsymbol{\mathsf{A}}}}$ is the conformation tensor whose components are
 \begin{equation} {{\boldsymbol{\mathsf{A}}}}=\left( \begin{array}{@{}ccc@{}} A_{zz} & A_{rz} & 0 \\ A_{rz} & A_{rr} & 0 \\ 0 & 0 & A_{\theta\theta} \\ \end{array} \right), \end{equation}
\begin{equation} {{\boldsymbol{\mathsf{A}}}}=\left( \begin{array}{@{}ccc@{}} A_{zz} & A_{rz} & 0 \\ A_{rz} & A_{rr} & 0 \\ 0 & 0 & A_{\theta\theta} \\ \end{array} \right), \end{equation}
and ![]() $tr({{\boldsymbol{\mathsf{A}}}})$ is the trace of
$tr({{\boldsymbol{\mathsf{A}}}})$ is the trace of ![]() ${{\boldsymbol{\mathsf{A}}}}$. The four non-zero components of
${{\boldsymbol{\mathsf{A}}}}$. The four non-zero components of ![]() ${{\boldsymbol{\mathsf{A}}}}$ are governed by
${{\boldsymbol{\mathsf{A}}}}$ are governed by
 $$\begin{gather} \frac{\partial A_{zz}}{\partial t} +v\frac{\partial A_{zz}}{\partial r}+u\frac{\partial A_{zz}}{\partial z}=2\frac{\partial u}{\partial z} A_{zz}+2\frac{\partial u}{\partial r}A_{rz}+\frac{1}{\lambda_c}\left(1-\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
$$\begin{gather} \frac{\partial A_{zz}}{\partial t} +v\frac{\partial A_{zz}}{\partial r}+u\frac{\partial A_{zz}}{\partial z}=2\frac{\partial u}{\partial z} A_{zz}+2\frac{\partial u}{\partial r}A_{rz}+\frac{1}{\lambda_c}\left(1-\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$ $$\begin{gather}\frac{\partial A_{rr}}{\partial t} +v\frac{\partial A_{rr}}{\partial r}+u\frac{\partial A_{rr}}{\partial z}=2\frac{\partial v}{\partial r} A_{rr}+2\frac{\partial v}{\partial z}A_{rz}+\frac{1}{\lambda_c}\left(1-\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
$$\begin{gather}\frac{\partial A_{rr}}{\partial t} +v\frac{\partial A_{rr}}{\partial r}+u\frac{\partial A_{rr}}{\partial z}=2\frac{\partial v}{\partial r} A_{rr}+2\frac{\partial v}{\partial z}A_{rz}+\frac{1}{\lambda_c}\left(1-\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$ $$\begin{gather}\frac{\partial A_{\theta\theta}}{\partial t} +v\frac{\partial A_{\theta\theta}}{\partial r}+u\frac{\partial A_{\theta\theta}}{\partial z}=2\frac{v}{r} A_{\theta\theta}+\frac{1}{\lambda_c}\left(1- \dfrac{A_{\theta\theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
$$\begin{gather}\frac{\partial A_{\theta\theta}}{\partial t} +v\frac{\partial A_{\theta\theta}}{\partial r}+u\frac{\partial A_{\theta\theta}}{\partial z}=2\frac{v}{r} A_{\theta\theta}+\frac{1}{\lambda_c}\left(1- \dfrac{A_{\theta\theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$ $$\begin{gather}\frac{\partial A_{rz}}{\partial t} +v\frac{\partial A_{rz}}{\partial r}+u\frac{\partial A_{rz}}{\partial z}=\frac{\partial v}{\partial z} A_{zz}+\frac{\partial u}{\partial r}-\frac{v}{r}A_{rz}+\frac{1}{\lambda_c}\left(-\frac{A_{rz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right). \end{gather}$$
$$\begin{gather}\frac{\partial A_{rz}}{\partial t} +v\frac{\partial A_{rz}}{\partial r}+u\frac{\partial A_{rz}}{\partial z}=\frac{\partial v}{\partial z} A_{zz}+\frac{\partial u}{\partial r}-\frac{v}{r}A_{rz}+\frac{1}{\lambda_c}\left(-\frac{A_{rz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right). \end{gather}$$ The surfactant concentration ![]() $\varGamma$ is governed by the time-dependent advection–diffusion equation (Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018)
$\varGamma$ is governed by the time-dependent advection–diffusion equation (Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018)
 \begin{equation} \frac{\partial \varGamma}{\partial t}+u\frac{\partial \varGamma}{\partial z}+\frac{\varGamma}{S\sqrt{1+S'^2}}\frac{\partial(Su_t)}{\partial z}+\mathcal{C} \varGamma u_n=\frac{D_s}{S\sqrt{1+S'^2}}\frac{\partial \left(\dfrac{S\varGamma'}{\sqrt{1+S'^2}}\right) }{\partial z}, \end{equation}
\begin{equation} \frac{\partial \varGamma}{\partial t}+u\frac{\partial \varGamma}{\partial z}+\frac{\varGamma}{S\sqrt{1+S'^2}}\frac{\partial(Su_t)}{\partial z}+\mathcal{C} \varGamma u_n=\frac{D_s}{S\sqrt{1+S'^2}}\frac{\partial \left(\dfrac{S\varGamma'}{\sqrt{1+S'^2}}\right) }{\partial z}, \end{equation}
where the prime ![]() $'$ denotes the partial derivative with respect to
$'$ denotes the partial derivative with respect to ![]() $z, D_s$ is the surface diffusion coefficient of the surfactant,
$z, D_s$ is the surface diffusion coefficient of the surfactant, ![]() $u_n$ and
$u_n$ and ![]() $u_t$ are the normal and tangential components of the velocity at the surface, i.e.
$u_t$ are the normal and tangential components of the velocity at the surface, i.e.
and ![]() $\mathcal {C}$ is the mean curvature given by
$\mathcal {C}$ is the mean curvature given by
with ![]() $''$ denoting the second-order derivative with respective to
$''$ denoting the second-order derivative with respective to ![]() $z$.
$z$.
At the thread surface ![]() $r=S(z,t)$, the kinematic condition must be satisfied, i.e.
$r=S(z,t)$, the kinematic condition must be satisfied, i.e.
and the force balance requires
where ![]() ${{\boldsymbol{\mathsf{T}}}}=-p{{\boldsymbol{\mathsf{I}}}}+\eta _s[\boldsymbol {\nabla }\boldsymbol {u} +(\boldsymbol {\nabla }\boldsymbol {u})^T]+\boldsymbol \tau _p$ is the stress tensor from the liquid phase but evaluated at the thread surface (the superscript
${{\boldsymbol{\mathsf{T}}}}=-p{{\boldsymbol{\mathsf{I}}}}+\eta _s[\boldsymbol {\nabla }\boldsymbol {u} +(\boldsymbol {\nabla }\boldsymbol {u})^T]+\boldsymbol \tau _p$ is the stress tensor from the liquid phase but evaluated at the thread surface (the superscript ![]() $T$ indicates the transpose),
$T$ indicates the transpose), ![]() $\boldsymbol n$ is the unit outward vector normal to the surface,
$\boldsymbol n$ is the unit outward vector normal to the surface, ![]() $\nabla _s$ is the surface gradient operator defined as
$\nabla _s$ is the surface gradient operator defined as ![]() $\nabla _s={{\boldsymbol{\mathsf{I}}}}_s\boldsymbol {\cdot }\boldsymbol {\nabla }=({{\boldsymbol{\mathsf{I}}}}-\boldsymbol n \boldsymbol n)\boldsymbol {\cdot }\boldsymbol {\nabla }$ and
$\nabla _s={{\boldsymbol{\mathsf{I}}}}_s\boldsymbol {\cdot }\boldsymbol {\nabla }=({{\boldsymbol{\mathsf{I}}}}-\boldsymbol n \boldsymbol n)\boldsymbol {\cdot }\boldsymbol {\nabla }$ and ![]() ${{\boldsymbol{\mathsf{T}}}}_s$ is the surface stress tensor modelled by the Boussinesq–Scriven approximation (Boussinesq Reference Boussinesq1913; Scriven Reference Scriven1960; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018)
${{\boldsymbol{\mathsf{T}}}}_s$ is the surface stress tensor modelled by the Boussinesq–Scriven approximation (Boussinesq Reference Boussinesq1913; Scriven Reference Scriven1960; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018)
where ![]() $\kappa _s$ and
$\kappa _s$ and ![]() $\mu _s$ are the surface dilatational and shear viscosities, respectively,
$\mu _s$ are the surface dilatational and shear viscosities, respectively, ![]() $\boldsymbol {u}_s$ is the velocity of the polymer solution at the surface and
$\boldsymbol {u}_s$ is the velocity of the polymer solution at the surface and ![]() $\sigma$ is the surface tension coefficient (hereafter, it is called the surface tension for short). Note that
$\sigma$ is the surface tension coefficient (hereafter, it is called the surface tension for short). Note that ![]() $\kappa _s, \mu _s$ and
$\kappa _s, \mu _s$ and ![]() $\sigma$ are all functions of the local surfactant concentration
$\sigma$ are all functions of the local surfactant concentration ![]() $\varGamma$. We simply assume that
$\varGamma$. We simply assume that ![]() $\kappa _s$ and
$\kappa _s$ and ![]() $\mu _s$ are linearly dependent on
$\mu _s$ are linearly dependent on ![]() $\varGamma$ (Ponce-Torres et al. Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021), i.e.
$\varGamma$ (Ponce-Torres et al. Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021), i.e.
where the subscript ![]() $r$ denotes the reference values. The dependence of the surface tension
$r$ denotes the reference values. The dependence of the surface tension ![]() $\sigma$ on the surfactant surface concentration
$\sigma$ on the surfactant surface concentration ![]() $\varGamma$ is assumed to be described by the Langmuir equation of state (Liao et al. Reference Liao, Franses and Basaran2006; Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021)
$\varGamma$ is assumed to be described by the Langmuir equation of state (Liao et al. Reference Liao, Franses and Basaran2006; Hameed et al. Reference Hameed, Siegal, Young, Li, Booty and Papageorgiou2008; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021)
where ![]() $\sigma _0$ is the surface tension of the clean surface,
$\sigma _0$ is the surface tension of the clean surface, ![]() $R_g$ is the universal gas constant,
$R_g$ is the universal gas constant, ![]() $T$ is the absolute temperature and
$T$ is the absolute temperature and ![]() $\varGamma _{\infty }$ is the maximum packing concentration of the surfactant. Introducing the surface pressure
$\varGamma _{\infty }$ is the maximum packing concentration of the surfactant. Introducing the surface pressure ![]() $\varPi (\varGamma )=\sigma _0-\sigma (\varGamma )$, the combination of (2.17a,b) and (2.18) gives the following dependence
$\varPi (\varGamma )=\sigma _0-\sigma (\varGamma )$, the combination of (2.17a,b) and (2.18) gives the following dependence
As a matter of fact, the dependence of the surface viscosities on the surface pressure diverges. For instance, it was found in the experiments that the surface shear viscosity ![]() $\mu _s$ often increases exponentially with the surface pressure
$\mu _s$ often increases exponentially with the surface pressure ![]() $\varPi$ (Fuller & Vermant Reference Fuller and Vermant2012; Manikantan & Squires Reference Manikantan and Squires2020). The
$\varPi$ (Fuller & Vermant Reference Fuller and Vermant2012; Manikantan & Squires Reference Manikantan and Squires2020). The ![]() $\varPi$-dependent surface viscosities have been shown to lead to surprising consequences in lubrication flows and affect significantly the deformation and breakup of droplets (Manikantan & Squires Reference Manikantan and Squires2017; Singh & Narsimhan Reference Singh and Narsimhan2021, Reference Singh and Narsimhan2022; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022). They may also affect the dynamics of liquid jets and threads, which remains an open problem to be explored.
$\varPi$-dependent surface viscosities have been shown to lead to surprising consequences in lubrication flows and affect significantly the deformation and breakup of droplets (Manikantan & Squires Reference Manikantan and Squires2017; Singh & Narsimhan Reference Singh and Narsimhan2021, Reference Singh and Narsimhan2022; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022). They may also affect the dynamics of liquid jets and threads, which remains an open problem to be explored.
The substitution of (2.16) into (2.15) yields
 \begin{align} &-{{\boldsymbol{\mathsf{T}}}}\boldsymbol{\cdot}{\boldsymbol n}+\nabla_s \sigma-{\boldsymbol n}(\nabla_s \boldsymbol{\cdot} {\boldsymbol n}) \sigma+\nabla_s \left[(\kappa_s-\mu_s)(\nabla_s\boldsymbol{\cdot} {\boldsymbol u}_s)\right]\nonumber\\ &\quad -{\boldsymbol n}(\nabla_s \boldsymbol{\cdot} {\boldsymbol n})(\kappa_s-\mu_s)(\nabla_s\boldsymbol{\cdot}{\boldsymbol u}_s)+\nabla_s\boldsymbol{\cdot}\left\{\mu_s\left[(\nabla_s{\boldsymbol u}_s)\boldsymbol{\cdot} {\boldsymbol I}_s+ {\boldsymbol I}_s\boldsymbol{\cdot} (\nabla_s {\boldsymbol u}_s)^T\right]\right\}=0. \end{align}
\begin{align} &-{{\boldsymbol{\mathsf{T}}}}\boldsymbol{\cdot}{\boldsymbol n}+\nabla_s \sigma-{\boldsymbol n}(\nabla_s \boldsymbol{\cdot} {\boldsymbol n}) \sigma+\nabla_s \left[(\kappa_s-\mu_s)(\nabla_s\boldsymbol{\cdot} {\boldsymbol u}_s)\right]\nonumber\\ &\quad -{\boldsymbol n}(\nabla_s \boldsymbol{\cdot} {\boldsymbol n})(\kappa_s-\mu_s)(\nabla_s\boldsymbol{\cdot}{\boldsymbol u}_s)+\nabla_s\boldsymbol{\cdot}\left\{\mu_s\left[(\nabla_s{\boldsymbol u}_s)\boldsymbol{\cdot} {\boldsymbol I}_s+ {\boldsymbol I}_s\boldsymbol{\cdot} (\nabla_s {\boldsymbol u}_s)^T\right]\right\}=0. \end{align}After some algebraic operations, the force balance in the normal direction is written as
 \begin{align} &p-\frac{1}{1+S'^2}\left[2\eta_s\frac{\partial v}{\partial r}-2\eta_s\left(\frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)+2\eta_s S'^2\frac{\partial u}{\partial z}+S'^2\tau_{zz}-2S'\tau_{rz}+\tau_{rr}\right]\nonumber\\ &\quad=\mathcal{C}\left[\sigma+(\kappa_s-\mu_s) \left(\frac{(Su_t)'}{S\sqrt{1+S'^2}}+\mathcal{C} u_n\right)\right]\nonumber\\ &\qquad+\frac{2\mu_s}{1+S'^2}\left[\frac{S'u_t+u_n}{S^2}- \frac{S''}{1+S'^2}\left(\frac{\partial (u_t)}{\partial z}-\frac{S''u_n}{1+S'^2}\right)\right], \end{align}
\begin{align} &p-\frac{1}{1+S'^2}\left[2\eta_s\frac{\partial v}{\partial r}-2\eta_s\left(\frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)+2\eta_s S'^2\frac{\partial u}{\partial z}+S'^2\tau_{zz}-2S'\tau_{rz}+\tau_{rr}\right]\nonumber\\ &\quad=\mathcal{C}\left[\sigma+(\kappa_s-\mu_s) \left(\frac{(Su_t)'}{S\sqrt{1+S'^2}}+\mathcal{C} u_n\right)\right]\nonumber\\ &\qquad+\frac{2\mu_s}{1+S'^2}\left[\frac{S'u_t+u_n}{S^2}- \frac{S''}{1+S'^2}\left(\frac{\partial (u_t)}{\partial z}-\frac{S''u_n}{1+S'^2}\right)\right], \end{align}and in the tangential direction as
 \begin{align}
&\frac{1}{\sqrt{1+S'^2}}\left[2\eta_sS'\left(\frac{\partial
v}{\partial r}-\frac{\partial u}{\partial
z}\right)+\eta_s\left(1-S'^2\right)\left(\frac{\partial
v}{\partial z}+\frac{\partial u}{\partial
r}\right)\right.\nonumber\\
&\quad +\left.S'\left(\tau_{rr}-\tau_{zz}\right)
+(1-S'^2)\tau_{rz}\right]\nonumber\\
&\quad =\frac{\partial \sigma}{\partial z}+\frac{\partial }{\partial
z}\left[(\kappa_s-\mu_s)\left(\frac{(Su_t)'}{S\sqrt{1+S'^2}}+\mathcal{C}
u_n\right)\right]\nonumber\\
&\qquad +\frac{\sqrt{1+S'^2}}{S}\frac{\partial }{\partial
z}\left[\frac{2\mu_sS}{1+S'^2}\left(\frac{\partial
u_t}{\partial z}-\frac{u_nS''}{1+S'^2}\right)\right]\nonumber\\
&\qquad-\frac{2\mu_sS'}{\sqrt{1+S'^2}}\left[\frac{S'u_t+u_n}{S^2}-
\frac{S''}{1+S'^2}\left(\frac{\partial u_t}{\partial
z}-\frac{S'' u_n}{1+S'^2}\right)\right].
\end{align}
\begin{align}
&\frac{1}{\sqrt{1+S'^2}}\left[2\eta_sS'\left(\frac{\partial
v}{\partial r}-\frac{\partial u}{\partial
z}\right)+\eta_s\left(1-S'^2\right)\left(\frac{\partial
v}{\partial z}+\frac{\partial u}{\partial
r}\right)\right.\nonumber\\
&\quad +\left.S'\left(\tau_{rr}-\tau_{zz}\right)
+(1-S'^2)\tau_{rz}\right]\nonumber\\
&\quad =\frac{\partial \sigma}{\partial z}+\frac{\partial }{\partial
z}\left[(\kappa_s-\mu_s)\left(\frac{(Su_t)'}{S\sqrt{1+S'^2}}+\mathcal{C}
u_n\right)\right]\nonumber\\
&\qquad +\frac{\sqrt{1+S'^2}}{S}\frac{\partial }{\partial
z}\left[\frac{2\mu_sS}{1+S'^2}\left(\frac{\partial
u_t}{\partial z}-\frac{u_nS''}{1+S'^2}\right)\right]\nonumber\\
&\qquad-\frac{2\mu_sS'}{\sqrt{1+S'^2}}\left[\frac{S'u_t+u_n}{S^2}-
\frac{S''}{1+S'^2}\left(\frac{\partial u_t}{\partial
z}-\frac{S'' u_n}{1+S'^2}\right)\right].
\end{align}3. One-dimensional model
If the radius of the perturbed thread varies gradually along the axial direction, the thread can be considered as a slender body and a 1-D analysis can be applied (Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a; Eggers & Villermaux Reference Eggers and Villermaux2008). The equations for the 1-D model are derived in Appendix A. Taking the thread radius ![]() $R$, the capillary time
$R$, the capillary time ![]() $t_c=\sqrt {\rho R^3/\sigma _0}$, the zero-shear viscosity
$t_c=\sqrt {\rho R^3/\sigma _0}$, the zero-shear viscosity ![]() $\eta _0=\eta _s+\eta _p$, the surface tension of the clear surface
$\eta _0=\eta _s+\eta _p$, the surface tension of the clear surface ![]() $\sigma _0$, the capillary force
$\sigma _0$, the capillary force ![]() $\sigma _0/R$ and the maximum packing concentration of the surfactant
$\sigma _0/R$ and the maximum packing concentration of the surfactant ![]() $\varGamma _\infty$ as the scales of length, time, viscosity, surface tension, pressure and surfactant concentration, respectively, the 1-D equations are non-dimensionalized as
$\varGamma _\infty$ as the scales of length, time, viscosity, surface tension, pressure and surfactant concentration, respectively, the 1-D equations are non-dimensionalized as
 \begin{gather}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial
z}= \frac{3\beta
Oh}{S^2}\frac{\partial\left(S^2\dfrac{\partial u}{\partial
z}\right)}{\partial z}+\frac{1}{S^2}
\frac{\partial\left[S^2\left(\tau_{zz}-\tau_{rr}
\right)\right]}{\partial z}\nonumber\\
-\frac{\partial}{\partial
z}\left\{\mathcal{C}\left[\sigma+\frac{Oh\left(\kappa_s-\mu_s\right)}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial
z}\right)\right]\right\}\nonumber\\
{\bigcirc{\kern-6pt 1}} \qquad \ \qquad \qquad {\bigcirc{\kern-6pt 2}} \nonumber\\
+\frac{2}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial
z}\left[\frac{Oh(\kappa_s-\mu_s)}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial z}\right)\right]\right\}\nonumber\\
\qquad {\bigcirc{\kern-6pt 3}} \qquad \ \ \qquad \qquad \qquad {\bigcirc{\kern-6pt 4}} \nonumber\\
+\frac{5Oh}{S^2}\frac{\partial }{\partial
z}\left(\mu_sS\frac{\partial u}{\partial z}\right), \nonumber\\
\qquad \quad \ {\bigcirc{\kern-6pt 5}}
\end{gather}
\begin{gather}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial
z}= \frac{3\beta
Oh}{S^2}\frac{\partial\left(S^2\dfrac{\partial u}{\partial
z}\right)}{\partial z}+\frac{1}{S^2}
\frac{\partial\left[S^2\left(\tau_{zz}-\tau_{rr}
\right)\right]}{\partial z}\nonumber\\
-\frac{\partial}{\partial
z}\left\{\mathcal{C}\left[\sigma+\frac{Oh\left(\kappa_s-\mu_s\right)}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial
z}\right)\right]\right\}\nonumber\\
{\bigcirc{\kern-6pt 1}} \qquad \ \qquad \qquad {\bigcirc{\kern-6pt 2}} \nonumber\\
+\frac{2}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial
z}\left[\frac{Oh(\kappa_s-\mu_s)}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial z}\right)\right]\right\}\nonumber\\
\qquad {\bigcirc{\kern-6pt 3}} \qquad \ \ \qquad \qquad \qquad {\bigcirc{\kern-6pt 4}} \nonumber\\
+\frac{5Oh}{S^2}\frac{\partial }{\partial
z}\left(\mu_sS\frac{\partial u}{\partial z}\right), \nonumber\\
\qquad \quad \ {\bigcirc{\kern-6pt 5}}
\end{gather} $$\begin{gather} \tau_{zz}=\frac{(1-\beta)Oh}{De}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather} \tau_{zz}=\frac{(1-\beta)Oh}{De}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{rr}=\frac{(1-\beta)Oh}{De}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{rr}=\frac{(1-\beta)Oh}{De}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{zz}}{\partial t}+u\frac{\partial A_{zz}}{\partial z}-2 A_{zz}\frac{\partial u}{\partial z}\right) =1-\frac{A_{zz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{zz}}{\partial t}+u\frac{\partial A_{zz}}{\partial z}-2 A_{zz}\frac{\partial u}{\partial z}\right) =1-\frac{A_{zz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{rr}}{\partial t}+u\frac{\partial A_{rr}}{\partial z}+ A_{rr}\frac{\partial u}{\partial z}\right)=1-\frac{A_{rr}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{rr}}{\partial t}+u\frac{\partial A_{rr}}{\partial z}+ A_{rr}\frac{\partial u}{\partial z}\right)=1-\frac{A_{rr}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}\frac{\partial \varGamma}{\partial t}+\frac{1}{S}\frac{\partial (Su\varGamma)}{\partial z}-\frac{\mathcal{C} \varGamma}{2S}\frac{\partial (S^2u)}{\partial z}=\frac{1}{Pe}\frac{1}{S}\frac{\partial \left(S\dfrac{\partial \varGamma}{\partial z}\right)}{\partial z}, \end{gather}$$
$$\begin{gather}\frac{\partial \varGamma}{\partial t}+\frac{1}{S}\frac{\partial (Su\varGamma)}{\partial z}-\frac{\mathcal{C} \varGamma}{2S}\frac{\partial (S^2u)}{\partial z}=\frac{1}{Pe}\frac{1}{S}\frac{\partial \left(S\dfrac{\partial \varGamma}{\partial z}\right)}{\partial z}, \end{gather}$$where
 $$\begin{gather}\mathcal{C}=\frac{1}{S\sqrt{1+\left(\dfrac{\partial S}{\partial z}\right)^2}}-\frac{\dfrac{\partial^2S}{\partial z^2}}{\left[1+\left(\dfrac{\partial S}{\partial z}\right)^2\right]^{3/2}}, \end{gather}$$
$$\begin{gather}\mathcal{C}=\frac{1}{S\sqrt{1+\left(\dfrac{\partial S}{\partial z}\right)^2}}-\frac{\dfrac{\partial^2S}{\partial z^2}}{\left[1+\left(\dfrac{\partial S}{\partial z}\right)^2\right]^{3/2}}, \end{gather}$$
Note that the same symbols are used to denote both the dimensional and the dimensionless quantities for brevity. The dimensionless numbers appearing in the above 1-D equations are the Ohnesorge number ![]() $Oh={\eta _0}/{\sqrt {\rho \sigma _0R}}$ representing the relative importance of bulk viscosity and capillarity, the solvent to solution viscosity ratio
$Oh={\eta _0}/{\sqrt {\rho \sigma _0R}}$ representing the relative importance of bulk viscosity and capillarity, the solvent to solution viscosity ratio ![]() $\beta ={\eta _s}/{\eta _0}$, the Deborah number
$\beta ={\eta _s}/{\eta _0}$, the Deborah number ![]() $De={\lambda _c}/{t_c}$ measuring the relative importance of elasticity and capillarity, the surface Péclet number
$De={\lambda _c}/{t_c}$ measuring the relative importance of elasticity and capillarity, the surface Péclet number ![]() $Pe={R^2}/{t_c D_s}$ measuring the relative importance of surface convection and surface diffusion in surfactant transport, the elasticity number
$Pe={R^2}/{t_c D_s}$ measuring the relative importance of surface convection and surface diffusion in surfactant transport, the elasticity number ![]() $E={R_gT\varGamma _{\infty }}/{\sigma _0}$ measuring the activity of the surfactant or the sensitivity of the surface tension to changes in the surfactant concentration (in order to distinguish from the elasticity of the viscoelastic liquid, hereafter it is called the Marangoni number, as referred to in Ponce-Torres et al. Reference Ponce-Torres, Herrada, Montanero and Vega2016; Martínez-Calvo et al. Reference Martínez-Calvo, Rivero-Rodríguez, Scheid and Sevilla2020; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022) and the dilatational Boussinesq number
$E={R_gT\varGamma _{\infty }}/{\sigma _0}$ measuring the activity of the surfactant or the sensitivity of the surface tension to changes in the surfactant concentration (in order to distinguish from the elasticity of the viscoelastic liquid, hereafter it is called the Marangoni number, as referred to in Ponce-Torres et al. Reference Ponce-Torres, Herrada, Montanero and Vega2016; Martínez-Calvo et al. Reference Martínez-Calvo, Rivero-Rodríguez, Scheid and Sevilla2020; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022) and the dilatational Boussinesq number ![]() $B_{\kappa \infty }={\kappa _s(\varGamma =\varGamma _\infty )}/{\eta _0 R}=({\kappa _{sr}}/{\eta _0 R})({\varGamma _\infty }/{\varGamma _r})$ and the shear Boussinesq number
$B_{\kappa \infty }={\kappa _s(\varGamma =\varGamma _\infty )}/{\eta _0 R}=({\kappa _{sr}}/{\eta _0 R})({\varGamma _\infty }/{\varGamma _r})$ and the shear Boussinesq number ![]() $B_{\mu \infty }={\mu _s(\varGamma =\varGamma _\infty )}/{\eta _0 R}=({\mu _{sr}}/{\eta _0 R})({\varGamma _\infty }/{\varGamma _r})$ measuring the relative importance of surface and bulk viscosities.
$B_{\mu \infty }={\mu _s(\varGamma =\varGamma _\infty )}/{\eta _0 R}=({\mu _{sr}}/{\eta _0 R})({\varGamma _\infty }/{\varGamma _r})$ measuring the relative importance of surface and bulk viscosities.
Equation (3.1) expresses the volume conservation, (3.2) is the 1-D momentum equation, (3.3)–(3.6) are the constitutive equations for the FENE-P viscoelastic model and (3.7) expresses the surfactant mass conservation. On the right-hand side of (3.2), the first term is the viscous force from the solvent, the second term is the viscoelastic force from the polymer and the rest of the terms, numbered ![]() ${\bigcirc{\kern-6pt 1}}$–
${\bigcirc{\kern-6pt 1}}$–![]() ${\bigcirc{\kern-6pt 5}}$, are all related to the surfactant, indicating that the surfactant influences the nonlinear dynamics of the viscoelastic thread in a complicated way. Specifically, term
${\bigcirc{\kern-6pt 5}}$, are all related to the surfactant, indicating that the surfactant influences the nonlinear dynamics of the viscoelastic thread in a complicated way. Specifically, term ![]() ${\bigcirc{\kern-6pt 1}}$ is the capillary force, term
${\bigcirc{\kern-6pt 1}}$ is the capillary force, term ![]() ${\bigcirc{\kern-6pt 3}}$ is the Marangoni stress resulting from the spatial non-uniformity of the surface tension and terms
${\bigcirc{\kern-6pt 3}}$ is the Marangoni stress resulting from the spatial non-uniformity of the surface tension and terms ![]() ${\bigcirc{\kern-6pt 2}}$,
${\bigcirc{\kern-6pt 2}}$, ![]() ${\bigcirc{\kern-6pt 4}}$ and
${\bigcirc{\kern-6pt 4}}$ and ![]() ${\bigcirc{\kern-6pt 5}}$ are the surface viscous stresses associated with surface dilatational and shear deformations. If the surface dilatational viscosity
${\bigcirc{\kern-6pt 5}}$ are the surface viscous stresses associated with surface dilatational and shear deformations. If the surface dilatational viscosity ![]() $\kappa _s$ is equal to the surface shear viscosity
$\kappa _s$ is equal to the surface shear viscosity ![]() $\mu _s$, both term
$\mu _s$, both term ![]() ${\bigcirc{\kern-6pt 2}}$ and term
${\bigcirc{\kern-6pt 2}}$ and term ![]() ${\bigcirc{\kern-6pt 4}}$ vanish and the momentum equation (3.2) is, fortunately, reduced. On the left-hand side of (3.7), the full curvature is preserved. If the slender body approximation is considered, (3.7) is simplified as
${\bigcirc{\kern-6pt 4}}$ vanish and the momentum equation (3.2) is, fortunately, reduced. On the left-hand side of (3.7), the full curvature is preserved. If the slender body approximation is considered, (3.7) is simplified as
 \begin{equation} \frac{\partial(\varGamma^2)}{\partial t}+\frac{\partial(\varGamma^2u)}{\partial z}=\frac{2}{Pe}\frac{\varGamma}{S}\frac{\partial \left(S\dfrac{\partial \varGamma}{\partial z}\right)}{\partial z}. \end{equation}
\begin{equation} \frac{\partial(\varGamma^2)}{\partial t}+\frac{\partial(\varGamma^2u)}{\partial z}=\frac{2}{Pe}\frac{\varGamma}{S}\frac{\partial \left(S\dfrac{\partial \varGamma}{\partial z}\right)}{\partial z}. \end{equation} When the finite extensibility ![]() $L$ approaches infinity (polymer chains are infinitely extensible), the Oldroyd-B viscoelastic model is recovered, for which (3.1) and (3.2) and (3.7) remain unchanged, but the constitutive equations (3.3)–(3.6) reduce to
$L$ approaches infinity (polymer chains are infinitely extensible), the Oldroyd-B viscoelastic model is recovered, for which (3.1) and (3.2) and (3.7) remain unchanged, but the constitutive equations (3.3)–(3.6) reduce to
If the Deborah number is set to be zero, the 1-D model reduces to that for Newtonian viscous liquid threads covered with insoluble surfactants, as proposed by Martínez-Calvo & Sevilla (Reference Martínez-Calvo and Sevilla2018) and Wee et al. (Reference Wee, Wagoner, Garg, Kamat and Basaran2021). In addition, if the surfactant concentration ![]() $\varGamma$ is set to zero, the 1-D model reduces to that for surfactant-free viscoelastic threads of FENE-P type as built in Fontelos & Li (Reference Fontelos and Li2004).
$\varGamma$ is set to zero, the 1-D model reduces to that for surfactant-free viscoelastic threads of FENE-P type as built in Fontelos & Li (Reference Fontelos and Li2004).
4. Numerical results
The 1-D equations (3.1)–(3.7) are solved by using an implicit finite difference scheme with adaptive mesh refinement (Li & He Reference Li and He2021). Considering both accuracy and efficiency, the number of spatial discrete points is ![]() $1000$–
$1000$–![]() $1600$, and the time step varies between
$1600$, and the time step varies between ![]() $10^{-6}$ and
$10^{-6}$ and ![]() $0.005$. The convergence condition at each time step is that the maximum relative error is below
$0.005$. The convergence condition at each time step is that the maximum relative error is below ![]() $0.001$. The calculation stops when the dimensionless minimum radius of the thread is less than 0.001. The validity of the code is checked by comparing with the results in Fontelos & Li (Reference Fontelos and Li2004), Li & He (Reference Li and He2021) and Wee et al. (Reference Wee, Wagoner, Garg, Kamat and Basaran2021).
$0.001$. The calculation stops when the dimensionless minimum radius of the thread is less than 0.001. The validity of the code is checked by comparing with the results in Fontelos & Li (Reference Fontelos and Li2004), Li & He (Reference Li and He2021) and Wee et al. (Reference Wee, Wagoner, Garg, Kamat and Basaran2021).
At the initial time ![]() $t=0$, the thread is perturbed by a small cosinusoidal harmonic disturbance, i.e.
$t=0$, the thread is perturbed by a small cosinusoidal harmonic disturbance, i.e.
where ![]() $k$ is the dimensionless axial wavenumber and
$k$ is the dimensionless axial wavenumber and ![]() $\epsilon _0$ is the initial amplitude of the disturbance whose value is fixed to 0.01.
$\epsilon _0$ is the initial amplitude of the disturbance whose value is fixed to 0.01.
Due to spatial periodicity and symmetry, only a half-wavelength long segment of the thread needs to be calculated. Therefore, in the calculation, the domain is limited to ![]() $z\in [0,\ \lambda /2]$, where
$z\in [0,\ \lambda /2]$, where ![]() $\lambda =2{\rm \pi} /k$ is the dimensionless wavelength of the disturbance.The periodic boundary conditions are imposed at
$\lambda =2{\rm \pi} /k$ is the dimensionless wavelength of the disturbance.The periodic boundary conditions are imposed at ![]() $z=0$ and
$z=0$ and ![]() $z=\lambda /2$, i.e.
$z=\lambda /2$, i.e.
 \begin{align}
\left.\begin{array}{@{}c@{}} \displaystyle \dfrac{\partial
S}{\partial z}(z=0,t)=\dfrac{\partial S}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
u(z=0,t)=u\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial \tau_{zz}}{\partial
z}(z=0,t)=\dfrac{\partial \tau_{zz}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
\dfrac{\partial \tau_{rr}}{\partial
z}(z=0,t)=\dfrac{\partial \tau_{rr}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial A_{zz}}{\partial z}(z=0,t)=\dfrac{\partial
A_{zz}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
\dfrac{\partial A_{rr}}{\partial z}(z=0,t)=\dfrac{\partial
A_{rr}}{\partial z}\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial \varGamma}{\partial
z}(z=0,t)=\dfrac{\partial \varGamma}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0.
\end{array}\right\}
\end{align}
\begin{align}
\left.\begin{array}{@{}c@{}} \displaystyle \dfrac{\partial
S}{\partial z}(z=0,t)=\dfrac{\partial S}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
u(z=0,t)=u\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial \tau_{zz}}{\partial
z}(z=0,t)=\dfrac{\partial \tau_{zz}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
\dfrac{\partial \tau_{rr}}{\partial
z}(z=0,t)=\dfrac{\partial \tau_{rr}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial A_{zz}}{\partial z}(z=0,t)=\dfrac{\partial
A_{zz}}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0,\quad
\dfrac{\partial A_{rr}}{\partial z}(z=0,t)=\dfrac{\partial
A_{rr}}{\partial z}\left(z=\dfrac{\lambda}{2},t\right)=0,\\
\displaystyle \dfrac{\partial \varGamma}{\partial
z}(z=0,t)=\dfrac{\partial \varGamma}{\partial
z}\left(z=\dfrac{\lambda}{2},t\right)=0.
\end{array}\right\}
\end{align} There are in total ten dimensionless parameters involved in this problem: ![]() $Oh, \beta, De, L, Pe, E, B_{\kappa \infty }, B_{\mu \infty }, \varGamma _0$ and
$Oh, \beta, De, L, Pe, E, B_{\kappa \infty }, B_{\mu \infty }, \varGamma _0$ and ![]() $k$. The physical properties of surfactant-laden or viscoelastic fluids as well as the values of the dimensionless numbers considered in the literature are collected in table 1. As one can see, the properties span a wide range. We would like to consider a viscoelastic thread of moderate viscosity and moderate elasticity. Suppose the density
$k$. The physical properties of surfactant-laden or viscoelastic fluids as well as the values of the dimensionless numbers considered in the literature are collected in table 1. As one can see, the properties span a wide range. We would like to consider a viscoelastic thread of moderate viscosity and moderate elasticity. Suppose the density ![]() $\rho$ is
$\rho$ is ![]() $1000\ \textrm {kg\ m}^{-3}$, the zero-shear viscosity
$1000\ \textrm {kg\ m}^{-3}$, the zero-shear viscosity ![]() $\eta _0$ is
$\eta _0$ is ![]() $0.1\ \textrm {Pa s}$, the stress relaxation time
$0.1\ \textrm {Pa s}$, the stress relaxation time ![]() $\lambda _c$ is
$\lambda _c$ is ![]() $0.5\ \textrm {ms}$, the surface tension
$0.5\ \textrm {ms}$, the surface tension ![]() $\sigma _0$ is
$\sigma _0$ is ![]() $0.05\ \textrm {N\ m}^{-1}$ and the radius of the unperturbed thread
$0.05\ \textrm {N\ m}^{-1}$ and the radius of the unperturbed thread ![]() $R$ is
$R$ is ![]() $100\ \mathrm {\mu }\textrm {m}$. Then, the Ohnesorge number
$100\ \mathrm {\mu }\textrm {m}$. Then, the Ohnesorge number ![]() $Oh$ has a value of
$Oh$ has a value of ![]() $1.4$ and the Deborah number
$1.4$ and the Deborah number ![]() $De$ has a value of
$De$ has a value of ![]() $3.5$. The values of
$3.5$. The values of ![]() $Oh$ and
$Oh$ and ![]() $De$ are kept unchanged, since we focus on the effects of the surfactant on the dynamic behaviour of the viscoelastic thread. Without loss of generality, the solvent to solution viscosity ratio
$De$ are kept unchanged, since we focus on the effects of the surfactant on the dynamic behaviour of the viscoelastic thread. Without loss of generality, the solvent to solution viscosity ratio ![]() $\beta$ is fixed to 0.5 and the finite extensibility parameter
$\beta$ is fixed to 0.5 and the finite extensibility parameter ![]() $L$ takes a value of 5 for the FENE-P model. The surfactant surface diffusivity
$L$ takes a value of 5 for the FENE-P model. The surfactant surface diffusivity ![]() $D_s$ is about
$D_s$ is about ![]() $10^{-10}$–
$10^{-10}$–![]() $10^{-9}\ \textrm {m}^2\ \textrm{s}^{-1}$ (Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018). The surface Péclet number
$10^{-9}\ \textrm {m}^2\ \textrm{s}^{-1}$ (Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018). The surface Péclet number ![]() $Pe$ is of the order of magnitude of
$Pe$ is of the order of magnitude of ![]() $10^3$ to
$10^3$ to ![]() $10^6$, suggesting that surface convection is dominant in surfactant transport. In many studies, surface diffusion was reasonably neglected, i.e. the surface Péclet number was taken to be infinity (Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018; Alhushaybari & Uddin Reference Alhushaybari and Uddin2020; Martínez-Calvo et al. Reference Martínez-Calvo, Rivero-Rodríguez, Scheid and Sevilla2020; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021). In addition to a case of large surface Péclet number (
$10^6$, suggesting that surface convection is dominant in surfactant transport. In many studies, surface diffusion was reasonably neglected, i.e. the surface Péclet number was taken to be infinity (Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018; Alhushaybari & Uddin Reference Alhushaybari and Uddin2020; Martínez-Calvo et al. Reference Martínez-Calvo, Rivero-Rodríguez, Scheid and Sevilla2020; Wee et al. Reference Wee, Wagoner, Garg, Kamat and Basaran2021). In addition to a case of large surface Péclet number (![]() $Pe=10^5$), we will examine a case of moderate surface Péclet number (
$Pe=10^5$), we will examine a case of moderate surface Péclet number (![]() $Pe=1$), in which surface convection and surface diffusion are of equal importance. In small-scale applications such as microemulsions and nanoemulsions, the surface Péclet number can be order one (
$Pe=1$), in which surface convection and surface diffusion are of equal importance. In small-scale applications such as microemulsions and nanoemulsions, the surface Péclet number can be order one (![]() $O(1)$). We intend to discuss the effect of surfactant diffusivity on the nonlinear evolution of a viscoelastic thread via the moderate
$O(1)$). We intend to discuss the effect of surfactant diffusivity on the nonlinear evolution of a viscoelastic thread via the moderate ![]() $Pe$ case. The initial surfactant concentration
$Pe$ case. The initial surfactant concentration ![]() $\varGamma _0$ varies between 0 and 0.5. The range of the Marangoni number
$\varGamma _0$ varies between 0 and 0.5. The range of the Marangoni number ![]() $E$ is from 0 to 0.6. The surface shear and dilatational viscosities are
$E$ is from 0 to 0.6. The surface shear and dilatational viscosities are ![]() $10^{-5}$–
$10^{-5}$–![]() $10^{-4}\ \textrm {Pa\ s m}$ (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018) or much lower (
$10^{-4}\ \textrm {Pa\ s m}$ (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018) or much lower (![]() $\sim 10^{-8} \textrm {Pa\ s\ m}$) (Zell et al. Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014; Ponce-Torres et al. Reference Ponce-Torres, Rubio, Herrada, Eggers and Montanero2020). The Boussinesq numbers
$\sim 10^{-8} \textrm {Pa\ s\ m}$) (Zell et al. Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014; Ponce-Torres et al. Reference Ponce-Torres, Rubio, Herrada, Eggers and Montanero2020). The Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ range widely from 0 to
$B_{\mu \infty }$ range widely from 0 to ![]() $O(10^3)$. The larger the Boussinesq numbers, the more important the surface viscous stresses. We consider a relatively conservative range of
$O(10^3)$. The larger the Boussinesq numbers, the more important the surface viscous stresses. We consider a relatively conservative range of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ from 0 to 100. Moreover, we assume that
$B_{\mu \infty }$ from 0 to 100. Moreover, we assume that ![]() $B_{\kappa \infty }$ is equal to
$B_{\kappa \infty }$ is equal to ![]() $B_{\mu \infty }$. The measurement of surface shear and dilatational viscosities is an experimental challenge. Some experiments showed that the surface dilatational viscosity can be orders of magnitude larger than the surface shear viscosity and can be augmented by adsorption if the surfactant is soluble (Lucassen & van den Tempel Reference Lucassen and van den Tempel1972; Alvarez et al. Reference Alvarez, Anna, Saigal, Tilton and Walker2012; Singh & Narsimhan Reference Singh and Narsimhan2021, Reference Singh and Narsimhan2022; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022). The range of the axial wavenumber
$B_{\mu \infty }$. The measurement of surface shear and dilatational viscosities is an experimental challenge. Some experiments showed that the surface dilatational viscosity can be orders of magnitude larger than the surface shear viscosity and can be augmented by adsorption if the surfactant is soluble (Lucassen & van den Tempel Reference Lucassen and van den Tempel1972; Alvarez et al. Reference Alvarez, Anna, Saigal, Tilton and Walker2012; Singh & Narsimhan Reference Singh and Narsimhan2021, Reference Singh and Narsimhan2022; Herrada et al. Reference Herrada, Ponce-Torres, Rubio, Eggers and Montanero2022). The range of the axial wavenumber ![]() $k$ is from 0.3 to 0.9. All the values of the dimensionless numbers considered in the simulation are summarized in table 2. Finally, to facilitate simulation and analysis, a reference state is selected, in which
$k$ is from 0.3 to 0.9. All the values of the dimensionless numbers considered in the simulation are summarized in table 2. Finally, to facilitate simulation and analysis, a reference state is selected, in which ![]() $Oh=1.4, \beta =0.5, De=3.5, \varGamma _0=0.3, E=0.4, Pe=10^5, B_{\kappa \infty }=B_{\mu \infty }=0$ and
$Oh=1.4, \beta =0.5, De=3.5, \varGamma _0=0.3, E=0.4, Pe=10^5, B_{\kappa \infty }=B_{\mu \infty }=0$ and ![]() $L=5$ (FENE-P) or
$L=5$ (FENE-P) or ![]() $\infty$ (Oldroyd-B). The dimensionless numbers are fixed to the reference state unless specified otherwise.
$\infty$ (Oldroyd-B). The dimensionless numbers are fixed to the reference state unless specified otherwise.
Table 1. The physical properties of surfactant-laden fluids and viscoelastic fluids and the values of the dimensional numbers in the literature. The superscripts 0 and c denote the Boussinesq numbers at ![]() $\varGamma _0$ and the CMC, respectively.
$\varGamma _0$ and the CMC, respectively.

Table 2. The values of the dimensionless numbers considered in the simulation.

4.1. Linear instability analysis based on the 1-D model
In this subsection, a brief linear analysis is performed based on the present 1-D model. Following the normal mode method, the quantities are decomposed into a base and a perturbation part, i.e.
 \begin{align} (S, u, \tau_{zz}, \tau_{rr}, A_{zz}, A_{rr}, \varGamma)&=\left(1, 0, 0, 0, \frac{L^2}{L^2+3},\frac{L^2}{L^2+3}, \varGamma_0\right)\nonumber\\ &\quad +(\hat{S}, \hat{u}, \hat{\tau}_{zz}, \hat{\tau}_{rr}, \hat{A}_{zz}, \hat{A}_{rr}, \hat{\varGamma})\exp(\alpha t+jkz)+{\rm c.c.}, \end{align}
\begin{align} (S, u, \tau_{zz}, \tau_{rr}, A_{zz}, A_{rr}, \varGamma)&=\left(1, 0, 0, 0, \frac{L^2}{L^2+3},\frac{L^2}{L^2+3}, \varGamma_0\right)\nonumber\\ &\quad +(\hat{S}, \hat{u}, \hat{\tau}_{zz}, \hat{\tau}_{rr}, \hat{A}_{zz}, \hat{A}_{rr}, \hat{\varGamma})\exp(\alpha t+jkz)+{\rm c.c.}, \end{align}
where the hat denotes the initial amplitudes of the perturbation parts, ![]() $\alpha$ is the complex frequency with the real part
$\alpha$ is the complex frequency with the real part ![]() $\alpha _r$ the temporal growth rate and the imaginary part
$\alpha _r$ the temporal growth rate and the imaginary part ![]() $\alpha _i$ the speed of wave propagation,
$\alpha _i$ the speed of wave propagation, ![]() $j$ is the imaginary unit and ‘c.c.’ denotes the complex conjugate.
$j$ is the imaginary unit and ‘c.c.’ denotes the complex conjugate.
Linearizing the 1-D equations (3.1)–(3.7) and then substituting the decomposition (4.3) into the linearized equations, we obtain a set of linear homogeneous algebraic equations for the unknowns ![]() $(\hat {S}, \hat {u}, \hat {\tau }_{zz}, \hat {\tau }_{rr}, \hat {A}_{zz}, \hat {A}_{rr}, \hat {\varGamma })$. The determinant of the coefficient matrix of the equations has to be zero to ensure the system has non-trivial solutions, which yields the following dispersion relation:
$(\hat {S}, \hat {u}, \hat {\tau }_{zz}, \hat {\tau }_{rr}, \hat {A}_{zz}, \hat {A}_{rr}, \hat {\varGamma })$. The determinant of the coefficient matrix of the equations has to be zero to ensure the system has non-trivial solutions, which yields the following dispersion relation:
 \begin{align} \alpha+3\beta Ohk^2&={-}k^2(1-\beta)Oh\frac{L^2+3}{L^2} (\varXi_1-\varXi_2)-\frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}\nonumber\\ &\quad+\frac{\sigma_ik^2(1-k^2)}{2\alpha}-\frac{B_{\kappa\infty} +9B_{\mu\infty}}{2}\varGamma_0Ohk^2, \end{align}
\begin{align} \alpha+3\beta Ohk^2&={-}k^2(1-\beta)Oh\frac{L^2+3}{L^2} (\varXi_1-\varXi_2)-\frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}\nonumber\\ &\quad+\frac{\sigma_ik^2(1-k^2)}{2\alpha}-\frac{B_{\kappa\infty} +9B_{\mu\infty}}{2}\varGamma_0Ohk^2, \end{align}where
 $$\begin{gather} \varXi_1=\dfrac{\left| \begin{array}{cc} \dfrac{2L^2}{L^2+3} & \dfrac{2(L^2+3)}{L^4} \\ -\dfrac{L^2}{L^2+3} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \\ \end{array} \right| }{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2(L^2+3)}{L^4} \\ \dfrac{L^2+3}{L^4} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \end{array} \right|}, \end{gather}$$
$$\begin{gather} \varXi_1=\dfrac{\left| \begin{array}{cc} \dfrac{2L^2}{L^2+3} & \dfrac{2(L^2+3)}{L^4} \\ -\dfrac{L^2}{L^2+3} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \\ \end{array} \right| }{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2(L^2+3)}{L^4} \\ \dfrac{L^2+3}{L^4} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \end{array} \right|}, \end{gather}$$ $$\begin{gather}\varXi_2=\dfrac{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2L^2}{L^2+3} \\ \dfrac{L^2+3}{L^4} & -\dfrac{L^2}{L^2+3} \\ \end{array} \right| }{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2(L^2+3)}{L^4} \\ \dfrac{L^2+3}{L^4} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \end{array} \right|}, \end{gather}$$
$$\begin{gather}\varXi_2=\dfrac{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2L^2}{L^2+3} \\ \dfrac{L^2+3}{L^4} & -\dfrac{L^2}{L^2+3} \\ \end{array} \right| }{\left| \begin{array}{cc} De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{L^2+3}{L^4} & \dfrac{2(L^2+3)}{L^4} \\ \dfrac{L^2+3}{L^4} & De \alpha +\dfrac{L^2+3}{L^2}+\dfrac{2(L^2+3)}{L^4} \end{array} \right|}, \end{gather}$$
and ![]() $\sigma _i(=1+E\ln (1-\varGamma _0))$ is the initial surface tension corresponding to the initial surfactant concentration
$\sigma _i(=1+E\ln (1-\varGamma _0))$ is the initial surface tension corresponding to the initial surfactant concentration ![]() $\varGamma _0$. Note that the four terms on the right-hand side of (4.4) are related to the viscoelasticity of the polymer solution, the Marangoni stress, the surface tension and the surface shear and dilatational viscosities, respectively.
$\varGamma _0$. Note that the four terms on the right-hand side of (4.4) are related to the viscoelasticity of the polymer solution, the Marangoni stress, the surface tension and the surface shear and dilatational viscosities, respectively.
When the finite extensibility ![]() $L$ approaches infinity, the dispersion relation (4.4) reduces to that for the linear Jeffreys model and any nonlinear viscoelastic model (e.g. Oldroyd-B and FENE-P) that becomes the Jeffreys model after linearization, i.e.
$L$ approaches infinity, the dispersion relation (4.4) reduces to that for the linear Jeffreys model and any nonlinear viscoelastic model (e.g. Oldroyd-B and FENE-P) that becomes the Jeffreys model after linearization, i.e.
 \begin{align} \alpha+3\beta Ohk^2&={-}\frac{3k^2(1-\beta)Oh}{1+De\alpha}- \frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}\nonumber\\ &\quad+\frac{\sigma_ik^2(1-k^2)}{2\alpha}- \frac{B_{\kappa\infty}+9B_{\mu\infty}}{2}\varGamma_0Ohk^2. \end{align}
\begin{align} \alpha+3\beta Ohk^2&={-}\frac{3k^2(1-\beta)Oh}{1+De\alpha}- \frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}\nonumber\\ &\quad+\frac{\sigma_ik^2(1-k^2)}{2\alpha}- \frac{B_{\kappa\infty}+9B_{\mu\infty}}{2}\varGamma_0Ohk^2. \end{align} When the Deborah number ![]() $De$ is equal to zero, (4.7) reduces to the dispersion relation determining the linear instability characteristics of surfactant-laden Newtonian viscous threads (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018), i.e.
$De$ is equal to zero, (4.7) reduces to the dispersion relation determining the linear instability characteristics of surfactant-laden Newtonian viscous threads (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018), i.e.
 \begin{equation} \alpha+3 Ohk^2={-}\frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}+\frac{\sigma_ik^2(1 -k^2)}{2\alpha}-\frac{B_{\kappa\infty}+9B_{\mu\infty}}{2}\varGamma_0Ohk^2. \end{equation}
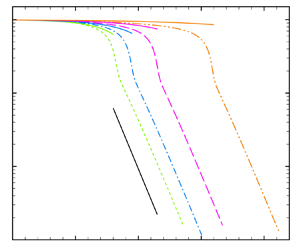
\begin{equation} \alpha+3 Ohk^2={-}\frac{k^2E\varGamma_0}{2(1-\varGamma_0) \left(\alpha+\dfrac{k^2}{Pe}\right)}+\frac{\sigma_ik^2(1 -k^2)}{2\alpha}-\frac{B_{\kappa\infty}+9B_{\mu\infty}}{2}\varGamma_0Ohk^2. \end{equation} The effect of the dimensionless numbers on the linear instability of the surfactant-covered viscoelastic thread is shown in figure 2. It can be seen that the temporal growth rate ![]() $\alpha _r$ decreases with the increase in the initial surfactant concentration
$\alpha _r$ decreases with the increase in the initial surfactant concentration ![]() $\varGamma _0$, the surface Péclet number
$\varGamma _0$, the surface Péclet number ![]() $Pe$, the Marangoni number
$Pe$, the Marangoni number ![]() $E$, the dilatational Boussinesq number
$E$, the dilatational Boussinesq number ![]() $B_{\kappa \infty }$ or the shear Boussinesq number
$B_{\kappa \infty }$ or the shear Boussinesq number ![]() $B_{\mu \infty }$ (see figures 2a–2f). In general, surfactants suppress the linear instability of viscoelastic threads, as they affect Newtonian viscous threads (Hansen et al. Reference Hansen, Peters and Meijer1999; Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018). The mechanism can be interpreted from several aspects: the presence of the surfactant lowers the surface tension and thereby the capillary force that destabilizes the viscoelastic thread; the Marangoni stress tends to eliminate the spatial non-uniformity of the surface tension and thereby suppresses the growth of the disturbance; the surface shear and dilatational viscosities and the resulting viscous stresses have a stabilizing effect on the viscoelastic thread.
$B_{\mu \infty }$ (see figures 2a–2f). In general, surfactants suppress the linear instability of viscoelastic threads, as they affect Newtonian viscous threads (Hansen et al. Reference Hansen, Peters and Meijer1999; Timmermans & Lister Reference Timmermans and Lister2002; Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018). The mechanism can be interpreted from several aspects: the presence of the surfactant lowers the surface tension and thereby the capillary force that destabilizes the viscoelastic thread; the Marangoni stress tends to eliminate the spatial non-uniformity of the surface tension and thereby suppresses the growth of the disturbance; the surface shear and dilatational viscosities and the resulting viscous stresses have a stabilizing effect on the viscoelastic thread.

Figure 2. The temporal growth rate ![]() $\alpha _{r}$ vs the axial wavenumber
$\alpha _{r}$ vs the axial wavenumber ![]() $k$. The effect of (a–b) the initial surfactant concentration
$k$. The effect of (a–b) the initial surfactant concentration ![]() $\varGamma _0$, (c) the surface Péclet number
$\varGamma _0$, (c) the surface Péclet number ![]() $Pe$, (d) the Marangoni number
$Pe$, (d) the Marangoni number ![]() $E$, (e) the dilatational Boussinesq number
$E$, (e) the dilatational Boussinesq number ![]() $B_{\kappa \infty }$, ( f) the shear Boussinesq number
$B_{\kappa \infty }$, ( f) the shear Boussinesq number ![]() $B_{\mu \infty }$ and (g) the finite extensibility parameter
$B_{\mu \infty }$ and (g) the finite extensibility parameter ![]() $L$. In (a),
$L$. In (a), ![]() $Pe=10^5$; in (b),
$Pe=10^5$; in (b), ![]() $Pe=1$. (a–f) The Oldroyd-B model (
$Pe=1$. (a–f) The Oldroyd-B model (![]() $L\rightarrow \infty$) and (g) the FENE-P model. The arrows denote the direction of a parameter increasing.
$L\rightarrow \infty$) and (g) the FENE-P model. The arrows denote the direction of a parameter increasing.
Comparing the large ![]() $Pe$ case in figure 2(a) with the moderate
$Pe$ case in figure 2(a) with the moderate ![]() $Pe$ case in figure 2(b), the temporal growth rate
$Pe$ case in figure 2(b), the temporal growth rate ![]() $\alpha _r$ is apparently more sensitive to the presence of the surfactant at larger values of
$\alpha _r$ is apparently more sensitive to the presence of the surfactant at larger values of ![]() $Pe$. Recall that the surface Péclet number
$Pe$. Recall that the surface Péclet number ![]() $Pe$ represents the relative importance of surface convection and surface diffusion in surfactant transport. At large values of
$Pe$ represents the relative importance of surface convection and surface diffusion in surfactant transport. At large values of ![]() $Pe$, surface convection is dominant, resulting in high non-uniformity of surfactant and thereby large Marangoni stress that suppresses the instability of the thread. This trend can also be seen in figure 2(c). The cutoff wavenumber
$Pe$, surface convection is dominant, resulting in high non-uniformity of surfactant and thereby large Marangoni stress that suppresses the instability of the thread. This trend can also be seen in figure 2(c). The cutoff wavenumber ![]() $k_c$, beyond which the thread is linearly stable (
$k_c$, beyond which the thread is linearly stable (![]() $\alpha _r\leq 0$), remains at unity no more in the presence of the surfactant. Analytically the cutoff wavenumber
$\alpha _r\leq 0$), remains at unity no more in the presence of the surfactant. Analytically the cutoff wavenumber ![]() $k_c$ can be obtained from the dispersion relation (4.4). Setting the complex frequency
$k_c$ can be obtained from the dispersion relation (4.4). Setting the complex frequency ![]() $\alpha$ in (4.4) to be zero, we have
$\alpha$ in (4.4) to be zero, we have
 \begin{equation} k_c=\sqrt{1-\frac{E\varGamma_0}{\sigma_i(1-\varGamma_0)}}. \end{equation}
\begin{equation} k_c=\sqrt{1-\frac{E\varGamma_0}{\sigma_i(1-\varGamma_0)}}. \end{equation}
Clearly, ![]() $k_c$ is strictly equal to unity only when
$k_c$ is strictly equal to unity only when ![]() $\varGamma _0$ is zero. As shown in figure 2,
$\varGamma _0$ is zero. As shown in figure 2, ![]() $k_c$ decreases (that is, the range of unstable axial wavenumbers is narrowed down) as
$k_c$ decreases (that is, the range of unstable axial wavenumbers is narrowed down) as ![]() $\varGamma _0, Pe$ or
$\varGamma _0, Pe$ or ![]() $E$ increases. However, this statement may not be true since the high-order terms are neglected in the 1-D model, as pointed out by Hansen et al. (Reference Hansen, Peters and Meijer1999), Timmermans & Lister (Reference Timmermans and Lister2002) and Martínez-Calvo & Sevilla (Reference Martínez-Calvo and Sevilla2018) in the study of Newtonian threads. The 2-D axisymmetric linear instability analysis has showed that the cutoff wavenumber remains at unity. The 1-D model may overestimate the suppressing effect of the surfactant on the thread instability at large wavenumbers near the cutoff. To eliminate the discrepancy, necessary high-order terms should be retained in the long wave approximation (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018), which is of interest but beyond the scope of the present research. Anyway, the 1-D model does not need to give results that agree with the 2-D instability analysis over the entire unstable wavenumber range. We can still get some insights into how surfactants affect the linear instability and nonlinear behaviour of viscoelastic threads via the 1-D model.
$E$ increases. However, this statement may not be true since the high-order terms are neglected in the 1-D model, as pointed out by Hansen et al. (Reference Hansen, Peters and Meijer1999), Timmermans & Lister (Reference Timmermans and Lister2002) and Martínez-Calvo & Sevilla (Reference Martínez-Calvo and Sevilla2018) in the study of Newtonian threads. The 2-D axisymmetric linear instability analysis has showed that the cutoff wavenumber remains at unity. The 1-D model may overestimate the suppressing effect of the surfactant on the thread instability at large wavenumbers near the cutoff. To eliminate the discrepancy, necessary high-order terms should be retained in the long wave approximation (Martínez-Calvo & Sevilla Reference Martínez-Calvo and Sevilla2018), which is of interest but beyond the scope of the present research. Anyway, the 1-D model does not need to give results that agree with the 2-D instability analysis over the entire unstable wavenumber range. We can still get some insights into how surfactants affect the linear instability and nonlinear behaviour of viscoelastic threads via the 1-D model.
A non-Newtonian viscoelastic thread possesses a higher temporal growth rate than its Newtonian viscous counterpart. That is, elasticity has a destabilizing effect on the linear instability of a thread (Brenn et al. Reference Brenn, Liu and Durst2000). It is found that finite extensibility affects viscoelastic threads in a different way. As shown in figure 2(g), the temporal growth rate ![]() $\alpha _r$ increases as the finite extensibility parameter
$\alpha _r$ increases as the finite extensibility parameter ![]() $L$ decreases, suggesting that the extensibility of polymer chains suppresses the instability of the thread.
$L$ decreases, suggesting that the extensibility of polymer chains suppresses the instability of the thread.
4.2. Nonlinear behaviour of a surfactant-covered Oldroyd-B viscoelastic thread
An Oldroyd-B viscoelastic liquid thread never breaks up because of its infinite extensibility. The 1-D models, the 2-D axisymmetric numerical simulations and the experiments have shown that a quasistatic beads-on-a-string structure is gradually formed during the nonlinear evolution of an Oldroyd-B viscoelastic thread (Chang et al. Reference Chang, Demekhin and Kalaidin1999; Ardekani et al. Reference Ardekani, Sharma and Mckinley2010; Tembely et al. Reference Tembely, Vadillo, Mackley and Soucemarianadin2012; Turkoz et al. Reference Turkoz, Lopez-Herrera, Eggers, Arnold and Deike2018). Moreover, the filament between two adjacent primary droplets, with an almost uniform thickness, thins exponentially in time at a rate of ![]() $1/3De$, and the flow in the filament is uniaxial extensional (Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a). The influence of other factors such as electric field, temperature, surfactant and exterior fluid phase on the dynamics of viscoelastic jets and threads has drawn attention in recent years (Eggers & Villermaux Reference Eggers and Villermaux2008; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). In the following, we examine how the presence of a surfactant monolayer affects the nonlinear behaviour of an Oldroyd-B viscoelastic thread.
$1/3De$, and the flow in the filament is uniaxial extensional (Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a). The influence of other factors such as electric field, temperature, surfactant and exterior fluid phase on the dynamics of viscoelastic jets and threads has drawn attention in recent years (Eggers & Villermaux Reference Eggers and Villermaux2008; Montanero & Gañán-Calvo Reference Montanero and Gañán-Calvo2020). In the following, we examine how the presence of a surfactant monolayer affects the nonlinear behaviour of an Oldroyd-B viscoelastic thread.
The effect of the initial surfactant concentration ![]() $\varGamma _0$ on the temporal evolution of the Oldroyd-B viscoelastic thread is shown in figure 3, where the large surface Péclet number case (
$\varGamma _0$ on the temporal evolution of the Oldroyd-B viscoelastic thread is shown in figure 3, where the large surface Péclet number case (![]() $Pe=10^5$) is considered and the surface dilatational and shear viscosities are turned off (
$Pe=10^5$) is considered and the surface dilatational and shear viscosities are turned off (![]() $B_{\kappa \infty }=B_{\mu \infty }=0$). As shown in figure 3(a), the radius of the Oldroyd-B viscoelastic thread at the midpoint
$B_{\kappa \infty }=B_{\mu \infty }=0$). As shown in figure 3(a), the radius of the Oldroyd-B viscoelastic thread at the midpoint ![]() $z=\lambda /2$ (where the centre of the filament is located), denoted by
$z=\lambda /2$ (where the centre of the filament is located), denoted by ![]() $S_{\lambda /2}$, first experiences a fast decrease and then enters a slow exponential thinning, regardless of the presence of the surfactant. The surfactant has a negligible influence on the
$S_{\lambda /2}$, first experiences a fast decrease and then enters a slow exponential thinning, regardless of the presence of the surfactant. The surfactant has a negligible influence on the ![]() $1/3De$ exponential thinning law of the filament. A local balance between the capillary and elastic forces is presumably established in the filament as in the absence of the surfactant. The first normal stress difference
$1/3De$ exponential thinning law of the filament. A local balance between the capillary and elastic forces is presumably established in the filament as in the absence of the surfactant. The first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ increases exponentially in time at the rate
$\tau _{zz}-\tau _{rr}$ increases exponentially in time at the rate ![]() $1/3De$, as shown in figure 3(b). It indicates that the surfactant plays a minimal role at the late stages of filament thinning. In contrast, the surfactant does greatly influence the evolution of the thread at the early stages. Most notably, the decrease of
$1/3De$, as shown in figure 3(b). It indicates that the surfactant plays a minimal role at the late stages of filament thinning. In contrast, the surfactant does greatly influence the evolution of the thread at the early stages. Most notably, the decrease of ![]() $S_{\lambda /2}$ is slowed down in the presence of the surfactant. As shown in figure 3(a), the filament needs increasingly more time to reach the uniaxial extension stage, as
$S_{\lambda /2}$ is slowed down in the presence of the surfactant. As shown in figure 3(a), the filament needs increasingly more time to reach the uniaxial extension stage, as ![]() $\varGamma _0$ increases. This trend is qualitatively in accordance with the linear prediction in figure 2(a). The temporal evolution of
$\varGamma _0$ increases. This trend is qualitatively in accordance with the linear prediction in figure 2(a). The temporal evolution of ![]() $S_{\lambda /2}$ predicted by linear theory is included in figure 3(a) for comparison (the solid lines). The 1-D linear theory turns out to underestimate the development of the disturbance as the nonlinear effects come into play.
$S_{\lambda /2}$ predicted by linear theory is included in figure 3(a) for comparison (the solid lines). The 1-D linear theory turns out to underestimate the development of the disturbance as the nonlinear effects come into play.

Figure 3. Effect of the initial surfactant concentration ![]() $\varGamma _0$ on the thinning of the Oldroyd-B viscoelastic thread. (a) The thread radius
$\varGamma _0$ on the thinning of the Oldroyd-B viscoelastic thread. (a) The thread radius ![]() $S$ and (b) the first normal stress difference
$S$ and (b) the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ at the midpoint
$\tau _{zz}-\tau _{rr}$ at the midpoint ![]() $z=\lambda /2$. Here,
$z=\lambda /2$. Here, ![]() $k=0.8$. The solid lines in (a) are the predictions of linear theory.
$k=0.8$. The solid lines in (a) are the predictions of linear theory.
To understand the negligible effect of the surfactant on the thinning of the viscoelastic thread at the late stages, the variation of the thread radius ![]() $S$, the surfactant concentration
$S$, the surfactant concentration ![]() $\varGamma$, the surface tension
$\varGamma$, the surface tension ![]() $\sigma$, the axial velocity
$\sigma$, the axial velocity ![]() $u$ and the first normal stress difference
$u$ and the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ along the thread are examined in figure 4(a) for the large surface Péclet number case (
$\tau _{zz}-\tau _{rr}$ along the thread are examined in figure 4(a) for the large surface Péclet number case (![]() $Pe=10^5$) and the initial surfactant concentration
$Pe=10^5$) and the initial surfactant concentration ![]() $\varGamma _0=0.3$ (the reference state). Obviously, at the observed time
$\varGamma _0=0.3$ (the reference state). Obviously, at the observed time ![]() $t=212$, the beads-on-a-string structure has been formed and an elasto-capillary balance has been established inside the filament. Note that the surfactant concentration
$t=212$, the beads-on-a-string structure has been formed and an elasto-capillary balance has been established inside the filament. Note that the surfactant concentration ![]() $\varGamma$ varies along the thread in a way quite similar to the thread radius
$\varGamma$ varies along the thread in a way quite similar to the thread radius ![]() $S$. As a matter of fact, at a value of the surface Péclet number as large as
$S$. As a matter of fact, at a value of the surface Péclet number as large as ![]() $10^5$, the diffusion term on the right-hand side of the surfactant advection–diffusion equation (3.7) or (3.11) is very small. Neglecting the diffusion term, (3.8) approximates to
$10^5$, the diffusion term on the right-hand side of the surfactant advection–diffusion equation (3.7) or (3.11) is very small. Neglecting the diffusion term, (3.8) approximates to
The above equation is the same in form with the volume conservation equation (3.1), implying that the spatio-temporal evolution of the surfactant concentration ![]() $\varGamma$ and the thread radius
$\varGamma$ and the thread radius ![]() $S$ follows the same discipline. Hence, we can write
$S$ follows the same discipline. Hence, we can write
where ![]() $a$ is a coefficient to be determined. Apparently,
$a$ is a coefficient to be determined. Apparently, ![]() $a=\varGamma _0$. The surface tension
$a=\varGamma _0$. The surface tension ![]() $\sigma$ in figure 4(a) is approximated as
$\sigma$ in figure 4(a) is approximated as
Most of surfactant molecules initially residing at the filament surface have been convected to the primary droplet before the thread enters the final elasto-capillary stage, due to the strong convection. The filament is almost free of surfactant in the elasto-capillary regime, with a nearly zero ![]() $\varGamma$ and a nearly unity
$\varGamma$ and a nearly unity ![]() $\sigma$. Due to the evacuation of the surfactant, the
$\sigma$. Due to the evacuation of the surfactant, the ![]() $1/3De$ exponential thinning law is maintained, the axial velocity
$1/3De$ exponential thinning law is maintained, the axial velocity ![]() $u$ goes linearly with
$u$ goes linearly with ![]() $z$ and the first normal stress difference
$z$ and the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ is spatially uniform in the filament, as illustrated in figure 4(a).
$\tau _{zz}-\tau _{rr}$ is spatially uniform in the filament, as illustrated in figure 4(a).

Figure 4. Variation of the thread radius ![]() $S$, the surfactant concentration
$S$, the surfactant concentration ![]() $\varGamma$, the surface tension
$\varGamma$, the surface tension ![]() $\sigma$, the axial velocity
$\sigma$, the axial velocity ![]() $u$ and the first normal stress difference
$u$ and the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ along the thread. In panel (a),
$\tau _{zz}-\tau _{rr}$ along the thread. In panel (a), ![]() $Pe=10^5$; in panel(b),
$Pe=10^5$; in panel(b), ![]() $Pe=1$. Here,
$Pe=1$. Here, ![]() $k=0.8$.
$k=0.8$.
For a viscoelastic thread with no surfactant, the shape of primary droplets is almost spherical under the action of surface tension (Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a). If the viscosity is small, primary droplets undergo shape oscillations until energy is dissipated (Ardekani et al. Reference Ardekani, Sharma and Mckinley2010; Li, Yin & Yin Reference Li, Yin and Yin2017). For the moderate viscosity considered in this problem, no oscillation takes place. On the other hand, the presence of the surfactant is found to alter the beads-on-a-string morphology to some extent. In figures 5(a) and 5(b), the thread profiles are plotted for different values of the initial surfactant concentration ![]() $\varGamma _0$ and a fixed value of the axial wavenumber
$\varGamma _0$ and a fixed value of the axial wavenumber ![]() $k=0.5$. It is shown that the surfactant leads to the stretch of the primary droplets in the axial direction. The primary droplets are spherical no more. They look like prolate spheroids in shape. Moreover, they deform more and more as the initial surfactant concentration
$k=0.5$. It is shown that the surfactant leads to the stretch of the primary droplets in the axial direction. The primary droplets are spherical no more. They look like prolate spheroids in shape. Moreover, they deform more and more as the initial surfactant concentration ![]() $\varGamma _0$ increases. The deformation may be caused by the Marangoni stress that tends to drive liquid from the small surface tension region (the primary droplets) to the large surface tension region (the filament).
$\varGamma _0$ increases. The deformation may be caused by the Marangoni stress that tends to drive liquid from the small surface tension region (the primary droplets) to the large surface tension region (the filament).

Figure 5. (a) Thread profiles for different values of the initial surfactant concentration ![]() $\varGamma _0$, where
$\varGamma _0$, where ![]() $k=0.5$.(b) Zoomed-in secondary droplets located at the midpoint
$k=0.5$.(b) Zoomed-in secondary droplets located at the midpoint ![]() $z=\lambda /2$, where
$z=\lambda /2$, where ![]() $t=100.85$ (
$t=100.85$ (![]() $\varGamma _0=0$),
$\varGamma _0=0$), ![]() $100.55$ (
$100.55$ (![]() $\varGamma _0=0.1$),
$\varGamma _0=0.1$), ![]() $105.1$ (
$105.1$ (![]() $\varGamma _0=0.2$) and
$\varGamma _0=0.2$) and ![]() $113.9$ (
$113.9$ (![]() $\varGamma _0=0.3$). (c) Dependence of the secondary droplet volume
$\varGamma _0=0.3$). (c) Dependence of the secondary droplet volume ![]() $V_s$ on
$V_s$ on ![]() $\varGamma _0$ and
$\varGamma _0$ and ![]() $k$.
$k$.
There is a secondary droplet between two adjacent primary ones, located at the midpoint ![]() $z=\lambda /2$. Increasing the surfactant concentration results in the decrease in the secondary droplet size, as illustrated in figure 5(b). The volume of the secondary droplet, denoted by
$z=\lambda /2$. Increasing the surfactant concentration results in the decrease in the secondary droplet size, as illustrated in figure 5(b). The volume of the secondary droplet, denoted by ![]() $V_s$, is shown in figure 5(c). Clearly,
$V_s$, is shown in figure 5(c). Clearly, ![]() $V_s$ decreases as the initial surfactant concentration
$V_s$ decreases as the initial surfactant concentration ![]() $\varGamma _0$ increases. When
$\varGamma _0$ increases. When ![]() $\varGamma _0$ is large enough, the secondary droplet can be completely removed. For instance, for the axial wavenumber
$\varGamma _0$ is large enough, the secondary droplet can be completely removed. For instance, for the axial wavenumber ![]() $k=0.7$, the secondary droplet disappears at a value of
$k=0.7$, the secondary droplet disappears at a value of ![]() $\varGamma _0$ as large as
$\varGamma _0$ as large as ![]() $0.3$. The calculation result shows that the secondary droplet begins to form at the late stages of filament thinning. The mechanism, responsible for the decrease in secondary droplet size, might lie in that the tiny amount of surfactant at the filament surface slightly weakens the local capillary force and thereby impedes the formation of secondary droplet. In figure 8 below, it is shown that the Marangoni stress also plays a role in reducing the secondary droplet size. In applications, surfactants may help eliminate unwelcome secondary droplets arising in viscoelastic threads, as long as surface convection is strong enough. It is also shown in figure 5(c) that the volume of the secondary droplet increases as the axial wavenumber
$0.3$. The calculation result shows that the secondary droplet begins to form at the late stages of filament thinning. The mechanism, responsible for the decrease in secondary droplet size, might lie in that the tiny amount of surfactant at the filament surface slightly weakens the local capillary force and thereby impedes the formation of secondary droplet. In figure 8 below, it is shown that the Marangoni stress also plays a role in reducing the secondary droplet size. In applications, surfactants may help eliminate unwelcome secondary droplets arising in viscoelastic threads, as long as surface convection is strong enough. It is also shown in figure 5(c) that the volume of the secondary droplet increases as the axial wavenumber ![]() $k$ decreases. The most unstable wavenumber
$k$ decreases. The most unstable wavenumber ![]() $k_{max}$ corresponding to the maximum growth rate is most probably dominant in nature. According to the 1-D linear result in figure 2(a), the most unstable wavenumber is generally small. For
$k_{max}$ corresponding to the maximum growth rate is most probably dominant in nature. According to the 1-D linear result in figure 2(a), the most unstable wavenumber is generally small. For ![]() $\varGamma _0=0, k_{max}=0.375$; as
$\varGamma _0=0, k_{max}=0.375$; as ![]() $\varGamma _0$ increases,
$\varGamma _0$ increases, ![]() $k_{max}$ decreases. On the other hand, the tendency in figure 5(c) suggests that the nonlinear evolution of the viscoelastic thread exposed to natural disturbances yields secondary droplets of large volume, at least larger than those for
$k_{max}$ decreases. On the other hand, the tendency in figure 5(c) suggests that the nonlinear evolution of the viscoelastic thread exposed to natural disturbances yields secondary droplets of large volume, at least larger than those for ![]() $k=0.4$.
$k=0.4$.
The moderate surface Péclet number case is examined in figure 6. At ![]() $Pe=1$, surface diffusion is comparable to surface convection and the motion of the surfactant is governed by both factors. The temporal evolution of the thread radius at the midpoint,
$Pe=1$, surface diffusion is comparable to surface convection and the motion of the surfactant is governed by both factors. The temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, is illustrated in figure 6(a) for different values of the initial surfactant concentration
$S_{\lambda /2}$, is illustrated in figure 6(a) for different values of the initial surfactant concentration ![]() $\varGamma _0$ and a fixed axial wavenumber
$\varGamma _0$ and a fixed axial wavenumber ![]() $k=0.9$. For a small value of
$k=0.9$. For a small value of ![]() $\varGamma _0$ equal to 0.1,
$\varGamma _0$ equal to 0.1, ![]() $S_{\lambda /2}$ decreases all the way and the thread evolves into a beads-on-a-string structure with no secondary droplet. At the large times the thinning of the filament is little influenced by the surfactant and basically follows the
$S_{\lambda /2}$ decreases all the way and the thread evolves into a beads-on-a-string structure with no secondary droplet. At the large times the thinning of the filament is little influenced by the surfactant and basically follows the ![]() $1/3De$ exponential law in time. The scenario is changed with
$1/3De$ exponential law in time. The scenario is changed with ![]() $\varGamma _0$ increasing, see the lines for
$\varGamma _0$ increasing, see the lines for ![]() $\varGamma _0$=0.3 and 0.5 in figure 6(a). At some instant,
$\varGamma _0$=0.3 and 0.5 in figure 6(a). At some instant, ![]() $S_{\lambda /2}$ begins to go upward, indicating that a secondary droplet is formed at the midpoint. Moreover, the size of the secondary droplet increases as
$S_{\lambda /2}$ begins to go upward, indicating that a secondary droplet is formed at the midpoint. Moreover, the size of the secondary droplet increases as ![]() $\varGamma _0$ increases. The predictions of linear theory are shown in figure 6(a) (the solid lines) for comparison.
$\varGamma _0$ increases. The predictions of linear theory are shown in figure 6(a) (the solid lines) for comparison.

Figure 6. (a) Effect of the initial surfactant concentration ![]() $\varGamma _0$ on the temporal evolution of the thread radius at the midpoint,
$\varGamma _0$ on the temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, where
$S_{\lambda /2}$, where ![]() $Pe=1$ and the solid lines are the predictions of linear theory. Spatial distribution of (b,c) the surfactant concentration
$Pe=1$ and the solid lines are the predictions of linear theory. Spatial distribution of (b,c) the surfactant concentration ![]() $\varGamma$ and (d,e) the surface tension
$\varGamma$ and (d,e) the surface tension ![]() $\sigma$ along the thread as time increases, where
$\sigma$ along the thread as time increases, where ![]() $\varGamma _0=0.3$. In (b) and (d),
$\varGamma _0=0.3$. In (b) and (d), ![]() $Pe=10^5$; in (c) and (e),
$Pe=10^5$; in (c) and (e), ![]() $Pe=1$. Here,
$Pe=1$. Here, ![]() $k=0.9$.
$k=0.9$.
The spatio-temporal evolution of the surfactant concentration ![]() $\varGamma$ and the surface tension
$\varGamma$ and the surface tension ![]() $\sigma$ is illustrated in figures 6(b)–6(e) for the large
$\sigma$ is illustrated in figures 6(b)–6(e) for the large ![]() $Pe$ case and the moderate
$Pe$ case and the moderate ![]() $Pe$ case, respectively, where the initial surfactant concentration
$Pe$ case, respectively, where the initial surfactant concentration ![]() $\varGamma _0$ is fixed to 0.3. Compared with the large
$\varGamma _0$ is fixed to 0.3. Compared with the large ![]() $Pe$ case, in the moderate
$Pe$ case, in the moderate ![]() $Pe$ case the surfactant layer remains almost equally dense over the entire thread due to the surface diffusion mechanism. Recall that the surface area of the thread tends to decrease all the way to minimize the surface energy. Reasonably, the surfactant concentration
$Pe$ case the surfactant layer remains almost equally dense over the entire thread due to the surface diffusion mechanism. Recall that the surface area of the thread tends to decrease all the way to minimize the surface energy. Reasonably, the surfactant concentration ![]() $\varGamma$ increases monotonically with time from its initial value
$\varGamma$ increases monotonically with time from its initial value ![]() $\varGamma _0$, and the surface tension
$\varGamma _0$, and the surface tension ![]() $\sigma$ decreases monotonically. Due to its abundance and non-uniform distribution at the filament surface, the surfactant affects significantly the thinning characteristics of the filament. An elasto-capillary balance fails to be established within the filament. Under the action of the capillary force and possibly the Marangoni stress as well, a small quantity of liquid is driven towards the midpoint
$\sigma$ decreases monotonically. Due to its abundance and non-uniform distribution at the filament surface, the surfactant affects significantly the thinning characteristics of the filament. An elasto-capillary balance fails to be established within the filament. Under the action of the capillary force and possibly the Marangoni stress as well, a small quantity of liquid is driven towards the midpoint ![]() $z=\lambda /2$ and forms a secondary droplet there.
$z=\lambda /2$ and forms a secondary droplet there.
For the case of moderate surface Péclet number ![]() $Pe=1$, the thread profiles are plotted in figure 7 for different values of the initial surfactant concentration
$Pe=1$, the thread profiles are plotted in figure 7 for different values of the initial surfactant concentration ![]() $\varGamma _0$ and the axial wavenumber
$\varGamma _0$ and the axial wavenumber ![]() $k=0.5$. Most interestingly, the secondary droplet at the midpoint gains weight as
$k=0.5$. Most interestingly, the secondary droplet at the midpoint gains weight as ![]() $\varGamma _0$ increases. This trend is opposite to the large
$\varGamma _0$ increases. This trend is opposite to the large ![]() $Pe$ case shown in figure 5. In addition, high-order secondary droplets appear in the filament when
$Pe$ case shown in figure 5. In addition, high-order secondary droplets appear in the filament when ![]() $\varGamma _0$ is sufficiently large, see the profile for
$\varGamma _0$ is sufficiently large, see the profile for ![]() $\varGamma _0=0.5$.
$\varGamma _0=0.5$.

Figure 7. The case of moderate surface Péclet number ![]() $Pe=1$. (a) Thread profiles for different values of the initial surfactant concentration
$Pe=1$. (a) Thread profiles for different values of the initial surfactant concentration ![]() $\varGamma _0$ and (b) zoomed-in secondary droplets at the midpoint
$\varGamma _0$ and (b) zoomed-in secondary droplets at the midpoint ![]() $z=\lambda /2$. Here,
$z=\lambda /2$. Here, ![]() $k=0.5$ and
$k=0.5$ and ![]() $t=100.85$ (
$t=100.85$ (![]() $\varGamma _0=0$),
$\varGamma _0=0$), ![]() $95.75$ (
$95.75$ (![]() $\varGamma _0=0.1$),
$\varGamma _0=0.1$), ![]() $99.4$ (
$99.4$ (![]() $\varGamma _0=0.3$) and
$\varGamma _0=0.3$) and ![]() $122.3$ (
$122.3$ (![]() $\varGamma _0=0.5$).
$\varGamma _0=0.5$).
The effect of the Marangoni stress is explored in figure 8 by comparing the case in which the Marangoni stress is taken into account with the case in which it is turned off. Figure 8(a) illustrates the temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, for the axial wavenumbers
$S_{\lambda /2}$, for the axial wavenumbers ![]() $k=0.8$ and
$k=0.8$ and ![]() $0.9$. For such large axial wavenumbers, no secondary droplet is formed in the beads-on-a-string structure. It can be seen that the Marangoni stress slows down the growth of the disturbance and delays the arrival of the elasto-capillary stage to a great extent. That is, the Marangoni stress acts as a resistance to the instability of the viscoelastic thread. On the other hand, the Marangoni stress has no significant effect on the exponential thinning law of the filament in the elasto-capillary regime (recall that this is the case of large surface Péclet number). The effect of the Marangoni stress on the thread profile is examined in figures 8(b) and 8(c). For small axial wavenumbers such as
$0.9$. For such large axial wavenumbers, no secondary droplet is formed in the beads-on-a-string structure. It can be seen that the Marangoni stress slows down the growth of the disturbance and delays the arrival of the elasto-capillary stage to a great extent. That is, the Marangoni stress acts as a resistance to the instability of the viscoelastic thread. On the other hand, the Marangoni stress has no significant effect on the exponential thinning law of the filament in the elasto-capillary regime (recall that this is the case of large surface Péclet number). The effect of the Marangoni stress on the thread profile is examined in figures 8(b) and 8(c). For small axial wavenumbers such as ![]() $k=0.5$ and
$k=0.5$ and ![]() $0.6$, a secondary droplet unavoidably appears at the midpoint of the filament. The Marangoni stress decreases the size of the secondary droplet to a certain extent. In addition, the Marangoni stress stretches the primary droplets in the axial direction and makes them more prolate, as illustrated previously in figure 5.
$0.6$, a secondary droplet unavoidably appears at the midpoint of the filament. The Marangoni stress decreases the size of the secondary droplet to a certain extent. In addition, the Marangoni stress stretches the primary droplets in the axial direction and makes them more prolate, as illustrated previously in figure 5.

Figure 8. Effect of the Marangoni stress. (a) Temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, for
$S_{\lambda /2}$, for ![]() $k=0.8$ and
$k=0.8$ and ![]() $0.9$; (b) and (c) thread profiles for
$0.9$; (b) and (c) thread profiles for ![]() $k=0.5$ and
$k=0.5$ and ![]() $0.6$, respectively. Solid lines: the Marangoni stress is taken into account; dotted lines: the Marangoni stress is turned off. In (b),
$0.6$, respectively. Solid lines: the Marangoni stress is taken into account; dotted lines: the Marangoni stress is turned off. In (b), ![]() $t=113.9$ (Marangoni) and
$t=113.9$ (Marangoni) and ![]() $92$ (no Marangoni); in (c),
$92$ (no Marangoni); in (c), ![]() $t=126.85$ (Marangoni) and
$t=126.85$ (Marangoni) and ![]() $104.6$ (no Marangoni).
$104.6$ (no Marangoni).
The primary droplets attain an almost static shape in the elasto-capillary regime. It is of interest to seek the static solution to the shape of primary droplets. For a surfactant-free viscoelastic thread, the static solution is a sphere (Clasen et al. Reference Clasen, Eggers, Fontelos, Li and McKinley2006a), as illustrated in figure 9(a). When the thread is covered with a surfactant monolayer, its primary droplets are spherical no more. The static solution can be readily obtained in some simplified cases. For instance, if we neglect the time-dependent term, the inertia, the viscoelastic stress and the surface shear and dilatational viscosities (in the primary droplet region this simplification is reasonable), the momentum equation (3.2) yields
In the large surface Péclet number case, the surface tension ![]() $\sigma$ can be approximated by (4.12). The substitution of (4.12) into (4.13) yields
$\sigma$ can be approximated by (4.12). The substitution of (4.12) into (4.13) yields
Note that both ![]() $\sigma$ and
$\sigma$ and ![]() $\mathcal {C}$ are functions of
$\mathcal {C}$ are functions of ![]() $S(z)$ only. So (4.14) is essentially an ordinary differential equation for
$S(z)$ only. So (4.14) is essentially an ordinary differential equation for ![]() $S$
$S$
An analytical solution to (4.14) or (4.15) may exist or not. We turn to numerical methods such as finite difference.

Figure 9. Shape of the primary droplet located at the origin ![]() $z=0$. The cases of (a) a surfactant-free viscoelastic thread, (b) a surfactant-covered viscoelastic thread with the Marangoni stress turned off and (c) a surfactant-covered viscoelastic thread with the Marangoni stress taken into account. The dotted lines denote an isolated spherical droplet of the same volume. The solid lines denote the primary droplets simulated by the 1-D model. The dashed lines denote the static solutions. Here,
$z=0$. The cases of (a) a surfactant-free viscoelastic thread, (b) a surfactant-covered viscoelastic thread with the Marangoni stress turned off and (c) a surfactant-covered viscoelastic thread with the Marangoni stress taken into account. The dotted lines denote an isolated spherical droplet of the same volume. The solid lines denote the primary droplets simulated by the 1-D model. The dashed lines denote the static solutions. Here, ![]() $k=0.8$.
$k=0.8$.
A static solution is plotted in figure 9(c). It is shown that the static solution agrees well with the 1-D numerical simulation. As outlined previously, the primary droplet exhibits a prolate spheroid profile under the action of the Marangoni stress. In contrast, when the Marangoni stress is turned off, the primary droplet becomes oblate, as illustrated in figure 9(b). That is, the primary droplet is stretched in the radial direction, due to the spatial non-uniformity of the surface tension.
The effect of the Marangoni number ![]() $E$ on the nonlinear evolution of the Oldroyd-B viscoelastic thread is shown in figure 10. As shown in figure 10(a), the Marangoni number
$E$ on the nonlinear evolution of the Oldroyd-B viscoelastic thread is shown in figure 10. As shown in figure 10(a), the Marangoni number ![]() $E$ prolongs the early stages of thread thinning. As the Marangoni number increases, the local capillary force decreases and the Marangoni stress increases. Both factors result in the decrease in the temporal growth rate of the initial disturbance, as predicted by linear theory. At the final stage, an elasto-capillary balance is established in the filament and the
$E$ prolongs the early stages of thread thinning. As the Marangoni number increases, the local capillary force decreases and the Marangoni stress increases. Both factors result in the decrease in the temporal growth rate of the initial disturbance, as predicted by linear theory. At the final stage, an elasto-capillary balance is established in the filament and the ![]() $1/3De$ exponential law is little influenced by the Marangoni number (recall that this is the large surface Péclet number case). On the other hand, the Marangoni number influences the beads-on-a-string morphology. Particularly, it decreases the size of the secondary droplet or even leads to the disappearance of the secondary droplet, as illustrated in figure 10(b). The capillary force at the filament surface decreases as the Marangoni number increases. This tendency might be responsible for the weight loss of the secondary droplet. The 1-D linear result in figure 2(d) shows that the most unstable wavenumber
$1/3De$ exponential law is little influenced by the Marangoni number (recall that this is the large surface Péclet number case). On the other hand, the Marangoni number influences the beads-on-a-string morphology. Particularly, it decreases the size of the secondary droplet or even leads to the disappearance of the secondary droplet, as illustrated in figure 10(b). The capillary force at the filament surface decreases as the Marangoni number increases. This tendency might be responsible for the weight loss of the secondary droplet. The 1-D linear result in figure 2(d) shows that the most unstable wavenumber ![]() $k_{max}$ decreases from 0.375 as the Marangoni number
$k_{max}$ decreases from 0.375 as the Marangoni number ![]() $E$ increases from zero. Figure 10(b) shows that the smaller the axial wavenumber, the larger the secondary droplet. So secondary droplets formed under natural excitations are predicted to possess volumes larger than those for
$E$ increases from zero. Figure 10(b) shows that the smaller the axial wavenumber, the larger the secondary droplet. So secondary droplets formed under natural excitations are predicted to possess volumes larger than those for ![]() $k=0.4$ in figure 10(b).
$k=0.4$ in figure 10(b).

Figure 10. Effect of the Marangoni number ![]() $E$ on the nonlinear behaviour of the Oldroyd-B viscoelastic thread. (a) Temporal evolution of the thread radius at the midpoint,
$E$ on the nonlinear behaviour of the Oldroyd-B viscoelastic thread. (a) Temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, where
$S_{\lambda /2}$, where ![]() $k=0.8$ and the solid lines are the predictions of linear theory. (b) Dependence of the secondary droplet volume
$k=0.8$ and the solid lines are the predictions of linear theory. (b) Dependence of the secondary droplet volume ![]() $V_s$ on
$V_s$ on ![]() $E$ and
$E$ and ![]() $k$. Note that for
$k$. Note that for ![]() $k=0.7$ and
$k=0.7$ and ![]() $E=0.4$ or
$E=0.4$ or ![]() $0.6$ the secondary droplet actually does not exist.
$0.6$ the secondary droplet actually does not exist.
The measurement of surface shear and dilatational viscosities is technically challenging due to the difficulty of separating the surface rheological effects from the Marangoni effects (Kamat et al. Reference Kamat, Wagoner, Thete and Basaran2018; Wee et al. Reference Wee, Wagoner, Kamat and Basaran2020). Several recent analytical and numerical studies on Newtonian threads have accounted for the surface viscosities and proposed possible routes to measuring the surface rheological properties (Wee et al. Reference Wee, Wagoner, Kamat and Basaran2020, Reference Wee, Wagoner, Garg, Kamat and Basaran2021). The effect of the surface viscosities on Newtonian threads are summarized in table 3. In the following, we examine their effect on the nonlinear dynamics of Oldroyd-B viscoelastic threads.
Table 3. The effects of surface viscosities on inviscid and viscous threads.

Figure 11 illustrates the temporal evolution of the thread radius ![]() $S$, the first normal stress difference
$S$, the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$, the extension rate
$\tau _{zz}-\tau _{rr}$, the extension rate ![]() $\dot {\varepsilon }$(
$\dot {\varepsilon }$(![]() $=\partial u/\partial z$) and the Trouton ratio
$=\partial u/\partial z$) and the Trouton ratio ![]() $\eta _E/\eta _0$(
$\eta _E/\eta _0$(![]() $=3\beta +(\tau _{zz}-\tau _{rr})/Oh\dot {\varepsilon }, \eta _E$: the elongational viscosity) at the midpoint
$=3\beta +(\tau _{zz}-\tau _{rr})/Oh\dot {\varepsilon }, \eta _E$: the elongational viscosity) at the midpoint ![]() $z=\lambda /2$ for the axial wavenumber
$z=\lambda /2$ for the axial wavenumber ![]() $k=0.8$, where a wide range of the Boussinesq numbers is considered. It is shown that the thinning of the viscoelastic thread can be delayed to an extraordinary extent at large values of the Boussinesq numbers, in agreement with the tendency predicted by linear theory in figures 2(e) and 2( f).
$k=0.8$, where a wide range of the Boussinesq numbers is considered. It is shown that the thinning of the viscoelastic thread can be delayed to an extraordinary extent at large values of the Boussinesq numbers, in agreement with the tendency predicted by linear theory in figures 2(e) and 2( f).

Figure 11. Effect of the Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ on the thinning behaviour of the Oldroyd-B viscoelastic thread, (a) the thread radius
$B_{\mu \infty }$ on the thinning behaviour of the Oldroyd-B viscoelastic thread, (a) the thread radius ![]() $S$, (b) the first normal stress difference
$S$, (b) the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$, (c) the extension rate
$\tau _{zz}-\tau _{rr}$, (c) the extension rate ![]() $\dot {\varepsilon }$ and (d) the Trouton ratio
$\dot {\varepsilon }$ and (d) the Trouton ratio ![]() $\eta _E/\eta _0$ at the midpoint
$\eta _E/\eta _0$ at the midpoint ![]() $z=\lambda /2$. The ordinate axis on the right is only for
$z=\lambda /2$. The ordinate axis on the right is only for ![]() $B_{\kappa \infty }=B_{\mu \infty }=100$ at extremely large times. Here,
$B_{\kappa \infty }=B_{\mu \infty }=100$ at extremely large times. Here, ![]() $k=0.8$.
$k=0.8$.
At large values of the Boussinesq numbers such as 10 and 100, the final stage of filament thinning is characterized by a uniaxial extensional flow no more. If the flow were uniaxial extensional, the extension rate ![]() $\dot {\varepsilon }$ would approach the constant
$\dot {\varepsilon }$ would approach the constant ![]() $2/3De$. However, as shown in figure 11(c), for
$2/3De$. However, as shown in figure 11(c), for ![]() $B_{\kappa \infty }=B_{\mu \infty }=10$ or
$B_{\kappa \infty }=B_{\mu \infty }=10$ or ![]() $100$, the extension rate oscillates violently with decreasing amplitude, possibly attributed to the interplay between the surface viscous stresses, the capillary force and the viscoelastic stresses as the thread enters the final stage. At the final stage, the filament thinning deviates from the
$100$, the extension rate oscillates violently with decreasing amplitude, possibly attributed to the interplay between the surface viscous stresses, the capillary force and the viscoelastic stresses as the thread enters the final stage. At the final stage, the filament thinning deviates from the ![]() $1/3De$ exponential law. Meanwhile, the temporal evolution of the first normal stress difference
$1/3De$ exponential law. Meanwhile, the temporal evolution of the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ does not follow exactly the
$\tau _{zz}-\tau _{rr}$ does not follow exactly the ![]() $1/3De$ exponential law, as shown in figure 11(b). The Trouton ratio
$1/3De$ exponential law, as shown in figure 11(b). The Trouton ratio ![]() $\eta _E/\eta _0$ behaves weirdly as well, see figure 11(d). In general, at large Boussinesq numbers, the surface viscous stresses enter the dominant force balance and affect the thinning of the filament significantly.
$\eta _E/\eta _0$ behaves weirdly as well, see figure 11(d). In general, at large Boussinesq numbers, the surface viscous stresses enter the dominant force balance and affect the thinning of the filament significantly.
An interesting phenomenon is observed at moderate Boussinesq numbers. As shown in figure 11(a), for ![]() $B_{\kappa \infty }=B_{\mu \infty }=1$, the thread radius at the midpoint,
$B_{\kappa \infty }=B_{\mu \infty }=1$, the thread radius at the midpoint, ![]() $S_{\lambda /2}$, begins to increase at some instant, indicating that a secondary droplet is formed. This is a delicate situation, for the secondary droplet disappears when the Boussinesq numbers increase a little. There seems to be a narrow window of
$S_{\lambda /2}$, begins to increase at some instant, indicating that a secondary droplet is formed. This is a delicate situation, for the secondary droplet disappears when the Boussinesq numbers increase a little. There seems to be a narrow window of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ near
$B_{\mu \infty }$ near ![]() $O(1)$ for the appearance of secondary droplet. The surface viscosities prompt the formation of secondary droplet when they are small but suppress it when they are large.
$O(1)$ for the appearance of secondary droplet. The surface viscosities prompt the formation of secondary droplet when they are small but suppress it when they are large.
The role of the surface viscous stresses at the final stage of thread thinning can be better understood by defining the filament Ohnesorge number ![]() $Oh^S_{1f}=\mu _s(\rho \sigma R^3_f)^{-1/2}$, where the surface shear viscosity
$Oh^S_{1f}=\mu _s(\rho \sigma R^3_f)^{-1/2}$, where the surface shear viscosity ![]() $\mu _s$, the surface tension
$\mu _s$, the surface tension ![]() $\sigma$ and the filament radius
$\sigma$ and the filament radius ![]() $R_f$ are all evaluated at the midpoint
$R_f$ are all evaluated at the midpoint ![]() $z=\lambda /2$. The filament Ohnesorge number
$z=\lambda /2$. The filament Ohnesorge number ![]() $Oh^S_{1f}$ represents the ratio of the surface viscous stresses to the capillary force in the filament. The evolution of
$Oh^S_{1f}$ represents the ratio of the surface viscous stresses to the capillary force in the filament. The evolution of ![]() $Oh^S_{1f}$ in time is shown in figures 12(a) and 12(b) for
$Oh^S_{1f}$ in time is shown in figures 12(a) and 12(b) for ![]() $B_{\kappa \infty }=B_{\mu \infty }=0.1$ and
$B_{\kappa \infty }=B_{\mu \infty }=0.1$ and ![]() $B_{\kappa \infty }=B_{\mu \infty }=10$, respectively, where the thread radius
$B_{\kappa \infty }=B_{\mu \infty }=10$, respectively, where the thread radius ![]() $S_{\lambda /2}$ and the surfactant concentration
$S_{\lambda /2}$ and the surfactant concentration ![]() $\varGamma _{\lambda /2}$ are plotted as well. As illustrated in the figure, before the final stage,
$\varGamma _{\lambda /2}$ are plotted as well. As illustrated in the figure, before the final stage, ![]() $Oh^S_{1f}$ increases slowly and
$Oh^S_{1f}$ increases slowly and ![]() $S_{\lambda /2}$ and
$S_{\lambda /2}$ and ![]() $\varGamma _{\lambda /2}$ decrease rapidly with time increasing; in contrast, at the final stage,
$\varGamma _{\lambda /2}$ decrease rapidly with time increasing; in contrast, at the final stage, ![]() $Oh^S_{1f}$ increases rapidly and
$Oh^S_{1f}$ increases rapidly and ![]() $S_{\lambda /2}$ and
$S_{\lambda /2}$ and ![]() $\varGamma _{\lambda /2}$ decrease slowly with time increasing. For the large surface Péclet number case (
$\varGamma _{\lambda /2}$ decrease slowly with time increasing. For the large surface Péclet number case (![]() $Pe=10^5$) considered in figure 12, the increase in
$Pe=10^5$) considered in figure 12, the increase in ![]() $Oh^S_{1f}$ at the final stage, similar to the decrease in
$Oh^S_{1f}$ at the final stage, similar to the decrease in ![]() $S_{\lambda /2}$ or
$S_{\lambda /2}$ or ![]() $\varGamma _{\lambda /2}$, seems to follow an almost exponential law in time, especially for small Boussinesq numbers. For
$\varGamma _{\lambda /2}$, seems to follow an almost exponential law in time, especially for small Boussinesq numbers. For ![]() $B_{\kappa \infty }=B_{\mu \infty }=0.1, Oh^S_{1f}$ can reach
$B_{\kappa \infty }=B_{\mu \infty }=0.1, Oh^S_{1f}$ can reach ![]() $O$(1). For
$O$(1). For ![]() $B_{\kappa \infty }=B_{\mu \infty }=10, Oh^S_{1f}$, which is already larger than unity at the initial time, can be
$B_{\kappa \infty }=B_{\mu \infty }=10, Oh^S_{1f}$, which is already larger than unity at the initial time, can be ![]() $O$(
$O$(![]() $10^2$) at the final time. The surface viscous stresses can still be large in the filament and compete with the capillary force and the viscoelastic stresses, even though surfactant molecules are almost swept away from the filament for large surface Péclet numbers.
$10^2$) at the final time. The surface viscous stresses can still be large in the filament and compete with the capillary force and the viscoelastic stresses, even though surfactant molecules are almost swept away from the filament for large surface Péclet numbers.

Figure 12. Temporal evolution of the filament Ohnesorge number ![]() $Oh^S_{1f}$, the thread radius
$Oh^S_{1f}$, the thread radius ![]() $S$ and the surfactant concentration
$S$ and the surfactant concentration ![]() $\varGamma$ at the midpoint
$\varGamma$ at the midpoint ![]() $\lambda /2$. In (a),
$\lambda /2$. In (a), ![]() $B_{\kappa \infty }=B_{\mu \infty }=0.1$; in (b),
$B_{\kappa \infty }=B_{\mu \infty }=0.1$; in (b), ![]() $B_{\kappa \infty }=B_{\mu \infty }=10$. Here,
$B_{\kappa \infty }=B_{\mu \infty }=10$. Here, ![]() $k=0.8$.
$k=0.8$.
The effect of the surface viscosities on the morphology of the Oldroyd-B viscoelastic thread is further examined in figure 13, where the thread profiles are plotted for different values of the axial wavenumber ![]() $k$. The two distinct roles of the surface viscosities can be more clearly seen in the figure. For instance, for
$k$. The two distinct roles of the surface viscosities can be more clearly seen in the figure. For instance, for ![]() $k=0.7$, there exists a secondary droplet at the midpoint when the surface viscosities are absent (
$k=0.7$, there exists a secondary droplet at the midpoint when the surface viscosities are absent (![]() $B_{\kappa \infty }=B_{\mu \infty }=0$).With the Boussinesq numbers
$B_{\kappa \infty }=B_{\mu \infty }=0$).With the Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ increasing from zero, the secondary droplet is continuously shrunk. When the surface viscosities are sufficiently large, the secondary droplet completely disappears, see the thread profile for
$B_{\mu \infty }$ increasing from zero, the secondary droplet is continuously shrunk. When the surface viscosities are sufficiently large, the secondary droplet completely disappears, see the thread profile for ![]() $B_{\kappa \infty }=B_{\mu \infty }=100$, reflecting the suppression effect of the surface viscosities on secondary droplets. The same phenomenon occurs at smaller axial wavenumbers, see the thread profiles for
$B_{\kappa \infty }=B_{\mu \infty }=100$, reflecting the suppression effect of the surface viscosities on secondary droplets. The same phenomenon occurs at smaller axial wavenumbers, see the thread profiles for ![]() $k=0.3$ to
$k=0.3$ to ![]() $0.6$. This trend is easily understood, considering that large surface viscosities create large surface viscous stresses that tend to hinder the formation of secondary droplets. For larger axial wavenumbers
$0.6$. This trend is easily understood, considering that large surface viscosities create large surface viscous stresses that tend to hinder the formation of secondary droplets. For larger axial wavenumbers ![]() $k=0.8$ and
$k=0.8$ and ![]() $0.9$, the thread evolves into a beads-on-a-string structure with no secondary droplet, in the absence of surface viscosities. However, at
$0.9$, the thread evolves into a beads-on-a-string structure with no secondary droplet, in the absence of surface viscosities. However, at ![]() $B_{\kappa \infty }=B_{\mu \infty }=1$, the surface viscosities cause the appearance of a secondary droplet at the midpoint. Then, the surface viscosities try to shrink the secondary droplet and eventually lead to its disappearance, see the thread profiles for
$B_{\kappa \infty }=B_{\mu \infty }=1$, the surface viscosities cause the appearance of a secondary droplet at the midpoint. Then, the surface viscosities try to shrink the secondary droplet and eventually lead to its disappearance, see the thread profiles for ![]() $B_{\kappa \infty }=B_{\mu \infty }=100$. The formation of secondary droplet at large axial wavenumbers and moderate surface viscosities seems odd. It possibly results from the interplay between the inertial, capillary and surface viscous forces.
$B_{\kappa \infty }=B_{\mu \infty }=100$. The formation of secondary droplet at large axial wavenumbers and moderate surface viscosities seems odd. It possibly results from the interplay between the inertial, capillary and surface viscous forces.

Figure 13. Thread profiles for different values of the Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ and different values of the axial wavenumber
$B_{\mu \infty }$ and different values of the axial wavenumber ![]() $k$. The insets illustrate the zoomed-in secondary droplet located at the midpoint
$k$. The insets illustrate the zoomed-in secondary droplet located at the midpoint ![]() ${z=\lambda /2}$.
${z=\lambda /2}$.
It is also found that surface viscosities can deform primary droplets. As shown in figure 13, the primary droplets are continuously stretched in the axial direction as the shear and dilatational Boussinesq numbers increase. At a value of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ as large as
$B_{\mu \infty }$ as large as ![]() $100$, the shape of the primary droplets becomes singular. The corner regions connecting the filament to the primary droplets get stretched. The shape resembles a cone in the 3-D space. From a physical point of view, the capillary force fails to overcome the surface viscous stresses and cannot help the primary droplets maintain their spheroidal shape at high surface viscosities.
$100$, the shape of the primary droplets becomes singular. The corner regions connecting the filament to the primary droplets get stretched. The shape resembles a cone in the 3-D space. From a physical point of view, the capillary force fails to overcome the surface viscous stresses and cannot help the primary droplets maintain their spheroidal shape at high surface viscosities.
In the 1-D momentum equation (3.2), the terms numbered ![]() ${\bigcirc{\kern-6pt 2}}$,
${\bigcirc{\kern-6pt 2}}$, ![]() ${\bigcirc{\kern-6pt 4}}$ and
${\bigcirc{\kern-6pt 4}}$ and ![]() ${\bigcirc{\kern-6pt 5}}$ represent the surface viscous stresses. If the shear and dilatational viscosities are not equal, terms
${\bigcirc{\kern-6pt 5}}$ represent the surface viscous stresses. If the shear and dilatational viscosities are not equal, terms ![]() ${\bigcirc{\kern-6pt 2}}$ and
${\bigcirc{\kern-6pt 2}}$ and ![]() ${\bigcirc{\kern-6pt 4}}$ are non-zero. These two terms make the simulation more difficult. To simplify the calculation, one strategy is to apply the slender body approximation to the full curvature in
${\bigcirc{\kern-6pt 4}}$ are non-zero. These two terms make the simulation more difficult. To simplify the calculation, one strategy is to apply the slender body approximation to the full curvature in ![]() ${\bigcirc{\kern-6pt 2}}$ and
${\bigcirc{\kern-6pt 2}}$ and ![]() ${\bigcirc{\kern-6pt 4}}$, i.e.
${\bigcirc{\kern-6pt 4}}$, i.e.
The accuracy of this simplification is checked in figure 14 by comparing the slender body approximation with the full-curvature case. It is shown in figure 14(a) that the simplification does not lead to any significant difference in the temporal evolution of the Oldroyd-B viscoelastic thread. In figures 14(b) and 14(c), the slender body approximation seems to predict smaller secondary droplets and less spherical primary droplets. Note that ![]() $B_{\kappa \infty }$ is taken to be smaller than
$B_{\kappa \infty }$ is taken to be smaller than ![]() $B_{\mu \infty }$. If
$B_{\mu \infty }$. If ![]() $B_{\kappa \infty }$ is larger than
$B_{\kappa \infty }$ is larger than ![]() $B_{\mu \infty }$, the trends in figures 14(b) and 14(c) are presumably opposite, since the signs of
$B_{\mu \infty }$, the trends in figures 14(b) and 14(c) are presumably opposite, since the signs of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ in terms
$B_{\mu \infty }$ in terms ![]() ${\bigcirc{\kern-6pt 2}}$ and
${\bigcirc{\kern-6pt 2}}$ and ![]() ${\bigcirc{\kern-6pt 4}}$ of (3.2) are opposite.
${\bigcirc{\kern-6pt 4}}$ of (3.2) are opposite.

Figure 14. Comparison of the slender body approximation (solid lines) and the full-curvature (dotted lines) case. (a) Temporal evolution of the thread radius at the midpoint, ![]() $S_{\lambda /2}$, for
$S_{\lambda /2}$, for ![]() $k=0.8$ and
$k=0.8$ and ![]() $0.9$, where
$0.9$, where ![]() $B_{\kappa \infty }=1$ and
$B_{\kappa \infty }=1$ and ![]() $B_{\mu \infty }=10$; (b) and (c) thread profiles for
$B_{\mu \infty }=10$; (b) and (c) thread profiles for ![]() $k=0.7$ and
$k=0.7$ and ![]() $k=0.8$, respectively, where
$k=0.8$, respectively, where ![]() $B_{\kappa \infty }=0.1$ and
$B_{\kappa \infty }=0.1$ and ![]() $B_{\mu \infty }=1$.
$B_{\mu \infty }=1$.
4.3. Nonlinear behaviour of a surfactant-covered FENE-P viscoelastic thread
Different from Oldroyd-B viscoelastic threads, viscoelastic threads of FENE-P type break up in finite time, owing to finite extensibility of polymer chains. The nonlinear behaviour of a FENE-P viscoelastic thread free of surfactant is represented in figure 15. As shown in figure 15(a), the ![]() $1/3De$ exponential thinning law is valid no more for the FENE-P model. At the nonlinear stages, the elastic force in the filament fails to balance the capillary force, and the dynamics of the thread is dominated by inertia, capillarity and viscoelasticity. In such a case, the minimum radius of the thread decreases linearly in time until pinch-off. For smaller values of the finite extensibility
$1/3De$ exponential thinning law is valid no more for the FENE-P model. At the nonlinear stages, the elastic force in the filament fails to balance the capillary force, and the dynamics of the thread is dominated by inertia, capillarity and viscoelasticity. In such a case, the minimum radius of the thread decreases linearly in time until pinch-off. For smaller values of the finite extensibility ![]() $L$, the minimum thread radius
$L$, the minimum thread radius ![]() $S_{min}$ decreases faster and pinch-off occurs earlier. Meanwhile, the location of
$S_{min}$ decreases faster and pinch-off occurs earlier. Meanwhile, the location of ![]() $S_{min}$, denoted by
$S_{min}$, denoted by ![]() $z_{min}$, moves from the midpoint
$z_{min}$, moves from the midpoint ![]() $z_{\lambda /2}$ to the corner region connecting the filament to the primary droplet, although the thickness of the filament appears to be uniform (Fontelos & Li Reference Fontelos and Li2004). The pinch-off time, denoted by
$z_{\lambda /2}$ to the corner region connecting the filament to the primary droplet, although the thickness of the filament appears to be uniform (Fontelos & Li Reference Fontelos and Li2004). The pinch-off time, denoted by ![]() $t_p$, is diagrammed in figure 15(b). It can be seen that
$t_p$, is diagrammed in figure 15(b). It can be seen that ![]() $t_p$ decreases as
$t_p$ decreases as ![]() $L$ decreases. On the other hand,
$L$ decreases. On the other hand, ![]() $t_p$ depends greatly on the axial wavenumber, or rather, on the growth rate predicted by linear theory. The thread profiles are plotted in figures 15(c) and 15(d) for a relatively large axial wavenumber
$t_p$ depends greatly on the axial wavenumber, or rather, on the growth rate predicted by linear theory. The thread profiles are plotted in figures 15(c) and 15(d) for a relatively large axial wavenumber ![]() $k=0.8$ and a relatively small axial wavenumber
$k=0.8$ and a relatively small axial wavenumber ![]() $k=0.3$, respectively. It is found that finite extensibility may alter the beads-on-a-string morphology to a certain extent. In the case of
$k=0.3$, respectively. It is found that finite extensibility may alter the beads-on-a-string morphology to a certain extent. In the case of ![]() $k=0.8$, a tiny secondary droplet arises at the midpoint when
$k=0.8$, a tiny secondary droplet arises at the midpoint when ![]() $L$ is sufficiently small, say
$L$ is sufficiently small, say ![]() $L=2$. In the case of
$L=2$. In the case of ![]() $k=0.3$, small extensibility may lead to large deformation of secondary droplet, see the thread profile for
$k=0.3$, small extensibility may lead to large deformation of secondary droplet, see the thread profile for ![]() $L=5$. In the following, we examine briefly the effect of surfactants on the nonlinear behaviour of FENE-P viscoelastic liquid threads.
$L=5$. In the following, we examine briefly the effect of surfactants on the nonlinear behaviour of FENE-P viscoelastic liquid threads.

Figure 15. Effect of the finite extensibility parameter ![]() $L$ on the nonlinear behaviour of a FENE-P viscoelastic thread free of surfactant. (a) The minimum thread radius
$L$ on the nonlinear behaviour of a FENE-P viscoelastic thread free of surfactant. (a) The minimum thread radius ![]() $S_{min}$ (the lower lines) and its location
$S_{min}$ (the lower lines) and its location ![]() $z_{min}$ (the upper lines) for different values of
$z_{min}$ (the upper lines) for different values of ![]() $L$, where
$L$, where ![]() $k=0.8$. (b) The pinch-off time
$k=0.8$. (b) The pinch-off time ![]() $t_p$ vs
$t_p$ vs ![]() $L$ for different values of
$L$ for different values of ![]() $k$. Thread profiles for (c)
$k$. Thread profiles for (c) ![]() $k=0.8$ and (d)
$k=0.8$ and (d) ![]() $k=0.3$ for different values of
$k=0.3$ for different values of ![]() $L$.
$L$.
Figure 16 illustrates the effect of the initial surfactant concentration ![]() $\varGamma _0$ on the thinning of the FENE-P viscoelastic thread. It can be seen from figure 16(a) that the surfactant retards the pinch-off of the thread. This is mainly because the decrease in the minimum thread radius
$\varGamma _0$ on the thinning of the FENE-P viscoelastic thread. It can be seen from figure 16(a) that the surfactant retards the pinch-off of the thread. This is mainly because the decrease in the minimum thread radius ![]() $S_{min}$ at the early stages is decelerated with increasing
$S_{min}$ at the early stages is decelerated with increasing ![]() $\varGamma _0$, which is basically a linear effect. At the final stage, the influence of the surfactant is limited, for most of the surfactant molecules are swept away from the filament for the large surface Péclet number case considered, as discussed in the Oldroyd-B model. In figure 16(b), close to the pinch-off time
$\varGamma _0$, which is basically a linear effect. At the final stage, the influence of the surfactant is limited, for most of the surfactant molecules are swept away from the filament for the large surface Péclet number case considered, as discussed in the Oldroyd-B model. In figure 16(b), close to the pinch-off time ![]() $t_p, S_{min}$ goes to zero almost in the same way as
$t_p, S_{min}$ goes to zero almost in the same way as ![]() $\varGamma _0$ varies, only that
$\varGamma _0$ varies, only that ![]() $S_{min}$ decreases a little faster at larger values of
$S_{min}$ decreases a little faster at larger values of ![]() $\varGamma _0$.
$\varGamma _0$.

Figure 16. Effect of the initial surfactant concentration ![]() $\varGamma _0$ on the thinning of the FENE-P viscoelastic thread. (a) Temporal evolution of the minimum thread radius
$\varGamma _0$ on the thinning of the FENE-P viscoelastic thread. (a) Temporal evolution of the minimum thread radius ![]() $S_{min}$ and (b)
$S_{min}$ and (b) ![]() $S_{min}$ vs the time to the pinching
$S_{min}$ vs the time to the pinching ![]() $t_p-t$ for different values of
$t_p-t$ for different values of ![]() $\varGamma _0$. Here,
$\varGamma _0$. Here, ![]() $k=0.8$.
$k=0.8$.
The effect of surfactant surface diffusion on the nonlinear behaviour of the FENE-P viscoelastic thread is explored by considering the moderate surface Péclet number case ![]() $Pe=1$. The result is illustrated in figure 17. As shown in figure 17(a), similar to the large
$Pe=1$. The result is illustrated in figure 17. As shown in figure 17(a), similar to the large ![]() $Pe$ case (
$Pe$ case (![]() $Pe=10^5$), in the moderate
$Pe=10^5$), in the moderate ![]() $Pe$ case the pinch-off of the FENE-P viscoelastic thread is retarded by increasing the initial surfactant concentration
$Pe$ case the pinch-off of the FENE-P viscoelastic thread is retarded by increasing the initial surfactant concentration ![]() $\varGamma _0$, owing to the suppression effect of the surfactant on the temporal growth rate of the initial disturbance. At the nonlinear stages, the minimum thread radius
$\varGamma _0$, owing to the suppression effect of the surfactant on the temporal growth rate of the initial disturbance. At the nonlinear stages, the minimum thread radius ![]() $S_{min}$ approaches zero at different speeds for different values of
$S_{min}$ approaches zero at different speeds for different values of ![]() $\varGamma _0$, as illustrated in figure 17(b). Unfortunately, no common trend can be found, suggesting that the surfactant affects the pinch-off of the viscoelastic thread in a complicated way.
$\varGamma _0$, as illustrated in figure 17(b). Unfortunately, no common trend can be found, suggesting that the surfactant affects the pinch-off of the viscoelastic thread in a complicated way.

Figure 17. The case of moderate surface Péclet number ![]() $Pe=1$. (a) Temporal evolution of the minimum thread radius
$Pe=1$. (a) Temporal evolution of the minimum thread radius ![]() $S_{min}$ and (b)
$S_{min}$ and (b) ![]() $S_{min}$ vs the time to the pinching
$S_{min}$ vs the time to the pinching ![]() $t_p-t$ for distinct values of the initial surfactant concentration
$t_p-t$ for distinct values of the initial surfactant concentration ![]() $\varGamma _0$. (c) Spatial variation of the thread radius
$\varGamma _0$. (c) Spatial variation of the thread radius ![]() $S$, the surfactant concentration
$S$, the surfactant concentration ![]() $\varGamma$, the surface tension
$\varGamma$, the surface tension ![]() $\sigma$, the axial velocity
$\sigma$, the axial velocity ![]() $u$ and the first normal stress difference
$u$ and the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ along the thread. In (a–c),
$\tau _{zz}-\tau _{rr}$ along the thread. In (a–c), ![]() $k=0.8$. In (c), the solid lines are for
$k=0.8$. In (c), the solid lines are for ![]() $\varGamma _0=0.3$ (the time instant
$\varGamma _0=0.3$ (the time instant ![]() $t=110.795$) and the dotted lines are for
$t=110.795$) and the dotted lines are for ![]() $\varGamma _0=0$ (
$\varGamma _0=0$ (![]() $t=94.48$).(d) Thread profiles for
$t=94.48$).(d) Thread profiles for ![]() $k=0.8$ and distinct values of
$k=0.8$ and distinct values of ![]() $\varGamma _0$, where the inset is the zoomed-in filament and secondary droplet regions. (e) Thread profiles for
$\varGamma _0$, where the inset is the zoomed-in filament and secondary droplet regions. (e) Thread profiles for ![]() $k=0.4$ and distinct values of
$k=0.4$ and distinct values of ![]() $\varGamma _0$.
$\varGamma _0$.
The variation of the thread radius ![]() $S$, the surfactant concentration
$S$, the surfactant concentration ![]() $\varGamma$, the surface tension
$\varGamma$, the surface tension ![]() $\sigma$, the axial velocity
$\sigma$, the axial velocity ![]() $u$ and the first normal stress difference
$u$ and the first normal stress difference ![]() $\tau _{zz}-\tau _{rr}$ along the thread is illustrated in figure 17(c) for the axial wavenumber
$\tau _{zz}-\tau _{rr}$ along the thread is illustrated in figure 17(c) for the axial wavenumber ![]() $k=0.8$ and the initial surfactant concentration
$k=0.8$ and the initial surfactant concentration ![]() $\varGamma _0=0$ and
$\varGamma _0=0$ and ![]() $0.3$. The spatial variation of
$0.3$. The spatial variation of ![]() $u$ and
$u$ and ![]() $\tau _{zz}-\tau _{rr}$ suggests that a tiny secondary droplet arises at the midpoint
$\tau _{zz}-\tau _{rr}$ suggests that a tiny secondary droplet arises at the midpoint ![]() $z=\lambda /2$ in the absence of the surfactant (
$z=\lambda /2$ in the absence of the surfactant (![]() $\varGamma _0=0$), although it is almost invisible from the thread profile. In the presence of the surfactant, i.e.
$\varGamma _0=0$), although it is almost invisible from the thread profile. In the presence of the surfactant, i.e. ![]() $\varGamma _0=0.3$, the volume of the secondary droplet is visibly increased. Due to surface diffusion, surfactant molecules cover the entire thread densely. Particularly in the neighbourhood of the secondary droplet, the surfactant concentration
$\varGamma _0=0.3$, the volume of the secondary droplet is visibly increased. Due to surface diffusion, surfactant molecules cover the entire thread densely. Particularly in the neighbourhood of the secondary droplet, the surfactant concentration ![]() $\varGamma$ is close to unity and the surface tension
$\varGamma$ is close to unity and the surface tension ![]() $\sigma$ is very small. Correspondingly, the viscoelastic force in the neighbourhood of the secondary droplet is small and the secondary droplet deforms greatly from spherical.
$\sigma$ is very small. Correspondingly, the viscoelastic force in the neighbourhood of the secondary droplet is small and the secondary droplet deforms greatly from spherical.
The effect of the initial surfactant concentration ![]() $\varGamma _0$ on the beads-on-a-string morphology in the moderate
$\varGamma _0$ on the beads-on-a-string morphology in the moderate ![]() $Pe$ case can be seen from figures 17(d) and 17(e) for the relatively large axial wavenumber
$Pe$ case can be seen from figures 17(d) and 17(e) for the relatively large axial wavenumber ![]() $k=0.8$ and the relatively small axial wavenumber
$k=0.8$ and the relatively small axial wavenumber ![]() $k=0.4$, respectively. For both wavenumbers, the secondary droplet at the midpoint gains weight and exhibits a more singular shape as
$k=0.4$, respectively. For both wavenumbers, the secondary droplet at the midpoint gains weight and exhibits a more singular shape as ![]() $\varGamma _0$ increases. Meanwhile, the thickness of the filament becomes more non-uniform. Pinch-off always occurs at the corner region where the filament joins the primary droplet. For the relatively small axial wavenumber
$\varGamma _0$ increases. Meanwhile, the thickness of the filament becomes more non-uniform. Pinch-off always occurs at the corner region where the filament joins the primary droplet. For the relatively small axial wavenumber ![]() $k=0.4$, higher-order generations of secondary droplets can be formed at sufficiently large values of
$k=0.4$, higher-order generations of secondary droplets can be formed at sufficiently large values of ![]() $\varGamma _0$ (see the thread profile for
$\varGamma _0$ (see the thread profile for ![]() $\varGamma _0=0.5$).
$\varGamma _0=0.5$).
The effect of the Marangoni stress on the pinch-off of the FENE-P viscoelastic thread is examined in figure 18, by comparing the case in which the Marangoni stress is taken into account with the case in which the Marangoni stress is turned off. As seen in figure 18(a), for the relatively large axial wavenumber ![]() $k=0.8$, the pinch-off of the viscoelastic thread occurs much earlier when the Marangoni stress is turned off. Note that the two lines intersect with each other near
$k=0.8$, the pinch-off of the viscoelastic thread occurs much earlier when the Marangoni stress is turned off. Note that the two lines intersect with each other near ![]() $S_{min}=0.53$ and
$S_{min}=0.53$ and ![]() $t_p-t=23$. Before intersecting, the minimum thread radius
$t_p-t=23$. Before intersecting, the minimum thread radius ![]() $S_{min}$ decreases much more rapidly in the absence of the Marangoni stress. In contrast, from the intersection point, it takes
$S_{min}$ decreases much more rapidly in the absence of the Marangoni stress. In contrast, from the intersection point, it takes ![]() $S_{min}$ the same time in two cases to decrease to zero. In general, the Marangoni stress greatly delays the pinch-off of the FENE-P viscoelastic thread. The thread profiles prior to pinch-off are plotted in figures 18(b) and 18(c) for
$S_{min}$ the same time in two cases to decrease to zero. In general, the Marangoni stress greatly delays the pinch-off of the FENE-P viscoelastic thread. The thread profiles prior to pinch-off are plotted in figures 18(b) and 18(c) for ![]() $k=0.8$ and
$k=0.8$ and ![]() $0.3$, respectively. For both axial wavenumbers, the primary droplets have been axially stretched by the Marangoni stress before the pinch-off takes place. The secondary droplets remain singular in shape when the Marangoni stress is absent. It indicates that the Marangoni stress has little to do with the non-spherical shape of secondary droplets. The deformation of secondary droplets possibly results from small local surface tension. On the other hand, the Marangoni stress affects secondary droplets by reducing their size.
$0.3$, respectively. For both axial wavenumbers, the primary droplets have been axially stretched by the Marangoni stress before the pinch-off takes place. The secondary droplets remain singular in shape when the Marangoni stress is absent. It indicates that the Marangoni stress has little to do with the non-spherical shape of secondary droplets. The deformation of secondary droplets possibly results from small local surface tension. On the other hand, the Marangoni stress affects secondary droplets by reducing their size.

Figure 18. Effect of the Marangoni stress on the nonlinear behaviour of the FENE-P viscoelastic thread.(a) The minimum thread radius ![]() $S_{min}$ vs the time to the pinching
$S_{min}$ vs the time to the pinching ![]() $t_p-t$ for
$t_p-t$ for ![]() $k=0.8$. Thread profiles for(b)
$k=0.8$. Thread profiles for(b) ![]() $k=0.8$ and (c)
$k=0.8$ and (c) ![]() $k=0.3$.
$k=0.3$.
Figure 19 shows the effect of the Marangoni number ![]() $E$ on the pinch-off of the FENE-P viscoelastic thread. At the early stages, the thinning of the thread can be greatly slowed down by increasing the value of
$E$ on the pinch-off of the FENE-P viscoelastic thread. At the early stages, the thinning of the thread can be greatly slowed down by increasing the value of ![]() $E$, owing to the suppression effect of the Marangoni number on the linear instability of the thread. At the late stages, from approximately
$E$, owing to the suppression effect of the Marangoni number on the linear instability of the thread. At the late stages, from approximately ![]() $S_{min}=0.45$ and
$S_{min}=0.45$ and ![]() $t_p-t=21$, the effect of the Marangoni number becomes quite limited. Recall that in the large surface Péclet number case of the Oldroyd-B viscoelastic thread, surfactant molecules are continuously convected to the primary droplet and not many remain at the filament surface. The situation is similar for the FENE-P viscoelastic thread.
$t_p-t=21$, the effect of the Marangoni number becomes quite limited. Recall that in the large surface Péclet number case of the Oldroyd-B viscoelastic thread, surfactant molecules are continuously convected to the primary droplet and not many remain at the filament surface. The situation is similar for the FENE-P viscoelastic thread.

Figure 19. Effect of the Marangoni number ![]() $E$ on the pinch-off of the FENE-P viscoelastic thread. The minimum thread radius
$E$ on the pinch-off of the FENE-P viscoelastic thread. The minimum thread radius ![]() $S_{min}$ vs the time to the pinching
$S_{min}$ vs the time to the pinching ![]() $t_p-t$. Here,
$t_p-t$. Here, ![]() $k=0.8$.
$k=0.8$.
In addition to the Marangoni number ![]() $E$, the Boussinesq numbers
$E$, the Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ may greatly delay the pinch-off of the FENE-P viscoelastic thread, as illustrated in figure 20(a). At relatively small values of
$B_{\mu \infty }$ may greatly delay the pinch-off of the FENE-P viscoelastic thread, as illustrated in figure 20(a). At relatively small values of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ such as 0.1 and 1, the surface viscosities slow down the growth of the initial disturbance at the early stages. At relatively large values of
$B_{\mu \infty }$ such as 0.1 and 1, the surface viscosities slow down the growth of the initial disturbance at the early stages. At relatively large values of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ 10 and 100, the surface viscosities tend to inhibit the pinch-off of the viscoelastic thread. The thread profiles for the axial wavenumber
$B_{\mu \infty }$ 10 and 100, the surface viscosities tend to inhibit the pinch-off of the viscoelastic thread. The thread profiles for the axial wavenumber ![]() $k=0.3$ and several values of
$k=0.3$ and several values of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ are plotted in figure 20(b). Like in Oldroyd-B threads, the surface viscous stresses may lead to the axial stretch of primary droplets. When
$B_{\mu \infty }$ are plotted in figure 20(b). Like in Oldroyd-B threads, the surface viscous stresses may lead to the axial stretch of primary droplets. When ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ are large, e.g.
$B_{\mu \infty }$ are large, e.g. ![]() $B_{\kappa \infty }=B_{\mu \infty }=10$, the corner connecting the filament to the primary droplet is axially stretched and the primary droplet is greatly deformed. On the other hand, for this small axial wavenumber, the secondary droplet located at the midpoint loses weight under the action of the surface viscous stresses. At sufficiently large values of
$B_{\kappa \infty }=B_{\mu \infty }=10$, the corner connecting the filament to the primary droplet is axially stretched and the primary droplet is greatly deformed. On the other hand, for this small axial wavenumber, the secondary droplet located at the midpoint loses weight under the action of the surface viscous stresses. At sufficiently large values of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$, the secondary droplet disappears.
$B_{\mu \infty }$, the secondary droplet disappears.

Figure 20. Effect of the Boussinesq numbers ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }$ on the pinch-off of the FENE-P viscoelastic thread. (a) The minimum thread radius
$B_{\mu \infty }$ on the pinch-off of the FENE-P viscoelastic thread. (a) The minimum thread radius ![]() $S_{min}$ vs the time to the pinching
$S_{min}$ vs the time to the pinching ![]() $t_p-t$ for
$t_p-t$ for ![]() $k=0.8$. (b) Thread profiles for different values of
$k=0.8$. (b) Thread profiles for different values of ![]() $B_{\kappa \infty }$ and
$B_{\kappa \infty }$ and ![]() $B_{\mu \infty }, k=0.3$.
$B_{\mu \infty }, k=0.3$.
5. Conclusion
Based on the slender body theory, we develop a 1-D model to numerically study the effect of an insoluble surfactant monolayer on the nonlinear dynamics of a non-Newtonian viscoelastic thread of Oldroyd-B or FENE-P type. In particular, we take into account the surface rheological properties of the surfactant. There are five dimensionless numbers related to the surfactant, i.e. the initial surfactant concentration, the Marangoni number, the surface Péclet number, the dilatational Boussinesq number and the shear Boussinesq number. The effect of these dimensionless numbers on the dynamics of the viscoelastic thread initially perturbed by a small harmonic disturbance is examined one by one.
The 1-D linear instability result shows that the temporal growth rate of the disturbance can be decreased by increasing the initial surfactant concentration, the Marangoni number, the surface Péclet number, the dilatational Boussinesq number or the shear Boussinesq number. That is, the presence of the surfactant suppresses the linear instability of the viscoelastic thread in all ways. The suppression effect of the surfactant is profound. It can greatly postpone the late nonlinear stages of thread thinning.
The surface Péclet number plays an important role in the nonlinear evolution of the viscoelastic thread. At large values of the surface Péclet number, the surfactant has a negligible influence on the exponential thinning of the Oldroyd-B viscoelastic thread, owing to the evacuation of surfactant molecules from the filament under the dominance of surface convection. On the other hand, the surfactant may affect the beads-on-a-string structure in two ways: it decreases the size of the secondary droplet or even remove it completely when the initial surfactant concentration or the Marangoni number is large enough; it stretches the primary droplet in the axial direction and leads to its deformation from a spherical to a prolate shape. In these phenomena, the Marangoni stress plays a role. At moderate values of the surface Péclet number, surfactant molecules are distributed over the filament due to surface diffusion, leading to the formation of secondary droplet in the filament.
At large values of the shear and dilatational Boussinesq numbers, the thinning of the viscoelastic thread can be greatly delayed by the surface viscous stresses. At the final stage, besides the capillary and elastic forces, the surface viscous stresses enter the dominant force balance in the filament. The filament follows the ![]() $1/3De$ exponential law no more. On the other hand, the surface viscous stresses can lead to the decrease in the secondary droplet size. When the Boussinesq numbers are sufficiently large, the secondary droplet disappears. Larger surface viscous stresses also lead to larger deformation of primary droplets.
$1/3De$ exponential law no more. On the other hand, the surface viscous stresses can lead to the decrease in the secondary droplet size. When the Boussinesq numbers are sufficiently large, the secondary droplet disappears. Larger surface viscous stresses also lead to larger deformation of primary droplets.
The pinch-off of the FENE-P viscoelastic thread can be greatly delayed by the presence of the surfactant. Prior to pinch-off, the decrease in the minimum thread radius is little influenced by the surfactant, if the surface Péclet number is large. However, when surface diffusion is important, the surfactant affects the pinch-off of the thread in a complicated way. The effect of the surfactant on the beads-on-a-string morphology of the FENE-P viscoelastic thread is similar to that on the Oldroyd-B viscoelastic thread.
According to the 1-D simulation, for surfactant-covered viscoelastic threads, the corner region connecting the primary droplet to the filament may possess self-similarity. An exploration of self-similar solutions may be performed in the future, taking into account the Marangoni stress and/or the surface rheological properties. Another open problem is the deformation of primary droplets driven by the surface viscous stresses. The singular shape of primary droplets is rare and deserves more investigation. In addition, it is of interest to develop an improved 1-D model with all necessary high-order terms included. The numerical simulation of the 2-D axisymmetric nonlinear dynamics of surfactant-covered viscoelastic threads needs to be carried out to verify the 1-D results.
Acknowledgements
We thank all the reviewers for their constructive comments and suggestions.
Funding
F.L. was supported by the National Natural Science Foundation of China (nos 12272373 and 11621202). D.H. was supported by the National Natural Science Foundation of China (no. 12172317), Guangdong Basic and Applied Basic Research Foundation (grant no. 2022A1515011784), and Shenzhen Science and Technology Program (no. JCYJ20210324125601005).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Derivation of the 1-D equations
The characteristic length in the radial direction, ![]() $l_r$, is assumed to be much smaller than the characteristic length in the axial direction,
$l_r$, is assumed to be much smaller than the characteristic length in the axial direction, ![]() $l_z$, i.e.
$l_z$, i.e.
where ![]() $\varepsilon$ is a small parameter. The balance of the capillary, inertial and viscoelastic forces gives
$\varepsilon$ is a small parameter. The balance of the capillary, inertial and viscoelastic forces gives
Use the scales
 \begin{equation}
\left.\begin{array}{@{}c@{}} \displaystyle r=l_r\tilde{r},\
z=l_z\tilde{z}, t=l_t\tilde{t}, \ S=l_r\tilde{S},
v=\dfrac{l_r}{l_t}\tilde{v}, u=\dfrac{l_z}{l_t}\tilde{u},
\sigma=\sigma_0\tilde{\sigma},\ p=\dfrac{\rho
l^2_z}{l^2_t}\tilde{p},\\
\displaystyle \tau_{rr}=\dfrac{\rho l^2_z}{l^2_t}\tilde{\tau}_{rr},
\tau_{\theta\theta}=\dfrac{\rho
l^2_z}{l^2_t}\tilde{\tau}_{\theta\theta},
\tau_{zz}=\dfrac{\rho l^2_z}{l^2_t}\tilde{\tau}_{zz},
\tau_{rz}=\dfrac{\rho l^3_z}{l_rl^2_t}\tilde{\tau}_{rz},
\varGamma=\varGamma_{\infty}\tilde{\varGamma},
\end{array}\right\}
\end{equation}
\begin{equation}
\left.\begin{array}{@{}c@{}} \displaystyle r=l_r\tilde{r},\
z=l_z\tilde{z}, t=l_t\tilde{t}, \ S=l_r\tilde{S},
v=\dfrac{l_r}{l_t}\tilde{v}, u=\dfrac{l_z}{l_t}\tilde{u},
\sigma=\sigma_0\tilde{\sigma},\ p=\dfrac{\rho
l^2_z}{l^2_t}\tilde{p},\\
\displaystyle \tau_{rr}=\dfrac{\rho l^2_z}{l^2_t}\tilde{\tau}_{rr},
\tau_{\theta\theta}=\dfrac{\rho
l^2_z}{l^2_t}\tilde{\tau}_{\theta\theta},
\tau_{zz}=\dfrac{\rho l^2_z}{l^2_t}\tilde{\tau}_{zz},
\tau_{rz}=\dfrac{\rho l^3_z}{l_rl^2_t}\tilde{\tau}_{rz},
\varGamma=\varGamma_{\infty}\tilde{\varGamma},
\end{array}\right\}
\end{equation}where the tilde denotes the corresponding dimensionless quantities. Hereafter the tilde is dropped for brevity.
The continuity, momentum and constitutive equations (2.1)–(2.10) are non-dimensionalized as
 $$\begin{gather}\begin{aligned} \frac{\partial v}{\partial t}+v\frac{\partial v}{\partial r} +u\frac{\partial v}{\partial z} & ={-}\frac{1}{\varepsilon^2} \frac{\partial p}{\partial r}+\frac{\beta}{\varepsilon^2} \left(\frac{\partial^2v}{\partial r^2}+\frac{1}{r} \frac{\partial v}{\partial r}-\frac{v}{r^2}\right) +\beta \frac{\partial^2v}{\partial z^2}\\ & \quad +\frac{1}{\varepsilon^2} \left(\frac{\partial \tau_{rr}}{\partial r}+ \frac{\partial \tau_{rz}}{\partial z}+\frac{\tau_{rr}- \tau_{\theta\theta}}{r}\right), \end{aligned} \end{gather}$$
$$\begin{gather}\begin{aligned} \frac{\partial v}{\partial t}+v\frac{\partial v}{\partial r} +u\frac{\partial v}{\partial z} & ={-}\frac{1}{\varepsilon^2} \frac{\partial p}{\partial r}+\frac{\beta}{\varepsilon^2} \left(\frac{\partial^2v}{\partial r^2}+\frac{1}{r} \frac{\partial v}{\partial r}-\frac{v}{r^2}\right) +\beta \frac{\partial^2v}{\partial z^2}\\ & \quad +\frac{1}{\varepsilon^2} \left(\frac{\partial \tau_{rr}}{\partial r}+ \frac{\partial \tau_{rz}}{\partial z}+\frac{\tau_{rr}- \tau_{\theta\theta}}{r}\right), \end{aligned} \end{gather}$$ $$\begin{gather}\tau_{zz}=\frac{1-\beta}{De}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{zz}=\frac{1-\beta}{De}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{rr}=\frac{1-\beta}{De}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{rr}=\frac{1-\beta}{De}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{\theta\theta}=\frac{1-\beta}{De}\left(\frac{A_{\theta \theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{\theta\theta}=\frac{1-\beta}{De}\left(\frac{A_{\theta \theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{rz}=\frac{1-\beta}{De}\frac{A_{rz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}\tau_{rz}=\frac{1-\beta}{De}\frac{A_{rz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{zz}}{\partial t}+v\frac{\partial A_{zz}}{\partial r}+u\frac{\partial A_{zz}}{\partial z}-\frac{2}{\varepsilon^2}A_{rz}\frac{\partial u}{\partial r}-2A_{zz}\frac{\partial u}{\partial z}\right)=1-\frac{A_{zz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{zz}}{\partial t}+v\frac{\partial A_{zz}}{\partial r}+u\frac{\partial A_{zz}}{\partial z}-\frac{2}{\varepsilon^2}A_{rz}\frac{\partial u}{\partial r}-2A_{zz}\frac{\partial u}{\partial z}\right)=1-\frac{A_{zz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{rr}}{\partial t}+v\frac{\partial A_{rr}}{\partial r}+u\frac{\partial A_{rr}}{\partial z}-2A_{rr}\frac{\partial v}{\partial r}-2A_{rz}\frac{\partial v}{\partial z}\right)=1-\frac{A_{rr}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{rr}}{\partial t}+v\frac{\partial A_{rr}}{\partial r}+u\frac{\partial A_{rr}}{\partial z}-2A_{rr}\frac{\partial v}{\partial r}-2A_{rz}\frac{\partial v}{\partial z}\right)=1-\frac{A_{rr}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{\theta\theta}}{\partial t}+v\frac{\partial A_{\theta\theta}}{\partial r}+u\frac{\partial A_{\theta\theta}}{\partial z}-2A_{\theta\theta}\frac{v}{r}\right)=1- \frac{A_{\theta\theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{\theta\theta}}{\partial t}+v\frac{\partial A_{\theta\theta}}{\partial r}+u\frac{\partial A_{\theta\theta}}{\partial z}-2A_{\theta\theta}\frac{v}{r}\right)=1- \frac{A_{\theta\theta}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{rz}}{\partial t}+v\frac{\partial A_{rz}}{\partial r}+u\frac{\partial A_{rz}}{\partial z}-A_{rr}\frac{\partial u}{\partial r}-\varepsilon^2A_{zz}\frac{\partial v}{\partial z}\right)={-}\frac{A_{rz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{rz}}{\partial t}+v\frac{\partial A_{rz}}{\partial r}+u\frac{\partial A_{rz}}{\partial z}-A_{rr}\frac{\partial u}{\partial r}-\varepsilon^2A_{zz}\frac{\partial v}{\partial z}\right)={-}\frac{A_{rz}}{1-\dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}, \end{gather}$$
where ![]() $De={\lambda _c}/{l_t}$ and
$De={\lambda _c}/{l_t}$ and ![]() $\beta ={\eta _s}/{\eta _0}={\eta _s}/({\eta _s+\eta _p})$.
$\beta ={\eta _s}/{\eta _0}={\eta _s}/({\eta _s+\eta _p})$.
The non-dimensionalized advection–diffusion equation for the surfactant is
 \begin{align} &\frac{\partial \varGamma }{\partial t}+u\frac{\partial \varGamma }{\partial z}+\frac{\varGamma}{S\sqrt{1+\varepsilon^2 S'^2}}\frac{\partial\left(\dfrac{S(u+\varepsilon^2 vS')}{\sqrt{1+\varepsilon^2 S'^2}}\right)}{\partial z}+\mathcal{C} \varGamma \frac{v-uS'}{\sqrt{1+\varepsilon^2 S'^2}}\nonumber\\ &\quad =\frac{1}{Pe}\frac{1}{S\sqrt{1+S'^2}}\frac{\partial \left(\dfrac{S\varGamma'}{\sqrt{1+\varepsilon^2 S'^2}}\right)}{\partial z}, \end{align}
\begin{align} &\frac{\partial \varGamma }{\partial t}+u\frac{\partial \varGamma }{\partial z}+\frac{\varGamma}{S\sqrt{1+\varepsilon^2 S'^2}}\frac{\partial\left(\dfrac{S(u+\varepsilon^2 vS')}{\sqrt{1+\varepsilon^2 S'^2}}\right)}{\partial z}+\mathcal{C} \varGamma \frac{v-uS'}{\sqrt{1+\varepsilon^2 S'^2}}\nonumber\\ &\quad =\frac{1}{Pe}\frac{1}{S\sqrt{1+S'^2}}\frac{\partial \left(\dfrac{S\varGamma'}{\sqrt{1+\varepsilon^2 S'^2}}\right)}{\partial z}, \end{align}
where ![]() $Pe={l^2_z}/{D_sl_t}$ and
$Pe={l^2_z}/{D_sl_t}$ and ![]() $\mathcal {C}={1}/{S\sqrt {1+\varepsilon ^2 S'^2}}-{\varepsilon ^2 S''}/{(1+\varepsilon ^2 S'^2)^{3/2}}$.
$\mathcal {C}={1}/{S\sqrt {1+\varepsilon ^2 S'^2}}-{\varepsilon ^2 S''}/{(1+\varepsilon ^2 S'^2)^{3/2}}$.
The non-dimensionalized kinematic boundary condition at the surface ![]() $r=S(z,t)$ has the same form with the dimensional one, i.e.
$r=S(z,t)$ has the same form with the dimensional one, i.e.
The normal and tangential force balance at the surface is non-dimensionalized as
 \begin{align} &p-\frac{1}{1+\varepsilon^2 S'^2}\left[2\beta \frac{\partial v}{\partial r}-2\beta S'\left(\varepsilon^2 \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)+2\beta \varepsilon^2 S'^2\frac{\partial u}{\partial z}+\varepsilon^2S'^2\tau_{zz}-2S'\tau_{rz}+\tau_{rr}\right]\nonumber\\ &\quad=\mathcal{C}\left[\sigma+\left(B_{\kappa\infty} \kappa_s-B_{\mu\infty}\mu_s\right)\left(\frac{(Su_t)'}{S\sqrt{1+ \varepsilon^2S'^2}}+\mathcal{C} u_n\right)\right]\nonumber\\ &\qquad+\frac{2B_{\mu\infty}\mu_s}{1+\varepsilon^2 S'^2}\left[\frac{S'u_t+u_n}{S^2}-\frac{\varepsilon^2 S''}{1+\varepsilon^2S'^2}\left(\frac{\partial (u_t)}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right], \end{align}
\begin{align} &p-\frac{1}{1+\varepsilon^2 S'^2}\left[2\beta \frac{\partial v}{\partial r}-2\beta S'\left(\varepsilon^2 \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)+2\beta \varepsilon^2 S'^2\frac{\partial u}{\partial z}+\varepsilon^2S'^2\tau_{zz}-2S'\tau_{rz}+\tau_{rr}\right]\nonumber\\ &\quad=\mathcal{C}\left[\sigma+\left(B_{\kappa\infty} \kappa_s-B_{\mu\infty}\mu_s\right)\left(\frac{(Su_t)'}{S\sqrt{1+ \varepsilon^2S'^2}}+\mathcal{C} u_n\right)\right]\nonumber\\ &\qquad+\frac{2B_{\mu\infty}\mu_s}{1+\varepsilon^2 S'^2}\left[\frac{S'u_t+u_n}{S^2}-\frac{\varepsilon^2 S''}{1+\varepsilon^2S'^2}\left(\frac{\partial (u_t)}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right], \end{align}and
 \begin{align} &\frac{1}{\left(1+\varepsilon^2S'^2\right)}\left[2\varepsilon^2 \beta S'\left(\frac{\partial v}{\partial r}-\frac{\partial u}{\partial z}\right)+\beta\left(1-\varepsilon^2 S'^2\right)\left(\varepsilon^2 \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)\right]\nonumber\\ &\qquad+\frac{1}{(1+\varepsilon^2S'^2)} [\varepsilon^2(\tau_{rr}-\tau_{zz})S'+ (1-\varepsilon^2S'^2)\tau_{rz}] \nonumber\\ &\quad =\varepsilon^2\frac{\partial \sigma}{\partial z} +\varepsilon^2\frac{\partial}{\partial z} \left[(B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s) \left(\frac{(Su_t)'}{S\sqrt{1+\varepsilon^2 S'^2}}\right)+\mathcal{C} u_n\right]\nonumber\\ &\qquad +\frac{\varepsilon^2\sqrt{1+\varepsilon^2 S'^2}}{S}\frac{\partial}{\partial z}\left[\frac{2B_{\mu\infty}\mu_s S}{1+\varepsilon^2 S'^2}\left(\frac{\partial u_t}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right]\nonumber\\ &\qquad-\frac{2\varepsilon^2B_{\mu\infty}\mu_sS'}{\sqrt{1+\varepsilon^2 S'^2}}\left[\frac{S'u_t+u_n}{S^2}-\frac{\varepsilon^2 S''}{1+\varepsilon^2 S'^2}\left(\frac{\partial u_t}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right], \end{align}
\begin{align} &\frac{1}{\left(1+\varepsilon^2S'^2\right)}\left[2\varepsilon^2 \beta S'\left(\frac{\partial v}{\partial r}-\frac{\partial u}{\partial z}\right)+\beta\left(1-\varepsilon^2 S'^2\right)\left(\varepsilon^2 \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right)\right]\nonumber\\ &\qquad+\frac{1}{(1+\varepsilon^2S'^2)} [\varepsilon^2(\tau_{rr}-\tau_{zz})S'+ (1-\varepsilon^2S'^2)\tau_{rz}] \nonumber\\ &\quad =\varepsilon^2\frac{\partial \sigma}{\partial z} +\varepsilon^2\frac{\partial}{\partial z} \left[(B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s) \left(\frac{(Su_t)'}{S\sqrt{1+\varepsilon^2 S'^2}}\right)+\mathcal{C} u_n\right]\nonumber\\ &\qquad +\frac{\varepsilon^2\sqrt{1+\varepsilon^2 S'^2}}{S}\frac{\partial}{\partial z}\left[\frac{2B_{\mu\infty}\mu_s S}{1+\varepsilon^2 S'^2}\left(\frac{\partial u_t}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right]\nonumber\\ &\qquad-\frac{2\varepsilon^2B_{\mu\infty}\mu_sS'}{\sqrt{1+\varepsilon^2 S'^2}}\left[\frac{S'u_t+u_n}{S^2}-\frac{\varepsilon^2 S''}{1+\varepsilon^2 S'^2}\left(\frac{\partial u_t}{\partial z}-\frac{\varepsilon^2 S'' u_n}{1+\varepsilon^2 S'^2}\right)\right], \end{align}
where ![]() $B_{\kappa \infty }={\kappa _{s\infty }}/{l_r\eta _0}$ with
$B_{\kappa \infty }={\kappa _{s\infty }}/{l_r\eta _0}$ with ![]() $\kappa _{s\infty }$ the surface dilatational viscosity at
$\kappa _{s\infty }$ the surface dilatational viscosity at ![]() $\varGamma =\varGamma _\infty, B_{\mu \infty }={\mu _{s\infty }}/{l_r\eta _0}$ with
$\varGamma =\varGamma _\infty, B_{\mu \infty }={\mu _{s\infty }}/{l_r\eta _0}$ with ![]() $\mu _{s\infty }$ the surface shear viscosity at
$\mu _{s\infty }$ the surface shear viscosity at ![]() $\varGamma =\varGamma _\infty$ and
$\varGamma =\varGamma _\infty$ and ![]() $\sigma =1+E\ln (1-\varGamma )$ with
$\sigma =1+E\ln (1-\varGamma )$ with ![]() $E={R_gT\varGamma _\infty }/{\sigma _0}$.
$E={R_gT\varGamma _\infty }/{\sigma _0}$.
Expand the quantities into Taylor series of ![]() $\varepsilon r$
$\varepsilon r$
Substituting the expansions (A19)–(A29) into the kinematic condition (A16), the leading order yields
Thus
Substituting the expansions (A19)–(A29) into (A4)–(A14), we have ![]() $\tau _{rz0}=0, \tau _{rr0}=\tau _{\theta \theta 0}, A_{rz0}=0, A_{rr0}=A_{\theta \theta 0}$ and
$\tau _{rz0}=0, \tau _{rr0}=\tau _{\theta \theta 0}, A_{rz0}=0, A_{rr0}=A_{\theta \theta 0}$ and
 $$\begin{gather}\tau_{zz0}=\frac{1-\beta}{De}\left(\frac{A_{zz0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{zz0}=\frac{1-\beta}{De}\left(\frac{A_{zz0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{rr0}=\frac{1-\beta}{De}\left(\frac{A_{rr0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{rr0}=\frac{1-\beta}{De}\left(\frac{A_{rr0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{zz0}}{\partial t}+u_0\frac{\partial A_{zz0}}{\partial z}-2 A_{zz0}\frac{\partial u_0}{\partial z}\right)=1-\frac{A_{zz0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{zz0}}{\partial t}+u_0\frac{\partial A_{zz0}}{\partial z}-2 A_{zz0}\frac{\partial u_0}{\partial z}\right)=1-\frac{A_{zz0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}, \end{gather}$$ $$\begin{gather}De\left(\frac{\partial A_{rr0}}{\partial t}+u_0\frac{\partial A_{rr0}}{\partial z}+ A_{rr0}\frac{\partial u_0}{\partial z}\right)=1-\frac{A_{rr0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}, \end{gather}$$
$$\begin{gather}De\left(\frac{\partial A_{rr0}}{\partial t}+u_0\frac{\partial A_{rr0}}{\partial z}+ A_{rr0}\frac{\partial u_0}{\partial z}\right)=1-\frac{A_{rr0}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}}_0)}{L^2}}, \end{gather}$$
where ![]() $tr({{\boldsymbol{\mathsf{A}}}}_0)=A_{zz0}+2A_{rr0}$.
$tr({{\boldsymbol{\mathsf{A}}}}_0)=A_{zz0}+2A_{rr0}$.
The surfactant conservation equation (A15) at ![]() $O(1)$ gives
$O(1)$ gives
The normal force balance (A17) at ![]() $O(1)$ gives
$O(1)$ gives
 \begin{align} p_0&=\tau_{rr0}-\beta\frac{\partial u_0}{\partial z}\nonumber\\ &\quad +\mathcal{C}\left[\sigma+\frac{B_{\kappa\infty} \kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial(u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial z}\right)\right]-\frac{B_{\mu\infty}\mu_s}{S}\frac{\partial u_0}{\partial z}. \end{align}
\begin{align} p_0&=\tau_{rr0}-\beta\frac{\partial u_0}{\partial z}\nonumber\\ &\quad +\mathcal{C}\left[\sigma+\frac{B_{\kappa\infty} \kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial(u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial z}\right)\right]-\frac{B_{\mu\infty}\mu_s}{S}\frac{\partial u_0}{\partial z}. \end{align} The derivative of (A38) with respect to ![]() $z$ is
$z$ is
 \begin{align}
-\frac{\partial p_0}{\partial
z}&={-}\frac{\partial\tau_{rr0}}{\partial
z}+\beta\frac{\partial^2 u_0}{\partial z^2}\nonumber\\
&\quad -\frac{\partial}{\partial
z}\left[\!\mathcal{C}\left(\!\sigma+\frac{B_{\kappa\infty}
\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\!\frac{\partial(u_0S)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial
z}\!\right)\!\right)\!\right]+B_{\mu\infty}\frac{\partial}{\partial
z}\left[\frac{\mu_su'_0}{S}\right].
\end{align}
\begin{align}
-\frac{\partial p_0}{\partial
z}&={-}\frac{\partial\tau_{rr0}}{\partial
z}+\beta\frac{\partial^2 u_0}{\partial z^2}\nonumber\\
&\quad -\frac{\partial}{\partial
z}\left[\!\mathcal{C}\left(\!\sigma+\frac{B_{\kappa\infty}
\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\!\frac{\partial(u_0S)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial
z}\!\right)\!\right)\!\right]+B_{\mu\infty}\frac{\partial}{\partial
z}\left[\frac{\mu_su'_0}{S}\right].
\end{align} The tangential force balance (A18) at ![]() $O(\varepsilon ^2)$ gives
$O(\varepsilon ^2)$ gives
 \begin{align} \beta u_2+ \tau_{rz2}&=\frac{3\beta S'}{S}\frac{\partial u_0}{\partial z}+\frac{\beta }{2}\frac{\partial^2 u_0 }{\partial z^2}-\frac{S'}{S}\left(\tau_{rr0}-\tau_{zz0}\right)\nonumber\\ &\quad \frac{1}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial z} \left[\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S} \left(\frac{\partial(u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{2 B_{\mu \infty}}{S^2}\frac{\partial (\mu_sSu'_0)}{\partial z}+\frac{B_{\mu\infty}\mu_s}{S^2} \frac{\partial u_0}{\partial z}S'. \end{align}
\begin{align} \beta u_2+ \tau_{rz2}&=\frac{3\beta S'}{S}\frac{\partial u_0}{\partial z}+\frac{\beta }{2}\frac{\partial^2 u_0 }{\partial z^2}-\frac{S'}{S}\left(\tau_{rr0}-\tau_{zz0}\right)\nonumber\\ &\quad \frac{1}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial z} \left[\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S} \left(\frac{\partial(u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial(u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{2 B_{\mu \infty}}{S^2}\frac{\partial (\mu_sSu'_0)}{\partial z}+\frac{B_{\mu\infty}\mu_s}{S^2} \frac{\partial u_0}{\partial z}S'. \end{align}Substituting (A39) and (A40) into (A32) yields
 \begin{align} \frac{ \partial u_0}{\partial t}+u_0\frac{\partial u_0}{\partial z}&=\frac{3\beta}{S^2}\frac{\partial (S^2u'_0)}{\partial z}+\frac{1}{S^2}\frac{\partial [S^2(\tau_{zz0}-\tau_{rr0})]}{\partial z}\nonumber\\ &\quad -\frac{\partial}{\partial z}\left\{\mathcal{C}\left[\sigma+\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial (u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial (u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{2}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial z}\left[\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial (u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial (u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{5B_{\mu\infty}}{S^2}\frac{\partial (\mu_sSu'_0)}{\partial z}. \end{align}
\begin{align} \frac{ \partial u_0}{\partial t}+u_0\frac{\partial u_0}{\partial z}&=\frac{3\beta}{S^2}\frac{\partial (S^2u'_0)}{\partial z}+\frac{1}{S^2}\frac{\partial [S^2(\tau_{zz0}-\tau_{rr0})]}{\partial z}\nonumber\\ &\quad -\frac{\partial}{\partial z}\left\{\mathcal{C}\left[\sigma+\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial (u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial (u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{2}{S}\left\{\frac{\partial \sigma}{\partial z}+\frac{\partial}{\partial z}\left[\frac{B_{\kappa\infty}\kappa_s-B_{\mu\infty}\mu_s}{S}\left(\frac{\partial (u_0S)}{\partial z}-\frac{\mathcal{C}}{2}\frac{\partial (u_0S^2)}{\partial z}\right)\right]\right\}\nonumber\\ &\quad +\frac{5B_{\mu\infty}}{S^2}\frac{\partial (\mu_sSu'_0)}{\partial z}. \end{align} Equations (A31), (A33)–(A37) and (A41) constitute the 1-D model. Dropping the subscript ![]() $0$, we have
$0$, we have
 \begin{gather}
\rho\left(\frac{\partial u}{\partial t}+u\frac{\partial
u}{\partial z}\right)=\frac{3\eta_s}{S^2}\frac{\partial
\left(S^2u'\right)}{\partial
z}+\frac{1}{S^2}\frac{\partial\left[S^2\left(\tau_{zz}-\tau_{rr}\right)\right]}{\partial z}\nonumber\\
-\frac{\partial}{\partial z}\left\{\mathcal{C}\left[\sigma+\frac{\kappa_s-\mu_s}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial z}\right)\right]\right\}\nonumber\\
+\frac{2}{S}\left\{\frac{\partial \sigma}{\partial
z}+\frac{\partial}{\partial
z}\left[\frac{\kappa_s-\mu_s}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial
z}\right)\right]\right\} \nonumber\\
+\frac{5}{S^2}\frac{\partial }{\partial
z}\left(\mu_sS\frac{\partial u}{\partial z}\right),
\end{gather}
\begin{gather}
\rho\left(\frac{\partial u}{\partial t}+u\frac{\partial
u}{\partial z}\right)=\frac{3\eta_s}{S^2}\frac{\partial
\left(S^2u'\right)}{\partial
z}+\frac{1}{S^2}\frac{\partial\left[S^2\left(\tau_{zz}-\tau_{rr}\right)\right]}{\partial z}\nonumber\\
-\frac{\partial}{\partial z}\left\{\mathcal{C}\left[\sigma+\frac{\kappa_s-\mu_s}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial z}\right)\right]\right\}\nonumber\\
+\frac{2}{S}\left\{\frac{\partial \sigma}{\partial
z}+\frac{\partial}{\partial
z}\left[\frac{\kappa_s-\mu_s}{S}\left(\frac{\partial(uS)}{\partial
z}-\frac{\mathcal{C}}{2}\frac{\partial(uS^2)}{\partial
z}\right)\right]\right\} \nonumber\\
+\frac{5}{S^2}\frac{\partial }{\partial
z}\left(\mu_sS\frac{\partial u}{\partial z}\right),
\end{gather} $$\begin{gather} \tau_{zz}=\frac{\eta_p}{\lambda_c}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather} \tau_{zz}=\frac{\eta_p}{\lambda_c}\left(\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\tau_{rr}=\frac{\eta_p}{\lambda_c}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$
$$\begin{gather}\tau_{rr}=\frac{\eta_p}{\lambda_c}\left(\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}-1\right), \end{gather}$$ $$\begin{gather}\frac{\partial A_{zz}}{\partial t}+u\frac{\partial A_{zz}}{\partial z}-2\frac{\partial u}{\partial z}A_{zz} =\frac{1}{\lambda_c}\left(1-\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
$$\begin{gather}\frac{\partial A_{zz}}{\partial t}+u\frac{\partial A_{zz}}{\partial z}-2\frac{\partial u}{\partial z}A_{zz} =\frac{1}{\lambda_c}\left(1-\frac{A_{zz}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$ $$\begin{gather}\frac{\partial A_{rr}}{\partial t}+u\frac{\partial A_{rr}}{\partial z}+\frac{\partial u}{\partial z}A_{rr}=\frac{1}{\lambda_c}\left(1-\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
$$\begin{gather}\frac{\partial A_{rr}}{\partial t}+u\frac{\partial A_{rr}}{\partial z}+\frac{\partial u}{\partial z}A_{rr}=\frac{1}{\lambda_c}\left(1-\frac{A_{rr}}{1- \dfrac{tr({{\boldsymbol{\mathsf{A}}}})}{L^2}}\right), \end{gather}$$
where ![]() $tr({{\boldsymbol{\mathsf{A}}}})=A_{zz}+2A_{rr}$ and
$tr({{\boldsymbol{\mathsf{A}}}})=A_{zz}+2A_{rr}$ and ![]() $\mathcal {C}, \kappa _s, \mu _s$ and
$\mathcal {C}, \kappa _s, \mu _s$ and ![]() $\sigma$ are given in (2.13) and (2.17a,b)–(2.18), respectively.
$\sigma$ are given in (2.13) and (2.17a,b)–(2.18), respectively.