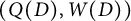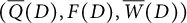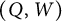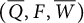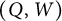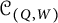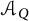1 Introduction
Since having been introduced by Fomin and Zelevinsky in the year 2000 [Reference Derksen, Weyman and ZelevinskyFZ02], cluster algebras have been seeing a tremendous development. It is believed that the coordinate rings of several algebraic varieties related to semisimple groups have cluster structures. This has been verified for various cases, such as double Bruhat cells [Reference Fomin and ZelevinskyBFZ05], partial flag varieties and their associated unipotent radicals [Reference Geuenich, Labardini-Fragoso and Miranda-OlveraGLS08], and Richardson varieties of complete flag varieties [Reference LeclercLec16]. An important and early example is the Grassmannians [Reference ScottS06]. In this paper, we study the quivers with potentials associated with Grassmannian cluster algebras.
Recall that, as a subalgebra of a rational function field, a (skew-symmetric) cluster algebra is generated by cluster variables in various seeds, where a seed is a pair consisting of a quiver and a set of indeterminates in the rational function field. Different seeds are related by an operation so-called mutation. In some sense, the rich combinatorial structures on cluster algebras are given by mutations. There is a representation-theoretic interpretation of quiver mutations given by Derksen, Weyman, and Zelevinsky [Reference Chang and ZhuDWZ08]. They introduced the notion of quivers with potentials and their decorated representations, where potentials can be considered as sum of cycles in the quiver, and the mutations of decorated representations can be viewed as a generalization of Bernstein–Gelfand–Ponomarev reflection functors.
On the other hand, the Postnikov diagram D, which is a certain planar graph on a disk, corresponds to a special cluster in a Grassmannian cluster algebra, which consists of Plücker coordinates. The strands of the diagram cut the disk into some oriented regions and alternating oriented regions. Then the quiver
$Q(D)$
of D can be viewed as certain dual of the Postnikov diagram, with the alternating oriented regions as the vertices and the crossings of the strands as the arrows.
It is proved by Scott [Reference ScottS06] that the mutation of the quiver
$Q(D)$
at a vertex with two arrows going out and two arrows going in is compatible with a transformation on the Postnikov diagram D, called geometric exchange, at an alternating oriented quadrilateral cell. By viewing the boundary regions as frozen vertices, we get an iced quiver
$(\overline {Q}(D),F)$
. Note that each oriented region in D yields a fundamental cycle with minimal length up to cyclically equivalence in the quiver. Then we define the potential
$\overline {W}(D)$
for the iced quiver as an alternating sum of these fundamental cycles. We then have the following theorem, which is a certain generalization of the result in [Reference ScottS06] (see Theorem 3.4 for more details).
Theorem 1.1 The geometric exchanges of the Postnikov diagram D are compatible with the mutations of
$(Q,W)$
and
$(\overline {Q}(D),F,\overline {W}(D))$
up to right equivalence.
Note that the concept of the mutation of an iced quiver with potential (IQP) we used here is the one recently introduced by Pressland in [Reference PresslandP18]. We should also say that besides the work of Scott mentioned above, there already exist some other related works which compare the mutations of the quivers with other operations, like that stated in the above theorem. For example, Vitória compared in [Reference YangV09] the mutation of the quiver with potential (QP) and the Seiberg duality; Buan, Iyama, Reiten, and Smith proved in [Reference Buan, Iyama, Reiten and ScottBIRS11] that the mutations of cluster tilting objects in the generalized cluster category arising from
$(Q,W)$
and the mutations of the QPs are compatible, whereas Pressland proved the case for iced quivers with potentials [Reference PresslandP18]; and Baur, King, and Marsh proved that the boundary algebra of the dimer algebra arising from a Postnikov diagram is invariant under the geometric exchange [Reference Baur, King and MarshBKM16]. Note that the completion of the dimer algebra is isomorphic to the Jacobian algebra of the IQP associated with the Postnikov diagram.
The above theorem allows us to define the quivers with potentials (up to right equivalence and mutation equivalence) for a Grassmannian cluster algebra by considering a fixed Postnikov diagram. Note that the mutation of a QP can only be operated at a vertex which is not involved in 2-cycles, and even when the initial quiver has no 2-cycles, there may appear 2-cycles after mutations [Reference Chang and ZhuDWZ08]. A QP is called nondegenerate if there exist no 2-cycles after any iterated mutations. A more “generic” condition called rigidity implies the nondegeneration. So a rigid QP can be viewed as a kind of “good” QP, respecting to the mutations. We study the rigidity of the QP of a Grassmannian cluster algebra (see Theorem 3.14).
Theorem 1.2 The QP
$(Q,W)$
associated with a Grassmannian cluster algebra is rigid, and it is the unique rigid QP with underlying quiver Q up to right equivalence and mutation equivalence.
We would like to mention that the rigidity of
$(Q,W)$
has already been studied by several authors such as Buan, Iyama, Reiten, and Smith [Reference Buan, Iyama, Reiten and ScottBIRS11] by using an algebraic method, and Kulkarni [Reference KulkarniK19] by using a topological method. The method we used in this paper is also topological, which is different from that used in [Reference KulkarniK19]. In fact, Kulkarni got the rigidity for a larger class of quivers with potentials arising from dimer models, whereas we only consider the Grassmannian cluster algebras and get the conclusion by explicitly describing a special QP. This description is also used in the proof for the uniqueness of the rigid QP of a Grassmannian cluster algebra.
The problem of classifying all nondegenerate (or rigid) potentials on a 2-acyclic quiver is systematically studied in [Reference Geiß, Leclerc and SchröerGLS16], where they proved that most quivers arising from triangulations of surfaces have unique nondegenerate potentials up to right equivalence. On the other hand, there do exist 2-acyclic quivers arising from surfaces admits infinitely many nondegenerate potentials that are pairwise not right-equivalent (see, for example, in more recent work [Reference Geiß, Labardini-Fragoso and SchröerGLM20]). We also refer the reader to [Reference Geiß, Labardini-Fragoso and SchröerGLM20] for detailed explanations on how this classification problem plays a role in algebraic geometry and in symplectic geometry.
We can easily get the following corollary from the above theorem.
Corollary 1.3 Inside the mutation-equivalent class of QP of a Grassmannian cluster algebra, the quiver determines the potentials up to right equivalence. More precisely, assume that
$(Q',W')$
and
$(Q,W)$
are two quivers with potentials of a Grassmannian cluster algebra. Then:
-
(1)
$(Q',W')$
is right-equivalent to
$(Q,W)$
if
$Q'\cong Q$
; -
(2)
$(Q',W')$
is right-equivalent to
$(Q^{op},W^{op})$
if
$Q'\cong Q^{op}$
.
As an application, we also consider the cluster automorphism group associated with the Grassmannian cluster algebras introduced in [Reference Assem, Schiffler and ShramchenkoASS12] and the auto-equivalence group of the corresponding cluster category. It is proved in [Reference Assem, Schiffler and ShramchenkoASS12, Reference Berenstein, Fomin and ZelevinskyBIRS09] that if the cluster algebra is of acyclic type, then the cluster automorphism group is isomorphic to the auto-equivalence group of the corresponding cluster category. We provide a similar isomorphism between these two groups for the Grassmannian cluster algebra with trivial coefficients (see Theorem 4.5). Note that most of Grassmannian cluster algebras are nonacyclic.
Theorem 1.4 Let
$(Q,W)$
be a QP for a Grassmannian cluster algebra. Then the auto-equivalence group of the generalized cluster category
$\mathcal {C}_{(Q,W)}$
is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra
$\mathcal {A}_{Q}$
with trivial coefficients.
In fact, we have a more general result: this isomorphism is valid for a generalized cluster category whose potentials are determined by the quivers. Note that, on the one hand, these two groups describe both the symmetries of the cluster structures in the category and the algebra, respectively. On the other hand, the cluster structure in the cluster algebra only depends on the quiver, rather than the potential over the quiver. So we conjecture that these two groups are isomorphic for all generalized cluster categories (see Conjecture 4.2). We also conjecture that the quivers always determine the potentials in the mutation-equivalent classes of quivers with potentials (see Conjecture 4.3).
The paper is organized as follows: In Section 2, we recall some preliminaries on cluster algebras, quivers with potentials, and Grassmannian cluster algebras. In Section 3, we define the quivers with potentials for Grassmannian cluster algebras and prove their rigidity and uniqueness. Section 4 is devoted to an application of our main results to the generalized cluster categories, namely, we prove the isomorphism between the auto-equivalence group of the category and the cluster automorphism group in Section 4.2.
2 Conventions
Throughout the paper, we use
$\mathbb {Z}$
as the set of integers,
$\mathbb {N}$
as the set of positive integers, and
$\mathbb {C}$
as the set of complex numbers. Arrows in a quiver are composed from right to left, that is, we write a path
$j\stackrel {\beta }\rightarrow i \stackrel {\alpha }\rightarrow k$
as
$\alpha \beta $
.
2.1 Preliminaries
In this section, we briefly recall some definitions on quivers with potentials and Grassmannian cluster algebras.
2.2 Quivers with potentials
The references of this subsection are [Reference Buan, Iyama, Reiten and ScottBIRS11, Reference Chang and ZhuDWZ08, Reference Geiß, Leclerc and SchröerGLS16, Reference PresslandP18], especially [Reference PresslandP18] for the case of IQPs.
2.2.1 Quivers
Recall that a quiver is a quadruple
$Q=(Q_0,Q_1,s,t)$
, consisting of a finite set of vertices
$Q_0$
, of a finite set of arrows
$Q_1$
, and of two maps
$s, t$
from
$Q_1$
to
$Q_0$
which map each arrow
$\alpha $
to its source
$s(\alpha )$
and its target
$t(\alpha )$
, respectively. An iced quiver is a pair
$(Q,F)$
where Q is a quiver and
$F=(F_0,F_1,s,t)$
is a subquiver (not necessarily full) of Q, where
$F_0\subseteq Q_0$
and
$F_1\subseteq Q_1$
. The vertices in
$F_0$
are called the frozen vertices, whereas the vertices in
$Q_0\setminus F_0$
are called the exchangeable vertices. The arrows in
$F_1$
are called the frozen arrows, whereas the arrows in
$Q_1\setminus F_1$
are called the unfrozen arrows. The full subquiver of Q with vertex set
$Q_0\setminus F_0$
is called the principal part of Q, denoted by
$Q^{pr}$
.
Let
$(Q,F)$
be an iced quiver without loops nor 2-cycles. A mutation of
$(Q,F)$
at exchangeable vertex i is an iced quiver
$(\mu _i(Q),F)$
, where
$\mu _i(Q)$
is obtained from Q by:
-
• inserting a new unfrozen arrow
$\gamma : j\to k$
for each path
$j\stackrel {\beta }\rightarrow i \stackrel {\alpha }\rightarrow k$
; -
• inverting all arrows passing through i;
-
• removing the arrows in a maximal set of pairwise disjoint
$2$
-cycles (
$2$
-cycles moves).
2.2.2 Cluster algebras
Let
$(Q,F)$
be an iced quiver with
$Q_0 = \{1, 2, \ldots , n+m\}$
and
$F_0 = \{n+1, n+2, \ldots , n+m\}$
. By associating with each vertex
$i \in Q_0$
an indeterminate element
$x_i$
, one gets a set
$\tilde {{\mathbf x}}=\{x_1, x_2,\ldots , x_{n+m}\}=\{x_1, x_2, \ldots , x_{n}\}\sqcup \{x_{n+1}, x_{n+2}, \ldots , x_{n+m}\}={\mathbf x}\sqcup \scriptstyle $
. We call the triple
$\Sigma =(Q,F,\tilde {{\mathbf x}})$
a seed. An element in
${\mathbf x}$
(resp. in
$\scriptstyle $
) is called a cluster variable (resp. coefficient variable), and
${\mathbf x}$
is called a cluster.
Let
$x_i$
be a cluster variable, and the mutation of the seed
$\Sigma $
at
$x_i$
is a new seed
$\mu _i(\Sigma )=(\mu _i(Q),F,\mu _i({\mathbf x}))$
, where
$\mu _i({\mathbf x}) = ({\mathbf x} \setminus \{x_i\}) \sqcup \{x^{\prime }_i\}$
with
$$ \begin{align} x_i x_i^\prime = \prod_{\substack{\alpha\in Q_1; \\ s(\alpha)=i}} x_{t(\alpha)} + \prod_{\substack{\alpha\in Q_1; \\ t(\alpha)=i}} x_{s(\alpha)}. \end{align} $$
Denote by
${\mathscr {X}}$
the union of all possible clusters obtained from an initial seed
$\Sigma =(Q,F,\tilde {{\mathbf x}})$
by iterated mutations. Let
$\mathbb {P}$
be the free abelian group (written multiplicatively) generated by the elements of
$\scriptstyle $
. Let
$\mathcal {F}=\mathbb {Q} \mathbb {P}(x_{1},x_{2},\ldots ,x_{n})$
be the field of rational functions in n independent variables with coefficients in
$\mathbb {Q} \mathbb {P}$
. The cluster algebra
$\mathcal {A}_{(Q,F)}$
is a
$\mathbb {Z}\mathbb {P}$
-subalgebra of
$\mathcal {F}$
generated by cluster variables in
${\mathscr {X}}$
, that is,
$$\begin{align*}\mathcal{A}_{(Q,F)}=\mathbb{Z}\mathbb{P}[\mathscr{X}].\end{align*}$$
2.2.3 Quivers with potentials
Let
$(Q,F)$
be an iced quiver without loops. We denote by
$\mathbb {C}\langle Q\rangle $
the path algebra of Q over
$\mathbb {C}$
. By
$\textrm{length}(p)$
, we denote the length of a path p in
$\mathbb {C}\langle Q\rangle $
. The complete path algebra
$\mathbb {C}\langle \langle Q\rangle \rangle $
is the completion of
$\mathbb {C}\langle Q\rangle $
with respect to the ideal
$\mathfrak {m}$
generated by the arrows of Q. A potential W on Q is an element in the closure
$\textrm{Pot}(Q)$
of the space generated by all cycles in Q. We say that two potentials W and
$W'$
are cyclically equivalent if
$W-W'$
belongs to the closure C of the space generated by all differences
$\alpha _s \cdots \alpha _2 \alpha _1 - \alpha _1\alpha _{s} \cdots \alpha _2$
coming from cycles
$\alpha _s \cdots \alpha _2\alpha _1$
. Denote by
$[l]$
the set of cycles which are cyclically equivalent to a cycle l. We call a triple
$(Q,F,W)$
an IQP, if no two terms in
$W\in \textrm{Pot}(Q)$
are cyclically equivalent. Moreover, if each term in W includes at least one unfrozen arrow, then we call the IQP irredundant. If
$F=\emptyset $
, then we call the pair
$(Q,W)$
a QP, and as for the quiver, we also view a QP as a special IQP.
2.2.4 Jacobian algebras
For an arrow
$\alpha $
of Q, we define
$\partial _\alpha : \textrm{Pot}(Q) \to \mathbb {C}\langle \langle Q\rangle \rangle $
the cyclic derivative with respect to
$\alpha $
, which is the unique continuous linear map that sends a cycle l to the sum
$\sum _{l=p\alpha q} pq$
taken over all decompositions of the cycle l. Let
$J(Q,F,W)$
be the closure of the ideal of
$\mathbb {C}\langle Q\rangle $
generated by cyclic derivatives in
$\{\partial _\alpha W,\alpha ~{\textrm {unfrozen}} \}.$
We call
$J(Q,F,W)$
the (frozen) Jacobian ideal of
$(Q,F,W)$
and call the quotient
$$ \begin{align*}\mathcal{P}(Q,F,W)=\mathbb{C}\langle \langle Q\rangle\rangle/J(Q,F,W)\end{align*} $$
the (frozen) Jacobian algebra of
$(Q,F,W)$
.
For an IQP
$(Q,F,W)$
, we call it trivial if each term in W is a
$2$
-cycle and
$\mathcal {P}(Q,F,W)$
is a product of copies of
$\mathbb {C}$
, and we say it is reduced if each term of W includes at least one unfrozen arrow and
$\partial _\beta W\in \mathfrak {m}^2$
for any unfrozen arrow
$\beta $
.
2.2.5 Right-equivalences and reductions
Two IQPs
$(Q,F,W)$
and
$(Q',F',W')$
are right-equivalent if Q and
$Q'$
have the same set of vertices and frozen vertices, and there exists an algebra isomorphism
$\varphi :\mathbb {C}\langle \langle Q\rangle \rangle \rightarrow \mathbb {C}\langle \langle Q'\rangle \rangle $
whose restriction on vertices is the identity map,
$\phi (\mathbb {C}\langle \langle F\rangle \rangle )=\mathbb {C}\langle \langle F'\rangle \rangle $
, and
$\varphi (W)$
and W are cyclically equivalent. Such an isomorphism
$\varphi $
is called a right-equivalence.
It is proved in [Reference PresslandP18, Theorem 3.6] (in [Reference Chang and ZhuDWZ08, Theorem 4.6] that for QP) that, for any irredundant IQP
$(Q,F,W)$
, there exist a reduced IQP
$(Q_{\mathrm {red}},F_{\mathrm {red}},W_{\mathrm {red}})$
such that the Jacobian algebras
$\mathcal {P}(Q,F,W)$
and
$\mathcal {P}(Q_{\mathrm {red}},F_{\mathrm {red}},W_{\mathrm {red}})$
are isomorphic. Furthermore, the right-equivalence class of
$(Q_{\mathrm {red}},F_{\mathrm {red}},W_{\mathrm {red}})$
is determined by the right-equivalence class of
$(Q,F,W)$
. The operation to producing
$(Q_{\mathrm {red}},F_{\mathrm {red}},W_{\mathrm {red}})$
is called the reduction, which consists of the following steps (see Lemma 3.14 of [Reference PresslandP18] and the proof of Theorem 3.6 of [Reference PresslandP18]):
Step I: we can write
$$ \begin{align} W=\sum_{i=1}^M\alpha_i\beta_i+\sum_{i=M+1}^N\alpha_i(\beta_i+p_i) +W_1 \end{align} $$
up to right equivalence, for some arrows
$\alpha _i$
and
$\beta _i$
and elements
$p_i\in \mathfrak {m}^2$
, where:
-
•
$\alpha _i$
is unfrozen for all
$1\leq i\leq N$
, and
$\beta _i$
is frozen if and only if
$i>M$
, -
• the arrows
$\alpha _i$
and
$\beta _i$
with
$1\leq i\leq M$
each appear exactly once in the expression, -
• the arrows
$\beta _i$
, for
$1\leq i\leq N$
, do not appear in any of the
$p_j$
, and -
• the arrows
$\alpha _i$
and
$\beta _i$
, for
$1\leq i\leq N$
, do not appear in the potential
$W_1$
, which has no length
$2$
terms.
Step II: Let
$Q'$
be the subquiver of Q consisting of all vertices and those arrows which are not
$\alpha _i$
and
$\beta _i, 1\leq i\leq M$
, and
$$ \begin{align*}W'=\sum_{i=M+1}^N\alpha_i(\beta_i+p_i) +W_1.\end{align*} $$
Then
$(Q',F,W')$
is an IQP.
Step III: Let
$(Q_{\mathrm {red}},F_{\mathrm {red}})$
be the iced quiver obtained from
$(Q',F)$
by deleting
$\beta _i$
and freezing
$\alpha _i$
for each
$M+1\leq i\leq N$
. Let
$$ \begin{align*}W_{\mathrm{red}}=\sum_{i=M+1}^N \alpha_ip_i +W_1.\end{align*} $$
Then
$(Q_{\mathrm {red}},F_{\mathrm {red}},W_{\mathrm {red}})$
is the reduced IQP we want.
2.2.6 Mutations of iced quivers with potentials
Let
$(Q,F,W)$
be an irredundant IQP, and let i be an exchangeable vertex of Q such that there is no
$2$
-cycles at i and no cycle occurring in the decomposition of W starts and ends at i. The premutation
$\widetilde {\mu }_i(Q,F,W)$
of
$(Q,F,W)$
is a new QP
$(\widetilde {\mu }_i(Q),\widetilde {\mu }_i(F),\widetilde {\mu }_i(W))=(\widetilde {Q},\widetilde {F},\widetilde {W})$
defined as follows. The new iced quiver
$(\widetilde {Q},\widetilde {F})$
is obtained from
$(Q,F)$
by:
-
• adding a new unfrozen arrow
$[\alpha \beta ]: j\to k$
for each path
$j\stackrel {\beta }\rightarrow i \stackrel {\alpha }\rightarrow k$
; -
• replacing each arrow
$\alpha $
incident to i with an arrow
$\alpha ^*$
in the opposite direction.
The new potential
$\widetilde {W}$
is the sum of two potentials
$\widetilde {W}_1$
and
$\widetilde {W}_2$
. The potential
$\widetilde {W}_1$
is obtained by replacing each factor
$\alpha _p\alpha _{p+1}$
by
$[\alpha _p\alpha _{p+1}]$
with
$s(\alpha _p)=t(\alpha _{p+1})=i$
for any cyclic path
$\alpha _1\cdots \alpha _s$
occurring in the expansion of
$W.$
The potential
$\widetilde {W}_2$
is given by
$$ \begin{align*}\widetilde{W}_2=\sum_{\alpha,\beta}[\alpha\beta]\beta^{*}\alpha^{*},\end{align*} $$
where the sum ranges over all pairs of arrows
$\alpha $
and
$\beta $
with
$s(\alpha )=t(\beta )=i$
. Then
$\widetilde {\mu }_i(Q,F,W)$
is an irredundant IQP. We denote by
$\mu _i(Q,F,W)$
the reduced part of
$\widetilde {\mu }_i(Q,F,W)$
, and call
$\mu _i$
the mutation of
$(Q,F,W)$
at the vertex i. We call two IQPs mutation-equivalent if one can be obtained from another by iterated mutations. Note that the mutation equivalence is an equivalent relation on the set of right-equivalence classes of IQPs.
2.3 Grassmannian cluster algebras
We recall in this subsection some definitions on Grassmannian cluster algebras, and we refer to [Reference PostnikovP06, Reference ScottS06] for more details on Postnikov diagrams and Grassmannian cluster algebras, respectively.
Let
$\mbox {Gr}(k,n)$
be the Grassmannian of k-planes in
$\mathbb {C}^n$
, and let
$\mathbb {C}[\mbox {Gr}(k,n)]$
be its homogeneous coordinate ring. When
$k=2$
, Fomin and Zelevinsky proved that
$\mathbb {C}[\mbox {Gr}(k,n)]$
has a cluster algebra structure [Reference Fomin and ZelevinskyFZ03]. Scott generalized this result to the case of any Grassmannian
$\mbox {Gr}(k,n)$
, where the proof relies on a correspondence between a special kind of clusters in the cluster algebra and certain planar diagram.
2.3.1 Postnikov diagrams
For
$k, n\in \mathbb {N}$
with
$k < n$
, a
$(k,n)$
-Postnikov diagram D is a collection of n oriented paths, called strands, in a disk with n marked points on its boundary, labeled by
$1, 2, \ldots , n$
in clockwise orientation. The strands, which are labeled by
$1 \leqslant i \leqslant n$
, start at point i and end at point
$i+k$
. These strands obey the following conditions:
-
• Any two strands cross transversely, and there are no triple crossings between strands.
-
• No strand intersects itself.
-
• There are finitely many crossing points.
-
• Following any given strand, the other strands alternately cross it from left to right and from right to left.
-
• For any two strands i and j, the configuration shown in Figure 1 is forbidden.
Figure 1: Forbidden crossing.
Postnikov diagrams are identified up to isotopy. We say that a Postnikov diagram is of reduced type if no untwisting move shown in Figure 2 can be applied to it.
Figure 2: Untwisting move.
The fourth condition ensures that the strands divide the disk into two types of regions: oriented regions, where all the strands on their sides circle clockwise or anticlockwise, and alternating oriented regions, where the adjacent strands alternate directions. A region is said to be internal if it is not adjacent to the boundary of the disk, and the other regions are referred to as boundary regions. A boundary region contains a part of boundary as side is viewed as an alternating oriented region. Denote by
$\mathfrak {R}_o(D)$
and
$\mathfrak {R}_a(D)$
the set of all oriented regions and alternating oriented regions in D, respectively. See Figure 3 for an example of
$(3,7)$
-Postnikov diagram.
Figure 3: A
$(3,7)$
-Postnikov diagram.
Given a Postnikov diagram D and an alternating oriented quadrilateral cell R inside D, a new Postnikov diagram
$\widetilde {\mu }_{R}(D)$
is constructed by the local rearrangement shown in Figure 4. We call
$\widetilde {\mu }_{R}$
a pre-geometric exchange at R. Note that there may appear new configurations in
$\widetilde {\mu }_{R}(D)$
as shown in the left side of Figure 2. Let
$\mu _{R}(D)$
be the Postnikov diagram obtained from
$\widetilde {\mu }_{R}(D)$
after untwisting these new configurations. We call
$\mu _{R}$
a geometric exchange at R. Note that if D is of reduced type, then so is
$\mu _{R}(D)$
.
Figure 4: Pregeometric exchange.
2.3.2 Grassmannian cluster algebras
For a Postnikov diagram D, one may associate it with a quiver
$\overline {Q}(D)$
, whose vertices are indexed by
$\mathfrak {R}_a(D)$
, and whose arrows correspond to crossings of stands that bound two alternating regions, with orientation inherited from that of the stands (see Figure 5). Let
$(\overline {Q}(D),F(D))$
be an iced quiver, where the exchangeable vertices of
$\overline {Q}(D)$
are given by internal regions in
$\mathfrak {R}_a(D)$
, whereas the frozen vertices correspond to the boundary regions in
$\mathfrak {R}_a(D)$
, and the frozen arrows are all the arrows connecting two boundary alternating oriented regions, which are shown in red in Figure 5. We denote by
$Q(D)$
the principal part of
$\overline {Q}(D)$
.
Figure 5: Arrow orientations in the quiver
$\overline {Q}(D)$
.
Example 1 See Figure 6 for the quiver
$(\overline {Q}(D),F(D))$
associated with the Postnikov diagram D in Figure 3.
Figure 6: The iced quiver
$(\overline {Q}(D),F(D))$
of the Postnikov diagram D in Figure 3, where the red arrows are the frozen arrows.
It has been proved in [Reference ScottS06] that the coordinate ring
$\mathbb {C}[\mbox {Gr}(k,n)]$
has a cluster algebra structure, more precisely, the localization of
$\mathbb {C}[\mbox {Gr}(k,n)]$
at consecutive Plücker coordinates is isomorphic to the complexification of
$\mathcal {A}_{(\overline {Q}(D),F)}$
as cluster algebras.
Remark 2.1 Note that the frozen arrows in the iced quiver
$(\overline {Q}(D),F(D))$
have no influence on the “cluster structure” of the cluster algebra
${\mathcal {A}}_{(\overline {Q}(D),F(D))}$
. However, these arrows appear naturally in the (Frobenius) categorification of the cluster algebras in [Reference Baur, King and MarshBKM16, Reference Geuenich, Labardini-Fragoso and Miranda-OlveraGLS08, Reference Jensen, King and SuJKS16]. In particular, it is proved by Buar, King, and Marsh in [Reference Baur, King and MarshBKM16] that
$(\overline {Q}(D),F(D))$
is the Gabriel quiver of the endomorphism algebra of the cluster tilting object in the Frobenius category (see Section 4 for more information about this).
3 Quivers with potentials of Grassmannian cluster algebras
We introduce in this section two quivers with potentials
$(\overline {Q}(D),F(D),\overline {W}(D))$
and
$(Q(D),W(D))$
for each Postnikov diagram D, and verify the compatibility of geometric exchanges of D and the mutations of these quivers with potentials. This ensures we may define quivers with potentials
$(Q,W)$
and IQP
$(\overline {Q},F,\overline {W})$
for a Grassmannian cluster algebra up to mutation equivalence. Then we prove the rigidity of
$(Q, W)$
and the finiteness of the dimension of the corresponding Jacobian algebra
$\mathcal {P}(Q, W)$
. We also show that
$(Q, W)$
is the unique rigid QP over the quiver Q of the Grassmannian cluster algebras up to right equivalence, and for each QP in the mutation class of
$(Q, W)$
, we show that the quiver determines the potentials up to right equivalence.
3.1 The definition
We write
$C.W.$
(resp.
$A.C.W.$
) for clockwise (resp. anticlockwise) for brevity. Then each oriented region r, bounded by m stands in
$D,$
is either
$C.W.$
or
$A.C.W.$
, and it yields a unique fundamental cycle (up to cyclic equivalence)
$\omega _r$
of length m in the quiver (see Figure 7 for example). We call
$\omega _r$
the internal fundamental cycles if r is an internal region, and boundary fundamental cycles if r is a boundary region.
Figure 7: The fundamental cycle, where the horizonal dashed line is the boundary of the diagram, and other dashed lines are the strands. The omitted part is at the interior of the diagram. The regions are anticlockwise. When the regions are clockwise, the figures occur in the opposite sense, which means inverting the orientations of the strands and the arrows simultaneously. The first cycle is an internal fundamental cycle, whereas the second one is a boundary fundamental cycle.
Definition 3.1 For the quivers
$Q(D)$
and
$(\overline {Q}(D),F(D))$
, let
$W(D)$
and
$\overline {W}(D)$
be potentials in the corresponding quivers, which are signed sums of representatives of fundamental cycles in the quivers, that is,
$$ \begin{align*} W=\sum\limits_{\begin{array}{c} r\in\mathfrak{R}_o(D)~C.W. \\ \textrm{internal region} \\ \end{array}} {\omega_r}-\sum\limits_{\begin{array}{c} r\in\mathfrak{R}_o(D)~A.C.W. \\ \textrm{internal region} \\ \end{array}} {\omega_r}\in \textrm{Pot}(Q),~~~~~~~ \end{align*} $$
$$ \begin{align*} \overline{W}=\sum\limits_{r\,\in\,\mathfrak{R}_o(D)~C.W.} {\omega_r}-\sum\limits_{r\,\in\,\mathfrak{R}_o(D)~A.C.W.}{\omega_r}\in \textrm{Pot}(\overline{Q}). \end{align*} $$
It is obvious that there are no two cyclically equivalent cycles appearing in the potential simultaneously, and there is at least one unfrozen arrow in each term of the potential. So
$(Q(D),W(D))$
is a QP and
$(\overline {Q}(D),F(D),\overline {W}(D))$
is an IQP. Note that these (iced) QPs are also reduced by definition.
Remark 3.2 In a more general setting of dimer models, the potentials are always picked in such signed sum over the fundamental cycles. In particular, in the settings of Grassmannian cluster algebras, the IQP
$(\overline {Q}(D),F(D),\overline {W}(D))$
has been introduced and studied in [Reference Baur, King and MarshBKM16, Reference PresslandP18]. The Jacobian algebra of the IQP is realized in [Reference Baur, King and MarshBKM16] as the endomorphism algebra of the cluster tilting object in the JKS’s Frobenius category.
In order to prove that mutations of
$(Q(D),W(D))$
and
$(\overline {Q}(D),F,\overline {W}(D))$
are compatible with geometric exchanges of the Postnikov diagrams D, we need the following lemma.
Lemma 3.3 Let D be a Postnikov diagram. Let
$\varepsilon : \mathfrak {R}_o(D) \rightarrow \{\pm 1\}$
be a function on the set of oriented regions in D. Define potentials
$$ \begin{align*} W_\varepsilon(D)=\sum\limits_{\begin{array}{c} r\in\mathfrak{R}_o(D)~C.W. \\ \mathrm{ internal region} \\ \end{array}} \varepsilon(r){\omega_r}-\sum\limits_{\begin{array}{c} r\in\mathfrak{R}_o(D)~A.C.W. \\ \textrm{ internal region} \\ \end{array}} \varepsilon(r){\omega_r}\in \textrm{ Pot}(Q), \end{align*} $$
$$ \begin{align*} \overline{W}_\varepsilon(D)=\sum\limits_{r\,\in\,\mathfrak{R}_o(D)~C.W.} \varepsilon(r){\omega_r}-\sum\limits_{r\,\in\,\mathfrak{R}_o(D)~A.C.W.} \varepsilon(r){\omega_r}\in \textrm{ Pot}(\overline{Q}). \end{align*} $$
Then
$(Q(D),W_\varepsilon (D))$
and
$(\overline {Q}(D),F(D),\overline {W}_\varepsilon (D))$
) are right-equivalent to
$(Q(D),W(D))$
and
$(\overline {Q}(D),F(D),\overline {W}(D))$
, respectively.
Proof We only deal with the case of
$Q(D)$
, and the case of
$\overline {Q}(D)$
is similar. Because the underlying graph of
$Q(D)$
is a planar graph with nontrivial boundary, as stated for the QP arising from surfaces in Section 10 of [Reference Labardini-FragosoL16], for any
$\varepsilon ,$
there exists a function
$$ \begin{align*}\epsilon: Q_1(D) \rightarrow \{\pm 1\}\end{align*} $$
on the arrows of
$Q(D)$
such that, for any r with
$\omega _r=\alpha _m \cdots \alpha _2 \alpha _1$
, we have
$$ \begin{align*}\prod\limits_{i=1}^{m} \epsilon(\alpha_i)=\varepsilon(r).\end{align*} $$
So the map
$$ \begin{align*}\phi:Q_1(D)\rightarrow Q_1(D), \alpha \mapsto \epsilon(\alpha)\alpha\end{align*} $$
induces an algebra isomorphism
$\Phi $
from
$\mathbb {C}\langle \langle Q(D)\rangle \rangle $
to
$\mathbb {C}\langle \langle Q(D)\rangle \rangle $
which maps
$W(D)$
to
$W_\varepsilon (D)$
. Then
$\Phi $
is a right equivalence which completes the proof.
Now, we are ready to give the main result in this subsection.
Theorem 3.4 Let D be a reduced Postnikov diagram with an alternating oriented quadrilateral cell R, which associates with an exchangeable vertex a in the quiver
$Q(D)$
. Then the mutations of
$(Q(D),W(D))$
and
$(\overline {Q}(D),F(D),\overline {W}(D))$
are compatible with the geometric exchanges of the Postnikov diagram. More precisely, up to right equivalence, we have:
-
(1)
$\mu _{a}(Q(D))=Q(\mu _{R}(D))$
and
$\mu _{a}(W(D))=W(\mu _{R}(D))$
; -
(2)
${\mu }_{a}(\overline {Q}(D),F(D))=(\overline {Q}(\mu _{R}(D)),F(\mu _{R}(D)))$
and
$\mu _{a}(\overline {W}(D))=\overline {W}(\mu _{R}(D))$
.
Proof Note that
$(Q(D),W(D))$
is the “principal part” of
$(\overline {Q}(D),F(D),\overline {W}(D))$
, where
$Q(D)$
is the principal part quiver of
$(\overline {Q}(D),F(D))$
and
$W(D)$
is obtained from
$\overline {W}(D)$
by deleting the potentials which contain the frozen arrows. Thus, the statement (1) follows from the statement (2). So we only prove the statement (2).
Since R is a quadrilateral cell in D, there are four arrows
$\alpha ,\beta ,\gamma ,\delta $
in the quiver
$(\overline {Q}(D),F(D))$
whose endings are the associated vertex a. On the other hand, since a is exchangeable, these arrows are all unfrozen. Without loss of generality, we assume that
$a=s(\alpha )=t(\beta )$
. Let
$\omega _r=\alpha \beta p$
be a fundamental cycle in
$\overline {W}(D)$
corresponding to an oriented region r of D that contains both
$\alpha $
and
$\beta $
, where p is a path from
$t(\alpha )$
to
$s(\beta )$
.
Up to rotations and reflections, there are essentially three possibilities of
$\omega _r$
, which are shown in Figure 8. If
$\textrm{length}(p)=1$
, then the local configuration of D is as shown in Figure 8a,c, where the arrow p is unfrozen in Figure 8a, whereas it is frozen in Figure 8c. If length(p)
$>1$
, then the local configuration is as shown in Figure 8b, where the length of the path p is at least 2 and it may contain frozen arrows.
Figure 8: Local configuration of a fundamental circle through the vertex a up to rotations and reflections. The path p in the first picture is an unfrozen arrow, whereas the path p in the third picture is a frozen arrow. The path p in the second picture is a path with length at least 2.
Now, we consider the local configuration of D around a depicted in the first picture of Figure 9, which contains all the above three possibilities. We only prove the result for this situation. Other situations can be proved similarly.
Figure 9: Mutations and geometric exchanges.
Up to a cyclic equivalence, we may write the potential
$$ \begin{align*}\overline{W}(D)=\zeta\alpha \delta-s\gamma\delta + \xi\gamma \beta-\eta\alpha\beta-\xi t+\overline{W}'(D) ,\end{align*} $$
where
$\textrm{length}(s)\geqslant 2$
,
$\textrm{length}(t)\geqslant 2$
, and each cycle in
$\overline {W}'(D)$
does not contain any of the following arrows
$\alpha ,\beta ,\gamma ,\delta ,\xi ,\zeta $
, and
$\eta $
. Then, by a pregeometric exchange
$\widetilde {\mu }_R$
on D and a premutation
$\widetilde {\mu }_a$
on
$(\overline {Q}(D),F(D))$
, we obtain the second picture in Figure 9. Note that the new arrows appearing in the iced quiver
$\widetilde {\mu }_{a}(\overline {Q}(D)),\widetilde {\mu }_{a}(F(D))$
are all unfrozen. Meanwhile, by applying the premutation
$\widetilde {\mu }_a$
on
$\overline {W}(D)$
, we get a new potential
$$ \begin{align*}\begin{array}{rcl} \widetilde{\mu}_a(\overline{W}(D)) & = & \zeta[\alpha\delta]+\delta^*\alpha^*[\alpha\delta]-s[\gamma\delta]-\delta^*\gamma^*[\gamma\delta] +\xi[\gamma\beta]\\ & & +\beta^*\gamma^*[\gamma\beta]-\eta[\alpha\beta]-\beta^*\alpha^*[\alpha\beta] -\xi t+\overline{W}'(D). \end{array}\end{align*} $$
Note that
$\overline {W}'(D)$
is not changed because a is not an end point of any arrow appearing in each potential of
$\overline {W}'(D)$
.
Recall the processes of the reduction of an IQP stated in Section 2.1, to reduce the IQP
$(\widetilde {\mu }_a(\overline {Q}(D)),\widetilde {\mu }_{a}(F(D)),\widetilde {\mu }_a(\overline {W}(D)))$
, we should firstly find a right equivalence and use it to rewrite the potential as the canonical form (2.2). Let us consider a unitriangular automorphism
$\phi $
on
$\mathbb {C}\langle \langle \widetilde {\mu }_a(\overline {Q}(D))\rangle \rangle $
, where
$$ \begin{align*}\phi([\gamma\beta])=[\gamma\beta]+t,\phi(\xi)=\xi-\beta^*\gamma^*,\phi([\alpha\beta])=-[\alpha\beta],\phi(u)=u\end{align*} $$
for other arrows u in
$\widetilde {\mu }_a((\overline {Q}(D))$
. Then
$$ \begin{align*}\begin{array}{rcl} \phi(\widetilde{\mu}_a(\overline{W}(D))) & = & \xi[\gamma\beta]\\ & & +[\alpha\delta](\zeta+\delta^*\alpha^*)+[\alpha\beta] (\eta+\beta^*\alpha^*)\\ & & +\beta^*\gamma^*t-s[\gamma\delta]-\delta^*\gamma^*[\gamma\delta]+\overline{W}'(D). \end{array}\end{align*} $$
On the one hand, note that
$\phi $
gives a right equivalence between the IQPs
$$ \begin{align*}(\widetilde{\mu}_a(\overline{Q}(D)),\widetilde{\mu}_a(F(D)), \widetilde{\mu}_a(\overline{W}(D)))\end{align*} $$
and
$$ \begin{align*}(\widetilde{\mu}_a(\overline{Q}(D)),\widetilde{\mu}_a(F(D)), \phi(\widetilde{\mu}_a(\overline{W}(D)))),\end{align*} $$
in particular,
$$ \begin{align*}\phi(\mathbb{C}\langle \langle F(D)\rangle\rangle)=\mathbb{C}\langle \langle \tilde{\mu}_a(F(D))\rangle\rangle.\end{align*} $$
On the other hand,
$\phi (\widetilde {\mu }_a(\overline {W}(D)))$
is of the canonical form (2.2) with the reduced part
$$ \begin{align*}\phi(\widetilde{\mu}_a(\overline{W}(D)))_{\mathrm{red}}=[\alpha\delta]\delta^*\alpha^*+[\alpha\beta]\beta^*\alpha^* +\beta^*\gamma^*t-s[\gamma\delta]-\delta^*\gamma^*[\gamma\delta]+\overline{W}'(D).\end{align*} $$
Then, after the reduction, we get the mutation
$$ \begin{align*}(\mu_a(\overline{Q}(D)),\mu_a(F(D)),\mu_a(\overline{W}(D))),\end{align*} $$
where the iced quiver
$(\mu _a(\overline {Q}(D)),\mu _a(F(D)))$
is obtained from
$(\widetilde {\mu }_a(\overline {Q}(D)),\widetilde {\mu }_a(F(D)))$
by deleting the arrows
$\xi $
,
$[\gamma \beta ]$
,
$\zeta $
, and
$\eta $
, and freezing the arrows
$[\alpha \beta ]$
and
$[\alpha \delta ]$
. Note that this iced quiver is exactly the iced quiver of the final Postnikov diagram
$\mu _{R}(D)$
depicted in the third picture of Figure 9, that is, we have
$\overline {Q}(\mu _{R}(D))=\mu _a(\overline {Q}(D))$
.
On the other hand, by the definition,
$$ \begin{align*}\overline{W}(\mu_R(D))=-[\alpha\delta]\delta^*\alpha^*+[\alpha\beta]\beta^*\alpha^* -\beta^*\gamma^*t-s[\gamma\delta]+\delta^*\gamma^*[\gamma\delta]+\overline{W}'(D).\end{align*} $$
Furthermore, by Lemma 3.3, there is a sign change of arrows
$\epsilon $
on
$\mathbb {C}\langle \langle \mu _a(\overline {Q}(D))\rangle \rangle $
such that
$$ \begin{align*}\epsilon(\mu_a(\overline{W}(D)))=\epsilon(\phi(\widetilde{\mu}_a(\overline{W}(D)))_{red})=\overline{W}(\mu_{R}(D))\end{align*} $$
up to the equality
$\mu _a(\overline {Q}(D))=\overline {Q}(\mu _{R}(D))$
. So, by the right-equivalent
$\epsilon \phi $
, we obtain the final mutation
$\mu _{a}(\overline {Q}(D),F(D),\overline {W}(D))$
, as well as the desired equalities
$$ \begin{align*}(\mu_{a}(\overline{Q}(D)),\mu_{a}(F(D))=(\overline{Q}(\mu_{R}(D)),F(\mu_{R}(D))) \mbox{~and~} \mu_{a}(\overline{W}(D))=\overline{W}(\mu_{R}(D)).\end{align*} $$
The compatibility stated in the above theorem ensures the following definition.
Definition 3.5 Let D be any
$(k,n)$
-Postnikov diagram, and let
$\mathbb {C}[Gr(k,n)]$
be the Grassmannian cluster algebra. We call:
-
• a QP which is mutation-equivalent to
$(Q(D),W(D))$
a QP of
$\mathbb {C}[Gr(k,n)]$
, and denote it by
$(Q,W)$
; -
• an IQP which is mutation-equivalent to
$(\overline {Q}(D),F(D),\overline {W}(D))$
an IQP of
$\mathbb {C}[Gr(k,n)]$
, and denote it by
$(\overline {Q},F,\overline {W})$
.
3.2 Rigidity and finite dimension
We prove in this subsection that each QP of a Grassmannian cluster algebra
$\mathbb {C}[Gr(k,n)]$
is rigid and Jacobi-finite. We would like to mention that the techniques used in this subsection to describe the properties of the quivers with potentials associated with Grassmannian cluster algebras is inspired by the work of Labardini for the surface cluster algebras [Reference Labardini-FragosoL09, Reference Labardini-FragosoL16]. The philosophy behind this is that as for the surface cluster algebras, some quivers of the Grassmannian cluster algebras are “two-dimensional,” which implies that they can be embedded into a disk. Notice that these quivers are the dual of the Postnikov diagrams. Therefore, from this point of view, our main results in Section 3, especially the uniqueness of the rigid QP, and thus the following application to the cluster automorphism groups, can be established in a more general settings, for example, for the cluster algebras arising from the dimer models [Reference BroomheadB12], from the unipotent groups [Reference Berenstein, Fomin and ZelevinskyBIRS09], and from the double Bruhat cells [Reference Fomin and ZelevinskyFZ07]. However, we restrict our interests to the Grassmannian cluster algebras in this paper.
Recall that a QP
$(Q,W)$
is said to be
$2$
-acyclic if there are no
$2$
-cycles in the quiver. Note that there may appear
$2$
-cycles in the quiver of
$\mu _i(Q,W)$
after mutations, even if
$(Q,W)$
is
$2$
-acyclic. If all possible iterations of mutations are
$2$
-acyclic, then we say that
$(Q,W)$
is nondegenerate. We call
$(Q,W)$
rigid if every cycle in Q is cyclically equivalent to an element of the Jacobian ideal
$J(Q,W)$
. It is known that a rigid QP is always nondegenerate [Reference Chang and ZhuDWZ08]. We call
$(Q,W)$
Jacobi-finite if the Jacobian algebra
$\mathcal {P}(Q,W)$
is finite-dimensional.
For the further study, we need some special Postnikov diagram (see Figure 10), where the diagrams depend on the parities of k and n, and any pair
$(k,n)$
matches a unique diagram shown in these figures. These diagrams are of special importance, and they are used by Scott as the initial diagrams, which give the initial quivers of the Grassmannian cluster algebras [Reference ScottS06].
Figure 10: Initial Postnikov diagram.
Denote by
$(\overline {Q}_{\textrm {ini}},F_{\textrm {ini}},\overline {W}_{\textrm {ini}})$
and
$(Q_{\textrm {ini}},W_{\textrm {ini}})$
the IQP and the QP associated with the initial Postnikov diagram, respectively. In what follows, we always assume that both k and n are odd. The statements and the proofs for the other cases are similar. The quiver Q is certain grid as shown in Figure 11, where we endow the points of the quiver with coordinates, and label the position of a fundamental cycle by its row Rj and column Ci. For example, the bottom-left fundamental cycle lies at R1 row and C1 column. We denote by
$a(i,j)$
the vertex with coordinate
$(i,j)$
.
Figure 11: Initial quiver
$Q_{\textrm {ini}}$
(k odd, n odd).
Let l be a path which forms a cycle in
$Q_{\textrm {ini}}$
. Let
$a(i_1,j_1)$
be a vertex on l, and we say that it is a leftmost vertex of l if
$i_1\leqslant i$
for any vertex
$a(i,j)$
on l. Similarly, we define the rightmost vertex, lowest vertex, and highest vertex of l as
$a(i_2,j_2)$
,
$a(i_3,j_3)$
, and
$a(i_4,j_4)$
respectively. We call
$width(l)=i_2-i_1$
the width of l, and call
$height(l)=j_4-j_3$
the height of l.
Lemma 3.6 Let l be a cycle in
$Q_{\textrm {ini}}$
with end point
$(i_0,j_0)$
. There exists a positive integer m such that
$l-\omega ^m\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
for any fundamental cycle
$\omega $
with end point
$(i_0,j_0)$
.
Proof Without loss of generality, we may assume that
$(i_0,j_0)$
is at the top-left corner of
$\omega $
. So
$\omega $
is located at
$R(j_0-1)$
and
$Ci_0$
of
$Q_{\textrm {ini}}$
. The proof is proceeded in two steps.
Step 1: We claim that there exists a cycle
$\xi $
satisfying the following conditions:
-
(1) the end point of
$\xi $
is
$(i_0,j_0)$
; -
(2)
$l-\xi \in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
; -
(3) any highest vertex of
$\xi $
is located at the top of the
$j_0$
-th level of
$Q_{\textrm {ini}}$
.
Let
$a=a(i,j)$
be a highest vertex of l. If
$j=2$
, then l itself already satisfies the conditions of
$\xi $
. So we assume that
$j \geq 2$
. Then, up to the left–right symmetries, we may assume that the local configuration of l is as in Figure 12, where the bold arrows form a subpath of a cycle which is cyclically equivalent to l. Now, we construct a new cycle
$l'$
from l with end point
$(i_0,j_0)$
such that
$l-l'\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
.
Figure 12: Local configuration neighboring the highest vertex a of a cycle.
Note that we may assume that none of the end points of
$\gamma $
is
$(i_0,j_0)$
. Otherwise, a is already located at the top of the
$j_0$
-th level of
$Q_{\textrm {ini}}$
, so it is unnecessary to consider such a. Therefore,
$\delta \gamma \beta $
is a subpath of l, and we may write
$l= q \delta \gamma \beta p$
with p and q the subpaths of l, where p and q maybe trivial paths. Let
$l"= q\nu \mu \rho p$
. Then the end point of
$l"$
is still the
$(i_0,j_0)$
, and
$l-l"= q(\delta \gamma \beta -\nu \mu \rho )p=p(\partial _\alpha W_{\textrm {ini}})q\in J(Q_{\textrm {ini}},W_{\textrm {ini}}).$
If a is still a vertex on
$l"$
, we repeat the above construction until a is never a vertex on a cycle
$l'$
, which makes sense since the length of l is finite. The final cycle
$l'$
is what we want. Note that the cycle
$l'$
has the following properties:
-
(1)
$l-l'\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
; -
(2) a is never a highest vertex of
$l'$
; -
(3) no new highest vertex arises in
$l'$
with respect to l.
Thus, by inductively constructing the cycle
$l'$
, we may find a cycle
$\xi $
satisfies the conditions in the claim.
Step 2: For the cycle
$\xi $
produced in Step I, we consider the lowest, the leftmost, and the rightmost vertices, similar to the analysis used in Step I, and we obtain a cycle
$\zeta $
such that:
-
(1) the end point of
$\zeta $
is
$(i_0,j_0)$
; -
(2)
$l-\zeta \in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
; -
(3)
$\zeta $
lies at
$R(j_0-1)$
and
$Ci_0$
, with
$width(\zeta )=height(\zeta )=1$
.
By item
$(3)$
,
$\zeta $
is a power of a fundamental cycle
$\omega '$
which lies at
$R(j_0-1)$
and
$Ci_0$
. By the assumption of
$\omega $
, it is a fundamental cycle starting at
$(i_0,j_0)$
and lies at
$R(j_0-1)$
and
$Ci_0$
. So we have
$\omega '=\omega $
by item
$(1)$
. Therefore, we have proved that there exists a positive integer m such that
$l-\omega ^m\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
.
Theorem 3.7 Any QP
$(Q,W)$
of a Grassmannian cluster algebra is rigid.
Because the QP-mutations preserve rigidity, it suffices to prove the theorem for the initial QP
$(Q_{\textrm {ini}},W_{\textrm {ini}})$
. So we have to show that any cycle in
$Q_{\textrm {ini}}$
is cyclically equivalent to a cycle in the Jacobian ideal
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. This is easy for the case
$k=2$
or
$k=n-2$
. Now, we assume that
$k \neq 2$
and
$k \neq n-2$
. The following lemma is useful.
Lemma 3.8 Let
$\omega _1$
and
$\omega _2$
be two fundamental cycles of
$Q_{\textrm {ini}}$
sharing a common arrow
$\alpha $
. For any positive integer m, if
$\omega ^m_2$
is cyclically equivalent to an element in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
, then
$\omega ^m_1$
is also cyclically equivalent to an element in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
.
Proof Recall that C is the closure of the span of all elements of the form
$$ \begin{align*}\alpha_s\cdots\alpha_2\alpha_1-\alpha_1\alpha_s\cdots\alpha_2,\end{align*} $$
where
$\alpha _s\cdots \alpha _2\alpha _1$
is a cycle. Since
$\omega ^m_2$
is cyclically equivalent to an element in the ideal
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
, there is a potential
$\omega \in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
such that
$\omega ^m_2-\omega \in C$
. Assume that
$\alpha p_1$
(resp.
$\alpha p_2$
) is the fundamental cycle which is cyclically equivalent to
$\omega _1$
(resp.
$\omega _2$
), where
$p_1$
and
$p_2$
are paths with head
$t(\alpha )$
and tail
$h(\alpha )$
. Then we use the partial derivation
$\partial _\alpha $
to obtain that
$$ \begin{align*}\alpha p_1-\alpha p_2\in J(Q_{\textrm{ini}},W_{\textrm{ini}}).\end{align*} $$
Moreover, since
$\alpha p_1-\alpha p_2$
is a factor of
$(\alpha p_1)^m-(\alpha p_2)^m$
,
$$ \begin{align*}(\alpha p_1)^m-(\alpha p_2)^m\in J(Q_{\textrm{ini}},W_{\textrm{ini}}).\end{align*} $$
Note that
$(\alpha p_2)^m-\omega ^m_2\in C$
and
$\omega ^m_2-\omega \in C$
, and thus
$(\alpha p_2)^m-\omega \in C$
. Therefore,
$$ \begin{align*}\omega^m_1-[(\alpha p_1)^m-(\alpha p_2)^m+\omega]=[\omega^m_1-(\alpha p_1)^m]+[(\alpha p_2)^m-\omega]\in C,\end{align*} $$
where
$(\alpha p_1)^m-(\alpha p_2)^m+\omega \in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. This completes the proof.
Proof Proof of the theorem: We divide the proof into three steps.
Step 1: See Figure 11, and note that there exist an arrow
$\alpha $
and a fundamental cycle
$\alpha p$
such that the only fundamental cycles that contain
$\alpha $
are those in the cyclically equivalent set
$[\alpha p]$
. Actually, one may always choose the arrow
$\alpha $
from
$a(2,1)$
to
$a(1,1)$
and the bottom-left fundamental cycle of the quiver. So
$$ \begin{align*}(\alpha p)^m=(\alpha \partial_\alpha {W})^m\in J(Q_{\textrm{ini}},W_{\textrm{ini}})\end{align*} $$
for any positive integer m. That means that, for any fundamental cycle
$\omega _1$
in
$[\alpha p]$
and any positive integer m,
$\omega _1^m$
is cyclically equivalent to an element in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
.
Step 2: For any fundamental cycle
$\omega _2$
and any positive integer m, by recursively using Lemma 3.8, we find a fundamental cycle
$\omega _1$
appearing in Step I, such that
$\omega ^m_2$
is cyclically equivalent
$\omega ^m_1$
. Thus,
$\omega ^m_2$
is cyclically equivalent to an element in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
.
Step 3: For any cycle l in
$\overline {Q}_{\textrm {ini}}$
, by Lemma 3.6, there is a power
$\omega ^m_2$
of fundamental cycle with
$l-\omega ^{m}_2\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. By Step II, there is an element
$\omega ^m_1$
in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
such that
$\omega ^m_2-\omega ^m_1\in C$
. That is,
$$ \begin{align*}l-[l-\omega^m_2+\omega^m_1]=\omega^m_2-\omega^m_1\in C,\end{align*} $$
where
$l-\omega ^m_2+\omega ^m_1\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. This means that l is cyclically equivalent to an element in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. Thus, the QP
$(Q_{\textrm {ini}},W_{\textrm {ini}})$
is rigid.
Remark 3.9 Similar to the rigidity of a QP, one may also consider the rigidity for an IQP, which is defined in [Reference PresslandP18]. It is easy to see that
$(\overline {Q}_{\textrm {ini}},F,\overline {W}_{\textrm {ini}})$
is not rigid. In particular, any fundamental cycle in
$(\overline {Q}_{\textrm {ini}},F,\overline {W}_{\textrm {ini}})$
is not cyclically equivalent to a cycle in
$J(\overline {Q}_{\textrm {ini}},F,\overline {W}_{\textrm {ini}})$
.
Theorem 3.10 For each QP
$(Q,W)$
of the Grassmannian cluster algebra, the Jacobian algebra
$\mathcal {P}(Q,W)$
is finite-dimensional.
Proof Since the Jacobi-finiteness of an QP is invariant under QP-mutations, we only prove this for the initial QP
$(Q_{\textrm {ini}},W_{\textrm {ini}})$
. We have to prove that if the length of a cycle l is large enough, then the cycle belongs to the Jacobian ideal.
By Lemma 3.6, there exist a fundamental cycle
$\omega $
and a positive integer m such that
$l-\omega ^m\in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. On the other hand, note that, by the construction of
$\omega $
, we have
$\textrm{length}(l)=m~\textrm{length}(\omega )$
. So we only need to show that, for any fundamental cycle
$\omega $
, there is a positive integer n such that
$$ \begin{align*}\omega^n\in J(Q_{\textrm{ini}},W_{\textrm{ini}}).\end{align*} $$
This can be done by iteratively using the relations in
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
. For example, we consider
$\omega ^n$
with
$\omega $
shown in Figure 13, where the end points of fundamental cycles
$\omega $
,
$\omega _1$
, and
$\omega _2$
are a, a, and b, respectively. Then we have
$$ \begin{align*}\omega^n-\omega_1^n \in J(Q_{\textrm{ini}},W_{\textrm{ini}}),\end{align*} $$
$$ \begin{align*}\omega_1^n-\delta\omega_2^{n-1}\gamma\beta\alpha \in J(Q_{\textrm{ini}},W_{\textrm{ini}}),\end{align*} $$
and thus
$$ \begin{align*}\omega^n-\delta\omega_2^{n-1}\gamma\beta\alpha \in J(Q_{\textrm{ini}},W_{\textrm{ini}}).\end{align*} $$
As long as n is large enough, repeating this process, we can find a fundamental cycle
$\omega '$
locating at the row
$R1$
, which belongs to
$J(Q_{\textrm {ini}},W_{\textrm {ini}})$
, such that
$$ \begin{align*}\omega^n-q(\omega')^{n'}p \in J(Q_{\textrm{ini}},W_{\textrm{ini}}),\end{align*} $$
where
$n'$
is a positive integer, and p and q are paths in
$Q_{\textrm {ini}}$
. Therefore,
$\omega ^n \in J(Q_{\textrm {ini}},W_{\textrm {ini}})$
, which completes the proof.
Remark 3.11 Unlike the case for the QP
$(Q_{\textrm {ini}},W_{\textrm {ini}})$
, the IQP
$(\overline {Q}_{\textrm {ini}},F,\overline {W}_{\textrm {ini}})$
is not Jacobi-finite. In particular, any power of a fundamental cycle of
$\overline {Q}_{ini}$
is nonzero in the Jacobian algebra
$\mathcal {P}(\overline {Q}_{\textrm {ini}},F,\overline {W}_{\textrm {ini}})$
.
3.3 The uniqueness
We study in this subsection the uniqueness of the QPs of a Grassmannian cluster algebra. This is based on a general result of Geiß, Labardini, and Schröer [Reference Geiß, Leclerc and SchröerGLS16]. They give a criterion which guarantees the uniqueness of a nondegenerate QP.
We first recall some definitions in [Reference Geiß, Leclerc and SchröerGLS16]. If W is a finite potential, i.e., the potential with finite items in the its expansion, then we denote by
$\textrm{long}(W)$
the length of the longest cycle appearing in W. For a nonzero element
$u\in \mathbb {C}\langle Q\rangle $
, denote by
$\textrm{short}(u)$
the unique integer such that
$u\in \mathfrak {m}^{\textrm{short}(u)}$
but
$u\notin \mathfrak {m}^{\textrm{short}(u)+1}$
, where
$\mathfrak {m}$
is the ideal generated by all arrows. We also set
$\textrm{short}(0)=+\infty $
(see [Reference Geiß, Leclerc and SchröerGLS16, Section 2.5]). The following two propositions are important for our main result.
Figure 13: Jacobi-finiteness of the QP.
Proposition 3.12 [Reference Geiß, Leclerc and SchröerGLS16, Proposition 2.4]
Let
$(Q,W)$
be a QP over a quiver Q, and let I be a subset of
$Q_0$
such that the following hold:
-
(1) The full subquiver
$Q|_I$
of Q with vertex set I contains exactly m arrows
$\alpha _1,\ldots ,\alpha _m$
; -
(2)
$l:=\alpha _1\ldots \alpha _m$
is a cycle in Q; -
(3) The vertices
$s(\alpha _1),\ldots ,s(\alpha _m)$
are pairwise different; -
(4) W is nondegenerate.
Then the cycle l appears in W.
Proposition 3.13 [Reference Geiß, Leclerc and SchröerGLS16, Theorem 8.20]
Suppose that
$(Q,W)$
is a QP over a quiver Q that satisfies the following three properties:
-
(1) W is a finite potential;
-
(2) Every cycle l in Q of length greater than
$\textrm{ long}(W)$
is cyclically equivalent to an element of the form
$\sum _{\alpha \in Q_1}\eta _\alpha \partial _\alpha W$
with
$\textrm{ short}(\eta _\alpha )+\textrm{ short}(\partial _\alpha W)\geqslant \textrm{ length}(l)$
for all
$\alpha \in Q_1$
; -
(3) Every nondegenerate potential on Q is right-equivalent to
$W+W'$
for some potential
$W'$
with
$\textrm{ short}(W')> \textrm{ long}(W)$
.
Then W is nondegenerate, and every nondegenerate QP on Q is right-equivalent to W.
Theorem 3.14 Let Q be a quiver of a Grassmannian cluster algebra, then the QP
$(Q,{W})$
is the unique nondegenerate QP on Q up to right equivalence, and thus the unique rigid QP on Q up to right equivalence.
Proof By Theorem 3.7,
$(Q,{W})$
is rigid, so if it is unique as a nondegenerate QP, then it must be unique as a rigid QP. Since the mutations of two right-equivalent QPs are still right-equivalent, we only need to prove the theorem for the initial QP.
To do this, we check that the conditions
$(1)$
–
$(3)$
in Proposition 3.13 hold for
$(Q_{\textrm {ini}},{W}_{\textrm {ini}})$
. The condition
$(1)$
is clear. Since the cluster algebra of
$Gr(2,n)$
is of acyclic type, so there is a unique rigid QP. Otherwise, there exists at least one internal fundamental cycle on
$Q_{\textrm {ini}}$
, and
$\textrm{long}({W}_{\textrm {ini}})=4$
. We prove the condition
$(2)$
in two steps (see Figure 11).
Step I: Let
$\omega $
be a fundamental cycle of
$Q_{\textrm {ini}}$
, and let m be a positive integer number. We claim that
$\omega ^m$
is cyclically equivalent to
$\sum _{\alpha \in Q_1} \eta _\alpha \partial _\alpha {W}_{\textrm {ini}}$
, where the length of a path appearing in nonzero
$\eta _\alpha $
is
$4m-3$
, and the length of all paths appearing in
$\partial _\alpha {W}_{\textrm {ini}}$
is
$3$
.
We prove this by induction on the level of
$\omega $
. Assume that the level of
$\omega $
is
$2$
and
$\alpha $
be the bottom arrow of
$\omega $
, then it is cyclically equivalent to
$\alpha \partial _\alpha {W}_{\textrm {ini}}$
. Moreover,
$$ \begin{align*}\omega^m \mbox{~ is~ cyclically~ equivalent~ to ~}((\alpha\partial_\alpha {W}_{\textrm{ini}})^{m-1}\alpha)\partial_\alpha {W}_{\textrm{ini}},\end{align*} $$
where
$\eta _\alpha =(\alpha \partial _\alpha {W}_{\textrm {ini}})^{m-1}\alpha $
and
$\partial _\alpha {W}_{\textrm {ini}}$
satisfy the conditions in the claim.
Now, let
$\omega $
be a fundamental cycle located at level t. Assume that the claim holds for the fundamental cycle
$\alpha \rho \nu \mu $
, which is located at level
$t-1$
(see Figure 14). Here, we only consider the clockwise cycle
$\alpha \rho \nu \mu $
, and another case is similar. So we may assume that
$(\alpha \rho \nu \mu )^m$
is cyclically equivalent to a potential
$\sum _{\alpha '\in Q_1} \eta _{\alpha '}\partial _{\alpha '}{W}_{\textrm {ini}}$
satisfying the claim. Then
$\omega ^m$
is cyclically equivalent to
$(\alpha \delta \gamma \beta )^m$
, which equals to
$(\alpha \rho \nu \mu -\alpha \partial _\alpha {W}_{\textrm {ini}})^m$
.
Figure 14: Uniqueness of the QP.
Note that we may write the expansion of
$(\alpha \rho \nu \mu -\alpha \partial _\alpha {W}_{\textrm {ini}})^m$
as the form of
$(\alpha \rho \nu \mu )^m+\sum _k S_k$
, where
$S_k$
is a multiplication of
$\alpha \rho \nu \mu $
and
$-\alpha \partial _\alpha {W}_{\textrm {ini}}$
with the term
$-\alpha \partial _\alpha {W}_{\textrm {ini}}$
appearing in it at least once. We write
$S_k=S^{\prime }_k\alpha \partial _\alpha {W}_{\textrm {ini}}S^{\prime \prime }_k$
, where
$S^{\prime }_k$
and
$S^{\prime \prime }_k$
are multiplications (maybe empty) of
$\alpha \rho \nu \mu $
and
$-\alpha \partial _\alpha {W}_{\textrm {ini}}$
. Then
$S_k-S^{\prime \prime }_kS^{\prime }_k\alpha \partial _\alpha {W}_{\textrm {ini}} \in C$
. Thus,
$$ \begin{align*} \begin{aligned} & (\alpha\delta\gamma\beta)^m-[\sum_{\alpha'\in Q_1} \eta_{\alpha'}\partial_{\alpha'}{W}_{\textrm{ini}}+({\textstyle\sum}_k S^{\prime\prime}_kS^{\prime}_k\alpha)\partial_\alpha {W}_{\textrm{ini}}]\\ =&[(\alpha\rho\nu\mu)^m+{\textstyle\sum}_k S_k]-[\sum_{\alpha'\in Q_1} \eta_{\alpha'}\partial_{\alpha'}{W}_{\textrm{ini}}+({\textstyle\sum}_k S^{\prime\prime}_kS^{\prime}_k\alpha)\partial_\alpha {W}_{\textrm{ini}}] \\ =& [(\alpha\rho\nu\mu)^m-\sum_{\alpha'\in Q_1} \eta_{\alpha'}\partial_{\alpha'}{W}_{\textrm{ini}}]+{\textstyle\sum}_k (S_k-S^{\prime\prime}_kS^{\prime}_k\alpha\partial_\alpha {W}_{\textrm{ini}}) \in C.\\ \end{aligned} \end{align*} $$
So
$(\alpha \delta \gamma \beta )^m$
, and therefore
$\omega ^m$
is cyclically equivalent to
$$ \begin{align*}\sum_{\alpha'\in Q_1} \eta_{\alpha'}\partial_{\alpha'}{W}_{\textrm{ini}}+({\textstyle\sum}_k S^{\prime\prime}_kS^{\prime}_k\alpha)\partial_\alpha {W}_{\textrm{ini}},\end{align*} $$
which satisfies the conditions in the claim.
To sum up, for any fundamental cycle
$\omega $
and any positive integer number m,
$\omega ^m$
is cyclically equivalent to
$\sum \eta _\alpha \partial _\alpha {W}_{\textrm {ini}}$
, where
$\eta _\alpha =0$
or each path in
$\eta _\alpha $
has length
$4m-3$
, and each path in
$\partial _\alpha {W}_{\textrm {ini}}$
has length
$3$
. So
$\textrm{short}(\eta _\alpha )=+\infty $
or
$4m-3$
, and
$\textrm{short}(\partial _\alpha {W}_{\textrm {ini}})=3$
. Therefore,
$$ \begin{align*}\textrm{short}(\eta_\alpha)+\textrm{short}(\partial_\alpha {W}_{\textrm{ini}})\geqslant 4m = \textrm{length}(\omega^m),\end{align*} $$
and the condition
$(2)$
holds for
$\omega ^m$
.
Step II: Let l be a cycle of Q. We use the notations appearing in Lemma 3.6. In particular,
$l'$
is the new cycle which shares an arrow
$\alpha $
with l, and p and q are two subpaths of l such that
$l=l'\pm q \partial _\alpha {W}_{\textrm {ini}}p$
. At last, we find a fundamental cycle
$\omega $
with
$$ \begin{align*}l-\omega^m \in J(Q,{W}_{\textrm{ini}}).\end{align*} $$
Assume that
$l'$
is cyclically equivalent to
$\sum \eta _{\alpha '}\partial _{\alpha '}{W}_{\textrm {ini}}$
and condition
$(2)$
holds for
$l'$
, that is,
$$ \begin{align*}\textrm{short}(\eta_{\alpha'})+\textrm{short}(\partial_{\alpha'} W)\geqslant \textrm{length}(l').\end{align*} $$
On the other hand, by the construction of
$l'$
given in Lemma 3.6, we have
$$ \begin{align*}\textrm{length}(l)=\textrm{length}(l')\mbox{~and~}\textrm{length}(l)=\textrm{length}(pq)+\textrm{short}(\partial_\alpha {W}_{\textrm{ini}}).\end{align*} $$
Therefore, l is cyclically equivalent to
$\sum \eta _{\alpha '}\partial _{\alpha '}{W}_{\textrm {ini}}\pm pq \partial _\alpha {W}_{\textrm {ini}}$
, which satisfies the condition
$(2)$
. This proves the condition
$(2)$
for all cycles over Q.
Finally, the condition
$(3)$
follows immediately from the following two observations. By Proposition 3.12, all of the fundamental cycles appear in
${W}_{\textrm {ini}}$
. For any cycle l, excepting the fundamental cycles,
$\textrm{length}(l)> 4=\textrm{long}({W}_{\textrm {ini}})$
.
4 Applications
4.1 Categorification
An “additive categorification” of a cluster algebra has been well studied in recent years. Roughly speaking, it lifts a cluster algebra structure on a categorical level, that is, one may find a cluster structure (see [Reference Berenstein, Fomin and ZelevinskyBIRS09] for precise definition) on the category. Such category always has a duality property called
$2$
-Calabi–Yau property. In particular, the cluster category is an important example of
$2$
-Calabi–Yau triangulated category with cluster structure, which gives a categorification for the cluster algebra of acyclic type with trivial coefficients. In [Reference AmiotA09], for a QP
$(Q,W)$
, Amiot constructed a generalized cluster category
$\mathcal {C}_{(Q,W)}$
.
Some stably
$2$
-Calabi–Yau Frobenius category also has cluster structure (see [Reference Berenstein, Fomin and ZelevinskyBIRS09, Reference Fu and KellerFK09]), which gives categorification of a cluster algebra with nontrivial coefficients. In our context, such Frobenius category is always certain subcategory of module categories. For the cluster algebra structure on the coordinate ring
$$ \begin{align} \mathbb{C}[\mbox{Gr}(k,n)] / (\phi_{\{1,2,\ldots ,k\}} - 1) \end{align} $$
of the affine open cell in the Grassmannian, where
$\phi _{\{1,2,\ldots ,k\}}$
is the consecutive Plücker coordinate indexed by k-subset
$\{1,2,\ldots ,k\}$
, Geiss, Leclerc, and Schröer have given in [Reference Geuenich, Labardini-Fragoso and Miranda-OlveraGLS08] a categorification in terms of a subcategory
$\operatorname {\textrm{Sub}} Q_k$
of the category of finite-dimensional modules over the preprojective algebra of type
$A_{n-1}$
. Note that the cluster coefficient
$\phi _{\{1,2,\ldots ,k\}}$
in
$\mathbb {C}[\mbox {Gr}(k,n)]$
is not realized in the category. More recently, Jensen, King, and Su (JKS) [Reference Jensen, King and SuJKS16] have given a full and direct categorification of the cluster structure on
$\mathbb {C}[\mbox {Gr}(k,n)]$
, using the category
$\operatorname {CM}(B)$
of (maximal) Cohen–Macaulay modules over the completion of an algebra B, which is a quotient of the preprojective algebra of type
$\tilde {A}_{n-1}$
.
Remark 4.1 It has been proved in [Reference Baur, King and MarshBKM16] that, for a cluster tilting object T in
$CM(B)$
corresponding to a Postnikov diagram, the cluster-tilted algebra
$\textrm{End}(T)$
is isomorphic to the Jacobian algebra
$\mathcal {P}(\overline {Q},F,\overline {W})$
. Note that
$CM(B)$
is Hom-infinite and
$\textrm{End}(T)$
is of infinite dimension, which is compatible with the Hom-infiniteness of
$\mathcal {P}(\overline {Q},F,\overline {W})$
(see Remark 3.11).
On the other hand, Amiot, Reiten, and Todorov showed in [Reference Amiot, Reiten and TodorovART11] that the generalized cluster category has some “ubiquity” (see also in [Reference AmiotA11, Reference Amiot, Iyama and ReitenAIR15, Reference VitóriaY18]). In our situation, this means that the stable categories of both
$\textrm{Sub} Q_k$
and
$\operatorname {CM}(B)$
are equivalent to a generalized cluster category, which is exactly the generalized cluster category defined by the QP
$(Q,W)$
.
4.2 Auto-equivalence groups and cluster automorphism groups
Recall that for a cluster algebra
$\mathcal {A}$
, we call an algebra automorphism f a cluster automorphism, if it maps a cluster
${\mathbf x}$
to a cluster
${\mathbf x}'$
, and is compatible with the mutations of the clusters. Equivalently, an algebra automorphism f is a cluster automorphism if and only if
$Q'\cong Q$
or
$Q'\cong Q^{op}$
, where
$Q'$
and Q are the associated quivers of
${\mathbf x}'$
and
${\mathbf x}$
, respectively. We refer to [Reference Assem, Schiffler and ShramchenkoASS12, Reference Buan, Iyama, Reiten and SmithCZ16, Reference Chang and ZhuCZ16b] for the details of cluster automorphisms.
Let
$\mathcal {C}$
be a
$2$
-Calabi–Yau triangulated category with cluster structure. In particular, there is a cluster tilting object T and a cluster map
$\phi $
which sends cluster tilting objects, which are reachable by iterated mutations from T in category
$\mathcal {C},$
to clusters in algebra
$\mathcal {A}_{\phi (T)}$
, where
$\mathcal {A}_{\phi (T)}$
is the cluster algebra with initial cluster
$\phi (T)$
. In fact,
$\mathcal {A}_{\phi (T)}$
is the cluster algebra defined by the Gabriel quiver of
$\textrm{End}_{\mathcal {C}}(T)$
.
Denote by
$\textrm{Aut}_T(\mathcal {C})$
a quotient group consisting of the (covariant and contravariant) triangulated auto-equivalence on
$\mathcal {C}$
that maps T to a cluster tilting object which is reachable from T itself, where we view two equivalences F and
$F'$
the same if
$F(T)\cong F(T')$
.
Let F be an auto-equivalence in
$\textrm{Aut}_T(\mathcal {C})$
. Denote by Q and
$Q'$
the Gabriel quivers of
$\textrm{End}_{\mathcal {C}}(T)$
and
$\textrm{End}_{\mathcal {C}}(F(T))$
, respectively. Then Q is naturally isomorphic to
$Q'$
since F is a triangulated equivalence. Moreover, since
$F(T)$
is reachable from T,
$\phi (F(T))$
is a cluster in
$\mathcal {A}_{\phi (T)}$
, so there is a cluster automorphism f in
$\textrm{Aut}(\mathcal {A}_{\phi (T)})$
which maps
$\phi (T)$
to
$\phi (F(T))$
. Thus,
$\textrm{Aut}_T(\mathcal {C})$
can be viewed as a subgroup of
$\textrm{Aut}(\mathcal {A}_{\phi (T)})$
. Conversely, we have the following.
Conjecture 4.2 There is a natural isomorphism
$\textrm{ Aut}_T(\mathcal {C})\cong \textrm{ Aut}(\mathcal {A}_{\phi (T)})$
.
If
$\mathcal {C}$
is algebraic and Q is acyclic, then Keller and Reiten proved in [Reference Keller and ReitenKR08] that
$\mathcal {C}$
is a (classical) cluster category. Then the conjecture has been verified in [Reference Assem, Schiffler and ShramchenkoASS12, Section 3] and [Reference Buan, Iyama, Reiten and ScottBIRS11, Theorem 2.3]. For the case of generalized cluster categories, the conjecture is related to the following conjecture, which says that the quivers determine the potentials up to right equivalences.
Conjecture 4.3 Let
$(Q,W)$
be a nondegenerate QP. Assume that
$(Q',W')$
is a QP which is mutation-equivalent to
$(Q,W)$
. Then:
-
(1)
$(Q',W')$
is right-equivalent to
$(Q,W)$
if
$Q'\cong Q$
; -
(2)
$(Q',W')$
is right-equivalent to
$(Q^{op},W^{op})$
if
$Q'\cong Q^{op}$
.
Proposition 4.4 If Conjecture 4.3 is true for a Jacobi-finite QP
$(Q,W)$
, then Conjecture 4.2 is true for the generalized cluster category
$\mathcal {C}_{(Q,W)}$
.
Proof Since
$(Q,W)$
is Jacobi-finite, recall from [Reference AmiotA09] that there is a canonical cluster titling object T in
$\mathcal {C}_{(Q,W)}$
whose endomorphism algebra is isomorphic to the Jacobian algebra
$J(Q,W)$
. Because we already have
$$ \begin{align*}\textrm{Aut}_T(\mathcal{C}_{(Q,W)})\subset \textrm{Aut}(\mathcal{A}_{\phi(T)}),\end{align*} $$
it suffices to show that any cluster automorphism f can be lifted as an auto-equivalence on
$\mathcal {C}$
which maps the canonical cluster tilting object to a reachable one. Assume that f maps
$\phi (T)$
to a cluster
$\mu (\phi (T))$
with quiver
$Q'\cong Q$
, where
$\mu (\phi (T))$
is obtained from
$\phi (T)$
by iterated mutations. Denote by
$(Q',W')=\mu (Q,W)$
the QP obtained from
$(Q,W)$
by the same steps of mutations.
On the one hand, by [Reference Keller and YangKY11, Theorem 3.2], there is an equivalence
$\Phi $
from
$\mathcal {C}_{(Q,W)}$
to
$\mathcal {C}_{(Q',W')}$
which maps T to
$\mu (T')$
, where
$T'$
is the canonical cluster tilting object in
$\mathcal {C}_{(Q',W')}$
whose endomorphism algebra is isomorphic to
$J(Q',W')$
.
On the other hand, Conjecture 4.3 ensures that there is a right equivalence between
$(Q',W')$
and
$(Q,W)$
, and then by [Reference Keller and YangKY11, Lemma 2.9], there is a covariant equivalence
$\Psi $
from
$\mathcal {C}_{(Q',W')}$
to
$\mathcal {C}_{(Q,W)}$
. Note that
$\Psi $
maps
$T'$
to T, and thus maps
$\mu (T')$
to
$\mu (T)$
, since the mutations are obtained by exchanged triangles (see, e.g., [Reference Berenstein, Fomin and ZelevinskyBIRS09]) and the equivalence
$\Psi $
is triangulated. Finally, the auto-equivalence
$\Psi \Phi $
is what we wanted, which gives a lift of f. We have a similar proof for the case
$Q'\cong Q^{op}$
. See the following diagram for the equivalences.
Theorem 4.5 For the nondegenerate QPs arising from the Grassmannians cluster algebra, Conjecture 4.3 is true. So, for the associated generalized cluster category
$\mathcal {C}$
, we have an isomorphism
$\textrm{ Aut}_T(\mathcal {C})\cong \textrm{ Aut}(\mathcal {A}_{\phi (T)})$
.
Proof Let
$(Q,W)$
be a nondegenerate QP of the Grassmannians cluster algebra, and let
$(Q',W')$
be a QP which is mutation-equivalent to
$(Q,W)$
. Then
$(Q',W')$
is nondegenerate. On the other hand, Theorem 3.14 implies that
$(Q,W)$
is the unique nondegenerate QP on Q, up to right equivalence. So
$(Q',W')$
is right-equivalent to
$(Q,W)$
if
$Q\cong Q'$
. Note that
$(Q^{op},W^{op})$
also has the nondegenerate uniqueness property since
$(Q,W)$
does. Thus, similarly,
$(Q',W')$
is also right-equivalent to
$(Q^{op},W^{op})$
, if
$Q'\cong Q^{op}$
. So Conjecture 4.3 is true, and
$\textrm{Aut}_T(\mathcal {C})\cong \textrm{Aut}(\mathcal {A}_{\phi (T)})$
.
Remark 4.6 For the QPs arising from a marked Riemann surface with some “technical conditions,” [Reference Geiß, Leclerc and SchröerGLS16, Theorem 1.4] ensures the nondegenerate uniqueness. So we have a similar isomorphism as in Theorem 4.5 for this case.
Acknowledgment
The authors would like to thank Dong Yang and Bin Zhu for useful discussions, Claire Amiot and Jeanne Scott for explaining their works in [Reference Amiot, Iyama and ReitenAIR15, Reference ScottS06], respectively, and Bernhard Keller and Osamu Iyama for pointing us to the references [Reference AmiotA09, Reference Amiot, Iyama and ReitenAIR15]. Part of the work was done when the first author visited the University of Connecticut from 2017 to 2018, and he thanks the university and especially Professor Ralf Schiffler for hospitality and providing him an excellent working environment.
