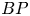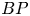1. Introduction
The projective Stiefel manifolds have been of interest in connection with a varied spectrum of topological questions. On one hand, they are useful in studying equivariant maps between the Stiefel manifolds [Reference Petrović and Prvulović17], and on the other, they form a part of an obstruction theory for constructing sections of multiples of a given line bundle [Reference Astey, Gitler, Micha and Pastor3]. In the real case, they play an important role in the immersion problem for real projective spaces [Reference Smith19].
In this paper, we consider the complex projective Stiefel manifolds $PW_{n,k}$![]() , defined as the quotient of the complex Stiefel manifold $W_{n,k}$
, defined as the quotient of the complex Stiefel manifold $W_{n,k}$![]() by the $S^{1}$
by the $S^{1}$![]() -action. Recall that $W_{n,k}$
-action. Recall that $W_{n,k}$![]() is the space of orthonormal $k$
is the space of orthonormal $k$![]() -frames in ${{\mathbb {C}}}^{n}$
-frames in ${{\mathbb {C}}}^{n}$![]() , and the group $S^{1}$
, and the group $S^{1}$![]() acts on $W_{n,k}$
acts on $W_{n,k}$![]() by vector-wise multiplication using $S^{1} \subset {{\mathbb {C}}}$
by vector-wise multiplication using $S^{1} \subset {{\mathbb {C}}}$![]() , whose orbit space is the complex projective Stiefel manifold $PW_{n,k}$
, whose orbit space is the complex projective Stiefel manifold $PW_{n,k}$![]() . The cohomology of $PW_{n,k}$
. The cohomology of $PW_{n,k}$![]() with ${{\mathbb {Z}}}/p$
with ${{\mathbb {Z}}}/p$![]() -coefficients was computed in [Reference Astey, Gitler, Micha and Pastor3], which is analogous to the ${{\mathbb {Z}}}/2$
-coefficients was computed in [Reference Astey, Gitler, Micha and Pastor3], which is analogous to the ${{\mathbb {Z}}}/2$![]() -computation for real projective Stiefel manifolds in [Reference Gitler and Handel11]. Among other applications, this has been used to prove the non-existence of $S^{1}$
-computation for real projective Stiefel manifolds in [Reference Gitler and Handel11]. Among other applications, this has been used to prove the non-existence of $S^{1}$![]() -equivariant maps between Stiefel manifolds [Reference Petrović and Prvulović17].
-equivariant maps between Stiefel manifolds [Reference Petrović and Prvulović17].
A natural idea here is that extending the computations to generalized cohomology theories would yield further results about equivariant maps. We follow through along these lines and compute the $BP$![]() -cohomology as (theorem 4.4).
-cohomology as (theorem 4.4).
Theorem A The $BP$![]() -cohomology of $PW_{n,k}$
-cohomology of $PW_{n,k}$![]() is described as
is described as
where $\gamma _j$![]() 's are of degree $2j-1,$
's are of degree $2j-1,$![]() $x$
$x$![]() is of degree $2,$
is of degree $2,$![]() and $I$
and $I$![]() is the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$
is the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$![]() .
.
The method used to compute the $BP$![]() -cohomology is the homotopy fixed point spectral sequence. This works for any complex oriented cohomology theory, where the class $x$
-cohomology is the homotopy fixed point spectral sequence. This works for any complex oriented cohomology theory, where the class $x$![]() comes from the choice of complex orientation. Consequently, the $K$
comes from the choice of complex orientation. Consequently, the $K$![]() -theory of the complex projective Stiefel manifold has an analogous formula, which was computed in [Reference Gondhali13] using the Hodgkin spectral sequence for the cohomology of homogeneous spaces. The same method is also likely to work for $P_\ell W_{n,k}$
-theory of the complex projective Stiefel manifold has an analogous formula, which was computed in [Reference Gondhali13] using the Hodgkin spectral sequence for the cohomology of homogeneous spaces. The same method is also likely to work for $P_\ell W_{n,k}$![]() , the quotient by a variant of the $S^{1}$
, the quotient by a variant of the $S^{1}$![]() -action, whose cohomology was computed in [Reference Basu and Subhash5]. Here, $\ell$
-action, whose cohomology was computed in [Reference Basu and Subhash5]. Here, $\ell$![]() refers to a tuple of integers $(l_1,\,\ldots,\, l_k)$
refers to a tuple of integers $(l_1,\,\ldots,\, l_k)$![]() and the action of $S^{1}$
and the action of $S^{1}$![]() is given by $z\cdot (v_1,\,\ldots,\,v_k)=(z^{l_1}v_1,\,\ldots,\, z^{l_k}v_k)$
is given by $z\cdot (v_1,\,\ldots,\,v_k)=(z^{l_1}v_1,\,\ldots,\, z^{l_k}v_k)$![]() .
.
We observe that the $BP$![]() -cohomology ring of $PW_{n,k}$
-cohomology ring of $PW_{n,k}$![]() is just the extension of coefficients from ${{\mathbb {Z}}}_{(p)}$
is just the extension of coefficients from ${{\mathbb {Z}}}_{(p)}$![]() in ordinary cohomology to ${{\mathbb {Z}}}_{(p)}[v_1,\,v_2,\,\ldots ]$
in ordinary cohomology to ${{\mathbb {Z}}}_{(p)}[v_1,\,v_2,\,\ldots ]$![]() in $BP$
in $BP$![]() -cohomology. Therefore, the primary multiplicative structure does not yield new results for equivariant maps between Stiefel manifolds. However, $BP$
-cohomology. Therefore, the primary multiplicative structure does not yield new results for equivariant maps between Stiefel manifolds. However, $BP$![]() has the action of Adams operations [Reference Araki2], which yield the following new result on equivariant maps (see theorem 5.3).
has the action of Adams operations [Reference Araki2], which yield the following new result on equivariant maps (see theorem 5.3).
Theorem B Suppose that $m,\,n,\,l,\, k$![]() are positive integers satisfying
are positive integers satisfying
(1) $n-k< m-l$
 and there is an $s$
and there is an $s$ such that $m<2^{s}+m-l\leq n$
such that $m<2^{s}+m-l\leq n$ .
.(2) $2$
 divides all the binomial coefficients $\binom {n}{n-k+1},\,\ldots,\, \binom {n}{m-l}$
divides all the binomial coefficients $\binom {n}{n-k+1},\,\ldots,\, \binom {n}{m-l}$ .
.(3) $2$
 does not divide $\binom {m}{m-l+1}$
does not divide $\binom {m}{m-l+1}$ and $2\nmid m-l$
and $2\nmid m-l$ .
.Then, there is no $S^{1}$
 -equivariant map from $W_{n,k}$
-equivariant map from $W_{n,k}$ to $W_{m,l}$
to $W_{m,l}$ .
.
We also obtain some new results using the action of Steenrod operations on $H^{\ast } PW_{n,k}$![]() . We point out that the analysis of equivariant maps on Stiefel manifolds also leads to results in topological combinatorics [Reference Basu and Kundu4].
. We point out that the analysis of equivariant maps on Stiefel manifolds also leads to results in topological combinatorics [Reference Basu and Kundu4].
1.1 Organization
In § 2, we discuss the construction of the homotopy fixed point spectral sequence, proving results about the convergence and the differentials in the case of projective Stiefel manifolds. In § 3, we describe the cohomology of the Stiefel manifold over generalized cohomology theories, and then specialize to $BP$![]() . In § 4, we complete the calculation of the spectral sequence and describe the $BP$
. In § 4, we complete the calculation of the spectral sequence and describe the $BP$![]() -cohomology of $PW_{n,k}$
-cohomology of $PW_{n,k}$![]() . In § 5, we discuss the applications to equivariant maps between Stiefel manifolds.
. In § 5, we discuss the applications to equivariant maps between Stiefel manifolds.
2. Homotopy fixed point spectral sequence
The purpose of this section is to set up the computational tools for the following sections. The main idea here is the homotopy fixed point spectral sequence for (naive) $G$![]() -equivariant spectra: for a spectrum $Z$
-equivariant spectra: for a spectrum $Z$![]() with a $G$
with a $G$![]() -action, there is a spectral sequence with $E_2$
-action, there is a spectral sequence with $E_2$![]() -page $H^{s}(G;\pi _{t} Z)$
-page $H^{s}(G;\pi _{t} Z)$![]() which converges to $\pi _{t-s} Z^{hG}$
which converges to $\pi _{t-s} Z^{hG}$![]() [Reference Dugger10] (see also [Reference Greenlees and May12]).
[Reference Dugger10] (see also [Reference Greenlees and May12]).
The principal example for our paper is when $G$![]() acts on a function spectrum $F(X,\,E)$
acts on a function spectrum $F(X,\,E)$![]() for a spectrum $E$
for a spectrum $E$![]() and a based $G$
and a based $G$![]() -space $X$
-space $X$![]() . Let us make this more precise. Let $E$
. Let us make this more precise. Let $E$![]() be a spectrum so that the reduced $E$
be a spectrum so that the reduced $E$![]() -cohomology of based spaces is computed as (note here that the cohomological grading is negative of the usual homotopy grading)
-cohomology of based spaces is computed as (note here that the cohomological grading is negative of the usual homotopy grading)
Here we use the notation $[-,\,-]$![]() for the homotopy classes of maps between spectra. We follow the construction of function spectra in [Reference May14]. If $X$
for the homotopy classes of maps between spectra. We follow the construction of function spectra in [Reference May14]. If $X$![]() has a $G$
has a $G$![]() -action, the function spectrum $F(X,\,E)$
-action, the function spectrum $F(X,\,E)$![]() is a spectrum with $G$
is a spectrum with $G$![]() -action (that is, a $G$
-action (that is, a $G$![]() -spectrum indexed over a trivial $G$
-spectrum indexed over a trivial $G$![]() -universe). We write $[-,\,-]^{G}_{tr}$
-universe). We write $[-,\,-]^{G}_{tr}$![]() for the equivariant homotopy classes in the category of spectra with $G$
for the equivariant homotopy classes in the category of spectra with $G$![]() -action, and $F^{G}_{tr}(-,\,-)$
-action, and $F^{G}_{tr}(-,\,-)$![]() for the equivariant function spectrum with $G$
for the equivariant function spectrum with $G$![]() -action. We have the following result regarding this construction.
-action. We have the following result regarding this construction.
Proposition 2.1 [Reference May14, Ch. XVI, §1, (1.9)]
Let $X$![]() be a based $G$
be a based $G$![]() -space, and $E$
-space, and $E$![]() a spectrum. Then,
a spectrum. Then,
For a free $G$![]() -space $X$
-space $X$![]() we may apply proposition 2.1 by adding a disjoint base-point. The homotopy fixed points of a spectrum $Z$
we may apply proposition 2.1 by adding a disjoint base-point. The homotopy fixed points of a spectrum $Z$![]() with $G$
with $G$![]() -action are $Z^{hG} = F^{G}_{tr}(EG_+,\,Z)^{G}$
-action are $Z^{hG} = F^{G}_{tr}(EG_+,\,Z)^{G}$![]() . We know that for a free $G$
. We know that for a free $G$![]() -space $X$
-space $X$![]() , the projection $X\times EG\to X$
, the projection $X\times EG\to X$![]() is a $G$
is a $G$![]() -equivalence. Therefore, we have the following equivalence of spectra.
-equivalence. Therefore, we have the following equivalence of spectra.
Corollary 2.2 Let $X$![]() be a free $G$
be a free $G$![]() -space, and $E$
-space, and $E$![]() a spectrum. Then
a spectrum. Then
In this paper, we apply corollary 2.2 to the case $X=W_{n,k}$![]() , the Stiefel manifold of $k$
, the Stiefel manifold of $k$![]() -orthogonal vectors in ${{\mathbb {C}}}^{n}$
-orthogonal vectors in ${{\mathbb {C}}}^{n}$![]() . This action is free and the quotient space is the projective Stiefel manifold $PW_{n,k}$
. This action is free and the quotient space is the projective Stiefel manifold $PW_{n,k}$![]() .
.
Corollary 2.3 Let $E$![]() be a spectrum. There is an equivalence of spectra
be a spectrum. There is an equivalence of spectra
We attempt to understand $F^{S^{1}}_{tr}({W_{n,k}}_+,\, E)^{hS^{1}}$![]() via the homotopy fixed point spectral sequence. For a spectrum $Z$
via the homotopy fixed point spectral sequence. For a spectrum $Z$![]() with $S^{1}$
with $S^{1}$![]() -action, we follow the exposition in [Reference Bruner and Rognes8] replacing homology with homotopy groups. We have a $S^{1}$
-action, we follow the exposition in [Reference Bruner and Rognes8] replacing homology with homotopy groups. We have a $S^{1}$![]() -equivariant filtration of $ES^{1}$
-equivariant filtration of $ES^{1}$![]() given by
given by
so that
We index the filtration of $ES^{1}$![]() as
as

so that
where the action of $S^{1}$![]() on $S^{2r}$
on $S^{2r}$![]() is the trivial action. The filtration on the induced tower of fibrations is written as
is the trivial action. The filtration on the induced tower of fibrations is written as
so that

We may now follow [Reference Bruner and Rognes8] to obtain a conditionally convergent spectral sequence [Reference Boardman6].
Proposition 2.4 Let $Z$![]() be a homotopy commutative ring spectrum with $S^{1}$
be a homotopy commutative ring spectrum with $S^{1}$![]() -action. There is a conditionally convergent multiplicative spectral sequence
-action. There is a conditionally convergent multiplicative spectral sequence
In this expression, the group cohomology $H^{\ast }(S^{1};\pi _t Z)$![]() of $S^{1}$
of $S^{1}$![]() with coefficients in the discrete group $\pi _t Z$
with coefficients in the discrete group $\pi _t Z$![]() equals ${{\mathbb {Z}}}[y] \otimes \pi _t Z$
equals ${{\mathbb {Z}}}[y] \otimes \pi _t Z$![]() with $|y|=(2,\,0)$
with $|y|=(2,\,0)$![]() .
.
Example 2.5 If $Z=E$![]() with trivial $S^{1}$
with trivial $S^{1}$![]() -action, the homotopy fixed point spectrum $Z^{hS^{1}} \simeq F(BS^{1}_+,\, E)$
-action, the homotopy fixed point spectrum $Z^{hS^{1}} \simeq F(BS^{1}_+,\, E)$![]() . In this case, the homotopy fixed point spectral sequence becomes
. In this case, the homotopy fixed point spectral sequence becomes
Making identifications $E^{n}({{\mathbb {C}}}P^{\infty }) \cong \pi _{-n}F({{\mathbb {C}}}P^{\infty }_+,\,E)$![]() , we observe that this reduces to the Atiyah-Hirzebruch spectral sequence for ${{\mathbb {C}}}P^{\infty }$
, we observe that this reduces to the Atiyah-Hirzebruch spectral sequence for ${{\mathbb {C}}}P^{\infty }$![]() . If $E$
. If $E$![]() is complex orientable, the class $y$
is complex orientable, the class $y$![]() becomes a permanent cycle.
becomes a permanent cycle.
Next we specialize to the case $Z=F^{S^{1}}_{tr}(X_+,\, E)$![]() where $X$
where $X$![]() is a free $S^{1}$
is a free $S^{1}$![]() -space, and $E$
-space, and $E$![]() is a spectrum. The homotopy groups of $F^{S^{1}}_{tr}(X_+,\,E)$
is a spectrum. The homotopy groups of $F^{S^{1}}_{tr}(X_+,\,E)$![]() in proposition 2.4 are computed by forgetting the $S^{1}$
in proposition 2.4 are computed by forgetting the $S^{1}$![]() action, and thus we have
action, and thus we have
On the other hand, we apply corollary 2.2 to deduce
We now switch the sign of the $t$![]() -grading in the spectral sequence of proposition 2.4 to obtain a conditionally convergent multiplicative spectral sequence
-grading in the spectral sequence of proposition 2.4 to obtain a conditionally convergent multiplicative spectral sequence
We summarize these facts together in the theorem below. For the rest of the section, $X$![]() is a free $S^{1}$
is a free $S^{1}$![]() -space and $E$
-space and $E$![]() a homotopy commutative ring spectrum.
a homotopy commutative ring spectrum.
Proposition 2.6 There is a conditionally convergent multiplicative spectral sequence
(1) If $E$
 is complex orientable, the class $y$
is complex orientable, the class $y$ is a permanent cycle.
is a permanent cycle.(2) The differential $d_r$
 changes the grading by $(s,\,t)\mapsto (s+r,\, t-r+1)$
changes the grading by $(s,\,t)\mapsto (s+r,\, t-r+1)$ .
.(3) If $X,$
 $X/S^{1}$
$X/S^{1}$ are finite CW complexes, and $E$
are finite CW complexes, and $E$ is complex orientable, the spectral sequence is strongly convergent.
is complex orientable, the spectral sequence is strongly convergent.
Proof. The degree of the differentials follow from the construction of the exact couple for the spectral sequence. We also have the map $X_+\to S^{0}$![]() which gives a map $E \to F^{S^{1}}_{tr}(X_+,\,E)$
which gives a map $E \to F^{S^{1}}_{tr}(X_+,\,E)$![]() which is $S^{1}$
which is $S^{1}$![]() -equivariant. Thus we have a map between the homotopy fixed point spectral sequences which maps the classes $y$
-equivariant. Thus we have a map between the homotopy fixed point spectral sequences which maps the classes $y$![]() to one another, and so, (1) follows from the identification in example 2.5.
to one another, and so, (1) follows from the identification in example 2.5.
It remains to prove (3). For this, we show that for $k$![]() sufficiently large, $y^{k}$
sufficiently large, $y^{k}$![]() lies in the image of a differential. It will then follow that for $r$
lies in the image of a differential. It will then follow that for $r$![]() sufficiently large the classes $y^{m}$
sufficiently large the classes $y^{m}$![]() and their $\pi _\ast E$
and their $\pi _\ast E$![]() multiples are $0$
multiples are $0$![]() in the $E_r$
in the $E_r$![]() -page for $m\geq k$
-page for $m\geq k$![]() . Therefore, the $E_r$
. Therefore, the $E_r$![]() -page will be concentrated in the columns between $1$
-page will be concentrated in the columns between $1$![]() and $k$
and $k$![]() , and $E_\infty =E_r$
, and $E_\infty =E_r$![]() by increasing $r$
by increasing $r$![]() further if necessary. Hence, the spectral sequence converges strongly [Reference Boardman6, theorem 7.4].
further if necessary. Hence, the spectral sequence converges strongly [Reference Boardman6, theorem 7.4].
The space $X/S^{1}$![]() being finite dimensional implies that the classifying map $X/S^{1} \to BS^{1}$
being finite dimensional implies that the classifying map $X/S^{1} \to BS^{1}$![]() (for the $S^{1}$
(for the $S^{1}$![]() -bundle $X\to X/S^{1}$
-bundle $X\to X/S^{1}$![]() ) factors through a finite skeleton. Hence, we have an equivariant map $X\to S({{\mathbb {C}}}^{k+1})$
) factors through a finite skeleton. Hence, we have an equivariant map $X\to S({{\mathbb {C}}}^{k+1})$![]() for some $k$
for some $k$![]() , and thus a map $F^{S^{1}}_{tr}(S({{\mathbb {C}}}^{k+1})_+,\,E) \to F^{S^{1}}_{tr}(X_+,\,E)$
, and thus a map $F^{S^{1}}_{tr}(S({{\mathbb {C}}}^{k+1})_+,\,E) \to F^{S^{1}}_{tr}(X_+,\,E)$![]() . As $E$
. As $E$![]() is complex orientable,
is complex orientable,
for some choice of complex orientation $y$![]() . Observe that the homotopy fixed point spectral sequence for the space $ES^{1}$
. Observe that the homotopy fixed point spectral sequence for the space $ES^{1}$![]() as in example 2.5 matches with the Atiyah-Hirzebruch spectral sequence for ${{\mathbb {C}}}P^{\infty }$
as in example 2.5 matches with the Atiyah-Hirzebruch spectral sequence for ${{\mathbb {C}}}P^{\infty }$![]() . It follows that the class $y$
. It follows that the class $y$![]() represents the complex orientation in the $E_2$
represents the complex orientation in the $E_2$![]() -page. For $S({{\mathbb {C}}}^{k+1})$
-page. For $S({{\mathbb {C}}}^{k+1})$![]() and hence also for $X$
and hence also for $X$![]() via the equivariant map $X \to S({{\mathbb {C}}}^{k+1})$
via the equivariant map $X \to S({{\mathbb {C}}}^{k+1})$![]() , the class $y$
, the class $y$![]() represents a nilpotent class whose $k+ 1$
represents a nilpotent class whose $k+ 1$![]() -power is $0$
-power is $0$![]() . Therefore, $y^{k+1}$
. Therefore, $y^{k+1}$![]() must lie in the image of a differential, and (3) follows.
must lie in the image of a differential, and (3) follows.
Example 2.7 Suppose that $E= HR$![]() for a commutative ring $R$
for a commutative ring $R$![]() , the Eilenberg-MacLane spectrum with $\pi _0 HR =R$
, the Eilenberg-MacLane spectrum with $\pi _0 HR =R$![]() . In this case the spectral sequence in proposition 2.6 matches the Serre spectral sequence (from the $E^{2}$
. In this case the spectral sequence in proposition 2.6 matches the Serre spectral sequence (from the $E^{2}$![]() -page onwards) associated to the fibration
-page onwards) associated to the fibration
obtained by identifying the homotopy orbits space $X_{hS^{1}} \simeq X/S^{1}$![]() , and the classifying space $BS^{1} \simeq {{\mathbb {C}}}P^{\infty }$
, and the classifying space $BS^{1} \simeq {{\mathbb {C}}}P^{\infty }$![]() . In this case, the spectral sequence is strongly convergent from the corresponding result for the Serre spectral sequence. Moreover, due to the fact that $X/S^{1}$
. In this case, the spectral sequence is strongly convergent from the corresponding result for the Serre spectral sequence. Moreover, due to the fact that $X/S^{1}$![]() is a finite complex, the $E_\infty$
is a finite complex, the $E_\infty$![]() -page vanishes beyond the dimension of $X/S^{1}$
-page vanishes beyond the dimension of $X/S^{1}$![]() .
.
Next we provide a method to compute the differentials in the spectral sequence of proposition 2.6. In the tower of fibrations used to construct the spectral sequence, the spectrum at the bottom of the tower is $F^{S^{1}}_{tr}(S^{1}\times X_+,\,E)^{S^{1}} \simeq F(X_+,\,E)$![]() .
.

Let $Q$![]() denote the homotopy cofibre of the map $X \to X/S^{1}$
denote the homotopy cofibre of the map $X \to X/S^{1}$![]() . In the category of spectra, $F(\Sigma ^{-1} Q,\, E)\simeq \Sigma F(Q,\,E)$
. In the category of spectra, $F(\Sigma ^{-1} Q,\, E)\simeq \Sigma F(Q,\,E)$![]() is the homotopy cofibre of the map $F(X/S^{1}_+,\, E)\to F(X_+,\,E)$
is the homotopy cofibre of the map $F(X/S^{1}_+,\, E)\to F(X_+,\,E)$![]() . In view of the commutative square
. In view of the commutative square

we obtain coherent maps $P_k: \Sigma F(Q,\, E) {\to } \Sigma F^{S^{1}}_{tr}(Q(k),\, E)^{S^{1}}$![]() , where $Q(k)= [S({{\mathbb {C}}}^{k+1})/S({{\mathbb {C}}})] \wedge X_+$
, where $Q(k)= [S({{\mathbb {C}}}^{k+1})/S({{\mathbb {C}}})] \wedge X_+$![]() is the $S^{1}$
is the $S^{1}$![]() -equivariant homotopy cofibre of $X\times S({{\mathbb {C}}}) \to X\times S({{\mathbb {C}}}^{k+1})$
-equivariant homotopy cofibre of $X\times S({{\mathbb {C}}}) \to X\times S({{\mathbb {C}}}^{k+1})$![]() . Projecting onto the first factor gives a map $Q(k)\to S({{\mathbb {C}}}^{k+1})/S({{\mathbb {C}}})$
. Projecting onto the first factor gives a map $Q(k)\to S({{\mathbb {C}}}^{k+1})/S({{\mathbb {C}}})$![]() which gives a map
which gives a map
Let an element $x \in E^{n}(X)$![]() be represented by the map $S^{-n} \stackrel {x}{\to } F(X_+,\,E)$
be represented by the map $S^{-n} \stackrel {x}{\to } F(X_+,\,E)$![]() . Our hypothesis about such an $x$
. Our hypothesis about such an $x$![]() is a factorization in the following commutative diagram for $0\leq k \leq \infty$
is a factorization in the following commutative diagram for $0\leq k \leq \infty$![]() .
.

Before applying this hypothesis we note
Proposition 2.8 Suppose that the composite $S^{-n} \stackrel {x}{\to } F(X_+,\,E) \to \Sigma F^{S^{1}}_{tr} (Q(k), E)^{S^{1}}$![]() is null-homotopic. Then, $d_r(x)=0$
is null-homotopic. Then, $d_r(x)=0$![]() for $r\leq 2k+1$
for $r\leq 2k+1$![]() .
.
Proof. The statement follows from the fact that the composite being null-homotopic implies that $x$![]() lifts in the tower of fibrations to $F^{S^{1}}_{tr}(S({{\mathbb {C}}}^{k+1})\times X_+,\, E)^{S^{1}}$
lifts in the tower of fibrations to $F^{S^{1}}_{tr}(S({{\mathbb {C}}}^{k+1})\times X_+,\, E)^{S^{1}}$![]() .
.
Example 2.9 In the case $E=HR$![]() , the spectral sequence is the Serre spectral sequence of the fibration $X \to X/S^{1} \to {{\mathbb {C}}}P^{\infty }$
, the spectral sequence is the Serre spectral sequence of the fibration $X \to X/S^{1} \to {{\mathbb {C}}}P^{\infty }$![]() according to example 2.7. Note that
according to example 2.7. Note that
so in the diagram (2.1) $y$![]() may be non-trivial only when $n$
may be non-trivial only when $n$![]() is odd, and $k\geq \frac {n+1}{2}$
is odd, and $k\geq \frac {n+1}{2}$![]() . If $n$
. If $n$![]() is odd and (2.1) holds for $k=\frac {n+1}{2}$
is odd and (2.1) holds for $k=\frac {n+1}{2}$![]() , the class $x$
, the class $x$![]() is transgressive, and $d_{n+1}(x)$
is transgressive, and $d_{n+1}(x)$![]() is the composite
is the composite

We assume now that $E$![]() is connective, and that (2.1) holds for $k=\infty$
is connective, and that (2.1) holds for $k=\infty$![]() . In this case we have
. In this case we have
Proposition 2.10 Suppose that (2.1) holds for $k=\infty$![]() and that $E$
and that $E$![]() is connective. Then, $d_r(x)=0$
is connective. Then, $d_r(x)=0$![]() if $r\leq n$
if $r\leq n$![]() . Further, $d_{n+1}(x)= d^{H}_{n+1}(q_H(x)),$
. Further, $d_{n+1}(x)= d^{H}_{n+1}(q_H(x)),$![]() where $q_H$
where $q_H$![]() is the map $E\to H\pi _0 E,$
is the map $E\to H\pi _0 E,$![]() and $d^{H}_{n+1}$
and $d^{H}_{n+1}$![]() is the $(n+1)^{th}$
is the $(n+1)^{th}$![]() differential for the spectral sequence of proposition 2.6 for $H\pi _0 E$
differential for the spectral sequence of proposition 2.6 for $H\pi _0 E$![]() . (Here we observe that the spectral sequence is one of $\pi _0 E$
. (Here we observe that the spectral sequence is one of $\pi _0 E$![]() -modules, so this allows us to interpret the last statement.)
-modules, so this allows us to interpret the last statement.)
Proof. We observe that $E$![]() is connective implies that $\Sigma F({{\mathbb {C}}}P^{k},\, E)$
is connective implies that $\Sigma F({{\mathbb {C}}}P^{k},\, E)$![]() is $(-2k + 1)$
is $(-2k + 1)$![]() -connective (that is, the homotopy groups are $0$
-connective (that is, the homotopy groups are $0$![]() in degree $\leq -2k$
in degree $\leq -2k$![]() ). Therefore, the composite
). Therefore, the composite
is trivial for degree reasons if $-n\leq -2k$![]() . From the commutative square
. From the commutative square

we deduce that the composite in the lower row is trivial. Hence, from proposition 2.8 we get that $d_r(x)=0$![]() if $r\leq n$
if $r\leq n$![]() .
.
Via the map $q_H : E \to H\pi _0 E$![]() , we observe that (2.1) also holds for $q_H(x)$
, we observe that (2.1) also holds for $q_H(x)$![]() when we replace $E$
when we replace $E$![]() by $H\pi _0 E$
by $H\pi _0 E$![]() . Therefore, in the associated spectral sequence $d_r^{H}(q_H(x))=0$
. Therefore, in the associated spectral sequence $d_r^{H}(q_H(x))=0$![]() if $r\leq n$
if $r\leq n$![]() and $d_{n+1}^{H}(q_H(x))$
and $d_{n+1}^{H}(q_H(x))$![]() is described in the formula in example 2.9. Also we need to only assume $n$
is described in the formula in example 2.9. Also we need to only assume $n$![]() is odd, as the result is vacuously true in the other case. We fix $k=\frac {n+1}{2}$
is odd, as the result is vacuously true in the other case. We fix $k=\frac {n+1}{2}$![]() so that $n=2k-1$
so that $n=2k-1$![]() . With this choice of $n$
. With this choice of $n$![]() and $k$
and $k$![]() ,
,
It follows that the composite of $y$![]() to $\Sigma F({{\mathbb {C}}}P^{k},\, E)$
to $\Sigma F({{\mathbb {C}}}P^{k},\, E)$![]() lifts to $y_k: S^{-n} \to \Sigma F({{\mathbb {C}}}P^{k}/{{\mathbb {C}}}P^{k-1},\,E)$
lifts to $y_k: S^{-n} \to \Sigma F({{\mathbb {C}}}P^{k}/{{\mathbb {C}}}P^{k-1},\,E)$![]() .
.
The differential $d_{n+1}(x)$![]() may be described as the composite
may be described as the composite
where $\chi$![]() is a lift of $x$
is a lift of $x$![]() along the map $F^{S^{1}}_{tr} (S({{\mathbb {C}}}^{k})\times X_+,\, E)^{S^{1}} \to F(X_+,\,E)$
along the map $F^{S^{1}}_{tr} (S({{\mathbb {C}}}^{k})\times X_+,\, E)^{S^{1}} \to F(X_+,\,E)$![]() . We expand this in the diagram below
. We expand this in the diagram below

Observe that the bottom square is a homotopy pullback square of spectra as the homotopy fibre of both the vertical maps are $F^{S^{1}}_{tr}(Q(k-1),\, E)^{S^{1}}$![]() . Therefore, the map $\chi$
. Therefore, the map $\chi$![]() is determined from $x$
is determined from $x$![]() and the map $S^{-n} \to \Sigma F^{S^{1}}_{tr} ([S({{\mathbb {C}}}^{\infty })/S({{\mathbb {C}}}^{k})]\wedge X_+,\, E)^{S^{1}}$
and the map $S^{-n} \to \Sigma F^{S^{1}}_{tr} ([S({{\mathbb {C}}}^{\infty })/S({{\mathbb {C}}}^{k})]\wedge X_+,\, E)^{S^{1}}$![]() . This may now be computed using the lift of $y$
. This may now be computed using the lift of $y$![]() to $\Sigma F ({{\mathbb {C}}}P^{\infty }/{{\mathbb {C}}}P^{k-1},\, E)^{S^{1}}$
to $\Sigma F ({{\mathbb {C}}}P^{\infty }/{{\mathbb {C}}}P^{k-1},\, E)^{S^{1}}$![]() as its restriction to ${{\mathbb {C}}}P^{k-1}$
as its restriction to ${{\mathbb {C}}}P^{k-1}$![]() is $0$
is $0$![]() . We may now compute $d_{n+1}(x)$
. We may now compute $d_{n+1}(x)$![]() via the following commutative diagram
via the following commutative diagram

The middle vertical map is the one which quotients out the factor $X$![]() , and this also induces the right vertical map. Under the identification $\Sigma F({{\mathbb {C}}}P^{k}/{{\mathbb {C}}}P^{k-1},\,E) \simeq \Sigma ^{-2k+1} E$
, and this also induces the right vertical map. Under the identification $\Sigma F({{\mathbb {C}}}P^{k}/{{\mathbb {C}}}P^{k-1},\,E) \simeq \Sigma ^{-2k+1} E$![]() , and $\pi _{-n} \Sigma ^{-2k+1} E \cong \pi _0 E$
, and $\pi _{-n} \Sigma ^{-2k+1} E \cong \pi _0 E$![]() , we identify $y_k$
, we identify $y_k$![]() with $d_{n+1}^{H}(x)$
with $d_{n+1}^{H}(x)$![]() .
.
3. The cohomology of $W_{n,k}$
In this section, we calculate the generalized cohomology of $W_{n,k}$![]() with respect to a complex oriented spectrum $E$
with respect to a complex oriented spectrum $E$![]() . Later in the section, we specialize to $E=BP$
. Later in the section, we specialize to $E=BP$![]() , the spectrum for Brown-Peterson cohomology.
, the spectrum for Brown-Peterson cohomology.
Recall that a complex orientation for a homotopy commutative ring spectrum $E$![]() is a class $x\in \tilde {E}^{2}({{\mathbb {C}}}P^{\infty })$
is a class $x\in \tilde {E}^{2}({{\mathbb {C}}}P^{\infty })$![]() , which restricts to a generator of the free rank one $\pi _0 E$
, which restricts to a generator of the free rank one $\pi _0 E$![]() -module $\tilde {E}^{2}(S^{2})\cong E^{0}(pt)$
-module $\tilde {E}^{2}(S^{2})\cong E^{0}(pt)$![]() . For a complex oriented spectrum $E$
. For a complex oriented spectrum $E$![]() , we have [Reference Adams1]
, we have [Reference Adams1]
For the complex Stiefel manifold, the classical computations of their cohomology [Reference Mimura and Toda15] proceeds using the Serre spectral sequence as for other homogeneous spaces. It is proved that the cohomology of $W_{n,k}$![]() is an exterior algebra with generators in degrees $2n-2k+1,\, 2n-2k+3,\, \ldots,\, 2n-1$
is an exterior algebra with generators in degrees $2n-2k+1,\, 2n-2k+3,\, \ldots,\, 2n-1$![]() . The Stiefel manifold also has a filtration
. The Stiefel manifold also has a filtration

where the inclusion $W_{n-1,k-1} \hookrightarrow W_{n,k}$![]() is given by adding the last vector $e_n$
is given by adding the last vector $e_n$![]() . The filtration quotients are computed using the following homotopy pushout ([Reference Whitehead20, chapter IV] defines the maps in the diagram below, and [Reference Mosher and Tangora16, Ch. 5, proposition 2] proves the entirely analogous result in the real case)
. The filtration quotients are computed using the following homotopy pushout ([Reference Whitehead20, chapter IV] defines the maps in the diagram below, and [Reference Mosher and Tangora16, Ch. 5, proposition 2] proves the entirely analogous result in the real case)

In order to construct $\mu _n$![]() one defines
one defines
by $(z,\,L) \mapsto A(z,\,L)$![]() , where $A(z,\,L):{{\mathbb {C}}}^{n} \to {{\mathbb {C}}}^{n}$
, where $A(z,\,L):{{\mathbb {C}}}^{n} \to {{\mathbb {C}}}^{n}$![]() is the unitary transformation which multiplies the elements of $L$
is the unitary transformation which multiplies the elements of $L$![]() by $z$
by $z$![]() and fixes the orthogonal complement. The map $\mu _n$
and fixes the orthogonal complement. The map $\mu _n$![]() is induced by matrix multiplication in $U(n)$
is induced by matrix multiplication in $U(n)$![]() and the left action on $W_{n,k}$
and the left action on $W_{n,k}$![]() . From the construction of $\mu$
. From the construction of $\mu$![]() and the fact that $W_{n,k}\cong U(n)/U(n-k)$
and the fact that $W_{n,k}\cong U(n)/U(n-k)$![]() , one obtains the induced map
, one obtains the induced map
It follows from (3.1) that
In the case of ordinary cohomology, the exterior algebra generators for the cohomology of $W_{n,k}$![]() pullback under $\mu _{n,k}$
pullback under $\mu _{n,k}$![]() to $\Sigma x^{i-1}$
to $\Sigma x^{i-1}$![]() ($\Sigma : H^{\ast } X \to H^{\ast } \Sigma X$
($\Sigma : H^{\ast } X \to H^{\ast } \Sigma X$![]() is the suspension isomorphism). We now use this filtration to prove analogous results for the $E$
is the suspension isomorphism). We now use this filtration to prove analogous results for the $E$![]() -cohomology of $W_{n,k}$
-cohomology of $W_{n,k}$![]() .
.
Proposition 3.1 Let $E$![]() be a complex oriented cohomology theory, such that there is no $2$
be a complex oriented cohomology theory, such that there is no $2$![]() -torsion in $E^{\ast }(pt)$
-torsion in $E^{\ast }(pt)$![]() . Then,
. Then,
is an exterior algebra with $|z_i| = 2i-1$![]() . These generators satisfy
. These generators satisfy
( 1) The inclusion $W_{n-1,k-1} \hookrightarrow W_{n,k}$![]() sends $z_i$
sends $z_i$![]() to $z_i$
to $z_i$![]() if $n-k+1 \leq i \leq n-1$
if $n-k+1 \leq i \leq n-1$![]() and sends $z_n$
and sends $z_n$![]() to $0$
to $0$![]() .
.
( 2) $\mu _{n,k}^{\ast } (z_i)=\Sigma x^{i-1}$![]() .
.
Proof. We prove the results by induction on $k$![]() , constructing the generators $z_i$
, constructing the generators $z_i$![]() along the way. For $k=1$
along the way. For $k=1$![]() , the Stiefel manifold is the sphere $S^{2n-1}$
, the Stiefel manifold is the sphere $S^{2n-1}$![]() , and in this case, we know that the $E$
, and in this case, we know that the $E$![]() -cohomology is the exterior algebra on one generator. This starts the induction.
-cohomology is the exterior algebra on one generator. This starts the induction.
In the induction step, we know that $E^{\ast }(W_{n-1,k-1})$![]() is as described in this proposition, and attempt to derive the same for $E^{\ast }(W_{n,k})$
is as described in this proposition, and attempt to derive the same for $E^{\ast }(W_{n,k})$![]() via the pushout (3.1). This gives us the following maps between long exact sequences corresponding to the columns of (3.1).
via the pushout (3.1). This gives us the following maps between long exact sequences corresponding to the columns of (3.1).

We now justify the various identifications described in (3.2). The fact that $E$![]() is complex oriented implies $E^{\ast }({{\mathbb {C}}}P^{n-1}) \to E^{\ast } ({{\mathbb {C}}}P^{n-2})$
is complex oriented implies $E^{\ast }({{\mathbb {C}}}P^{n-1}) \to E^{\ast } ({{\mathbb {C}}}P^{n-2})$![]() is surjective, and the induction hypothesis gives us that $E^{\ast }(W_{n-1,k-1})$
is surjective, and the induction hypothesis gives us that $E^{\ast }(W_{n-1,k-1})$![]() is a free $E^{\ast }(pt)$
is a free $E^{\ast }(pt)$![]() -module. This implies that
-module. This implies that
is surjective. This implies the identifications in the bottom row of (3.2). Note that the map $\Sigma ({{\mathbb {C}}}P^{n-2}_+)\times W_{n-1,k-1} \to W_{n-1,k-1}$![]() has a section corresponding to the inclusion of the base-point of $\Sigma ({{\mathbb {C}}}P^{n-2}_+)$
has a section corresponding to the inclusion of the base-point of $\Sigma ({{\mathbb {C}}}P^{n-2}_+)$![]() , and thus, the map induced on $E$
, and thus, the map induced on $E$![]() -cohomology is injective. The identifications on the top follow from the ones of the bottom row, and the fact that $E^{r} (W_{n-1,k-1}) \to E^{r}(\Sigma ({{\mathbb {C}}}P^{n-2}_+)\times W_{n-1,k-1})$
-cohomology is injective. The identifications on the top follow from the ones of the bottom row, and the fact that $E^{r} (W_{n-1,k-1}) \to E^{r}(\Sigma ({{\mathbb {C}}}P^{n-2}_+)\times W_{n-1,k-1})$![]() is injective. It follows that we have short exact sequences
is injective. It follows that we have short exact sequences
For $n-k+1 \leq i \leq n-1$![]() , we choose $z_i \in E^{2i-1}(W_{n,k})$
, we choose $z_i \in E^{2i-1}(W_{n,k})$![]() so that they map to $z_i$
so that they map to $z_i$![]() under $i^{\ast }$
under $i^{\ast }$![]() . The class $z_n$
. The class $z_n$![]() is chosen so that it maps to $\Sigma x^{n-1}$
is chosen so that it maps to $\Sigma x^{n-1}$![]() under $\mu _{n,n-1}$
under $\mu _{n,n-1}$![]() . From (3.2), it follows that $z_n$
. From (3.2), it follows that $z_n$![]() is a generator for the ideal of $E^{\ast }(W_{n,k})$
is a generator for the ideal of $E^{\ast }(W_{n,k})$![]() given by image of $j^{\ast }$
given by image of $j^{\ast }$![]() . By the construction (1) and (2) follow. As the classes $z_i$
. By the construction (1) and (2) follow. As the classes $z_i$![]() are in odd degree and $E^{\ast }(pt)$
are in odd degree and $E^{\ast }(pt)$![]() has no $2$
has no $2$![]() -torsion, we have $z_i^{2}=0$
-torsion, we have $z_i^{2}=0$![]() , and (3.2) implies that $E^{\ast }(W_{n,k})$
, and (3.2) implies that $E^{\ast }(W_{n,k})$![]() additively matches with the exterior algebra on the $z_i$
additively matches with the exterior algebra on the $z_i$![]() . The result now follows by induction on $k$
. The result now follows by induction on $k$![]() .
.
We now proceed to define the generators of the exterior algebra $E^{\ast }(W_{n,k})$![]() in a strict fashion which will satisfy (1) and (2) of proposition 3.1. From the proof, we note that for any classes $z_i$
in a strict fashion which will satisfy (1) and (2) of proposition 3.1. From the proof, we note that for any classes $z_i$![]() satisfying (2), $E^{\ast }(W_{n,k}) \cong \Lambda _{E^{\ast }(pt)}(z_{n-k+1},\,\ldots,\, z_n)$
satisfying (2), $E^{\ast }(W_{n,k}) \cong \Lambda _{E^{\ast }(pt)}(z_{n-k+1},\,\ldots,\, z_n)$![]() . Although the results in the following will have analogous consequences for any complex oriented $E$
. Although the results in the following will have analogous consequences for any complex oriented $E$![]() , we fix our attention to the case $E=BP$
, we fix our attention to the case $E=BP$![]() , which will be used in the following sections. Recall [Reference Ravenel18]
, which will be used in the following sections. Recall [Reference Ravenel18]
where $v_i$![]() denotes the Araki generators [Reference Ravenel18, A2.2.2] that lie in degree $-2(p^{i}-1)$
denotes the Araki generators [Reference Ravenel18, A2.2.2] that lie in degree $-2(p^{i}-1)$![]() . We also fix from now on $x\in \widetilde {BP}^{2}({{\mathbb {C}}}P^{\infty })$
. We also fix from now on $x\in \widetilde {BP}^{2}({{\mathbb {C}}}P^{\infty })$![]() to denote the fixed orientation for a $p$
to denote the fixed orientation for a $p$![]() -typical formal group law over $BP^{\ast }(pt)$
-typical formal group law over $BP^{\ast }(pt)$![]() . We also assume that $x$
. We also assume that $x$![]() is such that it maps to the first Chern class under the map $\lambda : BP\to H{{\mathbb {Z}}}_{(p)}$
is such that it maps to the first Chern class under the map $\lambda : BP\to H{{\mathbb {Z}}}_{(p)}$![]() .
.
The method of choosing the generators $y_j$![]() for $BP^{\ast } (W_{n,k})$
for $BP^{\ast } (W_{n,k})$![]() is by relating them to the $BP$
is by relating them to the $BP$![]() -Chern classes $c_j^{BP}$
-Chern classes $c_j^{BP}$![]() [Reference Conner and Floyd9]. We start with the case $k=n$
[Reference Conner and Floyd9]. We start with the case $k=n$![]() , when $W_{n,n}= U(n)$
, when $W_{n,n}= U(n)$![]() . Recall that $H^{*}(U(n);{{\mathbb {Z}}}_{(p)})=\Lambda _{{{\mathbb {Z}}}_{(p)}}(y^{H}_1,\,\ldots,\, y^{H}_n)$
. Recall that $H^{*}(U(n);{{\mathbb {Z}}}_{(p)})=\Lambda _{{{\mathbb {Z}}}_{(p)}}(y^{H}_1,\,\ldots,\, y^{H}_n)$![]() with $|y^{H}_j|=2j-1$
with $|y^{H}_j|=2j-1$![]() , and in Serre spectral sequence for the fibration
, and in Serre spectral sequence for the fibration
$y^{H}_j$![]() transgresses to the $j^{th}$
transgresses to the $j^{th}$![]() -Chern class $c_j^{H}$
-Chern class $c_j^{H}$![]() . This follows from [Reference Borel7] which identifies the transgression for the above spectral sequence. We also know that $A^{*}(y_j^{H})=\Sigma x_H^{j-1}$
. This follows from [Reference Borel7] which identifies the transgression for the above spectral sequence. We also know that $A^{*}(y_j^{H})=\Sigma x_H^{j-1}$![]() , where $A:\Sigma ({{\mathbb {C}}}P^{n-1}_+) \to U(n)$
, where $A:\Sigma ({{\mathbb {C}}}P^{n-1}_+) \to U(n)$![]() is induced from $(z,\,L)\mapsto A(z,\,L)$
is induced from $(z,\,L)\mapsto A(z,\,L)$![]() , and $x_H$
, and $x_H$![]() is the first $H$
is the first $H$![]() -Chern class of the canonical line bundle over ${{\mathbb {C}}}P^{\infty }$
-Chern class of the canonical line bundle over ${{\mathbb {C}}}P^{\infty }$![]() . Write $\sigma : \Sigma U(n) \to BU(n)$
. Write $\sigma : \Sigma U(n) \to BU(n)$![]() for the adjoint of the equivalence $U(n) \simeq \Omega BU(n)$
for the adjoint of the equivalence $U(n) \simeq \Omega BU(n)$![]() , and form the composite diagram
, and form the composite diagram

For a cohomology theory $E$![]() , denote by $\phi _E^{\ast }$
, denote by $\phi _E^{\ast }$![]() (respectively $\sigma _E^{\ast }$
(respectively $\sigma _E^{\ast }$![]() ) the map induced by $\phi$
) the map induced by $\phi$![]() (respectively $\sigma$
(respectively $\sigma$![]() ) on $E$
) on $E$![]() -cohomology. We have $\phi ^{*}_H(c_j)=\Sigma ^{2} x_H^{j-1}$
-cohomology. We have $\phi ^{*}_H(c_j)=\Sigma ^{2} x_H^{j-1}$![]() as $\sigma ^{*}_H(c_j)= \Sigma y_j^{H}$
as $\sigma ^{*}_H(c_j)= \Sigma y_j^{H}$![]() .
.
Proposition 3.2 There are classes $\tau _j \in BP^{2j} (BU(n))$![]() of the form
of the form
for $\nu _k \in BP^{\ast }(pt)$![]() , such that
, such that
The standard map $BU(n)\to BU(n+1)$![]() classifying the canonical bundle plus a trivial bundle sends $\tau _j$
classifying the canonical bundle plus a trivial bundle sends $\tau _j$![]() to $\tau _j$
to $\tau _j$![]() for $j\leq n$
for $j\leq n$![]() , and $\tau _{n+1}$
, and $\tau _{n+1}$![]() to $0$
to $0$![]() . Define $y_j^{BP} \in BP^{2j-1}(U(n))$
. Define $y_j^{BP} \in BP^{2j-1}(U(n))$![]() by the formula $\Sigma y_j^{BP} = \sigma _{BP}^{\ast } \tau _j$
by the formula $\Sigma y_j^{BP} = \sigma _{BP}^{\ast } \tau _j$![]() . Then,
. Then,
( 1) The classes $y_1^{BP},\, \ldots,\, y_n^{BP}$![]() are generators for the exterior algebra $BP^{\ast }(U(n))$
are generators for the exterior algebra $BP^{\ast }(U(n))$![]() .
.
( 2) $\lambda (y_j^{BP}) = y_j^{H}$![]() . (That is, the classes $y_j^{BP}$
. (That is, the classes $y_j^{BP}$![]() are lifts of the cohomology classes $y_j^{H}$
are lifts of the cohomology classes $y_j^{H}$![]() to $BP$
to $BP$![]() .)
.)
Proof. We note that using proposition 3.1, it suffices to prove the statements about $\tau _j$![]() . Consider the following commutative diagram
. Consider the following commutative diagram

We have $\lambda (c^{BP}_j)=c_j$![]() , and also that $\lambda$
, and also that $\lambda$![]() maps the complex orientation of $BP$
maps the complex orientation of $BP$![]() to that of $H$
to that of $H$![]() . It readily follows that $\phi ^{*}_{BP}(c^{BP}_j) - \Sigma ^{2}x^{j-1}$
. It readily follows that $\phi ^{*}_{BP}(c^{BP}_j) - \Sigma ^{2}x^{j-1}$![]() lies in the kernel of $\lambda$
lies in the kernel of $\lambda$![]() , which is the ideal $(v_1,\,v_2,\,\ldots )$
, which is the ideal $(v_1,\,v_2,\,\ldots )$![]() . As
. As
the left vertical arrow of (3.3) is an isomorphism in degree $2n$![]() . It follows that $\phi _{BP}^{\ast }(c_n^{BP}) = \Sigma ^{2} x^{n-1}$
. It follows that $\phi _{BP}^{\ast }(c_n^{BP}) = \Sigma ^{2} x^{n-1}$![]() , and so, $\tau _n^{BP}=c_n^{BP}$
, and so, $\tau _n^{BP}=c_n^{BP}$![]() maps to the element of $BP^{\ast }(\Sigma ^{2} ({{\mathbb {C}}}P^{n-1}_+))$
maps to the element of $BP^{\ast }(\Sigma ^{2} ({{\mathbb {C}}}P^{n-1}_+))$![]() required by the proposition.
required by the proposition.
We proceed to construct the $\tau _j$![]() such that $\phi _{BP}^{\ast } \tau _j=\Sigma ^{2} x^{j-1}$
such that $\phi _{BP}^{\ast } \tau _j=\Sigma ^{2} x^{j-1}$![]() . Starting from $j=n$
. Starting from $j=n$![]() , suppose that $\tau _{j+1}$
, suppose that $\tau _{j+1}$![]() has already been defined. We now have $\phi _{BP}^{\ast } (c_j^{BP})-\Sigma ^{2} x^{j-1} \in (v_1,\,v_2,\,\ldots )$
has already been defined. We now have $\phi _{BP}^{\ast } (c_j^{BP})-\Sigma ^{2} x^{j-1} \in (v_1,\,v_2,\,\ldots )$![]() . For degree reasons we have
. For degree reasons we have
for some $\rho _k \in (v_1,\,v_2,\,\ldots )$![]() . Rearranging terms and substituting the formula for $\tau _k$
. Rearranging terms and substituting the formula for $\tau _k$![]() , we obtain an equation
, we obtain an equation
where $\nu _k$![]() is a $BP^{\ast }(pt)$
is a $BP^{\ast }(pt)$![]() -linear combination of the classes $\rho _k$
-linear combination of the classes $\rho _k$![]() in the preceeding equation. It follows that $\tau _j=c_j^{BP} + \sum _{k>j} \nu _k c_k^{BP}$
in the preceeding equation. It follows that $\tau _j=c_j^{BP} + \sum _{k>j} \nu _k c_k^{BP}$![]() satisfies the required criteria. We note that $\phi _{BP}^{\ast }$
satisfies the required criteria. We note that $\phi _{BP}^{\ast }$![]() has image in $BP^{\ast } (\Sigma ^{2} ({{\mathbb {C}}}P^{n-1}_+))$
has image in $BP^{\ast } (\Sigma ^{2} ({{\mathbb {C}}}P^{n-1}_+))$![]() which is a suspension. It follows that the decomposable elements over $BP^{\ast }(pt)$
which is a suspension. It follows that the decomposable elements over $BP^{\ast }(pt)$![]() map to $0$
map to $0$![]() under $\phi _{BP}^{\ast }$
under $\phi _{BP}^{\ast }$![]() . Also the formula $\phi _{BP}^{\ast }(\tau _j)=\Sigma ^{2} x^{j-1}$
. Also the formula $\phi _{BP}^{\ast }(\tau _j)=\Sigma ^{2} x^{j-1}$![]() implies that $\phi _{BP}^{\ast }$
implies that $\phi _{BP}^{\ast }$![]() induces an isomorphism when restricted to the module of indecomposables. This shows that the elements $\nu _k$
induces an isomorphism when restricted to the module of indecomposables. This shows that the elements $\nu _k$![]() are unique, and so the classes $\tau _k$
are unique, and so the classes $\tau _k$![]() are coherently defined over $n$
are coherently defined over $n$![]() as required in the proposition.
as required in the proposition.
We now provide a strict definition for the generators of $BP^{\ast }(W_{n,k})$![]() following proposition 3.2. Recall that there are maps
following proposition 3.2. Recall that there are maps
where $i$![]() adds the vector $e_n$
adds the vector $e_n$![]() at the end, and $q$
at the end, and $q$![]() forgets the last vector. We have already seen in (3.2) that $i^{\ast }$
forgets the last vector. We have already seen in (3.2) that $i^{\ast }$![]() is surjective in $BP$
is surjective in $BP$![]() -cohomology. We also note that $q^{\ast }$
-cohomology. We also note that $q^{\ast }$![]() is injective. For, $q^{\ast }$
is injective. For, $q^{\ast }$![]() applied to the generators of $BP^{\ast }(W_{n,k-1})$
applied to the generators of $BP^{\ast }(W_{n,k-1})$![]() as in proposition 3.1 together with a generator of $BP^{\ast }(S^{2n-2k+1})=BP^{\ast }(W_{n-k+1,1})$
as in proposition 3.1 together with a generator of $BP^{\ast }(S^{2n-2k+1})=BP^{\ast }(W_{n-k+1,1})$![]() satisfies (2) of proposition 3.1. This provides a tuple of exterior algebra generators for $BP^{\ast }(W_{n,k})$
satisfies (2) of proposition 3.1. This provides a tuple of exterior algebra generators for $BP^{\ast }(W_{n,k})$![]() . Therefore, the quotient map $\pi : U(n)\to W_{n,k}$
. Therefore, the quotient map $\pi : U(n)\to W_{n,k}$![]() is injective in $BP$
is injective in $BP$![]() -cohomology.
-cohomology.
Proposition 3.3 With notations as above, $\pi ^{\ast }$![]() maps $BP^{\ast } (W_{n,k})$
maps $BP^{\ast } (W_{n,k})$![]() to the subalgebra of $BP^{\ast }(U(n))$
to the subalgebra of $BP^{\ast }(U(n))$![]() generated by the classes $y_{n-k+1}^{BP},\, \ldots,\, y_n^{BP}$
generated by the classes $y_{n-k+1}^{BP},\, \ldots,\, y_n^{BP}$![]() .
.
Proof. We have a diagram of fibrations

which induces the commutative diagram

From the construction of the classes $y_j^{BP}$![]() we have $\pi ^{\ast } \alpha (\tau _j)=\delta (y_j^{BP})$
we have $\pi ^{\ast } \alpha (\tau _j)=\delta (y_j^{BP})$![]() . On the other hand, if $j>n-k$
. On the other hand, if $j>n-k$![]() , the class $\alpha (\tau _j)$
, the class $\alpha (\tau _j)$![]() maps to $0$
maps to $0$![]() in $BP^{\ast }(BU(n-k))$
in $BP^{\ast }(BU(n-k))$![]() . The map $BP^{\ast } BU(n)\to BP^{\ast } BU(n-k)$
. The map $BP^{\ast } BU(n)\to BP^{\ast } BU(n-k)$![]() is the map on $BP$
is the map on $BP$![]() -cohomology associated to the standard inclusion $BU(n-k)\to BU(n)$
-cohomology associated to the standard inclusion $BU(n-k)\to BU(n)$![]() classifying the sum of the canonical bundle with $k$
classifying the sum of the canonical bundle with $k$![]() -copies of a trivial bundle. This maps $c_j^{BP}$
-copies of a trivial bundle. This maps $c_j^{BP}$![]() to $0$
to $0$![]() for $j>k$
for $j>k$![]() , and hence, from the formula in proposition 3.2, the classes $\tau _j$
, and hence, from the formula in proposition 3.2, the classes $\tau _j$![]() to $0$
to $0$![]() if $j>k$
if $j>k$![]() . It follows that for $j>k$
. It follows that for $j>k$![]() , there are classes $y_j \in BP^{\ast }(W_{n,k})$
, there are classes $y_j \in BP^{\ast }(W_{n,k})$![]() such that $\alpha (\tau _j)= \delta (y_j)$
such that $\alpha (\tau _j)= \delta (y_j)$![]() , and from (3.4) that $\pi ^{\ast }(y_j)= y_j^{BP}$
, and from (3.4) that $\pi ^{\ast }(y_j)= y_j^{BP}$![]() . Also the property $\phi _{BP}^{\ast }(\tau _j)=\Sigma ^{2} x^{j-1}$
. Also the property $\phi _{BP}^{\ast }(\tau _j)=\Sigma ^{2} x^{j-1}$![]() implies that the classes $y_j$
implies that the classes $y_j$![]() satisfy (2) of proposition 3.1. This result follows readily.
satisfy (2) of proposition 3.1. This result follows readily.
4. $BP$ -cohomology of $PW_{n,k}$
-cohomology of $PW_{n,k}$
In this section, we describe the $BP$![]() -cohomology ring of $PW_{n,k}$
-cohomology ring of $PW_{n,k}$![]() using the homotopy fixed point spectral sequence (proposition 2.6). This is a strongly convergent spectral sequence
using the homotopy fixed point spectral sequence (proposition 2.6). This is a strongly convergent spectral sequence
Recall that
by proposition 3.3. We start with a proposition describing the initial differential on the classes $y_j$![]() .
.
Proposition 4.1 In the spectral sequence (4.1) , the differentials on $y_j$![]() are described by
are described by

Proof. The proof will follow from the existence of a diagram as in (2.1). We have the commutative diagram

in which the rows are fibrations [Reference Astey, Gitler, Micha and Pastor3]. The map $f$![]() classifies the $n$
classifies the $n$![]() -fold Whitney sum of universal canonical complex line bundle. It leads to the following commutative diagram
-fold Whitney sum of universal canonical complex line bundle. It leads to the following commutative diagram

Suppose that the class $\tau _j$![]() of proposition 3.2 is mapped to $\psi _j$
of proposition 3.2 is mapped to $\psi _j$![]() under $f^{*}$
under $f^{*}$![]() . In the first row, the image of $y_j$
. In the first row, the image of $y_j$![]() and image of $\tau _j$
and image of $\tau _j$![]() coincide (proposition 3.2 and (3.4)), hence, the same must happen in the bottom row leading to the following homotopy commutative diagram
coincide (proposition 3.2 and (3.4)), hence, the same must happen in the bottom row leading to the following homotopy commutative diagram

The Whitney sum formula for Chern classes over $BP$![]() -cohomology implies that $f^{\ast } (c_j^{BP})= \binom {n}{j} x^{j}$
-cohomology implies that $f^{\ast } (c_j^{BP})= \binom {n}{j} x^{j}$![]() . The description of $\tau _j$
. The description of $\tau _j$![]() in proposition 3.2 now leads to the following form for $\psi _j$
in proposition 3.2 now leads to the following form for $\psi _j$![]()

Now apply proposition 2.10 to get $d_r(y_j)=0$![]() if $r<2j$
if $r<2j$![]() , and $d_{2j}y_j$
, and $d_{2j}y_j$![]() is determined from the corresponding spectral sequence over $H{{\mathbb {Z}}}_{(p)}$
is determined from the corresponding spectral sequence over $H{{\mathbb {Z}}}_{(p)}$![]() . This may be computed as in [Reference Astey, Gitler, Micha and Pastor3] to be $d_{2j} y_j= \binom {n}{j}x^{j}$
. This may be computed as in [Reference Astey, Gitler, Micha and Pastor3] to be $d_{2j} y_j= \binom {n}{j}x^{j}$![]() . Hence the result follows.
. Hence the result follows.
We now proceed to compute the $E_\infty$![]() -page of the spectral sequence. The main idea here is that (4.2) may be used to determine all the differentials on the classes $y_j$
-page of the spectral sequence. The main idea here is that (4.2) may be used to determine all the differentials on the classes $y_j$![]() .
.
Proposition 4.2 The $E_\infty$![]() -page of the spectral sequence (4.1) is given by
-page of the spectral sequence (4.1) is given by
where $\gamma _j$![]() are certain elements in $BP^{*}(W_{n,k})$
are certain elements in $BP^{*}(W_{n,k})$![]() with $\text {deg}(\gamma _j)=2j-1,$
with $\text {deg}(\gamma _j)=2j-1,$![]() and $I$
and $I$![]() is the ideal of $BP^{*}[[x]]$
is the ideal of $BP^{*}[[x]]$![]() generated by the set $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$
generated by the set $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$![]() .
.
Proof. The class $x$![]() is a permanent cycle by proposition 2.6. The multiplicative structure determines all the differentials once they are known on the classes $y_j$
is a permanent cycle by proposition 2.6. The multiplicative structure determines all the differentials once they are known on the classes $y_j$![]() . We notice that $E_{2n+1}$
. We notice that $E_{2n+1}$![]() is the $E_\infty$
is the $E_\infty$![]() -page because $d_{2n}(y_n)= x^{n}$
-page because $d_{2n}(y_n)= x^{n}$![]() (proposition 4.1) and so all the higher powers of $x$
(proposition 4.1) and so all the higher powers of $x$![]() are killed in the $E_{2n}$
are killed in the $E_{2n}$![]() -page.
-page.
From proposition 4.1, we see that the first non-trivial differential is $d_{2(n-k+1)}$![]() and the generator $y_{n-k+1}$
and the generator $y_{n-k+1}$![]() and all its multiples do not survive to the next page since
and all its multiples do not survive to the next page since
For the $y_j$![]() of higher degree, it may happen that the first non-trivial differential on it
of higher degree, it may happen that the first non-trivial differential on it
may be zero. This precisely happens when $\binom {n}{j}$![]() lies in the ideal generated by $\binom {n}{i}$
lies in the ideal generated by $\binom {n}{i}$![]() for $n-k+1\leq i < j$
for $n-k+1\leq i < j$![]() inside ${{\mathbb {Z}}}_{(p)}$
inside ${{\mathbb {Z}}}_{(p)}$![]() . This condition may be interpreted in terms of $p$
. This condition may be interpreted in terms of $p$![]() -adic valuations of these numbers. We then obtain a multiple $p^{s} y_j$
-adic valuations of these numbers. We then obtain a multiple $p^{s} y_j$![]() on which the differential is $0$
on which the differential is $0$![]() , determined by the formula $s+v_p(\binom {n}{j})= \min _{n-k+1\leq i < j}v_p(\binom {n}{i})$
, determined by the formula $s+v_p(\binom {n}{j})= \min _{n-k+1\leq i < j}v_p(\binom {n}{i})$![]() . The class $p^{s} y_j$
. The class $p^{s} y_j$![]() may now support higher order differentials. Their formula is determined by computing $p^{s}\psi _j$
may now support higher order differentials. Their formula is determined by computing $p^{s}\psi _j$![]() using (4.2) in the form of (2.1)
using (4.2) in the form of (2.1)

for $N> 2j$![]() . According to the formula (4.3), the next possible differential is
. According to the formula (4.3), the next possible differential is
We now rectify this class as $p^{s}y_j - p^{s} \nu _{j+1} y_{j+1}$![]() and obtain a cycle. This process continues until we reach the $E_{2n+1}$
and obtain a cycle. This process continues until we reach the $E_{2n+1}$![]() -page following which there are no further non-zero differentials.
-page following which there are no further non-zero differentials.
We now formalize the above process by writing down a series of modifications to produce the element $\gamma _j$![]() . Starting with $\gamma _{j}^{(2)}:= y_{j}$
. Starting with $\gamma _{j}^{(2)}:= y_{j}$![]() , in $r$
, in $r$![]() -th step of the modification, the modified element will be denoted by $\gamma _{j}^{(r)}$
-th step of the modification, the modified element will be denoted by $\gamma _{j}^{(r)}$![]() . Below we describe transformations, exactly one of which will be performed to produce $\gamma _{j}^{(r+1)}$
. Below we describe transformations, exactly one of which will be performed to produce $\gamma _{j}^{(r+1)}$![]() from $\gamma _{j}^{(r)}$
from $\gamma _{j}^{(r)}$![]() .
.
(1) If $d_r\gamma _{j}^{(r)}=0$
 , then it survives to the next page and we call that element $\gamma _{j}^{(r+1)}$
, then it survives to the next page and we call that element $\gamma _{j}^{(r+1)}$ .
.(2) If $r=2j$
 and $\gamma _{j}^{(2j)}=y_{j}$
and $\gamma _{j}^{(2j)}=y_{j}$ and $d_r(\gamma _{j}^{(r)}) = \binom {n}{j} x^{j}$
and $d_r(\gamma _{j}^{(r)}) = \binom {n}{j} x^{j}$ . Define $s$
. Define $s$ by the formula $s+v_p(\binom {n}{j})= \min _{n-k+1\leq i < j}v_p(\binom {n}{i})$
by the formula $s+v_p(\binom {n}{j})= \min _{n-k+1\leq i < j}v_p(\binom {n}{i})$ , and declare $\gamma _{j}^{(r+1)}=p^{s} \gamma _{j}^{(r)}$
, and declare $\gamma _{j}^{(r+1)}=p^{s} \gamma _{j}^{(r)}$ .
.(3) If $r>2j$
 , and $d_r(\gamma _j^{(r)})\neq 0$
, and $d_r(\gamma _j^{(r)})\neq 0$ , then we know $r$
, then we know $r$ is even, and there is a $BP^{\ast }$
is even, and there is a $BP^{\ast }$ -multiple of $y_{\frac {r}{2}}$
-multiple of $y_{\frac {r}{2}}$ mapped by $d_r$
mapped by $d_r$ onto the same class (this follows from the formula for $\psi _j$
onto the same class (this follows from the formula for $\psi _j$ in the same way as demonstrated for $p^{s}y_j$
in the same way as demonstrated for $p^{s}y_j$ above). That is, $d_r(\gamma _j^{(r)})= \lambda d_{r}(y_{\frac {r}{2}})$
above). That is, $d_r(\gamma _j^{(r)})= \lambda d_{r}(y_{\frac {r}{2}})$ for some $\lambda \in BP^{\ast }(pt)$
for some $\lambda \in BP^{\ast }(pt)$ . We declare $\gamma _{j}^{(r+1)}=\gamma _{j}^{(r)}-\lambda y_{\frac {r}{2}}$
. We declare $\gamma _{j}^{(r+1)}=\gamma _{j}^{(r)}-\lambda y_{\frac {r}{2}}$ .
.
We finally write $\gamma _j = \gamma _j^{(2n+1)}$![]() which survives to the $E_\infty$
which survives to the $E_\infty$![]() -page. Hence, we have shown that the $0$
-page. Hence, we have shown that the $0$![]() -th column of the $E_\infty$
-th column of the $E_\infty$![]() -page is $\Lambda _{BP^{*}}(\gamma _{n-k+2},\,\ldots,\,\gamma _n)$
-page is $\Lambda _{BP^{*}}(\gamma _{n-k+2},\,\ldots,\,\gamma _n)$![]() . Also on the $E_\infty$
. Also on the $E_\infty$![]() -page the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$
-page the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$![]() goes to $0$
goes to $0$![]() , as each of the generators are hit by the differentials $d_{2j}(y_j)$
, as each of the generators are hit by the differentials $d_{2j}(y_j)$![]() . This completes the proof.
. This completes the proof.
It remains now to solve the additive and multiplicative extension problems to obtain $BP^{\ast } PW_{n,k}$![]() from the expression in proposition 4.2. In the following lemma, we show that the part $BP^{\ast }(pt)[x]/I$
from the expression in proposition 4.2. In the following lemma, we show that the part $BP^{\ast }(pt)[x]/I$![]() forms a subalgebra of $BP^{\ast } PW_{n,k}$
forms a subalgebra of $BP^{\ast } PW_{n,k}$![]() . Recall the fibration $W_{n,k}\to PW_{n,k}\stackrel {p_k}{\to }{{\mathbb {C}}}P^{\infty }$
. Recall the fibration $W_{n,k}\to PW_{n,k}\stackrel {p_k}{\to }{{\mathbb {C}}}P^{\infty }$![]() . We prove
. We prove
Lemma 4.3 The kernel of the map $p^{*}:BP^{*}({{\mathbb {C}}}P^{\infty })\to BP^{*}(PW_{n,k})$![]() contains the ideal $I$
contains the ideal $I$![]() generated by $\{\binom {n}{j}x^{j} \vert n-k< j \leq n \}$
generated by $\{\binom {n}{j}x^{j} \vert n-k< j \leq n \}$![]() in $BP^{*}(pt)[[x]]$
in $BP^{*}(pt)[[x]]$![]() .
.
Proof. The proof goes by induction on $k$![]() . For $k=1$
. For $k=1$![]() , the fibration is up to homotopy the following sequence
, the fibration is up to homotopy the following sequence
so that the kernel of $p_1^{*}$![]() is the ideal generated by $x^{n}$
is the ideal generated by $x^{n}$![]() , satisfying the statement of the lemma. Suppose that the lemma is true for $PW_{n,k-1}$
, satisfying the statement of the lemma. Suppose that the lemma is true for $PW_{n,k-1}$![]() . To show the result for $PW_{n,k}$
. To show the result for $PW_{n,k}$![]() , we consider the diagram
, we consider the diagram

In the above diagram, $f$![]() classifies the bundle $n\gamma$
classifies the bundle $n\gamma$![]() where $\gamma$
where $\gamma$![]() is the canonical line bundle over ${{\mathbb {C}}}P^{\infty }$
is the canonical line bundle over ${{\mathbb {C}}}P^{\infty }$![]() , and $q$
, and $q$![]() is induced by the $S^{1}$
is induced by the $S^{1}$![]() -equivariant projection $W_{n,k}\to W_{n,k-1}$
-equivariant projection $W_{n,k}\to W_{n,k-1}$![]() . The three squares in the diagram are homotopy pullbacks. Our aim is to understand the kernel of $q^{*}$
. The three squares in the diagram are homotopy pullbacks. Our aim is to understand the kernel of $q^{*}$![]() . We see that $PW_{n,k}\to PW_{n,k-1}$
. We see that $PW_{n,k}\to PW_{n,k-1}$![]() is, up to homotopy, the sphere bundle associated to the complex bundle classified by the map $T_{n,k-1}$
is, up to homotopy, the sphere bundle associated to the complex bundle classified by the map $T_{n,k-1}$![]() . This is because $BU(n-k)$
. This is because $BU(n-k)$![]() is (up to homotopy) the sphere bundle of the canonical $n-k+1$
is (up to homotopy) the sphere bundle of the canonical $n-k+1$![]() -plane bundle over $BU(n-k+1)$
-plane bundle over $BU(n-k+1)$![]() . As $BP$
. As $BP$![]() is complex oriented, we obtain a Gysin sequence
is complex oriented, we obtain a Gysin sequence
It follows that the kernel of $q^{\ast }$![]() is the ideal generated by $e^{BP}(T_{n,k-1})$
is the ideal generated by $e^{BP}(T_{n,k-1})$![]() in $BP^{\ast } PW_{n,k-1}$
in $BP^{\ast } PW_{n,k-1}$![]() . The bundle $T_{n,k-1}$
. The bundle $T_{n,k-1}$![]() is obtained by lifting the composite $PW_{n,k-1} \stackrel {p_{k-1}}{\to } {{\mathbb {C}}}P^{\infty } \stackrel {n\gamma }{\to } BU(n)$
is obtained by lifting the composite $PW_{n,k-1} \stackrel {p_{k-1}}{\to } {{\mathbb {C}}}P^{\infty } \stackrel {n\gamma }{\to } BU(n)$![]() to $BU(n-k)$
to $BU(n-k)$![]() so that $T_{n,k-1} + (k-1)\epsilon = np_{k-1}^{\ast } \gamma$
so that $T_{n,k-1} + (k-1)\epsilon = np_{k-1}^{\ast } \gamma$![]() . We readily compute $e^{BP}$
. We readily compute $e^{BP}$![]() as the top $BP$
as the top $BP$![]() -Chern class
-Chern class
Therefore, $\binom {n}{n-k+1}x^{n-k+1}$![]() lies in the kernel of $p_k^{\ast }: BP^{\ast } {{\mathbb {C}}}P^{\infty } \to BP^{\ast } PW_{n,k}$
lies in the kernel of $p_k^{\ast }: BP^{\ast } {{\mathbb {C}}}P^{\infty } \to BP^{\ast } PW_{n,k}$![]() . By the inductive formula for the kernel of $p_{k-1}^{\ast } : BP^{\ast } {{\mathbb {C}}}P^{\infty } \to BP^{\ast } PW_{n,k-1}$
. By the inductive formula for the kernel of $p_{k-1}^{\ast } : BP^{\ast } {{\mathbb {C}}}P^{\infty } \to BP^{\ast } PW_{n,k-1}$![]() , the proof is now complete.
, the proof is now complete.
We now apply lemma 4.3 and proposition 4.2 to complete the calculation of $BP^{\ast } PW_{n,k}$![]() .
.
Theorem 4.4 For every prime $p,$![]() the $BP$
the $BP$![]() -cohomology algebra of $PW_{n,k}$
-cohomology algebra of $PW_{n,k}$![]() is described additively by $BP^{\ast }(pt)$
is described additively by $BP^{\ast }(pt)$![]() -module
-module
where $\gamma _j$![]() 's are of degree $2j-1,$
's are of degree $2j-1,$![]() $x$
$x$![]() is of degree $2,$
is of degree $2,$![]() and $I$
and $I$![]() is the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$
is the ideal generated by $\{\binom {n}{j}x^{j}\vert n-k< j\leq n \}$![]() . This isomorphism is also multiplicative if $p\neq 2$
. This isomorphism is also multiplicative if $p\neq 2$![]() .
.
Proof. Lemma 4.3 implies that $p^{\ast }$![]() induces a ring map of $BP^{\ast }$
induces a ring map of $BP^{\ast }$![]() -modules $BP^{\ast }(pt)[[x]]/I \to BP^{\ast }(PW_{n,k})$
-modules $BP^{\ast }(pt)[[x]]/I \to BP^{\ast }(PW_{n,k})$![]() . Choosing representatives for generators $\gamma _j$
. Choosing representatives for generators $\gamma _j$![]() of proposition 4.2 in the $E_\infty$
of proposition 4.2 in the $E_\infty$![]() -page we obtain a $BP^{\ast }(pt)$
-page we obtain a $BP^{\ast }(pt)$![]() -module map $\Lambda _{BP^{*}(pt)}(\gamma _{n-k+2},\,\ldots,\,\gamma _n)$
-module map $\Lambda _{BP^{*}(pt)}(\gamma _{n-k+2},\,\ldots,\,\gamma _n)$![]() to $BP^{\ast } PW_{n,k}$
to $BP^{\ast } PW_{n,k}$![]() . The multiplication as a bilinear map on these factors gives a map
. The multiplication as a bilinear map on these factors gives a map
of $BP^{\ast }(pt)$![]() -modules. This is an isomorphism by proposition 4.2 and the multiplicative structure of the spectral sequence (4.1). Further if $p\neq 2$
-modules. This is an isomorphism by proposition 4.2 and the multiplicative structure of the spectral sequence (4.1). Further if $p\neq 2$![]() , we have $\gamma _j^{2}=0$
, we have $\gamma _j^{2}=0$![]() as $\gamma _j$
as $\gamma _j$![]() lies in odd degree. Therefore, the isomorphism is also multiplicative.
lies in odd degree. Therefore, the isomorphism is also multiplicative.
We observe that in theorem 4.4, we do not expect the isomorphism to be multiplicative when $p=2$![]() , as it does not even hold over $H{{\mathbb {Z}}}/p$
, as it does not even hold over $H{{\mathbb {Z}}}/p$![]() ([Reference Astey, Gitler, Micha and Pastor3]).
([Reference Astey, Gitler, Micha and Pastor3]).
5. Equivariant maps between Stiefel manifolds
In this section, we demonstrate how the computations of $BP$![]() -cohomology operations may be used to rule out $S^{1}$
-cohomology operations may be used to rule out $S^{1}$![]() -equivariant maps between the Stiefel manifolds. The results of [Reference Petrović and Prvulović17] can be improved in this way.
-equivariant maps between the Stiefel manifolds. The results of [Reference Petrović and Prvulović17] can be improved in this way.
5.1 Applications using Steenrod operations
We start with an example using Steenrod operations in ${{\mathbb {Z}}}/2$![]() -cohomology. The Steenrod operations on $H^{\ast }(PW_{n,k};{{\mathbb {Z}}}/2)$
-cohomology. The Steenrod operations on $H^{\ast }(PW_{n,k};{{\mathbb {Z}}}/2)$![]() are described in [Reference Astey, Gitler, Micha and Pastor3, theorem 1.2]. We have from [Reference Petrović and Prvulović17] that if there is an $S^{1}$
are described in [Reference Astey, Gitler, Micha and Pastor3, theorem 1.2]. We have from [Reference Petrović and Prvulović17] that if there is an $S^{1}$![]() -equivariant map from $W_{n,k}$
-equivariant map from $W_{n,k}$![]() to $W_{m,l}$
to $W_{m,l}$![]() with $n-k=m-l$
with $n-k=m-l$![]() , then
, then
which is then used to rule out such equivariant maps in many cases when $n-k=m-l$![]() and $n>m$
and $n>m$![]() [Reference Petrović and Prvulović17, theorem 3.10]. The Steenrod operations allow us to rule out equivariant maps for cases where the above divisibility is valid. An example is given in the theorem below.
[Reference Petrović and Prvulović17, theorem 3.10]. The Steenrod operations allow us to rule out equivariant maps for cases where the above divisibility is valid. An example is given in the theorem below.
Theorem 5.1 Suppose $r \equiv -1,$![]() $-2,$
$-2,$![]() or $3\pmod {9}$
or $3\pmod {9}$![]() and $r \equiv 2,$
and $r \equiv 2,$![]() $1,$
$1,$![]() or $-2\pmod {7},$
or $-2\pmod {7},$![]() and $m=16 r -2$
and $m=16 r -2$![]() . Then, there is no $S^{1}$
. Then, there is no $S^{1}$![]() -equivariant map from $W_{m-3,7}$
-equivariant map from $W_{m-3,7}$![]() to $W_{m,10}$
to $W_{m,10}$![]() .
.
Proof. Write $n=m-3$![]() , $k=7$
, $k=7$![]() and $l=10$
and $l=10$![]() . Observe that the following are satisfied by these integers
. Observe that the following are satisfied by these integers
(1) $m,\,l$
 even and $n,\,k$
even and $n,\,k$ odd, and $m-l=n-k$
odd, and $m-l=n-k$ .
.(2) $2$
 divides both $\binom {m}{m-l+1}$
divides both $\binom {m}{m-l+1}$ , $\binom {n}{n-k+1}$
, $\binom {n}{n-k+1}$ but $4$
but $4$ does not divide either.
does not divide either.(3) $\binom {n}{n-k+1} \vert \binom {m}{m-l+1}$
 .
.
An $S^{1}$![]() -equivariant map $f$
-equivariant map $f$![]() from $W_{n,k}$
from $W_{n,k}$![]() to $W_{m,l}$
to $W_{m,l}$![]() induces a map of fibration sequences
induces a map of fibration sequences

~
We compare the associated Serre spectral sequences with ${{\mathbb {Z}}}$![]() -coefficients in the case $n-k=m-l$
-coefficients in the case $n-k=m-l$![]() . The condition (2) implies that $f^{*}(y_{m-l+1})=cy_{n-k+1}$
. The condition (2) implies that $f^{*}(y_{m-l+1})=cy_{n-k+1}$![]() , where $c$
, where $c$![]() is odd. This is because in those spectral sequences $y_j$
is odd. This is because in those spectral sequences $y_j$![]() transgresses to $\binom {n}{j}x^{j}$
transgresses to $\binom {n}{j}x^{j}$![]() and $\binom {m}{j}x^{j}$
and $\binom {m}{j}x^{j}$![]() respectively. The classes $y_{n-k+1}$
respectively. The classes $y_{n-k+1}$![]() and $y_{m-l+1}$
and $y_{m-l+1}$![]() also survive in the ${{\mathbb {Z}}}/2$
also survive in the ${{\mathbb {Z}}}/2$![]() -cohomology spectral sequence by (2), and we have $f^{*}(y_{m-l+1})=y_{n-k+1}$
-cohomology spectral sequence by (2), and we have $f^{*}(y_{m-l+1})=y_{n-k+1}$![]() . [Reference Astey, Gitler, Micha and Pastor3, Theorem 1.2] implies
. [Reference Astey, Gitler, Micha and Pastor3, Theorem 1.2] implies
and
This is a contradiction.
5.2 Results using $BP$ -operations
-operations
We have seen how Steenrod squares yield some results on non-existence of $S^{1}$![]() -equivariant maps between complex Stiefel manifolds. We now derive stronger results using $BP$
-equivariant maps between complex Stiefel manifolds. We now derive stronger results using $BP$![]() -theory and cohomology operations associated to it. The operations we use here are the Adams operations defined via [Reference Araki2, 2.4]. These are multiplicative, stable operations with the formula
-theory and cohomology operations associated to it. The operations we use here are the Adams operations defined via [Reference Araki2, 2.4]. These are multiplicative, stable operations with the formula
where $a\in {{\mathbb {Z}}}_{(p)}^{\times }$![]() , and $[a]_{BP}$
, and $[a]_{BP}$![]() denotes the $a$
denotes the $a$![]() -series using the $BP$
-series using the $BP$![]() -formal group law. These operations act on the coefficient ring via $\Psi ^{a}_{BP}(v_i)=a^{p^{i}-1}v_i$
-formal group law. These operations act on the coefficient ring via $\Psi ^{a}_{BP}(v_i)=a^{p^{i}-1}v_i$![]() .
.
Denote the ideal $(v_1,\,v_2,\,\ldots )$![]() in $BP^{*}(pt)={{\mathbb {Z}}}_{(p)}[v_1,\,v_2,\,\ldots ]$
in $BP^{*}(pt)={{\mathbb {Z}}}_{(p)}[v_1,\,v_2,\,\ldots ]$![]() by $J$
by $J$![]() . We fix the $\{v_i \mid i \geq 1 \}$
. We fix the $\{v_i \mid i \geq 1 \}$![]() to be the Araki generators [Reference Ravenel18, A2.2.2]. The formal group law $\mu _{BP}$
to be the Araki generators [Reference Ravenel18, A2.2.2]. The formal group law $\mu _{BP}$![]() , associated to $BP$
, associated to $BP$![]() with respect to our chosen orientation is strictly isomorphic to the additive formal group law over $BP^{*}(pt)\otimes {{\mathbb {Q}}}$
with respect to our chosen orientation is strictly isomorphic to the additive formal group law over $BP^{*}(pt)\otimes {{\mathbb {Q}}}$![]() and the isomorphism is given by $BP\text {-log}$
and the isomorphism is given by $BP\text {-log}$![]() series. The choice of generators imply that the $BP\text {-log}$
series. The choice of generators imply that the $BP\text {-log}$![]() series has the form
series has the form
where $l_i$![]() are determined by the relations
are determined by the relations
with $l_0=1$![]() and $v_0=p$
and $v_0=p$![]() . This implies the formula
. This implies the formula
Now we consider the expression of [Reference Adams1, part II, proposition 7.5] $\pmod {J^{2}}$![]() to obtain the following relation for the $\text {exp}_{BP}$
to obtain the following relation for the $\text {exp}_{BP}$![]() -series
-series
This implies

where by $+_{BP}$![]() we mean the formal sum under the formal group law $\mu _{BP}$
we mean the formal sum under the formal group law $\mu _{BP}$![]() .
.
We now restrict our attention to $p=2$![]() , and obtain the following reduction for $\Psi ^{3}_{BP}$
, and obtain the following reduction for $\Psi ^{3}_{BP}$![]() (5.1) by applying (5.2) multiple times.
(5.1) by applying (5.2) multiple times.

We note that $\frac {1-3^{2^{i}-1}}{2(1-2^{2^{i}-1})}= \alpha _i$![]() lies in ${{\mathbb {Z}}}_{(2)}^{\times }$
lies in ${{\mathbb {Z}}}_{(2)}^{\times }$![]() , and in this notation we have
, and in this notation we have
We shall now determine the action of $\Psi ^{3}_{BP}$![]() on $BP^{*}(W_{n,k})=\Lambda _{BP^{*}}(y_{n-k+1},\,\ldots,\,y_n)$
on $BP^{*}(W_{n,k})=\Lambda _{BP^{*}}(y_{n-k+1},\,\ldots,\,y_n)$![]() modulo the ideal $I^{2}$
modulo the ideal $I^{2}$![]() , where $I$
, where $I$![]() is the ideal of $BP^{*}(W_{n,k})$
is the ideal of $BP^{*}(W_{n,k})$![]() generated by $y_{n-k+1},\,\ldots,\,y_n$
generated by $y_{n-k+1},\,\ldots,\,y_n$![]() .
.
Proposition 5.2
Proof. Recall the map $\mu _{n,k}:\Sigma [{{\mathbb {C}}}P^{n-1}/{{{\mathbb {C}}}P^{n-k+1}}]= \Sigma P_{n,k} \longrightarrow W_{n,k}$![]() , for which we had $\mu _{n,k}^{*}(y_j)=\Sigma x^{j-1}$
, for which we had $\mu _{n,k}^{*}(y_j)=\Sigma x^{j-1}$![]() . Hence this will give us the isomorphism
. Hence this will give us the isomorphism
By naturality of the Adams operations, $\Psi ^{3}_{BP}$![]() commutes with $\mu ^{*}_{n,k}$
commutes with $\mu ^{*}_{n,k}$![]() . The action of $\Psi ^{3}_{BP}$
. The action of $\Psi ^{3}_{BP}$![]() on $y_j$
on $y_j$![]() is determined up to $I^{2}$
is determined up to $I^{2}$![]() from the computation for $\Sigma x^{j-1}$
from the computation for $\Sigma x^{j-1}$![]() . The Adams operation being stable, commutes with the suspension, so it is enough to compute the action of $\Psi ^{3}_{BP}$
. The Adams operation being stable, commutes with the suspension, so it is enough to compute the action of $\Psi ^{3}_{BP}$![]() on $x^{j-1}$
on $x^{j-1}$![]() , which comes from the multiplicative structure and the formulas above.
, which comes from the multiplicative structure and the formulas above.

Hence the proposition follows.
We now use the action of $BP$![]() -Adams operations to prove new results about equivariant maps between complex Stiefel manifolds. We note from [Reference Petrović and Prvulović17] that the existence of a $S^{1}$
-Adams operations to prove new results about equivariant maps between complex Stiefel manifolds. We note from [Reference Petrović and Prvulović17] that the existence of a $S^{1}$![]() -equivariant map $W_{n,k}\to W_{m,l}$
-equivariant map $W_{n,k}\to W_{m,l}$![]() implies that $n-k\leq m-l$
implies that $n-k\leq m-l$![]() . It states a number of hypotheses on $n,\,k,\,m,\,l$
. It states a number of hypotheses on $n,\,k,\,m,\,l$![]() in the case $n-k=m-l$
in the case $n-k=m-l$![]() for which equivariant maps do not exist. Proposition 5.1 proves some further results for this case. We use $BP$
for which equivariant maps do not exist. Proposition 5.1 proves some further results for this case. We use $BP$![]() -operations to rule out equivariant maps in some cases where $n-k< m-l$
-operations to rule out equivariant maps in some cases where $n-k< m-l$![]() .
.
Theorem 5.3 Suppose that $m,\,n,\,l,\, k$![]() are positive integers satisfying
are positive integers satisfying
(1) $n-k< m-l$
 and there is an $s$
and there is an $s$ such that $m<2^{s}+m-l\leq n$
such that $m<2^{s}+m-l\leq n$ .
.(2) $2$
 divides all the binomial coefficients $\binom {n}{n-k+1},\,\ldots,\, \binom {n}{m-l}$
divides all the binomial coefficients $\binom {n}{n-k+1},\,\ldots,\, \binom {n}{m-l}$ .
.(3) $2$
 does not divide $\binom {m}{m-l+1}$
does not divide $\binom {m}{m-l+1}$ and $2\nmid m-l$
and $2\nmid m-l$ .
.Then, there is no $S^{1}$
 -equivariant map from $W_{n,k}$
-equivariant map from $W_{n,k}$ to $W_{m,l}$
to $W_{m,l}$ .
.
Proof. We assume the contrary that $g: W_{n,k} \to W_{m,l}$![]() is an $S^{1}$
is an $S^{1}$![]() -equivariant map. This induces a map of homotopy fixed point spectral sequences, and also a compatible map between the associated projective Stiefel manifolds. The formula for the differentials in the homotopy fixed point spectral sequence (proposition 4.1) and the fact that $\binom {n}{m-l+1}$
-equivariant map. This induces a map of homotopy fixed point spectral sequences, and also a compatible map between the associated projective Stiefel manifolds. The formula for the differentials in the homotopy fixed point spectral sequence (proposition 4.1) and the fact that $\binom {n}{m-l+1}$![]() must be odd due to the hypotheses (2) and (3), implies that the pullback satisfies
must be odd due to the hypotheses (2) and (3), implies that the pullback satisfies
for some $\beta \in {{\mathbb {Z}}}_{(2)}^{\times }$![]() and $p_j\in BP^{\ast }(pt)$
and $p_j\in BP^{\ast }(pt)$![]() . Note that $|y_j|=2j-1$
. Note that $|y_j|=2j-1$![]() and $|v_j|= 2-2^{j+1}$
and $|v_j|= 2-2^{j+1}$![]() . For degree reasons, the second term in the above expression will be of the form
. For degree reasons, the second term in the above expression will be of the form
where $k_j \in {{\mathbb {Z}}}_{(2)}$![]() .
.
Now we shall compute $\Psi ^{3}_{BP}(g^{*}(y_{m-l+1}))$![]() and $g^{*}(\Psi ^{3}_{BP}(y_{m-l+1}))$
and $g^{*}(\Psi ^{3}_{BP}(y_{m-l+1}))$![]() modulo the ideal $I^{2}+J^{2}$
modulo the ideal $I^{2}+J^{2}$![]() .
.

On the other hand, we have

Note that for degree reasons,
for some $\nu \in {{\mathbb {Z}}}_{(2)}$![]() . Since $\Psi ^{3}_{BP}(g^{*}(y_{m-l+1}))=g^{*}(\Psi ^{3}_{BP}(y_{m-l+1}))$
. Since $\Psi ^{3}_{BP}(g^{*}(y_{m-l+1}))=g^{*}(\Psi ^{3}_{BP}(y_{m-l+1}))$![]() , the coefficients for $y_{2^{s}+m-l}$
, the coefficients for $y_{2^{s}+m-l}$![]() (for $s$
(for $s$![]() as in (1)) in the expressions (5.4) and (5.5) must be the same modulo the ideal $I^{2}+J^{2}$
as in (1)) in the expressions (5.4) and (5.5) must be the same modulo the ideal $I^{2}+J^{2}$![]() . This implies
. This implies

This contradicts the fact that $\beta (m-l) \in {{\mathbb {Z}}}_{(2)}^{\times }$![]() . Hence no such $S^{1}$
. Hence no such $S^{1}$![]() -equivariant map $g$
-equivariant map $g$![]() can exist.
can exist.
Example 5.4 One may easily figure out values of $m,\,n,\,l,\,k$![]() for which the hypothesis of theorem 5.3 is satisfied. For example, putting $k=n$
for which the hypothesis of theorem 5.3 is satisfied. For example, putting $k=n$![]() and $m-l+1=2$
and $m-l+1=2$![]() , we obtain : If $n$
, we obtain : If $n$![]() is even and $\binom {m}{2}$
is even and $\binom {m}{2}$![]() odd, and there is some $s$
odd, and there is some $s$![]() such that $m<2^{s}+1 \leq n$
such that $m<2^{s}+1 \leq n$![]() , then, there is no $S^{1}$
, then, there is no $S^{1}$![]() -equivariant map from $W_{n,n}$
-equivariant map from $W_{n,n}$![]() to $W_{m,m-1}$
to $W_{m,m-1}$![]() .
.
Acknowledgments
The first author would like to thank Shilpa Gondhali for some helpful conversations during the initial part of this work. The second author would like to thank Aloke Kumar Ghosh. The research of the first author was supported by the SERB MATRICS grant 2018/000845.