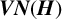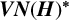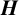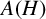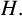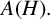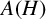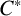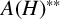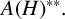1 Introduction
Let G be a locally compact group and let
$A(G)$
be the Fourier algebra associated with
$G.$
In 1973, Dunkl and Ramirez [Reference Dunkl and Ramirez9] introduced the notion of weakly almost periodic functionals on
$A(G)$
extending the classical notion of weakly almost periodic functions on locally compact abelian groups. In 1974, the space of uniformly continuous functionals was introduced by Granirer [Reference Granirer13], extending yet another classical notion of uniformly continuous functions. These spaces and their duals were well studied by many authors.
Let H be an ultraspherical hypergroup associated with a locally compact group G and a spherical projector
$\pi .$
Let
$A(H)$
denote the Fourier algebra corresponding to the ultraspherical hypergroup
$H.$
Also, let
$VN(H)$
denote the hypergroup von Neumann algebra of
$H.$
The algebra
$A(H),$
although introduced a decade ago, has not received much attention. For some of the recent contributions to
$A(H)$
, see for example, [Reference Degenfeld-Schonburg, Kaniuth and Lasser7, Reference Esmailvandi and Nemati10, Reference Esmailvandi and Nemati11, Reference Shravan Kumar23]. This paper is a continuation of the series of results obtained by the first and the second authors. The modest aim of this note is to contribute to the study of the dual and the bidual of
$A(H).$
The notion of weakly almost periodic functionals and uniformly continuous functionals on
$A(H)$
has been studied in a recent paper [Reference Esmailvandi and Nemati11]. In Section 3 of this paper, we show that the space of all uniformly continuous functionals forms a C*-algebra. This is Theorem 3.4. For the case of locally compact groups, the main ingredient in the proof of this is the fact that singletons are sets of spectral synthesis. In 2014, Degenfeld-Schonburg et al. [Reference Degenfeld-Schonburg, Kaniuth and Lasser7] produced examples of ultraspherical hypergroups for which singletons need not be sets of spectral synthesis for the corresponding Fourier algebra. Our idea is to show that the space of uniformly continuous functionals is the image of a C*-algebra under a C*-homomorphism.
In Section 4, we study the dual of
$VN(H).$
We characterize the existence of left and right identities for the dual of
$VN(H).$
We also characterize when the algebra
$VN(H)^{\ast }$
is semisimple. Then we take up the dual of the space of uniformly continuous functionals.
One of the classical results of Richard F. Arens says that if G is an infinite locally compact group, then the group algebra
$L^1(G)$
cannot be Arens regular. This result has been generalized to the Fourier algebra of a locally compact group by Lau [Reference Lau17] under the assumption that the group G is amenable. In Theorem 4.3, we prove that the Fourier algebra of an ultraspherical hypergroup is Arens regular if and only if H is finite under the assumption that
$A(H)$
has a bounded approximate identity.
Finally, in Section 5, we study unit elements in
$VN(H)^{\ast }.$
Our main aim in this section is to characterize when an element of
$A(H)^{**}$
is also an element of
$A(H)$
in terms of the unit elements.
2 Preliminaries
2.1 Hypergroups
We first recall the definition of a hypergroup. In [Reference Jewett15], Jewett calls a hypergroup a convo.
Definition 2.1. A nonempty locally compact Hausdorff space H is said to be a hypergroup if there exists a binary operation
$\ast $
on
$M(H),$
the space of all complex-valued bounded Radon measures on
$H,$
satisfying the following conditions.
-
(i)
$(M(H),\ast )$
is an algebra. -
(ii) For every
$x,y\in H$
,
$\delta _x\ast \delta _y$
is a probability measure and the mapping
$(x,y)\mapsto \delta _x\ast \delta _y$
is continuous from
$H\times H$
to
$M^1(H).$
-
(iii) There exists a unique element
$e\in H$
such that for all
$x\in H$
,
$\delta _x\ast \delta _e=\delta _e\ast \delta _x=\delta _x.$
-
(iv) There exists a unique homeomorphism
$x\mapsto x^-$
of H such that the following hold.-
(a)
$(x^-)^-=x$
for all
$x\in H.$
-
(b) If
$\widehat {\mu }$
is defined by
$\int _H f(x)\,d\widehat {\mu }(x)=\int _Hf(x^-)\,d\mu (x)$
for all
$f\in C_c(H),$
then
$\widehat {\delta _x\ast \delta _y}=\delta _{y^-}\ast \delta _{x^-}$
for all
$x,y\in H.$
-
(c) For every
$x,y\in H$
,
$\mbox {supp}(\delta _x\ast \delta _y)$
is compact. Further, the mapping
$(x,y)\mapsto \mbox {supp}(\delta _x\ast \delta _y)$
is continuous from
$H\times H$
to
$\mathcal {K}(H),$
where
$\mathcal {K}(H)$
denotes the space of all nonempty compact subsets of H equipped with the ‘Michael Topology’. See [Reference Michael21].
-
The following lemma is well known in the context of locally compact groups. As we cannot find any reference, we are providing a proof here.
Lemma 2.2. Let
$ H $
be a hypergroup. If every
$\sigma $
-compact open subhypergroup of H is compact, then H is compact.
Proof. The proof is by contradiction. Suppose that H is noncompact. Let
$H_0$
be the subhypergroup of H generated by a compact symmetric neighborhood of
$e.$
Then
$H_0$
is open and
$\sigma $
-compact and so under our hypothesis,
$H_0$
is compact. Choose
$x_1$
in H that is not in
$H_0$
. Then the union of
$H_0$
and
$\{x_1, (x_1)^-\}$
is again a compact symmetric neighborhood of e. Let
$H_1$
be the subhypergroup that it generates. Again,
$H_1$
is open and
$\sigma $
-compact and hence compact. Choose
$x_2$
in H that is not in
$H_1$
and let
$H_2$
be the subghypergroup generated by the union of
$H_1$
and
$\{x_2, (x_2)^-\}$
. As said earlier,
$H_2$
is compact. We can keep doing this infinitely, thereby obtaining a sequence
$x_n$
of elements from H and an increasing sequence
$H_n$
of open, compact subgroups with
$x_n$
in
$H_n$
but not in
$H_{n-1}$
. Let
$H'$
be the union of all the
$H_n$
. Then, once again,
$H'$
is an open
$\sigma $
-compact subhypergroup of H and hence is compact. So the sequence
$\{x_n\}$
must have a cluster point y in
$H'$
. But if y is in H, it is in
$H_k$
for some k, so
$H_k$
is a neighborhood of y that does not contain
$x_n$
for any
$n>k$
, which is a contradiction.
We now define the notion of a spherical projector on a locally compact group G [Reference Muruganandam22, Definition 2.1].
Definition 2.3. A map
$\pi :C_c(G)\rightarrow C_c(G)$
is called a spherical projector if it is linear and satisfies the following for all
$f,g\in C_c(G).$
- (i)
-
(a)
$\pi ^2=\pi $
and
$\pi $
is positivity preserving; -
(b)
$\pi (\pi (\,f)g)=\pi (\,f)\pi (g)$
; -
(c)
$\langle \pi (\,f),g \rangle =\langle f,\pi (g) \rangle $
; -
(d)
$\int _G\pi (\,f)(x)\,dx=\int _G f(x)\,d.$
-
-
(ii)
$\pi (\pi (\,f)*\pi (g))=\pi (\,f)*\pi (g)$
. -
(iii) Let
$\pi ^*:M(G)\rightarrow M(G)$
denote the transpose of
$\pi $
and let
$\mathcal {O}_x=\text {supp}(\pi ^*(\delta _x)), x\in G.$
Then for all
$x,y\in G:$
-
(a) either
$\mathcal {O}_x\cap \mathcal {O}_y=\emptyset $
or
$\mathcal {O}_x=\mathcal {O}_y;$
-
(b) if
$x\in \mathcal {O}_y\ \textrm{then}\ x^{-1}\in \mathcal {O}_{y^{-1}};$
-
(c) if
$\mathcal {O}_{xy}=\mathcal {O}_{e}\ \textrm{then}\ \mathcal {O}_y=\mathcal {O}_{x^{-1}};$
-
(d) the map
$x\mapsto \mathcal {O}_x$
from G to
$\mathcal {K}(G)$
is continuous.
-
Note that
$\pi $
extends to a norm decreasing linear map on various function spaces, including
$L^p(G),\ 1\leq p\leq \infty .$
A function f is called
$\pi $
-radial if
$\pi (\,f)=f$
and similarly, a measure
$\mu $
is called
$\pi $
-radial if
$\pi ^*(\,\mu )=\mu .$
Let
$ H = \{\dot {x}=\mathcal {O}_x: x \in G\}$
, equipped with the natural quotient topology under the quotient map
$ p: G\rightarrow H $
. We identify
$M(H)$
with the space of all
$ \pi ^* $
-radial measures in
$ M(G) $
, with the product defined by
$ \delta _{\dot x} \ast \delta _{\dot y}= \pi ^{\ast }(\pi ^{\ast }(\delta _{x} \ast \delta _{y} )) $
for all
$ x , y \in G $
. With this structure,
$ H $
becomes a locally compact hypergroup, called a spherical hypergroup [Reference Muruganandam22, Theorem 2.12]. A spherical hypergroup is further called an ultraspherical hypergroup if the modular function on G is
$\pi $
-radial.
The most common example of an ultraspherical hypergroup is the double coset hypergroup. Let G be a locally compact group containing a compact subgroup
$K.$
Define
$\pi :C_c(G)\rightarrow C_c(G)$
as
$$ \begin{align*} \pi(\,f)(x)=\int_K\int_K f(k^{\prime} xk)\,dk\,dk^{\prime}. \end{align*} $$
Then
$\pi $
defines a spherical projector and the resulting hypergroup is an ultraspherical hypergroup. Another interesting class of examples for ultraspherical hypergroups in the context of Lie groups is due to Damek and Ricci [Reference Damek and Ricci6]. The spherical projector was called an average projector in [Reference Damek and Ricci6].
A left Haar measure on a hypergroup H is a nonzero regular Borel measure m such that
$p_x*m=m$
for all
$x\in H.$
In this note, by a Haar measure, we mean a left Haar measure. It is well known that commutative (or compact or discrete) hypergroups admit a Haar measure. In fact, a Haar measure on a hypergroup (if it exists) is unique up to a scalar multiple [Reference Jewett15]. It remains an open question whether every locally compact hypergroup admits a Haar measure. It is shown in [Reference Muruganandam22] that a Haar measure exists on an ultraspherical hypergroup.
2.2 Fourier algebra
Let G be a locally compact group with a fixed Haar measure denoted by
$dx.$
Let
$A(G)$
and
$B(G)$
denote the Fourier and Fourier–Stieltjes algebras, respectively, introduced by Eymard [Reference Eymard12] in his seminal paper. Let H be an ultraspherical hypergroup associated to a locally compact group G and a spherical projector
$\pi .$
The map
$\pi $
extends to be a norm decreasing contraction on
$A(G).$
The Fourier algebra of an ultraspherical hypergroup is defined as the range of
$\pi $
inside
$A(G).$
The algebra
$A(H)$
is commutative, semisimple, regular and Tauberian, and the character space
$\Delta (A(H))$
of
$A(H)$
can be canonically identified with H. The Fourier–Stieltjes algebra of H is defined as the algebra of all
$\pi $
-radial functions in
$B(G).$
For more details on these algebras, see [Reference Muruganandam22].
Let
$\lambda $
denote the left regular representation of H on
$L^2(H)$
given by
$$ \begin{align*} \lambda(\dot{x})(\,f)(\dot{y})=f(\dot{x}^-\ast\dot{y})\quad (\dot{x},\dot{y}\in H, f\in L^2(H)). \end{align*} $$
This can be extended to
$L^1(H)$
by
$\lambda (\,f)(g)=f*g$
for all
$f\in L^1(H)$
and
$g\in L^2(H)$
. Let
$C^*_{\lambda }(H)$
denote the completion of
$\lambda (L^1(H))$
in
$B(L^2(H))$
which is called the reduced
$C^*$
-algebra of H. The von Neumann algebra generated by
$\{\lambda (\dot {x}): \dot {x}\in H\}$
is called the von Neumann algebra of H, and is denoted by
$VN(H)$
. Note that
$VN(H)$
is isometrically isomorphic to the dual of
$A(H)$
. Moreover,
$A(H)$
can be considered as an ideal of
$B_{\lambda }(H)$
, where
$B_{\lambda }(H)$
is the dual of
$C_{\lambda }^*(H).$
We denote by
$\langle \cdot ,\cdot \rangle _0$
the duality between
$C_{\lambda }^*(H)$
and
$B_{\lambda }(H).$
Let
$ q :C^{*}_{\lambda }(H)\longrightarrow C^{*}_{\lambda }(H)^{**} $
be the canonical embedding and
$ i : C^{*}_{\lambda }(H)\longrightarrow VN(H) $
be the inclusion map. Then, by [Reference Dixmier8, Proposition 12.1.5], there exists an ultraweakly continuous
$ * $
-homomorphism
$ \tilde {i} $
from
$ C^{*}_{\lambda }(H)^{**} $
onto
$ VN(H) $
such that
$$ \begin{align*} \tilde{i} q (T) = i (T) = T \quad (T \in C^{*}_{\lambda}(H)). \end{align*} $$
The following lemma is a simple and useful observation, which is a consequence of [Reference Dixmier8, 12.1.5] and [Reference Dixmier8, 12.1.3(ii)].
Lemma 2.4. If
$T\in C_{\lambda }^{\ast }(H)$
and
$u\in A(H),$
then
$\langle T,u\rangle _0=\langle u,\tilde {i}(T) \rangle .$
Let K be a subhypergroup of an ultraspherical hypergroup H and let
$ L=p^{-1}(K).$
Then L is a closed subgroup of G and the pair
$(L,\pi |_{L})$
defines the ultraspherical hypergroup
$K.$
It follows from [Reference Muruganandam22, Theorem 3.10] that
$A(H)$
and
$A(K)$
can be identified with
$A_{\pi }(G)$
and
$A_{\pi |_{L}}(L)$
as Banach spaces, respectively.
2.3 Arens product
Let
$ \mathcal {A} $
be a commutative Banach algebra. For any
$ a \in \mathcal {A} $
, let
$ \rho _a: \mathcal {A}\longrightarrow \mathcal {A} $
be the mapping defined by
$ \rho _a (b)= ba $
for
$ b \in \mathcal {A} $
. An element
$ a \in \mathcal A $
is called weakly completely continuous if
$ \rho _a $
is a weakly compact operator on
$\mathcal A $
and
$ \mathcal {A} $
is called weakly completely continuous if every
$ a \in \mathcal {A} $
is weakly completely continuous.
The Arens products on
$ \mathcal {A}^{**} $
are defined by the following three steps. For
$u, v\in \mathcal {A}$
,
$T\in \mathcal {A}^*$
and
$m,n \in \mathcal {A}^{**},$
we define
$T\cdot u,u \cdot T$
,
$m\cdot T, T\cdot m \in \mathcal {A}^*$
and
$m \square n, m \diamondsuit n \in \mathcal {A}^{**}$
as follows:
$$ \begin{align*} \langle T \cdot u , v\rangle&= \langle T , uv\rangle,\quad \langle u \cdot T , v\rangle= \langle T , uv\rangle \\ \langle m \cdot T , u \rangle &= \langle m , T \cdot u \rangle,\quad \langle T \cdot m , u\rangle = \langle m , u \cdot T \rangle\\ \langle m n , T \rangle &= \langle m\ , n \cdot T \rangle,\quad \langle m \diamondsuit n , T\rangle = \langle n , T \cdot m \rangle. \end{align*} $$
$ \mathcal {A} $
is said to be Arens regular if
$ \square $
and
$ \diamondsuit $
coincide on
$ \mathcal {A}^{**} $
.
Let
$ X $
be a closed topologically invariant subspace of
$ V N(H) $
containing
$ \lambda (\dot {e}) $
. A linear functional
$ m\in X^{*} $
is called a topologically invariant mean on X if
$$ \begin{align*} \lVert m \rVert =\langle m, \lambda({\dot{e}}) \rangle =1 \quad\mbox{and}\quad \langle m, u \cdot T\rangle = u(\dot{e}) \langle m,T \rangle \end{align*} $$
for every
$ T\in X $
,
$ u \in A(H).$
We denote by
$TIM(\widehat {H})$
the set of all topologically invariant means on
$VN(H)$
. It is shown in [Reference Shravan Kumar23] that
$ VN(H) $
always admits a topologically invariant mean.
Throughout this paper, G will denote a locally compact group,
$\pi $
a spherical projector and H an ultraspherical hypergroup associated with G and
$\pi .$
3 Uniformly continuous functionals
In this section, we study the space of all uniformly continuous functionals on
$A(H).$
We first show that this space is a
$C^*$
-algebra. The results of this section, corresponding to locally compact groups, can be found in [Reference Granirer14]. We begin with a simple lemma. This is motivated by [Reference Muruganandam22, Theorem 3.9].
Lemma 3.1. The mapping
$\pi ^*$
is a
$\text {weak}^*$
–
$\text {weak}^*$
-continuous isomorphism from
$VN(H)$
onto
$VN_{\pi }(G).$
Proof. Let
$\psi :VN_{\pi }(G)\rightarrow VN(H)$
be defined as
$\psi (T)=T|_{L^2(H)}.$
It is shown by Muruganandam [Reference Muruganandam22] that
$\psi $
is a *-isomorphism and therefore
$\psi ^{-1}$
is also a *-isomorphism. Thus, to prove this lemma, it would be enough to show that
$\pi ^*=\psi ^{-1}.$
Since
$\{\lambda _H(\,f):f\in C_c(H)\}$
is
$\text {weak}^*$
-dense in
$VN(H)$
, it would suffice to show that
$\pi ^*(\lambda _H(\,f))=\psi ^{-1}(\lambda _H(\,f))$
for all
$f\in C_c(H).$
Let
$f\in C_c(H).$
Then there exists a unique radial element
$\widetilde {f}\in C_c(G)$
such that
${\pi (\widetilde {f})=f.}$
Further,
$\psi (\lambda _G(\widetilde {f}))=\lambda _H(\,f).$
Hence, for
$u\in A(G),$
we have
$$ \begin{align*} \langle u,\pi^*(\lambda_H(\,f))\rangle &= \langle \pi(u),\lambda_H(\,f) \rangle = \int_H \pi(u)(\dot{x}) f(\dot{x})\,d\dot{x} \\ &= \int_G \pi(u)(x)\widetilde{f}(x)\,dx = \int_G u(x)\pi(\widetilde{f})(x)\,dx \\ &= \int_G u(x) \widetilde{f}(x)\,dx = \langle u,\lambda_G(\widetilde{f}) \rangle = \langle u ,\psi^{-1}(\lambda_H)(\,f) \rangle. \end{align*} $$
Hence, the lemma is proved.
Definition 3.2. Let
$ T\in VN(H) $
. Then the support of
$ T,$
denoted supp
$(T) $
, is the closed set consisting of all elements
$ x \in H $
such that for every neighbourhood
$ U_{x} $
of
$ x $
, there exists
$ v \in A(H) $
with supp
$ (v) \subseteq U_{x} $
and
$ \langle T , v\rangle \neq 0.$
Let
$UCB(\widehat {H}) $
denote the closed linear span of
$ \{u \cdot T : u \in A(H), T \in VN(H)\}.$
The elements in
$ UCB(\widehat {H}) $
are called uniformly continuous functionals on
$ A(H).$
Let
$$ \begin{align*} UC_c(\widehat{H})=\{T\in VN(H): \mbox{supp}(T)\mbox{ is compact}\}. \end{align*} $$
Remark 3.3. It can be shown as in the group case that if
$T\in UC_c(\widehat {H})$
, then there exists
$u\in A(H)$
such that
$\mbox { supp}(u)$
is compact and
$u \cdot T=T.$
Thus, it follows that
$UC_c(\widehat {H})$
is dense in
$UCB(\widehat {H}).$
Here is our first main result. This is an analogue of [Reference Granirer14, Proposition 2]. In this proof,
$\iota $
will denote the canonical inclusion of
$A(H)$
inside
$A(G).$
Theorem 3.4. The space
$ UCB(\widehat {H})$
is a
$ C^* $
-subalgebra of
$VN(H).$
Proof. Our first claim is
$\pi ^*(UC_c(\widehat {H}))=UC_c(\widehat {G})\cap VN_{\pi }(G).$
Let
$ T \in UC_c(\widehat H) $
. Then, by Remark 3.3, there exists
$ u \in A(H) \cap C_c(H) $
such that
$ u \cdot T = T $
. Let
$ \widetilde u \in A(G) \cap C_c(G) $
with
$ \pi (\,\widetilde u\,) = u $
. Then, for
$ w \in A(G) $
, we have
$$ \begin{align*} \langle w , \pi^*(T)\rangle & = \langle w , \pi^*(u \cdot T)\rangle = \langle \pi (w) , u \cdot T \rangle\\ &= \langle \pi (w) \cdot u , T \rangle = \langle \pi (w) \cdot \pi(\,\widetilde u\,), T \rangle\\ &=\langle \pi (w \cdot \pi(\,\widetilde u\,)) , T \rangle =\langle w \cdot \iota(\pi(\,\widetilde u\,)), \pi^* ( T ) \rangle\\ &=\langle w , \iota(\pi(\,\widetilde u\,)) \cdot\pi^* ( T ) \rangle. \end{align*} $$
Therefore,
$\pi ^*(T) = \iota (\pi (\,\widetilde u\,))\cdot \pi ^* ( T )\in UC_c(\widehat G) \cap VN_{\pi } (G).$
We now prove the other inclusion. Let
$\widetilde {T}\in UC_c(\widehat {G})\cap VN_{\pi }(G).$
By Lemma 3.1, there is a unique
$T\in VN(H)$
such that
$\pi ^*(T)=\widetilde {T}.$
Choose
$v\in A_{\pi }(G)$
such that
$\text {supp}(v)$
is compact and
$v\equiv 1$
on some open set containing
$\text {supp}(\widetilde {T}).$
It is clear that
$v.\widetilde {T}=\widetilde {T}$
and
$\pi (v).T\in UC_c(\widehat {H}).$
Now, for any
$w\in A(G),$
we have
$$ \begin{align*} \langle w,\pi^*(\pi(v) \cdot T) \rangle &= \langle \pi(w),\pi(v) \cdot T \rangle = \langle\pi(v) \cdot \pi(w),T \rangle \\ &= \langle \pi(\pi(v) \cdot w),T \rangle = \langle \pi(v) \cdot w,\pi^*(T) \rangle \\ &= \langle w,\pi(v) \cdot \pi^*(T) \rangle = \langle w ,v \cdot \widetilde{T} \rangle = \langle w,\widetilde{T}\rangle. \end{align*} $$
Therefore,
$\pi ^*(\pi (v) \cdot T)=\widetilde {T}.$
Since
$\pi (v) \cdot T \in UC_c(\widehat H),$
the converse follows.
Our second claim is
$\pi ^*(UCB(\widehat {H}))=UCB(\widehat {G})\cap VN_{\pi }(G).$
Let
$\psi $
be the map defined in Lemma 3.1. As
$\pi ^*$
is a *-isomorphism between
$VN(H)$
and
$VN_{\pi }(G),$
it follows that
$\pi ^*$
is a closed map. Hence, by the first claim,
$\pi ^*(UCB(\widehat {H}))$
is a closed subspace of
$VN_{\pi }(G)$
containing
$UC_c(\widehat {G})\cap VN_{\pi }(G).$
Since
$UC_c(\widehat {G})\cap VN_{\pi }(G)$
is dense in
$UCB(\widehat {G})\cap VN_{\pi }(G),$
it follows that
$\pi ^*(UCB(\widehat {H}))=UCB(\widehat {G})\cap VN_{\pi }(G).$
Thus, we have
$\psi (UCB(\widehat {G})\cap VN_{\pi }(G))=UCB(\widehat {H}).$
Since
$UCB(\widehat {G})$
and
$VN_{\pi }(G)$
are C*-algebras and also as
$\psi $
is a *-isomorphism, it follows that
$UCB(\widehat {H})$
is a C*-algebra.
Remark 3.5. The above theorem of course extends [Reference Granirer14, Proposition 2]. However, our proof makes use of the same method.
For an ultraspherical hypergroup
$H,$
let
$$ \begin{align*} C(\widehat{H}) = \{ T \in VN(H) : T C^*_{\lambda} (H) \cup C^*_{\lambda} (H) T \subseteq C^*_{\lambda} (H)\}. \end{align*} $$
Our next result says that the space
$C(\widehat {H})$
is a
$C^*$
-algebra. For the case of locally compact groups, see [Reference Granirer14]. As the proof of Proposition 3.6 follows the same lines as in [Reference Granirer14], we omit the proof.
Proposition 3.6. Let
$ H $
be an ultraspherical hypergroup. Then
$ C(\widehat {H})$
is a
$ C^* $
-subalgebra of
$ VN(H) $
containing
$ UCB(\widehat {H}) $
.
Before we proceed to the next result, here is some notation. Let
$ \mathcal {A} $
be a
$ C^* $
-algebra. We let
$ w^{\sim } $
denote the topology on
$\mathcal {A}^{*} $
such that
$ w^{\sim }- \lim \nolimits _{\alpha } f_{\alpha } =f $
in
$\mathcal {A}^{*} $
means:
-
(i)
$ \langle f_{\alpha } , a \rangle \longrightarrow \langle f , a \rangle $
for each
$ a \in \mathcal {A} $
; -
(ii)
$ \lVert f_{\alpha } \rVert \longrightarrow \lVert f \rVert $
.
We write
$$ \begin{align*} M_{\ell}(\mathcal{A}) &= \{ m \in \mathcal{A}^{**} : m \mathcal{A} \subseteq \mathcal{A} \},\\ M_{r}(\mathcal{A}) &= \{ m \in \mathcal{A}^{**} : \mathcal{A} m \subseteq \mathcal{A} \},\\ M_{\ell+r}(\mathcal{A}) &= M_{\ell}(\mathcal{A}) +M_{r}(\mathcal{A}). \end{align*} $$
Our next result gives a characterization of when the algebras
$C(\widehat {H})$
and
$VN(H)$
are equal under the assumption that the underlying group is amenable. The proof of this is an adaptation of the proof given in [Reference Granirer14] for the case of locally compact groups.
Theorem 3.7. Let
$ H $
be an ultraspherical hypergroup on an amenable locally compact group
$ G $
. Then
$ C(\widehat {H}) = VN(H) $
if and only if
$ H $
is compact.
Proof. If
$ H $
is compact, then
$ 1 \in A(H) $
and therefore
$VN(H) = 1 \cdot VN(H) \subseteq UCB(\widehat {H}) $
. Hence, by Proposition 3.6,
$C(\widehat {H})=VN(H).$
Suppose that
$C(\widehat {H})=VN(H).$
To show that H is compact, by Lemma 2.2, it is enough to show that each
$\sigma $
-compact open subhypergroup K of H is compact.
Let K be a
$\sigma $
-compact open subhypergroup of
$H.$
It follows from [Reference Muruganandam22, Definition 2.1] and [Reference Jewett15, Lemma 13.1C] that the set
$L=p^{-1}(K)$
is a noncompact
$\sigma $
-compact subgroup of
$G.$
Since G is amenable, it follows that L is amenable and hence by [Reference Degenfeld-Schonburg, Kaniuth and Lasser7, Lemma 3.7],
$A(K)$
possesses a bounded approximate identity
$(e_n)_{n\in \mathbb {N}}\subseteq P(K)\cap C_c(K)$
bounded by 1. Now, by [Reference Shravan Kumar23, Lemma 5.1], we can assume that
$(e_n)_n\subseteq A(H).$
Note that since G is amenable, by [Reference Esmailvandi and Nemati10, Theorem 3.4],
$\mathbf {1}_K\in B_{\lambda }(H).$
It is easy to see that
$e_n\longrightarrow \mathbf {1}_K$
uniformly on compacta on H and since
$(e_n)_n$
is bounded, we conclude that
$e_n\longrightarrow \mathbf {1}_K$
in
$ \sigma (B_{\lambda }(H) , C^{*}_{\lambda }(H)).$
Note that
$$ \begin{align*}\lVert e_n\rVert \longrightarrow 1 = \mathbf{1}_K(\dot{e})= \lVert \mathbf{1}_K\rVert \end{align*} $$
and so
$e_n \longrightarrow \mathbf {1}_K $
in the
$ w^{\sim } $
-topology on
$ B_{\lambda }(H) = C^{*}_{\lambda }(H)^{*}.$
Hence, it follows from [Reference Akeman and Walter1, Proposition 2] that
$$ \begin{align*} \langle m , e_n \rangle \longrightarrow \langle m , \mathbf{1}_K\rangle, \quad (m \in M_{\ell+r}(C^{*}_{\lambda}(H))). \end{align*} $$
Now, using the fact that
$C(\widehat {H})=VN(H)$
, it can be shown as in [Reference Granirer14] that
$\tilde {i}(M_{\ell +r}(C^{*}_{\lambda }(H))) = VN(H).$
As a consequence, it follows from Lemma 2.4 that the sequence
$\{e_n\}$
is a weak Cauchy sequence in
$A(H).$
Since
$A(H)$
is the predual of the von Neumann algebra
$VN(H),$
it is weakly sequentially complete and hence there exists
$u\in A(H)$
such that
$e_n\rightarrow u$
in the weak topology. As
$e_n\rightarrow \mathbf {1}_K$
uniformly on compacta, it follows that
$\mathbf {1}_K\in A(H).$
Thus, K is compact.
4 The dual of
$VN(H)$
and
$UCB(\widehat {H})$
In this section, we study the dual of
$VN(H).$
Our first two results generalize [Reference Lau17, Proposition 3.2].
Proposition 4.1. Let H be an ultraspherical hypergroup on a locally compact group
$G.$
Then
$VN(H)^{\ast }$
has a right identity if and only if
$ G $
is amenable.
Proof. Note that, by [Reference Degenfeld-Schonburg, Kaniuth and Lasser7, Lemma 3.7], amenability of G implies the existence of a bounded approximate identity in
$A(H),$
which is further equivalent to the existence of a right identity in
$ VN(H)^{\ast }$
by [Reference Bonsall and Duncan3, Proposition III.28.7, page 146].
For the converse, let
$ E $
be a right identity in
$ VN(H)^{\ast }$
. Then, by Goldstine’s theorem, there is a net
$ (e_{\alpha })_{\alpha \in I} $
in
$ A(H) $
with
$ \Vert e_{\alpha }\Vert \leq \Vert E\Vert $
such that
$$ \begin{align*} \text{weak}^{*}\text{-}\lim_{\alpha} e_{\alpha}=E. \end{align*} $$
Thus, for every
$ a \in A(H) , T \in VN(H) $
, we have
$$ \begin{align*}\langle a , T\rangle = \langle E \square a , T\rangle = \lim_{\alpha} \langle e_{\alpha} a , T\rangle. \end{align*} $$
Hence,
$ (e_{\alpha })_{\alpha \in I} $
is a bounded weak approximate identity for
$ A(H) $
. Thus, by [Reference Bonsall and Duncan3, Proposition I.11.4, page 58],
$ A(H) $
has a bounded approximate identity. Therefore,
$ G $
is amenable, by [Reference Alaghmandan2, Theorem 4.4].
Proposition 4.2. Let H be an ultraspherical hypergroup on an amenable locally compact group
$ G $
. Then
$ VN(H)^{\ast }$
has a left identity if and only if
$ H $
is compact.
Proof. If
$ H $
is compact, then
$ 1 \in A(H)$
. Therefore,
$ A(H) $
has an identity. Now, since
$ A(H) $
is in the centre of
$ VN(H)^{\ast }$
and Arens multiplication
$ (\square ) $
is weak
$ ^{*} $
continuous from the left, it follows that the identity of
$ A(H) $
is also the identity for
$ VN(H)^{\ast }$
. Conversely, if
$ H $
is not compact, then
$ UCB(\widehat {H}) $
is a closed proper subspace of
$ VN(H) $
, by Proposition 3.6 and Theorem 3.7. Hence, by the Hahn–Banach theorem, there exists a nonzero
$ m \in VN(H)^{*} $
such that
$m=0 $
on
$ UCB(\widehat {H}) $
. So,
$ m \square T =0 $
for each
$ T \in VN(H) $
. It follows that
$ n \square m =0 $
for each
$ n \in VN(H)^{*} $
. Therefore,
$ VN(H)^{*} $
cannot have a left identity.
Our next result characterizes Arens regularity of
$A(H)$
when the underlying group is amenable. For the corresponding on locally compact groups, see [Reference Lau17, Proposition 3.3]. We denote by
$ W(\widehat {H}) $
the set of all
$T $
in
$VN(H)$
such that the map
$ u\longrightarrow u \cdot T $
from
$A(H) $
into
$V N(H)$
is weakly compact.
Theorem 4.3. Let
$ H $
be an ultraspherical hypergroup for which
$A(H)$
has a bounded approximate identity. Then
$A(H)$
is Arens regular if and only if
$ H $
is finite.
Proof. Let
$ A(H) $
be Arens regular. Then, it follows from [Reference Dales and Lau5, Theorem 3.14] that
$ W(\widehat {H})=VN(H)$
and hence
$VN(H)$
has a unique topologically invariant mean. Therefore,
$ H $
is discrete by [Reference Shravan Kumar23, Theorem 1.7]. Now, since
$ A(H) $
is the predual of the von Neumann algebra
$ VN(H), $
it is weakly sequentially complete. Finally, [Reference Dales4, Theorem 2.9.39] implies that
$A(H)$
is unital, and thus H must be finite.
Conversely, if H is finite, then
$A(H)$
is finite dimensional. In particular,
$A(H)$
is reflexive. It then follows that
$VN(H)^{\ast }$
is a commutative Banach algebra, which is equivalent to saying that
$A(H)$
is Arens regular.
In the next result, we characterize semisimplicity of the algebra
$VN(H)^{\ast }$
assuming that the locally compact group G is amenable. See [Reference Lau17, Theorem 3.4] for the case of locally compact groups.
Proposition 4.4. The Banach algebra
$VN(H)^{\ast }$
is semisimple if and only if
$ H $
is finite.
Proof. Suppose that
$VN(H)^{\ast }$
is semisimple. Let
$$ \begin{align*} \mathcal{I}= \{ m\in VN(H)^{\ast}: \langle m, \lambda(\dot{e})\rangle=0 \ \text{and} \ m\square v= v(\dot{e})m \ \text{for each} \ v \in A(H)\}. \end{align*} $$
We first claim that
$\mathcal {I}$
is an ideal in
$ VN(H)^{\ast } $
. Indeed, let
$m\in \mathcal {I}$
and
$n\in VN(H)^{\ast }.$
Then,
$$ \begin{align*} \langle n\square m, \lambda(\dot{e})\rangle= \langle n,m\square \lambda(\dot{e}) \rangle =\langle n, \langle m, \lambda(\dot{e})\rangle\lambda(\dot{e})\rangle =\langle n, \lambda(\dot{e})\rangle \langle m, \lambda(\dot{e})\rangle= 0. \end{align*} $$
Similarly,
$\langle m\square n, \lambda (\dot {e})\rangle =0.$
Now, let
$v\in A(H).$
Then,
$$ \begin{align*} (n\square m)\square v=n\square(m\square v)= v(\dot{e})(n\square m). \end{align*} $$
Using the fact that
$A(H)$
is in the centre of
$VN(H)^{\ast }$
, one can show that
$$ \begin{align*} (m\square n)\square v=v(\dot{e})(m\square n). \end{align*} $$
Thus,
$\mathcal {I}$
is an ideal in
$ VN(H)^{\ast } $
.
Let
$m,n\in \mathcal {I}.$
Then, for each
$T\in VN(H)$
, we have
$$ \begin{align*} \langle m\square n , T \rangle = \langle m , n \cdot T \rangle = \langle m , \lambda(\dot{e}) \rangle \langle n, T \rangle=0, \end{align*} $$
that is,
$m\square n=0.$
In particular,
$ \mathcal {I} $
is nil and hence, by [Reference Dales4, Proposition 1.5.6],
${\mathcal {I} \subseteq Rad(VN(H)^{\ast }).}$
If
$m_1$
and
$m_2$
are any two distinct elements of
$TIM(\widehat {H}),$
then it is clear that
$m_1-m_2\in \mathcal {I}.$
In particular,
$\mathcal {I}\neq \emptyset ,$
which forces us to conclude that
$VN(H)^{\ast }$
is not semisimple, which is a contradiction. Therefore,
$TIM(\widehat {H})$
is a singleton and hence, by [Reference Shravan Kumar24, Theorem 1.7], H is discrete.
We finally claim that H is finite. We show this by contradiction. Suppose that H is not finite. Let
$\mathcal {I}$
denote the annihilator of
$UCB(\widehat {H})$
in
$VN(H)^{\ast }.$
Then, as earlier, one can show that
$\mathcal {I}$
is a nonzero ideal contained in
$Rad(VN(H)^{\ast }),$
which will again force us to conclude that
$VN(H)^{\ast }$
is not semisimple.
For the converse, if
$ H $
is finite, then
$A(H)$
is reflexive and hence
$VN(H)^{\ast }$
is semisimple.
For a Banach algebra
$ \mathcal {A }$
, we denote by
$ \text {Rad}(\mathcal A) $
the radical of
$\mathcal {A } $
. Let
$$ \begin{align*} C^{*}_{\lambda}(H)^{\perp} = \{m \in VN(H)^{\ast}: \langle m , T\rangle = 0~ \text{ for each }T \in C^{*}_{\lambda}(H) \}. \end{align*} $$
Proposition 4.5. The space
$C^{*}_{\lambda }(H)^{\perp }$
is a weak*-closed ideal in
$VN(H)^{\ast }$
containing
$\text {Rad}(VN(H)^{\ast }).$
Furthermore, the Banach algebra
$ VN(H)^{\ast }/C^{\ast }_{\lambda }(H)^{\perp } $
is isometrically isomorphic to
$ B_{\lambda }(H). $
Proof. Let
$ n \in VN(H)^{\ast }$
and let
$T\in C^{*}_{\lambda }(H). $
Then,
$n\square T \in C^{*}_{\lambda }(H) $
by [Reference Esmailvandi and Nemati10, Proposition 4.6]. Hence, for each
$ m\in C^{*}_{\lambda }(H)^{\perp }$
and
$T\in C^{*}_{\lambda }(H),$
we have
$$ \begin{align*} \langle m\square n, T\rangle = \langle m, n \square T\rangle =0. \end{align*} $$
This implies that
$C^{*}_{\lambda }(H)^{\perp }$
is a right ideal. Since
$C^{*}_{\lambda }(H)^{\perp }$
is weak*-closed by [Reference Megginson19, Proposition 2.6.6], a simple weak
$ ^*$
approximation argument gives that
$C^{*}_{\lambda }(H)^{\perp }$
is an ideal.
Let
$P:VN(H)^{\ast }/C^{\ast }_{\lambda }(H)^{\perp }\longrightarrow B_{\lambda }(H)$
be defined by
$$ \begin{align*} P(m+C^{*}_{\lambda}(H)^{\perp})(T) =\langle \psi, T\rangle \quad(T \in C^{*}_{\lambda}(H)), \end{align*} $$
where
$ \psi \in B_{\lambda }(H) $
is the restriction of
$ m $
on
$ C^{*}_{\lambda }(H). $
Then, since
$ B_{\lambda }(H)= C^{*}_{\lambda }(H)^*$
, the map P is an isometric isomorphism by [Reference Megginson19, Theorem 1.10.16]. Since the Arens product on
$B_{\lambda }(H)$
agrees with the pointwise multiplication [Reference Esmailvandi and Nemati10, Proposition 4.12], it follows that P is an algebra isomorphism.
Finally, as P is an epimorphism of the Banach algebra
$VN(H)^{\ast }/C^{\ast }_{\lambda }(H)^{\perp }$
onto the semisimple Banach algebra
$B_{\lambda }(H),$
it follows from [Reference Bonsall and Duncan3, Proposition III. 25.10, page 131] that
$\text {Rad} (VN(H)^{\ast })\subseteq C^{\ast }_{\lambda }(H)^{\perp }.$
Proposition 4.6. The spaces
$C^{\ast }_{\lambda }(H)^{\perp }$
and
$\text {Rad}(VN(H)^{\ast })$
are equal if and only if the ultraspherical hypergroup H is discrete.
Proof. If
$ H $
is discrete, then
$ C^{*}_{\lambda }(H)= UCB(\widehat {H}) $
by [Reference Esmailvandi and Nemati10, Proposition 4.4]. Now let
$ m,n \in C^{*}_{\lambda }(H)^{\perp }$
and let
$ (v_{\alpha }) $
be a net in
$ A(H) $
such that
$\text {weak}^*$
-
$\lim \nolimits _{\alpha }v_{\alpha }=m.$
Then we have
$$ \begin{align*} \langle m\square n , T\rangle = \lim\limits_{\alpha}\langle v_{\alpha} \square n , T\rangle = \lim\limits_{\alpha}\langle n , v_{\alpha} \cdot T\rangle =0 \quad (T\in VN(H) ), \end{align*} $$
and hence
$ (C^{*}_{\lambda }(H)^{\perp })^2=\{0\},$
which implies that
$ C^{*}_{\lambda }(H)^{\perp } \subseteq \mathrm {Rad} (VN(H)^{\ast }).$
It then follows from Proposition 4.5 that
$ C^{*}_{\lambda }(H)^{\perp } = \mathrm {Rad} (VN(H)^{\ast }).$
For the converse, suppose that
$ H $
is not discrete. Then
$ \lambda (\dot {e}) \notin C^{*}_{\lambda }(H) $
by [Reference Esmailvandi and Nemati10, Corollary 4.8]. Now choose
$m\in VN(H)^{\ast }$
such that
$\langle m , \lambda (\dot {e}) \rangle \neq 0$
and
$ \langle m , T \rangle = 0$
for each
$ T \in C^{*}_{\lambda }(H). $
If
$ C^{*}_{\lambda }(H)^{\perp } = \mathrm {Rad} (VN(H)^{\ast })$
, then
$ 0 \neq m \in \mathrm {Rad} (VN(H)^{\ast }),$
which is impossible since
$\text {Rad} (VN(H)^{\ast }) \subseteq \text {ker} \lambda (\dot {e}).$
We finish this section with an analogue of Proposition 4.4 for
$UCB(\widehat {H})^{\ast }.$
For the corresponding result for the case of locally compact groups, see [Reference Lau, Loy and Willis18, Theorem 5.6].
Proposition 4.7. The Banach algebra
$ UCB(\widehat {H})^{\ast }$
is semisimple if and only if
$ H $
is discrete.
Proof. If
$ H $
is discrete, then
$ UCB(\widehat {H}) = C^{\ast }_{\lambda }(H) $
by [Reference Esmailvandi and Nemati10, Proposition 4.6] and hence
$ UCB(\widehat {H})^{\ast } = B_{\lambda }(H)$
which is semisimple.
For the converse, let
$$ \begin{align*} \mathcal{I}= \{ m\in UCB(\widehat{H})^{\ast}: \langle m, \lambda(\dot{e})\rangle=0 \text{ and } m\square v= v(\dot{e})m \ \text{for each} \ v \in A(H)\}. \end{align*} $$
By repeating the arguments as in the proof of Proposition 4.4, one can deduce that
$\mathcal {I}$
is a closed ideal of
$UCB(\widehat {H})^{\ast }$
and is contained in
$\text {Rad}(UCB(\widehat {H})^{\ast }).$
However then,
$\mathcal {I}=0$
by semisimplicity of
$UCB(\widehat {H})^{\ast }.$
By [Reference Esmailvandi and Nemati10, Lemma 4.5], the set of topologically invariant means on
$UCB(\widehat {H})$
is nonempty. Further, as the difference of any two topologically invariant means on
$UCB(\widehat {H})$
lies in
$\mathcal {I},$
we conclude that
$UCB(\widehat {H})$
has a unique topologically invariant mean. Hence, by [Reference Esmailvandi and Nemati10, Proposition 4.6], H is discrete.
5 Unit elements
In this section, we study the unit elements in
$VN(H)^{\ast }$
in the spirit of [Reference Miao20]. The proofs given are modifications of the proofs given in [Reference Miao20]. Our main aim in this section is to characterize when an element of the double dual of
$A(H)$
belongs to
$A(H).$
Let
$ H $
be an ultraspherical hypergroup on a locally compact group
$ G $
. Let
$ K$
be an open and closed subhypergroup of
$ H $
. Then, by [Reference Shravan Kumar23, Lemma 5.1], the restriction map
$ u\longrightarrow u|_{K} $
is a norm decreasing algebra homomorphism from
$ A(H) $
onto
$ A(K) $
, denoted by
$ P_{K} $
.
Let
$ H $
be an ultraspherical hypergroup on an amenable locally compact group
$ G, $
let
$ \mathcal {E}= \mathcal {E}(A(H))$
denote the set of all right identities of the Banach algebra
$ A(H)^{**} $
that are the cluster points of all approximate identities in
$ A(H) $
bounded by
$ 1 $
.
Remark 5.1. If
$ \mathcal X $
is a Banach space and if
$ P $
is a bounded projection, then
$ P^* $
is a projection and
$ P^*(\mathcal X^*) $
is identified by
$P(\mathcal X)^* $
.
Definition 5.2. Let
$ \mathcal {B} $
be a closed subalgebra of a Banach algebra
$ \mathcal {A} $
and let
$ {P: \mathcal {A}\longrightarrow \mathcal {B} }$
be a bounded projection. Let
$ E $
be a right unit of
$ \mathcal {B}^{**} $
in
$ \mathcal {A}^{**}. $
A right unit
$ \widetilde {E} $
of
$ \mathcal {A}^{**}$
is called an extension of
$ E $
if
$ \langle \widetilde {E} , P^*(\,f) \rangle = \langle E , P^*(\,f) \rangle $
holds for all
$ f \in \mathcal {A}^*.$
Lemma 5.3. Let
$ H $
be an ultraspherical hypergroup on an amenable locally compact group
$ G $
. Let
$ K $
be an open subhypergroup of
$ H $
. Then every right unit of
$ A(K)^{**} $
in
$ A(H)^{**} $
can be extended to a right unit of
$ A(H)^{**}.$
In particular,
$A(H)^{**}$
has a unique right unit if and only if
$ H $
is compact.
Proof. Since
$ G $
is amenable,
$A(H)$
has a bounded approximate identity, by [Reference Degenfeld-Schonburg, Kaniuth and Lasser7, Lemma 3.7]. Since
$ A(K) $
is a closed ideal of
$ A(H) $
and
$ P_{K}:A(H)\longrightarrow A(K) $
is a bounded projection which is also a multiplier, it now follows from [Reference Miao20, Theorem
$2.3$
] that every right unit of
$A(K)^{**}$
in
$A(H)^{**}$
can be extended to a right unit of
$A(H)^{**}.$
Let
$ E $
be a right identity of
$ A(H)^{**} $
and
$ (e_{\alpha }) $
be a bounded approximate identity of
$ A(H) $
associated with
$ E $
. If
$ H $
is compact, then
$ 1 \in A(H) $
and
$\lim _{\alpha } \Vert e_{\alpha } -1\Vert =0 $
. Then, for each
$ T \in A(H)^* $
and each
$ m \in A(H)^{**} $
, we have
$$ \begin{align*} \langle E \square m , T \rangle &= \lim_{\alpha} \langle e_{\alpha} \square m , T\rangle \\ &= \lim_{\alpha} \langle e_{\alpha} , m \cdot T\rangle \\ &= \lim_{\alpha} \langle m \cdot T , 1\rangle \\ &=\langle m , T \rangle. \end{align*} $$
Thus,
$ E $
is also a left unit for
$ (A(H)^{**} , \square ) $
, and hence
$ E $
is unique.
If
$ H $
is not compact, then there exists an open
$ \sigma $
-compact and noncompact subhypergroup
$ K $
of
$ H $
, by Lemma 2.2. It follows from the definition of the spherical hypergroup and by [Reference Jewett15, Lemma 13.1C] that the set
$ L=p^{-1}(K) $
is a
$ \sigma $
-compact and noncompact subgroup of
$G.$
Hence,
$A(L)$
has a sequential bounded approximate identity, which implies that
$A(K)$
must have a sequential bounded approximate identity
$\{e_n\}$
, by [Reference Degenfeld-Schonburg, Kaniuth and Lasser7, Lemma 3.7]. Towards a contradiction, suppose that
$ \{e_n \} $
has a unique weak
$ ^* $
cluster point denoted by
$ E $
. Then
$ \{e_n \} $
must be a weakly Cauchy sequence, and since
$ A(K) $
is weakly sequentially complete, we have
$\text {weak} $
-
$\lim \nolimits _{n} e_n = E. $
Therefore,
$ A(K) $
is unital, which is impossible since
$ K $
is not compact. Thus,
$ A(K)^{**} $
at least has two distinct right identities. Now, let
$ E_1 $
and
$ E_2 $
be distinct right units of
$ A(K)^{**} $
in
$ A(H)^{**} $
. Then, by [Reference Miao20, Theorem
$2.3$
],
$ E_1 $
and
$ E_2 $
can be extended to distinct right units for
$ A(H)^{**} $
, which is a contradiction.
Lemma 5.4. Let H be an ultraspherical hypergroup and let
$m\in A(H)^{**}.$
Suppose that for every open
$\sigma $
-compact subhypergroup K of H,
$P^{**}_{K}(m)\in A(K)$
. Then, for each
$n\in \mathbb {N},$
there exists a compact subset
$K_n$
of H such that
$|\langle m , T \rangle |<({1}/{n})$
for
$T\in UCB(\widehat {H})$
with
$\lVert T\rVert \leq 1$
and
$\text {supp}(T) \subseteq H\setminus K_n.$
Proof. Suppose to the contrary that the statement is false. By the same argument as in the proof of [Reference Miao20, Lemma 3.1], we can construct a sequence
$\{T_n\}$
in
$UCB(\widehat {H})$
and a sequence of symmetric, relatively compact neighbourhoods
$\{U_n\}$
of
$\dot {e}$
in H such that
$ U_n^2\subseteq U_{n+1} $
and:
-
(1)
$\text {supp}(T_n)\subseteq U_n$
and
$\text {supp}(T_{n+1})\subseteq H\setminus \overline {U_n}$
; -
(2)
$\lVert T_n\rVert \leq 1$
and
$|\langle m , T_n \rangle | \geq \epsilon .$
Let
$K=\bigcup _n U_n.$
Since
$U_n^2\subseteq U_{n+1}$
for each
$n,$
it follows that K is an open
$\sigma $
-compact subhypergroup of
$H.$
Therefore, by hypothesis,
$P^{**}_{K}(m)\in A(K).$
Now, by the density of the subspace
$A(H)\kern-1pt\cap\kern-1pt C_c(H)$
in
$ A(H),$
there exists an element
$v\in A(H)\kern-1pt\cap\kern-1pt C_c(H)$
such that
$\lVert P^{**}_{K}(m) -v\rVert _{A(H)}<{\epsilon }/{2}$
and
$\text {supp}(v)\subseteq K.$
Let V be a relatively compact neighbourhood of
$\text {supp}(v)$
in
$K.$
Then, for any
$T \in VN(H)$
with
$\lVert T\rVert \leq 1$
and
$\text {supp}(T) \subseteq H\setminus \overline {V},$
we have
$$ \begin{align*} \lvert \langle P^{**}_{K}(m) , T\rangle\rvert \leq\lvert \langle P^{**}_{K}(m)-v , T\rangle\rvert + \lvert \langle v , T\rangle\rvert \leq \lVert P^{**}_{K}(m) -v\rVert_{A(H)}<\frac{\epsilon}{2}. \end{align*} $$
Since
$ \overline {V}\subseteq K $
is compact and
$ \{U_n\} $
is an increasing sequence of open sets, there is an
$ n \in \mathbb {N} $
such that
$ \overline {V}\subseteq U_n $
. Hence, the inequality
$ \lvert \langle P^{**}_{K}(m) , T_{n+1}\rangle \rvert \leq {\epsilon }/{2} $
follows from the fact that
$\text {supp}(T_{n+1})\subseteq H\setminus \overline {U_n} \subseteq H\setminus \overline {V}.$
Now, we show that
$P^{*}_{K}(T_{n+1})=T_{n+1}. $
Let
$ u \in A(H)\cap C_c(H) $
be such that
$ \text {supp}(u)\cap K^{c}\neq \varnothing $
. Let
$ v \in A(H)\cap C_c(H) $
be such that
$ v(\dot {x})=1 $
for each
$ \dot {x}\in \text {supp}(u)\cap K^{c}$
and
$ \text {supp}(v) \subseteq K^c $
. Then,
$$ \begin{align*} \langle T_{n+1} , u\rangle &= \langle T_{n+1} , u|_{K}\rangle+\langle T_{n+1} , uv\rangle\\ &=\langle T_{n+1} , u|_{K}\rangle+\langle v\cdot T_{n+1} ,u\rangle \\ &=\langle T_{n+1} , u|_{K}\rangle\\ &= \langle T_{n+1} ,P_K (u)\rangle\\ &= \langle P^{*}_{K}(T_{n+1}) , u\rangle, \end{align*} $$
and since
$ \text {supp}(T_{n+1}) \cap \text {supp}(v)= \varnothing $
, we have
$ v\cdot T_{n+1}=0 $
, so the third equality holds. Hence, a simple approximation argument gives that
$ \langle T_{n+1} , u\rangle = \langle P^{*}_{K}(T_{n+1}) , u\rangle $
for all
$ u \in A(H). $
Therefore,
$$ \begin{align*} \lvert \langle P^{**}_{K}(m) , T_{n+1}\rangle \rvert = \lvert \langle m , P^{*}_{K}(T_{n+1}) \rangle \rvert = \lvert \langle m , T_{n+1} \rangle \rvert \geq \epsilon, \end{align*} $$
which is a contradiction.
Proposition 5.5. Let
$m\in A(H)^{**}.$
Suppose that for every open
$\sigma $
-compact subhypergroup K of H,
$P^{**}_{K}(m)$
is in
$A(K)$
. Then the restriction of m to
$UCB(\widehat {H})$
is in
$ A(H).$
Proof. By Lemma 5.4, for each
$n\in \mathbb {N}$
, there exists a compact subset
$K_n$
of H such that
$|\langle m , T \rangle |<({1}/{n})$
for
$T\in UCB(\widehat {H})$
with
$\lVert T\rVert \leq 1$
and supp
$(T) \subseteq H\setminus K_n.$
Let K be an open
$\sigma $
-compact subhypergroup of H containing all
$K_n$
. Then for each
$n\in \mathbb {N}$
,
$H\setminus K \subseteq H\setminus K_n.$
Hence, for each
$T \in UCB(\widehat {H})$
with
$\text {supp}(T) \subseteq H\setminus K,$
we have
$\langle m, T\rangle =0.$
Let
$T \in UCB(\widehat {H})$
,
$\dot {x}\in K,$
and let
$U_{\dot {x}}\subseteq K$
be a neighbourhood of
$ \dot {x} $
. Then for each
$ u \in A(H) $
with
$\text {supp}(u)\subseteq U_{\dot {x}} $
, we have
$P_K(u)=u $
. Consequently,
$$ \begin{align*} \langle T- P^{*}_{K}(T) , u \rangle =\langle T , u\rangle - \langle P^{*}_{K}(T) , u \rangle =0, \end{align*} $$
which implies that
$\text {supp}(T- P^{*}_{K}(T)) \subseteq H\setminus K. $
Therefore, for each
$ T \in UCB(\widehat {H}) $
, we have
$$ \begin{align*} \langle m , T\rangle= \langle m , T-P^{*}_{K}(T)\rangle+ \langle m , P^{*}_{K}(T)\rangle =\langle m , P^{*}_{K}(T)\rangle = \langle P^{**}_{K}( m) , T\rangle. \end{align*} $$
Since
$ P^{**}_{K}(m) $
is in
$ A(K)\subseteq A(H), $
the restriction of
$ m $
to
$ UCB(\widehat {H}) $
is in
$ A(H). $
With the preceding proposition at hand, we can now deduce the main result of this section.
Theorem 5.6. Let
$ H $
be an ultraspherical hypergroup on an amenable locally compact group
$ G $
. Then for an element
$ m \in A(H)^{**} ,\ m\in A(H)$
if and only if
$ A(H)\square m \subseteq A(H) $
and
$\ E \square m = m $
for all
$ E $
in
$ \mathcal {E}$
.
Proof. If
$ m\in A(H) $
, then
$ A(H)\square m \subseteq A(H) $
and for any
$ E $
in
$ \mathcal {E}, \ E \square m = m. $
We now prove the converse. Suppose that
$m \in A(H)^{**}$
is such that m satisfies the assumptions. If H is compact, then
$\mathbf {1}_H \in A(H),$
and hence
$m= \mathbf {1}_H \square m \in A(H).$
Let H be noncompact and let K be a
$\sigma $
-compact, open subhypergroup of
$H.$
Let
$\{K_i\}$
be an increasing sequence of compact subsets of K such that
$K=\bigcup _i K_i.$
Let
$L= p^{-1}(K).$
Then L is a
$\sigma $
-compact, open and closed subgroup of G and
$L= \bigcup _i p^{-1} (K_i).$
It follows from the amenability of L and [Reference Kaniuth and Lau16, Corollary
$\mathrm{2.7.3}$
] that there exists a sequence
$ \{u_i\} $
in
$ A(L) $
such that for each
$ i $
,
$ u_i=1 $
on
$ p^{-1} (K_i) $
and
$ \lVert u_i\rVert _{A(L)}\leq 1+{1}/{i} $
. Therefore,
$ u_i \longrightarrow \mathbf {1}_L $
in the
$ \sigma (B(L) , C^{*}(L)) $
topology. Hence, it follows from [Reference Kaniuth and Lau16, Theorem
$\mathrm{3.7.7}$
] that
$ \lVert u_i v-v\rVert _{A(L)}\longrightarrow 0 $
for all
$v \in A(L).$
Therefore, by identifying
$ A(K) $
with
$ A_{\pi |L}(L), $
the sequence
$ \{\pi (u_i)\} $
is in
$ A(K).$
Now, if
$ \dot {x}\in K_i $
, then
$ O_x\subseteq p^{-1}(K_i). $
So
$ u_i=1 $
on
$ O_x $
and since
$ \pi (\delta _x) $
is a probability measure, we have
$$ \begin{align*} \pi(u_i)(\dot{x})= \langle u_i, \pi(\delta_x) \rangle= \int_{O_x}^{}u_i(z)\,d\pi(\delta_x)(z)=1. \end{align*} $$
Further, for each
$v \in A(K),$
$$ \begin{align*} \lVert \pi (u_i) v-v\rVert_{A(K)}&= \lVert \pi (u_i) \pi (v)-\pi(v)\rVert_{A(K)}\\&= \lVert \pi (u_i v-v)\rVert_{A(K)}\\ &\leq \lVert u_i v-v\rVert_{A(L)}\longrightarrow 0. \end{align*} $$
By hypothesis,
$\pi ( u_i) \square m \in A(H) $
for all
$ i $
. Then, by using Lemma 5.3, we can show as in [Reference Miao20, Theorem 3.2] that
$ \{ \pi ( u_i) \square m \} $
is a weakly Cauchy sequence. Since
$ A(H) $
is the predual of the von Neumann algebra
$VN(H),$
it is weakly sequentially complete, and thus
$\{ \pi ( u_i) \square m\}$
converges weakly to a point in
$A(H).$
Let
$f\in L^1(H)$
with compact support. Using the fact that each
$\pi ( u_i)\in A(K),$
we have
$\langle \pi ( u_i) \square m , \lambda (f )\rangle = \langle \pi ( u_i) \square m , \lambda (\mathbf {1}_K f )\rangle .$
Now, for each
$u\in A(H)$
,
$$ \begin{align*} \langle P_K^{*}(\lambda(((\mathbf{1}_H - \mathbf{1}_K)f ))) , u \rangle = \langle \lambda((\mathbf{1}_H - \mathbf{ 1}_K)f) , P_K (u) \rangle =0. \end{align*} $$
Also,
$$ \begin{align*} \langle P_K^{*}(\lambda((\mathbf{1}_Kf))\cdot \pi( u_i)) , u \rangle &= \langle \lambda(\mathbf{1}_Kf) , \pi( u_i) P_K (u) \rangle\\ &= \langle \lambda(\mathbf{1}_Kf) , P_K (\pi( u_i)) u \rangle \\ &= \langle \lambda(\mathbf{1}_Kf) \cdot P_K (\pi( u_i)) , u \rangle. \end{align*} $$
Therefore,
$$ \begin{align*} \langle \pi( u_i) \square m , \lambda(\,f) \rangle &= \langle \pi( u_i) \square m , \lambda(\mathbf{1}_K f) \rangle= \langle m , \lambda(\mathbf{1}_K f) \cdot \pi( u_i)\rangle\\ &=\langle m , \lambda(\mathbf{1}_Kf)\cdot P_K (\pi( u_i)) \rangle =\langle m , P_K^{*}(\lambda(\mathbf{1}_Kf)\cdot \pi( u_i))\rangle\\ &=\langle P_K^{**}(m) , \lambda(\mathbf{1}_Kf)\cdot \pi( u_i)\rangle \longrightarrow \langle P_K^{**}(m) , \lambda(\mathbf{1}_Kf)\rangle\\ &=\langle P_K^{**}(m) , \lambda(\,f)\rangle, \end{align*} $$
since
$\text {supp}(\mathbf {1}_Kf) \subset K_i$
for some
$i.$
Thus,
$\pi ( u_i) \square m\xrightarrow {w} P_K^{**}(m),$
which implies that
$ P_K^{**}(m) \in \overline {A(H)}^w=A(H). $
Since each
$\pi ( u_i) \square m \in A(K) $
and
$ A(K) $
is a closed convex subset of
$ A(H), $
we have
$ P_K^{**}(m) \in A(K).$
Let
$ m|_{UCB(\widehat {H})}=u $
. Then, by Proposition 5.5,
$ u \in A(H).$
Since G is amenable,
$A(H)$
has a bounded approximate identity, say
$\{ e_{\alpha }\}.$
It is easy to see that
$e_{\alpha } \square m \longrightarrow E\square m $
in the
$\sigma (A(H)^{**} , A(H)^{*})$
-topology for some
$ E \in \mathcal {E} $
. By assumption
$E\square m = m.$
Hence,
$e_{\alpha } \square m \longrightarrow m.$
Since
$e_{\alpha } \square m = e_{\alpha } u$
and
$e_{\alpha } u \longrightarrow u$
in norm, thus
$u= m.$
In fact, for each
$ T\in VN(H),$
we have
$$ \begin{align*} \langle e_{\alpha} \square m , T \rangle = \langle m ,e_{\alpha} \cdot T \rangle = \langle u ,e_{\alpha} \cdot T \rangle =\langle u e_{\alpha} , T \rangle, \end{align*} $$
so
$e_{\alpha } \square m= e_{\alpha } u $
. Therefore,
$ m \in A(H) $
.
Corollary 5.7. Let
$ H $
be a discrete ultraspherical hypergroup on an amenable locally compact group
$ G $
and
$m \in A(H)^{**} $
. Then,
$m \in A(H)$
if and only if
$ \ E \square m = m $
for each
$ E \in \mathcal {E}.$
Proof. If
$ H $
is discrete, then
$ A(H) $
is an ideal in
$ A(H)^{**} $
by [Reference Esmailvandi and Nemati11, Proposition
$2.7$
]. Hence, the result follows from Theorem 5.6.
Corollary 5.8. Let
$ H $
be an ultraspherical hypergroup on an amenable locally compact group
$ G $
. If
$ m \in \mathfrak {Z}(A(H)^{**} ) $
and
$ A(H)\square m\subseteq A(H), $
then
$ m \in A(H). $
In particular, if
$ H $
is discrete, then
$ \mathfrak {Z}(A(H)^{**} )=A(H). $
Acknowledgements
The authors would like to thank the anonymous referee for his/her useful comments and also for pointing out the mistakes which helped in improving the quality of the paper. The first author would like to thank Michael Leinert for providing him the paper [Reference Jewett15]. This research for the second author was in part supported by a grant from IPM (No. 1401170411). The third author would like to thank the Science and Engineering Board, India, for the MATRICS project fund with the Project No:MTR/2018/000849.
