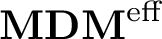1 Introduction
The Gysin triangle (see [Reference Voevodsky26, Prop.3.5.4]) in Voevodsky’s category of motives
$\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$
is a remarkable result which is a motivic analogue of the purity theorem of étale cohomology [Reference Artin, Grothendieck and Verdier1, Reference Bloch and Esnault4, XVI, Thm.3.7]. In this article, we shall prove a generalisation of Voevodsky’s theorem in the setting of motives of modulus pairs. Our theorem is an analogue of the Gysin triangle of (log-)crystalline cohomology (see [Reference Nakkajima and Shiho21, exact sequence (2.18.8.2)]). As a corollary, we give a remarkable equivalence which claims that the essential parts of a motive with modulus are the p-torsion part and the Voevodsky part. Our proof uses the smooth blow-up formula in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
(see [Reference Kahn, Saito and Yamazaki17]) and a new weighted smooth blow-up formula (see Section 4).
To formulate his Gysin triangle, Voevodsky uses a smooth variety and a smooth closed subvariety. To formulate our Gysin triangle in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
we replace the smooth variety by a modulus pair with smooth total space and a modulus whose support is a strict normal crossing divisor and replace the closed subvariety by a prime smooth Cartier divisor which intersects the modulus properly.
Situation 1.1. Let
$\overline {M}$
be a smooth scheme over a field,
$M^\infty \subset \overline {M}$
an effective Cartier divisor and
$\overline {Z} \subset \overline {M}$
a smooth integral closed subscheme not contained in
$M^\infty $
such that the support
$|M^{\infty } + \overline {Z}|$
is a strict normal crossings divisor on
$\overline {M}$
. Write
$Z^\infty $
for the intersection product of
$M^\infty $
and
$\overline {Z}$
.
Our main goal is the following two theorems.
Theorem 1.2 Tame Gysin triangle
In the notation of Situation 1.1, there exists a distinguished triangle
$$ \begin{align*} \underline{\mathbf{M}}(\overline{M},M^\infty + \overline{Z}) \to \underline{\mathbf{M}}(\overline{M},M^\infty) \to \underline{\mathbf{M}}(\overline{Z},Z^\infty)(1)[2] \to \underline{\mathbf{M}}(\overline{M},M^\infty + \overline{Z})[1], \end{align*} $$
in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
.
Theorem 1.2 leads to the following.
Corollary 1.3 Theorem 7.1
Let X be a smooth variety over k which has a compactification
$\overline {X}$
such that
$\overline {X}$
is smooth and
$|\overline {X}\backslash X|$
is a strict normal crossing divisor on
$\overline {X}$
; then the unit
$$ \begin{align*} \underline{\mathbf{M}}(\overline{X},|\overline{X}\backslash X|_{{\operatorname{red}}}) \to {\underline{\omega}}^{{\operatorname{eff}}}({\textbf{{M}}}(X)) \end{align*} $$
of the adjunction
${\underline {\omega }}_{{\operatorname {eff}}}:\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}} \rightleftarrows \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}:{\underline {\omega }}^{\operatorname {eff}}$
is an isomorphism.
Moreover, as an application of this corollary we get the following equivalence, which philosophically has been expected since the beginning of the theory of motives with modulus.
Corollary 1.4 Corollary 8.8
If the base field k has characteristic
$p \geq 2$
for any modulus pair
$(\overline {M},M^{\infty })$
such that
$\overline {M}$
is smooth and
$M^\infty _{\operatorname {red}}$
is strict normal crossing, then there is an isomorphism in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}(k,\mathbb {Z}[1/p])$
$$ \begin{align*} {\underline{\mathbf{M}}(\overline{M},M^{\infty})}_{\mathbb{Z}[1/p]} \simeq {\underline{\mathbf{M}}(\overline{M},M^\infty_{\operatorname{red}})}_{\mathbb{Z}[1/p]}. \end{align*} $$
Definition 1.5. We define
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
as the smallest full triangulated subcategory of
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
which contains all of the proper modulus pairs and is closed under small coproducts.
The category
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
is equivalent to the category in [Reference Kahn, Miyazaki, Saito and Yamazaki14, Definition 3.2.4] because of [Reference Kahn, Miyazaki, Saito and Yamazaki14, Threorem 3.3.1(2), Theorem 5.2.2].
Theorem 1.6 Theorem 8.9
If the base field k has characteristic
$p \geq 2$
and admits log resolution of singularities and R is commutative ring containing
$1/p$
, then
$$ \begin{align*} \operatorname{\mathbf{MDM}^{\operatorname{eff}}}(k,R) \simeq \operatorname{\mathbf{DM}}^{\operatorname{eff}}(k,R). \end{align*} $$
Let us discuss the relationship between our results and other work.
1.1 Relationship to the Gysin triangle for (log-)crystalline cohomology
First let us state the Gysin triangle for crystalline cohomology and a comparison theorem between rigid cohomology and crystalline cohomology.
Theorem 1.7 [Reference Nakkajima and Shiho21, Eq.2.18.8.2], [Reference Shiho22]
Let W be the Witt ring of the base field, let K be the fractional field of W and set
$S=\operatorname {Spec} W$
. Consider the pushforward functors
$f_{-/S}: Sh(-/S)_{\text {crys}}\to Sh_{\operatorname {Zar}}(S)$
from the (log-)crystalline sites of log schemes over S to the Zariski site of S and the structure sheaves
$\mathcal {O}_{-/S}$
on
$(-/S)_{\text {crys}}$
. In the notation of Situation 1.1, there is a long exact sequence of Zariski sheaves on S:
$$ \begin{align*} \cdots \rightarrow R^{n-2}f_{\overline{Z}/S} &(\mathcal{O}_{\overline{Z}/W})(-1) \rightarrow R^{n}f_{\overline{M}/S}(\mathcal{O}_{\overline{M}/S}) \\[3pt] &\rightarrow R^{n}f_{(\overline{M},\overline{Z}/S)}(\mathcal{O}_{(\overline{M},\overline{Z})/S}) \rightarrow R^{n-1}f_{\overline{Z}/S}(\mathcal{O}_{\overline{Z}/S})(-1) \rightarrow\cdots \end{align*} $$
and we have a natural and functorial isomorphism
$$ \begin{align*} comp: H^i_{\text{crys}}((\overline{M},\overline{Z})/W)\otimes_{W}K \simeq H^i_{\text{rig}}(\overline{M}\backslash \overline{Z}/K). \end{align*} $$
Expectation 1.8. We expect that there exists an exact ‘crystalline realisation functor’
$$\begin{align*}\mathbb{R}\Gamma_{crys}:\operatorname{\mathbf{MDM}^{\operatorname{eff}}}(k,W) \to D(W)\end{align*}$$
satisfying
$$ \begin{align*} \mathbb{R}\Gamma_{crys}\bigl(\underline{\mathbf{M}}(\overline{M},\emptyset)\bigr) \simeq \mathbb{R}\Gamma\bigl(S,\mathbb{R}f_{\overline{M}/S}(\mathcal{O}_{\overline{M}/S})\bigr) \text{ and } \end{align*} $$
$$ \begin{align*} \mathbb{R}\Gamma_{crys}\bigl(\underline{\mathbf{M}}(\overline{M},\overline{Z})\bigr) \simeq \mathbb{R}\Gamma\bigl(S,\mathbb{R}f_{(\overline{M},\overline{Z})/S}(\mathcal{O}_{(\overline{M},\overline{Z})/S})\bigr). \end{align*} $$
In this case, the tame Gysin triangle Theorem 1.2 would be a motivic lifting of the first claim of Theorem 1.7.
Now consider rigid cohomology. Milne–Ramachandran [Reference Miyazaki19] constructFootnote 1 a rigid realisation
$$ \begin{align*} \mathbb{R}\Gamma_{rig} :\operatorname{\mathbf{DM}}^{\operatorname{eff}}(k,K) \to D(K) \end{align*} $$
satisfying
$$ \begin{align*} \mathbb{R}\Gamma_{rig}(M(X)) = \mathbb{R}\Gamma_{rig}(X) \end{align*} $$
for X smooth where the right-hand side is Besser’s rigid complex. By Corollary 1.6 the functor
${{\underline {\omega }}^{\operatorname {eff}}}_K:\operatorname {\mathbf {DM}}^{\operatorname {eff}}(k,K)\to \operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}_{{\operatorname {prop}}}(k,K) $
is an equivalence, with quasi-inverse
${\underline {\omega }}_{{\operatorname {eff}}, K}$
. Since
${\underline {\omega }}_{{\operatorname {eff}}}$
sends
$\underline {\mathbf {M}}(\overline {M},M^\infty _{\operatorname {red}})$
to
${\textbf {{M}}}(\overline {M} \backslash M^\infty )$
, the second claim of Theorem 1.7 produces a natural isomorphism of functors
In this light, if Expectation 1.8 holds, then the equivalence
${\underline {\omega }}^{\operatorname {eff}}$
of Corollary 1.6 will be a motivic lifting of the isomorphism
$comp$
of Theorem 1.7.
Remark 1.9. Binda–Park–Østvær constructed in [Reference Binda and Merici6, Section 1.3.2] a framework which is analogous to
$\operatorname {\mathbf {\underline {M}DM}}^{{\operatorname {eff}}}$
called log motives, and they are pursuing the construction of a log-crystalline realisation functor in their framework. It would be very interesting to investigate the relationship between log motives and motives with modulus in the future.
1.2 Relationship to Miyazaki’s works on higher Chow groups with modulus
In [Reference Binda and Saito8] Binda–Saito define higher Chow groups with modulus generalising additive higher Chow groups (see [Reference Binda and Saito9]). Miyazaki proves that after inverting p, higher Chow groups with modulus become independent of the modulus.
Theorem 1.10. [Reference Milne and Ramachandran20, Theorem 5.1] If the base field has characteristic p, then for any modulus pair
$(\overline {M},M^\infty )$
, we have an isomorphism
$$ \begin{align*}{\operatorname{CH}}^i(\overline{M}|M^\infty,j,\mathbb{Z}[1/p]) \simeq {\operatorname{CH}}^i(\overline{M}|M_{\operatorname{red}}^\infty,j,\mathbb{Z}[1/p]).\end{align*} $$
On the other hand, it is expected that Voevodsky’s isomorphism [Reference Voevodsky26, Cor.4.2.9]
$$ \begin{align} {\operatorname{CH}}^{n{-}i}(X, j{-}2i) \cong \hom_{\operatorname{\mathbf{DM}}^{\operatorname{eff}}}(\mathbb{Z}(i)[j], M^c_{gm}(X)) \end{align} $$
can be generalised to a relationship between higher Chow groups with modulus and
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
. If this is the case, then the equivalence of Corollary 1.6 can be seen as an analogue of Miyazaki’s independence result.
1.3 Relationship to reciprocity sheaves
If the base field k has characteristic p, then for a Nisnevich reciprocity sheaf F (see [Reference Koizumi15]), the kernel of the canonical surjective morphism
$F \to \text {H}_0(F)$
must be p-primary torsion (see [Reference Bloch and Esnault4, Corollary 3.10]). In fact, Kahn–Saito–Yamazaki prove an equivalence of categories
${\operatorname {\mathbf {Rec}}}_{\operatorname {Nis}}[\frac {1}{p}] \simeq \operatorname {\mathbf {HI}}_{\operatorname {Nis}}[\frac {1}{p}]$
between the category of reciprocity sheaves and the category of homotopy invariant Nisnevich sheaves with transfers (see [Reference Kelly and Saito16, Corollary 3.2.6]).
On the other hand, there is a tower of fully faithful functors
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}} \overset {i_{\operatorname {rec}}^{\operatorname {Nis}}}{\hookrightarrow } {\operatorname {\mathbf {Rec}}}_{\operatorname {Nis}} \overset {\omega ^{\operatorname {\mathbf {CI}}}_{\operatorname {rec}}}{\hookrightarrow } {\operatorname {\mathbf {CI}}}_{\operatorname {Nis}}^{sp}$
(see [Reference Kelly and Saito16, Thm.3.6.6], [Reference Kelly and Saito16, Cor.3.8.2], [Reference Binda, Park and Østvær7]). In analogy to the fact that the heart of
$\operatorname {\mathbf {DM}}^{\operatorname {eff}}$
is
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}}$
(see [Reference Voevodsky26, Thm.3.1.12]), it is expected that the heart of
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
is
${\operatorname {\mathbf {CI}}}_{\operatorname {Nis}}^{sp}$
(the log version of this story is proved by Binda–Merici [Reference Besser5, Theorem 5.7]). By definition, the composition
$\omega ^{\operatorname {\mathbf {CI}}}_{\operatorname {rec}} \circ i_{\operatorname {rec}}^{\operatorname {Nis}}$
is compatible with
$\omega ^{\operatorname {eff}}:\operatorname {\mathbf {DM}}^{\operatorname {eff}} \to \operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
. If we assume that the heart of
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
is
${\operatorname {\mathbf {CI}}}_{\operatorname {Nis}}^{sp}$
, then Corollary 1.6 implies an equivalence
${\operatorname {\mathbf {CI}}}_{\operatorname {Nis}}^{sp}[\frac {1}{p}] \cong \operatorname {\mathbf {HI}}_{\operatorname {Nis}}[\frac {1}{p}]$
. Then the two inclusions
$i_{\operatorname {rec}}^{\operatorname {Nis}}[\frac {1}{p}]$
and
$\omega ^{\operatorname {\mathbf {CI}}}_{\operatorname {rec}}[\frac {1}{p}]$
become equivalences, so Corollary 1.6 can be seen as an analogue of this story.
2 Definition and Preparation
In this article, we work over a perfect field k. As in [Reference Kahn, Miyazaki, Saito and Yamazaki12, Definition 1.3.1] we write
$\operatorname {\mathbf {\underline {M}Cor}}$
for the category of modulus pairs and left proper admissible correspondences. We write
$$ \begin{align*} \mathbb{Z}_{\operatorname{tr}}:\operatorname{\mathbf{\underline{M}Cor}} \to PSh(\operatorname{\mathbf{\underline{M}Cor}}) \end{align*} $$
for the associated representable additive presheaf functor.
We set
$\operatorname {\mathbf {\underline {M}NST}}$
to be the category of Nisnevich sheaves on
$\operatorname {\mathbf {\underline {M}Cor}}$
defined in [Reference Kahn, Miyazaki, Saito and Yamazaki12, Definition 4.5.2].
We define
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
to be the Verdier quotient of
${\textbf {D}}(\operatorname {\mathbf {\underline {M}NST}})$
by the smallest localising subcategory containing all complexes of the form (CI) for
${\mathfrak {M}}\in \operatorname {\mathbf {\underline {M}Cor}}$
,
$$ \begin{align*} \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}\otimes \square) \to \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}). \end{align*} $$
Note that complexes of the following form are quasi-isomorphic to zero in
$D(\operatorname {\mathbf {\underline {M}NST}})$
: (MV) for
$\mathfrak {M}\in \operatorname {\mathbf {\underline {M}Cor}}$
and an elementary Nisnevich coverFootnote
2
$(\mathfrak {U},\mathfrak {V})$
of
$\mathfrak {M}$
,
$$ \begin{align*} \mathbb{Z}_{\operatorname{tr}}(\mathfrak{U}\times_{\mathfrak{M}}\mathfrak{V}) \to \mathbb{Z}_{\operatorname{tr}}(\mathfrak{U}) \oplus \mathbb{Z}_{\operatorname{tr}}(\mathfrak{V}) \to \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}). \end{align*} $$
We define
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
to be the smallest subcategory of
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
containing the objects
$\underline {\mathbf {M}}(\overline {M},M^{\infty })$
for modulus pair
$(\overline {M}, M^{\infty })$
such that
$\overline {M}$
is proper and closed under isomorphisms, direct sums, shifts and cones.
We have a functor
$$ \begin{align*} \underline{\omega}:\operatorname{\mathbf{\underline{M}Cor}} \to \operatorname{\mathbf{Cor}} \end{align*} $$
with
$\underline {\omega }(\overline {M},M^{\infty }) = M^{\circ }:=\overline {M} ~\backslash ~ M^{\infty }$
. This functor
$\underline {\omega }$
induces a triangulated functor
$$ \begin{align*} \underline{\omega}_{\text{eff}}: \operatorname{\mathbf{\underline{M}DM}}^{\operatorname{eff}} \to \operatorname{\mathbf{DM}}^{{\operatorname{eff}}}. \end{align*} $$
Definition 2.1. In Situation 1.1, we define the closed Thom space as
$$ \begin{align*} Th(N_ZM,cl) := \operatorname{Cone}\bigg( &\underline{\mathbf{M}}(\mathbb{P}(N_{\overline{Z}}\overline{M} \oplus \mathcal{O}), \pi^* Z^\infty + \{\infty\}_{\overline{Z}}) \\ \to &\underline{\mathbf{M}}(\mathbb{P}(N_{\overline{Z}}\overline{M} \oplus \mathcal{O}), \pi^* Z^\infty) \bigg ) \end{align*} $$
in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
, where
$\pi : \mathbb {P}(N_{\overline {Z}}\overline {M} \oplus \mathcal {O}) \to \overline {Z}$
is the canonical projection.
Notice that the closed Thom space is a lifting of Voevodsky’s Thom spaces in the sense that
$\underline {\omega }_{{\operatorname {eff}}}$
sends
$Th(N_Z M, cl)$
to
$Th(N_{Z^{\circ }} M^\circ )$
.
For a smooth variety and a vector bundle E on X, Voevodsky defined the Thom space in
$\operatorname {\mathbf {DM}}^{\operatorname {eff}}$
:
$$ \begin{align*} Th_X(E)=\operatorname{Cone}(\mathbb{P}_X(E\oplus \mathcal{O})\backslash \{\infty\}_X \to \mathbb{P}_X(E\oplus \mathcal{O})). \end{align*} $$
Remark 2.2. Note that
$Th(N_Z M)$
is a direct summand of
$\underline {\mathbf {M}}(\mathbb {P}(N_{\overline {Z}}\overline {M} \oplus \mathcal {O}), \pi ^* Z^\infty )$
since
$\underline {\mathbf {M}}(\mathbb {P}(\mathcal {O}), \pi ^* Z^\infty ) \simeq \underline {\mathbf {M}}(\overline {Z},Z^\infty )$
(cf. [Reference Kahn, Saito and Yamazaki17, Lemma 6]). In fact, by the projective bundle formula [Reference Kahn, Miyazaki, Saito and Yamazaki14, Theorem 7.3.2], the closed Thom spaces are just Tate twists:
$Th(N_ZM, cl) \cong \underline {\mathbf {M}}(\overline {Z}, Z^\infty )(1)[2]$
.
Remark 2.3. For any proper birational morphism of schemes
$f:X \to Y$
and effective Cartier divisors
$Y^\infty \subset Y$
and
$X^\infty =f^*Y^\infty $
satisfying
$Y \backslash Y^\infty \simeq X \backslash X^\infty $
, there is an isomorphism
$$ \begin{align*} \underline{\mathbf{M}}(Y,Y^\infty) \simeq \underline{\mathbf{M}}(X,X^\infty) \end{align*} $$
in
$\operatorname {\mathbf {\underline {M}Cor}}$
(cf. [Reference Kahn, Miyazaki, Saito and Yamazaki12, Proposition 1.9.2.(b)]).
The following basic homological algebra result will be useful.
Lemma 2.4. Consider a commutative diagram.
in an additive category
$\mathcal {A}$
such that all horizontal and vertical compositions are zero. Suppose we have a triangulated functor
$\Phi :K^b(\mathcal {A}) \to T$
to some triangulated category T such that (the complexes associated to) all three columns and two of the rows are sent to zero in T. Then the (the complex associated to) the third row is sent to zero in T as well.
Proof. Clear.
3 Excision
In this section we prove some basic excision results and prove that Thom spaces are invariant under change of étale neighbourhood.
Let
$M=(\overline {M},M^{\infty })$
and
$Z=(\overline {Z},Z^\infty )$
be as in Situation 1.1. For
$n\in \mathbb {Z}_{\geq 0}$
we define a presheaf on
$\operatorname {\mathbf {\underline {M}Cor}}$
,
$$ \begin{align*} C_{nZ}^{M} = \operatorname{Coker}\bigl(\mathbb{Z}_{\operatorname{tr}}(\overline{U},U^{\infty}) \hookrightarrow \mathbb{Z}_{\operatorname{tr}}(\overline{M},M^{\infty} + n\overline{Z})\bigr), \end{align*} $$
where
$\overline {U} = \overline {M} \setminus \overline {Z}$
,
$U^\infty = M^\infty |_{\overline {U}}$
and
$\mathbb {Z}_{\operatorname {tr}}(\overline {U},U^{\infty }) \to \mathbb {Z}_{\operatorname {tr}}(\overline {M},M^{\infty } + n\overline {Z})$
is induced by the open immersion
$\overline {U} \to \overline {M}$
.
For a morphism
$f:(\overline {M},M^{\infty }) \to (\overline {N},N^\infty )$
induced by a morphism of schemes
$\overline {f}:\overline {M} \to \overline {N}$
, we call f minimal if we have
$M^\infty =\overline {f}^*N^\infty $
.
Proposition 3.1. Let
$f:{(\overline {N},N^{\infty })} \to (\overline {M},M^{\infty })$
be an étale morphism (i.e., f is induced by an étale morphism
$\overline {f}:\overline {N} \to \overline {M}$
and is minimal). If
$\overline {f}^{-1}\overline {Z} \to \overline {Z}$
is an isomorphism, then for any
$n\in \mathbb {Z}_{\geq 0}$
, the natural morphism
$C_{nf^{-1}Z}^{N} \to C_{nZ}^{M}$
is a isomorphism in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
.
Proof. Let
$\overline {V}=\overline {N} \backslash f^{-1}\overline {Z}$
. We have a diagram in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
.
The left-hand square is homotopy Cartesian in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
by the definition of
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
. So we get the claim.
Theorem 3.2. Let
$f:{(\overline {N},N^{\infty })} \to (\overline {M},M^{\infty })$
be an étale morphism. If
$\overline {f}^{-1}\overline {Z} \to \overline {Z}$
is an isomorphism, then for any
$n \geq m \geq 0$
there is a diagram in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
,
such that
$\text {Coker}(i_N) \to \text {Coker}(i_M)$
is an isomorphism in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
.
Proof. We consider the following commutative diagram in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
:
where
$i_M$
is the natural map and
$c_M$
is the unique map determined by
$i_M$
. Now all columns and the two top rows are exact. Now by the nine lemma, we get that the bottom row is also exact. The morphisms
$i_M$
and
$\overline {f}$
induce the commutative diagram
By Proposition 3.1, the vertical morphisms become isomorphisms in
$\operatorname {\mathbf {\underline {M}DM}}^{{\operatorname {eff}}}$
. Hence, the map between the cokernels of the two horizontal presheaf monomorphims becomes isomorphisms in
$\operatorname {\mathbf {\underline {M}DM}}^{{\operatorname {eff}}}$
.
Corollary 3.3. In the situation of Theorem 3.2, Thom spaces are isomorphic
$$ \begin{align*} Th(N_{f^{-1}\overline{Z}}N,cl) \simeq Th(N_{\overline{Z}}M,cl). \end{align*} $$
Proof. In the situation of Theorem 3.2, for any
$n\in \{0,1\}$
the natural morphism
$$ \begin{align*}\overline{f}:(\mathbb{P}(N_{f^{-1}\overline{Z}}\overline{N} \oplus \mathcal{O}), \pi^{\prime*} Z^{\prime\infty} +n\{\infty\}_{f^{-1}\overline{Z}})\to(\mathbb{P}(N_{\overline{Z}}\overline{M} \oplus \mathcal{O}), \pi^* Z^\infty +n\{\infty\}_{\overline{Z}})\end{align*} $$
is minimal étale morphism where
$Z^{\prime \infty }:=f^{-1}\overline {Z}.N^{\infty }$
and
$\pi '$
is the projection
$\mathbb {P}(N_{f^{-1}\overline {Z}}\overline {N} \oplus \mathcal {O}) \to f^{-1}\overline {Z}$
. Moreover,
$\overline {f}$
induces an isomorphism
$\{\infty \}_{f^{-1}\overline {Z}} \simeq \{\infty \}_{\overline {Z}}$
since
$f^{-1}\overline {Z} \simeq \overline {Z}$
. By Proposition 3.1 and Theorem 3.2, we obtain the claim.
4 Blow-up formula with weight
4.1 Introduction
Kelly–Saito proved a blow-up formula for motives with modulus (see [Reference Kahn, Saito and Yamazaki17]), but to construct a tame Gysin map we need another formula, namely, Theorem 4.2. In this section, we calculate some motives of Fano surfaces with modulus, and then we construct the formula which we need. We begin with the notation that we will need to perform the deformation to the normal cone technique.
Notation 4.1. In Situation 1.1, we use the following notation:
$$ \begin{align*} M &:= (\overline{M},M^\infty),\\ Z &:= (\overline{Z},Z^\infty), \\ \overline{B}_M^{(\overline{Z})}\xrightarrow{\pi_M}\overline{M}\times\mathbb{P}^1 &: \text{the blow-up of } \overline{M}\times\mathbb{P}^1 \text{ at }\overline{Z}\times \{0\}, \\ B_M^\infty &:= \pi_M^*(M^\infty\times \mathbb{P}^1+\overline{M}\times \{\infty\}), \\ W_M &: \text{the strict transform of }\overline{Z}\times\mathbb{P}^1 \text{ w.r.t. }\overline{B}_M \to \overline{M}\times\mathbb{P}^1, \\ B_{M,cl}^{(\overline{Z})} &:= (\overline{B}_M^{(\overline{Z})},B_M^\infty + W_M),\\ \overline{U}_M &:= \overline{M}\times\mathbb{P}^1 ~ \backslash ~{\overline{Z}\times \mathbb{P}^1}, \\ \overline{E}_M^{(\overline{Z})} &:= \text{the exceptional divisor of }\pi_M, \\ E_{M,cl}^{(\overline{Z})} &:=\bigl(\overline{E}_M,(\overline{E}_M\cap B_M^\infty) + (\overline{E}_M\cap W_M)\bigr). \end{align*} $$
The goal of this section is to prove the following theorem.
Theorem 4.2. In the notation of Situation 1.1, there exists a distinguished triangle in
$\operatorname {\mathbf {\underline {M}DM}}^{{\operatorname {eff}}}$
.
$$ \begin{align*} \underline{\mathbf{M}}(E_{M,cl}^{(\overline{Z})}) \to \underline{\mathbf{M}}(Z)\oplus \underline{\mathbf{M}}(B_{M,cl}^{(\overline{Z})}) \to \underline{\mathbf{M}}(M\otimes{\overline{\square}}) \xrightarrow{+}. \end{align*} $$
4.2 Special case
Let
$H_0, H_1, H_2$
be the hyperplanes on
$\mathbb {P}^2$
given by
$\{[0:\star :\star ]\}$
,
$\{[\star :0:\star ]\}$
,
$\{[\star :\star :0]\}$
. We set
$b:B\to \mathbb {P}^2 $
to be the blow-up of
$\mathbb {P}^2$
along
$H_0\cap H_1$
and set
$\widetilde {H_0}, \widetilde {H_1}, \widetilde {H_2}$
to be the strict transforms of
$H_0, H_1, H_2$
. We set
$$ \begin{align*} B_{cl}:=(B,\widetilde{H_0}+\widetilde{H_2}) \qquad \text{ and }\qquad E_{cl}:=(E,E\cap \widetilde{H_0}), \qquad \end{align*} $$
where E is the exceptional divisor of the blow-up.
Proposition 4.3. There is a split distinguished triangle
$$ \begin{align} \underline{\mathbf{M}}(E_{cl}) \xrightarrow{ \begin{bmatrix} p & i\\ \end{bmatrix}} \underline{\mathbf{M}}(\operatorname{Spec} k) \oplus \underline{\mathbf{M}}(B_{cl}) \xrightarrow{ \begin{bmatrix} j \\ -b \end{bmatrix}}\underline{\mathbf{M}}(\mathbb{P}^2,H_2) \underset{0}{\xrightarrow{+}} \end{align} $$
in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
, where
$i,j$
are the natural closed immersions and p is the natural projection
$E \to \operatorname {Spec} k$
.
Proof. Since
$B_{cl}$
has a projection to
$E_{cl}$
which is a cube bundle, i is an isomorphism. Additionally, j is an isomorphism since
$(\mathbb {P}^2,H_2)$
is contractible [Reference Kahn, Saito and Yamazaki17, Lemma 10].
4.3 Proof of Theorem 4.2
Theorem 4.4. There is a distinguished triangle
$$ \begin{align*} \underline{\mathbf{M}}(E_{(\mathbb{A}^1,\emptyset),cl}^{(\{0\})}) \to \underline{\mathbf{M}}(\{0\})\oplus \underline{\mathbf{M}}(B_{(\mathbb{A}^1,\emptyset),cl}^{(\{0\})}) \to \underline{\mathbf{M}}((\mathbb{A}^1,\emptyset)\otimes{\overline{\square}}) \xrightarrow{+}. \end{align*} $$
A log version of the argument below appeared independently in Binda–Park–Østvær (see [Reference Binda and Merici6, Proposition 7.2.5]).
Proof. We set T to be the blow-up of
$\mathbb {P}^2$
at
$H_0\cap H_2$
and let f be the exceptional divisor and
$h_i$
be the strict transforms of the
$H_i$
. We set
$T'$
to be the blow-up of T at
$h_0 \cap h_1$
and let e be the exceptional divisor, the
$\widetilde {h_i}$
be strict transforms of the
$h_i$
and
$\widetilde {f}$
be the strict transform of f. In particular,
$T'$
is the same as the blow-up of B at
$\widetilde {H_0} \cap \widetilde {H_2}$
. The fans of these toric varieties are as follows:
The following triangle is isomorphic to it in Proposition 4.3, since this is obtained by blowing up inside the modulus:
$$ \begin{align} \underline{\mathbf{M}}(E_{cl}) \to \underline{\mathbf{M}}(\operatorname{Spec} k) \oplus \underline{\mathbf{M}}(T', \widetilde{h_2} + \widetilde{h_0} + \widetilde{f}) \to \underline{\mathbf{M}}(T,h_2+f) \underset{0}{\xrightarrow{+}}. \end{align} $$
Notice that there is a canonical isomorphism of toric surfaces
$T \setminus h_2 \cong \mathbf {A}^1 \times \mathbf {P}^1$
inducing an isomorphism of modulus pairs
$(T \setminus h_2, f \setminus (f \cap h_2)) \cong (\mathbf {A}^1,\emptyset ) \otimes {\overline {\square }}$
. Furthermore, pulling back the square that give rise to (4.2) along
$\mathbf {A}^1 \times \mathbf {P}^1 \to T$
produces the triangle in the statement.
Since
$\{T \setminus h_2 \to T, T \setminus h_0 \to T\}$
is a Zariski covering, by Mayer–Vietoris, to show that the triangle in the statement is distinguished, it suffices to show that the triangle associated to
$T, T \setminus h_0$
and
$T \setminus (h_0 \cup h_2)$
is distinguished; cf. Lemma 2.4. We have just seen that the triangle associated to T is an isomorphic distinguished triangle (4.2). On the other hand, since the centre of the blow-up is contained in
$h_0$
, the triangle coming from
$T \setminus h_0$
and
$T \setminus (h_0 \cup h_2)$
is trivially distinguished.
Theorem 4.5. For any modulus pair
$(\overline {Y}, Y^\infty ) \in \operatorname {\mathbf {\underline {M}Cor}}$
such that
$\overline {Y}$
is smooth and
$Y^\infty $
is a strict normal crossing divisor, there is a distinguished triangle
$$ \begin{align*} \underline{\mathbf{M}}(E_{Y\otimes(\mathbb{A}^1,\emptyset),*}^{(Y\otimes\{0\})}) \to \underline{\mathbf{M}}(Y\otimes\{0\})\oplus \underline{\mathbf{M}}(B_{Y\otimes(\mathbb{A}^1,\emptyset),*}^{(Y\otimes\{0\})}) \to \underline{\mathbf{M}}(Y\otimes(\mathbb{A}^1,\emptyset)\otimes{\overline{\square}}) \xrightarrow{+}. \end{align*} $$
Proof. Since
$$ \begin{align*} B_{Y\otimes(\mathbb{A}^1,\emptyset),cl}^{(Y\otimes\{0\})}= Y\otimes B_{(\mathbb{A}^1,\emptyset),cl}^{(\{0\})}, \end{align*} $$
the triangle in the statement is the triangle from Theorem 4.4 tensored by
$(\overline {Y}, Y^\infty )$
.
Situation 4.6. Let
$f:(\overline {N},N^\infty ) \to (\overline {M},M^\infty )$
be an étale morphism (i.e., f is induced by an étale morphism
$\overline {f}:\overline {N} \to \overline {M}$
and is minimal) such that f induces an isomorphism
$f^{-1}\overline {Z} \to \overline {Z}$
.
Notation 4.7. In Situation 4.6, we pull back everything from Notation 4.1 along f. That is, we set
$$ \begin{align*} N, f^{-1}Z, \overline{B}_N^{(f^{-1}\overline{Z})}, \pi_N, B_N^\infty, W_N, B_{N,cl}^{(f^{-1}\overline{Z})}, \overline{U}_N, U_N, \overline{E}_N^{(f^{-1}\overline{Z})}, E_{N,cl}^{(f^{-1}\overline{Z})} \end{align*} $$
to be the pullbacks of
$$ \begin{align*} M, Z, \overline{B}_M^{(\overline{Z})}, \pi_M, B_M^\infty, W_M, B_{M,op}^{(\overline{Z})}, B_{M,cl}^{(\overline{Z})}, \overline{U}_M, U_M, \overline{E}_M^{(\overline{Z})}, E_{M,op}^{(, \overline{Z})}, E_{M,cl}^{(\overline{Z})} \end{align*} $$
along
$\overline {f}: \overline {N} \to \overline {M}$
. Explicitly,
$$ \begin{align*} N &:= (\overline{N}, N^\infty), \\ f^{-1}Z &:= (f^{-1}\overline{Z},f^{-1}Z\cdot_{\overline{N}} N^\infty) \\ \overline{B}_N^{(f^{-1}\overline{Z})}\xrightarrow{\pi_N}\overline{N}\times\mathbb{P}^1 &:\text{the blow-up of } \overline{N}\times\mathbb{P}^1 \text{ along } f^{-1}\overline{Z}\times \{0\}, \\ B_N^\infty &:= \pi_N^*(N^\infty\times \mathbb{P}^1 + \overline{N}\times\{\infty\}) \\ W_N &:\text{the strict transform of }f^{-1}\overline{Z}\times\mathbb{P}^1 \text{ w.r.t. }\overline{B}_N \to \overline{N}\times\mathbb{P}^1, \\ B_{N,cl}^{(f^{-1}\overline{Z})}&:=(\overline{B}_N,B_N^\infty + W_N), \\ \overline{U}_N &:= \overline{N}\times\mathbb{P}^1 ~ \backslash ~{f^{-1}\overline{Z}\times \mathbb{P}^1}, \\ U_N &:=(\overline{U}_N,\overline{U}_N \cap (N^\infty\times \mathbb{P}^1 + \overline{N}\times\{\infty\})) \\ \overline{E}_N^{(f^{-1}\overline{Z})} &:\text{the exceptional divisor of }\pi_N, \\ E_{N,cl}^{(f^{-1}\overline{Z})} &:= (\overline{E}_N,\overline{E}_N\cap B_N^\infty + (W_N\cap\overline{E}_N)). \end{align*} $$
Proof. All morphisms in the square are minimal. By definition,
$(B_{M,cl}^{(\overline {Z})} ~ \backslash ~ U_M) = (W_M \cup \overline {E}_M)$
,
$(B_{N,cl}^{(f^{-1}\overline {Z})} ~ \backslash ~ U_N) = (W_N \cup \overline {E}_N)$
.
Corollary 4.9. In Situation 4.6 and Notation 4.7, the image under the functor
$\underline {\mathbf {M}}$
of the square
is a homotopy Cartesian in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
.
Notation 4.10. In Notation 4.1, consider the following ‘weighted’ blow-up formulas:
$$ \begin{align*} &(WBU)_{Z\to M}^{cl}:\\ &\quad \text{ the object } \underline{\mathbf{M}} \left (E_{M,cl}^{(\overline{Z})} {\to} Z \oplus B_{M,cl}^{(\overline{Z})} {\to} M\otimes{\overline{\square}} \right ) \text{ is isomorphic to zero in }\operatorname{\mathbf{\underline{M}DM}}^{\operatorname{eff}}. \end{align*} $$
Proposition 4.11. In Situation 4.6,
$(WBU)_{Z\to M}^*$
is true if and only if
$(WBU)_{f^{-1}Z\to N}^*$
is true.
Proof. The following diagram commutes in
$\operatorname {\mathbf {\underline {M}Cor}}$
:
By Corollary 4.9, we know the lower square is a homotopy Cartesian in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
, so the outer square is a homotopy Cartesian iff the upper square is.
The following lemma is proved in [Reference Kahn, Saito and Yamazaki17].
Lemma 4.12 [Reference Kahn, Saito and Yamazaki17, Lemma 8]
In Situation 1.1, up to replacing
$\overline {M}, \overline {Z}, M^{\infty }$
by
$\overline {V}, \overline {V} \cap \overline {Z}, \overline {V} \cap M^{\infty }$
for some open neighborhood
$x \in \overline {V}$
, there exists an étale morphism
$q:\overline {M} \to \mathbb {A}^{m}$
such that
$\overline {Z} = q^{-1}(\mathbb {A}^{m-1}\times \{0\})$
and
$M^{\infty } = q^{-1}(\{T_1^{d_1} \ldots T_s^{d_s} = 0\})$
where
$T_{i}$
are the coordinates of
$\mathbb {A}^{m}$
.
Now we have enough pieces to prove Theorem 4.2.
Proof of Theorem 4.2. For any open covering
$\{\overline {U}_i \to \overline {M}\}_i$
, by the Mayer–Vietoris sequence we obtain that
$(WBU)_{Z\to M}^*$
is true if
$(WBU)_{Z\cap \overline {U}\to (\overline {U},\overline {U}\cap M^\infty )}^*$
is true for all open subschemes
$\overline {U} \subset \overline {U}_i$
for all i. By Proposition 4.11 and Lemma 4.12, we can reduce the claim to the case
$(WBU)_{Z\otimes \{0\} \to Z\otimes (\mathbb {A}^1,\emptyset )}^*$
, but this was proved in Theorem 4.5.
5 Construction of the Tame Gysin map
5.1 Notation
We continue with
$\mathfrak {M}=(\overline {M},M^{\infty })$
and
$\mathfrak {Z}=(\overline {Z},Z^{\infty })$
satisfying the hypotheses of Situation 1.1. We furthermore drop all of the indexes ‘M’ from the notation of Notation 4.1. So
$$ \begin{align*} \overline{B}:\text{is the blow-up of } \overline{M} \times \mathbb{P}^1 \text{ along } \overline{Z} \times \{0\} \text{ and } \end{align*} $$
$$ \begin{align*} E:\text{is the exceptional divisor of }q, \end{align*} $$
so we have a Cartesian square
We put
$$ \begin{align*} \mathfrak{B}:= (\overline{B},q^*(M^\infty\times\mathbb{P}^1+\overline{M}\times \{\infty\})), \end{align*} $$
$$ \begin{align*} \mathfrak{B}_{Z,cl}:= (\overline{B},q^*(M^\infty\times\mathbb{P}^1+\overline{M}\times \{\infty\})+\widetilde{(\overline{Z}\times\mathbb{P}^1))} \end{align*} $$
$$ \begin{align*} \mathfrak{E}_{Z,cl}:=(\mathbb{P}(N_{Z}M\oplus \mathcal{O}),\pi^*Z^\infty + \mathbb{P}(0 \oplus \mathcal{O})). \end{align*} $$
Theorem 5.1. There is a distinguished triangle in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
$$ \begin{align*} \underline{\mathbf{M}}(\mathfrak{E}_{Z,cl}) \to \underline{\mathbf{M}}(B_{Z,cl})\oplus \underline{\mathbf{M}}(\mathfrak{Z}) \to \underline{\mathbf{M}}(\mathfrak{M}\otimes {\overline{\square}}) \xrightarrow{+} \end{align*} $$
and isomorphism
$$ \begin{align*} Th(N_ZM,cl) = \operatorname{Cone}(\underline{\mathbf{M}}(\mathfrak{E}_{Z,cl}) \to \underline{\mathbf{M}}(\mathfrak{E }_{})) \simeq \operatorname{Cone}(\underline{\mathbf{M}}(\mathfrak{B}_{Z,cl}) \to \underline{\mathbf{M}}(\mathfrak{B}_{})). \end{align*} $$
Proof. The first claim is Theorem 4.2; the second claim follows from the first and the blow-up formula
$$ \begin{align*} \underline{\mathbf{M}}(\mathfrak{E}) \to \underline{\mathbf{M}}(\mathfrak{B } )\oplus \underline{\mathbf{M}}(\mathfrak{Z}) \to \underline{\mathbf{M}}(\mathfrak{M}\otimes {\overline{\square}}) \xrightarrow{+} \end{align*} $$
proved in [Reference Kahn, Saito and Yamazaki17, Theorem, page 1].
5.2 Geometrical study
We write
$i_1$
for the natural embedding of schemes
$\overline {M}\times \{1\}$
to
$\overline {B}$
. The embedding
$i_1$
defines
$i:\mathfrak {M}_{} \to \mathfrak {B}_{}$
and
$\tilde {i}:\mathfrak {M}_{Z,cl} \to \mathfrak {B}_{Z,cl}$
in
$\operatorname {\mathbf {\underline {M}Cor}}$
.
The diagram gives us the morphism
$\mathbb {Z}_{\operatorname {tr}}(\mathfrak {M}/\mathfrak {M}_{Z,cl}) \to \mathbb {Z}_{\operatorname {tr}}(\mathfrak {B}/\mathfrak {B}_{Z,cl})$
in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
where we write
$$ \begin{align*} \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}/\mathfrak{M}_{Z,cl}) := coker\bigg ( \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}_{Z,cl}) \to \mathbb{Z}_{\operatorname{tr}}(\mathfrak{M}) \bigg ) \end{align*} $$
etc., in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
. Note that since
$\mathfrak {M}_{Z,cl} \to \mathfrak {M}$
are monomorphisms, the image of
$\mathbb {Z}_{\operatorname {tr}}(\mathfrak {M}/\mathfrak {M}_{Z,cl})$
in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
is the cone of the image of
$\mathbb {Z}_{\operatorname {tr}}(\mathfrak {M}_{Z,cl}) \to \mathbb {Z}_{\operatorname {tr}}(\mathfrak {M})$
. Composing with the isomorphism
$$ \begin{align*} \mathbb{Z}_{\operatorname{tr}}(\mathfrak{B}/\mathfrak{B}_{Z,cl}) \stackrel{\sim}{\leftarrow} \mathbb{Z}_{\operatorname{tr}}(\mathfrak{E}/\mathfrak{E}_{Z,cl}) = Th(N_ZM,cl) \end{align*} $$
from Theorem 5.1, one gets a morphism
$$ \begin{align*} \beta(\mathfrak{M}/Z,cl) : \underline{\mathbf{M}}(\mathfrak{M}_{}/\mathfrak{M}_{Z,cl}) \to \mathbb{Z}_{\operatorname{tr}}(\mathfrak{B}/\mathfrak{B}_{Z,cl}) \to Th(N_ZM,cl). \end{align*} $$
We call this morphism the closed Gysin map associated with
$\mathfrak {M}$
and Z.
Lemma 5.2. We have the following:
-
(0)
$\beta \bigl ((\mathbb {A}^{1},\emptyset )/\{0\},cl\bigr ): \underline {\mathbf {M}}((\mathbb {A}^{1},\emptyset )/(\mathbb {A}^1,\{0\})) \to Th(N_{\{0\}}(\mathbb {A}^1,\emptyset ),cl)$
is an isomorphism. -
(1) For any étale morphism
$e:\mathfrak {M}'=(\overline {M}',e^{*}M^{\infty }) \to \mathfrak {M}$
, set
$\mathfrak {Z}'=(e^{-1}\overline {Z},e^{*}Z^{\infty })$
. Then the diagram commutes. -
(2) For any modulus pair
$\mathfrak {Y}=(\overline {Y},Y^{\infty })$
with
$\overline {Y}$
smooth and
$Y^\infty $
a strict normal crossing divisor, we have
$$ \begin{align*} \beta(\mathfrak{M}\otimes \mathfrak{Y}/\mathfrak{Z} \otimes \mathfrak{Y},cl) = \beta(\mathfrak{M}/\mathfrak{Z},cl) \otimes Id_{\underline{M}(\mathfrak{Y})}. \end{align*} $$
Proof. Part 1. We take
$$ \begin{align*} \overline{B}':\text{blow-up of } \overline{M}' \times \mathbb{P}^{1} \text{ with along } e^{-1}\overline{Z} \times \{0\}, \end{align*} $$
and
$$ \begin{align*} \mathfrak{B}'=\bigl(\overline{B}',{q'}^{*}(e^{*}M^{\infty}\times \mathbb{P}^{1}) + {q'}^{*}(\overline{M}'\times \{\infty\})\bigr), \end{align*} $$
$$ \begin{align*} \mathfrak{B}^{\prime}_{\mathfrak{Z}',cl}=\bigl(\overline{B}',{q'}^{*}(e^{*}M^{\infty}\times \mathbb{P}^{1}) + {q'}^{*}(\overline{M}'\times \{\infty\})+\widetilde{(\overline{Z}'\times \mathbb{P}^1)}\bigr). \end{align*} $$
Since the morphism e is étale,
$e^{-1}\overline {Z}$
is also smooth. Now there is a natural map
$\mathfrak {B}' \to \mathfrak {B}$
and we have the following commutative diagram in
$\operatorname {\mathbf {\underline {M}Cor}}$
:
The diagram gives us the commutative diagram in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
:
The same argument shows that the square
is commutative.
Part 2. The blow-up of
$\overline {M}\times \overline {Y}\times \mathbb {P}^{1}$
along
$\overline {Z}\times \overline {Y}\times \{0\}$
is isomorphic to
$\overline {B} \times \overline {Y}$
, so the proof is complete.
Part 0. Set
$\eta _{op}$
(respectively
$\eta _{cl}$
) to be the composition of the
$1$
-section
$\mathbb {A}^1 \times \{1\} \hookrightarrow \overline {B}_{\{0\}}$
(respectively
$(\mathbb {A}^1 \setminus \{0\}) \times \{1\} \hookrightarrow \overline {B}_{\{0\}}$
) and the retraction
$\overline {B}_{\{0\}}\to \overline {E}_{\{0\}}$
(see the diagrams below on the left). Note that these are open immersions. Let
$\eta _{0,cl}, \eta _1$
be the induced morphisms on modulus pairs (see the square below on the right).
Since both of right-hand squares satisfy the condition of Proposition 3.1, these squares are homotopy Cartesian in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
.
6 Proof of main theorems
In this section, we use the notation of Section 5.1 and we prove that the Gysin maps defined in Section 5.2
$$ \begin{align*} \beta(\mathfrak{M}/\mathfrak{Z},cl): \underline{\mathbf{M}}(\mathfrak{M}_{}/\mathfrak{M}_{\mathfrak{Z},cl}) \to Th(N_ZM,cl) \end{align*} $$
are isomorphisms.
Lemma 6.1. The Gysin map
$\beta (\mathfrak {M}/\mathfrak {Z},*)$
is an isomorphism if there is an open Zariski cover
$\{\overline {V}_i \to \overline {M}\}_{i = 1}^l$
such that for all i the Gysin maps
$\beta ( (\overline {V},\overline {V} \cap M^\infty )/(\overline {V} \cap \overline {Z}, \overline {V} \cap M^\infty \cap \overline {Z}))$
associated to the intersections
$\overline {V} = \cap _{j \in J} \overline {V}_j$
are isomorphisms for all nonempty
$J \subseteq I$
.
Proof. By induction on l it suffices to consider the
$l = 2$
case. We take an open covering
$\overline {V}_1\cup \overline {V}_2 = \overline {M}$
. Now we set
$$ \begin{align*} {\mathfrak{V}_{\mathfrak{Z},12,cl}} =(\overline{V}_{12}, \overline{V}_{12} \cap M^{\infty} + \overline{V}_{12} \cap \overline{Z}). \end{align*} $$
We have the following diagram in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
:
where the compositions of all columns and the two top rows are zero and the bottom row maps are uniquely determined by the middle row maps.
By Lemma 2.4 we get the following distinguished triangle in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
:
$$ \begin{align*} \underline{\mathbf{M}}(\mathfrak{V}_{\mathfrak{Z},12,*}/{\mathfrak{V}_{\mathfrak{Z},12,*}}) \to \underline{\mathbf{M}}(\mathfrak{V}_{\mathfrak{Z},1,*}/{\mathfrak{V}_{\mathfrak{Z},1,*}}) \oplus \underline{\mathbf{M}}(\mathfrak{V}_{\mathfrak{Z},2,*}/{\mathfrak{V}_{\mathfrak{Z},2,*}}) \to \underline{\mathbf{M}}(\mathfrak{M}_{\mathfrak{Z}}/{\mathfrak{M}_{\mathfrak{Z}}}) \xrightarrow{+}. \end{align*} $$
The same argument can be applied for Thom space, so we obtain the following distinguished triangle in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
:
$$ \begin{align*} Th(N_{Z_{12}}\mathfrak{V}_{12},*) \to Th(N_{Z_{1}}\mathfrak{V}_{1},*) \oplus Th(N_{Z_{2}}\mathfrak{V}_{2},*) \to Th(N_{Z}\mathfrak{M},*) \xrightarrow{+}. \end{align*} $$
By Lemma 5.2, we know that Gysin maps are compatible with open immersions, so the proof follows from the triangulated category axioms.
Lemma 6.2. In the situation Theorem 3.2,
$\beta ((\overline {N},N^\infty )/(f^{-1}\overline {Z},Z^{\prime \infty },cl)$
is an isomorphism if and only if
$\beta ((\overline {M},M^\infty )/(\overline {Z},Z^\infty ),cl) $
is an isomorphism.
Proof. by Lemma 3.2. (1), we have the following commutative diagram:
where the vertical maps are isomorphisms by Theorem 3.2 and Corollary 3.3. So if one of the horizon maps is an isomorphism, then the other is also an isomorphism.
Now we have a proof of the main theorem.
Proof that the Gysin triangles are distinguished in
$\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}}$
It suffices to show the Gysin morphisms are isomorphisms. By Lemma 6.1, Lemma 6.2 and Lemma 4.12, we can assume that there is an étale map
$\overline {f}: \overline {M} \to \mathbb {A}^m$
such that
$M^\infty = \overline {f}^*E$
and
$\overline {Z} = \overline {f}^*(\mathbb {A}^{m-1} \times \{0\})$
where
$$ \begin{align*} (\mathbb{A}^{1},d_{{1}}\{0\}) \otimes (\mathbb{A}^{1},d_{{2}}\{0\}) \otimes \cdots \otimes (\mathbb{A}^{1},\emptyset) = (\mathbb{A}^m,E), \end{align*} $$
and we write
$E_{0} = E \times _{\mathbb {A}^{m}} (\mathbb {A}^{m-1}\times \{0\})$
so
$$ \begin{align*} (\mathbb{A}^{1},d_{{1}}\{0\}) \otimes (\mathbb{A}^{1},d_{{2}}\{0\}) \otimes \cdots \otimes \{0\}=(\mathbb{A}^{m-1} {\times} \{0\},E_{0}). \end{align*} $$
Now we have a Cartesian cubic diagram
By the above diagram, we know that
$f_{Z}:(\overline {Z},Z^\infty ) \to (\mathbb {A}^{m-1}\times \{0\},E_{0})$
is a minimal étale map. Now we consider the fibre product
$$ \begin{align*} \overline{X} ~:=~ \overline{M} \times_{\mathbb{A}^m} (\overline{Z} \times_{\operatorname{Spec} k} \mathbb{A}^1 ) \end{align*} $$
and
$$ \begin{align*} X^\infty ~:=~ \overline{\pi}^*M^\infty, \end{align*} $$
where
$\overline {\pi }$
is a canonical morphism
$\overline {X} \to \overline {M}$
. Now by [Reference Suslin and Voevodsky23, Theorem 4.10], we have a diagram
$(\Omega )$
in
$\operatorname {\mathbf {Sm}}(k)$
,
where
$i:\overline {X}' \to \overline {X}$
is an open immersion and
$p_{2}^{-1}(\overline {Z}\times \{0\})= \overline {Z}$
. By Lemma 6.2,
$\beta (\mathfrak {M}/\mathfrak {M}_{\mathfrak {Z}},cl)$
is an isomorphism if and only if
$\beta _{cl}: (\underline {\mathbf {M}}\Bigl ((\overline {Z},Z^\infty ) \otimes (\mathbb {A}^1,\emptyset ) \Bigr ) / \underline {\mathbf {M}}\Bigl ((\overline {Z},Z^\infty ) \otimes (\mathbb {A}^1,\{0\})\Bigr )) \to Th(N_{Z}\mathbb {A}^1_Z,cl)$
is an isomorphism. By Lemma 5.2 (2), this
$\beta _{cl}$
is the image of
$ \underline {\mathbf {M}}((\mathbb {A}^1, \emptyset ) / (\mathbb {A}^1, \{0\})) \to Th(N_{\{0\}}\mathbb {A}^1,cl)$
under
$(\overline {Z}, Z^\infty ) \otimes -$
. But this is an isomorphism by Lemma 5.2(0).
7 Application
Heuristically, the motive with modulus
$M(\overline {X}, X^\infty )$
is a placeholder which represents the cohomology of
$X^\circ = \overline {X} \setminus X^\infty $
whose ramification along the support of
$X^\infty $
is bounded by the multiplicities of
$X^\infty $
. In particular, the case when
$X^\infty $
is reduced corresponds to tamely ramified cohomology classes. On the other hand, there are concrete connections between tame class field theory and Voevodsky’s
$\operatorname {\mathbf {DM}}^{\operatorname {eff}}$
(cf. the relationship between the tame fundamental group and Suslin homology demonstrated by Geisser, Schmidt and Speiß). In this section we show that these two points of view are compatible.
Theorem 7.1. Let X be a smooth variety over k which has a compactification
$\overline {X}$
such that
$\overline {X}$
is smooth and
$|\overline {X}\backslash X|$
is a strict normal crossing divisor on
$\overline {X}$
. Then the unit
$$ \begin{align*} \underline{\mathbf{M}}(\overline{X},|\overline{X}\backslash X|_{{\operatorname{red}}}) \to {\underline{\omega}}^{{\operatorname{eff}}}({\textbf{{M}}}(X)) \end{align*} $$
of the adjunction
${\underline {\omega }}_{{\operatorname {eff}}}:\operatorname {\mathbf {\underline {M}DM}}^{\operatorname {eff}} \rightleftarrows \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}:{\underline {\omega }}^{\operatorname {eff}}$
is an isomorphism.
Lemma 7.2. The functor
${\underline {\omega }}_{\operatorname {eff}}$
sends the tame Gysin map
$g_{\mathfrak {Z}}\mathfrak {M}$
to Gysin map
$g_{Z^{\circ }}M^{\circ }$
of [Reference Voevodsky26, Thm.3.5.4].
Proof of Lemma 7.2. By using excision [Reference Voevodsky24, Proposition 5.18], Voevodsky’s construction of the Gysin map [Reference Voevodsky25] can be restated in terms of the deformation space obtained by blowing up
$Z^\circ \times \{0\}$
in
$X^\circ \times \mathbb {P}^1$
. The definition of the tame Gysin map is given only by geometrical morphisms. Our construction corresponds to Voevodsky’s construction under the functor
${\underline {\omega }}_{\operatorname {eff}}$
.
Proof of Theorem 7.1. Take
$$ \begin{align*} |\overline{X}\backslash X|_{{\operatorname{red}}} = \Sigma_{i=1}^{n} V_i \end{align*} $$
where each
$V_i$
is a smooth effective Cartier divisor. We prove the claim by induction on n.
Let us suppose
$n=1$
and write V for
$|\overline {X}\backslash X|_{{\operatorname {red}}} = V_1$
. We have the Gysin triangle in
$\operatorname {\mathbf {DM}}^{\operatorname {eff}}$
for the closed immersion
$V \hookrightarrow \overline {X}$
,
$$ \begin{align*} {\textbf{{M}}}(\overline{X} \backslash V) \to {\textbf{{M}}}(\overline{X}) \xrightarrow{g_{V}\overline{X}} {\textbf{{M}}}(V)(1)[2] \xrightarrow{+} {\textbf{{M}}}(\overline{X} \backslash V)[1]. \end{align*} $$
Since the unit
${\operatorname {Id}} \to {\underline {\omega }}^{\operatorname {eff}}{\underline {\omega }}_{{\operatorname {eff}}}$
is a natural transformation, we get a morphism of distinguished triangles
where the vertical arrows are the unit morphisms. Since
$\overline {X}$
and V are proper smooth over k,
$(2)$
and
$(3)$
are isomorphisms (cf. [Reference Kahn, Miyazaki, Saito and Yamazaki14, Theorem 6.3.1]). So
$(1)$
is also an isomorphism.
Now we take
$$ \begin{align*} U = \overline{X} \backslash\bigcup_{i=1}^{n-1}V_i \end{align*} $$
and
$$ \begin{align*} W= V_n ~~\backslash(\bigcup_{i=1}^{n-1} V_n\cap V_i). \end{align*} $$
It is easy to see that
$U~\backslash W = \overline {X} ~\backslash \bigcup _{i=1}^{n}V_i$
. Now the divisor
$\Sigma _{i=1}^{n} V_i$
is a strict normal crossing divisor, so
$V_n\cdot _{\overline {X}} V_i = |V_n \cap V_i |_{{\operatorname {red}}}$
. So we get
By induction,
$(5)$
and
$(6)$
are isomorphisms. So the claim is proved.□
8 The case of
$\mathbb {Z}[1/p]$
-coefficients
In this section, we suppose that the base field has characteristic p. The main objective of this section is to show that the non-Voevodsky part of
$\operatorname {\mathbf {MDM}}^{\operatorname {eff}}$
is all
$p^\infty $
-torsion in the sense that the kernel of
$\omega _{{\operatorname {eff}}} :\operatorname {\mathbf {MDM}}^{{\operatorname {eff}}} \to \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$
is contained in the kernel of
$\operatorname {\mathbf {MDM}}^{{\operatorname {eff}}} \to \operatorname {\mathbf {MDM}}^{{\operatorname {eff}}}[1/p]$
.
For a natural number
$l \in \mathbb {N}$
and an integer
$n \in \mathbb {Z}_{\geq 0}$
, we define a presheaf
$\mathbb {Z}[1/p]_{\text {tr}}({\overline {\square }}^{(l/p^{n})}) \in PSh(\operatorname {\mathbf {\underline {M}Cor}},\mathbb {Z}[1/p])$
as
$$ \begin{align*} \mathbb{Z}[1/p]_{\text{tr}}({\overline{\square}}^{(l/p^{n})}):(\overline{M},M^{\infty}) \mapsto {\operatorname{\mathbf{\underline{M}Cor}}} \big((\overline{M},p^nM^{\infty}),(\mathbb{P}^1,l\{\infty\})\big) \otimes \mathbb{Z}[1/p]. \end{align*} $$
Let us define morphisms
$$ \begin{align*} &V^{(n)}:\mathbb{Z}[1/p]_{\text{tr}}({\overline{\square}}^{(l/p^{n})}) \to \mathbb{Z}[1/p]_{\text{tr}}({\overline{\square}}^{(l/p^{n+1})}),\\ &F^{(n)}:\mathbb{Z}[1/p]_{\text{tr}}({\overline{\square}}^{(l/p^{n+1})}) \to \mathbb{Z}[1/p]_{\text{tr}}({\overline{\square}}^{(l/p^{n})}), \end{align*} $$
$$ \begin{align*} \text{satisfying} \hspace{15pt} V^{(n)} \circ F^{(n)} = p\cdot id, \hspace{15pt} F^{(n)} \circ V^{(n)} = p\cdot id. \end{align*} $$
We use the morphism of modulus pairs
$\tilde {\pi }: (\mathbb {P}^1,lp\{\infty \})\to (\mathbb {P}^1,l\{\infty \}) $
defined by
. Note, this is a minimal morphism which is finite flat on the total space and therefore has a well-defined transpose
$\tilde {\pi }^{\text {t}}: (\mathbb {P}^1,l\{\infty \}) \to (\mathbb {P}^1,lp\{\infty \}) $
as follows.
Lemma 8.1. For a minimal finite flat morphism
$g:(\overline {X},X^\infty ) \to (\overline {Y},Y^\infty )$
, we denote by
$g^\circ $
the morphism
$\overline {X}\backslash X^\infty \to \overline {Y}\backslash Y^\infty $
giving rise to g. Then the transpose correspondence
${g^{\circ }}^{\text {t}}\in \operatorname {\mathbf {Cor}}(\overline {Y}\backslash Y^\infty ,\overline {X}\backslash X^\infty )$
lies in the subgroup
$\operatorname {\mathbf {\underline {M}Cor}}\bigl ((\overline {Y},Y^\infty ),(\overline {X},X^\infty )\bigr )$
.
We write
$g^t$
for
$g^{\circ t}$
considered as a morphism of modulus pairs.
Proof. It is left proper because g is finite and admissible because g is minimal.
Definition 8.2. For a modulus pair
$(\overline {M},M^{\infty })$
, we define
$V^{(n)}(\overline {M},M^{\infty })$
as the morphism given by
$$ \begin{align*} \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^nM^{\infty}),(\mathbb{P}^1,l\{\infty\})\big) &= \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^{n+1}M^{\infty}),(\mathbb{P}^1,lp\{\infty\})\big)\\ &\xrightarrow{\tilde{\pi} \circ -} \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^{n+1}M^{\infty}),(\mathbb{P}^1,l\{\infty\})\big) \end{align*} $$
and
$F^{(n)}(\overline {M},M^{\infty })$
as the morphism given by
$$ \begin{align*} \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^{n+1}M^{\infty}),(\mathbb{P}^1,l\{\infty\})\big) &\xrightarrow{\tilde{\pi}^{\text{t}} \circ -} \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^{n+1}M^{\infty}),(\mathbb{P}^1,lp\{\infty\})\big)\\ &= \operatorname{\mathbf{\underline{M}Cor}}\big((\overline{M},p^{n}M^{\infty}),(\mathbb{P}^1,l\{\infty\})\big). \end{align*} $$
Lemma 8.3.
$V^{(n)} \circ F^{(n)} = p\cdot id$
and
$F^{(n)} \circ V^{(n)} = p\cdot id$
.
Proof. We write
$\pi $
for the morphism
$\mathbb {A}^1 \to \mathbb {A}^1$
given by the morphism of k-algebras
. To prove the claim, it is enough to prove that
$\pi \circ \pi ^{t} = p\cdot id \in \operatorname {\mathbf {Cor}}(\mathbb {A}^1,\mathbb {A}^1)$
and
$\pi ^t \circ \pi = p\cdot id\in \operatorname {\mathbf {Cor}}(\mathbb {A}^1,\mathbb {A}^1)$
. Since
$\pi $
is a flat, finite, surjective morphism with degree p, it follows that
$\pi \circ \pi ^{t} = p\cdot id \in \operatorname {\mathbf {Cor}}(\mathbb {A}^1,\mathbb {A}^1)$
is true. So the problem is the other equality.
We need the following lemma.
Lemma 8.4. The flat pullback
$(\text {id}\times \pi )^{*}:Z^{1}(\mathbb {A}^{1}\times \mathbb {A}^{1})\to Z^{1}(\mathbb {A}^{1}\times \mathbb {A}^{1})$
sends
$\Gamma _{\pi }$
to
$p\cdot \text {id}$
, where
$\Gamma _{\pi }$
is the graph of
$\pi $
; that is,
$\Gamma _{\pi }:\mathbb {A}^{1}\to \mathbb {A}^{1}\times \mathbb {A}^{1}; a \mapsto (a,a^{p})$
.
Proof of Lemma 8.4. The ideal of
$k[x]\otimes _kk[y]$
corresponding to
$\Gamma _\pi $
is
$(x^{p}-y)$
. Now
$\text {id}\times \pi $
comes from the k-morphism
$k[x]\otimes _k k[y] \to k[x]\otimes _k k[y]; x \mapsto x ,~y\mapsto y^{p}.$
So the pullback of the ideal sheaf
$(\text {id}\times \pi )^{*}((x^{p}-y))$
is the ideal sheaf
$(x^{p}-y^{p})$
, but
$\text {ch}(k)=p$
, so this is equal to
$(x-y)^{p}$
. The ideal
$(x-y)$
corresponds to the diagonal morphism
$\Delta _{\mathbb {A}^{1}}$
; that is, the identity morphism in in
$\operatorname {\mathbf {Cor}}(\mathbb {A}^{1},\mathbb {A}^{1})$
.
Now we recall
$\pi $
and
$\pi ^{t}$
in
$\operatorname {\mathbf {Cor}}(\mathbb {A}^{1},\mathbb {A}^{1})$
. The map
$\pi $
is the graph map
$\Gamma _{\pi }:\mathbb {A}^{1} \to \mathbb {A}^{1} \times \mathbb {A}^{1}; a \mapsto (a,a^{p})$
and
$\pi ^{t}$
is the map
$\psi :\mathbb {A}^{1}\to \mathbb {A}^{1}\times \mathbb {A}^{1}; b \to (b^{p},b)$
. We recall the composition
$\pi ^{t} \circ \pi $
:
$$ \begin{align*} \pi^{t} \circ \pi = p_{13*}((\Gamma_{\pi}\times\mathbb{A}^{1})\cdot_{\mathbb{A}^{1}\times\mathbb{A}^{1}\times\mathbb{A}^{1}}(\mathbb{A}^{1}\times\psi)). \end{align*} $$
Now
$\Gamma _{\pi }\times \mathbb {A}^{1}$
and
$\mathbb {A}^{1}\times \psi $
are effective Cartier divisors and they are intersect properly, so
$$ \begin{align*} (\Gamma_{\pi}\times\mathbb{A}^{1})\times_{\mathbb{A}^{1}\times\mathbb{A}^{1}\times\mathbb{A}^{1}}(\mathbb{A}^{1}\times\psi)=(\Gamma_{\pi}\times\mathbb{A}^{1})\cdot_{\mathbb{A}^{1}\times\mathbb{A}^{1}\times\mathbb{A}^{1}}(\mathbb{A}^{1}\times\psi). \end{align*} $$
Now this is denoted by V. Then we have following diagram:
By definition, we get
$$ \begin{align} p_{13} \circ (\mathbb{A}^{1}\times\psi)=\text{id}_{\mathbb{A}^{1}\times\mathbb{A}^{1}} \end{align} $$
and
$$ \begin{align} p_{12}\circ(\mathbb{A}^{1}\times\psi) = \text{id}_{\mathbb{A}^{1}}\times\pi. \end{align} $$
The equality (8.2) claims that V is the flat pullback
$(id_{\mathbb {A}^{1}} \times \pi )^{*}(\Gamma _{\pi })$
. By Lemma 8.4 and [Reference Fulton11, Propostion 7.1] we get
$$ \begin{align*} V=p\cdot\text{id}. \end{align*} $$
By (8.1) we get that
$\pi ^{t}\circ \pi =p_{13*}(V) = V$
. Therefore,
$\pi ^{t}\circ \pi =p\cdot \text {id}$
in
$\operatorname {\mathbf {Cor}}(\mathbb {A}^{1},\mathbb {A}^{1})$
.
We consider two colimits
and
in the category
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
where the transition maps are
$V^{(n)}:\mathbb {Z}[1/p]_{\text {tr}}({\overline {\square }}^{(l/p^{n})}) \to \mathbb {Z}[1/p]_{\text {tr}}({\overline {\square }}^{(l/p^{n+1})})$
and
${\underline {\omega }}^*\pi :{\underline {\omega }}^*\mathbb {Z}[1/p]_{\text {tr}}(\mathbb {A}^1) \to {\underline {\omega }}^*\mathbb {Z}[1/p]_{\text {tr}}(\mathbb {A}^1)$
and the morphism
given by the natural immersions
$\mathbb {Z}[1/p]_{\text {tr}}({\overline {\square }}^{(l/p^{n})})\to {\underline {\omega }}^*\mathbb {Z}[1/p]_{\text {tr}}(\mathbb {A}^1)$
.
Lemma 8.5. There are the following isomorphisms in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
:
Proof. The prime p is invertible in
$\mathbb {Z}[1/p]$
, so by Lemma 8.3, morphisms
$V^{(n)}$
are isomorphisms. Similarly, the morphism
$\pi :\mathbb {Z}[1/p]_{\text {tr}}(\mathbb {A}^1)\to \mathbb {Z}[1/p]_{\text {tr}}(\mathbb {A}^1)$
is an isomorphism. So the claim follows.
Lemma 8.6. I is an isomorphism.
Proof. The problem is surjectivity. By [Reference Kahn, Miyazaki, Saito and Yamazaki12, Lemma 1.1.3],
$$ \begin{align*} \operatorname{\mathbf{Cor}}(\overline{M}\backslash M^{\infty}, \mathbb{A}^1) = \bigcup_{n}\operatorname{\mathbf{\underline{M}Cor}}((\overline{M},p^{n}M^{\infty}),(\mathbb{P}^{1},l\{\infty\})). \end{align*} $$
Hence, for any elementary correspondence
$W\in \operatorname {\mathbf {Cor}}(\overline {M}\backslash M^{\infty },\mathbb {A}^1)$
, there is an integer n such that
$W\in \operatorname {\mathbf {\underline {M}Cor}}((\overline {M},p^{n}M^{\infty }),(\mathbb {P}^{1},l\{\infty \}))$
.
This lemma implies the following theorem, which only holds in positive characteristic.
Theorem 8.7. For any
$l\in \mathbb {Z}_{\geq 1}$
,
$\underline {\mathbf {M}}((\mathbb {P}^1,\{\infty \})/(\mathbb {P}^1,l\{\infty \}))\otimes \mathbb {Z}[1/p]=0$
.
Proof. Since
$\mathbb {Z}[1/p]$
is a flat
$\mathbb {Z}$
-module, it is enough to show that the natural morphism
$\mathbb {Z}[1/p]_{\text {tr}}(\mathbb {P}^1,l\{\infty \}) \to \mathbb {Z}[1/p]_{\text {tr}}(\mathbb {P}^1,\{\infty \})$
is an isomorphism. There is a commutative diagram
in
$PSh(\operatorname {\mathbf {\underline {M}Cor}})$
, where vertical maps are natural inclusions and horizontal maps are isomophisms given by Lemma 8.5. By Lemma 8.6 we know that I is an isomorphism. So the natural inclusion
$\mathbb {Z}[1/p]_{{\operatorname {tr}}}({\overline {\square }}^{(l)}) \to \underline {\omega }^*\mathbb {Z}[1/p]_{{\operatorname {tr}}}(\mathbb {A}^1)$
is also an isomophism for all
$l \geq 1$
. The result now follows from the sequence of inclusions
$\mathbb {Z}[1/p]_{{\operatorname {tr}}}({\overline {\square }}^{(l)}) \hookrightarrow \mathbb {Z}[1/p]_{{\operatorname {tr}}}({\overline {\square }}) \hookrightarrow \underline {\omega }^*\mathbb {Z}[1/p]_{{\operatorname {tr}}}(\mathbb {A}^1)$
.
Corollary 8.8. For any modulus pair
$(\overline {M},M^{\infty })$
such that
$\overline {M}$
is smooth and
$M^\infty _{\operatorname {red}}$
is strict normal crossing,
$$ \begin{align*} \underline{\mathbf{M}}(\overline{M},M^{\infty})\otimes\mathbb{Z}[1/p] \simeq \underline{\mathbf{M}}(\overline{M},M^\infty_{\operatorname{red}})\otimes\mathbb{Z}[1/p]. \end{align*} $$
Proof. Set
$M^\infty =\Sigma _{k=1}^{n} n_k V_k$
where
$V_k$
are smooth Cartier divisors. We take
$M^\infty _i := n_1 V_1 + \cdots n_i V_i + \Sigma _{k=i+1}^{n} V_k$
. It is enough to prove
$\underline {\mathbf {M}}(\overline {M},M^\infty _{i})\otimes \mathbb {Z}[1/p] \simeq \underline {\mathbf {M}}(\overline {M},M^\infty _{i-1})\otimes \mathbb {Z}[1/p]$
. By the Mayer–Vietoris sequence, we can replace
$\underline {\mathbf {M}}(\overline {M},M^\infty _{i})\otimes \mathbb {Z}[1/p]$
by
$\underline {\mathbf {M}}(\overline {U},\overline {U}\cap M^\infty _{i})\otimes \mathbb {Z}[1/p]$
where
$\overline {U}$
has a local chart
$q:\overline {U} \to \mathbb {A}^m$
such that
$\overline {U}\cap V_i=q^{-1}(\mathbb {A}^{m-1}\times \{0\})$
and
$\overline {U}\cap (M^\infty _{i}-n_iV_i)=q^{-1}(\{T_1^{d_1}.....T_j^{d_s}=0\})$
where
$T_l$
are the coordinates of
$\mathbb {A}^m$
. Replace
$\underline {\mathbf {M}}(\overline {M},M^\infty _{i})\otimes \mathbb {Z}[1/p]$
by
$\underline {\mathbf {M}}(\overline {U},\overline {U}\cap M^\infty _{i})\otimes \mathbb {Z}[1/p]$
. In this case we have a diagram
$(\Omega )$
used in the proof of the tame Gysin triangle. By Proposition 3.1, the cone of the natural morphisms
$\underline {\mathbf {M}}(\overline {M},M^\infty _{i})\otimes \mathbb {Z}[1/p] \to \underline {\mathbf {M}}(\overline {M},M^\infty _{i-1})\otimes \mathbb {Z}[1/p]$
is isomorphic to
$\underline {\mathbf {M}}\Bigl ((V_i,V_i^\infty ) \otimes (\mathbb {A}^1,\{0\}) \Bigr ) / \underline {\mathbf {M}}\Bigl ((V_i,V_i^\infty ) \otimes (\mathbb {A}^1,n_i\{0\})\Bigr )\otimes \mathbb {Z}[1/p]$
where
$V_i^\infty =V_i\cdot _{\overline {M}}(n_1 V_1 + \cdots n_{i-1} V_{i-1} + \Sigma _{k=i+1}^{n} V_k)$
. Proposition 3.1 and Theorem 8.7 claim
$(\mathbb {A}^1,\{0\})/(\mathbb {A}^1,n_i\{0\}) \otimes \mathbb {Z}[1/p]=0$
we win.
By this corollary and Theorem 7.1, we get the following theorem.
Theorem 8.9 Corollary 1.6
If the base field k has characteristic p and admits log resolution of singularities, then there is an equivalence
$$ \begin{align*} \omega_{{\operatorname{eff}}}[1/p]:\operatorname{\mathbf{MDM}^{\operatorname{eff}}}[1/p] \overset{\cong}{\longrightarrow} \operatorname{\mathbf{DM}}^{{\operatorname{eff}}}[1/p]. \end{align*} $$
Proof. We omit
$[1/p]$
. Since we assume the base field k admits log resolution of singularities, any modulus pair is isomorphic to a modulus pair which has a smooth total space and strictly normal crossing divisor modulus. Now
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$
is compactly generated by the
$\underline {\mathbf {M}}(\overline {M},M^{\infty })$
[Reference Kahn, Miyazaki, Saito and Yamazaki13, Theorem 1(2)] and both
$\omega _{\operatorname {eff}}$
and
$\omega ^{{\operatorname {eff}}}$
commute with all sums (the latter because
$\omega _{\operatorname {eff}}$
sends compact generators to compact objects), so it suffices to know that
$\underline {\mathbf {M}}(\overline {M},M^{\infty }) \to \omega _{\operatorname {eff}}\omega ^{\operatorname {eff}} \underline {\mathbf {M}}(\overline {M},M^{\infty })$
is an isomorphism when
$\overline {M}$
is smooth and proper and
$M^\infty $
is a strict normal crossing divisor. If
$M^\infty $
is reduced, Theorem 7.1 implies the claim. By Corollary 8.8, it is also true when
$M^\infty $
is not reduced.
Acknowledgements
We thank an anonymous referee for many suggestions which improved the readability of this article.
Next, I thank those members of motives with modulus school, especially Federico Binda, Shane Kelly, Hiroyasu Miyazaki and Shuji Saito.
I must also thank Jun Koizumi, a master student in Tokyo University, who pointed out a mistake in the proof of the open Gysin triangles [Reference Kahn, Saito and Yamazaki18].
Competing Interest
None.
