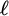1 Introduction
The idea of expanding structures in a given language with new operations and relations definable in some way is pervasive in Algebra and Model Theory. If we focus on operations defined by systems of equations on algebraic structures we arrive at the notion of Algebraic Expansions [Reference Campercholi and Vaggione10]. Restricting to this kind of definability has the advantage of producing well-behaved expansions that can be studied with ‘universal-algebraic’ techniques (e.g., sheaf representations). We describe these expansions in more detail.
Let
![]() $\tau $
be an algebraic language. Given a class of
$\tau $
be an algebraic language. Given a class of
![]() $\tau $
-algebras
$\tau $
-algebras
![]() $\mathcal {K}$
and a system of equations of the form
$\mathcal {K}$
and a system of equations of the form
 $$ \begin{align*} s_{1}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) & = t_{1}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) \\ & \hspace{2mm} \vdots \\ s_{k}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) & = t_{k}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) \end{align*} $$
$$ \begin{align*} s_{1}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) & = t_{1}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) \\ & \hspace{2mm} \vdots \\ s_{k}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) & = t_{k}(x_{1},\dots,x_{n},z_{1},\dots,z_{m}) \end{align*} $$
we can consider the class
![]() $\mathcal {A}$
of those algebras in
$\mathcal {A}$
of those algebras in
![]() $\mathcal {K}$
for which, given values for the x’s, there are unique values for the z’s such that all equalities hold. We say that
$\mathcal {K}$
for which, given values for the x’s, there are unique values for the z’s such that all equalities hold. We say that
![]() $\mathcal {A}$
is an Algebraically Expandable (AE) subclass of
$\mathcal {A}$
is an Algebraically Expandable (AE) subclass of
![]() $\mathcal {K}$
given that the members of
$\mathcal {K}$
given that the members of
![]() $\mathcal {A}$
can be expanded with the operations defined by the system of equations. For example, let
$\mathcal {A}$
can be expanded with the operations defined by the system of equations. For example, let
![]() $\mathcal {K}$
be the class of
$\mathcal {K}$
be the class of
![]() $\{\mathbin {\rightarrow },1\}$
-subreducts of Boolean algebras, and consider the system of equations
$\{\mathbin {\rightarrow },1\}$
-subreducts of Boolean algebras, and consider the system of equations
 $$ \begin{align*} &\qquad\qquad\qquad\quad z \mathbin{\rightarrow} x_1 = 1, \\ &\qquad\qquad\qquad\quad z \mathbin{\rightarrow} x_2 = 1, \\ &((x_1 \mathbin{\rightarrow} z) \mathbin{\rightarrow} (x_2 \mathbin{\rightarrow} z)) \mathbin{\rightarrow} (x_2 \mathbin{\rightarrow} z) = 1. \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\quad z \mathbin{\rightarrow} x_1 = 1, \\ &\qquad\qquad\qquad\quad z \mathbin{\rightarrow} x_2 = 1, \\ &((x_1 \mathbin{\rightarrow} z) \mathbin{\rightarrow} (x_2 \mathbin{\rightarrow} z)) \mathbin{\rightarrow} (x_2 \mathbin{\rightarrow} z) = 1. \end{align*} $$
The class
![]() $\mathcal {A}$
in this case is the class of algebras in
$\mathcal {A}$
in this case is the class of algebras in
![]() $\mathcal {K}$
where every two elements have a meet with respect to the ordering induced by
$\mathcal {K}$
where every two elements have a meet with respect to the ordering induced by
![]() $\mathbin {\rightarrow }$
. Expanding
$\mathbin {\rightarrow }$
. Expanding
![]() $\mathcal {A}$
with the meet operation yields a class term-equivalent to the class of generalized Boolean algebras.
$\mathcal {A}$
with the meet operation yields a class term-equivalent to the class of generalized Boolean algebras.
In the setting of Abstract Logic expansions by new connectives are a common theme as well, in particular, expansions of a logic L with connectives determined in some way by L. As we know, there is a long-standing and fruitful interplay between Logic and Algebra, so it is natural to consider what, if any, is the logical counterpart of AE-classes. As we shall see, for the case of an algebraizable logic L which has as its equivalent algebraic semantics a quasivariety
![]() $\mathcal {Q}$
, the AE-subclasses of
$\mathcal {Q}$
, the AE-subclasses of
![]() $\mathcal {Q}$
are in correspondence with the family of a specific kind of expansions of L, which we call algebraic expansions. The notion of an algebraic expansion of a logic turns out to be quite natural, we think, and interestingly it falls into the general framework of expansions by implicit connectives studied by Caicedo in [Reference Caicedo5]. An immediate consequence is that algebraic expansions are again algebraizable. The algebraic expansions of L are naturally pre-ordered by morphisms that preserve the language of L. It turns out that (modulo the equivalence relation induced by the pre-ordering) this is a lattice. Furthermore, this lattice is dually isomorphic to the lattice of AE-subclasses of
$\mathcal {Q}$
are in correspondence with the family of a specific kind of expansions of L, which we call algebraic expansions. The notion of an algebraic expansion of a logic turns out to be quite natural, we think, and interestingly it falls into the general framework of expansions by implicit connectives studied by Caicedo in [Reference Caicedo5]. An immediate consequence is that algebraic expansions are again algebraizable. The algebraic expansions of L are naturally pre-ordered by morphisms that preserve the language of L. It turns out that (modulo the equivalence relation induced by the pre-ordering) this is a lattice. Furthermore, this lattice is dually isomorphic to the lattice of AE-subclasses of
![]() $\mathcal {Q}$
under inclusion.
$\mathcal {Q}$
under inclusion.
Besides introducing the notion of algebraic expansions of a logic we analyze two particular cases:
![]() $\ell $
-groups and perfect MV-algebras. In both cases we obtain full descriptions of the AE-classes, and thus, of the algebraic expansions of their corresponding logics. We show that in both cases there is a continuum of expansions, and the lattices are isomorphic to
$\ell $
-groups and perfect MV-algebras. In both cases we obtain full descriptions of the AE-classes, and thus, of the algebraic expansions of their corresponding logics. We show that in both cases there is a continuum of expansions, and the lattices are isomorphic to
![]() $\mathbf {2}^\omega \oplus \mathbf {1}$
and
$\mathbf {2}^\omega \oplus \mathbf {1}$
and
![]() $\mathbf {2}^\omega \oplus \mathbf {2}$
, in the former and latter cases respectively.
$\mathbf {2}^\omega \oplus \mathbf {2}$
, in the former and latter cases respectively.
In the next section we summarize all the basic definitions and properties of the theory of AE-classes needed for this article. In Section 3 we give the formal definition of algebraic expansion of a logic, and prove the fundamental results linking them with AE-classes (Theorems 3.1 and 3.2). In Section 4 we characterize the AE-classes of abelian
![]() $\ell $
-groups and the algebraic expansions of their corresponding logic. Finally, in Section 5, we translate the results from Section 4 to their analogs for perfect MV-algebras. This completely describes the algebraic expansions of the associated logic.
$\ell $
-groups and the algebraic expansions of their corresponding logic. Finally, in Section 5, we translate the results from Section 4 to their analogs for perfect MV-algebras. This completely describes the algebraic expansions of the associated logic.
2 Preliminaries
In this section we introduce fundamental definitions, establish notation, and present several basic facts needed in the sequel. We assume familiarity with basic Universal Algebra, Model Theory, and Abstract Algebraic Logic (see, e.g., [Reference Burris and Sankappanavar4, Reference Hodges19, Reference Font15], respectively).
2.1 Notation and basic definitions
Throughout this article algebras are considered as models of first-order languages without relations. For example, abelian
![]() $\ell $
-groups are algebras in the language
$\ell $
-groups are algebras in the language
![]() $\tau _{\mathcal {G}} := \{+,-,0,\vee ,\wedge \}$
. As is customary we use bold letters (
$\tau _{\mathcal {G}} := \{+,-,0,\vee ,\wedge \}$
. As is customary we use bold letters (
![]() $\mathbf {A}, \mathbf {B}, \mathbf {C}, \ldots $
) for algebraic structures and italic letters (
$\mathbf {A}, \mathbf {B}, \mathbf {C}, \ldots $
) for algebraic structures and italic letters (
![]() $A, B, C, \ldots $
) for the underlying sets. For algebras
$A, B, C, \ldots $
) for the underlying sets. For algebras
![]() $\mathbf {A}$
and
$\mathbf {A}$
and
![]() $\mathbf {B}$
we write
$\mathbf {B}$
we write
![]() $\mathbf {A} \subseteq \mathbf {B}$
whenever
$\mathbf {A} \subseteq \mathbf {B}$
whenever
![]() $\mathbf {A}$
is a subalgebra of
$\mathbf {A}$
is a subalgebra of
![]() $\mathbf {B}$
.
$\mathbf {B}$
.
Given a structure
![]() $\mathbf {A}$
in a language
$\mathbf {A}$
in a language
![]() $\tau $
and a term
$\tau $
and a term
![]() $t(x_1,\ldots ,x_n)$
in the same language, we write
$t(x_1,\ldots ,x_n)$
in the same language, we write
![]() $t^{\mathbf {A}}(\bar {a})$
for the value of the term upon assigning elements
$t^{\mathbf {A}}(\bar {a})$
for the value of the term upon assigning elements
![]() $a_1,\ldots ,a_n$
from A to the variables
$a_1,\ldots ,a_n$
from A to the variables
![]() $x_1,\ldots ,x_n$
. We may omit the superscript
$x_1,\ldots ,x_n$
. We may omit the superscript
![]() $\mathbf {A}$
if there is no risk of confusion.
$\mathbf {A}$
if there is no risk of confusion.
Given a (first-order) formula
![]() $\varphi $
, we say that
$\varphi $
, we say that
![]() $\varphi $
is:
$\varphi $
is:
-
• an identity if it has the form
 $\forall \bar {x} (p(\bar {x}) = q(\bar {x}))$
, where p and q are terms,
$\forall \bar {x} (p(\bar {x}) = q(\bar {x}))$
, where p and q are terms, -
• a quasi-identity if it has the form
 $\forall \bar {x} (\alpha (\bar {x}) \mathbin {\boldsymbol {\rightarrow }} \beta (\bar {x}))$
,Footnote
1
where
$\forall \bar {x} (\alpha (\bar {x}) \mathbin {\boldsymbol {\rightarrow }} \beta (\bar {x}))$
,Footnote
1
where
 $\alpha $
is a finite conjunction of term-equalities and
$\alpha $
is a finite conjunction of term-equalities and
 $\beta $
is a term-equality,
$\beta $
is a term-equality, -
• universal if it has the form
 $\forall \bar {x} \psi $
, where
$\forall \bar {x} \psi $
, where
 $\psi $
is quantifier-free,
$\psi $
is quantifier-free, -
• existential if it has the form
 $\exists \bar {x} \psi $
, where
$\exists \bar {x} \psi $
, where
 $\psi $
is quantifier-free.
$\psi $
is quantifier-free.
A sentence is a formula with no free variables. If
![]() $\Sigma $
is a set of sentences,
$\Sigma $
is a set of sentences,
![]() $\mathop {\mathrm {Mod}}(\Sigma )$
denotes the class of all models that satisfy the sentences in
$\mathop {\mathrm {Mod}}(\Sigma )$
denotes the class of all models that satisfy the sentences in
![]() $\Sigma $
.
$\Sigma $
.
Whenever we consider a class
![]() $\mathcal {K}$
of algebras, we assume that all algebras in
$\mathcal {K}$
of algebras, we assume that all algebras in
![]() $\mathcal {K}$
have the same language. Given a class
$\mathcal {K}$
have the same language. Given a class
![]() $\mathcal {K}$
of algebras, we define the usual class operators:
$\mathcal {K}$
of algebras, we define the usual class operators:
-
•
 $\mathsf {I}(\mathcal {K})$
denotes the class of isomorphic images of members of
$\mathsf {I}(\mathcal {K})$
denotes the class of isomorphic images of members of
 $\mathcal {K}$
,
$\mathcal {K}$
, -
•
 $\mathsf {H}(\mathcal {K})$
denotes the class of homomorphic images of members of
$\mathsf {H}(\mathcal {K})$
denotes the class of homomorphic images of members of
 $\mathcal {K}$
,
$\mathcal {K}$
, -
•
 $\mathsf {S}(\mathcal {K})$
denotes the class of subalgebras of members of
$\mathsf {S}(\mathcal {K})$
denotes the class of subalgebras of members of
 $\mathcal {K}$
,
$\mathcal {K}$
, -
•
 $\mathsf {P}(\mathcal {K})$
denotes the class of direct products with factors in
$\mathsf {P}(\mathcal {K})$
denotes the class of direct products with factors in
 $\mathcal {K}$
,
$\mathcal {K}$
, -
•
 $\mathsf {P_U}(\mathcal {K})$
denotes the class of ultraproducts with factors in
$\mathsf {P_U}(\mathcal {K})$
denotes the class of ultraproducts with factors in
 $\mathcal {K}$
.
$\mathcal {K}$
.
If
![]() $\mathsf {O}$
is one of the above operators and
$\mathsf {O}$
is one of the above operators and
![]() $\mathcal {K} = \{\mathbf {A}_1,\ldots , \mathbf {A}_n\}$
, we write
$\mathcal {K} = \{\mathbf {A}_1,\ldots , \mathbf {A}_n\}$
, we write
![]() $\mathsf {O}(\mathbf {A}_1,\ldots ,\mathbf {A}_n)$
instead of
$\mathsf {O}(\mathbf {A}_1,\ldots ,\mathbf {A}_n)$
instead of
![]() $\mathsf {O}(\mathcal {K})$
.
$\mathsf {O}(\mathcal {K})$
.
Let
![]() $\mathcal {K}$
be a class of algebras of the same language. We say that
$\mathcal {K}$
be a class of algebras of the same language. We say that
![]() $\mathcal {K}$
is a variety (or equational class) if it can be axiomatized using a set of identities; equivalently, by Birkhoff’s theorem,
$\mathcal {K}$
is a variety (or equational class) if it can be axiomatized using a set of identities; equivalently, by Birkhoff’s theorem,
![]() $\mathcal {K}$
is a variety if and only if it is closed under
$\mathcal {K}$
is a variety if and only if it is closed under
![]() $\mathsf {H}$
,
$\mathsf {H}$
,
![]() $\mathsf {S}$
, and
$\mathsf {S}$
, and
![]() $\mathsf {P}$
. The smallest variety containing
$\mathsf {P}$
. The smallest variety containing
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\mathsf {HSP}(\mathcal {K})$
and is denoted by
$\mathsf {HSP}(\mathcal {K})$
and is denoted by
![]() $\mathsf {V}(\mathcal {K})$
. A quasivariety is a class of algebras that can be axiomatized by a set of quasi-identities. By Mal’cev’s theorem, the class
$\mathsf {V}(\mathcal {K})$
. A quasivariety is a class of algebras that can be axiomatized by a set of quasi-identities. By Mal’cev’s theorem, the class
![]() $\mathcal {K}$
is a quasivariety if and only if
$\mathcal {K}$
is a quasivariety if and only if
![]() $\mathcal {K}$
is closed under
$\mathcal {K}$
is closed under
![]() $\mathsf {I}$
,
$\mathsf {I}$
,
![]() $\mathsf {S}$
,
$\mathsf {S}$
,
![]() $\mathsf {P}$
, and
$\mathsf {P}$
, and
![]() $\mathsf {P_U}$
; the smallest quasivariety containing
$\mathsf {P_U}$
; the smallest quasivariety containing
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\mathsf {ISPP_U}(\mathcal {K})$
, also denoted by
$\mathsf {ISPP_U}(\mathcal {K})$
, also denoted by
![]() $\mathsf {Q}(\mathcal {K})$
. Finally, recall that
$\mathsf {Q}(\mathcal {K})$
. Finally, recall that
![]() $\mathcal {K}$
is universal if it can be axiomatized by a set of universal sentences, which is equivalent to
$\mathcal {K}$
is universal if it can be axiomatized by a set of universal sentences, which is equivalent to
![]() $\mathcal {K}$
being closed under
$\mathcal {K}$
being closed under
![]() $\mathsf {I}$
,
$\mathsf {I}$
,
![]() $\mathsf {S}$
, and
$\mathsf {S}$
, and
![]() $\mathsf {P_U}$
. Moreover, the smallest universal class containing
$\mathsf {P_U}$
. Moreover, the smallest universal class containing
![]() $\mathcal {K}$
is given by
$\mathcal {K}$
is given by
![]() $\mathsf {ISP_U}(\mathcal {K})$
.
$\mathsf {ISP_U}(\mathcal {K})$
.
Given a class
![]() $\mathcal {K}$
and two sentences
$\mathcal {K}$
and two sentences
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
, we say that
$\psi $
, we say that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are equivalent in
$\psi $
are equivalent in
![]() $\mathcal {K}$
, and write
$\mathcal {K}$
, and write
![]() $\varphi \mathrel {\sim } \psi $
in
$\varphi \mathrel {\sim } \psi $
in
![]() $\mathcal {K}$
, if for every
$\mathcal {K}$
, if for every
![]() $\mathbf {A} \in \mathcal {K}$
we have that
$\mathbf {A} \in \mathcal {K}$
we have that
![]() $\mathbf {A} \vDash \varphi $
if and only if
$\mathbf {A} \vDash \varphi $
if and only if
![]() $\mathbf {A} \vDash \psi $
.
$\mathbf {A} \vDash \psi $
.
2.2 Algebraically expandable classes
In order to define algebraically expandable classes [Reference Campercholi and Vaggione10], one of the fundamental notions in this article, we need to introduce the special type of sentences that axiomatize them. An equational function definition sentence (EFD-sentence for short) in the language
![]() $\tau $
is a sentence of the form
$\tau $
is a sentence of the form
 $$ \begin{align} \forall x_1 \ldots x_n \exists! z_1 \ldots z_m \, \mathop{\boldsymbol{\bigwedge}}\limits_{i=1}^k s_i(\bar{x},\bar{z}) = t_i(\bar{x},\bar{z}), \end{align} $$
$$ \begin{align} \forall x_1 \ldots x_n \exists! z_1 \ldots z_m \, \mathop{\boldsymbol{\bigwedge}}\limits_{i=1}^k s_i(\bar{x},\bar{z}) = t_i(\bar{x},\bar{z}), \end{align} $$
where
![]() $s_i,t_i$
are
$s_i,t_i$
are
![]() $\tau $
-terms,
$\tau $
-terms,
![]() $n \geq 0$
, and
$n \geq 0$
, and
![]() $m \geq 1$
. Suppose
$m \geq 1$
. Suppose
![]() $\varphi $
is the EFD-sentence in (1). Observe that
$\varphi $
is the EFD-sentence in (1). Observe that
![]() $\varphi $
is valid in a structure
$\varphi $
is valid in a structure
![]() $\mathbf {A}$
if and only if the system of equations
$\mathbf {A}$
if and only if the system of equations
 $\displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
defines a (total) function
$\displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
defines a (total) function
![]() $F\colon A^n \to A^m$
. If
$F\colon A^n \to A^m$
. If
![]() $\pi _j\colon A^m \to A$
is the j-th projection function, we write
$\pi _j\colon A^m \to A$
is the j-th projection function, we write
![]() $[\varphi ]_j^{\mathbf {A}} := \pi _j \circ F$
for
$[\varphi ]_j^{\mathbf {A}} := \pi _j \circ F$
for
![]() $j \in \{1,\ldots ,m\}$
.
$j \in \{1,\ldots ,m\}$
.
Let
![]() $\varphi $
be as in (1). We define:
$\varphi $
be as in (1). We define:
-
•
 $E(\varphi ) := \displaystyle \forall \bar {x} \exists \bar {z} \, \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
,
$E(\varphi ) := \displaystyle \forall \bar {x} \exists \bar {z} \, \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
, -
•
 $U(\varphi ) := \displaystyle \forall \bar {x} \bar {y} \bar {z} \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {y}) = t_i(\bar {x},\bar {y}) \boldsymbol {\land } \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z}) \mathbin {\boldsymbol {\rightarrow }} \bar {y} = \bar {z}$
.
$U(\varphi ) := \displaystyle \forall \bar {x} \bar {y} \bar {z} \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {y}) = t_i(\bar {x},\bar {y}) \boldsymbol {\land } \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z}) \mathbin {\boldsymbol {\rightarrow }} \bar {y} = \bar {z}$
.
The following basic facts are used without explicit reference throughout the article.
-
•
 $\varphi $
is equivalent to
$\varphi $
is equivalent to
 $E(\varphi ) \boldsymbol {\land } U(\varphi )$
.
$E(\varphi ) \boldsymbol {\land } U(\varphi )$
. -
•
 $U(\varphi )$
is (equivalent to) a conjunction of quasi-identities.
$U(\varphi )$
is (equivalent to) a conjunction of quasi-identities. -
•
 $E(\varphi )$
is preserved by homomorphic images, that is, for any surjective homomorphism
$E(\varphi )$
is preserved by homomorphic images, that is, for any surjective homomorphism
 $f: \mathbf {A} \to \mathbf {B}$
, if
$f: \mathbf {A} \to \mathbf {B}$
, if
 $\mathbf {A} \vDash E(\varphi )$
, then
$\mathbf {A} \vDash E(\varphi )$
, then
 $\mathbf {B} \vDash E(\varphi )$
.
$\mathbf {B} \vDash E(\varphi )$
.
A class of algebras
![]() $\mathcal {K}$
is an algebraically expandable class (AE-class for short) if there is a set of EFD-sentences
$\mathcal {K}$
is an algebraically expandable class (AE-class for short) if there is a set of EFD-sentences
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\mathcal {K} = \mathop {\mathrm {Mod}}(\Sigma )$
. Let
$\mathcal {K} = \mathop {\mathrm {Mod}}(\Sigma )$
. Let
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {C}$
be classes of algebras,
$\mathcal {C}$
be classes of algebras,
![]() $\mathcal {K} \subseteq \mathcal {C}$
. We say that
$\mathcal {K} \subseteq \mathcal {C}$
. We say that
![]() $\mathcal {K}$
is an AE-subclass of
$\mathcal {K}$
is an AE-subclass of
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $\mathcal {K}$
is axiomatizable by EFD-sentences relative to
$\mathcal {K}$
is axiomatizable by EFD-sentences relative to
![]() $\mathcal {C}$
, that is,
$\mathcal {C}$
, that is,
![]() $\mathcal {K} = \mathcal {C} \cap \mathop {\mathrm {Mod}}(\Sigma )$
for some set
$\mathcal {K} = \mathcal {C} \cap \mathop {\mathrm {Mod}}(\Sigma )$
for some set
![]() $\Sigma $
of EFD-sentences. The reader should be aware that
$\Sigma $
of EFD-sentences. The reader should be aware that
![]() $\mathcal {K}$
may be an AE-subclass of
$\mathcal {K}$
may be an AE-subclass of
![]() $\mathcal {C}$
, but fail to be an AE-class itself.
$\mathcal {C}$
, but fail to be an AE-class itself.
Let
![]() $\mathcal {Q}$
be a quasivariety in the language
$\mathcal {Q}$
be a quasivariety in the language
![]() $\tau $
and let
$\tau $
and let
![]() $\Sigma $
be a set of EFD-sentences. There is an obvious expansion of the AE-subclass
$\Sigma $
be a set of EFD-sentences. There is an obvious expansion of the AE-subclass
![]() $\mathcal {K} := \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma )$
of
$\mathcal {K} := \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma )$
of
![]() $\mathcal {Q}$
obtained by skolemizing the existential quantifiers in
$\mathcal {Q}$
obtained by skolemizing the existential quantifiers in
![]() $\Sigma $
. More precisely, for each
$\Sigma $
. More precisely, for each
![]() $\varphi \in \Sigma $
of the form
$\varphi \in \Sigma $
of the form
 $\forall x_1 \ldots x_n \exists ! z_1 \ldots z_m \, \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
consider new n-ary function symbols
$\forall x_1 \ldots x_n \exists ! z_1 \ldots z_m \, \mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
consider new n-ary function symbols
![]() $f_1^\varphi , \ldots , f_m^\varphi $
and the set of identities
$f_1^\varphi , \ldots , f_m^\varphi $
and the set of identities
Let
![]() $\tau _\Sigma $
be the expansion of
$\tau _\Sigma $
be the expansion of
![]() $\tau $
obtained by adding the
$\tau $
obtained by adding the
![]() $f_j^\varphi $
’s for each
$f_j^\varphi $
’s for each
![]() $\varphi \in \Sigma $
, and put
$\varphi \in \Sigma $
, and put
Define
where
![]() $\Gamma $
is a set of quasi-identities axiomatizing
$\Gamma $
is a set of quasi-identities axiomatizing
![]() $\mathcal {Q}$
. We call
$\mathcal {Q}$
. We call
![]() $\mathcal {Q}^\Sigma $
an algebraic expansion of
$\mathcal {Q}^\Sigma $
an algebraic expansion of
![]() $\mathcal {Q}$
. Note that
$\mathcal {Q}$
. Note that
![]() $\mathcal {Q}^\Sigma $
is a quasivariety over the language
$\mathcal {Q}^\Sigma $
is a quasivariety over the language
![]() $\tau _\Sigma $
whose members are precisely the expansions of the members of
$\tau _\Sigma $
whose members are precisely the expansions of the members of
![]() $\mathcal {K}$
. A fact worth mentioning is that if
$\mathcal {K}$
. A fact worth mentioning is that if
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
are two sets of EFD-sentences with the same models in
$\Sigma '$
are two sets of EFD-sentences with the same models in
![]() $\mathcal {Q}$
, then the quasivarieties
$\mathcal {Q}$
, then the quasivarieties
![]() $\mathcal {Q}^\Sigma $
and
$\mathcal {Q}^\Sigma $
and
![]() $\mathcal {Q}^{\Sigma '}$
are term-equivalent (see [Reference Campercholi and Vaggione11, Theorem 5]).
$\mathcal {Q}^{\Sigma '}$
are term-equivalent (see [Reference Campercholi and Vaggione11, Theorem 5]).
We conclude this section with a preservation result for EFD-sentences needed in the sequel. Recall that a structure
![]() $\mathbf {A}$
is finitely subdirectly irreducible if its diagonal congruence is meet-irreducible in the congruence lattice of
$\mathbf {A}$
is finitely subdirectly irreducible if its diagonal congruence is meet-irreducible in the congruence lattice of
![]() $\mathbf {A}$
. We write
$\mathbf {A}$
. We write
![]() $\mathcal {K}_{\mathrm {fsi}}$
for the class of finitely subdirectly irreducible members of
$\mathcal {K}_{\mathrm {fsi}}$
for the class of finitely subdirectly irreducible members of
![]() $\mathcal {K}$
. A variety is arithmetical provided that it is both congruence distributive and congruence permutable.
$\mathcal {K}$
. A variety is arithmetical provided that it is both congruence distributive and congruence permutable.
Lemma 2.1. Let
![]() $\mathcal {V}$
be an arithmetical variety such that
$\mathcal {V}$
be an arithmetical variety such that
![]() $\mathcal {V}_{\mathrm {fsi}} \cup \{\text {trivial algebras}\}$
is a universal class, and let
$\mathcal {V}_{\mathrm {fsi}} \cup \{\text {trivial algebras}\}$
is a universal class, and let
![]() $\mathbf {A} \in \mathcal {V}$
. If
$\mathbf {A} \in \mathcal {V}$
. If
![]() $\varphi $
is an EFD-sentence such that
$\varphi $
is an EFD-sentence such that
![]() $\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \varphi $
, then
$\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \varphi $
, then
![]() $\mathbf {A} \vDash \varphi $
.
$\mathbf {A} \vDash \varphi $
.
Proof By [Reference Gramaglia and Vaggione18, Theorem 5.1]
![]() $\mathbf {A}$
has a global representation with factors in
$\mathbf {A}$
has a global representation with factors in
![]() $\mathsf {H}(\mathbf {A})_{\mathrm {fsi}}$
, and by [Reference Volger25] global representations preserve EFD-sentences.
$\mathsf {H}(\mathbf {A})_{\mathrm {fsi}}$
, and by [Reference Volger25] global representations preserve EFD-sentences.
3 The algebraic expansions of a logic
Following [Reference Font15, Definition 1.5] we take a (sentential) logic to be a pair
![]() $L := \langle \tau , \vdash _L\rangle $
where
$L := \langle \tau , \vdash _L\rangle $
where
![]() $\tau $
is an algebraic language and
$\tau $
is an algebraic language and
![]() $\vdash _L$
is a substitution-invariant consequence operator on the set of
$\vdash _L$
is a substitution-invariant consequence operator on the set of
![]() $\tau $
-formulas. We refer the reader to [Reference Font15] for definitions and results about abstract algebraic logic not explicitly mentioned in this article. Important disclaimer: all logics considered in the sequel are assumed to be finitary.
$\tau $
-formulas. We refer the reader to [Reference Font15] for definitions and results about abstract algebraic logic not explicitly mentioned in this article. Important disclaimer: all logics considered in the sequel are assumed to be finitary.
Let
![]() $L := \langle \tau _L, \vdash _L\rangle $
and
$L := \langle \tau _L, \vdash _L\rangle $
and
![]() $L' := \langle \tau _{L'}, \vdash _{L'}\rangle $
be logics. Recall that
$L' := \langle \tau _{L'}, \vdash _{L'}\rangle $
be logics. Recall that
![]() $L'$
is an expansion of L if
$L'$
is an expansion of L if
![]() $\tau \subseteq \tau '$
and
$\tau \subseteq \tau '$
and
![]() $\mathord {\vdash _{L}} \subseteq \mathord {\vdash _{L'}}$
.
$\mathord {\vdash _{L}} \subseteq \mathord {\vdash _{L'}}$
.
Suppose L is algebraizable and let
![]() $\Delta (x,y)$
be a set of equivalence formulas for L. Given a finite set of
$\Delta (x,y)$
be a set of equivalence formulas for L. Given a finite set of
![]() $\tau $
-formulas
$\tau $
-formulas
![]() $\Phi (\bar {x},\bar {z})$
in variables
$\Phi (\bar {x},\bar {z})$
in variables
![]() $x_1,\ldots ,x_n, z_1,\ldots ,z_m$
,
$x_1,\ldots ,x_n, z_1,\ldots ,z_m$
,
![]() $n,m\in \omega $
, let
$n,m\in \omega $
, let
![]() $\tau _\Phi $
be the language obtained by expanding
$\tau _\Phi $
be the language obtained by expanding
![]() $\tau $
with new n-ary function symbols
$\tau $
with new n-ary function symbols
![]() $f^\Phi _1, \ldots , f^\Phi _m$
. Next, define
$f^\Phi _1, \ldots , f^\Phi _m$
. Next, define
![]() $L^\Phi := \langle \tau _\Phi , \vdash _{L^\Phi }\rangle $
, where
$L^\Phi := \langle \tau _\Phi , \vdash _{L^\Phi }\rangle $
, where
![]() $\vdash _{L^\Phi }$
is the least substitution-invariant consequence operator containing
$\vdash _{L^\Phi }$
is the least substitution-invariant consequence operator containing
![]() $\vdash _L$
such that
$\vdash _L$
such that
(
![]() $\Delta (\bar {y},\bar {z})$
is shorthand for
$\Delta (\bar {y},\bar {z})$
is shorthand for
![]() $\bigcup _{j=1}^m \Delta (y_j,z_j)$
.) We say that
$\bigcup _{j=1}^m \Delta (y_j,z_j)$
.) We say that
![]() $L^\Phi $
is the algebraic expansion of L by
$L^\Phi $
is the algebraic expansion of L by
![]() $\Phi $
. Recall that if
$\Phi $
. Recall that if
![]() $\Delta '(x,y)$
is another set of equivalence formulas for L, then
$\Delta '(x,y)$
is another set of equivalence formulas for L, then
![]() $\Delta (x,y) \dashv \vdash _L \Delta '(x,y)$
. Thus, the expansion
$\Delta (x,y) \dashv \vdash _L \Delta '(x,y)$
. Thus, the expansion
![]() $L^\Phi $
does not depend on the choice of the set of equivalence formulas.
$L^\Phi $
does not depend on the choice of the set of equivalence formulas.
Given a set
![]() $\Sigma $
of finite sets of
$\Sigma $
of finite sets of
![]() $\tau $
-formulas, define
$\tau $
-formulas, define
![]() $L^\Sigma := \langle \tau _\Sigma , \vdash _{L^\Sigma }\rangle $
, where
$L^\Sigma := \langle \tau _\Sigma , \vdash _{L^\Sigma }\rangle $
, where
![]() $\tau _\Sigma := \bigcup \{\tau _\Phi : \Phi \in \Sigma \}$
and
$\tau _\Sigma := \bigcup \{\tau _\Phi : \Phi \in \Sigma \}$
and
![]() $\vdash _{L^\Sigma }$
is the least substitution-invariant consequence operator containing
$\vdash _{L^\Sigma }$
is the least substitution-invariant consequence operator containing
![]() $\vdash _{L^\Phi }$
for every
$\vdash _{L^\Phi }$
for every
![]() $\Phi \in \Sigma $
. (Of course, we assume that the new symbols for each
$\Phi \in \Sigma $
. (Of course, we assume that the new symbols for each
![]() $L^\Phi $
are different.) The logic
$L^\Phi $
are different.) The logic
![]() $L^\Sigma $
is called the algebraic expansion of L by
$L^\Sigma $
is called the algebraic expansion of L by
![]() $\Sigma $
.
$\Sigma $
.
Observe that, in the definition of
![]() $L^\Phi $
, for the case
$L^\Phi $
, for the case
![]() $m = 0$
condition
$m = 0$
condition
![]() $\mathrm {U}_\Phi $
holds vacuously, so
$\mathrm {U}_\Phi $
holds vacuously, so
![]() $L^\Phi $
is just the axiomatic extension of L by
$L^\Phi $
is just the axiomatic extension of L by
![]() $\Phi $
. Hence, axiomatic extensions of L are algebraic expansions of L.
$\Phi $
. Hence, axiomatic extensions of L are algebraic expansions of L.
As mentioned in the introduction, in [Reference Caicedo5] Caicedo studies expansions of finitely algebraizable logics where the behaviour of the new connectives is determined by the added axioms and rules. More precisely, let
![]() $L := \langle \tau , \vdash \rangle $
be an algebraizable logic with equivalence formulas
$L := \langle \tau , \vdash \rangle $
be an algebraizable logic with equivalence formulas
![]() $\Delta (x,y)$
, and let F be a set, disjoint from
$\Delta (x,y)$
, and let F be a set, disjoint from
![]() $\tau $
, of function symbols. Following [Reference Caicedo5], an expansion
$\tau $
, of function symbols. Following [Reference Caicedo5], an expansion
![]() $L(F)$
is said to be an expansion of L by implicit connectives provided that
$L(F)$
is said to be an expansion of L by implicit connectives provided that
where
![]() $F'$
is a copy of F disjoint from
$F'$
is a copy of F disjoint from
![]() $\tau $
and F, the logic
$\tau $
and F, the logic
![]() $L(F')$
is the copy of
$L(F')$
is the copy of
![]() $L(F)$
in the language
$L(F)$
in the language
![]() $\tau \cup F'$
, and
$\tau \cup F'$
, and
![]() $L(F) \cup L(F')$
is the logic in the language
$L(F) \cup L(F')$
is the logic in the language
![]() $\tau \cup F \cup F'$
whose consequence operator is the least substitution invariant consequence operator containing
$\tau \cup F \cup F'$
whose consequence operator is the least substitution invariant consequence operator containing
![]() $\vdash _{L(F)}$
and
$\vdash _{L(F)}$
and
![]() $\vdash _{L(F')}$
.
$\vdash _{L(F')}$
.
It is easy to see that the expansion
![]() $L^\Sigma $
defined above is in fact an expansion of L by implicit connectives (where
$L^\Sigma $
defined above is in fact an expansion of L by implicit connectives (where
![]() $(\mathrm {E}_\Phi )$
and
$(\mathrm {E}_\Phi )$
and
![]() $(\mathrm {U}_\Phi )$
correspond to new axioms and rules, respectively). As an immediate consequence of this fact we have that
$(\mathrm {U}_\Phi )$
correspond to new axioms and rules, respectively). As an immediate consequence of this fact we have that
![]() $L^\Sigma $
is algebraizable with the same equivalence formulas and defining equations as L [Reference Caicedo5, Theorem 1]. Furthermore, the equivalent algebraic semantics of
$L^\Sigma $
is algebraizable with the same equivalence formulas and defining equations as L [Reference Caicedo5, Theorem 1]. Furthermore, the equivalent algebraic semantics of
![]() $L^\Sigma $
is the expected one [Reference Caicedo5, Corollary 2], which in this case turns out to be an algebraic expansion of the equivalent algebraic semantics of L. The details are worked out next.
$L^\Sigma $
is the expected one [Reference Caicedo5, Corollary 2], which in this case turns out to be an algebraic expansion of the equivalent algebraic semantics of L. The details are worked out next.
Let
![]() $\mathcal {Q}$
be the equivalent algebraic semantics of L via the set of equivalence formulas
$\mathcal {Q}$
be the equivalent algebraic semantics of L via the set of equivalence formulas
![]() $\Delta (x,y)$
and the set of defining equations
$\Delta (x,y)$
and the set of defining equations
![]() $\varepsilon (x)$
. Given a finite set
$\varepsilon (x)$
. Given a finite set
![]() $\Phi (\bar {x},\bar {z})$
of
$\Phi (\bar {x},\bar {z})$
of
![]() $\tau $
-formulas, let
$\tau $
-formulas, let
![]() $e(\Phi )$
be the EFD-sentence
$e(\Phi )$
be the EFD-sentence
![]() $\forall \bar {x} \exists ! \bar {z} \, \mathop {\boldsymbol {\bigwedge }}\limits \varepsilon (\Phi (\bar {x},\bar {z}))$
. For
$\forall \bar {x} \exists ! \bar {z} \, \mathop {\boldsymbol {\bigwedge }}\limits \varepsilon (\Phi (\bar {x},\bar {z}))$
. For
![]() $\Sigma $
a set of finite sets of
$\Sigma $
a set of finite sets of
![]() $\tau $
-formulas define
$\tau $
-formulas define
![]() $e(\Sigma ) := \{e(\Phi ): \Phi \in \Sigma \}$
. Now, Corollary 2 of [Reference Caicedo5] says that the algebraic expansion
$e(\Sigma ) := \{e(\Phi ): \Phi \in \Sigma \}$
. Now, Corollary 2 of [Reference Caicedo5] says that the algebraic expansion
![]() $\mathcal {Q}^{e(\Sigma )}$
is the equivalent algebraic semantics of
$\mathcal {Q}^{e(\Sigma )}$
is the equivalent algebraic semantics of
![]() $L^\Sigma $
. Thus, for each algebraic expansion of L we have a corresponding algebraic expansion of
$L^\Sigma $
. Thus, for each algebraic expansion of L we have a corresponding algebraic expansion of
![]() $\mathcal {Q}$
. Of course, we can also go in the other direction. Given an EFD-sentence
$\mathcal {Q}$
. Of course, we can also go in the other direction. Given an EFD-sentence
![]() $\varphi := \forall \bar {x} \exists ! \bar {z} \, \alpha (\bar {x},\bar {z})$
, put
$\varphi := \forall \bar {x} \exists ! \bar {z} \, \alpha (\bar {x},\bar {z})$
, put
![]() $d(\varphi ) := \Delta (\alpha (\bar {x},\bar {z}))$
. Here and in the sequel
$d(\varphi ) := \Delta (\alpha (\bar {x},\bar {z}))$
. Here and in the sequel
![]() $\Delta (\alpha (\bar {x},\bar {z}))$
abbreviates
$\Delta (\alpha (\bar {x},\bar {z}))$
abbreviates
![]() $\bigcup _{i=1}^k \Delta (s_i(\bar {x},\bar {z}),t_i(\bar {x},\bar {z}))$
if
$\bigcup _{i=1}^k \Delta (s_i(\bar {x},\bar {z}),t_i(\bar {x},\bar {z}))$
if
![]() $\alpha (\bar {x},\bar {z})$
is the conjunction of equations
$\alpha (\bar {x},\bar {z})$
is the conjunction of equations
 $\mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
. For a set
$\mathop {\boldsymbol {\bigwedge }}\limits _{i=1}^k s_i(\bar {x},\bar {z}) = t_i(\bar {x},\bar {z})$
. For a set
![]() $\Sigma $
of EFD-sentences, we write
$\Sigma $
of EFD-sentences, we write
![]() $d(\Sigma )$
for the set
$d(\Sigma )$
for the set
![]() $\{d(\varphi ): \varphi \in \Sigma \}$
. Again, it is straightforward to check that
$\{d(\varphi ): \varphi \in \Sigma \}$
. Again, it is straightforward to check that
![]() $\mathcal {Q}^\Sigma $
is the equivalent algebraic semantics of
$\mathcal {Q}^\Sigma $
is the equivalent algebraic semantics of
![]() $L^{d(\Sigma )}$
. Furthermore,
$L^{d(\Sigma )}$
. Furthermore,
-
•
 $L^\Sigma = L^{d(e(\Sigma ))}$
,
$L^\Sigma = L^{d(e(\Sigma ))}$
, -
•
 $\mathcal {Q}^\Sigma = \mathcal {Q}^{e(d(\Sigma ))}$
$\mathcal {Q}^\Sigma = \mathcal {Q}^{e(d(\Sigma ))}$
for suitable
![]() $\Sigma $
’s. This establishes a direct correspondence between algebraic expansions of a logic and those of its equivalent algebraic semantics. Theorem 3.2 explores this connection in greater detail. In the sequel, to avoid cumbersome notation, given a logic L and a set
$\Sigma $
’s. This establishes a direct correspondence between algebraic expansions of a logic and those of its equivalent algebraic semantics. Theorem 3.2 explores this connection in greater detail. In the sequel, to avoid cumbersome notation, given a logic L and a set
![]() $\Sigma $
of EFD-sentences we write
$\Sigma $
of EFD-sentences we write
![]() $L^\Sigma $
instead of
$L^\Sigma $
instead of
![]() $L^{d(\Sigma )}$
.
$L^{d(\Sigma )}$
.
For future reference, the facts above are summarized in the following:
Theorem 3.1. Let L be a finitely algebraizable logic with equivalent algebraic semantics
![]() $\mathcal {Q}$
. Let
$\mathcal {Q}$
. Let
![]() $\Sigma $
be a set of EFD-sentences in the language of
$\Sigma $
be a set of EFD-sentences in the language of
![]() $\mathcal {Q}$
. Then the algebraic expansion
$\mathcal {Q}$
. Then the algebraic expansion
![]() $L^\Sigma $
is algebraizable with the same equivalence formulas and defining equations as L, and its equivalent algebraic semantics is the quasivariety
$L^\Sigma $
is algebraizable with the same equivalence formulas and defining equations as L, and its equivalent algebraic semantics is the quasivariety
![]() $\mathcal {Q}^\Sigma $
. Moreover, there is a one-to-one correspondence between the algebraic expansions of L and the algebraic expansions of
$\mathcal {Q}^\Sigma $
. Moreover, there is a one-to-one correspondence between the algebraic expansions of L and the algebraic expansions of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
We conclude this section with an example of a logic that has an expansion by implicit connectives that is not algebraic. Let
![]() $L_{\mathrm {int}}$
be the Intuitionistic Logic and let
$L_{\mathrm {int}}$
be the Intuitionistic Logic and let
![]() $L_{\mathrm {int}}^S$
be the extension of
$L_{\mathrm {int}}^S$
be the extension of
![]() $L_{\mathrm {int}}$
by the implicit connective S defined in [Reference Caicedo and Cignoli7, Example 5.2]. The equivalent algebraic semantics of
$L_{\mathrm {int}}$
by the implicit connective S defined in [Reference Caicedo and Cignoli7, Example 5.2]. The equivalent algebraic semantics of
![]() $L_{\mathrm {int}}^S$
is the variety
$L_{\mathrm {int}}^S$
is the variety
![]() $\mathcal {H}^S$
of Heyting algebras with successor. It is not hard to show that the class of Heyting-reducts of algebras in
$\mathcal {H}^S$
of Heyting algebras with successor. It is not hard to show that the class of Heyting-reducts of algebras in
![]() $\mathcal {H}^S$
is not an AE-subclass of
$\mathcal {H}^S$
is not an AE-subclass of
![]() $\mathcal {H}$
. Thus, by Theorem 3.1,
$\mathcal {H}$
. Thus, by Theorem 3.1,
![]() $L_{\mathrm {int}}^S$
cannot be an algebraic expansion of
$L_{\mathrm {int}}^S$
cannot be an algebraic expansion of
![]() $L_{\mathrm {int}}$
.
$L_{\mathrm {int}}$
.
3.1 The lattice of algebraic expansions
Let L be a finitely algebraizable logic with equivalent algebraic semantics
![]() $\mathcal {Q}$
. The AE-subclasses of the quasivariety
$\mathcal {Q}$
. The AE-subclasses of the quasivariety
![]() $\mathcal {Q}$
are naturally (lattice-)ordered by inclusion. In the current section we show how this ordering translates to the algebraic expansions of
$\mathcal {Q}$
are naturally (lattice-)ordered by inclusion. In the current section we show how this ordering translates to the algebraic expansions of
![]() $\mathcal {Q}$
, and thus to the algebraic expansions of L. For this we need to look into interpretations between logics and between classes of algebras.
$\mathcal {Q}$
, and thus to the algebraic expansions of L. For this we need to look into interpretations between logics and between classes of algebras.
Fix a countably infinite set of variables
![]() $X := \{x_1,x_2,\ldots \}$
; given a language
$X := \{x_1,x_2,\ldots \}$
; given a language
![]() $\tau $
we write
$\tau $
we write
![]() $Tm(\tau )$
for the set of
$Tm(\tau )$
for the set of
![]() $\tau $
-terms over the variables in X. Let
$\tau $
-terms over the variables in X. Let
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
be two expansions of a language
$\tau _2$
be two expansions of a language
![]() $\tau $
. A
$\tau $
. A
![]() $\tau $
-translation from
$\tau $
-translation from
![]() $\tau _1$
into
$\tau _1$
into
![]() $\tau _2$
is a function
$\tau _2$
is a function
![]() $T\colon \tau _1 \to Tm(\tau _2)$
such that T maps each symbol of arity n to a term in the variables
$T\colon \tau _1 \to Tm(\tau _2)$
such that T maps each symbol of arity n to a term in the variables
![]() $x_1,\ldots ,x_n$
, and
$x_1,\ldots ,x_n$
, and
![]() $T(f) = f(x_1,\ldots ,x_n)$
for every n-ary symbol
$T(f) = f(x_1,\ldots ,x_n)$
for every n-ary symbol
![]() $f \in \tau $
.
$f \in \tau $
.
Let
![]() $\mathcal {K}_1$
and
$\mathcal {K}_1$
and
![]() $\mathcal {K}_2$
be two classes of algebras over
$\mathcal {K}_2$
be two classes of algebras over
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
, respectively. A
$\tau _2$
, respectively. A
![]() $\tau $
-interpretation of
$\tau $
-interpretation of
![]() $\mathcal {K}_1$
in
$\mathcal {K}_1$
in
![]() $\mathcal {K}_2$
is a
$\mathcal {K}_2$
is a
![]() $\tau $
-translation
$\tau $
-translation
![]() $T\colon \tau _1 \to Tm(\tau _2)$
such that for every member
$T\colon \tau _1 \to Tm(\tau _2)$
such that for every member
![]() $\mathbf {A} := (A,\{g^{\mathbf {A}}: g \in \tau _2\})$
in
$\mathbf {A} := (A,\{g^{\mathbf {A}}: g \in \tau _2\})$
in
![]() $\mathcal {K}_2$
, the algebra
$\mathcal {K}_2$
, the algebra
![]() $\mathbf {A}^T := (A,\{T(f)^{\mathbf {A}}: f \in \tau _1\})$
belongs to
$\mathbf {A}^T := (A,\{T(f)^{\mathbf {A}}: f \in \tau _1\})$
belongs to
![]() $\mathcal {K}_1$
. If T and S are
$\mathcal {K}_1$
. If T and S are
![]() $\tau $
-interpretations of
$\tau $
-interpretations of
![]() $\mathcal {K}_1$
in
$\mathcal {K}_1$
in
![]() $\mathcal {K}_2$
and
$\mathcal {K}_2$
and
![]() $\mathcal {K}_2$
in
$\mathcal {K}_2$
in
![]() $\mathcal {K}_1$
, respectively, such that the maps
$\mathcal {K}_1$
, respectively, such that the maps
![]() $\mathbf {A} \mapsto \mathbf {A}^T$
and
$\mathbf {A} \mapsto \mathbf {A}^T$
and
![]() $\mathbf {A} \mapsto \mathbf {A}^S$
are mutually inverse, we say that
$\mathbf {A} \mapsto \mathbf {A}^S$
are mutually inverse, we say that
![]() $\mathcal {K}_1$
and
$\mathcal {K}_1$
and
![]() $\mathcal {K}_2$
are
$\mathcal {K}_2$
are
![]() $\tau $
-term-equivalent.
$\tau $
-term-equivalent.
We turn now to maps between logics. A
![]() $\tau $
-translation T from
$\tau $
-translation T from
![]() $\tau _1$
into
$\tau _1$
into
![]() $\tau _2$
extends in a natural way to a mapping from
$\tau _2$
extends in a natural way to a mapping from
![]() $Tm(\tau _1)$
to
$Tm(\tau _1)$
to
![]() $Tm(\tau _2)$
:
$Tm(\tau _2)$
:
-
•
 $T(x) = x$
for every variable
$T(x) = x$
for every variable
 $x \in X$
;
$x \in X$
; -
•
 $T(f(\varphi _1,\ldots ,\varphi _n)) = T(f)(T(\varphi _1),\ldots ,T(\varphi _n))$
for f in
$T(f(\varphi _1,\ldots ,\varphi _n)) = T(f)(T(\varphi _1),\ldots ,T(\varphi _n))$
for f in
 $\tau _1$
of arity n and
$\tau _1$
of arity n and
 $\varphi _1, \ldots \varphi _n$
in
$\varphi _1, \ldots \varphi _n$
in
 $Tm(\tau _1)$
.
$Tm(\tau _1)$
.
Given a set
![]() $\Gamma $
of
$\Gamma $
of
![]() $\tau _1$
-terms we write
$\tau _1$
-terms we write
![]() $T(\Gamma )$
for
$T(\Gamma )$
for
![]() $\{T(\varphi ): \varphi \in \Gamma \}$
.
$\{T(\varphi ): \varphi \in \Gamma \}$
.
Let
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
be expansions of a language
$\tau _2$
be expansions of a language
![]() $\tau $
, and suppose
$\tau $
, and suppose
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are logics in
$L_2$
are logics in
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
, respectively. A
$\tau _2$
, respectively. A
![]() $\tau $
-morphism from
$\tau $
-morphism from
![]() $L_1$
to
$L_1$
to
![]() $L_2$
is a
$L_2$
is a
![]() $\tau $
-translation from
$\tau $
-translation from
![]() $\tau _1$
into
$\tau _1$
into
![]() $\tau _2$
such that
$\tau _2$
such that
for
![]() $\Gamma \cup \{\varphi \} \subseteq Tm(\tau _1)$
. We say that
$\Gamma \cup \{\varphi \} \subseteq Tm(\tau _1)$
. We say that
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are
$L_2$
are
![]() $\tau $
-bimorphic, and write
$\tau $
-bimorphic, and write
![]() $L_1 \leftrightarrows _\tau L_2$
, provided there exist a
$L_1 \leftrightarrows _\tau L_2$
, provided there exist a
![]() $\tau $
-morphism from
$\tau $
-morphism from
![]() $L_1$
to
$L_1$
to
![]() $L_2$
and a
$L_2$
and a
![]() $\tau $
-morphism from
$\tau $
-morphism from
![]() $L_2$
to
$L_2$
to
![]() $L_1$
.
$L_1$
.
The following result shows the connection between the above defined relations.
Theorem 3.2. Let L be a finitely algebraizable logic in the language
![]() $\tau $
with equivalent algebraic semantics
$\tau $
with equivalent algebraic semantics
![]() $\mathcal {Q}$
. Let
$\mathcal {Q}$
. Let
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
be two sets of EFD-sentences in
$\Sigma '$
be two sets of EFD-sentences in
![]() $\tau $
.
$\tau $
.
-
1. The following are equivalent:
-
(i) There is a
 $\tau $
-morphism from
$\tau $
-morphism from
 $L^{\Sigma '}$
to
$L^{\Sigma '}$
to
 $L^\Sigma $
.
$L^\Sigma $
. -
(ii) There is a
 $\tau $
-interpretation of
$\tau $
-interpretation of
 $\mathcal {Q}^{\Sigma '}$
in
$\mathcal {Q}^{\Sigma '}$
in
 $\mathcal {Q}^\Sigma $
.
$\mathcal {Q}^\Sigma $
. -
(iii)
 $\mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ) \subseteq \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ')$
.
$\mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ) \subseteq \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ')$
.
-
-
2. The following are equivalent:
-
(i)
 $L^{\Sigma '}$
and
$L^{\Sigma '}$
and
 $L^\Sigma $
are
$L^\Sigma $
are
 $\tau $
-bimorphic.
$\tau $
-bimorphic. -
(ii)
 $\mathcal {Q}^{\Sigma '}$
and
$\mathcal {Q}^{\Sigma '}$
and
 $\mathcal {Q}^\Sigma $
are
$\mathcal {Q}^\Sigma $
are
 $\tau $
-term-equivalent.
$\tau $
-term-equivalent. -
(iii)
 $\mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ) = \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ')$
.
$\mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ) = \mathcal {Q} \cap \mathop {\mathrm {Mod}}(\Sigma ')$
.
-
Proof The proofs of all equivalences are routine with the exception of the implication
![]() $(iii)\mathord {\Rightarrow }(ii)$
, which follows from the proof of [Reference Campercholi and Vaggione11, Theorem 5].
$(iii)\mathord {\Rightarrow }(ii)$
, which follows from the proof of [Reference Campercholi and Vaggione11, Theorem 5].
A word of caution: it is not true in general that two bimorphic algebraizable logics have term-equivalent algebraic semantics. For example, let
![]() $C := \langle \tau , \vdash \rangle $
be the Classical Propositional Logic and let
$C := \langle \tau , \vdash \rangle $
be the Classical Propositional Logic and let
![]() $C_e = \langle \tau \cup \{e\}, \vdash _e \rangle $
where e is a new constant symbol and
$C_e = \langle \tau \cup \{e\}, \vdash _e \rangle $
where e is a new constant symbol and
![]() $\vdash _e$
is the least substitution invariant consequence operator containing
$\vdash _e$
is the least substitution invariant consequence operator containing
![]() $\vdash $
. Clearly
$\vdash $
. Clearly
![]() $C_e$
is algebraizable with equivalent algebraic semantics
$C_e$
is algebraizable with equivalent algebraic semantics
![]() $\mathcal {B}_e$
, the class of pointed Boolean algebras. It is straightforward to check that
$\mathcal {B}_e$
, the class of pointed Boolean algebras. It is straightforward to check that
![]() $C_e \leftrightarrows _{\tau } C$
; however,
$C_e \leftrightarrows _{\tau } C$
; however,
![]() $\mathcal {B}_e$
is obviously not
$\mathcal {B}_e$
is obviously not
![]() $\tau $
-term-equivalent to the class of Boolean algebras.
$\tau $
-term-equivalent to the class of Boolean algebras.
Let L be a logic algebraized by a quasivariety
![]() $\mathcal {Q}$
. As is the case for any quasivariety, the AE subclasses of
$\mathcal {Q}$
. As is the case for any quasivariety, the AE subclasses of
![]() $\mathcal {Q}$
form a lattice
$\mathcal {Q}$
form a lattice
![]() $\Lambda $
under inclusion. In the light of Theorem 3.2, the algebraic expansions of L modulo
$\Lambda $
under inclusion. In the light of Theorem 3.2, the algebraic expansions of L modulo
![]() $\leftrightarrows $
, ordered by morphisms, form a lattice as well, dually isomorphic to
$\leftrightarrows $
, ordered by morphisms, form a lattice as well, dually isomorphic to
![]() $\Lambda $
. Thus, classifying the algebraically expandable classes of
$\Lambda $
. Thus, classifying the algebraically expandable classes of
![]() $\mathcal {Q}$
yields a classification of all algebraic expansions of L up to
$\mathcal {Q}$
yields a classification of all algebraic expansions of L up to
![]() $\leftrightarrows $
.
$\leftrightarrows $
.
3.2 Some examples
When the AE-subclasses of a quasivariety are known, Theorem 3.2 immediately gives a description of the algebraic expansions of the corresponding logic. We present here three examples.
3.2.1 The primal case
An algebra
![]() $\mathbf {A}$
is called primal if it is finite and every function
$\mathbf {A}$
is called primal if it is finite and every function
![]() $f\colon A^n \to A$
for
$f\colon A^n \to A$
for
![]() $n \geq 1$
is a term-operation of
$n \geq 1$
is a term-operation of
![]() $\mathbf {A}$
. It is proved in [Reference Campercholi and Vaggione10, Theorem 13] that the only AE-subclasses of
$\mathbf {A}$
. It is proved in [Reference Campercholi and Vaggione10, Theorem 13] that the only AE-subclasses of
![]() $\mathsf {V}(\mathbf {A})$
for a primal
$\mathsf {V}(\mathbf {A})$
for a primal
![]() $\mathbf {A}$
are
$\mathbf {A}$
are
![]() $\mathsf {V}(\mathbf {A})$
and the class of trivial algebras. Thus, the only (modulo
$\mathsf {V}(\mathbf {A})$
and the class of trivial algebras. Thus, the only (modulo
![]() $\leftrightarrows $
) algebraic expansions of a logic L algebraized by such a variety are L itself and the inconsistent logic. This applies, e.g., to Classical Propositional Logic and m-valued Post’s logic.
$\leftrightarrows $
) algebraic expansions of a logic L algebraized by such a variety are L itself and the inconsistent logic. This applies, e.g., to Classical Propositional Logic and m-valued Post’s logic.
3.2.2 Gödel logic
Recall that Gödel Logic
![]() $L_G$
is the extension of Intuitionistic Logic by the prelinearity axiom
$L_G$
is the extension of Intuitionistic Logic by the prelinearity axiom
![]() $(x \mathbin {\rightarrow } y) \vee (y \mathbin {\rightarrow } x)$
. It is known that the equivalent algebraic semantics of
$(x \mathbin {\rightarrow } y) \vee (y \mathbin {\rightarrow } x)$
. It is known that the equivalent algebraic semantics of
![]() $L_G$
is the variety
$L_G$
is the variety
![]() $\mathcal {H}_G$
of Gödel algebras, also known as prelinear Heyting algebras. The only AE-subclasses of
$\mathcal {H}_G$
of Gödel algebras, also known as prelinear Heyting algebras. The only AE-subclasses of
![]() $\mathcal {H}_G$
are its subvarieties [Reference Campercholi8]. Thus, the algebraic expansions of
$\mathcal {H}_G$
are its subvarieties [Reference Campercholi8]. Thus, the algebraic expansions of
![]() $L_G$
agree with its axiomatic extensions.
$L_G$
agree with its axiomatic extensions.
3.2.3 The implicative fragment of classical logic
Let
![]() $L_\to $
be the implicative fragment of classical propositional logic. The equivalent algebraic semantics of
$L_\to $
be the implicative fragment of classical propositional logic. The equivalent algebraic semantics of
![]() $L_\to $
is the variety
$L_\to $
is the variety
![]() $\mathcal {I}$
of implication algebras. Recall that disjunction is expressible in terms of
$\mathcal {I}$
of implication algebras. Recall that disjunction is expressible in terms of
![]() $\mathbin {\rightarrow }$
, and thus for
$\mathbin {\rightarrow }$
, and thus for
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $1 \leq i \leq n$
$1 \leq i \leq n$
 $$ \begin{align*}s_i^n(x_1,\ldots,x_n) := \bigvee_{j=1,j\ne i}^n x_j\end{align*} $$
$$ \begin{align*}s_i^n(x_1,\ldots,x_n) := \bigvee_{j=1,j\ne i}^n x_j\end{align*} $$
is an
![]() $\{\mathbin {\rightarrow }\}$
-term. For each
$\{\mathbin {\rightarrow }\}$
-term. For each
![]() $n \geq 2$
let
$n \geq 2$
let
 $$ \begin{align*}\Phi_n := \{z \mathbin{\rightarrow} s_i^n(\bar{x}): i \in \{1,\ldots,n\}\} \cup \bigg\{\bigvee_{i=1}^n (s_i^n(\bar{x}) \mathbin{\rightarrow} z)\bigg\}.\end{align*} $$
$$ \begin{align*}\Phi_n := \{z \mathbin{\rightarrow} s_i^n(\bar{x}): i \in \{1,\ldots,n\}\} \cup \bigg\{\bigvee_{i=1}^n (s_i^n(\bar{x}) \mathbin{\rightarrow} z)\bigg\}.\end{align*} $$
By definition,
![]() $L_\to ^{\Phi _n}$
is the least expansion of
$L_\to ^{\Phi _n}$
is the least expansion of
![]() $L_\to $
that satisfies
$L_\to $
that satisfies
![]() $(\mathrm {E}_{\Phi _n})$
and
$(\mathrm {E}_{\Phi _n})$
and
![]() $(\mathrm {U}_{\Phi _n})$
. However, condition
$(\mathrm {U}_{\Phi _n})$
. However, condition
![]() $(\mathrm {U}_{\Phi _n})$
is already true for
$(\mathrm {U}_{\Phi _n})$
is already true for
![]() $L_\to $
. Thus
$L_\to $
. Thus
![]() $L_\to ^{\Phi _n}$
is the expansion of
$L_\to ^{\Phi _n}$
is the expansion of
![]() $L_\to $
by the following axioms:
$L_\to $
by the following axioms:
 $\mu _n(\bar {x}) \mathbin {\rightarrow } s_i^n(\bar {x})$
for
$\mu _n(\bar {x}) \mathbin {\rightarrow } s_i^n(\bar {x})$
for
 $i \in \{1,\ldots ,n\}$
,
$i \in \{1,\ldots ,n\}$
, $\bigvee _{i=1}^n (s_i^n(\bar {x}) \mathbin {\rightarrow } \mu _n(\bar {x}))$
,
$\bigvee _{i=1}^n (s_i^n(\bar {x}) \mathbin {\rightarrow } \mu _n(\bar {x}))$
,
where
![]() $\mu _n$
is a new n-ary symbol.
$\mu _n$
is a new n-ary symbol.
By the characterization of the AE-subclasses of
![]() $\mathcal {I}$
given in [Reference Campercholi9, Theorem 13] it follows from Theorem 3.2 that, up to
$\mathcal {I}$
given in [Reference Campercholi9, Theorem 13] it follows from Theorem 3.2 that, up to
![]() $\leftrightarrows $
, the consistent algebraic expansions of
$\leftrightarrows $
, the consistent algebraic expansions of
![]() $L_\to $
are
$L_\to $
are
where
![]() $L < L'$
means that there is an
$L < L'$
means that there is an
![]() $\{\to \}$
-morphism from L to
$\{\to \}$
-morphism from L to
![]() $L'$
but there is no
$L'$
but there is no
![]() $\{\to \}$
-morphism from
$\{\to \}$
-morphism from
![]() $L'$
to
$L'$
to
![]() $L'$
. Observe that
$L'$
. Observe that
![]() $\mu _2$
is the classical conjunction and, more generally, we have that
$\mu _2$
is the classical conjunction and, more generally, we have that
![]() $\mu _n(\bar {x}) = \bigwedge _{i=1}^n s_i^n(\bar {x})$
.
$\mu _n(\bar {x}) = \bigwedge _{i=1}^n s_i^n(\bar {x})$
.
Example 3 of [Reference Caicedo5] shows classical negation is implicitly definable in
![]() $L_\to $
. Since none of the algebraic expansions of
$L_\to $
. Since none of the algebraic expansions of
![]() $L_\to $
has classical negation as a term, we have another example of an expansion by implicit connectives that is not algebraic.
$L_\to $
has classical negation as a term, we have another example of an expansion by implicit connectives that is not algebraic.
4 Algebraic expansions of abelian
 $\ell $
-groups and the Logic of Equilibrium
$\ell $
-groups and the Logic of Equilibrium
In this section we give a complete description of the AE-classes of abelian
![]() $\ell $
-groups. In particular, we show that they form a lattice isomorphic to
$\ell $
-groups. In particular, we show that they form a lattice isomorphic to
![]() $\mathbf {1} \oplus \mathbf {2}^\omega $
(here, and in the sequel,
$\mathbf {1} \oplus \mathbf {2}^\omega $
(here, and in the sequel,
![]() $\mathbf {A} \oplus \mathbf {B}$
denotes the ordinal sum of
$\mathbf {A} \oplus \mathbf {B}$
denotes the ordinal sum of
![]() $\mathbf {A}$
and
$\mathbf {A}$
and
![]() $\mathbf {B}$
where
$\mathbf {B}$
where
![]() $\mathbf {B}$
goes on top of
$\mathbf {B}$
goes on top of
![]() $\mathbf {A}$
). In view of Theorem 3.2 this produces a complete characterization of the algebraic expansions of the Logic of Equilibrium [Reference Galli, Lewin and Sagastume16, Reference Metcalfe, Olivetti and Gabbay21].
$\mathbf {A}$
). In view of Theorem 3.2 this produces a complete characterization of the algebraic expansions of the Logic of Equilibrium [Reference Galli, Lewin and Sagastume16, Reference Metcalfe, Olivetti and Gabbay21].
Recall that an abelian
![]() $\ell $
-group is a structure in the language
$\ell $
-group is a structure in the language
![]() $\tau _{\mathcal {G}} := \{+,-,0,\vee ,\wedge \}$
such that:
$\tau _{\mathcal {G}} := \{+,-,0,\vee ,\wedge \}$
such that:
-
•
 $(A,+,-,0)$
is an abelian group,
$(A,+,-,0)$
is an abelian group, -
•
 $(A,\vee ,\wedge )$
is a lattice,
$(A,\vee ,\wedge )$
is a lattice, -
•
 $a + (b \vee c) = (a + b) \vee (a + c)$
for every
$a + (b \vee c) = (a + b) \vee (a + c)$
for every
 $a,b,c \in A$
.
$a,b,c \in A$
.
Clearly abelian
![]() $\ell $
-groups form a variety, which we denote by
$\ell $
-groups form a variety, which we denote by
![]() $\mathcal {G}$
. We write
$\mathcal {G}$
. We write
![]() $\mathcal {G}_{\mathrm {to}}$
to denote its subclass of totally ordered members. Since all
$\mathcal {G}_{\mathrm {to}}$
to denote its subclass of totally ordered members. Since all
![]() $\ell $
-groups in this article are abelian, we sometimes omit the word abelian. In the following lemma we collect some well-known properties that are needed in the sequel (see, e.g., [Reference Glass17, Reference Weinberg26]).
$\ell $
-groups in this article are abelian, we sometimes omit the word abelian. In the following lemma we collect some well-known properties that are needed in the sequel (see, e.g., [Reference Glass17, Reference Weinberg26]).
Lemma 4.1.
-
1. The variety
 $\mathcal {G}$
is arithmetical, that is, every member of
$\mathcal {G}$
is arithmetical, that is, every member of
 $\mathcal {G}$
has permutable and distributive congruences.
$\mathcal {G}$
has permutable and distributive congruences. -
2. For every nontrivial
 $\mathbf {A} \in \mathcal {G}_{\mathrm {to}}$
we have
$\mathbf {A} \in \mathcal {G}_{\mathrm {to}}$
we have
 $\mathsf {ISP_U}(\mathbf {A}) = \mathcal {G}_{\mathrm {to}}$
.
$\mathsf {ISP_U}(\mathbf {A}) = \mathcal {G}_{\mathrm {to}}$
. -
3. An abelian
 $\ell $
-group is finitely subdirectly irreducible if and only if it is nontrivial and totally ordered.
$\ell $
-group is finitely subdirectly irreducible if and only if it is nontrivial and totally ordered. -
4. For every nontrivial
 $\mathbf {A} \in \mathcal {G}$
we have
$\mathbf {A} \in \mathcal {G}$
we have
 $\mathsf {Q}(\mathbf {A}) = \mathsf {V}(\mathbf {A}) = \mathcal {G}$
.
$\mathsf {Q}(\mathbf {A}) = \mathsf {V}(\mathbf {A}) = \mathcal {G}$
.
4.1 AE-classes of abelian
 $\ell $
-groups
$\ell $
-groups
We proceed to characterize EFD-sentences modulo equivalence in
![]() $\mathcal {G}$
. We first reduce the problem to totally ordered abelian
$\mathcal {G}$
. We first reduce the problem to totally ordered abelian
![]() $\ell $
-groups.
$\ell $
-groups.
Lemma 4.2. Given EFD-sentences
![]() $\varphi , \psi $
, if
$\varphi , \psi $
, if
![]() $\varphi \mathrel {\sim } \psi $
in
$\varphi \mathrel {\sim } \psi $
in
![]() $\mathcal {G}_{\mathrm {to}}$
, then
$\mathcal {G}_{\mathrm {to}}$
, then
![]() $\varphi \mathrel {\sim } \psi $
in
$\varphi \mathrel {\sim } \psi $
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof Suppose
![]() $\varphi \mathrel {\sim } \psi $
in
$\varphi \mathrel {\sim } \psi $
in
![]() $\mathcal {G}_{\mathrm {to}}$
; take a nontrivial
$\mathcal {G}_{\mathrm {to}}$
; take a nontrivial
![]() $\mathbf {A}$
in
$\mathbf {A}$
in
![]() $\mathcal {G}$
, and assume
$\mathcal {G}$
, and assume
![]() $\mathbf {A} \vDash \varphi $
. On the one hand, since
$\mathbf {A} \vDash \varphi $
. On the one hand, since
![]() $U(\varphi )$
is a quasi-identity, Lemma 4.1(4) implies that
$U(\varphi )$
is a quasi-identity, Lemma 4.1(4) implies that
![]() $\mathsf {H}(\mathbf {A}) \vDash U(\varphi )$
. On the other hand,
$\mathsf {H}(\mathbf {A}) \vDash U(\varphi )$
. On the other hand,
![]() $\mathsf {H}(\mathbf {A}) \vDash E(\varphi )$
because
$\mathsf {H}(\mathbf {A}) \vDash E(\varphi )$
because
![]() $E(\varphi )$
is preserved by homomorphic images. Hence
$E(\varphi )$
is preserved by homomorphic images. Hence
![]() $\mathsf {H}(\mathbf {A}) \vDash \varphi $
and, in particular,
$\mathsf {H}(\mathbf {A}) \vDash \varphi $
and, in particular,
![]() $\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \varphi $
. As, by Lemma 4.1(3), every member in
$\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \varphi $
. As, by Lemma 4.1(3), every member in
![]() $\mathsf {H}(\mathbf {A})_{\mathrm {fsi}}$
is totally ordered, we have
$\mathsf {H}(\mathbf {A})_{\mathrm {fsi}}$
is totally ordered, we have
![]() $\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \psi $
. So, using Lemma 2.1, we are done.
$\mathsf {H}(\mathbf {A})_{\mathrm {fsi}} \vDash \psi $
. So, using Lemma 2.1, we are done.
For each positive integer k define
Our next step is to show that every EFD-sentence is equivalent to a
![]() $\delta _k$
in
$\delta _k$
in
![]() $\mathcal {G}$
, which is accomplished in Theorem 4.12.
$\mathcal {G}$
, which is accomplished in Theorem 4.12.
Recall that an
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
is divisible if for every
$\mathbf {G}$
is divisible if for every
![]() $g \in G$
and every positive integer n, there exists
$g \in G$
and every positive integer n, there exists
![]() $h \in G$
such that
$h \in G$
such that
![]() $g = nh$
. Given a divisible
$g = nh$
. Given a divisible
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {D}$
, since
$\mathbf {D}$
, since
![]() $\ell $
-groups are torsion-free, we have that
$\ell $
-groups are torsion-free, we have that
![]() $\delta _k$
holds in
$\delta _k$
holds in
![]() $\mathbf {D}$
for all k; thus, we can define the expansion
$\mathbf {D}$
for all k; thus, we can define the expansion
The next result shows that the only functions defined by EFD-sentences in these expansions are term-operations.
Theorem 4.3. Let
![]() $\mathbf {D}$
be a totally ordered divisible
$\mathbf {D}$
be a totally ordered divisible
![]() $\ell $
-group and let
$\ell $
-group and let
![]() $\varphi $
be an EFD-sentence that holds in
$\varphi $
be an EFD-sentence that holds in
![]() $\mathbf {D}$
. Then, the functions
$\mathbf {D}$
. Then, the functions
![]() $[\varphi ]_1^{\mathbf {D}}, \ldots , [\varphi ]_m^{\mathbf {D}}$
defined by
$[\varphi ]_1^{\mathbf {D}}, \ldots , [\varphi ]_m^{\mathbf {D}}$
defined by
![]() $\varphi $
on
$\varphi $
on
![]() $\mathbf {D}$
are term-functions on
$\mathbf {D}$
are term-functions on
![]() $\overline {\mathbf {D}}$
.
$\overline {\mathbf {D}}$
.
The above theorem can be derived from [Reference Caicedo6, Theorem 20]. We provide a different proof that relies on the characterization of existentially closed algebras in
![]() $\mathcal {G}_{\mathrm {to}}$
.
$\mathcal {G}_{\mathrm {to}}$
.
Given a class
![]() $\mathcal {K}$
of algebras closed under isomorphisms and
$\mathcal {K}$
of algebras closed under isomorphisms and
![]() $\mathbf {A} \in \mathcal {K}$
, we say that
$\mathbf {A} \in \mathcal {K}$
, we say that
![]() $\mathbf {A}$
is existentially closed in
$\mathbf {A}$
is existentially closed in
![]() $\mathcal {K}$
if for every
$\mathcal {K}$
if for every
![]() $\mathbf {B} \in \mathcal {K}$
such that
$\mathbf {B} \in \mathcal {K}$
such that
![]() $\mathbf {A} \subseteq \mathbf {B}$
, every existential formula
$\mathbf {A} \subseteq \mathbf {B}$
, every existential formula
![]() $\varphi (\bar {x})$
, and every
$\varphi (\bar {x})$
, and every
![]() $\bar {a} \in A^n$
$\bar {a} \in A^n$
The next proposition characterizes the existentially closed members of the class of totally ordered
![]() $\ell $
-groups.
$\ell $
-groups.
Proposition 4.4. Given a totally ordered
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
, we have that
$\mathbf {G}$
, we have that
![]() $\mathbf {G}$
is existentially closed in
$\mathbf {G}$
is existentially closed in
![]() $\mathcal {G}_{\mathrm {to}}$
if and only if
$\mathcal {G}_{\mathrm {to}}$
if and only if
![]() $\mathbf {G}$
is divisible.
$\mathbf {G}$
is divisible.
Proof The result follows from [Reference Robinson24, Theorem 3.1.13] when considering totally ordered
![]() $\ell $
-groups as structures of the language
$\ell $
-groups as structures of the language
![]() $\tau := \{S,\leq \}$
, where S is a ternary relation symbol interpreted as the graph of the addition operation and
$\tau := \{S,\leq \}$
, where S is a ternary relation symbol interpreted as the graph of the addition operation and
![]() $\leq $
is a binary relation symbol interpreted as the ordering relation. Now, since the operations
$\leq $
is a binary relation symbol interpreted as the ordering relation. Now, since the operations
![]() $+, -, \vee , \wedge $
are definable by quantifier-free
$+, -, \vee , \wedge $
are definable by quantifier-free
![]() $\tau $
-formulas, the statement follows.
$\tau $
-formulas, the statement follows.
Corollary 4.5. Let
![]() $\mathbf {D} \subseteq \mathbf {G}$
be totally ordered
$\mathbf {D} \subseteq \mathbf {G}$
be totally ordered
![]() $\ell $
-groups and assume
$\ell $
-groups and assume
![]() $\mathbf {D}$
is divisible. Then, for every EFD-sentence
$\mathbf {D}$
is divisible. Then, for every EFD-sentence
![]() $\varphi $
we have that
$\varphi $
we have that
![]() $\mathbf {G} \vDash \varphi $
implies
$\mathbf {G} \vDash \varphi $
implies
![]() $\mathbf {D} \vDash \varphi $
.
$\mathbf {D} \vDash \varphi $
.
Proof Suppose
![]() $\mathbf {G}$
satisfies the EFD-sentence
$\mathbf {G}$
satisfies the EFD-sentence
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $U(\varphi )$
is universal, we have
$U(\varphi )$
is universal, we have
![]() $\mathbf {D} \vDash \varphi $
, and the fact that
$\mathbf {D} \vDash \varphi $
, and the fact that
![]() $\mathbf {D}$
is existentially closed implies
$\mathbf {D}$
is existentially closed implies
![]() $\mathbf {D} \vDash E(\varphi )$
.
$\mathbf {D} \vDash E(\varphi )$
.
Corollary 4.6. If
![]() $\varphi $
is an EFD-sentence with a nontrivial model in
$\varphi $
is an EFD-sentence with a nontrivial model in
![]() $\mathcal {G}$
, then every totally ordered divisible
$\mathcal {G}$
, then every totally ordered divisible
![]() $\ell $
-group satisfies
$\ell $
-group satisfies
![]() $\varphi $
.
$\varphi $
.
Proof Assume
![]() $\mathbf {H}$
is a nontrivial model of
$\mathbf {H}$
is a nontrivial model of
![]() $\varphi $
and let
$\varphi $
and let
![]() $\mathbf {H}'$
be a nontrivial totally ordered homomorphic image of
$\mathbf {H}'$
be a nontrivial totally ordered homomorphic image of
![]() $\mathbf {H}$
. Clearly
$\mathbf {H}$
. Clearly
![]() $\mathbf {H}' \vDash E(\varphi )$
and, since
$\mathbf {H}' \vDash E(\varphi )$
and, since
![]() $\mathsf {Q}(\mathbf {H})$
is the class of all
$\mathsf {Q}(\mathbf {H})$
is the class of all
![]() $\ell $
-groups, we have
$\ell $
-groups, we have
![]() $\mathbf {H}' \vDash U(\varphi )$
. Hence
$\mathbf {H}' \vDash U(\varphi )$
. Hence
![]() $\mathbf {H}' \vDash \varphi $
. By Lemma 4.1, we know that
$\mathbf {H}' \vDash \varphi $
. By Lemma 4.1, we know that
![]() $\mathsf {ISP_U}(\mathbf {H}') = \mathcal {G}_{\mathrm {to}}$
. Thus, if
$\mathsf {ISP_U}(\mathbf {H}') = \mathcal {G}_{\mathrm {to}}$
. Thus, if
![]() $\mathbf {D}$
is a totally ordered divisible
$\mathbf {D}$
is a totally ordered divisible
![]() $\ell $
-group, there is
$\ell $
-group, there is
![]() $\mathbf {G} \in \mathsf {P_U}(\mathbf {H}')$
such that
$\mathbf {G} \in \mathsf {P_U}(\mathbf {H}')$
such that
![]() $\mathbf {D} \subseteq \mathbf {G}$
. Finally, Corollary 4.5 yields
$\mathbf {D} \subseteq \mathbf {G}$
. Finally, Corollary 4.5 yields
![]() $\mathbf {D} \vDash \varphi $
.
$\mathbf {D} \vDash \varphi $
.
After this sequence of results we are ready to present:
Proof of Theorem 4.3 Assume
![]() $\mathbf {D} \vDash \varphi $
for some EFD-sentence
$\mathbf {D} \vDash \varphi $
for some EFD-sentence
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbf {D}$
nontrivial. Let
$\mathbf {D}$
nontrivial. Let
![]() $\overline {\mathbf {D}}$
be as in (2). Observe that
$\overline {\mathbf {D}}$
be as in (2). Observe that
![]() $\mathsf {V}(\overline {\mathbf {D}})$
is arithmetical since arithmeticity is witnessed by a Pixley term (see [Reference Burris and Sankappanavar4, Theorem 12.5]).
$\mathsf {V}(\overline {\mathbf {D}})$
is arithmetical since arithmeticity is witnessed by a Pixley term (see [Reference Burris and Sankappanavar4, Theorem 12.5]).
We prove first that
![]() $\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}} \vDash \varphi $
. Since all divisions are basic operations of
$\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}} \vDash \varphi $
. Since all divisions are basic operations of
![]() $\overline {\mathbf {D}}$
, we have that the algebras in
$\overline {\mathbf {D}}$
, we have that the algebras in
![]() $\mathsf {SP_U}(\overline {\mathbf {D}})$
are totally ordered divisible
$\mathsf {SP_U}(\overline {\mathbf {D}})$
are totally ordered divisible
![]() $\ell $
-groups, and Corollary 4.6 produces
$\ell $
-groups, and Corollary 4.6 produces
![]() $\mathsf {SP_U}(\overline {\mathbf {D}}) \vDash \varphi $
. Clearly
$\mathsf {SP_U}(\overline {\mathbf {D}}) \vDash \varphi $
. Clearly
![]() $\mathsf {HSP_U}(\overline {\mathbf {D}}) \vDash E(\varphi )$
and, since
$\mathsf {HSP_U}(\overline {\mathbf {D}}) \vDash E(\varphi )$
and, since
![]() $\mathcal {G} = \mathsf {Q}(\mathbf {D}) \vDash U(\varphi )$
, it follows that
$\mathcal {G} = \mathsf {Q}(\mathbf {D}) \vDash U(\varphi )$
, it follows that
![]() $\mathsf {HSP_U}(\overline {\mathbf {D}})$
satisfies
$\mathsf {HSP_U}(\overline {\mathbf {D}})$
satisfies
![]() $U(\varphi )$
as well. Thus,
$U(\varphi )$
as well. Thus,
![]() $\mathsf {HSP_U}(\overline {\mathbf {D}}) \vDash \varphi $
, and we are done since
$\mathsf {HSP_U}(\overline {\mathbf {D}}) \vDash \varphi $
, and we are done since
![]() $\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}} \subseteq \mathsf {HSP_U}(\overline {\mathbf {D}})$
by Jónsson’s lemma (see [Reference Jónsson20]).
$\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}} \subseteq \mathsf {HSP_U}(\overline {\mathbf {D}})$
by Jónsson’s lemma (see [Reference Jónsson20]).
Since
![]() $\ell $
-group congruences are compatible with division operations, we have that the congruences of algebras in
$\ell $
-group congruences are compatible with division operations, we have that the congruences of algebras in
![]() $\mathsf {V}(\overline {\mathbf {D}})$
agree with the congruences of their
$\mathsf {V}(\overline {\mathbf {D}})$
agree with the congruences of their
![]() $\ell $
-group reducts. Now, an algebra
$\ell $
-group reducts. Now, an algebra
![]() $\mathbf {A} \in \mathsf {V}(\overline {\mathbf {D}})$
is finitely subdirectly irreducible if and only if its diagonal congruence is meet irreducible in its congruence lattice. Thus,
$\mathbf {A} \in \mathsf {V}(\overline {\mathbf {D}})$
is finitely subdirectly irreducible if and only if its diagonal congruence is meet irreducible in its congruence lattice. Thus,
![]() $\mathbf {A}$
is finitely subdirectly irreducible if and only if
$\mathbf {A}$
is finitely subdirectly irreducible if and only if
![]() $\mathbf {A}|_{\tau _{\mathcal {G}}}$
is finitely subdirectly irreducible, which in turn is equivalent to
$\mathbf {A}|_{\tau _{\mathcal {G}}}$
is finitely subdirectly irreducible, which in turn is equivalent to
![]() $\mathbf {A}|_{\tau _{\mathcal {G}}}$
being totally ordered. Therefore, the class
$\mathbf {A}|_{\tau _{\mathcal {G}}}$
being totally ordered. Therefore, the class
![]() $\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}}$
is universal, and by Lemma 2.1 we have
$\mathsf {V}(\overline {\mathbf {D}})_{\mathrm {fsi}}$
is universal, and by Lemma 2.1 we have
![]() $\mathsf {V}(\overline {\mathbf {D}}) \vDash \varphi $
. The proof concludes applying [Reference Campercholi and Vaggione11, Lemma 3], which states that if an EFD-sentence
$\mathsf {V}(\overline {\mathbf {D}}) \vDash \varphi $
. The proof concludes applying [Reference Campercholi and Vaggione11, Lemma 3], which states that if an EFD-sentence
![]() $\varphi $
holds in a variety
$\varphi $
holds in a variety
![]() $\mathcal {V}$
, then there are terms that agree with the functions defined by
$\mathcal {V}$
, then there are terms that agree with the functions defined by
![]() $\varphi $
on each member of
$\varphi $
on each member of
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
Given a positive integer k and a term
![]() $t(\bar {x})$
in
$t(\bar {x})$
in
![]() $\tau _{\mathcal {G}}$
, let
$\tau _{\mathcal {G}}$
, let
Observe that
![]() $U(\delta _{k,t})$
is valid in
$U(\delta _{k,t})$
is valid in
![]() $\mathcal {G}$
because abelian
$\mathcal {G}$
because abelian
![]() $\ell $
-groups are torsion-free.
$\ell $
-groups are torsion-free.
We denote by
![]() $\mathcal {D}$
the class of expansions
$\mathcal {D}$
the class of expansions
![]() $\overline {\mathbf {D}}$
of divisible
$\overline {\mathbf {D}}$
of divisible
![]() $\ell $
-groups
$\ell $
-groups
![]() $\mathbf {D} \in \mathcal {G}$
. We write
$\mathbf {D} \in \mathcal {G}$
. We write
![]() $\tau _{\mathcal {D}}$
for the language of the algebras in the class
$\tau _{\mathcal {D}}$
for the language of the algebras in the class
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 4.7. Given a term
![]() $s(\bar {x})$
in
$s(\bar {x})$
in
![]() $\tau _{\mathcal {D}}$
, there is a term
$\tau _{\mathcal {D}}$
, there is a term
![]() $t(\bar {x})$
in
$t(\bar {x})$
in
![]() $\tau _{\mathcal {G}}$
and a positive integer k such that
$\tau _{\mathcal {G}}$
and a positive integer k such that
![]() $k \, s(\bar {x}) = t(\bar {x})$
is valid in
$k \, s(\bar {x}) = t(\bar {x})$
is valid in
![]() $\mathcal {D}$
. Hence, for any divisible
$\mathcal {D}$
. Hence, for any divisible
![]() $\mathbf {D} \in \mathcal {G}$
the term-function
$\mathbf {D} \in \mathcal {G}$
the term-function
![]() $s^{\overline {\mathbf {D}}}$
agrees with the function
$s^{\overline {\mathbf {D}}}$
agrees with the function
![]() $[\delta _{k,t}]^{\mathbf {D}}$
.
$[\delta _{k,t}]^{\mathbf {D}}$
.
Proof It follows by induction on the structure of
![]() $s(\bar {x})$
.
$s(\bar {x})$
.
Lemma 4.8. Let
![]() $\varphi $
be an EFD-sentence with a nontrivial model in
$\varphi $
be an EFD-sentence with a nontrivial model in
![]() $\mathcal {G}$
. Then there are positive integers
$\mathcal {G}$
. Then there are positive integers
![]() $k_1, \dots , k_m$
and terms
$k_1, \dots , k_m$
and terms
![]() $t_1, \dots , t_m$
in
$t_1, \dots , t_m$
in
![]() $\tau _{\mathcal {G}}$
such that
$\tau _{\mathcal {G}}$
such that
 $\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j,t_j}$
in
$\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j,t_j}$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof Fix
![]() $\varphi := \forall x_1 \dots x_n \exists ! z_1 \dots z_m \, \alpha (\bar {x},\bar {z})$
. Note that
$\varphi := \forall x_1 \dots x_n \exists ! z_1 \dots z_m \, \alpha (\bar {x},\bar {z})$
. Note that
![]() $\mathcal {G} \vDash U(\varphi )$
since
$\mathcal {G} \vDash U(\varphi )$
since
![]() $\varphi $
has a nontrivial model in
$\varphi $
has a nontrivial model in
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {G}$
has no proper subquasivarieties. Let
$\mathcal {G}$
has no proper subquasivarieties. Let
![]() $\mathbf {D}$
be a nontrivial totally ordered divisible
$\mathbf {D}$
be a nontrivial totally ordered divisible
![]() $\ell $
-group. By Corollary 4.6, we have that
$\ell $
-group. By Corollary 4.6, we have that
![]() $\mathbf {D} \vDash \varphi $
. So Theorem 4.3 provides terms
$\mathbf {D} \vDash \varphi $
. So Theorem 4.3 provides terms
![]() $s_1, \dots , s_m$
in
$s_1, \dots , s_m$
in
![]() $\tau _{\mathcal {D}}$
such that
$\tau _{\mathcal {D}}$
such that
![]() $[\varphi ]_j^{\mathbf {D}} = s_j^{\overline {\mathbf {D}}}$
for
$[\varphi ]_j^{\mathbf {D}} = s_j^{\overline {\mathbf {D}}}$
for
![]() $j \in \{1,\dots ,m\}$
. Moreover, by Lemma 4.7, there are positive integers
$j \in \{1,\dots ,m\}$
. Moreover, by Lemma 4.7, there are positive integers
![]() $k_1,\dots ,k_m$
and terms
$k_1,\dots ,k_m$
and terms
![]() $t_1, \dots , t_m$
in
$t_1, \dots , t_m$
in
![]() $\tau _{\mathcal {G}}$
such that
$\tau _{\mathcal {G}}$
such that
![]() $s_j^{\overline {\mathbf {D}}} = [\delta _{k_j,t_j}]^{\mathbf {D}}$
. This shows that
$s_j^{\overline {\mathbf {D}}} = [\delta _{k_j,t_j}]^{\mathbf {D}}$
. This shows that
 $\mathbf {D} \vDash \forall \bar {x} \bar {z} \, ( \alpha (\bar {x},\bar {z}) \mathbin {\boldsymbol {\leftrightarrow }} \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m k_jz_j = t_j(\bar {x}) )$
, and again using that
$\mathbf {D} \vDash \forall \bar {x} \bar {z} \, ( \alpha (\bar {x},\bar {z}) \mathbin {\boldsymbol {\leftrightarrow }} \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m k_jz_j = t_j(\bar {x}) )$
, and again using that
![]() $\mathcal {G}$
has no proper subquasivarieties, we have
$\mathcal {G}$
has no proper subquasivarieties, we have
 $\mathcal {G} \vDash \forall \bar {x} \bar {z} \, (\alpha (\bar {x},\bar {z}) \mathbin {\boldsymbol {\leftrightarrow }} \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m k_jz_j = t_j(\bar {x}))$
. Finally, since
$\mathcal {G} \vDash \forall \bar {x} \bar {z} \, (\alpha (\bar {x},\bar {z}) \mathbin {\boldsymbol {\leftrightarrow }} \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m k_jz_j = t_j(\bar {x}))$
. Finally, since
![]() $\mathcal {G}$
satisfies
$\mathcal {G}$
satisfies
![]() $U(\varphi )$
and
$U(\varphi )$
and
![]() $U(\delta _{k_j,t_j})$
for
$U(\delta _{k_j,t_j})$
for
![]() $j \in \{1,\dots ,m\}$
, it follows that
$j \in \{1,\dots ,m\}$
, it follows that
 $\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j,t_j}$
in
$\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j,t_j}$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
In the following, by a system of linear inequalities we mean a finite conjunction of inequalities of the form
![]() $a_1x_1 + \dots + a_nx_n \geq 0$
where
$a_1x_1 + \dots + a_nx_n \geq 0$
where
![]() $a_1,\dots ,a_n$
are integers. (Note that such a system can be written as a conjunction of equations in
$a_1,\dots ,a_n$
are integers. (Note that such a system can be written as a conjunction of equations in
![]() $\tau _{\mathcal {G}}$
.)
$\tau _{\mathcal {G}}$
.)
We say that a system of linear inequalities
![]() $\alpha (\bar {x})$
is full-dimensional on an abelian
$\alpha (\bar {x})$
is full-dimensional on an abelian
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
if there is no
$\mathbf {G}$
if there is no
![]() $(a_1,\dots ,a_n) \in \mathbb {Z}^n \setminus \{\bar {0}\}$
such that
$(a_1,\dots ,a_n) \in \mathbb {Z}^n \setminus \{\bar {0}\}$
such that
![]() $\mathbf {G} \vDash \forall \bar {x} \, (\alpha (\bar {x}) \mathbin {\boldsymbol {\rightarrow }} \sum a_ix_i \,{=}\, 0)$
. That is, the system
$\mathbf {G} \vDash \forall \bar {x} \, (\alpha (\bar {x}) \mathbin {\boldsymbol {\rightarrow }} \sum a_ix_i \,{=}\, 0)$
. That is, the system
![]() $\alpha (\bar {x})$
imposes no linear dependencies on its solutions in
$\alpha (\bar {x})$
imposes no linear dependencies on its solutions in
![]() $\mathbf {G}$
. Observe that Lemma 4.1(4) implies that
$\mathbf {G}$
. Observe that Lemma 4.1(4) implies that
![]() $\alpha (\bar {x})$
is full-dimensional on some nontrivial
$\alpha (\bar {x})$
is full-dimensional on some nontrivial
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
if and only if it is full-dimensional on every nontrivial
$\mathbf {G}$
if and only if it is full-dimensional on every nontrivial
![]() $\ell $
-group. Hence, we say that
$\ell $
-group. Hence, we say that
![]() $\alpha (\bar {x})$
is full-dimensional provided it is full-dimensional on some nontrivial
$\alpha (\bar {x})$
is full-dimensional provided it is full-dimensional on some nontrivial
![]() $\ell $
-group.
$\ell $
-group.
Lemma 4.9. A system of linear inequalities
![]() $\alpha (\bar {x})$
is full-dimensional if and only if for every totally ordered
$\alpha (\bar {x})$
is full-dimensional if and only if for every totally ordered
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
the set
$\mathbf {G}$
the set
![]() $\{\bar {g} \in G^n: \mathbf {G} \vDash \alpha (\bar {g})\}$
generates
$\{\bar {g} \in G^n: \mathbf {G} \vDash \alpha (\bar {g})\}$
generates
![]() $\mathbf {G}^n$
as an abelian group.
$\mathbf {G}^n$
as an abelian group.
Proof Assume
![]() $\alpha (\bar {x})$
is a full-dimensional system of linear inequalities and let
$\alpha (\bar {x})$
is a full-dimensional system of linear inequalities and let
![]() $S_{\mathbf {G}} := \{\bar {g} \in G^n: \mathbf {G} \vDash \alpha (\bar {g})\}$
for any totally ordered
$S_{\mathbf {G}} := \{\bar {g} \in G^n: \mathbf {G} \vDash \alpha (\bar {g})\}$
for any totally ordered
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
. Let
$\mathbf {G}$
. Let
![]() $\mathbf {Q}$
and
$\mathbf {Q}$
and
![]() $\mathbf {Z}$
denote the
$\mathbf {Z}$
denote the
![]() $\ell $
-groups of rational and integer numbers, respectively. First observe that
$\ell $
-groups of rational and integer numbers, respectively. First observe that
![]() $S_{\mathbf {Z}} = S_{\mathbf {Q}} \cap Z^n$
. Note also that
$S_{\mathbf {Z}} = S_{\mathbf {Q}} \cap Z^n$
. Note also that
![]() $S_{\mathbf {G}}$
is closed under linear combinations whose coefficients are non-negative integers, and
$S_{\mathbf {G}}$
is closed under linear combinations whose coefficients are non-negative integers, and
![]() $S_{\mathbf {Q}}$
is closed under non-negative rational linear combinations.
$S_{\mathbf {Q}}$
is closed under non-negative rational linear combinations.
We start by proving that
![]() $S_{\mathbf {Z}}$
generated
$S_{\mathbf {Z}}$
generated
![]() $\mathbf {Z}^n$
as an abelian group. Let V be the
$\mathbf {Z}^n$
as an abelian group. Let V be the
![]() $\mathbf {Q}$
-vector subspace of
$\mathbf {Q}$
-vector subspace of
![]() $\mathbf {Q}^n$
generated by
$\mathbf {Q}^n$
generated by
![]() $S_{\mathbf {Q}}$
. Observe that
$S_{\mathbf {Q}}$
. Observe that
![]() $V = Q^n$
; otherwise, there would exist integers
$V = Q^n$
; otherwise, there would exist integers
![]() $a_1, \ldots , a_n$
, not all zero, such that
$a_1, \ldots , a_n$
, not all zero, such that
![]() $V \subseteq \{\bar {x} \in Q^n: \sum a_ix_i = 0\}$
, contradicting the fact that
$V \subseteq \{\bar {x} \in Q^n: \sum a_ix_i = 0\}$
, contradicting the fact that
![]() $\alpha (\bar {x})$
is full-dimensional. Since
$\alpha (\bar {x})$
is full-dimensional. Since
![]() $V = Q^n$
, the solution set
$V = Q^n$
, the solution set
![]() $S_{\mathbf {Q}}$
contains a
$S_{\mathbf {Q}}$
contains a
![]() $\mathbf {Q}$
-basis of
$\mathbf {Q}$
-basis of
![]() $\mathbf {Q}^n$
, which, multiplied by a suitable positive integer, yields a
$\mathbf {Q}^n$
, which, multiplied by a suitable positive integer, yields a
![]() $\mathbf {Q}$
-basis
$\mathbf {Q}$
-basis
![]() $\{\bar {b}_1,\dots ,\bar {b}_n\} \subseteq S_{\mathbf {Z}}$
. Since
$\{\bar {b}_1,\dots ,\bar {b}_n\} \subseteq S_{\mathbf {Z}}$
. Since
![]() $S_{\mathbf {Z}}$
is closed under positive integer linear combinations,
$S_{\mathbf {Z}}$
is closed under positive integer linear combinations,
![]() $\bar {b} := \sum \bar {b}_i \in S_{\mathbf {Z}}$
. Now, let
$\bar {b} := \sum \bar {b}_i \in S_{\mathbf {Z}}$
. Now, let
![]() $\bar {c} \in Z^n$
be arbitrary and write
$\bar {c} \in Z^n$
be arbitrary and write
![]() $\bar {c} = \sum r_i\bar {b}_i$
for suitable rational numbers
$\bar {c} = \sum r_i\bar {b}_i$
for suitable rational numbers
![]() $r_i$
. Let k be a positive integer such that
$r_i$
. Let k be a positive integer such that
![]() $k \geq -r_i$
for all i. Then
$k \geq -r_i$
for all i. Then
![]() $k \bar {b} + \bar {c} = \sum _i (k+r_i)\bar {b}_i \in S_{\mathbf {Q}}$
, since it is a positive linear combination of elements in
$k \bar {b} + \bar {c} = \sum _i (k+r_i)\bar {b}_i \in S_{\mathbf {Q}}$
, since it is a positive linear combination of elements in
![]() $S_{\mathbf {Q}}$
. Thus
$S_{\mathbf {Q}}$
. Thus
![]() $k\bar {b} + \bar {c} \in S_{\mathbf {Q}} \cap Z^n = S_{\mathbf {Z}}$
, and so
$k\bar {b} + \bar {c} \in S_{\mathbf {Q}} \cap Z^n = S_{\mathbf {Z}}$
, and so
![]() $\bar {c} = (k\bar {b}+\bar {c}) - k\bar {b}$
belongs to the abelian group generated by
$\bar {c} = (k\bar {b}+\bar {c}) - k\bar {b}$
belongs to the abelian group generated by
![]() $S_{\mathbf {Z}}$
.
$S_{\mathbf {Z}}$
.
We prove now that
![]() $S_{\mathbf {G}}$
generates
$S_{\mathbf {G}}$
generates
![]() $\mathbf {G}^n$
as an abelian group for any totally ordered group
$\mathbf {G}^n$
as an abelian group for any totally ordered group
![]() $\mathbf {G}$
. For any
$\mathbf {G}$
. For any
![]() $\bar {a} \in Z^n$
and
$\bar {a} \in Z^n$
and
![]() $g \in G$
we write
$g \in G$
we write
![]() $\bar {a}g := (a_1g, \dots , a_ng)$
. Note that if
$\bar {a}g := (a_1g, \dots , a_ng)$
. Note that if
![]() $\bar {a} \in S_{\mathbf {Z}}$
and g is a non-negative member of G, then
$\bar {a} \in S_{\mathbf {Z}}$
and g is a non-negative member of G, then
![]() $\bar {a}g \in S_{\mathbf {G}}$
. Fix
$\bar {a}g \in S_{\mathbf {G}}$
. Fix
![]() $j \in \{1,\ldots ,n\}$
, and let
$j \in \{1,\ldots ,n\}$
, and let
![]() $\bar {e}_j \in Z^n$
be such that
$\bar {e}_j \in Z^n$
be such that
![]() $e_{ji} = 1$
if
$e_{ji} = 1$
if
![]() $i = j$
and
$i = j$
and
![]() $e_{ji} = 0$
otherwise. We write
$e_{ji} = 0$
otherwise. We write
![]() $\bar {e}_j = \sum k_l\bar {a}_l$
for integers
$\bar {e}_j = \sum k_l\bar {a}_l$
for integers
![]() $k_l$
and
$k_l$
and
![]() $\bar {a}_l \in S_{\mathbf {Z}}$
. Hence, if
$\bar {a}_l \in S_{\mathbf {Z}}$
. Hence, if
![]() $g \in G$
,
$g \in G$
,
![]() $g \geq 0$
, then
$g \geq 0$
, then
![]() $\bar {e}_jg = \sum k_l \bar {a}_lg$
is an integer linear combination of solutions
$\bar {e}_jg = \sum k_l \bar {a}_lg$
is an integer linear combination of solutions
![]() $\bar {a}_lg \in S_{\mathbf {G}}$
. This proves that
$\bar {a}_lg \in S_{\mathbf {G}}$
. This proves that
![]() $S_{\mathbf {G}}$
generates
$S_{\mathbf {G}}$
generates
![]() $\bar {e}_jg$
for all j and all
$\bar {e}_jg$
for all j and all
![]() $g \in G$
,
$g \in G$
,
![]() $g \geq 0$
. Now it follows easily that any
$g \geq 0$
. Now it follows easily that any
![]() $\bar {g} \in G^n$
is generated by elements in
$\bar {g} \in G^n$
is generated by elements in
![]() $S_{\mathbf {G}}$
.
$S_{\mathbf {G}}$
.
The converse implication is straightforward.
Lemma 4.10. Let
![]() $t(\bar {x})$
be a term in
$t(\bar {x})$
be a term in
![]() $\tau _{\mathcal {G}}$
. There are full-dimensional systems of linear inequalities
$\tau _{\mathcal {G}}$
. There are full-dimensional systems of linear inequalities
![]() $\alpha _1(\bar {x}), \dots , \alpha _m(\bar {x})$
and terms
$\alpha _1(\bar {x}), \dots , \alpha _m(\bar {x})$
and terms
![]() $t_1(\bar {x}), \dots , t_m(\bar {x})$
, which are integer linear combinations of the variables
$t_1(\bar {x}), \dots , t_m(\bar {x})$
, which are integer linear combinations of the variables
![]() $x_1, \ldots , x_n$
, such that for all
$x_1, \ldots , x_n$
, such that for all
![]() $\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
and all
$\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
and all
![]() $\bar {g} \in G^n$
we have
$\bar {g} \in G^n$
we have
 $$ \begin{align} t^{\mathbf{G}}(\bar{g}) = \begin{cases} t_1^{\mathbf{G}}(\bar{g}), & \text{if } \alpha_1(\bar{g}) \text{ holds in } \mathbf{G}, \\ \;\; \vdots \\ t_m^{\mathbf{G}}(\bar{g}), & \text{if } \alpha_m(\bar{g}) \text{ holds in } \mathbf{G}. \end{cases} \end{align} $$
$$ \begin{align} t^{\mathbf{G}}(\bar{g}) = \begin{cases} t_1^{\mathbf{G}}(\bar{g}), & \text{if } \alpha_1(\bar{g}) \text{ holds in } \mathbf{G}, \\ \;\; \vdots \\ t_m^{\mathbf{G}}(\bar{g}), & \text{if } \alpha_m(\bar{g}) \text{ holds in } \mathbf{G}. \end{cases} \end{align} $$
Proof Fix a
![]() $\tau _{\mathcal {G}}$
-term
$\tau _{\mathcal {G}}$
-term
![]() $t(\bar {x})$
. We show first that there are full-dimensional systems
$t(\bar {x})$
. We show first that there are full-dimensional systems
![]() $\alpha _1(\bar {x}), \dots , \alpha _m(\bar {x})$
and abelian group terms
$\alpha _1(\bar {x}), \dots , \alpha _m(\bar {x})$
and abelian group terms
![]() $t_1(\bar {x}), \dots , t_m(\bar {x})$
such that (3) holds for
$t_1(\bar {x}), \dots , t_m(\bar {x})$
such that (3) holds for
![]() $\mathbf {G} = \mathbf {R}$
, the
$\mathbf {G} = \mathbf {R}$
, the
![]() $\ell $
-group of real numbers.
$\ell $
-group of real numbers.
Using the way the lattice and group operations interact, we may assume
![]() $t(\bar {x}) = s(u_1(\bar {x}),\dots ,u_p(\bar {x}))$
where
$t(\bar {x}) = s(u_1(\bar {x}),\dots ,u_p(\bar {x}))$
where
![]() $u_1(\bar {x}),\dots ,u_p(\bar {x})$
are abelian group terms (i.e., linear combinations of variables with integer coefficients) and
$u_1(\bar {x}),\dots ,u_p(\bar {x})$
are abelian group terms (i.e., linear combinations of variables with integer coefficients) and
![]() $s(\bar {y})$
is a lattice term. For each permutation
$s(\bar {y})$
is a lattice term. For each permutation
![]() $\sigma $
of
$\sigma $
of
![]() $\{1,\ldots ,p\}$
let
$\{1,\ldots ,p\}$
let
![]() $\alpha _\sigma (\bar {x})$
be the system of linear inequalities expressing that
$\alpha _\sigma (\bar {x})$
be the system of linear inequalities expressing that
![]() $u_{\sigma (1)}(\bar {x}) \leq \dots \leq u_{\sigma (p)}(\bar {x})$
. Since
$u_{\sigma (1)}(\bar {x}) \leq \dots \leq u_{\sigma (p)}(\bar {x})$
. Since
![]() $\mathbf {R}$
is totally ordered, for each
$\mathbf {R}$
is totally ordered, for each
![]() $\sigma $
there is
$\sigma $
there is
![]() $j_\sigma \in \{1,\ldots ,p\}$
such that
$j_\sigma \in \{1,\ldots ,p\}$
such that
![]() $t^{\mathbf {R}}(\bar {r}) = u_{j_\sigma }^{\mathbf {R}}(\bar {r})$
for all
$t^{\mathbf {R}}(\bar {r}) = u_{j_\sigma }^{\mathbf {R}}(\bar {r})$
for all
![]() $\bar {r}$
such that
$\bar {r}$
such that
![]() $\alpha _\sigma (\bar {r})$
.
$\alpha _\sigma (\bar {r})$
.
Next, for each
![]() $\sigma $
let
$\sigma $
let
![]() $S_\sigma := \{\bar {r} \in R^n: \alpha _\sigma (\bar {r})\}$
. As each
$S_\sigma := \{\bar {r} \in R^n: \alpha _\sigma (\bar {r})\}$
. As each
![]() $\bar {r} \in R^n$
satisfies at least one
$\bar {r} \in R^n$
satisfies at least one
![]() $\alpha _\sigma (\bar {x})$
, we have that
$\alpha _\sigma (\bar {x})$
, we have that
![]() $R^n = \bigcup _\sigma S_\sigma $
. Let
$R^n = \bigcup _\sigma S_\sigma $
. Let
![]() $\{\sigma _1,\dots ,\sigma _m\}$
be the set of permutations
$\{\sigma _1,\dots ,\sigma _m\}$
be the set of permutations
![]() $\sigma $
such that
$\sigma $
such that
![]() $S_\sigma $
has nonempty interior. Note that
$S_\sigma $
has nonempty interior. Note that
![]() $\alpha _{\sigma _j}(\bar {x})$
is full-dimensional on
$\alpha _{\sigma _j}(\bar {x})$
is full-dimensional on
![]() $\mathbf {R}$
for all
$\mathbf {R}$
for all
![]() $j \in \{1,\ldots ,m\}$
(and thus on every
$j \in \{1,\ldots ,m\}$
(and thus on every
![]() $\ell $
-groups). Since each
$\ell $
-groups). Since each
![]() $S_\sigma $
is a closed subset of
$S_\sigma $
is a closed subset of
![]() $R^n$
, by a simple topological argument, we have
$R^n$
, by a simple topological argument, we have
![]() $R^n = S_{\sigma _1} \cup \dots \cup S_{\sigma _m}$
. So, defining
$R^n = S_{\sigma _1} \cup \dots \cup S_{\sigma _m}$
. So, defining
![]() $\alpha _j(\bar {x}) := \alpha _{\sigma _j}(\bar {x})$
and
$\alpha _j(\bar {x}) := \alpha _{\sigma _j}(\bar {x})$
and
![]() $t_j(\bar {x}) := u_{\sigma _j}(\bar {x})$
for
$t_j(\bar {x}) := u_{\sigma _j}(\bar {x})$
for
![]() $j \in \{1,\dots ,m\}$
, we have established (3) in the case
$j \in \{1,\dots ,m\}$
, we have established (3) in the case
![]() $\mathbf {G} = \mathbf {R}$
. To conclude we show that the same
$\mathbf {G} = \mathbf {R}$
. To conclude we show that the same
![]() $\alpha _j$
’s and
$\alpha _j$
’s and
![]() $t_j$
’s work for any
$t_j$
’s work for any
![]() $\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
. In fact, note that (3) holds if and only if
$\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
. In fact, note that (3) holds if and only if
![]() $\mathbf {G}$
satisfies the following universal formulas:
$\mathbf {G}$
satisfies the following universal formulas:
-
•
 $\forall \bar {x} \, (\alpha _j(\bar {x}) \mathbin {\boldsymbol {\rightarrow }} t(\bar {x}) = t_j(\bar {x}))$
for
$\forall \bar {x} \, (\alpha _j(\bar {x}) \mathbin {\boldsymbol {\rightarrow }} t(\bar {x}) = t_j(\bar {x}))$
for
 $j \in \{1,\dots ,m\}$
,
$j \in \{1,\dots ,m\}$
, -
•
 $\forall \bar {x} \, (\alpha _1(\bar {x}) \boldsymbol {\lor } \dots \boldsymbol {\lor } \alpha _m(\bar {x}))$
.
$\forall \bar {x} \, (\alpha _1(\bar {x}) \boldsymbol {\lor } \dots \boldsymbol {\lor } \alpha _m(\bar {x}))$
.
Since these formulas hold in
![]() $\mathbf {R}$
, Lemma 4.1(2) says that they must hold in
$\mathbf {R}$
, Lemma 4.1(2) says that they must hold in
![]() $\mathbf {G}$
.
$\mathbf {G}$
.
Lemma 4.11. Given a positive integer k and a
![]() $\tau _{\mathcal {G}}$
-term t, there is a positive integer
$\tau _{\mathcal {G}}$
-term t, there is a positive integer
![]() $k'$
such that
$k'$
such that
![]() $\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
$\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof Fix a positive integer k and a
![]() $\tau _{\mathcal {G}}$
-term t; let
$\tau _{\mathcal {G}}$
-term t; let
![]() $\alpha _j(\bar {x})$
and
$\alpha _j(\bar {x})$
and
![]() $t_j(\bar {x})$
for
$t_j(\bar {x})$
for
![]() $j \in \{1,\ldots ,m\}$
be as in Lemma 4.10. Suppose
$j \in \{1,\ldots ,m\}$
be as in Lemma 4.10. Suppose
![]() $t_j(\bar {x}) = a_{j1}x_1 + \dots + a_{jn}x_n$
, and let d be the greatest common divisor of the set
$t_j(\bar {x}) = a_{j1}x_1 + \dots + a_{jn}x_n$
, and let d be the greatest common divisor of the set
![]() $\{k\} \cup \{a_{ji}: i \in \{1,\dots ,n\}, j \in \{1,\ldots ,m\}\}$
. Define
$\{k\} \cup \{a_{ji}: i \in \{1,\dots ,n\}, j \in \{1,\ldots ,m\}\}$
. Define
![]() $k'$
by
$k'$
by
![]() $k = dk'$
; we prove that
$k = dk'$
; we prove that
![]() $\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
$\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
![]() $\mathcal {G}$
. Observe that, due to Lemma 4.2, it suffices to show that
$\mathcal {G}$
. Observe that, due to Lemma 4.2, it suffices to show that
![]() $\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
$\delta _{k,t} \mathrel {\sim } \delta _{k'}$
in
![]() $\mathcal {G}_{\mathrm {to}}$
.
$\mathcal {G}_{\mathrm {to}}$
.
Take
![]() $\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
and assume
$\mathbf {G} \in \mathcal {G}_{\mathrm {to}}$
and assume
![]() $\mathbf {G} \vDash \delta _{k,t}$
. We claim that
$\mathbf {G} \vDash \delta _{k,t}$
. We claim that
![]() $t_j(\bar {g})$
is divisible by k for every
$t_j(\bar {g})$
is divisible by k for every
![]() $\bar {g} \in G^n$
and
$\bar {g} \in G^n$
and
![]() $j \in \{1,\dots ,m\}$
. Indeed, given
$j \in \{1,\dots ,m\}$
. Indeed, given
![]() $\bar {g} \in G^n$
and
$\bar {g} \in G^n$
and
![]() $j \in \{1,\dots ,m\}$
, by Lemma 4.9, we can write
$j \in \{1,\dots ,m\}$
, by Lemma 4.9, we can write
![]() $\bar {g} = \sum b_l \bar {g}_l$
for some integers
$\bar {g} = \sum b_l \bar {g}_l$
for some integers
![]() $b_l$
and some
$b_l$
and some
![]() $\bar {g}_l \in G^n$
such that
$\bar {g}_l \in G^n$
such that
![]() $\mathbf {G} \vDash \alpha _j(\bar {g}_l)$
. Note that
$\mathbf {G} \vDash \alpha _j(\bar {g}_l)$
. Note that
![]() $t(\bar {g}_l) = t_j(\bar {g}_l)$
for each l. Since
$t(\bar {g}_l) = t_j(\bar {g}_l)$
for each l. Since
![]() $\mathbf {G} \vDash \delta _{k,t}$
, for each l there is
$\mathbf {G} \vDash \delta _{k,t}$
, for each l there is
![]() $h_l \in G$
such that
$h_l \in G$
such that
![]() $k h_l = t(\bar {g}_l) = t_j(\bar {g}_l)$
. Thus
$k h_l = t(\bar {g}_l) = t_j(\bar {g}_l)$
. Thus
which proves the claim.
Now write
![]() $d = kc + \sum _{i,j} a_{ji}c_{ji}$
for suitable integers c and
$d = kc + \sum _{i,j} a_{ji}c_{ji}$
for suitable integers c and
![]() $c_{ji}$
. Then, for any
$c_{ji}$
. Then, for any
![]() $g \in G$
,
$g \in G$
,
where
![]() $\bar {g}_j := (c_{j1}g,\dots ,c_{jn}g)$
. Since each
$\bar {g}_j := (c_{j1}g,\dots ,c_{jn}g)$
. Since each
![]() $t_j(\bar {g}_j)$
is divisible by k, it follows that there is
$t_j(\bar {g}_j)$
is divisible by k, it follows that there is
![]() $g' \in G$
such that
$g' \in G$
such that
![]() $dg = kg'$
. Thus
$dg = kg'$
. Thus
![]() $dg = dk'g'$
, so
$dg = dk'g'$
, so
![]() $d(g-k'g') = 0$
and, since
$d(g-k'g') = 0$
and, since
![]() $\mathbf {G}$
is torsion-free,
$\mathbf {G}$
is torsion-free,
![]() $g = k'g'$
. This proves that
$g = k'g'$
. This proves that
![]() $\mathbf {G} \vDash \delta _{k'}$
.
$\mathbf {G} \vDash \delta _{k'}$
.
Conversely, assume any element in
![]() $\mathbf {G}$
is divisible by
$\mathbf {G}$
is divisible by
![]() $k'$
, and fix
$k'$
, and fix
![]() $\bar {g} := (g_1,\dots ,g_n) \in G^n$
. We prove that
$\bar {g} := (g_1,\dots ,g_n) \in G^n$
. We prove that
![]() $t(\bar {g})$
is divisible by k. Let
$t(\bar {g})$
is divisible by k. Let
![]() $j \in \{1,\dots ,m\}$
be such that
$j \in \{1,\dots ,m\}$
be such that
![]() $t(\bar {g}) = t_j(\bar {g})$
. Since each
$t(\bar {g}) = t_j(\bar {g})$
. Since each
![]() $a_{ji}$
is divisible by d, there is
$a_{ji}$
is divisible by d, there is
![]() $g' \in G$
such that
$g' \in G$
such that
![]() $t_j(\bar {g}) = d g'$
. Now, since
$t_j(\bar {g}) = d g'$
. Now, since
![]() $g'$
is divisible by
$g'$
is divisible by
![]() $k'$
, there is
$k'$
, there is
![]() $g'' \in G$
such that
$g'' \in G$
such that
![]() $g' = k'g''$
. Putting all together we obtain
$g' = k'g''$
. Putting all together we obtain
![]() $t(\bar {g}) = t_j(\bar {g}) = dg' = dk'g'' = kg''$
.
$t(\bar {g}) = t_j(\bar {g}) = dg' = dk'g'' = kg''$
.
We are now ready to present our characterization of EFD-sentences in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Theorem 4.12. Given an EFD-sentence
![]() $\varphi $
with a nontrivial model in
$\varphi $
with a nontrivial model in
![]() $\mathcal {G}$
there is a positive integer k such that
$\mathcal {G}$
there is a positive integer k such that
![]() $\varphi \mathrel {\sim } \delta _k$
in
$\varphi \mathrel {\sim } \delta _k$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof Given
![]() $\varphi $
, combining Lemmas 4.8 and 4.11, we have that there are positive integers
$\varphi $
, combining Lemmas 4.8 and 4.11, we have that there are positive integers
![]() $k_1,\dots ,k_m$
such that
$k_1,\dots ,k_m$
such that
 $\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j}$
in
$\varphi \mathrel {\sim } \displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j}$
in
![]() $\mathcal {G}$
. Now take
$\mathcal {G}$
. Now take
![]() $k := k_1 \cdots k_m$
, and note that
$k := k_1 \cdots k_m$
, and note that
 $\displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j}$
is equivalent to
$\displaystyle \mathop {\boldsymbol {\bigwedge }}\limits _{j=1}^m \delta _{k_j}$
is equivalent to
![]() $\delta _k$
in
$\delta _k$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Given a set S of prime numbers, let
![]() $\Sigma _S := \{\delta _p: p \in S\}$
. Since for an
$\Sigma _S := \{\delta _p: p \in S\}$
. Since for an
![]() $\ell $
-group divisibility by k is equivalent to divisibility by the prime factors of k, we have the following:
$\ell $
-group divisibility by k is equivalent to divisibility by the prime factors of k, we have the following:
Theorem 4.13. Every set of EFD-sentences either has only trivial models or is equivalent over
![]() $\mathcal {G}$
to
$\mathcal {G}$
to
![]() $\Sigma _S$
for some set S of prime numbers. Furthermore, the map
$\Sigma _S$
for some set S of prime numbers. Furthermore, the map
![]() $S \mapsto \Sigma _S$
is one-to-one, and thus, the lattice of AE-subclasses of
$S \mapsto \Sigma _S$
is one-to-one, and thus, the lattice of AE-subclasses of
![]() $\mathcal {G}$
is isomorphic to
$\mathcal {G}$
is isomorphic to
![]() $\mathbf {1} \oplus \mathbf {2}^\omega $
.
$\mathbf {1} \oplus \mathbf {2}^\omega $
.
4.2 The algebraic expansions of the Logic of Equilibrium
As shown in [Reference Galli, Lewin and Sagastume16, Theorem 17] the variety
![]() $\mathcal {G}$
of abelian
$\mathcal {G}$
of abelian
![]() $\ell $
-groups is the equivalent algebraic semantics of the Logic of Equilibrium
$\ell $
-groups is the equivalent algebraic semantics of the Logic of Equilibrium
![]() $Bal$
in the language
$Bal$
in the language
![]() $\{\to ,{}^+\}$
whose consequence operator is defined in [Reference Galli, Lewin and Sagastume16, Section 2]. The derived connectives
$\{\to ,{}^+\}$
whose consequence operator is defined in [Reference Galli, Lewin and Sagastume16, Section 2]. The derived connectives
 $0 := x \mathbin {\rightarrow } x ,\hspace{8.6pc} x \vee y := (x \mathbin {\rightarrow } y)^+ + x$
,
$0 := x \mathbin {\rightarrow } x ,\hspace{8.6pc} x \vee y := (x \mathbin {\rightarrow } y)^+ + x$
, $-x := x \mathbin {\rightarrow } 0, \hspace{8pc} x \wedge y :=\,{-}\,(-x \vee -y)$
,
$-x := x \mathbin {\rightarrow } 0, \hspace{8pc} x \wedge y :=\,{-}\,(-x \vee -y)$
, $x + y := \,{-}\,x \mathbin {\rightarrow } y$
,
$x + y := \,{-}\,x \mathbin {\rightarrow } y$
,
form a complete set for
![]() $Bal$
since
$Bal$
since
![]() $\varphi (x \mathbin {\rightarrow } y,\bar {z}) \dashv \vdash \varphi (-x + y,\bar {z})$
and
$\varphi (x \mathbin {\rightarrow } y,\bar {z}) \dashv \vdash \varphi (-x + y,\bar {z})$
and
![]() $\varphi (x^+,\bar {z}) \dashv \vdash \varphi (x \vee 0,\bar {z})$
for any formula
$\varphi (x^+,\bar {z}) \dashv \vdash \varphi (x \vee 0,\bar {z})$
for any formula
![]() $\varphi $
. This allows us to say that
$\varphi $
. This allows us to say that
![]() $\mathcal {G}$
is the equivalent algebraic semantics of
$\mathcal {G}$
is the equivalent algebraic semantics of
![]() $Bal$
via equivalence formulas
$Bal$
via equivalence formulas
![]() $\Delta (x,y) = \{x \mathbin {\rightarrow } y\}$
and defining equations
$\Delta (x,y) = \{x \mathbin {\rightarrow } y\}$
and defining equations
![]() $\varepsilon (x) = \{x = 0\}$
.
$\varepsilon (x) = \{x = 0\}$
.
Given a prime number p, the algebraic expansion of
![]() $Bal$
corresponding to the EFD-sentence
$Bal$
corresponding to the EFD-sentence
![]() $\delta _p$
is, by definition, obtained from
$\delta _p$
is, by definition, obtained from
![]() $Bal$
by adding a unary function symbol
$Bal$
by adding a unary function symbol
![]() $\mathsf {d}_p$
to the langauge of
$\mathsf {d}_p$
to the langauge of
![]() $Bal$
, the rule
$Bal$
, the rule
![]() $\mathrm {U}_{\{x \mathbin {\rightarrow } pz\}}$
, and the axiom:
$\mathrm {U}_{\{x \mathbin {\rightarrow } pz\}}$
, and the axiom:
Since the rule
![]() $\mathrm {U}_{\{x \mathbin {\rightarrow } pz\}}$
is derivable in
$\mathrm {U}_{\{x \mathbin {\rightarrow } pz\}}$
is derivable in
![]() $Bal$
, the expansion is obtained simply by adding
$Bal$
, the expansion is obtained simply by adding
![]() $A_p$
. For a set S of prime numbers define
$A_p$
. For a set S of prime numbers define
![]() $Bal^S$
as the expansion of
$Bal^S$
as the expansion of
![]() $Bal$
by the axioms
$Bal$
by the axioms
![]() $\{A_p: p \in S\}$
. Note that, since
$\{A_p: p \in S\}$
. Note that, since
![]() $Bal^S$
is an axiomatic expansion of
$Bal^S$
is an axiomatic expansion of
![]() $Bal$
, its equivalent algebraic semantics is a variety. These expansions were also considered in [Reference Caicedo6, Section 7] where it is proved that every implicit connective in the logic
$Bal$
, its equivalent algebraic semantics is a variety. These expansions were also considered in [Reference Caicedo6, Section 7] where it is proved that every implicit connective in the logic
![]() $Bal^{Primes}$
is explicit.
$Bal^{Primes}$
is explicit.
Recall that an expansion
![]() $L' := \langle \tau ', \vdash _{L'}\rangle $
of a logic
$L' := \langle \tau ', \vdash _{L'}\rangle $
of a logic
![]() $L := \langle \tau ,\vdash _L\rangle $
is called conservative provided that for each set of
$L := \langle \tau ,\vdash _L\rangle $
is called conservative provided that for each set of
![]() $\tau $
-formulas
$\tau $
-formulas
![]() $\Gamma \cup \{\varphi \}$
we have that
$\Gamma \cup \{\varphi \}$
we have that
![]() $\Gamma \vdash _{L'} \varphi $
implies
$\Gamma \vdash _{L'} \varphi $
implies
![]() $\Gamma \vdash _L \varphi $
.
$\Gamma \vdash _L \varphi $
.
Theorem 4.14.
-
1. Every algebraic expansion of
 $Bal$
is
$Bal$
is
 $\tau _{\mathcal {G}}$
-bimorphic to exactly one of the following:
$\tau _{\mathcal {G}}$
-bimorphic to exactly one of the following:-
• Inconsistent Logic,
-
•
 $Bal^S$
for some set S of prime numbers.
$Bal^S$
for some set S of prime numbers.
-
-
2. The algebraic expansions of
 $Bal$
form a lattice isomorphic to
$Bal$
form a lattice isomorphic to
 $\mathbf {2}^\omega \oplus \mathbf {1}$
when ordered by
$\mathbf {2}^\omega \oplus \mathbf {1}$
when ordered by
 $\tau _{\mathcal {G}}$
-morphisms.
$\tau _{\mathcal {G}}$
-morphisms. -
3. Given sets
 $S,S'$
of prime numbers with
$S,S'$
of prime numbers with
 $S \subseteq S'$
, the expansion
$S \subseteq S'$
, the expansion
 $Bal^{S'}$
is conservative over
$Bal^{S'}$
is conservative over
 $Bal^S$
.
$Bal^S$
.
Proof Items 1. and 2. follow from Theorems 3.2 and 4.13. We prove 3.
Fix sets of prime numbers
![]() $S \subseteq S'$
, and let
$S \subseteq S'$
, and let
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\mathcal {V}'$
be the equivalent algebraic semantics of
$\mathcal {V}'$
be the equivalent algebraic semantics of
![]() $Bal^S$
and
$Bal^S$
and
![]() $Bal^{S'}\kern-1.2pt$
, respectively. Since
$Bal^{S'}\kern-1.2pt$
, respectively. Since
![]() $Bal^{S'}$
is finitary, to prove 3. it is enough to show that any quasi-identity in the language of
$Bal^{S'}$
is finitary, to prove 3. it is enough to show that any quasi-identity in the language of
![]() $\mathcal {V}$
valid in
$\mathcal {V}$
valid in
![]() $\mathcal {V}'$
is also valid in
$\mathcal {V}'$
is also valid in
![]() $\mathcal {V}$
. Let
$\mathcal {V}$
. Let
![]() $\mathbf {Q}_S$
be the
$\mathbf {Q}_S$
be the
![]() $\ell $
-group of rational numbers expanded with the divisions by the primes in S. It is not hard to show that
$\ell $
-group of rational numbers expanded with the divisions by the primes in S. It is not hard to show that
![]() $\mathbf {Q}_S$
generates
$\mathbf {Q}_S$
generates
![]() $\mathcal {V}$
as a quasivariety, that is,
$\mathcal {V}$
as a quasivariety, that is,
![]() $\mathsf {Q}(\mathbf {Q}_S) = \mathcal {V}$
. Now let
$\mathsf {Q}(\mathbf {Q}_S) = \mathcal {V}$
. Now let
![]() $\varphi $
be a quasi-identity in the language of
$\varphi $
be a quasi-identity in the language of
![]() $\mathcal {V}$
that is valid in
$\mathcal {V}$
that is valid in
![]() $\mathcal {V}'$
. Then, we have that
$\mathcal {V}'$
. Then, we have that
![]() $\mathbf {Q}_{S'} \vDash \varphi $
, and thus,
$\mathbf {Q}_{S'} \vDash \varphi $
, and thus,
![]() $\mathbf {Q}_S \vDash \varphi $
. Since
$\mathbf {Q}_S \vDash \varphi $
. Since
![]() $\mathsf {Q}(\mathbf {Q}_S) = \mathcal {V}$
, the proof is finished.
$\mathsf {Q}(\mathbf {Q}_S) = \mathcal {V}$
, the proof is finished.
5 Algebraic expansions of perfect MV-algebras and their logic
The class of MV-algebras is the equivalent algebraic semantics of Łukasiewicz infinite-valued logic and has been extensively studied [Reference Cignoli, D’Ottaviano and Mundici12]. In this section we characterize the AE-subclasses of the variety generated by perfect MV-algebras, and thus, by Theorem 3.2, we also obtain a full description of lattice of algebraic expansions of
![]() $L_{\mathcal {P}}$
, the Logic of Perfect MV-Algebras (see, e.g., [Reference Belluce, Di Nola and Gerla1]). Our approach is to export the results for abelian
$L_{\mathcal {P}}$
, the Logic of Perfect MV-Algebras (see, e.g., [Reference Belluce, Di Nola and Gerla1]). Our approach is to export the results for abelian
![]() $\ell $
-groups to perfect MV-algebras, exploiting the connection between these two classes (see [Reference Di Nola and Lettieri13, Reference Mundici22, Reference Mundici23]).
$\ell $
-groups to perfect MV-algebras, exploiting the connection between these two classes (see [Reference Di Nola and Lettieri13, Reference Mundici22, Reference Mundici23]).
Concerning notation and basic facts of MV-algebras we follow [Reference Cignoli, D’Ottaviano and Mundici12]; in particular, we consider MV-algebras in the language
![]() $\tau _{\mathcal {MV}} := \{+,\neg ,0\}$
. Let
$\tau _{\mathcal {MV}} := \{+,\neg ,0\}$
. Let
![]() $\mathbf {A}$
be an MV-algebra; the radical of
$\mathbf {A}$
be an MV-algebra; the radical of
![]() $\mathbf {A}$
is the intersection of all maximal ideals of
$\mathbf {A}$
is the intersection of all maximal ideals of
![]() $\mathbf {A}$
, which is denoted by
$\mathbf {A}$
, which is denoted by
![]() $\mathop {\mathrm {rad}} \mathbf {A}$
. We say that
$\mathop {\mathrm {rad}} \mathbf {A}$
. We say that
![]() $\mathbf {A}$
is perfect if it is nontrivial and
$\mathbf {A}$
is perfect if it is nontrivial and
![]() $A = \mathop {\mathrm {rad}} \mathbf {A} \cup \neg \mathop {\mathrm {rad}} \mathbf {A}$
, where
$A = \mathop {\mathrm {rad}} \mathbf {A} \cup \neg \mathop {\mathrm {rad}} \mathbf {A}$
, where
![]() $\neg \mathop {\mathrm {rad}} \mathbf {A} := \{\neg a: a \in \mathop {\mathrm {rad}} \mathbf {A}\}$
. The class of perfect MV-algebras is denoted by
$\neg \mathop {\mathrm {rad}} \mathbf {A} := \{\neg a: a \in \mathop {\mathrm {rad}} \mathbf {A}\}$
. The class of perfect MV-algebras is denoted by
![]() $\mathcal {P}$
; we write
$\mathcal {P}$
; we write
![]() $\mathcal {P}_{\mathrm {to}}$
for its subclass of totally ordered members.
$\mathcal {P}_{\mathrm {to}}$
for its subclass of totally ordered members.
5.1 EFD-sentences in perfect MV-algebras
As shown by Theorem 4.13, every EFD-sentence of
![]() $\ell $
-groups is equivalent to some
$\ell $
-groups is equivalent to some
![]() $\delta _k$
. Of course, each of these sentences induces the inverse function of multiplication by some positive integer. Next, for each k we introduce a term whose interpretation plays the role of multiplication by k in
$\delta _k$
. Of course, each of these sentences induces the inverse function of multiplication by some positive integer. Next, for each k we introduce a term whose interpretation plays the role of multiplication by k in
![]() $\mathsf {V}(\mathcal {P})$
, namely
$\mathsf {V}(\mathcal {P})$
, namely
Thus, division by k in
![]() $\mathsf {V}(\mathcal {P})$
is embodied by the function induced by the EFD-sentence
$\mathsf {V}(\mathcal {P})$
is embodied by the function induced by the EFD-sentence
Both of these operations enjoy some natural algebraic properties whose proofs we omit as they are easy exercises.
Lemma 5.1. Let
![]() $\mathbf {A} \in \mathcal {P}$
.
$\mathbf {A} \in \mathcal {P}$
.
-
1. For every
 $a \in A$
we have
$a \in A$
we have  $$ \begin{align*}\mathsf{t}_k^{\mathbf{A}}(a) = \begin{cases} a^k, & \text{ if } a \in \neg \mathop{\mathrm{rad}} \mathbf{A}, \\ ka, & \text{ if } a \in \mathop{\mathrm{rad}} \mathbf{A}. \end{cases}\end{align*} $$
$$ \begin{align*}\mathsf{t}_k^{\mathbf{A}}(a) = \begin{cases} a^k, & \text{ if } a \in \neg \mathop{\mathrm{rad}} \mathbf{A}, \\ ka, & \text{ if } a \in \mathop{\mathrm{rad}} \mathbf{A}. \end{cases}\end{align*} $$
-
2. The term-function
 $\mathsf {t}_k^{\mathbf {A}}$
is a one-to-one endomorphism of
$\mathsf {t}_k^{\mathbf {A}}$
is a one-to-one endomorphism of
 $\mathbf {A}$
.
$\mathbf {A}$
. -
3. The following are equivalent:
-
(i)
 $\mathsf {t}_k^{\mathbf {A}}$
is surjective.
$\mathsf {t}_k^{\mathbf {A}}$
is surjective. -
(ii)
 $\mathbf {A} \vDash \varepsilon _k$
.
$\mathbf {A} \vDash \varepsilon _k$
. -
(iii) For every
 $a \in \mathop {\mathrm {rad}} \mathbf {A}$
, there is
$a \in \mathop {\mathrm {rad}} \mathbf {A}$
, there is
 $b \in \mathop {\mathrm {rad}} \mathbf {A}$
such that
$b \in \mathop {\mathrm {rad}} \mathbf {A}$
such that
 $kb = a$
.
$kb = a$
. -
(iv) For every
 $a \in \neg \mathop {\mathrm {rad}} \mathbf {A}$
, there is
$a \in \neg \mathop {\mathrm {rad}} \mathbf {A}$
, there is
 $b \in \neg \mathop {\mathrm {rad}} \mathbf {A}$
such that
$b \in \neg \mathop {\mathrm {rad}} \mathbf {A}$
such that
 $b^k = a$
.
$b^k = a$
.
-
-
4. If
 $\mathbf {A} \vDash \varepsilon _k$
, then
$\mathbf {A} \vDash \varepsilon _k$
, then
 $[\varepsilon _k]^{\mathbf {A}}$
is an automorphism, which is the inverse of
$[\varepsilon _k]^{\mathbf {A}}$
is an automorphism, which is the inverse of
 $\mathsf {t}_k^{\mathbf {A}}$
.
$\mathsf {t}_k^{\mathbf {A}}$
.
Given the close connection between
![]() $\ell $
-groups and perfect MV-algebras, it is hardly surprising that a version of Theorem 4.13 holds for
$\ell $
-groups and perfect MV-algebras, it is hardly surprising that a version of Theorem 4.13 holds for
![]() $\mathsf {V}(\mathcal {P})$
when we take
$\mathsf {V}(\mathcal {P})$
when we take
![]() $\varepsilon _k$
in place of
$\varepsilon _k$
in place of
![]() $\delta _k$
. Even though the proof we discovered is nontrivial, for reasons of brevity we only outline its key steps.
$\delta _k$
. Even though the proof we discovered is nontrivial, for reasons of brevity we only outline its key steps.
Theorem 5.2. For every EFD-sentence
![]() $\varphi $
in
$\varphi $
in
![]() $\tau _{\mathcal {MV}}$
with a model in
$\tau _{\mathcal {MV}}$
with a model in
![]() $\mathcal {P}$
either
$\mathcal {P}$
either
![]() $\varphi \mathrel {\sim } \forall x \, 2x = x$
in
$\varphi \mathrel {\sim } \forall x \, 2x = x$
in
![]() $\mathsf {V}(\mathcal {P})$
or there is a positive integer k such that
$\mathsf {V}(\mathcal {P})$
or there is a positive integer k such that
![]() $\varphi \mathrel {\sim } \varepsilon _k$
in
$\varphi \mathrel {\sim } \varepsilon _k$
in
![]() $\mathsf {V}(\mathcal {P})$
.
$\mathsf {V}(\mathcal {P})$
.
Sketch of proof.
The key to translate our classification of EFD-sentences for
![]() $\ell $
-groups to perfect MV-algebras is that the positive cone of an
$\ell $
-groups to perfect MV-algebras is that the positive cone of an
![]() $\ell $
-group and the radical of a perfect MV-algebra are, essentially, the same thing.
$\ell $
-group and the radical of a perfect MV-algebra are, essentially, the same thing.
Given an abelian
![]() $\ell $
-group
$\ell $
-group
![]() $\mathbf {G}$
, its positive cone is the subset
$\mathbf {G}$
, its positive cone is the subset
![]() $G^+ := \{x \in G: x \geq 0\}$
. We define the algebraic structure
$G^+ := \{x \in G: x \geq 0\}$
. We define the algebraic structure
![]() where
where
![]() . We write
. We write
![]() $\mathcal {C}$
for the class of positive cones of abelian
$\mathcal {C}$
for the class of positive cones of abelian
![]() $\ell $
-groups considered as algebras in the language
$\ell $
-groups considered as algebras in the language
![]() . The members of
. The members of
![]() $\mathcal {C}$
are known as cancellative hoops; see, e.g., [Reference Blok and Ferreirim3, Reference Ferreirim14]. Given a cancellative hoop
$\mathcal {C}$
are known as cancellative hoops; see, e.g., [Reference Blok and Ferreirim3, Reference Ferreirim14]. Given a cancellative hoop
![]() $\mathbf {A}$
, there is (up to isomorphism) a unique abelian
$\mathbf {A}$
, there is (up to isomorphism) a unique abelian
![]() $\ell $
-group whose positive cone is isomorphic to
$\ell $
-group whose positive cone is isomorphic to
![]() $\mathbf {A}$
(see [Reference Birkhoff2, Chapter XIV]); we write
$\mathbf {A}$
(see [Reference Birkhoff2, Chapter XIV]); we write
![]() $\mathbf {A}^*$
for this
$\mathbf {A}^*$
for this
![]() $\ell $
-group.
$\ell $
-group.
By means of a syntactical translation argument we can apply Theorem 4.12 to obtain the following:
-
(1) For every EFD-sentence
 $\psi $
in
$\psi $
in
 $\tau _{\mathcal {C}}$
with a nontrivial model there is a positive integer k such that
$\tau _{\mathcal {C}}$
with a nontrivial model there is a positive integer k such that
 $\psi \mathrel {\sim } \delta _{k}$
in
$\psi \mathrel {\sim } \delta _{k}$
in
 $\mathcal {C}$
.Footnote
2
$\mathcal {C}$
.Footnote
2
In what follows let
![]() $\varphi := \forall \bar {x} \exists ! \bar {z} \, \alpha (\bar {x},\bar {z})$
denote a fixed but arbitrary EFD-sentence in
$\varphi := \forall \bar {x} \exists ! \bar {z} \, \alpha (\bar {x},\bar {z})$
denote a fixed but arbitrary EFD-sentence in
![]() $\tau _{\mathcal {MV}}$
with a model in
$\tau _{\mathcal {MV}}$
with a model in
![]() $\mathcal {P}$
. If the two-element MV-algebra is the only model of
$\mathcal {P}$
. If the two-element MV-algebra is the only model of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal {P}$
, it is easy to see that
$\mathcal {P}$
, it is easy to see that
![]() $\varphi \mathrel {\sim } \forall x \, 2x = x$
in
$\varphi \mathrel {\sim } \forall x \, 2x = x$
in
![]() $\mathsf {V}(\mathcal {P})$
. So, assume
$\mathsf {V}(\mathcal {P})$
. So, assume
![]() $\varphi $
has a non-Boolean model in
$\varphi $
has a non-Boolean model in
![]() $\mathcal {P}$
. By an argument analogous to the one in the proof of Lemma 4.2 it suffices to show that
$\mathcal {P}$
. By an argument analogous to the one in the proof of Lemma 4.2 it suffices to show that
![]() $\varphi $
is equivalent to some
$\varphi $
is equivalent to some
![]() $\varepsilon _k$
in
$\varepsilon _k$
in
![]() $\mathcal {P}_{\mathrm {to}}$
. We begin by showing that
$\mathcal {P}_{\mathrm {to}}$
. We begin by showing that
![]() $\varphi $
can be rewritten in a way such that it is evaluated just in the radical. Again, this is proved by a syntactical manipulation, and it turns out to be the most technically challenging part of the whole argument.
$\varphi $
can be rewritten in a way such that it is evaluated just in the radical. Again, this is proved by a syntactical manipulation, and it turns out to be the most technically challenging part of the whole argument.
-
(2) There is an EFD-sentence
 $\varphi ^{\mathrm {R}} := \forall \bar {x} \exists ! \bar {z} \, \alpha ^{\mathrm {R}}(\bar {x},\bar {z})$
in
$\varphi ^{\mathrm {R}} := \forall \bar {x} \exists ! \bar {z} \, \alpha ^{\mathrm {R}}(\bar {x},\bar {z})$
in
 $\tau _{\mathcal {MV}}$
such that
$\tau _{\mathcal {MV}}$
such that
 $\varphi \mathrel {\sim } \varphi ^{\mathrm {R}}$
in
$\varphi \mathrel {\sim } \varphi ^{\mathrm {R}}$
in
 $\mathcal {P}_{\mathrm {to}}$
and for every
$\mathcal {P}_{\mathrm {to}}$
and for every
 $\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
and every
$\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
and every
 $\bar {a} \in A^n$
the following holds:
$\bar {a} \in A^n$
the following holds:-
(i) if
 $\bar {a} \in (\mathop {\mathrm {rad}} \mathbf {A})^n$
and
$\bar {a} \in (\mathop {\mathrm {rad}} \mathbf {A})^n$
and
 $\mathbf {A} \vDash \alpha (\bar {a},\bar {b})$
for some
$\mathbf {A} \vDash \alpha (\bar {a},\bar {b})$
for some
 $\bar {b} \in A^m$
, then
$\bar {b} \in A^m$
, then
 $\bar {b} \in (\mathop {\mathrm {rad}} \mathbf {A})^m$
,
$\bar {b} \in (\mathop {\mathrm {rad}} \mathbf {A})^m$
, -
(ii) if
 $\bar {a} \not \in (\mathop {\mathrm {rad}} \mathbf {A})^n$
we have that
$\bar {a} \not \in (\mathop {\mathrm {rad}} \mathbf {A})^n$
we have that
 $\mathbf {A} \vDash \alpha (\bar {a},\bar {0})$
and
$\mathbf {A} \vDash \alpha (\bar {a},\bar {0})$
and
 $\bar {z} = \bar {0}$
is the unique solution to
$\bar {z} = \bar {0}$
is the unique solution to
 $\alpha (\bar {a},\bar {z})$
in
$\alpha (\bar {a},\bar {z})$
in
 $\mathbf {A}$
.
$\mathbf {A}$
.
-
Given
![]() $\mathbf {A} \in \mathcal {MV}$
, we define
$\mathbf {A} \in \mathcal {MV}$
, we define
![]() . Via this shorthand we can interpret
. Via this shorthand we can interpret
![]() $\tau _{\mathcal {C}}$
-terms in MV-algebras. The radical of
$\tau _{\mathcal {C}}$
-terms in MV-algebras. The radical of
![]() $\mathbf {A}$
is closed under
$\mathbf {A}$
is closed under
![]() $+$
and
$+$
and
![]() . Moreover,
. Moreover,
![]() is a cancellative hoop (see [Reference Di Nola and Lettieri13, Lemma 3.2]). The special properties of
is a cancellative hoop (see [Reference Di Nola and Lettieri13, Lemma 3.2]). The special properties of
![]() $\varphi ^{\mathrm {R}}$
allow us to exchange it for a sentence to be evaluated on
$\varphi ^{\mathrm {R}}$
allow us to exchange it for a sentence to be evaluated on
![]() $\mathop {\mathbf {rad}} \mathbf {A}$
.
$\mathop {\mathbf {rad}} \mathbf {A}$
.
-
(3) There is an EFD-sentence
 $\psi $
in the language
$\psi $
in the language
 $\tau _{\mathcal {C}}$
such that:
$\tau _{\mathcal {C}}$
such that:
 $\mathbf {A} \vDash \varphi ^{\mathrm {R}} \Leftrightarrow \mathop {\mathbf {rad}} \mathbf {A} \vDash \psi $
for all
$\mathbf {A} \vDash \varphi ^{\mathrm {R}} \Leftrightarrow \mathop {\mathbf {rad}} \mathbf {A} \vDash \psi $
for all
 $\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.
$\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.
Combining (1)–(3) yields
-
(4) There is a positive integer k such that
 $\mathbf {A} \vDash \varphi \Leftrightarrow \mathop {\mathbf {rad}} \mathbf {A} \vDash \delta _k$
for all
$\mathbf {A} \vDash \varphi \Leftrightarrow \mathop {\mathbf {rad}} \mathbf {A} \vDash \delta _k$
for all
 $\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.
$\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.
Finally, the equivalence between
![]() $(ii)$
and
$(ii)$
and
![]() $(iii)$
in Lemma 5.1.3 gives us
$(iii)$
in Lemma 5.1.3 gives us
-
(5)
 $\mathop {\mathbf {rad}} \mathbf {A} \vDash \delta _k \Leftrightarrow \mathbf {A} \vDash \varepsilon _k$
for all
$\mathop {\mathbf {rad}} \mathbf {A} \vDash \delta _k \Leftrightarrow \mathbf {A} \vDash \varepsilon _k$
for all
 $\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.⊣
$\mathbf {A} \in \mathcal {P}_{\mathrm {to}}$
.⊣
5.2 The algebraic expansions of
 $L_{\mathcal {P}}$
$L_{\mathcal {P}}$
The Logic
![]() $L_{\mathcal {P}}$
of Perfect MV-Algebras [Reference Di Nola and Lettieri13] is the extension of Łukasiewicz Logic by the axiom
$L_{\mathcal {P}}$
of Perfect MV-Algebras [Reference Di Nola and Lettieri13] is the extension of Łukasiewicz Logic by the axiom
![]() $2x^2 \mathbin {\leftrightarrow } (2x)^2$
(recall that
$2x^2 \mathbin {\leftrightarrow } (2x)^2$
(recall that
![]() $x \mathbin {\leftrightarrow } y := (\neg x + y) \wedge (\neg y + x)$
). As the name suggests, the equivalent algebraic semantics of
$x \mathbin {\leftrightarrow } y := (\neg x + y) \wedge (\neg y + x)$
). As the name suggests, the equivalent algebraic semantics of
![]() $L_{\mathcal {P}}$
is the variety
$L_{\mathcal {P}}$
is the variety
![]() $\mathsf {V}(\mathcal {P})$
.
$\mathsf {V}(\mathcal {P})$
.
Given a prime number p, the algebraic expansion of
![]() $L_{\mathcal {P}}$
corresponding to the EFD-sentence
$L_{\mathcal {P}}$
corresponding to the EFD-sentence
![]() $\varepsilon _p$
is, by definition, obtained from
$\varepsilon _p$
is, by definition, obtained from
![]() $L_{\mathcal {P}}$
by adding a unary function symbol
$L_{\mathcal {P}}$
by adding a unary function symbol
![]() $\mathsf {d}_p$
to the language of
$\mathsf {d}_p$
to the language of
![]() $L_{\mathcal {P}}$
, the axiom:
$L_{\mathcal {P}}$
, the axiom:
and the rule
![]() $\mathrm {U}_{\{((kz \wedge \neg 2z^2) \vee z^k) \leftrightarrow x\}}$
. However, since this rule is derivable in
$\mathrm {U}_{\{((kz \wedge \neg 2z^2) \vee z^k) \leftrightarrow x\}}$
. However, since this rule is derivable in
![]() $L_{\mathcal {P}}$
, the expansion is obtained simply by adding
$L_{\mathcal {P}}$
, the expansion is obtained simply by adding
![]() $D_p$
.
$D_p$
.
For a set S of prime numbers define
![]() $L_{\mathcal {P}}^S$
as the expansion of
$L_{\mathcal {P}}^S$
as the expansion of
![]() $L_{\mathcal {P}}$
by the axioms
$L_{\mathcal {P}}$
by the axioms
![]() $\{D_p: p \in S\}$
. Note that, by the comment above,
$\{D_p: p \in S\}$
. Note that, by the comment above,
![]() $L_{\mathcal {P}}^S$
is the algebraic expansion of
$L_{\mathcal {P}}^S$
is the algebraic expansion of
![]() $L_{\mathcal {P}}$
corresponding to the AE-class axiomatized by
$L_{\mathcal {P}}$
corresponding to the AE-class axiomatized by
![]() $\Sigma _S := \{\varepsilon _p: p \in S\}$
. Thus, the equivalent algebraic semantics
$\Sigma _S := \{\varepsilon _p: p \in S\}$
. Thus, the equivalent algebraic semantics
![]() $\mathsf {V}(\mathcal {P})^{\Sigma _S}$
of
$\mathsf {V}(\mathcal {P})^{\Sigma _S}$
of
![]() $L_{\mathcal {P}}^S$
is a variety.
$L_{\mathcal {P}}^S$
is a variety.
Theorem 5.3.
-
1. Every algebraic expansion of
 $L_{\mathcal {P}}$
is
$L_{\mathcal {P}}$
is
 $\tau _{\mathcal {MV}}$
-bimorphic to exactly one of the following:
$\tau _{\mathcal {MV}}$
-bimorphic to exactly one of the following:-
• Inconsistent Logic,
-
• Classical Propositional Logic,
-
•
 $L_{\mathcal {P}}^S$
for some set S of prime numbers.
$L_{\mathcal {P}}^S$
for some set S of prime numbers.
-
-
2. The algebraic expansions of
 $L_{\mathcal {P}}$
form a lattice isomorphic to
$L_{\mathcal {P}}$
form a lattice isomorphic to
 $\mathbf {2}^\omega \oplus \mathbf {2}$
when ordered by
$\mathbf {2}^\omega \oplus \mathbf {2}$
when ordered by
 $\tau _{\mathcal {MV}}$
-morphisms.
$\tau _{\mathcal {MV}}$
-morphisms. -
3. Given sets
 $S,S'$
of prime numbers with
$S,S'$
of prime numbers with
 $S \subseteq S'$
, the expansion
$S \subseteq S'$
, the expansion
 $L_{\mathcal {P}}^{S'}$
is conservative over
$L_{\mathcal {P}}^{S'}$
is conservative over
 $L_{\mathcal {P}}^S$
.
$L_{\mathcal {P}}^S$
.
Proof Items 1. and 2. follow from Theorems 3.2 and 5.2. To prove 3. let
![]() $\mathbf {D}_S$
be the expansion of
$\mathbf {D}_S$
be the expansion of
![]() $\Gamma (\mathbf {Z} \mathbin {\vec {\times }} \mathbf {Q}, (1,0))$
by the operations
$\Gamma (\mathbf {Z} \mathbin {\vec {\times }} \mathbf {Q}, (1,0))$
by the operations
![]() $\mathsf {d}_p$
for
$\mathsf {d}_p$
for
![]() $p \in S$
. (Where
$p \in S$
. (Where
![]() $\Gamma $
is Mundici’s functor and
$\Gamma $
is Mundici’s functor and
![]() $\mathbin {\vec {\times }}$
is the lexicographical product; see [Reference Cignoli, D’Ottaviano and Mundici12].) Now the proof follows the argument of that of 3. in Theorem 4.14 with
$\mathbin {\vec {\times }}$
is the lexicographical product; see [Reference Cignoli, D’Ottaviano and Mundici12].) Now the proof follows the argument of that of 3. in Theorem 4.14 with
![]() $\mathbf {D}_S$
in place of
$\mathbf {D}_S$
in place of
![]() $\mathbf {Q}_S$
.
$\mathbf {Q}_S$
.
Acknowledgment
The last author was supported by the I+D+I research project PID2019-110843GA-I00 funded by the Ministry of Science and Innovation of Spain.