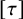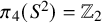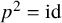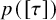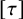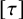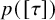1 Introduction
In this paper, we study the energy-minimizing and critical almost complex structures, as a continuation of [Reference He5], with respect to the energy functional
where
![]() ${\mathcal J}_g$
is the space of almost complex structures which are compatible with g. We call these objects biharmonic almost complex structures, as these objects are tensor-valued versions of biharmonic maps. The first result of the paper is the following.
${\mathcal J}_g$
is the space of almost complex structures which are compatible with g. We call these objects biharmonic almost complex structures, as these objects are tensor-valued versions of biharmonic maps. The first result of the paper is the following.
Theorem 1.1. A
![]() $W^{2, 2}$
-biharmonic almost complex structure on
$W^{2, 2}$
-biharmonic almost complex structure on
![]() $(M^4, g)$
is smooth. Moreover, on any compact almost Hermitian manifold
$(M^4, g)$
is smooth. Moreover, on any compact almost Hermitian manifold
![]() $(M^4, g)$
, there always exist minimizers of the energy functional
$(M^4, g)$
, there always exist minimizers of the energy functional
![]() ${\mathcal E}_2(J)$
which are smooth biharmonic almost complex structures. All such energy minimizers form a compact set.
${\mathcal E}_2(J)$
which are smooth biharmonic almost complex structures. All such energy minimizers form a compact set.
The existence of energy-minimizing almost complex structures is a standard practice of calculus of variations. The proof of smooth regularity in Theorem 1.1 is inspired by the theory of biharmonic maps in Chang-Wang-Yang [Reference Chang, Wang and Yang1]. There are subtle differences due to the nature of tensor-valued functions. We will present the smooth regularity for a much more general system in a paper together with Jiang [Reference He and Jiang6].
Our second result concerns the existence of energy-minimizing almost complex structures in a fixed homotopy class. The topology of M will play an important role in the following. Let A denote the set of homotopy classes of almost complex structures on M, so the first Chern class gives a map
Donaldson [Reference Donaldson3, Section 6] defined a map
![]() $p: A\rightarrow A$
with
$p: A\rightarrow A$
with
![]() $p^2=\text {id}$
and
$p^2=\text {id}$
and
![]() $c_1\circ p=c_1$
using the fact that
$c_1\circ p=c_1$
using the fact that
![]() $\pi _4(S^2)=\mathbb {Z}_2$
. First, we discuss the case that M is simply connected. If M is not spin, then
$\pi _4(S^2)=\mathbb {Z}_2$
. First, we discuss the case that M is simply connected. If M is not spin, then
![]() $\sigma =p(\sigma )$
(see [Reference Teichner11]), and it is uniquely determined by its first Chern class. If M is spin, then the pair,
$\sigma =p(\sigma )$
(see [Reference Teichner11]), and it is uniquely determined by its first Chern class. If M is spin, then the pair,
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
, is uniquely determined by its first Chern class.
$p(\sigma )$
, is uniquely determined by its first Chern class.
Theorem 1.2. Let
![]() $(M^4, g)$
be a compact, simply connected almost Hermitian four manifold. If M is nonspin, then every homotopy class contains an energy-minimizing biharmonic almost complex structure. If M is spin, there exists an energy-minimizing biharmonic almost complex structure in the pair of homotopy classes (
$(M^4, g)$
be a compact, simply connected almost Hermitian four manifold. If M is nonspin, then every homotopy class contains an energy-minimizing biharmonic almost complex structure. If M is spin, there exists an energy-minimizing biharmonic almost complex structure in the pair of homotopy classes (
![]() $\sigma $
,
$\sigma $
,
![]() $p(\sigma )$
).
$p(\sigma )$
).
Theorem 1.2 can be stated as, for a compact simply connected almost Hermitian four manifold, given its first Chern class
![]() $c_1$
, there exists an energy-minimizing biharmonic almost complex structure in the homotopy classes (possibly one or two) determined by
$c_1$
, there exists an energy-minimizing biharmonic almost complex structure in the homotopy classes (possibly one or two) determined by
![]() $c_1$
. When M is not necessarily simply connected, we have the following.
$c_1$
. When M is not necessarily simply connected, we have the following.
Theorem 1.3. Given a pair of homotopy classes
![]() $(\sigma , p(\sigma ))$
on
$(\sigma , p(\sigma ))$
on
![]() $(M, g)$
, there exists an energy-minimizing biharmonic almost complex structure in the pair.
$(M, g)$
, there exists an energy-minimizing biharmonic almost complex structure in the pair.
As a comparison, despite much progress in the study of biharmonic maps and polyharmonic maps in the last two decades, the general existence result remains very limited. We briefly discuss the new input in the proof of Theorem 1.3. Recall the classic [Reference Sacks and Uhlenbeck12] on the existence of harmonic two-spheres. Sacks-Uhlenbeck [Reference Sacks and Uhlenbeck12] considered a perturbation elliptic system for harmonic maps and one technical core is the bubble analysis. The system for biharmonic almost complex structures is fourth order, and a natural perturbed biharmonic system becomes much more complicated. We are not able to prove a regularity result for such a system. This obstructs us from adopting Sacks-Uhlenbeck’s approach using a perturbed biharmonic system. Instead, we analyze an energy-minimizing sequence directly in a fixed homotopy class. We get a weak limit in
![]() $W^{2, 2}$
. Using the special structure of the almost complex structure, we can argue that the weak limit satisfies the elliptic system weakly for biharmonic almost complex structures, and hence it is smooth by [Reference He and Jiang6, Theorem 2, Corollary 1]. The main difficulty, as in other similar situations, is to understand what exactly happens if the convergence fails to be strongly in
$W^{2, 2}$
. Using the special structure of the almost complex structure, we can argue that the weak limit satisfies the elliptic system weakly for biharmonic almost complex structures, and hence it is smooth by [Reference He and Jiang6, Theorem 2, Corollary 1]. The main difficulty, as in other similar situations, is to understand what exactly happens if the convergence fails to be strongly in
![]() $W^{2, 2}$
. A major technical result is an
$W^{2, 2}$
. A major technical result is an
![]() $\epsilon $
-regularity for an energy-minimizing sequence in a fixed homotopy class. We prove that if the convergence of a weakly convergent energy-minimizing subsequence fails to be strongly in
$\epsilon $
-regularity for an energy-minimizing sequence in a fixed homotopy class. We prove that if the convergence of a weakly convergent energy-minimizing subsequence fails to be strongly in
![]() $W^{2, 2}$
, then there must be energy concentration around finitely many isolated points. The
$W^{2, 2}$
, then there must be energy concentration around finitely many isolated points. The
![]() $\epsilon $
regularity for a minimizing sequence is very different from the classical
$\epsilon $
regularity for a minimizing sequence is very different from the classical
![]() $\epsilon $
-regularity in the theory of harmonic maps since there is no elliptic system to be dealt with.
$\epsilon $
-regularity in the theory of harmonic maps since there is no elliptic system to be dealt with.
A technical tool we develop in the paper is an extension theorem for almost complex structures in
![]() $W^{2, 2}$
, with precisely controlled behavior in the neck region. The classical extension theorems developed by Schoen-Uhlenbeck [Reference Schoen and Uhlenbeck13], Luckhaus [Reference Luckhaus10] and Lin [Reference Lin9] played an essential role in the setting of
$W^{2, 2}$
, with precisely controlled behavior in the neck region. The classical extension theorems developed by Schoen-Uhlenbeck [Reference Schoen and Uhlenbeck13], Luckhaus [Reference Luckhaus10] and Lin [Reference Lin9] played an essential role in the setting of
![]() $W^{1, p}$
maps, which do not extend to
$W^{1, p}$
maps, which do not extend to
![]() $W^{2, 2}$
(see Simon [Reference Simon14, Section 2.6, 2.7]). Motivated by these classical methods in the harmonic maps, we analyze the defect measure as in Lin [Reference Lin9]. We prove an
$W^{2, 2}$
(see Simon [Reference Simon14, Section 2.6, 2.7]). Motivated by these classical methods in the harmonic maps, we analyze the defect measure as in Lin [Reference Lin9]. We prove an
![]() $\epsilon $
-regularity theorem for a minimizing sequence in
$\epsilon $
-regularity theorem for a minimizing sequence in
![]() $W^{2, 2}$
for defect measure, by modifying techniques in Schoen-Uhlenbeck [Reference Schoen and Uhlenbeck13] and Lin [Reference Lin9] in a rather subtle way. The method developed should be useful in energy-minimizing problems in the setting of
$W^{2, 2}$
for defect measure, by modifying techniques in Schoen-Uhlenbeck [Reference Schoen and Uhlenbeck13] and Lin [Reference Lin9] in a rather subtle way. The method developed should be useful in energy-minimizing problems in the setting of
![]() $W^{k, 2}$
for
$W^{k, 2}$
for
![]() $k\geq 2$
.
$k\geq 2$
.
Recently, together with He-Jiang-Lin [Reference He, Jiang and Lin7], we apply this method to study the existence of biharmonic maps and polyharmonic maps. Among others, we prove the
![]() $\epsilon $
-regularity holds for an energy-minimizing sequence for a polyharmonic functional, and a weak limit is a polyharmonic map. Given the target manifold having trivial homotopy, we prove the existence of an energy-minimizing m-harmonic map in each homotopy class, which solves a longstanding open question for polyharmonic maps.
$\epsilon $
-regularity holds for an energy-minimizing sequence for a polyharmonic functional, and a weak limit is a polyharmonic map. Given the target manifold having trivial homotopy, we prove the existence of an energy-minimizing m-harmonic map in each homotopy class, which solves a longstanding open question for polyharmonic maps.
Theorem 1.3 does not answer what would precisely happen if we restrict to each homotopy class. We will discuss an intuitive conjectural picture regarding the existence problem in the pair
![]() $(\sigma , p(\sigma ))$
, which is closely related to the study of extrinsic biharmonic maps.
$(\sigma , p(\sigma ))$
, which is closely related to the study of extrinsic biharmonic maps.
2 Existence of an energy minimizer
In this section we prove the existence of an energy-minimizing biharmonic almost complex structure on
![]() $(M, g)$
and derive the Euler-Lagrange equation. We recall the definition of the Sobolev spaces of almost complex structures.
$(M, g)$
and derive the Euler-Lagrange equation. We recall the definition of the Sobolev spaces of almost complex structures.
Definition 2.1. Given an almost Hermitian manifold
![]() $(M, g)$
with compatible almost complex structures in
$(M, g)$
with compatible almost complex structures in
![]() ${\mathcal J}_g$
, we define
${\mathcal J}_g$
, we define
![]() $W^{k, p}({\mathcal J}_g)$
to be the subspace of
$W^{k, p}({\mathcal J}_g)$
to be the subspace of
![]() $W^{k, p}(T^*M\otimes TM)$
consisting of those sections
$W^{k, p}(T^*M\otimes TM)$
consisting of those sections
![]() $J\in W^{k, p}(T^*M\otimes TM)$
, satisfying the compatible condition almost everywhere,
$J\in W^{k, p}(T^*M\otimes TM)$
, satisfying the compatible condition almost everywhere,
We have the following.
Theorem 2.2. Let
![]() $(M, g, {\mathcal J}_g)$
be a compact Hermitian manifold with compatible almost complex structures. Then there exists an energy minimizer of
$(M, g, {\mathcal J}_g)$
be a compact Hermitian manifold with compatible almost complex structures. Then there exists an energy minimizer of
![]() ${\mathcal E}_2(J)$
in
${\mathcal E}_2(J)$
in
![]() $W^{2, 2}({\mathcal J}_g)$
, satisfying the Euler-Lagrangian equation in the weak sense as in (2.5). Moreover, energy minimizers form a sequential compact set in
$W^{2, 2}({\mathcal J}_g)$
, satisfying the Euler-Lagrangian equation in the weak sense as in (2.5). Moreover, energy minimizers form a sequential compact set in
![]() $W^{2, 2}$
.
$W^{2, 2}$
.
Proof. We only prove the existence of
![]() $W^{2, 2}$
energy minimizer of
$W^{2, 2}$
energy minimizer of
![]() ${\mathcal E}_2(J)$
over
${\mathcal E}_2(J)$
over
![]() $W^{2, 2}({\mathcal J}_g).$
We will derive the Euler-Lagrange equation later. This is a standard practice of calculus of variations. Take an energy-minimizing sequence
$W^{2, 2}({\mathcal J}_g).$
We will derive the Euler-Lagrange equation later. This is a standard practice of calculus of variations. Take an energy-minimizing sequence
![]() $J_k\in W^{2, 2}({\mathcal J}_g)$
, such that
$J_k\in W^{2, 2}({\mathcal J}_g)$
, such that
Since
![]() $J_k\in W^{2, 2}(TM\otimes T^*M)$
, it follows from Kondrachov compactness that a subsequence, still denoted by
$J_k\in W^{2, 2}(TM\otimes T^*M)$
, it follows from Kondrachov compactness that a subsequence, still denoted by
![]() $J_k$
, converges strongly in
$J_k$
, converges strongly in
![]() $W^{1, 2}(T^*M\otimes TM)$
and weakly in
$W^{1, 2}(T^*M\otimes TM)$
and weakly in
![]() $W^{2, 2}(T^*M\otimes TM)$
. Denote the limit by
$W^{2, 2}(T^*M\otimes TM)$
. Denote the limit by
![]() $J_0\in W^{2, 2}(TM\otimes T^*M)$
. The strong convergence in
$J_0\in W^{2, 2}(TM\otimes T^*M)$
. The strong convergence in
![]() $W^{1, 2}$
implies, in particular, that
$W^{1, 2}$
implies, in particular, that
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
almost everywhere; therefore,
$J_0$
almost everywhere; therefore,
![]() $J_0$
satisfies the compatible condition (2.1) almost everywhere. Hence,
$J_0$
satisfies the compatible condition (2.1) almost everywhere. Hence,
![]() $J_0\in W^{2, 2}({\mathcal J}_g)$
. The weak convergence in
$J_0\in W^{2, 2}({\mathcal J}_g)$
. The weak convergence in
![]() $W^{2, 2}$
implies that
$W^{2, 2}$
implies that
This forces that
![]() ${\mathcal E}_2(J_0)=\min {\mathcal E}_2(J)$
, and
${\mathcal E}_2(J_0)=\min {\mathcal E}_2(J)$
, and
![]() $J_0$
is an energy minimizer. Moreover, this also implies that the convergence
$J_0$
is an energy minimizer. Moreover, this also implies that the convergence
![]() $J_k\rightarrow J_0$
is strongly in
$J_k\rightarrow J_0$
is strongly in
![]() $W^{2, 2}$
and that the set of all energy minimizers is compact.
$W^{2, 2}$
and that the set of all energy minimizers is compact.
Straightforward computation gives the Euler-Lagrange equation in smooth setting
An equivalent form is
![]() $[\Delta ^2 J, J]=0$
. By
$[\Delta ^2 J, J]=0$
. By
![]() $J^2=-id$
, we can rewrite the equation as,
$J^2=-id$
, we can rewrite the equation as,
where Q is given by
We need to be more careful when working in
![]() $W^{2, 2}({\mathcal J}_g)$
to derive equations for weak solutions. For any
$W^{2, 2}({\mathcal J}_g)$
to derive equations for weak solutions. For any
![]() $A\in TM\rightarrow TM$
, it is convenient to define its adjoint
$A\in TM\rightarrow TM$
, it is convenient to define its adjoint
![]() $A^*$
as follows.
$A^*$
as follows.
Hence, g-compatibility can be written as
![]() $A+A^*=0$
. For any
$A+A^*=0$
. For any
![]() $J\in {\mathcal J}_g$
, the tangent space
$J\in {\mathcal J}_g$
, the tangent space
![]() ${\mathcal S}_J$
of J can be described as the endomorphisms
${\mathcal S}_J$
of J can be described as the endomorphisms
![]() $S: TM\rightarrow TM$
as
$S: TM\rightarrow TM$
as
Clearly,
![]() $S\in {\mathcal S}_J$
, and then
$S\in {\mathcal S}_J$
, and then
![]() $JS$
is in
$JS$
is in
![]() ${\mathcal S}_J$
as well. The adjoint can be directly carried over for Sobolev spaces. Necessary properties of the adjoint endomorphism are summarized in [Reference He and Jiang6, Proposition 4.1]. For any
${\mathcal S}_J$
as well. The adjoint can be directly carried over for Sobolev spaces. Necessary properties of the adjoint endomorphism are summarized in [Reference He and Jiang6, Proposition 4.1]. For any
![]() $S\in {\mathcal S}_J\cap L^\infty $
, it is direct to check that
$S\in {\mathcal S}_J\cap L^\infty $
, it is direct to check that
![]() $J(t)=J \exp (tSJ)$
gives a path in
$J(t)=J \exp (tSJ)$
gives a path in
![]() ${\mathcal J}_g\cap L^\infty $
for
${\mathcal J}_g\cap L^\infty $
for
![]() $|t|<<1$
, with
$|t|<<1$
, with
![]() $\partial _t J(0)=S$
.
$\partial _t J(0)=S$
.
Proposition 2.3. A critical point of
![]() ${\mathcal E}_2(J)$
on
${\mathcal E}_2(J)$
on
![]() $W^{2, 2}({\mathcal J}_g)$
satisfies the Euler-Lagrange equation (2.3) in the following weak sense. For any
$W^{2, 2}({\mathcal J}_g)$
satisfies the Euler-Lagrange equation (2.3) in the following weak sense. For any
![]() $T\in W^{2, 2}(T^*M\otimes TM)\cap L^\infty $
, we have
$T\in W^{2, 2}(T^*M\otimes TM)\cap L^\infty $
, we have
where we write
Proof. Assume that
![]() $T\in W^{2, 2}(\Gamma (T^*M\otimes TM))\cap L^\infty $
. Denote
$T\in W^{2, 2}(\Gamma (T^*M\otimes TM))\cap L^\infty $
. Denote
![]() $R=T+JTJ$
and
$R=T+JTJ$
and
![]() $S=R-R^*$
. Then S satisfies
$S=R-R^*$
. Then S satisfies
![]() $SJ+JS=0, S+S^*=0$
. Taking variation in the form
$SJ+JS=0, S+S^*=0$
. Taking variation in the form
![]() $J(t)=J\exp (tSJ)$
for small
$J(t)=J\exp (tSJ)$
for small
![]() $|t|<<1$
, we have
$|t|<<1$
, we have
![]() $\int _M (\Delta J, \Delta S)dv=0.$
Since J is g-compatible, this implies
$\int _M (\Delta J, \Delta S)dv=0.$
Since J is g-compatible, this implies
![]() $\int _M (\Delta J, \Delta R)dv=0$
. In other words, we have
$\int _M (\Delta J, \Delta R)dv=0$
. In other words, we have
For
![]() $J\in W^{2, 2}$
, we compute
$J\in W^{2, 2}$
, we compute
Since J is g-compatible, it is straightforward to check that
 $$ \begin{align*} (\Delta J, J \Delta T J)=&(J\Delta J J, \Delta T)\nonumber \\ (\Delta J, \Delta J T J)=&(\Delta J \Delta J J, T). \end{align*} $$
$$ \begin{align*} (\Delta J, J \Delta T J)=&(J\Delta J J, \Delta T)\nonumber \\ (\Delta J, \Delta J T J)=&(\Delta J \Delta J J, T). \end{align*} $$
Hence, we get that
where we have
However, we use
![]() $\Delta (J^2)=0$
to conclude that
$\Delta (J^2)=0$
to conclude that
 $$ \begin{align*} &\Delta J J+J\Delta J+2\nabla_p J\nabla_p J=0 \nonumber \\ &J\Delta J J=\Delta J-2J\nabla_p J\nabla_p J. \end{align*} $$
$$ \begin{align*} &\Delta J J+J\Delta J+2\nabla_p J\nabla_p J=0 \nonumber \\ &J\Delta J J=\Delta J-2J\nabla_p J\nabla_p J. \end{align*} $$
We compute that
Hence, we get that
We denote
![]() $A_0=2A$
, with
$A_0=2A$
, with
Together with (2.6), we have
This completes the proof.
Proposition 2.3 is equivalent to (2.2) for
![]() $J\in W^{2, 2}$
when (2.2) is understood as a weak solution in the form that
$J\in W^{2, 2}$
when (2.2) is understood as a weak solution in the form that
An almost complex structure
![]() $J\in W^{2, 2}({\mathcal J}_g)$
is called a weak biharmonic almost complex structure if it satisfies (2.8) or its equivalent form (2.5). The equivalent descriptions below will be useful as well.
$J\in W^{2, 2}({\mathcal J}_g)$
is called a weak biharmonic almost complex structure if it satisfies (2.8) or its equivalent form (2.5). The equivalent descriptions below will be useful as well.
Proposition 2.4. A weak biharmonic almost complex satisfies the following.
where
![]() $T\in \Gamma (TM\otimes T^*M)$
. Or equivalently, we have the following.
$T\in \Gamma (TM\otimes T^*M)$
. Or equivalently, we have the following.
As a consequence, the weak limit of a sequence of biharmonic almost complex structure with bounded
![]() $W^{2, 2}$
norm is biharmonic.
$W^{2, 2}$
norm is biharmonic.
Proof. To derive (2.9), we take
![]() $T=\tilde T J$
in (2.8) and observe that
$T=\tilde T J$
in (2.8) and observe that
Similarly, we have
This gives (2.10). Suppose a sequence of weak biharmonic almost complex structures
![]() $J_k$
, with bounded
$J_k$
, with bounded
![]() $W^{2, 2}$
norm, converges weakly in
$W^{2, 2}$
norm, converges weakly in
![]() $W^{2, 2}$
to
$W^{2, 2}$
to
![]() $J_0$
and strongly in
$J_0$
and strongly in
![]() $W^{1, 2}$
. By passing to the limit,
$W^{1, 2}$
. By passing to the limit,
![]() $J_0$
satisfies (2.10). More precisely, for any fixed smooth T, we have
$J_0$
satisfies (2.10). More precisely, for any fixed smooth T, we have
The strong convergence
![]() $J_k\rightarrow J_0$
in
$J_k\rightarrow J_0$
in
![]() $L^2$
implies that
$L^2$
implies that
Together, this implies that
Similarly, we have
This completes the proof.
He-Jiang [Reference He and Jiang6, Theorem 2, Corollary 1] proved a smooth regularity for a general elliptic system. As a result, we have the following.
Theorem 2.5. A
![]() $W^{2, 2}$
weak solution of biharmonic almost complex structure in dimension four is smooth.
$W^{2, 2}$
weak solution of biharmonic almost complex structure in dimension four is smooth.
3 Biharmonic almost complex structures in a homotopy class
A fundamental problem in the theory of harmonic maps is finding harmonic maps in a fixed homotopy class. Similarly, we would like to ask the same question for biharmonic almost complex structures. We shall see that the topology of M plays a very important role. The following famous example about almost complex structures on a
![]() $K3$
surface constructed by Donaldson [Reference Donaldson3] serves as an important example. We recall relevant discussions. A compatible almost complex structure J on an oriented Riemannian four-manifold M can be considered as a section of the associated
$K3$
surface constructed by Donaldson [Reference Donaldson3] serves as an important example. We recall relevant discussions. A compatible almost complex structure J on an oriented Riemannian four-manifold M can be considered as a section of the associated
![]() $SO(4)/U(2)$
-bundle over M (the sphere bundle of
$SO(4)/U(2)$
-bundle over M (the sphere bundle of
![]() $\Lambda ^2_+$
, known as the ‘twistor space’). Let A denote the set of homotopy classes of almost complex structures, so the first Chern class gives a map
$\Lambda ^2_+$
, known as the ‘twistor space’). Let A denote the set of homotopy classes of almost complex structures, so the first Chern class gives a map
Donaldson [Reference Donaldson3, Section 6] defined a map
![]() $p: A\rightarrow A$
with
$p: A\rightarrow A$
with
![]() $p^2=\text {id}$
and
$p^2=\text {id}$
and
![]() $c_1\circ p=c_1$
as follows. For
$c_1\circ p=c_1$
as follows. For
![]() $\sigma \in A$
,
$\sigma \in A$
,
![]() $p(\sigma )$
agrees with
$p(\sigma )$
agrees with
![]() $\sigma $
outside a small ball in M, and over this ball, the two compare by the nonzero element of
$\sigma $
outside a small ball in M, and over this ball, the two compare by the nonzero element of
We need the following general result about
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )\in A$
, which we have learned from Teichner through mathoverflow [Reference Teichner11].
$p(\sigma )\in A$
, which we have learned from Teichner through mathoverflow [Reference Teichner11].
Lemma 3.1. If M is simply connected and nonspin, then the first Chern class determines a unique homotopy class of an almost complex structure. When M is simply connected and spin, the first Chern class determines a pair of homotopy classes
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
.
$p(\sigma )$
.
The main result in this section is to prove Theorem 1.3. The proof consists of several steps. Let
![]() $J_k\in \sigma $
be a minimizing sequence such that
$J_k\in \sigma $
be a minimizing sequence such that
![]() ${\mathcal E}_2(J_k)\rightarrow E_0$
. A direct computation shows that
${\mathcal E}_2(J_k)\rightarrow E_0$
. A direct computation shows that
![]() $J_k$
has uniformly bounded
$J_k$
has uniformly bounded
![]() $W^{2, 2}$
norm. Hence, we can assume that
$W^{2, 2}$
norm. Hence, we can assume that
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
weakly in
$J_0$
weakly in
![]() $W^{2, 2}$
and strongly in
$W^{2, 2}$
and strongly in
![]() $W^{1, 2}$
, in particular
$W^{1, 2}$
, in particular
![]() $J_0\in W^{2, 2}({\mathcal J}_g)$
. First, we have the following.
$J_0\in W^{2, 2}({\mathcal J}_g)$
. First, we have the following.
Lemma 3.2. The limit
![]() $J_0$
is a smooth biharmonic almost complex structure.
$J_0$
is a smooth biharmonic almost complex structure.
Proof. We only need to prove that
![]() $J_0$
is a weak biharmonic almost complex structure satisfying (2.10). Let
$J_0$
is a weak biharmonic almost complex structure satisfying (2.10). Let
![]() $J_k$
be a minimizing sequence and
$J_k$
be a minimizing sequence and
![]() $J_0$
be its weak limit in
$J_0$
be its weak limit in
![]() $W^{2, 2}({\mathcal J}_g)$
. For any fixed smooth
$W^{2, 2}({\mathcal J}_g)$
. For any fixed smooth
![]() ${T\in \Gamma (TM\otimes T^*M)}$
, consider
${T\in \Gamma (TM\otimes T^*M)}$
, consider
Note that for
![]() $|t|$
sufficiently small,
$|t|$
sufficiently small,
![]() $S_t$
has small
$S_t$
has small
![]() $L^\infty $
norm and we construct
$L^\infty $
norm and we construct
We compute, for
![]() $|t|$
sufficiently small,
$|t|$
sufficiently small,
where the term
![]() $O(t^2)$
denotes the terms of higher order in t. We have
$O(t^2)$
denotes the terms of higher order in t. We have
![]() $|O(t^2)|\leq Ct^2$
for a uniformly bounded constant C (assuming t is small). A quick way to see (3.1) is to write the (matrix) expansion of
$|O(t^2)|\leq Ct^2$
for a uniformly bounded constant C (assuming t is small). A quick way to see (3.1) is to write the (matrix) expansion of
![]() $J_k(t)$
as
$J_k(t)$
as
Since
![]() $J_k$
is a minimizing sequence, hence when
$J_k$
is a minimizing sequence, hence when
![]() $k\rightarrow \infty $
, we have
$k\rightarrow \infty $
, we have
Hence, for
![]() $|t|$
sufficiently small,
$|t|$
sufficiently small,
In particular, this implies that
Similar as in (2.10) and (2.11), we use the fact
to conclude that
Since
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
weakly in
$J_0$
weakly in
![]() $W^{2, 2}$
and strongly in
$W^{2, 2}$
and strongly in
![]() $W^{1, 2}$
, the above implies that
$W^{1, 2}$
, the above implies that
By Proposition 2.4,
![]() $J_0$
is a weak biharmonic almost complex structure. Hence it is smooth by regularity results in [Reference He and Jiang6].
$J_0$
is a weak biharmonic almost complex structure. Hence it is smooth by regularity results in [Reference He and Jiang6].
An important question is to understand the homotopy class of
![]() $J_0$
. To proceed, we need the following fact about the first Chern class.
$J_0$
. To proceed, we need the following fact about the first Chern class.
Lemma 3.3 (Wood [Reference Wood16]).
Given a compact almost Hermitian manifold
![]() $(M, g, J, \omega )$
, then the first Chern class can be represented by the following 2-form
$(M, g, J, \omega )$
, then the first Chern class can be represented by the following 2-form
![]() $\gamma $
such that
$\gamma $
such that
where
![]() ${\mathcal R}(\omega )$
is the curvature operator acting on the Kähler form
${\mathcal R}(\omega )$
is the curvature operator acting on the Kähler form
![]() $\omega $
.
$\omega $
.
Lemma 3.3 has the following important consequence.
Lemma 3.4. The first Chern class
![]() $c_1(J_0)=c_1(J_k)$
for
$c_1(J_0)=c_1(J_k)$
for
![]() $J_k\in \sigma $
.
$J_k\in \sigma $
.
Proof. The first Chern class
![]() $c_1(J)$
is the deformation invariant, and hence it remains the same in the homotopy class
$c_1(J)$
is the deformation invariant, and hence it remains the same in the homotopy class
![]() $\sigma $
. By Lemma 3.3, the first Chern class is represented by the 2-form
$\sigma $
. By Lemma 3.3, the first Chern class is represented by the 2-form
![]() $\gamma $
. We write
$\gamma $
. We write
![]() $\gamma _k$
for
$\gamma _k$
for
![]() $J_k$
and
$J_k$
and
![]() $\gamma _0$
for
$\gamma _0$
for
![]() $J_0$
. Since
$J_0$
. Since
![]() $J_k$
converges strongly to
$J_k$
converges strongly to
![]() $J_0$
in
$J_0$
in
![]() $W^{1, 2}$
, then for any smooth two form
$W^{1, 2}$
, then for any smooth two form
![]() $\zeta $
, (3.2) implies that
$\zeta $
, (3.2) implies that
It follows that
![]() $[\gamma _k]=[\gamma _0]\in H^2(M, \mathbb {Z})$
.
$[\gamma _k]=[\gamma _0]\in H^2(M, \mathbb {Z})$
.
Hence, the fist Chern class remains unchanged for the weak limit. If M is simply connected and nonspin, Lemma 3.1 implies that
![]() $J_0$
is in the homotopy class
$J_0$
is in the homotopy class
![]() $\sigma $
.
$\sigma $
.
Lemma 3.5. If M is simply connected and nonspin, then every homotopy class contains an energy-minimizing biharmonic almost complex structure.
If M is simply connected and spin, the situation is more complicated. By Lemma 3.1,
![]() $J_0$
is either in the class
$J_0$
is either in the class
![]() $\sigma $
or in
$\sigma $
or in
![]() $p(\sigma )$
. In the former case,
$p(\sigma )$
. In the former case,
![]() $J_0$
is an energy-minimizing biharmonic almost complex structure in
$J_0$
is an energy-minimizing biharmonic almost complex structure in
![]() $\sigma $
; in the later case, we prove that there is an energy-minimizing biharmonic almost complex structure in
$\sigma $
; in the later case, we prove that there is an energy-minimizing biharmonic almost complex structure in
![]() $p(\sigma )$
. To achieve this, we consider the homotopy class
$p(\sigma )$
. To achieve this, we consider the homotopy class
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
simultaneously. We consider
$p(\sigma )$
simultaneously. We consider
![]() $\inf _{J\in \sigma } {\mathcal E}_2(J)$
and
$\inf _{J\in \sigma } {\mathcal E}_2(J)$
and
![]() $\inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
. We assume that
$\inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
. We assume that
![]() $\inf _{J\in \sigma } {\mathcal E}_2(J)\geq \inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
. A minimizing sequence
$\inf _{J\in \sigma } {\mathcal E}_2(J)\geq \inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
. A minimizing sequence
![]() $J_k$
in
$J_k$
in
![]() $p(\sigma )$
will have a weak limit
$p(\sigma )$
will have a weak limit
![]() $J_0$
and
$J_0$
and
![]() ${\mathcal E}_2(J_0)\geq \inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
, since
${\mathcal E}_2(J_0)\geq \inf _{J\in p(\sigma )}{\mathcal E}_2(J)$
, since
![]() $J_0$
is either in
$J_0$
is either in
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
. This will force that
$p(\sigma )$
. This will force that
![]() $J_0$
is an energy-minimizing biharmonic almost complex structure.
$J_0$
is an energy-minimizing biharmonic almost complex structure.
Lemma 3.6. If M is simply connected and spin, then for each first Chern class c of an almost complex structure, at least one homotopy class (among two homotopy classes corresponding to c) contains an energy-minimizing biharmonic almost complex structures.
When M is not necessarily simply connected, Lemma 3.1 does not hold anymore. We need more precise control of weak convergence to obtain the following.
Lemma 3.7. Let
![]() $J_k$
be an energy-minimizing sequence of
$J_k$
be an energy-minimizing sequence of
![]() ${\mathcal E}_2(J)$
in the homotopy class
${\mathcal E}_2(J)$
in the homotopy class
![]() $\sigma $
. Then the weak limit
$\sigma $
. Then the weak limit
![]() $J_0$
(of a convergent subsequence) lies in either
$J_0$
(of a convergent subsequence) lies in either
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
.
$p(\sigma )$
.
The key is to prove a version of
![]() $\epsilon $
-regularity for the minimizing sequence
$\epsilon $
-regularity for the minimizing sequence
![]() $J_k$
. As a consequence,
$J_k$
. As a consequence,
![]() $J_k$
converges strongly in
$J_k$
converges strongly in
![]() $W^{2, 2}$
to
$W^{2, 2}$
to
![]() $J_0$
except around finitely many isolated points. This will imply that the homotopy class of
$J_0$
except around finitely many isolated points. This will imply that the homotopy class of
![]() $J_0$
is either
$J_0$
is either
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
.
$p(\sigma )$
.
Now we are ready to state and prove the
![]() $\epsilon $
-regularity for the minimizing sequence
$\epsilon $
-regularity for the minimizing sequence
![]() $J_k$
(see Lemma 3.8 and Lemma 3.9). Fix a sufficiently small positive number
$J_k$
(see Lemma 3.8 and Lemma 3.9). Fix a sufficiently small positive number
![]() $\epsilon _0$
, which depends only on
$\epsilon _0$
, which depends only on
![]() $(M, g)$
and will be specified later. Let
$(M, g)$
and will be specified later. Let
![]() $\iota $
be the injectivity radius of
$\iota $
be the injectivity radius of
![]() $(M, g)$
. Suppose a minimizing sequence
$(M, g)$
. Suppose a minimizing sequence
![]() $J_k\in \sigma $
converges weakly to
$J_k\in \sigma $
converges weakly to
![]() $J_0$
in
$J_0$
in
![]() $W^{2, 2}$
and strongly in
$W^{2, 2}$
and strongly in
![]() $W^{1, 2}$
. For
$W^{1, 2}$
. For
![]() $r\in (0, \iota )$
,
$r\in (0, \iota )$
,
![]() $p\in M$
and
$p\in M$
and
![]() $J\in W^{2, 2}$
, denote
$J\in W^{2, 2}$
, denote
 $$ \begin{align} &E(r, p)=\int_{B_r(p)}|\Delta J|^2 dv \nonumber \\ &F(r, p)=\int_{B_r(p)} (|\nabla^2J|^2+|\nabla J|^4)dv. \end{align} $$
$$ \begin{align} &E(r, p)=\int_{B_r(p)}|\Delta J|^2 dv \nonumber \\ &F(r, p)=\int_{B_r(p)} (|\nabla^2J|^2+|\nabla J|^4)dv. \end{align} $$
We write
![]() $E_0(r, p), F_0(r, p), E_k(r, p), F_k(r, p)$
correspondingly for
$E_0(r, p), F_0(r, p), E_k(r, p), F_k(r, p)$
correspondingly for
![]() $J_0$
and
$J_0$
and
![]() $J_k$
. Set
$J_k$
. Set
![]() ${\mathcal S}_r=\{p\in M: \liminf _{k\rightarrow \infty } F_k(r, p)\geq \epsilon _0\}.$
Clearly,
${\mathcal S}_r=\{p\in M: \liminf _{k\rightarrow \infty } F_k(r, p)\geq \epsilon _0\}.$
Clearly,
![]() ${\mathcal S}_r\subset {\mathcal S}_s$
for
${\mathcal S}_r\subset {\mathcal S}_s$
for
![]() $r<s$
. Denote
$r<s$
. Denote
We introduce the measures which are all totally bounded,
 $$ \begin{align}\begin{cases} & \!\!\!\!\!d\mu_k=(|\nabla^2J_k|^2+|\nabla J_k|^4)dv\\ &\!\!\!\!\! d\mu_0=(|\nabla^2 J_0|^2+|\nabla J_0|^4)dv\\ & \!\!\!\!\! d\xi_k=|\Delta J_k|^2dv\\ &\!\!\!\!\! d\xi_0=|\Delta J_0|^2dv. \end{cases}\end{align} $$
$$ \begin{align}\begin{cases} & \!\!\!\!\!d\mu_k=(|\nabla^2J_k|^2+|\nabla J_k|^4)dv\\ &\!\!\!\!\! d\mu_0=(|\nabla^2 J_0|^2+|\nabla J_0|^4)dv\\ & \!\!\!\!\! d\xi_k=|\Delta J_k|^2dv\\ &\!\!\!\!\! d\xi_0=|\Delta J_0|^2dv. \end{cases}\end{align} $$
By passing to a subsequence,
![]() $\mu _k$
converges weakly to a positive Radon measure
$\mu _k$
converges weakly to a positive Radon measure
![]() $\mu $
, and
$\mu $
, and
![]() $\xi _k$
converges weakly to a positive Radon measure
$\xi _k$
converges weakly to a positive Radon measure
![]() $\xi $
. By Fatou’s lemma, there exist positive Radon measures
$\xi $
. By Fatou’s lemma, there exist positive Radon measures
![]() $\nu $
and
$\nu $
and
![]() $\lambda $
(called the defect measure [Reference Lin8, Reference Lin9]), such that
$\lambda $
(called the defect measure [Reference Lin8, Reference Lin9]), such that
 $$\begin{align*}\begin{cases} &\!\!\!\!\! d\mu=d\nu+d\mu_0\\ &\!\!\!\!\! d\xi=d\lambda+d\xi_0. \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} &\!\!\!\!\! d\mu=d\nu+d\mu_0\\ &\!\!\!\!\! d\xi=d\lambda+d\xi_0. \end{cases}\end{align*}$$
Certainly,
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
strongly in
$J_0$
strongly in
![]() $W^{2, 2}$
if and only if either
$W^{2, 2}$
if and only if either
![]() $\nu \equiv 0$
or
$\nu \equiv 0$
or
![]() $\lambda \equiv 0$
. But
$\lambda \equiv 0$
. But
![]() $\nu $
and
$\nu $
and
![]() $\lambda $
are not necessarily the same in general. The interplay between two defect measures
$\lambda $
are not necessarily the same in general. The interplay between two defect measures
![]() $\nu $
and
$\nu $
and
![]() $\lambda $
makes our discussions below more complicated than the theory of the harmonic maps, where only the measure
$\lambda $
makes our discussions below more complicated than the theory of the harmonic maps, where only the measure
![]() $|\nabla u|^2dv$
comes to play. We have the following.
$|\nabla u|^2dv$
comes to play. We have the following.
Lemma 3.8. The support of
![]() $\nu $
equals
$\nu $
equals
![]() ${\mathcal S}$
, which contains at most finitely many points.
${\mathcal S}$
, which contains at most finitely many points.
Proof. First, it is straightforward to see that
![]() ${\mathcal S}$
is contained in the support of
${\mathcal S}$
is contained in the support of
![]() $\nu $
. Since
$\nu $
. Since
![]() $J_0$
is smooth, we have for any
$J_0$
is smooth, we have for any
![]() $x\in M$
,
$x\in M$
,
![]() $\lim _{r\rightarrow 0}\mu _0(B_r(x))=0.$
If
$\lim _{r\rightarrow 0}\mu _0(B_r(x))=0.$
If
![]() $x\in {\mathcal S}$
, then
$x\in {\mathcal S}$
, then
This shows that
![]() ${\mathcal S}$
is contained in the support of
${\mathcal S}$
is contained in the support of
![]() $\nu $
.
$\nu $
.
Next, we claim the following. For
![]() $r\in (0, r_0]$
, where
$r\in (0, r_0]$
, where
![]() $r_0$
is a fixed, sufficiently small number, if
$r_0$
is a fixed, sufficiently small number, if
![]() $\mu (B_{2r}(p))<\epsilon _0$
, then
$\mu (B_{2r}(p))<\epsilon _0$
, then
![]() $\nu \equiv 0$
in
$\nu \equiv 0$
in
![]() $B_{r/2}(p)$
.
$B_{r/2}(p)$
.
We sketch the idea of the proof briefly. If
![]() $\mu (B_{2r}(p))<\epsilon _0$
for
$\mu (B_{2r}(p))<\epsilon _0$
for
![]() $\epsilon _0$
sufficiently small, then after passing to a subsequence, we have
$\epsilon _0$
sufficiently small, then after passing to a subsequence, we have
for sufficiently large k. This implies that
![]() $J_k$
is close to its average in
$J_k$
is close to its average in
![]() $B_{2r}$
and the same discussion holds for
$B_{2r}$
and the same discussion holds for
![]() $J_0$
. In particular,
$J_0$
. In particular,
![]() $J_k$
and
$J_k$
and
![]() $J_0$
, when restricted in
$J_0$
, when restricted in
![]() $B_r$
, are homotopy to each other. The key is to construct a new ‘almost minimizing’ sequence
$B_r$
, are homotopy to each other. The key is to construct a new ‘almost minimizing’ sequence
![]() $\tilde J_k$
in the same homotopy class such that
$\tilde J_k$
in the same homotopy class such that
![]() $\tilde J_k=J_0$
inside
$\tilde J_k=J_0$
inside
![]() $B_{r/2}(p)$
and
$B_{r/2}(p)$
and
![]() $\tilde J_k=J_k$
outside
$\tilde J_k=J_k$
outside
![]() $B_r(p)$
, while the behavior in the annulus region is precisely controlled. This would imply
$B_r(p)$
, while the behavior in the annulus region is precisely controlled. This would imply
![]() $\nu , \lambda \equiv 0$
in
$\nu , \lambda \equiv 0$
in
![]() $B_{r/2}(p)$
.
$B_{r/2}(p)$
.
Suppose at the moment, the claim is established. If p is in the support of
![]() $\nu $
, then
$\nu $
, then
![]() $\mu (B_{2r}(p))\geq \epsilon _0$
for all sufficiently small r. Hence
$\mu (B_{2r}(p))\geq \epsilon _0$
for all sufficiently small r. Hence
![]() $p\in {\mathcal S}$
. Since the total energy is bounded, it follows that
$p\in {\mathcal S}$
. Since the total energy is bounded, it follows that
![]() ${\mathcal S}$
contains, at most, finitely many isolated points. We complete the proof given Lemma 3.9 below, where we establish the claim.
${\mathcal S}$
contains, at most, finitely many isolated points. We complete the proof given Lemma 3.9 below, where we establish the claim.
First, we specify the choice of
![]() $r_0$
. We can do the scaling
$r_0$
. We can do the scaling
![]() $g_r=r^{-2}g$
for
$g_r=r^{-2}g$
for
![]() $r\leq r_0$
. We choose
$r\leq r_0$
. We choose
![]() $r_0$
sufficiently small, such that
$r_0$
sufficiently small, such that
![]() $g_r$
is sufficiently close to the Euclidean metric in the ball
$g_r$
is sufficiently close to the Euclidean metric in the ball
![]() $B_2(p)$
(we identify
$B_2(p)$
(we identify
![]() $B_2(p)$
with the Euclidean ball
$B_2(p)$
with the Euclidean ball
![]() $B_2$
equipped with the metric
$B_2$
equipped with the metric
![]() $g_r$
) such that
$g_r$
) such that
 $$ \begin{align} |g_{ij}-\delta_{ij}|+\sum_{k=1}^4|D^k g_{ij}|<\delta_0,\end{align} $$
$$ \begin{align} |g_{ij}-\delta_{ij}|+\sum_{k=1}^4|D^k g_{ij}|<\delta_0,\end{align} $$
where
![]() $\delta _0$
measures how close the metric
$\delta _0$
measures how close the metric
![]() $g_r$
is with respect to the Euclidean metric in
$g_r$
is with respect to the Euclidean metric in
![]() $B_2$
. We also assume that
$B_2$
. We also assume that
![]() $g_{ij}(0)=\delta _{ij}, \partial g_{ij}(0)=0$
.
$g_{ij}(0)=\delta _{ij}, \partial g_{ij}(0)=0$
.
Note that we choose
![]() $r_0, \delta _0$
and
$r_0, \delta _0$
and
![]() $\epsilon _0$
uniformly for any point
$\epsilon _0$
uniformly for any point
![]() $p\in M$
. The constants
$p\in M$
. The constants
![]() $r_0, \delta _0$
and
$r_0, \delta _0$
and
![]() $\epsilon _0$
are all fixed. Since r will also be fixed and the energy functionals are scaling invariant, we consider
$\epsilon _0$
are all fixed. Since r will also be fixed and the energy functionals are scaling invariant, we consider
![]() $(M, g_r)$
instead of
$(M, g_r)$
instead of
![]() $(M, g)$
. In other words, we can assume that, by scaling if necessary, g satisfies (3.5) in any geodesic ball
$(M, g)$
. In other words, we can assume that, by scaling if necessary, g satisfies (3.5) in any geodesic ball
![]() $B_2(p)\subset M$
such that the injectivity radius of
$B_2(p)\subset M$
such that the injectivity radius of
![]() $(M, g)$
is bigger than
$(M, g)$
is bigger than
![]() $2$
. We identify
$2$
. We identify
![]() $(B_2(p), g)$
with the Euclidean ball
$(B_2(p), g)$
with the Euclidean ball
![]() $(B_2, g)$
via the exponential map
$(B_2, g)$
via the exponential map
![]() $\exp _p: T_pM\rightarrow M$
. Over
$\exp _p: T_pM\rightarrow M$
. Over
![]() $(B_2, g)$
, the tangent bundle is trivial and we write
$(B_2, g)$
, the tangent bundle is trivial and we write
![]() $J: TM\rightarrow TM$
over
$J: TM\rightarrow TM$
over
![]() $(B_2, g)$
as a matrix-value function
$(B_2, g)$
as a matrix-value function
![]() $J(x)$
. We use
$J(x)$
. We use
![]() $\nabla , \nabla ^2$
, etc. to denote covariant derivatives of with respect to g over
$\nabla , \nabla ^2$
, etc. to denote covariant derivatives of with respect to g over
![]() $B_2$
. We will also use
$B_2$
. We will also use
![]() $D, D^2$
to denote the Euclidean derivatives over
$D, D^2$
to denote the Euclidean derivatives over
![]() $B_2$
. After this choice of the scaling and local coordinates, an almost complex structure J over
$B_2$
. After this choice of the scaling and local coordinates, an almost complex structure J over
![]() $(B_2, g)$
is a matrix-valued function, which we still denote as J. We establish the main technical lemma.
$(B_2, g)$
is a matrix-valued function, which we still denote as J. We establish the main technical lemma.
Lemma 3.9. Suppose
![]() $\mu (B_{2}(p))\leq \epsilon _0$
. Then
$\mu (B_{2}(p))\leq \epsilon _0$
. Then
![]() $\nu \equiv 0$
in
$\nu \equiv 0$
in
![]() $B_{1}(p)$
.
$B_{1}(p)$
.
The proof of this lemma involves a construction of a sequence of ‘almost energy-minimizing’ almost complex structures
![]() $\tilde J_k$
in
$\tilde J_k$
in
![]() $\sigma $
such that
$\sigma $
such that
 $$ \begin{align} \tilde J_k(x)=\begin{cases} &\!\!\!\! J_k(x), x\in M\setminus B_1(p)\\ &\!\!\!\! J_0(x), x\in B_{1-j^{-1}}(p), \end{cases} \end{align} $$
$$ \begin{align} \tilde J_k(x)=\begin{cases} &\!\!\!\! J_k(x), x\in M\setminus B_1(p)\\ &\!\!\!\! J_0(x), x\in B_{1-j^{-1}}(p), \end{cases} \end{align} $$
where
![]() $k\geq k_j=k(j)$
is sufficiently large depending on j. In the end, we will let
$k\geq k_j=k(j)$
is sufficiently large depending on j. In the end, we will let
![]() $j\rightarrow \infty $
(and
$j\rightarrow \infty $
(and
![]() $k_j\rightarrow \infty $
accordingly) to get an almost energy-minimizing subsequence. Such a construction is a type of extension of an almost complex structure which equals
$k_j\rightarrow \infty $
accordingly) to get an almost energy-minimizing subsequence. Such a construction is a type of extension of an almost complex structure which equals
![]() $J_k$
in
$J_k$
in
![]() $M\setminus B_1(p)$
and which equals
$M\setminus B_1(p)$
and which equals
![]() $J_0$
in
$J_0$
in
![]() $B_{1-j^{-1}}(p)$
. The construction happens in a small annulus
$B_{1-j^{-1}}(p)$
. The construction happens in a small annulus
![]() $B_1(p)\setminus B_{1-j^{-1}}(p)$
. The small energy condition
$B_1(p)\setminus B_{1-j^{-1}}(p)$
. The small energy condition
![]() $\mu (B_{2}(p))\leq \epsilon _0$
plays a very important role. In particular, this implies that
$\mu (B_{2}(p))\leq \epsilon _0$
plays a very important role. In particular, this implies that
![]() $\tilde J_k$
is still in
$\tilde J_k$
is still in
![]() $\sigma $
, using a theorem of White [Reference White15].
$\sigma $
, using a theorem of White [Reference White15].
The construction involves several delicate choices of small constants and cutoff functions. We shall first briefly explain the process of construction, leaving details to be proved below. We work on
![]() $(B_2, g)$
. Let
$(B_2, g)$
. Let
![]() $\psi _j: [0, \infty )\rightarrow [0, 1]$
be a smooth cutoff function depending on j such that
$\psi _j: [0, \infty )\rightarrow [0, 1]$
be a smooth cutoff function depending on j such that
 $$\begin{align*}\psi_j(s)= \begin{cases} &\!\!\!\! 1, s\geq 1\\ &\!\!\!\! 0, s\leq 1-j^{-1} \end{cases} \end{align*}$$
$$\begin{align*}\psi_j(s)= \begin{cases} &\!\!\!\! 1, s\geq 1\\ &\!\!\!\! 0, s\leq 1-j^{-1} \end{cases} \end{align*}$$
with bounds
![]() $|\psi ^{'}_j|\leq 3j, |\psi ^{"}_j|\leq 10 j^2$
. For
$|\psi ^{'}_j|\leq 3j, |\psi ^{"}_j|\leq 10 j^2$
. For
![]() $x\in B_2$
, we denote
$x\in B_2$
, we denote
Note that
 $$ \begin{align} J_{k,\, j}(x)=\begin{cases}& \!\!\!\!\! J_k(x), |x|\geq 1\\ &\!\!\!\!\! J_0(x), |x|\leq 1-j^{-1}. \end{cases} \end{align} $$
$$ \begin{align} J_{k,\, j}(x)=\begin{cases}& \!\!\!\!\! J_k(x), |x|\geq 1\\ &\!\!\!\!\! J_0(x), |x|\leq 1-j^{-1}. \end{cases} \end{align} $$
We extend
![]() $J_{k,\, j}$
to M such that it equals
$J_{k,\, j}$
to M such that it equals
![]() $J_k$
outside
$J_k$
outside
![]() $B_1(p)$
. Note that
$B_1(p)$
. Note that
![]() $J_{k,\, j}$
might not even be invertible for some points
$J_{k,\, j}$
might not even be invertible for some points
![]() $|x|\in (1-j^{-1}, 1)$
since the convergence of
$|x|\in (1-j^{-1}, 1)$
since the convergence of
![]() $J_k\rightarrow J_0$
does not imply the convergence in
$J_k\rightarrow J_0$
does not imply the convergence in
![]() $L^\infty $
. To overcome this difficulty, we construct a smooth approximation of
$L^\infty $
. To overcome this difficulty, we construct a smooth approximation of
![]() $J_{k,\, j}$
using a local average technique (a modification of mollifier).
$J_{k,\, j}$
using a local average technique (a modification of mollifier).
Let
![]() $\phi (x)=\phi (|x|)$
be a nonnegative smooth radial cutoff function which is supported in
$\phi (x)=\phi (|x|)$
be a nonnegative smooth radial cutoff function which is supported in
![]() $B=B_1$
with
$B=B_1$
with
![]() $\int _B \phi dx=1$
. For any given J and
$\int _B \phi dx=1$
. For any given J and
![]() $\rho>0$
, we denote
$\rho>0$
, we denote
 $$ \begin{align} J_\rho(x)=\int_{B_\rho (x)}\phi_\rho(y-x) J(y)dy=\int_{B} \phi(z)J(x+\rho z)dz, \end{align} $$
$$ \begin{align} J_\rho(x)=\int_{B_\rho (x)}\phi_\rho(y-x) J(y)dy=\int_{B} \phi(z)J(x+\rho z)dz, \end{align} $$
where we use the notation,
![]() $\phi _\rho (x)=\rho ^{-4} \phi \left (\frac {x}{\rho }\right ). $
When
$\phi _\rho (x)=\rho ^{-4} \phi \left (\frac {x}{\rho }\right ). $
When
![]() $\rho =0$
,
$\rho =0$
,
![]() $\phi _\rho $
is the delta-function and
$\phi _\rho $
is the delta-function and
![]() $J_\rho (x)=J(x)$
(this is also clear from the second equality in (3.8)). Certainly,
$J_\rho (x)=J(x)$
(this is also clear from the second equality in (3.8)). Certainly,
![]() $J_\rho $
is the smooth approximation of J, and
$J_\rho $
is the smooth approximation of J, and
![]() $J_\rho $
converges to J (in a certain norm depending on the regularity of J) when
$J_\rho $
converges to J (in a certain norm depending on the regularity of J) when
![]() $\rho \rightarrow 0$
. However, such a smooth approximation does not preserve (3.7) in general. Hence, we allow
$\rho \rightarrow 0$
. However, such a smooth approximation does not preserve (3.7) in general. Hence, we allow
![]() $\rho $
to be dependent of
$\rho $
to be dependent of
![]() $|x|$
and we write
$|x|$
and we write
![]() $\rho : [0, 2]\rightarrow [0, 1]$
. Such a technique is a modification of Schoen-Uhlenbeck [Reference Sacks and Uhlenbeck12]. The support of
$\rho : [0, 2]\rightarrow [0, 1]$
. Such a technique is a modification of Schoen-Uhlenbeck [Reference Sacks and Uhlenbeck12]. The support of
![]() $\rho $
is contained in
$\rho $
is contained in
![]() $(1-j^{-1}, 1)$
. In other words,
$(1-j^{-1}, 1)$
. In other words,
We choose
![]() $\rho (1-(2j)^{-1})=\max \rho =\bar \rho $
, where
$\rho (1-(2j)^{-1})=\max \rho =\bar \rho $
, where
![]() $\bar \rho $
is a small positive number and it can be chosen such that
$\bar \rho $
is a small positive number and it can be chosen such that
![]() $4C_0\bar \rho j^2=1$
, where
$4C_0\bar \rho j^2=1$
, where
![]() $C_0$
is a uniform constant, specified below. By choosing
$C_0$
is a uniform constant, specified below. By choosing
![]() $\bar \rho $
, we require the derivatives of
$\bar \rho $
, we require the derivatives of
![]() $\rho $
satisfying
$\rho $
satisfying
For
![]() $x\in B_2$
, we also denote
$x\in B_2$
, we also denote
![]() $\rho (x)=\rho (|x|)$
. The choice of the function
$\rho (x)=\rho (|x|)$
. The choice of the function
![]() $\rho $
depends crucially on the cutoff function
$\rho $
depends crucially on the cutoff function
![]() $\psi _j$
, and this is the first key point in our construction.
$\psi _j$
, and this is the first key point in our construction.
Given such a function
![]() $\rho $
, we construct, for
$\rho $
, we construct, for
![]() $x\in B=B_1$
,
$x\in B=B_1$
,
 $$ \begin{align} J_{k,\, j,\,\rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_{k,\, j}(y)dy=\int_B \phi(z) J_{k,\, j}(x+\rho(x)z)dz. \end{align} $$
$$ \begin{align} J_{k,\, j,\,\rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_{k,\, j}(y)dy=\int_B \phi(z) J_{k,\, j}(x+\rho(x)z)dz. \end{align} $$
By the choice of
![]() $\rho (x)$
, which is zero when
$\rho (x)$
, which is zero when
![]() $1\leq |x|\leq 2$
or
$1\leq |x|\leq 2$
or
![]() $|x|\leq 1-j^{-1}$
,
$|x|\leq 1-j^{-1}$
,
![]() $J_{k, j, \rho (x)}$
can be extended to M and satisfies (3.7). Similarly, we denote
$J_{k, j, \rho (x)}$
can be extended to M and satisfies (3.7). Similarly, we denote
 $$ \begin{align} &J_{0,\, \rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_0(y)dy=\int_B \phi(z)J_0(x+\rho(x)z)dz. \nonumber \\ &J_{k,\,\rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_k(y)dy=\int_B \phi(z)J_k(x+\rho(x)z)dz. \end{align} $$
$$ \begin{align} &J_{0,\, \rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_0(y)dy=\int_B \phi(z)J_0(x+\rho(x)z)dz. \nonumber \\ &J_{k,\,\rho(x)}(x)=\int_{B_{\rho(x)}(x)}\phi_\rho(y-x)J_k(y)dy=\int_B \phi(z)J_k(x+\rho(x)z)dz. \end{align} $$
Note that
![]() $J_{0,\,\rho (x)}(x)$
,
$J_{0,\,\rho (x)}(x)$
,
![]() $J_{k, \, \rho (x)}(x)$
and
$J_{k, \, \rho (x)}(x)$
and
![]() $J_{k,\, j,\,\rho (x)}(x)$
are neither almost complex structures nor compatible with the metric g in general. It is straightforward to see that
$J_{k,\, j,\,\rho (x)}(x)$
are neither almost complex structures nor compatible with the metric g in general. It is straightforward to see that
![]() $J_{0,\,\rho (x)}(x)$
is close to
$J_{0,\,\rho (x)}(x)$
is close to
![]() $J_0(x)$
given
$J_0(x)$
given
![]() $\bar \rho $
is sufficiently small (
$\bar \rho $
is sufficiently small (
![]() $J_0$
is smooth and
$J_0$
is smooth and
![]() $J_{0, \, \rho }$
is a standard approximation). We will also show that
$J_{0, \, \rho }$
is a standard approximation). We will also show that
![]() $J_{k, \,\rho (x)}(x)$
is close to an almost complex structure and it is almost compatible with the metric g, using the Poincare inequality and small energy assumption. One difficulty is to prove that
$J_{k, \,\rho (x)}(x)$
is close to an almost complex structure and it is almost compatible with the metric g, using the Poincare inequality and small energy assumption. One difficulty is to prove that
![]() $J_{k,\, j, \,\rho }$
is also close to an almost complex structure, with a suitable choice of
$J_{k,\, j, \,\rho }$
is also close to an almost complex structure, with a suitable choice of
![]() $\rho $
and
$\rho $
and
![]() $\bar \rho $
and
$\bar \rho $
and
![]() $k=k(\bar \rho , j)$
. The dependence of k on
$k=k(\bar \rho , j)$
. The dependence of k on
![]() $\bar \rho $
and j is inevitable. In particular, we need to choose
$\bar \rho $
and j is inevitable. In particular, we need to choose
![]() $\rho $
depending on
$\rho $
depending on
![]() $\psi _j$
.
$\psi _j$
.
Once we construct
![]() $J_{k,\, j, \,\rho }$
, we use the technique in [Reference He5] to construct a unique almost complex structure
$J_{k,\, j, \,\rho }$
, we use the technique in [Reference He5] to construct a unique almost complex structure
![]() $\tilde J_k$
using
$\tilde J_k$
using
![]() $J_{k,\, j,\, \rho }$
, such that it is compatible with g. We assert that
$J_{k,\, j,\, \rho }$
, such that it is compatible with g. We assert that
which implies that
![]() $\tilde J_k\in \sigma $
using a theorem of White [Reference White15, Theorem 2 and Section 6].
$\tilde J_k\in \sigma $
using a theorem of White [Reference White15, Theorem 2 and Section 6].
Here comes another essential point of the proof. By the construction,
![]() $\tilde J_k$
equals
$\tilde J_k$
equals
![]() $J_k$
outside
$J_k$
outside
![]() $B_1$
and agrees with
$B_1$
and agrees with
![]() $J_0$
in
$J_0$
in
![]() $B_{1-j^{-1}}$
. If
$B_{1-j^{-1}}$
. If
![]() $\tilde J_k$
is an energy-minimizing sequence in
$\tilde J_k$
is an energy-minimizing sequence in
![]() $\sigma $
, this implies that
$\sigma $
, this implies that
![]() $\lambda \equiv 0$
in
$\lambda \equiv 0$
in
![]() $B_{1}$
and completes the proof. Unfortunately, we are not able to prove
$B_{1}$
and completes the proof. Unfortunately, we are not able to prove
 $$ \begin{align} \int_{B_1\setminus B_{1-j^{-1}}}|\Delta \tilde J_{k}|^2dv\rightarrow 0 \end{align} $$
$$ \begin{align} \int_{B_1\setminus B_{1-j^{-1}}}|\Delta \tilde J_{k}|^2dv\rightarrow 0 \end{align} $$
for
![]() $k\geq k_j$
and
$k\geq k_j$
and
![]() $j\rightarrow \infty $
. Instead, we prove the following inequality approximately.
$j\rightarrow \infty $
. Instead, we prove the following inequality approximately.
 $$ \begin{align} \int_{B_1\setminus B_{1-j^{-1}}}|\Delta \tilde J_{k}|^2dv\lessapprox C \int_{B_{1}\setminus B_{1-j^{-1}}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
$$ \begin{align} \int_{B_1\setminus B_{1-j^{-1}}}|\Delta \tilde J_{k}|^2dv\lessapprox C \int_{B_{1}\setminus B_{1-j^{-1}}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
Given (3.15) and the fact that
![]() $\{J_k\}$
is an energy-minimizing sequence, we can obtain that
$\{J_k\}$
is an energy-minimizing sequence, we can obtain that
Since the defect measure
![]() $\nu (\partial B_1)$
can be strictly positive on
$\nu (\partial B_1)$
can be strictly positive on
![]() $\partial B_1$
, this does not directly lead to the conclusion
$\partial B_1$
, this does not directly lead to the conclusion
![]() $\lambda \equiv 0$
. However, the construction above actually works on any ball
$\lambda \equiv 0$
. However, the construction above actually works on any ball
![]() $B_r\subset B_2$
,
$B_r\subset B_2$
,
![]() $r\in [1/4, 7/4]$
(replacing
$r\in [1/4, 7/4]$
(replacing
![]() $B_1$
by
$B_1$
by
![]() $B_r$
), and the arguments can be directly carried over. Hence, we will prove for
$B_r$
), and the arguments can be directly carried over. Hence, we will prove for
![]() $r\in [1/4, 7/4]$
,
$r\in [1/4, 7/4]$
,
In particular, we have for
![]() $r\in [3/2, 7/4]$
,
$r\in [3/2, 7/4]$
,
Since
![]() $\nu $
is a totally bounded positive Radon measure, then
$\nu $
is a totally bounded positive Radon measure, then
![]() $\nu (\partial B_r)=0$
for infinitely many r (actually
$\nu (\partial B_r)=0$
for infinitely many r (actually
![]() $\nu (\partial B_r)>0$
for at most countably many r). Hence, this proves that
$\nu (\partial B_r)>0$
for at most countably many r). Hence, this proves that
![]() $\lambda \equiv 0$
in
$\lambda \equiv 0$
in
![]() $B_{3/2}$
. It is then a standard practice to prove that
$B_{3/2}$
. It is then a standard practice to prove that
![]() $\nu \equiv 0$
in
$\nu \equiv 0$
in
![]() $B_1$
.
$B_1$
.
We state two versions of the Poincare inequality which are needed in the proof. For
![]() $f\in W^{1, 2}(B_R), B_R\subset \mathbb {R}^n$
, denote
$f\in W^{1, 2}(B_R), B_R\subset \mathbb {R}^n$
, denote
![]() $\underline {f}$
to be its average in the ball,
$\underline {f}$
to be its average in the ball,
Then we have
where C is a uniform dimensional constant. Suppose
![]() $\phi $
is a cutoff function supported in
$\phi $
is a cutoff function supported in
![]() $B_R$
such that
$B_R$
such that
![]() $\int _{B_R}\phi (y)dy=1$
. We denote
$\int _{B_R}\phi (y)dy=1$
. We denote
and then we have
We should mention that f can be taken as vector-valued and matrix-valued functions as a direct generalization. Now we carry out the details to prove Lemma 3.9.
Proof.
Step one: the construction of an ‘almost’ almost complex structure
![]() $J_{k, j, \rho (x)}$
.
$J_{k, j, \rho (x)}$
.
Note that J is g-compatible if
![]() $J+J^*=0$
. With the localization over
$J+J^*=0$
. With the localization over
![]() $B_2$
, J is g-compatible if
$B_2$
, J is g-compatible if
![]() $(J+g J^t g^{-1})(x)=0$
holds as a matrix-valued equation for all
$(J+g J^t g^{-1})(x)=0$
holds as a matrix-valued equation for all
![]() $x\in B_2$
, where
$x\in B_2$
, where
![]() $J^t$
is the transpose of J. If J is compatible with g, then
$J^t$
is the transpose of J. If J is compatible with g, then
![]() $J_\rho $
is almost g-compatible if
$J_\rho $
is almost g-compatible if
![]() $\bar \rho $
is sufficiently small (we assume that
$\bar \rho $
is sufficiently small (we assume that
![]() $|J|$
is bounded, of course). We estimate
$|J|$
is bounded, of course). We estimate
 $$ \begin{align} |(J_\rho+gJ_\rho^t g^{-1})(x)|=&\left|\int_{B_\rho(x)}\phi_\rho(y-x) (J(y)+g(x)J^t(y)g^{-1}(x))dy\right| \nonumber \\ \leq &\rho^{-4}\int_{B_\rho}\left|J(y)+g(x)J^t(y)g^{-1}(x)\right|dy \nonumber \\ \leq &\rho^{-4}\int_{B_\rho} \left|-g(y)J^t(y)g^{-1}(y)+g(x)J^t(y)g^{-1}(x)\right|dy \nonumber \\ \leq& C\delta_0 \bar \rho, \end{align} $$
$$ \begin{align} |(J_\rho+gJ_\rho^t g^{-1})(x)|=&\left|\int_{B_\rho(x)}\phi_\rho(y-x) (J(y)+g(x)J^t(y)g^{-1}(x))dy\right| \nonumber \\ \leq &\rho^{-4}\int_{B_\rho}\left|J(y)+g(x)J^t(y)g^{-1}(x)\right|dy \nonumber \\ \leq &\rho^{-4}\int_{B_\rho} \left|-g(y)J^t(y)g^{-1}(y)+g(x)J^t(y)g^{-1}(x)\right|dy \nonumber \\ \leq& C\delta_0 \bar \rho, \end{align} $$
where we use the facts
![]() $|g(x)-g(y)|\leq C\delta _0\bar \rho \,\, \mbox {for}\,\, |y-x|\leq \rho $
and
$|g(x)-g(y)|\leq C\delta _0\bar \rho \,\, \mbox {for}\,\, |y-x|\leq \rho $
and
It is clear that (3.21) holds for all the cases
![]() $J=J_0,\, J_k\, \mbox {and}\, J_{k,\, j}$
.
$J=J_0,\, J_k\, \mbox {and}\, J_{k,\, j}$
.
Next we show that
![]() $J_{k,\, j,\,\rho }$
is ‘almost’ an almost complex structure in the sense that
$J_{k,\, j,\,\rho }$
is ‘almost’ an almost complex structure in the sense that
![]() $|J_{k,\, j,\,\rho }J_{k,\,j,\,\rho }+\text {id}|$
is very small pointwise. Now we specify
$|J_{k,\, j,\,\rho }J_{k,\,j,\,\rho }+\text {id}|$
is very small pointwise. Now we specify
![]() $\rho $
further and discuss the properties of
$\rho $
further and discuss the properties of
![]() $J_{k,\, j,\,\rho }$
. For
$J_{k,\, j,\,\rho }$
. For
![]() ${|x|\in [0, 1-j^{-1}]\cup [1, 2]}$
, since
${|x|\in [0, 1-j^{-1}]\cup [1, 2]}$
, since
![]() $\rho (x)=0$
, we have
$\rho (x)=0$
, we have
 $$ \begin{align} J_{k,\,j, \,\rho(x)}(x)=J_{k,\, j}(x)=\begin{cases} &\!\!\!\! J_k(x), |x|\in [1, 2],\\ &\!\!\!\! J_0(x), |x|\in [0, 1-j^{-1}].\end{cases}\end{align} $$
$$ \begin{align} J_{k,\,j, \,\rho(x)}(x)=J_{k,\, j}(x)=\begin{cases} &\!\!\!\! J_k(x), |x|\in [1, 2],\\ &\!\!\!\! J_0(x), |x|\in [0, 1-j^{-1}].\end{cases}\end{align} $$
Fix
![]() $\delta _1>0$
sufficiently small (which can be taken as
$\delta _1>0$
sufficiently small (which can be taken as
![]() $j^{-1}$
). We write
$j^{-1}$
). We write
![]() $(1-j^{-1}, 1)$
as three subintervals
$(1-j^{-1}, 1)$
as three subintervals
The discussions in each subinterval are different. We choose
![]() $\rho $
such that
$\rho $
such that
 $$ \begin{align} \begin{cases} &\!\!\!\! \rho(1-(2j)^{-1})=\bar \rho\\ &\!\!\!\! \rho(1-j^{-1}+\delta_1 j^{-1})=\rho(1-\delta_1 j^{-1})=\delta_1 \bar\rho\\ &\!\!\!\! \rho(s)<\delta_1\bar \rho, s\in (1-j^{-1}, 1-j^{-1}+\delta_1 j^{-1})\cup (1-\delta_1 j^{-1}, 1)\\ &\!\!\!\! \rho(s)\geq \delta_1\bar \rho, s\in (1-j^{-1}+\delta_1 j^{-1}, 1-\delta_1 j^{-1}). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} &\!\!\!\! \rho(1-(2j)^{-1})=\bar \rho\\ &\!\!\!\! \rho(1-j^{-1}+\delta_1 j^{-1})=\rho(1-\delta_1 j^{-1})=\delta_1 \bar\rho\\ &\!\!\!\! \rho(s)<\delta_1\bar \rho, s\in (1-j^{-1}, 1-j^{-1}+\delta_1 j^{-1})\cup (1-\delta_1 j^{-1}, 1)\\ &\!\!\!\! \rho(s)\geq \delta_1\bar \rho, s\in (1-j^{-1}+\delta_1 j^{-1}, 1-\delta_1 j^{-1}). \end{cases} \end{align} $$
Let
![]() $h(s)$
be a smooth nonnegative function supported over
$h(s)$
be a smooth nonnegative function supported over
![]() $[0, 2]$
, satisfying the following.
$[0, 2]$
, satisfying the following.
 $$ \begin{align} &h(1)=1=\max h, \text{and}\; h(s)=h(2-s), \nonumber \\ &h(j^{-1})=j^{-1}, \; h'(s)\geq 0, s\in [0, 1], \nonumber \\ &|h^{'}|+|h^{"}|\leq C_0. \end{align} $$
$$ \begin{align} &h(1)=1=\max h, \text{and}\; h(s)=h(2-s), \nonumber \\ &h(j^{-1})=j^{-1}, \; h'(s)\geq 0, s\in [0, 1], \nonumber \\ &|h^{'}|+|h^{"}|\leq C_0. \end{align} $$
Denote
![]() $\rho (s)= \bar \rho \; h(2+2j(s-1))$
. Then
$\rho (s)= \bar \rho \; h(2+2j(s-1))$
. Then
![]() $\rho (s)$
is supported in
$\rho (s)$
is supported in
![]() $[1-j^{-1}, 1]$
, satisfying (3.23). We now choose
$[1-j^{-1}, 1]$
, satisfying (3.23). We now choose
![]() $\bar \rho $
such that
$\bar \rho $
such that
For
![]() $|x|\in (1-j^{-1}, 1-j^{-1}+\delta _1 j^{-1}]$
, we have
$|x|\in (1-j^{-1}, 1-j^{-1}+\delta _1 j^{-1}]$
, we have
Using
![]() $\psi _j(1-j^{-1})=0$
and
$\psi _j(1-j^{-1})=0$
and
![]() $|\psi ^{'}_j|\leq 3j$
, we get
$|\psi ^{'}_j|\leq 3j$
, we get
We compute
 $$ \begin{align*} |J_{k,\, j,\,\rho(x)}(x)-J_{0,\, \rho(x)}(x)|=\left|\int_B\phi(z)\psi_j(|x+\rho(x)z)|(J_0-J_k)(x+\rho(x)z)dz\right|\leq 100 \delta_1. \end{align*} $$
$$ \begin{align*} |J_{k,\, j,\,\rho(x)}(x)-J_{0,\, \rho(x)}(x)|=\left|\int_B\phi(z)\psi_j(|x+\rho(x)z)|(J_0-J_k)(x+\rho(x)z)dz\right|\leq 100 \delta_1. \end{align*} $$
Similarly, for
![]() $|x|\in [1-\delta _1 j^{-1}, 1)$
, we have
$|x|\in [1-\delta _1 j^{-1}, 1)$
, we have
We can estimate
where
![]() $C_1=C_1(\max |\nabla J_0|)$
is a uniform constant. We derive
$C_1=C_1(\max |\nabla J_0|)$
is a uniform constant. We derive
This implies that
![]() $J_{k,\, j,\,\rho (x)}$
is close to an almost complex structure for
$J_{k,\, j,\,\rho (x)}$
is close to an almost complex structure for
![]() $|x|\in (1-j^{-1}, 1-j^{-1}+\delta _1 j^{-1})$
, provided that
$|x|\in (1-j^{-1}, 1-j^{-1}+\delta _1 j^{-1})$
, provided that
![]() $100\delta _1+C_1 \bar \rho $
is sufficiently small. Since
$100\delta _1+C_1 \bar \rho $
is sufficiently small. Since
![]() $|\nabla J_k|$
might not be uniformly bounded, we do not have an effective pointwise estimate on
$|\nabla J_k|$
might not be uniformly bounded, we do not have an effective pointwise estimate on
![]() $|J_{k,\,\rho (x)}(x)-J_k(x)|$
as above. Instead, we apply the Poincare inequality (3.20) in the ball
$|J_{k,\,\rho (x)}(x)-J_k(x)|$
as above. Instead, we apply the Poincare inequality (3.20) in the ball
![]() $B_\rho (x)$
to
$B_\rho (x)$
to
![]() $J(y)$
with
$J(y)$
with
![]() $ J_{*}=J_\rho (x)=\int _{B_\rho (x)} \phi _\rho (y-x) J(y)dy, $
$ J_{*}=J_\rho (x)=\int _{B_\rho (x)} \phi _\rho (y-x) J(y)dy, $
 $$ \begin{align} \rho^{-4}\int_{B_{\rho}(x)} |J(y)-J_\rho(x)|^2 dv\leq C\rho^{-2}\int_{B_\rho(x)}|DJ(y)|^2dy, \end{align} $$
$$ \begin{align} \rho^{-4}\int_{B_{\rho}(x)} |J(y)-J_\rho(x)|^2 dv\leq C\rho^{-2}\int_{B_\rho(x)}|DJ(y)|^2dy, \end{align} $$
Replacing J by
![]() $J_k$
, we can get that
$J_k$
, we can get that
 $$ \begin{align} \rho^{-4}\int_{B_\rho(x)}|J_k(y)-J_{k,\,\rho(x)}(x)|^2dy\leq C\rho^{-2}\int_{B_\rho(x)}|DJ_k(y)|^2dy. \end{align} $$
$$ \begin{align} \rho^{-4}\int_{B_\rho(x)}|J_k(y)-J_{k,\,\rho(x)}(x)|^2dy\leq C\rho^{-2}\int_{B_\rho(x)}|DJ_k(y)|^2dy. \end{align} $$
By the Hölder inequality, we see that
 $$\begin{align*}\rho^{-2}\int_{B_\rho(x)}|DJ_k(y)|^2dy\leq C\left(\int_{B_\rho(x)}|DJ_k|^4dy\right)^{\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\rho^{-2}\int_{B_\rho(x)}|DJ_k(y)|^2dy\leq C\left(\int_{B_\rho(x)}|DJ_k|^4dy\right)^{\frac{1}{2}}. \end{align*}$$
Using the fact that
![]() $\nabla J=DJ+\partial g*J$
and (3.5), it follows that
$\nabla J=DJ+\partial g*J$
and (3.5), it follows that
 $$ \begin{align} \rho^{-4}\int_{B_\rho(x)}|J_k(y)-J_{k,\,\rho(x)}(x)|^2dy\leq C\left(\int_{B_\rho(x)}|DJ_k|^4dy\right)^{\frac{1}{2}}\leq C(\sqrt{\epsilon_0}+\sqrt{\delta_0}). \end{align} $$
$$ \begin{align} \rho^{-4}\int_{B_\rho(x)}|J_k(y)-J_{k,\,\rho(x)}(x)|^2dy\leq C\left(\int_{B_\rho(x)}|DJ_k|^4dy\right)^{\frac{1}{2}}\leq C(\sqrt{\epsilon_0}+\sqrt{\delta_0}). \end{align} $$
Hence, (3.30) implies that there are many ys in
![]() $B_{\rho }(x)$
such that
$B_{\rho }(x)$
such that
In particular, this implies that
Using (3.25) and the above, we get that
Next we consider
![]() $|x|\in (1-j^{-1}+\delta _1j^{-1}, 1-\delta _1 j^{-1})$
, where
$|x|\in (1-j^{-1}+\delta _1j^{-1}, 1-\delta _1 j^{-1})$
, where
![]() $\rho (x)\geq \delta _1\bar \rho $
. We compute
$\rho (x)\geq \delta _1\bar \rho $
. We compute
We have
 $$\begin{align*}\int_B \phi(z) |(J_0-J_k)(x+\rho(x)z)|dz\leq &{\rho(x)}^{-4} \int_{B_{\rho(x)}(x)}|J_0(y)-J_k(y)|dy \nonumber \\ \leq&C\rho^{-2}\|J_0-J_k\|_{L^2(B_{3/2})}. \nonumber\end{align*}$$
$$\begin{align*}\int_B \phi(z) |(J_0-J_k)(x+\rho(x)z)|dz\leq &{\rho(x)}^{-4} \int_{B_{\rho(x)}(x)}|J_0(y)-J_k(y)|dy \nonumber \\ \leq&C\rho^{-2}\|J_0-J_k\|_{L^2(B_{3/2})}. \nonumber\end{align*}$$
Since
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
strongly in
$J_0$
strongly in
![]() $W^{1, 2}$
and
$W^{1, 2}$
and
![]() $\rho \geq \delta _1\bar \rho $
for
$\rho \geq \delta _1\bar \rho $
for
![]() $|x|\in (1-j^{-1}+\delta _1j^{-1}, 1-\delta _1 j^{-1})$
, we can choose
$|x|\in (1-j^{-1}+\delta _1j^{-1}, 1-\delta _1 j^{-1})$
, we can choose
![]() $k_0=k_0(\delta _1, \bar \rho )$
sufficiently large such that
$k_0=k_0(\delta _1, \bar \rho )$
sufficiently large such that
Hence, we get, for
![]() $k\geq k_0$
,
$k\geq k_0$
,
 $$ \begin{align} {\rho}^{-4} \int_{B_{\rho(x)}(x)}|J_0(y)-J_k(y)|dy\leq \bar\rho. \end{align} $$
$$ \begin{align} {\rho}^{-4} \int_{B_{\rho(x)}(x)}|J_0(y)-J_k(y)|dy\leq \bar\rho. \end{align} $$
Using (3.33) and (3.32), we have that, for
![]() $k\geq k_0$
,
$k\geq k_0$
,
This together with (3.26) implies that, for
![]() $k\geq k_0$
,
$k\geq k_0$
,
and in particular, we have
Step two: construction of almost complex structure
![]() $\tilde J_k$
by projecting
$\tilde J_k$
by projecting
![]() $J_{k, \;j, \;\rho (x)}$
w.r.t g.
$J_{k, \;j, \;\rho (x)}$
w.r.t g.
Next we construct a sequence
![]() $\tilde J_k(x)$
using
$\tilde J_k(x)$
using
![]() $J_{k,\, j, \,\rho (x)}(x)$
by the technique we have used in [Reference He5, see (4.15), (4.16)]. We briefly recall the construction. In the following, we consider
$J_{k,\, j, \,\rho (x)}(x)$
by the technique we have used in [Reference He5, see (4.15), (4.16)]. We briefly recall the construction. In the following, we consider
![]() $k\geq k_j$
for each j. For
$k\geq k_j$
for each j. For
![]() $|x|\in [0, 1-j^{-1}]\cup [1, 2]$
,
$|x|\in [0, 1-j^{-1}]\cup [1, 2]$
,
![]() $\rho =0$
, and we have
$\rho =0$
, and we have
 $$ \begin{align}\tilde J_k=J_{k,\, j, \, \rho}=J_{k,\, j}= \begin{cases} J_0,\, |x|\leq 1-j^{-1}\\ J_k,\, |x|\geq 1 \end{cases}\end{align} $$
$$ \begin{align}\tilde J_k=J_{k,\, j, \, \rho}=J_{k,\, j}= \begin{cases} J_0,\, |x|\leq 1-j^{-1}\\ J_k,\, |x|\geq 1 \end{cases}\end{align} $$
Now consider
![]() $|x|\in (1-j^{-1}, 1)$
. Let
$|x|\in (1-j^{-1}, 1)$
. Let
![]() $S_{g}(x)$
and
$S_{g}(x)$
and
![]() $A_{g}(x)$
be the g-symmetric and g-skew symmetric part of
$A_{g}(x)$
be the g-symmetric and g-skew symmetric part of
![]() $J_{k,\, j, \,\rho (x)}(x)$
, respectively. We have by (3.21)
$J_{k,\, j, \,\rho (x)}(x)$
, respectively. We have by (3.21)
It follows that
Note that
![]() $-A_{g}^2$
is g-symmetric and that it is close to the identity matrix pointwise; in particular, it is positive definite. Denote
$-A_{g}^2$
is g-symmetric and that it is close to the identity matrix pointwise; in particular, it is positive definite. Denote
![]() $Q_{g}$
to be the g-symmetric matrix such that
$Q_{g}$
to be the g-symmetric matrix such that
![]() $Q_{g}^2=-A_{g}^2$
. Note that
$Q_{g}^2=-A_{g}^2$
. Note that
![]() $Q_{g}$
is uniquely determined and it commutes with
$Q_{g}$
is uniquely determined and it commutes with
![]() $A_g$
. Denote
$A_g$
. Denote
![]() $\tilde J_{k}(x)=Q_{g}^{-1}(x)A_{g}(x)$
for
$\tilde J_{k}(x)=Q_{g}^{-1}(x)A_{g}(x)$
for
![]() $x\in B_2$
. Then
$x\in B_2$
. Then
![]() $\tilde J_{k}(x)$
is a g-compatible almost complex structure in
$\tilde J_{k}(x)$
is a g-compatible almost complex structure in
![]() $B_2$
. We extend
$B_2$
. We extend
![]() $\tilde J_k$
to M by simply putting
$\tilde J_k$
to M by simply putting
![]() $\tilde J_k=J_k$
on
$\tilde J_k=J_k$
on
![]() $M\setminus B_{1}(p)$
. Now we establish (3.13). We only need to consider over
$M\setminus B_{1}(p)$
. Now we establish (3.13). We only need to consider over
![]() $B_1(p)$
. Note that the
$B_1(p)$
. Note that the
![]() $L^\infty $
norm of
$L^\infty $
norm of
![]() $J_{k,\, j}, Q_g, A_g, Q_g^{-1}$
and
$J_{k,\, j}, Q_g, A_g, Q_g^{-1}$
and
![]() $1/|Q_{g}^{-1}|$
are all uniformly bounded by a dimensional constant. Since
$1/|Q_{g}^{-1}|$
are all uniformly bounded by a dimensional constant. Since
![]() $Q_g^2=-A_g^2$
and
$Q_g^2=-A_g^2$
and
![]() $|A_g^2+\text {id}|\ll 1$
, we have the following expansion of the matrix.
$|A_g^2+\text {id}|\ll 1$
, we have the following expansion of the matrix.
 $$ \begin{align} Q_g=\sqrt{\text{id}-(\text{id}+A_g^2)}=\sum_{l=0}^\infty \binom{1/2}{l}(\text{id}+A_g^2)^l. \end{align} $$
$$ \begin{align} Q_g=\sqrt{\text{id}-(\text{id}+A_g^2)}=\sum_{l=0}^\infty \binom{1/2}{l}(\text{id}+A_g^2)^l. \end{align} $$
We can compute directly that
![]() $|\nabla Q_g|\leq C|A_g||\nabla A_g|\leq C|\nabla A_g|$
. Hence, we obtain
$|\nabla Q_g|\leq C|A_g||\nabla A_g|\leq C|\nabla A_g|$
. Hence, we obtain
![]() $|\nabla \tilde J_k|\leq C|\nabla A_g|.$
We also need (using
$|\nabla \tilde J_k|\leq C|\nabla A_g|.$
We also need (using
![]() $\nabla g=0$
)
$\nabla g=0$
)
We compute
Hence, we have
Moreover, we have
![]() $|\nabla A_g|\leq |\nabla J_{k, j, \rho }|+|\nabla S_g|\leq C|\nabla J_{k, j, \rho }|$
. It follows that
$|\nabla A_g|\leq |\nabla J_{k, j, \rho }|+|\nabla S_g|\leq C|\nabla J_{k, j, \rho }|$
. It follows that
 $$\begin{align*}\int_B |\nabla \tilde J_k|^4dv\leq C\int_B \left(\int_B |\nabla J_{k, j}(x+\rho(x)z)|^4dz\right)dv_x\leq C \int_{B_{3/2}} |\nabla J_{k, j}|^4dv. \end{align*}$$
$$\begin{align*}\int_B |\nabla \tilde J_k|^4dv\leq C\int_B \left(\int_B |\nabla J_{k, j}(x+\rho(x)z)|^4dz\right)dv_x\leq C \int_{B_{3/2}} |\nabla J_{k, j}|^4dv. \end{align*}$$
Since
![]() $\nabla J_{k, j}=\nabla J_k+(1-\psi _j)(\nabla J_0-\nabla J_k)-(J_0-J_k) \nabla \psi _j$
and
$\nabla J_{k, j}=\nabla J_k+(1-\psi _j)(\nabla J_0-\nabla J_k)-(J_0-J_k) \nabla \psi _j$
and
![]() $|\nabla \psi _j|\leq 3j$
, it follows that
$|\nabla \psi _j|\leq 3j$
, it follows that
 $$ \begin{align} \int_{B_{3/2}} |\nabla J_{k, j}|^4dv\leq C \int_{B_2} (|\nabla J_k|^4+|\nabla J_0|^4) dv+C j^4\int_B |J_0-J_k|^4dv. \end{align} $$
$$ \begin{align} \int_{B_{3/2}} |\nabla J_{k, j}|^4dv\leq C \int_{B_2} (|\nabla J_k|^4+|\nabla J_0|^4) dv+C j^4\int_B |J_0-J_k|^4dv. \end{align} $$
Using the Sobolev inequality, we know that
By choosing
![]() $k_j=k(j)$
sufficiently large such that for
$k_j=k(j)$
sufficiently large such that for
![]() $k\geq k_j$
, we can assume that
$k\geq k_j$
, we can assume that
This establishes (3.13) and hence
![]() $\tilde J_k$
and
$\tilde J_k$
and
![]() $J_k$
are in the same homotopy class, for
$J_k$
are in the same homotopy class, for
![]() $k\geq k_j$
.
$k\geq k_j$
.
Step three: the comparison of
![]() $J_k$
and
$J_k$
and
![]() $\tilde J_k$
implies
$\tilde J_k$
implies
![]() $\lambda (B_1)\leq C\nu (\partial B_1)$
.
$\lambda (B_1)\leq C\nu (\partial B_1)$
.
Fix
![]() $\epsilon>0$
. Since
$\epsilon>0$
. Since
![]() $J_k$
is an energy-minimizing sequence, for k sufficiently large we have,
$J_k$
is an energy-minimizing sequence, for k sufficiently large we have,
By the construction of
![]() $\tilde J_k$
, we get
$\tilde J_k$
, we get
 $$ \begin{align*} \int_{B_1}|\Delta J_k|^2 dv\leq \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\int_{B_{1-j^{-1}}} |\Delta J_0|^2 dv+\epsilon. \end{align*} $$
$$ \begin{align*} \int_{B_1}|\Delta J_k|^2 dv\leq \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\int_{B_{1-j^{-1}}} |\Delta J_0|^2 dv+\epsilon. \end{align*} $$
By taking
![]() $j\rightarrow \infty $
(hence
$j\rightarrow \infty $
(hence
![]() $k\geq k_j\rightarrow \infty $
), we get (since
$k\geq k_j\rightarrow \infty $
), we get (since
![]() $B_1$
is open)
$B_1$
is open)
 $$ \begin{align*} \lambda(B_1)+\int_{B_{1}}|\Delta J_0|^2 dv\leq \liminf \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\int_{B_{1-j^{-1}}} |\Delta J_0|^2 dv+\epsilon. \end{align*} $$
$$ \begin{align*} \lambda(B_1)+\int_{B_{1}}|\Delta J_0|^2 dv\leq \liminf \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\int_{B_{1-j^{-1}}} |\Delta J_0|^2 dv+\epsilon. \end{align*} $$
Hence, we get
 $$ \begin{align*} \lambda(B_1)\leq \liminf_{j\rightarrow \infty} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\epsilon. \end{align*} $$
$$ \begin{align*} \lambda(B_1)\leq \liminf_{j\rightarrow \infty} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv+\epsilon. \end{align*} $$
Since
![]() $\epsilon>0$
is arbitrary, we have established the estimate
$\epsilon>0$
is arbitrary, we have established the estimate
 $$ \begin{align} \lambda(B_1)\leq \liminf_{j\rightarrow \infty} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv. \end{align} $$
$$ \begin{align} \lambda(B_1)\leq \liminf_{j\rightarrow \infty} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv. \end{align} $$
Now we need estimates as in (3.15) to control the right-hand side of (3.38). Recall that we have the unique decomposition
![]() $J_{k,\, j, \,\rho }=A_g+S_g$
and
$J_{k,\, j, \,\rho }=A_g+S_g$
and
![]() $\tilde J_k=Q_g^{-1}A_g$
, where
$\tilde J_k=Q_g^{-1}A_g$
, where
![]() $Q_g$
is the unique square root of
$Q_g$
is the unique square root of
![]() $-A_g^2$
. Using (3.35), we have
$-A_g^2$
. Using (3.35), we have
It follows that
Hence, we obtain
 $$ \begin{align} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\int_{B_{1}\setminus B_{1-j^{-1}}}\left( |\Delta J_{k, \, j, \,\rho}|^2+|\nabla J_{k,\, j, \,\rho}|^4\right)dv. \end{align} $$
$$ \begin{align} \int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\int_{B_{1}\setminus B_{1-j^{-1}}}\left( |\Delta J_{k, \, j, \,\rho}|^2+|\nabla J_{k,\, j, \,\rho}|^4\right)dv. \end{align} $$
We compute
 $$ \begin{align*} |\nabla J_{k,\,j}|=&|\nabla J_k+(1-\psi_j)(\nabla J_0-\nabla J_k)-\nabla \psi_j (J_0-J_k)| \nonumber \\ =&|\psi_j \nabla J_k+(1-\psi_j)\nabla J_0-\nabla \psi_j (J_0-J_k)| \nonumber \\ \leq& |\nabla J_k|+|\nabla J_0|+Cj |J_0-J_k|. \end{align*} $$
$$ \begin{align*} |\nabla J_{k,\,j}|=&|\nabla J_k+(1-\psi_j)(\nabla J_0-\nabla J_k)-\nabla \psi_j (J_0-J_k)| \nonumber \\ =&|\psi_j \nabla J_k+(1-\psi_j)\nabla J_0-\nabla \psi_j (J_0-J_k)| \nonumber \\ \leq& |\nabla J_k|+|\nabla J_0|+Cj |J_0-J_k|. \end{align*} $$
Similarly, we compute
 $$ \begin{align*} |\Delta J_{k,\,j}|=&|\Delta J_k+\Delta [(1-\psi_j)( J_0-J_k)]| \nonumber \\ \leq& |\nabla^2 J_k|+|\nabla^2 J_0|+Cj^2 (|J_0-J_k|+|\nabla J_0-\nabla J_k|). \end{align*} $$
$$ \begin{align*} |\Delta J_{k,\,j}|=&|\Delta J_k+\Delta [(1-\psi_j)( J_0-J_k)]| \nonumber \\ \leq& |\nabla^2 J_k|+|\nabla^2 J_0|+Cj^2 (|J_0-J_k|+|\nabla J_0-\nabla J_k|). \end{align*} $$
Write
![]() $y=x+\rho (x)z$
. Then we have
$y=x+\rho (x)z$
. Then we have
 $$\begin{align*}\left|\frac{\partial y_i}{\partial x_j}\right|\leq C(1+|\rho^{'}|), \left|\frac{\partial^2 y_i}{\partial x_j \partial x_k}\right|\leq C(1+|\rho^{'}|+|\rho^{"}|). \end{align*}$$
$$\begin{align*}\left|\frac{\partial y_i}{\partial x_j}\right|\leq C(1+|\rho^{'}|), \left|\frac{\partial^2 y_i}{\partial x_j \partial x_k}\right|\leq C(1+|\rho^{'}|+|\rho^{"}|). \end{align*}$$
Using
![]() $|\rho ^{'}|+|\rho ^{"}|\leq 1$
,
$|\rho ^{'}|+|\rho ^{"}|\leq 1$
,
![]() $|\psi ^{'}_j|+|\psi ^{"}_j|\leq 20j^2$
, we can then get
$|\psi ^{'}_j|+|\psi ^{"}_j|\leq 20j^2$
, we can then get
 $$ \begin{align*} |\nabla J_{k,\, j, \,\rho}|=&\left|\int_B \phi(z) \nabla_x J_{k,\, j}(x+\rho(x)z)dz\right|\nonumber \\ \leq &C\int_B \phi(z)|\nabla_z J_{k,\, j}| (1+|\rho^{'}|)dz\nonumber \\ \leq& C\int_{B_1} \phi(z)\left(|\nabla J_k|+|\nabla J_0|+j |J_0-J_k|\right)dz, \end{align*} $$
$$ \begin{align*} |\nabla J_{k,\, j, \,\rho}|=&\left|\int_B \phi(z) \nabla_x J_{k,\, j}(x+\rho(x)z)dz\right|\nonumber \\ \leq &C\int_B \phi(z)|\nabla_z J_{k,\, j}| (1+|\rho^{'}|)dz\nonumber \\ \leq& C\int_{B_1} \phi(z)\left(|\nabla J_k|+|\nabla J_0|+j |J_0-J_k|\right)dz, \end{align*} $$
where the function is evaluated at
![]() $y=x+\rho (x)z$
. For any open set
$y=x+\rho (x)z$
. For any open set
![]() $U\subset B_2$
, denote
$U\subset B_2$
, denote
![]() $U_{\bar \rho }=\{x: \text {dist}(x, U)<\bar \rho \}$
. We have
$U_{\bar \rho }=\{x: \text {dist}(x, U)<\bar \rho \}$
. We have
 $$ \begin{align} \int_{U}|\nabla J_{k,\, j, \,\rho}|^4dv_x\leq& C\int_{U}\left(\int_{B_1} \phi(z)\left(|\nabla J_k|(y)+|\nabla J_0|(y)+j |J_0-J_k|(y)\right)dz\right)^4dv_x \nonumber \\ \leq &C\int_{U_{\bar\rho}} (|\nabla J_k|^4+|\nabla J_0|^4+j^4 |J_0-J_k|^4)dv, \end{align} $$
$$ \begin{align} \int_{U}|\nabla J_{k,\, j, \,\rho}|^4dv_x\leq& C\int_{U}\left(\int_{B_1} \phi(z)\left(|\nabla J_k|(y)+|\nabla J_0|(y)+j |J_0-J_k|(y)\right)dz\right)^4dv_x \nonumber \\ \leq &C\int_{U_{\bar\rho}} (|\nabla J_k|^4+|\nabla J_0|^4+j^4 |J_0-J_k|^4)dv, \end{align} $$
where we have used a standard technique to estimate the
![]() $L^p$
norm of mollifier approximation (see [Reference Gilbarg and Trudinger4, Lemma 7.2, (7.15)]). Similarly, we compute
$L^p$
norm of mollifier approximation (see [Reference Gilbarg and Trudinger4, Lemma 7.2, (7.15)]). Similarly, we compute
 $$ \begin{align*} |\Delta J_{k,\, j, \,\rho}|=&\left|\int_B \phi(z) \Delta_x \left(J_{k,\, j}(x+\rho(x)z)\right)dz\right| \nonumber \\ \leq &C\int_B \phi(z)\left(|\nabla^2 J_k|+|\nabla^2 J_0|+j^2(|\nabla J_0-\nabla J_k|+|J_0-J_k|)\right) dz. \end{align*} $$
$$ \begin{align*} |\Delta J_{k,\, j, \,\rho}|=&\left|\int_B \phi(z) \Delta_x \left(J_{k,\, j}(x+\rho(x)z)\right)dz\right| \nonumber \\ \leq &C\int_B \phi(z)\left(|\nabla^2 J_k|+|\nabla^2 J_0|+j^2(|\nabla J_0-\nabla J_k|+|J_0-J_k|)\right) dz. \end{align*} $$
It follows that
 $$ \begin{align} \int_{U}|\Delta J_{k,\, j, \,\rho}|^2dv_x\leq C \int_{U_{\bar \rho}} \left(|\nabla^2 J_k|^2+|\nabla^2 J_0|^2+j^4|J_0-J_k|^2+j^4|\nabla J_0-\nabla J_k|^2\right)dv_x. \end{align} $$
$$ \begin{align} \int_{U}|\Delta J_{k,\, j, \,\rho}|^2dv_x\leq C \int_{U_{\bar \rho}} \left(|\nabla^2 J_k|^2+|\nabla^2 J_0|^2+j^4|J_0-J_k|^2+j^4|\nabla J_0-\nabla J_k|^2\right)dv_x. \end{align} $$
Take
![]() $U=B_1\setminus B_{1-j^{-1}}$
in the above. We obtain,
$U=B_1\setminus B_{1-j^{-1}}$
in the above. We obtain,
 $$ \begin{align} \int_{U} (|\nabla J_{k,\, j, \,\rho}|^4+|\nabla^2 J_{k,\, j, \,\rho}|^2)dv\leq C\int_{U_{\bar \rho}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv+C(R_1+R_2), \end{align} $$
$$ \begin{align} \int_{U} (|\nabla J_{k,\, j, \,\rho}|^4+|\nabla^2 J_{k,\, j, \,\rho}|^2)dv\leq C\int_{U_{\bar \rho}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv+C(R_1+R_2), \end{align} $$
where the remainder terms read,
 $$ \begin{align*} R_1=&\int_{U_{\bar \rho}} (|\nabla J_0|^4+|\Delta J_0|^2 )dv, \nonumber \\ R_2=&j^4\int_{U_{\bar \rho}} (|J_0-J_k|^2+|J_0-J_k|^4+|\nabla J_0-\nabla J_k|^2)dv. \end{align*} $$
$$ \begin{align*} R_1=&\int_{U_{\bar \rho}} (|\nabla J_0|^4+|\Delta J_0|^2 )dv, \nonumber \\ R_2=&j^4\int_{U_{\bar \rho}} (|J_0-J_k|^2+|J_0-J_k|^4+|\nabla J_0-\nabla J_k|^2)dv. \end{align*} $$
Recall we assume that
![]() $k\geq k_j$
, such that (3.37) holds. Hence,
$k\geq k_j$
, such that (3.37) holds. Hence,
![]() $R_2\leq j^{-1}$
. Certainly when
$R_2\leq j^{-1}$
. Certainly when
![]() $j\rightarrow \infty $
, the Lebesgue measure
$j\rightarrow \infty $
, the Lebesgue measure
![]() $U_{\bar \rho }\rightarrow 0$
and hence
$U_{\bar \rho }\rightarrow 0$
and hence
![]() $R_1\rightarrow 0$
. By (3.42), we obtain
$R_1\rightarrow 0$
. By (3.42), we obtain
 $$ \begin{align} \liminf_{j\rightarrow \infty}\int_{B_1\setminus B_{1-j^{-1}}}(|\nabla J_{k,\, j, \,\rho}|^4+|\Delta J_{k,\, j, \,\rho}|^2)dv\leq C\liminf_{j\rightarrow\infty}\int_{U_{\bar \rho}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
$$ \begin{align} \liminf_{j\rightarrow \infty}\int_{B_1\setminus B_{1-j^{-1}}}(|\nabla J_{k,\, j, \,\rho}|^4+|\Delta J_{k,\, j, \,\rho}|^2)dv\leq C\liminf_{j\rightarrow\infty}\int_{U_{\bar \rho}} (|\nabla^2 J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
Hence, we obtain, by (3.39) and (3.43),
 $$ \begin{align} \liminf_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\liminf_{j\rightarrow \infty}\int_{U_{\bar\rho}} (|\nabla^2J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
$$ \begin{align} \liminf_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\liminf_{j\rightarrow \infty}\int_{U_{\bar\rho}} (|\nabla^2J_k|^2+|\nabla J_k|^4)dv. \end{align} $$
Note that
![]() $U=B_{1}\setminus B_{1-j^{-1}}$
,
$U=B_{1}\setminus B_{1-j^{-1}}$
,
![]() $\bar \rho =j^{-2}/10$
. Fix
$\bar \rho =j^{-2}/10$
. Fix
![]() $\epsilon>0$
. Denote
$\epsilon>0$
. Denote
For any j sufficiently large,
![]() $U_{\bar \rho }\subset \overline {B_{1,\,\epsilon }}$
. Hence, we have
$U_{\bar \rho }\subset \overline {B_{1,\,\epsilon }}$
. Hence, we have
 $$\begin{align*}\lim_{k\rightarrow\infty}\int_{\overline{B_{1,\,\epsilon}}} (|\nabla^2J_k|^2+|\nabla J_k|^4)dv=\lim_{k\rightarrow\infty}\mu_k(\overline{B_{1,\,\epsilon}})\leq \mu(\overline{B_{1,\,\epsilon}}), \end{align*}$$
$$\begin{align*}\lim_{k\rightarrow\infty}\int_{\overline{B_{1,\,\epsilon}}} (|\nabla^2J_k|^2+|\nabla J_k|^4)dv=\lim_{k\rightarrow\infty}\mu_k(\overline{B_{1,\,\epsilon}})\leq \mu(\overline{B_{1,\,\epsilon}}), \end{align*}$$
where we use the fact that
![]() $\mu _k$
converges to
$\mu _k$
converges to
![]() $\mu $
weakly and
$\mu $
weakly and
![]() $\overline {B_{1,\,\epsilon }}$
is a closed set. Together with (3.44), we get that
$\overline {B_{1,\,\epsilon }}$
is a closed set. Together with (3.44), we get that
 $$ \begin{align} \lim_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\mu(\overline{B_{1,\,\epsilon}}). \end{align} $$
$$ \begin{align} \lim_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\mu(\overline{B_{1,\,\epsilon}}). \end{align} $$
Note that
![]() $\cap _{\epsilon>0} \overline {B_{1,\,\epsilon }}=\partial B_1$
. We obtain
$\cap _{\epsilon>0} \overline {B_{1,\,\epsilon }}=\partial B_1$
. We obtain
![]() $\lim _{\epsilon \rightarrow 0}\mu (\overline {B_{1,\,\epsilon }})=\nu (\partial B_1).$
With (3.45), we obtain
$\lim _{\epsilon \rightarrow 0}\mu (\overline {B_{1,\,\epsilon }})=\nu (\partial B_1).$
With (3.45), we obtain
 $$ \begin{align} \lim_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\nu(\partial B_1). \end{align} $$
$$ \begin{align} \lim_{j\rightarrow \infty}\int_{B_{1}\setminus B_{1-j^{-1}}}|\Delta \tilde J_k|^2dv\leq C\nu(\partial B_1). \end{align} $$
Hence, we have obtained the desired estimate
If we replace
![]() $B_1$
by
$B_1$
by
![]() $B_r$
, for
$B_r$
, for
![]() $1\leq r\leq \frac {3}{2}$
, replace
$1\leq r\leq \frac {3}{2}$
, replace
![]() $B_{1}\setminus B_{1-j^{-1}}$
by
$B_{1}\setminus B_{1-j^{-1}}$
by
![]() $B_{r}\setminus B_{r-j^{-1}}$
and apply the same arguments as in the proof (3.47), we obtain
$B_{r}\setminus B_{r-j^{-1}}$
and apply the same arguments as in the proof (3.47), we obtain
Since
![]() $\nu $
is totally bounded, this implies that
$\nu $
is totally bounded, this implies that
![]() $\lambda (B_r)\equiv 0$
for
$\lambda (B_r)\equiv 0$
for
![]() $r\leq 3/2$
. This completes the proof of Lemma 3.9.
$r\leq 3/2$
. This completes the proof of Lemma 3.9.
With Lemma 3.9, we prove Lemma 3.7, which asserts that the homotopy class of
![]() $J_0$
is either
$J_0$
is either
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
, for a minimizing sequence
$p(\sigma )$
, for a minimizing sequence
![]() $J_k$
in
$J_k$
in
![]() $\sigma $
.
$\sigma $
.
Proof of Lemma 3.7.
Lemma 3.9 implies that
![]() $J_k$
converges to
$J_k$
converges to
![]() $J_0$
strongly in
$J_0$
strongly in
![]() $W^{2, 2}(M\backslash U_{r/2})$
, where U is the collection of finitely many disjoint geodesic balls
$W^{2, 2}(M\backslash U_{r/2})$
, where U is the collection of finitely many disjoint geodesic balls
![]() $B(p_i)$
,
$B(p_i)$
,
![]() $i=1, \cdots N$
with radius
$i=1, \cdots N$
with radius
![]() $r/2$
, for any sufficiently small positive number r. Moreover, for any point
$r/2$
, for any sufficiently small positive number r. Moreover, for any point
![]() $p\in M\backslash U_r$
, we have that
$p\in M\backslash U_r$
, we have that
 $$\begin{align*}\int_{B_{r/2}(p)} |\nabla J_k|^4+|\nabla^2 J_k|^2 \leq \epsilon_0. \end{align*}$$
$$\begin{align*}\int_{B_{r/2}(p)} |\nabla J_k|^4+|\nabla^2 J_k|^2 \leq \epsilon_0. \end{align*}$$
Hence, we can construct
![]() $\tilde J_k$
such that
$\tilde J_k$
such that
 $$ \begin{align*} &\tilde J_k(p)= J_0(p), p\in M\backslash U_{2r}, \nonumber \\ &\tilde J_k(p)=J_k(p), p\in U_{r/2} \end{align*} $$
$$ \begin{align*} &\tilde J_k(p)= J_0(p), p\in M\backslash U_{2r}, \nonumber \\ &\tilde J_k(p)=J_k(p), p\in U_{r/2} \end{align*} $$
and
This implies that
![]() $\tilde J_k$
is in
$\tilde J_k$
is in
![]() $\sigma $
. In short, we construct
$\sigma $
. In short, we construct
![]() $\tilde J_k$
in the same homotopy class which coincides
$\tilde J_k$
in the same homotopy class which coincides
![]() $J_0$
over
$J_0$
over
![]() $M\backslash U_{2r}$
, where the convergence is strongly in
$M\backslash U_{2r}$
, where the convergence is strongly in
![]() $W^{2, 2}$
.
$W^{2, 2}$
.
Given a homotopy class
![]() $\sigma $
of almost complex structures on M, we recall the construction of
$\sigma $
of almost complex structures on M, we recall the construction of
![]() $p(\sigma )$
(see Donaldson [Reference Donaldson3, Section 6]). A compatible almost complex structure J on an oriented Riemannian four-manifold M can be considered as a section of the associated
$p(\sigma )$
(see Donaldson [Reference Donaldson3, Section 6]). A compatible almost complex structure J on an oriented Riemannian four-manifold M can be considered as a section of the associated
![]() $SO(4)/U(2)$
-bundle over M (the sphere bundle of
$SO(4)/U(2)$
-bundle over M (the sphere bundle of
![]() $\Lambda ^2_+$
, known as the ‘twistor space’). Suppose there are two almost complex structures
$\Lambda ^2_+$
, known as the ‘twistor space’). Suppose there are two almost complex structures
![]() $J_1$
and
$J_1$
and
![]() $J_2$
, which agree each other outside a small ball in M. Over this ball B,
$J_2$
, which agree each other outside a small ball in M. Over this ball B,
![]() $J_1$
and
$J_1$
and
![]() $J_2$
compare by a map from
$J_2$
compare by a map from
![]() $S^4$
to the fibre of the twistor bundle, hence defining an element in
$S^4$
to the fibre of the twistor bundle, hence defining an element in
![]() $[S^4, S^2]=\mathbb {Z}/2$
. If
$[S^4, S^2]=\mathbb {Z}/2$
. If
![]() $\sigma $
is a homotopy class,
$\sigma $
is a homotopy class,
![]() $p(\sigma )$
agrees with
$p(\sigma )$
agrees with
![]() $\sigma $
outside a small ball, and over the ball the two compare by the nonzero element of
$\sigma $
outside a small ball, and over the ball the two compare by the nonzero element of
![]() $[S^4, S^2]=\mathbb {Z}/2$
. Hence, if
$[S^4, S^2]=\mathbb {Z}/2$
. Hence, if
![]() $J_1$
and
$J_1$
and
![]() $J_2$
agree outside a small ball, then either they are in the same homotopy class or their homotopy classes are related by the map p.
$J_2$
agree outside a small ball, then either they are in the same homotopy class or their homotopy classes are related by the map p.
Applying this to
![]() $\tilde J_k$
and
$\tilde J_k$
and
![]() $J_0$
above, the homotopy classes differ by the composition
$J_0$
above, the homotopy classes differ by the composition
![]() $p^k$
, for some
$p^k$
, for some
![]() $k\leq N$
. Since
$k\leq N$
. Since
![]() $p\circ p=id$
, it follows that
$p\circ p=id$
, it follows that
![]() $J_0$
is either in
$J_0$
is either in
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
.
$p(\sigma )$
.
Theorem 1.3 follows as an immediate consequence of Lemma 3.7.
Proof of Theorem 1.3.
Given a pair of homotopy classes
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
, choose a minimizing sequence
$p(\sigma )$
, choose a minimizing sequence
![]() $J_k$
of bi-energy functional over
$J_k$
of bi-energy functional over
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
with respect to
$p(\sigma )$
with respect to
![]() $(M, g)$
. By passing to a subsequence, we assume that
$(M, g)$
. By passing to a subsequence, we assume that
![]() $J_k$
remains in homotopy class
$J_k$
remains in homotopy class
![]() $\sigma $
and it converges to a biharmonic almost complex structure
$\sigma $
and it converges to a biharmonic almost complex structure
![]() $J_0$
weakly in
$J_0$
weakly in
![]() $W^{2, 2}$
. Either
$W^{2, 2}$
. Either
![]() $J_0$
is in
$J_0$
is in
![]() $\sigma $
or in
$\sigma $
or in
![]() $p(\sigma )$
. Hence, there is an energy-minimizing biharmonic almost complex structure in the pair
$p(\sigma )$
. Hence, there is an energy-minimizing biharmonic almost complex structure in the pair
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
. Indeed, in this case, since
$p(\sigma )$
. Indeed, in this case, since
![]() $J_k$
is a minimizing sequence over
$J_k$
is a minimizing sequence over
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
, and all
$p(\sigma )$
, and all
![]() $J_k$
remains in
$J_k$
remains in
![]() $\sigma $
, the limit
$\sigma $
, the limit
![]() $J_0$
has to be in
$J_0$
has to be in
![]() $\sigma $
as well since no extra energy can be concentrated.
$\sigma $
as well since no extra energy can be concentrated.
4 An intuitive conjectural picture
A
![]() $K3$
surface is a compact simply connected complex surface S with trivial canonical bundle. Let
$K3$
surface is a compact simply connected complex surface S with trivial canonical bundle. Let
![]() $\sigma $
denote the homotopy class of the standard complex structures on S with
$\sigma $
denote the homotopy class of the standard complex structures on S with
![]() $c_1=0$
. S. Donaldson [Reference Donaldson3, Corollary 6.5] proved, using his polynomial invariants, the following.
$c_1=0$
. S. Donaldson [Reference Donaldson3, Corollary 6.5] proved, using his polynomial invariants, the following.
Theorem 4.1 (Donaldson).
The homotopy class
![]() $p(\sigma )$
on S with
$p(\sigma )$
on S with
![]() $c_1=0$
does not contain any integrable representative.
$c_1=0$
does not contain any integrable representative.
Theorem 1.3 does not specify precisely whether
![]() $\sigma $
or
$\sigma $
or
![]() $p(\sigma )$
contains an energy-minimizing biharmonic almost complex structure. There could be a couple options, as follows.
$p(\sigma )$
contains an energy-minimizing biharmonic almost complex structure. There could be a couple options, as follows.
-
1. Both
 $\sigma $
and
$\sigma $
and
 $p(\sigma )$
contain an energy-minimizing biharmonic almost complex structure, which might or might not have the same energy.
$p(\sigma )$
contain an energy-minimizing biharmonic almost complex structure, which might or might not have the same energy. -
2. Only one homotopy contains an energy-minimizing biharmonic almost complex structure, while the other does not.
We believe the following and Theorem 4.1 serves as an example.
Conjecture 4.2. Given two homotopy classes
![]() $\sigma $
and
$\sigma $
and
![]() $p(\sigma )$
on M, exactly one homotopy class among the pair
$p(\sigma )$
on M, exactly one homotopy class among the pair
![]() $(\sigma , p(\sigma ))$
contains an energy-minimizing biharmonic almost complex structure. Suppose
$(\sigma , p(\sigma ))$
contains an energy-minimizing biharmonic almost complex structure. Suppose
![]() $\sigma $
is the class containing a minimizer. Then
$\sigma $
is the class containing a minimizer. Then
![]() $p(\sigma )$
does not contain a minimizer, and a minimizing sequence in
$p(\sigma )$
does not contain a minimizer, and a minimizing sequence in
![]() $p(\sigma )$
converges weakly in
$p(\sigma )$
converges weakly in
![]() $W^{2, 2}$
to a minimizer in
$W^{2, 2}$
to a minimizer in
![]() $\sigma $
, which bubbles off a nonconstant biharmonic map from
$\sigma $
, which bubbles off a nonconstant biharmonic map from
![]() $\mathbb {R}^4$
to
$\mathbb {R}^4$
to
![]() $S^2$
with a nontrivial relative homotopy class.
$S^2$
with a nontrivial relative homotopy class.
In the process of energy-minimizing, the formation of a bubble gives a nonconstant extrinsic biharmonic map from
![]() $\mathbb {R}^4$
to
$\mathbb {R}^4$
to
![]() $S^2$
by a blowup argument. But it does not seem to be straightforward to specify its relative homotopy class, even though it is intuitive that it should correspond to the nonzero element in
$S^2$
by a blowup argument. But it does not seem to be straightforward to specify its relative homotopy class, even though it is intuitive that it should correspond to the nonzero element in
![]() $\pi _4(S^2)$
topologically. We believe the following.
$\pi _4(S^2)$
topologically. We believe the following.
Conjecture 4.3. In the nontrivial (relative) homotopy class of
![]() $\mathbb {R}^4$
to
$\mathbb {R}^4$
to
![]() $S^2$
corresponding to the nonzero element
$S^2$
corresponding to the nonzero element
![]() $\pi _4(S^2)$
, there exists an energy-minimizing extrinsic biharmonic map. For maps from
$\pi _4(S^2)$
, there exists an energy-minimizing extrinsic biharmonic map. For maps from
![]() $S^4$
to
$S^4$
to
![]() $S^2$
in the homotopy class corresponding to nonzero element
$S^2$
in the homotopy class corresponding to nonzero element
![]() $\pi _4(S^2)$
, there exists no energy-minimizing extrinsic biharmonic maps.
$\pi _4(S^2)$
, there exists no energy-minimizing extrinsic biharmonic maps.
Acknowledgements
The author thanks Ruiqi Jiang for proofreading the paper. The author is very grateful for the suggestions and comments of the referee.
Competing interest
The authors have no competing interest to declare.
Data availability statement
None.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by grants from NSF, Grant no. 1611797.