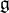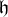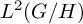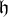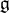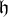1 Introduction
Let
$X=G/H$
be a homogeneous space of a Lie group G. This article is the fourth one in our series of papers [Reference Benoist and Kobayashi1, Reference Benoist and Kobayashi2, Reference Benoist and Kobayashi3] dealing with the harmonic analysis on the homogeneous spaces X and more precisely with the regular representation of G in
$L^2(X)$
. This representation is often denoted as
${\mathrm {Ind}}_{{H}}^G(1)$
and called ‘the induced representation of the trivial character of
${H}$
’. The aim of this series of papers is to find various necessary and sufficient conditions for this representation to be G-tempered, for example, to be weakly contained in the regular representation in
$L^2(G)$
. We proved in [Reference Benoist and Kobayashi1, Reference Benoist and Kobayashi2] a criterion (1.1) below by an analytic and dynamical approach when G is real reductive and accomplished in [Reference Benoist and Kobayashi3] a classification of all the pairs
$(G,H)$
of real reductive Lie groups for which
$L^2(X)$
is nontempered. We refer to the introduction of both [Reference Benoist and Kobayashi1] and [Reference Benoist and Kobayashi2] for some motivations and perspectives on this question.
In this article, we find a striking relationship of this question with other disciplines, such as a topological condition concerning the ‘limit subalgebras’ and a geometric condition concerning coadjoint orbits. The relationship is perfect when G is complex reductive (Theorem 1.6). For the proof, we explore the temperedness of
$L^2(X)$
beyond reductive setting (Theorem 1.1).
1.1 Real homogeneous spaces
We extend the criterion in [Reference Benoist and Kobayashi1, Reference Benoist and Kobayashi2] for the temperedness of
$L^2(X)$
to the general setting where X is a homogeneous of a real Lie group, which is not necessarily reductive.
In the first two papers [Reference Benoist and Kobayashi1] and [Reference Benoist and Kobayashi2], we first noticed that the property of
$L^2(G/H)$
being tempered depends only on the pair
of Lie algebras and introduced for an
-module V and
, the quantity:
$$ \begin{align*} \rho_V(Y) &:= \text{half the sum of the absolute values of the} \\ &\quad\quad \ \text{real part of the eigenvalues of } Y \text{ in } V. \end{align*} $$
We found the following temperedness criterion when G is a connected semisimple Lie group with finite center, and H is a connected closed subgroup:
This criterion (1.1) was proven in [Reference Benoist and Kobayashi1], when
is assumed to be semisimple by a dynamical approach and was extended in [Reference Benoist and Kobayashi2] to arbitrary
${\mathfrak {h}}$
by an idea of ‘domination of G-spaces’. Developing the techniques in a more general setting, we extend (1.1) without any reductivity assumptions of
${\mathfrak {g}}$
and
${\mathfrak {h}}$
:
Theorem 1.1 see Theorem 3.1
Let G be a real algebraic Lie group and H an algebraic subgroup. We fix maximal reductive subgroups
$G_{\operatorname {s}}$
and
$H_{\operatorname {s}}$
of G and H, respectively, such that
$H_{\operatorname {s}} \subset G_{\operatorname {s}}$
. Then one has the equivalence:
$$\begin{align*}L^2(G/H) \ \mathrm{is} \ G_{\operatorname{s}}\mbox{-}\mathrm{tempered} \ \Leftrightarrow \ \rho_{\mathfrak{g}_{\operatorname{s}}} \le 2 \rho_{\mathfrak{g}/\mathfrak{h}} \ \mathrm{on} \ {\mathfrak{h}}_{\operatorname{s}}. \end{align*}$$
By
$G_s$
-tempered, we mean tempered as a representation of
$G_s$
, or, equivalently, tempered as a representation of the semisimple Lie group
$[G_s,G_s]$
. When G is not semisimple, this notion happens to be much more useful than the temperedness as a representation of G.
Theorem 1.1 (and its further generalisation to the Hilbert bundle valued case) serves as a ‘tool’ in proving the relationship with other disciplines, which is formulated in Theorem 1.6 below.
1.2 Temperedness condition and the orbit philosophy
We discuss what the orbit philosophy suggests about the geometry of coadjoint orbits ‘corresponding to’ the temperedness condition of
$L^2(G/H)$
.
Let
${\mathfrak {g}}$
be a Lie algebra and
${\mathfrak {g}}^{\ast }$
be its dual. Let G be a connected Lie group with Lie algebra
. We denote by
$\widehat G$
the unitary dual of G, for example, the set of equivalence classes of irreducible unitary representations of G. The orbit philosophy due to Kirillov-Kostant-Duflo expects an intimate connection of the unitary dual
$\widehat G$
with the set of coadjoint orbits
${\mathfrak {g}}^{\ast }/\operatorname {Ad}^{\ast }(G)$
. This works perfectly for simply connected nilpotent groups but does not exactly for semisimple Lie groups. Nevertheless,
${\mathfrak {g}}^{\ast }/\operatorname {Ad}^{\ast }(G)$
may be considered to be a fairly good approximation as a parameter set of
$\widehat G$
. As an expected functionality, the orbit philosophy also suggests that the disintegration of
$L^2(G/H)$
would be supported on the subset of
$\widehat G$
‘corresponding to’ the closure of
$\operatorname {Ad}^{\ast } (G){\mathfrak {h}}^{\perp }/\operatorname {Ad}^{\ast }(G)$
, where:
On the other hand, for a connected semisimple Lie group G, loosely speaking, irreducible tempered representations of G are supposed to be obtained as ‘geometric quantisation’ of semisimple coadjoint orbits having amenable isotropy subgroups. Thus, one expects that the temperedness of the unitary representation
$L^2(G/H)$
may be characterised by its ‘classical limit’ in the geometry of coadjoint orbits via the orbit philosophy. When G is a complex Lie group, we formulate a precise criterion below from this viewpoint.
1.3 Complex homogeneous spaces
In the third paper [Reference Benoist and Kobayashi3], and in this one, we extend and deepen the theory of tempered homogeneous spaces with a focus on the complex setting.
Suppose
is a semisimple Lie algebra. Via the Killing form:
$$ \begin{align*} K(X,Y):={\mathrm{tr}}({\mathrm{ad}}X\,{\mathrm{ad}}Y), \end{align*} $$
we identify
with
and
with the orthogonal subspace of
in
with respect to K. An element
is called regular if its centraliser
in
has minimal dimension, for example,
. We denote by
, the set of regular elements X of
and set:
In the third paper [Reference Benoist and Kobayashi3], we found yet another but more geometric tempered criterion for
$L^2(G/H)$
when both
${\mathfrak {g}}$
and
${\mathfrak {h}}$
are assumed to be complex semisimple Lie algebras. As we see in Proposition 2.10, this geometric criterion can be reformulated as
. In the present paper, we extend this criterion to all complex Lie subalgebras
of
.
Theorem 1.2. Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. Then one has the equivalence:
Since the set
is Zariski open in
, one always has the equivalence:
and, thus, Theorem 1.2 fits well into the aforementioned orbit philosophy.
One sees from [Reference Benoist and Kobayashi2, Corollary 5.6] that Theorem 1.2 for complex Lie groups yields the sufficiency of the temperedness in the real setting as well:
Corollary 1.3. Let G be a real semisimple algebraic Lie group and H an algebraic subgroup. If
, then
$L^2 (G/H)$
is tempered.
Remark 1.4.
-
(1) The implications
$\Longrightarrow $
in (1.2) and (1.5) are not always true for a real semisimple Lie group G. For instance, when G is not
$\mathbb { R}$
-split and H is a maximal compact subgroup, the representation
$L^2(G/H)$
is tempered, but
is empty. Another example is given by
$G/H=SL(3, \mathbb { H})/SL(2,\mathbb { H})$
. -
(2) Let
${\mathfrak {g}}_{ame}$
denote the set of elements in
${\mathfrak {g}}$
with amenable stabiliser for the adjoint action of G. For reductive H, by [Reference Benoist and Kobayashi3, Theorem 1.5] and Lemma 2.14 below, one has the implication: (1.4)The converse implication (1.4) does not always hold, even for semisimple symmetric spaces ([Reference Benoist and Kobayashi3, Section 8.5]).
By (1.1), our main task for Theorem 1.2 will be to prove the following.
Proposition 1.5. Let
be a complex semisimple Lie algebra and
a complex Lie subalgebra. Then one has the equivalence:
1.4 The equivalent conditions
We now introduce two other conditions that we will prove to be equivalent to (1.5).
We suppose that
is a complex semisimple Lie algebra and
is a complex Lie subalgebra. Let us think of
as a point in the variety
$\mathcal { L}$
of all Lie subalgebras of
. One surprising feature of the equivalence (1.5) is that the left-hand side is a closed condition on
, while the right-hand side is an open condition on
. Since both conditions are invariant by conjugation by G, this remark suggests to work with the adjoint orbit closure of
. As we will see, this new point of view will be very fruitful, first by suggesting new striking conditions equivalent to (1.5), and eventually by leading to a proof of (1.5).
Let
${\mathrm {Ad}} G$
be the adjoint group, let
be the
${\mathrm {Ad}}G$
-orbit of
in
$\mathcal { L}$
and
be the closure of this orbit. We introduce also the following two G-invariant algebraic subvarieties of
$\mathcal { L}$
:
We recall that a Lie subalgebra is said to be unipotent if all its elements are nilpotent.
As we mentioned, we will prove the equivalence (1.5) by showing simultaneously the equivalence to other striking conditions that we introduce now. Let H be the closure of the connected subgroup of G with Lie subalgebra
.
-
-
, -
-
, -
-
, -
-
, such that
, -
-
To refer to these conditions, we might say informally that:
-
-
is a tempered Lie subalgebra, -
-
satisfies the
$\rho $
-inequality, -
-
admits a solvable limit algebra, -
-
has a transversal maximal unipotent, -
-
meets a regular orbit.
Theorem 1.6. Let
be a complex semisimple Lie algebra and
a complex Lie subalgebra. Then the following five conditions are equivalent:
The proof of Theorem 1.6 will last up to Section 5.5.
Corollary 1.7. Let
be a complex semisimple Lie algebra. The set
$\mathcal { L}_{sla}$
of Lie subalgebras
satisfying
is both closed and open in
$\mathcal { L}$
.
Proof. Corollary 1.7 follows from the following two remarks: the condition
is closed, while the condition
is open.
Corollary 1.8. Let
be a complex semisimple Lie algebra and
a complex Lie subalgebra. Choose
. Then one has the equivalence:
The equivalence (1.6) can be reformulated as follows:
Although the statement (1.6) is purely a structure theorem of Lie subalgebras, our proof of (1.6) relies on the theory of unitary representations via Theorem 1.6. We would like to point out that we are not aware of a more direct proof of (1.6).
1.5 Strategy of proof and organisation
We now explain the strategy of the proof of Theorem 1.6. Since we already know from (1.1) the equivalence:
it remains to prove the equivalences:
All these statements are purely algebraic, and we will prove these implications by algebraic methods in Chapter 2 except for the implication:
The proof of this implication (1.10) is more delicate and will be given in Chapter 5. It will use an induction argument that reduces to the case where
is semisimple. The induction argument will involve unitary representation theory and a parabolic subgroup
$G_0$
of G containing H. This will force us to deal with algebraic groups G, which are not semisimple.
The proof will also use the analytic interpretation of
as a temperedness criterion and the disintegration of the unitary representation
$L^2(G_0/H)$
. Indeed, we will spend Chapters 3 and 4 proving the extension of the temperedness criterion (1.1) that we need. This extension (Theorem 1.1) is valid for any real algebraic Lie group G and any real algebraic subgroup H. The proof of this extension will rely on the Hertz majoration principle for unitary representations.
In this paper, the expressions ‘Zariski open’, ‘Zariski closed’ and ‘Zariski dense’ will refer to the Zariski topology, while ‘open’, ‘closed’ and ‘dense’ will refer to the Lie group topology.
2 Sla, Tmu and Orb
In this chapter, we focus on the proof of the implications in (1.9) that uses only algebraic tools. That is all of them except for the implication (1.10).
2.1 Sla and Tmu
We begin with the easiest of all these equivalences.
Proposition 2.1. Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. Then, one has the equivalence:
Proof. Proof of the direct implication. Since we assume
, there exists a sequence
$(g_n)_{n\geq 1}$
in G, such that the limit:
exists and is a solvable Lie subalgebra of
. Since
is solvable, there exists a Borel subalgebra
of
containing
. Let
be a maximal unipotent subalgebra of
, which is opposite to
, so that one has
. In particular, one has
and, for n large,
. This proves
.
Proof of the converse implication. Since we assume
, there exists a maximal unipotent subalgebra
of
, such that
. Let
be the Borel subalgebra containing
, let
be a Cartan subalgebra of
, so that
and let
be the maximal unipotent subalgebra of
, which is opposite to
and normalised by
. Let
be the root system of
in
. We write
$\Delta =\Delta ^+ \cup \Delta ^-$
, where
$\Delta ^+$
and
$\Delta ^-$
are, respectively, the roots of
in
and
. Choose an element
in the positive Weyl chamber, this means that for all
$\alpha \in \Delta ^+$
, one has
${\textbf Re}(\alpha (X))>0$
. Since
, the limit:
exists and is a subalgebra of
. In particular, this Lie algebra
is solvable. This proves
.
Corollary 2.2. Let
be a complex semisimple Lie algebra. Then, the set of subalgebras
satisfying
is open in
$\mathcal { L}$
.
Proof. The condition
is clearly an open condition.
2.2 Related Lie subalgebras
We now explain why we can often assume that
.
Lemma 2.3. Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. Let G be a Lie group with Lie algebra
and
$H_1=H$
be the smallest closed subgroup of G, whose Lie algebra contains
. Set
and
.
Then, one has the equivalences:
Proof. Proof of the direct implication in
$(i)$
. This follows from the inclusion
.
Proof of the converse implication in
$(i)$
. Since we assume
, there exists a sequence
$(g_n)_{n\geq 1}$
in G, such that the limit
exists and is a solvable Lie subalgebra of
. Then, after extraction, the limit
exists and satisfies:
In particular, the limit
is a solvable Lie subalgebra of
. This proves
.
$(ii)$
, this follows from
$(i)$
and the inclusions
.
2.3 Sla and Orb
The proof of the following equivalence is still purely algebraic but slightly more tricky.
Proposition 2.4. Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. Then, one has the equivalence:
Proof. For the direct implication
$\Longrightarrow $
. Since we assume
, there exists a sequence
$(g_n)_{n\geq 1}$
in G, such that the limit
exists and is a solvable Lie subalgebra of
. Since
is solvable, there exists a Borel subalgebra
of
containing
. Since the orthogonal of
is the maximal unipotent subalgebra:
the orthogonal
also contains
. By a result of Dynkin (see [Reference Collingwood and McGovern6, Theorem 4.1.6]), the Lie algebra
always contains regular elements of
, the orthogonal
also contains regular elements of
. Since the set
is open, for n large, the orthogonal
contains regular elements and
too. This proves
.
The proof of the converse implication will rely on the following two lemmas.
Lemma 2.5. Let
be a complex semisimple Lie algebra and
be a parabolic subalgebra, where
is a reductive Lie subalgebra and
is the unipotent radical of
.
Let
be an element of
with
and
. If X is regular in
, then
is regular in
.
Let r be the rank of
. We recall that the set
of regular elements of
is the set of elements
whose centraliser in
has dimension
. Similarly, the set
of regular element of
is the set of elements
whose centraliser in
has dimension
. This set may not be equal to
. For instance, when
is a Borel subalgebra, then
is a Cartan subalgebra of
and one has
.
Lemma 2.6. Let
be a complex semisimple Lie algebra,
a complex Lie subalgebra and
. Then there exists
, such that
and
.
As in Section 1.2, we denote by G a connected Lie group with Lie algebra
. Such a Lie group has a unique structure of complex algebraic Lie group.
Proof. To prove Lemma 2.6, we introduce the Zariski closure
$A\subset G$
of the one-parameter subgroup
$\{e^{tX}\mid t\in \mathbb { C}\}$
. This group A is Abelian.
Note that, for all a in A, the Lie subalgebra
is orthogonal to X. Therefore, all Lie subalgebra
in the orbit closure
are orthogonal to X. This orbit closure
is an A-invariant subvariety of the projective algebraic variety
$\mathcal { L}$
. By Borel fixed point theorem [Reference Borel4, Theorem 10.6], the solvable group A has a fixed point in this subvariety. This means that there exists
in
, such that
. In particular,
.
Proof. For the converse implication
$\Longleftarrow $
in Proposition 2.4, we argue by induction on the dimension of
. We assume that
contains a regular element X, and we want to prove
. By Corollary 2.2 and Lemma 2.6, we can also assume that X normalises
, for example, that
. In particular, the sum
is a Lie subalgebra of
. By Lemma 2.3 (i), we may and do assume that:
Let
be a parabolic subalgebra of
of minimal dimension containing
and
the unipotent radical of
. By minimality of
, the image of
in
is reductive. Therefore, we can write
, where
is a semisimple Lie subalgebra and
is the unipotent radical of
. We can then write
, where
is a reductive Lie subalgebra containing
. We sum up this discussion by the inclusions:
Since X is in
$\widetilde {\mathfrak h} \subset \mathfrak q$
, we can decompose X as
with
and
. By Lemma 2.5, the element
is regular in
. Since
is the orthogonal of
with respect to the Killing form K, one has:
This proves that
is orthogonal to
.
We now claim that
. Indeed, if
, one has the equalities
, and this Lie algebra is semisimple by the assumption that
. Therefore, the Killing form restricted to
is nondegenerate. This contradicts the assumption
.
Therefore, one has
. The normaliser
of
in G has Lie algebra
. We have seen that the intersection
is nonempty. Therefore, by induction hypothesis, the orbit closure
contains a solvable Lie algebra and the orbit closure
also contains a solvable Lie algebra. This proves
.
2.4 Rho and Sla
In this section, we will prove the following implication, which is still purely algebraic. The proof of the converse will be much more delicate.
We will in fact prove a stronger statement.
Proposition 2.7. Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. Then, one has the implication:
More precisely, if
satisfies
, then every Lie algebra
in
satisfies
.
It will be useful to introduce the following two G-invariant subsets of
$\mathcal { L}$
.
Remark 2.8. We have the following nice characterisation of closed orbits in
$\mathcal { L}$
.
Proof. Proposition 2.7 follows from Lemma 2.9 below and from the fact that the orbit closure always contains a closed G-orbit.
Lemma 2.9. Let
be a complex semisimple Lie algebra. Then,
-
(i)
$\mathcal { L}_{rho}$
is closed in
$\mathcal { L}$
. -
(ii) Let
be a complex Lie subalgebra with
closed. Then,
Proof.
$(i)$
The map
is continuous on the set
. Let
be a sequence that converges to a Lie algebra
. We want to prove that
. Let
. We can find a sequence
converging to
$Y_\infty $
. Therefore, one has:
This proves that
is in
$\mathcal { L}_{rho}$
.
$(ii)$
Proof of the direct implication in (ii). Since
is solvable, it is included in a Borel Lie subalgebra
. Note that
satisfies the
$\rho $
-inequality, more precisely, one has the equality
, for all Y in
. Therefore,
also satisfies
.
$(ii)$
Proof of the converse implication in (ii). Let
be a Lie subalgebra with
closed and which satisfies
. We want to prove that
is solvable. By replacing
a few times with its derived subalgebra
if necessary, we may assume that
. Let
be the normaliser of
and
be the unipotent radical of
. By assumption,
is a parabolic Lie subalgebra. The projection of
in the reductive Lie algebra
is an ideal, and, hence, is a semisimple Lie algebra. Therefore, we can write
, where
is a semisimple Lie subalgebra and
is the unipotent radical of
. We then write
, where
is a reductive Lie subalgebra containing
. Let
be the opposite unipotent subalgebra, which is opposite to
and normalised by
, so that
. Fix Y in
. Since
normalises
, one has:
Since
is dual to
as an
-module, one has:
Combining (2.10) and (2.11), and using the
$\rho $
-inequality, one gets:
Since this is true for all Y in the semisimple Lie algebra
, one must have
. This proves that
is solvable.
2.5 Reductive homogeneous spaces
In this section, we check Theorem 1.6 for
reductive by relying on the previous papers of this series. We will prove:
Proposition 2.10. Let
be a complex semisimple Lie algebra and
a complex reductive Lie subalgebra. The following conditions are equivalent:
Remark 2.11. Since
is semisimple and
is reductive, one has a decomposition
with respect to the Killing form, and the orthogonal complement
is isomorphic to the quotient
as an
-module.
The proof uses the condition
that we introduced in [Reference Benoist and Kobayashi3] and proven to be equivalent to
. It is defined by:
According to our conventions, ‘dense’ means ‘dense for the vector space topology’, but we could also have used the Zariski topology in this definition.
Proof. For Proposition 2.10.
-
⋆ The equivalence
is proven in [Reference Benoist and Kobayashi1, Theorem 4.1] for all real semisimple Lie algebra
and all real reductive Lie subalgebra
. -
⋆ The equivalence
has been proven in the previous sections for all complex Lie subalgebra
. -
⋆ The equivalence
is proven in [Reference Benoist and Kobayashi3, Theorem 1.6] for all complex semisimple Lie algebra
and all complex reductive Lie subalgebra
. -
⋆ The equivalence
is proven in Proposition 2.12 below.
Proposition 2.12. Let
be a complex semisimple Lie algebra and
be a complex reductive Lie subalgebra. Then, one has the equivalence:
We will need the following lemma which relates the centraliser in
and the centraliser in
.
Lemma 2.13. Let
be a real semisimple Lie algebra,
a real reductive Lie subalgebra and regard
via the Killing form as before. Let:
Then, for every
$X_0$
in
, one has
Note that Lemma 2.13 applied to
implies that
is Abelian if
. Indeed, when
, one has
and
.
This lemma is a special case of the following general lemma for coadjoint orbits of real Lie algebras which is well known when
.
Lemma 2.14. Let
be a real Lie algebra and
be a real Lie subalgebra. Let
be the dual of
and
. We set:
Then, for every
$f_0$
in
, one has
.
Here,
denotes the stabiliser of f in
and
, its stabiliser in
.
Proof. To prove Lemma 2.14, we fix
and two elements
$Y_0$
and
$Z_0$
in
. We want to prove that
. We write:
where
is a complementary vector subspace.
For all
, for
$t\in \mathbb { R}$
small enough, the element
$f_t:=f_0+tf$
is also in the open set
. Choose a linear projection
. By the local inversion theorem, the map:
is a local diffeomorphism near
$(Y_0,0)$
. Let
$t\mapsto Y_t$
be the differentiable curve near
$0$
starting from
$Y_0$
given by
$\Phi (Y_t,t)=(0,t)$
. Since for t small the linear map
is an isomorphism, it satisfies:
For the same reason, there exists a differentiable curve
$t\mapsto Z_t$
near
$0$
starting from
$Z_0$
, such that:
They satisfy the equality
$f_t([Y_t,Z_t])=0$
whose derivative at
$t=0$
gives:
$$ \begin{align*}f([Y_0,Z_0])+f_0([Y^{\prime}_0,Z_0])+f_0([Y_0,Z^{\prime}_0])=0.\\[-16pt] \end{align*} $$
Since both
$Y_0$
and
$Z_0$
stabilise
$f_0$
, the last two terms are zero. One deduces:
This proves that
$[Y_0,Z_0]$
is in
as required.
The following lemma will also be useful.
Lemma 2.15. Let
be a complex semisimple Lie algebra and
be a complex reductive Lie subalgebra. Then the set:
is Zariski dense in
.
Proof. There exists a compact real form
of
, such that
is defined over
$\mathbb { R}$
. Since
, the vector space
is Zariski dense in
. Since all elements of
are semisimple, this proves Lemma 2.15.
Proof. We can now give the proof of Proposition 2.12.
Proof of the converse implication. Since the Zariski open set
meets the orthogonal
for the Killing form, the intersection
is dense in
. By Lemma 2.13 applied with the zero subalgebra, every
$X_0$
in
has an Abelian centraliser in
. In particular, every
$X_0$
in
has an Aabelian centraliser in
. This proves
.
Proof of the direct implication. Let
The set:
is nonempty and Zariski open in
. By assumption, the set:
is dense in
. Since it is also closed in
, one has
. Therefore, by Lemma 2.15, the set
contains a semisimple element
$X_0$
. The centraliser
is then a reductive Lie algebra. By Lemma 2.13, the Lie algebra
is included in
, which is an Abelian Lie algebra. Therefore, the Lie algebra
itself is Abelian. Since
$X_0$
is semisimple, this centraliser is a Cartan subalgebra and
$X_0$
is regular in
. This proves
.
3 Real algebraic homogeneous spaces
The proof of the last remaining implication (1.10) will last up to the end of this paper. Because of the induction method which involves parabolic subgroups, we need to extend the temperedness criterion of [Reference Benoist and Kobayashi2] to nonsemisimple groups G. This extension will be valid for all real algebraic groups.
3.1 Notations
Let G be a real algebraic Lie group and H be an algebraic Lie subgroup. We write
$G=LU$
and
$H=SV$
, where
$S\subset L$
are reductive subgroups and where V and U are the unipotent radicals of H and G. Note that, in general, one does not have the inclusion
$V\subset U$
. We denote by
,
,
,
, etc. the corresponding Lie algebras.
We consider the following conditions:
We recall that L-tempered means tempered as a representation of L or equivalently as a representation of the semisimple Lie group
$[L,L]$
.
Note that, when G itself is semisimple, these conditions are exactly those given in Section 1.4.
Theorem 3.1. Let G be a real algebraic Lie group and H be an algebraic Lie subgroup. One has the equivalence,
Remark 3.2. For real algebraic groups, the last condition
is not always equivalent to the first two, but it is often the case. For instance, we will see in Theorem 5.1, that this is true for complex algebraic Lie groups.
In the induction process, we will have to work with slightly more general representations than the regular representation
$L^2(G/H)$
. Let W be a finite-dimensional algebraic representation of H. We will have to deal with the (
$L^2$
-)induced representation:
$$ \begin{align*}{\mathrm{Ind}}_H^G(L^2(W))\simeq L^2(G\times_H W), \end{align*} $$
where
$G\times _HW$
is the G-equivariant bundle over
$G/H$
with fibre W, see [Reference Benoist and Kobayashi2, Section 2.1] for a more precise definition. This is why we also introduce the following two conditions.
The following theorem is a generalisation of our Theorem 3.6 in [Reference Benoist and Kobayashi2], where we assumed that G is semisimple.
Theorem 3.3. Let G be a real algebraic Lie group, H be an algebraic Lie subgroup and W a finite-dimensional algebraic representation of H. One has the equivalence,
We have assumed here that G and H are algebraic only to avoid uninteresting technicalities. It is not difficult to get rid of this assumption.
The proof of Theorem 3.3 follows the same line as in [Reference Benoist and Kobayashi2, Theorem 3.6].
In this Chapter 3, we will prove the direct implication
$\Longrightarrow $
.
In Chapter 4, we will prove the converse implication
$\Longleftarrow $
.
3.2 The Herz majoration principle
We first recall a few lemmas on tempered representations and on induced representations.
The first lemma is a variation on the Herz majoration principle.
Lemma 3.4. Let G be a real algebraic Lie group, L be a reductive algebraic Lie subgroup of G and H be a closed subgroup of G. If the regular representation in
$L^2(G/H)$
is L-tempered, then the induced representation
$\Pi ={\operatorname {Ind}}_H^G(\pi )$
is also L-tempered for any unitary representation
$\pi $
of H.
Proof. See for instance [Reference Benoist and Kobayashi2, Lemma 3.2].
The second lemma will prevent us from worrying about connected components of H and will allow us to assume that
$H=[H,H]$
.
Lemma 3.5. Let G be a real algebraic Lie group, L be a reductive algebraic subgroup of G and
$H'\subset H$
be two closed subgroups of G.
-
1) If
$L^2(G/H)$
is L-tempered, then
$L^2(G/H')$
is L-tempered. -
2) The converse is true when
$H'$
is normal in H and
$H/H'$
is amenable (for instance, finite, compact or Abelian).
Proof. See [Reference Benoist and Kobayashi2, Proposition 3.1].
The third lemma is good to keep in mind.
Lemma 3.6. Let
$Q=LU$
be a real algebraic Lie group which is a semidirect product of a reductive subgroup L and its unipotent radical U. Let
$\pi _0$
be a unitary representation of Q which is L-tempered and trivial on U. Then the representation
$\pi _0$
is also Q-tempered.
Proof. See [Reference Benoist and Kobayashi2, Lemma 4.3].
This lemma is useful for a parabolic subgroup Q of a semisimple Lie group G. In this case, the induced representation
${\mathrm {Ind}}_Q^G(\pi _0)$
is also G-tempered.
3.3 Decay of matrix coefficients
We now recall the control of the matrix coefficients of tempered representations of a reductive Lie group.
In the sequel, it will be more comfortable to deal with a reductive group L than just with a semisimple group even though, in the temperedness condition, the center
$Z_L$
of L plays no role.
So, let L be a real reductive algebraic Lie group. We fix a maximal compact subgroup K of L and denote by
$\Xi $
the Harish-Chandra spherical function on L. By definition,
$\Xi $
is the matrix coefficient of a normalised K-invariant vector
$v_0$
of the spherical unitary principal representation
$\pi _0={{\operatorname {Ind}}}_P^L({\textbf 1}_P)$
, where P is a minimal parabolic subgroup of L. That is:
$$ \begin{align} \Xi(\ell)=\langle\pi_0(\ell)v_0,v_0\rangle \; ,\;\; \mathrm{for \ all} \ \ell \ \mathrm{in} \ L. \end{align} $$
Since P is amenable, the representation
$\pi _0$
is L-tempered.
Proposition 3.7 [Reference Cowling, Haagerup and Howe7]
Let L be a real algebraic reductive Lie group and
$\pi $
be a unitary representation of L. The following are equivalent:
-
(i) the representation
$\pi $
is tempered, -
(ii) for every K-finite vector v in
${\mathcal H}_\pi $
, for every
$\ell $
in L, one has:
$$ \begin{align*} |\langle \pi(\ell)v,v\rangle |\leq \Xi(\ell)\, \| v\|^2\dim \langle K v\rangle. \end{align*} $$
See [Reference Cowling, Haagerup and Howe7, Theorems 1, 2 and Corollary]. See also [Reference Howe and Tan8] and [Reference Nevo10] for other applications of Proposition 3.7.
For the regular representation in an L-space, this proposition becomes:
Corollary 3.8. Let L be a real algebraic reductive Lie group and X be a locally compact space endowed with a continuous action of L preserving a Radon measure
${\mathrm {vol}}$
. The regular representation of L in
$L^2(X)$
is L-tempered if and only if, for any K-invariant compact subset C of X, one has:
$$ \begin{align} {\mathrm{vol}} (\ell\, C\cap C)\leq {\mathrm{vol}}( C)\;\Xi(\ell) \; ,\;\;\mathrm{for \ all} \ \ell \ \mathrm{in} \ L. \end{align} $$
Recall that the notation
$\ell \, C$
denotes the set
$\ell \, C: =\{\ell x\in X: x\in C\}$
.
3.4 The rho function
We now explain, following [Reference Benoist and Kobayashi2, Section 2.3] how to deal with the functions
$\rho _V$
occurring in the temperedness criterion.
Let H be a real algebraic Lie group,
its Lie algebra and V be a real algebraic finite-dimensional representation of H. For each element Y in
, we consider the eigenvalues of Y in V and we denote by
$V_+$
and
$V_-$
the largest vector subspaces of V on which the real part of all the eigenvalues of Y are respectively positive and negative, and we set:
$$ \begin{align*} \rho_V(Y) := \tfrac12\,\operatorname{\mathrm{Tr}}(Y|_{V_+})- \tfrac12\,\operatorname{\mathrm{Tr}}(Y|_{V_-}). \end{align*} $$
Let
be a maximal split Abelian Lie subalgebra of
(i.e. the Lie subalgebra of a maximal split torus A of H). The function
$\rho _V$
on
is completely determined by its restriction to
. Let
$P_V$
be the set of weights of
in V and, for all
$\alpha $
in
$P_V$
, let
$m_\alpha :=\dim V_{\alpha }$
be the dimension of the corresponding weight space. Then one has the equality:
For example, when
is semisimple and
via the adjoint action, our function
is equal on each positive Weyl chamber
of
to the sum of the corresponding positive roots (i.e. to twice the usual ‘
$\rho $
’ linear form).
The functions
$\rho _V$
occur in the volume estimate of Corollary 3.8 through the following Lemma.
Lemma 3.9. Let
$V=\mathbb { R}^d$
. Let
be an Abelian split Lie subalgebra of
${\mathrm {End}}(V)$
and C be a compact neighborhood of
$0$
in V. Then there exist constants
$m_{_C }>0$
,
$M_{_C }> 0$
, such that
Proof. This is [Reference Benoist and Kobayashi2, Lemma 2.8].
3.5 The direct implication
We first prove the direct implication in Theorem 3.3 which is:
Proposition 3.10. Let G be a real algebraic Lie group, H an algebraic Lie subgroup of G and W an algebraic representation of H. Let L be a maximal reductive subgroup of G containing a maximal reductive subgroup S of H.
If
$\Pi :={\operatorname {Ind}}_H^G(L^2(W))$
is L-tempered, then one has
on
.
Proof. This representation
$\Pi $
is also the regular representation of the G-space
$X:=G\times _HW$
. Let A be a maximal split torus of S and
be the Lie algebra of A. We choose an A-invariant decomposition
and small closed balls
and
$B_W\subset W$
centered at
$0$
. We can see
$B_W$
as a subset of X and the map:
$$ \begin{align*} B_0\times B_W \longrightarrow G\times_H W, \qquad (u,v)\mapsto \exp (u)v \end{align*} $$
is a homeomorphism onto its image C. Since
$\Pi $
is L-tempered, one has a bound as in (3.2):
$$ \begin{align} \langle\Pi(\ell )1_C,1_C\rangle\leq M_C\; \Xi(\ell) \;\;\;\mathrm{for \ all} \ \ell \ \mathrm{in} \ L. \end{align} $$
We will exploit this bound for elements
$\ell =e^Y$
with Y in
. In our coordinate system (3.4), we can choose the measure
$\nu _X$
to coincide with the Lebesgue measure on
. Taking into account the Radon–Nikodym derivative and the A-invariance of
, one computes as in [Reference Benoist and Kobayashi2, Section 3.3],
and therefore, using Lemma 3.9, one deduces:
Combining (3.4) and (3.5) with known bounds for the spherical function
$\Xi $
as in [Reference Knapp9, Proposition 7.15], one gets, for suitable positive constants d,
$M_0$
,
Therefore, one has
as required.
4 Proof of temperedness for real groups
In this chapter, we prove the converse implication in Theorem 3.3 which is:
Proposition 4.1. Let G be a real algebraic Lie group, H an algebraic Lie subgroup of G and W an algebraic representation of H. Let L be a maximal reductive subgroup of G containing a maximal reductive subgroup S of H.
If
on
, then
$\Pi :={\operatorname {Ind}}_H^G(L^2(W))$
is L-tempered.
Recall that, when
$W=0$
, one has
$\Pi =L^2(G/H)$
.
4.1 Domination of G-spaces
The proof relies on the notion of domination of a G-action that we have introduced in [Reference Benoist and Kobayashi2] without giving it a name.
Here is the definition. Let G be a locally compact group. Let X and
$X_0$
be two locally compact spaces endowed with a continuous action of G and with a G-invariant class of measures
${\mathrm {vol}}_X$
and
${\mathrm {vol}}_{X_0}$
. Let
$\pi $
and
$\pi _0$
be the unitary regular representations of G in the Hilbert spaces of square-integrable half-densities
$L^2(X)$
and
$L^2(X_0)$
.
Definition 4.2 Domination of a G-space
We say that X is G-dominated by
$X_0$
if for every compactly supported bounded half-density v on X, there exists a compactly supported bounded half-density
$v_0$
on
$X_0$
, such that, for all g in G,
$$ \begin{align} |\langle\pi(g)v,v\rangle| \leq \langle\pi_0(g)v_0,v_0\rangle. \end{align} $$
Remark 4.3. When both measures
${\mathrm {vol}}_X$
and
${\mathrm {vol}}_{X_0}$
are G-invariant, the bound (4.1) means that, for every compact set
$C\subset X$
, there exists a constant
$\lambda>0$
and a compact set
$C_0\subset X_0$
, such that, for all g in G,
$$ \begin{align*} {\mathrm{vol}}(g\,C\cap C) \leq \lambda \,{\mathrm{vol}}(g\,C_0\cap C_0). \end{align*} $$
This definition is very much related to our temperedness question because of the following lemma.
Lemma 4.4. Let G be a real algebraic reductive Lie group and P be a minimal parabolic subgroup of G, and let X be a G-space. The regular representation of G in
$L^2(X)$
is G-tempered if and only if X is G-dominated by the flag variety
$X_0=G/P$
.
Proof. This lemma is a direct consequence of Corollary 3.8.
The following proposition gives us a nice situation where an action is dominating another one.
Proposition 4.5. Let
$F=SU$
be a real algebraic Lie group which is a semidirect product of a reductive subgroup S and its unipotent radical U. Let
$H=SV$
be an algebraic subgroup of F containing S, where
$V=U\cap H$
. Let Z be the F-space
$Z=F/H=U/V$
. Let
$Z_0:=Z$
be endowed with another F-action, where the S-action is the same, but the U-action is trivial.
Then Z is F-dominated by
$Z_0$
.
Proof. This is [Reference Benoist and Kobayashi2, Corollary 4.6].
4.2 Inducing a dominated action
The following proposition tells us that the induction of actions preserves the domination.
Proposition 4.6. Let G be a locally compact group and F a closed subgroup of G. Let Z and
$Z_0$
be two locally compact F-spaces with G-invariant class of measures. Let
$X:=G\times _F Z$
and
$X_0:= G\times _F Z_0$
be the two induced G-spaces.
If Z is F-dominated by
$Z_0$
, then X is G-dominated by
$X_0$
.
Proof. The proof of Proposition 4.6 is an adaptation of [Reference Benoist and Kobayashi2, Proposition 4.9], where G was an algebraic semisimple group. We assume to simplify that the measures on Z and
$Z_0$
are G-invariant. This avoids complicating the formulas with the square roots of a Radon-Nikodym derivative. The projection:
$$ \begin{align*}G\rightarrow X':=G/F \end{align*} $$
is a G-equivariant principal bundle with structure group F. We fix a Borel measurable trivialisation of this principal bundle:
$$ \begin{align} G\simeq X'\times F, \end{align} $$
which sends relatively compact subsets to relatively compact subsets. The action of G by left multiplication through this trivialisation can be read as:
$$ \begin{align*} g\,(x',f)=(gx',\sigma_F(g,x')f) \;\;\;\;\mathrm{for \ all}\ g\in G, x'\in X' \ \mathrm{and} \ f\in F, \end{align*} $$
where
$\sigma _F\colon G\times X'\rightarrow F$
is a Borel measurable cocycle. This trivialisation (4.2) induces a trivialisation of the associated bundles
$$ \begin{align*} X= G\times _F Z &\simeq X' \times Z\, , \\ X_0 = G \times_F Z_0 &\simeq X' \times Z_0\,. \end{align*} $$
We start with a compact set C of X. Through the first trivialisation, this compact set is included in a product of two compact sets
$C'\subset X'$
and
$D\subset Z$
:
$$ \begin{align} C\subset C'\times D\;. \end{align} $$
Since Z is F-dominated by
$Z_0$
, there exists
$\lambda>0$
and a compact subset
$D_0\subset Z_0$
, such that, for all f in F,
$$ \begin{align*} {\mathrm{vol}}_Z(f\,D\cap D) \leq \lambda \,{\mathrm{vol}}_{Z_0}(f\,D_0\cap D_0). \end{align*} $$
We compute, for g in G,
$$ \begin{align*} {\mathrm{vol}}_X(g\, C\cap C) &\leq \int_{gC'\cap C'}{\mathrm{vol}}_Z(\sigma_F(g,g^{-1} x')D\cap D)\,\mathrm{d} x'\\ &\leq \lambda \int_{gC'\cap C'}{\mathrm{vol}}_{Z_0}(\sigma_F(g,g^{-1} x')D_0\cap D_0)\,\mathrm{d} x'\\ &\leq \lambda \,{\mathrm{vol}}_{X_0}(g\, C_0\cap C_0), \end{align*} $$
where
$\mathrm {d}x'$
is a G-invariant measure on
$X'$
and
$C_0$
is a compact subset of
$X_0\simeq X'\times Z_0$
, which contains
$C'\times D_0$
.
4.3 The converse implication
We conclude the proof of the converse implication in Theorem 3.3, by reducing it to the case where G is reductive, which was proven in [Reference Benoist and Kobayashi2, Theorem 3.6].
We will need the following lemma on the structure of nilpotent homogeneous spaces. See [Reference Benoist and Kobayashi2, Lemma 4.7] for a similar statement. We recall that a unipotent Lie group is an algebraic nilpotent Lie group with no torus factor.
Lemma 4.7. Let U be a real unipotent Lie group, V a unipotent subgroup and
their Lie algebra.
-
(1) There exists a real vector subspace
, such that
and the exponential map induces a polynomial bijection
. -
(2) Moreover, if
is invariant by a reductive subgroup
, one can choose
to be S-invariant.
Proof. We prove Lemma 4.7 by induction on
$\dim U$
. Let Z be the center of U and
its Lie algebra.
First case:
. In this case, we apply the induction assumption to the Lie algebra
and its Lie subalgebra
. This gives us an S-invariant subspace
of
, such that
and:
is a bijection. We denote by
the projection and choose
to be any S-invariant vector subspace of
$\pi ^{-1}\mathfrak m'$
, such that
.
Second case:
. In this case, we apply the induction assumption to the Lie algebra
and its subalgebra
. This gives us an S-invariant subspace
of
, such that
and:
is a bijection. We denote by
the projection and choose
. The identifications
and
$U'/V'\simeq U/VZ$
prove that the exponential map
is bijective.
Proof. We distinguish two cases in the proof of Proposition 4.1.
First case:
$W= \{0\}$
. In this case, one has
$\Pi =L^2(G/H)$
. We denote by U and V the unipotent radical of G and H, so that we have the equalities
$G=LU$
and
$H=SV$
. We have the inclusion
$S\subset L$
, but the group V might not be included in U. We introduce the unipotent group
$V':=VU\cap L$
and the algebraic groups
$F:=HU$
and
$F':=F\cap L$
so that we have the equality
$F'=SV'$
and the inclusions:
$$ \begin{align*} H=SV\subset F=F'U\subset G=LU\,. \end{align*} $$
Let:
$$ \begin{align*} Z:=F/H, \end{align*} $$
and let
$Z_0$
be the F-space Z endowed with the same S-action but with a trivial
$VU$
-action. One can easily describe
$Z_0$
. Indeed, let
,
,…be the Lie algebras of U, V,… By Lemma 4.7,
$Z_0$
can be identified with the S-module
, as is seen from the following isomorphisms:
According to Proposition 4.5, the F-space Z is dominated by
$Z_0$
. We introduce now the two induced G-spaces:
$$ \begin{align*} X:=G\times_F Z=G/H\;\;\;\mathrm{and}\;\;\; X_0:= G\times_F Z_0\,. \end{align*} $$
According to Proposition 4.6, the G-space X is dominated by
$X_0$
. Hence:
$$ \begin{align*} \mathrm{the} \ L\mbox{-}\mathrm{space} \ X=G/H \ \mathrm{is \ dominated \ by \ the} \ L\mbox{-}\mathrm{space} \ X_0=L\times_{F'}W'. \end{align*} $$
By assumption one has:
Since
this can be rewritten as:
Since L is reductive, we can apply [Reference Benoist and Kobayashi2, Theorem 3.6]. This tells us that the representation
$L^2(L\times _{F'}W')$
is L-tempered.
Therefore, since the L-space X is L-dominated by
$X_0$
, the representation of L in
$L^2(G/H)$
is L-tempered, as required.
Second case:
$W\neq \{0\}$
. In this case, one has
$\Pi =L^2(G\times _H W)$
. For w in W, we denote by
$H_w$
the stabiliser of w in H. We write
$H_w=S_wU_w$
with
$S_w$
reductive and
$U_w$
the unipotent radical. Since the action of H on W is algebraic, there exists a Borel measurable subset
$T\subset W$
which meets each of these H-orbits in exactly one point. We can assume that for each w in T, one has
$S_w\subset S$
. Let
$\mu $
be a probability measure on W with positive density and
$\nu $
be the probability measure on
$T\simeq S\backslash W$
given as the image of
$\mu $
. One has an integral decomposition of the regular representation:
$$ \begin{align} L^2(G\times_H W) =\int_T^{\oplus}L^2(G/H_w)\,\mathrm{d}\nu(w). \end{align} $$
Since the direct integral of tempered representations is tempered, we only need to prove that, for
$\nu $
-almost all w in T,
$$ \begin{align} L^2(G/H_w)\;\;\mbox{is} \ L\mbox{-}\mathrm{tempered.} \end{align} $$
We can choose w in the Zariski open set, where dim
$H_w$
is minimal. According to [Reference Benoist and Kobayashi2, Lemma 3.9], for such a w,
Our assumption implies that one has the inequality on
:
Thanks to (4.6), this can be rewritten as:
Then the first case tells us that for such w, the representation of L in
$L^2(G/H_w)$
is tempered. This proves (4.5) as required.
4.4 Using parabolic subgroups
The aim of this section is to explain how, when dealing with a quotient
$G/H$
of real algebraic groups, one can, using parabolic subgroups, reduce to the case where the unipotent radical V of H is included in the unipotent radical U of G. This reduction method will be used in Chapter 5 for complex Lie groups.
Let G be a real algebraic Lie group and H a real algebraic subgroup of G. We write
$G=LU$
and
$H=SV$
, where U and V are the unipotent radicals of G and H, and where S and L are reductive algebraic subgroups. We can manage so that
$S\subset L$
, but we cannot always assume that V is included in U. For instance, this is not possible when G is reductive and H is not. We fix a parabolic subgroup
$G_0$
of G that contains H and which is minimal with this property. We denote by
$U_0\supset U$
the unipotent radical of
$G_0$
.
Lemma 4.8. One has the inclusion
$V\subset U_0$
. Moreover, we can choose a reductive subgroup
$L_0\subset G_0$
, such that
$G_0=L_0U_0$
and
$S\subset L_0$
.
Proof. The group
$V_0:=U_0\cap H$
is a unipotent normal subgroup of H. The quotient
$S':=H/V_0$
is an algebraic subgroup of the reductive group
$G_0/U_0$
, which is not contained in any proper parabolic subgroup of
$G_0/U_0$
. Therefore, by [Reference Bourbaki5, Section VIII.10], this group
$S'$
is reductive and the group
$V_0$
is the unipotent radical V of H. This proves the inclusion
$V\subset U_0$
.
Since maximal reductive subgroups
$L_0$
of
$G_0$
are
$U_0$
-conjugate, one can choose
$L_0$
containing S.
We introduce the
$L_0$
-module
. The following two lemmas will be useful in our induction process.
Proposition 4.9. Keep this notation. The following are equivalent:
-
(i)
$L^2(G/H)$
is L-tempered; -
(ii)
as a function on
; -
(iii)
$L^2(G_0/H)$
is
$L_0$
-tempered; -
(iv)
as a function on
; -
(v)
$L^2(L_0\times _SW_0)$
is
$L_0$
-tempered.
Proof. Proof of the equivalence between (i) and (ii) and of the equivalence between (iii) and (iv). This is Theorem 3.1.
Proof of the equivalence between (ii) and (iv). Write
, where
. The equivalence follows from the equalities
and
. Proof of the equivalence between (iv) and (v). This follows from Theorem 3.3 and the equality
.
The following lemma will also be useful in this reduction process.
Lemma 4.10. Keep this notation. The following are equivalent:
-
(i) the orbit closure
contains a solvable Lie algebra; -
(ii) the orbit closure
contains a solvable Lie algebra.
Proof. Lemma 4.10 follows from the compactness of
$G/G_0$
.
5 Complex algebraic homogeneous spaces
The aim of this chapter is to prove the last remaining implication in Theorem 1.6, which is the converse of Proposition 2.7. We keep the notation of the previous Chapters 3 and 4. We assume in this chapter that both G and H are complex algebraic Lie groups but do not assume G to be semisimple.
5.1 The equivalence for G algebraic
We first state the extension of Theorem 1.6, which relates temperedness to the existence of solvable limit algebras for a general algebraic group G. This extension will be useful because of the induction process in the proof. We still use the notation in Section 3.1.
Theorem 5.1. Let G be a complex algebraic Lie group and H be a complex algebraic subgroup. Then one has the equivalences,
Proof. The first equivalence in Theorem 5.1 follows from Theorem 3.1. We split the proof of the second equivalence into Propositions 5.4 and 5.7.
Corollary 5.2. Let G be a complex algebraic Lie group, H be a complex algebraic subgroup and
. Then one has the equivalence,
This equivalence says that if a Lie subalgebra admits one solvable limit, then all its limit Lie algebras also admit a solvable limit.
Proof. More precisely, Corollary 5.2 is a corollary of Propositions 5.4 and 5.7. Indeed, if
satisfies
, then by Proposition 5.7, it satisfies
. Then by Proposition 5.4, all limit subalgebras
also satisfy
.
Remark 5.3. The set of Lie subalgebras
in
satisfying
is closed. Indeed, this follows from the
$Rho$
-condition in Theorem 5.1.
5.2 Rho and Sla
We extend Proposition 2.7 to general algebraic groups G.
Proposition 5.4. Let
be an algebraic complex Lie algebra and
be a complex Lie subalgebra. Then, one has the implication:
More precisely, if
satisfies
, then every Lie algebra
in
satisfies
.
Remark 5.5. In Propositions 5.4 and 5.7, the assumption that
is algebraic, which means that it is the Lie algebra of a complex algebraic Lie group, can easily be removed. We will not need it.
Proof. Proposition 5.4 follows from Lemma 5.6 below and from the fact that the orbit closure always contains a closed G-orbit.
We denote again by
$\mathcal { L}_{rho}$
the set of Lie subalgebras
of
that satisfy
.
Lemma 5.6. Let
be an algebraic complex Lie algebra. Then,
-
(i)
$\mathcal { L}_{rho}$
is closed in
$\mathcal { L}$
. -
(ii) Let
be a complex Lie subalgebra with
closed. Then,
Proof. Lemma 5.6 is a straightforward extension of Lemma 2.9. We write
with
reductive and
the unipotent radical.
$(i)$
Same as for Lemma 2.9.
$(ii)$
Proof of the direct implication in (ii). Same as for Lemma 2.9, but note that for
with
a Borel subalgebra of
, one has
.
$(ii)$
Proof of the converse implication in (ii) We may assume that
. Let
be the normaliser of
. By assumption,
is a parabolic Lie subalgebra of
and
is an ideal of
. Let
be a parabolic subalgebra of
containing
and which is minimal with this property. We can write
and
, where
is a reductive Lie algebra, where
is the unipotent radical of
, where
is an ideal of
and where
. By assumption, one has
. Then, by the equivalence
$(ii)\Leftrightarrow (iv)$
in Proposition 4.9, one also has
, for example,
But since
is an ideal in
, the right-hand side is null, and this inequality can be rewritten as
. This tells us that
is Abelian and
is solvable.
5.3 Sla and Rho
We are now able to prove the last remaining implication (1.10) by proving the following stronger Proposition 5.7, which is the converse to Proposition 5.4.
Proposition 5.7. Let
be a complex algebraic Lie algebra and
be a complex Lie subalgebra. Then, one has the implication:
Proof. Here is only the beginning of the proof of Proposition 5.7. This proof will be by induction on the dimension of
, reducing to the case where both
and
are semisimple that we discussed in Proposition 2.10. Using Lemma 3.5 and Theorem 3.1, we can replace
by
. Iterating this process finitely many times, we can assume that:
This condition ensures that
is an algebraic Lie subalgebra of
, so that we will be able to apply the strategy of Section 4.4. In Proposition 4.9 and Lemma 4.10, we have introduced an intermediate algebraic complex Lie algebra
, such that the unipotent radical
of
is included in the unipotent radical
of
, and for which we have the equivalences:
The proof will go on for two more sections.
5.4 Pushing down the Sla condition
We sum up the previous notation:
Notation. Let
$G_0=L_0U_0$
be an algebraic complex Lie group, where
$L_0$
is reductive and
$U_0$
is the unipotent radical of
$G_0$
. Let
$H=SV$
be a connected algebraic complex Lie subgroup, where S is reductive and V is the unipotent radical of H. Assume that
$S\subset L_0$
and
$V\subset U_0$
, and let
$W_0:=U_0/V$
. For w in
$W_0$
, we denote by
$S_w$
the stabiliser of w in S. Let
,
,…,
be the corresponding Lie algebras.
As we have seen, we could also add the assumption
, but it will not be used except at the very end of Section 5.5.
Lemma 5.8. Keep this notation. If
satisfies
, then there exists a nonempty Zariski open set
$W_0'\subset W_0$
, such that for all w in
$W_0'$
,
satisfies
Proof. We first give the proof of Lemma 5.8. By Lemma 4.7, there exists an S-invariant vector subspace
, such that
and the map
is a bijection.
By assumption, there exists a sequence
$g_n\in G_0$
, such that the limit:
exists and is a solvable Lie subalgebra of
.
Since V normalises
, we can assume that:
We denote by
$w_n\in W_0$
the image
$w_n:={\mathrm {exp }}(X_n)$
. The stabiliser
of
$w_n$
in
is also the centraliser of
$X_n$
in
. Therefore, one has the equality:
Therefore, after extraction, the limit
exists and is a Lie subalgebra of
. In particular, this limit
is solvable. Therefore, there exists a maximal unipotent Lie algebra
of
, such that:
and, for n large, one also has
We have found at least one point
$w_0$
in
$W_0$
whose stabiliser
is transversal to a maximal unipotent subalgebra
of
. For such a subalgebra
, the set:
is a nonempty Zariski open subset of
$W_0$
.
By the equivalence of
$Sla$
and
$Tmu$
proven in Proposition 2.1, and since
is reductive, for all w in
$W_0'$
, the stabiliser
satisfies
.
5.5 Pushing up the Rho condition
We now explain how a disintegration argument allows us to push the
$Rho$
-condition from
up to
. It is very surprising that we need this analytic argument to relate these two algebraic conditions.
Proof. We can now end the proof of Proposition 5.7. We keep the notation of Sections 4.4 and 5.4, and we go on to the proof by induction on the dimension of G.
First case:
$L_0\neq G$
. We want to prove the condition
. We first check that the regular representation of
$L_0$
in
$L^2(L_0\times _S W_0)$
is tempered. We argue as in the second case of Section 4.3. As in (4.4), we write the representation
$L^2(L_0\times _S W_0)$
as an integral of
$L^2(L_0/S_w)$
so that we only need to prove that, for Lebesgue almost all w in
$W_0$
, the representation:
$$ \begin{align} L^2(L_0/S_w) \;\;\mbox{is} \ L_0\mbox{-}\mathrm{tempered.} \end{align} $$
Note that the nonempty Zariski open set
$W^{\prime }_0$
introduced in Lemma 5.8 has full Lebesgue measure. We have seen in Lemma 5.8 that:
Since
$\dim L_0 <\dim G$
, our induction assumption implies that:
And, therefore, by Theorem 3.1,
This proves (5.4) and the representation of
$L_0$
in
$L^2(L_0\times _S W_0)$
is tempered.
Finally, using Proposition 4.9, one deduces that
$L^2(G/H)$
is
$L_0$
-tempered, or equivalently
satisfies
.
Second case:
$L_0= G$
. In this case, both G and H must be reductive. As we have seen in Lemma 3.5, we can assume that
. We can also assume that
. Therefore, one is reduced to the case where both
and
are semisimple, which was settled in Proposition 2.10. This ends the proof of Proposition 5.7.
This also ends simultaneously the proofs of Theorems 1.2, 1.6 and 5.1.
5.6 Comments and perspectives
We conclude by a few remaining questions.
5.6.1 Openness of the Sla condition
Question 5.9. Let
be a complex Lie algebra. Is the set of Lie subalgebras
satisfying
, an open set?
We have seen that this set is closed in Remark 5.3, and we have seen that this set is open when
is semisimple in Corollary 1.7.
5.6.2 Regular finite-dimensional representation
Let
be a complex semisimple Lie algebra and
be a complex Lie subalgebra. We denote by
the set of finite-dimensional irreducible representations V of
whose highest weight is regular. We now consider the condition:
Question 5.10. Does one have the equivalence
?
We know that the implication
$\Longrightarrow $
is true.
We also know that the converse
$\Longleftarrow $
is true when
is reductive.
5.6.3 Parabolic induction of tempered representation
The strategy we followed in this series of paper could be simplified if we knew the answer to the following.
Conjecture 5.11. Let G be a real algebraic semisimple group,
$Q=LU$
be a parabolic subgroup and
$\pi $
be a unitary representation of Q. Does one have:
$$ \begin{align*} \pi \ \mathrm{is} \ L\mbox{-}\mathrm{tempered} \Longleftrightarrow {\mathrm{Ind}}_Q^G \pi \ \mathrm{is}\ G\mbox{-}\mathrm{tempered.}\\[-15pt] \end{align*} $$
We know that the implication
$\Longleftarrow $
is true.
We have seen the implication
$\Longrightarrow $
when
$\pi |_U$
is trivial in Lemma 3.6.
We have checked the implication
$\Longrightarrow $
when
$G={\mathrm {SL}}(n,\mathbb { R})$
and
${\mathrm {SL}}(n,\mathbb { C})$
.
Acknowledgements
The authors are grateful to the Institut des Hautes Etudes Scientifiques (IHES) and to The University of Tokyo for their support. The second author was partially supported by Japan Society for the Promotion of Science (JSPS) Kakenhi Grant Number JP18H03669.
Competing Interests
None.
