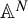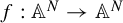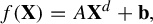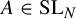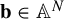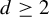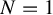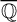1 Introduction
The unicritical polynomials
![]() $f(z)=z^d+c$
have been a test-bed in complex holomorphic dynamics, in part because much in dynamics is determined by the orbits of the critical points, and these polynomials have the fewest possible critical points. Along similar lines, in studying regular polynomial endomorphisms of
$f(z)=z^d+c$
have been a test-bed in complex holomorphic dynamics, in part because much in dynamics is determined by the orbits of the critical points, and these polynomials have the fewest possible critical points. Along similar lines, in studying regular polynomial endomorphisms of
![]() $\mathbb {C}^N$
(that is, polynomial maps which extend regularly to
$\mathbb {C}^N$
(that is, polynomial maps which extend regularly to
![]() $\mathbb {P}^N_{\mathbb {C}}$
) it makes sense again to consider those with the simplest possible critical locus, which in this case would consist of N hyperplanes intersecting properly (ignoring multiplicity for now). After a suitable change of variables, such a map has the form
$\mathbb {P}^N_{\mathbb {C}}$
) it makes sense again to consider those with the simplest possible critical locus, which in this case would consist of N hyperplanes intersecting properly (ignoring multiplicity for now). After a suitable change of variables, such a map has the form
with
![]() $A\in \operatorname {SL}_N(\mathbb {C})$
and
$A\in \operatorname {SL}_N(\mathbb {C})$
and
![]() $\mathbf {b}\in \mathbb {C}^N$
. We identify f with its extension to
$\mathbf {b}\in \mathbb {C}^N$
. We identify f with its extension to
![]() $\mathbb {P}^N_{\mathbb {C}}$
, and write
$\mathbb {P}^N_{\mathbb {C}}$
, and write
![]() $f|_H$
for the restriction of f to the plane at infinity (which is the dth-power map followed by multiplication by A, a minimally critical endomorphism of
$f|_H$
for the restriction of f to the plane at infinity (which is the dth-power map followed by multiplication by A, a minimally critical endomorphism of
![]() $\mathbb {P}^{N-1}$
in the sense of [Reference Ingram10]).
$\mathbb {P}^{N-1}$
in the sense of [Reference Ingram10]).
Write
![]() $L(f)$
for the sum of Lyapunov exponents of f with respect to its invariant measure. It follows from general result of Bedford and Jonsson [Reference Benedetto, Ingram, Jones and Levy2] on regular polynomial endomorphisms that
$L(f)$
for the sum of Lyapunov exponents of f with respect to its invariant measure. It follows from general result of Bedford and Jonsson [Reference Benedetto, Ingram, Jones and Levy2] on regular polynomial endomorphisms that
and our first result is a similar lower bound which becomes arbitrarily large for certain parameters.
Theorem 1 For f as in (1), we have
and
Explicit error terms, which are continuous and plurisubharmonic on
![]() $\operatorname {SL}_N(\mathbb {C})$
, are given in the proof.
$\operatorname {SL}_N(\mathbb {C})$
, are given in the proof.
Note that Favre [Reference Favre7, Theorem C] has characterized the variation of the Lyapunov exponent in a family of maps over a punctured disk, and from this one might deduce many examples of lower bounds on Lyapunov exponents in one-parameter families which become arbitrarily large as one approaches a boundary point.
Before we continue, note that by [Reference Benedetto, Ingram, Jones and Levy2, Theorem 3.2] we have an equality,
where G is Green’s function for f, and
is the critical measure of f. The aforementioned bound of Bedford and Jonsson follows from the non-negativity of the integral. The locus of pairs
![]() $(A, \mathbf {b})$
where the integral in (2) vanishes is a natural generalization of the Mandelbrot set, and contains the image of
$(A, \mathbf {b})$
where the integral in (2) vanishes is a natural generalization of the Mandelbrot set, and contains the image of
![]() $\operatorname {SL}_N(\mathbb {C})$
by
$\operatorname {SL}_N(\mathbb {C})$
by
![]() $A\mapsto (A, \mathbf {0})$
. The following corollary, then, gives a sort of generalization of the compactness of the Mandelbrot set.
$A\mapsto (A, \mathbf {0})$
. The following corollary, then, gives a sort of generalization of the compactness of the Mandelbrot set.
Corollary 2 Let
![]() $\mathcal {M}\subseteq \operatorname {SL}_N(\mathbb {C})\times \mathbb {C}^N$
be the set of pairs
$\mathcal {M}\subseteq \operatorname {SL}_N(\mathbb {C})\times \mathbb {C}^N$
be the set of pairs
![]() $(A, \mathbf {b})$
for which
$(A, \mathbf {b})$
for which
for
![]() $f(\mathbf {X})=A\mathbf {X}^d+\mathbf {b}$
. Then the projection
$f(\mathbf {X})=A\mathbf {X}^d+\mathbf {b}$
. Then the projection
![]() $\mathcal {M}\to \operatorname {SL}_N(\mathbb {C})$
is proper.
$\mathcal {M}\to \operatorname {SL}_N(\mathbb {C})$
is proper.
In the arithmetic context, the critical height of a morphism
![]() $f:\mathbb {P}^N\to \mathbb {P}^N\!,$
denoted
$f:\mathbb {P}^N\to \mathbb {P}^N\!,$
denoted
![]() $\hat {h}_{\mathrm {crit}}(f),$
is the appropriate analogue of the sum of Lyapunov exponents. Extrapolating from a definition of Silverman [Reference Silverman19, p. 101], we defined in [Reference Ingram12] a critical height
$\hat {h}_{\mathrm {crit}}(f),$
is the appropriate analogue of the sum of Lyapunov exponents. Extrapolating from a definition of Silverman [Reference Silverman19, p. 101], we defined in [Reference Ingram12] a critical height
![]() $\hat {h}_{\mathrm {crit}}(f)$
for an endomorphism
$\hat {h}_{\mathrm {crit}}(f)$
for an endomorphism
![]() $f:\mathbb {P}^N\to \mathbb {P}^N$
defined over
$f:\mathbb {P}^N\to \mathbb {P}^N$
defined over
![]() $\overline {\mathbb {Q}}$
, with the property that post-critically finite (PCF) maps all have
$\overline {\mathbb {Q}}$
, with the property that post-critically finite (PCF) maps all have
![]() $\hat {h}_{\mathrm {crit}}(f)=0$
. Specifically, we set
$\hat {h}_{\mathrm {crit}}(f)=0$
. Specifically, we set
where
![]() $C_f$
is the critical locus of f, and
$C_f$
is the critical locus of f, and
![]() $\hat {h}_f$
is the canonical height function associated to f (constructed for subvarieties by Zhang [Reference Zhang21], but note that our canonical height for divisors here and in [Reference Ingram10, Reference Ingram12] is Zhang’s height times the degree of the divisor). Just as Silverman conjectured [Reference Silverman19, p. 101] in dimension 1 that the moduli height is an ample Weil height away from the Lattès maps, confirmed in [Reference Ingram10], it is natural to conjecture [Reference Ingram12] that
$\hat {h}_f$
is the canonical height function associated to f (constructed for subvarieties by Zhang [Reference Zhang21], but note that our canonical height for divisors here and in [Reference Ingram10, Reference Ingram12] is Zhang’s height times the degree of the divisor). Just as Silverman conjectured [Reference Silverman19, p. 101] in dimension 1 that the moduli height is an ample Weil height away from the Lattès maps, confirmed in [Reference Ingram10], it is natural to conjecture [Reference Ingram12] that
![]() $\hat {h}_{\mathrm {crit}}$
is an ample Weil height away from some proper, Zariski closed subset of moduli space. Theorem 3, the arithmetic analogue of Theorem 1, proves this conjecture for fibres of the family (1) over
$\hat {h}_{\mathrm {crit}}$
is an ample Weil height away from some proper, Zariski closed subset of moduli space. Theorem 3, the arithmetic analogue of Theorem 1, proves this conjecture for fibres of the family (1) over
![]() $\operatorname {SL}_N$
, with some uniformity as the fibre varies.
$\operatorname {SL}_N$
, with some uniformity as the fibre varies.
Theorem 3 For
![]() $f:\mathbb {P}^N\to \mathbb {P}^N$
of the form (1) defined over
$f:\mathbb {P}^N\to \mathbb {P}^N$
of the form (1) defined over
![]() $\overline {\mathbb {Q}}$
(with
$\overline {\mathbb {Q}}$
(with
![]() $d\geq 2$
), we have explicit constants
$d\geq 2$
), we have explicit constants
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, depending just on N and d, such that
$C_2$
, depending just on N and d, such that
and
In particular, the critical height is a moduli height for algebraic families in which A is fixed.
Note that the error term in the lower bound comes from a slightly better error term involving both
![]() $h(A)$
and
$h(A)$
and
![]() $h(A^{-1})$
.
$h(A^{-1})$
.
For our next statement, recall that an endomorphism
![]() $f:\mathbb {P}^N\to \mathbb {P}^N$
is post-critically finite if and only if the post-critical locus
$f:\mathbb {P}^N\to \mathbb {P}^N$
is post-critically finite if and only if the post-critical locus
is algebraic, where
![]() $C_f$
is again defined by the vanishing of the determinant of the Jacobian of f.
$C_f$
is again defined by the vanishing of the determinant of the Jacobian of f.
Corollary 4 Fix
![]() $B\geq 0$
. For
$B\geq 0$
. For
![]() $A\in \operatorname {SL}_N(\overline {\mathbb {Q}})$
with
$A\in \operatorname {SL}_N(\overline {\mathbb {Q}})$
with
![]() $h(A)\leq B$
, the set of
$h(A)\leq B$
, the set of
![]() $\mathbf {b}\in \overline {\mathbb {Q}}^N$
for which (1) is PCF is a set of bounded height, with bound depending just on
$\mathbf {b}\in \overline {\mathbb {Q}}^N$
for which (1) is PCF is a set of bounded height, with bound depending just on
![]() $d, N$
, and B.
$d, N$
, and B.
When
![]() $N=1$
, McMullen [Reference McMullen16, Theorem 2.2] (building on work of Thurston) showed that the only non-isotrivial families of PCF rational functions are the flexible Lattès examples. The next result gives a statement in this direction for families of the form (1).
$N=1$
, McMullen [Reference McMullen16, Theorem 2.2] (building on work of Thurston) showed that the only non-isotrivial families of PCF rational functions are the flexible Lattès examples. The next result gives a statement in this direction for families of the form (1).
Theorem 5 Let k be an algebraically closed field of characteristic
![]() $0$
or
$0$
or
![]() $p>d$
. There is no algebraic family over k of PCF maps of the form (1) with A constant, but
$p>d$
. There is no algebraic family over k of PCF maps of the form (1) with A constant, but
![]() $\mathbf {b}$
non-constant.
$\mathbf {b}$
non-constant.
Compare with [Reference Ingram10, Theorem 3], which proves a similar result for a broader class of maps, but with restrictions on the degree. There are also cases in which we know that the induced family
![]() $f|_H(\mathbf {X})=A\mathbf {X}^d$
, if PCF, must be constant (or at least isotrivial), and in those cases we get more out of Theorem 5.
$f|_H(\mathbf {X})=A\mathbf {X}^d$
, if PCF, must be constant (or at least isotrivial), and in those cases we get more out of Theorem 5.
Corollary 6 On
![]() $\mathbb {P}^N_{\mathbb {C}}$
with
$\mathbb {P}^N_{\mathbb {C}}$
with
![]() $N=2$
or
$N=2$
or
![]() $d\geq N^2-N+1$
, any algebraic family of PCF maps of the form (1) is isotrivial.
$d\geq N^2-N+1$
, any algebraic family of PCF maps of the form (1) is isotrivial.
In the same cases, Corollary 4 can also be improved.
Corollary 7 For fixed
![]() $d\geq N^2-N+1$
(or
$d\geq N^2-N+1$
(or
![]() $d\geq 2$
if
$d\geq 2$
if
![]() $N=2$
), PCF maps
$N=2$
), PCF maps
![]() $f:\mathbb {P}^N\to \mathbb {P}^N$
of the form (1) have conjugacy representatives contained in a set of bounded height.
$f:\mathbb {P}^N\to \mathbb {P}^N$
of the form (1) have conjugacy representatives contained in a set of bounded height.
As alluded to above, this discussion fits into a larger framework. Let
![]() $\textsf{M}_d^N$
be the moduli space of endomorphisms of
$\textsf{M}_d^N$
be the moduli space of endomorphisms of
![]() $\mathbb {P}^N$
, and let
$\mathbb {P}^N$
, and let
![]() ${\textsf{P}}_d^N\subseteq {\textsf{M}}_d^N$
be the space of regular polynomial endomorphisms, that is, elements of
${\textsf{P}}_d^N\subseteq {\textsf{M}}_d^N$
be the space of regular polynomial endomorphisms, that is, elements of
![]() ${\textsf{M}}_d^N$
with an invariant hyperplane. Restriction to the hyperplane gives a surjective morphism
${\textsf{M}}_d^N$
with an invariant hyperplane. Restriction to the hyperplane gives a surjective morphism
![]() $\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
. Given that one always deserves a better understanding of
$\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
. Given that one always deserves a better understanding of
![]() $\textsf{M}_d^{N-1}$
than one has of
$\textsf{M}_d^{N-1}$
than one has of
![]() $\textsf{M}_d^N$
, it makes sense to approach
$\textsf{M}_d^N$
, it makes sense to approach
![]() ${\textsf{P}}_d^N\subseteq \textsf{M}_d^N$
by looking at what happens in fibres of the restriction map, and then thinking about how that relative behaviour varies as we vary the fibre.
${\textsf{P}}_d^N\subseteq \textsf{M}_d^N$
by looking at what happens in fibres of the restriction map, and then thinking about how that relative behaviour varies as we vary the fibre.
In relation to the discussion of Silverman’s conjecture in [Reference Ingram10, Reference Ingram12], note that on the relative moduli space
![]() $\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
of regular polynomial endomorphisms, the function
$\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
of regular polynomial endomorphisms, the function
gives a non-negative function interacting nicely with iteration,
and vanishing precisely on those maps whose critical orbits are in some sense no more complex than they need be, given the behaviour at infinity. We offer a conjecture on this relative critical height which, while weaker than Silverman’s, is perhaps also more approachable. A sufficiently precise version of this conjecture, combined with a version of Silverman’s conjecture in dimension one lower, ought to allow one to conclude Silverman’s conjecture for regular polynomial endomorphisms.
Conjecture 8 (The relative critical height is a relative moduli height) For any ample Weil heights
![]() $h_{\textsf{P}_d^N}$
and
$h_{\textsf{P}_d^N}$
and
![]() $h_{\textsf{M}_d^{N-1}}$
on
$h_{\textsf{M}_d^{N-1}}$
on
![]() $\textsf{P}_d^N$
and
$\textsf{P}_d^N$
and
![]() $\textsf{M}_d^{N-1}$
, we have
$\textsf{M}_d^{N-1}$
, we have
Theorem 3 gives a result in this direction for morphisms of a certain form. Note also that a case of Conjecture 8 appears to follow from the results in [Reference Ingram9], but unfortunately with an incompatible definition of the critical height. It remains to be seen if those results can be translated into the terms of the present paper.
We conclude with a few questions about the relative moduli space
![]() $\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
, generalizing the results above.
$\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
, generalizing the results above.
Question 9 Let
![]() $\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
be a relative moduli space of regular polynomial endomorphisms, and let
$\pi :\textsf{P}_d^N\to \textsf{M}_d^{N-1}$
be a relative moduli space of regular polynomial endomorphisms, and let
![]() $\mathcal {M}\subseteq \textsf{P}_d^N$
be the locus where
$\mathcal {M}\subseteq \textsf{P}_d^N$
be the locus where
![]() $L(f)=L(f|_H)+\log d$
. Is
$L(f)=L(f|_H)+\log d$
. Is
![]() $\pi :\mathcal {M}\to \textsf{M}_d^{N-1}$
proper?
$\pi :\mathcal {M}\to \textsf{M}_d^{N-1}$
proper?
An affirmative answer to Question 9 would immediately answer the complex case of the following question on PCF maps (which Theorem 5 answers negatively for maps of the form (1)).
Question 10 (Relative rigidity) Let k be an algebraically closed field of characteristic 0 or
![]() $p>d$
. Can there be an algebraic curve in the PCF locus in
$p>d$
. Can there be an algebraic curve in the PCF locus in
![]() $\textsf{P}_d^{N}$
over k which is contained in a fibre of the projection
$\textsf{P}_d^{N}$
over k which is contained in a fibre of the projection
![]() $\pi :\textsf{P}_d^{N}\to \textsf{M}_d^{N-1}$
?
$\pi :\textsf{P}_d^{N}\to \textsf{M}_d^{N-1}$
?
Of course, if
![]() $\Gamma \subseteq \textsf{P}_d^{N}$
is an algebraic curve in the PCF locus, not contained in a fibre of
$\Gamma \subseteq \textsf{P}_d^{N}$
is an algebraic curve in the PCF locus, not contained in a fibre of
![]() $\pi $
, then
$\pi $
, then
![]() $\pi (\Gamma )\subseteq \textsf{M}_d^{N-1}$
is an algebraic curve of PCF maps. In the case
$\pi (\Gamma )\subseteq \textsf{M}_d^{N-1}$
is an algebraic curve of PCF maps. In the case
![]() $N=2$
, then, a negative answer to Question 10 would imply that any non-trivial algebraic one-parameter family of PCF regular polynomial endomorphisms of
$N=2$
, then, a negative answer to Question 10 would imply that any non-trivial algebraic one-parameter family of PCF regular polynomial endomorphisms of
![]() $\mathbb {P}^2$
restricts to the line at infinity as a flexible Lattès family. The apparent rarity of PCF maps in several variables (see, for example, [Reference Ingram, Ramadas and Silverman13]), in fact, makes it likely that a stronger statement is true.
$\mathbb {P}^2$
restricts to the line at infinity as a flexible Lattès family. The apparent rarity of PCF maps in several variables (see, for example, [Reference Ingram, Ramadas and Silverman13]), in fact, makes it likely that a stronger statement is true.
It is somewhat illustrative to consider Question 10 in the case
![]() $N=1$
. Note that
$N=1$
. Note that
![]() $\mathbb {P}^0$
is a single point, and over an algebraically closed field so is
$\mathbb {P}^0$
is a single point, and over an algebraically closed field so is
![]() $\textsf{M}_d^0$
for each
$\textsf{M}_d^0$
for each
![]() $d\geq 2$
. In particular, any curve in the PCF locus of
$d\geq 2$
. In particular, any curve in the PCF locus of
![]() $\textsf{P}_d^1$
is contained in the unique fibre of the map
$\textsf{P}_d^1$
is contained in the unique fibre of the map
![]() $\textsf{P}_d^{1}\to \textsf{M}_d^{0}$
, and so the expected negative answer to Question 10 simply asserts that there are no non-isotrivial families of PCF polynomials in one variable.
$\textsf{P}_d^{1}\to \textsf{M}_d^{0}$
, and so the expected negative answer to Question 10 simply asserts that there are no non-isotrivial families of PCF polynomials in one variable.
Similarly, the unique (up to conjugacy) endomorphism of
![]() $\mathbb {P}^0$
of degree d has critical height 0, and so Conjecture 8 above asserts that the critical height is a moduli height for polynomials of one variable, which is also true [Reference Ingram8].
$\mathbb {P}^0$
of degree d has critical height 0, and so Conjecture 8 above asserts that the critical height is a moduli height for polynomials of one variable, which is also true [Reference Ingram8].
Before proceeding, we briefly mention the connection between this paper and [Reference Ingram10]. In [Reference Ingram10] we show that the critical height is a moduli height for maps of the form
![]() $f(\mathbf {X})=A\mathbf {X}^d$
in projective coordinates (one d is sufficiently large compared to the dimension), and in the present paper we consider the subclass of these maps fixing one of the ramified hyperplanes. The main novelty in this special case is that we are able to conclude local results (that is, over
$f(\mathbf {X})=A\mathbf {X}^d$
in projective coordinates (one d is sufficiently large compared to the dimension), and in the present paper we consider the subclass of these maps fixing one of the ramified hyperplanes. The main novelty in this special case is that we are able to conclude local results (that is, over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathbb {C}_p$
) which eluded us in [Reference Ingram10]. At the same time, the results of Theorems 3 and 5 have the benefit of applying to all degrees, but the drawback of depending on the behaviour at infinity, while the results in [Reference Ingram10] were absolute. These relative results can of course be combined with the results of [Reference Ingram10] applied to the map restricted to the invariant hyperplane, and we have demonstrated that in various places. In general, the estimate needed to deduce the results in this note are somewhat more delicate than those in [Reference Ingram10], and have at least the potential to be extended to regular polynomial endomorphisms in general.
$\mathbb {C}_p$
) which eluded us in [Reference Ingram10]. At the same time, the results of Theorems 3 and 5 have the benefit of applying to all degrees, but the drawback of depending on the behaviour at infinity, while the results in [Reference Ingram10] were absolute. These relative results can of course be combined with the results of [Reference Ingram10] applied to the map restricted to the invariant hyperplane, and we have demonstrated that in various places. In general, the estimate needed to deduce the results in this note are somewhat more delicate than those in [Reference Ingram10], and have at least the potential to be extended to regular polynomial endomorphisms in general.
In §2 we work over an algebraically closed field, complete with respect to some absolute value, and prove most of the technical lemmas. Section 3 introduces a ‘relative rate of escape’ for a hypersurface under a map of the form (1), which we then use to prove Theorem 1 and Corollary 2, as well as a statement of good reduction. Section 4 contains the proofs of Theorem 3 and Corollary 4. Finally, in §5 we delve deeper into the case
![]() $N=2$
, bootstrapping some results from what is known about critical dynamics in one variable.
$N=2$
, bootstrapping some results from what is known about critical dynamics in one variable.
2 Estimates on pulling back and pushing forward
Let K be an algebraically closed field, complete with respect to some absolute value
![]() $|\cdot |$
. We write
$|\cdot |$
. We write
![]() $\|x_1, \ldots ,x_n\|=\max \{|x_1|, \ldots , |x_n|\}$
, and
$\|x_1, \ldots ,x_n\|=\max \{|x_1|, \ldots , |x_n|\}$
, and
![]() $\log ^+ x = \max \{\log x, 0\}$
. Note that the triangle and ultrametric inequalities combine to give the following estimate, of which we make liberal use:
$\log ^+ x = \max \{\log x, 0\}$
. Note that the triangle and ultrametric inequalities combine to give the following estimate, of which we make liberal use:
Note that an absolute value is non-archimedean precisely if
![]() $\log ^+|n|=0$
for all
$\log ^+|n|=0$
for all
![]() $n\in \mathbb {Z}$
. To avoid unnecessary case distinctions in several places, we adopt the conventions that
$n\in \mathbb {Z}$
. To avoid unnecessary case distinctions in several places, we adopt the conventions that
![]() $\log 0 = -\infty $
, and that
$\log 0 = -\infty $
, and that
![]() $-\infty < x< \infty $
and
$-\infty < x< \infty $
and
![]() $\infty + x = \infty $
for all real numbers x.
$\infty + x = \infty $
for all real numbers x.
Before continuing, we comment on various numbered constants
![]() $c_i$
that appear in the arguments below. Throughout, these constants have always been chosen to be non-negative, to simplify the manipulation of inequalities (sometimes at the cost of optimal bounds). Moreover, the constants
$c_i$
that appear in the arguments below. Throughout, these constants have always been chosen to be non-negative, to simplify the manipulation of inequalities (sometimes at the cost of optimal bounds). Moreover, the constants
![]() $c_i$
depend only on d (the degree of the endomorphisms f under consideration) and N (the dimension of the ambient space). Finally, these constants will all have value 0, except in the case of archimedean absolute values, or p-adic absolute values for
$c_i$
depend only on d (the degree of the endomorphisms f under consideration) and N (the dimension of the ambient space). Finally, these constants will all have value 0, except in the case of archimedean absolute values, or p-adic absolute values for
![]() $p\leq d$
.
$p\leq d$
.
Given a homogeneous form F with coefficients in K, we set
![]() $\|F\|$
to be the largest absolute value of a coefficient of F, in other words the Gauss norm when
$\|F\|$
to be the largest absolute value of a coefficient of F, in other words the Gauss norm when
![]() $|\cdot |$
is non-archimedean. In [Reference Ingram12] we used the Mahler measure at the archimedean places, which is more natural, but turns out to be less convenient for the estimates in this note, which follows [Reference Ingram10] closely.
$|\cdot |$
is non-archimedean. In [Reference Ingram12] we used the Mahler measure at the archimedean places, which is more natural, but turns out to be less convenient for the estimates in this note, which follows [Reference Ingram10] closely.
Lemma 11 For
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $F_i$
be a homogeneous form in
$F_i$
be a homogeneous form in
![]() $N+1$
variables. Then
$N+1$
variables. Then
 $$ \begin{align*}-2N\sum_{i=1}^n\deg(F_i)\log^+|2|\leq \log\bigg\|\prod_{i=1}^{n}F_i\bigg\|-\sum_{i=1}^{n}\log\|F_{i}\|\leq 2N\sum_{i=1}^n\deg(F_i)\log^+|2|.\end{align*} $$
$$ \begin{align*}-2N\sum_{i=1}^n\deg(F_i)\log^+|2|\leq \log\bigg\|\prod_{i=1}^{n}F_i\bigg\|-\sum_{i=1}^{n}\log\|F_{i}\|\leq 2N\sum_{i=1}^n\deg(F_i)\log^+|2|.\end{align*} $$
Let
![]() $F_{i, j}$
be homogeneous forms in
$F_{i, j}$
be homogeneous forms in
![]() $N+1$
variables such that, for each
$N+1$
variables such that, for each
![]() $1\leq i\leq n$
, the form
$1\leq i\leq n$
, the form
![]() $\prod _{j=1}^{m_i}F_{i, j}$
has degree
$\prod _{j=1}^{m_i}F_{i, j}$
has degree
![]() $\delta $
. Then
$\delta $
. Then
 $$ \begin{align}\log\bigg\|\sum_{i=1}^n \prod_j^{m_i} F_{i, j}\bigg\|\leq\max_{1\leq i\leq n}\sum_{j=1}^{m_i}\log\|F_{i, j}\|+\log^+|n|+ 2N\delta \log^+|2|.\end{align} $$
$$ \begin{align}\log\bigg\|\sum_{i=1}^n \prod_j^{m_i} F_{i, j}\bigg\|\leq\max_{1\leq i\leq n}\sum_{j=1}^{m_i}\log\|F_{i, j}\|+\log^+|n|+ 2N\delta \log^+|2|.\end{align} $$
Proof. If
![]() $|\cdot |$
is non-archimedean, then these claims follow from the Gauss lemma and the ultrametric inequality (and note that the error terms containing
$|\cdot |$
is non-archimedean, then these claims follow from the Gauss lemma and the ultrametric inequality (and note that the error terms containing
![]() $\log ^+|m|$
, for m an integer, vanish).
$\log ^+|m|$
, for m an integer, vanish).
In the archimedean case, we recall the logarithmic Mahler measure of F, defined as
where
![]() $\mu $
is the usual normalized Haar measure on the unit circle in each variable. On the one hand, it is clear from the definition that
$\mu $
is the usual normalized Haar measure on the unit circle in each variable. On the one hand, it is clear from the definition that
![]() $m(FG)=m(F)+m(G)$
. On the other, it turns out that the Mahler measure is not too different from
$m(FG)=m(F)+m(G)$
. On the other, it turns out that the Mahler measure is not too different from
![]() $\log \|F\|$
, as pointed out by Mahler [Reference Mahler15]. Specifically,
$\log \|F\|$
, as pointed out by Mahler [Reference Mahler15]. Specifically,
Notice
 $$ \begin{align*} \log\bigg\|\prod_{i=1}^{n}F_i\bigg\|&\leq m\bigg(\prod_{i=1}^{n}F_i\bigg)+N\deg\bigg(\prod_{i=1}^nF_i\bigg)\log 2\\ &=\sum_{i=1}^nm(F_i)+N\sum_{i=1}^n\deg(F_i)\log 2 \end{align*} $$
$$ \begin{align*} \log\bigg\|\prod_{i=1}^{n}F_i\bigg\|&\leq m\bigg(\prod_{i=1}^{n}F_i\bigg)+N\deg\bigg(\prod_{i=1}^nF_i\bigg)\log 2\\ &=\sum_{i=1}^nm(F_i)+N\sum_{i=1}^n\deg(F_i)\log 2 \end{align*} $$
 $$\begin{align*}&\leq \sum_{i=1}^n \log\|F_i\|+N\sum_{i=1}^n\bigg(\frac{1}{2}\log(\deg(F_i)+1)+\deg(F_i)\log 2\bigg)\\ &\leq \sum_{i=1}^n \log\|F_i\|+2N\log 2\bigg(\sum_{i=1}^n\deg(F_i)\bigg) \end{align*}$$
$$\begin{align*}&\leq \sum_{i=1}^n \log\|F_i\|+N\sum_{i=1}^n\bigg(\frac{1}{2}\log(\deg(F_i)+1)+\deg(F_i)\log 2\bigg)\\ &\leq \sum_{i=1}^n \log\|F_i\|+2N\log 2\bigg(\sum_{i=1}^n\deg(F_i)\bigg) \end{align*}$$
using the estimates
![]() $\log (1+x)\leq x$
, for
$\log (1+x)\leq x$
, for
![]() $x\geq 0$
, and
$x\geq 0$
, and
![]() $\tfrac 12\leq \log 2$
.
$\tfrac 12\leq \log 2$
.
The inequality in the other direction is derived similarly.
For (3), by the triangle inequality,
 $$ \begin{align*} \log\bigg\|\sum_{i=1}^n \prod_j^{m_i} F_{i, j}\bigg\|&\leq \max_{1\leq i\leq n}\log\bigg\|\prod_j^{m_i} F_{i, j}\bigg\|+\log n\\ &\leq \max_{1\leq i\leq n}m\bigg(\prod_j^{m_i} F_{i, j}\bigg)+N\delta\log 2+\log n\\ &=\max_{1\leq i\leq n}\sum_j^{m_i}m( F_{i, j})+N\delta\log 2+\log n\\ &\leq \max_{1\leq i\leq n}\sum_j^{m_i}\log\| F_{i, j}\|+\max_{1\leq i\leq n}\sum_j^{m_i}\frac{N}{2}\log(\deg(F_{i, j})+1)\\ &\quad +\,N\delta\log 2+\log n, \end{align*} $$
$$ \begin{align*} \log\bigg\|\sum_{i=1}^n \prod_j^{m_i} F_{i, j}\bigg\|&\leq \max_{1\leq i\leq n}\log\bigg\|\prod_j^{m_i} F_{i, j}\bigg\|+\log n\\ &\leq \max_{1\leq i\leq n}m\bigg(\prod_j^{m_i} F_{i, j}\bigg)+N\delta\log 2+\log n\\ &=\max_{1\leq i\leq n}\sum_j^{m_i}m( F_{i, j})+N\delta\log 2+\log n\\ &\leq \max_{1\leq i\leq n}\sum_j^{m_i}\log\| F_{i, j}\|+\max_{1\leq i\leq n}\sum_j^{m_i}\frac{N}{2}\log(\deg(F_{i, j})+1)\\ &\quad +\,N\delta\log 2+\log n, \end{align*} $$
which gives the desired bound again using
![]() $\log (1+x)\leq x$
and
$\log (1+x)\leq x$
and
![]() $\tfrac 12\leq \log 2$
.
$\tfrac 12\leq \log 2$
.
Let H denote the hyperplane of
![]() $\mathbb {P}^N$
defined by
$\mathbb {P}^N$
defined by
![]() $X_{N+1}=0$
, and for any effective divisor D on
$X_{N+1}=0$
, and for any effective divisor D on
![]() $\mathbb {P}^N$
intersecting H properly, and defined by
$\mathbb {P}^N$
intersecting H properly, and defined by
![]() $F=0$
, set
$F=0$
, set
This definition does not depend on the choice of homogeneous form F representing D, and
![]() $\lambda (D)\geq 0$
. For some intuition, observe that on
$\lambda (D)\geq 0$
. For some intuition, observe that on
![]() $\mathbb {P}^1$
we have
$\mathbb {P}^1$
we have
for the divisor
![]() $[z]$
corresponding to the point
$[z]$
corresponding to the point
![]() $z\in \mathbb {P}^1_K\setminus \{\infty \}$
. We will also define, for a divisor D defined by the homogeneous form
$z\in \mathbb {P}^1_K\setminus \{\infty \}$
. We will also define, for a divisor D defined by the homogeneous form
![]() $F(\mathbf {X})=\sum _{i=0}^{\deg (F)} X_{N+1}^kF_k(X_1, \ldots , X_N)$
, the quantity
$F(\mathbf {X})=\sum _{i=0}^{\deg (F)} X_{N+1}^kF_k(X_1, \ldots , X_N)$
, the quantity
provided that D does not contain H or
![]() $(0, 0, \ldots , 1)$
, in which case we have
$(0, 0, \ldots , 1)$
, in which case we have
![]() $F_{\deg (D)}=F(0, 0, \ldots , 1)\neq 0$
. Note that it follows immediately from the definitions that
$F_{\deg (D)}=F(0, 0, \ldots , 1)\neq 0$
. Note that it follows immediately from the definitions that
but there is no bound in the other direction.
Remark 12 Although it is most efficient and transparent here to work in terms of homogeneous forms, it is worth noting that what we are doing fits into the framework of the geometry of arithmetic varieties as studied in arithmetic intersection theory. More concretely, if the absolute value on K is non-archimedean, then K has a ring of integers
![]() $\mathcal {O}\subseteq K$
, and the morphism
$\mathcal {O}\subseteq K$
, and the morphism
![]() $f:\mathbb {P}^N_K\to \mathbb {P}^N_K$
extends to a rational map of schemes
$f:\mathbb {P}^N_K\to \mathbb {P}^N_K$
extends to a rational map of schemes
![]() $f:\mathbb {P}^N_{\mathcal {O}}\dashrightarrow \mathbb {P}^N_{\mathcal {O}}$
. The homogeneous form
$f:\mathbb {P}^N_{\mathcal {O}}\dashrightarrow \mathbb {P}^N_{\mathcal {O}}$
. The homogeneous form
![]() $F(\mathbf {X})\in \mathcal {O}[X_1, \ldots , X_{N+1}]$
now defines an effective divisor
$F(\mathbf {X})\in \mathcal {O}[X_1, \ldots , X_{N+1}]$
now defines an effective divisor
![]() $\mathbb {P}^N_{\mathcal {O}}$
, specifically
$\mathbb {P}^N_{\mathcal {O}}$
, specifically
![]() $\overline {D}-\log _v\|F\|\mathbb {P}_{k}^N$
, where
$\overline {D}-\log _v\|F\|\mathbb {P}_{k}^N$
, where
![]() $\overline {D}$
is the Zariski closure of the divisor defined by F on the generic fibre,
$\overline {D}$
is the Zariski closure of the divisor defined by F on the generic fibre,
![]() $\mathbb {P}_{k}^N$
is the special fibre, and
$\mathbb {P}_{k}^N$
is the special fibre, and
![]() $\log _v$
is normalized so that
$\log _v$
is normalized so that
![]() $\log _v|\pi |=-1$
for any uniformizer
$\log _v|\pi |=-1$
for any uniformizer
![]() $\pi $
of the maximal ideal of
$\pi $
of the maximal ideal of
![]() $\mathcal {O}$
. Our estimates on how
$\mathcal {O}$
. Our estimates on how
![]() $\log \|F\|$
changes under pulling back by (some model of) f now correspond to estimates on the difference between
$\log \|F\|$
changes under pulling back by (some model of) f now correspond to estimates on the difference between
![]() $f^*\overline {D}$
and
$f^*\overline {D}$
and
![]() $\overline {f^* D}$
, for divisors D on the generic fibre (but there appears to be no simpler way of making these estimates than to reduce things to computations involving homogeneous forms). Our estimates on pushing forward are somewhat more fraught in this context, since
$\overline {f^* D}$
, for divisors D on the generic fibre (but there appears to be no simpler way of making these estimates than to reduce things to computations involving homogeneous forms). Our estimates on pushing forward are somewhat more fraught in this context, since
![]() $f:\mathbb {P}^N_{\mathcal {O}}\dashrightarrow \mathbb {P}^N_{\mathcal {O}}$
is generally not a morphism, but proceeding as in [Reference Ingram12] we may work with integral models, and recover something similar. All of these subtleties are eliminated by taking this more elementary approach.
$f:\mathbb {P}^N_{\mathcal {O}}\dashrightarrow \mathbb {P}^N_{\mathcal {O}}$
is generally not a morphism, but proceeding as in [Reference Ingram12] we may work with integral models, and recover something similar. All of these subtleties are eliminated by taking this more elementary approach.
Lemma 13 For effective divisors
![]() $D_i$
,
$D_i$
,
![]() $1\leq i\leq n$
, not containing H we have
$1\leq i\leq n$
, not containing H we have
 $$ \begin{align} -4N\sum_{i=1}^n\deg(D_i)\log^+|2| &\leq \lambda\bigg(\sum_{i=1}^n D_i\bigg)- \sum_{i=1}^n\lambda(D_i)\nonumber\\ &\leq 4N\sum_{i=1}^n\deg(D_i)\log^+|2|, \end{align} $$
$$ \begin{align} -4N\sum_{i=1}^n\deg(D_i)\log^+|2| &\leq \lambda\bigg(\sum_{i=1}^n D_i\bigg)- \sum_{i=1}^n\lambda(D_i)\nonumber\\ &\leq 4N\sum_{i=1}^n\deg(D_i)\log^+|2|, \end{align} $$
and if the
![]() $D_i$
do not contain the origin, we also have
$D_i$
do not contain the origin, we also have
 $$ \begin{align} \mu\bigg(\sum_{i=1}^n D_i\bigg)\geq\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|-(n-1)\log^+\bigg|\sum_{i=1}^n\deg(D_i)\bigg|. \end{align} $$
$$ \begin{align} \mu\bigg(\sum_{i=1}^n D_i\bigg)\geq\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|-(n-1)\log^+\bigg|\sum_{i=1}^n\deg(D_i)\bigg|. \end{align} $$
Finally, if
![]() $\mu (D)\geq 0$
, then
$\mu (D)\geq 0$
, then
for any form
![]() $F(\mathbf {X})=\sum _{i=0}^{\deg (F)} X_{N+1}^iF_i(X_1, \ldots , X_N)$
defining D.
$F(\mathbf {X})=\sum _{i=0}^{\deg (F)} X_{N+1}^iF_i(X_1, \ldots , X_N)$
defining D.
Proof. Claim (5) follows immediately from Lemma 11.
For (6) in the non-archimedean case, the proof is similar to that of the Gauss lemma.
Specifically, let
![]() $D_i$
be defined by
$D_i$
be defined by
![]() $F_i=0$
, with
$F_i=0$
, with
 $$ \begin{align*}F_i(\mathbf{X})=\sum_{j=0}^{\deg(F_i)}X_{N+1}^jF_{i, j}(X_1, \ldots, X_N),\end{align*} $$
$$ \begin{align*}F_i(\mathbf{X})=\sum_{j=0}^{\deg(F_i)}X_{N+1}^jF_{i, j}(X_1, \ldots, X_N),\end{align*} $$
and choose
![]() $k_i$
minimally so that
$k_i$
minimally so that
Now, for
![]() $\delta =\sum _{i=1}^n\deg (D_i)$
we have
$\delta =\sum _{i=1}^n\deg (D_i)$
we have
![]() $\sum _{i=1}^n D_i$
defined by the vanishing of
$\sum _{i=1}^n D_i$
defined by the vanishing of
 $$ \begin{align*}\sum_{\ell = 0}^{\delta}X_{N+1}^\ell G_{\ell}\end{align*} $$
$$ \begin{align*}\sum_{\ell = 0}^{\delta}X_{N+1}^\ell G_{\ell}\end{align*} $$
where
 $$ \begin{align*}G_\ell= \sum_{j_1+\cdots +j_n=\ell}\prod_{i=1}^nF_{i, j_i}.\end{align*} $$
$$ \begin{align*}G_\ell= \sum_{j_1+\cdots +j_n=\ell}\prod_{i=1}^nF_{i, j_i}.\end{align*} $$
Note that the number of summands is the number of solutions to
![]() $j_1+\cdots + j_n=\ell $
satisfying
$j_1+\cdots + j_n=\ell $
satisfying
![]() $0\leq j_i\leq \deg (F_i)$
for all
$0\leq j_i\leq \deg (F_i)$
for all
![]() $0\leq i \leq n$
, which we crudely estimate as at most
$0\leq i \leq n$
, which we crudely estimate as at most
![]() $(\ell +1)^{n-1}$
. Then we have, by Lemma 11,
$(\ell +1)^{n-1}$
. Then we have, by Lemma 11,
 $$ \begin{align*} \log\|G_\ell\| &\leq\max_{j_1+\cdots +j_n=\ell}\sum_{i=1}^{n}(\log\|F_{i, j_i}\|+2N(\deg(D_i)-j_i)\log^+|2|)\\ &\quad+(n-1)\log^+|\ell+1|. \end{align*} $$
$$ \begin{align*} \log\|G_\ell\| &\leq\max_{j_1+\cdots +j_n=\ell}\sum_{i=1}^{n}(\log\|F_{i, j_i}\|+2N(\deg(D_i)-j_i)\log^+|2|)\\ &\quad+(n-1)\log^+|\ell+1|. \end{align*} $$
Choosing
![]() $j_1+\cdots +j_n=\ell $
maximizing the right-hand side, we have
$j_1+\cdots +j_n=\ell $
maximizing the right-hand side, we have
 $$ \begin{align*} \log|G_{\delta}|-\log\|G_\ell\|&\geq \sum_{i=1}^n(\log|F_{i, \deg(F_i)}|-\log\|F_{i, j_i}\|)\\ &\quad -\,2N\sum_{i=1}^n(\deg(D_i)-j_i)\log^+|2| - (n-1)\log^+|\ell+1|\\ &\geq \sum_{i=1}^n(\mu(D_i)-2N\log^+|2|)(\deg(D_i)-j_i)\\ &\quad -\,(n-1)\log^+|\ell+1|\\ &\geq \big(\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|\big)\sum_{i=1}^n(\deg(D_i)-j_i)\\ &\quad -\,(n-1)\log^+|\ell+1|\\ &=\big(\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|\big)(\delta-\ell)\\ &\quad -\,(n-1)\log^+|\ell+1|. \end{align*} $$
$$ \begin{align*} \log|G_{\delta}|-\log\|G_\ell\|&\geq \sum_{i=1}^n(\log|F_{i, \deg(F_i)}|-\log\|F_{i, j_i}\|)\\ &\quad -\,2N\sum_{i=1}^n(\deg(D_i)-j_i)\log^+|2| - (n-1)\log^+|\ell+1|\\ &\geq \sum_{i=1}^n(\mu(D_i)-2N\log^+|2|)(\deg(D_i)-j_i)\\ &\quad -\,(n-1)\log^+|\ell+1|\\ &\geq \big(\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|\big)\sum_{i=1}^n(\deg(D_i)-j_i)\\ &\quad -\,(n-1)\log^+|\ell+1|\\ &=\big(\min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|\big)(\delta-\ell)\\ &\quad -\,(n-1)\log^+|\ell+1|. \end{align*} $$
Dividing both sides by
![]() $\delta -\ell $
and taking the minimum over
$\delta -\ell $
and taking the minimum over
![]() $0\leq \ell <\delta $
gives
$0\leq \ell <\delta $
gives
 $$ \begin{align*} \mu\bigg(\sum_{i=1}^n D_i\bigg)\geq \min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|-(n-1)\max_{0\leq \ell < \delta}\bigg(\frac{\log^+|\ell+1|}{\delta-\ell}\bigg). \end{align*} $$
$$ \begin{align*} \mu\bigg(\sum_{i=1}^n D_i\bigg)\geq \min_{1\leq i\leq n}\mu(D_i)-2N\log^+|2|-(n-1)\max_{0\leq \ell < \delta}\bigg(\frac{\log^+|\ell+1|}{\delta-\ell}\bigg). \end{align*} $$
Note that the maximum in the last term is attained at
![]() $\ell =\delta -1$
.
$\ell =\delta -1$
.
The last claim is simply due to the fact that
![]() $\mu (D)\geq 0$
implies
$\mu (D)\geq 0$
implies
for all
![]() $0\leq k<\deg (D)$
, whence
$0\leq k<\deg (D)$
, whence
![]() $\log \|F\|=\log |F_{\deg (D)}|$
.
$\log \|F\|=\log |F_{\deg (D)}|$
.
We will fix a block matrix
 $$ \begin{align}L=\begin{pmatrix}A & \mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix},\end{align} $$
$$ \begin{align}L=\begin{pmatrix}A & \mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix},\end{align} $$
where A is
![]() $N\times N$
,
$N\times N$
,
![]() $\mathbf {b}$
is
$\mathbf {b}$
is
![]() $N\times 1$
, and
$N\times 1$
, and
![]() $\mathbf {0}$
is the
$\mathbf {0}$
is the
![]() $1\times N$
zero vector, and use the same symbol to denote the resulting linear map
$1\times N$
zero vector, and use the same symbol to denote the resulting linear map
![]() $L:\mathbb {P}^{N}\to \mathbb {P}^{N}\!.$
Note that the inverse map/matrix is given by
$L:\mathbb {P}^{N}\to \mathbb {P}^{N}\!.$
Note that the inverse map/matrix is given by
 $$ \begin{align*}L^{-1}=\begin{pmatrix}A^{-1} & -A^{-1}\mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}L^{-1}=\begin{pmatrix}A^{-1} & -A^{-1}\mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix}.\end{align*} $$
We will also write
![]() $\phi $
for the power map of degree d on
$\phi $
for the power map of degree d on
![]() $\mathbb {P}^{N}\!,$
so that
$\mathbb {P}^{N}\!,$
so that
Note that endomorphisms of
![]() $\mathbb {P}^N$
of the form under consideration, described in (1), are precisely those of the form
$\mathbb {P}^N$
of the form under consideration, described in (1), are precisely those of the form
![]() $f=L\circ \phi $
.
$f=L\circ \phi $
.
We will be interested in the behaviour of the quantities
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
under pushing-forward and pulling-back divisors by f, and so consequently by L and by
$\mu $
under pushing-forward and pulling-back divisors by f, and so consequently by L and by
![]() $\phi $
. First, the power map.
$\phi $
. First, the power map.
Lemma 14 For
![]() $\phi $
as above, and any effective divisor D,
$\phi $
as above, and any effective divisor D,
and
Proof. Let F be some homogeneous form whose vanishing defines D. For the pullback, notice that
![]() $\phi ^* D$
is defined by
$\phi ^* D$
is defined by
![]() $F(X_1^d, \ldots , X_{N+1}^d)$
. The coefficients of this homogeneous form are exactly those of F (associated to different monomials), and so we certainly have
$F(X_1^d, \ldots , X_{N+1}^d)$
. The coefficients of this homogeneous form are exactly those of F (associated to different monomials), and so we certainly have
![]() $\|F\|=\|F(X_1^d, \ldots , X_{N+1}^d)\|$
. The claim about
$\|F\|=\|F(X_1^d, \ldots , X_{N+1}^d)\|$
. The claim about
![]() $\lambda (\phi ^*D)$
follows immediately, while the claim about
$\lambda (\phi ^*D)$
follows immediately, while the claim about
![]() $\mu (\phi ^* D)$
follows once we note that
$\mu (\phi ^* D)$
follows once we note that
![]() $\phi ^* D$
has degree
$\phi ^* D$
has degree
![]() $d\deg (D)$
.
$d\deg (D)$
.
Now consider the pushforward. For any tuple
![]() $\mathbf {\zeta }=(\zeta _1, \ldots , \zeta _N)$
of dth roots of unity, let
$\mathbf {\zeta }=(\zeta _1, \ldots , \zeta _N)$
of dth roots of unity, let
![]() $D_{\mathbf {\zeta }}$
be the divisor defined by the vanishing of
$D_{\mathbf {\zeta }}$
be the divisor defined by the vanishing of
![]() $F_{\mathbf {\zeta }}(X_1, \ldots , X_{N+1})=F(\zeta _1X_1, \ldots , \zeta _NX_N, X_{N+1})$
, noting that
$F_{\mathbf {\zeta }}(X_1, \ldots , X_{N+1})=F(\zeta _1X_1, \ldots , \zeta _NX_N, X_{N+1})$
, noting that
 $$ \begin{align*}\phi^*\phi_* D=\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}.\end{align*} $$
$$ \begin{align*}\phi^*\phi_* D=\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}.\end{align*} $$
Also, note that
![]() $\lambda (D_{\mathbf {\zeta }})=\lambda (D)$
and
$\lambda (D_{\mathbf {\zeta }})=\lambda (D)$
and
![]() $\mu (D_{\mathbf {\zeta }})=\mu (D)$
, since the coefficients of
$\mu (D_{\mathbf {\zeta }})=\mu (D)$
, since the coefficients of
![]() $F_{\mathbf {\zeta }}$
are the coefficients of F multiplied by various roots of unity. By (5) of Lemma 13 and the estimates for the pullback above, we have
$F_{\mathbf {\zeta }}$
are the coefficients of F multiplied by various roots of unity. By (5) of Lemma 13 and the estimates for the pullback above, we have
 $$ \begin{align*} \lambda(\phi_*D)&=\lambda(\phi^*\phi_*D)\\ &=\lambda\bigg(\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}\bigg)\\ &\leq \sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}\lambda(D_{\mathbf{\zeta}})+4N\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1} \deg(D_{\mathbf{\zeta}})\log^+|2| \\ &= d^N\lambda(D)+4Nd^{N}\deg(D)\log^+|2| \end{align*} $$
$$ \begin{align*} \lambda(\phi_*D)&=\lambda(\phi^*\phi_*D)\\ &=\lambda\bigg(\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}\bigg)\\ &\leq \sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}\lambda(D_{\mathbf{\zeta}})+4N\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1} \deg(D_{\mathbf{\zeta}})\log^+|2| \\ &= d^N\lambda(D)+4Nd^{N}\deg(D)\log^+|2| \end{align*} $$
and, by the essentially the same calculation,
Meanwhile,
 $$ \begin{align*} \mu(\phi_* D)&= d\mu(\phi^*\phi_* D)\\ &= d\mu\bigg(\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}\bigg)\\ &\geq d\min\{\mu(D_{\mathbf{\zeta}})\}-2dN\log^+|2|-d(d^N-1)\log^+\bigg|\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}\deg(D_{\mathbf{\zeta}})\bigg|\\ &= d\mu(D)-2dN\log^+|2|-d(d^N-1)\log^+|d^N\deg(D)|.\\[-37pt] \end{align*} $$
$$ \begin{align*} \mu(\phi_* D)&= d\mu(\phi^*\phi_* D)\\ &= d\mu\bigg(\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}D_{\mathbf{\zeta}}\bigg)\\ &\geq d\min\{\mu(D_{\mathbf{\zeta}})\}-2dN\log^+|2|-d(d^N-1)\log^+\bigg|\sum_{\zeta_1^d=\cdots =\zeta_{N}^d=1}\deg(D_{\mathbf{\zeta}})\bigg|\\ &= d\mu(D)-2dN\log^+|2|-d(d^N-1)\log^+|d^N\deg(D)|.\\[-37pt] \end{align*} $$
Next we will estimate
![]() $\lambda (L^*D)$
and
$\lambda (L^*D)$
and
![]() $\lambda (L_*D)$
, and
$\lambda (L_*D)$
, and
![]() $\mu (L^*D)$
and
$\mu (L^*D)$
and
![]() $\mu (L_*D)$
. But since our error terms will depend on the matrices representing these linear maps, it makes sense to introduce some Néron functions on matrices. The following lemma is easy to check, and left to the reader.
$\mu (L_*D)$
. But since our error terms will depend on the matrices representing these linear maps, it makes sense to introduce some Néron functions on matrices. The following lemma is easy to check, and left to the reader.
Lemma 15 For a matrix A with (
![]() $i, j$
)th entry
$i, j$
)th entry
![]() $A_{i, j}$
, let
$A_{i, j}$
, let
![]() $\|A\|=\max _{i, j}|A_{i, j}|$
. Let
$\|A\|=\max _{i, j}|A_{i, j}|$
. Let
![]() $\lambda :\operatorname {SL}_{N}(K)\to \mathbb {R}$
be defined by
$\lambda :\operatorname {SL}_{N}(K)\to \mathbb {R}$
be defined by
and
![]() $\xi :\operatorname {SL}_{N}(K)\to \mathbb {R}$
by
$\xi :\operatorname {SL}_{N}(K)\to \mathbb {R}$
by
Then the functions
![]() $\lambda $
and
$\lambda $
and
![]() $\xi $
are non-negative, and satisfy
$\xi $
are non-negative, and satisfy
and
Lemma 14 describes the behaviour certain quantities associated to divisors under pushing forward or pulling back by the power map, and now we present a corresponding result relative to linear maps. These estimates are very similar to those in the proof of [Reference Ingram10, Lemma 10], but the precise bounds depend on the special form of the matrix L.
Lemma 16 For
L as in (7), and any effective divisor D, we have
 $$ \begin{align*} &-\deg(D)(\log\|L\|-\log\|A\| +\lambda(L)+c_2) - c_1 \leq \lambda(L^* D)-\lambda(D) \\ &\quad \leq \deg(D)(\log\|L\|-\log\|A\|+\lambda(A)+c_2) + c_1 \end{align*} $$
$$ \begin{align*} &-\deg(D)(\log\|L\|-\log\|A\| +\lambda(L)+c_2) - c_1 \leq \lambda(L^* D)-\lambda(D) \\ &\quad \leq \deg(D)(\log\|L\|-\log\|A\|+\lambda(A)+c_2) + c_1 \end{align*} $$
and
 $$ \begin{align*} &-\deg(D)(\log\|L\|-\log\|A\| +\lambda(A)+c_2) - c_1 \leq \lambda(L_* D)-\lambda(D) \\ &\quad \leq \deg(D)(\log\|L\|-\log\|A\| +\lambda(L)+c_2) + c_1. \end{align*} $$
$$ \begin{align*} &-\deg(D)(\log\|L\|-\log\|A\| +\lambda(A)+c_2) - c_1 \leq \lambda(L_* D)-\lambda(D) \\ &\quad \leq \deg(D)(\log\|L\|-\log\|A\| +\lambda(L)+c_2) + c_1. \end{align*} $$
Proof. Choose a defining homogeneous form F for D. Any homogeneous form
![]() $F(\mathbf {X})=\sum c_mm(\mathbf {X})$
is a linear combination of at most
$F(\mathbf {X})=\sum c_mm(\mathbf {X})$
is a linear combination of at most
![]() $\binom {\deg (F)+N}{N}$
monomials of degree
$\binom {\deg (F)+N}{N}$
monomials of degree
![]() $\deg (F)$
, and so we have, for any
$\deg (F)$
, and so we have, for any
![]() $B\in \operatorname {SL}_{N+1}(K)$
,
$B\in \operatorname {SL}_{N+1}(K)$
,
 $$ \begin{align} \log\|F(B\mathbf{X})\|&= \log\bigg\|\sum c_m m(B\mathbf{X})\bigg\|\nonumber \\ &\leq \log\max \|c_m m(B\mathbf{X})\| + \log^+\bigg|\binom{\deg(F)+N}{N}\bigg| \nonumber \\ &\leq \log\|F\|+\deg(F)\log\|B\|+\deg(F)\log^+|N+1|\nonumber\\ &\quad +\deg(F)\log^+|2|+N\log^+|2| \end{align} $$
$$ \begin{align} \log\|F(B\mathbf{X})\|&= \log\bigg\|\sum c_m m(B\mathbf{X})\bigg\|\nonumber \\ &\leq \log\max \|c_m m(B\mathbf{X})\| + \log^+\bigg|\binom{\deg(F)+N}{N}\bigg| \nonumber \\ &\leq \log\|F\|+\deg(F)\log\|B\|+\deg(F)\log^+|N+1|\nonumber\\ &\quad +\deg(F)\log^+|2|+N\log^+|2| \end{align} $$
by the triangle inequality. On the other hand, by (8) we have
 $$ \begin{align*} \log\|F\|&=\log\|F(BB^{-1}\mathbf{X})\|\\ &\leq \log\|F(B\mathbf{X})\|+\deg(F)\log\|B^{-1}\|+\deg(F)\log^+|N+1|\\ &\quad +\deg(F)\log^+|2|+N\log^+|2|\\ &\leq \log\|F(B\mathbf{X})\| +\deg(F)\lambda(B)-\deg(F)\log\|B\|\\ &\quad +\deg(F)\log^+|N+1|+\deg(F)\log^+|2|+N\log^+|2|. \end{align*} $$
$$ \begin{align*} \log\|F\|&=\log\|F(BB^{-1}\mathbf{X})\|\\ &\leq \log\|F(B\mathbf{X})\|+\deg(F)\log\|B^{-1}\|+\deg(F)\log^+|N+1|\\ &\quad +\deg(F)\log^+|2|+N\log^+|2|\\ &\leq \log\|F(B\mathbf{X})\| +\deg(F)\lambda(B)-\deg(F)\log\|B\|\\ &\quad +\deg(F)\log^+|N+1|+\deg(F)\log^+|2|+N\log^+|2|. \end{align*} $$
Now for L of the form (7), note that if
![]() $F|_H(X_1, \ldots , X_N)=F(X_1, \ldots , X_N, 0)$
, then
$F|_H(X_1, \ldots , X_N)=F(X_1, \ldots , X_N, 0)$
, then
![]() $(F\circ L)|_H=(F|_H)\circ A$
, so for D defined by
$(F\circ L)|_H=(F|_H)\circ A$
, so for D defined by
![]() $F=0$
we have
$F=0$
we have
 $$ \begin{align*} \lambda(L^*D)&=\log\|F\circ L\| - \log\|F_0\circ A\|\\ &\leq \log\|F\|+\deg(F)\log\|L\|+\deg(F)\log^+|N+1| \\ &\quad +\deg(F)\log^+|2|+N\log^+|2|\\ &\quad -\log\|F_0\| +\deg(F)\lambda(A)-\deg(F)\log\|A\|\\ &\quad +\deg(F)\log^+|N|+\deg(F)\log^+|2|+(N-1)\log^+|2|\\ &=\lambda(D)+\deg(F)(\log\|L\|-\log\|A\|+\log^+|4N(N+1)| +\lambda(A))\\ &\quad + (2N-1)\log^+|2|. \end{align*} $$
$$ \begin{align*} \lambda(L^*D)&=\log\|F\circ L\| - \log\|F_0\circ A\|\\ &\leq \log\|F\|+\deg(F)\log\|L\|+\deg(F)\log^+|N+1| \\ &\quad +\deg(F)\log^+|2|+N\log^+|2|\\ &\quad -\log\|F_0\| +\deg(F)\lambda(A)-\deg(F)\log\|A\|\\ &\quad +\deg(F)\log^+|N|+\deg(F)\log^+|2|+(N-1)\log^+|2|\\ &=\lambda(D)+\deg(F)(\log\|L\|-\log\|A\|+\log^+|4N(N+1)| +\lambda(A))\\ &\quad + (2N-1)\log^+|2|. \end{align*} $$
Similarly,
 $$ \begin{align*} \lambda(L^*D)&=\log\|F\circ L\| - \log\|F_0\circ A\|\\ &\geq \log\|F\|-\deg(F)\lambda(L)+\deg(F)\log\|L\|\\ &\quad -\deg(F)\log^+|N+1|-\deg(F)\log^+|2|-N\log^+|2|\\ &\quad - \log\|F_0\|-\deg(F)\log\|A\|-\deg(F)\log^+|N|\\ &\quad -\deg(F)\log^+|2|-(N-1)\log^+|2|\\ &=\lambda(D)-\deg(D)(\lambda(L)+\log\|L\|-\log\|A\|+\log^+|4N(N+1)|)\\ &\quad - (2N-1)\log^+|2|. \end{align*} $$
$$ \begin{align*} \lambda(L^*D)&=\log\|F\circ L\| - \log\|F_0\circ A\|\\ &\geq \log\|F\|-\deg(F)\lambda(L)+\deg(F)\log\|L\|\\ &\quad -\deg(F)\log^+|N+1|-\deg(F)\log^+|2|-N\log^+|2|\\ &\quad - \log\|F_0\|-\deg(F)\log\|A\|-\deg(F)\log^+|N|\\ &\quad -\deg(F)\log^+|2|-(N-1)\log^+|2|\\ &=\lambda(D)-\deg(D)(\lambda(L)+\log\|L\|-\log\|A\|+\log^+|4N(N+1)|)\\ &\quad - (2N-1)\log^+|2|. \end{align*} $$
The bounds for
![]() $\lambda (L_*D)$
follow immediately from writing
$\lambda (L_*D)$
follow immediately from writing
![]() $D=L^ *L_*D$
.
$D=L^ *L_*D$
.
Lemma 16 gives estimates on
![]() $\lambda (L_* D)-\lambda (D)$
which depend on L, as one might expect. However, by analogy with
$\lambda (L_* D)-\lambda (D)$
which depend on L, as one might expect. However, by analogy with
![]() $z\mapsto z+c$
, one might also expect much more uniform estimates once D is sufficiently ‘large’ with respect to the coefficients of L, estimates which depend only on the behaviour at infinity. The rest of the section is more technical, and gives such estimates.
$z\mapsto z+c$
, one might also expect much more uniform estimates once D is sufficiently ‘large’ with respect to the coefficients of L, estimates which depend only on the behaviour at infinity. The rest of the section is more technical, and gives such estimates.
Lemma 17 For
![]() $\mathbf {c}=(c_1, \ldots , c_N)\in K^N$
, let
$\mathbf {c}=(c_1, \ldots , c_N)\in K^N$
, let
be the translation-by-
![]() $\mathbf {c}$
map, let D be a divisor not containing H or the origin, and let
$\mathbf {c}$
map, let D be a divisor not containing H or the origin, and let
 $$ \begin{align*} c_3= \begin{cases} (N+2)\log 2+\log N & \text{if } |\cdot| \text{ is archimedean,}\\ \dfrac{\log p}{p-1} & \text{if } |\cdot| \text{ is } p\text{-adic,} \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} c_3= \begin{cases} (N+2)\log 2+\log N & \text{if } |\cdot| \text{ is archimedean,}\\ \dfrac{\log p}{p-1} & \text{if } |\cdot| \text{ is } p\text{-adic,} \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
If
then
![]() $T_{\mathbf {c}}^*D$
also does not contain H or the origin, and we have
$T_{\mathbf {c}}^*D$
also does not contain H or the origin, and we have
Proof. If D is defined by the vanishing of
then
![]() $T_{\mathbf {c}}^*D$
is defined by the vanishing of
$T_{\mathbf {c}}^*D$
is defined by the vanishing of
which we would like to write as
With a view to computing
![]() $\mu (T_{\mathbf {c}}^*D)$
, note that
$\mu (T_{\mathbf {c}}^*D)$
, note that
and so
 $$ \begin{align} \nonumber\log |E_{\deg(D)}-F_{\deg(D)}|&= \log|F(c_1, \ldots, c_N, 1)-F_{\deg(D)}|\\ \nonumber &=\log\bigg|\sum_{k=1}^{\deg(D)} F_{\deg(D)-k}(\mathbf{c})\bigg|\\ \nonumber &\leq \max_{1\leq k\leq \deg(D)}\bigg(k\log\|\mathbf{c}\|+\log\|F_{\deg(D)-k}\|\\ \nonumber &\quad +\log^+\bigg|\binom{\deg(F_{\deg(F)-k})+N}{N}\bigg|\bigg)+\log^+|\deg(D)|\\ \nonumber &\leq \max_{1\leq k\leq \deg(D)}(k\mu(D)-kc_3-k2\log^+|\deg(D)|\\ \nonumber &\quad +\log\|F_{\deg(D)-k}\|+k(N+1)\log^+|2|)\\ \nonumber &\quad +\log^+|\deg(D)|\\ \nonumber & < \log|F_{\deg(D)}|+\log^+|\deg(D)|\\ &\quad -\min_{1\leq k\leq \deg(D)}k(c_3+2\log^+\!|\deg(D)|\!-\!(N+1)\log^+|2|)\nonumber\\ &\leq \log|F_{\deg(D)}|-\log^+|2|, \end{align} $$
$$ \begin{align} \nonumber\log |E_{\deg(D)}-F_{\deg(D)}|&= \log|F(c_1, \ldots, c_N, 1)-F_{\deg(D)}|\\ \nonumber &=\log\bigg|\sum_{k=1}^{\deg(D)} F_{\deg(D)-k}(\mathbf{c})\bigg|\\ \nonumber &\leq \max_{1\leq k\leq \deg(D)}\bigg(k\log\|\mathbf{c}\|+\log\|F_{\deg(D)-k}\|\\ \nonumber &\quad +\log^+\bigg|\binom{\deg(F_{\deg(F)-k})+N}{N}\bigg|\bigg)+\log^+|\deg(D)|\\ \nonumber &\leq \max_{1\leq k\leq \deg(D)}(k\mu(D)-kc_3-k2\log^+|\deg(D)|\\ \nonumber &\quad +\log\|F_{\deg(D)-k}\|+k(N+1)\log^+|2|)\\ \nonumber &\quad +\log^+|\deg(D)|\\ \nonumber & < \log|F_{\deg(D)}|+\log^+|\deg(D)|\\ &\quad -\min_{1\leq k\leq \deg(D)}k(c_3+2\log^+\!|\deg(D)|\!-\!(N+1)\log^+|2|)\nonumber\\ &\leq \log|F_{\deg(D)}|-\log^+|2|, \end{align} $$
since the minimum in (11) is attained with
![]() $k=1$
(the term in parentheses being non-negative). So we get
$k=1$
(the term in parentheses being non-negative). So we get
and also
![]() $E_{\deg (D)}\neq 0$
, which is equivalent to
$E_{\deg (D)}\neq 0$
, which is equivalent to
![]() $T^*_{\mathbf {c}}D$
not containing the origin.
$T^*_{\mathbf {c}}D$
not containing the origin.
In order to obtain a lower bound on
![]() $\mu (T^*_{\mathbf {c}})$
, we now need an upper bound on
$\mu (T^*_{\mathbf {c}})$
, we now need an upper bound on
![]() $\|E_s\|$
for
$\|E_s\|$
for
![]() $s<\deg (D)$
. We can expand each
$s<\deg (D)$
. We can expand each
![]() $F_\ell \circ T_{\mathbf {c}}$
as a polynomial in
$F_\ell \circ T_{\mathbf {c}}$
as a polynomial in
![]() $X_{N+1}$
in a fairly simple manner, namely by
$X_{N+1}$
in a fairly simple manner, namely by
 $$ \begin{align*}F_\ell\circ T_{\mathbf{c}} (\mathbf{X})=\sum_{j=0}^{\deg(F_\ell)}\frac{X_{N+1}^j}{j!}\bigg(\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}\bigg|_{X_{N+1}=0}\bigg).\end{align*} $$
$$ \begin{align*}F_\ell\circ T_{\mathbf{c}} (\mathbf{X})=\sum_{j=0}^{\deg(F_\ell)}\frac{X_{N+1}^j}{j!}\bigg(\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}\bigg|_{X_{N+1}=0}\bigg).\end{align*} $$
By the chain rule, if we write
 $$ \begin{align*}F_{i, k_1, \ldots, k_j}=\frac{\partial^jF_i}{\partial X_{k_1}\cdots \partial X_{k_j}},\end{align*} $$
$$ \begin{align*}F_{i, k_1, \ldots, k_j}=\frac{\partial^jF_i}{\partial X_{k_1}\cdots \partial X_{k_j}},\end{align*} $$
then
 $$ \begin{align}\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0)=\sum_{k_1, \ldots, k_j=1}^Nc_{k_1}\cdots c_{k_j}F_{\ell, k_1, \ldots, k_j}(X_1, \ldots, X_N).\end{align} $$
$$ \begin{align}\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0)=\sum_{k_1, \ldots, k_j=1}^Nc_{k_1}\cdots c_{k_j}F_{\ell, k_1, \ldots, k_j}(X_1, \ldots, X_N).\end{align} $$
For any homogeneous form H,
 $$ \begin{align*}\log\bigg\|\frac{\partial^j H}{\partial X_{k_1}\cdots \partial X_{k_j}}\bigg\| \leq \log\|H\|+j\log^+|\deg(H)|,\end{align*} $$
$$ \begin{align*}\log\bigg\|\frac{\partial^j H}{\partial X_{k_1}\cdots \partial X_{k_j}}\bigg\| \leq \log\|H\|+j\log^+|\deg(H)|,\end{align*} $$
and so each summand on the right-hand side of (12) satisfies
Summing over all terms on the right in (12) then gives
 $$ \begin{align*} &\log\bigg\|\frac{1}{j!}\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0)\bigg\|\\ & \quad \leq \log\|F_{\ell}\|+j(\log\|\mathbf{c}\|+\log^+|\deg(D)-\ell|+\log^+|N|)+\log^+\bigg|\frac{1}{j!}\bigg|. \end{align*} $$
$$ \begin{align*} &\log\bigg\|\frac{1}{j!}\frac{\partial^j (F_\ell\circ T_{\mathbf{c}})}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0)\bigg\|\\ & \quad \leq \log\|F_{\ell}\|+j(\log\|\mathbf{c}\|+\log^+|\deg(D)-\ell|+\log^+|N|)+\log^+\bigg|\frac{1}{j!}\bigg|. \end{align*} $$
At this point, we note that if
![]() $|\cdot |$
is not a p-adic absolute value, for any prime integer p, then
$|\cdot |$
is not a p-adic absolute value, for any prime integer p, then
![]() $\log ^+|{1}/{j!}|=0$
. If
$\log ^+|{1}/{j!}|=0$
. If
![]() $|\cdot |$
is the p-adic absolute value,
$|\cdot |$
is the p-adic absolute value,
 $$ \begin{align*} \log^+\bigg|\frac{1}{j!}\bigg|=\sum_{t=1}^\infty\bigg\lfloor \frac{j}{p^t}\bigg\rfloor\log p \leq j\bigg(\frac{\log p}{p-1}\bigg) \end{align*} $$
$$ \begin{align*} \log^+\bigg|\frac{1}{j!}\bigg|=\sum_{t=1}^\infty\bigg\lfloor \frac{j}{p^t}\bigg\rfloor\log p \leq j\bigg(\frac{\log p}{p-1}\bigg) \end{align*} $$
by Legendre’s formula, and so either way
 $$ \begin{align*} \log^+\bigg|\frac{1}{j!}\bigg|\leq jc_4, \end{align*} $$
$$ \begin{align*} \log^+\bigg|\frac{1}{j!}\bigg|\leq jc_4, \end{align*} $$
where
 $$ \begin{align*} c_4=\begin{cases} \dfrac{\log p}{p-1} & \text{if } |\cdot| \text{ is } p\text{-adic,}\\ 0 & \text{otherwise.}\end{cases} \end{align*} $$
$$ \begin{align*} c_4=\begin{cases} \dfrac{\log p}{p-1} & \text{if } |\cdot| \text{ is } p\text{-adic,}\\ 0 & \text{otherwise.}\end{cases} \end{align*} $$
Now, comparing coefficients of
![]() $X_{N+1}^s$
, we have
$X_{N+1}^s$
, we have
 $$ \begin{align*}E_s(X_1, \ldots, X_N)=\sum_{j=0}^s\frac{1}{j!}\frac{\partial^j F_{s-j}\circ T_{\mathbf{c}}}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0),\end{align*} $$
$$ \begin{align*}E_s(X_1, \ldots, X_N)=\sum_{j=0}^s\frac{1}{j!}\frac{\partial^j F_{s-j}\circ T_{\mathbf{c}}}{\partial X_{N+1}^j}(X_1, \ldots, X_N, 0),\end{align*} $$
whence
 $$ \begin{align} \log\|E_s\|&\leq \max_{0\leq j\leq s}\{\log\|F_{s-j}\|+j(\log\|\mathbf{c}\|+\log^+|\deg(D)|+\log^+|N|+c_4)\}\nonumber\\ &\quad +\log^+|s+1|\nonumber\\ &\leq \max_{0\leq j\leq s}\{\log|F_{\deg(D)}|-(\deg(D)-s+j) \mu(D)\nonumber\\ &\quad +j(\mu(D)-c_3-2\log^+|\deg(D)|+\log^+ |\deg(D)|+\log^+|N|+c_4)\}\nonumber \\ &\quad +\log^+|\deg(D)|\nonumber\\ &\leq \log|E_{\deg(D)}|+\log^+|2|-(\deg(D)-s)\mu(D)+\log^+|\deg(D)|, \end{align} $$
$$ \begin{align} \log\|E_s\|&\leq \max_{0\leq j\leq s}\{\log\|F_{s-j}\|+j(\log\|\mathbf{c}\|+\log^+|\deg(D)|+\log^+|N|+c_4)\}\nonumber\\ &\quad +\log^+|s+1|\nonumber\\ &\leq \max_{0\leq j\leq s}\{\log|F_{\deg(D)}|-(\deg(D)-s+j) \mu(D)\nonumber\\ &\quad +j(\mu(D)-c_3-2\log^+|\deg(D)|+\log^+ |\deg(D)|+\log^+|N|+c_4)\}\nonumber \\ &\quad +\log^+|\deg(D)|\nonumber\\ &\leq \log|E_{\deg(D)}|+\log^+|2|-(\deg(D)-s)\mu(D)+\log^+|\deg(D)|, \end{align} $$
since
But (13) for all
![]() $0\leq s<\deg (D)$
gives
$0\leq s<\deg (D)$
gives
![]() $\mu (T^*_{\mathbf {c}}D)\geq \mu (D)-\log ^+|\deg (D)|-\log ^+|2|$
.
$\mu (T^*_{\mathbf {c}}D)\geq \mu (D)-\log ^+|\deg (D)|-\log ^+|2|$
.
Lemma 17 effectively gives estimates on pushing forward or pulling back by L, in the special case where A is the identity matrix. It turns out that, with a little more work, this special case gives us the general case.
Lemma 18 Let
let D be an effective divisor of degree at least
![]() $1$
, not containing the origin, and suppose that
$1$
, not containing the origin, and suppose that
Then
and
 $$ \begin{align} &\lambda(D)-\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2| \nonumber\\ &\quad\leq \lambda(L_*D)\nonumber\\ &\quad\leq\lambda(D)+\deg(D)(\log\|A\|+\log^+|2N|)+N\log^+|2|. \end{align} $$
$$ \begin{align} &\lambda(D)-\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2| \nonumber\\ &\quad\leq \lambda(L_*D)\nonumber\\ &\quad\leq\lambda(D)+\deg(D)(\log\|A\|+\log^+|2N|)+N\log^+|2|. \end{align} $$
Proof. Note that
![]() $L_*=(L^{-1})^*$
, and that
$L_*=(L^{-1})^*$
, and that
 $$ \begin{align*}L^{-1}=\begin{pmatrix} A^{-1} & -A^{-1}\mathbf{b}\\ \mathbf{0} & 1 \end{pmatrix}=\begin{pmatrix} A^{-1} &\mathbf{0}\\ \mathbf{0} & 1 \end{pmatrix}\begin{pmatrix} I & -\mathbf{b}\\ \mathbf{0} & 1 \end{pmatrix}=: L_0^{-1}T_{-\mathbf{b}}. \end{align*} $$
$$ \begin{align*}L^{-1}=\begin{pmatrix} A^{-1} & -A^{-1}\mathbf{b}\\ \mathbf{0} & 1 \end{pmatrix}=\begin{pmatrix} A^{-1} &\mathbf{0}\\ \mathbf{0} & 1 \end{pmatrix}\begin{pmatrix} I & -\mathbf{b}\\ \mathbf{0} & 1 \end{pmatrix}=: L_0^{-1}T_{-\mathbf{b}}. \end{align*} $$
So
![]() $L_*=(L^{-1})^*=T_{-\mathbf {b}}^*(L_{0}^{-1})^*$
.
$L_*=(L^{-1})^*=T_{-\mathbf {b}}^*(L_{0}^{-1})^*$
.
First, note that
![]() $\mu ((L_0^{-1})^* D)$
can be estimated as follows. If D is defined by the vanishing of
$\mu ((L_0^{-1})^* D)$
can be estimated as follows. If D is defined by the vanishing of
![]() $F=\sum _{i=0}^{\deg (F)}F_iX_{N+1}^i$
, then
$F=\sum _{i=0}^{\deg (F)}F_iX_{N+1}^i$
, then
![]() $(L_0^{-1})^*D$
is defined by the vanishing of
$(L_0^{-1})^*D$
is defined by the vanishing of
![]() $\sum _{i=0}^{\deg (F)} X_{N+1}^iF_i\circ A^{-1}$
. From (10), we have, for any
$\sum _{i=0}^{\deg (F)} X_{N+1}^iF_i\circ A^{-1}$
. From (10), we have, for any
![]() $0\leq k<\deg (D)$
,
$0\leq k<\deg (D)$
,
 $$ \begin{align*} \log|F_{\deg(D)}|-\log\|F_k\circ A^{-1}\| & \geq \log|F_{\deg(D)}|-\log\|F_k\|-\deg(F_k)(\log\|A^{-1}\|\\ &\quad +\log^+|N|+\log^+|2|)-(N-1)\log^+|2| \\ &\geq(\deg(D)-k)\mu(D)-\deg(F_k)(\log\|A^{-1}\|\\ &\quad +\log^+|N|+N\log^+|2|)\\ &\geq(\deg(D)-k)(\mu(D)-c_5-\log\|A^{-1}\|) \end{align*} $$
$$ \begin{align*} \log|F_{\deg(D)}|-\log\|F_k\circ A^{-1}\| & \geq \log|F_{\deg(D)}|-\log\|F_k\|-\deg(F_k)(\log\|A^{-1}\|\\ &\quad +\log^+|N|+\log^+|2|)-(N-1)\log^+|2| \\ &\geq(\deg(D)-k)\mu(D)-\deg(F_k)(\log\|A^{-1}\|\\ &\quad +\log^+|N|+N\log^+|2|)\\ &\geq(\deg(D)-k)(\mu(D)-c_5-\log\|A^{-1}\|) \end{align*} $$
(noting that this is trivially true if
![]() $F_k=0$
), whence
$F_k=0$
), whence
Combined with (14), this gives
and so by Lemma 17 we have
 $$ \begin{align}\mu(L_*D)&=\mu(T_{-\mathbf{b}}^*(L_0^{-1})^* D)\geq \mu((L_0^{-1})^* D)-\log^+|\deg(D)|-\log^+|2| \nonumber\\ &\geq \mu(D)-\log^+|\deg(D)|-\log^+|2|-c_5-\log\|A^{-1}\|\geq 0, \end{align} $$
$$ \begin{align}\mu(L_*D)&=\mu(T_{-\mathbf{b}}^*(L_0^{-1})^* D)\geq \mu((L_0^{-1})^* D)-\log^+|\deg(D)|-\log^+|2| \nonumber\\ &\geq \mu(D)-\log^+|\deg(D)|-\log^+|2|-c_5-\log\|A^{-1}\|\geq 0, \end{align} $$
proving (15).
Since
![]() $A^{-1}\in \operatorname {SL}_N(K)$
we have
$A^{-1}\in \operatorname {SL}_N(K)$
we have
and so by (14) we have
![]() $\mu (D)\geq 0$
, hence
$\mu (D)\geq 0$
, hence
![]() $\lambda (D)=\log |F_{\deg (D)}|-\log \|F_0\|$
. Similarly, by the computations giving (17) we have
$\lambda (D)=\log |F_{\deg (D)}|-\log \|F_0\|$
. Similarly, by the computations giving (17) we have
 $$ \begin{align*} \lambda(L_* D)&= \log|F_{\deg(D)}|-\log\|F_0\circ A^{-1}\|\\ &\geq \log|F_{\deg(D)}| - \log\|F_0\| -\deg(D)\log\|A^{-1}\|- \deg(D)\log^+|2N|\\ &\quad -N\log^+|2|\\ &=\lambda(D)-\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2|. \end{align*} $$
$$ \begin{align*} \lambda(L_* D)&= \log|F_{\deg(D)}|-\log\|F_0\circ A^{-1}\|\\ &\geq \log|F_{\deg(D)}| - \log\|F_0\| -\deg(D)\log\|A^{-1}\|- \deg(D)\log^+|2N|\\ &\quad -N\log^+|2|\\ &=\lambda(D)-\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2|. \end{align*} $$
Also,
 $$ \begin{align*} \lambda(L_* D)&= \log|F_{\deg(D)}|-\log\|F_0\circ A^{-1}\|\\ &\leq \log|F_{\deg(D)}| - \log\|F_0\| +\deg(D)\log\|A\|+ \deg(D)\log^+|2N|\\ &\quad +\,N\log^+|2|\\ &=\lambda(D)+\deg(D)(\log\|A\|+\log^+|2N|)+N\log^+|2|.\\[-37pt] \end{align*} $$
$$ \begin{align*} \lambda(L_* D)&= \log|F_{\deg(D)}|-\log\|F_0\circ A^{-1}\|\\ &\leq \log|F_{\deg(D)}| - \log\|F_0\| +\deg(D)\log\|A\|+ \deg(D)\log^+|2N|\\ &\quad +\,N\log^+|2|\\ &=\lambda(D)+\deg(D)(\log\|A\|+\log^+|2N|)+N\log^+|2|.\\[-37pt] \end{align*} $$
3 The relative rate of escape
We continue in the context of the previous section. That is, K is an algebraically closed field, complete with respect to some absolute value
![]() $|\cdot |$
.
$|\cdot |$
.
Let f be as in (1), and let D be an effective divisor not containing H. We set
whenever this limit exists, but we will prove that it always does (subject to the constraints above).
Lemma 19 The limit in (18) exists, is non-negative for effective divisors D, and we have
and
as well as
 $$ \begin{align} &-\frac{\deg(D)}{d-1}(\log\|L\| - \log\|A\|+\log^+|4N(N+1)| \nonumber\\ &\quad+\lambda(A)+4Nd\log^+|2|)-\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|\nonumber\\ & \qquad \leq \Delta_f(D)-\lambda(D)\nonumber\\ & \qquad \leq \frac{\deg(D)}{d-1}(\log\|L\|-\log\|A\|+\log^+|4N(N+1)|\nonumber\\ &\quad\qquad+\lambda(L)+4Nd\log^+|2|)+\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align} $$
$$ \begin{align} &-\frac{\deg(D)}{d-1}(\log\|L\| - \log\|A\|+\log^+|4N(N+1)| \nonumber\\ &\quad+\lambda(A)+4Nd\log^+|2|)-\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|\nonumber\\ & \qquad \leq \Delta_f(D)-\lambda(D)\nonumber\\ & \qquad \leq \frac{\deg(D)}{d-1}(\log\|L\|-\log\|A\|+\log^+|4N(N+1)|\nonumber\\ &\quad\qquad+\lambda(L)+4Nd\log^+|2|)+\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align} $$
Furthermore, if D is preperiodic for f, then
![]() $\Delta _f(D)=0$
.
$\Delta _f(D)=0$
.
Proof. We will first show that the limit exists, for which we apply Lemmas 14 and 16. Specifically,
 $$ \begin{align*} \bigg|\frac{\lambda(f_*D)}{d^{N}}-\lambda(D)\bigg|&\leq \bigg|\frac{\lambda(L_*\phi_*D)}{d^{N}}- \frac{\lambda(\phi_*D)}{d^N}\bigg|+\bigg|\frac{\lambda(\phi_*D)}{d^N}-\lambda(D)\bigg|\\ &\leq d^{-N}\deg(\phi_*D)(\log\|L\|-\log\|A\|+\lambda(L)+\lambda(A)+c_2)\\ &\quad +\,d^{-N}c_1+4N\deg(D)\log^+|2|\\ &= \deg(D)(d^{-1}(\log\|L\|-\log\|A\| +\lambda(L)+\lambda(A)+c_2)\\ &\quad +\,4N\log^+|2|)+d^{-N}c_1. \end{align*} $$
$$ \begin{align*} \bigg|\frac{\lambda(f_*D)}{d^{N}}-\lambda(D)\bigg|&\leq \bigg|\frac{\lambda(L_*\phi_*D)}{d^{N}}- \frac{\lambda(\phi_*D)}{d^N}\bigg|+\bigg|\frac{\lambda(\phi_*D)}{d^N}-\lambda(D)\bigg|\\ &\leq d^{-N}\deg(\phi_*D)(\log\|L\|-\log\|A\|+\lambda(L)+\lambda(A)+c_2)\\ &\quad +\,d^{-N}c_1+4N\deg(D)\log^+|2|\\ &= \deg(D)(d^{-1}(\log\|L\|-\log\|A\| +\lambda(L)+\lambda(A)+c_2)\\ &\quad +\,4N\log^+|2|)+d^{-N}c_1. \end{align*} $$
Since
![]() $\deg (f_*D)=d^{N-1}\deg (D)$
, a standard telescoping sum argument gives
$\deg (f_*D)=d^{N-1}\deg (D)$
, a standard telescoping sum argument gives
 $$ \begin{align*} \bigg|\frac{\lambda(f_*^kD)}{d^{Nk}}-\lambda(D)\bigg| &\leq \sum_{j=0}^{k-1} \bigg|\frac{\lambda(f_*^{j+1}D)}{d^{N(j+1)}}- \frac{\lambda(f_*^jD)}{d^{Nj}}\bigg|\\ &\leq \sum_{j=0}^{k-1}d^{-Nj}\deg(f_*^{j}D)(d^{-1}(\log\|L\|-\log\|A\|\\ &\quad +\,\lambda(L) +\lambda(A)+c_2)+4N\log^+|2|)\\ &\quad +\,c_1\sum_{j=0}^{k-1}d^{-N(j+1)}\\ &= \bigg(\frac{1-d^{-k}}{1-d^{-1}}\bigg)\deg(D)(d^{-1}(\log\|L\|-\log\|A\|+\lambda(L)\\ &\quad +\,\lambda(A))+c_2)\\ &\quad +\bigg(\frac{1-d^{-Nk}}{d^N-1}\bigg)c_1. \end{align*} $$
$$ \begin{align*} \bigg|\frac{\lambda(f_*^kD)}{d^{Nk}}-\lambda(D)\bigg| &\leq \sum_{j=0}^{k-1} \bigg|\frac{\lambda(f_*^{j+1}D)}{d^{N(j+1)}}- \frac{\lambda(f_*^jD)}{d^{Nj}}\bigg|\\ &\leq \sum_{j=0}^{k-1}d^{-Nj}\deg(f_*^{j}D)(d^{-1}(\log\|L\|-\log\|A\|\\ &\quad +\,\lambda(L) +\lambda(A)+c_2)+4N\log^+|2|)\\ &\quad +\,c_1\sum_{j=0}^{k-1}d^{-N(j+1)}\\ &= \bigg(\frac{1-d^{-k}}{1-d^{-1}}\bigg)\deg(D)(d^{-1}(\log\|L\|-\log\|A\|+\lambda(L)\\ &\quad +\,\lambda(A))+c_2)\\ &\quad +\bigg(\frac{1-d^{-Nk}}{d^N-1}\bigg)c_1. \end{align*} $$
The difference
![]() $d^{-Nk}\lambda (f_*^kD)-\lambda (D)$
is thus the partial sum of an absolutely convergent series, and hence the limit in (18) exists. The above calculation, with slightly more care to distinguish the terms in the upper and lower bounds, and with
$d^{-Nk}\lambda (f_*^kD)-\lambda (D)$
is thus the partial sum of an absolutely convergent series, and hence the limit in (18) exists. The above calculation, with slightly more care to distinguish the terms in the upper and lower bounds, and with
![]() $k\to \infty $
, now gives (19).
$k\to \infty $
, now gives (19).
For linearity, note that in the non-archimedean case
![]() $\lambda (D+E)=\lambda (D)+\lambda (E)$
by the Gauss lemma, and so
$\lambda (D+E)=\lambda (D)+\lambda (E)$
by the Gauss lemma, and so
![]() $\Delta _f$
is linear as well. In the archimedean case, note that Lemma 13 gives
$\Delta _f$
is linear as well. In the archimedean case, note that Lemma 13 gives
 $$ \begin{align*} \Delta_f(D+E)&= \lim_{k\to\infty}\frac{\lambda(f_*^k D+f_*^kE)}{d^{Nk}}\\ &= \lim_{k\to\infty}\frac{\lambda(f_*^k D)+\lambda(f_*^kE)+O(\deg(f_*^k D+f_*^kE))}{d^{Nk}}\\ &= \bigg(\lim_{k\to\infty}\frac{\lambda(f_*^k D)}{d^{Nk}}+\lim_{k\to\infty}\frac{\lambda(f_*^k E)}{d^{Nk}}+\lim_{k\to\infty}\frac{d^{(N-1)k}O(\deg(D+E))}{d^{Nk}}\bigg)\\ &= \Delta_f(D)+\Delta_f(E). \end{align*} $$
$$ \begin{align*} \Delta_f(D+E)&= \lim_{k\to\infty}\frac{\lambda(f_*^k D+f_*^kE)}{d^{Nk}}\\ &= \lim_{k\to\infty}\frac{\lambda(f_*^k D)+\lambda(f_*^kE)+O(\deg(f_*^k D+f_*^kE))}{d^{Nk}}\\ &= \bigg(\lim_{k\to\infty}\frac{\lambda(f_*^k D)}{d^{Nk}}+\lim_{k\to\infty}\frac{\lambda(f_*^k E)}{d^{Nk}}+\lim_{k\to\infty}\frac{d^{(N-1)k}O(\deg(D+E))}{d^{Nk}}\bigg)\\ &= \Delta_f(D)+\Delta_f(E). \end{align*} $$
We have
![]() $\lambda (D)\geq 0$
, for D effective, and so
$\lambda (D)\geq 0$
, for D effective, and so
![]() $\Delta _f(D)\geq 0$
.
$\Delta _f(D)\geq 0$
.
The formula
![]() $\Delta _f(f_*D)=d^N\Delta _f(D)$
follows immediately from the definition and, now that we have linearity, we can compute
$\Delta _f(f_*D)=d^N\Delta _f(D)$
follows immediately from the definition and, now that we have linearity, we can compute
For the final claim, suppose that D is preperiodic and, without loss of generality, irreducible. Then for some
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $k\geq 1$
, the divisors
$k\geq 1$
, the divisors
![]() $f_*^{n+k}D$
and
$f_*^{n+k}D$
and
![]() $f_*^nD$
are supported on the same irreducible hypersurface. Comparing degrees, we have
$f_*^nD$
are supported on the same irreducible hypersurface. Comparing degrees, we have
That in turn gives
by linearity, and so
![]() $\Delta _f(D)=0$
.
$\Delta _f(D)=0$
.
Remark 20 In [Reference Ingram10] we defined a homogeneous escape rate
![]() $G_{F}(\Phi )$
for homogeneous forms
$G_{F}(\Phi )$
for homogeneous forms
![]() $\Phi $
and affine maps
$\Phi $
and affine maps
![]() $F(\mathbf {X})=A\mathbf {X}^d$
. If we choose a lift F for f, if
$F(\mathbf {X})=A\mathbf {X}^d$
. If we choose a lift F for f, if
![]() $F_h$
is the homogeneous part of F (that is, with
$F_h$
is the homogeneous part of F (that is, with
![]() $\mathbf {b}$
replaced by
$\mathbf {b}$
replaced by
![]() $\mathbf {0}$
), and
$\mathbf {0}$
), and
![]() $\Phi _h=\Phi (X_0, \ldots , X_{N-1}, 0)$
, then we can check from the properties in Lemma 19 and [Reference Ingram10, Lemma 10] that for D defined by
$\Phi _h=\Phi (X_0, \ldots , X_{N-1}, 0)$
, then we can check from the properties in Lemma 19 and [Reference Ingram10, Lemma 10] that for D defined by
![]() $\Phi =0$
, we have
$\Phi =0$
, we have
One virtue of the function
![]() $\Delta _f$
is that it does not depend on choosing models of f and D.
$\Delta _f$
is that it does not depend on choosing models of f and D.
Remark 21 In some sense it is more natural, in the case
![]() $K=\mathbb {C}$
, to work in terms of
$K=\mathbb {C}$
, to work in terms of
 $$ \begin{align*}\lambda_{\mathrm{m}}(D)=\int \log\bigg|\frac{F(X_1, \ldots, X_{N+1})}{F(X_1, \ldots, X_{N}\!\:\,\!, 0)}\bigg|\,d\mu(\mathbf{X}),\end{align*} $$
$$ \begin{align*}\lambda_{\mathrm{m}}(D)=\int \log\bigg|\frac{F(X_1, \ldots, X_{N+1})}{F(X_1, \ldots, X_{N}\!\:\,\!, 0)}\bigg|\,d\mu(\mathbf{X}),\end{align*} $$
where
![]() $\mu $
is normalized Haar measure on the appropriate power of the unit circle, instead of
$\mu $
is normalized Haar measure on the appropriate power of the unit circle, instead of
![]() $\lambda $
as defined above, naively in terms of the coefficients of a defining form. As noted in Lemma 11, using inequality (4) (due to Mahler [Reference Mahler15]), we have
$\lambda $
as defined above, naively in terms of the coefficients of a defining form. As noted in Lemma 11, using inequality (4) (due to Mahler [Reference Mahler15]), we have
with the implied constant depending only on N and d. It then follows that, for fixed D,
So the limit (18) using either
![]() $\lambda _{\mathrm {m}}$
or
$\lambda _{\mathrm {m}}$
or
![]() $\lambda $
defines the same function
$\lambda $
defines the same function
![]() $\Delta _f$
.
$\Delta _f$
.
Along similar lines, still over
![]() $\mathbb {C}$
, we can easily check, post hoc, that
$\mathbb {C}$
, we can easily check, post hoc, that
 $$ \begin{align*}\Delta_f(D)=\int\log\bigg|\frac{F(X_1, \ldots, X_{N+1})}{F(X_1, \ldots, X_{N}\!\:\,\!, 0)}\bigg|\,d\mu_f(\mathbf{X})\end{align*} $$
$$ \begin{align*}\Delta_f(D)=\int\log\bigg|\frac{F(X_1, \ldots, X_{N+1})}{F(X_1, \ldots, X_{N}\!\:\,\!, 0)}\bigg|\,d\mu_f(\mathbf{X})\end{align*} $$
for any homogeneous form F defining D, where
![]() $\mu _f$
is the invariant measure associated to f (see, for example, [Reference Ingram10, Lemma 11]). From this and [Reference Benedetto, Ingram, Jones and Levy2, Theorem 3.2] we have
$\mu _f$
is the invariant measure associated to f (see, for example, [Reference Ingram10, Lemma 11]). From this and [Reference Benedetto, Ingram, Jones and Levy2, Theorem 3.2] we have
from which we derive our main results over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Lemma 19 gives an estimate of the form
where the implied constant is explicit, but depends on L. The next lemma shows that, once
![]() $\mu (D)$
is large enough, we can estimate
$\mu (D)$
is large enough, we can estimate
![]() $\Delta _f(D)$
from below in terms of
$\Delta _f(D)$
from below in terms of
![]() $\lambda (D)$
, with an error term that is much more uniform, depending only on the submatrix A. This submatrix represents the restriction of L to the hyperplane at infinity, and so this can be seen as an assertion that all such maps with the same restriction to infinity are, near infinity, very similar (a philosophy which applies in general to regular polynomial endomorphisms).
$\lambda (D)$
, with an error term that is much more uniform, depending only on the submatrix A. This submatrix represents the restriction of L to the hyperplane at infinity, and so this can be seen as an assertion that all such maps with the same restriction to infinity are, near infinity, very similar (a philosophy which applies in general to regular polynomial endomorphisms).
Lemma 22 Let
 $$ \begin{align*}c_8 = \begin{cases} \dfrac{2(N-1)(d^{N+1}-d+1)}{(d-d^{1/2})} & \text{if } |\cdot| \text{ is archimedean},\\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*}c_8 = \begin{cases} \dfrac{2(N-1)(d^{N+1}-d+1)}{(d-d^{1/2})} & \text{if } |\cdot| \text{ is archimedean},\\ 0 & \text{otherwise}, \end{cases} \end{align*} $$
suppose that
 $$ \begin{align}&(d-1)\log^+\|\mathbf{b}\|>c_8(d^{1/2}-1)+c_3+c_5+\log\|A^{-1}\|+d\xi(A)\nonumber\\ &\quad +(2dN+1)\log^+|2|+(2N-2+dN(d^N-1))\log^+|d|,\end{align} $$
$$ \begin{align}&(d-1)\log^+\|\mathbf{b}\|>c_8(d^{1/2}-1)+c_3+c_5+\log\|A^{-1}\|+d\xi(A)\nonumber\\ &\quad +(2dN+1)\log^+|2|+(2N-2+dN(d^N-1))\log^+|d|,\end{align} $$
and suppose further that D is a non-zero effective divisor with
Then
Proof. Let S be the set of effective divisors of degree at least 1 meeting condition (22), and let (for
![]() $x\in \mathbb {R}^+$
)
$x\in \mathbb {R}^+$
)
if
![]() $|\cdot |$
is archimedean,
$|\cdot |$
is archimedean,
![]() $\psi =0$
otherwise. Note that
$\psi =0$
otherwise. Note that
![]() $\psi (1)=0$
, and we have chosen
$\psi (1)=0$
, and we have chosen
![]() $c_8$
so that
$c_8$
so that
![]() $\psi '(x)\geq 0$
for
$\psi '(x)\geq 0$
for
![]() $x\geq 1$
, whence
$x\geq 1$
, whence
![]() $\psi (x)\geq 0$
for all
$\psi (x)\geq 0$
for all
![]() $x\geq 1$
. Similarly, let
$x\geq 1$
. Similarly, let
 $$ \begin{align*}\omega(x)&=dc_8(-1+x^{1/2(N-1)})-c_8(-1+d^{1/2}x^{1/2(N-1)})\\ &\quad-(d^{N+1}-d+1)\log x+c_8(d^{1/2}-1)\end{align*} $$
$$ \begin{align*}\omega(x)&=dc_8(-1+x^{1/2(N-1)})-c_8(-1+d^{1/2}x^{1/2(N-1)})\\ &\quad-(d^{N+1}-d+1)\log x+c_8(d^{1/2}-1)\end{align*} $$
if
![]() $|\cdot |$
is archimedean, and
$|\cdot |$
is archimedean, and
![]() $\omega =0$
otherwise, and note that
$\omega =0$
otherwise, and note that
![]() $\omega (x)\geq 0$
for
$\omega (x)\geq 0$
for
![]() $x\geq 1$
.
$x\geq 1$
.
Now, for
![]() $D\in S$
not containing the origin, we have from Lemma 14 that
$D\in S$
not containing the origin, we have from Lemma 14 that
 $$ \begin{align*} \mu(\phi_*D)&\geq d\mu(D)-d(d^N-1)\log^+|\deg(D)|-2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &\geq d\log^+\|\mathbf{b}\|+dc_8(-1+\deg(D)^{1/2(N-1)})-d\xi(A) \\ &\quad -\,d(d^N-1)\log^+|\deg(D)|-2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &=d\log^+\|\mathbf{b}\|+\psi(\deg(D))+2\log^+|\deg(D)|-d\xi(A)\\ &\quad -\,2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &\geq d\log^+\|\mathbf{b}\|+2\log^+|d^{N-1}\deg(D)|-2\log^+|d^{N-1}|-d\xi(A)\\ &\quad -\,2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &= \log^+ \|\mathbf{b}\| +c_3+c_5+\log\|A^{-1}\|+2\log^+|\deg(\phi_*D)|\\ &\quad +\,(d-1)\log^+\|\mathbf{b}\|-c_3-c_5-\log\|A^{-1}\|-d\xi(A)\\ &\quad -\,(2N-2+dN(d^N-1))\log^+|d|-2dN\log^+|2|\\ &>\log^+\|\mathbf{b}\|+c_3+c_5+\log\|A^{-1}\|+2\log^+|\deg(\phi_*D)|, \end{align*} $$
$$ \begin{align*} \mu(\phi_*D)&\geq d\mu(D)-d(d^N-1)\log^+|\deg(D)|-2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &\geq d\log^+\|\mathbf{b}\|+dc_8(-1+\deg(D)^{1/2(N-1)})-d\xi(A) \\ &\quad -\,d(d^N-1)\log^+|\deg(D)|-2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &=d\log^+\|\mathbf{b}\|+\psi(\deg(D))+2\log^+|\deg(D)|-d\xi(A)\\ &\quad -\,2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &\geq d\log^+\|\mathbf{b}\|+2\log^+|d^{N-1}\deg(D)|-2\log^+|d^{N-1}|-d\xi(A)\\ &\quad -\,2dN\log^+|2|-dN(d^N-1)\log^+|d|\\ &= \log^+ \|\mathbf{b}\| +c_3+c_5+\log\|A^{-1}\|+2\log^+|\deg(\phi_*D)|\\ &\quad +\,(d-1)\log^+\|\mathbf{b}\|-c_3-c_5-\log\|A^{-1}\|-d\xi(A)\\ &\quad -\,(2N-2+dN(d^N-1))\log^+|d|-2dN\log^+|2|\\ &>\log^+\|\mathbf{b}\|+c_3+c_5+\log\|A^{-1}\|+2\log^+|\deg(\phi_*D)|, \end{align*} $$
given (21). It follows from this and Lemma 18 that
 $$ \begin{align*} \mu(f_*D)&= \mu(L_*\phi_*D)\\ &\geq \mu(\phi_*D)-\log^+|\deg(\phi_*D)|-\log^+|2|-c_5-\log\|A^{-1}\|\\ &= d\mu(D)-(d^{N+1}-d+1)\log^+|\deg(D)|-(N-1)\log^+|d|\\ &\quad -\,(2dN+1)\log^+|2|-dN(d^N-1)\log^+|d|-c_5-\log\|A^{-1}\|\\ &\geq d\log^+ \|\mathbf{b}\|+dc_8(-1+\deg(D)^{1/2(N-1)})-d\xi(A)\\ &\quad -\,(d^{N+1}-d+1)\log^+|\deg(D)|-(2dN+1)\log^+|2|\\ &\quad -\,(dN(d^N-1)+(N-1))\log^+|d|-c_5-\log\|A^{-1}\|\\ &= \log^+\|\mathbf{b}\|+c_8(-1+\deg(\phi_*D)^{1/2(N-1)})-\xi(A)+\omega(\deg(D))\\ &\quad -\,c_8(d^{1/2}-1)+(d-1)\log^+\|\mathbf{b}\|-(d-1)\xi(A)-(2dN+1)\log^+|2|\\ &\quad -\,(dN(d^N-1)+(N-1))\log^+|d|-c_5-\log\|A^{-1}\|\\ &>\log^+\|\mathbf{b}\|+c_8(-1+\deg(\phi_*D)^{1/2(N-1)})-\xi(A) \end{align*} $$
$$ \begin{align*} \mu(f_*D)&= \mu(L_*\phi_*D)\\ &\geq \mu(\phi_*D)-\log^+|\deg(\phi_*D)|-\log^+|2|-c_5-\log\|A^{-1}\|\\ &= d\mu(D)-(d^{N+1}-d+1)\log^+|\deg(D)|-(N-1)\log^+|d|\\ &\quad -\,(2dN+1)\log^+|2|-dN(d^N-1)\log^+|d|-c_5-\log\|A^{-1}\|\\ &\geq d\log^+ \|\mathbf{b}\|+dc_8(-1+\deg(D)^{1/2(N-1)})-d\xi(A)\\ &\quad -\,(d^{N+1}-d+1)\log^+|\deg(D)|-(2dN+1)\log^+|2|\\ &\quad -\,(dN(d^N-1)+(N-1))\log^+|d|-c_5-\log\|A^{-1}\|\\ &= \log^+\|\mathbf{b}\|+c_8(-1+\deg(\phi_*D)^{1/2(N-1)})-\xi(A)+\omega(\deg(D))\\ &\quad -\,c_8(d^{1/2}-1)+(d-1)\log^+\|\mathbf{b}\|-(d-1)\xi(A)-(2dN+1)\log^+|2|\\ &\quad -\,(dN(d^N-1)+(N-1))\log^+|d|-c_5-\log\|A^{-1}\|\\ &>\log^+\|\mathbf{b}\|+c_8(-1+\deg(\phi_*D)^{1/2(N-1)})-\xi(A) \end{align*} $$
since
![]() $\omega (\deg (D))\geq 0$
and
$\omega (\deg (D))\geq 0$
and
 $$ \begin{align*} (d-1)\log^+\|\mathbf{b}\|&\geq c_8(d^{1/2}-1)+(d-1)\xi(A)+(2dN+1)\log^+|2|\\ &\quad+(dN(d^N-1)+(N-1))\log^+|d|+c_5+\log\|A^{-1}\|. \end{align*} $$
$$ \begin{align*} (d-1)\log^+\|\mathbf{b}\|&\geq c_8(d^{1/2}-1)+(d-1)\xi(A)+(2dN+1)\log^+|2|\\ &\quad+(dN(d^N-1)+(N-1))\log^+|d|+c_5+\log\|A^{-1}\|. \end{align*} $$
In other words, S is closed under the action of
![]() $f_*$
.
$f_*$
.
On the other hand, since
![]() $\phi _*D$
satisfies the hypotheses of Lemma 18, we also have
$\phi _*D$
satisfies the hypotheses of Lemma 18, we also have
 $$ \begin{align*} \lambda(f_*D)&=\lambda(L_* \phi_* D)\\ &\geq \lambda(\phi_*D)-\deg(\phi_*D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2| \\ &= d^N\lambda(D)-d^{N-1}\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2|. \end{align*} $$
$$ \begin{align*} \lambda(f_*D)&=\lambda(L_* \phi_* D)\\ &\geq \lambda(\phi_*D)-\deg(\phi_*D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2| \\ &= d^N\lambda(D)-d^{N-1}\deg(D)(\log\|A^{-1}\|+\log^+|2N|)-N\log^+|2|. \end{align*} $$
As S is closed under
![]() $f_*$
, we can iterate this, giving
$f_*$
, we can iterate this, giving
for
![]() $D\in S$
and
$D\in S$
and
![]() $k\geq 1$
, from which the lower bound on
$k\geq 1$
, from which the lower bound on
![]() $\Delta _f(D)$
follows.
$\Delta _f(D)$
follows.
The next lemma, a lower bound on the relative escape rate of the critical divisor of f, is the main ingredient in the results of this paper.
Lemma 23 Let f be as in (1), let
![]() $C_f=\sum _{i=1}^N(d-1)H_i$
be the finite part of the critical divisor, and let
$C_f=\sum _{i=1}^N(d-1)H_i$
be the finite part of the critical divisor, and let
 $$ \begin{align*} c_9= &\max\bigg\{0, \frac{1}{d-1}\log^+|2N|+\frac{N}{d^N-1}\log^+|2|-\frac{1}{N(d-1)}\log^+|N!|, \\ & \frac{c_8(d^{1/2}-1)+c_3+c_5+(2dN+1)\kern-1pt\log^+|2|+(2N-2+dN(d^N-1))\kern-0.7pt\log^+|d|}{d-1}\!\bigg\}\kern-1.5pt. \end{align*} $$
$$ \begin{align*} c_9= &\max\bigg\{0, \frac{1}{d-1}\log^+|2N|+\frac{N}{d^N-1}\log^+|2|-\frac{1}{N(d-1)}\log^+|N!|, \\ & \frac{c_8(d^{1/2}-1)+c_3+c_5+(2dN+1)\kern-1pt\log^+|2|+(2N-2+dN(d^N-1))\kern-0.7pt\log^+|d|}{d-1}\!\bigg\}\kern-1.5pt. \end{align*} $$
Then
Proof. First, note that
![]() $\Delta _f(C_f)$
,
$\Delta _f(C_f)$
,
![]() $\lambda (A)$
,
$\lambda (A)$
,
![]() $\xi (A)$
, and
$\xi (A)$
, and
![]() $c_9$
are all non-negative, and so our conclusion holds trivially if
$c_9$
are all non-negative, and so our conclusion holds trivially if
![]() $\log ^+\|\mathbf {b}\|=0$
. We will, therefore, assume throughout that
$\log ^+\|\mathbf {b}\|=0$
. We will, therefore, assume throughout that
![]() $\log ^+\|\mathbf {b}\|=\log \|\mathbf {b}\|>0$
.
$\log ^+\|\mathbf {b}\|=\log \|\mathbf {b}\|>0$
.
Let
![]() $B_i=L_* H_i=(L^{-1})^*H_i$
, noting that the finite part of the branch locus of f is supported exactly on the
$B_i=L_* H_i=(L^{-1})^*H_i$
, noting that the finite part of the branch locus of f is supported exactly on the
![]() $B_i$
. The hyperplanes
$B_i$
. The hyperplanes
![]() $B_i$
, for
$B_i$
, for
![]() $1\leq i\leq N$
, are defined by the linear forms
$1\leq i\leq N$
, are defined by the linear forms
![]() $g_i$
whose coefficients make up the first N rows of
$g_i$
whose coefficients make up the first N rows of
![]() $L^{-1}$
, which we recall is given by
$L^{-1}$
, which we recall is given by
 $$ \begin{align*}L^{-1}=\begin{pmatrix}A^{-1} & -A^{-1}\mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}L^{-1}=\begin{pmatrix}A^{-1} & -A^{-1}\mathbf{b} \\ \mathbf{0} & 1 \end{pmatrix}.\end{align*} $$
Now, note that
and so there is some i such that the ith entry
![]() $b_i'$
of
$b_i'$
of
![]() $\mathbf {b}'=-A^{-1}\mathbf {b}$
satisfies
$\mathbf {b}'=-A^{-1}\mathbf {b}$
satisfies
 $$ \begin{align*} \log\|g_i\| &\geq \log|b_i'|\\ &\geq \log\|\mathbf{b}\|-\log\|A\|-\log^+|N|. \end{align*} $$
$$ \begin{align*} \log\|g_i\| &\geq \log|b_i'|\\ &\geq \log\|\mathbf{b}\|-\log\|A\|-\log^+|N|. \end{align*} $$
On the other hand,
![]() $\log \|g_i|_H\|\leq \log \|A^{-1}\|$
, and so we have
$\log \|g_i|_H\|\leq \log \|A^{-1}\|$
, and so we have
Note also
![]() $b_i'=g_{i, \deg (g_i)}$
in the notation of the definition of
$b_i'=g_{i, \deg (g_i)}$
in the notation of the definition of
![]() $\mu $
, and so we also have
$\mu $
, and so we also have
 $$ \begin{align*} \mu(B_i)&\geq \log\|\mathbf{b}\|-\xi(A)\\ &=\log\|\mathbf{b}\|-\xi(A)+c_8(-1+\deg(B_i)^{1/2(N-1)}), \end{align*} $$
$$ \begin{align*} \mu(B_i)&\geq \log\|\mathbf{b}\|-\xi(A)\\ &=\log\|\mathbf{b}\|-\xi(A)+c_8(-1+\deg(B_i)^{1/2(N-1)}), \end{align*} $$
given that
![]() $\deg (B_i)=1$
. Evidently, condition (22) in Lemma 22 is met, and so if (21) is satisfied as well, then we have
$\deg (B_i)=1$
. Evidently, condition (22) in Lemma 22 is met, and so if (21) is satisfied as well, then we have
 $$ \begin{align*} \Delta_f(B_i)&\geq \log\|\mathbf{b}\|-\frac{1}{N(d-1)}\lambda(A^{-1})+\frac{1}{N(d-1)}\log^+|N!|-\xi(A)\\ &\quad-\frac{1}{d-1}\log^+|2N| -\frac{N}{d^N-1}\log^+|2|, \end{align*} $$
$$ \begin{align*} \Delta_f(B_i)&\geq \log\|\mathbf{b}\|-\frac{1}{N(d-1)}\lambda(A^{-1})+\frac{1}{N(d-1)}\log^+|N!|-\xi(A)\\ &\quad-\frac{1}{d-1}\log^+|2N| -\frac{N}{d^N-1}\log^+|2|, \end{align*} $$
which is stronger than
If, on the other hand, we fail to meet (21), then
 $$ \begin{align*} (d-1)\log\|\mathbf{b}\|-\frac{1}{N}\lambda(A^{-1})-d\xi(A) &\leq (d-1)\log\|\mathbf{b}\|-\log\|A^{-1}\|-d\xi(A)\\ &\leq c_8(d^{1/2}-1)+c_3+c_5+(2dN+1)\log^+|2|\\ &\quad +\,(2N-2+dN(d^N-1))\log^+|d| \\ & \leq (d-1)c_9, \end{align*} $$
$$ \begin{align*} (d-1)\log\|\mathbf{b}\|-\frac{1}{N}\lambda(A^{-1})-d\xi(A) &\leq (d-1)\log\|\mathbf{b}\|-\log\|A^{-1}\|-d\xi(A)\\ &\leq c_8(d^{1/2}-1)+c_3+c_5+(2dN+1)\log^+|2|\\ &\quad +\,(2N-2+dN(d^N-1))\log^+|d| \\ & \leq (d-1)c_9, \end{align*} $$
in which case (23) is true simply because
![]() $\Delta _f(B_i)\geq 0$
.
$\Delta _f(B_i)\geq 0$
.
Inequality (23), combined with the non-negativity of
![]() $\Delta _f$
, gives
$\Delta _f$
, gives
 $$ \begin{align*} \Delta_f(C_f)&= \sum_{j=1}^N(d-1)\Delta_f(H_j) \\ &\geq (d-1)\Delta_f(H_i)\\ &=\frac{d-1}{d^N}\Delta_f(f_*H_i) \\ &= \frac{d-1}{d^N}\Delta_f(d^{N-1}B_i) \\ &\geq \frac{d-1}{d}\log^+\|\mathbf{b}\|-\frac{1}{Nd}\lambda(A^{-1})-\xi(A)-\frac{d-1}{d}c_9.\\[-39pt] \end{align*} $$
$$ \begin{align*} \Delta_f(C_f)&= \sum_{j=1}^N(d-1)\Delta_f(H_j) \\ &\geq (d-1)\Delta_f(H_i)\\ &=\frac{d-1}{d^N}\Delta_f(f_*H_i) \\ &= \frac{d-1}{d^N}\Delta_f(d^{N-1}B_i) \\ &\geq \frac{d-1}{d}\log^+\|\mathbf{b}\|-\frac{1}{Nd}\lambda(A^{-1})-\xi(A)-\frac{d-1}{d}c_9.\\[-39pt] \end{align*} $$
Although Lemma 23 is the key ingredient in our main results, one might wish to record the corresponding bound in the other direction, an immediate consequence of results already shown.
Lemma 24 There is a bound of the form
 $$ \begin{align*} \Delta_f(C_f)&\leq N(N+2)\log^+\|\mathbf{b}\|+(N+1)\lambda(A)+N\log^+|(N+1)!|+\log^+|N!|\\ &\quad+N\log^+|4N(N+1)| +\bigg(4N^2d+\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align*} $$
$$ \begin{align*} \Delta_f(C_f)&\leq N(N+2)\log^+\|\mathbf{b}\|+(N+1)\lambda(A)+N\log^+|(N+1)!|+\log^+|N!|\\ &\quad+N\log^+|4N(N+1)| +\bigg(4N^2d+\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align*} $$
Proof. Note that
![]() $C_f$
is defined by the monomial equation
$C_f$
is defined by the monomial equation
and so
![]() $\lambda (C_f)=0$
. By Lemma 19, or more precisely (19) therein, we have
$\lambda (C_f)=0$
. By Lemma 19, or more precisely (19) therein, we have
 $$ \begin{align*}\Delta_f(C_f)&\leq \frac{\deg(C_f)}{d-1}(\log\|L\|-\log\|A\|+\log^+|4N(N+1)|\\[4pt]&\quad+\lambda(L)+4Nd\log^+|2|)+\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align*} $$
$$ \begin{align*}\Delta_f(C_f)&\leq \frac{\deg(C_f)}{d-1}(\log\|L\|-\log\|A\|+\log^+|4N(N+1)|\\[4pt]&\quad+\lambda(L)+4Nd\log^+|2|)+\bigg(\frac{2N-1}{d^N-1}\bigg)\log^+|2|. \end{align*} $$
Now, since
![]() $A\in \operatorname {SL}_N(K)$
, we have
$A\in \operatorname {SL}_N(K)$
, we have
![]() $-({1}/{N})\log ^+|N!|\leq \log \|A\|$
, and so
$-({1}/{N})\log ^+|N!|\leq \log \|A\|$
, and so
Also, we have
 $$ \begin{align*} \lambda(L) & = (N+1)\log\|L\|+\log^+|(N+1)!|\\[4pt] &\leq (N+1)\log^+\|\mathbf{b}\|+\frac{N+1}{N}\log^+|N!|+(N+1)\log\|A\|+\log^+|(N+1)!| \\[4pt] &= (N+1)\log^+\|\mathbf{b}\|+\frac{N+1}{N}\lambda(A)+\log^+|(N+1)!|. \end{align*} $$
$$ \begin{align*} \lambda(L) & = (N+1)\log\|L\|+\log^+|(N+1)!|\\[4pt] &\leq (N+1)\log^+\|\mathbf{b}\|+\frac{N+1}{N}\log^+|N!|+(N+1)\log\|A\|+\log^+|(N+1)!| \\[4pt] &= (N+1)\log^+\|\mathbf{b}\|+\frac{N+1}{N}\lambda(A)+\log^+|(N+1)!|. \end{align*} $$
The claim follows, since
![]() $\deg (C_f)=N(d-1)$
.
$\deg (C_f)=N(d-1)$
.
Thus, with a view to fixing A, we have
which proves Theorem 1. Indeed, the error terms can be made explicit in terms of
![]() $\lambda (A)$
,
$\lambda (A)$
,
![]() $\lambda (A^{-1})$
, and
$\lambda (A^{-1})$
, and
![]() $\xi (A)$
, all non-negative functions on
$\xi (A)$
, all non-negative functions on
![]() $\operatorname {SL}_N(K)$
, which are plurisubharmonic and continuous when
$\operatorname {SL}_N(K)$
, which are plurisubharmonic and continuous when
![]() $K=\mathbb {C}$
. The following proposition also proves Corollary 2, recalling (20).
$K=\mathbb {C}$
. The following proposition also proves Corollary 2, recalling (20).
Proposition 25 In the case
![]() $K=\mathbb {C}$
, the map
$K=\mathbb {C}$
, the map
by
is continuous, plurisubharmonic, and proper. In particular, if
then the projection
![]() $\pi :\mathcal {M}\to \operatorname {SL}_{N+1}(\mathbb {C})$
is proper.
$\pi :\mathcal {M}\to \operatorname {SL}_{N+1}(\mathbb {C})$
is proper.
Proof. Note that, by (20), the set
![]() $\mathcal {M}$
is equivalently defined as the set of pairs for which
$\mathcal {M}$
is equivalently defined as the set of pairs for which
![]() $\Delta _f(C_f)=0$
.
$\Delta _f(C_f)=0$
.
For any
![]() $k\geq 0$
, the function
$k\geq 0$
, the function
is continuous and plurisubharmonic, since there is a homogeneous form defining
![]() $f^k_*C_f$
whose coefficients are polynomials in the entries of A and
$f^k_*C_f$
whose coefficients are polynomials in the entries of A and
![]() $\mathbf {b}$
. But from Lemma 19, these functions converge uniformly on compact subsets to
$\mathbf {b}$
. But from Lemma 19, these functions converge uniformly on compact subsets to
![]() $\Delta _f(C_f)$
, and so
$\Delta _f(C_f)$
, and so
![]() $f\mapsto \Delta _f(C_f)$
is continuous and plurisubharmonic. This part of the result can also be accessed by work of Basanelli and Berteloot [Reference Bedford and Jonsson1, §1.4] (see also [Reference Dinh and Sibony5]).
$f\mapsto \Delta _f(C_f)$
is continuous and plurisubharmonic. This part of the result can also be accessed by work of Basanelli and Berteloot [Reference Bedford and Jonsson1, §1.4] (see also [Reference Dinh and Sibony5]).
Now, on any compact
![]() $E\subseteq \operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {R}$
the functions
$E\subseteq \operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {R}$
the functions
![]() $\lambda (A)$
and
$\lambda (A)$
and
![]() $\xi (A)$
are bounded, and so Lemma 23 gives, for
$\xi (A)$
are bounded, and so Lemma 23 gives, for
![]() $(A, \mathbf {b})\in \mathcal {M}$
,
$(A, \mathbf {b})\in \mathcal {M}$
,
for
![]() $\Delta _f(C_f)$
in the projection of the second coordinate of E. Since
$\Delta _f(C_f)$
in the projection of the second coordinate of E. Since
![]() $\operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {C}^N\to \operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {R}$
is continuous, it is also proper.
$\operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {C}^N\to \operatorname {SL}_{N+1}(\mathbb {C})\times \mathbb {R}$
is continuous, it is also proper.
We end with a generalization of the observation that, if
![]() $z^d+c$
is PCF, then c is an algebraic integer. We recall that a morphism
$z^d+c$
is PCF, then c is an algebraic integer. We recall that a morphism
![]() $f:\mathbb {P}^N_K\to \mathbb {P}^N_K$
, with K complete with respect to a non-archimedean absolute value, has good reduction if and only if f extends to a scheme morphism
$f:\mathbb {P}^N_K\to \mathbb {P}^N_K$
, with K complete with respect to a non-archimedean absolute value, has good reduction if and only if f extends to a scheme morphism
![]() $\overline {f}:\mathbb {P}^N_R\to \mathbb {P}^N_R$
over the ring of integers R. Equivalently, if we choose homogeneous forms representing f, whose coefficients are integral and not all contained in the maximal ideal, then f has good reduction if and only if the resultant of these homogeneous forms is a unit.
$\overline {f}:\mathbb {P}^N_R\to \mathbb {P}^N_R$
over the ring of integers R. Equivalently, if we choose homogeneous forms representing f, whose coefficients are integral and not all contained in the maximal ideal, then f has good reduction if and only if the resultant of these homogeneous forms is a unit.
Proposition 26 Let K be an algebraically closed field, complete with respect to a non-archimedean absolute value which is not p-adic for any
![]() $p\leq \max \{d, N!\}$
, with ring of integers R. Then any PCF map of the form (1) with
$p\leq \max \{d, N!\}$
, with ring of integers R. Then any PCF map of the form (1) with
![]() $A\in \operatorname {SL}_N(R)$
has good reduction.
$A\in \operatorname {SL}_N(R)$
has good reduction.
Good reduction has various dynamical consequences. For example, if
![]() $f:\mathbb {P}^N\to \mathbb {P}^N$
has good reduction, and
$f:\mathbb {P}^N\to \mathbb {P}^N$
has good reduction, and
![]() $f(P)=P$
, then any eigenvalue
$f(P)=P$
, then any eigenvalue
![]() $\lambda $
of the action of f on the tangent space at P satisfies
$\lambda $
of the action of f on the tangent space at P satisfies
![]() $|\lambda |\leq 1$
(so, in a strong sense, periodic points are non-repelling).
$|\lambda |\leq 1$
(so, in a strong sense, periodic points are non-repelling).
Proof Proof of Proposition 26
For
![]() $A\in \operatorname {SL}_N(R)$
, we claim that f has good reduction if and only if the entries of
$A\in \operatorname {SL}_N(R)$
, we claim that f has good reduction if and only if the entries of
![]() $\mathbf {b}$
are integral. To see this, note that if the entries of
$\mathbf {b}$
are integral. To see this, note that if the entries of
![]() $\mathbf {b}$
are integral, then the entries of the matrix
$\mathbf {b}$
are integral, then the entries of the matrix
![]() $L=(\begin {smallmatrix}A & \mathbf {b} \\ \mathbf {0} & 1\end {smallmatrix})$
are integral, and are the coefficients of some homogeneous forms
$L=(\begin {smallmatrix}A & \mathbf {b} \\ \mathbf {0} & 1\end {smallmatrix})$
are integral, and are the coefficients of some homogeneous forms
![]() $F_i(\mathbf {X})=\sum _{j=1}^{N+1} L_{i, j}X_{j-1}^d$
defining f. If all entries are in the maximal ideal, then we could not have
$F_i(\mathbf {X})=\sum _{j=1}^{N+1} L_{i, j}X_{j-1}^d$
defining f. If all entries are in the maximal ideal, then we could not have
![]() $\det (A)=1$
, and so f has good reduction if and only if the resultant of these forms is a unit. But by [Reference Lang14, Theorem 3.13, p. 399] these homogeneous forms have resultant
$\det (A)=1$
, and so f has good reduction if and only if the resultant of these forms is a unit. But by [Reference Lang14, Theorem 3.13, p. 399] these homogeneous forms have resultant
If, on the other hand, the entries of
![]() $\mathbf {b}$
are non-integral, then for
$\mathbf {b}$
are non-integral, then for
![]() $\pi $
a uniformizer of the absolute value, there is some
$\pi $
a uniformizer of the absolute value, there is some
![]() $\varepsilon>0$
so that the entries of
$\varepsilon>0$
so that the entries of
![]() $\pi ^\varepsilon L$
are integral, and at least one is a unit. We have
$\pi ^\varepsilon L$
are integral, and at least one is a unit. We have
![]() $\det (\pi ^\varepsilon L)=\pi ^{(N+1)\varepsilon }$
not a unit, and so by the same argument as above, f has bad reduction.
$\det (\pi ^\varepsilon L)=\pi ^{(N+1)\varepsilon }$
not a unit, and so by the same argument as above, f has bad reduction.
Now, given our assumptions on the absolute value, we have
![]() $\xi (A)=0$
and
$\xi (A)=0$
and
![]() $\log \|A^{-1}\|=0$
, and Lemma 23 gives
$\log \|A^{-1}\|=0$
, and Lemma 23 gives
If f is PCF, and hence
![]() $\Delta _f(C_f)=0$
, it follows that
$\Delta _f(C_f)=0$
, it follows that
![]() $\log ^+\|\mathbf {b}\|=0$
, and so the entries of
$\log ^+\|\mathbf {b}\|=0$
, and so the entries of
![]() $\mathbf {b}$
are integral.
$\mathbf {b}$
are integral.
4 Global results
We now change context so that K is a field with a collection of inequivalent absolute values
![]() $M_K$
with weights
$M_K$
with weights
![]() $n_v$
such that the product formula holds for
$n_v$
such that the product formula holds for
![]() $\alpha \in K^*$
, that is,
$\alpha \in K^*$
, that is,
Our main example is when K is a number field,
![]() $M_K$
is the standard set of absolute values, and
$M_K$
is the standard set of absolute values, and
![]() $n_v=[K_v:\mathbb {Q}_v]/[K:\mathbb {Q}]$
. For any absolute value
$n_v=[K_v:\mathbb {Q}_v]/[K:\mathbb {Q}]$
. For any absolute value
![]() $|\cdot |_v$
on K we may apply results from the previous section to an algebraically closed completion of K, with respect to v, and all quantities thereby obtained now acquire a subscript v.
$|\cdot |_v$
on K we may apply results from the previous section to an algebraically closed completion of K, with respect to v, and all quantities thereby obtained now acquire a subscript v.
For a divisor D on
![]() $\mathbb {P}^N_K$
defined by the vanishing of the homogeneous form
$\mathbb {P}^N_K$
defined by the vanishing of the homogeneous form
![]() $F(\mathbf {X})\in K[X_1, \ldots , X_{N+1}]$
, let
$F(\mathbf {X})\in K[X_1, \ldots , X_{N+1}]$
, let
that is, let the height of D be the height of the tuple of coefficients as a point in the appropriate dual projective space. Note that, by (24), this definition is independent of the choice of form defining D, while (4) can be used to relate this height to the height used by Philippon [Reference Philippon17], which we used in [Reference Ingram12], and then to that of Faltings [Reference Faltings6] (see [Reference Soulé20]).
Then we see immediately that for D not containing H,
Writing
![]() $\hat {h}_f(D)$
for the canonical height of D relative to f, so
$\hat {h}_f(D)$
for the canonical height of D relative to f, so
we then have
(see also [Reference Bedford and Jonsson1
Reference Bassanelli and Berteloot3, Reference Bedford and Jonsson1
Reference Bombieri and Gubler4]). Note that in [Reference Ingram12], a different naive height was used on divisors, but since the heights differ by at most
![]() $O(\deg (D))$
, the canonical height is the same (see Remark 21). Also note the one subtlety here, that
$O(\deg (D))$
, the canonical height is the same (see Remark 21). Also note the one subtlety here, that
![]() $(f_*D)|_H = d(f|_H)_* D|_H\!,$
so that
$(f_*D)|_H = d(f|_H)_* D|_H\!,$
so that
![]() $\hat {h}_{f|_H}((f_*D)|_H)=d^N\hat {h}_{f|_H}(D|_H)$
, despite
$\hat {h}_{f|_H}((f_*D)|_H)=d^N\hat {h}_{f|_H}(D|_H)$
, despite
![]() $\dim (H)=N-1$
.
$\dim (H)=N-1$
.
Note that since
![]() $f^*H=dH$
, it follows readily that for
$f^*H=dH$
, it follows readily that for
![]() $C_f$
as above,
$C_f$
as above,
![]() $C_f+(d-1)H$
is the ramification divisor of f, and
$C_f+(d-1)H$
is the ramification divisor of f, and
![]() $\hat {h}_{\mathrm {crit}}(f)=\hat {h}_f(C_f)$
. In particular, we have
$\hat {h}_{\mathrm {crit}}(f)=\hat {h}_f(C_f)$
. In particular, we have
We may now proceed with the proofs of the global results.
Proof of Theorem 3. Let K be a number field, and let f be as in (1), with coefficients in K. At each place v of
![]() $K,$
with subscripts denoting dependence on the corresponding absolute value, we have from Lemma 23 that
$K,$
with subscripts denoting dependence on the corresponding absolute value, we have from Lemma 23 that
Summing over all places, we obtain the desired bound once we note that
 $$ \begin{gather*} \sum_{v\in M_K}n_v\log^+\|\mathbf{b}\|_v=h_{\mathbb{P}^N}(\mathbf{b}),\\ \sum_{v\in M_K}n_v\lambda_v(A)=Nh_{\operatorname{PGL}_{N+1}}(A)+\log N!,\\ \sum_{v\in M_K}n_v\xi(A)=h_{\operatorname{PGL}_{N+1}}(A)+h_{\operatorname{PGL}_{N+1}}(A^{-1})+\log N, \end{gather*} $$
$$ \begin{gather*} \sum_{v\in M_K}n_v\log^+\|\mathbf{b}\|_v=h_{\mathbb{P}^N}(\mathbf{b}),\\ \sum_{v\in M_K}n_v\lambda_v(A)=Nh_{\operatorname{PGL}_{N+1}}(A)+\log N!,\\ \sum_{v\in M_K}n_v\xi(A)=h_{\operatorname{PGL}_{N+1}}(A)+h_{\operatorname{PGL}_{N+1}}(A^{-1})+\log N, \end{gather*} $$
and
while
![]() $\sum _{v\in M_K}n_vc_{9, v}$
is some explicit constant depending just on N and d. Note that this last upper bound contains the sum
$\sum _{v\in M_K}n_vc_{9, v}$
is some explicit constant depending just on N and d. Note that this last upper bound contains the sum
![]() $\sum _{p\leq d}({\log p}/({p-1}))$
, a sum over primes, which can be explicitly bounded above in terms of d using estimates of Rosser and Schoenfeld [Reference Rosser and Schoenfeld18].
$\sum _{p\leq d}({\log p}/({p-1}))$
, a sum over primes, which can be explicitly bounded above in terms of d using estimates of Rosser and Schoenfeld [Reference Rosser and Schoenfeld18].
Similarly, the upper bound on
![]() $\hat {h}_{\mathrm {crit}}(f)-\hat {h}_{\mathrm {crit}}(f|_H)$
comes from summing the estimates in Lemma 24 over all places.
$\hat {h}_{\mathrm {crit}}(f)-\hat {h}_{\mathrm {crit}}(f|_H)$
comes from summing the estimates in Lemma 24 over all places.
Note that the terms
![]() $\hat {h}_{\mathrm {crit}}(f)$
and
$\hat {h}_{\mathrm {crit}}(f)$
and
![]() $\hat {h}_{\mathrm {crit}}(f|_H)$
in Theorem 3 are independent of choice of coordinates, while the terms
$\hat {h}_{\mathrm {crit}}(f|_H)$
in Theorem 3 are independent of choice of coordinates, while the terms
![]() $h(\mathbf {b})$
and
$h(\mathbf {b})$
and
![]() $h(A)$
are not. Indeed, it is possible to take
$h(A)$
are not. Indeed, it is possible to take
![]() $h(\mathbf {b})\to \infty $
within a conjugacy class, which might seem troubling at first for a lower bound on an invariant of the class, but note that this would result in the error term increasing as well.
$h(\mathbf {b})\to \infty $
within a conjugacy class, which might seem troubling at first for a lower bound on an invariant of the class, but note that this would result in the error term increasing as well.
Proof Proof of Theorem 5
Suppose our putative algebraic family is defined over the variety
![]() $V/k$
, and let
$V/k$
, and let
![]() $K=k(V)$
be the function field, so that we may think of f as a single map with coefficients in K. There exists a set
$K=k(V)$
be the function field, so that we may think of f as a single map with coefficients in K. There exists a set
![]() $M_K$
of inequivalent absolute values such that the elements of height zero are precisely the constants (namely, we can take
$M_K$
of inequivalent absolute values such that the elements of height zero are precisely the constants (namely, we can take
![]() $M_K$
to be the collection of absolute values corresponding to vanishing of functions on irreducible divisors on any normal, projective variety
$M_K$
to be the collection of absolute values corresponding to vanishing of functions on irreducible divisors on any normal, projective variety
![]() $V'$
birational to V [Reference Bombieri and Gubler4, Lemma 1.4.10, p. 12]).
$V'$
birational to V [Reference Bombieri and Gubler4, Lemma 1.4.10, p. 12]).
All of these absolute values are non-archimedean, and none are p-adic, and since A is constant we have by Proposition 26 that the entries of
![]() $\mathbf {b}$
are integral. In other words, given any irreducible divisor on
$\mathbf {b}$
are integral. In other words, given any irreducible divisor on
![]() $V'$
, the functions
$V'$
, the functions
![]() $b_i$
do not have a pole along
$b_i$
do not have a pole along
![]() $V'$
, and since the divisor was arbitrary, the
$V'$
, and since the divisor was arbitrary, the
![]() $b_i$
are all constant.
$b_i$
are all constant.
Finally, we note that the results in the previous sections allow for explicit estimates on the difference between the canonical height and the naive height of a divisor. Such results appear in [Reference Ingram10], but here (and with regular polynomial endomorphisms in general) it seems to make more sense to think in terms of relative quantities.
Proposition 27 Let D be an effective divisor on
![]() $\mathbb {P}^N\!,$
and f as in (1). Also, write
$\mathbb {P}^N\!,$
and f as in (1). Also, write
and
Then
Proof. Similar to the other results in this section, this is just a matter of summing (19) over all places.
5 The cases
 $d>N^2-N+1$
and
$d>N^2-N+1$
and
 $N=2$
$N=2$
Here we make a few remarks on cases in which the relative results in the introduction become absolute, largely by leveraging the results in [Reference Ingram10].
Proposition 28 Let
![]() $d>N^2-N+1$
or
$d>N^2-N+1$
or
![]() $N=2$
. Then the PCF maps of the form (1) are a set of bounded height, up to conjugation.
$N=2$
. Then the PCF maps of the form (1) are a set of bounded height, up to conjugation.
Proof. If f of the form (1) is PCF, then so is
![]() $f|_H$
, which is a minimally critical endomorphism in the sense of [Reference Ingram10]. If
$f|_H$
, which is a minimally critical endomorphism in the sense of [Reference Ingram10]. If
![]() $d>N^2-N+1=(N-1)^2+(N-1)+1$
, then the main result of [Reference Ingram10] shows that
$d>N^2-N+1=(N-1)^2+(N-1)+1$
, then the main result of [Reference Ingram10] shows that
![]() $f|_H$
is conjugate to a map of the form
$f|_H$
is conjugate to a map of the form
![]() $B\mathbf {X}^d$
with
$B\mathbf {X}^d$
with
![]() $h_{\operatorname {PGL}_{N}}(B)$
bounded in terms of d and N. We can extend this change of coordinates to
$h_{\operatorname {PGL}_{N}}(B)$
bounded in terms of d and N. We can extend this change of coordinates to
![]() $\mathbb {P}^N$
and choose a lift of B to
$\mathbb {P}^N$
and choose a lift of B to
![]() $\operatorname {SL}_N\!,$
and thereby replace f by a map
$\operatorname {SL}_N\!,$
and thereby replace f by a map
![]() $f(\mathbf {X})=A\mathbf {X}^d+\mathbf {b}$
with
$f(\mathbf {X})=A\mathbf {X}^d+\mathbf {b}$
with
![]() $h(A)$
bounded. But now Theorem 3 gives us that
$h(A)$
bounded. But now Theorem 3 gives us that
![]() $h(\mathbf {b})$
is bounded as well (in terms of d and N).
$h(\mathbf {b})$
is bounded as well (in terms of d and N).
In the case
![]() $N=2$
we may extend this to
$N=2$
we may extend this to
![]() $d=2, 3$
by the main result of [Reference Bassanelli and Berteloot3]. Here,
$d=2, 3$
by the main result of [Reference Bassanelli and Berteloot3]. Here,
![]() $f|_H$
is a minimally critical (bicritical) endomorphism of
$f|_H$
is a minimally critical (bicritical) endomorphism of
![]() $\mathbb {P}^1$
which is PCF, and hence has bounded moduli height. It is not a priori obvious that this map will be conjugate to something of the form
$\mathbb {P}^1$
which is PCF, and hence has bounded moduli height. It is not a priori obvious that this map will be conjugate to something of the form
![]() $B\mathbf {X}^d$
with
$B\mathbf {X}^d$
with
![]() $B\in \operatorname {PGL}_2$
of bounded height, but this follows from [Reference Ingram10, Lemma 15] and [Reference Silverman19, Lemma 6.32, p. 102]. The rest of the argument is now the same.
$B\in \operatorname {PGL}_2$
of bounded height, but this follows from [Reference Ingram10, Lemma 15] and [Reference Silverman19, Lemma 6.32, p. 102]. The rest of the argument is now the same.
Remark 29 There are, of course, a bevy of examples of PCF endomorphisms of the form (1) with
![]() $\mathbf {b}=\mathbf {0}$
, but we expect examples with
$\mathbf {b}=\mathbf {0}$
, but we expect examples with
![]() $\mathbf {b}\neq \mathbf {0}$
to be quite rare. As such, it would be interesting to compute exhaustive lists of examples defined over
$\mathbf {b}\neq \mathbf {0}$
to be quite rare. As such, it would be interesting to compute exhaustive lists of examples defined over
![]() $\mathbb {Q}$
, say, in the case
$\mathbb {Q}$
, say, in the case
![]() $N=2$
, which brings us to the question of how explicit the bounds in Proposition 28 can be made.
$N=2$
, which brings us to the question of how explicit the bounds in Proposition 28 can be made.
The bounds for
![]() $h(\mathbf {b})$
can be made completely explicit, in terms of
$h(\mathbf {b})$
can be made completely explicit, in terms of
![]() $h(A)$
, by a careful tracing through the proof of Theorem 3. In the case
$h(A)$
, by a careful tracing through the proof of Theorem 3. In the case
![]() $d=2$
, bounds for
$d=2$
, bounds for
![]() $h(A)$
are made concrete in [Reference Bassanelli and Berteloot3], and so the exhaustive list implied by Proposition 28 could actually be computed (but not easily). In the case
$h(A)$
are made concrete in [Reference Bassanelli and Berteloot3], and so the exhaustive list implied by Proposition 28 could actually be computed (but not easily). In the case
![]() $d\geq 3$
, the results in [Reference Bassanelli and Berteloot3] do not imply anything quite so explicit, but we note that a more direct argument gives effective constants when
$d\geq 3$
, the results in [Reference Bassanelli and Berteloot3] do not imply anything quite so explicit, but we note that a more direct argument gives effective constants when
![]() $d\geq 4$
(see [Reference Ingram10]).
$d\geq 4$
(see [Reference Ingram10]).
Proposition 30 Let
![]() $d>N^2-N+1$
or
$d>N^2-N+1$
or
![]() $N=2$
. Then there are no algebraic families of PCF maps of the form (1) over
$N=2$
. Then there are no algebraic families of PCF maps of the form (1) over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Proof. If
![]() $d>N^2-N+1$
, then again the results of [Reference Ingram10] apply to the restriction
$d>N^2-N+1$
, then again the results of [Reference Ingram10] apply to the restriction
![]() $f|_H$
. So if f is a PCF family, then
$f|_H$
. So if f is a PCF family, then
![]() $f|_H$
is also a PCF family, and by [Reference Ingram10, Theorem 3] must be isotrivial. Extending this change of coordinates to
$f|_H$
is also a PCF family, and by [Reference Ingram10, Theorem 3] must be isotrivial. Extending this change of coordinates to
![]() $\mathbb {P}^N$
, we may replace f by a conjugate family (perhaps after a finite extension of the function field) so that
$\mathbb {P}^N$
, we may replace f by a conjugate family (perhaps after a finite extension of the function field) so that
![]() $f|_H$
is constant. Theorem 5 now applies to show that all coefficients of f are constant. If
$f|_H$
is constant. Theorem 5 now applies to show that all coefficients of f are constant. If
![]() $N=2$
the argument is the same, except now in the case
$N=2$
the argument is the same, except now in the case
![]() $d=2, 3$
we must use Thurston’s result to conclude that the family
$d=2, 3$
we must use Thurston’s result to conclude that the family
![]() $f|_H$
of PCF endomorphisms of
$f|_H$
of PCF endomorphisms of
![]() $\mathbb {P}^1$
is isotrivial.
$\mathbb {P}^1$
is isotrivial.
In positive characteristic, we may still apply the results of [Reference Ingram10] and prove a version of Proposition 5 when
![]() $d>N^2-N+1$
. In the case
$d>N^2-N+1$
. In the case
![]() $N=2$
,
$N=2$
,
![]() $d=3$
we are out of luck, but the remaining case
$d=3$
we are out of luck, but the remaining case
![]() $N=d=2$
can be treated in odd characteristic by the exact same proof, and an appeal to the rigidity of PCF quadratic endomorphisms of
$N=d=2$
can be treated in odd characteristic by the exact same proof, and an appeal to the rigidity of PCF quadratic endomorphisms of
![]() $\mathbb {P}^1$
in odd characteristic [Reference Bassanelli and Berteloot3].
$\mathbb {P}^1$
in odd characteristic [Reference Bassanelli and Berteloot3].
Proposition 31 In characteristic
![]() $p\neq 2$
, there are no algebraic families of quadratic PCF maps
$p\neq 2$
, there are no algebraic families of quadratic PCF maps
![]() $f:\mathbb {P}^2\to \mathbb {P}^2$
of the form (1).
$f:\mathbb {P}^2\to \mathbb {P}^2$
of the form (1).