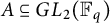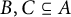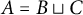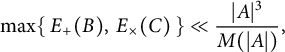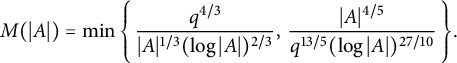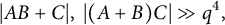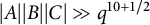1 Introduction
Let
![]() ${\mathbb F}_q$
denote a finite field of order q and characteristic p, and let
${\mathbb F}_q$
denote a finite field of order q and characteristic p, and let
![]() $M_2({\mathbb F}_q)$
be the set of two-by-two matrices with entries in
$M_2({\mathbb F}_q)$
be the set of two-by-two matrices with entries in
![]() ${\mathbb F}_q$
. We write
${\mathbb F}_q$
. We write
![]() $X\ll Y$
to mean
$X\ll Y$
to mean
![]() $X\leq CY$
for some absolute constant
$X\leq CY$
for some absolute constant
![]() $C>0$
and use
$C>0$
and use
![]() $X\sim Y$
if
$X\sim Y$
if
![]() $Y\ll X\ll Y$
.
$Y\ll X\ll Y$
.
Given subsets
![]() $A, B\subseteq M_2({\mathbb F}_q)$
, we define the sum set
$A, B\subseteq M_2({\mathbb F}_q)$
, we define the sum set
![]() $A+B$
to be the set
$A+B$
to be the set
![]() $\{a+b: (a, b)\in A\times B\}$
and similarly define the product set
$\{a+b: (a, b)\in A\times B\}$
and similarly define the product set
![]() $AB$
. In this paper, we study various questions closely related to the sum-product problem over
$AB$
. In this paper, we study various questions closely related to the sum-product problem over
![]() $M_2({\mathbb F}_q)$
, which is to determine nontrivial lower bounds on the quantity
$M_2({\mathbb F}_q)$
, which is to determine nontrivial lower bounds on the quantity
![]() $\max \{\,|A+A|,\, |AA|\,\}$
, under natural conditions on sets
$\max \{\,|A+A|,\, |AA|\,\}$
, under natural conditions on sets
![]() $A\subseteq M_2({\mathbb F}_q)$
.
$A\subseteq M_2({\mathbb F}_q)$
.
A result in this direction was proved by Karabulut et al. in [Reference Karabulut, Koh, Pham, Shen and Vinh4, Theorem 1.12], showing that if
![]() $A\subseteq M_2({\mathbb F}_q)$
satisfies
$A\subseteq M_2({\mathbb F}_q)$
satisfies
![]() $|A|\gg q^3$
then
$|A|\gg q^3$
then
 $$ \begin{align} \max\{\,|A+A|,\, |AA|\,\}\gg \min\left\{\,\frac{|A|^2}{q^{7/2}},\, q^{2}|A|^{1/2}\,\right\}. \end{align} $$
$$ \begin{align} \max\{\,|A+A|,\, |AA|\,\}\gg \min\left\{\,\frac{|A|^2}{q^{7/2}},\, q^{2}|A|^{1/2}\,\right\}. \end{align} $$
A closely related quantity is the additive energy
![]() $E_+(A, B)$
defined as the number of quadruples
$E_+(A, B)$
defined as the number of quadruples
![]() $(a, a^{\prime }, b, b^{\prime })\in A^2\times B^2$
such that
$(a, a^{\prime }, b, b^{\prime })\in A^2\times B^2$
such that
![]() $a + b = a^{\prime } + b^{\prime }$
. The multiplicative energy
$a + b = a^{\prime } + b^{\prime }$
. The multiplicative energy
![]() $E_{\times }(A, B)$
is defined in a similar manner. We also use, for example,
$E_{\times }(A, B)$
is defined in a similar manner. We also use, for example,
![]() $E_+(A) = E_+(A, A)$
. For
$E_+(A) = E_+(A, A)$
. For
![]() $\lambda \in M_2({\mathbb F}_q)$
, we define the representation function
$\lambda \in M_2({\mathbb F}_q)$
, we define the representation function
![]() $r_{A B}(\lambda ) = |\{\,(a, b)\in A\times B: a b = \lambda \,\}|$
. Note that
$r_{A B}(\lambda ) = |\{\,(a, b)\in A\times B: a b = \lambda \,\}|$
. Note that
![]() $r_{A B}$
is supported on the set
$r_{A B}$
is supported on the set
![]() $AB$
and so we have the identities
$AB$
and so we have the identities
A standard application of the Cauchy–Schwarz inequality gives
 $$ \begin{align} |A+B|\ge \frac{|A|^2|B|^2}{E_+(A, B)},\; |AB|\ge \frac{|A|^2|B|^2}{E_{\times}(A, B)}. \end{align} $$
$$ \begin{align} |A+B|\ge \frac{|A|^2|B|^2}{E_+(A, B)},\; |AB|\ge \frac{|A|^2|B|^2}{E_{\times}(A, B)}. \end{align} $$
Thus, if either
![]() $E_+(A, B)$
or
$E_+(A, B)$
or
![]() $E_{\times }(A, B)$
is small, then
$E_{\times }(A, B)$
is small, then
![]() $\max (|A+B|, |AB|)$
is big. This motivates the study of energy estimates.
$\max (|A+B|, |AB|)$
is big. This motivates the study of energy estimates.
Balog and Wooley [Reference Balog and Wooley2] initiated the investigation into a type of energy variant of the sum-product problem by proving that given a finite set
![]() $A\subset \mathbb {R}$
, one may write
$A\subset \mathbb {R}$
, one may write
![]() $A= B \sqcup C$
such that
$A= B \sqcup C$
such that
![]() $\max \{E_+(B), E_{\times }(C)\}\ll |A|^{3-\delta }(\log |A|)^{1-\delta }$
for
$\max \{E_+(B), E_{\times }(C)\}\ll |A|^{3-\delta }(\log |A|)^{1-\delta }$
for
![]() $\delta =2/33$
. In the prime field setting, they also provided similar results, namely:
$\delta =2/33$
. In the prime field setting, they also provided similar results, namely:
-
(1) If
 $|A|\le p^{\frac {101}{161}}(\log p)^{\frac {71}{161}}$
, then
$|A|\le p^{\frac {101}{161}}(\log p)^{\frac {71}{161}}$
, then  $$\begin{align*}\max\{E_+(B), E_{\times}(C)\}\ll |A|^{3-\delta}(\log |A|)^{1-\delta/2}, ~~\delta=4/101.\end{align*}$$
$$\begin{align*}\max\{E_+(B), E_{\times}(C)\}\ll |A|^{3-\delta}(\log |A|)^{1-\delta/2}, ~~\delta=4/101.\end{align*}$$
-
(2) If
 $|A|> p^{\frac {101}{161}}(\log p)^{\frac {71}{161}}$
, then
$|A|> p^{\frac {101}{161}}(\log p)^{\frac {71}{161}}$
, then  $$\begin{align*}\max\{E_+(B), E_{\times}(C)\}\ll |A|^{3}(|A|/p)^{1/15}(\log |A|)^{14/15}.\end{align*}$$
$$\begin{align*}\max\{E_+(B), E_{\times}(C)\}\ll |A|^{3}(|A|/p)^{1/15}(\log |A|)^{14/15}.\end{align*}$$
These results have been improved by Rudnev, Shkredov, and Stevens in [Reference Rudnev, Shkredov and Stevens10]. In particular, they increased
![]() $\delta $
from
$\delta $
from
![]() $2/33$
to
$2/33$
to
![]() $1/4$
over the reals, and from
$1/4$
over the reals, and from
![]() $4/101$
to
$4/101$
to
![]() $1/5$
over prime fields. We note that this type of result has many applications in different areas, for instance, bounding exponential sums [Reference Mohammadi and Stevens5, Reference Roche-Newton, Shparlinski and Winterhof8, Reference Shkredov12–Reference Swaenepoel and Winterhof15] or studying structures in Heisenberg groups [Reference Anh, Ham, Koh, Pham and Vinh1, Reference Hegyvári and Hennecart3].
$1/5$
over prime fields. We note that this type of result has many applications in different areas, for instance, bounding exponential sums [Reference Mohammadi and Stevens5, Reference Roche-Newton, Shparlinski and Winterhof8, Reference Shkredov12–Reference Swaenepoel and Winterhof15] or studying structures in Heisenberg groups [Reference Anh, Ham, Koh, Pham and Vinh1, Reference Hegyvári and Hennecart3].
The main goals of this paper are to study energy variants of the sum-product problem, and to obtain new exponents on two moderate expanding functions in the matrix ring
![]() $M_2({\mathbb F}_q)$
. While the results in [Reference Balog and Wooley2, Reference Rudnev, Shkredov and Stevens10] mainly relies on a number of earlier results on the sum-product problem or Rudnev’s point–plane incidence bound [Reference Rudnev9], our proofs rely on graph theoretic methods. It follows from our results in the next section that there exists a different phenomenon between problems over finite fields and over the matrix ring
$M_2({\mathbb F}_q)$
. While the results in [Reference Balog and Wooley2, Reference Rudnev, Shkredov and Stevens10] mainly relies on a number of earlier results on the sum-product problem or Rudnev’s point–plane incidence bound [Reference Rudnev9], our proofs rely on graph theoretic methods. It follows from our results in the next section that there exists a different phenomenon between problems over finite fields and over the matrix ring
![]() $M_2(\mathbb {F}_q)$
.
$M_2(\mathbb {F}_q)$
.
2 Main results
Our first theorem is on an energy decomposition of a set of matrices in
![]() $M_2(\mathbb {F}_q)$
.
$M_2(\mathbb {F}_q)$
.
Theorem 2.1 Given
![]() $A\subseteq GL_2({\mathbb F}_q)$
, there exist disjoint subsets
$A\subseteq GL_2({\mathbb F}_q)$
, there exist disjoint subsets
![]() $B, C\subseteq A$
such that
$B, C\subseteq A$
such that
![]() $A = B \sqcup C$
and
$A = B \sqcup C$
and
 $$\begin{align*}\max\{E_{+}(B), E_{\times}(C)\}\ll \frac{|A|^3}{M(|A|)}, \end{align*}$$
$$\begin{align*}\max\{E_{+}(B), E_{\times}(C)\}\ll \frac{|A|^3}{M(|A|)}, \end{align*}$$
where
 $$ \begin{align} M(|A|) = \min\Bigg\{\,\frac{q^{4/3}}{|A|^{1/3}(\log|A|)^{2/3}},\, \frac{|A|^{4/5}}{q^{13/5}(\log|A|)^{27/10}}\,\Bigg\}. \end{align} $$
$$ \begin{align} M(|A|) = \min\Bigg\{\,\frac{q^{4/3}}{|A|^{1/3}(\log|A|)^{2/3}},\, \frac{|A|^{4/5}}{q^{13/5}(\log|A|)^{27/10}}\,\Bigg\}. \end{align} $$
It follows from this theorem that for any set A of matrices in
![]() $M_2(\mathbb {F}_q)$
, we always can find a subset with either small additive energy or small multiplicative energy. By the Cauchy–Schwarz inequality, we have the following direct consequence on a sum-product estimate, namely, for
$M_2(\mathbb {F}_q)$
, we always can find a subset with either small additive energy or small multiplicative energy. By the Cauchy–Schwarz inequality, we have the following direct consequence on a sum-product estimate, namely, for
![]() $A\subseteq GL_2(\mathbb {F}_q)$
, we have
$A\subseteq GL_2(\mathbb {F}_q)$
, we have
By a direct computation, one can check that this is better than the estimate (1.1) in the range
![]() $|A|\ll q^{3+5/8}/(\log |A|)^{1/2}$
.
$|A|\ll q^{3+5/8}/(\log |A|)^{1/2}$
.
In the next theorem, we show that the lower bound of (2.2) can be improved by a direct energy estimate.
Theorem 2.2 Let
![]() $A, B\subseteq M_2({\mathbb F}_q)$
and
$A, B\subseteq M_2({\mathbb F}_q)$
and
![]() $C\subseteq GL_2({\mathbb F}_q)$
. Then
$C\subseteq GL_2({\mathbb F}_q)$
. Then
 $$\begin{align*}E_+(A, B) \ll \frac{|A|^2|BC|^2}{q^4} + q^{13/2}\frac{|A||BC|}{|C|}. \end{align*}$$
$$\begin{align*}E_+(A, B) \ll \frac{|A|^2|BC|^2}{q^4} + q^{13/2}\frac{|A||BC|}{|C|}. \end{align*}$$
Corollary 2.3 For
![]() $A\subseteq M_2({\mathbb F}_q)$
, with
$A\subseteq M_2({\mathbb F}_q)$
, with
![]() $|A|\gg q^{3}$
, we have
$|A|\gg q^{3}$
, we have
 $$ \begin{align} \max\{\,|A+A|,\, |AA|\,\}\gg \min\left\{\,\frac{|A|^2}{q^{13/4}},\, q^{4/3}|A|^{2/3}\,\right\}. \end{align} $$
$$ \begin{align} \max\{\,|A+A|,\, |AA|\,\}\gg \min\left\{\,\frac{|A|^2}{q^{13/4}},\, q^{4/3}|A|^{2/3}\,\right\}. \end{align} $$
In addition, if
![]() $|AA|\ll |A|$
and
$|AA|\ll |A|$
and
![]() $|A|\gg q^{3+1/2}$
, then
$|A|\gg q^{3+1/2}$
, then
If
![]() $|AA|\ll |A|$
and
$|AA|\ll |A|$
and
![]() $|A|\gg q^{3+2/5}$
, then
$|A|\gg q^{3+2/5}$
, then
We point out that the arguments of the proof of Corollary 2.3 could be used iteratively to give stronger results for expansion of k-fold sum sets
![]() $A + \cdots + A$
of sets
$A + \cdots + A$
of sets
![]() $A\subseteq M_2(F_q)$
with
$A\subseteq M_2(F_q)$
with
![]() $|AA|\ll |A|$
, as k gets larger.
$|AA|\ll |A|$
, as k gets larger.
We remark that the estimate (2.3) improves (1.1) in the range
![]() $|A|\ll q^{3+5/8}$
and is stronger than (2.2) in the range of
$|A|\ll q^{3+5/8}$
and is stronger than (2.2) in the range of
![]() $|A|\gg q^{13/4}$
. We also note that our assumption to get the estimate (2.4) is reasonable. For instance, let G be a subgroup of
$|A|\gg q^{13/4}$
. We also note that our assumption to get the estimate (2.4) is reasonable. For instance, let G be a subgroup of
![]() $\mathbb {F}_q^*$
, and let A be the set of matrices with determinants in G, then we have
$\mathbb {F}_q^*$
, and let A be the set of matrices with determinants in G, then we have
![]() $|A|\sim q^3\cdot |G|$
and
$|A|\sim q^3\cdot |G|$
and
![]() $|AA|=|A|$
.
$|AA|=|A|$
.
It has been proved in [Reference Karabulut, Koh, Pham, Shen and Vinh4, Theorems 1.8 and 1.9] that for
![]() $A, B, C\subseteq M_2(\mathbb {F}_q)$
, if
$A, B, C\subseteq M_2(\mathbb {F}_q)$
, if
![]() $|A||B||C|\ge q^{11}$
, then we have
$|A||B||C|\ge q^{11}$
, then we have
In the following theorem, we provide improvements of these results.
Theorem 2.4 Let
![]() $A, B, C \subseteq M_2({\mathbb F}_q)$
, we have
$A, B, C \subseteq M_2({\mathbb F}_q)$
, we have
 $$\begin{align*}|AB+C|\gg \min \left\lbrace\, q^4,\, \frac{|A||B||C|}{q^{13/2}} \,\right\rbrace. \end{align*}$$
$$\begin{align*}|AB+C|\gg \min \left\lbrace\, q^4,\, \frac{|A||B||C|}{q^{13/2}} \,\right\rbrace. \end{align*}$$
If
![]() $C\subseteq GL_2(\mathbb {F}_q)$
, the same conclusion holds for
$C\subseteq GL_2(\mathbb {F}_q)$
, the same conclusion holds for
![]() $(A+B)C$
, i.e.,
$(A+B)C$
, i.e.,
 $$\begin{align*}|(A+B)C|\gg \min \left\lbrace\, q^4,\, \frac{|A||B||C|}{q^{13/2}} \,\right\rbrace. \end{align*}$$
$$\begin{align*}|(A+B)C|\gg \min \left\lbrace\, q^4,\, \frac{|A||B||C|}{q^{13/2}} \,\right\rbrace. \end{align*}$$
In particular:
-
(1) If
 $|A||B||C|\gg q^{10 + 1/2}$
, then
$|A||B||C|\gg q^{10 + 1/2}$
, then
 $|AB + C|\gg q^4.$
$|AB + C|\gg q^4.$
-
(2) If
 $|A||B||C|\gg q^{10 + 1/2}$
and
$|A||B||C|\gg q^{10 + 1/2}$
and
 $C\subseteq GL_2(\mathbb {F}_q)$
, then
$C\subseteq GL_2(\mathbb {F}_q)$
, then
 $|(A+B)C|\gg q^4.$
$|(A+B)C|\gg q^4.$
The condition
![]() $C\subseteq GL_2(\mathbb {F}_q)$
is necessary, since, for instance, one can take C being the set of matrices with zero determinant and
$C\subseteq GL_2(\mathbb {F}_q)$
is necessary, since, for instance, one can take C being the set of matrices with zero determinant and
![]() $A=B=M_2(\mathbb {F}_q)$
, then
$A=B=M_2(\mathbb {F}_q)$
, then
![]() $|(A+B)C|\sim q^3$
and
$|(A+B)C|\sim q^3$
and
![]() $|A||B||C|\sim q^{11}$
.
$|A||B||C|\sim q^{11}$
.
We expect that the exponent
![]() $q^{10 + 1/2}$
, in the final conclusions of the above theorem, could be further improved to
$q^{10 + 1/2}$
, in the final conclusions of the above theorem, could be further improved to
![]() $q^{10}$
, which, as we shall demonstrate, is sharp. For
$q^{10}$
, which, as we shall demonstrate, is sharp. For
![]() $AB+C$
, let A and B be the set of lower triangular matrices in
$AB+C$
, let A and B be the set of lower triangular matrices in
![]() $M_2({\mathbb F}_q)$
and for arbitrary
$M_2({\mathbb F}_q)$
and for arbitrary
![]() $0<\delta <1$
, let
$0<\delta <1$
, let
![]() $X\subseteq {\mathbb F}_q$
be any set with
$X\subseteq {\mathbb F}_q$
be any set with
![]() $|X|= q^{1-\delta }$
, and let
$|X|= q^{1-\delta }$
, and let
 $$\begin{align*}C = \left\{\,\begin{pmatrix} c_1 & c_2 \\ c_3 & c_4 \end{pmatrix}:c_1, c_3, c_4\in {\mathbb F}_q, c_2\in X\,\right\}. \end{align*}$$
$$\begin{align*}C = \left\{\,\begin{pmatrix} c_1 & c_2 \\ c_3 & c_4 \end{pmatrix}:c_1, c_3, c_4\in {\mathbb F}_q, c_2\in X\,\right\}. \end{align*}$$
Then
![]() $|A||B||C| = q^{10-\delta }$
and
$|A||B||C| = q^{10-\delta }$
and
![]() $|AB+C| = |C| = q^{4-\delta }$
.
$|AB+C| = |C| = q^{4-\delta }$
.
For
![]() $(A+B)C$
, the construction is as follows: For arbitrary k, let
$(A+B)C$
, the construction is as follows: For arbitrary k, let
![]() $q=p^k$
, and let V be the set of elements corresponding to a
$q=p^k$
, and let V be the set of elements corresponding to a
![]() $(k-1)$
-dimensional vector space over
$(k-1)$
-dimensional vector space over
![]() ${\mathbb F}_p$
in
${\mathbb F}_p$
in
![]() ${\mathbb F}_q$
. Thus, we have
${\mathbb F}_q$
. Thus, we have
![]() $|V| = p^{k-1} = q^{1-1/k}$
. Now, let
$|V| = p^{k-1} = q^{1-1/k}$
. Now, let
 $$\begin{align*}A = B = \left\{\,\begin{pmatrix} x_1 & x_2 \\ x_3 & x_4 \end{pmatrix}:x_1, x_2\in V, x_3, x_4\in {\mathbb F}_q\,\right\}, \end{align*}$$
$$\begin{align*}A = B = \left\{\,\begin{pmatrix} x_1 & x_2 \\ x_3 & x_4 \end{pmatrix}:x_1, x_2\in V, x_3, x_4\in {\mathbb F}_q\,\right\}, \end{align*}$$
and
 $$\begin{align*}C = \left\{\,\begin{pmatrix} c_1 & c_2 \\ c_3 & c_4 \end{pmatrix}:c_1, c_3\in {\mathbb F}_q, c_2, c_4\in {\mathbb F}_p\,\right\}. \end{align*}$$
$$\begin{align*}C = \left\{\,\begin{pmatrix} c_1 & c_2 \\ c_3 & c_4 \end{pmatrix}:c_1, c_3\in {\mathbb F}_q, c_2, c_4\in {\mathbb F}_p\,\right\}. \end{align*}$$
Note that
![]() $A+B = A=B$
and so
$A+B = A=B$
and so
 $$\begin{align*}(A+B)C = AC = \left\{\,\begin{pmatrix} y_1 & y_2 \\ y_3 & y_4 \end{pmatrix}:y_1, y_3, y_4\in {\mathbb F}_q, y_2\in V\,\right\}, \end{align*}$$
$$\begin{align*}(A+B)C = AC = \left\{\,\begin{pmatrix} y_1 & y_2 \\ y_3 & y_4 \end{pmatrix}:y_1, y_3, y_4\in {\mathbb F}_q, y_2\in V\,\right\}, \end{align*}$$
where we have used that
![]() $V\cdot {\mathbb F}_p + V\cdot {\mathbb F}_p = V+V = V.$
$V\cdot {\mathbb F}_p + V\cdot {\mathbb F}_p = V+V = V.$
Thus,
![]() $|A||B||C| = (q^2\cdot q^{2-2/k})^2 \cdot (q^2\cdot q^{2/k}) = q^{10-2/k}$
while
$|A||B||C| = (q^2\cdot q^{2-2/k})^2 \cdot (q^2\cdot q^{2/k}) = q^{10-2/k}$
while
![]() $|(A+B)C| = q^{4-1/k}$
.
$|(A+B)C| = q^{4-1/k}$
.
Also, we remark here that in the setting of finite fields, our approach and that of Karabulut et al. in [Reference Karabulut, Koh, Pham, Shen and Vinh4] imply the same result. Namely, for
![]() $A,B,C \subseteq \mathbb {F}_q$
, we have
$A,B,C \subseteq \mathbb {F}_q$
, we have
![]() $|(A+B)C|, |AB+C| \gg q$
whenever
$|(A+B)C|, |AB+C| \gg q$
whenever
![]() $|A||B||C| \gg q^2$
. However, this is not true in the matrix ring. Let us briefly sketch the proof. For
$|A||B||C| \gg q^2$
. However, this is not true in the matrix ring. Let us briefly sketch the proof. For
![]() $\lambda \in AB +C$
, write
$\lambda \in AB +C$
, write
By the Cauchy–Schwarz inequality, we have
 $$\begin{align*}(|A||B||C|)^2 = \left(\sum_{\lambda\in AB+C} t(\lambda)\right)^2 \leq |AB +C|\sum_{\lambda\in AB+C} t(\lambda)^2. \end{align*}$$
$$\begin{align*}(|A||B||C|)^2 = \left(\sum_{\lambda\in AB+C} t(\lambda)\right)^2 \leq |AB +C|\sum_{\lambda\in AB+C} t(\lambda)^2. \end{align*}$$
Thus, the main task is to bound
![]() $\sum _{\lambda }t(\lambda )^2$
, i.e., the number of tuples
$\sum _{\lambda }t(\lambda )^2$
, i.e., the number of tuples
![]() $(a, b, c, a', b', c')\in (A\times B\times C)^2$
such that
$(a, b, c, a', b', c')\in (A\times B\times C)^2$
such that
![]() $ab+c=a'b'+c'$
. In [Reference Karabulut, Koh, Pham, Shen and Vinh4], instead of bounding
$ab+c=a'b'+c'$
. In [Reference Karabulut, Koh, Pham, Shen and Vinh4], instead of bounding
![]() $\sum _{\lambda }t(\lambda )^2$
, they bounded the number of quadruples
$\sum _{\lambda }t(\lambda )^2$
, they bounded the number of quadruples
![]() $(a, b, c, \lambda )\in A\times B\times C\times (AB+C)$
such that
$(a, b, c, \lambda )\in A\times B\times C\times (AB+C)$
such that
![]() $ab+c=\lambda $
. These two approaches imply the same lower bounds for
$ab+c=\lambda $
. These two approaches imply the same lower bounds for
![]() $(A+B)C$
and
$(A+B)C$
and
![]() $AB+C$
when
$AB+C$
when
![]() $A, B, C\subset \mathbb {F}_q$
, but in the matrix rings, bounding
$A, B, C\subset \mathbb {F}_q$
, but in the matrix rings, bounding
![]() $\sum _{\lambda }t(\lambda )^2$
is more effective. In other words, there exists a different phenomenon between problems over finite fields and over the matrix ring
$\sum _{\lambda }t(\lambda )^2$
is more effective. In other words, there exists a different phenomenon between problems over finite fields and over the matrix ring
![]() $M_2(\mathbb {F}_q)$
.
$M_2(\mathbb {F}_q)$
.
We now state a corollary of the above theorem with
![]() $C=AA$
which might be of independent interest.
$C=AA$
which might be of independent interest.
Corollary 2.5 Let
![]() $A\subset M_2({\mathbb F}_q)$
with
$A\subset M_2({\mathbb F}_q)$
with
![]() $|A|\gg q^{3+ 7/16}$
, then
$|A|\gg q^{3+ 7/16}$
, then
Let
![]() $A, B, C, D\subseteq M_2({\mathbb F}_q)$
, our last theorem is devoted for the solvability of the equation
$A, B, C, D\subseteq M_2({\mathbb F}_q)$
, our last theorem is devoted for the solvability of the equation
Let
![]() $\mathcal {J}(A,B,C,D)$
denote the number of solutions to this equation.
$\mathcal {J}(A,B,C,D)$
denote the number of solutions to this equation.
One can check that by using Lemma 4.1 and Theorem 4.2 from [Reference Karabulut, Koh, Pham, Shen and Vinh4], one has
 $$ \begin{align} \left\vert \mathcal{J}(A,B,C,D)-\frac{|A||B||C||D|}{q^4} \right\vert\ll q^{7/2}(|A||B||C||D|)^{1/2}. \end{align} $$
$$ \begin{align} \left\vert \mathcal{J}(A,B,C,D)-\frac{|A||B||C||D|}{q^4} \right\vert\ll q^{7/2}(|A||B||C||D|)^{1/2}. \end{align} $$
Thus, when
![]() $|A||B||C||D|\gg q^{15}$
, then
$|A||B||C||D|\gg q^{15}$
, then
![]() $\mathcal {J}(A,B,C,D)\sim \frac {|A||B||C||D|}{q^4}$
. We refer the interested reader to [Reference Sárközy11] for a result on this problem over finite fields. In our last theorem, we are interested in bounding
$\mathcal {J}(A,B,C,D)\sim \frac {|A||B||C||D|}{q^4}$
. We refer the interested reader to [Reference Sárközy11] for a result on this problem over finite fields. In our last theorem, we are interested in bounding
![]() $\mathcal {J}(A,B,C,D)$
from above when
$\mathcal {J}(A,B,C,D)$
from above when
![]() $|A||B||C||D|$
is smaller.
$|A||B||C||D|$
is smaller.
Theorem 2.6 Let
![]() $A, B, C, D\subseteq M_2({\mathbb F}_q)$
, and let
$A, B, C, D\subseteq M_2({\mathbb F}_q)$
, and let
![]() $\mathcal {J}(A,B,C,D)$
denote the number of solutions to equation (2.6). Then, we have
$\mathcal {J}(A,B,C,D)$
denote the number of solutions to equation (2.6). Then, we have
 $$ \begin{align*} \mathcal{J}(A,B,C,D) \ll \frac{|A||B|^{1/2}|C||D|}{q^2} + q^{13/4} (|A||B||C||D|)^{1/2}. \end{align*} $$
$$ \begin{align*} \mathcal{J}(A,B,C,D) \ll \frac{|A||B|^{1/2}|C||D|}{q^2} + q^{13/4} (|A||B||C||D|)^{1/2}. \end{align*} $$
Assume
![]() $|A|=|B|=|C|=|D|$
, the upper bound of this theorem is stronger than that of (2.7) when
$|A|=|B|=|C|=|D|$
, the upper bound of this theorem is stronger than that of (2.7) when
![]() $|A|\ll q^{11/3}$
.
$|A|\ll q^{11/3}$
.
2.1 Structure
The rest of this paper is structured as follows: In Section 3, we prove a preliminary lemma, which is one of the key ingredients in the proof of our energy decomposition theorem. Section 4 is devoted to proving Theorem 2.1. The proofs of Theorem 2.2 and Corollary 2.3 will be presented in Section 5. Section 6 contains proofs of Theorem 2.4, Corollary 2.5, and Theorem 2.6.
3 A preliminary lemma
Given sets
![]() $A, B, C, D, E, F\subseteq M_2({\mathbb F}_q)$
, let
$A, B, C, D, E, F\subseteq M_2({\mathbb F}_q)$
, let
![]() $\mathcal {I}(A, B, C, D, E, F)$
be the number of solutions
$\mathcal {I}(A, B, C, D, E, F)$
be the number of solutions
The main purpose of this section is to prove an estimate for
![]() $\mathcal {I}(A, B, C, D, E, F)$
, which is one of the key ingredients in the proof of Theorem 2.1.
$\mathcal {I}(A, B, C, D, E, F)$
, which is one of the key ingredients in the proof of Theorem 2.1.
Proposition 3.1 We have
 $$\begin{align*}\bigg|\mathcal{I}(A, B, C, D, E, F) - \frac{|A||B||C||D||E||F|}{q^4}\bigg| \ll q^{13/2}\sqrt{|A||B||C||D||E||F|}\,. \end{align*}$$
$$\begin{align*}\bigg|\mathcal{I}(A, B, C, D, E, F) - \frac{|A||B||C||D||E||F|}{q^4}\bigg| \ll q^{13/2}\sqrt{|A||B||C||D||E||F|}\,. \end{align*}$$
To prove Proposition 3.1, we define the sum-product digraph
![]() $G=(V, E)$
with the vertex set
$G=(V, E)$
with the vertex set
![]() $V=M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)$
, and there is a directed edge going from
$V=M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)$
, and there is a directed edge going from
![]() $(a, e, c)$
to
$(a, e, c)$
to
![]() $(b, f, d)$
if and only if
$(b, f, d)$
if and only if
![]() $ab+ ef = c+d$
. The setting of this digraph is a generalization of that in [Reference Karabulut, Koh, Pham, Shen and Vinh4, Section 4.1]
$ab+ ef = c+d$
. The setting of this digraph is a generalization of that in [Reference Karabulut, Koh, Pham, Shen and Vinh4, Section 4.1]
Let G be a digraph on n vertices. Suppose that G is regular of degree d, i.e., the in-degree and out-degree of each vertex are equal to d. Let
![]() $m_G$
be the adjacency matrix of G, where
$m_G$
be the adjacency matrix of G, where
![]() $(m_G)_{ij}=1$
if and only if there is a directed edge from i to j. Let
$(m_G)_{ij}=1$
if and only if there is a directed edge from i to j. Let
![]() $\mu _1=d, \mu _2, \ldots , \mu _n$
be the eigenvalues of
$\mu _1=d, \mu _2, \ldots , \mu _n$
be the eigenvalues of
![]() $m_G$
. Notice that these eigenvalues can be complex numbers, and for all
$m_G$
. Notice that these eigenvalues can be complex numbers, and for all
![]() $2\le i\le n$
, we have
$2\le i\le n$
, we have
![]() $|\mu _i|\le d$
. Define
$|\mu _i|\le d$
. Define
![]() $\mu (G):=\max _{|\mu _i|\ne d}|\mu _i|$
. This value is referred to as the second largest eigenvalue of
$\mu (G):=\max _{|\mu _i|\ne d}|\mu _i|$
. This value is referred to as the second largest eigenvalue of
![]() $m_G$
.
$m_G$
.
A digraph G is called an
![]() $(n, d, \mu )$
-digraph if G is a d-regular digraph of n vertices, and the second largest eigenvalue of
$(n, d, \mu )$
-digraph if G is a d-regular digraph of n vertices, and the second largest eigenvalue of
![]() $m_G$
is at most
$m_G$
is at most
![]() $\mu $
.
$\mu $
.
We recall the following lemma from [Reference Vu16] on the distribution of edges between two vertex sets on an
![]() $(n, d, \mu )$
-digraph.
$(n, d, \mu )$
-digraph.
Lemma 3.2 Let
![]() $G = (V, E)$
be an
$G = (V, E)$
be an
![]() $(n, d, \mu )$
-digraph. For any two sets
$(n, d, \mu )$
-digraph. For any two sets
![]() $B, C \subseteq V$
, the number of directed edges from B to C, denoted by
$B, C \subseteq V$
, the number of directed edges from B to C, denoted by
![]() $e(B, C)$
satisfies
$e(B, C)$
satisfies
With Lemma 3.2 in hand, to prove Proposition 3.1, it is enough to study properties of the sum-product digraph G.
Definition 3.1 Let
![]() $a, b \in M_2(\mathbb {F}_q)$
. We say they are equivalent, if whenever the ith row of a is not all-zero, neither is the ith row of b and vice versa, for
$a, b \in M_2(\mathbb {F}_q)$
. We say they are equivalent, if whenever the ith row of a is not all-zero, neither is the ith row of b and vice versa, for
![]() $1\leq i \leq 2$
.
$1\leq i \leq 2$
.
Proposition 3.3 The sum product graph G is a
![]() $(q^{12},\, q^8,\, c\cdot q^{13/2})$
-digraph, for some positive constant c.
$(q^{12},\, q^8,\, c\cdot q^{13/2})$
-digraph, for some positive constant c.
Proof The number of vertices is
![]() $|M_2(\mathbb {F}_q)|^3 = q^{12}$
. Moreover, for each vertex
$|M_2(\mathbb {F}_q)|^3 = q^{12}$
. Moreover, for each vertex
![]() $(a, e, c)$
, with each choice of
$(a, e, c)$
, with each choice of
![]() $(b, f)$
, d is determined uniquely from
$(b, f)$
, d is determined uniquely from
![]() $d = ab + ef - c$
. Thus, there are
$d = ab + ef - c$
. Thus, there are
![]() $|M_2(\mathbb {F}_q)|^2 = q^8$
directed edges going out of each vertex. The number of incoming directed edges can be argued in the same way. To conclude, the digraph G is
$|M_2(\mathbb {F}_q)|^2 = q^8$
directed edges going out of each vertex. The number of incoming directed edges can be argued in the same way. To conclude, the digraph G is
![]() $q^8$
-regular. Let
$q^8$
-regular. Let
![]() $m_G$
denote the adjacency matrix of G. It remains to bound the magnitude of the second largest eigenvalue of the adjacency matrix of G, i.e.,
$m_G$
denote the adjacency matrix of G. It remains to bound the magnitude of the second largest eigenvalue of the adjacency matrix of G, i.e.,
![]() $\mu (m_G)$
.
$\mu (m_G)$
.
In the next step, we are going to show that
![]() $m_G$
is a normal matrix, i.e.,
$m_G$
is a normal matrix, i.e.,
![]() $m_G^Tm_G=m_Gm_G^T$
, where
$m_G^Tm_G=m_Gm_G^T$
, where
![]() $m_G^T$
is the conjugate transpose of
$m_G^T$
is the conjugate transpose of
![]() $m_G$
. For a normal matrix m, we know that if
$m_G$
. For a normal matrix m, we know that if
![]() $\lambda $
is an eigenvalue of m, then
$\lambda $
is an eigenvalue of m, then
![]() $|\lambda |^2$
is an eigenvalue of
$|\lambda |^2$
is an eigenvalue of
![]() $mm^T$
and
$mm^T$
and
![]() $m^Tm$
. Thus, for a normal matrix m, it is enough to give an upper bound for the second largest eigenvalue of
$m^Tm$
. Thus, for a normal matrix m, it is enough to give an upper bound for the second largest eigenvalue of
![]() $mm^T$
or
$mm^T$
or
![]() $m^Tm$
.
$m^Tm$
.
There is a simple way to check whenever G is normal. For any two vertices u and v, let
![]() $\mathcal {N}^+(u,v)$
be the set of vertices w such that
$\mathcal {N}^+(u,v)$
be the set of vertices w such that
![]() $\overrightarrow {uw}, \overrightarrow {vw}$
are directed edges, and
$\overrightarrow {uw}, \overrightarrow {vw}$
are directed edges, and
![]() $\mathcal {N}^-(u, v)$
be the set of vertices
$\mathcal {N}^-(u, v)$
be the set of vertices
![]() $w'$
such that
$w'$
such that
![]() $\overrightarrow {w'u}, \overrightarrow {w'v}$
are directed edges. It is not hard to check that
$\overrightarrow {w'u}, \overrightarrow {w'v}$
are directed edges. It is not hard to check that
![]() $m_G$
is normal if and only if
$m_G$
is normal if and only if
![]() $|\mathcal {N}^+(u,v)| = |\mathcal {N}^-(u,v)|$
for any two vertices u and v.
$|\mathcal {N}^+(u,v)| = |\mathcal {N}^-(u,v)|$
for any two vertices u and v.
Given two vertices
![]() $(a, e, c)$
and
$(a, e, c)$
and
![]() $(a^{\prime }, e^{\prime }, c^{\prime })$
, where
$(a^{\prime }, e^{\prime }, c^{\prime })$
, where
![]() $(a, e, c) \neq (a^{\prime }, e^{\prime }, c^{\prime })$
, the number of
$(a, e, c) \neq (a^{\prime }, e^{\prime }, c^{\prime })$
, the number of
![]() $(x,y,z)$
that lies in the common outgoing neighborhood of both vertices is characterized by
$(x,y,z)$
that lies in the common outgoing neighborhood of both vertices is characterized by

For each pair
![]() $(x, y)$
satisfying this equation, z is determined uniquely. Thus, the problem is reduced to computing the number of such pairs
$(x, y)$
satisfying this equation, z is determined uniquely. Thus, the problem is reduced to computing the number of such pairs
![]() $(x, y)$
.
$(x, y)$
.
For convenience, let
![]() $\bar {a} = a - a^{\prime }$
,
$\bar {a} = a - a^{\prime }$
,
![]() $\bar {c} = c - c^{\prime }$
, and
$\bar {c} = c - c^{\prime }$
, and
![]() $\bar {e} = e - e^{\prime }$
. Also, let
$\bar {e} = e - e^{\prime }$
. Also, let
![]() $t = \begin {pmatrix} \bar {a} & \bar {e}\end {pmatrix}_{2\times 4}$
. Then, the above relation is equivalent to
$t = \begin {pmatrix} \bar {a} & \bar {e}\end {pmatrix}_{2\times 4}$
. Then, the above relation is equivalent to
 $$ \begin{align} \begin{pmatrix} \bar{a} & \bar{e}\end{pmatrix} \begin{pmatrix} x \\ y\end{pmatrix} = t \begin{pmatrix} x \\ y\end{pmatrix}_{4\times 2}= \bar{c}\,. \end{align} $$
$$ \begin{align} \begin{pmatrix} \bar{a} & \bar{e}\end{pmatrix} \begin{pmatrix} x \\ y\end{pmatrix} = t \begin{pmatrix} x \\ y\end{pmatrix}_{4\times 2}= \bar{c}\,. \end{align} $$
We now have the following cases:
-
• (Case 1:
 $\operatorname {\mathrm {rank}}(t) = 0$
) Note that in this case, we need
$\operatorname {\mathrm {rank}}(t) = 0$
) Note that in this case, we need
 $a = a^{\prime }$
,
$a = a^{\prime }$
,
 $c = c^{\prime }$
, and
$c = c^{\prime }$
, and
 $e = e^{\prime }$
, which is a contradiction to our assumption that
$e = e^{\prime }$
, which is a contradiction to our assumption that
 $(a, e, c) \neq (a^{\prime }, e^{\prime }, c^{\prime })$
. Thus, we simply exclude this case.
$(a, e, c) \neq (a^{\prime }, e^{\prime }, c^{\prime })$
. Thus, we simply exclude this case. -
• (Case 2:
 $\operatorname {\mathrm {rank}}(t) = 1$
) As t is not an all-zero matrix, there is at least one nonzero row. Without loss of generality, assume it is the first row. Then,
$\operatorname {\mathrm {rank}}(t) = 1$
) As t is not an all-zero matrix, there is at least one nonzero row. Without loss of generality, assume it is the first row. Then, ${t = \begin {pmatrix} a_1 & a_2 & e_1 & e_2 \\ \alpha a_1 & \alpha a_2 & \alpha e_1 & \alpha e_2\end {pmatrix}}$
, where
${t = \begin {pmatrix} a_1 & a_2 & e_1 & e_2 \\ \alpha a_1 & \alpha a_2 & \alpha e_1 & \alpha e_2\end {pmatrix}}$
, where
 $(a_1, a_2, e_1, e_2) \neq \textbf {0}$
and
$(a_1, a_2, e_1, e_2) \neq \textbf {0}$
and
 $\alpha \in \mathbb {F}_q$
.
$\alpha \in \mathbb {F}_q$
.-
– (Case 2.1:
 $\operatorname {\mathrm {rank}}(\bar {c}) = 2$
) In this case, there is no solution, as
$\operatorname {\mathrm {rank}}(\bar {c}) = 2$
) In this case, there is no solution, as
 $\operatorname {\mathrm {rank}}\left (t \begin {pmatrix} x \\ y\end {pmatrix}\right ) \leq \operatorname {\mathrm {rank}}(t) = 1$
but
$\operatorname {\mathrm {rank}}\left (t \begin {pmatrix} x \\ y\end {pmatrix}\right ) \leq \operatorname {\mathrm {rank}}(t) = 1$
but
 $\operatorname {\mathrm {rank}}(\bar {c}) = 2$
.
$\operatorname {\mathrm {rank}}(\bar {c}) = 2$
. -
– (Case 2.2:
 $\operatorname {\mathrm {rank}}(\bar {c}) = 1$
) Let
$\operatorname {\mathrm {rank}}(\bar {c}) = 1$
) Let
 $x = \begin {pmatrix} x_1 & x_2 \\ x_3 & x_4 \end {pmatrix}$
,
$x = \begin {pmatrix} x_1 & x_2 \\ x_3 & x_4 \end {pmatrix}$
,
 $y = \begin {pmatrix} y_1 & y_2 \\ y_3 & y_4 \end {pmatrix}$
. We discuss two sub-cases:
$y = \begin {pmatrix} y_1 & y_2 \\ y_3 & y_4 \end {pmatrix}$
. We discuss two sub-cases:(a)
 $\bar {c} = \begin {pmatrix} c_1 & c_2 \\ \alpha c_1 & \alpha c_2 \end {pmatrix}$
with the same factor
$\bar {c} = \begin {pmatrix} c_1 & c_2 \\ \alpha c_1 & \alpha c_2 \end {pmatrix}$
with the same factor
 $\alpha $
, where
$\alpha $
, where
 $(c_1, c_2) \neq (0, 0)$
.
$(c_1, c_2) \neq (0, 0)$
.In this case, we have the following set of equations:
Since we assume $$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = c_1, \\ a_1 x_2 + a_2 x_4 + e_1 y_2 + e_2 y_4 = c_2. \end{cases} \, \end{align*} $$
$$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = c_1, \\ a_1 x_2 + a_2 x_4 + e_1 y_2 + e_2 y_4 = c_2. \end{cases} \, \end{align*} $$
 $(a_1, a_2, e_1, e_2) \neq \textbf {0}$
, without loss of generality, let
$(a_1, a_2, e_1, e_2) \neq \textbf {0}$
, without loss of generality, let
 $a_1 \neq 0$
. Then, which means that for each
$a_1 \neq 0$
. Then, which means that for each $$ \begin{align*} \begin{cases} x_1 = (a_1)^{-1}(c_1 -a_2 x_3 -e_1 y_1 - e_2 y_3), \\ x_2 = (a_1)^{-1}(c_2 - a_2 x_4 - e_1 y_2 - e_2 y_4), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} x_1 = (a_1)^{-1}(c_1 -a_2 x_3 -e_1 y_1 - e_2 y_3), \\ x_2 = (a_1)^{-1}(c_2 - a_2 x_4 - e_1 y_2 - e_2 y_4), \end{cases} \end{align*} $$
 $(x_3, y_1, y_3)$
there is a unique
$(x_3, y_1, y_3)$
there is a unique
 $x_1$
and for each
$x_1$
and for each
 $(x_4, y_2, y_4)$
there is a unique
$(x_4, y_2, y_4)$
there is a unique
 $x_2$
. Thus, there are
$x_2$
. Thus, there are
 $q^6$
different
$q^6$
different
 $(x,y,z)$
solutions.
$(x,y,z)$
solutions.
(b) In all other sub-cases, there is no solution. If
 $\bar {c} = \begin {pmatrix} c_1 & c_2 \\ \beta c_1 & \beta c_2 \end {pmatrix}$
, where
$\bar {c} = \begin {pmatrix} c_1 & c_2 \\ \beta c_1 & \beta c_2 \end {pmatrix}$
, where
 $\beta \neq \alpha $
and
$\beta \neq \alpha $
and
 $(c_1, c_2) \neq (0, 0)$
, then we get the following two equations: which obviously do not have any solution.
$(c_1, c_2) \neq (0, 0)$
, then we get the following two equations: which obviously do not have any solution. $$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = c_1, \\ \alpha a_1 x_1 + \alpha a_2 x_3 + \alpha e_1 y_1 + \alpha e_2 y_3 = \beta c_1, \end{cases}\, \end{align*} $$
$$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = c_1, \\ \alpha a_1 x_1 + \alpha a_2 x_3 + \alpha e_1 y_1 + \alpha e_2 y_3 = \beta c_1, \end{cases}\, \end{align*} $$
Otherwise,
 $\bar {c} = \begin {pmatrix} \beta c_1 & \beta c_2 \\ c_1 & c_2 \end {pmatrix}$
, where
$\bar {c} = \begin {pmatrix} \beta c_1 & \beta c_2 \\ c_1 & c_2 \end {pmatrix}$
, where
 $(c_1, c_2) \neq (0, 0)$
. Note that if
$(c_1, c_2) \neq (0, 0)$
. Note that if
 $\alpha \neq 0$
, then
$\alpha \neq 0$
, then
 $\beta \neq \alpha ^{-1}$
, because this case is covered in Case 2.2(a) implicitly. We get the following equations. which obviously do not have any solution. Notice that
$\beta \neq \alpha ^{-1}$
, because this case is covered in Case 2.2(a) implicitly. We get the following equations. which obviously do not have any solution. Notice that $$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = \beta c_1, \\ \alpha a_1 x_1 + \alpha a_2 x_3 + \alpha e_1 y_1 + \alpha e_2 y_3 = c_1, \end{cases}\, \end{align*} $$
$$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = \beta c_1, \\ \alpha a_1 x_1 + \alpha a_2 x_3 + \alpha e_1 y_1 + \alpha e_2 y_3 = c_1, \end{cases}\, \end{align*} $$
 $\alpha = 0$
or
$\alpha = 0$
or
 $\beta = 0$
corresponds to t and
$\beta = 0$
corresponds to t and
 $\bar {c}$
not being equivalent.
$\bar {c}$
not being equivalent.
-
– (Case 2.3:
 $\operatorname {\mathrm {rank}}(\bar {c}) = 0$
) This case is similar to the Case 2.2(a), except
$\operatorname {\mathrm {rank}}(\bar {c}) = 0$
) This case is similar to the Case 2.2(a), except
 $c_1 = c_2 = 0$
. We have the following two equations: Following the same analysis, we conclude there are
$c_1 = c_2 = 0$
. We have the following two equations: Following the same analysis, we conclude there are $$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = 0, \\ a_1 x_2 + a_2 x_4 + e_1 y_2 + e_2 y_4 =0. \end{cases}\, \end{align*} $$
$$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 + e_1 y_1 + e_2 y_3 = 0, \\ a_1 x_2 + a_2 x_4 + e_1 y_2 + e_2 y_4 =0. \end{cases}\, \end{align*} $$
 $q^6$
solutions.
$q^6$
solutions.
-
-
• (Case 3:
 $\operatorname {\mathrm {rank}}(t) = 2$
) In this case, we always have solutions, for any
$\operatorname {\mathrm {rank}}(t) = 2$
) In this case, we always have solutions, for any
 $\bar {c}$
.
$\bar {c}$
.-
– (Case 3.1:
 $\operatorname {\mathrm {rank}}(\bar {a}) = 2$
or
$\operatorname {\mathrm {rank}}(\bar {a}) = 2$
or
 $\operatorname {\mathrm {rank}}(\bar {e}) = 2$
) In this case, let us look back on equation (3.1). If
$\operatorname {\mathrm {rank}}(\bar {e}) = 2$
) In this case, let us look back on equation (3.1). If
 $\operatorname {\mathrm {rank}}(\bar {a}) = 2$
, then we can rewrite (3.1) as
$\operatorname {\mathrm {rank}}(\bar {a}) = 2$
, then we can rewrite (3.1) as
 $\bar {a}x = \bar {c} - \bar {e} y$
. Observe that, for any
$\bar {a}x = \bar {c} - \bar {e} y$
. Observe that, for any
 $y\in M_2(\mathbb {F}_q)$
, there is a unique x. Thus, the number of solutions is
$y\in M_2(\mathbb {F}_q)$
, there is a unique x. Thus, the number of solutions is
 $q^4$
. The case where
$q^4$
. The case where
 $\operatorname {\mathrm {rank}}(\bar {e}) = 2$
is similar.
$\operatorname {\mathrm {rank}}(\bar {e}) = 2$
is similar. -
– (Case 3.2:
 $\operatorname {\mathrm {rank}}(\bar {a}) \leq 1$
and
$\operatorname {\mathrm {rank}}(\bar {a}) \leq 1$
and
 $\operatorname {\mathrm {rank}}(\bar {e}) \leq 1$
) In this case, it is not hard to observe that t must be one of the following four types:
$\operatorname {\mathrm {rank}}(\bar {e}) \leq 1$
) In this case, it is not hard to observe that t must be one of the following four types:-
(i)
 $\begin {pmatrix} a_1 & a_2 & e_1 & e_2 \\ \alpha a_1 & \alpha a_2 &\beta e_1 &\beta e_2\end {pmatrix}$
, where
$\begin {pmatrix} a_1 & a_2 & e_1 & e_2 \\ \alpha a_1 & \alpha a_2 &\beta e_1 &\beta e_2\end {pmatrix}$
, where
 $(a_1, a_2), (e_1, e_2)\neq (0,0)$
,
$(a_1, a_2), (e_1, e_2)\neq (0,0)$
,
 $\alpha \neq \beta $
,
$\alpha \neq \beta $
,
 $(\alpha , \beta ) \neq (0,0)$
.
$(\alpha , \beta ) \neq (0,0)$
. -
(ii)
 $\begin {pmatrix} \alpha a_1 & \alpha a_2 &\beta e_1 &\beta e_2 \\ a_1 & a_2 & e_1 & e_2 \end {pmatrix}$
, where
$\begin {pmatrix} \alpha a_1 & \alpha a_2 &\beta e_1 &\beta e_2 \\ a_1 & a_2 & e_1 & e_2 \end {pmatrix}$
, where
 $(a_1, a_2), (e_1, e_2) \neq (0,0)$
,
$(a_1, a_2), (e_1, e_2) \neq (0,0)$
,
 $\alpha \neq \beta $
,
$\alpha \neq \beta $
,
 $(\alpha , \beta ) \neq (0,0)$
.
$(\alpha , \beta ) \neq (0,0)$
. -
(iii)
 $\begin {pmatrix} a_1 & a_2 &0 &0 \\ 0& 0 & e_1 & e_2 \end {pmatrix}$
, where
$\begin {pmatrix} a_1 & a_2 &0 &0 \\ 0& 0 & e_1 & e_2 \end {pmatrix}$
, where
 $(a_1, a_2),(e_1, e_2) \neq (0,0)$
.
$(a_1, a_2),(e_1, e_2) \neq (0,0)$
. -
(iv)
 $\begin {pmatrix} 0 & 0 & e_1 & e_2 \\ a_1& a_2 & 0 & 0 \end {pmatrix}$
, where
$\begin {pmatrix} 0 & 0 & e_1 & e_2 \\ a_1& a_2 & 0 & 0 \end {pmatrix}$
, where
 $(a_1, a_2), (e_1, e_2)\neq (0,0)$
.
$(a_1, a_2), (e_1, e_2)\neq (0,0)$
.
Since
 $(i)$
and
$(i)$
and
 $(ii)$
are symmetric and so is
$(ii)$
are symmetric and so is
 $(iii)$
and
$(iii)$
and
 $(iv)$
, we only argue for
$(iv)$
, we only argue for
 $(i)$
and
$(i)$
and
 $(iii)$
. For
$(iii)$
. For
 $(iii)$
, reusing notations from Case 2.2(a), we have
$(iii)$
, reusing notations from Case 2.2(a), we have  $$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 = c_1, \\ a_1 x_2 + a_2 x_4 = c_2, \\ e_1 y_1 + e_2 y_3 = c_3, \\ e_1 y_2 + e_2 y_4 = c_4. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} a_1 x_1 + a_2 x_3 = c_1, \\ a_1 x_2 + a_2 x_4 = c_2, \\ e_1 y_1 + e_2 y_3 = c_3, \\ e_1 y_2 + e_2 y_4 = c_4. \end{cases} \end{align*} $$
As
 $(a_1, a_2) \neq (0,0)$
and
$(a_1, a_2) \neq (0,0)$
and
 $(e_1, e_2) \neq (0,0)$
, without loss of generality, we assume
$(e_1, e_2) \neq (0,0)$
, without loss of generality, we assume
 $a_1 \neq 0$
and
$a_1 \neq 0$
and
 $e_1 \neq 0$
. Then, it means for each
$e_1 \neq 0$
. Then, it means for each
 $(x_3, x_4, y_3, y_4)$
there is a unique
$(x_3, x_4, y_3, y_4)$
there is a unique
 $(x_1, x_2, y_1, y_2)$
. Thus, the system has
$(x_1, x_2, y_1, y_2)$
. Thus, the system has
 $q^4$
solutions.
$q^4$
solutions.For
 $(i)$
, we have Again, assume
$(i)$
, we have Again, assume
 $a_1 \neq 0$
and
$a_1 \neq 0$
and
 $e_1 \neq 0$
. Now, take
$e_1 \neq 0$
. Now, take
 , we get
, we get
 $(\alpha - \beta )(e_1 y_1 + e_2 y_3) = \alpha c_1 - c_3 $
. As
$(\alpha - \beta )(e_1 y_1 + e_2 y_3) = \alpha c_1 - c_3 $
. As
 $\alpha \neq \beta $
, this means
$\alpha \neq \beta $
, this means
 $e_1 y_1 + e_2 y_3 = (\alpha - \beta )^{-1}(\alpha c_1 - c_3)$
. Thus, for each
$e_1 y_1 + e_2 y_3 = (\alpha - \beta )^{-1}(\alpha c_1 - c_3)$
. Thus, for each
 $y_3$
, there is a unique
$y_3$
, there is a unique
 $y_1$
. Similarly, compute
$y_1$
. Similarly, compute
 , and we get
, and we get
 $ a_1 x_1 + a_2 x_3 = (\beta - \alpha )^{-1}(\beta c_1 - c_3)$
, which means that for each
$ a_1 x_1 + a_2 x_3 = (\beta - \alpha )^{-1}(\beta c_1 - c_3)$
, which means that for each
 $x_3$
, we get a unique
$x_3$
, we get a unique
 $x_1$
. We can do the same for
$x_1$
. We can do the same for
 and
and
 and conclude that there are
and conclude that there are
 $q^4$
solutions.
$q^4$
solutions.
-
-
Observe that all cases are disjoint and they together enumerate all possible relations between vertices
![]() $(a, e, c)$
and
$(a, e, c)$
and
![]() $(a^{\prime }, e^{\prime }, c^{\prime })$
. We computed
$(a^{\prime }, e^{\prime }, c^{\prime })$
. We computed
![]() $\mathcal {N}^+((a, e, c), (a^{\prime }, e^{\prime }, c^{\prime }))$
above and the computation for
$\mathcal {N}^+((a, e, c), (a^{\prime }, e^{\prime }, c^{\prime }))$
above and the computation for
![]() $\mathcal {N}^-((a, e, c), (a^{\prime }, e^{\prime }, c^{\prime }))$
is the same. Thus, we know
$\mathcal {N}^-((a, e, c), (a^{\prime }, e^{\prime }, c^{\prime }))$
is the same. Thus, we know
![]() $m_G$
is normal. Note that each entry of
$m_G$
is normal. Note that each entry of
![]() $m_Gm_G^T$
can be interpreted as counting the number of common outgoing neighbors between two vertices. We can write
$m_Gm_G^T$
can be interpreted as counting the number of common outgoing neighbors between two vertices. We can write
![]() $m_Gm_G^T$
as
$m_Gm_G^T$
as
 $$ \begin{align*} \begin{aligned} m_Gm_G^T &= q^8 I + 0 E_{21} + q^6 E_{22a} + 0 E_{22b} + q^6 E_{23} + q^4 E_{31} + q^4 E_{32} \\ &=(q^8 - q^4)I + q^4 J - q^4 E_{21} + (q^6 - q^4)E_{22a}\\ &\qquad\qquad -q^4 E_{22b} + (q^6 - q^4) E_{23} + (q^4 - q^4) E_{31} + (q^4 - q^4) E_{32} \\ &= (q^8 - q^4)I + q^4 J - q^4 E_{21} + (q^6 - q^4)E_{22a}- q^4 E_{22b} + (q^6 - q^4) E_{23}\,, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} m_Gm_G^T &= q^8 I + 0 E_{21} + q^6 E_{22a} + 0 E_{22b} + q^6 E_{23} + q^4 E_{31} + q^4 E_{32} \\ &=(q^8 - q^4)I + q^4 J - q^4 E_{21} + (q^6 - q^4)E_{22a}\\ &\qquad\qquad -q^4 E_{22b} + (q^6 - q^4) E_{23} + (q^4 - q^4) E_{31} + (q^4 - q^4) E_{32} \\ &= (q^8 - q^4)I + q^4 J - q^4 E_{21} + (q^6 - q^4)E_{22a}- q^4 E_{22b} + (q^6 - q^4) E_{23}\,, \end{aligned} \end{align*} $$
where I is the identity matrix, J is the all one matrix and
![]() $E_{ij}$
s are adjacency matrices, specifying which entries are involved. For example, for Case 2.3, all pairs
$E_{ij}$
s are adjacency matrices, specifying which entries are involved. For example, for Case 2.3, all pairs
![]() $(a,e,c), (a^{\prime }, e^{\prime }, c^{\prime })$
with
$(a,e,c), (a^{\prime }, e^{\prime }, c^{\prime })$
with
![]() $c = c^{\prime }$
and
$c = c^{\prime }$
and
![]() $\operatorname {\mathrm {rank}}(t) = 1$
are involved. Thus, the
$\operatorname {\mathrm {rank}}(t) = 1$
are involved. Thus, the
![]() $E_{23}$
is an adjacency matrix of size
$E_{23}$
is an adjacency matrix of size
![]() $q^{12}\times q^{12}$
(containing all triples
$q^{12}\times q^{12}$
(containing all triples
![]() $(a,e,c)$
), with pairs of vertices satisfying this property marked 1 and all others marked 0.
$(a,e,c)$
), with pairs of vertices satisfying this property marked 1 and all others marked 0.
Finally, observe that each subgraph defined by the corresponding adjacency matrix
![]() $E_{ij}$
is regular. This is due to the fact that the condition does not depend on specific value of
$E_{ij}$
is regular. This is due to the fact that the condition does not depend on specific value of
![]() $(a,e,c)$
. Starting from any vertex
$(a,e,c)$
. Starting from any vertex
![]() $(a,e,c)$
, we can get to all possible
$(a,e,c)$
, we can get to all possible
![]() $\bar {a}, \bar {e},\bar {c}$
by subtracting the correct
$\bar {a}, \bar {e},\bar {c}$
by subtracting the correct
![]() $(a^{\prime }, e^{\prime }, c^{\prime })$
. Thus, for each case, we get the same number of
$(a^{\prime }, e^{\prime }, c^{\prime })$
. Thus, for each case, we get the same number of
![]() $(a^{\prime }, e^{\prime }, c^{\prime })$
that satisfies the condition.
$(a^{\prime }, e^{\prime }, c^{\prime })$
that satisfies the condition.
Let
![]() $\kappa _{ij}$
be the maximum number of 1s in a row in
$\kappa _{ij}$
be the maximum number of 1s in a row in
![]() $E_{ij}$
. Obviously,
$E_{ij}$
. Obviously,
![]() $\kappa _{ij}$
is an upper bound on the largest eigenvalue of
$\kappa _{ij}$
is an upper bound on the largest eigenvalue of
![]() $E_{ij}$
. It is not difficult to see that
$E_{ij}$
. It is not difficult to see that
![]() $\kappa _{21} \ll q^9$
,
$\kappa _{21} \ll q^9$
,
![]() $\kappa _{22a} \ll q^7$
,
$\kappa _{22a} \ll q^7$
,
![]() $\kappa _{22b} \ll q^8$
and
$\kappa _{22b} \ll q^8$
and
![]() $\kappa _{23}\ll q^5$
. For example, in Case 2.1, we have
$\kappa _{23}\ll q^5$
. For example, in Case 2.1, we have
![]() $\operatorname {\mathrm {rank}}(t) = 1$
and
$\operatorname {\mathrm {rank}}(t) = 1$
and
![]() $\operatorname {\mathrm {rank}}(\bar {c}) = 2$
. For a fixed
$\operatorname {\mathrm {rank}}(\bar {c}) = 2$
. For a fixed
![]() $(a, e,c)$
, the former implies that there are
$(a, e,c)$
, the former implies that there are
![]() $O(q^5)$
possibilities for
$O(q^5)$
possibilities for
![]() $a^{\prime }$
and
$a^{\prime }$
and
![]() $e^{\prime }$
while the latter implies there are
$e^{\prime }$
while the latter implies there are
![]() $O(q^4)$
possibilities for
$O(q^4)$
possibilities for
![]() $c^{\prime }$
. Altogether, there are
$c^{\prime }$
. Altogether, there are
![]() $O(q^9)$
possibilities for
$O(q^9)$
possibilities for
![]() $(a^{\prime }, e^{\prime }, c^{\prime })$
in Case 2.1. Because the graph induced by
$(a^{\prime }, e^{\prime }, c^{\prime })$
in Case 2.1. Because the graph induced by
![]() $E_{21}$
is regular, we have
$E_{21}$
is regular, we have
![]() $\kappa _{21}\ll q^9$
. Other cases can be deduced accordingly.
$\kappa _{21}\ll q^9$
. Other cases can be deduced accordingly.
The rest follows from a routine computation: let
![]() $v_2$
be an eigenvector corresponding to
$v_2$
be an eigenvector corresponding to
![]() $\mu (G)$
. Then, because G is regular and connected (easy to see, there is no isolated vertex),
$\mu (G)$
. Then, because G is regular and connected (easy to see, there is no isolated vertex),
![]() $v_2$
is orthogonal to the all 1 vector, which means
$v_2$
is orthogonal to the all 1 vector, which means
![]() $J\cdot v_2 = \mathbf {0}$
. We now have
$J\cdot v_2 = \mathbf {0}$
. We now have
 $$ \begin{align*} \begin{aligned} \mu(m_G)^2 v_2 = m_Gm_G^T \cdot v_2 &= (q^8-q^4)I\cdot v_2 + (- q^4 E_{21} + (q^6 - q^4)E_{22a} - q^4 E_{22b} + (q^6 - q^4) E_{23}) \cdot v_2 \\ &= ((q^8 - q^4)- q^4 \kappa_{21} + (q^6 - q^4) \kappa_{22a} - q^4 \kappa_{22b} + (q^6 - q^4)\kappa_{23})\cdot v_2\\ &\ll q^{13} \cdot v_2 \,. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mu(m_G)^2 v_2 = m_Gm_G^T \cdot v_2 &= (q^8-q^4)I\cdot v_2 + (- q^4 E_{21} + (q^6 - q^4)E_{22a} - q^4 E_{22b} + (q^6 - q^4) E_{23}) \cdot v_2 \\ &= ((q^8 - q^4)- q^4 \kappa_{21} + (q^6 - q^4) \kappa_{22a} - q^4 \kappa_{22b} + (q^6 - q^4)\kappa_{23})\cdot v_2\\ &\ll q^{13} \cdot v_2 \,. \end{aligned} \end{align*} $$
Thus,
![]() $\mu (m_G)\ll q^{13/2}$
.
$\mu (m_G)\ll q^{13/2}$
.
4 Proof of Theorem 2.1
To prove Theorem 2.1, we will also need several technical results. A proof of the following inequality may be found in [Reference Roche-Newton, Shparlinski and Winterhof8, Lemma 2.4].
Lemma 4.1 Let
![]() $V_1, \dots , V_k$
be subsets of an abelian group. Then
$V_1, \dots , V_k$
be subsets of an abelian group. Then
 $$ \begin{align*} E_{+}\bigg(\bigsqcup_{i=1}^{k}V_i\bigg) \leq \bigg(\sum_{i=1}^k E_{+}(V_i)^{1/4}\bigg)^4. \end{align*} $$
$$ \begin{align*} E_{+}\bigg(\bigsqcup_{i=1}^{k}V_i\bigg) \leq \bigg(\sum_{i=1}^k E_{+}(V_i)^{1/4}\bigg)^4. \end{align*} $$
The following lemma is taken from [Reference Mohammadi and Stevens5] and may also be extracted from [Reference Roche-Newton, Shparlinski and Winterhof8, Reference Rudnev, Shkredov and Stevens10]. Lemma 4.2 is slightly different to its analogs over commutative rings as highlighted by the duality of the inequalities (4.5) and (4.6).
Lemma 4.2 Let
![]() $X \subseteq GL_2(\mathbb {F}_q)$
. There exist sets
$X \subseteq GL_2(\mathbb {F}_q)$
. There exist sets
![]() $X_*\subset X$
,
$X_*\subset X$
,
![]() $D \subset XX$
, as well as numbers
$D \subset XX$
, as well as numbers
![]() $\tau $
and
$\tau $
and
![]() $\kappa $
satisfying
$\kappa $
satisfying
 $$ \begin{align} \frac{E_{\times}(X)}{\tau^2\cdot \log |X|}\ll |D| \ll (\log|X|)^6 \frac{|X_*|^4}{E_{\times}(X)}, \end{align} $$
$$ \begin{align} \frac{E_{\times}(X)}{\tau^2\cdot \log |X|}\ll |D| \ll (\log|X|)^6 \frac{|X_*|^4}{E_{\times}(X)}, \end{align} $$
 $$ \begin{align} |X_*|^2 \gg \frac{E_{\times}(X)}{|X| (\log|X|)^{7/2}}, \end{align} $$
$$ \begin{align} |X_*|^2 \gg \frac{E_{\times}(X)}{|X| (\log|X|)^{7/2}}, \end{align} $$
 $$ \begin{align} \kappa \gg \frac{|D|\tau}{|X_*|(\log|X|)^2}, \end{align} $$
$$ \begin{align} \kappa \gg \frac{|D|\tau}{|X_*|(\log|X|)^2}, \end{align} $$
such that either
or
We need a dyadic pigeonhole argument, which can be found in [Reference Murphy and Petridis6, Lemma 18].
Lemma 4.3 For
![]() $\Omega \subseteq M_2(\mathbb {F}_q)$
, let
$\Omega \subseteq M_2(\mathbb {F}_q)$
, let
![]() $w,f: \Omega \rightarrow \mathbb {R}^+$
with
$w,f: \Omega \rightarrow \mathbb {R}^+$
with
![]() $f(x) \leq M, \;\forall x\in \Omega $
. Let
$f(x) \leq M, \;\forall x\in \Omega $
. Let
![]() $W = \sum _{x\in \Omega } w(x)$
. If
$W = \sum _{x\in \Omega } w(x)$
. If
![]() $\sum _{x\in \Omega } f(x) w(x) \geq K,$
then there exists a subset
$\sum _{x\in \Omega } f(x) w(x) \geq K,$
then there exists a subset
![]() $D \subset \Omega $
and a number
$D \subset \Omega $
and a number
![]() $\tau $
such that
$\tau $
such that
![]() $\tau \leq f(x) < 2\tau $
for all
$\tau \leq f(x) < 2\tau $
for all
![]() $x\in D$
and
$x\in D$
and
![]() $K/(2W) \leq \tau \leq M\,.$
Moreover,
$K/(2W) \leq \tau \leq M\,.$
Moreover,
Proof of Lemma 4.2
We use the identities in (1.2) and apply Lemma 4.3, by taking
![]() $\Omega = X X, \, f = w = r_{XX},\, M = |X|,\, K = E_{\times }(X)$
, and
$\Omega = X X, \, f = w = r_{XX},\, M = |X|,\, K = E_{\times }(X)$
, and
![]() $W = |X|^2$
, to find a set
$W = |X|^2$
, to find a set
![]() $D \subset XX$
and a number
$D \subset XX$
and a number
![]() $\tau $
, satisfying (4.1), such that
$\tau $
, satisfying (4.1), such that
![]() $D = \{\, \lambda \in XX: \tau \leq r_{XX}(\lambda ) < 2\tau \,\}\,$
and
$D = \{\, \lambda \in XX: \tau \leq r_{XX}(\lambda ) < 2\tau \,\}\,$
and
Define
![]() $P_1 = \{\,(x,y)\in X\times X: xy \in D\,\}$
and
$P_1 = \{\,(x,y)\in X\times X: xy \in D\,\}$
and
![]() $A_x = \{\,y: (x,y)\in P_1\,\}$
for
$A_x = \{\,y: (x,y)\in P_1\,\}$
for
![]() $x \in X$
. By the definition of D, we know that
$x \in X$
. By the definition of D, we know that
![]() $\tau |D| \leq |P_1| < 2\tau |D|$
. We can use Lemma 4.3 again with
$\tau |D| \leq |P_1| < 2\tau |D|$
. We can use Lemma 4.3 again with
![]() $\Omega = X, f(x) = |A_x|, w = 1, M = W = |X|$
, and
$\Omega = X, f(x) = |A_x|, w = 1, M = W = |X|$
, and
![]() $K = |P_1|$
to find a set
$K = |P_1|$
to find a set
![]() $V\subset X$
and a number
$V\subset X$
and a number
![]() $\kappa _1$
such that
$\kappa _1$
such that
![]() $V = \{\,x\in X: \kappa _1 \leq |A_x| < 2\kappa _1\,\}\,$
and
$V = \{\,x\in X: \kappa _1 \leq |A_x| < 2\kappa _1\,\}\,$
and
Now, we split the analysis into two cases based on
![]() $|V|$
:
$|V|$
:
Case 1 (
![]() $|V| \geq \kappa _1 (\log |X|)^{-1/2}$
): In this case, we simply set
$|V| \geq \kappa _1 (\log |X|)^{-1/2}$
): In this case, we simply set
![]() $X_* = V$
and
$X_* = V$
and
![]() $\kappa = \kappa _1$
. For each
$\kappa = \kappa _1$
. For each
![]() $x\in V$
, there are at least
$x\in V$
, there are at least
![]() $\kappa _1$
different y such that
$\kappa _1$
different y such that
![]() $x y \in D$
. Therefore,
$x y \in D$
. Therefore,
![]() $r_{DX^{-1}}(x) \geq \kappa \;\forall x \in X_*$
.
$r_{DX^{-1}}(x) \geq \kappa \;\forall x \in X_*$
.
Case 2 (
![]() $|V| < \kappa _1 (\log |X|)^{-1/2}$
): In this case, we find another pair
$|V| < \kappa _1 (\log |X|)^{-1/2}$
): In this case, we find another pair
![]() $U, \kappa _2$
that satisfies
$U, \kappa _2$
that satisfies
![]() $|U| \gg \kappa _2 (\log |X|)^{-1/2}$
and set
$|U| \gg \kappa _2 (\log |X|)^{-1/2}$
and set
![]() $X_* = U$
and
$X_* = U$
and
![]() $\kappa = \kappa _2$
. Let
$\kappa = \kappa _2$
. Let
![]() $P_2 = \{\,(x,y)\in P_1: x\in V\,\}$
and
$P_2 = \{\,(x,y)\in P_1: x\in V\,\}$
and
![]() $B_y = \{\,x: (x,y)\in P_2\,\}$
. By definition, we have
$B_y = \{\,x: (x,y)\in P_2\,\}$
. By definition, we have
![]() $|P_2| \geq |V|\kappa _1$
. We apply Lemma 4.3 again, with
$|P_2| \geq |V|\kappa _1$
. We apply Lemma 4.3 again, with
![]() $\Omega = X, f(y) = |B_y|, w = 1, K = |P_2|$
and
$\Omega = X, f(y) = |B_y|, w = 1, K = |P_2|$
and
![]() $W = M =|X|$
to get
$W = M =|X|$
to get
![]() $U \subset X$
and a number
$U \subset X$
and a number
![]() $\kappa _2$
such that
$\kappa _2$
such that
![]() $U = \{\,y\in X: \kappa _2 \leq |B_y| < 2\kappa _2\,\}\,$
and
$U = \{\,y\in X: \kappa _2 \leq |B_y| < 2\kappa _2\,\}\,$
and
Combining this inequality with the assumption of this case (
![]() $\kappa _1 \geq |V|(\log |X|)^{1/2}$
) and
$\kappa _1 \geq |V|(\log |X|)^{1/2}$
) and
![]() $|V| \geq \kappa _2$
, we conclude
$|V| \geq \kappa _2$
, we conclude
![]() $|U| \gg \kappa _2 (\log |X|)^{-1/2}$
. We can then argue similarly as in Case 1 to conclude
$|U| \gg \kappa _2 (\log |X|)^{-1/2}$
. We can then argue similarly as in Case 1 to conclude
![]() $r_{X^{-1}D}(x) \geq \kappa \;\forall x \in X_*$
.
$r_{X^{-1}D}(x) \geq \kappa \;\forall x \in X_*$
.
Now, (4.4) follows from either of (4.8) or (4.9). To prove (4.3), we first note that in either of the cases above we have
![]() $|X_*|\gg \kappa (\log |X|)^{-1/2}$
. Then using the lower bound on
$|X_*|\gg \kappa (\log |X|)^{-1/2}$
. Then using the lower bound on
![]() $\kappa $
, (4.7) and (4.1), we have
$\kappa $
, (4.7) and (4.1), we have
![]() $|X_*|^2\gg |D|\tau (\log |X|)^{-5/2}\gg E_{\times }(X)/(|X|\log |X|)^{7/2}$
as required. Finally, to deduce the required upper bound on
$|X_*|^2\gg |D|\tau (\log |X|)^{-5/2}\gg E_{\times }(X)/(|X|\log |X|)^{7/2}$
as required. Finally, to deduce the required upper bound on
![]() $|D|$
in (4.2) note that, as shown above,
$|D|$
in (4.2) note that, as shown above,
![]() $|D|\tau \ll |X_*|^2(\log |X|)^{5/2}$
, which with (4.7) implies
$|D|\tau \ll |X_*|^2(\log |X|)^{5/2}$
, which with (4.7) implies
![]() $|D|E_{\times }(X)(\log |X|)^{-1}\ll (|D|\tau )^2\ll |X_*|^4(\log |X|)^5$
.
$|D|E_{\times }(X)(\log |X|)^{-1}\ll (|D|\tau )^2\ll |X_*|^4(\log |X|)^5$
.
Lemma 4.4 Let
![]() $X\subseteq GL_2({\mathbb F}_q)$
. Then there exists
$X\subseteq GL_2({\mathbb F}_q)$
. Then there exists
![]() $X_*\subseteq X$
, with
$X_*\subseteq X$
, with
 $$\begin{align*}|X_*| \gg \frac{E_{\times}(X)^{1/2}}{|X|^{1/2}(\log |X|)^{7/4}}, \end{align*}$$
$$\begin{align*}|X_*| \gg \frac{E_{\times}(X)^{1/2}}{|X|^{1/2}(\log |X|)^{7/4}}, \end{align*}$$
such that
 $$ \begin{align} E_{+}(X_*) \ll \frac{|X_*|^4|X|^6(\log|X|)^2}{q^4 E_{\times}(X)^2} + \frac{q^{13/2}|X_*|^3|X|(\log|X|)^5}{E_{\times}(X)}. \end{align} $$
$$ \begin{align} E_{+}(X_*) \ll \frac{|X_*|^4|X|^6(\log|X|)^2}{q^4 E_{\times}(X)^2} + \frac{q^{13/2}|X_*|^3|X|(\log|X|)^5}{E_{\times}(X)}. \end{align} $$
Proof We apply Lemma 4.2 to the set X and henceforth assume its full statement, keeping the same notation. Without loss of generality, assume
![]() $r_{X^{-1}D}(x) \geq \kappa \;\forall x\in X_*$
. Thus,
$r_{X^{-1}D}(x) \geq \kappa \;\forall x\in X_*$
. Thus,
 $$ \begin{align*} E_{+}(X_*) &= |\{(x_1, x_2, x_3, x_4)\in X_*^4: x_1 + x_2 = x_3 + x_4\}|\\ &\leq \kappa^{-2}|\{(d_1, d_2, x_1, x_2, y_1, y_2)\in D^2\times X_*^2 \times X^2: x_1 + y_1^{-1} d_1 = x_2 + y_2^{-1} d_2 \}|\\ &= \kappa^{-2} \mathcal{I}(X^{-1}, D, -X_*, -X^{-1}, D, X_*). \end{align*} $$
$$ \begin{align*} E_{+}(X_*) &= |\{(x_1, x_2, x_3, x_4)\in X_*^4: x_1 + x_2 = x_3 + x_4\}|\\ &\leq \kappa^{-2}|\{(d_1, d_2, x_1, x_2, y_1, y_2)\in D^2\times X_*^2 \times X^2: x_1 + y_1^{-1} d_1 = x_2 + y_2^{-1} d_2 \}|\\ &= \kappa^{-2} \mathcal{I}(X^{-1}, D, -X_*, -X^{-1}, D, X_*). \end{align*} $$
Then applying Proposition 3.1 and (4.4), we obtain
 $$ \begin{align*} E_{+}(X_*) &\ll \kappa^{-2}\cdot\bigg( \frac{(|D||X||X_*|)^{2}}{q^4} + q^{13/2}|D||X||X_*|\bigg)\\ &\ll\frac{|X_*|^4|X|^2(\log|X|)^2}{q^4\tau^2} + \frac{q^{13/2}|X_*|^3|X|(\log|X|)^4}{|D|\tau^2}\,. \end{align*} $$
$$ \begin{align*} E_{+}(X_*) &\ll \kappa^{-2}\cdot\bigg( \frac{(|D||X||X_*|)^{2}}{q^4} + q^{13/2}|D||X||X_*|\bigg)\\ &\ll\frac{|X_*|^4|X|^2(\log|X|)^2}{q^4\tau^2} + \frac{q^{13/2}|X_*|^3|X|(\log|X|)^4}{|D|\tau^2}\,. \end{align*} $$
Finally, applying (4.1) and (4.2), we obtain the required bound in (4.10) for
![]() $E_{+}(X_*)$
.
$E_{+}(X_*)$
.
We are now ready to prove Theorem 2.1.
Proof of Theorem 2.1
We begin by describing an algorithm, which constructs two sequences of sets
![]() $A = S_1 \supseteq S_2 \supseteq \cdots \supseteq S_{k+1}$
and
$A = S_1 \supseteq S_2 \supseteq \cdots \supseteq S_{k+1}$
and
![]() $\emptyset = T_0 \subseteq T_1 \subseteq \cdots \subseteq T_{k}$
such that
$\emptyset = T_0 \subseteq T_1 \subseteq \cdots \subseteq T_{k}$
such that
![]() $ S_{i} \sqcup T_{i-1} = A$
, for
$ S_{i} \sqcup T_{i-1} = A$
, for
![]() $i = 1, \dots , k+1$
.
$i = 1, \dots , k+1$
.
Let
![]() $1\leq M\leq |A|$
be a parameter. At any step
$1\leq M\leq |A|$
be a parameter. At any step
![]() $i\geq 1$
, if
$i\geq 1$
, if
![]() $E_{\times }(S_i)\leq |A|^3/M$
the algorithm halts. Otherwise if
$E_{\times }(S_i)\leq |A|^3/M$
the algorithm halts. Otherwise if
through a use of Lemma 4.4, with
![]() $X=S_i$
, we identify a set
$X=S_i$
, we identify a set
![]() $V_i:= X_* \subseteq S_i$
, with
$V_i:= X_* \subseteq S_i$
, with
 $$ \begin{align} |V_i| \gg \frac{E_{\times}(S_i)^{1/2}}{|S_i|^{1/2}(\log|A|)^{7/4}}> \frac{|A|}{M^{1/2}(\log|A|)^{7/4}} \end{align} $$
$$ \begin{align} |V_i| \gg \frac{E_{\times}(S_i)^{1/2}}{|S_i|^{1/2}(\log|A|)^{7/4}}> \frac{|A|}{M^{1/2}(\log|A|)^{7/4}} \end{align} $$
and
 $$ \begin{align} E_{+}(V_i)\ll \frac{|V_i|^4|S_i|^6(\log|S_i|)^2}{q^4 E_{\times}(S_i)^2} + \frac{q^{13/2}|V_i|^3|S_i|(\log|S_i|)^5}{E_{\times}(S_i)}. \end{align} $$
$$ \begin{align} E_{+}(V_i)\ll \frac{|V_i|^4|S_i|^6(\log|S_i|)^2}{q^4 E_{\times}(S_i)^2} + \frac{q^{13/2}|V_i|^3|S_i|(\log|S_i|)^5}{E_{\times}(S_i)}. \end{align} $$
We then set
![]() $S_{i+1} = S_i \setminus V_i$
,
$S_{i+1} = S_i \setminus V_i$
,
![]() $T_{i+1} = T_i \sqcup V_i$
and repeat this process for the step
$T_{i+1} = T_i \sqcup V_i$
and repeat this process for the step
![]() $i+1$
. From (4.12), we deduce
$i+1$
. From (4.12), we deduce
![]() $|V_i|\gg |A|^{1/2}(\log |A|)^{-7/4}$
and so the cardinality of each
$|V_i|\gg |A|^{1/2}(\log |A|)^{-7/4}$
and so the cardinality of each
![]() $S_i$
monotonically decreases. This in turn implies that this process indeed terminates after a finite number of iterations k. We set
$S_i$
monotonically decreases. This in turn implies that this process indeed terminates after a finite number of iterations k. We set
![]() $B = S_{k+1}$
and
$B = S_{k+1}$
and
![]() $C = T_k$
, noting that
$C = T_k$
, noting that
![]() $A = B\sqcup C$
and that
$A = B\sqcup C$
and that
We apply the inequalities (4.11), (4.12) and
![]() $|S_i| \leq |A|$
, to (4.13), to get
$|S_i| \leq |A|$
, to (4.13), to get
 $$ \begin{align*} E_{+}(V_i) &\ll M^2|V_i|^4q^{-4}(\log|A|)^2 + M|A|^{-2}|V_i|^3 q^{13/2} (\log|A|)^5 \\ &\ll \big(M^2 q^{-4}(\log|A|)^2 + M^{3/2}|A|^{-3}q^{13/2}(\log|A|)^{27/4}\big)\cdot|V_i|^4. \end{align*} $$
$$ \begin{align*} E_{+}(V_i) &\ll M^2|V_i|^4q^{-4}(\log|A|)^2 + M|A|^{-2}|V_i|^3 q^{13/2} (\log|A|)^5 \\ &\ll \big(M^2 q^{-4}(\log|A|)^2 + M^{3/2}|A|^{-3}q^{13/2}(\log|A|)^{27/4}\big)\cdot|V_i|^4. \end{align*} $$
Then, observing that
 $$ \begin{align*} C = T_k = \bigsqcup_{i=1}^{k} V_i \subseteq A, \end{align*} $$
$$ \begin{align*} C = T_k = \bigsqcup_{i=1}^{k} V_i \subseteq A, \end{align*} $$
we use Lemma 4.1 to obtain
 $$ \begin{align*} E_{+}(C) &\ll (M^2q^{-4}(\log|A|)^2 + M^{3/2}|A|^{-3}q^{13/2}(\log|A|)^{27/4}) \bigg(\sum_{i=1}^k|V_i|\bigg)^4 \\ &\leq M^{2}|A|^4q^{-4}(\log|A|)^{2} + M^{3/2}|A|q^{13/2}(\log|A|)^{27/4}. \end{align*} $$
$$ \begin{align*} E_{+}(C) &\ll (M^2q^{-4}(\log|A|)^2 + M^{3/2}|A|^{-3}q^{13/2}(\log|A|)^{27/4}) \bigg(\sum_{i=1}^k|V_i|\bigg)^4 \\ &\leq M^{2}|A|^4q^{-4}(\log|A|)^{2} + M^{3/2}|A|q^{13/2}(\log|A|)^{27/4}. \end{align*} $$
Note that Lemma 4.1 is applicable because
![]() $M_2({\mathbb F}_q)$
is an abelian group under addition. Comparing this with (4.14), we see the choice
$M_2({\mathbb F}_q)$
is an abelian group under addition. Comparing this with (4.14), we see the choice
![]() $M = M(|A|)$
, given by (2.1) is optimal.
$M = M(|A|)$
, given by (2.1) is optimal.
5 Proofs of Theorem 2.2 and Corollary 2.3
Proof of Theorem 2.2
We proceed similarly to the proof of [Reference Roche-Newton, Rudnev and Shkredov7, Theorem 6]. Note that
 $$ \begin{align*} E_+(A, B) &= |C|^{-2}|\{\,(a, a^{\prime}, b, b^{\prime}, c, c^{\prime})\in A^2\times B^2\times C^2: a + b c c^{-1} = a^{\prime} + b^{\prime} c^{\prime} (c^{\prime})^{-1}\,\}|\\ &\leq |C|^{-2}|\{\,(a, a^{\prime}, s, s^{\prime}, c, c^{\prime})\in A^2\times (BC)^2\times (C^{-1})^2: a + s c = a^{\prime} + s^{\prime} c^{\prime}\,\}|. \end{align*} $$
$$ \begin{align*} E_+(A, B) &= |C|^{-2}|\{\,(a, a^{\prime}, b, b^{\prime}, c, c^{\prime})\in A^2\times B^2\times C^2: a + b c c^{-1} = a^{\prime} + b^{\prime} c^{\prime} (c^{\prime})^{-1}\,\}|\\ &\leq |C|^{-2}|\{\,(a, a^{\prime}, s, s^{\prime}, c, c^{\prime})\in A^2\times (BC)^2\times (C^{-1})^2: a + s c = a^{\prime} + s^{\prime} c^{\prime}\,\}|. \end{align*} $$
The required result then follows by applying Proposition 3.1.
Proof of Corollary 2.3
Since
![]() $|A|\gg q^3$
, we may assume
$|A|\gg q^3$
, we may assume
![]() $A\subseteq GL_2({\mathbb F}_q)$
. We use Theorem 2.2, with
$A\subseteq GL_2({\mathbb F}_q)$
. We use Theorem 2.2, with
![]() $A=B=C$
and apply the lower bound on
$A=B=C$
and apply the lower bound on
![]() $E_+(A)$
given by (1.3) to obtain (2.3). To prove (2.4), we follow the same process and apply the assumption
$E_+(A)$
given by (1.3) to obtain (2.3). To prove (2.4), we follow the same process and apply the assumption
![]() $|AA|\ll |A|$
, to obtain
$|AA|\ll |A|$
, to obtain
which gives the required result.
To prove (2.5), we use Theorem 2.2, to get
 $$\begin{align*}\frac{|A+A|^2|A|^2}{|A+A+A|}\leq E_{+}(A+A, A) \ll \frac{|A+A|^2|A|^2}{q^4} + q^{13/2}|A+A|. \end{align*}$$
$$\begin{align*}\frac{|A+A|^2|A|^2}{|A+A+A|}\leq E_{+}(A+A, A) \ll \frac{|A+A|^2|A|^2}{q^4} + q^{13/2}|A+A|. \end{align*}$$
Recalling (5.1), this rearranges to
 $$\begin{align*}|A+A+A|\gg \min\left\{q^4, \frac{|A+A||A|^2}{q^{13/2}}\right\}\gg \min\left\{q^4, \frac{|A|^2}{q^{5/2}}, \frac{|A|^5}{q^{13}}\right\}. \end{align*}$$
$$\begin{align*}|A+A+A|\gg \min\left\{q^4, \frac{|A+A||A|^2}{q^{13/2}}\right\}\gg \min\left\{q^4, \frac{|A|^2}{q^{5/2}}, \frac{|A|^5}{q^{13}}\right\}. \end{align*}$$
The required result then easily follows.
6 Proofs of Theorem 2.4, Corollary 2.5, and Theorem 2.6
Proof of Theorem 2.4
For
![]() $\lambda \in AB +C$
, write
$\lambda \in AB +C$
, write
By the Cauchy–Schwarz inequality, we have
 $$\begin{align*}(|A||B||C|)^2 = \left(\sum_{\lambda\in AB+C} t(\lambda)\right)^2 \leq |AB +C|\sum_{\lambda\in AB+C} t(\lambda)^2. \end{align*}$$
$$\begin{align*}(|A||B||C|)^2 = \left(\sum_{\lambda\in AB+C} t(\lambda)\right)^2 \leq |AB +C|\sum_{\lambda\in AB+C} t(\lambda)^2. \end{align*}$$
Further noting that
We apply Proposition 3.1 to obtain
 $$\begin{align*}|AB + C|\gg \min\left\{\,q^4,\, \frac{|A||B||C|}{q^{13/2}}\,\right\}. \end{align*}$$
$$\begin{align*}|AB + C|\gg \min\left\{\,q^4,\, \frac{|A||B||C|}{q^{13/2}}\,\right\}. \end{align*}$$
This immediately implies the required result.
For the set
![]() $(A+B)C$
, as above we have
$(A+B)C$
, as above we have
 $$\begin{align*}|(A+B)C|\ge \frac{|A|^2|B|^2|C|^2}{|\{\,(a, b, c, a', b', c')\in (A\times B\times C)^2\colon (a+b)c=(a'+b')c'\,\}|}. \end{align*}$$
$$\begin{align*}|(A+B)C|\ge \frac{|A|^2|B|^2|C|^2}{|\{\,(a, b, c, a', b', c')\in (A\times B\times C)^2\colon (a+b)c=(a'+b')c'\,\}|}. \end{align*}$$
To estimate the denominator, we follow the argument in the proof of Proposition 3.1. In particular, we first define a graph G with the vertex set
![]() $V=M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)$
, and there is a direct edge going from
$V=M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)\times M_2(\mathbb {F}_q)$
, and there is a direct edge going from
![]() $(a, e, c)$
to
$(a, e, c)$
to
![]() $(b, f, d)$
if
$(b, f, d)$
if
![]() $b a+e f=c+d$
. The only difference here compared to that graph in Section 3 is that we switch between
$b a+e f=c+d$
. The only difference here compared to that graph in Section 3 is that we switch between
![]() $b a$
and
$b a$
and
![]() $a b$
. By using a similar argument as in Section 3, we have this graph is a
$a b$
. By using a similar argument as in Section 3, we have this graph is a
![]() $(q^{12}, q^8,c q^{13/2})$
-digraph, where c is a positive constant.
$(q^{12}, q^8,c q^{13/2})$
-digraph, where c is a positive constant.
To bound the denominator, we observe that the equation
gives us a direct edge from
![]() $(c, -b', -ac )$
to
$(c, -b', -ac )$
to
![]() $(b, c', a'c')$
. So, let
$(b, c', a'c')$
. So, let
![]() $U:=\{(c, -b', -ac)\colon a\in A, c\in C, b'\in B\}$
and
$U:=\{(c, -b', -ac)\colon a\in A, c\in C, b'\in B\}$
and
![]() $W=\{(b, c', a'c')\colon b\in B, c'\in C, a'\in A\}$
. Since
$W=\{(b, c', a'c')\colon b\in B, c'\in C, a'\in A\}$
. Since
![]() $C\subseteq GL_2(\mathbb {F}_q)$
, we have
$C\subseteq GL_2(\mathbb {F}_q)$
, we have
![]() $|U|=|W|=|A||B||C|$
. So applying Lemma 3.2, the number of edges from U to W is at most
$|U|=|W|=|A||B||C|$
. So applying Lemma 3.2, the number of edges from U to W is at most
 $$\begin{align*}\frac{|A|^2|B|^2|C|^2}{q^4}+q^{13/2}|A||B||C|. \end{align*}$$
$$\begin{align*}\frac{|A|^2|B|^2|C|^2}{q^4}+q^{13/2}|A||B||C|. \end{align*}$$
In other words,
 $$\begin{align*}|\{\,(a, b, c, a', b', c')\in (A\times B\times C)^2\colon (a+b)c=(a'+b')c'\,\}|\ll \frac{|A|^2|B|^2|C|^2}{q^4}+q^{13/2}|A||B||C|, \end{align*}$$
$$\begin{align*}|\{\,(a, b, c, a', b', c')\in (A\times B\times C)^2\colon (a+b)c=(a'+b')c'\,\}|\ll \frac{|A|^2|B|^2|C|^2}{q^4}+q^{13/2}|A||B||C|, \end{align*}$$
and we get the desired estimate.
Proof of Corollary 2.5
It follows from Theorem 2.4 that
and
Note that by Corollary 2.3, if
![]() $|A|\gg q^{3+7/16}$
, we have
$|A|\gg q^{3+7/16}$
, we have
Hence, one of the conditions in (6.1) or (6.2) is satisfied, which in turn gives the required estimate.
Proof of Theorem 2.6
By the Cauchy–Schwarz inequality and Proposition 3.1, we have
 $$ \begin{align*} \mathcal{J}(A,B,C,D) &= |\{\,(a, b, c, d)\in A\times B \times C\times D: a+b = c d\,\}|\\ &\leq |B|^{1/2}|\{\,(a, a^{\prime}, c, c^{\prime}, d, d^{\prime}) \in A^2 \times C^2 \times D^2: c d - a = c^{\prime} d^{\prime} - a^{\prime}\,\}|^{1/2}\\ &\ll \frac{|A||B|^{1/2}|C||D|}{q^2} + q^{13/4} (|A||B||C||D|)^{1/2}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \mathcal{J}(A,B,C,D) &= |\{\,(a, b, c, d)\in A\times B \times C\times D: a+b = c d\,\}|\\ &\leq |B|^{1/2}|\{\,(a, a^{\prime}, c, c^{\prime}, d, d^{\prime}) \in A^2 \times C^2 \times D^2: c d - a = c^{\prime} d^{\prime} - a^{\prime}\,\}|^{1/2}\\ &\ll \frac{|A||B|^{1/2}|C||D|}{q^2} + q^{13/4} (|A||B||C||D|)^{1/2}.\\[-42pt] \end{align*} $$