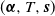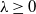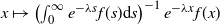1. Introduction
A phase-type distribution corresponds to the law of
![]() $Y\;:\!=\;\inf\{t\ge 0\;:\;J_t=\star\}$
where
$Y\;:\!=\;\inf\{t\ge 0\;:\;J_t=\star\}$
where
![]() $\{J_t\}_{t\ge 0}$
is a Markov jump process with state space
$\{J_t\}_{t\ge 0}$
is a Markov jump process with state space
![]() $\{1,\dots,p\}\cup \{\star\}$
, with
$\{1,\dots,p\}\cup \{\star\}$
, with
![]() $\{1,\dots,p\}$
assumed to be transient states and
$\{1,\dots,p\}$
assumed to be transient states and
![]() $\{\star\}$
absorbing. If
$\{\star\}$
absorbing. If
![]() $\{J_t\}_{t\ge 0}$
has a block-partitioned initial distribution
$\{J_t\}_{t\ge 0}$
has a block-partitioned initial distribution
![]() $(\boldsymbol{\pi}, 0)$
and intensity matrix given by
$(\boldsymbol{\pi}, 0)$
and intensity matrix given by
 \begin{equation}\left[\begin{matrix}A\;\;\;\;\;\;\;&\boldsymbol{{b}}\\[5pt]\textbf{0}\;\;\;\;\;\;\;&0\end{matrix}\right]\quad\mbox{with}\quad\boldsymbol{{b}}=-A\textbf{1},\end{equation}
\begin{equation}\left[\begin{matrix}A\;\;\;\;\;\;\;&\boldsymbol{{b}}\\[5pt]\textbf{0}\;\;\;\;\;\;\;&0\end{matrix}\right]\quad\mbox{with}\quad\boldsymbol{{b}}=-A\textbf{1},\end{equation}
where
![]() $\textbf{0}$
represents a p-dimensional row vector of 0s and
$\textbf{0}$
represents a p-dimensional row vector of 0s and
![]() $\textbf{1}$
a p-dimensional column vector of 1s, then we say that the phase-type distribution is of parameters
$\textbf{1}$
a p-dimensional column vector of 1s, then we say that the phase-type distribution is of parameters
![]() $(\boldsymbol{\pi}, A)$
. Via simple probabilistic arguments, it can be shown that the density function of a phase-type distribution of parameters
$(\boldsymbol{\pi}, A)$
. Via simple probabilistic arguments, it can be shown that the density function of a phase-type distribution of parameters
![]() $(\boldsymbol{\pi},A)$
is of the form
$(\boldsymbol{\pi},A)$
is of the form
Indeed, the vector
![]() $\boldsymbol{\pi}e^{Ax}$
yields the probabilities of
$\boldsymbol{\pi}e^{Ax}$
yields the probabilities of
![]() $\{J_t\}_{t\ge 0}$
being in some state
$\{J_t\}_{t\ge 0}$
being in some state
![]() $\{1,\dots, p\}$
at time x, and
$\{1,\dots, p\}$
at time x, and
![]() $\boldsymbol{{b}}$
corresponds to the intensity vector of an absorption happening immediately after. Phase-type distributions were first introduced in [Reference Jensen14] with the aim of constructing a robust and tractable class of distributions on
$\boldsymbol{{b}}$
corresponds to the intensity vector of an absorption happening immediately after. Phase-type distributions were first introduced in [Reference Jensen14] with the aim of constructing a robust and tractable class of distributions on
![]() $\mathbb{R}_+$
to be used in econometric problems. A more comprehensive study of phase-type distributions was carried on by Neuts [Reference Neuts15, Reference Neuts16], whose work popularized their use in more general stochastic models.
$\mathbb{R}_+$
to be used in econometric problems. A more comprehensive study of phase-type distributions was carried on by Neuts [Reference Neuts15, Reference Neuts16], whose work popularized their use in more general stochastic models.
On the other hand, a matrix-exponential distribution of dimension
![]() $p\ge 1$
is an absolutely continuous distribution on
$p\ge 1$
is an absolutely continuous distribution on
![]() $(0,\infty)$
whose density function can be written as
$(0,\infty)$
whose density function can be written as
where
![]() $\boldsymbol{\alpha}=(\alpha_1,\dots,\alpha_p)$
is a p-dimensional row vector,
$\boldsymbol{\alpha}=(\alpha_1,\dots,\alpha_p)$
is a p-dimensional row vector,
![]() $T=\{t_{ij}\}_{i,j\in\{1,\dots,p\}}$
is a
$T=\{t_{ij}\}_{i,j\in\{1,\dots,p\}}$
is a
![]() $(p\times p) $
-dimensional square matrix, and
$(p\times p) $
-dimensional square matrix, and
![]() $\boldsymbol{{s}}=(s_1,\dots,s_p)^\intercal$
is a p-dimensional column vector, all with complex entries. If the dimension need not be specified, we refer to such a distribution simply as matrix-exponential. It follows from (2) and (3) that the class of phase-type distributions is a subset of those that are matrix-exponential, with the inclusion being strict (see [Reference O’Cinneide17] for details on the latter).
$\boldsymbol{{s}}=(s_1,\dots,s_p)^\intercal$
is a p-dimensional column vector, all with complex entries. If the dimension need not be specified, we refer to such a distribution simply as matrix-exponential. It follows from (2) and (3) that the class of phase-type distributions is a subset of those that are matrix-exponential, with the inclusion being strict (see [Reference O’Cinneide17] for details on the latter).
Matrix-exponential distributions were first studied in [Reference Cox8, Reference Cox9] through the concept of complex-valued transition probabilities. More precisely, these papers showed that certain systems with complex-valued elements can be formally studied by analytical means without assigning a specific physical interpretation to their components. While their method provided mathematical rigour to systems ‘driven’ by complex-valued intensity matrices, it failed to provide a physical meaning to each individual component, as opposed to the case of Markov jump processes with genuine intensity matrices. Later on, it was proved in [Reference Bladt and Neuts5, Reference O’Cinneide17] that matrix-exponential distributions have an interpretation in terms of a Markov process with continuous state space, as opposed to the finite-state-space one that phase-type distributions enjoy. Even after the discovery of these physical interpretations of matrix-exponential distributions, however, properties of this class of distributions are still not as well understood as they are for its phase-type counterpart. One of the main reasons for this is that processes with continuous state space are more difficult to handle, so that studying matrix-exponential distributions by physical means requires a more sophisticated framework. For example, this is the case in [Reference Asmussen and Bladt2, Reference Bean and Nielsen4, Reference Bean, Nguyen, Nielsen and Peralta3], where the theory of piecewise deterministic Markov processes is used to study models with matrix-exponential components. Thus, having a finite-state system interpretation for matrix-exponential distributions available may potentially lead to the discovery of new properties, as has traditionally been the case for phase-type distributions.
Functions of the form (3) also play an important role in control theory, more specifically, in the topic of single-input–single-output (SISO) linear systems. Such systems are described by a column-vector function
![]() $\boldsymbol{{x}}\;:\;\mathbb{R}_+\rightarrow \mathbb{R}^p$
and
$\boldsymbol{{x}}\;:\;\mathbb{R}_+\rightarrow \mathbb{R}^p$
and
![]() $y\;:\;\mathbb{R}_+\rightarrow \mathbb{R}$
which satisfy the ordinary differential equations
$y\;:\;\mathbb{R}_+\rightarrow \mathbb{R}$
which satisfy the ordinary differential equations
 \begin{align*}\frac{\textrm{d} \boldsymbol{{x}}(t)}{\textrm{d} t} & = T_0\boldsymbol{{x}}(t) + \boldsymbol{{b}}_0u(t),\\[5pt]y(t)& = \boldsymbol{\alpha}_0 \boldsymbol{{x}}(t);\end{align*}
\begin{align*}\frac{\textrm{d} \boldsymbol{{x}}(t)}{\textrm{d} t} & = T_0\boldsymbol{{x}}(t) + \boldsymbol{{b}}_0u(t),\\[5pt]y(t)& = \boldsymbol{\alpha}_0 \boldsymbol{{x}}(t);\end{align*}
here u is called the input function,
![]() $\boldsymbol{{x}}$
the state function, and y the output function. SISO linear systems which produce a nonnegative output from a nonnegative input are said to be externally positive. It can be shown [Reference Farina and Rinaldi12, Theorem 1] that if
$\boldsymbol{{x}}$
the state function, and y the output function. SISO linear systems which produce a nonnegative output from a nonnegative input are said to be externally positive. It can be shown [Reference Farina and Rinaldi12, Theorem 1] that if
![]() $\boldsymbol{{x}}(0)=\textbf{0}$
, then the output function takes the form
$\boldsymbol{{x}}(0)=\textbf{0}$
, then the output function takes the form
where
![]() $h_0(z)=\boldsymbol{\alpha}_0e^{T_0z}\boldsymbol{{s}}_0$
. From this, one can deduce that the system is externally positive if and only if
$h_0(z)=\boldsymbol{\alpha}_0e^{T_0z}\boldsymbol{{s}}_0$
. From this, one can deduce that the system is externally positive if and only if
![]() $h_0$
is a nonnegative function. If, additionally,
$h_0$
is a nonnegative function. If, additionally,
![]() $h_0$
is bounded, then
$h_0$
is bounded, then
![]() $h_0$
is essentially a scaled matrix-exponential density function. This nicely links the theory of externally positive SISO linear systems with that of matrix-exponential distributions, both of which share some fundamental research questions, such as the positive realization and minimality problems. See [Reference Commault and Mocanu7] for a detailed account of the duality of phase-type and matrix-exponential distributions in control theory.
$h_0$
is essentially a scaled matrix-exponential density function. This nicely links the theory of externally positive SISO linear systems with that of matrix-exponential distributions, both of which share some fundamental research questions, such as the positive realization and minimality problems. See [Reference Commault and Mocanu7] for a detailed account of the duality of phase-type and matrix-exponential distributions in control theory.
In this paper we give a physical interpretation to each element of the parameters
![]() $(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
associated to the matrix-exponential density function (3) satisfying the following conditions:
$(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
associated to the matrix-exponential density function (3) satisfying the following conditions:
-
A1. The elements of
 $\boldsymbol{\alpha}$
, T and
$\boldsymbol{\alpha}$
, T and
 $\boldsymbol{{s}}$
are real.
$\boldsymbol{{s}}$
are real. -
A2. The dominant eigenvalue of T, denoted by
 $\sigma_0$
, is real and strictly negative.
$\sigma_0$
, is real and strictly negative.
Since it can be shown that for a given matrix-exponential density of the form (3) the parameters
![]() $(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
can be chosen is such a way that A1 and A2 hold (see [Reference Asmussen and Bladt1]), the interpretation that we develop essentially completes the picture laid out in [Reference Cox8, Reference Cox9]. Our method, inspired by the recent work in [Reference Völlering18], provides a transparent interpretation of
$(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
can be chosen is such a way that A1 and A2 hold (see [Reference Asmussen and Bladt1]), the interpretation that we develop essentially completes the picture laid out in [Reference Cox8, Reference Cox9]. Our method, inspired by the recent work in [Reference Völlering18], provides a transparent interpretation of
![]() $(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
in terms of a finite-state Markov jump process. To do so, we employ the technique known as exponential tilting, which means that we focus on the density proportional to
$(\boldsymbol{\alpha}, T, \boldsymbol{{s}})$
in terms of a finite-state Markov jump process. To do so, we employ the technique known as exponential tilting, which means that we focus on the density proportional to
![]() $e^{-\lambda \cdot}f(\!\cdot\!)$
for large enough
$e^{-\lambda \cdot}f(\!\cdot\!)$
for large enough
![]() $\lambda>0$
. After we perform this transformation, we construct a Markov jump process on a finite state space formed by two groups: the original states and the anti-states, the latter being a copy of the former. Heuristically, jumps within the set of original states or within the set of anti-states occur according to the off-diagonal nonnegative ‘jump intensities’ of T, while jumps between the original and the anti-states occur according to the negative ‘jump intensities’ of T. Eventual absorption or termination happens, and each realization ‘carries’ a positive or negative sign depending only on its initial and final state. Our main contribution is to show that this mechanism yields the exponentially tilted matrix-exponential distribution, and, by reverting the exponential tilting, to provide some probabilistic insight into the original matrix-exponential distribution as well.
$\lambda>0$
. After we perform this transformation, we construct a Markov jump process on a finite state space formed by two groups: the original states and the anti-states, the latter being a copy of the former. Heuristically, jumps within the set of original states or within the set of anti-states occur according to the off-diagonal nonnegative ‘jump intensities’ of T, while jumps between the original and the anti-states occur according to the negative ‘jump intensities’ of T. Eventual absorption or termination happens, and each realization ‘carries’ a positive or negative sign depending only on its initial and final state. Our main contribution is to show that this mechanism yields the exponentially tilted matrix-exponential distribution, and, by reverting the exponential tilting, to provide some probabilistic insight into the original matrix-exponential distribution as well.
The structure of the paper is as follows. In Section 2 we provide a brief exposition on exponential tilting and how it affects the representation of a matrix-exponential distribution. In Section 3 we present our main results, Theorem 3.2 and Corollary 3.1, where we give a precise interpretation of an exponentially tilted matrix-exponential density in terms of a Markov jump process. Finally, in Section 4 we provide methods to recover formulae and probabilistic interpretations for matrix-exponential distributions for which the assumptions A1 and A2 hold, based on the results of their exponentially tilted versions.
2. Preliminaries
Exponential tilting, also known as the Escher transform, is a technique which transforms any probability density function f with support on
![]() $[0,\infty)$
into a new probability density function
$[0,\infty)$
into a new probability density function
![]() $f_\lambda$
defined by
$f_\lambda$
defined by
where
![]() $\lambda\ge 0$
is the tilting rate. The use of exponential tilting goes back at least to [Reference Escher11], where it was used to build upon Cramér’s classical actuarial models [Reference Cramér10]. Later on, the exponential tilting method played a prominent role in the theory of option pricing [Reference Gerber and Shiu13].
$\lambda\ge 0$
is the tilting rate. The use of exponential tilting goes back at least to [Reference Escher11], where it was used to build upon Cramér’s classical actuarial models [Reference Cramér10]. Later on, the exponential tilting method played a prominent role in the theory of option pricing [Reference Gerber and Shiu13].
The exponentially tilted version of a matrix-exponential distribution has a simple form which happens to be matrix-exponential itself. To see this, notice that if f is of the form (3), then
where we used the fact that
![]() $T-\lambda I$
has eigenvalues with strictly negative real parts and thus
$T-\lambda I$
has eigenvalues with strictly negative real parts and thus
![]() $e^{(T-\lambda I) r}$
vanishes as
$e^{(T-\lambda I) r}$
vanishes as
![]() $r\rightarrow\infty$
. Thus,
$r\rightarrow\infty$
. Thus,
implying that
![]() $f_\lambda$
corresponds to the density function of a matrix-exponential distribution of parameters
$f_\lambda$
corresponds to the density function of a matrix-exponential distribution of parameters
![]() $\left(\tfrac{\boldsymbol{\alpha}}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}, T-\lambda I, \boldsymbol{{s}}\right)$
.
$\left(\tfrac{\boldsymbol{\alpha}}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}, T-\lambda I, \boldsymbol{{s}}\right)$
.
Recall that the parameters
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
need not have a probabilistic meaning in terms of a finite-state-space Markov chain, as opposed to the parameters associated to phase-type distributions. For instance, the parameters
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
need not have a probabilistic meaning in terms of a finite-state-space Markov chain, as opposed to the parameters associated to phase-type distributions. For instance, the parameters
 \begin{equation}\boldsymbol{\alpha}=\left(1,0, 0\right), \quad T=\left[\begin{array}{r@{\quad}r@{\quad}r}-1 & -1 & 2/3 \\[5pt]1 & -1 & -2/3 \\[5pt]0 & 0 & -1\end{array}\right], \quad \boldsymbol{{s}}=\left[\begin{array}{r}4/3 \\[5pt]2/3 \\[5pt]1\end{array}\right]\end{equation}
\begin{equation}\boldsymbol{\alpha}=\left(1,0, 0\right), \quad T=\left[\begin{array}{r@{\quad}r@{\quad}r}-1 & -1 & 2/3 \\[5pt]1 & -1 & -2/3 \\[5pt]0 & 0 & -1\end{array}\right], \quad \boldsymbol{{s}}=\left[\begin{array}{r}4/3 \\[5pt]2/3 \\[5pt]1\end{array}\right]\end{equation}
yield a valid matrix-exponential distribution whose density function is given by
![]() $f(x)=\tfrac{2}{3}e^{-x}(1+\cos\!(x))$
, and where the dominant eigenvalue of T is
$f(x)=\tfrac{2}{3}e^{-x}(1+\cos\!(x))$
, and where the dominant eigenvalue of T is
![]() $-1$
(see [Reference Bladt and Nielsen6, Example 4.5.21] for details). In the following section we show how to assign a probabilistic meaning to the exponentially tilted version of (5), and more generally to those having the properties A1 and A2, in terms of a finite-state Markov jump process.
$-1$
(see [Reference Bladt and Nielsen6, Example 4.5.21] for details). In the following section we show how to assign a probabilistic meaning to the exponentially tilted version of (5), and more generally to those having the properties A1 and A2, in terms of a finite-state Markov jump process.
3. Main results
Let
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
be parameters associated to a p-dimensional matrix-exponential distribution which have the properties A1 and A2. For
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
be parameters associated to a p-dimensional matrix-exponential distribution which have the properties A1 and A2. For
![]() $1\le i,j\le p$
denote by
$1\le i,j\le p$
denote by
![]() $t_{ij}$
the (i, j) entry of T, and denote by
$t_{ij}$
the (i, j) entry of T, and denote by
![]() $s_i$
the ith entry of
$s_i$
the ith entry of
![]() $\boldsymbol{{s}}$
. For
$\boldsymbol{{s}}$
. For
![]() $\ell\in\{+,-\}$
, define the
$\ell\in\{+,-\}$
, define the
![]() $(p\times p)$
-dimensional matrix
$(p\times p)$
-dimensional matrix
![]() $T^{\ell}=\left\{t_{ij}^{\ell}\right\}_{1 \le i,j\le p}$
and the p-dimensional column vector
$T^{\ell}=\left\{t_{ij}^{\ell}\right\}_{1 \le i,j\le p}$
and the p-dimensional column vector
![]() $\boldsymbol{{s}}^{\ell}=\left(s^\ell_1,\dots, s^\ell_p\right)^\intercal$
where
$\boldsymbol{{s}}^{\ell}=\left(s^\ell_1,\dots, s^\ell_p\right)^\intercal$
where
 \begin{align*}t_{ij}^\pm&=\max\{0,\pm t_{ij}\}\quad \forall\,i\neq j,\\[5pt]t_{ii}^\pm&=\pm \min\{0, \pm t_{ii}\}\quad\forall\, i,\mbox{ and}\\[5pt]s_i^\pm&=\max\{0,\pm s_i\}\quad\forall\, i.\end{align*}
\begin{align*}t_{ij}^\pm&=\max\{0,\pm t_{ij}\}\quad \forall\,i\neq j,\\[5pt]t_{ii}^\pm&=\pm \min\{0, \pm t_{ii}\}\quad\forall\, i,\mbox{ and}\\[5pt]s_i^\pm&=\max\{0,\pm s_i\}\quad\forall\, i.\end{align*}
It follows that
![]() $T^+$
has nonnegative off-diagonal elements and nonpositive diagonal elements,
$T^+$
has nonnegative off-diagonal elements and nonpositive diagonal elements,
![]() $T^-$
is a nonnegative matrix,
$T^-$
is a nonnegative matrix,
![]() $\boldsymbol{{s}}^+$
and
$\boldsymbol{{s}}^+$
and
![]() $\boldsymbol{{s}}^-$
are nonnegative column vectors,
$\boldsymbol{{s}}^-$
are nonnegative column vectors,
![]() $T=T^+-T^-$
, and
$T=T^+-T^-$
, and
![]() $\boldsymbol{{s}}=\boldsymbol{{s}}^+-\boldsymbol{{s}}^-$
. Now, let
$\boldsymbol{{s}}=\boldsymbol{{s}}^+-\boldsymbol{{s}}^-$
. Now, let
 \begin{equation*}\lambda_0=\min\!\left\{r\ge 0\;:\; s^+_i+s^-_i+\sum_{j=1}^p (t^+_{ij} + t^-_{ij}) \le r \mbox{ for all }1\le i\le p\right\}.\end{equation*}
\begin{equation*}\lambda_0=\min\!\left\{r\ge 0\;:\; s^+_i+s^-_i+\sum_{j=1}^p (t^+_{ij} + t^-_{ij}) \le r \mbox{ for all }1\le i\le p\right\}.\end{equation*}
For some fixed
![]() $\lambda\ge\lambda_0$
, consider a (possibly) terminating Markov jump process
$\lambda\ge\lambda_0$
, consider a (possibly) terminating Markov jump process
![]() $\{\varphi_t^\lambda\}_{t\ge 0}$
driven by the block-partitioned subintensity matrix
$\{\varphi_t^\lambda\}_{t\ge 0}$
driven by the block-partitioned subintensity matrix
 \begin{align}G=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}T^+-\lambda I & T^-&\boldsymbol{{s}}^+&\boldsymbol{{s}}^-\\[5pt]T^-& T^+-\lambda I & \boldsymbol{{s}}^-&\boldsymbol{{s}}^+\\[5pt]\textbf{0}&\textbf{0} & 0& 0\\[5pt]\textbf{0}&\textbf{0} & 0& 0 \end{array}\right]\end{align}
\begin{align}G=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}T^+-\lambda I & T^-&\boldsymbol{{s}}^+&\boldsymbol{{s}}^-\\[5pt]T^-& T^+-\lambda I & \boldsymbol{{s}}^-&\boldsymbol{{s}}^+\\[5pt]\textbf{0}&\textbf{0} & 0& 0\\[5pt]\textbf{0}&\textbf{0} & 0& 0 \end{array}\right]\end{align}
evolving on the state space
![]() $\mathcal{E}=\mathcal{E}^o\cup \mathcal{E}^a\cup\{\Delta^o\}\cup\{\Delta^a\}$
where
$\mathcal{E}=\mathcal{E}^o\cup \mathcal{E}^a\cup\{\Delta^o\}\cup\{\Delta^a\}$
where
![]() $\mathcal{E}^o\;:\!=\;\{1^o,2^o,\dots,p^o\}$
and
$\mathcal{E}^o\;:\!=\;\{1^o,2^o,\dots,p^o\}$
and
![]() $\mathcal{E}^a=\{1^a,2^a,\dots,p^a\}$
. The state space
$\mathcal{E}^a=\{1^a,2^a,\dots,p^a\}$
. The state space
![]() $\mathcal{E}$
may be thought as the union of two sets: a collection of original states
$\mathcal{E}$
may be thought as the union of two sets: a collection of original states
![]() $\mathcal{E}^o\cup\{\Delta^o\}$
and a collection of anti-states
$\mathcal{E}^o\cup\{\Delta^o\}$
and a collection of anti-states
![]() $\mathcal{E}^a\cup\{\Delta^a\}$
, where both
$\mathcal{E}^a\cup\{\Delta^a\}$
, where both
![]() $\Delta^o$
and
$\Delta^o$
and
![]() $\Delta^a$
are absorbing. In the case
$\Delta^a$
are absorbing. In the case
![]() $\lambda>\lambda_0$
, the process
$\lambda>\lambda_0$
, the process
![]() $\{\varphi_t^\lambda\}_{t\ge 0}$
alternates between sojourn times in
$\{\varphi_t^\lambda\}_{t\ge 0}$
alternates between sojourn times in
![]() $\mathcal{E}^o$
and
$\mathcal{E}^o$
and
![]() $\mathcal{E}^a$
up until one of the following happens: (a) get absorbed into
$\mathcal{E}^a$
up until one of the following happens: (a) get absorbed into
![]() $\Delta^o$
, (b) get absorbed into
$\Delta^o$
, (b) get absorbed into
![]() $\Delta^a$
, or (c) undergo termination due to the defect of (6). If
$\Delta^a$
, or (c) undergo termination due to the defect of (6). If
![]() $\lambda=\lambda_0$
, the states
$\lambda=\lambda_0$
, the states
![]() $\mathcal{E}^o\cup\mathcal{E}^a$
may or may not be transient, their status depending on the values of T.
$\mathcal{E}^o\cup\mathcal{E}^a$
may or may not be transient, their status depending on the values of T.
In Theorem 3.1 we establish a link between the absorption probabilities of
![]() $\{\varphi_t^\lambda\}_{t\ge 0}$
and the vector
$\{\varphi_t^\lambda\}_{t\ge 0}$
and the vector
![]() $e^{(T-\lambda I) x}\boldsymbol{{s}}$
appearing in the exponentially tilted matrix-exponential density (4). More specifically, we express each element in
$e^{(T-\lambda I) x}\boldsymbol{{s}}$
appearing in the exponentially tilted matrix-exponential density (4). More specifically, we express each element in
![]() $e^{(T-\lambda I) x}\boldsymbol{{s}}$
as the sum of some positive density function and some negative density function, where the positive density is associated to an absorption of
$e^{(T-\lambda I) x}\boldsymbol{{s}}$
as the sum of some positive density function and some negative density function, where the positive density is associated to an absorption of
![]() $\{\varphi_t^\lambda\}_{t\ge 0}$
to
$\{\varphi_t^\lambda\}_{t\ge 0}$
to
![]() $\Delta^o$
, while the negative density function corresponds to an absorption of
$\Delta^o$
, while the negative density function corresponds to an absorption of
![]() $\{\varphi_t^\lambda\}_{t\ge 0}$
to
$\{\varphi_t^\lambda\}_{t\ge 0}$
to
![]() $\Delta^a$
. To shorten notation, from now on we denote by
$\Delta^a$
. To shorten notation, from now on we denote by
![]() $\mathbb{P}_j$
(
$\mathbb{P}_j$
(
![]() $\mathbb{E}_j$
),
$\mathbb{E}_j$
),
![]() $j\in\mathcal{E}$
, the probability measure (expectation) associated to
$j\in\mathcal{E}$
, the probability measure (expectation) associated to
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
conditional on the event
$\{\varphi^\lambda_t\}_{t\ge 0}$
conditional on the event
![]() $\{\varphi^\lambda_0=j\}$
.
$\{\varphi^\lambda_0=j\}$
.
Theorem 3.1. Let
![]() $\lambda\ge \lambda_0$
be such that the states
$\lambda\ge \lambda_0$
be such that the states
![]() $\mathcal{E}^o\cup\mathcal{E}^a$
are transient. Define
$\mathcal{E}^o\cup\mathcal{E}^a$
are transient. Define
Then, for
![]() $i\in \{1,\dots, p\}$
and
$i\in \{1,\dots, p\}$
and
![]() $x\ge 0$
,
$x\ge 0$
,
 \begin{align} = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\textrm{d} x, \end{align}
\begin{align} = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\textrm{d} x, \end{align}
where
![]() $\boldsymbol{{e}}_i$
denotes the column vector with 1 as its ith entry and 0 elsewhere, and
$\boldsymbol{{e}}_i$
denotes the column vector with 1 as its ith entry and 0 elsewhere, and
![]() $\beta(j)\;:\!=\;{\unicode[Times]{x1D7D9}}\{j=\Delta^o\}-{\unicode[Times]{x1D7D9}}\{j=\Delta^a\}$
. Moreover,
$\beta(j)\;:\!=\;{\unicode[Times]{x1D7D9}}\{j=\Delta^o\}-{\unicode[Times]{x1D7D9}}\{j=\Delta^a\}$
. Moreover,
 \begin{align} = (\textbf{0},\boldsymbol{{e}}_i^\intercal)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\textrm{d} x.\end{align}
\begin{align} = (\textbf{0},\boldsymbol{{e}}_i^\intercal)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\textrm{d} x.\end{align}
Proof. The block structure of (6) implies that
 \begin{align*}\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o) & = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}^+\\[5pt]\boldsymbol{{s}}^-\end{matrix}\right]\textrm{d} x,\\[5pt]\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^a) & = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}^-\\[5pt]\boldsymbol{{s}}^+\end{matrix}\right]\textrm{d} x;\end{align*}
\begin{align*}\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o) & = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}^+\\[5pt]\boldsymbol{{s}}^-\end{matrix}\right]\textrm{d} x,\\[5pt]\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^a) & = (\boldsymbol{{e}}_i^\intercal,\textbf{0})\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}^-\\[5pt]\boldsymbol{{s}}^+\end{matrix}\right]\textrm{d} x;\end{align*}
therefore, the right-hand side of (8) is equal to (9). Next, we prove that (8) holds.
Define the collection of
![]() $(p\times p)$
-dimensional matrices
$(p\times p)$
-dimensional matrices
![]() $\{\Phi_{oa}(x)\}_{x\ge 0}$
,
$\{\Phi_{oa}(x)\}_{x\ge 0}$
,
![]() $\{\Phi_{ao}(x)\}_{x\ge 0}$
,
$\{\Phi_{ao}(x)\}_{x\ge 0}$
,
![]() $\{\Phi_{oo}(x)\}_{x\ge 0}$
, and
$\{\Phi_{oo}(x)\}_{x\ge 0}$
, and
![]() $\{\Phi_{aa}(x)\}_{x\ge 0}$
by
$\{\Phi_{aa}(x)\}_{x\ge 0}$
by
 \begin{align*}(\Phi_{oa}(x))_{ij}& =\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^a) ,\qquad(\Phi_{ao}(x))_{ij} =\mathbb{P}_{i^a}(\tau>x, \varphi_x^\lambda=j^o) ,\\[5pt](\Phi_{oo}(x))_{ij}& =\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^o) ,\qquad(\Phi_{aa}(x))_{ij} =\mathbb{P}_{i^a}(\tau>x, \varphi_x^\lambda=j^a) ,\end{align*}
\begin{align*}(\Phi_{oa}(x))_{ij}& =\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^a) ,\qquad(\Phi_{ao}(x))_{ij} =\mathbb{P}_{i^a}(\tau>x, \varphi_x^\lambda=j^o) ,\\[5pt](\Phi_{oo}(x))_{ij}& =\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^o) ,\qquad(\Phi_{aa}(x))_{ij} =\mathbb{P}_{i^a}(\tau>x, \varphi_x^\lambda=j^a) ,\end{align*}
for all
![]() $i,j\in\{1,\dots,p\}$
. By the symmetry of the subintensity matrix G it is clear that for all
$i,j\in\{1,\dots,p\}$
. By the symmetry of the subintensity matrix G it is clear that for all
![]() $x\ge 0$
,
$x\ge 0$
,
![]() $\Phi_{oa}(x)=\Phi_{ao}(x)$
and
$\Phi_{oa}(x)=\Phi_{ao}(x)$
and
![]() $\Phi_{oo}(x)=\Phi_{aa}(x)$
, even if their probabilistic interpretations differ. For all
$\Phi_{oo}(x)=\Phi_{aa}(x)$
, even if their probabilistic interpretations differ. For all
![]() $x\ge 0$
, let
$x\ge 0$
, let
![]() $\Phi_{o}(x)\;:\!=\;\Phi_{oo}(x)-\Phi_{oa}(x)$
and
$\Phi_{o}(x)\;:\!=\;\Phi_{oo}(x)-\Phi_{oa}(x)$
and
![]() $\Phi_{a}(x)\;:\!=\;\Phi_{aa}(x)-\Phi_{ao}(x)$
. Define
$\Phi_{a}(x)\;:\!=\;\Phi_{aa}(x)-\Phi_{ao}(x)$
. Define
Then, for
![]() $i,j\in\{1,\dots,p\}$
,
$i,j\in\{1,\dots,p\}$
,
 \begin{align}\boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{e}}_j&=\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^o) - \mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^a)\nonumber\\[5pt]&=\left\{\mathbb{P}_{i^o}(\gamma>x,\tau>x, \varphi_x^\lambda=j^o) + \mathbb{P}_{i^o}(\gamma\le x,\tau>x, \varphi_x^\lambda=j^o) \right\}\nonumber\\[5pt] &\quad - \left\{\mathbb{P}_{i^o}(\gamma>x,\tau>x, \varphi_x^\lambda=j^a) + \mathbb{P}_{i^o}(\gamma\le x,\tau>x, \varphi_x^\lambda=j^a)\right\} \nonumber\\[5pt]& = \left\{\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o) + \int_{0}^x \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \tau>x, \varphi_x^\lambda=j^o)\right\}\nonumber\\[5pt] &\quad -\left\{\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^a) + \int_{0}^x \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \tau>x, \varphi_x^\lambda=j^a)\right\}\nonumber\\[5pt]& = \mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o)\nonumber\\[5pt]&\quad + \int_{0}^x \sum_{k=1}^p \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a) \mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^o)\nonumber \\[5pt]&\quad - \int_{0}^x \sum_{k=1}^p \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a) \mathbb{P}_{k^a }(\tau>x-r, \varphi_{x-r}^\lambda=j^a),\end{align}
\begin{align}\boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{e}}_j&=\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^o) - \mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=j^a)\nonumber\\[5pt]&=\left\{\mathbb{P}_{i^o}(\gamma>x,\tau>x, \varphi_x^\lambda=j^o) + \mathbb{P}_{i^o}(\gamma\le x,\tau>x, \varphi_x^\lambda=j^o) \right\}\nonumber\\[5pt] &\quad - \left\{\mathbb{P}_{i^o}(\gamma>x,\tau>x, \varphi_x^\lambda=j^a) + \mathbb{P}_{i^o}(\gamma\le x,\tau>x, \varphi_x^\lambda=j^a)\right\} \nonumber\\[5pt]& = \left\{\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o) + \int_{0}^x \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \tau>x, \varphi_x^\lambda=j^o)\right\}\nonumber\\[5pt] &\quad -\left\{\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^a) + \int_{0}^x \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \tau>x, \varphi_x^\lambda=j^a)\right\}\nonumber\\[5pt]& = \mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o)\nonumber\\[5pt]&\quad + \int_{0}^x \sum_{k=1}^p \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a) \mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^o)\nonumber \\[5pt]&\quad - \int_{0}^x \sum_{k=1}^p \mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a) \mathbb{P}_{k^a }(\tau>x-r, \varphi_{x-r}^\lambda=j^a),\end{align}
where in the last equality we used that
![]() $\{\gamma>x, \varphi_x^\lambda=j^a\}=\varnothing$
and the Markov property of
$\{\gamma>x, \varphi_x^\lambda=j^a\}=\varnothing$
and the Markov property of
![]() $\{\varphi_{x}^\lambda\}_{x\ge 0}$
. Note that all the elements in (12) correspond to transition probabilities or intensities that can be expressed in matricial form as follows:
$\{\varphi_{x}^\lambda\}_{x\ge 0}$
. Note that all the elements in (12) correspond to transition probabilities or intensities that can be expressed in matricial form as follows:
 \begin{align*}\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o)&=\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)x}\boldsymbol{{e}}_j,\\[5pt]\mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a)&= \boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\textrm{d} r,\\[5pt]\mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^o) & = \boldsymbol{{e}}_k^\intercal \Phi_{ao}(x-r)\boldsymbol{{e}}_j,\\[5pt]\mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^a) & = \boldsymbol{{e}}_k^\intercal \Phi_{aa}(x-r)\boldsymbol{{e}}_j.\end{align*}
\begin{align*}\mathbb{P}_{i^o}(\gamma>x, \varphi_x^\lambda=j^o)&=\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)x}\boldsymbol{{e}}_j,\\[5pt]\mathbb{P}_{i^o}(\gamma\in[r,r+\textrm{d} r], \varphi_\gamma^\lambda=k^a)&= \boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\textrm{d} r,\\[5pt]\mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^o) & = \boldsymbol{{e}}_k^\intercal \Phi_{ao}(x-r)\boldsymbol{{e}}_j,\\[5pt]\mathbb{P}_{k^a}(\tau>x-r, \varphi_{x-r}^\lambda=j^a) & = \boldsymbol{{e}}_k^\intercal \Phi_{aa}(x-r)\boldsymbol{{e}}_j.\end{align*}
Substituting these expressions into (12) and using the identity
![]() $I=\sum_{k=1}^p \boldsymbol{{e}}_k\boldsymbol{{e}}_k^\intercal$
gives
$I=\sum_{k=1}^p \boldsymbol{{e}}_k\boldsymbol{{e}}_k^\intercal$
gives
 \begin{align*}\boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{e}}_j & = \boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)x}\boldsymbol{{e}}_j + \int_{0}^x \sum_{k=1}^p \left(\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\right) \left(\boldsymbol{{e}}_k^\intercal \Phi_{ao}(x-r)\boldsymbol{{e}}_j\right) \textrm{d} r\\[5pt]& \quad- \int_{0}^x \sum_{k=1}^p \left(\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\right) \left(\boldsymbol{{e}}_k^\intercal \Phi_{aa}(x-r)\boldsymbol{{e}}_j\right)\textrm{d} r\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}T^-\left[\Phi_{ao}(x-r)-\Phi_{aa}(x-r)\right]\textrm{d} r\right)\boldsymbol{{e}}_j\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}T^-\left[\Phi_{oa}(x-r)-\Phi_{oo}(x-r)\right]\textrm{d} r\right)\boldsymbol{{e}}_j\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}(\!-T^-)\Phi_{o}(x-r)\textrm{d} r\right)\boldsymbol{{e}}_j,\end{align*}
\begin{align*}\boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{e}}_j & = \boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)x}\boldsymbol{{e}}_j + \int_{0}^x \sum_{k=1}^p \left(\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\right) \left(\boldsymbol{{e}}_k^\intercal \Phi_{ao}(x-r)\boldsymbol{{e}}_j\right) \textrm{d} r\\[5pt]& \quad- \int_{0}^x \sum_{k=1}^p \left(\boldsymbol{{e}}_i^\intercal e^{(T^+-\lambda I)r}T^-\boldsymbol{{e}}_k\right) \left(\boldsymbol{{e}}_k^\intercal \Phi_{aa}(x-r)\boldsymbol{{e}}_j\right)\textrm{d} r\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}T^-\left[\Phi_{ao}(x-r)-\Phi_{aa}(x-r)\right]\textrm{d} r\right)\boldsymbol{{e}}_j\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}T^-\left[\Phi_{oa}(x-r)-\Phi_{oo}(x-r)\right]\textrm{d} r\right)\boldsymbol{{e}}_j\\[5pt]& = \boldsymbol{{e}}_i^\intercal\!\left(e^{(T^+-\lambda I)x} + \int_{0}^xe^{(T^+-\lambda I)r}(\!-T^-)\Phi_{o}(x-r)\textrm{d} r\right)\boldsymbol{{e}}_j,\end{align*}
so that
![]() $\{\Phi_{o}(x)\}_{x\ge 0}$
is the bounded solution to the matrix-integral equation
$\{\Phi_{o}(x)\}_{x\ge 0}$
is the bounded solution to the matrix-integral equation
By [Reference Bean, Nguyen, Nielsen and Peralta3, Theorem 3.10],
The Markov property implies that
 \begin{align*}&\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad = \sum_{k=1}^p \mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=k^o)\mathbb{P}_{k^o}(\tau\in[x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad\quad+\sum_{k=1}^p\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=k^a)\mathbb{P}_{k^a}(\tau\in[x, x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad = \sum_{k=1}^p (\boldsymbol{{e}}_i^\intercal\Phi_{oo}(x)\boldsymbol{{e}}_k)(\boldsymbol{{e}}_k^\intercal \boldsymbol{{s}}^+)\textrm{d} x + \sum_{k=1}^p (\boldsymbol{{e}}_i^\intercal\Phi_{oa}(x)\boldsymbol{{e}}_k)(\boldsymbol{{e}}_k^\intercal \boldsymbol{{s}}^-\textrm{d} x)\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal (\Phi_{oo}(x)\boldsymbol{{s}}^+ + \Phi_{oa}(x)\boldsymbol{{s}}^-)\textrm{d} x.\end{align*}
\begin{align*}&\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad = \sum_{k=1}^p \mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=k^o)\mathbb{P}_{k^o}(\tau\in[x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad\quad+\sum_{k=1}^p\mathbb{P}_{i^o}(\tau>x, \varphi_x^\lambda=k^a)\mathbb{P}_{k^a}(\tau\in[x, x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o)\\[5pt]&\quad = \sum_{k=1}^p (\boldsymbol{{e}}_i^\intercal\Phi_{oo}(x)\boldsymbol{{e}}_k)(\boldsymbol{{e}}_k^\intercal \boldsymbol{{s}}^+)\textrm{d} x + \sum_{k=1}^p (\boldsymbol{{e}}_i^\intercal\Phi_{oa}(x)\boldsymbol{{e}}_k)(\boldsymbol{{e}}_k^\intercal \boldsymbol{{s}}^-\textrm{d} x)\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal (\Phi_{oo}(x)\boldsymbol{{s}}^+ + \Phi_{oa}(x)\boldsymbol{{s}}^-)\textrm{d} x.\end{align*}
Similarly,
Thus,
 \begin{align*}&\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o) - \mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^a)\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal ([\Phi_{oo}(x)\boldsymbol{{s}}^+ + \Phi_{oa}(x)\boldsymbol{{s}}^-]-[\Phi_{oa}(x)\boldsymbol{{s}}^+ + \Phi_{oo}(x)\boldsymbol{{s}}^-])\textrm{d} x\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal ([\Phi_{oo}(x)-\Phi_{oa}(x)]\boldsymbol{{s}}^+ - [\Phi_{oo}(x)-\Phi_{oa}(x)]\boldsymbol{{s}}^-)\textrm{d} x\\[5pt]& \quad = \boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{s}}\textrm{d} x = \boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\textrm{d} x,\end{align*}
\begin{align*}&\mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^o) - \mathbb{P}_{i^o}(\tau\in [x,x+\textrm{d} x], \varphi_\tau^\lambda=\Delta^a)\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal ([\Phi_{oo}(x)\boldsymbol{{s}}^+ + \Phi_{oa}(x)\boldsymbol{{s}}^-]-[\Phi_{oa}(x)\boldsymbol{{s}}^+ + \Phi_{oo}(x)\boldsymbol{{s}}^-])\textrm{d} x\\[5pt]&\quad = \boldsymbol{{e}}_i^\intercal ([\Phi_{oo}(x)-\Phi_{oa}(x)]\boldsymbol{{s}}^+ - [\Phi_{oo}(x)-\Phi_{oa}(x)]\boldsymbol{{s}}^-)\textrm{d} x\\[5pt]& \quad = \boldsymbol{{e}}_i^\intercal\Phi_{o}(x)\boldsymbol{{s}}\textrm{d} x = \boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\textrm{d} x,\end{align*}
so that (8) holds. Analogous arguments follow for (10) and (11), which completes the proof.
Heuristically, Equations (8) and (10) imply that initiating
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
in the anti-state
$\{\varphi^\lambda_t\}_{t\ge 0}$
in the anti-state
![]() $i^a$
has the opposite effect, in terms of sign, to initiating in the original state
$i^a$
has the opposite effect, in terms of sign, to initiating in the original state
![]() $i^o$
. In the following we exploit this fact to provide a probabilistic interpretation not only for the elements of
$i^o$
. In the following we exploit this fact to provide a probabilistic interpretation not only for the elements of
![]() $e^{(T-\lambda I)x}\boldsymbol{{s}}$
, but also for the exponentially tilted matrix-exponential density
$e^{(T-\lambda I)x}\boldsymbol{{s}}$
, but also for the exponentially tilted matrix-exponential density
![]() $\boldsymbol{\alpha} e^{(T-\lambda I)x}\boldsymbol{{s}}$
.
$\boldsymbol{\alpha} e^{(T-\lambda I)x}\boldsymbol{{s}}$
.
Define
![]() $w^+$
and
$w^+$
and
![]() $w^-$
by
$w^-$
by
and define
![]() $\boldsymbol{\alpha}^+=(\alpha_1^+,\dots,\alpha_p^+)$
and
$\boldsymbol{\alpha}^+=(\alpha_1^+,\dots,\alpha_p^+)$
and
![]() $\boldsymbol{\alpha}^-=(\alpha_1^-,\dots,\alpha_p^-)$
by
$\boldsymbol{\alpha}^-=(\alpha_1^-,\dots,\alpha_p^-)$
by
 \begin{align*}\alpha^{\pm}_{i}=\left\{\begin{array}{c@{\quad}c@{\quad}c}\frac{1}{w^\pm}\max\{0,\pm\alpha_i\}&\mbox{if}&w^\pm>0,\\[5pt]0&\mbox{if}& w^\pm=0.\end{array}\right.\end{align*}
\begin{align*}\alpha^{\pm}_{i}=\left\{\begin{array}{c@{\quad}c@{\quad}c}\frac{1}{w^\pm}\max\{0,\pm\alpha_i\}&\mbox{if}&w^\pm>0,\\[5pt]0&\mbox{if}& w^\pm=0.\end{array}\right.\end{align*}
If
![]() $w^\pm>0$
, then
$w^\pm>0$
, then
![]() $\boldsymbol{\alpha}^\pm$
is a probability vector, and in general,
$\boldsymbol{\alpha}^\pm$
is a probability vector, and in general,
In some sense,
![]() $(w^+ + w^-)^{-1}\boldsymbol{\alpha}$
can be thought as a mixture of the probability vectors
$(w^+ + w^-)^{-1}\boldsymbol{\alpha}$
can be thought as a mixture of the probability vectors
![]() $\boldsymbol{\alpha}^+$
and
$\boldsymbol{\alpha}^+$
and
![]() $\boldsymbol{\alpha}^-$
, with the latter contributing ‘negative mass’. Fortunately, this ‘negative mass’ in the context of
$\boldsymbol{\alpha}^-$
, with the latter contributing ‘negative mass’. Fortunately, this ‘negative mass’ in the context of
![]() $\boldsymbol{\alpha} e^{(T-\lambda I)x}\boldsymbol{{s}}$
can be given a precise probabilistic interpretation by means of anti-states as follows.
$\boldsymbol{\alpha} e^{(T-\lambda I)x}\boldsymbol{{s}}$
can be given a precise probabilistic interpretation by means of anti-states as follows.
Theorem 3.2. Let
![]() $f_\lambda(x)=(\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}})^{-1}\boldsymbol{\alpha}e^{(T-\lambda I)x}\boldsymbol{{s}}$
,
$f_\lambda(x)=(\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}})^{-1}\boldsymbol{\alpha}e^{(T-\lambda I)x}\boldsymbol{{s}}$
,
![]() $x\ge 0$
, be the density of the exponentially tilted matrix-exponential distribution of parameters
$x\ge 0$
, be the density of the exponentially tilted matrix-exponential distribution of parameters
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
. Define the vectors
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
. Define the vectors
and suppose
![]() $\varphi_0^\lambda\sim (\widehat{\boldsymbol{\alpha}}^+, \widehat{\boldsymbol{\alpha}}^-)$
. Then
$\varphi_0^\lambda\sim (\widehat{\boldsymbol{\alpha}}^+, \widehat{\boldsymbol{\alpha}}^-)$
. Then
 \begin{align} = \frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left((\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\right)\textrm{d} x,\end{align}
\begin{align} = \frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left((\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\right)\textrm{d} x,\end{align}
where
![]() $\tau$
and
$\tau$
and
![]() $\beta(\!\cdot\!)$
are defined as in Theorem 3.1.
$\beta(\!\cdot\!)$
are defined as in Theorem 3.1.
Proof. Equation (13) implies that
 \begin{align}f_\lambda(x)&= \frac{1}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\sum_{i=1}^p w^+\alpha^+_{i}\!\left(\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right) + \sum_{i=1}^p w^-\alpha^-_i\left(-\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right)\right)\nonumber\\[5pt]& = \frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\sum_{i=1}^p \tfrac{w^+}{w^++w^-}\alpha^+_i \left(\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right) + \sum_{i=1}^p \tfrac{w^-}{w^++w^-}\alpha^-_i\left(-\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right)\right).\end{align}
\begin{align}f_\lambda(x)&= \frac{1}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\sum_{i=1}^p w^+\alpha^+_{i}\!\left(\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right) + \sum_{i=1}^p w^-\alpha^-_i\left(-\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right)\right)\nonumber\\[5pt]& = \frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\sum_{i=1}^p \tfrac{w^+}{w^++w^-}\alpha^+_i \left(\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right) + \sum_{i=1}^p \tfrac{w^-}{w^++w^-}\alpha^-_i\left(-\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}\right)\right).\end{align}
Equality (14) follows from (16), (8), and (10). Equality (15) follows from (16), (9), and (11).
Example 3.1. Let
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
be the matrix-exponential parameters corresponding to (5). As noted previously, these parameters by themselves lack a probabilistic interpretation, so we apply Theorem 3.1 to construct one. For such parameters we take the tilting parameter
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
be the matrix-exponential parameters corresponding to (5). As noted previously, these parameters by themselves lack a probabilistic interpretation, so we apply Theorem 3.1 to construct one. For such parameters we take the tilting parameter
![]() $\lambda\;:\!=\;\lambda_0=2$
, leading to the block-partitioned matrices
$\lambda\;:\!=\;\lambda_0=2$
, leading to the block-partitioned matrices


and
![]() $w^+=1$
,
$w^+=1$
,
![]() $w^-=0$
. We can then verify that
$w^-=0$
. We can then verify that
 \begin{align*}&\frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left((\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\right)\\[5pt]&\qquad=\frac{1}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}} \left(\frac{2}{3}e^{-3x}(1+\cos\!(x))\right)=\frac{e^{-2x}}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\frac{2}{3} e^{-x}(1+\cos\!(x))\right),\end{align*}
\begin{align*}&\frac{(w^++w^-)}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left((\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+-\lambda I & T^-\\[5pt]T^-& T^+-\lambda I\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right]\right)\\[5pt]&\qquad=\frac{1}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}} \left(\frac{2}{3}e^{-3x}(1+\cos\!(x))\right)=\frac{e^{-2x}}{\boldsymbol{\alpha}(\lambda I-T)^{-1}\boldsymbol{{s}}}\left(\frac{2}{3} e^{-x}(1+\cos\!(x))\right),\end{align*}
the latter corresponding to the exponentially tilted matrix-exponential density function
![]() $f(x)=\tfrac{2}{3} e^{-x}(1+\cos\!(x))$
.
$f(x)=\tfrac{2}{3} e^{-x}(1+\cos\!(x))$
.
A probabilistic interpretation of
![]() $f_\lambda$
alternative to that of (14) is the following.
$f_\lambda$
alternative to that of (14) is the following.
Corollary 3.1. Define
![]() $\boldsymbol{{d}}= (d_1,\dots,d_p)^\intercal\;:\!=\;-(T^+-\lambda I)\textbf{1} - T^-\textbf{1}$
to be the termination intensities vector from
$\boldsymbol{{d}}= (d_1,\dots,d_p)^\intercal\;:\!=\;-(T^+-\lambda I)\textbf{1} - T^-\textbf{1}$
to be the termination intensities vector from
![]() $\mathcal{E}^o$
or
$\mathcal{E}^o$
or
![]() $\mathcal{E}^a$
, and define
$\mathcal{E}^a$
, and define
![]() $\boldsymbol{{q}}^\pm=(q_1^\pm,\dots,q_p^\pm)^\intercal$
by
$\boldsymbol{{q}}^\pm=(q_1^\pm,\dots,q_p^\pm)^\intercal$
by
 \begin{equation*}q^\pm_i=\left\{\begin{array}{c@{\quad}c@{\quad}c}\frac{s^\pm_i}{d_i}&{\textit{if}} &d_i>0,\\[5pt] 0& {\textit{if}}&d_i=0.\end{array}\right.\end{equation*}
\begin{equation*}q^\pm_i=\left\{\begin{array}{c@{\quad}c@{\quad}c}\frac{s^\pm_i}{d_i}&{\textit{if}} &d_i>0,\\[5pt] 0& {\textit{if}}&d_i=0.\end{array}\right.\end{equation*}
Let
![]() $\bar{q}\;:\;\mathcal{E}^o\cup\mathcal{E}^a\mapsto \mathbb{R}$
be defined by
$\bar{q}\;:\;\mathcal{E}^o\cup\mathcal{E}^a\mapsto \mathbb{R}$
be defined by
Then
where
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
and
$\{\varphi^\lambda_t\}_{t\ge 0}$
and
![]() $\tau$
are defined as in Theorem 3.2.
$\tau$
are defined as in Theorem 3.2.
Proof. First, notice that the jump mechanism of
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
described in (6) implies that for
$\{\varphi^\lambda_t\}_{t\ge 0}$
described in (6) implies that for
![]() $i\in\{1,\dots,p\}$
,
$i\in\{1,\dots,p\}$
,
 \begin{align*}\mathbb{P}(\varphi^\lambda_\tau=\Delta^o\mid \tau, \varphi^\lambda_{\tau^-}=i^o)&=q_i^+,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^a\mid \tau, \varphi^\lambda_{\tau^-}=i^o)&=q_i^-,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^o\mid \tau, \varphi^\lambda_{\tau^-}=i^a)&=q_i^-,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^a\mid \tau, \varphi^\lambda_{\tau^-}=i^a)&=q_i^+,\end{align*}
\begin{align*}\mathbb{P}(\varphi^\lambda_\tau=\Delta^o\mid \tau, \varphi^\lambda_{\tau^-}=i^o)&=q_i^+,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^a\mid \tau, \varphi^\lambda_{\tau^-}=i^o)&=q_i^-,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^o\mid \tau, \varphi^\lambda_{\tau^-}=i^a)&=q_i^-,\\[5pt]\mathbb{P}(\varphi^\lambda_\tau=\Delta^a\mid \tau, \varphi^\lambda_{\tau^-}=i^a)&=q_i^+,\end{align*}
which in turn implies that
Consequently,
 \begin{align*}\mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \beta(\varphi_\tau^\lambda)\right]&=\mathbb{E}\!\left[\mathbb{E}\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \beta(\varphi_\tau^\lambda)\mid \tau,\varphi^\lambda_{\tau^-}\right]\right]\\[5pt]& = \mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\}\mathbb{E}\!\left[\beta(\varphi_\tau^\lambda)\mid \tau,\varphi^\lambda_{\tau^-}\right]\right]\\[5pt]& =\mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \bar{q}\big(\varphi^\lambda_{\tau^-}\big)\right],\end{align*}
\begin{align*}\mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \beta(\varphi_\tau^\lambda)\right]&=\mathbb{E}\!\left[\mathbb{E}\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \beta(\varphi_\tau^\lambda)\mid \tau,\varphi^\lambda_{\tau^-}\right]\right]\\[5pt]& = \mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\}\mathbb{E}\!\left[\beta(\varphi_\tau^\lambda)\mid \tau,\varphi^\lambda_{\tau^-}\right]\right]\\[5pt]& =\mathbb{E}\!\left[{\unicode[Times]{x1D7D9}}\{\tau\in [x,x+\textrm{d} x]\} \bar{q}\big(\varphi^\lambda_{\tau^-}\big)\right],\end{align*}
and the result follows from (14).
Though closely related, the interpretation provided by Corollary 3.1 is more suitable than that of Theorem 3.2 for Monte Carlo applications. Indeed, a realization of
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
may get absorbed in
$\{\varphi^\lambda_t\}_{t\ge 0}$
may get absorbed in
![]() $\Delta^o$
,
$\Delta^o$
,
![]() $\Delta^a$
or terminated. If termination occurs, such a realization contributes nothing to the term in the right-hand side of (14). In contrast, by observing the process until its exit time from
$\Delta^a$
or terminated. If termination occurs, such a realization contributes nothing to the term in the right-hand side of (14). In contrast, by observing the process until its exit time from
![]() $\mathcal{E}^o\cup\mathcal{E}^a$
and disregarding its landing point as in Corollary 3.1, we make sure that each realization contributes towards the mass in the right-hand side of (17).
$\mathcal{E}^o\cup\mathcal{E}^a$
and disregarding its landing point as in Corollary 3.1, we make sure that each realization contributes towards the mass in the right-hand side of (17).
4. Recovering the untilted distribution
Once the exponentially tilted density
![]() $f_\lambda$
of a matrix-exponential distribution of parameters
$f_\lambda$
of a matrix-exponential distribution of parameters
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
has a tractable known form, say as in (15), in principle it is straightforward to recover the original untilted density f by taking
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
has a tractable known form, say as in (15), in principle it is straightforward to recover the original untilted density f by taking
 \begin{align}f(x)& =(\boldsymbol{\alpha}(\lambda I-T)\boldsymbol{{s}})e^{\lambda x} f_{\lambda}(x)\nonumber\\[5pt]& = (w^++w^-)(\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+ \;\;\;\;\;\;& T^-\\[5pt]T^- \;\;\;\;\;\;& T^+\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right],\qquad x\ge 0.\end{align}
\begin{align}f(x)& =(\boldsymbol{\alpha}(\lambda I-T)\boldsymbol{{s}})e^{\lambda x} f_{\lambda}(x)\nonumber\\[5pt]& = (w^++w^-)(\widehat{\boldsymbol{\alpha}}^+,\widehat{\boldsymbol{\alpha}}^-)\exp\!\left(\left[\begin{matrix}T^+ \;\;\;\;\;\;& T^-\\[5pt]T^- \;\;\;\;\;\;& T^+\end{matrix}\right] x\right)\left[\begin{matrix}\boldsymbol{{s}}\\[5pt]-\boldsymbol{{s}}\end{matrix}\right],\qquad x\ge 0.\end{align}
While (18) is a legitimate matrix-exponential representation of f, it has two drawbacks:
-
1. The matrix
 $\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]$
may no longer be a subintensity matrix.
$\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]$
may no longer be a subintensity matrix. -
2. The dominant eigenvalue of
 $\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]$
may be nonnegative.
$\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]$
may be nonnegative.
The first item may affect the probabilistic interpretation of f, while the second one may make integration of certain functions (with respect to the density f) more difficult to handle. For instance, in the context of Example 3.1, the matrix

is not a subintensity matrix since some row sums are strictly positive, and it has 0 as its dominant eigenvalue. Having 0 as an eigenvalue implies that some entries of
![]() $\exp\!\left(\left(\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right)x\right)$
may potentially be of order
$\exp\!\left(\left(\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right)x\right)$
may potentially be of order
![]() $e^{0\cdot x}=1$
, meaning that the matrix integral
$e^{0\cdot x}=1$
, meaning that the matrix integral
may only be well-defined for functions
![]() $h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
that decrease to 0 fast enough. In comparison,
$h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
that decrease to 0 fast enough. In comparison,
![]() $\exp\!(Tx)$
with T as in (5) has entries of order
$\exp\!(Tx)$
with T as in (5) has entries of order
![]() $e^{\sigma_0 x}=e^{-x}$
or less, so that
$e^{\sigma_0 x}=e^{-x}$
or less, so that
is well-defined and finite for every function
![]() $h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
of order
$h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
of order
![]() $e^{-\rho x}$
for any
$e^{-\rho x}$
for any
![]() $\rho>-1$
. This apparent disagreement between the applicability of (19) and (20) vanishes when we multiply
$\rho>-1$
. This apparent disagreement between the applicability of (19) and (20) vanishes when we multiply
![]() $\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)$
by
$\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)$
by
![]() $\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
. Indeed, in the context of Example 3.1 it can be verified that the elements of the vector
$\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
. Indeed, in the context of Example 3.1 it can be verified that the elements of the vector
![]() $\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
are at most of order
$\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
are at most of order
![]() $e^{-x}$
, with the higher-order terms of
$e^{-x}$
, with the higher-order terms of
![]() $\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)$
cancelling each other when we multiply the matrix function by
$\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)$
cancelling each other when we multiply the matrix function by
![]() $\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
.
$\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
.
In the general case, this cancellation of higher-order terms is implied by Theorem 3.1 via the following arguments. If
![]() $\sigma_0$
is the dominant eigenvalue of T and has multiplicity
$\sigma_0$
is the dominant eigenvalue of T and has multiplicity
![]() $m_0$
, then the order of
$m_0$
, then the order of
![]() $\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}$
is at most
$\boldsymbol{{e}}_i^\intercal e^{(T-\lambda I)x}\boldsymbol{{s}}$
is at most
![]() $x^{m_0}e^{(\sigma_0-\lambda) x}$
. By (9) and (11), the elements of
$x^{m_0}e^{(\sigma_0-\lambda) x}$
. By (9) and (11), the elements of
![]() $\exp\!\left(\left[\begin{smallmatrix}T^+ -\lambda I& T^-\\[5pt]T^-& T^+-\lambda I\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
are also of order less than or equal to
$\exp\!\left(\left[\begin{smallmatrix}T^+ -\lambda I& T^-\\[5pt]T^-& T^+-\lambda I\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
are also of order less than or equal to
![]() $x^{m_0}e^{(\sigma_0-\lambda) x}$
. Finally, if we multiply the previous by
$x^{m_0}e^{(\sigma_0-\lambda) x}$
. Finally, if we multiply the previous by
![]() $e^{\lambda x}$
, then we get that
$e^{\lambda x}$
, then we get that
![]() $\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
is of order at most
$\exp\!\left(\left[\begin{smallmatrix}T^+ & T^-\\[5pt]T^-& T^+\end{smallmatrix}\right]x\right)\left[\begin{smallmatrix}\boldsymbol{{s}}\\[5pt] -\boldsymbol{{s}}\end{smallmatrix}\right]$
is of order at most
![]() $x^{m_0}e^{\sigma_0 x}$
, which coincides with the order of
$x^{m_0}e^{\sigma_0 x}$
, which coincides with the order of
![]() $e^{Tx}$
.
$e^{Tx}$
.
In terms of expectations, (14) and (17) provide alternative ways to recover properties of any matrix-exponential density f of parameters
![]() $(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
in terms of the exponentially tilted density
$(\boldsymbol{\alpha},T,\boldsymbol{{s}})$
in terms of the exponentially tilted density
![]() $f_\lambda$
. Indeed, for any function
$f_\lambda$
. Indeed, for any function
![]() $h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
of order
$h\;:\;\mathbb{R}_+\mapsto\mathbb{R}_+$
of order
![]() $e^{-\rho x}$
or less,
$e^{-\rho x}$
or less,
![]() $\rho>\sigma_0$
, we have that
$\rho>\sigma_0$
, we have that
where
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
and
$\{\varphi^\lambda_t\}_{t\ge 0}$
and
![]() $\tau$
are as in Theorem 3.2. Existence and finiteness of the first moment of
$\tau$
are as in Theorem 3.2. Existence and finiteness of the first moment of
![]() $h(\tau)e^{\lambda \tau} \beta(\varphi^\lambda_\tau)$
in (22) is guaranteed by noting that the order
$h(\tau)e^{\lambda \tau} \beta(\varphi^\lambda_\tau)$
in (22) is guaranteed by noting that the order
![]() $e^{-\rho+\lambda}$
of
$e^{-\rho+\lambda}$
of
![]() $h(x)e^{\lambda x}$
is dominated by that of
$h(x)e^{\lambda x}$
is dominated by that of
![]() $f_\lambda$
. Notice that, as opposed to the formula in (18), the representations (22) and (23) still have probabilistic interpretations in terms of the Markov jump process
$f_\lambda$
. Notice that, as opposed to the formula in (18), the representations (22) and (23) still have probabilistic interpretations in terms of the Markov jump process
![]() $\{\varphi^\lambda_t\}_{t\ge 0}$
.
$\{\varphi^\lambda_t\}_{t\ge 0}$
.
Acknowledgements
I wish to thank the editor and anonymous reviewer for their constructive comments, which helped me to improve the manuscript.
Funding information
The author acknowledges funding from the Australian Research Council Discovery Project DP180103106 and the Swiss National Science Foundation Project 200021.191984.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.