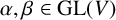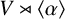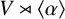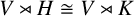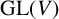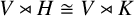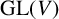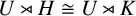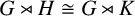1. Introduction
We fix throughout a prime number p and write F for the field with p elements and V for an F-vector space of finite dimension
![]() $n>0$
. Given an automorphism
$n>0$
. Given an automorphism
![]() $\alpha $
of V, we may consider the semidirect product
$\alpha $
of V, we may consider the semidirect product
![]() $G_\alpha =V\rtimes \langle \alpha \rangle $
, where
$G_\alpha =V\rtimes \langle \alpha \rangle $
, where
Likewise, given
![]() $\beta \in \mathrm {GL}(V)$
, we have the semidirect product
$\beta \in \mathrm {GL}(V)$
, we have the semidirect product
![]() $G_\beta =V\rtimes \langle \beta \rangle $
. It is well known that if
$G_\beta =V\rtimes \langle \beta \rangle $
. It is well known that if
![]() $\langle \alpha \rangle $
and
$\langle \alpha \rangle $
and
![]() $\langle \beta \rangle $
are conjugate subgroups of
$\langle \beta \rangle $
are conjugate subgroups of
![]() $\mathrm {GL}(V)$
, then
$\mathrm {GL}(V)$
, then
![]() $G_\alpha $
is isomorphic to
$G_\alpha $
is isomorphic to
![]() $G_\beta $
. In Theorem 4.1, we prove the converse: if
$G_\beta $
. In Theorem 4.1, we prove the converse: if
![]() $G_\alpha \cong G_\beta $
, then
$G_\alpha \cong G_\beta $
, then
![]() $\langle \alpha \rangle $
and
$\langle \alpha \rangle $
and
![]() $\langle \beta \rangle $
must be conjugate in
$\langle \beta \rangle $
must be conjugate in
![]() $\mathrm {GL}(V)$
. Here
$\mathrm {GL}(V)$
. Here
![]() $\langle \alpha \rangle $
and
$\langle \alpha \rangle $
and
![]() $\langle \beta \rangle $
are conjugate if and only if
$\langle \beta \rangle $
are conjugate if and only if
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\beta ^i$
for some integer i coprime to the order of
$\beta ^i$
for some integer i coprime to the order of
![]() $\beta $
, that is, such that
$\beta $
, that is, such that
![]() $\langle \beta ^i\rangle =\langle \beta \rangle $
. The proof of Theorem 4.1 is somewhat subtle. A more transparent argument is given in Theorem 5.2, provided
$\langle \beta ^i\rangle =\langle \beta \rangle $
. The proof of Theorem 4.1 is somewhat subtle. A more transparent argument is given in Theorem 5.2, provided
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are unipotent, in which case,
$\beta $
are unipotent, in which case,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
must themselves be similar. Theorem 4.1 seems to be exceptional in the realm of group theory, in the sense that any changes to the given linear algebra setting will tend to make it fail, as explained below.
$\beta $
must themselves be similar. Theorem 4.1 seems to be exceptional in the realm of group theory, in the sense that any changes to the given linear algebra setting will tend to make it fail, as explained below.
Given an arbitrary group G, its holomorph is
![]() $\mathrm {Hol}(G)=G\rtimes \mathrm {Aut}(G)$
, where
$\mathrm {Hol}(G)=G\rtimes \mathrm {Aut}(G)$
, where
For a subgroup H of
![]() $\mathrm {Aut}(G)$
, we have the relative holomorph
$\mathrm {Aut}(G)$
, we have the relative holomorph
![]() $\mathrm {Hol}(G,H)=G\rtimes H$
, viewed as a subgroup of
$\mathrm {Hol}(G,H)=G\rtimes H$
, viewed as a subgroup of
![]() $\mathrm {Hol}(G)$
. If K is also a subgroup of
$\mathrm {Hol}(G)$
. If K is also a subgroup of
![]() $\mathrm {Aut}(G)$
, it is well known that if H and K are conjugate in
$\mathrm {Aut}(G)$
, it is well known that if H and K are conjugate in
![]() $\mathrm {Aut}(G)$
, then
$\mathrm {Aut}(G)$
, then
![]() $\mathrm {Hol}(G,H)$
and
$\mathrm {Hol}(G,H)$
and
![]() $\mathrm {Hol}(G,K)$
are conjugate in
$\mathrm {Hol}(G,K)$
are conjugate in
![]() $\mathrm {Hol}(G)$
, and hence isomorphic. The converse is false in general. In Example 6.4, we exhibit nonisomorphic noncyclic subgroups H and K of
$\mathrm {Hol}(G)$
, and hence isomorphic. The converse is false in general. In Example 6.4, we exhibit nonisomorphic noncyclic subgroups H and K of
![]() $\mathrm {GL}(V)$
such that
$\mathrm {GL}(V)$
such that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
, provided p is odd and
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
, provided p is odd and
![]() $n\geq 2$
. The case
$n\geq 2$
. The case
![]() $p=2$
and
$p=2$
and
![]() $n\geq 4$
is dealt with in Example 6.5. Moreover, Example 6.3 gives nonconjugate, noncyclic, abelian subgroups H and K of
$n\geq 4$
is dealt with in Example 6.5. Moreover, Example 6.3 gives nonconjugate, noncyclic, abelian subgroups H and K of
![]() $\mathrm {GL}(V)$
such that
$\mathrm {GL}(V)$
such that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
for any
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
for any
![]() $n\geq 6$
. However, in Corollary 3.4, we show that if H and K are abelian subgroups of
$n\geq 6$
. However, in Corollary 3.4, we show that if H and K are abelian subgroups of
![]() $\mathrm {GL}(V)$
such that
$\mathrm {GL}(V)$
such that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
and the sum of all subspaces
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
and the sum of all subspaces
![]() $(h-1)V$
, with
$(h-1)V$
, with
![]() $h\in H$
, is equal to V, then H is necessarily conjugate to K. Furthermore, according to Proposition 5.3,
$h\in H$
, is equal to V, then H is necessarily conjugate to K. Furthermore, according to Proposition 5.3,
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
always forces
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
always forces
![]() $H\cong K$
when H and K are abelian. Example 6.2 shows that Theorem 4.1 fails, in general, if V is replaced by a free module U over
$H\cong K$
when H and K are abelian. Example 6.2 shows that Theorem 4.1 fails, in general, if V is replaced by a free module U over
![]() ${\mathbb {Z}}/p^m{\mathbb {Z}}$
of finite rank n. Indeed, when
${\mathbb {Z}}/p^m{\mathbb {Z}}$
of finite rank n. Indeed, when
![]() $p=2, m=3, n=4$
, we exhibit an explicit automorphism
$p=2, m=3, n=4$
, we exhibit an explicit automorphism
![]() $\alpha $
of U such that
$\alpha $
of U such that
![]() $\mathrm {Hol}(U,\alpha )\cong \mathrm {Hol}(U,\beta )$
for exactly two conjugacy classes of cyclic subgroups
$\mathrm {Hol}(U,\alpha )\cong \mathrm {Hol}(U,\beta )$
for exactly two conjugacy classes of cyclic subgroups
![]() $\langle \beta \rangle $
of
$\langle \beta \rangle $
of
![]() $\mathrm {GL}(U)$
. When used in conjunction with Lemma 3.3, Examples 6.2 and 6.3 reveal instances when
$\mathrm {GL}(U)$
. When used in conjunction with Lemma 3.3, Examples 6.2 and 6.3 reveal instances when
![]() $\mathrm {Hol}(G,H)\cong \mathrm {Hol}(G,K)$
but no isomorphism between them sends G back into itself.
$\mathrm {Hol}(G,H)\cong \mathrm {Hol}(G,K)$
but no isomorphism between them sends G back into itself.
If we completely abandon our requirements on V, Example 6.6 gives a sufficient criterion for a group G to admit cyclic subgroups H and K such that
![]() $\mathrm {Hol}(G,H)\cong \mathrm {Hol}(G,K)$
, but H and K are not conjugate in
$\mathrm {Hol}(G,H)\cong \mathrm {Hol}(G,K)$
, but H and K are not conjugate in
![]() $\mathrm {Aut}(G)$
. This is illustrated with various instances of such G, H and K. Finally, Example 6.7 lists a few groups G such that the existence of an isomorphism between
$\mathrm {Aut}(G)$
. This is illustrated with various instances of such G, H and K. Finally, Example 6.7 lists a few groups G such that the existence of an isomorphism between
![]() $\mathrm {Hol}(G,H)$
and
$\mathrm {Hol}(G,H)$
and
![]() $\mathrm {Hol}(G,K)$
, for arbitrary subgroups H and K of
$\mathrm {Hol}(G,K)$
, for arbitrary subgroups H and K of
![]() $\mathrm {Aut}(G)$
, forces H to be similar to K.
$\mathrm {Aut}(G)$
, forces H to be similar to K.
The holomorph of a group appeared early in the literature to produce examples of complete groups, that is, groups having trivial centre and only inner automorphisms. In 1908, Miller [Reference Miller10] showed that the holomorph of any finite abelian group of odd order is complete, based on prior work of Burnside [Reference Burnside2]. Miller’s result was extended to show that the holomorph, or a relative holomorph, of other classes of abelian groups, not necessarily finite, is also complete (see [Reference Bekker1, Reference Clay4, Reference Hsu6, Reference Peremans13]). A long-standing problem in this regard was the existence of complete groups of odd order, settled positively by Dark [Reference Dark5] in 1975.
We are concerned here with a specific case of the general problem of finding necessary and sufficient conditions for two semidirect products
![]() $A\rtimes _f B$
and
$A\rtimes _f B$
and
![]() $C\rtimes _g D$
to be isomorphic, where
$C\rtimes _g D$
to be isomorphic, where
![]() $f:B\to \mathrm {Aut}(A)$
and
$f:B\to \mathrm {Aut}(A)$
and
![]() $g:D\to \mathrm {Aut}(C)$
are homomorphisms. No general answer is known. When
$g:D\to \mathrm {Aut}(C)$
are homomorphisms. No general answer is known. When
![]() $A=C$
and
$A=C$
and
![]() $B=D$
, this problem was investigated by Taunt [Reference Taunt14] and Kuzennyi [Reference Kuzennyi9]. If
$B=D$
, this problem was investigated by Taunt [Reference Taunt14] and Kuzennyi [Reference Kuzennyi9]. If
![]() $B=\mathrm {Aut}(A)$
,
$B=\mathrm {Aut}(A)$
,
![]() $D=\mathrm {Aut}(C)$
, and f and g are the identity maps, Mills showed in [Reference Mills11, Reference Mills12] respectively that
$D=\mathrm {Aut}(C)$
, and f and g are the identity maps, Mills showed in [Reference Mills11, Reference Mills12] respectively that
![]() $\mathrm {Hol}(A)\cong \mathrm {Hol}(C)$
forces
$\mathrm {Hol}(A)\cong \mathrm {Hol}(C)$
forces
![]() $A\cong C$
when both A and C are finitely generated abelian groups and when A or C are finite abelian groups. Mills [Reference Mills11] also pointed out that when
$A\cong C$
when both A and C are finitely generated abelian groups and when A or C are finite abelian groups. Mills [Reference Mills11] also pointed out that when
![]() $n\geq 3$
, the nonisomorphic dihedral and generalised quaternion groups of order
$n\geq 3$
, the nonisomorphic dihedral and generalised quaternion groups of order
![]() $4n$
have isomorphic holomorphs. A proof can be found in Kohl’s paper [Reference Kohl7, Proposition 3.10]. In Miller’s work [Reference Miller10], the holomorph of a group G is viewed as the normaliser in the symmetric group
$4n$
have isomorphic holomorphs. A proof can be found in Kohl’s paper [Reference Kohl7, Proposition 3.10]. In Miller’s work [Reference Miller10], the holomorph of a group G is viewed as the normaliser in the symmetric group
![]() $S(G)$
of the left (or right) regular representation of G. Miller referred to the normaliser in
$S(G)$
of the left (or right) regular representation of G. Miller referred to the normaliser in
![]() $S(G)$
of
$S(G)$
of
![]() $\mathrm {Hol}(G)$
as the multiple holomorph, say
$\mathrm {Hol}(G)$
as the multiple holomorph, say
![]() $M(G)$
, of G. The quotient group
$M(G)$
, of G. The quotient group
![]() $T(G)=M(G)/\mathrm {Hol}(G)$
has interesting properties and has received considerable attention recently. The structure of
$T(G)=M(G)/\mathrm {Hol}(G)$
has interesting properties and has received considerable attention recently. The structure of
![]() $T(G)$
was determined by Kohl [Reference Kohl8] for dihedral and generalised quaternion groups, and by Caranti and Dalla Volta [Reference Caranti and Dalla Volta3] for finite perfect groups with trivial centre.
$T(G)$
was determined by Kohl [Reference Kohl8] for dihedral and generalised quaternion groups, and by Caranti and Dalla Volta [Reference Caranti and Dalla Volta3] for finite perfect groups with trivial centre.
The conjugacy of subgroups H and K of
![]() $\mathrm {Aut}(G)$
is an obvious sufficient condition for
$\mathrm {Aut}(G)$
is an obvious sufficient condition for
![]() $\mathrm {Hol}(G,H)$
to be isomorphic to
$\mathrm {Hol}(G,H)$
to be isomorphic to
![]() $\mathrm {Hol}(G,K)$
, and in the present paper, we show that it is also necessary, provided H and K are cyclic and
$\mathrm {Hol}(G,K)$
, and in the present paper, we show that it is also necessary, provided H and K are cyclic and
![]() $G=V$
. Our examples show that one cannot deviate much from the stated hypotheses for the necessity of conjugacy to hold. One may use our results in the classification, up to isomorphism, of the relative holomorphs of an elementary abelian group such as V. This is a difficult problem, as attested by one of its simplest cases [Reference Vera López and Ortiz de Elguea15], namely when
$G=V$
. Our examples show that one cannot deviate much from the stated hypotheses for the necessity of conjugacy to hold. One may use our results in the classification, up to isomorphism, of the relative holomorphs of an elementary abelian group such as V. This is a difficult problem, as attested by one of its simplest cases [Reference Vera López and Ortiz de Elguea15], namely when
![]() $p=2$
and
$p=2$
and
![]() $n=4$
, in which case, there are 138 relative holomorphs.
$n=4$
, in which case, there are 138 relative holomorphs.
2. Background from linear algebra
Given
![]() $\alpha \in \mathrm {End}(V)$
, we write
$\alpha \in \mathrm {End}(V)$
, we write
![]() $m_\alpha \in F[X]$
for the minimal polynomial of
$m_\alpha \in F[X]$
for the minimal polynomial of
![]() $\alpha $
. Given a group G and
$\alpha $
. Given a group G and
![]() $g\in G$
, we let
$g\in G$
, we let
![]() $o(g)$
stand for the order of g.
$o(g)$
stand for the order of g.
Lemma 2.1. Let
![]() $\alpha \in \mathrm {GL}(V)$
. Then
$\alpha \in \mathrm {GL}(V)$
. Then
![]() $p\nmid o(\alpha )$
if and only if
$p\nmid o(\alpha )$
if and only if
![]() $m_\alpha $
is square-free.
$m_\alpha $
is square-free.
Proof. Let
![]() $m=o(\alpha )$
. Then m is the smallest natural number such that
$m=o(\alpha )$
. Then m is the smallest natural number such that
![]() $m_\alpha \mid (X^m-1).$
Now
$m_\alpha \mid (X^m-1).$
Now
![]() $X^m-1$
and its formal derivative, namely
$X^m-1$
and its formal derivative, namely
![]() $mX^{m-1}$
, are relatively prime if and only if
$mX^{m-1}$
, are relatively prime if and only if
![]() $p\nmid m$
.
$p\nmid m$
.
Lemma 2.2. Let
![]() $\alpha \in \mathrm {GL}(V)$
. Then
$\alpha \in \mathrm {GL}(V)$
. Then
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\alpha ^p$
if and only if
$\alpha ^p$
if and only if
![]() $p\nmid o(\alpha )$
.
$p\nmid o(\alpha )$
.
Proof. If
![]() $p\mid o(\alpha )$
, then
$p\mid o(\alpha )$
, then
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^p$
have different orders, whence they are not similar.
$\alpha ^p$
have different orders, whence they are not similar.
Suppose
![]() $p\nmid o(\alpha )$
. Then by Lemma 2.1, the invariant factors of
$p\nmid o(\alpha )$
. Then by Lemma 2.1, the invariant factors of
![]() $\alpha $
are all square-free. Thus, the rational canonical form of
$\alpha $
are all square-free. Thus, the rational canonical form of
![]() $\alpha $
is the direct sum of companion matrices
$\alpha $
is the direct sum of companion matrices
![]() $C_f$
to square-free monic polynomials
$C_f$
to square-free monic polynomials
![]() $f\in F[X]$
. Let
$f\in F[X]$
. Let
![]() $f\in F[X]$
be an invariant factor of
$f\in F[X]$
be an invariant factor of
![]() $\alpha $
of degree d. Since every irreducible polynomial over F has distinct roots in any splitting field and f is square-free, it follows that f has distinct roots in a splitting field, say K. In particular,
$\alpha $
of degree d. Since every irreducible polynomial over F has distinct roots in any splitting field and f is square-free, it follows that f has distinct roots in a splitting field, say K. In particular,
![]() $C_f$
is similar in
$C_f$
is similar in
![]() $\mathrm {GL}_d(K)$
to a diagonal matrix
$\mathrm {GL}_d(K)$
to a diagonal matrix
![]() $\mathrm {diag}(\lambda _1,\ldots ,\lambda _d)$
. Thus,
$\mathrm {diag}(\lambda _1,\ldots ,\lambda _d)$
. Thus,
![]() $C_f^p$
is similar in
$C_f^p$
is similar in
![]() $\mathrm {GL}_d(K)$
to
$\mathrm {GL}_d(K)$
to
![]() $\mathrm {diag}(\lambda _1^p,\ldots ,\lambda _d^p)$
. Now the map
$\mathrm {diag}(\lambda _1^p,\ldots ,\lambda _d^p)$
. Now the map
![]() $\Omega :K\to K$
given by
$\Omega :K\to K$
given by
![]() $\Omega (k)=k^p$
, for
$\Omega (k)=k^p$
, for
![]() $k\in K,$
is an automorphism of K with fixed field F. We also write
$k\in K,$
is an automorphism of K with fixed field F. We also write
![]() $\Omega $
for the associated automorphism
$\Omega $
for the associated automorphism
![]() $K[X]\to K[X]$
. Since
$K[X]\to K[X]$
. Since
![]() $f\in F[X]$
,
$f\in F[X]$
,
![]() $f=\Omega (f)= (X-\lambda _1^p)\cdots (X-\lambda _d^p)$
is the minimal polynomial of
$f=\Omega (f)= (X-\lambda _1^p)\cdots (X-\lambda _d^p)$
is the minimal polynomial of
![]() $C_f^p$
. Thus,
$C_f^p$
. Thus,
![]() $C_f^p$
is similar to
$C_f^p$
is similar to
![]() $C_f$
in
$C_f$
in
![]() $\mathrm {GL}_d(F)$
, whence
$\mathrm {GL}_d(F)$
, whence
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^p$
have the same rational canonical form.
$\alpha ^p$
have the same rational canonical form.
Given a field K, and K-vector spaces
![]() $V_1$
and
$V_1$
and
![]() $V_2$
with automorphisms
$V_2$
with automorphisms
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
, respectively, we say that
$\alpha _2$
, respectively, we say that
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
are similar if there is an isomorphism
$\alpha _2$
are similar if there is an isomorphism
![]() $f:V_1\to V_2$
such that
$f:V_1\to V_2$
such that
![]() $f\alpha _1 f^{-1}=\alpha _2$
.
$f\alpha _1 f^{-1}=\alpha _2$
.
Lemma 2.3. Let R be a principal ideal domain, M a nonzero finitely generated torsion R-module and
![]() $q\in R$
an irreducible element. Then the isomorphism type of M is completely determined by the composition length of M and the isomorphism type of
$q\in R$
an irreducible element. Then the isomorphism type of M is completely determined by the composition length of M and the isomorphism type of
![]() $N=qM$
. In particular, if K is a field, W is a nonzero finite dimensional K-vector space,
$N=qM$
. In particular, if K is a field, W is a nonzero finite dimensional K-vector space,
![]() $q\in K[X]$
is irreducible, and
$q\in K[X]$
is irreducible, and
![]() $u,v\in \mathrm {End}(W)$
are such that
$u,v\in \mathrm {End}(W)$
are such that
![]() $u|_{q(u)W}$
and
$u|_{q(u)W}$
and
![]() $v|_{q(v)W}$
are similar, then u and v are similar.
$v|_{q(v)W}$
are similar, then u and v are similar.
Proof. For any
![]() $r\in R$
, set
$r\in R$
, set
Let
![]() $(q_1^{a_1}\cdots q_s^{a_s})$
be the annihilating ideal of M, where
$(q_1^{a_1}\cdots q_s^{a_s})$
be the annihilating ideal of M, where
![]() $q_1,\ldots ,q_s$
are nonassociate irreducible elements of R and each
$q_1,\ldots ,q_s$
are nonassociate irreducible elements of R and each
![]() $a_i\geq 1$
. If q is nonassociate to every
$a_i\geq 1$
. If q is nonassociate to every
![]() $q_i$
, then
$q_i$
, then
![]() $M=N$
and there is nothing to do. We assume henceforth that q is associate to some
$M=N$
and there is nothing to do. We assume henceforth that q is associate to some
![]() $q_i$
, say
$q_i$
, say
![]() $q_1$
. Then
$q_1$
. Then
![]() $M_{q_j}=N_{q_j}$
for every
$M_{q_j}=N_{q_j}$
for every
![]() $j>1$
. Moreover,
$j>1$
. Moreover,
![]() $M=M_{q_1}\oplus \cdots \oplus M_{q_s}.$
$M=M_{q_1}\oplus \cdots \oplus M_{q_s}.$
It remains to show that the isomorphism type of
![]() $M_q=M_{q_1}$
is determined by that of
$M_q=M_{q_1}$
is determined by that of
![]() $N_q$
and the composition length of M. There exists a unique sequence of nonnegative integers
$N_q$
and the composition length of M. There exists a unique sequence of nonnegative integers
![]() $(e_1,e_2,\ldots )$
, which is eventually 0, and such that
$(e_1,e_2,\ldots )$
, which is eventually 0, and such that
![]() $M_q=U_1\oplus U_2\oplus \cdots ,$
where each
$M_q=U_1\oplus U_2\oplus \cdots ,$
where each
![]() $U_i$
is the direct sum of
$U_i$
is the direct sum of
![]() $e_i$
cyclic submodules with annihilating ideal
$e_i$
cyclic submodules with annihilating ideal
![]() $(q^i)$
. The corresponding sequence for
$(q^i)$
. The corresponding sequence for
![]() $N_q$
is clearly
$N_q$
is clearly
![]() $(e_2,e_3,\ldots )$
. Thus,
$(e_2,e_3,\ldots )$
. Thus,
![]() $e_2,e_3,\ldots $
are determined by the isomorphism type of N. Moreover, the composition length of M is equal to the sum of the composition lengths of the
$e_2,e_3,\ldots $
are determined by the isomorphism type of N. Moreover, the composition length of M is equal to the sum of the composition lengths of the
![]() $M_{q_j}$
,
$M_{q_j}$
,
![]() $j>1$
, plus
$j>1$
, plus
![]() $e_1+2e_2+3e_3+\cdots $
, so
$e_1+2e_2+3e_3+\cdots $
, so
![]() $e_1$
is determined by the composition length of M and the isomorphism type of N. This proves the first statement.
$e_1$
is determined by the composition length of M and the isomorphism type of N. This proves the first statement.
As for the second, take
![]() $R=K[X]$
, and view
$R=K[X]$
, and view
![]() $M=W$
and
$M=W$
and
![]() $N=q(u)W$
as R-modules via u. The similarity types of u and
$N=q(u)W$
as R-modules via u. The similarity types of u and
![]() $u|_N$
are completely determined by the isomorphism types of M and N, respectively, as R-modules. Moreover, in the above notation,
$u|_N$
are completely determined by the isomorphism types of M and N, respectively, as R-modules. Moreover, in the above notation,
![]() $e_2,e_3,\ldots $
are determined by the isomorphism type of N, and
$e_2,e_3,\ldots $
are determined by the isomorphism type of N, and
so
![]() $e_1$
is determined by the fixed quantities
$e_1$
is determined by the fixed quantities
![]() $\dim _K M$
and
$\dim _K M$
and
![]() $\mathrm {deg\,} q$
, together with the isomorphism type of N as R-module. This proves the second statement.
$\mathrm {deg\,} q$
, together with the isomorphism type of N as R-module. This proves the second statement.
3. Background from group theory
Given a group G with subgroups H and K, we say that H and K are conjugate in G if there is
![]() $g\in G$
such that
$g\in G$
such that
![]() $gHg^{-1}=K$
, in which case, we write
$gHg^{-1}=K$
, in which case, we write
![]() $H\sim K$
.
$H\sim K$
.
Lemma 3.1. Let G be a group and suppose that
![]() $H_1,H_2$
are conjugate subgroups of
$H_1,H_2$
are conjugate subgroups of
![]() $\mathrm {Aut}(G)$
. Then
$\mathrm {Aut}(G)$
. Then
![]() $\mathrm {Hol}(G,H_1)$
and
$\mathrm {Hol}(G,H_1)$
and
![]() $\mathrm {Hol}(G,H_2)$
are conjugate subgroups of
$\mathrm {Hol}(G,H_2)$
are conjugate subgroups of
![]() $\mathrm {Hol}(G)$
, and are therefore isomorphic.
$\mathrm {Hol}(G)$
, and are therefore isomorphic.
Proof. By assumption, there is
![]() $\gamma \in \mathrm {Aut}(G)$
such that
$\gamma \in \mathrm {Aut}(G)$
such that
![]() $\gamma H_1\gamma ^{-1}=H_2$
. Then
$\gamma H_1\gamma ^{-1}=H_2$
. Then
![]() $\gamma \in \mathrm {Hol}(G)$
and we have
$\gamma \in \mathrm {Hol}(G)$
and we have
![]() $\gamma G\gamma ^{-1}=\gamma (G)=G$
inside
$\gamma G\gamma ^{-1}=\gamma (G)=G$
inside
![]() $\mathrm {Hol}(G)$
. Therefore,
$\mathrm {Hol}(G)$
. Therefore,
Lemma 3.2. Let G be a finite group having a normal subgroup N with
![]() $\gcd (|G/N|,|N|)=1$
. Then any subgroup K of G such that
$\gcd (|G/N|,|N|)=1$
. Then any subgroup K of G such that
![]() $|K|$
is a factor of
$|K|$
is a factor of
![]() $|N|$
must be included in N. In particular, if
$|N|$
must be included in N. In particular, if
![]() $x\in G$
is such that
$x\in G$
is such that
![]() $o(x)$
is a factor of
$o(x)$
is a factor of
![]() $|N|$
, then
$|N|$
, then
![]() $x\in N$
.
$x\in N$
.
Proof. As
![]() $KN/N\cong K/(K\cap N)$
, we have
$KN/N\cong K/(K\cap N)$
, we have
![]() $|KN/N|\mid |K|$
. However,
$|KN/N|\mid |K|$
. However,
![]() $KN/N$
is a subgroup of
$KN/N$
is a subgroup of
![]() $G/N$
, so
$G/N$
, so
![]() $|KN/N|\mid |G/N|$
. Since
$|KN/N|\mid |G/N|$
. Since
![]() $\gcd (|G/N|,|N|)=1$
, we infer that
$\gcd (|G/N|,|N|)=1$
, we infer that
![]() $KN/N$
is trivial, so
$KN/N$
is trivial, so
![]() $K\subseteq N$
.
$K\subseteq N$
.
Lemma 3.3. Let A be an abelian group, and let H and K be subgroups of
![]() $\mathrm {Aut}(A)$
. Suppose that
$\mathrm {Aut}(A)$
. Suppose that
![]() $f:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
is an isomorphism such that
$f:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
is an isomorphism such that
![]() $f(A)=A$
. Then
$f(A)=A$
. Then
![]() $H\sim K$
. In particular, if A is finite and abelian, and
$H\sim K$
. In particular, if A is finite and abelian, and
![]() $\gcd (|A|,|H|)=1$
, then
$\gcd (|A|,|H|)=1$
, then
![]() $\mathrm {Hol}(A,H)\cong \mathrm {Hol}(A,K)$
forces
$\mathrm {Hol}(A,H)\cong \mathrm {Hol}(A,K)$
forces
![]() $H\sim K$
.
$H\sim K$
.
Proof. By hypothesis, f restricts to an automorphism u of A and induces an isomorphism
![]() $g:\mathrm {Hol}(A,H)/A\to \mathrm {Hol}(A,K)/A$
. Moreover, there are isomorphisms
$g:\mathrm {Hol}(A,H)/A\to \mathrm {Hol}(A,K)/A$
. Moreover, there are isomorphisms
![]() $i:H\to \mathrm {Hol}(A,H)/A$
and
$i:H\to \mathrm {Hol}(A,H)/A$
and
![]() $j:K\to \mathrm {Hol}(A,K)/A$
. Let
$j:K\to \mathrm {Hol}(A,K)/A$
. Let
![]() $v:H\to K$
be the isomorphism given by
$v:H\to K$
be the isomorphism given by
![]() $v=j^{-1}gi$
.
$v=j^{-1}gi$
.
Given any
![]() $h\in H$
, we have
$h\in H$
, we have
![]() $f(h)=b k$
for unique
$f(h)=b k$
for unique
![]() $b\in A$
and
$b\in A$
and
![]() $k\in K$
and, by definition,
$k\in K$
and, by definition,
![]() $v(h)=k$
. Since A is abelian, conjugation by
$v(h)=k$
. Since A is abelian, conjugation by
![]() $k=v(h)$
and
$k=v(h)$
and
![]() $bk=f(h)$
agree on A. Thus, for any
$bk=f(h)$
agree on A. Thus, for any
![]() $a\in A$
,
$a\in A$
,
Therefore,
![]() $u h u^{-1}=v(h)$
for all
$u h u^{-1}=v(h)$
for all
![]() $h\in H$
. As v is an isomorphism, we infer
$h\in H$
. As v is an isomorphism, we infer
![]() $u H u^{-1}=K$
, which proves the first part. As for the second, suppose that A is finite and abelian,
$u H u^{-1}=K$
, which proves the first part. As for the second, suppose that A is finite and abelian,
![]() $\gcd (|A|,|H|)=1$
, and that
$\gcd (|A|,|H|)=1$
, and that
![]() $s:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
is an isomorphism. Then
$s:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
is an isomorphism. Then
![]() $s(A)$
is a normal subgroup of
$s(A)$
is a normal subgroup of
![]() $\mathrm {Hol}(A,K)$
of order
$\mathrm {Hol}(A,K)$
of order
![]() $|A|$
, where
$|A|$
, where
![]() $|A|$
is relatively prime to
$|A|$
is relatively prime to
![]() $|H|=|K|=|\mathrm {Hol}(A,K)/A|$
. It follows from Lemma 3.2 that
$|H|=|K|=|\mathrm {Hol}(A,K)/A|$
. It follows from Lemma 3.2 that
![]() $s(A)=A$
, whence
$s(A)=A$
, whence
![]() $H\sim K$
by the first part.
$H\sim K$
by the first part.
The condition that A be abelian is not necessary for the second part of Lemma 3.3, although we will not require this more powerful result. The condition that
![]() $f(A)=A$
cannot be removed with impunity from the first part of Lemma 3.3, as Examples 6.2 and 6.3 show.
$f(A)=A$
cannot be removed with impunity from the first part of Lemma 3.3, as Examples 6.2 and 6.3 show.
Corollary 3.4. Let A be a finite (additive) abelian group and let H and K be abelian subgroups of
![]() $\mathrm {Aut}(A)$
. Suppose that
$\mathrm {Aut}(A)$
. Suppose that
![]() $\mathrm {Hol}(A,H)\cong \mathrm {Hol}(A,K)$
and that the sum of all subgroups
$\mathrm {Hol}(A,H)\cong \mathrm {Hol}(A,K)$
and that the sum of all subgroups
![]() $(h-1)(A)$
, as h runs through H, is equal to A. Then
$(h-1)(A)$
, as h runs through H, is equal to A. Then
![]() $H\sim K$
.
$H\sim K$
.
Proof. Let
![]() $f:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
be an isomorphism. The stated hypotheses imply that the derived subgroup of
$f:\mathrm {Hol}(A,H)\to \mathrm {Hol}(A,K)$
be an isomorphism. The stated hypotheses imply that the derived subgroup of
![]() $\mathrm {Hol}(A,H)$
(respectively
$\mathrm {Hol}(A,H)$
(respectively
![]() $\mathrm {Hol}(A,K)$
) is A (respectively a subgroup of A). Thus, f maps A inside of A. However A is finite, so
$\mathrm {Hol}(A,K)$
) is A (respectively a subgroup of A). Thus, f maps A inside of A. However A is finite, so
![]() $f(A)=A$
and Lemma 3.3 applies.
$f(A)=A$
and Lemma 3.3 applies.
Examples 6.2 and 6.3 show that Corollary 3.4 fails if the condition on H is removed.
4. Isomorphism of relative holomorphs forces conjugacy of the complements
We are ready to prove our main result.
Theorem 4.1. If
![]() $\alpha ,\beta \in \mathrm {GL}(V)$
, then
$\alpha ,\beta \in \mathrm {GL}(V)$
, then
![]() $\mathrm {Hol}(V,\alpha )\cong \mathrm {Hol}(V,\beta )$
if and only if
$\mathrm {Hol}(V,\alpha )\cong \mathrm {Hol}(V,\beta )$
if and only if
![]() $\langle \alpha \rangle \sim \langle \beta \rangle $
.
$\langle \alpha \rangle \sim \langle \beta \rangle $
.
Proof. For
![]() $\pi \in \mathrm {GL}(V)$
, set
$\pi \in \mathrm {GL}(V)$
, set
![]() $G_\pi =\mathrm {Hol}(V,\pi )$
and let
$G_\pi =\mathrm {Hol}(V,\pi )$
and let
![]() $V_\pi =[G_\pi ,G_\pi ]$
be the derived subgroup of
$V_\pi =[G_\pi ,G_\pi ]$
be the derived subgroup of
![]() $G_\pi $
. We readily see that
$G_\pi $
. We readily see that
![]() $V_\pi =(\pi -1)(V)$
.
$V_\pi =(\pi -1)(V)$
.
If
![]() $\langle \alpha \rangle \kern1.3pt{\sim}\kern1.3pt \langle \beta \rangle $
, then
$\langle \alpha \rangle \kern1.3pt{\sim}\kern1.3pt \langle \beta \rangle $
, then
![]() $G_\alpha \kern1.3pt{\cong}\kern1.3pt G_\beta $
by Lemma 3.1. Suppose next
$G_\alpha \kern1.3pt{\cong}\kern1.3pt G_\beta $
by Lemma 3.1. Suppose next
![]() $G_\alpha \kern1.3pt{\cong}\kern1.3pt G_\beta $
. If
$G_\alpha \kern1.3pt{\cong}\kern1.3pt G_\beta $
. If
![]() ${\gcd (p,o(\alpha ))\kern1.3pt{=}\kern1.3pt1}$
, then
${\gcd (p,o(\alpha ))\kern1.3pt{=}\kern1.3pt1}$
, then
![]() $\langle \alpha \rangle \sim \langle \beta \rangle $
by Lemma 3.3. We suppose henceforth that
$\langle \alpha \rangle \sim \langle \beta \rangle $
by Lemma 3.3. We suppose henceforth that
![]() $p\mid o(\alpha )$
.
$p\mid o(\alpha )$
.
There is a group isomorphism, say
![]() $f:G_\alpha \to G_\beta $
, sending
$f:G_\alpha \to G_\beta $
, sending
![]() $V_\alpha $
onto
$V_\alpha $
onto
![]() $V_\beta $
. We have
$V_\beta $
. We have
![]() $f(\alpha )=w\gamma $
for unique
$f(\alpha )=w\gamma $
for unique
![]() $w\in V$
and
$w\in V$
and
![]() $\gamma \in \langle \beta \rangle $
. It is clear that the subspaces
$\gamma \in \langle \beta \rangle $
. It is clear that the subspaces
![]() $V_\alpha $
and
$V_\alpha $
and
![]() $V_\beta $
are invariant under
$V_\beta $
are invariant under
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
, respectively. A calculation analogous to (3.1) shows that
$\gamma $
, respectively. A calculation analogous to (3.1) shows that
![]() $\alpha |_{V_\alpha }$
is similar to
$\alpha |_{V_\alpha }$
is similar to
![]() $\gamma |_{V_\beta }$
. Indeed, let
$\gamma |_{V_\beta }$
. Indeed, let
![]() $u:V_\alpha \to V_\beta $
be the isomorphism of F-vector spaces induced by f. Then for any
$u:V_\alpha \to V_\beta $
be the isomorphism of F-vector spaces induced by f. Then for any
![]() $v\in V_\alpha $
,
$v\in V_\alpha $
,
so that
![]() $u\alpha |_{V_\alpha } u^{-1}=\gamma |_{V_\beta }$
, as claimed.
$u\alpha |_{V_\alpha } u^{-1}=\gamma |_{V_\beta }$
, as claimed.
Since
![]() $f(V_\alpha )=V_\beta $
, we see that f also induces an isomorphism
$f(V_\alpha )=V_\beta $
, we see that f also induces an isomorphism
![]() $g:G_\alpha /V_\alpha \to G_\beta /V_\beta $
. As
$g:G_\alpha /V_\alpha \to G_\beta /V_\beta $
. As
![]() $V\cap \langle \alpha \rangle $
is trivial, we have
$V\cap \langle \alpha \rangle $
is trivial, we have
![]() $ o(\beta )=o(\alpha )=o(V_\alpha \alpha )=o(g(V_\alpha \alpha ))=o(V_\beta w \gamma ). $
Let m denote this common number. Since
$ o(\beta )=o(\alpha )=o(V_\alpha \alpha )=o(g(V_\alpha \alpha ))=o(V_\beta w \gamma ). $
Let m denote this common number. Since
![]() $\gamma \in \langle \beta \rangle $
, we see that
$\gamma \in \langle \beta \rangle $
, we see that
![]() $o(\gamma )\mid m$
. Set
$o(\gamma )\mid m$
. Set
Then,
Suppose first that
![]() $p\mid o(\gamma )$
. Then (4.1) implies
$p\mid o(\gamma )$
. Then (4.1) implies
![]() $(V_\beta w \gamma )^{o(\gamma )}=V_{\beta }$
. Thus,
$(V_\beta w \gamma )^{o(\gamma )}=V_{\beta }$
. Thus,
![]() $m\mid o(\gamma )$
and therefore
$m\mid o(\gamma )$
and therefore
![]() $m=o(\gamma )$
, whence
$m=o(\gamma )$
, whence
![]() $\langle \gamma \rangle =\langle \beta \rangle $
. It follows that
$\langle \gamma \rangle =\langle \beta \rangle $
. It follows that
![]() $G_\beta =G_\gamma $
and
$G_\beta =G_\gamma $
and
![]() $V_\beta =V_\gamma $
. Thus,
$V_\beta =V_\gamma $
. Thus,
![]() $\alpha |_{V_\alpha }$
is similar to
$\alpha |_{V_\alpha }$
is similar to
![]() $\gamma |_{V_\gamma }$
, which implies that
$\gamma |_{V_\gamma }$
, which implies that
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\gamma $
by Lemma 2.3.
$\gamma $
by Lemma 2.3.
Suppose next that
![]() $p\nmid o(\gamma )$
. Then
$p\nmid o(\gamma )$
. Then
![]() $p\nmid o(\gamma |_{V_\beta })$
. As
$p\nmid o(\gamma |_{V_\beta })$
. As
![]() $\alpha |_{V_\alpha }$
is similar to
$\alpha |_{V_\alpha }$
is similar to
![]() $\gamma |_{V_\beta }$
, we deduce that
$\gamma |_{V_\beta }$
, we deduce that
![]() $p\nmid o(\alpha |_{V_\alpha })$
.
$p\nmid o(\alpha |_{V_\alpha })$
.
The map
![]() $f^{-1}:G_\beta \to G_\alpha $
is also an isomorphism, and
$f^{-1}:G_\beta \to G_\alpha $
is also an isomorphism, and
![]() $f^{-1}(\beta )=z\delta $
for unique
$f^{-1}(\beta )=z\delta $
for unique
![]() $z\in V$
and
$z\in V$
and
![]() $\delta \in \langle \alpha \rangle $
. If
$\delta \in \langle \alpha \rangle $
. If
![]() $p\mid o(\delta )$
, we may deduce, as above, that
$p\mid o(\delta )$
, we may deduce, as above, that
![]() $\beta $
is similar to
$\beta $
is similar to
![]() $\delta $
, where
$\delta $
, where
![]() $\langle \delta \rangle =\langle \alpha \rangle $
. Suppose next that
$\langle \delta \rangle =\langle \alpha \rangle $
. Suppose next that
![]() $p\nmid o(\delta )$
, which implies, as above, that
$p\nmid o(\delta )$
, which implies, as above, that
![]() $p\nmid o(\beta |_{V_\beta })$
.
$p\nmid o(\beta |_{V_\beta })$
.
Now (4.1) implies
![]() $m\mid o(\gamma )p$
. Since
$m\mid o(\gamma )p$
. Since
![]() $p\mid o(\alpha )$
, then p and
$p\mid o(\alpha )$
, then p and
![]() $o(\gamma )$
are relatively prime factors of m, so
$o(\gamma )$
are relatively prime factors of m, so
![]() $o(\gamma )p \mid m$
and therefore
$o(\gamma )p \mid m$
and therefore
![]() $m=o(\gamma )p$
. Thus,
$m=o(\gamma )p$
. Thus,
![]() $\gamma =\beta ^{pj}$
, where
$\gamma =\beta ^{pj}$
, where
![]() $j\in {\mathbb {Z}}$
and
$j\in {\mathbb {Z}}$
and
![]() $\gcd (pj,m)=p$
. We may thus write
$\gcd (pj,m)=p$
. We may thus write
![]() $pj=p^s k$
, where
$pj=p^s k$
, where
![]() $s\geq 1$
and
$s\geq 1$
and
![]() $k\in {\mathbb {Z}}$
is relatively prime to m. Therefore,
$k\in {\mathbb {Z}}$
is relatively prime to m. Therefore,
![]() $\langle \beta \rangle =\langle \beta ^k\rangle $
,
$\langle \beta \rangle =\langle \beta ^k\rangle $
,
![]() $V_\beta =V_{\beta ^k}$
and
$V_\beta =V_{\beta ^k}$
and
![]() $o(\beta |_{V_\beta })=o(\beta ^k|_{V_\beta })$
. Since
$o(\beta |_{V_\beta })=o(\beta ^k|_{V_\beta })$
. Since
![]() $\gamma =(\beta ^k)^{p^s}$
and
$\gamma =(\beta ^k)^{p^s}$
and
![]() $p\nmid o(\beta ^k|_{V_\beta })$
, Lemma 2.2 implies that
$p\nmid o(\beta ^k|_{V_\beta })$
, Lemma 2.2 implies that
![]() $\beta ^k|_{V_\beta }$
is similar to
$\beta ^k|_{V_\beta }$
is similar to
![]() $\gamma |_{V_\beta }$
. However,
$\gamma |_{V_\beta }$
. However,
![]() $\gamma |_{V_\beta }$
is similar to
$\gamma |_{V_\beta }$
is similar to
![]() $\alpha |_{V_\alpha }$
, so
$\alpha |_{V_\alpha }$
, so
![]() $\beta ^k|_{V_{\beta ^k}}$
is similar to
$\beta ^k|_{V_{\beta ^k}}$
is similar to
![]() $\alpha |_{V_\alpha }$
. By Lemma 2.3,
$\alpha |_{V_\alpha }$
. By Lemma 2.3,
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\beta ^k$
.
$\beta ^k$
.
5. The unipotent case
For a group G, its lower central series
![]() $G^1,G^2,\ldots $
is inductively defined by
$G^1,G^2,\ldots $
is inductively defined by
![]() $G^1=G$
and
$G^1=G$
and
![]() $G^{i+1}=[G,G^{i}]$
,
$G^{i+1}=[G,G^{i}]$
,
![]() $i\geq 1$
. If
$i\geq 1$
. If
![]() $G^{i+1}=1$
for some
$G^{i+1}=1$
for some
![]() $i\geq 1$
, we say that G is nilpotent, and the smallest such i is called the nilpotency class of G. It is well known that every finite p-group is nilpotent.
$i\geq 1$
, we say that G is nilpotent, and the smallest such i is called the nilpotency class of G. It is well known that every finite p-group is nilpotent.
Given an additive abelian group A and an endomorphism
![]() $\alpha $
of A, we say that
$\alpha $
of A, we say that
![]() $\alpha $
is unipotent if
$\alpha $
is unipotent if
![]() $\alpha =1+\beta $
, with
$\alpha =1+\beta $
, with
![]() $\beta \in \mathrm {End}(A)$
nilpotent.
$\beta \in \mathrm {End}(A)$
nilpotent.
Lemma 5.1. Let A be a nontrivial finite abelian p-group. Let
![]() $\alpha \in \mathrm {Aut}(A)$
and set
$\alpha \in \mathrm {Aut}(A)$
and set
![]() $G_\alpha =\mathrm {Hol}(A,\alpha )$
. Then
$G_\alpha =\mathrm {Hol}(A,\alpha )$
. Then
![]() $G_\alpha $
is nilpotent
$G_\alpha $
is nilpotent
![]() $\Leftrightarrow \alpha $
is unipotent
$\Leftrightarrow \alpha $
is unipotent
![]() $\Leftrightarrow $
the order of
$\Leftrightarrow $
the order of
![]() $\alpha $
is a power of p.
$\alpha $
is a power of p.
Proof. It is readily seen that the proper terms of the lower central series of
![]() $G_\alpha $
are
$G_\alpha $
are
![]() $(\alpha -1)^i A$
,
$(\alpha -1)^i A$
,
![]() $i\geq 1$
, so
$i\geq 1$
, so
![]() $G_\alpha $
is nilpotent
$G_\alpha $
is nilpotent
![]() $\Leftrightarrow \alpha $
is unipotent. If the order of
$\Leftrightarrow \alpha $
is unipotent. If the order of
![]() $\alpha $
is a power of p, then
$\alpha $
is a power of p, then
![]() $G_\alpha $
is a p-group, and hence nilpotent. Suppose
$G_\alpha $
is a p-group, and hence nilpotent. Suppose
![]() $\alpha $
is unipotent, so
$\alpha $
is unipotent, so
![]() $\alpha =1+\beta $
, with
$\alpha =1+\beta $
, with
![]() $\beta \in \mathrm {End}(A)$
nilpotent, and therefore
$\beta \in \mathrm {End}(A)$
nilpotent, and therefore
![]() $\beta ^{p^m}=0$
for some
$\beta ^{p^m}=0$
for some
![]() $m\geq 0$
. We show by induction on m that this implies that the order of
$m\geq 0$
. We show by induction on m that this implies that the order of
![]() $1+\beta $
is a power of p. The case
$1+\beta $
is a power of p. The case
![]() $m=0$
is trivial. Suppose
$m=0$
is trivial. Suppose
![]() $m>0$
and the result is true for
$m>0$
and the result is true for
![]() $m-1$
. We have
$m-1$
. We have
![]() $p^\ell A=0$
for some
$p^\ell A=0$
for some
![]() $\ell \geq 1$
. Since
$\ell \geq 1$
. Since
![]() $p^\ell \mid \binom {p^\ell }{i}$
for
$p^\ell \mid \binom {p^\ell }{i}$
for
![]() $0<i<p$
, we have
$0<i<p$
, we have
![]() $(1+\beta )^{p^\ell }=1+\beta ^p\gamma $
for some
$(1+\beta )^{p^\ell }=1+\beta ^p\gamma $
for some
![]() $\gamma \in {\mathbb {Z}}[\beta ]$
. As
$\gamma \in {\mathbb {Z}}[\beta ]$
. As
![]() ${(\beta ^p\gamma )^{p^{m-1}}=0}$
, the order of
${(\beta ^p\gamma )^{p^{m-1}}=0}$
, the order of
![]() $(1+\beta )^{p^\ell }$
is a power of p, and hence so is that of
$(1+\beta )^{p^\ell }$
is a power of p, and hence so is that of
![]() $1+\beta $
.
$1+\beta $
.
Theorem 5.2. Suppose
![]() $\alpha ,\beta \in \mathrm {GL}(V)$
are unipotent and
$\alpha ,\beta \in \mathrm {GL}(V)$
are unipotent and
![]() $\mathrm {Hol}(V,\alpha )\cong \mathrm {Hol}(V,\beta )$
. Then
$\mathrm {Hol}(V,\alpha )\cong \mathrm {Hol}(V,\beta )$
. Then
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\beta $
.
$\beta $
.
Proof. Set
![]() $G_\alpha =\mathrm {Hol}(V,\alpha )$
and
$G_\alpha =\mathrm {Hol}(V,\alpha )$
and
![]() $G_\beta =\mathrm {Hol}(V,\beta )$
. Then
$G_\beta =\mathrm {Hol}(V,\beta )$
. Then
![]() $G_\alpha $
and
$G_\alpha $
and
![]() $G_\beta $
are nilpotent by Lemma 5.1, and we let m be the common nilpotency class of
$G_\beta $
are nilpotent by Lemma 5.1, and we let m be the common nilpotency class of
![]() $G_\alpha $
and
$G_\alpha $
and
![]() $G_\beta $
.
$G_\beta $
.
As indicated earlier, the proper terms of the lower central series of
![]() $G_\alpha $
(respectively
$G_\alpha $
(respectively
![]() $G_\beta $
) are
$G_\beta $
) are
![]() $(\alpha -1)^i V$
(respectively
$(\alpha -1)^i V$
(respectively
![]() $(\beta -1)^i V$
),
$(\beta -1)^i V$
),
![]() $i\geq 1$
.
$i\geq 1$
.
There is basis of V relative to which the matrix of
![]() $\alpha $
(respectively
$\alpha $
(respectively
![]() $\beta $
) is the direct sum of
$\beta $
) is the direct sum of
![]() $e_1,\ldots ,e_m$
(respectively
$e_1,\ldots ,e_m$
(respectively
![]() $f_1,\ldots ,f_m$
) Jordan blocks with eigenvalue 1 of sizes
$f_1,\ldots ,f_m$
) Jordan blocks with eigenvalue 1 of sizes
![]() $1,\ldots , m$
, respectively. Thus,
$1,\ldots , m$
, respectively. Thus,
This yields a basis of
![]() $(\alpha -1)V$
(respectively
$(\alpha -1)V$
(respectively
![]() $(\beta -1)V$
) relative to which the matrix of
$(\beta -1)V$
) relative to which the matrix of
![]() $\alpha $
(respectively
$\alpha $
(respectively
![]() $\beta $
) is the direct sum of
$\beta $
) is the direct sum of
![]() $e_2,\ldots ,e_m$
(respectively
$e_2,\ldots ,e_m$
(respectively
![]() $f_2,\ldots ,f_m$
) Jordan blocks with eigenvalue 1 of sizes
$f_2,\ldots ,f_m$
) Jordan blocks with eigenvalue 1 of sizes
![]() $1,\ldots , m-1$
. Since
$1,\ldots , m-1$
. Since
![]() $[G_\alpha ,G_\alpha ]=(\alpha -1)V$
(respectively
$[G_\alpha ,G_\alpha ]=(\alpha -1)V$
(respectively
![]() $[G_\beta ,G_\beta ]=(\beta -1)V$
), it follows that
$[G_\beta ,G_\beta ]=(\beta -1)V$
), it follows that
Continuing in this way, we see that the column vector with entries
![]() ${e_1-f_1,\ldots , e_m-f_m}$
is annihilated by the upper triangular matrix with equal entries along each superdiagonal, these entries being
${e_1-f_1,\ldots , e_m-f_m}$
is annihilated by the upper triangular matrix with equal entries along each superdiagonal, these entries being
![]() $1,2,\ldots ,m$
, in each successive superdiagonal. As this matrix is invertible, we see that
$1,2,\ldots ,m$
, in each successive superdiagonal. As this matrix is invertible, we see that
![]() $e_1=f_1,\ldots , e_m=f_m$
, whence
$e_1=f_1,\ldots , e_m=f_m$
, whence
![]() $\alpha $
is similar to
$\alpha $
is similar to
![]() $\beta $
.
$\beta $
.
Proposition 5.3. Suppose H and K are abelian subgroups of
![]() $\mathrm {GL}(V)$
such that
$\mathrm {GL}(V)$
such that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
. Then
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,K)$
. Then
![]() $H\cong K$
.
$H\cong K$
.
Proof. Set
![]() $V_H=[\mathrm {Hol}(V,H),\mathrm {Hol}(V,H)]$
and
$V_H=[\mathrm {Hol}(V,H),\mathrm {Hol}(V,H)]$
and
![]() $V_K=[\mathrm {Hol}(V,K),\mathrm {Hol}(V,K)]$
, which are subgroups of V. Let
$V_K=[\mathrm {Hol}(V,K),\mathrm {Hol}(V,K)]$
, which are subgroups of V. Let
![]() $f:\mathrm { Hol}(V,H)\to \mathrm {Hol}(V,K)$
be an isomorphism. Then f restricts to an isomorphism between
$f:\mathrm { Hol}(V,H)\to \mathrm {Hol}(V,K)$
be an isomorphism. Then f restricts to an isomorphism between
![]() $V_H$
and
$V_H$
and
![]() $V_K$
. This yields an isomorphism between
$V_K$
. This yields an isomorphism between
![]() $\mathrm {Hol}(V,H)/V_H$
and
$\mathrm {Hol}(V,H)/V_H$
and
![]() $\mathrm {Hol}(V,K)/V_K$
. However,
$\mathrm {Hol}(V,K)/V_K$
. However,
Here
![]() $V/V_H\cong V/V_K$
, as both are F-vector spaces of the same dimension, so the uniqueness part of the fundamental theorem of finite abelian groups yields
$V/V_H\cong V/V_K$
, as both are F-vector spaces of the same dimension, so the uniqueness part of the fundamental theorem of finite abelian groups yields
![]() $H\cong K$
.
$H\cong K$
.
6. Examples
Given a group G and
![]() $x,y\in G$
, we set
$x,y\in G$
, we set
![]() ${}^x y=xyx^{-1}$
. If H and N are groups such that H acts on N by automorphisms via a homomorphism
${}^x y=xyx^{-1}$
. If H and N are groups such that H acts on N by automorphisms via a homomorphism
![]() $T:H\to \mathrm {Aut}(N)$
, we may consider the semidirect product
$T:H\to \mathrm {Aut}(N)$
, we may consider the semidirect product
![]() $N\rtimes _{T} H$
, where
$N\rtimes _{T} H$
, where
![]() $ {}^h x=hxh^{-1}=T(h)(x),\ h\in H,x\in N. $
$ {}^h x=hxh^{-1}=T(h)(x),\ h\in H,x\in N. $
There is a slight generalisation of Theorem 4.1 to a semidirect product
![]() $V\rtimes _T\langle \alpha \rangle $
, where the action of
$V\rtimes _T\langle \alpha \rangle $
, where the action of
![]() $\langle \alpha \rangle $
on V is not necessarily faithful. We omit the details of the proof, which is similar to that of Theorem 4.1 but notationally more complicated.
$\langle \alpha \rangle $
on V is not necessarily faithful. We omit the details of the proof, which is similar to that of Theorem 4.1 but notationally more complicated.
We let
![]() $U_n(p)$
stand for the subgroup of
$U_n(p)$
stand for the subgroup of
![]() $\mathrm {GL}_n(p)$
consisting of all upper triangular matrices with 1 values along the main diagonal. For later reference, we observe that
$\mathrm {GL}_n(p)$
consisting of all upper triangular matrices with 1 values along the main diagonal. For later reference, we observe that
![]() $U_3(p)=\mathrm {Heis}(p)$
, the Heisenberg group over F.
$U_3(p)=\mathrm {Heis}(p)$
, the Heisenberg group over F.
Throughout this section, we set
![]() $R={\mathbb {Z}}/p^m{\mathbb {Z}}$
, where
$R={\mathbb {Z}}/p^m{\mathbb {Z}}$
, where
![]() $m\geq 1$
, and let U be a free R-module of finite rank
$m\geq 1$
, and let U be a free R-module of finite rank
![]() $n>0$
. Given a subgroup H of
$n>0$
. Given a subgroup H of
![]() $\mathrm {GL}_n(R)$
, taking
$\mathrm {GL}_n(R)$
, taking
![]() $U=R^n$
, we may consider the semidirect product
$U=R^n$
, we may consider the semidirect product
![]() $U\rtimes _T H$
, where T is the homomorphism
$U\rtimes _T H$
, where T is the homomorphism
![]() $H\hookrightarrow \mathrm {GL}_n(R)\to \mathrm {GL}(U)$
, and
$H\hookrightarrow \mathrm {GL}_n(R)\to \mathrm {GL}(U)$
, and
![]() $\mathrm {GL}_n(R)\to \mathrm {GL}(U)$
is the isomorphism associated to the canonical basis of U, so that
$\mathrm {GL}_n(R)\to \mathrm {GL}(U)$
is the isomorphism associated to the canonical basis of U, so that
![]() ${}^h v=h\cdot v$
is the product of the
${}^h v=h\cdot v$
is the product of the
![]() $n\times n$
matrix h by the vector v of length n. It is clear that
$n\times n$
matrix h by the vector v of length n. It is clear that
![]() $U\rtimes _T H\cong \mathrm {Hol}(U,T(H))$
, and we will write
$U\rtimes _T H\cong \mathrm {Hol}(U,T(H))$
, and we will write
![]() $\mathrm {Hol}(U,H)=U\rtimes _T H$
from now on.
$\mathrm {Hol}(U,H)=U\rtimes _T H$
from now on.
Lemma 6.1. Let H be a subgroup of
![]() $\mathrm {GL}_n(R)$
and set
$\mathrm {GL}_n(R)$
and set
![]() $U=R^n$
. Suppose there are subgroups W and K of
$U=R^n$
. Suppose there are subgroups W and K of
![]() $\mathrm {Hol}(U,H)$
such that W is normal,
$\mathrm {Hol}(U,H)$
such that W is normal,
![]() $W\cong U$
,
$W\cong U$
,
![]() $\mathrm {Hol}(U,H)=WK$
and
$\mathrm {Hol}(U,H)=WK$
and
![]() $W\cap K$
is trivial. Assume that the homomorphism
$W\cap K$
is trivial. Assume that the homomorphism
![]() $K\to \mathrm {GL}(W)$
arising from the conjugation action of K on W is faithful. Fix an R-basis
$K\to \mathrm {GL}(W)$
arising from the conjugation action of K on W is faithful. Fix an R-basis
![]() $B=\{w_1,\ldots ,w_n\}$
of W, and let L be the image of the corresponding homomorphism
$B=\{w_1,\ldots ,w_n\}$
of W, and let L be the image of the corresponding homomorphism
![]() $v:K\to \mathrm {GL}(W)\to \mathrm {GL}_n(R)$
. Then
$v:K\to \mathrm {GL}(W)\to \mathrm {GL}_n(R)$
. Then
![]() $\mathrm {Hol}(U,H)\cong \mathrm {Hol}(U,L)$
.
$\mathrm {Hol}(U,H)\cong \mathrm {Hol}(U,L)$
.
Proof. For
![]() $w\in W$
, let
$w\in W$
, let
![]() $[w]_B\in U$
be the coordinates of w relative to B. Thus, the map
$[w]_B\in U$
be the coordinates of w relative to B. Thus, the map
![]() $u:W\to U$
, given by
$u:W\to U$
, given by
![]() $w\mapsto [w]_B$
, is an isomorphism. By assumption, the map
$w\mapsto [w]_B$
, is an isomorphism. By assumption, the map
![]() $K\to L$
, given by
$K\to L$
, given by
![]() $k\mapsto v(k)$
is an isomorphism. Consider the map
$k\mapsto v(k)$
is an isomorphism. Consider the map
![]() $f:W\rtimes K\to \mathrm {Hol}(U,L)$
given by
$f:W\rtimes K\to \mathrm {Hol}(U,L)$
given by
![]() $wk\mapsto u(w)v(k)$
. We claim that f is an isomorphism. It suffices to verify that f maps
$wk\mapsto u(w)v(k)$
. We claim that f is an isomorphism. It suffices to verify that f maps
![]() ${}^k w$
into
${}^k w$
into
![]() ${}^{v(k)} u(w)$
, that is,
${}^{v(k)} u(w)$
, that is,
![]() $[{}^k w]_B=v(k)\cdot [w]_B$
. To see this, observe that by definition, if
$[{}^k w]_B=v(k)\cdot [w]_B$
. To see this, observe that by definition, if
![]() $k\in K$
and
$k\in K$
and
![]() $1\leq j\leq n$
, then
$1\leq j\leq n$
, then
 $$ \begin{align*} {}^k w_i=\underset{1\leq j\leq n}\sum v(k)_{ji}w_j, \end{align*} $$
$$ \begin{align*} {}^k w_i=\underset{1\leq j\leq n}\sum v(k)_{ji}w_j, \end{align*} $$
so that
![]() $[{}^k w_i]_B$
is the ith column of
$[{}^k w_i]_B$
is the ith column of
![]() $v(k)$
, that is,
$v(k)$
, that is,
![]() $[{}^k w_i]_B=v(k)\cdot [w_i]_B$
. As K acts linearly on W, it follows that
$[{}^k w_i]_B=v(k)\cdot [w_i]_B$
. As K acts linearly on W, it follows that
![]() $[{}^k w]_B=v(k)\cdot [w]_B$
.
$[{}^k w]_B=v(k)\cdot [w]_B$
.
Example 6.2. Take
![]() $p=2$
and
$p=2$
and
![]() $m=3$
, so that
$m=3$
, so that
![]() $R={\mathbb {Z}}/8{\mathbb {Z}}$
, and further take
$R={\mathbb {Z}}/8{\mathbb {Z}}$
, and further take
![]() $n=4$
and
$n=4$
and
![]() $U=R^4$
, whose elements are viewed as column vectors. Let
$U=R^4$
, whose elements are viewed as column vectors. Let
 $$ \begin{align*} A=\begin{pmatrix} 3 & -1 & 1 & -2\\0 & 3 & -3 & 1\\0 & 3 & 4 & 3\\2 & 0 & -2 & 3\end{pmatrix}\in\mathrm{GL}_4(R), \end{align*} $$
$$ \begin{align*} A=\begin{pmatrix} 3 & -1 & 1 & -2\\0 & 3 & -3 & 1\\0 & 3 & 4 & 3\\2 & 0 & -2 & 3\end{pmatrix}\in\mathrm{GL}_4(R), \end{align*} $$
and set
![]() $G=\mathrm {Hol}(U,A)=U\rtimes \langle A\rangle $
, where
$G=\mathrm {Hol}(U,A)=U\rtimes \langle A\rangle $
, where
![]() $ AvA^{-1}=A\cdot v, $
the product of A by the column vector
$ AvA^{-1}=A\cdot v, $
the product of A by the column vector
![]() $v\in U$
. Then for
$v\in U$
. Then for
![]() $S\in \mathrm {GL}_4(R)$
, we have
$S\in \mathrm {GL}_4(R)$
, we have
![]() $G\cong \mathrm {Hol}(U,S)$
if and only if
$G\cong \mathrm {Hol}(U,S)$
if and only if
![]() $\langle S\rangle \sim \langle A\rangle $
or
$\langle S\rangle \sim \langle A\rangle $
or
![]() $\langle S\rangle \sim \langle B\rangle $
, where
$\langle S\rangle \sim \langle B\rangle $
, where
![]() $\langle B\rangle \not \sim \langle A\rangle $
and
$\langle B\rangle \not \sim \langle A\rangle $
and
 $$ \begin{align} B=\begin{pmatrix} -1 & -2 & 2 & 4\\0 & 3 & -3 & 1\\0 & 3 & 4 & 3\\1 & 0 & -2 & 3\end{pmatrix}\in\mathrm{GL}_4(R). \end{align} $$
$$ \begin{align} B=\begin{pmatrix} -1 & -2 & 2 & 4\\0 & 3 & -3 & 1\\0 & 3 & 4 & 3\\1 & 0 & -2 & 3\end{pmatrix}\in\mathrm{GL}_4(R). \end{align} $$
Indeed, for
![]() $M\in \mathrm {GL}_4(R)$
, we denote by
$M\in \mathrm {GL}_4(R)$
, we denote by
![]() $\overline {M}$
the image of M under the canonical projection
$\overline {M}$
the image of M under the canonical projection
![]() $\mathrm {GL}_4(R)\to \mathrm {GL}_4(F)$
. The characteristic polynomial of
$\mathrm {GL}_4(R)\to \mathrm {GL}_4(F)$
. The characteristic polynomial of
![]() $\overline {A}$
is
$\overline {A}$
is
![]() $f(X)= (X+1)^2(X^2+X+1)$
. Thus, the minimal polynomial of
$f(X)= (X+1)^2(X^2+X+1)$
. Thus, the minimal polynomial of
![]() $\overline {A}$
is
$\overline {A}$
is
![]() $f(X)$
or
$f(X)$
or
![]() $g(X)= (X+1)(X^2+X+1)=X^3+1$
. In the latter case,
$g(X)= (X+1)(X^2+X+1)=X^3+1$
. In the latter case,
![]() $\overline {A}$
has order 3, which is easily seen to be false. Thus, the minimal polynomial of
$\overline {A}$
has order 3, which is easily seen to be false. Thus, the minimal polynomial of
![]() $\overline {A}$
is
$\overline {A}$
is
![]() $f(X)$
. As the degree of
$f(X)$
. As the degree of
![]() $f(X)$
is the size of
$f(X)$
is the size of
![]() $\overline {A}$
, it follows that
$\overline {A}$
, it follows that
![]() $\overline {A}$
is similar to the companion matrix of
$\overline {A}$
is similar to the companion matrix of
![]() $f(X)$
, or the direct sum of the companion matrices of
$f(X)$
, or the direct sum of the companion matrices of
![]() $f_1(X)=X^2+1$
and
$f_1(X)=X^2+1$
and
![]() $f_2(X)=X^2+X+1$
. Thus, the order of
$f_2(X)=X^2+X+1$
. Thus, the order of
![]() $\overline {A}$
is 6, whence the order of A is a multiple of 6. The same comments apply to B. In particular,
$\overline {A}$
is 6, whence the order of A is a multiple of 6. The same comments apply to B. In particular,
![]() $\overline {A}$
is similar to
$\overline {A}$
is similar to
![]() $\overline {B}$
. However,
$\overline {B}$
. However,
![]() $\langle A\rangle \not \sim \langle B\rangle $
, since the determinant of A is
$\langle A\rangle \not \sim \langle B\rangle $
, since the determinant of A is
![]() $-$
1 and that of B is 3. Thus, every odd power of B has determinant 3, so no odd power of B is similar to A. Therefore,
$-$
1 and that of B is 3. Thus, every odd power of B has determinant 3, so no odd power of B is similar to A. Therefore,
![]() $\langle A\rangle $
and
$\langle A\rangle $
and
![]() $\langle B\rangle $
are not conjugate in
$\langle B\rangle $
are not conjugate in
![]() $\mathrm {GL}_4(R)$
.
$\mathrm {GL}_4(R)$
.
We next show that
![]() $\mathrm {Hol}(U,A)\cong \mathrm {Hol}(U,B)$
. For this purpose, note that
$\mathrm {Hol}(U,A)\cong \mathrm {Hol}(U,B)$
. For this purpose, note that
 $$ \begin{align*} A^2=\begin{pmatrix} -3 & -3 & -2 & -2\\2 & 0 & 1 & -3\\-2 & -3 & 1 & 0\\4 & 0 & 4 & -1\end{pmatrix}, \quad A^3=\begin{pmatrix} 3 & 4 & 2 & -1\\0 & 1 & 4 & -2\\2 & 4 & 3 & 4\\2 & 0 & -2 & 1\end{pmatrix}, \quad A^6=\begin{pmatrix} 3 & 0 & -2 & 4\\4 & 1 & 4 & 4\\4 & 0 & -3 & -2\\4 & 0 & 4 & -1\end{pmatrix}, \end{align*} $$
$$ \begin{align*} A^2=\begin{pmatrix} -3 & -3 & -2 & -2\\2 & 0 & 1 & -3\\-2 & -3 & 1 & 0\\4 & 0 & 4 & -1\end{pmatrix}, \quad A^3=\begin{pmatrix} 3 & 4 & 2 & -1\\0 & 1 & 4 & -2\\2 & 4 & 3 & 4\\2 & 0 & -2 & 1\end{pmatrix}, \quad A^6=\begin{pmatrix} 3 & 0 & -2 & 4\\4 & 1 & 4 & 4\\4 & 0 & -3 & -2\\4 & 0 & 4 & -1\end{pmatrix}, \end{align*} $$
which confirms that the order of
![]() $\overline {A}$
is 6. Moreover,
$\overline {A}$
is 6. Moreover,
 $$ \begin{align*} A^{12}=\begin{pmatrix} 1 & 0 & 0 & 4\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}, \end{align*} $$
$$ \begin{align*} A^{12}=\begin{pmatrix} 1 & 0 & 0 & 4\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}, \end{align*} $$
so the order of A is 24. Set
![]() $G=\mathrm {Hol}(U,A)$
,
$G=\mathrm {Hol}(U,A)$
,
 $$ \begin{align*} x=\begin{pmatrix} -1 \\0\\0\\ 1\end{pmatrix}\in U,\quad y=(x,A^{12})\in G, \end{align*} $$
$$ \begin{align*} x=\begin{pmatrix} -1 \\0\\0\\ 1\end{pmatrix}\in U,\quad y=(x,A^{12})\in G, \end{align*} $$
where this notation will be used to avoid confusion when dealing with elements of G which are neither in U nor in
![]() $\langle A\rangle $
. We further let W be the subgroup of G generated by
$\langle A\rangle $
. We further let W be the subgroup of G generated by
![]() $[G,G]$
and y. As W contains
$[G,G]$
and y. As W contains
![]() $[G,G]$
, it is a normal subgroup of G. We claim that W is abelian and, in fact, isomorphic to U. To see this, note that
$[G,G]$
, it is a normal subgroup of G. We claim that W is abelian and, in fact, isomorphic to U. To see this, note that
![]() $[G,G]$
is the subgroup of U generated by the columns of
$[G,G]$
is the subgroup of U generated by the columns of
![]() $A-1$
, say
$A-1$
, say
![]() $f_1,f_2,f_3,f_4$
. Thus, W is abelian if and only if
$f_1,f_2,f_3,f_4$
. Thus, W is abelian if and only if
![]() $A^{12}$
commutes with
$A^{12}$
commutes with
![]() $[G,G]$
, which means that
$[G,G]$
, which means that
![]() $A^{12}$
fixes the columns of
$A^{12}$
fixes the columns of
![]() $A-1$
, that is,
$A-1$
, that is,
![]() $(A^{12}-1)(A-1)=0,$
which is true as the fourth row of
$(A^{12}-1)(A-1)=0,$
which is true as the fourth row of
![]() $A-1$
is annihilated by 4. Row reducing
$A-1$
is annihilated by 4. Row reducing
![]() $A-1$
, we find that
$A-1$
, we find that
![]() $\langle f_1,f_2,f_3,f_4\rangle =\langle f_1\rangle \oplus \langle f_2\rangle \oplus \langle f_3\rangle \oplus \langle f_4\rangle ,$
where
$\langle f_1,f_2,f_3,f_4\rangle =\langle f_1\rangle \oplus \langle f_2\rangle \oplus \langle f_3\rangle \oplus \langle f_4\rangle ,$
where
![]() $f_2,f_3,f_4$
have order 8 and
$f_2,f_3,f_4$
have order 8 and
![]() $f_1$
has order 4. In particular, this yields
$f_1$
has order 4. In particular, this yields
![]() $[G,G]\cong C_8^3\times C_4$
and
$[G,G]\cong C_8^3\times C_4$
and
![]() $G/[G,G]\cong C_2\times C_{24}$
. Moreover,
$G/[G,G]\cong C_2\times C_{24}$
. Moreover,
whence
![]() $W\cong U$
and
$W\cong U$
and
![]() $W/[G,G]\cong C_2$
. Note that W is complemented by
$W/[G,G]\cong C_2$
. Note that W is complemented by
![]() $K=\langle A\rangle $
in G, since their intersection is trivial, so their product has the right order. Also,
$K=\langle A\rangle $
in G, since their intersection is trivial, so their product has the right order. Also,
![]() $x,f_2,f_3,f_4$
are the columns of an invertible matrix, say Q, so they generate U.
$x,f_2,f_3,f_4$
are the columns of an invertible matrix, say Q, so they generate U.
The conjugation action of
![]() $\langle A\rangle $
on W is faithful, for if
$\langle A\rangle $
on W is faithful, for if
![]() $A^i$
acts trivially on W, then
$A^i$
acts trivially on W, then
![]() $(A^i-1)Q=0$
, whence
$(A^i-1)Q=0$
, whence
![]() $A^i=1$
. Let M be the matrix of the conjugation action of A on W relative to the R-basis
$A^i=1$
. Let M be the matrix of the conjugation action of A on W relative to the R-basis
![]() $\{y,f_2,f_3,f_4\}$
. We claim that
$\{y,f_2,f_3,f_4\}$
. We claim that
![]() $M=B$
, as given in (6.1). Indeed, denoting by
$M=B$
, as given in (6.1). Indeed, denoting by
![]() $C_i(P)$
the i-column of a matrix P,
$C_i(P)$
the i-column of a matrix P,
 $$ \begin{align*} {}^A f_i&=A\cdot f_i=A\cdot C_i(A-1)=C_i(A(A-1))=(A-1) C_i(A)\\&=A_{1i} f_1+A_{2i} f_2+A_{3i} f_3+ A_{4i} f_4 \end{align*} $$
$$ \begin{align*} {}^A f_i&=A\cdot f_i=A\cdot C_i(A-1)=C_i(A(A-1))=(A-1) C_i(A)\\&=A_{1i} f_1+A_{2i} f_2+A_{3i} f_3+ A_{4i} f_4 \end{align*} $$
for all
![]() $i\in \{2,3,4\}$
. Recalling that
$i\in \{2,3,4\}$
. Recalling that
![]() $y^2=f_1$
, it follows that M and B share the last three columns. Let us verify that M and B share the first column. To see this, observe that
$y^2=f_1$
, it follows that M and B share the last three columns. Let us verify that M and B share the first column. To see this, observe that
Here, the definition of x gives
![]() $(A-1)x= -f_1+f_4,$
where
$(A-1)x= -f_1+f_4,$
where
![]() $f_1=y^2$
, so
$f_1=y^2$
, so
![]() ${}^A y=y^{-2}f_4 y=y^{-1}f_4$
, so the first columns of M and B are identical. It follows from Lemma 6.1 that
${}^A y=y^{-2}f_4 y=y^{-1}f_4$
, so the first columns of M and B are identical. It follows from Lemma 6.1 that
![]() $\mathrm {Hol}(U,A)\cong \mathrm {Hol}(U,B)$
.
$\mathrm {Hol}(U,A)\cong \mathrm {Hol}(U,B)$
.
Let
![]() $S\in \mathrm {GL}_4(R)$
and suppose that
$S\in \mathrm {GL}_4(R)$
and suppose that
![]() $H=\mathrm {Hol}(U,S)$
is isomorphic to G. We proceed to show that
$H=\mathrm {Hol}(U,S)$
is isomorphic to G. We proceed to show that
![]() $\langle S\rangle \sim \langle A\rangle $
or
$\langle S\rangle \sim \langle A\rangle $
or
![]() $\langle S\rangle \sim \langle B\rangle $
. By hypothesis, we have an isomorphism
$\langle S\rangle \sim \langle B\rangle $
. By hypothesis, we have an isomorphism
![]() $\Delta :H\to G$
. Here, U is a normal subgroup of H containing
$\Delta :H\to G$
. Here, U is a normal subgroup of H containing
![]() $[H,H]$
; U is complemented in H by the cyclic subgroup
$[H,H]$
; U is complemented in H by the cyclic subgroup
![]() $\langle S\rangle $
of order 24; and relative to the canonical basis of U, the matrix of the action of S on U by conjugation is S.
$\langle S\rangle $
of order 24; and relative to the canonical basis of U, the matrix of the action of S on U by conjugation is S.
Set
![]() $N=\Delta (U)$
and
$N=\Delta (U)$
and
![]() $T=\Delta (S)$
. Then N is a normal subgroup of G isomorphic to U containing
$T=\Delta (S)$
. Then N is a normal subgroup of G isomorphic to U containing
![]() $[G,G]$
; N is complemented in G by the cyclic subgroup
$[G,G]$
; N is complemented in G by the cyclic subgroup
![]() $\langle T\rangle $
of order 24; and relative to some R-basis of N, the matrix of the action of T on N by conjugation is S.
$\langle T\rangle $
of order 24; and relative to some R-basis of N, the matrix of the action of T on N by conjugation is S.
As indicated above,
![]() $[G,G]\cong C_8^3\times C_4$
, so
$[G,G]\cong C_8^3\times C_4$
, so
![]() $N/[G,G]\cong C_2$
. As
$N/[G,G]\cong C_2$
. As
![]() $G/[G,G]\cong C_2\times C_{24}$
, it follows that there are exactly three normal subgroups of G containing
$G/[G,G]\cong C_2\times C_{24}$
, it follows that there are exactly three normal subgroups of G containing
![]() $[G,G]$
as a subgroup of index 2, and N must be one of them. The first possibility is
$[G,G]$
as a subgroup of index 2, and N must be one of them. The first possibility is
![]() $N=U$
, in which case,
$N=U$
, in which case,
![]() $\langle S\rangle \sim \langle A\rangle $
by Lemma 3.3. The second possibility is
$\langle S\rangle \sim \langle A\rangle $
by Lemma 3.3. The second possibility is
which cannot be. It remains to analyse the third possibility, namely
![]() $N=W$
. Since
$N=W$
. Since
![]() $G=W\rtimes \langle T\rangle $
, the order of T modulo W is also 24. As
$G=W\rtimes \langle T\rangle $
, the order of T modulo W is also 24. As
![]() $G=W\rtimes \langle A\rangle $
, it follows that
$G=W\rtimes \langle A\rangle $
, it follows that
![]() $T=w A^i$
, where
$T=w A^i$
, where
![]() $w\in W$
and
$w\in W$
and
![]() $i\in {\mathbb {Z}}$
is relatively prime to 24. Since
$i\in {\mathbb {Z}}$
is relatively prime to 24. Since
![]() $M=B$
, the conjugation action of T on W relative to the R-basis
$M=B$
, the conjugation action of T on W relative to the R-basis
![]() $\{y,f_2,f_3,f_4\}$
of W is
$\{y,f_2,f_3,f_4\}$
of W is
![]() $B^i$
. However, relative to some R-basis of W, the matrix of the conjugation action of T on W is S. Thus, S is similar to
$B^i$
. However, relative to some R-basis of W, the matrix of the conjugation action of T on W is S. Thus, S is similar to
![]() $B^i$
with
$B^i$
with
![]() $\gcd (24,i)=1$
, as required.
$\gcd (24,i)=1$
, as required.
Example 6.3. Suppose that
![]() $n\geq 6$
and set
$n\geq 6$
and set
![]() $V=F^n$
. Then there are abelian subgroups H and L of
$V=F^n$
. Then there are abelian subgroups H and L of
![]() $U_n(p)$
such that
$U_n(p)$
such that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
but
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
but
![]() $H\not \sim L$
in
$H\not \sim L$
in
![]() $\mathrm {GL}_n(p)$
.
$\mathrm {GL}_n(p)$
.
Indeed, suppose first that
![]() $n=6$
and let
$n=6$
and let
![]() $\{v_1,v_2,v_3,v_4,v_5,v_6\}$
be the canonical basis of V. For
$\{v_1,v_2,v_3,v_4,v_5,v_6\}$
be the canonical basis of V. For
![]() $A\in M_3(F)$
, set
$A\in M_3(F)$
, set
 $$ \begin{align*} S_A=\begin{pmatrix} I_3 & A\\0 & I_3\end{pmatrix}\in U_6(p), \end{align*} $$
$$ \begin{align*} S_A=\begin{pmatrix} I_3 & A\\0 & I_3\end{pmatrix}\in U_6(p), \end{align*} $$
and let
 $$ \begin{align*} A_1=\begin{pmatrix} 1 & 0 & 0 \\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}, \quad A_2=\begin{pmatrix} 0 & 1 & 0 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad A_3=\begin{pmatrix} 0 & 0 & 1 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \end{align*} $$
$$ \begin{align*} A_1=\begin{pmatrix} 1 & 0 & 0 \\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}, \quad A_2=\begin{pmatrix} 0 & 1 & 0 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad A_3=\begin{pmatrix} 0 & 0 & 1 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \end{align*} $$
![]() $T_H$
be the additive subgroup of
$T_H$
be the additive subgroup of
![]() $M_3(F)$
generated by
$M_3(F)$
generated by
![]() $A_1,A_2,A_3$
, and H the subgroup of
$A_1,A_2,A_3$
, and H the subgroup of
![]() $U_6(p)$
generated by
$U_6(p)$
generated by
![]() $S_{A_1},S_{A_2},S_{A_3}$
.
$S_{A_1},S_{A_2},S_{A_3}$
.
Let W be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_1,v_2,v_3,S_{A_1},S_{A_2},S_{A_3}$
. Then
$v_1,v_2,v_3,S_{A_1},S_{A_2},S_{A_3}$
. Then
![]() $W\cong V$
. Moreover, W is a normal subgroup of
$W\cong V$
. Moreover, W is a normal subgroup of
![]() $\mathrm {Hol}(V,H)$
. Let K be the subgroup of
$\mathrm {Hol}(V,H)$
. Let K be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_4,v_5,v_6$
. We see that
$v_4,v_5,v_6$
. We see that
![]() $K\cong H$
and
$K\cong H$
and
![]() $\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
$\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
![]() $v_4,v_5,v_6$
relative to the basis
$v_4,v_5,v_6$
relative to the basis
![]() $\{v_1,v_2,v_3,S_{A_1},S_{A_2},S_{A_3}\}$
are respectively equal to
$\{v_1,v_2,v_3,S_{A_1},S_{A_2},S_{A_3}\}$
are respectively equal to
![]() $S_{B_1},S_{B_2},S_{B_3}$
, where
$S_{B_1},S_{B_2},S_{B_3}$
, where
![]() $B_i$
is the opposite of the matrix formed by the ith columns of
$B_i$
is the opposite of the matrix formed by the ith columns of
![]() $A_1,A_2,A_3$
, in that order, for
$A_1,A_2,A_3$
, in that order, for
![]() $i\in \{1,2,3\}$
. Thus,
$i\in \{1,2,3\}$
. Thus,
 $$ \begin{align*} B_1=\begin{pmatrix} -1 & 0 & 0 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad B_2=\begin{pmatrix} 0 & -1 & 0 \\-1 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad B_3=\begin{pmatrix} 0 & 0 & -1 \\0 & 0 & 0\\-1 & 0 & 0\end{pmatrix}, \end{align*} $$
$$ \begin{align*} B_1=\begin{pmatrix} -1 & 0 & 0 \\0 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad B_2=\begin{pmatrix} 0 & -1 & 0 \\-1 & 0 & 0\\0 & 0 & 0\end{pmatrix}, \quad B_3=\begin{pmatrix} 0 & 0 & -1 \\0 & 0 & 0\\-1 & 0 & 0\end{pmatrix}, \end{align*} $$
so the action of K on W is faithful. Let L be the subgroup of
![]() $U_6(p)$
generated by
$U_6(p)$
generated by
![]() $S_{B_1},S_{B_2},S_{B_3}$
, so that
$S_{B_1},S_{B_2},S_{B_3}$
, so that
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
by Lemma 6.1. Let
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
by Lemma 6.1. Let
![]() $T_L$
be the additive subgroup of
$T_L$
be the additive subgroup of
![]() $M_3(p)$
generated by
$M_3(p)$
generated by
![]() $B_1,B_2,B_3$
.
$B_1,B_2,B_3$
.
Suppose, if possible, that
![]() $H\sim L$
in
$H\sim L$
in
![]() $\mathrm {GL}_6(p)$
. Then, there is
$\mathrm {GL}_6(p)$
. Then, there is
![]() $X\in \mathrm {GL}_6(p)$
such that
$X\in \mathrm {GL}_6(p)$
such that
![]() $X H X^{-1}=L$
. Thus, X gives rise to the isomorphism
$X H X^{-1}=L$
. Thus, X gives rise to the isomorphism
![]() $f:\mathrm {Hol}(V,H)\to \mathrm {Hol}(V,L)$
given by
$f:\mathrm {Hol}(V,H)\to \mathrm {Hol}(V,L)$
given by
![]() $vh\mapsto (X\cdot v)(X h X^{-1})$
. Then f must map the centre of
$vh\mapsto (X\cdot v)(X h X^{-1})$
. Then f must map the centre of
![]() $\mathrm {Hol}(V,H)$
onto the centre of
$\mathrm {Hol}(V,H)$
onto the centre of
![]() $\mathrm {Hol}(V,L)$
. However, both centres are equal to
$\mathrm {Hol}(V,L)$
. However, both centres are equal to
![]() $\langle v_1,v_2,v_3\rangle $
, so
$\langle v_1,v_2,v_3\rangle $
, so
 $$ \begin{align*} X=\begin{pmatrix} Y & Q\\0 & Z\end{pmatrix}, \end{align*} $$
$$ \begin{align*} X=\begin{pmatrix} Y & Q\\0 & Z\end{pmatrix}, \end{align*} $$
where
![]() $Y,Z\in \mathrm {GL}_3(p)$
and
$Y,Z\in \mathrm {GL}_3(p)$
and
![]() $Q\in M_3(F)$
. Then
$Q\in M_3(F)$
. Then
![]() $X H X^{-1}=L$
gives
$X H X^{-1}=L$
gives
![]() $Y T_H Z^{-1}=T_L$
. However, all matrices in
$Y T_H Z^{-1}=T_L$
. However, all matrices in
![]() $T_L$
have rank at most 2, whereas
$T_L$
have rank at most 2, whereas
![]() $T_H$
has a matrix of rank 3. We deduce that
$T_H$
has a matrix of rank 3. We deduce that
![]() $H\not \sim L$
in
$H\not \sim L$
in
![]() $\mathrm {GL}_6(p)$
.
$\mathrm {GL}_6(p)$
.
In general, take
![]() $m=\lceil n/2\rceil $
, for
$m=\lceil n/2\rceil $
, for
![]() $A\in M_m(F)$
, set
$A\in M_m(F)$
, set
 $$ \begin{align*} S_A=\begin{pmatrix} I_m & A\\0 & I_{n-m}\end{pmatrix}\in U_n(p), \end{align*} $$
$$ \begin{align*} S_A=\begin{pmatrix} I_m & A\\0 & I_{n-m}\end{pmatrix}\in U_n(p), \end{align*} $$
and let
![]() $A_1,\ldots , A_{n-m}\in M_{m,n-m}(p)$
be defined as follows:
$A_1,\ldots , A_{n-m}\in M_{m,n-m}(p)$
be defined as follows:
![]() $A_1=\mathrm {diag}(1,\ldots ,1)$
, where the number of 1 values is
$A_1=\mathrm {diag}(1,\ldots ,1)$
, where the number of 1 values is
![]() $n-m$
,
$n-m$
,
![]() $A_2=E^{1,2},\ldots , A_{n-m}=E^{1,n-m}$
, where
$A_2=E^{1,2},\ldots , A_{n-m}=E^{1,n-m}$
, where
![]() $E^{i,j}$
is the matrix having a 1 in position
$E^{i,j}$
is the matrix having a 1 in position
![]() $(i,j)$
and 0 elsewhere. We can then continue as above, noting that all matrices in
$(i,j)$
and 0 elsewhere. We can then continue as above, noting that all matrices in
![]() $T_L$
have rank at most 2, whereas
$T_L$
have rank at most 2, whereas
![]() $T_H$
has a matrix of rank
$T_H$
has a matrix of rank
![]() $n-m\geq 3$
.
$n-m\geq 3$
.
We will refer to a group G as admitting if there exist nonconjugate subgroups H and K of
![]() $\mathrm {Aut}(G)$
such that
$\mathrm {Aut}(G)$
such that
![]() $\mathrm {Hol}(N,H)\cong \mathrm {Hol}(N,K)$
. We will say that G is highly admitting if there exist nonisomorphic subgroups H and K of
$\mathrm {Hol}(N,H)\cong \mathrm {Hol}(N,K)$
. We will say that G is highly admitting if there exist nonisomorphic subgroups H and K of
![]() $\mathrm {Aut}(G)$
such that
$\mathrm {Aut}(G)$
such that
![]() $\mathrm {Hol}(N,H)\cong \mathrm {Hol}(N,K)$
.
$\mathrm {Hol}(N,H)\cong \mathrm {Hol}(N,K)$
.
Example 6.4. Suppose that p is odd and
![]() $n\geq 2$
. Then V is highly admitting.
$n\geq 2$
. Then V is highly admitting.
Indeed, suppose first
![]() $n=2$
and set
$n=2$
and set
![]() $V=F^2$
. Let
$V=F^2$
. Let
![]() $\{v_1,v_2\}$
be the canonical basis of V and let H be the subgroup of
$\{v_1,v_2\}$
be the canonical basis of V and let H be the subgroup of
![]() $\mathrm {GL}_2(p)$
generated by
$\mathrm {GL}_2(p)$
generated by
 $$ \begin{align*} A=\begin{pmatrix} -1 & 0\\ 0 & 1\end{pmatrix}, \quad B=\begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} A=\begin{pmatrix} -1 & 0\\ 0 & 1\end{pmatrix}, \quad B=\begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix}. \end{align*} $$
Since
![]() $o(B)=p$
,
$o(B)=p$
,
![]() $o(A)=2$
and
$o(A)=2$
and
![]() ${}^A B=B^{-1}$
, we see that H is the dihedral group of order
${}^A B=B^{-1}$
, we see that H is the dihedral group of order
![]() $2p$
.
$2p$
.
Let W be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_1,B$
. Then
$v_1,B$
. Then
![]() $W\cong V$
. Moreover, W is a normal subgroup of
$W\cong V$
. Moreover, W is a normal subgroup of
![]() $\mathrm {Hol}(V,H)$
. Let K be the subgroup of
$\mathrm {Hol}(V,H)$
. Let K be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_2,A$
. Clearly,
$v_2,A$
. Clearly,
![]() $K\cong C_{2p}$
is not isomorphic to H, and
$K\cong C_{2p}$
is not isomorphic to H, and
![]() $\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
$\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
![]() $v_2$
and A relative to the basis
$v_2$
and A relative to the basis
![]() $\{v_1,B\}$
are respectively equal to
$\{v_1,B\}$
are respectively equal to
 $$ \begin{align*} \begin{pmatrix} 1 & -1\\ 0 & 1\end{pmatrix}, \quad \begin{pmatrix} -1 & 0\\ 0 & -1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & -1\\ 0 & 1\end{pmatrix}, \quad \begin{pmatrix} -1 & 0\\ 0 & -1\end{pmatrix}. \end{align*} $$
The subgroup of
![]() $\mathrm {GL}_2(p)$
generated by these matrices, say L, is isomorphic to
$\mathrm {GL}_2(p)$
generated by these matrices, say L, is isomorphic to
![]() $C_{2p}$
, so the action of K on W is faithful. It follows from Lemma 6.1 that
$C_{2p}$
, so the action of K on W is faithful. It follows from Lemma 6.1 that
![]() $\mathrm {Hol}(V,L)\cong \mathrm {Hol}(V,H)$
, even though L is not isomorphic to H.
$\mathrm {Hol}(V,L)\cong \mathrm {Hol}(V,H)$
, even though L is not isomorphic to H.
The general case when
![]() $\{v_1,\ldots ,v_n\}$
is the canonical basis of V follows by extending
$\{v_1,\ldots ,v_n\}$
is the canonical basis of V follows by extending
![]() $A,B$
so that they fix
$A,B$
so that they fix
![]() $v_3,\ldots ,v_n$
.
$v_3,\ldots ,v_n$
.
In addition to proving that V is highly admitting when
![]() $n\geq 2$
and p is odd, this example shows that even though
$n\geq 2$
and p is odd, this example shows that even though
![]() $\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
and the Sylow p-subgroup of H is conjugate to the Sylow p-subgroup of L, this conjugation cannot be extended to all of H and L.
$\mathrm {Hol}(V,H)\cong \mathrm {Hol}(V,L)$
and the Sylow p-subgroup of H is conjugate to the Sylow p-subgroup of L, this conjugation cannot be extended to all of H and L.
We next provide an analogue of Example 6.4 when
![]() $p=2$
, provided
$p=2$
, provided
![]() $n\geq 4$
.
$n\geq 4$
.
Example 6.5. Suppose that
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $p=2$
. Then V is highly admitting.
$p=2$
. Then V is highly admitting.
Indeed, suppose first
![]() $n=4$
and set
$n=4$
and set
![]() $V=F^4$
. Let
$V=F^4$
. Let
![]() $\{v_1,v_2,v_3,v_4\}$
be the canonical basis of V and let H be the subgroup of
$\{v_1,v_2,v_3,v_4\}$
be the canonical basis of V and let H be the subgroup of
![]() $\mathrm {GL}(V)$
generated by
$\mathrm {GL}(V)$
generated by
 $$ \begin{align*} X=\begin{pmatrix} 0 & 0 & 0 & 1\\0 & 0 & 1 & 0\\0 & 1 & 0 & 0\\1 & 0 & 0 & 0\end{pmatrix}, \quad Y=\begin{pmatrix} 0 & 0 & 0 & 1\\0 & 0 & 1 & 1\\1 & 1 & 0 & 0\\1 & 0 & 0 & 0\end{pmatrix}, \quad Z=\begin{pmatrix} 0 & 0 & 0 & 1\\1 & 0 & 1 & 1\\1 & 1 & 0 & 1\\1 & 0 & 0 & 0\end{pmatrix}. \end{align*} $$
$$ \begin{align*} X=\begin{pmatrix} 0 & 0 & 0 & 1\\0 & 0 & 1 & 0\\0 & 1 & 0 & 0\\1 & 0 & 0 & 0\end{pmatrix}, \quad Y=\begin{pmatrix} 0 & 0 & 0 & 1\\0 & 0 & 1 & 1\\1 & 1 & 0 & 0\\1 & 0 & 0 & 0\end{pmatrix}, \quad Z=\begin{pmatrix} 0 & 0 & 0 & 1\\1 & 0 & 1 & 1\\1 & 1 & 0 & 1\\1 & 0 & 0 & 0\end{pmatrix}. \end{align*} $$
Then
![]() $H\cong C_2^3$
. Let W be the subgroup of
$H\cong C_2^3$
. Let W be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_1+v_4,v_2+v_3,X,Z$
. Then
$v_1+v_4,v_2+v_3,X,Z$
. Then
![]() $W\cong V$
. Moreover, W is a normal subgroup of
$W\cong V$
. Moreover, W is a normal subgroup of
![]() $\mathrm {Hol}(V,H)$
. Let K be the subgroup of
$\mathrm {Hol}(V,H)$
. Let K be the subgroup of
![]() $\mathrm {Hol}(V,H)$
generated by
$\mathrm {Hol}(V,H)$
generated by
![]() $v_1,Y$
. We see that
$v_1,Y$
. We see that
![]() $K\cong D_{8}$
and
$K\cong D_{8}$
and
![]() $\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
$\mathrm {Hol}(V,H)=W\rtimes K$
. When K acts on W by conjugation, the matrices corresponding to the actions of
![]() $v_1,Y$
relative to the basis
$v_1,Y$
relative to the basis
![]() $\{v_1+v_4,v_2+v_3,X,Z\}$
are respectively equal to
$\{v_1+v_4,v_2+v_3,X,Z\}$
are respectively equal to
 $$ \begin{align*} \begin{pmatrix} 1 & 0 & 1 & 1\\0 & 1 & 0 & 1\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & 0 & 0 & 0\\1 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 0 & 1 & 1\\0 & 1 & 0 & 1\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & 0 & 0 & 0\\1 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}. \end{align*} $$
The subgroup of
![]() $\mathrm {GL}_4(2)$
generated by these matrices, say L, is isomorphic to
$\mathrm {GL}_4(2)$
generated by these matrices, say L, is isomorphic to
![]() $D_{8}$
, so the action of K on W is faithful. It follows from Lemma 6.1 that
$D_{8}$
, so the action of K on W is faithful. It follows from Lemma 6.1 that
![]() $\mathrm {Hol}(V,L)\cong \mathrm {Hol}(V,H)$
even though L is not isomorphic to H.
$\mathrm {Hol}(V,L)\cong \mathrm {Hol}(V,H)$
even though L is not isomorphic to H.
The general case when
![]() $\{v_1,\ldots ,v_n\}$
is the canonical basis of V follows by extending
$\{v_1,\ldots ,v_n\}$
is the canonical basis of V follows by extending
![]() $X,Y,Z$
so that they fix
$X,Y,Z$
so that they fix
![]() $v_5,\ldots ,v_n$
.
$v_5,\ldots ,v_n$
.
Example 6.6. Conditions (C1)–(C3) below ensure that a group G admits automorphisms
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
such that
$\beta $
such that
![]() $\mathrm {Hol}(G,\alpha )\cong \mathrm {Hol}(G,\beta )$
but
$\mathrm {Hol}(G,\alpha )\cong \mathrm {Hol}(G,\beta )$
but
![]() $\langle \alpha \rangle \not \sim \langle \beta \rangle $
.
$\langle \alpha \rangle \not \sim \langle \beta \rangle $
.
Let G be a group having elements x and y such that:
-
(C1)
 $o(x)=o(y)$
;
$o(x)=o(y)$
; -
(C2)
 $o(x)=o(x Z(G))$
and
$o(x)=o(x Z(G))$
and
 $o(y)=o(y Z(G))$
(so that
$o(y)=o(y Z(G))$
(so that
 $\langle x\rangle \cap Z(G)=1=\langle y\rangle \cap Z(G)$
);
$\langle x\rangle \cap Z(G)=1=\langle y\rangle \cap Z(G)$
); -
(C3) there is no automorphism of G that sends
 $x^i$
to
$x^i$
to
 $yz$
for any i relatively prime to the order of x and any
$yz$
for any i relatively prime to the order of x and any
 $z\in Z(G)$
(this means that when
$z\in Z(G)$
(this means that when
 $\mathrm {Aut}(G)$
acts on
$\mathrm {Aut}(G)$
acts on
 $\mathrm {Inn}(G)$
by conjugation, the subgroups generated by
$\mathrm {Inn}(G)$
by conjugation, the subgroups generated by
 $i(x)$
and
$i(x)$
and
 $i(y)$
are in different orbits, where
$i(y)$
are in different orbits, where
 $i(g)\in \mathrm {Inn}(G)$
is the inner automorphism associated to
$i(g)\in \mathrm {Inn}(G)$
is the inner automorphism associated to
 $g\in G$
).
$g\in G$
).
Let
![]() $\alpha =i(x)$
and
$\alpha =i(x)$
and
![]() $\beta =i(y)$
. By condition (C2),
$\beta =i(y)$
. By condition (C2),
![]() $\mathrm {Hol}(G,\alpha )=G\times \langle u\rangle $
, where
$\mathrm {Hol}(G,\alpha )=G\times \langle u\rangle $
, where
![]() $u=x^{-1}\alpha $
has the same order as x, and
$u=x^{-1}\alpha $
has the same order as x, and
![]() $\mathrm {Hol}(G,\beta )=G\times \langle v\rangle $
, where
$\mathrm {Hol}(G,\beta )=G\times \langle v\rangle $
, where
![]() $v=y^{-1}\beta $
has the same order as y. Thus,
$v=y^{-1}\beta $
has the same order as y. Thus,
![]() $\mathrm {Hol}(G,\alpha )\cong \mathrm {Hol}(G,\beta )$
by condition (C1). Also,
$\mathrm {Hol}(G,\alpha )\cong \mathrm {Hol}(G,\beta )$
by condition (C1). Also,
![]() $\langle \alpha \rangle $
and
$\langle \alpha \rangle $
and
![]() $\langle \beta \rangle $
are not conjugate subgroups of
$\langle \beta \rangle $
are not conjugate subgroups of
![]() $\mathrm {Aut}(G)$
by condition (C3).
$\mathrm {Aut}(G)$
by condition (C3).
Many groups satisfy conditions (C1)–(C3). A centreless group G having cyclic subgroups of the same order that are not in the same
![]() $\mathrm {Aut}(G)$
-orbit meets conditions (C1)–(C3). For instance:
$\mathrm {Aut}(G)$
-orbit meets conditions (C1)–(C3). For instance:
![]() $S_n$
,
$S_n$
,
![]() $n\geq 4$
, taking
$n\geq 4$
, taking
![]() $x=(1,2)$
and
$x=(1,2)$
and
![]() $y=(1,2)(3,4)$
, and looking at the size of their centralisers; a free group on
$y=(1,2)(3,4)$
, and looking at the size of their centralisers; a free group on
![]() $n\geq 2$
generators
$n\geq 2$
generators
![]() $x_1,\ldots ,x_n$
, taking
$x_1,\ldots ,x_n$
, taking
![]() $x=x_1$
and
$x=x_1$
and
![]() $y=[x_1,x_2]$
. The general linear group
$y=[x_1,x_2]$
. The general linear group
![]() $\mathrm {GL}_n(p)$
, with
$\mathrm {GL}_n(p)$
, with
![]() $n\geq 4$
and p odd, is not centreless and satisfies conditions (C1)–(C3), taking
$n\geq 4$
and p odd, is not centreless and satisfies conditions (C1)–(C3), taking
![]() $x=\mathrm {diag}(-1,1,\ldots ,1)$
and
$x=\mathrm {diag}(-1,1,\ldots ,1)$
and
![]() $y=\mathrm {diag}(-1,-1,1,\ldots ,1)$
, and looking at the size of their centralisers.
$y=\mathrm {diag}(-1,-1,1,\ldots ,1)$
, and looking at the size of their centralisers.
As another example, assume
![]() $m\geq 2$
and let
$m\geq 2$
and let
![]() $G=\mathrm {Hol}(V,\alpha )$
, where
$G=\mathrm {Hol}(V,\alpha )$
, where
![]() $\alpha $
acts on V, with respect to some basis, via the direct sum of m copies of the matrix
$\alpha $
acts on V, with respect to some basis, via the direct sum of m copies of the matrix
![]() $ (\begin {smallmatrix} 1 & 1\\ 0 & 1\end {smallmatrix}), $
where
$ (\begin {smallmatrix} 1 & 1\\ 0 & 1\end {smallmatrix}), $
where
![]() $n=2m$
. Thus, the order of G is
$n=2m$
. Thus, the order of G is
![]() $p^{2m+1}$
. As an abstract group,
$p^{2m+1}$
. As an abstract group,
The simplest example occurs when
![]() $m=2$
and
$m=2$
and
![]() $p=2$
, in which case,
$p=2$
, in which case,
![]() $|G|=32$
. In this case, G can also be described as a Sylow 2-subgroup P of
$|G|=32$
. In this case, G can also be described as a Sylow 2-subgroup P of
![]() $\mathrm {GL}_2({\mathbb {Z}}/4{\mathbb {Z}})$
. Indeed, let N be the kernel of the canonical map
$\mathrm {GL}_2({\mathbb {Z}}/4{\mathbb {Z}})$
. Indeed, let N be the kernel of the canonical map
![]() $\mathrm { GL}_2({\mathbb {Z}}/4{\mathbb {Z}})\to \mathrm {GL}_2({\mathbb {Z}}/2{\mathbb {Z}})$
, which consists of all 16 matrices of the form
$\mathrm { GL}_2({\mathbb {Z}}/4{\mathbb {Z}})\to \mathrm {GL}_2({\mathbb {Z}}/2{\mathbb {Z}})$
, which consists of all 16 matrices of the form
![]() $1+X$
, where
$1+X$
, where
![]() $X\in M_2(2{\mathbb {Z}}/4{\mathbb {Z}})$
. Then
$X\in M_2(2{\mathbb {Z}}/4{\mathbb {Z}})$
. Then
![]() $N\cong C_2^4$
, and N is generated by
$N\cong C_2^4$
, and N is generated by
 $$ \begin{align*} B=\begin{pmatrix} 1 & 2\\ 0 & 1\end{pmatrix},\quad C=\begin{pmatrix} 1 & 2\\ 2 & 1\end{pmatrix},\quad D=\begin{pmatrix} -1 & 0\\ 0 & 1\end{pmatrix},\quad E=\begin{pmatrix} -1 & 0\\ 0 & -1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} B=\begin{pmatrix} 1 & 2\\ 0 & 1\end{pmatrix},\quad C=\begin{pmatrix} 1 & 2\\ 2 & 1\end{pmatrix},\quad D=\begin{pmatrix} -1 & 0\\ 0 & 1\end{pmatrix},\quad E=\begin{pmatrix} -1 & 0\\ 0 & -1\end{pmatrix}. \end{align*} $$
Defining
![]() $A\in P$
by
$A\in P$
by
 $$ \begin{align*} A=\begin{pmatrix} 0 & 1\\ 1 & 0\end{pmatrix}, \end{align*} $$
$$ \begin{align*} A=\begin{pmatrix} 0 & 1\\ 1 & 0\end{pmatrix}, \end{align*} $$
we see that
Using the notation from (6.2), the centre of G is generated by all
![]() $x_{2i-1}$
. Take
$x_{2i-1}$
. Take
![]() $x=x_2$
and y as given. Then x and y have order p, which remains the same modulo
$x=x_2$
and y as given. Then x and y have order p, which remains the same modulo
![]() $Z(G)$
. The centraliser of
$Z(G)$
. The centraliser of
![]() $x^i$
, when
$x^i$
, when
![]() $p\nmid i$
, is the subgroup T generated by all
$p\nmid i$
, is the subgroup T generated by all
![]() $x_j$
. The centraliser of
$x_j$
. The centraliser of
![]() $yz$
, when
$yz$
, when
![]() $z\in Z(G)$
, is equal to
$z\in Z(G)$
, is equal to
![]() $Z(G)\langle y\rangle $
. Here,
$Z(G)\langle y\rangle $
. Here,
![]() $|T|=p^{2m}$
and
$|T|=p^{2m}$
and
![]() $|Z(G)\langle y\rangle |=p^{m+1}$
. Since
$|Z(G)\langle y\rangle |=p^{m+1}$
. Since
![]() $m\geq 2$
, it follows that T cannot be mapped into
$m\geq 2$
, it follows that T cannot be mapped into
![]() $Z(G)\langle y\rangle $
by any automorphism of G, so x and y meet the required conditions. Note that if
$Z(G)\langle y\rangle $
by any automorphism of G, so x and y meet the required conditions. Note that if
![]() $m=1$
, then
$m=1$
, then
![]() $G=\mathrm {Heis}(p)$
, in which case, G does not satisfy conditions (C1)–(C3). Indeed, if p is odd, then any two noncentral elements of G produce subgroups of inner automorphisms of order p that are in the same
$G=\mathrm {Heis}(p)$
, in which case, G does not satisfy conditions (C1)–(C3). Indeed, if p is odd, then any two noncentral elements of G produce subgroups of inner automorphisms of order p that are in the same
![]() $\mathrm {Aut}(G)$
-orbit; if
$\mathrm {Aut}(G)$
-orbit; if
![]() $p=2$
, then
$p=2$
, then
![]() $G=D_8$
, and
$G=D_8$
, and
![]() $D_8$
is nonadmitting (see Example 6.7 below).
$D_8$
is nonadmitting (see Example 6.7 below).
Our last example discusses instances of nonadmitting finite groups.
Example 6.7. (a) Suppose that
![]() $n=2$
and
$n=2$
and
![]() $p=2$
. Then V is nonadmitting.
$p=2$
. Then V is nonadmitting.
Indeed, every proper subgroup of
![]() $\mathrm {GL}(V)\cong S_3$
is cyclic, and all cyclic subgroups of
$\mathrm {GL}(V)\cong S_3$
is cyclic, and all cyclic subgroups of
![]() $S_3$
of the same order are conjugate in
$S_3$
of the same order are conjugate in
![]() $S_3$
.
$S_3$
.
(b) Suppose that
![]() $n=3$
and
$n=3$
and
![]() $p=2$
. Then V is nonadmitting.
$p=2$
. Then V is nonadmitting.
Indeed, set
![]() $V=F^3$
and let
$V=F^3$
and let
![]() $\{v_1,v_2,v_3\}$
be the canonical basis of V. It is known that the only cases, when
$\{v_1,v_2,v_3\}$
be the canonical basis of V. It is known that the only cases, when
![]() $\mathrm {GL}_3(2)$
has subgroups of the same order that are not conjugate, occur for orders 4, 12 and 24, and that there are three conjugacy classes of groups of order 4 and two conjugacy classes of groups of orders 12 and 24. In order 4, let H and K respectively consist of all matrices of the form
$\mathrm {GL}_3(2)$
has subgroups of the same order that are not conjugate, occur for orders 4, 12 and 24, and that there are three conjugacy classes of groups of order 4 and two conjugacy classes of groups of orders 12 and 24. In order 4, let H and K respectively consist of all matrices of the form
 $$ \begin{align*} \begin{pmatrix} 1 & 0 & *\\ 0 & 1 & *\\ 0 & 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & * & *\\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 0 & *\\ 0 & 1 & *\\ 0 & 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & * & *\\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix}. \end{align*} $$
Note that
![]() $G_1=\mathrm {Hol}(V,H)$
is not isomorphic to
$G_1=\mathrm {Hol}(V,H)$
is not isomorphic to
![]() $G_2=\mathrm {Hol}(V,K)$
, since
$G_2=\mathrm {Hol}(V,K)$
, since
![]() $[G_1,G_1]=\langle v_1,v_2\rangle $
and
$[G_1,G_1]=\langle v_1,v_2\rangle $
and
![]() $[G_2,G_2]=\langle v_1\rangle $
(this gives a quick way to verify that
$[G_2,G_2]=\langle v_1\rangle $
(this gives a quick way to verify that
![]() $H\not \sim K$
). Next, let J be the subgroup generated by the upper triangular Jordan block with eigenvalue 1. Thus, J is cyclic of order 4. Set
$H\not \sim K$
). Next, let J be the subgroup generated by the upper triangular Jordan block with eigenvalue 1. Thus, J is cyclic of order 4. Set
![]() $G_3=\mathrm {Hol}(V,J)$
. Then
$G_3=\mathrm {Hol}(V,J)$
. Then
![]() $[G_3,G_3]=\langle v_1,v_2\rangle $
, but
$[G_3,G_3]=\langle v_1,v_2\rangle $
, but
![]() $G_3$
is nilpotent of class 3 and
$G_3$
is nilpotent of class 3 and
![]() $G_1$
is nilpotent of class 2. Thus,
$G_1$
is nilpotent of class 2. Thus,
![]() $G_3$
is not isomorphic to
$G_3$
is not isomorphic to
![]() $G_1$
or to
$G_1$
or to
![]() $G_2$
.
$G_2$
.
In order 24, let H and K respectively consist of all matrices of the form
 $$ \begin{align*} \begin{pmatrix} A & u\\ 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & w\\ 0 & A\end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} A & u\\ 0 & 1\end{pmatrix}, \quad \begin{pmatrix} 1 & w\\ 0 & A\end{pmatrix}, \end{align*} $$
where
![]() $A\in \mathrm {GL}_2(2)$
, u is a column vector of length 2 and w is a row vector of length 2. Observe that
$A\in \mathrm {GL}_2(2)$
, u is a column vector of length 2 and w is a row vector of length 2. Observe that
![]() $G_1=\mathrm {Hol}(V,H)$
is not isomorphic to
$G_1=\mathrm {Hol}(V,H)$
is not isomorphic to
![]() $G_2=\mathrm {Hol}(V,K)$
, since
$G_2=\mathrm {Hol}(V,K)$
, since
![]() $[G_1,G_1]=\langle v_1,v_2\rangle \rtimes A_4$
and
$[G_1,G_1]=\langle v_1,v_2\rangle \rtimes A_4$
and
![]() $[G_2,G_2]=V\rtimes A_4$
(this gives a quick way to verify that
$[G_2,G_2]=V\rtimes A_4$
(this gives a quick way to verify that
![]() $H\not \sim K$
).
$H\not \sim K$
).
In order 12, the situation is as above, but with
![]() $A\in \langle C\rangle $
, where C is the companion matrix of the polynomial
$A\in \langle C\rangle $
, where C is the companion matrix of the polynomial
![]() $t^2+t+1\in F[t]$
. The outcome is the same.
$t^2+t+1\in F[t]$
. The outcome is the same.
(c) In addition to the group
![]() $C_2^3$
discussed above, every other group of order 8 is nonadmitting. These cases are easily verified and we omit the details.
$C_2^3$
discussed above, every other group of order 8 is nonadmitting. These cases are easily verified and we omit the details.
(d) In addition to the group
![]() $C_8$
mentioned above, every cyclic group
$C_8$
mentioned above, every cyclic group
![]() $C_{p^n}$
is nonadmitting. The case when p is odd is trivial, and the case when
$C_{p^n}$
is nonadmitting. The case when p is odd is trivial, and the case when
![]() $p=2$
requires routine calculations that we omit.
$p=2$
requires routine calculations that we omit.
Acknowledgements
We thank Eamonn O’Brien for Magma calculations and Allen Herman for useful discussions.