Statistical Congresses
In the 19th century, a series of statistical congresses began; congresses in Brussels in 1853 and in St. Petersburg in 1872 were particularly important for demographic, and especially twin, research. At that time, it was feared that in most countries the registers were defective in essential facts, but those of Belgium and Sweden were perhaps the most effective for scientific inquiries. Arosenius (Reference Arosenius and Koren1918) presented a thorough description of the genesis of the official statistics in Sweden. Among other things, he describes in detail how demographic statistics was formed in the 18th century and the step-by-step creation of Statistiska Centralbyrån (Statistics Sweden).
Levi (Reference Levi1854, p. 5) gave a detailed presentation of the suggestions accepted at the Brussels congress:
[T]here ought to be an annual registry of population, exhibiting the births by sex, by age of both parents, legitimate and illegitimate, number of twins, stillborn, marriages and divorces, by months. The deaths, by sex, by age, and by months, distinguishing among dead children, till three years of age, the legitimate from the illegitimate. The deaths by month, with the causes of death, and the profession of the deceased; marriages, with the age of the parties, their condition, profession, and number of children, distinguishing the legitimate and those acknowledged as such. Considering the extreme importance of a uniform nomenclature of diseases equally applicable to all countries, the attention of learned men is to be called to the question for further consideration at some future congress.
According to Brown (Reference Brown1872), at the congress in St. Petersburg the principal discussion was related to the movements of the population and how these should be registered. Among the facts to be recorded were multiple births, the sex and number of children born alive or still-born, whether legitimate or not, and the age of the mother at the date of the births. Later, Westergaard (Reference Westergaard1932) devoted an entire chapter in his history of statistics to the presentation of the statistical congresses in the middle of the 19th century.
Recently, Randeraad (Reference Randeraad2011, p. 51) directed attention to, and even criticism of, the international statistical congresses in the second half of the 19th century. He stated that it would be overly simplistic to assume that they were an outright success. In fact, no more congresses were held after 1876. Furthermore, he stressed that:
More importantly, by then it was clear that the aspirations of the early congresses had been too high. International uniformity in statistics was evidently not a goal that could be reached overnight. Much of this failure to bring about rapid change can be explained by the difficulties in realizing effective knowledge transfers, in other words effective communication, in an age that was not fully prepared for truly international activities. It has been shown that the second half of the nineteenth century was a period of numerous experiments in internationalism, but at the same time rampant nationalism nipped many initiatives in the bud.
Papers Before Hellin
Hellin's (Reference Hellin1895) paper can be considered a central milestone in the history of twin research, and one can divide the research into studies before and after Hellin. Spengler (Reference Spengler1848) presented birth data, including data concerning multiple births, for Mecklenburg-Schwerin for the period 1777–1847, presented here in Table 1 and Figure 1.
TABLE 1 Demographic Data From Mecklenburg-Schwerin Based on Spengler Data (1848)
FIGURE 1 Temporal trends in TWR and Hellin-transformed TRR (HRR) (Spengler, Reference Spengler1848). The confidence band of HRR indicates a good agreement between TWR and HRR.
Veit (Reference Veit1855) found in a data set from Prussia (1826–1849) one twin maternity per 89, one triplet maternity per 7,910 and one quadruplet maternity per 371,126 total maternities. It is notable that 892 = 7,921 and 893 = 704,969, but he did not give the relation between the twinning rate (TWR), triplet rate (TRR) and quadruplet rate (QUR). The Veit data are presented in Table 2.
TABLE 2 Data from Prussia, 1826–1849, According to Veit (Reference Veit1855)
Bertillon (Reference Bertillon1874) considered multiple maternity data from different countries in central Europe. He anticipated Hellin's law because he presented the number of twin maternities in relation to one triplet maternity.
Shortly after the congresses in Brussels (1853) and St. Petersburg (1872), Neefe (Reference Neefe1877) published his classical work. He stressed how important the above-mentioned statistical congresses were for the standardization of the demographic registers in different countries, and he used the new possibilities that the improved birth registers offered. Despite the other contemporaneous studies published, our opinion is that the history of twin research starts from his publication. Neefe analyzed a long series of problems connected to twinning, which have been shown to be central in later studies. He considered inter alia: (1) the rates of twin and higher multiple maternities, (2) the crude birth rates among single and multiple maternities, (3) the regional and seasonal variations in the TWRs, (4) the rates of live and stillbirths among the twins, (5) the sex composition of the set of the multiple maternities, (6) the sex ratio among single and multiple maternities, and (7) the effect of such influential factors as the age of the parents, the marital status of the mothers, urban and rural regions, and the seasonality. In addition, he considered the birth weights and premature births among the multiples and the mortality among the multiples and their mothers. This list indicates clearly that Neefe introduced a thorough research program for twin studies. It is important in this study to stress that Neefe did not anticipate Hellin's law (Fellman & Eriksson, Reference Fellman and Eriksson2009a).
During the second half of the 19th century, Statistics Sweden published in Statistisk Tidskrift extensive time series about demographic data. The data were given separately for the different counties of Sweden and contained the size of the population, the number of births and twin, triplet, and quadruplet sets (Fellman & Eriksson Reference Fellman and Eriksson2009a). Berg (Reference Berg1880) published a rigorous study of the multiple maternities in Sweden, 1869–1878. Because his study was published in Swedish, it did not receive the attention deserved. For our research team, having Swedish as their native language, Berg's results have been invaluable.
Strassmann (Reference Strassmann1889) analyzed data published by Veit (Reference Veit1855) concerning single and higher maternities and noted that there is one twin maternity per 891 and one triplet maternity per 892 total maternities.
Drejer (Reference Drejer1895) was apparently unaware of Hellin (Reference Hellin1895), but referred to Strassmann (Reference Strassmann1889) and stated that Strassmann had noted the relation between the rates of twin and triplet maternities. Drejer was dubious about the regularity between the rates. He stressed that under such circumstances the rule had to also hold for higher multiple maternities, but he could not find any clear indication of this being the case (Fellman & Eriksson, Reference Fellman and Eriksson2009a).
Hellin's Contribution
Hellin (Reference Hellin1895) observed an empirical relationship between the rates of twins and triplets. He stated that among human beings there is on average one twin maternity per 89 singleton maternities, one triplet maternity per (89)2 singleton maternities, one quadruplet maternity per (89)3 singleton maternities, and in general, within the range of the possibility, one x-tuplet maternity per (89)χ-1 singleton maternities. Strassmann related the number of multiple maternities to the number of all maternities, while Hellin related the number of multiple maternities to the number of single maternities. Both, however, used the same relation, 1:89. This is understandable because the relation between single maternities and all maternities is very close to one.
Fellman and Eriksson (Reference Fellman and Eriksson2009a) stressed that Hellin cited the articles by Veit (Reference Veit1855) and Strassmann (Reference Strassmann1889). Although Strassmann had already presented his version of Hellin's law, Hellin did not mention this fact. He only stated that, according to Strassmann, in Germany the number of single maternities per one twin maternity varies between 70 and 84. Today, one usually follows Strassmann and considers rates of multiple maternities with respect to all maternities. Although it seems that Strassmann noted the law before Hellin, Hellin's additional contribution was that he gave the law a general form.
Disposition
This text consists of the following parts. In the Methods section, the statistical formulae needed for the analyses are presented. In the Results, we give our analyses of the classical pre-Hellin data sets. In addition, in order to study recent data we also analyzed some data collected by our research team in earlier studies. After 1970, the TRR and the Hellin-transformed triplet rate (HRR) show excesses, but this is mainly caused by the influence of the artificial reproduction technologies (ARTs); in particular, the use of fertility-enhancing drugs. However, discrepancies in data obtained during the era of fertility treatments are of less interest when Hellin's law is considered because now no natural stochastic model is applicable (Eriksson & Fellman, Reference Eriksson and Fellman2007).
Here, we particularly consider how the association between TWR and TRR varies in time series. According to Hellin's law, one can study the fundamental relation between TWR and TRR. This should follow a parabolic model. However, linear models are easier to analyze, and therefore one can study the association between TWR and
$HRR = \sqrt {TRR} $
. Jenkins (Reference Jenkins1927) studied the linear association between TRR and TWR
2. However, we assume that TWR is more exact and prefer to keep TWR untransformed. In the Discussion section, we present results concerning Hellin's law in the literature and give our comments and alternative analyses.
Methods
A problem hindering the discussion of Hellin's law is that the law is a mathematical rule concerning theoretical rates, but all checks of the law are based on empirically obtained rates, and no exact proof to support the law can be obtained. In fact, one can only determine whether the inconsistencies are too large or not explained by random errors. Fellman and Eriksson (Reference Fellman and Eriksson2009b) gave a detailed presentation of the statistical analyses of Hellin's law. The central formulae are offered below.
Let the theoretical TRR be r. In studying the random errors of the obtained TRR, and particularly of the square root of the TRR, there are two possibilities. The first is to estimate the standard deviation (SD) of the TRR and construct a confidence interval (CI) for r. The square root is a monotone-increasing function, and consequently, one can construct the CI for
$\sqrt r $
by a square root transformation of the limits of the CI for r.
Let the observed TRR be
$\hat{r}$
, Then
$S{D_{\hat{r}}} = \sqrt {\frac{{r(1 - r)}}{n}} $
and the standard CI of r is
$$\begin{equation}
\left( {\hat{r} - k\sqrt {\frac{{\hat{r}(1 - \hat{r})}}{n}} ,\quad \hat{r} + k\sqrt {\frac{{\hat{r}(1 - \hat{r})}}{n}} } \right),
\end{equation}$$
where the factor k defines the confidence level. Hence, for
$\sqrt r $
the corresponding transformed CI is
$$\begin{equation}
\left( {\sqrt {\hat{r} - k\sqrt {\frac{{\hat{r}(1 - \hat{r})}}{n}} } ,\quad \sqrt {\hat{r} + k\sqrt {\frac{{\hat{r}(1 - \hat{r})}}{n}} } } \right).
\end{equation}$$
The second is to estimate the SD of
$\sqrt {\hat{r}} $
and to use it in order to obtain the CI for
$\sqrt r $
. If we use the general approximate formula
$Var( {f(z)} ) \approx {( {\frac{{df}}{{dz}}} )^2}Var(z)$
, we obtain (Fellman & Eriksson, Reference Fellman and Eriksson2004)
$$\begin{equation}
Var\left( {\sqrt {\hat{r}} } \right) \approx {\left( {\frac{1}{{2\sqrt r }}} \right)^2}Var(\hat{r}) = \frac{1}{{4r}}\frac{{r(1 - r)}}{n} = \frac{{1 - r}}{{4n}}
\end{equation}$$
and
$S{D_{\sqrt {\hat{r}} }} \approx \sqrt {\frac{{1 - r}}{{4n}}} $
. Now, the alternative CI for
$\sqrt r $
is
$$\begin{equation}
\left( {\sqrt {\hat{r}} - k\sqrt {\frac{{1 - \hat{r}}}{{4n}}} ,\quad \sqrt {\hat{r}} + k\sqrt {\frac{{1 - \hat{r}}}{{4n}}} } \right).
\end{equation}$$
Although formula (3) is only an approximate one, Fellman and Eriksson (Reference Fellman and Eriksson2009b) proved that for large data sets the difference between the alternative CIs (2) and (4) is minute and both CIs are good alternatives. In the empirical analyses, we use the standard CI for TWR and the CI (2) for HRR.
Results
Pre-Hellin Data
We start with the application of our CI formulae presented in the Method section on the Spengler and the Veit data given in Tables 1 and 2. We present in Figure 1 the temporal trend for the Mecklenburg–Schwerin data. One observes that compared with Hellin's law there is a slight deficit in HRR. However, according to the broad confidence band of HRR, this deficit is almost negligible.
Figure 2 shows the temporal trends in TWR and HRR obtained from the Veit (Reference Veit1855) data. The confidence band of HRR indicates that TWR and HRR show good agreement for the whole period.
FIGURE 2 Temporal trends in twinning rate (TWR) and Hellin-transformed triplet rate (HRR) in Prussia, 1826–1849. The confidence band of HRR indicates a good agreement between TWR and HRR.
Temporal Trends
In Figure 3a–d, we present the temporal trends of TWR and HRR in Sweden (1754–2000), in the Netherlands (1950–2003), in England and Wales (1938–2003), and in Portugal (1930–2011). The Portuguese data were from Fuster et al. (Reference Fuster, Santos, Roman-Busto and Manuel Magalhaes2013). Figure 3a and b includes 95% CI bands for HRR. During the 20th century, the populations show a similar temporal pattern. It can be seen that up to 1870 in Sweden the TWR and HRR rates are comparable, while between 1871 and 1970 the TWR is superior. The excess after 1970 is mainly caused by the influence of ARTs, particularly the use of fertility-enhancing drugs, this being more marked for TRR than for TWR. When Hellin's law is considered, discrepancies in data obtained during the era of fertility treatments are of less interest because now no natural stochastic model is applicable (Eriksson & Fellman, Reference Eriksson and Fellman2007). Consequently, one should compare the rates of the multiple maternities and analyze Hellin's law only for data before the 1970s.
FIGURE 3 Temporal variation in twinning rate (TWR) and Hellin-transformed TRR (HRR). Sweden (1754–2000) is presented in (a) the Netherlands (1950–2003) in (b) England and Wales (1938–2003) in (c) and Portugal (1930–2011) in (d).
Discrepancies in the Linearity of Hellin's Law
Following Jenkins (Reference Jenkins1927, Reference Jenkins1929) and Jenkins and Gwin (Reference Jenkins and Gwin1940), we studied the association between HRR and TWR. Our opinion is that the best model is obtained when HRR is a linear function of TWR. The association between the TWR and the HRR is based on the different populations presented in Figure 3. We assume models without intercepts and consider the model HRR = βTWR. The parameter value indicates when the HRR shows an excess or deficit relative to TWR. Hellin's law holds if the parameter β = 1. If β < 1 then there is a deficit of triplet sets and if β > 1 there is an excess of triplet sets. For all populations in Figure 3, there is a slight shortage of HRR during the medium period and an excess during the last periods. The results are given in Table 3.
TABLE 3 Association Between TWR and HRR in the Time Series Presented in Figure 3
Alternative models
In the literature, there have been several attempts to improve Hellin's law. Allen and Firschein (Reference Allen and Firschein1957) first gave a theoretical argument for the law and went on to modify it. Their initial argument for the law was that it is a mean of a stochastic model for DZ rates. If the probability for an extra ovulation, yielding a twin set, is p, the probability for two extras, yielding a triplet maternity, is p 2, and so on. They stated that the agreement of Hellin's law with birth statistics is not entirely coincidental and that it fits data partly because of underlying truth and partly because its two major defects tend to cancel each other. They improved the formula to include both monozygotic and multizygotic maternities. However, the obtained expected frequencies were not in concordance with the observed ones (Fellman & Eriksson, Reference Fellman and Eriksson2009a).
Allen (Reference Allen1960) proposed one method based on the zygosity of the twin pairs and the triplet sets. Bulmer (Reference Bulmer1970) later discussed this method, which requires information about the sexes of the twin pairs and the triplet sets. Let the monozygotic TWR be M and the dizygotic be D. According to the Allen-Bulmer model, the improved Hellin's formula is R = k 1 M 2 + 2MD + k 3 D2 , where R is the TRR. For k 1 = k 3 = 1, Hellin's law is obtained. Based on empirical data, the factors k 1 and k 3 should be estimated by the formulae
$$\begin{eqnarray*}
{k_{1}} = \frac{{\rm total\,number\,of\,monozygotic\,twins}}{{\sum {{N_{i}}M_{i}^{2}} }}
\end{eqnarray*}$$
and
$$\begin{eqnarray*}
{k_{3}} = \frac{{\rm total\,number\,of\,dizygotic\,twins}}{{\sum {{N_i}D_i^2} }}.
\end{eqnarray*}$$
Using data from England and Wales, the United States and Italy, Bulmer (Reference Bulmer1970) obtained the empirical formula for HRRAB R = 1.36M 2 + 2MD + 0.47D 2. This formula can be written
$$\begin{eqnarray*}
R &=& 1.36{M^2} + 2MD + 0.47{D^2} = {M^2} + 2MD + {D^2} \\
&&+\, 0.36{M^2} - 0.53{D^2} = {(M + D)^2} + 0.36{M^2}\\
&&-\, 0.53{D^2} = {W^2} + 0.36{M^2} - 0.53{D^2}.
\end{eqnarray*}$$
With respect to Hellin's law, the correction is 0.36M2 –0.53D2 . This is negative if D ≥ 0.82 M. The dizygotic rate D is almost always greater than the monozygotic rate M, and consequently, a deficit in the triplet rate in comparison with Hellin's law is common. Fellman and Eriksson (Reference Fellman and Eriksson2004) studied multiple maternities in Sweden for the period 1869–1878 (Berg, Reference Berg1880) and, in addition, decade data for the period 1901–1960. They followed Allen and Bulmer when they studied multiple maternities for the period 1869–1960 in Sweden. They applied Weinberg's law and obtained the dizygotic (D) and monozygotic (M) twinning rates. Numerically, they obtained the estimated model HRRFE = 1.39M 2 + 2MD + 0.44D 2. The parameter estimates differed only slightly from Bulmer's, and they observed also that their parameters satisfy the conditions k 1 > 1 and k 3 < 1. According to their formula, a deficit of triplet sets compared with Hellin's law is obtained if D ≥ 0.84M. In fact, according to the data analyzed, D ≈ 2.89M and the deficit is obvious. The results are presented graphically in Figure 4. This figure includes the TWR and the HRR estimated according to Hellin's law, Bulmer's model and the Fellman–Eriksson model.
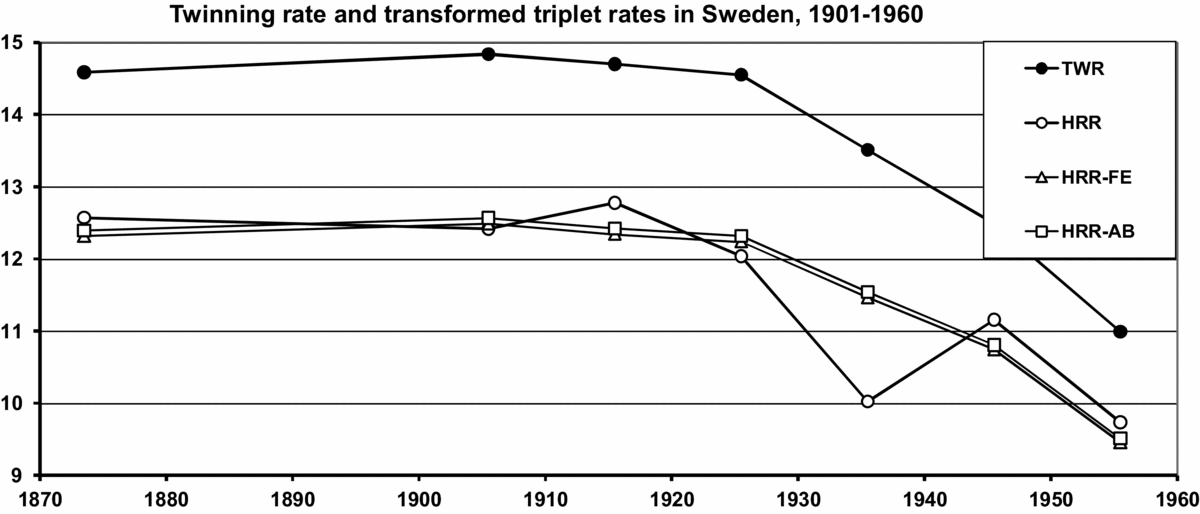
FIGURE 4 TWR and the transformed triplet rates: the Hellin-transformed TRR (HRR), the Allen–Bulmer model HRR AB and the Fellman–Eriksson model HRRFE (Fellman & Eriksson, Reference Fellman and Eriksson2004).
Discussion
Our intention here was not to give an exhaustive list of publications, but to present such papers where pre-Hellin authors provided data suitable for Hellin's law and where post-Hellin authors analyzed and commented on the strengths and weaknesses of the law. The interest in Hellin's law is mainly a result of its being approximately correct, but showing discrepancies that are difficult to explain and/or eliminate.
It is a common agreement that the main argument for Hellin's law is that the probabilities of additional ovulations and the fissions of fertilized eggs can be explained by stochastic models (see, e.g., Allen & Firschein, Reference Allen and Firschein1957; Fellman, Reference Fellman2017; Fellman & Eriksson, Reference Fellman and Eriksson2009a; Jenkins, Reference Jenkins1927; Reference Jenkins1929; Jenkins & Gwin, Reference Jenkins and Gwin1940; Zeleny, Reference Zeleny1921). Consequently, in large data sets, the averages could be stable and formulated by a mathematical relation (Hellin's law). In a short note, Zeleny (Reference Zeleny1921) discussed Hellin's law. He stated that from the statistical relations it would appear that triplets are produced by the coincidence of two independent processes occurring with equal frequencies. One of these processes by itself gives rise to twins. This relation would apply to any mode of origin of multiple births or to different combinations of these provided that each followed the rule. In fact, he considered the Strassmann version, where the rates are related to the total number of maternities. He also referred to the Veit (Reference Veit1855) data and found startlingly good agreement with the law. His analyses yielded him the honor by which some authors later renamed the law the Hellin-Zeleny law.
The arguments for the discrepancies are that after the fertilizations there is a long process influenced by disturbing factors. For instance, Jenkins (Reference Jenkins1927) and Komai and Fukuoka (Reference Komai and Fukuoka1936) assumed that differential mortality of twins and triplets in utero could be one such disturbing factor. Consequently, the final result shows only a weak resemblance to the outcome of a stochastic process. This seems to be the main cause of the discrepancies between Hellin's law and empirical findings. Fellman and Eriksson (Reference Fellman and Eriksson1993) gave a mathematical proof that Hellin's law cannot hold as a general rule. However, it is still of special interest to obtain and explain a surplus or deficit in the rates of higher multiple maternities when Hellin's law is used as a benchmark.
Jenkins (Reference Jenkins1927) stated that Hellin's law should be considered as a first approximation. He based his own model on the rates of monozygotic (MZ) and dizygotic (DZ) twinning. The rate of DZ twinning is strongly dependent on maternal age, and consequently he stressed that the relation between TWR and TRR should hold only for age-specific rates. Therefore, he assumed that the age-specific TRRs are the squared age-specific TWRs. Consequently, for the total TRR he obtained the formula
$$\begin{equation}
TRR = \frac{1}{n}{\sum\limits_i {\left( {TW{R_i}} \right)} ^2}{n_i},
\end{equation}$$
where ni
is the number of mothers in age group number i and n is the total number of mothers. His stochastic model indicated at least that Hellin's law holds approximately within maternal age groups, but for the total rates, Hellin's law does not hold. Discrepancies within a maternal age group he ascribed to differential mortality of twins and triplets in utero. In addition, Jenkins stated that the proposed model did not give the correct proportion of same-sex and opposite-sex triplet sets. Later, Jenkins (Reference Jenkins1929) returned to the model and gave some suggestions on how it could be improved. Jenkins and Gwin (Reference Jenkins and Gwin1940) attempted a rigorous treatment of the live-births statistics with the classification of the data according to the age groups of the mothers. The rule so derived deviated markedly from Hellin's law. They considered U.S. data for the periods 1923–1924 and 1927–1936. Partly missing stillbirths caused them some problems. They presented U.S. data in a graph with TWR2
as abscissa and TRR as ordinate. If Hellin's law holds, this curve should be linear. The same can be said if the graph has TWR as abscissa and
$\sqrt {TRR} $
as ordinate. As an alternative, Jenkins (Reference Jenkins1927) presented TRR as a function of TWR. According to Hellin's law, this curve is a parabola. However, graphs containing linear curves are easier to interpret.
In his monograph concerning twinning, Dahlberg (Reference Dahlberg1926) gave only short comments concerning triplet rates and Hellin's law. He presented twin and triplet data from Finland (1878–1916) grouped according to maternal age. Jenkins and Gwin (Reference Jenkins and Gwin1940) used Dahlberg's data for Finland (1878–1916), but they did not include the extreme TRR for the age group 45+ in their analyses. Fellman and Eriksson (Reference Fellman and Eriksson2009b) used Finnish official registers and confirmed the view that Dahlberg's data contained a misprint. Hence, in their alternative analyses, Fellman and Eriksson used the corrected data.
Sarkar (Reference Sarkar1945) studied the TWR in India and Ceylon (Sri Lanka). Sarkar's study is based on hospital data. This situation reduces the relevance of the study, a fact that Sarkar recognized. However, in connection with this study his paper is interesting because he defined the TWR as 1:n and the triplet rate as 1:m2 , that is, he indirectly used a modified Hellin's law without any reference to Hellin. In analyzing his results, one finds a deficit of triplet maternities (m > n). In addition, it is observed that in Ceylon the TWR was low (1:161.1), yielding the TWR 6.21 per 1,000. In Ceylon, the TRR followed Hellin's law more exactly because it was 1:154.42 . The Ceylon findings must be considered consistent because the total number of maternities was as high as 1,620,077.
In his study of the rates of multiple maternities for total ‘white’ and ‘colored’ in U.S. populations (1922–1936), Strandskov (Reference Strandskov1945) evaluated how well his data satisfied Hellin's law. Applying χ 2 tests, he found that in none of the three populations tested did the observed plural birth frequencies agree closely with Hellin's law.
Jenkins (Reference Jenkins1927; Reference Jenkins1929), Jenkins and Gwin (Reference Jenkins and Gwin1940), Allen (Reference Allen1960), Bulmer (Reference Bulmer1970), and later Fellman and Eriksson (Reference Fellman and Eriksson2004) have tried to modify the law in order to improve it. These attempts are presented in Figure 4. It can be seen that the models HRR, HRRAB and HRRFE are rather consistent and too low with respect to Hellin's law. Consequently, the attempts have not improved the TWR models.
One application of Hellin's law is comparisons between TWR and HRR, that is, the square root of TRR, the cubic root of quadruplet rates (QUR), and so on (Fellman & Eriksson, Reference Fellman and Eriksson2006). Fellman and Eriksson (Reference Fellman and Eriksson2004) considered the correlation between the TWR and HRR in Sweden. After elimination of temporal factors, they found that the correlation was positive, but not very strong. These findings indicate that Hellin's law cannot be considered exact. In fact, Hellin's law presupposes strong correlations, but even strong correlations do not prove Hellin's law.
Inspired by the results given by Zeleny, Greulich (Reference Greulich1930) analyzed the association between the TWR, TRR and QUR. Greulich refers only to Zeleny and never to Hellin. He starts with data given by Veit (Reference Veit1855), Guzzoni (1889), and Arey (Reference Arey1925). He observed good agreement between the TWR and TRR, but Veit's data for QUR differs markedly. Starting with these findings, he introduced a large project. He collected data from 21 different countries and built his analyses on these data. Despite large variations in the rates obtained for the different countries, he noted a close approach to Zeleny's law. He closed his study with the statement that if Zeleny's hypothesis has any basis in fact it must of necessity apply to conceptions and not to confinements.
Peller (Reference Peller1946) stressed that the deviation of the actual figures from expectation must not obscure the fact that Hellin's law comes pretty close to reality. Neither should the rule be condemned just because it cannot be explained. On the contrary, attempts should be made at correction and explanation. Peller based his study on models that he constructed for recurrent multiple maternities within sibships. As an application of this model, he obtained an alternative rule for the relationship between the numbers of twin sets and sets of higher multiple maternities. Although his starting point was different, the formulae obtained differed only slightly from Hellin's law. Peller was the first, at least indirectly, to connect Hellin's law to inter-individual variation in the chances for multiple maternities among mothers. Later, Eriksson (1973) considered recurrent twin maternities and gave a modified model. When he applied his model on family series for Åland (Finland), he obtained better congruence with Hellin's law than with Peller's formulae (Fellman & Eriksson, Reference Fellman and Eriksson2009b).
Das (Reference Das1953) formulated Hellin's law such that ‘the frequency of twin confinements bears to that of total confinements a ratio which is equal to the ratio borne by the frequency of the triplet confinements to that of the twin confinements’. This modified definition is in congruence with Strassmann's version of the law. He reviewed of earlier studies concerning Hellin's law and stressed the discrepancies presented in them. Furthermore, he considered data for more than 300 million births and showed that Hellin's law was inexact for triplets and does not hold for quintuplets. Consequently, Das concluded that Hellin's law has no sound basis and that exceptions to the rule have been the rule. In a later paper, Das (Reference Das1955) developed his model for the frequencies of twins and higher multiple maternities. Based on this theory, he also considered the relation TRR = (TWR)2. His mathematical analyses of the model did not support Hellin's law (Fellman & Eriksson, Reference Fellman and Eriksson2009a).
Fellman and Eriksson (Reference Fellman and Eriksson1993) gave a mathematical proof that Hellin's law cannot hold in general. If one aggregates heterogeneous data, the fluctuations are smoothed out, but the relation between the TWR and the TRR is not linear, and consequently, the aggregated and the disaggregated data cannot simultaneously satisfy Hellin's law. Jenkins (Reference Jenkins1927) noted that Hellin's law can be assumed only for disaggregated data and that the discrepancy between Hellin's law and the observed aggregated data demands the use of his formula. In fact, Jenkins’ formula coincides mathematically with the integral proposed by Fellman and Eriksson (Reference Fellman and Eriksson1993). However, Jenkins did not explain the disagreement between Hellin's law for aggregated and disaggregated data. Fellman (Reference Fellman2017) studied the seasonality of multiple maternities and applied Hellin's law to compare the seasonality of twin and triplet rates. The triplet sets are very rare and consequently suitable data containing sufficiently large sets for statistical analyses of monthly triplet births are difficult to obtain (Elster & Bleyl, Reference Elster and Bleyl1991; James, Reference James1980).
The history of the studies of Hellin's law shows a long series of attempts in order to reduce discrepancies between the observed data and Hellin's law. Some studies give improved results, but some cannot eliminate obtained discrepancies in the data. In conclusion, one can note that every ‘improved’ model has the same weakness as Hellin's law. The models are mathematically exact, but the analyses are based on empirical data. Hence, the question remains, are the improvements general or do they depend on the specific data considered?
Acknowledgments
We are grateful to the personnel at the National Library of Health Sciences at the University of Helsinki (Terkko) for providing us ― my late friend and colleague Aldur W. Eriksson and myself ― with copies of old publications concerning twin studies in the 19th century, which are otherwise difficult to obtain.
