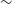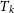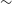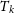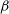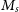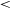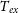1. Introduction
Star formation is one of the fundamental processes in the cosmos. Stars are born in dense cold places called cloud cores. Cores are classified as prestellar or protostellar depending on whether they contain an embedded protostar. Along with gravity, other effects like turbulence, magnetic field, rotation, and temperature form a complex enviornment prior to the star formation (Barranco & Goodman, Reference Barranco and Goodman1998; Kudoh & Basu, Reference Kudoh and Basu2014; Dunham et al., Reference Dunham, Offner and Pineda2016; André, Reference André2017; Dobashi et al., Reference Dobashi, Shimoikura and Nakamura2018; Caselli et al., Reference Caselli, Pineda and Zhao2019; Koley & Roy, Reference Koley and Roy2019; Dobashi et al., Reference Dobashi, Shimoikura and Ochiai2019; Tokuda et al., Reference Tokuda, Fujishiro and Tachihara2020; Sahu et al., Reference Sahu, Liu and Liu2021; Koley et al., Reference Koley, Roy and Menten2021, Reference Koley, Roy, Momjian, Sarma and Datta2022; Koley, Reference Koley2023). Therefore, studying these quantities are very much essential for a complete understanding of the star formation process. Dust continuum emission provides the line-of-sight averaged temperature of the core (Schnee et al., Reference Schnee, Enoch and Noriega-Crespo2010). Apart from that, ammonia molecule is also used to probe the temperature of the molecular cloud; hence it is often called an “interstellar thermometer”. Ammonia molecule exhibits several hyperfine lines. Here, due to the several well-separated lines, measurements of essential parameters like excitation temperature (
![]() $T_{ex}$
), kinetic temperature (
$T_{ex}$
), kinetic temperature (
![]() $T_{k}$
), optical depth (
$T_{k}$
), optical depth (
![]() $\tau$
), column density (N), etc., have been possible (Walmsley & Ungerechts, Reference Walmsley and Ungerechts1983; Mangum & Shirley, Reference Mangum and Shirley2015). In addition to these parameters, if one assumes that the non-thermal broadening is caused due to turbulence, then from this spectral study, turbulence measurement is also possible; in particular, about the nature of the turbulence and its scale-dependent behaviour. For several decades, temperature measurements have been carried out using ammonia molecules in low- and high-mass prestellar cores and star-forming regions, both from single-dish and from interferometric telescopes (Barranco & Goodman, Reference Barranco and Goodman1998; Pillai et al., Reference Pillai, Wyrowski, Carey and Menten2006; Dirienzo et al., Reference Dirienzo, Brogan and Indebetouw2015; Krieger et al., Reference Krieger, Ott and Beuther2017). Although from several studies, it has been argued that in interferometric telescopes a significant amount of flux is resolved out in the prestellar cores (Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Roy et al., Reference Roy, Datta, Momjian and Sarma2011; Koley, Reference Koley2022); for tracing the internal cold dense structures, interferometric observations are generally more effective than single-dish studies (Barranco & Goodman, Reference Barranco and Goodman1998; Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Dobashi et al., Reference Dobashi, Shimoikura and Nakamura2018; Tokuda et al., Reference Tokuda, Fujishiro and Tachihara2020; Sahu et al., Reference Sahu, Liu and Liu2021).
$\tau$
), column density (N), etc., have been possible (Walmsley & Ungerechts, Reference Walmsley and Ungerechts1983; Mangum & Shirley, Reference Mangum and Shirley2015). In addition to these parameters, if one assumes that the non-thermal broadening is caused due to turbulence, then from this spectral study, turbulence measurement is also possible; in particular, about the nature of the turbulence and its scale-dependent behaviour. For several decades, temperature measurements have been carried out using ammonia molecules in low- and high-mass prestellar cores and star-forming regions, both from single-dish and from interferometric telescopes (Barranco & Goodman, Reference Barranco and Goodman1998; Pillai et al., Reference Pillai, Wyrowski, Carey and Menten2006; Dirienzo et al., Reference Dirienzo, Brogan and Indebetouw2015; Krieger et al., Reference Krieger, Ott and Beuther2017). Although from several studies, it has been argued that in interferometric telescopes a significant amount of flux is resolved out in the prestellar cores (Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Roy et al., Reference Roy, Datta, Momjian and Sarma2011; Koley, Reference Koley2022); for tracing the internal cold dense structures, interferometric observations are generally more effective than single-dish studies (Barranco & Goodman, Reference Barranco and Goodman1998; Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Dobashi et al., Reference Dobashi, Shimoikura and Nakamura2018; Tokuda et al., Reference Tokuda, Fujishiro and Tachihara2020; Sahu et al., Reference Sahu, Liu and Liu2021).
In this work, we study the internal structures of the central region of L1517B core with the Jansky Very Large Array (VLA) radio telescope. This core was observed previously with several single-dish telescopes using different molecules (Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a; Chitsazzadeh, Reference Chitsazzadeh2014; Megías et al., Reference Megías, Jiménez-Serra and Marítn-Pintado2023), where the field of view was larger than our study. Here, we particularly concentrate on the central dense region of the core using the high spatial resolution interferometric telescope.
In Section 2, we present the observation and data analysis of our work. In Section 3, we mention the ammonia line fitting using pyspeckit code (Ginsburg & Mirocha, Reference Ginsburg and Mirocha2011). In Section 4, we discuss the main results. At last, in Section 5, we summarise our main findings.
2. Observation and data analysis
All the observational data were taken from the VLA archival data centre. These observations were carried out in 2013 from March 20 to 26 over three observing sessions using the VLA D configuration in the K band (proposal id: VLA-13A/394). Right ascension (R.A.) and declination (Dec.) of the pointing centre is
![]() $04{^{\rm h}} 55{^{\rm m}} 18.00^{s}\;$
and
$04{^{\rm h}} 55{^{\rm m}} 18.00^{s}\;$
and
![]() $\;+30{^\circ} 37^{\prime} 46.99{''}$
, respectively (epoch J2000). The primary objective of this study is to analyse the internal structures of the central region of the core using NH
$\;+30{^\circ} 37^{\prime} 46.99{''}$
, respectively (epoch J2000). The primary objective of this study is to analyse the internal structures of the central region of the core using NH
![]() $_{3}$
(J, K = 1,1 and 2,2) spectral lines. Rest frequencies of these lines are 23.69449550 GHz and 23.722633600 GHz, respectively. The bandpass calibrator was 3C48 (0137 + 331) for this observation, whereas J0414 + 3418 was used as a phase calibrator. Channel resolution was
$_{3}$
(J, K = 1,1 and 2,2) spectral lines. Rest frequencies of these lines are 23.69449550 GHz and 23.722633600 GHz, respectively. The bandpass calibrator was 3C48 (0137 + 331) for this observation, whereas J0414 + 3418 was used as a phase calibrator. Channel resolution was
![]() $\sim$
3.906 kHz (
$\sim$
3.906 kHz (
![]() $\sim$
0.049 km sec
$\sim$
0.049 km sec
![]() $^{-1}$
) with a total number of channels was 2048. For every 4 min 24 s of source observation, phase calibrator, J0414 + 3418 was observed for almost 1 minute 45 s. In each observing session, bandpass calibrator, 3C48 was observed for
$^{-1}$
) with a total number of channels was 2048. For every 4 min 24 s of source observation, phase calibrator, J0414 + 3418 was observed for almost 1 minute 45 s. In each observing session, bandpass calibrator, 3C48 was observed for
![]() $\sim$
9 min 54 s. After observing almost 5 h and 18 min on the source, the achieved RMS noise was
$\sim$
9 min 54 s. After observing almost 5 h and 18 min on the source, the achieved RMS noise was
![]() $\sim$
2 mJy beam
$\sim$
2 mJy beam
![]() $^{-1}$
. This value of RMS noise represents the RMS noise per channel. Initial flagging and calibration were done using the scripted Common Astronomy Software Applications (CASA) pipeline (scripted pipeline version 1.4.2) of the National Radio Astronomy Observatory (NRAO)Footnote
1
. Additional flagging was needed due to the bad amplitude gain of a few antennas. We would like to emphasise that we have not done the hanning smoothing of the UV data while calibrating using the scripted pipeline. With the calibrated data produced by the pipeline, we performed the cleaning with the CASA task TCLEAN (CASA version 5.3.0). Please note that, we ran it separately for the NH
$^{-1}$
. This value of RMS noise represents the RMS noise per channel. Initial flagging and calibration were done using the scripted Common Astronomy Software Applications (CASA) pipeline (scripted pipeline version 1.4.2) of the National Radio Astronomy Observatory (NRAO)Footnote
1
. Additional flagging was needed due to the bad amplitude gain of a few antennas. We would like to emphasise that we have not done the hanning smoothing of the UV data while calibrating using the scripted pipeline. With the calibrated data produced by the pipeline, we performed the cleaning with the CASA task TCLEAN (CASA version 5.3.0). Please note that, we ran it separately for the NH
![]() $_{3}$
(J, K = 1,1) and NH
$_{3}$
(J, K = 1,1) and NH
![]() $_{3}$
(J, K = 2,2) lines. Here, we used the deconvolver “multiscale” with the scales 3.2′′, 6.4′′, 12.8′′, 25.6′′, and 51.2′′, respectively, to pick up all the structures. We used the robust parameter, ROBUST = + 2 for natural weighting. The synthesised beam that is convolved with the clean components is
$_{3}$
(J, K = 2,2) lines. Here, we used the deconvolver “multiscale” with the scales 3.2′′, 6.4′′, 12.8′′, 25.6′′, and 51.2′′, respectively, to pick up all the structures. We used the robust parameter, ROBUST = + 2 for natural weighting. The synthesised beam that is convolved with the clean components is
![]() $\sim$
4.01′′
$\sim$
4.01′′
![]() $\times$
3.37′′ with a position angle of + 52.02
$\times$
3.37′′ with a position angle of + 52.02
![]() ${^\circ}$
. Final image cubes (both for 1,1 and 2,2 lines) produced after cleaning are used to study the core using the simultaneous fitting of these lines. Here we would like to point out that due to the use of interferometric-only observations, our data are lacking a contribution from extended NH
${^\circ}$
. Final image cubes (both for 1,1 and 2,2 lines) produced after cleaning are used to study the core using the simultaneous fitting of these lines. Here we would like to point out that due to the use of interferometric-only observations, our data are lacking a contribution from extended NH
![]() $_{3}$
emissions. This effect may affect the determination of parameters that depend on the absolute intensity of the lines, such as the column density of NH
$_{3}$
emissions. This effect may affect the determination of parameters that depend on the absolute intensity of the lines, such as the column density of NH
![]() $_{3}$
. However, it may be less severe for parameters that are dependent on the line ratio, such as the kinetic temperature (
$_{3}$
. However, it may be less severe for parameters that are dependent on the line ratio, such as the kinetic temperature (
![]() $T_{k}$
) of the gas.
$T_{k}$
) of the gas.
3. Line fitting
For fitting the NH
![]() $_{3}$
(J, K = 1,1) and NH
$_{3}$
(J, K = 1,1) and NH
![]() $_{3}$
(J, K = 2,2) lines and in turn obtaining different useful informations mentioned earlier, we use the pyspeckit code (Ginsburg & Mirocha, Reference Ginsburg and Mirocha2011). This code is based on the nonlinear gradient descent algorithm (MPFIT, Markwardt (Reference Markwardt, Bohlender, Durand and Dowler2009)), where various useful parameters are obtained after comparing the simulated and observed brightness temperature (
$_{3}$
(J, K = 2,2) lines and in turn obtaining different useful informations mentioned earlier, we use the pyspeckit code (Ginsburg & Mirocha, Reference Ginsburg and Mirocha2011). This code is based on the nonlinear gradient descent algorithm (MPFIT, Markwardt (Reference Markwardt, Bohlender, Durand and Dowler2009)), where various useful parameters are obtained after comparing the simulated and observed brightness temperature (
![]() $T_{B}$
) of the lines. For a detailed discussion regarding the fitting, we refer the study of Friesen et al. (Reference Friesen and Pineda2017). Initial guesses in terms of kinetic (
$T_{B}$
) of the lines. For a detailed discussion regarding the fitting, we refer the study of Friesen et al. (Reference Friesen and Pineda2017). Initial guesses in terms of kinetic (
![]() $T_{k}$
) or rotational temperature (
$T_{k}$
) or rotational temperature (
![]() $T_{rot}$
), excitation temperature (
$T_{rot}$
), excitation temperature (
![]() $T_{ex}$
), para column density (
$T_{ex}$
), para column density (
![]() $N_{para}$
), ortho ratio (
$N_{para}$
), ortho ratio (
![]() $F_{ortho}$
), centre velocity (
$F_{ortho}$
), centre velocity (
![]() $v_{c}$
), and the velocity dispersion (
$v_{c}$
), and the velocity dispersion (
![]() $\sigma_{total}$
) of the line have to be put in the fitting. As the line modelling crucially depends on the centre velocity (
$\sigma_{total}$
) of the line have to be put in the fitting. As the line modelling crucially depends on the centre velocity (
![]() $v_{c}$
), its initial guess has been calculated from the moment map of the cube before the fitting. We note that the final results do not alter as long as the initial parameters are within a reliable range. We would also like to point out that we took only those pixels where the signal-to-noise ratio (SNR) of the NH
$v_{c}$
), its initial guess has been calculated from the moment map of the cube before the fitting. We note that the final results do not alter as long as the initial parameters are within a reliable range. We would also like to point out that we took only those pixels where the signal-to-noise ratio (SNR) of the NH
![]() $_{3}$
(1,1) emission is greater than 5.5. In the modelling, it is assumed that
$_{3}$
(1,1) emission is greater than 5.5. In the modelling, it is assumed that
![]() $T_{ex}$
is the same for both (1,1) and (2,2) lines. Out of different types of fitters, we use the fittype = ′
cold
$T_{ex}$
is the same for both (1,1) and (2,2) lines. Out of different types of fitters, we use the fittype = ′
cold
![]() $\_$
ammonia
′, which makes the assumption that for typically low temperature in the prestellar cores, only (1,1), (2,2), and (2,1) lines of para-NH
$\_$
ammonia
′, which makes the assumption that for typically low temperature in the prestellar cores, only (1,1), (2,2), and (2,1) lines of para-NH
![]() $_{3}$
are occupied (Krieger et al., Reference Krieger, Ott and Beuther2017; Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). It is also assumed that the ortho-to-para ratio of ammonia is 1. This code fits pixel-wise spectra and finally forms a cube, where various fitted parameters and their associated errors are stored in different planes, which are further used for detailed analysing the core. For a detailed understanding of the different energy levels of NH
$_{3}$
are occupied (Krieger et al., Reference Krieger, Ott and Beuther2017; Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). It is also assumed that the ortho-to-para ratio of ammonia is 1. This code fits pixel-wise spectra and finally forms a cube, where various fitted parameters and their associated errors are stored in different planes, which are further used for detailed analysing the core. For a detailed understanding of the different energy levels of NH
![]() $_{3}$
lines, we refer the works of Walmsley & Ungerechts (Reference Walmsley and Ungerechts1983) and Mangum & Shirley (Reference Mangum and Shirley2015).
$_{3}$
lines, we refer the works of Walmsley & Ungerechts (Reference Walmsley and Ungerechts1983) and Mangum & Shirley (Reference Mangum and Shirley2015).
4. Results
4.1. Integrated intensity emission & column density
Left panel of Figure 1 shows the overplot of integrated intensity map of NH
![]() $_{3}$
(1,1) emission both in colour and contour plots. Likewise, the right panel of Figure 1 shows the overplot of integrated intensity map of NH
$_{3}$
(1,1) emission both in colour and contour plots. Likewise, the right panel of Figure 1 shows the overplot of integrated intensity map of NH
![]() $_{3}$
(2,2) emission both in colour and contour plots. Based on these figures, it is apparent that NH
$_{3}$
(2,2) emission both in colour and contour plots. Based on these figures, it is apparent that NH
![]() $_{3}$
(2,2) emission is less spread than NH
$_{3}$
(2,2) emission is less spread than NH
![]() $_{3}$
(1,1) emission. This is supported by the previous single-dish observation of this core (Chitsazzadeh, Reference Chitsazzadeh2014). From these figures, it is also noticeable that NH
$_{3}$
(1,1) emission. This is supported by the previous single-dish observation of this core (Chitsazzadeh, Reference Chitsazzadeh2014). From these figures, it is also noticeable that NH
![]() $_{3}$
(1,1) and (2,2) emissions are centrally concentrated, but the peak positions of the integrated intensity maps have a slight offset compared to the dust and H
$_{3}$
(1,1) and (2,2) emissions are centrally concentrated, but the peak positions of the integrated intensity maps have a slight offset compared to the dust and H
![]() $_{2}$
column density maps where the peaks of them are identical (Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a; Megías et al., Reference Megías, Jiménez-Serra and Marítn-Pintado2023). The location of the dust peak is
$_{2}$
column density maps where the peaks of them are identical (Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a; Megías et al., Reference Megías, Jiménez-Serra and Marítn-Pintado2023). The location of the dust peak is
![]() $04{^{\rm h}} 55{^{\rm m}} 17.60^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 17.60^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 44.00{''}$
, whereas the peaks of the NH
$\;+30{^\circ} 37^{\prime} 44.00{''}$
, whereas the peaks of the NH
![]() $_{3}$
(1,1) and (2,2) integrated intensity maps are
$_{3}$
(1,1) and (2,2) integrated intensity maps are
![]() $04{^{\rm h}} 55{^{\rm m}} 18.31^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 18.31^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 42.38{''}$
and
$\;+30{^\circ} 37^{\prime} 42.38{''}$
and
![]() $04{^{\rm h}} 55{^{\rm m}} 18.06^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 18.06^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 41.34{''}$
, respectively. It is interesting to note that, the central region of the core is close-to-round in shape, rather than a filament-like structure (Kauffmann et al., Reference Kauffmann, Bertoldi, Bourke and Evans2008; Dobashi et al., Reference Dobashi, Shimoikura and Nakamura2018). Since the shape of the central region of the core is round, an average of various essential parameters can be calculated over concentric circles to obtain the radially averaged profiles of the essential parameters. On the other hand, if the structure had elongated, an average would have to be performed over successive ellipses (with a fixed aspect ratio and position angle). From the line fitting using pyspeckit code, we obtain the column density map of ammonia emission in the L1517B core, which is shown in the left panel of Figure 2. Using this distribution, we obtain the radially averaged profile of column density in the core. Here, we would also like to point out that, we consider the peak position of the dust continuum emission as the centre of the core. This is because the peak of dust and the peak of H
$\;+30{^\circ} 37^{\prime} 41.34{''}$
, respectively. It is interesting to note that, the central region of the core is close-to-round in shape, rather than a filament-like structure (Kauffmann et al., Reference Kauffmann, Bertoldi, Bourke and Evans2008; Dobashi et al., Reference Dobashi, Shimoikura and Nakamura2018). Since the shape of the central region of the core is round, an average of various essential parameters can be calculated over concentric circles to obtain the radially averaged profiles of the essential parameters. On the other hand, if the structure had elongated, an average would have to be performed over successive ellipses (with a fixed aspect ratio and position angle). From the line fitting using pyspeckit code, we obtain the column density map of ammonia emission in the L1517B core, which is shown in the left panel of Figure 2. Using this distribution, we obtain the radially averaged profile of column density in the core. Here, we would also like to point out that, we consider the peak position of the dust continuum emission as the centre of the core. This is because the peak of dust and the peak of H
![]() $_{2}$
column density match well in this core (Megías et al., Reference Megías, Jiménez-Serra and Marítn-Pintado2023). And for converting the angular scale into the physical distance on the plane of the sky, we take 159 pc distance of the L1517B core (Galli et al., Reference Galli, Loinard and Bouy2019). Right panel of Figure 2 represents the radially averaged column density profile. From this figure, it indicates that the peak column density of NH
$_{2}$
column density match well in this core (Megías et al., Reference Megías, Jiménez-Serra and Marítn-Pintado2023). And for converting the angular scale into the physical distance on the plane of the sky, we take 159 pc distance of the L1517B core (Galli et al., Reference Galli, Loinard and Bouy2019). Right panel of Figure 2 represents the radially averaged column density profile. From this figure, it indicates that the peak column density of NH
![]() $_{3}$
is
$_{3}$
is
![]() $\sim$
10
$\sim$
10
![]() $^{15}$
cm
$^{15}$
cm
![]() $^{-2}$
and decreases towards the outer edge. We also note that the distance where the column density decreases by a factor of 2 of its peak value is at radius
$^{-2}$
and decreases towards the outer edge. We also note that the distance where the column density decreases by a factor of 2 of its peak value is at radius
![]() $\sim$
0.016 pc.
$\sim$
0.016 pc.

Figure 1. Left: Integrated intensity map of NH
![]() $_{3}$
(1,1) emission both in colour and contour plots (integrated over main and satellite lines). The contour levels are 0.30, 1.30, 2.30, 3.30, 4.30, 5.30, and 6.30 K.km sec
$_{3}$
(1,1) emission both in colour and contour plots (integrated over main and satellite lines). The contour levels are 0.30, 1.30, 2.30, 3.30, 4.30, 5.30, and 6.30 K.km sec
![]() $^{-1}$
, respectively. Right: Integrated intensity map of NH
$^{-1}$
, respectively. Right: Integrated intensity map of NH
![]() $_{3}$
(2,2) emission both in colour and contour plots. The contour levels are 0.02, 0.06, 0.10, 0.14, 0.18, and 0.22 K.km sec
$_{3}$
(2,2) emission both in colour and contour plots. The contour levels are 0.02, 0.06, 0.10, 0.14, 0.18, and 0.22 K.km sec
![]() $^{-1}$
, respectively.
$^{-1}$
, respectively.

Figure 2. Left: Column density (log
![]() $_{10}$
N(NH
$_{10}$
N(NH
![]() $_{3}$
)) distribution of the L1517B core. Right: Radial profile of log
$_{3}$
)) distribution of the L1517B core. Right: Radial profile of log
![]() $_{10}$
N(NH
$_{10}$
N(NH
![]() $_{3}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
$_{3}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
![]() $\sigma$
uncertainties of the mean values. Two dashed red lines intersect the curve at the point where column density drops by a factor of two, which is at 0.016 pc.
$\sigma$
uncertainties of the mean values. Two dashed red lines intersect the curve at the point where column density drops by a factor of two, which is at 0.016 pc.
4.2. Spectral properties across the core
In Figure 3, we show the spectra of NH
![]() $_{3}$
(1,1) and (2,2) lines towards different positions inside the core. For example, we show the spectra towards the dust peak position. Similarly, we also plot the spectra towards the peaks of NH
$_{3}$
(1,1) and (2,2) lines towards different positions inside the core. For example, we show the spectra towards the dust peak position. Similarly, we also plot the spectra towards the peaks of NH
![]() $_{3}$
(1,1) and (2,2) emissions. Here, it is interesting to note that the blue-skewed profile that is observed in the (1,1) spectra is not due to the collapse (Myers et al., Reference Myers, Mardones, Tafalla, Williams and Wilner1996) or any other cloud dynamics (Evans, Reference Evans Neal1999), rather it is the intrinsic closely separated lines caused by the hyperfine splitting. Here, we would like to point out that all the calibrated data and the pyspeckit results are obtained from the original data. No hanning smoothing has been performed in the entire analysis except for these spectra in Figure 3. As a simple matter of making the spectra more visible, we use the CASA viewer task to smooth the spectra in Figure 3.
$_{3}$
(1,1) and (2,2) emissions. Here, it is interesting to note that the blue-skewed profile that is observed in the (1,1) spectra is not due to the collapse (Myers et al., Reference Myers, Mardones, Tafalla, Williams and Wilner1996) or any other cloud dynamics (Evans, Reference Evans Neal1999), rather it is the intrinsic closely separated lines caused by the hyperfine splitting. Here, we would like to point out that all the calibrated data and the pyspeckit results are obtained from the original data. No hanning smoothing has been performed in the entire analysis except for these spectra in Figure 3. As a simple matter of making the spectra more visible, we use the CASA viewer task to smooth the spectra in Figure 3.

Figure 3. Upper panel: Left: Integrated intensity map of NH
![]() $_{3}$
(1,1) emission in colour plot. Here, different circles marked with numerical numbers denote the positions where the spectra of (1,1) and (2,2) lines are shown in the following figures. Right: Spectra of NH
$_{3}$
(1,1) emission in colour plot. Here, different circles marked with numerical numbers denote the positions where the spectra of (1,1) and (2,2) lines are shown in the following figures. Right: Spectra of NH
![]() $_{3}$
(1,1) and (2,2) lines (after hanning smoothing with kernel width 11) towards the dust peak position (
$_{3}$
(1,1) and (2,2) lines (after hanning smoothing with kernel width 11) towards the dust peak position (
![]() $04{^{\rm h}} 55{^{\rm m}} 17.60^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 17.60^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 44.00{''}$
) marked by 1 in the left figure. Here, the red dashed vertical line corresponds to the systematic velocity of the core, which is + 5.79 km sec
$\;+30{^\circ} 37^{\prime} 44.00{''}$
) marked by 1 in the left figure. Here, the red dashed vertical line corresponds to the systematic velocity of the core, which is + 5.79 km sec
![]() $^{-1}$
. Lower panel: Left: Same as uper panel right figure but towards the NH
$^{-1}$
. Lower panel: Left: Same as uper panel right figure but towards the NH
![]() $_{3}$
(1,1) peak position (
$_{3}$
(1,1) peak position (
![]() $04{^{\rm h}} 55{^{\rm m}} 18.31^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 18.31^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 42.38{''}$
) marked by 2 in the uper panel left figure. Right: Same as left but towards the NH
$\;+30{^\circ} 37^{\prime} 42.38{''}$
) marked by 2 in the uper panel left figure. Right: Same as left but towards the NH
![]() $_{3}$
(2,2) peak position (
$_{3}$
(2,2) peak position (
![]() $04{^{\rm h}} 55{^{\rm m}} 18.06^{s}\;$
,
$04{^{\rm h}} 55{^{\rm m}} 18.06^{s}\;$
,
![]() $\;+30{^\circ} 37^{\prime} 41.34{''}$
) marked by 3 in the uper panel left figure.
$\;+30{^\circ} 37^{\prime} 41.34{''}$
) marked by 3 in the uper panel left figure.
Now, we discuss the Left panel of Figure 4, where we show the velocity field across the region. From this figure, it appears that there is an indication of overall velocity gradient from north-east to south-west direction. This might be caused due to the rotational motion of the core. However, the exact pattern is more complex than a continuous increase or decrease in velocity of equal magnitude. Velocity gradient across the core was noticed in the earlier single-dish observations with the NH
![]() $_{3}$
(1,1) and N
$_{3}$
(1,1) and N
![]() $_{2}\textrm{H}^{+}$
(1-0) lines where the fields of view were larger than our study (Goodman et al., Reference Goodman, Benson, Fuller and Myers1993; Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a; Chitsazzadeh, Reference Chitsazzadeh2014). Right panel of Figure 4 shows the overplot of the local velocity gradient and velocity field across the region. Here, in the colour plot we subtract the systematic velocity of the core (+ 5.79 km sec
$_{2}\textrm{H}^{+}$
(1-0) lines where the fields of view were larger than our study (Goodman et al., Reference Goodman, Benson, Fuller and Myers1993; Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a; Chitsazzadeh, Reference Chitsazzadeh2014). Right panel of Figure 4 shows the overplot of the local velocity gradient and velocity field across the region. Here, in the colour plot we subtract the systematic velocity of the core (+ 5.79 km sec
![]() $^{-1}$
) from the velocity field. Now, in order to measure the overall velocity gradient, we first calculate the velocity gradient at each position and finally obtain the overall gradient in this region. Detailed discussion regarding the calculation of local and overall velocity gradient is mentioned in Appendix A. From the analysis, we obtain the overall velocity gradient,
$^{-1}$
) from the velocity field. Now, in order to measure the overall velocity gradient, we first calculate the velocity gradient at each position and finally obtain the overall gradient in this region. Detailed discussion regarding the calculation of local and overall velocity gradient is mentioned in Appendix A. From the analysis, we obtain the overall velocity gradient,
![]() ${\psi}$
${\psi}$
![]() $\sim$
1.10 km sec
$\sim$
1.10 km sec
![]() $^{-1}$
pc
$^{-1}$
pc
![]() $^{-1}$
and direction,
$^{-1}$
and direction,
![]() $\theta_{\hat{\psi}}$
$\theta_{\hat{\psi}}$
![]() $\sim$
127
$\sim$
127
![]() $^{\circ}$
west of north. This value is similar to the earlier single-dish observations studied by Goodman et al. (Reference Goodman, Benson, Fuller and Myers1993) and Tafalla et al. (Reference Tafalla, Myers, Caselli and Walmsley2004a), where the measured values were 1.52 and 1.10 km sec
$^{\circ}$
west of north. This value is similar to the earlier single-dish observations studied by Goodman et al. (Reference Goodman, Benson, Fuller and Myers1993) and Tafalla et al. (Reference Tafalla, Myers, Caselli and Walmsley2004a), where the measured values were 1.52 and 1.10 km sec
![]() $^{-1}$
pc
$^{-1}$
pc
![]() $^{-1}$
, respectively. However, this value is one order smaller than the L1544 core, where the value is
$^{-1}$
, respectively. However, this value is one order smaller than the L1544 core, where the value is
![]() $\sim$
9.0 km sec
$\sim$
9.0 km sec
![]() $^{-1} $
pc
$^{-1} $
pc
![]() $^{-1}$
based on the interferometric (VLA) observations of NH
$^{-1}$
based on the interferometric (VLA) observations of NH
![]() $_{3}$
(1,1) and (2,2) lines (Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007).
$_{3}$
(1,1) and (2,2) lines (Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007).

Figure 4. Left: Centre velocity (
![]() $V_{c}$
) distribution of the L1517B core. Right: Overplot of velocity fields and velocity gradient vectors (10′′ corresponds to a gradient of 89.28 km sec
$V_{c}$
) distribution of the L1517B core. Right: Overplot of velocity fields and velocity gradient vectors (10′′ corresponds to a gradient of 89.28 km sec
![]() $^{-1}$
pc
$^{-1}$
pc
![]() $^{-1}$
) across the region. Here, the systematic velocity of the core (+ 5.79 km sec
$^{-1}$
) across the region. Here, the systematic velocity of the core (+ 5.79 km sec
![]() $^{-1}$
) has been subtracted from the centre velocity. The black solid arrow on the right bottom corner represents the overall velocity gradient (
$^{-1}$
) has been subtracted from the centre velocity. The black solid arrow on the right bottom corner represents the overall velocity gradient (
![]() $\hat\psi$
$\hat\psi$
![]() $\sim$
1.10 km sec
$\sim$
1.10 km sec
![]() $^{-1}$
pc
$^{-1}$
pc
![]() $^{-1}$
, 10′′ corresponds to 1.0 km sec
$^{-1}$
, 10′′ corresponds to 1.0 km sec
![]() $^{-1}$
pc
$^{-1}$
pc
![]() $^{-1}$
) and its direction (
$^{-1}$
) and its direction (
![]() $\theta_{\hat{\psi}}$
$\theta_{\hat{\psi}}$
![]() $\sim$
127
$\sim$
127
![]() $^{\circ}$
west of north).
$^{\circ}$
west of north).
If there is a strict continuous velocity gradient of equal magnitude across the region, it is possible to conclude strongly that the region is rotating. However, in our region, both visually and in terms of the magnitude of the overall velocity gradient, it appears to be a rotation, despite not meeting the strict criteria of smooth and continuous velocity variation. It is also true that there are many challenges associated with the analysis and fitting of real astronomical data. Consequently, obtaining a smooth variation of velocity across the region is extremely difficult. Therefore, in the following, we calculate the ratio of rotational energy to gravitational potential energy, assuming that the velocity gradient is the cause of rotation. This enables us to gain a rough understanding of the role of rotation in this region if the overall velocity gradient is caused by the rotation. The parameter
![]() $\beta$
, which is the ratio of the rotational energy to the gravitational energy (Goodman et al., Reference Goodman, Benson, Fuller and Myers1993) is defined by the formula:
$\beta$
, which is the ratio of the rotational energy to the gravitational energy (Goodman et al., Reference Goodman, Benson, Fuller and Myers1993) is defined by the formula:
Here, I is the moment of inertia,
![]() $\omega$
is the angular velocity, G is the gravitational constant, M is the mass, R is the radius of the core, p and q are unit-less numbers, which vary depending on the geometry and the density profile of the system (Kauffmann et al., Reference Kauffmann, Pillai and Goldsmith2013). The value of
$\omega$
is the angular velocity, G is the gravitational constant, M is the mass, R is the radius of the core, p and q are unit-less numbers, which vary depending on the geometry and the density profile of the system (Kauffmann et al., Reference Kauffmann, Pillai and Goldsmith2013). The value of
![]() $\left(\frac{\textit{p}}{\textit{q}}\right)$
is 0.66 for a constant density sphere. However, when the density profile varies as
$\left(\frac{\textit{p}}{\textit{q}}\right)$
is 0.66 for a constant density sphere. However, when the density profile varies as
![]() $r^{-2}$
with fixed M and R, this value is 0.22, which is one third of the earlier one (see Appendix B). From the fitting of observed continuum emission, Tafalla et al. (Reference Tafalla, Myers, Caselli and Walmsley2004a) showed that the number density of this core is not constant rather follows a power law:
$r^{-2}$
with fixed M and R, this value is 0.22, which is one third of the earlier one (see Appendix B). From the fitting of observed continuum emission, Tafalla et al. (Reference Tafalla, Myers, Caselli and Walmsley2004a) showed that the number density of this core is not constant rather follows a power law:
![]() $n(r) = \frac{n_{0}} {1+(\frac{r}{r_{0}})^{2.5}}$
. Here, r is the radial distance,
$n(r) = \frac{n_{0}} {1+(\frac{r}{r_{0}})^{2.5}}$
. Here, r is the radial distance,
![]() $n_{0}$
= 2.2
$n_{0}$
= 2.2
![]() $\times$
10
$\times$
10
![]() $^{5}$
cm
$^{5}$
cm
![]() $^{-3}$
and
$^{-3}$
and
![]() $r_{0}$
= 35.00′′ or 0.027 pc. Since we are only analysing the central 0.025 pc region inside the core, we consider
$r_{0}$
= 35.00′′ or 0.027 pc. Since we are only analysing the central 0.025 pc region inside the core, we consider
![]() $\frac{p}{q}$
= 0.66 for our analysis, which will not lead to a significant difference in the result. Likewise, we consider only the enclosed mass within the radius of 0.025 pc. From the work of Benson & Myers (Reference Benson and Myers1989), the mass of the core is
$\frac{p}{q}$
= 0.66 for our analysis, which will not lead to a significant difference in the result. Likewise, we consider only the enclosed mass within the radius of 0.025 pc. From the work of Benson & Myers (Reference Benson and Myers1989), the mass of the core is
![]() $\sim$
0.50
$\sim$
0.50
![]() ${\textrm{M}_ \odot }$
, where it was assumed a radius of
${\textrm{M}_ \odot }$
, where it was assumed a radius of
![]() $\sim$
0.068 pc (assuming 159 pc distance) based on the observation of NH
$\sim$
0.068 pc (assuming 159 pc distance) based on the observation of NH
![]() $_{3}$
(1,1) line. Now, according to the power law of density (
$_{3}$
(1,1) line. Now, according to the power law of density (
![]() $r^{-2.5}$
), the mass enclosed in a radius of 0.025 pc is
$r^{-2.5}$
), the mass enclosed in a radius of 0.025 pc is
![]() $\sim$
0.30
$\sim$
0.30
![]() ${\textrm{M}_ \odot }$
. Furthermore, the value of
${\textrm{M}_ \odot }$
. Furthermore, the value of
![]() $\omega$
is obtained from
$\omega$
is obtained from
![]() $\psi$
after considering the inclination angle (i) of
$\psi$
after considering the inclination angle (i) of
![]() $\omega$
to the line-of-sight. However, for a single measurement, we have not taken into account this statistical correction. This correction factor is small and will not significantly affect the value of
$\omega$
to the line-of-sight. However, for a single measurement, we have not taken into account this statistical correction. This correction factor is small and will not significantly affect the value of
![]() $\beta$
(Goodman et al., Reference Goodman, Benson, Fuller and Myers1993). After putting all these in Equation 1, we finally obtain
$\beta$
(Goodman et al., Reference Goodman, Benson, Fuller and Myers1993). After putting all these in Equation 1, we finally obtain
![]() $\beta$
equals to
$\beta$
equals to
![]() $\sim$
5
$\sim$
5
![]() $\times$
10
$\times$
10
![]() $^{-3}$
. From this value, it indicates that rotation has no effect on the gas dynamics, at least inside the central region of the core.
$^{-3}$
. From this value, it indicates that rotation has no effect on the gas dynamics, at least inside the central region of the core.
After that, we show the spatial distribution and the radially averaged profile of total velocity dispersion (
![]() $\sigma_{\text{total,1D}}$
) in the left and right panels of Figure 5. Here, we would like to point out that we have corrected the
$\sigma_{\text{total,1D}}$
) in the left and right panels of Figure 5. Here, we would like to point out that we have corrected the
![]() $\sigma_{\text{total,1D}}$
due to the channel resolution effect, which means
$\sigma_{\text{total,1D}}$
due to the channel resolution effect, which means
![]() $\sigma_{\text{total,1D}}$
=
$\sigma_{\text{total,1D}}$
=
![]() $\sqrt{\sigma_{\text{total,1D fit}}^{2}-(\frac{\Delta \text{ch}}{2.35})^{2}}$
. Here,
$\sqrt{\sigma_{\text{total,1D fit}}^{2}-(\frac{\Delta \text{ch}}{2.35})^{2}}$
. Here,
![]() $\sigma_{\text{total,1D fit}}$
is the resulting velocity dispersion from the fit and
$\sigma_{\text{total,1D fit}}$
is the resulting velocity dispersion from the fit and
![]() $\Delta \text{ch}$
is the channel resolution of the observation (Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). From the right figure, it indicates that there is a slight variation of
$\Delta \text{ch}$
is the channel resolution of the observation (Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). From the right figure, it indicates that there is a slight variation of
![]() $\sigma_{\text{total,1D}}$
with a mean value of
$\sigma_{\text{total,1D}}$
with a mean value of
![]() $\sim$
0.07 km sec
$\sim$
0.07 km sec
![]() $^{-1}$
. We note that this value is lower than that reported earlier from the single-dish study with the same NH
$^{-1}$
. We note that this value is lower than that reported earlier from the single-dish study with the same NH
![]() $_{3}$
line emissions, where
$_{3}$
line emissions, where
![]() $\sigma_{\text{total,1D}}$
was
$\sigma_{\text{total,1D}}$
was
![]() $\sim$
0.09 km sec
$\sim$
0.09 km sec
![]() $^{-1}$
(Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a,Reference Tafalla, Myers, Caselli and Walmsleyb). Now, it is important to check whether this total (thermal and non-thermal) motion and the magnetic field (B) are capable of preventing the collapse. For that we calculate a parameter W, which is defined by the formula:
$^{-1}$
(Tafalla et al., Reference Tafalla, Myers, Caselli and Walmsley2004a,Reference Tafalla, Myers, Caselli and Walmsleyb). Now, it is important to check whether this total (thermal and non-thermal) motion and the magnetic field (B) are capable of preventing the collapse. For that we calculate a parameter W, which is defined by the formula:

Figure 5. Left: Distribution of total velocity dispersion (
![]() $\sigma_{\text{total,1D}}$
) of the L1517B core. Right: Radial profile of
$\sigma_{\text{total,1D}}$
) of the L1517B core. Right: Radial profile of
![]() $\sigma_{\text{total,1D}}$
inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
$\sigma_{\text{total,1D}}$
inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
![]() $\sigma$
uncertainties of the mean values. Here, the red dashed horizontal line represents the line at which
$\sigma$
uncertainties of the mean values. Here, the red dashed horizontal line represents the line at which
![]() $\sigma_{\text{total,1D}}$
is 0.07 km sec
$\sigma_{\text{total,1D}}$
is 0.07 km sec
![]() $^{-1}$
.
$^{-1}$
.
Here,
![]() $\in_{k}$
is total kinetic energy of the system, which is
$\in_{k}$
is total kinetic energy of the system, which is
![]() $\frac{3}{2}$
$\frac{3}{2}$
![]() $M\sigma_{\text{total,1D}}^{2}$
,
$M\sigma_{\text{total,1D}}^{2}$
,
![]() $\Lambda_{B}$
is the magnetic energy of the system, which is
$\Lambda_{B}$
is the magnetic energy of the system, which is
![]() $\frac{B^{2}}{6R^{3}}$
, and
$\frac{B^{2}}{6R^{3}}$
, and
![]() $\Phi_{v}$
is the potential energy of the system which is equal to -
$\Phi_{v}$
is the potential energy of the system which is equal to -
![]() $q\frac{GM^{2}}{R}$
. A value of W equal to 1 indicates a state of virial equilibrium, and a value less than 1 indicates possible gravitational contraction. Kirk et al. (Reference Kirk, Ward-Thompson and Crutcher2006) estimated the magnetic field (B) in L1517B prestellar core using the Chandrasekhar & Fermi (CF) method and obtained
$q\frac{GM^{2}}{R}$
. A value of W equal to 1 indicates a state of virial equilibrium, and a value less than 1 indicates possible gravitational contraction. Kirk et al. (Reference Kirk, Ward-Thompson and Crutcher2006) estimated the magnetic field (B) in L1517B prestellar core using the Chandrasekhar & Fermi (CF) method and obtained
![]() $\sim$
30
$\sim$
30
![]() $\pm$
10
$\pm$
10
![]() $\mu$
G. We take this value of B in our analysis. We also consider the M and R values in the same manner as described above. After putting all these values we finally obtain W equals to 0.55. We note that, due to the uncertainties of M, B,
$\mu$
G. We take this value of B in our analysis. We also consider the M and R values in the same manner as described above. After putting all these values we finally obtain W equals to 0.55. We note that, due to the uncertainties of M, B,
![]() $\sigma_{\text{total,1D}}$
, and R, this parameter W will vary. For example, if we take B = 20
$\sigma_{\text{total,1D}}$
, and R, this parameter W will vary. For example, if we take B = 20
![]() $\mu$
G instead of 30
$\mu$
G instead of 30
![]() $\mu$
G, we obtain W equals to 0.41. Similarly, if we take B = 40
$\mu$
G, we obtain W equals to 0.41. Similarly, if we take B = 40
![]() $\mu$
G, the value of W becomes 0.75. Thus, we can say that this central region may be in a stage of contraction. This is also supported by the previous work of Fu et al. (Reference Fu, Gao and Lou2011).
$\mu$
G, the value of W becomes 0.75. Thus, we can say that this central region may be in a stage of contraction. This is also supported by the previous work of Fu et al. (Reference Fu, Gao and Lou2011).
4.3. Temperature
In the left and right panels of Figure 6, we show the pixel-wise kinetic temperature (
![]() $T_{k}$
) distribution and the radially averaged profile of
$T_{k}$
) distribution and the radially averaged profile of
![]() $T_{k}$
in the core. From the right figure, it indicates that radially averaged
$T_{k}$
in the core. From the right figure, it indicates that radially averaged
![]() $T_{k}$
values vary slightly with a mean value of
$T_{k}$
values vary slightly with a mean value of
![]() $\sim$
9 K. Therefore, we can argue that there is no such prominent radial temperature gradient exist in the central region of the core. We would like to pint out that, in other highly compact cores (TMC-1C and L1544) (Schnee & Goodman, Reference Schnee and Goodman2005; Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Sipilä et al., Reference Sipilä, Caselli, Redaelli and Spezzano2022), where the central density is
$\sim$
9 K. Therefore, we can argue that there is no such prominent radial temperature gradient exist in the central region of the core. We would like to pint out that, in other highly compact cores (TMC-1C and L1544) (Schnee & Goodman, Reference Schnee and Goodman2005; Crapsi et al., Reference Crapsi, Caselli, Walmsley and Tafalla2007; Sipilä et al., Reference Sipilä, Caselli, Redaelli and Spezzano2022), where the central density is
![]() $\sim$
10
$\sim$
10
![]() $^{6.5-7.0}$
cm
$^{6.5-7.0}$
cm
![]() $^{-3}$
, it has been observed using dust SED (spectral energy distribution) fitting and using the ammonia line that there is a sharp decrease in central kinetic temperature up to
$^{-3}$
, it has been observed using dust SED (spectral energy distribution) fitting and using the ammonia line that there is a sharp decrease in central kinetic temperature up to
![]() $\sim$
6 K. However, in some other prestellar cores, where the central density is
$\sim$
6 K. However, in some other prestellar cores, where the central density is
![]() $\sim$
10
$\sim$
10
![]() $^{5.0-5.5}$
cm
$^{5.0-5.5}$
cm
![]() $^{-3}$
, similar to this prestellar core, earlier studies did not find any such sharp decrease in kinetic temperature inside the central region of the prestellar core (Ruoskanen et al., Reference Ruoskanen, Harju and Juvela2011; Chitsazzadeh, Reference Chitsazzadeh2014; Pineda et al., Reference Pineda, Harju and Caselli2022). It is possible that the surrounding environment (in terms of the radiation field) of these highly compact prestellar cores differs from that of the other prestellar cores, which do not experience a sharp drop in kinetic temperature.
$^{-3}$
, similar to this prestellar core, earlier studies did not find any such sharp decrease in kinetic temperature inside the central region of the prestellar core (Ruoskanen et al., Reference Ruoskanen, Harju and Juvela2011; Chitsazzadeh, Reference Chitsazzadeh2014; Pineda et al., Reference Pineda, Harju and Caselli2022). It is possible that the surrounding environment (in terms of the radiation field) of these highly compact prestellar cores differs from that of the other prestellar cores, which do not experience a sharp drop in kinetic temperature.

Figure 6. Left: Kinetic temperature (
![]() $T_{k}$
) distribution of the L1517B core. Right: Radial profile of kinetic temperature (
$T_{k}$
) distribution of the L1517B core. Right: Radial profile of kinetic temperature (
![]() $T_{k}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
$T_{k}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
![]() $\sigma$
uncertainties of the mean values. Here, the red dashed horizontal line represents the line at which
$\sigma$
uncertainties of the mean values. Here, the red dashed horizontal line represents the line at which
![]() $T_{k}$
is 9.0 K
$T_{k}$
is 9.0 K
In Figure 7, we show the spatial distribution and radially averaged profile of excitation temperature (
![]() $T_{ex}$
). From these figures, it shows that
$T_{ex}$
). From these figures, it shows that
![]() $T_{ex}$
increases from the outside to the inside the central nucleus of the core with a peak value of
$T_{ex}$
increases from the outside to the inside the central nucleus of the core with a peak value of
![]() $\sim$
5.6 K. It indicates that due to the increase of the density towards the inner core or nucleus,
$\sim$
5.6 K. It indicates that due to the increase of the density towards the inner core or nucleus,
![]() $T_{ex}$
is more strongly coupled with
$T_{ex}$
is more strongly coupled with
![]() $T_{k}$
.
$T_{k}$
.

Figure 7. Left: Excitation temperature (
![]() $T_{ex}$
) distribution of the L1517B core. Right: Radial profile of
$T_{ex}$
) distribution of the L1517B core. Right: Radial profile of
![]() $T_{ex}$
inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
$T_{ex}$
inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
![]() $\sigma$
uncertainties of the mean values.
$\sigma$
uncertainties of the mean values.
4.4. Turbulence
Turbulence can be studied from the spectral analysis if one assumes that the non-thermal broadening is caused due to turbulence. If this is the case, then it is obtained by the formula:
Here,
![]() $\sigma_{\text{total,1D}}$
is the total velocity dispersion of the observed line, whereas
$\sigma_{\text{total,1D}}$
is the total velocity dispersion of the observed line, whereas
![]() $\sigma_{\text{th,1D}}$
and
$\sigma_{\text{th,1D}}$
and
![]() $\sigma_{\text{nth,1D}}$
are the thermal and non-thermal broadenings of the line. Distribution of
$\sigma_{\text{nth,1D}}$
are the thermal and non-thermal broadenings of the line. Distribution of
![]() $\sigma_{\text{total,1D}}$
is obtained from the output of
$\sigma_{\text{total,1D}}$
is obtained from the output of
![]() $\textit{pyspeckit}$
code whereas, pixel-wise
$\textit{pyspeckit}$
code whereas, pixel-wise
![]() $\sigma_{\text{th,1D}}$
can be calculated from the measured
$\sigma_{\text{th,1D}}$
can be calculated from the measured
![]() $T_{k}$
by the formula (Sepúlveda et al., Reference Sepúlveda, Estalella and Anglada2020):
$T_{k}$
by the formula (Sepúlveda et al., Reference Sepúlveda, Estalella and Anglada2020):
Here,
![]() $k_{B}$
is the Boltzmann constant,
$k_{B}$
is the Boltzmann constant,
![]() $m_{H}$
is the mass of the hydrogen atom,
$m_{H}$
is the mass of the hydrogen atom,
![]() $T_{k}$
is the kinetic temperature and
$T_{k}$
is the kinetic temperature and
![]() $\mu_{NH_{3}}$
= 17 is the molecular mass of the NH
$\mu_{NH_{3}}$
= 17 is the molecular mass of the NH
![]() $_{3}$
molecule.
$_{3}$
molecule.
In Figure 8, we show the radially averaged
![]() $\sigma_{\text{nth,1D}}$
profile. From this figure, it appears that the radially averaged values vary slightly with a mean value of 0.03 km sec
$\sigma_{\text{nth,1D}}$
profile. From this figure, it appears that the radially averaged values vary slightly with a mean value of 0.03 km sec
![]() $^{-1}$
. To check whether the
$^{-1}$
. To check whether the
![]() $\sigma_{\text{nth,1D}}$
has any inherent length-scale dependency, we fit the profile with
$\sigma_{\text{nth,1D}}$
has any inherent length-scale dependency, we fit the profile with
![]() $A r^{\alpha}$
, where A is the magnitude in km sec
$A r^{\alpha}$
, where A is the magnitude in km sec
![]() $^{-1}$
, r is the length scale in pc and
$^{-1}$
, r is the length scale in pc and
![]() $\alpha$
is the power law index. The values of A and
$\alpha$
is the power law index. The values of A and
![]() $\alpha$
come out to be 0.026
$\alpha$
come out to be 0.026
![]() $\pm$
0.001 km sec
$\pm$
0.001 km sec
![]() $^{-1}$
and - 0.030
$^{-1}$
and - 0.030
![]() $\pm$
0.008, respectively. These values indicate that there is no prominent length-scale dependence on turbulence. Now, if we consider that the turbulence is isotropic, then total three dimensional velocity dispersion
$\pm$
0.008, respectively. These values indicate that there is no prominent length-scale dependence on turbulence. Now, if we consider that the turbulence is isotropic, then total three dimensional velocity dispersion
![]() $\sigma_{\text{nth,3D}}$
can be obtained from
$\sigma_{\text{nth,3D}}$
can be obtained from
![]() $\sigma_{\text{nth,1D}}$
after multiplying
$\sigma_{\text{nth,1D}}$
after multiplying
![]() $\sqrt{3}$
. On the other hand, sound speed
$\sqrt{3}$
. On the other hand, sound speed
![]() $c_{s}$
can also be obtained by:
$c_{s}$
can also be obtained by:
Here,
![]() $\mu_{\text{gas}}$
= 2.37 is the average mass of molecular gas. We then finally obtain the sonic Mach number
$\mu_{\text{gas}}$
= 2.37 is the average mass of molecular gas. We then finally obtain the sonic Mach number
![]() $M_{s}$
by the formula:
$M_{s}$
by the formula:
From this analysis, radially averaged mean value of
![]() $ T_{k}$
is
$ T_{k}$
is
![]() $\sim$
9 K, and radially average mean value of
$\sim$
9 K, and radially average mean value of
![]() $\sigma_{\text{nth,1D}}$
is
$\sigma_{\text{nth,1D}}$
is
![]() $\sim$
0.03 km sec
$\sim$
0.03 km sec
![]() $^{-1}$
. Therefore,
$^{-1}$
. Therefore,
![]() $M_{s}$
$M_{s}$
![]() $\sim$
0.3 inside this central region of the core. From the value of
$\sim$
0.3 inside this central region of the core. From the value of
![]() $M_{s}$
, it indicates that turbulence is subsonic in nature. This result supports previous observational studies as well as the theoretical ideas of the dissipation of turbulence near the ambipolar diffusion scale, which is close to the size of the prestellar core (
$M_{s}$
, it indicates that turbulence is subsonic in nature. This result supports previous observational studies as well as the theoretical ideas of the dissipation of turbulence near the ambipolar diffusion scale, which is close to the size of the prestellar core (
![]() $\sim$
0.1 pc) (Barranco & Goodman, Reference Barranco and Goodman1998; Stahler & Palla, Reference Stahler and Palla2004; Schnee et al., Reference Schnee, Caselli and Goodman2007; Koley, Reference Koley2022). However, a recent observational study reveals interesting results, where they argue that although the turbulence (or perturbed MHD Alfven wave) is dissipated in neutral near the outer edge of the core, ions still carry the turbulence inside the core, and in turn, they have wider line width compared to the neutrals (Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). In the future, more observational studies including N
$\sim$
0.1 pc) (Barranco & Goodman, Reference Barranco and Goodman1998; Stahler & Palla, Reference Stahler and Palla2004; Schnee et al., Reference Schnee, Caselli and Goodman2007; Koley, Reference Koley2022). However, a recent observational study reveals interesting results, where they argue that although the turbulence (or perturbed MHD Alfven wave) is dissipated in neutral near the outer edge of the core, ions still carry the turbulence inside the core, and in turn, they have wider line width compared to the neutrals (Pineda et al., Reference Pineda, Schmiedeke and Caselli2021). In the future, more observational studies including N
![]() $_{2}\textrm{H}^{+}$
, will ascertain the detailed nature of the turbulence inside the prestellar core.
$_{2}\textrm{H}^{+}$
, will ascertain the detailed nature of the turbulence inside the prestellar core.

Figure 8. Radial profile of non-thermal velocity dispersion (
![]() $\sigma_{\text{nth,1D}}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
$\sigma_{\text{nth,1D}}$
) inside the core. Grey squares are the mean values for successive concentric circles around the centre, whereas the vertical blue lines on both sides are the 1
![]() $\sigma$
uncertainties of the mean values. Here, red solid line is the best fitted
$\sigma$
uncertainties of the mean values. Here, red solid line is the best fitted
![]() $\sigma_{\text{nth,1D}}$
curve.
$\sigma_{\text{nth,1D}}$
curve.
5. Conclusions
In this work, we analysis the central region of the prestellar core L1517B with NH
![]() $_{3}$
(1,1) and (2,2) lines with the Jansky VLA telescope. Our observations and analysis reveal the following:
$_{3}$
(1,1) and (2,2) lines with the Jansky VLA telescope. Our observations and analysis reveal the following:
-
(1) The central region of the core is close-to-round in shape obtained both from NH
 $_{3}$
(1,1) and (2,2) observations.
$_{3}$
(1,1) and (2,2) observations. -
(2) Column density of NH
 $_{3}$
decreases from the centre of the core to the edge, with a peak value of
$_{3}$
decreases from the centre of the core to the edge, with a peak value of
 $\sim$
10
$\sim$
10
 $^{15}$
cm
$^{15}$
cm
 $^{-2}$
and the distance where it decreases by a factor 2 is at radius 0.016 pc.
$^{-2}$
and the distance where it decreases by a factor 2 is at radius 0.016 pc. -
(3) There is an overall velocity gradient (
 ${\psi}$
${\psi}$
 $\sim$
1.10 km sec
$\sim$
1.10 km sec
 $^{-1}$
pc
$^{-1}$
pc
 $^{-1}$
) from the north-east to south-west direction (
$^{-1}$
) from the north-east to south-west direction (
 $\theta_{\hat{\psi}}$
$\theta_{\hat{\psi}}$
 $\sim$
127
$\sim$
127
 $^{\circ}$
west of north) in this region, which may cause due to the rotation of the core. This value of
$^{\circ}$
west of north) in this region, which may cause due to the rotation of the core. This value of
 ${\psi}$
is similar to the earlier single-dish observation obtained from NH
${\psi}$
is similar to the earlier single-dish observation obtained from NH
 $_{3}$
emission. After assuming the velocity gradient caused due to rotation, we calculate the parameter
$_{3}$
emission. After assuming the velocity gradient caused due to rotation, we calculate the parameter
 $\beta$
, which is defined by the ratio of rotational energy to the gravitational potential energy and obtain
$\beta$
, which is defined by the ratio of rotational energy to the gravitational potential energy and obtain
 $\beta$
equals to
$\beta$
equals to
 $\sim$
5
$\sim$
5
 $\times$
10
$\times$
10
 $^{-3}$
, which indicates that rotation has no significant effect on gas dynamics, at least inside the central region of the core.
$^{-3}$
, which indicates that rotation has no significant effect on gas dynamics, at least inside the central region of the core. -
(4) We find that the total velocity dispersion (
 $\sigma_{\text{total,1D}}$
) varies slightly with mean value of 0.07 km sec
$\sigma_{\text{total,1D}}$
) varies slightly with mean value of 0.07 km sec
 $^{-1}$
. It is slightly smaller than the previously measured value of
$^{-1}$
. It is slightly smaller than the previously measured value of
 $\sim$
0.09 km sec
$\sim$
0.09 km sec
 $^{-1}$
from single-dish observation.
$^{-1}$
from single-dish observation. -
(5) We perform the virial analysis including the magnetic field taken from the previous study and conclude that the central region could be in a stage of collapse.
-
(6) Kinetic temperature (
 $T_{k}$
) of this central region is nearly constant with a mean value of
$T_{k}$
) of this central region is nearly constant with a mean value of
 $\sim$
9 K. No sharp decrease of the
$\sim$
9 K. No sharp decrease of the
 $T_{k}$
has been observed inside the nucleus of the prestellar core.
$T_{k}$
has been observed inside the nucleus of the prestellar core. -
(7) We observe that the excitation temperature (
 $T_{ex}$
) increases towards the nucleus of the core with a peak value of
$T_{ex}$
) increases towards the nucleus of the core with a peak value of
 $\sim$
5.6 K. It suggests that due to the increase in the density towards the inner core or nucleus,
$\sim$
5.6 K. It suggests that due to the increase in the density towards the inner core or nucleus,
 $T_{ex}$
is more strongly coupled with
$T_{ex}$
is more strongly coupled with
 $T_{k}$
.
$T_{k}$
. -
(8) We study the turbulence in this core and find that turbulence is subsonic in nature (sonic Mach number,
 $M_{s}$
$M_{s}$
 $<$
1) and has no prominent length-scale dependence. This is supported by earlier studies in several prestellar cores.
$<$
1) and has no prominent length-scale dependence. This is supported by earlier studies in several prestellar cores.
Acknowledgements
We thank the reviewer for insightful comments and valuable suggestions that have helped in improving this paper significantly. AK gratefully acknowledges support from ANID BASAL project FB210003. The author would like to acknowledge the Indian Institute of Science, Bangalore, India, where most of the research was conducted while AK was working there as a Research Associate (RA). AK would also like to extend his deepest gratitude to Prof. Nirupam Roy for introducing him to the study of ammonia during his earlier research.
Telescope: Jansky Very Large Array Telescope (VLA).
Software: Aplpy (Robitaille & Bressert, Reference Robitaille and Bressert2012), Astropy (Astropy Collaboration et al., Reference Robitaille and Tollerud2013), CARTA (Comrie et al., Reference Comrie, Wang and Hsu2021), CASA (Common Astronomy Software Applications package-National Radio Astronomical Observatory), Matplotlib (Hunter, Reference Hunter2007), PySpeckit (Ginsburg & Mirocha, Reference Ginsburg and Mirocha2011), Scousepy (Henshaw et al., Reference Henshaw, Longmore and Kruijssen2016, Reference Henshaw, Ginsburg and Haworth2019).
Data availability
All data used in this study are available publicly from the VLA online archive. Authors will be happy to share all the reduced data and the velocity gradient code on reasonable request.
Appendix A. Calculation of velocity gradient
We calculate the local velocity gradient in each pixel as well as the overall velocity gradient in this region based on the method described below. Firstly, we calculate the local velocity gradient of each pixel using its neighbouring pixels according to their weightages, which are based on the distance from that particular pixel and the uncertainties of their centre velocities. For example, while calculating the local gradient of a particular pixel (m,n), we take all the other (i,j) pixels in this region, and the weight function f(i,j) has been given as follows:
Here,
![]() $\Delta V_{c_{i,j}}$
is the uncertainty of the centre velocity of the i,j pixel and
$\Delta V_{c_{i,j}}$
is the uncertainty of the centre velocity of the i,j pixel and
![]() $R_{i,j-m,n}$
is the distance between i,j and m,n pixel. We take the value of the full width at half maximum (FWHM) of the Gaussian function is 4.6 for the following reason. The beam size of this observation is
$R_{i,j-m,n}$
is the distance between i,j and m,n pixel. We take the value of the full width at half maximum (FWHM) of the Gaussian function is 4.6 for the following reason. The beam size of this observation is
![]() $\sim$
4.01′′(
$\sim$
4.01′′(
![]() $\theta_{major}$
)
$\theta_{major}$
)
![]() $\times$
3.37′′(
$\times$
3.37′′(
![]() $\theta_{minor}$
), and therefore, the effective beam size is
$\theta_{minor}$
), and therefore, the effective beam size is
![]() $\sqrt{\theta_{major} \times \theta_{minor}}$
= 3.68′′. On the other hand, the pixel size in our image cube is 0.80′′. That is why, we take the FWHM is equal to 4.6 pixels.
$\sqrt{\theta_{major} \times \theta_{minor}}$
= 3.68′′. On the other hand, the pixel size in our image cube is 0.80′′. That is why, we take the FWHM is equal to 4.6 pixels.
From the pyspeckit result, we obtain the pixel-wise centre velocity (
![]() ${V_{c}}$
) and its associated error (
${V_{c}}$
) and its associated error (
![]() $\Delta{V_{c}}$
). Therefore, the horizontal component of the local velocity gradient of a pixel (m,n) is obtained by the formula:
$\Delta{V_{c}}$
). Therefore, the horizontal component of the local velocity gradient of a pixel (m,n) is obtained by the formula:
Similarly, the vertical component of the local velocity gradient of a pixel (m,n) is
Therefore, the magnitude of the local velocity gradient at the pixel (m,n) is as follows:
 \begin{equation}\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local}} = \displaystyle\sqrt{\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,x}}^{2}+\;\;\;\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,y}}^{2} }\end{equation}
\begin{equation}\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local}} = \displaystyle\sqrt{\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,x}}^{2}+\;\;\;\left( \frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,y}}^{2} }\end{equation}
and the direction of the local velocity gradient at the pixel (m, n) is
 \begin{equation}\theta_{m,n\;local}= tan^{-1}\left(\frac{\left(\frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,y}}}{\left(\frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,x}}}\right)\end{equation}
\begin{equation}\theta_{m,n\;local}= tan^{-1}\left(\frac{\left(\frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,y}}}{\left(\frac{dV_{c}}{dR}\right)_{{m,n}_{\;local,x}}}\right)\end{equation}
On the other hand, for the overall velocity gradient, we first calculate the velocity gradient at each pixel (m,n) using the other pixels (i,j) and then obtain the average value as well as direction of the velocity gradient. In this case, we use the following weight function:
Appendix B. Ratio of rotational energy to gravitational energy for a spherical system of non-uniform density
Ratio of rotational energy to gravitational energy is defined by the parameter
![]() $\beta$
:
$\beta$
:
Here, I is the moment of inertia, w is the rotational velocity, G is the gravitational constant, R is the radius of the spherical system, p and q are unit-less numbers, which vary depending on the density profile of the spherical system (Kauffmann et al., Reference Kauffmann, Pillai and Goldsmith2013).
We consider a solid sphere of radius R, mass M, and density
![]() ${\rho}(r)$
=
${\rho}(r)$
=
![]() $K{\rho}_{0}r^{-\alpha}$
(neglect singularity at r = 0). Now, for calculating the moment of inertia (I), we consider the solid sphere as the sum of consecutive spherical shells of infinitesimal thickness, one of which radius is r and thickness is dr.
$K{\rho}_{0}r^{-\alpha}$
(neglect singularity at r = 0). Now, for calculating the moment of inertia (I), we consider the solid sphere as the sum of consecutive spherical shells of infinitesimal thickness, one of which radius is r and thickness is dr.
Now, the moment of inertia of that spherical shell is
Then, the total moment of inertia of the solid sphere becomes
Similarly, for calculating the gravitational potential energy, we consider that a sphere of radius r is already formed and we want to add a thin spherical shell on top of that whose thickness is dr and mass is dm(r), then potential energy is
Now, the total total potential energy becomes
For
![]() $\alpha$
= 0,
$\alpha$
= 0,
![]() $I=\dfrac{2}{5}MR^{2}$
and
$I=\dfrac{2}{5}MR^{2}$
and
![]() $U=-\dfrac{3}{5}\dfrac{GM}{R^{2}}$
, so
$U=-\dfrac{3}{5}\dfrac{GM}{R^{2}}$
, so
![]() $\dfrac{p}{q}$
= 0.66. Similarly, for
$\dfrac{p}{q}$
= 0.66. Similarly, for
![]() $\alpha$
= 2,
$\alpha$
= 2,
![]() $I=\dfrac{2}{9}MR^{2}$
and
$I=\dfrac{2}{9}MR^{2}$
and
![]() $U=-\dfrac{GM}{R^{2}}$
, so
$U=-\dfrac{GM}{R^{2}}$
, so
![]() $\dfrac{p}{q}$
= 0.22.
$\dfrac{p}{q}$
= 0.22.