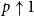 $p\uparrow 1$ limit
$p\uparrow 1$ limitPublished online by Cambridge University Press: 14 December 2022
Let
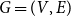 $G=(V,E)$
be a countable graph. The Bunkbed graph of
$G=(V,E)$
be a countable graph. The Bunkbed graph of
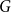 $G$
is the product graph
$G$
is the product graph
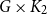 $G \times K_2$
, which has vertex set
$G \times K_2$
, which has vertex set
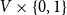 $V\times \{0,1\}$
with “horizontal” edges inherited from
$V\times \{0,1\}$
with “horizontal” edges inherited from
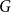 $G$
and additional “vertical” edges connecting
$G$
and additional “vertical” edges connecting
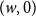 $(w,0)$
and
$(w,0)$
and
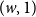 $(w,1)$
for each
$(w,1)$
for each
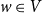 $w \in V$
. Kasteleyn’s Bunkbed conjecture states that for each
$w \in V$
. Kasteleyn’s Bunkbed conjecture states that for each
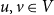 $u,v \in V$
and
$u,v \in V$
and
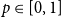 $p\in [0,1]$
, the vertex
$p\in [0,1]$
, the vertex
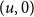 $(u,0)$
is at least as likely to be connected to
$(u,0)$
is at least as likely to be connected to
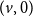 $(v,0)$
as to
$(v,0)$
as to
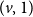 $(v,1)$
under Bernoulli-
$(v,1)$
under Bernoulli-
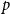 $p$
bond percolation on the bunkbed graph. We prove that the conjecture holds in the
$p$
bond percolation on the bunkbed graph. We prove that the conjecture holds in the
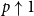 $p \uparrow 1$
limit in the sense that for each finite graph
$p \uparrow 1$
limit in the sense that for each finite graph
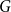 $G$
there exists
$G$
there exists
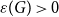 $\varepsilon (G)\gt 0$
such that the bunkbed conjecture holds for
$\varepsilon (G)\gt 0$
such that the bunkbed conjecture holds for
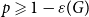 $p \geqslant 1-\varepsilon (G)$
.
$p \geqslant 1-\varepsilon (G)$
.