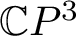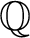Given a real algebraic variety X, we denote by
![]() $\mathbb {C} X$
the set of its complex points and by
$\mathbb {C} X$
the set of its complex points and by
![]() $\mathbb {R} X$
the set of its real points. Recall that the signature
$\mathbb {R} X$
the set of its real points. Recall that the signature
![]() $\sigma (M)$
of an even-dimensional oriented compact smooth manifold M is defined to be
$\sigma (M)$
of an even-dimensional oriented compact smooth manifold M is defined to be
![]() $0$
if
$0$
if
![]() $\dim M=4n +2$
and to be the signature on the (symmetric) intersection form on
$\dim M=4n +2$
and to be the signature on the (symmetric) intersection form on
![]() $H_{2n}(M;\mathbb {Q})$
if
$H_{2n}(M;\mathbb {Q})$
if
![]() $\dim M=4n$
. The Euler characteristic with closed support (or Borel–Moore Euler characteristic) of a topological space M is denoted by
$\dim M=4n$
. The Euler characteristic with closed support (or Borel–Moore Euler characteristic) of a topological space M is denoted by
![]() $\chi ^{c}(M)$
.
$\chi ^{c}(M)$
.
1 Statement
1.1 Context
A real algebraic variety X is said to satisfy
![]() $\chi =\sigma $
if
$\chi =\sigma $
if
This definition is motivated by the old empirical observation that an important proportion of known real algebraic varieties satisfy
![]() $\chi =\sigma $
, in particular among compact nonsingular M-varieties. By the Smith–Thom inequality (see for example [Reference Mangolte15, §3.2]), any real algebraic variety X satisfies
$\chi =\sigma $
, in particular among compact nonsingular M-varieties. By the Smith–Thom inequality (see for example [Reference Mangolte15, §3.2]), any real algebraic variety X satisfies
 $$ \begin{align*} \sum_{i} \beta_{i}(\mathbb{R} X)\le \sum_{i} \beta_{i}(\mathbb{C} X), \end{align*} $$
$$ \begin{align*} \sum_{i} \beta_{i}(\mathbb{R} X)\le \sum_{i} \beta_{i}(\mathbb{C} X), \end{align*} $$
where
![]() $\beta _{i}$
denotes the ith Betti number with
$\beta _{i}$
denotes the ith Betti number with
![]() $\mathbb {Z}/2\mathbb {Z}$
-coefficients. Furthermore, the difference between the two sides is even, and we say that X is an
$\mathbb {Z}/2\mathbb {Z}$
-coefficients. Furthermore, the difference between the two sides is even, and we say that X is an
![]() $(M-i)$
-variety if
$(M-i)$
-variety if
 $$ \begin{align*} \sum_{i} \beta_{i}(\mathbb{C} X)- \sum_{i} \beta_{i}(\mathbb{R} X)=2i. \end{align*} $$
$$ \begin{align*} \sum_{i} \beta_{i}(\mathbb{C} X)- \sum_{i} \beta_{i}(\mathbb{R} X)=2i. \end{align*} $$
If X is a compact and nonsingular M-variety, Rokhlin congruence [Reference Degtyarev and Kharlamov6, 2.7.1] asserts that
yet almost all known examples of nonsingular compact M-varieties satisfy the stronger inequality
![]() $\chi (\mathbb {R} X)=\sigma (\mathbb {C} X)$
. If many examples among M-surfaces not satisfying this equality are known (see, for example, [Reference Degtyarev and Kharlamov6, Reference Mangolte15]), all nonsingular compact M-varieties of dimension at least 3 that I knowFootnote
1
satisfy
$\chi (\mathbb {R} X)=\sigma (\mathbb {C} X)$
. If many examples among M-surfaces not satisfying this equality are known (see, for example, [Reference Degtyarev and Kharlamov6, Reference Mangolte15]), all nonsingular compact M-varieties of dimension at least 3 that I knowFootnote
1
satisfy
![]() $\chi =\sigma $
. A heuristic explanation of this fact is the following: A large class of known real algebraic varieties is obtained by gluing ‘basic real algebraic varieties’ satisfying
$\chi =\sigma $
. A heuristic explanation of this fact is the following: A large class of known real algebraic varieties is obtained by gluing ‘basic real algebraic varieties’ satisfying
![]() $\chi =\sigma $
, a property that is preserved under gluing. This latter statement is the content of Proposition 2.1, which is an elementary observation relying on deep results about motivic nearby fibers and limit mixed Hodge structures. By ‘basic real algebraic varieties’, we mean, for example, real projective spaces or more generally real toric varieties.
$\chi =\sigma $
, a property that is preserved under gluing. This latter statement is the content of Proposition 2.1, which is an elementary observation relying on deep results about motivic nearby fibers and limit mixed Hodge structures. By ‘basic real algebraic varieties’, we mean, for example, real projective spaces or more generally real toric varieties.
As an application of this observation, we prove Theorem 1.2: Real algebraic varieties constructed out of nonsingular tropical varieties satisfy
![]() $\chi =\sigma $
. This generalizes the case of complete intersections, originally proved by Itenberg [Reference Itenberg10] for hypersurfaces of dimension
$\chi =\sigma $
. This generalizes the case of complete intersections, originally proved by Itenberg [Reference Itenberg10] for hypersurfaces of dimension
![]() $2$
, by Bertrand [Reference Bertrand2] for hypersurfaces of higher dimensions, and then by Bihan and Bertrand [Reference Bertrand and Bihan3] for any complete intersections. Theorem 1.2 is actually about potentially noncompact algebraic varieties, and we first briefly recall the extension of the signature to all complex algebraic varieties.
$2$
, by Bertrand [Reference Bertrand2] for hypersurfaces of higher dimensions, and then by Bihan and Bertrand [Reference Bertrand and Bihan3] for any complete intersections. Theorem 1.2 is actually about potentially noncompact algebraic varieties, and we first briefly recall the extension of the signature to all complex algebraic varieties.
Given a field
![]() $\mathbb {K}$
, the Grothendieck group
$\mathbb {K}$
, the Grothendieck group
![]() $K_{0}(Var_{\mathbb {K}})$
is the abelian group generated by isomorphism classes
$K_{0}(Var_{\mathbb {K}})$
is the abelian group generated by isomorphism classes
![]() $[X]$
of algebraic varieties over k modulo the scissor relation
$[X]$
of algebraic varieties over k modulo the scissor relation
for any closed algebraic subvariety Y of X. Considering the product
turns
![]() $K_{0}(Var_{\mathbb {K}})$
into a commutative ring with
$K_{0}(Var_{\mathbb {K}})$
into a commutative ring with
![]() $0=[\emptyset ]$
and
$0=[\emptyset ]$
and
![]() $1=[pt]$
. It it is not too difficult to show (see, for example, [Reference Peters17, Lecture 1]) that when
$1=[pt]$
. It it is not too difficult to show (see, for example, [Reference Peters17, Lecture 1]) that when
![]() $\mathbb {K}=\mathbb {R}$
or
$\mathbb {K}=\mathbb {R}$
or
![]() $\mathbb {C}$
, the Euler characteristic with closed support provides a ring morphism
$\mathbb {C}$
, the Euler characteristic with closed support provides a ring morphism
 $$ \begin{align*} \chi^{c}: K_{0}(Var_{\mathbb{K}})& \longrightarrow \mathbb{Z} \\ X&\longmapsto \chi^{c}(\mathbb{K} X). \end{align*} $$
$$ \begin{align*} \chi^{c}: K_{0}(Var_{\mathbb{K}})& \longrightarrow \mathbb{Z} \\ X&\longmapsto \chi^{c}(\mathbb{K} X). \end{align*} $$
Such a ring (or group) morphism is called a motivic invariant. It is a much less obvious result that the signature of nonsingular projective complex algebraic varieties extends to a motivic invariant
This is a consequence of the combination of the two following facts:
-
• The signature of a nonsingular projective complex algebraic manifold is the evaluation at
 $1$
of its Hirzebruch genus; this is the Hodge index theorem (see, for example, [Reference Voisin21, Theorem 6.33]).
$1$
of its Hirzebruch genus; this is the Hodge index theorem (see, for example, [Reference Voisin21, Theorem 6.33]). -
• The Hirzebruch genus extends to a motivic invariant
 $\chi _{y}: K_{0}(Var_{\mathbb {C}})\to \mathbb {Z}[y]$
(see, for example, [Reference Peters and Steenbrink18, Remark 5.6]), since
$\chi _{y}: K_{0}(Var_{\mathbb {C}})\to \mathbb {Z}[y]$
(see, for example, [Reference Peters and Steenbrink18, Remark 5.6]), since
 $\chi _{y}$
is in its turn a specialization of the Hodge–Euler polynomial.
$\chi _{y}$
is in its turn a specialization of the Hodge–Euler polynomial.
Using the scissor relation, it easy to check that, as already mentioned, basic real algebraic varieties satisfy
![]() $\chi =\sigma $
.
$\chi =\sigma $
.
Example 1.1. One computes easily that
![]() $\chi ^{c}(\mathbb {R})=-1$
. On the other hand, one has
$\chi ^{c}(\mathbb {R})=-1$
. On the other hand, one has
 $$ \begin{align*} 0=\sigma\left(\mathbb{C}P^{1}\right)=\sigma(\mathbb{C})+\sigma(pt)=\sigma(\mathbb{C})+1. \end{align*} $$
$$ \begin{align*} 0=\sigma\left(\mathbb{C}P^{1}\right)=\sigma(\mathbb{C})+\sigma(pt)=\sigma(\mathbb{C})+1. \end{align*} $$
Hence we deduce that
![]() $\chi ^{c}(\mathbb {R})=\sigma (\mathbb {C})=-1$
; that is to say,
$\chi ^{c}(\mathbb {R})=\sigma (\mathbb {C})=-1$
; that is to say,
![]() $\mathbb {C}$
satisfies
$\mathbb {C}$
satisfies
![]() $\chi =\sigma $
. Since both
$\chi =\sigma $
. Since both
![]() $\chi ^{c}$
and
$\chi ^{c}$
and
![]() $\sigma $
are ring morphisms, we deduce that
$\sigma $
are ring morphisms, we deduce that
![]() $\chi ^{c}(\mathbb {R}^{n})=\sigma (\mathbb {C}^{n})=(-1)^{n}$
. In other words, real affine spaces satisfy
$\chi ^{c}(\mathbb {R}^{n})=\sigma (\mathbb {C}^{n})=(-1)^{n}$
. In other words, real affine spaces satisfy
![]() $\chi =\sigma $
. By the scissor relation again, this implies that any real algebraic variety with a stratification by real affine spaces satisfies
$\chi =\sigma $
. By the scissor relation again, this implies that any real algebraic variety with a stratification by real affine spaces satisfies
![]() $\chi =\sigma $
. In particular, all Grassmannians, and more generally all real flag varieties, satisfy
$\chi =\sigma $
. In particular, all Grassmannians, and more generally all real flag varieties, satisfy
![]() $\chi =\sigma $
. The case of real toric varieties – that is, equipped with the standard real structure induced by the complex conjugation on
$\chi =\sigma $
. The case of real toric varieties – that is, equipped with the standard real structure induced by the complex conjugation on
![]() $\mathbb {C}^{*}$
– can be handled similarly. One has
$\mathbb {C}^{*}$
– can be handled similarly. One has
Hence a real torus
![]() $(\mathbb {C}^{*})^{n}$
satisfies
$(\mathbb {C}^{*})^{n}$
satisfies
![]() $\chi =\sigma $
, and so does any real toric variety, since it admits a stratification by real tori.
$\chi =\sigma $
, and so does any real toric variety, since it admits a stratification by real tori.
1.2 Real approximations of
 $\mathbb {Q}$
-nonsingular tropical varieties
$\mathbb {Q}$
-nonsingular tropical varieties
Given a fan
![]() $\Delta \subset \mathbb {R}^{n}$
, we denote by
$\Delta \subset \mathbb {R}^{n}$
, we denote by
![]() $Tor_{\mathbb {C}}(\Delta )$
the complex toric variety defined by
$Tor_{\mathbb {C}}(\Delta )$
the complex toric variety defined by
![]() $\Delta $
[Reference Fulton8]. In this note we consider only fans
$\Delta $
[Reference Fulton8]. In this note we consider only fans
![]() $\Delta $
for which
$\Delta $
for which
![]() $Tor_{\mathbb {C}}(\Delta )$
is nonsingular, in which case we can also consider the tropical toric variety
$Tor_{\mathbb {C}}(\Delta )$
is nonsingular, in which case we can also consider the tropical toric variety
![]() $Tor_{\mathbb {T}}(\Delta )$
defined by
$Tor_{\mathbb {T}}(\Delta )$
defined by
![]() $\Delta $
[Reference Bittner5, Reference Mikhalkin and Rau16]. In what follows, we use the notions defined in [Reference Itenberg, Katzarkov, Mikhalkin and Zharkov11] of
$\Delta $
[Reference Bittner5, Reference Mikhalkin and Rau16]. In what follows, we use the notions defined in [Reference Itenberg, Katzarkov, Mikhalkin and Zharkov11] of
![]() $\mathbb {Q}$
-nonsingular tropical varieties of
$\mathbb {Q}$
-nonsingular tropical varieties of
![]() $Tor_{\mathbb {T}}(\Delta )$
and of tropical limits of nonsingular analytic families
$Tor_{\mathbb {T}}(\Delta )$
and of tropical limits of nonsingular analytic families
![]() $X\subset \mathbb {C}P^{N}\times D^{*}$
of algebraic subvarieties of
$X\subset \mathbb {C}P^{N}\times D^{*}$
of algebraic subvarieties of
![]() $\mathbb {C}P^{N}$
over the punctured unit disk
$\mathbb {C}P^{N}$
over the punctured unit disk
![]() $D^{*}\subset \mathbb {C}$
. For such a family, we denote by
$D^{*}\subset \mathbb {C}$
. For such a family, we denote by
![]() $X_{t}$
the member of the family corresponding to
$X_{t}$
the member of the family corresponding to
![]() $t\in D^{*}$
.
$t\in D^{*}$
.
Theorem 1.2. Let
![]() $\Delta $
be a fan defining a nonsingular projective toric variety
$\Delta $
be a fan defining a nonsingular projective toric variety
![]() $Tor_{\mathbb {C}}(\Delta )$
. Suppose that
$Tor_{\mathbb {C}}(\Delta )$
. Suppose that
![]() $X\subset Tor_{\mathbb {C}}(\Delta )\times D^{*}$
is a nonsingular real analytic family of algebraic subvarieties of
$X\subset Tor_{\mathbb {C}}(\Delta )\times D^{*}$
is a nonsingular real analytic family of algebraic subvarieties of
![]() $Tor_{\mathbb {C}}(\Delta )$
, admitting a
$Tor_{\mathbb {C}}(\Delta )$
, admitting a
![]() $\mathbb {Q}$
-nonsingular tropical limit in
$\mathbb {Q}$
-nonsingular tropical limit in
![]() $Tor_{\mathbb {T}}(\Delta )$
. Then for any subfan
$Tor_{\mathbb {T}}(\Delta )$
. Then for any subfan
![]() $\delta $
of
$\delta $
of
![]() $\Delta $
and any
$\Delta $
and any
![]() $t_{0}\in \mathbb {R} D^{*}$
small enough, the real analytic variety
$t_{0}\in \mathbb {R} D^{*}$
small enough, the real analytic variety
![]() $X_{t_{0}}\cap Tor_{\mathbb {C}}(\delta )$
satisfies
$X_{t_{0}}\cap Tor_{\mathbb {C}}(\delta )$
satisfies
![]() $\chi =\sigma $
.
$\chi =\sigma $
.
As already mentioned, the case of compact hypersurfaces was earlier proved by Itenberg [Reference Itenberg10] and Bertrand [Reference Bertrand2]. This was generalized to possibly noncompact complete intersections by Bertand and Bihan [Reference Bertrand and Bihan3], who used motivic aspects of
![]() $\chi ^{c}$
and
$\chi ^{c}$
and
![]() $\sigma $
to reduce to the case of hypersurfaces. The strategy in each of these three papers is then to separately compute
$\sigma $
to reduce to the case of hypersurfaces. The strategy in each of these three papers is then to separately compute
![]() $\chi ^{c}$
and
$\chi ^{c}$
and
![]() $\sigma $
and to check that both numbers coincide. Alternative proofs using tropical homology were proposed in the case of complete intersections by Arnal [Reference Arnal1] (still by equating two separate computations), and by Renaudineau and Shaw [Reference Renaudineau and Shaw20]. In this latter work, the equality
$\sigma $
and to check that both numbers coincide. Alternative proofs using tropical homology were proposed in the case of complete intersections by Arnal [Reference Arnal1] (still by equating two separate computations), and by Renaudineau and Shaw [Reference Renaudineau and Shaw20]. In this latter work, the equality
![]() $\chi ^{c}(\mathbb {R} X_{t})=\sigma (\mathbb {C} X_{t})$
is a consequence of a much stronger result: It follows from the existence of a spectral sequence starting from the tropical homology of the tropical limit of X and converging to the homology of
$\chi ^{c}(\mathbb {R} X_{t})=\sigma (\mathbb {C} X_{t})$
is a consequence of a much stronger result: It follows from the existence of a spectral sequence starting from the tropical homology of the tropical limit of X and converging to the homology of
![]() $\mathbb {R} X$
. Results from [Reference Renaudineau and Shaw20] have recently been generalized to any real analytic family admitting a
$\mathbb {R} X$
. Results from [Reference Renaudineau and Shaw20] have recently been generalized to any real analytic family admitting a
![]() $\mathbb {Q}$
-nonsingular tropical limit by Rau, Renaudineau, and Shaw [Reference Rau, Renaudineau and Shaw19].
$\mathbb {Q}$
-nonsingular tropical limit by Rau, Renaudineau, and Shaw [Reference Rau, Renaudineau and Shaw19].
Hence in a sense all previous proofs of Theorem 1.2 are based on separate computations of both
![]() $\chi ^{c}$
and
$\chi ^{c}$
and
![]() $\sigma $
. Our proof uses a different strategy: Both quantities satisfy the same gluing relations under totally real semistable degenerations by Proposition 2.1, while the tropical nonsingularity assumption ensures that all pieces involved in the gluing satisfy
$\sigma $
. Our proof uses a different strategy: Both quantities satisfy the same gluing relations under totally real semistable degenerations by Proposition 2.1, while the tropical nonsingularity assumption ensures that all pieces involved in the gluing satisfy
![]() $\chi =\sigma $
.
$\chi =\sigma $
.
Note that in the case of hypersurfaces, the methods of Itenberg, Bertrand, and Bertand and Bihan do not work in the tropical-geometry framework but rather in the dual setup of unimodular subdivisions of polytopes. It is interesting that their proof also applies to nonregular (or nonconvex) subdivisions – that is to say, real combinatorial hypersurfaces (see [Reference Itenberg and Shustin12] for a definition) also satisfy
![]() $\chi =\sigma $
. Our proof of Theorem 1.2, as well as the proofs by Arnal, Renaudineau and Shaw, and Rau, Renaudineau, and Shaw do not seem to extend to real combinatorial hypersurfaces.
$\chi =\sigma $
. Our proof of Theorem 1.2, as well as the proofs by Arnal, Renaudineau and Shaw, and Rau, Renaudineau, and Shaw do not seem to extend to real combinatorial hypersurfaces.
2 Proof
2.1 Real semistable degenerations
Let
![]() $f:X\to D$
be a proper analytic map from a nonsingular complex algebraic manifold X to the unit disk
$f:X\to D$
be a proper analytic map from a nonsingular complex algebraic manifold X to the unit disk
![]() $D\subset \mathbb {C}$
such that
$D\subset \mathbb {C}$
such that
-
•
 $X_{t}$
is a nonsingular algebraic manifold for all
$X_{t}$
is a nonsingular algebraic manifold for all
 $t\in D^{*}$
and
$t\in D^{*}$
and -
•
 $X_{0}=f^{-1}(0)$
is a reduced algebraic variety with nonsingular components crossing normally.
$X_{0}=f^{-1}(0)$
is a reduced algebraic variety with nonsingular components crossing normally.
Such a map is called a semistable degeneration (of
![]() $X_{t}$
for
$X_{t}$
for
![]() $t\ne 0$
). Denoting by
$t\ne 0$
). Denoting by
![]() $(E_{i})_{i\in J}$
the irreducible components of
$(E_{i})_{i\in J}$
the irreducible components of
![]() $X_{0}$
, we define for
$X_{0}$
, we define for
![]() $I\subset J$
$I\subset J$
 $$ \begin{align*} E_{I}^{\circ} =\bigcap_{i\in I}E_{i}\setminus \bigcup_{j\notin J}E_{j}. \end{align*} $$
$$ \begin{align*} E_{I}^{\circ} =\bigcap_{i\in I}E_{i}\setminus \bigcup_{j\notin J}E_{j}. \end{align*} $$
Suppose now that X is real and that f is real when D is equipped with the standard complex conjugation. We say that f is totally real if each irreducible component of
![]() $X_{0}$
is real.
$X_{0}$
is real.
Proposition 2.1. Let
![]() $f:X\to D$
be a totally real semistable degeneration. Then for any
$f:X\to D$
be a totally real semistable degeneration. Then for any
![]() $t\in \mathbb {R} D^{*}$
small enough,
$t\in \mathbb {R} D^{*}$
small enough,
 $$ \begin{align*} \sigma(\mathbb{C} X_{t})=\sum_{\emptyset \ne I\subset J}2^{\lvert I\rvert-1}\sigma\left(\mathbb{C} E^{o}_{I}\right) \qquad \text{and}\qquad \chi^{c}(\mathbb{R} X_{t})=\sum_{\emptyset \ne I\subset J}2^{\lvert I\rvert-1}\chi^{c}\left(\mathbb{R} E^{o}_{I}\right). \end{align*} $$
$$ \begin{align*} \sigma(\mathbb{C} X_{t})=\sum_{\emptyset \ne I\subset J}2^{\lvert I\rvert-1}\sigma\left(\mathbb{C} E^{o}_{I}\right) \qquad \text{and}\qquad \chi^{c}(\mathbb{R} X_{t})=\sum_{\emptyset \ne I\subset J}2^{\lvert I\rvert-1}\chi^{c}\left(\mathbb{R} E^{o}_{I}\right). \end{align*} $$
In particular,
![]() $X_{t}$
satisfies
$X_{t}$
satisfies
![]() $\chi =\sigma $
as soon as all
$\chi =\sigma $
as soon as all
![]() $E^{o}_{I}$
s satisfy
$E^{o}_{I}$
s satisfy
![]() $\chi =\sigma $
.
$\chi =\sigma $
.
Proof. The statement about the signature follows from deep results on motivic nearby fibers and limit mixed Hodge structures. We refer to [Reference Katz and Stapledon14, §§1 and 3] for a concise exposition of what is needed here, and to [Reference Denef and Loeser7, §3], [Reference Brugallé, Itenberg, Mikhalkin and Shaw4, §2], and [Reference Peters and Steenbrink18, §11] for more details. Recall first that the Hirzebruch genus
![]() $\chi _{y}(Y)$
of a projective nonsingular complex algebraic variety is the polynomial in y defined by
$\chi _{y}(Y)$
of a projective nonsingular complex algebraic variety is the polynomial in y defined by
 $$ \begin{align*} \chi_{y}(Y)=\sum_{p\ge 0}\left(\sum_{q\ge 0}(-1)^{q}h^{p,q}(Y) \right) y^{p}, \end{align*} $$
$$ \begin{align*} \chi_{y}(Y)=\sum_{p\ge 0}\left(\sum_{q\ge 0}(-1)^{q}h^{p,q}(Y) \right) y^{p}, \end{align*} $$
and that it satisfies
![]() $\chi _{1}(Y)=\sigma (Y)$
by the Hodge index theorem. The Hirzebruch genus turns out to be a motivic invariant – that is, it extends to a ring morphism
$\chi _{1}(Y)=\sigma (Y)$
by the Hodge index theorem. The Hirzebruch genus turns out to be a motivic invariant – that is, it extends to a ring morphism
![]() $\chi _{y}:K_{0}(Var_{\mathbb {C}})\to \mathbb {Z}[y]$
. In particular,
$\chi _{y}:K_{0}(Var_{\mathbb {C}})\to \mathbb {Z}[y]$
. In particular,
![]() $\sigma (Y)=\chi _{1}(Y)$
for any complex algebraic variety Y. The motivic nearby fiber of f, introduced by Denef and Loeser, is defined by
$\sigma (Y)=\chi _{1}(Y)$
for any complex algebraic variety Y. The motivic nearby fiber of f, introduced by Denef and Loeser, is defined by
 $$ \begin{align*} \psi_{f}=\sum_{\emptyset \ne I\subset J} \left[E^{o}_{I}\right](1- [\mathbb{C}])^{\lvert I\rvert-1} \in K_{0}(Var_{\mathbb{C}}), \end{align*} $$
$$ \begin{align*} \psi_{f}=\sum_{\emptyset \ne I\subset J} \left[E^{o}_{I}\right](1- [\mathbb{C}])^{\lvert I\rvert-1} \in K_{0}(Var_{\mathbb{C}}), \end{align*} $$
and satisfies the great property
![]() $\chi _{y}\left (\psi _{f}\right )=\chi _{y}(X_{t})$
for
$\chi _{y}\left (\psi _{f}\right )=\chi _{y}(X_{t})$
for
![]() $t\ne 0$
. So one has
$t\ne 0$
. So one has
 $$ \begin{align*} \chi_{y}(X_{t})=\sum_{\emptyset \ne I\subset J} \chi_{y}\left(E^{o}_{I}\right) \left(2-\chi_{y}\left(\mathbb{C}P^{1}\right)\right)^{\lvert I\rvert-1} =\sum_{\emptyset \ne I\subset J} (1+y)^{\lvert I\rvert-1}\chi_{y}\left(E^{o}_{I}\right). \end{align*} $$
$$ \begin{align*} \chi_{y}(X_{t})=\sum_{\emptyset \ne I\subset J} \chi_{y}\left(E^{o}_{I}\right) \left(2-\chi_{y}\left(\mathbb{C}P^{1}\right)\right)^{\lvert I\rvert-1} =\sum_{\emptyset \ne I\subset J} (1+y)^{\lvert I\rvert-1}\chi_{y}\left(E^{o}_{I}\right). \end{align*} $$
The first statement of the proposition is obtained by evaluating this identity at
![]() $y=1$
.
$y=1$
.
The statement about the Euler characteristic follows from the observation that
![]() $\mathbb {R} X_{t}$
is the disjoint union of coverings of
$\mathbb {R} X_{t}$
is the disjoint union of coverings of
![]() $\mathbb {R} E^{o}_{I}$
of degree
$\mathbb {R} E^{o}_{I}$
of degree
![]() $2^{\lvert I\rvert -1}$
, with I ranging over all possible sets
$2^{\lvert I\rvert -1}$
, with I ranging over all possible sets
![]() $\emptyset \ne I\subset J$
. Indeed, by assumption one can locally express X in coordinates at a point of
$\emptyset \ne I\subset J$
. Indeed, by assumption one can locally express X in coordinates at a point of
![]() $\mathbb {R} E^{o}_{I}$
as the solutions of the equation
$\mathbb {R} E^{o}_{I}$
as the solutions of the equation
where
![]() $\alpha $
is the deformation parameter, with
$\alpha $
is the deformation parameter, with
![]() $\alpha =0$
corresponding to the central fiber
$\alpha =0$
corresponding to the central fiber
![]() $X_{0}$
. Given a nonzero
$X_{0}$
. Given a nonzero
![]() $\alpha $
, the corresponding smooth fiber of f is locally given in
$\alpha $
, the corresponding smooth fiber of f is locally given in
![]() $\mathbb {R}^{n}=\mathbb {R}^{\lvert I\rvert }\times \mathbb {R}^{n-\lvert I\rvert }$
by the solutions of this equation. This set is homeomorphic to the disjoint union of
$\mathbb {R}^{n}=\mathbb {R}^{\lvert I\rvert }\times \mathbb {R}^{n-\lvert I\rvert }$
by the solutions of this equation. This set is homeomorphic to the disjoint union of
![]() $2^{\lvert I\rvert -1}$
copies of
$2^{\lvert I\rvert -1}$
copies of
 $\mathbb {R}_{\ge 0}^{\lvert I\rvert }\times \mathbb {R}^{n-\lvert I\rvert }$
, and the result follows.
$\mathbb {R}_{\ge 0}^{\lvert I\rvert }\times \mathbb {R}^{n-\lvert I\rvert }$
, and the result follows.
2.2 Proof of Theorem 1.2
Our proof combines Proposition 2.1 and [Reference Itenberg and Shustin11, §4] to reduce to an elementary computation for a complement of real hyperplane arrangements.
Recall that
![]() $\Delta \subset \mathbb {R}^{n}$
is a fan defining a nonsingular projective toric variety
$\Delta \subset \mathbb {R}^{n}$
is a fan defining a nonsingular projective toric variety
![]() $Tor_{\mathbb {C}}(\Delta )$
, and that
$Tor_{\mathbb {C}}(\Delta )$
, and that
![]() $f:X\to D^{*}$
is a nonsingular real analytic family of algebraic subvarieties of
$f:X\to D^{*}$
is a nonsingular real analytic family of algebraic subvarieties of
![]() $Tor_{\mathbb {C}}(\Delta )$
admitting a
$Tor_{\mathbb {C}}(\Delta )$
admitting a
![]() $\mathbb {Q}$
-nonsingular tropical limit V in
$\mathbb {Q}$
-nonsingular tropical limit V in
![]() $Tor_{\mathbb {T}}(\Delta )$
. Given torus orbits
$Tor_{\mathbb {T}}(\Delta )$
. Given torus orbits
![]() $\mathcal O_{\mathbb {C}}$
and
$\mathcal O_{\mathbb {C}}$
and
![]() $\mathcal O_{\mathbb {T}}$
of
$\mathcal O_{\mathbb {T}}$
of
![]() $Tor_{\mathbb {C}}(\Delta )$
and
$Tor_{\mathbb {C}}(\Delta )$
and
![]() $Tor_{\mathbb {T}}(\Delta )$
, respectively, corresponding to the same cone of
$Tor_{\mathbb {T}}(\Delta )$
, respectively, corresponding to the same cone of
![]() $\Delta $
, the intersection of
$\Delta $
, the intersection of
![]() $V\cap \mathcal O_{\mathbb {T}}$
is the tropical limit of
$V\cap \mathcal O_{\mathbb {T}}$
is the tropical limit of
![]() $X\cap (\mathcal O_{\mathbb {C}}\times D^{*})$
. Since both
$X\cap (\mathcal O_{\mathbb {C}}\times D^{*})$
. Since both
![]() $\sigma $
and
$\sigma $
and
![]() $\chi ^{c}$
are motivic invariants, it is enough to prove Theorem 1.2 in the case when
$\chi ^{c}$
are motivic invariants, it is enough to prove Theorem 1.2 in the case when
![]() $\delta =\{0\}$
– that is, when
$\delta =\{0\}$
– that is, when
![]() $Tor_{\mathbb {C}}(\delta )=(\mathbb {C}^{*})^{n}$
. In what follows, we define
$Tor_{\mathbb {C}}(\delta )=(\mathbb {C}^{*})^{n}$
. In what follows, we define
![]() $X^{o}=X\cap ((\mathbb {C}^{*})^{n} \times D^{*})$
and
$X^{o}=X\cap ((\mathbb {C}^{*})^{n} \times D^{*})$
and
![]() $V^{o}=V\cap \mathbb {R}^{n}$
.
$V^{o}=V\cap \mathbb {R}^{n}$
.
By [Reference Itenberg and Shustin11, Proposition 51] (see also [Reference Helm and Katz9, Proposition 2.3] and [Reference Katz and Stapledon13, Lemma 7.9] in a slightly different realm), after shrinking D if necessary and after a base change
![]() $t\mapsto \pm t^{d}$
, one can extend the real family
$t\mapsto \pm t^{d}$
, one can extend the real family
![]() $X^{o}$
over
$X^{o}$
over
![]() $0$
to a real semistable degeneration
$0$
to a real semistable degeneration
![]() $f:\overline X^{o}\to D$
such that any irreducible component of
$f:\overline X^{o}\to D$
such that any irreducible component of
![]() $E_{I}^{\circ }$
of the central fiber
$E_{I}^{\circ }$
of the central fiber
 $\overline X^{o}_{0}$
is isomorphic to the complement of a hyperplane arrangement in some
$\overline X^{o}_{0}$
is isomorphic to the complement of a hyperplane arrangement in some
![]() $\mathbb {C}P^{m}$
. When d is even, the sign in the base change is chosen so that the real fiber
$\mathbb {C}P^{m}$
. When d is even, the sign in the base change is chosen so that the real fiber
![]() $X_{t_{0}}$
lifts to a real fiber (that is, it is the sign of
$X_{t_{0}}$
lifts to a real fiber (that is, it is the sign of
![]() $t_{0}$
). Since the complex conjugation on
$t_{0}$
). Since the complex conjugation on
![]() $(\mathbb {C}^{*})^{n}$
induces, via the the tropicalization procedure, the identity map on
$(\mathbb {C}^{*})^{n}$
induces, via the the tropicalization procedure, the identity map on
![]() $\mathbb {R}^{n}$
, the semistable degeneration
$\mathbb {R}^{n}$
, the semistable degeneration
![]() $f:\overline X^{o}\to D$
is totally real. In particular, each irreducible component of
$f:\overline X^{o}\to D$
is totally real. In particular, each irreducible component of
![]() $E_{I}^{\circ }$
is the complement of a real hyperplane arrangement in some
$E_{I}^{\circ }$
is the complement of a real hyperplane arrangement in some
![]() $\mathbb {C}P^{m}$
equipped with the standard complex conjugation.
$\mathbb {C}P^{m}$
equipped with the standard complex conjugation.
Hence, thanks to Proposition 2.1, the proof of Theorem 1.2 reduces to verifying that these latter complements satisfy
![]() $\chi =\sigma $
. This is easily done by a double induction on m and the number k of hyperplanes in the arrangement.
$\chi =\sigma $
. This is easily done by a double induction on m and the number k of hyperplanes in the arrangement.
-
(1) The case
 $m=0$
holds trivially.
$m=0$
holds trivially. -
(2) Assume that this is true for
 $m-1$
and any k, and let us prove by induction on k that it is also true for m and any k.
$m-1$
and any k, and let us prove by induction on k that it is also true for m and any k.-
(a) One checks easily that the case
 $k=0$
holds (see Example 1.1).
$k=0$
holds (see Example 1.1). -
(b) By definition, the complement
 $\mathcal A$
of k real hyperplanes in
$\mathcal A$
of k real hyperplanes in
 $\mathbb {C}P^{m}$
is obtained by removing the complement
$\mathbb {C}P^{m}$
is obtained by removing the complement
 $\mathcal A^{\prime \prime }$
of
$\mathcal A^{\prime \prime }$
of
 $k-1$
real hyperplanes in
$k-1$
real hyperplanes in
 $\mathbb {C}P^{m-1}$
to the complement
$\mathbb {C}P^{m-1}$
to the complement
 $\mathcal A^{\prime }$
of
$\mathcal A^{\prime }$
of
 $k-1$
real hyperplanes in
$k-1$
real hyperplanes in
 $\mathbb {C}P^{m}$
. By induction and the scissor relation, we have
$\mathbb {C}P^{m}$
. By induction and the scissor relation, we have  $$ \begin{align*} \chi^{c}(\mathbb{R} \mathcal A)=\chi^{c}(\mathbb{R} \mathcal A^{\prime})-\chi^{c}(\mathbb{R} \mathcal A^{\prime\prime}) = \sigma^{c}(\mathbb{C} \mathcal A^{\prime})-\sigma^{c}(\mathbb{C} \mathcal A^{\prime\prime})= \sigma^{c}(\mathbb{C} \mathcal A). \end{align*} $$
$$ \begin{align*} \chi^{c}(\mathbb{R} \mathcal A)=\chi^{c}(\mathbb{R} \mathcal A^{\prime})-\chi^{c}(\mathbb{R} \mathcal A^{\prime\prime}) = \sigma^{c}(\mathbb{C} \mathcal A^{\prime})-\sigma^{c}(\mathbb{C} \mathcal A^{\prime\prime})= \sigma^{c}(\mathbb{C} \mathcal A). \end{align*} $$
-
Now the proof of Theorem 1.2 is complete.□
3 Further comments
We end this note with a couple of remarks. First, dropping compactness or the M-condition, one easily constructs real algebraic varieties which do not satisfy
![]() $\chi =\sigma $
. For example,
$\chi =\sigma $
. For example,
![]() $X=\mathbb {C}^{*}$
equipped with the real structure
$X=\mathbb {C}^{*}$
equipped with the real structure
 $\tau (z)=\frac {1}{z}$
is an M-curve and satisfies
$\tau (z)=\frac {1}{z}$
is an M-curve and satisfies
 $$ \begin{align*} \chi^{c}(\mathbb{R} X)=\chi\left(S^{1}\right)=0\ne -2= \sigma(\mathbb{C}^{*}), \end{align*} $$
$$ \begin{align*} \chi^{c}(\mathbb{R} X)=\chi\left(S^{1}\right)=0\ne -2= \sigma(\mathbb{C}^{*}), \end{align*} $$
and a quadric ellipsoid X in
![]() $\mathbb {C}P^{3}$
satisfies
$\mathbb {C}P^{3}$
satisfies
More generally, Gudkov–Kharlamov–Krakhnov congruence [Reference Degtyarev and Kharlamov6, 2.7.1] implies that a nonsingular compact
![]() $(M-1)$
-varietyFootnote
2
cannot satisfy
$(M-1)$
-varietyFootnote
2
cannot satisfy
![]() $\chi =\sigma $
.
$\chi =\sigma $
.
Lastly, the Viro conjecture for M-surfaces states that such a projective and simply connected M-surface X satisfies
which is equivalent in this case to the inequality
I do not know any M-variety,Footnote 3 projective or not, singular or not, which does not satisfy
 $$ \begin{align*} \chi^{c}(\mathbb{R} X)\le \sigma(\mathbb{C} X) &\text{ if }\dim X = 0,3\bmod 4, \\ \chi^{c}(\mathbb{R} X)\ge \sigma(\mathbb{C} X) &\text{ if } \dim X = 1,2\bmod 4. \end{align*} $$
$$ \begin{align*} \chi^{c}(\mathbb{R} X)\le \sigma(\mathbb{C} X) &\text{ if }\dim X = 0,3\bmod 4, \\ \chi^{c}(\mathbb{R} X)\ge \sigma(\mathbb{C} X) &\text{ if } \dim X = 1,2\bmod 4. \end{align*} $$
Acknowledgment
This work is partially supported by the TROPICOUNT grant of Région Pays de la Loire, and the ANR project ENUMGEOM NR-18-CE40-0009-02. I am grateful to Ilia Itenberg for drawing my attention to the classifications of real cubic hypersurfaces of dimension
![]() $3$
and
$3$
and
![]() $4$
, which helped me in improving the last remark of this note.
$4$
, which helped me in improving the last remark of this note.
Competing Interest
None.