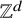1 Introduction
Higher-dimensional partitions are classical combinatorial objects introduced by MacMahon over a century ago. While the concept itself is a straightforward generalization of the usual (1-dimensional) integer partitions, the problems related to it are very challenging. For (2-dimensional) plane partitions, MacMahon obtained his celebrated enumerative formulas [Reference MacMahonMac16] (cf. [Reference StanleySta99, Ch. 7]). For general d-dimensional partitions, he only conjectured a formula of the volume generating function, which was later computed to be incorrect [Reference Atkin, Bratley, Macdonald and McKayABMM67].
Despite long interest and many connections to various fields including algebra, combinatorics, geometry, probability and statistical physics, the subject remains rather mysterious – very little is known about d-dimensional partitions for
![]() $d \ge 3$
(e.g., according to Stanley [Reference StanleySta99, Ch. 7.20], ‘almost nothing significant is known’). See [Reference Atkin, Bratley, Macdonald and McKayABMM67, Reference KnuthKnu70, Reference GovindarajanGov13] on some computational and enumerative aspects; [Reference Mustonen and RajeshMR03, Reference Balakrishnan, Govindarajan and PrabhakarBGP12, Reference Destainville and GovindarajanDG15] on asymptotic data and connections to physics; [Reference Behrend, Bryan and SzendrőiBBS13, Reference NekrasovNek17, Reference Cao and KoolCK18] on further aspects particularly related to the theory of Donaldson–Thomas invariants. A few more remarks and some early references can also be found in [Reference StanleySta71].
$d \ge 3$
(e.g., according to Stanley [Reference StanleySta99, Ch. 7.20], ‘almost nothing significant is known’). See [Reference Atkin, Bratley, Macdonald and McKayABMM67, Reference KnuthKnu70, Reference GovindarajanGov13] on some computational and enumerative aspects; [Reference Mustonen and RajeshMR03, Reference Balakrishnan, Govindarajan and PrabhakarBGP12, Reference Destainville and GovindarajanDG15] on asymptotic data and connections to physics; [Reference Behrend, Bryan and SzendrőiBBS13, Reference NekrasovNek17, Reference Cao and KoolCK18] on further aspects particularly related to the theory of Donaldson–Thomas invariants. A few more remarks and some early references can also be found in [Reference StanleySta71].
At the same time, the theory of plane partitions has greatly developed; see [Reference AndrewsAnd98, Reference StanleySta99, Reference Krattenthaler, Hersh, Lam, Pylyavskyy and ReinerKrat16] and many references therein. Its success mainly comes from the theory of symmetric functions, especially by using the Robinson–Schensted–Knuth (RSK) correspondence and Schur polynomials. The lack of tools for higher-dimensional generalizations makes it difficult to approach them, and here, one can try to develop analogous methods. This paper is in this direction.
Let us summarize our results.
1.1 Higher-dimensional partitions and hypermatrices
First, we present a natural bijection between d-dimensional arrays of nonnegative integers and d-dimensional partitions; see Section 3. Roughly speaking, any d-dimensional partition can be viewed as a hypermatrix of largest paths for some source weight hypermatrix. The bijection has nice properties which relate natural statistics for both objects. We then give a number of applications.
1.2 Corner-hook volume and interpretation of MacMahon’s numbers
One of the main consequences of this bijection is the multivariable generating series presented in Theorem 4.1 whose specializations allow to explicitly compute generating functions for certain statistics on d-dimensional partitions. In particular, we introduce two statistics on d-dimensional partitions: corners
![]() $\mathrm {cor}(\cdot )$
and corner-hook volume
$\mathrm {cor}(\cdot )$
and corner-hook volume
![]() $|\cdot |_{ch}$
(see Sections 3.3 and 5 for definitions) with generating functions shown below.
$|\cdot |_{ch}$
(see Sections 3.3 and 5 for definitions) with generating functions shown below.
Theorem 1.1 (Corner-hook generating function, cf. Corollary 5.4).
We have the following generating function:
 $$ \begin{align*}\sum_{\pi} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^{\infty} {(1 - t q^n)^{-\binom{n + d - 2}{d-1}}}, \end{align*} $$
$$ \begin{align*}\sum_{\pi} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^{\infty} {(1 - t q^n)^{-\binom{n + d - 2}{d-1}}}, \end{align*} $$
where the sum runs over d-dimensional partitions
![]() $\pi $
.
$\pi $
.
For
![]() $d = 2$
, this formula is equidistributed with Stanley’s trace generating function [Reference StanleySta99, Thm. 7.20.1], but the statistics are not identical. MacMahon conjectured [Reference MacMahonMac16] that the generating function defined as
$d = 2$
, this formula is equidistributed with Stanley’s trace generating function [Reference StanleySta99, Thm. 7.20.1], but the statistics are not identical. MacMahon conjectured [Reference MacMahonMac16] that the generating function defined as
 $$ \begin{align*} \sum_{n = 0}^{\infty} m_d(n)\, q^n := \prod_{n = 1}^{\infty} {(1 - q^n)^{-\binom{n + d - 2}{d-1}}} \end{align*} $$
$$ \begin{align*} \sum_{n = 0}^{\infty} m_d(n)\, q^n := \prod_{n = 1}^{\infty} {(1 - q^n)^{-\binom{n + d - 2}{d-1}}} \end{align*} $$
gives the volume generating function
![]() $\sum _{\pi } q^{|\pi |}$
for d-dimensional partitions. This was shown to be incorrect for
$\sum _{\pi } q^{|\pi |}$
for d-dimensional partitions. This was shown to be incorrect for
![]() $d \ge 3$
[Reference Atkin, Bratley, Macdonald and McKayABMM67]. However, from Theorem 1.1, we obtain the following interpretation of MacMahon’s numbers
$d \ge 3$
[Reference Atkin, Bratley, Macdonald and McKayABMM67]. However, from Theorem 1.1, we obtain the following interpretation of MacMahon’s numbers
![]() $m_d(n)$
, thus showing that (instead of the volume) they count d-dimensional partitions via the corner-hook volume statistic so that
$m_d(n)$
, thus showing that (instead of the volume) they count d-dimensional partitions via the corner-hook volume statistic so that
More generally, we also prove results for generating functions over partitions with fixed shape.
Theorem 1.2 (Corner-hook generating function with fixed shape, cf. Theorem 5.2).
Let
![]() $\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following generating function:
$\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following generating function:
 $$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - t q^{i_1 + \ldots + i_d - d + 1}\right)^{-1}}, \end{align*} $$
$$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - t q^{i_1 + \ldots + i_d - d + 1}\right)^{-1}}, \end{align*} $$
where the sum runs over d-dimensional partitions
![]() $\pi $
whose shape is contained in
$\pi $
whose shape is contained in
![]() $\rho $
.
$\rho $
.
1.3 d-dimensional Grothendieck polynomials
To develop tools for studying d-dimensional partitions, one might be looking for analogues of Schur polynomials whose specializations allow to enumerate them. We work in a slightly different direction. In Section 6, we define higher-dimensional analogues of dual stable Grothendieck polynomials. These new functions are indexed by shapes of d-dimensional partitions, and in specializations they compute the number of such partitions. For
![]() $d = 2$
, they turn into the dual stable Grothendieck polynomials (indexed by partitions) known as K-theoretic analogues of Schur polynomials introduced in [Reference Lam and PylyavskyyLP07] (see also [Reference YeliussizovYel17, Reference YeliussizovYel19] for more on these functions).
$d = 2$
, they turn into the dual stable Grothendieck polynomials (indexed by partitions) known as K-theoretic analogues of Schur polynomials introduced in [Reference Lam and PylyavskyyLP07] (see also [Reference YeliussizovYel17, Reference YeliussizovYel19] for more on these functions).
Let us illustrate our results in the special case for (3-dimensional) solid partitions. We define the polynomials (see Equation (8))
![]() $g_{\pi }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
in three sets of variables indexed by plane partitions
$g_{\pi }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
in three sets of variables indexed by plane partitions
![]() $\{\pi \}$
. These polynomials enumerate solid partitions within a given shape. For example, we have
$\{\pi \}$
. These polynomials enumerate solid partitions within a given shape. For example, we have
We show that the following generating series identity holds.
Theorem 1.3 (Cauchy–Littlewood-type identity for 3d Grothendieck polynomials, cf. Corollary 6.5).
We have
 $$ \begin{align*}\sum_{\pi} g_{\pi}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{a} \prod_{j = 1}^{b} \prod_{k = 1}^{c} \frac{1}{1 - x_i y_j z_k}, \end{align*} $$
$$ \begin{align*}\sum_{\pi} g_{\pi}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{a} \prod_{j = 1}^{b} \prod_{k = 1}^{c} \frac{1}{1 - x_i y_j z_k}, \end{align*} $$
where the sum runs over plane partitions
![]() $\pi $
with shape inside the rectangle
$\pi $
with shape inside the rectangle
![]() $b \times c$
and
$b \times c$
and
![]() $\mathbf {x} = (x_1,\ldots , x_a), \mathbf {y} = (y_1,\ldots , y_b), \mathbf {z} = (z_1,\ldots , z_c).$
$\mathbf {x} = (x_1,\ldots , x_a), \mathbf {y} = (y_1,\ldots , y_b), \mathbf {z} = (z_1,\ldots , z_c).$
It is known that dual stable Grothendieck polynomials (for
![]() $d = 2$
) are symmetric (in
$d = 2$
) are symmetric (in
![]() $\mathbf {x}$
). As we show, this is no longer the case for
$\mathbf {x}$
). As we show, this is no longer the case for
![]() $d \ge 3$
. However, we prove that these new functions are quasisymmetric (cf. Proposition 6.9), the next known class containing symmetric functions (see, for example, [Reference StanleySta99, Ch. 7.19]).
$d \ge 3$
. However, we prove that these new functions are quasisymmetric (cf. Proposition 6.9), the next known class containing symmetric functions (see, for example, [Reference StanleySta99, Ch. 7.19]).
1.4 Last passage percolation in
 $\mathbb {Z}^{d}$
$\mathbb {Z}^{d}$
It turns out that these problems are closely related to the directed last passage percolation model with geometric weights in
![]() $\mathbb {Z}^d$
(see [Reference MartinMar06] for a survey on this probabilistic model). We prove that d-dimensional Grothendieck polynomials naturally compute distribution formulas for this model (see Theorem 7.1). See Section 7 for details.
$\mathbb {Z}^d$
(see [Reference MartinMar06] for a survey on this probabilistic model). We prove that d-dimensional Grothendieck polynomials naturally compute distribution formulas for this model (see Theorem 7.1). See Section 7 for details.
2 Preliminary definitions
We use the following basic notation:
![]() $\mathbb {N}$
is the set of nonnegative integers;
$\mathbb {N}$
is the set of nonnegative integers;
![]() $\mathbb {Z}_+$
is the set of positive integers;
$\mathbb {Z}_+$
is the set of positive integers;
![]() $\{\mathbf {e}_1, \ldots , \mathbf {e}_d\}$
is the standard basis of
$\{\mathbf {e}_1, \ldots , \mathbf {e}_d\}$
is the standard basis of
![]() $\mathbb {Z}^d$
; and
$\mathbb {Z}^d$
; and
![]() $[n] := \{1, \ldots , n \}$
.
$[n] := \{1, \ldots , n \}$
.
A d-dimensional
![]() $\mathbb {N}$
-hypermatrix is an array
$\mathbb {N}$
-hypermatrix is an array
![]() $\left (a_{i_1, \ldots , i_d}\right )_{i_1, \ldots , i_d \ge 1}$
of nonnegative integers with only finitely many nonzero elements. A d-dimensional partition is a d-dimensional
$\left (a_{i_1, \ldots , i_d}\right )_{i_1, \ldots , i_d \ge 1}$
of nonnegative integers with only finitely many nonzero elements. A d-dimensional partition is a d-dimensional
![]() $\mathbb {N}$
-hypermatrix
$\mathbb {N}$
-hypermatrix
![]() $\left (\pi _{i_1, \ldots , i_d} \right )$
such that
$\left (\pi _{i_1, \ldots , i_d} \right )$
such that
Let
![]() $\mathcal {M}^{(d)}$
be the set of d-dimensional
$\mathcal {M}^{(d)}$
be the set of d-dimensional
![]() $\mathbb {N}$
-hypermatrices and
$\mathbb {N}$
-hypermatrices and
![]() $\mathcal {P}^{(d)}$
be the set of d-dimensional partitions. For
$\mathcal {P}^{(d)}$
be the set of d-dimensional partitions. For
![]() $\pi = (\pi _{i_1, \ldots , i_d}) \in \mathcal {P}^{(d)}$
, the volume (or size) of
$\pi = (\pi _{i_1, \ldots , i_d}) \in \mathcal {P}^{(d)}$
, the volume (or size) of
![]() $\pi $
denoted by
$\pi $
denoted by
![]() $|\pi |$
is defined as
$|\pi |$
is defined as
Any partition
![]() $\pi $
is uniquely determined by its diagram
$\pi $
is uniquely determined by its diagram
![]() $D(\pi )$
which is the set
$D(\pi )$
which is the set
The shape of
![]() $\pi $
denoted by
$\pi $
denoted by
![]() $\mathrm {sh}(\pi )$
is the set
$\mathrm {sh}(\pi )$
is the set
Note that
![]() $\mathrm {sh}(\pi )$
is a diagram of some
$\mathrm {sh}(\pi )$
is a diagram of some
![]() $(d-1)$
-dimensional partition. Let
$(d-1)$
-dimensional partition. Let
be the set of
![]() $[n_1] \times \cdots \times [n_d]\ \mathbb {N}$
-hypermatrices and
$[n_1] \times \cdots \times [n_d]\ \mathbb {N}$
-hypermatrices and
be the set of boxed d-dimensional partitions.
For
![]() $d = 2,3$
, partitions are called plane partitions and solid partitions.Footnote
1
$d = 2,3$
, partitions are called plane partitions and solid partitions.Footnote
1
Let us note that for a set
![]() $\rho \subset \mathbb {Z}^d_+$
, the following three conditions are equivalent:
$\rho \subset \mathbb {Z}^d_+$
, the following three conditions are equivalent:
-
(1) The set
 $\rho $
is the shape of some d-dimensional partition.
$\rho $
is the shape of some d-dimensional partition. -
(2) The set
 $\rho $
is the diagram of some
$\rho $
is the diagram of some
 $(d-1)$
-dimensional partition.
$(d-1)$
-dimensional partition. -
(3) The set
 $\rho $
is finite and has the property that if
$\rho $
is finite and has the property that if
 $\mathbf {i} \in \mathbb {Z}^d_+$
and
$\mathbf {i} \in \mathbb {Z}^d_+$
and
 $\ell \in [d]$
satisfy
$\ell \in [d]$
satisfy
 $\mathbf {i} + \mathbf {e}_{\ell } \in \rho $
, then
$\mathbf {i} + \mathbf {e}_{\ell } \in \rho $
, then
 $\mathbf {i} \in \rho $
.
$\mathbf {i} \in \rho $
.
Sometimes we will identify a partition with its diagram (but never with its shape).
3 A bijection between d-dimensional
 $\mathbb {N}$
-hypermatrices and partitions
$\mathbb {N}$
-hypermatrices and partitions
3.1 Last passage hypermatrix
A lattice path in
![]() $\mathbb {Z}^d$
is called directed if it uses only steps of the form
$\mathbb {Z}^d$
is called directed if it uses only steps of the form
![]() $\mathbf {i} \to \mathbf {i} + \mathbf {e}_\ell $
for
$\mathbf {i} \to \mathbf {i} + \mathbf {e}_\ell $
for
![]() $\mathbf {i} \in \mathbb {Z}^d$
and
$\mathbf {i} \in \mathbb {Z}^d$
and
![]() $\ell \in [d]$
. Given a d-dimensional
$\ell \in [d]$
. Given a d-dimensional
![]() $\mathbb {N}$
-hypermatrix
$\mathbb {N}$
-hypermatrix
![]() $A = (a_{i_1, \ldots , i_d})$
, define the last passage times Footnote
2
$A = (a_{i_1, \ldots , i_d})$
, define the last passage times Footnote
2
 $$ \begin{align*} G_{i_1, \ldots, i_d} := \max_{\Pi\, :\, (i_1, \ldots, i_d) \to (\infty,\ldots,\infty)} \sum_{(j_1, \ldots, j_d) \in \Pi} a_{j_1, \ldots, j_d}, \end{align*} $$
$$ \begin{align*} G_{i_1, \ldots, i_d} := \max_{\Pi\, :\, (i_1, \ldots, i_d) \to (\infty,\ldots,\infty)} \sum_{(j_1, \ldots, j_d) \in \Pi} a_{j_1, \ldots, j_d}, \end{align*} $$
where the maximum is over directed lattice paths
![]() $\Pi $
which start at
$\Pi $
which start at
![]() $(i_1, \ldots , i_d) \in \mathbb {Z}^d_+$
. It is easy to see that the following recurrence relation holds:
$(i_1, \ldots , i_d) \in \mathbb {Z}^d_+$
. It is easy to see that the following recurrence relation holds:
Notice that the hypermatrix
![]() $G = (G_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+} \in \mathcal {P}^{(d)}$
is a d-dimensional partition.
$G = (G_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+} \in \mathcal {P}^{(d)}$
is a d-dimensional partition.
3.2 The bijection
Define the map
![]() $\Phi : \mathcal {M}^{(d)} \to \mathcal {P}^{(d)}$
as follows:
$\Phi : \mathcal {M}^{(d)} \to \mathcal {P}^{(d)}$
as follows:
Let
![]() $\rho \subset \mathbb {Z}^d_+$
be a shape of some d-dimensional partition (or a diagram of a
$\rho \subset \mathbb {Z}^d_+$
be a shape of some d-dimensional partition (or a diagram of a
![]() $(d-1)$
-dimensional partition). Let
$(d-1)$
-dimensional partition). Let
be the set of d-dimensional partitions whose shape is a subset of
![]() $\rho $
and the largest entry is at most n. Let
$\rho $
and the largest entry is at most n. Let
be the set of d-dimensional
![]() $\mathbb {N}$
-hypermatrices whose support (i.e., the set of indices corresponding to positive entries) lies inside
$\mathbb {N}$
-hypermatrices whose support (i.e., the set of indices corresponding to positive entries) lies inside
![]() $\rho $
and whose largest last passage time is at most n.
$\rho $
and whose largest last passage time is at most n.
Theorem 3.1. The map
![]() $\Phi $
defines a bijection between the sets
$\Phi $
defines a bijection between the sets
![]() $\mathcal {M}(\rho , n)$
and
$\mathcal {M}(\rho , n)$
and
![]() $\mathcal {P}(\rho , n)$
.
$\mathcal {P}(\rho , n)$
.
Proof. Let
![]() $A = (a_{\mathbf {i}}) \in \mathcal {M}(\rho , n)$
. By construction of the map, it is not difficult to see that
$A = (a_{\mathbf {i}}) \in \mathcal {M}(\rho , n)$
. By construction of the map, it is not difficult to see that
![]() $\pi = \Phi (A) \in \mathcal {P}(\rho , n)$
. Indeed, we have the largest last passage time
$\pi = \Phi (A) \in \mathcal {P}(\rho , n)$
. Indeed, we have the largest last passage time
![]() $\pi _{1,\ldots , 1} \le n$
, and
$\pi _{1,\ldots , 1} \le n$
, and
![]() $\mathrm {sh}(\pi ) \subseteq \rho $
since if
$\mathrm {sh}(\pi ) \subseteq \rho $
since if
![]() $a_{\mathbf {i}}> 0$
, then
$a_{\mathbf {i}}> 0$
, then
![]() $\mathbf {i} \in \rho $
.
$\mathbf {i} \in \rho $
.
Conversely, given
![]() $\pi \in \mathcal {P}(\rho , n)$
, to reconstruct the inverse map
$\pi \in \mathcal {P}(\rho , n)$
, to reconstruct the inverse map
![]() $\Phi ^{-1}$
, using the recurrence (1) we define the hypermatrix
$\Phi ^{-1}$
, using the recurrence (1) we define the hypermatrix
![]() $A = (a_{\mathbf {i}})$
given by
$A = (a_{\mathbf {i}})$
given by
Let
![]() $G = (G_{\mathbf {i}}) = \Phi (A)$
. Let us check that
$G = (G_{\mathbf {i}}) = \Phi (A)$
. Let us check that
![]() $G = \pi $
and
$G = \pi $
and
![]() $A \in \mathcal {M}(\rho , n)$
. Since
$A \in \mathcal {M}(\rho , n)$
. Since
![]() $\mathrm {sh}(\pi ) \subseteq \rho $
, we have
$\mathrm {sh}(\pi ) \subseteq \rho $
, we have
![]() $a_{\mathbf {i}} = 0$
for all
$a_{\mathbf {i}} = 0$
for all
![]() $\mathbf {i} \not \in \rho $
(in particular,
$\mathbf {i} \not \in \rho $
(in particular,
![]() $A \in \mathcal {M}(\rho , \infty )$
). Hence,
$A \in \mathcal {M}(\rho , \infty )$
). Hence,
![]() $G_{\mathbf {i}} = \pi _{\mathbf {i}} = 0$
for all
$G_{\mathbf {i}} = \pi _{\mathbf {i}} = 0$
for all
![]() $\mathbf {i} \not \in \rho $
. Consider the directed graph
$\mathbf {i} \not \in \rho $
. Consider the directed graph
![]() $\Gamma $
on the vertex set
$\Gamma $
on the vertex set
![]() $\rho $
and edges
$\rho $
and edges
![]() $\mathbf {i} \to \mathbf {i} + \mathbf {e}_{\ell }$
(when
$\mathbf {i} \to \mathbf {i} + \mathbf {e}_{\ell }$
(when
![]() $\mathbf {i} + \mathbf {e}_{\ell } \in \rho $
) for
$\mathbf {i} + \mathbf {e}_{\ell } \in \rho $
) for
![]() $\ell \in [d]$
. Then
$\ell \in [d]$
. Then
![]() $\Gamma $
is acyclic (i.e., has no directed cycles). Notice that
$\Gamma $
is acyclic (i.e., has no directed cycles). Notice that
![]() $a_{\mathbf {i}} = \pi _{\mathbf {i}} = G_{\mathbf {i}}$
if a vertex
$a_{\mathbf {i}} = \pi _{\mathbf {i}} = G_{\mathbf {i}}$
if a vertex
![]() $\mathbf {i} \in \Gamma $
has no outgoing edges. Since
$\mathbf {i} \in \Gamma $
has no outgoing edges. Since
![]() $\Gamma $
is acyclic, we can sort its vertices in linear order
$\Gamma $
is acyclic, we can sort its vertices in linear order
![]() $(\mathbf {i}^{(1)}, \ldots , \mathbf {i}^{(m)})$
so that the edges go only in one direction
$(\mathbf {i}^{(1)}, \ldots , \mathbf {i}^{(m)})$
so that the edges go only in one direction
![]() $\mathbf {i}^{(\ell )} \to \mathbf {i}^{(k)}$
for
$\mathbf {i}^{(\ell )} \to \mathbf {i}^{(k)}$
for
![]() $\ell < k$
. We already noticed that
$\ell < k$
. We already noticed that
![]() $\pi _{\mathbf {i}^{(m)}} = G_{\mathbf {i}^{(m)}}$
. Then inductively on
$\pi _{\mathbf {i}^{(m)}} = G_{\mathbf {i}^{(m)}}$
. Then inductively on
![]() $\ell = m-1,\ldots , 1$
, we have
$\ell = m-1,\ldots , 1$
, we have
Therefore,
![]() $\pi = G$
. In particular,
$\pi = G$
. In particular,
![]() $G_{1,\ldots , 1} \le n$
and hence,
$G_{1,\ldots , 1} \le n$
and hence,
![]() $A \in \mathcal {M}(\rho , n)$
.
$A \in \mathcal {M}(\rho , n)$
.
Corollary 3.2. The map
![]() $\Phi $
defines a bijection between each of the following pairs of sets:
$\Phi $
defines a bijection between each of the following pairs of sets:
-
(i)
 $\mathcal {M}([n_1]\times \cdots \times [n_d], n_{d+1})$
and
$\mathcal {M}([n_1]\times \cdots \times [n_d], n_{d+1})$
and
 $\mathcal {P}(n_1,\ldots , n_{d+1})$
$\mathcal {P}(n_1,\ldots , n_{d+1})$
-
(ii)
 $\mathcal {M}(n_1, \ldots , n_d)$
and
$\mathcal {M}(n_1, \ldots , n_d)$
and
 $\mathcal {P}(n_1,\ldots , n_{d}, \infty )$
$\mathcal {P}(n_1,\ldots , n_{d}, \infty )$
-
(iii)
 $\mathcal {M}(\rho , \infty )$
and
$\mathcal {M}(\rho , \infty )$
and
 $\mathcal {P}(\rho , \infty )$
$\mathcal {P}(\rho , \infty )$
-
(iv)
 $\mathcal {M}^{(d)}$
and
$\mathcal {M}^{(d)}$
and
 $\mathcal {P}^{(d)}$
.
$\mathcal {P}^{(d)}$
.
Remark 1. The item (i) above states that the number of boxed d-dimensional partitions with diagrams inside the box
![]() $[n_1] \times \cdots \times [n_{d+1}]$
is equal to the number of
$[n_1] \times \cdots \times [n_{d+1}]$
is equal to the number of
![]() $[n_1]\times \cdots \times [n_d]\ \mathbb {N}$
-hypermatrices whose largest last passage time is at most
$[n_1]\times \cdots \times [n_d]\ \mathbb {N}$
-hypermatrices whose largest last passage time is at most
![]() $n_{d+1}$
.
$n_{d+1}$
.
Remark 2. The map
![]() $\Phi ^{-1}$
is essentially Stanley’s ‘transfer map’ between order and chain poset polytopes [Reference StanleySta86a], specific to d-dimensional partitions. For
$\Phi ^{-1}$
is essentially Stanley’s ‘transfer map’ between order and chain poset polytopes [Reference StanleySta86a], specific to d-dimensional partitions. For
![]() $d = 2$
, the map
$d = 2$
, the map
![]() $\Phi $
gives a bijection between
$\Phi $
gives a bijection between
![]() $\mathbb {N}$
-hypermatrices and plane partitions. This bijection is essentially equivalent (up to diagram rotations) to the one studied in [Reference YeliussizovYel21a, Reference YeliussizovYel21b]. Note that one can construct d-dimensional partitions G dynamically using an insertion type procedure as in RSK, similarly as in [Reference YeliussizovYel21a, Reference YeliussizovYel21b] for
$\mathbb {N}$
-hypermatrices and plane partitions. This bijection is essentially equivalent (up to diagram rotations) to the one studied in [Reference YeliussizovYel21a, Reference YeliussizovYel21b]. Note that one can construct d-dimensional partitions G dynamically using an insertion type procedure as in RSK, similarly as in [Reference YeliussizovYel21a, Reference YeliussizovYel21b] for
![]() $d = 2$
; we plan to address this in more detail in [Reference Amanov and YeliussizovAY23+]. Note also that similar largest path (last passage time) properties hold for RSK as well; see [Reference PakPak01, Reference SaganSag01].
$d = 2$
; we plan to address this in more detail in [Reference Amanov and YeliussizovAY23+]. Note also that similar largest path (last passage time) properties hold for RSK as well; see [Reference PakPak01, Reference SaganSag01].
3.3 Corners and the inverse map
 $\Phi ^{-1}$
$\Phi ^{-1}$
Now we are going to describe the inverse map
![]() $\Phi ^{-1}$
more concretely using a structure of d-dimensional partitions.
$\Phi ^{-1}$
more concretely using a structure of d-dimensional partitions.
Given a partition
![]() $\pi \in \mathcal {P}^{(d)}$
, define the set of corners as follows:
$\pi \in \mathcal {P}^{(d)}$
, define the set of corners as follows:
(Here
![]() $\{\mathbf {e}_{\ell }\}$
is the standard basis in
$\{\mathbf {e}_{\ell }\}$
is the standard basis in
![]() $\mathbb {Z}^{d+1}$
.) Let
$\mathbb {Z}^{d+1}$
.) Let
![]() $\mathrm {cor}(\pi ) := |\mathrm {Cor}(\pi )|$
be the number of corners of
$\mathrm {cor}(\pi ) := |\mathrm {Cor}(\pi )|$
be the number of corners of
![]() $\pi $
. Define also the set of top corners as follows:
$\pi $
. Define also the set of top corners as follows:
Let
![]() $\mathrm {cr}(\pi ) := |\mathrm {Cr}(\pi )|$
be the number of top corners of
$\mathrm {cr}(\pi ) := |\mathrm {Cr}(\pi )|$
be the number of top corners of
![]() $\pi $
. More intuitively, a top corner (resp. corner) of
$\pi $
. More intuitively, a top corner (resp. corner) of
![]() $\pi $
is an element removable from the diagram of (resp. the shape of)
$\pi $
is an element removable from the diagram of (resp. the shape of)
![]() $\pi $
. Note that the set of top corners
$\pi $
. Note that the set of top corners
![]() $\mathrm {Cr}(\pi )$
uniquely determines the partition
$\mathrm {Cr}(\pi )$
uniquely determines the partition
![]() $\pi $
.
$\pi $
.
Example 3.3. Let
![]() $d = 2$
and
$d = 2$
and
![]() $\pi $
be the plane partition given in Figure 1. We then have
$\pi $
be the plane partition given in Figure 1. We then have
 $$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}\\ \mathrm{Cr}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k),(i,j,k+1) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,2), (2,2,3)\}, \end{align*} $$
$$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}\\ \mathrm{Cr}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k),(i,j,k+1) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,2), (2,2,3)\}, \end{align*} $$
where corners in Figure 1 correspond to local configurations
![]() and top corners correspond to the configurations
and top corners correspond to the configurations
![]() .
.

Figure 1 A plane partition
![]() $\pi \in \mathcal {P}^{(2)}$
whose
$\pi \in \mathcal {P}^{(2)}$
whose
![]() $\mathrm {sh}(\pi )$
is the diagram of the partition
$\mathrm {sh}(\pi )$
is the diagram of the partition
![]() $(3,2)$
; its boxed diagram presentation as a pile of cubes in
$(3,2)$
; its boxed diagram presentation as a pile of cubes in
![]() $\mathbb {R}^3$
; and boxes of this diagram which correspond to corners.
$\mathbb {R}^3$
; and boxes of this diagram which correspond to corners.
Consider the corner projection map
![]() $\varphi : \mathcal {P}^{(d)} \to \mathcal {M}^{(d)}$
given by
$\varphi : \mathcal {P}^{(d)} \to \mathcal {M}^{(d)}$
given by
![]() $\pi \mapsto (a_{\mathbf {i}})$
, where
$\pi \mapsto (a_{\mathbf {i}})$
, where
Lemma 3.4. We have:
![]() $\varphi = \Phi ^{-1}$
.
$\varphi = \Phi ^{-1}$
.
Proof. The key observation is that
![]() $(\mathbf {i}, i_{d+1}) \in \mathrm {Cor}(\pi )$
if and only if
$(\mathbf {i}, i_{d+1}) \in \mathrm {Cor}(\pi )$
if and only if
![]() $\pi _{\mathbf {i}} \ge i_{d+1}> \pi _{\mathbf {i} + \mathbf {e}_\ell }$
for all
$\pi _{\mathbf {i}} \ge i_{d+1}> \pi _{\mathbf {i} + \mathbf {e}_\ell }$
for all
![]() $\ell \in [d]$
. Hence,
$\ell \in [d]$
. Hence,
which gives
![]() $\Phi ^{-1} : \pi \mapsto (a_{\mathbf {i}})$
.
$\Phi ^{-1} : \pi \mapsto (a_{\mathbf {i}})$
.
We will also use the following properties relating shapes of partitions and top corners.
Lemma 3.5. Let
![]() $\rho \subset \mathbb {Z}^d_+$
be a shape of a d-dimensional partition,
$\rho \subset \mathbb {Z}^d_+$
be a shape of a d-dimensional partition,
![]() $A = (a_{\mathbf {i}}) \in \mathcal {M}^{}(\rho , \infty )$
and
$A = (a_{\mathbf {i}}) \in \mathcal {M}^{}(\rho , \infty )$
and
![]() $\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{}(\rho ,\infty )$
. The following are equivalent:
$\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{}(\rho ,\infty )$
. The following are equivalent:
-
(a)
 $a_{\mathbf {i}}> 0$
for all
$a_{\mathbf {i}}> 0$
for all
 $(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$
$(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$
-
(b)
 $\mathrm {sh}(\pi ) = \rho $
.
$\mathrm {sh}(\pi ) = \rho $
.
Proof. Let
![]() $(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$
. Assume (a) holds. Since
$(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$
. Assume (a) holds. Since
![]() $A \in \mathcal {M}^{}(\rho , \infty )$
, we have
$A \in \mathcal {M}^{}(\rho , \infty )$
, we have
![]() $a_{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
for all
$a_{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
for all
![]() $\ell \in [d]$
. Therefore,
$\ell \in [d]$
. Therefore,
![]() $\pi _{\mathbf {i}} = a_{\mathbf {i}}> 0$
and
$\pi _{\mathbf {i}} = a_{\mathbf {i}}> 0$
and
![]() $\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
. Hence,
$\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
. Hence,
![]() $\mathrm {sh}(\pi ) = \rho $
.
$\mathrm {sh}(\pi ) = \rho $
.
Assume (b) holds. Then we have
![]() $\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
for all
$\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$
for all
![]() $\ell \in [d]$
. Therefore,
$\ell \in [d]$
. Therefore,
![]() $a_{\mathbf {i}} = \pi _{\mathbf {i}}> 0$
.
$a_{\mathbf {i}} = \pi _{\mathbf {i}}> 0$
.
4 Multivariate identities
4.1 Main formulas
Let
![]() $(x_{i_1,\ldots , i_d})$
be indeterminate variables.
$(x_{i_1,\ldots , i_d})$
be indeterminate variables.
Theorem 4.1. Let
![]() $\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following multivariate generating function identities:
$\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following multivariate generating function identities:
 $$ \begin{align} \sum_{{\pi \in \mathcal{P}^{(d)}, \atop \, \mathrm{sh}(\pi) \subseteq \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}} ,\qquad\qquad\qquad\ \ \qquad \end{align} $$
$$ \begin{align} \sum_{{\pi \in \mathcal{P}^{(d)}, \atop \, \mathrm{sh}(\pi) \subseteq \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}} ,\qquad\qquad\qquad\ \ \qquad \end{align} $$
 $$ \begin{align} \sum_{ {\pi \in \mathcal{P}^{(d)},\atop \, \mathrm{sh}(\pi) = \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}, \end{align} $$
$$ \begin{align} \sum_{ {\pi \in \mathcal{P}^{(d)},\atop \, \mathrm{sh}(\pi) = \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}, \end{align} $$
where
![]() $\mathrm {Cr}(\rho ) := \mathrm {Cr}(\text {the partition whose diagram is } \rho )$
.
$\mathrm {Cr}(\rho ) := \mathrm {Cr}(\text {the partition whose diagram is } \rho )$
.
It is convenient to define weights of hypermatrices and partitions as follows. Given a hypermatrix
![]() $A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{(d)}$
, we associate to it a multivariable monomial weight
$A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{(d)}$
, we associate to it a multivariable monomial weight
 $$ \begin{align*}w_A := \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}}.\end{align*} $$
$$ \begin{align*}w_A := \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}}.\end{align*} $$
Given a partition
![]() $\pi \in \mathcal {P}^{(d)}$
, we associate to it a multivariable monomial weight
$\pi \in \mathcal {P}^{(d)}$
, we associate to it a multivariable monomial weight
 $$ \begin{align*}w(\pi) := \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d}. \end{align*} $$
$$ \begin{align*}w(\pi) := \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d}. \end{align*} $$
The following lemma shows that the bijection
![]() $\Phi $
is weight-preserving.
$\Phi $
is weight-preserving.
Lemma 4.2. Let
![]() $A = (a_{\mathbf {i}}) \in \mathcal {M}^{(d)}$
and
$A = (a_{\mathbf {i}}) \in \mathcal {M}^{(d)}$
and
![]() $\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{(d)}$
. Then
$\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{(d)}$
. Then
![]() $w_A = w(\pi )$
.
$w_A = w(\pi )$
.
Proof. Using the corner projection map
![]() $\varphi = \Phi ^{-1}$
, by Lemma 3.4, we have
$\varphi = \Phi ^{-1}$
, by Lemma 3.4, we have
 $$ \begin{align*} w_A &= \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &=\prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{|\{i_{d+1} : (i_1,\ldots,i_d, i_{d+1}) \in \mathrm{Cor}(\pi) \}|} \\ &=\prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \\ &= w(\pi), \end{align*} $$
$$ \begin{align*} w_A &= \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &=\prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{|\{i_{d+1} : (i_1,\ldots,i_d, i_{d+1}) \in \mathrm{Cor}(\pi) \}|} \\ &=\prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \\ &= w(\pi), \end{align*} $$
which gives what is needed.
Proof of Theorem 4.1.
First, note that
 $$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots,i_d) \in \rho} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$
$$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots,i_d) \in \rho} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$
On the other hand, using Corollary 3.2 (iii) and Lemma 4.2, we have
 $$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty)} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$
$$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty)} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$
and hence the identity (4) follows.
Let
![]() $\overline {\mathcal {M}}(\rho , \infty ) = \{A \in \mathcal {M}(\rho , \infty ) : \mathbf {i} \in \mathrm {Cr}(\rho ) \implies a_{\mathbf {i}}> 0\}$
. Similarly, note that
$\overline {\mathcal {M}}(\rho , \infty ) = \{A \in \mathcal {M}(\rho , \infty ) : \mathbf {i} \in \mathrm {Cr}(\rho ) \implies a_{\mathbf {i}}> 0\}$
. Similarly, note that
 $$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$
$$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$
On the other hand, using Lemma 3.5 we have
 $$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty), \mathrm{sh}(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$
$$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty), \mathrm{sh}(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$
and hence, the identity (5) follows.
4.2 Some special cases
Let us list a few immediate special cases of the above formulas.
Corollary 4.3 (Boxed case).
For any
![]() $n_1,\ldots , n_d \ge 0$
, we have
$n_1,\ldots , n_d \ge 0$
, we have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots,n_d, \infty)}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots,n_d, \infty)}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}. \end{align*} $$
Corollary 4.4 (Solid partitions,
 $d = 3$
).
$d = 3$
).
Let
![]() $\rho $
be a plane partition. We have
$\rho $
be a plane partition. We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}} \prod_{(i, j, k) \in \mathrm{Cr}(\rho)} x^{}_{i j k}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}} \prod_{(i, j, k) \in \mathrm{Cr}(\rho)} x^{}_{i j k}. \end{align*} $$
For
![]() $d = 2$
we obtain the following new identity for plane partitions.
$d = 2$
we obtain the following new identity for plane partitions.
Corollary 4.5 (Plane partitions,
 $d = 2$
).
$d = 2$
).
Let
![]() $\lambda $
be a partition. We have
$\lambda $
be a partition. We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi)= D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}} \prod_{(i, j) \in \mathrm{Cr}(\lambda)} x^{}_{i j}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi)= D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}} \prod_{(i, j) \in \mathrm{Cr}(\lambda)} x^{}_{i j}. \end{align*} $$
Remark 3. For
![]() $d = 2$
, the formula in the special rectangular case (with
$d = 2$
, the formula in the special rectangular case (with
![]() $x_{ij} = x_{i} y_j$
up to rotation of diagrams of plane partitions) was proved in [Reference YeliussizovYel21b].
$x_{ij} = x_{i} y_j$
up to rotation of diagrams of plane partitions) was proved in [Reference YeliussizovYel21b].
5 MacMahon’s numbers and statistics
5.1 Corner-hook volume
Let
![]() $\pi \in \mathcal {P}^{(d)}$
be a d-dimensional partition. For each point
$\pi \in \mathcal {P}^{(d)}$
be a d-dimensional partition. For each point
![]() $(i_1,\ldots ,i_d)$
, define the cohook length
$(i_1,\ldots ,i_d)$
, define the cohook length
Define now the corner-hook volume statistic
![]() $|\cdot |_{ch} : \mathcal {P}^{(d)} \to \mathbb {N}$
, computed as follows:
$|\cdot |_{ch} : \mathcal {P}^{(d)} \to \mathbb {N}$
, computed as follows:
 $$ \begin{align*}|\pi|_{ch} := \sum_{(\mathbf{i}, i_{d+1})\, \in\, \mathrm{Cor}(\pi)} \mathrm{ch}(\mathbf{i}). \end{align*} $$
$$ \begin{align*}|\pi|_{ch} := \sum_{(\mathbf{i}, i_{d+1})\, \in\, \mathrm{Cor}(\pi)} \mathrm{ch}(\mathbf{i}). \end{align*} $$
Example 5.1. Let
![]() $d = 2$
and
$d = 2$
and
![]() $\pi $
be the plane partition given in Figure 1. Recall that
$\pi $
be the plane partition given in Figure 1. Recall that
 $$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}, \end{align*} $$
$$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}, \end{align*} $$
and hence, we have
Theorem 5.2. Let
![]() $\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following generating functions:
$\rho \subset \mathbb {Z}^d_+$
be a fixed shape of a d-dimensional partition. We have the following generating functions:
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}, \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}, \end{align*} $$
where
 $$ \begin{align*}|\rho|_{cr} := \sum_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} \mathrm{ch}(i_1,\ldots,i_d). \end{align*} $$
$$ \begin{align*}|\rho|_{cr} := \sum_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} \mathrm{ch}(i_1,\ldots,i_d). \end{align*} $$
Proof. In Theorem 4.1 set
![]() $x_{i_1,\ldots , i_d} = t q^{i_1 + \ldots + i_d - d + 1}$
.
$x_{i_1,\ldots , i_d} = t q^{i_1 + \ldots + i_d - d + 1}$
.
Corollary 5.3 (Boxed version).
We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_d, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_d, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}. \end{align*} $$
Corollary 5.4 (Full generating function).
We have
 $$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$
$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$
Corollary 5.5 (Interpretation of MacMahon’s numbers).
We have
 $$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - q^{n})^{-\binom{n + d - 2}{d - 1}} = \sum_{n = 0}^{\infty} m_d(n) q^n, \end{align*} $$
$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - q^{n})^{-\binom{n + d - 2}{d - 1}} = \sum_{n = 0}^{\infty} m_d(n) q^n, \end{align*} $$
and hence,
(i.e.,
![]() $m_d(n)$
is the number of d-dimensional partitions whose corner-hook volume is n).
$m_d(n)$
is the number of d-dimensional partitions whose corner-hook volume is n).
Corollary 5.6 (Pyramid partitions).
Let
![]() $\Delta _d({m})$
be a d-dimensional partition whose diagram is
$\Delta _d({m})$
be a d-dimensional partition whose diagram is
![]() $D(\Delta _{d}({m})) = \{(i_1,\ldots , i_{d+1}) : \mathbb {Z}^{d+1}_+ : i_1 + \cdots + i_{d+1} - d \le m\}$
. We have
$D(\Delta _{d}({m})) = \{(i_1,\ldots , i_{d+1}) : \mathbb {Z}^{d+1}_+ : i_1 + \cdots + i_{d+1} - d \le m\}$
. We have
 $$ \begin{align*}\sum_{\pi \in \mathcal{P}^{}(D(\Delta_{d-1}({m})), \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^m (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$
$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{}(D(\Delta_{d-1}({m})), \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^m (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$
Corollary 5.7 (
 $q = 1$
specialization).
$q = 1$
specialization).
We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} &= {\left( 1 - t \right)^{-|\rho|}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} &= t^{\mathrm{cr}(\rho)} {\left( 1 - t \right)^{-|\rho|}}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} &= {\left( 1 - t \right)^{-|\rho|}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} &= t^{\mathrm{cr}(\rho)} {\left( 1 - t \right)^{-|\rho|}}. \end{align*} $$
Then the number of
![]() $\pi \in \mathcal {P}^{(d)}$
of shape
$\pi \in \mathcal {P}^{(d)}$
of shape
![]() $\rho $
with k corners is equal to
$\rho $
with k corners is equal to
![]() $\binom {k - \mathrm {cr}(\rho ) + |\rho | - 1}{|\rho | - 1}$
.
$\binom {k - \mathrm {cr}(\rho ) + |\rho | - 1}{|\rho | - 1}$
.
5.2 Solid partitions,
 $d = 3$
$d = 3$
Let us restate some of these results for solid partitions. Let
![]() $\pi \in \mathcal {P}^{(3)}$
be a solid partition. We then have
$\pi \in \mathcal {P}^{(3)}$
be a solid partition. We then have
 $$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k,\ell)\in \mathrm{Cor}(\pi)} (i + j + k - 2). \end{align*} $$
$$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k,\ell)\in \mathrm{Cor}(\pi)} (i + j + k - 2). \end{align*} $$
Corollary 5.8. Let
![]() $\rho $
be a fixed plane partition. We have
$\rho $
be a fixed plane partition. We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}, \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}, \end{align*} $$
and, in particular, the boxed version
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, n_3, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, n_3, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}. \end{align*} $$
5.3 Plane partitions,
 $d = 2$
$d = 2$
Similarly, let us restate some of these results for plane partitions. Let
![]() $\pi \in \mathcal {P}^{(2)}$
be a plane partition. We then have
$\pi \in \mathcal {P}^{(2)}$
be a plane partition. We then have
 $$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k)\in \mathrm{Cor}(\pi)} (i + j - 1). \end{align*} $$
$$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k)\in \mathrm{Cor}(\pi)} (i + j - 1). \end{align*} $$
Corollary 5.9. Let
![]() $\lambda $
be a fixed partition. We have
$\lambda $
be a fixed partition. We have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) = D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\lambda)} q^{|\lambda|_{cr}} \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}}, \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) = D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\lambda)} q^{|\lambda|_{cr}} \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}}, \end{align*} $$
and, in particular, the boxed version
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}}. \end{align*} $$
Let us compare the last boxed formula with known results. The following trace generating function is known for plane partitions (see, for example, [Reference StanleySta99, Thm 7.20.1]):
 $$ \begin{align*}\prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}} = \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{tr}(\pi)} q^{|\pi|}, \end{align*} $$
$$ \begin{align*}\prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}} = \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{tr}(\pi)} q^{|\pi|}, \end{align*} $$
where
![]() $\mathrm {tr}(\pi ) := \sum _{i} \pi _{i,i}$
is the trace of a plane partition. Therefore, in this case, we actually have the following equidistribution result.
$\mathrm {tr}(\pi ) := \sum _{i} \pi _{i,i}$
is the trace of a plane partition. Therefore, in this case, we actually have the following equidistribution result.
Theorem 5.10 (Equidistribution of (tr, vol) and (cor, ch-vol) for plane partitions).
We have
Remark 4. Up to a rotation of coordinates, this equidistribution result was proved by the second author in [Reference YeliussizovYel21b]. We also have a direct bijective argument for (a stronger version of) this identity which is somewhat long and will be addressed elsewhere.
Remark 5. The formulas in Theorem 5.2 can be viewed as higher-dimensional analogues of the well-known formula
 $$ \begin{align*}\sum_{\mathrm{sh}(\pi) = \lambda} q^{|\pi|} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$
$$ \begin{align*}\sum_{\mathrm{sh}(\pi) = \lambda} q^{|\pi|} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$
where
![]() $\lambda $
is a (usual) partition,
$\lambda $
is a (usual) partition,
![]() $h_{\lambda }(i,j) := \lambda _i - i + \lambda ^{\prime }_j - j + 1$
are hook lengths and the sum runs over weak reverse plane partitions
$h_{\lambda }(i,j) := \lambda _i - i + \lambda ^{\prime }_j - j + 1$
are hook lengths and the sum runs over weak reverse plane partitions
![]() $\pi $
; see [Reference StanleySta99, Ch. 7.22]. Its combinatorial proof is known as the Hillman–Grassl correspondence [Reference Hillman and GrasslHG76]. Now, setting
$\pi $
; see [Reference StanleySta99, Ch. 7.22]. Its combinatorial proof is known as the Hillman–Grassl correspondence [Reference Hillman and GrasslHG76]. Now, setting
![]() $x_{i j} = q^{h_{\lambda }(i,j)}$
in Corollary 4.5 gives
$x_{i j} = q^{h_{\lambda }(i,j)}$
in Corollary 4.5 gives
 $$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \lambda} q^{|\pi|_h} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$
$$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \lambda} q^{|\pi|_h} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$
where the sum runs over plane partitions
![]() $\pi $
and
$\pi $
and
 $$ \begin{align*}|\pi|_h := \sum_{(i,j,k) \in \mathrm{Cor}(\pi)} h_{\lambda}(i,j). \end{align*} $$
$$ \begin{align*}|\pi|_h := \sum_{(i,j,k) \in \mathrm{Cor}(\pi)} h_{\lambda}(i,j). \end{align*} $$
These formulas give another interesting equidistribution result.
Remark 6. There are various enumeration and generating function formulas known for classes of symmetric plane partitions; see [Reference StanleySta86b]. Similarly, one can define classes of symmetries of diagrams for d-dimensional partitions. Are there any explicit corner-hook generating functions over symmetric d-dimensional partitions as in Theorem 5.2?
5.4 Other statistics
Theorem 4.1 is a source for many statistics over d-dimensional partitions, whose generating functions can be computed explicitly by taking appropriate specializations. For instance, another interesting statistic
![]() $|\cdot |_{c} : \mathcal {P}^{(d)} \to \mathbb {N}$
is given by
$|\cdot |_{c} : \mathcal {P}^{(d)} \to \mathbb {N}$
is given by
 $$ \begin{align*}|\pi|_c := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} i_1, \quad \pi \in \mathcal{P}^{(d)}. \end{align*} $$
$$ \begin{align*}|\pi|_c := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} i_1, \quad \pi \in \mathcal{P}^{(d)}. \end{align*} $$
Then via the substitution
![]() $x_{i_1,\ldots , i_d} = q^{i_1}$
we obtain the following generating function:
$x_{i_1,\ldots , i_d} = q^{i_1}$
we obtain the following generating function:
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_{d}, \infty)} q^{|\pi|_c} = \prod_{i = 1}^{n_1} (1 - q^{i})^{-n_2\cdots n_d}. \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_{d}, \infty)} q^{|\pi|_c} = \prod_{i = 1}^{n_1} (1 - q^{i})^{-n_2\cdots n_d}. \end{align*} $$
Another curious statistic is given by
 $$ \begin{align*}|\pi|_p := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} (i_1 + 2 \, i_2 + \ldots + d \, i_d), \quad \pi \in \mathcal{P}^{(d)} \end{align*} $$
$$ \begin{align*}|\pi|_p := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} (i_1 + 2 \, i_2 + \ldots + d \, i_d), \quad \pi \in \mathcal{P}^{(d)} \end{align*} $$
for which via the substitution
![]() $x_{i_1,\ldots , i_d} = q^{i_1 + 2 i_2 + \ldots + d i_d}$
we obtain the following generating function:
$x_{i_1,\ldots , i_d} = q^{i_1 + 2 i_2 + \ldots + d i_d}$
we obtain the following generating function:
 $$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_p} = \prod_{n = 1}^{\infty} (1 - q^{n})^{-p(n, d)}, \end{align*} $$
$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_p} = \prod_{n = 1}^{\infty} (1 - q^{n})^{-p(n, d)}, \end{align*} $$
where
![]() $p(n, d)$
is the number of integer partitions of n into d distinct parts.
$p(n, d)$
is the number of integer partitions of n into d distinct parts.
6 d-dimensional Grothendieck polynomials
From now on, we specialize
![]() $x_{i_1,\ldots , i_d} = x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}$
.
$x_{i_1,\ldots , i_d} = x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}$
.
6.1 Definitions
Let
![]() $\pi $
be a d-dimensional partition. Define the set
$\pi $
be a d-dimensional partition. Define the set
which can be viewed as a shape of
![]() $\pi $
with respect to the first coordinate. Note that if
$\pi $
with respect to the first coordinate. Note that if
![]() $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
, then
$\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
, then
![]() $\mathrm {sh}_1(\pi )$
is a diagram of
$\mathrm {sh}_1(\pi )$
is a diagram of
![]() $(d-1)$
-dimensional partition from
$(d-1)$
-dimensional partition from
![]() $\mathcal {P}(n_2,\ldots , n_{d+1}).$
Concretely,
$\mathcal {P}(n_2,\ldots , n_{d+1}).$
Concretely,
![]() $\mathrm {sh}_1(\pi )$
is the diagram of the partition
$\mathrm {sh}_1(\pi )$
is the diagram of the partition
![]() $(\pi _{1,i_2,\ldots ,i_d})$
. For example, if
$(\pi _{1,i_2,\ldots ,i_d})$
. For example, if
![]() $\pi $
is the plane partition in Figure 1, then
$\pi $
is the plane partition in Figure 1, then
![]() $\mathrm {sh}_1(\pi )$
corresponds to the partition
$\mathrm {sh}_1(\pi )$
corresponds to the partition
![]() $(4,3,2)$
, which is the first row of
$(4,3,2)$
, which is the first row of
![]() $\pi $
.
$\pi $
.
Throughout this section, let us assume that
![]() $n_1, \ldots , n_d$
are fixed and we have the sets of variables
$n_1, \ldots , n_d$
are fixed and we have the sets of variables
Definition 6.1. Let
![]() $\rho $
be a
$\rho $
be a
![]() $(d-1)$
-dimensional partition from the set
$(d-1)$
-dimensional partition from the set
![]() $\mathcal {P}(n_2,\ldots ,n_{d+1})$
. Define the d-dimensional Grothendieck polynomials in d sets of variables as follows:
$\mathcal {P}(n_2,\ldots ,n_{d+1})$
. Define the d-dimensional Grothendieck polynomials in d sets of variables as follows:
 $$ \begin{align} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align} $$
$$ \begin{align} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align} $$
where the sum runs over d-dimensional partitions
![]() $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
with
$\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
with
![]() $\mathrm {sh}_1(\pi ) = \rho $
(here
$\mathrm {sh}_1(\pi ) = \rho $
(here
![]() $\rho $
is identified with its diagram).
$\rho $
is identified with its diagram).
In the specialization
![]() $x^{(k)}_{i} = 1$
for all
$x^{(k)}_{i} = 1$
for all
![]() $k \ge 2$
, we simply denote these polynomials by
$k \ge 2$
, we simply denote these polynomials by
![]() $g_{\rho }(\mathbf {x}) = g_{\rho }(x_1,x_2,\ldots )$
in one set of variables
$g_{\rho }(\mathbf {x}) = g_{\rho }(x_1,x_2,\ldots )$
in one set of variables
![]() $\mathbf {x}^{(1)} = \mathbf {x} = (x_1,\ldots , x_{n_1})$
so that
$\mathbf {x}^{(1)} = \mathbf {x} = (x_1,\ldots , x_{n_1})$
so that
 $$ \begin{align} g_{\rho}(\mathbf{x}^{}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) := |\{\mathbf{i} : (i, \mathbf{i}) \in \mathrm{Cor}(\pi) \}| \end{align} $$
$$ \begin{align} g_{\rho}(\mathbf{x}^{}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) := |\{\mathbf{i} : (i, \mathbf{i}) \in \mathrm{Cor}(\pi) \}| \end{align} $$
and the sum runs over
![]() $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
.
$\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$
.
6.2 Examples
Example 6.2. Consider the case
![]() $d = 2$
. Let
$d = 2$
. Let
![]() $\lambda \in \mathcal {P}(n_2, n_3)$
be a partition and
$\lambda \in \mathcal {P}(n_2, n_3)$
be a partition and
![]() $\mathbf {x}^{(1)} = \mathbf {x}, \mathbf {x}^{(2)} = \mathbf {y}$
. Then (7) becomes
$\mathbf {x}^{(1)} = \mathbf {x}, \mathbf {x}^{(2)} = \mathbf {y}$
. Then (7) becomes
 $$ \begin{align*}g_{\lambda}(\mathbf{x}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) = |\{(j,k) : (i, j, k) \in \mathrm{Cor}(\pi) \}|, \end{align*} $$
$$ \begin{align*}g_{\lambda}(\mathbf{x}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) = |\{(j,k) : (i, j, k) \in \mathrm{Cor}(\pi) \}|, \end{align*} $$
and the sum runs over plane partitions
![]() $\pi \in \mathcal {P}(n_1,n_2,n_3)$
. Let us transpose
$\pi \in \mathcal {P}(n_1,n_2,n_3)$
. Let us transpose
![]() $\pi $
to
$\pi $
to
![]() $\pi '$
via cyclic shift of the diagram so that
$\pi '$
via cyclic shift of the diagram so that
![]() $(i,j,k) \in D(\pi ) \iff (j,k, i) \in D(\pi ')$
. Note that
$(i,j,k) \in D(\pi ) \iff (j,k, i) \in D(\pi ')$
. Note that
![]() $\mathrm {sh}_1(\pi ) = \mathrm {sh}(\pi ') = \lambda $
and
$\mathrm {sh}_1(\pi ) = \mathrm {sh}(\pi ') = \lambda $
and
![]() $c_i(\pi )$
is equal to the number of columns of
$c_i(\pi )$
is equal to the number of columns of
![]() $\pi '$
(viewed as a 2d array) containing the entry
$\pi '$
(viewed as a 2d array) containing the entry
![]() $i \in [n_1]$
; see Figure 2. This shows that
$i \in [n_1]$
; see Figure 2. This shows that
![]() $\{g_{\lambda }(\mathbf {x})\}$
are the dual stable Grothendieck polynomials introducedFootnote
3
in [Reference Lam and PylyavskyyLP07], but phrased in a slightly different yet equivalent form.
$\{g_{\lambda }(\mathbf {x})\}$
are the dual stable Grothendieck polynomials introducedFootnote
3
in [Reference Lam and PylyavskyyLP07], but phrased in a slightly different yet equivalent form.

Figure 2 A plane partition
![]() $\pi $
and its transpose
$\pi $
and its transpose
![]() $\pi '$
of the shape
$\pi '$
of the shape
![]() $\lambda = (432)$
with the corresponding diagrams in which the corner boxes of
$\lambda = (432)$
with the corresponding diagrams in which the corner boxes of
![]() $\pi $
are highlighted.
$\pi $
are highlighted.
More generally, (6) becomes
 $$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$
$$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$
which by rescaling
![]() $\tilde g_{\lambda }(\mathbf {x}; \mathbf {y}) = \mathbf {y}^{\lambda } g_{\lambda }(\mathbf {x}; \mathbf {y}^{-1})$
gives the refined version of dual stable Grothendieck polynomials introduced in [Reference Galashin, Grinberg and LiuGGL16], where it was shown that these polynomials are symmetric in the variables
$\tilde g_{\lambda }(\mathbf {x}; \mathbf {y}) = \mathbf {y}^{\lambda } g_{\lambda }(\mathbf {x}; \mathbf {y}^{-1})$
gives the refined version of dual stable Grothendieck polynomials introduced in [Reference Galashin, Grinberg and LiuGGL16], where it was shown that these polynomials are symmetric in the variables
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
Example 6.3. Let
![]() $d = 3$
,
$d = 3$
,
![]() $(n_1,n_2,n_3,n_4) = (3,2,2,2)$
and
$(n_1,n_2,n_3,n_4) = (3,2,2,2)$
and
![]() $\mathbf {x}^{(1)} = \mathbf {x} = (x_1,x_2,x_3)$
,
$\mathbf {x}^{(1)} = \mathbf {x} = (x_1,x_2,x_3)$
,
![]() $\mathbf {x}^{(2)} = \mathbf {y} = (y_1,y_2)$
,
$\mathbf {x}^{(2)} = \mathbf {y} = (y_1,y_2)$
,
![]() $\mathbf {x}^{(3)} = \mathbf {z} = (z_1,z_2)$
. Note that in this case,
$\mathbf {x}^{(3)} = \mathbf {z} = (z_1,z_2)$
. Note that in this case,
![]() $3$
-dimensional Grothendieck polynomials are indexed by plane partitions and defined as sums over solid partitions. Consider a few examples.
$3$
-dimensional Grothendieck polynomials are indexed by plane partitions and defined as sums over solid partitions. Consider a few examples.
(a) Let
![]() . Then we have
. Then we have
 $$ \begin{align*} g_\rho(\mathbf{x};\mathbf{y};\mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{1}x_{2}^{2} + x_{1}x_{3}^{2} + x_{2}^{2}x_{3} + x_{2}x_{3}^{2} + 2 x_{1}x_{2}x_{3}) \cdot y_{1}^{3}z_{1}^{2}z_{2}\\ &+ (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{1}x_{2} + x_{1}x_{3} + x_{2}x_{3}) \cdot y_{1}^{2}z_{1}z_{2}, \end{align*} $$
$$ \begin{align*} g_\rho(\mathbf{x};\mathbf{y};\mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{1}x_{2}^{2} + x_{1}x_{3}^{2} + x_{2}^{2}x_{3} + x_{2}x_{3}^{2} + 2 x_{1}x_{2}x_{3}) \cdot y_{1}^{3}z_{1}^{2}z_{2}\\ &+ (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{1}x_{2} + x_{1}x_{3} + x_{2}x_{3}) \cdot y_{1}^{2}z_{1}z_{2}, \end{align*} $$
which coincides with the ordinary dual stable Grothendieck polynomial indexed by the partition
![]() $\lambda = (2,1)$
(i.e., in this case, we have
$\lambda = (2,1)$
(i.e., in this case, we have
![]() $g_{\lambda }(\mathbf {x}) = g_\rho (\mathbf {x}, \mathbf {1}, \mathbf {1})$
).
$g_{\lambda }(\mathbf {x}) = g_\rho (\mathbf {x}, \mathbf {1}, \mathbf {1})$
).
(b) Let
![]() . Then we have
. Then we have
 $$ \begin{align*} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{2}^{2}x_{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} + 2 x_{1}x_{2}x_{3} \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} \\ & + (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + 2 x_{1}x_{2} + 2 x_{1}x_{3} + 2 x_{2}x_{3}) \cdot y_{1}y_{2}z_{1}z_{2}, \end{align*} $$
$$ \begin{align*} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{2}^{2}x_{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} + 2 x_{1}x_{2}x_{3} \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} \\ & + (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + 2 x_{1}x_{2} + 2 x_{1}x_{3} + 2 x_{2}x_{3}) \cdot y_{1}y_{2}z_{1}z_{2}, \end{align*} $$
and in particular,
(c) Let
![]() . Then we have
. Then we have
 $$ \begin{align*} g_{\rho}(\mathbf{x},\mathbf{y},\mathbf{z}) &= (3 x_{1}^{2}x_{2}x_{3} + 3 x_{1}x_{2}^{2}x_{3} + 2 x_{1}x_{2}x_{3}^{2} + x_{1}^{2}x_{2}^{2} + x_{1}^{2}x_{3}^{2} + x_{2}^{2}x_{3}^{2} + x_{1}^{3}x_{2} + x_{1}^{3}x_{3} + x_{2}^{3}x_{3})\cdot y_{1}^{3}y_{2}z_{1}^{3}z_{2}\\ &+ (4 x_{1}x_{2}x_{3} + 2 x_{1}^{2}x_{2} + 2 x_{1}^{2}x_{3} + 2 x_{2}^{2}x_{3} + 3 x_{1}x_{2}^{2} + 3 x_{1}x_{3}^{2} + 3 x_{2}x_{3}^{2} + x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2}. \end{align*} $$
$$ \begin{align*} g_{\rho}(\mathbf{x},\mathbf{y},\mathbf{z}) &= (3 x_{1}^{2}x_{2}x_{3} + 3 x_{1}x_{2}^{2}x_{3} + 2 x_{1}x_{2}x_{3}^{2} + x_{1}^{2}x_{2}^{2} + x_{1}^{2}x_{3}^{2} + x_{2}^{2}x_{3}^{2} + x_{1}^{3}x_{2} + x_{1}^{3}x_{3} + x_{2}^{3}x_{3})\cdot y_{1}^{3}y_{2}z_{1}^{3}z_{2}\\ &+ (4 x_{1}x_{2}x_{3} + 2 x_{1}^{2}x_{2} + 2 x_{1}^{2}x_{3} + 2 x_{2}^{2}x_{3} + 3 x_{1}x_{2}^{2} + 3 x_{1}x_{3}^{2} + 3 x_{2}x_{3}^{2} + x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2}. \end{align*} $$
Figure 3 illustrates a few examples of solid partitions contributing to the last expansion.

Figure 3 Each picture here represents a solid partition as a filling of a diagram of some plane partition with numbers written on top of each box (to make entries of inner boxes visible, some facets are removed). On the left, we have
![]() $\mathrm {sh}_{1}\!(\pi ) = \rho $
. The next two are solid partitions
$\mathrm {sh}_{1}\!(\pi ) = \rho $
. The next two are solid partitions
![]() $\pi ^{(1)}$
and
$\pi ^{(1)}$
and
![]() $\pi ^{(2)}$
represented as fillings of diagrams of plane partitions
$\pi ^{(2)}$
represented as fillings of diagrams of plane partitions
 and
and
 ; each has the weight
; each has the weight
![]() $w(\pi ^{(i)}) = x_2^2x_3 \cdot y_1^2 y_2 z_1^2 z_2$
; and both have the same
$w(\pi ^{(i)}) = x_2^2x_3 \cdot y_1^2 y_2 z_1^2 z_2$
; and both have the same
![]() $\mathrm {sh}_1(\pi ^{(i)}) =\rho $
(
$\mathrm {sh}_1(\pi ^{(i)}) =\rho $
(
![]() $i = 1,2$
) displayed on the left.
$i = 1,2$
) displayed on the left.
6.3 Properties
We now prove some properties of d-dimensional Grothendieck polynomials.
Theorem 6.4 (Cauchy–Littlewood-type identity).
Let
![]() $\eta \in \mathcal {P}(n_2,\ldots , n_d)$
be a
$\eta \in \mathcal {P}(n_2,\ldots , n_d)$
be a
![]() $(d-2)$
-dimensional partition. Let
$(d-2)$
-dimensional partition. Let
![]() $n \times \eta $
be a
$n \times \eta $
be a
![]() $(d-1)$
-dimensional partition with the diagram
$(d-1)$
-dimensional partition with the diagram
![]() $D(n \times \eta ) = \{(i, \mathbf {i}) : i \in [n], \mathbf {i} \in D(\eta ) \}$
. Then we have the following generating series:
$D(n \times \eta ) = \{(i, \mathbf {i}) : i \in [n], \mathbf {i} \in D(\eta ) \}$
. Then we have the following generating series:
 $$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
$$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
Proof. Notice that we have
 $$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(\eta, \infty)} \sum_{\mathrm{sh}_1(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi). \end{align*} $$
$$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(\eta, \infty)} \sum_{\mathrm{sh}_1(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi). \end{align*} $$
On the other hand, from Theorem 4.1, we have
 $$ \begin{align*} \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1} \end{align*} $$
$$ \begin{align*} \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1} \end{align*} $$
which gives the result.
Corollary 6.5. We have
 $$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2,\ldots, n_d, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
$$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2,\ldots, n_d, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
Lemma 6.6 (Simple branching rule).
We have
Proof. Given a d-dimensional partition
![]() $\tau $
with
$\tau $
with
![]() $\mathrm {sh}_1(\tau ) = \pi $
, it contributes to the l.h.s. the weight
$\mathrm {sh}_1(\tau ) = \pi $
, it contributes to the l.h.s. the weight
![]() $\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )}$
(see Equation (7)). Let us form the new partition
$\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )}$
(see Equation (7)). Let us form the new partition
![]() $\eta \subseteq \pi $
with the diagram
$\eta \subseteq \pi $
with the diagram
so that
![]() $\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )} = \prod _{i = 1}^{n} x_i^{c_{i}(\eta )}$
, which contributes to the r.h.s. In other words, remove from
$\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )} = \prod _{i = 1}^{n} x_i^{c_{i}(\eta )}$
, which contributes to the r.h.s. In other words, remove from
![]() $D(\tau )$
the points with the first coordinate
$D(\tau )$
the points with the first coordinate
![]() $1$
, then decrease by
$1$
, then decrease by
![]() $1$
the first coordinates for the remaining points. It is not difficult to see that this defines a proper weight-preserving bijection between both sides of the equation.
$1$
the first coordinates for the remaining points. It is not difficult to see that this defines a proper weight-preserving bijection between both sides of the equation.
Denote
![]() $1^k = (1,\ldots , 1)$
with k ones.
$1^k = (1,\ldots , 1)$
with k ones.
Proposition 6.7 (Boxed specialization).
We have
Proof. Denote
![]() $B = [n_2] \times \cdots \times [n_{d+1}]$
. Let
$B = [n_2] \times \cdots \times [n_{d+1}]$
. Let
![]() $\rho $
be a partition diagram inside B. From the definition of g, we immediately obtain that
$\rho $
be a partition diagram inside B. From the definition of g, we immediately obtain that
Therefore, using the branching formula above, we get
 $$ \begin{align*} g_{B}(1^{n_1 + 1}; 1^{n_2}; \ldots; 1^{n_d}) &= \sum_{\rho \subseteq B} g_{\rho}(1^{n_1}; 1^{n_2}; \ldots; 1^{n_d}) \\ &= \sum_{\rho \subseteq B} |\{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})\, :\, \mathrm{sh}_1(\pi) = \rho \}| \\ &=|\mathcal{P}(n_1,\ldots, n_{d+1})|, \end{align*} $$
$$ \begin{align*} g_{B}(1^{n_1 + 1}; 1^{n_2}; \ldots; 1^{n_d}) &= \sum_{\rho \subseteq B} g_{\rho}(1^{n_1}; 1^{n_2}; \ldots; 1^{n_d}) \\ &= \sum_{\rho \subseteq B} |\{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})\, :\, \mathrm{sh}_1(\pi) = \rho \}| \\ &=|\mathcal{P}(n_1,\ldots, n_{d+1})|, \end{align*} $$
which gives what is needed.
6.4 Quasisymmetry
It is known that the dual stable Grothendieck polynomials
![]() $g_{\lambda }(\mathbf {x})$
are symmetric in
$g_{\lambda }(\mathbf {x})$
are symmetric in
![]() $\mathbf {x}$
(in the case
$\mathbf {x}$
(in the case
![]() $d = 2$
). As Example 6.3 shows, the generalized polynomials
$d = 2$
). As Example 6.3 shows, the generalized polynomials
![]() $g_{\rho }$
are not necessarily symmetric for
$g_{\rho }$
are not necessarily symmetric for
![]() $d \ge 3$
. However, as we show in this subsection, these polynomials are always quasisymmetric.
$d \ge 3$
. However, as we show in this subsection, these polynomials are always quasisymmetric.
Definition 6.8. A polynomial
![]() $f \in \mathbb {Z}[x_1,\ldots , x_n]$
is called quasisymmetric if for all
$f \in \mathbb {Z}[x_1,\ldots , x_n]$
is called quasisymmetric if for all
![]() $1 \le \ell _1 < \cdots < \ell _k \le n$
,
$1 \le \ell _1 < \cdots < \ell _k \le n$
,
![]() $1 \le j_1 < \cdots < j_k \le n$
, and
$1 \le j_1 < \cdots < j_k \le n$
, and
![]() $a_1,\ldots , a_k \in \mathbb {Z}_+$
, we have
$a_1,\ldots , a_k \in \mathbb {Z}_+$
, we have
where
![]() $[\mathbf {x}^{\alpha }] f$
denotes the coefficient of the monomial
$[\mathbf {x}^{\alpha }] f$
denotes the coefficient of the monomial
![]() $\mathbf {x}^{\alpha }$
in f.
$\mathbf {x}^{\alpha }$
in f.
Proposition 6.9. We have:
![]() $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
is quasisymmetric in the variables
$g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
is quasisymmetric in the variables
![]() $\mathbf {x}^{(1)}$
.
$\mathbf {x}^{(1)}$
.
Proof. To simplify notation, let us denote
![]() $\mathbf {x}^{(1)} = \mathbf {x} = (x_1, x_2,\ldots )$
. We need to show that for all
$\mathbf {x}^{(1)} = \mathbf {x} = (x_1, x_2,\ldots )$
. We need to show that for all
![]() $a_1,\ldots , a_k \in \mathbb {Z}_+$
,
$a_1,\ldots , a_k \in \mathbb {Z}_+$
,
![]() $1 \le \ell _1 < \cdots < \ell _k \le n_1$
,
$1 \le \ell _1 < \cdots < \ell _k \le n_1$
,
![]() $1 \le j_1 < \cdots < j_k \le n_1$
, we have
$1 \le j_1 < \cdots < j_k \le n_1$
, we have
(where the indeterminates
![]() $\mathbf {x}^{(2)}, \ldots , \mathbf {x}^{(d)}$
are regarded as constants). Let L and R be the sets of d-dimensional partitions which contribute to the l.h.s. and r.h.s., respectively. We are going to construct a weight-preserving bijection
$\mathbf {x}^{(2)}, \ldots , \mathbf {x}^{(d)}$
are regarded as constants). Let L and R be the sets of d-dimensional partitions which contribute to the l.h.s. and r.h.s., respectively. We are going to construct a weight-preserving bijection
![]() $\phi : L \to R$
.
$\phi : L \to R$
.
Let
![]() $\pi \in L$
for which we have
$\pi \in L$
for which we have
![]() $\pi \in \mathcal {P}(n_1,\ldots ,n_{d+1})$
with
$\pi \in \mathcal {P}(n_1,\ldots ,n_{d+1})$
with
![]() $\mathrm {sh}_1(\pi ) = D(\rho )$
and
$\mathrm {sh}_1(\pi ) = D(\rho )$
and
![]() $w(\pi ) = x^{a_1}_{\ell _1} \cdots x^{a_{k}}_{\ell _k} \times w'$
, where
$w(\pi ) = x^{a_1}_{\ell _1} \cdots x^{a_{k}}_{\ell _k} \times w'$
, where
![]() $w'$
is the remaining product which does not contain the variables
$w'$
is the remaining product which does not contain the variables
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
For a hypermatrix
![]() $X = ({x}_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d}_+}$
, define the slices
$X = ({x}_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d}_+}$
, define the slices
![]() $X^{(\ell )} = (x_{\ell ,\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d-1}_+}$
. Let
$X^{(\ell )} = (x_{\ell ,\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d-1}_+}$
. Let
![]() $|X|$
denote the sum of the entries of X.
$|X|$
denote the sum of the entries of X.
Let
![]() $A = (a_{\mathbf {i}}) = \Phi ^{-1}(\pi ) \in \mathcal {M}(n_1,\ldots , n_d)$
. Note that
$A = (a_{\mathbf {i}}) = \Phi ^{-1}(\pi ) \in \mathcal {M}(n_1,\ldots , n_d)$
. Note that
![]() $A^{(\ell )} \in \mathcal {M}(n_2,\ldots , n_d)$
for
$A^{(\ell )} \in \mathcal {M}(n_2,\ldots , n_d)$
for
![]() $\ell \in [n_1]$
. Since
$\ell \in [n_1]$
. Since
![]() $\Phi $
preserves weights (i.e.,
$\Phi $
preserves weights (i.e.,
![]() $w_A = w(\pi )$
; see Lemma 4.2), we must have
$w_A = w(\pi )$
; see Lemma 4.2), we must have
![]() $A^{(\ell )} \ne \mathbf {0}$
iff
$A^{(\ell )} \ne \mathbf {0}$
iff
![]() $\ell \in \{\ell _1,\ldots , \ell _k \}$
. We then have
$\ell \in \{\ell _1,\ldots , \ell _k \}$
. We then have
 $$ \begin{align*}w(\pi) = w_A = \prod_{i = 1}^{n_1} x_i^{|A^{(i)}|} \prod_{\mathbf{i} = (i_2,\ldots, i_d)} (x^{(2)}_{i_2} \cdots x^{(d)}_{i_d})^{a_{i,\mathbf{i}}} = \prod_{i = 1}^{k} x_{\ell_i}^{a_i} \times w'. \end{align*} $$
$$ \begin{align*}w(\pi) = w_A = \prod_{i = 1}^{n_1} x_i^{|A^{(i)}|} \prod_{\mathbf{i} = (i_2,\ldots, i_d)} (x^{(2)}_{i_2} \cdots x^{(d)}_{i_d})^{a_{i,\mathbf{i}}} = \prod_{i = 1}^{k} x_{\ell_i}^{a_i} \times w'. \end{align*} $$
Let us now construct another hypermatrix
![]() $B = (b_{\mathbf {i}}) \in \mathcal {M}(n_1,\ldots , n_d)$
so that
$B = (b_{\mathbf {i}}) \in \mathcal {M}(n_1,\ldots , n_d)$
so that
![]() $B^{(j)} \ne \mathbf {0}$
iff
$B^{(j)} \ne \mathbf {0}$
iff
![]() ${j \in \{j_1,\ldots ,j_k\}}$
and
${j \in \{j_1,\ldots ,j_k\}}$
and
![]() $B^{(j_i)} = A^{(\ell _i)}$
for all
$B^{(j_i)} = A^{(\ell _i)}$
for all
![]() $i \in [k]$
. Let
$i \in [k]$
. Let
![]() $\pi ' = \Phi (B)$
. We then clearly have
$\pi ' = \Phi (B)$
. We then clearly have
 $$ \begin{align*}w(\pi') = w_B = \prod_{i = 1}^{k} x_{j_i}^{a_i} \times w'. \end{align*} $$
$$ \begin{align*}w(\pi') = w_B = \prod_{i = 1}^{k} x_{j_i}^{a_i} \times w'. \end{align*} $$
Let us show that
![]() $\mathrm {sh}_1(\pi ') = D(\rho ) = \mathrm {sh}_1(\pi )$
. Recall that
$\mathrm {sh}_1(\pi ') = D(\rho ) = \mathrm {sh}_1(\pi )$
. Recall that
![]() $\mathrm {sh}_1(\pi ')$
is the diagram of the partition
$\mathrm {sh}_1(\pi ')$
is the diagram of the partition
![]() $(\pi ^{\prime }_{1,i_2,\ldots ,i_d})$
. By definition of
$(\pi ^{\prime }_{1,i_2,\ldots ,i_d})$
. By definition of
![]() $\Phi $
, each entry
$\Phi $
, each entry
![]() $\pi ^{\prime }_{1,i_2,\ldots ,i_d} $
is the largest weight of a directed path from
$\pi ^{\prime }_{1,i_2,\ldots ,i_d} $
is the largest weight of a directed path from
![]() $(1,i_2,\ldots , i_d)$
to
$(1,i_2,\ldots , i_d)$
to
![]() $(n_1,\ldots , n_d)$
through the hypermatrix B. This holds as the maximum of
$(n_1,\ldots , n_d)$
through the hypermatrix B. This holds as the maximum of
![]() $\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$
among all paths
$\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$
among all paths
![]() $\Pi : (1,i_2,\ldots , i_d) \to \infty ^d$
is achieved for some path that passes through
$\Pi : (1,i_2,\ldots , i_d) \to \infty ^d$
is achieved for some path that passes through
![]() $(n_1,\ldots , n_d)$
, as any other path could be redirected to
$(n_1,\ldots , n_d)$
, as any other path could be redirected to
![]() $(n_1,\ldots , n_d)$
from the point where it first leaves the box
$(n_1,\ldots , n_d)$
from the point where it first leaves the box
![]() $[n_1] \times \cdots \times [n_d]$
without lowering
$[n_1] \times \cdots \times [n_d]$
without lowering
![]() $\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$
. Similarly, each entry
$\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$
. Similarly, each entry
![]() $\pi _{1,i_2,\ldots ,i_d} $
is the largest weight of a directed path from
$\pi _{1,i_2,\ldots ,i_d} $
is the largest weight of a directed path from
![]() $(1,i_2,\ldots , i_d)$
to
$(1,i_2,\ldots , i_d)$
to
![]() $(n_1,\ldots , n_d)$
through the hypermatrix A. In addition, note that when taking the maximum over lattice paths, we can ‘skip’ zero slices
$(n_1,\ldots , n_d)$
through the hypermatrix A. In addition, note that when taking the maximum over lattice paths, we can ‘skip’ zero slices
![]() $A^{(\ell )} = \mathbf {0}$
. We then have
$A^{(\ell )} = \mathbf {0}$
. We then have
 $$ \begin{align*} \pi_{1,i_2,\ldots,i_d} &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(\ell,\mathbf{i}) \in \Pi, \, \ell \in \{\ell_1,\ldots, \ell_k \}} a_{(\ell, \mathbf{i}) } \\ &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(j,\mathbf{i}) \in \Pi, \, j \in \{j_1,\ldots, j_k \}} b_{(j, \mathbf{i}) } \\ &= \pi^{\prime}_{1,i_2,\ldots,i_d}. \end{align*} $$
$$ \begin{align*} \pi_{1,i_2,\ldots,i_d} &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(\ell,\mathbf{i}) \in \Pi, \, \ell \in \{\ell_1,\ldots, \ell_k \}} a_{(\ell, \mathbf{i}) } \\ &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(j,\mathbf{i}) \in \Pi, \, j \in \{j_1,\ldots, j_k \}} b_{(j, \mathbf{i}) } \\ &= \pi^{\prime}_{1,i_2,\ldots,i_d}. \end{align*} $$
Hence
![]() $\pi ' \in R$
, we can set
$\pi ' \in R$
, we can set
![]() $\phi : \pi \mapsto \pi '$
and it is a well-defined bijection between L and R.
$\phi : \pi \mapsto \pi '$
and it is a well-defined bijection between L and R.
Note also that d-dimensional Grothendieck polynomials satisfy the stability:
![]() $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
does not change for
$g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
does not change for
![]() $n_1 \to n_1 + 1$
and
$n_1 \to n_1 + 1$
and
![]() $x^{(1)}_{n_1+1} = 0$
(i.e., if we add an extra
$x^{(1)}_{n_1+1} = 0$
(i.e., if we add an extra
![]() $0$
at the end of
$0$
at the end of
![]() $\mathbf {x}^{(1)}$
). Therefore,
$\mathbf {x}^{(1)}$
). Therefore,
![]() $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
can be treated as a quasisymmetric function in infinitely many variables
$g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$
can be treated as a quasisymmetric function in infinitely many variables
![]() $\mathbf {x}^{(1)}$
(The stability is just the projective limit of quasisymmetric functions).
$\mathbf {x}^{(1)}$
(The stability is just the projective limit of quasisymmetric functions).
Let us define the boxed polynomials
 $$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align*} $$
$$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align*} $$
which are bounded versions of the Cauchy product as by Corollary 4.3; we have
 $$ \begin{align*}\lim_{n_{d+1} \to \infty} F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
$$ \begin{align*}\lim_{n_{d+1} \to \infty} F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$
These polynomials can also be expanded as follows:
 $$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} \sum_{\mathrm{sh}_{1}(\pi) = \rho} w(\pi) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}). \end{align*} $$
$$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} \sum_{\mathrm{sh}_{1}(\pi) = \rho} w(\pi) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}). \end{align*} $$
Corollary 6.10 (Full quasisymmetry of boxed polynomials).
We have:
![]() $ F_{(n_1,\ldots , n_{d+ 1})} $
is quasisymmetric in each set of the variables
$ F_{(n_1,\ldots , n_{d+ 1})} $
is quasisymmetric in each set of the variables
![]() $\mathbf {x}^{(1)}, \ldots , \mathbf {x}^{(d)}$
independently.
$\mathbf {x}^{(1)}, \ldots , \mathbf {x}^{(d)}$
independently.
Proof. The quasisymmetry in
![]() $\mathbf {x}^{(1)}$
is immediate from the previous proposition. The same holds for any other set of variables by noting that the definitions of
$\mathbf {x}^{(1)}$
is immediate from the previous proposition. The same holds for any other set of variables by noting that the definitions of
![]() $\mathrm {Cor}(\pi )$
and weights
$\mathrm {Cor}(\pi )$
and weights
![]() $w(\pi )$
are symmetric in the first d coordinates, and hence we may repeat the proof by ‘rotation’ (i.e., moving any coordinate to the position of the first one).
$w(\pi )$
are symmetric in the first d coordinates, and hence we may repeat the proof by ‘rotation’ (i.e., moving any coordinate to the position of the first one).
Definition 6.11. Let
![]() $A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{}(n_1,\ldots , n_d)$
. For each
$A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{}(n_1,\ldots , n_d)$
. For each
![]() $\ell \in [d]$
, consider the hypermatrices
$\ell \in [d]$
, consider the hypermatrices
![]() $B^{(\ell )}_{i} = (a_{i_1,\ldots ,i_d})_{i_{\ell } = i}$
(i.e., slices of A with fixed
$B^{(\ell )}_{i} = (a_{i_1,\ldots ,i_d})_{i_{\ell } = i}$
(i.e., slices of A with fixed
![]() $\ell $
-th coordinate). Define the vectors
$\ell $
-th coordinate). Define the vectors
where
![]() $|B|$
denotes the sum of entries of B. For example, if
$|B|$
denotes the sum of entries of B. For example, if
![]() $d = 2$
, then
$d = 2$
, then
![]() $s_{1}(A)$
is the vector of row sums of A, and
$s_{1}(A)$
is the vector of row sums of A, and
![]() $s_{2}(A)$
is the column sums of A. Let us also say that A is a packed hypermatrix if for each
$s_{2}(A)$
is the column sums of A. Let us also say that A is a packed hypermatrix if for each
![]() $\ell \in [d]$
, the sequence
$\ell \in [d]$
, the sequence
![]() $s_{\ell }(A)$
does not contain zeros between its positive entries. Denote by
$s_{\ell }(A)$
does not contain zeros between its positive entries. Denote by
![]() $\mathrm {pack}(A)$
the packed hypermatrix formed from A by removing its zero slices
$\mathrm {pack}(A)$
the packed hypermatrix formed from A by removing its zero slices
![]() $B^{(\ell )}_i = \mathbf {0}$
.
$B^{(\ell )}_i = \mathbf {0}$
.
Note that for any
![]() $A \in \mathcal {M}(n_1,\ldots , n_d)$
, we have
$A \in \mathcal {M}(n_1,\ldots , n_d)$
, we have
 $$ \begin{align*}w_A = \prod_{\ell = 1}^d \left(\mathbf{x}^{(\ell)} \right)^{s_{\ell}(A)}, \end{align*} $$
$$ \begin{align*}w_A = \prod_{\ell = 1}^d \left(\mathbf{x}^{(\ell)} \right)^{s_{\ell}(A)}, \end{align*} $$
where for a set of variables
![]() $\mathbf {x} = (x_1,x_2,\ldots )$
and a vector
$\mathbf {x} = (x_1,x_2,\ldots )$
and a vector
![]() $s = (s_1, s_2,\ldots )$
, we use the notation
$s = (s_1, s_2,\ldots )$
, we use the notation
![]() ${\mathbf {x}^{s} = x_1^{s_1} x_2^{s_2} \cdots }$
.
${\mathbf {x}^{s} = x_1^{s_1} x_2^{s_2} \cdots }$
.
For a composition
![]() $\alpha = (\alpha _1,\ldots , \alpha _k) \in \mathbb {Z}^k_+$
, recall the monomial quasisymmetric functions
$\alpha = (\alpha _1,\ldots , \alpha _k) \in \mathbb {Z}^k_+$
, recall the monomial quasisymmetric functions
Note that they form a basis of the algebra of quasisymmetric functions.
It is easy to see that
 $$ \begin{align*}F_{(n_1,\ldots,n_d, \infty)} = \sum_{A \in \mathcal{M}(n_1,\ldots,n_d)} w_A = \sum_{{\alpha^{(1)}, \ldots, \alpha^{(d)} \atop \text{compositions}} } m^{}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, (\mathbf{x}^{(1)})^{\alpha^{(1)}} \cdots (\mathbf{x}^{(d)})^{\alpha^{(d)}}, \end{align*} $$
$$ \begin{align*}F_{(n_1,\ldots,n_d, \infty)} = \sum_{A \in \mathcal{M}(n_1,\ldots,n_d)} w_A = \sum_{{\alpha^{(1)}, \ldots, \alpha^{(d)} \atop \text{compositions}} } m^{}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, (\mathbf{x}^{(1)})^{\alpha^{(1)}} \cdots (\mathbf{x}^{(d)})^{\alpha^{(d)}}, \end{align*} $$
where
![]() $m^{}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$
is the number of
$m^{}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$
is the number of
![]() $A \in \mathcal {M}(n_1,\ldots , n_d)$
with
$A \in \mathcal {M}(n_1,\ldots , n_d)$
with
![]() $s_{\ell }(A) = \alpha ^{(\ell )} \in \mathbb {N}^{n_{\ell }}$
. The following result is a finite boxed version of this expansion.
$s_{\ell }(A) = \alpha ^{(\ell )} \in \mathbb {N}^{n_{\ell }}$
. The following result is a finite boxed version of this expansion.
Theorem 6.12 (Monomial basis expansion of boxed polynomials).
We have
 $$ \begin{align*}F_{(n_1,\ldots,n_{d+1})} = \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}), \end{align*} $$
$$ \begin{align*}F_{(n_1,\ldots,n_{d+1})} = \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}), \end{align*} $$
where the sum runs over compositions
![]() $\alpha ^{(1)}, \ldots , \alpha ^{(d)}$
such that
$\alpha ^{(1)}, \ldots , \alpha ^{(d)}$
such that
![]() $|\alpha ^{(i)}| = |\alpha ^{(j)}|$
for all
$|\alpha ^{(i)}| = |\alpha ^{(j)}|$
for all
![]() $i,j$
, and the coefficient
$i,j$
, and the coefficient
![]() $m^{(n_{d+1})}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$
is equal to the number of packed hypermatrices
$m^{(n_{d+1})}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$
is equal to the number of packed hypermatrices
![]() $A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
such that
$A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
such that
![]() $s_{\ell }(A) = \alpha ^{(\ell )}$
for all
$s_{\ell }(A) = \alpha ^{(\ell )}$
for all
![]() $\ell \in [d]$
.
$\ell \in [d]$
.
Proof. Note that replacing a hypermatrix A by
![]() $\mathrm {pack}(A)$
does not change its last passage time
$\mathrm {pack}(A)$
does not change its last passage time
![]() $G_{1,\ldots , 1}$
. Let
$G_{1,\ldots , 1}$
. Let
![]() $P \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
be a packed hypermatrix and let
$P \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
be a packed hypermatrix and let
![]() $M(P)$
be the set of hypermatrices
$M(P)$
be the set of hypermatrices
![]() $A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
such that
$A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$
such that
![]() $\mathrm {pack}(A) = P$
. Let
$\mathrm {pack}(A) = P$
. Let
![]() $s_{\ell }(P) = \alpha ^{(\ell )}$
. Then (by an argument as in Proposition 6.9) it is not difficult to obtain that we have
$s_{\ell }(P) = \alpha ^{(\ell )}$
. Then (by an argument as in Proposition 6.9) it is not difficult to obtain that we have
Therefore, we obtain
 $$ \begin{align*} F_{(n_1,\ldots,n_{d+1})} &= \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} w(\pi) \\ &= \sum_{A \in \mathcal{M}([n_1] \times \cdots \times [n_d], n_{d+1})} w_A \\ &= \sum_{P \text{ packed}} \sum_{A \in M(P)} w_A \\ &= \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}) \end{align*} $$
$$ \begin{align*} F_{(n_1,\ldots,n_{d+1})} &= \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} w(\pi) \\ &= \sum_{A \in \mathcal{M}([n_1] \times \cdots \times [n_d], n_{d+1})} w_A \\ &= \sum_{P \text{ packed}} \sum_{A \in M(P)} w_A \\ &= \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}) \end{align*} $$
as needed.
Remark 7. For
![]() $d = 2$
, packed matrices appear in the algebra of matrix quasisymmetric functions; see [Reference Duchamp, Hivert and ThibonDHT02].
$d = 2$
, packed matrices appear in the algebra of matrix quasisymmetric functions; see [Reference Duchamp, Hivert and ThibonDHT02].
6.5 Some remarks
Remark 8 (Dual stable Grothendieck polynomials,
 $d = 2$
).
$d = 2$
).
Recall that in this case (see Example 6.2), we get the following definition of polynomials
![]() $g_{\lambda }(\mathbf {x}; \mathbf {y})$
indexed by partitions
$g_{\lambda }(\mathbf {x}; \mathbf {y})$
indexed by partitions
![]() $\lambda $
. We define
$\lambda $
. We define
 $$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$
$$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$
where the sum runs over plane partitions
![]() $\pi $
. The polynomials
$\pi $
. The polynomials
![]() $g_{\lambda }(\mathbf {x}; \mathbf {y})$
are generalizations of dual stable Grothendieck polynomials which correspond to the specialization
$g_{\lambda }(\mathbf {x}; \mathbf {y})$
are generalizations of dual stable Grothendieck polynomials which correspond to the specialization
![]() $g_{\lambda }(\mathbf {x}) = g_{\lambda }(\mathbf {x}; \mathbf {1})$
. In fact,
$g_{\lambda }(\mathbf {x}) = g_{\lambda }(\mathbf {x}; \mathbf {1})$
. In fact,
![]() $g_{\lambda }(\mathbf {x}; \mathbf {y})$
is symmetric in
$g_{\lambda }(\mathbf {x}; \mathbf {y})$
is symmetric in
![]() $\mathbf {x}$
. The Cauchy–Littlewood-type identity in Corollary 6.5 becomes
$\mathbf {x}$
. The Cauchy–Littlewood-type identity in Corollary 6.5 becomes
 $$ \begin{align*}\sum_{\lambda \in \mathcal{P}(n_2, \infty)} g_{\lambda}(\mathbf{x}; \mathbf{y}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \frac{1}{1 - x_i y_j}, \end{align*} $$
$$ \begin{align*}\sum_{\lambda \in \mathcal{P}(n_2, \infty)} g_{\lambda}(\mathbf{x}; \mathbf{y}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \frac{1}{1 - x_i y_j}, \end{align*} $$
which was proved in [Reference YeliussizovYel21a, Reference YeliussizovYel21b]. The boxed specialization formula in Proposition 6.7 becomes the following:
the number of plane partitions inside the box
![]() $[n_1] \times [n_2] \times [n_3]$
, for which there is also the famous MacMahon boxed product formula
$[n_1] \times [n_2] \times [n_3]$
, for which there is also the famous MacMahon boxed product formula
 $$ \begin{align*}|\mathcal{P}(n_1, n_2, n_3)| = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \frac{i + j + k - 1}{i + j + k - 2}. \end{align*} $$
$$ \begin{align*}|\mathcal{P}(n_1, n_2, n_3)| = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \frac{i + j + k - 1}{i + j + k - 2}. \end{align*} $$
Using determinantal formulas for dual stable Grothendieck polynomials [Reference YeliussizovYel17], we also have the following ‘coincidence’ formula (see [Reference YeliussizovYel21a, Lemma 3.4], [Reference YeliussizovYel21b, Lemma 6.9]) connecting them with the Schur polynomials
![]() $\{s_{\lambda } \}$
as follows:
$\{s_{\lambda } \}$
as follows:
Remark 9 (3d Grothendieck polynomials,
 $d = 3$
).
$d = 3$
).
In this case, we get the following definition of polynomials
![]() $g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
indexed by plane partitions
$g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
indexed by plane partitions
![]() $\rho $
. We define
$\rho $
. We define
 $$ \begin{align} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x_{i} y_{j} z_{k}, \end{align} $$
$$ \begin{align} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x_{i} y_{j} z_{k}, \end{align} $$
where the sum runs over solid partitions
![]() $\pi \in \mathcal {P}(n_1,n_2,n_3,n_4)$
. Note also that if
$\pi \in \mathcal {P}(n_1,n_2,n_3,n_4)$
. Note also that if
![]() $\rho $
satisfies
$\rho $
satisfies
![]() $D(\rho ) = \{(1,i,j) : (i,j) \in D(\lambda )\}$
where
$D(\rho ) = \{(1,i,j) : (i,j) \in D(\lambda )\}$
where
![]() $\lambda $
is a partition, we then have
$\lambda $
is a partition, we then have
![]() $g_{\rho }(\mathbf {x}; \mathbf {1}; \mathbf {z}) = g_{\lambda }(\mathbf {x}; \mathbf {z})$
reduces to the 2d case discussed above. The polynomials
$g_{\rho }(\mathbf {x}; \mathbf {1}; \mathbf {z}) = g_{\lambda }(\mathbf {x}; \mathbf {z})$
reduces to the 2d case discussed above. The polynomials
![]() $g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
are quasisymmetric in
$g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$
are quasisymmetric in
![]() $\mathbf {x}$
. The Cauchy–Littlewood-type identity in Corollary 6.5 becomes
$\mathbf {x}$
. The Cauchy–Littlewood-type identity in Corollary 6.5 becomes
 $$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2, n_3, \infty)} g_{\rho}(\mathbf{x}^{}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \left(1 - x^{}_{i} y_j z_k \right)^{-1}. \end{align*} $$
$$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2, n_3, \infty)} g_{\rho}(\mathbf{x}^{}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \left(1 - x^{}_{i} y_j z_k \right)^{-1}. \end{align*} $$
The boxed specialization formula becomes the following:
the number of solid partitions inside the box
![]() $[n_1] \times [n_2] \times [n_3] \times [n_4]$
.
$[n_1] \times [n_2] \times [n_3] \times [n_4]$
.
Remark 10 (On higher-dimensional Schur polynomials and SSYT).
Note that the d-dimensional Grothendieck polynomials
![]() $g_{\rho }(\mathbf {x})$
are inhomogeneous. It is well known that for
$g_{\rho }(\mathbf {x})$
are inhomogeneous. It is well known that for
![]() $d = 2$
, we have
$d = 2$
, we have
![]() $g_{\lambda } = s_{\lambda } + \text {lower degree terms}$
. By analogy, the top degree homogeneous component of
$g_{\lambda } = s_{\lambda } + \text {lower degree terms}$
. By analogy, the top degree homogeneous component of
![]() $g_{\rho }(\mathbf {x})$
denoted by
$g_{\rho }(\mathbf {x})$
denoted by
![]() $s_{\rho }(\mathbf {x})$
can be viewed as a higher-dimensional analogue of Schur polynomials. It sums over a subset of d-dimensional partitions which are analogous to semistandard Young tableaux (SSYT) for the case
$s_{\rho }(\mathbf {x})$
can be viewed as a higher-dimensional analogue of Schur polynomials. It sums over a subset of d-dimensional partitions which are analogous to semistandard Young tableaux (SSYT) for the case
![]() $d = 2$
. By Proposition 6.9,
$d = 2$
. By Proposition 6.9,
![]() $\{s_{\rho }\}$
are also quasisymmetric polynomials. Are there any interesting properties of these functions and tableaux?
$\{s_{\rho }\}$
are also quasisymmetric polynomials. Are there any interesting properties of these functions and tableaux?
7 Last passage percolation in
 $\mathbb {Z}^{d}$
$\mathbb {Z}^{d}$
In this section, we consider a directed last passage percolation model with geometric weights and show its connections with d-dimensional Grothendieck polynomials studied in the previous section.
Let
![]() $W = (w_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+}$
be a random hypermatrix with i.i.d. entries
$W = (w_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+}$
be a random hypermatrix with i.i.d. entries
![]() $w_{\mathbf {i}}$
which have geometric distribution with parameter
$w_{\mathbf {i}}$
which have geometric distribution with parameter
![]() $q \in (0,1)$
; that is,
$q \in (0,1)$
; that is,
Define the last passage times as follows:
where the maximum is over directed lattice paths
![]() $\Pi $
from
$\Pi $
from
![]() $(1,\ldots , 1)$
to
$(1,\ldots , 1)$
to
![]() $\mathbf {i}$
.
$\mathbf {i}$
.
Now we are going to show that d-dimensional Grothendieck polynomials naturally appear in distribution formulas for this model.
Theorem 7.1. Let
![]() $n_1,\ldots , n_d \in \mathbb {Z}_+$
and
$n_1,\ldots , n_d \in \mathbb {Z}_+$
and
![]() $\rho \in \mathcal {P}(n_2,\ldots , n_{d}, \infty )$
be a
$\rho \in \mathcal {P}(n_2,\ldots , n_{d}, \infty )$
be a
![]() $(d-1)$
-dimensional partition. Denote
$(d-1)$
-dimensional partition. Denote
![]() $\mathbf {n} = (n_2 + 1,\ldots , n_{d} + 1)$
and
$\mathbf {n} = (n_2 + 1,\ldots , n_{d} + 1)$
and
![]() $N = n_1 \cdots n_{d}$
. We have the following joint distribution formula:
$N = n_1 \cdots n_{d}$
. We have the following joint distribution formula:
 $$ \begin{align*} \mathrm{Prob}\left( G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) = (1 - q)^{N}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
$$ \begin{align*} \mathrm{Prob}\left( G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) = (1 - q)^{N}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
Proof. Let us flip and truncate the hypermatrix W to get
![]() $W' =(w^{\prime }_{\mathbf {i}}) = (w_{(n_1 + 1,\mathbf {n}) - \mathbf {i}} )_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$
.
$W' =(w^{\prime }_{\mathbf {i}}) = (w_{(n_1 + 1,\mathbf {n}) - \mathbf {i}} )_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$
.
Let
![]() $\pi = (\pi _{\mathbf {i}}) \in \mathcal {P}(n_1,\ldots , n_d, \infty )$
and
$\pi = (\pi _{\mathbf {i}}) \in \mathcal {P}(n_1,\ldots , n_d, \infty )$
and
![]() $(a_{\mathbf {i}}) = \Phi ^{-1}(\pi )$
. We obtain
$(a_{\mathbf {i}}) = \Phi ^{-1}(\pi )$
. We obtain
 $$ \begin{align*}\mathrm{Prob}(W' = \Phi^{-1}(\pi)) = \prod_{\mathbf{i} \in [n_1] \times \cdots \times [n_{d}]} \mathrm{Prob}(w^{\prime}_{\mathbf{i}} = a_{\mathbf{i}}) = (1-q)^{N} q^{S(\pi)}, \end{align*} $$
$$ \begin{align*}\mathrm{Prob}(W' = \Phi^{-1}(\pi)) = \prod_{\mathbf{i} \in [n_1] \times \cdots \times [n_{d}]} \mathrm{Prob}(w^{\prime}_{\mathbf{i}} = a_{\mathbf{i}}) = (1-q)^{N} q^{S(\pi)}, \end{align*} $$
where
![]() $S(\pi ) = \sum _{\mathbf {i}} a_{\mathbf {i}}$
. Note that
$S(\pi ) = \sum _{\mathbf {i}} a_{\mathbf {i}}$
. Note that
where we defined
![]() $c_{i}(\pi ) = |\{ \mathbf {i} : (i, \mathbf {i}) \in \mathrm {Cor}(\pi ) \}|$
. Then from (7), we have
$c_{i}(\pi ) = |\{ \mathbf {i} : (i, \mathbf {i}) \in \mathrm {Cor}(\pi ) \}|$
. Then from (7), we have
 $$ \begin{align*} (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}) &= (1 - q)^{N} \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} q^{c_1(\pi) + \ldots + c_{n_1}(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} (1 - q)^{N} q^{S(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(W' = \Phi^{-1}(\pi)), \end{align*} $$
$$ \begin{align*} (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}) &= (1 - q)^{N} \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} q^{c_1(\pi) + \ldots + c_{n_1}(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} (1 - q)^{N} q^{S(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(W' = \Phi^{-1}(\pi)), \end{align*} $$
where the sum runs over
![]() $\pi \in \mathcal {P}(n_1,\ldots , n_d, \infty )$
.
$\pi \in \mathcal {P}(n_1,\ldots , n_d, \infty )$
.
Note that we have
![]() $\Phi (W') = (G((n_1 + 1, \mathbf {n}) - \mathbf {i}))_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$
since the maximum of
$\Phi (W') = (G((n_1 + 1, \mathbf {n}) - \mathbf {i}))_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$
since the maximum of
![]() $\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$
among all paths
$\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$
among all paths
![]() $\Pi : \mathbf {j} \to \infty ^d$
is achieved for some path that passes through
$\Pi : \mathbf {j} \to \infty ^d$
is achieved for some path that passes through
![]() $(n_1 + 1, \mathbf {n})$
and therefore equals the maximum of
$(n_1 + 1, \mathbf {n})$
and therefore equals the maximum of
![]() $\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$
among all paths
$\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$
among all paths
![]() $\Pi : \mathbf {j} \to (n_1 + 1, \mathbf {n})$
. Therefore, now we get
$\Pi : \mathbf {j} \to (n_1 + 1, \mathbf {n})$
. Therefore, now we get
 $$ \begin{align*} \mathrm{Prob}\left(G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(\Phi(W') = \pi) \\ &= (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \end{align*} $$
$$ \begin{align*} \mathrm{Prob}\left(G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(\Phi(W') = \pi) \\ &= (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \end{align*} $$
as needed.
Remark 11. The same proof (with slight modifications) works in a more general case if
![]() $(w_{\mathbf {i}})$
are independent geometric random variables with different parameters
$(w_{\mathbf {i}})$
are independent geometric random variables with different parameters
![]() $x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \in (0,1)$
. Then the corresponding probability will be proportional to the d-dimensional Grothendieck polynomial
$x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \in (0,1)$
. Then the corresponding probability will be proportional to the d-dimensional Grothendieck polynomial
![]() $g_{\rho }$
of variables
$g_{\rho }$
of variables
![]() $x^{(\ell )}_{i}$
. As it was pointed out by one of the referees, a proof can also be given using an analogue of Gelfand–Tsetlin patterns and conditioning as in [Reference Motegi and ScrimshawMS20] for
$x^{(\ell )}_{i}$
. As it was pointed out by one of the referees, a proof can also be given using an analogue of Gelfand–Tsetlin patterns and conditioning as in [Reference Motegi and ScrimshawMS20] for
![]() $d = 2$
.
$d = 2$
.
Corollary 7.2 (Single point distribution formula).
We have
 $$ \begin{align*}\mathrm{Prob}(G(n_1,\ldots, n_d) \le n) = (1 - q)^{N}\, g_{[n_2] \times \cdots \times [n_d] \times [n]}(1,\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
$$ \begin{align*}\mathrm{Prob}(G(n_1,\ldots, n_d) \le n) = (1 - q)^{N}\, g_{[n_2] \times \cdots \times [n_d] \times [n]}(1,\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
Proof. Follows by combining the theorem with Lemma 6.6.
Corollary 7.3 (The case
 $d = 2$
).
$d = 2$
).
Let
![]() $\lambda \in \mathcal {P}(n_2, \infty )$
be a partition. We have
$\lambda \in \mathcal {P}(n_2, \infty )$
be a partition. We have
 $$ \begin{align*} \mathrm{Prob}\left(G(n_1, n_2 + 1 - i) = \lambda_i \, :\, i \in [n_2] \right) = (1 - q)^{n_1 n_2}\, g_{\lambda}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
$$ \begin{align*} \mathrm{Prob}\left(G(n_1, n_2 + 1 - i) = \lambda_i \, :\, i \in [n_2] \right) = (1 - q)^{n_1 n_2}\, g_{\lambda}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$
Remark 12. This formula (which shows that dual stable Grothendieck polynomials arise naturally in the last passage percolation model) was proved in [Reference YeliussizovYel21a] and in a more general case with different parameters in [Reference YeliussizovYel20]. Note that in this case we can obtain many determinantal formulas.
Remark 13. Theorem 7.1 suggests a probability distribution on the set
![]() $\mathcal {P}(n_2,\ldots , n_{d}, \infty )$
of
$\mathcal {P}(n_2,\ldots , n_{d}, \infty )$
of
![]() $(d-1)$
-dimensional partitions defined as follows:
$(d-1)$
-dimensional partitions defined as follows:
 $$ \begin{align*}\mathrm{Prob}_{g}(\rho) := (1 - q)^{n_1 \cdots n_d}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \qquad \rho \in \mathcal{P}(n_2,\ldots, n_{d}, \infty). \end{align*} $$
$$ \begin{align*}\mathrm{Prob}_{g}(\rho) := (1 - q)^{n_1 \cdots n_d}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \qquad \rho \in \mathcal{P}(n_2,\ldots, n_{d}, \infty). \end{align*} $$
Remark 14. Using Kingman’s subadditivity theorem, one can show that there is a deterministic limit shape
![]() $\psi : \mathbb {R}^{d}_{\ge 0} \to \mathbb {R}_{\ge 0}$
(see [Reference MartinMar06]) such that as
$\psi : \mathbb {R}^{d}_{\ge 0} \to \mathbb {R}_{\ge 0}$
(see [Reference MartinMar06]) such that as
![]() $n \to \infty $
, we have a.s. convergence
$n \to \infty $
, we have a.s. convergence
The case
![]() $d = 2$
is exactly solvable and
$d = 2$
is exactly solvable and
![]() $\psi (x,y) = (x + y + 2\sqrt {qxy})/(1 - q)$
; moreover, the point fluctuations around the shape are of order
$\psi (x,y) = (x + y + 2\sqrt {qxy})/(1 - q)$
; moreover, the point fluctuations around the shape are of order
![]() $n^{1/3}$
and tend to the Tracy-Widom distribution [Reference JohanssonJoh00]. However, much less is known for
$n^{1/3}$
and tend to the Tracy-Widom distribution [Reference JohanssonJoh00]. However, much less is known for
![]() $d \ge 3$
.
$d \ge 3$
.
8 Concluding remarks and open questions
8.1 Asymptotics
MacMahon’s numbers
![]() $m_d(n)$
have the following asymptotics [Reference Balakrishnan, Govindarajan and PrabhakarBGP12]:
$m_d(n)$
have the following asymptotics [Reference Balakrishnan, Govindarajan and PrabhakarBGP12]:
where
![]() $\zeta $
is the Riemann zeta function (which is computed based on the explicit formula for the generating function). Let
$\zeta $
is the Riemann zeta function (which is computed based on the explicit formula for the generating function). Let
![]() $p_d(n)$
be the number of d-dimensional partitions of volume n. Supported by numerical experiments for solid partitions, it was conjectured in [Reference Mustonen and RajeshMR03] that
$p_d(n)$
be the number of d-dimensional partitions of volume n. Supported by numerical experiments for solid partitions, it was conjectured in [Reference Mustonen and RajeshMR03] that
![]() $p_3(n)$
has the same asymptotics as
$p_3(n)$
has the same asymptotics as
![]() $m_3(n)$
. However, later computations reported in [Reference Destainville and GovindarajanDG15] suggest that this is not the case and that
$m_3(n)$
. However, later computations reported in [Reference Destainville and GovindarajanDG15] suggest that this is not the case and that
![]() $p_3(n)$
is asymptotically larger than
$p_3(n)$
is asymptotically larger than
![]() $m_3(n)$
, despite the fact that
$m_3(n)$
, despite the fact that
![]() $m_3(n) = p_3(n)$
for
$m_3(n) = p_3(n)$
for
![]() $n \le 5$
and
$n \le 5$
and
![]() $m_3(n)> p_3(n)$
for the next many values of n [Reference Atkin, Bratley, Macdonald and McKayABMM67, Reference Destainville and GovindarajanDG15]; cf. the sequences A000293, A000294 in [OEIS]). See also [Reference EkhadEkh12] and a useful resource [Reference GovindarajanGov] for more related data. Using our interpretation for
$m_3(n)> p_3(n)$
for the next many values of n [Reference Atkin, Bratley, Macdonald and McKayABMM67, Reference Destainville and GovindarajanDG15]; cf. the sequences A000293, A000294 in [OEIS]). See also [Reference EkhadEkh12] and a useful resource [Reference GovindarajanGov] for more related data. Using our interpretation for
![]() $m_d(n)$
(Corollary 5.5) and bounds on the corner-hook volume, it was shown in [Reference YeliussizovYel23] that
$m_d(n)$
(Corollary 5.5) and bounds on the corner-hook volume, it was shown in [Reference YeliussizovYel23] that
![]() $p_d(n) < dn \cdot m_d(dn)$
, and obtaining a more accurate comparison between these sequences (e.g., by showing that
$p_d(n) < dn \cdot m_d(dn)$
, and obtaining a more accurate comparison between these sequences (e.g., by showing that
![]() $\log p_d(n) \sim \log m_d(\alpha n)$
for some
$\log p_d(n) \sim \log m_d(\alpha n)$
for some
![]() $\alpha $
) will be important for understanding the asymptotics of
$\alpha $
) will be important for understanding the asymptotics of
![]() $p_d(n)$
.
$p_d(n)$
.
8.2 d-dimensional Grothendieck polynomials
Are there any (algebraic, determinantal) formulas for d-dimensional Grothendieck polynomials? They will be important for at least two applications: enumeration of boxed higher-dimensional partitions and computing distribution formulas (or performing asymptotic analysis) for the last passage percolation problem discussed above. Note that for
![]() $d = 2$
, there are several determinantal formulas (Jacobi-Trudi, bialternant types) known; see, for example, [Reference YeliussizovYel17, Reference Amanov and YeliussizovAY22, Reference IwaoIwa20, Reference KimKim22, Reference Hwang, Jang, Kim, Song and SongHJKSS21, Reference IwaoIwa21].
$d = 2$
, there are several determinantal formulas (Jacobi-Trudi, bialternant types) known; see, for example, [Reference YeliussizovYel17, Reference Amanov and YeliussizovAY22, Reference IwaoIwa20, Reference KimKim22, Reference Hwang, Jang, Kim, Song and SongHJKSS21, Reference IwaoIwa21].
Acknowledgements
We are grateful to Askar Dzhumadil’daev, Suresh Govindarajan and Igor Pak for useful conversations. We are also grateful to the referees for their careful reading of the text and many useful comments. This research was supported by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (No. AP14871710).
Competing interest
The authors have no competing interest to declare.