No CrossRef data available.
Published online by Cambridge University Press: 07 September 2023
Working in homotopy type theory, we introduce the notion of n-exactness for a short sequence 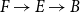 $F\to E\to B$ of pointed types and show that any fiber sequence
$F\to E\to B$ of pointed types and show that any fiber sequence  $F\hookrightarrow E \twoheadrightarrow B$ of arbitrary types induces a short sequence
$F\hookrightarrow E \twoheadrightarrow B$ of arbitrary types induces a short sequence
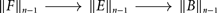
that is n-exact at 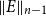 $\| E\|_{n-1}$. We explain how the indexing makes sense when interpreted in terms of n-groups, and we compare our definition to the existing definitions of an exact sequence of n-groups for
$\| E\|_{n-1}$. We explain how the indexing makes sense when interpreted in terms of n-groups, and we compare our definition to the existing definitions of an exact sequence of n-groups for  $n=1,2$. As the main application, we obtain the long n-exact sequence of homotopy n-groups of a fiber sequence.
$n=1,2$. As the main application, we obtain the long n-exact sequence of homotopy n-groups of a fiber sequence.