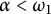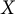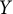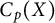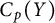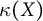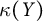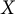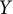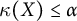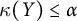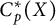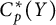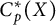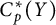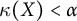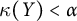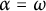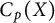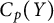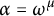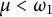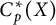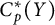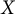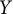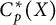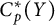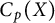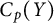1 Introduction
For a Tychonov space
![]() $X$
, we define
$X$
, we define
![]() $C(X)$
to be the set of real-valued continuous functions in
$C(X)$
to be the set of real-valued continuous functions in
![]() $X$
and
$X$
and
![]() $C^*(X)$
to be the subset of bounded functions in
$C^*(X)$
to be the subset of bounded functions in
![]() $C(X)$
. If we endow
$C(X)$
. If we endow
![]() $C(X)$
and
$C(X)$
and
![]() $C^*(X)$
with the topology of pointwise convergence, we denote that by
$C^*(X)$
with the topology of pointwise convergence, we denote that by
![]() $C_p(X)$
and
$C_p(X)$
and
![]() $C_p^*(X)$
. These function spaces are topological vector spaces that are dense subspaces of
$C_p^*(X)$
. These function spaces are topological vector spaces that are dense subspaces of
![]() $\mathbb {R}^X$
. We define spaces
$\mathbb {R}^X$
. We define spaces
![]() $X$
and
$X$
and
![]() $Y$
to be
$Y$
to be
![]() $l_p$
-equivalent if
$l_p$
-equivalent if
![]() $C_p(X)$
and
$C_p(X)$
and
![]() $C_p(Y)$
are linearly homeomorphic and
$C_p(Y)$
are linearly homeomorphic and
![]() $l_p^*$
-equivalent if
$l_p^*$
-equivalent if
![]() $C_p^*(X)$
and
$C_p^*(X)$
and
![]() $C_p^*(Y)$
are linearly homeomorphic. Function spaces with the topology of pointwise convergence have been widely investigated. For the results achieved, we refer to [Reference Arhangel’skii2, Reference Baars and de Groot8, Reference van Mill15, Reference Tkachuk18–Reference Tkachuk21].
$C_p^*(Y)$
are linearly homeomorphic. Function spaces with the topology of pointwise convergence have been widely investigated. For the results achieved, we refer to [Reference Arhangel’skii2, Reference Baars and de Groot8, Reference van Mill15, Reference Tkachuk18–Reference Tkachuk21].
In this paper, we will focus on linear homeomorphisms between function spaces of metric spaces and the linear equivalence of the scattered height of the underlying spaces. For a scattered metric space
![]() $X$
,
$X$
,
![]() $\kappa (X)$
denotes the scattered height of
$\kappa (X)$
denotes the scattered height of
![]() $X$
(see Section 2 for a formal definition). The following result for
$X$
(see Section 2 for a formal definition). The following result for
![]() $l_p$
-equivalent metric spaces can be found in [Reference Baars and de Groot8, Theorem 4.1.15].
$l_p$
-equivalent metric spaces can be found in [Reference Baars and de Groot8, Theorem 4.1.15].
Theorem 1.1 Let
![]() $\alpha < \omega _1$
be a prime component, and let
$\alpha < \omega _1$
be a prime component, and let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $l_p$
-equivalent metric spaces. Then
$l_p$
-equivalent metric spaces. Then
![]() $\kappa (X) \leq \alpha $
if and only if
$\kappa (X) \leq \alpha $
if and only if
![]() $\kappa (Y) \leq \alpha $
.
$\kappa (Y) \leq \alpha $
.
The notion of “support,” introduced in [Reference Arhangel’skii1] by Arhangel’skii, was very important in proving results for
![]() $l_p$
-equivalent spaces. In particular, Lemmas 2.2 and 2.3 in the next section formulate properties of the support function that were key in the proof of Theorem 1.1. Although the support function is also defined for continuous linear functions
$l_p$
-equivalent spaces. In particular, Lemmas 2.2 and 2.3 in the next section formulate properties of the support function that were key in the proof of Theorem 1.1. Although the support function is also defined for continuous linear functions
![]() $\phi : C_p^*(X) \to C_p^*(Y)$
, both Lemmas 2.2 and 2.3 are not true in this case. Therefore, a different approach is required to derive the equivalent of Theorem 1.1, for
$\phi : C_p^*(X) \to C_p^*(Y)$
, both Lemmas 2.2 and 2.3 are not true in this case. Therefore, a different approach is required to derive the equivalent of Theorem 1.1, for
![]() $l_p^*$
-equivalent spaces. For this, the notion of
$l_p^*$
-equivalent spaces. For this, the notion of
![]() $\varepsilon $
-supported sets and Lemma 2.5, the alternative for Lemma 2.3, were introduced in [Reference Baars, de Groot and Pelant10]. In addition to that, we also need an alternative for Lemma 2.2. For the purposes of this paper, it will turn out that Lemma 2.8 suffices as that alternative (see Section 2 for more details). These are amongst the essential ingredients to prove the following 30-year-old problem (see [Reference Baars, de Groot, van Mill and Pelant9] or [Reference Baars and de Groot8], Conjecture 4.6.8).
$\varepsilon $
-supported sets and Lemma 2.5, the alternative for Lemma 2.3, were introduced in [Reference Baars, de Groot and Pelant10]. In addition to that, we also need an alternative for Lemma 2.2. For the purposes of this paper, it will turn out that Lemma 2.8 suffices as that alternative (see Section 2 for more details). These are amongst the essential ingredients to prove the following 30-year-old problem (see [Reference Baars, de Groot, van Mill and Pelant9] or [Reference Baars and de Groot8], Conjecture 4.6.8).
Theorem 1.2 Let
![]() $\alpha < \omega _1$
be a prime component, and let
$\alpha < \omega _1$
be a prime component, and let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $l_p^*$
-equivalent metric spaces. Then:
$l_p^*$
-equivalent metric spaces. Then:
-
(a)
 $\kappa (X) \leq \alpha $
if and only if
$\kappa (X) \leq \alpha $
if and only if
 $\kappa (Y) \leq \alpha $
.
$\kappa (Y) \leq \alpha $
. -
(b)
 $\kappa (X) < \alpha $
if and only if
$\kappa (X) < \alpha $
if and only if
 $\kappa (Y) < \alpha $
.
$\kappa (Y) < \alpha $
.
We will also show, for metric spaces
![]() $X$
and
$X$
and
![]() $Y$
, that if
$Y$
, that if
![]() $C_p^*(X)$
and
$C_p^*(X)$
and
![]() $C_p^*(Y)$
are linearly homeomorphic, then
$C_p^*(Y)$
are linearly homeomorphic, then
![]() $X$
is scattered if and only if
$X$
is scattered if and only if
![]() $Y$
is scattered. Since Theorem 1.2 will only be derived in this paper for
$Y$
is scattered. Since Theorem 1.2 will only be derived in this paper for
![]() $\alpha < \omega _1$
, this result does not directly follow from it.
$\alpha < \omega _1$
, this result does not directly follow from it.
Theorem 1.2(a) shows that Theorem 1.1 also holds for
![]() $l_p^*$
-equivalent spaces. In [Reference Baars, de Groot, van Mill and Pelant9], Theorem 1.2(b) was proved for
$l_p^*$
-equivalent spaces. In [Reference Baars, de Groot, van Mill and Pelant9], Theorem 1.2(b) was proved for
![]() $\alpha = \omega $
and, therefore, Theorem 1.2(b) generalizes this result for all prime components. The proof in [Reference Baars, de Groot, van Mill and Pelant9] for
$\alpha = \omega $
and, therefore, Theorem 1.2(b) generalizes this result for all prime components. The proof in [Reference Baars, de Groot, van Mill and Pelant9] for
![]() $\alpha = \omega $
made use of techniques that seem to be unsuitable for the general case. The techniques in this paper also provide an alternative proof of the original result for
$\alpha = \omega $
made use of techniques that seem to be unsuitable for the general case. The techniques in this paper also provide an alternative proof of the original result for
![]() $\alpha = \omega $
.
$\alpha = \omega $
.
Theorem 1.2(b) shows that
![]() $C_p^*([1,\omega ^2))$
and
$C_p^*([1,\omega ^2))$
and
![]() $C_p^*([1, \omega ^{\omega }))$
are not linearly homeomorphic, where
$C_p^*([1, \omega ^{\omega }))$
are not linearly homeomorphic, where
![]() $[1,\alpha )$
is the ordinal space
$[1,\alpha )$
is the ordinal space
![]() $\{\beta : 1 \leq \beta <\alpha \}$
with the order topology. However by the classification results in [Reference Baars and de Groot6],
$\{\beta : 1 \leq \beta <\alpha \}$
with the order topology. However by the classification results in [Reference Baars and de Groot6],
![]() $C_p([1,\omega ^2))$
and
$C_p([1,\omega ^2))$
and
![]() $C_p([1, \omega ^{\omega }))$
are linearly homeomorphic which shows that Theorem 1.2(b) cannot always be true for
$C_p([1, \omega ^{\omega }))$
are linearly homeomorphic which shows that Theorem 1.2(b) cannot always be true for
![]() $l_p$
-equivalent metric spaces. One might think that for
$l_p$
-equivalent metric spaces. One might think that for
![]() $l_p$
-equivalent metric spaces, Theorem 1.2(b) is not true for all prime components
$l_p$
-equivalent metric spaces, Theorem 1.2(b) is not true for all prime components
![]() $\alpha < \omega _1$
. In this paper, we will show this is not the case. For
$\alpha < \omega _1$
. In this paper, we will show this is not the case. For
![]() $l_p$
-equivalent metric spaces, it is true for some prime components
$l_p$
-equivalent metric spaces, it is true for some prime components
![]() $\alpha < \omega _1$
but not for all.
$\alpha < \omega _1$
but not for all.
Theorem 1.3 Let
![]() $0< \alpha < \omega _1$
be a prime component, and let
$0< \alpha < \omega _1$
be a prime component, and let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $l_p$
-equivalent metric spaces.
$l_p$
-equivalent metric spaces.
-
(a) If
 $\alpha = \omega ^{\mu }$
with
$\alpha = \omega ^{\mu }$
with
 $\mu = 0$
or
$\mu = 0$
or
 $\mu $
a limit ordinal, then
$\mu $
a limit ordinal, then
 $\kappa (X) < \alpha $
if and only if
$\kappa (X) < \alpha $
if and only if
 $\kappa (Y) < \alpha $
.
$\kappa (Y) < \alpha $
. -
(b) For all other
 $\alpha $
,
$\alpha $
,
 $\kappa (X) < \alpha $
if and only if
$\kappa (X) < \alpha $
if and only if
 $\kappa (Y) < \alpha $
is not always true.
$\kappa (Y) < \alpha $
is not always true.
We will conclude this paper by showing that Theorems 1.1 and 1.2(a) do not hold for arbitrary Tychonov spaces, but that it remains an open question whether this is the case for Theorems 1.2(b) and 1.3(a).
2 The support function
Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, and let
$Y$
be Tychonov spaces, and let
![]() $\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function. For
$\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function. For
![]() $y \in Y$
, the map
$y \in Y$
, the map
![]() $\psi _y: C_p(X)\rightarrow \mathbb {R}$
defined by
$\psi _y: C_p(X)\rightarrow \mathbb {R}$
defined by
![]() $\psi _y (f)= \phi (f)(y)$
is continuous and linear. This means
$\psi _y (f)= \phi (f)(y)$
is continuous and linear. This means
![]() $\psi _y \in L(X)$
, the dual space of
$\psi _y \in L(X)$
, the dual space of
![]() $C_p(X)$
. Since the evaluation mappings
$C_p(X)$
. Since the evaluation mappings
![]() $\xi _x$
(
$\xi _x$
(
![]() $x \in X$
) defined by
$x \in X$
) defined by
![]() $\xi _x (f) = f(x)$
for
$\xi _x (f) = f(x)$
for
![]() $f \in C_p(X)$
form a Hamel basis for
$f \in C_p(X)$
form a Hamel basis for
![]() $L(X)$
, there are
$L(X)$
, there are
![]() $x_1, \ldots , x_n \in X$
and
$x_1, \ldots , x_n \in X$
and
![]() $\lambda _{x_1}^y, \ldots , \lambda _{x_n}^y \in \mathbb {R} \kern2pt{\backslash}\kern2pt \{0\}$
such that
$\lambda _{x_1}^y, \ldots , \lambda _{x_n}^y \in \mathbb {R} \kern2pt{\backslash}\kern2pt \{0\}$
such that
![]() $\psi _y = \sum _{i=1}^{n}\lambda _{x_i}^y \xi _{x_i}$
. This means that for every
$\psi _y = \sum _{i=1}^{n}\lambda _{x_i}^y \xi _{x_i}$
. This means that for every
![]() $f \in C_p(X)$
,
$f \in C_p(X)$
,
![]() $\phi (f)(y) = \sum _{i=1}^{n}\lambda _{x_i}^y f(x_i)$
. We define the support of
$\phi (f)(y) = \sum _{i=1}^{n}\lambda _{x_i}^y f(x_i)$
. We define the support of
![]() $y$
to be
$y$
to be
![]() $\{x_1, \ldots , x_n \}$
and we denote that by
$\{x_1, \ldots , x_n \}$
and we denote that by
![]() $\textrm {supp}_{\phi }(y)$
or simply by
$\textrm {supp}_{\phi }(y)$
or simply by
![]() $\textrm {supp}(y)$
if the subscript can be omitted without confusion. For
$\textrm {supp}(y)$
if the subscript can be omitted without confusion. For
![]() $B \subseteq Y$
, we denote
$B \subseteq Y$
, we denote
![]() $\bigcup _{y \in B} \textrm {supp}(y)$
by
$\bigcup _{y \in B} \textrm {supp}(y)$
by
![]() $\textrm {supp}_{\phi }(B)$
or
$\textrm {supp}_{\phi }(B)$
or
![]() $\textrm {supp} (B)$
. The following lemma is well known (see [Reference van Mill15, Lemma 6.8.2]).
$\textrm {supp} (B)$
. The following lemma is well known (see [Reference van Mill15, Lemma 6.8.2]).
Lemma 2.1 Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, let
$Y$
be Tychonov spaces, let
![]() $\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function, and let
$\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function, and let
![]() $y \in Y$
.
$y \in Y$
.
-
(a) If
 $f,g \in C_p(X)$
coincide on
$f,g \in C_p(X)$
coincide on
 $\mathrm{supp}_{\phi }(y)$
, then
$\mathrm{supp}_{\phi }(y)$
, then
 $\phi (f)(y) = \phi (g)(y)$
.
$\phi (f)(y) = \phi (g)(y)$
. -
(b) If
 $\phi $
is a homeomorphism, then
$\phi $
is a homeomorphism, then
 $y \in \mathrm{supp}_{\phi ^{-1}}(\mathrm{supp}_{\phi }(y))$
.
$y \in \mathrm{supp}_{\phi ^{-1}}(\mathrm{supp}_{\phi }(y))$
.
Similarly, the support function can be defined for continuous linear functions between
![]() $C_p^*(X)$
and
$C_p^*(X)$
and
![]() $C_p^*(Y)$
and Lemma 2.1 holds for continuous linear functions
$C_p^*(Y)$
and Lemma 2.1 holds for continuous linear functions
![]() $\phi : C_p^*(X)\rightarrow C_p^*(Y)$
. For more information on the support function, we refer to [Reference Baars and de Groot8] and [Reference van Mill15, Chapter 6].
$\phi : C_p^*(X)\rightarrow C_p^*(Y)$
. For more information on the support function, we refer to [Reference Baars and de Groot8] and [Reference van Mill15, Chapter 6].
The following two lemmas were key in the proof of Theorem 1.1.
Lemma 2.2 [Reference Arhangel’skii1]
Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, and let
$Y$
be Tychonov spaces, and let
![]() $\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function. If
$\phi : C_p(X)\rightarrow C_p(Y)$
be a continuous linear function. If
![]() $A \subseteq Y$
is bounded, then
$A \subseteq Y$
is bounded, then
![]() $\mathrm{supp}(A) \subseteq X$
is bounded.
$\mathrm{supp}(A) \subseteq X$
is bounded.
Lemma 2.3 [Reference Baars and de Groot7]
Let
![]() $X$
and
$X$
and
![]() $Y$
be normal spaces, and let
$Y$
be normal spaces, and let
![]() $\phi : C_p(X)\to C_p(Y)$
be a continuous linear function. Let
$\phi : C_p(X)\to C_p(Y)$
be a continuous linear function. Let
![]() $\mathcal {V}$
be a locally finite family of open sets in
$\mathcal {V}$
be a locally finite family of open sets in
![]() $X$
, and let
$X$
, and let
![]() $y_0 \in Y$
be of countable character. Then there are a neighborhood
$y_0 \in Y$
be of countable character. Then there are a neighborhood
![]() $U$
of
$U$
of
![]() $y_0$
and a finite subset
$y_0$
and a finite subset
![]() $\mathcal {W} \subseteq \mathcal {V}$
such that
$\mathcal {W} \subseteq \mathcal {V}$
such that
![]() $\mathrm{supp}(U) \cap \bigcup \{V \in \mathcal {V}: V \notin \mathcal {W} \}= \emptyset $
.
$\mathrm{supp}(U) \cap \bigcup \{V \in \mathcal {V}: V \notin \mathcal {W} \}= \emptyset $
.
Examples in [Reference Baars and de Groot8, Reference Baars, van Mill and Tkachuk12] show that both Lemmas 2.2 and 2.3 do not hold for continuous linear functions
![]() $\phi : C_p^*(X)\rightarrow C_p^*(Y)$
. Therefore, a new approach is required to prove Theorem 1.2. For continuous linear functions
$\phi : C_p^*(X)\rightarrow C_p^*(Y)$
. Therefore, a new approach is required to prove Theorem 1.2. For continuous linear functions
![]() $\phi : C_p^*(X)\rightarrow C_p^*(Y)$
,
$\phi : C_p^*(X)\rightarrow C_p^*(Y)$
,
![]() $\varepsilon $
-supported sets and an alternative for Lemma 2.3 were introduced in [Reference Baars, de Groot and Pelant10].
$\varepsilon $
-supported sets and an alternative for Lemma 2.3 were introduced in [Reference Baars, de Groot and Pelant10].
Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, and let
$Y$
be Tychonov spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
![]() $A \subseteq X$
,
$A \subseteq X$
,
![]() $B \subseteq Y$
and
$B \subseteq Y$
and
![]() $\varepsilon> 0$
. We define
$\varepsilon> 0$
. We define
![]() $B$
to be
$B$
to be
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $A$
if for each
$A$
if for each
![]() $y \in B$
,
$y \in B$
,
The following lemma is straightforward.
Lemma 2.4 Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, and let
$Y$
be Tychonov spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
![]() $A \subseteq X$
,
$A \subseteq X$
,
![]() $B \subseteq Y$
and
$B \subseteq Y$
and
![]() $\varepsilon> 0$
be such that
$\varepsilon> 0$
be such that
![]() $B$
is
$B$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $A$
.
$A$
.
-
(a) If
 $D \subseteq B$
, then
$D \subseteq B$
, then
 $D$
is
$D$
is
 $\varepsilon $
-supported on
$\varepsilon $
-supported on
 $A$
.
$A$
. -
(b) If
 $A \subseteq C$
, then
$A \subseteq C$
, then
 $B$
is
$B$
is
 $\varepsilon $
-supported on
$\varepsilon $
-supported on
 $C$
.
$C$
. -
(c) If
 $\delta> 0$
and
$\delta> 0$
and
 $C \subseteq X$
are such that
$C \subseteq X$
are such that
 $B$
is
$B$
is
 $\delta $
-supported on
$\delta $
-supported on
 $C$
, then
$C$
, then
 $B$
is
$B$
is
 $\varepsilon + \delta $
-supported on
$\varepsilon + \delta $
-supported on
 $A \cap C.$
$A \cap C.$
-
(d) If
 $D \subseteq Y$
is
$D \subseteq Y$
is
 $\varepsilon $
-supported on
$\varepsilon $
-supported on
 $A$
, then
$A$
, then
 $B \cup D $
is
$B \cup D $
is
 $\varepsilon $
-supported on
$\varepsilon $
-supported on
 $A.$
$A.$
The next lemma on
![]() $\varepsilon $
-supported sets can be found in [Reference Baars, de Groot and Pelant10]. This lemma is the alternative for Lemma 2.3 that we need in the proof of Theorem 1.2.
$\varepsilon $
-supported sets can be found in [Reference Baars, de Groot and Pelant10]. This lemma is the alternative for Lemma 2.3 that we need in the proof of Theorem 1.2.
Lemma 2.5 Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces, and let
$Y$
be metric spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
![]() $\mathcal {V}$
be a locally finite family of open sets in
$\mathcal {V}$
be a locally finite family of open sets in
![]() $X$
, and let
$X$
, and let
![]() $y \in Y$
. For every
$y \in Y$
. For every
![]() $\varepsilon>0$
, there are a neighborhood
$\varepsilon>0$
, there are a neighborhood
![]() $U$
of
$U$
of
![]() $y$
and a finite subset
$y$
and a finite subset
![]() $\mathcal {W} \subseteq \mathcal {V}$
such that
$\mathcal {W} \subseteq \mathcal {V}$
such that
![]() $U$
is
$U$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
$\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
We need the following corollary to Lemma 2.5.
Corollary 2.6 Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces, and let
$Y$
be metric spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
![]() $\mathcal {V}$
be a locally finite family of open sets in
$\mathcal {V}$
be a locally finite family of open sets in
![]() $X$
, and let
$X$
, and let
![]() $K \subseteq Y$
be compact. For every
$K \subseteq Y$
be compact. For every
![]() $\varepsilon>0$
, there is a finite subset
$\varepsilon>0$
, there is a finite subset
![]() $\mathcal {W} \subseteq \mathcal {V}$
such that
$\mathcal {W} \subseteq \mathcal {V}$
such that
![]() $K$
is
$K$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
$\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
Proof For every
![]() $y \in K$
, there are, by Lemma 2.5, a neighborhood
$y \in K$
, there are, by Lemma 2.5, a neighborhood
![]() $U_y \subseteq Y$
of
$U_y \subseteq Y$
of
![]() $y$
and a finite subset
$y$
and a finite subset
![]() $\mathcal {W}_y \subseteq \mathcal {V}$
such that
$\mathcal {W}_y \subseteq \mathcal {V}$
such that
![]() $U_y$
is
$U_y$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W}_y \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
. Since
$\bigcup \mathcal {W}_y \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
. Since
![]() $K$
is compact, there is a finite subset
$K$
is compact, there is a finite subset
![]() $F \subseteq K$
such that
$F \subseteq K$
such that
![]() $K \subseteq \bigcup \{U_y: y \in F \}$
. Let
$K \subseteq \bigcup \{U_y: y \in F \}$
. Let
![]() $\mathcal {W} = \bigcup \{\mathcal {W}_y: y \in F \}$
. Then
$\mathcal {W} = \bigcup \{\mathcal {W}_y: y \in F \}$
. Then
![]() $\mathcal {W}$
is a finite subset of
$\mathcal {W}$
is a finite subset of
![]() $\mathcal {V}$
. Let
$\mathcal {V}$
. Let
![]() $y \in F$
. Since
$y \in F$
. Since
![]() $U_y$
is
$U_y$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W}_y \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
, we have by Lemma 2.4(b),
$\bigcup \mathcal {W}_y \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
, we have by Lemma 2.4(b),
![]() $U_y$
is
$U_y$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
. Then, by Lemma 2.4(d),
$\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
. Then, by Lemma 2.4(d),
![]() $\bigcup \{U_y: y \in F \}$
is
$\bigcup \{U_y: y \in F \}$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
, and hence, by Lemma 2.4(a),
$\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
, and hence, by Lemma 2.4(a),
![]() $K$
is
$K$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
$\bigcup \mathcal {W} \cup (X \kern2pt{\backslash}\kern2pt \bigcup \mathcal {V})$
.
For a Tychonov space
![]() $X$
and an ordinal
$X$
and an ordinal
![]() $\alpha $
, we define
$\alpha $
, we define
![]() $X^{(\alpha )}$
, the
$X^{(\alpha )}$
, the
![]() $\alpha $
th derivative of
$\alpha $
th derivative of
![]() $X$
by transfinite induction as follows:
$X$
by transfinite induction as follows:
-
(a)
 $X^{(0)}=X$
and
$X^{(0)}=X$
and
 $X^{(1)}=\{x \in X : x \text { is an accumulation point of } X \}$
.
$X^{(1)}=\{x \in X : x \text { is an accumulation point of } X \}$
. -
(b) If
 $\alpha $
is a successor, say
$\alpha $
is a successor, say
 $\alpha = \beta +1$
, then
$\alpha = \beta +1$
, then
 $X^{(\alpha )}= (X^{(\beta )})^{(1)}$
.
$X^{(\alpha )}= (X^{(\beta )})^{(1)}$
. -
(c) If
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $X^{(\alpha )}= \bigcap _{\beta < \alpha } X^{(\beta )}$
.
$X^{(\alpha )}= \bigcap _{\beta < \alpha } X^{(\beta )}$
.
For each ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $X^{(\alpha )}$
is a closed subset of
$X^{(\alpha )}$
is a closed subset of
![]() $X$
. A Tychonov space
$X$
. A Tychonov space
![]() $X$
is defined to be scattered if there exists an ordinal
$X$
is defined to be scattered if there exists an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $X^{(\alpha )} = \emptyset $
. The scattered height
$X^{(\alpha )} = \emptyset $
. The scattered height
![]() $\kappa (X)$
of a scattered space
$\kappa (X)$
of a scattered space
![]() $X$
is defined to be the smallest ordinal
$X$
is defined to be the smallest ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $X^{(\alpha )} = \emptyset $
.
$X^{(\alpha )} = \emptyset $
.
Theorem 2.7 [Reference Semadeni16, Theorem 8.5.2 and Proposition 8.5.5]
Let
![]() $X$
be a topological space. Then there exists an ordinal
$X$
be a topological space. Then there exists an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $X^{(\alpha )} = X^{(\alpha +1)}$
. For this
$X^{(\alpha )} = X^{(\alpha +1)}$
. For this
![]() $\alpha $
,
$\alpha $
,
![]() $X^{(\alpha )}$
is closed and dense in itself and
$X^{(\alpha )}$
is closed and dense in itself and
![]() $X \kern2pt{\backslash}\kern2pt X^{(\alpha )}$
is scattered. In particular,
$X \kern2pt{\backslash}\kern2pt X^{(\alpha )}$
is scattered. In particular,
![]() $X$
is scattered if and only if
$X$
is scattered if and only if
![]() $X^{(\alpha )} = \emptyset $
. Moreover, if
$X^{(\alpha )} = \emptyset $
. Moreover, if
![]() $X$
is second countable and scattered, then it is countable.
$X$
is second countable and scattered, then it is countable.
As mentioned in the introduction, Lemma 2.2 does not hold for continuous linear functions
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
. Instead, we will use the following lemma in the proof of Theorem 1.2.
$\phi : C_p^*(X)\to C_p^*(Y)$
. Instead, we will use the following lemma in the proof of Theorem 1.2.
Lemma 2.8 Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces, and let
$Y$
be metric spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a continuous linear function. Let
![]() $A \subseteq X$
be closed and scattered. Then, for every
$A \subseteq X$
be closed and scattered. Then, for every
![]() $K \subseteq Y$
compact and
$K \subseteq Y$
compact and
![]() $\varepsilon> 0,$
there is
$\varepsilon> 0,$
there is
![]() $L \subseteq A$
compact such that
$L \subseteq A$
compact such that
![]() $K$
is
$K$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt A)$
.
$L \cup (X \kern2pt{\backslash}\kern2pt A)$
.
Proof Let
![]() $\kappa (A) = \alpha $
. We will prove the lemma by transfinite induction on
$\kappa (A) = \alpha $
. We will prove the lemma by transfinite induction on
![]() $\alpha $
. For
$\alpha $
. For
![]() $\alpha =0,$
we have
$\alpha =0,$
we have
![]() $A = \emptyset $
. Then, for
$A = \emptyset $
. Then, for
![]() $L = \emptyset $
, the lemma follows. For
$L = \emptyset $
, the lemma follows. For
![]() $\alpha> 0$
, assume the lemma is true for every
$\alpha> 0$
, assume the lemma is true for every
![]() $\beta < \alpha $
.
$\beta < \alpha $
.
First, suppose that
![]() $\alpha $
is a limit ordinal. Since
$\alpha $
is a limit ordinal. Since
![]() $A^{(\alpha )} = \emptyset $
, the family
$A^{(\alpha )} = \emptyset $
, the family
![]() $\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt A^{(\beta )}: \beta < \alpha \}$
is an open cover of
$\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt A^{(\beta )}: \beta < \alpha \}$
is an open cover of
![]() $X$
. Let
$X$
. Let
![]() $\mathcal {U}$
be a locally finite open cover of
$\mathcal {U}$
be a locally finite open cover of
![]() $X$
such that
$X$
such that
![]() $\{\overline {U}: U \in \mathcal {U}\}$
refines
$\{\overline {U}: U \in \mathcal {U}\}$
refines
![]() $\mathcal {V}$
. By Corollary 2.6, there is a finite subset
$\mathcal {V}$
. By Corollary 2.6, there is a finite subset
![]() $\mathcal {W} \subseteq \mathcal {U}$
such that
$\mathcal {W} \subseteq \mathcal {U}$
such that
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $\bigcup \mathcal {W}$
. Let
$\bigcup \mathcal {W}$
. Let
![]() $F = \bigcup \{\overline {U}: U \in \mathcal {W}\} \cap A$
. Then
$F = \bigcup \{\overline {U}: U \in \mathcal {W}\} \cap A$
. Then
![]() $F$
is closed and since
$F$
is closed and since
![]() $\mathcal {W}$
is finite, there is
$\mathcal {W}$
is finite, there is
![]() $\beta < \alpha $
such that
$\beta < \alpha $
such that
![]() $F \subseteq A \kern2pt{\backslash}\kern2pt A^{(\beta )}$
. This implies
$F \subseteq A \kern2pt{\backslash}\kern2pt A^{(\beta )}$
. This implies
![]() $F^{(\beta )} = \emptyset $
, hence
$F^{(\beta )} = \emptyset $
, hence
![]() $F$
is scattered. By the induction hypothesis, there is
$F$
is scattered. By the induction hypothesis, there is
![]() $L \subseteq F$
compact such that
$L \subseteq F$
compact such that
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt F)$
. Note that
$L \cup (X \kern2pt{\backslash}\kern2pt F)$
. Note that
![]() $(L \cup (X \kern2pt{\backslash}\kern2pt F)) \cap \bigcup W \subseteq L \cup (X \kern2pt{\backslash}\kern2pt A)$
. So, by Lemma 2.4(b) and (c), the set
$(L \cup (X \kern2pt{\backslash}\kern2pt F)) \cap \bigcup W \subseteq L \cup (X \kern2pt{\backslash}\kern2pt A)$
. So, by Lemma 2.4(b) and (c), the set
![]() $K$
is
$K$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt A)$
.
$L \cup (X \kern2pt{\backslash}\kern2pt A)$
.
Second, suppose that
![]() $\alpha = \beta +1$
is a successor ordinal. Since
$\alpha = \beta +1$
is a successor ordinal. Since
![]() $A^{(\alpha )} = \emptyset $
and
$A^{(\alpha )} = \emptyset $
and
![]() $A$
is closed,
$A$
is closed,
![]() $A^{(\beta )}$
is a closed and discrete subset of
$A^{(\beta )}$
is a closed and discrete subset of
![]() $X$
. Then
$X$
. Then
![]() $\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt G: G \subseteq A^{(\beta )} \textrm { cofinite} \}$
is an open cover of
$\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt G: G \subseteq A^{(\beta )} \textrm { cofinite} \}$
is an open cover of
![]() $X$
. Let
$X$
. Let
![]() $\mathcal {U}$
be a locally finite open cover of
$\mathcal {U}$
be a locally finite open cover of
![]() $X$
such that
$X$
such that
![]() $\{\overline {U}: U \in \mathcal {U}\}$
refines
$\{\overline {U}: U \in \mathcal {U}\}$
refines
![]() $\mathcal {V}$
. By Corollary 2.6, there is a finite subset
$\mathcal {V}$
. By Corollary 2.6, there is a finite subset
![]() $\mathcal {W} \subseteq \mathcal {U}$
such that
$\mathcal {W} \subseteq \mathcal {U}$
such that
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $\bigcup \mathcal {W}$
. Let
$\bigcup \mathcal {W}$
. Let
![]() $F = \bigcup \{\overline {U}: U \in \mathcal {W}\} \cap A$
. Then
$F = \bigcup \{\overline {U}: U \in \mathcal {W}\} \cap A$
. Then
![]() $F$
is closed and since
$F$
is closed and since
![]() $\mathcal {W}$
is finite, there is
$\mathcal {W}$
is finite, there is
![]() $G \subseteq A^{(\beta )}$
cofinite such that
$G \subseteq A^{(\beta )}$
cofinite such that
![]() $F \subseteq A \kern2pt{\backslash}\kern2pt G$
. This implies that
$F \subseteq A \kern2pt{\backslash}\kern2pt G$
. This implies that
![]() $F^{(\beta )} = F \cap A^{(\beta )}$
is finite.
$F^{(\beta )} = F \cap A^{(\beta )}$
is finite.
Let
![]() $\{U_n:n \in \mathbb {N}\}$
be an open neighborhood base of
$\{U_n:n \in \mathbb {N}\}$
be an open neighborhood base of
![]() $F^{(\beta )}$
in
$F^{(\beta )}$
in
![]() $X$
such that for every
$X$
such that for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\overline {U}_{n+1} \subseteq U_n$
. Let
$\overline {U}_{n+1} \subseteq U_n$
. Let
![]() $(\varepsilon _n)_{n \in \mathbb {N}}$
be a sequence of positive numbers such that
$(\varepsilon _n)_{n \in \mathbb {N}}$
be a sequence of positive numbers such that
![]() $\sum _{n=1}^{\infty } \varepsilon _n = \varepsilon /2$
. For every
$\sum _{n=1}^{\infty } \varepsilon _n = \varepsilon /2$
. For every
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $F_n = F \kern2pt{\backslash}\kern2pt U_n$
. Then
$F_n = F \kern2pt{\backslash}\kern2pt U_n$
. Then
![]() $F_n$
is closed in
$F_n$
is closed in
![]() $X$
,
$X$
,
![]() $F_{n-1} \subseteq F_n$
and
$F_{n-1} \subseteq F_n$
and
![]() $F_n^{(\beta )} = \emptyset $
. Hence, by the induction hypothesis, there is
$F_n^{(\beta )} = \emptyset $
. Hence, by the induction hypothesis, there is
![]() $L_n \subseteq F_n$
compact such that
$L_n \subseteq F_n$
compact such that
![]() $K$
is
$K$
is
![]() $\varepsilon _n$
-supported on
$\varepsilon _n$
-supported on
![]() $L_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. For
$L_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. For
![]() $n \in \mathbb {N}$
, we inductively define
$n \in \mathbb {N}$
, we inductively define
![]() $\widehat {L}_n$
by
$\widehat {L}_n$
by
![]() $\widehat {L}_1 =L_1$
and for
$\widehat {L}_1 =L_1$
and for
![]() $n>1$
,
$n>1$
,
![]() $\widehat {L}_n = \widehat {L}_{n-1} \cup (L_n \cap \overline {U_{n-1}})$
. Note that
$\widehat {L}_n = \widehat {L}_{n-1} \cup (L_n \cap \overline {U_{n-1}})$
. Note that
![]() $L_n \cap \overline {U_{n-1}} \subseteq L_n$
,
$L_n \cap \overline {U_{n-1}} \subseteq L_n$
,
![]() $\widehat {L}_n \subseteq F_n$
and
$\widehat {L}_n \subseteq F_n$
and
![]() $\widehat {L}_n$
is compact.
$\widehat {L}_n$
is compact.
Claim 1 For every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $K$
is
$K$
is
![]() $\sum _{m=1}^n \varepsilon _m$
-supported on
$\sum _{m=1}^n \varepsilon _m$
-supported on
![]() $\widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
.
$\widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
.
We will prove the claim by induction on
![]() $n$
. Clearly the claim holds for
$n$
. Clearly the claim holds for
![]() $n=1$
. Let
$n=1$
. Let
![]() $n>1$
and assume that the claim holds for every
$n>1$
and assume that the claim holds for every
![]() $m < n$
. By the induction hypothesis, the set
$m < n$
. By the induction hypothesis, the set
![]() $K$
is
$K$
is
![]() $\sum _{m=1}^{n-1} \varepsilon _m$
-supported on
$\sum _{m=1}^{n-1} \varepsilon _m$
-supported on
![]() $\widehat {L}_{n-1} \cup (X \kern2pt{\backslash}\kern2pt F_{n-1})$
. We also have that
$\widehat {L}_{n-1} \cup (X \kern2pt{\backslash}\kern2pt F_{n-1})$
. We also have that
![]() $K$
is
$K$
is
![]() $\varepsilon _n$
-supported on
$\varepsilon _n$
-supported on
![]() $L_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. Since
$L_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. Since
we have by Lemma 2.4(b) and (c) that
![]() $K$
is
$K$
is
![]() $\sum _{m=1}^n \varepsilon _m$
-supported on
$\sum _{m=1}^n \varepsilon _m$
-supported on
![]() $\widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. This proves the claim.
$\widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
. This proves the claim.
Let
![]() $L = \bigcup _{n=1}^{\infty } \widehat {L}_n \cup F^{(\beta )}$
.
$L = \bigcup _{n=1}^{\infty } \widehat {L}_n \cup F^{(\beta )}$
.
Claim 2
-
(a) For every
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $L \cap F_n = \widehat {L}_n \cup ((\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n)$
.
$L \cap F_n = \widehat {L}_n \cup ((\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n)$
. -
(b)
 $L \subseteq F$
is compact.
$L \subseteq F$
is compact. -
(c)
 $K$
is
$K$
is
 $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
 $L \cup (X \kern2pt{\backslash}\kern2pt F)$
.
$L \cup (X \kern2pt{\backslash}\kern2pt F)$
.
Clearly
![]() $\widehat {L}_n \subseteq L \cap F_n$
and
$\widehat {L}_n \subseteq L \cap F_n$
and
![]() $(\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n \subseteq L \cap F_n$
. Let
$(\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n \subseteq L \cap F_n$
. Let
![]() $x \in L \cap F_n$
. Since
$x \in L \cap F_n$
. Since
![]() $F_n \cap F^{(\beta )} = \emptyset $
, we have
$F_n \cap F^{(\beta )} = \emptyset $
, we have
![]() $x \in \bigcup _{n=1}^{\infty } \widehat {L}_n$
. Let
$x \in \bigcup _{n=1}^{\infty } \widehat {L}_n$
. Let
![]() $m = \min \{k \in \mathbb {N}: x \in \widehat {L}_k\}$
. Then
$m = \min \{k \in \mathbb {N}: x \in \widehat {L}_k\}$
. Then
![]() $x \in F_m$
and hence
$x \in F_m$
and hence
![]() $x \notin U_m$
. If
$x \notin U_m$
. If
![]() $m \leq n$
, then
$m \leq n$
, then
![]() $x \in \widehat {L}_m \subseteq \widehat {L}_n$
and we are done. If
$x \in \widehat {L}_m \subseteq \widehat {L}_n$
and we are done. If
![]() $m>n$
, then
$m>n$
, then
![]() $x \notin \widehat {L}_{m-1}$
and hence
$x \notin \widehat {L}_{m-1}$
and hence
![]() $x \in L_m \cap \overline {U_{m-1}}$
. If
$x \in L_m \cap \overline {U_{m-1}}$
. If
![]() $m-1>n$
, then
$m-1>n$
, then
![]() $\overline {U_{m-1}} \subseteq U_n$
. Since
$\overline {U_{m-1}} \subseteq U_n$
. Since
![]() $x \in F_n$
, we have
$x \in F_n$
, we have
![]() $x \notin U_n$
which is a contradiction. If
$x \notin U_n$
which is a contradiction. If
![]() $m = n+1$
, then
$m = n+1$
, then
![]() $x \notin \widehat {L}_n$
and hence
$x \notin \widehat {L}_n$
and hence
![]() $x \in L_{n+1} \cap \overline {U_n} \subseteq \overline {U_n}$
. But then
$x \in L_{n+1} \cap \overline {U_n} \subseteq \overline {U_n}$
. But then
![]() $x \in (\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n$
which proves part (a) of the claim.
$x \in (\widehat {L}_{n+1} \cap \overline {U_n})\kern2pt{\backslash}\kern2pt U_n$
which proves part (a) of the claim.
For (b), note that by (a), we have
![]() $L \cap F_n$
is compact. Let
$L \cap F_n$
is compact. Let
![]() $\mathcal {V}$
be an open cover of
$\mathcal {V}$
be an open cover of
![]() $L$
. Then, for every
$L$
. Then, for every
![]() $x \in F^{(\beta )}$
, there is
$x \in F^{(\beta )}$
, there is
![]() $V_x \in \mathcal {V}$
such that
$V_x \in \mathcal {V}$
such that
![]() $x \in V_x$
. Let
$x \in V_x$
. Let
![]() $n \in \mathbb {N}$
be such that
$n \in \mathbb {N}$
be such that
![]() $U_n \subseteq \bigcup \{V_x: x \in F^{(\beta )}\}$
. Since
$U_n \subseteq \bigcup \{V_x: x \in F^{(\beta )}\}$
. Since
![]() $L \cap F_n$
is compact, there is a finite subset
$L \cap F_n$
is compact, there is a finite subset
![]() $\mathcal {W} \subseteq \mathcal {V}$
such that
$\mathcal {W} \subseteq \mathcal {V}$
such that
![]() $L \cap F_n \subseteq \bigcup \mathcal {W}$
. But then
$L \cap F_n \subseteq \bigcup \mathcal {W}$
. But then
![]() $L \subseteq \bigcup \mathcal {W} \cup \bigcup \{V_x: x \in F^{(\beta )}\}$
, hence
$L \subseteq \bigcup \mathcal {W} \cup \bigcup \{V_x: x \in F^{(\beta )}\}$
, hence
![]() $L$
is compact.
$L$
is compact.
For
![]() $y \in K$
,
$y \in K$
,
![]() $\textrm {supp}(y)$
is finite, hence there is
$\textrm {supp}(y)$
is finite, hence there is
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $\textrm {supp}(y) \cap (F \kern2pt{\backslash}\kern2pt F^{(\beta )}) \subseteq F_n$
. Let
$\textrm {supp}(y) \cap (F \kern2pt{\backslash}\kern2pt F^{(\beta )}) \subseteq F_n$
. Let
![]() $H_n = \widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
and
$H_n = \widehat {L}_n \cup (X \kern2pt{\backslash}\kern2pt F_n)$
and
![]() $H = L \cup (X \kern2pt{\backslash}\kern2pt F)$
. By Claim 1, we have
$H = L \cup (X \kern2pt{\backslash}\kern2pt F)$
. By Claim 1, we have
![]() $\sum \{ | \lambda _x^y | : x \in \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H_n \} < \sum _{m=1}^n \varepsilon _m <\varepsilon /2$
. Since
$\sum \{ | \lambda _x^y | : x \in \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H_n \} < \sum _{m=1}^n \varepsilon _m <\varepsilon /2$
. Since
![]() $ \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H \subseteq \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H_n$
, we have
$ \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H \subseteq \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H_n$
, we have
![]() $\sum \{ | \lambda _x^y | : x \in \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H \} < \varepsilon /2$
. So
$\sum \{ | \lambda _x^y | : x \in \textrm {supp} (y) \kern2pt{\backslash}\kern2pt H \} < \varepsilon /2$
. So
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $H$
which proves part (c) of the claim.
$H$
which proves part (c) of the claim.
Now, we can conclude that
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $\bigcup \mathcal {W}$
and, by Claim 2, that
$\bigcup \mathcal {W}$
and, by Claim 2, that
![]() $K$
is
$K$
is
![]() $\varepsilon /2$
-supported on
$\varepsilon /2$
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt F)$
. Note that
$L \cup (X \kern2pt{\backslash}\kern2pt F)$
. Note that
![]() $(L \cup (X \kern2pt{\backslash}\kern2pt F)) \cap \bigcup W \subseteq L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Then, by Lemma 2.4(b) and (c), the set
$(L \cup (X \kern2pt{\backslash}\kern2pt F)) \cap \bigcup W \subseteq L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Then, by Lemma 2.4(b) and (c), the set
![]() $K$
is
$K$
is
![]() $\varepsilon $
-supported on
$\varepsilon $
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Since by Claim 2,
$L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Since by Claim 2,
![]() $L$
is compact, this proves the lemma.
$L$
is compact, this proves the lemma.
3 Linear
 ${\boldsymbol{k}}$
-mappings
${\boldsymbol{k}}$
-mappings
Let
![]() $X$
and
$X$
and
![]() $Y$
be Tychonov spaces, let
$Y$
be Tychonov spaces, let
![]() $E$
be a linear subspace of
$E$
be a linear subspace of
![]() $C_p(X),$
and let
$C_p(X),$
and let
![]() $\phi : E \to C_p(Y)$
be a continuous linear function. Let
$\phi : E \to C_p(Y)$
be a continuous linear function. Let
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $F = \phi (E) \subseteq C_p(Y)$
. We define
$F = \phi (E) \subseteq C_p(Y)$
. We define
![]() $\phi $
to be a linear
$\phi $
to be a linear
![]() $k$
-mapping if, for every
$k$
-mapping if, for every
![]() $f \in E$
satisfying
$f \in E$
satisfying
![]() $f(E) \subseteq [-1,1]$
, we have
$f(E) \subseteq [-1,1]$
, we have
![]() $\phi (f)(Y) \subseteq [-k,k]$
. If
$\phi (f)(Y) \subseteq [-k,k]$
. If
![]() $\phi : E \to F$
is a linear homeomorphism, we define
$\phi : E \to F$
is a linear homeomorphism, we define
![]() $\phi $
to be a linear
$\phi $
to be a linear
![]() $k$
-homeomorphism if both
$k$
-homeomorphism if both
![]() $\phi : E \to F$
and
$\phi : E \to F$
and
![]() $\phi ^{-1}: F \to E$
are linear
$\phi ^{-1}: F \to E$
are linear
![]() $k$
-mappings. In that case, we define
$k$
-mappings. In that case, we define
![]() $\phi : E \to C_p(Y)$
to be a linear
$\phi : E \to C_p(Y)$
to be a linear
![]() $k$
-embedding.
$k$
-embedding.
If we endow
![]() $C^*(X)$
with the topology of uniform convergence, we denote that by
$C^*(X)$
with the topology of uniform convergence, we denote that by
![]() $C_u^*(X)$
. For
$C_u^*(X)$
. For
![]() $f \in C^*(X)$
, we define
$f \in C^*(X)$
, we define
![]() $\|f\| = \sup _{x \in X} |f(x)|$
. Let
$\|f\| = \sup _{x \in X} |f(x)|$
. Let
![]() $\phi : C_p^*(X)\rightarrow C_p^*(Y)$
be a continuous linear function. By the Closed Graph Theorem,
$\phi : C_p^*(X)\rightarrow C_p^*(Y)$
be a continuous linear function. By the Closed Graph Theorem,
![]() $\phi : C_u^*(X)\rightarrow C_u^*(Y)$
is also continuous. This means there exist
$\phi : C_u^*(X)\rightarrow C_u^*(Y)$
is also continuous. This means there exist
![]() $k \in \mathbb {N}$
such that for each
$k \in \mathbb {N}$
such that for each
![]() $f \in C^*(X)$
,
$f \in C^*(X)$
,
![]() $\| \phi (f) \| \leq k \cdot \|f\|$
. Hence, for this
$\| \phi (f) \| \leq k \cdot \|f\|$
. Hence, for this
![]() $k,$
it turns out that
$k,$
it turns out that
![]() $\phi $
is a linear
$\phi $
is a linear
![]() $k$
-mapping. Similarly, if
$k$
-mapping. Similarly, if
![]() $\phi $
is a linear homeomorphism (embedding), there is
$\phi $
is a linear homeomorphism (embedding), there is
![]() $k \in \mathbb {N}$
such that for each
$k \in \mathbb {N}$
such that for each
![]() $f \in C^*(X)$
,
$f \in C^*(X)$
,
![]() $\frac {1}{k} \|f\| \leq \| \phi (f) \| \leq k \cdot \|f\|$
. For this
$\frac {1}{k} \|f\| \leq \| \phi (f) \| \leq k \cdot \|f\|$
. For this
![]() $k$
, we have that
$k$
, we have that
![]() $\phi $
is a linear
$\phi $
is a linear
![]() $k$
-homeomorphism (embedding).
$k$
-homeomorphism (embedding).
If there exists a linear
![]() $k$
-homeomorphism between linear subspaces
$k$
-homeomorphism between linear subspaces
![]() $E$
and
$E$
and
![]() $F$
of
$F$
of
![]() $C_p(X)$
and
$C_p(X)$
and
![]() $C_p(Y)$
or
$C_p(Y)$
or
![]() $C_u^*(X)$
and
$C_u^*(X)$
and
![]() $C_u^*(Y)$
, we denote this by
$C_u^*(Y)$
, we denote this by
![]() $E \stackrel {k}{\sim } F$
.
$E \stackrel {k}{\sim } F$
.
For each ordinal
![]() $\alpha $
, let
$\alpha $
, let
![]() $[1,\alpha ]$
be the compact ordinal space
$[1,\alpha ]$
be the compact ordinal space
![]() $\{\beta : 1 \leq \beta \leq \alpha \}$
with the order topology. By Corollary 8.6.7 in [Reference Semadeni16], the space
$\{\beta : 1 \leq \beta \leq \alpha \}$
with the order topology. By Corollary 8.6.7 in [Reference Semadeni16], the space
![]() $[1,\alpha ]$
is scattered. We define
$[1,\alpha ]$
is scattered. We define
![]() $C_{u,0}^*([1, \alpha ])= \{f \in C_u^*([1, \alpha ]): f(\alpha ) =0\}$
. In [Reference Bessaga and Pelczyński13], Bessaga and Pelczyński found the following:
$C_{u,0}^*([1, \alpha ])= \{f \in C_u^*([1, \alpha ]): f(\alpha ) =0\}$
. In [Reference Bessaga and Pelczyński13], Bessaga and Pelczyński found the following:
Lemma 3.1 Let
![]() $\alpha \geq \omega $
be an ordinal. Then
$\alpha \geq \omega $
be an ordinal. Then
![]() $C_{u,0}^*([1, \alpha ]) \stackrel {2}{\sim } C_u^*([1, \alpha ])$
.
$C_{u,0}^*([1, \alpha ]) \stackrel {2}{\sim } C_u^*([1, \alpha ])$
.
Lemma 3.2 Let
![]() $\alpha , \beta \geq \omega $
be ordinals, let
$\alpha , \beta \geq \omega $
be ordinals, let
![]() $\{ U_n : n \in \mathbb {N}\}$
be a clopen decreasing base at
$\{ U_n : n \in \mathbb {N}\}$
be a clopen decreasing base at
![]() $\alpha $
with
$\alpha $
with
![]() $U_1 =[1,\alpha ]$
, and let
$U_1 =[1,\alpha ]$
, and let
![]() $\{ V_n : n \in \mathbb {N}\}$
be a clopen decreasing base at
$\{ V_n : n \in \mathbb {N}\}$
be a clopen decreasing base at
![]() $\beta $
with
$\beta $
with
![]() $V_1 =[1,\beta ]$
. If
$V_1 =[1,\beta ]$
. If
![]() $k \in \mathbb {N}$
is such that for every
$k \in \mathbb {N}$
is such that for every
![]() $n \in \mathbb {N}$
, there is a linear
$n \in \mathbb {N}$
, there is a linear
![]() $k$
-embedding from
$k$
-embedding from
![]() $C_u^*(U_n \kern2pt{\backslash}\kern2pt U_{n+1})$
to
$C_u^*(U_n \kern2pt{\backslash}\kern2pt U_{n+1})$
to
![]() $C_u^*(V_n \kern2pt{\backslash}\kern2pt V_{n+1})$
, then there is a linear
$C_u^*(V_n \kern2pt{\backslash}\kern2pt V_{n+1})$
, then there is a linear
![]() $4k$
-embedding from
$4k$
-embedding from
![]() $C_u^*([1, \alpha ])$
to
$C_u^*([1, \alpha ])$
to
![]() $C_u^*([1, \beta ])$
.
$C_u^*([1, \beta ])$
.
Proof For
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $\theta _n: C_u^*(U_n \kern2pt{\backslash}\kern2pt U_{n+1}) \to C_u^*(V_n \kern2pt{\backslash}\kern2pt V_{n+1})$
be a linear
$\theta _n: C_u^*(U_n \kern2pt{\backslash}\kern2pt U_{n+1}) \to C_u^*(V_n \kern2pt{\backslash}\kern2pt V_{n+1})$
be a linear
![]() $k$
-embedding.
$k$
-embedding.
Define
![]() $\theta : C_{u,0}^*([1, \alpha ]) \to C_{u,0}^*([1, \beta ])$
by
$\theta : C_{u,0}^*([1, \alpha ]) \to C_{u,0}^*([1, \beta ])$
by
Since each
![]() $\theta _n$
is a linear
$\theta _n$
is a linear
![]() $k$
-mapping,
$k$
-mapping,
![]() $\theta $
is well defined. Since, for every
$\theta $
is well defined. Since, for every
![]() $f \in C_{u,0}^*([1, \alpha ]),$
we have
$f \in C_{u,0}^*([1, \alpha ]),$
we have
![]() $\frac {1}{k} \|f\| \leq \| \theta (f)\| \leq k \|f\|$
it follows that
$\frac {1}{k} \|f\| \leq \| \theta (f)\| \leq k \|f\|$
it follows that
![]() $\theta $
is a linear
$\theta $
is a linear
![]() $k$
-embedding. By Lemma 3.1, it then follows there is a linear
$k$
-embedding. By Lemma 3.1, it then follows there is a linear
![]() $4k$
-embedding from
$4k$
-embedding from
![]() $C_u^*([1,\alpha ])$
to
$C_u^*([1,\alpha ])$
to
![]() $C_u^*([1,\beta ])$
.
$C_u^*([1,\beta ])$
.
In [Reference Dugundji14], Dugundji proved the following:
Theorem 3.3 Let
![]() $X$
be a metric space, and let
$X$
be a metric space, and let
![]() $A$
be a closed subspace of
$A$
be a closed subspace of
![]() $X$
. Then there exists a continuous linear function
$X$
. Then there exists a continuous linear function
![]() $\phi : C_p(A) \to C_p(X)$
such that, for every
$\phi : C_p(A) \to C_p(X)$
such that, for every
![]() $f \in C_p(A),$
we have
$f \in C_p(A),$
we have
![]() $\phi (f)|_A = f$
and
$\phi (f)|_A = f$
and
![]() $\phi (f)(X) \subseteq \mathrm{conv}(f(A))$
the convex hull of
$\phi (f)(X) \subseteq \mathrm{conv}(f(A))$
the convex hull of
![]() $f(A)$
.
$f(A)$
.
Dugundji’s theorem is used in the proof of the following lemma. A version of this lemma was embedded in the proof of Theorem 1.1 (see [Reference Baars and de Groot8, Theorem 4.1.15 on p. 147]).
Lemma 3.4 Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces, and let
$Y$
be metric spaces, and let
![]() $\phi : C_p(X)\to C_p(Y)$
be a linear homeomorphism. Let
$\phi : C_p(X)\to C_p(Y)$
be a linear homeomorphism. Let
![]() $K \subseteq Y$
be compact, and let
$K \subseteq Y$
be compact, and let
![]() $L = \overline {\mathrm{supp}(K)}$
. Then there exists a linear embedding
$L = \overline {\mathrm{supp}(K)}$
. Then there exists a linear embedding
![]() $\theta : C_p(K) \to C_p(L)$
.
$\theta : C_p(K) \to C_p(L)$
.
Proof By Theorem 3.3, there is a continuous linear function
![]() $\psi : C_p(L) \to C_p(X)$
such that, for every
$\psi : C_p(L) \to C_p(X)$
such that, for every
![]() $f \in C_p(L),$
we have
$f \in C_p(L),$
we have
![]() $\psi (f)|_L = f$
and a continuous linear function
$\psi (f)|_L = f$
and a continuous linear function
![]() $\zeta : C_p(K) \to C_p(Y)$
such that, for every
$\zeta : C_p(K) \to C_p(Y)$
such that, for every
![]() $g \in C_p(K),$
we have
$g \in C_p(K),$
we have
![]() $\zeta (g)|_K = g$
. Define
$\zeta (g)|_K = g$
. Define
![]() $\theta : C_p(K) \to C_p(L)$
by
$\theta : C_p(K) \to C_p(L)$
by
![]() $\theta (g) = (\phi ^{-1} (\zeta (g))|_L$
and
$\theta (g) = (\phi ^{-1} (\zeta (g))|_L$
and
![]() $\vartheta : C_p(L) \to C_p(K)$
by
$\vartheta : C_p(L) \to C_p(K)$
by
![]() $\vartheta (f) = (\phi (\psi (f))|_K$
. Then
$\vartheta (f) = (\phi (\psi (f))|_K$
. Then
![]() $\theta $
and
$\theta $
and
![]() $\vartheta $
are well-defined continuous linear mappings.
$\vartheta $
are well-defined continuous linear mappings.
Let
![]() $g \in C_p(K),$
and let
$g \in C_p(K),$
and let
![]() $h = \psi (\theta (g)) - \phi ^{-1}( \zeta (g))$
. Then
$h = \psi (\theta (g)) - \phi ^{-1}( \zeta (g))$
. Then
Since
![]() $\textrm {supp}(K) \subseteq L$
, we have
$\textrm {supp}(K) \subseteq L$
, we have
![]() $h|_{\textrm {supp}(K)}=0$
. Hence, by Lemma 2.1(a),
$h|_{\textrm {supp}(K)}=0$
. Hence, by Lemma 2.1(a),
![]() $\phi (h)|_K =0$
. Therefore,
$\phi (h)|_K =0$
. Therefore,
and hence
![]() $\vartheta (\theta (g)) = g$
. So
$\vartheta (\theta (g)) = g$
. So
![]() $\theta $
is injective and
$\theta $
is injective and
![]() $\vartheta \circ \theta = \textrm {id}_K$
. This implies that
$\vartheta \circ \theta = \textrm {id}_K$
. This implies that
![]() $\theta $
is a linear embedding.
$\theta $
is a linear embedding.
By Lemma 2.2, the subspace
![]() $L \subseteq X$
in Lemma 3.4 is compact. This fact is essential in the proof of Theorem 1.1. Although it can be shown that Lemma 3.4 also holds for linear homeomorphisms
$L \subseteq X$
in Lemma 3.4 is compact. This fact is essential in the proof of Theorem 1.1. Although it can be shown that Lemma 3.4 also holds for linear homeomorphisms
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
, we cannot guarantee in this case that
$\phi : C_p^*(X)\to C_p^*(Y)$
, we cannot guarantee in this case that
![]() $L$
is compact. Therefore, a different approach is required to prove Theorem 1.2. Instead of Lemma 3.4, we will use Lemma 3.6 applied to the compact set
$L$
is compact. Therefore, a different approach is required to prove Theorem 1.2. Instead of Lemma 3.4, we will use Lemma 3.6 applied to the compact set
![]() $L$
in Lemma 2.8. But first, we need the following corollary to Dugundji’s theorem.
$L$
in Lemma 2.8. But first, we need the following corollary to Dugundji’s theorem.
Lemma 3.5 Let
![]() $X$
be a metric space, and let
$X$
be a metric space, and let
![]() $A$
be a closed subspace of
$A$
be a closed subspace of
![]() $X$
. Then there is a continuous linear 1-mapping
$X$
. Then there is a continuous linear 1-mapping
![]() $\phi : C_p^*(A) \to C_p^*(X)$
such that, for every
$\phi : C_p^*(A) \to C_p^*(X)$
such that, for every
![]() $f \in C_p^*(A),$
we have
$f \in C_p^*(A),$
we have
![]() $\phi (f)|_A = f$
.
$\phi (f)|_A = f$
.
Proof By Theorem 3.3, there is a continuous linear function
![]() $\psi : C_p(A) \to C_p(X)$
such that, for every
$\psi : C_p(A) \to C_p(X)$
such that, for every
![]() $f \in C_p(A),$
we have
$f \in C_p(A),$
we have
![]() $\psi (f)|_A = f$
and
$\psi (f)|_A = f$
and
![]() $\psi (f)(X) \subseteq \textrm {conv}(f(A))$
. For
$\psi (f)(X) \subseteq \textrm {conv}(f(A))$
. For
![]() $f \in C_p^*(A)$
, let
$f \in C_p^*(A)$
, let
![]() $k =\|f\|$
. Then
$k =\|f\|$
. Then
![]() $f(A) \subseteq [-k,k]$
and hence
$f(A) \subseteq [-k,k]$
and hence
![]() $\psi (f)(X) \subseteq \textrm {conv}(f(A)) \subseteq [-k,k]$
. This implies
$\psi (f)(X) \subseteq \textrm {conv}(f(A)) \subseteq [-k,k]$
. This implies
![]() $\psi (f) \in C_p^*(X)$
and
$\psi (f) \in C_p^*(X)$
and
![]() $\|\psi (f)\| \leq \|f\|$
. So
$\|\psi (f)\| \leq \|f\|$
. So
![]() $\phi = \psi |_{C_p^*(A)}:C_p^*(A) \to C_p^*(X)$
is a linear 1-mapping.
$\phi = \psi |_{C_p^*(A)}:C_p^*(A) \to C_p^*(X)$
is a linear 1-mapping.
The next lemma is motivated by Lemma 3.4 in [Reference Baars3].
Lemma 3.6 Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces, and let
$Y$
be metric spaces, and let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a linear
$\phi : C_p^*(X)\to C_p^*(Y)$
be a linear
![]() $k$
-homeomorphism. Let
$k$
-homeomorphism. Let
![]() $K \subseteq Y$
be compact, and let
$K \subseteq Y$
be compact, and let
![]() $L \subseteq X$
be such that
$L \subseteq X$
be such that
![]() $K$
is
$K$
is
![]() $\frac {1}{4k}$
-supported on
$\frac {1}{4k}$
-supported on
![]() $L$
. Then there exists a linear
$L$
. Then there exists a linear
![]() $2k$
-embedding
$2k$
-embedding
![]() $\theta : C_u^*(K) \to C_u^*(L).$
$\theta : C_u^*(K) \to C_u^*(L).$
Proof By Lemma 3.5 and the Closed Graph Theorem, there is a continuous linear 1-mapping
![]() $\psi : C_u^*(L) \to C_u^*(X)$
such that, for every
$\psi : C_u^*(L) \to C_u^*(X)$
such that, for every
![]() $f \in C_u^*(L),$
we have
$f \in C_u^*(L),$
we have
![]() $\psi (f)|_L = f$
and there is a continuous linear 1-mapping
$\psi (f)|_L = f$
and there is a continuous linear 1-mapping
![]() $\zeta : C_u^*(K) \to C_u^*(Y)$
such that, for every
$\zeta : C_u^*(K) \to C_u^*(Y)$
such that, for every
![]() $g \in C_u^*(K),$
we have
$g \in C_u^*(K),$
we have
![]() $\zeta (g)|_K = g$
. Define
$\zeta (g)|_K = g$
. Define
![]() $\theta : C_u^*(K) \to C_u^*(L)$
by
$\theta : C_u^*(K) \to C_u^*(L)$
by
![]() $\theta (g) = (\phi ^{-1} (\zeta (g))|_L$
and
$\theta (g) = (\phi ^{-1} (\zeta (g))|_L$
and
![]() $\vartheta : C_u^*(L) \to C_u^*(K)$
by
$\vartheta : C_u^*(L) \to C_u^*(K)$
by
![]() $\vartheta (f) = (\phi (\psi (f))|_K$
. Then
$\vartheta (f) = (\phi (\psi (f))|_K$
. Then
![]() $\theta $
and
$\theta $
and
![]() $\vartheta $
are continuous and linear. Since
$\vartheta $
are continuous and linear. Since
![]() $\psi $
and
$\psi $
and
![]() $\zeta $
are linear 1-mappings and
$\zeta $
are linear 1-mappings and
![]() $\phi $
and
$\phi $
and
![]() $\phi ^{-1}$
are linear
$\phi ^{-1}$
are linear
![]() $k$
-mappings, we conclude that
$k$
-mappings, we conclude that
![]() $\theta $
and
$\theta $
and
![]() $\vartheta $
are linear
$\vartheta $
are linear
![]() $k$
-mappings.
$k$
-mappings.
Claim For every
![]() $g \in C_u^*(K),$
we have
$g \in C_u^*(K),$
we have
![]() $\| ( \vartheta ( \theta (g)) - g \| \leq \frac {1}{2} \|g\|$
.
$\| ( \vartheta ( \theta (g)) - g \| \leq \frac {1}{2} \|g\|$
.
Let
![]() $h = \psi (\theta (g)) - \phi ^{-1}( \zeta (g))$
. Since
$h = \psi (\theta (g)) - \phi ^{-1}( \zeta (g))$
. Since
![]() $\psi $
is a linear 1-mapping and
$\psi $
is a linear 1-mapping and
![]() $\theta $
is a linear
$\theta $
is a linear
![]() $k$
-mapping it follows that
$k$
-mapping it follows that
![]() $\psi \circ \theta $
is a linear
$\psi \circ \theta $
is a linear
![]() $k$
-mapping. Hence
$k$
-mapping. Hence
![]() $\|\psi (\theta (g))\| \leq k \|g\|$
. Since
$\|\psi (\theta (g))\| \leq k \|g\|$
. Since
![]() $\zeta $
is a linear 1-mapping and
$\zeta $
is a linear 1-mapping and
![]() $\phi ^{-1}$
is a linear
$\phi ^{-1}$
is a linear
![]() $k$
-mapping, it follows that
$k$
-mapping, it follows that
![]() $\phi ^{-1} \circ \zeta $
is a linear
$\phi ^{-1} \circ \zeta $
is a linear
![]() $k$
-mapping. Hence
$k$
-mapping. Hence
![]() $\|\phi ^{-1}( \zeta (g))\| \leq k \|g\|$
. This implies
$\|\phi ^{-1}( \zeta (g))\| \leq k \|g\|$
. This implies
![]() $\|h\| \leq \|\psi (\theta (g))\| + \|\phi ^{-1}( \zeta (g))\| \leq 2k\|g\|$
.
$\|h\| \leq \|\psi (\theta (g))\| + \|\phi ^{-1}( \zeta (g))\| \leq 2k\|g\|$
.
Note that
![]() $h|_L = \psi (\theta (g))|_L - \phi ^{-1}( \zeta (g))|_L = \theta (g) - \theta (g)= 0$
. Then, for
$h|_L = \psi (\theta (g))|_L - \phi ^{-1}( \zeta (g))|_L = \theta (g) - \theta (g)= 0$
. Then, for
![]() $z \in K$
,
$z \in K$
,
 $$ \begin{align*} |\phi(h)(z)| & = |\sum \{ \lambda_x^z h(x) : x \in \textrm{supp} (z)\}| \leq \sum \{ |\lambda_x^z| \cdot |h(x)| : x \in \textrm{supp} (z)\} \\ & \leq \sum \{ |\lambda_x^z|\cdot |h(x)| : x \in \textrm{supp} (z) \cap L \} + \sum \{ |\lambda_x^z| \cdot |h(x)| : x \in \textrm{supp} (z) \kern2pt{\backslash}\kern2pt L \} \\ & \leq 0 + \sum \{ |\lambda_x^z| : x \in \textrm{supp} (z) \kern2pt{\backslash}\kern2pt L \} \cdot \|h\| < \frac{1}{4k} \cdot 2k \|g\| = \frac{1}{2} \|g\|. \end{align*} $$
$$ \begin{align*} |\phi(h)(z)| & = |\sum \{ \lambda_x^z h(x) : x \in \textrm{supp} (z)\}| \leq \sum \{ |\lambda_x^z| \cdot |h(x)| : x \in \textrm{supp} (z)\} \\ & \leq \sum \{ |\lambda_x^z|\cdot |h(x)| : x \in \textrm{supp} (z) \cap L \} + \sum \{ |\lambda_x^z| \cdot |h(x)| : x \in \textrm{supp} (z) \kern2pt{\backslash}\kern2pt L \} \\ & \leq 0 + \sum \{ |\lambda_x^z| : x \in \textrm{supp} (z) \kern2pt{\backslash}\kern2pt L \} \cdot \|h\| < \frac{1}{4k} \cdot 2k \|g\| = \frac{1}{2} \|g\|. \end{align*} $$
This implies
![]() $\| \phi (h)|_K \| \leq \frac {1}{2} \|g\|$
. Since
$\| \phi (h)|_K \| \leq \frac {1}{2} \|g\|$
. Since
 $$ \begin{align*} \phi(h)|_K & = \phi(\psi (\theta(g)))|_K - \phi(\phi^{-1}( \zeta(g)))|_K \\ & = \vartheta(\theta(g)) - \zeta(g)|_K = \vartheta(\theta(g)) - g, \end{align*} $$
$$ \begin{align*} \phi(h)|_K & = \phi(\psi (\theta(g)))|_K - \phi(\phi^{-1}( \zeta(g)))|_K \\ & = \vartheta(\theta(g)) - \zeta(g)|_K = \vartheta(\theta(g)) - g, \end{align*} $$
this proves the claim.
Let
![]() $g \in C_u^*(K)$
and suppose
$g \in C_u^*(K)$
and suppose
![]() $\theta (g) = 0$
. Then
$\theta (g) = 0$
. Then
![]() $\vartheta ( \theta (g)) = 0$
, and hence, it follows by the claim that
$\vartheta ( \theta (g)) = 0$
, and hence, it follows by the claim that
![]() $\|g\| = \| ( \vartheta ( \theta (g)) - g \| \leq \frac {1}{2} \|g\|$
. So
$\|g\| = \| ( \vartheta ( \theta (g)) - g \| \leq \frac {1}{2} \|g\|$
. So
![]() $g = 0,$
and hence,
$g = 0,$
and hence,
![]() $\theta $
is one-to-one. For
$\theta $
is one-to-one. For
![]() $g \in C_u^*(K)$
, since
$g \in C_u^*(K)$
, since
![]() $\vartheta $
is a linear
$\vartheta $
is a linear
![]() $k$
-mapping, we have by the claim
$k$
-mapping, we have by the claim
Hence
![]() $\|g\| \leq 2k \|\theta (g)\|$
. Since
$\|g\| \leq 2k \|\theta (g)\|$
. Since
![]() $\theta $
is a linear
$\theta $
is a linear
![]() $k$
-mapping, it follows that
$k$
-mapping, it follows that
![]() $\frac {1}{2k} \|g\| \leq \|\theta (g)\| \leq 2k\|g\|$
. Hence,
$\frac {1}{2k} \|g\| \leq \|\theta (g)\| \leq 2k\|g\|$
. Hence,
![]() $\theta $
is a linear
$\theta $
is a linear
![]() $2k$
-embedding.
$2k$
-embedding.
4 Main results
We define an ordinal
![]() $\alpha $
to be a prime component if, for every
$\alpha $
to be a prime component if, for every
![]() $\beta < \alpha $
, we have
$\beta < \alpha $
, we have
![]() $\beta + \alpha = \alpha $
. If
$\beta + \alpha = \alpha $
. If
![]() $\alpha> 0$
is a prime component, then
$\alpha> 0$
is a prime component, then
![]() $\alpha = \omega ^{\mu }$
for some ordinal
$\alpha = \omega ^{\mu }$
for some ordinal
![]() $\mu $
(see [Reference Sierpiński17, Theorem 1, p. 320]). By Theorem 8.6.6 in [Reference Semadeni16], for the ordinal space
$\mu $
(see [Reference Sierpiński17, Theorem 1, p. 320]). By Theorem 8.6.6 in [Reference Semadeni16], for the ordinal space
![]() $X = [1,\omega ^{\mu }]$
, we have the equality
$X = [1,\omega ^{\mu }]$
, we have the equality
![]() $X^{(\mu )} = \{\omega ^{\mu }\}$
. It is well known that, for every ordinal
$X^{(\mu )} = \{\omega ^{\mu }\}$
. It is well known that, for every ordinal
![]() $\alpha ,$
there is a largest prime component
$\alpha ,$
there is a largest prime component
![]() $\omega ^{\mu }$
such that
$\omega ^{\mu }$
such that
![]() $\omega ^\mu \leq \alpha$
(see [Reference Sierpiński17, p. 282]). We then have
$\omega ^\mu \leq \alpha$
(see [Reference Sierpiński17, p. 282]). We then have
![]() $\omega ^{\mu } \leq \alpha < \omega ^{\mu +1}$
. Note that if
$\omega ^{\mu } \leq \alpha < \omega ^{\mu +1}$
. Note that if
![]() $X$
is a first countable space and
$X$
is a first countable space and
![]() $\mu < \omega _1$
is such that
$\mu < \omega _1$
is such that
![]() $X^{(\mu )} \neq \emptyset $
, then there is
$X^{(\mu )} \neq \emptyset $
, then there is
![]() $K \subseteq X$
such that
$K \subseteq X$
such that
![]() $K$
is homeomorphic to
$K$
is homeomorphic to
![]() $[1,\omega ^{\mu }]$
(see, for example, Lemma 4.1.8 in [Reference Baars and de Groot8]).
$[1,\omega ^{\mu }]$
(see, for example, Lemma 4.1.8 in [Reference Baars and de Groot8]).
Bessaga and Pelczyński [Reference Bessaga and Pelczyński13] found the following:
Theorem 4.1
-
(a) If
 $\omega \leq \alpha \leq \gamma < \omega _1$
, then
$\omega \leq \alpha \leq \gamma < \omega _1$
, then
 $C_u^*([1,\alpha ]) \sim C_u^*([1,\gamma ])$
if and only if
$C_u^*([1,\alpha ]) \sim C_u^*([1,\gamma ])$
if and only if
 $\gamma < \alpha ^{\omega }$
.
$\gamma < \alpha ^{\omega }$
. -
(b) If
 $\theta : C_u^*([1,\omega ^{\mu }])\rightarrow C_u^*([1,\omega ^{\nu }])$
is a linear embedding with
$\theta : C_u^*([1,\omega ^{\mu }])\rightarrow C_u^*([1,\omega ^{\nu }])$
is a linear embedding with
 $\mu ,\nu \geq 1$
and
$\mu ,\nu \geq 1$
and
 $\mu $
is a prime component, then
$\mu $
is a prime component, then
 $\mu \leq \nu $
.
$\mu \leq \nu $
.
In [Reference Baars and de Groot6], it was shown that the same isomorphic classification as in Theorem 4.1(a) holds for linear homeomorphisms between function spaces
![]() $C_p([1,\alpha ])$
. We are now in a position to proof Theorems 1.2 and 1.3. In both proofs, we will need the following:
$C_p([1,\alpha ])$
. We are now in a position to proof Theorems 1.2 and 1.3. In both proofs, we will need the following:
Theorem 4.2 [Reference Semadeni16, Theorem 8.6.10]
Let
![]() $X$
be a countable compact Hausdorff space. Then there is an ordinal
$X$
be a countable compact Hausdorff space. Then there is an ordinal
![]() $\alpha < \omega _1$
such that
$\alpha < \omega _1$
such that
![]() $X$
is homeomorphic to
$X$
is homeomorphic to
![]() $[1,\alpha ]$
.
$[1,\alpha ]$
.
Proof of Theorem 1.2
Let
![]() $\phi : C_p^*(X)\to C_p^*(Y)$
be a linear homeomorphism. Let
$\phi : C_p^*(X)\to C_p^*(Y)$
be a linear homeomorphism. Let
![]() $k \in \mathbb {N}$
be such that
$k \in \mathbb {N}$
be such that
![]() $\phi $
is linear
$\phi $
is linear
![]() $k$
-homeomorphism. Clearly, we have
$k$
-homeomorphism. Clearly, we have
![]() $X = \emptyset $
if and only
$X = \emptyset $
if and only
![]() $Y = \emptyset $
, so (a) holds for
$Y = \emptyset $
, so (a) holds for
![]() $\alpha = 0$
and (b) holds for
$\alpha = 0$
and (b) holds for
![]() $\alpha = 1$
. Note that for
$\alpha = 1$
. Note that for
![]() $\alpha = 0$
, there is nothing to prove for (b). For
$\alpha = 0$
, there is nothing to prove for (b). For
![]() $\alpha = 1$
, (a) follows from Theorem 2.2 in [Reference Baars, de Groot, van Mill and Pelant9], so we may assume that
$\alpha = 1$
, (a) follows from Theorem 2.2 in [Reference Baars, de Groot, van Mill and Pelant9], so we may assume that
![]() $\alpha \geq \omega $
.
$\alpha \geq \omega $
.
For (a), assume that
![]() $\kappa (X) \leq \alpha $
and
$\kappa (X) \leq \alpha $
and
![]() $\kappa (Y)> \alpha $
. Since
$\kappa (Y)> \alpha $
. Since
![]() $Y^{(1)} \neq \emptyset ,$
we have by the above that
$Y^{(1)} \neq \emptyset ,$
we have by the above that
![]() $X^{(1)} \neq \emptyset $
, hence
$X^{(1)} \neq \emptyset $
, hence
![]() $X$
is not discrete. Since
$X$
is not discrete. Since
![]() $Y^{(\alpha )} \neq \emptyset $
, there is
$Y^{(\alpha )} \neq \emptyset $
, there is
![]() $K \subseteq Y$
such that
$K \subseteq Y$
such that
![]() $K$
is homeomorphic to
$K$
is homeomorphic to
![]() $[1,\omega ^{\alpha }]$
in
$[1,\omega ^{\alpha }]$
in
![]() $Y$
. Since
$Y$
. Since
![]() $X$
is scattered, we can find by Lemma 2.8, a compact subset
$X$
is scattered, we can find by Lemma 2.8, a compact subset
![]() $L$
of
$L$
of
![]() $X$
such that
$X$
such that
![]() $K$
is
$K$
is
![]() $\frac {1}{4k}$
-supported on
$\frac {1}{4k}$
-supported on
![]() $L$
. Since
$L$
. Since
![]() $X$
is not discrete, we may assume, by Lemma 2.4(b), that
$X$
is not discrete, we may assume, by Lemma 2.4(b), that
![]() $L$
is infinite. By Lemma 3.6, there is a linear embedding
$L$
is infinite. By Lemma 3.6, there is a linear embedding
![]() $\theta : C_u^*(K) \to C_u^*(L)$
. Since
$\theta : C_u^*(K) \to C_u^*(L)$
. Since
![]() $L^{(\alpha )} = \emptyset $
, we conclude that
$L^{(\alpha )} = \emptyset $
, we conclude that
![]() $L$
is a compact scattered metric space. Therefore, by Theorem 2.7,
$L$
is a compact scattered metric space. Therefore, by Theorem 2.7,
![]() $L$
is countable, and hence, by Theorem 4.2, there is
$L$
is countable, and hence, by Theorem 4.2, there is
![]() $\omega \leq \gamma < \omega ^{\alpha }$
such that
$\omega \leq \gamma < \omega ^{\alpha }$
such that
![]() $L$
is homeomorphic to
$L$
is homeomorphic to
![]() $[1,\gamma ]$
. Let
$[1,\gamma ]$
. Let
![]() $\omega ^{\mu } < \omega _1$
be a prime component such that
$\omega ^{\mu } < \omega _1$
be a prime component such that
![]() $\omega ^{\mu } \leq \gamma < \omega ^{\mu +1}$
. Then
$\omega ^{\mu } \leq \gamma < \omega ^{\mu +1}$
. Then
![]() $L^{(\mu )} \neq \emptyset $
and since
$L^{(\mu )} \neq \emptyset $
and since
![]() $L^{(\alpha )} = \emptyset $
it follows that
$L^{(\alpha )} = \emptyset $
it follows that
![]() $\mu < \alpha $
. Since
$\mu < \alpha $
. Since
![]() $\gamma < (\omega ^{\mu })^{\omega }$
, we have, by Theorem 4.1(a), that
$\gamma < (\omega ^{\mu })^{\omega }$
, we have, by Theorem 4.1(a), that
![]() $C_u^*([1,\omega ^{\mu }]) \sim C_u^*([1,\gamma ]),$
and hence, there exists a linear embedding from
$C_u^*([1,\omega ^{\mu }]) \sim C_u^*([1,\gamma ]),$
and hence, there exists a linear embedding from
![]() $C_u^*([1,\omega ^{\alpha }])$
to
$C_u^*([1,\omega ^{\alpha }])$
to
![]() $C_u^*([1,\omega ^{\mu }])$
. But then by Theorem 4.1(b),
$C_u^*([1,\omega ^{\mu }])$
. But then by Theorem 4.1(b),
![]() $\alpha \leq \mu $
. Contradiction. This proves (a).
$\alpha \leq \mu $
. Contradiction. This proves (a).
For (b), assume that
![]() $\kappa (X) < \alpha $
and
$\kappa (X) < \alpha $
and
![]() $\kappa (Y) \geq \alpha $
. Let
$\kappa (Y) \geq \alpha $
. Let
![]() $\kappa (X) =\beta < \alpha $
. Let
$\kappa (X) =\beta < \alpha $
. Let
![]() $(\alpha _i)_{i \in \mathbb {N}}$
be an increasing sequence of ordinals such that
$(\alpha _i)_{i \in \mathbb {N}}$
be an increasing sequence of ordinals such that
![]() $\alpha _i \to \alpha $
and
$\alpha _i \to \alpha $
and
![]() $\alpha _i> \beta $
for every
$\alpha _i> \beta $
for every
![]() $i \in \mathbb {N}$
. Let
$i \in \mathbb {N}$
. Let
![]() $K_i$
be a closed copy of
$K_i$
be a closed copy of
![]() $[1,\omega ^{\alpha _i}]$
in
$[1,\omega ^{\alpha _i}]$
in
![]() $Y$
. Since
$Y$
. Since
![]() $X$
is scattered, by Lemma 2.8, there is a compact subset
$X$
is scattered, by Lemma 2.8, there is a compact subset
![]() $L_i$
of
$L_i$
of
![]() $X$
such that
$X$
such that
![]() $K_i$
is
$K_i$
is
![]() $\frac {1}{4k}$
-supported on
$\frac {1}{4k}$
-supported on
![]() $L_i$
. As in the proof of (a), we may assume that
$L_i$
. As in the proof of (a), we may assume that
![]() $L_i$
is infinite and, since
$L_i$
is infinite and, since
![]() $L_i^{(\beta )} = \emptyset $
, there is
$L_i^{(\beta )} = \emptyset $
, there is
![]() $\omega \leq \gamma _i < \omega ^{\beta }$
such that
$\omega \leq \gamma _i < \omega ^{\beta }$
such that
![]() $L_i$
is homeomorphic to
$L_i$
is homeomorphic to
![]() $[1,\gamma _i]$
. But then
$[1,\gamma _i]$
. But then
![]() $L_i$
can be seen as a closed subset of
$L_i$
can be seen as a closed subset of
![]() $[1,\omega ^{\beta }],$
and hence, by Lemma 3.5, there is a linear 1-embedding from
$[1,\omega ^{\beta }],$
and hence, by Lemma 3.5, there is a linear 1-embedding from
![]() $C_u^*(L_i)$
to
$C_u^*(L_i)$
to
![]() $C_u^*([1,\omega ^{\beta }])$
. By Lemma 3.6, there is a linear
$C_u^*([1,\omega ^{\beta }])$
. By Lemma 3.6, there is a linear
![]() $2k$
-embedding
$2k$
-embedding
![]() $\theta _i: C_u^*(K_i) \to C_u^*(L_i)$
, and hence, there is a linear
$\theta _i: C_u^*(K_i) \to C_u^*(L_i)$
, and hence, there is a linear
![]() $2k$
-embedding
$2k$
-embedding
![]() $\psi _i : C_u^*([1,\omega ^{\alpha _i}]) \to C_u^*([1,\omega ^{\beta }])$
.
$\psi _i : C_u^*([1,\omega ^{\alpha _i}]) \to C_u^*([1,\omega ^{\beta }])$
.
Let
![]() $S = \{x_i: i \in \mathbb {N}\} \cup \{x_0\}$
be a convergent sequence, where
$S = \{x_i: i \in \mathbb {N}\} \cup \{x_0\}$
be a convergent sequence, where
![]() $x_i \to x_0$
. Let
$x_i \to x_0$
. Let
![]() $A$
be the compact space defined by replacing
$A$
be the compact space defined by replacing
![]() $x_i$
in
$x_i$
in
![]() $S$
by a copy
$S$
by a copy
![]() $A_i$
of
$A_i$
of
![]() $[1,\omega ^{\alpha _i}]$
, and let
$[1,\omega ^{\alpha _i}]$
, and let
![]() $B$
be the compact space defined by replacing
$B$
be the compact space defined by replacing
![]() $x_i$
in
$x_i$
in
![]() $S$
by a copy
$S$
by a copy
![]() $B_i$
of
$B_i$
of
![]() $[1,\omega ^{\beta }]$
. Then
$[1,\omega ^{\beta }]$
. Then
![]() $A$
is homeomorphic to
$A$
is homeomorphic to
![]() $[1,\omega ^{\alpha }]$
and
$[1,\omega ^{\alpha }]$
and
![]() $B$
is homeomorphic to
$B$
is homeomorphic to
![]() $[1,\omega ^{\beta +1}]$
. By Lemma 3.2, it now follows that there is a linear
$[1,\omega ^{\beta +1}]$
. By Lemma 3.2, it now follows that there is a linear
![]() $8k$
-embedding from
$8k$
-embedding from
![]() $C_u^*([1,\omega ^{\alpha }])$
to
$C_u^*([1,\omega ^{\alpha }])$
to
![]() $C_u^*([1,\omega ^{\beta +1}])$
. But then, by Theorem 4.1(b),
$C_u^*([1,\omega ^{\beta +1}])$
. But then, by Theorem 4.1(b),
![]() $\alpha \leq \beta +1$
. Since
$\alpha \leq \beta +1$
. Since
![]() $\beta < \alpha $
, we then have
$\beta < \alpha $
, we then have
![]() $\alpha = \beta +1$
. But
$\alpha = \beta +1$
. But
![]() $\alpha $
is a prime component and hence a limit ordinal. Contradiction. This proves (b).
$\alpha $
is a prime component and hence a limit ordinal. Contradiction. This proves (b).
Proof of Theorem 1.3
For (a), let
![]() $\phi : C_p(X)\to C_p(Y)$
be a linear homeomorphism. Since
$\phi : C_p(X)\to C_p(Y)$
be a linear homeomorphism. Since
![]() $X = \emptyset $
, if and only
$X = \emptyset $
, if and only
![]() $Y = \emptyset $
, (a) holds for
$Y = \emptyset $
, (a) holds for
![]() $\mu =1$
. For
$\mu =1$
. For
![]() $\alpha = \omega ^{\mu }$
with
$\alpha = \omega ^{\mu }$
with
![]() $\mu $
a limit ordinal, let
$\mu $
a limit ordinal, let
![]() $(\mu _i)_{i \in \mathbb {N}}$
be a strictly increasing sequence of ordinals such that
$(\mu _i)_{i \in \mathbb {N}}$
be a strictly increasing sequence of ordinals such that
![]() $\mu _i \to \mu $
. Let
$\mu _i \to \mu $
. Let
![]() $\beta = \kappa (X)$
and assume that
$\beta = \kappa (X)$
and assume that
![]() $\kappa (X) < \alpha $
and
$\kappa (X) < \alpha $
and
![]() $\kappa (Y) \geq \alpha $
. Let
$\kappa (Y) \geq \alpha $
. Let
![]() $i \in \mathbb {N}$
be such that
$i \in \mathbb {N}$
be such that
![]() $\beta < \omega ^{\mu _i}$
. Let
$\beta < \omega ^{\mu _i}$
. Let
![]() $\alpha _i = \omega ^{\mu _i}$
and
$\alpha _i = \omega ^{\mu _i}$
and
![]() $\alpha _{i+1} = \omega ^{\mu _{i+1}}$
. Let
$\alpha _{i+1} = \omega ^{\mu _{i+1}}$
. Let
![]() $K$
be a closed copy of
$K$
be a closed copy of
![]() $[1,\omega ^{\alpha _{i+1}}]$
in
$[1,\omega ^{\alpha _{i+1}}]$
in
![]() $Y$
, and let
$Y$
, and let
![]() $L = \overline {\textrm {supp}_{\phi }(K)}$
. By Lemma 2.1(b), we have
$L = \overline {\textrm {supp}_{\phi }(K)}$
. By Lemma 2.1(b), we have
![]() $K \subseteq \textrm {supp}_{\phi ^{-1}}(\textrm {supp}_{\phi }(K)) \subseteq \textrm {supp}_{\phi ^{-1}} (L)$
, and hence
$K \subseteq \textrm {supp}_{\phi ^{-1}}(\textrm {supp}_{\phi }(K)) \subseteq \textrm {supp}_{\phi ^{-1}} (L)$
, and hence
![]() $L$
is infinite. By Lemma 2.2,
$L$
is infinite. By Lemma 2.2,
![]() $L$
is compact. Hence, by Lemma 3.4 and the Closed Graph Theorem, there is a linear embedding
$L$
is compact. Hence, by Lemma 3.4 and the Closed Graph Theorem, there is a linear embedding
![]() $\theta : C_u^*(K) \to C_u^*(L)$
. Since
$\theta : C_u^*(K) \to C_u^*(L)$
. Since
![]() $L^{(\beta )} = \emptyset $
, as in the proof of Theorem 1.2(a), there is
$L^{(\beta )} = \emptyset $
, as in the proof of Theorem 1.2(a), there is
![]() $\omega \leq \gamma < \omega ^{\beta }$
such that
$\omega \leq \gamma < \omega ^{\beta }$
such that
![]() $L$
is homeomorphic to
$L$
is homeomorphic to
![]() $[1,\gamma ]$
. But then
$[1,\gamma ]$
. But then
![]() $L$
can be seen as a closed subset of
$L$
can be seen as a closed subset of
![]() $[1,\omega ^{\alpha _i}]$
, and hence, by Lemma 3.5, there is a linear embedding from
$[1,\omega ^{\alpha _i}]$
, and hence, by Lemma 3.5, there is a linear embedding from
![]() $C_u^*([1,\omega ^{\alpha _{i+1}}])$
to
$C_u^*([1,\omega ^{\alpha _{i+1}}])$
to
![]() $C_u^*([1,\omega ^{\alpha _i}])$
. Since
$C_u^*([1,\omega ^{\alpha _i}])$
. Since
![]() $\alpha _{i+1}$
is a prime component, it then follows by Theorem 4.1(b) that
$\alpha _{i+1}$
is a prime component, it then follows by Theorem 4.1(b) that
![]() $\alpha _{i+1} \leq \alpha _i$
. Contradiction, which proves (a).
$\alpha _{i+1} \leq \alpha _i$
. Contradiction, which proves (a).
For (b), let
![]() $\alpha = \omega ^{\mu } < \omega _1$
be a prime component with
$\alpha = \omega ^{\mu } < \omega _1$
be a prime component with
![]() $\mu \geq 1$
a successor ordinal. Suppose
$\mu \geq 1$
a successor ordinal. Suppose
![]() $\mu = \sigma +1$
and
$\mu = \sigma +1$
and
![]() $\beta = \omega ^{\sigma }$
. Then
$\beta = \omega ^{\sigma }$
. Then
![]() $\beta \geq 1$
is a prime component and
$\beta \geq 1$
is a prime component and
![]() $\alpha = \beta \cdot \omega $
. For every
$\alpha = \beta \cdot \omega $
. For every
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $X_n = [1, \omega ^{\beta \cdot n}]$
. Let
$X_n = [1, \omega ^{\beta \cdot n}]$
. Let
![]() $X = \bigoplus _{n=1}^{\infty } X_n$
be the topological sum of the spaces
$X = \bigoplus _{n=1}^{\infty } X_n$
be the topological sum of the spaces
![]() $X_n$
, and let
$X_n$
, and let
![]() $Y = X_1 \times \mathbb {N}$
. By Theorem 4.1(a), we have, for every
$Y = X_1 \times \mathbb {N}$
. By Theorem 4.1(a), we have, for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $C_p(X_n) \sim C_p(X_1)$
. Therefore,
$C_p(X_n) \sim C_p(X_1)$
. Therefore,
![]() $C_p(X) \sim C_p(Y)$
. Note that for every
$C_p(X) \sim C_p(Y)$
. Note that for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\kappa (X_n) = \beta \cdot n +1$
. This implies
$\kappa (X_n) = \beta \cdot n +1$
. This implies
![]() $\kappa (Y) = \beta +1 < \alpha $
and
$\kappa (Y) = \beta +1 < \alpha $
and
![]() $\kappa (X) = \beta \cdot \omega = \alpha $
.
$\kappa (X) = \beta \cdot \omega = \alpha $
.
Remark 4.3 Theorems 1.1–1.3(a) are true for prime components. The question is if these results also hold for ordinals that are not a prime component. For such ordinals
![]() $\alpha $
, let
$\alpha $
, let
![]() $\omega ^{\mu }$
be the largest prime component such that
$\omega ^{\mu }$
be the largest prime component such that
![]() $\omega ^{\mu } \leq \alpha $
, and let
$\omega ^{\mu } \leq \alpha $
, and let
![]() $\beta = \omega ^{\mu }$
. Then
$\beta = \omega ^{\mu }$
. Then
![]() $\beta < \alpha < \beta \cdot \omega $
, and hence
$\beta < \alpha < \beta \cdot \omega $
, and hence
![]() $\omega ^{\beta } < \omega ^{\alpha } < \omega ^{\beta \cdot \omega }$
.
$\omega ^{\beta } < \omega ^{\alpha } < \omega ^{\beta \cdot \omega }$
.
Let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $l_p$
-equivalent metric spaces, and suppose
$l_p$
-equivalent metric spaces, and suppose
![]() $\alpha = \beta +1$
. If
$\alpha = \beta +1$
. If
![]() $\kappa (X) < \alpha $
, then
$\kappa (X) < \alpha $
, then
![]() $\kappa (X) \leq \beta $
. Since
$\kappa (X) \leq \beta $
. Since
![]() $\beta $
is a prime component, we have by Theorem 1.1 that
$\beta $
is a prime component, we have by Theorem 1.1 that
![]() $\kappa (Y) \leq \beta ,$
and hence
$\kappa (Y) \leq \beta ,$
and hence
![]() $\kappa (Y) < \alpha $
. This implies that Theorem 1.3 also holds for
$\kappa (Y) < \alpha $
. This implies that Theorem 1.3 also holds for
![]() $\alpha = \beta +1$
with
$\alpha = \beta +1$
with
![]() $\beta $
a prime component. By the same reasoning, Theorem 1.2(b) also holds for
$\beta $
a prime component. By the same reasoning, Theorem 1.2(b) also holds for
![]() $\alpha = \beta +1$
with
$\alpha = \beta +1$
with
![]() $\beta $
a prime component.
$\beta $
a prime component.
Now assume
![]() $\alpha> \beta +1$
. By Theorem 4.1(a), we have
$\alpha> \beta +1$
. By Theorem 4.1(a), we have
![]() $C_u^*([1,\omega ^{\beta }]) \sim C_u^*([1,\omega ^{\alpha }])$
. As mentioned above, the same isomorphic classification holds for function spaces
$C_u^*([1,\omega ^{\beta }]) \sim C_u^*([1,\omega ^{\alpha }])$
. As mentioned above, the same isomorphic classification holds for function spaces
![]() $C_p(X)$
, where
$C_p(X)$
, where
![]() $X$
is a countable compact ordinal space (see [Reference Baars and de Groot6]). Therefore,
$X$
is a countable compact ordinal space (see [Reference Baars and de Groot6]). Therefore,
![]() $C_p([1,\omega ^{\beta }]) \sim C_p([1,\omega ^{\alpha }])$
. Since
$C_p([1,\omega ^{\beta }]) \sim C_p([1,\omega ^{\alpha }])$
. Since
![]() $\kappa ([1,\omega ^{\alpha }]) = \alpha +1> \alpha $
and
$\kappa ([1,\omega ^{\alpha }]) = \alpha +1> \alpha $
and
![]() $\kappa ([1,\omega ^{\beta }]) = \beta +1 < \alpha $
, it follows that Theorems 1.1–1.3 do not always hold.
$\kappa ([1,\omega ^{\beta }]) = \beta +1 < \alpha $
, it follows that Theorems 1.1–1.3 do not always hold.
In Theorem 4.6, we will show that if
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $l_p^*$
-equivalent spaces, then
$l_p^*$
-equivalent spaces, then
![]() $X$
is scattered if and only
$X$
is scattered if and only
![]() $Y$
is scattered. This result does not directly follow from Theorem 1.2 since we have only proved it for prime components
$Y$
is scattered. This result does not directly follow from Theorem 1.2 since we have only proved it for prime components
![]() $\alpha < \omega _1$
. To prove Theorem 4.6, we need the following notion and result from [Reference Baars5].
$\alpha < \omega _1$
. To prove Theorem 4.6, we need the following notion and result from [Reference Baars5].
For a metric space
![]() $X$
and an ordinal
$X$
and an ordinal
![]() $\alpha $
, we define
$\alpha $
, we define
![]() $X^{\{\alpha \}}$
by transfinite induction as follows:
$X^{\{\alpha \}}$
by transfinite induction as follows:
-
(a)
 $X^{\{0\}}=X.$
$X^{\{0\}}=X.$
-
(b) If
 $\alpha $
is a successor, say
$\alpha $
is a successor, say
 $\alpha = \beta +1$
, then
$\alpha = \beta +1$
, then
 $x \in X^{\{\alpha \}}$
if and only if for every neighborhood
$x \in X^{\{\alpha \}}$
if and only if for every neighborhood
 $U$
of
$U$
of
 $x$
,
$x$
,
 $U \cap X^{\{\beta \}}$
is not compact.
$U \cap X^{\{\beta \}}$
is not compact. -
(c) If
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $X^{\{\alpha \}}= \bigcap _{\beta < \alpha } X^{\{\beta \}}$
.
$X^{\{\alpha \}}= \bigcap _{\beta < \alpha } X^{\{\beta \}}$
.
For each ordinal
![]() $\alpha $
, it turns out that
$\alpha $
, it turns out that
![]() $X^{\{\alpha \}}$
is a closed subset of
$X^{\{\alpha \}}$
is a closed subset of
![]() $X$
. The following result can be found in [Reference Baars5].
$X$
. The following result can be found in [Reference Baars5].
Theorem 4.4 Let
![]() $X$
and
$X$
and
![]() $Y$
be
$Y$
be
![]() $l_p^*$
-equivalent metric spaces, and let
$l_p^*$
-equivalent metric spaces, and let
![]() $\alpha $
be an ordinal. Then
$\alpha $
be an ordinal. Then
![]() $X^{\{\alpha \}} = \emptyset $
if and only if
$X^{\{\alpha \}} = \emptyset $
if and only if
![]() $Y^{\{\alpha \}}= \emptyset $
.
$Y^{\{\alpha \}}= \emptyset $
.
In the proof of Theorem 4.6, we also need the following lemma on non-scattered spaces.
Lemma 4.5 Let
![]() $X$
be a non-scattered Tychonov space, and let
$X$
be a non-scattered Tychonov space, and let
![]() $\alpha $
be an ordinal such that
$\alpha $
be an ordinal such that
![]() $X^{\{\alpha \}} = \emptyset $
. Then
$X^{\{\alpha \}} = \emptyset $
. Then
![]() $X$
contains a compact non-scattered subspace.
$X$
contains a compact non-scattered subspace.
Proof Let
![]() $C = \bigcap _{\beta } Y^{(\beta )}$
. By Theorem 2.7, we have
$C = \bigcap _{\beta } Y^{(\beta )}$
. By Theorem 2.7, we have
![]() $C \neq \emptyset $
, and hence
$C \neq \emptyset $
, and hence
![]() $\alpha>0$
. Note that for every
$\alpha>0$
. Note that for every
![]() $x \in C$
and every neighborhood
$x \in C$
and every neighborhood
![]() $U$
of
$U$
of
![]() $x,$
we have
$x,$
we have
![]() $\overline {U} \cap C$
is not scattered. We will proof the lemma by transfinite induction on
$\overline {U} \cap C$
is not scattered. We will proof the lemma by transfinite induction on
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha =1$
, then
$\alpha =1$
, then
![]() $Y$
is locally compact. Pick
$Y$
is locally compact. Pick
![]() $x \in C$
, and let
$x \in C$
, and let
![]() $U$
be a neighborhood of
$U$
be a neighborhood of
![]() $x$
such that
$x$
such that
![]() $\overline {U}$
is compact. Then
$\overline {U}$
is compact. Then
![]() $\overline {U} \cap C$
is a compact non-scattered subspace of
$\overline {U} \cap C$
is a compact non-scattered subspace of
![]() $Y$
.
$Y$
.
Let
![]() $\alpha>1$
and assume the lemma is true for every non-scattered Tychonov space
$\alpha>1$
and assume the lemma is true for every non-scattered Tychonov space
![]() $Z$
and every
$Z$
and every
![]() $\beta < \alpha $
such that
$\beta < \alpha $
such that
![]() $Z^{\{\beta \}} = \emptyset $
. Pick
$Z^{\{\beta \}} = \emptyset $
. Pick
![]() $x \in C$
, and let
$x \in C$
, and let
![]() $\beta = \min \{\gamma \leq \alpha : x \notin X^{\{\gamma \}}\}$
. Since
$\beta = \min \{\gamma \leq \alpha : x \notin X^{\{\gamma \}}\}$
. Since
![]() $x \notin X^{\{\alpha \}}$
,
$x \notin X^{\{\alpha \}}$
,
![]() $\beta $
is well defined. Clearly,
$\beta $
is well defined. Clearly,
![]() $\beta>0$
and
$\beta>0$
and
![]() $\beta $
is a successor ordinal, say
$\beta $
is a successor ordinal, say
![]() $\beta = \gamma +1$
. Since
$\beta = \gamma +1$
. Since
![]() $x \notin X^{\{\beta \}}$
, there exists a neighborhood
$x \notin X^{\{\beta \}}$
, there exists a neighborhood
![]() $U$
of
$U$
of
![]() $x$
such that
$x$
such that
![]() $\overline {U} \cap X^{\{\delta \}}$
is compact. If
$\overline {U} \cap X^{\{\delta \}}$
is compact. If
![]() $\overline {U} \cap C$
is compact we are done, so let’s assume that
$\overline {U} \cap C$
is compact we are done, so let’s assume that
![]() $\overline {U} \cap C$
is not compact. Then there is
$\overline {U} \cap C$
is not compact. Then there is
![]() $z \in (\overline {U} \cap C) \kern2pt{\backslash}\kern2pt X^{\{\delta \}}$
. Let
$z \in (\overline {U} \cap C) \kern2pt{\backslash}\kern2pt X^{\{\delta \}}$
. Let
![]() $V$
be a neighborhood of
$V$
be a neighborhood of
![]() $z$
such that
$z$
such that
![]() $\overline {V} \cap X^{\{\delta \}}=\emptyset $
. Then
$\overline {V} \cap X^{\{\delta \}}=\emptyset $
. Then
![]() $\overline {V} \cap C$
is not scattered and
$\overline {V} \cap C$
is not scattered and
![]() $(\overline {V} \cap C)^{\{\delta \}} = \emptyset $
. By the induction hypothesis,
$(\overline {V} \cap C)^{\{\delta \}} = \emptyset $
. By the induction hypothesis,
![]() $\overline {V} \cap C$
contains a compact non-scattered subspace which proves the lemma.
$\overline {V} \cap C$
contains a compact non-scattered subspace which proves the lemma.
We will now prove the following:
Theorem 4.6 Let X and Y be
![]() $l_p^*$
-equivalent metric spaces. Then X is scattered if and only if Y is scattered.
$l_p^*$
-equivalent metric spaces. Then X is scattered if and only if Y is scattered.
Proof Let
![]() $\phi : C_p^*(X) \to C_p^*(Y)$
be a linear homeomorphism. Then there is
$\phi : C_p^*(X) \to C_p^*(Y)$
be a linear homeomorphism. Then there is
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() $\phi $
is a linear
$\phi $
is a linear
![]() $k$
-homeomorphism. Assume that
$k$
-homeomorphism. Assume that
![]() $X$
is scattered and that
$X$
is scattered and that
![]() $Y$
is not scattered. Let
$Y$
is not scattered. Let
![]() $\alpha>0$
be an ordinal such that
$\alpha>0$
be an ordinal such that
![]() $X^{(\alpha )} = \emptyset $
. Then
$X^{(\alpha )} = \emptyset $
. Then
![]() $X^{\{\alpha \}} = \emptyset $
, since
$X^{\{\alpha \}} = \emptyset $
, since
![]() $X^{\{\alpha \}} \subseteq X^{(\alpha )}$
. From Theorem 4.4, it then follows that
$X^{\{\alpha \}} \subseteq X^{(\alpha )}$
. From Theorem 4.4, it then follows that
![]() $Y^{\{\alpha \}} = \emptyset $
.
$Y^{\{\alpha \}} = \emptyset $
.
Since
![]() $Y$
is not-scattered, by Lemma 4.5,
$Y$
is not-scattered, by Lemma 4.5,
![]() $Y$
contains a compact non-scattered subspace
$Y$
contains a compact non-scattered subspace
![]() $K$
. Since
$K$
. Since
![]() $X$
is scattered, there is, by Lemma 2.8, a compact subset
$X$
is scattered, there is, by Lemma 2.8, a compact subset
![]() $L$
of
$L$
of
![]() $X$
such that
$X$
such that
![]() $K$
is
$K$
is
![]() $\frac {1}{4k}$
-supported on
$\frac {1}{4k}$
-supported on
![]() $L$
. Then, by Lemma 3.6, there is a linear embedding
$L$
. Then, by Lemma 3.6, there is a linear embedding
![]() $\theta : C_u^*(K) \to C_u^*(L)$
. As in the proof of Theorem 1.2, we may assume that
$\theta : C_u^*(K) \to C_u^*(L)$
. As in the proof of Theorem 1.2, we may assume that
![]() $L$
is infinite and that there is
$L$
is infinite and that there is
![]() $\omega \leq \gamma < \omega _1$
such that
$\omega \leq \gamma < \omega _1$
such that
![]() $L$
is homeomorphic to
$L$
is homeomorphic to
![]() $[1,\gamma ]$
.
$[1,\gamma ]$
.
Let
![]() $\omega ^{\mu } < \omega _1$
be a prime component such that
$\omega ^{\mu } < \omega _1$
be a prime component such that
![]() $\omega ^{\mu } \leq \gamma < \omega ^{\mu +1}$
, and let
$\omega ^{\mu } \leq \gamma < \omega ^{\mu +1}$
, and let
![]() $\beta> \mu +1$
be a prime component. Since
$\beta> \mu +1$
be a prime component. Since
![]() $K$
is a compact non-scattered metric space, we have
$K$
is a compact non-scattered metric space, we have
![]() $K^{(\beta )} \neq \emptyset $
, and hence, it contains a copy of
$K^{(\beta )} \neq \emptyset $
, and hence, it contains a copy of
![]() $[1,\omega ^{\beta }]$
and so, by Lemma 3.5, there exists a linear embedding from
$[1,\omega ^{\beta }]$
and so, by Lemma 3.5, there exists a linear embedding from
![]() $C_u^*([1,\omega ^{\beta }])$
to
$C_u^*([1,\omega ^{\beta }])$
to
![]() $C_u^*(K)$
. By Theorem 4.1(a), we have
$C_u^*(K)$
. By Theorem 4.1(a), we have
![]() $C_u^*([1,\omega ^{\mu }]) \sim C_u^*([1,\gamma ]),$
and hence, there exists a linear embedding from
$C_u^*([1,\omega ^{\mu }]) \sim C_u^*([1,\gamma ]),$
and hence, there exists a linear embedding from
![]() $C_u^*([1,\omega ^{\beta }])$
to
$C_u^*([1,\omega ^{\beta }])$
to
![]() $C_u^*([1,\omega ^{\mu }])$
. But then by Theorem 4.1(b),
$C_u^*([1,\omega ^{\mu }])$
. But then by Theorem 4.1(b),
![]() $\beta \leq \mu $
. Contradiction, which shows that
$\beta \leq \mu $
. Contradiction, which shows that
![]() $Y$
is scattered.
$Y$
is scattered.
Remark 4.7 Theorem 4.6 also holds for
![]() $l_p$
-equivalent first countable paracompact spaces (see [Reference Baars4]). The proof of Theorem 4.6 does not work for all first countable paracompact
$l_p$
-equivalent first countable paracompact spaces (see [Reference Baars4]). The proof of Theorem 4.6 does not work for all first countable paracompact
![]() $l_p^*$
-equivalent spaces. The reason for this is the use of Lemma 3.6. This lemma makes essential use of Dugundji’s theorem 3.3 for metric spaces. The proof of Theorem 4.6 for
$l_p^*$
-equivalent spaces. The reason for this is the use of Lemma 3.6. This lemma makes essential use of Dugundji’s theorem 3.3 for metric spaces. The proof of Theorem 4.6 for
![]() $l_p$
-equivalent first countable paracompact spaces in [Reference Baars4] does not need Dugundji’s theorem. A careful examination of the proofs of Lemma 2.5 in [Reference Baars, de Groot and Pelant10], Corollary 2.6 and Lemma 2.8 shows that these results do hold for first countable paracompact spaces.
$l_p$
-equivalent first countable paracompact spaces in [Reference Baars4] does not need Dugundji’s theorem. A careful examination of the proofs of Lemma 2.5 in [Reference Baars, de Groot and Pelant10], Corollary 2.6 and Lemma 2.8 shows that these results do hold for first countable paracompact spaces.
Question 4.8 Let X and Y be
![]() $l_p^*$
-equivalent first countable paracompact spaces. Is it true that X is scattered if and only if Y is scattered?
$l_p^*$
-equivalent first countable paracompact spaces. Is it true that X is scattered if and only if Y is scattered?
The results in this paper do hold for ordinals
![]() $\alpha < \omega _1$
. For ordinals
$\alpha < \omega _1$
. For ordinals
![]() $\alpha> \omega _1$
, the approach in this paper does not seem to work, but for
$\alpha> \omega _1$
, the approach in this paper does not seem to work, but for
![]() $\alpha = \omega _1$
it does.
$\alpha = \omega _1$
it does.
Proof Theorem 4.1.17 in [Reference Baars and de Groot8] shows that Theorem 1.1 holds for
![]() $\alpha = \omega _1$
.
$\alpha = \omega _1$
.
Let
![]() $X$
and
$X$
and
![]() $Y$
be metric spaces. Suppose
$Y$
be metric spaces. Suppose
![]() $\kappa (X) < \omega _1$
. Then there is a prime component
$\kappa (X) < \omega _1$
. Then there is a prime component
![]() $\omega ^{\mu }$
, with
$\omega ^{\mu }$
, with
![]() $\mu <\omega _1$
a limit ordinal, such that
$\mu <\omega _1$
a limit ordinal, such that
![]() $\kappa (X) < \omega ^{\mu }$
. So if
$\kappa (X) < \omega ^{\mu }$
. So if
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $l_p$
-equivalent or
$l_p$
-equivalent or
![]() $l_p^*$
-equivalent, we then have, by Theorem 1.2(b) or Theorem 1.3(a), that
$l_p^*$
-equivalent, we then have, by Theorem 1.2(b) or Theorem 1.3(a), that
![]() $\kappa (Y) < \omega ^{\mu } <\omega _1$
. Therefore, Theorems 1.2(b) and 1.3(a) hold for
$\kappa (Y) < \omega ^{\mu } <\omega _1$
. Therefore, Theorems 1.2(b) and 1.3(a) hold for
![]() $\alpha = \omega _1$
.
$\alpha = \omega _1$
.
This leaves us with Theorem 1.2(a) for
![]() $\alpha =\omega _1$
. Let
$\alpha =\omega _1$
. Let
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
![]() $\phi : C_p^*(X) \to C_p^*(Y)$
be a linear
$\phi : C_p^*(X) \to C_p^*(Y)$
be a linear
![]() $k$
-homeomorphism. Suppose
$k$
-homeomorphism. Suppose
![]() $\kappa (X) \leq \omega _1$
and
$\kappa (X) \leq \omega _1$
and
![]() $\kappa (Y)> \omega _1$
. Let
$\kappa (Y)> \omega _1$
. Let
![]() $y \in Y^{(\omega _1)}$
, and let
$y \in Y^{(\omega _1)}$
, and let
![]() $\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt X^{(\alpha )}: \alpha < \omega _1\}$
. Then
$\mathcal {V} = \{X \kern2pt{\backslash}\kern2pt X^{(\alpha )}: \alpha < \omega _1\}$
. Then
![]() $\mathcal {V}$
is an open cover of
$\mathcal {V}$
is an open cover of
![]() $X$
. Let
$X$
. Let
![]() $\mathcal {W}$
be a locally finite open cover of
$\mathcal {W}$
be a locally finite open cover of
![]() $X$
such that
$X$
such that
![]() $\{\overline {W}: W \in \mathcal {W}\}$
refines
$\{\overline {W}: W \in \mathcal {W}\}$
refines
![]() $\mathcal {V}$
. By Lemma 2.5, there are a neighborhood
$\mathcal {V}$
. By Lemma 2.5, there are a neighborhood
![]() $U$
of
$U$
of
![]() $y$
and a finite subset
$y$
and a finite subset
![]() $\mathcal {F} \subseteq \mathcal {W}$
such that
$\mathcal {F} \subseteq \mathcal {W}$
such that
![]() $U$
is
$U$
is
![]() $\frac {1}{8k}$
-supported on
$\frac {1}{8k}$
-supported on
![]() $\bigcup \mathcal {F}$
. Let
$\bigcup \mathcal {F}$
. Let
![]() $A = \bigcup \{\overline {W}: W \in \mathcal {F}\}$
. Then
$A = \bigcup \{\overline {W}: W \in \mathcal {F}\}$
. Then
![]() $A$
is closed and since
$A$
is closed and since
![]() $\mathcal {F}$
is finite, there is
$\mathcal {F}$
is finite, there is
![]() $\beta < \omega _1$
such that
$\beta < \omega _1$
such that
![]() $A \subseteq X \kern2pt{\backslash}\kern2pt X^{(\beta )}$
. So
$A \subseteq X \kern2pt{\backslash}\kern2pt X^{(\beta )}$
. So
![]() $A^{(\beta )} = \emptyset $
. Let
$A^{(\beta )} = \emptyset $
. Let
![]() $\sigma $
be a prime component such that
$\sigma $
be a prime component such that
![]() $\beta < \sigma < \omega _1$
. Then
$\beta < \sigma < \omega _1$
. Then
![]() $U$
contains a closed copy
$U$
contains a closed copy
![]() $K$
of
$K$
of
![]() $[1, \omega ^{\sigma }]$
. By Lemma 2.8, there is
$[1, \omega ^{\sigma }]$
. By Lemma 2.8, there is
![]() $L \subseteq A$
compact such that
$L \subseteq A$
compact such that
![]() $K$
is
$K$
is
![]() $\frac {1}{8k}$
-supported on
$\frac {1}{8k}$
-supported on
![]() $L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Then, by Lemma 2.4(a), (b), and (c), we have that
$L \cup (X \kern2pt{\backslash}\kern2pt A)$
. Then, by Lemma 2.4(a), (b), and (c), we have that
![]() $K$
is
$K$
is
![]() $\frac {1}{4k}$
-supported on
$\frac {1}{4k}$
-supported on
![]() $L$
. Then, as in the proof of Theorem 1.2(a), there is
$L$
. Then, as in the proof of Theorem 1.2(a), there is
![]() $\omega \leq \gamma < \omega ^{\alpha }$
such that
$\omega \leq \gamma < \omega ^{\alpha }$
such that
![]() $L$
is homeomorphic to
$L$
is homeomorphic to
![]() $[1, \gamma ]$
and there is a linear embedding from
$[1, \gamma ]$
and there is a linear embedding from
![]() $C_u^*(K) \to C_u^*(L)$
. As in the proof of Theorem 1.2(a), this gives a contradiction. Hence, Theorem 1.2(a) holds for
$C_u^*(K) \to C_u^*(L)$
. As in the proof of Theorem 1.2(a), this gives a contradiction. Hence, Theorem 1.2(a) holds for
![]() $\alpha = \omega _1$
.
$\alpha = \omega _1$
.
The following question remains open:
Question 4.10 Let X and Y be
![]() $l_p$
-equivalent or
$l_p$
-equivalent or
![]() $l_p^*$
-equivalent metric spaces. For which ordinals
$l_p^*$
-equivalent metric spaces. For which ordinals
![]() $\alpha> \omega _1$
are Theorem 1.1, Theorem 1.2, or Theorem 1.3 true?
$\alpha> \omega _1$
are Theorem 1.1, Theorem 1.2, or Theorem 1.3 true?
We conclude this paper by showing that Theorem 1.1 and Theorem 1.2(a) do not hold for arbitrary Tychonov spaces. It remains an open question if the same holds for Theorems 1.2(b) and 1.3(a).
Example 4.11 For every prime component, such that
![]() $\omega \leq \alpha < \omega _1$
, there are Tychonov spaces
$\omega \leq \alpha < \omega _1$
, there are Tychonov spaces
![]() $X$
and
$X$
and
![]() $Y$
such that:
$Y$
such that:
-
(a)
 $X$
and
$X$
and
 $Y$
are
$Y$
are
 $l_p$
-equivalent.
$l_p$
-equivalent. -
(b)
 $X$
and
$X$
and
 $Y$
are
$Y$
are
 $l_p^*$
-equivalent.
$l_p^*$
-equivalent. -
(c)
 $\kappa (X) = \alpha +1$
and
$\kappa (X) = \alpha +1$
and
 $\kappa (Y) = \alpha .$
$\kappa (Y) = \alpha .$
Proof Let
![]() $(\alpha _i)_{i \in \mathbb {N}}$
be an increasing sequence of limit ordinals such that
$(\alpha _i)_{i \in \mathbb {N}}$
be an increasing sequence of limit ordinals such that
![]() $\alpha _i \to \alpha $
. Let
$\alpha _i \to \alpha $
. Let
![]() $Z = [1,\omega ^{\alpha }),$
and for every
$Z = [1,\omega ^{\alpha }),$
and for every
![]() $i \in \mathbb {N}$
, let
$i \in \mathbb {N}$
, let
![]() $Z_i = [1,\omega ^{\alpha _i}]$
. Then
$Z_i = [1,\omega ^{\alpha _i}]$
. Then
![]() $Z$
is homeomorphic to the topological sum
$Z$
is homeomorphic to the topological sum
![]() $\bigoplus _{i=1}^{\infty } Z_i$
. We have
$\bigoplus _{i=1}^{\infty } Z_i$
. We have
![]() $\kappa (Z) = \alpha $
and for every
$\kappa (Z) = \alpha $
and for every
![]() $i \in \mathbb {N}$
,
$i \in \mathbb {N}$
,
![]() $\kappa (Z_i) = \alpha _i +1$
. Let
$\kappa (Z_i) = \alpha _i +1$
. Let
![]() $z_i$
be the unique point in
$z_i$
be the unique point in
![]() $Z_i^{(\alpha _i)}$
, and let
$Z_i^{(\alpha _i)}$
, and let
![]() $D = \{z_i: i \in \mathbb {N}\}$
. Then
$D = \{z_i: i \in \mathbb {N}\}$
. Then
![]() $D$
is a countable closed and discrete subset of
$D$
is a countable closed and discrete subset of
![]() $Z$
.
$Z$
.
Let
![]() $\beta Z$
be the Čech–Stone compactification of
$\beta Z$
be the Čech–Stone compactification of
![]() $Z$
, and let
$Z$
, and let
![]() $Z^* = \beta Z \kern2pt{\backslash}\kern2pt Z$
, the Čech–Stone remainder of
$Z^* = \beta Z \kern2pt{\backslash}\kern2pt Z$
, the Čech–Stone remainder of
![]() $X$
. Note that
$X$
. Note that
![]() $D$
is
$D$
is
![]() $C^*$
-embedded in
$C^*$
-embedded in
![]() $Z$
and that the closure
$Z$
and that the closure
![]() $\mathrm {cl}_{\beta Z}{D}$
of
$\mathrm {cl}_{\beta Z}{D}$
of
![]() $D$
in
$D$
in
![]() $\beta Z$
is
$\beta Z$
is
![]() $\beta D$
which is canonically homeomorphic to
$\beta D$
which is canonically homeomorphic to
![]() $\beta \mathbb {N}$
. Let
$\beta \mathbb {N}$
. Let
![]() $u\in \mathrm {cl}_{\beta Z} D$
, and let
$u\in \mathrm {cl}_{\beta Z} D$
, and let
![]() $X$
be the subspace
$X$
be the subspace
![]() $Z \cup \{u\}$
of
$Z \cup \{u\}$
of
![]() $\beta Z$
. Then
$\beta Z$
. Then
![]() $\tilde u = \{A\subseteq \mathbb {N}: u\in \mathrm {cl}_{\beta Z} \{z_i : i\in A\}\}$
is an ultrafilter on
$\tilde u = \{A\subseteq \mathbb {N}: u\in \mathrm {cl}_{\beta Z} \{z_i : i\in A\}\}$
is an ultrafilter on
![]() $\mathbb {N}$
, and hence a point in
$\mathbb {N}$
, and hence a point in
![]() $\mathbb {N}^*$
. Let
$\mathbb {N}^*$
. Let
![]() $S = \mathbb {N} \cup \{\tilde u\} \subseteq \beta \mathbb {N}$
, and let
$S = \mathbb {N} \cup \{\tilde u\} \subseteq \beta \mathbb {N}$
, and let
![]() $Y = Z \oplus S$
.
$Y = Z \oplus S$
.
In [Reference Baars and van Mill11], it was shown that
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $l_p$
-equivalent. In fact, the proof shows that there is
$l_p$
-equivalent. In fact, the proof shows that there is
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() $C_p(X) \stackrel {k}{\sim } C_p(Y)$
. Hence,
$C_p(X) \stackrel {k}{\sim } C_p(Y)$
. Hence,
![]() $X$
and
$X$
and
![]() $Y$
are also
$Y$
are also
![]() $l_p^*$
-equivalent. Note that
$l_p^*$
-equivalent. Note that
![]() $\kappa (X) = \alpha +1$
and
$\kappa (X) = \alpha +1$
and
![]() $\kappa (Y) = \alpha $
.
$\kappa (Y) = \alpha $
.
Question 4.12 Let
![]() $\alpha < \omega _1$
be a prime component. Are there
$\alpha < \omega _1$
be a prime component. Are there
![]() $l_p^*$
-equivalent Tychonov spaces
$l_p^*$
-equivalent Tychonov spaces
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $\kappa (X) < \alpha $
and
$\kappa (X) < \alpha $
and
![]() $\kappa (Y) \geq \alpha $
?
$\kappa (Y) \geq \alpha $
?
Question 4.13 Let
![]() $\alpha = \omega ^{\mu } < \omega _1$
be a prime component with
$\alpha = \omega ^{\mu } < \omega _1$
be a prime component with
![]() $\mu $
a limit ordinal. Are there
$\mu $
a limit ordinal. Are there
![]() $l_p$
-equivalent Tychonov spaces
$l_p$
-equivalent Tychonov spaces
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $\kappa (X) < \alpha $
and
$\kappa (X) < \alpha $
and
![]() $\kappa (Y) \geq \alpha $
?
$\kappa (Y) \geq \alpha $
?