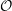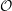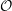1 Introduction
This paper continues the study of categories
![]() ${\mathcal{O}}$
over quantizations of symplectic resolutions started in [Reference Braden, Licata, Proudfoot and WebsterBLPW16].
${\mathcal{O}}$
over quantizations of symplectic resolutions started in [Reference Braden, Licata, Proudfoot and WebsterBLPW16].
Our base field is
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $X$
be a symplectic algebraic variety with form
$X$
be a symplectic algebraic variety with form
![]() $\unicode[STIX]{x1D714}$
. We assume that
$\unicode[STIX]{x1D714}$
. We assume that
![]() $X$
is equipped with a
$X$
is equipped with a
![]() $\mathbb{C}^{\times }$
-action that has the following two properties.
$\mathbb{C}^{\times }$
-action that has the following two properties.
-
∙ The algebra
 $\mathbb{C}[X]$
is finitely generated. Furthermore, the weights of
$\mathbb{C}[X]$
is finitely generated. Furthermore, the weights of
 $\mathbb{C}^{\times }$
in
$\mathbb{C}^{\times }$
in
 $\mathbb{C}[X]$
are non-negative, and the zero-weight component consists of scalars.
$\mathbb{C}[X]$
are non-negative, and the zero-weight component consists of scalars. -
∙ The torus
 $\mathbb{C}^{\times }$
rescales the symplectic form with a positive weight, i.e., there is an integer
$\mathbb{C}^{\times }$
rescales the symplectic form with a positive weight, i.e., there is an integer
 $d>0$
such that
$d>0$
such that
 $t.\unicode[STIX]{x1D714}=t^{d}\unicode[STIX]{x1D714}$
for all
$t.\unicode[STIX]{x1D714}=t^{d}\unicode[STIX]{x1D714}$
for all
 $t\in \mathbb{C}^{\times }$
.
$t\in \mathbb{C}^{\times }$
.
Set
 $X_{0}:=\operatorname{Spec}(\mathbb{C}[X])$
, so that the algebras
$X_{0}:=\operatorname{Spec}(\mathbb{C}[X])$
, so that the algebras
![]() $\mathbb{C}[X_{0}]$
and
$\mathbb{C}[X_{0}]$
and
![]() $\mathbb{C}[X]$
are identified. We say that
$\mathbb{C}[X]$
are identified. We say that
![]() $X$
is a conical symplectic resolution (of
$X$
is a conical symplectic resolution (of
![]() $X_{0}$
) if the natural morphism
$X_{0}$
) if the natural morphism
 $X\rightarrow X_{0}$
is projective and birational.
$X\rightarrow X_{0}$
is projective and birational.
A classical example is as follows. Let
![]() $G$
be a semisimple algebraic group and let
$G$
be a semisimple algebraic group and let
 $T\subset B\subset G$
be a maximal torus and a Borel subgroup. Set
$T\subset B\subset G$
be a maximal torus and a Borel subgroup. Set
 $X:=T^{\ast }(G/B)$
and equip it with the
$X:=T^{\ast }(G/B)$
and equip it with the
![]() $\mathbb{C}^{\times }$
-action by fiberwise dilations. The corresponding variety
$\mathbb{C}^{\times }$
-action by fiberwise dilations. The corresponding variety
![]() $X_{0}$
is the nilpotent cone in
$X_{0}$
is the nilpotent cone in
![]() $\mathfrak{g}^{\ast }$
, and the morphism
$\mathfrak{g}^{\ast }$
, and the morphism
 $X\rightarrow X_{0}$
is the Springer resolution.
$X\rightarrow X_{0}$
is the Springer resolution.
In the general situation, to
 $\unicode[STIX]{x1D706}\in H_{DR}^{2}(X)$
we can assign a quantization,
$\unicode[STIX]{x1D706}\in H_{DR}^{2}(X)$
we can assign a quantization,
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
, of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
, of
![]() ${\mathcal{O}}_{X}$
that is a sheaf (in the conical topology on
${\mathcal{O}}_{X}$
that is a sheaf (in the conical topology on
![]() $X$
: by an open subset one means a Zariski open
$X$
: by an open subset one means a Zariski open
![]() $\mathbb{C}^{\times }$
-stable subset) of filtered algebras with
$\mathbb{C}^{\times }$
-stable subset) of filtered algebras with
 $\operatorname{gr}{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}={\mathcal{O}}_{X}$
and some additional conditions. So far
$\operatorname{gr}{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}={\mathcal{O}}_{X}$
and some additional conditions. So far
![]() $\unicode[STIX]{x1D703}$
is just an element of notation. For example, in the case
$\unicode[STIX]{x1D703}$
is just an element of notation. For example, in the case
 $X=T^{\ast }(G/B)$
, the sheaf
$X=T^{\ast }(G/B)$
, the sheaf
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
is the microlocalization of the sheaf of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
is the microlocalization of the sheaf of
![]() $\unicode[STIX]{x1D706}-\unicode[STIX]{x1D70C}$
-twisted differential operators on
$\unicode[STIX]{x1D706}-\unicode[STIX]{x1D70C}$
-twisted differential operators on
![]() $G/B$
.
$G/B$
.
Now suppose that on
![]() $X$
we have a Hamiltonian action of a torus
$X$
we have a Hamiltonian action of a torus
![]() $T$
with finitely many fixed points. The action lifts to a Hamiltonian action on
$T$
with finitely many fixed points. The action lifts to a Hamiltonian action on
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
. A one-parameter subgroup
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
. A one-parameter subgroup
 $\unicode[STIX]{x1D708}:\mathbb{C}^{\times }\rightarrow T$
is said to be generic if the number of fixed points for
$\unicode[STIX]{x1D708}:\mathbb{C}^{\times }\rightarrow T$
is said to be generic if the number of fixed points for
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
in
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
in
![]() $X$
is finite. The set of generic one-parameter subgroups is the complement in
$X$
is finite. The set of generic one-parameter subgroups is the complement in
 $\operatorname{Hom}(\mathbb{C}^{\times },T)$
to finitely many hyperplanes (to be called walls). The connected components of the complement to the walls in
$\operatorname{Hom}(\mathbb{C}^{\times },T)$
to finitely many hyperplanes (to be called walls). The connected components of the complement to the walls in
 $\operatorname{Hom}(\mathbb{C}^{\times },T)\otimes _{\mathbb{Z}}\mathbb{R}$
will be called chambers.
$\operatorname{Hom}(\mathbb{C}^{\times },T)\otimes _{\mathbb{Z}}\mathbb{R}$
will be called chambers.
Now fix a generic one-parameter subgroup
 $\unicode[STIX]{x1D708}:\mathbb{C}^{\times }\rightarrow T$
. Consider its attracting locus
$\unicode[STIX]{x1D708}:\mathbb{C}^{\times }\rightarrow T$
. Consider its attracting locus
![]() $Y$
in
$Y$
in
![]() $X$
, i.e., the set of all
$X$
, i.e., the set of all
![]() $x\in X$
such that the limit
$x\in X$
such that the limit
 $\lim _{t\rightarrow 0}t.x$
exists. Then
$\lim _{t\rightarrow 0}t.x$
exists. Then
![]() $Y$
is the Lagrangian subvariety in
$Y$
is the Lagrangian subvariety in
![]() $X$
whose irreducible components are closures of affine spaces labelled by
$X$
whose irreducible components are closures of affine spaces labelled by
![]() $X^{T}$
. We define the category
$X^{T}$
. We define the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
as the category of all coherent
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
as the category of all coherent
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules supported on
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules supported on
![]() $Y$
that admit a weakly
$Y$
that admit a weakly
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure. This definition is equivalent to the definition appearing in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 3.3]. In the case of
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure. This definition is equivalent to the definition appearing in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 3.3]. In the case of
 $X=T^{\ast }(G/B)$
, we recover a version of the classical Bernstein–Gelfand–Gelfand (BGG) category
$X=T^{\ast }(G/B)$
, we recover a version of the classical Bernstein–Gelfand–Gelfand (BGG) category
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
One of the main results of [Reference Braden, Licata, Proudfoot and WebsterBLPW16] is that the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is highest weight with simple objects labelled by
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is highest weight with simple objects labelled by
![]() $X^{T}$
. For an order that is a part of a highest-weight structure, one can take the usual (contraction) order
$X^{T}$
. For an order that is a part of a highest-weight structure, one can take the usual (contraction) order
![]() ${\leqslant}_{\unicode[STIX]{x1D708}}$
on the fixed points produced from
${\leqslant}_{\unicode[STIX]{x1D708}}$
on the fixed points produced from
![]() $\unicode[STIX]{x1D708}$
. Being highest weight with respect to a given order means certain upper triangularity properties, just as in the BGG case.
$\unicode[STIX]{x1D708}$
. Being highest weight with respect to a given order means certain upper triangularity properties, just as in the BGG case.
Our first result about the categories
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
establishes more structure on them. Namely, take
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
establishes more structure on them. Namely, take
![]() $\unicode[STIX]{x1D708}_{0}$
lying in the closure of the chamber containing
$\unicode[STIX]{x1D708}_{0}$
lying in the closure of the chamber containing
![]() $\unicode[STIX]{x1D708}$
. Then
$\unicode[STIX]{x1D708}$
. Then
![]() $\unicode[STIX]{x1D708}_{0}$
defines a pre-order
$\unicode[STIX]{x1D708}_{0}$
defines a pre-order
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
on
$\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
on
![]() $X^{T}$
, by contraction of the irreducible components of
$X^{T}$
, by contraction of the irreducible components of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. This pre-order is refined by
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. This pre-order is refined by
![]() ${\leqslant}_{\unicode[STIX]{x1D708}}$
. We show, in Theorem 6.3, that the category
${\leqslant}_{\unicode[STIX]{x1D708}}$
. We show, in Theorem 6.3, that the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
becomes standardly stratified in the sense of [Reference Losev and WebsterLW15] with respect to
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
becomes standardly stratified in the sense of [Reference Losev and WebsterLW15] with respect to
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
. Roughly speaking, this means some additional upper-triangularity properties.
$\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
. Roughly speaking, this means some additional upper-triangularity properties.
The main result of this paper concerns certain derived functors introduced in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.2] that relate categories
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
and
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
and
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with different generic
${\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with different generic
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
. The functors were called shuffling in [Reference Braden, Licata, Proudfoot and WebsterBLPW16], but in this paper we call them cross-walling, because they are supposed to be Koszul dual to functors called wall-crossing in [Reference Bezrukavnikov and LosevBL13] (and twisting in [Reference Braden, Proudfoot and WebsterBPW16]). We show that the cross-walling functor
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
. The functors were called shuffling in [Reference Braden, Licata, Proudfoot and WebsterBLPW16], but in this paper we call them cross-walling, because they are supposed to be Koszul dual to functors called wall-crossing in [Reference Bezrukavnikov and LosevBL13] (and twisting in [Reference Braden, Proudfoot and WebsterBPW16]). We show that the cross-walling functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
is an equivalence of triangulated categories proving a conjecture of Braden et al. Moreover, we show that the cross-walling functors define an action of the Deligne groupoid of the real hyperplane arrangement given by the walls in
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
is an equivalence of triangulated categories proving a conjecture of Braden et al. Moreover, we show that the cross-walling functors define an action of the Deligne groupoid of the real hyperplane arrangement given by the walls in
 $\operatorname{Hom}(\mathbb{C}^{\times },T)\otimes _{\mathbb{Z}}\mathbb{R}$
on the categories
$\operatorname{Hom}(\mathbb{C}^{\times },T)\otimes _{\mathbb{Z}}\mathbb{R}$
on the categories
 $D^{b}({\mathcal{O}}_{?}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
; see § 7.2. Recall that by the Deligne groupoid of a real hyperplane arrangement in
$D^{b}({\mathcal{O}}_{?}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
; see § 7.2. Recall that by the Deligne groupoid of a real hyperplane arrangement in
![]() $\mathbb{C}^{n}$
one means the full subgroupoid in the fundamental groupoid of the hyperplane complement
$\mathbb{C}^{n}$
one means the full subgroupoid in the fundamental groupoid of the hyperplane complement
![]() $\mathfrak{X}$
whose objects are points in
$\mathfrak{X}$
whose objects are points in
![]() $\mathfrak{X}\,\cap \,\mathbb{R}^{n}$
, one per chamber. This establishes another conjecture of Braden et al. (there is a stronger version taking a Weyl group into account; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Theorem 8.13]). We also show that both the long wall-crossing and the long cross-walling functors realize the Ringel duality, which implies [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 8.24].
$\mathfrak{X}\,\cap \,\mathbb{R}^{n}$
, one per chamber. This establishes another conjecture of Braden et al. (there is a stronger version taking a Weyl group into account; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Theorem 8.13]). We also show that both the long wall-crossing and the long cross-walling functors realize the Ringel duality, which implies [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 8.24].
In order to prove these claims we examine an interplay between the cross-walling functors and the standardly stratified structures. This interplay is of independent interest; it will be used in a subsequent paper to provide combinatorial recipes to determine the supports of the global sections of the irreducible objects in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
in the case when
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
in the case when
![]() $X$
is a Gieseker moduli space.
$X$
is a Gieseker moduli space.
The paper is organized as follows. In § 2 we will recall some generalities on symplectic resolutions and their quantizations following [Reference Braden, Proudfoot and WebsterBPW16]. In § 3 we recall generalities of standardly stratified categories mostly following [Reference Losev and WebsterLW15]. Section 4 deals with categories
![]() ${\mathcal{O}}$
of symplectic resolutions. Here we follow [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Reference LosevLos17]. These three sections basically contain no new results. In § 5 we introduce a ‘parabolic induction’, one of the main tools to study the categories
${\mathcal{O}}$
of symplectic resolutions. Here we follow [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Reference LosevLos17]. These three sections basically contain no new results. In § 5 we introduce a ‘parabolic induction’, one of the main tools to study the categories
![]() ${\mathcal{O}}$
. In particular, we apply the parabolic induction in § 6 to introduce standardly stratified structures on those categories. In § 7 we study cross-walling functors proving all results about them mentioned before. In the appendix we discuss some analogies between our work and that of Maulik and Okounkov [Reference Maulik and OkounkovMO12].
${\mathcal{O}}$
. In particular, we apply the parabolic induction in § 6 to introduce standardly stratified structures on those categories. In § 7 we study cross-walling functors proving all results about them mentioned before. In the appendix we discuss some analogies between our work and that of Maulik and Okounkov [Reference Maulik and OkounkovMO12].
2 Symplectic resolutions and their quantizations
2.1 Conical symplectic resolutions and their deformations
Let
![]() $X_{0}$
be a normal Poisson affine variety equipped with an action of
$X_{0}$
be a normal Poisson affine variety equipped with an action of
![]() $\mathbb{C}^{\times }$
such that the grading on
$\mathbb{C}^{\times }$
such that the grading on
![]() $\mathbb{C}[X_{0}]$
is positive (meaning that the graded component
$\mathbb{C}[X_{0}]$
is positive (meaning that the graded component
![]() $\mathbb{C}[X_{0}]_{i}$
is zero when
$\mathbb{C}[X_{0}]_{i}$
is zero when
![]() $i<0$
, and
$i<0$
, and
 $\mathbb{C}[X_{0}]_{0}=\mathbb{C}$
) and there is a positive integer
$\mathbb{C}[X_{0}]_{0}=\mathbb{C}$
) and there is a positive integer
![]() $d$
such that
$d$
such that
 $\{\mathbb{C}[X_{0}]_{i},\mathbb{C}[X_{0}]_{j}\}\subset \mathbb{C}[X_{0}]_{i+j-d}$
. By a symplectic resolution of singularities of
$\{\mathbb{C}[X_{0}]_{i},\mathbb{C}[X_{0}]_{j}\}\subset \mathbb{C}[X_{0}]_{i+j-d}$
. By a symplectic resolution of singularities of
![]() $X_{0}$
, we mean a pair
$X_{0}$
, we mean a pair
![]() $(X,\unicode[STIX]{x1D70C})$
of:
$(X,\unicode[STIX]{x1D70C})$
of:
-
∙ a symplectic algebraic variety
 $X$
(with form
$X$
(with form
 $\unicode[STIX]{x1D714}$
);
$\unicode[STIX]{x1D714}$
); -
∙ a morphism
 $\unicode[STIX]{x1D70C}$
of Poisson varieties that is a projective resolution of singularities.
$\unicode[STIX]{x1D70C}$
of Poisson varieties that is a projective resolution of singularities.
Below we assume that
![]() $(X,\unicode[STIX]{x1D70C})$
is a symplectic resolution of singularities. Besides, we will assume that
$(X,\unicode[STIX]{x1D70C})$
is a symplectic resolution of singularities. Besides, we will assume that
![]() $(X,\unicode[STIX]{x1D70C})$
is conical meaning that the
$(X,\unicode[STIX]{x1D70C})$
is conical meaning that the
![]() $\mathbb{C}^{\times }$
-action lifts to
$\mathbb{C}^{\times }$
-action lifts to
![]() $X$
in such a way that
$X$
in such a way that
![]() $\unicode[STIX]{x1D70C}$
is equivariant. This
$\unicode[STIX]{x1D70C}$
is equivariant. This
![]() $\mathbb{C}^{\times }$
-action will be called contracting later on.
$\mathbb{C}^{\times }$
-action will be called contracting later on.
Note that
 $\unicode[STIX]{x1D70C}^{\ast }:\mathbb{C}[X_{0}]\rightarrow \mathbb{C}[X]$
is an isomorphism because
$\unicode[STIX]{x1D70C}^{\ast }:\mathbb{C}[X_{0}]\rightarrow \mathbb{C}[X]$
is an isomorphism because
![]() $X_{0}$
is normal. By the Grauert–Riemenschneider theorem, we have
$X_{0}$
is normal. By the Grauert–Riemenschneider theorem, we have
 $H^{i}(X,{\mathcal{O}}_{X})=0$
for
$H^{i}(X,{\mathcal{O}}_{X})=0$
for
![]() $i>0$
. By results of Kaledin, [Reference KaledinKal06b, Theorem 2.3],
$i>0$
. By results of Kaledin, [Reference KaledinKal06b, Theorem 2.3],
![]() $X_{0}$
has finitely many symplectic leaves.
$X_{0}$
has finitely many symplectic leaves.
Remark 2.1. Note that if
![]() $X_{0}^{\prime }$
is an affine Poisson variety and its normalization
$X_{0}^{\prime }$
is an affine Poisson variety and its normalization
![]() $X_{0}$
has finitely many leaves, then so does
$X_{0}$
has finitely many leaves, then so does
![]() $X_{0}^{\prime }$
. It follows that any affine Poisson algebraic variety
$X_{0}^{\prime }$
. It follows that any affine Poisson algebraic variety
![]() $X_{0}^{\prime }$
admitting a symplectic resolution
$X_{0}^{\prime }$
admitting a symplectic resolution
![]() $X$
has finitely many leaves.
$X$
has finitely many leaves.
We will be interested in deformations
![]() $\hat{X}/\mathfrak{p}$
, where
$\hat{X}/\mathfrak{p}$
, where
![]() $\mathfrak{p}$
is a finite-dimensional vector space, and
$\mathfrak{p}$
is a finite-dimensional vector space, and
![]() $\hat{X}$
is a symplectic scheme over
$\hat{X}$
is a symplectic scheme over
![]() $\mathfrak{p}$
with symplectic form
$\mathfrak{p}$
with symplectic form
 $\hat{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6FA}^{2}(\hat{X}/\mathfrak{p})$
that specializes to
$\hat{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6FA}^{2}(\hat{X}/\mathfrak{p})$
that specializes to
![]() $\unicode[STIX]{x1D714}$
and also with a
$\unicode[STIX]{x1D714}$
and also with a
![]() $\mathbb{C}^{\times }$
-action on
$\mathbb{C}^{\times }$
-action on
![]() $\hat{X}$
having the following properties:
$\hat{X}$
having the following properties:
-
∙ the morphism
 $\hat{X}\rightarrow \mathfrak{p}$
is
$\hat{X}\rightarrow \mathfrak{p}$
is
 $\mathbb{C}^{\times }$
-equivariant;
$\mathbb{C}^{\times }$
-equivariant; -
∙ the restriction of the action to
 $X$
coincides with the contracting action;
$X$
coincides with the contracting action; -
∙
 $t.\hat{\unicode[STIX]{x1D714}}:=t^{d}\hat{\unicode[STIX]{x1D714}}$
.
$t.\hat{\unicode[STIX]{x1D714}}:=t^{d}\hat{\unicode[STIX]{x1D714}}$
.
It turns out that there is a universal such deformation
![]() $\tilde{X}$
over
$\tilde{X}$
over
 $\tilde{\mathfrak{p}}:=H^{2}(X,\mathbb{C})$
(any other deformation is obtained via the pull-back with respect to a linear map
$\tilde{\mathfrak{p}}:=H^{2}(X,\mathbb{C})$
(any other deformation is obtained via the pull-back with respect to a linear map
![]() $\mathfrak{p}\rightarrow \tilde{\mathfrak{p}}$
). Moreover, the deformation
$\mathfrak{p}\rightarrow \tilde{\mathfrak{p}}$
). Moreover, the deformation
![]() $\tilde{X}$
is trivial in the category of
$\tilde{X}$
is trivial in the category of
![]() $C^{\infty }$
-manifolds. This result is due to Namikawa [Reference NamikawaNam08, Lemmas 12 and 22 and Proposition 13].
$C^{\infty }$
-manifolds. This result is due to Namikawa [Reference NamikawaNam08, Lemmas 12 and 22 and Proposition 13].
Now we are going to review some structural features of conical symplectic resolutions mostly due to Kaledin and Namikawa.
First of all, let us point out that
![]() $X$
has no odd cohomology [Reference Braden, Proudfoot and WebsterBPW16, Proposition 2.5].
$X$
has no odd cohomology [Reference Braden, Proudfoot and WebsterBPW16, Proposition 2.5].
For
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
, let us write
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
, let us write
![]() $X_{\unicode[STIX]{x1D706}}$
for the corresponding fiber of
$X_{\unicode[STIX]{x1D706}}$
for the corresponding fiber of
![]() $\tilde{X}\rightarrow \tilde{\mathfrak{p}}$
. It turns out that, for
$\tilde{X}\rightarrow \tilde{\mathfrak{p}}$
. It turns out that, for
![]() $\unicode[STIX]{x1D706}$
Zariski generic,
$\unicode[STIX]{x1D706}$
Zariski generic,
![]() $X_{\unicode[STIX]{x1D706}}$
is affine and independent of the choice of a conical symplectic resolution
$X_{\unicode[STIX]{x1D706}}$
is affine and independent of the choice of a conical symplectic resolution
![]() $X$
. This shows that the groups
$X$
. This shows that the groups
 $H^{i}(X,\mathbb{Z})$
are independent of the choice of
$H^{i}(X,\mathbb{Z})$
are independent of the choice of
![]() $X$
. Furthermore, if
$X$
. Furthermore, if
![]() $X,X^{\prime }$
are two conical symplectic resolutions of
$X,X^{\prime }$
are two conical symplectic resolutions of
![]() $X$
, then there are open subvarieties
$X$
, then there are open subvarieties
 $X^{0}\subset X,{X^{\prime }}^{0}\subset X^{\prime }$
with complements of codimension bigger than
$X^{0}\subset X,{X^{\prime }}^{0}\subset X^{\prime }$
with complements of codimension bigger than
![]() $1$
that are isomorphic; see, e.g., [Reference Braden, Proudfoot and WebsterBPW16, Proposition 2.18]. This allows us to identify the Picard groups
$1$
that are isomorphic; see, e.g., [Reference Braden, Proudfoot and WebsterBPW16, Proposition 2.18]. This allows us to identify the Picard groups
 $\operatorname{Pic}(X)=\operatorname{Pic}(X^{\prime })$
. Moreover, the Chern class map defines an isomorphism
$\operatorname{Pic}(X)=\operatorname{Pic}(X^{\prime })$
. Moreover, the Chern class map defines an isomorphism
 $\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X)\xrightarrow[{}]{{\sim}}H^{2}(X,\mathbb{C})$
. The isomorphisms
$\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X)\xrightarrow[{}]{{\sim}}H^{2}(X,\mathbb{C})$
. The isomorphisms
 $\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X)\xrightarrow[{}]{{\sim}}H^{2}(X,\mathbb{C})$
,
$\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X)\xrightarrow[{}]{{\sim}}H^{2}(X,\mathbb{C})$
,
 $\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X^{\prime })\xrightarrow[{}]{{\sim}}H^{2}(X^{\prime },\mathbb{C})$
intertwine the identifications
$\mathbb{C}\,\otimes _{\mathbb{Z}}\operatorname{Pic}(X^{\prime })\xrightarrow[{}]{{\sim}}H^{2}(X^{\prime },\mathbb{C})$
intertwine the identifications
 $\operatorname{Pic}(X)\cong \operatorname{Pic}(X^{\prime })$
,
$\operatorname{Pic}(X)\cong \operatorname{Pic}(X^{\prime })$
,
 $H^{2}(X,\mathbb{C})\cong H^{2}(X^{\prime },\mathbb{C})$
. Let
$H^{2}(X,\mathbb{C})\cong H^{2}(X^{\prime },\mathbb{C})$
. Let
![]() $\tilde{\mathfrak{p}}_{\mathbb{Z}}$
be the image of
$\tilde{\mathfrak{p}}_{\mathbb{Z}}$
be the image of
![]() $\operatorname{Pic}(X)$
in
$\operatorname{Pic}(X)$
in
 $H^{2}(X,\mathbb{C})$
.
$H^{2}(X,\mathbb{C})$
.
Set
 $\tilde{\mathfrak{p}}_{\mathbb{R}}:=\mathbb{R}\otimes _{\mathbb{Z}}\tilde{\mathfrak{p}}_{\mathbb{Z}}$
. There is a finite group
$\tilde{\mathfrak{p}}_{\mathbb{R}}:=\mathbb{R}\otimes _{\mathbb{Z}}\tilde{\mathfrak{p}}_{\mathbb{Z}}$
. There is a finite group
![]() $W$
acting on
$W$
acting on
![]() $\tilde{\mathfrak{p}}_{\mathbb{R}}$
as a reflection group, such that the movable cone
$\tilde{\mathfrak{p}}_{\mathbb{R}}$
as a reflection group, such that the movable cone
![]() $C$
of
$C$
of
![]() $X$
(that does not depend on the choice of a resolution) is a fundamental chamber for
$X$
(that does not depend on the choice of a resolution) is a fundamental chamber for
![]() $W$
. We can partition
$W$
. We can partition
![]() $C$
into the union of cones
$C$
into the union of cones
 $C_{1},\ldots ,C_{m}$
(with disjoint interiors) such that the possible conical symplectic resolutions of
$C_{1},\ldots ,C_{m}$
(with disjoint interiors) such that the possible conical symplectic resolutions of
![]() $X_{0}$
are in one-to-one correspondence with
$X_{0}$
are in one-to-one correspondence with
 $C_{1},\ldots ,C_{m}$
in such a way that the cone corresponding to a resolution
$C_{1},\ldots ,C_{m}$
in such a way that the cone corresponding to a resolution
![]() $X^{\prime }$
is its ample cone. Let
$X^{\prime }$
is its ample cone. Let
 $H_{1},\ldots ,H_{k}$
be the hyperplanes spanned by the codimension-
$H_{1},\ldots ,H_{k}$
be the hyperplanes spanned by the codimension-
![]() $1$
faces of the cones
$1$
faces of the cones
 $C_{1},\ldots ,C_{m}$
. Set
$C_{1},\ldots ,C_{m}$
. Set
 $$\begin{eqnarray}{\mathcal{H}}_{\mathbb{C}}:=\mathop{\bigcup }_{1\leqslant i\leqslant k,w\in W}w(\mathbb{C}\otimes _{\mathbb{R}}H_{i}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{\mathbb{C}}:=\mathop{\bigcup }_{1\leqslant i\leqslant k,w\in W}w(\mathbb{C}\otimes _{\mathbb{R}}H_{i}).\end{eqnarray}$$
Then
![]() $X_{\unicode[STIX]{x1D706}}$
is affine if and only if
$X_{\unicode[STIX]{x1D706}}$
is affine if and only if
![]() $\unicode[STIX]{x1D706}\not \in {\mathcal{H}}_{\mathbb{C}}$
. The results in this paragraph are due to Namikawa [Reference NamikawaNam15].
$\unicode[STIX]{x1D706}\not \in {\mathcal{H}}_{\mathbb{C}}$
. The results in this paragraph are due to Namikawa [Reference NamikawaNam15].
For
![]() $\unicode[STIX]{x1D703}\not \in {\mathcal{H}}_{\mathbb{C}}$
, we will write
$\unicode[STIX]{x1D703}\not \in {\mathcal{H}}_{\mathbb{C}}$
, we will write
![]() $X^{\unicode[STIX]{x1D703}}$
for the resolution corresponding to the ample cone containing
$X^{\unicode[STIX]{x1D703}}$
for the resolution corresponding to the ample cone containing
 $W\unicode[STIX]{x1D703}\,\cap \,C$
. Further, if
$W\unicode[STIX]{x1D703}\,\cap \,C$
. Further, if
 $w\unicode[STIX]{x1D703}\in C$
, we will choose a different identification of
$w\unicode[STIX]{x1D703}\in C$
, we will choose a different identification of
 $H^{2}(X^{\unicode[STIX]{x1D703}},\mathbb{C})$
with
$H^{2}(X^{\unicode[STIX]{x1D703}},\mathbb{C})$
with
![]() $\tilde{\mathfrak{p}}$
, one twisted by
$\tilde{\mathfrak{p}}$
, one twisted by
![]() $w$
(so that the ample cone actually contains
$w$
(so that the ample cone actually contains
![]() $\unicode[STIX]{x1D703}$
).
$\unicode[STIX]{x1D703}$
).
2.2 Quantizations
We will study quantizations of
 $X,X_{0},\tilde{X}$
. By a quantization of
$X,X_{0},\tilde{X}$
. By a quantization of
![]() $X_{0}$
, we mean a filtered algebra
$X_{0}$
, we mean a filtered algebra
![]() ${\mathcal{A}}$
together with an isomorphism
${\mathcal{A}}$
together with an isomorphism
 $\operatorname{gr}{\mathcal{A}}\cong \mathbb{C}[X_{0}]$
of graded Poisson algebras. By a quantization of
$\operatorname{gr}{\mathcal{A}}\cong \mathbb{C}[X_{0}]$
of graded Poisson algebras. By a quantization of
 $X=X^{\unicode[STIX]{x1D703}}$
, we mean a sheaf
$X=X^{\unicode[STIX]{x1D703}}$
, we mean a sheaf
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
of filtered algebras in the conical topology on
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
of filtered algebras in the conical topology on
![]() $X$
(in this topology, ‘open’ means Zariski open and
$X$
(in this topology, ‘open’ means Zariski open and
![]() $\mathbb{C}^{\times }$
-stable) that is complete and separated with respect to the filtration together with an isomorphism
$\mathbb{C}^{\times }$
-stable) that is complete and separated with respect to the filtration together with an isomorphism
 $\operatorname{gr}{\mathcal{A}}^{\unicode[STIX]{x1D703}}\cong {\mathcal{O}}_{X^{\unicode[STIX]{x1D703}}}$
(of sheaves of graded Poisson algebras). A quantization
$\operatorname{gr}{\mathcal{A}}^{\unicode[STIX]{x1D703}}\cong {\mathcal{O}}_{X^{\unicode[STIX]{x1D703}}}$
(of sheaves of graded Poisson algebras). A quantization
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of the universal deformation
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of the universal deformation
![]() $\tilde{X}^{\unicode[STIX]{x1D703}}$
is:
$\tilde{X}^{\unicode[STIX]{x1D703}}$
is:
-
∙ a filtered sheaf of
 $\mathbb{C}[\tilde{\mathfrak{p}}]$
-algebras (with a complete and separated filtration), where the induced filtration on
$\mathbb{C}[\tilde{\mathfrak{p}}]$
-algebras (with a complete and separated filtration), where the induced filtration on
 $\mathbb{C}[\tilde{\mathfrak{p}}]$
coincides with the natural one, where
$\mathbb{C}[\tilde{\mathfrak{p}}]$
coincides with the natural one, where
 $\deg \tilde{\mathfrak{p}}=d$
;
$\deg \tilde{\mathfrak{p}}=d$
; -
∙ together with an isomorphism
 $\operatorname{gr}\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\tilde{X}^{\unicode[STIX]{x1D703}}}$
of graded Poisson
$\operatorname{gr}\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\tilde{X}^{\unicode[STIX]{x1D703}}}$
of graded Poisson
 $\mathbb{C}[\tilde{\mathfrak{p}}]$
-algebras.
$\mathbb{C}[\tilde{\mathfrak{p}}]$
-algebras.
Note that we can specialize a quantization
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
to a point in
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
to a point in
![]() $\tilde{\mathfrak{p}}$
getting a quantization of
$\tilde{\mathfrak{p}}$
getting a quantization of
![]() $X$
.
$X$
.
A result of Bezrukavnikov and Kaledin [Reference Bezrukavnikov and KaledinBK04] (with ramifications given in [Reference LosevLos12, § 2]) shows that quantizations
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
are parameterized (up to an isomorphism) by the points in
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
are parameterized (up to an isomorphism) by the points in
![]() $\tilde{\mathfrak{p}}$
. More precisely, there is a canonical quantization
$\tilde{\mathfrak{p}}$
. More precisely, there is a canonical quantization
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of
![]() $\tilde{X}^{\unicode[STIX]{x1D703}}$
such that the quantization of
$\tilde{X}^{\unicode[STIX]{x1D703}}$
such that the quantization of
![]() $X^{\unicode[STIX]{x1D703}}$
corresponding to
$X^{\unicode[STIX]{x1D703}}$
corresponding to
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
is the specialization of
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
is the specialization of
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
to
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
to
![]() $\unicode[STIX]{x1D706}$
. The quantization
$\unicode[STIX]{x1D706}$
. The quantization
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
has the following important property: there is an anti-automorphism,
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
has the following important property: there is an anti-automorphism,
![]() $\unicode[STIX]{x1D70D}$
(to be called the parity anti-automorphism), that preserves the filtration, is the identity on the associated graded algebra, preserves
$\unicode[STIX]{x1D70D}$
(to be called the parity anti-automorphism), that preserves the filtration, is the identity on the associated graded algebra, preserves
 $\tilde{\mathfrak{p}}^{\ast }\subset \unicode[STIX]{x1D6E4}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}})$
and induces
$\tilde{\mathfrak{p}}^{\ast }\subset \unicode[STIX]{x1D6E4}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}})$
and induces
![]() $-1$
on
$-1$
on
![]() $\tilde{\mathfrak{p}}^{\ast }$
. It follows that
$\tilde{\mathfrak{p}}^{\ast }$
. It follows that
![]() ${\mathcal{A}}_{-\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
is isomorphic to
${\mathcal{A}}_{-\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
is isomorphic to
 $({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
.
$({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
.
We set
 $\tilde{{\mathcal{A}}}:=\unicode[STIX]{x1D6E4}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}),{\mathcal{A}}_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
, so that
$\tilde{{\mathcal{A}}}:=\unicode[STIX]{x1D6E4}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}),{\mathcal{A}}_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
, so that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is the specialization of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is the specialization of
![]() $\tilde{{\mathcal{A}}}$
to
$\tilde{{\mathcal{A}}}$
to
![]() $\unicode[STIX]{x1D706}$
. It follows from [Reference Braden, Proudfoot and WebsterBPW16, § 3.3] that the algebras
$\unicode[STIX]{x1D706}$
. It follows from [Reference Braden, Proudfoot and WebsterBPW16, § 3.3] that the algebras
![]() $\tilde{{\mathcal{A}}},{\mathcal{A}}_{\unicode[STIX]{x1D706}}$
are independent of the choice of
$\tilde{{\mathcal{A}}},{\mathcal{A}}_{\unicode[STIX]{x1D706}}$
are independent of the choice of
![]() $\unicode[STIX]{x1D703}$
. From
$\unicode[STIX]{x1D703}$
. From
 $H^{i}(X^{\unicode[STIX]{x1D703}},{\mathcal{O}}_{X^{\unicode[STIX]{x1D703}}})=0$
, we deduce that the higher cohomologies of both
$H^{i}(X^{\unicode[STIX]{x1D703}},{\mathcal{O}}_{X^{\unicode[STIX]{x1D703}}})=0$
, we deduce that the higher cohomologies of both
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
and
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
and
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
vanish and also that
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
vanish and also that
![]() $\tilde{{\mathcal{A}}}$
is a quantization of
$\tilde{{\mathcal{A}}}$
is a quantization of
![]() $\mathbb{C}[\tilde{X}]$
and
$\mathbb{C}[\tilde{X}]$
and
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is a quantization of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is a quantization of
 $\mathbb{C}[X]=\mathbb{C}[X_{0}]$
. Also, we note that
$\mathbb{C}[X]=\mathbb{C}[X_{0}]$
. Also, we note that
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is the specialization of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
is the specialization of
![]() $\tilde{{\mathcal{A}}}$
at
$\tilde{{\mathcal{A}}}$
at
![]() $\unicode[STIX]{x1D706}$
and that
$\unicode[STIX]{x1D706}$
and that
 ${\mathcal{A}}_{-\unicode[STIX]{x1D706}}\cong {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}$
. Also, we have
${\mathcal{A}}_{-\unicode[STIX]{x1D706}}\cong {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}$
. Also, we have
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}}\cong {\mathcal{A}}_{w\unicode[STIX]{x1D706}}$
for all
${\mathcal{A}}_{\unicode[STIX]{x1D706}}\cong {\mathcal{A}}_{w\unicode[STIX]{x1D706}}$
for all
 $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}},w\in W$
; see [Reference Braden, Proudfoot and WebsterBPW16, § 3.3].
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}},w\in W$
; see [Reference Braden, Proudfoot and WebsterBPW16, § 3.3].
2.3 Localization and translation equivalences
Consider the categories
 $\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
of coherent
$\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
of coherent
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules and
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules and
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
of finitely generated
${\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
of finitely generated
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-modules. Recall that an
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-modules. Recall that an
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module
![]() $M$
is called coherent if it can be equipped with a complete and separated
$M$
is called coherent if it can be equipped with a complete and separated
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module filtration such that
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module filtration such that
![]() $\operatorname{gr}M$
is coherent (such a filtration is called good).
$\operatorname{gr}M$
is coherent (such a filtration is called good).
We have functors between these categories, the global section functor
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}:\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
and its left adjoint, the localization functor
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}:\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
and its left adjoint, the localization functor
 $\operatorname{Loc}_{\unicode[STIX]{x1D706}}:{\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}\rightarrow \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}),N\mapsto {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}}}N$
. We can also consider their derived functors
$\operatorname{Loc}_{\unicode[STIX]{x1D706}}:{\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}\rightarrow \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}),N\mapsto {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}}}N$
. We can also consider their derived functors
 $R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}:D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
and
$R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}:D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
and
 $L\operatorname{Loc}_{\unicode[STIX]{x1D706}}:D^{-}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\rightarrow D^{-}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
.
$L\operatorname{Loc}_{\unicode[STIX]{x1D706}}:D^{-}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\rightarrow D^{-}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
.
We will need a partial answer to the question of when
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}},\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
are mutually quasi-inverse equivalences (in this case we will say that abelian localization holds for
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}},\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
are mutually quasi-inverse equivalences (in this case we will say that abelian localization holds for
![]() $(\unicode[STIX]{x1D706},\unicode[STIX]{x1D703})$
); see [Reference Braden, Proudfoot and WebsterBPW16, Corollary 5.17].
$(\unicode[STIX]{x1D706},\unicode[STIX]{x1D703})$
); see [Reference Braden, Proudfoot and WebsterBPW16, Corollary 5.17].
Lemma 2.2. Let
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
and
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
and
![]() $\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
be ample for
$\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
be ample for
![]() $X^{\unicode[STIX]{x1D703}}$
. Then there is
$X^{\unicode[STIX]{x1D703}}$
. Then there is
![]() $n_{0}\in \mathbb{Z}$
such that
$n_{0}\in \mathbb{Z}$
such that
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}:\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\rightleftarrows {\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}\text{-}\!\operatorname{mod}:\operatorname{Loc}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}$
are mutually quasi-inverse equivalences for all
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}:\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\rightleftarrows {\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}\text{-}\!\operatorname{mod}:\operatorname{Loc}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}$
are mutually quasi-inverse equivalences for all
![]() $n\geqslant n_{0}$
.
$n\geqslant n_{0}$
.
Let us proceed to translation equivalences. When
![]() $\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
, we have an equivalence
$\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
, we have an equivalence
 $\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})$
. This equivalence is given by tensoring with the
$\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})$
. This equivalence is given by tensoring with the
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
-
${\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
-
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-bimodule to be denoted by
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-bimodule to be denoted by
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
. This bimodule is the unique quantization of the line bundle
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
. This bimodule is the unique quantization of the line bundle
![]() ${\mathcal{O}}(\unicode[STIX]{x1D712})$
corresponding to
${\mathcal{O}}(\unicode[STIX]{x1D712})$
corresponding to
![]() $\unicode[STIX]{x1D712}$
. Similarly, we can define the
$\unicode[STIX]{x1D712}$
. Similarly, we can define the
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
-bimodule
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
-bimodule
![]() $\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
quantizing the extension to
$\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
quantizing the extension to
![]() $\tilde{X}$
of the line bundle corresponding to
$\tilde{X}$
of the line bundle corresponding to
![]() $\unicode[STIX]{x1D712}$
[Reference Braden, Proudfoot and WebsterBPW16, § 5.1]. Clearly,
$\unicode[STIX]{x1D712}$
[Reference Braden, Proudfoot and WebsterBPW16, § 5.1]. Clearly,
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
is the specialization of
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
is the specialization of
![]() $\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
.
$\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
.
We write
 ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})},\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
for the global sections of
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})},\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
for the global sections of
 ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}},\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
, respectively. It is not known, in general, whether the bimodule
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}},\tilde{{\mathcal{A}}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
, respectively. It is not known, in general, whether the bimodule
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
is independent of
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
is independent of
![]() $\unicode[STIX]{x1D703}$
. For an affine subspace
$\unicode[STIX]{x1D703}$
. For an affine subspace
![]() $\mathfrak{p}\subset \tilde{\mathfrak{p}}$
, we set
$\mathfrak{p}\subset \tilde{\mathfrak{p}}$
, we set
 ${\mathcal{A}}_{\mathfrak{p},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}:=\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}\,\otimes _{\mathbb{C}[\tilde{\mathfrak{p}}]}\mathbb{C}[\mathfrak{p}])$
.
${\mathcal{A}}_{\mathfrak{p},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}:=\unicode[STIX]{x1D6E4}({\mathcal{A}}_{\tilde{\mathfrak{p}},\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}\,\otimes _{\mathbb{C}[\tilde{\mathfrak{p}}]}\mathbb{C}[\mathfrak{p}])$
.
Lemma 2.3. Suppose that
 $H^{1}(X,{\mathcal{O}}(\unicode[STIX]{x1D712}))=0$
. Let
$H^{1}(X,{\mathcal{O}}(\unicode[STIX]{x1D712}))=0$
. Let
![]() $\mathfrak{p}\subset \tilde{\mathfrak{p}}$
be an affine subspace. Then
$\mathfrak{p}\subset \tilde{\mathfrak{p}}$
be an affine subspace. Then
 ${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}:=\tilde{{\mathcal{A}}}_{\mathfrak{p},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{\mathbb{C}[\mathfrak{p}]}\mathbb{C}_{\unicode[STIX]{x1D706}}$
.
${\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}:=\tilde{{\mathcal{A}}}_{\mathfrak{p},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{\mathbb{C}[\mathfrak{p}]}\mathbb{C}_{\unicode[STIX]{x1D706}}$
.
The proof repeats that of [Reference Bezrukavnikov and LosevBL13, Lemma 5.6(1)].
Let us provide a sufficient condition on
![]() $z\in \mathbb{C}$
for the algebras
$z\in \mathbb{C}$
for the algebras
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
to be simple, to have finite homological dimension and also for the localization theorem to hold.
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
to be simple, to have finite homological dimension and also for the localization theorem to hold.
Lemma 2.4. Let
![]() $\unicode[STIX]{x1D712}$
be ample and
$\unicode[STIX]{x1D712}$
be ample and
 $H^{1}(X,{\mathcal{O}}(\unicode[STIX]{x1D712}))=0$
. Then the following are true.
$H^{1}(X,{\mathcal{O}}(\unicode[STIX]{x1D712}))=0$
. Then the following are true.
-
(1) There are finitely many elements
 $z_{1},\ldots ,z_{k}\in \mathbb{C}$
such that
$z_{1},\ldots ,z_{k}\in \mathbb{C}$
such that
 $\operatorname{Loc}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is an equivalence provided
$\operatorname{Loc}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is an equivalence provided
 $z_{i}-z\not \in \mathbb{Z}_{{\geqslant}0}$
for every
$z_{i}-z\not \in \mathbb{Z}_{{\geqslant}0}$
for every
 $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
. -
(2) For a Weil generic
 $z$
, the algebra
$z$
, the algebra
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple.
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple. -
(3) For a Zariski generic
 $z\in \mathbb{C}$
, the algebra
$z\in \mathbb{C}$
, the algebra
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has finite homological dimension. This dimension does not exceed
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has finite homological dimension. This dimension does not exceed
 $\dim X$
.
$\dim X$
.
Proof. Let us prove (1); the proof is similar in spirit to those of [Reference Braden, Proudfoot and WebsterBPW16, § 5.3]. The localization holds for all parameters of the form
 $\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712}$
with
 $n\in \mathbb{Z}_{{\geqslant}0}$
if and only if the bimodules
$n\in \mathbb{Z}_{{\geqslant}0}$
if and only if the bimodules
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})},{\mathcal{A}}_{\ell ,-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+n+1)\unicode[STIX]{x1D712}}$
define mutually inverse Morita equivalences; see [Reference Braden, Proudfoot and WebsterBPW16, § 5.3]. Note that by Lemma 2.3,
${\mathcal{A}}_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})},{\mathcal{A}}_{\ell ,-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+n+1)\unicode[STIX]{x1D712}}$
define mutually inverse Morita equivalences; see [Reference Braden, Proudfoot and WebsterBPW16, § 5.3]. Note that by Lemma 2.3,
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}={\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712}}$
.
${\mathcal{A}}_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}={\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+n)\unicode[STIX]{x1D712}}$
.
The set, say
![]() $Z$
, of
$Z$
, of
![]() $z\in \mathbb{C}$
such that
$z\in \mathbb{C}$
such that
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
and
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
and
 ${\mathcal{A}}_{\ell ,-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+1)\unicode[STIX]{x1D712}}$
are mutually inverse Morita equivalences is Zariski open. The reason is that
${\mathcal{A}}_{\ell ,-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}|_{\unicode[STIX]{x1D706}+(z+1)\unicode[STIX]{x1D712}}$
are mutually inverse Morita equivalences is Zariski open. The reason is that
 $\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in Z\}$
is the locus
$\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in Z\}$
is the locus
 $\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
, where the natural homomorphisms (given by multiplication)
$\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
, where the natural homomorphisms (given by multiplication)
 $$\begin{eqnarray}{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712},-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712}}}{\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\rightarrow {\mathcal{A}}_{\ell },{\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{{\mathcal{A}}_{\ell }}{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712},-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\rightarrow {\mathcal{A}}_{\ell +\unicode[STIX]{x1D712}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712},-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712}}}{\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\rightarrow {\mathcal{A}}_{\ell },{\mathcal{A}}_{\ell ,\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\,\otimes _{{\mathcal{A}}_{\ell }}{\mathcal{A}}_{\ell +\unicode[STIX]{x1D712},-\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}\rightarrow {\mathcal{A}}_{\ell +\unicode[STIX]{x1D712}}\end{eqnarray}$$
are isomorphisms. This locus is open by Proposition 2.6 below. It is non-empty by [Reference Braden, Proudfoot and WebsterBPW16, § 5.3]. Let
 $z_{1},\ldots ,z_{k}$
be the points in
$z_{1},\ldots ,z_{k}$
be the points in
![]() $Z$
. So, we see that localization holds for
$Z$
. So, we see that localization holds for
![]() $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
if and only if
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
if and only if
 $(z+\mathbb{Z}_{{\geqslant}0})\,\cap \,\mathbb{Z}=\varnothing$
. This finishes the proof of (1).
$(z+\mathbb{Z}_{{\geqslant}0})\,\cap \,\mathbb{Z}=\varnothing$
. This finishes the proof of (1).
Let us prove (2):
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple for a Weil generic
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple for a Weil generic
![]() $z$
. Equivalently, we need to show that the
$z$
. Equivalently, we need to show that the
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\otimes {\mathcal{A}}_{-\unicode[STIX]{x1D706}-z\unicode[STIX]{x1D712}}$
-module
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\otimes {\mathcal{A}}_{-\unicode[STIX]{x1D706}-z\unicode[STIX]{x1D712}}$
-module
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple. By (1), abelian localization holds for the parameter
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is simple. By (1), abelian localization holds for the parameter
 $(\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},-\unicode[STIX]{x1D706}+(-z)\unicode[STIX]{x1D712})$
and the variety
$(\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},-\unicode[STIX]{x1D706}+(-z)\unicode[STIX]{x1D712})$
and the variety
 $X^{\unicode[STIX]{x1D703}}\times X^{\unicode[STIX]{x1D703}}$
when
$X^{\unicode[STIX]{x1D703}}\times X^{\unicode[STIX]{x1D703}}$
when
![]() $z$
is Weil generic. The module
$z$
is Weil generic. The module
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
localizes to
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
localizes to
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
. The latter is simple because it is supported on the diagonal in
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
. The latter is simple because it is supported on the diagonal in
 $X^{\unicode[STIX]{x1D703}}\times X^{\unicode[STIX]{x1D703}}$
and has rank 1. This finishes the proof of simplicity of
$X^{\unicode[STIX]{x1D703}}\times X^{\unicode[STIX]{x1D703}}$
and has rank 1. This finishes the proof of simplicity of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
for a Weil generic
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
for a Weil generic
![]() $z$
.
$z$
.
Let us proceed to (3). The homological dimension of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
does not exceed that of
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}$
does not exceed that of
 $\operatorname{gr}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}={\mathcal{O}}_{X}$
. The homological dimension of the latter does not exceed
$\operatorname{gr}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}={\mathcal{O}}_{X}$
. The homological dimension of the latter does not exceed
![]() $\dim X$
(as any quasicoherent sheaf has injective resolution of length at most
$\dim X$
(as any quasicoherent sheaf has injective resolution of length at most
![]() $\dim X$
). The algebra
$\dim X$
). The algebra
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has homological dimension equal to that of
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has homological dimension equal to that of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\pm \unicode[STIX]{x1D703}}$
provided localization holds for
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\pm \unicode[STIX]{x1D703}}$
provided localization holds for
 $(\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},\pm \unicode[STIX]{x1D703})$
. Now our claim easily follows from (1) applied to both these situations.◻
$(\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},\pm \unicode[STIX]{x1D703})$
. Now our claim easily follows from (1) applied to both these situations.◻
We will also need the following general lemma, whose proof is completely analogous to that of [Reference Bezrukavnikov and LosevBL13, Lemma 5.7].
Lemma 2.5. Let
![]() $\ell$
denote a one-dimensional vector space. Let
$\ell$
denote a one-dimensional vector space. Let
![]() $\mathfrak{A}_{\ell }$
be a filtered
$\mathfrak{A}_{\ell }$
be a filtered
![]() $\mathbb{C}[\ell ]$
-algebra such that
$\mathbb{C}[\ell ]$
-algebra such that
![]() $\ell ^{\ast }$
has degree
$\ell ^{\ast }$
has degree
![]() $d$
and
$d$
and
![]() $\operatorname{gr}\mathfrak{A}_{\ell }$
is commutative and finitely generated. Let
$\operatorname{gr}\mathfrak{A}_{\ell }$
is commutative and finitely generated. Let
![]() $M_{\ell }$
be a finitely generated
$M_{\ell }$
be a finitely generated
![]() $\mathfrak{A}_{\ell }$
-module. Then there is an open subset
$\mathfrak{A}_{\ell }$
-module. Then there is an open subset
![]() $\ell ^{0}\subset \ell$
such that
$\ell ^{0}\subset \ell$
such that
 $\mathbb{C}[\ell ^{0}]\,\otimes _{\mathbb{C}[\ell ]}M_{\ell }$
is a free
$\mathbb{C}[\ell ^{0}]\,\otimes _{\mathbb{C}[\ell ]}M_{\ell }$
is a free
![]() $\mathbb{C}[\ell ^{0}]$
-module.
$\mathbb{C}[\ell ^{0}]$
-module.
2.4 Harish-Chandra bimodules
Let us introduce the notion of a Harish-Chandra, shortly, a HC bimodule. Let
![]() ${\mathcal{A}},{\mathcal{A}}^{\prime }$
be two
${\mathcal{A}},{\mathcal{A}}^{\prime }$
be two
![]() $\mathbb{Z}_{{\geqslant}0}$
-filtered algebras. Suppose we have a fixed isomorphism
$\mathbb{Z}_{{\geqslant}0}$
-filtered algebras. Suppose we have a fixed isomorphism
 $\operatorname{gr}{\mathcal{A}}\cong \operatorname{gr}{\mathcal{A}}^{\prime }$
of graded algebras. Further, suppose that
$\operatorname{gr}{\mathcal{A}}\cong \operatorname{gr}{\mathcal{A}}^{\prime }$
of graded algebras. Further, suppose that
 $A:=\operatorname{gr}{\mathcal{A}}=\operatorname{gr}{\mathcal{A}}^{\prime }$
is finitely generated and commutative. Let
$A:=\operatorname{gr}{\mathcal{A}}=\operatorname{gr}{\mathcal{A}}^{\prime }$
is finitely generated and commutative. Let
![]() ${\mathcal{B}}$
be an
${\mathcal{B}}$
be an
![]() ${\mathcal{A}}^{\prime }$
-
${\mathcal{A}}^{\prime }$
-
![]() ${\mathcal{A}}$
-bimodule. We say that
${\mathcal{A}}$
-bimodule. We say that
![]() ${\mathcal{B}}$
is HC if it is equipped with a bimodule filtration (called good) such that
${\mathcal{B}}$
is HC if it is equipped with a bimodule filtration (called good) such that
![]() $\operatorname{gr}{\mathcal{B}}$
is a finitely generated
$\operatorname{gr}{\mathcal{B}}$
is a finitely generated
![]() $A$
-module (meaning that the left and the right actions of
$A$
-module (meaning that the left and the right actions of
![]() $A$
coincide). Note that a HC bimodule is automatically finitely generated as a left and as a right module.
$A$
coincide). Note that a HC bimodule is automatically finitely generated as a left and as a right module.
An example is as follows: let
 ${\mathcal{A}}:={\mathcal{A}}_{\unicode[STIX]{x1D706}},{\mathcal{A}}^{\prime }:={\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}$
and
${\mathcal{A}}:={\mathcal{A}}_{\unicode[STIX]{x1D706}},{\mathcal{A}}^{\prime }:={\mathcal{A}}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D712}}$
and
 ${\mathcal{B}}:={\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
. Then
${\mathcal{B}}:={\mathcal{A}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}}^{(\unicode[STIX]{x1D703})}$
. Then
![]() ${\mathcal{B}}$
is HC; see [Reference Braden, Proudfoot and WebsterBPW16, § 6.3].
${\mathcal{B}}$
is HC; see [Reference Braden, Proudfoot and WebsterBPW16, § 6.3].
Below we will need a result about the supports of HC bimodules in the parameter spaces. Namely, suppose that
![]() $\mathfrak{p}$
is a finite-dimensional vector space and let
$\mathfrak{p}$
is a finite-dimensional vector space and let
![]() ${\mathcal{A}}$
be a filtered
${\mathcal{A}}$
be a filtered
![]() $\mathbb{C}[\mathfrak{p}]$
-algebra such that
$\mathbb{C}[\mathfrak{p}]$
-algebra such that
![]() $\mathfrak{p}$
has degree
$\mathfrak{p}$
has degree
![]() $d>0$
and
$d>0$
and
 $[{\mathcal{A}}_{{\leqslant}i},{\mathcal{A}}_{{\leqslant}j}]\subset {\mathcal{A}}_{{\leqslant}i+j-d}$
. Further, suppose that
$[{\mathcal{A}}_{{\leqslant}i},{\mathcal{A}}_{{\leqslant}j}]\subset {\mathcal{A}}_{{\leqslant}i+j-d}$
. Further, suppose that
 $\operatorname{gr}{\mathcal{A}}/(\mathfrak{p})$
is finitely generated and the corresponding Poisson scheme
$\operatorname{gr}{\mathcal{A}}/(\mathfrak{p})$
is finitely generated and the corresponding Poisson scheme
![]() $X_{0}$
has finitely many symplectic leaves.
$X_{0}$
has finitely many symplectic leaves.
Now let
![]() ${\mathcal{B}}$
be a Harish-Chandra
${\mathcal{B}}$
be a Harish-Chandra
![]() ${\mathcal{A}}$
-bimodule. Define its right
${\mathcal{A}}$
-bimodule. Define its right
![]() $\mathfrak{p}$
-support
$\mathfrak{p}$
-support
 $\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
as the set of all
$\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
as the set of all
![]() $p\in \mathfrak{p}$
such that
$p\in \mathfrak{p}$
such that
 ${\mathcal{B}}\,\otimes _{\mathbb{C}[\mathfrak{p}]}\mathbb{C}_{p}\neq 0$
. Similarly, we can define the
${\mathcal{B}}\,\otimes _{\mathbb{C}[\mathfrak{p}]}\mathbb{C}_{p}\neq 0$
. Similarly, we can define the
![]() $\mathfrak{p}$
-support of
$\mathfrak{p}$
-support of
![]() $\operatorname{gr}{\mathcal{B}}$
(where the associated graded algebra is taken with respect to a good filtration) to be denoted by
$\operatorname{gr}{\mathcal{B}}$
(where the associated graded algebra is taken with respect to a good filtration) to be denoted by
 $\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})$
. The following proposition generalizes [Reference Bezrukavnikov and LosevBL13, Proposition 5.15].
$\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})$
. The following proposition generalizes [Reference Bezrukavnikov and LosevBL13, Proposition 5.15].
Proposition 2.6. The subset
 $\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})\subset \mathfrak{p}$
is Zariski closed. The associated cone of
$\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})\subset \mathfrak{p}$
is Zariski closed. The associated cone of
 $\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
coincides with
$\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
coincides with
 $\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})$
.
$\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})$
.
Proof. The proof generalizes that of [Reference Bezrukavnikov and LosevBL13, Proposition 5.15]. Namely, to
![]() ${\mathcal{B}}$
we can assign its associated variety
${\mathcal{B}}$
we can assign its associated variety
 $\operatorname{V}({\mathcal{B}})\subset X_{0}$
defined as the support of the finitely generated
$\operatorname{V}({\mathcal{B}})\subset X_{0}$
defined as the support of the finitely generated
![]() $\mathbb{C}[X_{0}]$
-module
$\mathbb{C}[X_{0}]$
-module
 $\operatorname{gr}{\mathcal{B}}/\mathfrak{p}\operatorname{gr}{\mathcal{B}}$
. It is easy to see that
$\operatorname{gr}{\mathcal{B}}/\mathfrak{p}\operatorname{gr}{\mathcal{B}}$
. It is easy to see that
 $\operatorname{gr}{\mathcal{B}}/\mathfrak{p}\operatorname{gr}{\mathcal{B}}$
is a Poisson module.
$\operatorname{gr}{\mathcal{B}}/\mathfrak{p}\operatorname{gr}{\mathcal{B}}$
is a Poisson module.
Let us order the symplectic leaves of
![]() $X_{0}$
:
$X_{0}$
:
 ${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{k}$
in such a way that
${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{k}$
in such a way that
 ${\mathcal{L}}_{i}\subset \overline{{\mathcal{L}}}_{j}$
implies that
${\mathcal{L}}_{i}\subset \overline{{\mathcal{L}}}_{j}$
implies that
![]() $i\leqslant j$
. We prove our claim by induction on
$i\leqslant j$
. We prove our claim by induction on
![]() $k$
such that
$k$
such that
 $\operatorname{V}({\mathcal{B}})\subset \bigcup _{i\leqslant k}{\mathcal{L}}_{i}$
. The base,
$\operatorname{V}({\mathcal{B}})\subset \bigcup _{i\leqslant k}{\mathcal{L}}_{i}$
. The base,
![]() $k=1$
, follows from the observation that
$k=1$
, follows from the observation that
![]() ${\mathcal{L}}_{1}$
is a single point, in which case
${\mathcal{L}}_{1}$
is a single point, in which case
![]() ${\mathcal{B}}$
is finitely generated as a module over
${\mathcal{B}}$
is finitely generated as a module over
![]() $\mathbb{C}[\mathfrak{p}]$
.
$\mathbb{C}[\mathfrak{p}]$
.
Now suppose that we know our claim for all
![]() ${\mathcal{B}}^{\prime }$
with
${\mathcal{B}}^{\prime }$
with
 $\operatorname{V}({\mathcal{B}}^{\prime })\subset \bigcup _{i\leqslant k-1}{\mathcal{L}}_{i}$
. Pick
$\operatorname{V}({\mathcal{B}}^{\prime })\subset \bigcup _{i\leqslant k-1}{\mathcal{L}}_{i}$
. Pick
![]() ${\mathcal{B}}$
with
${\mathcal{B}}$
with
 $\operatorname{V}({\mathcal{B}})\subset \bigcup _{i\leqslant k}{\mathcal{L}}_{i}$
.
$\operatorname{V}({\mathcal{B}})\subset \bigcup _{i\leqslant k}{\mathcal{L}}_{i}$
.
Equip
![]() ${\mathcal{B}}$
with a good filtration and consider the Rees bimodule
${\mathcal{B}}$
with a good filtration and consider the Rees bimodule
![]() ${\mathcal{B}}_{\hbar }$
. Pick
${\mathcal{B}}_{\hbar }$
. Pick
![]() $x\in {\mathcal{L}}_{k}$
and consider the completion
$x\in {\mathcal{L}}_{k}$
and consider the completion
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
at
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
at
![]() $x$
. It decomposes as
$x$
. It decomposes as
 ${\mathcal{B}}_{\hbar }^{\wedge _{x}}=\mathbb{A}_{\hbar }^{\wedge _{0}}\,\widehat{\otimes }_{\mathbb{C}[\hbar ]}\,\text{}\underline{{\mathcal{B}}}_{\hbar }$
, where
${\mathcal{B}}_{\hbar }^{\wedge _{x}}=\mathbb{A}_{\hbar }^{\wedge _{0}}\,\widehat{\otimes }_{\mathbb{C}[\hbar ]}\,\text{}\underline{{\mathcal{B}}}_{\hbar }$
, where
![]() $\mathbb{A}_{\hbar }$
is the homogenized Weyl algebra of the tangent space
$\mathbb{A}_{\hbar }$
is the homogenized Weyl algebra of the tangent space
![]() $T_{x}{\mathcal{L}}_{i}$
that is embedded into
$T_{x}{\mathcal{L}}_{i}$
that is embedded into
![]() ${\mathcal{A}}_{\hbar }^{\wedge _{x}}$
(compare, for example, [Reference Bezrukavnikov and LosevBL13, § 5.4]) and
${\mathcal{A}}_{\hbar }^{\wedge _{x}}$
(compare, for example, [Reference Bezrukavnikov and LosevBL13, § 5.4]) and
![]() $\text{}\underline{{\mathcal{B}}}_{\hbar }$
is the centralizer of
$\text{}\underline{{\mathcal{B}}}_{\hbar }$
is the centralizer of
![]() $\mathbb{A}_{\hbar }^{\wedge _{0}}$
in
$\mathbb{A}_{\hbar }^{\wedge _{0}}$
in
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
. By the choice of
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
. By the choice of
![]() $x$
and
$x$
and
![]() ${\mathcal{L}}_{k}$
, we see that
${\mathcal{L}}_{k}$
, we see that
![]() $\text{}\underline{{\mathcal{B}}}_{\hbar }$
is finitely generated over
$\text{}\underline{{\mathcal{B}}}_{\hbar }$
is finitely generated over
![]() $\mathbb{C}[[\mathfrak{p},\hbar ]]$
. It follows that the right
$\mathbb{C}[[\mathfrak{p},\hbar ]]$
. It follows that the right
![]() $\mathbb{C}[[\mathfrak{p},\hbar ]]$
-support of
$\mathbb{C}[[\mathfrak{p},\hbar ]]$
-support of
![]() $\text{}\underline{{\mathcal{B}}}_{\hbar }$
(that is the same as the support of
$\text{}\underline{{\mathcal{B}}}_{\hbar }$
(that is the same as the support of
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
) is the closed subscheme of the formal neighborhood of
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
) is the closed subscheme of the formal neighborhood of
![]() $0$
in
$0$
in
![]() $\mathfrak{p}\oplus \mathbb{C}$
whose intersection with
$\mathfrak{p}\oplus \mathbb{C}$
whose intersection with
![]() $\mathfrak{p}$
coincides with the
$\mathfrak{p}$
coincides with the
![]() $\mathbb{C}[[\mathfrak{p}]]$
-support of
$\mathbb{C}[[\mathfrak{p}]]$
-support of
 $(\operatorname{gr}{\mathcal{B}})^{\wedge _{x}}$
. We note that
$(\operatorname{gr}{\mathcal{B}})^{\wedge _{x}}$
. We note that
![]() ${\mathcal{B}}_{\hbar }$
comes with the Euler derivation
${\mathcal{B}}_{\hbar }$
comes with the Euler derivation
![]() $\hbar \unicode[STIX]{x2202}_{\hbar }$
. This derivation extends to
$\hbar \unicode[STIX]{x2202}_{\hbar }$
. This derivation extends to
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
. We deduce that the support of
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
. We deduce that the support of
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
is the formal neighborhood at
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
is the formal neighborhood at
![]() $0$
of a closed subvariety
$0$
of a closed subvariety
 $Z\subset \mathfrak{p}\oplus \mathbb{C}$
that is stable with respect to the
$Z\subset \mathfrak{p}\oplus \mathbb{C}$
that is stable with respect to the
![]() $\mathbb{C}^{\times }$
-action on
$\mathbb{C}^{\times }$
-action on
 $\mathfrak{p}\oplus \mathbb{C},t.(p,\unicode[STIX]{x1D6FC})=(t^{d}p,t\unicode[STIX]{x1D6FC})$
. Let
$\mathfrak{p}\oplus \mathbb{C},t.(p,\unicode[STIX]{x1D6FC})=(t^{d}p,t\unicode[STIX]{x1D6FC})$
. Let
![]() $Z_{1}$
be the intersection of
$Z_{1}$
be the intersection of
![]() $Z$
with
$Z$
with
 $\mathfrak{p}\times \{1\}$
. Let us check that
$\mathfrak{p}\times \{1\}$
. Let us check that
 $Z_{1}\subset \operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
. Indeed, let
$Z_{1}\subset \operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
. Indeed, let
![]() $z\in Z_{1}$
and
$z\in Z_{1}$
and
![]() $D$
be the formal neighborhood of
$D$
be the formal neighborhood of
![]() $0$
in
$0$
in
![]() $\mathbb{C}z$
. Then
$\mathbb{C}z$
. Then
 $({\mathcal{B}}_{\hbar }^{\wedge _{x}})\,\otimes _{\mathbb{C}[[\mathfrak{p},\hbar ]]}\mathbb{C}[D]$
coincides with
$({\mathcal{B}}_{\hbar }^{\wedge _{x}})\,\otimes _{\mathbb{C}[[\mathfrak{p},\hbar ]]}\mathbb{C}[D]$
coincides with
![]() $({\mathcal{B}}_{z_{1}})_{\hbar }^{\wedge _{x}}$
. This implies that
$({\mathcal{B}}_{z_{1}})_{\hbar }^{\wedge _{x}}$
. This implies that
 $Z_{1}\subset \operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
.
$Z_{1}\subset \operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})$
.
Moreover, consider
 $Z_{0}=Z\,\cap \,(\mathfrak{p}\times \{0\})$
. It coincides with the asymptotic cone of
$Z_{0}=Z\,\cap \,(\mathfrak{p}\times \{0\})$
. It coincides with the asymptotic cone of
![]() $Z_{1}$
, and the formal neighborhood of
$Z_{1}$
, and the formal neighborhood of
![]() $0$
in
$0$
in
![]() $Z_{0}$
is the support of
$Z_{0}$
is the support of
 $(\operatorname{gr}{\mathcal{B}})^{\wedge _{x}}$
.
$(\operatorname{gr}{\mathcal{B}})^{\wedge _{x}}$
.
Now let
![]() $I$
be the annihilator of
$I$
be the annihilator of
![]() ${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
in
${\mathcal{B}}_{\hbar }^{\wedge _{x}}$
in
![]() $\mathbb{C}[\mathfrak{p},\hbar ]$
. The corresponding subvariety in
$\mathbb{C}[\mathfrak{p},\hbar ]$
. The corresponding subvariety in
![]() $\mathfrak{p}\oplus \mathbb{C}$
is
$\mathfrak{p}\oplus \mathbb{C}$
is
![]() $Z$
. Let
$Z$
. Let
![]() $I_{1},I_{0}$
be the specializations of
$I_{1},I_{0}$
be the specializations of
![]() $I$
to
$I$
to
 $\hbar =1,\hbar =0$
, respectively. Note that
$\hbar =1,\hbar =0$
, respectively. Note that
 $({\mathcal{B}}I_{1})_{\hbar }^{\wedge _{x}}=0$
. It follows that
$({\mathcal{B}}I_{1})_{\hbar }^{\wedge _{x}}=0$
. It follows that
 $\operatorname{V}({\mathcal{B}}I_{1})\subset \bigcup _{i\leqslant k-1}{\mathcal{L}}_{i}$
. So,
$\operatorname{V}({\mathcal{B}}I_{1})\subset \bigcup _{i\leqslant k-1}{\mathcal{L}}_{i}$
. So,
 $\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}}I_{1})$
is a closed subvariety in
$\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}}I_{1})$
is a closed subvariety in
![]() $\mathfrak{p}$
and its asymptotic cone is
$\mathfrak{p}$
and its asymptotic cone is
 $\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}({\mathcal{B}}I_{1}))$
. Similarly to the proof of [Reference Bezrukavnikov and LosevBL13, Proposition 5.15], we see that
$\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}({\mathcal{B}}I_{1}))$
. Similarly to the proof of [Reference Bezrukavnikov and LosevBL13, Proposition 5.15], we see that
 $\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})=\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}}I_{1})\cup Z_{1}$
and
$\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}})=\operatorname{Supp}_{\mathfrak{p}}^{r}({\mathcal{B}}I_{1})\cup Z_{1}$
and
 $\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})=\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}({\mathcal{B}}I_{1}))\cup Z_{0}$
. Our claim follows.◻
$\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}{\mathcal{B}})=\operatorname{Supp}_{\mathfrak{p}}(\operatorname{gr}({\mathcal{B}}I_{1}))\cup Z_{0}$
. Our claim follows.◻
3 Standardly stratified categories
Here we recall the notion of a standardly stratified category following [Reference Losev and WebsterLW15, § 2] that is a refinement of the first definition of a standardly stratified category given in [Reference Cline, Parshall and ScottCPS96].
3.1 Definition
Let
![]() $\mathbb{K}$
be a field. Let
$\mathbb{K}$
be a field. Let
![]() ${\mathcal{C}}$
be a
${\mathcal{C}}$
be a
![]() $\mathbb{K}$
-linear abelian category equivalent to the category of finite-dimensional modules over a split unital associative finite-dimensional
$\mathbb{K}$
-linear abelian category equivalent to the category of finite-dimensional modules over a split unital associative finite-dimensional
![]() $\mathbb{K}$
-algebra. We will write
$\mathbb{K}$
-algebra. We will write
![]() ${\mathcal{T}}$
for an indexing set for the simple objects of
${\mathcal{T}}$
for an indexing set for the simple objects of
![]() ${\mathcal{C}}$
. Let us write
${\mathcal{C}}$
. Let us write
![]() $L(\unicode[STIX]{x1D70F})$
for the simple object indexed by
$L(\unicode[STIX]{x1D70F})$
for the simple object indexed by
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{T}}$
and
$\unicode[STIX]{x1D70F}\in {\mathcal{T}}$
and
![]() $P(\unicode[STIX]{x1D70F})$
for the projective cover of
$P(\unicode[STIX]{x1D70F})$
for the projective cover of
![]() $L(\unicode[STIX]{x1D70F})$
.
$L(\unicode[STIX]{x1D70F})$
.
The additional structure of a standardly stratified category on
![]() ${\mathcal{C}}$
is a partial pre-order
${\mathcal{C}}$
is a partial pre-order
![]() ${\leqslant}$
on
${\leqslant}$
on
![]() ${\mathcal{T}}$
that should satisfy axioms (SS1) and (SS2) to be explained below. Let us write
${\mathcal{T}}$
that should satisfy axioms (SS1) and (SS2) to be explained below. Let us write
![]() $\unicode[STIX]{x1D6EF}$
for the set of equivalence classes of
$\unicode[STIX]{x1D6EF}$
for the set of equivalence classes of
![]() ${\leqslant}$
; this is a poset (with partial order again denoted by
${\leqslant}$
; this is a poset (with partial order again denoted by
![]() ${\leqslant}$
) that comes with a natural surjection
${\leqslant}$
) that comes with a natural surjection
 $\unicode[STIX]{x1D71A}:{\mathcal{T}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}$
. The pre-order
$\unicode[STIX]{x1D71A}:{\mathcal{T}}{\twoheadrightarrow}\unicode[STIX]{x1D6EF}$
. The pre-order
![]() ${\leqslant}$
defines a filtration on
${\leqslant}$
defines a filtration on
![]() ${\mathcal{C}}$
by Serre subcategories indexed by
${\mathcal{C}}$
by Serre subcategories indexed by
![]() $\unicode[STIX]{x1D6EF}$
. Namely, to
$\unicode[STIX]{x1D6EF}$
. Namely, to
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}$
we assign the subcategory
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}$
we assign the subcategory
![]() ${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
that is the Serre span of the simples
${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
that is the Serre span of the simples
![]() $L(\unicode[STIX]{x1D70F})$
with
$L(\unicode[STIX]{x1D70F})$
with
 $\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\leqslant \unicode[STIX]{x1D709}$
. Define
$\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\leqslant \unicode[STIX]{x1D709}$
. Define
![]() ${\mathcal{C}}_{{<}\unicode[STIX]{x1D709}}$
analogously and let
${\mathcal{C}}_{{<}\unicode[STIX]{x1D709}}$
analogously and let
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
denote the quotient
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
denote the quotient
 ${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}/{\mathcal{C}}_{{<}\unicode[STIX]{x1D709}}$
. Let
${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}/{\mathcal{C}}_{{<}\unicode[STIX]{x1D709}}$
. Let
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
denote the quotient functor
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
denote the quotient functor
 ${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}{\twoheadrightarrow}{\mathcal{C}}_{\unicode[STIX]{x1D709}}$
. Let us write
${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}{\twoheadrightarrow}{\mathcal{C}}_{\unicode[STIX]{x1D709}}$
. Let us write
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}:{\mathcal{C}}_{\unicode[STIX]{x1D709}}\rightarrow {\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
for the left adjoint functor of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}:{\mathcal{C}}_{\unicode[STIX]{x1D709}}\rightarrow {\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
for the left adjoint functor of
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
; it exists because
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
; it exists because
![]() ${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
is equivalent to the category of modules over a finite-dimensional associative algebra and
${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
is equivalent to the category of modules over a finite-dimensional associative algebra and
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is a quotient functor (and so is given by taking Hom from a suitable bimodule). Also, we write
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is a quotient functor (and so is given by taking Hom from a suitable bimodule). Also, we write
![]() $\operatorname{gr}{\mathcal{C}}$
for
$\operatorname{gr}{\mathcal{C}}$
for
 $\bigoplus _{\unicode[STIX]{x1D709}}{\mathcal{C}}_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6E5}$
for
$\bigoplus _{\unicode[STIX]{x1D709}}{\mathcal{C}}_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6E5}$
for
 $\bigoplus _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}:\operatorname{gr}{\mathcal{C}}\rightarrow {\mathcal{C}}$
. Finally, for
$\bigoplus _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}:\operatorname{gr}{\mathcal{C}}\rightarrow {\mathcal{C}}$
. Finally, for
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D709})$
, we write
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D709})$
, we write
![]() $L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
for
$L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
for
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}(L(\unicode[STIX]{x1D70F}))$
,
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}(L(\unicode[STIX]{x1D70F}))$
,
![]() $P_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
for the projective cover of
$P_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
for the projective cover of
![]() $L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
in
$L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
and
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
and
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
for
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
for
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(P_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
. The object
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(P_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
. The object
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
is called standard. The object
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
is called standard. The object
 $\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}):=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
is called proper standard.
$\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}):=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
is called proper standard.
The axioms to be satisfied by
![]() $({\mathcal{C}},\leqslant )$
in order to give a standardly stratified structure are as follows.
$({\mathcal{C}},\leqslant )$
in order to give a standardly stratified structure are as follows.
-
(SS1) The functor
 $\unicode[STIX]{x1D6E5}:\operatorname{gr}{\mathcal{C}}\rightarrow {\mathcal{C}}$
is exact.
$\unicode[STIX]{x1D6E5}:\operatorname{gr}{\mathcal{C}}\rightarrow {\mathcal{C}}$
is exact. -
(SS2) The kernel of
 $P(\unicode[STIX]{x1D70F}){\twoheadrightarrow}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
has a filtration with successive quotients
$P(\unicode[STIX]{x1D70F}){\twoheadrightarrow}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
has a filtration with successive quotients
 $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}^{\prime })$
, where
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}^{\prime })$
, where
 $\unicode[STIX]{x1D70F}^{\prime }>\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}^{\prime }>\unicode[STIX]{x1D70F}$
.
Note that (SS1) allows us to identify
 $K_{0}(\operatorname{gr}{\mathcal{C}})$
and
$K_{0}(\operatorname{gr}{\mathcal{C}})$
and
![]() $K_{0}({\mathcal{C}})$
by means of
$K_{0}({\mathcal{C}})$
by means of
![]() $\unicode[STIX]{x1D6E5}$
. If (SS2) holds as well, then we also have the identification of
$\unicode[STIX]{x1D6E5}$
. If (SS2) holds as well, then we also have the identification of
 $K_{0}(\operatorname{gr}{\mathcal{C}}\text{-}\!\operatorname{proj})$
and
$K_{0}(\operatorname{gr}{\mathcal{C}}\text{-}\!\operatorname{proj})$
and
 $K_{0}({\mathcal{C}}\text{-}\!\operatorname{proj})$
.
$K_{0}({\mathcal{C}}\text{-}\!\operatorname{proj})$
.
If all quotient categories
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
are equivalent to
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
are equivalent to
![]() $\operatorname{Vect}$
, then we recover the classical definition of a highest-weight category. On the opposite end, if we take the trivial pre-order on
$\operatorname{Vect}$
, then we recover the classical definition of a highest-weight category. On the opposite end, if we take the trivial pre-order on
![]() ${\mathcal{T}}$
, then there is no additional structure.
${\mathcal{T}}$
, then there is no additional structure.
3.2 (Proper) standardly filtered objects
We say that an object in
![]() ${\mathcal{C}}$
is standardly filtered if it admits a filtration whose successive quotients are standard. The notion of a proper standardly filtered object is introduced in a similar fashion. The categories of the standardly filtered objects and of the proper standardly filtered objects will be denoted by
${\mathcal{C}}$
is standardly filtered if it admits a filtration whose successive quotients are standard. The notion of a proper standardly filtered object is introduced in a similar fashion. The categories of the standardly filtered objects and of the proper standardly filtered objects will be denoted by
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6E5}}$
and
${\mathcal{C}}^{\unicode[STIX]{x1D6E5}}$
and
![]() ${\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
. Note that (SS1) implies that
${\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
. Note that (SS1) implies that
 ${\mathcal{C}}^{\unicode[STIX]{x1D6E5}}\subset {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
${\mathcal{C}}^{\unicode[STIX]{x1D6E5}}\subset {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
Also, note that in a standardly stratified category the following hold:
 $$\begin{eqnarray}\displaystyle & \operatorname{Ext}_{{\mathcal{C}}}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(N))\neq 0\Rightarrow \unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Ext}_{{\mathcal{C}}}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(N))\neq 0\Rightarrow \unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \operatorname{Ext}_{{\mathcal{C}}}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(N))=\operatorname{Ext}_{{\mathcal{C}}_{\unicode[STIX]{x1D709}}}^{i}(M,N). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Ext}_{{\mathcal{C}}}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(N))=\operatorname{Ext}_{{\mathcal{C}}_{\unicode[STIX]{x1D709}}}^{i}(M,N). & \displaystyle\end{eqnarray}$$
3.3 Subcategories and quotients
Suppose that
![]() ${\mathcal{C}}$
is standardly stratified.
${\mathcal{C}}$
is standardly stratified.
Let
![]() $\unicode[STIX]{x1D6EF}_{0}$
be a poset ideal in
$\unicode[STIX]{x1D6EF}_{0}$
be a poset ideal in
![]() $\unicode[STIX]{x1D6EF}$
. Let
$\unicode[STIX]{x1D6EF}$
. Let
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
denote the Serre span of the simples
${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
denote the Serre span of the simples
![]() $L(\unicode[STIX]{x1D70F})$
with
$L(\unicode[STIX]{x1D70F})$
with
 $\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\in \unicode[STIX]{x1D6EF}_{0}$
. Then
$\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\in \unicode[STIX]{x1D6EF}_{0}$
. Then
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
is a standardly stratified category with pre-order on
${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
is a standardly stratified category with pre-order on
 ${\mathcal{T}}_{0}:=\unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D6EF}_{0})$
restricted from
${\mathcal{T}}_{0}:=\unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D6EF}_{0})$
restricted from
![]() $\unicode[STIX]{x1D6EF}$
. Note that, for
$\unicode[STIX]{x1D6EF}$
. Note that, for
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{T}}_{0}$
, we have
$\unicode[STIX]{x1D70F}\in {\mathcal{T}}_{0}$
, we have
 $\overline{\unicode[STIX]{x1D6E5}}_{\unicode[STIX]{x1D6EF}_{0}}(\unicode[STIX]{x1D70F})=\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}_{0}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
, where the subscript
$\overline{\unicode[STIX]{x1D6E5}}_{\unicode[STIX]{x1D6EF}_{0}}(\unicode[STIX]{x1D70F})=\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6EF}_{0}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
, where the subscript
![]() $\unicode[STIX]{x1D6EF}_{0}$
refers to the objects computed in
$\unicode[STIX]{x1D6EF}_{0}$
refers to the objects computed in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
.
${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
.
The embedding
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}:{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}^{\overline{\unicode[STIX]{x1D6E5}}}{\hookrightarrow}{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
admits a left adjoint functor
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}:{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}^{\overline{\unicode[STIX]{x1D6E5}}}{\hookrightarrow}{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
admits a left adjoint functor
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
: to an object
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
: to an object
 $M\in {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
, this functor assigns the maximal quotient lying in
$M\in {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
, this functor assigns the maximal quotient lying in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
The following lemma will be of importance in the sequel.
Lemma 3.1. The natural functor
 $D^{-}({\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}})\rightarrow D^{-}({\mathcal{C}})$
is a fully faithful embedding.
$D^{-}({\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}})\rightarrow D^{-}({\mathcal{C}})$
is a fully faithful embedding.
Proof. Let
![]() $P_{\bullet }$
be a projective resolution (in
$P_{\bullet }$
be a projective resolution (in
![]() ${\mathcal{C}}$
) of
${\mathcal{C}}$
) of
 $M\in {\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. Then
$M\in {\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. Then
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}P_{\bullet }$
is easily seen to be exact. So, it is a projective resolution of
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}P_{\bullet }$
is easily seen to be exact. So, it is a projective resolution of
![]() $M$
in
$M$
in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. It follows that for
${\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. It follows that for
 $M,N\in {\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
, we have
$M,N\in {\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
, we have
 $$\begin{eqnarray}\operatorname{Ext}_{{\mathcal{C}}}^{i}(M,N)=\operatorname{Ext}_{{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}}^{i}(M,N).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{{\mathcal{C}}}^{i}(M,N)=\operatorname{Ext}_{{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}}^{i}(M,N).\end{eqnarray}$$
This completes the proof.◻
Now let
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
be the quotient category
${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
be the quotient category
![]() ${\mathcal{C}}/{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. Let
${\mathcal{C}}/{\mathcal{C}}_{\unicode[STIX]{x1D6EF}_{0}}$
. Let
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}$
denote the quotient functor
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}$
denote the quotient functor
 ${\mathcal{C}}\rightarrow {\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
and let
${\mathcal{C}}\rightarrow {\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
and let
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
be its left adjoint. The category
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
be its left adjoint. The category
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
is standardly stratified with pre-order on
${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
is standardly stratified with pre-order on
 ${\mathcal{T}}^{0}:={\mathcal{T}}\setminus {\mathcal{T}}_{0}$
restricted from
${\mathcal{T}}^{0}:={\mathcal{T}}\setminus {\mathcal{T}}_{0}$
restricted from
![]() ${\mathcal{T}}$
. For
${\mathcal{T}}$
. For
 $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}^{0}:=\unicode[STIX]{x1D6EF}\setminus \unicode[STIX]{x1D6EF}_{0}$
, let
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}^{0}:=\unicode[STIX]{x1D6EF}\setminus \unicode[STIX]{x1D6EF}_{0}$
, let
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{0}$
denote the standardization functor for
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{0}$
denote the standardization functor for
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
. Then we have
${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
. Then we have
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{0}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Let us also point out that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{0}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Let us also point out that
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
defines a full embedding
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6EF}_{0}}^{!}$
defines a full embedding
 $({\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}})^{\overline{\unicode[STIX]{x1D6E5}}}{\hookrightarrow}{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
whose image coincides with the full subcategory
$({\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}})^{\overline{\unicode[STIX]{x1D6E5}}}{\hookrightarrow}{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
whose image coincides with the full subcategory
![]() ${\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}},{\mathcal{T}}^{0}}$
consisting of all objects that admit a filtration with successive quotients
${\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}},{\mathcal{T}}^{0}}$
consisting of all objects that admit a filtration with successive quotients
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
with
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
with
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{T}}^{0}$
. This embedding sends
$\unicode[STIX]{x1D70F}\in {\mathcal{T}}^{0}$
. This embedding sends
![]() $\unicode[STIX]{x1D6E5}^{0}(\unicode[STIX]{x1D70F})$
to
$\unicode[STIX]{x1D6E5}^{0}(\unicode[STIX]{x1D70F})$
to
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
,
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
,
![]() $P^{0}(\unicode[STIX]{x1D70F})$
to
$P^{0}(\unicode[STIX]{x1D70F})$
to
![]() $P(\unicode[STIX]{x1D70F})$
(here
$P(\unicode[STIX]{x1D70F})$
(here
 $\unicode[STIX]{x1D6E5}^{0}(\unicode[STIX]{x1D70F}),P^{0}(\unicode[STIX]{x1D70F})$
are the standard and projective objects in
$\unicode[STIX]{x1D6E5}^{0}(\unicode[STIX]{x1D70F}),P^{0}(\unicode[STIX]{x1D70F})$
are the standard and projective objects in
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
labelled by
${\mathcal{C}}^{\unicode[STIX]{x1D6EF}_{0}}$
labelled by
![]() $\unicode[STIX]{x1D70F}$
).
$\unicode[STIX]{x1D70F}$
).
3.4 Opposite category
Let
![]() ${\mathcal{C}}$
be a standardly stratified category. It turns out that the opposite category
${\mathcal{C}}$
be a standardly stratified category. It turns out that the opposite category
![]() ${\mathcal{C}}^{\text{opp}}$
is also standardly stratified with the same pre-order
${\mathcal{C}}^{\text{opp}}$
is also standardly stratified with the same pre-order
![]() ${\leqslant}$
; see [Reference Losev and WebsterLW15, § 2.2]. The standard and proper standard objects for
${\leqslant}$
; see [Reference Losev and WebsterLW15, § 2.2]. The standard and proper standard objects for
![]() ${\mathcal{C}}^{\text{opp}}$
are denoted by
${\mathcal{C}}^{\text{opp}}$
are denoted by
![]() $\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F})$
and
![]() $\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F})$
. When viewed as objects of
$\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F})$
. When viewed as objects of
![]() ${\mathcal{C}}$
, they are called costandard and proper costandard. The right adjoint functor to
${\mathcal{C}}$
, they are called costandard and proper costandard. The right adjoint functor to
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
will be denoted by
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
will be denoted by
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
and we write
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
and we write
![]() $\unicode[STIX]{x1D6FB}$
for
$\unicode[STIX]{x1D6FB}$
for
![]() $\bigoplus _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
. So, we have
$\bigoplus _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
. So, we have
 $\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FB}(L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
and
$\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FB}(L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
and
 $\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FB}(I_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
, where
$\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FB}(I_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F}))$
, where
![]() $I_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
is the injective envelope of
$I_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
is the injective envelope of
![]() $L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
in
$L_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70F})$
in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
.
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
.
Let us write
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D6FB}},{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6FB}}}$
for the subcategories of costandardly filtered objects. We have the following standard lemma.
${\mathcal{C}}^{\unicode[STIX]{x1D6FB}},{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6FB}}}$
for the subcategories of costandardly filtered objects. We have the following standard lemma.
Lemma 3.2 (Lemma 2.5 in [Reference Losev and WebsterLW15]).
The following are true.
-
(1)
 $\dim \operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}),\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F}^{\prime }))=\dim \operatorname{Ext}^{i}(\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F}^{\prime }))=\unicode[STIX]{x1D6FF}_{i,0}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}^{\prime }}$
.
$\dim \operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}),\overline{\unicode[STIX]{x1D6FB}}(\unicode[STIX]{x1D70F}^{\prime }))=\dim \operatorname{Ext}^{i}(\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D70F}^{\prime }))=\unicode[STIX]{x1D6FF}_{i,0}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}^{\prime }}$
. -
(2) For
 $N\in {\mathcal{C}}$
, we have
$N\in {\mathcal{C}}$
, we have
 $N\in {\mathcal{C}}^{\unicode[STIX]{x1D6FB}}$
(respectively,
$N\in {\mathcal{C}}^{\unicode[STIX]{x1D6FB}}$
(respectively,
 $N\in {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6FB}}}$
) if and only if
$N\in {\mathcal{C}}^{\overline{\unicode[STIX]{x1D6FB}}}$
) if and only if
 $\operatorname{Ext}^{1}(\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),N)=0$
(respectively,
$\operatorname{Ext}^{1}(\overline{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70F}),N)=0$
(respectively,
 $\operatorname{Ext}^{1}(\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}),N)=0$
) for all
$\operatorname{Ext}^{1}(\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F}),N)=0$
) for all
 $\unicode[STIX]{x1D70F}$
. Similar characterizations hold for
$\unicode[STIX]{x1D70F}$
. Similar characterizations hold for
 ${\mathcal{C}}^{\unicode[STIX]{x1D6E5}},{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
${\mathcal{C}}^{\unicode[STIX]{x1D6E5}},{\mathcal{C}}^{\overline{\unicode[STIX]{x1D6E5}}}$
.
Let us also note the following fact.
Lemma 3.3. Suppose that (SS1) holds as well as the following weaker version of (SS2):
![]() $P(\unicode[STIX]{x1D70F})$
admits an epimorphism onto
$P(\unicode[STIX]{x1D70F})$
admits an epimorphism onto
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
and the kernel admits a filtration with subquotients of the form
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})$
and the kernel admits a filtration with subquotients of the form
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M_{\unicode[STIX]{x1D709}})$
for
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M_{\unicode[STIX]{x1D709}})$
for
 $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})$
and
 $M_{\unicode[STIX]{x1D709}}\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
(unlike in (SS2), we do not require
$M_{\unicode[STIX]{x1D709}}\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
(unlike in (SS2), we do not require
![]() $M_{\unicode[STIX]{x1D709}}$
to be projective; note that we do not require that the labels
$M_{\unicode[STIX]{x1D709}}$
to be projective; note that we do not require that the labels
![]() $\unicode[STIX]{x1D709}$
are ordered either). Then
$\unicode[STIX]{x1D709}$
are ordered either). Then
![]() ${\mathcal{C}}$
is standardly stratified if and only if the right adjoint
${\mathcal{C}}$
is standardly stratified if and only if the right adjoint
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
of
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
of
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is exact for all
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is exact for all
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Proof. It remains to show that if
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
is exact, then (SS2) holds. Note that the weaker version of (SS2) implies that if
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}$
is exact, then (SS2) holds. Note that the weaker version of (SS2) implies that if
 $\operatorname{Ext}^{1}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(M^{\prime }))\neq 0$
, then
$\operatorname{Ext}^{1}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M),\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(M^{\prime }))\neq 0$
, then
![]() $\unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}^{\prime }$
. So, we can assume in our filtration that every
$\unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}^{\prime }$
. So, we can assume in our filtration that every
![]() $\unicode[STIX]{x1D709}$
appears at most once.
$\unicode[STIX]{x1D709}$
appears at most once.
Set
 $\unicode[STIX]{x1D6EF}_{0}:=\{\unicode[STIX]{x1D709}^{\prime }\in \unicode[STIX]{x1D6EF}\mid \unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}\}$
. The object
$\unicode[STIX]{x1D6EF}_{0}:=\{\unicode[STIX]{x1D709}^{\prime }\in \unicode[STIX]{x1D6EF}\mid \unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}\}$
. The object
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}(P(\unicode[STIX]{x1D70F}))$
is projective in
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}(P(\unicode[STIX]{x1D70F}))$
is projective in
![]() ${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
if
${\mathcal{C}}_{{\leqslant}\unicode[STIX]{x1D709}}$
if
 $\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\leqslant \unicode[STIX]{x1D709}$
and is zero otherwise. It is filtered with
$\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\leqslant \unicode[STIX]{x1D709}$
and is zero otherwise. It is filtered with
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(M_{\unicode[STIX]{x1D709}^{\prime }})$
for
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{\prime }}(M_{\unicode[STIX]{x1D709}^{\prime }})$
for
![]() $\unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}$
. Since
$\unicode[STIX]{x1D709}^{\prime }\leqslant \unicode[STIX]{x1D709}$
. Since
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
has an exact right adjoint, the object
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
has an exact right adjoint, the object
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}(P(\unicode[STIX]{x1D70F})))$
is projective. But this object is
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D6EF}_{0}}^{!}(P(\unicode[STIX]{x1D70F})))$
is projective. But this object is
![]() $M_{\unicode[STIX]{x1D709}}$
. So,
$M_{\unicode[STIX]{x1D709}}$
. So,
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M_{\unicode[STIX]{x1D709}})$
is the sum of standard objects and (SS2) follows.◻
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}(M_{\unicode[STIX]{x1D709}})$
is the sum of standard objects and (SS2) follows.◻
3.5 Compatible standardly stratified structures
Now suppose that
![]() ${\mathcal{C}}$
is a highest-weight category with set of simples
${\mathcal{C}}$
is a highest-weight category with set of simples
![]() ${\mathcal{T}}$
and partial order
${\mathcal{T}}$
and partial order
![]() ${\leqslant}$
. Consider a pre-order
${\leqslant}$
. Consider a pre-order
![]() $\preccurlyeq$
on
$\preccurlyeq$
on
![]() ${\mathcal{T}}$
refined by
${\mathcal{T}}$
refined by
![]() ${\leqslant}$
, meaning that
${\leqslant}$
, meaning that
![]() $\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}^{\prime }$
implies that
$\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}^{\prime }$
implies that
![]() $\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70F}^{\prime }$
. We say that
$\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70F}^{\prime }$
. We say that
![]() $\preccurlyeq$
is standardly stratified if
$\preccurlyeq$
is standardly stratified if
![]() $({\mathcal{C}},\preccurlyeq )$
is a standardly stratified category. The corresponding standardly stratified structure will be called compatible with the initial highest-weight structure.
$({\mathcal{C}},\preccurlyeq )$
is a standardly stratified category. The corresponding standardly stratified structure will be called compatible with the initial highest-weight structure.
The following lemma gives a criterion for
![]() $\preccurlyeq$
to be standardly stratified. Namely, pick an equivalence class
$\preccurlyeq$
to be standardly stratified. Namely, pick an equivalence class
![]() $\unicode[STIX]{x1D709}$
for
$\unicode[STIX]{x1D709}$
for
![]() $\preccurlyeq$
. Let
$\preccurlyeq$
. Let
![]() $\unicode[STIX]{x1D71A}$
be the surjection from
$\unicode[STIX]{x1D71A}$
be the surjection from
![]() ${\mathcal{T}}$
to the set
${\mathcal{T}}$
to the set
![]() $\unicode[STIX]{x1D6EF}$
of equivalence classes for
$\unicode[STIX]{x1D6EF}$
of equivalence classes for
![]() $\preccurlyeq$
. Set
$\preccurlyeq$
. Set
 ${\mathcal{T}}_{0}:=\{\unicode[STIX]{x1D70F}\mid \unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\preccurlyeq \unicode[STIX]{x1D709}\}$
. Since
${\mathcal{T}}_{0}:=\{\unicode[STIX]{x1D70F}\mid \unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})\preccurlyeq \unicode[STIX]{x1D709}\}$
. Since
![]() ${\leqslant}$
refines
${\leqslant}$
refines
![]() $\preccurlyeq$
, we see that
$\preccurlyeq$
, we see that
![]() ${\mathcal{T}}_{0}$
is a poset ideal for
${\mathcal{T}}_{0}$
is a poset ideal for
![]() ${\leqslant}$
. For the same reason,
${\leqslant}$
. For the same reason,
![]() $\unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D709})$
is an interval for
$\unicode[STIX]{x1D71A}^{-1}(\unicode[STIX]{x1D709})$
is an interval for
![]() ${\leqslant}$
. It follows that the subquotient
${\leqslant}$
. It follows that the subquotient
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
of
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
of
![]() ${\mathcal{C}}$
corresponding to
${\mathcal{C}}$
corresponding to
![]() $\unicode[STIX]{x1D709}$
has a natural highest-weight structure.
$\unicode[STIX]{x1D709}$
has a natural highest-weight structure.
Let
 $\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}:{\mathcal{C}}_{{\mathcal{T}}_{0}}{\hookrightarrow}{\mathcal{C}}$
be an inclusion. For a standardly filtered object
$\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}:{\mathcal{C}}_{{\mathcal{T}}_{0}}{\hookrightarrow}{\mathcal{C}}$
be an inclusion. For a standardly filtered object
![]() $M\in {\mathcal{C}}$
, define an object
$M\in {\mathcal{C}}$
, define an object
 $M(\unicode[STIX]{x1D709})\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
as
$M(\unicode[STIX]{x1D709})\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
as
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}\circ \unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{!}(M)$
. The object
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}\circ \unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{!}(M)$
. The object
![]() $M(\unicode[STIX]{x1D709})$
is standardly filtered.
$M(\unicode[STIX]{x1D709})$
is standardly filtered.
Similarly, for a costandardly filtered object
![]() $N$
, we can define
$N$
, we can define
![]() $N(\unicode[STIX]{x1D709})$
in a similar way (but we need to use the right adjoint
$N(\unicode[STIX]{x1D709})$
in a similar way (but we need to use the right adjoint
![]() $\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{\ast }$
instead of the left adjoint
$\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{\ast }$
instead of the left adjoint
![]() $\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{!}$
).
$\unicode[STIX]{x1D704}_{{\mathcal{T}}_{0}}^{!}$
).
Lemma 3.4. The following are equivalent.
-
(1) The partial order
 $\preccurlyeq$
is standardly stratified.
$\preccurlyeq$
is standardly stratified. -
(2) For any projective
 $P\in {\mathcal{C}}$
and any injective
$P\in {\mathcal{C}}$
and any injective
 $I\in {\mathcal{C}}$
, the objects
$I\in {\mathcal{C}}$
, the objects
 $P(\unicode[STIX]{x1D709}),I(\unicode[STIX]{x1D709})\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
are projective and injective, respectively.
$P(\unicode[STIX]{x1D709}),I(\unicode[STIX]{x1D709})\in {\mathcal{C}}_{\unicode[STIX]{x1D709}}$
are projective and injective, respectively.
Proof. If (1) holds, then (2) is just (SS2) for
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{C}}^{\text{opp}}$
.
${\mathcal{C}}^{\text{opp}}$
.
Since
![]() $I(\unicode[STIX]{x1D709})$
is injective in
$I(\unicode[STIX]{x1D709})$
is injective in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
, for any injective object
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
, for any injective object
![]() $I\in {\mathcal{C}}$
, we see that
$I\in {\mathcal{C}}$
, we see that
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
sends injective objects in
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
sends injective objects in
![]() ${\mathcal{C}}_{{\mathcal{T}}_{0}}$
to injective objects in
${\mathcal{C}}_{{\mathcal{T}}_{0}}$
to injective objects in
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
. It follows that
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
. It follows that
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
, the left adjoint to
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
, the left adjoint to
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
, is exact, which is (SS1).◻
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
, is exact, which is (SS1).◻
Conversely, let
![]() ${\mathcal{C}}$
be a standardly stratified category with respect to a pre-order
${\mathcal{C}}$
be a standardly stratified category with respect to a pre-order
![]() $\preccurlyeq$
. Suppose that each
$\preccurlyeq$
. Suppose that each
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
is highest weight with respect to an order
${\mathcal{C}}_{\unicode[STIX]{x1D709}}$
is highest weight with respect to an order
![]() ${\leqslant}_{\unicode[STIX]{x1D709}}$
for all
${\leqslant}_{\unicode[STIX]{x1D709}}$
for all
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}$
. Then
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D6EF}$
. Then
![]() ${\mathcal{C}}$
is highest weight with respect to the order
${\mathcal{C}}$
is highest weight with respect to the order
![]() ${\leqslant}$
defined as follows:
${\leqslant}$
defined as follows:
![]() $\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}^{\prime }$
if and only if either
$\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}^{\prime }$
if and only if either
![]() $\unicode[STIX]{x1D70F}\prec \unicode[STIX]{x1D70F}^{\prime }$
or
$\unicode[STIX]{x1D70F}\prec \unicode[STIX]{x1D70F}^{\prime }$
or
![]() $\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}^{\prime }$
and
$\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D70F}^{\prime }$
and
![]() $\unicode[STIX]{x1D70F}\leqslant _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D70F}^{\prime }$
for
$\unicode[STIX]{x1D70F}\leqslant _{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D70F}^{\prime }$
for
 $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})$
.
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D70F})$
.
4 Categories
 ${\mathcal{O}}$
${\mathcal{O}}$
4.1 Cartan subquotient: algebra level
Let
 ${\mathcal{A}}=\bigcup _{i\in \mathbb{Z}}{\mathcal{A}}_{{\leqslant}i}$
be a filtered associative algebra (with a complete and separated filtration) such that
${\mathcal{A}}=\bigcup _{i\in \mathbb{Z}}{\mathcal{A}}_{{\leqslant}i}$
be a filtered associative algebra (with a complete and separated filtration) such that
 $[{\mathcal{A}}_{{\leqslant}i},{\mathcal{A}}_{{\leqslant}j}]\subset {\mathcal{A}}_{{\leqslant}i+j-d}$
for some
$[{\mathcal{A}}_{{\leqslant}i},{\mathcal{A}}_{{\leqslant}j}]\subset {\mathcal{A}}_{{\leqslant}i+j-d}$
for some
 $d\in \mathbb{Z}_{{>}0}$
. The algebra
$d\in \mathbb{Z}_{{>}0}$
. The algebra
![]() $\operatorname{gr}{\mathcal{A}}$
is commutative and we require that it is finitely generated.
$\operatorname{gr}{\mathcal{A}}$
is commutative and we require that it is finitely generated.
Suppose that
![]() ${\mathcal{A}}$
is equipped with a pro-rational Hamiltonian
${\mathcal{A}}$
is equipped with a pro-rational Hamiltonian
![]() $\mathbb{C}^{\times }$
-action
$\mathbb{C}^{\times }$
-action
![]() $\unicode[STIX]{x1D708}$
that preserves the filtration (pro-rational means that the action of
$\unicode[STIX]{x1D708}$
that preserves the filtration (pro-rational means that the action of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
![]() ${\mathcal{A}}/{\mathcal{A}}_{{\leqslant}i}$
is rational for all
${\mathcal{A}}/{\mathcal{A}}_{{\leqslant}i}$
is rational for all
![]() $i$
). Let
$i$
). Let
![]() $h\in {\mathcal{A}}$
be the image of
$h\in {\mathcal{A}}$
be the image of
![]() $1$
under the comoment map and let
$1$
under the comoment map and let
![]() ${\mathcal{A}}^{i}$
denote the
${\mathcal{A}}^{i}$
denote the
![]() $i$
th graded component, so that
$i$
th graded component, so that
 ${\mathcal{A}}^{i}:=\{a\mid [h,a]=ia\}$
. We set
${\mathcal{A}}^{i}:=\{a\mid [h,a]=ia\}$
. We set
 ${\mathcal{A}}^{{\geqslant}0}:=\bigoplus _{i\geqslant 0}{\mathcal{A}}^{i},{\mathcal{A}}^{{>}0}:=\bigoplus _{i>0}{\mathcal{A}}^{i},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}):={\mathcal{A}}^{{\geqslant}0}/({\mathcal{A}}^{{\geqslant}0}\,\cap \,{\mathcal{A}}{\mathcal{A}}^{{>}0})$
. Note that
${\mathcal{A}}^{{\geqslant}0}:=\bigoplus _{i\geqslant 0}{\mathcal{A}}^{i},{\mathcal{A}}^{{>}0}:=\bigoplus _{i>0}{\mathcal{A}}^{i},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}):={\mathcal{A}}^{{\geqslant}0}/({\mathcal{A}}^{{\geqslant}0}\,\cap \,{\mathcal{A}}{\mathcal{A}}^{{>}0})$
. Note that
 ${\mathcal{A}}^{{\geqslant}0}\,\cap \,{\mathcal{A}}{\mathcal{A}}^{{>}0}$
is a two-sided ideal in
${\mathcal{A}}^{{\geqslant}0}\,\cap \,{\mathcal{A}}{\mathcal{A}}^{{>}0}$
is a two-sided ideal in
![]() ${\mathcal{A}}^{{\geqslant}0}$
. We have a natural isomorphism
${\mathcal{A}}^{{\geqslant}0}$
. We have a natural isomorphism
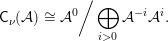 $$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\cong {\mathcal{A}}^{0}\bigg/\bigoplus _{i>0}{\mathcal{A}}^{-i}{\mathcal{A}}^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\cong {\mathcal{A}}^{0}\bigg/\bigoplus _{i>0}{\mathcal{A}}^{-i}{\mathcal{A}}^{i}.\end{eqnarray}$$
The algebra
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
inherits a filtration from
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
inherits a filtration from
![]() ${\mathcal{A}}$
. This filtration is complete and separated as any two-sided ideal in
${\mathcal{A}}$
. This filtration is complete and separated as any two-sided ideal in
![]() ${\mathcal{A}}^{0}$
is closed with respect to the topology induced by the filtration; compare [Reference LosevLos11, Lemma 2.4.4]. The algebra
${\mathcal{A}}^{0}$
is closed with respect to the topology induced by the filtration; compare [Reference LosevLos11, Lemma 2.4.4]. The algebra
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is commutative and, being a quotient of
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is commutative and, being a quotient of
 $(\operatorname{gr}{\mathcal{A}})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, finitely generated.
$(\operatorname{gr}{\mathcal{A}})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, finitely generated.
Let us note that the definitions of
 ${\mathcal{A}}^{{>}0},{\mathcal{A}}^{{\geqslant}0},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
make sense even if the action
${\mathcal{A}}^{{>}0},{\mathcal{A}}^{{\geqslant}0},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
make sense even if the action
![]() $\unicode[STIX]{x1D708}$
is not Hamiltonian.
$\unicode[STIX]{x1D708}$
is not Hamiltonian.
4.2 Categories
 ${\mathcal{O}}$
: algebra level
${\mathcal{O}}$
: algebra level
Let
![]() ${\mathcal{A}}$
be as in § 4.1 and assume that the filtration mentioned there is by
${\mathcal{A}}$
be as in § 4.1 and assume that the filtration mentioned there is by
![]() $\mathbb{Z}_{{\geqslant}0}$
. By the category
$\mathbb{Z}_{{\geqslant}0}$
. By the category
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
, we mean the full subcategory of the category
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
, we mean the full subcategory of the category
![]() ${\mathcal{A}}\text{-}\!\operatorname{mod}$
of the finitely generated
${\mathcal{A}}\text{-}\!\operatorname{mod}$
of the finitely generated
![]() ${\mathcal{A}}$
-modules consisting of all modules such that
${\mathcal{A}}$
-modules consisting of all modules such that
![]() ${\mathcal{A}}^{{>}0}$
acts locally nilpotently. We have the Verma module functor
${\mathcal{A}}^{{>}0}$
acts locally nilpotently. We have the Verma module functor
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
given by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
given by
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N):={\mathcal{A}}\,\otimes _{{\mathcal{A}}^{{\geqslant}0}}N=({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}N$
. Note that if
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N):={\mathcal{A}}\,\otimes _{{\mathcal{A}}^{{\geqslant}0}}N=({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}N$
. Note that if
![]() $h$
acts on
$h$
acts on
![]() $N$
with eigenvalue
$N$
with eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
(so that
$\unicode[STIX]{x1D6FC}$
(so that
![]() $N$
is a single generalized
$N$
is a single generalized
![]() $h$
-eigenspace), then
$h$
-eigenspace), then
![]() $h$
acts locally finitely on
$h$
acts locally finitely on
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
with eigenvalues in
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
with eigenvalues in
 $\unicode[STIX]{x1D6FC}+\mathbb{Z}_{{\leqslant}0}$
. The generalized eigenspace with eigenvalue
$\unicode[STIX]{x1D6FC}+\mathbb{Z}_{{\leqslant}0}$
. The generalized eigenspace with eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
coincides with
$\unicode[STIX]{x1D6FC}$
coincides with
 $({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}N=N$
(note that
$({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}N=N$
(note that
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is identified with
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is identified with
 $({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
). The module
$({\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
). The module
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
has the maximal submodule that does not intersect
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
has the maximal submodule that does not intersect
![]() $N$
; the quotient is denoted by
$N$
; the quotient is denoted by
![]() $L_{\unicode[STIX]{x1D708}}(N)$
. Note that
$L_{\unicode[STIX]{x1D708}}(N)$
. Note that
![]() $L_{\unicode[STIX]{x1D708}}(N)$
is simple provided
$L_{\unicode[STIX]{x1D708}}(N)$
is simple provided
![]() $N$
is simple. Conversely, any simple object
$N$
is simple. Conversely, any simple object
![]() $L$
in
$L$
in
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is of the form
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
is of the form
![]() $L_{\unicode[STIX]{x1D708}}(N)$
for a unique simple
$L_{\unicode[STIX]{x1D708}}(N)$
for a unique simple
 $N\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\text{-}\!\operatorname{mod}$
; this simple
$N\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})\text{-}\!\operatorname{mod}$
; this simple
![]() $N$
coincides with the annihilator
$N$
coincides with the annihilator
![]() $L^{{\mathcal{A}}^{{>}0}}$
of
$L^{{\mathcal{A}}^{{>}0}}$
of
![]() ${\mathcal{A}}^{{>}0}$
in
${\mathcal{A}}^{{>}0}$
in
![]() $L$
.
$L$
.
Assume now that
 $\dim \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})<\infty$
. Let
$\dim \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})<\infty$
. Let
 $N_{1},\ldots ,N_{r}$
be the full list of the simple
$N_{1},\ldots ,N_{r}$
be the full list of the simple
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
-modules. Let
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
-modules. Let
 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r}$
be the eigenvalues of
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r}$
be the eigenvalues of
![]() $h$
on these modules (note that
$h$
on these modules (note that
![]() $h$
maps into the center of
$h$
maps into the center of
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
). We define a partial order
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
). We define a partial order
![]() ${\leqslant}$
on the set
${\leqslant}$
on the set
 $N_{1},\ldots ,N_{r}$
by setting
$N_{1},\ldots ,N_{r}$
by setting
 $N_{i}\leqslant N_{j}$
if
$N_{i}\leqslant N_{j}$
if
 $\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FC}_{i}\in \mathbb{Z}_{{>}0}$
or
$\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FC}_{i}\in \mathbb{Z}_{{>}0}$
or
![]() $i=j$
. Using the order, it is easy to prove the following.
$i=j$
. Using the order, it is easy to prove the following.
Lemma 4.1. Under the assumption
 $\dim \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})<\infty$
, the following are true.
$\dim \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})<\infty$
, the following are true.
-
(1) The modules
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
have finite length.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N)$
have finite length. -
(2) The simple
 $L_{\unicode[STIX]{x1D708}}(N_{i})$
appears in the composition series of
$L_{\unicode[STIX]{x1D708}}(N_{i})$
appears in the composition series of
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
with multiplicity
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
with multiplicity
 $1$
and as a quotient. Further, if
$1$
and as a quotient. Further, if
 $L_{\unicode[STIX]{x1D708}}(N_{j})$
appears in the composition series of
$L_{\unicode[STIX]{x1D708}}(N_{j})$
appears in the composition series of
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
, then
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
, then
 $N_{j}\leqslant N_{i}$
.
$N_{j}\leqslant N_{i}$
. -
(3) All modules in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
have finite length and all generalized eigenspaces for
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
have finite length and all generalized eigenspaces for
 $h$
are finite dimensional.
$h$
are finite dimensional. -
(4) The category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
consists of all
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
consists of all
 ${\mathcal{A}}$
-modules with locally nilpotent action of
${\mathcal{A}}$
-modules with locally nilpotent action of
 ${\mathcal{A}}^{{>}0}$
, locally finite action of
${\mathcal{A}}^{{>}0}$
, locally finite action of
 $h$
and finite-dimensional generalized eigenspaces for
$h$
and finite-dimensional generalized eigenspaces for
 $h$
.
$h$
.
Also, an argument similar to that in [Reference Ginzburg, Guay, Opdam and RouquierGGOR03, § 2.4] implies that
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
has enough projectives.
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
has enough projectives.
Now let us describe the opposite category. The opposite algebra
![]() ${\mathcal{A}}^{\text{opp}}$
is also graded. Consider the category
${\mathcal{A}}^{\text{opp}}$
is also graded. Consider the category
 ${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
. By (4.1), we have a natural identification
${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
. By (4.1), we have a natural identification
 $\mathsf{C}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})\cong \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})^{\text{opp}}$
(indeed, the
$\mathsf{C}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})\cong \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})^{\text{opp}}$
(indeed, the
![]() $i$
th graded component for
$i$
th graded component for
![]() $\unicode[STIX]{x1D708}$
is the same as the
$\unicode[STIX]{x1D708}$
is the same as the
![]() $-i$
th graded component for
$-i$
th graded component for
![]() $-\unicode[STIX]{x1D708}$
). For a module
$-\unicode[STIX]{x1D708}$
). For a module
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
, we define its restricted dual
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
, we define its restricted dual
![]() $M^{(\ast )}$
as
$M^{(\ast )}$
as
 $\bigoplus _{\unicode[STIX]{x1D6FC}}M_{\unicode[STIX]{x1D6FC}}^{\ast }$
, where
$\bigoplus _{\unicode[STIX]{x1D6FC}}M_{\unicode[STIX]{x1D6FC}}^{\ast }$
, where
![]() $M_{\unicode[STIX]{x1D6FC}}$
stands for the generalized eigenspace for
$M_{\unicode[STIX]{x1D6FC}}$
stands for the generalized eigenspace for
![]() $h$
with eigenvalue
$h$
with eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
. Note that
$\unicode[STIX]{x1D6FC}$
. Note that
 $M^{(\ast )}\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
by (4) of Lemma 4.1. Similarly, for
$M^{(\ast )}\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
by (4) of Lemma 4.1. Similarly, for
 $M^{\prime }\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
, we can form
$M^{\prime }\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
, we can form
![]() ${M^{\prime }}^{(\ast )}$
and this will be an object of
${M^{\prime }}^{(\ast )}$
and this will be an object of
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
. The functors of taking the restricted dual define mutually inverse contravariant equivalences between
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
. The functors of taking the restricted dual define mutually inverse contravariant equivalences between
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
and
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
and
 ${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
.
${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}^{\text{opp}})$
.
Using these equivalences, one can introduce dual Verma modules
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N):=\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}^{\text{opp}}(N^{\ast })^{(\ast )}\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
. Equivalently,
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N):=\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}^{\text{opp}}(N^{\ast })^{(\ast )}\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
. Equivalently,
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N)=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N)$
. Here we take the restricted Hom, so that
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N)=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N)$
. Here we take the restricted Hom, so that
 $\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N)=\bigoplus _{i}\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}(({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}})_{i},N)$
. Indeed, the functors
$\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N)=\bigoplus _{i}\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}(({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}})_{i},N)$
. Indeed, the functors
 $\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}})}(\bullet ,\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}^{\text{opp}}(N^{\ast })^{(\ast )})$
and
$\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}})}(\bullet ,\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}^{\text{opp}}(N^{\ast })^{(\ast )})$
and
 $\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}})}(\bullet ,\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N))$
are isomorphic.
$\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}})}(\bullet ,\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}^{\text{restr}}({\mathcal{A}}/{\mathcal{A}}^{{<}0}{\mathcal{A}},N))$
are isomorphic.
4.3 Case of quantizations of symplectic resolutions
Now let
![]() $X$
be a conical symplectic resolution of an affine variety
$X$
be a conical symplectic resolution of an affine variety
![]() $X_{0}$
. Let
$X_{0}$
. Let
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
stand for the algebra of global sections of the filtered quantization
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
stand for the algebra of global sections of the filtered quantization
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
of
![]() $X$
corresponding to
$X$
corresponding to
 $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}:=H^{2}(X,\mathbb{C})$
. Assume that we have a Hamiltonian action
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}:=H^{2}(X,\mathbb{C})$
. Assume that we have a Hamiltonian action
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
![]() $X$
with finitely many fixed points that commutes with the contracting
$X$
with finitely many fixed points that commutes with the contracting
![]() $\mathbb{C}^{\times }$
-action. This action lifts to a Hamiltonian action on a quantization and hence gives rise to a Hamiltonian action on
$\mathbb{C}^{\times }$
-action. This action lifts to a Hamiltonian action on a quantization and hence gives rise to a Hamiltonian action on
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
again denoted by
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
again denoted by
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
The following results were obtained in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 5].
Proposition 4.2. Fix
![]() $\unicode[STIX]{x1D706}^{\circ }\in \tilde{\mathfrak{p}}$
and pick
$\unicode[STIX]{x1D706}^{\circ }\in \tilde{\mathfrak{p}}$
and pick
![]() $\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}$
such that
$\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}$
such that
![]() $X_{\unicode[STIX]{x1D712}}$
is affine. Then, for a Zariski generic
$X_{\unicode[STIX]{x1D712}}$
is affine. Then, for a Zariski generic
 $\unicode[STIX]{x1D706}\in \ell :=\{\unicode[STIX]{x1D706}^{\circ }+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
, we have the following.
$\unicode[STIX]{x1D706}\in \ell :=\{\unicode[STIX]{x1D706}^{\circ }+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
, we have the following.
-
(1) There is a natural isomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\xrightarrow[{}]{{\sim}}\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\xrightarrow[{}]{{\sim}}\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. -
(2) The category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is highest weight, where the standard objects are
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is highest weight, where the standard objects are
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
, costandard objects are
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N_{i})$
, costandard objects are
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N_{i})$
,
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(N_{i})$
,
 $N_{i}\in \operatorname{Irr}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}))$
. The order is given as explained before Lemma 4.1.
$N_{i}\in \operatorname{Irr}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}))$
. The order is given as explained before Lemma 4.1. -
(3) The natural functor
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
is a full embedding.
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
is a full embedding.
The image of the embedding in (3) is the category
 $D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
of all complexes whose homologies lie in
$D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
of all complexes whose homologies lie in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
.
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
.
We also have the category
![]() ${\mathcal{O}}$
on the level of sheaves. Following [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 3.3], consider the category
${\mathcal{O}}$
on the level of sheaves. Following [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 3.3], consider the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
. It consists of all coherent
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
. It consists of all coherent
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules that come with a good filtration stable under
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-modules that come with a good filtration stable under
![]() $h$
and that are supported on the contracting locus
$h$
and that are supported on the contracting locus
![]() $Y$
for
$Y$
for
![]() $\unicode[STIX]{x1D708}$
in
$\unicode[STIX]{x1D708}$
in
![]() $X$
, i.e.,
$X$
, i.e.,
 $Y:=\{x\in X\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}(t).x\text{ exists}\}$
. Note that
$Y:=\{x\in X\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}(t).x\text{ exists}\}$
. Note that
![]() $Y$
is a Lagrangian subvariety.
$Y$
is a Lagrangian subvariety.
The translation equivalences preserve categories
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}$
and so do
${\mathcal{O}}_{\unicode[STIX]{x1D708}}$
and so do
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\operatorname{Loc}$
; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Lemma 3.17 and Corollary 3.19].
$\operatorname{Loc}$
; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Lemma 3.17 and Corollary 3.19].
Lemma 4.3. A coherent
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module supported on
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module supported on
![]() $Y$
lies in
$Y$
lies in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
if and only if it can be made weakly
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
if and only if it can be made weakly
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant (which, by definition, means that the module is equipped with a
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant (which, by definition, means that the module is equipped with a
![]() $\mathbb{C}^{\times }$
-action that is compatible with the action of
$\mathbb{C}^{\times }$
-action that is compatible with the action of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
via
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
via
![]() $\unicode[STIX]{x1D708}$
).
$\unicode[STIX]{x1D708}$
).
Proof. We may assume that abelian localization holds for
![]() $(\unicode[STIX]{x1D706},\unicode[STIX]{x1D703})$
. Let
$(\unicode[STIX]{x1D706},\unicode[STIX]{x1D703})$
. Let
![]() $Y_{0}$
be the
$Y_{0}$
be the
![]() $\unicode[STIX]{x1D708}$
-contracting locus in
$\unicode[STIX]{x1D708}$
-contracting locus in
![]() $X_{0}$
, so that
$X_{0}$
, so that
 $Y=\unicode[STIX]{x1D70C}^{-1}(Y_{0})$
. For
$Y=\unicode[STIX]{x1D70C}^{-1}(Y_{0})$
. For
 $M\in \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
, we have
$M\in \operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
, we have
 $\operatorname{Supp}(M)\subset Y$
if and only if
$\operatorname{Supp}(M)\subset Y$
if and only if
 $\operatorname{Supp}(\unicode[STIX]{x1D6E4}(M))\subset Y_{0}$
. So, it is enough to check that a finitely generated module
$\operatorname{Supp}(\unicode[STIX]{x1D6E4}(M))\subset Y_{0}$
. So, it is enough to check that a finitely generated module
![]() $M_{0}$
supported on
$M_{0}$
supported on
![]() $Y_{0}$
lies in
$Y_{0}$
lies in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
if and only if it admits a weakly
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
if and only if it admits a weakly
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure.
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure.
Suppose that
 $M_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. Then
$M_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. Then
![]() $h$
acts locally finitely on
$h$
acts locally finitely on
![]() $M_{0}$
. Pick any map
$M_{0}$
. Pick any map
 $\unicode[STIX]{x1D711}:\mathbb{C}\rightarrow \mathbb{Z}$
such that
$\unicode[STIX]{x1D711}:\mathbb{C}\rightarrow \mathbb{Z}$
such that
 $\unicode[STIX]{x1D711}(z+1)=\unicode[STIX]{x1D711}(z)+1$
. Then we define a grading on
$\unicode[STIX]{x1D711}(z+1)=\unicode[STIX]{x1D711}(z)+1$
. Then we define a grading on
![]() $M_{0}$
by requiring that the generalized
$M_{0}$
by requiring that the generalized
![]() $z$
-eigenspace for
$z$
-eigenspace for
![]() $h$
has degree
$h$
has degree
![]() $\unicode[STIX]{x1D711}(z)$
. This gives a required weakly
$\unicode[STIX]{x1D711}(z)$
. This gives a required weakly
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure.
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure.
Conversely, assume that
![]() $M_{0}$
has a weakly
$M_{0}$
has a weakly
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure. We can pick a
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant structure. We can pick a
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant good filtration on
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-equivariant good filtration on
![]() $M_{0}$
. Since
$M_{0}$
. Since
 $\operatorname{Supp}(M_{0})\subset Y_{0}$
, we see that the weights of
$\operatorname{Supp}(M_{0})\subset Y_{0}$
, we see that the weights of
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
in
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
in
![]() $M_{0}$
are bounded from above. It follows that
$M_{0}$
are bounded from above. It follows that
![]() ${\mathcal{A}}^{{>}0}$
acts locally nilpotently. So,
${\mathcal{A}}^{{>}0}$
acts locally nilpotently. So,
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
.◻
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
.◻
Again, we assume that
![]() $\unicode[STIX]{x1D708}$
is generic. Pick an ample class
$\unicode[STIX]{x1D708}$
is generic. Pick an ample class
 $\unicode[STIX]{x1D712}\in \operatorname{Pic}(X)$
. Using equivalences
$\unicode[STIX]{x1D712}\in \operatorname{Pic}(X)$
. Using equivalences
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
for
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
for
![]() $n\gg 0$
, we can carry the highest-weight structure from
$n\gg 0$
, we can carry the highest-weight structure from
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
to
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
to
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
. However, we can use a different partial order getting the same collection of standard objects. Namely, for
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
. However, we can use a different partial order getting the same collection of standard objects. Namely, for
 $p\in X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, let
$p\in X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, let
![]() $Y_{p}$
denote the contracting component of
$Y_{p}$
denote the contracting component of
![]() $p$
,
$p$
,
 $Y_{p}:=\{x\in X\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}(t)x=p\}$
. Define the pre-order
$Y_{p}:=\{x\in X\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}(t)x=p\}$
. Define the pre-order
![]() $p^{\prime }\preccurlyeq p$
on
$p^{\prime }\preccurlyeq p$
on
![]() $X^{T}$
given by
$X^{T}$
given by
![]() $p^{\prime }\preccurlyeq p$
if and only if
$p^{\prime }\preccurlyeq p$
if and only if
![]() $p^{\prime }\in \overline{Y_{p}}$
(we will see that this is indeed a pre-order in Lemma 6.1 that covers a more general situation below).
$p^{\prime }\in \overline{Y_{p}}$
(we will see that this is indeed a pre-order in Lemma 6.1 that covers a more general situation below).
Define the partial order
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}}$
on
$\preccurlyeq _{\unicode[STIX]{x1D708}}$
on
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
by taking the transitive closure of the relation
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
by taking the transitive closure of the relation
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}}$
. Set
$\preccurlyeq _{\unicode[STIX]{x1D708}}$
. Set
 $Y_{\preccurlyeq p}:=\bigcup _{p^{\prime }\preccurlyeq p}Y_{p^{\prime }}$
; this is a closed Lagrangian subvariety in
$Y_{\preccurlyeq p}:=\bigcup _{p^{\prime }\preccurlyeq p}Y_{p^{\prime }}$
; this is a closed Lagrangian subvariety in
![]() $X$
. Further, set
$X$
. Further, set
 $$\begin{eqnarray}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})_{\preccurlyeq p}:=\{M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\mid \operatorname{Supp}(M)\subset Y_{\preccurlyeq p}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})_{\preccurlyeq p}:=\{M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\mid \operatorname{Supp}(M)\subset Y_{\preccurlyeq p}\}.\end{eqnarray}$$
Here, as usual, we write
 $\operatorname{Supp}(M)$
for the support of
$\operatorname{Supp}(M)$
for the support of
![]() $\operatorname{gr}M$
in
$\operatorname{gr}M$
in
![]() $X$
, where the associated graded algebra is taken with respect to a good filtration.
$X$
, where the associated graded algebra is taken with respect to a good filtration.
It turns out that
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is a highest-weight category with respect to this order. The standard objects are localizations of Verma modules
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is a highest-weight category with respect to this order. The standard objects are localizations of Verma modules
 $\operatorname{Loc}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N))\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 5.3].
$\operatorname{Loc}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(N))\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
; see [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 5.3].
Below we will need to understand the structure of the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
in the case when
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
in the case when
![]() $X$
splits into the product
$X$
splits into the product
 $X^{1}\times X^{2}$
of two conical symplectic resolutions. Both
$X^{1}\times X^{2}$
of two conical symplectic resolutions. Both
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D703}$
are naturally pairs
$\unicode[STIX]{x1D703}$
are naturally pairs
 $(\unicode[STIX]{x1D706}^{1},\unicode[STIX]{x1D706}^{2}),(\unicode[STIX]{x1D703}^{1},\unicode[STIX]{x1D703}^{2})$
.
$(\unicode[STIX]{x1D706}^{1},\unicode[STIX]{x1D706}^{2}),(\unicode[STIX]{x1D703}^{1},\unicode[STIX]{x1D703}^{2})$
.
Lemma 4.4. The functor
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{1}}^{1\unicode[STIX]{x1D703}^{1}})\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{2}}^{2\unicode[STIX]{x1D703}^{2}})\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
defined by
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{1}}^{1\unicode[STIX]{x1D703}^{1}})\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{2}}^{2\unicode[STIX]{x1D703}^{2}})\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
defined by
 $M\boxtimes N\rightarrow M\otimes N$
is an equivalence of highest-weight categories.
$M\boxtimes N\rightarrow M\otimes N$
is an equivalence of highest-weight categories.
Proof. Note that we have
 $$\begin{eqnarray}\dim \text{Ext}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}}^{i}(P^{1}(p_{1})\boxtimes P^{2}(p_{2}),L^{1}(p_{1}^{\prime })\boxtimes L^{2}(p_{2}^{\prime }))=\unicode[STIX]{x1D6FF}_{i,0}\unicode[STIX]{x1D6FF}_{p_{1},p_{1}^{\prime }}\unicode[STIX]{x1D6FF}_{p_{2},p_{2}^{\prime }},\end{eqnarray}$$
$$\begin{eqnarray}\dim \text{Ext}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}}^{i}(P^{1}(p_{1})\boxtimes P^{2}(p_{2}),L^{1}(p_{1}^{\prime })\boxtimes L^{2}(p_{2}^{\prime }))=\unicode[STIX]{x1D6FF}_{i,0}\unicode[STIX]{x1D6FF}_{p_{1},p_{1}^{\prime }}\unicode[STIX]{x1D6FF}_{p_{2},p_{2}^{\prime }},\end{eqnarray}$$
where
 $p_{i},p_{i}^{\prime }\in X^{i\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},i=1,2,$
and
$p_{i},p_{i}^{\prime }\in X^{i\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},i=1,2,$
and
![]() $P^{i},L^{i}$
stand for the projective and simple objects in the categories
$P^{i},L^{i}$
stand for the projective and simple objects in the categories
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{i}}^{i\unicode[STIX]{x1D703}^{i}})$
. Indeed, (4.2) is clear for the categories on the level of algebras and on the level of sheaves it follows from the localization argument. The objects
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{i}}^{i\unicode[STIX]{x1D703}^{i}})$
. Indeed, (4.2) is clear for the categories on the level of algebras and on the level of sheaves it follows from the localization argument. The objects
 $L^{1}(p_{1}^{\prime })\boxtimes L^{2}(p_{2}^{\prime })$
are the simples in
$L^{1}(p_{1}^{\prime })\boxtimes L^{2}(p_{2}^{\prime })$
are the simples in
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
. It follows that the objects
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
. It follows that the objects
 $P^{1}(p_{1})\boxtimes P^{2}(p_{2})$
are the indecomposable projectives.◻
$P^{1}(p_{1})\boxtimes P^{2}(p_{2})$
are the indecomposable projectives.◻
4.4 Holonomic modules
In this section, we recall some results from [Reference LosevLos17]. Let
![]() $X_{0}$
be a Poisson variety with finitely many symplectic leaves. Following [Reference LosevLos17], we say that a subvariety
$X_{0}$
be a Poisson variety with finitely many symplectic leaves. Following [Reference LosevLos17], we say that a subvariety
 $Y_{0}\subset X_{0}$
is isotropic if its intersection with every leaf is isotropic in the leaf. For example, when
$Y_{0}\subset X_{0}$
is isotropic if its intersection with every leaf is isotropic in the leaf. For example, when
![]() $X_{0}$
admits a symplectic resolution of singularities
$X_{0}$
admits a symplectic resolution of singularities
![]() $(X,\unicode[STIX]{x1D70C})$
, then
$(X,\unicode[STIX]{x1D70C})$
, then
 $Y_{0}\subset X_{0}$
is isotropic if and only if
$Y_{0}\subset X_{0}$
is isotropic if and only if
 $\unicode[STIX]{x1D70C}^{-1}(Y_{0})$
is isotropic; see [Reference LosevLos17, Lemma 5.1].
$\unicode[STIX]{x1D70C}^{-1}(Y_{0})$
is isotropic; see [Reference LosevLos17, Lemma 5.1].
Now let
 $X,X_{0},\unicode[STIX]{x1D708}$
be as in § 4.3. Let
$X,X_{0},\unicode[STIX]{x1D708}$
be as in § 4.3. Let
 $Y_{0}\subset X_{0}$
be the contracting locus of
$Y_{0}\subset X_{0}$
be the contracting locus of
![]() $\unicode[STIX]{x1D708}$
. Then
$\unicode[STIX]{x1D708}$
. Then
 $\unicode[STIX]{x1D70C}^{-1}(Y_{0})=Y$
. We conclude that
$\unicode[STIX]{x1D70C}^{-1}(Y_{0})=Y$
. We conclude that
 $Y_{0}\subset X_{0}$
is isotropic.
$Y_{0}\subset X_{0}$
is isotropic.
Let us proceed to holonomic
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-modules. We say that a finitely generated
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-modules. We say that a finitely generated
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-module is holonomic if its support in
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-module is holonomic if its support in
![]() $X_{0}$
is holonomic. In particular, any module in
$X_{0}$
is holonomic. In particular, any module in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is supported on
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is supported on
![]() $Y_{0}$
and so is holonomic.
$Y_{0}$
and so is holonomic.
For holonomic modules, we have the following result; see [Reference LosevLos17, Theorems 1.2 and 1.3].
Proposition 4.5. Let
![]() $N$
be a holonomic
$N$
be a holonomic
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-module and
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-module and
![]() ${\mathcal{I}}$
be its annihilator. Then
${\mathcal{I}}$
be its annihilator. Then
 $\operatorname{GK}\!\text{-}\!\dim {\mathcal{A}}_{\unicode[STIX]{x1D706}}/{\mathcal{I}}=2\operatorname{GK}\!\text{-}\!\dim N$
, where
$\operatorname{GK}\!\text{-}\!\dim {\mathcal{A}}_{\unicode[STIX]{x1D706}}/{\mathcal{I}}=2\operatorname{GK}\!\text{-}\!\dim N$
, where
 $\operatorname{GK}\!\text{-}\!\dim$
stands for the Gelfand–Kirillov (GK) dimension.
$\operatorname{GK}\!\text{-}\!\dim$
stands for the Gelfand–Kirillov (GK) dimension.
We will need a consequence of this proposition and Lemma 2.4.
Corollary 4.6. Let
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}$
be as in Lemma 2.4. Then, for a Weil generic
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D712}$
be as in Lemma 2.4. Then, for a Weil generic
![]() $z$
and any non-zero holonomic
$z$
and any non-zero holonomic
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
-module
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
-module
![]() $M$
, we have
$M$
, we have
 $\operatorname{GK}\!\text{-}\!\dim M=\frac{1}{2}\dim X$
.
$\operatorname{GK}\!\text{-}\!\dim M=\frac{1}{2}\dim X$
.
Let us provide one more example of holonomic modules. Let
![]() ${\mathcal{B}}$
be a HC
${\mathcal{B}}$
be a HC
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-bimodule. Then it is a holonomic
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
-bimodule. Then it is a holonomic
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}}\otimes {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}$
-module (its support is the diagonal in
${\mathcal{A}}_{\unicode[STIX]{x1D706}}\otimes {\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}$
-module (its support is the diagonal in
 $X_{0}\times X_{0}$
that is easily seen to be isotropic).
$X_{0}\times X_{0}$
that is easily seen to be isotropic).
5 Parabolic induction
5.1 Hamiltonian actions and fixed point components
Suppose that we have a Hamiltonian action
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\mathbb{C}^{\times }$
on
$\mathbb{C}^{\times }$
on
 $X=X^{\unicode[STIX]{x1D703}}$
that commutes with the contracting action of
$X=X^{\unicode[STIX]{x1D703}}$
that commutes with the contracting action of
![]() $\mathbb{C}^{\times }$
. By the universality of the deformations, the Hamiltonian action extends to both
$\mathbb{C}^{\times }$
. By the universality of the deformations, the Hamiltonian action extends to both
![]() $\tilde{X}^{\unicode[STIX]{x1D703}}$
and
$\tilde{X}^{\unicode[STIX]{x1D703}}$
and
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
. Since
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
. Since
 $H_{DR}^{1}(X)=0$
, we see that the actions on
$H_{DR}^{1}(X)=0$
, we see that the actions on
![]() $\tilde{X}^{\unicode[STIX]{x1D703}},\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
are Hamiltonian as well. For the action on
$\tilde{X}^{\unicode[STIX]{x1D703}},\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
are Hamiltonian as well. For the action on
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
, this means, by definition, that there is a
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
, this means, by definition, that there is a
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-invariant element
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-invariant element
![]() $h\in \tilde{{\mathcal{A}}}$
such that the derivation
$h\in \tilde{{\mathcal{A}}}$
such that the derivation
![]() $[h,\cdot ]$
of
$[h,\cdot ]$
of
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
coincides with the derivation induced by the
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
coincides with the derivation induced by the
![]() $\mathbb{C}^{\times }$
-action.
$\mathbb{C}^{\times }$
-action.
Proposition 5.1. The fixed point subvariety
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is itself a conical symplectic resolution.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is itself a conical symplectic resolution.
Proof. The proof is in two steps.
Step 1. Let us take an irreducible component
![]() $Z$
of
$Z$
of
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. Assume for the time being that
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. Assume for the time being that
 $\dim \unicode[STIX]{x1D70C}(Z)=\dim Z$
. Apply the Stein decomposition to the projective morphism
$\dim \unicode[STIX]{x1D70C}(Z)=\dim Z$
. Apply the Stein decomposition to the projective morphism
 $Z\rightarrow \unicode[STIX]{x1D70C}(Z)$
: it factors through a birational morphism
$Z\rightarrow \unicode[STIX]{x1D70C}(Z)$
: it factors through a birational morphism
 $Z\rightarrow Z_{0}:=\operatorname{Spec}(\mathbb{C}[Z])$
and a finite dominant morphism
$Z\rightarrow Z_{0}:=\operatorname{Spec}(\mathbb{C}[Z])$
and a finite dominant morphism
 $Z_{0}\rightarrow \unicode[STIX]{x1D70C}(Z)$
. The morphism
$Z_{0}\rightarrow \unicode[STIX]{x1D70C}(Z)$
. The morphism
 $Z\rightarrow Z_{0}$
is a symplectic resolution of singularities. It is conical because
$Z\rightarrow Z_{0}$
is a symplectic resolution of singularities. It is conical because
![]() $\unicode[STIX]{x1D70C}(Z)$
is a closed
$\unicode[STIX]{x1D70C}(Z)$
is a closed
![]() $\mathbb{C}^{\times }$
-stable subvariety of
$\mathbb{C}^{\times }$
-stable subvariety of
![]() $X_{0}$
. So, it is enough to check that indeed
$X_{0}$
. So, it is enough to check that indeed
 $\dim \unicode[STIX]{x1D70C}(Z)=\dim Z$
.
$\dim \unicode[STIX]{x1D70C}(Z)=\dim Z$
.
Step 2. Pick a Zariski generic one-dimensional subspace
![]() $\ell \subset \tilde{\mathfrak{p}}$
. Consider the irreducible component
$\ell \subset \tilde{\mathfrak{p}}$
. Consider the irreducible component
![]() $Z_{\ell }$
of
$Z_{\ell }$
of
![]() $X_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
containing
$X_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
containing
![]() $Z$
, a one-dimensional smooth deformation of
$Z$
, a one-dimensional smooth deformation of
![]() $Z$
over
$Z$
over
![]() $\ell$
. So,
$\ell$
. So,
![]() $\tilde{\unicode[STIX]{x1D70C}}(Z_{\ell })$
is an irreducible scheme over
$\tilde{\unicode[STIX]{x1D70C}}(Z_{\ell })$
is an irreducible scheme over
![]() $\ell$
. The fiber over zero is
$\ell$
. The fiber over zero is
![]() $\unicode[STIX]{x1D70C}(Z)$
. But, over
$\unicode[STIX]{x1D70C}(Z)$
. But, over
![]() $\ell \setminus \{0\}$
, the map
$\ell \setminus \{0\}$
, the map
 $Z_{\ell }\rightarrow \tilde{\unicode[STIX]{x1D70C}}(Z_{\ell })$
is an isomorphism. It follows that
$Z_{\ell }\rightarrow \tilde{\unicode[STIX]{x1D70C}}(Z_{\ell })$
is an isomorphism. It follows that
 $\dim \unicode[STIX]{x1D70C}(Z)=\dim \unicode[STIX]{x1D70C}(Z_{\ell })-1=\dim Z_{\ell }-1=\dim Z$
. This completes the proof.◻
$\dim \unicode[STIX]{x1D70C}(Z)=\dim \unicode[STIX]{x1D70C}(Z_{\ell })-1=\dim Z_{\ell }-1=\dim Z$
. This completes the proof.◻
We also note that the irreducible components of
![]() $X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
are in a natural bijection with those of
$X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
are in a natural bijection with those of
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
.
5.2 Cartan subquotient: sheaf level
We start with a symplectic variety
![]() $X$
equipped with a
$X$
equipped with a
![]() $\mathbb{C}^{\times }$
-action that rescales the symplectic form and also with a commuting Hamiltonian action
$\mathbb{C}^{\times }$
-action that rescales the symplectic form and also with a commuting Hamiltonian action
![]() $\unicode[STIX]{x1D708}$
. Of course, it still makes sense to speak about quantizations of
$\unicode[STIX]{x1D708}$
. Of course, it still makes sense to speak about quantizations of
![]() $X$
that are Hamiltonian for
$X$
that are Hamiltonian for
![]() $\unicode[STIX]{x1D708}$
. We want to construct a quantization
$\unicode[STIX]{x1D708}$
. We want to construct a quantization
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
of
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
starting from a Hamiltonian quantization
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
starting from a Hamiltonian quantization
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
of
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
of
![]() $X$
.
$X$
.
The variety
![]() $X$
can be covered by
$X$
can be covered by
![]() $(\mathbb{C}^{\times })^{2}$
-stable open affine subvarieties. Pick such a subvariety
$(\mathbb{C}^{\times })^{2}$
-stable open affine subvarieties. Pick such a subvariety
![]() $X^{\prime }$
with
$X^{\prime }$
with
 $(X^{\prime })^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\neq \varnothing$
. We remark that the open subsets of the form
$(X^{\prime })^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\neq \varnothing$
. We remark that the open subsets of the form
 $(X^{\prime })^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
form a base of the Zariski topology on
$(X^{\prime })^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
form a base of the Zariski topology on
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
.
The following proposition defines the sheaf
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
.
Proposition 5.2. The following hold.
-
(1) Suppose that the contracting
 $\unicode[STIX]{x1D708}$
-locus in
$\unicode[STIX]{x1D708}$
-locus in
 $X^{\prime }$
is a complete intersection defined by homogeneous (for
$X^{\prime }$
is a complete intersection defined by homogeneous (for
 $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
) equations of positive weight. Then the algebra
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
) equations of positive weight. Then the algebra
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
is a quantization of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
is a quantization of
 $\mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
.
$\mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. -
(2) There is a unique sheaf
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
in the conical topology on
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
in the conical topology on
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
whose sections on
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
whose sections on
 ${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
with
${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
with
 $X^{\prime }$
as above coincide with
$X^{\prime }$
as above coincide with
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
. This sheaf is a quantization of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
. This sheaf is a quantization of
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. -
(3) If
 $X^{\prime }$
is a
$X^{\prime }$
is a
 $(\mathbb{C}^{\times })^{2}$
-stable open affine subvariety, then
$(\mathbb{C}^{\times })^{2}$
-stable open affine subvariety, then
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})({X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})=\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})({X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})=\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
.
Proof. Let us prove (1). To simplify the notation, we write
![]() ${\mathcal{A}}$
for
${\mathcal{A}}$
for
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime })$
. The algebra
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime })$
. The algebra
![]() ${\mathcal{A}}$
is Noetherian because it is complete and separated with respect to a filtration whose associated graded algebra is Noetherian. Let us show that
${\mathcal{A}}$
is Noetherian because it is complete and separated with respect to a filtration whose associated graded algebra is Noetherian. Let us show that
 $\operatorname{gr}({\mathcal{A}}{\mathcal{A}}^{{>}0})=\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
; this will complete the proof of (1).
$\operatorname{gr}({\mathcal{A}}{\mathcal{A}}^{{>}0})=\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
; this will complete the proof of (1).
In the proof, it is more convenient to deal with
![]() $\hbar$
-adically completed homogenized quantizations. Namely, let
$\hbar$
-adically completed homogenized quantizations. Namely, let
![]() ${\mathcal{A}}_{\hbar }$
stand for the
${\mathcal{A}}_{\hbar }$
stand for the
![]() $\hbar$
-adic completion of
$\hbar$
-adic completion of
![]() $R_{\hbar }({\mathcal{A}})$
. The claim that
$R_{\hbar }({\mathcal{A}})$
. The claim that
 $\operatorname{gr}{\mathcal{A}}{\mathcal{A}}^{{>}0}=\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
is equivalent to the condition that
$\operatorname{gr}{\mathcal{A}}{\mathcal{A}}^{{>}0}=\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
is equivalent to the condition that
 ${\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
is
${\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
is
![]() $\hbar$
-saturated in
$\hbar$
-saturated in
![]() ${\mathcal{A}}_{\hbar }$
, meaning that
${\mathcal{A}}_{\hbar }$
, meaning that
 $\hbar a\in {\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
implies that
$\hbar a\in {\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
implies that
 $a\in {\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
.
$a\in {\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
.
Recall that we assume that there are
![]() $\unicode[STIX]{x1D708}$
-homogeneous elements
$\unicode[STIX]{x1D708}$
-homogeneous elements
 $f_{1},\ldots ,f_{k}\in \mathbb{C}[X^{\prime }]^{{>}0}$
that form a regular sequence generating the ideal
$f_{1},\ldots ,f_{k}\in \mathbb{C}[X^{\prime }]^{{>}0}$
that form a regular sequence generating the ideal
 $\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
. We can lift those elements to homogeneous
$\mathbb{C}[X^{\prime }]\mathbb{C}[X^{\prime }]^{{>}0}$
. We can lift those elements to homogeneous
 $\tilde{f}_{1},\ldots ,\tilde{f}_{k}\in {\mathcal{A}}_{\hbar ,>0}$
. We claim that these elements still generate
$\tilde{f}_{1},\ldots ,\tilde{f}_{k}\in {\mathcal{A}}_{\hbar ,>0}$
. We claim that these elements still generate
 ${\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
. Indeed, it is enough to check that
${\mathcal{A}}_{\hbar }{\mathcal{A}}_{\hbar ,>0}$
. Indeed, it is enough to check that
 ${\mathcal{A}}_{\hbar ,>0}\subset \operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. For a homogeneous element
${\mathcal{A}}_{\hbar ,>0}\subset \operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. For a homogeneous element
 $f\in {\mathcal{A}}_{\hbar ,>0}\setminus \hbar {\mathcal{A}}_{\hbar }$
, we can find homogeneous elements
$f\in {\mathcal{A}}_{\hbar ,>0}\setminus \hbar {\mathcal{A}}_{\hbar }$
, we can find homogeneous elements
 $g_{1},\ldots ,g_{k}$
such that
$g_{1},\ldots ,g_{k}$
such that
 $f-\sum _{i=1}^{k}g_{i}\tilde{f}_{i}$
still has the same
$f-\sum _{i=1}^{k}g_{i}\tilde{f}_{i}$
still has the same
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-weight and is divisible by
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-weight and is divisible by
![]() $\hbar$
. Divide by
$\hbar$
. Divide by
![]() $\hbar$
and repeat the argument. Since the
$\hbar$
and repeat the argument. Since the
![]() $\hbar$
-adic topology is complete and separated, we see that
$\hbar$
-adic topology is complete and separated, we see that
 $f\in \operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. So, it is enough to check that
$f\in \operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. So, it is enough to check that
 $\operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
is
$\operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
is
![]() $\hbar$
-saturated.
$\hbar$
-saturated.
Pick elements
 $\tilde{h}_{1},\ldots ,\tilde{h}_{k}$
such that
$\tilde{h}_{1},\ldots ,\tilde{h}_{k}$
such that
 $\sum _{j=1}^{k}\tilde{h}_{j}\tilde{f}_{j}$
is divisible by
$\sum _{j=1}^{k}\tilde{h}_{j}\tilde{f}_{j}$
is divisible by
![]() $\hbar$
. Let
$\hbar$
. Let
 $h_{j}\in \mathbb{C}[X^{\prime }]$
be congruent to
$h_{j}\in \mathbb{C}[X^{\prime }]$
be congruent to
![]() $\tilde{h}_{j}$
modulo
$\tilde{h}_{j}$
modulo
![]() $\hbar$
, so that
$\hbar$
, so that
 $\sum _{j=1}^{k}h_{j}f_{j}=0$
. Since
$\sum _{j=1}^{k}h_{j}f_{j}=0$
. Since
 $f_{1},\ldots ,f_{k}$
form a regular sequence, we see that there are elements
$f_{1},\ldots ,f_{k}$
form a regular sequence, we see that there are elements
 $h_{ij}\in \mathbb{C}[X^{\prime }]$
such that
$h_{ij}\in \mathbb{C}[X^{\prime }]$
such that
 $h_{j^{\prime }j}=-h_{jj^{\prime }}$
and
$h_{j^{\prime }j}=-h_{jj^{\prime }}$
and
 $h_{j}=\sum _{\ell =1}^{k}h_{j\ell }f_{\ell }$
. Lift the elements
$h_{j}=\sum _{\ell =1}^{k}h_{j\ell }f_{\ell }$
. Lift the elements
![]() $h_{jj^{\prime }}$
to
$h_{jj^{\prime }}$
to
 $\tilde{h}_{jj^{\prime }}\in {\mathcal{A}}_{\hbar }$
with
$\tilde{h}_{jj^{\prime }}\in {\mathcal{A}}_{\hbar }$
with
 $\tilde{h}_{jj^{\prime }}=-\tilde{h}_{j^{\prime }j}$
. So, we have
$\tilde{h}_{jj^{\prime }}=-\tilde{h}_{j^{\prime }j}$
. So, we have
 $\tilde{h}_{j}=\sum _{\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }+\hbar \tilde{h}_{j}^{\prime }$
for some
$\tilde{h}_{j}=\sum _{\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }+\hbar \tilde{h}_{j}^{\prime }$
for some
 $\tilde{h}_{j}^{\prime }\in {\mathcal{A}}_{\hbar }$
. It follows that
$\tilde{h}_{j}^{\prime }\in {\mathcal{A}}_{\hbar }$
. It follows that
 $\sum _{j=1}^{k}\tilde{h}_{j}\tilde{f}_{j}=\hbar \sum _{j=1}^{k}\tilde{h}_{j}^{\prime }\tilde{f}_{j}+\sum _{j,\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }\tilde{f}_{j}$
. But
$\sum _{j=1}^{k}\tilde{h}_{j}\tilde{f}_{j}=\hbar \sum _{j=1}^{k}\tilde{h}_{j}^{\prime }\tilde{f}_{j}+\sum _{j,\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }\tilde{f}_{j}$
. But
 $\sum _{j,\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }\tilde{f}_{j}=\sum _{j<\ell }\tilde{h}_{j\ell }[\tilde{f}_{\ell },\tilde{f}_{j}]$
. The bracket is divisible by
$\sum _{j,\ell =1}^{k}\tilde{h}_{j\ell }\tilde{f}_{\ell }\tilde{f}_{j}=\sum _{j<\ell }\tilde{h}_{j\ell }[\tilde{f}_{\ell },\tilde{f}_{j}]$
. The bracket is divisible by
![]() $\hbar$
. But
$\hbar$
. But
 $(1/\hbar )[\tilde{f}_{\ell },\tilde{f}_{j}]$
is still in
$(1/\hbar )[\tilde{f}_{\ell },\tilde{f}_{j}]$
is still in
![]() ${\mathcal{A}}_{\hbar ,>0}$
and so in
${\mathcal{A}}_{\hbar ,>0}$
and so in
 $\operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. This finishes the proof of (1).
$\operatorname{Span}_{{\mathcal{A}}_{\hbar }}(\tilde{f}_{1},\ldots ,\tilde{f}_{k})$
. This finishes the proof of (1).
Let us proceed to the proof of (2). Let us show that we can choose a covering of
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
by
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
by
![]() ${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, where
${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, where
![]() $X^{\prime }$
is as in (1). This is easily reduced to the affine case. Here the existence of such a covering is deduced from the Luna slice theorem applied to a fixed point for
$X^{\prime }$
is as in (1). This is easily reduced to the affine case. Here the existence of such a covering is deduced from the Luna slice theorem applied to a fixed point for
![]() $\unicode[STIX]{x1D708}$
. In more detail, for a fixed point
$\unicode[STIX]{x1D708}$
. In more detail, for a fixed point
![]() $x$
, we can choose an open affine neighborhood
$x$
, we can choose an open affine neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
 $X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
with an étale morphism
$X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
with an étale morphism
 $U\rightarrow T_{x}X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
such that
$U\rightarrow T_{x}X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
such that
 $\unicode[STIX]{x1D70B}^{-1}(U)\cong U\times _{T_{x}X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}T_{x}X$
, where
$\unicode[STIX]{x1D70B}^{-1}(U)\cong U\times _{T_{x}X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}T_{x}X$
, where
![]() $\unicode[STIX]{x1D70B}$
stands for the quotient morphism for the action
$\unicode[STIX]{x1D70B}$
stands for the quotient morphism for the action
![]() $\unicode[STIX]{x1D708}$
. The subset
$\unicode[STIX]{x1D708}$
. The subset
![]() $\unicode[STIX]{x1D70B}^{-1}(U)$
then obviously satisfies the requirements in (1).
$\unicode[STIX]{x1D70B}^{-1}(U)$
then obviously satisfies the requirements in (1).
It is easy to see that the algebras
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
form a presheaf with respect to the covering
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
form a presheaf with respect to the covering
![]() ${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
(obviously, if
${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
(obviously, if
![]() $X^{\prime },X^{\prime \prime }$
satisfy our assumptions, then their intersection does). Since the subsets
$X^{\prime },X^{\prime \prime }$
satisfy our assumptions, then their intersection does). Since the subsets
![]() ${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
form a base of topology on
${X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
form a base of topology on
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, it is enough to show that the algebras
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, it is enough to show that the algebras
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
form a sheaf with respect to the covering. This is easily deduced from the two straightforward claims:
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
form a sheaf with respect to the covering. This is easily deduced from the two straightforward claims:
-
∙
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
is complete and separated with respect to the filtration (here we use an easy claim that, being finitely generated, the ideal
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
is complete and separated with respect to the filtration (here we use an easy claim that, being finitely generated, the ideal
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime })^{{>}0}$
is closed);
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime })^{{>}0}$
is closed); -
∙ the algebras
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))=\mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
do form a sheaf: the structure sheaf
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))=\mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
do form a sheaf: the structure sheaf
 ${\mathcal{O}}_{X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}}$
.
${\mathcal{O}}_{X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}}$
.
For example, suppose that
 $X^{\prime }=\bigcup X_{i}^{\prime }$
is a covering and
$X^{\prime }=\bigcup X_{i}^{\prime }$
is a covering and
 $a_{i}\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X_{i}^{\prime }))$
. We claim that the elements
$a_{i}\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X_{i}^{\prime }))$
. We claim that the elements
![]() $a_{i}$
glue to an element of
$a_{i}$
glue to an element of
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
provided the restrictions of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
provided the restrictions of
![]() $a_{i},a_{j}$
to
$a_{i},a_{j}$
to
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X_{i}^{\prime }\,\cap \,X_{j}^{\prime }))$
agree. Let
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X_{i}^{\prime }\,\cap \,X_{j}^{\prime }))$
agree. Let
![]() $d$
be the common filtration degree of the elements
$d$
be the common filtration degree of the elements
![]() $a_{i}$
. We can find a homogeneous element
$a_{i}$
. We can find a homogeneous element
 $f\in \mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
of degree
$f\in \mathbb{C}[{X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
of degree
![]() $d$
such that the degree-
$d$
such that the degree-
![]() $d$
part of
$d$
part of
![]() $a_{i}$
is
$a_{i}$
is
![]() $f|_{X_{i}^{\prime }}$
. Lift
$f|_{X_{i}^{\prime }}$
. Lift
![]() $f$
to an element
$f$
to an element
 $a\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
and replace
$a\in \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
and replace
![]() $a_{i}$
with
$a_{i}$
with
![]() $a_{i}-a$
. This reduces the degree by
$a_{i}-a$
. This reduces the degree by
![]() $1$
. Now we can use the descending induction on the degree (that makes sense because the filtrations involved are complete and separated).
$1$
. Now we can use the descending induction on the degree (that makes sense because the filtrations involved are complete and separated).
The proof of (2) is now complete.
To prove (3), it is enough to assume that
![]() $X$
is affine. Let
$X$
is affine. Let
![]() $\unicode[STIX]{x1D70B}$
denote the categorical quotient map
$\unicode[STIX]{x1D70B}$
denote the categorical quotient map
 $X\rightarrow X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. It is easy to see that, for every open
$X\rightarrow X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. It is easy to see that, for every open
![]() $(\mathbb{C}^{\times })^{2}$
-stable affine subvariety
$(\mathbb{C}^{\times })^{2}$
-stable affine subvariety
![]() $X^{\prime }$
that intersects
$X^{\prime }$
that intersects
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
non-trivially, and any point
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
non-trivially, and any point
 $x\in {X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, there is some
$x\in {X^{\prime }}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, there is some
![]() $\mathbb{C}^{\times }$
-stable open affine subvariety
$\mathbb{C}^{\times }$
-stable open affine subvariety
 $Z\subset X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
with
$Z\subset X/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
with
 $x\in \unicode[STIX]{x1D70B}^{-1}(Z)\subset X^{\prime }$
. So, we can assume, in addition, that all covering affine subsets
$x\in \unicode[STIX]{x1D70B}^{-1}(Z)\subset X^{\prime }$
. So, we can assume, in addition, that all covering affine subsets
![]() $X^{i}$
are of the form
$X^{i}$
are of the form
![]() $\unicode[STIX]{x1D70B}^{-1}(?)$
. Moreover, we can assume that they are all principal (and so are given by non-vanishing of
$\unicode[STIX]{x1D70B}^{-1}(?)$
. Moreover, we can assume that they are all principal (and so are given by non-vanishing of
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-invariant and
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-invariant and
![]() $\mathbb{C}^{\times }$
-semi-invariant elements of
$\mathbb{C}^{\times }$
-semi-invariant elements of
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X)$
). Then all algebras
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X)$
). Then all algebras
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
are obtained from
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{\prime }))$
are obtained from
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X))$
by microlocalization. By standard properties of microlocalization, the algebra
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X))$
by microlocalization. By standard properties of microlocalization, the algebra
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X))$
is the only algebra with these properties. Hence, (3) follows.◻
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X))$
is the only algebra with these properties. Hence, (3) follows.◻
5.3 Comparison between algebra and sheaf levels
Now let us assume that
![]() $X$
is a conical symplectic resolution of
$X$
is a conical symplectic resolution of
![]() $X_{0}$
. We write
$X_{0}$
. We write
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
for the quantization of
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
for the quantization of
![]() $X$
corresponding to
$X$
corresponding to
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
for its algebra of global sections. By the construction, for any
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
for its algebra of global sections. By the construction, for any
 $\unicode[STIX]{x1D706}\in H^{2}(X)$
, there are a natural homomorphism
$\unicode[STIX]{x1D706}\in H^{2}(X)$
, there are a natural homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
as well as a natural homomorphism
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
as well as a natural homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}])\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{O}}_{X}))=\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. Our goal in this section is to prove the following result.
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}])\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{O}}_{X}))=\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. Our goal in this section is to prove the following result.
Proposition 5.3. For a Zariski generic
![]() $\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
, the homomorphism
$\unicode[STIX]{x1D706}\in \tilde{\mathfrak{p}}$
, the homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
is an isomorphism.
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
is an isomorphism.
In the proof, we will need a lemma describing some properties of the natural morphism
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
.
Lemma 5.4. The morphism
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is projective and its image is the reduced scheme of
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is projective and its image is the reduced scheme of
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. Further, the scheme
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. Further, the scheme
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
has finitely many symplectic leaves.
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
has finitely many symplectic leaves.
Proof. Let
![]() $Y_{0}$
denote the contracting locus for the action of
$Y_{0}$
denote the contracting locus for the action of
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
on
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
on
![]() $X_{0}$
; we view
$X_{0}$
; we view
![]() $Y_{0}$
as a subscheme of
$Y_{0}$
as a subscheme of
![]() $X_{0}$
with the defining ideal
$X_{0}$
with the defining ideal
 $\mathbb{C}[X_{0}]\mathbb{C}[X_{0}]^{{>}0}$
, so that
$\mathbb{C}[X_{0}]\mathbb{C}[X_{0}]^{{>}0}$
, so that
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))=Y_{0}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. The embedding
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))=Y_{0}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. The embedding
 $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}{\hookrightarrow}Y_{0}$
gives rise to the morphism
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}{\hookrightarrow}Y_{0}$
gives rise to the morphism
 $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. The ideal of
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. The ideal of
![]() $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
in
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
in
![]() $\mathbb{C}[Y_{0}]$
contains all elements of positive degree with respect to
$\mathbb{C}[Y_{0}]$
contains all elements of positive degree with respect to
![]() $\unicode[STIX]{x1D708}$
. Therefore, the morphism
$\unicode[STIX]{x1D708}$
. Therefore, the morphism
 $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is also an embedding. It is a bijection on the level of points because the action on
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is also an embedding. It is a bijection on the level of points because the action on
![]() $Y_{0}$
is contracting and the fixed points in
$Y_{0}$
is contracting and the fixed points in
![]() $Y_{0}$
are precisely
$Y_{0}$
are precisely
![]() $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. So,
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. So,
 $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
. On the other hand, the morphism
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
. On the other hand, the morphism
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
we study is the composition of the surjective projective morphism
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
we study is the composition of the surjective projective morphism
 $\unicode[STIX]{x1D70C}:X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
and the closed embedding
$\unicode[STIX]{x1D70C}:X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
and the closed embedding
 $X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}{\hookrightarrow}\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. It follows that
$X_{0}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}{\hookrightarrow}\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
. It follows that
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is projective with image
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
is projective with image
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
.
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
.
We see that
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
admits a symplectic resolution
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))_{\text{red}}$
admits a symplectic resolution
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
(see Proposition 5.1), so it has finitely many leaves.◻
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
(see Proposition 5.1), so it has finitely many leaves.◻
Proof of Proposition 5.3.
Recall that
![]() $\tilde{X}$
denotes the universal deformation of
$\tilde{X}$
denotes the universal deformation of
![]() $X$
over
$X$
over
![]() $\tilde{\mathfrak{p}}$
and let
$\tilde{\mathfrak{p}}$
and let
![]() $\tilde{X}_{0}$
be its affinization. Consider the natural homomorphism
$\tilde{X}_{0}$
be its affinization. Consider the natural homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[\tilde{X}_{0}])\rightarrow \mathbb{C}[\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. It is an isomorphism outside of
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[\tilde{X}_{0}])\rightarrow \mathbb{C}[\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. It is an isomorphism outside of
![]() ${\mathcal{H}}_{\mathbb{C}}$
(defined by (2.1)) since
${\mathcal{H}}_{\mathbb{C}}$
(defined by (2.1)) since
 $\tilde{X}\rightarrow \tilde{X}_{0}$
is an isomorphism precisely outside that locus. Now consider the canonical quantization
$\tilde{X}\rightarrow \tilde{X}_{0}$
is an isomorphism precisely outside that locus. Now consider the canonical quantization
![]() $\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of
$\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}$
of
![]() $\tilde{X}$
. Similarly to § 5.2,
$\tilde{X}$
. Similarly to § 5.2,
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}})$
is a quantization of
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}})$
is a quantization of
![]() $\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. The equality
$\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. The equality
 $H^{i}(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0,i>0$
(that is a consequence of Proposition 5.1) implies that
$H^{i}(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0,i>0$
(that is a consequence of Proposition 5.1) implies that
 $H^{i}(\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0,i>0$
. It follows that
$H^{i}(\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0,i>0$
. It follows that
 $\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))=\mathbb{C}[\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. Also, there are a natural epimorphism
$\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))=\mathbb{C}[\tilde{X}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]$
. Also, there are a natural epimorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[\tilde{X}_{0}]){\twoheadrightarrow}\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
and a natural homomorphism
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[\tilde{X}_{0}]){\twoheadrightarrow}\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
and a natural homomorphism
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
. The resulting homomorphism
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
. The resulting homomorphism
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is, on the one hand, the associated graded homomorphism of the homomorphism
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is, on the one hand, the associated graded homomorphism of the homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
and, on the other hand, an isomorphism over
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
and, on the other hand, an isomorphism over
![]() $\tilde{\mathfrak{p}}\setminus {\mathcal{H}}_{\mathbb{C}}$
. We deduce that the supports of the associated graded modules of the kernel and the cokernel of
$\tilde{\mathfrak{p}}\setminus {\mathcal{H}}_{\mathbb{C}}$
. We deduce that the supports of the associated graded modules of the kernel and the cokernel of
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
are supported on
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
are supported on
![]() ${\mathcal{H}}_{\mathbb{C}}$
as
${\mathcal{H}}_{\mathbb{C}}$
as
![]() $\mathbb{C}[\tilde{\mathfrak{p}}]$
-modules.
$\mathbb{C}[\tilde{\mathfrak{p}}]$
-modules.
Now let us check that this kernel and the cokernel are HC bimodules over
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
. For the kernel, it is obvious. For the cokernel, we need to check that
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
. For the kernel, it is obvious. For the cokernel, we need to check that
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is a HC
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is a HC
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
-bimodule. This will follow if we check that
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
-bimodule. This will follow if we check that
 $\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]=[\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))]/(\tilde{\mathfrak{p}})$
is finitely generated over
$\mathbb{C}[X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}]=[\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))]/(\tilde{\mathfrak{p}})$
is finitely generated over
 $[\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})]/(\tilde{\mathfrak{p}})$
. The latter algebra is a quotient of
$[\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})]/(\tilde{\mathfrak{p}})$
. The latter algebra is a quotient of
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}])$
. Now the claim about the cokernel follows from Lemma 5.4.
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}])$
. Now the claim about the cokernel follows from Lemma 5.4.
Also, thanks to Lemma 5.4,
 $\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
has finitely many symplectic leaves. It follows that
$\operatorname{Spec}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\mathbb{C}[X_{0}]))$
has finitely many symplectic leaves. It follows that
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
satisfies the assumptions of Proposition 2.6. Applying this proposition to the kernel and the cokernel above, we see that their supports in
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})$
satisfies the assumptions of Proposition 2.6. Applying this proposition to the kernel and the cokernel above, we see that their supports in
![]() $\mathfrak{p}$
are closed subvarieties whose asymptotic cones lie in
$\mathfrak{p}$
are closed subvarieties whose asymptotic cones lie in
![]() ${\mathcal{H}}_{\mathbb{C}}$
. So, for a Zariski generic parameter
${\mathcal{H}}_{\mathbb{C}}$
. So, for a Zariski generic parameter
![]() $\unicode[STIX]{x1D706}$
, the homomorphism
$\unicode[STIX]{x1D706}$
, the homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})_{\unicode[STIX]{x1D706}}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))_{\unicode[STIX]{x1D706}}$
is an isomorphism.
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})_{\unicode[STIX]{x1D706}}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))_{\unicode[STIX]{x1D706}}$
is an isomorphism.
We note that
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is flat over
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}}^{\unicode[STIX]{x1D703}}))$
is flat over
![]() $\mathfrak{p}$
and the specialization at
$\mathfrak{p}$
and the specialization at
![]() $\unicode[STIX]{x1D706}$
coincides with
$\unicode[STIX]{x1D706}$
coincides with
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
; this is because
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
; this is because
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is a symplectic resolution; see Proposition 5.1. Further,
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is a symplectic resolution; see Proposition 5.1. Further,
 $\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})_{\unicode[STIX]{x1D706}}=\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. This implies the claim of the proposition.◻
$\mathsf{C}_{\unicode[STIX]{x1D708}}(\tilde{{\mathcal{A}}})_{\unicode[STIX]{x1D706}}=\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. This implies the claim of the proposition.◻
5.4 Correspondence between parameters
Our next goal is to understand how to recover the periods of the direct summands
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
from that of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
from that of
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
. We will assume that
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
. We will assume that
 $H^{i}(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0$
for
$H^{i}(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })},{\mathcal{O}})=0$
for
![]() $i>0$
, but we will not require that of
$i>0$
, but we will not require that of
![]() $X$
. The period map still makes sense for
$X$
. The period map still makes sense for
![]() $X$
; see [Reference Bezrukavnikov and KaledinBK04, § 4]. Consider the decomposition
$X$
; see [Reference Bezrukavnikov and KaledinBK04, § 4]. Consider the decomposition
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=\bigsqcup _{i}X_{i}^{0}$
into connected components. Let
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=\bigsqcup _{i}X_{i}^{0}$
into connected components. Let
![]() $Y_{i}$
denote the contracting locus of
$Y_{i}$
denote the contracting locus of
![]() $X_{i}^{0}$
and let
$X_{i}^{0}$
and let
![]() ${\mathcal{A}}_{i}^{\unicode[STIX]{x1D703}0}$
be the restriction of
${\mathcal{A}}_{i}^{\unicode[STIX]{x1D703}0}$
be the restriction of
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
to
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
to
![]() $X_{i}^{0}$
. To determine the period of
$X_{i}^{0}$
. To determine the period of
![]() ${\mathcal{A}}_{i}^{\unicode[STIX]{x1D703}0}$
, we will quantize
${\mathcal{A}}_{i}^{\unicode[STIX]{x1D703}0}$
, we will quantize
![]() $Y_{i}$
and then use results from [Reference Baranovsky, Ginzburg, Kaledin and PecharichBGKP16] on quantizations of line bundles on Lagrangian subvarieties.
$Y_{i}$
and then use results from [Reference Baranovsky, Ginzburg, Kaledin and PecharichBGKP16] on quantizations of line bundles on Lagrangian subvarieties.
First of all, let us consider the case when
![]() $X$
is affine and so is quantized by a single algebra,
$X$
is affine and so is quantized by a single algebra,
![]() ${\mathcal{A}}$
. We will quantize the contracting locus
${\mathcal{A}}$
. We will quantize the contracting locus
![]() $Y$
by a single
$Y$
by a single
![]() ${\mathcal{A}}$
-
${\mathcal{A}}$
-
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
-bimodule; this bimodule is
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
-bimodule; this bimodule is
 ${\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0}$
.
${\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0}$
.
Lemma 5.5. Under the above assumptions,
 $\operatorname{gr}{\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0}=\mathbb{C}[Y]$
.
$\operatorname{gr}{\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0}=\mathbb{C}[Y]$
.
Proof. This was established in the proof of Proposition 5.2. More precisely, the case when
![]() $Y$
is a complete intersection given by
$Y$
is a complete intersection given by
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-semi-invariant elements of positive weight follows from the proof of assertion (1), while the general case follows similarly to the proof of (3).◻
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
-semi-invariant elements of positive weight follows from the proof of assertion (1), while the general case follows similarly to the proof of (3).◻
Now let us consider the non-affine case. Let us cover
 $X\setminus \bigcup _{k\neq i}X_{k}^{0}$
with
$X\setminus \bigcup _{k\neq i}X_{k}^{0}$
with
![]() $(\mathbb{C}^{\times })^{2}$
-stable open affine subsets
$(\mathbb{C}^{\times })^{2}$
-stable open affine subsets
![]() $X^{j}$
. We may assume that
$X^{j}$
. We may assume that
 $X^{j}\,\cap \,Y_{i}=\varnothing$
or
$X^{j}\,\cap \,Y_{i}=\varnothing$
or
 $X^{j}\,\cap \,Y_{i}=\unicode[STIX]{x1D70B}_{i}^{-1}(X^{j}\,\cap \,X_{i}^{0})$
, where
$X^{j}\,\cap \,Y_{i}=\unicode[STIX]{x1D70B}_{i}^{-1}(X^{j}\,\cap \,X_{i}^{0})$
, where
 $\unicode[STIX]{x1D70B}_{i}:Y_{i}\rightarrow X_{i}^{0}$
is the projection. For this, we first choose some covering by
$\unicode[STIX]{x1D70B}_{i}:Y_{i}\rightarrow X_{i}^{0}$
is the projection. For this, we first choose some covering by
![]() $(\mathbb{C}^{\times })^{2}$
-stable open affine subsets. Then we delete
$(\mathbb{C}^{\times })^{2}$
-stable open affine subsets. Then we delete
 $Y_{i}\setminus \unicode[STIX]{x1D70B}_{i}^{-1}(X^{j}\,\cap \,X_{i}^{0})$
from each
$Y_{i}\setminus \unicode[STIX]{x1D70B}_{i}^{-1}(X^{j}\,\cap \,X_{i}^{0})$
from each
![]() $X^{j}$
; we still have a covering. We cover the remainder of each
$X^{j}$
; we still have a covering. We cover the remainder of each
![]() $X^{j}$
by subsets that are pre-images of open affine subsets on
$X^{j}$
by subsets that are pre-images of open affine subsets on
 $X^{j}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
that do not intersect
$X^{j}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
that do not intersect
 $X_{j}^{0}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. It is easy to see that this covering has the required properties. Let us replace
$X_{j}^{0}/\!/\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
. It is easy to see that this covering has the required properties. Let us replace
![]() $X$
with the union of
$X$
with the union of
![]() $X^{j}$
that intersect
$X^{j}$
that intersect
![]() $Y_{i}$
.
$Y_{i}$
.
After this replacement, we can quantize
![]() $Y_{i}$
by an
$Y_{i}$
by an
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
-
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
-
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
-bimodule. We have natural
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
-bimodule. We have natural
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})$
-
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})$
-
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})(X^{j}\,\cap \,X_{i}^{0})$
-bimodule structures on
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})(X^{j}\,\cap \,X_{i}^{0})$
-bimodule structures on
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})^{{>}0}$
and glue the bimodules corresponding to different
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{j})^{{>}0}$
and glue the bimodules corresponding to different
![]() $j$
together along the intersections
$j$
together along the intersections
 $X^{i}\,\cap \,X^{j}$
(we have homomorphisms
$X^{i}\,\cap \,X^{j}$
(we have homomorphisms
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})\rightarrow {\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})$
that give rise to
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})\rightarrow {\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})$
that give rise to
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})^{{>}0}\rightarrow {\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})^{{>}0}$
and to
${\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i})^{{>}0}\rightarrow {\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})/{\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j}){\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j})^{{>}0}$
and to
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}))\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j}))$
). Similarly to the proof of (2) in Proposition 5.2, we get a sheaf of
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}))\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}}(X^{i}\,\cap \,X^{j}))$
). Similarly to the proof of (2) in Proposition 5.2, we get a sheaf of
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
-
${\mathcal{A}}^{\unicode[STIX]{x1D703}}$
-
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
-bimodules on
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
-bimodules on
![]() $Y_{i}$
that we denote by
$Y_{i}$
that we denote by
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}/{\mathcal{A}}^{\unicode[STIX]{x1D703}}{\mathcal{A}}^{\unicode[STIX]{x1D703},>0}$
. The following is a direct consequence of the construction.
${\mathcal{A}}^{\unicode[STIX]{x1D703}}/{\mathcal{A}}^{\unicode[STIX]{x1D703}}{\mathcal{A}}^{\unicode[STIX]{x1D703},>0}$
. The following is a direct consequence of the construction.
Lemma 5.6. The associated graded bimodule of
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}/{\mathcal{A}}^{\unicode[STIX]{x1D703}}{\mathcal{A}}^{\unicode[STIX]{x1D703},>0}$
coincides with the
${\mathcal{A}}^{\unicode[STIX]{x1D703}}/{\mathcal{A}}^{\unicode[STIX]{x1D703}}{\mathcal{A}}^{\unicode[STIX]{x1D703},>0}$
coincides with the
![]() ${\mathcal{O}}_{X}$
-
${\mathcal{O}}_{X}$
-
![]() ${\mathcal{O}}_{X_{i}^{0}}$
-bimodule
${\mathcal{O}}_{X_{i}^{0}}$
-bimodule
![]() ${\mathcal{O}}_{Y_{i}}$
.
${\mathcal{O}}_{Y_{i}}$
.
Now we want to interpret
![]() $Y$
as a Lagrangian subvariety in
$Y$
as a Lagrangian subvariety in
 $X\times X^{0}$
(we still use
$X\times X^{0}$
(we still use
![]() $X$
as in the paragraph preceding Lemma 5.6 and so can write
$X$
as in the paragraph preceding Lemma 5.6 and so can write
![]() $Y$
instead of
$Y$
instead of
![]() $Y_{i}$
and
$Y_{i}$
and
![]() $X^{0}$
instead of
$X^{0}$
instead of
![]() $X_{i}^{0}$
). Namely, let
$X_{i}^{0}$
). Namely, let
![]() $\unicode[STIX]{x1D704}$
denote the inclusion
$\unicode[STIX]{x1D704}$
denote the inclusion
 $Y{\hookrightarrow}X$
and
$Y{\hookrightarrow}X$
and
![]() $\unicode[STIX]{x1D70B}$
be the projection
$\unicode[STIX]{x1D70B}$
be the projection
 $Y\rightarrow X^{0}$
. We embed
$Y\rightarrow X^{0}$
. We embed
![]() $Y$
into
$Y$
into
 $X\times X^{0}$
via
$X\times X^{0}$
via
![]() $(\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B})$
. We equip
$(\unicode[STIX]{x1D704},\unicode[STIX]{x1D70B})$
. We equip
 $X\times X^{0}$
with the symplectic form
$X\times X^{0}$
with the symplectic form
 $(\unicode[STIX]{x1D714},-\unicode[STIX]{x1D714}^{0})$
, where
$(\unicode[STIX]{x1D714},-\unicode[STIX]{x1D714}^{0})$
, where
![]() $\unicode[STIX]{x1D714}^{0}$
is the restriction of
$\unicode[STIX]{x1D714}^{0}$
is the restriction of
![]() $\unicode[STIX]{x1D714}$
to
$\unicode[STIX]{x1D714}$
to
![]() $X^{0}$
. With respect to this symplectic form,
$X^{0}$
. With respect to this symplectic form,
![]() $Y$
is a Lagrangian subvariety. Further,
$Y$
is a Lagrangian subvariety. Further,
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
is a quantization of
${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
is a quantization of
 $X\times X^{0}$
with period
$X\times X^{0}$
with period
 $(\unicode[STIX]{x1D706},-\unicode[STIX]{x1D706}^{0})$
, where
$(\unicode[STIX]{x1D706},-\unicode[STIX]{x1D706}^{0})$
, where
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{0}$
are periods of
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{0}$
are periods of
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
.
${\mathcal{A}}^{\unicode[STIX]{x1D703}},\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})$
.
Proposition 5.7. The period
![]() $\unicode[STIX]{x1D706}^{0}$
coincides with
$\unicode[STIX]{x1D706}^{0}$
coincides with
 $\unicode[STIX]{x1D704}^{0\ast }(\unicode[STIX]{x1D706}+c_{1}(K_{Y})/2)\in H^{2}(X^{0})=H^{2}(Y)$
, where
$\unicode[STIX]{x1D704}^{0\ast }(\unicode[STIX]{x1D706}+c_{1}(K_{Y})/2)\in H^{2}(X^{0})=H^{2}(Y)$
, where
![]() $K_{Y}$
denotes the canonical class of
$K_{Y}$
denotes the canonical class of
![]() $Y$
and
$Y$
and
![]() $\unicode[STIX]{x1D704}^{0}$
is the inclusion
$\unicode[STIX]{x1D704}^{0}$
is the inclusion
 $X^{0}{\hookrightarrow}X$
.
$X^{0}{\hookrightarrow}X$
.
Proof. The period of
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
coincides with
${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
coincides with
 $p_{1}(\unicode[STIX]{x1D706})-p_{2}(\unicode[STIX]{x1D706}^{0})$
, where
$p_{1}(\unicode[STIX]{x1D706})-p_{2}(\unicode[STIX]{x1D706}^{0})$
, where
 $p_{1}^{\ast }:X\times X^{0}\rightarrow X,p_{2}^{\ast }:X\times X^{0}\rightarrow X^{0}$
are the projections. So, the pull-back of the period to
$p_{1}^{\ast }:X\times X^{0}\rightarrow X,p_{2}^{\ast }:X\times X^{0}\rightarrow X^{0}$
are the projections. So, the pull-back of the period to
![]() $Y$
is
$Y$
is
 $\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D706}^{0})$
. The structure sheaf of
$\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D706}^{0})$
. The structure sheaf of
![]() $Y$
admits a quantization to an
$Y$
admits a quantization to an
 ${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
-bimodule. By [Reference Baranovsky, Ginzburg, Kaledin and PecharichBGKP16, Equation (1.1.3) and Theorem 1.1.4], we have
${\mathcal{A}}^{\unicode[STIX]{x1D703}}\,\widehat{\otimes }\,\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}^{\unicode[STIX]{x1D703}})^{\text{opp}}$
-bimodule. By [Reference Baranovsky, Ginzburg, Kaledin and PecharichBGKP16, Equation (1.1.3) and Theorem 1.1.4], we have
 $\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D706}^{0})=-\frac{1}{2}c_{1}(K_{Y})$
. Restricting this equality to
$\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D706}^{0})=-\frac{1}{2}c_{1}(K_{Y})$
. Restricting this equality to
![]() $X^{0}$
, we get the equality required in the proposition.◻
$X^{0}$
, we get the equality required in the proposition.◻
5.5 Parabolic induction functor
Let
![]() $X$
be a conical symplectic resolution of
$X$
be a conical symplectic resolution of
![]() $X_{0}$
. We assume that
$X_{0}$
. We assume that
![]() $X$
comes with a Hamiltonian action of a torus
$X$
comes with a Hamiltonian action of a torus
![]() $T$
. Let
$T$
. Let
![]() $\mathfrak{C}$
stand for
$\mathfrak{C}$
stand for
 $\operatorname{Hom}(\mathbb{C}^{\times },T)$
. We introduce a pre-order
$\operatorname{Hom}(\mathbb{C}^{\times },T)$
. We introduce a pre-order
![]() $\prec ^{\unicode[STIX]{x1D706}}$
on
$\prec ^{\unicode[STIX]{x1D706}}$
on
![]() $\mathfrak{C}$
as follows:
$\mathfrak{C}$
as follows:
![]() $\unicode[STIX]{x1D708}\prec ^{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D708}^{\prime }$
if:
$\unicode[STIX]{x1D708}\prec ^{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D708}^{\prime }$
if:
-
(i)
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})={\mathcal{A}}_{\unicode[STIX]{x1D706}}{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
; and
${\mathcal{A}}_{\unicode[STIX]{x1D706}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})={\mathcal{A}}_{\unicode[STIX]{x1D706}}{\mathcal{A}}_{\unicode[STIX]{x1D706}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
; and -
(ii) the natural action of
 $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
on
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
on
 $\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is trivial.
$\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
is trivial.
The pre-order extends naturally to
 $\mathfrak{C}_{\mathbb{Q}}:=\mathbb{Q}\,\otimes _{\mathbb{Z}}\mathfrak{C}$
.
$\mathfrak{C}_{\mathbb{Q}}:=\mathbb{Q}\,\otimes _{\mathbb{Z}}\mathfrak{C}$
.
The following lemma explains why this ordering is important.
Lemma 5.8. Suppose that
![]() $\unicode[STIX]{x1D708}\prec \unicode[STIX]{x1D708}^{\prime }$
. Then
$\unicode[STIX]{x1D708}\prec \unicode[STIX]{x1D708}^{\prime }$
. Then
 $\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))=\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. Further, let
$\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))=\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
. Further, let
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}:\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}:\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
,
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod}$
,
 $\text{}\underline{\unicode[STIX]{x1D6E5}}:\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})\text{-}\!\operatorname{mod}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}$
be the Verma module functors. We have
$\text{}\underline{\unicode[STIX]{x1D6E5}}:\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})\text{-}\!\operatorname{mod}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})\text{-}\!\operatorname{mod}$
be the Verma module functors. We have
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}\circ \text{}\underline{\unicode[STIX]{x1D6E5}}$
.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}\circ \text{}\underline{\unicode[STIX]{x1D6E5}}$
.
Proof. Let us write
![]() ${\mathcal{A}}$
for
${\mathcal{A}}$
for
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
.
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
.
Let us prove that
 $\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}))=\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
. Condition (i) produces an epimorphism
$\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}))=\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
. Condition (i) produces an epimorphism
 ${\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}{\twoheadrightarrow}{\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
. By (ii), the latter gives rise to an algebra epimorphism
${\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}{\twoheadrightarrow}{\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
. By (ii), the latter gives rise to an algebra epimorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}){\twoheadrightarrow}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
that induces
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}){\twoheadrightarrow}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
that induces
 $\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})){\twoheadrightarrow}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}})){\twoheadrightarrow}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
.
To show that
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}\,\circ \,\text{}\underline{\unicode[STIX]{x1D6E5}}\cong \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}$
, we note that the right-hand side is
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}\,\circ \,\text{}\underline{\unicode[STIX]{x1D6E5}}\cong \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}^{\prime }}$
, we note that the right-hand side is
 ${\mathcal{A}}/I_{r}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})}\bullet$
, while the left-hand side is
${\mathcal{A}}/I_{r}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})}\bullet$
, while the left-hand side is
 ${\mathcal{A}}/I_{\ell }\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})}\bullet$
, where we write
${\mathcal{A}}/I_{\ell }\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})}\bullet$
, where we write
![]() $I_{\ell },I_{r}$
for the ideals of
$I_{\ell },I_{r}$
for the ideals of
![]() ${\mathcal{A}}$
in the left- and the right-hand sides of the equality in (i).◻
${\mathcal{A}}$
in the left- and the right-hand sides of the equality in (i).◻
The lemma shows that the Verma module functor can be studied in stages. This is what we mean by the parabolic induction.
Here is an example of two one-parameter subgroups that are comparable with respect to
![]() $\prec ^{\unicode[STIX]{x1D706}}$
. Pick one-parameter subgroups
$\prec ^{\unicode[STIX]{x1D706}}$
. Pick one-parameter subgroups
 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D705}:\mathbb{C}^{\times }\rightarrow T$
.
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D705}:\mathbb{C}^{\times }\rightarrow T$
.
Lemma 5.9. For
![]() $m\gg 0$
, we have
$m\gg 0$
, we have
 $\unicode[STIX]{x1D708}\prec ^{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D708}^{\prime }:=m\unicode[STIX]{x1D708}+\unicode[STIX]{x1D705}$
for all
$\unicode[STIX]{x1D708}\prec ^{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D708}^{\prime }:=m\unicode[STIX]{x1D708}+\unicode[STIX]{x1D705}$
for all
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Proof. Let us write
![]() ${\mathcal{A}}$
for
${\mathcal{A}}$
for
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
. Let us prove the inclusion
${\mathcal{A}}_{\unicode[STIX]{x1D706}}$
. Let us prove the inclusion
 ${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
that will imply that
${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
that will imply that
 ${\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
.
${\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
.
The algebra
 $\operatorname{gr}({\mathcal{A}}^{{\geqslant}0,\unicode[STIX]{x1D708}})=\mathbb{C}[X_{0}]^{{\geqslant}0,\unicode[STIX]{x1D708}}$
is finitely generated, as in the proof of [Reference Gordon and LosevGL14, Lemma 3.1.2]. So, we can choose finitely many
$\operatorname{gr}({\mathcal{A}}^{{\geqslant}0,\unicode[STIX]{x1D708}})=\mathbb{C}[X_{0}]^{{\geqslant}0,\unicode[STIX]{x1D708}}$
is finitely generated, as in the proof of [Reference Gordon and LosevGL14, Lemma 3.1.2]. So, we can choose finitely many
![]() $T$
-semi-invariant generators of the ideal
$T$
-semi-invariant generators of the ideal
 $\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}}$
in
$\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}}$
in
 $\mathbb{C}[X_{0}]^{{\geqslant}0,\unicode[STIX]{x1D708}}$
, say
$\mathbb{C}[X_{0}]^{{\geqslant}0,\unicode[STIX]{x1D708}}$
, say
 $f_{1},\ldots ,f_{k}$
. Let
$f_{1},\ldots ,f_{k}$
. Let
 $\tilde{f}_{1},\ldots ,\tilde{f}_{k}$
denote their lifts to
$\tilde{f}_{1},\ldots ,\tilde{f}_{k}$
denote their lifts to
![]() $T$
-semi-invariant elements in
$T$
-semi-invariant elements in
![]() ${\mathcal{A}}$
; these lifts are generators of the ideal
${\mathcal{A}}$
; these lifts are generators of the ideal
![]() ${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}$
in
${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}$
in
![]() ${\mathcal{A}}^{{\geqslant}0,\unicode[STIX]{x1D708}}$
. Let
${\mathcal{A}}^{{\geqslant}0,\unicode[STIX]{x1D708}}$
. Let
 $a_{1},\ldots ,a_{k}>0$
be their weights for
$a_{1},\ldots ,a_{k}>0$
be their weights for
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
 $b_{1},\ldots ,b_{k}$
be their weights for
$b_{1},\ldots ,b_{k}$
be their weights for
![]() $\unicode[STIX]{x1D705}$
. Take
$\unicode[STIX]{x1D705}$
. Take
 $m\in \mathbb{Z}^{{>}0}$
such that
$m\in \mathbb{Z}^{{>}0}$
such that
 $ma_{i}+b_{i}>0$
for all
$ma_{i}+b_{i}>0$
for all
![]() $i$
. The elements
$i$
. The elements
 $\tilde{f}_{1},\ldots ,\tilde{f}_{k}$
then lie in
$\tilde{f}_{1},\ldots ,\tilde{f}_{k}$
then lie in
![]() ${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
and so
${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
and so
 ${\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
.
${\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\subset {\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
.
The inclusion
 ${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}\subset {\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})$
is proved in a similar fashion. So, we get the equality in (i).
${\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}^{\prime }}\subset {\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}+({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D708}^{\prime }})$
is proved in a similar fashion. So, we get the equality in (i).
Let us check that
![]() $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
acts trivially on
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
acts trivially on
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
. We get
$\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})$
. We get
 $$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})=\big({\mathcal{A}}/{\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\oplus ({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D705}})\big)^{\unicode[STIX]{x1D708}^{\prime }(\mathbb{C}^{\times })}.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}})=\big({\mathcal{A}}/{\mathcal{A}}({\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}}\oplus ({\mathcal{A}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})^{{>}0,\unicode[STIX]{x1D705}})\big)^{\unicode[STIX]{x1D708}^{\prime }(\mathbb{C}^{\times })}.\end{eqnarray}$$
Note that the expression in brackets is independent of
![]() $m$
and the weights of
$m$
and the weights of
![]() $\unicode[STIX]{x1D708}$
are all non-negative. From here it is easy to deduce that the invariants with respect to
$\unicode[STIX]{x1D708}$
are all non-negative. From here it is easy to deduce that the invariants with respect to
![]() $\unicode[STIX]{x1D708}^{\prime }(\mathbb{C}^{\times })$
coincide with the invariants for
$\unicode[STIX]{x1D708}^{\prime }(\mathbb{C}^{\times })$
coincide with the invariants for
 $\unicode[STIX]{x1D708}(\mathbb{C}^{\times })\unicode[STIX]{x1D705}(\mathbb{C}^{\times })$
for
$\unicode[STIX]{x1D708}(\mathbb{C}^{\times })\unicode[STIX]{x1D705}(\mathbb{C}^{\times })$
for
![]() $m$
large enough.◻
$m$
large enough.◻
6 Standardly stratified structures on categories
 ${\mathcal{O}}$
${\mathcal{O}}$
In this section, we introduce a family of standardly stratified structures on the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
that are compatible in the sense of § 3.5 with the highest-weight structure recalled in § 4.3.
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
that are compatible in the sense of § 3.5 with the highest-weight structure recalled in § 4.3.
6.1 Main result
Suppose that we have a Hamiltonian action of a torus
![]() $T$
on
$T$
on
![]() $X$
(commuting with the contracting action) such that the fixed point set
$X$
(commuting with the contracting action) such that the fixed point set
![]() $X^{T}$
is finite. Let
$X^{T}$
is finite. Let
 $\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{N}$
be the characters of the
$\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{N}$
be the characters of the
![]() $T$
-action on
$T$
-action on
 $$\begin{eqnarray}\bigoplus _{p\in X^{T}}T_{p}X.\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{p\in X^{T}}T_{p}X.\end{eqnarray}$$
The kernels
 $\ker \unicode[STIX]{x1D712}_{i},i=1,\ldots ,N,$
partition the cocharacter space
$\ker \unicode[STIX]{x1D712}_{i},i=1,\ldots ,N,$
partition the cocharacter space
 $\operatorname{Hom}(\mathbb{C}^{\times },T)\,\otimes _{\mathbb{Z}}\mathbb{R}$
into polyhedral cones to be called chambers. If
$\operatorname{Hom}(\mathbb{C}^{\times },T)\,\otimes _{\mathbb{Z}}\mathbb{R}$
into polyhedral cones to be called chambers. If
![]() $\unicode[STIX]{x1D708}$
lies in the interior of a chamber (i.e.,
$\unicode[STIX]{x1D708}$
lies in the interior of a chamber (i.e.,
 $\langle \unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D708}\rangle \neq 0$
for all
$\langle \unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D708}\rangle \neq 0$
for all
![]() $i$
), then
$i$
), then
 $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=X^{T}$
. Such one-parameter subgroups will be called generic. Otherwise,
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}=X^{T}$
. Such one-parameter subgroups will be called generic. Otherwise,
![]() $X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is infinite.
$X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
is infinite.
Let
![]() $\unicode[STIX]{x1D708}$
be a generic one-parameter subgroup of
$\unicode[STIX]{x1D708}$
be a generic one-parameter subgroup of
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D708}_{0}$
be a one-parameter subgroup lying in the closure of the chamber containing
$\unicode[STIX]{x1D708}_{0}$
be a one-parameter subgroup lying in the closure of the chamber containing
![]() $\unicode[STIX]{x1D708}$
. In this case we will write
$\unicode[STIX]{x1D708}$
. In this case we will write
![]() $\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Our goal is to produce a standardly stratified structure on
$\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Our goal is to produce a standardly stratified structure on
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
corresponding to
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
corresponding to
![]() $\unicode[STIX]{x1D708}_{0}$
. The first step is to define a pre-order on
$\unicode[STIX]{x1D708}_{0}$
. The first step is to define a pre-order on
![]() $X^{T}$
from
$X^{T}$
from
![]() $\unicode[STIX]{x1D708}_{0}$
.
$\unicode[STIX]{x1D708}_{0}$
.
Let
 $Z_{1},\ldots ,Z_{k}$
be the irreducible (
$Z_{1},\ldots ,Z_{k}$
be the irreducible (
![]() $=$
connected) components of
$=$
connected) components of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. We define a partial order
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. We define a partial order
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
on the set
$\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
on the set
 $\{Z_{1},\ldots ,Z_{k}\}$
as the transitive closure of the relation
$\{Z_{1},\ldots ,Z_{k}\}$
as the transitive closure of the relation
 $Z_{i}\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z_{j}$
specified by
$Z_{i}\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z_{j}$
specified by
 $Z_{i}\,\cap \,\overline{Y_{j}}\neq \varnothing$
, where
$Z_{i}\,\cap \,\overline{Y_{j}}\neq \varnothing$
, where
![]() $Y_{j}$
is the contracting locus of
$Y_{j}$
is the contracting locus of
![]() $Z_{j}$
, i.e.,
$Z_{j}$
, i.e.,
 $$\begin{eqnarray}Y_{j}=\Big\{x\in X|\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x\in Z_{j}\Big\}.\end{eqnarray}$$
$$\begin{eqnarray}Y_{j}=\Big\{x\in X|\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x\in Z_{j}\Big\}.\end{eqnarray}$$
For
 $p,p^{\prime }\in X^{T}$
, we set
$p,p^{\prime }\in X^{T}$
, we set
 $p\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
if
$p\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
if
 $p\in Z_{i},p^{\prime }\in Z_{j}$
with
$p\in Z_{i},p^{\prime }\in Z_{j}$
with
 $Z_{i}\prec _{\unicode[STIX]{x1D708}_{0}}Z_{j}$
.
$Z_{i}\prec _{\unicode[STIX]{x1D708}_{0}}Z_{j}$
.
Lemma 6.1.
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
is a partial order on
$\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
is a partial order on
 $\{Z_{1},\ldots ,Z_{k}\}$
.
$\{Z_{1},\ldots ,Z_{k}\}$
.
Proof. We only need to check that the relation
 $\preccurlyeq :=\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
does not contain cycles:
$\preccurlyeq :=\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
does not contain cycles:
 $Z_{i_{1}}\preccurlyeq Z_{i_{2}}\preccurlyeq \cdots \preccurlyeq Z_{i_{s}}\preccurlyeq Z_{i_{1}}$
implies that
$Z_{i_{1}}\preccurlyeq Z_{i_{2}}\preccurlyeq \cdots \preccurlyeq Z_{i_{s}}\preccurlyeq Z_{i_{1}}$
implies that
 $i_{1}=i_{2}=\cdots =i_{s}$
.
$i_{1}=i_{2}=\cdots =i_{s}$
.
We can find a smooth projective compactification of
![]() $X$
with an action of
$X$
with an action of
![]() $\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })$
; denote it by
$\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })$
; denote it by
![]() $X^{c}$
. Then the closures
$X^{c}$
. Then the closures
 $Z_{i}^{c},i=1,\ldots ,k,$
are still irreducible components of
$Z_{i}^{c},i=1,\ldots ,k,$
are still irreducible components of
 $X^{c\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
(there may be other components). Moreover,
$X^{c\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
(there may be other components). Moreover,
![]() $Y_{i}$
is an open subset in the contracting locus
$Y_{i}$
is an open subset in the contracting locus
![]() $Y_{i}^{c}$
of
$Y_{i}^{c}$
of
![]() $\overline{Z}_{i}$
and so
$\overline{Z}_{i}$
and so
![]() $\overline{Y}_{i}$
is open and dense in
$\overline{Y}_{i}$
is open and dense in
![]() $\overline{Y_{i}^{c}}$
. We can define the relation
$\overline{Y_{i}^{c}}$
. We can define the relation
![]() $\preccurlyeq ^{c}$
in
$\preccurlyeq ^{c}$
in
![]() $X^{c}$
instead of
$X^{c}$
instead of
![]() $X$
. Clearly,
$X$
. Clearly,
 $Z_{i}\preccurlyeq Z_{j}\Rightarrow Z_{i}^{c}\preccurlyeq ^{c}Z_{j}^{c}$
. So, if
$Z_{i}\preccurlyeq Z_{j}\Rightarrow Z_{i}^{c}\preccurlyeq ^{c}Z_{j}^{c}$
. So, if
![]() $\preccurlyeq ^{c}$
contains no cycles, neither does
$\preccurlyeq ^{c}$
contains no cycles, neither does
![]() $\preccurlyeq$
. The relation
$\preccurlyeq$
. The relation
![]() $\preccurlyeq ^{c}$
contains no cycles by [Reference Bialynicki-BirulaBia76].◻
$\preccurlyeq ^{c}$
contains no cycles by [Reference Bialynicki-BirulaBia76].◻
Lemma 6.2. The relation
![]() $p\preccurlyeq _{\unicode[STIX]{x1D708}}p^{\prime }$
implies that
$p\preccurlyeq _{\unicode[STIX]{x1D708}}p^{\prime }$
implies that
 $p\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
.
$p\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
.
Proof. In the proof, we can assume that
![]() $p\in \overline{Y}_{p^{\prime }}$
. In this case, what we need to check is that
$p\in \overline{Y}_{p^{\prime }}$
. In this case, what we need to check is that
![]() $\unicode[STIX]{x1D708}_{0}$
contracts
$\unicode[STIX]{x1D708}_{0}$
contracts
![]() $Y_{p^{\prime }}$
to the irreducible component
$Y_{p^{\prime }}$
to the irreducible component
![]() $Z$
of
$Z$
of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
containing
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
containing
![]() $p^{\prime }$
. We can replace
$p^{\prime }$
. We can replace
![]() $X$
with a
$X$
with a
![]() $T$
-stable affine neighborhood of
$T$
-stable affine neighborhood of
![]() $p^{\prime }$
. Applying the Luna slice theorem to
$p^{\prime }$
. Applying the Luna slice theorem to
![]() $T$
and
$T$
and
![]() $p^{\prime }$
, we see that
$p^{\prime }$
, we see that
![]() $Y_{p^{\prime }}$
is
$Y_{p^{\prime }}$
is
![]() $T$
-equivariantly isomorphic to a
$T$
-equivariantly isomorphic to a
![]() $T$
-module such that all weights of
$T$
-module such that all weights of
![]() $\unicode[STIX]{x1D708}$
are positive. Since
$\unicode[STIX]{x1D708}$
are positive. Since
![]() $\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
$\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
![]() $\unicode[STIX]{x1D708}$
, we see that all weights of
$\unicode[STIX]{x1D708}$
, we see that all weights of
![]() $\unicode[STIX]{x1D708}_{0}$
are non-negative. This implies our claim.◻
$\unicode[STIX]{x1D708}_{0}$
are non-negative. This implies our claim.◻
Let us proceed to the main result of this section.
Theorem 6.3. Suppose that
![]() $\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
$\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
![]() $\unicode[STIX]{x1D708}$
. Then
$\unicode[STIX]{x1D708}$
. Then
 $({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}),\preccurlyeq _{\unicode[STIX]{x1D708}_{0}})$
is a standardly stratified category.
$({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}),\preccurlyeq _{\unicode[STIX]{x1D708}_{0}})$
is a standardly stratified category.
In the proof, we will always assume that
 $\unicode[STIX]{x1D708}=m\unicode[STIX]{x1D708}_{0}+\unicode[STIX]{x1D705}$
for a fixed
$\unicode[STIX]{x1D708}=m\unicode[STIX]{x1D708}_{0}+\unicode[STIX]{x1D705}$
for a fixed
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $m\gg 0$
.
$m\gg 0$
.
Let us explain our scheme of proof of Theorem 6.3. We will start by describing the associated graded category
 $\operatorname{gr}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
; we will show that this category is
$\operatorname{gr}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
; we will show that this category is
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{C}}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
and that, under the identifications
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{C}}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
and that, under the identifications
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
and
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
and
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{C}}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}))$
(where
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{C}}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}))$
(where
![]() $\unicode[STIX]{x1D712}$
is ample and
$\unicode[STIX]{x1D712}$
is ample and
![]() $n\gg 0$
) the standardization functor becomes the Verma module functor
$n\gg 0$
) the standardization functor becomes the Verma module functor
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Using this, we will check that the standardization functor is exact confirming (SS1); this reduces to the claim that the right
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Using this, we will check that the standardization functor is exact confirming (SS1); this reduces to the claim that the right
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
-module
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})$
-module
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})_{{>}0,\unicode[STIX]{x1D708}_{0}}$
is projective. Finally, we will use Lemma 3.4 to complete the proof.
${\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}})_{{>}0,\unicode[STIX]{x1D708}_{0}}$
is projective. Finally, we will use Lemma 3.4 to complete the proof.
Below we will write
![]() $\unicode[STIX]{x1D706}^{+}$
for
$\unicode[STIX]{x1D706}^{+}$
for
![]() $\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}$
with
![]() $n\gg 0$
.
$n\gg 0$
.
6.2 Associated graded category
The goal of this part is to prove the following proposition.
Proposition 6.4. Let
![]() $Z$
be an irreducible component of
$Z$
be an irreducible component of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. The subquotient
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. The subquotient
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})_{Z}$
is equivalent to
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})_{Z}$
is equivalent to
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})|_{Z})$
as an abelian category so that the functors
${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})|_{Z})$
as an abelian category so that the functors
![]() $\unicode[STIX]{x1D70B}_{Z}^{!}$
and
$\unicode[STIX]{x1D70B}_{Z}^{!}$
and
![]() $\unicode[STIX]{x1D70B}_{Z}^{\ast }$
get identified with
$\unicode[STIX]{x1D70B}_{Z}^{\ast }$
get identified with
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
and
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
, respectively.
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
, respectively.
In order to prove this proposition, we need to understand the ‘highest weights’ of modules in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
. We can identify
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
. We can identify
 $\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
with
$\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
with
 $\mathbb{C}[(X^{\unicode[STIX]{x1D703}})^{T}]$
. Let
$\mathbb{C}[(X^{\unicode[STIX]{x1D703}})^{T}]$
. Let
![]() $\ell$
denote the line
$\ell$
denote the line
 $\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
. Let
$\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
. Let
 $\unicode[STIX]{x1D6F7}_{\ell }:\mathfrak{t}\rightarrow {\mathcal{A}}_{\ell ,\leqslant d}$
be a quantum comoment map for the action of
$\unicode[STIX]{x1D6F7}_{\ell }:\mathfrak{t}\rightarrow {\mathcal{A}}_{\ell ,\leqslant d}$
be a quantum comoment map for the action of
![]() $T$
on
$T$
on
![]() ${\mathcal{A}}_{\ell }$
. Note that
${\mathcal{A}}_{\ell }$
. Note that
![]() $\unicode[STIX]{x1D6F7}_{\ell }$
is defined up to adding a linear function
$\unicode[STIX]{x1D6F7}_{\ell }$
is defined up to adding a linear function
 $\mathfrak{t}\rightarrow \operatorname{Aff}(\ell ,\mathbb{C})$
, where
$\mathfrak{t}\rightarrow \operatorname{Aff}(\ell ,\mathbb{C})$
, where
 $\operatorname{Aff}(\ell ,\mathbb{C})$
stands for the space of affine functions
$\operatorname{Aff}(\ell ,\mathbb{C})$
stands for the space of affine functions
![]() $\ell \rightarrow \mathbb{C}$
. Then we have a linear function
$\ell \rightarrow \mathbb{C}$
. Then we have a linear function
 $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}:\mathfrak{t}\rightarrow \mathbb{C}$
defined as the composition
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}:\mathfrak{t}\rightarrow \mathbb{C}$
defined as the composition
 $\unicode[STIX]{x1D702}_{p}\circ \unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
, where the quantum comoment map
$\unicode[STIX]{x1D702}_{p}\circ \unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
, where the quantum comoment map
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is viewed as a map
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is viewed as a map
 $\mathfrak{t}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, by
$\mathfrak{t}\rightarrow {\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
, by
![]() $\unicode[STIX]{x1D711}$
we denote the natural homomorphism
$\unicode[STIX]{x1D711}$
we denote the natural homomorphism
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))$
and
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))$
and
![]() $\unicode[STIX]{x1D702}_{p}$
stands for the projection
$\unicode[STIX]{x1D702}_{p}$
stands for the projection
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))\rightarrow \mathbb{C}$
to the one-dimensional quotient corresponding to
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))\rightarrow \mathbb{C}$
to the one-dimensional quotient corresponding to
 $p\in X^{T}$
. By the construction,
$p\in X^{T}$
. By the construction,
![]() $\mathfrak{t}$
acts on the top degree component of
$\mathfrak{t}$
acts on the top degree component of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p)$
by the character
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p)$
by the character
![]() $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
. We are going to investigate the properties of
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
. We are going to investigate the properties of
![]() $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
.
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
.
Lemma 6.5. The following are true.
-
(1) The function
 $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
is affine in
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
is affine in
 $z$
.
$z$
. -
(2) Let
 $\mathfrak{t}_{0}\subset \mathfrak{t}$
be the Lie subalgebra spanned by the face containing
$\mathfrak{t}_{0}\subset \mathfrak{t}$
be the Lie subalgebra spanned by the face containing
 $\unicode[STIX]{x1D708}_{0}$
with
$\unicode[STIX]{x1D708}_{0}$
with
 $\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. If
$\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. If
 $p,p^{\prime }$
lie in the connected component of
$p,p^{\prime }$
lie in the connected component of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
, then
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
, then
 $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p},c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p^{\prime }}$
coincide on
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p},c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p^{\prime }}$
coincide on
 $\mathfrak{t}_{0}$
.
$\mathfrak{t}_{0}$
. -
(3) For two points
 $p,p^{\prime }\in X^{T}$
, the linear part of the difference
$p,p^{\prime }\in X^{T}$
, the linear part of the difference
 $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}-c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p^{\prime }}$
equals
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}-c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p^{\prime }}$
equals
 $z(\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})-\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712}))$
, where
$z(\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})-\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712}))$
, where
 $\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
(respectively,
$\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
(respectively,
 $\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712})$
) is the character of the action of
$\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712})$
) is the character of the action of
 $T$
on the fiber
$T$
on the fiber
 ${\mathcal{O}}(\unicode[STIX]{x1D712})_{p}$
(respectively, on
${\mathcal{O}}(\unicode[STIX]{x1D712})_{p}$
(respectively, on
 ${\mathcal{O}}(\unicode[STIX]{x1D712})_{p^{\prime }}$
). Note that
${\mathcal{O}}(\unicode[STIX]{x1D712})_{p^{\prime }}$
). Note that
 $\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
depends on the choice of the
$\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
depends on the choice of the
 $T$
-equivariant structure on
$T$
-equivariant structure on
 ${\mathcal{O}}(\unicode[STIX]{x1D712})$
but the difference does not.
${\mathcal{O}}(\unicode[STIX]{x1D712})$
but the difference does not.
Proof. We can consider the universal function
 $c^{p}:\mathfrak{t}\rightarrow \mathbb{C}[\ell ]$
, the composition of the quantum comoment map
$c^{p}:\mathfrak{t}\rightarrow \mathbb{C}[\ell ]$
, the composition of the quantum comoment map
 $\unicode[STIX]{x1D6F7}:\mathfrak{t}\rightarrow ({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})_{{\leqslant}d}$
, the natural homomorphism
$\unicode[STIX]{x1D6F7}:\mathfrak{t}\rightarrow ({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})_{{\leqslant}d}$
, the natural homomorphism
 ${\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
and the projection
${\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
and the projection
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})){\twoheadrightarrow}\mathbb{C}[\ell ]$
corresponding to
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})){\twoheadrightarrow}\mathbb{C}[\ell ]$
corresponding to
![]() $p$
. Note that
$p$
. Note that
 $\operatorname{im}c^{p}\in \operatorname{Aff}(\ell ,\mathbb{C})$
and that
$\operatorname{im}c^{p}\in \operatorname{Aff}(\ell ,\mathbb{C})$
and that
![]() $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
is the specialization of
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
is the specialization of
![]() $c^{p}$
to
$c^{p}$
to
![]() $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
. This implies (1).
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
. This implies (1).
Let us proceed to (2). By Lemma 5.9,
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
factors through
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
factors through
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. The image of
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
. The image of
![]() $\unicode[STIX]{x1D6F7}(\mathfrak{t}_{0})$
in
$\unicode[STIX]{x1D6F7}(\mathfrak{t}_{0})$
in
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
is central and so, for any
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
is central and so, for any
![]() $\unicode[STIX]{x1D709}\in \mathfrak{t}_{0}$
, the projection of
$\unicode[STIX]{x1D709}\in \mathfrak{t}_{0}$
, the projection of
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D709})$
to the direct summand corresponding to any component of
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D709})$
to the direct summand corresponding to any component of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
is constant. This implies (2).
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
is constant. This implies (2).
Let us prove (3). Let us write
![]() $X_{\mathbb{C}\unicode[STIX]{x1D712}}$
for
$X_{\mathbb{C}\unicode[STIX]{x1D712}}$
for
 $\mathbb{C}\unicode[STIX]{x1D712}\times _{\tilde{\mathfrak{p}}}X$
. The linear part of the map
$\mathbb{C}\unicode[STIX]{x1D712}\times _{\tilde{\mathfrak{p}}}X$
. The linear part of the map
![]() $c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
coincides with the composition of
$c_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{p}$
coincides with the composition of
 $\unicode[STIX]{x1D707}^{\ast }:\mathfrak{t}^{\ast }\rightarrow \mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
and the projection
$\unicode[STIX]{x1D707}^{\ast }:\mathfrak{t}^{\ast }\rightarrow \mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}$
and the projection
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathbb{C}[z]$
corresponding to
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })}\rightarrow \mathbb{C}[z]$
corresponding to
![]() $p$
. So, this linear part is
$p$
. So, this linear part is
![]() $z\unicode[STIX]{x1D707}(p_{1})$
, where
$z\unicode[STIX]{x1D707}(p_{1})$
, where
 $p_{1}\in X_{\unicode[STIX]{x1D712}}^{T}$
is the point corresponding to
$p_{1}\in X_{\unicode[STIX]{x1D712}}^{T}$
is the point corresponding to
![]() $p$
(see the end of § 5.1). We now need to show that
$p$
(see the end of § 5.1). We now need to show that
 $\unicode[STIX]{x1D707}(p_{1})-\unicode[STIX]{x1D707}(p_{1}^{\prime })=\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})-\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712})$
.
$\unicode[STIX]{x1D707}(p_{1})-\unicode[STIX]{x1D707}(p_{1}^{\prime })=\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})-\unicode[STIX]{x1D6FC}_{p^{\prime }}(\unicode[STIX]{x1D712})$
.
Let us choose a
![]() $T\times \mathbb{C}^{\times }$
-equivariant structure on
$T\times \mathbb{C}^{\times }$
-equivariant structure on
![]() ${\mathcal{O}}(\unicode[STIX]{x1D712})$
. Let
${\mathcal{O}}(\unicode[STIX]{x1D712})$
. Let
![]() ${\mathcal{L}}$
denote a unique
${\mathcal{L}}$
denote a unique
![]() $T\times \mathbb{C}^{\times }$
-equivariant extension of
$T\times \mathbb{C}^{\times }$
-equivariant extension of
![]() ${\mathcal{O}}(\unicode[STIX]{x1D712})$
to
${\mathcal{O}}(\unicode[STIX]{x1D712})$
to
![]() $X_{\mathbb{C}\unicode[STIX]{x1D712}}$
. According to [Reference KaledinKal06a], the complement
$X_{\mathbb{C}\unicode[STIX]{x1D712}}$
. According to [Reference KaledinKal06a], the complement
![]() ${\mathcal{L}}^{\times }$
of the zero section in
${\mathcal{L}}^{\times }$
of the zero section in
![]() ${\mathcal{L}}$
is a symplectic variety with a Hamiltonian action of
${\mathcal{L}}$
is a symplectic variety with a Hamiltonian action of
![]() $\mathbb{C}^{\times }$
, whose moment map
$\mathbb{C}^{\times }$
, whose moment map
![]() $\unicode[STIX]{x1D707}_{\mathbb{C}^{\times }}$
is the projection
$\unicode[STIX]{x1D707}_{\mathbb{C}^{\times }}$
is the projection
 ${\mathcal{L}}^{\times }\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
. The
${\mathcal{L}}^{\times }\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
. The
![]() $T$
-equivariant structure on
$T$
-equivariant structure on
![]() ${\mathcal{L}}$
induces a moment map
${\mathcal{L}}$
induces a moment map
![]() $\unicode[STIX]{x1D707}_{T}$
for the action of
$\unicode[STIX]{x1D707}_{T}$
for the action of
![]() $T$
on
$T$
on
![]() ${\mathcal{L}}^{\times }$
; the induced moment map on
${\mathcal{L}}^{\times }$
; the induced moment map on
 $X=\unicode[STIX]{x1D707}_{\mathbb{C}^{\times }}^{-1}(0)/\!/\mathbb{C}^{\times }$
coincides with the original one. Let us pick
$X=\unicode[STIX]{x1D707}_{\mathbb{C}^{\times }}^{-1}(0)/\!/\mathbb{C}^{\times }$
coincides with the original one. Let us pick
 $p\in X^{T}$
, consider the corresponding fixed point line
$p\in X^{T}$
, consider the corresponding fixed point line
 $P\subset X_{\mathbb{C}\unicode[STIX]{x1D712}}^{T}$
and let
$P\subset X_{\mathbb{C}\unicode[STIX]{x1D712}}^{T}$
and let
![]() $\tilde{P}$
be its pre-image in
$\tilde{P}$
be its pre-image in
![]() ${\mathcal{L}}^{\times }$
. The latter is easily seen to be a symplectic subvariety in
${\mathcal{L}}^{\times }$
. The latter is easily seen to be a symplectic subvariety in
![]() ${\mathcal{L}}^{\times }$
. This symplectic variety is nothing else but
${\mathcal{L}}^{\times }$
. This symplectic variety is nothing else but
![]() $T^{\ast }\mathbb{C}^{\times }$
, where the zero section
$T^{\ast }\mathbb{C}^{\times }$
, where the zero section
![]() $\mathbb{C}^{\times }$
is the pre-image of
$\mathbb{C}^{\times }$
is the pre-image of
![]() $p$
in
$p$
in
![]() ${\mathcal{L}}^{\times }$
. The action of
${\mathcal{L}}^{\times }$
. The action of
![]() $T$
on the base
$T$
on the base
![]() $\mathbb{C}^{\times }$
is induced by the character
$\mathbb{C}^{\times }$
is induced by the character
![]() $\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
. We conclude that the restriction of
$\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
. We conclude that the restriction of
![]() $\unicode[STIX]{x1D707}_{T}$
to
$\unicode[STIX]{x1D707}_{T}$
to
![]() $P\cong \mathbb{C}$
is also given by (the differential of)
$P\cong \mathbb{C}$
is also given by (the differential of)
![]() $\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
. This shows the claim in the previous paragraph and completes the proof of the lemma.◻
$\unicode[STIX]{x1D6FC}_{p}(\unicode[STIX]{x1D712})$
. This shows the claim in the previous paragraph and completes the proof of the lemma.◻
We need one more lemma; see [Reference Maulik and OkounkovMO12, § 3.2.4].
Lemma 6.6. Let
 $p,p^{\prime }\in X^{T}$
be such that
$p,p^{\prime }\in X^{T}$
be such that
 $p\prec _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
and let
$p\prec _{\unicode[STIX]{x1D708}_{0}}p^{\prime }$
and let
![]() $\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}^{\prime }$
be the characters of
$\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}^{\prime }$
be the characters of
![]() $T$
in the fibers
$T$
in the fibers
 ${\mathcal{O}}(\unicode[STIX]{x1D712})_{p},{\mathcal{O}}(\unicode[STIX]{x1D712})_{p^{\prime }}$
. Then
${\mathcal{O}}(\unicode[STIX]{x1D712})_{p},{\mathcal{O}}(\unicode[STIX]{x1D712})_{p^{\prime }}$
. Then
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D708}_{0}\rangle <\langle \unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D708}_{0}\rangle$
.
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D708}_{0}\rangle <\langle \unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D708}_{0}\rangle$
.
Now we are ready to prove Proposition 6.4.
Proof of Proposition 6.4.
In the proof, we can replace
![]() $\unicode[STIX]{x1D706}$
with
$\unicode[STIX]{x1D706}$
with
![]() $\unicode[STIX]{x1D706}^{+}$
and, thanks to abelian localization, deal with algebras instead of sheaves.
$\unicode[STIX]{x1D706}^{+}$
and, thanks to abelian localization, deal with algebras instead of sheaves.
Let us produce an exact functor
 $$\begin{eqnarray}\unicode[STIX]{x1D71B}_{Z}:{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}{\twoheadrightarrow}{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D71B}_{Z}:{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}{\twoheadrightarrow}{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z}).\end{eqnarray}$$
Let
![]() $h_{0}$
be the image of
$h_{0}$
be the image of
![]() $1$
under the quantum comoment map for
$1$
under the quantum comoment map for
![]() $\unicode[STIX]{x1D708}_{0}$
. For
$\unicode[STIX]{x1D708}_{0}$
. For
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
, let
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
, let
![]() $\unicode[STIX]{x1D71B}_{Z}(M)$
be the generalized eigenspace for
$\unicode[STIX]{x1D71B}_{Z}(M)$
be the generalized eigenspace for
![]() $h_{0}$
with eigenvalue
$h_{0}$
with eigenvalue
![]() $c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
, where
$c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
, where
![]() $p\in Z$
(this depends only on
$p\in Z$
(this depends only on
![]() $Z$
by Lemma 6.5(2)). Lemma 6.5(3) and the choice of
$Z$
by Lemma 6.5(2)). Lemma 6.5(3) and the choice of
![]() $\unicode[STIX]{x1D706}^{+}$
imply that, for any eigenvalue
$\unicode[STIX]{x1D706}^{+}$
imply that, for any eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $h_{0}$
in
$h_{0}$
in
 $M:=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p^{\prime })$
, where
$M:=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p^{\prime })$
, where
![]() $p^{\prime }\in Z^{\prime }$
with
$p^{\prime }\in Z^{\prime }$
with
![]() $Z^{\prime }\preccurlyeq Z$
, we have
$Z^{\prime }\preccurlyeq Z$
, we have
 $\unicode[STIX]{x1D6FC}-c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})\in \mathbb{Z}_{{\leqslant}0}$
. It follows that the similar conclusion is true for any
$\unicode[STIX]{x1D6FC}-c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})\in \mathbb{Z}_{{\leqslant}0}$
. It follows that the similar conclusion is true for any
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
. So,
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
. So,
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
annihilates
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
annihilates
![]() $\unicode[STIX]{x1D71B}_{Z}(M)$
and therefore
$\unicode[STIX]{x1D71B}_{Z}(M)$
and therefore
![]() $\unicode[STIX]{x1D71B}_{Z}$
is an exact functor
$\unicode[STIX]{x1D71B}_{Z}$
is an exact functor
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
. From Lemma 6.6, it follows that
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
. From Lemma 6.6, it follows that
![]() $c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
is not an eigenvalue of
$c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
is not an eigenvalue of
![]() $h_{0}$
on
$h_{0}$
on
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p^{\prime })$
with
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p^{\prime })$
with
![]() $p^{\prime }\in Z^{\prime }$
and
$p^{\prime }\in Z^{\prime }$
and
![]() $Z^{\prime }\prec Z$
. We conclude that
$Z^{\prime }\prec Z$
. We conclude that
![]() $\unicode[STIX]{x1D71B}_{Z}$
annihilates
$\unicode[STIX]{x1D71B}_{Z}$
annihilates
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\prec Z}$
. Also, we note that, for
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\prec Z}$
. Also, we note that, for
 $N\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
, we have
$N\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
, we have
 $\unicode[STIX]{x1D71B}_{Z}\circ \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(N)\cong N$
. We conclude that the essential image of
$\unicode[STIX]{x1D71B}_{Z}\circ \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(N)\cong N$
. We conclude that the essential image of
![]() $\unicode[STIX]{x1D71B}_{Z}$
is
$\unicode[STIX]{x1D71B}_{Z}$
is
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
and that
${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
and that
![]() $\unicode[STIX]{x1D71B}_{Z}$
descends to an equivalence
$\unicode[STIX]{x1D71B}_{Z}$
descends to an equivalence
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}/{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\prec Z}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
.
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}/{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\prec Z}\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
.
It remains to check that
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0},Z}$
is the left adjoint of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0},Z}$
is the left adjoint of
![]() $\unicode[STIX]{x1D71B}_{Z}$
, while
$\unicode[STIX]{x1D71B}_{Z}$
, while
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0},Z}$
is the right adjoint of
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0},Z}$
is the right adjoint of
![]() $\unicode[STIX]{x1D71B}_{Z}$
. To show the former, note that
$\unicode[STIX]{x1D71B}_{Z}$
. To show the former, note that
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M),N)=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,N^{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M),N)=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,N^{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}})\end{eqnarray}$$
for
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
and
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})|_{Z})$
and
 $N\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
. The right-hand side coincides with
$N\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq Z}$
. The right-hand side coincides with
 $\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,\unicode[STIX]{x1D71B}_{Z}(N))$
because the eigenvalue of
$\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,\unicode[STIX]{x1D71B}_{Z}(N))$
because the eigenvalue of
![]() $h_{0}$
on
$h_{0}$
on
![]() $M$
is
$M$
is
![]() $c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
and
$c_{\unicode[STIX]{x1D706}^{+}}^{p}(h_{0})$
and
![]() $\unicode[STIX]{x1D71B}_{Z}(N)$
is annihilated by
$\unicode[STIX]{x1D71B}_{Z}(N)$
is annihilated by
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
. This shows that
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
. This shows that
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0},Z}$
is the left adjoint of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0},Z}$
is the left adjoint of
![]() $\unicode[STIX]{x1D71B}_{Z}$
. A similar argument (based on an observation that
$\unicode[STIX]{x1D71B}_{Z}$
. A similar argument (based on an observation that
![]() $\unicode[STIX]{x1D71B}_{Z}(N)$
embeds into
$\unicode[STIX]{x1D71B}_{Z}(N)$
embeds into
 $N/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}N$
) shows that
$N/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}N$
) shows that
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0},Z}$
is the right adjoint of
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0},Z}$
is the right adjoint of
![]() $\unicode[STIX]{x1D71B}_{Z}$
.◻
$\unicode[STIX]{x1D71B}_{Z}$
.◻
6.3 Algebras and bimodules
Here we will introduce certain algebras and bimodules that will be needed in several proofs below. Recall that
![]() $\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
is ample for
$\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
is ample for
![]() $X^{\unicode[STIX]{x1D703}}$
and that
$X^{\unicode[STIX]{x1D703}}$
and that
![]() $\ell$
stands for
$\ell$
stands for
 $\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
.
$\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
.
Set
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}:={\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
. This is an
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}:={\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{{>}0,\unicode[STIX]{x1D708}_{0}}$
. This is an
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
-
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
-
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-bimodule that comes with a
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-bimodule that comes with a
![]() $\mathbb{Z}$
-grading induced by
$\mathbb{Z}$
-grading induced by
![]() $\unicode[STIX]{x1D708}_{0}$
.
$\unicode[STIX]{x1D708}_{0}$
.
For a Zariski generic
![]() $z$
, Proposition 5.3 yields the direct sum decomposition
$z$
, Proposition 5.3 yields the direct sum decomposition
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})=\bigoplus _{Z}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
, where
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})=\bigoplus _{Z}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
, where
![]() $Z$
runs over the connected components of
$Z$
runs over the connected components of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. Therefore, for a Zariski generic
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. Therefore, for a Zariski generic
![]() $z$
,
$z$
,
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}$
splits into the direct sum
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}$
splits into the direct sum
 $\bigoplus _{Z}{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
, where
$\bigoplus _{Z}{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
, where
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}:={\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}e_{Z}$
and
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}:={\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}e_{Z}$
and
![]() $e_{Z}$
stands for the idempotent in
$e_{Z}$
stands for the idempotent in
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
corresponding to
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
corresponding to
![]() $Z$
. Note that the latter direct sum decomposition respects the grading.
$Z$
. Note that the latter direct sum decomposition respects the grading.
Let us write
![]() ${\mathcal{B}}_{\ell }^{+}$
for
${\mathcal{B}}_{\ell }^{+}$
for
 ${\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{>}0,\unicode[STIX]{x1D708}_{0}}$
so that
${\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{>}0,\unicode[STIX]{x1D708}_{0}}$
so that
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}$
is the specialization of
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}$
is the specialization of
![]() ${\mathcal{B}}_{\ell }^{+}$
to
${\mathcal{B}}_{\ell }^{+}$
to
 $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\in \ell$
. We will need a
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\in \ell$
. We will need a
![]() $\mathbb{C}[\ell ]$
-algebra
$\mathbb{C}[\ell ]$
-algebra
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
and an
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
and an
![]() ${\mathcal{A}}_{\ell }$
-
${\mathcal{A}}_{\ell }$
-
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-bimodule
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-bimodule
![]() ${\mathcal{B}}_{\ell }^{+}|_{Z}$
that specialize to
${\mathcal{B}}_{\ell }^{+}|_{Z}$
that specialize to
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z},{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
for a Zariski generic
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z},{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
for a Zariski generic
![]() $z$
. Recall that we have a natural homomorphism
$z$
. Recall that we have a natural homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
. The kernel and the cokernel of the homomorphism of the associated graded algebras are supported at
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
. The kernel and the cokernel of the homomorphism of the associated graded algebras are supported at
![]() $0\in \mathbb{C}\unicode[STIX]{x1D712}$
; this follows from the proof of Proposition 5.3.
$0\in \mathbb{C}\unicode[STIX]{x1D712}$
; this follows from the proof of Proposition 5.3.
Let
![]() $I_{Z}$
denote the kernel of the composition of the homomorphism
$I_{Z}$
denote the kernel of the composition of the homomorphism
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
with the projection
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
with the projection
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})){\twoheadrightarrow}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})$
. We set
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})){\twoheadrightarrow}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})$
. We set
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })/I_{Z}$
and
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })/I_{Z}$
and
 ${\mathcal{B}}_{\ell }^{+}|_{Z}={\mathcal{B}}_{\ell }^{+}/{\mathcal{B}}_{\ell }^{+}I_{Z}$
. Note that the bimodule
${\mathcal{B}}_{\ell }^{+}|_{Z}={\mathcal{B}}_{\ell }^{+}/{\mathcal{B}}_{\ell }^{+}I_{Z}$
. Note that the bimodule
![]() ${\mathcal{B}}_{\ell }^{+}|_{Z}$
inherits a grading from
${\mathcal{B}}_{\ell }^{+}|_{Z}$
inherits a grading from
![]() ${\mathcal{B}}_{\ell }^{+}$
.
${\mathcal{B}}_{\ell }^{+}$
.
Lemma 6.7. For a Zariski generic
![]() $z$
, the specializations of
$z$
, the specializations of
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z},{\mathcal{B}}_{\ell }^{+}|_{Z}$
to
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z},{\mathcal{B}}_{\ell }^{+}|_{Z}$
to
![]() $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
coincide with
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
coincide with
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z},{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z},{\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
.
Proof. It is enough to check the claim about
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
. Lemma 2.5 applied to
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
. Lemma 2.5 applied to
 $\mathfrak{A}_{\ell }=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
shows that
$\mathfrak{A}_{\ell }=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
shows that
 $I_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })/I_{Z}$
as well as the cokernel of
$I_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })/I_{Z}$
as well as the cokernel of
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
are generically free over
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}}))$
are generically free over
![]() $\mathbb{C}[\ell ]$
. From here we deduce that for a Zariski generic
$\mathbb{C}[\ell ]$
. From here we deduce that for a Zariski generic
![]() $z$
, the specialization of
$z$
, the specialization of
![]() $I_{Z}$
to
$I_{Z}$
to
![]() $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
coincides with the kernel of
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
coincides with the kernel of
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}){\twoheadrightarrow}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))$
. Now the claim of the present lemma is a consequence of Proposition 5.3.◻
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}){\twoheadrightarrow}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}}))$
. Now the claim of the present lemma is a consequence of Proposition 5.3.◻
The algebra
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
is filtered; the filtration is induced from
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
is filtered; the filtration is induced from
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
. The bimodule
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
. The bimodule
![]() ${\mathcal{B}}_{\ell }^{+}|_{Z}$
is also filtered with the filtration induced from
${\mathcal{B}}_{\ell }^{+}|_{Z}$
is also filtered with the filtration induced from
![]() ${\mathcal{B}}_{\ell }^{+}$
. We will need some information about the associated graded algebra
${\mathcal{B}}_{\ell }^{+}$
. We will need some information about the associated graded algebra
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
and the associated graded bimodule
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
and the associated graded bimodule
 $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
. The facts we need about the former are gathered in the following lemma.
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
. The facts we need about the former are gathered in the following lemma.
Lemma 6.8. The following are true.
-
(1) The fiber of
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
over
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
over
 $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
 $\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
.
$\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
. -
(2) The scheme
 $\text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\operatorname{Spec}(\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})$
is equidimensional over
$\text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\operatorname{Spec}(\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})$
is equidimensional over
 $\mathbb{C}\unicode[STIX]{x1D712}$
.
$\mathbb{C}\unicode[STIX]{x1D712}$
. -
(3) The fiber
 $\text{}\underline{Z}$
of
$\text{}\underline{Z}$
of
 $\text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
$\text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
 $0$
has finitely many symplectic leaves.
$0$
has finitely many symplectic leaves.
Proof. We have a natural homomorphism
 $$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})\end{eqnarray}$$
that is an isomorphism generically; this follows from Lemma 6.7. The kernel of its associated graded homomorphism is supported at
![]() $0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Moreover, the induced homomorphism of fibers
$0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Moreover, the induced homomorphism of fibers
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})|_{Z}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})|_{Z})$
is a filtration-preserving isomorphism for a Zariski generic
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})|_{Z}\rightarrow \unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})|_{Z})$
is a filtration-preserving isomorphism for a Zariski generic
![]() $\unicode[STIX]{x1D706}\in \ell$
. It follows that the cokernel of the associated graded homomorphism of (6.1) is also supported at
$\unicode[STIX]{x1D706}\in \ell$
. It follows that the cokernel of the associated graded homomorphism of (6.1) is also supported at
![]() $0$
. Hence, (1) follows.
$0$
. Hence, (1) follows.
Let us prove (2). We have
 $\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})=\mathbb{C}[Z_{\mathbb{C}\unicode[STIX]{x1D712}}]$
. This algebra is finite over
$\operatorname{gr}\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})=\mathbb{C}[Z_{\mathbb{C}\unicode[STIX]{x1D712}}]$
. This algebra is finite over
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
. It follows that if we equip
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
. It follows that if we equip
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
with the filtration restricted from
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
with the filtration restricted from
 $\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})$
, then the reduced scheme of the associated graded algebra does not change. Therefore, the dimension of the zero fiber of
$\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell }^{\unicode[STIX]{x1D703}})|_{Z})$
, then the reduced scheme of the associated graded algebra does not change. Therefore, the dimension of the zero fiber of
 $\operatorname{Spec}(\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
equals
$\operatorname{Spec}(\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
equals
![]() $\dim Z$
. Hence, (2) follows.
$\dim Z$
. Hence, (2) follows.
Let us prove (3). We have a fiberwise resolution of singularities morphism
 $Z_{\mathbb{C}\unicode[STIX]{x1D712}}\rightarrow \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
that is an isomorphism over
$Z_{\mathbb{C}\unicode[STIX]{x1D712}}\rightarrow \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
that is an isomorphism over
![]() $\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
. Since the morphism
$\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
. Since the morphism
![]() $Z\rightarrow \text{}\underline{Z}$
is a symplectic resolution of singularities, by Remark 2.1, we conclude that
$Z\rightarrow \text{}\underline{Z}$
is a symplectic resolution of singularities, by Remark 2.1, we conclude that
![]() $\text{}\underline{Z}$
has finitely many symplectic leaves.◻
$\text{}\underline{Z}$
has finitely many symplectic leaves.◻
Let us proceed to study the
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\otimes \operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-bimodule
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\otimes \operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-bimodule
 $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
.
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
.
Lemma 6.9. The following are true.
-
(1) The support of
 $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
in
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
in
 $X_{0,\mathbb{C}\unicode[STIX]{x1D712}}\times \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
lies in
$X_{0,\mathbb{C}\unicode[STIX]{x1D712}}\times \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}$
lies in  $$\begin{eqnarray}{\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\Big\{(x,z)\in X_{0,\mathbb{C}\unicode[STIX]{x1D712}}\times \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}|\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x=z\Big\}.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\Big\{(x,z)\in X_{0,\mathbb{C}\unicode[STIX]{x1D712}}\times \text{}\underline{Z}_{\mathbb{C}\unicode[STIX]{x1D712}}|\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x=z\Big\}.\end{eqnarray}$$
-
(2) The fiber of
 ${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
 $\unicode[STIX]{x1D712}$
coincides with
$\unicode[STIX]{x1D712}$
coincides with
 $Y_{\unicode[STIX]{x1D712},Z}:=\{(x,z)\in X_{\unicode[STIX]{x1D712}}\times Z_{\unicode[STIX]{x1D712}}\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x=z\}$
.
$Y_{\unicode[STIX]{x1D712},Z}:=\{(x,z)\in X_{\unicode[STIX]{x1D712}}\times Z_{\unicode[STIX]{x1D712}}\mid \lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)x=z\}$
. -
(3) The fiber of
 ${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
over
 $0$
is an isotropic subvariety in
$0$
is an isotropic subvariety in
 $X_{0}\times \text{}\underline{Z}$
.
$X_{0}\times \text{}\underline{Z}$
. -
(4) The fiber of
 $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
over
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
over
 $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
 $\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
.
$\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
.
Proof. Parts (1) and (2) are straightforward.
Let us prove (3). Recall, see [Reference LosevLos17, § 5.1], that a subvariety of
 $X_{0}\times \text{}\underline{Z}$
is isotropic if and only if its pre-image in
$X_{0}\times \text{}\underline{Z}$
is isotropic if and only if its pre-image in
![]() $X\times Z$
is. The pre-image of the zero fiber of
$X\times Z$
is. The pre-image of the zero fiber of
![]() ${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
in
${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
in
![]() $X\times Z$
consists of all points
$X\times Z$
consists of all points
![]() $(\tilde{x},\tilde{x}^{\prime })$
such that
$(\tilde{x},\tilde{x}^{\prime })$
such that
 $\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)\tilde{x}$
exists and
$\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)\tilde{x}$
exists and
 $\unicode[STIX]{x1D70C}(\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)\tilde{x})=\unicode[STIX]{x1D70C}(\tilde{x}^{\prime })$
. The claim that this locus is isotropic easily reduces to checking that
$\unicode[STIX]{x1D70C}(\lim _{t\rightarrow 0}\unicode[STIX]{x1D708}_{0}(t)\tilde{x})=\unicode[STIX]{x1D70C}(\tilde{x}^{\prime })$
. The claim that this locus is isotropic easily reduces to checking that
 $(\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C})^{-1}(X_{\text{diag}})\,\cap \,X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\times Z$
is isotropic. But
$(\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C})^{-1}(X_{\text{diag}})\,\cap \,X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\times Z$
is isotropic. But
 $(\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C})^{-1}(X_{\text{diag}})\subset X\times X$
is isotropic while
$(\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C})^{-1}(X_{\text{diag}})\subset X\times X$
is isotropic while
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\times Z$
is symplectic. These two observations imply our claim. We conclude that the zero fiber of
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\times Z$
is symplectic. These two observations imply our claim. We conclude that the zero fiber of
![]() ${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
is isotropic.
${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
is isotropic.
Let us prove (4). Let us check that the kernel of the natural epimorphism
 $$\begin{eqnarray}\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}_{0}}{\twoheadrightarrow}\operatorname{gr}{\mathcal{B}}_{\ell }^{+}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}_{0}}{\twoheadrightarrow}\operatorname{gr}{\mathcal{B}}_{\ell }^{+}\end{eqnarray}$$
is supported at
![]() $0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Consider the
$0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Consider the
![]() $\hbar$
-adic completion
$\hbar$
-adic completion
![]() ${\mathcal{A}}_{\ell ,\hbar }$
of
${\mathcal{A}}_{\ell ,\hbar }$
of
![]() $R_{\hbar }({\mathcal{A}})$
. Let
$R_{\hbar }({\mathcal{A}})$
. Let
![]() ${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}$
denote the (completed) localization of
${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}$
denote the (completed) localization of
![]() ${\mathcal{A}}_{\ell ,\hbar }$
to
${\mathcal{A}}_{\ell ,\hbar }$
to
![]() $\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
. Then
$\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
. Then
 ${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}/{\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}({\mathcal{A}}_{\ell ,\hbar }^{{>}0,\unicode[STIX]{x1D708}^{\prime }})^{\text{reg}}$
coincides with the (micro)localization of
${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}/{\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}({\mathcal{A}}_{\ell ,\hbar }^{{>}0,\unicode[STIX]{x1D708}^{\prime }})^{\text{reg}}$
coincides with the (micro)localization of
 ${\mathcal{A}}_{\ell ,\hbar }/{\mathcal{A}}_{\ell ,\hbar }({\mathcal{A}}_{\ell ,\hbar })^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
. On the other hand, over
${\mathcal{A}}_{\ell ,\hbar }/{\mathcal{A}}_{\ell ,\hbar }({\mathcal{A}}_{\ell ,\hbar })^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
. On the other hand, over
![]() $\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
, the ideal
$\mathbb{C}^{\times }\unicode[STIX]{x1D712}$
, the ideal
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
is a locally complete intersection (given by elements of positive
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
is a locally complete intersection (given by elements of positive
![]() $\unicode[STIX]{x1D708}^{\prime }$
-weight); compare the proof of (2) in Proposition 5.2. As in the proof of (1) of Proposition 5.2, this implies that
$\unicode[STIX]{x1D708}^{\prime }$
-weight); compare the proof of (2) in Proposition 5.2. As in the proof of (1) of Proposition 5.2, this implies that
 ${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}/{\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}({\mathcal{A}}_{\ell ,\hbar }^{{>}0,\unicode[STIX]{x1D708}^{\prime }})^{\text{reg}}$
is flat over
${\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}/{\mathcal{A}}_{\ell ,\hbar }^{\text{reg}}({\mathcal{A}}_{\ell ,\hbar }^{{>}0,\unicode[STIX]{x1D708}^{\prime }})^{\text{reg}}$
is flat over
![]() $\mathbb{C}[[\hbar ]]$
. So, the
$\mathbb{C}[[\hbar ]]$
. So, the
![]() $\hbar$
-torsion in
$\hbar$
-torsion in
 ${\mathcal{A}}_{\ell ,\hbar }/{\mathcal{A}}_{\ell ,\hbar }({\mathcal{A}}_{\ell ,\hbar })_{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
is supported at
${\mathcal{A}}_{\ell ,\hbar }/{\mathcal{A}}_{\ell ,\hbar }({\mathcal{A}}_{\ell ,\hbar })_{{>}0,\unicode[STIX]{x1D708}^{\prime }}$
is supported at
![]() $0$
. This implies the claim in the beginning of the paragraph.
$0$
. This implies the claim in the beginning of the paragraph.
Part (1) of Lemma 6.8 implies that the fiber over
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\operatorname{gr}I_{Z}$
is the kernel of
$\operatorname{gr}I_{Z}$
is the kernel of
 $\mathbb{C}[X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}]\rightarrow \mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
. So,
$\mathbb{C}[X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}]\rightarrow \mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
. So,
 $(\operatorname{gr}{\mathcal{B}}_{\ell }^{+})_{\unicode[STIX]{x1D712}}/(\operatorname{gr}{\mathcal{B}}_{\ell }^{+})_{\unicode[STIX]{x1D712}}(\operatorname{gr}I_{Z})_{\unicode[STIX]{x1D712}}=\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
and we get an epimorphism
$(\operatorname{gr}{\mathcal{B}}_{\ell }^{+})_{\unicode[STIX]{x1D712}}/(\operatorname{gr}{\mathcal{B}}_{\ell }^{+})_{\unicode[STIX]{x1D712}}(\operatorname{gr}I_{Z})_{\unicode[STIX]{x1D712}}=\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
and we get an epimorphism
 $\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]\rightarrow (\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}$
of
$\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]\rightarrow (\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}$
of
 $\mathbb{C}[X_{\unicode[STIX]{x1D712}}]\otimes \mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
-modules. The Gabber involutivity theorem implies that the support of
$\mathbb{C}[X_{\unicode[STIX]{x1D712}}]\otimes \mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
-modules. The Gabber involutivity theorem implies that the support of
 $(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}$
in
$(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}$
in
 $X_{\unicode[STIX]{x1D712}}\times Z_{\unicode[STIX]{x1D712}}$
is coisotropic (if this bimodule is non-zero). Since
$X_{\unicode[STIX]{x1D712}}\times Z_{\unicode[STIX]{x1D712}}$
is coisotropic (if this bimodule is non-zero). Since
![]() $Y_{\unicode[STIX]{x1D712},Z}$
is Lagrangian, it follows that either
$Y_{\unicode[STIX]{x1D712},Z}$
is Lagrangian, it follows that either
 $(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}=\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
or
$(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}=\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
or
 $(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}=0$
. The latter is not the case because
$(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z})_{\unicode[STIX]{x1D712}}=0$
. The latter is not the case because

To finish this section, let us point out that the conclusions of this section also hold for the following bimodules:
 $$\begin{eqnarray}{\mathcal{B}}_{\ell }^{-}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{<}0,\unicode[STIX]{x1D708}_{0}},\quad {\mathcal{B}}_{\ell }^{+,o}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }^{{>}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\ell },\quad {\mathcal{B}}_{\ell }^{-,o}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\ell }^{-}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{<}0,\unicode[STIX]{x1D708}_{0}},\quad {\mathcal{B}}_{\ell }^{+,o}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }^{{>}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\ell },\quad {\mathcal{B}}_{\ell }^{-,o}:={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\ell }.\end{eqnarray}$$
6.4 Standardization functor
According to Proposition 6.4, under the identification of
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
and
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
and
 $\operatorname{gr}_{\unicode[STIX]{x1D708}_{0}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with
$\operatorname{gr}_{\unicode[STIX]{x1D708}_{0}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
with
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, the standardization functor
${\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, the standardization functor
 $\operatorname{gr}_{\unicode[STIX]{x1D708}_{0}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
becomes
$\operatorname{gr}_{\unicode[STIX]{x1D708}_{0}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
becomes
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Recall that we write
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Recall that we write
![]() $\unicode[STIX]{x1D706}^{+}$
for
$\unicode[STIX]{x1D706}^{+}$
for
![]() $\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D706}+n\unicode[STIX]{x1D712}$
with
![]() $n\gg 0$
and
$n\gg 0$
and
![]() $\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
ample. The goal of this section is to prove the following claim.
$\unicode[STIX]{x1D712}\in \tilde{\mathfrak{p}}_{\mathbb{Z}}$
ample. The goal of this section is to prove the following claim.
Proposition 6.10. The functor
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}:{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is exact.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}:{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is exact.
Since
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(\bullet )={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}\bullet$
, this proposition is a direct consequence of the following claim.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(\bullet )={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}\bullet$
, this proposition is a direct consequence of the following claim.
Proposition 6.11. For a Zariski generic
![]() $z$
, the right
$z$
, the right
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-module
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-module
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is projective.
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is projective.
Proof. The proof is in several steps.
Step 1. The claim will follow if we show that, for a Zariski generic
![]() $z$
,
$z$
,
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
is a projective
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
is a projective
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module. This will follow if we check that
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module. This will follow if we check that
 $$\begin{eqnarray}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z})=0\quad \text{for }i>0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z})=0\quad \text{for }i>0.\end{eqnarray}$$
Here and below we abuse the notation and write
![]() $\operatorname{Ext}^{i}$
for the restricted
$\operatorname{Ext}^{i}$
for the restricted
![]() $\operatorname{Ext}$
, i.e., the direct sum of the Ext spaces from graded components of
$\operatorname{Ext}$
, i.e., the direct sum of the Ext spaces from graded components of
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
. Indeed, (6.2) implies that
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z}$
. Indeed, (6.2) implies that
 $\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z},M)=0$
when
$\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{+}|_{Z},M)=0$
when
![]() $i>0$
for any right
$i>0$
for any right
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module
![]() $M$
.
$M$
.
Step 2. By Lemma 2.5,
![]() ${\mathcal{B}}_{\ell }^{+}|_{Z}$
is generically free over
${\mathcal{B}}_{\ell }^{+}|_{Z}$
is generically free over
![]() $\mathbb{C}[\ell ]$
. We deduce that, for a Zariski generic
$\mathbb{C}[\ell ]$
. We deduce that, for a Zariski generic
![]() $z$
, the left-hand side of (6.2) is the specialization to
$z$
, the left-hand side of (6.2) is the specialization to
![]() $\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}$
of
 $$\begin{eqnarray}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\ell }^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\ell }^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}).\end{eqnarray}$$
For a Zariski generic
![]() $z$
, the algebra
$z$
, the algebra
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}=\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})|_{Z})$
has homological dimension not exceeding
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}=\unicode[STIX]{x1D6E4}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D703}})|_{Z})$
has homological dimension not exceeding
![]() $\dim Z$
; see (3) of Lemma 2.4. So, (6.2) will follow if we check that, for every
$\dim Z$
; see (3) of Lemma 2.4. So, (6.2) will follow if we check that, for every
![]() $i$
, the module in (6.3) is torsion over
$i$
, the module in (6.3) is torsion over
![]() $\mathbb{C}[\ell ]$
.
$\mathbb{C}[\ell ]$
.
Step 3. So, we are proving that (6.3) is torsion over
![]() $\mathbb{C}[\ell ]$
. To this end, we will need the category
$\mathbb{C}[\ell ]$
. To this end, we will need the category
![]() ${\mathcal{C}}$
of all finitely generated
${\mathcal{C}}$
of all finitely generated
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-
![]() ${\mathcal{A}}_{\ell }$
-bimodules whose associated variety lies in the subvariety
${\mathcal{A}}_{\ell }$
-bimodules whose associated variety lies in the subvariety
![]() ${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
from Lemma 6.9. We will see below that the restricted Ext spaces from
${\hat{Y}}_{\mathbb{C}\unicode[STIX]{x1D712}}$
from Lemma 6.9. We will see below that the restricted Ext spaces from
![]() ${\mathcal{B}}_{\ell }^{+}|_{Z}$
to
${\mathcal{B}}_{\ell }^{+}|_{Z}$
to
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
lie in this category.
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
lie in this category.
Thanks to (3) of Lemma 6.9, for
![]() $M\in {\mathcal{C}}$
, the specialization
$M\in {\mathcal{C}}$
, the specialization
![]() $M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is a holonomic
$M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
is a holonomic
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\text{opp}}\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module; see § 4.4. We conclude that, for a Weil generic
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\text{opp}}\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
-module; see § 4.4. We conclude that, for a Weil generic
![]() $z$
, the specialization
$z$
, the specialization
![]() $M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has GK dimension equal to
$M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
has GK dimension equal to
 $\frac{1}{2}(\dim X+\dim Z)$
(provided
$\frac{1}{2}(\dim X+\dim Z)$
(provided
 $M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\neq 0$
); this follows from Corollary 4.6 (applied to the algebra
$M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\neq 0$
); this follows from Corollary 4.6 (applied to the algebra
 ${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\text{opp}}\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
that is the algebra of global sections of a conical symplectic resolution).
${\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{\text{opp}}\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})|_{Z}$
that is the algebra of global sections of a conical symplectic resolution).
Step 4. Now let
![]() $M$
be an object in
$M$
be an object in
![]() ${\mathcal{C}}$
. Suppose that
${\mathcal{C}}$
. Suppose that
![]() $M$
has a good filtration such that
$M$
has a good filtration such that
![]() $\operatorname{gr}M$
is torsion over
$\operatorname{gr}M$
is torsion over
![]() $\mathbb{C}[\mathbb{C}\unicode[STIX]{x1D712}]$
. We claim that
$\mathbb{C}[\mathbb{C}\unicode[STIX]{x1D712}]$
. We claim that
![]() $M$
is torsion over
$M$
is torsion over
![]() $\mathbb{C}[\ell ]$
. Lemma 2.5 implies that
$\mathbb{C}[\ell ]$
. Lemma 2.5 implies that
![]() $M$
is generically free over
$M$
is generically free over
![]() $\mathbb{C}[\ell ]$
. The associated graded bimodule
$\mathbb{C}[\ell ]$
. The associated graded bimodule
![]() $\operatorname{gr}M$
is supported on the zero fiber of
$\operatorname{gr}M$
is supported on the zero fiber of
 $\widehat{Y}_{\mathbb{C}\unicode[STIX]{x1D712}}\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
. The dimension of the latter does not exceed
$\widehat{Y}_{\mathbb{C}\unicode[STIX]{x1D712}}\rightarrow \mathbb{C}\unicode[STIX]{x1D712}$
. The dimension of the latter does not exceed
 $\frac{1}{2}(\dim X+\dim Z)$
; see (3) of Lemma 6.9. We conclude that the GK dimension of
$\frac{1}{2}(\dim X+\dim Z)$
; see (3) of Lemma 6.9. We conclude that the GK dimension of
![]() $M$
does not exceed
$M$
does not exceed
 $\frac{1}{2}(\dim X+\dim Z)$
. On the other hand, since
$\frac{1}{2}(\dim X+\dim Z)$
. On the other hand, since
![]() $M$
is generically free over
$M$
is generically free over
![]() $\mathbb{C}[\ell ]$
, if
$\mathbb{C}[\ell ]$
, if
![]() $M$
is not torsion, then we have
$M$
is not torsion, then we have
 $M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\neq 0$
for a Weil generic
$M_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}\neq 0$
for a Weil generic
![]() $z$
. So, the GK dimension of a Weil generic fiber of
$z$
. So, the GK dimension of a Weil generic fiber of
![]() $M$
coincides with that of
$M$
coincides with that of
![]() $M$
. It follows that we have quotients of
$M$
. It follows that we have quotients of
![]() $M$
with arbitrarily large GK multiplicity. But the GK multiplicity of
$M$
with arbitrarily large GK multiplicity. But the GK multiplicity of
![]() $M$
is not less than that of any quotient of
$M$
is not less than that of any quotient of
![]() $M$
. We arrive at a contradiction.
$M$
. We arrive at a contradiction.
Step 5. It remains to show that (6.3) lies in
![]() ${\mathcal{C}}$
and has a good filtration like in Step 4. Recall that
${\mathcal{C}}$
and has a good filtration like in Step 4. Recall that
![]() $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
is a finitely generated
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
is a finitely generated
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\otimes \operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-module supported on
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\otimes \operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
-module supported on
![]() $\widehat{Y}_{\mathbb{C}\unicode[STIX]{x1D712}}$
by (1) of Lemma 6.9. Also, note that (6.3) has a filtration with
$\widehat{Y}_{\mathbb{C}\unicode[STIX]{x1D712}}$
by (1) of Lemma 6.9. Also, note that (6.3) has a filtration with
 $$\begin{eqnarray}\operatorname{gr}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\ell }^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})\text{ is a subquotient of }\text{Ext}_{\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}}^{i}(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z},\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{gr}\operatorname{Ext}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}^{\text{opp}}}^{i}({\mathcal{B}}_{\ell }^{+}|_{Z},\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z})\text{ is a subquotient of }\text{Ext}_{\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}}^{i}(\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z},\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}).\end{eqnarray}$$
This implies that (6.3) is in
![]() ${\mathcal{C}}$
. Let us show that the right-hand side of (6.4) is supported at
${\mathcal{C}}$
. Let us show that the right-hand side of (6.4) is supported at
![]() $0\in \mathbb{C}\unicode[STIX]{x1D712}$
(when
$0\in \mathbb{C}\unicode[STIX]{x1D712}$
(when
![]() $i>0$
). Indeed, the specialization of
$i>0$
). Indeed, the specialization of
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
to
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })|_{Z}$
to
![]() $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
![]() $\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
(see (1) of Lemma 6.8), while the specialization of
$\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
(see (1) of Lemma 6.8), while the specialization of
 $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
is
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}|_{Z}$
is
![]() $\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
(by (4) of Lemma 6.9). It follows that the specialization of the right-hand side of (6.4) to
$\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
(by (4) of Lemma 6.9). It follows that the specialization of the right-hand side of (6.4) to
![]() $\unicode[STIX]{x1D712}$
coincides with
$\unicode[STIX]{x1D712}$
coincides with
 $$\begin{eqnarray}\operatorname{Ext}_{\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]}^{i}(\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}],\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]}^{i}(\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}],\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]).\end{eqnarray}$$
But
![]() $\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
is a projective
$\mathbb{C}[Y_{\unicode[STIX]{x1D712},Z}]$
is a projective
![]() $\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
-module and so the fiber at
$\mathbb{C}[Z_{\unicode[STIX]{x1D712}}]$
-module and so the fiber at
![]() $\unicode[STIX]{x1D712}$
vanishes.
$\unicode[STIX]{x1D712}$
vanishes.
This completes the proof. ◻
6.5 Filtration on projectives
We finish the proof of Theorem 6.3 using Lemma 3.4. In order to do this, note that the functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\bullet )=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})}^{\text{restr}}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o},\bullet ):{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}))\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\bullet )=\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})}^{\text{restr}}({\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o},\bullet ):{\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}))\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})\end{eqnarray}$$
is exact for a Zariski generic
![]() $z\in \mathbb{C}$
, where
$z\in \mathbb{C}$
, where
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o}={\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
. Indeed, completely analogously to Proposition 6.11,
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o}={\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}$
. Indeed, completely analogously to Proposition 6.11,
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o}$
is a projective
${\mathcal{B}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}}^{-,o}$
is a projective
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-module for a Zariski generic
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}})$
-module for a Zariski generic
![]() $z$
.
$z$
.
The category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is highest weight with respect to the order
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is highest weight with respect to the order
![]() ${\leqslant}_{\unicode[STIX]{x1D708}}$
. It follows that it satisfies the conditions of Lemma 3.3. Together with the exactness of
${\leqslant}_{\unicode[STIX]{x1D708}}$
. It follows that it satisfies the conditions of Lemma 3.3. Together with the exactness of
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
, this implies that
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
, this implies that
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is standardly stratified with respect to the pre-order
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
is standardly stratified with respect to the pre-order
![]() $\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
. This finishes the proof of Theorem 6.3.
$\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}$
. This finishes the proof of Theorem 6.3.
Let us record a result that follows from the claim that the right
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-module
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-module
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}$
and the left
${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}$
and the left
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-module
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-module
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}$
are projective.
${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}$
are projective.
Lemma 6.12. For
 $M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
, we have
$M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M)={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}^{L}M,\quad \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(M)=R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o},M).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M)={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}^{L}M,\quad \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(M)=R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o},M).\end{eqnarray}$$
7 Cross-walling functors
7.1 Definition and basic properties
We have a functor
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
. This functor is an embedding. Indeed, we can assume that
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
. This functor is an embedding. Indeed, we can assume that
![]() $\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
is an equivalence
$\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
is an equivalence
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})),D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
. This equivalence intertwines
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})),D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
. This equivalence intertwines
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
with the analogous functor
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
with the analogous functor
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
. Modifying
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
. Modifying
![]() $\unicode[STIX]{x1D706}$
further (so that
$\unicode[STIX]{x1D706}$
further (so that
![]() $\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
is still an equivalence), we get
$\operatorname{Loc}_{\unicode[STIX]{x1D706}}$
is still an equivalence), we get
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})){\hookrightarrow}D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
by (3) of Proposition 4.2.
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})){\hookrightarrow}D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
by (3) of Proposition 4.2.
The image of
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
clearly lies in the full subcategory
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
clearly lies in the full subcategory
 $D_{\text{hol}}^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
of all complexes with holonomic homology (recall that a coherent
$D_{\text{hol}}^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
of all complexes with holonomic homology (recall that a coherent
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module is called holonomic if its support is Lagrangian; note that by the Gabber involutivity theorem, the support is always coisotropic). It was checked in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.2] that the functor
${\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}$
-module is called holonomic if its support is Lagrangian; note that by the Gabber involutivity theorem, the support is always coisotropic). It was checked in [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.2] that the functor
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})){\hookrightarrow}D_{\text{hol}}^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
admits both left adjoint
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})){\hookrightarrow}D_{\text{hol}}^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
admits both left adjoint
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}^{!}$
and right adjoint
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}^{!}$
and right adjoint
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}^{\ast }$
.
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}^{\ast }$
.
For two generic one-parameter subgroups
 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }:\mathbb{C}^{\times }\rightarrow T$
, we define the cross-walling functor (shuffling functor from [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.2]) by setting
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }:\mathbb{C}^{\times }\rightarrow T$
, we define the cross-walling functor (shuffling functor from [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.2]) by setting
 $$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}\,\circ \,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}\,\circ \,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
So, the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is uniquely characterized by a bi-functorial isomorphism
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is uniquely characterized by a bi-functorial isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M,N)=\operatorname{Hom}_{D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))}(M,N).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M,N)=\operatorname{Hom}_{D^{b}(\operatorname{Coh}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))}(M,N).\end{eqnarray}$$
Note that the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
admits a right adjoint functor
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
admits a right adjoint functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
. Also, note that there is a natural functor morphism
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
. Also, note that there is a natural functor morphism
 $$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\circ \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\circ \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\end{eqnarray}$$
induced by the adjunction morphism
 $\operatorname{id}\rightarrow \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}$
.
$\operatorname{id}\rightarrow \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}$
.
When
 $\operatorname{Loc}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}$
are abelian equivalences, we can carry the functor
$\operatorname{Loc}_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D706}}$
are abelian equivalences, we can carry the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
to
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
to
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))$
. Obviously, this functor can be realized as
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))$
. Obviously, this functor can be realized as
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
, where
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{!}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
, where
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
now stands for the inclusion
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}}$
now stands for the inclusion
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})){\hookrightarrow}D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
.
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})){\hookrightarrow}D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})$
.
Let us finish this section by discussing the case of products, where we have
 $X=X^{1}\times X^{2}$
. Recall that we have an identification
$X=X^{1}\times X^{2}$
. Recall that we have an identification
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{1}}^{1\unicode[STIX]{x1D703}^{1}})\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{2}}^{2\unicode[STIX]{x1D703}^{2}})$
; see Lemma 4.4. The following claim follows from Lemma 4.4 and (7.1).
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{1}}^{1\unicode[STIX]{x1D703}^{1}})\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{2}}^{2\unicode[STIX]{x1D703}^{2}})$
; see Lemma 4.4. The following claim follows from Lemma 4.4 and (7.1).
Lemma 7.1. Under the identification of the previous paragraph, we have
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{1}\boxtimes \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{2}$
.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{1}\boxtimes \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{2}$
.
7.2 Main results
Let us start with some notation. Pick two generic one-parameter subgroups
 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }:\mathbb{C}^{\times }\rightarrow T$
. Define
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }:\mathbb{C}^{\times }\rightarrow T$
. Define
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })\in \mathbb{Z}_{{\geqslant}0}$
as the number of
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })\in \mathbb{Z}_{{\geqslant}0}$
as the number of
![]() $T$
-weights in
$T$
-weights in
 $\bigoplus _{p\in X^{T}}T_{p}X$
that are positive on
$\bigoplus _{p\in X^{T}}T_{p}X$
that are positive on
![]() $\unicode[STIX]{x1D708}$
and negative on
$\unicode[STIX]{x1D708}$
and negative on
![]() $\unicode[STIX]{x1D708}^{\prime }$
. Note that
$\unicode[STIX]{x1D708}^{\prime }$
. Note that
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime })\geqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime \prime })$
and
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })+\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime })\geqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime \prime })$
and
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708})$
. We will say that a sequence
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime })=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708})$
. We will say that a sequence
 $\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
of generic one-parameter subgroups of
$\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
of generic one-parameter subgroups of
![]() $T$
is reduced if
$T$
is reduced if
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{k})=\sum _{i=1}^{k-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{i},\unicode[STIX]{x1D708}_{i+1})$
. We say that a reduced sequence
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{k})=\sum _{i=1}^{k-1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{i},\unicode[STIX]{x1D708}_{i+1})$
. We say that a reduced sequence
 $\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
is maximal reduced if
$\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
is maximal reduced if
![]() $\unicode[STIX]{x1D708}_{i},\unicode[STIX]{x1D708}_{i+1}$
lie in chambers separated by a single wall.
$\unicode[STIX]{x1D708}_{i},\unicode[STIX]{x1D708}_{i+1}$
lie in chambers separated by a single wall.
Lemma 7.2. Every reduced sequence can be completed to a maximal reduced one.
Proof. We need to check that generic
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are included in a maximal reduced sequence. Pick sufficiently general
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are included in a maximal reduced sequence. Pick sufficiently general
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
in their chambers so that the interval joining
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
in their chambers so that the interval joining
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
does not intersect pairwise intersections of walls. Let
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
does not intersect pairwise intersections of walls. Let
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{0},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}_{k}$
be one-parameter subgroups from the chambers intersected by that interval taken in order. Then
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{0},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}_{k}$
be one-parameter subgroups from the chambers intersected by that interval taken in order. Then
 $\unicode[STIX]{x1D708}_{0},\ldots ,\unicode[STIX]{x1D708}_{k}$
is easily seen to be a maximal reduced sequence.◻
$\unicode[STIX]{x1D708}_{0},\ldots ,\unicode[STIX]{x1D708}_{k}$
is easily seen to be a maximal reduced sequence.◻
Now we are ready to state the main results.
Theorem 7.3. The functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence for any
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence for any
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
. Moreover, for any reduced sequence
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
. Moreover, for any reduced sequence
 $\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
, the natural functor morphism
$\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{k}$
, the natural functor morphism
 $$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}_{1}\rightarrow \unicode[STIX]{x1D708}_{k}}\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}_{k-1}\rightarrow \unicode[STIX]{x1D708}_{k}}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}_{k-2}\rightarrow \unicode[STIX]{x1D708}_{k-1}}\,\circ \,\cdots \circ \mathfrak{CW}_{\unicode[STIX]{x1D708}_{1}\rightarrow \unicode[STIX]{x1D708}_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{CW}_{\unicode[STIX]{x1D708}_{1}\rightarrow \unicode[STIX]{x1D708}_{k}}\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}_{k-1}\rightarrow \unicode[STIX]{x1D708}_{k}}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}_{k-2}\rightarrow \unicode[STIX]{x1D708}_{k-1}}\,\circ \,\cdots \circ \mathfrak{CW}_{\unicode[STIX]{x1D708}_{1}\rightarrow \unicode[STIX]{x1D708}_{2}}\end{eqnarray}$$
is an isomorphism.
This theorem proves several conjectures of Braden et al. (stated in a previous version of [Reference Braden, Licata, Proudfoot and WebsterBLPW16]). The claim that the functors
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
yield an action of the Deligne groupoid of the hyperplane arrangement given by the non-generic one-parameter subgroups is established as in [Reference Braden, Proudfoot and WebsterBPW16, § 6.4].
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
yield an action of the Deligne groupoid of the hyperplane arrangement given by the non-generic one-parameter subgroups is established as in [Reference Braden, Proudfoot and WebsterBPW16, § 6.4].
Our next main result (that plays a crucial role in the proof of Theorem 7.3) concerns an interplay between the equivalences
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
and the standardly stratified structures on the categories involved. In order to state the result, we need some more notation.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
and the standardly stratified structures on the categories involved. In order to state the result, we need some more notation.
Pick
 $\unicode[STIX]{x1D708}_{0}:\mathbb{C}^{\times }\rightarrow T$
. Recall that for a generic
$\unicode[STIX]{x1D708}_{0}:\mathbb{C}^{\times }\rightarrow T$
. Recall that for a generic
![]() $\unicode[STIX]{x1D708}$
and some
$\unicode[STIX]{x1D708}$
and some
![]() $\unicode[STIX]{x1D708}_{0}$
, we write
$\unicode[STIX]{x1D708}_{0}$
, we write
![]() $\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
if
$\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
if
![]() $\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
$\unicode[STIX]{x1D708}_{0}$
lies in the closure of the chamber containing
![]() $\unicode[STIX]{x1D708}$
. We write
$\unicode[STIX]{x1D708}$
. We write
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
for the cross-walling functor between categories
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
for the cross-walling functor between categories
![]() ${\mathcal{O}}$
for
${\mathcal{O}}$
for
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
.
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
.
Proposition 7.4. Let
![]() $\unicode[STIX]{x1D708}$
be generic with
$\unicode[STIX]{x1D708}$
be generic with
![]() $\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. The following are true.
$\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. The following are true.
-
(1) If
 $\unicode[STIX]{x1D708}^{\prime }$
is generic with
$\unicode[STIX]{x1D708}^{\prime }$
is generic with
 $\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
, then
$\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
, then
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\cong \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
and
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\cong \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}$
and
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\cong \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Here
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\cong \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}$
. Here
 $\text{}\underline{\mathfrak{CW}}^{\ast }$
stands for the right adjoint of
$\text{}\underline{\mathfrak{CW}}^{\ast }$
stands for the right adjoint of
 $\text{}\underline{\mathfrak{CW}}$
.
$\text{}\underline{\mathfrak{CW}}$
. -
(2) The functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is a Ringel duality.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is a Ringel duality.
We will recall a definition of the Ringel duality in the next section.
In particular, (2) implies the shuffling part of [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 8.24] (the twisting part will be proved in the next section).
7.3 Ringel duality, homological duality and long wall-crossing
Let
![]() ${\mathcal{C}}_{1},{\mathcal{C}}_{2}$
be two highest-weight categories. Consider the full subcategories
${\mathcal{C}}_{1},{\mathcal{C}}_{2}$
be two highest-weight categories. Consider the full subcategories
 ${\mathcal{C}}_{1}^{\unicode[STIX]{x1D6E5}}\subset {\mathcal{C}}_{1},{\mathcal{C}}_{2}^{\unicode[STIX]{x1D6FB}}\subset {\mathcal{C}}_{2}$
of standardly filtered and of costandardly filtered objects. We say that
${\mathcal{C}}_{1}^{\unicode[STIX]{x1D6E5}}\subset {\mathcal{C}}_{1},{\mathcal{C}}_{2}^{\unicode[STIX]{x1D6FB}}\subset {\mathcal{C}}_{2}$
of standardly filtered and of costandardly filtered objects. We say that
![]() ${\mathcal{C}}_{2}$
is Ringel dual to
${\mathcal{C}}_{2}$
is Ringel dual to
![]() ${\mathcal{C}}_{1}$
if there is an equivalence
${\mathcal{C}}_{1}$
if there is an equivalence
 ${\mathcal{C}}_{1}^{\unicode[STIX]{x1D6E5}}\xrightarrow[{}]{{\sim}}{\mathcal{C}}_{2}^{\unicode[STIX]{x1D6FB}}$
of exact categories (and we write
${\mathcal{C}}_{1}^{\unicode[STIX]{x1D6E5}}\xrightarrow[{}]{{\sim}}{\mathcal{C}}_{2}^{\unicode[STIX]{x1D6FB}}$
of exact categories (and we write
![]() ${\mathcal{C}}_{1}^{\vee }$
for
${\mathcal{C}}_{1}^{\vee }$
for
![]() ${\mathcal{C}}_{2}$
). This equivalence is known to extend to a derived equivalence
${\mathcal{C}}_{2}$
). This equivalence is known to extend to a derived equivalence
 ${\mathcal{R}}:D^{b}({\mathcal{C}}_{1})\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{C}}_{2})$
to be called the Ringel duality functor. The functor
${\mathcal{R}}:D^{b}({\mathcal{C}}_{1})\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{C}}_{2})$
to be called the Ringel duality functor. The functor
![]() ${\mathcal{R}}$
maps standards to costandards, projectives to tiltings and tiltings to injectives. So, we can identify highest-weight posets of
${\mathcal{R}}$
maps standards to costandards, projectives to tiltings and tiltings to injectives. So, we can identify highest-weight posets of
![]() ${\mathcal{C}}_{1},{\mathcal{C}}_{2}$
as sets (they will have the opposite orders). In this section, we will describe the category
${\mathcal{C}}_{1},{\mathcal{C}}_{2}$
as sets (they will have the opposite orders). In this section, we will describe the category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})^{\vee }$
.
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})^{\vee }$
.
Consider the functor
 $D:=\operatorname{RHom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}(\bullet ,{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
. It defines an equivalence
$D:=\operatorname{RHom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}(\bullet ,{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
. It defines an equivalence
 $D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
. Note that
$D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
. Note that
 $\operatorname{Supp}H^{i}(DM)\subset \operatorname{Supp}M$
for all
$\operatorname{Supp}H^{i}(DM)\subset \operatorname{Supp}M$
for all
![]() $i$
. Also, note that
$i$
. Also, note that
 $H^{i}(DM)$
is weakly
$H^{i}(DM)$
is weakly
![]() $T$
-equivariant provided
$T$
-equivariant provided
![]() $M$
is. Using Lemma 4.3, we see that
$M$
is. Using Lemma 4.3, we see that
![]() $D$
restricts to an equivalence
$D$
restricts to an equivalence
 $D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
. So, we get a derived equivalence
$D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
. So, we get a derived equivalence
 $D:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))^{\text{opp}}$
.
$D:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))^{\text{opp}}$
.
Proposition 7.5. There is a labeling preserving highest-weight equivalence
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})^{\vee }\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})^{\text{opp}}$
that intertwines
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})^{\vee }\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})^{\text{opp}}$
that intertwines
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
 $D[\frac{1}{2}\dim X]$
.
$D[\frac{1}{2}\dim X]$
.
We start with a technical lemma. Pick
 $p\in X^{T}$
. It uniquely deforms to a
$p\in X^{T}$
. It uniquely deforms to a
![]() $T$
-fixed point in any
$T$
-fixed point in any
![]() $X_{\unicode[STIX]{x1D712}}$
that we again denote by
$X_{\unicode[STIX]{x1D712}}$
that we again denote by
![]() $p$
. Let
$p$
. Let
![]() $Y_{\unicode[STIX]{x1D712},p}$
denote the
$Y_{\unicode[STIX]{x1D712},p}$
denote the
![]() $\unicode[STIX]{x1D708}$
-contracting locus for
$\unicode[STIX]{x1D708}$
-contracting locus for
![]() $p$
in
$p$
in
![]() $X_{\unicode[STIX]{x1D712}}$
.
$X_{\unicode[STIX]{x1D712}}$
.
Lemma 7.6. The object
 $D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{+}}(p))$
is concentrated in homological degree
$D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{+}}(p))$
is concentrated in homological degree
 $\frac{1}{2}\dim X$
and, moreover, its characteristic cycle (an element of the vector space with basis formed by the irreducible components of the contracting variety
$\frac{1}{2}\dim X$
and, moreover, its characteristic cycle (an element of the vector space with basis formed by the irreducible components of the contracting variety
![]() $Y$
) coincides with the class of
$Y$
) coincides with the class of
 $\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D712},p}}\,\cap \,X$
.
$\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D712},p}}\,\cap \,X$
.
Proof. Let us prove the first claim. Set
 $\ell :=\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
. What we need to prove is that
$\ell :=\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712}\mid z\in \mathbb{C}\}$
. What we need to prove is that
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{\prime }},{\mathcal{A}}_{\unicode[STIX]{x1D706}^{\prime }})=0$
provided
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{\prime }},{\mathcal{A}}_{\unicode[STIX]{x1D706}^{\prime }})=0$
provided
 $i\neq \frac{1}{2}\dim X$
for a Zariski generic
$i\neq \frac{1}{2}\dim X$
for a Zariski generic
![]() $\unicode[STIX]{x1D706}^{\prime }\in \ell$
. Our claim will follow if we show that the support of
$\unicode[STIX]{x1D706}^{\prime }\in \ell$
. Our claim will follow if we show that the support of
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
in
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
in
![]() $\mathbb{C}\unicode[STIX]{x1D712}$
is finite and that the
$\mathbb{C}\unicode[STIX]{x1D712}$
is finite and that the
![]() $\mathbb{C}[\ell ]$
-module
$\mathbb{C}[\ell ]$
-module
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
is generically free. Here we write
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
is generically free. Here we write
 $\unicode[STIX]{x1D6E5}_{\ell }={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{>}0}$
.
$\unicode[STIX]{x1D6E5}_{\ell }={\mathcal{A}}_{\ell }/{\mathcal{A}}_{\ell }{\mathcal{A}}_{\ell }^{{>}0}$
.
The right
![]() ${\mathcal{A}}_{\ell }$
-modules
${\mathcal{A}}_{\ell }$
-modules
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
are filtered with
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
are filtered with
 $\operatorname{gr}\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
being a subquotient of
$\operatorname{gr}\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\ell },{\mathcal{A}}_{\ell })$
being a subquotient of
 $\operatorname{Ext}^{i}(\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell },\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
. The claim about generic freeness follows from Lemma 2.5. Also, to prove the claim in the previous paragraph that the support is finite, it is enough to prove that
$\operatorname{Ext}^{i}(\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell },\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
. The claim about generic freeness follows from Lemma 2.5. Also, to prove the claim in the previous paragraph that the support is finite, it is enough to prove that
 $\operatorname{Ext}^{i}(\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell },\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
is supported at 0 as in Step 4 of the proof of Proposition 6.11.
$\operatorname{Ext}^{i}(\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell },\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
is supported at 0 as in Step 4 of the proof of Proposition 6.11.
Set
 $\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X]_{\mathbb{C}\unicode[STIX]{x1D712}}^{{>}0}$
. We have
$\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}:=\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X]_{\mathbb{C}\unicode[STIX]{x1D712}}^{{>}0}$
. We have
 $\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}{\twoheadrightarrow}\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell }$
. Moreover, the kernel is supported at 0; see the proof of (4) of Lemma 6.9. So, it is enough to show that the support of
$\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}{\twoheadrightarrow}\operatorname{gr}\unicode[STIX]{x1D6E5}_{\ell }$
. Moreover, the kernel is supported at 0; see the proof of (4) of Lemma 6.9. So, it is enough to show that the support of
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}},\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
is at 0 when
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}},\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}])$
is at 0 when
 $i\neq \frac{1}{2}\dim X$
. This follows from the observation that, generically over
$i\neq \frac{1}{2}\dim X$
. This follows from the observation that, generically over
![]() $\mathbb{C}\unicode[STIX]{x1D712}$
, the ideal
$\mathbb{C}\unicode[STIX]{x1D712}$
, the ideal
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0}$
is a locally complete intersection in a smooth variety.
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0}$
is a locally complete intersection in a smooth variety.
The argument above also implies that the associated graded module of
 $D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{+}}(p))$
coincides with that of
$D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}^{+}}(p))$
coincides with that of
 $\operatorname{Ext}^{(1/2)\dim X}(\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}(p)|_{\unicode[STIX]{x1D712}},\mathbb{C}[X_{\unicode[STIX]{x1D712}}])$
. The latter is just the class of the contracting component
$\operatorname{Ext}^{(1/2)\dim X}(\unicode[STIX]{x1D6E5}_{\mathbb{C}\unicode[STIX]{x1D712}}(p)|_{\unicode[STIX]{x1D712}},\mathbb{C}[X_{\unicode[STIX]{x1D712}}])$
. The latter is just the class of the contracting component
![]() $Y_{\unicode[STIX]{x1D712},p}$
(defined as the sum of components of
$Y_{\unicode[STIX]{x1D712},p}$
(defined as the sum of components of
 $X\,\cap \,\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D712},p}}$
with obvious multiplicities).◻
$X\,\cap \,\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D712},p}}$
with obvious multiplicities).◻
Proof of Proposition 7.5.
We write
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
for
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
for
 $D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p))[\frac{1}{2}\dim X]$
; thanks to Lemma 7.6, this is an object in
$D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p))[\frac{1}{2}\dim X]$
; thanks to Lemma 7.6, this is an object in
 ${\mathcal{O}}({\mathcal{A}}_{-\unicode[STIX]{x1D706}})$
(and not just a complex in its derived category). We have
${\mathcal{O}}({\mathcal{A}}_{-\unicode[STIX]{x1D706}})$
(and not just a complex in its derived category). We have
 $\operatorname{End}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee })=\mathbb{C}$
and
$\operatorname{End}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee })=\mathbb{C}$
and
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee },\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p^{\prime })^{\vee })=0$
if
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee },\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p^{\prime })^{\vee })=0$
if
![]() $i>0$
or
$i>0$
or
![]() $p\leqslant ^{\unicode[STIX]{x1D703}}p^{\prime }$
. We remark that the orders
$p\leqslant ^{\unicode[STIX]{x1D703}}p^{\prime }$
. We remark that the orders
![]() ${\leqslant}^{\unicode[STIX]{x1D703}}$
and
${\leqslant}^{\unicode[STIX]{x1D703}}$
and
![]() ${\leqslant}^{-\unicode[STIX]{x1D703}}$
can be refined to opposite partial orders (by the values of the real moment maps for the actions of
${\leqslant}^{-\unicode[STIX]{x1D703}}$
can be refined to opposite partial orders (by the values of the real moment maps for the actions of
 $\mathbb{S}^{1}\subset \unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
); compare with [Reference GordonGor08, § 5.4]. So, it only remains to prove that the characteristic cycle of
$\mathbb{S}^{1}\subset \unicode[STIX]{x1D708}(\mathbb{C}^{\times })$
); compare with [Reference GordonGor08, § 5.4]. So, it only remains to prove that the characteristic cycle of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
consists of the contracting components
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
consists of the contracting components
![]() $Y_{p^{\prime }}$
with
$Y_{p^{\prime }}$
with
 ${p^{\prime }\leqslant }^{-\unicode[STIX]{x1D703}}p$
. The characteristic cycle of
${p^{\prime }\leqslant }^{-\unicode[STIX]{x1D703}}p$
. The characteristic cycle of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
coincides with
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(p)^{\vee }$
coincides with
 $\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D703},p}}\,\cap \,X$
by Lemma 7.6. But the characteristic cycle of
$\overline{\mathbb{C}^{\times }Y_{\unicode[STIX]{x1D703},p}}\,\cap \,X$
by Lemma 7.6. But the characteristic cycle of
![]() $\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D706}}(p)$
is the same. Our claim follows.◻
$\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D706}}(p)$
is the same. Our claim follows.◻
Now we can establish a connection between the long wall-crossing functor from [Reference Bezrukavnikov and LosevBL13, § 4.1] and the Ringel duality. Pick
![]() $N\gg 0$
and set
$N\gg 0$
and set
 $\unicode[STIX]{x1D706}^{-}:=\unicode[STIX]{x1D706}-N\unicode[STIX]{x1D703}$
so that the analogs of (1) and (2) hold for
$\unicode[STIX]{x1D706}^{-}:=\unicode[STIX]{x1D706}-N\unicode[STIX]{x1D703}$
so that the analogs of (1) and (2) hold for
![]() $(\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D703})$
. We can consider the functor
$(\unicode[STIX]{x1D706}^{-},\unicode[STIX]{x1D703})$
. We can consider the functor
 $\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}:D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}\text{-}\!\operatorname{mod})$
given by
$\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}:D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}\text{-}\!\operatorname{mod})\rightarrow D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}\text{-}\!\operatorname{mod})$
given by
 ${\mathcal{A}}_{\unicode[STIX]{x1D706},-N\unicode[STIX]{x1D712}}^{(-\unicode[STIX]{x1D703})}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}}}^{L}\bullet$
. This is the long twisting functor from [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.1]: it is an equivalence, see [Reference Braden, Proudfoot and WebsterBPW16, § 6.4]. Since
${\mathcal{A}}_{\unicode[STIX]{x1D706},-N\unicode[STIX]{x1D712}}^{(-\unicode[STIX]{x1D703})}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}}}^{L}\bullet$
. This is the long twisting functor from [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.1]: it is an equivalence, see [Reference Braden, Proudfoot and WebsterBPW16, § 6.4]. Since
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706},-N\unicode[STIX]{x1D712}}^{(-\unicode[STIX]{x1D703})}$
is a HC bimodule, the functor
${\mathcal{A}}_{\unicode[STIX]{x1D706},-N\unicode[STIX]{x1D712}}^{(-\unicode[STIX]{x1D703})}$
is a HC bimodule, the functor
 $\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
restricts to an equivalence
$\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
restricts to an equivalence
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}))$
.
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}))$
.
The following proposition implies the twisting part of [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 8.24].
Proposition 7.7. There is a labelling preserving highest-weight equivalence
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})^{\vee }$
that intertwines
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}})\xrightarrow[{}]{{\sim}}{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})^{\vee }$
that intertwines
 $\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
and
$\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
and
![]() ${\mathcal{R}}$
.
${\mathcal{R}}$
.
Proof. In [Reference Bezrukavnikov and LosevBL13, § 4.3], we have established a
![]() $t$
-exact equivalence
$t$
-exact equivalence
 $D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
that intertwines
$D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{-}}\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D_{\text{hol}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\text{opp}}\text{-}\!\operatorname{mod})^{\text{opp}}$
that intertwines
 $\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
and
$\mathfrak{WC}_{\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}^{-}}$
and
 $D[\frac{1}{2}\dim X]$
(there we were dealing with the case when
$D[\frac{1}{2}\dim X]$
(there we were dealing with the case when
![]() $X$
is a Nakajima quiver variety, but the proof works in the general case as well). Now we are done by Proposition 7.5.◻
$X$
is a Nakajima quiver variety, but the proof works in the general case as well). Now we are done by Proposition 7.5.◻
7.4 Proof of (1) of Proposition 7.4
In this section, we prove (1) of Proposition 7.4. Our proof is based on the computation of the derived tensor product of certain bimodules.
The bimodules we are interested in are as follows:
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}:={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}},{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}:={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}},{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}}.\end{eqnarray}$$
The former is a
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
-bimodule and the latter is a
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
-bimodule and the latter is a
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
-
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
-
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-bimodule.
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
-bimodule.
Lemma 7.8. We have
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
.
${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
.
Proof. Note that
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}+{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}})=\bigg({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\bigg/\bigoplus _{i>0}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{-i}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{i}\bigg)_{0}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}={\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}/({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{<}0,\unicode[STIX]{x1D708}_{0}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}+{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{{>}0,\unicode[STIX]{x1D708}_{0}})=\bigg({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\bigg/\bigoplus _{i>0}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{-i}{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{i}\bigg)_{0}=\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}).\end{eqnarray}$$
So, we just need to check that the higher Tor spaces vanish.
Set
 $\ell :=\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
. We can consider the bimodules
$\ell :=\{\unicode[STIX]{x1D706}+z\unicode[STIX]{x1D712},z\in \mathbb{C}\}$
. We can consider the bimodules
 ${\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+}$
and form the derived tensor product
${\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+}$
and form the derived tensor product
 ${\mathcal{B}}_{\ell }^{-,o}\otimes ^{{\mathcal{A}}_{\ell }}{\mathcal{B}}_{\ell }^{+}$
. Similarly to Step 2 of the proof of Proposition 6.11, we just need to check that each
${\mathcal{B}}_{\ell }^{-,o}\otimes ^{{\mathcal{A}}_{\ell }}{\mathcal{B}}_{\ell }^{+}$
. Similarly to Step 2 of the proof of Proposition 6.11, we just need to check that each
 $\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is torsion over
$\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is torsion over
![]() $\mathbb{C}[\ell ]$
.
$\mathbb{C}[\ell ]$
.
The bimodules
 $\operatorname{Tor}_{i}^{\operatorname{gr}{\mathcal{A}}_{\ell }}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
are all supported at
$\operatorname{Tor}_{i}^{\operatorname{gr}{\mathcal{A}}_{\ell }}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
are all supported at
![]() $0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Indeed, the fiber of
$0\in \mathbb{C}\unicode[STIX]{x1D712}$
. Indeed, the fiber of
![]() $\operatorname{gr}{\mathcal{B}}_{\ell }^{+}$
over
$\operatorname{gr}{\mathcal{B}}_{\ell }^{+}$
over
![]() $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
![]() $\mathbb{C}[Y_{\unicode[STIX]{x1D712}}]$
, while the fiber of
$\mathbb{C}[Y_{\unicode[STIX]{x1D712}}]$
, while the fiber of
![]() $\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
equals
$\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
equals
![]() $\mathbb{C}[Y_{\unicode[STIX]{x1D712}}^{-}]$
; compare (4) of Lemma 6.9. Here
$\mathbb{C}[Y_{\unicode[STIX]{x1D712}}^{-}]$
; compare (4) of Lemma 6.9. Here
 $Y_{\unicode[STIX]{x1D712}}^{-}:=\{(x,z)\in X_{\unicode[STIX]{x1D712}}\times X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\mid \lim _{t\rightarrow \infty }\unicode[STIX]{x1D708}_{0}(t)x=z\}$
and
$Y_{\unicode[STIX]{x1D712}}^{-}:=\{(x,z)\in X_{\unicode[STIX]{x1D712}}\times X_{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}\mid \lim _{t\rightarrow \infty }\unicode[STIX]{x1D708}_{0}(t)x=z\}$
and
![]() $Y_{\unicode[STIX]{x1D712}}$
is defined similarly. The varieties
$Y_{\unicode[STIX]{x1D712}}$
is defined similarly. The varieties
![]() $Y_{\unicode[STIX]{x1D712}}$
and
$Y_{\unicode[STIX]{x1D712}}$
and
![]() $Y_{\unicode[STIX]{x1D712}}^{-}$
intersect transversally, hence our claim. Note that
$Y_{\unicode[STIX]{x1D712}}^{-}$
intersect transversally, hence our claim. Note that
 $$\begin{eqnarray}\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})\text{ is a subquotient of }\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})\text{ is a subquotient of }\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})\end{eqnarray}$$
(as
 $\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
-bimodules). We conclude that
$\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}})$
-bimodules). We conclude that
 $\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is supported at
$\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is supported at
![]() $0$
. We want to deduce from here that
$0$
. We want to deduce from here that
 $\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is torsion over
$\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is torsion over
![]() $\mathbb{C}[\ell ]$
.
$\mathbb{C}[\ell ]$
.
Thanks to Proposition 2.6, the previous claim will follow if we check that
 $\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is a Harish-Chandra
$\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is a Harish-Chandra
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
-bimodule. We have an epimorphism
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
-bimodule. We have an epimorphism
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}{\twoheadrightarrow}\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
. So, it is enough to prove that the left and the right actions of
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}{\twoheadrightarrow}\operatorname{gr}\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
. So, it is enough to prove that the left and the right actions of
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
on
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
on
 $\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
coincide. We have
$\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
coincide. We have
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}_{0}}{\twoheadrightarrow}\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
. So, the action of
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]/\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{{>}0,\unicode[STIX]{x1D708}_{0}}{\twoheadrightarrow}\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
. So, the action of
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
on
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
on
![]() $\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
(from the right) is restricted from the
$\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o}$
(from the right) is restricted from the
![]() $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
-action (from the left). It follows that the left
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
-action (from the left). It follows that the left
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
-action on
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
-action on
 $\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
is restricted from the
$\operatorname{Tor}_{i}^{\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]}(\operatorname{gr}{\mathcal{B}}_{\ell }^{-,o},\operatorname{gr}{\mathcal{B}}_{\ell }^{+})$
is restricted from the
![]() $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
-action (we take the Tor of modules over the commutative ring
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
-action (we take the Tor of modules over the commutative ring
![]() $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
). For similar reasons, the same is true for the right action. So,
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]$
). For similar reasons, the same is true for the right action. So,
 $\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is a
$\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{-,o},{\mathcal{B}}_{\ell }^{+})$
is a
 $\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
-module. Hence,
$\mathbb{C}[X_{\mathbb{C}\unicode[STIX]{x1D712}}]^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
-module. Hence,
 $\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{+,o},{\mathcal{B}}_{\ell }^{-})$
is indeed a HC
$\operatorname{Tor}_{i}^{{\mathcal{A}}_{\ell }}({\mathcal{B}}_{\ell }^{+,o},{\mathcal{B}}_{\ell }^{-})$
is indeed a HC
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
-bimodule.◻
$\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\ell })$
-bimodule.◻
Proof Proposition 7.4(1).
Let us show that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\circ \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
; the other isomorphism is similar.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\circ \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
; the other isomorphism is similar.
We need to establish a bifunctorial isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N))\end{eqnarray}$$
for
 $M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod}),N\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
.
$M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod}),N\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
.
By the definition of
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
, we have
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
, we have
 $$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(N)).\end{eqnarray}$$
On the other hand,

The first equality holds thanks to Lemma 6.12.
Note that
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
. Indeed, this is true for
${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
. Indeed, this is true for
 $M=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M^{\prime })$
, where
$M=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M^{\prime })$
, where
 $M^{\prime }\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, because, by Lemma 7.8, we have
$M^{\prime }\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, because, by Lemma 7.8, we have
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}^{L}M^{\prime }=M^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M={\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}{\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{+}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}^{L}M^{\prime }=M^{\prime }.\end{eqnarray}$$
Since the objects of the form
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M^{\prime })$
span
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}(M^{\prime })$
span
 $D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})$
, we deduce that
$D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})$
, we deduce that
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
for all
${\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})$
for all
 $M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})$
. It follows that
$M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})$
. It follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M,N)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M,N)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\text{-}\!\operatorname{mod})}({\mathcal{B}}_{\unicode[STIX]{x1D706}^{+}}^{-,o}\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}M,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle \xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}\text{-}\!\operatorname{mod})}(M,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}(\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N)).\end{eqnarray}$$
7.5 Proof of (2) of Proposition 7.4
In this section, we prove (2) of Proposition 7.4.
Pick some parameter
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Lemma 7.9. We have a bifunctorial isomorphism
 $$\begin{eqnarray}R\operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M,N)=D(M)\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}N.\end{eqnarray}$$
$$\begin{eqnarray}R\operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M,N)=D(M)\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}N.\end{eqnarray}$$
Proof. Equation (7.1) implies that the left-hand side is
 $R\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,N)$
. The claim is now standard.◻
$R\operatorname{Hom}_{D^{b}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(M,N)$
. The claim is now standard.◻
One can compute
 $D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))$
. The following claim was obtained in the proof of Proposition 7.5 (and is a formal corollary of that proposition).
$D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))$
. The following claim was obtained in the proof of Proposition 7.5 (and is a formal corollary of that proposition).
Lemma 7.10. We have
 $D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)[-\frac{1}{2}\dim X]$
.
$D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)[-\frac{1}{2}\dim X]$
.
Corollary 7.11. We have
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)[\frac{1}{2}\dim X]$
.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)[\frac{1}{2}\dim X]$
.
Proof. We have
 $$\begin{eqnarray}\displaystyle R\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k]) & = & \displaystyle D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k]\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k-{\textstyle \frac{1}{2}}\dim X].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R\operatorname{Hom}_{{\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k]) & = & \displaystyle D(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p))\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k]\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[k-{\textstyle \frac{1}{2}}\dim X].\nonumber\end{eqnarray}$$
It follows from Lemma 7.8 that the last expression is zero unless
![]() $p=p^{\prime }$
and
$p=p^{\prime }$
and
 $k=\frac{1}{2}\dim X$
, in which case it is one dimensional. Set
$k=\frac{1}{2}\dim X$
, in which case it is one dimensional. Set
 $M:=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[-\frac{1}{2}\dim X]$
. This object lies in
$M:=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })[-\frac{1}{2}\dim X]$
. This object lies in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
because any projective
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
because any projective
![]() $P$
in that category is standardly filtered and hence
$P$
in that category is standardly filtered and hence
 $\operatorname{Hom}(P,M[k])=0$
for
$\operatorname{Hom}(P,M[k])=0$
for
![]() $k\neq 0$
. From
$k\neq 0$
. From
 $\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),M)=0$
for
$\operatorname{Ext}^{i}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),M)=0$
for
![]() $i>0$
, it follows that
$i>0$
, it follows that
![]() $M$
is costandardly filtered. Now from
$M$
is costandardly filtered. Now from
 $\dim \operatorname{Hom}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),M)=\unicode[STIX]{x1D6FF}_{p,p^{\prime }}$
it follows that
$\dim \operatorname{Hom}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}(p),M)=\unicode[STIX]{x1D6FF}_{p,p^{\prime }}$
it follows that
 $M=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)$
.◻
$M=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)$
.◻
Let us proceed to the proof of (2).
Recall, see § 4.2, that
 ${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})^{\text{opp}}$
via
${\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})\cong {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})^{\text{opp}}$
via
 $N\mapsto N^{(\ast )}$
(the restricted dual).
$N\mapsto N^{(\ast )}$
(the restricted dual).
Lemma 7.12. For
 $M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}),N\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
, we have a bifunctorial isomorphism
$M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}),N\in {\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
, we have a bifunctorial isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}}(M,N^{(\ast )})=(M\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N)^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}}(M,N^{(\ast )})=(M\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N)^{\ast }.\end{eqnarray}$$
Proof. The space on the right is that of
![]() $\mathbb{K}$
-bilinear maps
$\mathbb{K}$
-bilinear maps
 $M\times N\rightarrow \mathbb{K}$
satisfying
$M\times N\rightarrow \mathbb{K}$
satisfying
 $\langle ma,n\rangle =\langle m,an\rangle$
. So, we have a homomorphism from the left-hand side to the right-hand side that to an
$\langle ma,n\rangle =\langle m,an\rangle$
. So, we have a homomorphism from the left-hand side to the right-hand side that to an
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}$
-linear map
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}$
-linear map
 $\unicode[STIX]{x1D711}:M\rightarrow N^{(\ast )}$
assigns the linear map
$\unicode[STIX]{x1D711}:M\rightarrow N^{(\ast )}$
assigns the linear map
 $\langle m,n\rangle _{\unicode[STIX]{x1D711}}:=\langle \unicode[STIX]{x1D711}(m),n\rangle$
. This homomorphism is clearly bifunctorial and injective. So, it remains to prove that it is surjective. By the five lemma, it is enough to prove the surjectivity when both
$\langle m,n\rangle _{\unicode[STIX]{x1D711}}:=\langle \unicode[STIX]{x1D711}(m),n\rangle$
. This homomorphism is clearly bifunctorial and injective. So, it remains to prove that it is surjective. By the five lemma, it is enough to prove the surjectivity when both
![]() $M,N$
are projective. We will do this in the case when
$M,N$
are projective. We will do this in the case when
![]() $M,N$
are standardly filtered. When
$M,N$
are standardly filtered. When
![]() $N$
is standardly filtered, the object
$N$
is standardly filtered, the object
![]() $N^{(\ast )}$
is costandardly filtered. So, the left-hand side has dimension
$N^{(\ast )}$
is costandardly filtered. So, the left-hand side has dimension
 $\sum _{p\in X^{T}}[M:\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)][N:\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)]$
. By a direct analog of Lemma 7.8, the functor
$\sum _{p\in X^{T}}[M:\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)][N:\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)]$
. By a direct analog of Lemma 7.8, the functor
 $$\begin{eqnarray}\bullet \otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}?:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))\times D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow D^{b}(\operatorname{Vect})\end{eqnarray}$$
$$\begin{eqnarray}\bullet \otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}^{L}?:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))\times D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow D^{b}(\operatorname{Vect})\end{eqnarray}$$
is acyclic on standardly filtered objects and also
 $\dim \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })=\unicode[STIX]{x1D6FF}_{pp^{\prime }}$
. It follows that the dimension of the right-hand side of (7.8) is also
$\dim \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p^{\prime })=\unicode[STIX]{x1D6FF}_{pp^{\prime }}$
. It follows that the dimension of the right-hand side of (7.8) is also
 $\sum _{p\in X^{T}}[M:\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)][N:\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)]$
.◻
$\sum _{p\in X^{T}}[M:\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}^{\text{opp}}(p)][N:\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)]$
.◻
Lemma 7.12 implies that
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}}(M,N^{(\ast )})=(M\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N)^{\ast },\quad M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})),N\in D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}}(M,N^{(\ast )})=(M\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N)^{\ast },\quad M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}})),N\in D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})).\end{eqnarray}$$
So, we get the following bifunctorial isomorphism:
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}(M),N)=D(M)\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))}(D(M),N^{(\ast )})^{\ast }\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(N,D^{(\ast )}(M))^{\ast }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}(M),N)=D(M)\,\otimes _{{\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}}N & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}^{\text{opp}}))}(D(M),N^{(\ast )})^{\ast }\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(N,D^{(\ast )}(M))^{\ast }.\nonumber\end{eqnarray}$$
Here we write
 $D^{(\ast )}(M)$
for
$D^{(\ast )}(M)$
for
 $(D(M))^{(\ast )}$
. Note that
$(D(M))^{(\ast )}$
. Note that
![]() $D^{(\ast )}$
is an equivalence. So, the functor
$D^{(\ast )}$
is an equivalence. So, the functor
 ${\mathcal{F}}:=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}\,\circ \,(D^{(\ast )})^{-1}$
satisfies
${\mathcal{F}}:=\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}\,\circ \,(D^{(\ast )})^{-1}$
satisfies
 $$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}({\mathcal{F}}N^{\prime },N)\cong \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(N,N^{\prime })^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}({\mathcal{F}}N^{\prime },N)\cong \operatorname{Hom}_{D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))}(N,N^{\prime })^{\ast }.\end{eqnarray}$$
From here, it is easy to see that
![]() ${\mathcal{F}}$
is fully faithful. Also,
${\mathcal{F}}$
is fully faithful. Also,
![]() ${\mathcal{F}}$
has a right adjoint:
${\mathcal{F}}$
has a right adjoint:
 ${\mathcal{F}}^{\ast }=D^{(\ast )}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }$
. Since
${\mathcal{F}}^{\ast }=D^{(\ast )}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }$
. Since
![]() ${\mathcal{F}}$
is fully faithful, the adjunction morphism
${\mathcal{F}}$
is fully faithful, the adjunction morphism
 $\operatorname{id}\rightarrow {\mathcal{F}}^{\ast }\circ {\mathcal{F}}$
is an isomorphism. It follows from (7.9) that the adjoint
$\operatorname{id}\rightarrow {\mathcal{F}}^{\ast }\circ {\mathcal{F}}$
is an isomorphism. It follows from (7.9) that the adjoint
![]() ${\mathcal{F}}^{\ast }$
is also fully faithful. So, we conclude that
${\mathcal{F}}^{\ast }$
is also fully faithful. So, we conclude that
![]() ${\mathcal{F}},{\mathcal{F}}^{\ast }$
are mutually inverse equivalences. Therefore,
${\mathcal{F}},{\mathcal{F}}^{\ast }$
are mutually inverse equivalences. Therefore,
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}$
is an equivalence of triangulated categories.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}$
is an equivalence of triangulated categories.
By Corollary 7.11,
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
sends
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
sends
![]() $\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)$
to
$\unicode[STIX]{x1D6E5}_{-\unicode[STIX]{x1D708}}(p)$
to
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)$
. Since
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}}(p)$
. Since
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is an equivalence, it follows that
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is an equivalence, it follows that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is a Ringel duality functor. This finishes the proof of (2).
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}^{\ast }[\frac{1}{2}\dim X]$
is a Ringel duality functor. This finishes the proof of (2).
7.6 Short cross-walling functors are equivalences
Let
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
be two generic one-parameter subgroups. We say that
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
be two generic one-parameter subgroups. We say that
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are neighbors if the chambers containing them share a codimension-one face. We will show that if
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are neighbors if the chambers containing them share a codimension-one face. We will show that if
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are neighbors, then
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
are neighbors, then
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
(a short wall-crossing functor) is an equivalence.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
(a short wall-crossing functor) is an equivalence.
We will prove a stronger result. Let
 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Let
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Let
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
denote the cross-walling functor
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
denote the cross-walling functor
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})))$
.
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})))$
.
Lemma 7.13. If
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence, then so is
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence, then so is
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
.
The claim that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence will follow. Indeed, for the action of
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is an equivalence will follow. Indeed, for the action of
![]() $T$
on
$T$
on
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
, the one-parameter subgroups
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
, the one-parameter subgroups
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
lie in the opposite chambers. Thanks to (2) of Proposition 7.4, the functor
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }$
lie in the opposite chambers. Thanks to (2) of Proposition 7.4, the functor
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is the sum of Ringel dualities with various shifts; in particular, it is an equivalence.
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
is the sum of Ringel dualities with various shifts; in particular, it is an equivalence.
Proof of Lemma 7.13.
Recall that, according to (1) of Proposition 7.4,
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\\ \displaystyle \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\\ \displaystyle \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\cong \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }.\end{array}\end{eqnarray}$$
It follows that both
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
respect the filtrations
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
respect the filtrations
 $$\begin{eqnarray}D_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z}^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\subset D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})),\quad D_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z}^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\subset D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})),\end{eqnarray}$$
$$\begin{eqnarray}D_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z}^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\subset D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})),\quad D_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z}^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\subset D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})),\end{eqnarray}$$
where
![]() $Z$
runs over the poset of the connected components of
$Z$
runs over the poset of the connected components of
 $X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. Recall, see Lemma 3.1, that
$X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })}$
. Recall, see Lemma 3.1, that
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z})$
is a full subcategory in
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})_{\preccurlyeq _{\unicode[STIX]{x1D708}_{0}}Z})$
is a full subcategory in
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
. Moreover, the associated graded categories are just
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
. Moreover, the associated graded categories are just
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
,
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
,
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
by Proposition 6.4. It follows from (7.10) that the functors
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
by Proposition 6.4. It follows from (7.10) that the functors
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))\rightleftarrows D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
induced by
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))\rightleftarrows D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{0}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})))$
induced by
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
are
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
are
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
. The latter are mutually quasi-inverse equivalences. So, if
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
. The latter are mutually quasi-inverse equivalences. So, if
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}(K)=0$
for some
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}(K)=0$
for some
 $K\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, then
$K\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
, then
![]() $K=0$
. Applying this for
$K=0$
. Applying this for
![]() $K$
being the cone of the adjunction morphism
$K$
being the cone of the adjunction morphism
 $M\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M$
, we see that
$M\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M$
, we see that
 $M\xrightarrow[{}]{{\sim}}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M$
. Similarly, we get that
$M\xrightarrow[{}]{{\sim}}\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}M$
. Similarly, we get that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N\xrightarrow[{}]{{\sim}}N$
. We conclude that
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }N\xrightarrow[{}]{{\sim}}N$
. We conclude that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
are mutually inverse equivalences.◻
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
are mutually inverse equivalences.◻
7.7 Proof of Theorem 7.3
The following theorem is a crucial step in the proof of (and also a special case of) Theorem 7.3.
Theorem 7.14. Let
![]() $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
be three generic one-parameter subgroups forming a reduced sequence (in this order) such that
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
be three generic one-parameter subgroups forming a reduced sequence (in this order) such that
![]() $\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
are neighbors. Then
$\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
are neighbors. Then
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\xrightarrow[{}]{{\sim}}\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
.
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\xrightarrow[{}]{{\sim}}\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
.
A key step in the proof is the next proposition. Let
![]() $\bar{\unicode[STIX]{x1D708}}$
be a generic one-parameter subgroup that is a neighbor of
$\bar{\unicode[STIX]{x1D708}}$
be a generic one-parameter subgroup that is a neighbor of
![]() $\unicode[STIX]{x1D708}$
and such that the sequence
$\unicode[STIX]{x1D708}$
and such that the sequence
 $\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
is reduced (note that here we can have
$\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
is reduced (note that here we can have
![]() $\bar{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}^{\prime }$
). Let
$\bar{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}^{\prime }$
). Let
![]() $\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}$
be such that
$\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}$
be such that
 $\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}}{\rightsquigarrow}\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{2}$
and
$\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}}{\rightsquigarrow}\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{2}$
and
![]() $\unicode[STIX]{x1D708}_{1}$
lies on the wall between
$\unicode[STIX]{x1D708}_{1}$
lies on the wall between
![]() $\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}}$
, while
$\unicode[STIX]{x1D708},\bar{\unicode[STIX]{x1D708}}$
, while
![]() $\unicode[STIX]{x1D708}_{2}$
lies on the wall between
$\unicode[STIX]{x1D708}_{2}$
lies on the wall between
![]() $\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
. Below we will write
$\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
. Below we will write
![]() ${\mathcal{A}}$
instead of
${\mathcal{A}}$
instead of
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
.
${\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}$
.
Proposition 7.15. For
 $M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}}))),N\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))$
, the natural homomorphism
$M\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}}))),N\in D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))$
, the natural homomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\rightarrow \operatorname{Hom}_{{\mathcal{A}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{{\mathcal{A}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\rightarrow \operatorname{Hom}_{{\mathcal{A}}}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\end{eqnarray}$$
is an isomorphism.
We will give a proof of Proposition 7.15 after a series of auxiliary results.
We start by giving an alternative interpretation of the homomorphism (7.11). Below we identify all categories
 $D^{b}({\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}))$
with
$D^{b}({\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}))$
with
 $D_{{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
so that the functors
$D_{{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
so that the functors
![]() $\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}$
become the inclusions. So, we will omit the functors
$\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}$
become the inclusions. So, we will omit the functors
![]() $\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}$
and get natural transformations
$\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}$
and get natural transformations
 $\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}^{\ast }\rightarrow \operatorname{id}$
.
$\unicode[STIX]{x1D704}_{\tilde{\unicode[STIX]{x1D708}}}^{\ast }\rightarrow \operatorname{id}$
.
Lemma 7.16. For
 $\tilde{M}\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod}),{\tilde{N}}\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
, there are bifunctorial isomorphisms
$\tilde{M}\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod}),{\tilde{N}}\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
, there are bifunctorial isomorphisms
 $$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},{\tilde{N}})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }{\tilde{N}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }{\tilde{N}})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }{\tilde{N}}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},{\tilde{N}})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }{\tilde{N}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }{\tilde{N}})\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\tilde{M},\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }{\tilde{N}}) & \displaystyle \nonumber\end{eqnarray}$$
making the following diagram commutative.

The proof is straightforward.
Consider the
![]() ${\mathcal{A}}$
-
${\mathcal{A}}$
-
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})$
-bimodule
$\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})$
-bimodule
 ${\mathcal{B}}^{1}:={\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}_{1}}$
and the
${\mathcal{B}}^{1}:={\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}_{1}}$
and the
![]() $\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})$
-
$\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})$
-
![]() ${\mathcal{A}}$
-bimodule
${\mathcal{A}}$
-bimodule
 ${\mathcal{B}}^{2}:={\mathcal{A}}/{\mathcal{A}}^{{<}0,\unicode[STIX]{x1D708}_{2}}{\mathcal{A}}$
so that
${\mathcal{B}}^{2}:={\mathcal{A}}/{\mathcal{A}}^{{<}0,\unicode[STIX]{x1D708}_{2}}{\mathcal{A}}$
so that
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(\bullet )={\mathcal{B}}^{1}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}\bullet$
and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(\bullet )={\mathcal{B}}^{1}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}\bullet$
and
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(\bullet )=R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})}({\mathcal{B}}^{2},\bullet )$
by Lemma 6.12. Set
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(\bullet )=R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})}({\mathcal{B}}^{2},\bullet )$
by Lemma 6.12. Set
 ${\mathcal{Q}}:={\mathcal{B}}^{2}\otimes _{{\mathcal{A}}}^{L}{\mathcal{B}}^{1}$
. This is an object in
${\mathcal{Q}}:={\mathcal{B}}^{2}\otimes _{{\mathcal{A}}}^{L}{\mathcal{B}}^{1}$
. This is an object in
 $D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})$
(the notation ‘Mod’ stands for the category of all modules).
$D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})$
(the notation ‘Mod’ stands for the category of all modules).
Let
![]() $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}$
denote the inclusion
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}$
denote the inclusion
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))=D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod}){\hookrightarrow}D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
. So, we get the right adjoint functor
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))=D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod}){\hookrightarrow}D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
. So, we get the right adjoint functor
 $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }:D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})\rightarrow D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
. Also, we consider the homological duality functor
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }:D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})\rightarrow D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
. Also, we consider the homological duality functor
 $\text{}\underline{D}:D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{mod})$
.
$\text{}\underline{D}:D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})\text{-}\!\operatorname{mod})\xrightarrow[{}]{{\sim}}D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{mod})$
.
Lemma 7.17. For
 $M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})\text{-}\!\operatorname{mod}),N\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
, there are bifunctorial isomorphisms
$M\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})\text{-}\!\operatorname{mod}),N\in D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}}^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{mod})$
, there are bifunctorial isomorphisms
 $$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},N\boxtimes \text{}\underline{D}M), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{Mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }(N)\boxtimes \text{}\underline{D}M) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},N\boxtimes \text{}\underline{D}M), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{Mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N))\xrightarrow[{}]{{\sim}}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }(N)\boxtimes \text{}\underline{D}M) & \displaystyle \nonumber\end{eqnarray}$$
making the following diagram commutative.

Proof. First of all, there is a functor isomorphism
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\,\circ \,\,\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}$
intertwining the morphisms
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\,\circ \,\,\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}$
intertwining the morphisms
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\,\circ \,\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast },\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\rightarrow \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}$
. This was established in the proof of (1) of Proposition 7.4 (recall that on
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\,\circ \,\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast },\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}\rightarrow \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}$
. This was established in the proof of (1) of Proposition 7.4 (recall that on
 $D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
, the functor
$D_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}}^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})$
, the functor
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
coincides with
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
coincides with
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
and a similar claim holds for
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
and a similar claim holds for
![]() $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
).
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }$
).
The claim of the lemma is now a consequence of the following bifunctorial isomorphisms (and similar isomorphisms with
![]() $N$
replaced with
$N$
replaced with
![]() $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N$
):
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N$
):
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)) & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}({\mathcal{B}}^{1}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}M,R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})}({\mathcal{B}}^{2},N))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{Mod})}({\mathcal{Q}}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}M,N)\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},N\boxtimes \text{}\underline{D}M).\hspace{59.75095pt}\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)) & = & \displaystyle \operatorname{Hom}_{D^{b}({\mathcal{A}}\text{-}\!\operatorname{mod})}({\mathcal{B}}^{1}\,\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}M,R\operatorname{Hom}_{\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})}({\mathcal{B}}^{2},N))\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\text{-}\!\operatorname{Mod})}({\mathcal{Q}}\otimes _{\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})}^{L}M,N)\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},N\boxtimes \text{}\underline{D}M).\hspace{59.75095pt}\square\nonumber\end{eqnarray}$$
Now we will need to get some information about
 ${\mathcal{Q}}\in D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})$
.
${\mathcal{Q}}\in D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})$
.
Lemma 7.18. We have
 $H_{\bullet }({\mathcal{Q}})\in {\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
.
$H_{\bullet }({\mathcal{Q}})\in {\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
.
Proof. The proof is in several steps.
Step 1. Note that both bimodules
![]() ${\mathcal{B}}^{1}$
and
${\mathcal{B}}^{1}$
and
![]() ${\mathcal{B}}^{2}$
are weakly
${\mathcal{B}}^{2}$
are weakly
![]() $T$
-equivariant. So,
$T$
-equivariant. So,
![]() $H_{\bullet }({\mathcal{Q}})$
is weakly
$H_{\bullet }({\mathcal{Q}})$
is weakly
![]() $T$
-equivariant as well. Let us check that the numbers
$T$
-equivariant as well. Let us check that the numbers
 $\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle ,-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
are bounded from above for all
$\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle ,-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
are bounded from above for all
![]() $T$
-weights
$T$
-weights
![]() $\unicode[STIX]{x1D6FC}$
appearing in
$\unicode[STIX]{x1D6FC}$
appearing in
![]() $H_{\bullet }({\mathcal{Q}})$
. Let us prove this claim for
$H_{\bullet }({\mathcal{Q}})$
. Let us prove this claim for
![]() $\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle$
; the proof for
$\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle$
; the proof for
 $-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
is similar. Recall that
$-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
is similar. Recall that
 ${\mathcal{B}}^{1}={\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}_{1}}$
. Choose a projective weakly
${\mathcal{B}}^{1}={\mathcal{A}}/{\mathcal{A}}{\mathcal{A}}^{{>}0,\unicode[STIX]{x1D708}_{1}}$
. Choose a projective weakly
![]() $T$
-equivariant
$T$
-equivariant
![]() ${\mathcal{A}}$
-module resolution for
${\mathcal{A}}$
-module resolution for
![]() ${\mathcal{B}}^{2}$
. We see that
${\mathcal{B}}^{2}$
. We see that
![]() $H_{\bullet }({\mathcal{Q}})$
is also the homology of a complex whose terms are direct sums of several copies of
$H_{\bullet }({\mathcal{Q}})$
is also the homology of a complex whose terms are direct sums of several copies of
![]() ${\mathcal{B}}^{1}$
with twisted
${\mathcal{B}}^{1}$
with twisted
![]() $T$
-actions. Our claim follows.
$T$
-actions. Our claim follows.
Step 2. Now let us check that
![]() $H_{\bullet }({\mathcal{Q}})$
is the union of objects in
$H_{\bullet }({\mathcal{Q}})$
is the union of objects in
 $$\begin{eqnarray}{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}).\end{eqnarray}$$
Consider the action of
![]() $(\mathbb{C}^{\times })^{2}$
on
$(\mathbb{C}^{\times })^{2}$
on
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
by
$\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
by
![]() $\unicode[STIX]{x1D708}_{1}\times \unicode[STIX]{x1D708}_{2}$
so that the first copy of
$\unicode[STIX]{x1D708}_{1}\times \unicode[STIX]{x1D708}_{2}$
so that the first copy of
![]() $\mathbb{C}^{\times }$
acts trivially on the second factor and vice versa. Since the numbers
$\mathbb{C}^{\times }$
acts trivially on the second factor and vice versa. Since the numbers
 $\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle ,-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
are bounded from above, so is their sum. So, the
$\langle \unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D6FC}\rangle ,-\langle \unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D6FC}\rangle$
are bounded from above, so is their sum. So, the
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
-submodule of
$\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
-submodule of
![]() $H_{\bullet }({\mathcal{Q}})$
generated by any finite collection of
$H_{\bullet }({\mathcal{Q}})$
generated by any finite collection of
 $(\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2})$
-homogeneous elements lies in
$(\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2})$
-homogeneous elements lies in
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
. By Lemma 4.4, the latter category coincides with
${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
. By Lemma 4.4, the latter category coincides with
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
. The category
${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
. The category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
coincides with (7.12). This is because
${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{-\unicode[STIX]{x1D708}_{2}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
coincides with (7.12). This is because
![]() $\unicode[STIX]{x1D708}^{\prime }$
and
$\unicode[STIX]{x1D708}^{\prime }$
and
![]() $\unicode[STIX]{x1D708}_{1}$
lie in one half-space with respect to the wall containing
$\unicode[STIX]{x1D708}_{1}$
lie in one half-space with respect to the wall containing
![]() $\unicode[STIX]{x1D708}_{2}$
(and hence
$\unicode[STIX]{x1D708}_{2}$
(and hence
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))={\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))$
), and
${\mathcal{O}}_{\unicode[STIX]{x1D708}_{1}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))={\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))$
), and
![]() $\unicode[STIX]{x1D708},-\unicode[STIX]{x1D708}_{2}$
also lie in one half-space with respect to the wall containing
$\unicode[STIX]{x1D708},-\unicode[STIX]{x1D708}_{2}$
also lie in one half-space with respect to the wall containing
![]() $\unicode[STIX]{x1D708}_{1}$
. It is here that we use our choice of the one-parameter subgroups involved.
$\unicode[STIX]{x1D708}_{1}$
. It is here that we use our choice of the one-parameter subgroups involved.
Step 3. Now we claim that each
![]() $H_{i}({\mathcal{Q}})$
is actually the direct sum of objects in (7.12). Set
$H_{i}({\mathcal{Q}})$
is actually the direct sum of objects in (7.12). Set
 $\tilde{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}$
. Note that all weight spaces for
$\tilde{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}$
. Note that all weight spaces for
![]() $\tilde{\unicode[STIX]{x1D708}}$
in
$\tilde{\unicode[STIX]{x1D708}}$
in
![]() $H_{i}(Q)$
are finite dimensional and the weights are bounded from above. Indeed, it is enough to check this for
$H_{i}(Q)$
are finite dimensional and the weights are bounded from above. Indeed, it is enough to check this for
 $\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1})$
because
$\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1})$
because
 $$\begin{eqnarray}\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}}({\mathcal{B}}^{2},{\mathcal{B}}^{1})\text{ is a subquotient of }\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{gr}\operatorname{Tor}_{i}^{{\mathcal{A}}}({\mathcal{B}}^{2},{\mathcal{B}}^{1})\text{ is a subquotient of }\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1}).\end{eqnarray}$$
Note that
 $\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1})$
is a finitely generated module over
$\operatorname{Tor}_{i}^{\mathbb{C}[X_{0}]}(\operatorname{gr}{\mathcal{B}}^{2},\operatorname{gr}{\mathcal{B}}^{1})$
is a finitely generated module over
 $\mathbb{C}[X_{0}]/\mathbb{C}[X_{0}](\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}_{1}}+\mathbb{C}[X]^{{<}0,\unicode[STIX]{x1D708}_{2}})$
. The eigencharacters of
$\mathbb{C}[X_{0}]/\mathbb{C}[X_{0}](\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}_{1}}+\mathbb{C}[X]^{{<}0,\unicode[STIX]{x1D708}_{2}})$
. The eigencharacters of
![]() $\tilde{\unicode[STIX]{x1D708}}$
on the latter are all non-negative. The zero eigenspace is easily seen to be finite dimensional. Since the algebra
$\tilde{\unicode[STIX]{x1D708}}$
on the latter are all non-negative. The zero eigenspace is easily seen to be finite dimensional. Since the algebra
 $\mathbb{C}[X_{0}]/\mathbb{C}[X_{0}](\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}_{1}}+\mathbb{C}[X]^{{<}0,\unicode[STIX]{x1D708}_{2}})$
is finitely generated, every eigenspace is finite dimensional. This shows that the weights of the
$\mathbb{C}[X_{0}]/\mathbb{C}[X_{0}](\mathbb{C}[X_{0}]^{{>}0,\unicode[STIX]{x1D708}_{1}}+\mathbb{C}[X]^{{<}0,\unicode[STIX]{x1D708}_{2}})$
is finitely generated, every eigenspace is finite dimensional. This shows that the weights of the
![]() $\tilde{\unicode[STIX]{x1D708}}$
-action on
$\tilde{\unicode[STIX]{x1D708}}$
-action on
![]() $H_{i}({\mathcal{Q}})$
are bounded from above and all eigenspaces are finite dimensional.
$H_{i}({\mathcal{Q}})$
are bounded from above and all eigenspaces are finite dimensional.
Let
![]() $h$
denote the image of
$h$
denote the image of
![]() $1$
under the quantum comoment map for the actions of
$1$
under the quantum comoment map for the actions of
![]() $\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}$
on
$\unicode[STIX]{x1D708}_{1}-\unicode[STIX]{x1D708}_{2}$
on
 $\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
. The element
$\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\otimes \mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}$
. The element
![]() $h$
preserves the grading coming from the
$h$
preserves the grading coming from the
![]() $\tilde{\unicode[STIX]{x1D708}}$
-action and hence acts locally finitely on
$\tilde{\unicode[STIX]{x1D708}}$
-action and hence acts locally finitely on
![]() $H_{i}({\mathcal{Q}})$
. For
$H_{i}({\mathcal{Q}})$
. For
 $z\in \mathbb{C},j\in \mathbb{Z}$
, let
$z\in \mathbb{C},j\in \mathbb{Z}$
, let
 $H_{i}({\mathcal{Q}})[z,j]$
denote the generalized
$H_{i}({\mathcal{Q}})[z,j]$
denote the generalized
![]() $z$
-eigenspace for
$z$
-eigenspace for
![]() $h$
in the component of degree
$h$
in the component of degree
![]() $j$
. So,
$j$
. So,
 $M_{z}:=\bigoplus _{j}H_{i}({\mathcal{Q}})[z+j,j]$
is a submodule in
$M_{z}:=\bigoplus _{j}H_{i}({\mathcal{Q}})[z+j,j]$
is a submodule in
![]() $H_{i}({\mathcal{Q}})$
and
$H_{i}({\mathcal{Q}})$
and
 $H_{i}({\mathcal{Q}})=\bigoplus _{z\in \mathbb{C}}M_{z}$
. By (4) of Lemma 4.1,
$H_{i}({\mathcal{Q}})=\bigoplus _{z\in \mathbb{C}}M_{z}$
. By (4) of Lemma 4.1,
![]() $M_{z}$
lies in (7.12).
$M_{z}$
lies in (7.12).
Step 4. To check that
![]() $H_{i}({\mathcal{Q}})$
lies in (7.12), it is enough to show that
$H_{i}({\mathcal{Q}})$
lies in (7.12), it is enough to show that
 $$\begin{eqnarray}\dim \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\,\otimes \,\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},I[k])<\infty\end{eqnarray}$$
$$\begin{eqnarray}\dim \operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\,\otimes \,\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{Mod})}({\mathcal{Q}},I[k])<\infty\end{eqnarray}$$
for any indecomposable injective object
![]() $I$
in (7.12) and any integer
$I$
in (7.12) and any integer
![]() $k$
. Recall, see Lemma 7.17, that
$k$
. Recall, see Lemma 7.17, that
 $$\begin{eqnarray}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\,\otimes \,\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{mod})}({\mathcal{Q}},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N\boxtimes \text{}\underline{D}M)=\operatorname{Hom}_{D^{b}({\mathcal{A}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(M)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{D^{b}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})\,\otimes \,\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}\text{-}\!\operatorname{mod})}({\mathcal{Q}},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N\boxtimes \text{}\underline{D}M)=\operatorname{Hom}_{D^{b}({\mathcal{A}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(M)).\end{eqnarray}$$
The right-hand side is finite dimensional. Now we remark that any indecomposable injective in (7.12) is a product of the indecomposable injectives in the factors; this follows from Lemma 4.4. Both
 $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }:D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))$
and
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }:D^{b}({\mathcal{O}}_{-\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}})))$
and
 $\text{}\underline{D}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}))$
are equivalences. So, any injective in (7.12) has the form
$\text{}\underline{D}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})))\rightarrow D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}))$
are equivalences. So, any injective in (7.12) has the form
 $N\boxtimes \text{}\underline{D}(M)$
.◻
$N\boxtimes \text{}\underline{D}(M)$
.◻
Proof of Proposition 7.15.
We claim that the bottom row of the commutative diagram in Lemma 7.17 is an isomorphism. For this, we note that both
![]() ${\mathcal{Q}}$
and
${\mathcal{Q}}$
and
 $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N\boxtimes \text{}\underline{D}M$
lie in
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }N\boxtimes \text{}\underline{D}M$
lie in
 $D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}))$
. Furthermore, on
$D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}}))$
. Furthermore, on
 $N\boxtimes \text{}\underline{D}M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
, the functor
$N\boxtimes \text{}\underline{D}M\in {\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}(\mathsf{C}_{\unicode[STIX]{x1D708}_{2}}({\mathcal{A}}))\boxtimes {\mathcal{O}}_{\unicode[STIX]{x1D708}}(\mathsf{C}_{\unicode[STIX]{x1D708}_{1}}({\mathcal{A}})^{\text{opp}})$
, the functor
![]() $\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\boxtimes \operatorname{id}$
coincides with
$\text{}\underline{\unicode[STIX]{x1D704}}_{\unicode[STIX]{x1D708}^{\prime }}^{\ast }\boxtimes \operatorname{id}$
coincides with
 $\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\boxtimes \operatorname{id}=\text{}\underline{\mathfrak{CW}}_{(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708})\rightarrow (\unicode[STIX]{x1D708}^{\prime \prime },\unicode[STIX]{x1D708})}^{\ast }$
; the last equality holds thanks to Lemma 7.1. So, the claim in the beginning of the proof follows.◻
$\text{}\underline{\mathfrak{CW}}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\boxtimes \operatorname{id}=\text{}\underline{\mathfrak{CW}}_{(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708})\rightarrow (\unicode[STIX]{x1D708}^{\prime \prime },\unicode[STIX]{x1D708})}^{\ast }$
; the last equality holds thanks to Lemma 7.1. So, the claim in the beginning of the proof follows.◻
Proof of Theorem 7.14.
First of all, we claim that, in the notation of Proposition 7.15, the natural morphism
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)$
is an isomorphism. Indeed, let
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D708}_{2}}(N)$
is an isomorphism. Indeed, let
![]() $C$
be the cone. Then, by Proposition 7.15, we have
$C$
be the cone. Then, by Proposition 7.15, we have
 $R\operatorname{Hom}_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),C)=0$
. Since all standard objects in
$R\operatorname{Hom}_{{\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M),C)=0$
. Since all standard objects in
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
are of the form
${\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}})$
are of the form
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M)$
, we see that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}_{1}}(M)$
, we see that
![]() $C=0$
.
$C=0$
.
Now the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }$
is an isomorphism on all costandard objects in
$\mathfrak{CW}_{\unicode[STIX]{x1D708}^{\prime }\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }\,\circ \,\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }\rightarrow \mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime \prime }}^{\ast }$
is an isomorphism on all costandard objects in
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}({\mathcal{A}})$
. So, it is an isomorphism.◻
${\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime \prime }}({\mathcal{A}})$
. So, it is an isomorphism.◻
Proof of Theorem 7.3.
The part about the isomorphism of functors follows from Theorem 7.14 and easy induction. The claim that
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
is an equivalence now follows from the existence of a maximal reduced decomposition and Lemma 7.13.◻
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}^{\ast }$
is an equivalence now follows from the existence of a maximal reduced decomposition and Lemma 7.13.◻
Acknowledgements
I would like to thank Roman Bezrukavnikov and Andrei Okounkov for numerous stimulating discussions. I am also grateful to Justin Hilburn and Nick Proudfoot for their comments on a preliminary version of this text. I would also like to thank the reviewers for their comments that helped me to improve the exposition. My work was partially supported by the NSF under Grant DMS-1161584.
Appendix A Comparison to [Reference Maulik and OkounkovMO12]
In [Reference Maulik and OkounkovMO12], Maulik and Okounkov gave a geometric construction of
![]() $R$
-matrices. In this section, we will argue that the cross-walling functors should be viewed as a categorical version of their construction.
$R$
-matrices. In this section, we will argue that the cross-walling functors should be viewed as a categorical version of their construction.
A.1 Stable envelopes and Verma modules
Namely, let
![]() $X$
be a conical symplectic resolution equipped with a Hamiltonian action of a torus
$X$
be a conical symplectic resolution equipped with a Hamiltonian action of a torus
![]() $T$
. We assume that
$T$
. We assume that
![]() $T$
has finitely many fixed points in
$T$
has finitely many fixed points in
![]() $X$
(although this is not required in [Reference Maulik and OkounkovMO12]). Given a cocharacter
$X$
(although this is not required in [Reference Maulik and OkounkovMO12]). Given a cocharacter
![]() $\unicode[STIX]{x1D708}$
, Maulik and Okounkov [Reference Maulik and OkounkovMO12, § 3.5] constructed a map
$\unicode[STIX]{x1D708}$
, Maulik and Okounkov [Reference Maulik and OkounkovMO12, § 3.5] constructed a map
 $\mathsf{Stab}_{\unicode[STIX]{x1D708}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
that becomes an isomorphism on the localized equivariant cohomology (here
$\mathsf{Stab}_{\unicode[STIX]{x1D708}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
that becomes an isomorphism on the localized equivariant cohomology (here
![]() $\mathbb{C}^{\times }$
stands for the contracting torus). The map enjoys a certain transitivity property. Namely, pick
$\mathbb{C}^{\times }$
stands for the contracting torus). The map enjoys a certain transitivity property. Namely, pick
![]() $\unicode[STIX]{x1D708}_{0}$
with
$\unicode[STIX]{x1D708}_{0}$
with
![]() $\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Then we get maps
$\unicode[STIX]{x1D708}{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
. Then we get maps
 $\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
and
$\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
and
 $\text{}\underline{\mathsf{Stab}}_{\unicode[STIX]{x1D708}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })})$
. We have the following equality [Reference Maulik and OkounkovMO12, Lemma 3.6.1]:
$\text{}\underline{\mathsf{Stab}}_{\unicode[STIX]{x1D708}}:H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})\rightarrow H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}_{0}(\mathbb{C}^{\times })})$
. We have the following equality [Reference Maulik and OkounkovMO12, Lemma 3.6.1]:
 $\mathsf{Stab}_{\unicode[STIX]{x1D708}}=\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathsf{Stab}}_{\unicode[STIX]{x1D708}}$
.
$\mathsf{Stab}_{\unicode[STIX]{x1D708}}=\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\mathsf{Stab}}_{\unicode[STIX]{x1D708}}$
.
Following the original intuition of Okounkov, we would like to claim that the functor
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}$
should be viewed as a categorical version of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}$
should be viewed as a categorical version of
![]() $\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
. Namely, pick a generic cocharacter
$\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
. Namely, pick a generic cocharacter
![]() $\tilde{\unicode[STIX]{x1D708}}$
such that
$\tilde{\unicode[STIX]{x1D708}}$
such that
![]() $\tilde{\unicode[STIX]{x1D708}}{\rightsquigarrow}\unicode[STIX]{x1D708}$
. We replace
$\tilde{\unicode[STIX]{x1D708}}{\rightsquigarrow}\unicode[STIX]{x1D708}$
. We replace
 $H_{T\times \mathbb{C}^{\times }}^{\ast }(X),H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})$
with
$H_{T\times \mathbb{C}^{\times }}^{\ast }(X),H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{\unicode[STIX]{x1D708}(\mathbb{C}^{\times })})$
with
 ${\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}),{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
so that we have an exact functor
${\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}),{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
so that we have an exact functor
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow {\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
. An analog of the claim that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}:{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\rightarrow {\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
. An analog of the claim that
![]() $\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
is an isomorphism after localization is that
$\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
is an isomorphism after localization is that
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}$
lifts the equivalence
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D708}}$
lifts the equivalence
 ${\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}\operatorname{gr}{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
(where the filtration is taken with respect to
${\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}(\mathsf{C}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}\operatorname{gr}{\mathcal{O}}_{\tilde{\unicode[STIX]{x1D708}}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}})$
(where the filtration is taken with respect to
![]() $\unicode[STIX]{x1D708}$
); see § 6.4. Lemma 5.8 provides a transitivity result.
$\unicode[STIX]{x1D708}$
); see § 6.4. Lemma 5.8 provides a transitivity result.
A.2
 $R$
-matrices
$R$
-matrices
Pick generic cocharacters
![]() $\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}$
. Maulik and Okounkov [Reference Maulik and OkounkovMO12, § 4] defined an automorphism
$\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}$
. Maulik and Okounkov [Reference Maulik and OkounkovMO12, § 4] defined an automorphism
![]() $R_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
of
$R_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
of
 $H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{T})_{\text{loc}}$
as
$H_{T\times \mathbb{C}^{\times }}^{\ast }(X^{T})_{\text{loc}}$
as
 $\mathsf{Stab}_{\unicode[STIX]{x1D708}^{\prime }}^{-1}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
(here and below
$\mathsf{Stab}_{\unicode[STIX]{x1D708}^{\prime }}^{-1}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
(here and below
 $\bullet _{\text{loc}}:=\bullet \,\otimes _{\mathbb{C}[\mathfrak{t}\times \mathbb{C}]}\mathbb{C}(\mathfrak{t}\times \mathbb{C})$
).
$\bullet _{\text{loc}}:=\bullet \,\otimes _{\mathbb{C}[\mathfrak{t}\times \mathbb{C}]}\mathbb{C}(\mathfrak{t}\times \mathbb{C})$
).
We could also consider the automorphism
 $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:=\mathsf{Stab}_{\unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}}^{-1}$
of
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:=\mathsf{Stab}_{\unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}}^{-1}$
of
 $H_{T\times \mathbb{C}^{\times }}^{\ast }(X)_{\text{loc}}$
. The transitivity result quoted in the last section implies that if
$H_{T\times \mathbb{C}^{\times }}^{\ast }(X)_{\text{loc}}$
. The transitivity result quoted in the last section implies that if
 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
, then
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime }{\rightsquigarrow}\unicode[STIX]{x1D708}_{0}$
, then
 $$\begin{eqnarray}\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}=\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\tilde{R}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}=\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}\,\circ \,\text{}\underline{\tilde{R}}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}\,\circ \,\mathsf{Stab}_{\unicode[STIX]{x1D708}_{0}}^{-1}.\end{eqnarray}$$
We would like to argue that the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
should be viewed as a categorical version of
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}:D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))\xrightarrow[{}]{{\sim}}D^{b}({\mathcal{O}}_{\unicode[STIX]{x1D708}^{\prime }}({\mathcal{A}}_{\unicode[STIX]{x1D706}^{+}}))$
should be viewed as a categorical version of
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
. A part of our reasons for this is Proposition 7.4. Part (1) of that proposition should be viewed as a categorical analog of (A.1). To interpret part (2) of that proposition, we note that using
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
. A part of our reasons for this is Proposition 7.4. Part (1) of that proposition should be viewed as a categorical analog of (A.1). To interpret part (2) of that proposition, we note that using
![]() $\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
we can define a basis in
$\mathsf{Stab}_{\unicode[STIX]{x1D708}}$
we can define a basis in
 $H_{T\times \mathbb{C}^{\times }}^{\ast }(X)_{\text{loc}}$
called the stable basis; it consists of the images of the classes of the fixed points. The map
$H_{T\times \mathbb{C}^{\times }}^{\ast }(X)_{\text{loc}}$
called the stable basis; it consists of the images of the classes of the fixed points. The map
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
intertwines the stable bases for
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
intertwines the stable bases for
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D708}^{\prime }$
. In particular, the stable basis for
$\unicode[STIX]{x1D708}^{\prime }$
. In particular, the stable basis for
![]() $-\unicode[STIX]{x1D708}$
should be viewed as the opposite to
$-\unicode[STIX]{x1D708}$
should be viewed as the opposite to
![]() $\unicode[STIX]{x1D708}$
, and the map
$\unicode[STIX]{x1D708}$
, and the map
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}$
intertwines these two bases. Part (2) of Proposition 7.4 should be viewed as a categorical analog of this.
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow -\unicode[STIX]{x1D708}}$
intertwines these two bases. Part (2) of Proposition 7.4 should be viewed as a categorical analog of this.
By its very definition, the map
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
satisfies the braid relations; compare [Reference Maulik and OkounkovMO12, § 4.1.8]. A categorical analog of this is Theorem 7.3.
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
satisfies the braid relations; compare [Reference Maulik and OkounkovMO12, § 4.1.8]. A categorical analog of this is Theorem 7.3.
The map
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
and the functor
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
and the functor
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
share some further similarities. For example, using [Reference Maulik and OkounkovMO12, Theorem 4.6.1], one can prove that
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
share some further similarities. For example, using [Reference Maulik and OkounkovMO12, Theorem 4.6.1], one can prove that
![]() $\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
commutes with the action of the convolution algebra of the Steinberg variety
$\tilde{R}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
commutes with the action of the convolution algebra of the Steinberg variety
 $X\times _{X_{0}}X$
. On the other hand, it is not difficult to show that the functors
$X\times _{X_{0}}X$
. On the other hand, it is not difficult to show that the functors
 $\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
commute with the functors of taking derived tensor products with Harish-Chandra bimodules; compare [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.3].
$\mathfrak{CW}_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
commute with the functors of taking derived tensor products with Harish-Chandra bimodules; compare [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 8.3].
We do not know if the map
![]() $R_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
itself has a categorical analog.
$R_{\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D708}^{\prime }}$
itself has a categorical analog.
A.3 Possible formal connection
Let us speculate on how one could formally pass from our categorical constructions to those of [Reference Maulik and OkounkovMO12]. We can consider the categories of weakly
![]() $T$
-equivariant objects
$T$
-equivariant objects
![]() ${\mathcal{O}}_{?}^{T}$
in
${\mathcal{O}}_{?}^{T}$
in
![]() ${\mathcal{O}}_{?}$
. Via taking the characteristic cycle, see, e.g., [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 6.1],
${\mathcal{O}}_{?}$
. Via taking the characteristic cycle, see, e.g., [Reference Braden, Licata, Proudfoot and WebsterBLPW16, § 6.1],
 $K_{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}}^{T}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
gets identified with
$K_{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}}^{T}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}}))$
gets identified with
 $H_{T}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
, where
$H_{T}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
, where
![]() $Y_{\unicode[STIX]{x1D708}}$
is the contracting locus for
$Y_{\unicode[STIX]{x1D708}}$
is the contracting locus for
![]() $\unicode[STIX]{x1D708}$
. The category
$\unicode[STIX]{x1D708}$
. The category
 ${\mathcal{O}}_{\unicode[STIX]{x1D708}}^{T}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is expected to be standard Koszul; compare [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 5.14]. Under the corresponding additional graded lift, the
${\mathcal{O}}_{\unicode[STIX]{x1D708}}^{T}({\mathcal{A}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D703}})$
is expected to be standard Koszul; compare [Reference Braden, Licata, Proudfoot and WebsterBLPW16, Conjecture 5.14]. Under the corresponding additional graded lift, the
![]() $K_{0}$
should be identified with
$K_{0}$
should be identified with
 $H_{T\times \mathbb{C}^{\times }}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
. Up to localization,
$H_{T\times \mathbb{C}^{\times }}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
. Up to localization,
 $H_{T\times \mathbb{C}^{\times }}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
coincides with
$H_{T\times \mathbb{C}^{\times }}^{\text{top}}(Y_{\unicode[STIX]{x1D708}})$
coincides with
 $H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
. We expect that the functors above in this section have graded lifts and it is possible that on the level of the
$H_{T\times \mathbb{C}^{\times }}^{\ast }(X)$
. We expect that the functors above in this section have graded lifts and it is possible that on the level of the
![]() $K_{0}$
they give maps constructed by Maulik and Okounkov (or some close relatives of those).
$K_{0}$
they give maps constructed by Maulik and Okounkov (or some close relatives of those).