1 Introduction
One of the most classical results in representation theory is Schur–Weyl duality, one half of which is the statement that the algebra homomorphism
$$\begin{align*}\mathbb{C} \mathfrak{S}_r \to \operatorname{\mathrm{End}}_{\mathrm{GL}(V)}(V^{\otimes r}) \end{align*}$$
is surjective, where
$\mathfrak {S}_r$
is the symmetric group on r letters, acting on
$V^{\otimes r}$
by permutation of the factors. If one replaces the general linear group by the orthogonal group, the analogous statement is that one has a surjective algebra homomorphism
$$\begin{align*}\textrm{ Br}_r \to \operatorname{\mathrm{End}}_{\mathrm{O}(V)}(V^{\otimes r}), \end{align*}$$
where
$\textrm { Br}_r$
is the Brauer algebra.
A more modern approach to the above involves considering morphisms between different powers of the natural module V to rephrase the results in terms of monoidal categories. More precisely, there is a full and essentially surjective functor
$$\begin{align*}\mathscr{OB}(N) \to \mathrm{GL}(V)\textrm{-mod} \end{align*}$$
from the oriented Brauer category to the category of finite-dimensional rational
$\mathrm {GL}(V)$
-modules, where
$N = \dim V$
. See, for example, [Reference Comes and WilsonCW12, Th. 4.7.1], although the idea essentially goes back to Turaev [Reference TuraevTur89]. Similarly, one has a full and essentially surjective functor
$$\begin{align*}\mathscr{B}(N) \to \mathrm{O}(V)\textrm{-mod}, \end{align*}$$
where
$\mathscr {B}(N)$
is the Brauer category. See, for example, [Reference Lehrer and ZhangLZ15, Th. 4.8]. The categories
$\mathscr {OB}(N)$
and
$\mathscr {B}(N)$
are defined for any choice of parameter
$N \in \mathbb {C}$
. Their additive Karoubi envelopes are Deligne’s interpolating categories for the general linear and orthogonal groups [Reference DeligneDel07].
Since the orthogonal group is not simply connected, it is natural to want to extend the above picture to its double cover, the pin group
$\mathrm {Pin}(V)$
, or the identity component, the spin group
$\mathrm {Spin}(V)$
. This desire is further underlined by the importance of the spin group in other areas of representation theory and physics. A first step in this direction is the recent work of Wenzl [Reference WenzlWen20] describing the endomorphism algebra of
$S^{\otimes r}$
, where S is the spin module. (In fact, [Reference WenzlWen20] works with representations of quantized enveloping algebra.) Other partial results were obtained in [Reference Orellana and WenzlOW02, Reference WenzlWen12]. In type D, see also [Reference HoweHow95, Th. 4.3.4.1] and [Reference AboumradAbo22, Th. 3.6] for similar results. The goal of the current paper is to develop the monoidal category approach and find a spin analogue of the Brauer category, allowing one to describe morphisms between all tensor products of the spin and vector modules.
After recalling and developing, in Sections 2 to 4, some of the representation theory of the spin and pin groups, we introduce the spin Brauer category
$\mathscr {SB}(d,D;\kappa )$
in Section 5. Here,
$d,D$
are elements of the ground field and
$\kappa \in \{\pm 1\}$
. Our definition of this strict monoidal category is diagrammatic, given via a presentation in terms of generators and relations. Whereas the Brauer category has one generating object, which should be thought of as a formal version of the natural module, the spin Brauer category has an additional generating object corresponding to the spin module. The parameters d and D are the categorical dimensions of the two generating objects. We then describe, in Theorem 6.1, a functor
$$\begin{align*}\mathbf{F} \colon \mathscr{SB}(N, \sigma_N 2^{n}; \kappa_N) \to {\mathrm{G}}(V)\textrm{-mod}, \end{align*}$$
where
$N = \dim V$
,
$n=\lfloor \frac {N}{2} \rfloor $
,
$\sigma _N, \kappa _N \in \{\pm 1\}$
depend on N (see Equation (6.1)), and
$$\begin{align*}{\mathrm{G}}(V) := \begin{cases} \mathrm{Pin}(V) & \text{if } N \text{ is even}, \\ \mathrm{Spin}(V) & \text{if } N \text{ is odd}. \end{cases} \end{align*}$$
(See Remarks 2.5 and 4.9 for an explanation of why we split into these cases.)
We prove that the functor
$\mathbf {F}$
is full (Theorem 7.9), essentially surjective after passing to the Karoubi envelope (Theorem 8.1) and that its kernel is precisely the tensor ideal of negligible morphisms (Theorem 8.3). This implies that the category
${\mathrm {G}}(V)\textrm { -mod}$
is equivalent to the semisimplification of the Karoubi envelope of
$\mathscr {SB}(N, \sigma _N 2^n; \kappa _N)$
. The Karoubi envelope of
$\mathscr {SB}(d,D;\kappa )$
should be thought of as an interpolating category for the spin and pin groups, in the spirit of Deligne’s interpolating categories [Reference DeligneDel07].
Both the oriented Brauer category and the Brauer category have affine analogues, defined in [Reference Brundan, Comes, Nash and ReynoldsBCNR17, Reference Rui and SongRS19]. In Section 9, we define an affine version
$\mathscr {ASB}(d,D;\kappa )$
of the spin Brauer category, together with functors (Theorem 9.8)
$$\begin{align*}\mathscr{ASB}(N, \sigma_N 2^n; \kappa_N) \to \mathscr{End}_{\mathbb{C}}({\mathrm{G}}(V)\textrm{-mod}) \quad \text{and} \quad \mathscr{ASB}(N, \sigma_N 2^n; \kappa_N) \to \mathscr{End}_{\mathbb{C}}(\mathfrak{so}(V)\textrm{-Mod}), \end{align*}$$
where
$\mathscr {End}_{\mathbb {C}}(\mathcal {C})$
denotes the monoidal category of
$\mathbb {C}$
-linear endofunctors of a
$\mathbb {C}$
-linear category
$\mathcal {C}$
, with natural transformations as morphisms, and
$\mathfrak {so}(V)\textrm { -Mod}$
denotes the category of all
$\mathfrak {so}(V)$
-modules. This functor yields tools for studying the translation functors given by tensoring with the spin and vector modules. Such translation functors have proved to be extremely useful in representation theory. Finally, in Theorem 10.1, we show that the image of the induced algebra homomorphism
is
$Z(\mathfrak {so}(V))^{{\mathrm {G}}(V)}$
, where
$Z(\mathfrak {so}(V))$
is the centre of the universal enveloping algebra
$U(\mathfrak {so}(V))$
.
The results of the current paper bring the power of diagrammatic techniques to the study of the representation theory of the spin and pin groups. As such, they lead to many natural directions of future research. We plan to develop a quantum analogue of our results, replacing the spin group by the quantized enveloping algebra
$U_q(\mathfrak {so}(n))$
. Such a quantum version would also suggest an approach to webs of types B and D, and so should be related to recent work of Bodish and Wu [Reference Bodish and WuBW23].
2 The spin representation
In this section, we recall the explicit construction of the most important representation theoretic ingredient in the current paper: the spin representation. Throughout this section, we work over the field
$\mathbb {C}$
of complex numbers.
2.1 The Clifford algebra
Let V be a vector space of finite dimension N, and let
$\Phi _V \colon V \times V \to \mathbb {C}$
be a nondegenerate symmetric bilinear form. Let
$$ \begin{align} \mathrm{Cl} = \mathrm{Cl}(V) := T(V)/ \left( vw+wv - 2 \Phi_V(v, w) : v,w \in V \right) \end{align} $$
denote the Clifford algebra associated to V. Here,
$T(V)$
is the tensor algebra on V. The algebra
$\mathrm {Cl}$
is
$(\mathbb {Z}/2\mathbb {Z})$
-graded by declaring that elements of V are odd (that is, have degree
$\bar 1$
). We let
$\deg x \in \mathbb {Z}/2\mathbb {Z}$
denote the degree of a homogeneous element
$x \in \mathrm {Cl}$
.
The factor of
$2$
in Equation (2.1) is chosen to make some later formulas slightly cleaner. For instance, for
$v \in V$
with
$\Phi _V(v,v) = 1$
, we have
$v^2 = 1$
. Note, however, that not all elements of V are invertible when
$N \ge 2$
. For example, if
$v \in V$
satisfies
$\Phi _V(v,v) = 0$
, then v is not invertible.
Since, over the complex numbers, any nondegenerate symmetric form is equivalent to the standard one, we may fix an orthonormal basis
$e_1,\dotsc ,e_N$
of V. Then, in
$\mathrm {Cl}$
, we have
$$ \begin{align} e_i e_j + e_j e_i = 2 \delta_{ij}. \end{align} $$
Let
$$ \begin{align} n = \left\lfloor \frac{N}{2} \right\rfloor \in \mathbb{N}, \quad \text{so that} \quad N = \begin{cases} 2n & \text{if } N \text{ is even}, \\ 2n+1 & \text{if } N \text{ is odd}. \end{cases} \end{align} $$
Now, define
$$ \begin{align} \psi_j := \tfrac{1}{2} \left( e_{2j-1} + \sqrt{-1} e_{2j} \right),\qquad \psi_j^\dagger : = \tfrac{1}{2} \left( e_{2j-1} - \sqrt{-1} e_{2j} \right), \qquad 1 \le j \le n. \end{align} $$
Then we have
$$\begin{align*}\Phi_V(\psi_i, \psi_j) = 0, \quad \Phi_V(\psi_i^\dagger, \psi_j^\dagger) = 0, \quad \Phi_V(\psi_i, \psi_j^\dagger) = \tfrac{1}{2} \delta_{ij},\qquad 1 \le i,j \le n, \end{align*}$$
and so
$$ \begin{align} \psi_i \psi_j + \psi_j \psi_i = 0 = \psi_i^\dagger \psi_j^\dagger + \psi_j^\dagger \psi_i^\dagger, \qquad \psi_i \psi_j^\dagger + \psi_j^\dagger \psi_i = \delta_{ij},\qquad 1 \le i,j \le n. \end{align} $$
When N is even, Equation (2.5) gives a presentation of
$\mathrm {Cl}$
. When N is odd, we need to include the additional relations
$$ \begin{align} \psi_i e_N + e_N \psi_i=0=\psi_i^\dagger e_N + e_N \psi_i^\dagger, \qquad e_{N}^2=1, \qquad 1\le i \le n, \end{align} $$
to obtain a presentation of
$\mathrm {Cl}$
.
2.2 Clifford modules
The algebra
$\mathrm {Cl}$
is semisimple. If N is even, then the algebra
$\mathrm {Cl}$
has a unique simple module up to isomorphism. If N is odd, then
$\mathrm {Cl}$
has exactly two simple modules. We will now describe these.
Let
$$\begin{align*}S := \Lambda(W) = \bigoplus_{r=0}^n \Lambda^r(W),\qquad \text{where}\quad W = \operatorname{\mathrm{span}}_{\mathbb{C}} \{ \psi_i^\dagger : 1 \le i \le n \}. \end{align*}$$
As a
$\mathbb {C}$
-module, S has basis
$$ \begin{align} \begin{gathered} x_I := \psi_{i_1}^\dagger \wedge \psi_{i_2}^\dagger \wedge \dotsb \wedge \psi_{i_k}^\dagger,\\ I = \{i_1,\dotsc,i_k\} \subseteq [n],\quad i_1 < i_2 < \dotsc < i_k,\quad 0 \le k \le n, \end{gathered} \end{align} $$
where
$$\begin{align*}[n]=\{1,2,\dotsc,n\}, \end{align*}$$
a notation we use throughout. In particular,
$$ \begin{align} \dim_{\mathbb{C}}(S) = 2^n. \end{align} $$
We will now construct a
$\mathrm {Cl}$
-module structure on S. If N is even, we turn S into a
$\mathrm {Cl}$
-module by defining
$$ \begin{align} \psi_i^\dagger x_I = \psi_i^\dagger \wedge x_I,\qquad \psi_i x_I = \begin{cases} (-1)^{|\{ j \in I : j<i \}|} x_{I \setminus \{i\}} & \text{if } i \in I, \\ 0 & \text{if } i \notin I, \end{cases} \qquad I \subseteq [n],\ 1 \le i \le n. \end{align} $$
It is straightforward to verify that the relations (2.5) are satisfied.
If N is odd, then we define two
$\mathrm {Cl}$
-module structures on S, depending on a choice of
$\varepsilon \in \{\pm 1\}$
. We again use the action defined in Equation (2.9) and additionally define
$$ \begin{align} e_{2n+1} x_I = \varepsilon (-1)^{|I|} x_I. \end{align} $$
It is straightforward to verify that relations (2.6) are satisfied.
For both even and odd N, the
$\mathrm {Cl}$
-modules defined above are called the spin modules. If N is even, then S is the unique simple
$\mathrm {Cl}$
-module. If N is odd, then the two modules constructed above are the two nonisomorphic simple
$\mathrm {Cl}$
-modules. In both cases,
$\mathrm {Cl}$
is semisimple.
Remark 2.1. An equivalent construction of the spin module is as
$\mathrm {Cl}/A$
, where A is the left ideal generated by the
$\psi _j$
,
$1 \le j \le n$
, if N is even, and is the left ideal generated by the
$\psi _j$
,
$1 \le j \le n$
, and
$e_N-\varepsilon $
if N is odd.
We conclude this subsection with a technical lemma that will be used in the proof of Theorem 6.1. Suppose N is odd, and let
$$ \begin{align} \psi_0 = \tfrac{1}{\sqrt{2}} e_N,\qquad \psi_{-i}=\psi_i^\dagger, \quad i \in [n]. \end{align} $$
Lemma 2.2. Suppose N is odd. For all permutations
$\varpi $
of
$\{-n,1-n,\cdots ,n-1,n\}$
, we have
$$ \begin{align} \psi_{\varpi(-n)}\psi_{\varpi(1-n)} \dotsm \psi_{\varpi(n-1)}\psi_{\varpi(n)} x_I = \begin{cases} \frac{\varepsilon}{\sqrt{2}} \operatorname{sgn}(\varpi) x_I & \text{if } I=I_\varpi, \\ 0 & \text{otherwise}, \end{cases} \end{align} $$
where
$I_\varpi =\{i \in [n] : \varpi ^{-1}(-i) < \varpi ^{-1}(i)\}$
.
Proof. For
$i=1,2,\ldots ,n$
, let
$$\begin{align*}A_i = \begin{cases} \psi_{-i}\psi_i & \text{if } i \in I_\varpi, \\ \psi_i \psi_{-i} & \text{if } i \notin I_\varpi. \end{cases} \end{align*}$$
We compare the products
$\psi _{\varpi (-n)}\psi _{\varpi (1-n)} \dotsm \psi _{\varpi (n-1)}\psi _{\varpi (n)}$
and
$\psi _0 A_1 A_2 \dotsm A_n$
. They are both a product of
$\psi _{-n},\psi _{1-n},\ldots ,\psi _n$
in some order. For each
$i\in [n]$
, the elements
$\psi _i$
and
$\psi _{-i}$
appear in the same order in each of these two products. Therefore, we can pass from one to the other by swapping adjacent pairs
$\psi _i$
and
$\psi _j$
for
$i\neq \pm j$
. In the Clifford algebra, each of these swaps introduces a minus sign since
$\psi _i\psi _j=-\psi _j\psi _i$
for
$i\neq \pm j$
. So, in order to compare
$\psi _{\varpi (-n)} \psi _{\varpi (1-n)} \dotsm \psi _{\varpi (n-1)}\psi _{\varpi (n)}$
and
$\psi _0 A_1 A_2 \dotsm A_n$
in
$\mathrm {Cl}$
, we need to compute the sign of the permutation by which these two orderings of the indices differ.
The sign of the permutation sending
$(\varpi (-n),\varpi (1-n),\ldots ,\varpi (n))$
to
$(-n,1-n,\ldots ,n)$
is
$\operatorname {sgn}(\varpi )$
. A reduced expression of the permutation sending
$(-n,1-n,\cdots ,n)$
to
$(0,-1,1,-2,2,\dotsc ,-n,n)$
is a product of
$1 + 3 + \dotsb + (2n-1) = n^2$
simple transpositions. Therefore, its sign is
$(-1)^{n^2} = (-1)^n$
. The sign of the permutation sending
$(0,-1,1,-2,2,\dotsc ,-n,n)$
to the order of the indices in the product
$\psi _0 A_1 A_2 \dotsm A_n$
is
$(-1)^{n-|I_\varpi |}$
. Hence, we obtain the identity
$$\begin{align*}\psi_{\varpi(-n)}\psi_{\varpi(1-n)} \dotsm \psi_{\varpi(n-1)}\psi_{\varpi(n)} = \operatorname{sgn}(\varpi)(-1)^{|I_\varpi|} \psi_0 A_1 A_2 \dotsm A_n. \end{align*}$$
From Equations (2.9) and (2.10), we have
$A_i x_{I_\varpi }=x_{I_\varpi }$
and
$\psi _0 x_{I_\varpi }=\varepsilon (-1)^{|I_\varpi |}/\sqrt {2}$
. This completes the proof of Equation (2.12) when
$I=I_\varpi $
. On the other hand, when
$I \ne I_\varpi $
, we have
$A_i x_I = 0$
for any
$i \in (I \setminus I_\varpi ) \cup (I_\varpi \setminus I)$
.
2.3 The pin and spin groups
Recall that
$\mathrm {Cl}$
is
$(\mathbb {Z}/2\mathbb {Z})$
-graded. Define
$$ \begin{align} \mathrm{GPin}(V) := \{ g \in \mathrm{Cl}(V)^\times : g \text{ is homogeneous and } gVg^{-1} = V\}, \end{align} $$
and let
$$ \begin{align} \iota \colon \mathrm{Cl}(V) \to \mathrm{Cl}(V) \end{align} $$
be the unique antiautomorphism of
$\mathrm {Cl}(V)$
that is the identity on elements of V. Then the spinor norm on
$\mathrm {GPin}(V)$
is the group homomorphism given by
$$\begin{align*}\mathrm{GPin}(V) \to \mathbb{C}^\times,\quad g \mapsto g \iota(g). \end{align*}$$
The pin group associated to V, equipped with its nondegenerate symmetric bilinear form, is the subgroup of
$\mathrm {GPin}(V)$
consisting of elements of spinor norm one:
$$ \begin{align} \mathrm{Pin}(V) := \{g \in \mathrm{GPin}(V) : g \iota(g) = 1\}. \end{align} $$
The corresponding spin group is
$$ \begin{align} \mathrm{Spin}(V) := \mathrm{Pin}(V) \cap \mathrm{Cl}_{\bar{0}}, \end{align} $$
where
$\mathrm {Cl}_{\bar {0}}$
is the even part of
$\mathrm {Cl}$
.
We will need the following analogue of the Cartan–Dieudonné theorem for the pin and spin groups. Note that if
$v\in V$
satisfies
$\Phi _V(v,v)=1$
, then
$v\in \mathrm {Pin}(V)$
.
Theorem 2.3. Suppose
$N\geq 1$
. Then
$$ \begin{align} \mathrm{Pin}(V) = \{ v_1 v_2 \dotsm v_k : k \in \mathbb{N},\ v_i \in V,\ \Phi_V(v_i,v_i)=1\ \forall\ 1 \le i \le k \} \subseteq \mathrm{Cl}(V)^\times, \end{align} $$
$$ \begin{align} \mathrm{Spin}(V) = \{ v_1 v_2 \dotsm v_k : k \in 2\mathbb{N},\ v_i \in V,\ \Phi_V(v_i,v_i)=1\ \forall\ 1 \le i \le k \} \subseteq \mathrm{Pin}(V). \end{align} $$
Proof. First, we prove Equation (2.17). We will deduce this from the usual Cartan–Dieudonné theorem, which states that the orthogonal group
$\mathrm {O}(V)$
is generated by reflections (linear transformations that act as
$-1$
on a vector of nonzero length and fix its orthogonal complement).
There is a homomorphism
$p \colon \mathrm {Pin}(V)\to \mathrm {O}(V)$
given by the following action of
$\mathrm {Pin}(V)$
on V:
$$ \begin{align} p(g)(v)=(-1)^{\deg g} g v g^{-1} \end{align} $$
for
$g\in \mathrm {Pin}(V)$
and
$v\in V$
. Indeed, conjugate
$uv+vu=2\Phi _V(u,v)$
by g to get
$\Phi _V(p(g)(u),p(g)(v)) = \Phi _V(u,v)$
. This shows that the image of p lies in
$\mathrm {O}(V)$
.
Since
$v^2 = \Phi _V(v,v)$
, we have
$$\begin{align*}v^{-1} = \Phi_V(v,v)^{-1} v \qquad \text{for } v \in V,\quad \Phi_V(v,v) \ne 0. \end{align*}$$
Then, for
$w \in V$
, we have
$$\begin{align*}-vwv^{-1} \overset{(2.1)}{=} wvv^{-1} - 2 \Phi_V(v,w) v^{-1} = w - 2\Phi_V(v,w) v^{-1} = w - 2 \frac{\Phi_V(v,w)}{\Phi_V(v,v)} v. \end{align*}$$
Thus, if
$\Phi _V(v,v) \ne 0$
, then
$p(v)$
is reflection across the hyperplane orthogonal to v.
Let
$g\in \mathrm {Pin} (V)$
. By the Cartan–Dieudonné theorem, there exist
$v_1,v_2,\dotsc ,v_k\in V$
with
$\Phi _V(v_i,v_i)=1$
, such that
$p(g)=p(v_1 v_2 \dotsm v_k)$
. Therefore,
$g^{-1} v_1v_2\cdots v_k\in \ker p$
. If
$x\in \ker p$
, then
$xvx^{-1}=(-1)^{\deg x} v$
for all
$v\in V$
. Since V generates
$\mathrm {Cl}$
, this implies
$xyx^{-1}=(-1)^{(\deg x)(\deg y)}y$
for all homogeneous
$y\in \mathrm {Cl}$
. This is the condition that x lies in the supercentre of
$\mathrm {Cl}$
(where we consider
$\mathrm {Cl}$
as a superalgebra via its
$(\mathbb {Z}/2\mathbb {Z})$
-grading), which we claim consists only of scalars. Indeed, for
$I \subseteq [n]$
, write
$e_I=\prod _{i\in I}e_i$
. (Pick one order of the product for each I; it does not matter which one.) Suppose
$\sum _{I \subseteq [n]}a_I e_I$
is in the supercentre. (In particular, it must be purely even or purely odd.) Now, suppose
$I \subseteq [n]$
is nonempty, and pick
$i \in I$
. Comparing the coefficients of
$e_{I \setminus \{i\}}$
on both sides of the equation
$$\begin{align*}\left( \sum_{I \subseteq [n]} a_I e_I \right)e_i = (-1)^{|I|} e_i \left( \sum_{I \subseteq [n]} a_I e_I \right) \end{align*}$$
yields
$a_I=0$
.
The only scalars lying in
$\mathrm {Pin}(V)$
are
$\pm 1$
. Hence,
$g^{-1} v_1 v_2 \dotsm v_k = \pm 1$
. If
$g^{-1} v_1 v_2 \dotsm v_k = 1$
; we are done. If
$g^{-1} v_1 v_2 \dotsm v_k = -1$
, then pick
$w \in V$
with
$\Phi _V(w,w)=1$
, and write
$-1=w(-w)$
. Then we have
$g = v_1 v_2 \dotsm v_{k+2}$
with
$v_{k+1}=w$
and
$v_{k+2}=-w$
, and we are done.
Finally, Equation (2.18) follows from Equation (2.17) by noting that each
$v_i$
lies in
$\mathrm {Cl}_{\bar {1}}$
.
Remark 2.4 (Low values of N).
It will be important for some of the inductive arguments in the paper that we allow
$N \in \{0,1,2\}$
, even though, in some ways, these behave differently than the cases
$N \ge 3$
. Let
$C_2$
denote the cyclic group on
$2$
elements. Then we have the following:
-
• When
$N=0$
,
$\mathrm {Pin}(V) = \mathrm {Spin}(V) = \{\pm 1\} \cong C_2$
. -
• When
$N=1$
,
$\mathrm {Pin}(V) = \{\pm 1, \pm v\} \cong C_2 \times C_2$
, where
$v \in V$
satisfies
$\Phi _V(v,v)=1$
(so that
$v^2=1$
), and
$\mathrm {Spin}(V) = \{\pm 1\} \cong C_2$
. -
• When
$N=2$
, we have an isomorphism (2.20)where
$$ \begin{align} \mathbb{G}_m \xrightarrow{\cong} \mathrm{Spin}(V),\qquad t \mapsto t + (t^{-1}-t) \psi_1^\dagger \psi_1, \end{align} $$
$\mathbb {G}_m$
is the multiplicative group. Next, note that
$\mathrm {Pin}(V) = \mathrm {Spin}(V) \sqcup \mathrm {Spin}(V) e_1$
and conjugation by
$e_1$
corresponds, under the above isomorphism, to inversion on
$\mathbb {G}_m$
. Thus,
$\mathrm {Pin}(V) \cong \mathbb {G}_m \rtimes C_2$
, where the nontrivial element of
$C_2$
acts on
$\mathbb {G}_m$
by inversion.
Implicit in the proof of Theorem 2.3 is a short exact sequence (for all
$N \in \mathbb {N}$
)
$$\begin{align*}\{1\} \to \{\pm 1\} \to \mathrm{Pin}(V)\to \mathrm{O}(V) \to \{1\}. \end{align*}$$
Restricting to
$\mathrm {Spin}(V)$
yields another short exact sequence
$$\begin{align*}\{1\} \to \{\pm 1\} \to \mathrm{Spin}(V)\to \mathrm{SO}(V) \to \{1\}. \end{align*}$$
The group
$\mathrm {Spin}(V)$
is connected for
$N \ge 2$
. This explains why the image of the third map above lies in the connected group
$\mathrm {SO}(V)$
, and realises
$\mathrm {Spin}(V)$
as the universal cover of
$\mathrm {SO}(V)$
for
$N\geq 3$
.
Remark 2.5. If N is odd, then the element
$e_1 e_2 \dotsm e_N \in \mathrm {Pin}(V) \setminus \mathrm {Spin}(V)$
is central, and
$\mathrm {Pin}(V)$
is generated by
$\mathrm {Spin}(V)$
and this central element. In this case, the difference between the representation theory of
$\mathrm {Pin}(V)$
and
$\mathrm {Spin}(V)$
is not significant. We will focus on
$\mathrm {Spin}(V)$
-modules when N is odd; see Remark 4.9.
3 Special orthogonal Lie algebras
In this section, we collect some basic facts about the special orthogonal Lie algebra
$\mathfrak {so}(V)$
. Since
$\mathfrak {so}(V)$
is the zero Lie algebra when
$N \le 1$
, we assume throughout this section that
$N \ge 2$
.
The Lie algebra
$\mathrm {Lie}(\mathrm {Cl}^\times )$
is
$\mathrm {Cl}$
with the commutator Lie bracket. The inclusion
$\mathrm {Spin}(V) \hookrightarrow \mathrm {Cl}^\times $
induces an inclusion
$\mathrm {Lie}(\mathrm {Spin}(V)) \hookrightarrow \mathrm {Cl}$
. The image of this inclusion is
$$\begin{align*}\mathrm{Cl}^2 := \operatorname{\mathrm{span}}_{\mathbb{C}} \{ uv-vu : u,v \in V\} \subseteq \mathrm{Cl}. \end{align*}$$
The group homomorphism
$\mathrm {Spin}(V)\to \mathrm {SO}(V)$
induces an isomorphism of Lie algebras. Under the identification of
$\mathrm {Lie}(\mathrm {Spin}(V))$
with
$\mathrm {Cl}^2$
above, this isomorphism is
$$ \begin{align} \gamma \colon \mathrm{Cl}^2\to \mathfrak{so}(V), \qquad \gamma(uv-vu)=4M_{u,v}, \end{align} $$
where
$M_{u,v}\in \mathfrak {so}(V)$
is defined by
$$ \begin{align} M_{u,v} w = \Phi_V(v,w) u - \Phi_V(u,w) v. \end{align} $$
3.1 Type D (even N)
We suppose throughout this subsection that
$N=2n$
is even, and we continue to assume that
$N \ge 2$
. Note that
-
• when
$n=1$
,
$\mathfrak {so}(V)$
is a one-dimensional abelian Lie algebra, and -
• when
$n \ge 2$
,
$\mathfrak {so}(V)$
is the semisimple Lie algebra of type
$D_n$
.
For
$A \in \operatorname {\mathrm {Mat}}_n(\mathbb {C})$
, let
$A'$
denote the flip of A in the antidiagonal. More precisely,
$$ \begin{align} \text{if } \quad A = (a_{ij})_{i,j=1}^n \quad \text{then} \quad A' = (a_{n-j+1,n-i+1})_{i,j=1}^n. \end{align} $$
Note that
$(AB)' = B' A'$
for
$A,B \in \operatorname {\mathrm {Mat}}_n(\mathbb {C})$
. In the ordered basis
$\psi _1, \dotsc , \psi _n, \psi _n^\dagger , \dotsc , \psi _1^\dagger $
of V, the matrices of
$\mathfrak {so}(V)$
are those of the form
$$\begin{align*}\begin{pmatrix} A & B \\ C & -A' \end{pmatrix} ,\qquad A,B,C \in \operatorname{\mathrm{Mat}}_n(\mathbb{C}),\ B' = -B,\ C' = -C. \end{align*}$$
The Cartan subalgebra
$\mathfrak {h}$
consists of the diagonal matrices. For
$1 \le i \le n$
, define
$$\begin{align*}\epsilon_i \in \mathfrak{h}^*,\quad \epsilon_i( \operatorname{\mathrm{diag}}(a_1,\dotsc,a_n, -a_n,\dotsc,-a_1) ) = a_i. \end{align*}$$
Let
$E_{ij}$
,
$1 \le i,j \le n$
denote the usual matrix units of
$\operatorname {\mathrm {Mat}}_n(\mathbb {C})$
, and define, for
$1 \le i,j \le n$
,
$$ \begin{align} A_{ij} = \begin{pmatrix} E_{ij} & 0 \\ 0 & -E_{ij}^{\prime} \end{pmatrix} ,\ B_{ij} = \begin{pmatrix} 0 & E_{i,n-j+1} - E_{j,n-i+1} \\ 0 & 0 \end{pmatrix} ,\ C_{ij} = \begin{pmatrix} 0 & 0 \\ E_{n-i+1,j} - E_{n-j+1,i} & 0 \end{pmatrix}. \end{align} $$
Then the
$A_{ij}$
,
$B_{ij}$
and
$C_{ij}$
are the root vectors, with corresponding roots
$\epsilon _i - \epsilon _j$
,
$\epsilon _i + \epsilon _j$
and
$-\epsilon _i - \epsilon _j$
, respectively. We choose the positive system of roots given by
$$\begin{align*}\epsilon_i \pm \epsilon_j,\quad 1 \le i < j \le n. \end{align*}$$
Thus, the positive root spaces of
$\mathfrak {so}(V)$
are spanned by
$$\begin{align*}A_{ij},\quad B_{ij},\quad 1 \le i < j \le n. \end{align*}$$
It is straightforward to verify, recalling the definition (3.2) of
$M_{u,v}$
, that
$$\begin{align*}2 M_{\psi_i,\psi_j^\dagger} = A_{ij},\quad 2 M_{\psi_i,\psi_j} = B_{ij},\quad 2 M_{\psi_i^\dagger,\psi_j^\dagger} = C_{ij},\qquad 1 \le i,j \le n. \end{align*}$$
Thus, the positive root vectors are
$$\begin{align*}2 M_{\psi_i,\psi_j^\dagger},\quad 2 M_{\psi_i,\psi_j},\quad 1 \le i < j \le n. \end{align*}$$
The images under the isomorphism
$\gamma ^{-1}$
, given in Equation (3.1), of these elements are
$$ \begin{align} \psi_i \psi_j^\dagger,\quad \psi_i \psi_j,\quad 1 \le i < j \le n. \end{align} $$
We also have that
$$ \begin{align} \gamma^{-1}(A_{ii}) = \gamma^{-1} \left( 2 M_{\psi_i,\psi_i^\dagger} \right) = \tfrac{1}{2} (\psi_i \psi_i^\dagger - \psi_i^\dagger \psi_i) \overset{(2.5)}{=} \psi_i \psi_i^\dagger - \tfrac{1}{2}, \quad 1 \le i \le n. \end{align} $$
For
$n \ge 2$
, the dominant integral weights are those weights of the form
$$ \begin{align} \begin{gathered} \lambda = \sum_{i=1}^n \lambda_i \epsilon_i,\quad \lambda_1 \ge \lambda_2 \ge \dotsb \ge \lambda_{n-1} \ge |\lambda_n|, \\ \text{such that} \quad (\lambda_i \in \tfrac{1}{2} + \mathbb{Z} \text{ for all } 1 \le i \le n) \quad \text{or} \quad (\lambda_i \in \mathbb{Z} \text{ for all } 1 \le i \le n). \end{gathered} \end{align} $$
For
$n=1$
, we adopt the convention that the set of dominant integral weights is
$\frac {1}{2}\mathbb {Z} \epsilon _1$
.
Remark 3.1 (
$N=2$
).
When
$N=2$
,
$$\begin{align*}\mathfrak{so}(V) = \left\{ \begin{pmatrix} a_1 & 0 \\ 0 & -a_1 \end{pmatrix} : a_1 \in \mathbb{C} \right\} \end{align*}$$
is a one-dimensional abelian Lie algebra. For
$z \in \mathbb {C}$
, we call the one-dimensional representation
$z \epsilon _1 \colon \mathfrak {so}(V) \to \mathbb {C} \cong \operatorname {\mathrm {End}}_{\mathbb {C}}(\mathbb {C})$
the simple highest-weight
$\mathfrak {so}(V)$
-module with highest weight
$z \epsilon _1$
since this will often allow us to make uniform statements for
$N \ge 2$
.
3.2 Type B (odd N)
We suppose throughout this subsection that
$N=2n+1$
is odd so that
$\mathfrak {so}(V)$
is the simple Lie algebra of type
$B_n$
. We continue to assume that
$N \ge 2$
, that is,
$n \ge 1$
.
In the ordered basis
$\psi _1,\dotsc ,\psi _n,\frac {1}{\sqrt {2}} e_{2n+1},\psi _n^\dagger ,\dotsc \psi _1^\dagger $
, the matrices of
$\mathfrak {so}(V)$
are those of the form
$$\begin{align*}\begin{pmatrix} A & u & B & \\ -v^{\textrm{ t}} & 0 & -u^{\textrm{ t}} \\ C & v & -A' \end{pmatrix} , \qquad u,v \in \mathbb{C}^n,\ A,B,C \in \operatorname{\mathrm{Mat}}_n(\mathbb{C}),\ B' = -B,\ C' = -C, \end{align*}$$
where the notation
$A'$
is defined in Equation (3.3). The Cartan subalgebra
$\mathfrak {h}$
consists of the diagonal matrices. For
$1 \le i \le n$
, define
$$\begin{align*}\epsilon_i \in \mathfrak{h}^*,\quad \epsilon_i( \operatorname{\mathrm{diag}}(a_1,\dotsc,a_n,0,-a_n,\dotsc,-a_1) ) = a_i. \end{align*}$$
Recall that
$E_{ij}$
,
$1 \le i,j \le n$
, denote the usual matrix units of
$\operatorname {\mathrm {Mat}}_n(\mathbb {C})$
and let
$u_i$
be the element of
$\mathbb {C}^n$
with a
$1$
in the i-th position and
$0$
in all other positions. Then define, for
$1 \le i,j \le n$
,
$$ \begin{align} \begin{gathered} A_{ij} = \begin{pmatrix} E_{ij} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -E_{ij}^{\prime} \end{pmatrix} ,\quad X_i = \begin{pmatrix} 0 & u_i & 0 \\ 0 & 0 & -u_{n-i+1}^{\textrm{ t}}\\ 0 & 0 & 0 \end{pmatrix} ,\quad Y_i = \begin{pmatrix} 0 & 0 & 0 \\ -u_i^{\textrm{ t}} & 0 & 0 \\ 0 & u_{n-i+1} & 0 \end{pmatrix} , \\ B_{ij} = \begin{pmatrix} 0 & 0 & E_{i,n-j+1} - E_{j,n-i+1} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} ,\quad C_{ij} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 &0 \\ E_{n-i+1,j} - E_{n-j+1,i} & 0 & 0 \end{pmatrix}. \end{gathered} \end{align} $$
Then the
$A_{ij}$
,
$B_{ij}$
,
$C_{ij}$
,
$X_i$
and
$Y_i$
are the root vectors, with corresponding roots
$\epsilon _i - \epsilon _j$
,
$\epsilon _i + \epsilon _j$
,
$-\epsilon _i - \epsilon _j$
,
$\epsilon _i$
and
$-\epsilon _i$
, respectively. We choose the positive system of roots given by
$$\begin{align*}\epsilon_i \pm \epsilon_j,\quad \epsilon_k, \qquad 1 \le i < j \le n,\quad 1 \le k \le n. \end{align*}$$
Thus, the positive root spaces of
$\mathfrak {so}(V)$
are spanned by
$$\begin{align*}A_{ij},\qquad B_{ij},\qquad X_k,\qquad 1 \le i < j \le n,\quad 1 \le k \le n. \end{align*}$$
It is straightforward to verify, recalling the definition (3.2) of
$M_{u,v}$
, that we have
$$\begin{align*}2M_{\psi_i,\psi_j^\dagger} = A_{ij},\quad 2M_{\psi_i,\psi_j} = B_{ij},\quad 2M_{\psi_i^\dagger,\psi_j^\dagger} = C_{ij},\quad \sqrt{2} M_{\psi_i,e_{2n+1}} = X_i,\quad \sqrt{2} M_{\psi_i^\dagger,e_{2n+1}} = Y_i. \end{align*}$$
Thus, the positive root vectors are
$$\begin{align*}2M_{\psi_i, \psi_j^\dagger},\qquad 2M_{\psi_i,\psi_j},\qquad \sqrt{2} M_{\psi_k,e_{2n+1}},\qquad 1 \le i < j \le n,\quad 1 \le k \le n. \end{align*}$$
The images under the isomorphism
$\gamma ^{-1}$
, given in Equation (3.1), of these elements are
$$\begin{align*}\psi_i \psi_j^\dagger,\quad \psi_i \psi_j,\quad \tfrac{1}{\sqrt{2}} \psi_k e_{2n+1},\qquad 1 \le i < j \le n,\quad 1 \le k \le n. \end{align*}$$
We also have that
$$ \begin{align} \gamma^{-1}(A_{ii}) = \gamma^{-1} \left( 2 M_{\psi_i,\psi_i^\dagger} \right) = \tfrac{1}{2} (\psi_i \psi_i^\dagger - \psi_i^\dagger \psi_i) \overset{(2.5)}{=} \psi_i \psi_i^\dagger - \tfrac{1}{2}, \quad 1 \le i \le n. \end{align} $$
The dominant integral weights are those weights of the form
$$ \begin{align} \begin{gathered} \lambda = \sum_{i=1}^n \lambda_i \epsilon_i,\quad \lambda_1 \ge \lambda_2 \ge \dotsb \ge \lambda_{n-1} \ge \lambda_n \ge 0, \\ \text{such that} \quad (\lambda_i \in \tfrac{1}{2} + \mathbb{Z} \text{ for all } 1 \le i \le n) \quad \text{or} \quad (\lambda_i \in \mathbb{Z} \text{ for all } 1 \le i \le n). \end{gathered} \end{align} $$
4 Representations of pin and spin groups
In this section, we collect some facts about representations of the pin and spin groups that will be important for us.
4.1 The spin and vector modules
Recall the
$\mathrm {Cl}$
-module S introduced in Section 2.2. By restriction, S is a
$\mathrm {Pin}(V)$
-module and a
$\mathrm {Spin}(V)$
-module. Passing to the Lie algebra, we obtain a
$\mathfrak {so}(V)$
-module structure on S, most conveniently computed via the isomorphism
$\gamma $
obtained in (3.1). With respect to the Cartan subalgebras introduced in Sections 3.1 and 3.2, the vectors
$x_I$
for
$I \subseteq [n]$
are all weight vectors.
First, suppose that N is even. As
$\mathfrak {so}(V)$
-modules and as
$\mathrm {Spin}(V)$
-modules, we have a decomposition
$$ \begin{align} S = S^+ \oplus S^-,\qquad S^+ = \operatorname{\mathrm{span}}_{\mathbb{C}} \{ x_I : |I| \text{ is even} \},\qquad S^- = \operatorname{\mathrm{span}}_{\mathbb{C}} \{ x_I : |I| \text{ is odd} \}. \end{align} $$
When
$N \ge 2$
, we also see that
$S^+$
is a simple highest-weight
$\mathfrak {so}(V)$
-module with highest-weight vector
$x_\varnothing $
of weight
$\frac {1}{2}(\epsilon _1 + \dotsb + \epsilon _n)$
and that
$S^-$
is a simple highest-weight
$\mathfrak {so}(V)$
-module with highest-weight vector
$x_{\{n\}}$
of weight
$\frac {1}{2}(\epsilon _1 + \dotsb + \epsilon _{n-1} - \epsilon _n)$
. As a
$\mathrm {Pin}(V)$
-module, S remains simple; see Proposition 4.4 below.
Now, suppose that N is odd. In this case, there are two choices of a
$\mathrm {Cl}$
-module structure on S depending on the choice of
$\varepsilon \in \{\pm 1\}$
, as in Equation (2.10), but they give rise to isomorphic
$\mathrm {Spin}(V)$
-modules. In this case, there is a unique highest-weight vector
$x_\varnothing $
, so the spin module S is a simple
$\mathfrak {so}(V)$
-module of highest weight
$\frac {1}{2}(\epsilon _1 + \dotsb + \epsilon _n)$
.
We view V as a
$\mathrm {Pin}(V)$
-module with action
$$ \begin{align} g \cdot v := gvg^{-1},\qquad g \in \mathrm{Pin}(V),\ v \in V. \end{align} $$
As a representation of
$\mathfrak {so}(V)$
, V is simple with highest weight
$\epsilon _1$
if
$N\geq 3$
.
Remark 4.1 (Low values of N).
As noted in Remark 2.4, the cases
$N \le 2$
behave differently than the cases
$N \ge 3$
.
-
• When
$N=0$
, we have
$V=S^-=0$
and
$S^+$
is the nontrivial one-dimensional module for
$\mathrm {Pin}(V) \cong C_2$
. Of course, S is the trivial module for the trivial group
$\mathrm {Spin}(V)$
and the zero Lie algebra
$\mathfrak {so}(V)$
. -
• When
$N=1$
, we have that V is the trivial
$\mathrm {Pin}(V)$
-module. We also have that S is the nontrivial one-dimensional module for
$\mathrm {Spin}(V) \cong C_2$
. The
$\mathrm {Pin}(V)$
-module structure on S depends on the choice of
$\varepsilon \in \{\pm 1\}$
, as in (2.10). -
• When
$N=2$
, recall the isomorphism
$\mathbb {G}_m \cong \mathrm {Spin}(V)$
of (2.20). Let
$L_r$
,
$r \in \mathbb {Z}$
, denote the one-dimensional
$\mathbb {G}_m$
-module with action
$t \cdot v = t^r v$
,
$t \in \mathbb {G}_m$
,
$v \in L_r$
. Since we have
$$\begin{align*}\left( t + (t^{-1}-t) \psi_1^\dagger \psi_1 \right) x_\varnothing = t x_\varnothing,\qquad \left( t + (t^{-1}-t) \psi_1^\dagger \psi_1 \right) x_{\{1\}} = t^{-1} x_{\{1\}}, \end{align*}$$
$S^\pm \cong L_{\pm 1}$
. We also have
$V \cong L_{-2} \oplus L_2$
. As
$\mathfrak {so}(V)$
-modules, we have
$L_r = L \left ( \frac {r}{2} \epsilon _1 \right )$
. Both V and S are simple as modules for
$\mathrm {Pin}(V) \cong \mathbb {G}_m \rtimes C_2$
, with the generator of
$C_2$
interchanging the summands
$L_r$
and
$L_{-r}$
.
4.2 Classification of simple modules
When
$N \le 1$
, the groups
$\mathrm {Spin}(V)$
and
$\mathrm {Pin}(V)$
are finite (see Remark 2.4), and their representation theory is straightforward. Therefore, we assume in this subsection that
$N \ge 2$
.
We have an exact sequence of groups
$$ \begin{align} \{1\} \to \mathrm{Spin}(V) \to \mathrm{Pin}(V) \xrightarrow{\pi} \{\pm 1\} \to \{1\}, \end{align} $$
where
$\{\pm 1\}$
is the cyclic group of order
$2$
, written multiplicatively, and
$\pi (g) = (-1)^{\deg g}$
. The finite-dimensional representation theory of
$\mathrm {Pin}(V)$
can be described in terms of the representation theory of
$\mathrm {Spin}(V)$
using Clifford theory. Since
$\mathrm {Pin}(V)$
and
$\mathrm {Spin}(V)$
are reductive, their categories of finite-dimensional representations are both semisimple, and so it suffices to describe their simple modules. We begin with a discussion of the representation theory of
$\mathrm {Spin}(V)$
.
The group
$\mathrm {Spin}(V)$
is connected and reductive. Let H denote its abstract Cartan. This is canonically isomorphic to the abelianisation of every Borel subgroup of
$\mathrm {Spin}(V)$
. Write
$X^\ast (H)=\operatorname {\mathrm {Hom}}(H,\mathbb {G}_m)$
for the weight lattice of
$\mathrm {Spin}(V)$
. Dominance is defined in the usual way from any choice of Borel subgroup. We write
$X^\ast (H)^+$
for the subset of dominant weights.
The choice of Borel subalgebra of
$\mathfrak {so}(V)$
spanned by the
$A_{ij}$
,
$B_{ij}$
, and
$X_k$
, for
$1 \leq i < j \leq n$
and
$1 \leq k \leq n$
(the
$X_k$
only appearing in type B) induces an isomorphism
$X^\ast (H)\otimes _{\mathbb {Z}} \mathbb {C} \cong \mathfrak {h}^\ast $
, which we use to write down elements of
$X^\ast (H)$
as linear combinations of
$\epsilon _1,\epsilon _2,\dotsc ,\epsilon _n$
.
Write
$\mathrm {Irr}(\mathrm {Spin}(V))$
for the set of isomorphism classes of finite-dimensional simple
$\mathrm {Spin}(V)$
-modules. These are classified by highest weight theory. Explicitly, there is an isomorphism
$X^\ast (H)^+ \cong \mathrm {Irr}(\mathrm {Spin}(V))$
,
$\lambda \mapsto L(\lambda )$
, characterised by the following fact: For all Borel subgroups B of
$\mathrm {Spin}(V)$
, there exists nonzero
$v\in L(\lambda )$
such that
$bv=\lambda (b)v$
for all
$b\in B$
.
The group
$\mathrm {Pin}(V)$
acts on
$\mathrm {Spin}(V)$
by conjugation. For
$g \in \mathrm {Pin}(V)$
and W a
$\mathrm {Spin}(V)$
-module, we let
$W^g$
denote the
$\mathrm {Spin}(V)$
-module that is equal to W as a vector space but with the twisted action
$$ \begin{align} h \cdot w = \left( ghg^{-1} \right) w,\qquad h \in \mathrm{Spin}(V),\ w \in W^g, \end{align} $$
where the juxtaposition
$hw$
denotes the action of
$h \in \mathrm {Spin}(V)$
on
$w \in W$
.
The group
$\mathrm {Pin}(V)$
also acts by conjugation on H and hence by precomposition on
$X^\ast (H)^+ \cong \mathrm {Irr}(\mathrm {Spin}(V))$
. We let
$g \lambda $
denote the result of
$g \in \mathrm {Pin}(V)$
acting on
$\lambda \in X^\ast (H)$
. The subgroup
$\mathrm {Spin}(V)$
acts trivially, so this descends to an action of the quotient
$\pi _0(\mathrm {Pin}(V)) \cong \{\pm 1\}$
. For
$\lambda \in X^\ast (H)^+$
and
$g \in \mathrm {Pin}(V)$
, we have
$$\begin{align*}L(\lambda)^g \cong L(g \lambda). \end{align*}$$
In particular, up to isomorphism,
$L(\lambda )^g$
depends only on
$\lambda $
and the class of g in
$\pi _0(\mathrm {Pin}(V))$
.
To pass between representations of
$\mathrm {Spin}(V)$
and
$\mathrm {Pin}(V)$
, we use the biadjoint pair of restriction and induction functors
$$ \begin{align} \operatorname{\mathrm{Res}} \colon \mathrm{Pin}(V)\textrm{-mod} \to \mathrm{Spin}(V)\textrm{-mod} \qquad \text{and} \qquad \operatorname{\mathrm{Ind}} \colon \mathrm{Spin}(V)\textrm{-mod} \to \mathrm{Pin}(V)\textrm{-mod}, \end{align} $$
where
$G\textrm { -mod}$
denotes the category of finite-dimensional modules of an algebraic group G. These satisfy
$$ \begin{align} \operatorname{\mathrm{Res}} \circ \operatorname{\mathrm{Ind}}(W) \cong W \oplus W^P, \end{align} $$
where P is any element of
$\mathrm {Pin}(V) \setminus \mathrm {Spin}(V)$
. In order to make explicit computations, we will fix
$$ \begin{align} P = \begin{cases} e_1 e_2 \dotsm e_N & \text{if } N \text{ is odd}, \\ e_1 e_2 \dotsm e_{N-1} & \text{if } N \text{ is even}. \end{cases} \end{align} $$
Proposition 4.2. Let W be a simple
$\mathrm {Pin}(V)$
-module. Then there exists a unique
$\pi _0(\mathrm {Pin}(V))$
-orbit
$\mathcal {O}$
on
$X^\ast (H)^+$
such that
$$ \begin{align} \operatorname{\mathrm{Res}}(W) \cong \bigoplus_{\lambda\in \mathcal{O}} L(\lambda). \end{align} $$
Furthermore, given an orbit
$\mathcal {O}$
, the number of nonisomorphic simple
$\mathrm {Pin}(V)$
-modules W satisfying Equation (4.8) is equal to the size of the stabiliser of
$\pi _0(\mathrm {Pin}(V))$
acting on an element of
$\mathcal {O}$
.
Proof. By Frobenius reciprocity, every simple
$\mathrm {Pin}(V)$
-module is a simple summand of
$\operatorname {\mathrm {Ind}}(M)$
for some simple
$\mathrm {Spin}(V)$
-module M. Thus, it suffices to prove the result for such simple summands.
Suppose M is a simple
$\mathrm {Spin}(V)$
-module. By Frobenius reciprocity,
$$\begin{align*}\dim \operatorname{\mathrm{Hom}}_{\mathrm{Pin}(V)}(\operatorname{\mathrm{Ind}}(M),\operatorname{\mathrm{Ind}}(M)) = \dim \operatorname{\mathrm{Hom}}_{\mathrm{Spin}(V)}(M,\operatorname{\mathrm{Res}} \circ \operatorname{\mathrm{Ind}}(M)) \end{align*}$$
which, by Equation (4.6), is equal to two if
$M \cong M^P$
, and is equal to one otherwise. In the former case,
$\operatorname {\mathrm {Ind}} M$
is of the form
$W_1 \oplus W_2$
with
$W_1$
,
$W_2$
nonisomorphic simple modules satisfying
$\operatorname {\mathrm {Res}}(W_1) \cong \operatorname {\mathrm {Res}}(W_2) \cong M$
. Thus,
$W_1$
and
$W_2$
satisfy Equation (4.8), with the orbit
$\mathcal {O}$
having one element, namely M. In the latter case,
$W=\operatorname {\mathrm {Ind}}(M)$
is simple and also satisfies Equation (4.8) by Equation (4.6). The final statement of the proposition also follows from this discussion.
Remark 4.3. It follows from Proposition 4.2 that the simple
$\mathrm {Pin}(V)$
-modules are:
-
•
$\operatorname {\mathrm {Ind}}(M)$
for a simple
$\mathrm {Spin}(V)$
-module M with
$M^P \not \cong M$
, -
• the two simple summands of
$\operatorname {\mathrm {Ind}}(M)$
for a simple
$\mathrm {Spin}(V)$
-module M with
$M^P \cong M$
.
In particular, if
$\mathcal {O}$
is an orbit of size two, then the unique simple
$\mathrm {Pin}(V)$
-module W satisfying Equation (4.8) is
$\operatorname {\mathrm {Ind}} (L(\lambda ))$
, where
$\lambda $
is any element of
$\mathcal {O}$
.
We let
$\mathrm {triv}^0$
denote the trivial
$\mathrm {Pin}(V)$
-module and let
$\mathrm {triv}^1$
be the one-dimensional module with action given by
$g v = (-1)^{\deg g} v$
,
$v \in \mathrm {triv}^1$
. If M is a simple
$\mathrm {Spin}(V)$
-module fixed under the
$\mathrm {Pin}(V)$
-action (i.e.,
$M^g \cong M$
as
$\mathrm {Spin}(V)$
-modules for
$g \in \mathrm {Pin}(V)$
), and
$M'$
and
$M^{\prime \prime }$
are its two lifts to a
$\mathrm {Pin}(V)$
-module, then these are related by
$$ \begin{align} M' \otimes \mathrm{triv}^1 \cong M^{\prime\prime}. \end{align} $$
We now study the action of
$\pi _0(\mathrm {Pin}(V))$
on
$\mathrm {Irr}(\mathrm {Spin}(V))\cong X^\ast (H)^+$
. When N is even, define
$$ \begin{align} \tilde{\lambda} := \lambda_1 \epsilon_1 + \dotsb + \lambda_{n-1} \epsilon_{n-1} - \lambda_n \epsilon_n \qquad \text{for } \lambda = \lambda_1 \epsilon_1 + \dotsb + \lambda_{n-1} \epsilon_{n-1} + \lambda_n \epsilon_n. \end{align} $$
Proposition 4.4. If N is odd, then
$\pi _0(\mathrm {Pin}(V))$
acts trivially on
$\mathrm {Irr}(\mathrm {Spin}(V))\cong X^\ast (H)^+$
. If N is even, the action of the nontrivial element
$P \in \pi _0(\mathrm {Pin}(V))$
is
$P \lambda = \tilde {\lambda }$
.
Proof. If N is odd, then P is central and so there is nothing to do. From now on, suppose
$N=2n$
is even. Then
$$ \begin{align} P e_i P^{-1} = (-1)^{\delta_{iN}} e_i ,\qquad 1 \le i \le N. \end{align} $$
It follows that
$$ \begin{align} P \psi_n P^{-1} = \psi_n^\dagger,\quad P \psi_n^\dagger P^{-1} = \psi_n,\quad P \psi_i P^{-1} = \psi_i,\quad P \psi_i^\dagger P^{-1} = \psi_i^\dagger,\quad 1 \le i < n. \end{align} $$
Hence, conjugation by P preserves the set of positive root vectors (3.5) and acts on the elements (3.6) of the Cartan subalgebra of
$\mathfrak {so}(V)$
as
$$ \begin{gather*} P \left( \psi_i \psi_i^\dagger - \tfrac{1}{2} \right) P^{-1} = \psi_i \psi_i^\dagger - \tfrac{1}{2},\qquad 1 \le i < n, \\ P \left( \psi_n \psi_n^\dagger - \tfrac{1}{2} \right) P^{-1} = \psi_n^\dagger \psi_n - \tfrac{1}{2} \overset{(2.5)}{=} - \left( \psi_n \psi_n^\dagger - \tfrac{1}{2} \right).\\[-37pt] \end{gather*} $$
For the remainder of this subsection, we assume that N is even. It follows from Proposition 4.4 that, for any dominant integral weight
$\lambda $
, we have
$$ \begin{align} L(\lambda)^P \cong L(\tilde{\lambda}) \quad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align} $$
In particular, for
$N \ge 2$
,
$$ \begin{align} (S^\pm)^P \cong S^\mp \quad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align} $$
For all even N,
$$ \begin{align} S^P \cong S,\quad V^P \cong V \quad \text{as } \mathrm{Spin}(V)\text{-modules}, \end{align} $$
since
$V = L(-\epsilon _1) \oplus L(\epsilon _1)$
when
$N=2$
(see Remark 4.1), and
$V = L(\epsilon _1)$
for
$N \ge 3$
. Note that, when
$N \ge 4$
,
$$\begin{align*}S \cong \operatorname{\mathrm{Ind}} \left( L \left( \tfrac{1}{2} \epsilon_1 + \tfrac{1}{2} \epsilon_2 + \dotsb + \tfrac{1}{2} \epsilon_{n-1} \pm \tfrac{1}{2} \epsilon_n \right) \right). \end{align*}$$
Lemma 4.5. Suppose N is even. Let
$M_1$
and
$M_2$
be two simple
$\mathrm {Pin}(V)$
-modules whose restrictions to
$\mathrm {Spin}(V)$
are isomorphic. Then, for all
$r\geq 1$
, the multiplicities of
$M_1$
and
$M_2$
in
$S^{\otimes r}$
are equal.
Proof. Since
$S \cong \operatorname {\mathrm {Ind}}(S^\pm )$
is self-dual, we have, for
$i \in \{1,2\}$
,
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathrm{Pin}(V)}(S^{\otimes r},M_i) &\cong \operatorname{\mathrm{Hom}}_{\mathrm{Pin}(V)}(S, S^{\otimes (r-1)}\otimes M_i) \\&\cong \operatorname{\mathrm{Hom}}_{\mathrm{Pin}(V)} \left( \operatorname{\mathrm{Ind}}(S^+), S^{\otimes (r-1)} \otimes M_i \right) \cong \operatorname{\mathrm{Hom}}_{\mathrm{Spin}(V)} (S^+, S^{\otimes(r-1)} \otimes M_i), \end{align*} $$
where we used Frobenius reciprocity in the final isomorphism. Since
$M_1$
and
$M_2$
are isomorphic upon restriction to
$\mathrm {Spin}(V)$
, the result follows.
4.3 Invariant bilinear form
For a subset I of
$[n]$
, we let
$I^\complement = [n]\setminus I$
denote its complement. Define a bilinear form on S by
$$ \begin{align} \Phi_S(x_I, x_J) = \begin{cases} (-1)^{\binom{|I|}{2} + nN|I| + |\{(i,j)\in I\times I^\complement : i>j\}|} & \text{if } J = I^\complement, \\ 0 & \text{otherwise}, \end{cases} \end{align} $$
and extending by bilinearity.
Lemma 4.6. We have
$$ \begin{align} \Phi_S(v x, y) = (-1)^{nN} \Phi_S(x, v y), \qquad x,y \in S,\quad v \in V \subseteq \mathrm{Cl}. \end{align} $$
Proof. Since both sides of Equation (4.17) are linear in v, x and y, it suffices to prove that
$$ \begin{align} \Phi_S(\psi_k^\dagger x_I, x_J) = (-1)^{nN} \Phi_S(x_I, \psi_k^\dagger x_J) \quad \text{and} \quad \Phi_S(\psi_k x_I, x_J) = (-1)^{nN} \Phi_S(x_I, \psi_k x_J), \end{align} $$
for all
$1 \le k \le n$
and
$I,J \subseteq [n]$
, and, if N is odd, that
$$ \begin{align} \Phi_S(e_{2n+1} x_I, x_J) = (-1)^n \Phi_S(x_I, e_{2n+1} x_J), \end{align} $$
for all
$I,J \subseteq [n]$
.
For
$I,J \subseteq [n]$
, define
$$ \begin{align} \sigma_{I,J} := (-1)^{|\{ (i,j) \in I \times J : i> j \}|}. \end{align} $$
Then, for
$I,J,I_1,J_1,I_2,J_2 \subseteq [n]$
, with
$I \cap J = I_1 \cap I_2 = J_1 \cap J_2 = \varnothing $
, we have
$$ \begin{align} \sigma_{I,J} = (-1)^{|I||J|} \sigma_{J,I},\qquad \sigma_{I_1 \sqcup I_2, J} = \sigma_{I_1,J} \sigma_{I_2,J},\qquad \sigma_{I,J_1 \sqcup J_2} = \sigma_{I,J_1} \sigma_{I,J_2}. \end{align} $$
First, note that both sides of the first equation in (4.18) are zero unless
$I \cap J = \varnothing $
and
$I \cup J = \{1,\dotsc ,k-1,k+1,\dotsc ,n\}$
. Thus, we assume that I and J satisfy these two conditions. Then
$$\begin{align*}\Phi_S(\psi_k^\dagger x_I, x_J) \overset{(2.9)}{=} \sigma_{\{k\},I} \Phi_S(x_{I \cup \{k\}}, x_J) \overset{(4.16)}{\underset{(4.21)}{=}} (-1)^{\binom{|I|+1}{2} + nN(|I|+1)} \sigma_{\{k\},I} \sigma_{I,J} \sigma_{\{k\},J} \end{align*}$$
and
$$\begin{align*}\Phi_S(x_I, \psi_k^\dagger x_J) \overset{(2.9)}{=} \sigma_{\{k\},J} \Phi_S(x_I, x_{J \cup \{k\}}) \overset{(4.16)}{\underset{(4.21)}{=}} (-1)^{\binom{|I|}{2} + nN|I|} \sigma_{\{k\},J} \sigma_{I,J} \sigma_{I,\{k\}}. \end{align*}$$
Since
$$ \begin{align} \sigma_{I,\{k\}} \sigma_{\{k\},I} = (-1)^{|I|} \qquad \text{and} \qquad \binom{|I|}{2} + |I| = \binom{|I|+1}{2}, \end{align} $$
the first equality in (4.18) follows.
Next, note that both sides of the second equality in Equation (4.18) are zero unless
$I \cap J = \{k\}$
and
$I \cup J = [n]$
. Thus, we assume that I and J satisfy these two conditions. Then
$$ \begin{align*} \Phi_S(\psi_k x_I, x_J) &\overset{(2.9)}{=} \sigma_{\{k\},I} \Phi_S(x_{I \setminus \{k\}}, x_J) \\& \overset{(4.16)}{=} (-1)^{\binom{|I|-1}{2} + nN(|I|-1)} \sigma_{\{k\},I} \sigma_{I \setminus \{k\}, J} \overset{(4.21)}{=} (-1)^{\binom{|I|-1}{2} + nN(|I|-1)} \sigma_{\{k\},I} \sigma_{I,J} \sigma_{\{k\}, J} \end{align*} $$
and
$$ \begin{align*} \Phi_S(x_I, \psi_k x_J) \overset{(2.9)}{=} &\sigma_{\{k\}, J} \Phi_S(x_I, x_{J \setminus \{k\}}) \\ & \overset{(4.16)}{=} (-1)^{\binom{|I|}{2} + nN|I|} \sigma_{\{k\}, J} \sigma_{I,J \setminus \{k\}} \overset{(4.21)}{=} (-1)^{\binom{|I|}{2} + nN|I|} \sigma_{\{k\}, J} \sigma_{I,J} \sigma_{I,\{k\}}. \end{align*} $$
Using the second equality in Equation (4.22) with
$|I|$
replaced by
$|I|-1$
then implies the second equality in Equation (4.18).
Now, suppose that N is odd. To prove Equation (4.19), we assume that
$I \cap J = \varnothing $
and
$I \cup J = [n]$
, since otherwise both sides are zero. Then we have
$$\begin{align*}\Phi_S(e_{2n+1} x_I, x_J) \overset{(2.10)}{=} \pm (-1)^{|I|} \Phi_S(x_I, x_J) = \pm (-1)^{n + |J|} \Phi_S(x_I, x_J) \overset{(2.10)}{=} (-1)^n \Phi_S(x_I, e_{2n+1} x_J), \end{align*}$$
as desired.
As in the introduction, define
$$ \begin{align} {\mathrm{G}}(V) := \begin{cases} \mathrm{Pin}(V) & \text{if } N \text{ is even}, \\ \mathrm{Spin}(V) & \text{if } N \text{ is odd}. \end{cases} \end{align} $$
Corollary 4.7. We have
$$ \begin{align} \Phi_S(gx,gy) = \Phi_S(x,y)\qquad \text{for all } g \in {\mathrm{G}}(V),\ x,y \in S, \end{align} $$
$$ \begin{align} \Phi_S(Xx,y) = - \Phi_S(x,Xy) \qquad \text{for all } X \in \mathfrak{so}(V),\ x,y \in S. \end{align} $$
Proof. When
$N<2$
, the identity (4.24) is trivial, since
${\mathrm {G}}(V)=\{\pm 1\}$
, acting by the scalar
$\{\pm 1\}$
on S. Now, suppose
$N \geq 2$
. Let
$v_1,\dotsc ,v_k \in V$
satisfy
$\Phi _V(v_i,v_i) = 1$
for all
$1 \le i \le k$
. Then, for
$x,y \in S$
, it follows from (4.17) that
$$ \begin{align*} \Phi_S(v_1 v_2 \dotsm v_k x, v_1 v_2 \dotsm v_k y) &= \begin{cases} \Phi_S(x, v_k \dotsm v_1 v_1 \dotsm v_k y) & \text{if } N=2n, \\ (-1)^{kn} \Phi_S(x, v_k \dotsm v_1 v_1 \dotsm v_k y) & \text{if } N=2n+1, \end{cases} \\ &= \begin{cases} \Phi_S(x,y) & \text{if } N=2n, \\ (-1)^{kn} \Phi_S(x,y) & \text{if } N=2n+1. \end{cases} \end{align*} $$
Thus, Equation (4.24) follows from Equations (2.17) and (2.18). The identity (4.25) follows from Equation (4.24) by differentiating.
Proposition 4.8. We have
$$ \begin{align} \Phi_S(x,y) = (-1)^{\binom{n}{2} + nN} \Phi_S(y,x) \qquad \text{for all } x,y \in S. \end{align} $$
Proof. Since
$\Phi _S(x_I,x_J) = 0 = \Phi _S(x_J,x_I)$
unless
$I \cup J = [n]$
and
$I \cap J = \varnothing $
, we assume that I and J satisfy these two conditions. Then, defining
$\sigma _{I,J}$
as in Equation (4.20), we have
$$ \begin{align*} \Phi_S(x_J, x_I) \overset{(4.16)}{=} (-1)^{\binom{|J|}{2} + nN|J|} \sigma_{J,I} \overset{(4.21)}{=} &(-1)^{\binom{|J|}{2} + nN|J| + |I||J|} \sigma_{I,J} \\ &\overset{(4.16)}{=} (-1)^{\binom{|J|}{2}+\binom{|I|}{2}+nN(|I|+|J|)+|I||J|} \Phi_S(x_I,x_J). \end{align*} $$
Then the result follows from the fact that
$nN(|I|+|J|) = n^2 N \equiv nN$
modulo
$2$
and that
$\binom {|I|}{2} + \binom {|J|}{2} + |I||J| = \binom {n}{2}$
.
Remark 4.9. Corollary 4.7 implies that S is self-dual. Since S is also simple, as noted above,
$\Phi _S$
is the unique invariant bilinear form on S, up to scalar multiple. On the other hand, if
$N \equiv 3 \pmod {4}$
, then S is not self-dual as a
$\mathrm {Pin}(V)$
-module, and so there is no
$\mathrm {Pin}(V)$
-invariant bilinear form on S. This is our main motivation for defining
${\mathrm {G}}(V)$
to be
$\mathrm {Spin}(V)$
when N is odd; see also Remark 2.5.
4.4 Tensor product decompositions
We now recall some tensor product decompositions that will be important for us. For a weight
$\mathrm {Spin}(V)$
-module M, we let
$\operatorname {\mathrm {wt}}(M)$
denote its set of weights. Thus, for example, when
$N \ge 2$
,
$$\begin{align*}\operatorname{\mathrm{wt}}(S) = \left\{ \left( \pm \tfrac{1}{2}, \dotsc, \pm \tfrac{1}{2} \right) \right\}. \end{align*}$$
For the next result, recall, from Section 3.1, that the set of dominant integral weights is
$\frac {1}{2}\mathbb {Z}\epsilon _1$
when
$N=2$
.
Lemma 4.10. Suppose
$N \ge 2$
, and let
$\lambda $
be a dominant integral weight. Then
$$\begin{align*}S \otimes L(\lambda) \cong \bigoplus_{\epsilon \in \operatorname{\mathrm{wt}}(S)} L(\lambda+\epsilon) \quad \text{as } \mathrm{Spin}(V)\text{-modules}, \end{align*}$$
where we define
$L(\lambda +\epsilon )$
to be zero if
$\lambda +\epsilon $
is not dominant.
Proof. For
$N=2$
, this is a straightforward direct computation using the description of S in Remark 4.1. For
$N \ge 3$
, it is a standard application of the Weyl character formula.
Corollary 4.11.
-
(a) If
$N=2$
, then (4.27)
$$ \begin{align} S \otimes V \cong S \oplus \operatorname{\mathrm{Ind}} \left( L \left( \tfrac{3}{2} \epsilon_1 \right) \right) \quad \text{as } \mathrm{Pin}(V)\text{-modules}. \end{align} $$
-
(b) If
$N=2n+1 \ge 3$
(type
$B_n$
), then (4.28)
$$ \begin{align} S \otimes V \cong S \otimes L(\epsilon_1) \cong S \oplus L \left( \tfrac{3}{2} \epsilon_1 + \tfrac{1}{2} \epsilon_2 + \dotsb + \tfrac{1}{2} \epsilon_n \right) \quad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align} $$
-
(c) If
$N=2n \ge 4$
(type
$D_n$
), then (4.29)
$$ \begin{align} S \otimes V \cong S \otimes L(\epsilon_1) \cong S \oplus \operatorname{\mathrm{Ind}} \left( L \left( \tfrac{3}{2} \epsilon_1 + \tfrac{1}{2} \epsilon_2 + \dotsb + \tfrac{1}{2} \epsilon_n \right) \right) \quad \text{as } \mathrm{Pin}(V)\text{-modules}. \end{align} $$
Proof. Part (a) is a direct computation using Remark 4.1. Parts (b) and (c) follow from Lemma 4.10 and 3.7 and 3.10, where the appearance of
$\operatorname {\mathrm {Ind}}$
in part (c) follows from Remark 4.3.
Proposition 4.12.
-
(a) If
$N=2n+1$
(type
$B_n$
), we have (4.30)and
$$ \begin{align} \Lambda^k(V) \cong \Lambda^{N-k}(V) \quad \text{as } \mathrm{Pin}(V)\text{-modules}, \quad 0 \le k \le n, \end{align} $$
$\Lambda ^k(V)$
is simple for
$0 \le k \le N$
. Furthermore, if
$n \ge 1$
, we have (4.31)
$$ \begin{align} \Lambda^k(V) \cong \Lambda^{N-k}(V) \cong L(\epsilon_1 + \dotsb + \epsilon_k) \quad \text{as } \mathrm{Spin}(V)\text{-modules}, \quad 0 \le k \le n. \end{align} $$
-
(b) If
$N=2n$
(type
$D_n$
), we have (4.32)and
$$ \begin{align} \Lambda^k(V) \not\cong \Lambda^{N-k}(V) \quad \text{as } \mathrm{Pin}(V)\text{-modules},\quad 0 \le k < n, \end{align} $$
$\Lambda ^k(V)$
is simple for
$0 \le k \le N$
. Furthermore, if
$n \ge 2$
, we have (4.33)
$$ \begin{align} \Lambda^k(V) \cong \Lambda^{N-k}(V) \cong L(\epsilon_1 + \dotsb + \epsilon_k),\qquad 0 \le k \le n, \end{align} $$
(4.34)as
$$ \begin{align} \Lambda^n(V) \cong L(\epsilon_1 + \dotsb + \epsilon_{n-1} + \epsilon_n) \oplus L(\epsilon_1 + \dotsb + \epsilon_{n-1} - \epsilon_n) \end{align} $$
$\mathrm {Spin}(V)$
-modules.
Proof. For
$N \le 2$
, the results follow from straightforward computations using the explicit descriptions of V and S given in Remark 4.1.
Now, suppose that
$N \ge 3$
. A proof that
$\Lambda ^k(V) \cong L(\epsilon _1 + \dotsb + \epsilon _k)$
as
$\mathfrak {so}(V)$
-modules, and hence as
$\mathrm {Spin}(V)$
-modules, for the given ranges on k can be found, for instance, in [Reference CarterCar05, Th. 13.9, Th. 13.11]. (The ranges on k are slightly more restrictive there, since those results relate exterior powers to fundamental modules, but the proofs give the isomorphisms for our ranges on k.) To prove Equation (4.34), one notes that
$\epsilon _1 + \dotsb + \epsilon _{n-1} \pm \epsilon _n$
are both weights that appear in
$\Lambda ^n(V)$
. Furthermore, they are highest weights since adding any simple root produces a weight that does not appear in
$\Lambda ^n(V)$
. Hence,
$\Lambda ^n(V)$
contains a submodule isomorphic to the right-hand side of Equation (4.34). A straightforward application of the Weyl dimension formula then shows that this submodule is all of
$\Lambda ^n(V)$
.
Next, note that we have a pairing of
$\Lambda ^k(V)$
with
$\Lambda ^{N-k}(V)$
given by the composition
$$\begin{align*}\Lambda^k(V) \otimes \Lambda^{N-k}(V) \xrightarrow{\wedge} \Lambda^{N}(V) \xrightarrow{\cong} \mathbb{C}. \end{align*}$$
This is a
$\mathrm {Spin}(V)$
-module homomorphism and so identifies
$\Lambda ^{N-k}(V)$
with the dual of
$\Lambda ^k(V)$
. Since
$\Lambda ^k(V)$
is self-dual, this yields an isomorphism of
$\Lambda ^{N-k}(V)$
with
$\Lambda ^k(V)$
as
$\mathrm {Spin}(V)$
-modules.
In type
$B_n$
, the element P, defined in Equation (4.7), acts trivially on V, and so the actions of P on
$\Lambda ^k(V)$
and
$\Lambda ^{N-k}(V)$
are also trivial. This completes the proof of Equation (4.30).
In type
$D_n$
, the highest-weight spaces of
$\Lambda ^k(V)$
and
$\Lambda ^{N-k}(V)$
,
$1 \le k < n$
, are spanned, respectively, by
$$\begin{align*}v_k := \psi_1 \wedge \psi_2 \wedge \dotsb \wedge \psi_k \quad \text{and} \quad w_k := \psi_1 \wedge \psi_2 \wedge \dotsb \wedge \psi_n \wedge \psi_n^\dagger \wedge \dotsb \wedge \psi_{k+1}^\dagger. \end{align*}$$
By Equation (4.12), the action of P on these highest-weight vectors is given by
$$\begin{align*}P \cdot v_k = v_k,\qquad P \cdot w_k = - w_k. \end{align*}$$
Thus,
$\Lambda ^k(V) \not \cong \Lambda ^{N-k}(V)$
as
$\mathrm {Pin}(V)$
-modules.
Corollary 4.13.
-
(a) When
$N=2n+1$
(type
$B_n$
), we have (4.35)
$$ \begin{align} S^{\otimes 2} \cong \bigoplus_{k=0}^n \Lambda^k(V) \qquad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align} $$
-
(b) When
$N=2n$
(type
$D_n$
), we have (4.36)
$$ \begin{align} S^{\otimes 2} \cong \bigoplus_{k=0}^{2n} \Lambda^k(V) \qquad \text{as } \mathrm{Pin}(V)\text{-modules}. \end{align} $$
Proof.
-
(a) When
$N=1$
, it follows immediately from the descriptions of S and V given in Remark 4.1 that
$S^{\otimes 2} \cong \mathrm {triv}^0 \cong \Lambda ^0(V)$
. For
$N \ge 3$
, it follows from Lemma 4.10 that
$$\begin{align*}S^{\otimes 2} \cong \bigoplus_{k=0}^n L(\epsilon_1 + \dotsb + \epsilon_k) \cong \bigoplus_{k=0}^n \Lambda^k(V) \qquad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align*}$$
-
(b) When
$N=0$
, it follows immediately from the descriptions of S and V given in Remark 4.1 that
$S^{\otimes 2} \cong \mathrm {triv}^0 \cong \Lambda ^0(V)$
. Now, suppose
$N=2$
. Then, in the notation of Remark 4.1, we have as modules for
$$\begin{align*}S^{\otimes 2} \cong L_{-2} \oplus L_2 \oplus L_0^{\oplus 2} \end{align*}$$
$\mathrm {Spin}(V) \cong \mathbb {G}_m$
. As
$\mathrm {Pin}(V)$
-modules, the summand
$L_{-2} \oplus L_2$
is isomorphic to
$\Lambda ^1(V) \cong V$
. It remains to show that the summand
$L_0^{\oplus 2}$
contains the trivial
$\mathrm {Pin}(V)$
-module
$\Lambda ^0(V)$
and the nontrivial
$\mathrm {Pin}(V)$
-module
$\Lambda ^2(V)$
. As modules for the subgroup
$C_2 \subseteq \mathbb {G}_m \rtimes C_2 \cong \mathrm {Pin}(V)$
, S decomposes as a sum of the trivial module and the nontrivial
$C_2$
-module. Hence,
$S^{\otimes 2}$
contains two copies of the trivial
$C_2$
-module and two copies of the nontrivial
$C_2$
-module. Since the summand
$L_{-2} \oplus L_2$
contains one of each, we are done.
For
$N \ge 4$
, it follows from Lemma 4.10 and Proposition 4.12(b) that as
$$ \begin{align*} S^{\otimes 2} &\cong (S^+ \otimes S) \oplus (S^- \otimes S) \\ &\cong \left( \bigoplus_{k=0}^n L(\epsilon_1 + \dotsb + \epsilon_k) \right) \oplus \left( L(\epsilon_1 + \dotsb + \epsilon_{n-1} - \epsilon_n) \oplus \bigoplus_{k=0}^{n-1} L(\epsilon_1 + \dotsb + \epsilon_k) \right) \\ &\cong \bigoplus_{k=0}^{2n} \Lambda^k(V), \end{align*} $$
$\mathrm {Spin}(V)$
-modules. The result then follows from Lemma 4.5 and Proposition 4.12(b).
5 The spin Brauer category
In this section, we introduce our main category of interest. We work over an arbitrary commutative ring
$\Bbbk $
in which
$2$
is invertible. (Note, however, that Definition 5.1 below does not require that
$2$
is invertible.)
Definition 5.1. For
$d,D \in \Bbbk $
and
$\kappa \in \{\pm 1\}$
, the spin Brauer category
$\mathscr {SB}(d,D;\kappa )$
is the strict
$\Bbbk $
-linear monoidal category presented as follows. The generating objects are
$\mathsf {S}$
and
$\mathsf {V}$
, whose identity morphisms we depict by a black strand and a dotted blue strand:
The generating morphisms are
To state the defining relations, we will use the convention that a relation involving
$r \ge 1$
dashed red strands (as in Equation (5.1)) means we impose the
$2^r$
relations obtained from replacing each such strand with either a black strand or a dotted blue strand. The defining relations on morphisms are then as follows:
This concludes the definition of
$\mathscr {SB}(d,D;\kappa )$
.
The third and fourth relations in Equation (5.1) imply that
$\mathscr {SB}(d,D;\kappa )$
is a rigid monoidal category, with the objects
$\mathsf {S}$
and
$\mathsf {V}$
being self-dual. The first, second and sixth relations in Equation (5.1), together with Equation (5.2) imply that
$\mathscr {SB}(d,D;\kappa )$
is symmetric monoidal, with symmetry given by the crossings. Then Equation (5.3) implies that
$\mathscr {SB}(d,D;\kappa )$
is strict pivotal, with duality given by rotating diagrams through
$180\deg $
. This means that diagrams are isotopy invariant, and so rotated versions of all the defining relations hold. For example, we have
Throughout this document, we will refer to a relation by its equation number even when we are, in fact, using a rotated version of that relation.
We introduce other trivalent morphisms by successive clockwise rotation:
Since
$\mathscr {SB}(d,D;\kappa )$
is strict pivotal, the trivalent morphisms are also related in the natural way by counterclockwise rotation:
Lemma 5.2. We have
Proof. The first relation in Equation (5.9) is simply a rewriting of Equation (5.4), using Equation (5.8). Then, composing on the bottom of the first relation in Equation (5.9) with 
and using the first relation in Equation (5.1) gives the second relation in Equation (5.9). For the third relation in Equation (5.9), we compute
Remark 5.3. The need for the choice of
$\kappa \in \{\pm 1 \}$
in the definition of the spin Brauer category arises from that fact that, under the incarnation functor to be defined in Section 6, the objects
$\mathsf {S}$
and
$\mathsf {V}$
will be sent to the spin and vector representations, respectively, of
$\mathrm {Pin}(N)$
or
$\mathrm {Spin}(N)$
. For some values of N, the trivial representation and the vector representation either both live in the symmetric square or both live in the exterior square of the spin representation. In this case, we can take
$\kappa =1$
. However, for other values of N, one of the trivial or vector representations lives in the symmetric square while the other lives in the exterior square. In this case, we need to take
$\kappa =-1$
. See Equation (6.1) and Theorem 6.1 for details.
It will also sometimes be convenient to draw horizontal strands. Since
$\mathscr {SB}(d,D;\kappa )$
is strict pivotal, the meaning of diagrams containing such strands is unambiguous. For example,
Lemma 5.4. We have
Proof. We compute
Since we have assumed that
$2$
is invertible in the ground ring
$\Bbbk $
, the result follows.
Let
$\mathcal {C}^{\mathrm {op}}$
denote the opposite of a category
$\mathcal {C}$
, and let
$\mathcal {C}^{\mathrm {rev}}$
denote the reverse of a monoidal category
$\mathcal {C}$
, where we reverse the order of the tensor product. We have an isomorphism of monoidal categories
$$ \begin{align} \mathscr{SB}(d,D;\kappa) \to \mathscr{SB}(d,D;\kappa)^{\mathrm{op}} \end{align} $$
that is the identity on objects and reflects morphisms in the horizontal axis. We also have an isomorphism of monoidal categories
$$ \begin{align} \mathscr{SB}(d,D;\kappa) \to \mathscr{SB}(d,D;\kappa)^{\mathrm{rev}} \end{align} $$
that is the identity on objects and reflects morphisms in the vertical axis.
Lemma 5.5. We have
Proof. By (5.5), we have
Then Equation (5.14) follows after composing on top with 
and using Equations (5.2), (5.1) and (5.9).
It will be convenient to introduce a shorthand for multiple strands:
The first two relations in Equations (5.1) imply that we can interpret any element of the symmetric group
$\mathfrak {S}_r$
on r strands as a morphism in
$\operatorname {\mathrm {End}}_{\mathscr {SB}(d,D;\kappa )}(\mathsf {V}^{\otimes r})$
. For a permutation
$g \in \mathfrak {S}_r$
, let
$\operatorname {sgn}(g)$
denote its sign. Then define the antisymmetrizer
where we label the strands by r when we wish to emphasize how many there are. Thus, for example,
It follows from Equation (5.15) that the antisymmetrizer (5.16) is 
when
$r=0$
. It also follows directly from the definition that
Proposition 5.6. Suppose that r is a positive integer such that either
-
• r is even and invertible, or
-
• r is odd and
$r-d$
is invertible.
Then
Proof. We have
Thus,
If r is even, then the coefficient on the left-hand side above is
$2r$
and so Equation (5.18) follows when r is invertible. If r is odd, then the coefficient is
$2(r-d)$
and Equation (5.18) follows as long as
$r - d$
is invertible.
Remark 5.7. Note that the case
$r=d \in 2 \mathbb {N} +1$
is not covered by Proposition 5.6. In fact, the diagram in Equation (5.18) is not zero in this case; see Remark 8.5.
Definition 5.8. For
$d \in 2\mathbb {N} + 1$
, let
$\overline {\mathscr {SB}}(d,D;\kappa )$
denote the quotient of
$\mathscr {SB}(d,D;\kappa )$
by the relation
For
$d \notin 2\mathbb {N}+1$
, let
$\overline {\mathscr {SB}}(d,D;\kappa ) = \mathscr {SB}(d,D;\kappa )$
.
The next result gives sufficient conditions under which all closed diagrams in
$\overline {\mathscr {SB}}(d,D;\kappa )$
can be reduced to a multiple of the empty diagram 
.
Proposition 5.9. Suppose that
$\Bbbk $
is a
$\mathbb {Q}$
-algebra and
$r-d$
is invertible for all
$r \in (2\mathbb {N} + 1) \setminus \{d\}$
. (For instance, this is satisfied when
$\Bbbk $
is a field of characteristic zero.) Then 
.
Proof. We give an algorithm to simplify any diagram in 
to a scalar multiple of the identity. Throughout, we freely use our observations about isotopy invariance of diagrams in 
, as discussed immediately after the definition of
$\mathscr {SB}(d,D;\kappa )$
. We proceed by induction on the number of trivalent vertices in the diagram.
Suppose we have a closed diagram with at least one trivalent vertex. Consider the black curve that is part of that trivalent vertex. Since every trivalent vertex has exactly two black strings incident to it, this curve is part of a loop. Our first goal is to remove all self-intersections of this loop, and make the interior of this loop empty. We can separate all other black strands from this loop and remove self-intersections of this loop using Equations (5.1) and (5.2). We separate all other dotted blue strands that do not have any trivalent vertices on this loop in the same manner. We can then use the same techniques, in addition to Equation (5.4), to ensure the interior of this loop is empty. Let r be the number of trivalent vertices on this loop.
Unless
$r=d$
and d is an odd number, we have
where A is a linear combination of diagrams with fewer than r dotted blue strands attached to the black circle. Since
$\Bbbk $
is a
$\mathbb {Q}$
-algebra,
$r!$
is invertible in
$\Bbbk $
. We can then use this relation to write our diagram as a linear combination of diagrams with fewer trivalent vertices, as is our inductive goal.
Suppose instead that
$r=d$
is an odd positive integer. Since the total number of trivalent vertices is even, there must be another black loop with a trivalent vertex. We can repeat the process discussed above with that loop, and can either rewrite in terms of diagrams with fewer trivalent vertices, or that other loop also has r trivalent vertices, in which case we end up with a subdiagram of the form
Then we have
where again A is a linear combination of diagrams with fewer trivalent vertices, and we proceed as before.
This completes the inductive step and reduces us to considering the case where there are zero trivalent vertices. In this case, the relations (5.1) (which are the same as in the Brauer category) suffice to rewrite our diagrams as a disjoint union of circles, which are evaluated as scalars by (5.6).
Remark 5.10.
-
(a) Note that Proposition 5.9 does not imply that
is a free
$\Bbbk $
-module of rank one. Rather, it states that it is spanned by . A priori, this endomorphism algebra could be a quotient of
$\Bbbk $
. However, see Corollary 6.2 for conditions that insure it is free of rank one. -
(b) When d is an odd positive integer, the authors believe that Proposition 5.9 is false when
$\overline {\mathscr {SB}}(d,D;\kappa )$
is replaced by
$\mathscr {SB}(d,D;\kappa )$
because of the condition on r in Proposition 5.6 (see Remark 5.7). For instance, if
$d=3$
, the authors do not now how to reduce the diagrams to a scalar multiple of the empty diagram without the additional relation (5.19).
is a free 
. A priori, this endomorphism algebra could be a quotient of 
without the additional relation (Lemma 5.11. We have
Proof. We have
Remark 5.12. The image of the relation (5.20) under the incarnation functor to be defined in Theorem 6.1 corresponds to [Reference WenzlWen20, Lem. 1.3], which plays a key role in the arguments of that paper. Note that our
$\beta $
, defined in Equation (6.15), is equal to
$2C$
, where C is defined in [Reference WenzlWen20, §1.4].
We conclude this section with two lemmas that will be needed in the sequel.
Lemma 5.13. We have
where we interpret the right-hand side as 
when
$r=0$
.
Proof. We prove the result by induction on r. The base case
$r=0$
is immediate. (The case
$r=1$
is the first relation in Equation (5.6).) For the inductive step, note that, by the standard decomposition of
$S_{r+1}$
as a union of right
$S_r$
-cosets, we have
Thus,
by the inductive hypothesis.
Lemma 5.14. We have
where we interpret the right-hand side as 
when
$r=0$
.
Proof. We prove the result by induction on r. The base case
$r=0$
is precisely the second relation in Equation (5.6). Now suppose the result holds for some
$r \ge 0$
. Using Equation (5.22), we have
Now,
Starting from Equation (5.24), repeated use of Equation (5.25) gives
Since
it follows that
by the inductive hypothesis.
6 The incarnation functor
In this section, we relate the spin Brauer category to the representation theory of the spin and pin groups. Throughout this section, we assume
$\Bbbk = \mathbb {C}$
.
Fix an vector space V of finite dimension N, equipped with a nondegenerate symmetric bilinear form
$\Phi _V$
, and let
$n = \left \lfloor \frac {N}{2} \right \rfloor $
. Recall the definition of
${\mathrm {G}}(V)$
from Equation (4.23), the spin
${\mathrm {G}}(V)$
-module S and the vector
${\mathrm {G}}(V)$
-module V from Section 4.1, and the bilinear form
$\Phi _S$
on S defined in Equation (4.16). Let
$$ \begin{align} \sigma_N := (-1)^{\binom{n}{2} + nN}, \qquad \kappa_N := (-1)^{nN}, \end{align} $$
$$ \begin{align} \mathscr{SB}(V) := \mathscr{SB}(N,\sigma_N 2^n; \kappa_N), \qquad \overline{\mathscr{SB}}(V) = \overline{\mathscr{SB}}(N,\sigma_N 2^n; \kappa_N). \end{align} $$
(Recall that
$\sigma _N$
is the sign appearing in Equation (4.26), describing the symmetry of the form
$\Phi _S$
.)
Fix a basis
$\mathbf {B}_S$
of S, and let
$\mathbf {B}_S^\vee = \{x^\vee : x \in \mathbf {B}_S\}$
denote the left dual basis with respect to
$\Phi _S$
, defined by
$$\begin{align*}\Phi_S(x^\vee, y) = \delta_{x,y},\qquad x,y \in \mathbf{B}_S. \end{align*}$$
We fix a basis
$\mathbf {B}_V$
of V and define the left dual basis
$\mathbf {B}_V^\vee = \{v^\vee : v \in V\}$
similarly. Then we have
${\mathrm {G}}(V)$
-module homomorphisms
$$ \begin{align} \Phi_S^\vee &\colon \Bbbk \to S \otimes S,& \lambda &\mapsto \lambda \sum_{x \in \mathbf{B}_S} x \otimes x^\vee,\quad \lambda \in \Bbbk, \end{align} $$
$$ \begin{align} \Phi_V^\vee &\colon \Bbbk \to V \otimes V,& \lambda &\mapsto \lambda \sum_{v \in \mathbf{B}_V} v \otimes v^\vee,\quad \lambda \in \Bbbk. \end{align} $$
These are independent of the choices of bases.
It follows from Proposition 4.8 and the fact that the form
$\Phi _V$
is symmetric that the left dual bases of
$\mathbf {B}_V^\vee $
and
$\mathbf {B}_S^\vee $
are given by
$$ \begin{align} (v^\vee)^\vee = v,\quad v \in \mathbf{B}_V, \qquad \text{and} \qquad (x^\vee)^\vee = \sigma_N x,\quad x \in \mathbf{B}_S, \end{align} $$
respectively.
For any
$\Bbbk $
-modules U and W, we define the linear map
$$ \begin{align} \operatorname{\mathrm{flip}} = \operatorname{\mathrm{flip}}_{U,W} \colon U \otimes W \to W \otimes U,\qquad u \otimes w \mapsto w \otimes u, \end{align} $$
extended by linearity. If U and W are
${\mathrm {G}}(V)$
-modules, then
$\operatorname {\mathrm {flip}}$
is a homomorphism of
${\mathrm {G}}(V)$
-modules. We also let
$$ \begin{align} \tau \colon V \otimes S \to S,\quad v \otimes x \mapsto vx, \end{align} $$
denote the homomorphism of
${\mathrm {G}}(V)$
-modules induced by multiplication in the Clifford algebra
$\mathrm {Cl}(V)$
; see Remark 2.1.
Theorem 6.1. There is a unique monoidal functor
$$\begin{align*}\mathbf{F} \colon \mathscr{SB}(V) \to {\mathrm{G}}(V)\textrm{-mod} \end{align*}$$
given on objects by
$\mathsf {S} \mapsto S$
,
$\mathsf {V} \mapsto V$
and on morphisms by
Furthermore, we have
We call
$\mathbf {F}$
the incarnation functor.
Proof. We first show that Equations (6.8) to (6.10) indeed yield a functor
$\mathbf {F}$
. We must show that
$\mathbf {F}$
respects the relations of Definition 5.1. The fifth relation in Equation (5.1) follows from Proposition 4.8 and the fact that
$\Phi _V$
is symmetric. The remaining relations in Equation (5.1) are straightforward. Relation (5.2) is also straightforward.
The image under
$\mathbf {F}$
of the left-hand side of Equation (5.3) is the map
$S \to S \otimes V$
given by
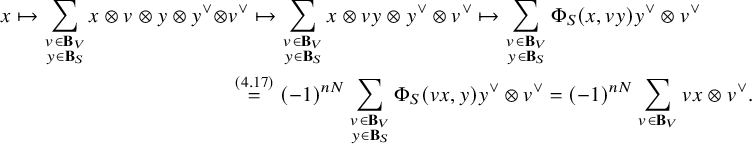$$ \begin{align*} x \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} x \otimes v \otimes y \otimes y^\vee \otimes &v^\vee \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} x \otimes vy \otimes y^\vee \otimes v^\vee \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} \Phi_S(x,vy) y^\vee \otimes v^\vee \\ & \overset{(4.17)}{=} (-1)^{nN} \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} \Phi_S(vx,y) y^\vee \otimes v^\vee = (-1)^{nN} \sum_{v \in \mathbf{B}_V} vx \otimes v^\vee. \end{align*} $$
On the other hand, the image under
$\mathbf {F}$
of the diagram in the right-hand side of Equation (5.3) is the map given by
$$ \begin{align*} & x \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} y \otimes v \otimes v^\vee \otimes y^\vee \otimes x \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} y \otimes v \otimes v^\vee y^\vee \otimes x \mapsto \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} \Phi_S(v^\vee y^\vee, x) y \otimes v \\ &\quad \overset{(4.17)}{=} (-1)^{nN} \sum_{\substack{v \in \mathbf{B}_V \\ y \in \mathbf{B}_S}} \Phi_S(y^\vee, v^\vee x) y \otimes v = (-1)^{nN} \sum_{v \in \mathbf{B}_V} v^\vee x \otimes v \overset{(6.5)}{=} (-1)^{nN} \sum_{v \in \mathbf{B}_V} v x \otimes v^\vee. \end{align*} $$
Since
$\kappa _N=(-1)^{nN}$
,
$\mathbf {F}$
respects relation (5.3).
The image under
$\mathbf {F}$
of the left-hand side of Equation (5.4) is the map
$S \otimes V \mapsto S$
given by
$$\begin{align*}x \otimes v \mapsto v \otimes x \mapsto vx. \end{align*}$$
On the other hand, the image under
$\mathbf {F}$
of the right-hand side of Equation (5.4) is the map given by
$$ \begin{align*} x \otimes v \mapsto \sum_{y \in \mathbf{B}_S} x \otimes v \otimes y \otimes y^\vee \mapsto \sum_{y \in \mathbf{B}_S} x \otimes vy &\otimes y^\vee \mapsto \sum_{y \in \mathbf{B}_S} \Phi_S(x,vy) y^\vee \\ &\overset{(4.17)}{=} (-1)^{nN} \sum_{y \in \mathbf{B}_S} \Phi_S(vx,y) y^\vee = (-1)^{nN} vx. \end{align*} $$
Thus,
$\mathbf {F}$
respects Equation (5.4).
The image under
$\mathbf {F}$
of the left-hand side of relation (5.5) is the map
$V \otimes V \otimes S \to S$
given by
$$\begin{align*}v \otimes w \otimes x \mapsto (vw+wv)x \overset{(2.1)}{=} 2 \Phi_V(v,w) x, \end{align*}$$
which agrees with the image under
$\mathbf {F}$
of the right-hand side of Equation (5.5).
For the first relation in Equation (5.6), we use the fact that
$\Phi _V$
is symmetric and that
$\dim _\Bbbk (V) = N$
to compute
Finally, for the second relation in Equation (5.6), we use Proposition 4.8 and the fact that
$\dim _\Bbbk (S) = 2^n$
to compute
It remains to prove that, for any functor as in the first sentence of the theorem, we have Equation (6.10). Suppose that
Then, for all
$z \in \mathbf {B}_S$
, we have
It follows that
$a_{xz} = \delta _{xz}$
for all
$x,z \in \mathbf {B}_S$
, and so 
. The proof that 
is analogous.
Corollary 6.2. Let
$\Bbbk _0=\mathbb {Q}[d,D][\frac {1}{d-1},\frac {1}{d-3},\frac {1}{d-5},\ldots ]$
, and suppose that
$\Bbbk $
is a commutative
$\Bbbk _0$
-algebra. (In particular, this holds when
$\Bbbk $
is a field of characteristic zero and
$d \notin 2\mathbb {N}+1$
.) Then
Proof. It suffices to prove the result when
$\Bbbk =\Bbbk _0$
, since the general result then follows after extending scalars from
$\Bbbk _0$
to
$\Bbbk $
. By Proposition 5.9, we have 
for some ideal I of
$\Bbbk _0$
. (This is where we use our assumption that
$d-1, d-3, \dotsc $
are invertible.) Suppose there exists a nonzero element
$f(d,D)\in I$
. Then there exists a positive integer n such that
$f \left ( 2n,(-1)^{\binom {n}{2}} 2^{2n} \right ) \neq 0$
. Viewing
$\mathbb {C}$
as a
$\Bbbk _0$
-module via the map
$d \mapsto 2n$
,
$D \mapsto (-1)^{\binom {n}{2}} 2^{2n}$
, we can extend scalars in
$\mathscr {SB}(d,D;1)$
and we then have an incarnation functor
$$\begin{align*}\mathscr{SB}(d,D;1) \otimes_{\Bbbk_0} \mathbb{C} \to {\mathrm{G}}(V)\textrm{-mod}. \end{align*}$$
This functor sends 
to a nonzero element of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(\mathrm {triv}^0)$
, which is a contradiction.
Our next goal is to show that the incarnation functor factors through
$\overline {\mathscr {SB}}(V)$
.
Lemma 6.3. When N is an odd positive integer, we have
Proof. Let
$$\begin{align*}Y = \{-n,1-n,\dotsc,n\}. \end{align*}$$
In what follows, we will use the fact that
$$ \begin{align} \Phi_S(x_I, x_I^\vee) \overset{(4.26)}{=} (-1)^{\binom{n}{2} + n(2n+1)} \Phi_S(x_I^\vee, x_I) = (-1)^{\binom{n+1}{2}} \qquad \text{for all } I \subseteq [n]. \end{align} $$
Recall the definition of
$\psi _i$
for
$i \le 0$
from Equation (2.11). The dual of the ordered basis
$\{\psi _{-n},\psi _{1-n},\ldots ,\psi _{n}\}$
of V is
$\{2\psi _{n},2\psi _{n-1},\dotsc ,2\psi _{-n}\}$
. Therefore, by Equations (5.7) and (6.10),
Thus,
is the map
$$ \begin{align*} 1 &\mapsto \sum_{I \subseteq [n]} x_I \otimes x_I^\vee \\ &\mapsto 2^N \sum_{I \subseteq [n]} \sum_{i_{-n},i_{1-n},\dotsc,i_n=-n}^n \psi_{-i_n}\otimes \psi_{-i_{n-1}} \otimes \dotsb \otimes \psi_{-i_{-n}} \otimes \psi_{i_{-n}} \dotsm \psi_{i_{n-1}} \psi_{i_n} x_I \otimes x_I^\vee \\ &\mapsto 2^N \sum_{I \subseteq [n]} \sum_{i_{-n},i_{1-n},\dotsc,i_n=-n}^n \Phi_S(\psi_{i_{-n}} \dotsm \psi_{i_{n-1}} \psi_{i_n} x_I, x_I^\vee) \psi_{-i_n}\otimes \psi_{-i_{n-1}} \otimes \dotsb \otimes \psi_{-i_{-n}}. \end{align*} $$
Applying the antisymmetrizer 
, which annihilates any terms for which the map
$j \mapsto i_j$
is not some permutation
$\varpi \in \mathfrak {S}_Y$
, we obtain
where, in the last equality, we re-indexed the summation, noting that the sign of the permutation
$\varpi (-j) \mapsto -\varpi \varpi '(j)$
is
$\operatorname {sgn}(\omega ')$
.
We now apply
to obtain
$$ \begin{align*} 2^{N-1/2} \varepsilon (-1)^{\binom{n+1}{2}} N! \sum_{\varpi \in \mathfrak{S}_Y} &\sum_{I \subseteq [n]} \operatorname{sgn}(\varpi) \Phi_S(\psi_{\varpi(-n)} \psi_{\varpi(1-n)} \psi_{\varpi(n)} x_I, x_I^\vee) \\ &\overset{(2.12)}{=} 2^{N-1} (-1)^{\binom{n+1}{2}} N! \sum_{\varpi \in \mathfrak{S}_Y} \Phi_S(x_{I_\varpi}, x_{I_\varpi}^\vee) \overset{(2.12)}{=} 2^{N-1} (N!)^2.\\[-51pt] \end{align*} $$
Theorem 6.4. The incarnation functor
$\mathbf {F}$
of Theorem 6.1 factors through
$\overline {\mathscr {SB}}(V)$
.
Proof. If N is even, there is nothing to prove, since
$\overline {\mathscr {SB}}(V) = \mathscr {SB}(V)$
in this case. Therefore, we suppose that N is odd. The images under
$\mathbf {F}$
of the two sides of Equation (5.19) are endomorphisms of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(\Lambda ^N(V))$
, which is one dimensional. Therefore, there exists a scalar
$a \in \Bbbk $
such
We then have
It follows that
$a = 2^{N-1} (N!)^2$
, as desired.
Lemma 6.5. We have
where
$$ \begin{align} \beta := \sum_{i=1}^N e_i \otimes e_i \in \mathrm{Cl}^{\otimes 2}. \end{align} $$
Proof. Using Equation (5.9), we see that Equation (6.13) follows from the part of the proof of Theorem 6.1 where we verified Equation (5.4). Then we have
Remark 6.6. There are other possible incarnation functors. In particular, for
$m,k \in \mathbb {N}$
, let
$\mathrm {OSp}(m|2k)$
be the corresponding orthosymplectic supergroup, defined to be the supergroup preserving a nondegenerate supersymmetric bilinear form
$\Phi _W$
on a vector superspace W whose even part has dimension m and odd part has dimension
$2k$
. Then there is a unique monoidal functor
$$\begin{align*}\mathscr{SB}(N,\sigma_N (m-2k) 2^n;\kappa_N) \to ({\mathrm{G}}(V) \times \mathrm{OSp}(m|2k))\textrm{-mod} \end{align*}$$
given on objects by
$\mathsf {S} \mapsto S \otimes W$
,
$\mathsf {V} \mapsto V$
, and on morphisms by
where we now use the super analogue of the map
$\operatorname {\mathrm {flip}}$
of Equation (6.6), given by
$u \otimes w \mapsto (-1)^{\bar {u} \bar {w}} w \otimes u$
, where
$\bar {v}$
is the parity of a homogeneous vector v. The proof of the existence and uniqueness of this functor is similar to that of Theorem 6.1, as is the proof that it factors through
$\overline {\mathscr {SB}}(N,\sigma _N(m-2k)2^n; \kappa _N)$
.
Corollary 6.7. Suppose that
$\Bbbk $
is a
$\mathbb {Q}$
-algebra and d is an odd positive integer. Then
Proof. The proof is analogous to that of Corollary 6.2, using the extra incarnation functors of Remark 6.6.
Remark 6.8. When
$\Bbbk $
is a field of characteristic not equal to two, we have an incarnation functor from
$\mathscr {SB}(V)$
to the category of tilting modules for the group
${\mathrm {G}}(V)$
, given in an analogous manner to Theorem 6.1. This functor exists since our constructions can be carried out over
$\mathbb {Z}[\frac {1}{2}]$
, the defining and spin representations are tilting away from characteristic two, and the category of tilting modules is closed under tensor products. The restriction on the characteristic is necessary since the module V is not tilting in characteristic two. We expect that this incarnation functor is full.
7 Fullness of the incarnation functor
In the current section, we prove that the incarnation functor of Theorem 6.1 is full. Until the statement of Theorem 7.8, we assume that
$N \ge 2$
.
Recall the element
$\beta \in \mathrm {Cl}^{\otimes 2}$
from (6.15). We define a barbell to be any element of the form
$1^{\otimes t} \otimes \beta \otimes 1^{r-t-2} \in \mathrm {Cl}^{\otimes r}$
,
$0 \le t \le r-2$
,
$r \ge 2$
. The action of a barbell yields an element of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
.
Lemma 7.1. The action of the barbell
$\beta $
generates
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S\otimes S)$
.
Proof. By Corollary 4.13 and Proposition 4.12, the
${\mathrm {G}}(V)$
-module
$S \otimes S$
is multiplicity free and, by [Reference WenzlWen20, Lem. 1.2], the action of
$\beta $
has a different eigenvalue on each summand. (There is a typo in [Reference WenzlWen20, Lem. 1.2(b)]; the index j should run from
$0$
to k inclusive.)
Lemma 7.2. For all
$k \ge 0$
, the morphism
lies in the subalgebra of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes 2k})$
generated by barbells, where the thick cup and cap labelled by k denote k nested cups and caps, respectively.
Proof. We have
By Lemma 7.1, the innermost 
can be written as a polynomial in
Next, note that
A straightforward proof by induction, using Equation (5.14), shows that
is in the image of the barbells. Thus, the lemma follows by induction.
Lemma 7.3. Let
$r\in \mathbb {N}$
, and let
$\lambda =(\lambda _1,\lambda _2,\ldots ,\lambda _n)$
be a dominant integral weight with
$\lambda _1 = \frac {r}{2}$
. Then
$L(\lambda )$
is a direct summand of the
$\mathrm {Spin}(V)$
-module
$S^{\otimes r}$
.
Proof. We prove this by induction on r, the base case
$r=0$
being trivial. Suppose
$r \geq 1$
, and let
$\lambda =(\lambda _1,\lambda _2,\ldots ,\lambda _n)$
with
$\lambda _1=\frac {r}{2}$
. Let k be the largest index for which
$\lambda _k> 0$
. Let
$\epsilon = \left ( \frac {1}{2}, \dotsc , \frac {1}{2}, -\frac {1}{2}, \dotsc , -\frac {1}{2} \right )$
, where there are k occurrences of
$\frac {1}{2}$
. It then follows directly from the characterisations (3.7) and (3.10) of dominant integral weights that
$\lambda -\epsilon $
is dominant integral. By the inductive hypothesis,
$L(\lambda -\epsilon )$
is a direct summand of
$S^{\otimes (r-1)}$
. Lemma 4.10 implies that
$L(\lambda )$
is a summand of
$S \otimes L(\lambda -\epsilon )$
, hence is a direct summand of
$S^{\otimes r}$
, as required.
Corollary 7.4. Suppose N is even, and let r be a positive integer. Let
$\lambda =(\lambda _1,\lambda _2,\dotsc ,\lambda _n)$
be a dominant integral weight with
$\lambda _1=\frac {r}{2}$
, and let M be a simple
$\mathrm {Pin}(V)$
-module whose restriction to
$\mathrm {Spin}(V)$
contains
$L(\lambda )$
as submodule. Then M is a summand of the
$\mathrm {Pin}(V)$
-module
$S^{\otimes r}$
.
Remark 7.5. Note that the condition
$r>0$
in Corollary 7.4 is necessary since
$\mathrm {triv}^1$
is not a summand of the trivial
$\mathrm {Pin}(V)$
-module
$S^{\otimes 0}$
. However, when N is even,
$\mathrm {triv}^1$
is a summand of
$S^{\otimes r}$
for
$r \in 2\mathbb {N}$
,
$r> 0$
by Lemma 4.5.
Let
$r \in \mathbb {N}$
. For
$N> 2$
, let
$X_r$
be the
$\mathrm {Spin}(V)$
-submodule of
$S^{\otimes r}$
that is the sum of all simple summands of highest weight
$\lambda $
with
$\lambda _1 = \frac {r}{2}$
. For
$N=2$
, let
$X_r$
be the
$\mathrm {Spin}(V)$
-submodule of
$S^{\otimes r}$
that is the sum of all simple summands of highest weight
$\lambda _1 = \pm \frac {r}{2}$
. It follows from Remark 4.3 and Proposition 4.4 that
$X_r$
is also
${\mathrm {G}}(V)$
-submodule.
Recall the definition of
$A_{ij}$
from Equations 3.4 and 3.8, and let
$Y_r$
be the
$\frac {r}{2}$
-eigenspace of
$A_{11}$
on
$X_r$
. Since
$\lambda _1 \le \frac {r}{2}$
for all weights
$\lambda $
appearing as a highest weight in
$S^{\otimes r}$
,
$Y_r$
is also the
$\frac {r}{2}$
-eigenspace of
$A_{11}$
on
$S^{\otimes r}$
. Recall the definition of the elements
$x_I \in S$
from Equation (2.7). It follows from Equations 3.6 and 3.9 that the space
$Y_r$
is the span of all
$x_{I_1} \otimes x_{I_2} \otimes \dotsb \otimes x_{I_r}$
, where
$1 \in I_i$
for all i.
Let
$$\begin{align*}W = \begin{cases} \operatorname{\mathrm{span}}_\Bbbk \left\{ \psi_2,\psi_3,\dotsc,\psi_n,\psi_n^\dagger,\dotsc,\psi_3^\dagger,\psi_2^\dagger \right\} \subseteq V & \text{if } N \in 2\mathbb{N}, \\ \operatorname{\mathrm{span}}_\Bbbk \left\{ \psi_2,\psi_3,\dotsc,\psi_n,e_N,\psi_n^\dagger,\dotsc,\psi_3^\dagger,\psi_2^\dagger \right\} \subseteq V & \text{if } N \in 2\mathbb{N} + 1, \end{cases} \end{align*}$$
where we adopt the convention that
$W = \{0\}$
when
$N=2$
. We have a natural inclusion of groups
${\mathrm {G}}(W) \subseteq {\mathrm {G}}(V)$
. Since the actions of
$A_{11}$
and
${\mathrm {G}}(W)$
on V commute,
$Y_r$
is a
${\mathrm {G}}(W)$
-submodule of V. Let
$S_W$
be the spin module for
${\mathrm {G}}(W)$
. Then
$x_I$
,
$I \subseteq \{2,3,\dotsc ,n\}$
, is a basis for
$S_W$
. It is straightforward to verify that the map
$$ \begin{align} Y_r \to S_W^{\otimes r},\quad x_{I_1} \otimes \dotsb \otimes x_{I_r} \mapsto x_{I_1 \setminus \{1\}} \otimes \dotsb \otimes x_{I_r \setminus \{1\}}, \end{align} $$
is an isomorphism of
${\mathrm {G}}(W)$
-modules.
Lemma 7.6. For every
$f \in \operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(X_r)$
, we have
$f(Y_r) \subseteq Y_r$
. Furthermore, restriction to
$Y_r$
yields an isomorphism of
$\Bbbk $
-modules
$$ \begin{align} \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(X_r) \xrightarrow{\cong} \operatorname{\mathrm{End}}_{{\mathrm{G}}(W)}(Y_r). \end{align} $$
Proof. The first assertion follows from the fact that any element of
$f \in \operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(X_r)$
commutes with the action of
$A_{11}$
, hence leaves the eigenspace
$Y_r$
invariant. Since
${\mathrm {G}}(W)$
is a subgroup of
${\mathrm {G}}(V)$
, it follows that the restriction of f lies in
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(Y_r)$
. Thus, we have a homomorphism of
$\Bbbk $
-modules
$$ \begin{align} \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(X_r) \to \operatorname{\mathrm{End}}_{{\mathrm{G}}(W)}(Y_r). \end{align} $$
Our goal is to show that this linear map is an isomorphism. The result is trivial if
$N=2$
, and so we assume
$N>2$
.
Since
${\mathrm {G}}(V)$
-mod is a semisimple category, any element of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(X_r)$
is determined by its action on highest-weight vectors. An analogous statement holds for
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(Y_r)$
. Therefore, to see that Equation (7.3) is injective, it suffices to show that the space of highest-weight vectors of the
${\mathrm {G}}(V)$
-module
$X_r$
is equal to the space of highest-weight vectors of the
${\mathrm {G}}(W)$
-module
$Y_r$
.
First, suppose that v is a highest-weight vector in
$X_r$
of weight
$(\lambda _1,\dotsc ,\lambda _n)$
. Then
$v \in Y_r$
, since
$\lambda _1 = \frac {r}{2}$
by definition of
$X_r$
. Since the inclusion
${\mathrm {G}}(W) \subseteq {\mathrm {G}}(V)$
respects upper triangularity, it follows that v is a highest-weight vector of the
${\mathrm {G}}(W)$
-module
$Y_r$
. Conversely, suppose v is a highest-weight vector in the
${\mathrm {G}}(W)$
-module
$Y_r$
. Then, since
$[A_{11},A_{12}] = A_{12}$
, we have
$$\begin{align*}A_{11} A_{12} v = A_{12} A_{11} v + [A_{11},A_{12}] v = \left( \tfrac{r}{2}+1 \right) A_{12} v. \end{align*}$$
Since there are no nonzero
$w \in S^{\otimes r}$
satisfying
$A_{11}w = (\frac {r}{2}+1)w$
, we have
$A_{12}(v)=0$
. If
$\mathfrak {n}$
and
$\mathfrak {n}'$
are the subalgebras of strictly upper-triangular matrices in
$\mathfrak {so}(V)$
and
$\mathfrak {so}(W)$
, respectively, then
$\mathfrak {n}$
is generated by
$\mathfrak {n}'$
and
$A_{12}$
. Hence,
$\mathfrak {n}$
annihilates v, and so v is a highest-weight vector in
$X_r$
. This completes the argument that Equation (7.3) is injective.
To finish the proof of the lemma, it suffices to show that the dimensions of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(X_r)$
and
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(Y_r)$
are equal. Since
${\mathrm {G}}(V)$
-mod and
${\mathrm {G}}(W)$
-mod are both semisimple categories, these endomorphism algebras are isomorphic to products of matrix algebras. To see that their dimensions are equal, it is enough to show that the identification of highest-weight spaces given above preserves multiplicities of weights. This, in turn, follows from the fact that two highest-weight vectors in
$X_r$
have equal
${\mathrm {G}}(V)$
-weights if and only if they have equal
${\mathrm {G}}(W)$
-weights, since the highest weights in
$X_r$
are constrained to have
$\lambda _1 = \frac {r}{2}$
.
Since
$X_r$
is a sum of isotypic components of
$S^{\otimes r}$
, any endomorphism of
$S^{\otimes r}$
leaves
$X_r$
invariant. Therefore, restriction to
$X_r$
yields a natural projection
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r}) \twoheadrightarrow \operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(X_r)$
. We thus have a surjective composite of
$\Bbbk $
-module homomorphisms
$$ \begin{align} \Psi_r \colon \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(S^{\otimes r}) \twoheadrightarrow \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(X_r) \xrightarrow[(7.2)]{\cong} \operatorname{\mathrm{End}}_{{\mathrm{G}}(W)}(Y_r) \xrightarrow{\cong} \operatorname{\mathrm{End}}_{{\mathrm{G}}(W)}(S_W^{\otimes r}), \end{align} $$
where the final isomorphism is induced by Equation (7.1).
Lemma 7.7. For
$0 \le t \le r-2$
,
$r \ge 2$
, we have
$$\begin{align*}\Psi_r \left( 1^{\otimes r} \otimes \beta \otimes 1^{\otimes (t-r-2)} \right) = 1^{\otimes r} \otimes \beta_W \otimes 1^{\otimes (t-r-2)}, \end{align*}$$
where
$\beta _W = \sum _{i=3}^N e_i \otimes e_i$
is the barbell for W. (By convention,
$\beta _W = 0$
if
$N=2$
.)
Proof. Using Equation (2.4), we compute that
$$ \begin{align} e_1 \otimes e_1 + e_2 \otimes e_2 = 2 ( \psi_1 \otimes \psi_1^\dagger + \psi_1^\dagger \otimes \psi_1 ). \end{align} $$
Now, suppose that
$I_1,I_2, \dotsc , I_r \subseteq [n]$
satisfy
$1 \in I_k$
for all
$1 \le k \le r$
. Then
$$ \begin{align*} \left( 1^{\otimes t} \otimes \psi_1 \otimes \psi_1^\dagger \otimes 1^{\otimes (r-t-2)} \right) &(x_{I_1} \otimes x_{I_2} \otimes \dotsb \otimes x_{I_r}) = 0 \\ &\qquad = \left( 1^{\otimes t} \otimes \psi_1^\dagger \otimes \psi_1 \otimes 1^{\otimes (r-t-2)} \right) (x_{I_1} \otimes x_{I_2} \otimes \dotsb \otimes x_{I_r}). \end{align*} $$
Thus, the result follows from Equation (7.5).
For the remainder of this section, we drop the assumption that
$N \ge 2$
.
Theorem 7.8. Suppose
$r,r_1,r_2 \in \mathbb {N}$
.
-
(a) The incarnation functor
$\mathbf {F}$
induces a surjection
$$\begin{align*}\operatorname{\mathrm{Hom}}_{\mathscr{SB}(V)}(\mathsf{S}^{\otimes r_1}, \mathsf{S}^{\otimes r_2}) \twoheadrightarrow \operatorname{\mathrm{Hom}}_{{\mathrm{G}}(V)}(S^{\otimes r_1}, S^{\otimes r_2}). \end{align*}$$
-
(b) The algebra
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
is generated by barbells.
Proof. Since the components of the weights of
$S^{\otimes r}$
lie in
$\frac {r}{2} + \mathbb {Z}$
, we have
$\operatorname {\mathrm {Hom}}_{{\mathrm {G}}(V)}(S^{\otimes r_1}, S^{\otimes r_2}) = 0$
when
$r_1+r_2 \notin 2\mathbb {Z}$
. Thus, for statement (a), we will assume for the remainder of this proof that
$r_1 + r_2 \in 2\mathbb {Z}$
.
We have a commutative diagram
where the horizontal maps are the usual isomorphisms that hold in any rigid monoidal category. In particular, the top horizontal map is the
$\Bbbk $
-linear isomorphism given on diagrams by
where the rectangles denote some diagram. Therefore, part (a) holds for
$r_1,r_2 \in \mathbb {N}$
if and only if it holds for all other
$r_1',r_2' \in \mathbb {N}$
satisfying
$r_1 + r_2 = r_1' + r_2'$
. It also follows that, for
$0 \le k \le \frac {r}{2}$
,
where, as in Lemma 7.2, the thick cup and cap labelled by k denote k nested cups and caps, respectively.
We now prove the theorem by induction on
$N = \dim V$
. The base cases are
$N=0$
and
$N=1$
. In these cases, S is one-dimensional, and so
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
only consists of scalars, which makes the theorem trivial in these cases.
Now, suppose that
$N \ge 2$
and that the result holds for
$0 \le \dim V < N$
. For
$r \in \mathbb {N}$
, let
$F(r)$
be the statement that (a) holds for all
$r_1+r_2 = 2r$
and that (b) holds. By the argument given above,
$F(r)$
is equivalent to the statement that (a) holds for some
$r_1,r_2 \in \mathbb {N}$
satisfying
$r_1+r_2=2r$
and that (b) holds. We will prove that
$F(r)$
holds for all
$r \in \mathbb {N}$
by induction on r. The base of the induction consists of the cases
$r \leq 2$
. The cases
$r \leq 1$
are trivial as S is a simple
${\mathrm {G}}(V)$
-module, and so
$\operatorname {\mathrm {Hom}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
consists of scalar multiples of the identity. The case
$r=2$
follows from Lemma 7.1.
Now, suppose that
$r \ge 3$
, and that
$F(k)$
holds for all
$k<r$
. Recall the surjective
$\Bbbk $
-linear map
$$\begin{align*}\Psi_r \colon \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(S^{\otimes r}) \twoheadrightarrow \operatorname{\mathrm{End}}_{{\mathrm{G}}(W)}(S_W^{\otimes r}) \end{align*}$$
defined in Equation (7.4). The kernel of
$\Psi _r$
consists of all elements of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
that factor through simple modules with highest weights
$\lambda $
with
$\lambda _1<r/2$
(when
$N>2$
) or
$-r/2 < \lambda _1 < r_2$
(when
$N=2$
). By Corollary 7.4 and Remark 7.5, these simple modules are precisely the simple modules that occur as summands in
$S^{\otimes (r-2k)}$
for
$0 < k \leq \frac {r}{2}$
. Therefore,
$\ker \Psi _r$
is the sum of all images of all compositions
$$\begin{align*}\operatorname{\mathrm{Hom}}_{{\mathrm{G}}(V)}(S^{\otimes r},S^{\otimes (r-2k)}) \times \operatorname{\mathrm{Hom}}_{{\mathrm{G}}(V)}(S^{\otimes (r-2k)},S^{\otimes r}) \to \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(S^{\otimes r}),\qquad 0 < k \leq \frac{r}{2}. \end{align*}$$
It follows from Equation (7.7), Equation (7.8), Lemma 7.2 and the inductive hypothesis that
$\ker \Psi _r$
is generated by barbells and hence is in the image of
$\mathbf {F}$
.
By the inductive hypothesis for our induction on N, barbells generate
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(S_W^{\otimes r})$
. By Lemma 7.7, every barbell in
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(S_W^{\otimes r})$
is in the image of
$\Psi _r$
. Thus, if U denotes the subalgebra of
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes r})$
generated by barbells, we have
$\Psi _r(U) = \operatorname {\mathrm {End}}_{{\mathrm {G}}(W)}(S_W^{\otimes r})$
. Since
$\Psi _r$
is surjective, this implies that
$$\begin{align*}U + \ker \Psi_r = \operatorname{\mathrm{End}}_{{\mathrm{G}}(V)}(S^{\otimes r}). \end{align*}$$
The subspace U lies in the image of
$\mathbf {F}$
since all barbells do. This completes the proof of the statement
$F(r)$
.
Theorem 7.9. The incarnation functor
$\mathbf {F}$
is full.
Proof. We must show that
$$\begin{align*}\mathbf{F} \colon \operatorname{\mathrm{Hom}}_{\mathscr{SB}(V)}(\mathsf{X}, \mathsf{Y}) \to \operatorname{\mathrm{Hom}}_{{\mathrm{G}}(V)}(\mathbf{F}(\mathsf{X}), \mathbf{F}(\mathsf{Y})) \end{align*}$$
is surjective for all objects
$\mathsf {X}$
and
$\mathsf {Y}$
in
$\mathscr {SB}(V)$
. By the first relation in Equation (5.1), we have mutually inverse isomorphisms
Therefore, it suffices to consider the case where
$\mathsf {X} = \mathsf {S}^{\otimes k_1} \otimes \mathsf {V}^{\otimes l_1}$
and
$\mathsf {Y} = \mathsf {S}^{\otimes k_2} \otimes \mathsf {V}^{\otimes l_2}$
for some
$k_1,l_1,k_2,l_2 \in \mathbb {N}$
. Consider an arbitrary morphism
$$\begin{align*}f \in \operatorname{\mathrm{Hom}}_{{\mathrm{G}}(V)} \left( S^{\otimes k_1} \otimes V^{\otimes l_1}, S^{\otimes k_2} \otimes V^{\otimes l_2} \right). \end{align*}$$
Define
By Theorem 7.8(a), there exists a
$g' \in \operatorname {\mathrm {Hom}}_{\mathscr {SB}(V)}(\mathsf {S}^{\otimes (k_1+2l_1)}, \mathsf {S}^{\otimes (k_2+2l_2)})$
such that
$\mathbf {F}(g') = f'$
. Let
Using Proposition 5.6 with
$r=2$
, we have
It follows that
$$\begin{align*}\mathbf{F}(g) = D^{l_1 + l_2} f, \end{align*}$$
completing the proof.
8 Essential surjectivity of the incarnation functor
In this section, we prove that, after passing to the additive Karoubi envelope, the incarnation functor is essentially surjective, that is, it induces a surjection on isomorphism classes of objects. We then give explicit descriptions of some important idempotents. When discussing the incarnation functor, we always assume that
$\Bbbk =\mathbb {C}$
.
Let
$\operatorname {\mathrm {Kar}}(\overline {\mathscr {SB}}(d,D;\kappa ))$
be the additive Karoubi envelope (that is, the idempotent completion of the additive envelope) of
$\mathscr {SB}(d,D;\kappa )$
. Since
${\mathrm {G}}(V)\textrm { -mod}$
is additive and idempotent complete,
$\mathbf {F}$
induces a monoidal functor
$$ \begin{align} \operatorname{\mathrm{Kar}}(\mathbf{F}) \colon \operatorname{\mathrm{Kar}} \big( \overline{\mathscr{SB}}(V) \big) \to {\mathrm{G}}(V)\textrm{-mod}. \end{align} $$
Theorem 8.1. For all
$N \in \mathbb {N}$
, the functor
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
is essentially surjective.
Proof. The spin module S is a self-dual faithful
${\mathrm {G}}(V)$
-module. Hence, it is a tensor generator of
${\mathrm {G}}(V)\textrm { -mod}$
. Let M be a simple
${\mathrm {G}}(V)$
-module. The above implies that M is a direct summand of
$S^{\otimes k}$
for some k. By Theorem 7.8(a), the idempotent in
$\operatorname {\mathrm {End}}_{{\mathrm {G}}(V)}(S^{\otimes k})$
projecting onto M is in the image of the incarnation functor
$\mathbf {F}$
, hence M is in the essential image of
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
. Since
${\mathrm {G}}(V)\textrm { -mod}$
is semisimple, this completes the proof that
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
is essentially surjective.
Remark 8.2. The Lie algebra of
${\mathrm {G}}(V)$
is
$\mathfrak {so}(V)$
. Passage to the Lie algebra induces a functor
${\mathrm {G}}(V)\textrm { -mod} \to \mathfrak {so}(V)\textrm { -mod}$
, where
$\mathfrak {so}(V)\textrm { -mod}$
denotes the category of finite-dimensional
$\mathfrak {so}(V)$
-modules. We can compose the incarnation functor
$\mathbf {F}$
with this passage to the Lie algebra to yield a functor
$\mathbf {F}' \colon \mathscr {SB}(V) \to \mathfrak {so}(V)\textrm { -mod}$
, which factors through
$\overline {\mathscr {SB}}(V)$
. However, while we have shown in Theorems 7.9 and 8.1 that
$\mathbf {F}$
is full and
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
is essentially surjective, the functor
$\mathbf {F}'$
is not full and the functor
$\operatorname {\mathrm {Kar}}(\mathbf {F}')$
is not essentially surjective when N is even. For example, as
$\mathfrak {so}(V)$
-modules,
$\Lambda ^N(V)$
is isomorphic to the trivial module. But this isomorphism is not contained in the image of
$\mathbf {F}'$
since
$\Lambda ^N(V)$
is nontrivial as a
$\mathrm {Pin}(V)$
-module when N is even, by Equation (4.33). The functor
$\operatorname {\mathrm {Kar}}(\mathbf {F}')$
is not essentially surjective since there are modules for
$\mathfrak {so}(V)$
that are not the restriction of
${\mathrm {G}}(V)$
-modules; an example is either of the two summands of the spin module S. This is our main motivation for considering the larger group
$\mathrm {Pin}(V)$
when N is even.
It is straightforward to verify that
$\mathscr {SB}(d,D;\kappa )$
is a spherical pivotal category, hence so is its idempotent completion
$\operatorname {\mathrm {Kar}}(\mathscr {SB}(d,D;\kappa ))$
. (We refer the reader to [Reference SelingerSel11, §4.4.3] for the definition of a spherical pivotal category.) In any spherical pivotal category
$\mathcal {C}$
, we have a trace map 
. In terms of string diagrams, this corresponds to closing a diagram off to the right or left:
where the second equality follows from the axioms of a spherical category. We say that a morphism
$f \in \operatorname {\mathrm {Hom}}_{\mathcal {C}}(X,Y)$
is negligible if
$\operatorname {\mathrm {Tr}}(f \circ g) = 0$
for all
$g \in \operatorname {\mathrm {Hom}}_{\mathcal {C}}(Y,X)$
. The negligible morphisms form a two-sided tensor ideal
$\mathscr {N}$
of
$\mathcal {C}$
, and the quotient
$\mathcal {C}/\mathscr {N}$
is called the semisimplification of
$\mathcal {C}$
.
Theorem 8.3. For all
$N \in \mathbb {N}$
, the kernel of the functor
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
of Equation (8.1) is equal to the tensor ideal of negligible morphisms of
$\operatorname {\mathrm {Kar}}(\overline {\mathscr {SB}}(V))$
. The functor
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
induces an equivalence of categories from the semisimplification of
$\operatorname {\mathrm {Kar}}(\overline {\mathscr {SB}}(V))$
to
${\mathrm {G}}(V)\textrm { -mod}$
.
Proof. By Theorems 7.9 and 8.1 the functor
$\operatorname {\mathrm {Kar}}(\mathbf {F})$
is full and essentially surjective. It follows from Proposition 5.9 and [Reference Savage and WestburySW, Prop. 6.9] that its kernel is the tensor ideal of negligible morphisms.
We spend the rest of this section explicitly constructing idempotents in the spin Brauer category that correspond, under the incarnation functor, to projections onto the simple summands of the tensor products
$S^{\otimes 2}$
, as in Corollary 4.13, and onto the summand S in
$S \otimes V$
. For the rest of this section, we assume that
$\Bbbk $
is a field of characteristic zero. For statements involving the incarnation functor, we assume that
$\Bbbk = \mathbb {C}$
.
Recall the definition of the antisymmetrizer (5.16). If
$D \ne 0$
, define
Proposition 8.4.
-
(a) If
$d \notin 2\mathbb {N} + 1$
, then
$\pi _r \pi _s = 0$
for all
$r \ne s$
. -
(b) If
$d \in 2\mathbb {N} + 1$
, then
$\pi _r \pi _s = 0$
for all
$r \ne s$
,
$0 \le r+s < d$
. -
(c) If
$d \notin \{0,1,\dotsc ,r-1\}$
, then
$\pi _r^2 = \pi _r$
. -
(d) If
$d=N$
,
$D = \sigma _N 2^n$
, and
$0 \le r \le N$
, then
$\mathbf {F}(\pi _r)$
is the projection
$S^{\otimes 2} \twoheadrightarrow \Lambda ^r(V)$
with respect to the decompositions of Corollary 4.13.
Proof. Recall that, for
$r,s \in \mathbb {N}$
, an
$(r,s)$
-shuffle is a permutation g of the set
$\{1,\dotsc ,r+s\}$
such that
$$\begin{align*}g(1) < \dotsb < g(r) \quad \text{and} \quad g(r+1) < \dotsb g(r+s). \end{align*}$$
The set
$\textrm { Sh}(r,s)$
of
$(r,s)$
-shuffles is a complete set of representatives of the left cosets of the subgroup
$\mathfrak {S}_r \times \mathfrak {S}_s$
of
$\mathfrak {S}_{r+s}$
. Thus, we have
for some
$c_a \in \Bbbk $
,
$1 \le a \le \min (r,s)$
.
We now prove (a) by induction on
$r+s$
. Suppose
$d \notin 2\mathbb {N}+1$
and
$r \ne s$
. It suffices to show that
For the base case
$r+s=1$
, the result follows immediately from the
$r=1$
case of Equation (5.18). Now, suppose
$r + s> 1$
. Then, for
$1 \le a \le \min (r,s)$
, we have
where the last equality follows from the inductive hypothesis. Therefore,
and the result follows. The proof of (b) is identical, except that the first equality in Equation (8.5) uses the assumption that
$r+s < d$
.
Next, we prove (c). We first show, by induction on r, that
The base case
$r=0$
follows immediately from the second relation in Equation (5.6). Now, assume
$r> 1$
and that the result holds for
$r-1$
. Then, for
$a \ge 1$
,
Thus,
and (8.6) follows.
Now, taking the trace of both sides of Equation (8.6), we see that
Thus, by Equations 5.23 and 5.21, we have
$$\begin{align*}b_r d(d-1) \dotsm (d-r+1) = D (r!)^2 d(d-1) \dotsb (d-r+1), \end{align*}$$
and so
$b_r = D(r!)^2$
.
Finally, to prove (d), note that
$F(\pi _r)$
is an idempotent
$\mathrm {Pin}(V)$
-module homomorphism
$S^{\otimes 2} \to \Lambda ^r(V) \to S^{\otimes 2}$
. Since its trace is nonzero by Equation (5.23), the result follows from Corollary 4.13.
For
$N \ge 1$
, we have
$$ \begin{align} V^{\otimes 2} \cong S^2(V) \oplus \Lambda^2(V),\qquad S^2(V) \cong \mathrm{triv}^0 \oplus W,\qquad \text{as } \mathrm{Pin}(V)\text{-modules}. \end{align} $$
When
$N=1$
, we have
$W = \Lambda ^2(V) = 0$
. For
$N \ge 2$
, the
$\mathrm {Pin}(V)$
-modules W and
$\Lambda ^2(V)$
are simple. We have
$$ \begin{align} \Lambda^2(V) = \mathrm{triv}^1 \quad \text{and} \quad W = \operatorname{\mathrm{Ind}}(L(2\epsilon_1)) \quad \text{when } N=2. \end{align} $$
Moreover, when
$N \ge 3$
, we have
$$ \begin{align} W \cong L(2 \epsilon_1), \qquad \Lambda^2(V) \cong \begin{cases} L(\epsilon_1 + \epsilon_2) & \text{if } N> 3, \\ L(\epsilon_1) & \text{if } N = 3, \end{cases} \qquad \text{as } \mathrm{Spin}(V)\text{-modules}. \end{align} $$
Remark 8.5. Suppose
$d=N$
is odd. It follows from Proposition 8.4(d), Proposition 4.12 and Corollary 4.13 that
$\mathbf {F}(\pi _0)$
and
$\mathbf {F}(\pi _N)$
are both the projection from
$S^{\otimes 2}$
onto its trivial
$\mathrm {Pin}(V)$
-module summand. It follows that
$\mathbf {F}(\pi _0 \pi _N) \ne 0$
, and so
$\pi _0 \pi _N \ne 0$
. This shows that the equality in (5.18) fails when
$r = d$
is odd.
Proposition 8.6. If
$d \ne 0$
, the morphisms
are orthogonal idempotents. When
$d=N \ge 1$
and
$D = \sigma _N 2^n$
, their images under the incarnation functor
$\mathbf {F}$
are the projections onto the summands
$\mathrm {triv}^0$
, W, and
$\Lambda ^2(V)$
, respectively, of
$V^{\otimes 2}$
.
Proof. The proof that these are orthogonal idempotents is a straightforward diagrammatic computation, analogous to the corresponding computation in the Brauer category. Since the images under
$\mathbf {F}$
of
are the symmetrizer and antisymmetrizer, respectively, and the first morphism in Equation (8.11) clearly factors through the trivial module, the final statement in the proposition follows.
Recall the decomposition of
$S \otimes V$
given in Corollary 4.11.
Lemma 8.7. If
$d \ne 0$
, the morphism
is an idempotent. When
$d=N \ge 1$
and
$D = \sigma _N 2^n$
, its image under the incarnation functor
$\mathbf {F}$
is the projection onto the summand S of
$S \otimes V$
.
Proof. We have
Thus, the morphism (8.12) is an idempotent. When
$d=N$
and
$D = \sigma _N 2^n$
, its image under
$\mathbf {F}$
is a morphism
$S \otimes V \to S \to S \otimes V$
. Thus, it is the projection onto the summand S of
$S \otimes V$
as long as it is nonzero. Recalling the trace map of (8.2), we have
and the result follows.
9 The affine spin Brauer category
In this section, we define an affine version of the spin Brauer category, together with an affine incarnation functor. This can be thought of as a spin version of the affine Brauer category introduced in [Reference Rui and SongRS19].
Definition 9.1. For
$d,D \in \Bbbk $
and
$\kappa \in \{\pm 1\}$
, the affine spin Brauer category is the strict
$\Bbbk $
-linear monoidal category
$\mathscr {ASB}(d,D;\kappa )$
obtained from
$\mathscr {SB}(d,D;\kappa )$
by adjoining two additional generating morphisms
which we call dots, subject to the relations
Let
$\overline {\mathscr {ASB}}(d,D;\kappa )$
denote the quotient of
$\mathscr {ASB}(d,D;\kappa )$
by Equation (5.19).
Proposition 9.2. The following relations hold in
$\mathscr {ASB}(d,D;\kappa )$
:
Proof. Relations (9.5) and (9.7) follow from rotating Equations (9.1) and (9.3) using cups and caps. The first relation in (9.6) follows from the first relation in Equation (9.2) after composing on the top and bottom with 
. The second relation in Equation (9.6) follows similarly from the second relation in Equation (9.2).
To prove Equation (9.8), we compute
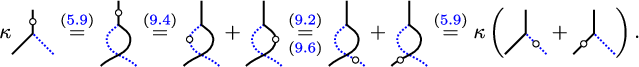
The symmetries (5.12) and (5.13) can be extended to
$\mathscr {ASB}(d,D;\kappa )$
. Precisely, we have an isomorphism of monoidal categories
$$ \begin{align} \mathscr{ASB}(d,D;\kappa) \to \mathscr{ASB}(d,D;\kappa)^{\mathrm{op}} \end{align} $$
that is the identity on objects and reflects morphisms in the horizontal axis. We also have an isomorphism of monoidal categories
$$ \begin{align} \mathscr{ASB}(d,D;\kappa) \to \mathscr{ASB}(d,D;\kappa)^{\mathrm{rev}} \end{align} $$
that is the identity on objects and, on morphisms, reflects diagrams in the vertical axis and multiplies dots by
$-1$
.
Our goal in the remainder of this section is to define an affine version of the incarnation functor of Section 6. Since our construction will be based on the Lie algebra
$\mathfrak {so}(V)$
, we assume throughout that
$N \ge 2$
and we work over the ground field
$\Bbbk = \mathbb {C}$
. However, see Remark 9.9 for the cases
$N=0$
and
$N=1$
.
Let
$\mathbf {B}_{\mathfrak {so}(V)}$
be a basis of
$\mathfrak {so}(V)$
, and let
$\{X^\vee : X \in \mathbf {B}_{\mathfrak {so}(V)}\}$
denote the dual basis with respect to the symmetric bilinear form
$$\begin{align*}\langle X,Y \rangle = \tfrac{1}{2} \operatorname{\mathrm{tr}}(XY),\qquad X,Y \in \mathfrak{so}(V), \end{align*}$$
where
$\operatorname {\mathrm {tr}}$
denotes the usual trace on the space of linear operators on V. We have
Thus, if we take the basis
$$\begin{align*}\mathbf{B}_{\mathfrak{so}(V)} = \{M_{e_i,e_j} : 1 \le i < j \le N\}, \end{align*}$$
then
$$\begin{align*}M_{e_i,e_j}^\vee = M_{e_j,e_i} = - M_{e_i,e_j},\qquad 1 \le i < j \le N. \end{align*}$$
Define
$$ \begin{align} \Omega = \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} X \otimes X^\vee = \sum_{1 \le i < j \le N} M_{e_i,e_j} \otimes M_{e_j,e_i} \in \mathfrak{so}(V) \otimes \mathfrak{so}(V), \end{align} $$
$$ \begin{align} C = \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} X X^\vee = \sum_{1 \le i < j \le N} M_{e_i,e_j} M_{e_j,e_i} \in U(\mathfrak{so}(V)). \end{align} $$
The elements
$\Omega $
and C are both independent of the chosen basis
$\mathbf {B}_{\mathfrak {so}(V)}$
. Note that C is the Casimir element and we have
$$ \begin{align} \Omega = \tfrac{1}{2}(\Delta(C) - C \otimes 1 - 1 \otimes C), \end{align} $$
where
$\Delta $
is the standard coproduct on
$\mathfrak {so}(V)$
. Define
$$ \begin{align} \tilde{\Omega} := 2 \Omega + C \otimes 1 = \Delta(C) - 1 \otimes C. \end{align} $$
The nondegenerate form
$\langle \cdot ,\cdot \rangle $
remains nondegenerate when restricted to
$\mathfrak {h}$
, hence induces a pairing
$\langle \cdot ,\cdot \rangle \colon \mathfrak {h}^\ast \times \mathfrak {h}^\ast \to \mathbb {C}$
, which we denote by the same symbol.
Lemma 9.3. The element C acts on the simple
$\mathrm {Spin}(V)$
-module
$L(\lambda )$
of highest weight
$\lambda $
as
$\langle \lambda , \lambda + 2\rho \rangle $
, where
$$ \begin{align} \rho = \frac{1}{2} \sum_{i=1}^n \left( N - 2i \right) \epsilon_i. \end{align} $$
Proof. This is well known. See, for example, [Reference CarterCar05, Prop. 11.36].
Corollary 9.4. The action of C commutes with the action of
$\mathrm {Pin}(V)$
.
Proof. Note that, if
$N=2n$
, and
$\tilde {\lambda }$
is defined as in Equation (4.10), then
$\langle \lambda , \lambda + 2 \rho \rangle = \langle \tilde {\lambda }, \tilde {\lambda } + 2 \rho \rangle $
. Thus, C acts on the simple
$\mathrm {Pin}(V)$
-module
$\operatorname {\mathrm {Ind}}(L(\lambda ))$
as
$\langle \lambda , \lambda + 2 \rho \rangle $
. Then the corollary follows from the fact that
$\mathrm {Pin}(V)\textrm { -mod}$
is a semisimple category.
Lemma 9.5. We have
$$ \begin{align} \beta^2 (x \otimes y) = \left( N - 8 \Omega \right) (x \otimes y) \qquad \text{for all } x,y \in S. \end{align} $$
Proof. Throughout this proof, we view all elements of
$\mathfrak {so}(V) \otimes \mathfrak {so}(V)$
as operators on
$S \otimes S$
. Then we have, via (3.1),
$M_{e_i,e_j} = \frac {1}{2} e_i e_j$
for
$i\neq j$
. Thus,
$$\begin{align*}\Omega = \frac{1}{4} \sum_{1 \le i<j \le N}e_i e_j \otimes e_j e_i. \end{align*}$$
On the other hand,
$$\begin{align*}\beta^2 = \sum_{i,j=1}^N e_i e_j \otimes e_i e_j \overset{(2.2)}{=} N - 2 \sum_{1 \le i<j \le N} e_i e_j \otimes e_j e_i = N - 8 \Omega.\\[-51pt] \end{align*}$$
Lemma 9.6. The element C acts as
-
(a)
$k(N-k)$
on
$L(\epsilon _1 + \dotsb + \epsilon _k)$
,
$0 \le k \le n$
; -
(b)
$\frac {N(N-1)}{8}$
on the spin representation S; -
(c)
$2N$
on
$L(2 \epsilon _1)$
; -
(d)
$\frac {N^2}{4}$
on
$L(\epsilon _1 + \dotsb + \epsilon _{n-1} - \epsilon _n)$
when
$N=2n \ge 4$
(i.e., type
$D_n$
); -
(e)
$\frac {N(N+7)}{8}$
on
$L \left ( \frac {3}{2} \epsilon _1 + \frac {1}{2} \epsilon _2 + \dotsb + \frac {1}{2} \epsilon _n \right )$
,
$n \ge 2$
; -
(f)
$\frac {N(N+7)}{8}$
on
$L \left ( \frac {3}{2} \epsilon _1 + \frac {1}{2} \epsilon _2 + \dotsb + \frac {1}{2} \epsilon _{n-1} - \frac {1}{2} \epsilon _n \right )$
when
$N=2n \ge 4$
(i.e., type
$D_n$
).
Proof. These are all direct computations using Lemma 9.3. First, note that
$\epsilon _1,\dotsc ,\epsilon _n$
is an orthonormal basis of
$\mathfrak {h}^*$
. (It is dual to the orthonormal basis
$A_{11},\dotsc ,A_{nn}$
of
$\mathfrak {h}$
.)
-
(a) We have
$$\begin{align*}\left\langle \sum_{i=1}^k \epsilon_i, \sum_{i=1}^k \epsilon_i + 2 \rho \right\rangle = k + \sum_{i=1}^k (N-2i) = k+kN-k(k+1) = k(N-k). \end{align*}$$
-
(b) In type
$D_n$
, so that
$N=2n$
, we have
$S^\pm = L \big (\frac {1}{2}( \epsilon _1 + \dotsb + \epsilon _{n-1} \pm \epsilon _n) \big )$
. Then we compute In type
$$\begin{align*}\left\langle \frac{1}{2} \sum_{i=1}^{n-1} \epsilon_i \pm \frac{1}{2} \epsilon_n, \frac{1}{2} \sum_{i=1}^{n-1} \epsilon_i \pm \frac{1}{2} \epsilon_n + 2 \rho \right\rangle = \frac{n}{4} + \frac{1}{2} \sum_{i=1}^{n-1} (N-2i) = \frac{N(N-1)}{8}. \end{align*}$$
$B_n$
, so that
$N=2n+1$
, we have
$S = L \big ( \frac {1}{2}(\epsilon _1 + \dotsb + \epsilon _n) \big )$
, and we compute
$$\begin{align*}\left\langle \frac{1}{2} \sum_{i=1}^n \epsilon_i, \frac{1}{2} \sum_{i=1}^n \epsilon_i + 2 \rho \right\rangle = \frac{n}{4} + \frac{1}{2} \sum_{i=1}^n (N-2i) = \frac{n}{4} + \frac{nN-n(n+1)}{2} = \frac{N(N-1)}{8}. \end{align*}$$
-
(c) We compute
$$\begin{align*}\langle 2 \epsilon_1, 2 \epsilon_1 + 2\rho \rangle = 4 + 2(N-2) = 2N. \end{align*}$$
-
(d) We compute
$$\begin{align*}\left\langle \sum_{i=1}^{n-1} \epsilon_i - \epsilon_n, \sum_{i=1}^{n-1} \epsilon_i - \epsilon_n + 2 \rho \right\rangle = n + \sum_{i=1}^{n-1} (N-2i) = n + (n-1)N - n(n-1) = \frac{N^2}{4}. \end{align*}$$
-
(e) We compute
When,
$$ \begin{align*} \left\langle \frac{3}{2} \epsilon_1 + \frac{1}{2} \sum_{i=2}^n \epsilon_i, \frac{3}{2} + \frac{1}{2} \sum_{i=2}^n \epsilon_i + 2 \rho \right\rangle = \frac{n+8}{4} + \frac{3}{2}(N-2) + \frac{1}{2} \sum_{i=2}^n (N-2i) \\ = \frac{2Nn-2n^2+4N-n}{4}. \end{align*} $$
$N=2n+1$
, we have On the other hand, when
$$\begin{align*}2Nn-2n^2+4N-n = (2n+1)(n+4) = \frac{N(N+7)}{2}. \end{align*}$$
$N=2n$
, we have
$$\begin{align*}2Nn-2n^2+4N-n = n(2n+7) = \frac{N(N+7)}{2}. \end{align*}$$
-
(f) This computation is almost identical to the previous one, using the fact that the
$\epsilon _n$
component of
$\rho $
is zero when
$N=2n$
.
The following lemma will play a key role in our proof that the affine incarnation functor satisfies the dot-crossing relations (9.1) and (9.2). It will describe the image of
under our affine incarnation functor.
Lemma 9.7. For any
$M_1,M_2,M_3 \in \mathfrak {so}(V)\textrm { -mod}$
, we have
$$ \begin{align} (1 \otimes \Delta)(\tilde{\Omega}) - (\operatorname{\mathrm{flip}} \otimes 1) \circ (1 \otimes \tilde{\Omega}) \circ (\operatorname{\mathrm{flip}} \otimes 1) = 2 \Omega \otimes 1 \quad \text{as operators on } M_1 \otimes M_2 \otimes M_3, \end{align} $$
where
$\Delta $
is the usual coproduct of
$\mathfrak {so}(V)$
given by
$\Delta (X) = X \otimes 1 + 1 \otimes X$
.
Proof. For
$m_1 \in M_1$
,
$m_2 \in M_2$
,
$m_3 \in M_3$
, we have
$$ \begin{align*} &\big( (1 \otimes \Delta)(\tilde{\Omega}) \big) (m_1 \otimes m_2 \otimes m_3) \\ &\qquad\quad = \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} (2 X m_1 \otimes X^\vee m_2 \otimes m_3 + 2X m_1 \otimes m_2 \otimes X^\vee m_3 + X X^\vee m_1 \otimes m_2 \otimes m_3) \end{align*} $$
and
$$ \begin{align*} (\operatorname{\mathrm{flip}} \otimes 1) \circ (1 \otimes \tilde{\Omega}) \circ (\operatorname{\mathrm{flip}} \otimes 1) &(m_1 \otimes m_2 \otimes m_3) \\ &\qquad = \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} (2 X m_1 \otimes m_2 \otimes X^\vee m_3 + XX^\vee m_1 \otimes m_2 \otimes m_3). \end{align*} $$
Subtracting these two sums proves the lemma.
For a
$\Bbbk $
-linear category
$\mathcal {C}$
, let
$\mathscr {End}_\Bbbk (\mathcal {C})$
denote the strict monoidal category of
$\Bbbk $
-linear endofunctors and natural transformations. An action of a monoidal category
$\mathcal {D}$
on a category
$\mathcal {C}$
is a monoidal functor
$\mathcal {D} \to \mathscr {End}_\Bbbk (\mathcal {C})$
. It follows immediately from Theorem 6.1 that
$\mathscr {SB}(V)$
acts on
${\mathrm {G}}(V)\textrm { -mod}$
via
$$\begin{align*}X \mapsto \mathbf{F}(X) \otimes -,\quad f \mapsto \mathbf{F}(f) \otimes -, \end{align*}$$
for objects X and morphisms f in
$\mathscr {SB}(V)$
. The following result extends this action to
$$ \begin{align} \mathscr{ASB}(V) := \mathscr{ASB}(N, \sigma_N 2^n; \kappa_N). \end{align} $$
Let
$\overline {\mathscr {ASB}}(V)$
denote the quotient of
$\mathscr {ASB}(V)$
by Equation (5.19).
Theorem 9.8. There is a unique monoidal functor
$\hat {\mathbf {F}} \colon \mathscr {ASB}(V) \to \mathscr {End}_{\mathbb {C}}({\mathrm {G}}(V)\textrm { -mod})$
given on objects by
$\mathsf {S} \mapsto S \otimes -$
,
$\mathsf {V} \mapsto V \otimes -$
, and on morphisms by
and 
, 
are the natural transformations with components
for
$M \in \mathfrak {so}(V)\textrm { -mod}$
, where
$\tilde {\Omega }$
is the element defined in Equation (9.14). The functor
$\hat {\mathbf {F}}$
factors through
$\overline {\mathscr {ASB}}(V)$
.
Proof. When N is odd, the functor
$\hat {\mathbf {F}}$
factors respects the relation (5.19) since
$\mathbf {F}$
does. It follows from Corollary 9.4 that 
is a natural transformation of the functor
$S \otimes -$
and that 
is a natural transformation of the functor
$V \otimes -$
. Thus, it remains to verify that
$\hat {\mathbf {F}}$
respects the relations (9.1) to (9.4). Throughout, M will denote an arbitrary object in
${\mathrm {G}}(V)\textrm { -mod}$
.
First relation in Equation (9.1). Composing on the top of the first relation in Equation (9.1) with the invertible morphism 
, then using the fifth relation in Equation (5.1), we see that the first relation in (9.1) is equivalent to
By Lemma 9.7, the image under
$\hat {\mathbf {F}}$
of the left-hand side of Equation (9.20) is the natural endomorphism of the functor
$V \otimes V \otimes -$
given by
$2 \Omega \otimes -$
. Recall the decompositions (8.8) and (8.10). Let
$1_\lambda \colon V^{\otimes 2} \to V^{\otimes 2}$
denote the projection onto the summand isomorphic to
$L(\lambda )$
as a
$\mathrm {Spin}(V)$
-module. Recall also that
$V = L(\epsilon _1)$
. When
$N>3$
, it follows from (9.13) and Lemma 9.6 that
$2\Omega $
acts on
$V^{\otimes 2}$
as
$$ \begin{align*} 2 \Omega(u \otimes v) &= C(u \otimes v) - Cu \otimes v - u \otimes Cv \\ &= (2N 1_{2 \epsilon_1} + 2(N-2) 1_{\epsilon_1 + \epsilon_2})(u \otimes v) - (N-1) (u \otimes v) - (N-1) (u \otimes v) \\ &= \big( 2(1-N) 1_0 + 2 ( 1_{2 \epsilon_1} - 1_{\epsilon_1 + \epsilon_2}) \big) (u \otimes v). \end{align*} $$
On the other hand, since
$d=N$
, it follows from Proposition 8.6 that
The cases
$N=2$
and
$N=3$
are analogous. Thus,
$\hat {\mathbf {F}}$
respects the first relation in (9.1).
Second relation in Equation (9.1). Composing on the top of the second relation in Equation (9.1) with the invertible morphism 
, then using Equation (5.3) and the first relation in Equation (5.1), we see that the second relation in Equation (9.1) is equivalent to
Thus, the fact that
$\hat {\mathbf {F}}$
respects the second relation in (9.1) follows from Lemma 9.7 and (6.14) and (9.16).
Relations (9.2). Composing on the top of the first relation in Equation (9.2) with the invertible morphism 
, then using Equation (5.9) and the first relation in Equation (5.1), we see that the first relation in (9.2) is equivalent to
By Lemma 9.7, the image under
$\hat {\mathbf {F}}$
of the left-hand side of Equation (9.21) is the natural endomorphism of the functor
$S \otimes V \otimes -$
given by
$2 \Omega \otimes -$
. When
$N \ge 3$
, we have, from Corollary 4.11,
$$\begin{align*}S \otimes V \cong S \otimes L(\epsilon_1) \cong S \oplus W, \end{align*}$$
where
$$\begin{align*}W = \begin{cases} L \left( \tfrac{3}{2} \epsilon_1 + \tfrac{1}{2} \epsilon_2 + \dotsb + \tfrac{1}{2} \epsilon_n \right) & \text{if } N=2n+1, \\ \operatorname{\mathrm{Ind}} \left( L \left( \tfrac{3}{2} \epsilon_1 + \tfrac{1}{2} \epsilon_2 + \dotsb + \tfrac{1}{2} \epsilon_n \right) \right) & \text{if } N=2n. \end{cases} \end{align*}$$
Then, as in our verification of the first relation in Equation (9.1), we use Equation (9.13) and Lemma 9.6 to compute that
$2 \Omega $
acts on
$S \otimes V$
as
$$\begin{align*}\tfrac{N(N-1)}{8} 1_S + \tfrac{N(N+7)}{8} 1_W - \tfrac{N(N-1)}{8} - (N-1) = 1 - N 1_S. \end{align*}$$
By Lemma 8.7, this is the also the action on
$S \otimes V$
of the image under
$\mathbf {F}$
of the left-hand side of Equation (9.21). The case
$N=2$
is similar. Thus,
$\hat {\mathbf {F}}$
respects the first relation in Equation (9.2). The proof that
$\hat {\mathbf {F}}$
respects the second relation in Equation (9.2) is almost identical.
Relations (9.3). Let U denote either V or S. The image under
$\hat {\mathbf {F}}$
of the left-hand side of relations (9.3) is the natural transformation with components
$U \otimes U \otimes M \to U \otimes U \otimes M$
given by
$$ \begin{align*} u \otimes v \otimes m &\mapsto \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} \left( 2\Phi_U(Xu \otimes X^\vee v) m + 2\Phi_U(Xu \otimes v) X^\vee m + \Phi_U(X X^\vee u, v) m \right) \\ &= -\sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} \left(2\Phi_U(u \otimes Xv) X^\vee m + \Phi_U(u, X X^\vee v) m \right), \end{align*} $$
where the equality follows from Equation (4.25) in the case
$U=S$
and from the definition of
$\mathfrak {so}(V)$
in the case
$U=V$
. Since the last sum above is precisely the image under
$\hat {\mathbf {F}}$
of the right-hand side of relations (9.3), we see that
$\hat {\mathbf {F}}$
preserves these relations.
Relation (9.4). We will show that, for any homomorphism
$f \colon U_1 \otimes U_2 \to W$
of
${\mathrm {G}}(V)$
-modules, we have
$$ \begin{align} \tilde{\Omega} \circ (f \otimes 1) = (f \otimes 1) \circ \big( (1 \otimes \Delta)(\tilde{\Omega}) + (1 \otimes \tilde{\Omega}) \big) \colon U_1 \otimes U_2 \otimes M \to W \otimes M, \end{align} $$
for any
$M \in {\mathrm {G}}(V)\textrm { -mod}$
. Then the fact that
$\hat {\mathbf {F}}$
respects Equation (9.4) follows from taking
$f = \tau $
, given by Equation (6.7). To prove Equation (9.22), we compute
$$ \begin{align*} \tilde{\Omega} \circ &(f \otimes 1)(u_1 \otimes u_2 \otimes m) = \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} \left( 2Xf(u_1 \otimes u_2) \otimes X^\vee m + X X^\vee f(u_1 \otimes u_2) \otimes m \right) \\ &\begin{aligned} = (f \otimes 1) \sum_{X \in \mathbf{B}_{\mathfrak{so}(V)}} \left( 2Xu_1 \otimes u_2 \otimes X^\vee m + 2u_1 \otimes Xu_2 \otimes X^\vee m + XX^\vee u_1 \otimes u_2 \otimes m \right. \\ \left. + 2Xu_1 \otimes X^\vee u_2 \otimes m + u_1 \otimes XX^\vee u_2 \otimes m \right) \end{aligned} \\ &= (f \otimes 1) \circ \big( (1 \otimes \Delta)(\tilde{\Omega}) + (1 \otimes \tilde{\Omega}) \big) (u_1 \otimes u_2 \otimes m), \end{align*} $$
proving Equation (9.22).
Remark 9.9. Although we assumed above that
$N \ge 2$
, one can define the affine incarnation functor for
$N=0$
and
$N=1$
. In these cases, the functor is defined as in Theorem 9.8, except that both dots are sent to the zero natural transformation.
Remark 9.10. Replacing
$\mathbf {F}$
by the functor
$\mathbf {F}' \colon \mathscr {SB}(V) \to \mathfrak {so}(V)\textrm { -mod}$
of Remark 8.2, we can define an affine version
$\hat {\mathbf {F}}' \colon \mathscr {ASB}(V) \to \mathscr {End}_\Bbbk (\mathfrak {so}(V)\textrm { -Mod})$
of that functor, defined in the same way as
$\hat {\mathbf {F}}$
. Here, we choose to work with the category
$\mathfrak {so}(V)\textrm { -Mod}$
of all
$\mathfrak {so}(V)$
-modules (as opposed to just finite-dimensional ones) for reasons that will be become apparent in Section 10.
10 Central elements
We assume throughout this section that
$\Bbbk = \mathbb {C}$
. Let
$\mathfrak {g}=\mathfrak {so}(V)$
and let
$Z(\mathfrak {g})$
be the centre of its universal enveloping algebra
$U(\mathfrak {g})$
. This centre is identified with the endomorphism algebra of the identity functor
$\operatorname {\mathrm {Id}}_{\mathfrak {g}\textrm { -Mod}}$
. Precisely, evaluation on the identity element of the regular representation of
$U(\mathfrak {g})$
defines a canonical algebra isomorphism
$\operatorname {\mathrm {End}}(\operatorname {\mathrm {Id}}_{\mathfrak {g}\textrm { -Mod}}) \xrightarrow {\cong } Z(\mathfrak {g})$
. (It is here that we need to consider all
$\mathfrak {so}(V)$
-modules, not just finite-dimensional ones; see Remark 9.10.) It follows that the affine incarnation functor
$$\begin{align*}\hat{\mathbf{F}}' \colon \mathscr{ASB}(V) \to \mathscr{End}_{\mathbb{C}}(\mathfrak{g}\textrm{ -Mod}) \end{align*}$$
of Remark 9.10 induces a homomorphism
The goal of this section is to describe the image of
$\chi $
. We will prove the following result.
Theorem 10.1. The image of
$\chi $
is equal to
$Z(\mathfrak {g})^{{\mathrm {G}}(V)}$
.
We first entertain a discussion of the structure of
$Z(\mathfrak {g})$
, which is given by the Harish-Chandra isomorphism. Recall that, for
$\lambda \in X^\ast (H)^+$
,
$L(\lambda )$
is the simple highest-weight
$\mathfrak {g}$
-module with highest weight
$\lambda $
. By Schur’s lemma, any
$z \in Z(\mathfrak {g})$
acts on
$L(\lambda )$
by a scalar. The Harish-Chandra isomorphism is an isomorphism of algebras
$$\begin{align*}\Gamma \colon Z(\mathfrak{g})\to \mathbb{C}[\mathfrak{h}^\ast]^W, \qquad z\mapsto (f_z:\mathfrak{h}^\ast\to \mathbb{C}), \end{align*}$$
where W is the Weyl group, uniquely characterised by the identity
$$\begin{align*}z v = f_z(\lambda+\rho) v, \end{align*}$$
for all
$z\in Z(\mathfrak {g})$
and
$v\in L(\lambda )$
. The Harish-Chandra isomorphism
$\Gamma $
is equivariant with respect to the natural actions of
${\mathrm {G}}(V)$
on both sides by conjugation. Since
$\mathrm {Spin}(V)$
acts trivially on
$Z(\mathfrak {g})$
, we have, by Proposition 4.4,
$$ \begin{align} Z(\mathfrak{g})^{{\mathrm{G}}(V)} = \begin{cases} Z(\mathfrak{g}) & \text{if } N \in 2\mathbb{N} + 1, \\ Z(\mathfrak{g})^P & \text{if } N \in 2\mathbb{N}, \end{cases} \end{align} $$
where P is as in Equation (4.7).
To simplify notation, we define
$x_i = A_{ii}$
for
$1 \le i \le n$
, where
$A_{ii}$
is defined as in Equations (3.4) and (3.8). If N is odd, then
$W=C_2^n \rtimes \mathfrak {S}_n$
and
$$\begin{align*}Z(\mathfrak{g})^{{\mathrm{G}}(V)} \overset{(10.1)}{=} Z(\mathfrak{g}) \cong \mathbb{C}[\mathfrak{h}^\ast]^W \cong \mathbb{C}[x_1,x_2,\dotsc,x_n]^{C_2^n \rtimes \mathfrak{S}_n}=\mathbb{C}[x_1^2,x_2^2,\dotsc,x_n^2]^{\mathfrak{S}_n}, \end{align*}$$
the ring of symmetric polynomials in
$x_1^2,x_2^2,\dotsc ,x_n^2$
. (Here
$C_2$
is the cyclic group on two elements.)
If N is even, then the action of
${\mathrm {G}}(V)$
on
$Z(\mathfrak {g})$
is no longer trivial; see Equation (4.13). Here the action of the component group of
${\mathrm {G}}(V)$
precisely compensates for the difference between the type B and type D Weyl groups. More precisely, we have
$$\begin{align*}Z(\mathfrak{g})^{{\mathrm{G}}(V)} \cong (\mathbb{C}[\mathfrak{h}^\ast]^W)^P \cong \mathbb{C}[x_1,x_2,\dotsc,x_n]^{C_2^n \rtimes \mathfrak{S}_n} = \mathbb{C}[x_1^2,x_2^2,\dotsc,x_n^2]^{\mathfrak{S}_n}, \end{align*}$$
where the first isomorphism arises from Equation (10.1) and the Harish-Chandra isomorphism, while the second isomorphism follows from the fact that W and
$\pi _0({\mathrm {G}}(V))$
generate the action of
$C_2^n \rtimes \mathfrak {S}_n$
, using Equation (4.13). So, in either case, we have the isomorphism
$$ \begin{align} Z(\mathfrak{g})^{{\mathrm{G}}(V)} \cong \mathbb{C}[x_1^2,x_2^2,\dotsc,x_n^2]^{\mathfrak{S}_n}. \end{align} $$
Define
Proposition 10.2. For each
$r \in \mathbb {N}$
,
$$\begin{align*}f_{z_r} \in (-1)^{\binom{n}{2}+nN} \sum_{\varsigma_1,\dotsc,\varsigma_n\in \{\pm 1\}} \left(\sum_{i=1}^n \varsigma_i x_i \right)^r + \mathbb{C}[\mathfrak{h}^\ast]_{<r}, \end{align*}$$
where
$\mathbb {C}[\mathfrak {h}^\ast ]_{<r}$
denotes the space of polynomial functions on
$\mathfrak {h}^\ast $
of degree strictly less than r.
Proof. Let v be a highest-weight vector of
$L(\lambda -\rho )$
, and let 
,
$I \subseteq [n]$
, be the right dual basis to
$x_I$
,
$I \subseteq [n]$
, defined by 
. Note that
Unravelling the definition of 
, we get
Note that
$$\begin{align*}\tilde{\Omega}=2\sum_{i=1}^n A_{ii}\otimes A_{ii} + \sum_{\alpha \in\Phi} X_\alpha \otimes Y_\alpha+C\otimes 1, \end{align*}$$
for some
$X_\alpha \in \mathfrak {g}_\alpha $
,
$Y_\alpha \in \mathfrak {g}_{-\alpha }$
, where
$\Phi $
is the set of roots of
$\mathfrak {g}$
Write
$\tilde {\Omega }^r$
in the form
$\tilde {\Omega }^r=\sum _j A_j\otimes B_j$
, where each term
$B_j$
is a monomial in a Poincaré–Birkhoff–Witt (PBW) basis of
$U(\mathfrak {g})\cong U(\mathfrak {n}^-)\otimes U(\mathfrak {h})\otimes U(\mathfrak {n}^+)$
. The terms with degree equal to r that give a nonzero contribution to Equation (10.5) are exactly the monomials involving only elements of
$\mathfrak {h}$
, and for these monomials, we compute
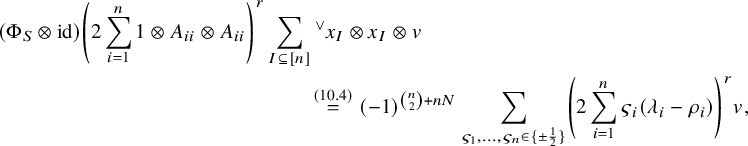
which is equal to
$(-1)^{\binom {n}{2}+nN} \sum _{\varsigma _1,\dotsc ,\varsigma _n\in \{\pm 1\}} \left (\sum _{i=1}^n \varsigma _i \lambda _i \right )^r$
modulo terms of degree strictly less than r in the
$\lambda _i$
. The remaining terms that give a nonzero contribution all have degree less than r, and so lie in
$\mathbb {C}[\mathfrak {h}^\ast ]_{<r}$
.
We pause to introduce some symmetric functions notation. Let
$\Lambda $
denote the ring of symmetric functions with coefficients in
$\mathbb {Q}$
. We use
$p_r$
and
$h_r$
to denote the power sum and complete symmetric functions, respectively, and
$\langle \cdot ,\cdot \rangle $
to denote the Hall inner product. Let
$m_\pi $
denote the monomial symmetric function associated to a partition
$\pi $
. Given a partition
$\pi =1^{m_1} 2^{m_2} \cdots $
, we define
$\delta (\pi )=(m_1,m_2,\dotsc )$
. This is a composition of the length,
$\ell (\pi )$
, of
$\pi $
.
For
$r \in \mathbb {N}$
, define the symmetric polynomial
$$ \begin{align} W_r(x_1,x_2,\dotsc,x_n) = \frac{1}{2^n} \sum_{\varsigma_1,\dotsc,\varsigma_n\in \{\pm 1\}} \left( \sum_{i=1}^n \varsigma_i \sqrt{x_i} \right)^{2r}. \end{align} $$
Taking the inverse limit over n, these define a symmetric function
$W_r \in \Lambda $
. In terms of the monomial symmetric functions, we have the expansion
$$ \begin{align} W_r= \sum_{\pi\vdash r} \binom{2r}{2\pi} m_{\pi}, \end{align} $$
where
$\binom {2r}{2\pi }$
is a multinomial coefficient and
$2\pi $
denotes the partition obtained from
$\pi $
by multiplying all parts by
$2$
.
Proposition 10.3. Let
$B_{2r}$
denote the
$(2r)$
-th Bernoulli number. Then
$$\begin{align*}\langle W_r, p_r\rangle = -2^{2r-1}(2^{2r}-1)B_{2r} \qquad \text{for all } r \in \mathbb{N}. \end{align*}$$
Proof. Begin with the generating function identity
$$\begin{align*}\sum_{k=1}^\infty \frac{p_k}{k}t^k = \log \left( \sum_{j=0}^\infty h_j t^j \right) = \sum_{m=0}^\infty \frac{(-1)^m}{m}\left( \sum_{j=1}^\infty h_j t^j \right)^m, \end{align*}$$
and expand it to obtain
$$\begin{align*}\frac{-p_r}{r} = \sum_{\pi\vdash r} \binom{\ell(\pi)}{\delta(\pi)} \frac{(-1)^{\ell(\pi)}}{\ell(\pi)} h_\pi, \end{align*}$$
where, again,
$\binom {\ell (\pi )}{\delta (\pi )}$
is a multinomial coefficient. Since the complete symmetric functions are dual to the monomial symmetric functions, this implies that
$$\begin{align*}\frac{-1}{r}\langle p_r,m_\pi\rangle = {\ell(\pi) \choose \delta(\pi)} \frac{(-1)^{\ell(\pi)}}{\ell(\pi)}. \end{align*}$$
The above equation, together with Equation (10.7), implies that
$$ \begin{align} \frac{-1}{r}\langle W_r,p_r\rangle = \sum_{\pi\vdash r} \binom{2r}{2\pi}{\ell(\pi) \choose \delta(\pi)} \frac{(-1)^{\ell(\pi)}}{\ell(\pi)}. \end{align} $$
We now compute
$$ \begin{align*} \log(\cosh(x)) = \log\left(1+\sum_{n=1}^\infty \frac{x^{2n}}{(2n)!}\right) &= \sum_{m=1}^\infty \frac{(-1)^m}{m}\left( \sum_{n=1}^\infty \frac{x^{2n}}{(2n)!} \right)^m \\ &\qquad \ = \sum_{m=1}^\infty \frac{(-1)^m}{m} \sum_{n_1,\dotsc,n_m=1}^\infty \frac{x^{2(n_1+\dotsb+n_m)}}{(2n_1)!(2n_2)!\dotsm(2n_m)!}. \end{align*} $$
Collect all terms with the same multiset
$\{n_1,n_2,\ldots ,n_m\}$
to make the inner sum into a sum over all partitions of length m, and we get
$$\begin{align*}\log(\cosh(x)) = \sum_{m=1}^\infty \frac{(-1)^m}{m} \sum_{\ell(\pi)=m} \binom{m}{\delta(\pi)} \frac{x^{2|\pi|}}{(2\pi_1)!\cdots (2\pi_m)!} = \sum_{r=1}^\infty \sum_{\pi \vdash r} \binom{2r}{2\pi} \binom{\ell(\pi)}{\delta(\pi)} \frac{(-1)^{\ell(\pi)}}{\ell(\pi)} \frac{x^{2r}}{(2r)!}. \end{align*}$$
Comparing this with Equation (10.8), we obtain
$$\begin{align*}\sum_{r=1}^\infty \frac{-1}{r}\langle W_r,p_r\rangle \frac{x^{2r}}{(2r)!} = \log(\cosh(x)). \end{align*}$$
Differentiating with respect to x gives
$$\begin{align*}\sum_{r=1}^\infty \frac{-2}{(2r)!} \langle W_r, p_r \rangle x^{2r-1} = \tanh(x) = \sum_{r=1}^\infty \frac{ 2^{2r}(2^{2r}-1)B_{2r}}{(2r)!} x^{2r-1}. \end{align*}$$
Comparing the coefficients of
$x^{2r-1}$
gives the desired result.
We use the following criterion for determining generators for
$\Lambda $
.
Proposition 10.4. Let
$q_1,q_2,\dotsc $
be elements of
$\Lambda $
with
$q_i$
of degree i and such that
$\langle q_i, p_i \rangle \neq 0$
for all i. Then the
$q_i$
are algebraically independent and generate
$\Lambda $
.
Proof. Let
$\Lambda ' = \mathbb {Q}[q_1',q_2',\dotsc ]$
be the polynomial algebra on indeterminates
$q_1',q_2',\dotsc $
, and consider the algebra homomorphism
$$\begin{align*}\alpha \colon \Lambda' \to \Lambda,\qquad q_i' \mapsto q_i,\quad i \ge 1. \end{align*}$$
Write
$\Lambda _r$
for the r-th graded piece of
$\Lambda $
, and let
$X_r$
be the subspace of
$\Lambda _r$
spanned by all products of terms of lower degrees. Define
$\Lambda _r'$
and
$X_r'$
similarly. It suffices to show that the induced map
$\alpha _r \colon \Lambda _r' \to \Lambda _r$
is an isomorphism for all
$r \in \mathbb {N}$
. We prove this by induction. The base case
$r=0$
is trivial.
Now, suppose
$r \ge 1$
. Since
$\Lambda \cong \mathbb {Q}[h_1,h_2,\dotsc ]$
, we know that
$X_r$
is of codimension 1 in
$\Lambda _r$
. If
$a,b \in \Lambda $
are of positive degree, then
$\langle ab,p_r\rangle = \langle a\otimes b, p_r\otimes 1+1\otimes p_r\rangle = 0$
. Therefore,
$\langle X_r, p_r \rangle = 0$
. In particular,
$q_r\notin X_r$
and, since
$X_r$
is of codimension 1 in
$\Lambda _r$
, this implies that
$\Lambda _r$
is spanned by
$X_r$
and
$q_r$
. Thus,
$\alpha _r$
is surjective. Since
$X_r$
and
$X_r'$
have the same dimension, it follows that
$\alpha _r$
is an isomorphism, as desired.
Corollary 10.5. The symmetric functions
$W_r$
,
$r \ge 1$
, are algebraically independent and generate
$\Lambda $
.
Proof. This follows from Propositions 10.3 and 10.4 and the fact that the even Bernoulli numbers are nonzero.
We can now prove Theorem 10.1.
Proof of Theorem 10.1.
We first show that the image of
$\chi $
lies in
$Z(\mathfrak {g})^{{\mathrm {G}}(V)}$
. By Equation (10.1), it suffices to consider the case where N is even. Let 
. We must show that
$(\Gamma \circ \chi )(a) \in (\mathbb {C}[\mathfrak {h}^\ast ]^W)^P$
. By Proposition 4.4, it suffices to show that
$$ \begin{align} (\Gamma \circ \chi)(a)(\lambda) = (\Gamma \circ \chi)(a)(\tilde{\lambda}) \end{align} $$
for all
$\lambda \in \mathfrak {h}^\ast $
, where
$\tilde {\lambda }$
is defined as in Equation (4.10). In fact, since the set of dominant integral
$\lambda $
for which
$\tilde {\lambda } \ne \lambda $
is Zariski dense in
$\mathfrak {h}$
*, it suffices to prove that Equation (10.9) holds for all such
$\lambda $
.
Suppose that
$\lambda $
is a dominant integral weight satisfying
$\tilde {\lambda } \neq \lambda $
. Then
$\operatorname {\mathrm {Ind}}(L(\lambda ))$
is a simple
$\mathrm {Pin}(V)$
-module by Proposition 4.2, and so
$\hat {\mathbf {F}}(a)$
acts on it by a scalar. The action of
$\hat {\mathbf {F}}(a)$
on
$\operatorname {\mathrm {Ind}}(L(\lambda ))$
is the same as the action of
$\hat {\mathbf {F}}'(a)$
on
$\operatorname {\mathrm {Res}} \circ \operatorname {\mathrm {Ind}}(L(\lambda ))\cong L(\lambda )\oplus L(\tilde {\lambda })$
. Therefore, Equation (10.9) holds, as desired.
It remains to prove that
$\chi $
surjects onto
$Z(\mathfrak {g})^{{\mathrm {G}}(V)}$
. But this follows from Proposition 10.2, Corollary 10.5 and the isomorphism (10.2).
Corollary 10.6. The elements
are algebraically independent.
Proof. This follows immediately from the fact that their images under
$\chi $
are algebraically independent by Proposition 10.2 and Corollary 10.5.
Given their role above, it would be interesting to further study the symmetric functions
$W_r$
. Recall that a symmetric function is Schur-positive if, when written as a linear combination of Schur functions, all coefficients are nonnegative. Computer computations suggest the following conjecture.
Conjecture 10.7. The symmetric functions
$W_r$
are Schur-positive.
Acknowledgements
A.S. is grateful for the support and hospitality of the Sydney Mathematical Research Institute (SMRI). The authors thank Elijah Bodish, Ben Webster and Geordie Williamson for helpful discussions. Several ideas in this paper were also influenced by [Reference DeligneDel].
Competing interest
The authors have no competing interest to declare.
Financial support
The research of P.M. was supported by Australian Research Council grant DE150101415. The research of A.S. was supported by Discovery Grant RGPIN-2023-03842 from the Natural Sciences and Engineering Research Council of Canada.
Open access
