No CrossRef data available.
Published online by Cambridge University Press: 13 December 2023
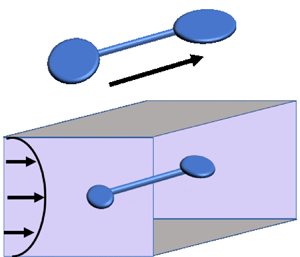
Considerable effort has been directed towards the characterization of chiral mesoscale structures, as shown in chiral protein assemblies and carbon nanotubes. Here, we establish a thermally driven hydrodynamic description for the actuation and separation of mesoscale chiral structures in a fluid medium. Cross-flow of a Newtonian liquid with a thermal gradient gives rise to an effective torque that propels each particle of a chiral suspension according to its handedness. In turn, the chiral suspension alters the liquid flow, which thus acquires a transverse (chiral) velocity component. Since observation of the predicted effects requires a low degree of sophistication, our work provides an efficient and inexpensive approach to test and calibrate chiral particle propulsion and separation strategies.