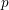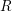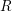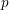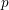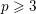1 Introduction
Let
![]() $p$
be a prime. A semiperfect ring is an
$p$
be a prime. A semiperfect ring is an
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $R$
such that the Frobenius endomorphism
$R$
such that the Frobenius endomorphism
![]() $\unicode[STIX]{x1D719}_{R}:R\rightarrow R$
is surjective. In the first part of this article we study the classification of
$\unicode[STIX]{x1D719}_{R}:R\rightarrow R$
is surjective. In the first part of this article we study the classification of
![]() $p$
-divisible groups over semiperfect rings by Dieudonné crystals and related objects. This was initiated in [Reference Scholze and WeinsteinSW13]. In the second part we draw conclusions for perfectoid rings.
$p$
-divisible groups over semiperfect rings by Dieudonné crystals and related objects. This was initiated in [Reference Scholze and WeinsteinSW13]. In the second part we draw conclusions for perfectoid rings.
1.1 Crystalline Dieudonné windows
Every semiperfect ring
![]() $R$
has a universal
$R$
has a universal
![]() $p$
-adic divided power extension
$p$
-adic divided power extension
![]() $A_{\operatorname{cris}}(R)$
. By a lemma of [Reference Scholze and WeinsteinSW13], this ring carries a natural structure of a frame
$A_{\operatorname{cris}}(R)$
. By a lemma of [Reference Scholze and WeinsteinSW13], this ring carries a natural structure of a frame
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)$
, which means that the Frobenius of
$\text{}\underline{A}_{\operatorname{cris}}(R)$
, which means that the Frobenius of
![]() $A_{\operatorname{cris}}(R)$
is divided by
$A_{\operatorname{cris}}(R)$
is divided by
![]() $p$
on the kernel of
$p$
on the kernel of
![]() $A_{\operatorname{cris}}(R)\rightarrow R$
. This is not clear a priori because in general
$A_{\operatorname{cris}}(R)\rightarrow R$
. This is not clear a priori because in general
![]() $A_{\operatorname{cris}}(R)$
has
$A_{\operatorname{cris}}(R)$
has
![]() $p$
-torsion.
$p$
-torsion.
The following result has been suggested in [Reference Scholze and WeinsteinSW13].
Theorem 1.1. Let
![]() $R$
be a semiperfect ring. There is a natural functor
$R$
be a semiperfect ring. There is a natural functor
from
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $R$
to windows over
$R$
to windows over
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)$
, such that the underlying module of
$\text{}\underline{A}_{\operatorname{cris}}(R)$
, such that the underlying module of
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)$
is given by the Dieudonné crystal of
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)$
is given by the Dieudonné crystal of
![]() $G$
.
$G$
.
See Theorem 6.3. The functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is a variant of the functor
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is a variant of the functor
![]() $\unicode[STIX]{x1D6F7}_{R}$
of [Reference LauLau13] from
$\unicode[STIX]{x1D6F7}_{R}$
of [Reference LauLau13] from
![]() $p$
-divisible groups to displays for an arbitrary
$p$
-divisible groups to displays for an arbitrary
![]() $p$
-adic ring
$p$
-adic ring
![]() $R$
, and of the functor
$R$
, and of the functor
![]() $\unicode[STIX]{x1D6F7}_{R}$
of [Reference LauLau14] from
$\unicode[STIX]{x1D6F7}_{R}$
of [Reference LauLau14] from
![]() $p$
-divisible groups to Dieudonné displays for a local Artin ring
$p$
-divisible groups to Dieudonné displays for a local Artin ring
![]() $R$
with perfect residue field.
$R$
with perfect residue field.
Our main result on the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
depends on the following boundedness condition. We call
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
depends on the following boundedness condition. We call
![]() $R$
balanced if
$R$
balanced if
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719}_{R})^{p}=0$
, and we call
$\operatorname{Ker}(\unicode[STIX]{x1D719}_{R})^{p}=0$
, and we call
![]() $R$
iso-balanced if there is a nilpotent ideal
$R$
iso-balanced if there is a nilpotent ideal
![]() $\mathfrak{a}\subseteq R$
such that
$\mathfrak{a}\subseteq R$
such that
![]() $R/\mathfrak{a}$
is balanced. Every
$R/\mathfrak{a}$
is balanced. Every
![]() $f$
-semiperfect ring in the sense of [Reference Scholze and WeinsteinSW13] is iso-balanced.
$f$
-semiperfect ring in the sense of [Reference Scholze and WeinsteinSW13] is iso-balanced.
Theorem 1.2. If
![]() $R$
is iso-balanced, the functor
$R$
is iso-balanced, the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.
See Theorem 7.10. Theorem 1.2 implies that for iso-balanced semiperfect rings the crystalline Dieudonné functor
is fully faithful up to isogeny. When
![]() $R$
is
$R$
is
![]() $f$
-semiperfect, this is proved in [Reference Scholze and WeinsteinSW13] using perfectoid spaces.
$f$
-semiperfect, this is proved in [Reference Scholze and WeinsteinSW13] using perfectoid spaces.
Assume that
![]() $R$
is a complete intersection in the sense that
$R$
is a complete intersection in the sense that
![]() $R$
is the quotient of a perfect ring by a regular sequence. Then
$R$
is the quotient of a perfect ring by a regular sequence. Then
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free, and windows over
$p$
-torsion free, and windows over
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)$
are equivalent to Dieudonné crystals over
$\text{}\underline{A}_{\operatorname{cris}}(R)$
are equivalent to Dieudonné crystals over
![]() $\operatorname{Spec}R$
with an admissible filtration in the sense of [Reference GrothendieckGro74]; this filtration is unique if it exists. Thus for complete intersections, Theorem 1.2 means that the functor
$\operatorname{Spec}R$
with an admissible filtration in the sense of [Reference GrothendieckGro74]; this filtration is unique if it exists. Thus for complete intersections, Theorem 1.2 means that the functor
![]() $\mathbb{D}_{R}$
is fully faithful and that its essential image consists of those Dieudonné crystals which admit an admissible filtration. Full faithfulness is already proved in [Reference Scholze and WeinsteinSW13] as an easy consequence of full faithfulness up to isogeny.
$\mathbb{D}_{R}$
is fully faithful and that its essential image consists of those Dieudonné crystals which admit an admissible filtration. Full faithfulness is already proved in [Reference Scholze and WeinsteinSW13] as an easy consequence of full faithfulness up to isogeny.
For a general semiperfect ring,
![]() $A_{\operatorname{cris}}(R)$
can have
$A_{\operatorname{cris}}(R)$
can have
![]() $p$
-torsion, and the functor
$p$
-torsion, and the functor
![]() $\mathbb{D}_{R}$
cannot be expected to be fully faithful. The phenomenon that passing from Dieudonné modules to windows can compensate for this failure is familiar from the classification of formal
$\mathbb{D}_{R}$
cannot be expected to be fully faithful. The phenomenon that passing from Dieudonné modules to windows can compensate for this failure is familiar from the classification of formal
![]() $p$
-divisible groups over arbitrary
$p$
-divisible groups over arbitrary
![]() $p$
-adic rings by nilpotent displays, and from the classification of arbitrary
$p$
-adic rings by nilpotent displays, and from the classification of arbitrary
![]() $p$
-divisible groups over local Artin rings by Dieudonné displays.
$p$
-divisible groups over local Artin rings by Dieudonné displays.
1.2 Dieudonné modules via lifts
The proof of Theorem 1.2 relies on another construction of Dieudonné modules, which is independent of the functors
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
. A lift of an
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
. A lift of an
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $R$
is a
$R$
is a
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free ring
$p$
-torsion free ring
![]() $A$
with
$A$
with
![]() $A/pA=R$
and with a Frobenius lift
$A/pA=R$
and with a Frobenius lift
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
. Then there is an evident frame structure
$\unicode[STIX]{x1D70E}:A\rightarrow A$
. Then there is an evident frame structure
![]() $\text{}\underline{A}$
and a functor
$\text{}\underline{A}$
and a functor
Here
![]() $\text{}\underline{A}$
-windows are equivalent to locally free Dieudonné modules over
$\text{}\underline{A}$
-windows are equivalent to locally free Dieudonné modules over
![]() $A$
in the usual sense. The functor
$A$
in the usual sense. The functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
also induces a functor
$\unicode[STIX]{x1D6F7}_{A}$
also induces a functor
![]() $\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}$
from commutative finite locally free
$\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}$
from commutative finite locally free
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $R$
to
$R$
to
![]() $p$
-torsion Dieudonné modules over
$p$
-torsion Dieudonné modules over
![]() $A$
which are of projective dimension less than or equal to
$A$
which are of projective dimension less than or equal to
![]() $1$
as
$1$
as
![]() $A$
-modules. In general the properties of
$A$
-modules. In general the properties of
![]() $\unicode[STIX]{x1D6F7}_{A}$
depend on the lift.
$\unicode[STIX]{x1D6F7}_{A}$
depend on the lift.
Theorem 1.3. If
![]() $R$
is a complete intersection or balanced semiperfect ring, there is a lift
$R$
is a complete intersection or balanced semiperfect ring, there is a lift
![]() $A$
of
$A$
of
![]() $R$
such that the functors
$R$
such that the functors
![]() $\unicode[STIX]{x1D6F7}_{A}$
and
$\unicode[STIX]{x1D6F7}_{A}$
and
![]() $\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}$
are equivalences.
$\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}$
are equivalences.
See Theorem 5.7 and Corollary 10.14. When
![]() $R$
is perfect, then
$R$
is perfect, then
![]() $A=W(R)$
is the unique lift of
$A=W(R)$
is the unique lift of
![]() $R$
, and Theorem 1.3 holds by a result of Gabber. The general case is reduced to the perfect case by a specialization argument along
$R$
, and Theorem 1.3 holds by a result of Gabber. The general case is reduced to the perfect case by a specialization argument along
![]() $R^{\flat }\rightarrow R$
, where
$R^{\flat }\rightarrow R$
, where
![]() $R^{\flat }$
is the limit perfection of
$R^{\flat }$
is the limit perfection of
![]() $R$
.
$R$
.
We note that for an arbitrary
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $R$
with a lift
$R$
with a lift
![]() $(A,\unicode[STIX]{x1D70E})$
the functor
$(A,\unicode[STIX]{x1D70E})$
the functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
gives an equivalence between formal
$\unicode[STIX]{x1D6F7}_{A}$
gives an equivalence between formal
![]() $p$
-divisible groups and nilpotent windows by [Reference ZinkZin01] and the extensions of [Reference ZinkZin02] provided by [Reference LauLau08, Reference LauLau13]. So the new aspect of Theorem 1.3 is that it applies to all
$p$
-divisible groups and nilpotent windows by [Reference ZinkZin01] and the extensions of [Reference ZinkZin02] provided by [Reference LauLau08, Reference LauLau13]. So the new aspect of Theorem 1.3 is that it applies to all
![]() $p$
-divisible groups.
$p$
-divisible groups.
The functors
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
and
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
and
![]() $\unicode[STIX]{x1D6F7}_{A}$
are related as follows. For every lift
$\unicode[STIX]{x1D6F7}_{A}$
are related as follows. For every lift
![]() $A$
of a semiperfect ring
$A$
of a semiperfect ring
![]() $R$
there is a natural homomorphism of frames
$R$
there is a natural homomorphism of frames
and the base change under
![]() $\unicode[STIX]{x1D718}$
of
$\unicode[STIX]{x1D718}$
of
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)$
coincides with
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)$
coincides with
![]() $\unicode[STIX]{x1D6F7}_{A}(G)$
.
$\unicode[STIX]{x1D6F7}_{A}(G)$
.
Lemma 1.4. If
![]() $R$
is a complete intersection or balanced semiperfect ring, there is a lift
$R$
is a complete intersection or balanced semiperfect ring, there is a lift
![]() $A$
of
$A$
of
![]() $R$
as in Theorem 1.3 such that
$R$
as in Theorem 1.3 such that
![]() $\unicode[STIX]{x1D718}$
induces an equivalence of the window categories.
$\unicode[STIX]{x1D718}$
induces an equivalence of the window categories.
See Proposition 5.10. Theorem 1.3 and Lemma 1.4 give Theorem 1.2 when
![]() $R$
is balanced or a complete intersection, and the general case follows by a deformation argument, using a weak version of lifts for iso-balanced rings, for which an analogue of Lemma 1.4 holds; see Proposition 7.8.
$R$
is balanced or a complete intersection, and the general case follows by a deformation argument, using a weak version of lifts for iso-balanced rings, for which an analogue of Lemma 1.4 holds; see Proposition 7.8.
1.3 Breuil–Kisin–Fargues modules
Now let
![]() $R$
be a perfectoid ring in the sense of [Reference Bhatt, Morrow and ScholzeBMS16]. This class of rings includes all perfect rings and all bounded open integrally closed subrings of perfectoid Tate rings in the sense of [Reference FontaineFon13]. Let
$R$
be a perfectoid ring in the sense of [Reference Bhatt, Morrow and ScholzeBMS16]. This class of rings includes all perfect rings and all bounded open integrally closed subrings of perfectoid Tate rings in the sense of [Reference FontaineFon13]. Let
![]() $R^{\flat }$
be the tilt of
$R^{\flat }$
be the tilt of
![]() $R$
, which is a perfect ring, and
$R$
, which is a perfect ring, and
![]() $A_{\inf }=W(R^{\flat })$
.
$A_{\inf }=W(R^{\flat })$
.
The kernel of the natural homomorphism
![]() $\unicode[STIX]{x1D703}:A_{\inf }\rightarrow R$
is generated by a non-zero divisor
$\unicode[STIX]{x1D703}:A_{\inf }\rightarrow R$
is generated by a non-zero divisor
![]() $\unicode[STIX]{x1D709}$
. In the following, a Breuil–Kisin–Fargues module for
$\unicode[STIX]{x1D709}$
. In the following, a Breuil–Kisin–Fargues module for
![]() $R$
is a finite projective
$R$
is a finite projective
![]() $A_{\inf }$
-module
$A_{\inf }$
-module
![]() $\mathfrak{M}$
with a linear map
$\mathfrak{M}$
with a linear map
![]() $\unicode[STIX]{x1D711}:\mathfrak{M}^{\unicode[STIX]{x1D70E}}\rightarrow \mathfrak{M}$
whose cokernel is annihilated by
$\unicode[STIX]{x1D711}:\mathfrak{M}^{\unicode[STIX]{x1D70E}}\rightarrow \mathfrak{M}$
whose cokernel is annihilated by
![]() $\unicode[STIX]{x1D709}$
.Footnote
1
As an application of Theorem 1.2 we obtain the following result.Footnote
2
$\unicode[STIX]{x1D709}$
.Footnote
1
As an application of Theorem 1.2 we obtain the following result.Footnote
2
Theorem 1.5. If
![]() $p\geqslant 3$
, for each perfectoid ring
$p\geqslant 3$
, for each perfectoid ring
![]() $R$
the category
$R$
the category
![]() $\operatorname{BT}(\operatorname{Spec}R)$
is equivalent to the category of Breuil–Kisin–Fargues modules for
$\operatorname{BT}(\operatorname{Spec}R)$
is equivalent to the category of Breuil–Kisin–Fargues modules for
![]() $R$
.
$R$
.
See Theorem 9.8. When
![]() $R={\mathcal{O}}_{C}$
for an algebraically closed perfectoid field
$R={\mathcal{O}}_{C}$
for an algebraically closed perfectoid field
![]() $C$
, the result is due to Fargues [Reference FarguesFar15, Reference FarguesFar13]. Theorem 1.5 is a variant of the classical equivalence between
$C$
, the result is due to Fargues [Reference FarguesFar15, Reference FarguesFar13]. Theorem 1.5 is a variant of the classical equivalence between
![]() $p$
-divisible groups over a mixed characteristic complete discrete valuation ring with perfect residue field and Breuil–Kisin modules.
$p$
-divisible groups over a mixed characteristic complete discrete valuation ring with perfect residue field and Breuil–Kisin modules.
To prove Theorem 1.5 we consider the ring
![]() $R/p$
, which is semiperfect and balanced. The universal
$R/p$
, which is semiperfect and balanced. The universal
![]() $p$
-adic divided power extension
$p$
-adic divided power extension
![]() $A_{\operatorname{cris}}(R)$
coincides with
$A_{\operatorname{cris}}(R)$
coincides with
![]() $A_{\operatorname{cris}}(R/p)$
as a ring and carries a natural frame structure. The equivalence of Theorem 1.2 for
$A_{\operatorname{cris}}(R/p)$
as a ring and carries a natural frame structure. The equivalence of Theorem 1.2 for
![]() $R/p$
(which is covered by Theorem 1.3 and Lemma 1.4 in this case) extends for
$R/p$
(which is covered by Theorem 1.3 and Lemma 1.4 in this case) extends for
![]() $p\geqslant 3$
to an equivalence
$p\geqslant 3$
to an equivalence
Moreover there is a base change functor
which is an equivalence for
![]() $p\geqslant 3$
by a descent from
$p\geqslant 3$
by a descent from
![]() $A_{\operatorname{cris}}$
to
$A_{\operatorname{cris}}$
to
![]() $A_{\inf }$
that generalizes the ‘descent from
$A_{\inf }$
that generalizes the ‘descent from
![]() $S$
to
$S$
to
![]() $\mathfrak{S}$
’ used in the classical case. Theorem 1.5 follows. One can expect that Theorem 1.5 also holds for
$\mathfrak{S}$
’ used in the classical case. Theorem 1.5 follows. One can expect that Theorem 1.5 also holds for
![]() $p=2$
, but the present proof does not extend to that case directly.
$p=2$
, but the present proof does not extend to that case directly.
As in the classical case, Theorem 1.5 induces a similar result for finite group schemes. Namely, a torsion Breuil–Kisin–Fargues module for
![]() $R$
is a triple
$R$
is a triple
![]() $(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
$(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
![]() $\mathfrak{M}$
is a
$\mathfrak{M}$
is a
![]() $p$
-torsion finitely presented
$p$
-torsion finitely presented
![]() $A_{\inf }$
-module of projective dimension less than or equal to
$A_{\inf }$
-module of projective dimension less than or equal to
![]() $1$
with linear maps
$1$
with linear maps
such that
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D713}\circ (1\otimes \unicode[STIX]{x1D711})$
are the multiplication maps. If
$\unicode[STIX]{x1D713}\circ (1\otimes \unicode[STIX]{x1D711})$
are the multiplication maps. If
![]() $R$
is
$R$
is
![]() $p$
-torsion free then
$p$
-torsion free then
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $\mathfrak{M}$
-regular and
$\mathfrak{M}$
-regular and
![]() $\unicode[STIX]{x1D713}$
is determined by
$\unicode[STIX]{x1D713}$
is determined by
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
Corollary 1.6 (Theorem 10.12).
If
![]() $p\geqslant 3$
, for each perfectoid ring
$p\geqslant 3$
, for each perfectoid ring
![]() $R$
the category of commutative finite locally free
$R$
the category of commutative finite locally free
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $R$
is equivalent to the category of torsion Breuil–Kisin–Fargues modules for
$R$
is equivalent to the category of torsion Breuil–Kisin–Fargues modules for
![]() $R$
.
$R$
.
2 Notation
We fix a prime
![]() $p$
.
$p$
.
An abelian group
![]() $A$
is called
$A$
is called
![]() $p$
-adically complete if
$p$
-adically complete if
![]() $A\cong \mathop{\varprojlim }\nolimits_{n}A/p^{n}A$
.
$A\cong \mathop{\varprojlim }\nolimits_{n}A/p^{n}A$
.
A PD extension is a surjective ring homomorphism whose kernel is equipped with divided powers. A
![]() $p$
-adic PD extension is a PD extension of
$p$
-adic PD extension is a PD extension of
![]() $p$
-adically complete rings such that the divided powers are compatible with the divided powers on
$p$
-adically complete rings such that the divided powers are compatible with the divided powers on
![]() $p\mathbb{Z}_{p}$
. Divided powers
$p\mathbb{Z}_{p}$
. Divided powers
![]() $\unicode[STIX]{x1D6FE}$
are also denoted by
$\unicode[STIX]{x1D6FE}$
are also denoted by
![]() $\unicode[STIX]{x1D6FE}_{n}(x)=x^{[n]}$
.
$\unicode[STIX]{x1D6FE}_{n}(x)=x^{[n]}$
.
Following [Reference LauLau10], a frame
![]() $\text{}\underline{S}\,=\,(S,\operatorname{Fil}S,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
consists of rings
$\text{}\underline{S}\,=\,(S,\operatorname{Fil}S,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
consists of rings
![]() $S$
and
$S$
and
![]() $R\,=\,S/\text{Fil}\,S$
such that
$R\,=\,S/\text{Fil}\,S$
such that
![]() $pS\,+\,\operatorname{Fil}S\,\subseteq \,\operatorname{Rad}S$
, together with a Frobenius lift
$pS\,+\,\operatorname{Fil}S\,\subseteq \,\operatorname{Rad}S$
, together with a Frobenius lift
![]() $\unicode[STIX]{x1D70E}\,:\,S\,\rightarrow \,S$
and a
$\unicode[STIX]{x1D70E}\,:\,S\,\rightarrow \,S$
and a
![]() $\unicode[STIX]{x1D70E}$
-linear map
$\unicode[STIX]{x1D70E}$
-linear map
![]() $\unicode[STIX]{x1D70E}_{1}\,:\,\operatorname{Fil}S\,\rightarrow \,S$
whose image generates the unit ideal.Footnote
3
A window over the frame
$\unicode[STIX]{x1D70E}_{1}\,:\,\operatorname{Fil}S\,\rightarrow \,S$
whose image generates the unit ideal.Footnote
3
A window over the frame
![]() $\text{}\underline{S}$
is a collection
$\text{}\underline{S}$
is a collection
![]() $\text{}\underline{M}=(M,\operatorname{Fil}M,F,F_{1})$
where
$\text{}\underline{M}=(M,\operatorname{Fil}M,F,F_{1})$
where
![]() $M$
is a finite projective
$M$
is a finite projective
![]() $S$
-module,
$S$
-module,
![]() $\operatorname{Fil}M\subseteq M$
is a submodule which takes the form
$\operatorname{Fil}M\subseteq M$
is a submodule which takes the form
![]() $\operatorname{Fil}M=L\oplus (\operatorname{Fil}S)T$
for some decomposition
$\operatorname{Fil}M=L\oplus (\operatorname{Fil}S)T$
for some decomposition
![]() $M=L\oplus T$
, and
$M=L\oplus T$
, and
![]() $F:M\rightarrow M$
and
$F:M\rightarrow M$
and
![]() $F_{1}:\operatorname{Fil}M\rightarrow M$
are
$F_{1}:\operatorname{Fil}M\rightarrow M$
are
![]() $\unicode[STIX]{x1D70E}$
-linear maps such that the image of
$\unicode[STIX]{x1D70E}$
-linear maps such that the image of
![]() $F_{1}$
generates
$F_{1}$
generates
![]() $M$
, and
$M$
, and
![]() $F_{1}(ax)=\unicode[STIX]{x1D70E}_{1}(a)F(x)$
for
$F_{1}(ax)=\unicode[STIX]{x1D70E}_{1}(a)F(x)$
for
![]() $a\in \operatorname{Fil}S$
and
$a\in \operatorname{Fil}S$
and
![]() $x\in M$
. We denote by
$x\in M$
. We denote by
![]() $\operatorname{Win}(\text{}\underline{S})$
the category of windows over
$\operatorname{Win}(\text{}\underline{S})$
the category of windows over
![]() $\text{}\underline{S}$
. A frame homomorphism
$\text{}\underline{S}$
. A frame homomorphism
![]() $\unicode[STIX]{x1D6FC}:\text{}\underline{S}\rightarrow \text{}\underline{S}^{\prime }$
is a ring homomorphism
$\unicode[STIX]{x1D6FC}:\text{}\underline{S}\rightarrow \text{}\underline{S}^{\prime }$
is a ring homomorphism
![]() $S\rightarrow S^{\prime }$
with
$S\rightarrow S^{\prime }$
with
![]() $\operatorname{Fil}S\rightarrow \operatorname{Fil}S^{\prime }$
such that
$\operatorname{Fil}S\rightarrow \operatorname{Fil}S^{\prime }$
such that
![]() $\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}_{1}^{\prime }\unicode[STIX]{x1D6FC}=u\cdot \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{1}$
for a unit
$\unicode[STIX]{x1D70E}_{1}^{\prime }\unicode[STIX]{x1D6FC}=u\cdot \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{1}$
for a unit
![]() $u\in S^{\prime }$
. There is a base change functor
$u\in S^{\prime }$
. There is a base change functor
![]() $\unicode[STIX]{x1D6FC}^{\ast }:\operatorname{Win}(\text{}\underline{S})\rightarrow \operatorname{Win}(\text{}\underline{S}^{\prime })$
. If this functor is an equivalence,
$\unicode[STIX]{x1D6FC}^{\ast }:\operatorname{Win}(\text{}\underline{S})\rightarrow \operatorname{Win}(\text{}\underline{S}^{\prime })$
. If this functor is an equivalence,
![]() $\unicode[STIX]{x1D6FC}$
is called crystalline.
$\unicode[STIX]{x1D6FC}$
is called crystalline.
A frame
![]() $\text{}\underline{S}$
is called a
$\text{}\underline{S}$
is called a
![]() $p$
-frame if
$p$
-frame if
![]() $p\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}$
on
$p\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}$
on
![]() $\operatorname{Fil}S$
, i.e. in the notation of [Reference LauLau10, Lemma 2.2] we have
$\operatorname{Fil}S$
, i.e. in the notation of [Reference LauLau10, Lemma 2.2] we have
![]() $\unicode[STIX]{x1D703}=p$
. A PD frame is a
$\unicode[STIX]{x1D703}=p$
. A PD frame is a
![]() $p$
-frame
$p$
-frame
![]() $\text{}\underline{S}$
where
$\text{}\underline{S}$
where
![]() $S\rightarrow R$
is a
$S\rightarrow R$
is a
![]() $p$
-adic PD extension such that
$p$
-adic PD extension such that
![]() $\unicode[STIX]{x1D70E}$
preserves the resulting divided powers on the ideal
$\unicode[STIX]{x1D70E}$
preserves the resulting divided powers on the ideal
![]() $\operatorname{Fil}S+pS$
. If in addition
$\operatorname{Fil}S+pS$
. If in addition
![]() $S$
is
$S$
is
![]() $p$
-torsion free, then
$p$
-torsion free, then
![]() $(S,\unicode[STIX]{x1D70E})$
is a frame for
$(S,\unicode[STIX]{x1D70E})$
is a frame for
![]() $R$
in the sense of [Reference ZinkZin01].
$R$
in the sense of [Reference ZinkZin01].
3 Dieudonné crystals and modules
In this section we fix notation and recall some standard results.
For a scheme
![]() $X$
on which
$X$
on which
![]() $p$
is nilpotent, or more generally a
$p$
is nilpotent, or more generally a
![]() $p$
-adic formal scheme, let
$p$
-adic formal scheme, let
![]() $\operatorname{BT}(X)$
be the category of
$\operatorname{BT}(X)$
be the category of
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $X$
, let
$X$
, let
![]() $\operatorname{D}(X)$
be the category of locally free Dieudonné crystals over
$\operatorname{D}(X)$
be the category of locally free Dieudonné crystals over
![]() $X$
, and let
$X$
, and let
![]() $\operatorname{DF}(X)$
be the category of locally free Dieudonné crystals
$\operatorname{DF}(X)$
be the category of locally free Dieudonné crystals
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() $X$
equipped with an admissible filtration
$X$
equipped with an admissible filtration
![]() $\operatorname{Fil}{\mathcal{M}}_{X}\subseteq {\mathcal{M}}_{X}$
as in [Reference GrothendieckGro74]; see [Reference Cais and LauCL14, Definition 2.4.1]. Let
$\operatorname{Fil}{\mathcal{M}}_{X}\subseteq {\mathcal{M}}_{X}$
as in [Reference GrothendieckGro74]; see [Reference Cais and LauCL14, Definition 2.4.1]. Let
be the contravariant crystalline Dieudonné functor defined in [Reference Mazur and MessingMM74] and in [Reference Berthelot, Breen and MessingBBM82], and let
be its extension defined by the Hodge filtration; see [Reference Cais and LauCL14, Proposition 2.4.3]. If
![]() $\text{}\underline{S}=(S,\operatorname{Fil}S,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
is a
$\text{}\underline{S}=(S,\operatorname{Fil}S,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
is a
![]() $p$
-torsion free PD frame as in § 2, the evaluation of the filtered Dieudonné crystal at
$p$
-torsion free PD frame as in § 2, the evaluation of the filtered Dieudonné crystal at
![]() $\text{}\underline{S}$
gives a contravariant functor
$\text{}\underline{S}$
gives a contravariant functor
where
![]() $M=\mathbb{D}(G)_{S}$
, the submodule
$M=\mathbb{D}(G)_{S}$
, the submodule
![]() $\operatorname{Fil}M\subseteq M$
is the inverse image of the Hodge filtration
$\operatorname{Fil}M\subseteq M$
is the inverse image of the Hodge filtration
![]() $\operatorname{Lie}(G)^{\ast }\subseteq \mathbb{D}(G)_{R}$
of
$\operatorname{Lie}(G)^{\ast }\subseteq \mathbb{D}(G)_{R}$
of
![]() $G$
,
$G$
,
![]() $F$
is induced by the Frobenius of
$F$
is induced by the Frobenius of
![]() $G$
, and
$G$
, and
![]() $F_{1}=p^{-1}F$
on
$F_{1}=p^{-1}F$
on
![]() $\operatorname{Fil}M$
; see [Reference LauLau14, Proposition 3.17] or [Reference Cais and LauCL14, Proposition 2.5.2].
$\operatorname{Fil}M$
; see [Reference LauLau14, Proposition 3.17] or [Reference Cais and LauCL14, Proposition 2.5.2].
3.1 Explicit Dieudonné modules
Let
![]() $R$
be an
$R$
be an
![]() $\mathbb{F}_{p}$
-algebra. A lift of
$\mathbb{F}_{p}$
-algebra. A lift of
![]() $R$
is a pair
$R$
is a pair
![]() $(A,\unicode[STIX]{x1D70E})$
where
$(A,\unicode[STIX]{x1D70E})$
where
![]() $A$
is a
$A$
is a
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free ring with
$p$
-torsion free ring with
![]() $R=A/pA$
, and
$R=A/pA$
, and
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
is a Frobenius lift.
$\unicode[STIX]{x1D70E}:A\rightarrow A$
is a Frobenius lift.
In the following let
![]() $(A,\unicode[STIX]{x1D70E})$
be a lift of
$(A,\unicode[STIX]{x1D70E})$
be a lift of
![]() $R$
. A (locally free) Dieudonné module over
$R$
. A (locally free) Dieudonné module over
![]() $A$
is a triple
$A$
is a triple
![]() $\text{}\underline{M}=(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
$\text{}\underline{M}=(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
![]() $M$
a finite projective
$M$
a finite projective
![]() $A$
-module and
$A$
-module and
![]() $\unicode[STIX]{x1D711}:M^{\unicode[STIX]{x1D70E}}\rightarrow M$
and
$\unicode[STIX]{x1D711}:M^{\unicode[STIX]{x1D70E}}\rightarrow M$
and
![]() $\unicode[STIX]{x1D713}:M\rightarrow M^{\unicode[STIX]{x1D70E}}$
are linear maps with
$\unicode[STIX]{x1D713}:M\rightarrow M^{\unicode[STIX]{x1D70E}}$
are linear maps with
![]() $\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}=p$
and
$\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}=p$
and
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}=p$
, where
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}=p$
, where
![]() $M^{\unicode[STIX]{x1D70E}}=M\otimes _{A,\unicode[STIX]{x1D70E}}A$
. We write
$M^{\unicode[STIX]{x1D70E}}=M\otimes _{A,\unicode[STIX]{x1D70E}}A$
. We write
![]() $\operatorname{DM}(A)$
for the category of Dieudonné modules over
$\operatorname{DM}(A)$
for the category of Dieudonné modules over
![]() $A$
.
$A$
.
Lemma 3.1. For
![]() $(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in \operatorname{DM}(A)$
the
$(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in \operatorname{DM}(A)$
the
![]() $R$
-module
$R$
-module
![]() $\operatorname{Coker}(\unicode[STIX]{x1D711})$
is projective.
$\operatorname{Coker}(\unicode[STIX]{x1D711})$
is projective.
Proof. Let
![]() $\bar{M}=M\otimes _{A}R$
. There is an exact sequence of finite projective
$\bar{M}=M\otimes _{A}R$
. There is an exact sequence of finite projective
![]() $R$
-modules
$R$
-modules
and we have to show that
![]() $\operatorname{Im}(\bar{\unicode[STIX]{x1D713}})$
is a direct summand of
$\operatorname{Im}(\bar{\unicode[STIX]{x1D713}})$
is a direct summand of
![]() $\bar{M}^{\unicode[STIX]{x1D70E}}$
. This holds if and only if for each maximal ideal
$\bar{M}^{\unicode[STIX]{x1D70E}}$
. This holds if and only if for each maximal ideal
![]() $\mathfrak{m}\subset R$
the base change of (3.4) to
$\mathfrak{m}\subset R$
the base change of (3.4) to
![]() $k=R/\mathfrak{m}$
is exact, or equivalently if the base change to
$k=R/\mathfrak{m}$
is exact, or equivalently if the base change to
![]() $k^{\operatorname{per}}$
is exact.
$k^{\operatorname{per}}$
is exact.
Let
![]() $\unicode[STIX]{x1D6E5}:A\rightarrow W(A)$
be the homomorphism with
$\unicode[STIX]{x1D6E5}:A\rightarrow W(A)$
be the homomorphism with
![]() $w_{n}\circ \unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D70E}^{n}$
, where
$w_{n}\circ \unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D70E}^{n}$
, where
![]() $w_{n}$
is the
$w_{n}$
is the
![]() $n$
th Witt polynomial; see [Reference BourbakiBou83, IX, § 1.2, Proposition 2]. The composition of
$n$
th Witt polynomial; see [Reference BourbakiBou83, IX, § 1.2, Proposition 2]. The composition of
![]() $\unicode[STIX]{x1D6E5}$
with the homomorphism
$\unicode[STIX]{x1D6E5}$
with the homomorphism
![]() $W(A)\rightarrow W(R)\rightarrow W(k^{\operatorname{per}})$
is a homomorphism
$W(A)\rightarrow W(R)\rightarrow W(k^{\operatorname{per}})$
is a homomorphism
![]() $A\rightarrow W(k^{\operatorname{per}})$
that commutes with
$A\rightarrow W(k^{\operatorname{per}})$
that commutes with
![]() $\unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70E}$
. Then
![]() $M\otimes _{A}W(k^{\operatorname{per}})$
is a Dieudonné module whose reduction mod
$M\otimes _{A}W(k^{\operatorname{per}})$
is a Dieudonné module whose reduction mod
![]() $p$
is (3.4)
$p$
is (3.4)
![]() $\otimes _{R}\,k^{\operatorname{per}}$
, which is therefore exact as required. ☐
$\otimes _{R}\,k^{\operatorname{per}}$
, which is therefore exact as required. ☐
We have a frame
![]() $\text{}\underline{A}=(A,pA,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
with
$\text{}\underline{A}=(A,pA,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
with
![]() $\unicode[STIX]{x1D70E}_{1}(pa)=\unicode[STIX]{x1D70E}(a)$
, and
$\unicode[STIX]{x1D70E}_{1}(pa)=\unicode[STIX]{x1D70E}(a)$
, and
![]() $\text{}\underline{A}$
is a
$\text{}\underline{A}$
is a
![]() $p$
-torsion free PD frame as defined in § 2. Using Lemma 3.1 one verifies that there is an equivalence of categories
$p$
-torsion free PD frame as defined in § 2. Using Lemma 3.1 one verifies that there is an equivalence of categories
defined by
![]() $N=\operatorname{Fil}M$
and
$N=\operatorname{Fil}M$
and
![]() $\unicode[STIX]{x1D711}(x\otimes 1)=F(x)$
for
$\unicode[STIX]{x1D711}(x\otimes 1)=F(x)$
for
![]() $x\in \operatorname{Fil}M$
; see [Reference Cais and LauCL14, Lemma 2.1.15] with
$x\in \operatorname{Fil}M$
; see [Reference Cais and LauCL14, Lemma 2.1.15] with
![]() $E=p$
. Thus the functor
$E=p$
. Thus the functor
![]() $\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
$\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
![]() $\text{}\underline{S}=\text{}\underline{A}$
can be viewed as a contravariant functor
$\text{}\underline{S}=\text{}\underline{A}$
can be viewed as a contravariant functor
In certain cases one can hope that
![]() $\unicode[STIX]{x1D6F7}_{A}$
is an equivalence of categories; see [Reference de JongdeJ93] for the case of complete regular local rings.
$\unicode[STIX]{x1D6F7}_{A}$
is an equivalence of categories; see [Reference de JongdeJ93] for the case of complete regular local rings.
Remark 3.2. The functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
always induces an equivalence between formal
$\unicode[STIX]{x1D6F7}_{A}$
always induces an equivalence between formal
![]() $p$
-divisible groups and
$p$
-divisible groups and
![]() $\unicode[STIX]{x1D711}$
-nilpotent Dieudonné modules, which correspond to
$\unicode[STIX]{x1D711}$
-nilpotent Dieudonné modules, which correspond to
![]() $F$
-nilpotent
$F$
-nilpotent
![]() $\text{}\underline{A}$
-windows. This follows from [Reference ZinkZin01] together with the extension of [Reference ZinkZin02, Theorem 9] to general base rings in [Reference LauLau08, Reference LauLau13].
$\text{}\underline{A}$
-windows. This follows from [Reference ZinkZin01] together with the extension of [Reference ZinkZin02, Theorem 9] to general base rings in [Reference LauLau08, Reference LauLau13].
4 Semiperfect rings
Let
![]() $p$
be a prime. Following [Reference Scholze and WeinsteinSW13], an
$p$
be a prime. Following [Reference Scholze and WeinsteinSW13], an
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $R$
is called semiperfect if the Frobenius endomorphism
$R$
is called semiperfect if the Frobenius endomorphism
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
is surjective. An isogeny of semiperfect rings is a surjective ring homomorphism whose kernel is annihilated by a power of
$\unicode[STIX]{x1D719}:R\rightarrow R$
is surjective. An isogeny of semiperfect rings is a surjective ring homomorphism whose kernel is annihilated by a power of
![]() $\unicode[STIX]{x1D719}$
. Let
$\unicode[STIX]{x1D719}$
. Let
![]() $R$
be semiperfect. There is a universal homomorphism
$R$
be semiperfect. There is a universal homomorphism
from a perfect ring to
![]() $R$
, and there is a universal
$R$
, and there is a universal
![]() $p$
-adic PD extension
$p$
-adic PD extension
Explicitly, we have
![]() $R^{\flat }=\varprojlim (R,\unicode[STIX]{x1D719})$
, and
$R^{\flat }=\varprojlim (R,\unicode[STIX]{x1D719})$
, and
![]() $A_{\operatorname{cris}}(R)$
is the
$A_{\operatorname{cris}}(R)$
is the
![]() $p$
-adic completion of the PD envelope of the natural map
$p$
-adic completion of the PD envelope of the natural map
![]() $W(R^{\flat })\rightarrow R$
. We will often write
$W(R^{\flat })\rightarrow R$
. We will often write
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
. Two classes of semiperfect rings will play a special role: complete intersections and balanced rings.
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
. Two classes of semiperfect rings will play a special role: complete intersections and balanced rings.
4.1 Complete intersection semiperfect rings
Definition 4.1. A semiperfect ring
![]() $R$
is called a complete intersection if
$R$
is called a complete intersection if
![]() $R\cong R_{0}/J_{0}$
where
$R\cong R_{0}/J_{0}$
where
![]() $R_{0}$
is a perfect ring and where the ideal
$R_{0}$
is a perfect ring and where the ideal
![]() $J_{0}$
is generated by a regular sequence.
$J_{0}$
is generated by a regular sequence.
Lemma 4.2. Let
![]() $R=R_{0}/J_{0}$
as in Definition 4.1 where
$R=R_{0}/J_{0}$
as in Definition 4.1 where
![]() $J_{0}$
is generated by the regular sequence
$J_{0}$
is generated by the regular sequence
![]() $\text{}\underline{u}=(u_{1},\ldots ,u_{r})$
. The natural homomorphism
$\text{}\underline{u}=(u_{1},\ldots ,u_{r})$
. The natural homomorphism
![]() $R_{0}\rightarrow R^{\flat }$
maps
$R_{0}\rightarrow R^{\flat }$
maps
![]() $\text{}\underline{u}$
to a regular sequence that generates the kernel of
$\text{}\underline{u}$
to a regular sequence that generates the kernel of
![]() $R^{\flat }\rightarrow R$
.
$R^{\flat }\rightarrow R$
.
Proof. Since the ideal
![]() $J_{0}$
is finitely generated, the
$J_{0}$
is finitely generated, the
![]() $J_{0}$
-adic topology of
$J_{0}$
-adic topology of
![]() $R_{0}$
coincides with the linear topology defined by the ideals
$R_{0}$
coincides with the linear topology defined by the ideals
![]() $\unicode[STIX]{x1D719}^{n}(J_{0})$
for
$\unicode[STIX]{x1D719}^{n}(J_{0})$
for
![]() $n\geqslant 0$
. Thus
$n\geqslant 0$
. Thus
![]() $R^{\flat }$
is the
$R^{\flat }$
is the
![]() $J_{0}$
-adic completion of
$J_{0}$
-adic completion of
![]() $R_{0}$
. Then the assertion is clear.☐
$R_{0}$
. Then the assertion is clear.☐
Remark 4.3. Lemma 4.2 implies that in Definition 4.1 one can take
![]() $R_{0}=R^{\flat }$
. It follows that for a complete intersection semiperfect ring
$R_{0}=R^{\flat }$
. It follows that for a complete intersection semiperfect ring
![]() $R$
the ring
$R$
the ring
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free; see for example [Reference Cais and LauCL14, Lemma 2.6.1].
$p$
-torsion free; see for example [Reference Cais and LauCL14, Lemma 2.6.1].
4.2 Balanced semiperfect rings
Definition 4.4. A semiperfect ring
![]() $R$
is called balanced if the ideal
$R$
is called balanced if the ideal
![]() $\bar{J}=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
satisfies
$\bar{J}=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
satisfies
![]() $\bar{J}^{p}=0$
, and
$\bar{J}^{p}=0$
, and
![]() $R$
is called iso-balanced if
$R$
is called iso-balanced if
![]() $R$
is isogenous to a balanced semiperfect ring.
$R$
is isogenous to a balanced semiperfect ring.
Lemma 4.5. For a homomorphism of semiperfect rings
![]() $\unicode[STIX]{x1D6FC}:R^{\prime }\rightarrow R$
where
$\unicode[STIX]{x1D6FC}:R^{\prime }\rightarrow R$
where
![]() $R$
is balanced we have
$R$
is balanced we have
![]() $\operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p}=\unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
.
$\operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p}=\unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
.
Proof. Clearly
![]() $\unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))\subseteq \operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p}$
. To prove the opposite inclusion, let
$\unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))\subseteq \operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p}$
. To prove the opposite inclusion, let
![]() $x_{1},\ldots ,x_{p}\in \operatorname{Ker}(\unicode[STIX]{x1D6FC})$
be given, and choose
$x_{1},\ldots ,x_{p}\in \operatorname{Ker}(\unicode[STIX]{x1D6FC})$
be given, and choose
![]() $y_{i}\in R^{\prime }$
with
$y_{i}\in R^{\prime }$
with
![]() $\unicode[STIX]{x1D719}(y_{i})=x_{i}$
. Then
$\unicode[STIX]{x1D719}(y_{i})=x_{i}$
. Then
![]() $\unicode[STIX]{x1D6FC}(y_{i})\in \bar{J}=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
. Since
$\unicode[STIX]{x1D6FC}(y_{i})\in \bar{J}=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
. Since
![]() $R$
is balanced we have
$R$
is balanced we have
![]() $\unicode[STIX]{x1D6FC}(\prod y_{i})=0$
, thus
$\unicode[STIX]{x1D6FC}(\prod y_{i})=0$
, thus
![]() $\prod x_{i}=\unicode[STIX]{x1D719}(\prod y_{i})\in \unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
as required.☐
$\prod x_{i}=\unicode[STIX]{x1D719}(\prod y_{i})\in \unicode[STIX]{x1D719}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
as required.☐
Lemma 4.6. A semiperfect ring
![]() $R$
is balanced if and only if the ideal
$R$
is balanced if and only if the ideal
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
satisfies
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
satisfies
![]() $J^{p}=\unicode[STIX]{x1D719}(J)$
.
$J^{p}=\unicode[STIX]{x1D719}(J)$
.
Proof. If
![]() $R$
is balanced then
$R$
is balanced then
![]() $J^{p}=\unicode[STIX]{x1D719}(J)$
by Lemma 4.5. The rest is clear.☐
$J^{p}=\unicode[STIX]{x1D719}(J)$
by Lemma 4.5. The rest is clear.☐
Remark 4.7. For every semiperfect ring
![]() $R$
there is a universal homomorphism to a balanced semiperfect ring
$R$
there is a universal homomorphism to a balanced semiperfect ring
![]() $R\rightarrow R^{\operatorname{bal}}$
, namely
$R\rightarrow R^{\operatorname{bal}}$
, namely
![]() $R^{\operatorname{bal}}=R^{\flat }/J^{\operatorname{bal}}$
where
$R^{\operatorname{bal}}=R^{\flat }/J^{\operatorname{bal}}$
where
![]() $J^{\operatorname{bal}}$
is the ascending union of the ideals
$J^{\operatorname{bal}}$
is the ascending union of the ideals
![]() $\unicode[STIX]{x1D719}^{-n}(J)^{p^{n}}$
for
$\unicode[STIX]{x1D719}^{-n}(J)^{p^{n}}$
for
![]() $n\geqslant 0$
. The ring
$n\geqslant 0$
. The ring
![]() $R$
is iso-balanced if and only if
$R$
is iso-balanced if and only if
![]() $R\rightarrow R^{\operatorname{bal}}$
is an isogeny.
$R\rightarrow R^{\operatorname{bal}}$
is an isogeny.
Lemma 4.8. Let
![]() $\unicode[STIX]{x1D70B}:R^{\prime }\rightarrow R$
be an isogeny of iso-balanced semiperfect rings. Then the ideal
$\unicode[STIX]{x1D70B}:R^{\prime }\rightarrow R$
be an isogeny of iso-balanced semiperfect rings. Then the ideal
![]() $\operatorname{Ker}(\unicode[STIX]{x1D70B})$
is nilpotent.
$\operatorname{Ker}(\unicode[STIX]{x1D70B})$
is nilpotent.
Proof. The composition
![]() $\unicode[STIX]{x1D6FC}:R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R\rightarrow R^{\operatorname{bal}}$
is an isogeny since
$\unicode[STIX]{x1D6FC}:R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R\rightarrow R^{\operatorname{bal}}$
is an isogeny since
![]() $R$
is iso-balanced. Lemma 4.5 implies that
$R$
is iso-balanced. Lemma 4.5 implies that
![]() $\operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p^{n}}=\unicode[STIX]{x1D719}^{n}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
, which is zero for large
$\operatorname{Ker}(\unicode[STIX]{x1D6FC})^{p^{n}}=\unicode[STIX]{x1D719}^{n}(\operatorname{Ker}(\unicode[STIX]{x1D6FC}))$
, which is zero for large
![]() $n$
.☐
$n$
.☐
Remark 4.9. A semiperfect ring
![]() $R$
is called
$R$
is called
![]() $f$
-semiperfect [Reference Scholze and WeinsteinSW13, Definition 4.1.2] if it is isogenous to the quotient of a perfect ring by a finitely generated ideal. Each
$f$
-semiperfect [Reference Scholze and WeinsteinSW13, Definition 4.1.2] if it is isogenous to the quotient of a perfect ring by a finitely generated ideal. Each
![]() $f$
-semiperfect ring
$f$
-semiperfect ring
![]() $R$
is iso-balanced. Indeed, assume that
$R$
is iso-balanced. Indeed, assume that
![]() $R=R_{0}/J_{0}$
where
$R=R_{0}/J_{0}$
where
![]() $R_{0}$
is perfect and
$R_{0}$
is perfect and
![]() $J_{0}=(a_{1},\ldots ,a_{r})$
is finitely generated. Let
$J_{0}=(a_{1},\ldots ,a_{r})$
is finitely generated. Let
![]() $J_{1}$
be the union of
$J_{1}$
be the union of
![]() $\unicode[STIX]{x1D719}^{-n}(J_{0})^{p^{n}}$
for
$\unicode[STIX]{x1D719}^{-n}(J_{0})^{p^{n}}$
for
![]() $n\geqslant 0$
. Then
$n\geqslant 0$
. Then
![]() $R_{0}/J_{1}$
is balanced. Explicitly,
$R_{0}/J_{1}$
is balanced. Explicitly,
![]() $J_{1}$
is generated by all monomials
$J_{1}$
is generated by all monomials
![]() $\prod a_{i}^{m_{i}}$
with
$\prod a_{i}^{m_{i}}$
with
![]() $m_{i}\in \mathbb{Z}[1/p]$
and
$m_{i}\in \mathbb{Z}[1/p]$
and
![]() $m_{i}\geqslant 0$
such that
$m_{i}\geqslant 0$
such that
![]() $\sum m_{i}=1$
, which implies that
$\sum m_{i}=1$
, which implies that
![]() $m_{i}\geqslant 1/r$
for at least one
$m_{i}\geqslant 1/r$
for at least one
![]() $i$
. Choose
$i$
. Choose
![]() $s$
such that
$s$
such that
![]() $p^{s}\geqslant r$
. Then
$p^{s}\geqslant r$
. Then
![]() $\unicode[STIX]{x1D719}^{s}(J_{1})\subseteq J_{0}$
, hence
$\unicode[STIX]{x1D719}^{s}(J_{1})\subseteq J_{0}$
, hence
![]() $R\rightarrow R_{0}/J_{1}$
is an isogeny.
$R\rightarrow R_{0}/J_{1}$
is an isogeny.
4.3 Lifts of semiperfect rings
Let
![]() $R$
be a semiperfect ring, and let
$R$
be a semiperfect ring, and let
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
Definition 4.10. A lift of
![]() $R$
is a
$R$
is a
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free ring
$p$
-torsion free ring
![]() $A$
with
$A$
with
![]() $A/pA=R$
which carries a ring endomorphism
$A/pA=R$
which carries a ring endomorphism
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
that induces
$\unicode[STIX]{x1D70E}:A\rightarrow A$
that induces
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
![]() $R$
.
$R$
.
Remark 4.11. The endomorphism
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
is unique if it exists. Indeed, the universal property of the ring of Witt vectors [Reference GrothendieckGro74, ch. IV, Proposition 4.3] gives a unique homomorphism
$\unicode[STIX]{x1D70E}:A\rightarrow A$
is unique if it exists. Indeed, the universal property of the ring of Witt vectors [Reference GrothendieckGro74, ch. IV, Proposition 4.3] gives a unique homomorphism
![]() $\unicode[STIX]{x1D713}:W(R^{\flat })\rightarrow A$
that induces the projection
$\unicode[STIX]{x1D713}:W(R^{\flat })\rightarrow A$
that induces the projection
![]() $R^{\flat }\rightarrow R$
modulo
$R^{\flat }\rightarrow R$
modulo
![]() $p$
, and we have
$p$
, and we have
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D713}$
by the universal property. Moreover
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D713}$
by the universal property. Moreover
![]() $\unicode[STIX]{x1D713}$
is surjective, and the uniqueness of
$\unicode[STIX]{x1D713}$
is surjective, and the uniqueness of
![]() $\unicode[STIX]{x1D70E}$
follows. This reasoning shows that lifts
$\unicode[STIX]{x1D70E}$
follows. This reasoning shows that lifts
![]() $A$
of
$A$
of
![]() $R$
correspond to closed ideals
$R$
correspond to closed ideals
![]() $J^{\prime }\subseteq W(R^{\flat })$
such that
$J^{\prime }\subseteq W(R^{\flat })$
such that
![]() $\unicode[STIX]{x1D70E}(J^{\prime })\subseteq J^{\prime }$
and
$\unicode[STIX]{x1D70E}(J^{\prime })\subseteq J^{\prime }$
and
![]() $J^{\prime }\cap pW(R^{\flat })=pJ^{\prime }$
and
$J^{\prime }\cap pW(R^{\flat })=pJ^{\prime }$
and
![]() $J^{\prime }/pJ^{\prime }=J$
.
$J^{\prime }/pJ^{\prime }=J$
.
Definition 4.12. A lift
![]() $A$
of
$A$
of
![]() $R$
is called straight if
$R$
is called straight if
![]() $A=W(R^{\flat })/J^{\prime }$
such that the set of all
$A=W(R^{\flat })/J^{\prime }$
such that the set of all
![]() $a\in J$
with
$a\in J$
with
![]() $[a]\in J^{\prime }$
generates
$[a]\in J^{\prime }$
generates
![]() $J$
.
$J$
.
Lemma 4.13. Let
![]() $R$
be a semiperfect ring which is a complete intersection or balanced, see Definitions 4.1 and 4.4. Then a straight lift of
$R$
be a semiperfect ring which is a complete intersection or balanced, see Definitions 4.1 and 4.4. Then a straight lift of
![]() $R$
exists.
$R$
exists.
Proof. If
![]() $R$
is a complete intersection,
$R$
is a complete intersection,
![]() $J$
is generated by a regular sequence
$J$
is generated by a regular sequence
![]() $(u_{1},\ldots ,u_{r})$
; see Lemma 4.2. Let
$(u_{1},\ldots ,u_{r})$
; see Lemma 4.2. Let
![]() $J^{\prime }=([u_{1}],\ldots ,[u_{r}])$
in
$J^{\prime }=([u_{1}],\ldots ,[u_{r}])$
in
![]() $W(R^{\flat })$
. The ring
$W(R^{\flat })$
. The ring
![]() $A=W(R^{\flat })/J^{\prime }$
is
$A=W(R^{\flat })/J^{\prime }$
is
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free with
$p$
-torsion free with
![]() $A/pA=R$
. The ideal
$A/pA=R$
. The ideal
![]() $J^{\prime }$
is stable under
$J^{\prime }$
is stable under
![]() $\unicode[STIX]{x1D70E}$
since
$\unicode[STIX]{x1D70E}$
since
![]() $\unicode[STIX]{x1D70E}([u_{i}])=[u_{i}]^{p}$
. Thus
$\unicode[STIX]{x1D70E}([u_{i}])=[u_{i}]^{p}$
. Thus
![]() $A$
is a straight lift of
$A$
is a straight lift of
![]() $R$
.
$R$
.
Assume that
![]() $R$
is balanced. Let
$R$
is balanced. Let
![]() $J^{\prime }\subseteq W(R^{\flat })$
be the set of all Witt vectors
$J^{\prime }\subseteq W(R^{\flat })$
be the set of all Witt vectors
![]() $a=(a_{0},a_{1},\ldots )$
with
$a=(a_{0},a_{1},\ldots )$
with
![]() $a_{i}\in \unicode[STIX]{x1D719}^{i}(J)$
. We claim that
$a_{i}\in \unicode[STIX]{x1D719}^{i}(J)$
. We claim that
![]() $J^{\prime }$
is an ideal. Indeed, the ring structure of
$J^{\prime }$
is an ideal. Indeed, the ring structure of
![]() $W(R^{\flat })$
is given by
$W(R^{\flat })$
is given by
![]() $(x_{0},x_{1},\ldots )\ast (y_{0},y_{1},\ldots )=(g_{0}^{\ast }(x,y),g_{1}^{\ast }(x,y),\ldots )$
where
$(x_{0},x_{1},\ldots )\ast (y_{0},y_{1},\ldots )=(g_{0}^{\ast }(x,y),g_{1}^{\ast }(x,y),\ldots )$
where
![]() $\ast$
is
$\ast$
is
![]() $+$
or
$+$
or
![]() $\times$
, with certain polynomials
$\times$
, with certain polynomials
![]() $g_{n}^{\ast }$
. If the variables
$g_{n}^{\ast }$
. If the variables
![]() $x_{i},y_{i}$
have degree
$x_{i},y_{i}$
have degree
![]() $p^{i}$
, then
$p^{i}$
, then
![]() $p_{n}^{+}$
is homogeneous of degree
$p_{n}^{+}$
is homogeneous of degree
![]() $p^{n}$
, and
$p^{n}$
, and
![]() $p_{n}^{\times }$
is bihomogeneous of bidegree
$p_{n}^{\times }$
is bihomogeneous of bidegree
![]() $(p^{n},p^{n})$
. Since
$(p^{n},p^{n})$
. Since
![]() $R$
is balanced we have
$R$
is balanced we have
![]() $\unicode[STIX]{x1D719}(J)=J^{p}$
; see Lemma 4.6. It follows that
$\unicode[STIX]{x1D719}(J)=J^{p}$
; see Lemma 4.6. It follows that
![]() $J^{\prime }$
is an ideal. We have
$J^{\prime }$
is an ideal. We have
![]() $J^{\prime }\cap pW(R^{\flat })=pJ^{\prime }$
, and
$J^{\prime }\cap pW(R^{\flat })=pJ^{\prime }$
, and
![]() $J^{\prime }$
is the closure of the ideal generated by the elements
$J^{\prime }$
is the closure of the ideal generated by the elements
![]() $[a]$
for all
$[a]$
for all
![]() $a\in J$
. Clearly
$a\in J$
. Clearly
![]() $J^{\prime }$
is stable under
$J^{\prime }$
is stable under
![]() $\unicode[STIX]{x1D70E}$
. Thus
$\unicode[STIX]{x1D70E}$
. Thus
![]() $A=W(R^{\flat })/J^{\prime }$
is a straight lift of
$A=W(R^{\flat })/J^{\prime }$
is a straight lift of
![]() $R$
.☐
$R$
.☐
Lemma 4.14. If
![]() $A$
is a lift of the semiperfect ring
$A$
is a lift of the semiperfect ring
![]() $R$
, then
$R$
, then
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
is surjective, and
$\unicode[STIX]{x1D70E}:A\rightarrow A$
is surjective, and
Proof. The first assertion holds because the natural
![]() $\unicode[STIX]{x1D70E}$
-equivariant homomorphism
$\unicode[STIX]{x1D70E}$
-equivariant homomorphism
![]() $W(R^{\flat })\rightarrow A$
is surjective, and
$W(R^{\flat })\rightarrow A$
is surjective, and
![]() $\unicode[STIX]{x1D70E}$
is bijective on
$\unicode[STIX]{x1D70E}$
is bijective on
![]() $W(R^{\flat })$
; see Remark 4.11. Let
$W(R^{\flat })$
; see Remark 4.11. Let
![]() $B=\varprojlim (A,\unicode[STIX]{x1D70E})$
. Since
$B=\varprojlim (A,\unicode[STIX]{x1D70E})$
. Since
![]() $A$
is
$A$
is
![]() $p$
-torsion free the same holds for
$p$
-torsion free the same holds for
![]() $B$
. We take the limit over
$B$
. We take the limit over
![]() $\unicode[STIX]{x1D70E}$
of the exact sequence
$\unicode[STIX]{x1D70E}$
of the exact sequence
![]() $0\rightarrow A\xrightarrow[{}]{}A\rightarrow A_{n}\rightarrow 0$
, where the first map is
$0\rightarrow A\xrightarrow[{}]{}A\rightarrow A_{n}\rightarrow 0$
, where the first map is
![]() $p^{n}$
. It follows that
$p^{n}$
. It follows that
![]() $B/p^{n}B=\varprojlim (A_{n},\unicode[STIX]{x1D70E})$
, which implies that
$B/p^{n}B=\varprojlim (A_{n},\unicode[STIX]{x1D70E})$
, which implies that
![]() $\mathop{\varprojlim }\nolimits_{n}(B/p^{n}B)\,=\,B$
; moreover
$\mathop{\varprojlim }\nolimits_{n}(B/p^{n}B)\,=\,B$
; moreover
![]() $B/pB\,=\,R^{\flat }$
. Therefore
$B/pB\,=\,R^{\flat }$
. Therefore
![]() $B=W(R^{\flat })$
.☐
$B=W(R^{\flat })$
.☐
5 Dieudonné modules via lifts
Let
![]() $R$
be a semiperfect ring and let
$R$
be a semiperfect ring and let
![]() $A$
be lift of
$A$
be lift of
![]() $R$
; see Definition 4.10.
$R$
; see Definition 4.10.
5.1 Frames associated to a lift
To the lift
![]() $A$
of
$A$
of
![]() $R$
we associate two frames. First, there is the
$R$
we associate two frames. First, there is the
![]() $p$
-torsion free PD frame
$p$
-torsion free PD frame
with
![]() $\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
; see § 3. Second, let
$\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
; see § 3. Second, let
Lemma 5.1. We have
![]() $\unicode[STIX]{x1D70E}(\tilde{\text{Fil}}\,A)\subseteq pA$
, and
$\unicode[STIX]{x1D70E}(\tilde{\text{Fil}}\,A)\subseteq pA$
, and
![]() $\tilde{\text{Fil}}\,A$
is a PD ideal of
$\tilde{\text{Fil}}\,A$
is a PD ideal of
![]() $A$
.
$A$
.
Proof. Since
![]() $\unicode[STIX]{x1D70E}$
is a lift of
$\unicode[STIX]{x1D70E}$
is a lift of
![]() $\unicode[STIX]{x1D719}$
, for
$\unicode[STIX]{x1D719}$
, for
![]() $a\in A$
we have
$a\in A$
we have
![]() $a\in \tilde{\text{Fil}}\,A$
if and only if
$a\in \tilde{\text{Fil}}\,A$
if and only if
![]() $\unicode[STIX]{x1D70E}(a)\in pA$
if and only if
$\unicode[STIX]{x1D70E}(a)\in pA$
if and only if
![]() $a^{p}\in pA$
. For
$a^{p}\in pA$
. For
![]() $a\in \tilde{\text{Fil}}\,A$
let
$a\in \tilde{\text{Fil}}\,A$
let
![]() $b=a^{p}/p\in A$
. We have to show that
$b=a^{p}/p\in A$
. We have to show that
![]() $b\in \tilde{\text{Fil}}\,A$
, or equivalently that
$b\in \tilde{\text{Fil}}\,A$
, or equivalently that
![]() $\unicode[STIX]{x1D70E}(b)\in pA$
. But
$\unicode[STIX]{x1D70E}(b)\in pA$
. But
![]() $\unicode[STIX]{x1D70E}(b)=\unicode[STIX]{x1D70E}(a)^{p}/p=p^{p-1}(\unicode[STIX]{x1D70E}(a)/p)^{p}$
.☐
$\unicode[STIX]{x1D70E}(b)=\unicode[STIX]{x1D70E}(a)^{p}/p=p^{p-1}(\unicode[STIX]{x1D70E}(a)/p)^{p}$
.☐
Since
![]() $R$
is semiperfect,
$R$
is semiperfect,
![]() $\unicode[STIX]{x1D70E}$
induces an isomorphism
$\unicode[STIX]{x1D70E}$
induces an isomorphism
![]() $A/\tilde{\text{Fil}}\,A\xrightarrow[{}]{{\sim}}R$
. By Lemma 5.1 we can define a
$A/\tilde{\text{Fil}}\,A\xrightarrow[{}]{{\sim}}R$
. By Lemma 5.1 we can define a
![]() $p$
-torsion free PD frame
$p$
-torsion free PD frame
with
![]() $\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
. The endomorphism
$\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
. The endomorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $A$
is a frame endomorphism
$A$
is a frame endomorphism
![]() $\unicode[STIX]{x1D70E}:\text{}\underline{A}\rightarrow \text{}\underline{A}$
over
$\unicode[STIX]{x1D70E}:\text{}\underline{A}\rightarrow \text{}\underline{A}$
over
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
, which factors into frame homomorphisms
$\unicode[STIX]{x1D719}:R\rightarrow R$
, which factors into frame homomorphisms
where
![]() $\unicode[STIX]{x1D704}$
is given by the identity on
$\unicode[STIX]{x1D704}$
is given by the identity on
![]() $A$
and by
$A$
and by
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
![]() $R$
, while
$R$
, while
![]() $\unicode[STIX]{x1D70B}$
is given by
$\unicode[STIX]{x1D70B}$
is given by
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $A$
and by the identity on
$A$
and by the identity on
![]() $R$
.
$R$
.
Lemma 5.2. The frame homomorphism
![]() $\unicode[STIX]{x1D70B}:\text{}\underline{A}/\unicode[STIX]{x1D719}\rightarrow \text{}\underline{A}$
is crystalline, i.e. it induces an equivalence of the window categories.
$\unicode[STIX]{x1D70B}:\text{}\underline{A}/\unicode[STIX]{x1D719}\rightarrow \text{}\underline{A}$
is crystalline, i.e. it induces an equivalence of the window categories.
Proof. Let
![]() $I$
be the kernel of the surjective homomorphism
$I$
be the kernel of the surjective homomorphism
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
. If we write
$\unicode[STIX]{x1D70E}:A\rightarrow A$
. If we write
![]() $A=W(R^{\flat })/J^{\prime }$
(see Remark 4.11) then
$A=W(R^{\flat })/J^{\prime }$
(see Remark 4.11) then
![]() $I=J^{\prime }/\unicode[STIX]{x1D70E}(J^{\prime })$
. Thus
$I=J^{\prime }/\unicode[STIX]{x1D70E}(J^{\prime })$
. Thus
![]() $\unicode[STIX]{x1D70E}=p\unicode[STIX]{x1D70E}_{1}$
is zero on
$\unicode[STIX]{x1D70E}=p\unicode[STIX]{x1D70E}_{1}$
is zero on
![]() $I$
. Since
$I$
. Since
![]() $A$
is
$A$
is
![]() $p$
-torsion free it follows that
$p$
-torsion free it follows that
![]() $\unicode[STIX]{x1D70E}_{1}:I\rightarrow I$
is zero, and the lemma follows from the general deformation lemma [Reference LauLau10, Theorem 3.2].☐
$\unicode[STIX]{x1D70E}_{1}:I\rightarrow I$
is zero, and the lemma follows from the general deformation lemma [Reference LauLau10, Theorem 3.2].☐
Remark 5.3. The divided powers on
![]() $\tilde{\text{Fil}}\,A$
, which exist by Lemma 5.1, induce divided powers on the ideal
$\tilde{\text{Fil}}\,A$
, which exist by Lemma 5.1, induce divided powers on the ideal
![]() $(\tilde{\text{Fil}}\,A)/pA=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
of
$(\tilde{\text{Fil}}\,A)/pA=\operatorname{Ker}(\unicode[STIX]{x1D719}:R\rightarrow R)$
of
![]() $R$
. Thus the given lift
$R$
. Thus the given lift
![]() $A$
of
$A$
of
![]() $R$
determines divided powers on
$R$
determines divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
.
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
.
Lemma 5.4. If
![]() $A$
is a straight lift of
$A$
is a straight lift of
![]() $R$
in the sense of Definition 4.12, then the associated divided powers on
$R$
in the sense of Definition 4.12, then the associated divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent.
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent.
Proof. Let
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
and
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
and
![]() $A=W(R^{\flat })/J^{\prime }$
. Since
$A=W(R^{\flat })/J^{\prime }$
. Since
![]() $A$
is straight, there are generators
$A$
is straight, there are generators
![]() $a_{i}$
of
$a_{i}$
of
![]() $J$
with
$J$
with
![]() $[a_{i}]\in J^{\prime }$
. The elements
$[a_{i}]\in J^{\prime }$
. The elements
![]() $b_{i}=\unicode[STIX]{x1D719}^{-1}(a_{i})+J$
of
$b_{i}=\unicode[STIX]{x1D719}^{-1}(a_{i})+J$
of
![]() $R$
generate the ideal
$R$
generate the ideal
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
. We claim that
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
. We claim that
![]() $b_{i}^{[p]}=0$
, which proves the lemma. The element
$b_{i}^{[p]}=0$
, which proves the lemma. The element
![]() $c_{i}=[\unicode[STIX]{x1D719}^{-1}(a_{i})]+J^{\prime }$
of
$c_{i}=[\unicode[STIX]{x1D719}^{-1}(a_{i})]+J^{\prime }$
of
![]() $A$
is an inverse image of
$A$
is an inverse image of
![]() $b_{i}$
. We have
$b_{i}$
. We have
![]() $c_{i}^{p}=[a_{i}]+J^{\prime }=0$
in
$c_{i}^{p}=[a_{i}]+J^{\prime }=0$
in
![]() $A$
, thus
$A$
, thus
![]() $c_{i}^{[p]}=0$
in
$c_{i}^{[p]}=0$
in
![]() $A$
, and thus
$A$
, and thus
![]() $b_{i}^{[p]}=0$
in
$b_{i}^{[p]}=0$
in
![]() $R$
.☐
$R$
.☐
5.2 Evaluation of crystals
We consider the functor
given by (3.3) for
![]() $\text{}\underline{S}=\text{}\underline{A}$
. Here
$\text{}\underline{S}=\text{}\underline{A}$
. Here
![]() $\operatorname{Win}(\text{}\underline{A})$
is equivalent to the category
$\operatorname{Win}(\text{}\underline{A})$
is equivalent to the category
![]() $\operatorname{DM}(A)$
of Dieudonné modules over
$\operatorname{DM}(A)$
of Dieudonné modules over
![]() $A$
by (3.5).
$A$
by (3.5).
Proposition 5.5. If the divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent, then the commutative diagram of categories
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent, then the commutative diagram of categories

is cartesian.
Proof. The diagram (5.3) commutes by the functoriality of
![]() $\unicode[STIX]{x1D6F7}_{A}$
with respect to the frame endomorphism
$\unicode[STIX]{x1D6F7}_{A}$
with respect to the frame endomorphism
![]() $\unicode[STIX]{x1D70E}:\text{}\underline{A}\rightarrow \text{}\underline{A}$
. The factorization (5.1) of
$\unicode[STIX]{x1D70E}:\text{}\underline{A}\rightarrow \text{}\underline{A}$
. The factorization (5.1) of
![]() $\unicode[STIX]{x1D70E}$
induces the following extension of (5.3).
$\unicode[STIX]{x1D70E}$
induces the following extension of (5.3).

Here
![]() $\unicode[STIX]{x1D70B}^{\ast }$
is an equivalence by Lemma 5.2. Thus (5.3) is equivalent to the left-hand square of (5.4). For a
$\unicode[STIX]{x1D70B}^{\ast }$
is an equivalence by Lemma 5.2. Thus (5.3) is equivalent to the left-hand square of (5.4). For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $\text{}\underline{M}=\unicode[STIX]{x1D6F7}_{\text{}\underline{A}/\unicode[STIX]{x1D719}}(G)$
in
$\text{}\underline{M}=\unicode[STIX]{x1D6F7}_{\text{}\underline{A}/\unicode[STIX]{x1D719}}(G)$
in
![]() $\operatorname{Win}(\text{}\underline{A}/\unicode[STIX]{x1D719})$
. Then
$\operatorname{Win}(\text{}\underline{A}/\unicode[STIX]{x1D719})$
. Then
![]() $M\,\otimes _{A}\,R$
is the value of
$M\,\otimes _{A}\,R$
is the value of
![]() $\mathbb{D}(G)$
at the PD extension
$\mathbb{D}(G)$
at the PD extension
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
. Thus lifts of the Hodge filtration of
$\unicode[STIX]{x1D719}:R\rightarrow R$
. Thus lifts of the Hodge filtration of
![]() $G$
under
$G$
under
![]() $\unicode[STIX]{x1D719}$
correspond to lifts of the Hodge filtration of
$\unicode[STIX]{x1D719}$
correspond to lifts of the Hodge filtration of
![]() $\text{}\underline{M}$
under
$\text{}\underline{M}$
under
![]() $\unicode[STIX]{x1D704}^{\ast }$
. The latter correspond to lifts of
$\unicode[STIX]{x1D704}^{\ast }$
. The latter correspond to lifts of
![]() $\text{}\underline{M}$
under
$\text{}\underline{M}$
under
![]() $\unicode[STIX]{x1D704}^{\ast }$
by [Reference LauLau10, Lemma 4.2], and the former correspond to lifts of
$\unicode[STIX]{x1D704}^{\ast }$
by [Reference LauLau10, Lemma 4.2], and the former correspond to lifts of
![]() $G$
under
$G$
under
![]() $\unicode[STIX]{x1D719}$
by the Grothendieck–Messing Theorem [Reference MessingMes72] since the divided powers on
$\unicode[STIX]{x1D719}$
by the Grothendieck–Messing Theorem [Reference MessingMes72] since the divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent.☐
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent.☐
Corollary 5.6. If the divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent, then the commutative diagram of categories
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent, then the commutative diagram of categories

is cartesian. ◻
Proof. Proposition 5.5 gives the following cartesian diagram.

The upper limit category is equivalent to
![]() $\operatorname{BT}(\operatorname{Spec}R^{\flat })$
by the obvious analogue of [Reference MessingMes72, ch. II, Lemma 4.16]; see also [Reference de JongdeJ95, Lemma 2.4.4]. Since we have
$\operatorname{BT}(\operatorname{Spec}R^{\flat })$
by the obvious analogue of [Reference MessingMes72, ch. II, Lemma 4.16]; see also [Reference de JongdeJ95, Lemma 2.4.4]. Since we have
![]() $\varprojlim (\text{}\underline{A},\unicode[STIX]{x1D70E})=\text{}\underline{W}(R^{\flat })$
by Lemma 4.14, the lower limit category is equivalent to
$\varprojlim (\text{}\underline{A},\unicode[STIX]{x1D70E})=\text{}\underline{W}(R^{\flat })$
by Lemma 4.14, the lower limit category is equivalent to
![]() $\operatorname{Win}(\text{}\underline{W}(R^{\flat }))$
by [Reference LauLau10, Lemma 2.12].☐
$\operatorname{Win}(\text{}\underline{W}(R^{\flat }))$
by [Reference LauLau10, Lemma 2.12].☐
Theorem 5.7. Let
![]() $R$
be a semiperfect ring with a lift
$R$
be a semiperfect ring with a lift
![]() $A$
such that the associated divided powers on
$A$
such that the associated divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent. Then the functor
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
given by Remark 5.3 are pointwise nilpotent. Then the functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
is an equivalence.
$\unicode[STIX]{x1D6F7}_{A}$
is an equivalence.
Remark 5.8. If
![]() $R$
is a complete intersection or balanced, there is a straight lift by Lemma 4.13, and the associated divided powers on
$R$
is a complete intersection or balanced, there is a straight lift by Lemma 4.13, and the associated divided powers on
![]() $\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent by Lemma 5.4. Thus Theorem 5.7 applies in these cases.
$\operatorname{Ker}(\unicode[STIX]{x1D719})$
are pointwise nilpotent by Lemma 5.4. Thus Theorem 5.7 applies in these cases.
Proof of Theorem 5.7.
Since
![]() $R^{\flat }$
is a perfect ring, the functor
$R^{\flat }$
is a perfect ring, the functor
![]() $\unicode[STIX]{x1D6F7}_{W(R^{\flat })}$
is an equivalence by a theorem of Gabber; see [Reference LauLau13, Theorem 6.4]. Every window over
$\unicode[STIX]{x1D6F7}_{W(R^{\flat })}$
is an equivalence by a theorem of Gabber; see [Reference LauLau13, Theorem 6.4]. Every window over
![]() $\text{}\underline{A}$
can be lifted to a window over
$\text{}\underline{A}$
can be lifted to a window over
![]() $\text{}\underline{W}(R^{\flat })$
. Indeed, the projections
$\text{}\underline{W}(R^{\flat })$
. Indeed, the projections
![]() $A\rightarrow R$
and
$A\rightarrow R$
and
![]() $W(R^{\flat })\rightarrow R^{\flat }\rightarrow R$
induce bijective maps of the sets of isomorphisms classes of finite projective modules, and thus the same holds for
$W(R^{\flat })\rightarrow R^{\flat }\rightarrow R$
induce bijective maps of the sets of isomorphisms classes of finite projective modules, and thus the same holds for
![]() $W(R^{\flat })\rightarrow A$
. Hence a normal representation of an
$W(R^{\flat })\rightarrow A$
. Hence a normal representation of an
![]() $\text{}\underline{A}$
-window in the sense of [Reference LauLau10, Lemma 2.6] can be lifted to
$\text{}\underline{A}$
-window in the sense of [Reference LauLau10, Lemma 2.6] can be lifted to
![]() $\text{}\underline{W}(R^{\flat })$
. Now Lemma 5.9 below applied to the diagram of Corollary 5.6 gives the result.◻
$\text{}\underline{W}(R^{\flat })$
. Now Lemma 5.9 below applied to the diagram of Corollary 5.6 gives the result.◻
Lemma 5.9. Let

be a cartesian diagram of additive categories or of groupoids. If
![]() $f$
is an equivalence and
$f$
is an equivalence and
![]() $\unicode[STIX]{x1D70B}$
is essentially surjective, then
$\unicode[STIX]{x1D70B}$
is essentially surjective, then
![]() $g$
is an equivalence.
$g$
is an equivalence.
Proof. The case of additive categories is reduced to the case of groupoids using that a homomorphism
![]() $u:X\rightarrow Y$
can be encoded by the automorphism
$u:X\rightarrow Y$
can be encoded by the automorphism
![]() $(\!\begin{smallmatrix}1 & 0\\ u & 1\end{smallmatrix}\!)$
of
$(\!\begin{smallmatrix}1 & 0\\ u & 1\end{smallmatrix}\!)$
of
![]() $X\oplus Y$
. Consider the groupoid case. We may assume that
$X\oplus Y$
. Consider the groupoid case. We may assume that
![]() ${\mathcal{A}}$
is equal to the fibered product of
${\mathcal{A}}$
is equal to the fibered product of
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() ${\mathcal{B}}$
over
${\mathcal{B}}$
over
![]() ${\mathcal{D}}$
, which is the category of triples
${\mathcal{D}}$
, which is the category of triples
![]() $(C,\unicode[STIX]{x1D6FF},B)$
with
$(C,\unicode[STIX]{x1D6FF},B)$
with
![]() $C\in {\mathcal{C}}$
,
$C\in {\mathcal{C}}$
,
![]() $B\in {\mathcal{B}}$
, and
$B\in {\mathcal{B}}$
, and
![]() $\unicode[STIX]{x1D6FF}:g(C)\cong \unicode[STIX]{x1D70B}(B)$
.
$\unicode[STIX]{x1D6FF}:g(C)\cong \unicode[STIX]{x1D70B}(B)$
.
(1) The functor
 $g$
is surjective on isomorphism classes: This holds for
$g$
is surjective on isomorphism classes: This holds for
 $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
 $f$
.
$f$
.(2) The functor
 $\unicode[STIX]{x1D713}$
is surjective on isomorphism classes: Let
$\unicode[STIX]{x1D713}$
is surjective on isomorphism classes: Let
 $C\in {\mathcal{C}}$
. Find
$C\in {\mathcal{C}}$
. Find
 $B\in {\mathcal{B}}$
and
$B\in {\mathcal{B}}$
and
 $\unicode[STIX]{x1D6FF}:g(C)\cong \unicode[STIX]{x1D70B}(B)$
. Then
$\unicode[STIX]{x1D6FF}:g(C)\cong \unicode[STIX]{x1D70B}(B)$
. Then
 $A=(C,\unicode[STIX]{x1D6FF},B)$
satisfies
$A=(C,\unicode[STIX]{x1D6FF},B)$
satisfies
 $\unicode[STIX]{x1D713}(A)=C$
.
$\unicode[STIX]{x1D713}(A)=C$
.(3) The functor
 $g$
is faithful: We have to show that if
$g$
is faithful: We have to show that if
 $C\in {\mathcal{C}}$
and
$C\in {\mathcal{C}}$
and
 $\unicode[STIX]{x1D6FE}\in \operatorname{Aut}(C)$
with
$\unicode[STIX]{x1D6FE}\in \operatorname{Aut}(C)$
with
 $g(\unicode[STIX]{x1D6FE})=\operatorname{id}$
then
$g(\unicode[STIX]{x1D6FE})=\operatorname{id}$
then
 $\unicode[STIX]{x1D6FE}=\operatorname{id}$
. Extend
$\unicode[STIX]{x1D6FE}=\operatorname{id}$
. Extend
 $C$
to
$C$
to
 $A=(C,\unicode[STIX]{x1D6FF},B)\in {\mathcal{A}}$
. Then
$A=(C,\unicode[STIX]{x1D6FF},B)\in {\mathcal{A}}$
. Then
 $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FE},\operatorname{id}_{B})$
lies in
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FE},\operatorname{id}_{B})$
lies in
 $\operatorname{Aut}(A)$
with
$\operatorname{Aut}(A)$
with
 $f(\unicode[STIX]{x1D6FC})=\operatorname{id}$
. Thus
$f(\unicode[STIX]{x1D6FC})=\operatorname{id}$
. Thus
 $\unicode[STIX]{x1D6FC}=\operatorname{id}$
and
$\unicode[STIX]{x1D6FC}=\operatorname{id}$
and
 $\unicode[STIX]{x1D6FE}=\operatorname{id}$
.
$\unicode[STIX]{x1D6FE}=\operatorname{id}$
.(4) The functor
 $g$
is full: Let
$g$
is full: Let
 $C,C^{\prime }\in {\mathcal{C}}$
and
$C,C^{\prime }\in {\mathcal{C}}$
and
 $\unicode[STIX]{x1D6FF}:g(C)\cong g(C^{\prime })$
. Extend
$\unicode[STIX]{x1D6FF}:g(C)\cong g(C^{\prime })$
. Extend
 $C^{\prime }$
to
$C^{\prime }$
to
 $A^{\prime }=(C^{\prime },\unicode[STIX]{x1D6FF}^{\prime },B^{\prime })\in {\mathcal{A}}$
. Let
$A^{\prime }=(C^{\prime },\unicode[STIX]{x1D6FF}^{\prime },B^{\prime })\in {\mathcal{A}}$
. Let
 $A=(C,\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF},B^{\prime })\in {\mathcal{A}}$
. Then
$A=(C,\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF},B^{\prime })\in {\mathcal{A}}$
. Then
 $f(A)=B^{\prime }=f(A^{\prime })$
, and
$f(A)=B^{\prime }=f(A^{\prime })$
, and
 $\operatorname{id}_{B^{\prime }}$
lifts to a unique
$\operatorname{id}_{B^{\prime }}$
lifts to a unique
 $\unicode[STIX]{x1D6FC}:A\cong A^{\prime }$
, which consists of
$\unicode[STIX]{x1D6FC}:A\cong A^{\prime }$
, which consists of
 $(\unicode[STIX]{x1D6FE},\operatorname{id}_{B^{\prime }})$
with
$(\unicode[STIX]{x1D6FE},\operatorname{id}_{B^{\prime }})$
with
 $\unicode[STIX]{x1D6FE}:C\cong C^{\prime }$
such that
$\unicode[STIX]{x1D6FE}:C\cong C^{\prime }$
such that
 $\unicode[STIX]{x1D6FF}^{\prime }\circ g(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}$
, thus
$\unicode[STIX]{x1D6FF}^{\prime }\circ g(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}$
, thus
 $g(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FF}$
. ☐
$g(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FF}$
. ☐
5.3 The passage to
 $A_{\operatorname{cris}}$
$A_{\operatorname{cris}}$
For a moment let
![]() $R$
be an arbitrary semiperfect ring. By the universal property of
$R$
be an arbitrary semiperfect ring. By the universal property of
![]() $A_{\operatorname{cris}}(R)$
there is a unique lift of
$A_{\operatorname{cris}}(R)$
there is a unique lift of
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
to a PD endomorphism
$\unicode[STIX]{x1D719}:R\rightarrow R$
to a PD endomorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $A_{\operatorname{cris}}(R)$
, and one verifies that
$A_{\operatorname{cris}}(R)$
, and one verifies that
![]() $\unicode[STIX]{x1D70E}$
is a Frobenius lift. Let
$\unicode[STIX]{x1D70E}$
is a Frobenius lift. Let
![]() $\operatorname{Fil}A_{\operatorname{cris}}(R)$
be the kernel of
$\operatorname{Fil}A_{\operatorname{cris}}(R)$
be the kernel of
![]() $A_{\operatorname{cris}}(R)\rightarrow R$
. By [Reference Scholze and WeinsteinSW13, Lemma 4.1.8] there is a unique functorial
$A_{\operatorname{cris}}(R)\rightarrow R$
. By [Reference Scholze and WeinsteinSW13, Lemma 4.1.8] there is a unique functorial
![]() $\unicode[STIX]{x1D70E}$
-linear map
$\unicode[STIX]{x1D70E}$
-linear map
![]() $\unicode[STIX]{x1D70E}_{1}:\operatorname{Fil}A_{\operatorname{cris}}(R)\rightarrow A_{\operatorname{cris}}(R)$
such that
$\unicode[STIX]{x1D70E}_{1}:\operatorname{Fil}A_{\operatorname{cris}}(R)\rightarrow A_{\operatorname{cris}}(R)$
such that
![]() $p\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}$
, which means that
$p\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}$
, which means that
is a
![]() $p$
-frame, and even a PD frame; see § 2. A homomorphism of semiperfect rings
$p$
-frame, and even a PD frame; see § 2. A homomorphism of semiperfect rings
![]() $R\rightarrow R^{\prime }$
induces a strict frame homomorphism
$R\rightarrow R^{\prime }$
induces a strict frame homomorphism
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}_{\operatorname{cris}}(R^{\prime })$
.
$\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}_{\operatorname{cris}}(R^{\prime })$
.
Assume now that
![]() $A$
is a lift of
$A$
is a lift of
![]() $R$
as earlier. The universal property of
$R$
as earlier. The universal property of
![]() $A_{\operatorname{cris}}(R)$
gives a homomorphism
$A_{\operatorname{cris}}(R)$
gives a homomorphism
![]() $\unicode[STIX]{x1D718}:A_{\operatorname{cris}}(R)\rightarrow A$
of extensions of
$\unicode[STIX]{x1D718}:A_{\operatorname{cris}}(R)\rightarrow A$
of extensions of
![]() $R$
, and
$R$
, and
![]() $\unicode[STIX]{x1D718}$
commutes with
$\unicode[STIX]{x1D718}$
commutes with
![]() $\unicode[STIX]{x1D70E}$
. Since
$\unicode[STIX]{x1D70E}$
. Since
![]() $A$
is
$A$
is
![]() $p$
-torsion free,
$p$
-torsion free,
![]() $\unicode[STIX]{x1D718}$
is a frame homomorphism
$\unicode[STIX]{x1D718}$
is a frame homomorphism
Proposition 5.10. If
![]() $A$
is a straight lift of
$A$
is a straight lift of
![]() $R$
in the sense of Definition 4.12, the frame homomorphism
$R$
in the sense of Definition 4.12, the frame homomorphism
![]() $\unicode[STIX]{x1D718}$
is crystalline.
$\unicode[STIX]{x1D718}$
is crystalline.
See also Proposition 7.8 below.
Proof. Let
![]() $N\subseteq A_{\operatorname{cris}}(R)$
be the kernel of
$N\subseteq A_{\operatorname{cris}}(R)$
be the kernel of
![]() $\unicode[STIX]{x1D718}$
. Since
$\unicode[STIX]{x1D718}$
. Since
![]() $A$
is
$A$
is
![]() $p$
-torsion free we have
$p$
-torsion free we have
![]() $N\cap p^{n}A_{\operatorname{cris}}(R)=p^{n}N$
. Since
$N\cap p^{n}A_{\operatorname{cris}}(R)=p^{n}N$
. Since
![]() $\unicode[STIX]{x1D718}$
is continuous for the
$\unicode[STIX]{x1D718}$
is continuous for the
![]() $p$
-adic topology and
$p$
-adic topology and
![]() $A$
is
$A$
is
![]() $p$
-adically complete,
$p$
-adically complete,
![]() $N$
is closed in the
$N$
is closed in the
![]() $p$
-adic topology of
$p$
-adic topology of
![]() $A_{\operatorname{cris}}(R)$
, and it follows that
$A_{\operatorname{cris}}(R)$
, and it follows that
![]() $N$
is
$N$
is
![]() $p$
-adically complete. We have an exact sequence
$p$
-adically complete. We have an exact sequence
![]() $0\rightarrow N/p\rightarrow A_{\operatorname{cris}}(R)/p\rightarrow R\rightarrow 0$
, and this is the PD envelope over
$0\rightarrow N/p\rightarrow A_{\operatorname{cris}}(R)/p\rightarrow R\rightarrow 0$
, and this is the PD envelope over
![]() $\mathbb{F}_{p}$
of the ideal
$\mathbb{F}_{p}$
of the ideal
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
Clearly
![]() $N$
is stable under
$N$
is stable under
![]() $\unicode[STIX]{x1D70E}_{1}$
. We claim that
$\unicode[STIX]{x1D70E}_{1}$
. We claim that
![]() $\unicode[STIX]{x1D70E}_{1}$
is nilpotent on
$\unicode[STIX]{x1D70E}_{1}$
is nilpotent on
![]() $N/p$
; cf. [Reference Scholze and WeinsteinSW13, Lemma 4.2.4]. Let
$N/p$
; cf. [Reference Scholze and WeinsteinSW13, Lemma 4.2.4]. Let
![]() $A=W(R^{\flat })/J^{\prime }$
. The hypothesis means that there are generators
$A=W(R^{\flat })/J^{\prime }$
. The hypothesis means that there are generators
![]() $a_{i}$
of
$a_{i}$
of
![]() $J$
such that
$J$
such that
![]() $[a_{i}]\in J^{\prime }$
. The ideal
$[a_{i}]\in J^{\prime }$
. The ideal
![]() $N/pN$
of
$N/pN$
of
![]() $A_{\operatorname{cris}}(R)/p$
is generated by the elements
$A_{\operatorname{cris}}(R)/p$
is generated by the elements
![]() $a_{i}^{[n]}$
for
$a_{i}^{[n]}$
for
![]() $n\geqslant 1$
. The elements
$n\geqslant 1$
. The elements
![]() $[a_{i}]^{[n]}\in N$
satisfy
$[a_{i}]^{[n]}\in N$
satisfy
see [Reference Scholze and WeinsteinSW13, Lemma 4.1.8]. Since the integer
![]() $(pn)!/(p\cdot n!)$
is divisible by
$(pn)!/(p\cdot n!)$
is divisible by
![]() $p$
when
$p$
when
![]() $n\geqslant p$
it follows that
$n\geqslant p$
it follows that
![]() $\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D70E}_{1}=0$
on
$\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D70E}_{1}=0$
on
![]() $N/pN$
.
$N/pN$
.
We consider the frames
![]() $\text{}\underline{B}_{n}=(A_{\operatorname{cris}}(R)/p^{n}N,\operatorname{Fil}A_{\operatorname{cris}}(R)/p^{n}N,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
for
$\text{}\underline{B}_{n}=(A_{\operatorname{cris}}(R)/p^{n}N,\operatorname{Fil}A_{\operatorname{cris}}(R)/p^{n}N,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
for
![]() $n\geqslant 0$
. Since
$n\geqslant 0$
. Since
![]() $\unicode[STIX]{x1D70E}_{1}$
is nilpotent on
$\unicode[STIX]{x1D70E}_{1}$
is nilpotent on
![]() $N/p^{n}N$
, the projection
$N/p^{n}N$
, the projection
![]() $\text{}\underline{B}_{n}\rightarrow \text{}\underline{B}_{0}=\text{}\underline{A}$
is crystalline by the general deformation lemma [Reference LauLau10, Theorem 3.2]. We have
$\text{}\underline{B}_{n}\rightarrow \text{}\underline{B}_{0}=\text{}\underline{A}$
is crystalline by the general deformation lemma [Reference LauLau10, Theorem 3.2]. We have
![]() $\varprojlim \text{}\underline{B}_{n}=\text{}\underline{A}_{\operatorname{cris}}(R)$
, and the proposition follows; see [Reference LauLau10, Lemma 2.12].☐
$\varprojlim \text{}\underline{B}_{n}=\text{}\underline{A}_{\operatorname{cris}}(R)$
, and the proposition follows; see [Reference LauLau10, Lemma 2.12].☐
Corollary 5.11. If the semiperfect ring
![]() $R$
admits a straight lift
$R$
admits a straight lift
![]() $A$
, there is an equivalence of categories
$A$
, there is an equivalence of categories
Proof. By Theorem 5.7 and Proposition 5.10 we have equivalences
Remark 5.12. When
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free, the equivalence (5.8) is given by the functor
$p$
-torsion free, the equivalence (5.8) is given by the functor
![]() $\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
$\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
![]() $\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}$
. A variant of this holds in general; see Corollary 6.5, which shows in particular that the equivalence (5.8) does not depend on the choice of the lift
$\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}$
. A variant of this holds in general; see Corollary 6.5, which shows in particular that the equivalence (5.8) does not depend on the choice of the lift
![]() $A$
.
$A$
.
Corollary 5.13. If
![]() $R$
is a complete intersection semiperfect ring, the functor
$R$
is a complete intersection semiperfect ring, the functor
![]() $\operatorname{DF}_{\operatorname{Spec}R}$
of (3.2) is an equivalence.
$\operatorname{DF}_{\operatorname{Spec}R}$
of (3.2) is an equivalence.
Proof. If
![]() $R$
is a complete intersection, the ring
$R$
is a complete intersection, the ring
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free; see Remark 4.3. Therefore we have a sequence of functors
$p$
-torsion free; see Remark 4.3. Therefore we have a sequence of functors
where
![]() $e$
is the evaluation functor, and the composition is
$e$
is the evaluation functor, and the composition is
![]() $\unicode[STIX]{x1D6F7}_{A}$
. The functor
$\unicode[STIX]{x1D6F7}_{A}$
. The functor
![]() $e$
is an equivalence; see [Reference Cais and LauCL14, Proposition 2.6.4]. Here no connection appears because
$e$
is an equivalence; see [Reference Cais and LauCL14, Proposition 2.6.4]. Here no connection appears because
![]() $R^{\flat }$
is perfect, and thus
$R^{\flat }$
is perfect, and thus
![]() $\unicode[STIX]{x1D6FA}_{R^{\flat }}=0$
. The functors
$\unicode[STIX]{x1D6FA}_{R^{\flat }}=0$
. The functors
![]() $\unicode[STIX]{x1D718}^{\ast }$
and
$\unicode[STIX]{x1D718}^{\ast }$
and
![]() $\unicode[STIX]{x1D6F7}_{A}$
are equivalences by Theorem 5.7 and Proposition 5.10. Thus
$\unicode[STIX]{x1D6F7}_{A}$
are equivalences by Theorem 5.7 and Proposition 5.10. Thus
![]() $\operatorname{DF}_{R}$
is an equivalence as well.☐
$\operatorname{DF}_{R}$
is an equivalence as well.☐
Lemma 5.14. If the semiperfect ring
![]() $R$
has a lift
$R$
has a lift
![]() $A$
, then the forgetful functor
$A$
, then the forgetful functor
![]() $\operatorname{D}(\operatorname{Spec}R)\rightarrow \operatorname{DF}(\operatorname{Spec}R)$
is fully faithful.
$\operatorname{D}(\operatorname{Spec}R)\rightarrow \operatorname{DF}(\operatorname{Spec}R)$
is fully faithful.
Proof. For a PD extension
![]() $S\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R$
of
$S\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R$
of
![]() $\mathbb{F}_{p}$
-algebras the Frobenius
$\mathbb{F}_{p}$
-algebras the Frobenius
![]() $\unicode[STIX]{x1D719}_{S}$
factors through a homomorphism
$\unicode[STIX]{x1D719}_{S}$
factors through a homomorphism
![]() $\unicode[STIX]{x1D719}_{S/R}:R\rightarrow S$
, i.e.
$\unicode[STIX]{x1D719}_{S/R}:R\rightarrow S$
, i.e.
![]() $\unicode[STIX]{x1D719}_{S/R}\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D719}_{S}$
. An object of
$\unicode[STIX]{x1D719}_{S/R}\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D719}_{S}$
. An object of
![]() $\operatorname{DF}(\operatorname{Spec}R)$
is a triple
$\operatorname{DF}(\operatorname{Spec}R)$
is a triple
![]() $({\mathcal{M}},F,V)\in \operatorname{D}(\operatorname{Spec}R)$
together with a direct summand of
$({\mathcal{M}},F,V)\in \operatorname{D}(\operatorname{Spec}R)$
together with a direct summand of
![]() ${\mathcal{M}}_{R}$
whose base change under each
${\mathcal{M}}_{R}$
whose base change under each
![]() $\unicode[STIX]{x1D719}_{S/R}$
is determined by
$\unicode[STIX]{x1D719}_{S/R}$
is determined by
![]() $({\mathcal{M}},F)$
; see [Reference Cais and LauCL14, Definition 2.4.1]. The lift
$({\mathcal{M}},F)$
; see [Reference Cais and LauCL14, Definition 2.4.1]. The lift
![]() $A$
of
$A$
of
![]() $R$
makes
$R$
makes
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
into a PD extension, which we write as
$\unicode[STIX]{x1D719}:R\rightarrow R$
into a PD extension, which we write as
![]() $S\rightarrow R$
; see Remark 5.3. The corresponding
$S\rightarrow R$
; see Remark 5.3. The corresponding
![]() $\unicode[STIX]{x1D719}_{S/R}$
is the identity of
$\unicode[STIX]{x1D719}_{S/R}$
is the identity of
![]() $R$
, and the lemma follows.☐
$R$
, and the lemma follows.☐
Corollary 5.13 together with Lemmas 4.13 and 5.14 gives the following.
Corollary 5.15 [Reference Scholze and WeinsteinSW13, Corollary 4.1.12].
If
![]() $R$
is a complete intersection semiperfect ring, the crystalline Dieudonné functor
$R$
is a complete intersection semiperfect ring, the crystalline Dieudonné functor
![]() $\mathbb{D}_{\operatorname{Spec}R}$
is fully faithful.
$\mathbb{D}_{\operatorname{Spec}R}$
is fully faithful.
6 Crystalline Dieudonné windows
In this section we associate to a
![]() $p$
-divisible group over an arbitrary semiperfect ring
$p$
-divisible group over an arbitrary semiperfect ring
![]() $R$
a window over the frame
$R$
a window over the frame
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)$
of (5.5).
$\text{}\underline{A}_{\operatorname{cris}}(R)$
of (5.5).
6.1 Relative deformation rings
We need a relative version of the universal deformation of a
![]() $p$
-divisible group. Let
$p$
-divisible group. Let
![]() $\unicode[STIX]{x1D6EC}\rightarrow R$
be a homomorphism of
$\unicode[STIX]{x1D6EC}\rightarrow R$
be a homomorphism of
![]() $\mathbb{F}_{p}$
-algebras. (More generally one could take
$\mathbb{F}_{p}$
-algebras. (More generally one could take
![]() $p$
-adic rings.)
$p$
-adic rings.)
Let
![]() $\operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
be the category of
$\operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
be the category of
![]() $\unicode[STIX]{x1D6EC}$
-algebras
$\unicode[STIX]{x1D6EC}$
-algebras
![]() $A$
equipped with a
$A$
equipped with a
![]() $\unicode[STIX]{x1D6EC}$
-linear homomorphism
$\unicode[STIX]{x1D6EC}$
-linear homomorphism
![]() $A\rightarrow R$
, and let
$A\rightarrow R$
, and let
![]() $\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}\subseteq \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
be the full subcategory of all
$\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}\subseteq \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
be the full subcategory of all
![]() $A$
such that
$A$
such that
![]() $A\rightarrow R$
is surjective and
$A\rightarrow R$
is surjective and
![]() $J_{A}=\operatorname{Ker}(A\rightarrow R)$
is a nilpotent ideal. For a
$J_{A}=\operatorname{Ker}(A\rightarrow R)$
is a nilpotent ideal. For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
we consider the deformation functor
$R$
we consider the deformation functor
where
![]() $\operatorname{Def}_{G}(A)$
is the set of isomorphism classes of deformations of
$\operatorname{Def}_{G}(A)$
is the set of isomorphism classes of deformations of
![]() $G$
to
$G$
to
![]() $A$
. If
$A$
. If
![]() $\unicode[STIX]{x1D6EC}=R$
, then
$\unicode[STIX]{x1D6EC}=R$
, then
![]() $\operatorname{Def}_{G}$
is pro-represented by the twisted power series ring
$\operatorname{Def}_{G}$
is pro-represented by the twisted power series ring
![]() $B=\unicode[STIX]{x1D6EC}[[Q]]\in \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
, where
$B=\unicode[STIX]{x1D6EC}[[Q]]\in \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
, where
![]() $Q$
is the projective
$Q$
is the projective
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $\operatorname{Lie}(G^{\vee })^{\ast }\otimes _{\unicode[STIX]{x1D6EC}}\operatorname{Lie}(G)^{\ast }$
; see [Reference LauLau14, Proposition 3.11].
$\operatorname{Lie}(G^{\vee })^{\ast }\otimes _{\unicode[STIX]{x1D6EC}}\operatorname{Lie}(G)^{\ast }$
; see [Reference LauLau14, Proposition 3.11].
Lemma 6.1. Assume that
![]() $G^{\prime }$
is a
$G^{\prime }$
is a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $\unicode[STIX]{x1D6EC}$
with an isomorphism
$\unicode[STIX]{x1D6EC}$
with an isomorphism
![]() $G^{\prime }\otimes _{\unicode[STIX]{x1D6EC}}R\cong G$
. If
$G^{\prime }\otimes _{\unicode[STIX]{x1D6EC}}R\cong G$
. If
![]() $B=\unicode[STIX]{x1D6EC}[[Q]]$
represents
$B=\unicode[STIX]{x1D6EC}[[Q]]$
represents
![]() $\operatorname{Def}_{G^{\prime }}:\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}}\rightarrow \operatorname{Set}$
, then
$\operatorname{Def}_{G^{\prime }}:\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}}\rightarrow \operatorname{Set}$
, then
![]() $B$
also represents
$B$
also represents
![]() $\operatorname{Def}_{G}:\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}\rightarrow \operatorname{Set}$
.
$\operatorname{Def}_{G}:\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}\rightarrow \operatorname{Set}$
.
Proof. For
![]() $A\in \operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}$
the fiber product
$A\in \operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R}$
the fiber product
![]() $A^{\prime }=A\times _{R}\unicode[STIX]{x1D6EC}$
lies in
$A^{\prime }=A\times _{R}\unicode[STIX]{x1D6EC}$
lies in
![]() $\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}}$
. Let
$\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D6EC}}$
. Let
![]() $\operatorname{LF}(A)$
denote the category of finite projective
$\operatorname{LF}(A)$
denote the category of finite projective
![]() $A$
-modules. Then the obvious functor
$A$
-modules. Then the obvious functor
![]() $\operatorname{LF}(A^{\prime })\rightarrow \operatorname{LF}(A)\times _{\operatorname{LF}(R)}\operatorname{LF}(\unicode[STIX]{x1D6EC})$
is an equivalence. It follows that the natural map
$\operatorname{LF}(A^{\prime })\rightarrow \operatorname{LF}(A)\times _{\operatorname{LF}(R)}\operatorname{LF}(\unicode[STIX]{x1D6EC})$
is an equivalence. It follows that the natural map
![]() $\operatorname{Def}_{G^{\prime }}(A^{\prime })\rightarrow \operatorname{Def}_{G}(A)$
is bijective, which proves the lemma.☐
$\operatorname{Def}_{G^{\prime }}(A^{\prime })\rightarrow \operatorname{Def}_{G}(A)$
is bijective, which proves the lemma.☐
Let
![]() $\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
be the category of all
$\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
be the category of all
![]() $A\in \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
such that
$A\in \operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
such that
![]() $A\rightarrow R$
is surjective and the ideal
$A\rightarrow R$
is surjective and the ideal
![]() $J_{A}$
is bounded nilpotent, i.e. there is an
$J_{A}$
is bounded nilpotent, i.e. there is an
![]() $n\geqslant 1$
with
$n\geqslant 1$
with
![]() $x^{n}=0$
for all
$x^{n}=0$
for all
![]() $x\in J_{A}$
. We define
$x\in J_{A}$
. We define
![]() $\operatorname{Def}_{G}:\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}\rightarrow \operatorname{Set}$
as before.
$\operatorname{Def}_{G}:\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}\rightarrow \operatorname{Set}$
as before.
Lemma 6.2. In the situation of Lemma 6.1 the functor
![]() $\operatorname{Def}_{G}$
on
$\operatorname{Def}_{G}$
on
![]() $\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
is also represented by
$\tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
is also represented by
![]() $B$
.
$B$
.
Proof. Let
![]() $A\in \tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
. We have to show that the natural map
$A\in \tilde{\operatorname{Nil}}_{\unicode[STIX]{x1D6EC}/R}$
. We have to show that the natural map
![]() $\operatorname{Hom}(B,A)\rightarrow \operatorname{Def}_{G}(A)$
is bijective. For each pair of homomorphisms
$\operatorname{Hom}(B,A)\rightarrow \operatorname{Def}_{G}(A)$
is bijective. For each pair of homomorphisms
![]() $f_{1},f_{2}:B\rightarrow A$
in
$f_{1},f_{2}:B\rightarrow A$
in
![]() $\operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
there is a finitely generated ideal
$\operatorname{Aug}_{\unicode[STIX]{x1D6EC}/R}$
there is a finitely generated ideal
![]() $\mathfrak{b}\subseteq J_{A}$
such that the projection
$\mathfrak{b}\subseteq J_{A}$
such that the projection
![]() $A\rightarrow \bar{A}=A/\mathfrak{b}$
equalizes
$A\rightarrow \bar{A}=A/\mathfrak{b}$
equalizes
![]() $f$
and
$f$
and
![]() $g$
. For each pair of deformations
$g$
. For each pair of deformations
![]() $G_{1},G_{2}$
of
$G_{1},G_{2}$
of
![]() $G$
over
$G$
over
![]() $A$
the reduction map
$A$
the reduction map
![]() $\operatorname{Hom}_{A}(G_{1},G_{2})\rightarrow \operatorname{End}_{R}(G)$
is injective with cokernel annihilated by
$\operatorname{Hom}_{A}(G_{1},G_{2})\rightarrow \operatorname{End}_{R}(G)$
is injective with cokernel annihilated by
![]() $p^{r}$
for some
$p^{r}$
for some
![]() $r$
; see [Reference LauLau14, Lemma 3.4]. Thus there is a unique isogeny
$r$
; see [Reference LauLau14, Lemma 3.4]. Thus there is a unique isogeny
![]() $\unicode[STIX]{x1D713}:G_{1}\rightarrow G_{2}$
which lifts
$\unicode[STIX]{x1D713}:G_{1}\rightarrow G_{2}$
which lifts
![]() $p^{r}\operatorname{id}_{G}$
. Its kernel is finitely presented; see [Reference LauLau14, Lemma 3.6]. Thus there is a finitely generated ideal
$p^{r}\operatorname{id}_{G}$
. Its kernel is finitely presented; see [Reference LauLau14, Lemma 3.6]. Thus there is a finitely generated ideal
![]() $\mathfrak{b}\subseteq A$
such that
$\mathfrak{b}\subseteq A$
such that
![]() $\operatorname{Ker}(\unicode[STIX]{x1D713})$
and
$\operatorname{Ker}(\unicode[STIX]{x1D713})$
and
![]() $G_{1}[p^{r}]$
coincide over
$G_{1}[p^{r}]$
coincide over
![]() $A/\mathfrak{b}$
, which means that
$A/\mathfrak{b}$
, which means that
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
map to the same element of
$G_{2}$
map to the same element of
![]() $\operatorname{Def}_{G}(A/\mathfrak{b})$
. Moreover
$\operatorname{Def}_{G}(A/\mathfrak{b})$
. Moreover
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
are equal as deformations of
$G_{2}$
are equal as deformations of
![]() $G$
if and only if they are equal as deformations of
$G$
if and only if they are equal as deformations of
![]() $G_{1}\otimes _{A}A/\mathfrak{b}$
. In view of these remarks it suffices to show that
$G_{1}\otimes _{A}A/\mathfrak{b}$
. In view of these remarks it suffices to show that
![]() $B(A)\rightarrow \operatorname{Def}_{G}(A)$
is bijective when
$B(A)\rightarrow \operatorname{Def}_{G}(A)$
is bijective when
![]() $R$
is replaced by
$R$
is replaced by
![]() $R^{\prime }=A/\mathfrak{b}$
for varying finitely generated ideals
$R^{\prime }=A/\mathfrak{b}$
for varying finitely generated ideals
![]() $\mathfrak{b}$
. Then
$\mathfrak{b}$
. Then
![]() $A$
lies in
$A$
lies in
![]() $\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R^{\prime }}$
, and the lemma follows from Lemma 6.1.☐
$\operatorname{Nil}_{\unicode[STIX]{x1D6EC}/R^{\prime }}$
, and the lemma follows from Lemma 6.1.☐
6.2 Construction of the crystalline window functor
Theorem 6.3. For semiperfect rings
![]() $R$
there are unique functors
$R$
there are unique functors
which are functorial in
![]() $R$
, such that the triple
$R$
, such that the triple
![]() $(M,\operatorname{Fil}M,F)$
is given by the filtered Dieudonné crystal
$(M,\operatorname{Fil}M,F)$
is given by the filtered Dieudonné crystal
![]() $\operatorname{DF}(G)$
of (3.2) as usual, i.e.
$\operatorname{DF}(G)$
of (3.2) as usual, i.e.
![]() $M=\mathbb{D}(G)_{A_{\operatorname{cris}}(R)}$
, the submodule
$M=\mathbb{D}(G)_{A_{\operatorname{cris}}(R)}$
, the submodule
![]() $\operatorname{Fil}M\subseteq M$
is the inverse image of the Hodge filtration
$\operatorname{Fil}M\subseteq M$
is the inverse image of the Hodge filtration
![]() $\operatorname{Lie}(G)^{\ast }\subseteq \mathbb{D}(G)_{R}$
, and
$\operatorname{Lie}(G)^{\ast }\subseteq \mathbb{D}(G)_{R}$
, and
![]() $F:M\rightarrow M$
is induced by
$F:M\rightarrow M$
is induced by
![]() $F:\unicode[STIX]{x1D719}^{\ast }\mathbb{D}(G)\rightarrow \mathbb{D}(G)$
.
$F:\unicode[STIX]{x1D719}^{\ast }\mathbb{D}(G)\rightarrow \mathbb{D}(G)$
.
The existence of such a functor has been suggested in [Reference Scholze and WeinsteinSW13, Remark 4.1.9]. We call
![]() $\text{}\underline{M}$
the crystalline Dieudonné window of
$\text{}\underline{M}$
the crystalline Dieudonné window of
![]() $G$
.
$G$
.
Proof. This is similar to [Reference LauLau14, Theorem 3.19].
Let
![]() $G\mapsto (M(G),\operatorname{Fil}M(G),F)$
be as defined in the theorem. We have to find a functorial map
$G\mapsto (M(G),\operatorname{Fil}M(G),F)$
be as defined in the theorem. We have to find a functorial map
![]() $F_{1}:\operatorname{Fil}M(G)\rightarrow M(G)$
which gives a window
$F_{1}:\operatorname{Fil}M(G)\rightarrow M(G)$
which gives a window
![]() $\text{}\underline{M}(G)$
, and verify that
$\text{}\underline{M}(G)$
, and verify that
![]() $F_{1}$
is unique. If
$F_{1}$
is unique. If
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free then
$p$
-torsion free then
![]() $F_{1}$
and thus
$F_{1}$
and thus
![]() $\text{}\underline{M}(G)$
are well defined; see [Reference LauLau14, Proposition 3.17]. This applies in particular when
$\text{}\underline{M}(G)$
are well defined; see [Reference LauLau14, Proposition 3.17]. This applies in particular when
![]() $R$
is perfect since then
$R$
is perfect since then
![]() $A_{\operatorname{cris}}(R)=W(R)$
.
$A_{\operatorname{cris}}(R)=W(R)$
.
In general let
![]() $\unicode[STIX]{x1D70B}:R^{\flat }\rightarrow R$
be the projection. We write
$\unicode[STIX]{x1D70B}:R^{\flat }\rightarrow R$
be the projection. We write
![]() $\unicode[STIX]{x1D70B}^{\ast }$
for the base change functor of modules or windows from
$\unicode[STIX]{x1D70B}^{\ast }$
for the base change functor of modules or windows from
![]() $W(R^{\flat })$
to
$W(R^{\flat })$
to
![]() $A_{\operatorname{cris}}(R)$
. Note that
$A_{\operatorname{cris}}(R)$
. Note that
![]() $p$
-divisible groups can be lifted under
$p$
-divisible groups can be lifted under
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
by [Reference IllusieIll85, Theorem 4.4], and thus
$\unicode[STIX]{x1D719}:R\rightarrow R$
by [Reference IllusieIll85, Theorem 4.4], and thus
![]() $p$
-divisible groups can be lifted under
$p$
-divisible groups can be lifted under
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $G\in \operatorname{BT}(\operatorname{Spec}R)$
be given. We choose a lift
$G\in \operatorname{BT}(\operatorname{Spec}R)$
be given. We choose a lift
![]() $G_{1}\in \operatorname{BT}(\operatorname{Spec}R^{\flat })$
of
$G_{1}\in \operatorname{BT}(\operatorname{Spec}R^{\flat })$
of
![]() $G$
. Then
$G$
. Then
![]() $M(G)=\unicode[STIX]{x1D70B}^{\ast }M(G_{1})$
as modules with
$M(G)=\unicode[STIX]{x1D70B}^{\ast }M(G_{1})$
as modules with
![]() $\operatorname{Fil}$
and
$\operatorname{Fil}$
and
![]() $F$
, and necessarily we have to define
$F$
, and necessarily we have to define
![]() $\text{}\underline{M}(G)=\unicode[STIX]{x1D70B}^{\ast }\text{}\underline{M}(G_{1})$
as windows. We have to show that this construction of
$\text{}\underline{M}(G)=\unicode[STIX]{x1D70B}^{\ast }\text{}\underline{M}(G_{1})$
as windows. We have to show that this construction of
![]() $F_{1}$
does not depend on the choice of
$F_{1}$
does not depend on the choice of
![]() $G_{1}$
, i.e. if
$G_{1}$
, i.e. if
![]() $G_{2}\in \operatorname{BT}(\operatorname{Spec}R^{\flat })$
is another lift of
$G_{2}\in \operatorname{BT}(\operatorname{Spec}R^{\flat })$
is another lift of
![]() $G$
, then the composite isomorphism of modules
$G$
, then the composite isomorphism of modules
preserves the homomorphisms
![]() $F_{1}$
defined on the outer terms by the windows
$F_{1}$
defined on the outer terms by the windows
![]() $\text{}\underline{M}(G_{i})$
.
$\text{}\underline{M}(G_{i})$
.
We want to lift the situation to perfect rings. More precisely, we claim that one can find a commutative diagram of rings

where
![]() $S$
and
$S$
and
![]() $S^{\prime }$
are perfect, and
$S^{\prime }$
are perfect, and
![]() $p$
-divisible groups
$p$
-divisible groups
![]() $H_{1},H_{2}\in \operatorname{BT}(\operatorname{Spec}S^{\prime })$
together with an isomorphism
$H_{1},H_{2}\in \operatorname{BT}(\operatorname{Spec}S^{\prime })$
together with an isomorphism
![]() $\unicode[STIX]{x1D6FC}:u^{\ast }H_{1}\cong u^{\ast }H_{2}$
over
$\unicode[STIX]{x1D6FC}:u^{\ast }H_{1}\cong u^{\ast }H_{2}$
over
![]() $S$
and isomorphisms
$S$
and isomorphisms
![]() $f^{\ast }H_{i}\cong G_{i}$
over
$f^{\ast }H_{i}\cong G_{i}$
over
![]() $R^{\flat }$
for
$R^{\flat }$
for
![]() $i=1,2$
such that
$i=1,2$
such that
![]() $\unicode[STIX]{x1D6FC}$
induces the given isomorphism
$\unicode[STIX]{x1D6FC}$
induces the given isomorphism
![]() $\unicode[STIX]{x1D70B}^{\ast }G_{1}\cong \unicode[STIX]{x1D70B}^{\ast }G_{2}$
over
$\unicode[STIX]{x1D70B}^{\ast }G_{1}\cong \unicode[STIX]{x1D70B}^{\ast }G_{2}$
over
![]() $R$
, i.e. the composition
$R$
, i.e. the composition
is the given isomorphism. Then the homomorphisms
![]() $F_{1}$
of
$F_{1}$
of
![]() $H_{1}$
and of
$H_{1}$
and of
![]() $H_{2}$
coincide over
$H_{2}$
coincide over
![]() $S$
since
$S$
since
![]() $S$
is perfect, and by base change under
$S$
is perfect, and by base change under
![]() $g$
it follows that the homomorphisms
$g$
it follows that the homomorphisms
![]() $F_{1}$
of
$F_{1}$
of
![]() $G_{1}$
and of
$G_{1}$
and of
![]() $G_{2}$
coincide over
$G_{2}$
coincide over
![]() $R$
as required.
$R$
as required.
Let us prove the claim. Let
![]() $G^{\prime }$
be a lift of
$G^{\prime }$
be a lift of
![]() $G$
to
$G$
to
![]() $R^{\flat }$
, for example
$R^{\flat }$
, for example
![]() $G^{\prime }=G_{1}$
. Let
$G^{\prime }=G_{1}$
. Let
![]() $B=R^{\flat }[[Q]]$
be the universal deformation ring of
$B=R^{\flat }[[Q]]$
be the universal deformation ring of
![]() $G^{\prime }$
as in § 6.1 and let
$G^{\prime }$
as in § 6.1 and let
![]() ${\mathcal{G}}$
over
${\mathcal{G}}$
over
![]() $B$
be the universal deformation. By Lemma 6.2,
$B$
be the universal deformation. By Lemma 6.2,
![]() $B$
represents the deformation functor
$B$
represents the deformation functor
![]() $\operatorname{Def}_{G}$
on the category
$\operatorname{Def}_{G}$
on the category
![]() $\tilde{\operatorname{Nil}}_{R^{\flat }/R}$
of augmented algebras
$\tilde{\operatorname{Nil}}_{R^{\flat }/R}$
of augmented algebras
![]() $R^{\flat }\rightarrow A\rightarrow R$
such that the kernel of
$R^{\flat }\rightarrow A\rightarrow R$
such that the kernel of
![]() $A\rightarrow R$
is bounded nilpotent. The system
$A\rightarrow R$
is bounded nilpotent. The system
![]() $(\unicode[STIX]{x1D719}^{n}:R\rightarrow R)_{n}$
is a pro-object of
$(\unicode[STIX]{x1D719}^{n}:R\rightarrow R)_{n}$
is a pro-object of
![]() $\tilde{\operatorname{Nil}}_{R^{\flat }/R}$
with limit
$\tilde{\operatorname{Nil}}_{R^{\flat }/R}$
with limit
![]() $R^{\flat }\rightarrow R$
in
$R^{\flat }\rightarrow R$
in
![]() $\operatorname{Aug}_{R^{\flat }/R}$
. Thus there are homomorphisms
$\operatorname{Aug}_{R^{\flat }/R}$
. Thus there are homomorphisms
![]() $\unicode[STIX]{x1D6FD}_{i}:B\rightarrow R^{\flat }$
in
$\unicode[STIX]{x1D6FD}_{i}:B\rightarrow R^{\flat }$
in
![]() $\operatorname{Aug}_{R^{\flat }/R}$
with
$\operatorname{Aug}_{R^{\flat }/R}$
with
![]() $\unicode[STIX]{x1D6FD}_{i}^{\ast }{\mathcal{G}}\cong G_{i}$
as deformations of
$\unicode[STIX]{x1D6FD}_{i}^{\ast }{\mathcal{G}}\cong G_{i}$
as deformations of
![]() $G$
over
$G$
over
![]() $R^{\flat }$
.
$R^{\flat }$
.
We put
![]() $S=R^{\flat }$
with
$S=R^{\flat }$
with
![]() $g=\unicode[STIX]{x1D70B}$
and
$g=\unicode[STIX]{x1D70B}$
and
![]() $S^{\prime }=B^{\operatorname{per}}=\varinjlim (B,\unicode[STIX]{x1D719})$
with
$S^{\prime }=B^{\operatorname{per}}=\varinjlim (B,\unicode[STIX]{x1D719})$
with
![]() $u=\unicode[STIX]{x1D6FD}_{1}^{\operatorname{per}}$
and
$u=\unicode[STIX]{x1D6FD}_{1}^{\operatorname{per}}$
and
![]() $f=\unicode[STIX]{x1D6FD}_{2}^{\operatorname{per}}$
. Let
$f=\unicode[STIX]{x1D6FD}_{2}^{\operatorname{per}}$
. Let
![]() $H_{1}$
be the base change of
$H_{1}$
be the base change of
![]() $G_{1}$
under
$G_{1}$
under
![]() $R^{\flat }\rightarrow B\rightarrow S^{\prime }$
and let
$R^{\flat }\rightarrow B\rightarrow S^{\prime }$
and let
![]() $H_{2}$
be the base change of
$H_{2}$
be the base change of
![]() ${\mathcal{G}}$
under
${\mathcal{G}}$
under
![]() $B\rightarrow S^{\prime }$
. Then
$B\rightarrow S^{\prime }$
. Then
![]() $u^{\ast }H_{1}\cong G_{1}\cong u^{\ast }H_{2}$
and
$u^{\ast }H_{1}\cong G_{1}\cong u^{\ast }H_{2}$
and
![]() $f^{\ast }H_{1}\cong G_{1}$
and
$f^{\ast }H_{1}\cong G_{1}$
and
![]() $f^{\ast }H_{2}\cong G_{2}$
as deformations of
$f^{\ast }H_{2}\cong G_{2}$
as deformations of
![]() $G$
. This proves the claim; the required equality of isomorphisms
$G$
. This proves the claim; the required equality of isomorphisms
![]() $\unicode[STIX]{x1D70B}^{\ast }G_{1}\cong \unicode[STIX]{x1D70B}^{\ast }G_{2}$
is automatic because the reduction map
$\unicode[STIX]{x1D70B}^{\ast }G_{1}\cong \unicode[STIX]{x1D70B}^{\ast }G_{2}$
is automatic because the reduction map
![]() $\operatorname{Hom}(G_{1},G_{2})\rightarrow \operatorname{End}(G)$
is injective.☐
$\operatorname{Hom}(G_{1},G_{2})\rightarrow \operatorname{End}(G)$
is injective.☐
The functors
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
are related with the functors
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
are related with the functors
![]() $\unicode[STIX]{x1D6F7}_{A}$
of (5.2) as follows.
$\unicode[STIX]{x1D6F7}_{A}$
of (5.2) as follows.
Lemma 6.4. If
![]() $A$
is a lift of the semiperfect ring
$A$
is a lift of the semiperfect ring
![]() $R$
, there is a natural isomorphism of
$R$
, there is a natural isomorphism of
![]() $\text{}\underline{A}$
-windows
$\text{}\underline{A}$
-windows
![]() $\unicode[STIX]{x1D718}^{\ast }\circ \unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)\cong \unicode[STIX]{x1D6F7}_{A}(G)$
, where
$\unicode[STIX]{x1D718}^{\ast }\circ \unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)\cong \unicode[STIX]{x1D6F7}_{A}(G)$
, where
![]() $\unicode[STIX]{x1D718}$
is defined in (5.6).
$\unicode[STIX]{x1D718}$
is defined in (5.6).
Proof. The functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
without
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
without
![]() $F_{1}$
is given by the Dieudonné crystal evaluated at
$F_{1}$
is given by the Dieudonné crystal evaluated at
![]() $A_{\operatorname{cris}}(R)$
. Thus the functor
$A_{\operatorname{cris}}(R)$
. Thus the functor
![]() $\unicode[STIX]{x1D718}^{\ast }\circ \unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
without
$\unicode[STIX]{x1D718}^{\ast }\circ \unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
without
![]() $F_{1}$
is given by the Dieudonné crystal evaluated at
$F_{1}$
is given by the Dieudonné crystal evaluated at
![]() $A$
. Since
$A$
. Since
![]() $A$
is
$A$
is
![]() $p$
-torsion free, for the frame
$p$
-torsion free, for the frame
![]() $\text{}\underline{A}$
the functor of forgetting
$\text{}\underline{A}$
the functor of forgetting
![]() $F_{1}$
is fully faithful, and the lemma follows.☐
$F_{1}$
is fully faithful, and the lemma follows.☐
Corollary 6.5. If the semiperfect ring
![]() $R$
admits a straight lift
$R$
admits a straight lift
![]() $A$
, the functor
$A$
, the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence and coincides with the equivalence of Corollary 5.11.
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence and coincides with the equivalence of Corollary 5.11.
Proof. If
![]() $A$
is a straight lift of
$A$
is a straight lift of
![]() $R$
, the functor
$R$
, the functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
is an equivalence by Theorem 5.7 together with Lemma 5.4, and the functor
$\unicode[STIX]{x1D6F7}_{A}$
is an equivalence by Theorem 5.7 together with Lemma 5.4, and the functor
![]() $\unicode[STIX]{x1D718}^{\ast }$
is an equivalence by Proposition 5.10. By Lemma 6.4 it follows that
$\unicode[STIX]{x1D718}^{\ast }$
is an equivalence by Proposition 5.10. By Lemma 6.4 it follows that
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence. The final assertion is clear.☐
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence. The final assertion is clear.☐
Remark 6.6. Corollary 6.5 is a special case of Theorem 7.10 below. Corollary 6.5 applies in particular when
![]() $R$
is a complete intersection or balanced; see Lemma 4.13. For complete intersections, Corollary 6.5 is essentially a restatement of Corollary 5.13, but the balanced case contains new information.
$R$
is a complete intersection or balanced; see Lemma 4.13. For complete intersections, Corollary 6.5 is essentially a restatement of Corollary 5.13, but the balanced case contains new information.
Corollary 6.7. If
![]() $R$
is an iso-balanced semiperfect ring, then the crystalline Dieudonné functor
$R$
is an iso-balanced semiperfect ring, then the crystalline Dieudonné functor
![]() $\mathbb{D}_{R}:\operatorname{BT}(\operatorname{Spec}R)\rightarrow \operatorname{D}(\operatorname{Spec}R)$
is fully faithful up to isogeny.
$\mathbb{D}_{R}:\operatorname{BT}(\operatorname{Spec}R)\rightarrow \operatorname{D}(\operatorname{Spec}R)$
is fully faithful up to isogeny.
For
![]() $f$
-semiperfect rings, this is [Reference Scholze and WeinsteinSW13, Theorem 4.1.4]; see Remark 4.9.
$f$
-semiperfect rings, this is [Reference Scholze and WeinsteinSW13, Theorem 4.1.4]; see Remark 4.9.
Proof. To prove the assertion we may replace
![]() $R$
by an isogenous ring; see [Reference Scholze and WeinsteinSW13, Proposition 4.1.5]. Thus we can assume that
$R$
by an isogenous ring; see [Reference Scholze and WeinsteinSW13, Proposition 4.1.5]. Thus we can assume that
![]() $R$
is balanced, so
$R$
is balanced, so
![]() $R$
has a straight lift. For
$R$
has a straight lift. For
![]() $G\in \operatorname{BT}(\operatorname{Spec}R)$
and
$G\in \operatorname{BT}(\operatorname{Spec}R)$
and
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)=\text{}\underline{M}=(M,\operatorname{Fil}M,F,F_{1})$
, the Dieudenné crystal
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}(G)=\text{}\underline{M}=(M,\operatorname{Fil}M,F,F_{1})$
, the Dieudenné crystal
![]() $\mathbb{D}(G)$
is given by the pair
$\mathbb{D}(G)$
is given by the pair
![]() $(M,F)$
. For
$(M,F)$
. For
![]() $G,G^{\prime }\in \operatorname{BT}(\operatorname{Spec}R)$
we have to show that the composition
$G,G^{\prime }\in \operatorname{BT}(\operatorname{Spec}R)$
we have to show that the composition
is bijective. The first map is bijective without
![]() $\otimes \mathbb{Q}$
by Corollary 6.5, the second map is bijective because the
$\otimes \mathbb{Q}$
by Corollary 6.5, the second map is bijective because the
![]() $A_{\operatorname{cris}}(R)$
-module
$A_{\operatorname{cris}}(R)$
-module
![]() $M$
is of finite type.☐
$M$
is of finite type.☐
7 The crystalline equivalence
In this section we extend Corollary 6.5 to arbitrary iso-balanced semiperfect rings. Let
![]() $R$
be a semiperfect ring, and let
$R$
be a semiperfect ring, and let
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
.
7.1 Weak lifts
We use a weak version of lifts which may have
![]() $p$
-torsion.
$p$
-torsion.
Definition 7.1. A weak lift of
![]() $R$
is a
$R$
is a
![]() $p$
-adically complete ring
$p$
-adically complete ring
![]() $A$
with
$A$
with
![]() $A/pA=R$
which carries a ring endomorphism
$A/pA=R$
which carries a ring endomorphism
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
that induces
$\unicode[STIX]{x1D70E}:A\rightarrow A$
that induces
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
![]() $R$
, and a
$R$
, and a
![]() $\unicode[STIX]{x1D70E}$
-linear map
$\unicode[STIX]{x1D70E}$
-linear map
![]() $\unicode[STIX]{x1D70E}_{1}:pA\rightarrow A$
with
$\unicode[STIX]{x1D70E}_{1}:pA\rightarrow A$
with
![]() $\unicode[STIX]{x1D70E}_{1}(p)=1$
.
$\unicode[STIX]{x1D70E}_{1}(p)=1$
.
Remark 7.2. The maps
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}_{1}$
are unique if they exist. This is analogous to Remark 4.11. There is a unique homomorphism
$\unicode[STIX]{x1D70E}_{1}$
are unique if they exist. This is analogous to Remark 4.11. There is a unique homomorphism
![]() $\unicode[STIX]{x1D713}:W(R^{\flat })\rightarrow A$
of extensions of
$\unicode[STIX]{x1D713}:W(R^{\flat })\rightarrow A$
of extensions of
![]() $R$
, and
$R$
, and
![]() $\unicode[STIX]{x1D713}$
commutes with
$\unicode[STIX]{x1D713}$
commutes with
![]() $\unicode[STIX]{x1D70E}$
. Since
$\unicode[STIX]{x1D70E}$
. Since
![]() $\unicode[STIX]{x1D713}$
is surjective,
$\unicode[STIX]{x1D713}$
is surjective,
![]() $\unicode[STIX]{x1D70E}$
is unique. Then
$\unicode[STIX]{x1D70E}$
is unique. Then
![]() $\unicode[STIX]{x1D70E}_{1}(px)=\unicode[STIX]{x1D70E}(x)$
is unique as well.
$\unicode[STIX]{x1D70E}_{1}(px)=\unicode[STIX]{x1D70E}(x)$
is unique as well.
By definition, a weak lift
![]() $A$
of
$A$
of
![]() $R$
gives a PD frame
$R$
gives a PD frame
![]() $\text{}\underline{A}=(A,pA,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
.
$\text{}\underline{A}=(A,pA,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
.
Definition 7.3. A weak lift
![]() $A$
of
$A$
of
![]() $R$
is called straight if
$R$
is called straight if
![]() $A=W(R^{\flat })/J^{\prime }$
such that
$A=W(R^{\flat })/J^{\prime }$
such that
![]() $J$
is generated by elements
$J$
is generated by elements
![]() $a$
with
$a$
with
![]() $[a]\in J^{\prime }$
.
$[a]\in J^{\prime }$
.
Lemma 7.4. For each straight weak lift
![]() $A$
of
$A$
of
![]() $R$
there is a unique homomorphism of PD frames
$R$
there is a unique homomorphism of PD frames
over the identity of
![]() $R$
.
$R$
.
Proof. The universal property of
![]() $A_{\operatorname{cris}}(R)$
gives a PD homomorphism
$A_{\operatorname{cris}}(R)$
gives a PD homomorphism
![]() $\unicode[STIX]{x1D718}:A_{\operatorname{cris}}\rightarrow A$
over the identity of
$\unicode[STIX]{x1D718}:A_{\operatorname{cris}}\rightarrow A$
over the identity of
![]() $R$
, and
$R$
, and
![]() $\unicode[STIX]{x1D718}$
commutes with
$\unicode[STIX]{x1D718}$
commutes with
![]() $\unicode[STIX]{x1D70E}$
. To show that
$\unicode[STIX]{x1D70E}$
. To show that
![]() $\unicode[STIX]{x1D718}$
is a frame homomorphism it suffices to verify that
$\unicode[STIX]{x1D718}$
is a frame homomorphism it suffices to verify that
![]() $\unicode[STIX]{x1D718}(\unicode[STIX]{x1D70E}_{1}(y))=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D718}(y))$
for generators
$\unicode[STIX]{x1D718}(\unicode[STIX]{x1D70E}_{1}(y))=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D718}(y))$
for generators
![]() $y$
of the ideal
$y$
of the ideal
![]() $\operatorname{Fil}A_{\operatorname{cris}}(R)$
. A set of generators of this ideal is formed by
$\operatorname{Fil}A_{\operatorname{cris}}(R)$
. A set of generators of this ideal is formed by
![]() $p$
and the elements
$p$
and the elements
![]() $[x]^{[n]}$
for generators
$[x]^{[n]}$
for generators
![]() $x\in J$
and
$x\in J$
and
![]() $n\geqslant 1$
. We have
$n\geqslant 1$
. We have
![]() $\unicode[STIX]{x1D718}(\unicode[STIX]{x1D70E}_{1}(p))=1=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D718}(p))$
, moreover (5.7) gives
$\unicode[STIX]{x1D718}(\unicode[STIX]{x1D70E}_{1}(p))=1=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D718}(p))$
, moreover (5.7) gives
and
Since the weak lift
![]() $A$
is straight, the generators
$A$
is straight, the generators
![]() $x$
of
$x$
of
![]() $J$
can be chosen such that
$J$
can be chosen such that
![]() $[x]\in J^{\prime }$
. Then
$[x]\in J^{\prime }$
. Then
![]() $\unicode[STIX]{x1D718}([x])=0$
, and (7.1) and (7.2) are both zero.☐
$\unicode[STIX]{x1D718}([x])=0$
, and (7.1) and (7.2) are both zero.☐
Next we observe that every semiperfect ring has many straight weak lifts.
Definition 7.5. A descending sequence of ideals
![]() $J_{0}\supseteq J_{1}\supseteq J_{2}\supseteq \cdots \,$
of
$J_{0}\supseteq J_{1}\supseteq J_{2}\supseteq \cdots \,$
of
![]() $R^{\flat }$
is called admissible if
$R^{\flat }$
is called admissible if
![]() $J_{0}=J$
and
$J_{0}=J$
and
![]() $J_{i}^{p}\subseteq J_{i+1}$
. In this case let
$J_{i}^{p}\subseteq J_{i+1}$
. In this case let
![]() $W(J_{\ast })\subseteq W(R^{\flat })$
be the set of all Witt vectors
$W(J_{\ast })\subseteq W(R^{\flat })$
be the set of all Witt vectors
![]() $a=(a_{0},a_{1},a_{2},\ldots )$
with
$a=(a_{0},a_{1},a_{2},\ldots )$
with
![]() $a_{i}\in J_{i}$
, which is an ideal by Lemma 7.6 below, and let
$a_{i}\in J_{i}$
, which is an ideal by Lemma 7.6 below, and let
![]() $A(J_{\ast })=W(R^{\flat })/W(J_{\ast })$
.
$A(J_{\ast })=W(R^{\flat })/W(J_{\ast })$
.
Lemma 7.6. Let
![]() $J_{\ast }$
be an admissible sequence of ideals of
$J_{\ast }$
be an admissible sequence of ideals of
![]() $R^{\flat }$
. Then
$R^{\flat }$
. Then
![]() $W(J_{\ast })$
is an ideal of
$W(J_{\ast })$
is an ideal of
![]() $W(R^{\flat })$
, and the ring
$W(R^{\flat })$
, and the ring
![]() $A(J_{\ast })$
is a straight weak lift of
$A(J_{\ast })$
is a straight weak lift of
![]() $R$
.
$R$
.
Let
![]() $\text{}\underline{A}(J_{\ast })=(A(J_{\ast }),pA(J_{\ast }),R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
be the corresponding PD frame.
$\text{}\underline{A}(J_{\ast })=(A(J_{\ast }),pA(J_{\ast }),R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
be the corresponding PD frame.
Proof. As in the proof of Lemma 4.13 we see that
![]() $W(J_{\ast })$
is an ideal. This ideal is closed in
$W(J_{\ast })$
is an ideal. This ideal is closed in
![]() $W(R^{\flat })$
, and thus
$W(R^{\flat })$
, and thus
![]() $A=A(J_{\ast })$
is
$A=A(J_{\ast })$
is
![]() $p$
-adically complete. Since
$p$
-adically complete. Since
![]() $J_{0}=J$
we have
$J_{0}=J$
we have
![]() $A/pA=R$
. Clearly
$A/pA=R$
. Clearly
![]() $W(J_{\ast })$
is stable under the endomorphism
$W(J_{\ast })$
is stable under the endomorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $W(R^{\flat })$
, so
$W(R^{\flat })$
, so
![]() $\unicode[STIX]{x1D70E}$
induces
$\unicode[STIX]{x1D70E}$
induces
![]() $\unicode[STIX]{x1D70E}:A\rightarrow A$
. We have
$\unicode[STIX]{x1D70E}:A\rightarrow A$
. We have
![]() $pA=pW(R^{\flat })/(W(J_{\ast })\cap pW(R^{\flat }))$
, and an element
$pA=pW(R^{\flat })/(W(J_{\ast })\cap pW(R^{\flat }))$
, and an element
![]() $a\in W(J_{\ast })$
lies in
$a\in W(J_{\ast })$
lies in
![]() $pW(R^{\flat })$
if and only if
$pW(R^{\flat })$
if and only if
![]() $a_{0}=0$
. Since the sequence
$a_{0}=0$
. Since the sequence
![]() $J_{\ast }$
is descending we have
$J_{\ast }$
is descending we have
![]() $\unicode[STIX]{x1D70E}_{1}(W(J_{\ast })\cap pW(R^{\flat }))\subseteq W(J_{\ast })$
, so
$\unicode[STIX]{x1D70E}_{1}(W(J_{\ast })\cap pW(R^{\flat }))\subseteq W(J_{\ast })$
, so
![]() $\unicode[STIX]{x1D70E}_{1}$
induces
$\unicode[STIX]{x1D70E}_{1}$
induces
![]() $\unicode[STIX]{x1D70E}_{1}:pA\rightarrow A$
. It follows that
$\unicode[STIX]{x1D70E}_{1}:pA\rightarrow A$
. It follows that
![]() $A$
is a weak lift, which is straight because for every
$A$
is a weak lift, which is straight because for every
![]() $a\in J$
we have
$a\in J$
we have
![]() $[a]\in W(J_{\ast })$
.☐
$[a]\in W(J_{\ast })$
.☐
Windows over
![]() $\text{}\underline{A}(J_{\ast })$
are insensitive to bounded variations of
$\text{}\underline{A}(J_{\ast })$
are insensitive to bounded variations of
![]() $J_{\ast }$
in the following sense.
$J_{\ast }$
in the following sense.
Lemma 7.7. Let
![]() $J_{\ast }$
and
$J_{\ast }$
and
![]() $J_{\ast }^{\prime }$
be two admissible sequences of ideals of
$J_{\ast }^{\prime }$
be two admissible sequences of ideals of
![]() $R^{\flat }$
such that there is an
$R^{\flat }$
such that there is an
![]() $n\geqslant 0$
with
$n\geqslant 0$
with
![]() $J_{i+n}^{\prime }\subseteq J_{i}\subseteq J_{i}^{\prime }$
for all
$J_{i+n}^{\prime }\subseteq J_{i}\subseteq J_{i}^{\prime }$
for all
![]() $i\geqslant 0$
. Then there is a natural frame homomorphism
$i\geqslant 0$
. Then there is a natural frame homomorphism
![]() $\unicode[STIX]{x1D70B}:\text{}\underline{A}(J_{\ast })\rightarrow \text{}\underline{A}(J_{\ast }^{\prime })$
, which is crystalline.
$\unicode[STIX]{x1D70B}:\text{}\underline{A}(J_{\ast })\rightarrow \text{}\underline{A}(J_{\ast }^{\prime })$
, which is crystalline.
Proof. The homomorphism
![]() $\unicode[STIX]{x1D70B}$
exists because
$\unicode[STIX]{x1D70B}$
exists because
![]() $J_{i}\subseteq J_{i}^{\prime }$
. Let
$J_{i}\subseteq J_{i}^{\prime }$
. Let
![]() $\mathfrak{a}=\operatorname{Ker}(\unicode[STIX]{x1D70B})=W(J_{\ast }^{\prime })/W(J_{\ast })$
. Then
$\mathfrak{a}=\operatorname{Ker}(\unicode[STIX]{x1D70B})=W(J_{\ast }^{\prime })/W(J_{\ast })$
. Then
![]() $\unicode[STIX]{x1D70E}_{1}$
induces an endomorphism of
$\unicode[STIX]{x1D70E}_{1}$
induces an endomorphism of
![]() $\mathfrak{a}$
, and
$\mathfrak{a}$
, and
![]() $(\unicode[STIX]{x1D70E}_{1})^{n}$
is zero on
$(\unicode[STIX]{x1D70E}_{1})^{n}$
is zero on
![]() $\mathfrak{a}$
because
$\mathfrak{a}$
because
![]() $J_{i+n}^{\prime }\subseteq J_{i}$
. The result follows from the deformation lemma [Reference LauLau10, Theorem 3.2] if we find a sequence of ideals
$J_{i+n}^{\prime }\subseteq J_{i}$
. The result follows from the deformation lemma [Reference LauLau10, Theorem 3.2] if we find a sequence of ideals
![]() $\mathfrak{a}=\mathfrak{a}_{0}\supseteq \cdots \supseteq \mathfrak{a}_{n}=0$
which are stable under
$\mathfrak{a}=\mathfrak{a}_{0}\supseteq \cdots \supseteq \mathfrak{a}_{n}=0$
which are stable under
![]() $\unicode[STIX]{x1D70E}_{1}$
such that
$\unicode[STIX]{x1D70E}_{1}$
such that
![]() $\unicode[STIX]{x1D70E}(\mathfrak{a}_{m})\subseteq \mathfrak{a}_{m+1}$
for
$\unicode[STIX]{x1D70E}(\mathfrak{a}_{m})\subseteq \mathfrak{a}_{m+1}$
for
![]() $m<n$
.
$m<n$
.
This sequence can be constructed as follows. We have
![]() $\unicode[STIX]{x1D719}^{n}(J_{i}^{\prime })\subseteq J_{i}^{\prime p^{n}}\subseteq J_{i+n}^{\prime }\subseteq J_{i}$
and thus
$\unicode[STIX]{x1D719}^{n}(J_{i}^{\prime })\subseteq J_{i}^{\prime p^{n}}\subseteq J_{i+n}^{\prime }\subseteq J_{i}$
and thus
![]() $J_{i}\subseteq J_{i}^{\prime }\subseteq \unicode[STIX]{x1D719}^{-n}(J_{i})$
. For each
$J_{i}\subseteq J_{i}^{\prime }\subseteq \unicode[STIX]{x1D719}^{-n}(J_{i})$
. For each
![]() $m$
with
$m$
with
![]() $0\leqslant m\leqslant n$
let
$0\leqslant m\leqslant n$
let
![]() $K_{m,i}=J_{i}^{\prime }\cap \unicode[STIX]{x1D719}^{m-n}(J_{i})$
. Then
$K_{m,i}=J_{i}^{\prime }\cap \unicode[STIX]{x1D719}^{m-n}(J_{i})$
. Then
![]() $K_{m,\ast }$
is an admissible sequence, moreover
$K_{m,\ast }$
is an admissible sequence, moreover
![]() $J_{i}^{\prime }=K_{0,i}\supseteq K_{1,i}\supseteq \cdots \supseteq K_{n,i}=J_{i}$
and thus
$J_{i}^{\prime }=K_{0,i}\supseteq K_{1,i}\supseteq \cdots \supseteq K_{n,i}=J_{i}$
and thus
![]() $W(J_{\ast }^{\prime })=W(K_{0,\ast })\supseteq \cdots \supseteq W(K_{n,\ast })=W(J_{\ast })$
. Let
$W(J_{\ast }^{\prime })=W(K_{0,\ast })\supseteq \cdots \supseteq W(K_{n,\ast })=W(J_{\ast })$
. Let
![]() $\mathfrak{a}_{m}=W(K_{m,\ast })/W(J_{\ast })$
. Then
$\mathfrak{a}_{m}=W(K_{m,\ast })/W(J_{\ast })$
. Then
![]() $\mathfrak{a}_{m}$
is stable under
$\mathfrak{a}_{m}$
is stable under
![]() $\unicode[STIX]{x1D70E}_{1}$
because
$\unicode[STIX]{x1D70E}_{1}$
because
![]() $K_{m,\ast }$
is a decreasing sequence; see the proof of Lemma 7.6. We have
$K_{m,\ast }$
is a decreasing sequence; see the proof of Lemma 7.6. We have
![]() $\unicode[STIX]{x1D70E}(\mathfrak{a}_{m})\subseteq \mathfrak{a}_{m+1}$
because
$\unicode[STIX]{x1D70E}(\mathfrak{a}_{m})\subseteq \mathfrak{a}_{m+1}$
because
![]() $\unicode[STIX]{x1D719}(K_{m,i})\subseteq K_{m+1,i}$
.☐
$\unicode[STIX]{x1D719}(K_{m,i})\subseteq K_{m+1,i}$
.☐
7.2 The passage to
 $A_{\operatorname{cris}}$
$A_{\operatorname{cris}}$
Proposition 7.8. Assume that
![]() $R$
is iso-balanced, and let
$R$
is iso-balanced, and let
![]() $J_{i}=J^{p^{i}}$
for all
$J_{i}=J^{p^{i}}$
for all
![]() $i$
. Then the frame homomorphism
$i$
. Then the frame homomorphism
![]() $\unicode[STIX]{x1D718}:\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}(J_{\ast })$
is crystalline.
$\unicode[STIX]{x1D718}:\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}(J_{\ast })$
is crystalline.
The homomorphism
![]() $\unicode[STIX]{x1D718}$
is given by Lemma 7.4. See also Proposition 5.10.
$\unicode[STIX]{x1D718}$
is given by Lemma 7.4. See also Proposition 5.10.
Proof. Let
![]() $R\rightarrow R^{\prime }$
be an isogeny with balanced
$R\rightarrow R^{\prime }$
be an isogeny with balanced
![]() $R^{\prime }$
whose kernel is annihilated by
$R^{\prime }$
whose kernel is annihilated by
![]() $\unicode[STIX]{x1D719}^{n}$
. Then
$\unicode[STIX]{x1D719}^{n}$
. Then
![]() $R^{\prime }=R^{\flat }/J^{\prime }$
with
$R^{\prime }=R^{\flat }/J^{\prime }$
with
![]() $\unicode[STIX]{x1D719}(J^{\prime })={J^{\prime }}^{p}$
and
$\unicode[STIX]{x1D719}(J^{\prime })={J^{\prime }}^{p}$
and
![]() $\unicode[STIX]{x1D719}^{n}(J^{\prime })\subseteq J\subseteq J^{\prime }$
. Let
$\unicode[STIX]{x1D719}^{n}(J^{\prime })\subseteq J\subseteq J^{\prime }$
. Let
![]() $K_{i}=J\cap \unicode[STIX]{x1D719}^{i}(J^{\prime })$
for
$K_{i}=J\cap \unicode[STIX]{x1D719}^{i}(J^{\prime })$
for
![]() $i\geqslant 0$
. The sequence
$i\geqslant 0$
. The sequence
![]() $K_{\ast }$
is admissible. For
$K_{\ast }$
is admissible. For
![]() $i\geqslant 0$
we have
$i\geqslant 0$
we have
![]() $K_{n+i}=\unicode[STIX]{x1D719}^{n+i}(J^{\prime })\subseteq J_{i}\subseteq K_{i}$
. Thus the natural frame homomorphism
$K_{n+i}=\unicode[STIX]{x1D719}^{n+i}(J^{\prime })\subseteq J_{i}\subseteq K_{i}$
. Thus the natural frame homomorphism
![]() $\unicode[STIX]{x1D70B}:\text{}\underline{A}(J_{\ast })\rightarrow \text{}\underline{A}(K_{\ast })$
is crystalline by Lemma 7.7, and it suffices to show that the composition
$\unicode[STIX]{x1D70B}:\text{}\underline{A}(J_{\ast })\rightarrow \text{}\underline{A}(K_{\ast })$
is crystalline by Lemma 7.7, and it suffices to show that the composition
is crystalline. Let
![]() $N=\operatorname{Ker}(\unicode[STIX]{x1D718}^{\prime })$
.
$N=\operatorname{Ker}(\unicode[STIX]{x1D718}^{\prime })$
.
Lemma 7.9.
(i) The
 $p$
-power torsion of
$p$
-power torsion of
 $A(K_{\ast })$
is annihilated by
$A(K_{\ast })$
is annihilated by
 $p^{n}$
.
$p^{n}$
.(ii) For
 $i\geqslant 0$
we have
$i\geqslant 0$
we have
 $N\cap p^{n+i}A_{\operatorname{cris}}(R)\subseteq p^{i}N$
, in particular the
$N\cap p^{n+i}A_{\operatorname{cris}}(R)\subseteq p^{i}N$
, in particular the
 $p$
-adic topology of
$p$
-adic topology of
 $N$
is induced by the
$N$
is induced by the
 $p$
-adic topology of
$p$
-adic topology of
 $A_{\operatorname{cris}}(R)$
.
$A_{\operatorname{cris}}(R)$
.(iii) The endomorphism
 $\unicode[STIX]{x1D70E}_{1}:N/pN\rightarrow N/pN$
is nilpotent.
$\unicode[STIX]{x1D70E}_{1}:N/pN\rightarrow N/pN$
is nilpotent.
Proof. Let
![]() $J_{i}^{\prime }=\unicode[STIX]{x1D719}^{i}(J^{\prime })$
. Then
$J_{i}^{\prime }=\unicode[STIX]{x1D719}^{i}(J^{\prime })$
. Then
![]() $J_{\ast }^{\prime }$
is an admissible sequence of ideals of
$J_{\ast }^{\prime }$
is an admissible sequence of ideals of
![]() $W(R^{\flat })$
with respect to
$W(R^{\flat })$
with respect to
![]() $R^{\prime }=R^{\flat }/J^{\prime }$
; note that
$R^{\prime }=R^{\flat }/J^{\prime }$
; note that
![]() $R^{\flat }={R^{\prime }}^{\flat }$
. We have
$R^{\flat }={R^{\prime }}^{\flat }$
. We have
![]() $K_{i}\subseteq J_{i}^{\prime }$
with equality for
$K_{i}\subseteq J_{i}^{\prime }$
with equality for
![]() $i\geqslant n$
, so there is a projection
$i\geqslant n$
, so there is a projection
![]() $A(K_{\ast })\rightarrow A(J_{\ast }^{\prime })$
whose kernel is annihilated by
$A(K_{\ast })\rightarrow A(J_{\ast }^{\prime })$
whose kernel is annihilated by
![]() $p^{n}$
. The ring
$p^{n}$
. The ring
![]() $A(J_{\ast }^{\prime })$
is the straight lift of
$A(J_{\ast }^{\prime })$
is the straight lift of
![]() $R^{\prime }$
constructed in Lemma 4.13, which is
$R^{\prime }$
constructed in Lemma 4.13, which is
![]() $p$
-torsion free. This proves (i), and (ii) follows.
$p$
-torsion free. This proves (i), and (ii) follows.
Let us prove (iii). The ring
![]() $A_{\operatorname{cris}}(R)$
is the
$A_{\operatorname{cris}}(R)$
is the
![]() $p$
-adic completion of a
$p$
-adic completion of a
![]() $W(R^{\flat })$
-algebra generated by the elements
$W(R^{\flat })$
-algebra generated by the elements
![]() $[x]^{[i]}$
for
$[x]^{[i]}$
for
![]() $x\in J$
and
$x\in J$
and
![]() $i\geqslant 1$
, and these elements map to zero in
$i\geqslant 1$
, and these elements map to zero in
![]() $A(K_{\ast })$
. Thus for each
$A(K_{\ast })$
. Thus for each
![]() $m\geqslant 1$
the image of
$m\geqslant 1$
the image of
![]() $N$
in
$N$
in
![]() $A_{\operatorname{cris}}(R)/p^{m}$
is generated as an ideal by
$A_{\operatorname{cris}}(R)/p^{m}$
is generated as an ideal by
![]() $W(K_{\ast })$
and the elements
$W(K_{\ast })$
and the elements
![]() $[x]^{[i]}$
. By (ii) it follows that
$[x]^{[i]}$
. By (ii) it follows that
![]() $N/pN$
is generated as an
$N/pN$
is generated as an
![]() $A_{\operatorname{cris}}(R)$
-module by
$A_{\operatorname{cris}}(R)$
-module by
![]() $W(K_{\ast })$
and the elements
$W(K_{\ast })$
and the elements
![]() $[x]^{[i]}$
. We check these elements separately.
$[x]^{[i]}$
. We check these elements separately.
First, the explicit formula (5.7) for
![]() $\unicode[STIX]{x1D70E}_{1}$
implies that for
$\unicode[STIX]{x1D70E}_{1}$
implies that for
![]() $x\in J$
the element
$x\in J$
the element
![]() $(\unicode[STIX]{x1D70E}_{1})^{2}([x]^{[i]})$
lies in
$(\unicode[STIX]{x1D70E}_{1})^{2}([x]^{[i]})$
lies in
![]() $pN$
; see the proof of Proposition 5.10. Second, since
$pN$
; see the proof of Proposition 5.10. Second, since
![]() $\unicode[STIX]{x1D719}^{i}(K_{n})=K_{n+i}$
for
$\unicode[STIX]{x1D719}^{i}(K_{n})=K_{n+i}$
for
![]() $i\geqslant 0$
, each element of
$i\geqslant 0$
, each element of
![]() $W(K_{\ast })/pW(K_{\ast })$
is represented by an element
$W(K_{\ast })/pW(K_{\ast })$
is represented by an element
![]() $a=(a_{0},a_{1},a_{2},\ldots )\in W(K_{\ast })$
with
$a=(a_{0},a_{1},a_{2},\ldots )\in W(K_{\ast })$
with
![]() $a_{i}=0$
for
$a_{i}=0$
for
![]() $i>n$
. Then
$i>n$
. Then
lies in
![]() $pN$
, using that
$pN$
, using that
![]() $a_{i}\in K_{i}\subseteq J$
. Thus
$a_{i}\in K_{i}\subseteq J$
. Thus
![]() $(\unicode[STIX]{x1D70E}_{1})^{n+2}$
is zero on
$(\unicode[STIX]{x1D70E}_{1})^{n+2}$
is zero on
![]() $N/pN$
, and Lemma 7.9 is proved. ☐
$N/pN$
, and Lemma 7.9 is proved. ☐
We continue the proof of Proposition 7.8. Since
![]() $A(K_{\ast })$
is
$A(K_{\ast })$
is
![]() $p$
-adically complete, the ideal
$p$
-adically complete, the ideal
![]() $N$
is closed in
$N$
is closed in
![]() $A_{\operatorname{cris}}(R)$
, and thus
$A_{\operatorname{cris}}(R)$
, and thus
![]() $N$
is
$N$
is
![]() $p$
-adically complete by Lemma 7.9(ii). Since
$p$
-adically complete by Lemma 7.9(ii). Since
![]() $\unicode[STIX]{x1D70E}_{1}:N\rightarrow N$
stabilizes
$\unicode[STIX]{x1D70E}_{1}:N\rightarrow N$
stabilizes
![]() $p^{m}N$
, the ring
$p^{m}N$
, the ring
![]() $A_{\operatorname{cris}}(R)/p^{m}N$
carries a natural frame structure, denoted by
$A_{\operatorname{cris}}(R)/p^{m}N$
carries a natural frame structure, denoted by
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N$
. We have
$\text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N$
. We have
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)/N=\text{}\underline{A}(K_{\ast })$
and
$\text{}\underline{A}_{\operatorname{cris}}(R)/N=\text{}\underline{A}(K_{\ast })$
and
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)=\varprojlim \text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N$
. This limit preserves the window categories by [Reference LauLau10, Lemma 2.12]. Thus it suffices to show that the frame homomorphism
$\text{}\underline{A}_{\operatorname{cris}}(R)=\varprojlim \text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N$
. This limit preserves the window categories by [Reference LauLau10, Lemma 2.12]. Thus it suffices to show that the frame homomorphism
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N\rightarrow \text{}\underline{A}(K_{\ast })$
is crystalline for each
$\text{}\underline{A}_{\operatorname{cris}}(R)/p^{m}N\rightarrow \text{}\underline{A}(K_{\ast })$
is crystalline for each
![]() $m$
. Since
$m$
. Since
![]() $\unicode[STIX]{x1D70E}_{1}:N/p^{m}N\rightarrow N/p^{m}N$
is nilpotent by Lemma 7.9(iii), this follows from [Reference LauLau10, Theorem 3.2].☐
$\unicode[STIX]{x1D70E}_{1}:N/p^{m}N\rightarrow N/p^{m}N$
is nilpotent by Lemma 7.9(iii), this follows from [Reference LauLau10, Theorem 3.2].☐
Theorem 7.10. If
![]() $R$
is an iso-balanced semiperfect ring, the functor
$R$
is an iso-balanced semiperfect ring, the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
of Theorem 6.3 is an equivalence of categories.
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
of Theorem 6.3 is an equivalence of categories.
Proof. By Corollary 6.5 the theorem holds for balanced rings. An isogeny from
![]() $R$
to a balanced ring has nilpotent kernel by Lemma 4.5. Therefore it suffices to show the following. Let
$R$
to a balanced ring has nilpotent kernel by Lemma 4.5. Therefore it suffices to show the following. Let
![]() $\unicode[STIX]{x1D70B}:R^{\prime }\rightarrow R$
be an isogeny of iso-balanced rings such that
$\unicode[STIX]{x1D70B}:R^{\prime }\rightarrow R$
be an isogeny of iso-balanced rings such that
![]() $\operatorname{Ker}(\unicode[STIX]{x1D70B})^{p}=0$
. If
$\operatorname{Ker}(\unicode[STIX]{x1D70B})^{p}=0$
. If
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence then so is
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence then so is
![]() $\unicode[STIX]{x1D6F7}_{R^{\prime }}^{\operatorname{cris}}$
.
$\unicode[STIX]{x1D6F7}_{R^{\prime }}^{\operatorname{cris}}$
.
To prove this we use some auxiliary frames. Let
![]() $J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
and
$J=\operatorname{Ker}(R^{\flat }\rightarrow R)$
and
![]() $J^{\prime }=\operatorname{Ker}(R^{\flat }\rightarrow R^{\prime })$
, thus
$J^{\prime }=\operatorname{Ker}(R^{\flat }\rightarrow R^{\prime })$
, thus
![]() $J^{p}\subseteq J^{\prime }\subseteq J$
. We define
$J^{p}\subseteq J^{\prime }\subseteq J$
. We define
![]() $J_{i}=J^{p^{i}}$
and
$J_{i}=J^{p^{i}}$
and
![]() $J_{i}^{\prime }={J^{\prime }}^{p^{i}}$
for
$J_{i}^{\prime }={J^{\prime }}^{p^{i}}$
for
![]() $i\geqslant 0$
, and we define
$i\geqslant 0$
, and we define
![]() $K_{0}=J^{\prime }$
and
$K_{0}=J^{\prime }$
and
![]() $K_{i}=J_{i}$
for
$K_{i}=J_{i}$
for
![]() $i\geqslant 1$
. Then
$i\geqslant 1$
. Then
![]() $J_{\ast }$
is an admissible sequence with respect to
$J_{\ast }$
is an admissible sequence with respect to
![]() $R$
, while
$R$
, while
![]() $K_{\ast }$
and
$K_{\ast }$
and
![]() $J_{\ast }^{\prime }$
are admissible sequences with respect to
$J_{\ast }^{\prime }$
are admissible sequences with respect to
![]() $R^{\prime }$
. There are obvious frame homomorphisms
$R^{\prime }$
. There are obvious frame homomorphisms
where
![]() $a$
lies over
$a$
lies over
![]() $\operatorname{id}_{R^{\prime }}$
and
$\operatorname{id}_{R^{\prime }}$
and
![]() $q$
lies over
$q$
lies over
![]() $\unicode[STIX]{x1D70B}$
. Here
$\unicode[STIX]{x1D70B}$
. Here
![]() $a$
is crystalline by Lemma 7.7, using that
$a$
is crystalline by Lemma 7.7, using that
![]() $K_{i+1}\subseteq J_{i}^{\prime }\subseteq K_{i}$
. We want to factor
$K_{i+1}\subseteq J_{i}^{\prime }\subseteq K_{i}$
. We want to factor
![]() $q$
over another frame
$q$
over another frame
![]() ${\mathcal{F}}=(A,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
with
${\mathcal{F}}=(A,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
with
![]() $A=A(K_{\ast })$
, thus
$A=A(K_{\ast })$
, thus
![]() $I$
is the kernel of
$I$
is the kernel of
![]() $A(K_{\ast })\rightarrow A(J_{\ast })\rightarrow R$
. We only have to define
$A(K_{\ast })\rightarrow A(J_{\ast })\rightarrow R$
. We only have to define
![]() $\unicode[STIX]{x1D70E}_{1}:I\rightarrow A$
. It is easy to see that the natural map
$\unicode[STIX]{x1D70E}_{1}:I\rightarrow A$
. It is easy to see that the natural map
![]() $\operatorname{Ker}(q)\rightarrow \operatorname{Ker}(\unicode[STIX]{x1D70B})$
is bijective and that
$\operatorname{Ker}(q)\rightarrow \operatorname{Ker}(\unicode[STIX]{x1D70B})$
is bijective and that
as a direct sum of ideals. We have
![]() $\operatorname{Ker}(q)^{p}=0$
, and
$\operatorname{Ker}(q)^{p}=0$
, and
![]() $\unicode[STIX]{x1D70E}(x)=0$
for
$\unicode[STIX]{x1D70E}(x)=0$
for
![]() $x\in \operatorname{Ker}(q)$
. We extend the homomorphism
$x\in \operatorname{Ker}(q)$
. We extend the homomorphism
![]() $\unicode[STIX]{x1D70E}_{1}$
and the divided powers defined on
$\unicode[STIX]{x1D70E}_{1}$
and the divided powers defined on
![]() $pA$
to
$pA$
to
![]() $I$
by
$I$
by
![]() $\unicode[STIX]{x1D70E}_{1}(x)=0$
and
$\unicode[STIX]{x1D70E}_{1}(x)=0$
and
![]() $x^{[p]}=0$
for
$x^{[p]}=0$
for
![]() $x\in \operatorname{Ker}(q)$
. This defines a PD frame
$x\in \operatorname{Ker}(q)$
. This defines a PD frame
![]() ${\mathcal{F}}$
as above. Together we have homomorphisms of PD frames
${\mathcal{F}}$
as above. Together we have homomorphisms of PD frames
over
![]() $R^{\prime }\xrightarrow[{}]{\operatorname{id}}R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R\xrightarrow[{}]{\operatorname{id}}R$
, where
$R^{\prime }\xrightarrow[{}]{\operatorname{id}}R^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}}R\xrightarrow[{}]{\operatorname{id}}R$
, where
![]() $c$
is given by
$c$
is given by
![]() $q$
and
$q$
and
![]() $b$
is given by
$b$
is given by
![]() $\operatorname{id}_{A}$
. Since
$\operatorname{id}_{A}$
. Since
![]() $\unicode[STIX]{x1D70E}_{1}$
is zero on
$\unicode[STIX]{x1D70E}_{1}$
is zero on
![]() $\operatorname{Ker}(c)=\operatorname{Ker}(q)$
,
$\operatorname{Ker}(c)=\operatorname{Ker}(q)$
,
![]() $c$
is crystalline by [Reference LauLau10, Theorem 3.2].
$c$
is crystalline by [Reference LauLau10, Theorem 3.2].
Since
![]() $A\rightarrow R$
is a
$A\rightarrow R$
is a
![]() $p$
-adic PD extension, the universal property of
$p$
-adic PD extension, the universal property of
![]() $A_{\operatorname{cris}}(R)$
gives a unique homomorphism
$A_{\operatorname{cris}}(R)$
gives a unique homomorphism
![]() $\tilde{\unicode[STIX]{x1D718}}:A_{\operatorname{cris}}(R)\rightarrow A$
of PD extensions of
$\tilde{\unicode[STIX]{x1D718}}:A_{\operatorname{cris}}(R)\rightarrow A$
of PD extensions of
![]() $R$
, and
$R$
, and
![]() $\tilde{\unicode[STIX]{x1D718}}$
commutes with
$\tilde{\unicode[STIX]{x1D718}}$
commutes with
![]() $\unicode[STIX]{x1D70E}$
. We claim that
$\unicode[STIX]{x1D70E}$
. We claim that
![]() $\tilde{\unicode[STIX]{x1D718}}$
is a frame homomorphism
$\tilde{\unicode[STIX]{x1D718}}$
is a frame homomorphism
![]() $\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow {\mathcal{F}}$
, i.e. that
$\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow {\mathcal{F}}$
, i.e. that
![]() $\tilde{\unicode[STIX]{x1D718}}$
commutes with
$\tilde{\unicode[STIX]{x1D718}}$
commutes with
![]() $\unicode[STIX]{x1D70E}_{1}$
. As in the proof of Lemma 7.4 it suffices to show that
$\unicode[STIX]{x1D70E}_{1}$
. As in the proof of Lemma 7.4 it suffices to show that
![]() $\tilde{\unicode[STIX]{x1D718}}(\unicode[STIX]{x1D70E}_{1}(y))=\unicode[STIX]{x1D70E}_{1}(\tilde{\unicode[STIX]{x1D718}}(y))$
when
$\tilde{\unicode[STIX]{x1D718}}(\unicode[STIX]{x1D70E}_{1}(y))=\unicode[STIX]{x1D70E}_{1}(\tilde{\unicode[STIX]{x1D718}}(y))$
when
![]() $y=[x]^{[n]}$
with
$y=[x]^{[n]}$
with
![]() $x\in J$
and
$x\in J$
and
![]() $n\geqslant 1$
. Let
$n\geqslant 1$
. Let
![]() $z=\tilde{\unicode[STIX]{x1D718}}([x])$
in
$z=\tilde{\unicode[STIX]{x1D718}}([x])$
in
![]() $A$
. Then
$A$
. Then
![]() $z\in \operatorname{Ker}(q)$
and thus
$z\in \operatorname{Ker}(q)$
and thus
![]() $z^{[np]}=0$
, moreover
$z^{[np]}=0$
, moreover
![]() $z^{[n]}\in \operatorname{Ker}(q)$
as well and thus
$z^{[n]}\in \operatorname{Ker}(q)$
as well and thus
![]() $\unicode[STIX]{x1D70E}_{1}(z^{[n]})=0$
. Therefore (7.1) and (7.2) with
$\unicode[STIX]{x1D70E}_{1}(z^{[n]})=0$
. Therefore (7.1) and (7.2) with
![]() $\tilde{\unicode[STIX]{x1D718}}$
in place of
$\tilde{\unicode[STIX]{x1D718}}$
in place of
![]() $\unicode[STIX]{x1D718}$
show that
$\unicode[STIX]{x1D718}$
show that
![]() $\tilde{\unicode[STIX]{x1D718}}(\unicode[STIX]{x1D70E}_{1}(y))=0$
and
$\tilde{\unicode[STIX]{x1D718}}(\unicode[STIX]{x1D70E}_{1}(y))=0$
and
![]() $\unicode[STIX]{x1D70E}_{1}(\tilde{\unicode[STIX]{x1D718}}(y))=0$
. Thus
$\unicode[STIX]{x1D70E}_{1}(\tilde{\unicode[STIX]{x1D718}}(y))=0$
. Thus
![]() $\tilde{\unicode[STIX]{x1D718}}$
is a frame homomorphism. Since
$\tilde{\unicode[STIX]{x1D718}}$
is a frame homomorphism. Since
![]() $a,b,c$
are PD homomorphisms, we obtain a commutative diagram of frames
$a,b,c$
are PD homomorphisms, we obtain a commutative diagram of frames

where the homomorphisms
![]() $\unicode[STIX]{x1D718}$
are given by Lemma 7.4, and
$\unicode[STIX]{x1D718}$
are given by Lemma 7.4, and
![]() $\unicode[STIX]{x1D718}^{\prime }=a\circ \unicode[STIX]{x1D718}$
. The two homomorphisms
$\unicode[STIX]{x1D718}^{\prime }=a\circ \unicode[STIX]{x1D718}$
. The two homomorphisms
![]() $\unicode[STIX]{x1D718}$
are crystalline by Proposition 7.8. Since
$\unicode[STIX]{x1D718}$
are crystalline by Proposition 7.8. Since
![]() $a$
and
$a$
and
![]() $c$
are crystalline, the same holds for
$c$
are crystalline, the same holds for
![]() $\unicode[STIX]{x1D718}^{\prime }$
and
$\unicode[STIX]{x1D718}^{\prime }$
and
![]() $\tilde{\unicode[STIX]{x1D718}}$
. We have the following commutative diagram of categories.
$\tilde{\unicode[STIX]{x1D718}}$
. We have the following commutative diagram of categories.

The functors
![]() $\operatorname{BT}(\operatorname{Spec}R^{\prime })\rightarrow \operatorname{Win}(\text{}\underline{A}(K_{\ast }))$
and
$\operatorname{BT}(\operatorname{Spec}R^{\prime })\rightarrow \operatorname{Win}(\text{}\underline{A}(K_{\ast }))$
and
![]() $\operatorname{BT}(\operatorname{Spec}R)\rightarrow \operatorname{Win}({\mathcal{F}})$
are given by the Dieudonné crystal with an additional
$\operatorname{BT}(\operatorname{Spec}R)\rightarrow \operatorname{Win}({\mathcal{F}})$
are given by the Dieudonné crystal with an additional
![]() $F_{1}$
. Since
$F_{1}$
. Since
![]() $\operatorname{Ker}(\unicode[STIX]{x1D70B})^{p}=0$
, the ideal
$\operatorname{Ker}(\unicode[STIX]{x1D70B})^{p}=0$
, the ideal
![]() $\operatorname{Ker}(\unicode[STIX]{x1D70B})$
can be equipped with the trivial divided powers. Then the projection
$\operatorname{Ker}(\unicode[STIX]{x1D70B})$
can be equipped with the trivial divided powers. Then the projection
![]() $A(K_{\ast })=A\rightarrow R^{\prime }$
is a homomorphism of PD extensions of
$A(K_{\ast })=A\rightarrow R^{\prime }$
is a homomorphism of PD extensions of
![]() $R$
. It follows that for
$R$
. It follows that for
![]() $G\in \operatorname{BT}(\operatorname{Spec}R)$
with associated
$G\in \operatorname{BT}(\operatorname{Spec}R)$
with associated
![]() $\text{}\underline{M}\in \operatorname{Win}({\mathcal{F}})$
there is a natural isomorphism
$\text{}\underline{M}\in \operatorname{Win}({\mathcal{F}})$
there is a natural isomorphism
![]() $M\otimes _{A}R^{\prime }\cong \mathbb{D}(G)_{R^{\prime }}$
. By the Grothendieck–Messing theorem [Reference MessingMes72] and its trivial counterpart for the frame homomorphism
$M\otimes _{A}R^{\prime }\cong \mathbb{D}(G)_{R^{\prime }}$
. By the Grothendieck–Messing theorem [Reference MessingMes72] and its trivial counterpart for the frame homomorphism
![]() $b$
in [Reference LauLau10, Lemma 4.2] it follows that the lifts of
$b$
in [Reference LauLau10, Lemma 4.2] it follows that the lifts of
![]() $G$
under
$G$
under
![]() $\unicode[STIX]{x1D70B}$
and the lifts of
$\unicode[STIX]{x1D70B}$
and the lifts of
![]() $\text{}\underline{M}$
under
$\text{}\underline{M}$
under
![]() $b$
coincide; cf. the proof of Proposition 5.5. Therefore if
$b$
coincide; cf. the proof of Proposition 5.5. Therefore if
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence, the same holds for
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence, the same holds for
![]() $\unicode[STIX]{x1D6F7}_{R^{\prime }}^{\operatorname{cris}}$
. This finishes the proof of Theorem 7.10.☐
$\unicode[STIX]{x1D6F7}_{R^{\prime }}^{\operatorname{cris}}$
. This finishes the proof of Theorem 7.10.☐
8 Perfectoid rings
We use the definition of perfectoid rings of [Reference Bhatt, Morrow and ScholzeBMS16] in a slightly different formulation. We begin with an easy remark on perfect rings.
Lemma 8.1. Let
![]() $S$
be a perfect ring and
$S$
be a perfect ring and
![]() $a\in S$
. Let
$a\in S$
. Let
![]() $J=(a^{p^{-\infty }})$
and
$J=(a^{p^{-\infty }})$
and
![]() $I=\operatorname{Ann}(a)$
. Then
$I=\operatorname{Ann}(a)$
. Then
![]() $J=\unicode[STIX]{x1D719}(J)$
and
$J=\unicode[STIX]{x1D719}(J)$
and
![]() $I=\unicode[STIX]{x1D719}(I)=\operatorname{Ann}(J)$
and
$I=\unicode[STIX]{x1D719}(I)=\operatorname{Ann}(J)$
and
![]() $I\cap J=0$
, thus we have an exact sequence
$I\cap J=0$
, thus we have an exact sequence
where the first map is the diagonal map and the second map is the difference. The element
![]() $a\in S/I$
is a non-zero divisor. If
$a\in S/I$
is a non-zero divisor. If
![]() $S$
is
$S$
is
![]() $a$
-adically complete, the same holds for
$a$
-adically complete, the same holds for
![]() $S/I$
.
$S/I$
.
Proof. Clearly
![]() $J=\unicode[STIX]{x1D719}(J)$
, moreover
$J=\unicode[STIX]{x1D719}(J)$
, moreover
![]() $I=\operatorname{Ann}(a)\subseteq \operatorname{Ann}(a^{p})=\unicode[STIX]{x1D719}(I)\subseteq I$
, and thus
$I=\operatorname{Ann}(a)\subseteq \operatorname{Ann}(a^{p})=\unicode[STIX]{x1D719}(I)\subseteq I$
, and thus
![]() $I=\unicode[STIX]{x1D719}(I)=\operatorname{Ann}(J)$
. Since
$I=\unicode[STIX]{x1D719}(I)=\operatorname{Ann}(J)$
. Since
![]() $S$
is reduced we have
$S$
is reduced we have
![]() $I\cap J=IJ=0$
, and (8.1) is exact. Since
$I\cap J=IJ=0$
, and (8.1) is exact. Since
![]() $I=\operatorname{Ann}(a)=\operatorname{Ann}(a^{2})$
the element
$I=\operatorname{Ann}(a)=\operatorname{Ann}(a^{2})$
the element
![]() $a\in S/I$
is a non-zero divisor. The last assertion follows from (8.1) because
$a\in S/I$
is a non-zero divisor. The last assertion follows from (8.1) because
![]() $S/J$
and
$S/J$
and
![]() $S/(I+J)$
are annihilated by
$S/(I+J)$
are annihilated by
![]() $a$
.☐
$a$
.☐
The exact sequence (8.1) can also be expressed by the following cartesian and cocartesian diagram of perfect rings.

The following is contained in [Reference Gabber and RameroGR17, Proposition 9.3.45].
Lemma 8.2. Let
![]() $S$
be a perfect ring and let
$S$
be a perfect ring and let
![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D709}_{1},\ldots )\in W(S)$
such that
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D709}_{1},\ldots )\in W(S)$
such that
![]() $\unicode[STIX]{x1D709}_{0},\ldots ,\unicode[STIX]{x1D709}_{r}$
generate the unit ideal of
$\unicode[STIX]{x1D709}_{0},\ldots ,\unicode[STIX]{x1D709}_{r}$
generate the unit ideal of
![]() $S$
. Then
$S$
. Then
![]() $\unicode[STIX]{x1D709}$
is a non-zero divisor, and for
$\unicode[STIX]{x1D709}$
is a non-zero divisor, and for
![]() $n\geqslant 0$
we have
$n\geqslant 0$
we have
In particular,
![]() $\unicode[STIX]{x1D709}W(S)$
is
$\unicode[STIX]{x1D709}W(S)$
is
![]() $p$
-adically closed in
$p$
-adically closed in
![]() $W(S)$
and
$W(S)$
and
![]() $p$
-adically complete.
$p$
-adically complete.
Proof. Using Lemma 8.1 with
![]() $a=\unicode[STIX]{x1D709}_{0}$
one reduces to the case where
$a=\unicode[STIX]{x1D709}_{0}$
one reduces to the case where
![]() $\unicode[STIX]{x1D709}_{0}=0$
or where
$\unicode[STIX]{x1D709}_{0}=0$
or where
![]() $\unicode[STIX]{x1D709}_{0}$
is a non-zero divisor. In the second case
$\unicode[STIX]{x1D709}_{0}$
is a non-zero divisor. In the second case
![]() $\unicode[STIX]{x1D709}$
is a non-zero divisor, and
$\unicode[STIX]{x1D709}$
is a non-zero divisor, and
![]() $\unicode[STIX]{x1D709}W(S)\cap p^{n}W(S)=p^{n}\unicode[STIX]{x1D709}W(S)$
. If
$\unicode[STIX]{x1D709}W(S)\cap p^{n}W(S)=p^{n}\unicode[STIX]{x1D709}W(S)$
. If
![]() $\unicode[STIX]{x1D709}_{0}=0$
then
$\unicode[STIX]{x1D709}_{0}=0$
then
![]() $\unicode[STIX]{x1D709}=p\unicode[STIX]{x1D709}^{\prime }$
, and the proof of (8.3) is finished by induction on
$\unicode[STIX]{x1D709}=p\unicode[STIX]{x1D709}^{\prime }$
, and the proof of (8.3) is finished by induction on
![]() $r$
. The last assertion follows easily.☐
$r$
. The last assertion follows easily.☐
Definition 8.3. For a perfect ring
![]() $S$
, an element
$S$
, an element
![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D709}_{1},\ldots )\in W(S)$
is called distinguished if
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D709}_{1},\ldots )\in W(S)$
is called distinguished if
![]() $\unicode[STIX]{x1D709}_{1}\in S$
is a unit and
$\unicode[STIX]{x1D709}_{1}\in S$
is a unit and
![]() $S$
is
$S$
is
![]() $\unicode[STIX]{x1D709}_{0}$
-adically complete.
$\unicode[STIX]{x1D709}_{0}$
-adically complete.
Remark 8.4. If a ring
![]() $R$
is complete with respect to some linear topology and
$R$
is complete with respect to some linear topology and
![]() $x\in R$
is topologically nilpotent, then
$x\in R$
is topologically nilpotent, then
![]() $R$
is also
$R$
is also
![]() $x$
-adically complete; see the proof of [SPA16, Tag 090T].
$x$
-adically complete; see the proof of [SPA16, Tag 090T].
Definition 8.5. A ring
![]() $R$
is called perfectoid if there is an isomorphism
$R$
is called perfectoid if there is an isomorphism
![]() $R\cong W(S)/\unicode[STIX]{x1D709}$
where
$R\cong W(S)/\unicode[STIX]{x1D709}$
where
![]() $S$
is perfect and
$S$
is perfect and
![]() $\unicode[STIX]{x1D709}\in W(S)$
is distinguished.
$\unicode[STIX]{x1D709}\in W(S)$
is distinguished.
Remark 8.6. Definition 8.5 is equivalent to [Reference Bhatt, Morrow and ScholzeBMS16, Definition 3.5]; moreover for
![]() $R=W(S)/\unicode[STIX]{x1D709}$
as in Definition 8.5 we have
$R=W(S)/\unicode[STIX]{x1D709}$
as in Definition 8.5 we have
canonically. Indeed, if
![]() $R=W(S)/\unicode[STIX]{x1D709}$
then
$R=W(S)/\unicode[STIX]{x1D709}$
then
![]() $R/p=S/\unicode[STIX]{x1D709}_{0}$
, the projective system
$R/p=S/\unicode[STIX]{x1D709}_{0}$
, the projective system
![]() $R/p\leftarrow R/p\leftarrow \cdots \,$
with arrows
$R/p\leftarrow R/p\leftarrow \cdots \,$
with arrows
![]() $\unicode[STIX]{x1D719}$
is identified with
$\unicode[STIX]{x1D719}$
is identified with
![]() $S/\unicode[STIX]{x1D709}_{0}\leftarrow S/\unicode[STIX]{x1D709}_{0}^{p}\leftarrow \cdots \,$
where the arrows are the projection maps, and (8.4) follows since
$S/\unicode[STIX]{x1D709}_{0}\leftarrow S/\unicode[STIX]{x1D709}_{0}^{p}\leftarrow \cdots \,$
where the arrows are the projection maps, and (8.4) follows since
![]() $S$
is
$S$
is
![]() $\unicode[STIX]{x1D709}_{0}$
-adically complete. Moreover
$\unicode[STIX]{x1D709}_{0}$
-adically complete. Moreover
![]() $R$
is
$R$
is
![]() $p$
-adically complete because this holds for
$p$
-adically complete because this holds for
![]() $W(S)$
and because
$W(S)$
and because
![]() $\unicode[STIX]{x1D709}W(S)$
is
$\unicode[STIX]{x1D709}W(S)$
is
![]() $p$
-adically closed by Lemma 8.2. If
$p$
-adically closed by Lemma 8.2. If
![]() $\unicode[STIX]{x1D70B}\in R$
is the image of
$\unicode[STIX]{x1D70B}\in R$
is the image of
![]() $[\unicode[STIX]{x1D709}_{0}^{1/p}]\in W(S)$
then
$[\unicode[STIX]{x1D709}_{0}^{1/p}]\in W(S)$
then
![]() $\unicode[STIX]{x1D70B}^{p}R=pR$
. Thus
$\unicode[STIX]{x1D70B}^{p}R=pR$
. Thus
![]() $R$
satisfies [Reference Bhatt, Morrow and ScholzeBMS16, Definition 3.5]. Conversely, if the latter holds, then
$R$
satisfies [Reference Bhatt, Morrow and ScholzeBMS16, Definition 3.5]. Conversely, if the latter holds, then
![]() $R=W(R^{\flat })/\unicode[STIX]{x1D709}$
where
$R=W(R^{\flat })/\unicode[STIX]{x1D709}$
where
![]() $R^{\flat }$
is perfect and
$R^{\flat }$
is perfect and
![]() $\unicode[STIX]{x1D709}$
is distinguished. See also [Reference Gabber and RameroGR17, 16.2.19].
$\unicode[STIX]{x1D709}$
is distinguished. See also [Reference Gabber and RameroGR17, 16.2.19].
Remark 8.7. If
![]() $R=W(S)/\unicode[STIX]{x1D709}$
is perfectoid then the ring
$R=W(S)/\unicode[STIX]{x1D709}$
is perfectoid then the ring
![]() $R/p=S/\unicode[STIX]{x1D709}_{0}$
is semiperfect and balanced (Definition 4.4). This is straightforward.
$R/p=S/\unicode[STIX]{x1D709}_{0}$
is semiperfect and balanced (Definition 4.4). This is straightforward.
Remark 8.8. The perfectoid ring
![]() $R=W(S)/\unicode[STIX]{x1D709}$
is
$R=W(S)/\unicode[STIX]{x1D709}$
is
![]() $p$
-torsion free if and only if
$p$
-torsion free if and only if
![]() $\unicode[STIX]{x1D709}_{0}\in S$
is a non-zero divisor. Indeed, since
$\unicode[STIX]{x1D709}_{0}\in S$
is a non-zero divisor. Indeed, since
![]() $p,\unicode[STIX]{x1D709}\in W(S)$
are regular elements, the kernels of
$p,\unicode[STIX]{x1D709}\in W(S)$
are regular elements, the kernels of
![]() $p:R\rightarrow R$
and of
$p:R\rightarrow R$
and of
![]() $\unicode[STIX]{x1D709}_{0}:S\rightarrow S$
are isomorphic.
$\unicode[STIX]{x1D709}_{0}:S\rightarrow S$
are isomorphic.
Remark 8.9. If
![]() $R=W(S)/\unicode[STIX]{x1D709}$
is perfectoid, the decomposition (8.2) of
$R=W(S)/\unicode[STIX]{x1D709}$
is perfectoid, the decomposition (8.2) of
![]() $S$
with respect to
$S$
with respect to
![]() $a=\unicode[STIX]{x1D709}_{0}$
gives a similar decomposition of
$a=\unicode[STIX]{x1D709}_{0}$
gives a similar decomposition of
![]() $R$
. More precisely, let
$R$
. More precisely, let
![]() $S_{1}=S/\operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
and
$S_{1}=S/\operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
and
![]() $S_{2}=S/(\unicode[STIX]{x1D709}_{0}^{p^{-\infty }})$
and
$S_{2}=S/(\unicode[STIX]{x1D709}_{0}^{p^{-\infty }})$
and
![]() $S_{12}=S_{1}\otimes _{S}S_{2}$
. Then
$S_{12}=S_{1}\otimes _{S}S_{2}$
. Then
![]() $\unicode[STIX]{x1D709}\in W(S_{i})$
is distinguished, and
$\unicode[STIX]{x1D709}\in W(S_{i})$
is distinguished, and
![]() $R_{i}=W(S_{i})/\unicode[STIX]{x1D709}$
is perfectoid. The sequence (8.1) gives an exact sequence
$R_{i}=W(S_{i})/\unicode[STIX]{x1D709}$
is perfectoid. The sequence (8.1) gives an exact sequence
Since
![]() $\unicode[STIX]{x1D709}$
is a non-zero divisor in
$\unicode[STIX]{x1D709}$
is a non-zero divisor in
![]() $W(S_{12})$
, we obtain an exact sequence
$W(S_{12})$
, we obtain an exact sequence
Here
![]() $R_{2}=S_{2}$
and
$R_{2}=S_{2}$
and
![]() $R_{12}=S_{12}$
are perfect, while
$R_{12}=S_{12}$
are perfect, while
![]() $R_{1}$
is
$R_{1}$
is
![]() $p$
-torsion free perfectoid.
$p$
-torsion free perfectoid.
As an easy consequence we observe the following.
Lemma 8.10. Every perfectoid ring
![]() $R$
is reduced.
$R$
is reduced.
Proof. By (8.6) we can assume that
![]() $R$
is either perfect (thus reduced) or
$R$
is either perfect (thus reduced) or
![]() $p$
-torsion free. For
$p$
-torsion free. For
![]() $\unicode[STIX]{x1D70B}\in R$
as in Remark 8.6 we have
$\unicode[STIX]{x1D70B}\in R$
as in Remark 8.6 we have
![]() $\unicode[STIX]{x1D70B}^{p}R=pR$
, and
$\unicode[STIX]{x1D70B}^{p}R=pR$
, and
![]() $\unicode[STIX]{x1D719}:R/\unicode[STIX]{x1D70B}\rightarrow R/p$
is bijective. Hence, if
$\unicode[STIX]{x1D719}:R/\unicode[STIX]{x1D70B}\rightarrow R/p$
is bijective. Hence, if
![]() $a\in R$
satisfies
$a\in R$
satisfies
![]() $a^{p}=0$
then
$a^{p}=0$
then
![]() $a=\unicode[STIX]{x1D70B}b$
. If
$a=\unicode[STIX]{x1D70B}b$
. If
![]() $R$
is
$R$
is
![]() $p$
-torsion free it follows that
$p$
-torsion free it follows that
![]() $b^{p}=0$
, thus
$b^{p}=0$
, thus
![]() $a\in \unicode[STIX]{x1D70B}^{n}R$
for all
$a\in \unicode[STIX]{x1D70B}^{n}R$
for all
![]() $n$
, whence
$n$
, whence
![]() $a=0$
.☐
$a=0$
.☐
We need the following form of tilting.
Lemma 8.11. Let
![]() $R$
be a perfectoid ring and
$R$
be a perfectoid ring and
![]() $B=R/p$
. The functor
$B=R/p$
. The functor
![]() $R^{\prime }\mapsto R^{\prime }/p$
from perfectoid
$R^{\prime }\mapsto R^{\prime }/p$
from perfectoid
![]() $R$
-algebras to
$R$
-algebras to
![]() $B$
-algebras has a left adjoint
$B$
-algebras has a left adjoint
![]() $B^{\prime }\mapsto {B^{\prime }}^{\sharp }$
. If
$B^{\prime }\mapsto {B^{\prime }}^{\sharp }$
. If
![]() $B^{\prime }$
is an étale
$B^{\prime }$
is an étale
![]() $B$
-algebra then
$B$
-algebra then
![]() $R^{\prime }={B^{\prime }}^{\sharp }$
is the unique
$R^{\prime }={B^{\prime }}^{\sharp }$
is the unique
![]() $p$
-adically complete
$p$
-adically complete
![]() $R$
-algebra such that
$R$
-algebra such that
![]() $R^{\prime }/p=B^{\prime }$
and
$R^{\prime }/p=B^{\prime }$
and
![]() $R/p^{n}\rightarrow R^{\prime }/p^{n}$
is étale for all
$R/p^{n}\rightarrow R^{\prime }/p^{n}$
is étale for all
![]() $n$
.
$n$
.
Proof. Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
where
$R=W(S)/\unicode[STIX]{x1D709}$
where
![]() $\unicode[STIX]{x1D709}$
is distinguished, thus
$\unicode[STIX]{x1D709}$
is distinguished, thus
![]() $S=B^{\flat }=\varprojlim (B,\unicode[STIX]{x1D719})$
, see Remark 8.6. For a
$S=B^{\flat }=\varprojlim (B,\unicode[STIX]{x1D719})$
, see Remark 8.6. For a
![]() $B$
-algebra
$B$
-algebra
![]() $B^{\prime }$
let
$B^{\prime }$
let
![]() ${B^{\prime }}^{\sharp }=W({B^{\prime }}^{\flat })/\unicode[STIX]{x1D709}$
. This defines the left adjoint functor. Assume that
${B^{\prime }}^{\sharp }=W({B^{\prime }}^{\flat })/\unicode[STIX]{x1D709}$
. This defines the left adjoint functor. Assume that
![]() $B\rightarrow B^{\prime }$
is étale and let
$B\rightarrow B^{\prime }$
is étale and let
![]() $R^{\prime }={B^{\prime }}^{\sharp }$
. We have to show that
$R^{\prime }={B^{\prime }}^{\sharp }$
. We have to show that
![]() $R^{\prime }/p=B^{\prime }$
and that
$R^{\prime }/p=B^{\prime }$
and that
![]() $R/p^{n}\rightarrow R^{\prime }/p^{n}$
is flat. Let
$R/p^{n}\rightarrow R^{\prime }/p^{n}$
is flat. Let
![]() $x_{n}\in R/p$
be the image of
$x_{n}\in R/p$
be the image of
![]() $\unicode[STIX]{x1D709}_{0}^{1/p^{n}}$
, so
$\unicode[STIX]{x1D709}_{0}^{1/p^{n}}$
, so
![]() $x_{n}(R/p)$
is the kernel of
$x_{n}(R/p)$
is the kernel of
![]() $\unicode[STIX]{x1D719}^{n}:R/p\rightarrow R/p$
. Since
$\unicode[STIX]{x1D719}^{n}:R/p\rightarrow R/p$
. Since
![]() $B\rightarrow B^{\prime }$
is étale, the diagram of rings
$B\rightarrow B^{\prime }$
is étale, the diagram of rings

is cocartesian, in particular
![]() $x_{n}B$
is the kernel of
$x_{n}B$
is the kernel of
![]() $\unicode[STIX]{x1D719}^{n}:B^{\prime }\rightarrow B^{\prime }$
. It follows that
$\unicode[STIX]{x1D719}^{n}:B^{\prime }\rightarrow B^{\prime }$
. It follows that
![]() $B^{\prime }={B^{\prime }}^{\flat }/\unicode[STIX]{x1D709}_{0}$
(see [Reference Grothendieck and DieudonnéGD60, ch. 0, Proposition 7.2.7]) and thus
$B^{\prime }={B^{\prime }}^{\flat }/\unicode[STIX]{x1D709}_{0}$
(see [Reference Grothendieck and DieudonnéGD60, ch. 0, Proposition 7.2.7]) and thus
![]() $R^{\prime }/p={B^{\prime }}^{\flat }/\unicode[STIX]{x1D709}_{0}=B^{\prime }$
. We have
$R^{\prime }/p={B^{\prime }}^{\flat }/\unicode[STIX]{x1D709}_{0}=B^{\prime }$
. We have
![]() $R/p^{n}=W(B^{\flat })/([\unicode[STIX]{x1D709}_{0}^{n}],p^{n},\unicode[STIX]{x1D709})$
and similarly for
$R/p^{n}=W(B^{\flat })/([\unicode[STIX]{x1D709}_{0}^{n}],p^{n},\unicode[STIX]{x1D709})$
and similarly for
![]() $R^{\prime }$
. For fixed
$R^{\prime }$
. For fixed
![]() $n$
let
$n$
let
In order to verify that
![]() $R/p^{n}\rightarrow R^{\prime }/p^{n}$
is flat it suffices to show that
$R/p^{n}\rightarrow R^{\prime }/p^{n}$
is flat it suffices to show that
![]() $C\rightarrow C^{\prime }$
is flat, or equivalently that
$C\rightarrow C^{\prime }$
is flat, or equivalently that
![]() $C/p\rightarrow C^{\prime }/p$
is flat and that the associated graded rings satisfy
$C/p\rightarrow C^{\prime }/p$
is flat and that the associated graded rings satisfy
![]() $\operatorname{gr}_{p}(C^{\prime })=\operatorname{gr}_{p}(C)\otimes _{C/p}C^{\prime }/p$
(local flatness criterion). But
$\operatorname{gr}_{p}(C^{\prime })=\operatorname{gr}_{p}(C)\otimes _{C/p}C^{\prime }/p$
(local flatness criterion). But
![]() $C/p=B^{\flat }/\unicode[STIX]{x1D709}_{0}^{n}\cong B/x_{r}^{n}$
when
$C/p=B^{\flat }/\unicode[STIX]{x1D709}_{0}^{n}\cong B/x_{r}^{n}$
when
![]() $p^{r}\geqslant n$
, and
$p^{r}\geqslant n$
, and
![]() $gr_{p}(C)\cong (C/p)[T]/T^{n}$
; and similarly for
$gr_{p}(C)\cong (C/p)[T]/T^{n}$
; and similarly for
![]() $C^{\prime }$
. The assertion follows.☐
$C^{\prime }$
. The assertion follows.☐
8.1 The ring
 $A_{\operatorname{cris}}$
for perfectoid rings
$A_{\operatorname{cris}}$
for perfectoid rings
Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
$R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
![]() $S$
is perfect and
$S$
is perfect and
![]() $\unicode[STIX]{x1D709}$
is distinguished. Let
$\unicode[STIX]{x1D709}$
is distinguished. Let
![]() $A_{\inf }(R)=W(S)$
and let
$A_{\inf }(R)=W(S)$
and let
![]() $A_{\operatorname{cris}}(R)\rightarrow R$
be the universal
$A_{\operatorname{cris}}(R)\rightarrow R$
be the universal
![]() $p$
-adic PD extension. We have
$p$
-adic PD extension. We have
![]() $A_{\operatorname{cris}}(R)=A_{\operatorname{cris}}(R/p)$
as rings. If
$A_{\operatorname{cris}}(R)=A_{\operatorname{cris}}(R/p)$
as rings. If
![]() $R$
is perfect then
$R$
is perfect then
![]() $A_{\operatorname{cris}}(R)=A_{\inf }(R)=W(R)$
. If
$A_{\operatorname{cris}}(R)=A_{\inf }(R)=W(R)$
. If
![]() $R$
is
$R$
is
![]() $p$
-torsion free, which means that the semiperfect ring
$p$
-torsion free, which means that the semiperfect ring
![]() $R/p$
is a complete intersection in the sense of Definition 4.1 (see Remark 8.8), then
$R/p$
is a complete intersection in the sense of Definition 4.1 (see Remark 8.8), then
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free. Let us verify that this also holds in general.
$p$
-torsion free. Let us verify that this also holds in general.
Proposition 8.12. Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring as above and
$R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring as above and
![]() $R_{i}=W(S_{i})/\unicode[STIX]{x1D709}$
as in Remark 8.9, for
$R_{i}=W(S_{i})/\unicode[STIX]{x1D709}$
as in Remark 8.9, for
![]() $i=1,2,12$
. We have an exact sequence
$i=1,2,12$
. We have an exact sequence
In particular, the ring
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free.
$p$
-torsion free.
Proof. Recall that
To simplify the notation, in the following we consider the empty index
![]() $\emptyset$
so that
$\emptyset$
so that
![]() $S_{\emptyset }=S$
and
$S_{\emptyset }=S$
and
![]() $S_{\emptyset 2}=S_{2}$
. For
$S_{\emptyset 2}=S_{2}$
. For
![]() $i=\emptyset$
or
$i=\emptyset$
or
![]() $i=1$
let
$i=1$
let
![]() $A_{i}$
be the PD envelope of
$A_{i}$
be the PD envelope of
![]() $[\unicode[STIX]{x1D709}_{0}]W(S_{i})\subseteq W(S_{i})$
relative to
$[\unicode[STIX]{x1D709}_{0}]W(S_{i})\subseteq W(S_{i})$
relative to
![]() $p\mathbb{Z}_{p}\subset \mathbb{Z}_{p}$
. Then
$p\mathbb{Z}_{p}\subset \mathbb{Z}_{p}$
. Then
![]() $A_{\operatorname{cris}}(R_{i})$
is the
$A_{\operatorname{cris}}(R_{i})$
is the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $A_{i}$
. The projection
$A_{i}$
. The projection
![]() $W(S_{i})\rightarrow W(S_{i2})$
extends to a PD homomorphism
$W(S_{i})\rightarrow W(S_{i2})$
extends to a PD homomorphism
![]() $g_{i}:A_{i}\rightarrow W(S_{i2})$
, and we have the following commutative diagram of rings, where
$g_{i}:A_{i}\rightarrow W(S_{i2})$
, and we have the following commutative diagram of rings, where
![]() $f_{i}$
is the canonical map.
$f_{i}$
is the canonical map.

We claim that
![]() $\operatorname{Coker}(f)\rightarrow \operatorname{Coker}(f_{1})$
is bijective,
$\operatorname{Coker}(f)\rightarrow \operatorname{Coker}(f_{1})$
is bijective,
![]() $f_{1}$
is injective, and
$f_{1}$
is injective, and
![]() $A_{1}$
is
$A_{1}$
is
![]() $p$
-torsion free. Assume this holds. The diagonal map
$p$
-torsion free. Assume this holds. The diagonal map
![]() $W(S)\rightarrow W(S_{1})\times W(S_{2})$
is injective, thus
$W(S)\rightarrow W(S_{1})\times W(S_{2})$
is injective, thus
![]() $W(S)\rightarrow W(S_{1})\times A$
is injective. Since
$W(S)\rightarrow W(S_{1})\times A$
is injective. Since
![]() $f_{1}$
is injective, it follows that
$f_{1}$
is injective, it follows that
![]() $f$
is injective. Consider the homomorphisms of complexes
$f$
is injective. Consider the homomorphisms of complexes
Here
![]() $f_{\ast }$
and
$f_{\ast }$
and
![]() $g_{\ast }\circ f_{\ast }$
are quasi-isomorphism, thus
$g_{\ast }\circ f_{\ast }$
are quasi-isomorphism, thus
![]() $g_{\ast }$
is a quasi-isomorphism. This remains true after
$g_{\ast }$
is a quasi-isomorphism. This remains true after
![]() $p$
-adic completion, and the lemma follows.
$p$
-adic completion, and the lemma follows.
To prove the claim we need a closer look on the construction of
![]() $A$
and
$A$
and
![]() $A_{1}$
. Let
$A_{1}$
. Let
![]() $\unicode[STIX]{x1D6EC}_{0}=\mathbb{Z}_{p}[T]$
and let
$\unicode[STIX]{x1D6EC}_{0}=\mathbb{Z}_{p}[T]$
and let
![]() $\unicode[STIX]{x1D6EC}=\mathbb{Z}_{p}\langle T\rangle$
be the PD polynomial algebra, i.e. the
$\unicode[STIX]{x1D6EC}=\mathbb{Z}_{p}\langle T\rangle$
be the PD polynomial algebra, i.e. the
![]() $\mathbb{Z}_{p}$
-subalgebra of
$\mathbb{Z}_{p}$
-subalgebra of
![]() $\mathbb{Q}_{p}[T]$
generated by
$\mathbb{Q}_{p}[T]$
generated by
![]() $T^{n}/n!$
for
$T^{n}/n!$
for
![]() $n\geqslant 1$
. Define
$n\geqslant 1$
. Define
![]() $\unicode[STIX]{x1D6EC}_{0}\rightarrow W(S)$
by
$\unicode[STIX]{x1D6EC}_{0}\rightarrow W(S)$
by
![]() $T\mapsto [\unicode[STIX]{x1D709}_{0}]$
. This extends to a PD homomorphism
$T\mapsto [\unicode[STIX]{x1D709}_{0}]$
. This extends to a PD homomorphism
![]() $\unicode[STIX]{x1D6EC}\rightarrow A$
, and the resulting homomorphisms
$\unicode[STIX]{x1D6EC}\rightarrow A$
, and the resulting homomorphisms
are surjective. Since
![]() $\unicode[STIX]{x1D709}_{0}$
is a non-zero divisor in
$\unicode[STIX]{x1D709}_{0}$
is a non-zero divisor in
![]() $S_{1}$
, the homomorphism
$S_{1}$
, the homomorphism
![]() $h_{1}$
is bijective, and
$h_{1}$
is bijective, and
![]() $A_{1}$
is torsion free.Footnote
4
$A_{1}$
is torsion free.Footnote
4
We consider the following ascending filtration of
![]() $\unicode[STIX]{x1D6EC}$
and the associated filtrations of
$\unicode[STIX]{x1D6EC}$
and the associated filtrations of
![]() $A$
and of
$A$
and of
![]() $A_{1}$
. For
$A_{1}$
. For
![]() $m\geqslant 0$
let
$m\geqslant 0$
let
![]() $F^{m}\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}\cap p^{-m}\mathbb{Z}_{p}[T]$
. Then
$F^{m}\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}\cap p^{-m}\mathbb{Z}_{p}[T]$
. Then
![]() $\unicode[STIX]{x1D6EC}=\bigcup F^{m}\unicode[STIX]{x1D6EC}$
, and
$\unicode[STIX]{x1D6EC}=\bigcup F^{m}\unicode[STIX]{x1D6EC}$
, and
![]() $\operatorname{gr}^{m}\unicode[STIX]{x1D6EC}=F^{m}\unicode[STIX]{x1D6EC}/F^{m-1}\unicode[STIX]{x1D6EC}$
is a free
$\operatorname{gr}^{m}\unicode[STIX]{x1D6EC}=F^{m}\unicode[STIX]{x1D6EC}/F^{m-1}\unicode[STIX]{x1D6EC}$
is a free
![]() $\unicode[STIX]{x1D6EC}_{0}/p$
-module of rank
$\unicode[STIX]{x1D6EC}_{0}/p$
-module of rank
![]() $1$
generated by
$1$
generated by
![]() $p^{-m}T^{d_{m}}$
where
$p^{-m}T^{d_{m}}$
where
![]() $d_{m}$
is minimal such that
$d_{m}$
is minimal such that
![]() $p^{m}$
divides
$p^{m}$
divides
![]() $d_{m}!$
. For
$d_{m}!$
. For
![]() $i=\emptyset$
or
$i=\emptyset$
or
![]() $1$
let
$1$
let
![]() $F^{m}A_{i}\subseteq A_{i}$
be the image of
$F^{m}A_{i}\subseteq A_{i}$
be the image of
![]() $W(S_{i})\otimes _{\unicode[STIX]{x1D6EC}_{0}}F^{m}\unicode[STIX]{x1D6EC}$
and let
$W(S_{i})\otimes _{\unicode[STIX]{x1D6EC}_{0}}F^{m}\unicode[STIX]{x1D6EC}$
and let
![]() $\operatorname{gr}^{m}A_{i}=F^{m}A_{i}/F^{m-1}A_{i}$
. The homomorphism
$\operatorname{gr}^{m}A_{i}=F^{m}A_{i}/F^{m-1}A_{i}$
. The homomorphism
![]() $h_{i}$
induces surjective maps
$h_{i}$
induces surjective maps
and surjective maps
which map
![]() $1\in S_{i}$
to
$1\in S_{i}$
to
![]() $(p^{-m}d_{m}!)\unicode[STIX]{x1D6FE}_{d_{m}}([\unicode[STIX]{x1D709}_{0}])$
. The transition homomorphisms
$(p^{-m}d_{m}!)\unicode[STIX]{x1D6FE}_{d_{m}}([\unicode[STIX]{x1D709}_{0}])$
. The transition homomorphisms
are injective because
Since
![]() $h_{1}$
is bijective it follows that
$h_{1}$
is bijective it follows that
![]() $F^{m}h_{1}$
is bijective for
$F^{m}h_{1}$
is bijective for
![]() $m\geqslant 0$
, which for
$m\geqslant 0$
, which for
![]() $m=0$
means that
$m=0$
means that
![]() $f_{1}:W(S_{1})\rightarrow A_{1}$
is injective, moreover
$f_{1}:W(S_{1})\rightarrow A_{1}$
is injective, moreover
![]() $\operatorname{gr}^{m}h_{1}$
is bijective for
$\operatorname{gr}^{m}h_{1}$
is bijective for
![]() $m\geqslant 1$
. We consider the following commutative diagram of surjective maps.
$m\geqslant 1$
. We consider the following commutative diagram of surjective maps.

We claim that
![]() $\operatorname{Ker}(S\rightarrow S_{1})=\operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
maps to zero in
$\operatorname{Ker}(S\rightarrow S_{1})=\operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
maps to zero in
![]() $\operatorname{gr}^{m}A$
. Indeed, choose
$\operatorname{gr}^{m}A$
. Indeed, choose
![]() $r$
such that
$r$
such that
![]() $p^{r}\geqslant d_{m}$
. For
$p^{r}\geqslant d_{m}$
. For
![]() $a\in \operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
we have
$a\in \operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
we have
![]() $b=a^{p^{-r}}\in \operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
and therefore
$b=a^{p^{-r}}\in \operatorname{Ann}(\unicode[STIX]{x1D709}_{0})$
and therefore
![]() $[a]\unicode[STIX]{x1D6FE}_{d_{m}}([\unicode[STIX]{x1D709}_{0}])=[b^{p^{r}-d_{m}}]\unicode[STIX]{x1D6FE}_{d_{m}}([b\unicode[STIX]{x1D709}_{0}])=0$
. It follows that
$[a]\unicode[STIX]{x1D6FE}_{d_{m}}([\unicode[STIX]{x1D709}_{0}])=[b^{p^{r}-d_{m}}]\unicode[STIX]{x1D6FE}_{d_{m}}([b\unicode[STIX]{x1D709}_{0}])=0$
. It follows that
![]() $\operatorname{gr}^{m}A\rightarrow \operatorname{gr}^{m}A_{1}$
is bijective for
$\operatorname{gr}^{m}A\rightarrow \operatorname{gr}^{m}A_{1}$
is bijective for
![]() $m\geqslant 1$
, and thus
$m\geqslant 1$
, and thus
![]() $A/F^{0}A\rightarrow A_{1}/F^{0}A_{1}$
is bijective, which means that
$A/F^{0}A\rightarrow A_{1}/F^{0}A_{1}$
is bijective, which means that
![]() $\operatorname{Coker}(f)\rightarrow \operatorname{Coker}(f_{1})$
is bijective as required.☐
$\operatorname{Coker}(f)\rightarrow \operatorname{Coker}(f_{1})$
is bijective as required.☐
9 Windows and modules for perfectoid rings
As earlier, let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
$R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
![]() $S$
is perfect and
$S$
is perfect and
![]() $\unicode[STIX]{x1D709}$
is distinguished. The rings
$\unicode[STIX]{x1D709}$
is distinguished. The rings
![]() $A_{\inf }(R)=W(S)$
and
$A_{\inf }(R)=W(S)$
and
![]() $A_{\operatorname{cris}}(R)$
carry natural frame structures:
$A_{\operatorname{cris}}(R)$
carry natural frame structures:
where
![]() $\operatorname{Fil}A_{\inf }(R)=\unicode[STIX]{x1D709}A_{\inf }(R)$
and
$\operatorname{Fil}A_{\inf }(R)=\unicode[STIX]{x1D709}A_{\inf }(R)$
and
![]() $\unicode[STIX]{x1D70E}_{1}^{\inf }(\unicode[STIX]{x1D709}a)=\unicode[STIX]{x1D70E}(a)$
, and
$\unicode[STIX]{x1D70E}_{1}^{\inf }(\unicode[STIX]{x1D709}a)=\unicode[STIX]{x1D70E}(a)$
, and
where
![]() $\operatorname{Fil}A_{\operatorname{cris}}(R)$
is the kernel of
$\operatorname{Fil}A_{\operatorname{cris}}(R)$
is the kernel of
![]() $A_{\operatorname{cris}}(R)\rightarrow R$
, and
$A_{\operatorname{cris}}(R)\rightarrow R$
, and
![]() $\unicode[STIX]{x1D70E}_{1}(a)=p^{-1}\unicode[STIX]{x1D70E}(a)$
; this is well defined since
$\unicode[STIX]{x1D70E}_{1}(a)=p^{-1}\unicode[STIX]{x1D70E}(a)$
; this is well defined since
![]() $A_{\operatorname{cris}}(R)$
is
$A_{\operatorname{cris}}(R)$
is
![]() $p$
-torsion free by Proposition 8.12. The natural map
$p$
-torsion free by Proposition 8.12. The natural map
![]() $A_{\inf }(R)\rightarrow A_{\operatorname{cris}}(R)$
is a frame homomorphism
$A_{\inf }(R)\rightarrow A_{\operatorname{cris}}(R)$
is a frame homomorphism
Indeed, let
![]() $c=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D709})$
in
$c=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D709})$
in
![]() $A_{\operatorname{cris}}(R)$
. Then
$A_{\operatorname{cris}}(R)$
. Then
![]() $c\equiv [\unicode[STIX]{x1D709}_{0}]^{p}/p+[\unicode[STIX]{x1D709}_{1}]^{p}$
mod
$c\equiv [\unicode[STIX]{x1D709}_{0}]^{p}/p+[\unicode[STIX]{x1D709}_{1}]^{p}$
mod
![]() $pA_{\operatorname{cris}}(R)$
and thus
$pA_{\operatorname{cris}}(R)$
and thus
![]() $c\equiv [\unicode[STIX]{x1D709}_{1}]^{p}$
mod
$c\equiv [\unicode[STIX]{x1D709}_{1}]^{p}$
mod
![]() $pA_{\operatorname{cris}}(R)+\operatorname{Fil}A_{\operatorname{cris}}(R)$
, so
$pA_{\operatorname{cris}}(R)+\operatorname{Fil}A_{\operatorname{cris}}(R)$
, so
![]() $c$
is a unit since
$c$
is a unit since
![]() $\unicode[STIX]{x1D709}_{1}$
is a unit. We have
$\unicode[STIX]{x1D709}_{1}$
is a unit. We have
![]() $\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D706}=c\cdot \unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D70E}_{1}$
on
$\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D706}=c\cdot \unicode[STIX]{x1D706}\circ \unicode[STIX]{x1D70E}_{1}$
on
![]() $\unicode[STIX]{x1D709}A_{\inf }(R)$
, so
$\unicode[STIX]{x1D709}A_{\inf }(R)$
, so
![]() $\unicode[STIX]{x1D706}$
is a
$\unicode[STIX]{x1D706}$
is a
![]() $c$
-homomorphism of frames in the sense of [Reference LauLau10]. If
$c$
-homomorphism of frames in the sense of [Reference LauLau10]. If
![]() $R$
is perfect,
$R$
is perfect,
![]() $\unicode[STIX]{x1D706}$
is the identity and
$\unicode[STIX]{x1D706}$
is the identity and
![]() $c=1$
.
$c=1$
.
9.1 Descent of windows under
 $\unicode[STIX]{x1D706}$
$\unicode[STIX]{x1D706}$
We need the following standard lemma. For a ring
![]() $A$
let
$A$
let
![]() $\operatorname{LF}(A)$
be the category of finite projective
$\operatorname{LF}(A)$
be the category of finite projective
![]() $A$
-modules.
$A$
-modules.
Lemma 9.1. Let
![]() $A_{1}\rightarrow A_{3}\leftarrow A_{2}$
be rings with surjective homomorphisms and
$A_{1}\rightarrow A_{3}\leftarrow A_{2}$
be rings with surjective homomorphisms and
![]() $A=A_{1}\times _{A_{3}}A_{2}$
. Then the corresponding diagram of categories
$A=A_{1}\times _{A_{3}}A_{2}$
. Then the corresponding diagram of categories

is
![]() $2$
-cartesian.
$2$
-cartesian.
Proof. For a flat
![]() $A$
-module
$A$
-module
![]() $M$
and
$M$
and
![]() $M_{i}=M\otimes _{A}A_{i}$
the natural map
$M_{i}=M\otimes _{A}A_{i}$
the natural map
![]() $M\rightarrow M_{1}\times _{M_{3}}M_{2}$
is bijective. Thus the functor
$M\rightarrow M_{1}\times _{M_{3}}M_{2}$
is bijective. Thus the functor
![]() $\operatorname{LF}(A)\rightarrow \operatorname{LF}(A_{1})\times _{\operatorname{LF}(A_{3})}\operatorname{LF}(A_{2})$
is fully faithful. For given
$\operatorname{LF}(A)\rightarrow \operatorname{LF}(A_{1})\times _{\operatorname{LF}(A_{3})}\operatorname{LF}(A_{2})$
is fully faithful. For given
![]() $M_{i}\in \operatorname{LF}(A_{i})$
and isomorphisms
$M_{i}\in \operatorname{LF}(A_{i})$
and isomorphisms
![]() $M_{1}\otimes _{A_{1}}A_{3}\cong M_{3}\cong M_{2}\otimes _{A_{2}}A_{3}$
let
$M_{1}\otimes _{A_{1}}A_{3}\cong M_{3}\cong M_{2}\otimes _{A_{2}}A_{3}$
let
![]() $M=M_{1}\times _{M_{3}}M_{2}$
. We have to show that
$M=M_{1}\times _{M_{3}}M_{2}$
. We have to show that
![]() $M\in \operatorname{LF}(A)$
and that
$M\in \operatorname{LF}(A)$
and that
![]() $M\otimes _{A}A_{i}\rightarrow M_{i}$
is bijective. One can choose a finite free
$M\otimes _{A}A_{i}\rightarrow M_{i}$
is bijective. One can choose a finite free
![]() $A$
-module
$A$
-module
![]() $F$
and compatible surjective maps
$F$
and compatible surjective maps
![]() $g_{i}:F_{i}\rightarrow M_{i}$
where
$g_{i}:F_{i}\rightarrow M_{i}$
where
![]() $F_{i}=F\otimes _{A}A_{i}$
. Indeed, clearly one can arrange that
$F_{i}=F\otimes _{A}A_{i}$
. Indeed, clearly one can arrange that
![]() $g_{1}$
or
$g_{1}$
or
![]() $g_{3}$
is surjective, and then take the direct sum. Next one can find compatible maps
$g_{3}$
is surjective, and then take the direct sum. Next one can find compatible maps
![]() $s_{i}:M_{i}\rightarrow F_{i}$
with
$s_{i}:M_{i}\rightarrow F_{i}$
with
![]() $g_{i}s_{i}=\operatorname{id}$
. Indeed, choose
$g_{i}s_{i}=\operatorname{id}$
. Indeed, choose
![]() $s_{1}$
, which induces
$s_{1}$
, which induces
![]() $s_{3}$
, and use that
$s_{3}$
, and use that
![]() $F_{2}\rightarrow F_{3}\times _{M_{3}}M_{2}$
is surjective to get
$F_{2}\rightarrow F_{3}\times _{M_{3}}M_{2}$
is surjective to get
![]() $s_{2}$
. This gives compatible isomorphisms
$s_{2}$
. This gives compatible isomorphisms
![]() $F_{i}\cong M_{i}\oplus \operatorname{Ker}(g_{i})$
, so
$F_{i}\cong M_{i}\oplus \operatorname{Ker}(g_{i})$
, so
![]() $M$
is a direct summand of
$M$
is a direct summand of
![]() $F$
, and the assertion follows.☐
$F$
, and the assertion follows.☐
Lemma 9.2. Let
![]() $R$
be a perfectoid ring. For
$R$
be a perfectoid ring. For
![]() $R_{1}$
,
$R_{1}$
,
![]() $R_{2}$
,
$R_{2}$
,
![]() $R_{12}$
as in Remark 8.9 the natural diagrams of window categories
$R_{12}$
as in Remark 8.9 the natural diagrams of window categories

and

are
![]() $2$
-cartesian.
$2$
-cartesian.
Proof. The rings
![]() $R$
,
$R$
,
![]() $R_{1}$
,
$R_{1}$
,
![]() $R_{2}$
,
$R_{2}$
,
![]() $R_{12}$
form a cartesian diagram with surjective maps, and the same holds for the associated rings
$R_{12}$
form a cartesian diagram with surjective maps, and the same holds for the associated rings
![]() $A_{\inf }$
and
$A_{\inf }$
and
![]() $A_{\operatorname{cris}}$
, the latter by Proposition 8.12. Thus the diagrams of frames that arise from (9.2) and (9.3) by deleting ‘
$A_{\operatorname{cris}}$
, the latter by Proposition 8.12. Thus the diagrams of frames that arise from (9.2) and (9.3) by deleting ‘
![]() $\operatorname{Win}$
’ are cartesian with surjective maps in all components. Using Lemma 9.1 the assertion follows easily.☐
$\operatorname{Win}$
’ are cartesian with surjective maps in all components. Using Lemma 9.1 the assertion follows easily.☐
Proposition 9.3. If
![]() $p\geqslant 3$
, for every perfectoid ring
$p\geqslant 3$
, for every perfectoid ring
![]() $R$
the functor
$R$
the functor
associated to (9.1) is an equivalence of categories.
Proof. By Lemma 9.2 we can assume that
![]() $R$
is either perfect or
$R$
is either perfect or
![]() $p$
-torsion free. In the perfect case
$p$
-torsion free. In the perfect case
![]() $\unicode[STIX]{x1D706}$
is bijective. Let
$\unicode[STIX]{x1D706}$
is bijective. Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
where
$R=W(S)/\unicode[STIX]{x1D709}$
where
![]() $S$
is perfect and
$S$
is perfect and
![]() $\unicode[STIX]{x1D709}$
is distinguished. If
$\unicode[STIX]{x1D709}$
is distinguished. If
![]() $R$
is
$R$
is
![]() $p$
-torsion free,
$p$
-torsion free,
![]() $(p,\unicode[STIX]{x1D709})$
is a regular sequence in
$(p,\unicode[STIX]{x1D709})$
is a regular sequence in
![]() $W(S)$
, and
$W(S)$
, and
![]() $\unicode[STIX]{x1D706}^{\ast }$
is an equivalence by [Reference Cais and LauCL14, Proposition 2.3.1] (which requires
$\unicode[STIX]{x1D706}^{\ast }$
is an equivalence by [Reference Cais and LauCL14, Proposition 2.3.1] (which requires
![]() $p\geqslant 3$
).☐
$p\geqslant 3$
).☐
9.2 Breuil–Kisin–Fargues modules
Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
be perfectoid as before. In the following we write
$R=W(S)/\unicode[STIX]{x1D709}$
be perfectoid as before. In the following we write
![]() $A_{\inf }=A_{\inf }(R)=W(S)$
.
$A_{\inf }=A_{\inf }(R)=W(S)$
.
Definition 9.4. A (locally free) Breuil–Kisin–Fargues module for
![]() $R$
is a pair
$R$
is a pair
![]() $(\mathfrak{M},\unicode[STIX]{x1D711})$
where
$(\mathfrak{M},\unicode[STIX]{x1D711})$
where
![]() $\mathfrak{M}$
is a finite projective
$\mathfrak{M}$
is a finite projective
![]() $A_{\inf }$
-module and where
$A_{\inf }$
-module and where
![]() $\unicode[STIX]{x1D711}:\mathfrak{M}^{\unicode[STIX]{x1D70E}}\rightarrow \mathfrak{M}$
is a linear map whose cokernel is annihilated by
$\unicode[STIX]{x1D711}:\mathfrak{M}^{\unicode[STIX]{x1D70E}}\rightarrow \mathfrak{M}$
is a linear map whose cokernel is annihilated by
![]() $\unicode[STIX]{x1D709}$
. We denote by
$\unicode[STIX]{x1D709}$
. We denote by
![]() $\operatorname{BK}(R)$
the category of Breuil–Kisin–Fargues modules for
$\operatorname{BK}(R)$
the category of Breuil–Kisin–Fargues modules for
![]() $R$
.
$R$
.
In the case
![]() $R={\mathcal{O}}_{K}$
for a perfectoid field
$R={\mathcal{O}}_{K}$
for a perfectoid field
![]() $K$
, free
$K$
, free
![]() $\unicode[STIX]{x1D711}$
-modules over
$\unicode[STIX]{x1D711}$
-modules over
![]() $A_{\inf }$
are studied by Fargues [Reference FarguesFar15] in analogy with the classical theory of Breuil–Kisin modules [Reference KisinKis06], and are called Breuil–Kisin–Fargues modules in [Reference Bhatt, Morrow and ScholzeBMS16]. Here we only consider minuscule
$A_{\inf }$
are studied by Fargues [Reference FarguesFar15] in analogy with the classical theory of Breuil–Kisin modules [Reference KisinKis06], and are called Breuil–Kisin–Fargues modules in [Reference Bhatt, Morrow and ScholzeBMS16]. Here we only consider minuscule
![]() $\unicode[STIX]{x1D711}$
-modules, which correspond to
$\unicode[STIX]{x1D711}$
-modules, which correspond to
![]() $p$
-divisible groups. When
$p$
-divisible groups. When
![]() $R$
is a perfect ring, then
$R$
is a perfect ring, then
![]() $A=W(R)$
, and
$A=W(R)$
, and
![]() $\operatorname{BK}(R)$
is the category of Dieudonné modules over
$\operatorname{BK}(R)$
is the category of Dieudonné modules over
![]() $R$
in the usual sense.
$R$
in the usual sense.
Lemma 9.5. For
![]() $(\mathfrak{M},\unicode[STIX]{x1D711})\in \operatorname{BK}(R)$
the
$(\mathfrak{M},\unicode[STIX]{x1D711})\in \operatorname{BK}(R)$
the
![]() $R$
-module
$R$
-module
![]() $\operatorname{Coker}(\unicode[STIX]{x1D711})$
is projective.
$\operatorname{Coker}(\unicode[STIX]{x1D711})$
is projective.
Proof. Cf. Lemma 3.1. Let
![]() $\mathfrak{N}=\mathfrak{M}^{\unicode[STIX]{x1D70E}}$
and
$\mathfrak{N}=\mathfrak{M}^{\unicode[STIX]{x1D70E}}$
and
![]() $\bar{\mathfrak{M}}=\mathfrak{M}\otimes _{A}R$
and
$\bar{\mathfrak{M}}=\mathfrak{M}\otimes _{A}R$
and
![]() $\bar{\mathfrak{N}}=\mathfrak{N}\otimes _{A}R$
. There is a unique linear map
$\bar{\mathfrak{N}}=\mathfrak{N}\otimes _{A}R$
. There is a unique linear map
![]() $\unicode[STIX]{x1D713}:\mathfrak{M}\rightarrow \mathfrak{M}^{\unicode[STIX]{x1D70E}}$
such that
$\unicode[STIX]{x1D713}:\mathfrak{M}\rightarrow \mathfrak{M}^{\unicode[STIX]{x1D70E}}$
such that
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}$
, and we obtain an exact sequence of finite projective
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}$
, and we obtain an exact sequence of finite projective
![]() $R$
-modules
$R$
-modules
We have to show that
![]() $\operatorname{Im}(\bar{\unicode[STIX]{x1D713}})$
is a direct summand of
$\operatorname{Im}(\bar{\unicode[STIX]{x1D713}})$
is a direct summand of
![]() $\bar{\mathfrak{N}}$
. This holds if and only if for each maximal ideal
$\bar{\mathfrak{N}}$
. This holds if and only if for each maximal ideal
![]() $\mathfrak{m}\subset R$
the base change of (9.5) to
$\mathfrak{m}\subset R$
the base change of (9.5) to
![]() $k=R/\mathfrak{m}$
is exact. We have
$k=R/\mathfrak{m}$
is exact. We have
![]() $p\in \mathfrak{m}$
, so
$p\in \mathfrak{m}$
, so
![]() $k$
is a perfect field of characteristic
$k$
is a perfect field of characteristic
![]() $p$
. The natural homomorphism
$p$
. The natural homomorphism
![]() $A\rightarrow A_{\inf }(k)=W(k)$
maps
$A\rightarrow A_{\inf }(k)=W(k)$
maps
![]() $\unicode[STIX]{x1D709}$
to
$\unicode[STIX]{x1D709}$
to
![]() $p$
. Thus
$p$
. Thus
![]() $\mathfrak{M}\otimes _{A}W(k)$
is a Dieudonné module over
$\mathfrak{M}\otimes _{A}W(k)$
is a Dieudonné module over
![]() $k$
, and it follows that the base change of (9.5) under
$k$
, and it follows that the base change of (9.5) under
![]() $R\rightarrow k$
is exact as required.☐
$R\rightarrow k$
is exact as required.☐
Lemma 9.5 implies that there is an equivalence of categories
given by
![]() $(M,\operatorname{Fil}M,F,F_{1})\mapsto (\mathfrak{M},\unicode[STIX]{x1D711})$
with
$(M,\operatorname{Fil}M,F,F_{1})\mapsto (\mathfrak{M},\unicode[STIX]{x1D711})$
with
![]() $\mathfrak{M}=\operatorname{Fil}M$
and
$\mathfrak{M}=\operatorname{Fil}M$
and
![]() $\unicode[STIX]{x1D711}(1\otimes x)=\unicode[STIX]{x1D709}F_{1}(x)$
, see [Reference Cais and LauCL14, Lemma 2.1.15]. The inverse functor is determined by
$\unicode[STIX]{x1D711}(1\otimes x)=\unicode[STIX]{x1D709}F_{1}(x)$
, see [Reference Cais and LauCL14, Lemma 2.1.15]. The inverse functor is determined by
![]() $M=\mathfrak{M}^{\unicode[STIX]{x1D70E}}$
and
$M=\mathfrak{M}^{\unicode[STIX]{x1D70E}}$
and
![]() $\operatorname{Fil}M=\{x\in M\mid \unicode[STIX]{x1D711}(x)\in \unicode[STIX]{x1D709}\mathfrak{M}\}$
and
$\operatorname{Fil}M=\{x\in M\mid \unicode[STIX]{x1D711}(x)\in \unicode[STIX]{x1D709}\mathfrak{M}\}$
and
![]() $F(x)=1\otimes \unicode[STIX]{x1D711}(x)$
for
$F(x)=1\otimes \unicode[STIX]{x1D711}(x)$
for
![]() $x\in M$
.
$x\in M$
.
Remark 9.6. The frame
![]() $\text{}\underline{A}_{\inf }(R)$
depends on the choice of
$\text{}\underline{A}_{\inf }(R)$
depends on the choice of
![]() $\unicode[STIX]{x1D709}$
, but the functor
$\unicode[STIX]{x1D709}$
, but the functor
defined as the composition of (9.4) and the inverse of (9.6) is independent of
![]() $\unicode[STIX]{x1D709}$
as is easily verified.
$\unicode[STIX]{x1D709}$
as is easily verified.
9.3
 $p$
-divisible groups over perfectoid rings
$p$
-divisible groups over perfectoid rings
Let
![]() $R$
be a perfectoid ring. The functor
$R$
be a perfectoid ring. The functor
![]() $\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
$\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
of (3.3) for
![]() $\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}(R)$
defined by evaluation of the crystalline Dieudonné module is a functor
$\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}(R)$
defined by evaluation of the crystalline Dieudonné module is a functor
Proposition 9.7. If
![]() $p\geqslant 3$
then the functor
$p\geqslant 3$
then the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.
Proof. Since the ring
![]() $A_{\operatorname{cris}}(R)=A_{\operatorname{cris}}(R/p)$
is torsion free by Proposition 8.12, there is another frame
$A_{\operatorname{cris}}(R)=A_{\operatorname{cris}}(R/p)$
is torsion free by Proposition 8.12, there is another frame
defined by
![]() $\operatorname{Fil}A_{\operatorname{cris}}(R/p)=\operatorname{Fil}A_{\operatorname{cris}}(R)+pA_{\operatorname{cris}}(R)$
and
$\operatorname{Fil}A_{\operatorname{cris}}(R/p)=\operatorname{Fil}A_{\operatorname{cris}}(R)+pA_{\operatorname{cris}}(R)$
and
![]() $\unicode[STIX]{x1D70E}_{1}(x)=p^{-1}\unicode[STIX]{x1D70E}(x)$
. The identity is a strict frame homomorphism
$\unicode[STIX]{x1D70E}_{1}(x)=p^{-1}\unicode[STIX]{x1D70E}(x)$
. The identity is a strict frame homomorphism
![]() $j:\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}_{\operatorname{cris}}(R/p)$
over the projection
$j:\text{}\underline{A}_{\operatorname{cris}}(R)\rightarrow \text{}\underline{A}_{\operatorname{cris}}(R/p)$
over the projection
![]() $\unicode[STIX]{x1D70B}:R\rightarrow R/p$
, and we obtain a commutative diagram of functors
$\unicode[STIX]{x1D70B}:R\rightarrow R/p$
, and we obtain a commutative diagram of functors

where
![]() $\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
is the functor
$\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
is the functor
![]() $\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
for
$\unicode[STIX]{x1D6F7}_{\text{}\underline{S}}$
for
![]() $\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}(R/p)$
. Here
$\text{}\underline{S}=\text{}\underline{A}_{\operatorname{cris}}(R/p)$
. Here
![]() $\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
coincides with the functor of Theorem 6.3, but this is not needed. Since
$\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
coincides with the functor of Theorem 6.3, but this is not needed. Since
![]() $R/p$
is a balanced semiperfect ring (see Remark 8.7), the functor
$R/p$
is a balanced semiperfect ring (see Remark 8.7), the functor
![]() $\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
is an equivalence by Corollary 5.11; see also Remark 5.12.
$\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}$
is an equivalence by Corollary 5.11; see also Remark 5.12.
For
![]() $G\in \operatorname{BT}(\operatorname{Spec}R/p)$
and
$G\in \operatorname{BT}(\operatorname{Spec}R/p)$
and
![]() $\text{}\underline{M}=\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}(G)$
there is a natural isomorphism of
$\text{}\underline{M}=\unicode[STIX]{x1D6F7}_{R/p}^{\operatorname{cris}}(G)$
there is a natural isomorphism of
![]() $R$
-modules
$R$
-modules
![]() $M\otimes _{A_{\operatorname{cris}}(R/p)}R\cong \mathbb{D}(G)_{R}$
. Since
$M\otimes _{A_{\operatorname{cris}}(R/p)}R\cong \mathbb{D}(G)_{R}$
. Since
![]() $p\geqslant 3$
, the divided powers on the ideal
$p\geqslant 3$
, the divided powers on the ideal
![]() $pR$
are topologically nilpotent. By the Grothendieck–Messing theorem [Reference MessingMes72] and by [Reference LauLau10, Lemma 4.2] it follows that lifts of
$pR$
are topologically nilpotent. By the Grothendieck–Messing theorem [Reference MessingMes72] and by [Reference LauLau10, Lemma 4.2] it follows that lifts of
![]() $G$
under
$G$
under
![]() $\unicode[STIX]{x1D70B}$
and lifts of
$\unicode[STIX]{x1D70B}$
and lifts of
![]() $\text{}\underline{M}$
under
$\text{}\underline{M}$
under
![]() $j$
correspond to lifts of the Hodge filtration in the same way. Therefore the functor
$j$
correspond to lifts of the Hodge filtration in the same way. Therefore the functor
![]() $\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.☐
$\unicode[STIX]{x1D6F7}_{R}^{\operatorname{cris}}$
is an equivalence.☐
Theorem 9.8. If
![]() $p\geqslant 3$
, for every perfectoid ring
$p\geqslant 3$
, for every perfectoid ring
![]() $R$
there is an equivalence
$R$
there is an equivalence
between
![]() $p$
-divisible groups and Breuil–Kisin–Fargues modules.
$p$
-divisible groups and Breuil–Kisin–Fargues modules.
Proof. We have a chain of functors
where the last equivalence is (9.6). For
![]() $p\geqslant 3$
the two arrows are equivalences by Propositions 9.7 and 9.3.☐
$p\geqslant 3$
the two arrows are equivalences by Propositions 9.7 and 9.3.☐
The equivalence of Theorem 9.8 is independent of the choice of the generator
![]() $\unicode[STIX]{x1D709}$
of the kernel of
$\unicode[STIX]{x1D709}$
of the kernel of
![]() $A_{\inf }\rightarrow R$
; see Remark 9.6.
$A_{\inf }\rightarrow R$
; see Remark 9.6.
10 Classification of finite group schemes
The equivalence between
![]() $p$
-divisible groups and Breuil–Kisin–Fargues modules over perfectoid rings induces a similar equivalence for finite group schemes. For a scheme
$p$
-divisible groups and Breuil–Kisin–Fargues modules over perfectoid rings induces a similar equivalence for finite group schemes. For a scheme
![]() $X$
let
$X$
let
![]() $\operatorname{pGr}(X)$
be the category of commutative finite locally free
$\operatorname{pGr}(X)$
be the category of commutative finite locally free
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $X$
.
$X$
.
10.1 A category of torsion modules
If
![]() $A$
is a
$A$
is a
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free ring, let
$p$
-torsion free ring, let
![]() $\operatorname{T}(A)$
be the category of finitely presented
$\operatorname{T}(A)$
be the category of finitely presented
![]() $A$
-modules of projective dimension less than or equal to
$A$
-modules of projective dimension less than or equal to
![]() $1$
which are annihilated by a power of
$1$
which are annihilated by a power of
![]() $p$
.
$p$
.
Lemma 10.1. For a homomorphism of
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free rings
$p$
-torsion free rings
![]() $A\rightarrow A^{\prime }$
and
$A\rightarrow A^{\prime }$
and
![]() $M\in \operatorname{T}(A)$
we have
$M\in \operatorname{T}(A)$
we have
![]() $M\otimes _{A}A^{\prime }\in \operatorname{T}(A^{\prime })$
.
$M\otimes _{A}A^{\prime }\in \operatorname{T}(A^{\prime })$
.
Proof. Let
![]() $0\rightarrow Q\xrightarrow[{}]{u}P\rightarrow M\rightarrow 0$
be exact where
$0\rightarrow Q\xrightarrow[{}]{u}P\rightarrow M\rightarrow 0$
be exact where
![]() $P$
and
$P$
and
![]() $Q$
are finite projective
$Q$
are finite projective
![]() $A$
-modules. Let
$A$
-modules. Let
![]() $p^{r}M=0$
. There is a homomorphism
$p^{r}M=0$
. There is a homomorphism
![]() $w:P\rightarrow Q$
such that
$w:P\rightarrow Q$
such that
![]() $uw=p^{r}$
and
$uw=p^{r}$
and
![]() $wu=p^{r}$
. Let
$wu=p^{r}$
. Let
![]() $Q^{\prime }=Q\otimes _{A}A^{\prime }$
etc. Since
$Q^{\prime }=Q\otimes _{A}A^{\prime }$
etc. Since
![]() $Q^{\prime }$
is
$Q^{\prime }$
is
![]() $p$
-torsion free it follows that
$p$
-torsion free it follows that
![]() $0\rightarrow Q^{\prime }\rightarrow P^{\prime }\rightarrow M^{\prime }\rightarrow 0$
is exact, thus
$0\rightarrow Q^{\prime }\rightarrow P^{\prime }\rightarrow M^{\prime }\rightarrow 0$
is exact, thus
![]() $M^{\prime }\in \operatorname{T}(A^{\prime })$
.☐
$M^{\prime }\in \operatorname{T}(A^{\prime })$
.☐
The category
![]() $\operatorname{T}(A)$
can be described in terms of the rings
$\operatorname{T}(A)$
can be described in terms of the rings
![]() $A/p^{n}$
as follows.
$A/p^{n}$
as follows.
Lemma 10.2. Let
![]() $A$
be a
$A$
be a
![]() $p$
-adically complete
$p$
-adically complete
![]() $p$
-torsion free ring,
$p$
-torsion free ring,
![]() $A_{n}=A/p^{n}$
. Let
$A_{n}=A/p^{n}$
. Let
![]() $M$
be a finite
$M$
be a finite
![]() $A$
-module annihilated by
$A$
-module annihilated by
![]() $p^{r}$
. We have
$p^{r}$
. We have
![]() $M\in \operatorname{T}(A)$
if and only if for every exact sequence
$M\in \operatorname{T}(A)$
if and only if for every exact sequence
![]() $0\rightarrow Q_{n}\rightarrow P_{n}\rightarrow M\rightarrow 0$
where
$0\rightarrow Q_{n}\rightarrow P_{n}\rightarrow M\rightarrow 0$
where
![]() $P_{n}$
is a finite projective
$P_{n}$
is a finite projective
![]() $A_{n}$
-module with
$A_{n}$
-module with
![]() $n\geqslant r$
, the
$n\geqslant r$
, the
![]() $A_{n-r}$
-module
$A_{n-r}$
-module
![]() $Q_{n}/p^{n-r}Q_{n}$
is finite projective.
$Q_{n}/p^{n-r}Q_{n}$
is finite projective.
Proof. Assume that
![]() $M\in \operatorname{T}(A)$
and let
$M\in \operatorname{T}(A)$
and let
![]() $0\rightarrow Q_{n}\rightarrow P_{n}\rightarrow M\rightarrow 0$
be as in the lemma. Choose a finite projective
$0\rightarrow Q_{n}\rightarrow P_{n}\rightarrow M\rightarrow 0$
be as in the lemma. Choose a finite projective
![]() $A$
-module
$A$
-module
![]() $P$
with
$P$
with
![]() $P/p^{n}=P_{n}$
and let
$P/p^{n}=P_{n}$
and let
![]() $Q$
be the kernel of
$Q$
be the kernel of
![]() $P\rightarrow M$
. Then
$P\rightarrow M$
. Then
![]() $Q$
is finite projective over
$Q$
is finite projective over
![]() $A$
, and
$A$
, and
![]() $Q_{n}=Q/p^{n}P$
. We have
$Q_{n}=Q/p^{n}P$
. We have
![]() $p^{n}P\subseteq p^{n-r}Q$
, and thus
$p^{n}P\subseteq p^{n-r}Q$
, and thus
![]() $Q_{n}/p^{n-r}=Q/p^{n-r}$
is finite projective over
$Q_{n}/p^{n-r}=Q/p^{n-r}$
is finite projective over
![]() $A_{n-r}$
. Conversely, assume that the condition on
$A_{n-r}$
. Conversely, assume that the condition on
![]() $M$
holds and let
$M$
holds and let
![]() $0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
be exact where
$0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
be exact where
![]() $P$
is finite projective over
$P$
is finite projective over
![]() $A$
. For
$A$
. For
![]() $n\geqslant r$
let
$n\geqslant r$
let
![]() $P_{n}=P/p^{n}$
and
$P_{n}=P/p^{n}$
and
![]() $Q_{n}=Q/p^{n}P$
. Then the
$Q_{n}=Q/p^{n}P$
. Then the
![]() $A_{n}$
-module
$A_{n}$
-module
![]() $\tilde{Q}_{n}=Q_{n+r}/p^{n}Q_{n+r}$
is finite projective, and we have
$\tilde{Q}_{n}=Q_{n+r}/p^{n}Q_{n+r}$
is finite projective, and we have
![]() $\tilde{Q}_{n+1}/p^{n}=\tilde{Q}_{n}$
. It follows that
$\tilde{Q}_{n+1}/p^{n}=\tilde{Q}_{n}$
. It follows that
![]() $Q=\varprojlim Q_{n}=\varprojlim \tilde{Q}_{n}$
is finite projective over
$Q=\varprojlim Q_{n}=\varprojlim \tilde{Q}_{n}$
is finite projective over
![]() $A$
.☐
$A$
.☐
The category
![]() $\operatorname{T}(A)$
satisfies fpqc descent in the following sense.
$\operatorname{T}(A)$
satisfies fpqc descent in the following sense.
Lemma 10.3. Let
![]() $A\rightarrow A^{\prime }$
be a homomorphism of
$A\rightarrow A^{\prime }$
be a homomorphism of
![]() $p$
-adically complete
$p$
-adically complete
![]() $p$
-torsion free rings such that
$p$
-torsion free rings such that
![]() $A/p\rightarrow A^{\prime }/p$
is faithfully flat. Let
$A/p\rightarrow A^{\prime }/p$
is faithfully flat. Let
![]() $A^{\prime \prime }$
and
$A^{\prime \prime }$
and
![]() $A^{\prime \prime \prime }$
be the
$A^{\prime \prime \prime }$
be the
![]() $p$
-adic completions of
$p$
-adic completions of
![]() $A^{\prime }\otimes _{A}A^{\prime }$
and
$A^{\prime }\otimes _{A}A^{\prime }$
and
![]() $A^{\prime }\otimes _{A}A^{\prime }\otimes _{A}A^{\prime }$
. Then
$A^{\prime }\otimes _{A}A^{\prime }\otimes _{A}A^{\prime }$
. Then
![]() $\operatorname{T}(A)$
is equivalent to the category of pairs
$\operatorname{T}(A)$
is equivalent to the category of pairs
![]() $(M^{\prime },\unicode[STIX]{x1D6FC})$
where
$(M^{\prime },\unicode[STIX]{x1D6FC})$
where
![]() $M^{\prime }\in \operatorname{T}(A^{\prime })$
and
$M^{\prime }\in \operatorname{T}(A^{\prime })$
and
![]() $\unicode[STIX]{x1D6FC}:M^{\prime }\otimes _{A}A^{\prime }\cong A^{\prime }\otimes _{A}M^{\prime }$
is an isomorphism that satisfies the usual cocycle condition over
$\unicode[STIX]{x1D6FC}:M^{\prime }\otimes _{A}A^{\prime }\cong A^{\prime }\otimes _{A}M^{\prime }$
is an isomorphism that satisfies the usual cocycle condition over
![]() $A^{\prime \prime \prime }$
.
$A^{\prime \prime \prime }$
.
Proof. Lemma 10.1 gives a functor
![]() $M\mapsto (M^{\prime },\unicode[STIX]{x1D6FC})$
. By the local flatness criterion
$M\mapsto (M^{\prime },\unicode[STIX]{x1D6FC})$
. By the local flatness criterion
![]() $A/p^{n}\rightarrow A^{\prime }/p^{n}$
is faithfully flat for each
$A/p^{n}\rightarrow A^{\prime }/p^{n}$
is faithfully flat for each
![]() $n$
. It follows that the functor
$n$
. It follows that the functor
![]() $M\mapsto (M^{\prime },\unicode[STIX]{x1D6FC})$
is fully faithful, moreover each
$M\mapsto (M^{\prime },\unicode[STIX]{x1D6FC})$
is fully faithful, moreover each
![]() $(M^{\prime },\unicode[STIX]{x1D6FC})$
with
$(M^{\prime },\unicode[STIX]{x1D6FC})$
with
![]() $M^{\prime }\in \operatorname{T}(A)$
comes from an
$M^{\prime }\in \operatorname{T}(A)$
comes from an
![]() $A$
-module
$A$
-module
![]() $M$
annihilated by a power of
$M$
annihilated by a power of
![]() $p$
, and it remains to show that
$p$
, and it remains to show that
![]() $M\in \operatorname{T}(A)$
. This is an easy consequence of Lemma 10.2.☐
$M\in \operatorname{T}(A)$
. This is an easy consequence of Lemma 10.2.☐
The category
![]() $\operatorname{T}(A)$
preserves projective limits of nilpotent immersions as follows.
$\operatorname{T}(A)$
preserves projective limits of nilpotent immersions as follows.
Lemma 10.4. Let
![]() $A=\mathop{\varprojlim }\nolimits_{n}\,A^{n}$
for a surjective system
$A=\mathop{\varprojlim }\nolimits_{n}\,A^{n}$
for a surjective system
![]() $A^{1}\leftarrow A^{2}\leftarrow \cdots \,$
of
$A^{1}\leftarrow A^{2}\leftarrow \cdots \,$
of
![]() $p$
-adically complete
$p$
-adically complete
![]() $p$
-torsion free rings such that
$p$
-torsion free rings such that
![]() $\operatorname{Ker}(A^{n+1}\rightarrow A^{n})$
is nilpotent for each
$\operatorname{Ker}(A^{n+1}\rightarrow A^{n})$
is nilpotent for each
![]() $n$
. Then the obvious functor
$n$
. Then the obvious functor
![]() $\unicode[STIX]{x1D70C}:\operatorname{T}(A)\rightarrow \mathop{\varprojlim }\nolimits_{n}\,\operatorname{T}(A^{n})$
is an equivalence.
$\unicode[STIX]{x1D70C}:\operatorname{T}(A)\rightarrow \mathop{\varprojlim }\nolimits_{n}\,\operatorname{T}(A^{n})$
is an equivalence.
Proof. For
![]() $M\in \operatorname{T}(A)$
let
$M\in \operatorname{T}(A)$
let
![]() $0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
be exact where
$0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
be exact where
![]() $P$
and
$P$
and
![]() $Q$
are finite projective over
$Q$
are finite projective over
![]() $A$
. By the proof of Lemma 10.1 the base change under
$A$
. By the proof of Lemma 10.1 the base change under
![]() $A\rightarrow A^{n}$
gives an exact sequence
$A\rightarrow A^{n}$
gives an exact sequence
![]() $0\rightarrow Q^{n}\rightarrow P^{n}\rightarrow M^{n}\rightarrow 0$
. Since
$0\rightarrow Q^{n}\rightarrow P^{n}\rightarrow M^{n}\rightarrow 0$
. Since
![]() $P=\mathop{\varprojlim }\nolimits_{n}\,P^{n}$
and
$P=\mathop{\varprojlim }\nolimits_{n}\,P^{n}$
and
![]() $Q=\mathop{\varprojlim }\nolimits_{n}\,Q^{n}$
it follows that
$Q=\mathop{\varprojlim }\nolimits_{n}\,Q^{n}$
it follows that
![]() $M=\mathop{\varprojlim }\nolimits_{n}\,M^{n}$
. In particular the functor
$M=\mathop{\varprojlim }\nolimits_{n}\,M^{n}$
. In particular the functor
![]() $\unicode[STIX]{x1D70C}$
is fully faithful.
$\unicode[STIX]{x1D70C}$
is fully faithful.
Conversely, let
![]() $M^{n}\in \operatorname{T}(A^{n})$
with isomorphisms
$M^{n}\in \operatorname{T}(A^{n})$
with isomorphisms
![]() $M^{n+1}\otimes _{A^{n+1}}A^{n}\cong M^{n}$
be given. Let
$M^{n+1}\otimes _{A^{n+1}}A^{n}\cong M^{n}$
be given. Let
![]() $M=\mathop{\varprojlim }\nolimits_{n}\,M^{n}$
and choose a homomorphism
$M=\mathop{\varprojlim }\nolimits_{n}\,M^{n}$
and choose a homomorphism
![]() $P\rightarrow M$
where
$P\rightarrow M$
where
![]() $P$
is finite projective over
$P$
is finite projective over
![]() $A$
such that
$A$
such that
![]() $P^{1}\rightarrow M^{1}$
is surjective,
$P^{1}\rightarrow M^{1}$
is surjective,
![]() $P^{n}=P\otimes _{A}A^{n}$
. Then
$P^{n}=P\otimes _{A}A^{n}$
. Then
![]() $P^{n}\rightarrow M^{n}$
is surjective by Nakayama’s lemma. The module
$P^{n}\rightarrow M^{n}$
is surjective by Nakayama’s lemma. The module
![]() $Q^{n}=\operatorname{Ker}(P^{n}\rightarrow M^{n})$
is finite projective over
$Q^{n}=\operatorname{Ker}(P^{n}\rightarrow M^{n})$
is finite projective over
![]() $A^{n}$
, and
$A^{n}$
, and
![]() $Q^{n}=Q^{n+1}\otimes _{A^{n+1}}A^{n}$
by the proof of Lemma 10.1. It follows that
$Q^{n}=Q^{n+1}\otimes _{A^{n+1}}A^{n}$
by the proof of Lemma 10.1. It follows that
![]() $Q=\mathop{\varprojlim }\nolimits_{n}\,Q^{n}$
is finite projective over
$Q=\mathop{\varprojlim }\nolimits_{n}\,Q^{n}$
is finite projective over
![]() $A$
, and
$A$
, and
![]() $0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
is exact, thus
$0\rightarrow Q\rightarrow P\rightarrow M\rightarrow 0$
is exact, thus
![]() $M\in \operatorname{T}(A)$
. The base change under
$M\in \operatorname{T}(A)$
. The base change under
![]() $A\rightarrow A^{n}$
of the last sequence remains exact, so
$A\rightarrow A^{n}$
of the last sequence remains exact, so
![]() $M^{n}=M\otimes _{A}A^{n}$
.☐
$M^{n}=M\otimes _{A}A^{n}$
.☐
10.2 Torsion Breuil–Kisin–Fargues modules
Let
![]() $R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
$R=W(S)/\unicode[STIX]{x1D709}$
be a perfectoid ring where
![]() $S$
is perfect and
$S$
is perfect and
![]() $\unicode[STIX]{x1D709}$
is distinguished. We write again
$\unicode[STIX]{x1D709}$
is distinguished. We write again
![]() $A_{\inf }=A_{\inf }(R)=W(S)$
, and
$A_{\inf }=A_{\inf }(R)=W(S)$
, and
![]() $\operatorname{Fil}A_{\inf }=\operatorname{Ker}(A_{\inf }\rightarrow R)=\unicode[STIX]{x1D709}A_{\inf }$
.
$\operatorname{Fil}A_{\inf }=\operatorname{Ker}(A_{\inf }\rightarrow R)=\unicode[STIX]{x1D709}A_{\inf }$
.
Definition 10.5. A torsion Breuil–Kisin–Fargues module for
![]() $R$
is a triple
$R$
is a triple
![]() $(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
$(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
![]() $\mathfrak{M}\in \operatorname{T}(A_{\inf })$
and where
$\mathfrak{M}\in \operatorname{T}(A_{\inf })$
and where
are linear maps such that
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D713}\circ (1\otimes \unicode[STIX]{x1D711})$
are the multiplication maps. We denote by
$\unicode[STIX]{x1D713}\circ (1\otimes \unicode[STIX]{x1D711})$
are the multiplication maps. We denote by
![]() $\operatorname{BK}_{\operatorname{tor}}(R)$
the category of torsion Breuil–Kisin–Fargues modules over
$\operatorname{BK}_{\operatorname{tor}}(R)$
the category of torsion Breuil–Kisin–Fargues modules over
![]() $R$
.
$R$
.
Remark 10.6. For a homomorphism of perfectoid rings
![]() $R\rightarrow R^{\prime }$
there is an obvious base change functor
$R\rightarrow R^{\prime }$
there is an obvious base change functor
![]() $\operatorname{BK}_{\operatorname{tor}}(R)\rightarrow \operatorname{BK}_{\operatorname{tor}}(R^{\prime })$
; see Lemma 10.1.
$\operatorname{BK}_{\operatorname{tor}}(R)\rightarrow \operatorname{BK}_{\operatorname{tor}}(R^{\prime })$
; see Lemma 10.1.
Remark 10.7. If
![]() $R$
is
$R$
is
![]() $p$
-torsion free,
$p$
-torsion free,
![]() $(p,\unicode[STIX]{x1D709})$
is a regular sequence in
$(p,\unicode[STIX]{x1D709})$
is a regular sequence in
![]() $A_{\inf }$
, thus
$A_{\inf }$
, thus
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $\mathfrak{M}$
-regular for each
$\mathfrak{M}$
-regular for each
![]() $\mathfrak{M}\in \operatorname{T}(A_{\inf })$
, and torsion Breuil–Kisin–Fargues are equivalent to pairs
$\mathfrak{M}\in \operatorname{T}(A_{\inf })$
, and torsion Breuil–Kisin–Fargues are equivalent to pairs
![]() $(\mathfrak{M},\unicode[STIX]{x1D711})$
where the cokernel of
$(\mathfrak{M},\unicode[STIX]{x1D711})$
where the cokernel of
![]() $\unicode[STIX]{x1D711}$
is annihilated by
$\unicode[STIX]{x1D711}$
is annihilated by
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Remark 10.8. For a locally free Breuil–Kisin–Fargues module
![]() $\text{}\underline{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711})$
as in Definition 9.4 there is a unique
$\text{}\underline{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711})$
as in Definition 9.4 there is a unique
![]() $\unicode[STIX]{x1D713}$
as in (10.1). In the following we will view
$\unicode[STIX]{x1D713}$
as in (10.1). In the following we will view
![]() $\text{}\underline{\mathfrak{M}}$
as a triple
$\text{}\underline{\mathfrak{M}}$
as a triple
![]() $(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
. A homomorphism
$(\mathfrak{M},\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
. A homomorphism
![]() $u:\text{}\underline{\mathfrak{M}}\rightarrow \text{}\underline{\mathfrak{M}}^{\prime }$
in
$u:\text{}\underline{\mathfrak{M}}\rightarrow \text{}\underline{\mathfrak{M}}^{\prime }$
in
![]() $\operatorname{BK}(R)$
is called an isogeny if it becomes bijective over
$\operatorname{BK}(R)$
is called an isogeny if it becomes bijective over
![]() $A[1/p]$
. Then
$A[1/p]$
. Then
![]() $u$
is injective, and its cokernel lies in
$u$
is injective, and its cokernel lies in
![]() $\operatorname{BK}_{\operatorname{tor}}(R)$
.
$\operatorname{BK}_{\operatorname{tor}}(R)$
.
Étale descent
By an abuse of notation, let
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
denote the site of all affine étale
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
denote the site of all affine étale
![]() $R/p$
-schemes, with surjective families as coverings. For an étale
$R/p$
-schemes, with surjective families as coverings. For an étale
![]() $R/p$
-algebra
$R/p$
-algebra
![]() $B^{\prime }$
there is a unique homomorphism of perfectoid rings
$B^{\prime }$
there is a unique homomorphism of perfectoid rings
![]() $R\rightarrow R^{\prime }$
with
$R\rightarrow R^{\prime }$
with
![]() $R^{\prime }/p=B^{\prime }$
; see Lemma 8.11. We define presheaves of rings
$R^{\prime }/p=B^{\prime }$
; see Lemma 8.11. We define presheaves of rings
![]() ${\mathcal{A}}_{\inf }$
and
${\mathcal{A}}_{\inf }$
and
![]() ${\mathcal{R}}$
on
${\mathcal{R}}$
on
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
by
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
by
For varying étale
![]() $R/p$
-algebras
$R/p$
-algebras
![]() $B^{\prime }$
, the categories
$B^{\prime }$
, the categories
![]() $\operatorname{LF}(R^{\prime })$
of locally free
$\operatorname{LF}(R^{\prime })$
of locally free
![]() $R^{\prime }$
-modules form a fibered category
$R^{\prime }$
-modules form a fibered category
![]() $\operatorname{LF}({\mathcal{R}})$
over
$\operatorname{LF}({\mathcal{R}})$
over
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
. Similarly we have fibered categories
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
. Similarly we have fibered categories
![]() $\operatorname{LF}({\mathcal{A}}_{\inf })$
,
$\operatorname{LF}({\mathcal{A}}_{\inf })$
,
![]() $\operatorname{T}({\mathcal{A}}_{\inf })$
,
$\operatorname{T}({\mathcal{A}}_{\inf })$
,
![]() $\operatorname{BK}({\mathcal{R}})$
,
$\operatorname{BK}({\mathcal{R}})$
,
![]() $\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
,
$\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
,
![]() $\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
, and
$\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
, and
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
over
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
over
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
; see Lemma 10.1 for
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
; see Lemma 10.1 for
![]() $\operatorname{T}({\mathcal{A}}_{\inf })$
.
$\operatorname{T}({\mathcal{A}}_{\inf })$
.
Lemma 10.9. The presheaves of rings
![]() ${\mathcal{A}}_{\inf }$
and
${\mathcal{A}}_{\inf }$
and
![]() ${\mathcal{R}}$
on
${\mathcal{R}}$
on
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
are sheaves. The fibered categories
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
are sheaves. The fibered categories
![]() $\operatorname{LF}({\mathcal{R}})$
,
$\operatorname{LF}({\mathcal{R}})$
,
![]() $\operatorname{LF}({\mathcal{A}}_{\inf })$
,
$\operatorname{LF}({\mathcal{A}}_{\inf })$
,
![]() $\operatorname{T}({\mathcal{A}}_{\inf })$
,
$\operatorname{T}({\mathcal{A}}_{\inf })$
,
![]() $\operatorname{BK}({\mathcal{R}})$
,
$\operatorname{BK}({\mathcal{R}})$
,
![]() $\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
,
$\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
,
![]() $\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
, and
$\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
, and
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
over
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
over
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
are stacks.
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
are stacks.
Proof. Let
![]() $x=[\unicode[STIX]{x1D709}_{0}]\in A:=A_{\inf }$
and let
$x=[\unicode[STIX]{x1D709}_{0}]\in A:=A_{\inf }$
and let
![]() $I=(x,p)$
as an ideal of
$I=(x,p)$
as an ideal of
![]() $A$
. Then
$A$
. Then
![]() $A$
is
$A$
is
![]() $I$
-adically complete. Let
$I$
-adically complete. Let
![]() $B=R/p$
. We fix a faithfully flat étale homomorphism
$B=R/p$
. We fix a faithfully flat étale homomorphism
![]() $B\rightarrow B^{\prime }$
and write
$B\rightarrow B^{\prime }$
and write
![]() $A^{\prime }=A_{\inf }(B^{\prime })$
and
$A^{\prime }=A_{\inf }(B^{\prime })$
and
![]() $A^{\prime \prime }=A_{\inf }(B^{\prime }\otimes _{B}B^{\prime })$
and
$A^{\prime \prime }=A_{\inf }(B^{\prime }\otimes _{B}B^{\prime })$
and
![]() $A^{\prime \prime \prime }=A_{\inf }(B^{\prime }\otimes _{B}B^{\prime }\otimes _{B}B^{\prime })$
. The reduction modulo
$A^{\prime \prime \prime }=A_{\inf }(B^{\prime }\otimes _{B}B^{\prime }\otimes _{B}B^{\prime })$
. The reduction modulo
![]() $I^{n}$
of
$I^{n}$
of
![]() $A\rightarrow A^{\prime }$
is étale, and the reductions modulo
$A\rightarrow A^{\prime }$
is étale, and the reductions modulo
![]() $I^{n}$
of
$I^{n}$
of
![]() $A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime \prime }$
and of
$A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime \prime }$
and of
![]() $A^{\prime }\otimes _{A}A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime \prime \prime }$
are isomorphisms. Since the category
$A^{\prime }\otimes _{A}A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime \prime \prime }$
are isomorphisms. Since the category
![]() $\operatorname{LF}(A)$
is equivalent to
$\operatorname{LF}(A)$
is equivalent to
![]() $\mathop{\varprojlim }\nolimits_{n}\,\operatorname{LF}(A/I^{n})$
, étale descent of locally free modules shows that
$\mathop{\varprojlim }\nolimits_{n}\,\operatorname{LF}(A/I^{n})$
, étale descent of locally free modules shows that
![]() ${\mathcal{A}}_{\inf }$
is a sheaf and
${\mathcal{A}}_{\inf }$
is a sheaf and
![]() $\operatorname{LF}({\mathcal{A}}_{\inf })$
and
$\operatorname{LF}({\mathcal{A}}_{\inf })$
and
![]() $\operatorname{BK}({\mathcal{R}})$
are stacks. A similar argument shows that
$\operatorname{BK}({\mathcal{R}})$
are stacks. A similar argument shows that
![]() ${\mathcal{R}}$
is a sheaf and that
${\mathcal{R}}$
is a sheaf and that
![]() $\operatorname{LF}({\mathcal{R}})$
,
$\operatorname{LF}({\mathcal{R}})$
,
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
, and
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
, and
![]() $\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
are stacks.
$\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})$
are stacks.
We claim that
![]() $A$
is
$A$
is
![]() $x$
-adically complete and that the quotients
$x$
-adically complete and that the quotients
![]() $A/x^{n}$
are
$A/x^{n}$
are
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free. Indeed, this is clear when
$p$
-torsion free. Indeed, this is clear when
![]() $R$
is perfect and thus
$R$
is perfect and thus
![]() $x=0$
, or when
$x=0$
, or when
![]() $R$
is torsion free; in that case
$R$
is torsion free; in that case
![]() $(x,p)$
is a regular sequence in
$(x,p)$
is a regular sequence in
![]() $A$
. In general, we use the exact sequence (8.5) where
$A$
. In general, we use the exact sequence (8.5) where
![]() $A=W(S)$
. Let
$A=W(S)$
. Let
![]() $A_{i}=W(S_{i})$
. Since
$A_{i}=W(S_{i})$
. Since
![]() $x$
is zero in
$x$
is zero in
![]() $A_{2}$
and in
$A_{2}$
and in
![]() $A_{12}$
we get an exact sequence
$A_{12}$
we get an exact sequence
![]() $0\rightarrow A/x^{n}\rightarrow A_{1}/x^{n}\oplus A_{2}\rightarrow A_{12}\rightarrow 0$
. Here all rings except possibly
$0\rightarrow A/x^{n}\rightarrow A_{1}/x^{n}\oplus A_{2}\rightarrow A_{12}\rightarrow 0$
. Here all rings except possibly
![]() $A/x^{n}$
are
$A/x^{n}$
are
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion free, thus the same holds for
$p$
-torsion free, thus the same holds for
![]() $A/x^{n}$
. The limit over
$A/x^{n}$
. The limit over
![]() $n$
shows that
$n$
shows that
![]() $A$
is
$A$
is
![]() $x$
-adically complete. The claim is proved.
$x$
-adically complete. The claim is proved.
Lemma 10.4 implies that
![]() $\operatorname{T}(A)$
is equivalent to
$\operatorname{T}(A)$
is equivalent to
![]() $\mathop{\varprojlim }\nolimits_{n}\operatorname{T}(A/x^{n})$
, and similarly for
$\mathop{\varprojlim }\nolimits_{n}\operatorname{T}(A/x^{n})$
, and similarly for
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $A^{\prime \prime }$
and
$A^{\prime \prime }$
and
![]() $A^{\prime \prime \prime }$
. The homomorphism
$A^{\prime \prime \prime }$
. The homomorphism
![]() $A/(x^{n},p)\rightarrow A^{\prime }/(x^{n},p)$
is faithfully flat étale, hence Lemma 10.3 implies that
$A/(x^{n},p)\rightarrow A^{\prime }/(x^{n},p)$
is faithfully flat étale, hence Lemma 10.3 implies that
![]() $\operatorname{T}(A/x^{n})$
is equivalent to the category of modules in
$\operatorname{T}(A/x^{n})$
is equivalent to the category of modules in
![]() $\operatorname{T}(A^{\prime }/x^{n})$
with a descent datum in
$\operatorname{T}(A^{\prime }/x^{n})$
with a descent datum in
![]() $\operatorname{T}(A^{\prime \prime }/x^{n})$
. This proves that
$\operatorname{T}(A^{\prime \prime }/x^{n})$
. This proves that
![]() $\operatorname{T}({\mathcal{A}})$
and
$\operatorname{T}({\mathcal{A}})$
and
![]() $\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
are stacks.☐
$\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
are stacks.☐
Let us now continue the discussion of Remark 10.8.
Lemma 10.10. For
![]() $\text{}\underline{\mathfrak{M}}\in \operatorname{BK}_{\operatorname{tor}}(R)$
, Zariski locally in
$\text{}\underline{\mathfrak{M}}\in \operatorname{BK}_{\operatorname{tor}}(R)$
, Zariski locally in
![]() $\operatorname{Spec}(R/p)$
there is an isogeny of locally free Breuil–Kisin–Fargues modules with cokernel
$\operatorname{Spec}(R/p)$
there is an isogeny of locally free Breuil–Kisin–Fargues modules with cokernel
![]() $\text{}\underline{\mathfrak{M}}$
.
$\text{}\underline{\mathfrak{M}}$
.
Proof. This is similar to [Reference KisinKis06, Lemma (2.3.4)]. We have to find locally in
![]() $\operatorname{Spec}(R/p)$
a surjective map
$\operatorname{Spec}(R/p)$
a surjective map
![]() $\text{}\underline{\mathfrak{N}}\rightarrow \text{}\underline{\mathfrak{M}}$
where
$\text{}\underline{\mathfrak{N}}\rightarrow \text{}\underline{\mathfrak{M}}$
where
![]() $\text{}\underline{\mathfrak{N}}$
is a locally free Breuil–Kisin–Fargues module. One can choose finite free
$\text{}\underline{\mathfrak{N}}$
is a locally free Breuil–Kisin–Fargues module. One can choose finite free
![]() $A$
-modules
$A$
-modules
![]() $Q$
and
$Q$
and
![]() $\mathfrak{N}$
of equal rank and a commutative diagram with surjective vertical maps
$\mathfrak{N}$
of equal rank and a commutative diagram with surjective vertical maps

such that
![]() $f\circ g$
and
$f\circ g$
and
![]() $g\circ (1\otimes f)$
are the multiplication maps. Assume that
$g\circ (1\otimes f)$
are the multiplication maps. Assume that
![]() $u:\mathfrak{N}^{\unicode[STIX]{x1D70E}}\rightarrow Q$
is an isomorphism with
$u:\mathfrak{N}^{\unicode[STIX]{x1D70E}}\rightarrow Q$
is an isomorphism with
![]() $\unicode[STIX]{x1D70C}u=\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D70B})$
. Then
$\unicode[STIX]{x1D70C}u=\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D70B})$
. Then
![]() $\text{}\underline{\mathfrak{N}}=(\mathfrak{N},fu,u^{-1}g)$
solves the problem. It is easy to see that
$\text{}\underline{\mathfrak{N}}=(\mathfrak{N},fu,u^{-1}g)$
solves the problem. It is easy to see that
![]() $u$
exists locally in
$u$
exists locally in
![]() $\operatorname{Spec}A$
and therefore also locally in
$\operatorname{Spec}A$
and therefore also locally in
![]() $\operatorname{Spec}(R/p)$
.☐
$\operatorname{Spec}(R/p)$
.☐
Lemma 10.11. For
![]() $H\in \operatorname{pGr}(\operatorname{Spec}R)$
, Zariski locally in
$H\in \operatorname{pGr}(\operatorname{Spec}R)$
, Zariski locally in
![]() $\operatorname{Spec}(R/p)$
there is an isogeny of
$\operatorname{Spec}(R/p)$
there is an isogeny of
![]() $p$
-divisible groups with kernel
$p$
-divisible groups with kernel
![]() $H$
.
$H$
.
Proof. We have to find locally in
![]() $\operatorname{Spec}(R/p)$
an embedding of
$\operatorname{Spec}(R/p)$
an embedding of
![]() $H$
into a
$H$
into a
![]() $p$
-divisible group. By [Reference Berthelot, Breen and MessingBBM82, Theorem 3.1.1] such an embedding exists Zariski locally in
$p$
-divisible group. By [Reference Berthelot, Breen and MessingBBM82, Theorem 3.1.1] such an embedding exists Zariski locally in
![]() $\operatorname{Spec}(R)$
, and therefore also Zariski locally in
$\operatorname{Spec}(R)$
, and therefore also Zariski locally in
![]() $\operatorname{Spec}(R/p)$
.☐
$\operatorname{Spec}(R/p)$
.☐
Theorem 10.12. If
![]() $p\geqslant 3$
, for every perfectoid ring
$p\geqslant 3$
, for every perfectoid ring
![]() $R$
there is an equivalence
$R$
there is an equivalence
Proof. This follows from Theorem 9.8 as in [Reference KisinKis06, Theorem (2.3.5)]. More precisely, let
![]() $\operatorname{pGr}(\operatorname{Spec}R)^{\circ }$
be the category of all
$\operatorname{pGr}(\operatorname{Spec}R)^{\circ }$
be the category of all
![]() $H\in \operatorname{pGr}(\operatorname{Spec}R)$
with are the kernel of an isogeny in
$H\in \operatorname{pGr}(\operatorname{Spec}R)$
with are the kernel of an isogeny in
![]() $\operatorname{BT}(\operatorname{Spec}R)$
, and let
$\operatorname{BT}(\operatorname{Spec}R)$
, and let
![]() $\operatorname{BK}_{\operatorname{tor}}(R)^{\circ }$
be the category of all
$\operatorname{BK}_{\operatorname{tor}}(R)^{\circ }$
be the category of all
![]() $\text{}\underline{\mathfrak{M}}\in \operatorname{BK}_{\operatorname{tor}}(R)$
which are the cokernel of an isogeny in
$\text{}\underline{\mathfrak{M}}\in \operatorname{BK}_{\operatorname{tor}}(R)$
which are the cokernel of an isogeny in
![]() $\operatorname{BK}(R)$
. The corresponding fibered categories
$\operatorname{BK}(R)$
. The corresponding fibered categories
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})^{\circ }$
and
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})^{\circ }$
and
![]() $\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})^{\circ }$
over
$\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})^{\circ }$
over
![]() $(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
have associated stacks
$(\operatorname{Spec}R/p)_{\acute{\text{e}}\text{t}}$
have associated stacks
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
and
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})$
and
![]() $\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
by Lemmas 10.10 and 10.11. Moreover
$\operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
by Lemmas 10.10 and 10.11. Moreover
![]() $\operatorname{pGr}(\operatorname{Spec}R)^{\circ }$
(respectively
$\operatorname{pGr}(\operatorname{Spec}R)^{\circ }$
(respectively
![]() $\operatorname{BK}_{\operatorname{tor}}(R)^{\circ }$
) is equivalent to the full subcategory of the derived category of the exact category
$\operatorname{BK}_{\operatorname{tor}}(R)^{\circ }$
) is equivalent to the full subcategory of the derived category of the exact category
![]() $\operatorname{BT}(\operatorname{Spec}R)$
(respectively
$\operatorname{BT}(\operatorname{Spec}R)$
(respectively
![]() $\operatorname{BK}(R)$
) whose objects are isogenies
$\operatorname{BK}(R)$
) whose objects are isogenies
![]() $G^{0}\rightarrow G^{1}$
(respectively isogenies
$G^{0}\rightarrow G^{1}$
(respectively isogenies
![]() $\text{}\underline{\mathfrak{M}}_{1}\rightarrow \text{}\underline{\mathfrak{M}}_{0}$
). Thus the equivalence of fibered categories
$\text{}\underline{\mathfrak{M}}_{1}\rightarrow \text{}\underline{\mathfrak{M}}_{0}$
). Thus the equivalence of fibered categories
![]() $\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})\cong \operatorname{BK}({\mathcal{R}})$
given by Theorem 9.8 induces an equivalence
$\operatorname{BT}(\operatorname{Spec}{\mathcal{R}})\cong \operatorname{BK}({\mathcal{R}})$
given by Theorem 9.8 induces an equivalence
![]() $\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})\cong \operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
. ☐
$\operatorname{pGr}(\operatorname{Spec}{\mathcal{R}})\cong \operatorname{BK}_{\operatorname{tor}}({\mathcal{R}})$
. ☐
10.3 Torsion Dieudonné modules
For completeness we record a similar classification of finite group schemes in the context of §§ 3 and 5.
Let
![]() $R$
be an
$R$
be an
![]() $\mathbb{F}_{p}$
-algebra and let
$\mathbb{F}_{p}$
-algebra and let
![]() $(A,\unicode[STIX]{x1D70E})$
be a lift of
$(A,\unicode[STIX]{x1D70E})$
be a lift of
![]() $R$
as in § 3. A torsion Dieudonné module over
$R$
as in § 3. A torsion Dieudonné module over
![]() $A$
is a triple
$A$
is a triple
![]() $\text{}\underline{M}=(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
$\text{}\underline{M}=(M,\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
where
![]() $M\in \operatorname{T}(A)$
and
$M\in \operatorname{T}(A)$
and
![]() $\unicode[STIX]{x1D711}:M^{\unicode[STIX]{x1D70E}}\rightarrow M$
and
$\unicode[STIX]{x1D711}:M^{\unicode[STIX]{x1D70E}}\rightarrow M$
and
![]() $\unicode[STIX]{x1D713}:M\rightarrow M^{\unicode[STIX]{x1D70E}}$
are linear maps with
$\unicode[STIX]{x1D713}:M\rightarrow M^{\unicode[STIX]{x1D70E}}$
are linear maps with
![]() $\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}=p$
and
$\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}=p$
and
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}=p$
. We write
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}=p$
. We write
![]() $\operatorname{DM}_{\operatorname{tor}}(A)$
for the category of torsion Dieudonné modules over
$\operatorname{DM}_{\operatorname{tor}}(A)$
for the category of torsion Dieudonné modules over
![]() $A$
.
$A$
.
An étale ring homomorphism
![]() $R\rightarrow R^{\prime }$
extends to a unique homomorphism of lifts
$R\rightarrow R^{\prime }$
extends to a unique homomorphism of lifts
![]() $(A,\unicode[STIX]{x1D70E})\rightarrow (A^{\prime },\unicode[STIX]{x1D70E})$
; each
$(A,\unicode[STIX]{x1D70E})\rightarrow (A^{\prime },\unicode[STIX]{x1D70E})$
; each
![]() $A/p^{r}\rightarrow A^{\prime }/p^{r}$
is the unique étale homomorphism that lifts
$A/p^{r}\rightarrow A^{\prime }/p^{r}$
is the unique étale homomorphism that lifts
![]() $R\rightarrow R^{\prime }$
.
$R\rightarrow R^{\prime }$
.
Lemma 10.13. The functors
![]() $\unicode[STIX]{x1D6F7}_{A^{\prime }}:\operatorname{BT}(\operatorname{Spec}R^{\prime })\rightarrow \operatorname{DM}(A^{\prime })$
of (3.6) for all étale
$\unicode[STIX]{x1D6F7}_{A^{\prime }}:\operatorname{BT}(\operatorname{Spec}R^{\prime })\rightarrow \operatorname{DM}(A^{\prime })$
of (3.6) for all étale
![]() $R$
-algebras
$R$
-algebras
![]() $R^{\prime }$
induce functors
$R^{\prime }$
induce functors
If all functors
![]() $\unicode[STIX]{x1D6F7}_{A^{\prime }}$
are equivalences, then so are the functors
$\unicode[STIX]{x1D6F7}_{A^{\prime }}$
are equivalences, then so are the functors
![]() $\unicode[STIX]{x1D6F7}_{A^{\prime }}^{\operatorname{tor}}$
.
$\unicode[STIX]{x1D6F7}_{A^{\prime }}^{\operatorname{tor}}$
.
Proof. The functor
![]() $\unicode[STIX]{x1D6F7}_{A}$
induces a functor from the category of all
$\unicode[STIX]{x1D6F7}_{A}$
induces a functor from the category of all
![]() $H\in \operatorname{pGr}(\operatorname{Spec}R)$
which are the kernel of an isogeny of
$H\in \operatorname{pGr}(\operatorname{Spec}R)$
which are the kernel of an isogeny of
![]() $p$
-divisible groups to the category of all
$p$
-divisible groups to the category of all
![]() $\mathfrak{M}\in \operatorname{DM}_{\operatorname{tor}}(A)$
which are the cokernel of an isogeny of locally free Dieudonné modules. For given
$\mathfrak{M}\in \operatorname{DM}_{\operatorname{tor}}(A)$
which are the cokernel of an isogeny of locally free Dieudonné modules. For given
![]() $H$
or
$H$
or
![]() $\mathfrak{M}$
, such isogenies exist locally in
$\mathfrak{M}$
, such isogenies exist locally in
![]() $\operatorname{Spec}R$
. The lemma follows by descent; see Lemma 10.3.☐
$\operatorname{Spec}R$
. The lemma follows by descent; see Lemma 10.3.☐
Corollary 10.14. For a semiperfect ring
![]() $R$
with a lift
$R$
with a lift
![]() $(A,\unicode[STIX]{x1D70E})$
as in Theorem 5.7, the functor
$(A,\unicode[STIX]{x1D70E})$
as in Theorem 5.7, the functor
![]() $\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}:\operatorname{pGr}(\operatorname{Spec}R)\rightarrow \operatorname{DM}_{\operatorname{tor}}(\text{}\underline{A})$
is an equivalence.
$\unicode[STIX]{x1D6F7}_{A}^{\operatorname{tor}}:\operatorname{pGr}(\operatorname{Spec}R)\rightarrow \operatorname{DM}_{\operatorname{tor}}(\text{}\underline{A})$
is an equivalence.
Proof. For each étale
![]() $R$
-algebra
$R$
-algebra
![]() $R^{\prime }$
with associated lift
$R^{\prime }$
with associated lift
![]() $A^{\prime }$
the resulting divided powers on the kernel of
$A^{\prime }$
the resulting divided powers on the kernel of
![]() $\unicode[STIX]{x1D719}:R^{\prime }\rightarrow R^{\prime }$
are induced from the divided powers on the kernel of
$\unicode[STIX]{x1D719}:R^{\prime }\rightarrow R^{\prime }$
are induced from the divided powers on the kernel of
![]() $\unicode[STIX]{x1D719}:R\rightarrow R$
and are thus pointwise nilpotent. Hence
$\unicode[STIX]{x1D719}:R\rightarrow R$
and are thus pointwise nilpotent. Hence
![]() $\unicode[STIX]{x1D6F7}_{A^{\prime }}$
is an equivalence by Theorem 5.7, and Lemma 10.13 applies. ☐
$\unicode[STIX]{x1D6F7}_{A^{\prime }}$
is an equivalence by Theorem 5.7, and Lemma 10.13 applies. ☐
Acknowledgements
The author thanks Peter Scholze and Thomas Zink for fruitful discussions and the referee for helpful comments.