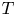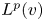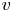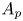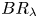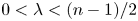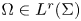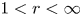1. Introduction
Let
be the Fourier transform of $f \in L^{1}( \mathbb {R}^{n} )$![]() and let $a_{+} = \max \{a,\,0\}$
and let $a_{+} = \max \{a,\,0\}$![]() denote the positive part of $a \in \mathbb {R}$
denote the positive part of $a \in \mathbb {R}$![]() . Given $\lambda > 0$
. Given $\lambda > 0$![]() , the Bochner–Riesz operator $BR_\lambda$
, the Bochner–Riesz operator $BR_\lambda$![]() is defined by
is defined by
These operators were first introduced by Bochner in [Reference Bochner6] and, since then, they have been widely studied (see [Reference Bourgain and Guth7–Reference Carro, Duoandikoetxea and Lorente9, Reference Christ14, Reference Grafakos22, Reference Kesler and Lacey27, Reference Tao40, Reference Vargas42]). The case $\lambda = 0$![]() corresponds to the so-called disc multiplier, which is unbounded on $L^{p}(\mathbb {R}^{n})$
corresponds to the so-called disc multiplier, which is unbounded on $L^{p}(\mathbb {R}^{n})$![]() if $n \geq 2$
if $n \geq 2$![]() and $p \ne 2$
and $p \ne 2$![]() (see [Reference Fefferman20]).
(see [Reference Fefferman20]).
When $\lambda > {(n - 1)}/2$![]() , it is well known that $BR_\lambda$
, it is well known that $BR_\lambda$![]() is controlled by the Hardy–Littlewood maximal operator $M$
is controlled by the Hardy–Littlewood maximal operator $M$![]() , defined for every locally integrable function $f$
, defined for every locally integrable function $f$![]() (i.e. $f \in L^{1}_{\text {loc}}(\mathbb {R}^{n})$
(i.e. $f \in L^{1}_{\text {loc}}(\mathbb {R}^{n})$![]() ) by
) by
where the supremum is taken overall cubes $Q \subseteq \mathbb {R}^{n}$![]() that contains $x \in \mathbb {R}^{n}$
that contains $x \in \mathbb {R}^{n}$![]() . As a consequence, all weighted inequalities for $M$
. As a consequence, all weighted inequalities for $M$![]() are also satisfied by $BR_\lambda$
are also satisfied by $BR_\lambda$![]() .
.
The value $\lambda = {n - 1}/{2}$![]() is called the critical index. In this case, Shi and Sun [Reference Shi and Sun38] proved that $BR_{{(n-1)}/2}$
is called the critical index. In this case, Shi and Sun [Reference Shi and Sun38] proved that $BR_{{(n-1)}/2}$![]() is bounded on $L^{p}(v)$
is bounded on $L^{p}(v)$![]() for every $1 < p < \infty$
for every $1 < p < \infty$![]() and $v \in A_p$
and $v \in A_p$![]() . The weak-type inequality for $p = 1$
. The weak-type inequality for $p = 1$![]() was first settled by Christ [Reference Christ16], who showed that $BR_{{(n-1)}/2}$
was first settled by Christ [Reference Christ16], who showed that $BR_{{(n-1)}/2}$![]() is bounded from $L^{1}(\mathbb {R}^{n})$
is bounded from $L^{1}(\mathbb {R}^{n})$![]() to $L^{1,\infty }(\mathbb {R}^{n})$
to $L^{1,\infty }(\mathbb {R}^{n})$![]() , and the corresponding weighted weak-type inequality was obtained by Vargas in [Reference Vargas42], where she proved that, indeed, $BR_{{(n-1)}/2}$
, and the corresponding weighted weak-type inequality was obtained by Vargas in [Reference Vargas42], where she proved that, indeed, $BR_{{(n-1)}/2}$![]() is bounded from $L^{1}(v)$
is bounded from $L^{1}(v)$![]() to $L^{1,\infty }(v)$
to $L^{1,\infty }(v)$![]() for every $v \in A_1$
for every $v \in A_1$![]() .
.
Below the critical index, that is $0 < \lambda < {(n-1)}/2$![]() , $BR_\lambda$
, $BR_\lambda$![]() is not bounded on $L^{p}({{\mathbb {R}^{n}}})$
is not bounded on $L^{p}({{\mathbb {R}^{n}}})$![]() for the whole range $1 < p < \infty$
for the whole range $1 < p < \infty$![]() . For instance, in dimension $n=2$
. For instance, in dimension $n=2$![]() , Carleson and Sjölin [Reference Carleson and Sjölin8] proved that $BR_\lambda$
, Carleson and Sjölin [Reference Carleson and Sjölin8] proved that $BR_\lambda$![]() is bounded on $L^{p}({{\mathbb {R}^{n}}})$
is bounded on $L^{p}({{\mathbb {R}^{n}}})$![]() if and only if $p > 1$
if and only if $p > 1$![]() and
and
or equivalently, $0 < \lambda < \frac 12$![]() and
and
Moreover, Seeger [Reference Seeger37] showed that the corresponding weak-type inequality at the endpoint $BR_\lambda : L^{4/{(3 + 2\lambda )}}({{\mathbb {R}^{n}}}) \rightarrow L^{4/{(3 + 2\lambda )},\, \infty }({{\mathbb {R}^{n}}})$![]() also holds.
also holds.
For higher dimensions, it is already well known that $BR_\lambda$![]() is not bounded on $L^{p}(\mathbb {R}^{n})$
is not bounded on $L^{p}(\mathbb {R}^{n})$![]() for $p \leq {2n}/{(n + 1 + 2\lambda )}$
for $p \leq {2n}/{(n + 1 + 2\lambda )}$![]() or $p \geq {2n}/{(n - 1 - 2\lambda )}$
or $p \geq {2n}/{(n - 1 - 2\lambda )}$![]() (see for instance [Reference Duoandikoetxea18, theorem 8.15] or [Reference Grafakos22, proposition 5.2.3]). Furthermore, it was conjectured the following:
(see for instance [Reference Duoandikoetxea18, theorem 8.15] or [Reference Grafakos22, proposition 5.2.3]). Furthermore, it was conjectured the following:
Conjecture 1.1 (Bochner–Riesz conjecture)
$BR_\lambda$![]() is bounded on $L^{p}(\mathbb {R}^{n})$
is bounded on $L^{p}(\mathbb {R}^{n})$![]() if $p > 1$
if $p > 1$![]() and
and
or equivalently, $0 < \lambda < {(n-1)}/2$![]() and
and
This has an equivalent formulation (see [Reference Lacey, Mena and Reguera29]): let $\chi _{[-1/4, 1/4]} \leq \phi \leq \chi _{[-1/2,1/2]}$![]() be a Schwartz function, and set $S_\tau$
be a Schwartz function, and set $S_\tau$![]() , $\tau > 0$
, $\tau > 0$![]() , to be the Fourier multiplier having as a symbol $\phi ((|\xi | - 1)/\tau )$
, to be the Fourier multiplier having as a symbol $\phi ((|\xi | - 1)/\tau )$![]() , $\xi \in \mathbb {R}^{n}$
, $\xi \in \mathbb {R}^{n}$![]() .
.
Conjecture 1.2 For $p > 1$![]() such that $n\big |\frac 1p - \frac 12 \big | < \frac 12$
such that $n\big |\frac 1p - \frac 12 \big | < \frac 12$![]() ,
,
with constant controlled by $C_\varepsilon \tau ^{-\varepsilon }$![]() for all $0 < \varepsilon < 1$
for all $0 < \varepsilon < 1$![]() .
.
However, the Bochner–Riesz conjecture only has been partially answered and the best results known are currently due to Guo, Oh, Wang, Wu and Zhang (see [Reference Guo, Oh, Wang, Wu and Zhang23]) where the authors used polynomial partitioning. Before them, the best known results followed from the work of [Reference Guth, Hickman and Iliopoulou24] (see also [Reference Wu43]). We thank the referee for this information.
Further, under the condition ${(n - 1)}/{(2(n + 1))} < \lambda < {(n-1)}/2$![]() , the corresponding weak-type inequality at the endpoint $BR_\lambda : L^{{2n}/{(n + 1 + 2\lambda )}} \rightarrow L^{{2n}/{(n + 1 + 2\lambda )},\, \infty }$
, the corresponding weak-type inequality at the endpoint $BR_\lambda : L^{{2n}/{(n + 1 + 2\lambda )}} \rightarrow L^{{2n}/{(n + 1 + 2\lambda )},\, \infty }$![]() was settled by Christ [Reference Christ15] and extended to $\lambda = {(n - 1)}/{(2(n + 1))}$
was settled by Christ [Reference Christ15] and extended to $\lambda = {(n - 1)}/{(2(n + 1))}$![]() by Tao [Reference Tao40], while it remains unknown for the range $0 < \lambda < {(n - 1)}/{(2(n + 1))}$
by Tao [Reference Tao40], while it remains unknown for the range $0 < \lambda < {(n - 1)}/{(2(n + 1))}$![]() . This is the so-called endpoint Bochner–Riesz conjecture (see [Reference Tao41]) and we observe that if it holds for some $\lambda$
. This is the so-called endpoint Bochner–Riesz conjecture (see [Reference Tao41]) and we observe that if it holds for some $\lambda$![]() , then by duality and interpolation the Bochner–Riesz conjecture holds for such $\lambda$
, then by duality and interpolation the Bochner–Riesz conjecture holds for such $\lambda$![]() as well.
as well.
In two recent papers [Reference Kesler and Lacey27, Reference Lacey, Mena and Reguera29], new weighted estimates for $BR_\lambda$![]() have been proved using the fact that the Bochner–Riesz operators can be dominated by sparse type operators. As far as we know, these are the best weighted estimates known together with the results for the $(2,2)$
have been proved using the fact that the Bochner–Riesz operators can be dominated by sparse type operators. As far as we know, these are the best weighted estimates known together with the results for the $(2,2)$![]() -strong type inequality in [Reference Carro, Duoandikoetxea and Lorente9, Reference Christ14]. We summarize them here in a suitable way for the following main results of this paper. To do so, first we need the following notion.
-strong type inequality in [Reference Carro, Duoandikoetxea and Lorente9, Reference Christ14]. We summarize them here in a suitable way for the following main results of this paper. To do so, first we need the following notion.
Definition 1.3 Given $0 \leq \alpha,\, \beta \leq 1$![]() and $1 \leq p < \infty$
and $1 \leq p < \infty$![]() , let us define the class of weights
, let us define the class of weights
where
Remark 1.4 $A_{p;(\alpha,\beta )} \subseteq A_p$![]() (see for instance [Reference Carro, Duoandikoetxea and Lorente9]) where $A_p$
(see for instance [Reference Carro, Duoandikoetxea and Lorente9]) where $A_p$![]() is the Muckenhoupt class of weights (see (2.1)). Besides, we observe that
is the Muckenhoupt class of weights (see (2.1)). Besides, we observe that
Let us start stating the result for dimension $n=2$![]() where the conjecture has completely been solved.
where the conjecture has completely been solved.
Proposition 1.5 Let $n=2$![]() and $0<\lambda <\frac 12$
and $0<\lambda <\frac 12$![]() .
.
(i) [Reference Carro, Duoandikoetxea and Lorente9, Reference Lacey, Mena and Reguera29] For every $\frac 43 \leq q_0 \leq 4$
 ,
\[ BR_\lambda: L^{q_0}(v) \longrightarrow L^{q_0}(v), \quad \forall v \in A_{q_0;\left( { {2\lambda}, {2\lambda}} \right)}. \]
,
\[ BR_\lambda: L^{q_0}(v) \longrightarrow L^{q_0}(v), \quad \forall v \in A_{q_0;\left( { {2\lambda}, {2\lambda}} \right)}. \]
(ii) [Reference Kesler and Lacey27, corollary 1.3]
\begin{align*} & BR_\lambda: L^{4/{(3 + 2\lambda)}}\left(v\right) \rightarrow L^{4/{(3 + 2\lambda)}, \infty}\left(v\right), \quad \forall v\nonumber\\ & \quad \in A_{4/{(3 + 2\lambda)};\left( {{2\lambda}/{(3 + 2\lambda)}, 0 } \right)} \hspace{2mm} (\text{i.e. } v^{{(3 + 2\lambda)}/{2\lambda}} \in A_1). \end{align*}
(iii) In particular, in this case, the operator norm is bounded by $c(n,\,\lambda ) \left \lVert {v}\right \rVert ^{{(7 + 4\lambda )}/4}_{A_1}$
 .
.
Further, for $n > 2$![]() we have the following result.
we have the following result.
Proposition 1.6 Let $0 < \lambda < {(n-1)}/2$![]() .
.
(i) [Reference Carro, Duoandikoetxea and Lorente9, Reference Lacey, Mena and Reguera29] If $q_0 = 2$
 or $q_0$
or $q_0$ is such that ${2n}/{(n+1)} < q_0 < 2$
is such that ${2n}/{(n+1)} < q_0 < 2$ and conjecture 1.2 holds with $p = q_0,$
and conjecture 1.2 holds with $p = q_0,$ \[ BR_\lambda: L^{q_0}(v) \longrightarrow L^{q_0}(v), \quad \forall v \in A_{q_0;\left( {{2\lambda}/{(n-1)},{2\lambda}/{(n-1)}} \right)}. \]
\[ BR_\lambda: L^{q_0}(v) \longrightarrow L^{q_0}(v), \quad \forall v \in A_{q_0;\left( {{2\lambda}/{(n-1)},{2\lambda}/{(n-1)}} \right)}. \]
(ii) And, by duality,
\[ BR_\lambda: L^{q_0'}(v) \longrightarrow L^{q_0'}(v), \quad \forall v \in A_{q_0';\left( {{2\lambda}/{(n-1)},{2\lambda}/{(n-1)}} \right)}. \]
(iii) [Reference Christ14] If ${(n-1)}/{(2(n+1))} < \lambda < {(n-1)}/2,$
 then
\[ BR_\lambda: L^{2}(v) \longrightarrow L^{2}(v), \quad \forall v \in A_{2;\left( {{(1 + 2\lambda)}/n,0} \right)}\cup A_{2; \left( {0, {(1 + 2\lambda)}/n} \right)}. \]
then
\[ BR_\lambda: L^{2}(v) \longrightarrow L^{2}(v), \quad \forall v \in A_{2;\left( {{(1 + 2\lambda)}/n,0} \right)}\cup A_{2; \left( {0, {(1 + 2\lambda)}/n} \right)}. \]
Now, set $\mathcal {M}(\mathbb {R}^{n})$![]() to be the set of all measurable functions on $\mathbb {R}^{n}$
to be the set of all measurable functions on $\mathbb {R}^{n}$![]() and let us consider for a positive and locally integrable function $w$
and let us consider for a positive and locally integrable function $w$![]() in $\mathbb {R}^{+}$
in $\mathbb {R}^{+}$![]() (i.e. $w\in L^{1}_{\text {loc}}(\mathbb {R}^{+})$
(i.e. $w\in L^{1}_{\text {loc}}(\mathbb {R}^{+})$![]() ) the primitive $W(t)=\int _0^{t} w(r){\rm d}r$
) the primitive $W(t)=\int _0^{t} w(r){\rm d}r$![]() . Given a sublinear operator $T$
. Given a sublinear operator $T$![]() defined over the function space
defined over the function space
we define the class
where $\mu _f$![]() and $f^{*}$
and $f^{*}$![]() are, respectively, the distribution function and the decreasing rearrangement of $f \in \mathcal {M}(\mathbb {R}^{n})$
are, respectively, the distribution function and the decreasing rearrangement of $f \in \mathcal {M}(\mathbb {R}^{n})$![]() defined by
defined by
Then, one can immediately see that
The original motivation of this paper was to study the class $\mathcal {W}(T)$![]() not only for the Bochner–Riesz operators but also for other interesting operators in harmonic analysis having in common some properties connected with weighted estimates; namely, for some $1 \leq p < \infty$
not only for the Bochner–Riesz operators but also for other interesting operators in harmonic analysis having in common some properties connected with weighted estimates; namely, for some $1 \leq p < \infty$![]() ,
,
for every positive and locally integrable function $v$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() belonging in $A_{p;(\alpha,\beta )}$
belonging in $A_{p;(\alpha,\beta )}$![]() for some $0 \leq \alpha,\,\beta \leq 1$
for some $0 \leq \alpha,\,\beta \leq 1$![]() . In particular, and as a consequence of our main results, we will obtain boundedness on weighted Lorentz spaces $\Lambda ^{p}(w)$
. In particular, and as a consequence of our main results, we will obtain boundedness on weighted Lorentz spaces $\Lambda ^{p}(w)$![]() , $0 < p < \infty$
, $0 < p < \infty$![]() , defined by
, defined by

Weighted type inequalities as in (1.4) are also satisfied by other operators such as the Hörmander Fourier multipliers $m\in M(s,\, l)$![]() with $l< n$
with $l< n$![]() (see [Reference Kurtz and Wheeden28]) among many others. And this is the starting point of this paper. We want to use the information about weighted estimates on Lebesgue spaces to study the class $\mathcal {W}(T)$
(see [Reference Kurtz and Wheeden28]) among many others. And this is the starting point of this paper. We want to use the information about weighted estimates on Lebesgue spaces to study the class $\mathcal {W}(T)$![]() and, as a consequence, to obtain boundedness on weighted Lorentz spaces. To this end, we need to adapt the ideas in [Reference Baena-Miret and Carro4] where the case $\alpha =\beta =1$
and, as a consequence, to obtain boundedness on weighted Lorentz spaces. To this end, we need to adapt the ideas in [Reference Baena-Miret and Carro4] where the case $\alpha =\beta =1$![]() was studied and applications to the case $\lambda ={(n-1)}/2$
was studied and applications to the case $\lambda ={(n-1)}/2$![]() (for the Bochner–Riesz operator) and the case $l = n$
(for the Bochner–Riesz operator) and the case $l = n$![]() (for the Hörmander multiplier) were considered. In particular, the following result was proved: if $T$
(for the Hörmander multiplier) were considered. In particular, the following result was proved: if $T$![]() satisfies that $T:L^{1}(v) \rightarrow L^{1, \infty }(v)$
satisfies that $T:L^{1}(v) \rightarrow L^{1, \infty }(v)$![]() , for every $v \in A_1$
, for every $v \in A_1$![]() , with constant less than or equal to $\varphi (||{v}||_{A_1})$
, with constant less than or equal to $\varphi (||{v}||_{A_1})$![]() , with $\varphi$
, with $\varphi$![]() an increasing function on $(0,\, \infty )$
an increasing function on $(0,\, \infty )$![]() , then (see (2.3) for the definition of the class $B_p^{{\mathcal{R}}}$
, then (see (2.3) for the definition of the class $B_p^{{\mathcal{R}}}$![]() , and definition 2.2 for $B^{*}_\infty$
, and definition 2.2 for $B^{*}_\infty$![]() )
)
for some universal constants $C_1,\, C_2>0$![]() .
.
We write $A \lesssim B$![]() , where $A$
, where $A$![]() , $B$
, $B$![]() are nonnegative quantities, if there exists a positive constant $C>0$
are nonnegative quantities, if there exists a positive constant $C>0$![]() , independent of $A$
, independent of $A$![]() and $B$
and $B$![]() , such that $A\leq C B$
, such that $A\leq C B$![]() . If $A\lesssim B$
. If $A\lesssim B$![]() and $B\lesssim A$
and $B\lesssim A$![]() , then we write $A\approx B$
, then we write $A\approx B$![]() .
.
Definition 1.7 We say that $f$![]() is quasi-decreasing, and we denote it by $f \approx \downarrow$
is quasi-decreasing, and we denote it by $f \approx \downarrow$![]() , if $f(t) \lesssim f(s)$
, if $f(t) \lesssim f(s)$![]() , $0< s\le t$
, $0< s\le t$![]() . If $-f$
. If $-f$![]() is quasi-decreasing we say that $f$
is quasi-decreasing we say that $f$![]() is quasi-increasing and we denote it by $f \approx \uparrow$
is quasi-increasing and we denote it by $f \approx \uparrow$![]() .
.
Hence, the inclusion in (1.5) can be reinterpreted (see (2.3) and (2.7)) to the existence of some $\varepsilon > 0$![]() so that if
so that if
then $w \in \mathcal {W}(T)$![]() . This motivates the next theorems that allows us to generalize the results in [Reference Baena-Miret and Carro4] to operators satisfying (1.4). Indeed, (1.5) turns out to be the case $p_0 = \alpha = 1$
. This motivates the next theorems that allows us to generalize the results in [Reference Baena-Miret and Carro4] to operators satisfying (1.4). Indeed, (1.5) turns out to be the case $p_0 = \alpha = 1$![]() of our second main result (see theorem 1.11). Our first main result is the following (see (2.2) for the definition of the class $B_p$
of our second main result (see theorem 1.11). Our first main result is the following (see (2.2) for the definition of the class $B_p$![]() , and definition 2.3 for $B^{*}_p$
, and definition 2.3 for $B^{*}_p$![]() ):
):
Theorem 1.8 Let $1 < p_0 < \infty,$![]() $0 \leq \alpha \leq 1,$
$0 \leq \alpha \leq 1,$![]() $0 < \beta \leq 1$
$0 < \beta \leq 1$![]() and let $T$
and let $T$![]() be a sublinear operator such that
be a sublinear operator such that
with constant less than or equal to $\varphi (||{v}||_{A_{1+\beta (p_0-1)}}),$![]() with $\varphi$
with $\varphi$![]() an increasing function on $(0,\, \infty )$
an increasing function on $(0,\, \infty )$![]() . Set
. Set
Then, $B_{{1}/{p_-}}\cap B_{ {p_+}}^{*} \subset \mathcal {W}(T),$![]() or equivalently, if there exists some $\varepsilon > 0$
or equivalently, if there exists some $\varepsilon > 0$![]() so that
so that
then $w \in \mathcal {W}(T)$![]() . Moreover, it holds that $\left \lVert {w}\right \rVert _{\mathcal {W}(T)} \leq \Phi (\left \lVert {w}\right \rVert _{B_{{1}/{p_-}}},\, \left \lVert {w}\right \rVert _{B_{ {p_+}}^{*}}),$
. Moreover, it holds that $\left \lVert {w}\right \rVert _{\mathcal {W}(T)} \leq \Phi (\left \lVert {w}\right \rVert _{B_{{1}/{p_-}}},\, \left \lVert {w}\right \rVert _{B_{ {p_+}}^{*}}),$![]() where $\Phi$
where $\Phi$![]() is an increasing function in each variable depending on $\varphi$
is an increasing function in each variable depending on $\varphi$![]() .
.
By taking $T=M\circ M$![]() with $M$
with $M$![]() the Hardy–Littlewood maximal operator, it is clear that the above result is false with $\varepsilon =0$
the Hardy–Littlewood maximal operator, it is clear that the above result is false with $\varepsilon =0$![]() since $T$
since $T$![]() satisfies the hypothesis of our theorem with $\alpha =1$
satisfies the hypothesis of our theorem with $\alpha =1$![]() and $\beta =1$
and $\beta =1$![]() but, although $w = 1$
but, although $w = 1$![]() satisfies the hypothesis, $T$
satisfies the hypothesis, $T$![]() is not of weak type $(1,\,1)$
is not of weak type $(1,\,1)$![]() .
.
Remark 1.9 Recall that a weight $v$![]() belongs to the reverse Hölder class $RH_q$
belongs to the reverse Hölder class $RH_q$![]() , $1 < q < \infty$
, $1 < q < \infty$![]() , if for every measurable cube $Q\subset \mathbb {R}^{n}$
, if for every measurable cube $Q\subset \mathbb {R}^{n}$![]() ,
,

It is known that $v \in A_p \cap RH_q$![]() if and only if $v^{q} \in A_{\tilde p}$
if and only if $v^{q} \in A_{\tilde p}$![]() with $\tilde p = q(p - 1) + 1$
with $\tilde p = q(p - 1) + 1$![]() (see for instance [Reference Johnson and Neugebauer26, (P6)]) so that when $\alpha > 0$
(see for instance [Reference Johnson and Neugebauer26, (P6)]) so that when $\alpha > 0$![]() ,
,
which keeps some symmetry with the class of weights $B_{1/{p_-}}\cap B_{p_+}^{*}$![]() .
.
As a consequence of theorem 1.8, we have the following result:
Corollary 1.10 Let $0 < p < \infty$![]() . Under the hypotheses of theorem 1.8, if there exists some $\varepsilon > 0$
. Under the hypotheses of theorem 1.8, if there exists some $\varepsilon > 0$![]() so that
so that
we have that
Our next main result reads as follows:
Theorem 1.11 Let $1 \leq p_0 < \infty,$![]() $0 < \alpha \leq 1,$
$0 < \alpha \leq 1,$![]() and let $T$
and let $T$![]() be a sublinear operator such that
be a sublinear operator such that
with constant less than or equal to $\varphi ( \left \lVert {v}\right \rVert _{A_1}),$![]() where $\varphi$
where $\varphi$![]() is an increasing function. Then, $B_{1/{p_0}}^{{\mathcal{R}}}\cap B_{{p_0}/{(1-\alpha )}}^{*} \subset \mathcal {W}(T),\,$
is an increasing function. Then, $B_{1/{p_0}}^{{\mathcal{R}}}\cap B_{{p_0}/{(1-\alpha )}}^{*} \subset \mathcal {W}(T),\,$![]() or equivalently, if there exists some $\varepsilon > 0$
or equivalently, if there exists some $\varepsilon > 0$![]() so that
so that
then $w \in \mathcal {W}(T)$![]() . Moreover,
. Moreover,

Corollary 1.12 Let $0 < p < \infty$![]() and let us assume the hypotheses of theorem 1.11.
and let us assume the hypotheses of theorem 1.11.
(a) If
then
(b) If
then
Remark 1.13 Although theorems 1.8 and 1.11 are stated with $T$![]() being a sublinear operator, which is enough for the applications that we present in § 4, they can be proved without this hypothesis. In fact, we only need this condition when applying interpolation in corollaries 1.10 and 1.12.
being a sublinear operator, which is enough for the applications that we present in § 4, they can be proved without this hypothesis. In fact, we only need this condition when applying interpolation in corollaries 1.10 and 1.12.
The paper is organized as follows. In § 2 we present some definitions, previous results and technical lemmas which shall be used later on, while § 3 contains our main results. The last section (see § 4) will be devoted to obtain estimates in the setting of weighted Lorentz spaces for the Bochner–Riesz operators in the critical range, among others, such as sparse operators, Hörmander multipliers with a limited regularity condition and rough operators with $\Omega \in L^{r}(\Sigma )$![]() .
.
2. Definitions, previous results and some technical lemmas
Given $0 < p,\, q < \infty$![]() , $w$
, $w$![]() a positive locally integrable function defined on $\mathbb {R}^{+}$
a positive locally integrable function defined on $\mathbb {R}^{+}$![]() and $W(t)=\int _0^{t} w(r)\,{\rm d}r$
and $W(t)=\int _0^{t} w(r)\,{\rm d}r$![]() , the weighted Lorentz space $\Lambda ^{p,q}(w)$
, the weighted Lorentz space $\Lambda ^{p,q}(w)$![]() is defined by the condition $||f||_{\Lambda ^{p,q}(w)} < \infty$
is defined by the condition $||f||_{\Lambda ^{p,q}(w)} < \infty$![]() where
where

where $\mu _f$![]() and $f^{*}$
and $f^{*}$![]() are, respectively, the distribution function and the decreasing rearrangement of $f$
are, respectively, the distribution function and the decreasing rearrangement of $f$![]() defined in (1.3). Observe that if $w=1$
defined in (1.3). Observe that if $w=1$![]() , $\Lambda ^{p,q}(w)$
, $\Lambda ^{p,q}(w)$![]() coincides with the more usual case $L^{p,q}$
coincides with the more usual case $L^{p,q}$![]() . We should also emphasize here that for $0 < q < \infty$
. We should also emphasize here that for $0 < q < \infty$![]() ,
,
and, similar, $\Lambda ^{p,\infty }(w) = \Lambda ^{1,\infty }(\tilde w)$![]() , with $\tilde W(t) \approx W(t)^{1/p}$
, with $\tilde W(t) \approx W(t)^{1/p}$![]() $\text {(or } \tilde {w}(t) \approx W(t)^{1/p - 1}w(t)\text {)}$
$\text {(or } \tilde {w}(t) \approx W(t)^{1/p - 1}w(t)\text {)}$![]() . Besides, these spaces satisfy the embeddings
. Besides, these spaces satisfy the embeddings
continuously for $0 < q_0 \leq q_1 \leq \infty$![]() . For further information about these notions and related topics see [Reference Bennett and Sharpley5, Reference Carro, Raposo and Soria12].
. For further information about these notions and related topics see [Reference Bennett and Sharpley5, Reference Carro, Raposo and Soria12].
We observe here that,
and

Let us consider the Hardy–Littlewood maximal operator $M$![]() , defined in (1.1). It is known [Reference Muckenhoupt34] that for every $1< p<\infty$
, defined in (1.1). It is known [Reference Muckenhoupt34] that for every $1< p<\infty$![]() ,
,
where

Moreover, by a weighted norm inequality due to Fefferman and Stein in [Reference Fefferman and Stein21], it was seen that, for $1 \leq p < \infty$![]() , the $A_p$
, the $A_p$![]() class also characterizes the weak-type boundedness
class also characterizes the weak-type boundedness
(see (1.2) for the definition of the class $A_1$![]() ).
).
Concerning the boundedness of $M$![]() on weighted Lorentz spaces we have (see [Reference Ariño and Muckenhoupt3]) that for every $p>0$
on weighted Lorentz spaces we have (see [Reference Ariño and Muckenhoupt3]) that for every $p>0$![]() ,
,
where
and $\left \lVert {M}\right \rVert _{\Lambda ^{p}(w)} := \left \lVert {M}\right \rVert _{\Lambda ^{p}(w) \rightarrow \Lambda ^{p}(w)}\lesssim \left \lVert {w}\right \rVert _{B_p}$![]() . Also, since for $\tilde {W}(t) \approx W(t)^{1/p}$
. Also, since for $\tilde {W}(t) \approx W(t)^{1/p}$![]() ,
,
we have that [Reference Carro, García del Amo and Soria10, Reference Carro and Soria13]
where $w\in B_p^{\mathcal{R}}$![]() is defined by
is defined by
Further, $||M||_{\Lambda ^{p, 1}(w) \longrightarrow \Lambda ^{p, \infty }(w)}\lesssim ||w||_{B_p^{{\mathcal{R}}}}$![]() and, for $0 < q < p < \infty$
and, for $0 < q < p < \infty$![]() , it is easy to see that $B_q^{\mathcal {R}} \subsetneq B_p \subsetneq B_p^{\mathcal {R}}$
, it is easy to see that $B_q^{\mathcal {R}} \subsetneq B_p \subsetneq B_p^{\mathcal {R}}$![]() with
with
Indeed, it is known that [Reference Ariño and Muckenhoupt3, Reference Neugebauer35] for $0 < p < \infty$![]() ,
,
Finally, we say that $w \in \Delta _2$![]() if there exists $C > 0$
if there exists $C > 0$![]() such that $W(2t) \leq C W(t)$
such that $W(2t) \leq C W(t)$![]() , for all $t > 0$
, for all $t > 0$![]() . Clearly, it holds that, for every $0 < p < \infty$
. Clearly, it holds that, for every $0 < p < \infty$![]() , $B_p^{{\mathcal{R}}} \subsetneq \Delta _2$
, $B_p^{{\mathcal{R}}} \subsetneq \Delta _2$![]() . Besides, for every $0 < p,\,q < \infty$
. Besides, for every $0 < p,\,q < \infty$![]() , if $w \in \Delta _2$
, if $w \in \Delta _2$![]() , then $\Lambda ^{p,q}(w)$
, then $\Lambda ^{p,q}(w)$![]() is a quasi-Banach r.i. function space (see [Reference Carro, Raposo and Soria12]).
is a quasi-Banach r.i. function space (see [Reference Carro, Raposo and Soria12]).
Let us recall now, that given a quasi-Banach r.i. space $\mathbb {X}$![]() , the associate space $\mathbb {X}'$
, the associate space $\mathbb {X}'$![]() is defined by the condition
is defined by the condition
Lemma 2.1 Let $0 < p \leq 1$![]() . If $w\in B_p^{{\mathcal{R}}},$
. If $w\in B_p^{{\mathcal{R}}},$![]() then for every measurable set $E \subseteq \mathbb {R}^{n},$
then for every measurable set $E \subseteq \mathbb {R}^{n},$![]()
Proof. It is known [Reference Carro, Raposo and Soria12, theorem 2.4.7] that

and hence
To prove our main results we need several estimates on the boundedness of the operators $M_\alpha f = M( f^{1/\alpha })^{\alpha }$![]() , $0 < \alpha \leq 1$
, $0 < \alpha \leq 1$![]() , on the corresponding associate spaces $(\Lambda ^{p}(w))'$
, on the corresponding associate spaces $(\Lambda ^{p}(w))'$![]() . To this end, the following classes of weights are going to be fundamental.
. To this end, the following classes of weights are going to be fundamental.
Definition 2.2 [Reference Neugebauer36]
A weight $w\in B^{*}_\infty$![]() if and only if
if and only if
Definition 2.3 [Reference Lai30, Reference Neugebauer36]
Let $0 < p < \infty$![]() . A weight $w \in B_p^{*}$
. A weight $w \in B_p^{*}$![]() if and only if
if and only if

It is known that [Reference Lai30, Reference Martín and Milman33] for every $0 < p < \infty$![]() ,
,
Besides, direct from the definition, for $0 < q \leq p < \infty$![]() ,
,
and, for every $0 < p < \infty$![]() ,
,
Indeed, (2.5) also holds for $p = \infty$![]() as the following result shows. Consequently, (2.6) is also true for this exponent.
as the following result shows. Consequently, (2.6) is also true for this exponent.
Lemma 2.4
Proof. Since $B_p^{*} \subseteq B_\infty ^{*}$![]() , by (2.5), it is enough to see that if $w \in B_\infty ^{*}$
, by (2.5), it is enough to see that if $w \in B_\infty ^{*}$![]() , then there exists some $p > 0$
, then there exists some $p > 0$![]() such that $w \in B_p^{*}$
such that $w \in B_p^{*}$![]() .
.
Let $\overline {W}:(0,\,\infty ) \rightarrow (0,\,\infty )$![]() be defined by
be defined by
where the last equality follows since $W$![]() is increasing. It was seen [Reference Agora, Carro and Soria1, lemma 2.6] that $w \in B_\infty ^{*}$
is increasing. It was seen [Reference Agora, Carro and Soria1, lemma 2.6] that $w \in B_\infty ^{*}$![]() is equivalent to the existence of some $t_0 \in (0,\,1)$
is equivalent to the existence of some $t_0 \in (0,\,1)$![]() such that $\overline {W}(t_0) < 1$
such that $\overline {W}(t_0) < 1$![]() . What's more, arguing similar as in [Reference Agora, Carro and Soria1, lemma 2.7], it can be seen that $w \in B_p^{*}$
. What's more, arguing similar as in [Reference Agora, Carro and Soria1, lemma 2.7], it can be seen that $w \in B_p^{*}$![]() is equivalent to the existence of some $t_1 \in (0,\,1)$
is equivalent to the existence of some $t_1 \in (0,\,1)$![]() such that $\overline {W}(t_1) < t_1^{{1/p}}$
such that $\overline {W}(t_1) < t_1^{{1/p}}$![]() . Therefore, given $w \in B_\infty ^{*}$
. Therefore, given $w \in B_\infty ^{*}$![]() and taking $p$
and taking $p$![]() large enough, it holds that $\overline {W}(t_0) < 1$
large enough, it holds that $\overline {W}(t_0) < 1$![]() implies $\overline {W}(t_0) < t_0^{{1/p}}$
implies $\overline {W}(t_0) < t_0^{{1/p}}$![]() .
.
Hence, from lemma 2.4, equivalences (2.4) and (2.5), and the definition of $B_p^{\mathcal {R}}$![]() , it follows immediately that for every $0 < p < \infty$
, it follows immediately that for every $0 < p < \infty$![]() , $0 < q \leq \infty$
, $0 < q \leq \infty$![]() ,
,
and
Example 2.5 (a) Let $0 < p < \infty$![]() and take $w(t) = t^{\gamma - 1}$
and take $w(t) = t^{\gamma - 1}$![]() , $t > 0$
, $t > 0$![]() . Then,
. Then,
with $\left \lVert {w}\right \rVert _{B_p} = \frac p{p - \gamma }$![]() and $\left \lVert {w}\right \rVert _{B_p^{R}} = 1$
and $\left \lVert {w}\right \rVert _{B_p^{R}} = 1$![]() . Moreover,
. Moreover,
with $\left \lVert {w}\right \rVert _{B_p^{*}} = \frac \gamma {\gamma - 1/p}$![]() and $\left \lVert {w}\right \rVert _{B_\infty ^{*}} = \frac 1\gamma$
and $\left \lVert {w}\right \rVert _{B_\infty ^{*}} = \frac 1\gamma$![]() .
.
(b) Let $1 \leq p < q < \infty$![]() and set, for every $m \in \mathbb {N}$
and set, for every $m \in \mathbb {N}$![]() ,
,
By induction on $m$![]() , it is easy to see that $w_m\in B_p^{\mathcal {R}}\cap B^{*}_q$
, it is easy to see that $w_m\in B_p^{\mathcal {R}}\cap B^{*}_q$![]() with
with
(c) Similarly, let $1 \leq p < q < \infty$![]() and set, for every $m \in \mathbb {N}$
and set, for every $m \in \mathbb {N}$![]() ,
,
Then, $\tilde w_m\in B_p^{\mathcal {R}}\cap B^{*}_q$![]() with
with
From the above results we are now ready to estimate the boundedness of $M_\alpha$![]() , $0 < \alpha \leq 1$
, $0 < \alpha \leq 1$![]() , on the associate spaces $\left (\Lambda ^{p}\left ( {w} \right )\right )'$
, on the associate spaces $\left (\Lambda ^{p}\left ( {w} \right )\right )'$![]() for $0 < p \leq 1$
for $0 < p \leq 1$![]() . First, the case $\alpha = 1$
. First, the case $\alpha = 1$![]() :
:
Proposition 2.6 [Reference Andersen2, Reference Baena-Miret and Carro4]
For every $0 < p < \infty,$![]()
For $0 < \alpha < 1$![]() , we need this technical lemma:
, we need this technical lemma:
Lemma 2.7 Let $0 < p \leq 1,$![]() $0 < \alpha < 1$
$0 < \alpha < 1$![]() and
and
If

then $||M_\alpha f ||_{(\Lambda ^{p}(w))'} \lesssim A_V ||f||_{(\Lambda ^{p}(w))'}$![]() . Moreover, if $M_{\alpha }: \left (\Lambda ^{p}\left ( {w} \right )\right )'\rightarrow \left (\Lambda ^{p}\left ( {w} \right )\right )',$
. Moreover, if $M_{\alpha }: \left (\Lambda ^{p}\left ( {w} \right )\right )'\rightarrow \left (\Lambda ^{p}\left ( {w} \right )\right )',$![]() and $w \in \Delta _2,$
and $w \in \Delta _2,$![]() then $A_V < \infty$
then $A_V < \infty$![]() .
.
Proof. Since
and $\int _0^{t}h^{*}(r)\,{\rm d}r$![]() is a concave function, we have that, for every $t > 0$
is a concave function, we have that, for every $t > 0$![]() ,
,
and hence
First assume that $A_V < \infty$![]() . Then,
. Then,

Conversely, the first observation is that since $Mf\le M(f^{1/\alpha } )^{\alpha }$![]() , the boundedness of $M_\alpha$
, the boundedness of $M_\alpha$![]() implies the boundedness of $M$
implies the boundedness of $M$![]() and hence, since $w \in \Delta _2$
and hence, since $w \in \Delta _2$![]() (so that $(\Lambda ^{p}(w))'$
(so that $(\Lambda ^{p}(w))'$![]() is a Banach space [Reference Carro, Raposo and Soria12]) we already know that the derivative of $V$
is a Banach space [Reference Carro, Raposo and Soria12]) we already know that the derivative of $V$![]() must satisfy ${\rm d}V \in B^{*}_\infty$
must satisfy ${\rm d}V \in B^{*}_\infty$![]() (see, for instance, [Reference Baena-Miret and Carro4]).
(see, for instance, [Reference Baena-Miret and Carro4]).
Now, since $V$![]() is concave, the function $\displaystyle f(r) = {V(r)}/{r}$
is concave, the function $\displaystyle f(r) = {V(r)}/{r}$![]() is decreasing and hence, if we take $g(x) = f(C_n|x|^{n})$
is decreasing and hence, if we take $g(x) = f(C_n|x|^{n})$![]() , $x \in \mathbb {R}^{n}$
, $x \in \mathbb {R}^{n}$![]() , where $C_n$
, where $C_n$![]() is the volume of the unit sphere in $\mathbb {R}^{n}$
is the volume of the unit sphere in $\mathbb {R}^{n}$![]() , we have that $g^{*} = f$
, we have that $g^{*} = f$![]() and thus
and thus

Lemma 2.8 Let $0 < p \leq 1$![]() and $0 < \alpha < 1$
and $0 < \alpha < 1$![]() . If $w \in B_{{1}/{((1 - \alpha )p)}}^{*},$
. If $w \in B_{{1}/{((1 - \alpha )p)}}^{*},$![]() then
then
Proof. Observe that, by lemma 2.7, it is enough to see that
and we have seen in the proof of lemma 2.7 that, in particular,

Now take $s > 0$![]() . By the Minkowski's inequality applied with the exponent ${1}/{\alpha } > 1$
. By the Minkowski's inequality applied with the exponent ${1}/{\alpha } > 1$![]() ,
,

Therefore, using that $V(t) \leq W(t)^{1/p}$![]() and the Minkowski's inequality again with exponent $1/ p \geq 1$
and the Minkowski's inequality again with exponent $1/ p \geq 1$![]() , we obtain that, for every $t > 0$
, we obtain that, for every $t > 0$![]() ,
,

and the result follows.
Lemma 2.9 Let $0 < p \leq 1$![]() and $0 < \alpha < 1$
and $0 < \alpha < 1$![]() . If $w \in B_{\frac 1{(1 - \alpha )p}}^{*},$
. If $w \in B_{\frac 1{(1 - \alpha )p}}^{*},$![]() then
then
Proof. Recall that $\Lambda ^{p,\,1}\left ( {w} \right ) = \Lambda^{1}\left( \tilde {w} \right)$![]() with $\tilde {w} = W^{1/p - 1}w$
with $\tilde {w} = W^{1/p - 1}w$![]() . Therefore, by lemma 2.8
. Therefore, by lemma 2.8
Now, integrating by parts and using the Minkowski's inequality we obtain that, for every $t > 0$![]() ,
,

and the result follows taking the supremum on $t$![]() .
.
To end this section, we present an extrapolation theorem that we shall need for our purposes (see [Reference Carro, Duoandikoetxea and Lorente9, theorem 2.7] and [Reference Duoandikoetxea19, theorem 7.1]).
Definition 2.10 Given $1 \leq p_0 < \infty$![]() and $0 \leq \alpha,\, \beta \leq 1$
and $0 \leq \alpha,\, \beta \leq 1$![]() , set
, set
and, for every $p \in (p_{-},\, p_{+})$![]() , take $0 \leq \alpha (p),\, \beta (p) \leq 1$
, take $0 \leq \alpha (p),\, \beta (p) \leq 1$![]() such that
such that
Theorem 2.11 Assume that for some family of pairs of functions $(f,\,g),$![]() for some $1 \leq p_0 < \infty$
for some $1 \leq p_0 < \infty$![]() and $0 \leq \alpha,\, \beta \leq 1,$
and $0 \leq \alpha,\, \beta \leq 1,$![]() $\alpha$
$\alpha$![]() and $\beta$
and $\beta$![]() not both identically zero, and for all $v \in A_{p_0;(\alpha, \beta )}$
not both identically zero, and for all $v \in A_{p_0;(\alpha, \beta )}$![]()
where $\varphi$![]() is an increasing function in $(0,\,\infty )$
is an increasing function in $(0,\,\infty )$![]() . Then, for every $p_- < q < p_0$
. Then, for every $p_- < q < p_0$![]() and for every $v \in A_{q;(\alpha (q), \beta (q))}$
and for every $v \in A_{q;(\alpha (q), \beta (q))}$![]() ,
,

with $r_q = 1 + \frac {\beta (q)}{\alpha (q)}(q-1)$![]() .
.
3. Proof of our main results
Proof of theorem 1.8. Assume first that $\alpha < 1$![]() (i.e. $p_+ < \infty$
(i.e. $p_+ < \infty$![]() ) and let $w \in B_{1/{p_-}} \cap B_{p_+}^{*}$
) and let $w \in B_{1/{p_-}} \cap B_{p_+}^{*}$![]() . We want to see that $w \in \mathcal {W}(T)$
. We want to see that $w \in \mathcal {W}(T)$![]() , or equivalently,
, or equivalently,
Since we have that $w \in B_{1/{p_-} }$![]() , we can define
, we can define

Then,
(i) $f(x)\leq R_{1/{p_-}}f(x)$
 a.e. $x \in {{\mathbb {R}^{n}}}$
a.e. $x \in {{\mathbb {R}^{n}}}$ ,
,(ii) $R(f^{p_-}) \in A_1$
 with $\left \lVert {R(f^{p_-})}\right \rVert _{A_1} \leq 2\left \lVert {M}\right \rVert _{\Lambda ^ {1/{p_-}}(w)}$
with $\left \lVert {R(f^{p_-})}\right \rVert _{A_1} \leq 2\left \lVert {M}\right \rVert _{\Lambda ^ {1/{p_-}}(w)}$ ,
,(iii) and, using the definition of $B_{1/{p_-}}$
 together with that $\Lambda ^{ 1/{p_-}} (w) \subset \Lambda ^{1/{p_-},\,\infty }(w)$
together with that $\Lambda ^{ 1/{p_-}} (w) \subset \Lambda ^{1/{p_-},\,\infty }(w)$ and $\Lambda ^{1/{p_-},\,\infty }(w)$
and $\Lambda ^{1/{p_-},\,\infty }(w)$ is a Banach space (see [Reference Soria39]),
\[ ||R_{1/{p_-}} f||_{\Lambda^{1,\infty}(w)} \leq \left(\sum_{k = 0}^{\infty} \frac{ || M^{k} (f^{p_-}) ||_{\Lambda^{1/{p_-},\infty }(w)} }{\left( 2||M||_{\Lambda^{1/{p_-} }(w)} \right)^{k} } \right)^{1/{p_-}} \leq 2^{1/{p_-}} ||f||_{\Lambda^{1}(w)}. \]
is a Banach space (see [Reference Soria39]),
\[ ||R_{1/{p_-}} f||_{\Lambda^{1,\infty}(w)} \leq \left(\sum_{k = 0}^{\infty} \frac{ || M^{k} (f^{p_-}) ||_{\Lambda^{1/{p_-},\infty }(w)} }{\left( 2||M||_{\Lambda^{1/{p_-} }(w)} \right)^{k} } \right)^{1/{p_-}} \leq 2^{1/{p_-}} ||f||_{\Lambda^{1}(w)}. \]
Moreover, using (2.6) we have that
with
and hence, we have that there exists some $p_- < q < p_0 \leq p_+$![]() such that $w \in B_{{p_-}/{(1 - \alpha (q))}}^{*}$
such that $w \in B_{{p_-}/{(1 - \alpha (q))}}^{*}$![]() and $0 < \alpha (q) < 1$
and $0 < \alpha (q) < 1$![]() , $0 < \beta (q) \leq 1$
, $0 < \beta (q) \leq 1$![]() . Besides, by theorem 2.11, we obtain that (2.8) holds with $g = Tf$
. Besides, by theorem 2.11, we obtain that (2.8) holds with $g = Tf$![]() . Hence, bylemma 2.8, since $w \in B_{{p_-}/{(1-\alpha (q)) }}^{*}$
. Hence, bylemma 2.8, since $w \in B_{{p_-}/{(1-\alpha (q)) }}^{*}$![]() , we can define, for an arbitrary nonnegative function $h \in (\Lambda ^{1/{p_-} }(w))'$
, we can define, for an arbitrary nonnegative function $h \in (\Lambda ^{1/{p_-} }(w))'$![]() ,
,

so that
(i) $h(x) \leq S_{\alpha (q)}h(x)$
 a.e. $x \in {{\mathbb {R}^{n}}}$
a.e. $x \in {{\mathbb {R}^{n}}}$ ,
,(ii) $S(h^{1/{\alpha (q)}}) \in A_1$
 with $\left \lVert {S(h^{1/{\alpha (q)}})}\right \rVert _{A_1}^{\alpha (q)} \leq 2\left \lVert {M_{\alpha (q)}}\right \rVert _{(\Lambda ^{1/{p_-}}(w))'}$
with $\left \lVert {S(h^{1/{\alpha (q)}})}\right \rVert _{A_1}^{\alpha (q)} \leq 2\left \lVert {M_{\alpha (q)}}\right \rVert _{(\Lambda ^{1/{p_-}}(w))'}$ ,
,(iii) and, since $(\Lambda ^{1/{p_-}}(w))'$
 is a Banach space (see [Reference Carro, Raposo and Soria12]),
\[ \lVert S_{\alpha(q)}h\rVert_{\left(\Lambda^{1/{p_-} }(w)\right)'} \leq \sum_{k = 0}^{\infty} \frac{ \left\lVert{ M_{\alpha(q)}^{k} h }\right\rVert_{\left(\Lambda^{1/{p_-}}\left( w \right)\right)' }}{\left( 2||M_{\alpha(q)}||_{\left(\Lambda^{1/{p_-}}\left( w \right)\right)'} \right)^{k} } \leq 2||h||_{\left(\Lambda^{1/{p_-} }(w)\right)'}. \]
is a Banach space (see [Reference Carro, Raposo and Soria12]),
\[ \lVert S_{\alpha(q)}h\rVert_{\left(\Lambda^{1/{p_-} }(w)\right)'} \leq \sum_{k = 0}^{\infty} \frac{ \left\lVert{ M_{\alpha(q)}^{k} h }\right\rVert_{\left(\Lambda^{1/{p_-}}\left( w \right)\right)' }}{\left( 2||M_{\alpha(q)}||_{\left(\Lambda^{1/{p_-}}\left( w \right)\right)'} \right)^{k} } \leq 2||h||_{\left(\Lambda^{1/{p_-} }(w)\right)'}. \]
Let $y > 0$![]() and observe that since $q - p_- = \beta (q)(q - 1)p_-$
and observe that since $q - p_- = \beta (q)(q - 1)p_-$![]() ,
,
and $v \in A_{q; (\alpha (q), \beta (q))}$![]() . Hence, for every $\gamma > 0$
. Hence, for every $\gamma > 0$![]() and since we know that (2.8) holds with $g = Tf$
and since we know that (2.8) holds with $g = Tf$![]() ,
,

Now, by the Hölder's inequality,

where in the last estimate we have used lemma 2.1. Therefore, by the properties of $R_{{1}/{p_-}}$![]() ,
,

Thus, taking the supremum in $y > 0$![]() and the infimum in $\gamma > 0$
and the infimum in $\gamma > 0$![]() ,
,

Finally, since
then (see [Reference Duoandikoetxea19, lemma 2.1])

so that
with

If $\alpha = 1$![]() , then $p_+ = \infty$
, then $p_+ = \infty$![]() and $w \in B_{1/{p_-}} \cap B^{*}_\infty$
and $w \in B_{1/{p_-}} \cap B^{*}_\infty$![]() . So, arguing identically as before but with $q = p_0$
. So, arguing identically as before but with $q = p_0$![]() and $\alpha (q) = 1$
and $\alpha (q) = 1$![]() , in addition to use proposition 2.6 instead of lemma 2.8 to define (3.1), we get that
, in addition to use proposition 2.6 instead of lemma 2.8 to define (3.1), we get that
with
Proof of corollary 1.10. Let $\tilde {w}:=W^{1/p-1}w$![]() . Hence, observe that
. Hence, observe that

Therefore, if $w\in B_{p/{p_-}} \cap B_{{p_+}/{p}}^{*}$![]() , by theorem 1.8, we have that
, by theorem 1.8, we have that
and hence
Now if $w\in B_{p/{p_-}} \cap B_{{p_+}/{p}}^{*}$![]() , there exists some $\delta > 0$
, there exists some $\delta > 0$![]() such that $w\in B_{{(p- \delta )}/{p_-}} \cap B_{{p_+}/{(p - \delta )}}^{*}$
such that $w\in B_{{(p- \delta )}/{p_-}} \cap B_{{p_+}/{(p - \delta )}}^{*}$![]() and $w\in B_{{(p+\delta )}/{p_-}} \cap B_{{p_+}/{(p+\delta )}}^{*}$
and $w\in B_{{(p+\delta )}/{p_-}} \cap B_{{p_+}/{(p+\delta )}}^{*}$![]() . Hence,
. Hence,
so that the result follows by interpolation on Lorentz spaces [Reference Carro, Raposo and Soria12, theorem 2.6.5].
Proof of theorem 1.11. The proof essentially follows the same steps as the proof of theorem 1.8 with few modifications. For the sake of completeness and the convenience of the reader, we have added a proof of it here.
Let $w \in B^{\mathcal {R}}_{1/{p_0}} \cap B_{{p_0}/{(1 - \alpha )}}^{*}$![]() . First, by lemma 2.9 (when $0 < \alpha < 1$
. First, by lemma 2.9 (when $0 < \alpha < 1$![]() ) and proposition 2.6 (when $\alpha = 1$
) and proposition 2.6 (when $\alpha = 1$![]() ) we can define, for an arbitrary nonnegative function $h \in (\Lambda ^{1/{p_0},\, 1}(w))'$
) we can define, for an arbitrary nonnegative function $h \in (\Lambda ^{1/{p_0},\, 1}(w))'$![]() ,
,

Then,
(i) $h(x) \leq R_{\alpha }h(x)$
 a.e. $x\in {{\mathbb {R}^{n}}}$
a.e. $x\in {{\mathbb {R}^{n}}}$ ,
,(ii) $R_{\alpha }h \in A_1$
 with $\left \lVert {R(h^{1/\alpha })}\right \rVert _{A_1}^{\alpha } \leq 2\left \lVert {M_\alpha }\right \rVert _{(\Lambda ^{1/{p_0},\,1}(w))'}$
with $\left \lVert {R(h^{1/\alpha })}\right \rVert _{A_1}^{\alpha } \leq 2\left \lVert {M_\alpha }\right \rVert _{(\Lambda ^{1/{p_0},\,1}(w))'}$ ,
,(iii) and, since $(\Lambda ^{1/{p_0},\, 1}(w))'$
 is a Banach space (see [Reference Carro, Raposo and Soria12]),
(3.2)\begin{equation} \lVert R_{\alpha}h\rVert_{\left(\Lambda^{1/{p_0}, 1}(w)\right)'} \leq 2 \left\lVert{h}\right\rVert_{\left(\Lambda^{1/{p_0}, 1}(w)\right)'}. \end{equation}
is a Banach space (see [Reference Carro, Raposo and Soria12]),
(3.2)\begin{equation} \lVert R_{\alpha}h\rVert_{\left(\Lambda^{1/{p_0}, 1}(w)\right)'} \leq 2 \left\lVert{h}\right\rVert_{\left(\Lambda^{1/{p_0}, 1}(w)\right)'}. \end{equation}
Let $y > 0$![]() and observe that $v = R( \chi _{\{Tf > y\}} ) \in A_1$
and observe that $v = R( \chi _{\{Tf > y\}} ) \in A_1$![]() . Then, we have
. Then, we have

where in the last estimate we have used the Hölder's inequality and the property (3.2) of $R_\alpha$![]() . Now, since $\Lambda ^{1/{p_0},\, 1}(w) = \Lambda ^{1}(\tilde w)$
. Now, since $\Lambda ^{1/{p_0},\, 1}(w) = \Lambda ^{1}(\tilde w)$![]() with $\tilde {W}(t)\approx W(t)^{p_0}$
with $\tilde {W}(t)\approx W(t)^{p_0}$![]() , by lemma 2.1
, by lemma 2.1

Thus,
and since

the result follows.
Proof of corollary 1.12. The proof follows the same pattern as in corollary 1.10.
4. Applications to the boundedness of operators
4.1 Bochner–Riesz $BR_\lambda$
Corollary 4.1 Let $n = 2,$![]() $0 < \lambda < \frac 12$
$0 < \lambda < \frac 12$![]() and $\frac 43 \leq q_0 \leq 4$
and $\frac 43 \leq q_0 \leq 4$![]() . If there exists some $\varepsilon >0$
. If there exists some $\varepsilon >0$![]() so that
so that
then $w\in \mathcal {W}(BR_\lambda ).$![]()
Proof. By proposition 1.5 (i), we have that $p_+=\frac {q_0}{1-2\lambda } \mbox { and } p_-= \frac {q_0}{1+2\lambda (q_0 - 1)}$![]() and the result follows by theorem 1.8.
and the result follows by theorem 1.8.
Corollary 4.2 Let $n = 2$![]() and $0 < \lambda < \frac 12$
and $0 < \lambda < \frac 12$![]() . If
. If
then $w\in \mathcal {W}(BR_\lambda ) \text { with } \left \lVert {w}\right \rVert _{\mathcal {W}(BR_\lambda )} \lesssim \left \lVert {w}\right \rVert _{B^{{\mathcal{R}}_{{(3+2\lambda )}/4}}}^{{(3+2\lambda )}/4} \left \lVert {w}\right \rVert _{B^{*}_{ 4/3}}^{{(7+4\lambda )}/{2\lambda }}.$![]()
Proof. By proposition 1.5 (ii), we have that $p_0= 4/{(3 + 2\lambda )} \mbox { and } \alpha = {2\lambda }/{(3 + 2\lambda )}$![]() and the result follows by theorem 1.11.
and the result follows by theorem 1.11.
Remark 4.3 As a first example of corollary 4.2, if we let $w_\lambda (t) = t^{{(2\lambda - 1)}/4 }$![]() , which clearly satisfies (4.1), then we conclude that $w_\lambda \in \mathcal {W}(BR_\lambda )$
, which clearly satisfies (4.1), then we conclude that $w_\lambda \in \mathcal {W}(BR_\lambda )$![]() ; that is, for this power weight, $BR_\lambda : \Lambda ^{1}(w_\lambda ) \rightarrow \Lambda ^{1,\infty }(w_\lambda )$
; that is, for this power weight, $BR_\lambda : \Lambda ^{1}(w_\lambda ) \rightarrow \Lambda ^{1,\infty }(w_\lambda )$![]() , or equivalently,
, or equivalently,
and, as expected, we obtain that the Bochner–Riesz conjecture holds for $BR_\lambda$![]() when $n = 2$
when $n = 2$![]() . Further, we also obtain spaces for which the boundedness of $BR_\lambda$
. Further, we also obtain spaces for which the boundedness of $BR_\lambda$![]() was not previously known. For instance, taking $w_m$
was not previously known. For instance, taking $w_m$![]() and $\tilde w_m$
and $\tilde w_m$![]() as in examples 2.5 (b) and (c), we have the inclusions
as in examples 2.5 (b) and (c), we have the inclusions

and the boundedness of

Corollary 4.4 Let $n > 2,$![]() $0 < \lambda < {(n-1)}/2$
$0 < \lambda < {(n-1)}/2$![]() and $q_0 = 2$
and $q_0 = 2$![]() or let $q_0$
or let $q_0$![]() be such that ${2n}/{(n+1)} < q_0 < 2$
be such that ${2n}/{(n+1)} < q_0 < 2$![]() and conjecture 1.2 holds with $p = q_0$
and conjecture 1.2 holds with $p = q_0$![]() . If $q \in \{q_0,\, q_0'\}$
. If $q \in \{q_0,\, q_0'\}$![]() and there exists some $\varepsilon >0$
and there exists some $\varepsilon >0$![]() so that
so that
then $w\in \mathcal {W}(BR_\lambda ).$![]()
Proof. By proposition 1.6 (i), we have that $p_+=\frac {q(n-1)}{n - 1 - 2\lambda }\mbox { and } p_-= \frac {q(n-1)}{n - 1 + 2\lambda (q-1)}$![]() for $q \in \{q_0,\, q_0'\}$
for $q \in \{q_0,\, q_0'\}$![]() , and the result follows by theorem 1.8.
, and the result follows by theorem 1.8.
Corollary 4.5 Let $n > 2$![]() and $\frac {n-1}{2(n+1)} < \lambda < {(n-1)}/2$
and $\frac {n-1}{2(n+1)} < \lambda < {(n-1)}/2$![]() . If
. If
or
then $w\in \mathcal {W}(BR_\lambda ).$![]()
4.2 Sparse operators
These operators have become very important due to its role in the so-called $A_2$![]() conjecture consisting in proving that if $T$
conjecture consisting in proving that if $T$![]() is a Calderón–Zygmund operator then
is a Calderón–Zygmund operator then
This result was first obtained by Hytönen [Reference Hytönen25] (see also [Reference Lerner31, Reference Lerner32]). Let us give the precise definition. A general dyadic grid $\mathcal {D}$![]() is a collection of cubes in $\mathbb {R}^{n}$
is a collection of cubes in $\mathbb {R}^{n}$![]() satisfying the following properties:
satisfying the following properties:
(i) For any cube $Q \in \mathcal {D}$
 , its side length is $2^{k}$
, its side length is $2^{k}$ for some $k \in \mathbb {Z}$
for some $k \in \mathbb {Z}$ .
.(ii) Every two cubes in $\mathcal {D}$
 are either disjoint or one is wholly contained in the other.
are either disjoint or one is wholly contained in the other.(iii) For every $k \in \mathbb {Z}$
 and given $x \in \mathbb {R}^{n}$
and given $x \in \mathbb {R}^{n}$ , there is only one cube in $\mathcal {D}$
, there is only one cube in $\mathcal {D}$ of side length $2^{k}$
of side length $2^{k}$ containing it.
containing it.
Let $0 < \eta < 1$![]() , a collection of cubes $\mathcal {S} \subset \mathcal {D}$
, a collection of cubes $\mathcal {S} \subset \mathcal {D}$![]() is called $\eta$
is called $\eta$![]() -sparse if, for every $Q\in \mathcal {S}$
-sparse if, for every $Q\in \mathcal {S}$![]() , there exist pairwise disjoint measurable sets $E_Q \subset Q$
, there exist pairwise disjoint measurable sets $E_Q \subset Q$![]() with $|E_Q| \geq \eta |Q|$
with $|E_Q| \geq \eta |Q|$![]() .
.
Definition 4.6 Let $1 \leq r < \infty$![]() . Given a sparse family of cubes $\mathcal {S} \subset \mathcal {D}$
. Given a sparse family of cubes $\mathcal {S} \subset \mathcal {D}$![]() , the sparse operator is defined by
, the sparse operator is defined by

The boundedness of $A_{1, \mathcal {S}}f$![]() over the Lorentz spaces $\Lambda ^{p}(w)$
over the Lorentz spaces $\Lambda ^{p}(w)$![]() was settled in [Reference Baena-Miret and Carro4]. Here we deal with the case $1 < r < \infty$
was settled in [Reference Baena-Miret and Carro4]. Here we deal with the case $1 < r < \infty$![]() . To do so, first we present the following restricted weak-type inequality for the sparse operator $\mathcal {A}_{r, \mathcal {S}}$
. To do so, first we present the following restricted weak-type inequality for the sparse operator $\mathcal {A}_{r, \mathcal {S}}$![]() . The proof follows by duality using the same ideas as in [Reference Carro, Grafakos and Soria11, theorem 4.1] with the obvious modifications.
. The proof follows by duality using the same ideas as in [Reference Carro, Grafakos and Soria11, theorem 4.1] with the obvious modifications.
Proposition 4.7 Given $1 < r < \infty$![]() and a weight $v \in A_1$
and a weight $v \in A_1$![]() . The sparse operator $\mathcal {A}_{r,\mathcal {S}}$
. The sparse operator $\mathcal {A}_{r,\mathcal {S}}$![]() satisfies the weak-type estimate
satisfies the weak-type estimate
Consequently, by theorem 1.11 and corollary 1.12:
Corollary 4.8 If
then $w\in \mathcal {W}(\mathcal {A}_{r,\mathcal {S}})$![]() with $\left \lVert {w}\right \rVert _{\mathcal {W}(A_{r,\mathcal {S}})} \lesssim \left \lVert {w}\right \rVert _{B_{1/r}^{{\mathcal{R}}}}^{1/r} \left \lVert {w}\right \rVert _{B^{*}_\infty }^{2}.$
with $\left \lVert {w}\right \rVert _{\mathcal {W}(A_{r,\mathcal {S}})} \lesssim \left \lVert {w}\right \rVert _{B_{1/r}^{{\mathcal{R}}}}^{1/r} \left \lVert {w}\right \rVert _{B^{*}_\infty }^{2}.$![]() Moreover, if for $0 < p < \infty$
Moreover, if for $0 < p < \infty$![]() ,
,
then
4.3 Hörmander multipliers
Let $m$![]() be a bounded function on $\mathbb {R}^{n}$
be a bounded function on $\mathbb {R}^{n}$![]() and consider the Fourier multiplier $T_m$
and consider the Fourier multiplier $T_m$![]() defined by
defined by
Set $s>1$![]() and let $\gamma =(\gamma _1,\, \ldots,\, \gamma _n)$
and let $\gamma =(\gamma _1,\, \ldots,\, \gamma _n)$![]() a multi-index of nonnegative integers with $|\gamma |=\gamma _1+\cdots +\gamma _n$
a multi-index of nonnegative integers with $|\gamma |=\gamma _1+\cdots +\gamma _n$![]() . It is said that $m\in M(s,\, l)$
. It is said that $m\in M(s,\, l)$![]() if
if

Proposition 4.9 [Reference Kurtz and Wheeden28]
Let $1 < s \leq 2,$![]() $n/s < l < n$
$n/s < l < n$![]() and $m \in M(s,\,l)$
and $m \in M(s,\,l)$![]() . Then:
. Then:
(i) If $v \in A_1,$
 \[ T_m:L^{1}(v^{ l/n}) \rightarrow L^{1,\infty}(v^{ l/n}), \]with constant less than or equal to $\varphi (\left \lVert {v}\right \rVert _{A_1}).$
\[ T_m:L^{1}(v^{ l/n}) \rightarrow L^{1,\infty}(v^{ l/n}), \]with constant less than or equal to $\varphi (\left \lVert {v}\right \rVert _{A_1}).$
 with $\varphi$
with $\varphi$ an increasing function.
an increasing function.(ii) If $v \in A_1,$
 \[ T_m:L^{ n/l}(v) \rightarrow L^{ n/l, \infty}(v), \]with constant less than or equal to ${\varphi }(\left \lVert {v}\right \rVert _{A_1}),$
\[ T_m:L^{ n/l}(v) \rightarrow L^{ n/l, \infty}(v), \]with constant less than or equal to ${\varphi }(\left \lVert {v}\right \rVert _{A_1}),$
 with ${\varphi }$
with ${\varphi }$ an increasing function.
an increasing function.
Consequently, by theorem 1.11 and corollary 1.12:
Corollary 4.10 Let $1 < s \leq 2,$![]() $n/s < l < n$
$n/s < l < n$![]() and $m \in M(s,\,l)$
and $m \in M(s,\,l)$![]() . If
. If
then $w \in \mathcal {W}(T_m).$![]() Moreover, if for $0 < p < \infty,$
Moreover, if for $0 < p < \infty,$![]()
then
4.4 Rough operators
Let $\Sigma =\Sigma _{n-1}=\{x\in \mathbb {R}^{n}: |x|=1\}$![]() and, for $1 < r < \infty$
and, for $1 < r < \infty$![]() , take $\Omega \in L^{r}(\Sigma )$
, take $\Omega \in L^{r}(\Sigma )$![]() to be a positive function homogeneous of degree zero such that $\int _\Sigma \Omega = 0$
to be a positive function homogeneous of degree zero such that $\int _\Sigma \Omega = 0$![]() . Let us consider the rough operator
. Let us consider the rough operator
whenever this limit exists almost everywhere and where $y'= y/{|y|}$![]() , $y\neq 0$
, $y\neq 0$![]() .
.
Proposition 4.11 [Reference Duoandikoetxea17]
If $v \in A_1$![]() ,
,
with constant less than or equal to $\varphi (\left \lVert {v}\right \rVert _{A_1}),$![]() with $\varphi$
with $\varphi$![]() an increasing function.
an increasing function.
Consequently, by theorem 1.11 and corollary 1.12:
Corollary 4.12 If
then $w \in \mathcal {W}(T_\Omega ).$![]() Moreover, for $0 < p < \infty,$
Moreover, for $0 < p < \infty,$![]() if
if
then
Also, if we assume that $\Omega$![]() satisfies the $L^{r}$
satisfies the $L^{r}$![]() -Dini condition, that is
-Dini condition, that is

with $\rho$![]() any rotation of $\Sigma$
any rotation of $\Sigma$![]() and $|\rho | = \sup _{x \in \Sigma }|\rho x - x|$
and $|\rho | = \sup _{x \in \Sigma }|\rho x - x|$![]() , we also have the following result:
, we also have the following result:
Proposition 4.13 [Reference Kurtz and Wheeden28]
If $v \in A_1,$![]()
with constant less than or equal to $\varphi (\left \lVert {v}\right \rVert _{A_1}),$![]() with $\varphi$
with $\varphi$![]() an increasing function.
an increasing function.
Consequently, by theorem 1.11 and corollary 1.12:
Corollary 4.14 If
then $w \in \mathcal {W}(T_\Omega ).$![]() Moreover, for $0 < p < \infty,$
Moreover, for $0 < p < \infty,$![]() if
if
then
Acknowledgments
The authors would like to thank the anonymous referee who provided useful, detailed and insightful comments on an earlier version of the manuscript. The authors were supported by grants MTM2016-75196-P and 2017SGR358 respectively.