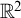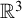1 Introduction
Let
![]() $k,n>0$
be natural numbers. An algebraic hypergraph
$k,n>0$
be natural numbers. An algebraic hypergraph
![]() $\Gamma $
of arity k on the Euclidean space
$\Gamma $
of arity k on the Euclidean space
![]() $\mathbb {R}^n$
is a subset of
$\mathbb {R}^n$
is a subset of
![]() $[\mathbb {R}^n]^k$
defined by a polynomial equation with real coefficients in
$[\mathbb {R}^n]^k$
defined by a polynomial equation with real coefficients in
![]() $kn$
unknowns; its elements are called hyperedges. A
$kn$
unknowns; its elements are called hyperedges. A
![]() $\Gamma $
-coloring is a (possibly partial) map c on
$\Gamma $
-coloring is a (possibly partial) map c on
![]() $\mathbb {R}^n$
such that there is no
$\mathbb {R}^n$
such that there is no
![]() $\Gamma $
-hyperedge on which
$\Gamma $
-hyperedge on which
![]() $\Gamma $
is constant by c. If there exists a total
$\Gamma $
is constant by c. If there exists a total
![]() $\Gamma $
-coloring whose range is countable, the chromatic number of
$\Gamma $
-coloring whose range is countable, the chromatic number of
![]() $\Gamma $
is countable; otherwise, the chromatic number of
$\Gamma $
is countable; otherwise, the chromatic number of
![]() $\Gamma $
is uncountable.
$\Gamma $
is uncountable.
This paper shows one result of comparing chromatic numbers for different algebraic hypergraphs in the context of choiceless set theory ZF+DC. It contributes to one of the numerous paths that balanced forcings in Geometric Set Theory [Reference Larson and Zapletal5] can lead to. In general, one can use balanced forcings to prove independence theorems in choiceless set theory concerning various
![]() $\Sigma ^2_1$
sentences.
$\Sigma ^2_1$
sentences.
In the context of ZFC theory, there has been a great deal of interest from people studying the partition/coloring problems on Euclidean spaces related to graphs and hypergraphs. Let
![]() $n\geq 2$
be a natural number. Let
$n\geq 2$
be a natural number. Let
![]() $\Gamma _n$
be the hypergraph of isosceles triangles on
$\Gamma _n$
be the hypergraph of isosceles triangles on
![]() $\mathbb {R}^n$
:
$\mathbb {R}^n$
:
![]() $\{x_0,x_1,x_2\} \in \Gamma _n \Longleftrightarrow d_n(x_0,x_1) = d_n(x_1,x_2)$
where
$\{x_0,x_1,x_2\} \in \Gamma _n \Longleftrightarrow d_n(x_0,x_1) = d_n(x_1,x_2)$
where
![]() $d_n$
is the Euclidean distance on
$d_n$
is the Euclidean distance on
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
![]() $\Gamma _n$
is an algebraic hypergraph arity three.
$\Gamma _n$
is an algebraic hypergraph arity three.
Fact 1.1 (ZFC)
[Reference Schmerl8] Let
![]() $n\geq 2$
be a natural number. The chromatic number of
$n\geq 2$
be a natural number. The chromatic number of
![]() $\Gamma _n$
is countable.
$\Gamma _n$
is countable.
Erdős and Kakutani conjectured that the conclusion of the theorem holds for all
![]() $n\geq 1$
, and proved the case for
$n\geq 1$
, and proved the case for
![]() $n=1$
[Reference Erdös and Kakutani2]. Given the Continuum Hypothesis, the theorem was proved by Kunen [Reference Kunen4]. Without the Continuum Hypothesis, the theorem was proved by Schmerl [Reference Schmerl8]. Later, Schmerl provided a complete classification [Reference Schmerl9]. The chromatic number of any algebraic hypergraph
$n=1$
[Reference Erdös and Kakutani2]. Given the Continuum Hypothesis, the theorem was proved by Kunen [Reference Kunen4]. Without the Continuum Hypothesis, the theorem was proved by Schmerl [Reference Schmerl8]. Later, Schmerl provided a complete classification [Reference Schmerl9]. The chromatic number of any algebraic hypergraph
![]() $\Gamma $
on a Euclidean space satisfies a trichotomy: ZFC proves exactly one of the following:
$\Gamma $
on a Euclidean space satisfies a trichotomy: ZFC proves exactly one of the following:
-
• The chromatic number is countable.
-
• The chromatic number is uncountable.
-
• There is a natural number
 $m\in \omega $
such that the chromatic number is countable if and only if
$m\in \omega $
such that the chromatic number is countable if and only if
 $2^{\aleph _0} \leq \aleph _m$
.
$2^{\aleph _0} \leq \aleph _m$
.
In addition, there is a computer program which, for a given algebraic equation, outputs the number m for the hypergraph given by the equation.
Now in the choiceless context, we realize that there are much finer differences between the chromatic numbers of different hypergraphs. It seems to be frequently the case that the countable chromatic number of one hypergraph doesn’t imply this number for another hypergraph, except for some obvious cases; e.g., for every n, the countable chromatic number of the hypergraph of isosceles triangles on
![]() $\mathbb {R}^{n+1}$
implies the one on
$\mathbb {R}^{n+1}$
implies the one on
![]() $\mathbb {R}^{n}$
. We notice that the dimension and the arity of a hypergraph play bigger roles for its chromatic number. The following is the main theorem of this paper.
$\mathbb {R}^{n}$
. We notice that the dimension and the arity of a hypergraph play bigger roles for its chromatic number. The following is the main theorem of this paper.
Theorem 1.2. It is consistent relative to an inaccessible cardinal that ZF+DC holds, and
![]() ${\Gamma _2}$
has countable chromatic number while
${\Gamma _2}$
has countable chromatic number while
![]() $\Gamma _3$
has uncountable chromatic number.
$\Gamma _3$
has uncountable chromatic number.
For this theorem, we will construct a model as a generic extension of the symmetric Solovay model. In fact, the conclusion for the model can be strengthened using the theorems of [Reference Larson and Zapletal5, Sections 9.1, 14.1, and 14.2]. We expect the theorem to hold for higher dimensions.
Conjecture 1.3. For every natural number
![]() $n \geq 2$
, it is consistent with ZF+DC that
$n \geq 2$
, it is consistent with ZF+DC that
![]() ${\Gamma _n}$
has countable chromatic number while
${\Gamma _n}$
has countable chromatic number while
![]() $\Gamma _{n+1}$
has uncountable chromatic number.
$\Gamma _{n+1}$
has uncountable chromatic number.
There are two main difficulties. The first is to invent a balanced forcing poset which will add a countable total
![]() $\Gamma _n$
-coloring. The second difficulty is to refine the poset so that it doesn’t add any countable total
$\Gamma _n$
-coloring. The second difficulty is to refine the poset so that it doesn’t add any countable total
![]() $\Gamma _{n+1}$
-coloring, often by investigating the geometric, algebraic, or combinatorial differences. For example, the core distinction to be used in this paper is that
$\Gamma _{n+1}$
-coloring, often by investigating the geometric, algebraic, or combinatorial differences. For example, the core distinction to be used in this paper is that
![]() $\Gamma _3$
satisfies Definition 6.13 for k at most
$\Gamma _3$
satisfies Definition 6.13 for k at most
![]() $4$
while
$4$
while
![]() $\Gamma _2$
satisfies Definition 6.13 for k at most
$\Gamma _2$
satisfies Definition 6.13 for k at most
![]() $3$
. We observe that similar distinction holds for every n and will be needed for handling the second difficulty. However, the first difficulty of getting a balanced poset increases with higher n. For example, if just adapting the poset that we use in this paper for
$3$
. We observe that similar distinction holds for every n and will be needed for handling the second difficulty. However, the first difficulty of getting a balanced poset increases with higher n. For example, if just adapting the poset that we use in this paper for
![]() $\mathbb {R}^3$
, the resulting poset won’t be balanced as Theorem 5.4 will fail due to higher dimension. Therefore, our approach does not generalize to separate the chromatic numbers for hypergraphs of isosceles triangles in dimension three and four. In comparison, the independence of the countable chromatic number for the hypergraph of rectangles between all dimensions has been established in [Reference Zapletal14]; the independence of the countable chromatic number between the hypergraph of rectangles and the hypergraph of equilateral triangles in all dimensions has been established in [Reference Zapletal13].
$\mathbb {R}^3$
, the resulting poset won’t be balanced as Theorem 5.4 will fail due to higher dimension. Therefore, our approach does not generalize to separate the chromatic numbers for hypergraphs of isosceles triangles in dimension three and four. In comparison, the independence of the countable chromatic number for the hypergraph of rectangles between all dimensions has been established in [Reference Zapletal14]; the independence of the countable chromatic number between the hypergraph of rectangles and the hypergraph of equilateral triangles in all dimensions has been established in [Reference Zapletal13].
All theorems and definitions in this paper take place in ZFC set theory; let V be a model of ZFC for this paper. The notation in this paper uses the set theoretic standard of [Reference Jech3], and in matters of geometric set theory [Reference Larson and Zapletal5]. Section 2 introduces the basics for DC, the symmetric Solovay model W, the
![]() $\mathbb {R}$
-analytic balanced forcing, and RCF. In Section 3, we construct a suitable poset P that adds a countable coloring for
$\mathbb {R}$
-analytic balanced forcing, and RCF. In Section 3, we construct a suitable poset P that adds a countable coloring for
![]() $\Gamma _2$
when forced over the model W. Section 4 introduces a natural notion of amalgamation positionFootnote
1
of pairs of real closed subfields of
$\Gamma _2$
when forced over the model W. Section 4 introduces a natural notion of amalgamation positionFootnote
1
of pairs of real closed subfields of
![]() $\mathbb {R}$
. Section 5 defines a notion of the analytic forcing with algebraic amalgamation of conditions; such forcing is cofinally balanced. Section 6 shows several open projections from some ordered hypergraphs; then we define the Cohen forcing to add a generic hyperedge for
$\mathbb {R}$
. Section 5 defines a notion of the analytic forcing with algebraic amalgamation of conditions; such forcing is cofinally balanced. Section 6 shows several open projections from some ordered hypergraphs; then we define the Cohen forcing to add a generic hyperedge for
![]() $\Gamma _3$
. Section 7 finally completes the proof of the main theorem.
$\Gamma _3$
. Section 7 finally completes the proof of the main theorem.
2 Preliminaries
2.1 Axiom of dependent choices (DC)
Definition 2.1. The axiom of dependent choices
![]() $(DC)$
: for every nonempty set X and every entire binary relation R on X, there exists a countable sequence in X such that every adjacent pairs are related.
$(DC)$
: for every nonempty set X and every entire binary relation R on X, there exists a countable sequence in X such that every adjacent pairs are related.
Theorem 2.2 [Reference Blair1]
Over ZF, DC is equivalent to the Baire category theorem for complete metric spaces.
DC is a fragment of AC on which the real analysis can be developed, possibly without paradoxical AC consequences such as the statement “there exists a set of reals that is not Lebesgue measurable.” The symmetric Solovay model [Reference Solovay10] is a model of ZF+DC that we use in this paper.
2.2 Symmetric Solovay model
Definition 2.3. If X is a set, then Coll
![]() $(\omega ,X)$
is the poset of finite partial functions from
$(\omega ,X)$
is the poset of finite partial functions from
![]() $\omega $
to X ordered by reverse extension; if
$\omega $
to X ordered by reverse extension; if
![]() $\kappa $
is a cardinal, then Coll
$\kappa $
is a cardinal, then Coll
![]() $(\omega ,< \kappa )$
is the finite support product of the posets Coll
$(\omega ,< \kappa )$
is the finite support product of the posets Coll
![]() $(\omega , \alpha )$
for all
$(\omega , \alpha )$
for all
![]() $\alpha \in \kappa $
.
$\alpha \in \kappa $
.
Any collapse poset obeys an important factoring rule.
Fact 2.4 [Reference Jech3, Corollary 26.11]
Let
![]() $\lambda $
be a cardinal and let P be a poset of cardinality
$\lambda $
be a cardinal and let P be a poset of cardinality
![]() $<\lambda $
. Suppose that
$<\lambda $
. Suppose that
![]() $G\subset $
Coll(
$G\subset $
Coll(
![]() $\omega ,\lambda $
) is a generic filter and in
$\omega ,\lambda $
) is a generic filter and in
![]() $V[G]$
,
$V[G]$
,
![]() $H\subset P$
is a filter generic over
$H\subset P$
is a filter generic over
![]() $V $
. Then there is a filter
$V $
. Then there is a filter
![]() $K \subset Coll(\omega , \lambda )$
generic over
$K \subset Coll(\omega , \lambda )$
generic over
![]() $V [H]$
such that
$V [H]$
such that
![]() $V [G] = V [H][K]$
.
$V [G] = V [H][K]$
.
Definition 2.5 [Reference Solovay10]
Let
![]() $\kappa $
be an inaccessible cardinal and let
$\kappa $
be an inaccessible cardinal and let
![]() $G\subset \mbox {Coll}(\omega , < \kappa )$
be a generic filter over V. In
$G\subset \mbox {Coll}(\omega , < \kappa )$
be a generic filter over V. In
![]() $V [G]$
, form HOD
$V [G]$
, form HOD
![]() $(V\cup \omega ^\omega )$
, the model of all sets hereditarily definable from reals and elements of the ground model. This is the symmetric Solovay model; we denote it by W.
$(V\cup \omega ^\omega )$
, the model of all sets hereditarily definable from reals and elements of the ground model. This is the symmetric Solovay model; we denote it by W.
The theory of the symmetric Solovay model has been fulled developed, including the following one:
Fact 2.6 [Reference Solovay10, Reference Stern11]
In W, ZF+DC holds, every set has the Baire property and is Lebesgue measurable, and there is no uncountable well-ordered sequence of distinct Borel sets of bounded Borel rank.
We will make use of the following technical facts in the paper.
Fact 2.7 [Reference Jech3, Section 26], [Reference Solovay10]
Let
![]() $\kappa $
be an inaccessible cardinal and let W be the symmetric Solovay extension of V associated with
$\kappa $
be an inaccessible cardinal and let W be the symmetric Solovay extension of V associated with
![]() $\kappa $
. Then the following hold in
$\kappa $
. Then the following hold in
![]() $W:$
$W:$
-
1. Eevery set is definable from parameters in
 $V \cup \omega ^\omega $
.
$V \cup \omega ^\omega $
. -
2. Whenever M is a generic extension of V by a partial order of cardinality smaller than
 $\kappa $
, then W is a symmetric Solovay extension of M.
$\kappa $
, then W is a symmetric Solovay extension of M. -
3. Whenever a is a set of ordinals, then
 $V [a]$
is a generic extension of V by a poset of cardinality smaller than
$V [a]$
is a generic extension of V by a poset of cardinality smaller than
 $\kappa $
.
$\kappa $
.
Fact 2.8 [Reference Larson and Zapletal5, Corollary 1.7.17], [Reference Solovay10]
Suppose that
![]() $\kappa $
is an inaccessible cardinal, X is a Polish space,
$\kappa $
is an inaccessible cardinal, X is a Polish space,
![]() $\phi ( x,\bar y)$
is a formula of set theory with all free variables displayed, and
$\phi ( x,\bar y)$
is a formula of set theory with all free variables displayed, and
![]() $\bar z$
is a sequence of sets of the same length as
$\bar z$
is a sequence of sets of the same length as
![]() $\bar y$
. The following are equivalent:
$\bar y$
. The following are equivalent:
-
1. Coll(
 $\omega ,< \kappa ) \Vdash \exists x \in X \ \phi (x,\bar z)$
.
$\omega ,< \kappa ) \Vdash \exists x \in X \ \phi (x,\bar z)$
. -
2. There exist a poset R of cardinality smaller than
 $\kappa $
and an R-name
$\kappa $
and an R-name
 $\sigma $
for an element of X such that
$\sigma $
for an element of X such that
 $R \Vdash $
Coll(
$R \Vdash $
Coll(
 $\omega , < \kappa ) \Vdash \phi (\sigma ,\bar z)$
.
$\omega , < \kappa ) \Vdash \phi (\sigma ,\bar z)$
.
2.3
 $\mathbb {R}$
-analytic balanced forcing
$\mathbb {R}$
-analytic balanced forcing
In this paper we deal with analytic forcings, a looser notion than Suslin forcings from the book [Reference Larson and Zapletal5, Section 5.2].
Definition 2.9. An analytic forcing is a poset
![]() $\langle P,\leq \rangle $
for which there is a Polish space X so that:
$\langle P,\leq \rangle $
for which there is a Polish space X so that:
-
1. P is an analytic subset of X.
-
2. The partial order relation
 $\leq $
is an analytic subset of
$\leq $
is an analytic subset of
 $X^2$
.
$X^2$
.
Being different from Suslin forcings, analytic forcings don’t require the incompatibility relation
![]() $\{\langle p_0, p_1\rangle \in P^2 : \forall q \in P \ q\not \leq p_0 \vee q\not \leq p_1\}$
to be also an analytic subset of
$\{\langle p_0, p_1\rangle \in P^2 : \forall q \in P \ q\not \leq p_0 \vee q\not \leq p_1\}$
to be also an analytic subset of
![]() $X^2$
. Note that the compatibility relation is automatically analytic.
$X^2$
. Note that the compatibility relation is automatically analytic.
Definition 2.10. An
![]() $\mathbb {R}$
-analytic forcing is an analytic forcing P such that:
$\mathbb {R}$
-analytic forcing is an analytic forcing P such that:
-
1. Each condition
 $p \in P$
is a structure in some fixed relational first order language whose universe
$p \in P$
is a structure in some fixed relational first order language whose universe
 $\mathrm {supp}(p)$
is a countable real closed subfield of
$\mathrm {supp}(p)$
is a countable real closed subfield of
 $\mathbb {R}$
.
$\mathbb {R}$
. -
2.
 $p_1 \leq p_0$
implies
$p_1 \leq p_0$
implies
 $p_1 \upharpoonright \mathrm {supp}(p_0) = p_0$
.
$p_1 \upharpoonright \mathrm {supp}(p_0) = p_0$
. -
3. For every countable set
 $a \subset \mathbb {R}$
and every condition
$a \subset \mathbb {R}$
and every condition
 $p_0 \in P$
there is a condition
$p_0 \in P$
there is a condition
 $p_1 \leq p_0$
such that
$p_1 \leq p_0$
such that
 $a \subset \mathrm {supp}(p_1)$
.
$a \subset \mathrm {supp}(p_1)$
. -
4. P is
 $\sigma $
-closed: whenever
$\sigma $
-closed: whenever
 $\langle p_n : n \in \omega \rangle $
is a descending sequence of conditions then
$\langle p_n : n \in \omega \rangle $
is a descending sequence of conditions then
 $\bigcup _n p_n \in P$
is their lower bound.
$\bigcup _n p_n \in P$
is their lower bound.
Thus, an
![]() $\mathbb {R}$
-analytic forcing adds a certain generic structure on
$\mathbb {R}$
-analytic forcing adds a certain generic structure on
![]() $\mathbb {R}$
which is the union of all (countable) structures in the generic filter. By quantifier counting procedure, one can check being an
$\mathbb {R}$
which is the union of all (countable) structures in the generic filter. By quantifier counting procedure, one can check being an
![]() $\mathbb {R}$
-analytic forcing is a
$\mathbb {R}$
-analytic forcing is a
![]() $\Pi ^1_2$
statement and therefore absolute throughout all forcing extensions by the Shoenfield absoluteness [Reference Jech3, Theorem 25.20].
$\Pi ^1_2$
statement and therefore absolute throughout all forcing extensions by the Shoenfield absoluteness [Reference Jech3, Theorem 25.20].
Balanced forcings are fully developed in the book [Reference Larson and Zapletal5, Section 5.2]. Intuitively speaking, a balanced condition is a condition
![]() $p_0$
such that, under some circumstance,
$p_0$
such that, under some circumstance,
![]() $\forall p_1,p_2\leq p_0\ \exists p_3\leq p_1,p_2 $
holds. Rigorously, one needs the notion of balanced pairs and balanced virtual conditionsFootnote
2
by taking the quotient of some equivalence relation on balanced pairs as [Reference Larson and Zapletal5, Definitions 5.1.6, 5.1.7, 5.2.1, and 5.2.5].
$\forall p_1,p_2\leq p_0\ \exists p_3\leq p_1,p_2 $
holds. Rigorously, one needs the notion of balanced pairs and balanced virtual conditionsFootnote
2
by taking the quotient of some equivalence relation on balanced pairs as [Reference Larson and Zapletal5, Definitions 5.1.6, 5.1.7, 5.2.1, and 5.2.5].
Definition 2.11 [Reference Larson and Zapletal5, Definition 5.2.10]
Let P be an analytic forcing. P is balanced if for every condition
![]() $p \in P$
there is a balanced virtual condition below p.
$p \in P$
there is a balanced virtual condition below p.
Definition 2.12 [Reference Larson and Zapletal5, Section 1.7]
Let P be an analytic forcing. Let
![]() $\kappa $
be an inaccessible cardinal. P is balanced cofinally below
$\kappa $
be an inaccessible cardinal. P is balanced cofinally below
![]() $\kappa $
if
$\kappa $
if
![]() $V_\kappa \models $
every forcing extension has a further extension in which P is balanced.
$V_\kappa \models $
every forcing extension has a further extension in which P is balanced.
Cofinally balanced analytic forcings do not add any well-ordered sequences of elements of the symmetric Solovay model:
Theorem 2.13 [Reference Larson and Zapletal5, Theorem 9.1.1]
Let
![]() $\kappa $
be an inaccessible cardinal. Let W be the symmetric Solovay model derived from
$\kappa $
be an inaccessible cardinal. Let W be the symmetric Solovay model derived from
![]() $\kappa $
. Let P be balanced cofinally below
$\kappa $
. Let P be balanced cofinally below
![]() $\kappa $
. Then in any P extension of W, every well-ordered sequence of elements of W belongs to W.
$\kappa $
. Then in any P extension of W, every well-ordered sequence of elements of W belongs to W.
As a consequence, any cofinally balanced analytic forcing has a limitation: there is no balanced analytic forcing for the hypergraph of right triangles, according to [Reference Zapletal12].
2.4 Real closed fields (RCF)
Consider the real closed field
![]() $\langle \mathbb {R}, +, \cdot , \leq \rangle $
: its ordering is invariant under addition and multiplication by positive elements, and every polynomial of odd degree has a root. Model theory of real closed fields (RCF) is well established in [Reference Marker6, Section 3.3]. We will make use of two key facts: real closed fields satisfy quantifier elimination [Reference Marker6, Theorem 3.3.15] and they are model complete [Reference Marker6, Corollary 3.3.16]: if
$\langle \mathbb {R}, +, \cdot , \leq \rangle $
: its ordering is invariant under addition and multiplication by positive elements, and every polynomial of odd degree has a root. Model theory of real closed fields (RCF) is well established in [Reference Marker6, Section 3.3]. We will make use of two key facts: real closed fields satisfy quantifier elimination [Reference Marker6, Theorem 3.3.15] and they are model complete [Reference Marker6, Corollary 3.3.16]: if
![]() $F\subset \mathbb {R}$
is a real closed subfield, then F is an elementary submodel of
$F\subset \mathbb {R}$
is a real closed subfield, then F is an elementary submodel of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
We have a model theoretic notion of “algebraic” in the context of real closed fields.
Definition 2.14. Let
![]() $m,n>0$
be natural numbers.
$m,n>0$
be natural numbers.
-
• If
 $x_0 \in \mathbb {R}$
is a point and
$x_0 \in \mathbb {R}$
is a point and
 $b \subset \mathbb {R}$
is a set, we say that
$b \subset \mathbb {R}$
is a set, we say that
 $x_0$
is an algebraic point over b if there is a polynomial
$x_0$
is an algebraic point over b if there is a polynomial
 $p(x, \bar y)$
with coefficients in
$p(x, \bar y)$
with coefficients in
 $\mathbb {Z}$
and a tuple
$\mathbb {Z}$
and a tuple
 $\bar y_0$
with each coordinate from
$\bar y_0$
with each coordinate from
 $ b$
such that
$ b$
such that
 $p(x_0, \bar y_0) = 0$
and
$p(x_0, \bar y_0) = 0$
and
 $\{x \in \mathbb {R} : p(x, \bar y_0) = 0\}$
is finite.
$\{x \in \mathbb {R} : p(x, \bar y_0) = 0\}$
is finite. -
• If
 $\bar x_0 \in \mathbb {R}^n$
is a point and
$\bar x_0 \in \mathbb {R}^n$
is a point and
 $b\subset \bigcup _ {m'\in m}\mathbb {R}^{m'}$
is a set, we say that
$b\subset \bigcup _ {m'\in m}\mathbb {R}^{m'}$
is a set, we say that
 $\bar x_0$
is an algebraic point over b if each coordinate of
$\bar x_0$
is an algebraic point over b if each coordinate of
 $\bar x_0$
is an algebraic point in
$\bar x_0$
is an algebraic point in
 $\mathbb {R}$
over the set
$\mathbb {R}$
over the set
 $\{\beta : \beta $
is a coordinate of some element in
$\{\beta : \beta $
is a coordinate of some element in
 $b \} \subset \mathbb {R}$
.
$b \} \subset \mathbb {R}$
. -
• If
 $A \subset \mathbb {R}^n$
is a set and
$A \subset \mathbb {R}^n$
is a set and
 $b \subset \mathbb {R}$
is a set, we say that A is an algebraic set over b if there is a polynomial
$b \subset \mathbb {R}$
is a set, we say that A is an algebraic set over b if there is a polynomial
 $p(\bar x, \bar y)$
with coefficients in
$p(\bar x, \bar y)$
with coefficients in
 $\mathbb {Z}$
and a tuple
$\mathbb {Z}$
and a tuple
 $\bar y_0$
with each coordinate from
$\bar y_0$
with each coordinate from
 $ b$
such that
$ b$
such that
 $A= \{\bar x \in \mathbb {R}^n : p(\bar x, \bar y_0) = 0\}$
.
$A= \{\bar x \in \mathbb {R}^n : p(\bar x, \bar y_0) = 0\}$
.
There is a fact that bridges between algebraic points and algebraic sets.
Fact 2.15. Let
![]() $n>0$
be a natural number. Let F be a real closed field. If
$n>0$
be a natural number. Let F be a real closed field. If
![]() $A \subset F^n$
is a finite set,
$A \subset F^n$
is a finite set,
![]() $b \subset F$
is a set, and A is an algebraic set over b, then every point in A is an algebraic point over b.
$b \subset F$
is a set, and A is an algebraic set over b, then every point in A is an algebraic point over b.
Proof Assume
![]() $A \subset F^n$
is a nonempty finite set,
$A \subset F^n$
is a nonempty finite set,
![]() $b \subset F$
is a set, and A is an algebraic set over b. Then there is a polynomial
$b \subset F$
is a set, and A is an algebraic set over b. Then there is a polynomial
![]() $p(\bar x, \bar y)$
with coefficients in
$p(\bar x, \bar y)$
with coefficients in
![]() $\mathbb {Z}$
and a tuple
$\mathbb {Z}$
and a tuple
![]() $\bar y_0$
with each coordinate from
$\bar y_0$
with each coordinate from
![]() $ b$
such that
$ b$
such that
![]() $A= \{\bar x \in \mathbb {R}^n : p(\bar x, \bar y_0) = 0\}$
. Fix a coordinate
$A= \{\bar x \in \mathbb {R}^n : p(\bar x, \bar y_0) = 0\}$
. Fix a coordinate
![]() $i\in n$
. Then the ith projection
$i\in n$
. Then the ith projection
![]() $A|_i = \{x\in \mathbb {R}^{\{i\}} : \exists \bar x \in \mathbb {R}^{n\setminus \{i\} }\ p(x, \bar x, \bar y_0) = 0\}$
has cardinality at least one and at most
$A|_i = \{x\in \mathbb {R}^{\{i\}} : \exists \bar x \in \mathbb {R}^{n\setminus \{i\} }\ p(x, \bar x, \bar y_0) = 0\}$
has cardinality at least one and at most
![]() $|A| < \infty $
. By quantifier elimination of the real closed field F, there is a quantifier-free formula
$|A| < \infty $
. By quantifier elimination of the real closed field F, there is a quantifier-free formula
![]() $\phi $
such that
$\phi $
such that
![]() $A|_i = \{x\in \mathbb {R}^{\{i\}} :\phi (x, \bar y_0)\}$
. We may assume that all atomic formulas appearing in
$A|_i = \{x\in \mathbb {R}^{\{i\}} :\phi (x, \bar y_0)\}$
. We may assume that all atomic formulas appearing in
![]() $\phi $
are of the form“
$\phi $
are of the form“
![]() $q(x, \bar y)>0$
” or “
$q(x, \bar y)>0$
” or “
![]() $q(x, \bar y)=0$
” for some polynomial q with integer coefficients. Let
$q(x, \bar y)=0$
” for some polynomial q with integer coefficients. Let
![]() $\{q_j : j \in k\}$
be a list of all polynomials appearing in
$\{q_j : j \in k\}$
be a list of all polynomials appearing in
![]() $\phi $
. Let
$\phi $
. Let
![]() $x_i\in A|_i$
. Let
$x_i\in A|_i$
. Let
![]() $a = \{j \in k: q_j(x_i, \bar y_0) = 0\}$
. Then
$a = \{j \in k: q_j(x_i, \bar y_0) = 0\}$
. Then
![]() $\psi (x, \bar y) = \sum _{j\in a} q_j^2 (x, \bar y) $
is a polynomial with single variable x such that
$\psi (x, \bar y) = \sum _{j\in a} q_j^2 (x, \bar y) $
is a polynomial with single variable x such that
![]() $\psi (x_i, \bar y_0) = 0$
where
$\psi (x_i, \bar y_0) = 0$
where
![]() $\bar y_0$
has every coordinate from
$\bar y_0$
has every coordinate from
![]() $ b$
.
$ b$
.
Finally,
![]() $\psi (x, \bar y_0) $
cannot be the zero polynomial. Suppose it is the zero polynomial for the sake of contradiction. Then for every
$\psi (x, \bar y_0) $
cannot be the zero polynomial. Suppose it is the zero polynomial for the sake of contradiction. Then for every
![]() $ j$
,
$ j$
,
![]() $q_j(x, \bar y_0)$
is the zero polynomial. Since
$q_j(x, \bar y_0)$
is the zero polynomial. Since
![]() $\phi (x, \bar y_0)$
is neither a tautology nor a contradiction as
$\phi (x, \bar y_0)$
is neither a tautology nor a contradiction as
![]() $0<|(A|_i) |<\infty $
, we can remove every
$0<|(A|_i) |<\infty $
, we can remove every
![]() $q_j(x, \bar y_0) = 0 $
inside the formula
$q_j(x, \bar y_0) = 0 $
inside the formula
![]() $\phi (x, \bar y_0)$
, so all atomic formulas appearing in
$\phi (x, \bar y_0)$
, so all atomic formulas appearing in
![]() $\phi (x, \bar y_0)$
are of the form“
$\phi (x, \bar y_0)$
are of the form“
![]() $q(x, \bar y_0)>0$
” for some polynomial q with integer coefficients. In any case, the set
$q(x, \bar y_0)>0$
” for some polynomial q with integer coefficients. In any case, the set
![]() $A|_i = \{x\in \mathbb {R}^{\{i\}} :\phi (x, \bar y_0)\}$
must be either empty or infinite, which is a contradiction. Hence
$A|_i = \{x\in \mathbb {R}^{\{i\}} :\phi (x, \bar y_0)\}$
must be either empty or infinite, which is a contradiction. Hence
![]() $\psi (x, \bar y_0) $
has finitely many roots. Hence the ith coordinate of each element in A is an algebraic point over b. Hence every point in A is an algebraic point over b.
$\psi (x, \bar y_0) $
has finitely many roots. Hence the ith coordinate of each element in A is an algebraic point over b. Hence every point in A is an algebraic point over b.
We note that the model theoretic notion of “algebraic” agrees with the field-theoretic notion of “algebraic” for real closed fields (RCF). It is also the case for algebraic closed fields (ACF) as [Reference Marker6, Proposition 3.2.15]. Because quantifier elimination is satisfied in both RCF and ACF, two proofs are the same.
Fact 2.16. Let
![]() $K \models $
RCF and
$K \models $
RCF and
![]() $A \subset K$
. Then
$A \subset K$
. Then
![]() $x $
is an algebraic point over A if and only if x is algebraic over the subfield of K generated by A.
$x $
is an algebraic point over A if and only if x is algebraic over the subfield of K generated by A.
3 Construction of the poset
Recall that
![]() $\Gamma _2$
is the hypergraph of isosceles triangles on
$\Gamma _2$
is the hypergraph of isosceles triangles on
![]() $\mathbb {R}^2$
. In this section, we will produce a balanced
$\mathbb {R}^2$
. In this section, we will produce a balanced
![]() $\mathbb {R}$
-analytic poset P adding a total
$\mathbb {R}$
-analytic poset P adding a total
![]() $\Gamma _2$
-coloring. The model for the main theorem of this paper will be a P-generic extension of the symmetric Solovay model. For any set
$\Gamma _2$
-coloring. The model for the main theorem of this paper will be a P-generic extension of the symmetric Solovay model. For any set
![]() $b \subset \mathbb {R}$
, let
$b \subset \mathbb {R}$
, let
![]() $E^L(b)$
be the set of lines in
$E^L(b)$
be the set of lines in
![]() $\mathbb {R}^2$
algebraic over b; let
$\mathbb {R}^2$
algebraic over b; let
![]() $E^O (b)$
be the set of circles in
$E^O (b)$
be the set of circles in
![]() $\mathbb {R}^2$
algebraic over b. For any map p from a subset of
$\mathbb {R}^2$
algebraic over b. For any map p from a subset of
![]() $\mathbb {R}^2$
to
$\mathbb {R}^2$
to
![]() $\omega $
and for any line
$\omega $
and for any line
![]() $l\subset \mathbb {R}^2$
, let
$l\subset \mathbb {R}^2$
, let
![]() $s(p, l)$
be the set
$s(p, l)$
be the set
![]() $\{i\in \omega : \mbox {there are points }y_0, y_1 $
in
$\{i\in \omega : \mbox {there are points }y_0, y_1 $
in
![]() $\mathrm {dom}(p)$
symmetricalFootnote
3
with respect to
$\mathrm {dom}(p)$
symmetricalFootnote
3
with respect to
![]() $ l $
and
$ l $
and
![]() $ p(y_0) = p(y_1) = i\}$
. Fix a Borel ideal
$ p(y_0) = p(y_1) = i\}$
. Fix a Borel ideal
![]() $I $
on
$I $
on
![]() $\omega $
that contains all finite sets and it is not generated by countably many sets. Most ideals that people use have such property, such as the summable ideals. The particular choice of the ideal seems unimportant.
$\omega $
that contains all finite sets and it is not generated by countably many sets. Most ideals that people use have such property, such as the summable ideals. The particular choice of the ideal seems unimportant.
Definition 3.1. Define P to be the poset of all conditions p such that:
-
1.
 $\mathrm {supp}(p)$
is a countable real closed subfield and
$\mathrm {supp}(p)$
is a countable real closed subfield and
 $\mathrm {supp}(p)^2 = \mathrm {dom}(p) \subset \mathbb {R}^2$
;
$\mathrm {supp}(p)^2 = \mathrm {dom}(p) \subset \mathbb {R}^2$
; -
2.
 $ p: \mathrm {dom}(p) \rightarrow \omega $
is a partial
$ p: \mathrm {dom}(p) \rightarrow \omega $
is a partial
 $\Gamma _2$
-coloring;
$\Gamma _2$
-coloring; -
3. (the symmetrical colors requirement) for each line
 $l \in E^L(\mathrm {supp}(p)) $
,
$l \in E^L(\mathrm {supp}(p)) $
,
 $s(p, l) \in I$
holds.
$s(p, l) \in I$
holds.
The ordering is defined by
![]() $p_1 \leq p_0$
if:
$p_1 \leq p_0$
if:
-
4.
 $\mathrm {dom}(p_1) \supset \mathrm {dom}(p_0)$
;
$\mathrm {dom}(p_1) \supset \mathrm {dom}(p_0)$
; -
5.
 $p_1\upharpoonright {\mathrm {dom}(p_0)} = p_0$
;
$p_1\upharpoonright {\mathrm {dom}(p_0)} = p_0$
; -
6. (the symmetrical colors invariant requirement) for each
 $l \in \ E^L(\mathrm {supp}(p_0)) $
,
$l \in \ E^L(\mathrm {supp}(p_0)) $
,
 $s(p_0, l) = s(p_1, l)$
holds;
$s(p_0, l) = s(p_1, l)$
holds; -
7. (the avoid center requirement) for each circle
 $e\in E^O(\mathrm {supp}(p_0))$
, for each point
$e\in E^O(\mathrm {supp}(p_0))$
, for each point
 $ x \ \in e \cap ( \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)), p_1(x) \neq p_0(t) $
holds where t is the center of e;
$ x \ \in e \cap ( \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)), p_1(x) \neq p_0(t) $
holds where t is the center of e; -
8. (the algebraic points requirement) for every finite set
 $ a \subset \mathrm {supp}(p_1)$
, the
$ a \subset \mathrm {supp}(p_1)$
, the
 $p_1$
-image of the set
$p_1$
-image of the set
 $\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
 $x $
is algebraic over
$x $
is algebraic over
 $\mathrm {supp}(p_0)\cup a\} $
is in
$\mathrm {supp}(p_0)\cup a\} $
is in
 $ I$
.
$ I$
.
First and foremost, one can check from Definition 3.1 that the underlying set and the ordering of the poset P are Borel (as each quantifier is quantifying over a countable set, by rewriting the definition if necessary). Automatically, the compatibility relation is also analytic. Therefore, the poset P is analytic. We will be checking that P is an
![]() $\mathbb {R}$
-analytic poset as Definition 2.10 for the rest of the section. For every condition
$\mathbb {R}$
-analytic poset as Definition 2.10 for the rest of the section. For every condition
![]() $p\in P$
, we have some useful real closure facts for
$p\in P$
, we have some useful real closure facts for
![]() $\mathrm {supp}(p)$
.
$\mathrm {supp}(p)$
.
Fact 3.2. Let
![]() $p\in P$
be a condition. Let
$p\in P$
be a condition. Let
![]() $x_0,x_1,x_2$
be distinct points in
$x_0,x_1,x_2$
be distinct points in
![]() $\mathrm {dom}(p) $
. Then the following hold:
$\mathrm {dom}(p) $
. Then the following hold:
-
1. The unique line that passes through
 $x_0,x_1$
is in
$x_0,x_1$
is in
 $E^L(\mathrm {supp}(p))$
.
$E^L(\mathrm {supp}(p))$
. -
2. The unique line that is the perpendicular bisector of the line segment from
 $x_0$
to
$x_0$
to
 $x_1$
is in
$x_1$
is in
 $E^L(\mathrm {supp}(p))$
.
$E^L(\mathrm {supp}(p))$
. -
3. The unique circle centered at
 $x_0$
passes through
$x_0$
passes through
 $x_1$
is in
$x_1$
is in
 $E^O(\mathrm {supp}(p))$
.
$E^O(\mathrm {supp}(p))$
. -
4. If
 $x_0,x_1,x_2$
are not colinear, the unique circle that passes through
$x_0,x_1,x_2$
are not colinear, the unique circle that passes through
 $x_0,x_1,x_2$
is in
$x_0,x_1,x_2$
is in
 $E^O(\mathrm {supp}(p))$
.
$E^O(\mathrm {supp}(p))$
. -
5. For all distinct line
 $(s)$
or circle
$(s)$
or circle
 $(s) \ e_0,e_1\in E^L(\mathrm {supp}(p))\cup E^O(\mathrm {supp}(p))$
,
$(s) \ e_0,e_1\in E^L(\mathrm {supp}(p))\cup E^O(\mathrm {supp}(p))$
,
 $e_0\cap e_1\subset \mathrm {dom}(p)$
holds.
$e_0\cap e_1\subset \mathrm {dom}(p)$
holds. -
6. For every line
 $e\in E^L(\mathrm {supp}(p))$
and every point
$e\in E^L(\mathrm {supp}(p))$
and every point
 $x\in \mathrm {dom}(p)\setminus e$
, the point that is symmetrical to x with respect to e is in
$x\in \mathrm {dom}(p)\setminus e$
, the point that is symmetrical to x with respect to e is in
 $\mathrm {dom}(p)$
.
$\mathrm {dom}(p)$
. -
7. For every circle
 $ e\in E^O(\mathrm {supp}(p))$
, the center of e is in
$ e\in E^O(\mathrm {supp}(p))$
, the center of e is in
 $\mathrm {dom}(p)$
.
$\mathrm {dom}(p)$
.
Proof Let us prove a few from above. Other proofs will be similar. Let
![]() $d_2$
be the Euclidean distance on
$d_2$
be the Euclidean distance on
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
For (3), the unique circle centered at
![]() $x_0$
passes through
$x_0$
passes through
![]() $x_1$
is the set
$x_1$
is the set
![]() $\{y\in \mathbb {R}^2: d_2(y, x_0) = d_2(x_1, x_0)\}$
, and clearly this set is a circle algebraic over
$\{y\in \mathbb {R}^2: d_2(y, x_0) = d_2(x_1, x_0)\}$
, and clearly this set is a circle algebraic over
![]() $\mathrm {supp}(p)$
since
$\mathrm {supp}(p)$
since
![]() $x_0,x_1$
are distinct points in
$x_0,x_1$
are distinct points in
![]() $\mathrm {dom}(p) $
; hence this set is in
$\mathrm {dom}(p) $
; hence this set is in
![]() $E^O(\mathrm {supp}(p))$
.
$E^O(\mathrm {supp}(p))$
.
For (4), it is easy to see that
![]() $\{y: d_2(y, x_0) = d_2(y, x_1) =d_2(y, x_2) \}$
is the set
$\{y: d_2(y, x_0) = d_2(y, x_1) =d_2(y, x_2) \}$
is the set
![]() $\{c\} $
for some
$\{c\} $
for some
![]() $c\in \mathbb {R}^2$
. As a consequence of Fact 2.15, c is in
$c\in \mathbb {R}^2$
. As a consequence of Fact 2.15, c is in
![]() $\mathrm {dom}(p)$
using the real closure property of
$\mathrm {dom}(p)$
using the real closure property of
![]() $\mathrm {supp}(p)$
and by definition of
$\mathrm {supp}(p)$
and by definition of
![]() $\mathrm {dom}(p) $
. Then the unique circle that passes through
$\mathrm {dom}(p) $
. Then the unique circle that passes through
![]() $x_0,x_1,x_2$
is just the unique circle centered at c that passes through
$x_0,x_1,x_2$
is just the unique circle centered at c that passes through
![]() $x_1$
, which is in
$x_1$
, which is in
![]() $E^O(\mathrm {supp}(p))$
by (3).
$E^O(\mathrm {supp}(p))$
by (3).
(5) uses the fact that the intersection of two algebraic sets is algebraic and Fact 2.15.
For (7), fix a circle
![]() $ e\in E^O(\mathrm {supp}(p))$
. We just need to somehow find three non-colinear points on
$ e\in E^O(\mathrm {supp}(p))$
. We just need to somehow find three non-colinear points on
![]() $e\cap \mathrm {dom}(p)$
, then as in the proof for (4), the center of e is in
$e\cap \mathrm {dom}(p)$
, then as in the proof for (4), the center of e is in
![]() $\mathrm {dom}(p)$
. Since
$\mathrm {dom}(p)$
. Since
![]() $\mathrm {supp}(p)$
contains all the rational points, there are densely many parallel lines algebraic over
$\mathrm {supp}(p)$
contains all the rational points, there are densely many parallel lines algebraic over
![]() $\mathrm {supp}(p)$
. In particular, there are two lines that intersect e at at least three points that are non-colinear, and they are also in
$\mathrm {supp}(p)$
. In particular, there are two lines that intersect e at at least three points that are non-colinear, and they are also in
![]() $\mathrm {dom}(p)$
by (5).
$\mathrm {dom}(p)$
by (5).
Other than the concrete proofs from above, one can also do much shorter proofs using the fact that
![]() $\mathrm {supp}(p)$
is an elementary submodel of
$\mathrm {supp}(p)$
is an elementary submodel of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Fact 3.3. P is not empty.
Proof Take any set
![]() $b \subset \mathbb {R}$
a nonempty countable real closed subfield of
$b \subset \mathbb {R}$
a nonempty countable real closed subfield of
![]() $\mathbb {R}$
. Just take an injection
$\mathbb {R}$
. Just take an injection
![]() $p:\mathrm {dom}(p) \rightarrow \omega $
where
$p:\mathrm {dom}(p) \rightarrow \omega $
where
![]() $\mathrm {dom}(p) = b^2 $
. It is easy to see that
$\mathrm {dom}(p) = b^2 $
. It is easy to see that
![]() $p\in P$
; therefore P is not empty.
$p\in P$
; therefore P is not empty.
Fact 3.4.
![]() $\langle P, \leq \rangle $
is transitive.
$\langle P, \leq \rangle $
is transitive.
Proof Assume
![]() $p_2 \leq p_1 \leq p_0 \in P$
. We want to prove that
$p_2 \leq p_1 \leq p_0 \in P$
. We want to prove that
![]() $p_2 \leq p_0 $
. We will see that checking Definition 3.1(4)–(7) is not more difficult than just looking at the definitions. For Definition 3.1(4) and (5), it’s clear that
$p_2 \leq p_0 $
. We will see that checking Definition 3.1(4)–(7) is not more difficult than just looking at the definitions. For Definition 3.1(4) and (5), it’s clear that
![]() $\mathrm {dom}(p_2) \supset \mathrm {dom}(p_0)$
and
$\mathrm {dom}(p_2) \supset \mathrm {dom}(p_0)$
and
![]() $p_2\upharpoonright {\mathrm {dom}(p_0)} = p_0$
. For Definition 3.1(6) the symmetrical colors invariant requirement: let
$p_2\upharpoonright {\mathrm {dom}(p_0)} = p_0$
. For Definition 3.1(6) the symmetrical colors invariant requirement: let
![]() $e \in E^L(\mathrm {supp}(p_0)) \subset E^L(\mathrm {supp}(p_1))$
; then
$e \in E^L(\mathrm {supp}(p_0)) \subset E^L(\mathrm {supp}(p_1))$
; then
![]() $s(p_0, e) = s(p_1, e) = s(p_2, e)$
holds because of the symmetrical colors invariant requirement for
$s(p_0, e) = s(p_1, e) = s(p_2, e)$
holds because of the symmetrical colors invariant requirement for
![]() $p_2 \leq p_1$
and
$p_2 \leq p_1$
and
![]() $p_1 \leq p_0$
.
$p_1 \leq p_0$
.
For Definition 3.1(7) the avoid center requirement: let
![]() $e\in E^O(\mathrm {supp}(p_0))$
; let
$e\in E^O(\mathrm {supp}(p_0))$
; let
![]() $ x \in e \cap ( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0))$
; let t be the center of the circle e. Then:
$ x \in e \cap ( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0))$
; let t be the center of the circle e. Then:
-
• either
 $ x \in e \cap ( \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0))$
: then by the avoid center requirement for
$ x \in e \cap ( \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0))$
: then by the avoid center requirement for
 $p_1\leq p_0$
,
$p_1\leq p_0$
,
 $p_2(x) = p_1(x) \neq p_0(t) $
;
$p_2(x) = p_1(x) \neq p_0(t) $
; -
• or
 $ x \in e \cap ( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_1))$
: then by the avoid center requirement for
$ x \in e \cap ( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_1))$
: then by the avoid center requirement for
 $p_2\leq p_1$
,
$p_2\leq p_1$
,
 $p_2(x) \neq p_1(t) = p_0(t) $
.
$p_2(x) \neq p_1(t) = p_0(t) $
.
In either case, the avoid center requirement is satisfied on
![]() $x\in e$
.
$x\in e$
.
For Definition 3.1(8) the algebraic points requirement: fix a finite set
![]() $ u \subset \mathrm {supp}(p_2)$
. Let v be an inclusion-maximal subset of
$ u \subset \mathrm {supp}(p_2)$
. Let v be an inclusion-maximal subset of
![]() $\mathrm {supp}(p_1)$
intersected with the algebraic closure of
$\mathrm {supp}(p_1)$
intersected with the algebraic closure of
![]() $\mathrm {supp}(p_0)\cup u$
, which is algebraically independent over
$\mathrm {supp}(p_0)\cup u$
, which is algebraically independent over
![]() $\mathrm {supp}(p_0)$
. Since the sets algebraically independent over
$\mathrm {supp}(p_0)$
. Since the sets algebraically independent over
![]() $\mathrm {supp}(p_0)$
form a matroid by [Reference Oxley7, Theorem 6.7.1], v is finite (and in fact
$\mathrm {supp}(p_0)$
form a matroid by [Reference Oxley7, Theorem 6.7.1], v is finite (and in fact
![]() $|v| \leq |u|$
). Let
$|v| \leq |u|$
). Let
-
•
 $a_1 =$
$a_1 =$
 $p_2^{\prime \prime }\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_1)$
:
$p_2^{\prime \prime }\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_1)$
:
 $x $
is algebraic over
$x $
is algebraic over
 $\mathrm {supp}(p_1)\cup u\}$
;
$\mathrm {supp}(p_1)\cup u\}$
; -
•
 $a_0 =$
$a_0 =$
 $p_1^{\prime \prime }\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$p_1^{\prime \prime }\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
 $x $
is algebraic over
$x $
is algebraic over
 $\mathrm {supp}(p_0)\cup u\}.$
$\mathrm {supp}(p_0)\cup u\}.$
Then
![]() $a_1\in I$
is by the algebraic points requirement for
$a_1\in I$
is by the algebraic points requirement for
![]() $p_2\leq p_1$
;
$p_2\leq p_1$
;
![]() $a_0 \subset p_1^{\prime \prime }\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$a_0 \subset p_1^{\prime \prime }\{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_0)\cup v\}\in I$
is by our choice of v and by the algebraic points requirement for
$\mathrm {supp}(p_0)\cup v\}\in I$
is by our choice of v and by the algebraic points requirement for
![]() $p_1\leq p_0$
. Hence
$p_1\leq p_0$
. Hence
![]() $p_2^{\prime \prime }\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
$p_2^{\prime \prime }\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_0)\cup u\} \subset a_0\cup a_1\in I$
.
$\mathrm {supp}(p_0)\cup u\} \subset a_0\cup a_1\in I$
.
Fact 3.5. P is
![]() $\sigma $
-closed.
$\sigma $
-closed.
Proof We will show that for any descending sequence
![]() $\{p_n\}_{n\in \omega }$
of conditions from P,
$\{p_n\}_{n\in \omega }$
of conditions from P,
![]() $ q = \bigcup _{n\in \omega } p_n \in P$
is their lower bound. For Definition 3.1(1),
$ q = \bigcup _{n\in \omega } p_n \in P$
is their lower bound. For Definition 3.1(1),
![]() $\mathbb {R} \supset \mathrm {supp}(q) = \mathrm {supp}(\bigcup _{n\in \omega } p_n) = \bigcup _{n\in \omega } \mathrm {supp}(p_n)$
is still a countable real closed subfield and
$\mathbb {R} \supset \mathrm {supp}(q) = \mathrm {supp}(\bigcup _{n\in \omega } p_n) = \bigcup _{n\in \omega } \mathrm {supp}(p_n)$
is still a countable real closed subfield and
![]() $\mathrm {supp}(q)^2 = \mathrm {dom}(q) \subset \mathbb {R}^2$
.
$\mathrm {supp}(q)^2 = \mathrm {dom}(q) \subset \mathbb {R}^2$
.
For Definition 3.1(2), if a q-monochromatic triple were found in
![]() $\mathrm {dom}(q)$
, the triple would be found in
$\mathrm {dom}(q)$
, the triple would be found in
![]() $\mathrm {dom}(p_n)$
for some n. But because
$\mathrm {dom}(p_n)$
for some n. But because
![]() $p_n\in P$
is a
$p_n\in P$
is a
![]() ${\Gamma _2}$
-coloring, the triple is not
${\Gamma _2}$
-coloring, the triple is not
![]() $p_n$
-monochromatic hence not q-monochromatic, which is a contradiction.
$p_n$
-monochromatic hence not q-monochromatic, which is a contradiction.
Observe that
![]() $E^L(\mathrm {supp}(q)) = E^L(\bigcup _n\mathrm {supp}(p_n))= \bigcup _n E^L(\mathrm {supp}(p_n))$
and
$E^L(\mathrm {supp}(q)) = E^L(\bigcup _n\mathrm {supp}(p_n))= \bigcup _n E^L(\mathrm {supp}(p_n))$
and
![]() $E^O(\mathrm {supp}(q)) = E^O(\bigcup _n \mathrm {supp}(p_n))= \bigcup _n E^O(\mathrm {supp}(p_n))$
. For Definition 3.1(3) the symmetrical colors requirement: let
$E^O(\mathrm {supp}(q)) = E^O(\bigcup _n \mathrm {supp}(p_n))= \bigcup _n E^O(\mathrm {supp}(p_n))$
. For Definition 3.1(3) the symmetrical colors requirement: let
![]() $l \in E^L(\mathrm {supp}(q)) $
, then
$l \in E^L(\mathrm {supp}(q)) $
, then
![]() $l \in E^L(\mathrm {supp}(p_n) )$
for some n. Then
$l \in E^L(\mathrm {supp}(p_n) )$
for some n. Then
![]() $s(q, l) = \bigcup _{n< i\in \omega } s(p_i, l) = s(p_n, l) \in I $
because for every
$s(q, l) = \bigcup _{n< i\in \omega } s(p_i, l) = s(p_n, l) \in I $
because for every
![]() $ i> n$
,
$ i> n$
,
![]() $s(p_i, l) = s(p_n, l) \in I $
by the symmetrical colors invariant requirement for
$s(p_i, l) = s(p_n, l) \in I $
by the symmetrical colors invariant requirement for
![]() $p_i \leq p_n$
.
$p_i \leq p_n$
.
For the rest of the proof, we will check
![]() $\forall n\: q \leq p_n $
holds. Fix a number n. Definition 3.1(4) and (5) is clear:
$\forall n\: q \leq p_n $
holds. Fix a number n. Definition 3.1(4) and (5) is clear:
![]() $\mathrm {dom}(q) \supset \mathrm {dom}(p_n)$
and
$\mathrm {dom}(q) \supset \mathrm {dom}(p_n)$
and
![]() $q \upharpoonright {\mathrm {dom}(p_n)} = p_n$
. For Definition 3.1(6) the symmetrical colors invariant requirement:
$q \upharpoonright {\mathrm {dom}(p_n)} = p_n$
. For Definition 3.1(6) the symmetrical colors invariant requirement:
![]() $s(q, l) = \bigcup _{n< i\in \omega } s(p_i, l) = s(p_n, l) $
because
$s(q, l) = \bigcup _{n< i\in \omega } s(p_i, l) = s(p_n, l) $
because
![]() $\forall i> n\ \ s(p_i, l) = s(p_n, l)$
by the symmetrical colors invariant requirement for
$\forall i> n\ \ s(p_i, l) = s(p_n, l)$
by the symmetrical colors invariant requirement for
![]() $p_i \leq p_n$
.
$p_i \leq p_n$
.
For Definition 3.1(7) the avoid center requirement: let
![]() $e\in E^O(\mathrm {supp}(p_n))$
be a circle and let t be the center of the circle e; then
$e\in E^O(\mathrm {supp}(p_n))$
be a circle and let t be the center of the circle e; then
![]() $t\in \mathrm {dom}(p_n) $
by Fact 3.2. Let
$t\in \mathrm {dom}(p_n) $
by Fact 3.2. Let
![]() $ x \in e \cap ( \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)) $
, then there is some
$ x \in e \cap ( \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)) $
, then there is some
![]() $m>n$
such that
$m>n$
such that
![]() $ x \in e \cap ( \mathrm {dom}(p_m)\setminus \mathrm {dom}(p_n)) $
. Then
$ x \in e \cap ( \mathrm {dom}(p_m)\setminus \mathrm {dom}(p_n)) $
. Then
![]() $p_m(x) \neq p_m(t)$
because the avoid center requirement is satisfied for
$p_m(x) \neq p_m(t)$
because the avoid center requirement is satisfied for
![]() $p_m \leq p_n$
. Then
$p_m \leq p_n$
. Then
![]() $q (x) = p_m(x) \neq p_m(t) = q(t) $
.
$q (x) = p_m(x) \neq p_m(t) = q(t) $
.
For Definition 3.1(8) the algebraic points requirement: fix a finite set
![]() $ a \subset \mathrm {supp}(q)$
. Find a number
$ a \subset \mathrm {supp}(q)$
. Find a number
![]() $m>n$
such that
$m>n$
such that
![]() $a\subset \mathrm {supp}(p_m)$
. Then the set
$a\subset \mathrm {supp}(p_m)$
. Then the set
![]() $ \{x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)$
:
$ \{x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_n)\cup a\}$
is a subset of
$\mathrm {supp}(p_n)\cup a\}$
is a subset of
![]() $\mathrm {dom}(p_m)$
since
$\mathrm {dom}(p_m)$
since
![]() $\mathrm {supp}(p_m)$
is a real closed field. Since
$\mathrm {supp}(p_m)$
is a real closed field. Since
![]() $ p_m \leq p_n$
, the
$ p_m \leq p_n$
, the
![]() $p_m$
-image of the set
$p_m$
-image of the set
![]() $\{x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)$
:
$\{x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p_n)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_n)\cup a\}$
equaling the q-image of the same set is in the ideal I.
$\mathrm {supp}(p_n)\cup a\}$
equaling the q-image of the same set is in the ideal I.
Theorem 3.6.
![]() $\forall x \in \mathbb {R}^2, \forall p \in P$
, there is a condition
$\forall x \in \mathbb {R}^2, \forall p \in P$
, there is a condition
![]() $ q \in P$
such that
$ q \in P$
such that
![]() $x\in \mathrm {dom} (q)$
and
$x\in \mathrm {dom} (q)$
and
![]() $ q \leq p $
hold.
$ q \leq p $
hold.
In fact, this theorem is a consequence of Theorem 5.4, but we still provide this shorter and tighter proof.
Proof Given a point
![]() $x \in \mathbb {R}^2$
, a condition
$x \in \mathbb {R}^2$
, a condition
![]() $p \in P$
. If
$p \in P$
. If
![]() $x\in \mathrm {dom}(p)$
, then there is nothing to do. So suppose
$x\in \mathrm {dom}(p)$
, then there is nothing to do. So suppose
![]() $x\notin \mathrm {dom}(p)$
. Choose a countable real closed field
$x\notin \mathrm {dom}(p)$
. Choose a countable real closed field
![]() $b\subset \mathbb {R}$
such that
$b\subset \mathbb {R}$
such that
![]() $\mathrm {supp}(p)\subset b $
and
$\mathrm {supp}(p)\subset b $
and
![]() $x\in b^2$
. We will extend the
$x\in b^2$
. We will extend the
![]() ${\Gamma _2}$
-coloring p to some q with
${\Gamma _2}$
-coloring p to some q with
![]() $\mathrm {dom}(q) = b^2$
.
$\mathrm {dom}(q) = b^2$
.
Fix any set
![]() $\pi \in I $
such that
$\pi \in I $
such that
![]() $\forall l \in E^L(\mathrm {supp}(p))\: \pi \setminus s(p, l)$
is infinite. It is possible because for every line
$\forall l \in E^L(\mathrm {supp}(p))\: \pi \setminus s(p, l)$
is infinite. It is possible because for every line
![]() $l \in E^L(\mathrm {supp}(p))$
,
$l \in E^L(\mathrm {supp}(p))$
,
![]() $s(p, l)\in I$
by the symmetrical colors requirement for p, and by the feature of our choice of I. Fix a point
$s(p, l)\in I$
by the symmetrical colors requirement for p, and by the feature of our choice of I. Fix a point
![]() $x \in b^2 \setminus \mathrm {dom}(p)$
. Note that there is at most one line or one circle
$x \in b^2 \setminus \mathrm {dom}(p)$
. Note that there is at most one line or one circle
![]() $e\in E^L(\mathrm {supp}(p)) \cup E^O(\mathrm {supp}(p))$
such that
$e\in E^L(\mathrm {supp}(p)) \cup E^O(\mathrm {supp}(p))$
such that
![]() $x \in e$
: using Fact 3.2(5), if there were different such
$x \in e$
: using Fact 3.2(5), if there were different such
![]() $e, e' \in E^L(\mathrm {supp}(p)) \cup E^O(\mathrm {supp}(p))$
that
$e, e' \in E^L(\mathrm {supp}(p)) \cup E^O(\mathrm {supp}(p))$
that
![]() $x\in e\cap e'$
, then x would be in
$x\in e\cap e'$
, then x would be in
![]() $\mathrm {dom}(p)$
which is a contradiction. Let’s define the set of allowed colors for the point x, denoted by
$\mathrm {dom}(p)$
which is a contradiction. Let’s define the set of allowed colors for the point x, denoted by
![]() $a(x)$
:
$a(x)$
:
-
• If x is on some line
 $e\in E^L(\mathrm {supp}(p)) $
, then let
$e\in E^L(\mathrm {supp}(p)) $
, then let
 $a(x) = \pi \setminus s( p, e) $
.
$a(x) = \pi \setminus s( p, e) $
. -
• If x is on some circle
 $e\in E^O(\mathrm {supp}(p))$
, then let
$e\in E^O(\mathrm {supp}(p))$
, then let
 $a(x) = \pi \setminus \{p(t)\} $
where t is the center of e.
$a(x) = \pi \setminus \{p(t)\} $
where t is the center of e.
Since I is an ideal, and by our choice of
![]() $\pi \in I$
, the set
$\pi \in I$
, the set
![]() $a(x) $
is infinite. Now just let
$a(x) $
is infinite. Now just let
![]() $q: b^2\rightarrow \omega $
be a map such that:
$q: b^2\rightarrow \omega $
be a map such that:
-
•
 $q\upharpoonright {\mathrm {dom}(p)} = p $
.
$q\upharpoonright {\mathrm {dom}(p)} = p $
. -
•
 $\forall x\in b^2 \setminus \mathrm {dom}(p),\: q (x) \in a(x)$
.
$\forall x\in b^2 \setminus \mathrm {dom}(p),\: q (x) \in a(x)$
. -
• q on
 $ b^2 \setminus \mathrm {dom}(p)$
is an injection.
$ b^2 \setminus \mathrm {dom}(p)$
is an injection.
Claim 3.7.
![]() $q \in P$
.
$q \in P$
.
Proof Definition 3.1(1) is satisfied as we required
![]() $\mathrm {supp}(q) = b\subset \mathbb {R} $
to be a countable real closed subfield and
$\mathrm {supp}(q) = b\subset \mathbb {R} $
to be a countable real closed subfield and
![]() $\mathrm {supp}(q)^2 = \mathrm {dom}(q) \subset \mathbb {R}^2$
.
$\mathrm {supp}(q)^2 = \mathrm {dom}(q) \subset \mathbb {R}^2$
.
For Definition 3.1(2), let’s check q is a
![]() ${\Gamma _2}$
-coloring for
${\Gamma _2}$
-coloring for
![]() $\mathrm {dom}(q)$
. Assume there are points
$\mathrm {dom}(q)$
. Assume there are points
![]() $ x,y,z\in \mathrm {dom}(q)$
such that
$ x,y,z\in \mathrm {dom}(q)$
such that
![]() $\{x,y,z\} \in {\Gamma _2}$
.
$\{x,y,z\} \in {\Gamma _2}$
.
Case 1: at least two points in
![]() $\{x,y,z\}$
are from
$\{x,y,z\}$
are from
![]() $\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
. Then
$\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
. Then
![]() $q"\{x,y,z\} $
is not a singleton because we required q to be an injection on
$q"\{x,y,z\} $
is not a singleton because we required q to be an injection on
![]() $b^2\setminus \mathrm {dom}(p) = \mathrm {dom}(q) \setminus \mathrm {dom}(p) $
.
$b^2\setminus \mathrm {dom}(p) = \mathrm {dom}(q) \setminus \mathrm {dom}(p) $
.
Case 2:
![]() $x,y,z \in \mathrm {dom}(p)$
. Then because p is a
$x,y,z \in \mathrm {dom}(p)$
. Then because p is a
![]() ${\Gamma _2}$
-coloring on
${\Gamma _2}$
-coloring on
![]() $\mathrm {dom}(p)$
,
$\mathrm {dom}(p)$
,
![]() $q"\{x,y,z\} = p"\{x,y,z\} $
is not a singleton.
$q"\{x,y,z\} = p"\{x,y,z\} $
is not a singleton.
Without loss of generality, we have the following case left.
Case 3:
![]() $x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p)$
and
$x \in \mathrm {dom}(q)\setminus \mathrm {dom}(p)$
and
![]() $y,z \in \mathrm {dom}(p)$
. We have two sub-cases depending on the pivot point of the isosceles triangle
$y,z \in \mathrm {dom}(p)$
. We have two sub-cases depending on the pivot point of the isosceles triangle
![]() $\{x,y,z\}$
.
$\{x,y,z\}$
.
Case 3.1: x is the pivot point. Then x is on the perpendicular bisector l of the line segment from y to z, and because
![]() $y,z \in \mathrm {dom}(p)$
, l was in
$y,z \in \mathrm {dom}(p)$
, l was in
![]() $ E^L(\mathrm {supp}(p))$
by Fact 3.2(2). But by the definition of
$ E^L(\mathrm {supp}(p))$
by Fact 3.2(2). But by the definition of
![]() $q(x)\in a(x)$
,
$q(x)\in a(x)$
,
![]() $q(x) \notin s(p, l) \ni p(y) = p(z)$
so
$q(x) \notin s(p, l) \ni p(y) = p(z)$
so
![]() $q(x) \neq p(y) = p(z) = q(y) = q(z)$
; hence
$q(x) \neq p(y) = p(z) = q(y) = q(z)$
; hence
![]() $\{x,y,z\}$
is not monochromatic by q.
$\{x,y,z\}$
is not monochromatic by q.
Case 3.2: y or z is the pivot point. Without loss of generality, let’s say
![]() $ y$
is the pivot point. Then
$ y$
is the pivot point. Then
![]() $ x$
is on the circle centered at
$ x$
is on the circle centered at
![]() $ y$
passing through
$ y$
passing through
![]() $ z$
, which was in
$ z$
, which was in
![]() $\mathrm {dom}(p)$
because of
$\mathrm {dom}(p)$
because of
![]() $ y, z \in \mathrm {dom}(p)$
and by Fact 3.2(3). But in the definition of
$ y, z \in \mathrm {dom}(p)$
and by Fact 3.2(3). But in the definition of
![]() $a(x)$
, we made sure
$a(x)$
, we made sure
![]() $q( x) \neq q( y) = p( y)$
; hence
$q( x) \neq q( y) = p( y)$
; hence
![]() $\{x,y,z\}$
is not monochromatic by q.
$\{x,y,z\}$
is not monochromatic by q.
For Definition 3.1(3) the symmetrical colors requirement, let
![]() $l \in E^L(\mathrm {supp}(q)) $
.
$l \in E^L(\mathrm {supp}(q)) $
.
Case 1:
![]() $l \in E^L(\mathrm {supp}(p)) $
. Then
$l \in E^L(\mathrm {supp}(p)) $
. Then
![]() $s(p, l) \in I$
since
$s(p, l) \in I$
since
![]() $p\in P$
; we also have
$p\in P$
; we also have
![]() $s(q, l) = s(p, l)$
that we will check later as Definition 3.1(6); hence
$s(q, l) = s(p, l)$
that we will check later as Definition 3.1(6); hence
![]() $s(q, l) \in I$
.
$s(q, l) \in I$
.
Case 2:
![]() $l \in E^L(\mathrm {supp}(q)) \setminus E^L(\mathrm {supp}(p)) $
. Then for any pair of points symmetrical with respect to l, at least one point in the pair has to be in
$l \in E^L(\mathrm {supp}(q)) \setminus E^L(\mathrm {supp}(p)) $
. Then for any pair of points symmetrical with respect to l, at least one point in the pair has to be in
![]() $\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
because otherwise it would be the case that
$\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
because otherwise it would be the case that
![]() $l \in E^L(\mathrm {supp}(p)) $
by Fact 3.2(2), which would lead to the previous case. Because of
$l \in E^L(\mathrm {supp}(p)) $
by Fact 3.2(2), which would lead to the previous case. Because of
![]() $q"(\mathrm {dom}(q)\setminus \mathrm {dom}(p))\in \pi $
,
$q"(\mathrm {dom}(q)\setminus \mathrm {dom}(p))\in \pi $
,
![]() $s(q, l) \subset \pi \in I$
holds; thus
$s(q, l) \subset \pi \in I$
holds; thus
![]() $s(q, l) \in I$
holds.
$s(q, l) \in I$
holds.
Claim 3.8.
![]() $q\leq p$
.
$q\leq p$
.
Proof For Definition 3.1(4) and (5), indeed
![]() $\mathrm {dom}(q) \supset \mathrm {dom}(p)$
and
$\mathrm {dom}(q) \supset \mathrm {dom}(p)$
and
![]() $q\upharpoonright {\mathrm {dom}(p)} = p$
. For Definition 3.1(6) the symmetrical colors invariant requirement, first of all, obviously
$q\upharpoonright {\mathrm {dom}(p)} = p$
. For Definition 3.1(6) the symmetrical colors invariant requirement, first of all, obviously
![]() $s(p, l) \subset s(q, l)$
. We will show that
$s(p, l) \subset s(q, l)$
. We will show that
![]() $s(q, l)\subset s(p, l)$
. Let
$s(q, l)\subset s(p, l)$
. Let
![]() $l \in E^L(\mathrm {supp}(p)) $
. Any pair of points that are symmetrical with respect to l has to be both in
$l \in E^L(\mathrm {supp}(p)) $
. Any pair of points that are symmetrical with respect to l has to be both in
![]() $\mathrm {dom}(p)$
or both in
$\mathrm {dom}(p)$
or both in
![]() $\mathrm {dom}(q) \setminus \mathrm {dom}(p) $
, again using Fact 3.2(6). For the pair of points that are both in
$\mathrm {dom}(q) \setminus \mathrm {dom}(p) $
, again using Fact 3.2(6). For the pair of points that are both in
![]() $\mathrm {dom}(q) \setminus \mathrm {dom}(p) $
, they have distinct q-colors since q is an injection on
$\mathrm {dom}(q) \setminus \mathrm {dom}(p) $
, they have distinct q-colors since q is an injection on
![]() $\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
. Then
$\mathrm {dom}(q)\setminus \mathrm {dom}(p)$
. Then
![]() $s(q, l)$
can’t include more colors than
$s(q, l)$
can’t include more colors than
![]() $s(p, l)$
does. Hence
$s(p, l)$
does. Hence
![]() $s(p, l) = s(q, l)$
.
$s(p, l) = s(q, l)$
.
For Definition 3.1(7) the avoid center requirement, suppose that
![]() $x\in \mathrm {dom}(q\setminus p)$
is a point and
$x\in \mathrm {dom}(q\setminus p)$
is a point and
![]() $e\in E^C(\mathrm {dom}(p))$
is an old circle such that
$e\in E^C(\mathrm {dom}(p))$
is an old circle such that
![]() $x\in e$
. Since
$x\in e$
. Since
![]() $q(x)\notin a(x)$
, it follows that
$q(x)\notin a(x)$
, it follows that
![]() $q(x)\neq p(y)$
where y is the center of e. For Definition 3.1(8) the algebraic points requirement, in fact we even have
$q(x)\neq p(y)$
where y is the center of e. For Definition 3.1(8) the algebraic points requirement, in fact we even have
![]() $q"(\mathrm {dom}(q) \setminus \mathrm {dom}(p)) \subset \pi \in I $
so that any subset of
$q"(\mathrm {dom}(q) \setminus \mathrm {dom}(p)) \subset \pi \in I $
so that any subset of
![]() $q"(\mathrm {dom}(q) \setminus \mathrm {dom}(p)) $
is in the ideal I by the property of an ideal.
$q"(\mathrm {dom}(q) \setminus \mathrm {dom}(p)) $
is in the ideal I by the property of an ideal.
This completes the proof of the theorem.
As a consequence, P forces the union of the generic filter to be a total
![]() $\Gamma _2$
-coloring.
$\Gamma _2$
-coloring.
4 Fields in amalgamation position
Mutual genericity is at the heart of the balanced forcing technology. In this section, we introduce an algebraic counterpart to it which has the advantage of removing the forcing relation when showing our poset to be balanced.
Definition 4.1. Let
![]() $F_0,F_1$
be real closed subfields of
$F_0,F_1$
be real closed subfields of
![]() $\mathbb {R}$
. We say that
$\mathbb {R}$
. We say that
![]() $F_0 , F_1$
are in amalgamation position if for every polynomial
$F_0 , F_1$
are in amalgamation position if for every polynomial
![]() $p(\bar {x}_0,\bar {x}_1 $
) with integer coefficients and all variables listed, and every pair of tuples
$p(\bar {x}_0,\bar {x}_1 $
) with integer coefficients and all variables listed, and every pair of tuples
![]() $\bar r_0$
from
$\bar r_0$
from
![]() $F_0$
and
$F_0$
and
![]() $\bar r_1$
from
$\bar r_1$
from
![]() $F_1$
such that
$F_1$
such that
![]() $p(\bar {r}_0,\bar {r}_1) = 0$
holds, and all open neighborhoods
$p(\bar {r}_0,\bar {r}_1) = 0$
holds, and all open neighborhoods
![]() $O_0$
and
$O_0$
and
![]() $O_1$
of
$O_1$
of
![]() $\bar {r}_0,\bar {r}_1$
respectively, there are tuples
$\bar {r}_0,\bar {r}_1$
respectively, there are tuples
![]() $\bar {r}_0^{\prime }\in O_0,\bar {r}_1^{\prime }\in O_1$
from
$\bar {r}_0^{\prime }\in O_0,\bar {r}_1^{\prime }\in O_1$
from
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $p(\bar {r}_0^{\prime },\bar {r}_1) = p(\bar {r}_0,\bar {r}_1^{\prime }) = 0$
.
$p(\bar {r}_0^{\prime },\bar {r}_1) = p(\bar {r}_0,\bar {r}_1^{\prime }) = 0$
.
With the help of quantifier elimination for real closed fields, the amalgamation position yields seemingly stronger consequences for the two fields than stated in the definition.
Proposition 4.2. Let
![]() $F_0,F_1$
be real closed subfields of
$F_0,F_1$
be real closed subfields of
![]() $\mathbb {R}$
in amalgamation position. Let
$\mathbb {R}$
in amalgamation position. Let
![]() $\phi (\bar {x}_0,\bar {x}_1)$
be a formula of real closed fields with all free variables listed. For every pair of tuples
$\phi (\bar {x}_0,\bar {x}_1)$
be a formula of real closed fields with all free variables listed. For every pair of tuples
![]() $\bar {r}_0$
from
$\bar {r}_0$
from
![]() $F_0$
and
$F_0$
and
![]() $\bar {r}_1$
from
$\bar {r}_1$
from
![]() $F_1$
such that
$F_1$
such that
![]() $\phi (\bar {r}_0,\bar {r}_1)$
holds, there are tuples
$\phi (\bar {r}_0,\bar {r}_1)$
holds, there are tuples
![]() $\bar {r}_0^{\prime },\bar {r}_1^{\prime }$
from
$\bar {r}_0^{\prime },\bar {r}_1^{\prime }$
from
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $\phi (\bar {r}_0^{\prime },\bar {r}_1) $
and
$\phi (\bar {r}_0^{\prime },\bar {r}_1) $
and
![]() $ \phi (\bar {r}_0,\bar {r}_1^{\prime }) $
both hold.
$ \phi (\bar {r}_0,\bar {r}_1^{\prime }) $
both hold.
Proof By the quantifier elimination for real closed fields, we can assume that
![]() $\phi $
is quantifier-free. We also assume that all atomic formulas appearing in it are of the form
$\phi $
is quantifier-free. We also assume that all atomic formulas appearing in it are of the form
![]() $p(\bar x_0, \bar x_1) = 0$
or
$p(\bar x_0, \bar x_1) = 0$
or
![]() $ p(\bar x_0, \bar x_1)>0 $
for some polynomial p with integer coefficients. Let
$ p(\bar x_0, \bar x_1)>0 $
for some polynomial p with integer coefficients. Let
![]() $\{p_i : i \in n\}$
be a list of all polynomials appearing in
$\{p_i : i \in n\}$
be a list of all polynomials appearing in
![]() $\phi $
. Take tuples
$\phi $
. Take tuples
![]() $\bar {r}_0$
from
$\bar {r}_0$
from
![]() $F_0$
and
$F_0$
and
![]() $\bar {r}_1$
from
$\bar {r}_1$
from
![]() $F_1$
such that
$F_1$
such that
![]() $\phi (\bar {r}_0,\bar {r}_1)$
holds. Let
$\phi (\bar {r}_0,\bar {r}_1)$
holds. Let
![]() $a = \{i \in n: p_i(\bar r_0, \bar r_1) \neq 0\}$
. Let
$a = \{i \in n: p_i(\bar r_0, \bar r_1) \neq 0\}$
. Let
![]() $O_0, O_1$
be open neighborhoods of
$O_0, O_1$
be open neighborhoods of
![]() $\bar r_0, \bar r_1$
respectively such that for all
$\bar r_0, \bar r_1$
respectively such that for all
![]() $i \in a$
, the polynomials
$i \in a$
, the polynomials
![]() $p_i$
have constant sign on
$p_i$
have constant sign on
![]() $O_0 \times O_1$
. Use the amalgamation position assumption as in Definition 4.1 to find tuples
$O_0 \times O_1$
. Use the amalgamation position assumption as in Definition 4.1 to find tuples
![]() $\bar r_0^{\prime }\in O_0$
and
$\bar r_0^{\prime }\in O_0$
and
![]() $\bar r_1^{\prime }\in O_1$
from
$\bar r_1^{\prime }\in O_1$
from
![]() $F_0 \cap F_1$
such that
$F_0 \cap F_1$
such that
![]() $\sum _{i\in n\setminus a} p_i^2 (\bar r_0^{\prime }, \bar r_1) = 0 = \sum _{i\in n\setminus a} p_i^2 (\bar r_0, \bar r_1^{\prime })$
. One can check that the tuples
$\sum _{i\in n\setminus a} p_i^2 (\bar r_0^{\prime }, \bar r_1) = 0 = \sum _{i\in n\setminus a} p_i^2 (\bar r_0, \bar r_1^{\prime })$
. One can check that the tuples
![]() $ \bar r_0^{\prime }, \bar r_1^{\prime }$
work as required.
$ \bar r_0^{\prime }, \bar r_1^{\prime }$
work as required.
Then we have a quick corollary as the following, although it is true without the amalgamation position requirement.
Corollary 4.3. Let
![]() $n>0$
be a natural number. Assume that
$n>0$
be a natural number. Assume that
![]() $F_0,F_1$
are real closed subfields of
$F_0,F_1$
are real closed subfields of
![]() $\mathbb {R}$
in amalgamation position and
$\mathbb {R}$
in amalgamation position and
![]() $A\subset \mathbb {R}^n$
is an algebraic set over both
$A\subset \mathbb {R}^n$
is an algebraic set over both
![]() $F_0$
and
$F_0$
and
![]() $F_1$
. Then
$F_1$
. Then
![]() $A\subset \mathbb {R}^n$
is an algebraic set over
$A\subset \mathbb {R}^n$
is an algebraic set over
![]() $F_0\cap F_1$
.
$F_0\cap F_1$
.
Proof Let
![]() $p_0,p_1$
be polynomials such that there are some tuples
$p_0,p_1$
be polynomials such that there are some tuples
![]() $\bar y_0$
from
$\bar y_0$
from
![]() $F_0$
,
$F_0$
,
![]() $\bar y_1$
from
$\bar y_1$
from
![]() $F_1$
,
$F_1$
,
![]() $\bar z$
from
$\bar z$
from
![]() $F_0\cap F_1$
so that
$F_0\cap F_1$
so that
![]() $A = \{\bar x : p_0(\bar x,\bar y_0, \bar z) = 0 \} = \{\bar x : p_1(\bar x,\bar y_1, \bar z) = 0 \}$
. Let
$A = \{\bar x : p_0(\bar x,\bar y_0, \bar z) = 0 \} = \{\bar x : p_1(\bar x,\bar y_1, \bar z) = 0 \}$
. Let
![]() $\phi (\bar y_0^{\prime }, \bar y_1^{\prime })$
be the formula
$\phi (\bar y_0^{\prime }, \bar y_1^{\prime })$
be the formula
![]() $\forall \bar x\ p_0(\bar x,\bar y_0^{\prime }, \bar z) = 0 \leftrightarrow p_1(\bar x,\bar y_1^{\prime }, \bar z) = 0 $
. Clearly,
$\forall \bar x\ p_0(\bar x,\bar y_0^{\prime }, \bar z) = 0 \leftrightarrow p_1(\bar x,\bar y_1^{\prime }, \bar z) = 0 $
. Clearly,
![]() $\phi (\bar y_0, \bar y_1)$
holds. By Proposition 4.2, there is a tuple
$\phi (\bar y_0, \bar y_1)$
holds. By Proposition 4.2, there is a tuple
![]() $\bar y_1^{\prime }$
from
$\bar y_1^{\prime }$
from
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $\phi (\bar y_0, \bar y_1^{\prime })$
holds. Then
$\phi (\bar y_0, \bar y_1^{\prime })$
holds. Then
![]() $A = \{\bar x : p_0(\bar x,\bar y_0, \bar z) = 0 \} = \{\bar x : p_1(\bar x,\bar y_1^{\prime }, \bar z) = 0 \}$
. Thus
$A = \{\bar x : p_0(\bar x,\bar y_0, \bar z) = 0 \} = \{\bar x : p_1(\bar x,\bar y_1^{\prime }, \bar z) = 0 \}$
. Thus
![]() $A\subset \mathbb {R}^n$
is an algebraic set over
$A\subset \mathbb {R}^n$
is an algebraic set over
![]() $F_0\cap F_1$
using the polynomial
$F_0\cap F_1$
using the polynomial
![]() $p_1$
and parameters
$p_1$
and parameters
![]() $\bar y_1^{\prime }, \bar z$
from
$\bar y_1^{\prime }, \bar z$
from
![]() $F_0\cap F_1$
.
$F_0\cap F_1$
.
Proposition 4.4. Let
![]() $F_0,F_1$
be real closed subfields of
$F_0,F_1$
be real closed subfields of
![]() $\mathbb {R}$
in amalgamation position. Let
$\mathbb {R}$
in amalgamation position. Let
![]() $n_0,n_1>0$
be natural numbers and
$n_0,n_1>0$
be natural numbers and
![]() $B\subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}$
be an algebraic set over
$B\subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}$
be an algebraic set over
![]() $F_0 \cap F_1$
. If
$F_0 \cap F_1$
. If
![]() $a_0 \subset F^{n_0}$
and
$a_0 \subset F^{n_0}$
and
![]() $a_1 \subset F^{n_1}$
are sets such that
$a_1 \subset F^{n_1}$
are sets such that
![]() $a_0 \times a_1 \subset B$
, then there are algebraic sets
$a_0 \times a_1 \subset B$
, then there are algebraic sets
![]() $A_0 \subset \mathbb {R}^{n_0}$
and
$A_0 \subset \mathbb {R}^{n_0}$
and
![]() $A_1 \subset \mathbb {R}^{n_1}$
algebraic over
$A_1 \subset \mathbb {R}^{n_1}$
algebraic over
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $a_0 \subset A_0$
,
$a_0 \subset A_0$
,
![]() $a_1 \subset A_1$
, and
$a_1 \subset A_1$
, and
![]() $A_0 \times A_1 \subset B$
.
$A_0 \times A_1 \subset B$
.
One can use a corollary to the Hilbert basis theorem as Fact 4.5 to see that there are inclusion-smallest algebraic sets over
![]() $F_0 \cap F_1$
which contain
$F_0 \cap F_1$
which contain
![]() $a_0$
and
$a_0$
and
![]() $a_1$
respectively, if there are any. The proof is to show that they in fact do work.
$a_1$
respectively, if there are any. The proof is to show that they in fact do work.
Fact 4.5 [Reference Marker6, Corollary 3.2.6]
If
![]() $X_i$
is Zariski closed for
$X_i$
is Zariski closed for
![]() $i \in \iota $
, then there is a finite
$i \in \iota $
, then there is a finite
![]() $\iota _0 \subset \iota $
such that
$\iota _0 \subset \iota $
such that
Now we prove Proposition 4.4.
Proof Let
![]() $p(\bar x_0, \bar x_1)$
be a polynomial with coefficients in
$p(\bar x_0, \bar x_1)$
be a polynomial with coefficients in
![]() $F_0 \cap F_1$
whose zero locus is the set B. By Fact 4.5, there exists a finite set
$F_0 \cap F_1$
whose zero locus is the set B. By Fact 4.5, there exists a finite set
![]() $b_0 \subset a_0$
such that
$b_0 \subset a_0$
such that
![]() $ \bigcap _{ \bar r_0\in a_0} \{ \bar r_1\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}= \bigcap _{ \bar r_0\in b_0} \{ \bar r_1\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}$
; denote the intersection by
$ \bigcap _{ \bar r_0\in a_0} \{ \bar r_1\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}= \bigcap _{ \bar r_0\in b_0} \{ \bar r_1\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}$
; denote the intersection by
![]() $C_1$
; let
$C_1$
; let
![]() $C_1^{\prime } = C_1\cap (F_0 \cap F_1)^{n_1}$
. Similarly, there exists a finite set
$C_1^{\prime } = C_1\cap (F_0 \cap F_1)^{n_1}$
. Similarly, there exists a finite set
![]() $c_1 \subset C_1^{\prime }$
such that
$c_1 \subset C_1^{\prime }$
such that
![]() $\bigcap _{ \bar r_1\in C_1^{\prime }} \{ \bar r_0\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}= \bigcap _{ \bar r_1\in c_1} \{ \bar r_0\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}$
; denote the intersection by
$\bigcap _{ \bar r_1\in C_1^{\prime }} \{ \bar r_0\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}= \bigcap _{ \bar r_1\in c_1} \{ \bar r_0\in \mathbb {R}^{n_1}: p(\bar r_0, \bar r_1) = 0\}$
; denote the intersection by
![]() $A_0$
.
$A_0$
.
It is clear that
![]() $A_0 \subset \mathbb {R}^{n_0}$
is an algebraic set over
$A_0 \subset \mathbb {R}^{n_0}$
is an algebraic set over
![]() $F_0 \cap F_1$
. It is also clear that
$F_0 \cap F_1$
. It is also clear that
![]() $a_0 \subset A_0$
: if
$a_0 \subset A_0$
: if
![]() $\bar r_0\in a_0$
, then
$\bar r_0\in a_0$
, then
![]() $ p(\bar r_0, \bar r_1) = 0$
for all
$ p(\bar r_0, \bar r_1) = 0$
for all
![]() $\bar r_1\in C_1$
, in particular for all
$\bar r_1\in C_1$
, in particular for all
![]() $\bar r_1\in c_1$
; by the definition of the set
$\bar r_1\in c_1$
; by the definition of the set
![]() $A_0$
,
$A_0$
,
![]() $\bar r_0\in A_0$
.
$\bar r_0\in A_0$
.
Claim
![]() $(A_0 \cap F^{n_0}_0)\times a_1 \subset B$
. To prove this, suppose that
$(A_0 \cap F^{n_0}_0)\times a_1 \subset B$
. To prove this, suppose that
![]() $\bar r_0 \in A_0 \cap F^{n_0}_0$
and
$\bar r_0 \in A_0 \cap F^{n_0}_0$
and
![]() $\bar r_1 \in a_1$
are points such that
$\bar r_1 \in a_1$
are points such that
![]() $ p(\bar r_0, \bar r_1) \neq 0$
holds for the sake of contradiction. Let
$ p(\bar r_0, \bar r_1) \neq 0$
holds for the sake of contradiction. Let
![]() $O\subset \mathbb {R}^{n_1 } $
be an open neighborhood of
$O\subset \mathbb {R}^{n_1 } $
be an open neighborhood of
![]() $\bar r_1$
such that
$\bar r_1$
such that
![]() $\{\bar r_0\} \times O$
contains no solutions of
$\{\bar r_0\} \times O$
contains no solutions of
![]() $p = 0$
. Use the amalgamation position as in Definition 4.1 to find a point
$p = 0$
. Use the amalgamation position as in Definition 4.1 to find a point
![]() $\bar r_1^{\prime }\in O $
from
$\bar r_1^{\prime }\in O $
from
![]() $F_0 \cap F_1$
such that
$F_0 \cap F_1$
such that
![]() $\forall \bar r_0^{\prime } \in b_0\ p(\bar r_0^{\prime }, \bar r_1^{\prime }) = 0$
holds. Thus
$\forall \bar r_0^{\prime } \in b_0\ p(\bar r_0^{\prime }, \bar r_1^{\prime }) = 0$
holds. Thus
![]() $\bar r_1^{\prime } \in C_1 $
. Adding
$\bar r_1^{\prime } \in C_1 $
. Adding
![]() $\bar r_1^{\prime }$
to the set
$\bar r_1^{\prime }$
to the set
![]() $c_1$
, the resulting set
$c_1$
, the resulting set
![]() $A_0$
would be smaller, excluding
$A_0$
would be smaller, excluding
![]() $\bar r_0$
from it. This contradicts the choice of the set
$\bar r_0$
from it. This contradicts the choice of the set
![]() $c_1$
.
$c_1$
.
By performing a symmetric argument, find an algebraic set
![]() $A_1 \subset \mathbb {R}^{n_1}$
over
$A_1 \subset \mathbb {R}^{n_1}$
over
![]() $F_0 \cap F_1$
such that
$F_0 \cap F_1$
such that
![]() $a_1 \subset A_1$
, and
$a_1 \subset A_1$
, and
![]() $(A_0 \cap F^{n_0})\times (A_1 \cap F^{n_1})\subset B$
holds. Then, the sets
$(A_0 \cap F^{n_0})\times (A_1 \cap F^{n_1})\subset B$
holds. Then, the sets
![]() $A_0, A_1$
are what we wanted:
$A_0, A_1$
are what we wanted:
![]() $a_0 \subset A_0, a_1 \subset A_1$
hold;
$a_0 \subset A_0, a_1 \subset A_1$
hold;
![]() $A_0 \times A_1 \subset B$
holds as
$A_0 \times A_1 \subset B$
holds as
![]() $(A_0 \cap (F_0 \cap F_1)^{n_0})\times (A_1 \cap (F_0 \cap F_1)^{n_1}) \subset B$
and because the real closed subfield
$(A_0 \cap (F_0 \cap F_1)^{n_0})\times (A_1 \cap (F_0 \cap F_1)^{n_1}) \subset B$
and because the real closed subfield
![]() $F_0 \cap F_1$
is an elementary submodel of
$F_0 \cap F_1$
is an elementary submodel of
![]() $\mathbb {R}$
by the model completeness of real closed fields.
$\mathbb {R}$
by the model completeness of real closed fields.
Corollary 4.6. If
![]() $F_0,F_1$
are real closed subfields of
$F_0,F_1$
are real closed subfields of
![]() $\mathbb {R}$
in amalgamation position,
$\mathbb {R}$
in amalgamation position,
![]() $n>1$
is a natural number, and
$n>1$
is a natural number, and
![]() $\bar {r} \in (F_1)^n$
is a point on
$\bar {r} \in (F_1)^n$
is a point on
![]() $a_0 \subset \mathbb {R}^n$
a line or a circle algebraic over
$a_0 \subset \mathbb {R}^n$
a line or a circle algebraic over
![]() $F_0$
, then
$F_0$
, then
![]() $\bar {r}$
or
$\bar {r}$
or
![]() $a_0$
is algebraic over
$a_0$
is algebraic over
![]() $F_0 \cap F_1$
.
$F_0 \cap F_1$
.
Proof Let us prove the case for lines. Assume
![]() $F_0, F_1$
are in amalgamation position and
$F_0, F_1$
are in amalgamation position and
![]() $\bar {r} \in (F_1)^n$
is a point on a line
$\bar {r} \in (F_1)^n$
is a point on a line
![]() $a_0$
algebraic over
$a_0$
algebraic over
![]() $F_0$
. Consider the set
$F_0$
. Consider the set
![]() $B \subset \mathbb {R}^{2n} \times \mathbb {R}^n$
consisting of all triples
$B \subset \mathbb {R}^{2n} \times \mathbb {R}^n$
consisting of all triples
![]() $(\bar x_0, \bar x_1, \bar x_2)$
of colinear n-tuples of reals. One can see that B is an algebraic set over
$(\bar x_0, \bar x_1, \bar x_2)$
of colinear n-tuples of reals. One can see that B is an algebraic set over
![]() $ \mathbb {Z} \subset F_0\cap F_1$
by writing down the polynomial equation defining B. Let
$ \mathbb {Z} \subset F_0\cap F_1$
by writing down the polynomial equation defining B. Let
![]() $a_1 = \{\bar {r}\}$
. Indeed,
$a_1 = \{\bar {r}\}$
. Indeed,
![]() $a_0 \times a_1 \subset B$
holds. By Proposition 4.4, there are algebraic sets
$a_0 \times a_1 \subset B$
holds. By Proposition 4.4, there are algebraic sets
![]() $A_0 \subset \mathbb {R}^{2n}$
and
$A_0 \subset \mathbb {R}^{2n}$
and
![]() $A_1 \subset \mathbb {R}^{n}$
algebraic over
$A_1 \subset \mathbb {R}^{n}$
algebraic over
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $a_0 \subset A_0$
,
$a_0 \subset A_0$
,
![]() $a_1 \subset A_1$
, and
$a_1 \subset A_1$
, and
![]() $A_0 \times A_1 \subset B$
. We can see specifically
$A_0 \times A_1 \subset B$
. We can see specifically
![]() $a_0\times A_1 \subset B$
holds. This means that
$a_0\times A_1 \subset B$
holds. This means that
![]() $A_1$
is included in the line
$A_1$
is included in the line
![]() $a_0$
by definition of B. Recall just now
$a_0$
by definition of B. Recall just now
![]() $\{\bar {r}\} = a_1 \subset A_1$
. If
$\{\bar {r}\} = a_1 \subset A_1$
. If
![]() $A_1$
has only one element, then it has to be
$A_1$
has only one element, then it has to be
![]() $\bar r$
, which therefore is an algebraic point over
$\bar r$
, which therefore is an algebraic point over
![]() $F_0 \cap F_1$
by Fact 2.15; if
$F_0 \cap F_1$
by Fact 2.15; if
![]() $A_1$
has at least two elements, then the line
$A_1$
has at least two elements, then the line
![]() $a_0\supset A_1$
is an algebraic set over
$a_0\supset A_1$
is an algebraic set over
![]() $F_0 \cap F_1$
, since
$F_0 \cap F_1$
, since
![]() $A_1$
is an algebraic set over
$A_1$
is an algebraic set over
![]() $F_0 \cap F_1$
and two elements in
$F_0 \cap F_1$
and two elements in
![]() $A_1$
will algebraically determine the line
$A_1$
will algebraically determine the line
![]() $a_0$
.
$a_0$
.
For the case for circles, we can instead just consider set
![]() $B \subset \mathbb {R}^{3n} \times \mathbb {R}^n$
consisting of all quadruples
$B \subset \mathbb {R}^{3n} \times \mathbb {R}^n$
consisting of all quadruples
![]() $(\bar x_0, \bar x_1, \bar x_2, \bar x_3 )$
of n-tuples of reals that belong to some circle. The rest of the proof will be the same.
$(\bar x_0, \bar x_1, \bar x_2, \bar x_3 )$
of n-tuples of reals that belong to some circle. The rest of the proof will be the same.
I further strengthen Proposition 4.4 as the following.
Proposition 4.7. Let
![]() $F_0,F_1$
be real closed subfields of
$F_0,F_1$
be real closed subfields of
![]() $\mathbb {R}$
in amalgamation position. Let
$\mathbb {R}$
in amalgamation position. Let
![]() $n_0,n_1>0$
be natural numbers,
$n_0,n_1>0$
be natural numbers,
![]() $f_0\subset F_0, f_1\subset F_1$
be finite sets, and
$f_0\subset F_0, f_1\subset F_1$
be finite sets, and
![]() $B\subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}$
be an algebraic set over
$B\subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}$
be an algebraic set over
![]() $(F_0 \cap F_1) \cup f_0\cup f_1$
. If
$(F_0 \cap F_1) \cup f_0\cup f_1$
. If
![]() $a_0 \subset F_0^{n_0}$
and
$a_0 \subset F_0^{n_0}$
and
![]() $a_1 \subset F_1^{n_1}$
are sets such that
$a_1 \subset F_1^{n_1}$
are sets such that
![]() $a_0 \times a_1 \subset B$
, then there are sets
$a_0 \times a_1 \subset B$
, then there are sets
![]() $A_0 \subset \mathbb {R}^{n_0}$
algebraic over
$A_0 \subset \mathbb {R}^{n_0}$
algebraic over
![]() $(F_0\cap F_1)\cup f_0$
and
$(F_0\cap F_1)\cup f_0$
and
![]() $A_1 \subset \mathbb {R}^{n_1}$
algebraic over
$A_1 \subset \mathbb {R}^{n_1}$
algebraic over
![]() $(F_0\cap F_1)\cup f_1$
such that
$(F_0\cap F_1)\cup f_1$
such that
![]() $a_0 \subset A_0$
,
$a_0 \subset A_0$
,
![]() $a_1 \subset A_1$
, and
$a_1 \subset A_1$
, and
![]() ${A_0 \times A_1 \subset B}$
.
${A_0 \times A_1 \subset B}$
.
Proof Fix some enumeration
![]() $\bar f_0\in \mathbb {R}^{|f_0|},\bar f_1\in \mathbb {R}^{|f_1|}$
for
$\bar f_0\in \mathbb {R}^{|f_0|},\bar f_1\in \mathbb {R}^{|f_1|}$
for
![]() $f_0$
,
$f_0$
,
![]() $f_1$
respectively. Since B is algebraic over
$f_1$
respectively. Since B is algebraic over
![]() $(F_0 \cap F_1) \cup f_0\cup f_1$
, find an algebraic set
$(F_0 \cap F_1) \cup f_0\cup f_1$
, find an algebraic set
![]() $C \subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}\times \mathbb {R}^{|f_0|}\times \mathbb {R}^{|f_1|}$
over
$C \subset \mathbb {R}^{n_0}\times \mathbb {R}^{n_1}\times \mathbb {R}^{|f_0|}\times \mathbb {R}^{|f_1|}$
over
![]() $F_0 \cap F_1$
such that the horizontal section
$F_0 \cap F_1$
such that the horizontal section
![]() $C^{ \bar f_0\times \bar f_1} = ( C^{\bar f_1})^{\bar f_0}$
equals the set B. Assume
$C^{ \bar f_0\times \bar f_1} = ( C^{\bar f_1})^{\bar f_0}$
equals the set B. Assume
![]() $a_0 \subset F_0^{n_0}$
and
$a_0 \subset F_0^{n_0}$
and
![]() $a_1 \subset F_1^{n_1}$
are sets such that
$a_1 \subset F_1^{n_1}$
are sets such that
![]() $a_0 \times a_1 \subset B$
. Then
$a_0 \times a_1 \subset B$
. Then
![]() $a_0 \times a_1 \times \{\bar f_0\} \times \{ \bar f_1\} \subset C$
by our choice of C, with
$a_0 \times a_1 \times \{\bar f_0\} \times \{ \bar f_1\} \subset C$
by our choice of C, with
![]() $a_0\times \{\bar f_0\} \subset F_0^{n_0 }\times F_0^ { |f_0|} $
and
$a_0\times \{\bar f_0\} \subset F_0^{n_0 }\times F_0^ { |f_0|} $
and
![]() $a_1\times \{\bar f_1\} \subset F_1^{n_1}\times F_1^ {|f_1|} $
. By Proposition 4.4, there are algebraic sets
$a_1\times \{\bar f_1\} \subset F_1^{n_1}\times F_1^ {|f_1|} $
. By Proposition 4.4, there are algebraic sets
![]() $A_0 \subset \mathbb {R}^{n_0}\times \mathbb {R}^{|f_0|}$
and
$A_0 \subset \mathbb {R}^{n_0}\times \mathbb {R}^{|f_0|}$
and
![]() $A_1 \subset \mathbb {R}^{n_1} \times \mathbb {R}^{|f_1|}$
over
$A_1 \subset \mathbb {R}^{n_1} \times \mathbb {R}^{|f_1|}$
over
![]() $F_0\cap F_1$
such that
$F_0\cap F_1$
such that
![]() $a_0 \times \{\bar f_0\} \subset A_0$
,
$a_0 \times \{\bar f_0\} \subset A_0$
,
![]() $a_1\times \{\bar f_1\} \subset A_1$
, and
$a_1\times \{\bar f_1\} \subset A_1$
, and
![]() $A_0 \times A_1 \subset C$
. Then we get the algebraic sets
$A_0 \times A_1 \subset C$
. Then we get the algebraic sets
![]() $A_0^{\bar f_0} \subset \mathbb {R}^{n_0}$
over
$A_0^{\bar f_0} \subset \mathbb {R}^{n_0}$
over
![]() $(F_0\cap F_1)\cup f_0$
and
$(F_0\cap F_1)\cup f_0$
and
![]() $A_1^{\bar f_1} \subset \mathbb {R}^{n_1}$
over
$A_1^{\bar f_1} \subset \mathbb {R}^{n_1}$
over
![]() $(F_0\cap F_1)\cup f_1$
such that
$(F_0\cap F_1)\cup f_1$
such that
![]() $a_0 \subset A_0^{\bar f_0}$
,
$a_0 \subset A_0^{\bar f_0}$
,
![]() $a_1 \subset A_1^{\bar f_1}$
, and
$a_1 \subset A_1^{\bar f_1}$
, and
![]() $A_0^{\bar f_0}\times A_1^{\bar f_1} \subset B$
, as wanted.
$A_0^{\bar f_0}\times A_1^{\bar f_1} \subset B$
, as wanted.
Corollary 4.8. Assume that
![]() $F_0,F_1$
are real closed subfields of
$F_0,F_1$
are real closed subfields of
![]() $\mathbb {R}$
in amalgamation position, that
$\mathbb {R}$
in amalgamation position, that
![]() $ x_0 \subset F_0$
,
$ x_0 \subset F_0$
,
![]() $ x_1 \subset F_1$
are finite sets, and that
$ x_1 \subset F_1$
are finite sets, and that
![]() ${y} \in F_1$
is a point. If y is an algebraic point over
${y} \in F_1$
is a point. If y is an algebraic point over
![]() $(F_0\cap F_1) \cup x_0 \cup x_1 $
, then y is an algebraic point over
$(F_0\cap F_1) \cup x_0 \cup x_1 $
, then y is an algebraic point over
![]() ${(F_0\cap F_1) \cup x_1 }$
.
${(F_0\cap F_1) \cup x_1 }$
.
Proof Let
![]() $B = \{0\} \times \{y\}$
which is algebraic over
$B = \{0\} \times \{y\}$
which is algebraic over
![]() $(F_0\cap F_1 )\cup x_0 \cup x_1 $
. Since
$(F_0\cap F_1 )\cup x_0 \cup x_1 $
. Since
![]() $\{0\} \times \{y\} \subset B = \{0\} \times \{y\}$
, by Proposition 4.7, we have
$\{0\} \times \{y\} \subset B = \{0\} \times \{y\}$
, by Proposition 4.7, we have
![]() $A_1 = \{y\}$
algebraic over
$A_1 = \{y\}$
algebraic over
![]() $(F_0\cap F_1) \cup x_1 $
. Therefore y is algebraic over
$(F_0\cap F_1) \cup x_1 $
. Therefore y is algebraic over
![]() $(F_0\cap F_1) \cup x_1 $
.
$(F_0\cap F_1) \cup x_1 $
.
Finally, using mutual genericity and the following proposition, we can build pairs of real closed subfields of
![]() $\mathbb {R}$
that are in amalgamation position.
$\mathbb {R}$
that are in amalgamation position.
Proposition 4.9. Whenever
![]() $V [G_0], V [G_1]$
are mutually generic extensions,
$V [G_0], V [G_1]$
are mutually generic extensions,
![]() $F_0 = \mathbb {R} \cap V [G_0]$
and
$F_0 = \mathbb {R} \cap V [G_0]$
and
![]() $F_1 = \mathbb {R} \cap V [G_1]$
are in amalgamation position.
$F_1 = \mathbb {R} \cap V [G_1]$
are in amalgamation position.
Proof Firstly and trivially,
![]() $\mathbb {R}$
remains to be a real closed field in any generic extension. Now work in the ground model V. Let
$\mathbb {R}$
remains to be a real closed field in any generic extension. Now work in the ground model V. Let
![]() $Q_0, Q_1$
be partial orders, let
$Q_0, Q_1$
be partial orders, let
![]() $\tau _0, \tau _1$
be their respective names for strings of reals, let p be a polynomial, and let
$\tau _0, \tau _1$
be their respective names for strings of reals, let p be a polynomial, and let
![]() $ O$
be a basic open set of a Euclidean space such that
$ O$
be a basic open set of a Euclidean space such that
![]() $Q_0 \Vdash \tau _0 \in O$
and
$Q_0 \Vdash \tau _0 \in O$
and
![]() $Q_0\times Q_1 \Vdash p(\tau _0, \tau _1) = 0$
holds. Let
$Q_0\times Q_1 \Vdash p(\tau _0, \tau _1) = 0$
holds. Let
![]() $\langle q_0^n : n \in \omega \rangle $
be a descending sequence of conditions in
$\langle q_0^n : n \in \omega \rangle $
be a descending sequence of conditions in
![]() $Q_0$
and let
$Q_0$
and let
![]() $\{ O_n \}_{n \in \omega }$
be a sequence of basic open neighborhoods such that
$\{ O_n \}_{n \in \omega }$
be a sequence of basic open neighborhoods such that
![]() $O = O_0, \bar O_{n+1} \subset O_n$
,
$O = O_0, \bar O_{n+1} \subset O_n$
,
![]() $O_{n+1}$
has a metric diameter at most
$O_{n+1}$
has a metric diameter at most
![]() $2^{-n}$
, and
$2^{-n}$
, and
![]() $q_0^n \Vdash \tau _0 \in O_n$
. The intersection
$q_0^n \Vdash \tau _0 \in O_n$
. The intersection
![]() $\bigcap _n O_n$
contains a single point
$\bigcap _n O_n$
contains a single point
![]() $\bar r $
. It will suffice to show that
$\bar r $
. It will suffice to show that
![]() $Q_1 \Vdash p(\bar r , \tau _1) = 0$
holds.
$Q_1 \Vdash p(\bar r , \tau _1) = 0$
holds.
If not, then by continuity of polynomial functions there has to be a number
![]() $n\in \omega $
and a condition
$n\in \omega $
and a condition
![]() $q_1 \in Q_1$
such that
$q_1 \in Q_1$
such that
![]() $q_1 \Vdash p\upharpoonright O_n\times \{\tau _1\}$
is never zero. Then, the condition
$q_1 \Vdash p\upharpoonright O_n\times \{\tau _1\}$
is never zero. Then, the condition
![]() $\langle q_0^n,q_1\rangle $
forces in the product that
$\langle q_0^n,q_1\rangle $
forces in the product that
![]() $p(\tau _0,\tau _1)\neq 0$
, contradicting the initial assumptions.
$p(\tau _0,\tau _1)\neq 0$
, contradicting the initial assumptions.
5 Forcing with algebraic amalgamation
This section bridges between an algebraic notion of amalgamation in posets and the forcing-theoretic balance.
Definition 5.1. An
![]() $\mathbb {R}$
-analytic forcing satisfies
$\mathbb {R}$
-analytic forcing satisfies
![]() $\mathbb {R}$
-amalgamation if for any pair of
$\mathbb {R}$
-amalgamation if for any pair of
![]() $ p_0, p_1 \in P $
such that the fields
$ p_0, p_1 \in P $
such that the fields
![]() $\mathrm {supp}(p_0)$
,
$\mathrm {supp}(p_0)$
,
![]() $\mathrm {supp}(p_1) \subset \mathbb {R}$
are in amalgamation position, the following (1) implies (2):
$\mathrm {supp}(p_1) \subset \mathbb {R}$
are in amalgamation position, the following (1) implies (2):
-
1.
 $p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
, and, writing
$p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
, and, writing
 $p_\cap $
for the common value,
$p_\cap $
for the common value,
 $p_\cap \in P$
,
$p_\cap \in P$
,
 $p_0\leq p_\cap $
,
$p_0\leq p_\cap $
,
 $p_1\leq p_\cap $
hold.
$p_1\leq p_\cap $
hold. -
2.
 $ p_0, p_1$
have a common lower bound in P.
$ p_0, p_1$
have a common lower bound in P.
By quantifier counting procedure, one can check that
![]() $\mathbb {R}$
-amalgamation is a
$\mathbb {R}$
-amalgamation is a
![]() $\Pi ^1_2$
statement and therefore absolute throughout all forcing extensions by the Shoenfield absoluteness [Reference Jech3, Theorem 25.20]. The main point in this section is that
$\Pi ^1_2$
statement and therefore absolute throughout all forcing extensions by the Shoenfield absoluteness [Reference Jech3, Theorem 25.20]. The main point in this section is that
![]() $\mathbb {R}$
-amalgamation implies forcing theoretic balance as Theorem 5.3. Unfortunately, we are not able to easily provide a typical connection and classification of balanced virtual conditions as in [Reference Larson and Zapletal5, Chapters 6–8] because our poset P does not satisfy (2)
$\mathbb {R}$
-amalgamation implies forcing theoretic balance as Theorem 5.3. Unfortunately, we are not able to easily provide a typical connection and classification of balanced virtual conditions as in [Reference Larson and Zapletal5, Chapters 6–8] because our poset P does not satisfy (2)
![]() $\Longrightarrow $
(1) in Definition 5.1. But this doesn’t affect the result of this paper.
$\Longrightarrow $
(1) in Definition 5.1. But this doesn’t affect the result of this paper.
Definition 5.2. Let P be an
![]() $\mathbb {R}$
-analytic forcing. A P-structure is a relational structure c that is total with universe
$\mathbb {R}$
-analytic forcing. A P-structure is a relational structure c that is total with universe
![]() $\mathbb {R}$
such that Coll
$\mathbb {R}$
such that Coll ![]() holds.
holds.
Theorem 5.3. Let P be an
![]() $\mathbb {R}$
-analytic forcing with
$\mathbb {R}$
-analytic forcing with
![]() $\mathbb {R}$
-amalgamation. Then the following hold:
$\mathbb {R}$
-amalgamation. Then the following hold:
-
1. If c is a P-structure, then the pair
 is balanced.
is balanced. -
2. If the Continuum Hypothesis holds, then P is balanced.
-
3. P is balanced cofinally below
 $\kappa $
for every inaccessible cardinal
$\kappa $
for every inaccessible cardinal
 $\kappa $
.
$\kappa $
.
Proof For (1), assume c is a P-structure. Then ![]() holds by definition. Let
holds by definition. Let
![]() $V [G_0], V [G_1]$
be mutually generic extensions and let
$V [G_0], V [G_1]$
be mutually generic extensions and let
![]() $p_0, p_1$
be conditions in P in the respective models
$p_0, p_1$
be conditions in P in the respective models
![]() $V [G_0], V [G_1]$
such that
$V [G_0], V [G_1]$
such that
![]() $p_0, p_1 \leq c$
holds. Since c is total,
$p_0, p_1 \leq c$
holds. Since c is total,
![]() $p_0, p_1$
are total as well, i.e.,
$p_0, p_1$
are total as well, i.e.,
![]() $\mathrm {supp}(p_0)= \mathbb {R}\cap V [G_0]$
and
$\mathrm {supp}(p_0)= \mathbb {R}\cap V [G_0]$
and
![]() $\mathrm {supp}(p_1)= \mathbb {R}\cap V [G_1]$
hold. We must show that
$\mathrm {supp}(p_1)= \mathbb {R}\cap V [G_1]$
hold. We must show that
![]() $p_0, p_1$
have a common lower bound in some ambient model. By Proposition 4.9, the fields
$p_0, p_1$
have a common lower bound in some ambient model. By Proposition 4.9, the fields
![]() $\mathrm {supp}(p_0)= \mathbb {R}\cap V [G_0]$
and
$\mathrm {supp}(p_0)= \mathbb {R}\cap V [G_0]$
and
![]() $\mathrm {supp}(p_1)= \mathbb {R}\cap V [G_1]$
are in amalgamation position. By the properties of the ordering of P,
$\mathrm {supp}(p_1)= \mathbb {R}\cap V [G_1]$
are in amalgamation position. By the properties of the ordering of P,
![]() $p_0 \upharpoonright V = p_1 \upharpoonright V = c $
holds. The
$p_0 \upharpoonright V = p_1 \upharpoonright V = c $
holds. The
![]() $\mathbb {R}$
-amalgamation applied in the model
$\mathbb {R}$
-amalgamation applied in the model
![]() $V [G_0, G_1]$
then implies that
$V [G_0, G_1]$
then implies that
![]() $p_0, p_1$
have a common lower bound as desired. Then by [Reference Larson and Zapletal5, Proposition 5.2.2], the pair
$p_0, p_1$
have a common lower bound as desired. Then by [Reference Larson and Zapletal5, Proposition 5.2.2], the pair ![]() is balanced.
is balanced.
For (2), let
![]() $p \in P$
be a condition and we will produce a balanced virtual condition below p. Use the Continuum Hypothesis (CH) assumption to enumerate all reals as
$p \in P$
be a condition and we will produce a balanced virtual condition below p. Use the Continuum Hypothesis (CH) assumption to enumerate all reals as
![]() $\{ r_\alpha \}_{\alpha \in \omega _1}$
, and by transfinite recursion on
$\{ r_\alpha \}_{\alpha \in \omega _1}$
, and by transfinite recursion on
![]() $\alpha \in \omega _1$
build conditions
$\alpha \in \omega _1$
build conditions
![]() $p_\alpha $
so that
$p_\alpha $
so that
![]() $p_0 = p, p_{\alpha +1} \leq p_\alpha $
,
$p_0 = p, p_{\alpha +1} \leq p_\alpha $
,
![]() $r_{\alpha } \in \mathrm {supp}(p_{\alpha +1})$
, and for limit ordinals
$r_{\alpha } \in \mathrm {supp}(p_{\alpha +1})$
, and for limit ordinals
![]() $\alpha $
,
$\alpha $
,
![]() $p_\alpha = \bigcup _{\beta \in \alpha } p_\beta $
. This is possible by Definition 2.10(3) and (4) and the result is a descending sequence of conditions in P. Let
$p_\alpha = \bigcup _{\beta \in \alpha } p_\beta $
. This is possible by Definition 2.10(3) and (4) and the result is a descending sequence of conditions in P. Let
![]() $c = \bigcup _{\alpha } p_\alpha $
. c is a relational structure on
$c = \bigcup _{\alpha } p_\alpha $
. c is a relational structure on
![]() $\mathbb {R}$
and by Definition 2.10(4), Coll
$\mathbb {R}$
and by Definition 2.10(4), Coll![]() and
and ![]() . Thus c is a P-structure. By (1) of the present theorem,
. Thus c is a P-structure. By (1) of the present theorem, ![]() is a balanced pair. By [Reference Larson and Zapletal5, Theorem 5.2.8]Footnote
4
, the
is a balanced pair. By [Reference Larson and Zapletal5, Theorem 5.2.8]Footnote
4
, the
![]() $ \equiv _b$
-class containing
$ \equiv _b$
-class containing ![]() contains a balanced virtual condition, which is stronger than p as desired.
contains a balanced virtual condition, which is stronger than p as desired.
For (3), for every inaccessible cardinal
![]() $\kappa $
, since
$\kappa $
, since
![]() $V_\kappa \models $
every forcing extension has a further extension in which CH holds, P is balanced cofinally below
$V_\kappa \models $
every forcing extension has a further extension in which CH holds, P is balanced cofinally below
![]() $\kappa $
.
$\kappa $
.
Now let the poset P be defined as Definition 3.1.
Theorem 5.4. P satisfies
![]() $\mathbb {R}$
-amalgamation.
$\mathbb {R}$
-amalgamation.
Once the theorem is verified, we can conclude that if the Continuum Hypothesis holds, then P is balancedFootnote
5
by Theorem 5.3. Before we prove Theorem 5.4, we need a few lemmas and a definition. Fix any pair of conditions
![]() $ p_0, p_1 \in P $
with
$ p_0, p_1 \in P $
with
![]() $\mathrm {supp}(p_0)$
and
$\mathrm {supp}(p_0)$
and
![]() $\mathrm {supp}(p_1)$
being in amalgamation position. Assume
$\mathrm {supp}(p_1)$
being in amalgamation position. Assume
![]() $p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
. Denote
$p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
. Denote
![]() $ p_\cup =p_0 \cup p_1 , p_\cap =p_0 \cap p_1 $
. Assume
$ p_\cup =p_0 \cup p_1 , p_\cap =p_0 \cap p_1 $
. Assume
![]() $p_\cap \in P$
,
$p_\cap \in P$
,
![]() $p_0\leq p_\cap $
,
$p_0\leq p_\cap $
,
![]() $p_1\leq p_\cap $
hold.
$p_1\leq p_\cap $
hold.
Lemma 5.5.
![]() $p_\cup $
is a partial
$p_\cup $
is a partial
![]() ${\Gamma _2}$
-coloring.
${\Gamma _2}$
-coloring.
Proof Assume that there is an hyperedge
![]() $\{x,y,z\} \in {{\Gamma _2}}$
, and
$\{x,y,z\} \in {{\Gamma _2}}$
, and
![]() $x,y \in \mathrm {dom}(p_0)$
,
$x,y \in \mathrm {dom}(p_0)$
,
![]() $z \in \mathrm {dom}(p_1)$
without loss of generality. We will show that
$z \in \mathrm {dom}(p_1)$
without loss of generality. We will show that
![]() $\{x,y,z\} $
is not monochromatic by
$\{x,y,z\} $
is not monochromatic by
![]() $p_\cup $
. There are three cases depending on which is the pivot point for the isosceles triangle.
$p_\cup $
. There are three cases depending on which is the pivot point for the isosceles triangle.
Case 1: z is the pivot point. Let l be the perpendicular bisector for the line segment from x to y. By Proposition 4.6,
![]() $z\in \mathrm {dom}(p_\cap )$
or the line l is algebraic over
$z\in \mathrm {dom}(p_\cap )$
or the line l is algebraic over
![]() $\mathrm {supp}(p_\cap )$
. If
$\mathrm {supp}(p_\cap )$
. If
![]() $z\in \mathrm {dom}(p_\cap )$
, then
$z\in \mathrm {dom}(p_\cap )$
, then
![]() $p_\cup ^{\prime \prime }\{x,y,z\} = p_0^{\prime \prime }\{x,y,z\}$
is not monochromatic since
$p_\cup ^{\prime \prime }\{x,y,z\} = p_0^{\prime \prime }\{x,y,z\}$
is not monochromatic since
![]() $p_0$
is a
$p_0$
is a
![]() ${\Gamma _2}$
-coloring on
${\Gamma _2}$
-coloring on
![]() $\mathrm {dom}(p_0) $
. Now assume that
$\mathrm {dom}(p_0) $
. Now assume that
![]() $z\notin \mathrm {dom}(p_\cap )$
and l is algebraic over
$z\notin \mathrm {dom}(p_\cap )$
and l is algebraic over
![]() $\mathrm {supp}(p_\cap )$
. If
$\mathrm {supp}(p_\cap )$
. If
![]() $p_0(x) = p_0(y)$
, then
$p_0(x) = p_0(y)$
, then
![]() $p_0(x) = p_0(y) \in s(p_0, l)$
. By Definition 3.1(6) the symmetrical colors invariant requirement, since
$p_0(x) = p_0(y) \in s(p_0, l)$
. By Definition 3.1(6) the symmetrical colors invariant requirement, since
![]() $p_0 \leq p_\cap \geq p_1$
,
$p_0 \leq p_\cap \geq p_1$
,
![]() $ s(p_0, l) = s( p_\cap , l) = s(p_1, l)$
, then there must have been
$ s(p_0, l) = s( p_\cap , l) = s(p_1, l)$
, then there must have been
![]() $x', y' \in \mathrm {dom}(p_\cap )$
such that
$x', y' \in \mathrm {dom}(p_\cap )$
such that
![]() $p_0(x) = p_0(y) = p_0(x') = p_0(y')$
. Since
$p_0(x) = p_0(y) = p_0(x') = p_0(y')$
. Since
![]() $p_1$
is a
$p_1$
is a
![]() $\Gamma _2$
-coloring,
$\Gamma _2$
-coloring,
![]() $p_1(z) \neq p_1(x') = p_1 (y') = p_0(x') = p_0(y') = p_0(x) = p_0(y)$
. Hence
$p_1(z) \neq p_1(x') = p_1 (y') = p_0(x') = p_0(y') = p_0(x) = p_0(y)$
. Hence
![]() $\{x,y,z\} $
is not monochromatic by
$\{x,y,z\} $
is not monochromatic by
![]() $p_\cup $
.
$p_\cup $
.
Case 2: y is the pivot point. Let O be the circle centered at y passing through x. By Proposition 4.6,
![]() $z\in \mathrm {dom}(p_\cap )$
or O is algebraic over
$z\in \mathrm {dom}(p_\cap )$
or O is algebraic over
![]() $\mathrm {supp}(p_\cap )$
. If
$\mathrm {supp}(p_\cap )$
. If
![]() $z\in \mathrm {dom}(p_\cap )$
,
$z\in \mathrm {dom}(p_\cap )$
,
![]() $p_\cup ^{\prime \prime }\{x,y,z\}= p_0^{\prime \prime }\{x,y,z\}$
is not monochromatic since
$p_\cup ^{\prime \prime }\{x,y,z\}= p_0^{\prime \prime }\{x,y,z\}$
is not monochromatic since
![]() $p_0$
is a
$p_0$
is a
![]() $\Gamma _2$
-coloring. Now assume that
$\Gamma _2$
-coloring. Now assume that
![]() $z\notin \mathrm {dom}(p_\cap )$
and O is algebraic over
$z\notin \mathrm {dom}(p_\cap )$
and O is algebraic over
![]() $\mathrm {supp}(p_\cap )$
. By Definition 3.1(7) the avoid center requirement,
$\mathrm {supp}(p_\cap )$
. By Definition 3.1(7) the avoid center requirement,
![]() $p_1(z) \neq p_1(y)$
. Hence
$p_1(z) \neq p_1(y)$
. Hence
![]() $\{x,y,z\} $
is not monochromatic by
$\{x,y,z\} $
is not monochromatic by
![]() $p_\cup $
.
$p_\cup $
.
Case 3: x is the pivot point. It’s the same argument as Case 2.
Definition 5.6. For every point
![]() $x \in \mathbb {R}^2\setminus \mathrm {dom}(p_\cup ) $
, define
$x \in \mathbb {R}^2\setminus \mathrm {dom}(p_\cup ) $
, define
![]() $d(p_0,p_1, x)$
the set of disallowed colors on x for
$d(p_0,p_1, x)$
the set of disallowed colors on x for
![]() $p_0,p_1$
:
$p_0,p_1$
:
where:
-
(S)
 $L = \{l\in E^L(\mathrm {supp}(p_\cup )): x\in l\}$
and
$L = \{l\in E^L(\mathrm {supp}(p_\cup )): x\in l\}$
and
 $S = \bigcup _{l\in L} s(p_\cup , l)$
;
$S = \bigcup _{l\in L} s(p_\cup , l)$
; -
(O)
 $O = \{o\in E^O(\mathrm {supp}(p_\cup )): $
the center of o is in
$O = \{o\in E^O(\mathrm {supp}(p_\cup )): $
the center of o is in
 $\mathrm {dom}(p_\cup )$
and
$\mathrm {dom}(p_\cup )$
and
 $x\in o\}$
,
$x\in o\}$
,
 $O^- = O\cap (E^O(\mathrm {supp}(p_0))\cup E^O(\mathrm {supp}(p_1)) )$
;
$O^- = O\cap (E^O(\mathrm {supp}(p_0))\cup E^O(\mathrm {supp}(p_1)) )$
; -
(T)
 $T = \bigcup _{o\in O^-}\{t: t \text { is the center of } o\}$
;
$T = \bigcup _{o\in O^-}\{t: t \text { is the center of } o\}$
; -
(R)
 $R = \{y \in \mathrm {dom}(p_\cup ) : $
that x and y are symmetrical with respect to l for some
$R = \{y \in \mathrm {dom}(p_\cup ) : $
that x and y are symmetrical with respect to l for some
 $l \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) \}$
.
$l \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) \}$
.
Lemma 5.7.
![]() $d(p_0,p_1, x)\in I$
.
$d(p_0,p_1, x)\in I$
.
Proof We start with the following claim.
Claim 5.8. For
![]() $i\in 2$
, if
$i\in 2$
, if
![]() $l\in E^L(\mathrm {supp}(p_i))$
, then
$l\in E^L(\mathrm {supp}(p_i))$
, then
![]() $s(p_\cup , l) = s(p_i, l) $
.
$s(p_\cup , l) = s(p_i, l) $
.
Proof We prove the case for
![]() $i=0$
and the proof for the other case is the same. We will rule out all the possible ways that
$i=0$
and the proof for the other case is the same. We will rule out all the possible ways that
![]() $s(p_\cup , l)$
can have more elements than
$s(p_\cup , l)$
can have more elements than
![]() $s(p_0, l)$
. Let
$s(p_0, l)$
. Let
![]() $x,y\in \mathrm {dom}(p_\cup )$
be a symmetrical pair of points with respect to l.
$x,y\in \mathrm {dom}(p_\cup )$
be a symmetrical pair of points with respect to l.
Case 1: at least one point from
![]() $\{x,y\} $
is in
$\{x,y\} $
is in
![]() $\mathrm {dom}(p_0) $
. Since
$\mathrm {dom}(p_0) $
. Since
![]() $l \in E^L(\mathrm {supp}(p_0)) $
and by Fact 3.2(6),
$l \in E^L(\mathrm {supp}(p_0)) $
and by Fact 3.2(6),
![]() $\{x,y\} \subset \mathrm {dom}(p_0)$
. So this case doesn’t witness any element in
$\{x,y\} \subset \mathrm {dom}(p_0)$
. So this case doesn’t witness any element in
![]() $s(p_\cup , l)\setminus s(p_0, l)$
.
$s(p_\cup , l)\setminus s(p_0, l)$
.
Case 2:
![]() $x,y\in \mathrm {dom}(p_1) \setminus \mathrm {dom}(p_0) $
.
$x,y\in \mathrm {dom}(p_1) \setminus \mathrm {dom}(p_0) $
.
Then
![]() $l\in E^L(\mathrm {supp}(p_1))$
by Fact 3.2(2). Then
$l\in E^L(\mathrm {supp}(p_1))$
by Fact 3.2(2). Then
![]() $l{\kern-1.5pt}\in{\kern-1.5pt} E^L(\mathrm {supp}(p_0)){\kern-1.5pt}\cap{\kern-1.5pt} E^L(\mathrm {supp}(p_1)) \subset E^L(\mathrm {supp}(p_\cap ))$
by Corollary 4.3. Since
$l{\kern-1.5pt}\in{\kern-1.5pt} E^L(\mathrm {supp}(p_0)){\kern-1.5pt}\cap{\kern-1.5pt} E^L(\mathrm {supp}(p_1)) \subset E^L(\mathrm {supp}(p_\cap ))$
by Corollary 4.3. Since
![]() $p_0, p_1 \leq p_\cap $
,
$p_0, p_1 \leq p_\cap $
,
![]() $s(p_0 , l) = s( p_\cap , l) = s(p_1, l)$
. Then
$s(p_0 , l) = s( p_\cap , l) = s(p_1, l)$
. Then
![]() $ p_1(x) = p_1(y) \rightarrow ( p_1(x),p_1(y) \in s(p_1 , l)= s(p_\cap , l) = s(p_0 , l) ) \rightarrow (p_1(x),p_1(y) \notin s(p_\cup , l)\setminus s(p_0, l) )$
holds. So this case doesn’t witness any element in
$ p_1(x) = p_1(y) \rightarrow ( p_1(x),p_1(y) \in s(p_1 , l)= s(p_\cap , l) = s(p_0 , l) ) \rightarrow (p_1(x),p_1(y) \notin s(p_\cup , l)\setminus s(p_0, l) )$
holds. So this case doesn’t witness any element in
![]() $s(p_\cup , l)\setminus s(p_0, l)$
.
$s(p_\cup , l)\setminus s(p_0, l)$
.
We have ruled out all possible ways that
![]() $s(p_\cup , l)$
can have more elements than
$s(p_\cup , l)$
can have more elements than
![]() $s(p_0, l)$
. Therefore
$s(p_0, l)$
. Therefore
![]() $s(p_0, l) = s(p_\cup , l)$
.
$s(p_0, l) = s(p_\cup , l)$
.
Part (S): Denote
![]() $L\cap (E^L(\mathrm {supp}(p_0))\cup E^L(\mathrm {supp}(p_1)))$
by
$L\cap (E^L(\mathrm {supp}(p_0))\cup E^L(\mathrm {supp}(p_1)))$
by
![]() $L^-$
. Observe that
$L^-$
. Observe that
![]() $L^-$
must be finite (in fact with cardinality two or less) using Fact 3.2(5). Let
$L^-$
must be finite (in fact with cardinality two or less) using Fact 3.2(5). Let
![]() $l\in L$
. If
$l\in L$
. If
![]() $l\in L^-$
, then
$l\in L^-$
, then
![]() $s(p_\cup , l) = s(p_0, l) \in I$
or
$s(p_\cup , l) = s(p_0, l) \in I$
or
![]() $s(p_\cup , l) = s(p_1, l)\in I$
by Claim 5.8. Therefore
$s(p_\cup , l) = s(p_1, l)\in I$
by Claim 5.8. Therefore
![]() $\bigcup _{l\in L^-} s( p_\cup , l)$
is in
$\bigcup _{l\in L^-} s( p_\cup , l)$
is in
![]() $ I$
.
$ I$
.
Now let’s investigate the set of lines
![]() $ L\setminus L^-$
. For every
$ L\setminus L^-$
. For every
![]() $l\in L\setminus L^-$
, let
$l\in L\setminus L^-$
, let
![]() $\Xi (l) = \{(y,z)\in \mathrm {dom}(p_0)\times \mathrm {dom} (p_1) : y,z$
are symmetrical with respect to
$\Xi (l) = \{(y,z)\in \mathrm {dom}(p_0)\times \mathrm {dom} (p_1) : y,z$
are symmetrical with respect to
![]() $l\}$
. In particular, we will look into the set
$l\}$
. In particular, we will look into the set
![]() $\Xi (l)|_1$
the projection of
$\Xi (l)|_1$
the projection of
![]() $\Xi (l)$
to the coordinate 1. We will show that every point in
$\Xi (l)$
to the coordinate 1. We will show that every point in
![]() $ \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} $
is algebraic over
$ \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} $
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a$
for some finite set
$\mathrm {supp}(p_\cap ) \cup a$
for some finite set
![]() $a \subset \mathrm {dom}(p_1)$
.
$a \subset \mathrm {dom}(p_1)$
.
Case S.1: the set
![]() $L\setminus L^-$
has cardinality one. Let
$L\setminus L^-$
has cardinality one. Let
![]() $l\in L\setminus L^-$
. If the set
$l\in L\setminus L^-$
. If the set
![]() $\Xi (l) $
has cardinality at most one, then
$\Xi (l) $
has cardinality at most one, then
![]() $s( p_\cup , l)$
is finite (in fact of cardinality at most
$s( p_\cup , l)$
is finite (in fact of cardinality at most
![]() $1$
), thus in the ideal I. Now suppose that
$1$
), thus in the ideal I. Now suppose that
![]() $|\Xi (l)|> 1 $
holds. Fix
$|\Xi (l)|> 1 $
holds. Fix
![]() $ (y,z)\in \Xi (l)$
. We will show that the set
$ (y,z)\in \Xi (l)$
. We will show that the set
![]() $\Xi (l)|_1$
consists of points algebraic over
$\Xi (l)|_1$
consists of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z\}$
. Notice that l is the perpendicular bisector of the line segment from x to y. Let
$\mathrm {supp}(p_\cap ) \cup \{z\}$
. Notice that l is the perpendicular bisector of the line segment from x to y. Let
![]() $ (y',z')\in \Xi (l)$
such that
$ (y',z')\in \Xi (l)$
such that
![]() $(y,z) \neq (y',z')$
. Then
$(y,z) \neq (y',z')$
. Then
![]() $ y', z' $
are symmetrical with respect to l. Then it’s easy to see that the point
$ y', z' $
are symmetrical with respect to l. Then it’s easy to see that the point
![]() $z'$
is algebraic over
$z'$
is algebraic over
![]() $\{y, z, y'\}$
, hence algebraic over
$\{y, z, y'\}$
, hence algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{y, z, y'\}$
. Then by Proposition 4.8, the point
$\mathrm {supp}(p_\cap ) \cup \{y, z, y'\}$
. Then by Proposition 4.8, the point
![]() $z'$
is algebraic over
$z'$
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z\}$
. Hence every point in
$\mathrm {supp}(p_\cap ) \cup \{z\}$
. Hence every point in
![]() $ \Xi (l)|_1$
is algebraic over
$ \Xi (l)|_1$
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z\}$
, i.e.,
$\mathrm {supp}(p_\cap ) \cup \{z\}$
, i.e.,
![]() $\Xi (l)|_1$
consists of points algebraic over
$\Xi (l)|_1$
consists of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z\}$
where
$\mathrm {supp}(p_\cap ) \cup \{z\}$
where
![]() $\{z\}\subset \mathrm {dom}(p_1)$
.
$\{z\}\subset \mathrm {dom}(p_1)$
.
Case S.2: the set
![]() $L\setminus L^-$
has cardinality more than one. Take distinct lines
$L\setminus L^-$
has cardinality more than one. Take distinct lines
![]() $l_0,l_1 \in L\setminus L^-$
. Take pairs of pointsFootnote
6
$l_0,l_1 \in L\setminus L^-$
. Take pairs of pointsFootnote
6
![]() $ (y,z)\in \Xi (l_0)$
and
$ (y,z)\in \Xi (l_0)$
and
![]() $ (y',z')\in \Xi (l_1)$
. Then
$ (y',z')\in \Xi (l_1)$
. Then
![]() $(y,z) \neq (y',z')$
. We see that x can be calculated from
$(y,z) \neq (y',z')$
. We see that x can be calculated from
![]() $\{y,z, y',z'\}$
using polynomials: x is the intersection of
$\{y,z, y',z'\}$
using polynomials: x is the intersection of
![]() $l_0,l_1$
, the perpendicular bisectors of the line segment
$l_0,l_1$
, the perpendicular bisectors of the line segment
![]() $(y,z)$
and the line segment
$(y,z)$
and the line segment
![]() $ (y',z')$
respectively. Then x is algebraic over
$ (y',z')$
respectively. Then x is algebraic over
![]() $ \{y,z, y',z'\}$
. If possible, take another pair of points
$ \{y,z, y',z'\}$
. If possible, take another pair of points
![]() $(y",z")\in \Xi (l_2)$
distinct from
$(y",z")\in \Xi (l_2)$
distinct from
![]() $(y,z),(y',z')$
for some line
$(y,z),(y',z')$
for some line
![]() $l_2 \in L\setminus L^-$
. The line
$l_2 \in L\setminus L^-$
. The line
![]() $l_2$
is not necessarily distinct from
$l_2$
is not necessarily distinct from
![]() $l_0,l_1$
. We will show that
$l_0,l_1$
. We will show that
![]() $z" $
is algebraic over
$z" $
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
.
$\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
.
The points
![]() $x,y",z" $
form an isosceles triangle. Let c be the circle centered at x passing through
$x,y",z" $
form an isosceles triangle. Let c be the circle centered at x passing through
![]() $y"$
. Then
$y"$
. Then
![]() $z"\in c$
holds. Since the point x is algebraic over
$z"\in c$
holds. Since the point x is algebraic over
![]() $\{y,z, y',z'\}$
, the set c is algebraic over
$\{y,z, y',z'\}$
, the set c is algebraic over
![]() $\{y, y', y",z,z'\}$
. Then c is algebraic over
$\{y, y', y",z,z'\}$
. Then c is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{y, y', y"\} \cup \{z,z'\}$
. By Corollary 4.8, there is a set
$\mathrm {supp}(p_\cap ) \cup \{y, y', y"\} \cup \{z,z'\}$
. By Corollary 4.8, there is a set
![]() $A_1$
algebraic over
$A_1$
algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z,z'\}$
such that
$\mathrm {supp}(p_\cap ) \cup \{z,z'\}$
such that
![]() $c\cap \mathrm {dom}(p_1) \subset A_1\subset c$
. Using Fact 3.2(4), if there are at least three points in
$c\cap \mathrm {dom}(p_1) \subset A_1\subset c$
. Using Fact 3.2(4), if there are at least three points in
![]() $A_1\cap \mathrm {dom}(p_1)$
, then c needs to be algebraic over
$A_1\cap \mathrm {dom}(p_1)$
, then c needs to be algebraic over
![]() $\mathrm {supp}(p_1)$
; then by Fact 3.2(7), c’s center point x is in
$\mathrm {supp}(p_1)$
; then by Fact 3.2(7), c’s center point x is in
![]() $\mathrm {dom}(p_1)$
, which is not the case. Therefore, there are at most two points (including
$\mathrm {dom}(p_1)$
, which is not the case. Therefore, there are at most two points (including
![]() $z"$
) in
$z"$
) in
![]() $A_1\cap \mathrm {dom}(p_1)$
. Then in the view of the real closed field
$A_1\cap \mathrm {dom}(p_1)$
. Then in the view of the real closed field
![]() $\mathrm {supp}(p_1)$
, the set
$\mathrm {supp}(p_1)$
, the set
![]() $ A_1\cap \mathrm {dom}(p_1)$
containing
$ A_1\cap \mathrm {dom}(p_1)$
containing
![]() $z"$
is algebraic over
$z"$
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
. By Fact 2.15,
$\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
. By Fact 2.15,
![]() $z" $
is algebraic over
$z" $
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
, where
$\mathrm {supp}(p_\cap ) \cup \{z, z'\}$
, where
![]() $\{z, z'\}\subset \mathrm {dom}(p_1)$
.
$\{z, z'\}\subset \mathrm {dom}(p_1)$
.
From both Case S.1 and Case S.2 above, we conclude that every point in
![]() $ \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} $
is algebraic over
$ \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} $
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a$
for some finite set
$\mathrm {supp}(p_\cap ) \cup a$
for some finite set
![]() $a \subset \mathrm {dom}(p_1)$
. Then the set
$a \subset \mathrm {dom}(p_1)$
. Then the set
![]() $p_1^{\prime \prime }( \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} )$
is in I since
$p_1^{\prime \prime }( \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} )$
is in I since
![]() $ p_1\leq p_\cap $
and by Definition 3.1(8). Then
$ p_1\leq p_\cap $
and by Definition 3.1(8). Then
![]() $S = \bigcup _{l\in L} s( p_\cup , l) =\bigcup _{l\in L^-\cup (L\setminus L^-)} s( p_\cup , l) $
$S = \bigcup _{l\in L} s( p_\cup , l) =\bigcup _{l\in L^-\cup (L\setminus L^-)} s( p_\cup , l) $
![]() $\subset \bigcup _{l\in L^-} s( p_\cup , l) \cup p_1^{\prime \prime }( \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} ) \in I$
holds. Thus
$\subset \bigcup _{l\in L^-} s( p_\cup , l) \cup p_1^{\prime \prime }( \bigcup _{l\in L\setminus L^-} \Xi (l) | _{1} ) \in I$
holds. Thus
![]() $S\in I$
holds.
$S\in I$
holds.
Part (T): Since
![]() $x\notin \mathrm {dom}(p_\cup )$
, it’s easy to see that
$x\notin \mathrm {dom}(p_\cup )$
, it’s easy to see that
![]() $O^-$
must be finite (in fact with cardinality two or less) using Fact 3.2(5). Then
$O^-$
must be finite (in fact with cardinality two or less) using Fact 3.2(5). Then
![]() $T = \bigcup _{o\in O^-}\{t: t$
is the center of
$T = \bigcup _{o\in O^-}\{t: t$
is the center of
![]() $o\}$
is finite, then
$o\}$
is finite, then
![]() $p_\cup ^{\prime \prime } T$
is finite, hence in I.
$p_\cup ^{\prime \prime } T$
is finite, hence in I.
Part (O): Observe that for every circle
![]() $o\in O\setminus O^-$
,
$o\in O\setminus O^-$
,
![]() $o\cap \mathrm {dom}(p_0)$
has cardinality at most two: otherwise, by Fact 3.2(4),
$o\cap \mathrm {dom}(p_0)$
has cardinality at most two: otherwise, by Fact 3.2(4),
![]() $o\in O^-$
holds which is a contradiction; similarly,
$o\in O^-$
holds which is a contradiction; similarly,
![]() $o\cap \mathrm {dom}(p_1)$
has cardinality at most two. If
$o\cap \mathrm {dom}(p_1)$
has cardinality at most two. If
![]() $ O\setminus O^-$
has cardinality at most one,
$ O\setminus O^-$
has cardinality at most one,
![]() $p_\cup ^{\prime \prime }\bigcup (O\setminus O^-)$
has cardinality at most four, hence is in the ideal I.
$p_\cup ^{\prime \prime }\bigcup (O\setminus O^-)$
has cardinality at most four, hence is in the ideal I.
Now assume
![]() $ O\setminus O^-$
has cardinality more than one. Let
$ O\setminus O^-$
has cardinality more than one. Let
![]() $o,o'\in O\setminus O^-$
be distinct circles. Then there are finite sets
$o,o'\in O\setminus O^-$
be distinct circles. Then there are finite sets
![]() $a_0\subset \mathrm {dom}(p_0),a_1\subset \mathrm {dom}(p_1) $
such that
$a_0\subset \mathrm {dom}(p_0),a_1\subset \mathrm {dom}(p_1) $
such that
![]() $ o,o'$
are algebraic over
$ o,o'$
are algebraic over
![]() $ a_0\cup a_1$
. We see that
$ a_0\cup a_1$
. We see that
![]() $ o\cap o' $
has cardinality one or two and contains the point x. Then
$ o\cap o' $
has cardinality one or two and contains the point x. Then
![]() $o\cap o' $
is algebraic over
$o\cap o' $
is algebraic over
![]() $ a_0\cup a_1$
, and by Fact 2.15, x is algebraic over
$ a_0\cup a_1$
, and by Fact 2.15, x is algebraic over
![]() $ a_0\cup a_1$
. Take a circle
$ a_0\cup a_1$
. Take a circle
![]() $o"\in O\setminus O^-$
. Then the center of
$o"\in O\setminus O^-$
. Then the center of
![]() $o" $
, denoted as
$o" $
, denoted as
![]() $t"$
, is in
$t"$
, is in
![]() $\mathrm {dom}(p_1)$
: if
$\mathrm {dom}(p_1)$
: if
![]() $t"\in \mathrm {dom}(p_0)$
were true,
$t"\in \mathrm {dom}(p_0)$
were true,
![]() $o" \in E^O(\mathrm {supp}(p_0)) \subset O^-$
by Fact 3.2(3), as a contradiction. Assume
$o" \in E^O(\mathrm {supp}(p_0)) \subset O^-$
by Fact 3.2(3), as a contradiction. Assume
![]() $o"\cap \mathrm {dom}(p_0) $
is not empty. We will show that
$o"\cap \mathrm {dom}(p_0) $
is not empty. We will show that
![]() $o"\cap \mathrm {dom}(p_0)$
is a set of points algebraic over
$o"\cap \mathrm {dom}(p_0)$
is a set of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_0$
.
$\mathrm {supp}(p_\cap ) \cup a_0$
.
The circle
![]() $o" $
is algebraic over the set
$o" $
is algebraic over the set
![]() $ \{t" , x\}$
. Then
$ \{t" , x\}$
. Then
![]() $o"$
is algebraic over
$o"$
is algebraic over
![]() $ a_0\cup a_1\cup \{t"\}$
since x is algebraic over
$ a_0\cup a_1\cup \{t"\}$
since x is algebraic over
![]() $ a_0\cup a_1$
. Then
$ a_0\cup a_1$
. Then
![]() $o"$
is algebraic over
$o"$
is algebraic over
![]() $ \mathrm {supp}(p_\cap ) \cup a_0\cup a_1\cup \{t"\}$
. By Corollary 4.8, there is a set
$ \mathrm {supp}(p_\cap ) \cup a_0\cup a_1\cup \{t"\}$
. By Corollary 4.8, there is a set
![]() $A_0$
algebraic over
$A_0$
algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_0$
such that
$\mathrm {supp}(p_\cap ) \cup a_0$
such that
![]() $o"\cap \mathrm {dom}(p_0) \subset A_0\subset o"$
. If there are at least three points in
$o"\cap \mathrm {dom}(p_0) \subset A_0\subset o"$
. If there are at least three points in
![]() $A_0\cap \mathrm {dom}(p_0)$
, then
$A_0\cap \mathrm {dom}(p_0)$
, then
![]() $t"\in \mathrm {dom}(p_0)$
, and then
$t"\in \mathrm {dom}(p_0)$
, and then
![]() $o"$
becomes algebraic over
$o"$
becomes algebraic over
![]() $\mathrm {supp}(p_0)$
, contradicting our assumption
$\mathrm {supp}(p_0)$
, contradicting our assumption
![]() $o"\notin O^-$
. Therefore, there are at most two points in
$o"\notin O^-$
. Therefore, there are at most two points in
![]() $A_0\cap \mathrm {dom}(p_0)$
. Then using Fact 2.15, the finite set
$A_0\cap \mathrm {dom}(p_0)$
. Then using Fact 2.15, the finite set
![]() $o"\cap \mathrm {dom}(p_0)\subset A_0\cap \mathrm {dom}(p_0)$
is a set of points algebraic over
$o"\cap \mathrm {dom}(p_0)\subset A_0\cap \mathrm {dom}(p_0)$
is a set of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_0$
.
$\mathrm {supp}(p_\cap ) \cup a_0$
.
By a symmetric argument, if
![]() $o"\cap \mathrm {dom}(p_1) $
is not empty, then
$o"\cap \mathrm {dom}(p_1) $
is not empty, then
![]() $o"\cap \mathrm {dom}(p_1)$
is a set of points algebraic over
$o"\cap \mathrm {dom}(p_1)$
is a set of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_1$
. Then
$\mathrm {supp}(p_\cap ) \cup a_1$
. Then
![]() $ \bigcup (O\setminus O^-)\cap \mathrm {dom}(p_0) $
is still a set of points algebraic over
$ \bigcup (O\setminus O^-)\cap \mathrm {dom}(p_0) $
is still a set of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_0$
;
$\mathrm {supp}(p_\cap ) \cup a_0$
;
![]() $ \bigcup (O\setminus O^-)\cap \mathrm {dom}(p_1) $
is still a set of points algebraic over
$ \bigcup (O\setminus O^-)\cap \mathrm {dom}(p_1) $
is still a set of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup a_1$
. Since
$\mathrm {supp}(p_\cap ) \cup a_1$
. Since
![]() $ p_0\leq p_\cap $
and
$ p_0\leq p_\cap $
and
![]() $ p_1\leq p_\cap $
, and by Definition 3.1(8),
$ p_1\leq p_\cap $
, and by Definition 3.1(8),
![]() $p_\cup ^{\prime \prime } \bigcup (O\setminus O^-) = p_0^{\prime \prime } \bigcup (O\setminus O^-) \cup p_1^{\prime \prime } \bigcup (O\setminus O^-) \in I$
holds.
$p_\cup ^{\prime \prime } \bigcup (O\setminus O^-) = p_0^{\prime \prime } \bigcup (O\setminus O^-) \cup p_1^{\prime \prime } \bigcup (O\setminus O^-) \in I$
holds.
Part (R): First consider
![]() $R\cap \mathrm {dom}(p_0)$
. Let
$R\cap \mathrm {dom}(p_0)$
. Let
![]() $y_0\in R\cap \mathrm {dom}(p_0)$
if possible. Then x and
$y_0\in R\cap \mathrm {dom}(p_0)$
if possible. Then x and
![]() $y_0$
are symmetrical with respect to
$y_0$
are symmetrical with respect to
![]() $l_0$
for some
$l_0$
for some
![]() $l_0 \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) $
. It can’t be the case
$l_0 \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) $
. It can’t be the case
![]() $l_0\in E^L(\mathrm {supp}(p_0))$
using Fact 3.2(6). Then
$l_0\in E^L(\mathrm {supp}(p_0))$
using Fact 3.2(6). Then
![]() $l_0\in E^L(\mathrm {supp}(p_1))\setminus E^L(\mathrm {supp}(p_0))$
holds. Then the point x can be calculated from
$l_0\in E^L(\mathrm {supp}(p_1))\setminus E^L(\mathrm {supp}(p_0))$
holds. Then the point x can be calculated from
![]() $y_0$
and
$y_0$
and
![]() $l_0$
. Take another point
$l_0$
. Take another point
![]() $y_1 \in R\cap \mathrm {dom}(p_0)$
different than
$y_1 \in R\cap \mathrm {dom}(p_0)$
different than
![]() $y_0$
if there is any. We will show that
$y_0$
if there is any. We will show that
![]() $y_1$
is algebraic over
$y_1$
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{y_0\}$
.
$\mathrm {supp}(p_\cap ) \cup \{y_0\}$
.
Since
![]() $y_1 \in R\cap \mathrm {dom}(p_0)$
,
$y_1 \in R\cap \mathrm {dom}(p_0)$
,
![]() $\exists l_1 \in E^L(\mathrm {supp}(p_1))\setminus E^L(\mathrm {supp}(p_0))$
that the points x and
$\exists l_1 \in E^L(\mathrm {supp}(p_1))\setminus E^L(\mathrm {supp}(p_0))$
that the points x and
![]() $y_1$
are symmetrical with respect to
$y_1$
are symmetrical with respect to
![]() $l_1$
. Then the point
$l_1$
. Then the point
![]() $y_1$
can be calculated from x and
$y_1$
can be calculated from x and
![]() $l_1$
. Since x can be calculated from
$l_1$
. Since x can be calculated from
![]() $y_0$
and
$y_0$
and
![]() $l_0$
,
$l_0$
,
![]() $y_1$
can be calculated from
$y_1$
can be calculated from
![]() $l_0, l_1, y_0$
. Let
$l_0, l_1, y_0$
. Let
![]() $f \subset \mathrm {supp}(p_1)$
be a finite set over which the sets
$f \subset \mathrm {supp}(p_1)$
be a finite set over which the sets
![]() $l_0, l_1$
are algebraic. Then the point
$l_0, l_1$
are algebraic. Then the point
![]() $y_1$
is algebraic over
$y_1$
is algebraic over
![]() $\mathrm {supp}(p_\cap )\cup \{y_0\}\cup f$
. Then by Proposition 4.8,
$\mathrm {supp}(p_\cap )\cup \{y_0\}\cup f$
. Then by Proposition 4.8,
![]() $y_1$
is algebraic over
$y_1$
is algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{y_0\}$
. Thus
$\mathrm {supp}(p_\cap ) \cup \{y_0\}$
. Thus
![]() $R\cap \mathrm {dom}(p_0) $
consists of points algebraic over
$R\cap \mathrm {dom}(p_0) $
consists of points algebraic over
![]() $\mathrm {supp}(p_\cap ) \cup \{y_0\}$
, where
$\mathrm {supp}(p_\cap ) \cup \{y_0\}$
, where
![]() $\{y_0\}\subset \mathrm {dom}{(p_0)}$
. Then
$\{y_0\}\subset \mathrm {dom}{(p_0)}$
. Then
![]() $p_0^{\prime \prime }(R\cap \mathrm {dom}(p_0)) \in I$
holds, since
$p_0^{\prime \prime }(R\cap \mathrm {dom}(p_0)) \in I$
holds, since
![]() $p_0\leq p_\cap $
and by Definition 3.1(8).
$p_0\leq p_\cap $
and by Definition 3.1(8).
Similarly,
![]() $p_1^{\prime \prime }(R\cap \mathrm {dom}(p_1))\in I$
. Then
$p_1^{\prime \prime }(R\cap \mathrm {dom}(p_1))\in I$
. Then
![]() $p_\cup ^{\prime \prime }R = p_0^{\prime \prime }(R\cap \mathrm {dom}(p_0))\cup p_1^{\prime \prime }(R\cap \mathrm {dom}(p_1))\in I$
holds since the ideal I is closed under finite union.
$p_\cup ^{\prime \prime }R = p_0^{\prime \prime }(R\cap \mathrm {dom}(p_0))\cup p_1^{\prime \prime }(R\cap \mathrm {dom}(p_1))\in I$
holds since the ideal I is closed under finite union.
Finally,
because we have shown that each part in the union is in I and the ideal I is closed under finite union.
Now we prove Theorem 5.4.
Proof Fix any pair of conditions
![]() $ p_0, p_1 \in P$
with
$ p_0, p_1 \in P$
with
![]() $\mathrm {supp}(p_0)$
and
$\mathrm {supp}(p_0)$
and
![]() $\mathrm {supp}(p_1)$
being in amalgamation position. Assume
$\mathrm {supp}(p_1)$
being in amalgamation position. Assume
![]() $p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
. Denote
$p_0 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) = p_1 \upharpoonright \mathrm {supp}(p_0)\cap \mathrm {supp}(p_1)$
. Denote
![]() $ p_\cup =p_0 \cup p_1 , p_\cap =p_0 \cap p_1 $
. Assume
$ p_\cup =p_0 \cup p_1 , p_\cap =p_0 \cap p_1 $
. Assume
![]() $p_\cap \in P$
and
$p_\cap \in P$
and
![]() $p_0\leq p_\cap $
and
$p_0\leq p_\cap $
and
![]() $p_1\leq p_\cap $
holds. Then by Lemma 5.5,
$p_1\leq p_\cap $
holds. Then by Lemma 5.5,
![]() $p_\cup $
is a partial
$p_\cup $
is a partial
![]() $\Gamma _2$
-coloring.
$\Gamma _2$
-coloring.
Let
![]() $ b \supset \mathrm {supp}(p_\cup )$
be a countable real closed subfield of
$ b \supset \mathrm {supp}(p_\cup )$
be a countable real closed subfield of
![]() $\mathbb {R}$
. We will extend
$\mathbb {R}$
. We will extend
![]() $p_\cup $
to some
$p_\cup $
to some
![]() $p_2 \in P$
with
$p_2 \in P$
with
![]() $ \mathrm {supp}(p_2) = b$
and
$ \mathrm {supp}(p_2) = b$
and
![]() $\mathrm {dom}(p_2) = b^2$
. Recall
$\mathrm {dom}(p_2) = b^2$
. Recall
![]() $d(p_0, p_1, x)$
from Definition 5.6, and by Lemma 5.7,
$d(p_0, p_1, x)$
from Definition 5.6, and by Lemma 5.7,
![]() $d(p_0,p_1, x)\in I$
. For every x, denote
$d(p_0,p_1, x)\in I$
. For every x, denote
![]() $d(p_0, p_1, x)$
as
$d(p_0, p_1, x)$
as
![]() $d(x) $
for the rest of the proof. Fix any set
$d(x) $
for the rest of the proof. Fix any set
![]() $\pi \in I $
that
$\pi \in I $
that
![]() $\forall x\in b^2 \setminus \mathrm {dom}(p_\cup ): \:\pi \setminus d( x)$
is infinite. It is possible by our choice of
$\forall x\in b^2 \setminus \mathrm {dom}(p_\cup ): \:\pi \setminus d( x)$
is infinite. It is possible by our choice of
![]() $\pi $
. Now just let
$\pi $
. Now just let
![]() $p_2$
be a map with domain
$p_2$
be a map with domain
![]() $b^2$
such that:
$b^2$
such that:
-
•
 $p_2\upharpoonright {\mathrm {dom}(p_\cup )} = p_\cup $
.
$p_2\upharpoonright {\mathrm {dom}(p_\cup )} = p_\cup $
. -
•
 $\forall x\in b^2 \setminus \mathrm {dom}(p_\cup ) ,\: p_2 (x) \in \pi \setminus d(x)$
.
$\forall x\in b^2 \setminus \mathrm {dom}(p_\cup ) ,\: p_2 (x) \in \pi \setminus d(x)$
. -
•
 $p_2$
on
$p_2$
on
 $b^2 \setminus \mathrm {dom}(p_\cup )$
is an injection.
$b^2 \setminus \mathrm {dom}(p_\cup )$
is an injection.
Claim 5.9.
![]() $p_2 \in P$
.
$p_2 \in P$
.
Proof Definition 3.1(1) is satisfied as we required
![]() $\mathrm {supp}(p_2) = b$
to be a countable real closed subfield of
$\mathrm {supp}(p_2) = b$
to be a countable real closed subfield of
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\mathrm {supp}(p_2)^2 = \mathrm {dom}(p_2) \subset \mathbb {R}^2$
.
$\mathrm {supp}(p_2)^2 = \mathrm {dom}(p_2) \subset \mathbb {R}^2$
.
For Definition 3.1(2), let’s check
![]() $p_2$
is a
$p_2$
is a
![]() ${\Gamma _2 }$
-coloring for
${\Gamma _2 }$
-coloring for
![]() $\mathrm {dom}(p_2)$
. Assume there are points
$\mathrm {dom}(p_2)$
. Assume there are points
![]() $ x,y,z\in \mathrm {dom}(p_2)$
such that
$ x,y,z\in \mathrm {dom}(p_2)$
such that
![]() $\{x,y,z\} \in {\Gamma _2 }$
.
$\{x,y,z\} \in {\Gamma _2 }$
.
Case 1: at least two points in
![]() $\{x,y,z\}$
are from
$\{x,y,z\}$
are from
![]() $\mathrm {dom}(p_2) \setminus (\mathrm {dom}(p_1)\cup \mathrm {dom}(p_0))$
. Then
$\mathrm {dom}(p_2) \setminus (\mathrm {dom}(p_1)\cup \mathrm {dom}(p_0))$
. Then
![]() $p_2^{\prime \prime }\{x,y,z\} $
is not a singleton because
$p_2^{\prime \prime }\{x,y,z\} $
is not a singleton because
![]() $p_2$
is injective on
$p_2$
is injective on
![]() $\mathrm {dom}(p_2) \setminus (\mathrm {dom}(p_1)\cup \mathrm {dom}(p_0))$
.
$\mathrm {dom}(p_2) \setminus (\mathrm {dom}(p_1)\cup \mathrm {dom}(p_0))$
.
Case 2: all points
![]() $x,y,z \in \mathrm {dom}(p_\cup )$
. Because
$x,y,z \in \mathrm {dom}(p_\cup )$
. Because
![]() $p_\cup $
is a
$p_\cup $
is a
![]() $\Gamma _2$
-coloring by Lemma 5.5,
$\Gamma _2$
-coloring by Lemma 5.5,
![]() $\{x,y,z\}$
is not monochromatic by
$\{x,y,z\}$
is not monochromatic by
![]() $p_2\supset p_\cup $
.
$p_2\supset p_\cup $
.
Case 3: precisely one point in
![]() $\{x,y,z\}$
are from
$\{x,y,z\}$
are from
![]() $\mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
; let x be such point, without the loss of generality.
$\mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
; let x be such point, without the loss of generality.
Case 3.1: x is the pivot point. Then x is on the perpendicular bisector l of the line segment from y to z, and because
![]() $y,z \in \mathrm {dom}(p_\cup )$
and by Fact 3.2(2), the line l is in the set
$y,z \in \mathrm {dom}(p_\cup )$
and by Fact 3.2(2), the line l is in the set
![]() $ E^L(\mathrm {supp}(p_\cup ))$
. Since we made
$ E^L(\mathrm {supp}(p_\cup ))$
. Since we made
![]() $p_2(x) \notin d(x)\supset S$
and by part (S) in Definition 5.6, it’s easy to see that
$p_2(x) \notin d(x)\supset S$
and by part (S) in Definition 5.6, it’s easy to see that
![]() $\{x,y,z\}$
is not monochromatic by
$\{x,y,z\}$
is not monochromatic by
![]() $p_2$
.
$p_2$
.
Case 3.2: x is not the pivot point. Then x is on the circle
![]() $o\in E^O(\mathrm {supp}(p_\cup ))$
centered at y passing through z or centered at z passing through y. Since we made
$o\in E^O(\mathrm {supp}(p_\cup ))$
centered at y passing through z or centered at z passing through y. Since we made
![]() $p_2(x) \notin d(x)\supset p_\cup ^{\prime \prime } (T\cup \bigcup (O\setminus O^-))$
and by part (T) (O) in Definition 5.6, it’s easy to see that
$p_2(x) \notin d(x)\supset p_\cup ^{\prime \prime } (T\cup \bigcup (O\setminus O^-))$
and by part (T) (O) in Definition 5.6, it’s easy to see that
![]() $\{x,y,z\}$
is not monochromatic by
$\{x,y,z\}$
is not monochromatic by
![]() $p_2$
.
$p_2$
.
For Definition 3.1(3) the symmetrical colors requirement, let
![]() $l\in E^L(\mathrm {supp}(p_2)) $
.
$l\in E^L(\mathrm {supp}(p_2)) $
.
Case 1:
![]() $l \in E^L(\mathrm {supp}(p_0)) $
. Then
$l \in E^L(\mathrm {supp}(p_0)) $
. Then
![]() $s(p_0, l) \in I$
by Definition 3.1, and
$s(p_0, l) \in I$
by Definition 3.1, and
![]() $s(p_2, l) = s(p_0, l)$
(that we will check later for Definition 3.1(6)), hence
$s(p_2, l) = s(p_0, l)$
(that we will check later for Definition 3.1(6)), hence
![]() $s(p_2, l) \in I$
holds.
$s(p_2, l) \in I$
holds.
Case 2:
![]() $l \in E^L(\mathrm {supp}(p_1)) $
.
$l \in E^L(\mathrm {supp}(p_1)) $
.
![]() $s(p_2, l) \in I$
holds for the same reason as Case 1.
$s(p_2, l) \in I$
holds for the same reason as Case 1.
Case 3:
![]() $l {\kern-1pt}\in{\kern-1pt} E^L(\mathrm {supp}(p_2)) \setminus (E^L(\mathrm {supp}(p_1)) {\kern-1pt}\cup{\kern-1pt} E^L(\mathrm {supp}(p_0)) )$
. For any pair of points symmetrical with respect to l, at least one of the pair’s coordinate has to be in
$l {\kern-1pt}\in{\kern-1pt} E^L(\mathrm {supp}(p_2)) \setminus (E^L(\mathrm {supp}(p_1)) {\kern-1pt}\cup{\kern-1pt} E^L(\mathrm {supp}(p_0)) )$
. For any pair of points symmetrical with respect to l, at least one of the pair’s coordinate has to be in
![]() $\mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup )$
because otherwise it would be the case
$\mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup )$
because otherwise it would be the case
![]() $l \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) $
by Fact 3.2(2). Then it’s easy to see
$l \in E^L(\mathrm {supp}(p_0)) \cup E^L(\mathrm {supp}(p_1)) $
by Fact 3.2(2). Then it’s easy to see
![]() $s(p_2, l) \subset p_2^{\prime \prime }( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup ) ) \subset \pi \in I$
. Hence
$s(p_2, l) \subset p_2^{\prime \prime }( \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup ) ) \subset \pi \in I$
. Hence
![]() $s(p_2, l) \in I$
because the ideal I is closed under subset.
$s(p_2, l) \in I$
because the ideal I is closed under subset.
Since we just checked the definition,
![]() $p_2\in P$
holds.
$p_2\in P$
holds.
Claim 5.10.
![]() $p_2 \leq p_0 $
and
$p_2 \leq p_0 $
and
![]() $p_2 \leq p_1 $
.
$p_2 \leq p_1 $
.
Proof We will prove
![]() $p_2 \leq p_0 $
, and the proof for
$p_2 \leq p_0 $
, and the proof for
![]() $p_2 \leq p_1 $
is the same. The items (4) and (5) in Definition 3.1 are obviously satisfied.
$p_2 \leq p_1 $
is the same. The items (4) and (5) in Definition 3.1 are obviously satisfied.
For Definition 3.1(6) the symmetrical colors invariant requirement, for each
![]() $l \in E^L(\mathrm {supp}(p_0)) $
, we want to show
$l \in E^L(\mathrm {supp}(p_0)) $
, we want to show
![]() $s(p_0, l) = s(p_2, l)$
. By Claim 5.8,
$s(p_0, l) = s(p_2, l)$
. By Claim 5.8,
![]() $s( p_\cup , l) = s(p_0, l) $
. So just need to show that
$s( p_\cup , l) = s(p_0, l) $
. So just need to show that
![]() $s( p_\cup , l) = s(p_2, l) $
. Let
$s( p_\cup , l) = s(p_2, l) $
. Let
![]() $x,y\in \mathrm {dom}(p_2)$
be a symmetrical pair of points with respect to l.
$x,y\in \mathrm {dom}(p_2)$
be a symmetrical pair of points with respect to l.
Case 1:
![]() $x,y\in \mathrm {dom}( p_\cup )$
. This case doesn’t witness any element in
$x,y\in \mathrm {dom}( p_\cup )$
. This case doesn’t witness any element in
![]() $s(p_2, l)\setminus s( p_\cup , l)$
.
$s(p_2, l)\setminus s( p_\cup , l)$
.
Case 2: one point from
![]() $\{x,y\} $
is in
$\{x,y\} $
is in
![]() $\mathrm {dom}(p_0) $
. Since
$\mathrm {dom}(p_0) $
. Since
![]() $l \in E^L(\mathrm {supp}(p_0)) $
and by Fact 3.2(6),
$l \in E^L(\mathrm {supp}(p_0)) $
and by Fact 3.2(6),
![]() $\{x,y\} \subset \mathrm {dom}(p_0)\subset \mathrm {dom}( p_\cup )$
. This leads to the previous case.
$\{x,y\} \subset \mathrm {dom}(p_0)\subset \mathrm {dom}( p_\cup )$
. This leads to the previous case.
Case 3:
![]() $x,y\in \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup ) $
, then
$x,y\in \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup ) $
, then
![]() $p_2(x)\neq p_2(y)$
since
$p_2(x)\neq p_2(y)$
since
![]() $p_2$
is an injection on
$p_2$
is an injection on
![]() $ \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
. So this case doesn’t witness any element in
$ \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
. So this case doesn’t witness any element in
![]() $s(p_2, l)\setminus s( p_\cup , l)$
.
$s(p_2, l)\setminus s( p_\cup , l)$
.
Case 4:
![]() $x \in \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
and
$x \in \mathrm {dom}(p_2) \setminus \mathrm {dom}(p_\cup )$
and
![]() $y\in \mathrm {dom}(p_1)$
without loss of generality. Because
$y\in \mathrm {dom}(p_1)$
without loss of generality. Because
![]() $ p_2(x) \notin R \ni p_2(y)$
as item (R) in Definition 5.6,
$ p_2(x) \notin R \ni p_2(y)$
as item (R) in Definition 5.6,
![]() $p_2(x)\neq p_2(y)$
holds. So this case doesn’t witness any element in
$p_2(x)\neq p_2(y)$
holds. So this case doesn’t witness any element in
![]() $s(p_2, l)\setminus s( p_\cup , l)$
.
$s(p_2, l)\setminus s( p_\cup , l)$
.
From above, we have ruled out all the possible ways that
![]() $s(p_2, l)$
can have more elements than
$s(p_2, l)$
can have more elements than
![]() $s( p_\cup , l)$
. Since trivially
$s( p_\cup , l)$
. Since trivially
![]() $s( p_\cup , l) \subset s(p_2, l)$
holds,
$s( p_\cup , l) \subset s(p_2, l)$
holds,
![]() $s( p_\cup , l) = s(p_2, l)$
holds.
$s( p_\cup , l) = s(p_2, l)$
holds.
For Definition 3.1(7) the avoid center requirement, let
![]() $x\in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
be a point, let
$x\in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
be a point, let
![]() $c\in E^O(\mathrm {supp}(p_0))$
be a circle, and let t be the center of the circle c. If
$c\in E^O(\mathrm {supp}(p_0))$
be a circle, and let t be the center of the circle c. If
![]() $x\in \mathrm {dom}(p_2)\setminus \mathrm {dom}( p_\cup ) $
, we made
$x\in \mathrm {dom}(p_2)\setminus \mathrm {dom}( p_\cup ) $
, we made
![]() $p_2(x) \notin d(x) \supset p_\cup ^{\prime \prime }T$
; by Definition 5.6 (T),
$p_2(x) \notin d(x) \supset p_\cup ^{\prime \prime }T$
; by Definition 5.6 (T),
![]() $T \ni t$
holds, then
$T \ni t$
holds, then
![]() $p_2(x) \neq p_0(t)$
holds. If
$p_2(x) \neq p_0(t)$
holds. If
![]() $x\in \mathrm {dom}(p_1) \setminus \mathrm {dom}(p_0)$
, by Case 2 in the proof of Lemma 5.5,
$x\in \mathrm {dom}(p_1) \setminus \mathrm {dom}(p_0)$
, by Case 2 in the proof of Lemma 5.5,
![]() $p_2(x) = p_1(x) \neq p_0(t)$
holds.
$p_2(x) = p_1(x) \neq p_0(t)$
holds.
For Definition 3.1(8) the algebraic points requirement, take a finite set
![]() $ u \subset \mathrm {supp}(p_2)$
. We will show that the
$ u \subset \mathrm {supp}(p_2)$
. We will show that the
![]() $p_2$
-image of the set
$p_2$
-image of the set
![]() $\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
$\{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_0)\cup u\} $
, denoted as B, is in
$\mathrm {supp}(p_0)\cup u\} $
, denoted as B, is in
![]() $ I$
. First observe that
$ I$
. First observe that
![]() $p_2^{\prime \prime }(\mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup )) \subset \pi \in I $
. Since ideal I is closed under union, once we have showed that the
$p_2^{\prime \prime }(\mathrm {dom}(p_2)\setminus \mathrm {dom}(p_\cup )) \subset \pi \in I $
. Since ideal I is closed under union, once we have showed that the
![]() $p_2$
-image of the set
$p_2$
-image of the set
![]() $B \cap \mathrm {dom}(p_1) $
is in
$B \cap \mathrm {dom}(p_1) $
is in
![]() $I $
, we are done. To do that, let v be an inclusion-maximal subset of
$I $
, we are done. To do that, let v be an inclusion-maximal subset of
![]() $\mathrm {supp}(p_1)$
intersected with the algebraic closure of
$\mathrm {supp}(p_1)$
intersected with the algebraic closure of
![]() $\mathrm {supp}(p_0)\cup u$
, which is algebraically independent over
$\mathrm {supp}(p_0)\cup u$
, which is algebraically independent over
![]() $\mathrm {supp}(p_0)$
. Since the sets algebraically independent over
$\mathrm {supp}(p_0)$
. Since the sets algebraically independent over
![]() $\mathrm {supp}(p_0)$
form a matroid by [Reference Oxley7, Theorem 6.7.1], v is finite (and in fact
$\mathrm {supp}(p_0)$
form a matroid by [Reference Oxley7, Theorem 6.7.1], v is finite (and in fact
![]() $|v| \leq |u|$
). Observe that
$|v| \leq |u|$
). Observe that
![]() $B \cap \mathrm {dom}(p_1) = \{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
$B \cap \mathrm {dom}(p_1) = \{x \in \mathrm {dom}(p_2)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_0)\cup u\} \cap \mathrm {dom}(p_1) = \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$\mathrm {supp}(p_0)\cup u\} \cap \mathrm {dom}(p_1) = \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_0)\cup v\} = \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$\mathrm {supp}(p_0)\cup v\} = \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_\cap )\cup v\}$
. This last equality is a consequence of amalgamation position: every
$\mathrm {supp}(p_\cap )\cup v\}$
. This last equality is a consequence of amalgamation position: every
![]() $x\in \mathrm {dom}(p_1)$
algebraic over
$x\in \mathrm {dom}(p_1)$
algebraic over
![]() $\mathrm {supp}(p_0)\cup v$
is algebraic over
$\mathrm {supp}(p_0)\cup v$
is algebraic over
![]() $\mathrm {supp}(p_\cap )\cup v$
by Corollary 4.8, because
$\mathrm {supp}(p_\cap )\cup v$
by Corollary 4.8, because
![]() $\mathrm {supp}(p_0)$
and
$\mathrm {supp}(p_0)$
and
![]() $\mathrm {supp}(p_1)$
are in amalgamation position with the intersection
$\mathrm {supp}(p_1)$
are in amalgamation position with the intersection
![]() $\mathrm {supp}(p_\cap )$
. Then we have
$\mathrm {supp}(p_\cap )$
. Then we have
![]() $p_2^{\prime \prime }(B \cap \mathrm {dom}(p_1) ) =p_1^{\prime \prime } (B \cap \mathrm {dom}(p_1) ) =p_1^{\prime \prime } \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
$p_2^{\prime \prime }(B \cap \mathrm {dom}(p_1) ) =p_1^{\prime \prime } (B \cap \mathrm {dom}(p_1) ) =p_1^{\prime \prime } \{x \in \mathrm {dom}(p_1)\setminus \mathrm {dom}(p_0)$
:
![]() $x $
is algebraic over
$x $
is algebraic over
![]() $\mathrm {supp}(p_\cap )\cup v\} \in I$
by Definition 3.1 (8) for
$\mathrm {supp}(p_\cap )\cup v\} \in I$
by Definition 3.1 (8) for
![]() $p_1\leq p_\cap $
.
$p_1\leq p_\cap $
.
Therefore,
![]() $p_2\leq p_0$
holds. Similarly,
$p_2\leq p_0$
holds. Similarly,
![]() $p_2\leq p_1$
holds as well.
$p_2\leq p_1$
holds as well.
As we have found a condition
![]() $p_2\in P$
extending
$p_2\in P$
extending
![]() $p_0$
and
$p_0$
and
![]() $p_1$
, it’s the end of the proof.
$p_1$
, it’s the end of the proof.
6 Open projections and hyperedge forcings
This section provides some open projections and hyperedge forcings in order to obtain Proposition 6.21, a key for distinguishing
![]() ${\Gamma }_2$
and
${\Gamma }_2$
and
![]() ${\Gamma }_3$
. Fix
${\Gamma }_3$
. Fix
![]() $n,m\in \omega $
. We say that G is an ordered hypergraph on
$n,m\in \omega $
. We say that G is an ordered hypergraph on
![]() $\mathbb {R}^n$
of arity m if
$\mathbb {R}^n$
of arity m if
![]() $G \subset (\mathbb {R}^n)^m$
. For
$G \subset (\mathbb {R}^n)^m$
. For
![]() $\iota $
a list of indexes in m, for
$\iota $
a list of indexes in m, for
![]() $A\subset (\mathbb {R}^n)^m$
a set, write
$A\subset (\mathbb {R}^n)^m$
a set, write
![]() $A|_\iota \subset (\mathbb {R}^n)^{\iota }$
to mean the projection of A into the coordinates mentioned in
$A|_\iota \subset (\mathbb {R}^n)^{\iota }$
to mean the projection of A into the coordinates mentioned in
![]() $\iota $
. If
$\iota $
. If
![]() $ G $
is a
$ G $
is a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $(\mathbb {R}^n)^m$
, then
$(\mathbb {R}^n)^m$
, then
![]() $ G $
is a Polish space in the inherited topology. We want to define the Cohen forcing associated with G.
$ G $
is a Polish space in the inherited topology. We want to define the Cohen forcing associated with G.
Definition 6.1. Let
![]() $ G $
be a
$ G $
be a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $(\mathbb {R}^n)^m$
. Equip
$(\mathbb {R}^n)^m$
. Equip
![]() $ G$
with its Polish topology. Let
$ G$
with its Polish topology. Let
![]() $P_G$
be the Cohen forcing associated with the space G (i.e.,
$P_G$
be the Cohen forcing associated with the space G (i.e.,
![]() $P_G$
is the poset of nonempty open subsets of
$P_G$
is the poset of nonempty open subsets of
![]() $ G $
ordered by reverse inclusion). We call
$ G $
ordered by reverse inclusion). We call
![]() $P_G$
the hyperedge forcing for G.
$P_G$
the hyperedge forcing for G.
We need some basic geometry and continuity for the later open projection claims.
Definition 6.2. A similarity of
![]() $\mathbb {R}^n$
is a bijection on
$\mathbb {R}^n$
is a bijection on
![]() $\mathbb {R}^n$
that multiplies all distances by some positive real number.
$\mathbb {R}^n$
that multiplies all distances by some positive real number.
![]() $\mbox {SIM}(\mathbb {R}^n)$
is the group of all similarities of
$\mbox {SIM}(\mathbb {R}^n)$
is the group of all similarities of
![]() $\mathbb {R}^n$
under the operation of composition.
$\mathbb {R}^n$
under the operation of composition.
Definition 6.3. Let
![]() $G\subset (\mathbb {R}^n)^m$
be a set. We say that G is invariant under similarities of
$G\subset (\mathbb {R}^n)^m$
be a set. We say that G is invariant under similarities of
![]() $\mathbb {R}^n$
if for every m-tuple
$\mathbb {R}^n$
if for every m-tuple
![]() $g\in G$
and every
$g\in G$
and every
![]() $s\in \mbox {SIM}(\mathbb {R}^n)$
a similarity of
$s\in \mbox {SIM}(\mathbb {R}^n)$
a similarity of
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
![]() $\bar {s}(g) \in G$
holds, where
$\bar {s}(g) \in G$
holds, where
![]() $\bar {s}$
is the bijection on
$\bar {s}$
is the bijection on
![]() $(\mathbb {R}^n)^m$
that each of its coordinate is the map s.
$(\mathbb {R}^n)^m$
that each of its coordinate is the map s.
Fact 6.4.
![]() $\mbox {SIM}(\mathbb {R}^n)$
is a Polish group with the pointwise convergence topology, with the compatible metric
$\mbox {SIM}(\mathbb {R}^n)$
is a Polish group with the pointwise convergence topology, with the compatible metric
 $$ \begin{align*} \delta(f,g) = \sum_{n=0}^{\infty} 2^{-n-1} \left( \frac{d(f(x_n) , g(x_n) )}{ 1 + d(f(x_n) , g(x_n) ) } + \frac{d(f^{-1}(x_n) , g^{-1}(x_n) )}{ 1 + d(f^{-1}(x_n) , g^{-1}(x_n) ) }\right), \end{align*} $$
$$ \begin{align*} \delta(f,g) = \sum_{n=0}^{\infty} 2^{-n-1} \left( \frac{d(f(x_n) , g(x_n) )}{ 1 + d(f(x_n) , g(x_n) ) } + \frac{d(f^{-1}(x_n) , g^{-1}(x_n) )}{ 1 + d(f^{-1}(x_n) , g^{-1}(x_n) ) }\right), \end{align*} $$
where
![]() $\{x_n\}_{n\in \omega }$
is dense in
$\{x_n\}_{n\in \omega }$
is dense in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Lemma 6.5. Fix distinct points
![]() $y_0,y_1\in \mathbb {R}^n$
. Then there is an open neighborhood
$y_0,y_1\in \mathbb {R}^n$
. Then there is an open neighborhood
![]() $U\subset (\mathbb {R}^n)^2$
of the origin and a continuous function
$U\subset (\mathbb {R}^n)^2$
of the origin and a continuous function
![]() $\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that each
$\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that each
![]() $\Psi (\delta _0,\delta _1)$
is a similarity of
$\Psi (\delta _0,\delta _1)$
is a similarity of
![]() $\mathbb {R}^n$
that moves
$\mathbb {R}^n$
that moves
![]() $y_0$
to
$y_0$
to
![]() $y_0 + \delta _0$
and
$y_0 + \delta _0$
and
![]() $y_1$
to
$y_1$
to
![]() $ y_1+\delta _1$
.
$ y_1+\delta _1$
.
Remark 6.6. The previous
![]() $\Psi $
being a continuous function is equivalent to “for any
$\Psi $
being a continuous function is equivalent to “for any
![]() $y\in \mathbb {R}^n$
, the map
$y\in \mathbb {R}^n$
, the map
![]() $ (\delta _0,\delta _1) \mapsto \Psi (\delta _0,\delta _1)(y)$
is continuous from U to
$ (\delta _0,\delta _1) \mapsto \Psi (\delta _0,\delta _1)(y)$
is continuous from U to
![]() $\mathbb {R}^n$
.”
$\mathbb {R}^n$
.”
With the remark, let’s prove the lemma.
Proof Take an open neighborhood
![]() $U\subset (\mathbb {R}^n)^2$
of the origin such that
$U\subset (\mathbb {R}^n)^2$
of the origin such that
![]() $(y_0,y_1) + U$
is a pair of two separate open balls in
$(y_0,y_1) + U$
is a pair of two separate open balls in
![]() $\mathbb {R}^n$
. For every
$\mathbb {R}^n$
. For every
![]() $(\delta _0,\delta _1) \in U$
, let
$(\delta _0,\delta _1) \in U$
, let
![]() $\Psi (\delta _0,\delta _1)$
be the similarity which is a composition of the following transformations:
$\Psi (\delta _0,\delta _1)$
be the similarity which is a composition of the following transformations:
-
1. shift by
 $\delta _0$
;
$\delta _0$
; -
2. rotation around
 $y_0 + \delta _0$
by the angle from the vector
$y_0 + \delta _0$
by the angle from the vector
 $y_1 - y_0 $
to the vector
$y_1 - y_0 $
to the vector
 $(y_1+ \delta _1) - (y_0+ \delta _0)$
;
$(y_1+ \delta _1) - (y_0+ \delta _0)$
; -
3. stretch by the ratio
 $\frac {d(y_0+ \delta _0,y_1+ \delta _1) }{d(y_0,y_1)}$
from the point
$\frac {d(y_0+ \delta _0,y_1+ \delta _1) }{d(y_0,y_1)}$
from the point
 $y_0 + \delta _0 $
.
$y_0 + \delta _0 $
.
By working out the explicit formula, one can observe that for every
![]() $y \in \mathbb {R}^n$
, the map
$y \in \mathbb {R}^n$
, the map
![]() $(\delta _0,\delta _1) \mapsto \Psi (\delta _0,\delta _1) (y)$
is continuous. Hence
$(\delta _0,\delta _1) \mapsto \Psi (\delta _0,\delta _1) (y)$
is continuous. Hence
![]() $\Psi $
is continuous on U.
$\Psi $
is continuous on U.
Proposition 6.7. Let
![]() $G\subset (\mathbb {R}^n)^m$
be
$G\subset (\mathbb {R}^n)^m$
be
![]() $G_\delta $
and invariant under similarities of
$G_\delta $
and invariant under similarities of
![]() $\mathbb {R}^n$
. Then the projection of G into any two coordinates is an open map to
$\mathbb {R}^n$
. Then the projection of G into any two coordinates is an open map to
![]() $(\mathbb {R}^n)^2$
.
$(\mathbb {R}^n)^2$
.
Proof For index convenience, we will only prove for the projection to the first two coordinates. The proof for any other case is identical. Denote the projection as
![]() $\mathrm {proj}: G \rightarrow G|_{0,1} $
. Take any open set
$\mathrm {proj}: G \rightarrow G|_{0,1} $
. Take any open set
![]() $ Q\subset (\mathbb {R}^n)^m$
so that
$ Q\subset (\mathbb {R}^n)^m$
so that
![]() $Q\cap G\neq \emptyset $
(so
$Q\cap G\neq \emptyset $
(so
![]() $Q\cap G$
is a relative open set in the Polish space G). Take any
$Q\cap G$
is a relative open set in the Polish space G). Take any
![]() $(y_0 ,y_1) \in \mathrm {proj}"G$
. Then
$(y_0 ,y_1) \in \mathrm {proj}"G$
. Then
![]() $(y_0 ,y_1) $
is the projection of some
$(y_0 ,y_1) $
is the projection of some
![]() $y = (y_i)_{i\in m} \in G$
. We just need to find an open set inside
$y = (y_i)_{i\in m} \in G$
. We just need to find an open set inside
![]() $\mathrm {proj}"G$
that includes
$\mathrm {proj}"G$
that includes
![]() $(y_0,y_1)$
.
$(y_0,y_1)$
.
By Lemma 6.5, take an open neighborhood
![]() $U\subset (\mathbb {R}^n)^2$
of the origin and a continuous function
$U\subset (\mathbb {R}^n)^2$
of the origin and a continuous function
![]() $\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that each
$\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that each
![]() $\Psi (\delta _0,\delta _1)$
is a similarity of
$\Psi (\delta _0,\delta _1)$
is a similarity of
![]() $\mathbb {R}^n$
that moves
$\mathbb {R}^n$
that moves
![]() $y_0$
to
$y_0$
to
![]() $y_0 + \delta _0$
and
$y_0 + \delta _0$
and
![]() $y_1$
to
$y_1$
to
![]() $ y_1+\delta _1$
. Consider the map
$ y_1+\delta _1$
. Consider the map
![]() $ \Psi ': U\to (\mathbb {R}^n)^{m-2}$
by
$ \Psi ': U\to (\mathbb {R}^n)^{m-2}$
by
![]() $ \Psi '(\delta _0,\delta _1) = (\Psi (\delta _0,\delta _1)(y_i) )_{2 \leq i\in m }$
, which is continuous too. Let
$ \Psi '(\delta _0,\delta _1) = (\Psi (\delta _0,\delta _1)(y_i) )_{2 \leq i\in m }$
, which is continuous too. Let
![]() $Q' = \Psi ^{\prime -1} (Q|_{2, 3, \dots , m-1 } )+ (y_0, y_1)$
, which is an open set by the continuity of
$Q' = \Psi ^{\prime -1} (Q|_{2, 3, \dots , m-1 } )+ (y_0, y_1)$
, which is an open set by the continuity of
![]() $\Psi '$
, and contains
$\Psi '$
, and contains
![]() $(y_0, y_1 )$
since as
$(y_0, y_1 )$
since as
![]() $\Psi ^{\prime -1} Q|_{2, 3, \dots , m-1 }$
contains the origin.
$\Psi ^{\prime -1} Q|_{2, 3, \dots , m-1 }$
contains the origin.
Further shrink
![]() $Q'$
:
$Q'$
:
![]() $Q" = Q'\cap \mathrm {proj}" (Q\cap G)$
. We will just show that
$Q" = Q'\cap \mathrm {proj}" (Q\cap G)$
. We will just show that
![]() $(y_0,y_1) \in Q" \subset \mathrm {proj}" (Q\cap G)$
. Clearly,
$(y_0,y_1) \in Q" \subset \mathrm {proj}" (Q\cap G)$
. Clearly,
![]() $(y_0,y_1) \in Q"$
still. Take an arbitrary
$(y_0,y_1) \in Q"$
still. Take an arbitrary
![]() $ y' \in Q"$
, and we will show that
$ y' \in Q"$
, and we will show that
![]() $y' \in \mathrm {proj}" (Q\cap G)$
. The point
$y' \in \mathrm {proj}" (Q\cap G)$
. The point
![]() $y'$
has the form
$y'$
has the form
![]() $y ' = (y_0 + \delta _0, y_1 + \delta _1)$
, for some
$y ' = (y_0 + \delta _0, y_1 + \delta _1)$
, for some
![]() $\delta _0,\delta _1$
. Let
$\delta _0,\delta _1$
. Let
![]() $y" = (\Psi (\delta _0,\delta _1)(y_i) )_{2 \leq i\in m }$
. Then
$y" = (\Psi (\delta _0,\delta _1)(y_i) )_{2 \leq i\in m }$
. Then
![]() $y' \times y" \in Q\cap G$
:
$y' \times y" \in Q\cap G$
:
-
•
 $y' \times y" \in G$
is because
$y' \times y" \in G$
is because
 $y'\times y"$
is coordinatewisely moved by a similarity of
$y'\times y"$
is coordinatewisely moved by a similarity of
 $\mathbb {R}^n$
from y and G is an ordered hypergraph on any Euclidean space invariant under similarities of
$\mathbb {R}^n$
from y and G is an ordered hypergraph on any Euclidean space invariant under similarities of
 $\mathbb {R}^n$
.
$\mathbb {R}^n$
. -
•
 $y' \times y" \in Q$
is because
$y' \times y" \in Q$
is because
 $y'\in Q|_{0,1}$
and
$y'\in Q|_{0,1}$
and
 $y" \in Q|_{2,3,\dots , m-1}$
by our choice of
$y" \in Q|_{2,3,\dots , m-1}$
by our choice of
 $Q'$
and
$Q'$
and
 $Q"$
.
$Q"$
.
Hence
![]() $ y' = \mathrm {proj}( y' \times y" ) \in \mathrm {proj}" (Q\cap G)$
. Then
$ y' = \mathrm {proj}( y' \times y" ) \in \mathrm {proj}" (Q\cap G)$
. Then
![]() $ Q" \subset \mathrm {proj}" (Q\cap G)$
. Hence
$ Q" \subset \mathrm {proj}" (Q\cap G)$
. Hence
![]() $\mathrm {proj}" (Q\cap G)$
is open. Hence
$\mathrm {proj}" (Q\cap G)$
is open. Hence
![]() $\mathrm {proj}$
is an open map.
$\mathrm {proj}$
is an open map.
For
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\bar {\Gamma }_n\subset (\mathbb {R}^n)^3$
be the ordered hypergraph on
$\bar {\Gamma }_n\subset (\mathbb {R}^n)^3$
be the ordered hypergraph on
![]() $\mathbb {R}^n$
such that:
$\mathbb {R}^n$
such that:
![]() $\forall \ x_0,x_1,x_2\in \mathbb {R}^n$
,
$\forall \ x_0,x_1,x_2\in \mathbb {R}^n$
,
![]() $( x_0,x_1,x_2) \in \bar \Gamma _n \Longleftrightarrow (d_n(x_0,x_1) = d_n(x_1,x_2)\wedge x_0\neq x_1\neq x_2\neq x_0)$
. Recall that
$( x_0,x_1,x_2) \in \bar \Gamma _n \Longleftrightarrow (d_n(x_0,x_1) = d_n(x_1,x_2)\wedge x_0\neq x_1\neq x_2\neq x_0)$
. Recall that
![]() $\Gamma _ n\subset [\mathbb {R}^n]^3$
is the hypergraph of isosceles triangles on
$\Gamma _ n\subset [\mathbb {R}^n]^3$
is the hypergraph of isosceles triangles on
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Fact 6.8.
![]() $\forall \ x_0,x_1,x_2\in \mathbb {R}^n$
distinct points,
$\forall \ x_0,x_1,x_2\in \mathbb {R}^n$
distinct points,
and
Corollary 6.9. The projection of
![]() $\bar {\Gamma }_3$
to any two coordinates is an open map.
$\bar {\Gamma }_3$
to any two coordinates is an open map.
Proof
![]() $\bar {\Gamma }_3 \subset (\mathbb {R}^n)^m$
is
$\bar {\Gamma }_3 \subset (\mathbb {R}^n)^m$
is
![]() $G_\delta $
and invariant under similarities of
$G_\delta $
and invariant under similarities of
![]() $\mathbb {R}^3$
. Then apply Proposition 6.7.
$\mathbb {R}^3$
. Then apply Proposition 6.7.
Let the ground model be V (of ZFC). According to Definition 6.1, consider the poset
![]() $P_{\bar {\Gamma }_3}$
to force over V. Let
$P_{\bar {\Gamma }_3}$
to force over V. Let
![]() $e = ( x_0,x_1,x_2)$
be
$e = ( x_0,x_1,x_2)$
be
![]() $P_{\bar {\Gamma }_3}$
-generic over V. Then
$P_{\bar {\Gamma }_3}$
-generic over V. Then
![]() $\{x_0,x_1,x_2\}$
form a
$\{x_0,x_1,x_2\}$
form a
![]() ${\Gamma }_3$
-hyperedge.
${\Gamma }_3$
-hyperedge.
Corollary 6.10. Each pair of points from
![]() $ e$
are mutually generic over V for the product forcing
$ e$
are mutually generic over V for the product forcing
![]() $P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
.
$P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
.
Proof We will prove that
![]() $x_0,x_1$
are mutually generic; the proof for any other pair is the same. In V, fix an arbitrary open dense set D of conditions in
$x_0,x_1$
are mutually generic; the proof for any other pair is the same. In V, fix an arbitrary open dense set D of conditions in
![]() $P_{ \mathbb {R}^3} \times P_{ \mathbb {R}^3} $
. Then
$P_{ \mathbb {R}^3} \times P_{ \mathbb {R}^3} $
. Then
![]() $\bigcup D \subset \mathbb {R}^3 \times \mathbb {R}^3 $
is an open dense set. Let
$\bigcup D \subset \mathbb {R}^3 \times \mathbb {R}^3 $
is an open dense set. Let
![]() $\mathrm {proj}$
denote the projection of
$\mathrm {proj}$
denote the projection of
![]() $\bar {\Gamma }_3$
to the first two coordinates. Because
$\bar {\Gamma }_3$
to the first two coordinates. Because
![]() $\mathrm {proj}$
is a continuous open map by Corollary 6.9,
$\mathrm {proj}$
is a continuous open map by Corollary 6.9,
![]() $\mathrm {proj}^{-1} (\bigcup D) $
is an open dense subset of
$\mathrm {proj}^{-1} (\bigcup D) $
is an open dense subset of
![]() $\bar {\Gamma }_3$
.
$\bar {\Gamma }_3$
.
Look in
![]() $V[e]$
. Because e is a generic tuple over V for the forcing
$V[e]$
. Because e is a generic tuple over V for the forcing
![]() $P_{\bar {\Gamma }_3 }$
,
$P_{\bar {\Gamma }_3 }$
,
![]() $e\in \mathrm {proj}^{-1} (\bigcup D)$
holds. Then
$e\in \mathrm {proj}^{-1} (\bigcup D)$
holds. Then
![]() $\mathrm {proj}(e) = (x_0, x_1) \in \bigcup D$
holds. Then there is some
$\mathrm {proj}(e) = (x_0, x_1) \in \bigcup D$
holds. Then there is some
![]() $d\in D $
that
$d\in D $
that
![]() $(x_0,x_1 )\in d$
. Hence
$(x_0,x_1 )\in d$
. Hence
![]() $(x_0, x_1)$
is generic over V for the product forcing
$(x_0, x_1)$
is generic over V for the product forcing
![]() $P_{ \mathbb {R}^3} \times P_{ \mathbb {R}^3} $
.
$P_{ \mathbb {R}^3} \times P_{ \mathbb {R}^3} $
.
We want to define a notion of duplication on an ordered hypergraph’s coordinate, and investigate a few relevant projection maps.
Definition 6.11. Let
![]() $G\subset (\mathbb {R}^n)^m$
be an ordered hypergraph. Define
$G\subset (\mathbb {R}^n)^m$
be an ordered hypergraph. Define
![]() $G^k\subset (\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1} = (\mathbb {R}^n)^{m + k-1} $
to be the ordered hypergraph of arity
$G^k\subset (\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1} = (\mathbb {R}^n)^{m + k-1} $
to be the ordered hypergraph of arity
![]() $m+k-1$
such that
$m+k-1$
such that
![]() $ (x_{0i}, x_j)_{i\in k, j\in m-1} \in G^k $
if
$ (x_{0i}, x_j)_{i\in k, j\in m-1} \in G^k $
if
![]() $ (\forall i\in k \: \ (x_{0i}, x_j)_{j \in m-1} \in G $
and
$ (\forall i\in k \: \ (x_{0i}, x_j)_{j \in m-1} \in G $
and
![]() $x_{0i}, i\in k \mbox { are in general position} )$
. We say that the hypergraph
$x_{0i}, i\in k \mbox { are in general position} )$
. We say that the hypergraph
![]() $G^k$
is obtained from G by duplicating its zeroth coordinate k times.
$G^k$
is obtained from G by duplicating its zeroth coordinate k times.
Recall that, for
![]() $d\in \omega $
, a set of points in a d-dimensional Euclidean space is in general linear position (or just general position) if no k of them lie in a
$d\in \omega $
, a set of points in a d-dimensional Euclidean space is in general linear position (or just general position) if no k of them lie in a
![]() $(k -2)$
-dimensional flat for
$(k -2)$
-dimensional flat for
![]() $k = 2, 3, \dots , d + 1.$
In particular for
$k = 2, 3, \dots , d + 1.$
In particular for
![]() $d = 3$
, four points are in general position if they are distinct, any three of them determine a plane, and any one of them is not on the plane determined by the other three. Since being in general position is an open relation,
$d = 3$
, four points are in general position if they are distinct, any three of them determine a plane, and any one of them is not on the plane determined by the other three. Since being in general position is an open relation,
![]() $G^k$
remains
$G^k$
remains
![]() $G_\delta $
if G is
$G_\delta $
if G is
![]() $G_\delta $
. Similarly, we could define the duplication on any other coordinate too, but this is not needed for this research effort.
$G_\delta $
. Similarly, we could define the duplication on any other coordinate too, but this is not needed for this research effort.
Proposition 6.12. Let
![]() $G\subset (\mathbb {R}^n)^m$
be
$G\subset (\mathbb {R}^n)^m$
be
![]() $G_\delta $
. Suppose the projection of G into all but the zeroth coordinate is an open map to the range space. Consider the hypergraph
$G_\delta $
. Suppose the projection of G into all but the zeroth coordinate is an open map to the range space. Consider the hypergraph
![]() $G^k$
obtained from G by duplicating its zeroth coordinate k times. Then the projection of
$G^k$
obtained from G by duplicating its zeroth coordinate k times. Then the projection of
![]() $G^k$
to the last m many coordinates is an open map to the space G.
$G^k$
to the last m many coordinates is an open map to the space G.
Proof Denote the projection of
![]() $G^k$
to the last m many coordinates as
$G^k$
to the last m many coordinates as
![]() $\mathrm {proj}$
.
$\mathrm {proj}$
.
Suppose the projection of G into all but the zeroth coordinate, denoted as
![]() $\mathrm {proj}'$
, is an open map to the range space. Take an open set
$\mathrm {proj}'$
, is an open map to the range space. Take an open set
![]() $Q = \Pi _{i\in k} Q_{0i} \times \Pi _{ j\in m-1}Q_{j} \subset (\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1}$
such that the relative open set
$Q = \Pi _{i\in k} Q_{0i} \times \Pi _{ j\in m-1}Q_{j} \subset (\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1}$
such that the relative open set
![]() $ Q\cap G^k$
is not empty. For each
$ Q\cap G^k$
is not empty. For each
![]() $i \in k$
, let
$i \in k$
, let
![]() $\mathrm {proj}_i$
be the projection of
$\mathrm {proj}_i$
be the projection of
![]() $(\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1}$
to all the coordinates in
$(\mathbb {R}^n)^{k }\times (\mathbb {R}^n)^{ m-1}$
to all the coordinates in
![]() $\{ 0i, j:j\in m-1\}$
. In fact, for each
$\{ 0i, j:j\in m-1\}$
. In fact, for each
![]() $i \in k$
,
$i \in k$
,
![]() $\mathrm {proj}_i^{\prime \prime }G^k$
is a copy of G. Then for each
$\mathrm {proj}_i^{\prime \prime }G^k$
is a copy of G. Then for each
![]() $i \in k$
,
$i \in k$
,
![]() $ (\mathrm {proj}'\circ \mathrm {proj}_i)" Q$
is open to the space
$ (\mathrm {proj}'\circ \mathrm {proj}_i)" Q$
is open to the space
![]() $\mathrm {rng}(\mathrm {proj}')$
, by the openness of
$\mathrm {rng}(\mathrm {proj}')$
, by the openness of
![]() $ \mathrm {proj}'$
from our assumption and the openness of
$ \mathrm {proj}'$
from our assumption and the openness of
![]() $\mathrm {proj}_i$
between Euclidean spaces. We claim
$\mathrm {proj}_i$
between Euclidean spaces. We claim
![]() $\mathrm {proj}"Q =( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. We will show both inclusions.
$\mathrm {proj}"Q =( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. We will show both inclusions.
-
⊂ Basically just chase definitions and quantifiers. Take an arbitrary point
 $y' \in \mathrm {proj}"Q $
. Then
$y' \in \mathrm {proj}"Q $
. Then
 $y'$
is a projection of some
$y'$
is a projection of some
 $y = (y_{0i},y_j)_{i\in k, j\in m-1} \in Q$
, so
$y = (y_{0i},y_j)_{i\in k, j\in m-1} \in Q$
, so
 $y'=(y_{0(k-1)}, y_{j} )_{j\in m-1} $
. Firstly, clearly
$y'=(y_{0(k-1)}, y_{j} )_{j\in m-1} $
. Firstly, clearly
 $y_{0(k-1)} \in Q_{0(k-1)}$
holds. For each
$y_{0(k-1)} \in Q_{0(k-1)}$
holds. For each
 $i \in k-1$
,
$i \in k-1$
,
 $ (y_{j} )_{j\in m-1} = (\mathrm {proj}'\circ \mathrm {proj}_i)(y) $
holds, Then
$ (y_{j} )_{j\in m-1} = (\mathrm {proj}'\circ \mathrm {proj}_i)(y) $
holds, Then
 $(y_{j} )_{j\in m-1} \in \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q $
. Lastly, clearly
$(y_{j} )_{j\in m-1} \in \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q $
. Lastly, clearly
 $y' \in \mathrm {rng}(\mathrm {proj})$
holds. Hence
$y' \in \mathrm {rng}(\mathrm {proj})$
holds. Hence
 $y'\in ( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
.
$y'\in ( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. -
⊃ Take an arbitrary point
 $y' \times y" \in ( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. For each
$y' \times y" \in ( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. For each
 $i \in k-1$
, since
$i \in k-1$
, since
 $y"\in (\mathrm {proj}'\circ \mathrm {proj}_i)" Q $
, there is some point
$y"\in (\mathrm {proj}'\circ \mathrm {proj}_i)" Q $
, there is some point
 $x_{0i} \in Q_{0i}$
such that
$x_{0i} \in Q_{0i}$
such that
 $ (x_{0i} ) \times y" \in G$
. Since
$ (x_{0i} ) \times y" \in G$
. Since
 $ y' \times y" \in \mathrm {rng}(\mathrm {proj}) = G$
is part of our assumption,
$ y' \times y" \in \mathrm {rng}(\mathrm {proj}) = G$
is part of our assumption,
 $ {(x_{0i})_{i \in k-1} }\times y' \times y" \in G^k$
by the definition of
$ {(x_{0i})_{i \in k-1} }\times y' \times y" \in G^k$
by the definition of
 $G^k$
. Then
$G^k$
. Then
 $\mathrm {proj}( {(x_{0i})_{i \in k-1} }\times y' \times y" ) = y' \times y"$
holds. Since clearly
$\mathrm {proj}( {(x_{0i})_{i \in k-1} }\times y' \times y" ) = y' \times y"$
holds. Since clearly
 ${(x_{0i})_{i \in k-1} }\times y' \times y" \in Q$
holds,
${(x_{0i})_{i \in k-1} }\times y' \times y" \in Q$
holds,
 $y' \times y" \in \mathrm {proj}"Q$
is true.
$y' \times y" \in \mathrm {proj}"Q$
is true.
Hence we have proved
![]() $\mathrm {proj}"Q =( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. The right-hand side of this equality, as we can see, is open in the range space
$\mathrm {proj}"Q =( Q_{0(k-1)}\times \bigcap _{i \in k-1} (\mathrm {proj}'\circ \mathrm {proj}_i)" Q ) \cap \mathrm {rng}(\mathrm {proj})$
. The right-hand side of this equality, as we can see, is open in the range space
![]() $\mathrm {rng}(\mathrm {proj})=G$
, then so is the left-hand side.
$\mathrm {rng}(\mathrm {proj})=G$
, then so is the left-hand side.
Given
![]() $G\subset (\mathbb {R}^n)^m$
,
$G\subset (\mathbb {R}^n)^m$
,
![]() $y_1, y_2, \ldots , y_{m-1} \in \mathbb {R}^n$
, for now we use an alternative notation for the horizontal section of G as
$y_1, y_2, \ldots , y_{m-1} \in \mathbb {R}^n$
, for now we use an alternative notation for the horizontal section of G as
![]() $G( -,y_1, y_2, \ldots , y_{m-1} ) := \{y_0\in \mathbb {R}^n:\: (y_0, y_1, y_2, \ldots , y_{m-1} )\in G \}$
.
$G( -,y_1, y_2, \ldots , y_{m-1} ) := \{y_0\in \mathbb {R}^n:\: (y_0, y_1, y_2, \ldots , y_{m-1} )\in G \}$
.
Definition 6.13. Let
![]() $G\subset (\mathbb {R}^n)^m$
. Let us say that G is stable against k vertices if the following holds. Whenever
$G\subset (\mathbb {R}^n)^m$
. Let us say that G is stable against k vertices if the following holds. Whenever
![]() $x = \{x_{i}\}_{i \in k} \subset \mathbb {R}^n$
is a set of points in general position, there is an open neighborhood
$x = \{x_{i}\}_{i \in k} \subset \mathbb {R}^n$
is a set of points in general position, there is an open neighborhood
![]() $U\subset (\mathbb {R}^n)^k$
of the origin and a continuous function
$U\subset (\mathbb {R}^n)^k$
of the origin and a continuous function
![]() $\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that for each
$\Psi : U \rightarrow \mbox {SIM}(\mathbb {R}^n)$
such that for each
![]() $ u = (u_i)_{i\in k} \in U$
:
$ u = (u_i)_{i\in k} \in U$
:
-
1.
 $\Psi ( u )$
is a similarity of
$\Psi ( u )$
is a similarity of
 $\mathbb {R}^n$
.
$\mathbb {R}^n$
. -
2.
 $\Psi (0)$
is the identity map.
$\Psi (0)$
is the identity map. -
3.
 $\forall y_1, y_2, \ldots , y_{m-1} \in \mathbb {R}^n$
, if
$\forall y_1, y_2, \ldots , y_{m-1} \in \mathbb {R}^n$
, if
 $G( -, y_1, y_2, \ldots , y_{m-1} ) \supset x$
, then:
$G( -, y_1, y_2, \ldots , y_{m-1} ) \supset x$
, then:-
•
 $\Psi ( u )$
moves the section
$\Psi ( u )$
moves the section
 $G( -, y_1, y_2, \ldots , y_{m-1} )$
to the section
$G( -, y_1, y_2, \ldots , y_{m-1} )$
to the section $G( -,\Psi (u)(y_1), \Psi (u)(y_2) ,\ldots , \Psi (u)(y_{m-1}) ) $
.
$G( -,\Psi (u)(y_1), \Psi (u)(y_2) ,\ldots , \Psi (u)(y_{m-1}) ) $
. -
•
 $G( -,\Psi (u)(y_1), \Psi (u)(y_2) ,\ldots , \Psi (u)(y_{m-1}) ) \supset \{x_i + u_i\}_{i\in k}$
.
$G( -,\Psi (u)(y_1), \Psi (u)(y_2) ,\ldots , \Psi (u)(y_{m-1}) ) \supset \{x_i + u_i\}_{i\in k}$
.
-
We call
![]() $\Psi $
a similarity function transferring points
$\Psi $
a similarity function transferring points
![]() $x_{i}, {i \in k}$
for G.
$x_{i}, {i \in k}$
for G.
Proposition 6.14. Let
![]() $G\subset (\mathbb {R}^n)^m$
be
$G\subset (\mathbb {R}^n)^m$
be
![]() $G_\delta $
, and consider the hypergraph
$G_\delta $
, and consider the hypergraph
![]() $G^k$
obtained from G by duplicating its zeroth coordinate k times. If G is stable against k vertices, then the projection of
$G^k$
obtained from G by duplicating its zeroth coordinate k times. If G is stable against k vertices, then the projection of
![]() $G^k$
into the first k many coordinates is an open map to the space
$G^k$
into the first k many coordinates is an open map to the space
![]() $(\mathbb {R}^n)^k$
.
$(\mathbb {R}^n)^k$
.
Proof Assume that G is stable against k vertices. Denote the mentioned projection by
![]() $\mathrm {proj}$
. Take a basic open set
$\mathrm {proj}$
. Take a basic open set
![]() $Q = \Pi _{i\in k} Q_{0i} \times \Pi _{j\in m-1}Q_j \subset (\mathbb {R}^n)^k\times (\mathbb {R}^n)^{m-1}$
such that the relative open set
$Q = \Pi _{i\in k} Q_{0i} \times \Pi _{j\in m-1}Q_j \subset (\mathbb {R}^n)^k\times (\mathbb {R}^n)^{m-1}$
such that the relative open set
![]() $Q\cap G^k \neq \emptyset $
. We want to show that
$Q\cap G^k \neq \emptyset $
. We want to show that
![]() $\mathrm {proj}"(Q\cap G^k)$
is open in
$\mathrm {proj}"(Q\cap G^k)$
is open in
![]() $(\mathbb {R}^n)^k $
. Take an arbitrary point
$(\mathbb {R}^n)^k $
. Take an arbitrary point
![]() $x' = (x_{0i})_{i\in k} \in \mathrm {proj}"(Q\cap G^k) $
, which is the projection of some point
$x' = (x_{0i})_{i\in k} \in \mathrm {proj}"(Q\cap G^k) $
, which is the projection of some point
![]() $x = (x_{0i}, x_j)_{i\in k, j\in m-1} \in Q\cap G^k$
. We want to find an open set around
$x = (x_{0i}, x_j)_{i\in k, j\in m-1} \in Q\cap G^k$
. We want to find an open set around
![]() $x'$
that is inside
$x'$
that is inside
![]() $\mathrm {proj}"(Q\cap G^k)$
.
$\mathrm {proj}"(Q\cap G^k)$
.
Since
![]() $\{x_{0i}:{i\in k}\} $
is a set of points in general position by the definition of
$\{x_{0i}:{i\in k}\} $
is a set of points in general position by the definition of
![]() $G^k$
, we obtain the open set U and the similarity function
$G^k$
, we obtain the open set U and the similarity function
![]() $\Psi $
on U transferring points
$\Psi $
on U transferring points
![]() $x_{0i}, {i \in k}$
for G, as described in Definition 6.13. Then the map
$x_{0i}, {i \in k}$
for G, as described in Definition 6.13. Then the map
![]() $u \mapsto (\Psi (u)(x_j) )_{ j \in m-1} $
, denoted as
$u \mapsto (\Psi (u)(x_j) )_{ j \in m-1} $
, denoted as
![]() $\Theta $
, is continuous from U to
$\Theta $
, is continuous from U to
![]() $ (\mathbb {R}^n)^{ m - 1}$
since
$ (\mathbb {R}^n)^{ m - 1}$
since
![]() $\Theta $
is coordinatewisely continuous by the pointwise convergence topology of the space
$\Theta $
is coordinatewisely continuous by the pointwise convergence topology of the space
![]() $\mbox {SIM}(\mathbb {R}^n)$
; and still
$\mbox {SIM}(\mathbb {R}^n)$
; and still
![]() $ \forall u\in U \ (x' + u) \times \Theta (u) \in G^k$
holds by the properties of
$ \forall u\in U \ (x' + u) \times \Theta (u) \in G^k$
holds by the properties of
![]() $\Psi $
in Definition 6.13. Let
$\Psi $
in Definition 6.13. Let
![]() $Q' = \Theta ^{-1}(\Pi _{j\in m-1} Q_j)$
. Move and shrink
$Q' = \Theta ^{-1}(\Pi _{j\in m-1} Q_j)$
. Move and shrink
![]() $Q'$
: let
$Q'$
: let
![]() $Q" = (Q'+x') \cap \Pi _{i\in k} Q_{0i}$
.
$Q" = (Q'+x') \cap \Pi _{i\in k} Q_{0i}$
.
By chasing the definition and quantifiers, we can check
![]() $x'\in Q"\cap \mathrm {rng}(\mathrm {proj}) \subset \mathrm {proj}"Q$
holds:
$x'\in Q"\cap \mathrm {rng}(\mathrm {proj}) \subset \mathrm {proj}"Q$
holds:
-
(∈) Clearly
 $x'\in \mathrm {rng}(\mathrm {proj})$
and
$x'\in \mathrm {rng}(\mathrm {proj})$
and
 $x'\in \Pi _{i\in k} Q_{0i}$
hold;
$x'\in \Pi _{i\in k} Q_{0i}$
hold;
 $x'\in x' + Q'$
holds as
$x'\in x' + Q'$
holds as
 $0\in Q'$
which is because: by Definition 6.13(2) and the definition of
$0\in Q'$
which is because: by Definition 6.13(2) and the definition of
 $\Theta $
,
$\Theta $
,
 $\Theta (0) = (x_j)_{j\in m-1} \in \Pi _{j\in m-1} Q_j $
holds, then
$\Theta (0) = (x_j)_{j\in m-1} \in \Pi _{j\in m-1} Q_j $
holds, then
 $0\in Q' = \Theta ^{-1}(\Pi _{j\in m-1} Q_j)$
.
$0\in Q' = \Theta ^{-1}(\Pi _{j\in m-1} Q_j)$
. -
(⊂) Whenever
 $ (x'+u) \in Q"\cap \mathrm {rng}(\mathrm {proj})$
,
$ (x'+u) \in Q"\cap \mathrm {rng}(\mathrm {proj})$
,
 $ (x'+u)\in \mathrm {proj}"Q$
holds since
$ (x'+u)\in \mathrm {proj}"Q$
holds since
 $ (x' + u) \times \Theta (u) \in G^k \cap Q$
.
$ (x' + u) \times \Theta (u) \in G^k \cap Q$
.
It follows that
![]() $\mathrm {proj}"Q$
is open in
$\mathrm {proj}"Q$
is open in
![]() $ \mathrm {rng}(\mathrm {proj})$
.
$ \mathrm {rng}(\mathrm {proj})$
.
Let
![]() $\bar {{\Gamma }}_3^4$
be the ordered hypergraph obtained from
$\bar {{\Gamma }}_3^4$
be the ordered hypergraph obtained from
![]() $\bar {\Gamma }_3 $
by duplicating its zeroth coordinate four times.
$\bar {\Gamma }_3 $
by duplicating its zeroth coordinate four times.
Corollary 6.15. The projection of
![]() $\bar {\Gamma }_3^4$
to the first four coordinates is an open map to
$\bar {\Gamma }_3^4$
to the first four coordinates is an open map to
![]() $(\mathbb {R}^3)^4$
.
$(\mathbb {R}^3)^4$
.
Proof We will check Definition 6.13 is satisfied for
![]() $\bar {\Gamma }_3$
, and then just use Proposition 6.14. To check Definition 6.13 that
$\bar {\Gamma }_3$
, and then just use Proposition 6.14. To check Definition 6.13 that
![]() $\bar {\Gamma }_3$
is stable against four vertices, let
$\bar {\Gamma }_3$
is stable against four vertices, let
![]() $x = \{x_{i}\}_{i \in 4} \subset \mathbb {R}^n$
be a set of points in general position. Then there is a unique sphere S that passes through all the points in x, with some center point c and some radius r, by elementary geometry. Take an open neighborhood
$x = \{x_{i}\}_{i \in 4} \subset \mathbb {R}^n$
be a set of points in general position. Then there is a unique sphere S that passes through all the points in x, with some center point c and some radius r, by elementary geometry. Take an open neighborhood
![]() $U\subset (\mathbb {R}^n)^4$
of the origin such that
$U\subset (\mathbb {R}^n)^4$
of the origin such that
![]() $\forall u = (u_i)_{i\in 4} \in U$
,
$\forall u = (u_i)_{i\in 4} \in U$
,
![]() $\{x_{i} + u_i:{i \in 4}\}$
still remains in general position. Let
$\{x_{i} + u_i:{i \in 4}\}$
still remains in general position. Let
![]() $ u = (u_i)_{i\in 4} \in U$
. Then there is a unique sphere
$ u = (u_i)_{i\in 4} \in U$
. Then there is a unique sphere
![]() $S'$
that passes through all the points in
$S'$
that passes through all the points in
![]() $\{x_{i}+u_i\}_{i \in 4}$
, with some center
$\{x_{i}+u_i\}_{i \in 4}$
, with some center
![]() $c'$
and some radius
$c'$
and some radius
![]() $r'$
. One can explicitly calculate that
$r'$
. One can explicitly calculate that
![]() $u\mapsto (c' - c, r'/r)$
is continuous to its image space. Define
$u\mapsto (c' - c, r'/r)$
is continuous to its image space. Define
![]() $\Psi (u)$
to be the similarity of
$\Psi (u)$
to be the similarity of
![]() $\mathbb {R}^3$
as a composition of the following maps:
$\mathbb {R}^3$
as a composition of the following maps:
-
• stretch from c by
 $r'/r$
;
$r'/r$
; -
• shift by
 $c' - c$
.
$c' - c$
.
As a consequence,
![]() $\Psi (u)$
is a similarity of
$\Psi (u)$
is a similarity of
![]() $\mathbb {R}^3$
that moves
$\mathbb {R}^3$
that moves
![]() $S $
to
$S $
to
![]() $S'$
. With the continuity of the map
$S'$
. With the continuity of the map
![]() $u\mapsto (c' - c, r'/r)$
and the continuity of the transformation between the Cartesian coordinates and spherical coordinates, one can check that
$u\mapsto (c' - c, r'/r)$
and the continuity of the transformation between the Cartesian coordinates and spherical coordinates, one can check that
![]() $\Psi $
is a continuous function with respect to the topology of its range
$\Psi $
is a continuous function with respect to the topology of its range
![]() $\mbox {SIM}(\mathbb {R}^3)$
.
$\mbox {SIM}(\mathbb {R}^3)$
.
For Definition 6.13 (2), it’s easy to see that
![]() $\Psi (0)$
is the identity map. Finally, let’s check Definition 6.13(3). Recall S is a unique sphere that
$\Psi (0)$
is the identity map. Finally, let’s check Definition 6.13(3). Recall S is a unique sphere that
![]() $x\subset S$
. Let
$x\subset S$
. Let
![]() $y_1, y_2$
be such that
$y_1, y_2$
be such that
![]() $\bar {\Gamma }_3^4( -,y_1,y_2) = S $
; then
$\bar {\Gamma }_3^4( -,y_1,y_2) = S $
; then
![]() $y_1$
is the center of S and
$y_1$
is the center of S and
![]() $y_2\in S$
. We have had S being mapped to
$y_2\in S$
. We have had S being mapped to
![]() $S'$
by
$S'$
by
![]() $\Psi (u)$
such that
$\Psi (u)$
such that
![]() $\{x_{i} + u_i:{i \in 4}\}\subset S'$
so
$\{x_{i} + u_i:{i \in 4}\}\subset S'$
so
![]() $S'$
is uniquely determined. Observe that
$S'$
is uniquely determined. Observe that
![]() $S' = G( -,\Psi (u)(y_1),\Psi (u)(y_2))$
, because
$S' = G( -,\Psi (u)(y_1),\Psi (u)(y_2))$
, because
-
• we must have
 $\Psi (u)$
maps
$\Psi (u)$
maps
 $y_1$
, the center of S, to
$y_1$
, the center of S, to
 $\Psi (u)(y_1)$
, the center of
$\Psi (u)(y_1)$
, the center of
 $S'$
;
$S'$
; -
• by
 $\Psi (u)"S=S'$
and
$\Psi (u)"S=S'$
and
 $y_2\in S$
,
$y_2\in S$
,
 $\Psi (u)(y_2)\in S'$
holds.
$\Psi (u)(y_2)\in S'$
holds.
Hence we have checked the following:
-
•
 $\Psi (u)$
moves
$\Psi (u)$
moves
 $G( -,y_1,y_2) = S $
to
$G( -,y_1,y_2) = S $
to
 $G( -,\Psi (u)(y_1),\Psi (u)(y_2)) = S' $
.
$G( -,\Psi (u)(y_1),\Psi (u)(y_2)) = S' $
. -
•
 $\{x_{i} + u_i:{i \in 4}\}\subset G( -,\Psi (u)(y_1),\Psi (u)(y_2)) =S'$
.
$\{x_{i} + u_i:{i \in 4}\}\subset G( -,\Psi (u)(y_1),\Psi (u)(y_2)) =S'$
.
Therefore,
![]() $\bar {\Gamma }_3$
is stable against four vertices. This completes the proof.
$\bar {\Gamma }_3$
is stable against four vertices. This completes the proof.
Corollary 6.16. The projection of
![]() $\bar {\Gamma }_3^4$
to the last three coordinates is an open map to the space
$\bar {\Gamma }_3^4$
to the last three coordinates is an open map to the space
![]() $\bar {\Gamma }_3$
.
$\bar {\Gamma }_3$
.
Proof It’s a direct consequence of Proposition 6.12.
Corollary 6.17. The projection of
![]() $\bar {\Gamma }_3^4$
to any two coordinates is an open map.
$\bar {\Gamma }_3^4$
to any two coordinates is an open map.
Proof We will use the fact that the composition of open maps is open. The projection to any two coordinates in the first four coordinates is an open map: by Corollary 6.15, the projection of
![]() $\bar {\Gamma }_3^4$
to the first four coordinates is an open map to the space
$\bar {\Gamma }_3^4$
to the first four coordinates is an open map to the space
![]() $(\mathbb {R}^3)^4$
; then just compose it with the projection map from
$(\mathbb {R}^3)^4$
; then just compose it with the projection map from
![]() $(\mathbb {R}^3)^4$
to any two coordinates.
$(\mathbb {R}^3)^4$
to any two coordinates.
The projection to any two coordinates in the last three coordinates is an open map: by Corollary 6.16, the projection of
![]() $\bar {\Gamma }_3^4$
to the last three coordinates is an open map to the space
$\bar {\Gamma }_3^4$
to the last three coordinates is an open map to the space
![]() $\bar {\Gamma }_3 $
; then just compose with the open map from Corollary 6.9.
$\bar {\Gamma }_3 $
; then just compose with the open map from Corollary 6.9.
The proof for the rest of the cases is the same, using the fact that
![]() $\bar {\Gamma }_3^4$
is invariant when permuting the first four coordinates.
$\bar {\Gamma }_3^4$
is invariant when permuting the first four coordinates.
Corollary 6.18. Let
![]() $e^4$
be generic over V for the poset
$e^4$
be generic over V for the poset
![]() $P_{\bar {\Gamma }_3 ^4} $
. Then the first four coordinate points from
$P_{\bar {\Gamma }_3 ^4} $
. Then the first four coordinate points from
![]() $ e^4$
are mutually generic over V for the product forcing
$ e^4$
are mutually generic over V for the product forcing
![]() $(P_{\mathbb {R}^3}) ^4$
.
$(P_{\mathbb {R}^3}) ^4$
.
Proof With the openness of each projection map in Corollary 6.15, the proof is similar to what we have done in Corollary 6.10.
Corollary 6.19. Let
![]() $e^4 = ( x_{0i}, x_1, x_{2} : i\in 4) $
be generic over V for the poset
$e^4 = ( x_{0i}, x_1, x_{2} : i\in 4) $
be generic over V for the poset
![]() $P_{\bar {\Gamma }_3 ^4} $
.
$P_{\bar {\Gamma }_3 ^4} $
.
![]() $\forall i\in 4$
,
$\forall i\in 4$
,
![]() $(x_{0i}, x_1, x_{2})$
is generic over V for the poset
$(x_{0i}, x_1, x_{2})$
is generic over V for the poset
![]() $P_{\bar {\Gamma }_3 } $
.
$P_{\bar {\Gamma }_3 } $
.
Proof By Corollary 6.16, it’s easy to see that
![]() $(x_{03}, x_1, x_{2})$
is generic over V for the poset
$(x_{03}, x_1, x_{2})$
is generic over V for the poset
![]() $P_{\bar {\Gamma }_3 } $
. Again using the fact that
$P_{\bar {\Gamma }_3 } $
. Again using the fact that
![]() $\bar {\Gamma }_3^4$
is invariant when permuting the first four coordinates, for every
$\bar {\Gamma }_3^4$
is invariant when permuting the first four coordinates, for every
![]() $ i\in 4$
,
$ i\in 4$
,
![]() $(x_{0i}, x_1, x_{2})$
is generic over V for the poset
$(x_{0i}, x_1, x_{2})$
is generic over V for the poset
![]() $P_{\bar {\Gamma }_3 } $
.
$P_{\bar {\Gamma }_3 } $
.
Corollary 6.20. Let
![]() $e^4$
be generic over V for the poset
$e^4$
be generic over V for the poset
![]() $P_{\bar {\Gamma }_3 ^4} $
. Then any two points from
$P_{\bar {\Gamma }_3 ^4} $
. Then any two points from
![]() $ e^4$
are mutually generic over V for the product forcing
$ e^4$
are mutually generic over V for the product forcing
![]() $P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
.
$P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
.
Proof Using the openness of the projection map in Corollary 6.17, the proof is similar to what we have done in Corollary 6.10.
The following is a key proposition for distinguishing
![]() ${\Gamma }_2$
and
${\Gamma }_2$
and
![]() ${\Gamma }_3$
.
${\Gamma }_3$
.
Proposition 6.21. There is no
![]() ${\Gamma }_2$
hyperedge in
${\Gamma }_2$
hyperedge in
![]() $V [e]$
with each vertex in
$V [e]$
with each vertex in
![]() $V [x_i]\setminus V$
respectively, where
$V [x_i]\setminus V$
respectively, where
![]() $e = ( x_0,x_1,x_2)$
is a
$e = ( x_0,x_1,x_2)$
is a
![]() $P_{\bar {\Gamma }_3}$
-generic hyperedge over V.
$P_{\bar {\Gamma }_3}$
-generic hyperedge over V.
Proof First of all, for distinct
![]() $ x_i,x_j$
from e, as Corollary 6.20,
$ x_i,x_j$
from e, as Corollary 6.20,
![]() $x_i$
and
$x_i$
and
![]() $x_j$
are mutually generic over V for the product forcing
$x_j$
are mutually generic over V for the product forcing
![]() $P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
; hence
$P_{\mathbb {R}^3} \times P_{\mathbb {R}^3} $
; hence
![]() $\: V[x_i] \cap V[x_j] = V$
, by basic theorem of product forcing.
$\: V[x_i] \cap V[x_j] = V$
, by basic theorem of product forcing.
Suppose towards the contradiction, in the ground model V, there is some condition
![]() $p\in P_{\bar \Gamma _3} $
forcing that there are
$p\in P_{\bar \Gamma _3} $
forcing that there are
![]() $\Gamma _2$
-connected points
$\Gamma _2$
-connected points
![]() $z_0 \in V[\dot {x}_ 0]\setminus V$
,
$z_0 \in V[\dot {x}_ 0]\setminus V$
,
![]() $z_1 \in V[\dot {x}_ 1]\setminus V$
and
$z_1 \in V[\dot {x}_ 1]\setminus V$
and
![]() $z_2 \in V[\dot {x}_ 2]\setminus V$
that are in
$z_2 \in V[\dot {x}_ 2]\setminus V$
that are in
![]() $\mathbb {R}^2$
. Strengthen the condition p if necessary to find
$\mathbb {R}^2$
. Strengthen the condition p if necessary to find
![]() $P_{\mathbb {R}^3}$
-names
$P_{\mathbb {R}^3}$
-names
![]() $\tau _0,\tau _1, \tau _2$
for elements of
$\tau _0,\tau _1, \tau _2$
for elements of
![]() $\mathbb {R}^2 \setminus V$
such that
$\mathbb {R}^2 \setminus V$
such that
![]() $p \Vdash \{\tau _0 /\dot {x}_0 ,\tau _1 / \dot {x}_ 1 , \tau _2 / \dot {x}_ 2\}\in \Gamma _2 $
. Strengthening p further, we may find disjoint basic open sets
$p \Vdash \{\tau _0 /\dot {x}_0 ,\tau _1 / \dot {x}_ 1 , \tau _2 / \dot {x}_ 2\}\in \Gamma _2 $
. Strengthening p further, we may find disjoint basic open sets
![]() $O_0,O_1, O_2\subset \mathbb {R}^3$
such that
$O_0,O_1, O_2\subset \mathbb {R}^3$
such that
![]() $p=(O_0\times O_1\times O_2)\cap \bar \Gamma _3$
and p decides the pivot point for the isosceles triangle
$p=(O_0\times O_1\times O_2)\cap \bar \Gamma _3$
and p decides the pivot point for the isosceles triangle
![]() $\{\tau _0 /\dot {x}_0 ,\tau _1 / \dot {x}_ 1 , \tau _2 / \dot {x}_ 2\}$
.
$\{\tau _0 /\dot {x}_0 ,\tau _1 / \dot {x}_ 1 , \tau _2 / \dot {x}_ 2\}$
.
Consider the hyperedge forcing
![]() $P_{\bar {\Gamma }_3^4}$
. Observe that
$P_{\bar {\Gamma }_3^4}$
. Observe that
![]() $\bar {\Gamma }_3^4 \cap (O_0^4\times O_1\times O_2) \neq \emptyset $
holds. Obtain a generic hyperedge
$\bar {\Gamma }_3^4 \cap (O_0^4\times O_1\times O_2) \neq \emptyset $
holds. Obtain a generic hyperedge
![]() $e^4 = ( x_{0i}, x_1, x_{2} : i\in 4) $
in
$e^4 = ( x_{0i}, x_1, x_{2} : i\in 4) $
in
![]() $O_0^4\times O_1\times O_2$
using the poset
$O_0^4\times O_1\times O_2$
using the poset
![]() $P_{\bar {\Gamma }_3^4}$
. Look into the model
$P_{\bar {\Gamma }_3^4}$
. Look into the model
![]() $V[e^4]$
. We have the following observations:
$V[e^4]$
. We have the following observations:
-
1. By Corollary 6.18, the points
 $ x_{0i} ,{i\in 4}$
are mutually Cohen generic for the product forcing
$ x_{0i} ,{i\in 4}$
are mutually Cohen generic for the product forcing
 $(P_{\mathbb {R}^3} )^4$
;
$(P_{\mathbb {R}^3} )^4$
;
 $V[{x}_{00},{x}_{01}] , V[{x}_{02},{x}_{03}]$
are also mutually generic extensions.
$V[{x}_{00},{x}_{01}] , V[{x}_{02},{x}_{03}]$
are also mutually generic extensions. -
2. By Corollary 6.19, for every
 $ i\in 4$
,
$ i\in 4$
,
 $(x_{0i}, x_1, x_{2})$
is generic for the poset
$(x_{0i}, x_1, x_{2})$
is generic for the poset
 $P_{\bar {\Gamma }_3}$
.
$P_{\bar {\Gamma }_3}$
. -
3. As a consequence of Corollary 6.20, the models obtained by adjoining each point from e pairwise intersect in V; using both item 1 and Corollary 6.20,
 $V[x_{0i}, i\in 4] $
and
$V[x_{0i}, i\in 4] $
and
 $V[x_1]$
are also mutually generic extensions, hence they intersect in V; the same holds for
$V[x_1]$
are also mutually generic extensions, hence they intersect in V; the same holds for
 $V[x_{0i}, i\in 4] $
and
$V[x_{0i}, i\in 4] $
and
 $V[x_2]$
.
$V[x_2]$
. -
4. By item 1, Corollary 6.20, and Proposition 4.9, the fields of reals in the models obtained by adjoining each point from e are pairwise in amalgamation position; the fields of reals
 $V[{x}_{00},{x}_{01}] \cap \mathbb {R} , V[{x}_{02},{x}_{03}]\cap \mathbb {R}$
are also in amalgamation position.
$V[{x}_{00},{x}_{01}] \cap \mathbb {R} , V[{x}_{02},{x}_{03}]\cap \mathbb {R}$
are also in amalgamation position.
As a consequence of observation item 3, the points in
![]() $\{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \} $
are pairwise distinct. With observation item 2 and by the forcing theorem applied to
$\{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \} $
are pairwise distinct. With observation item 2 and by the forcing theorem applied to
![]() $p\in P_{\bar {\Gamma }_3}$
earlier, for
$p\in P_{\bar {\Gamma }_3}$
earlier, for
![]() $i\in 4$
,
$i\in 4$
,
![]() $ \{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \} \in {\Gamma }_2$
holds. We have three complete cases depending on the pivot point of each isosceles triangle
$ \{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \} \in {\Gamma }_2$
holds. We have three complete cases depending on the pivot point of each isosceles triangle
![]() $ \{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \}$
for
$ \{ \tau _0 / {x}_{ 0i}, \tau _1 /{x}_{1} ,\tau _2 / {x}_ 2 \}$
for
![]() $i\in 4 $
.
$i\in 4 $
.
Case 1: for each
![]() $i\in 4$
,
$i\in 4$
,
![]() $\tau _0 / {x}_{ 0i}$
is the pivot point. Then there is a line l on which all the points
$\tau _0 / {x}_{ 0i}$
is the pivot point. Then there is a line l on which all the points
![]() $\tau _0 /{x}_{0i}, i\in 4$
are. Then
$\tau _0 /{x}_{0i}, i\in 4$
are. Then
![]() $l $
is algebraic over
$l $
is algebraic over
![]() $ \{\tau _0 / {x}_{00},\tau _0 / {x}_{01}\}\subset V[{x}_{00},{x}_{01}] \cap \mathbb {R}$
and over
$ \{\tau _0 / {x}_{00},\tau _0 / {x}_{01}\}\subset V[{x}_{00},{x}_{01}] \cap \mathbb {R}$
and over
![]() $\{\tau _0 / {x}_{02},\tau _0 / {x}_{03}\} \subset V[{x}_{02},{x}_{03}] \cap \mathbb {R}$
by Fact 3.2 (1). See that l is algebraic over the field
$\{\tau _0 / {x}_{02},\tau _0 / {x}_{03}\} \subset V[{x}_{02},{x}_{03}] \cap \mathbb {R}$
by Fact 3.2 (1). See that l is algebraic over the field
![]() $V\cap \mathbb {R}$
: l is algebraic over
$V\cap \mathbb {R}$
: l is algebraic over
![]() $ V[{x}_{00},{x}_{01}] \cap V[{x}_{02},{x}_{03}] \cap \mathbb {R}= V\cap \mathbb {R}$
by our observation item 4 and Corollary 4.3. Also see
$ V[{x}_{00},{x}_{01}] \cap V[{x}_{02},{x}_{03}] \cap \mathbb {R}= V\cap \mathbb {R}$
by our observation item 4 and Corollary 4.3. Also see
![]() $\tau _1 /{x}_{1}, \tau _2 /{x}_{2} \in V $
: since
$\tau _1 /{x}_{1}, \tau _2 /{x}_{2} \in V $
: since
![]() $\tau _1 /{x}_{1},\tau _2 /{x}_{2}$
are symmetrical with respect to l,
$\tau _1 /{x}_{1},\tau _2 /{x}_{2}$
are symmetrical with respect to l,
![]() $\tau _1 /{x}_{1} \in V[x_2]$
and
$\tau _1 /{x}_{1} \in V[x_2]$
and
![]() $\tau _2 /{x}_{2} \in V[x_1]$
hold by Fact 3.2(6); then
$\tau _2 /{x}_{2} \in V[x_1]$
hold by Fact 3.2(6); then
![]() $\tau _1 /{x}_{1} , \tau _2 /{x}_{2} \in V[x_2]\cap V[x_1] = V$
by our observation item 3. This is a contradiction to
$\tau _1 /{x}_{1} , \tau _2 /{x}_{2} \in V[x_2]\cap V[x_1] = V$
by our observation item 3. This is a contradiction to
![]() $\tau _1,\tau _2$
being forced not in V.
$\tau _1,\tau _2$
being forced not in V.
Case 2:
![]() $\tau _1 /{x}_{1} $
is always the pivot point. Then
$\tau _1 /{x}_{1} $
is always the pivot point. Then
![]() $\tau _1 /{x}_{1} $
is the center of the circle c on which all the points
$\tau _1 /{x}_{1} $
is the center of the circle c on which all the points
![]() $\tau _0 /{x}_{0i}, i\in 4$
are. Then
$\tau _0 /{x}_{0i}, i\in 4$
are. Then
![]() $\tau _1 /{x}_{1} \in V[x_{0i}:i\in 4] $
holds by Fact 3.2(3) and (7). Then
$\tau _1 /{x}_{1} \in V[x_{0i}:i\in 4] $
holds by Fact 3.2(3) and (7). Then
![]() $\tau _1 /{x}_{1} \in V[x_{0i}:i\in 4] \cap V[x_1] = V$
by our observation item 3. This is a contradiction to
$\tau _1 /{x}_{1} \in V[x_{0i}:i\in 4] \cap V[x_1] = V$
by our observation item 3. This is a contradiction to
![]() $\tau _1$
being forced not in V.
$\tau _1$
being forced not in V.
Case 3:
![]() $\tau _2 /{x}_{2} $
is always the pivot point. This case is handled the same as Case 2.
$\tau _2 /{x}_{2} $
is always the pivot point. This case is handled the same as Case 2.
Therefore, our initial assumption is impossible.
7 The independence theorem
This section is devoted to the proof of Theorem 1.2.
Lemma 7.1. For each
![]() $i\in 3$
, let
$i\in 3$
, let
![]() $V[G_i]$
be a generic extension over V such that:
$V[G_i]$
be a generic extension over V such that:
-
1.
 $V[G_i]$
for
$V[G_i]$
for
 $i\in 3$
form a
$i\in 3$
form a
 $\Delta $
-system with the root V.
$\Delta $
-system with the root V. -
2. There is no isosceles triangle in
 $\mathbb {R}^2$
with each vertex in each
$\mathbb {R}^2$
with each vertex in each
 $V[G_i]\setminus{\kern-1.5pt} V$
respectively.
$V[G_i]\setminus{\kern-1.5pt} V$
respectively. -
3.
 $P_i \in V [G_i]$
is a poset and
$P_i \in V [G_i]$
is a poset and
 $H_i \subset P_i$
is a filter such that
$H_i \subset P_i$
is a filter such that
 $H_i, i\in 3$
are mutually generic over the model
$H_i, i\in 3$
are mutually generic over the model
 $V [G_i: i\in 3]$
.
$V [G_i: i\in 3]$
.
Then:
-
4.
 $V [G_i][H_i], i\in 3$
form a
$V [G_i][H_i], i\in 3$
form a
 $\Delta $
-system with the root V.
$\Delta $
-system with the root V. -
5. There is no isosceles triangle in
 $\mathbb {R}^2$
with each vertex in
$\mathbb {R}^2$
with each vertex in
 $V [G_i][H_i]\setminus V$
respectively.
$V [G_i][H_i]\setminus V$
respectively.
Proof Let’s first show the
![]() $\Delta $
-system for (4). Fix
$\Delta $
-system for (4). Fix
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $x\in V [G_i][H_i]\cap V [G_j][H_j]$
. Then
$x\in V [G_i][H_i]\cap V [G_j][H_j]$
. Then
![]() $x\in V [G_i][H_i]\cap V [G_j][H_j] \subset V [G_i, G_j][H_i]\cap V [G_i, G_j][H_j] = V[G_i,G_j] $
. Then
$x\in V [G_i][H_i]\cap V [G_j][H_j] \subset V [G_i, G_j][H_i]\cap V [G_i, G_j][H_j] = V[G_i,G_j] $
. Then
![]() $x \in V[G_i,G_j] \cap V [G_i][H_i] = V[G_i]$
and
$x \in V[G_i,G_j] \cap V [G_i][H_i] = V[G_i]$
and
![]() $x \in V[G_i,G_j] \cap V [G_j][H_j] \kern1.3pt{=}\kern1.3pt V[G_j]$
. Then
$x \in V[G_i,G_j] \cap V [G_j][H_j] \kern1.3pt{=}\kern1.3pt V[G_j]$
. Then
![]() $x\kern1.3pt{\in}\kern1.3pt V[G_i] \kern1.3pt{\cap}\kern1.3pt V[G_j] \kern1.3pt{=}\kern1.3pt V$
. Thus
$x\kern1.3pt{\in}\kern1.3pt V[G_i] \kern1.3pt{\cap}\kern1.3pt V[G_j] \kern1.3pt{=}\kern1.3pt V$
. Thus
![]() $ V [G_i][H_i]\kern1.2pt{\cap}\kern1.2pt V [G_j][H_j] \subset V$
. Thus
$ V [G_i][H_i]\kern1.2pt{\cap}\kern1.2pt V [G_j][H_j] \subset V$
. Thus
![]() $ V [G_i][H_i]\cap V [G_j][H_j] = V$
.
$ V [G_i][H_i]\cap V [G_j][H_j] = V$
.
For (5), suppose towards a contradiction that for each
![]() $i\in 3$
,
$i\in 3$
,
![]() $p_i \in P_i$
is a condition and
$p_i \in P_i$
is a condition and
![]() $\tau _i$
are
$\tau _i$
are
![]() $P_i$
-names in
$P_i$
-names in
![]() $V [G_i]$
for elements of
$V [G_i]$
for elements of
![]() $\mathbb {R}^2$
which do not belong to V, and
$\mathbb {R}^2$
which do not belong to V, and
![]() $\langle p_0,p_1,p_2\rangle $
forces in
$\langle p_0,p_1,p_2\rangle $
forces in
![]() $P_0 \times P_1\times P_2$
that
$P_0 \times P_1\times P_2$
that
![]() $\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
. Strengthen
$\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
. Strengthen
![]() $\langle p_0,p_1,p_2\rangle $
to decide which of the points in the set
$\langle p_0,p_1,p_2\rangle $
to decide which of the points in the set
![]() $\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
is the pivot point for the isosceles triangle. To complete the proof, we will reach a contradiction in any case as below.
$\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
is the pivot point for the isosceles triangle. To complete the proof, we will reach a contradiction in any case as below.
Case 1:
![]() $\forall i\: p_i \Vdash \tau _i\in V[G_i]$
. Then
$\forall i\: p_i \Vdash \tau _i\in V[G_i]$
. Then
![]() $\forall i\: p_i \Vdash \tau _i\in V[G_i]\setminus V$
and
$\forall i\: p_i \Vdash \tau _i\in V[G_i]\setminus V$
and
![]() $\langle p_0,p_1,p_2\rangle $
forces that
$\langle p_0,p_1,p_2\rangle $
forces that
![]() $\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
, which is impossible by our assumption item 2.
$\{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
, which is impossible by our assumption item 2.
Case 2:
![]() $\exists i\ p_i \Vdash \tau _i\notin V[G_i]$
. Without loss of generality,
$\exists i\ p_i \Vdash \tau _i\notin V[G_i]$
. Without loss of generality,
![]() $p_0 \Vdash \tau _0\notin V[G_0]$
. So
$p_0 \Vdash \tau _0\notin V[G_0]$
. So
![]() $p_0 \Vdash \tau _0\in V[G_0][H_0]\setminus V[G_0]$
. Here comes a “duplication” technique again. For each
$p_0 \Vdash \tau _0\in V[G_0][H_0]\setminus V[G_0]$
. Here comes a “duplication” technique again. For each
![]() $k\in 4$
, let
$k\in 4$
, let
![]() $h_{0k}\subset P_0$
be mutually generic filters over
$h_{0k}\subset P_0$
be mutually generic filters over
![]() $V[G_0] $
containing the condition
$V[G_0] $
containing the condition
![]() $p_0$
. Let
$p_0$
. Let
![]() $h_{1}\subset P_1$
containing the condition
$h_{1}\subset P_1$
containing the condition
![]() $p_1$
and
$p_1$
and
![]() $h_{2}\subset P_2$
containing the condition
$h_{2}\subset P_2$
containing the condition
![]() $p_2$
be mutually generic filters over
$p_2$
be mutually generic filters over
![]() $V[G_{i}: i\in 3] [h_{0k}: k\in 4]$
. For each
$V[G_{i}: i\in 3] [h_{0k}: k\in 4]$
. For each
![]() $k\in 4$
, let
$k\in 4$
, let
![]() $y_{0k} = \tau _0 / h_{0k}, y_{1} = \tau _1 / h_{1}, y_{2} = \tau _2 / h_{2} \in \mathbb {R}^2$
be points. As
$y_{0k} = \tau _0 / h_{0k}, y_{1} = \tau _1 / h_{1}, y_{2} = \tau _2 / h_{2} \in \mathbb {R}^2$
be points. As
![]() $\langle p_0,p_1,p_2\rangle \Vdash \{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
, for each
$\langle p_0,p_1,p_2\rangle \Vdash \{\tau _0,\tau _1, \tau _2\} \in \Gamma _2$
, for each
![]() $ k\in 4, \{y_{0k}, y_1, y_2 \} \in \Gamma _2$
holds. We will reach a contradiction in two complementary cases, similar to the cases in the proof of Proposition 6.21.
$ k\in 4, \{y_{0k}, y_1, y_2 \} \in \Gamma _2$
holds. We will reach a contradiction in two complementary cases, similar to the cases in the proof of Proposition 6.21.
Case 2.1:
![]() $p_0$
forces that
$p_0$
forces that
![]() $\tau _0$
is not the pivot point. Then for each k,
$\tau _0$
is not the pivot point. Then for each k,
![]() $y_{0k}$
will not be the pivot point. Then
$y_{0k}$
will not be the pivot point. Then
![]() $y_j$
is the pivot point for
$y_j$
is the pivot point for
![]() $j=1$
or
$j=1$
or
![]() $j = 2$
. The point
$j = 2$
. The point
![]() $y_j$
, as the center of the circle passing through all points in
$y_j$
, as the center of the circle passing through all points in
![]() $\{y_{0k}\}_{k\in 4}$
, is algebraic over
$\{y_{0k}\}_{k\in 4}$
, is algebraic over
![]() $\{y_{0k}\}_{k\in 4}$
by Fact 3.2(7); hence
$\{y_{0k}\}_{k\in 4}$
by Fact 3.2(7); hence
![]() $y_j$
is in
$y_j$
is in
![]() $V [G_0][h_{0k}: k\in 4]$
. But also
$V [G_0][h_{0k}: k\in 4]$
. But also
![]() $y_j\in V[G_j]$
. Hence
$y_j\in V[G_j]$
. Hence
![]() $y_j\in V[G_j]\cap V [G_0][h_{0k}: k\in 4] = V$
, contradicting our initial assumption that
$y_j\in V[G_j]\cap V [G_0][h_{0k}: k\in 4] = V$
, contradicting our initial assumption that
![]() $\tau _j$
is forced to not belong to V.
$\tau _j$
is forced to not belong to V.
Case 2.2:
![]() $p_0$
forces that
$p_0$
forces that
![]() $\tau _0$
is the pivot point. Then for each k,
$\tau _0$
is the pivot point. Then for each k,
![]() $y_{0k}$
is the pivot point. Then the line l, which is the perpendicular bisector of the line segment from
$y_{0k}$
is the pivot point. Then the line l, which is the perpendicular bisector of the line segment from
![]() $y_1$
to
$y_1$
to
![]() $y_2$
, passes through
$y_2$
, passes through
![]() $y_{0k}$
for each k. Then
$y_{0k}$
for each k. Then
![]() $l $
is algebraic over
$l $
is algebraic over
![]() $ \{y_{00}, y_{01}\}\subset V[G_0][y_{00}, y_{01}] \cap \mathbb {R}$
and over
$ \{y_{00}, y_{01}\}\subset V[G_0][y_{00}, y_{01}] \cap \mathbb {R}$
and over
![]() $\{y_{02}, y_{03}\} \subset V[G_0][y_{02}, y_{03}] \cap \mathbb {R}$
by Fact 3.2(1). Then l must be algebraic over
$\{y_{02}, y_{03}\} \subset V[G_0][y_{02}, y_{03}] \cap \mathbb {R}$
by Fact 3.2(1). Then l must be algebraic over
![]() $ V[G_0][y_{00}, y_{01}] \cap V[G_0][y_{02}, y_{03}] \cap \mathbb {R}= V[G_0]\cap \mathbb {R}$
by Proposition 4.9 and Corollary 4.3. Also observe
$ V[G_0][y_{00}, y_{01}] \cap V[G_0][y_{02}, y_{03}] \cap \mathbb {R}= V[G_0]\cap \mathbb {R}$
by Proposition 4.9 and Corollary 4.3. Also observe
![]() $y_1 \in V[G_1],y_2 \in V[G_2] $
: since
$y_1 \in V[G_1],y_2 \in V[G_2] $
: since
![]() $y_1,y_2$
are symmetrical with respect to l,
$y_1,y_2$
are symmetrical with respect to l,
![]() $y_1 \in V[G_i:i\in 3][h_2]$
and
$y_1 \in V[G_i:i\in 3][h_2]$
and
![]() $y_2 \in V[G_i:i\in 3][h_1]$
hold by Fact 3.2(6);
$y_2 \in V[G_i:i\in 3][h_1]$
hold by Fact 3.2(6);
![]() $V[G_i:i\in 3][h_1]\cap V[G_i:i\in 3][h_2] = V[G_i:i\in 3]$
holds; then
$V[G_i:i\in 3][h_1]\cap V[G_i:i\in 3][h_2] = V[G_i:i\in 3]$
holds; then
![]() $y_1 \in V[G_i:i\in 3] \cap V[G_1][h_1]= V[G_1],y_2 \in V[G_i:i\in 3] \cap V[G_2][h_2] = V[G_2] $
hold.
$y_1 \in V[G_i:i\in 3] \cap V[G_1][h_1]= V[G_1],y_2 \in V[G_i:i\in 3] \cap V[G_2][h_2] = V[G_2] $
hold.
The line l algebraic over
![]() $V[G_0] \cap \mathbb {R}$
needs to contain some points in
$V[G_0] \cap \mathbb {R}$
needs to contain some points in
![]() $V[G_0] $
. See that l can’t contain any point in
$V[G_0] $
. See that l can’t contain any point in
![]() $V[G_0]\setminus V$
, because such a point would form an isosceles triangle with
$V[G_0]\setminus V$
, because such a point would form an isosceles triangle with
![]() $y_1,y_2$
contradicting the assumption item 2. Then l contains points with coordinates from
$y_1,y_2$
contradicting the assumption item 2. Then l contains points with coordinates from
![]() $V\cap \mathbb {R}$
by and must be algebraic over
$V\cap \mathbb {R}$
by and must be algebraic over
![]() $V\cap \mathbb {R}$
by Fact 3.2. Since
$V\cap \mathbb {R}$
by Fact 3.2. Since
![]() $y_1,y_2$
are symmetrical with l,
$y_1,y_2$
are symmetrical with l,
![]() $y_1 \in V[G_2]$
and
$y_1 \in V[G_2]$
and
![]() $y_2 \in V[G_1]$
, hence
$y_2 \in V[G_1]$
, hence
![]() $y_1,y_2\in V[G_2] \cap V[G_1] = V$
, contradicting our initial assumption that
$y_1,y_2\in V[G_2] \cap V[G_1] = V$
, contradicting our initial assumption that
![]() $\tau _1,\tau _2$
are forced to not belong to V.
$\tau _1,\tau _2$
are forced to not belong to V.
Now let the poset P be defined as Definition 3.1. The following gives us the ability of amalgamating three conditions in P.
Proposition 7.2. For arbitrary conditions
![]() $ p_0, p_1,p_2 \in P $
, with their common upper bound p, such that any pair of fields from
$ p_0, p_1,p_2 \in P $
, with their common upper bound p, such that any pair of fields from
![]() $\mathrm {supp}(p_0),\mathrm {supp}(p_1) , \mathrm {supp}(p_2) \subset \mathbb {R}$
is in amalgamation position and that
$\mathrm {supp}(p_0),\mathrm {supp}(p_1) , \mathrm {supp}(p_2) \subset \mathbb {R}$
is in amalgamation position and that
![]() $\{\mathrm {supp}(p_0),\mathrm {supp}(p_1) , \mathrm {supp}(p_2)\}$
forms a
$\{\mathrm {supp}(p_0),\mathrm {supp}(p_1) , \mathrm {supp}(p_2)\}$
forms a
![]() $\Delta $
-system with the root
$\Delta $
-system with the root
![]() $\mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) \cap \mathrm {supp}(p_2) = \mathrm {supp}(p)$
,
$\mathrm {supp}(p_0)\cap \mathrm {supp}(p_1) \cap \mathrm {supp}(p_2) = \mathrm {supp}(p)$
,
![]() $ p_0, p_1,p_2 $
have a common lower bound in P whenever:
$ p_0, p_1,p_2 $
have a common lower bound in P whenever:
-
1.
 $p_0 \upharpoonright \mathrm {supp}(p) = p_1 \upharpoonright \mathrm {supp}(p) = p_2 \upharpoonright \mathrm {supp}(p) $
, and
$p_0 \upharpoonright \mathrm {supp}(p) = p_1 \upharpoonright \mathrm {supp}(p) = p_2 \upharpoonright \mathrm {supp}(p) $
, and
 $p\in P$
,
$p\in P$
,
 $p_0\leq p$
,
$p_0\leq p$
,
 $p_1\leq p$
and
$p_1\leq p$
and
 $p_2\leq p$
hold.
$p_2\leq p$
hold. -
2. There is no isosceles triangle in
 $\mathbb {R}^2$
with each of its vertex in
$\mathbb {R}^2$
with each of its vertex in
 $\mathrm {dom}(p_0) \setminus \mathrm {dom}(p),\mathrm {dom}(p_1) \setminus \mathrm {dom}(p), \mathrm {dom}(p_2) \setminus \mathrm {dom}(p)$
respectively.
$\mathrm {dom}(p_0) \setminus \mathrm {dom}(p),\mathrm {dom}(p_1) \setminus \mathrm {dom}(p), \mathrm {dom}(p_2) \setminus \mathrm {dom}(p)$
respectively.
Proof First of all,
![]() $\forall i, j\in 3 , p_i \cup p_j$
is a
$\forall i, j\in 3 , p_i \cup p_j$
is a
![]() $\Gamma _2$
-coloring by Lemma 5.5. Since there is no isosceles triangle in
$\Gamma _2$
-coloring by Lemma 5.5. Since there is no isosceles triangle in
![]() $\mathbb {R}^2$
with each of its vertex in
$\mathbb {R}^2$
with each of its vertex in
![]() $\mathrm {dom}(p_0) \setminus \mathrm {dom}(p),\mathrm {dom}(p_1) \setminus \mathrm {dom}(p), \mathrm {dom}(p_2) \setminus \mathrm {dom}(p)$
respectively by item 2 in our assumption,
$\mathrm {dom}(p_0) \setminus \mathrm {dom}(p),\mathrm {dom}(p_1) \setminus \mathrm {dom}(p), \mathrm {dom}(p_2) \setminus \mathrm {dom}(p)$
respectively by item 2 in our assumption,
![]() $ p_0\cup p_1\cup p_2$
is a
$ p_0\cup p_1\cup p_2$
is a
![]() $\Gamma _2$
-coloring.
$\Gamma _2$
-coloring.
Now we will extend the
![]() $\Gamma _2$
-coloring
$\Gamma _2$
-coloring
![]() $ p_0\cup p_1\cup p_2$
. Let
$ p_0\cup p_1\cup p_2$
. Let
![]() $ b \supset \mathrm {supp}(p_0) \cup \mathrm {supp}(p_1) \cup \mathrm {supp}(p_2)$
be a countable real closed subfield of
$ b \supset \mathrm {supp}(p_0) \cup \mathrm {supp}(p_1) \cup \mathrm {supp}(p_2)$
be a countable real closed subfield of
![]() $\mathbb {R}$
. We will extend
$\mathbb {R}$
. We will extend
![]() $p_0 \cup p_1\cup p_2$
to some
$p_0 \cup p_1\cup p_2$
to some
![]() $p_3 \in P$
with
$p_3 \in P$
with
![]() $ \mathrm {supp}(p_3) = b$
and
$ \mathrm {supp}(p_3) = b$
and
![]() $\mathrm {dom}(p_3) = \mathrm {supp}(p_3) ^2 = b^2$
. For each point
$\mathrm {dom}(p_3) = \mathrm {supp}(p_3) ^2 = b^2$
. For each point
![]() $x \in b^2 \setminus (\mathrm {dom}(p_0) \cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2) ) $
, let
$x \in b^2 \setminus (\mathrm {dom}(p_0) \cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2) ) $
, let
![]() $d(x) = \bigcup _{i\neq j\in 3} d(p_i,p_j,x) $
where each
$d(x) = \bigcup _{i\neq j\in 3} d(p_i,p_j,x) $
where each
![]() $d(p_i,p_j,x) $
is the set of disallowed colors on x for
$d(p_i,p_j,x) $
is the set of disallowed colors on x for
![]() $p_i,p_j$
from Definition 5.6. Then
$p_i,p_j$
from Definition 5.6. Then
![]() $d(x)\in I$
holds as each
$d(x)\in I$
holds as each
![]() $d(p_i,p_j,x)\in I$
by Lemma 5.7. Fix any set
$d(p_i,p_j,x)\in I$
by Lemma 5.7. Fix any set
![]() $\pi \in I $
so that
$\pi \in I $
so that
![]() $\forall x\in b^2 \setminus (\mathrm {dom}(p_0) \cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2) ) : \:\pi \setminus d(x)$
is infinite, which is possible by our choice of the ideal I. Now just let
$\forall x\in b^2 \setminus (\mathrm {dom}(p_0) \cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2) ) : \:\pi \setminus d(x)$
is infinite, which is possible by our choice of the ideal I. Now just let
![]() $p_3$
be a map with domain
$p_3$
be a map with domain
![]() $b^2$
such that:
$b^2$
such that:
-
•
 $p_2\upharpoonright {\mathrm {dom}(p_0)\cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2)} = p_0 \cup p_1\cup p_2$
.
$p_2\upharpoonright {\mathrm {dom}(p_0)\cup \mathrm {dom}(p_1)\cup \mathrm {dom}(p_2)} = p_0 \cup p_1\cup p_2$
. -
•
 $\forall x\in b^2 \setminus ( \mathrm {dom}(p_0 ) \cup \mathrm {dom}( p_1) \cup \mathrm {dom}(p_2)),\: p_3 (x) \in \pi \setminus d(x)$
.
$\forall x\in b^2 \setminus ( \mathrm {dom}(p_0 ) \cup \mathrm {dom}( p_1) \cup \mathrm {dom}(p_2)),\: p_3 (x) \in \pi \setminus d(x)$
. -
•
 $p_3$
on
$p_3$
on
 $b^2 \setminus ( \mathrm {dom}(p_0 ) \cup \mathrm {dom}( p_1) \cup \mathrm {dom}(p_2))$
is an injection.
$b^2 \setminus ( \mathrm {dom}(p_0 ) \cup \mathrm {dom}( p_1) \cup \mathrm {dom}(p_2))$
is an injection.
Claim 7.3.
![]() $p_3 \in P$
and
$p_3 \in P$
and
![]() $p_3 \leq p_0,p_1,p_2$
hold.
$p_3 \leq p_0,p_1,p_2$
hold.
This completes the proof.
Theorem 7.4. Let
![]() $\kappa $
be an inaccessible cardinal. There is a model of ZF+DC in which
$\kappa $
be an inaccessible cardinal. There is a model of ZF+DC in which
![]() ${\Gamma _2}$
has countable chromatic number while for every non-meager set
${\Gamma _2}$
has countable chromatic number while for every non-meager set
![]() $A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle.
$A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle.
Proof Let W be the symmetric Solovay model derived from
![]() $\kappa $
, and the model we need is the P extension over W, in which
$\kappa $
, and the model we need is the P extension over W, in which
![]() ${\Gamma _2}$
has countable chromatic number by our construction of P. We will show that in this model, for every non-meager set
${\Gamma _2}$
has countable chromatic number by our construction of P. We will show that in this model, for every non-meager set
![]() $A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle.
$A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle.
Work in W. Suppose
![]() $p\in P$
is a condition and let
$p\in P$
is a condition and let
![]() $\tau $
be a P-name for a nonmeager subset of
$\tau $
be a P-name for a nonmeager subset of
![]() $\mathbb {R}^3$
. We will find a
$\mathbb {R}^3$
. We will find a
![]() $\Gamma _3$
-hyperedge e and a strengthening of the condition p which forces e to be a subset of
$\Gamma _3$
-hyperedge e and a strengthening of the condition p which forces e to be a subset of
![]() $\tau $
. By the definition of W and Fact 2.7(1), the condition p as well as the name
$\tau $
. By the definition of W and Fact 2.7(1), the condition p as well as the name
![]() $\tau $
must be definable from ground model parameters and an additional parameter
$\tau $
must be definable from ground model parameters and an additional parameter
![]() $z \in \omega ^\omega $
. Using Fact 2.7(3), let
$z \in \omega ^\omega $
. Using Fact 2.7(3), let
![]() $V [K]$
be an intermediate extension obtained by a forcing of cardinality smaller than
$V [K]$
be an intermediate extension obtained by a forcing of cardinality smaller than
![]() $\kappa $
with z,
$\kappa $
with z,
![]() $p \in V[K]$
and the Continuum Hypothesis holds in
$p \in V[K]$
and the Continuum Hypothesis holds in
![]() $V [K]$
. Then P is balanced in
$V [K]$
. Then P is balanced in
![]() $V[K]$
by Proposition 5.3(2).
$V[K]$
by Proposition 5.3(2).
Work in the model
![]() $V [K]$
. Let
$V [K]$
. Let
![]() $\bar {p} \leq p$
be a balanced virtual condition in the poset P. Consider the Cohen poset
$\bar {p} \leq p$
be a balanced virtual condition in the poset P. Consider the Cohen poset
![]() $P_{\mathbb {R}^3}$
consisting of nonempty open subsets of
$P_{\mathbb {R}^3}$
consisting of nonempty open subsets of
![]() ${\mathbb {R}^3}$
ordered by inclusion, with its name
${\mathbb {R}^3}$
ordered by inclusion, with its name
![]() $ \dot {x}_{gen}$
for a generic element of the space
$ \dot {x}_{gen}$
for a generic element of the space
![]() ${\mathbb {R}^3}$
. By a standard Solovay model argument using Fact 2.8 with Fact 2.4, there must be a condition
${\mathbb {R}^3}$
. By a standard Solovay model argument using Fact 2.8 with Fact 2.4, there must be a condition
![]() $O \in P_{\mathbb {R}^3}$
, a poset Q of cardinality smaller than
$O \in P_{\mathbb {R}^3}$
, a poset Q of cardinality smaller than
![]() $\kappa $
, and (with the convenience of product forcing) a
$\kappa $
, and (with the convenience of product forcing) a
![]() $P_{\mathbb {R}^3} \times Q$
-name
$P_{\mathbb {R}^3} \times Q$
-name
![]() $\sigma $
for a condition in the poset P stronger than
$\sigma $
for a condition in the poset P stronger than
![]() $\bar {p}$
such that
$\bar {p}$
such that
Otherwise, in the model W, the virtual condition
![]() $\bar {p} $
would force
$\bar {p} $
would force
![]() $\tau $
to be disjoint from the comeager set of points in
$\tau $
to be disjoint from the comeager set of points in
![]() $\mathbb {R}^3$
which are Cohen generic over the model
$\mathbb {R}^3$
which are Cohen generic over the model
![]() $V [K]$
, contradicting the initial assumption that the name
$V [K]$
, contradicting the initial assumption that the name
![]() $\tau $
forced to be a non-meager set.
$\tau $
forced to be a non-meager set.
Now recall the poset
![]() $P_{\bar \Gamma _3}$
according to Definition 6.1, and observe that
$P_{\bar \Gamma _3}$
according to Definition 6.1, and observe that
![]() $O^3$
is a condition in
$O^3$
is a condition in
![]() $P_{\bar \Gamma _3}$
. Over the ground model
$P_{\bar \Gamma _3}$
. Over the ground model
![]() $V[K]$
, let e be a generic hyperedge of the poset
$V[K]$
, let e be a generic hyperedge of the poset
![]() $P_{\bar \Gamma ^3}$
that meets
$P_{\bar \Gamma ^3}$
that meets
![]() $O^3$
. Identify e with set of its vertices. Observe that for each vertex
$O^3$
. Identify e with set of its vertices. Observe that for each vertex
![]() $x\in e$
, x is
$x\in e$
, x is
![]() $P_{\mathbb {R}^3}$
-generic, and each pair of vertices in e is mutually generic, by Corollary 6.10. Let
$P_{\mathbb {R}^3}$
-generic, and each pair of vertices in e is mutually generic, by Corollary 6.10. Let
![]() $H_x\subset Q$
for
$H_x\subset Q$
for
![]() $x \in e$
be filters mutually generic over the model
$x \in e$
be filters mutually generic over the model
![]() $V [K][e]$
. Work in the model
$V [K][e]$
. Work in the model
![]() $V [K][e][H_x : x \in e]$
. Use Proposition 6.21 and Lemma 7.1 to observe that:
$V [K][e][H_x : x \in e]$
. Use Proposition 6.21 and Lemma 7.1 to observe that:
-
• The models
 $V [K][x][H_x]$
for
$V [K][x][H_x]$
for
 $x \in e$
form a
$x \in e$
form a
 $\Delta $
-system with the root
$\Delta $
-system with the root
 $V[K]$
.
$V[K]$
. -
• There is no isosceles triangle in
 $\mathbb {R}^3$
with one vertex in each model
$\mathbb {R}^3$
with one vertex in each model
 $V [K][x][H_x]$
for
$V [K][x][H_x]$
for
 $x \in e$
respectively.
$x \in e$
respectively.
Claim 7.5. Whenever for each vertex
![]() $x\in e$
,
$x\in e$
,
![]() $p_x$
is a condition in
$p_x$
is a condition in
![]() $V [K][e][H_x]$
with
$V [K][e][H_x]$
with
![]() $ p_x \leq \bar {p}$
, the conditions
$ p_x \leq \bar {p}$
, the conditions
![]() $ p_x$
for
$ p_x$
for
![]() $x\in e$
have a common lower bound.
$x\in e$
have a common lower bound.
Proof Apply Proposition 7.2 after checking its assumptions.
For each
![]() $x\in e$
, write
$x\in e$
, write
![]() $p_x = \sigma / x$
, which is a condition in
$p_x = \sigma / x$
, which is a condition in
![]() $V [K][x][H_x]$
; by forcing theorem applied in the model
$V [K][x][H_x]$
; by forcing theorem applied in the model
![]() $V [K][x][H_x]$
,
$V [K][x][H_x]$
,
![]() $p_x\leq \bar {p}$
is a condition forcing
$p_x\leq \bar {p}$
is a condition forcing
![]() $x \in \tau $
. Then by Claim 7.5, let q be a lower bound of the conditions
$x \in \tau $
. Then by Claim 7.5, let q be a lower bound of the conditions
![]() $ p_x$
for
$ p_x$
for
![]() $x\in e$
. Thus we have produced a
$x\in e$
. Thus we have produced a
![]() $\Gamma _3$
-hyperedge e and a condition q stronger than p which forces all vertices of e to be in
$\Gamma _3$
-hyperedge e and a condition q stronger than p which forces all vertices of e to be in
![]() $\tau $
, as required.
$\tau $
, as required.
Finally, Theorem 1.2 is just a corollary of Theorem 7.4. Here is the proof of Theorem 1.2.
Proof Let
![]() $\kappa $
be an inaccessible cardinal. By Theorem 7.4, there is a model of ZF+DC in which
$\kappa $
be an inaccessible cardinal. By Theorem 7.4, there is a model of ZF+DC in which
![]() ${\Gamma _2}$
has countable chromatic number while for every non-meager set
${\Gamma _2}$
has countable chromatic number while for every non-meager set
![]() $A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle. Then immediately, in this model, the hypergraph
$A\subset \mathbb {R}^3$
, A contains all vertices of an isosceles triangle. Then immediately, in this model, the hypergraph
![]() $\Gamma _3$
has uncountable chromatic number: by Theorem 2.2, Baire Category Theorem holds for
$\Gamma _3$
has uncountable chromatic number: by Theorem 2.2, Baire Category Theorem holds for
![]() $\mathbb {R}^3$
due to DC; then when dividing the space
$\mathbb {R}^3$
due to DC; then when dividing the space
![]() $\mathbb {R}^3$
into countably many pieces, one of them has to be nonmeager; that piece contains all vertices of an isosceles triangle.
$\mathbb {R}^3$
into countably many pieces, one of them has to be nonmeager; that piece contains all vertices of an isosceles triangle.