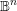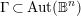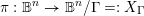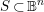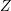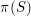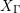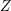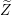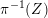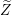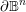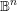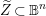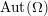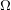Let
![]() $(X,ds_{X}^{2})$
be a complex hyperbolic space form of finite volume, i.e.,
$(X,ds_{X}^{2})$
be a complex hyperbolic space form of finite volume, i.e.,
![]() $X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
is the quotient of the complex unit ball
$X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
is the quotient of the complex unit ball
![]() $\mathbb{B}^{n}$
by a torsion-free lattice
$\mathbb{B}^{n}$
by a torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
, and
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
, and
![]() $ds_{X}^{2}$
be a canonical Kähler–Einstein metric on
$ds_{X}^{2}$
be a canonical Kähler–Einstein metric on
![]() $X$
. In [Reference Mok and EbenfeltMok10], motivated by the study of the Gauss map on subvarieties of
$X$
. In [Reference Mok and EbenfeltMok10], motivated by the study of the Gauss map on subvarieties of
![]() $X$
we considered the question of determining Zariski closures of images of totally geodesic complex submanifolds
$X$
we considered the question of determining Zariski closures of images of totally geodesic complex submanifolds
![]() $S\,\subset \,\mathbb{B}^{n}$
under the universal covering map
$S\,\subset \,\mathbb{B}^{n}$
under the universal covering map
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X$
. We proved that the Zariski closure
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X$
. We proved that the Zariski closure
![]() $Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\,\subset \,X$
must be a totally geodesic subset.
$Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\,\subset \,X$
must be a totally geodesic subset.
In place of
![]() $X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
one can more generally consider
$X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
one can more generally consider
![]() $\unicode[STIX]{x1D6FA}\Subset \mathbb{C}^{N}\,\subset \,M$
a bounded symmetric domain in the Harish-Chandra realization
$\unicode[STIX]{x1D6FA}\Subset \mathbb{C}^{N}\,\subset \,M$
a bounded symmetric domain in the Harish-Chandra realization
![]() $\unicode[STIX]{x1D6FA}\Subset \mathbb{C}^{N}$
and in the Borel embedding
$\unicode[STIX]{x1D6FA}\Subset \mathbb{C}^{N}$
and in the Borel embedding
![]() $\unicode[STIX]{x1D6FA}\,\subset \,M$
into its dual Hermitian symmetric manifold
$\unicode[STIX]{x1D6FA}\,\subset \,M$
into its dual Hermitian symmetric manifold
![]() $M$
of the compact type,
$M$
of the compact type,
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\unicode[STIX]{x1D6FA})$
a torsion-free lattice, and in place of a totally geodesic complex submanifold one may consider
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\unicode[STIX]{x1D6FA})$
a torsion-free lattice, and in place of a totally geodesic complex submanifold one may consider
![]() $S\,\subset \,\unicode[STIX]{x1D6FA}$
an irreducible algebraic subset, by which we mean an irreducible component of
$S\,\subset \,\unicode[STIX]{x1D6FA}$
an irreducible algebraic subset, by which we mean an irreducible component of
![]() $V\cap \unicode[STIX]{x1D6FA}$
, where
$V\cap \unicode[STIX]{x1D6FA}$
, where
![]() $V\,\subset \,M$
is a projective subvariety,
$V\,\subset \,M$
is a projective subvariety,
![]() $\dim (S)>0$
. In recent years, the question of finding Zariski closures
$\dim (S)>0$
. In recent years, the question of finding Zariski closures
![]() $Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!$
was posed in the area of functional transcendence theory in the form of the hyperbolic Ax–Lindemann–Weierstrass conjecture, when
$Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!$
was posed in the area of functional transcendence theory in the form of the hyperbolic Ax–Lindemann–Weierstrass conjecture, when
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\unicode[STIX]{x1D6FA})$
is an arithmetic lattice. The conjecture was formulated by Pila [Reference PilaPil11] in relation to the André–Oort conjecture in number theory using the method of Pila and Zannier (cf. [Reference Pila and ZannierPZ08]), and it is one of the two components for an unconditional affirmative resolution of the latter conjecture. By means of the method of o-minimality from model theory in mathematical logic in combination with other methods, the hyperbolic Ax–Lindemann–Weierstrass conjecture was resolved in the affirmative in the cocompact and arithmetic case by Ullmo and Yafaev [Reference Ullmo and YafaevUY14], for the moduli space
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\unicode[STIX]{x1D6FA})$
is an arithmetic lattice. The conjecture was formulated by Pila [Reference PilaPil11] in relation to the André–Oort conjecture in number theory using the method of Pila and Zannier (cf. [Reference Pila and ZannierPZ08]), and it is one of the two components for an unconditional affirmative resolution of the latter conjecture. By means of the method of o-minimality from model theory in mathematical logic in combination with other methods, the hyperbolic Ax–Lindemann–Weierstrass conjecture was resolved in the affirmative in the cocompact and arithmetic case by Ullmo and Yafaev [Reference Ullmo and YafaevUY14], for the moduli space
![]() $X={\mathcal{A}}_{g}$
of principally polarized Abelian varieties by Pila and Tsimerman [Reference Pila and TsimermanPT14], and in the general arithmetic case by Klingler, Ullmo and Yafaev [Reference Klingler, Ullmo and YafaevKUY16]. All these proofs relied heavily on the arithmeticity of the lattices being considered.
$X={\mathcal{A}}_{g}$
of principally polarized Abelian varieties by Pila and Tsimerman [Reference Pila and TsimermanPT14], and in the general arithmetic case by Klingler, Ullmo and Yafaev [Reference Klingler, Ullmo and YafaevKUY16]. All these proofs relied heavily on the arithmeticity of the lattices being considered.
In relation to [Reference Mok and EbenfeltMok10], the author was led to consider the same problem in complex differential geometry for arbitrary lattices. When
![]() $\unicode[STIX]{x1D6FA}$
is irreducible, in view of the arithmeticity theorem of Margulis [Reference MargulisMar84] only the complex unit ball
$\unicode[STIX]{x1D6FA}$
is irreducible, in view of the arithmeticity theorem of Margulis [Reference MargulisMar84] only the complex unit ball
![]() $\mathbb{B}^{n}$
admits nonarithmetic finite-volume quotients. In this article we resolve in the affirmative the analogue of the hyperbolic Ax–Lindemann–Weierstrass conjecture in the rank-1 case for arbitrary lattices
$\mathbb{B}^{n}$
admits nonarithmetic finite-volume quotients. In this article we resolve in the affirmative the analogue of the hyperbolic Ax–Lindemann–Weierstrass conjecture in the rank-1 case for arbitrary lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
. It serves as a starting point for tackling the analogous problem and other related problems (e.g. the hyperbolic Ax–Schanuel conjecture) for arbitrary and possibly reducible lattices (cf. Remark after the proof of Lemma 4.1).
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
. It serves as a starting point for tackling the analogous problem and other related problems (e.g. the hyperbolic Ax–Schanuel conjecture) for arbitrary and possibly reducible lattices (cf. Remark after the proof of Lemma 4.1).
We consider the problem from a completely different perspective using methods of several complex variables, algebraic geometry and Kähler geometry. In the case where
![]() $S\,\subset \,\mathbb{B}^{n}$
is totally geodesic, it was proved by Mok [Reference Mok and EbenfeltMok10, Main Theorem] that the Zariski closure
$S\,\subset \,\mathbb{B}^{n}$
is totally geodesic, it was proved by Mok [Reference Mok and EbenfeltMok10, Main Theorem] that the Zariski closure
![]() $Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!$
is necessarily ‘uniruled’ by pieces of totally geodesic complex submanifolds, and a lifting
$Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!$
is necessarily ‘uniruled’ by pieces of totally geodesic complex submanifolds, and a lifting
![]() $\widetilde{Z}$
of
$\widetilde{Z}$
of
![]() $Z$
to
$Z$
to
![]() $\mathbb{B}^{n}$
was shown to be totally geodesic from its asymptotic geometric behavior as
$\mathbb{B}^{n}$
was shown to be totally geodesic from its asymptotic geometric behavior as
![]() $\widetilde{Z}$
exits
$\widetilde{Z}$
exits
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}$
. For an arbitrary irreducible algebraic subvariety
$\unicode[STIX]{x2202}\mathbb{B}^{n}$
. For an arbitrary irreducible algebraic subvariety
![]() $S\,\subset \,\mathbb{B}^{n}$
we make use of the universal family
$S\,\subset \,\mathbb{B}^{n}$
we make use of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
over an irreducible component
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
over an irreducible component
![]() ${\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
, the Chow space of
${\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
, the Chow space of
![]() $\mathbb{P}^{n}$
, to construct by restriction and by descent a locally homogeneous holomorphic fiber bundle of projective varieties
$\mathbb{P}^{n}$
, to construct by restriction and by descent a locally homogeneous holomorphic fiber bundle of projective varieties
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
equipped with a tautological meromorphic foliation
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
equipped with a tautological meromorphic foliation
![]() $\mathscr{F}$
. In the case of compact ball quotients, by embedding
$\mathscr{F}$
. In the case of compact ball quotients, by embedding
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of some locally homogeneous projective bundle
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of some locally homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, which is necessarily projective algebraic, we are led to the study of the foliation
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, which is necessarily projective algebraic, we are led to the study of the foliation
![]() $\mathscr{F}$
on the projective variety
$\mathscr{F}$
on the projective variety
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
For noncompact complex ball quotients
![]() $X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
we make use of the existence of the minimal compactification even in the nonarithmetic case by the works of Siu and Yau [Reference Siu, Yau and YauSY82], which were shown to be projective by Mok [Reference MokMok12a], and the methods of compactification of complete Kähler manifolds of finite volume of [Reference Mok and ZhongMZ89] applied to
$X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
we make use of the existence of the minimal compactification even in the nonarithmetic case by the works of Siu and Yau [Reference Siu, Yau and YauSY82], which were shown to be projective by Mok [Reference MokMok12a], and the methods of compactification of complete Kähler manifolds of finite volume of [Reference Mok and ZhongMZ89] applied to
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
to show that
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
to show that
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
and hence
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
and hence
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective, and to show that the tautological foliation obtained by descent from the universal family
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective, and to show that the tautological foliation obtained by descent from the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
extends meromorphically to a compactification
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
extends meromorphically to a compactification
![]() $\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}$
. To complete the proof of Main Theorem we introduce a rescaling argument for Kähler submanifolds exiting
$\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}$
. To complete the proof of Main Theorem we introduce a rescaling argument for Kähler submanifolds exiting
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}$
by means of a result of Klembeck [Reference KlembeckKle78] according to which a certain standard complete Kähler metric on a strictly pseudoconvex domain is asymptotically of constant holomorphic sectional curvature. As a by-product of our proof of Main Theorem for arbitrary lattices
$\unicode[STIX]{x2202}\mathbb{B}^{n}$
by means of a result of Klembeck [Reference KlembeckKle78] according to which a certain standard complete Kähler metric on a strictly pseudoconvex domain is asymptotically of constant holomorphic sectional curvature. As a by-product of our proof of Main Theorem for arbitrary lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
we show that the Zariski closure
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
we show that the Zariski closure
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
of
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
of
![]() $\unicode[STIX]{x1D70B}(S)$
is uniruled by subvarieties belonging to
$\unicode[STIX]{x1D70B}(S)$
is uniruled by subvarieties belonging to
![]() ${\mathcal{K}}$
(in the precise sense of Definition 3.1).
${\mathcal{K}}$
(in the precise sense of Definition 3.1).
After earlier works the author’s interest in further pursuing the analytic and geometric approach to functional transcendence theory was rekindled after discussions with Jacob Tsimerman in Spring 2016; it transpired that a combination of our approach from the perspective of complex geometry with works of Pila and Tsimerman on the hyperbolic Ax–Schanuel conjecture from the perspective of o-minimal geometry might shed light on the not necessarily arithmetic analogue of the latter conjecture. The Ax–Schanuel theorem for Shimura varieties has now been established by Mok, Pila and Tsimerman [Reference Mok, Pila and TsimermanMPT19].
1 Introduction, background materials and statement of the main theorem
Let
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice and denote by
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice and denote by
![]() $X:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold. When
$X:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold. When
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
is an arithmetic lattice, by Satake [Reference SatakeSat60] and Baily and Borel [Reference Baily and BorelBB66]
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
is an arithmetic lattice, by Satake [Reference SatakeSat60] and Baily and Borel [Reference Baily and BorelBB66]
![]() $X$
admits a minimal compactification
$X$
admits a minimal compactification
![]() $\overline{X}_{\text{min}}$
by adjoining a finite number of normal isolated singularities. In general
$\overline{X}_{\text{min}}$
by adjoining a finite number of normal isolated singularities. In general
![]() $X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
is of finite volume with respect to the canonical Kähler–Einstein metric, and by Siu and Yau [Reference Siu, Yau and YauSY82],
$X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
is of finite volume with respect to the canonical Kähler–Einstein metric, and by Siu and Yau [Reference Siu, Yau and YauSY82],
![]() $X$
admits a compactification
$X$
admits a compactification
![]() $X\,\subset \,\overline{X}_{\text{min}}$
by adding a finite number of normal isolated singularities, where
$X\,\subset \,\overline{X}_{\text{min}}$
by adding a finite number of normal isolated singularities, where
![]() $\overline{X}_{\text{min}}$
is exactly the minimal compactification of Satake, Baily and Borel in the arithmetic case. The methods of Siu and Yau [Reference Siu, Yau and YauSY82] are transcendental, and they apply to complete Kähler manifolds of finite volume and of pinched negative sectional curvature. When
$\overline{X}_{\text{min}}$
is exactly the minimal compactification of Satake, Baily and Borel in the arithmetic case. The methods of Siu and Yau [Reference Siu, Yau and YauSY82] are transcendental, and they apply to complete Kähler manifolds of finite volume and of pinched negative sectional curvature. When
![]() $X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, Mok [Reference MokMok12a] proved that
$X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, Mok [Reference MokMok12a] proved that
![]() $\overline{X}_{\text{min}}$
is projective. For finite-volume complex ball quotients, by [Reference SatakeSat60], [Reference Baily and BorelBB66], [Reference Siu, Yau and YauSY82] and [Reference MokMok12a] we have the following.
$\overline{X}_{\text{min}}$
is projective. For finite-volume complex ball quotients, by [Reference SatakeSat60], [Reference Baily and BorelBB66], [Reference Siu, Yau and YauSY82] and [Reference MokMok12a] we have the following.
Theorem 1.1. Let
![]() $n\geqslant 2$
and denote by
$n\geqslant 2$
and denote by
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
the complex unit ball equipped with the canonical Kähler–Einstein metric
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
the complex unit ball equipped with the canonical Kähler–Einstein metric
![]() $ds_{\mathbb{B}^{n}}^{2}$
. Let
$ds_{\mathbb{B}^{n}}^{2}$
. Let
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice. Denote by
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice. Denote by
![]() $X:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold, of finite volume with respect to the canonical Kähler–Einstein metric
$X:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold, of finite volume with respect to the canonical Kähler–Einstein metric
![]() $ds_{X}^{2}$
induced from
$ds_{X}^{2}$
induced from
![]() $ds_{\mathbb{B}^{n}}^{2}$
. Then, there exists a projective variety
$ds_{\mathbb{B}^{n}}^{2}$
. Then, there exists a projective variety
![]() $\overline{X}_{\text{min}}$
such that
$\overline{X}_{\text{min}}$
such that
![]() $X=\overline{X}_{\text{min}}-\{p_{1},\ldots ,p_{m}\}$
, where each
$X=\overline{X}_{\text{min}}-\{p_{1},\ldots ,p_{m}\}$
, where each
![]() $p_{i}$
,
$p_{i}$
,
![]() $1\leqslant i\leqslant m$
, is a normal isolated singularity of
$1\leqslant i\leqslant m$
, is a normal isolated singularity of
![]() $\overline{X}_{\text{min}}$
.
$\overline{X}_{\text{min}}$
.
Here and henceforth, without loss of generality we choose the canonical Kähler–Einstein metric so that
![]() $(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
and hence
$(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
and hence
![]() $(X,ds_{X}^{2})$
are of constant holomorphic sectional curvature
$(X,ds_{X}^{2})$
are of constant holomorphic sectional curvature
![]() $-2$
. From now on
$-2$
. From now on
![]() $X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
will be equipped with the quasi-projective structure inherited from the projective variety
$X=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
will be equipped with the quasi-projective structure inherited from the projective variety
![]() $\overline{X}_{\text{min}}$
. To emphasize the dependence on the lattice
$\overline{X}_{\text{min}}$
. To emphasize the dependence on the lattice
![]() $\unicode[STIX]{x1D6E4}$
we will now write
$\unicode[STIX]{x1D6E4}$
we will now write
![]() $X_{\unicode[STIX]{x1D6E4}}$
for
$X_{\unicode[STIX]{x1D6E4}}$
for
![]() $X$
, and
$X$
, and
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
for
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
for
![]() $\overline{X}_{\text{min}}$
. In [Reference Mok and EbenfeltMok10] we consider Zariski closures of totally geodesic complex submanifolds on
$\overline{X}_{\text{min}}$
. In [Reference Mok and EbenfeltMok10] we consider Zariski closures of totally geodesic complex submanifolds on
![]() $X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, and we have proved the following main result.
$X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, and we have proved the following main result.
Theorem 1.2 [Reference Mok and EbenfeltMok10, Main Theorem].
Let
![]() $X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
be a complex ball quotient of finite volume with respect to
$X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
be a complex ball quotient of finite volume with respect to
![]() $ds_{X}^{2}$
, as in Theorem 1.1, and denote by
$ds_{X}^{2}$
, as in Theorem 1.1, and denote by
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
the universal covering map. Let
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
the universal covering map. Let
![]() $S\,\subset \,\mathbb{B}^{n}$
be a totally geodesic complex submanifold in
$S\,\subset \,\mathbb{B}^{n}$
be a totally geodesic complex submanifold in
![]() $(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
. Then, the Zariski closure
$(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
. Then, the Zariski closure
![]() $Z$
of
$Z$
of
![]() $\unicode[STIX]{x1D70B}(S)$
in
$\unicode[STIX]{x1D70B}(S)$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
$X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
Denoting by
![]() $\widetilde{Z}$
an irreducible component of
$\widetilde{Z}$
an irreducible component of
![]() $\unicode[STIX]{x1D70B}^{-1}(Z)\,\subset \,\mathbb{B}^{n}$
, in the above
$\unicode[STIX]{x1D70B}^{-1}(Z)\,\subset \,\mathbb{B}^{n}$
, in the above
![]() $Z\,\subset \,X$
is said to be a totally geodesic subset if and only if
$Z\,\subset \,X$
is said to be a totally geodesic subset if and only if
![]() $\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
is a totally geodesic (complex) submanifold with respect to the canonical Kähler–Einstein metric.
$\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
is a totally geodesic (complex) submanifold with respect to the canonical Kähler–Einstein metric.
In the current article we prove the Ax–Lindemann–Weierstrass theorem for not necessarily arithmetic finite-volume quotients of
![]() $\mathbb{B}^{n}$
,
$\mathbb{B}^{n}$
,
![]() $n\geqslant 2$
. A subvariety
$n\geqslant 2$
. A subvariety
![]() $S\,\subset \,\mathbb{B}^{n}$
is said to be an irreducible algebraic subset if and only if it is an irreducible component of the intersection
$S\,\subset \,\mathbb{B}^{n}$
is said to be an irreducible algebraic subset if and only if it is an irreducible component of the intersection
![]() $V\cap \mathbb{B}^{n}$
for some (irreducible) projective subvariety
$V\cap \mathbb{B}^{n}$
for some (irreducible) projective subvariety
![]() $V\,\subset \,\mathbb{P}^{n}$
, and an algebraic subset
$V\,\subset \,\mathbb{P}^{n}$
, and an algebraic subset
![]() $S\,\subset \,\mathbb{B}^{n}$
is the union of a finite number of irreducible algebraic subsets. Note that a totally geodesic complex submanifold of
$S\,\subset \,\mathbb{B}^{n}$
is the union of a finite number of irreducible algebraic subsets. Note that a totally geodesic complex submanifold of
![]() $\mathbb{B}^{n}$
is precisely a nonempty intersection of the form
$\mathbb{B}^{n}$
is precisely a nonempty intersection of the form
![]() $V\cap \mathbb{B}^{n}$
, where
$V\cap \mathbb{B}^{n}$
, where
![]() $V\,\subset \,\mathbb{P}^{n}$
is a projective linear subspace of
$V\,\subset \,\mathbb{P}^{n}$
is a projective linear subspace of
![]() $\mathbb{P}^{n}$
. In this article we prove the following main result generalizing Theorem 1.2.
$\mathbb{P}^{n}$
. In this article we prove the following main result generalizing Theorem 1.2.
Main Theorem. Let
![]() $n\geqslant 2$
and denote by
$n\geqslant 2$
and denote by
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
the complex unit ball equipped with the canonical Kähler–Einstein metric
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
the complex unit ball equipped with the canonical Kähler–Einstein metric
![]() $ds_{\mathbb{B}^{n}}^{2}$
. Let
$ds_{\mathbb{B}^{n}}^{2}$
. Let
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice. Denote by
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
be a torsion-free lattice. Denote by
![]() $X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold, of finite volume with respect to the canonical Kähler–Einstein metric
$X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
the quotient manifold, of finite volume with respect to the canonical Kähler–Einstein metric
![]() $g_{\unicode[STIX]{x1D6E4}}:=ds_{X_{\unicode[STIX]{x1D6E4}}}^{2}$
induced from
$g_{\unicode[STIX]{x1D6E4}}:=ds_{X_{\unicode[STIX]{x1D6E4}}}^{2}$
induced from
![]() $ds_{\mathbb{B}^{n}}^{2}$
and equipped with the structure of a quasi-projective manifold from
$ds_{\mathbb{B}^{n}}^{2}$
and equipped with the structure of a quasi-projective manifold from
![]() $X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
. Let
$X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map and denote by
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map and denote by
![]() $S\,\subset \,\mathbb{B}^{n}$
an irreducible algebraic subset. Then, the Zariski closure
$S\,\subset \,\mathbb{B}^{n}$
an irreducible algebraic subset. Then, the Zariski closure
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
of
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
of
![]() $\unicode[STIX]{x1D70B}(S)$
in
$\unicode[STIX]{x1D70B}(S)$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
$X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
For the proof of Main Theorem we will consider the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
over some irreducible component
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
over some irreducible component
![]() ${\mathcal{K}}$
of the Chow space of
${\mathcal{K}}$
of the Chow space of
![]() $\mathbb{P}^{n}$
and obtain by restriction to
$\mathbb{P}^{n}$
and obtain by restriction to
![]() $\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
and by descent to
$\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
and by descent to
![]() $X_{\unicode[STIX]{x1D6E4}}$
a locally homogeneous holomorphic fiber bundle
$X_{\unicode[STIX]{x1D6E4}}$
a locally homogeneous holomorphic fiber bundle
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
equipped with a tautological foliation. The fibered space
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
equipped with a tautological foliation. The fibered space
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
will be embedded as a locally homogeneous fiber subbundle of projective varieties in a certain locally homogeneous projective bundle
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
will be embedded as a locally homogeneous fiber subbundle of projective varieties in a certain locally homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, which implies in the compact case that
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, which implies in the compact case that
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is projective. For the finite-volume and noncompact case we will need to embed the total space
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is projective. For the finite-volume and noncompact case we will need to embed the total space
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
onto a quasi-projective variety. For this purpose we will need the following compactification result of Mok and Zhong [Reference Mok and ZhongMZ89] from Kähler geometry.
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
onto a quasi-projective variety. For this purpose we will need the following compactification result of Mok and Zhong [Reference Mok and ZhongMZ89] from Kähler geometry.
Theorem 1.3 [Reference Mok and ZhongMZ89].
Let
![]() $(X,g)$
be a complete Kähler manifold of finite volume, bounded sectional curvature and finite topological type, and denote by
$(X,g)$
be a complete Kähler manifold of finite volume, bounded sectional curvature and finite topological type, and denote by
![]() $\unicode[STIX]{x1D714}$
the Kähler form of
$\unicode[STIX]{x1D714}$
the Kähler form of
![]() $(X,g)$
. Suppose there exists on
$(X,g)$
. Suppose there exists on
![]() $(X,g)$
a Hermitian holomorphic line bundle
$(X,g)$
a Hermitian holomorphic line bundle
![]() $(L,h)$
whose curvature form
$(L,h)$
whose curvature form
![]() $\unicode[STIX]{x1D6E9}(L,h)$
satisfies
$\unicode[STIX]{x1D6E9}(L,h)$
satisfies
![]() $a\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D6E9}(L,h)\leqslant b\unicode[STIX]{x1D714}$
for some real constants
$a\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D6E9}(L,h)\leqslant b\unicode[STIX]{x1D714}$
for some real constants
![]() $a,b>0$
. For an integer
$a,b>0$
. For an integer
![]() $k\geqslant 0$
and for a holomorphic section
$k\geqslant 0$
and for a holomorphic section
![]() $s\in \unicode[STIX]{x1D6E4}(X,L^{k})$
, we say that
$s\in \unicode[STIX]{x1D6E4}(X,L^{k})$
, we say that
![]() $s$
is of the Nevanlinna class if and only if
$s$
is of the Nevanlinna class if and only if
![]() $\,\log ^{+}\Vert s\Vert _{h^{k}}:=\text{max}(\log \Vert s\Vert _{h^{k}},0)$
is integrable on
$\,\log ^{+}\Vert s\Vert _{h^{k}}:=\text{max}(\log \Vert s\Vert _{h^{k}},0)$
is integrable on
![]() $X$
. Then, denoting by
$X$
. Then, denoting by
![]() ${\mathcal{N}}(X,L^{k})\,\subset \,\unicode[STIX]{x1D6E4}(X,L^{k})$
the vector subspace consisting of holomorphic sections of the Nevanlinna class, we have
${\mathcal{N}}(X,L^{k})\,\subset \,\unicode[STIX]{x1D6E4}(X,L^{k})$
the vector subspace consisting of holomorphic sections of the Nevanlinna class, we have
![]() $\dim ({\mathcal{N}}(X,L^{k}))<\infty$
. Furthermore, there exists some
$\dim ({\mathcal{N}}(X,L^{k}))<\infty$
. Furthermore, there exists some
![]() $\ell >0$
such that
$\ell >0$
such that
![]() ${\mathcal{N}}(X,L^{\ell })$
has no base points and defines a holomorphic embedding
${\mathcal{N}}(X,L^{\ell })$
has no base points and defines a holomorphic embedding
![]() $\unicode[STIX]{x1D6F7}_{\ell }:X{\hookrightarrow}\mathbb{P}({\mathcal{N}}(X,L^{\ell })^{\ast })$
onto a dense Zariski open subset of some projective variety. In particular,
$\unicode[STIX]{x1D6F7}_{\ell }:X{\hookrightarrow}\mathbb{P}({\mathcal{N}}(X,L^{\ell })^{\ast })$
onto a dense Zariski open subset of some projective variety. In particular,
![]() $X$
is biholomorphic to a quasi-projective manifold.
$X$
is biholomorphic to a quasi-projective manifold.
For the study of
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
we will need the following basic result on Chow spaces of
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
we will need the following basic result on Chow spaces of
![]() $\mathbb{P}^{n}$
from Chow and van der Waerden [Reference Chow and van der WaerdenCvdW37]. More details will be given in § 2.
$\mathbb{P}^{n}$
from Chow and van der Waerden [Reference Chow and van der WaerdenCvdW37]. More details will be given in § 2.
Theorem 1.4. On the projective space
![]() $\mathbb{P}^{n}$
, for an integer
$\mathbb{P}^{n}$
, for an integer
![]() $r$
,
$r$
,
![]() $0\leqslant r<n$
, and a positive integer
$0\leqslant r<n$
, and a positive integer
![]() $d$
, denote by
$d$
, denote by
![]() ${\mathcal{Q}}={\mathcal{Q}}(n,r,d)$
the set of pure
${\mathcal{Q}}={\mathcal{Q}}(n,r,d)$
the set of pure
![]() $r$
-dimensional cycles
$r$
-dimensional cycles
![]() $W$
on
$W$
on
![]() $\mathbb{P}^{n}$
of degree
$\mathbb{P}^{n}$
of degree
![]() $d$
. Then,
$d$
. Then,
![]() ${\mathcal{Q}}$
admits canonically the structure of a projective subvariety of some projective space
${\mathcal{Q}}$
admits canonically the structure of a projective subvariety of some projective space
![]() $\mathbb{P}^{s}$
, where
$\mathbb{P}^{s}$
, where
![]() $s=s(n,r,d)$
. Moreover,
$s=s(n,r,d)$
. Moreover,
![]() $\text{Aut}(\mathbb{P}^{n})\cong \mathbb{P}\text{GL}(n+1,\mathbb{C})$
acts canonically on
$\text{Aut}(\mathbb{P}^{n})\cong \mathbb{P}\text{GL}(n+1,\mathbb{C})$
acts canonically on
![]() $\mathbb{P}^{s}$
preserving the subset
$\mathbb{P}^{s}$
preserving the subset
![]() ${\mathcal{Q}}\,\subset \,\mathbb{P}^{s}$
. Furthermore, the subset
${\mathcal{Q}}\,\subset \,\mathbb{P}^{s}$
. Furthermore, the subset
![]() $\,{\mathcal{W}}:=\{w=([W],x)\in {\mathcal{Q}}\times \mathbb{P}^{n}:x\in W\}\,\subset \,{\mathcal{Q}}\times \mathbb{P}^{n}\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}$
is a projective subvariety invariant under the natural action of
$\,{\mathcal{W}}:=\{w=([W],x)\in {\mathcal{Q}}\times \mathbb{P}^{n}:x\in W\}\,\subset \,{\mathcal{Q}}\times \mathbb{P}^{n}\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}$
is a projective subvariety invariant under the natural action of
![]() $\,\text{Aut}(\mathbb{P}^{n})$
on
$\,\text{Aut}(\mathbb{P}^{n})$
on
![]() $\,\mathbb{P}^{s}\times \mathbb{P}^{n}$
.
$\,\mathbb{P}^{s}\times \mathbb{P}^{n}$
.
Here an element
![]() $[W]\in {\mathcal{Q}}$
denotes an
$[W]\in {\mathcal{Q}}$
denotes an
![]() $r$
-cycle on
$r$
-cycle on
![]() $\mathbb{P}^{n}$
, which is neither necessarily irreducible nor reduced. As an
$\mathbb{P}^{n}$
, which is neither necessarily irreducible nor reduced. As an
![]() $r$
-cycle
$r$
-cycle
![]() $[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
, where
$[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
, where
![]() $s\geqslant 1$
and
$s\geqslant 1$
and
![]() $W_{i},1\leqslant i\leqslant s$
, are reduced and irreducible
$W_{i},1\leqslant i\leqslant s$
, are reduced and irreducible
![]() $r$
-dimensional subvarieties of
$r$
-dimensional subvarieties of
![]() $\mathbb{P}^{n}$
.
$\mathbb{P}^{n}$
.
In the proof of Main Theorem we will study pre-images of Zariski closures of the image of an algebraic subset on
![]() $\mathbb{B}^{n}$
under the universal covering map, for which we will need the following result of Klembeck [Reference KlembeckKle78] on the asymptotic behavior of complete Kähler metrics on strictly pseudoconvex domains.
$\mathbb{B}^{n}$
under the universal covering map, for which we will need the following result of Klembeck [Reference KlembeckKle78] on the asymptotic behavior of complete Kähler metrics on strictly pseudoconvex domains.
Theorem 1.5 (Klembeck [Reference KlembeckKle78]).
Let
![]() $U\,\subset \,\mathbb{C}^{n}$
be a domain,
$U\,\subset \,\mathbb{C}^{n}$
be a domain,
![]() $\unicode[STIX]{x1D70C}$
be a smooth real function on
$\unicode[STIX]{x1D70C}$
be a smooth real function on
![]() $U$
and
$U$
and
![]() $b$
be a point on
$b$
be a point on
![]() $U$
. Suppose
$U$
. Suppose
![]() $\unicode[STIX]{x1D70C}(b)=0$
and
$\unicode[STIX]{x1D70C}(b)=0$
and
![]() $d\unicode[STIX]{x1D70C}(x)\neq 0$
for any
$d\unicode[STIX]{x1D70C}(x)\neq 0$
for any
![]() $x\in U$
, and assume that
$x\in U$
, and assume that
![]() $\unicode[STIX]{x1D70C}$
is strictly plurisubharmonic on
$\unicode[STIX]{x1D70C}$
is strictly plurisubharmonic on
![]() $U$
, i.e.,
$U$
, i.e.,
![]() $\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D70C}>0$
on
$\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D70C}>0$
on
![]() $U$
. Let
$U$
. Let
![]() $U^{\prime }\,\subset \,U$
be the open subset defined by
$U^{\prime }\,\subset \,U$
be the open subset defined by
![]() $\unicode[STIX]{x1D70C}<0$
, and
$\unicode[STIX]{x1D70C}<0$
, and
![]() $s$
be the Kähler metric on
$s$
be the Kähler metric on
![]() $U^{\prime }$
with Kähler form given by
$U^{\prime }$
with Kähler form given by
![]() $\unicode[STIX]{x1D714}_{s}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\text{log}\,(-\unicode[STIX]{x1D70C}))$
. Then,
$\unicode[STIX]{x1D714}_{s}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\text{log}\,(-\unicode[STIX]{x1D70C}))$
. Then,
![]() $(U^{\prime },s)$
is asymptotically of constant holomorphic sectional curvature
$(U^{\prime },s)$
is asymptotically of constant holomorphic sectional curvature
![]() $-2$
at
$-2$
at
![]() $b$
, i.e., defining
$b$
, i.e., defining
![]() $\unicode[STIX]{x1D716}(x)\geqslant 0$
at
$\unicode[STIX]{x1D716}(x)\geqslant 0$
at
![]() $x\in U^{\prime }$
to be the smallest nonnegative number such that holomorphic sectional curvatures of
$x\in U^{\prime }$
to be the smallest nonnegative number such that holomorphic sectional curvatures of
![]() $(U^{\prime },s)$
at
$(U^{\prime },s)$
at
![]() $x$
are bounded between
$x$
are bounded between
![]() $-2-\unicode[STIX]{x1D716}(x)$
and
$-2-\unicode[STIX]{x1D716}(x)$
and
![]() $-2+\unicode[STIX]{x1D716}(x)$
, then
$-2+\unicode[STIX]{x1D716}(x)$
, then
![]() $\unicode[STIX]{x1D716}(x)\rightarrow 0$
as
$\unicode[STIX]{x1D716}(x)\rightarrow 0$
as
![]() $x\in U^{\prime }$
approaches
$x\in U^{\prime }$
approaches
![]() $b\in \unicode[STIX]{x2202}U^{\prime }\cap U$
.
$b\in \unicode[STIX]{x2202}U^{\prime }\cap U$
.
2 Construction of locally homogeneous projective fiber subbundles of projective bundles
Consider the standard inclusions
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. Let
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. Let
![]() $W_{0}\,\subset \,\mathbb{P}^{n}$
be an irreducible subvariety and
$W_{0}\,\subset \,\mathbb{P}^{n}$
be an irreducible subvariety and
![]() $S$
be an irreducible component of
$S$
be an irreducible component of
![]() $W_{0}\cap \mathbb{B}^{n}$
. Let
$W_{0}\cap \mathbb{B}^{n}$
. Let
![]() ${\mathcal{K}}$
be an irreducible component of the Chow space of
${\mathcal{K}}$
be an irreducible component of the Chow space of
![]() $\mathbb{P}^{n}$
to which the reduced cycle
$\mathbb{P}^{n}$
to which the reduced cycle
![]() $W_{0}$
belongs, written
$W_{0}$
belongs, written
![]() $[W_{0}]\in {\mathcal{K}}$
. The algebraic group
$[W_{0}]\in {\mathcal{K}}$
. The algebraic group
![]() $\text{Aut}(\mathbb{P}^{n})=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
acts on
$\text{Aut}(\mathbb{P}^{n})=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
acts on
![]() ${\mathcal{K}}$
naturally. Let
${\mathcal{K}}$
naturally. Let
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
be the universal family associated to
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
be the universal family associated to
![]() ${\mathcal{K}}$
, i.e.,
${\mathcal{K}}$
, i.e.,
![]() $\mathscr{U}=\{([W],x)\in {\mathcal{K}}\times \mathbb{P}^{n}:x\in W\}\,\subset \,{\mathcal{K}}\times \mathbb{P}^{n}$
, and
$\mathscr{U}=\{([W],x)\in {\mathcal{K}}\times \mathbb{P}^{n}:x\in W\}\,\subset \,{\mathcal{K}}\times \mathbb{P}^{n}$
, and
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
is induced from the canonical projection from
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
is induced from the canonical projection from
![]() ${\mathcal{K}}\times \mathbb{P}^{n}$
onto the first factor. For
${\mathcal{K}}\times \mathbb{P}^{n}$
onto the first factor. For
![]() $[W]\in {\mathcal{K}}$
we have
$[W]\in {\mathcal{K}}$
we have
![]() $[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
where
$[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
where
![]() $s=s(W)\geqslant 1$
and
$s=s(W)\geqslant 1$
and
![]() $W_{i},1\leqslant i\leqslant s$
are the reductions of the irreducible components of the pure
$W_{i},1\leqslant i\leqslant s$
are the reductions of the irreducible components of the pure
![]() $r$
-dimensional complex space
$r$
-dimensional complex space
![]() $W\,\subset \,\mathbb{P}^{n}$
. From the definition of
$W\,\subset \,\mathbb{P}^{n}$
. From the definition of
![]() ${\mathcal{K}}$
a general member
${\mathcal{K}}$
a general member
![]() $[W]\in {\mathcal{K}}$
is irreducible and reduced, i.e.,
$[W]\in {\mathcal{K}}$
is irreducible and reduced, i.e.,
![]() $s=1$
and
$s=1$
and
![]() $k_{1}=1$
. The canonical projection from
$k_{1}=1$
. The canonical projection from
![]() ${\mathcal{K}}\times \mathbb{P}^{n}$
to
${\mathcal{K}}\times \mathbb{P}^{n}$
to
![]() $\mathbb{P}^{n}$
restricted to
$\mathbb{P}^{n}$
restricted to
![]() $\mathscr{U}$
gives
$\mathscr{U}$
gives
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
, called the evaluation map of the universal family
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
, called the evaluation map of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, which realizes
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, which realizes
![]() $\mathscr{U}$
as the total space of a homogeneous holomorphic fiber bundle (with respect to Aut
$\mathscr{U}$
as the total space of a homogeneous holomorphic fiber bundle (with respect to Aut
![]() $(\mathbb{P}^{n})$
) with fibers isomorphic to
$(\mathbb{P}^{n})$
) with fibers isomorphic to
![]() $\mathscr{U}_{0}:=\unicode[STIX]{x1D707}^{-1}(0)$
. Hence, the map
$\mathscr{U}_{0}:=\unicode[STIX]{x1D707}^{-1}(0)$
. Hence, the map
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
is a holomorphic fibration with equidimensional fibers
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
is a holomorphic fibration with equidimensional fibers
![]() $\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D705})$
,
$\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D705})$
,
![]() $\unicode[STIX]{x1D705}=[W]$
. Each fiber
$\unicode[STIX]{x1D705}=[W]$
. Each fiber
![]() $\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D705})$
projects via the evaluation map
$\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D705})$
projects via the evaluation map
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
onto the support Supp
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
onto the support Supp
![]() $(W)=W_{1}\,\cup \,\cdots \,\cup \,W_{s}\,\subset \,\mathbb{P}^{n}$
of the cycles
$(W)=W_{1}\,\cup \,\cdots \,\cup \,W_{s}\,\subset \,\mathbb{P}^{n}$
of the cycles
![]() $W\,\subset \,\mathbb{P}^{n}$
belonging to
$W\,\subset \,\mathbb{P}^{n}$
belonging to
![]() ${\mathcal{K}}$
. (We will henceforth make no notational distinction between
${\mathcal{K}}$
. (We will henceforth make no notational distinction between
![]() $W$
and its support.) The holomorphic fibration
$W$
and its support.) The holomorphic fibration
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
defines naturally a foliation
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
defines naturally a foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $\mathscr{U}$
such that, at a smooth point
$\mathscr{U}$
such that, at a smooth point
![]() $u\in \mathscr{U}$
where
$u\in \mathscr{U}$
where
![]() $\unicode[STIX]{x1D70C}$
is a submersion,
$\unicode[STIX]{x1D70C}$
is a submersion,
![]() $\unicode[STIX]{x1D70C}(u)=:[W]\in {\mathcal{K}}$
, the germ of leaf of
$\unicode[STIX]{x1D70C}(u)=:[W]\in {\mathcal{K}}$
, the germ of leaf of
![]() $\mathscr{F}$
passing through
$\mathscr{F}$
passing through
![]() $u$
is just the germ of
$u$
is just the germ of
![]() $\widehat{W}:=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(u))$
at
$\widehat{W}:=\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(u))$
at
![]() $u$
,
$u$
,
![]() $\widehat{W}$
being the tautological lifting of
$\widehat{W}$
being the tautological lifting of
![]() $W$
to
$W$
to
![]() $\mathscr{U}$
. We have
$\mathscr{U}$
. We have
![]() $W=\unicode[STIX]{x1D707}(\widehat{W})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(u)))$
.
$W=\unicode[STIX]{x1D707}(\widehat{W})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(u)))$
.
Write
![]() $\mathscr{U}^{\prime }:=\mathscr{U}|_{\mathbb{B}^{n}}$
. The algebraic group
$\mathscr{U}^{\prime }:=\mathscr{U}|_{\mathbb{B}^{n}}$
. The algebraic group
![]() $\text{Aut}(\mathbb{P}^{n})$
acts on
$\text{Aut}(\mathbb{P}^{n})$
acts on
![]() $\mathscr{U}^{\prime }$
, hence the holomorphic fiber bundle
$\mathscr{U}^{\prime }$
, hence the holomorphic fiber bundle
![]() $\unicode[STIX]{x1D707}^{\prime }:\mathscr{U}^{\prime }\rightarrow \mathbb{B}^{n}$
is homogeneous under Aut
$\unicode[STIX]{x1D707}^{\prime }:\mathscr{U}^{\prime }\rightarrow \mathbb{B}^{n}$
is homogeneous under Aut
![]() $(\mathbb{B}^{n})$
, and it descends under the action of a torsion-free discrete subgroup
$(\mathbb{B}^{n})$
, and it descends under the action of a torsion-free discrete subgroup
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
to
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
to
![]() $X_{\unicode[STIX]{x1D6E4}}$
to give a complex space
$X_{\unicode[STIX]{x1D6E4}}$
to give a complex space
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}:=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}$
equipped with the evaluation map
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}:=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}$
equipped with the evaluation map
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, realizing the latter as a locally homogeneous holomorphic fiber bundle with fibers isomorphic to
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, realizing the latter as a locally homogeneous holomorphic fiber bundle with fibers isomorphic to
![]() $\mathscr{U}_{0}$
. The fiber bundle
$\mathscr{U}_{0}$
. The fiber bundle
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
will be our major object of study. In the case where
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
will be our major object of study. In the case where
![]() $X_{\unicode[STIX]{x1D6E4}}$
is compact, we will show that
$X_{\unicode[STIX]{x1D6E4}}$
is compact, we will show that
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is a projective variety by embedding
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
is a projective variety by embedding
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into some projective bundle
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into some projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. (Projective bundles are understood to be holomorphic.) By the Kodaira embedding theorem, we have the following well-known result on projective bundles.
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. (Projective bundles are understood to be holomorphic.) By the Kodaira embedding theorem, we have the following well-known result on projective bundles.
Proposition 2.1. Let
![]() $Z$
be a projective manifold and
$Z$
be a projective manifold and
![]() $A$
be an ample line bundle on
$A$
be an ample line bundle on
![]() $Z$
, and let
$Z$
, and let
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow Z$
be a projective bundle over
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow Z$
be a projective bundle over
![]() $Z$
. Denote by
$Z$
. Denote by
![]() $T_{\unicode[STIX]{x1D71B}}$
the relative tangent bundle of
$T_{\unicode[STIX]{x1D71B}}$
the relative tangent bundle of
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow Z$
. Then, for a sufficiently large integer
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow Z$
. Then, for a sufficiently large integer
![]() $k$
, the holomorphic line bundle
$k$
, the holomorphic line bundle
![]() $\text{det}(T_{\unicode[STIX]{x1D71B}})\otimes \unicode[STIX]{x1D71B}^{\ast }A^{k}$
is ample on
$\text{det}(T_{\unicode[STIX]{x1D71B}})\otimes \unicode[STIX]{x1D71B}^{\ast }A^{k}$
is ample on
![]() $\mathscr{P}$
. As a consequence,
$\mathscr{P}$
. As a consequence,
![]() $\mathscr{P}$
is a projective manifold.
$\mathscr{P}$
is a projective manifold.
We proceed to construct a projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
which admits
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
which admits
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
naturally as an embedded complex subspace. In what follows we denote by
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
naturally as an embedded complex subspace. In what follows we denote by
![]() $G:=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
the automorphism group of
$G:=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
the automorphism group of
![]() $\mathbb{P}^{n}$
, by
$\mathbb{P}^{n}$
, by
![]() $G_{0}:=\mathbb{P}U(n,1)\,\subset \,G$
the automorphism group of
$G_{0}:=\mathbb{P}U(n,1)\,\subset \,G$
the automorphism group of
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
, and by
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
, and by
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
a torsion-free lattice. We write
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
a torsion-free lattice. We write
![]() $P\,\subset \,G$
for the parabolic subgroup at
$P\,\subset \,G$
for the parabolic subgroup at
![]() $0\in \mathbb{P}^{n}$
, and
$0\in \mathbb{P}^{n}$
, and
![]() $K\,\subset \,G_{0}$
for the isotropy subgroup of
$K\,\subset \,G_{0}$
for the isotropy subgroup of
![]() $(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
at
$(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
at
![]() $0\in \mathbb{B}^{n}$
. Lie algebras of real or complex Lie groups will be denoted by corresponding fraktur characters, so that
$0\in \mathbb{B}^{n}$
. Lie algebras of real or complex Lie groups will be denoted by corresponding fraktur characters, so that
![]() $\mathfrak{g}$
stands for the Lie algebra of the complex Lie group
$\mathfrak{g}$
stands for the Lie algebra of the complex Lie group
![]() $G$
, and
$G$
, and
![]() $\mathfrak{g}_{0}$
for the Lie algebra of the real Lie group
$\mathfrak{g}_{0}$
for the Lie algebra of the real Lie group
![]() $G_{0}$
, etc. On the complex unit ball
$G_{0}$
, etc. On the complex unit ball
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
,
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
,
![]() $K=U(n)$
acts as a compact group of linear transformations on
$K=U(n)$
acts as a compact group of linear transformations on
![]() $\mathbb{C}^{n}$
extending to projective linear transformations on
$\mathbb{C}^{n}$
extending to projective linear transformations on
![]() $\mathbb{P}^{n}$
, and we denote by
$\mathbb{P}^{n}$
, and we denote by
![]() $K^{\mathbb{C}}$
its complexification, i.e.,
$K^{\mathbb{C}}$
its complexification, i.e.,
![]() $K^{\mathbb{C}}=\text{GL}(n,\mathbb{C})$
, preserving
$K^{\mathbb{C}}=\text{GL}(n,\mathbb{C})$
, preserving
![]() $\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
and acting as a group of automorphisms of
$\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
and acting as a group of automorphisms of
![]() $\mathbb{P}^{n}$
which restricts to
$\mathbb{P}^{n}$
which restricts to
![]() $\mathbb{C}^{n}$
to give the usual action of
$\mathbb{C}^{n}$
to give the usual action of
![]() $\text{GL}(n,\mathbb{C})$
on
$\text{GL}(n,\mathbb{C})$
on
![]() $\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. The complex Lie algebra
$\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. The complex Lie algebra
![]() $\mathfrak{g}$
, considered as the Lie algebra of holomorphic vector fields on
$\mathfrak{g}$
, considered as the Lie algebra of holomorphic vector fields on
![]() $\mathbb{P}^{n}$
, admits the Harish-Chandra decomposition
$\mathbb{P}^{n}$
, admits the Harish-Chandra decomposition
![]() $\mathfrak{g}=\mathfrak{m}^{+}\oplus \,\mathfrak{k}^{\mathbb{C}}\oplus \,\mathfrak{m}^{-}$
, where
$\mathfrak{g}=\mathfrak{m}^{+}\oplus \,\mathfrak{k}^{\mathbb{C}}\oplus \,\mathfrak{m}^{-}$
, where
![]() $\mathfrak{k}^{\mathbb{C}}=\mathfrak{k}\,\otimes _{\mathbb{R}}\mathbb{C}$
is the complexification of
$\mathfrak{k}^{\mathbb{C}}=\mathfrak{k}\,\otimes _{\mathbb{R}}\mathbb{C}$
is the complexification of
![]() $\mathfrak{k}$
, equivalently the Lie algebra of
$\mathfrak{k}$
, equivalently the Lie algebra of
![]() $K^{\mathbb{C}}$
,
$K^{\mathbb{C}}$
,
![]() $\mathfrak{m}^{-}\,\subset \,\mathfrak{g}$
is the Abelian Lie subalgebra consisting of holomorphic vector fields on
$\mathfrak{m}^{-}\,\subset \,\mathfrak{g}$
is the Abelian Lie subalgebra consisting of holomorphic vector fields on
![]() $\mathbb{P}^{n}$
vanishing to the order
$\mathbb{P}^{n}$
vanishing to the order
![]() ${\geqslant}2$
at
${\geqslant}2$
at
![]() $0\in \mathbb{P}^{n}$
, and
$0\in \mathbb{P}^{n}$
, and
![]() $\mathfrak{m}^{+}\,\subset \,\mathfrak{g}$
is the Abelian Lie subalgebra whose elements restrict to constant vector fields on
$\mathfrak{m}^{+}\,\subset \,\mathfrak{g}$
is the Abelian Lie subalgebra whose elements restrict to constant vector fields on
![]() $\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. The vector subspace
$\mathbb{C}^{n}\,\subset \,\mathbb{P}^{n}$
. The vector subspace
![]() $\mathfrak{p}:=\mathfrak{k}^{\mathbb{C}}\oplus \mathfrak{m}^{-}\,\subset \,\mathfrak{g}$
is the parabolic subalgebra at
$\mathfrak{p}:=\mathfrak{k}^{\mathbb{C}}\oplus \mathfrak{m}^{-}\,\subset \,\mathfrak{g}$
is the parabolic subalgebra at
![]() $0\in \mathbb{P}^{n}$
. Writing
$0\in \mathbb{P}^{n}$
. Writing
![]() $M^{+}=\exp (\mathfrak{m}^{+})$
and
$M^{+}=\exp (\mathfrak{m}^{+})$
and
![]() $M^{-}=\exp (\mathfrak{m}^{-})$
, the mapping
$M^{-}=\exp (\mathfrak{m}^{-})$
, the mapping
![]() $\unicode[STIX]{x1D706}:M^{+}\times K^{\mathbb{C}}\times M^{-}\rightarrow G$
defined by
$\unicode[STIX]{x1D706}:M^{+}\times K^{\mathbb{C}}\times M^{-}\rightarrow G$
defined by
![]() $\unicode[STIX]{x1D706}(m^{+},k,m^{-})=m^{+}km^{-}\in G$
maps
$\unicode[STIX]{x1D706}(m^{+},k,m^{-})=m^{+}km^{-}\in G$
maps
![]() $M^{+}\times K^{\mathbb{C}}\times M^{-}$
biholomorphically onto a dense open subset of
$M^{+}\times K^{\mathbb{C}}\times M^{-}$
biholomorphically onto a dense open subset of
![]() $G$
. We note that
$G$
. We note that
![]() $K^{\mathbb{C}}M^{-}=P$
is a Levi decomposition of
$K^{\mathbb{C}}M^{-}=P$
is a Levi decomposition of
![]() $P\,\subset \,G$
, with
$P\,\subset \,G$
, with
![]() $K^{\mathbb{C}}\,\subset \,P$
being a Levi factor. By means of
$K^{\mathbb{C}}\,\subset \,P$
being a Levi factor. By means of
![]() $\unicode[STIX]{x1D706}$
, and writing
$\unicode[STIX]{x1D706}$
, and writing
![]() $e\in G$
for the identity element, the orbit of
$e\in G$
for the identity element, the orbit of
![]() $0=eP\in G/P$
under
$0=eP\in G/P$
under
![]() $M^{+}$
is identified with
$M^{+}$
is identified with
![]() $M^{+}\cong \mathbb{C}^{n}$
, from which the Harish-Chandra realization
$M^{+}\cong \mathbb{C}^{n}$
, from which the Harish-Chandra realization
![]() $\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
arises as the obvious projection of
$\mathbb{B}^{n}\Subset \mathbb{C}^{n}$
arises as the obvious projection of
![]() $\unicode[STIX]{x1D706}^{-1}(G_{0})$
into
$\unicode[STIX]{x1D706}^{-1}(G_{0})$
into
![]() $M^{+}\cong \mathbb{C}^{n}$
. The description above applies in general to bounded symmetric domains, cf. Wolf [Reference WolfWol72] and Mok [Reference MokMok89].
$M^{+}\cong \mathbb{C}^{n}$
. The description above applies in general to bounded symmetric domains, cf. Wolf [Reference WolfWol72] and Mok [Reference MokMok89].
Let
![]() $E$
be a finite-dimensional complex vector space, and
$E$
be a finite-dimensional complex vector space, and
![]() $\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
be a projective linear representation. Introduce an equivalence relation
$\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
be a projective linear representation. Introduce an equivalence relation
![]() ${\sim}$
on
${\sim}$
on
![]() $G\times \mathbb{P}(E)$
by declaring
$G\times \mathbb{P}(E)$
by declaring
![]() $(g,e)\sim (g^{\prime },e^{\prime })$
;
$(g,e)\sim (g^{\prime },e^{\prime })$
;
![]() $g,g^{\prime }\in G$
,
$g,g^{\prime }\in G$
,
![]() $e,e^{\prime }\in E$
; if and only if there exists
$e,e^{\prime }\in E$
; if and only if there exists
![]() $p\in P$
such that
$p\in P$
such that
![]() $g^{\prime }=gp^{-1}$
and
$g^{\prime }=gp^{-1}$
and
![]() $e^{\prime }=pe$
, where
$e^{\prime }=pe$
, where
![]() $pe$
means
$pe$
means
![]() $\unicode[STIX]{x1D6F7}(p)e$
, and define
$\unicode[STIX]{x1D6F7}(p)e$
, and define
![]() $G\times _{P}\mathbb{P}(E)=(G\times \mathbb{P}(E))/\sim$
. Denote by
$G\times _{P}\mathbb{P}(E)=(G\times \mathbb{P}(E))/\sim$
. Denote by
![]() $[g,e]$
the equivalence class of
$[g,e]$
the equivalence class of
![]() $(g,e)$
with respect to
$(g,e)$
with respect to
![]() ${\sim}$
. The natural map
${\sim}$
. The natural map
![]() $\unicode[STIX]{x1D70F}:G\times _{P}\mathbb{P}(E)\rightarrow G/P$
defined by
$\unicode[STIX]{x1D70F}:G\times _{P}\mathbb{P}(E)\rightarrow G/P$
defined by
![]() $\unicode[STIX]{x1D70F}([g,e])=gP$
realizes
$\unicode[STIX]{x1D70F}([g,e])=gP$
realizes
![]() $G\times _{P}\mathbb{P}(E)$
as the total space of a projective bundle
$G\times _{P}\mathbb{P}(E)$
as the total space of a projective bundle
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow G/P=\mathbb{P}^{n}$
. Left multiplication on
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow G/P=\mathbb{P}^{n}$
. Left multiplication on
![]() $G$
induces a holomorphic action of
$G$
induces a holomorphic action of
![]() $G$
on
$G$
on
![]() $\mathscr{P}$
compatible with the natural transitive holomorphic action of
$\mathscr{P}$
compatible with the natural transitive holomorphic action of
![]() $G$
on
$G$
on
![]() $G/P=\mathbb{P}^{n}$
. By a homogeneous projective bundle on
$G/P=\mathbb{P}^{n}$
. By a homogeneous projective bundle on
![]() $\mathbb{P}^{n}$
we will always mean
$\mathbb{P}^{n}$
we will always mean
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
arising this way. We have
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
arising this way. We have
![]() $K=P\cap G_{0}$
. Defining
$K=P\cap G_{0}$
. Defining
![]() $G_{0}\times _{K}\mathbb{P}(E)$
analogously we have on
$G_{0}\times _{K}\mathbb{P}(E)$
analogously we have on
![]() $G_{0}\times _{K}\mathbb{P}(E)$
the structure of a smooth projective bundle
$G_{0}\times _{K}\mathbb{P}(E)$
the structure of a smooth projective bundle
![]() $\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }\rightarrow G_{0}/K=\mathbb{B}^{n}$
. The latter is a priori only a smooth projective bundle since
$\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }\rightarrow G_{0}/K=\mathbb{B}^{n}$
. The latter is a priori only a smooth projective bundle since
![]() $K$
is a real Lie group, but embedding
$K$
is a real Lie group, but embedding
![]() $G_{0}\times _{K}\mathbb{P}(E)$
canonically into
$G_{0}\times _{K}\mathbb{P}(E)$
canonically into
![]() $G\times _{P}\mathbb{P}(E)$
one identifies
$G\times _{P}\mathbb{P}(E)$
one identifies
![]() $G_{0}\times _{K}\mathbb{P}(E)$
as an open subset of
$G_{0}\times _{K}\mathbb{P}(E)$
as an open subset of
![]() $G\times _{P}\mathbb{P}(E)$
, and hence
$G\times _{P}\mathbb{P}(E)$
, and hence
![]() $\mathscr{P}^{\prime }$
as the restriction of
$\mathscr{P}^{\prime }$
as the restriction of
![]() $\mathscr{P}$
over
$\mathscr{P}$
over
![]() $\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
, so that
$\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
, so that
![]() $\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
inherits the structure of a (holomorphic) projective bundle over
$\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
inherits the structure of a (holomorphic) projective bundle over
![]() $\mathbb{B}^{n}$
. From now on we will identify
$\mathbb{B}^{n}$
. From now on we will identify
![]() $\mathscr{P}^{\prime }$
with
$\mathscr{P}^{\prime }$
with
![]() $\mathscr{P}|_{\mathbb{B}^{n}}$
. The fiber of
$\mathscr{P}|_{\mathbb{B}^{n}}$
. The fiber of
![]() $\mathscr{P}$
over a point
$\mathscr{P}$
over a point
![]() $x\in \mathbb{P}^{n}$
will be denoted by
$x\in \mathbb{P}^{n}$
will be denoted by
![]() $\mathscr{P}_{x}$
.
$\mathscr{P}_{x}$
.
Let
![]() $\unicode[STIX]{x1D708}:{\mathcal{E}}\rightarrow M$
be a locally trivial holomorphic fiber bundle over a complex manifold
$\unicode[STIX]{x1D708}:{\mathcal{E}}\rightarrow M$
be a locally trivial holomorphic fiber bundle over a complex manifold
![]() $M$
. By a locally trivial holomorphic fiber subbundle
$M$
. By a locally trivial holomorphic fiber subbundle
![]() ${\mathcal{E}}^{\prime }\,\subset \,{\mathcal{E}}$
we mean a subvariety
${\mathcal{E}}^{\prime }\,\subset \,{\mathcal{E}}$
we mean a subvariety
![]() ${\mathcal{E}}^{\prime }\,\subset \,{\mathcal{E}}$
such that, writing
${\mathcal{E}}^{\prime }\,\subset \,{\mathcal{E}}$
such that, writing
![]() ${\mathcal{E}}_{0}^{\prime }:={\mathcal{E}}_{0}\cap {\mathcal{E}}^{\prime }$
, and shrinking the neighborhoods
${\mathcal{E}}_{0}^{\prime }:={\mathcal{E}}_{0}\cap {\mathcal{E}}^{\prime }$
, and shrinking the neighborhoods
![]() $U$
if necessary, the trivializations
$U$
if necessary, the trivializations
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D708}^{-1}(U)\overset{\cong }{\longrightarrow }{\mathcal{E}}_{0}\times U$
can be chosen such that
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D708}^{-1}(U)\overset{\cong }{\longrightarrow }{\mathcal{E}}_{0}\times U$
can be chosen such that
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D708}^{-1}(U)\cap {\mathcal{E}}^{\prime })={\mathcal{E}}_{0}^{\prime }\times U\,\subset \,{\mathcal{E}}_{0}\times U$
, endowed with the canonical projection map
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D708}^{-1}(U)\cap {\mathcal{E}}^{\prime })={\mathcal{E}}_{0}^{\prime }\times U\,\subset \,{\mathcal{E}}_{0}\times U$
, endowed with the canonical projection map
![]() $\unicode[STIX]{x1D708}^{\prime }:{\mathcal{E}}^{\prime }\rightarrow M$
given by
$\unicode[STIX]{x1D708}^{\prime }:{\mathcal{E}}^{\prime }\rightarrow M$
given by
![]() $\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}|_{{\mathcal{E}}^{\prime }}$
. The adjective ‘locally trivial’ will be understood and omitted in what follows. For
$\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}|_{{\mathcal{E}}^{\prime }}$
. The adjective ‘locally trivial’ will be understood and omitted in what follows. For
![]() $M=X_{\unicode[STIX]{x1D6E4}}$
a holomorphic fiber (sub)bundle is said to be locally homogeneous if it descends from a homogeneous holomorphic fiber (sub)bundle on
$M=X_{\unicode[STIX]{x1D6E4}}$
a holomorphic fiber (sub)bundle is said to be locally homogeneous if it descends from a homogeneous holomorphic fiber (sub)bundle on
![]() $\mathbb{B}^{n}$
under the action of
$\mathbb{B}^{n}$
under the action of
![]() $G_{0}$
.
$G_{0}$
.
In order to embed
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into a projective bundle we will embed
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into a projective bundle we will embed
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
into a projective bundle
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
into a projective bundle
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
in such a way that
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
in such a way that
![]() $G$
acts canonically on
$G$
acts canonically on
![]() $\mathscr{P}$
. For this we need some basic facts about Chow
$\mathscr{P}$
. For this we need some basic facts about Chow
![]() $(\mathbb{P}^{n})$
. This is provided by the Chow coordinates (Chow and van der Waerden [Reference Chow and van der WaerdenCvdW37]). Fix an integer
$(\mathbb{P}^{n})$
. This is provided by the Chow coordinates (Chow and van der Waerden [Reference Chow and van der WaerdenCvdW37]). Fix an integer
![]() $r$
,
$r$
,
![]() $0<r<n$
, and an integer
$0<r<n$
, and an integer
![]() $d>0$
. For an irreducible and reduced
$d>0$
. For an irreducible and reduced
![]() $r$
-cycle
$r$
-cycle
![]() $W$
of degree
$W$
of degree
![]() $d$
consider the set
$d$
consider the set
![]() $\mathscr{F}$
of
$\mathscr{F}$
of
![]() $(r+1)$
-tuples
$(r+1)$
-tuples
![]() $(\unicode[STIX]{x1D6F1}_{1},\ldots ,\unicode[STIX]{x1D6F1}_{r+1})$
,
$(\unicode[STIX]{x1D6F1}_{1},\ldots ,\unicode[STIX]{x1D6F1}_{r+1})$
,
![]() $1\leqslant i\leqslant r+1$
, of hyperplanes
$1\leqslant i\leqslant r+1$
, of hyperplanes
![]() $\unicode[STIX]{x1D6F1}_{i}\,\subset \,\mathbb{P}^{n}$
, such that
$\unicode[STIX]{x1D6F1}_{i}\,\subset \,\mathbb{P}^{n}$
, such that
![]() $\unicode[STIX]{x1D6F1}_{1}\cap \cdots \cap \unicode[STIX]{x1D6F1}_{r+1}\cap W\neq \emptyset$
. Writing
$\unicode[STIX]{x1D6F1}_{1}\cap \cdots \cap \unicode[STIX]{x1D6F1}_{r+1}\cap W\neq \emptyset$
. Writing
![]() $\mathbb{P}^{n}=\mathbb{P}(H)$
,
$\mathbb{P}^{n}=\mathbb{P}(H)$
,
![]() $H\cong \mathbb{C}^{n+1}$
, hyperplanes
$H\cong \mathbb{C}^{n+1}$
, hyperplanes
![]() $\unicode[STIX]{x1D6F1}\,\subset \,\mathbb{P}(H)$
are parametrized by the dual projective space
$\unicode[STIX]{x1D6F1}\,\subset \,\mathbb{P}(H)$
are parametrized by the dual projective space
![]() $\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
. The set
$\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
. The set
![]() $\mathscr{F}\,\subset \,\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n}$
is then a hypersurface and it is the zero set of some
$\mathscr{F}\,\subset \,\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n}$
is then a hypersurface and it is the zero set of some
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{W}\in \unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},\unicode[STIX]{x1D716}_{1}^{\ast }{\mathcal{O}}(d)\otimes \cdots \otimes \unicode[STIX]{x1D716}_{r+1}^{\ast }{\mathcal{O}}(d))$
,
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{W}\in \unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},\unicode[STIX]{x1D716}_{1}^{\ast }{\mathcal{O}}(d)\otimes \cdots \otimes \unicode[STIX]{x1D716}_{r+1}^{\ast }{\mathcal{O}}(d))$
,
![]() $\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
, where
$\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
, where
![]() $\unicode[STIX]{x1D716}_{k}:\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n}\rightarrow \check{\mathbb{P}}^{n}$
is the canonical projection onto the
$\unicode[STIX]{x1D716}_{k}:\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n}\rightarrow \check{\mathbb{P}}^{n}$
is the canonical projection onto the
![]() $k$
th factor. Writing
$k$
th factor. Writing
![]() ${\mathcal{O}}(d,\ldots ,d)$
for
${\mathcal{O}}(d,\ldots ,d)$
for
![]() $\unicode[STIX]{x1D716}_{1}^{\ast }{\mathcal{O}}(d)\otimes \cdots \otimes \unicode[STIX]{x1D716}_{r+1}^{\ast }{\mathcal{O}}(d)$
,
$\unicode[STIX]{x1D716}_{1}^{\ast }{\mathcal{O}}(d)\otimes \cdots \otimes \unicode[STIX]{x1D716}_{r+1}^{\ast }{\mathcal{O}}(d)$
,
![]() $\unicode[STIX]{x1D70E}$
corresponds to a plurihomogeneous polynomial of multi-degree
$\unicode[STIX]{x1D70E}$
corresponds to a plurihomogeneous polynomial of multi-degree
![]() $(d,\ldots ,d)$
, which is called the Chow form of
$(d,\ldots ,d)$
, which is called the Chow form of
![]() $[W]$
, uniquely determined up to a nonzero multiplicative scalar. In the general case of
$[W]$
, uniquely determined up to a nonzero multiplicative scalar. In the general case of
![]() $[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
one defines
$[W]=k_{1}[W_{1}]+\cdots +k_{s}[W_{s}]$
one defines
![]() $\unicode[STIX]{x1D70E}_{W}=\unicode[STIX]{x1D70E}_{W_{1}}^{k_{1}}\cdots \unicode[STIX]{x1D70E}_{W_{s}}^{k_{s}}$
, which is again of multi-degree
$\unicode[STIX]{x1D70E}_{W}=\unicode[STIX]{x1D70E}_{W_{1}}^{k_{1}}\cdots \unicode[STIX]{x1D70E}_{W_{s}}^{k_{s}}$
, which is again of multi-degree
![]() $(d,\ldots ,d)$
. Writing
$(d,\ldots ,d)$
. Writing
![]() ${\mathcal{Q}}$
for the set of all
${\mathcal{Q}}$
for the set of all
![]() $r$
-cycles of degree
$r$
-cycles of degree
![]() $d$
in
$d$
in
![]() $\mathbb{P}^{n}$
, the mapping
$\mathbb{P}^{n}$
, the mapping
![]() $\unicode[STIX]{x1D6F9}$
associating
$\unicode[STIX]{x1D6F9}$
associating
![]() $[W]\in {\mathcal{Q}}$
to
$[W]\in {\mathcal{Q}}$
to
![]() $[\unicode[STIX]{x1D70E}_{W}]\in \mathbb{P}(J)$
,
$[\unicode[STIX]{x1D70E}_{W}]\in \mathbb{P}(J)$
,
![]() $J=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
, is injective, and we have defined the structure of a projective variety on
$J=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
, is injective, and we have defined the structure of a projective variety on
![]() ${\mathcal{Q}}$
by identifying it with
${\mathcal{Q}}$
by identifying it with
![]() $\unicode[STIX]{x1D6F9}({\mathcal{Q}})\,\subset \,\mathbb{P}(J)$
, noting that
$\unicode[STIX]{x1D6F9}({\mathcal{Q}})\,\subset \,\mathbb{P}(J)$
, noting that
![]() $G$
acts canonically on
$G$
acts canonically on
![]() $\mathbb{P}(J)$
. Restricting to an irreducible component
$\mathbb{P}(J)$
. Restricting to an irreducible component
![]() ${\mathcal{K}}$
of
${\mathcal{K}}$
of
![]() ${\mathcal{Q}}$
we summarize the relevant statements in the following lemma using the notation in the above.
${\mathcal{Q}}$
we summarize the relevant statements in the following lemma using the notation in the above.
Lemma 2.1. Let
![]() $r$
and
$r$
and
![]() $d$
be positive integers,
$d$
be positive integers,
![]() $1\leqslant r\leqslant n-1$
. Let
$1\leqslant r\leqslant n-1$
. Let
![]() ${\mathcal{K}}$
be an irreducible component of
${\mathcal{K}}$
be an irreducible component of
![]() $\text{Chow}(\mathbb{P}^{n})$
parametrizing
$\text{Chow}(\mathbb{P}^{n})$
parametrizing
![]() $r$
-cycles of degree
$r$
-cycles of degree
![]() $d$
in
$d$
in
![]() $\mathbb{P}^{n}$
. Then, writing
$\mathbb{P}^{n}$
. Then, writing
![]() $J:=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
, in which there are
$J:=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
, in which there are
![]() $\,r+1$
Cartesian factors of
$\,r+1$
Cartesian factors of
![]() $\check{\mathbb{P}}^{n}$
, the association of
$\check{\mathbb{P}}^{n}$
, the association of
![]() $[W]\in {\mathcal{K}}$
to
$[W]\in {\mathcal{K}}$
to
![]() $[\unicode[STIX]{x1D70E}_{W}]\in \mathbb{P}(J)$
, where
$[\unicode[STIX]{x1D70E}_{W}]\in \mathbb{P}(J)$
, where
![]() $\unicode[STIX]{x1D70E}_{W}\in J$
denotes the Chow form of
$\unicode[STIX]{x1D70E}_{W}\in J$
denotes the Chow form of
![]() $W$
(which is unique up to scaling constants), identifies
$W$
(which is unique up to scaling constants), identifies
![]() ${\mathcal{K}}$
as a projective subvariety of
${\mathcal{K}}$
as a projective subvariety of
![]() $\mathbb{P}(J)$
. Furthermore,
$\mathbb{P}(J)$
. Furthermore,
![]() $G$
leaves
$G$
leaves
![]() ${\mathcal{K}}\,\subset \,\mathbb{P}(J)$
invariant and acts holomorphically on
${\mathcal{K}}\,\subset \,\mathbb{P}(J)$
invariant and acts holomorphically on
![]() ${\mathcal{K}}$
.
${\mathcal{K}}$
.
We proceed to embed
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into a projective bundle. We have the following.
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
into a projective bundle. We have the following.
Proposition 2.2. Let
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
be the universal family for the irreducible component
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
be the universal family for the irreducible component
![]() ${\mathcal{K}}$
of
${\mathcal{K}}$
of
![]() $\,\text{ Chow}(\mathbb{P}^{n})$
,
$\,\text{ Chow}(\mathbb{P}^{n})$
,
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
be a torsion-free cocompact discrete subgroup,
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
be a torsion-free cocompact discrete subgroup,
![]() $X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
. Define
$X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
. Define
![]() $\mathscr{U}^{\prime }=\mathscr{U}|_{\mathbb{B}^{n}}$
and write
$\mathscr{U}^{\prime }=\mathscr{U}|_{\mathbb{B}^{n}}$
and write
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}:=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
for the induced locally homogeneous holomorphic fiber bundle on
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}:=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
for the induced locally homogeneous holomorphic fiber bundle on
![]() $X_{\unicode[STIX]{x1D6E4}}$
with fibers biholomorphic to
$X_{\unicode[STIX]{x1D6E4}}$
with fibers biholomorphic to
![]() $\mathscr{U}_{0}$
. Then, there exists a locally homogeneous projective bundle
$\mathscr{U}_{0}$
. Then, there exists a locally homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
such that
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
such that
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a locally homogeneous holomorphic fiber subbundle over
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a locally homogeneous holomorphic fiber subbundle over
![]() $X_{\unicode[STIX]{x1D6E4}}$
. Moreover, the total space
$X_{\unicode[STIX]{x1D6E4}}$
. Moreover, the total space
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a projective manifold, hence
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a projective manifold, hence
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a projective variety.
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a projective variety.
Proof. It suffices to show that
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
embeds into some homogeneous projective bundle
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
embeds into some homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}\,:\,\mathscr{P}\rightarrow \mathbb{P}^{n}$
such that
$\unicode[STIX]{x1D71B}\,:\,\mathscr{P}\rightarrow \mathbb{P}^{n}$
such that
![]() $\mathscr{U}$
is invariant under the action of
$\mathscr{U}$
is invariant under the action of
![]() $G$
on
$G$
on
![]() $\mathscr{P}$
. In this way, the restriction
$\mathscr{P}$
. In this way, the restriction
![]() $\unicode[STIX]{x1D707}^{\prime }:\mathscr{U}^{\prime }\rightarrow \mathbb{B}^{n}$
,
$\unicode[STIX]{x1D707}^{\prime }:\mathscr{U}^{\prime }\rightarrow \mathbb{B}^{n}$
,
![]() $\mathscr{U}^{\prime }:=\unicode[STIX]{x1D707}^{-1}(\mathbb{B}^{n})$
,
$\mathscr{U}^{\prime }:=\unicode[STIX]{x1D707}^{-1}(\mathbb{B}^{n})$
,
![]() $\unicode[STIX]{x1D707}^{\prime }=\unicode[STIX]{x1D707}|_{\mathscr{P}^{\prime }}$
is invariant under
$\unicode[STIX]{x1D707}^{\prime }=\unicode[STIX]{x1D707}|_{\mathscr{P}^{\prime }}$
is invariant under
![]() $G_{0}\,\subset \,G$
, and it descends under the action of
$G_{0}\,\subset \,G$
, and it descends under the action of
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
to give
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
to give
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}$
, which embeds as a locally homogeneous holomorphic fiber subbundle of the projective bundle
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}=\mathscr{U}^{\prime }/\unicode[STIX]{x1D6E4}$
, which embeds as a locally homogeneous holomorphic fiber subbundle of the projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. Given this, Proposition 2.1 implies the projectivity of
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. Given this, Proposition 2.1 implies the projectivity of
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
For the Chow component
![]() ${\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
whose members are
${\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
whose members are
![]() $r$
-cycles of degree
$r$
-cycles of degree
![]() $d$
in
$d$
in
![]() $\mathbb{P}^{n}$
, by Lemma 2.1, writing
$\mathbb{P}^{n}$
, by Lemma 2.1, writing
![]() $\mathbb{P}^{n}=:\mathbb{P}(H)$
,
$\mathbb{P}^{n}=:\mathbb{P}(H)$
,
![]() ${\mathcal{K}}$
embeds canonically into the projective space
${\mathcal{K}}$
embeds canonically into the projective space
![]() $\mathbb{P}(J):\cong \mathbb{P}^{N}$
, where
$\mathbb{P}(J):\cong \mathbb{P}^{N}$
, where
![]() $J=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
,
$J=\unicode[STIX]{x1D6E4}(\check{\mathbb{P}}^{n}\times \cdots \times \check{\mathbb{P}}^{n},{\mathcal{O}}(d,\ldots ,d))^{\ast }$
,
![]() $\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
. By definition
$\check{\mathbb{P}}^{n}=\mathbb{P}(H^{\ast })$
. By definition
![]() $\mathscr{U}\,\subset \,{\mathcal{K}}\times \mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{N}\times \mathbb{P}^{n}{\hookrightarrow}\mathbb{P}(J\otimes H)\cong :\mathbb{P}^{s}$
and hence
$\mathscr{U}\,\subset \,{\mathcal{K}}\times \mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{N}\times \mathbb{P}^{n}{\hookrightarrow}\mathbb{P}(J\otimes H)\cong :\mathbb{P}^{s}$
and hence
![]() $\mathscr{U}{\hookrightarrow}\mathbb{P}^{s}$
embeds canonically into
$\mathscr{U}{\hookrightarrow}\mathbb{P}^{s}$
embeds canonically into
![]() $\mathbb{P}^{s}$
. We have
$\mathbb{P}^{s}$
. We have
![]() $\mathscr{U}_{0}=\unicode[STIX]{x1D707}^{-1}(0)\,\subset \,\mathscr{U}\,\subset \,{\mathcal{K}}\,\times \,\mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{s}$
. Restricting the
$\mathscr{U}_{0}=\unicode[STIX]{x1D707}^{-1}(0)\,\subset \,\mathscr{U}\,\subset \,{\mathcal{K}}\,\times \,\mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{s}$
. Restricting the
![]() $G$
-action on
$G$
-action on
![]() $\mathbb{P}^{s}$
to the parabolic subgroup
$\mathbb{P}^{s}$
to the parabolic subgroup
![]() $P$
, written
$P$
, written
![]() $\unicode[STIX]{x1D6F7}:P\rightarrow \text{Aut}(\mathbb{P}^{s})$
, we obtain from the discussion preceding Lemma 2.1 a homogeneous projective bundle
$\unicode[STIX]{x1D6F7}:P\rightarrow \text{Aut}(\mathbb{P}^{s})$
, we obtain from the discussion preceding Lemma 2.1 a homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
equipped with a
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
equipped with a
![]() $G$
-action. The restriction
$G$
-action. The restriction
![]() $\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
is invariant under
$\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
is invariant under
![]() $G_{0}\,\subset \,G$
, hence it descends to
$G_{0}\,\subset \,G$
, hence it descends to
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. The mapping
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. The mapping
![]() $\unicode[STIX]{x1D711}(u)=(u,\unicode[STIX]{x1D707}(u))$
embeds
$\unicode[STIX]{x1D711}(u)=(u,\unicode[STIX]{x1D707}(u))$
embeds
![]() $\mathscr{U}$
into
$\mathscr{U}$
into
![]() $\mathscr{U}\times \mathbb{P}^{n}$
, and its image
$\mathscr{U}\times \mathbb{P}^{n}$
, and its image
![]() $\mathscr{U}^{\sharp }$
equipped with the projection onto
$\mathscr{U}^{\sharp }$
equipped with the projection onto
![]() $\mathbb{P}^{n}$
realizes
$\mathbb{P}^{n}$
realizes
![]() $\mathscr{U}^{\sharp }\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}=\mathscr{P}$
as a holomorphic fiber subbundle of
$\mathscr{U}^{\sharp }\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}=\mathscr{P}$
as a holomorphic fiber subbundle of
![]() $\mathscr{P}$
. Identifying
$\mathscr{P}$
. Identifying
![]() $\mathscr{U}$
with
$\mathscr{U}$
with
![]() $\mathscr{U}^{\sharp }$
and
$\mathscr{U}^{\sharp }$
and
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
with the projection of
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
with the projection of
![]() $\mathscr{U}^{\sharp }\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}$
onto the second factor
$\mathscr{U}^{\sharp }\,\subset \,\mathbb{P}^{s}\times \mathbb{P}^{n}$
onto the second factor
![]() $\mathbb{P}^{n}$
, we have realized
$\mathbb{P}^{n}$
, we have realized
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
as a locally homogeneous holomorphic fiber subbundle of
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
as a locally homogeneous holomorphic fiber subbundle of
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
. Proposition 2.2 follows.◻
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
. Proposition 2.2 follows.◻
In the case where
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice, we will study
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice, we will study
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
by constructing Hermitian metrics with positive curvature (1,1)-form on a homogeneous holomorphic line bundle on
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
by constructing Hermitian metrics with positive curvature (1,1)-form on a homogeneous holomorphic line bundle on
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
and prove quasi-projectivity by means of techniques of compactification of complete Kähler manifolds of finite volume.
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
and prove quasi-projectivity by means of techniques of compactification of complete Kähler manifolds of finite volume.
As a preparation we consider the general situation of a representation
![]() $\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
and the associated homogeneous projective bundle
$\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
and the associated homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
.
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
.
Writing
![]() $E:\cong \mathbb{C}^{m+1}$
we have
$E:\cong \mathbb{C}^{m+1}$
we have
![]() $\mathbb{P}\text{GL}(E)\cong \mathbb{P}\text{GL}(m+1,\mathbb{C})\cong \text{SL}(m+1,\mathbb{C})/Z$
, where
$\mathbb{P}\text{GL}(E)\cong \mathbb{P}\text{GL}(m+1,\mathbb{C})\cong \text{SL}(m+1,\mathbb{C})/Z$
, where
![]() $Z=\{\unicode[STIX]{x1D706}I_{m+1}:\unicode[STIX]{x1D706}^{m+1}=1\}.$
Recall that
$Z=\{\unicode[STIX]{x1D706}I_{m+1}:\unicode[STIX]{x1D706}^{m+1}=1\}.$
Recall that
![]() $K\cong U(n)$
is the isotropy subgroup of
$K\cong U(n)$
is the isotropy subgroup of
![]() $(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
at
$(\mathbb{B}^{n},ds_{\mathbb{B}^{n}}^{2})$
at
![]() $0\in \mathbb{B}^{n}$
,
$0\in \mathbb{B}^{n}$
,
![]() $K=P\,\cap \,G_{0}$
. Denoting by
$K=P\,\cap \,G_{0}$
. Denoting by
![]() $\unicode[STIX]{x1D6FC}:\text{SL}(m+1,\mathbb{C})\rightarrow \text{SL}(m+1,\mathbb{C})/Z\cong \mathbb{P}\text{GL}(E)$
the quotient map, let
$\unicode[STIX]{x1D6FC}:\text{SL}(m+1,\mathbb{C})\rightarrow \text{SL}(m+1,\mathbb{C})/Z\cong \mathbb{P}\text{GL}(E)$
the quotient map, let
![]() $Q\,\subset \,\text{SL}(m+1,\mathbb{C})$
be the subgroup
$Q\,\subset \,\text{SL}(m+1,\mathbb{C})$
be the subgroup
![]() $\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6F7}(K))$
. Now let
$\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6F7}(K))$
. Now let
![]() $\unicode[STIX]{x1D701}$
be a Hermitian Euclidean metric on the complex vector space
$\unicode[STIX]{x1D701}$
be a Hermitian Euclidean metric on the complex vector space
![]() $E$
which is invariant under the compact subgroup
$E$
which is invariant under the compact subgroup
![]() $Q\,\subset \,\text{GL}(E)$
. The metric
$Q\,\subset \,\text{GL}(E)$
. The metric
![]() $\unicode[STIX]{x1D701}$
induces on
$\unicode[STIX]{x1D701}$
induces on
![]() $\mathbb{P}(E)$
a Fubini–Study metric
$\mathbb{P}(E)$
a Fubini–Study metric
![]() $g_{c}$
with Kähler form
$g_{c}$
with Kähler form
![]() $\unicode[STIX]{x1D714}_{c}$
such that, with respect to the canonical projection
$\unicode[STIX]{x1D714}_{c}$
such that, with respect to the canonical projection
![]() $\unicode[STIX]{x1D6FD}:E-\{0\}\rightarrow \mathbb{P}(E)$
,
$\unicode[STIX]{x1D6FD}:E-\{0\}\rightarrow \mathbb{P}(E)$
,
![]() $\unicode[STIX]{x1D6FD}^{\ast }(\unicode[STIX]{x1D714}_{c})=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log \Vert w\Vert _{\unicode[STIX]{x1D701}}^{2}$
, where
$\unicode[STIX]{x1D6FD}^{\ast }(\unicode[STIX]{x1D714}_{c})=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\log \Vert w\Vert _{\unicode[STIX]{x1D701}}^{2}$
, where
![]() $w=(w_{1},\ldots ,w_{m+1})$
are Euclidean coordinates on
$w=(w_{1},\ldots ,w_{m+1})$
are Euclidean coordinates on
![]() $E$
and
$E$
and
![]() $\Vert w\Vert _{\unicode[STIX]{x1D701}}$
denotes the norm of
$\Vert w\Vert _{\unicode[STIX]{x1D701}}$
denotes the norm of
![]() $w$
measured in terms of
$w$
measured in terms of
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.
Restricting
![]() $\unicode[STIX]{x1D6F7}$
to
$\unicode[STIX]{x1D6F7}$
to
![]() $G_{0}\,\cap \,P=K$
, from
$G_{0}\,\cap \,P=K$
, from
![]() $\unicode[STIX]{x1D6F7}|_{K}:K\rightarrow \mathbb{P}\text{GL}(E)$
we obtain
$\unicode[STIX]{x1D6F7}|_{K}:K\rightarrow \mathbb{P}\text{GL}(E)$
we obtain
![]() $\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }=G_{0}\times _{K}\mathbb{P}(E)\rightarrow G/K=\mathbb{B}^{n}$
as a homogeneous projective bundle over
$\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }=G_{0}\times _{K}\mathbb{P}(E)\rightarrow G/K=\mathbb{B}^{n}$
as a homogeneous projective bundle over
![]() $\mathbb{B}^{n}$
such that
$\mathbb{B}^{n}$
such that
![]() $\mathscr{P}^{\prime }$
is identified with
$\mathscr{P}^{\prime }$
is identified with
![]() $\mathscr{P}|_{\mathbb{B}^{n}}$
. Since
$\mathscr{P}|_{\mathbb{B}^{n}}$
. Since
![]() $g_{c}$
is invariant under
$g_{c}$
is invariant under
![]() $Q$
, identifying
$Q$
, identifying
![]() $\mathbb{P}(E)$
with the fiber
$\mathbb{P}(E)$
with the fiber
![]() $\mathscr{P}_{0}=\unicode[STIX]{x1D71B}^{-1}(0)$
we have correspondingly a Fubini–Study metric
$\mathscr{P}_{0}=\unicode[STIX]{x1D71B}^{-1}(0)$
we have correspondingly a Fubini–Study metric
![]() $g_{0}$
on
$g_{0}$
on
![]() $\mathscr{P}_{0}$
. By the
$\mathscr{P}_{0}$
. By the
![]() $Q$
-invariance of
$Q$
-invariance of
![]() $g_{0}$
, the latter metric can be transported by means of
$g_{0}$
, the latter metric can be transported by means of
![]() $G_{0}$
-action to fibers
$G_{0}$
-action to fibers
![]() $\mathscr{P}_{x}$
over
$\mathscr{P}_{x}$
over
![]() $x\in \mathbb{B}^{n}$
, yielding thereby a
$x\in \mathbb{B}^{n}$
, yielding thereby a
![]() $G_{0}$
-invariant Hermitian metric
$G_{0}$
-invariant Hermitian metric
![]() $g$
on the relative tangent bundle
$g$
on the relative tangent bundle
![]() $T_{\unicode[STIX]{x1D71B}^{\prime }}$
. Denoting by
$T_{\unicode[STIX]{x1D71B}^{\prime }}$
. Denoting by
![]() $L$
the determinant line bundle det
$L$
the determinant line bundle det
![]() $(T_{\unicode[STIX]{x1D71B}^{\prime }})$
and writing
$(T_{\unicode[STIX]{x1D71B}^{\prime }})$
and writing
![]() $h$
for det
$h$
for det
![]() $(g)$
, we have a Hermitian holomorphic line bundle
$(g)$
, we have a Hermitian holomorphic line bundle
![]() $(L,h)$
on
$(L,h)$
on
![]() $\mathscr{P}^{\prime }$
which is invariant under the
$\mathscr{P}^{\prime }$
which is invariant under the
![]() $G_{0}$
-action described. The curvature form
$G_{0}$
-action described. The curvature form
![]() $\unicode[STIX]{x1D6E9}(L,h)$
, as a closed (1,1)-form on
$\unicode[STIX]{x1D6E9}(L,h)$
, as a closed (1,1)-form on
![]() $\mathscr{P}^{\prime }$
, is
$\mathscr{P}^{\prime }$
, is
![]() $G_{0}$
-invariant and positive when restricted to each of the fibers
$G_{0}$
-invariant and positive when restricted to each of the fibers
![]() $\mathscr{P}_{x},\,x\in \mathbb{B}^{n}$
. Let
$\mathscr{P}_{x},\,x\in \mathbb{B}^{n}$
. Let
![]() $(A,t)$
be a positive homogeneous Hermitian holomorphic line bundle on
$(A,t)$
be a positive homogeneous Hermitian holomorphic line bundle on
![]() $\mathbb{B}^{n}$
. By the
$\mathbb{B}^{n}$
. By the
![]() $G_{0}$
-invariance of
$G_{0}$
-invariance of
![]() $\unicode[STIX]{x1D703}$
and the compactness of the fibers
$\unicode[STIX]{x1D703}$
and the compactness of the fibers
![]() $\mathscr{P}_{x}\cong \mathbb{P}(E)$
, for a sufficiently large integer
$\mathscr{P}_{x}\cong \mathbb{P}(E)$
, for a sufficiently large integer
![]() $k$
,
$k$
,
![]() $\unicode[STIX]{x1D703}:=\unicode[STIX]{x1D6E9}(L\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }A)^{k},h\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(t))^{k})>0$
. Since
$\unicode[STIX]{x1D703}:=\unicode[STIX]{x1D6E9}(L\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }A)^{k},h\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(t))^{k})>0$
. Since
![]() $\unicode[STIX]{x1D703}$
is
$\unicode[STIX]{x1D703}$
is
![]() $G_{0}$
-invariant, for a torsion-free lattice
$G_{0}$
-invariant, for a torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}=\mathscr{P}/\unicode[STIX]{x1D6E4}\rightarrow X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, the Hermitian holomorphic line bundle
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}=\mathscr{P}/\unicode[STIX]{x1D6E4}\rightarrow X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
, the Hermitian holomorphic line bundle
![]() $(\unicode[STIX]{x1D6EC},s):=(L\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }A)^{k},h\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(t))^{k})$
descends to a positive line bundle on
$(\unicode[STIX]{x1D6EC},s):=(L\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }A)^{k},h\otimes ({\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(t))^{k})$
descends to a positive line bundle on
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
We summarize the discussion above to the following result which will be used in the case of finite-volume noncompact quotient manifolds.
Proposition 2.3. Let
![]() $E$
be a finite-dimensional complex vector space,
$E$
be a finite-dimensional complex vector space,
![]() $\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
be a representation,
$\unicode[STIX]{x1D6F7}:P\rightarrow \mathbb{P}\text{GL}(E)$
be a representation,
![]() $\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
be the associated homogeneous projective bundle on
$\unicode[STIX]{x1D71B}:\mathscr{P}\rightarrow \mathbb{P}^{n}$
be the associated homogeneous projective bundle on
![]() $\mathbb{P}^{n}$
, and write
$\mathbb{P}^{n}$
, and write
![]() $\mathscr{P}^{\prime }:=\mathscr{P}|_{\mathbb{B}^{n}}$
. Then, there exists a
$\mathscr{P}^{\prime }:=\mathscr{P}|_{\mathbb{B}^{n}}$
. Then, there exists a
![]() $G_{0}$
-invariant Hermitian holomorphic line bundle
$G_{0}$
-invariant Hermitian holomorphic line bundle
![]() $(\unicode[STIX]{x1D6EC},s)$
on
$(\unicode[STIX]{x1D6EC},s)$
on
![]() $\mathscr{P}^{\prime }$
whose curvature form
$\mathscr{P}^{\prime }$
whose curvature form
![]() $\unicode[STIX]{x1D703}$
is positive definite. Hence, given any torsion-free discrete subgroup
$\unicode[STIX]{x1D703}$
is positive definite. Hence, given any torsion-free discrete subgroup
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
![]() $(\unicode[STIX]{x1D6EC},s)$
descends to a locally homogeneous Hermitian holomorphic line bundle
$(\unicode[STIX]{x1D6EC},s)$
descends to a locally homogeneous Hermitian holomorphic line bundle
![]() $(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6E4}},s_{\unicode[STIX]{x1D6E4}})$
with positive curvature form
$(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6E4}},s_{\unicode[STIX]{x1D6E4}})$
with positive curvature form
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
.
We prove now an embedding theorem for
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
.
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
.
Proposition 2.4. For a torsion-free nonuniform lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
the total space
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
the total space
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
of the locally homogeneous projective bundle
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
of the locally homogeneous projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is biholomorphic to a dense Zariski open subset of some projective subvariety
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is biholomorphic to a dense Zariski open subset of some projective subvariety
![]() $V\,\subset \,\mathbb{P}^{\ell }$
of a projective space
$V\,\subset \,\mathbb{P}^{\ell }$
of a projective space
![]() $\mathbb{P}^{\ell }$
.
$\mathbb{P}^{\ell }$
.
Proof. By Proposition 2.3,
![]() $\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
is equipped with a homogeneous Hermitian holomorphic line bundle
$\mathscr{P}^{\prime }=\mathscr{P}|_{\mathbb{B}^{n}}$
is equipped with a homogeneous Hermitian holomorphic line bundle
![]() $(\unicode[STIX]{x1D6EC},s)$
whose curvature form
$(\unicode[STIX]{x1D6EC},s)$
whose curvature form
![]() $\unicode[STIX]{x1D703}$
is positive definite. We can now equip
$\unicode[STIX]{x1D703}$
is positive definite. We can now equip
![]() $\mathscr{P}^{\prime }$
with the Kähler form
$\mathscr{P}^{\prime }$
with the Kähler form
![]() $\unicode[STIX]{x1D703}$
, which descends to a Kähler form
$\unicode[STIX]{x1D703}$
, which descends to a Kähler form
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
. From the definition we have
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
. From the definition we have
Recall that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}$
is the Kähler form of the complete Kähler metric on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}$
is the Kähler form of the complete Kähler metric on
![]() $X_{\unicode[STIX]{x1D6E4}}$
with constant holomorphic sectional curvature
$X_{\unicode[STIX]{x1D6E4}}$
with constant holomorphic sectional curvature
![]() $-2$
. Replacing
$-2$
. Replacing
![]() $k$
by
$k$
by
![]() $k+1$
we may assume furthermore that
$k+1$
we may assume furthermore that
![]() $\unicode[STIX]{x1D703}>(n+1){\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})>{\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
. It follows that the length of any smooth curve
$\unicode[STIX]{x1D703}>(n+1){\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})>{\unicode[STIX]{x1D71B}^{\prime }}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
. It follows that the length of any smooth curve
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathscr{P}_{\unicode[STIX]{x1D6E4}}$
with respect to
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathscr{P}_{\unicode[STIX]{x1D6E4}}$
with respect to
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
dominates the length of the smooth curve
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}$
dominates the length of the smooth curve
![]() $\unicode[STIX]{x1D6FE}\,\circ \,\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:[0,1]\rightarrow X_{\unicode[STIX]{x1D6E4}}$
with respect to
$\unicode[STIX]{x1D6FE}\,\circ \,\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:[0,1]\rightarrow X_{\unicode[STIX]{x1D6E4}}$
with respect to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}$
. Since
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}$
. Since
![]() $(X_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
is a complete Kähler manifold, we conclude that
$(X_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
is a complete Kähler manifold, we conclude that
![]() $(\mathscr{P}_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}})$
is also a complete Kähler manifold.
$(\mathscr{P}_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}})$
is also a complete Kähler manifold.
We also equip
![]() $(\mathscr{P}_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}})$
with the Hermitian–Einstein positive line bundle
$(\mathscr{P}_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}})$
with the Hermitian–Einstein positive line bundle
![]() $(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6E4}},s_{\unicode[STIX]{x1D6E4}})$
. Since the Kähler form
$(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6E4}},s_{\unicode[STIX]{x1D6E4}})$
. Since the Kähler form
![]() $\unicode[STIX]{x1D703}$
on
$\unicode[STIX]{x1D703}$
on
![]() $\mathscr{P}^{\prime }$
is
$\mathscr{P}^{\prime }$
is
![]() $G_{0}$
-invariant, for any open subset
$G_{0}$
-invariant, for any open subset
![]() ${\mathcal{O}}\Subset \mathbb{B}^{n}$
and any
${\mathcal{O}}\Subset \mathbb{B}^{n}$
and any
![]() $\unicode[STIX]{x1D711}\in G_{0}$
, Volume
$\unicode[STIX]{x1D711}\in G_{0}$
, Volume
![]() $(\unicode[STIX]{x1D71B}^{-1}({\mathcal{O}}),\unicode[STIX]{x1D703})=\text{Volume}(\unicode[STIX]{x1D71B}^{-1}(\unicode[STIX]{x1D711}({\mathcal{O}})),\unicode[STIX]{x1D703})<\infty$
. Recall that
$(\unicode[STIX]{x1D71B}^{-1}({\mathcal{O}}),\unicode[STIX]{x1D703})=\text{Volume}(\unicode[STIX]{x1D71B}^{-1}(\unicode[STIX]{x1D711}({\mathcal{O}})),\unicode[STIX]{x1D703})<\infty$
. Recall that
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is of fiber dimension
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is of fiber dimension
![]() $s$
. Since both (1,1)-forms
$s$
. Since both (1,1)-forms
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714})$
are invariant under
$\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714})$
are invariant under
![]() $G_{0}$
, both
$G_{0}$
, both
![]() $\unicode[STIX]{x1D703}^{s+n}$
and
$\unicode[STIX]{x1D703}^{s+n}$
and
![]() $\unicode[STIX]{x1D703}^{s}\wedge (\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714}))^{n}$
are
$\unicode[STIX]{x1D703}^{s}\wedge (\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714}))^{n}$
are
![]() $G_{0}$
-invariant volume forms on
$G_{0}$
-invariant volume forms on
![]() $\mathscr{P}^{\prime }$
, and the function
$\mathscr{P}^{\prime }$
, and the function
![]() $h:\mathscr{P}^{\prime }\rightarrow \mathbb{R}$
defined by
$h:\mathscr{P}^{\prime }\rightarrow \mathbb{R}$
defined by
![]() $\unicode[STIX]{x1D703}^{s+n}(p)=h(p)\unicode[STIX]{x1D703}^{s}\wedge (\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714}))^{n}$
is a
$\unicode[STIX]{x1D703}^{s+n}(p)=h(p)\unicode[STIX]{x1D703}^{s}\wedge (\unicode[STIX]{x1D71B}^{\ast }(\unicode[STIX]{x1D714}))^{n}$
is a
![]() $G_{0}$
-invariant function on
$G_{0}$
-invariant function on
![]() $\mathscr{P}^{\prime }$
. Since any point
$\mathscr{P}^{\prime }$
. Since any point
![]() $p\in \mathscr{P}^{\prime }$
is equivalent under the action of
$p\in \mathscr{P}^{\prime }$
is equivalent under the action of
![]() $G_{0}$
to some point on
$G_{0}$
to some point on
![]() $\mathscr{P}_{0}$
, which is compact, we observe that there exists a constant
$\mathscr{P}_{0}$
, which is compact, we observe that there exists a constant
![]() $C_{0}>0$
such that
$C_{0}>0$
such that
![]() $0<h(p)\leqslant C_{0}$
for any
$0<h(p)\leqslant C_{0}$
for any
![]() $p\in \mathscr{P}^{\prime }$
. For any open subset
$p\in \mathscr{P}^{\prime }$
. For any open subset
![]() ${\mathcal{O}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
, by Fubini’s theorem we have
${\mathcal{O}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
, by Fubini’s theorem we have
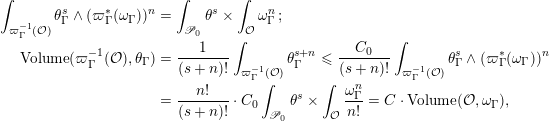 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s}\wedge (\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}))^{n} & = & \displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}\times \int _{{\mathcal{O}}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}^{n}\,;\nonumber\\ \displaystyle \text{Volume}(\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}}),\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}) & = & \displaystyle {\displaystyle \frac{1}{(s+n)!}}\displaystyle \int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s+n}\leqslant {\displaystyle \frac{C_{0}}{(s+n)!}}\int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s}\wedge (\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}))^{n}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{n!}{(s+n)!}}\cdot C_{0}\displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}\times \displaystyle \int _{{\mathcal{O}}}{\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}^{n}}{n!}}=C\cdot \text{Volume}({\mathcal{O}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s}\wedge (\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}))^{n} & = & \displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}\times \int _{{\mathcal{O}}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}^{n}\,;\nonumber\\ \displaystyle \text{Volume}(\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}}),\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}) & = & \displaystyle {\displaystyle \frac{1}{(s+n)!}}\displaystyle \int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s+n}\leqslant {\displaystyle \frac{C_{0}}{(s+n)!}}\int _{\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{-1}({\mathcal{O}})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6E4}}^{s}\wedge (\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\ast }(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}))^{n}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{n!}{(s+n)!}}\cdot C_{0}\displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}\times \displaystyle \int _{{\mathcal{O}}}{\displaystyle \frac{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}^{n}}{n!}}=C\cdot \text{Volume}({\mathcal{O}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}}),\nonumber\end{eqnarray}$$
where
![]() $C=n!/(s+n)!\cdot C_{0}\displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}$
. In particular,
$C=n!/(s+n)!\cdot C_{0}\displaystyle \int _{\mathscr{P}_{0}}\unicode[STIX]{x1D703}^{s}$
. In particular,
From the
![]() $G_{0}$
-invariance of
$G_{0}$
-invariance of
![]() $(\mathscr{P}^{\prime },\unicode[STIX]{x1D703})$
and the compactness of the fibers of
$(\mathscr{P}^{\prime },\unicode[STIX]{x1D703})$
and the compactness of the fibers of
![]() $\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }\rightarrow \mathbb{B}^{n}$
, it follows that
$\unicode[STIX]{x1D71B}^{\prime }:\mathscr{P}^{\prime }\rightarrow \mathbb{B}^{n}$
, it follows that
![]() $(\mathscr{P}^{\prime },\unicode[STIX]{x1D703})$
is of bounded sectional curvature. Since
$(\mathscr{P}^{\prime },\unicode[STIX]{x1D703})$
is of bounded sectional curvature. Since
![]() $X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective manifold (as in Theorem 1.1), it is of finite topological type. Hence,
$X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective manifold (as in Theorem 1.1), it is of finite topological type. Hence,
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is also of finite topological type. As a consequence, one can apply the embedding result on complete Kähler manifolds of finite volume given by Theorem 1.3 here (from Mok and Zhong [Reference Mok and ZhongMZ89]) to complete the proof of the proposition.◻
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is also of finite topological type. As a consequence, one can apply the embedding result on complete Kähler manifolds of finite volume given by Theorem 1.3 here (from Mok and Zhong [Reference Mok and ZhongMZ89]) to complete the proof of the proposition.◻
Without loss of generality we may assume
![]() $V$
to be normal, and we also write
$V$
to be normal, and we also write
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}:=V$
for the compactification of
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}:=V$
for the compactification of
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
as a normal projective variety. Since
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
as a normal projective variety. Since
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a proper holomorphic map, by the Riemann extension theorem and the normality of
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a proper holomorphic map, by the Riemann extension theorem and the normality of
![]() $\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
, it extends holomorphically to
$\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
, it extends holomorphically to
![]() $\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
, to be denoted as
$\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
, to be denoted as
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
.
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
.
We now return to our study of the locally homogeneous holomorphic fiber subbundle
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
of
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
of
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. We have the following result on
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. We have the following result on
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\subset \mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\subset \mathscr{P}_{\unicode[STIX]{x1D6E4}}$
.
Proposition 2.5. For a torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, identifying the total space of the locally homogeneous holomorphic projective bundle
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, identifying the total space of the locally homogeneous holomorphic projective bundle
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a quasi-projective variety by means of Proposition 2.4 and embedding
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a quasi-projective variety by means of Proposition 2.4 and embedding
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
![]() $\,\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety.
$\,\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety.
Proof. Let
![]() $\unicode[STIX]{x1D6F9}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\overset{\cong }{\longrightarrow }W\,\subset \,V\,\subset \,\mathbb{P}^{\ell }$
be a biholomorphism of
$\unicode[STIX]{x1D6F9}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\overset{\cong }{\longrightarrow }W\,\subset \,V\,\subset \,\mathbb{P}^{\ell }$
be a biholomorphism of
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
onto a Zariski open subset
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
onto a Zariski open subset
![]() $W$
of a projective subvariety
$W$
of a projective subvariety
![]() $V\,\subset \,\mathbb{P}^{\ell }$
, where
$V\,\subset \,\mathbb{P}^{\ell }$
, where
![]() $V$
is the topological closure of
$V$
is the topological closure of
![]() $W$
in
$W$
in
![]() $\mathbb{P}^{\ell }$
, and identify
$\mathbb{P}^{\ell }$
, and identify
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
with
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
with
![]() $W=\unicode[STIX]{x1D6F9}(\mathscr{P}_{\unicode[STIX]{x1D6E4}})$
, and write
$W=\unicode[STIX]{x1D6F9}(\mathscr{P}_{\unicode[STIX]{x1D6E4}})$
, and write
![]() $\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}:=V$
. Subsets of
$\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}:=V$
. Subsets of
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
will likewise be identified with their images under
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
will likewise be identified with their images under
![]() $\unicode[STIX]{x1D6F9}$
in
$\unicode[STIX]{x1D6F9}$
in
![]() $W$
. Recall that
$W$
. Recall that
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a projective bundle, and
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a projective bundle, and
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a holomorphic fiber subbundle with fibers
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is a holomorphic fiber subbundle with fibers
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}^{-1}(x)=:\mathscr{U}_{x}$
. Write
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}^{-1}(x)=:\mathscr{U}_{x}$
. Write
![]() $q:=\dim (\mathscr{U}_{x})$
for
$q:=\dim (\mathscr{U}_{x})$
for
![]() $x\in X_{\unicode[STIX]{x1D6E4}}$
, and denote by
$x\in X_{\unicode[STIX]{x1D6E4}}$
, and denote by
![]() $d$
the degree of
$d$
the degree of
![]() $\mathscr{U}_{x}\,\subset \,\mathscr{P}_{x}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathbb{P}^{\ell }$
as a projective subvariety. Denote by
$\mathscr{U}_{x}\,\subset \,\mathscr{P}_{x}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathbb{P}^{\ell }$
as a projective subvariety. Denote by
![]() $\widetilde{{\mathcal{H}}}$
the subset of Chow
$\widetilde{{\mathcal{H}}}$
the subset of Chow
![]() $(\mathbb{P}^{\ell })$
consisting of all pure
$(\mathbb{P}^{\ell })$
consisting of all pure
![]() $q$
-dimensional cycles in
$q$
-dimensional cycles in
![]() $\mathbb{P}^{\ell }$
of degree
$\mathbb{P}^{\ell }$
of degree
![]() $d$
. The continuous mapping
$d$
. The continuous mapping
![]() $\unicode[STIX]{x1D711}:X_{\unicode[STIX]{x1D6E4}}\rightarrow \widetilde{{\mathcal{H}}}$
defined by
$\unicode[STIX]{x1D711}:X_{\unicode[STIX]{x1D6E4}}\rightarrow \widetilde{{\mathcal{H}}}$
defined by
![]() $\unicode[STIX]{x1D711}(x)=[\mathscr{U}_{x}]\in \widetilde{{\mathcal{H}}}$
is a holomorphic mapping from the complex manifold
$\unicode[STIX]{x1D711}(x)=[\mathscr{U}_{x}]\in \widetilde{{\mathcal{H}}}$
is a holomorphic mapping from the complex manifold
![]() $X_{\unicode[STIX]{x1D6E4}}$
into some irreducible component
$X_{\unicode[STIX]{x1D6E4}}$
into some irreducible component
![]() ${\mathcal{H}}\,\subset \,\widetilde{{\mathcal{H}}}$
. Recall that
${\mathcal{H}}\,\subset \,\widetilde{{\mathcal{H}}}$
. Recall that
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
is normal and
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
is normal and
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}-X_{\unicode[STIX]{x1D6E4}}$
is a finite set. Since
$\overline{X_{\unicode[STIX]{x1D6E4}}}-X_{\unicode[STIX]{x1D6E4}}$
is a finite set. Since
![]() $X_{\unicode[STIX]{x1D6E4}}$
is of complex dimension
$X_{\unicode[STIX]{x1D6E4}}$
is of complex dimension
![]() $n\geqslant 2$
, by Hartogs’ extension the holomorphic map
$n\geqslant 2$
, by Hartogs’ extension the holomorphic map
![]() $\unicode[STIX]{x1D711}:X_{\unicode[STIX]{x1D6E4}}\rightarrow {\mathcal{H}}$
extends meromorphically to
$\unicode[STIX]{x1D711}:X_{\unicode[STIX]{x1D6E4}}\rightarrow {\mathcal{H}}$
extends meromorphically to
![]() $\unicode[STIX]{x1D711}^{\sharp }:\overline{X_{\unicode[STIX]{x1D6E4}}}\rightarrow {\mathcal{H}}$
.
$\unicode[STIX]{x1D711}^{\sharp }:\overline{X_{\unicode[STIX]{x1D6E4}}}\rightarrow {\mathcal{H}}$
.
Let
![]() ${\mathcal{Z}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}$
be the graph of the meromorphic map
${\mathcal{Z}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}$
be the graph of the meromorphic map
![]() $\unicode[STIX]{x1D711}^{\sharp }$
, i.e.,
$\unicode[STIX]{x1D711}^{\sharp }$
, i.e.,
![]() ${\mathcal{Z}}$
is the topological closure of
${\mathcal{Z}}$
is the topological closure of
![]() $\text{Graph}(\unicode[STIX]{x1D711})$
in
$\text{Graph}(\unicode[STIX]{x1D711})$
in
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}$
. Denote by
$\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}$
. Denote by
![]() $\unicode[STIX]{x1D6FC}:{\mathcal{V}}\rightarrow {\mathcal{H}}$
the universal family over
$\unicode[STIX]{x1D6FC}:{\mathcal{V}}\rightarrow {\mathcal{H}}$
the universal family over
![]() ${\mathcal{H}}\,\subset \,\text{Chow}(\mathbb{P}^{\ell })$
,
${\mathcal{H}}\,\subset \,\text{Chow}(\mathbb{P}^{\ell })$
,
![]() ${\mathcal{V}}\,\subset \,{\mathcal{H}}\times \mathbb{P}^{\ell }$
. Now let
${\mathcal{V}}\,\subset \,{\mathcal{H}}\times \mathbb{P}^{\ell }$
. Now let
![]() ${\mathcal{W}}\,\subset \,{\mathcal{Z}}\times \mathbb{P}^{\ell }$
be the total space of the pull-back of the universal family
${\mathcal{W}}\,\subset \,{\mathcal{Z}}\times \mathbb{P}^{\ell }$
be the total space of the pull-back of the universal family
![]() $\unicode[STIX]{x1D6FC}:{\mathcal{V}}\rightarrow {\mathcal{H}}$
by the canonical projection map
$\unicode[STIX]{x1D6FC}:{\mathcal{V}}\rightarrow {\mathcal{H}}$
by the canonical projection map
![]() $\unicode[STIX]{x1D6FD}:{\mathcal{Z}}\rightarrow {\mathcal{H}}$
, i.e., writing
$\unicode[STIX]{x1D6FD}:{\mathcal{Z}}\rightarrow {\mathcal{H}}$
, i.e., writing
![]() $C_{\unicode[STIX]{x1D702}}$
for the
$C_{\unicode[STIX]{x1D702}}$
for the
![]() $q$
-cycle in
$q$
-cycle in
![]() $\mathbb{P}^{\ell }$
represented by
$\mathbb{P}^{\ell }$
represented by
![]() $\unicode[STIX]{x1D702}\in {\mathcal{H}}$
we have
$\unicode[STIX]{x1D702}\in {\mathcal{H}}$
we have
![]() ${\mathcal{W}}=\{(x,\unicode[STIX]{x1D702},y)\in \overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}\times \mathbb{P}^{\ell }:(x,\unicode[STIX]{x1D702})\in {\mathcal{Z}},y\in C_{\unicode[STIX]{x1D702}}\}$
. Then, denoting by
${\mathcal{W}}=\{(x,\unicode[STIX]{x1D702},y)\in \overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}\times \mathbb{P}^{\ell }:(x,\unicode[STIX]{x1D702})\in {\mathcal{Z}},y\in C_{\unicode[STIX]{x1D702}}\}$
. Then, denoting by
![]() $\unicode[STIX]{x1D6FE}:\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}\times \mathbb{P}^{\ell }\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }$
the canonical projection, by the proper mapping theorem and Chow’s theorem,
$\unicode[STIX]{x1D6FE}:\overline{X_{\unicode[STIX]{x1D6E4}}}\times {\mathcal{H}}\times \mathbb{P}^{\ell }\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }$
the canonical projection, by the proper mapping theorem and Chow’s theorem,
![]() ${\mathcal{Q}}:=\unicode[STIX]{x1D6FE}({\mathcal{W}})\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }$
is projective. Consider the canonical projections
${\mathcal{Q}}:=\unicode[STIX]{x1D6FE}({\mathcal{W}})\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }$
is projective. Consider the canonical projections
![]() $\unicode[STIX]{x1D6FF}:{\mathcal{Q}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
and
$\unicode[STIX]{x1D6FF}:{\mathcal{Q}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
and
![]() $\unicode[STIX]{x1D706}:\overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }\rightarrow \mathbb{P}^{\ell }$
. Then, by the theorems above
$\unicode[STIX]{x1D706}:\overline{X_{\unicode[STIX]{x1D6E4}}}\times \mathbb{P}^{\ell }\rightarrow \mathbb{P}^{\ell }$
. Then, by the theorems above
![]() ${\mathcal{E}}:=\unicode[STIX]{x1D706}({\mathcal{Q}})\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is projective, and it contains
${\mathcal{E}}:=\unicode[STIX]{x1D706}({\mathcal{Q}})\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is projective, and it contains
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FF}^{-1}(X_{\unicode[STIX]{x1D6E4}}))=\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. Finally it follows from
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FF}^{-1}(X_{\unicode[STIX]{x1D6E4}}))=\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. Finally it follows from
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}={\mathcal{E}}\,\cap \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
that
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}={\mathcal{E}}\,\cap \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
that
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,{\mathcal{E}}$
is a dense Zariski open subset, and hence
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,{\mathcal{E}}$
is a dense Zariski open subset, and hence
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety, as desired.◻
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety, as desired.◻
3 Uniruling on Zariski closures of images of algebraic subsets under the uniformization map
Let
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
be a torsion-free lattice,
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
be a torsion-free lattice,
![]() $X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
,
$X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
,
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
be its minimal compactification, and
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
be its minimal compactification, and
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map. We consider an irreducible algebraic subset
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map. We consider an irreducible algebraic subset
![]() $S\,\subset \,\mathbb{B}^{n}$
of positive dimension and define
$S\,\subset \,\mathbb{B}^{n}$
of positive dimension and define
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
to be the Zariski closure of
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
to be the Zariski closure of
![]() $\unicode[STIX]{x1D70B}(S)$
in
$\unicode[STIX]{x1D70B}(S)$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
. To characterize
$X_{\unicode[STIX]{x1D6E4}}$
. To characterize
![]() $Z$
we will resort to studying meromorphic foliations on holomorphic fiber bundles over
$Z$
we will resort to studying meromorphic foliations on holomorphic fiber bundles over
![]() $X_{\unicode[STIX]{x1D6E4}}$
and on compactifications of total spaces of such fiber bundles. We start with some generalities about complex spaces (cf. Grauert, Peternell and Remmert [Reference Grauert, Peternell and RemmertGPR94, p. 100ff]) and about meromorphic foliations on them.
$X_{\unicode[STIX]{x1D6E4}}$
and on compactifications of total spaces of such fiber bundles. We start with some generalities about complex spaces (cf. Grauert, Peternell and Remmert [Reference Grauert, Peternell and RemmertGPR94, p. 100ff]) and about meromorphic foliations on them.
Let
![]() $(Y,{\mathcal{O}}_{Y})$
be a reduced irreducible complex space, assumed to be embedded as a subvariety of a complex manifold
$(Y,{\mathcal{O}}_{Y})$
be a reduced irreducible complex space, assumed to be embedded as a subvariety of a complex manifold
![]() $M$
. Let
$M$
. Let
![]() $\unicode[STIX]{x1D6FA}_{M}={\mathcal{O}}(T_{M}^{\ast })$
be the cotangent sheaf on
$\unicode[STIX]{x1D6FA}_{M}={\mathcal{O}}(T_{M}^{\ast })$
be the cotangent sheaf on
![]() $M$
, and
$M$
, and
![]() $\mathscr{I}_{Y}\,\subset \,{\mathcal{O}}_{M}$
be the ideal sheaf of
$\mathscr{I}_{Y}\,\subset \,{\mathcal{O}}_{M}$
be the ideal sheaf of
![]() $Y\,\subset \,M$
. Define now
$Y\,\subset \,M$
. Define now
![]() $\mathscr{S}\,\subset \,\unicode[STIX]{x1D6FA}_{M}$
to be the subsheaf spanned by
$\mathscr{S}\,\subset \,\unicode[STIX]{x1D6FA}_{M}$
to be the subsheaf spanned by
![]() $\mathscr{I}_{Y}\unicode[STIX]{x1D6FA}_{M}$
and
$\mathscr{I}_{Y}\unicode[STIX]{x1D6FA}_{M}$
and
![]() $\{df:f\in \mathscr{I}_{Y}\}$
. Then,
$\{df:f\in \mathscr{I}_{Y}\}$
. Then,
![]() $\mathscr{S}\,\subset \,\unicode[STIX]{x1D6FA}_{M}$
is a coherent subsheaf and
$\mathscr{S}\,\subset \,\unicode[STIX]{x1D6FA}_{M}$
is a coherent subsheaf and
![]() $\unicode[STIX]{x1D6FA}_{Y}:=\unicode[STIX]{x1D6FA}_{M}/\mathscr{S}$
is called the cotangent sheaf of
$\unicode[STIX]{x1D6FA}_{Y}:=\unicode[STIX]{x1D6FA}_{M}/\mathscr{S}$
is called the cotangent sheaf of
![]() $Y$
. The tangent sheaf
$Y$
. The tangent sheaf
![]() ${\mathcal{T}}_{Y}$
is by definition the coherent sheaf
${\mathcal{T}}_{Y}$
is by definition the coherent sheaf
![]() $\mathscr{H}om_{{\mathcal{O}}_{Y}}(\unicode[STIX]{x1D6FA}_{Y},{\mathcal{O}}_{Y})$
, which is naturally identified with a coherent subsheaf of
$\mathscr{H}om_{{\mathcal{O}}_{Y}}(\unicode[STIX]{x1D6FA}_{Y},{\mathcal{O}}_{Y})$
, which is naturally identified with a coherent subsheaf of
![]() ${\mathcal{T}}_{M}|_{Y}$
. The tangent sheaf
${\mathcal{T}}_{M}|_{Y}$
. The tangent sheaf
![]() ${\mathcal{T}}_{Y}$
on
${\mathcal{T}}_{Y}$
on
![]() $Y$
thus defined is unique up to isomorphisms independent of the embedding
$Y$
thus defined is unique up to isomorphisms independent of the embedding
![]() $Y\,\subset \,M$
. When the assumption
$Y\,\subset \,M$
. When the assumption
![]() $Y\,\subset \,M$
is dropped, the tangent sheaf
$Y\,\subset \,M$
is dropped, the tangent sheaf
![]() ${\mathcal{T}}_{Y}$
is defined using an atlas
${\mathcal{T}}_{Y}$
is defined using an atlas
![]() $\mathscr{U}=\{{U_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$
on
$\mathscr{U}=\{{U_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$
on
![]() $Y$
consisting of subvarieties of coordinate open sets by gluing together the tangent sheaves of
$Y$
consisting of subvarieties of coordinate open sets by gluing together the tangent sheaves of
![]() $U_{\unicode[STIX]{x1D6FC}}$
.
$U_{\unicode[STIX]{x1D6FC}}$
.
A meromorphic foliation
![]() $\mathscr{F}$
on a reduced irreducible complex space
$\mathscr{F}$
on a reduced irreducible complex space
![]() $Y$
is by definition given by a coherent subsheaf
$Y$
is by definition given by a coherent subsheaf
![]() ${\mathcal{T}}_{\mathscr{F}}$
of the tangent sheaf
${\mathcal{T}}_{\mathscr{F}}$
of the tangent sheaf
![]() ${\mathcal{T}}_{Y}$
such that, outside some subvariety
${\mathcal{T}}_{Y}$
such that, outside some subvariety
![]() $A\,\subsetneq \,Y$
,
$A\,\subsetneq \,Y$
,
![]() $A\supset \text{Sing}(Y)$
,
$A\supset \text{Sing}(Y)$
,
![]() ${\mathcal{T}}_{\mathscr{F}}|_{Y-A}$
is a locally free subsheaf and, writing
${\mathcal{T}}_{\mathscr{F}}|_{Y-A}$
is a locally free subsheaf and, writing
![]() ${\mathcal{T}}_{\mathscr{F}}|_{Y-A}:={\mathcal{O}}(F)$
for a holomorphic distribution
${\mathcal{T}}_{\mathscr{F}}|_{Y-A}:={\mathcal{O}}(F)$
for a holomorphic distribution
![]() $F\,\subset \,T_{Y-A}$
,
$F\,\subset \,T_{Y-A}$
,
![]() $F$
satisfies the involutive property
$F$
satisfies the involutive property
![]() $[F,F]=F$
. The tangent subsheaf of the meromorphic foliation
$[F,F]=F$
. The tangent subsheaf of the meromorphic foliation
![]() ${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is also uniquely determined subject to the conditions that
${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is also uniquely determined subject to the conditions that
![]() ${\mathcal{T}}_{\mathscr{F}}$
agrees with
${\mathcal{T}}_{\mathscr{F}}$
agrees with
![]() ${\mathcal{O}}(F)$
over
${\mathcal{O}}(F)$
over
![]() $Y-A$
and that
$Y-A$
and that
![]() ${\mathcal{T}}_{Y}/{\mathcal{T}}_{\mathscr{F}}$
is torsion-free, in which case
${\mathcal{T}}_{Y}/{\mathcal{T}}_{\mathscr{F}}$
is torsion-free, in which case
![]() ${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is said to be saturated. In what follows,
${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is said to be saturated. In what follows,
![]() ${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is always assumed saturated. The singular locus
${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
is always assumed saturated. The singular locus
![]() $\text{Sing}(\mathscr{F})\,\subset \,Y$
is the union of Sing
$\text{Sing}(\mathscr{F})\,\subset \,Y$
is the union of Sing
![]() $(Y)$
and the locus on Reg
$(Y)$
and the locus on Reg
![]() $(Y)$
over which
$(Y)$
over which
![]() $\mathscr{F}$
fails to be a locally free subsheaf. The subset
$\mathscr{F}$
fails to be a locally free subsheaf. The subset
![]() $\text{Sing}(\mathscr{F})\subsetneq Y$
is a subvariety, and we write
$\text{Sing}(\mathscr{F})\subsetneq Y$
is a subvariety, and we write
![]() $\text{Reg}(\mathscr{F}):=Y-\text{Sing}(\mathscr{F})$
. Given an irreducible complex-analytic subvariety
$\text{Reg}(\mathscr{F}):=Y-\text{Sing}(\mathscr{F})$
. Given an irreducible complex-analytic subvariety
![]() $Z\,\subset \,Y$
such that
$Z\,\subset \,Y$
such that
![]() $Z\,\cap \,\text{Reg}(\mathscr{F})\neq \emptyset$
, we say that
$Z\,\cap \,\text{Reg}(\mathscr{F})\neq \emptyset$
, we say that
![]() $Z$
is saturated with respect to
$Z$
is saturated with respect to
![]() $\mathscr{F}$
to mean that for any point
$\mathscr{F}$
to mean that for any point
![]() $z_{0}\in \text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})\neq \emptyset$
, the leaf
$z_{0}\in \text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})\neq \emptyset$
, the leaf
![]() ${\mathcal{L}}(z_{0})$
of
${\mathcal{L}}(z_{0})$
of
![]() $\mathscr{F}$
passing through
$\mathscr{F}$
passing through
![]() $z_{0}$
must necessarily lie on
$z_{0}$
must necessarily lie on
![]() $Z$
. When
$Z$
. When
![]() $Y$
is projective, we have the following result concerning Zariski closures of leaves of
$Y$
is projective, we have the following result concerning Zariski closures of leaves of
![]() $\mathscr{F}$
.
$\mathscr{F}$
.
Proposition 3.1. Let
![]() $Y$
be a reduced irreducible projective variety. Let
$Y$
be a reduced irreducible projective variety. Let
![]() $\mathscr{F}$
be a meromorphic foliation on
$\mathscr{F}$
be a meromorphic foliation on
![]() $Y$
,
$Y$
,
![]() $\text{ Sing}(\mathscr{F})\supset \text{Sing}(Y)$
be the singular locus of
$\text{ Sing}(\mathscr{F})\supset \text{Sing}(Y)$
be the singular locus of
![]() $\mathscr{F}$
, and write
$\mathscr{F}$
, and write
![]() $\text{Reg}(\mathscr{F}):=Y-\text{Sing}(\mathscr{F})$
. Denote by
$\text{Reg}(\mathscr{F}):=Y-\text{Sing}(\mathscr{F})$
. Denote by
![]() ${\mathcal{T}}_{Y}$
the tangent sheaf of
${\mathcal{T}}_{Y}$
the tangent sheaf of
![]() $Y$
, and by
$Y$
, and by
![]() ${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
the tangent subsheaf of
${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
the tangent subsheaf of
![]() $\mathscr{F}$
. Now let
$\mathscr{F}$
. Now let
![]() $y_{0}\in \text{Reg}(\mathscr{F})$
, and
$y_{0}\in \text{Reg}(\mathscr{F})$
, and
![]() ${\mathcal{L}}\,\subset \,\text{Reg}(\mathscr{F})$
be the leaf of
${\mathcal{L}}\,\subset \,\text{Reg}(\mathscr{F})$
be the leaf of
![]() $\mathscr{F}|_{\text{Reg}(\mathscr{F})}$
passing through
$\mathscr{F}|_{\text{Reg}(\mathscr{F})}$
passing through
![]() $y_{0}$
. Denote by
$y_{0}$
. Denote by
![]() $Z\,\subset \,Y$
the Zariski closure of
$Z\,\subset \,Y$
the Zariski closure of
![]() ${\mathcal{L}}$
. Then,
${\mathcal{L}}$
. Then,
![]() $Z$
is saturated with respect to the meromorphic foliation
$Z$
is saturated with respect to the meromorphic foliation
![]() $\mathscr{F}$
.
$\mathscr{F}$
.
Proof. Note first of all that
![]() ${\mathcal{L}}\not \subset \text{Sing}(Z)$
, otherwise the Zariski closure of
${\mathcal{L}}\not \subset \text{Sing}(Z)$
, otherwise the Zariski closure of
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $Y$
would be contained in Sing
$Y$
would be contained in Sing
![]() $(Z)\subsetneq Z$
, contradicting the assumption
$(Z)\subsetneq Z$
, contradicting the assumption
![]() $Z=\overline{{\mathcal{L}}}^{\mathscr{Z}\!ar}\!$
. On the projective subvariety
$Z=\overline{{\mathcal{L}}}^{\mathscr{Z}\!ar}\!$
. On the projective subvariety
![]() $Z\,\subset \,Y$
consider the coherent subsheaf
$Z\,\subset \,Y$
consider the coherent subsheaf
![]() $\mathscr{E}:={\mathcal{T}}_{\mathscr{F}}|_{Z}+{\mathcal{T}}_{Z}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
, where
$\mathscr{E}:={\mathcal{T}}_{\mathscr{F}}|_{Z}+{\mathcal{T}}_{Z}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
, where
![]() ${\mathcal{T}}_{\mathscr{F}}|_{Z}:={\mathcal{T}}_{\mathscr{F}}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Z},{\mathcal{T}}_{Y}|_{Z}:={\mathcal{T}}_{Y}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Z}$
. Let
${\mathcal{T}}_{\mathscr{F}}|_{Z}:={\mathcal{T}}_{\mathscr{F}}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Z},{\mathcal{T}}_{Y}|_{Z}:={\mathcal{T}}_{Y}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Z}$
. Let
![]() $\unicode[STIX]{x1D6F4}\,\subset \,Z$
be the union of Sing
$\unicode[STIX]{x1D6F4}\,\subset \,Z$
be the union of Sing
![]() $(Z)$
,
$(Z)$
,
![]() $\text{Sing}(\mathscr{F})\,\cap \,Z$
, and the locus of points
$\text{Sing}(\mathscr{F})\,\cap \,Z$
, and the locus of points
![]() $x\in \text{Reg}(Z)\,\cap \,\text{Reg}(Y)$
where
$x\in \text{Reg}(Z)\,\cap \,\text{Reg}(Y)$
where
![]() $\mathscr{E}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
fails to be a locally free subsheaf. Then,
$\mathscr{E}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
fails to be a locally free subsheaf. Then,
![]() $\unicode[STIX]{x1D6F4}\subsetneq Z$
is a projective subvariety and we must have
$\unicode[STIX]{x1D6F4}\subsetneq Z$
is a projective subvariety and we must have
![]() ${\mathcal{L}}\not \subset \unicode[STIX]{x1D6F4}$
, otherwise the Zariski closure of
${\mathcal{L}}\not \subset \unicode[STIX]{x1D6F4}$
, otherwise the Zariski closure of
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $Y$
would be contained in
$Y$
would be contained in
![]() $\unicode[STIX]{x1D6F4}\subsetneq Z$
, and we reach the same contradiction. Thus, there exists
$\unicode[STIX]{x1D6F4}\subsetneq Z$
, and we reach the same contradiction. Thus, there exists
![]() $y_{1}\in {\mathcal{L}}\,\cap \,\text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})$
such that the coherent subsheaf
$y_{1}\in {\mathcal{L}}\,\cap \,\text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})$
such that the coherent subsheaf
![]() $\mathscr{E}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
is a locally free subsheaf at
$\mathscr{E}\,\subset \,{\mathcal{T}}_{Y}|_{Z}$
is a locally free subsheaf at
![]() $y_{1}$
. On
$y_{1}$
. On
![]() $Z-\unicode[STIX]{x1D6F4}\,\subset \,\text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})\,\subset \,\text{Reg}(Z)\,\cap \,\text{Reg}(Y)$
we have
$Z-\unicode[STIX]{x1D6F4}\,\subset \,\text{Reg}(Z)\,\cap \,\text{Reg}(\mathscr{F})\,\subset \,\text{Reg}(Z)\,\cap \,\text{Reg}(Y)$
we have
![]() $\mathscr{E}|_{Z-\unicode[STIX]{x1D6F4}}={\mathcal{O}}(E)$
for some holomorphic vector subbundle
$\mathscr{E}|_{Z-\unicode[STIX]{x1D6F4}}={\mathcal{O}}(E)$
for some holomorphic vector subbundle
![]() $E\,\subset \,T_{Z-\unicode[STIX]{x1D6F4}}$
. Since
$E\,\subset \,T_{Z-\unicode[STIX]{x1D6F4}}$
. Since
![]() ${\mathcal{T}}_{\mathscr{F},y_{1}}\,\subset \,{\mathcal{T}}_{Z,y_{1}}$
we must have
${\mathcal{T}}_{\mathscr{F},y_{1}}\,\subset \,{\mathcal{T}}_{Z,y_{1}}$
we must have
![]() $E_{y_{1}}=T_{Z,y_{1}}$
, so that rank
$E_{y_{1}}=T_{Z,y_{1}}$
, so that rank
![]() $(E)=\dim (E_{y_{1}})=\dim (Z)$
. It follows that
$(E)=\dim (E_{y_{1}})=\dim (Z)$
. It follows that
![]() $E=T_{Z-\unicode[STIX]{x1D6F4}}$
. Writing
$E=T_{Z-\unicode[STIX]{x1D6F4}}$
. Writing
![]() ${\mathcal{T}}_{\mathscr{F}}|_{\text{Reg}(\mathscr{F})}={\mathcal{O}}(F)$
for some
${\mathcal{T}}_{\mathscr{F}}|_{\text{Reg}(\mathscr{F})}={\mathcal{O}}(F)$
for some
![]() $F\,\subset \,T_{Y}|_{\text{Reg}(\mathscr{F})}$
we must have
$F\,\subset \,T_{Y}|_{\text{Reg}(\mathscr{F})}$
we must have
![]() $F_{y}+T_{Z,y}=T_{Z,y}$
for all
$F_{y}+T_{Z,y}=T_{Z,y}$
for all
![]() $y\in Z-\unicode[STIX]{x1D6F4}$
, i.e.,
$y\in Z-\unicode[STIX]{x1D6F4}$
, i.e.,
![]() $F|_{Z-\unicode[STIX]{x1D6F4}}\,\subset \,T_{Z-\unicode[STIX]{x1D6F4}}$
. As a consequence,
$F|_{Z-\unicode[STIX]{x1D6F4}}\,\subset \,T_{Z-\unicode[STIX]{x1D6F4}}$
. As a consequence,
![]() $Z$
is saturated with respect to the meromorphic foliation
$Z$
is saturated with respect to the meromorphic foliation
![]() $\mathscr{F}$
, as desired.◻
$\mathscr{F}$
, as desired.◻
Let
![]() $M$
be a complex manifold,
$M$
be a complex manifold,
![]() $\unicode[STIX]{x1D70B}:\widetilde{M}\rightarrow M$
be a covering map, and
$\unicode[STIX]{x1D70B}:\widetilde{M}\rightarrow M$
be a covering map, and
![]() $Y\,\subset \,M$
be an irreducible subvariety. Let
$Y\,\subset \,M$
be an irreducible subvariety. Let
![]() ${\mathcal{H}}$
be a reduced irreducible complex space and
${\mathcal{H}}$
be a reduced irreducible complex space and
![]() ${\mathcal{R}}\,\subset \,{\mathcal{H}}\times \widetilde{M}$
be a subvariety such that the canonical projection
${\mathcal{R}}\,\subset \,{\mathcal{H}}\times \widetilde{M}$
be a subvariety such that the canonical projection
![]() $\unicode[STIX]{x1D70E}:{\mathcal{R}}\rightarrow {\mathcal{H}}$
is surjective and the fibers
$\unicode[STIX]{x1D70E}:{\mathcal{R}}\rightarrow {\mathcal{H}}$
is surjective and the fibers
![]() $\unicode[STIX]{x1D70E}^{-1}(t)=:\{t\}\times R_{t}$
are equidimensional. Denote by
$\unicode[STIX]{x1D70E}^{-1}(t)=:\{t\}\times R_{t}$
are equidimensional. Denote by
![]() $\unicode[STIX]{x1D708}:{\mathcal{H}}\times \widetilde{M}\rightarrow \widetilde{M}$
the canonical projection. We have the following notion of uniruling of subvarieties
$\unicode[STIX]{x1D708}:{\mathcal{H}}\times \widetilde{M}\rightarrow \widetilde{M}$
the canonical projection. We have the following notion of uniruling of subvarieties
![]() $Y\,\subset \,M$
. In what follows openness and denseness of subsets are defined in terms of the complex topology.
$Y\,\subset \,M$
. In what follows openness and denseness of subsets are defined in terms of the complex topology.
Definition 3.1. We say that
![]() $Y\,\subset \,M$
is uniruled by subvarieties belonging to
$Y\,\subset \,M$
is uniruled by subvarieties belonging to
![]() ${\mathcal{H}}$
if and only if there exists a dense open subset
${\mathcal{H}}$
if and only if there exists a dense open subset
![]() ${\mathcal{O}}\,\subset \,\text{Reg}(Y)$
for which the following statement
${\mathcal{O}}\,\subset \,\text{Reg}(Y)$
for which the following statement
![]() $(\sharp )$
holds for every point
$(\sharp )$
holds for every point
![]() $x_{0}\in {\mathcal{O}}$
.
$x_{0}\in {\mathcal{O}}$
.
![]() $(\sharp )$
There exist an open neighborhood
$(\sharp )$
There exist an open neighborhood
![]() $U_{x_{0}}\,\subset \,{\mathcal{O}}$
of
$U_{x_{0}}\,\subset \,{\mathcal{O}}$
of
![]() $x_{0}$
and a point
$x_{0}$
and a point
![]() $t_{0}\in \text{Reg}({\mathcal{H}})$
satisfying
$t_{0}\in \text{Reg}({\mathcal{H}})$
satisfying
![]() $(t_{0},x_{0})\in \text{Reg}({\mathcal{R}})$
, a complex submanifold
$(t_{0},x_{0})\in \text{Reg}({\mathcal{R}})$
, a complex submanifold
![]() ${\mathcal{S}}\,\subset \,{\mathcal{G}}\,\subset \,{\mathcal{H}}$
of some open subset
${\mathcal{S}}\,\subset \,{\mathcal{G}}\,\subset \,{\mathcal{H}}$
of some open subset
![]() ${\mathcal{G}}\,\subset \,{\mathcal{H}}$
and a smooth neighborhood
${\mathcal{G}}\,\subset \,{\mathcal{H}}$
and a smooth neighborhood
![]() $\mathscr{U}_{t_{0},x_{0}}\,\subset \,\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
of
$\mathscr{U}_{t_{0},x_{0}}\,\subset \,\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
of
![]() $(t_{0},x_{0})$
such that
$(t_{0},x_{0})$
such that
![]() $\unicode[STIX]{x1D70E}|_{\mathscr{U}_{t_{0},x_{0}}}:\mathscr{U}_{t_{0},x_{0}}\rightarrow {\mathcal{S}}$
is a holomorphic submersion and such that
$\unicode[STIX]{x1D70E}|_{\mathscr{U}_{t_{0},x_{0}}}:\mathscr{U}_{t_{0},x_{0}}\rightarrow {\mathcal{S}}$
is a holomorphic submersion and such that
![]() $\unicode[STIX]{x1D70B}\,\circ \,\unicode[STIX]{x1D708}|_{\mathscr{U}_{t_{0},x_{0}}}:\mathscr{U}_{t_{0},x_{0}}\rightarrow M$
maps
$\unicode[STIX]{x1D70B}\,\circ \,\unicode[STIX]{x1D708}|_{\mathscr{U}_{t_{0},x_{0}}}:\mathscr{U}_{t_{0},x_{0}}\rightarrow M$
maps
![]() $\mathscr{U}_{t_{0},x_{0}}$
biholomorphically onto
$\mathscr{U}_{t_{0},x_{0}}$
biholomorphically onto
![]() $U_{x_{0}}\,\subset \,Y\,\subset \,M$
.
$U_{x_{0}}\,\subset \,Y\,\subset \,M$
.
We will apply the notion of uniruling to the case where
![]() $M=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}=X_{\unicode[STIX]{x1D6E4}}$
is a complex ball quotient by a torsion-free lattice
$M=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}=X_{\unicode[STIX]{x1D6E4}}$
is a complex ball quotient by a torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
equipped with the quasi-projective structure given by
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$
equipped with the quasi-projective structure given by
![]() $X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
,
$X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
,
![]() ${\mathcal{H}}$
is some
${\mathcal{H}}$
is some
![]() $G$
-invariant irreducible subvariety of Chow
$G$
-invariant irreducible subvariety of Chow
![]() $(\mathbb{P}^{n})$
, and where
$(\mathbb{P}^{n})$
, and where
![]() $Y\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is an algebraic subvariety. We start with some preparation relating meromorphic foliations to meromorphic sections of Grassmann bundles.
$Y\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is an algebraic subvariety. We start with some preparation relating meromorphic foliations to meromorphic sections of Grassmann bundles.
Let
![]() $M$
be a complex manifold,
$M$
be a complex manifold,
![]() $Y\,\subset \,M$
be an irreducible subvariety, and
$Y\,\subset \,M$
be an irreducible subvariety, and
![]() ${\mathcal{T}}_{Y}\,\subset \,{\mathcal{T}}_{M}|_{Y}$
be the tangent sheaf of
${\mathcal{T}}_{Y}\,\subset \,{\mathcal{T}}_{M}|_{Y}$
be the tangent sheaf of
![]() $Y$
. Let
$Y$
. Let
![]() ${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
be the tangent sheaf of a meromorphic foliation
${\mathcal{T}}_{\mathscr{F}}\,\subset \,{\mathcal{T}}_{Y}$
be the tangent sheaf of a meromorphic foliation
![]() $\mathscr{F}$
of leaf dimension
$\mathscr{F}$
of leaf dimension
![]() $r$
,
$r$
,
![]() $0<r<\dim (M)$
, defined on
$0<r<\dim (M)$
, defined on
![]() $Y$
. Write
$Y$
. Write
![]() $B:=\text{Sing}(\mathscr{F})$
, and write
$B:=\text{Sing}(\mathscr{F})$
, and write
![]() $F\,\subset \,T_{Y-B}$
for the involutive holomorphic distribution such that
$F\,\subset \,T_{Y-B}$
for the involutive holomorphic distribution such that
![]() $T_{\mathscr{F}}={\mathcal{O}}(F)$
. Define the holomorphic section
$T_{\mathscr{F}}={\mathcal{O}}(F)$
. Define the holomorphic section
![]() $\unicode[STIX]{x1D711}:Y-B\rightarrow \text{Gr}(r,T_{M})$
by setting
$\unicode[STIX]{x1D711}:Y-B\rightarrow \text{Gr}(r,T_{M})$
by setting
![]() $\unicode[STIX]{x1D711}(y)=[F_{y}]\in \text{Gr}(r,T_{Y,y})\,\subset \,\text{Gr}(r,T_{M,y})$
. Since
$\unicode[STIX]{x1D711}(y)=[F_{y}]\in \text{Gr}(r,T_{Y,y})\,\subset \,\text{Gr}(r,T_{M,y})$
. Since
![]() $\mathscr{F}$
is locally finitely generated, at every point
$\mathscr{F}$
is locally finitely generated, at every point
![]() $y_{0}\in Y$
, there exist
$y_{0}\in Y$
, there exist
![]() $r$
holomorphic sections
$r$
holomorphic sections
![]() $\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{r}\in \unicode[STIX]{x1D6E4}(U,{\mathcal{T}}|_{{\mathcal{F}}})$
defined on some neighborhood
$\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{r}\in \unicode[STIX]{x1D6E4}(U,{\mathcal{T}}|_{{\mathcal{F}}})$
defined on some neighborhood
![]() $U$
of
$U$
of
![]() $y_{0}$
, such that
$y_{0}$
, such that
![]() $\unicode[STIX]{x1D712}_{1}(y^{\prime }),\ldots ,\unicode[STIX]{x1D712}_{r}(y^{\prime })$
span
$\unicode[STIX]{x1D712}_{1}(y^{\prime }),\ldots ,\unicode[STIX]{x1D712}_{r}(y^{\prime })$
span
![]() ${\mathcal{T}}_{\mathscr{F},y^{\prime }}$
at a general point
${\mathcal{T}}_{\mathscr{F},y^{\prime }}$
at a general point
![]() $y^{\prime }\in U-B$
. Then, by using Plücker coordinates, the formula
$y^{\prime }\in U-B$
. Then, by using Plücker coordinates, the formula
![]() $\unicode[STIX]{x1D6F7}(y)=[\unicode[STIX]{x1D712}_{1}(y)\wedge \cdots \wedge \unicode[STIX]{x1D712}_{r}(y)]\in \text{Gr}(r,T_{M,y})\,\subset \,\mathbb{P}(\unicode[STIX]{x1D6EC}^{r}T_{M,y})$
determines a unique meromorphic section over
$\unicode[STIX]{x1D6F7}(y)=[\unicode[STIX]{x1D712}_{1}(y)\wedge \cdots \wedge \unicode[STIX]{x1D712}_{r}(y)]\in \text{Gr}(r,T_{M,y})\,\subset \,\mathbb{P}(\unicode[STIX]{x1D6EC}^{r}T_{M,y})$
determines a unique meromorphic section over
![]() $U$
of
$U$
of
![]() $\text{Gr}(r,T_{M})$
extending
$\text{Gr}(r,T_{M})$
extending
![]() $\unicode[STIX]{x1D711}|_{U-B}$
. From uniqueness it follows that
$\unicode[STIX]{x1D711}|_{U-B}$
. From uniqueness it follows that
![]() $\unicode[STIX]{x1D711}$
extends meromorphically to
$\unicode[STIX]{x1D711}$
extends meromorphically to
![]() $\unicode[STIX]{x1D711}^{\flat }:Y{\dashrightarrow}\text{Gr}(r,T_{M})$
. We call
$\unicode[STIX]{x1D711}^{\flat }:Y{\dashrightarrow}\text{Gr}(r,T_{M})$
. We call
![]() $\unicode[STIX]{x1D711}^{\flat }$
the meromorphic section of
$\unicode[STIX]{x1D711}^{\flat }$
the meromorphic section of
![]() $\text{Gr}(r,T_{M})$
associated to
$\text{Gr}(r,T_{M})$
associated to
![]() $(Y,\mathscr{F})$
. We have the following lemma on meromorphic extensions of foliations.
$(Y,\mathscr{F})$
. We have the following lemma on meromorphic extensions of foliations.
Lemma 3.1. Let
![]() $M$
be a complex manifold,
$M$
be a complex manifold,
![]() $Y\,\subset \,M$
be an irreducible normal complex-analytic subvariety and
$Y\,\subset \,M$
be an irreducible normal complex-analytic subvariety and
![]() $A\,\subset \,Y$
be a complex-analytic subvariety containing
$A\,\subset \,Y$
be a complex-analytic subvariety containing
![]() $\text{ Sing}(Y)$
. Let
$\text{ Sing}(Y)$
. Let
![]() $\mathscr{F}$
be a meromorphic foliation on
$\mathscr{F}$
be a meromorphic foliation on
![]() $Y-A$
and
$Y-A$
and
![]() $T_{\mathscr{F}}\,\subset \,T_{Y-A}$
be its tangent sheaf. Let
$T_{\mathscr{F}}\,\subset \,T_{Y-A}$
be its tangent sheaf. Let
![]() $\unicode[STIX]{x1D711}^{\flat }:Y-A{\dashrightarrow}\text{Gr}(r,T_{M})$
be the meromorphic section associated to
$\unicode[STIX]{x1D711}^{\flat }:Y-A{\dashrightarrow}\text{Gr}(r,T_{M})$
be the meromorphic section associated to
![]() $(Y-A,\mathscr{F})$
. Then, the foliation
$(Y-A,\mathscr{F})$
. Then, the foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $Y-A$
admits a meromorphic extension to
$Y-A$
admits a meromorphic extension to
![]() $Y$
if and only if
$Y$
if and only if
![]() $\unicode[STIX]{x1D711}^{\flat }$
extends meromorphically from
$\unicode[STIX]{x1D711}^{\flat }$
extends meromorphically from
![]() $Y-A$
to
$Y-A$
to
![]() $Y$
.
$Y$
.
Proof. The forward implication has been established (without assuming
![]() $Y$
normal). Conversely, assume that
$Y$
normal). Conversely, assume that
![]() $\unicode[STIX]{x1D711}^{\flat }$
admits a meromorphic extension to
$\unicode[STIX]{x1D711}^{\flat }$
admits a meromorphic extension to
![]() $\unicode[STIX]{x1D711}^{\sharp }:Y{\dashrightarrow}\text{Gr}(r,T_{M})$
. Let
$\unicode[STIX]{x1D711}^{\sharp }:Y{\dashrightarrow}\text{Gr}(r,T_{M})$
. Let
![]() $H\,\subset \,Y$
be the subvariety of codimension
$H\,\subset \,Y$
be the subvariety of codimension
![]() ${\geqslant}2$
over which either
${\geqslant}2$
over which either
![]() $Y$
is singular or
$Y$
is singular or
![]() $\unicode[STIX]{x1D711}^{\sharp }$
fails to be holomorphic. Write
$\unicode[STIX]{x1D711}^{\sharp }$
fails to be holomorphic. Write
![]() $B:=\text{Sing}(\mathscr{F})\,\subset \,Y-A$
,
$B:=\text{Sing}(\mathscr{F})\,\subset \,Y-A$
,
![]() $\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}^{\sharp }|_{Y-H}$
, and
$\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}^{\sharp }|_{Y-H}$
, and
![]() $\unicode[STIX]{x1D6FC}:\text{Gr}(r,T_{M})\rightarrow M$
for the canonical projection. Let
$\unicode[STIX]{x1D6FC}:\text{Gr}(r,T_{M})\rightarrow M$
for the canonical projection. Let
![]() $F\,\subset \,T_{Y-H}$
be the distribution such that
$F\,\subset \,T_{Y-H}$
be the distribution such that
![]() $T_{\mathscr{F}}|_{Y-H}={\mathcal{O}}(F)$
and define
$T_{\mathscr{F}}|_{Y-H}={\mathcal{O}}(F)$
and define
![]() $Y^{\prime }\,\subset \,\text{Gr}(r,T_{M})$
to be the topological closure of
$Y^{\prime }\,\subset \,\text{Gr}(r,T_{M})$
to be the topological closure of
![]() $Y^{0}:=\unicode[STIX]{x1D713}(Y-H)$
. The universal rank-
$Y^{0}:=\unicode[STIX]{x1D713}(Y-H)$
. The universal rank-
![]() $r$
bundle on
$r$
bundle on
![]() $\text{Gr}(r,T_{M})$
restricts to
$\text{Gr}(r,T_{M})$
restricts to
![]() $Y^{\prime }$
to give a rank-
$Y^{\prime }$
to give a rank-
![]() $r$
holomorphic vector bundle
$r$
holomorphic vector bundle
![]() $F^{\prime }$
over
$F^{\prime }$
over
![]() $Y^{\prime }$
such that
$Y^{\prime }$
such that
![]() $F^{\prime }|_{Y^{0}}$
is the tautological lifting of the holomorphic rank-
$F^{\prime }|_{Y^{0}}$
is the tautological lifting of the holomorphic rank-
![]() $r$
vector subbundle
$r$
vector subbundle
![]() $F\,\subset \,T_{Y-H}$
. By the direct image theorem,
$F\,\subset \,T_{Y-H}$
. By the direct image theorem,
![]() $\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}(F^{\prime }))=:{\mathcal{E}}$
is a coherent sheaf on
$\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}(F^{\prime }))=:{\mathcal{E}}$
is a coherent sheaf on
![]() $Y$
such that
$Y$
such that
![]() ${\mathcal{E}}|_{Y-H}={\mathcal{O}}(F)$
and such that
${\mathcal{E}}|_{Y-H}={\mathcal{O}}(F)$
and such that
![]() ${\mathcal{E}}|_{Y-A-B}={\mathcal{T}}_{\mathscr{F}}|_{Y-A-B}$
. Since
${\mathcal{E}}|_{Y-A-B}={\mathcal{T}}_{\mathscr{F}}|_{Y-A-B}$
. Since
![]() $Y$
is normal, for any open subset
$Y$
is normal, for any open subset
![]() $U\,\subset \,Y$
and any
$U\,\subset \,Y$
and any
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(U,{\mathcal{E}})$
,
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(U,{\mathcal{E}})$
,
![]() $\unicode[STIX]{x1D70E}|_{U-H}\in \unicode[STIX]{x1D6E4}(U-H,{\mathcal{O}}(F))$
extends holomorphically to give
$\unicode[STIX]{x1D70E}|_{U-H}\in \unicode[STIX]{x1D6E4}(U-H,{\mathcal{O}}(F))$
extends holomorphically to give
![]() $\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6E4}(U,{\mathcal{T}}_{Y})$
. The coherent sheaf
$\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6E4}(U,{\mathcal{T}}_{Y})$
. The coherent sheaf
![]() ${\mathcal{E}}$
can thus be identified as a coherent subsheaf of
${\mathcal{E}}$
can thus be identified as a coherent subsheaf of
![]() ${\mathcal{T}}_{Y}$
and its double dual
${\mathcal{T}}_{Y}$
and its double dual
![]() ${\mathcal{E}}^{\ast \ast }$
is mapped canonically onto a coherent subsheaf
${\mathcal{E}}^{\ast \ast }$
is mapped canonically onto a coherent subsheaf
![]() $\mathscr{S}\,\subset \,{\mathcal{T}}_{Y}$
extending
$\mathscr{S}\,\subset \,{\mathcal{T}}_{Y}$
extending
![]() ${\mathcal{O}}(F)$
such that
${\mathcal{O}}(F)$
such that
![]() ${\mathcal{T}}_{Y}/\mathscr{S}$
is torsion-free and
${\mathcal{T}}_{Y}/\mathscr{S}$
is torsion-free and
![]() $\mathscr{S}|_{Y-A}={\mathcal{T}}_{\mathscr{F}}$
. As a consequence,
$\mathscr{S}|_{Y-A}={\mathcal{T}}_{\mathscr{F}}$
. As a consequence,
![]() $\mathscr{S}$
is the tangent sheaf of a meromorphic foliation
$\mathscr{S}$
is the tangent sheaf of a meromorphic foliation
![]() $\mathscr{F}^{\sharp }$
on
$\mathscr{F}^{\sharp }$
on
![]() $Y$
extending
$Y$
extending
![]() $\mathscr{F}$
, as desired.◻
$\mathscr{F}$
, as desired.◻
We return now to the study of Zariski closures of images of algebraic subsets
![]() $S\,\subset \,\mathbb{B}^{n}$
,
$S\,\subset \,\mathbb{B}^{n}$
,
![]() $n\geqslant 2$
, under the universal covering map
$n\geqslant 2$
, under the universal covering map
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
for a torsion-free lattice
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
for a torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
,
![]() $X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}$
. When
$X_{\unicode[STIX]{x1D6E4}}:=\mathbb{B}^{n}$
. When
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is not cocompact, we embed
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is not cocompact, we embed
![]() $X_{\unicode[STIX]{x1D6E4}}$
into its minimal compactification
$X_{\unicode[STIX]{x1D6E4}}$
into its minimal compactification
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
by adding a finite number of normal isolated singularities. Recall that
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
by adding a finite number of normal isolated singularities. Recall that
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
is projective and
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
is projective and
![]() $X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
inherits a canonical quasi-projective structure.
$X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
inherits a canonical quasi-projective structure.
Recall that the irreducible algebraic subset
![]() $S\,\subset \,\mathbb{B}^{n}$
in the statement of Main Theorem is an irreducible component of
$S\,\subset \,\mathbb{B}^{n}$
in the statement of Main Theorem is an irreducible component of
![]() $W_{0}\,\cap \,\mathbb{B}^{n}$
for some irreducible projective subvariety
$W_{0}\,\cap \,\mathbb{B}^{n}$
for some irreducible projective subvariety
![]() $W_{0}\,\subset \,\mathbb{P}^{n}$
. Consider the universal family
$W_{0}\,\subset \,\mathbb{P}^{n}$
. Consider the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, where
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, where
![]() ${\mathcal{K}}$
is an irreducible component of the Chow space of
${\mathcal{K}}$
is an irreducible component of the Chow space of
![]() $\mathbb{P}^{n}$
containing
$\mathbb{P}^{n}$
containing
![]() $[W_{0}]$
. By means of the stratification given by singular loci we are going to define a
$[W_{0}]$
. By means of the stratification given by singular loci we are going to define a
![]() $G$
-invariant irreducible subvariety
$G$
-invariant irreducible subvariety
![]() ${\mathcal{H}}\,\subset \,{\mathcal{K}}$
,
${\mathcal{H}}\,\subset \,{\mathcal{K}}$
,
![]() $[W_{0}]\in {\mathcal{H}}$
, such that
$[W_{0}]\in {\mathcal{H}}$
, such that
![]() $[W_{0}]$
is a smooth point of
$[W_{0}]$
is a smooth point of
![]() ${\mathcal{H}}$
, and consider the restriction over
${\mathcal{H}}$
, and consider the restriction over
![]() ${\mathcal{H}}$
of the universal family
${\mathcal{H}}$
of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, as follows. Write
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, as follows. Write
![]() ${\mathcal{K}}_{1}:={\mathcal{K}}$
, and consider the Zariski open subset
${\mathcal{K}}_{1}:={\mathcal{K}}$
, and consider the Zariski open subset
![]() ${\mathcal{K}}_{1}^{0}\,\subset \,{\mathcal{K}}_{1}$
consisting of smooth points
${\mathcal{K}}_{1}^{0}\,\subset \,{\mathcal{K}}_{1}$
consisting of smooth points
![]() $[F]\in {\mathcal{K}}$
such that
$[F]\in {\mathcal{K}}$
such that
![]() $F\,\subset \,\mathbb{P}^{n}$
is irreducible and reduced. In case
$F\,\subset \,\mathbb{P}^{n}$
is irreducible and reduced. In case
![]() $[W_{0}]\in {\mathcal{K}}_{1}^{0}$
we define
$[W_{0}]\in {\mathcal{K}}_{1}^{0}$
we define
![]() ${\mathcal{H}}={\mathcal{K}}_{1}={\mathcal{K}}$
. Otherwise
${\mathcal{H}}={\mathcal{K}}_{1}={\mathcal{K}}$
. Otherwise
![]() $[W_{0}]\in {\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
. Now let
$[W_{0}]\in {\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
. Now let
![]() ${\mathcal{K}}_{2}\subsetneq {\mathcal{K}}_{1}$
be an irreducible component of
${\mathcal{K}}_{2}\subsetneq {\mathcal{K}}_{1}$
be an irreducible component of
![]() ${\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
containing the point
${\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
containing the point
![]() $[W_{0}]$
. Since
$[W_{0}]$
. Since
![]() $G=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
is connected, the irreducible component
$G=\mathbb{P}\text{GL}(n+1,\mathbb{C})$
is connected, the irreducible component
![]() ${\mathcal{K}}_{2}$
of the
${\mathcal{K}}_{2}$
of the
![]() $G$
-invariant subvariety
$G$
-invariant subvariety
![]() ${\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
is also
${\mathcal{K}}_{1}-{\mathcal{K}}_{1}^{0}$
is also
![]() $G$
-invariant. Define now
$G$
-invariant. Define now
![]() ${\mathcal{K}}_{2}^{0}\,\subset \,{\mathcal{K}}_{2}$
to consist of all
${\mathcal{K}}_{2}^{0}\,\subset \,{\mathcal{K}}_{2}$
to consist of all
![]() $[F]\in {\mathcal{K}}_{2}$
such that
$[F]\in {\mathcal{K}}_{2}$
such that
![]() $F$
is irreducible and reduced. Iterating the process, we obtain a finite sequence of
$F$
is irreducible and reduced. Iterating the process, we obtain a finite sequence of
![]() $G$
-invariant irreducible subvarieties
$G$
-invariant irreducible subvarieties
![]() ${\mathcal{K}}_{m}\subsetneq \cdots \subsetneq {\mathcal{K}}_{1}={\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
such that
${\mathcal{K}}_{m}\subsetneq \cdots \subsetneq {\mathcal{K}}_{1}={\mathcal{K}}\,\subset \,\text{Chow}(\mathbb{P}^{n})$
such that
![]() $[W_{0}]$
is a smooth point on
$[W_{0}]$
is a smooth point on
![]() ${\mathcal{K}}_{m}$
. We define now
${\mathcal{K}}_{m}$
. We define now
![]() ${\mathcal{H}}={\mathcal{K}}_{m}$
and
${\mathcal{H}}={\mathcal{K}}_{m}$
and
![]() $\mathscr{V}:=\unicode[STIX]{x1D70C}^{-1}({\mathcal{K}}_{m})$
. Clearly
$\mathscr{V}:=\unicode[STIX]{x1D70C}^{-1}({\mathcal{K}}_{m})$
. Clearly
![]() ${\mathcal{H}}$
is also
${\mathcal{H}}$
is also
![]() $G$
-invariant. We denote by
$G$
-invariant. We denote by
![]() $\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
the restriction of the universal family
$\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
the restriction of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
over
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
over
![]() ${\mathcal{H}}\,\subset \,{\mathcal{K}}$
.
${\mathcal{H}}\,\subset \,{\mathcal{K}}$
.
A torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
acts properly discontinuously on
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
acts properly discontinuously on
![]() $\mathscr{V}^{\prime }=\mathscr{V}|_{\mathbb{B}^{n}}$
without fixed points, and we have a quotient space
$\mathscr{V}^{\prime }=\mathscr{V}|_{\mathbb{B}^{n}}$
without fixed points, and we have a quotient space
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}:=\mathscr{V}^{\prime }/\unicode[STIX]{x1D6E4}$
equipped with a map
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}:=\mathscr{V}^{\prime }/\unicode[STIX]{x1D6E4}$
equipped with a map
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}=\mathbb{B}^{n}/\unicode[STIX]{x1D6E4}$
,
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
, realizing
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
, realizing
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
as a locally homogeneous holomorphic fiber subbundle of
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. The foliation
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
. The foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $\mathscr{U}$
restricts to
$\mathscr{U}$
restricts to
![]() $\mathscr{V}=\unicode[STIX]{x1D70C}^{-1}({\mathcal{H}})$
, and we will use the same notation
$\mathscr{V}=\unicode[STIX]{x1D70C}^{-1}({\mathcal{H}})$
, and we will use the same notation
![]() $\mathscr{F}$
for the restriction to
$\mathscr{F}$
for the restriction to
![]() $\mathscr{V}$
. The foliation
$\mathscr{V}$
. The foliation
![]() $\mathscr{F}$
descends to a foliation
$\mathscr{F}$
descends to a foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
.
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
.
In the case of torsion-free nonuniform lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
we will be dealing with quasi-projective varieties
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
we will be dealing with quasi-projective varieties
![]() $X_{\unicode[STIX]{x1D6E4}}$
and we have to consider their minimal compactifications
$X_{\unicode[STIX]{x1D6E4}}$
and we have to consider their minimal compactifications
![]() $X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
together with projective compactifications of various holomorphic fiber bundles over
$X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
together with projective compactifications of various holomorphic fiber bundles over
![]() $X_{\unicode[STIX]{x1D6E4}}$
. Recall that
$X_{\unicode[STIX]{x1D6E4}}$
. Recall that
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is embedded as a locally homogeneous holomorphic fiber subbundle into
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}:\mathscr{U}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
is embedded as a locally homogeneous holomorphic fiber subbundle into
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
,
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective by Proposition 2.4 and
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective by Proposition 2.4 and
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective by Proposition 2.5. In fact, identifying
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}\,\subset \,\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
is quasi-projective by Proposition 2.5. In fact, identifying
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
as a subset of
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
as a subset of
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
, compactifying
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
, compactifying
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
to a projective variety
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
to a projective variety
![]() $\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
and extending the canonical projection
$\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
and extending the canonical projection
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
to a holomorphic map
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}:\mathscr{P}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
to a holomorphic map
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
, the topological closure
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
, the topological closure
![]() $\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is a projective subvariety. The same proof as in Proposition 2.5 shows that for the holomorphic fiber bundle
$\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is a projective subvariety. The same proof as in Proposition 2.5 shows that for the holomorphic fiber bundle
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, the topological closure
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, the topological closure
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is a projective subvariety, and we have
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\mathbb{P}^{\ell }$
is a projective subvariety, and we have
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
,
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
,
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }|_{\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}}$
. We need now to extend
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:=\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }|_{\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}}$
. We need now to extend
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
to a meromorphic foliation
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
to a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
. Denoting the normalization of a reduced irreducible complex space
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
. Denoting the normalization of a reduced irreducible complex space
![]() $Y$
by
$Y$
by
![]() $Y^{\mathfrak{n}}$
,
$Y^{\mathfrak{n}}$
,
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
induces a meromorphic foliation
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
induces a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
, and the aforementioned extension problem on
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
, and the aforementioned extension problem on
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
is equivalently the problem of extending
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
is equivalently the problem of extending
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
meromorphically from
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
meromorphically from
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
to
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
to
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}^{\mathfrak{n}}$
, hence we may apply Lemma 3.1. For the purpose of proving the meromorphic extension of
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}^{\mathfrak{n}}$
, hence we may apply Lemma 3.1. For the purpose of proving the meromorphic extension of
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
to
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\mathfrak{n}}$
to
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}^{\mathfrak{n}}$
we will need the following Hartogs-type extension theorem for meromorphic functions in Mok and Zhang [Reference Mok and ZhangMZ19, Lemma 7.4].
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}^{\mathfrak{n}}$
we will need the following Hartogs-type extension theorem for meromorphic functions in Mok and Zhang [Reference Mok and ZhangMZ19, Lemma 7.4].
Lemma 3.2. Let
![]() $B$
be an irreducible projective variety, and
$B$
be an irreducible projective variety, and
![]() $E\,\subset \,B$
be a subvariety of codimension
$E\,\subset \,B$
be a subvariety of codimension
![]() ${\geqslant}2$
. Let
${\geqslant}2$
. Let
![]() ${\mathcal{X}}$
be an irreducible projective variety and
${\mathcal{X}}$
be an irreducible projective variety and
![]() $\unicode[STIX]{x1D6FC}:{\mathcal{X}}\rightarrow B$
be a surjective morphism. Let
$\unicode[STIX]{x1D6FC}:{\mathcal{X}}\rightarrow B$
be a surjective morphism. Let
![]() $\unicode[STIX]{x1D6FA}\,\subset \,B$
be an open subset in the complex topology and
$\unicode[STIX]{x1D6FA}\,\subset \,B$
be an open subset in the complex topology and
![]() $f$
be a meromorphic function on
$f$
be a meromorphic function on
![]() ${\mathcal{X}}|_{\unicode[STIX]{x1D6FA}-E}:=\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FA}-E)$
. Then,
${\mathcal{X}}|_{\unicode[STIX]{x1D6FA}-E}:=\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FA}-E)$
. Then,
![]() $f$
extends to a meromorphic function on
$f$
extends to a meromorphic function on
![]() ${\mathcal{X}}|_{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FA})$
.
${\mathcal{X}}|_{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FA})$
.
Remark.
The main point of Lemma 3.2 is that
![]() $\unicode[STIX]{x1D6FC}^{-1}(E)\,\subset \,{\mathcal{X}}$
may have irreducible components of codimension 1 even though
$\unicode[STIX]{x1D6FC}^{-1}(E)\,\subset \,{\mathcal{X}}$
may have irreducible components of codimension 1 even though
![]() $E\,\subset \,B$
is of codimension
$E\,\subset \,B$
is of codimension
![]() ${\geqslant}2$
. Realizing
${\geqslant}2$
. Realizing
![]() ${\mathcal{X}}\,\subset \,\mathbb{P}^{m}$
as a projective subvariety and writing
${\mathcal{X}}\,\subset \,\mathbb{P}^{m}$
as a projective subvariety and writing
![]() $X_{t}:=\unicode[STIX]{x1D6FC}^{-1}(t)$
, we define
$X_{t}:=\unicode[STIX]{x1D6FC}^{-1}(t)$
, we define
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FA}-E{\dashrightarrow}{\mathcal{H}}$
by
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FA}-E{\dashrightarrow}{\mathcal{H}}$
by
![]() $\unicode[STIX]{x1D711}(t)=[\text{Graph}(f|_{X_{t}})]\in {\mathcal{H}}$
for a general point
$\unicode[STIX]{x1D711}(t)=[\text{Graph}(f|_{X_{t}})]\in {\mathcal{H}}$
for a general point
![]() $t\in \unicode[STIX]{x1D6FA}-E$
, where
$t\in \unicode[STIX]{x1D6FA}-E$
, where
![]() ${\mathcal{H}}\,\subset \,\text{Chow}(\mathbb{P}^{m}\times \mathbb{P}^{1})$
is some irreducible component. By Hartogs’ extension,
${\mathcal{H}}\,\subset \,\text{Chow}(\mathbb{P}^{m}\times \mathbb{P}^{1})$
is some irreducible component. By Hartogs’ extension,
![]() $\unicode[STIX]{x1D711}$
extends meromorphically to
$\unicode[STIX]{x1D711}$
extends meromorphically to
![]() $\unicode[STIX]{x1D711}^{\sharp }:\unicode[STIX]{x1D6FA}{\dashrightarrow}{\mathcal{H}}$
, and the meromorphic extension
$\unicode[STIX]{x1D711}^{\sharp }:\unicode[STIX]{x1D6FA}{\dashrightarrow}{\mathcal{H}}$
, and the meromorphic extension
![]() $f^{\sharp }:{\mathcal{X}}|_{\unicode[STIX]{x1D6FA}}{\dashrightarrow}\mathbb{P}^{1}$
of
$f^{\sharp }:{\mathcal{X}}|_{\unicode[STIX]{x1D6FA}}{\dashrightarrow}\mathbb{P}^{1}$
of
![]() $f:{\mathcal{X}}|_{\unicode[STIX]{x1D6FA}-E}{\dashrightarrow}\mathbb{P}^{1}$
is defined by pulling back the universal family over
$f:{\mathcal{X}}|_{\unicode[STIX]{x1D6FA}-E}{\dashrightarrow}\mathbb{P}^{1}$
is defined by pulling back the universal family over
![]() ${\mathcal{H}}$
by
${\mathcal{H}}$
by
![]() $\unicode[STIX]{x1D711}^{\sharp }$
and projecting to the
$\unicode[STIX]{x1D711}^{\sharp }$
and projecting to the
![]() $\mathbb{P}^{1}$
factor of
$\mathbb{P}^{1}$
factor of
![]() $\mathbb{P}^{m}\times \mathbb{P}^{1}$
. For details cf. Mok and Zhang [Reference Mok and ZhangMZ19, Lemma 7.4].
$\mathbb{P}^{m}\times \mathbb{P}^{1}$
. For details cf. Mok and Zhang [Reference Mok and ZhangMZ19, Lemma 7.4].
We deduce from Lemma 3.2 the following extension theorem for meromorphic foliations. We will apply the setting of Lemma 3.1 to the case where
![]() $\unicode[STIX]{x1D6FA}=B$
and where
$\unicode[STIX]{x1D6FA}=B$
and where
![]() $B$
and
$B$
and
![]() ${\mathcal{X}}$
are normal.
${\mathcal{X}}$
are normal.
Lemma 3.3. Let
![]() $B$
be a normal irreducible projective variety, and
$B$
be a normal irreducible projective variety, and
![]() $E\,\subset \,B$
be a subvariety of codimension
$E\,\subset \,B$
be a subvariety of codimension
![]() ${\geqslant}2$
. Let
${\geqslant}2$
. Let
![]() ${\mathcal{X}}$
be a normal irreducible projective variety and
${\mathcal{X}}$
be a normal irreducible projective variety and
![]() $\unicode[STIX]{x1D6FC}:{\mathcal{X}}\rightarrow B$
be a surjective morphism. Let
$\unicode[STIX]{x1D6FC}:{\mathcal{X}}\rightarrow B$
be a surjective morphism. Let
![]() $\mathscr{L}$
be a meromorphic foliation on
$\mathscr{L}$
be a meromorphic foliation on
![]() ${\mathcal{X}}|_{B-E}:=\unicode[STIX]{x1D6FC}^{-1}(B-E)$
. Then,
${\mathcal{X}}|_{B-E}:=\unicode[STIX]{x1D6FC}^{-1}(B-E)$
. Then,
![]() $\mathscr{L}$
extends to a meromorphic foliation on
$\mathscr{L}$
extends to a meromorphic foliation on
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Proof. Let
![]() $r$
be the leaf dimension of the meromorphic foliation
$r$
be the leaf dimension of the meromorphic foliation
![]() $\mathscr{L}$
on
$\mathscr{L}$
on
![]() ${\mathcal{X}}|_{B-E}$
. Identify the total space
${\mathcal{X}}|_{B-E}$
. Identify the total space
![]() ${\mathcal{X}}\,\subset \,\mathbb{P}^{N}$
as a projective subvariety of some projective space
${\mathcal{X}}\,\subset \,\mathbb{P}^{N}$
as a projective subvariety of some projective space
![]() $\mathbb{P}^{N}$
. The tangent sheaf
$\mathbb{P}^{N}$
. The tangent sheaf
![]() ${\mathcal{T}}_{{\mathcal{X}}}$
is a saturated coherent subsheaf of
${\mathcal{T}}_{{\mathcal{X}}}$
is a saturated coherent subsheaf of
![]() ${\mathcal{T}}_{\mathbb{P}^{N}}|_{{\mathcal{X}}}={\mathcal{O}}(T_{\mathbb{P}^{N}}|_{{\mathcal{X}}})$
. The meromorphic foliation
${\mathcal{T}}_{\mathbb{P}^{N}}|_{{\mathcal{X}}}={\mathcal{O}}(T_{\mathbb{P}^{N}}|_{{\mathcal{X}}})$
. The meromorphic foliation
![]() $\mathscr{L}$
on
$\mathscr{L}$
on
![]() ${\mathcal{X}}|_{B-E}$
corresponds to a saturated coherent subsheaf
${\mathcal{X}}|_{B-E}$
corresponds to a saturated coherent subsheaf
![]() ${\mathcal{T}}_{\mathscr{L}}\,\subset \,{\mathcal{T}}_{{\mathcal{X}}|_{B-E}}$
of rank
${\mathcal{T}}_{\mathscr{L}}\,\subset \,{\mathcal{T}}_{{\mathcal{X}}|_{B-E}}$
of rank
![]() $r$
such that, outside a complex-analytic subvariety
$r$
such that, outside a complex-analytic subvariety
![]() ${\mathcal{A}}\,\subset \,{\mathcal{X}}|_{B-E}$
of codimension
${\mathcal{A}}\,\subset \,{\mathcal{X}}|_{B-E}$
of codimension
![]() ${\geqslant}2$
containing the singularity set Sing
${\geqslant}2$
containing the singularity set Sing
![]() $({\mathcal{X}}|_{B-E})$
of the normal projective variety
$({\mathcal{X}}|_{B-E})$
of the normal projective variety
![]() ${\mathcal{X}}|_{B-E}$
,
${\mathcal{X}}|_{B-E}$
,
![]() ${\mathcal{T}}_{\mathscr{L}}|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}={\mathcal{O}}(L)$
for some rank-
${\mathcal{T}}_{\mathscr{L}}|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}={\mathcal{O}}(L)$
for some rank-
![]() $r$
integrable holomorphic distribution
$r$
integrable holomorphic distribution
![]() $L\,\subset \,T_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}$
. The holomorphic distribution
$L\,\subset \,T_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}$
. The holomorphic distribution
![]() $L$
then defines a holomorphic section
$L$
then defines a holomorphic section
![]() $\unicode[STIX]{x1D713}$
of the Grassmann bundle
$\unicode[STIX]{x1D713}$
of the Grassmann bundle
![]() $\text{Gr}(r,T_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}})\,\subset \,\text{Gr}(r,T_{\mathbb{P}^{N}}|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}})$
over
$\text{Gr}(r,T_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}})\,\subset \,\text{Gr}(r,T_{\mathbb{P}^{N}}|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}})$
over
![]() ${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
. Given a point
${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
. Given a point
![]() $x$
on the complex manifold
$x$
on the complex manifold
![]() ${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
,
${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
,
![]() $\unicode[STIX]{x1D713}(x)=[V(x)]$
for some
$\unicode[STIX]{x1D713}(x)=[V(x)]$
for some
![]() $r$
-dimensional linear subspace
$r$
-dimensional linear subspace
![]() $V(x)\,\subset \,T_{\mathbb{P}^{N},x}\cong \mathbb{C}^{N}$
. Denote by
$V(x)\,\subset \,T_{\mathbb{P}^{N},x}\cong \mathbb{C}^{N}$
. Denote by
![]() $\unicode[STIX]{x1D6F9}(x)$
the unique
$\unicode[STIX]{x1D6F9}(x)$
the unique
![]() $r$
-dimensional projective linear subspace in
$r$
-dimensional projective linear subspace in
![]() $\mathbb{P}^{N}$
passing through
$\mathbb{P}^{N}$
passing through
![]() $x$
such that
$x$
such that
![]() $T_{x}(\unicode[STIX]{x1D6F9}(x))=V(x)$
. Then,
$T_{x}(\unicode[STIX]{x1D6F9}(x))=V(x)$
. Then,
![]() $\unicode[STIX]{x1D6F9}:{\mathcal{X}}|_{B-E}-{\mathcal{A}}\rightarrow \mathscr{G}$
, where
$\unicode[STIX]{x1D6F9}:{\mathcal{X}}|_{B-E}-{\mathcal{A}}\rightarrow \mathscr{G}$
, where
![]() $\mathscr{G}$
is the Grassmannian of
$\mathscr{G}$
is the Grassmannian of
![]() $r$
-dimensional projective linear subspaces in
$r$
-dimensional projective linear subspaces in
![]() $\mathbb{P}^{N}$
;
$\mathbb{P}^{N}$
;
![]() $\mathscr{G}\cong \text{Gr}(r+1,\mathbb{C}^{N+1})$
.
$\mathscr{G}\cong \text{Gr}(r+1,\mathbb{C}^{N+1})$
.
We may identify
![]() $\mathscr{G}$
as a projective subvariety of
$\mathscr{G}$
as a projective subvariety of
![]() $\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
by means of the Plücker embedding. Write
$\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
by means of the Plücker embedding. Write
![]() $d:=\dim _{\mathbb{C}}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
. Make now a generic choice of homogeneous coordinates
$d:=\dim _{\mathbb{C}}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
. Make now a generic choice of homogeneous coordinates
![]() $[w_{0},\ldots ,w_{d}]$
on
$[w_{0},\ldots ,w_{d}]$
on
![]() $\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
so that
$\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))$
so that
![]() $\unicode[STIX]{x1D6F9}({\mathcal{X}}|_{B-E}-{\mathcal{A}})$
does not entirely lie on the hyperplane
$\unicode[STIX]{x1D6F9}({\mathcal{X}}|_{B-E}-{\mathcal{A}})$
does not entirely lie on the hyperplane
![]() $\{w_{0}=0\}$
of
$\{w_{0}=0\}$
of
![]() $\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))\cong \mathbb{P}^{d}$
. Then, writing
$\mathbb{P}(\unicode[STIX]{x1D6EC}^{r+1}(\mathbb{C}^{N+1}))\cong \mathbb{P}^{d}$
. Then, writing
![]() $z_{k}:=w_{k}/w_{0}$
for
$z_{k}:=w_{k}/w_{0}$
for
![]() $1\leqslant k\leqslant d$
, so that
$1\leqslant k\leqslant d$
, so that
![]() $(z_{1},\ldots ,z_{d})$
constitutes a system of inhomogeneous coordinates on
$(z_{1},\ldots ,z_{d})$
constitutes a system of inhomogeneous coordinates on
![]() $\mathbb{P}^{d}$
, we have
$\mathbb{P}^{d}$
, we have
![]() $\unicode[STIX]{x1D6F9}(x)=(\unicode[STIX]{x1D6F9}_{1}(x),\ldots ,\unicode[STIX]{x1D6F9}_{d}(x))$
, where each
$\unicode[STIX]{x1D6F9}(x)=(\unicode[STIX]{x1D6F9}_{1}(x),\ldots ,\unicode[STIX]{x1D6F9}_{d}(x))$
, where each
![]() $\unicode[STIX]{x1D6F9}_{k}$
is a meromorphic function on
$\unicode[STIX]{x1D6F9}_{k}$
is a meromorphic function on
![]() ${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
. By Hartogs’ extension each
${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
. By Hartogs’ extension each
![]() $\unicode[STIX]{x1D6F9}_{k},1\leqslant k\leqslant d$
, extends meromorphically to
$\unicode[STIX]{x1D6F9}_{k},1\leqslant k\leqslant d$
, extends meromorphically to
![]() ${\mathcal{X}}|_{B-E}$
. Denote by
${\mathcal{X}}|_{B-E}$
. Denote by
![]() $\unicode[STIX]{x1D6F9}_{k}^{\dagger },1\leqslant k\leqslant d$
, the meromorphic extension of
$\unicode[STIX]{x1D6F9}_{k}^{\dagger },1\leqslant k\leqslant d$
, the meromorphic extension of
![]() $\unicode[STIX]{x1D6F9}_{k}$
to
$\unicode[STIX]{x1D6F9}_{k}$
to
![]() ${\mathcal{X}}|_{B-E}$
. Then, by Lemma 3.2 each
${\mathcal{X}}|_{B-E}$
. Then, by Lemma 3.2 each
![]() $\unicode[STIX]{x1D6F9}_{k}^{\dagger },1\leqslant k\leqslant d$
, extends to a meromorphic function
$\unicode[STIX]{x1D6F9}_{k}^{\dagger },1\leqslant k\leqslant d$
, extends to a meromorphic function
![]() $\unicode[STIX]{x1D6F9}_{k}^{\sharp }$
on
$\unicode[STIX]{x1D6F9}_{k}^{\sharp }$
on
![]() ${\mathcal{X}}$
, yielding a meromorphic extension
${\mathcal{X}}$
, yielding a meromorphic extension
![]() $\unicode[STIX]{x1D6F9}^{\sharp }=(\unicode[STIX]{x1D6F9}_{1}^{\sharp },\ldots ,\unicode[STIX]{x1D6F9}_{d}^{\sharp })$
,
$\unicode[STIX]{x1D6F9}^{\sharp }=(\unicode[STIX]{x1D6F9}_{1}^{\sharp },\ldots ,\unicode[STIX]{x1D6F9}_{d}^{\sharp })$
,
![]() $\unicode[STIX]{x1D6F9}^{\sharp }:{\mathcal{X}}{\dashrightarrow}\mathbb{P}^{d}$
. Since the graph of
$\unicode[STIX]{x1D6F9}^{\sharp }:{\mathcal{X}}{\dashrightarrow}\mathbb{P}^{d}$
. Since the graph of
![]() $\unicode[STIX]{x1D6F9}^{\sharp }$
is obtained by taking the topological closure of the graph of
$\unicode[STIX]{x1D6F9}^{\sharp }$
is obtained by taking the topological closure of the graph of
![]() $\unicode[STIX]{x1D6F9}$
, and since
$\unicode[STIX]{x1D6F9}$
, and since
![]() $\unicode[STIX]{x1D6F9}({\mathcal{X}}|_{B-E}-{\mathcal{A}})\,\subset \,\mathscr{G}\,\subset \,\mathbb{P}^{d}$
, we have also
$\unicode[STIX]{x1D6F9}({\mathcal{X}}|_{B-E}-{\mathcal{A}})\,\subset \,\mathscr{G}\,\subset \,\mathbb{P}^{d}$
, we have also
![]() $\unicode[STIX]{x1D6F9}^{\sharp }:{\mathcal{X}}{\dashrightarrow}\mathscr{G}$
.
$\unicode[STIX]{x1D6F9}^{\sharp }:{\mathcal{X}}{\dashrightarrow}\mathscr{G}$
.
Finally, to apply Lemma 3.1 we need to extend the holomorphic section
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
$\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
![]() ${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
to a meromorphic section
${\mathcal{X}}|_{B-E}-{\mathcal{A}}$
to a meromorphic section
![]() $\unicode[STIX]{x1D713}^{\sharp }$
of
$\unicode[STIX]{x1D713}^{\sharp }$
of
![]() $\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
$\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
![]() ${\mathcal{X}}$
. Since
${\mathcal{X}}$
. Since
![]() $\unicode[STIX]{x1D6F9}(x)$
passes through
$\unicode[STIX]{x1D6F9}(x)$
passes through
![]() $x$
whenever
$x$
whenever
![]() $x$
belongs to the dense open subset
$x$
belongs to the dense open subset
![]() ${\mathcal{X}}|_{B-E}-{\mathcal{A}}\,\subset \,{\mathcal{X}}$
in the complex topology, it follows by continuity that at a point
${\mathcal{X}}|_{B-E}-{\mathcal{A}}\,\subset \,{\mathcal{X}}$
in the complex topology, it follows by continuity that at a point
![]() $y\in {\mathcal{X}}$
where
$y\in {\mathcal{X}}$
where
![]() $\unicode[STIX]{x1D6F9}^{\sharp }(y)$
is holomorphic,
$\unicode[STIX]{x1D6F9}^{\sharp }(y)$
is holomorphic,
![]() $\unicode[STIX]{x1D6F9}^{\sharp }(y)$
(which is well-defined) must pass through
$\unicode[STIX]{x1D6F9}^{\sharp }(y)$
(which is well-defined) must pass through
![]() $y$
, hence
$y$
, hence
![]() $\unicode[STIX]{x1D713}^{\sharp }$
can be defined at
$\unicode[STIX]{x1D713}^{\sharp }$
can be defined at
![]() $y$
by
$y$
by
![]() $\unicode[STIX]{x1D713}^{\sharp }(y)=[T_{y}(\unicode[STIX]{x1D6F9}^{\sharp }(y))]\in \text{Gr}(r,T_{y}(\mathbb{P}^{N}))$
. It follows that
$\unicode[STIX]{x1D713}^{\sharp }(y)=[T_{y}(\unicode[STIX]{x1D6F9}^{\sharp }(y))]\in \text{Gr}(r,T_{y}(\mathbb{P}^{N}))$
. It follows that
![]() $\unicode[STIX]{x1D713}^{\sharp }(y)$
is defined and holomorphic outside of a normal projective subvariety
$\unicode[STIX]{x1D713}^{\sharp }(y)$
is defined and holomorphic outside of a normal projective subvariety
![]() ${\mathcal{S}}$
of
${\mathcal{S}}$
of
![]() ${\mathcal{X}}$
of codimension
${\mathcal{X}}$
of codimension
![]() ${\geqslant}2$
and hence by Hartogs’ extension
${\geqslant}2$
and hence by Hartogs’ extension
![]() $\unicode[STIX]{x1D713}^{\sharp }$
is defined as a meromorphic section of
$\unicode[STIX]{x1D713}^{\sharp }$
is defined as a meromorphic section of
![]() $\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
$\text{Gr}(r,T_{\mathbb{P}^{N}})$
over
![]() ${\mathcal{X}}$
in such a way that
${\mathcal{X}}$
in such a way that
![]() $\unicode[STIX]{x1D713}^{\sharp }|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}\equiv \unicode[STIX]{x1D713}$
. By Lemma 3.1 the meromorphic foliation
$\unicode[STIX]{x1D713}^{\sharp }|_{{\mathcal{X}}|_{B-E}-{\mathcal{A}}}\equiv \unicode[STIX]{x1D713}$
. By Lemma 3.1 the meromorphic foliation
![]() $\mathscr{L}$
on
$\mathscr{L}$
on
![]() ${\mathcal{X}}|_{B-E}$
extends meromorphically to
${\mathcal{X}}|_{B-E}$
extends meromorphically to
![]() ${\mathcal{X}}$
.◻
${\mathcal{X}}$
.◻
We conclude this section with the following result on
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
and on the compactification
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
and on the compactification
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
for torsion-free lattices
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
for torsion-free lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
.
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
.
Proposition 3.2. Let
![]() ${\mathcal{K}}$
be an irreducible component of
${\mathcal{K}}$
be an irreducible component of
![]() $\,\text{ Chow}(\mathbb{P}^{n})$
,
$\,\text{ Chow}(\mathbb{P}^{n})$
,
![]() $[W_{0}]\in {\mathcal{K}}$
,
$[W_{0}]\in {\mathcal{K}}$
,
![]() $S\,\subset \,\mathbb{B}^{n}$
be an irreducible component of
$S\,\subset \,\mathbb{B}^{n}$
be an irreducible component of
![]() $W_{0}\,\cap \,\mathbb{B}^{n}$
, and
$W_{0}\,\cap \,\mathbb{B}^{n}$
, and
![]() $\mathscr{S}\,\subset \,\mathscr{U}$
be the tautological lifting of
$\mathscr{S}\,\subset \,\mathscr{U}$
be the tautological lifting of
![]() $S$
to
$S$
to
![]() $\mathscr{U}$
. Let
$\mathscr{U}$
. Let
![]() ${\mathcal{H}}\,\subset \,{\mathcal{K}}$
be a
${\mathcal{H}}\,\subset \,{\mathcal{K}}$
be a
![]() $G$
-invariant subvariety such that
$G$
-invariant subvariety such that
![]() $[W_{0}]\in {\mathcal{H}}$
and such that, denoting by
$[W_{0}]\in {\mathcal{H}}$
and such that, denoting by
![]() $\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
,
$\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
,
![]() $\unicode[STIX]{x1D708}:\mathscr{V}\rightarrow \mathbb{P}^{n}$
the restriction of the universal family
$\unicode[STIX]{x1D708}:\mathscr{V}\rightarrow \mathbb{P}^{n}$
the restriction of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
from
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
from
![]() $\mathscr{U}$
to
$\mathscr{U}$
to
![]() $\mathscr{V}$
, a general point of
$\mathscr{V}$
, a general point of
![]() $\mathscr{S}$
is a smooth point of
$\mathscr{S}$
is a smooth point of
![]() $\mathscr{V}$
. Then, denoting
$\mathscr{V}$
. Then, denoting
![]() $\unicode[STIX]{x1D708}|_{\mathbb{B}^{n}}$
by
$\unicode[STIX]{x1D708}|_{\mathbb{B}^{n}}$
by
![]() $\unicode[STIX]{x1D708}^{\prime }:\mathscr{V}^{\prime }\rightarrow \mathbb{B}^{n}$
, and by
$\unicode[STIX]{x1D708}^{\prime }:\mathscr{V}^{\prime }\rightarrow \mathbb{B}^{n}$
, and by
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
the locally homogeneous fiber bundle obtained from
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}:\mathscr{V}_{\unicode[STIX]{x1D6E4}}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
the locally homogeneous fiber bundle obtained from
![]() $\unicode[STIX]{x1D708}^{\prime }:\mathscr{V}^{\prime }\rightarrow \mathbb{B}^{n}$
by taking quotients with respect to
$\unicode[STIX]{x1D708}^{\prime }:\mathscr{V}^{\prime }\rightarrow \mathbb{B}^{n}$
by taking quotients with respect to
![]() $\unicode[STIX]{x1D6E4}$
, the tautological foliation
$\unicode[STIX]{x1D6E4}$
, the tautological foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $\mathscr{V}$
descends to a meromorphic foliation
$\mathscr{V}$
descends to a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. Moreover, when
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. Moreover, when
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice the topological closure
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice the topological closure
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective, and
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective, and
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
extends to a meromorphic foliation
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
extends to a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
. As a consequence, for any torsion-free lattice
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
. As a consequence, for any torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
the Zariski closure
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
the Zariski closure
![]() $Z$
of
$Z$
of
![]() $\unicode[STIX]{x1D70B}(S)$
in
$\unicode[STIX]{x1D70B}(S)$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
is uniruled by subvarieties belonging to
$X_{\unicode[STIX]{x1D6E4}}$
is uniruled by subvarieties belonging to
![]() ${\mathcal{H}}$
.
${\mathcal{H}}$
.
Proof of Proposition 3.2.
As in the second last paragraph preceding Lemma 3.2, we have seen that the tautological foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $\mathscr{V}$
descends to a meromorphic foliation
$\mathscr{V}$
descends to a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. When
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. When
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice, by the last paragraph preceding Lemma 3.2, the topological closure
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is a torsion-free nonuniform lattice, by the last paragraph preceding Lemma 3.2, the topological closure
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective. By Lemma 3.3 and passing to normalizations (as in the paragraph preceding Lemma 3.2) the meromorphic foliation
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective. By Lemma 3.3 and passing to normalizations (as in the paragraph preceding Lemma 3.2) the meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
extends to a meromorphic foliation
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
extends to a meromorphic foliation
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}^{\sharp }$
on
![]() $\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
.
$\overline{\mathscr{V}_{\unicode[STIX]{x1D6E4}}}$
.
For an arbitrary torsion-free lattice
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
it remains to establish the concluding sentence on the uniruling of
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
it remains to establish the concluding sentence on the uniruling of
![]() $Z$
by subvarieties belonging to
$Z$
by subvarieties belonging to
![]() ${\mathcal{H}}$
. Write
${\mathcal{H}}$
. Write
![]() $\widetilde{\unicode[STIX]{x1D70B}}:\mathscr{V}\rightarrow \mathscr{V}_{\unicode[STIX]{x1D6E4}}$
for the covering map induced from the universal covering map
$\widetilde{\unicode[STIX]{x1D70B}}:\mathscr{V}\rightarrow \mathscr{V}_{\unicode[STIX]{x1D6E4}}$
for the covering map induced from the universal covering map
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, and denote by
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
, and denote by
![]() $\mathscr{Z}\,\subset \,\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
$\mathscr{Z}\,\subset \,\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
![]() $\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})$
in
$\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})$
in
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. We observe that
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. We observe that
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=Z$
. In the notation as in § 2 denote by
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=Z$
. In the notation as in § 2 denote by
![]() $\overline{\mathscr{Z}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
the topological closure of
$\overline{\mathscr{Z}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
the topological closure of
![]() $\mathscr{Z}$
in the projective compactification
$\mathscr{Z}$
in the projective compactification
![]() $\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
of the projective bundle
$\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
of the projective bundle
![]() $\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
. The subset
$\mathscr{P}_{\unicode[STIX]{x1D6E4}}$
. The subset
![]() $\overline{\mathscr{Z}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective. Denote by
$\overline{\mathscr{Z}}\,\subset \,\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}$
is projective. Denote by
![]() $\overline{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}}:\overline{\mathscr{Z}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
the restriction of
$\overline{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}}:\overline{\mathscr{Z}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
the restriction of
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
to
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D6E4}}^{\sharp }:\overline{\mathscr{P}_{\unicode[STIX]{x1D6E4}}}\rightarrow \overline{X_{\unicode[STIX]{x1D6E4}}}$
to
![]() $\overline{\mathscr{Z}}$
. By the proper mapping theorem
$\overline{\mathscr{Z}}$
. By the proper mapping theorem
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=\overline{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}}(\overline{\mathscr{Z}})\,\cap \,X_{\unicode[STIX]{x1D6E4}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety containing
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=\overline{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}}(\overline{\mathscr{Z}})\,\cap \,X_{\unicode[STIX]{x1D6E4}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety containing
![]() $\unicode[STIX]{x1D70B}(S)$
, hence
$\unicode[STIX]{x1D70B}(S)$
, hence
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})\supset Z$
. Suppose
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})\supset Z$
. Suppose
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})\supsetneq Z$
. Then,
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})\supsetneq Z$
. Then,
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(Z)\,\cap \,\mathscr{Z}\subsetneq \mathscr{Z}$
is a quasi-projective subvariety of
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(Z)\,\cap \,\mathscr{Z}\subsetneq \mathscr{Z}$
is a quasi-projective subvariety of
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
containing
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
containing
![]() $\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})$
, contradicting with
$\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})$
, contradicting with
![]() $\mathscr{Z}:=\overline{\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})}^{\mathscr{Z}\!ar}$
. Hence,
$\mathscr{Z}:=\overline{\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})}^{\mathscr{Z}\!ar}$
. Hence,
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=Z$
by contradiction, as observed.
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})=Z$
by contradiction, as observed.
Recall that dim
![]() $(S)=:r$
and define
$(S)=:r$
and define
![]() $d:=\dim (Z)$
,
$d:=\dim (Z)$
,
![]() $e:=\dim (\mathscr{Z})$
. By Proposition 3.1,
$e:=\dim (\mathscr{Z})$
. By Proposition 3.1,
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
restricts to a meromorphic foliation on
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
restricts to a meromorphic foliation on
![]() $\mathscr{Z}$
which we denote by
$\mathscr{Z}$
which we denote by
![]() $\mathscr{E}$
. The singular locus
$\mathscr{E}$
. The singular locus
![]() $\text{Sing}(\mathscr{E})\subsetneq \mathscr{Z}$
of
$\text{Sing}(\mathscr{E})\subsetneq \mathscr{Z}$
of
![]() $\mathscr{E}$
is a subvariety containing
$\mathscr{E}$
is a subvariety containing
![]() $\text{Sing}(\mathscr{Z})$
. Write
$\text{Sing}(\mathscr{Z})$
. Write
![]() $\text{Reg}(\mathscr{E}):=\mathscr{Z}-\text{Sing}(\mathscr{E})\,\subset \,\text{Reg}(\mathscr{Z})$
and consider the open subset
$\text{Reg}(\mathscr{E}):=\mathscr{Z}-\text{Sing}(\mathscr{E})\,\subset \,\text{Reg}(\mathscr{Z})$
and consider the open subset
![]() $\unicode[STIX]{x1D6FA}:=\widetilde{\unicode[STIX]{x1D70B}}^{-1}(\text{Reg}(\mathscr{E}))\,\subset \,\mathscr{P}^{\prime }$
. Let
$\unicode[STIX]{x1D6FA}:=\widetilde{\unicode[STIX]{x1D70B}}^{-1}(\text{Reg}(\mathscr{E}))\,\subset \,\mathscr{P}^{\prime }$
. Let
![]() $\mathfrak{A}\,\subset \,\unicode[STIX]{x1D6FA}$
be the subvariety over which
$\mathfrak{A}\,\subset \,\unicode[STIX]{x1D6FA}$
be the subvariety over which
![]() $\text{rank}(d\unicode[STIX]{x1D70E})<e-r$
. Then
$\text{rank}(d\unicode[STIX]{x1D70E})<e-r$
. Then
![]() $\mathfrak{A}$
is invariant under
$\mathfrak{A}$
is invariant under
![]() $\unicode[STIX]{x1D70B}_{1}(Z)$
and it descends to a subvariety
$\unicode[STIX]{x1D70B}_{1}(Z)$
and it descends to a subvariety
![]() $\mathscr{A}\,\subset \,\text{Reg}(\mathscr{E})$
. Write
$\mathscr{A}\,\subset \,\text{Reg}(\mathscr{E})$
. Write
![]() $\unicode[STIX]{x1D706}:=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{Z}}$
. Define now
$\unicode[STIX]{x1D706}:=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{Z}}$
. Define now
![]() $\mathscr{B}\,\subset \,\mathscr{Z}$
to be the locus of points
$\mathscr{B}\,\subset \,\mathscr{Z}$
to be the locus of points
![]() $v\in \mathscr{Z}$
where (a)
$v\in \mathscr{Z}$
where (a)
![]() $v\in \text{Sing}(\mathscr{Z})$
, or (b)
$v\in \text{Sing}(\mathscr{Z})$
, or (b)
![]() $\unicode[STIX]{x1D706}(v)\in \text{Sing}(Z)$
, or (c)
$\unicode[STIX]{x1D706}(v)\in \text{Sing}(Z)$
, or (c)
![]() $v\in \text{Reg}(\mathscr{Z}),\unicode[STIX]{x1D706}(v)\in \text{Reg}(Z)$
but
$v\in \text{Reg}(\mathscr{Z}),\unicode[STIX]{x1D706}(v)\in \text{Reg}(Z)$
but
![]() $\unicode[STIX]{x1D706}|_{\text{Reg}(\mathscr{Z})\,\cap \,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(\text{Reg}(Z))}:\text{Reg}(\mathscr{Z})\,\cap \,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(\text{Reg}(Z))\rightarrow \text{Reg}(Z)$
fails to be a submersion at
$\unicode[STIX]{x1D706}|_{\text{Reg}(\mathscr{Z})\,\cap \,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(\text{Reg}(Z))}:\text{Reg}(\mathscr{Z})\,\cap \,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}^{-1}(\text{Reg}(Z))\rightarrow \text{Reg}(Z)$
fails to be a submersion at
![]() $v$
. Then,
$v$
. Then,
![]() $\mathscr{B}\,\subset \,\mathscr{Z}$
is a quasi-projective subvariety.
$\mathscr{B}\,\subset \,\mathscr{Z}$
is a quasi-projective subvariety.
Consider now
![]() $\mathscr{W}:=\text{Reg}(\mathscr{E})-\mathscr{A}-\mathscr{B}\,\subset \,\mathscr{Z}$
, which is dense in
$\mathscr{W}:=\text{Reg}(\mathscr{E})-\mathscr{A}-\mathscr{B}\,\subset \,\mathscr{Z}$
, which is dense in
![]() $\mathscr{Z}$
in the complex topology. Let
$\mathscr{Z}$
in the complex topology. Let
![]() $v$
be a point on
$v$
be a point on
![]() $\mathscr{W}\,\subset \,\mathscr{Z}$
,
$\mathscr{W}\,\subset \,\mathscr{Z}$
,
![]() $\unicode[STIX]{x1D706}(v)=:x$
. By the definition of universal families the restriction of
$\unicode[STIX]{x1D706}(v)=:x$
. By the definition of universal families the restriction of
![]() $\unicode[STIX]{x1D706}$
to each local leaf
$\unicode[STIX]{x1D706}$
to each local leaf
![]() ${\mathcal{L}}\,\subset \,\text{Reg}(\mathscr{E})$
of
${\mathcal{L}}\,\subset \,\text{Reg}(\mathscr{E})$
of
![]() $\mathscr{E}$
is an immersion into
$\mathscr{E}$
is an immersion into
![]() $X_{\unicode[STIX]{x1D6E4}}$
. Since
$X_{\unicode[STIX]{x1D6E4}}$
. Since
![]() $\unicode[STIX]{x1D706}:\mathscr{W}\rightarrow \text{Reg}(Z)$
is a submersion, there exists a
$\unicode[STIX]{x1D706}:\mathscr{W}\rightarrow \text{Reg}(Z)$
is a submersion, there exists a
![]() $(d-r)$
-dimensional complex submanifold
$(d-r)$
-dimensional complex submanifold
![]() $\mathscr{D}\,\subset \,\mathscr{W}_{0}$
of some open neighborhood
$\mathscr{D}\,\subset \,\mathscr{W}_{0}$
of some open neighborhood
![]() $\mathscr{W}_{0}$
of
$\mathscr{W}_{0}$
of
![]() $v$
in
$v$
in
![]() $\mathscr{W}$
such that
$\mathscr{W}$
such that
![]() $\mathscr{D}$
is biholomorphic to
$\mathscr{D}$
is biholomorphic to
![]() $\unicode[STIX]{x1D6E5}^{d-r}$
and
$\unicode[STIX]{x1D6E5}^{d-r}$
and
![]() $\unicode[STIX]{x1D706}|_{\mathscr{D}}:\mathscr{D}\rightarrow \text{Reg}(Z)$
is a holomorphic embedding onto a locally closed complex submanifold
$\unicode[STIX]{x1D706}|_{\mathscr{D}}:\mathscr{D}\rightarrow \text{Reg}(Z)$
is a holomorphic embedding onto a locally closed complex submanifold
![]() $N\,\subset \,\text{Reg}(Z)$
. Lifting
$N\,\subset \,\text{Reg}(Z)$
. Lifting
![]() $\mathscr{D}$
to
$\mathscr{D}$
to
![]() $\widetilde{\mathscr{D}}$
on any connected component of
$\widetilde{\mathscr{D}}$
on any connected component of
![]() $\unicode[STIX]{x1D6FA}$
and noting that
$\unicode[STIX]{x1D6FA}$
and noting that
![]() $\widetilde{\mathscr{D}}\,\cap \,\mathfrak{A}=\emptyset$
, shrinking
$\widetilde{\mathscr{D}}\,\cap \,\mathfrak{A}=\emptyset$
, shrinking
![]() $\widetilde{\mathscr{D}}$
if necessary we may assume that
$\widetilde{\mathscr{D}}$
if necessary we may assume that
![]() $\unicode[STIX]{x1D70E}$
maps
$\unicode[STIX]{x1D70E}$
maps
![]() $\widetilde{\mathscr{D}}$
biholomorphically onto some
$\widetilde{\mathscr{D}}$
biholomorphically onto some
![]() $(d-r)$
-dimensional complex submanifold
$(d-r)$
-dimensional complex submanifold
![]() ${\mathcal{S}}$
of some open subset
${\mathcal{S}}$
of some open subset
![]() ${\mathcal{G}}$
of
${\mathcal{G}}$
of
![]() ${\mathcal{H}}$
. Clearly, there exists a contractible open neighborhood
${\mathcal{H}}$
. Clearly, there exists a contractible open neighborhood
![]() $\widetilde{{\mathcal{O}}}$
of
$\widetilde{{\mathcal{O}}}$
of
![]() $\widetilde{\mathscr{D}}$
in
$\widetilde{\mathscr{D}}$
in
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
such that
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
such that
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
maps
$\widetilde{\unicode[STIX]{x1D70B}}$
maps
![]() $\widetilde{{\mathcal{O}}}$
biholomorphically onto a neighborhood
$\widetilde{{\mathcal{O}}}$
biholomorphically onto a neighborhood
![]() ${\mathcal{O}}$
of
${\mathcal{O}}$
of
![]() $v$
on Reg
$v$
on Reg
![]() $(\mathscr{E})$
and
$(\mathscr{E})$
and
![]() ${\mathcal{O}}$
is the disjoint union of local leaves of
${\mathcal{O}}$
is the disjoint union of local leaves of
![]() $\mathscr{E}=\mathscr{F}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{Z}}$
passing through points on
$\mathscr{E}=\mathscr{F}_{\unicode[STIX]{x1D6E4}}|_{\mathscr{Z}}$
passing through points on
![]() $\mathscr{D}$
, and such that
$\mathscr{D}$
, and such that
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}\,\circ \,\widetilde{\unicode[STIX]{x1D70B}}$
maps
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}\,\circ \,\widetilde{\unicode[STIX]{x1D70B}}$
maps
![]() $\widetilde{{\mathcal{O}}}$
biholomorphically onto a neighborhood
$\widetilde{{\mathcal{O}}}$
biholomorphically onto a neighborhood
![]() $U$
of
$U$
of
![]() $x=\unicode[STIX]{x1D706}(v)$
. Here we make take
$x=\unicode[STIX]{x1D706}(v)$
. Here we make take
![]() $N$
to be a complex submanifold of
$N$
to be a complex submanifold of
![]() $U$
and
$U$
and
![]() $U$
to be a disjoint union of
$U$
to be a disjoint union of
![]() $r$
-dimensional complex submanifolds
$r$
-dimensional complex submanifolds
![]() $L(y)\,\subset \,U$
passing through
$L(y)\,\subset \,U$
passing through
![]() $y\in N$
which are images under
$y\in N$
which are images under
![]() $\unicode[STIX]{x1D70B}\,\circ \,\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}\,\circ \,\widetilde{\unicode[STIX]{x1D70B}}$
of connected smooth open subsets of
$\unicode[STIX]{x1D70B}\,\circ \,\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}\,\circ \,\widetilde{\unicode[STIX]{x1D70B}}$
of connected smooth open subsets of
![]() $S_{\unicode[STIX]{x1D702}}\,\cap \,\widetilde{{\mathcal{O}}}$
, where
$S_{\unicode[STIX]{x1D702}}\,\cap \,\widetilde{{\mathcal{O}}}$
, where
![]() $S_{\unicode[STIX]{x1D702}}:=W_{\unicode[STIX]{x1D702}}\,\cap \,\mathbb{B}^{n}$
and
$S_{\unicode[STIX]{x1D702}}:=W_{\unicode[STIX]{x1D702}}\,\cap \,\mathbb{B}^{n}$
and
![]() $W_{\unicode[STIX]{x1D702}}$
belongs to
$W_{\unicode[STIX]{x1D702}}$
belongs to
![]() ${\mathcal{S}}\,\subset \,{\mathcal{H}}$
, and we have a uniruling of
${\mathcal{S}}\,\subset \,{\mathcal{H}}$
, and we have a uniruling of
![]() $\mathscr{Z}$
by subvarieties belonging to
$\mathscr{Z}$
by subvarieties belonging to
![]() ${\mathcal{H}}$
(cf. Definition 3.1), as desired.◻
${\mathcal{H}}$
(cf. Definition 3.1), as desired.◻
The uniruling of
![]() $Z$
by subvarieties belonging to
$Z$
by subvarieties belonging to
![]() ${\mathcal{H}}$
is the key statement in Proposition 3.2 which will allow us to establish Main Theorem in § 4 by analytic methods.
${\mathcal{H}}$
is the key statement in Proposition 3.2 which will allow us to establish Main Theorem in § 4 by analytic methods.
4 Proof of Main Theorem and generalizations
Proof of Main Theorem in the compact case.
Recall that
![]() $g=ds_{\mathbb{B}^{n}}^{2}$
is the canonical Kähler–Einstein metric with Kähler form
$g=ds_{\mathbb{B}^{n}}^{2}$
is the canonical Kähler–Einstein metric with Kähler form
![]() $\unicode[STIX]{x1D714}_{g}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (1-\Vert z\Vert ^{2}))$
, which is of constant holomorphic sectional curvature
$\unicode[STIX]{x1D714}_{g}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (1-\Vert z\Vert ^{2}))$
, which is of constant holomorphic sectional curvature
![]() $-2$
, and
$-2$
, and
![]() $X_{\unicode[STIX]{x1D6E4}}$
is endowed with the quotient metric
$X_{\unicode[STIX]{x1D6E4}}$
is endowed with the quotient metric
![]() $g_{\unicode[STIX]{x1D6E4}}=ds_{X_{\unicode[STIX]{x1D6E4}}}^{2}$
. Recall that dim
$g_{\unicode[STIX]{x1D6E4}}=ds_{X_{\unicode[STIX]{x1D6E4}}}^{2}$
. Recall that dim
![]() $(S)=r$
, and write dim
$(S)=r$
, and write dim
![]() $(Z)=d$
. When
$(Z)=d$
. When
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}=\text{Aut}(\mathbb{B}^{n})$
is cocompact, the proof that
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}=\text{Aut}(\mathbb{B}^{n})$
is cocompact, the proof that
![]() $Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset will now be deduced from Proposition 3.1, as follows. A general point
$Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset will now be deduced from Proposition 3.1, as follows. A general point
![]() $x\in S$
must be a smooth point on
$x\in S$
must be a smooth point on
![]() $\unicode[STIX]{x1D70B}^{-1}(Z)$
, otherwise
$\unicode[STIX]{x1D70B}^{-1}(Z)$
, otherwise
![]() $Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!\,\subset \,X\,\subset \,\text{Sing}(Z)\subsetneq Z$
, a plain contradiction. In particular, there is a unique irreducible component
$Z=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\!\,\subset \,X\,\subset \,\text{Sing}(Z)\subsetneq Z$
, a plain contradiction. In particular, there is a unique irreducible component
![]() $\widetilde{Z}$
of
$\widetilde{Z}$
of
![]() $\unicode[STIX]{x1D70B}^{-1}(Z)$
which contains
$\unicode[STIX]{x1D70B}^{-1}(Z)$
which contains
![]() $S$
.
$S$
.
Recall that
![]() $\mathscr{S}\,\subset \,\mathscr{V}$
is the tautological lifting of
$\mathscr{S}\,\subset \,\mathscr{V}$
is the tautological lifting of
![]() $S$
to the total space
$S$
to the total space
![]() $\mathscr{V}$
of the
$\mathscr{V}$
of the
![]() $G$
-invariant subfamily
$G$
-invariant subfamily
![]() $\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
of the universal family
$\unicode[STIX]{x1D70E}:\mathscr{V}\rightarrow {\mathcal{H}}$
of the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, and that
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
, and that
![]() $\mathscr{Z}:=\overline{\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})}^{\mathscr{Z}ar}\,\subset \,\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. By Proposition 3.1,
$\mathscr{Z}:=\overline{\widetilde{\unicode[STIX]{x1D70B}}(\mathscr{S})}^{\mathscr{Z}ar}\,\subset \,\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. By Proposition 3.1,
![]() $\mathscr{Z}$
is saturated with respect to the tautological foliation
$\mathscr{Z}$
is saturated with respect to the tautological foliation
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. By Proposition 3.2,
$\mathscr{V}_{\unicode[STIX]{x1D6E4}}$
. By Proposition 3.2,
![]() $Z=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})$
is uniruled by subvarieties belonging to
$Z=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z})$
is uniruled by subvarieties belonging to
![]() ${\mathcal{H}}$
in the sense of Definition 3.1. Consider the germ at some point
${\mathcal{H}}$
in the sense of Definition 3.1. Consider the germ at some point
![]() $b\in \unicode[STIX]{x2202}\widetilde{Z}$
of a complex submanifold
$b\in \unicode[STIX]{x2202}\widetilde{Z}$
of a complex submanifold
![]() $\unicode[STIX]{x1D6F4}$
which is the union of nonempty open subsets of a certain family of subvarieties
$\unicode[STIX]{x1D6F4}$
which is the union of nonempty open subsets of a certain family of subvarieties
![]() $W_{\unicode[STIX]{x1D702}}\,\subset \,\mathbb{P}^{n}$
belonging to
$W_{\unicode[STIX]{x1D702}}\,\subset \,\mathbb{P}^{n}$
belonging to
![]() ${\mathcal{H}}$
and which exits the boundary of
${\mathcal{H}}$
and which exits the boundary of
![]() $\mathbb{B}^{n}$
near
$\mathbb{B}^{n}$
near
![]() $b\in \unicode[STIX]{x2202}\widetilde{Z}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. We are going to prove that
$b\in \unicode[STIX]{x2202}\widetilde{Z}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. We are going to prove that
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset by exploiting the asymptotic total geodesy of
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset by exploiting the asymptotic total geodesy of
![]() $(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}})$
at
$(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}})$
at
![]() $b\in \unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
using asymptotic curvature properties resulting from Klembeck [Reference KlembeckKle78] (Theorem 1.5 here).
$b\in \unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
using asymptotic curvature properties resulting from Klembeck [Reference KlembeckKle78] (Theorem 1.5 here).
By Proposition 3.2,
![]() $\mathscr{Z}$
is uniruled by subvarieties belonging to
$\mathscr{Z}$
is uniruled by subvarieties belonging to
![]() ${\mathcal{H}}$
. In the notation there consider now the mapping
${\mathcal{H}}$
. In the notation there consider now the mapping
![]() $\unicode[STIX]{x1D6FD}:=\unicode[STIX]{x1D708}|_{\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})}:\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})\rightarrow \mathbb{P}^{n}$
. Note that dim
$\unicode[STIX]{x1D6FD}:=\unicode[STIX]{x1D708}|_{\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})}:\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})\rightarrow \mathbb{P}^{n}$
. Note that dim
![]() $(\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}}))=(d-r)+r=d$
and that the image
$(\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}}))=(d-r)+r=d$
and that the image
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}}))$
contains the open set
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}}))$
contains the open set
![]() $\widetilde{{\mathcal{O}}}\,\subset \,\widetilde{Z}$
. Since by construction
$\widetilde{{\mathcal{O}}}\,\subset \,\widetilde{Z}$
. Since by construction
![]() $\unicode[STIX]{x1D6FD}$
is a local biholomorphism into
$\unicode[STIX]{x1D6FD}$
is a local biholomorphism into
![]() $\widetilde{Z}$
at
$\widetilde{Z}$
at
![]() $\widetilde{v}\in \widetilde{Z}$
,
$\widetilde{v}\in \widetilde{Z}$
,
![]() $\unicode[STIX]{x1D6FD}$
must necessarily be an immersion into
$\unicode[STIX]{x1D6FD}$
must necessarily be an immersion into
![]() $\mathbb{P}^{n}$
at a general smooth point of
$\mathbb{P}^{n}$
at a general smooth point of
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
.
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
.
Observe that singularities of
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
are of complex codimension
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
are of complex codimension
![]() ${\geqslant}1$
while
${\geqslant}1$
while
![]() $\unicode[STIX]{x1D6FD}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})=\unicode[STIX]{x1D708}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})\,\cap \,\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
is a real hypersurface in
$\unicode[STIX]{x1D6FD}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})=\unicode[STIX]{x1D708}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})\,\cap \,\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
is a real hypersurface in
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
. It follows that, for a general point
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
. It follows that, for a general point
![]() $\widehat{b}\in \unicode[STIX]{x1D6FD}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})$
,
$\widehat{b}\in \unicode[STIX]{x1D6FD}^{-1}(\unicode[STIX]{x2202}\mathbb{B}^{n})$
,
![]() $\widehat{b}$
is a smooth point of
$\widehat{b}$
is a smooth point of
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
and
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
and
![]() $\unicode[STIX]{x1D6FD}$
is an immersion at
$\unicode[STIX]{x1D6FD}$
is an immersion at
![]() $\widehat{b}$
. Thus, for some open neighborhood
$\widehat{b}$
. Thus, for some open neighborhood
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
![]() $\widehat{b}$
in
$\widehat{b}$
in
![]() $\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
,
$\unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})$
,
![]() $\unicode[STIX]{x1D6FD}|_{{\mathcal{W}}}:{\mathcal{W}}\overset{\cong }{\longrightarrow }\unicode[STIX]{x1D6F4}\,\subset \,\mathbb{C}^{n}$
maps
$\unicode[STIX]{x1D6FD}|_{{\mathcal{W}}}:{\mathcal{W}}\overset{\cong }{\longrightarrow }\unicode[STIX]{x1D6F4}\,\subset \,\mathbb{C}^{n}$
maps
![]() ${\mathcal{W}}$
biholomorphically onto some complex submanifold
${\mathcal{W}}$
biholomorphically onto some complex submanifold
![]() $\unicode[STIX]{x1D6F4}\,\subset \,U$
of some open set
$\unicode[STIX]{x1D6F4}\,\subset \,U$
of some open set
![]() $U\,\subset \,\mathbb{C}^{n}$
,
$U\,\subset \,\mathbb{C}^{n}$
,
![]() $b\in U$
, such that
$b\in U$
, such that
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}$
is a nonempty open subset of
$\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}$
is a nonempty open subset of
![]() $\widetilde{Z}$
. One may say that
$\widetilde{Z}$
. One may say that
![]() $\widetilde{Z}$
is analytically continued by grafting
$\widetilde{Z}$
is analytically continued by grafting
![]() $\unicode[STIX]{x1D6F4}$
to
$\unicode[STIX]{x1D6F4}$
to
![]() $\widetilde{Z}$
at
$\widetilde{Z}$
at
![]() $\widehat{b}$
. For convenience we may assume that both
$\widehat{b}$
. For convenience we may assume that both
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}\,\subset \,\unicode[STIX]{x1D6F4}$
are connected, and that
$\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}\,\subset \,\unicode[STIX]{x1D6F4}$
are connected, and that
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}=\widetilde{Z}\,\cap \,U$
.
$\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}=\widetilde{Z}\,\cap \,U$
.
For easy reference we include a proof of the following well-known lemma.
Lemma 4.1. At a general point
![]() $b\in \unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
the function
$b\in \unicode[STIX]{x1D70E}^{-1}({\mathcal{S}})\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
the function
![]() $\unicode[STIX]{x1D711}:=\Vert z\Vert ^{2}-1$
of
$\unicode[STIX]{x1D711}:=\Vert z\Vert ^{2}-1$
of
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}=\{\unicode[STIX]{x1D711}=0\}$
must necessarily vanish exactly to the order 1.
$\unicode[STIX]{x2202}\mathbb{B}^{n}=\{\unicode[STIX]{x1D711}=0\}$
must necessarily vanish exactly to the order 1.
Proof. Otherwise
![]() $\unicode[STIX]{x1D711}$
vanishes to the order
$\unicode[STIX]{x1D711}$
vanishes to the order
![]() $k\geqslant 2$
on a neighborhood
$k\geqslant 2$
on a neighborhood
![]() $N$
of a general point
$N$
of a general point
![]() $b$
in
$b$
in
![]() $W_{\unicode[STIX]{x1D702}}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
and
$W_{\unicode[STIX]{x1D702}}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
and
![]() $-\unicode[STIX]{x1D711}|_{W_{\unicode[STIX]{x1D702}}}=\unicode[STIX]{x1D703}^{k}$
such that
$-\unicode[STIX]{x1D711}|_{W_{\unicode[STIX]{x1D702}}}=\unicode[STIX]{x1D703}^{k}$
such that
![]() $\unicode[STIX]{x1D703}\geqslant 0$
and
$\unicode[STIX]{x1D703}\geqslant 0$
and
![]() $d\unicode[STIX]{x1D703}(p)\neq 0$
for
$d\unicode[STIX]{x1D703}(p)\neq 0$
for
![]() $p\in N$
. We have
$p\in N$
. We have
 $$\begin{eqnarray}\displaystyle \sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711} & = & \displaystyle -\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}^{k}\nonumber\\ \displaystyle & = & \displaystyle -k\unicode[STIX]{x1D703}^{k-1}\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}-k(k-1)\unicode[STIX]{x1D703}^{k-2}\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\wedge \overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & = & \displaystyle -k\unicode[STIX]{x1D703}^{k-2}(\unicode[STIX]{x1D703}\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}+(k-1)\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\wedge \overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711} & = & \displaystyle -\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}^{k}\nonumber\\ \displaystyle & = & \displaystyle -k\unicode[STIX]{x1D703}^{k-1}\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}-k(k-1)\unicode[STIX]{x1D703}^{k-2}\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\wedge \overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & = & \displaystyle -k\unicode[STIX]{x1D703}^{k-2}(\unicode[STIX]{x1D703}\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}+(k-1)\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}\wedge \overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}).\nonumber\end{eqnarray}$$
At
![]() $p\in N$
we have
$p\in N$
we have
![]() $\unicode[STIX]{x1D703}(p)=0$
while
$\unicode[STIX]{x1D703}(p)=0$
while
![]() $\unicode[STIX]{x1D707}:=\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(p)\wedge \overline{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(p)}\geqslant 0$
and
$\unicode[STIX]{x1D707}:=\sqrt{-1}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(p)\wedge \overline{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(p)}\geqslant 0$
and
![]() $\unicode[STIX]{x1D707}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})>0$
whenever
$\unicode[STIX]{x1D707}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})>0$
whenever
![]() $\unicode[STIX]{x1D709}\in T_{p}^{1,0}(\mathbb{B}^{n})$
and
$\unicode[STIX]{x1D709}\in T_{p}^{1,0}(\mathbb{B}^{n})$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D709})\neq 0$
, hence
$\unicode[STIX]{x2202}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D709})\neq 0$
, hence
![]() $\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})<0$
. Thus, for
$\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})<0$
. Thus, for
![]() $x\in W_{\unicode[STIX]{x1D702}}\,\cap \,\mathbb{B}^{n}$
sufficiently close to
$x\in W_{\unicode[STIX]{x1D702}}\,\cap \,\mathbb{B}^{n}$
sufficiently close to
![]() $p$
, by continuity there also exists
$p$
, by continuity there also exists
![]() $\unicode[STIX]{x1D709}\in T_{x}^{1,0}(\mathbb{B}^{n})$
such that
$\unicode[STIX]{x1D709}\in T_{x}^{1,0}(\mathbb{B}^{n})$
such that
![]() $\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})<0$
, contradicting the plurisubharmonicity of
$\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}((1/\sqrt{-1})\unicode[STIX]{x1D709}\wedge \overline{\unicode[STIX]{x1D709}})<0$
, contradicting the plurisubharmonicity of
![]() $\unicode[STIX]{x1D711}$
, as desired.◻
$\unicode[STIX]{x1D711}$
, as desired.◻
Proof of Main Theorem in the compact case continued.
By Lemma 4.1 the function
![]() $\unicode[STIX]{x1D711}|_{\unicode[STIX]{x1D6F4}}$
vanishes on
$\unicode[STIX]{x1D711}|_{\unicode[STIX]{x1D6F4}}$
vanishes on
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
exactly to the order 1 at a general point
$\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
exactly to the order 1 at a general point
![]() $p\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Thus, shrinking
$p\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Thus, shrinking
![]() $\unicode[STIX]{x1D6F4}$
if necessary,
$\unicode[STIX]{x1D6F4}$
if necessary,
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}=\{x\in \unicode[STIX]{x1D6F4}:\unicode[STIX]{x1D711}<0\}=\widetilde{Z}\,\cap \,U\,\subset \,\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}=\{x\in \unicode[STIX]{x1D6F4}:\unicode[STIX]{x1D711}<0\}=\widetilde{Z}\,\cap \,U\,\subset \,\unicode[STIX]{x1D6F4}$
and
![]() $\unicode[STIX]{x1D711}$
is a defining function of
$\unicode[STIX]{x1D711}$
is a defining function of
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}\,\subset \,\unicode[STIX]{x1D6F4}$
along
$\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}\,\subset \,\unicode[STIX]{x1D6F4}$
along
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}=\unicode[STIX]{x2202}\widetilde{Z}\,\cap \,U$
. It follows from Klembeck [Reference KlembeckKle78] (Theorem 1.5 here) that
$\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}=\unicode[STIX]{x2202}\widetilde{Z}\,\cap \,U$
. It follows from Klembeck [Reference KlembeckKle78] (Theorem 1.5 here) that
![]() $(\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}})$
, where the Kähler form
$(\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}})$
, where the Kähler form
![]() $\unicode[STIX]{x1D714}_{g}$
of
$\unicode[STIX]{x1D714}_{g}$
of
![]() $(\mathbb{B}^{n},g)$
is given by
$(\mathbb{B}^{n},g)$
is given by
![]() $\unicode[STIX]{x1D714}_{g}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (-\unicode[STIX]{x1D711}))$
, is asymptotically of constant holomorphic sectional curvature
$\unicode[STIX]{x1D714}_{g}=\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (-\unicode[STIX]{x1D711}))$
, is asymptotically of constant holomorphic sectional curvature
![]() $-2$
at any boundary point
$-2$
at any boundary point
![]() $p\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. This implies that
$p\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. This implies that
![]() $(\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}})$
is asymptotically totally geodesic along
$(\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n},g|_{\unicode[STIX]{x1D6F4}\,\cap \,\mathbb{B}^{n}})$
is asymptotically totally geodesic along
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
.
$\unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
.
Finally we are going to deduce the total geodesy of
![]() $\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
and hence that
$\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
and hence that
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. Choose
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. Choose
![]() $R<\infty$
exceeding the diameter of the compact ball quotient
$R<\infty$
exceeding the diameter of the compact ball quotient
![]() $X_{\unicode[STIX]{x1D6E4}}$
. Then, denoting by
$X_{\unicode[STIX]{x1D6E4}}$
. Then, denoting by
![]() $B(a;r)\,\subset \,\mathbb{B}^{n}$
the geodesic ball with respect to the canonical Kähler–Einstein metric
$B(a;r)\,\subset \,\mathbb{B}^{n}$
the geodesic ball with respect to the canonical Kähler–Einstein metric
![]() $g$
of radius
$g$
of radius
![]() $r>0$
centered at
$r>0$
centered at
![]() $a\in \mathbb{B}^{n}$
, we have
$a\in \mathbb{B}^{n}$
, we have
![]() $\unicode[STIX]{x1D70B}(B(y;R))=X_{\unicode[STIX]{x1D6E4}}$
for any point
$\unicode[STIX]{x1D70B}(B(y;R))=X_{\unicode[STIX]{x1D6E4}}$
for any point
![]() $y$
in
$y$
in
![]() $\mathbb{B}^{n}$
. Take now any point
$\mathbb{B}^{n}$
. Take now any point
![]() $x\in \widetilde{Z}$
. Let
$x\in \widetilde{Z}$
. Let
![]() $x_{k},k\geqslant 0,$
be a sequence of points on
$x_{k},k\geqslant 0,$
be a sequence of points on
![]() $\widetilde{Z}$
such that
$\widetilde{Z}$
such that
![]() $x_{k}$
converges to
$x_{k}$
converges to
![]() $b\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. For any
$b\in \unicode[STIX]{x1D6F4}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. For any
![]() $k\geqslant 0$
, it follows from
$k\geqslant 0$
, it follows from
![]() $\unicode[STIX]{x1D70B}(B(x_{k};R))=X_{\unicode[STIX]{x1D6E4}}$
that there exists a point
$\unicode[STIX]{x1D70B}(B(x_{k};R))=X_{\unicode[STIX]{x1D6E4}}$
that there exists a point
![]() $y_{k}\in B(x_{k};R)$
such that
$y_{k}\in B(x_{k};R)$
such that
![]() $\unicode[STIX]{x1D70B}(y_{k})=\unicode[STIX]{x1D70B}(x)$
. In other words, there exists
$\unicode[STIX]{x1D70B}(y_{k})=\unicode[STIX]{x1D70B}(x)$
. In other words, there exists
![]() $\unicode[STIX]{x1D6FE}_{k}\in \unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6FE}_{k}\in \unicode[STIX]{x1D6E4}$
such that
![]() $\unicode[STIX]{x1D6FE}_{k}(x)=y_{k}$
. Denoting by
$\unicode[STIX]{x1D6FE}_{k}(x)=y_{k}$
. Denoting by
![]() $d(\cdot ;\cdot )$
the distance function with respect to
$d(\cdot ;\cdot )$
the distance function with respect to
![]() $g$
, we have
$g$
, we have
![]() $d(x_{k};y_{k})<R$
. Comparing the Kähler form
$d(x_{k};y_{k})<R$
. Comparing the Kähler form
![]() $\unicode[STIX]{x1D714}_{g}$
of
$\unicode[STIX]{x1D714}_{g}$
of
![]() $(\mathbb{B}^{n},g)$
with the Kähler form
$(\mathbb{B}^{n},g)$
with the Kähler form
![]() $\unicode[STIX]{x1D714}_{g_{e}}=(\sqrt{-1}/2)\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}$
of the Euclidean metric
$\unicode[STIX]{x1D714}_{g_{e}}=(\sqrt{-1}/2)\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}$
of the Euclidean metric
![]() $g_{e}$
we have
$g_{e}$
we have
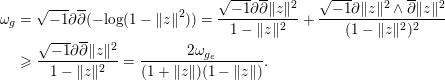 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{g} & = & \displaystyle \sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (1-\Vert z\Vert ^{2}))=\frac{\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{1-\Vert z\Vert ^{2}}+\frac{\sqrt{-1}\unicode[STIX]{x2202}\Vert z\Vert ^{2}\wedge \overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{(1-\Vert z\Vert ^{2})^{2}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{1-\Vert z\Vert ^{2}}=\frac{2\unicode[STIX]{x1D714}_{g_{e}}}{(1+\Vert z\Vert )(1-\Vert z\Vert )}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{g} & = & \displaystyle \sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(-\!\log (1-\Vert z\Vert ^{2}))=\frac{\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{1-\Vert z\Vert ^{2}}+\frac{\sqrt{-1}\unicode[STIX]{x2202}\Vert z\Vert ^{2}\wedge \overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{(1-\Vert z\Vert ^{2})^{2}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{\sqrt{-1}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}\Vert z\Vert ^{2}}{1-\Vert z\Vert ^{2}}=\frac{2\unicode[STIX]{x1D714}_{g_{e}}}{(1+\Vert z\Vert )(1-\Vert z\Vert )}.\nonumber\end{eqnarray}$$
Thus,
![]() $g\geqslant g_{e}/(1-\Vert z\Vert )$
on
$g\geqslant g_{e}/(1-\Vert z\Vert )$
on
![]() $\mathbb{B}^{n}$
. Since
$\mathbb{B}^{n}$
. Since
![]() $x_{k}$
converges in
$x_{k}$
converges in
![]() $\mathbb{C}^{n}$
to
$\mathbb{C}^{n}$
to
![]() $b$
, from
$b$
, from
![]() $d(x_{k};y_{k})<R$
we conclude that there exists a constant
$d(x_{k};y_{k})<R$
we conclude that there exists a constant
![]() $C>0$
such that we have
$C>0$
such that we have
as
![]() $k$
tends to
$k$
tends to
![]() $\infty$
, so that
$\infty$
, so that
![]() $y_{k}$
also converges in
$y_{k}$
also converges in
![]() $\mathbb{C}^{n}$
to
$\mathbb{C}^{n}$
to
![]() $b$
. On the other hand, by the invariance of
$b$
. On the other hand, by the invariance of
![]() $g$
under
$g$
under
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, holomorphic sectional curvatures at
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, holomorphic sectional curvatures at
![]() $x$
are the same as holomorphic sectional curvatures at
$x$
are the same as holomorphic sectional curvatures at
![]() $y_{k}=\unicode[STIX]{x1D6FE}_{k}(x)$
. From the last paragraph
$y_{k}=\unicode[STIX]{x1D6FE}_{k}(x)$
. From the last paragraph
![]() $(\widetilde{Z},g|_{\widetilde{Z}})$
is of constant holomorphic sectional curvature
$(\widetilde{Z},g|_{\widetilde{Z}})$
is of constant holomorphic sectional curvature
![]() $-2$
at
$-2$
at
![]() $x$
. Denoting by
$x$
. Denoting by
![]() $\unicode[STIX]{x1D70F}$
the second fundamental form of
$\unicode[STIX]{x1D70F}$
the second fundamental form of
![]() $\widetilde{Z}$
in
$\widetilde{Z}$
in
![]() $(\mathbb{B}^{n},g)$
, by the Gauss equation we have
$(\mathbb{B}^{n},g)$
, by the Gauss equation we have
where
![]() $\unicode[STIX]{x1D6FC}\in T_{x}^{1,0}(\widetilde{Z})$
and
$\unicode[STIX]{x1D6FC}\in T_{x}^{1,0}(\widetilde{Z})$
and
![]() $\Vert \cdot \Vert$
stands for norms measured with respect to Hermitian metrics induced from
$\Vert \cdot \Vert$
stands for norms measured with respect to Hermitian metrics induced from
![]() $g$
. It follows that
$g$
. It follows that
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=0$
at
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=0$
at
![]() $x$
for all
$x$
for all
![]() $\unicode[STIX]{x1D6FC}\in T_{x}^{1,0}$
, and hence
$\unicode[STIX]{x1D6FC}\in T_{x}^{1,0}$
, and hence
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime })=0$
for all
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime })=0$
for all
![]() $\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime }\in T_{x}^{1,0}$
by polarization. Since
$\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime }\in T_{x}^{1,0}$
by polarization. Since
![]() $x\in \widetilde{Z}$
is arbitrary,
$x\in \widetilde{Z}$
is arbitrary,
![]() $\unicode[STIX]{x1D70F}\equiv 0$
, and we conclude that
$\unicode[STIX]{x1D70F}\equiv 0$
, and we conclude that
![]() $\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
is totally geodesic with respect to
$\widetilde{Z}\,\subset \,\mathbb{B}^{n}$
is totally geodesic with respect to
![]() $g$
, as desired. The proof of Main Theorem for the case of cocompact torsion-free lattices
$g$
, as desired. The proof of Main Theorem for the case of cocompact torsion-free lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is complete.◻
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
is complete.◻
Remark.
Replacing
![]() $\mathbb{B}^{n}$
by a possibly reducible bounded symmetric domain
$\mathbb{B}^{n}$
by a possibly reducible bounded symmetric domain
![]() $\unicode[STIX]{x1D6FA}$
of higher rank, in the same setup we have a complex-analytic subvariety
$\unicode[STIX]{x1D6FA}$
of higher rank, in the same setup we have a complex-analytic subvariety
![]() $\widetilde{Z}\,\subset \,\unicode[STIX]{x1D6FA}$
exiting as a germ of complex submanifold at points
$\widetilde{Z}\,\subset \,\unicode[STIX]{x1D6FA}$
exiting as a germ of complex submanifold at points
![]() $b\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
belonging to some
$b\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
belonging to some
![]() $G_{0}$
-invariant subset
$G_{0}$
-invariant subset
![]() $E\,\subset \,\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. If the analytic continuation
$E\,\subset \,\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. If the analytic continuation
![]() $\widetilde{Z}\,\cup \,U$
by grafting a coordinate chart
$\widetilde{Z}\,\cup \,U$
by grafting a coordinate chart
![]() $U$
at
$U$
at
![]() $b$
happens to be transversal to the foliation of
$b$
happens to be transversal to the foliation of
![]() $E$
by maximal complex submanifolds (cf. Wolf [Reference WolfWol72]), then
$E$
by maximal complex submanifolds (cf. Wolf [Reference WolfWol72]), then
![]() $Z$
is strictly pseudoconvex at
$Z$
is strictly pseudoconvex at
![]() $b$
and the same rescaling argument shows that
$b$
and the same rescaling argument shows that
![]() $\widetilde{Z}$
is the image of a holomorphic isometry of some
$\widetilde{Z}$
is the image of a holomorphic isometry of some
![]() $\mathbb{B}^{m}$
and it is hence algebraic by Mok [Reference MokMok12b]. In general the rescaling argument shows that
$\mathbb{B}^{m}$
and it is hence algebraic by Mok [Reference MokMok12b]. In general the rescaling argument shows that
![]() $\widetilde{Z}$
decomposes near
$\widetilde{Z}$
decomposes near
![]() $b$
into a union of algebraic subsets which are images of holomorphic isometric embeddings of some
$b$
into a union of algebraic subsets which are images of holomorphic isometric embeddings of some
![]() $\mathbb{B}^{m}$
, which furnishes a starting point of our approach under preparation to the hyperbolic Ax–Lindemann–Weierstrass theorem for bounded symmetric domains applicable to nonarithmetic lattices.
$\mathbb{B}^{m}$
, which furnishes a starting point of our approach under preparation to the hyperbolic Ax–Lindemann–Weierstrass theorem for bounded symmetric domains applicable to nonarithmetic lattices.
For the proof of Main Theorem it remains to consider torsion-free nonuniform lattices
![]() $\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, i.e, the case where
$\unicode[STIX]{x1D6E4}\,\subset \,G_{0}$
, i.e, the case where
![]() $(X_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
is (necessarily) of finite volume but noncompact. In this case, in the notation of the proof of Main Theorem in the cocompact case, taking sequences of points
$(X_{\unicode[STIX]{x1D6E4}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E4}})$
is (necessarily) of finite volume but noncompact. In this case, in the notation of the proof of Main Theorem in the cocompact case, taking sequences of points
![]() $(x_{k})$
on
$(x_{k})$
on
![]() $\widetilde{Z}$
converging to points on
$\widetilde{Z}$
converging to points on
![]() $\widetilde{Z}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
, we have to take care of the possibility that
$\widetilde{Z}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
, we have to take care of the possibility that
![]() $\unicode[STIX]{x1D70B}(x_{k})\in X_{\unicode[STIX]{x1D6E4}}$
escapes to infinity. To deal with this situation we prove the following result ascertaining that the sequence
$\unicode[STIX]{x1D70B}(x_{k})\in X_{\unicode[STIX]{x1D6E4}}$
escapes to infinity. To deal with this situation we prove the following result ascertaining that the sequence
![]() $\{x_{k}\}$
may be chosen such that
$\{x_{k}\}$
may be chosen such that
![]() $\{\unicode[STIX]{x1D70B}(x_{k})\}$
lies on a compact subset of
$\{\unicode[STIX]{x1D70B}(x_{k})\}$
lies on a compact subset of
![]() $X_{\unicode[STIX]{x1D6E4}}$
.
$X_{\unicode[STIX]{x1D6E4}}$
.
Proposition 4.1. In the notation of Main Theorem let
![]() $S\,\subset \,\mathbb{B}^{n}$
be an irreducible algebraic subset and write
$S\,\subset \,\mathbb{B}^{n}$
be an irreducible algebraic subset and write
![]() $Z:=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. Let
$Z:=\overline{\unicode[STIX]{x1D70B}(S)}^{\mathscr{Z}ar}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. Let
![]() $\widetilde{Z}$
be an irreducible component of
$\widetilde{Z}$
be an irreducible component of
![]() $\unicode[STIX]{x1D70B}^{-1}(Z)$
. Suppose
$\unicode[STIX]{x1D70B}^{-1}(Z)$
. Suppose
![]() $b\in \unicode[STIX]{x2202}\mathbb{B}^{n}$
and let
$b\in \unicode[STIX]{x2202}\mathbb{B}^{n}$
and let
![]() $U\Subset \mathbb{C}^{n}$
be an open neighborhood of
$U\Subset \mathbb{C}^{n}$
be an open neighborhood of
![]() $b$
for which there exists a complex submanifold
$b$
for which there exists a complex submanifold
![]() $\unicode[STIX]{x1D6F4}\,\subset \,U$
of dimension
$\unicode[STIX]{x1D6F4}\,\subset \,U$
of dimension
![]() $d:=\dim (Z)$
such that:
$d:=\dim (Z)$
such that:
![]() $\text{(a)}$
$\text{(a)}$
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}$
is a nonempty connected open subset of
$\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}$
is a nonempty connected open subset of
![]() $\widetilde{Z}$
and
$\widetilde{Z}$
and
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
is connected;
$\unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
is connected;
![]() $\text{(b)}$
$\text{(b)}$
![]() $\unicode[STIX]{x1D6F4}$
is transversal to
$\unicode[STIX]{x1D6F4}$
is transversal to
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}$
at every point
$\unicode[STIX]{x2202}\mathbb{B}^{n}$
at every point
![]() $p\in \unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
. Let
$p\in \unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
. Let
![]() $\{U_{k}:0\leqslant k<\infty \}$
be a sequence of open neighborhoods of
$\{U_{k}:0\leqslant k<\infty \}$
be a sequence of open neighborhoods of
![]() $b$
in
$b$
in
![]() $\mathbb{C}^{n}$
,
$\mathbb{C}^{n}$
,
![]() $U_{0}=U$
, such that for each
$U_{0}=U$
, such that for each
![]() $k\geqslant 0$
,
$k\geqslant 0$
,
![]() $U_{k+1}\Subset U_{k}$
and
$U_{k+1}\Subset U_{k}$
and
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
is connected, and such that
$\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
is connected, and such that
![]() $\bigcap _{0\leqslant k<\infty }U_{k}=\overline{{\mathcal{O}}}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
for some open neighborhood
$\bigcap _{0\leqslant k<\infty }U_{k}=\overline{{\mathcal{O}}}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
for some open neighborhood
![]() ${\mathcal{O}}$
of
${\mathcal{O}}$
of
![]() $b$
in
$b$
in
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Then, there exists a compact subset
$\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Then, there exists a compact subset
![]() $Q\,\subset \,Z$
and a sequence of points
$Q\,\subset \,Z$
and a sequence of points
![]() $x_{k}\in U_{k}$
such that
$x_{k}\in U_{k}$
such that
![]() $\unicode[STIX]{x1D70B}(x_{k})\in Q$
for any
$\unicode[STIX]{x1D70B}(x_{k})\in Q$
for any
![]() $k\geqslant 0$
. As a consequence,
$k\geqslant 0$
. As a consequence,
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset.
For the proof of Proposition 4.1 we will need the following well-known statement about holomorphic functions on the unit ball for which we include a proof for easy reference.
Lemma 4.2. Let
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() $b\in \unicode[STIX]{x2202}\mathbb{B}^{n}$
, and
$b\in \unicode[STIX]{x2202}\mathbb{B}^{n}$
, and
![]() $U\Subset \mathbb{C}^{n}$
be a neighborhood of
$U\Subset \mathbb{C}^{n}$
be a neighborhood of
![]() $b$
. Suppose
$b$
. Suppose
![]() $f:\overline{U}\,\cap \,\overline{\mathbb{B}^{n}}\rightarrow \mathbb{C}$
is a continuous function which is holomorphic on
$f:\overline{U}\,\cap \,\overline{\mathbb{B}^{n}}\rightarrow \mathbb{C}$
is a continuous function which is holomorphic on
![]() $U\,\cap \,\mathbb{B}^{n}$
and vanishes on
$U\,\cap \,\mathbb{B}^{n}$
and vanishes on
![]() $\overline{U}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Then,
$\overline{U}\,\cap \,\unicode[STIX]{x2202}\mathbb{B}^{n}$
. Then,
![]() $f\equiv 0$
on
$f\equiv 0$
on
![]() $\overline{U}\,\cap \,\overline{\mathbb{B}^{n}}$
.
$\overline{U}\,\cap \,\overline{\mathbb{B}^{n}}$
.
Proof. Slicing by complex lines transversal to
![]() $\unicode[STIX]{x2202}\mathbb{B}^{n}$
at points
$\unicode[STIX]{x2202}\mathbb{B}^{n}$
at points
![]() $p\in U\,\cap \,\unicode[STIX]{x2202}B^{n}$
one reduces the problem to the case of
$p\in U\,\cap \,\unicode[STIX]{x2202}B^{n}$
one reduces the problem to the case of
![]() $n=1$
. By the Riemann mapping theorem it suffices to show that, for a continuous function
$n=1$
. By the Riemann mapping theorem it suffices to show that, for a continuous function
![]() $g:\overline{\unicode[STIX]{x1D6E5}}\rightarrow \mathbb{C}$
which is holomorphic on
$g:\overline{\unicode[STIX]{x1D6E5}}\rightarrow \mathbb{C}$
which is holomorphic on
![]() $\unicode[STIX]{x1D6E5}$
and vanishes on an open arc of
$\unicode[STIX]{x1D6E5}$
and vanishes on an open arc of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
, we must have
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
, we must have
![]() $g\equiv 0$
. To see this, replacing
$g\equiv 0$
. To see this, replacing
![]() $g$
by
$g$
by
![]() $g\,\circ \,\unicode[STIX]{x1D711}$
for some
$g\,\circ \,\unicode[STIX]{x1D711}$
for some
![]() $\unicode[STIX]{x1D711}\in \text{Aut}(\unicode[STIX]{x1D6E5})$
we may assume that
$\unicode[STIX]{x1D711}\in \text{Aut}(\unicode[STIX]{x1D6E5})$
we may assume that
![]() $g(\unicode[STIX]{x1D701})=0$
for
$g(\unicode[STIX]{x1D701})=0$
for
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
satisfying Re
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
satisfying Re
![]() $(\unicode[STIX]{x1D701})\geqslant 0$
. Then, the continuous function
$(\unicode[STIX]{x1D701})\geqslant 0$
. Then, the continuous function
![]() $h:\overline{\unicode[STIX]{x1D6E5}}\rightarrow \mathbb{C}$
defined by
$h:\overline{\unicode[STIX]{x1D6E5}}\rightarrow \mathbb{C}$
defined by
![]() $h(z):=g(z)g(-z)$
vanishes on
$h(z):=g(z)g(-z)$
vanishes on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
and it is holomorphic on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
and it is holomorphic on
![]() $\unicode[STIX]{x1D6E5}$
. By the maximum principle
$\unicode[STIX]{x1D6E5}$
. By the maximum principle
![]() $h\equiv 0$
and hence
$h\equiv 0$
and hence
![]() $g\equiv 0$
, as desired.◻
$g\equiv 0$
, as desired.◻
Proof of Proposition 4.1.
Denote by
![]() $\{q_{1},\ldots ,q_{m}\}$
the finite set of normal isolated singularities of
$\{q_{1},\ldots ,q_{m}\}$
the finite set of normal isolated singularities of
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
. For each
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
. For each
![]() $q_{i}$
,
$q_{i}$
,
![]() $1\leqslant i\leqslant m$
, let
$1\leqslant i\leqslant m$
, let
![]() $V_{i}$
be an open neighborhood of
$V_{i}$
be an open neighborhood of
![]() $q_{i}$
in
$q_{i}$
in
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
such that there is a biholomorphism
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
such that there is a biholomorphism
![]() $\unicode[STIX]{x1D706}_{i}:V_{i}\overset{\cong }{\longrightarrow }E_{i}\,\subset \,\mathbb{B}^{N_{i}}$
onto a subvariety
$\unicode[STIX]{x1D706}_{i}:V_{i}\overset{\cong }{\longrightarrow }E_{i}\,\subset \,\mathbb{B}^{N_{i}}$
onto a subvariety
![]() $E_{i}$
of the complex unit ball
$E_{i}$
of the complex unit ball
![]() $\mathbb{B}^{N_{i}}$
in
$\mathbb{B}^{N_{i}}$
in
![]() $\mathbb{C}^{N_{i}}$
,
$\mathbb{C}^{N_{i}}$
,
![]() $\unicode[STIX]{x1D708}(q_{i})=0$
. We assume without loss of generality that
$\unicode[STIX]{x1D708}(q_{i})=0$
. We assume without loss of generality that
![]() $\overline{V_{1}},\ldots ,\overline{V_{m}}$
are disjoint. Let
$\overline{V_{1}},\ldots ,\overline{V_{m}}$
are disjoint. Let
![]() $\{U_{k}:0\leqslant k<\infty \}$
be the sequence of open neighborhoods of
$\{U_{k}:0\leqslant k<\infty \}$
be the sequence of open neighborhoods of
![]() $b$
in
$b$
in
![]() $\mathbb{C}^{n}$
as in the statement of the proposition. Arguing by contradiction assume that there exists no compact subset
$\mathbb{C}^{n}$
as in the statement of the proposition. Arguing by contradiction assume that there exists no compact subset
![]() $Q\,\subset \,Z$
with the desired property as stated in the proposition. Let
$Q\,\subset \,Z$
with the desired property as stated in the proposition. Let
![]() $C\,\subset \,Z$
be the compact subset such that
$C\,\subset \,Z$
be the compact subset such that
![]() $Z-C$
is the disjoint union of the open subsets
$Z-C$
is the disjoint union of the open subsets
![]() $V_{i}\,\cap \,\widetilde{Z},1\leqslant i\leqslant m$
. By assumption, for
$V_{i}\,\cap \,\widetilde{Z},1\leqslant i\leqslant m$
. By assumption, for
![]() $k$
sufficiently large, say
$k$
sufficiently large, say
![]() $k\geqslant \ell$
,
$k\geqslant \ell$
,
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k})\,\subset \,Z-C=(V_{1}\,\cap \,\widetilde{Z})\,\cup \,\cdots \,\cup \,(V_{m}\,\cap \,\widetilde{Z})$
. Since
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k})\,\subset \,Z-C=(V_{1}\,\cap \,\widetilde{Z})\,\cup \,\cdots \,\cup \,(V_{m}\,\cap \,\widetilde{Z})$
. Since
![]() $\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
is connected for each
$\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
is connected for each
![]() $k\geqslant 0$
, we may assume that
$k\geqslant 0$
, we may assume that
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k})\,\subset \,V_{i}$
for one of the disjoint open sets
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k})\,\subset \,V_{i}$
for one of the disjoint open sets
![]() $V_{i}$
, say
$V_{i}$
, say
![]() $i=1$
, whenever
$i=1$
, whenever
![]() $k\geqslant \ell$
. Since
$k\geqslant \ell$
. Since
![]() $\unicode[STIX]{x1D706}_{1}:V_{1}\overset{\cong }{\longrightarrow }E_{1}\,\subset \,\mathbb{B}^{N_{1}}$
there exists a holomorphic function
$\unicode[STIX]{x1D706}_{1}:V_{1}\overset{\cong }{\longrightarrow }E_{1}\,\subset \,\mathbb{B}^{N_{1}}$
there exists a holomorphic function
![]() $h$
on
$h$
on
![]() $\mathbb{B}^{N_{1}}$
such that
$\mathbb{B}^{N_{1}}$
such that
![]() $h(0)=0$
and such that the holomorphic function
$h(0)=0$
and such that the holomorphic function
![]() $f:\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{\ell }\rightarrow \mathbb{C}$
defined by
$f:\unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{\ell }\rightarrow \mathbb{C}$
defined by
![]() $f:=h\,\circ \,\unicode[STIX]{x1D706}_{1}\,\circ \,\unicode[STIX]{x1D70B}$
is nonconstant. By assumption, for any sequence of points
$f:=h\,\circ \,\unicode[STIX]{x1D706}_{1}\,\circ \,\unicode[STIX]{x1D70B}$
is nonconstant. By assumption, for any sequence of points
![]() $x_{k}\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
,
$x_{k}\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
,
![]() $\unicode[STIX]{x1D70B}(x_{k})$
converges to
$\unicode[STIX]{x1D70B}(x_{k})$
converges to
![]() $q_{1}\in \overline{X_{\unicode[STIX]{x1D6E4}}}$
. It follows that
$q_{1}\in \overline{X_{\unicode[STIX]{x1D6E4}}}$
. It follows that
![]() $f(x)$
converges to
$f(x)$
converges to
![]() $0$
as
$0$
as
![]() $x\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{\ell }$
converges to some boundary point
$x\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{\ell }$
converges to some boundary point
![]() $p\in {\mathcal{O}}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
. By Lemma 4.2, such a holomorphic function must necessarily be identically zero, a plain contradiction. We have thus proven by contradiction that there is some compact subset
$p\in {\mathcal{O}}\,\subset \,\unicode[STIX]{x2202}\mathbb{B}^{n}\,\cap \,\unicode[STIX]{x1D6F4}$
. By Lemma 4.2, such a holomorphic function must necessarily be identically zero, a plain contradiction. We have thus proven by contradiction that there is some compact subset
![]() $Q\,\subset \,Z$
for which there exists some sequence of points
$Q\,\subset \,Z$
for which there exists some sequence of points
![]() $x_{k}\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
such that
$x_{k}\in \unicode[STIX]{x1D6F4}\,\cap \,\widetilde{Z}\,\cap \,U_{k}$
such that
![]() $\unicode[STIX]{x1D70B}(x_{k})\in Q$
for each
$\unicode[STIX]{x1D70B}(x_{k})\in Q$
for each
![]() $k$
. By the proof of Main Theorem in the compact case and by Proposition 4.1, this forces
$k$
. By the proof of Main Theorem in the compact case and by Proposition 4.1, this forces
![]() $\widetilde{Z}$
to be totally geodesic on an open neighborhood of some point
$\widetilde{Z}$
to be totally geodesic on an open neighborhood of some point
![]() $x\in Z$
, hence
$x\in Z$
, hence
![]() $Z=\unicode[STIX]{x1D70B}(\widetilde{Z})$
is a totally geodesic subset in
$Z=\unicode[STIX]{x1D70B}(\widetilde{Z})$
is a totally geodesic subset in
![]() $X_{\unicode[STIX]{x1D6E4}}$
, as desired.◻
$X_{\unicode[STIX]{x1D6E4}}$
, as desired.◻
Proof of Main Theorem continued.
Main Theorem was first proved for the case where
![]() $X_{\unicode[STIX]{x1D6E4}}$
is compact, and the case where
$X_{\unicode[STIX]{x1D6E4}}$
is compact, and the case where
![]() $X_{\unicode[STIX]{x1D6E4}}$
is noncompact has been incorporated in Proposition 4.1. The proof of Main Theorem is now complete.◻
$X_{\unicode[STIX]{x1D6E4}}$
is noncompact has been incorporated in Proposition 4.1. The proof of Main Theorem is now complete.◻
The proof of Main Theorem also yields readily the following result about the Zariski closure of unions of totally geodesic subsets of
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
.
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
.
Theorem 4.1. Let
![]() $A$
be any set of indices and
$A$
be any set of indices and
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
,
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
,
![]() $\unicode[STIX]{x1D6FC}\in A$
, be a family of closed totally geodesic subsets of
$\unicode[STIX]{x1D6FC}\in A$
, be a family of closed totally geodesic subsets of
![]() $X_{\unicode[STIX]{x1D6E4}}$
of positive dimension. Write
$X_{\unicode[STIX]{x1D6E4}}$
of positive dimension. Write
![]() $E:=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Then, the Zariski closure of
$E:=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Then, the Zariski closure of
![]() $E$
in
$E$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
is a union of finitely many totally geodesic subsets.
$X_{\unicode[STIX]{x1D6E4}}$
is a union of finitely many totally geodesic subsets.
Proof. Since the minimal compactification
![]() $X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
is obtained by adding a finite number of normal isolated singularities, by the Remmert–Stein extension theorem the topological closure in
$X_{\unicode[STIX]{x1D6E4}}\,\subset \,\overline{X_{\unicode[STIX]{x1D6E4}}}$
is obtained by adding a finite number of normal isolated singularities, by the Remmert–Stein extension theorem the topological closure in
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
of each
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
of each
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
,
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
,
![]() $\unicode[STIX]{x1D6FC}\in A$
, is necessarily a projective subvariety of
$\unicode[STIX]{x1D6FC}\in A$
, is necessarily a projective subvariety of
![]() $\overline{X_{\unicode[STIX]{x1D6E4}}}$
. Hence for any
$\overline{X_{\unicode[STIX]{x1D6E4}}}$
. Hence for any
![]() $\unicode[STIX]{x1D6FC}\in A$
,
$\unicode[STIX]{x1D6FC}\in A$
,
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety. Denote by
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a quasi-projective subvariety. Denote by
![]() $Z$
the Zariski closure of
$Z$
the Zariski closure of
![]() $E=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Write
$E=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Write
![]() $Z=Z_{1}\,\cup \,\cdots \,\cup \,Z_{m}$
for the decomposition of
$Z=Z_{1}\,\cup \,\cdots \,\cup \,Z_{m}$
for the decomposition of
![]() $Z$
into irreducible components. For
$Z$
into irreducible components. For
![]() $1\leqslant k\leqslant m$
we proceed to prove that
$1\leqslant k\leqslant m$
we proceed to prove that
![]() $Z_{k}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. For each dimension
$Z_{k}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. For each dimension
![]() $d$
,
$d$
,
![]() $1\leqslant d\leqslant \dim (Z_{k})$
, denote by
$1\leqslant d\leqslant \dim (Z_{k})$
, denote by
![]() $A(k,d)\,\subset \,A$
the set of indices
$A(k,d)\,\subset \,A$
the set of indices
![]() $\unicode[STIX]{x1D6FC}\in A$
such that
$\unicode[STIX]{x1D6FC}\in A$
such that
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,Z_{k}$
and
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\,\subset \,Z_{k}$
and
![]() $\dim (\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}})=d$
. Let
$\dim (\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}})=d$
. Let
![]() $E(k,d)$
be the union of
$E(k,d)$
be the union of
![]() $\{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A(k,d)\}$
and denote by
$\{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A(k,d)\}$
and denote by
![]() $Z(k,d)$
the Zariski closure of
$Z(k,d)$
the Zariski closure of
![]() $E(k,d)$
. Then, there exists some
$E(k,d)$
. Then, there exists some
![]() $d_{0}$
,
$d_{0}$
,
![]() $1\leqslant d_{0}\leqslant \dim (Z_{k})$
, such that
$1\leqslant d_{0}\leqslant \dim (Z_{k})$
, such that
![]() $Z(k,d_{0})=Z_{k}$
. Thus, replacing
$Z(k,d_{0})=Z_{k}$
. Thus, replacing
![]() $Z$
by
$Z$
by
![]() $Z_{k}$
and
$Z_{k}$
and
![]() $A$
by
$A$
by
![]() $A(k,d_{0})$
, for the proof of Theorem 4.1 without loss of generality we may assume that
$A(k,d_{0})$
, for the proof of Theorem 4.1 without loss of generality we may assume that
![]() $Z$
is irreducible and that all
$Z$
is irreducible and that all
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in A$
, are of the same complex dimension
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in A$
, are of the same complex dimension
![]() $d_{0}$
.
$d_{0}$
.
Consider now the Chow space
![]() ${\mathcal{K}}$
of all
${\mathcal{K}}$
of all
![]() $d_{0}$
-dimensional projective subspaces in
$d_{0}$
-dimensional projective subspaces in
![]() $\mathbb{P}^{n}$
and the universal family
$\mathbb{P}^{n}$
and the universal family
![]() $\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
$\unicode[STIX]{x1D70C}:\mathscr{U}\rightarrow {\mathcal{K}}$
,
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
. (In this case
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
. (In this case
![]() $\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
can be identified with the Grassmann bundle Gr
$\unicode[STIX]{x1D707}:\mathscr{U}\rightarrow \mathbb{P}^{n}$
can be identified with the Grassmann bundle Gr
![]() $(d_{0},T_{\mathbb{P}^{n}})$
.) Denote by
$(d_{0},T_{\mathbb{P}^{n}})$
.) Denote by
![]() ${\mathcal{L}}_{\unicode[STIX]{x1D6FC}}\,\subset \,\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
the tautological lifting of
${\mathcal{L}}_{\unicode[STIX]{x1D6FC}}\,\subset \,\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
the tautological lifting of
![]() $Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
to
$Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
to
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. Let
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. Let
![]() $\mathscr{Z}\,\subset \,\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
be the Zariski closure of
$\mathscr{Z}\,\subset \,\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
be the Zariski closure of
![]() $\bigcup _{\unicode[STIX]{x1D6FC}\in A}{\mathcal{L}}_{\unicode[STIX]{x1D6FC}}$
. Writing
$\bigcup _{\unicode[STIX]{x1D6FC}\in A}{\mathcal{L}}_{\unicode[STIX]{x1D6FC}}$
. Writing
![]() $\mathscr{Z}=\mathscr{Z}_{1}\,\cup \,\cdots \,\cup \,\mathscr{Z}_{s}$
for the decomposition of
$\mathscr{Z}=\mathscr{Z}_{1}\,\cup \,\cdots \,\cup \,\mathscr{Z}_{s}$
for the decomposition of
![]() $\mathscr{Z}$
into irreducible components and recalling that
$\mathscr{Z}$
into irreducible components and recalling that
![]() $Z$
is assumed now to be irreducible, there exists an integer
$Z$
is assumed now to be irreducible, there exists an integer
![]() $\ell$
,
$\ell$
,
![]() $1\leqslant \ell \leqslant s$
, such that
$1\leqslant \ell \leqslant s$
, such that
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z}_{\ell })=Z$
. Then,
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z}_{\ell })=Z$
. Then,
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z}_{\ell })\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is the Zariski closure
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6E4}}(\mathscr{Z}_{\ell })\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is the Zariski closure
![]() $Z$
of
$Z$
of
![]() $E=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Denote by
$E=\bigcup \{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}$
. Denote by
![]() $\mathscr{F}$
the tautological holomorphic foliation on
$\mathscr{F}$
the tautological holomorphic foliation on
![]() $\mathscr{U}$
and by
$\mathscr{U}$
and by
![]() $\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
the induced holomorphic foliation on
$\mathscr{F}_{\unicode[STIX]{x1D6E4}}$
the induced holomorphic foliation on
![]() $\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. In analogy to the proof of Proposition 3.1, there exists a point
$\mathscr{U}_{\unicode[STIX]{x1D6E4}}$
. In analogy to the proof of Proposition 3.1, there exists a point
![]() $e_{\ell }\in E\,\cap \,\text{Reg}(\mathscr{Z})\,\cap \,\mathscr{Z}_{\ell }$
such that
$e_{\ell }\in E\,\cap \,\text{Reg}(\mathscr{Z})\,\cap \,\mathscr{Z}_{\ell }$
such that
![]() $\mathscr{S}_{\ell }:={\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}+{\mathcal{T}}_{\mathscr{Z}_{\ell }}\,\subset \,{\mathcal{T}}_{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}$
is a locally free subsheaf at
$\mathscr{S}_{\ell }:={\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}+{\mathcal{T}}_{\mathscr{Z}_{\ell }}\,\subset \,{\mathcal{T}}_{\mathscr{U}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}$
is a locally free subsheaf at
![]() $e_{\ell }\in E$
(since the points to be excluded form a quasi-projective subvariety
$e_{\ell }\in E$
(since the points to be excluded form a quasi-projective subvariety
![]() $\mathscr{Q}_{\ell }\subsetneq \mathscr{Z}_{\ell }$
, which implies that
$\mathscr{Q}_{\ell }\subsetneq \mathscr{Z}_{\ell }$
, which implies that
![]() ${\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}+{\mathcal{T}}_{\mathscr{Z}_{\ell }}={\mathcal{T}}_{\mathscr{Z}_{\ell }}$
). It follows that
${\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}+{\mathcal{T}}_{\mathscr{Z}_{\ell }}={\mathcal{T}}_{\mathscr{Z}_{\ell }}$
). It follows that
![]() ${\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}\,\subset \,{\mathcal{T}}_{\mathscr{Z}_{\ell }}$
and
${\mathcal{T}}_{\mathscr{F}_{\unicode[STIX]{x1D6E4}}}|_{\mathscr{Z}_{\ell }}\,\subset \,{\mathcal{T}}_{\mathscr{Z}_{\ell }}$
and
![]() $Z$
is uniruled by subvarieties belonging to
$Z$
is uniruled by subvarieties belonging to
![]() ${\mathcal{K}}$
in the sense of Definition 3.1, and the proof of Main Theorem shows that
${\mathcal{K}}$
in the sense of Definition 3.1, and the proof of Main Theorem shows that
![]() $Z$
is a totally geodesic subset, as desired.◻
$Z$
is a totally geodesic subset, as desired.◻
Combining Main Theorem and Theorem 4.1 we finish with the following corollary.
Corollary 4.1. Let
![]() $A$
be any set of indices and
$A$
be any set of indices and
![]() $S_{\unicode[STIX]{x1D6FC}}\,\subset \,\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
be a family of algebraic subsets on the complex unit ball
$S_{\unicode[STIX]{x1D6FC}}\,\subset \,\mathbb{B}^{n}\,\subset \,\mathbb{P}^{n}$
be a family of algebraic subsets on the complex unit ball
![]() $\mathbb{B}^{n}$
of positive dimension. Let
$\mathbb{B}^{n}$
of positive dimension. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map and define
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow X_{\unicode[STIX]{x1D6E4}}$
be the universal covering map and define
![]() $E:=\bigcup \{\unicode[STIX]{x1D70B}(S_{\unicode[STIX]{x1D6FC}}):\unicode[STIX]{x1D6FC}\in A\}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. Then, the Zariski closure of
$E:=\bigcup \{\unicode[STIX]{x1D70B}(S_{\unicode[STIX]{x1D6FC}}):\unicode[STIX]{x1D6FC}\in A\}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. Then, the Zariski closure of
![]() $E$
in
$E$
in
![]() $X_{\unicode[STIX]{x1D6E4}}$
is a finite union of totally geodesic subsets.
$X_{\unicode[STIX]{x1D6E4}}$
is a finite union of totally geodesic subsets.
Proof. Denote by
![]() $Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
$Z\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
![]() $E$
. For each
$E$
. For each
![]() $\unicode[STIX]{x1D6FC}\in A$
denote by
$\unicode[STIX]{x1D6FC}\in A$
denote by
![]() $Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
$Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
the Zariski closure of
![]() $\unicode[STIX]{x1D70B}(S_{\unicode[STIX]{x1D6FC}})\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. By Main Theorem, for each
$\unicode[STIX]{x1D70B}(S_{\unicode[STIX]{x1D6FC}})\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. By Main Theorem, for each
![]() $\unicode[STIX]{x1D6FC}\in A$
,
$\unicode[STIX]{x1D6FC}\in A$
,
![]() $Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. Hence,
$Z_{\unicode[STIX]{x1D6FC}}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
is a totally geodesic subset. Hence,
![]() $Z$
is the Zariski closure of
$Z$
is the Zariski closure of
![]() $E^{\prime }=\bigcup \{Z_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. By Theorem 4.1,
$E^{\prime }=\bigcup \{Z_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in A\}\,\subset \,X_{\unicode[STIX]{x1D6E4}}$
. By Theorem 4.1,
![]() $Z$
is a finite union of totally geodesic subsets, as desired.◻
$Z$
is a finite union of totally geodesic subsets, as desired.◻
Acknowledgements
The author wishes to thank Laurent Clozel, Emmanuel Ullmo, Gisbert Wüstholz and Jonathan Pila for their invitations during which he has expounded on works revolving around Main Theorem of the current article, and for introducing him to problems in the interface between complex geometry and number theory.