1. Introduction
Fluid flow can be driven by various methods, such as buoyancy-driven (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Xia Reference Xia2013), surface-tension-driven (Levich & Krylov Reference Levich and Krylov1969; Kawamura et al. Reference Kawamura, Nishino, Matsumoto and Ueno2012), electromagnetic-driven (Schüssler Reference Schüssler2012; MacDonald & Mullan Reference MacDonald and Mullan2017) and vibration-driven (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998; Lappa Reference Lappa2009), which is essential for many practical applications, such as heat transfer and mixing. While buoyancy-driven convection is a common way to induce fluid flow, in certain extreme conditions such as microgravity, it becomes challenging to generate sufficient flow due to the negligible effect of gravity. However, alternative methods such as vibration can become significant for heat transport, and vibration can be possibly caused by many ways in microgravity such as spacecraft movement, astronaut activity (Bannister et al. Reference Bannister, Grodzka, Spradley, Bourgeois, Hedden and Facemire1973) or even manually imposed. Vibration can result in a supplementary fluid motion, making it an attractive way to control fluid flow and heat transfer in microgravity. In this context, thermal vibrational convection (TVC) arises when vibration is applied to a fluid system with a temperature gradient. The resulting body force causes relative fluid motion and increases the threshold for convective instability. Therefore, it is important to study the underlying flow physics of TVC as a potential way to drive fluid flow and heat transfer in microgravity. The present work focuses on investigating the effect of vibration on the structural transitions of the flow in TVC systems.
Many previous studies have focused on introducing vibration to the classical model of thermal convection, such as Rayleigh–Bénard (RB) convection, to understand how boundary layer disruption affects heat transport. There are many ways to disrupt the boundary layer, such as applying roughness (Zhang et al. Reference Zhang, Sun, Bao and Zhou2018; Jin et al. Reference Jin, Wu, Zhang, Liu and Zhou2022; Wu, Wang & Zhou Reference Wu, Wang and Zhou2022b), using a time-varying heating plate (Yang et al. Reference Yang, Chong, Wang, Verzicco, Shishkina and Lohse2020) or a spatially varying heating plate (Zhao et al. Reference Zhao, Zhang, Wang, Wu, Chong and Zhou2022), and so on (Yang et al. Reference Yang, Wang, Tang, Zhou and Dong2022a,Reference Yang, Zhang, Wang, Dong and Zhoub). In particular, vibration can either enhance or suppress convective heat transport depending on the mutual direction of the vibration axis and the temperature gradient (Savino, Monti & Piccirillo Reference Savino, Monti and Piccirillo1998; Cissé, Bardan & Mojtabi Reference Cissé, Bardan and Mojtabi2004). Wang, Zhou & Sun (Reference Wang, Zhou and Sun2020) applied horizontal vibrations to RB convection, and found that high-frequency vibration can significantly enhance the heat transport. This enhancement is achieved by vibration-induced boundary layer (BL) destabilisation, which breaks up the limitation of laminar BL for heat transport. In contrast, when vertical vibration is applied to the turbulent RB convection, the convective heat transport is suppressed (Wu et al. Reference Wu, Wang, Chong, Dong, Sun and Zhou2022a) by inducing the anti-gravity effect that stabilises thermal BL and enhances thermal limitation. In addition to studying global quantities, Wu et al. (Reference Wu, Dong, Wang and Zhou2021) distinguish vibration-generated oscillatory flows and fluctuating fields in oscillatory RB convection with periodic lateral boundary conditions by using the phase decomposition method. It is shown that vibration not only induces strong shear forces that breaks thermal BL and triggers massive plume emissions, but also generates an oscillatory flow that enhances the intensity of the turbulent fluctuating flows in the bulk zone.
The effect of vibration on vertical convection (VC) has also been studied. Vertical convection can be considered as RB convection with an extreme inclination angle of 
$90^{\circ }$ (Shishkina & Horn Reference Shishkina and Horn2016; Zwirner & Shishkina Reference Zwirner and Shishkina2018; Wang et al. Reference Wang, Liu, Verzicco, Shishkina and Lohse2021; Zhang, Ding & Xia Reference Zhang, Ding and Xia2021), which indeed can be encountered in some practical situations. A typical flow feature for VC systems is the stably stratified bulk region. Guo et al. (Reference Guo, Wang, Wu, Chong and Zhou2022) studied numerically the effect of vertical vibration on VC systems. They revealed a critical vibration frequency 
$\omega ^{*}$ beyond which heat transport enhancement is found. In addition to the heat transport properties, the influence of vibration on the existing flow structure is also worthy to be studied. In the pure VC, the hot plumes move upwards along the heating wall, the cold plumes move downwards along the cooling wall and the flow is self-organised to form the LSC. However, upon vibration, Bouarab et al. (Reference Bouarab, Mokhtari, Kaddeche, Henry, Botton and Medelfef2019) and Mokhtari et al. (Reference Mokhtari, Kaddeche, Henry, Bouarab, Medelfef and Botton2020) showed that the LSC in the VC systems can be reversed when the angle between the vibration direction and gravity falls within two critical vibration angles.
As mentioned above, there have been many studies that have considered the joint drive from both buoyancy and vibration. With the vibration as the only driving force, there are also extensive studies especially in the field of aerospace engineering. In a spacecraft experiment, the vibration frequency can reach up to 100 Hz (Marín et al. Reference Marín, Dubert, Simón, Ollé, Gavaldà and Ruiz2018; Dong et al. Reference Dong, Duan, Liu and Zhang2019) and a series of long-duration microgravity vibration experiments have been performed using spacecraft. Field experiments on TVC in microgravity can be traced back to that on the Apollo spacecraft (Grodzka, Fan & Hedden Reference Grodzka, Fan and Hedden1971; Bannister et al. Reference Bannister, Grodzka, Spradley, Bourgeois, Hedden and Facemire1973). Their experiments revealed that vibrations caused by the vibrating motion of the spacecraft and the astronauts significantly increased the heat transfer compared to the case with pure conduction (Grodzka & Bannister Reference Grodzka and Bannister1975). Using the ALICE-2 instrument on the MIR station, Garrabos et al. (Reference Garrabos, Beysens, Lecoutre, Dejoan, Polezhaev and Emelianov2007) studied the effect of linear harmonic vibration on temperature propagation with a point-like heat source in near-critical fluid. Using experimental equipment on the International Space Station (ISS), Braibanti et al. (Reference Braibanti2019) studied the response of binary mixtures to the onboard g-jitter and vibrational forcing, where the density difference is introduced by thermal and compositional variations. Their study suggests that g-jitter on the ISS actually has a limited effect on thermal diffusion, and that externally imposed constant frequency and amplitude are the main factors affecting diffusive processes. A number of experiments (Mialdun et al. Reference Mialdun, Ryzhkov, Melnikov and Shevtsova2008; Shevtsova et al. Reference Shevtsova, Gaponenko, Melnikov, Ryzhkov and Mialdun2010a,Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdunb) have been carried out in the microgravity environment emulated by the parabolic flight of the aircraft. It has been demonstrated that vibrations can induce convection in a non-uniformly heated fluid. This opens up a possible avenue for driving convection in microgravity environments.
The morphological change of flow structure in TVC systems due to the onset of convective instability is a key issue. Linear stability analysis based on mean flow dynamical equations have been performed to identify the relevant parameter characterising the intensity of the vibrational excitation, which is the vibrational Rayleigh number 
${{Ra}}_{vib}$ (Gershuni, Zhukhovitskii & Iurkov Reference Gershuni, Zhukhovitskii and Iurkov1970; Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1979). Gershuni, Zhukhovitskii & Yurkov (Reference Gershuni, Zhukhovitskii and Yurkov1982) examined the change of flow structure of the average vibrational convection under microgravity. When 
${{Ra}}_{vib}$ is less than the critical value 
${{Ra}}_{vib}^{*}$ (
${{Ra}}_{vib}^{*}$ depends on the fluid properties and boundary conditions), there is steady four-vortex structure. As 
${{Ra}}_{vib}$ increases, the four-vortex structure becomes an unstable mode and the structure transitions to a stable three-vortex structure. Crewdson & Lappa (Reference Crewdson and Lappa2021) performed a systematic parametric study of the mean velocity field that displaced a very regular columnar array of convective structures when the 
${{Ra}}_{vib} \geq 5 \times 10^{7}$. In a numerical study of vibration over a wide range of frequencies and amplitudes, Hirata, Sasaki & Tanigawa (Reference Hirata, Sasaki and Tanigawa2001) observed synchronous, subharmonic and non-periodic responses of the flow to vibrational excitations. The non-periodic response may be related to the transition between flow states. Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010b) performed the investigation of the effect of vibration on flow pattern bifurcation in a low-gravity environment using both two-dimensional (2-D) numerical modelling based on the averaging equations and three-dimensional (3-D) DNS of TVC.
At present, the unified constitutive law of heat transport in TVC has been revealed in our previous work (Wu et al. Reference Wu, Guo, Zhao, Wang, Chong and Zhou2022); however, the study on the morphological transition of flow structure in the turbulent state of TVC with microgravity is still lacking. To gain insight into this, a 2-D numerical study is carried out in a square enclosed domain with imposed temperature difference. The choice of a 2-D simulation as the first step in examining flow transition problems is a common practice to understand the physical mechanisms of TVC convection thanks to the much lower computational cost compared to the 3-D cases. With much fewer computational resources, one can simulate many cases to clearly capture the transition of the flow structure. Our aim is to study the transition of flow structure, especially in the unsteady and even turbulent state, and the associated statistical properties. The structure of this paper is organised as follows. In § 2, the governing equations of TVC in microgravity are given, and the numerical methods and parameters are described. In § 3, the flow structure transition in TVC is observed from the visualisation of instantaneous and mean flow field. In § 4, a quantitative analysis of statistical properties is given to characterise this transition and the transition phase is obtained. Finally, a brief conclusion is given in § 5.
2. Numerical methods
We carry out a series of DNS to study the vibration-driven thermal turbulence in a 2-D square domain, as illustrated in figure 1. The external harmonic vibration is applied to the convection cell in the horizontal direction, which is perpendicular to the direction of the temperature gradient. The normalisation is done by the scale of cell height 
$H$, the viscous diffusion time 
$H^{2} / \nu$, and the temperature difference 
$\varDelta$ between the top and bottom plates. Choosing the reference frame associated with the external vibration, the incompressible Oberbeck–Boussinesq equations for the TVC are given by (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998; Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010b)
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u} = 0 , \end{gather}
\begin{gather} \frac{\partial \boldsymbol{u}}{\partial t} +\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{u} ={-} \boldsymbol{\nabla} p + \boldsymbol{\nabla}^2 \boldsymbol{u} - {{a}} \omega^2 \cos(\omega t) T \boldsymbol{e}_{x}, \end{gather}
\begin{gather} \frac{\partial T}{\partial t} + \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} T = {{Pr}}^{{-}1} {\nabla}^{2} T , \end{gather}
where 
$\boldsymbol {u}=(u, w)$, 
$T$ and 
$p$ are the dimensionless flow velocity, temperature and kinematic pressure, respectively, and 
$\boldsymbol {e}_{x}$ is the unit vector along the horizontal direction. In (2.1)–(2.3), there are three control parameters, i.e. the Prandtl number 
${{Pr}}$, the dimensionless vibration amplitude 
${{a}}$ and the dimensionless angular frequency 
$\omega$:
\begin{equation} {{Pr}} = \frac{\nu}{\kappa}, \quad {{a}} = \frac{\alpha \Delta A}{H}, \quad \omega = \frac{\varOmega H^{2}}{\nu}, \end{equation}
where 
$A$ is the pulsating displacement, 
$\varOmega$ the angular frequency, and 
$\alpha$, 
$\nu$ and 
$\kappa$ are the coefficients of thermal expansion, kinematic viscosity and thermal diffusivity. Regarding the velocity boundary conditions, all solid boundaries are assumed to be impermeable and no-slip. For temperature, an adiabatic condition is maintained at the sidewalls, while a constant temperature is applied to the top and bottom plates, i.e. 
$T_{top} = 0$ and 
$T_{bot} = 1$, respectively.
Figure 1. Sketches of the 2-D convection cell with the coordinate systems. The bottom conducting plate is heated to the temperature 
$T_{bot}$, while the top conducting plate is cooled to the temperature 
$T_{top}$. The sidewalls are adiabatic. Vibration is applied to the cell in the horizontal direction. In the reference associated with vibration, an additional acceleration induced by vibration is introduced, i.e. 
$a \omega ^{2} \cos (\omega t)\boldsymbol {e}_x$ in dimensionless form.
In previous studies, the vibrational Rayleigh number 
$Ra_{{vib}}$, which is derived using the averaging approach under the condition of small amplitude and high frequency, has often been used to describe the averaged vibrational effects on convective flows. The derivation of the averaged equations of TVC are shown in Appendix A. From the averaged equations, one obtains the dimensionless control parameter 
$Ra_{{vib}}$, which is given by
\begin{equation} {{Ra}}_{vib} = \frac{(A \varOmega \alpha \Delta H)^{2}}{2 \nu \kappa}. \end{equation} Numerical simulations are performed using the in-house finite-difference code, which has been well validated in our previous studies (Wang et al. Reference Wang, Zhou and Sun2020; Wu et al. Reference Wu, Wang, Chong, Dong, Sun and Zhou2022a). A second-order finite-difference method is used for the spatial discretisation in a staggered grid. The third-order Runge–Kutta method combined with the second-order Crank–Nicholson scheme is used for time integration. The pressure Poisson equation is solved using the fast Fourier transform (FFT) method. More details on the numerical approach can be found from Zhang et al. (Reference Zhang, Xia, Dong, Wang and Zhou2019). In all runs, we fixed 
${{Pr}} = 4.38$, which corresponds to the working fluid of water. The dimensionless amplitude ranges from 
${{a}} = 0.001$ to 
${{a}} = 0.3$ and the dimensionless frequency ranges from 
$\omega = 10^2$ to 
$\omega = 10^7$. The grid spacing increases with increasing amplitude 
${{a}}$ and frequency 
$\omega$. For instance, the grid size is increased from 
$512 \times 512$ for 
$\omega = 10^2$ to 
$2048 \times 2048$ for 
$\omega = 10^7$ at fixed 
$a=0.1$, and from 
$1024 \times 1024$ for 
${{a}} = 0.001$ to 
$2048 \times 2048$ for 
${{a}} = 0.3$ at fixed 
$\omega =10^7$. The mesh is refined in the near-wall region to ensure accurate resolution of the near-wall dynamics within the oscillating Stokes layer. For simulation with high frequencies, the Stokes layer is resolved with at least 
$16$ meshes. For the time integration, we maintained the time step 
$\varDelta _{t} \leq \tau _\omega / 60$, where 
$\tau _\omega = 2 {\rm \pi}/ \omega$, such that the convective flows during each vibration period are resolved with at least 
$60$ time steps. Moreover, the mesh and time step are well chosen following the resolution requirements of Shishkina et al. (Reference Shishkina, Stevens, Grossmann and Lohse2010).
3. Transition of flow structure
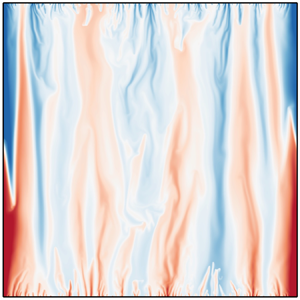
We analyse the flow structures through the visualisation of the temperature and velocity fields. Figure 2 shows the snapshots of the instantaneous temperature (colour) and velocity (vectors) fields for different vibration amplitudes (
$a=0.01,0.1$) and frequencies (
$\omega = 10^{3}, 10^{5}, 10^{7}$). As shown in figure 2(a), when the frequency is small (
$\omega = 10^{3}$ at 
$a=0.01$), a nearly stable temperature distribution is established in the bulk. When the frequency reaches 
$\omega = 10^{5}$, the morphology of the flow changes significantly, as shown in figure 2(b). The vibration destabilises the flow such that the flow state deviates from that of pure conduction, and eventually the temperature field changes from a nearly linear temperature distribution to one with a stack of columnar thermal plumes. As the vibration frequency is increased further to 
$\omega = 10^{7}$, more fragmented hot (cold) plumes are ejected from the thermal boundary layer which subsequently merge into the columnar thermal updrafts (downdrafts). The columnar structures also appear in the 3-D case shown in the supplementary material available at https://doi.org/10.1017/jfm.2023.666.
Figure 2. Instantaneous temperature (colour) and velocity (vectors) fields for two different 
$a$, which are (a–c) 
$a=0.01$ and (d–f) 
$a=0.1$, and for three different 
$\omega$, which are (a,d) 
$\omega =10^{3}$, (b,e) 
$\omega =10^{5}$ and (c,f) 
$\omega =10^{7}$. Note that the range of colour bar is different for each case to amplify the details in the flow structure.
Apart from the dependence on frequency, the effect of vibration amplitude on flow structure has also been shown in figure 2(d,f). As the amplitude increases to 
$a=0.1$ from 
$a=0.01$, the flow field becomes more chaotic as revealed by the more fragmented and irregular temperature structure. The difference caused by increasing amplitude can be even more pronounced for 
$\omega = 10^{7}$. The columnar thermal structure observed in the case 
$a=0.01$ has been broken down as 
$a$ is increased to 
$0.1$, and one observes the transition to a flywheel structure as shown in figure 2(f) (see supplementary movie 3), where the hot plume moves upwards on one side and the cold plume moves downwards on the other side. We also performed three 2-D simulations with periodic boundary condition for 
$\omega =10^{3}$, 
$\omega =10^{4}$, 
$\omega =10^{7}$ at fixed 
$a=0.1$, and the results are shown in the supplementary material. One observes that the columnar structure breaks down at sufficiently strong vibration. However, no flywheel structure can be observed in the case of lateral periodic boundary conditions. This indicates that the sidewall effect plays a crucial role on the formation of the flywheel structure in the columnar-broken regime.
Figure 3 shows more details of the instantaneous horizontal and vertical velocity fields. Note that the velocity is normalised by the characteristic vibration velocity 
$a \omega$. It is shown that at low forcing with periodic-circulation structure (e.g. at 
$\omega =10^{3}$ for 
$a=0.01$ and 
$a=0.1$ in figure 3a,d,g,j), the magnitude of the horizontal velocity is large near the top and bottom plates while the magnitude of the vertical one is large near the sidewalls. This circulation flips sign over a period of vibration. At moderate forcing with columnar structure (e.g. at 
$\omega =10^{5}$ for 
$a=0.01$ and 
$a=0.1$ in figure 3b,e,h,k, 
$\omega =10^{7}$ for 
$a=0.01$ in figure 3c,i), the vertical velocity in the bulk becomes strong. After the transition into the LSC structure with high forcing (e.g. at 
$\omega =10^{7}$ for 
$a=0.1$ in figure 3f,l), both horizontal and vertical velocities are significantly enhanced in the bulk.
Figure 3. Typical snapshots of the horizontal velocity 
$u / a \omega$ and vertical velocity 
$w / a \omega$ fields for two different 
$a$, which are (a–c,g–i) 
$a=0.01$ and (d–f,j–l) 
$a=0.1$, and for three different 
$\omega$, which are (a,d,g,j) 
$\omega =10^{3}$, (b,e,h,k) 
$\omega =10^{5}$ and (c,f,i,l) 
$\omega =10^{7}$.
To gain a deeper understanding on the flow structure, we examine the time-averaged fields of temperature (colour) and velocity (vectors) as shown in figure 4. The corresponding time-averaged velocity field is shown in figure 5. At small 
$\omega$, the four-roll structure for 
$a=0.01$ (figure 4a) and a three-roll structure for 
$a=0.1$ (figure 4d) are established in the flow, which is consistent with the previous observations of TVC in a microgravity environment (Mialdun et al. Reference Mialdun, Ryzhkov, Melnikov and Shevtsova2008; Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010b). The observed four-roll flow pattern in the flow field is a result of the superposition of two counter-rotating circulations (see supplementary movie 1), which are induced by the back-and-forth vibration. In figure 4(b,c,e), the clear footprint of the columnar thermal plume can also be seen in the time-averaged field. It signifies that the location of these heat transport channels are almost stable over time. We have applied adiabatic and no-slip boundary conditions to the side walls, resulting in the heat accumulation near the walls. As a result, the temperature near the side wall is relatively high or low. However, in the bulk, there is stronger mixing compared to the near-wall region, thus there is less temperature contrast for the hot and cold heat exchanger channels. The flow structure then evolves into the flywheel structure shown in figure 4(f).
Figure 4. Time-averaged temperature (colour) and velocity (vectors) fields for two different 
$a$, which are (a–c) 
$a=0.01$ and (d–f) 
$a=0.1$, and for three different 
$\omega$, which are (a,d) 
$\omega =10^{3}$, (b,e) 
$\omega =10^{5}$ and (c,f) 
$\omega =10^{7}$.
Figure 5. Time-averaged horizontal velocity 
$u / a \omega$ and vertical velocity 
$w / a \omega$ fields for two different 
$a$, which are (a–c,g–i) 
$a=0.01$ and (d–f,j–l) 
$a=0.1$, and for three different 
$\omega$, which are (a,d,g,j) 
$\omega =10^{3}$, (b,e,h,k) 
$\omega =10^{5}$ and (c,f,i,l) 
$\omega =10^{7}$.
To quantify the characteristics of the columnar structures, the time-averaged temperature field was examined. Applying a Fourier transform along the horizontal direction of the temperature fluctuations fields, one can extract the number of columnar structures 
$k_{m}$ in the vibrational convection. One observes that as 
$\omega$ increases, 
$k_{m}$ increases monotonically, specifically, at 
$a=0.01$, 
$k_{m}$ increases from 
$k_{m}=2$ for 
$\omega =10^{5}$ to 
$k_{m}=5$ for 
$\omega =10^{7}$, indicating that more columnar structures are formed under stronger vibrational driving forces. However, when the columnar structures are broken and the LSC is formed, 
$k_{m}$ dropped to 1.
4. Statistical properties in different flow states
4.1. Mean and standard deviation temperature profiles
As mentioned above, the global flow structure undergoes two kinds of transitions with the increasing control parameters 
$\omega$ at sufficiently large amplitude 
$a$. The first flow transition is characterised by a change from periodic circulating flow to a convective flow with columnar thermal structures, while the second transition is characterised by the emergence of flywheel structure. In this subsection, we quantify local statistics that correspond to the change of global flow structure.
Figure 6 depicts the temperature profiles at amplitudes 
$a=0.01$ and 
$a=0.1$ for various frequencies 
$\omega$. For small 
$\omega$, a linear distribution of temperature profiles is observed, which confirms the stable temperature distribution found in figures 2(a,d) and 4(a,d). As 
$\omega$ increases, the thermal BLs become distinctly visible near the top and bottom plates. Within the thermal BLs, the temperature decreases (increases) sharply from normalised temperature 
$T_{bot}=1$ (
$T_{top}=0$) in proximity to the bottom (top) plate to the bulk temperature. At the largest explored frequency 
$\omega$ of 
$a=0.1$, the temperature structure with thermal shortcut in the bulk is observed, reminiscent of that in RB convection (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Xia Reference Xia2013). Interestingly, at certain intermediate frequencies, the temperature change can be non-monotonic with an inversion layer existing at the junction between the bulk and the boundaries. This phenomenon is also observed in VC systems due to the presence of stable stratification in the bulk (Ravi, Henkes & Hoogendoorn Reference Ravi, Henkes and Hoogendoorn1994; Wang et al. Reference Wang, Liu, Verzicco, Shishkina and Lohse2021) and in the similarity solution of natural convection BL equations (Henkes & Hoogendoorn Reference Henkes and Hoogendoorn1989).
Figure 6. Vertical profiles of mean temperature for various 
$\omega$ at (a) 
$a=0.01$ and (b) 
$a=0.1$.
Next, the profiles of standard deviation (SD) for temperature 
$\sigma _{T}(z)$ are examined, which quantifies the temporal fluctuation of the temperature field, defined as follows:
\begin{equation} \sigma_{T}(z) = \left\langle \sqrt{\langle T^{2} \rangle_{t} - \langle T \rangle_{t}^{2}} \right \rangle_{x}, \end{equation}
where 
$\langle \boldsymbol{\cdot} \rangle _{t}$ and 
$\langle \boldsymbol{\cdot} \rangle _{x}$ are the time average and spatial average in the horizontal direction, respectively. The vertical profile of temperature fluctuations, 
$\sigma _T$, as a function of the vertical distance 
$z$ away from the bottom plate drawn up to the mid-height is shown in figure 7. As the frequency increases to sufficiently large values (
$\omega =10^5$), the location of the edge of the thermal BL becomes apparent. Additionally, a secondary peak at the mid-height is observed. The flow field shown in figure 4 suggests that this secondary peak is related to the presence of the recirculating flow. Visualised by supplementary movie 2, the merging of hot and cold columnar plumes leads to the intense mixing near the mid-height, which contributes to the significantly enhanced temperature fluctuation.
Figure 7. Vertical profiles of mean temperature SD 
$\sigma _{T}(z)$ for various 
$\omega$ at (a) 
$a=0.01$ and (b) 
$a=0.1$.
4.2. Profiles of velocity standard deviation
In addition to the temperature profiles, we examine the velocity fluctuation using the modulus of the SD of all velocity components 
$\sigma _{{vel}}$, which is calculated as
\begin{equation} \sigma_{vel}(z)=\sqrt{\sigma_u^2(z)+\sigma_w^2(z)}, \end{equation}
where 
$\sigma _u(z)$ and 
$\sigma _w(z)$ are the SDs of the horizontal and vertical velocities normalised by the pulsating velocity, respectively, with the following definitions:
\begin{equation} \sigma_u(z)=\frac{1}{a \omega}\left\langle\sqrt{\left\langle u^2\right\rangle_t-\langle u\rangle_t^2}\right\rangle_x, \quad \sigma_w(z)=\frac{1}{a \omega}\left\langle\sqrt{\left\langle w^2\right\rangle_t-\langle w\rangle_t^2}\right\rangle_x. \end{equation}
In figure 8, we show the 
$\sigma _{\boldsymbol {u}}(z)$ profiles at two different amplitudes, namely, 
$a = 0.01$ (figure 8a,c) and 
$a = 0.1$ (figure 8b,d). As 
$\omega$ increases, the velocity BL, defined by the height of the peak, becomes thinner. It is noteworthy that the magnitude of the peak near the BLs and the shape of the peak at different 
$\omega$ are similar (figure 8a,b). To further confirm the universal properties existing near the BL, we adopt the normalisation using the thickness of the Stokes layer. The disturbance generated by vibrational force near the top and bottom plates travels as a transverse wave in the region adjacent to the wall, and the penetration depth of this wave defines the Stokes layer, which is defined as 
$\delta _{\omega } = \sqrt {2\nu / \varOmega }$ (namely 
$\delta _{\omega } / H = \sqrt {2 / \omega }$). We then plot the 
$\sigma _{{vel}}(z)$ as a function of the normalised vertical distance 
$z\omega ^{0.5}$ in figure 8(c,d). The results show that the 
$\omega$-dependent peaks of 
$\sigma _{{vel}}(z)$ all collapse onto the same curve for 
$z\omega ^{0.5}\leq 1$. As the height progressively reaches the bulk region, the velocity fluctuations decrease (cases with columnar flow structure) due to the diminishing of the vibrating effect travelled by the walls. However, once the breaking of columnar flow takes place and flywheel structure emerges, the fluctuation 
$\sigma _{{vel}}(z)$ in the bulk increases significantly.
Figure 8. Mean velocity SD 
$\sigma _{{vel}}(z)$ as a function of the (a,b) normalised vertical distance 
$z$ and (c,d) 
$z \omega ^{0.5}$ under different vibration amplitude with (a,c) 
$a=0.01$ and (b,d) 
$a=0.1$.
To investigate the behaviour of velocity fluctuations, we examine the time evolution of temperature and velocity profiles at mid-height over forty vibration periods, as shown in figure 9. We consider three representative cases corresponding to different flow structures: periodic oscillating circulation, columnar structure and broken-columnar structure. For the cases with periodic oscillating circulation (small enough 
$\omega$ shown in figure 9a,b), the continuous reversal of the circulating flow due to simple harmonic vibration leads to periodic changes in temperature and velocity fluctuations, with the period of change matching the imposed vibrating period. As the columnar structure forms (figure 9c,d), the periodic signature fades and stable strips in the temporal map appear as a footprint of the stable columnar structure. When the frequency is further increased, reaching the regime with broken thermal columns, the strips vanish and fragmented plumes continuously travel near the sidewall (figure 9e). However, these temperature anomalies decouple from the region of large vertical velocities, with the maximum velocity occurring mainly in the bulk (figure 9f). Although the flywheel structure observed here resembles that in RB convection, they are essentially different because the flow structure here contains maximum vertical velocity in the bulk, rather than near the sidewalls (see figures 3f,i and 5f,i).
Figure 9. Temporal evolution of (a,c,e) temperature 
$T(x) \vert _{z=H/2}$ and (b,d,f) vertical velocity 
$w(x) \vert _{z=H/2}$ at the mid-height for three typical cases: (a,b) 
$a=0.01, \omega =10^{3}$ in periodic-circulation regime; (c,d) 
$a=0.01, \omega =10^{7}$ in columnar regime; and (e,f) 
$a=0.1, \omega =10^{7}$ in columnar-broken regime. Horizontal axis represents the time normalised by the vibration period 
$\tau _{\omega }$.
4.3. Local velocity standard deviations near the boundaries and at mid-height
We further examine the local velocity fluctuations at both the edge of BL and mid-height. The local velocity SD at the BL edge is evaluated as
\begin{equation} \sigma_{{vel},{BL}} = \sqrt{\sigma_{u}^{2} \vert_{z=\delta_{\omega}} + \sigma_{w}^{2}\vert_{z=\delta_{\omega}} } , \end{equation}and the one at mid-height as
\begin{equation} \sigma_{{vel},{mid}} = \sqrt{ \sigma_{u}^{2}\vert_{z=H/2} + \sigma_{w}^{2}\vert_{z=H/2} }. \end{equation}
In addition to the frequency 
$\omega$, we introduce 
$Ra_{vib}$, which is obtained from the averaging equation (see (A7)) and describes the averaged vibrational effects on convective flows and can be expressed as 
$Ra_{vib} = a^2 \omega ^2 Pr /2$, according to (A12). Our results show that the velocity fluctuations at the BL edge are primarily influenced by the vibration frequency rather than 
$Ra_{vib}$, as evidenced by the collapse of 
$\sigma _{{vel},{BL}}$ at small 
$\omega$ values (figure 10a,b). At positions close to the top and bottom plates, the disturbance generated by the oscillation propagates as a transverse wave, with a penetration depth given by 
$\delta _{\omega }/H$, which only depends on 
$\omega$. Therefore, the velocity fluctuations at small 
$\omega$ values exhibit a universal property across different amplitudes. As 
$\omega$ increases further, the slope of the lines becomes smaller and the curves tend to saturate at high 
$\omega$. This is probably caused by the fact that at high 
$\omega$, vibration destabilises the Stokes layer and the velocity fluctuations within the BL are dominated by turbulent fluctuations. The presence of turbulent fluctuations depending on the vibration amplitude may cause the deviations of the curves at high 
$\omega$.
Figure 10. (a,c) Mean velocity SD 
$\sigma _{{vel},{BL}}$ at the BL edge, and (b,d) 
$\sigma _{{vel},{mid}}$ at the mid-height as a function of (a,b) vibration frequency 
$\omega$ and (c,d) vibrational Rayleigh number 
${{Ra}}_{vib}$.
The parameter 
$Ra_{vib}$ is more relevant than 
$\omega$ in describing the local velocity SD at mid-height, 
$\sigma _{{vel},{mid}}$. Figure 10(b) shows that 
$\omega$ does not collapse the data well, whereas 
$Ra_{vib}$ effectively captures the trend of 
$\sigma _{{vel},{mid}}$ for different vibration parameters. The plot of 
$\sigma _{{vel},{mid}}$ versus 
$Ra_{vib}$ (figure 10d) reveals three distinct flow regimes. In regime I with periodic circulation structure, 
$\sigma _{{vel},{mid}}$ is not sensitive to changes in 
$Ra_{vib}$. In regime II with columnar structure, 
$\sigma _{{vel},{mid}}$ decreases monotonically with increasing 
$Ra_{vib}$, and the decrease in 
$\sigma _{{vel},{mid}}$ indicates that columnar plumes become more robust with increasing vibration intensity, leading to the formation of stable columnar structures. In regime III, 
$\sigma _{{vel},{mid}}$ suddenly increases sharply, which is associated with the breakdown of the columnar structure.
Then, we construct the phase diagram over the full parameter space (
$a,\omega$) for fixed 
$Pr = 4.38$. We use 
$\log _{10}\sigma _{{vel},{mid}}$ to determine the flow regime transitions and the colour of the symbol to represent the value of 
$\log _{10}\sigma _{{vel},{mid}}$. Based on the trend of 
$\log _{10}\sigma _{{vel},{mid}}$, we can clearly distinguish three regimes: the periodic-circulation regime (yellow-shaded area); the columnar regime (purple-shaded area); and the columnar-broken regime (orange-shaded area) (see figure 11a,b). We also examine the transition of the flow regime within the parameter framework of (
$a,Ra_{vib}$). As shown in figure 11(b), the transition from regime I to regime II can be well described by the vibrational Rayleigh number 
$Ra_{vib}$, which is the only one control parameter representing the vibrational intensity obtained from the averaged equations of TVC (see Appendix A). Our results show that the first flow transition occurs when 
$Ra_{vib}$ exceeds a critical value of 
$Ra_{vib,cr} \approx 2.19 \times 10^{6}$. However, the transition from regime II to regime III, that is, from columnar convective structure to LSC, cannot be fully described by 
$Ra_{vib}$.
Figure 11. Phase diagram in the (a) 
$(a,\omega )$ plane and in the (b) 
$(a, {{Ra}}_{vib})$ plane. The colour of the points denotes the value of 
$\log _{10} \sigma _{{vel},{mid}}$. Three different regimes are represented by different background colours: the periodic-circulation regime (regime I) coloured by yellow, the columnar regime (regime II) coloured by purple and the columnar-broken regime (regime III) coloured by orange.
4.4. Heat transfer properties
In this subsection, we discuss the heat transfer characteristics of the TVC system. The Nusselt number 
$Nu$ is plotted as a function of frequency 
$\omega$ and the vibrational Rayleigh number 
$Ra_{{vib}}$ in figure 12. Here, the Nusselt number 
$Nu$ is the ratio of the convective to conductive heat transport that characterises the global heat transport efficiency of the system and is calculated by 
$Nu= Pr \langle w T \rangle - \langle \partial T / \partial z \rangle$, where 
$w$ is the vertical velocity and 
$\langle \boldsymbol{\cdot} \rangle$ denotes the time and space averaging. It is found that for low vibration forcing at small 
$a$ and 
$\omega$, the heat transport is driven by pure conduction, i.e. 
$Nu=1$. With increasing 
$a$ and 
$\omega$, the vibration forcing becomes strong enough to trigger convective instability and enhance heat transport. The 
$Nu$ value increases with increasing 
$a$ or 
$\omega$. Further, we examine the dependency of 
$Nu$ on the 
$Ra_{{vib}}$. As shown in figure 12(b), the onset of convective heat transfer can be well described by 
$Ra_{{vib}}$. For small 
$Ra_{{vib}}$, the pure conduction dominates the heat transport, i.e. numerical data collapse together at the line of 
$Nu=1$ for different amplitudes 
$a$. When 
$Ra_{{vib}}$ exceeds a critical value, vibration-induced convection comes into play and thus affects the heat transport. A detailed discussion of the heat transfer properties, particularly the scaling properties, in TVC has been given in our previous work (Wu et al. Reference Wu, Guo, Zhao, Wang, Chong and Zhou2022).
Figure 12. 
$Nu$ as a function of (a) vibration frequency 
$\omega$, (b) vibrational Rayleigh number 
$Ra_{{vib}}$ at various amplitude 
$a$.
5. Conclusion
In summary, we employed direct numerical simulation to investigate the flow transition in a two-dimensional thermal vibrational convection (TVC) system. Our simulations covered a wide range of dimensionless amplitudes (
$0.001 \le a \le 0.3$) and frequencies (
$10^{3} \le \omega \le 10^{7}$), with a fixed Prandtl number (
$Pr = 4.38$). Our results indicate that there are three different regimes of flow in vibration-driven convection at different amplitudes and frequencies. Based on the analysis of temperature and velocity standard deviations, we classified these regimes as the periodic-circulation regime, the columnar regime, and the columnar-broken regime. Each regime features different flow structures and statistical properties. In regime I, periodic circulation reversal occurs with the imposed vibration frequency. In regime II, the columnar plume becomes the dominant flow structure. Strong oscillation triggers the emission of thermal plumes. These plumes merge and self-organise into columnar updrafts or downdrafts, becoming heat channels between the cold and hot plates. These heat columns are almost stationary over space and time, and they are robust. In regime III, breakdown of the heat columns occurs suddenly, and eventually, flywheel structures dominate. Consequently, temperature and velocity fluctuations increase sharply after this breakdown. We analyse the heat transfer properties of the system and the results show that vibration-driven flow can be used as a means to improve the heat transfer efficiency of the system in microgravity environments or in microfluidic systems where the effect buoyancy is absent.
Our study has demonstrated that horizontal vibrations can drive the fluid flow and reveal flow state transitions in microgravity TVC systems. In addition to its fundamental significance, understanding the transition of flow structure is also important for manipulating fluid devices with dedicated purposes, such as mixing two fluids with different densities. Further research is needed to fully comprehend the regime transitions, such as studying the effects of vibrations on low and very high 
$Pr$ values instead of fixing 
$Pr$ at 
$4.38$.
Supplementary material and movies
Supplementary material and movies are available at https://doi.org/10.1017/jfm.2023.666.
Funding
This work was supported by the Natural Science Foundation of China under grant nos 11988102, 11825204, 92052201, 12032016, 11732010, 12102246 and 91852202, the Shanghai Science and Technology Program under project no. 20ZR1419800, the Shanghai Pujiang program under grant no. 21PJ1404400, and China Postdoctoral Science Foundation under grant no. 2020M681259.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Derivation of the averaged equation
In a TVC system, the velocity, temperature and pressure fields can be decomposed into slow parts and fast parts:
\begin{equation} \boldsymbol{U} = \boldsymbol{\bar{U}} + \boldsymbol{U}^{'},\quad \theta= \bar{\theta}+ \theta^{'},\quad P= \bar{P} + P^{'} , \end{equation}
where 
$\boldsymbol {\bar {U}}=\langle \boldsymbol {U} \rangle _{\tau }$, 
$\bar {\theta }= \langle \theta \rangle _{\tau }$ and 
$\bar {P} = \langle P \rangle _{\tau }$ is averaged over one vibration period 
$\tau =2 {\rm \pi}/ \omega$. The average value of the fast parts over a vibration period is 0, i.e. 
$\langle \boldsymbol {U}^{'} \rangle _\tau =0$, 
$\langle \theta ^{'} \rangle _\tau =0$ and 
$\langle P^{'} \rangle _\tau =0$. And the Boussinesq equations of TVC can be written in the following form:
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\bar{U}} = 0 , \end{gather}
\begin{gather} \frac{\partial \boldsymbol{\bar{U}}}{\partial t} +\boldsymbol{\bar{U}} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{\bar{U}} ={-} \frac{1}{\rho} \boldsymbol{\nabla} \bar{P} + \nu \boldsymbol{\nabla}^2 \boldsymbol{\bar{U}} - \alpha A \varOmega^{2} \langle \theta^{'} \mathrm{cos}(\varOmega t)\rangle_{\tau} \boldsymbol{e}_{x} + \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{T}_{u}, \end{gather}
\begin{gather} \frac{\partial \bar{\theta}}{\partial t} + \boldsymbol{\bar{U}} \boldsymbol{\cdot} \boldsymbol{\nabla} \bar{\theta} = \kappa {\nabla}^{2} \bar{\theta} + \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{T}_{\theta}. \end{gather}
Here, 
$\boldsymbol {T}_{u} = - \langle \boldsymbol {U}^{'} \boldsymbol {U}^{'} \rangle _{\tau }$ and 
$T_{\theta } = - \langle \boldsymbol {U}^{'} \theta ^{'} \rangle _{\tau }$ are the vibrational stress and flux induced by the fast parts, respectively. In the limit of high frequency and small amplitude, the solutions for 
$\boldsymbol {U}^{'}$ and 
$\theta ^{'}$ can be obtained as follows (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998):
\begin{equation} \boldsymbol{U}^{\prime}={-}\alpha A \varOmega \sin (\varOmega t) \boldsymbol{N}, \quad \theta^{\prime}={-}\alpha A \cos (\varOmega t)(\boldsymbol{N} \boldsymbol{\cdot} \boldsymbol{\nabla}) \bar{\theta} . \end{equation}
Here, 
$\boldsymbol {N}=\bar {\theta } \boldsymbol {e}_{x}-\boldsymbol {\nabla } \varPhi$ with 
$\boldsymbol {\nabla } \boldsymbol{\cdot} N =0$ (
${\nabla }^{2} \varPhi = \boldsymbol {e}_{x} \boldsymbol{\cdot} \boldsymbol {\nabla } \varPhi$). Substituting the analytical solution of 
$\boldsymbol {U}^{\prime }$ and 
$\theta ^{'}$ in (A5a,b) into (A3) and (A4), one can obtain the averaged equations of TVC:
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\bar{U}} = 0 , \end{gather}
\begin{gather} \frac{\partial \boldsymbol{\bar{U}}}{\partial t} +\boldsymbol{\bar{U}} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{\bar{U}} ={-} \frac{1}{\rho} \boldsymbol{\nabla} \bar{P} + \nu \boldsymbol{\nabla}^2 \boldsymbol{\bar{U}} + \frac{\alpha^2 A^2 \varOmega^2}{2} (\boldsymbol{N} \boldsymbol{\cdot} \boldsymbol{\nabla}) (\bar{\theta} \boldsymbol{e}_{x} - \boldsymbol{N}) , \end{gather}
\begin{gather} \frac{\partial \bar{\theta}}{\partial t} + \boldsymbol{\bar{U}} \boldsymbol{\cdot} \boldsymbol{\nabla} \bar{\theta} = \kappa {\nabla}^{2} \bar{\theta} . \end{gather}
The normalisation is done by the scale of cell height 
$H$, the viscous diffusion time 
$H^{2}/ \nu$, and the temperature difference 
$\varDelta$ between the top and bottom plates. Equations (A6) and (A8) can be written as
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\bar{u}} = 0 , \end{gather}
\begin{gather} \frac{\partial \boldsymbol{\bar{u}}}{\partial t} +\boldsymbol{\bar{u}} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{\bar{u}} ={-} \boldsymbol{\nabla} \bar{p} + \boldsymbol{\nabla}^2 \boldsymbol{\bar{u}} + Ra_{{vib}} (\boldsymbol{N}^{*}\boldsymbol{\nabla})(\bar{T} \boldsymbol{e}_{x} - \boldsymbol{N}^{*}) , \end{gather}
\begin{gather} \frac{\partial \bar{T}}{\partial t} + \boldsymbol{\bar{u}} \boldsymbol{\cdot} \boldsymbol{\nabla} \bar{T} = Pr^{{-}1} {\nabla}^{2} \bar{T} . \end{gather}
Here, 
$\boldsymbol {N}^{*}$ is the dimensionless form of 
$\boldsymbol {N}$. Equation (A10) includes the vibrational Rayleigh number 
${{Ra}}_{vib}$, which describes the average vibrational effects on convective flows. The definition of 
${{Ra}}_{vib}$ can be expressed by the ratio of the conductive diffusion time scale 
$H^{2}/\kappa$ and the vibrational time scale 
$2\nu / (A \varOmega \alpha \varDelta )^{2}$:
\begin{equation} {{Ra}}_{vib} = \frac{(A \varOmega \alpha \Delta H)^{2}}{2 \nu \kappa}. \end{equation}
According to the definition of amplitude 
$a=\alpha A \varDelta / H$ and frequency 
$\omega = \varOmega H^2 / \nu$, 
${{Ra}}_{vib}$ can be further written as 
$Ra_{vib} = a^2 \omega ^2 Pr / 2$.
Open access
