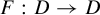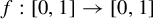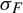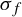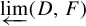1 Introduction
The present paper pertains to the notion of the natural extension of a map, introduced by Rohlin in [Reference Rohlin38]. Given a map
$f:X\to X$
on a compact metric space X, the natural extension of f is the homeomorphism
$\sigma _f$
defined on the inverse limit space
$\underleftarrow {\lim } (X,f)$
by
$\sigma _f(x_0,x_1,x_2,\ldots )=(f(x_0),x_0,x_1,x_2,\ldots )$
. (In the mathematical literature, this homeomorphism is also called the shift on the inverse limit
$\underleftarrow {\lim } (X,f)$
and was used prior to Rohlin’s work, for instance, in an example considered by Williams [Reference Williams42]. In our context, however, we want to emphasize the relation between non-invertible maps and their particular invertible extensions, and not merely consider a homeomorphism on the inverse limit space, and hence the use of the term natural extension seems more appropriate.) It gives the unique invertible map semi-conjugate to f, such that any other invertible map semi-conjugate to f is also semi-conjugate to
$\sigma _f$
. There exists a bijection between the set of invariant probability measures of f and
$\sigma _f$
, and the topological entropies of f and
$\sigma _f$
coincide [Reference Rohlin38]; see also [Reference Li30]. Natural extensions of non-invertible maps of branched 1-manifolds appear in the mathematical literature in the context of studying dynamics on surfaces, e.g. in hyperbolic attractors [Reference Williams43], Hénon attractors [Reference Barge3–Reference Barge and Holte5],
$C^0$
dynamics [Reference Boyland, de Carvalho and Hall12, Reference Boyland, de Carvalho and Hall14, Reference Bruin15], holomorphic dynamics [Reference Lyubich and Minsky31], complex dynamics [Reference Rempe-Gillen37], and rotation theory [Reference Boroński and Oprocha9, Reference Boyland, de Carvalho and Hall13, Reference Kwapisz29].
Our paper is motivated by a recent result of the first and last author [Reference Boroński and Štimac10], in which it has been shown that for a class of mildly dissipative plane homeomorphisms that contains positive Lebesgue measure subsets of Lozi and Hénon maps, the dynamics on their attractors is conjugate to natural extensions of densely branching dendrite maps. In that context, the question arose whether these homeomorphisms could be also conjugate to natural extensions of maps on some simpler one-dimensional spaces, such as the interval
$[0,1]$
. The homeomorphisms in question are transitive on their attractors, and sometimes even topologically mixing, and such properties are inherited by the respective dendrite maps. Therefore, it would seem as if the existence of dense orbits, together with density of the set of branch points in the dendrites, would force the corresponding inverse limit spaces to have a much richer topological structure than those of inverse limits of some simpler spaces, such as the interval, which has no branch points at all. This, in turn, would suggest that the above-mentioned simplification is not possible. In the present paper, however, we show that such an intuition is deceitful. In §4, we introduce the notion of a small folds property for interval maps (Definition 4.4), and then show that every map with that property can be factored through an arbitrary dendrite. More precisely, if
$f:[0, 1]\to [0, 1]$
is a continuous surjection with the small folds property and D is an arbitrary non-degenerate dendrite, then there are continuous surjections
$g:[0,1]\to D$
and
$h:D\to [0,1]$
such that
$h\circ g=f$
; see Lemma 4.5. It follows that if
$F=g\circ h$
, then the natural extensions
$\sigma _F$
and
$\sigma _f$
are conjugate. In particular, F is transitive on D and
$\underleftarrow {\lim } (D,F)$
is homeomorphic to the pseudo-arc if f has the same properties on
$[0,1]$
. W.R.R. Transue and the second author of the present paper constructed a transitive map f of
$[0,1]$
onto itself such that
$\varprojlim ([0,1],f)$
is homeomorphic to the pseudo-arc [Reference Minc and Transue33] (see also [Reference Drwiega and Oprocha19, Reference Kawamura, Tuncali and Tymchatyn26, Reference Kościelniak, Oprocha and Tuncali27] for related constructions). It is possible that this map has the small folds property, but it is not apparent how to prove it. However, in §5, we tweak the original construction from [Reference Minc and Transue33] to get a modified map f that does have the small folds property in addition to the properties promised by [Reference Minc and Transue33], see Theorem 5.7. This modified map f can be factored through any non-degenerate dendrite D creating interesting dynamics on D, see Theorem 5.8. The following theorem is a restatement of Theorem 5.8.
Theorem 1.1. For any non-degenerate dendrite D, there exist topologically mixing maps
$F : D \to D$
and
$f : [0, 1] \to [0, 1]$
such that the natural extensions
$\sigma _F : \underleftarrow {\lim } (D,F) \to \underleftarrow {\lim } (D,F)$
and
$\sigma _f : \underleftarrow {\lim } ([0, 1],f) \to \underleftarrow {\lim } ([0, 1],f)$
are conjugate. Moreover, the map f does not depend on a dendrite D and can be constructed so that
$\underleftarrow {\lim } (D,F)$
is homeomorphic to the pseudo-arc.
Note that the interval maps f such that
$\underleftarrow {\lim } ([0,1],f)$
is the pseudo-arc are generic in the closure of the subset of maps of the interval that have a dense set of periodic points [Reference Činč and Oprocha18]. Moreover, all such maps have infinite topological entropy by [Reference Mouron35] (see also [Reference Boroński and Oprocha11] for a stronger result). Consequently, the same is true for the maps
$F,\sigma _F$
and
$\sigma _f$
. This is noteworthy since, although any transitive interval map has positive entropy [Reference Blokh8], there do exist transitive zero entropy maps on dendrites [Reference Byszewski, Falniowski and Kwietniak16] (see also [Reference Acosta, Hernández-Gutiérrez, Naghmouchi and Oprocha1, Reference Baldwin2, Reference Hoehn and Mouron23, Reference Martínez-de-la-Vega, Martínez-Montejano and Mouron32] for related results). Note also that the class of dendrites is very rich. Every dendrite is locally connected, but there is a number of other properties with respect to which various elements of the class differ from each other, such as the properties of the subsets of end points and branch points. The set of end points in a dendrite can be finite, countably infinite, or even uncountable, and either be closed or not. The set of branch points do not need to be finite, but can be countably infinite and even dense in the dendrite. In addition, a branch point may separate the dendrite into infinitely many components. There exists a universal object in the class of all dendrites, the Ważewski dendrite
$D_\omega $
[Reference Wazewski40]; that is, any dendrite D embeds as a closed subset of
$D_\omega $
. In that context, below we formulate a stronger version of our main result Theorem 5.9.
Theorem 1.2. For any
$k\in \mathbb {N}$
and any dendrites
$D_1,D_2,\ldots ,D_k$
, there exist topologically mixing maps
$\{F_i : D_i \to D_i\}_{i=1}^{k}$
such that for any
$i,j\in \{1,2,\ldots ,k\}$
, we have:
-
(1)
$F_i$
and
$F_j$
are semi-conjugate; -
(2) the natural extensions
$\sigma _{F_i} $
and
$\sigma _{F_j}$
are conjugate; and -
(3) the inverse limits
$\underleftarrow {\lim } (D_i,F_i)$
and
$\underleftarrow {\lim } (D_j,F_j)$
are homeomorphic.
In addition,
$F_1$
can be chosen so that
$\underleftarrow {\lim } (D_i,F_i)$
is the pseudo-arc, for any
$i=1,2,\ldots , k$
.
The above theorems produce, what seems to be, a very surprising family of examples for the question of conjugacy between natural extensions of self-maps of distinct dendrites. These examples, however, do not provide any new pieces of information for Hénon or Lozi maps. Moreover, it seems rather implausible that, for parameter values considered in [Reference Boroński and Štimac10], these maps would semi-conjugate to interval maps with a small folds property, should any of them semi-conjugate to any interval map at all. In fact, it is known that for certain Hénon maps, this is never true [Reference Barge3]. Furthermore, Hénon and Lozi attractors discussed in [Reference Boroński and Štimac10] always contain non-degenerate arc components (such as branches of unstable manifolds), whereas the pseudo-arc contains no non-degenerate arcs at all. Moreover, as we have already mentioned, the interval maps f such that
$\underleftarrow {\lim } ([0,1],f)$
is the pseudo-arc, and their natural extensions
$\sigma _f$
have infinite topological entropy, but the Hénon and Lozi maps have finite entropy, bounded above by
$\log 2$
.
The paper is organized as follows. In §2, we give definitions and introduce notation that we need throughout the paper. In §3, we give some preliminary results on dendrites and prove a slightly stronger version of Whyburn’s theorem, see Theorem 3.10, that we need later on. In §4, we introduce the notion of a small folds property for interval maps (Definition 4.4), and then show that every map with that property can be factored through an arbitrary dendrite, see Lemma 4.5. In §5, we construct a transitive map f on
$[0,1]$
with the small folds property such that
$\varprojlim ([0,1],f)$
is homeomorphic to the pseudo-arc which, together with Lemma 4.5, implies our main results that this map f can be factored through any non-degenerate dendrite D, see Theorems 5.8 and 5.9. In §6, we give some remarks and further questions. Finally, for the reader’s convenience and to make this paper self-contained, we include Appendix A, where we cite three results from [Reference Minc and Transue33] needed in §5.
2 Preliminaries
In this paper, a map is a continuous function. Given a map
$f:X\to X$
on a compact metric space X, we let
$$ \begin{align} \underleftarrow{\lim} (X,f) = \{(x_0,x_1,\ldots,) \in X^{\mathbb{N}_0} : x_i\in X, x_i=f(x_{i+1}) \text{ for any } i \in {\mathbb{N}_0} \}, \end{align} $$
and call
$\underleftarrow {\lim } (X,f)$
the inverse limit of X with bonding map f, or inverse limit of f for short. It is equipped with metric induced from the product metric in
$X^{\mathbb {N}_0}$
. The map f is said to be transitive if for any two non-empty open sets
$U,V\subset X$
, there exists an
$n\in \mathbb {N}$
such that
$f^{n}(U)\cap V\neq \emptyset $
. The map f is said to be topologically mixing if for any two non-empty open sets
$U,V\subset X$
, there exists an
$N\in \mathbb {N}$
such that
$f^{n}(U)\cap V\neq \emptyset $
for all
$n>N$
. The map f is said to be topologically exact, or locally eventually onto, if for every non-empty open set U, there exists an n such that
$f^n(U)=X$
. It is evident from the definitions that topological exactness implies mixing, which implies transitivity. A map
$F:Y\to Y$
is said to be semi-conjugate to f if there exists a surjective map
$\varphi :Y\to X$
such that
$f\circ \varphi =\varphi \circ ~F$
. If in addition
$\varphi $
is a homeomorphism, then F is said to be conjugate to f. A continuum is a compact and connected metric space that contains at least two points. A dendrite is a locally connected continuum D such that for all
$x, y \in D$
, there exists a unique (possibly degenerate) arc in D with endpoints x and y. We denote this arc by
$xy$
. The arcs
$xy$
and
$yx$
are the same as sets. We assume that
$xy$
is oriented from x to y if this is needed. So, x and y are the first and the last points, respectively, of
$xy$
. An end point of D is a point e such that
$D\setminus \{e\}$
is connected. The set of all end points of D will by denoted by
$E_D$
. A branch point
$b\in D$
is a point such that
$D\setminus \{b\}$
has at least three components. For an arbitrary
$x\in D$
and arbitrary positive number
$\epsilon $
, by
$B_D(x,\epsilon )$
we will denote the open ball in D with center at x and radius
$\epsilon $
. In the present paper, a dendrite with finitely many branch points will be called a tree. It is well known that a dendrite D is a tree if and only if
$E_D$
is finite; see [Reference Nadler36, Exercise 10.48]. An arc is a dendrite with no branch points.
If x and y are real numbers, by
$[x,y]$
we understand the closed interval between x and y, regardless of whether
$x\le y$
or
$x\ge y$
. Similarly as in the case of dendrites, we use the order of endpoints to indicate the orientation of the interval. We do not use the notation
$xy=[x,y]$
in the context of real numbers, even though
$[x,y]$
is a dendrite.
The pseudo-arc is a fractal-like object first constructed by Knaster in 1922. It was rediscovered by Moise in 1948 [Reference Moise34], who constructed it as a hereditarily equivalent continuum distinct from the arc, and in the same year by Bing who obtained it to show that there exists a topologically homogeneous plane continuum, distinct from the circle [Reference Bing7]. (A space X is topologically homogeneous if for any
$y,z\in X$
there exists a homeomorphism
$H:X\to X$
such that
$H(y)=z$
.) Since then, the pseudo-arc received a lot of attention in the mathematical literature, mainly in topology, but it also appears in other branches of mathematics, such as dynamical systems, including smooth and even complex dynamics; see e.g. [Reference Chéritat17, Reference Handel21, Reference Herman22, Reference Ruiz del Portal39]. Several topological characterizations of the pseudo-arc are known. One of the most recent ones, by Hoehn and Oversteegen [Reference Hoehn and Oversteegen24] from 2016, states that the pseudo-arc is a unique topologically homogeneous plane non-separating continuum (see also [Reference Hoehn and Oversteegen25]).
3 Preliminary results on dendrites
G. T. Whyburn proved that every dendrite D can be expressed as
$D=E_D\cup \bigcup _{i=0}^{\infty }A_i$
, where
$(A_i)$
is a sequence of arcs such that
$\lim _{i\to \infty }\operatorname {diam}(A_i)=0$
; see [Reference Whyburn41, V, Equation (1.3)(iii), p. 89] and [Reference Nadler36, Corollary 10.28, p. 177]. Since we need a slightly stronger version of Whyburn’s theorem, we prove it below, see Theorem 3.10. We start with the following simple observation.
Proposition 3.1. Let T be a tree. Let
$p_0\in E_T$
and
$q_0,q_1,\ldots ,q_k$
be an enumeration of all points in
$E_T\!\setminus \!\{p_0\}$
. Then there exists a unique sequence of points
$p_1,\ldots ,p_{k}\in T\setminus E_T$
such that, if
$A_i=p_iq_i$
for all
$i=0,\ldots ,k$
, then
$A_i\cap \bigcup _{j=0}^{i-1}A_j=\{p_i\}$
for each
$i=1,\ldots ,k$
. Moreover,
$\bigcup _{j=0}^{k}A_j=T$
.
Proof. For each
$i=1,\ldots ,k$
, let
$p_i$
be the first point in the arc
$q_ip_0$
(oriented from
$q_i$
to
$p_0$
) such that
$p_i\in \bigcup _{j=0}^{i-1}q_jp_0$
. Observe that
$p_1,\ldots ,p_k$
satisfy the proposition.
Note that in the above proposition, the points
$p_1,\ldots ,p_k$
do not need to be distinct.
Now let D be a dendrite which is not a tree and let
$\mathcal {S}=(s_1,s_2,\ldots )$
be a sequence of points dense in D.
Proposition 3.2. There exists an infinite sequence of non-degenerate arcs
$A_0=p_0q_0, A_1=p_1q_1, A_2=p_2q_2,\ldots $
contained in D such that
$p_0,q_0\in E_D$
, and for each integer
$i\ge 1$
, the following statements are true:
-
(1) i
$q_i\in E_D \setminus \{p_0,q_0,\ldots ,q_{i-1}\}$
; -
(2) i
$A_i\cap \bigcup _{j=0}^{i-1}A_j=\{p_i\}$
and
$p_i\notin E_D$
; -
(3) i
$\bigcup _{j=0}^iA_j$
is a tree with endpoints
$p_0,q_0,\ldots ,q_i$
; and -
(4) i
$s_i\in \bigcup _{j=0}^{i}A_j$
.
Proof. Let
$A_0=p_0q_0$
, where
$p_0\ne q_0\in E_D$
. Since an arc is a tree, item
$(3)_0$
is satisfied. Let i be a positive integer. Suppose
$A_0=p_0q_0,\ldots ,A_{i-1}=p_{i-1}q_{i-1}$
have been constructed so that items
$(1)_{j}$
–
$(4)_{j}$
are satisfied for all integers j such that
$1\le j\le i-1$
. We will now construct
$A_i=p_iq_i$
so that items
$(1)_{i}$
–
$(4)_{i}$
are satisfied.
It is convenient to briefly outline this construction before actually choosing
$q_i$
. So, suppose some
$q_i\in E_D\setminus \{p_0,q_0,\ldots ,q_{i-1}\}$
has been selected. Then it follows from
$(3)_{i-1}$
that
$q_i\notin \bigcup _{j=0}^{i-1}A_j$
and
$p_0\in \bigcup _{j=0}^{i-1}A_j$
. Let
$p_i$
be the first point in the arc
$q_ip_0$
(oriented from
$q_i$
to
$p_0$
) such that
$p_i\in \bigcup _{j=0}^{i-1}A_j$
. Observe that items
$(1)_{i}$
–
$(3)_{i}$
are automatically satisfied. Thus, to complete the proof of the proposition, we need to strengthen the condition
$q_i\in E_D\setminus \{p_0,q_0,\ldots ,q_{i-1}\}$
in such a way that item
$(4)_{i}$
is also satisfied (with the choice of
$p_i$
as described above). We do that by considering the following three cases separately.
Case
$s_i\in \bigcup _{j=0}^{i-1}A_j$
. In this case, we may choose any
$q_i\in E_D\setminus \{p_0,q_0,\ldots ,q_{i-1}\}$
. (Notice that
$E_D\setminus \{p_0,q_0,\ldots ,q_{i-1}\}\ne \emptyset $
because D is no a tree.)
Case
$s_i\notin \bigcup _{j=0}^{i-1}A_j$
and
$s_i\in E_D$
. In this case, setting
$q_i=s_i$
clearly satisfies item
$(4)_{i}$
.
Case
$s_i\notin \bigcup _{j=0}^{i-1}A_j$
and
$s_i\in D\setminus E_D$
. In this case,
$D\setminus \{s_i\}$
is not connected by [Reference Nadler36, Theorem 10.7]. Since
$\bigcup _{j=0}^{i-1}A_j$
is connected, it is contained in one component of
$D\setminus \{s_i\}$
. Let
$D_0$
denote that component and let
$D_1$
be another component
$D\setminus \{s_i\}$
. Clearly,
$\operatorname {cl}(D_0)=D_0\cup \{s_i\}$
and
$\operatorname {cl}(D_1)=D_1\cup \{s_i\}$
are dendrites such that
$\operatorname {cl}(D_0)\cap \operatorname {cl}(D_1)=\{s_i\}$
. Since each non-degenerate metric continuum has at least two non-separating points (see [Reference Kuratowski28, Theorem 5, p. 177]), there exists
$q_i\in D_1$
such that
$\operatorname {cl}(D_1)\setminus \{q_i\}$
is connected. It follows that
$q_i\in E_D\setminus \bigcup _{j=0}^{i-1}A_j\subset E_D\setminus \{p_0,q_0,\ldots ,q_{i-1}\}$
. Finally, observe that
$s_i\in A_i=p_iq_i$
because
$p_i\in \bigcup _{j=0}^{i-1}A_j\subset D_0$
and
$q_i\in D_1$
.
Let
$A_0=p_0q_0, A_1=p_1q_1, A_2=p_2q_2,\ldots $
be as in the above proposition.
Corollary 3.3. For every
$a,b\in \bigcup _{j=0}^{\infty }A_j$
, there is an integer
$n\ge 0$
such that
$ab\subset \bigcup _{j=0}^{n}A_j$
.
Proposition 3.4. For every
$a,b\in D\setminus E_D$
, there is an integer
$n\ge 0$
such that
$ab\subset \bigcup _{j=0}^{n}A_j$
.
Proof. Since
$a,b\in D\setminus E_D$
, the arc
$ab$
can be extended from both ends to an arc
$a^{\prime }b^{\prime }\subset D$
so that
$a^{\prime }a\cap ab=\{a\}$
and
$ab\cap bb^{\prime }=\{b\}$
. Let
$D_a$
and
$D_b$
be dendrites contained in
$D\setminus ab$
such that
$a^{\prime }\in \operatorname {int}(D_a)$
and
$b^{\prime }\in \operatorname {int}(D_b)$
. Observe that each point of
$ab$
separates D between
$D_a$
and
$D_b$
. Since
$\mathcal {S}$
is dense in D, there are positive integers
$n_a$
and
$n_b$
such that
$s_{n_a}\in D_a$
and
$s_{n_b}\in D_b$
. Clearly,
$ab\subset s_{n_a}s_{n_b}$
. Set
$n=\max (n_a,n_b)$
. Condition Proposition 3.2(4) implies that both
$s_{n_a}$
and
$s_{n_b}$
belong to
$\bigcup _{j=0}^nA_j$
. So
$s_{n_a}s_{n_b}\subset \bigcup _{j=0}^nA_j$
since
$\bigcup _{j=0}^nA_j$
is a tree. Consequently,
$ab\subset \bigcup _{j=0}^nA_j$
.
Corollary 3.5.
$D\setminus E_D\subset \bigcup _{j=0}^\infty A_j$
.
Corollary 3.6. For each non-empty open set
$U\subset D$
, there is a non-negative integer i such that
$U\cap A_i$
contains a non-degenerate arc.
For every arc
$L\subset D\setminus E_D$
, let
$\nu (L)$
denote the least non-negative integer such that
$L\subset \bigcup _{j=0}^{\nu (L)}A_j$
.
Proposition 3.7. Let
$d_i$
be the supremum of diameters of arcs contained in
$D\setminus \bigcup _{j=0}^iA_j$
. Then
$\lim _{i\to \infty }d_i=0$
.
Proof. Clearly,
$d_i\le d_j$
for all integers i and j such that
$0\le j\le i$
.
Suppose the proposition is false. Then there is a positive number
$\epsilon $
such that
$d_i>\epsilon $
for all
$i=0,1,\ldots $
. It follows that for each i, there is an arc J contained in
$D\setminus \bigcup _{j=0}^iA_j$
such that
$\operatorname {diam}(J)>\epsilon $
. Let L be a subarc of J such that L is contained in the interior of J, but
$\operatorname {diam}(L)$
is still greater than
$\epsilon $
. Obviously,
$L\subset J\setminus E_D$
. So the following statement is true.
Claim. For each integer
$i\ge 0$
, there is an arc
$L\subset D\setminus (E_D\cup \bigcup _{j=0}^iA_j)$
such that
$\operatorname {diam}(L)>\epsilon $
.
Let
$L_0\subset D\setminus E_D$
be an arc with
$\operatorname {diam}(L_0)>\epsilon $
. Use the claim with
$i=\nu (L_0)$
to get
$L_1$
contained in
$D\setminus (E_D\cup \bigcup _{j=0}^{\nu (L_0)}A_j)$
such that
$\operatorname {diam}(L_1)>\epsilon $
. Continue using the claim repeatedly to obtain a sequence of arcs
$L_1,L_2,L_3,\ldots $
such that for each positive integer k,
$L_k\subset D\setminus (E_D\cup \bigcup _{j=0}^{\nu (L_{k-1})}A_j)$
and
$\operatorname {diam}(L_k)>\epsilon $
. Observe that the arcs
$L_0,L_1,L_2,L_3,\ldots $
are mutually disjoint and each of them has diameter greater than
$\epsilon $
, which is impossible in a dendrite. This contradiction completes the proof of the proposition.
For each positive integer i, let
$l(i)$
be the least non-negative integer such that
$p_i\in A_{l(i)}$
. Clearly,
$i>l(i)$
.
For each non-negative integer n and each positive integer i, let
$\mu (n,i)$
denote the set of those integers j such that
$1\le j\le i$
and
$l(j)=n$
. Clearly,
$\mu (n,i)=\emptyset $
if
$i\le n$
. Additionally, set
$\mu (n,0)=\emptyset $
.
We say that a non-negative integer n precedes i and write
$n\prec i$
if
$l^k(i)=n$
for some positive integer k. If n does not precede i, we write
$n\not \prec i$
.
Observe that
$0\prec i$
for all positive integers i.
The following two propositions easily follow from the construction and their proofs are left to the reader.
Proposition 3.8. There are no positive integers i and j such that
$l(j)\prec i\prec j$
. In particular, if
$l(i)=l(j)$
, then neither i precedes j nor j precedes i.
For each non-negative integer i, let
$C_i$
denote the component of
$D\setminus \{p_i\}$
containing
$A_i\setminus \{p_i\}$
.
Proposition 3.9. The following statements are true for each positive integer i.
-
(1)
$C_i$
is an open path connected set. -
(2)
$\operatorname {cl}(C_i)=C_i\cup \{p_i\}$
. -
(3)
$C_i\cap \bigcup _{j=0}^{i-1} A_j=\emptyset $
. -
(4) Let j be an integer greater than i. Then the following three statements are equivalent:
-
•
$A_j\cap C_i\ne \emptyset $
; -
•
$A_j\subset C_i$
; -
•
$i\prec j$
.
-
Theorem 3.10. (Whyburn)
$D=E_D\cup \bigcup _{i=0}^{\infty }A_i$
and
$\lim _{i\to \infty }\operatorname {diam}(C_i)=0$
.
Proposition 3.11. Let
$h_0:\bigcup _{j=0}^\infty A_j\to [0,1]$
such that
$\operatorname {diam}(h_0(A_i))\le 2^{-i}$
and
$h_0$
is continuous on
$\bigcup _{j=0}^{i}A_j$
for all non-negative integer i. Then there is a unique extension of
$h_0$
to a continuous mapping
$h:D\to [0,1]$
.
Proof.
Claim. For each
$x\in D$
and each non-negative integer i, there is a continuum
$K_i(x)\subset B_D(x,2^{-i})$
containing x in its interior such that
$|h_0(a)-h_0(b)|\le 2^{-i}$
for all
$a,b\in K_i(x)\cap \bigcup _{j=0}^\infty A_j$
.
Proof of the claim
If
$x\notin \bigcup _{j=0}^{i+1}A_j$
, set
$T=\emptyset $
. Otherwise, let
$T\subset \bigcup _{j=0}^{i+1}A_j$
be a tree containing x in its interior with respect to
$\bigcup _{j=0}^{i+1}A_j$
, and such that
$\operatorname {diam}(h_0(T))\le 2^{-(i+1)}$
. Clearly,
$Z=\operatorname {cl}(\bigcup _{j=0}^{i+1}A_j\setminus T)$
is a compact set not containing x. Let
$K_i(x)\subset B_D(x,2^{-i})\setminus Z$
be a continuum such that
$x\in \operatorname {int}(K_i(x))$
. Take any two points
$a,b\in K_i(x)\cap \bigcup _{j=0}^\infty A_j$
. To prove the claim, it remains to prove that
$|h_0(a)-h_0(b)|\le 2^{-i}$
.
There is an integer
$k>i+1$
such that
$ab\subset \bigcup _{j=0}^{k}A_j$
, see Corollary 3.3. Since
$ab\subset K_i(x)\subset D\setminus Z$
, we get the result that
$ab\subset T\cup \bigcup _{j=i+2}^{k}A_j$
. Set
$L_{i+1}=ab\cap T$
,
$L_{i+2}=ab\cap A_{i+2}$
,
$L_{i+3}=ab\cap A_{i+3}$
, …,
$L_{k}=ab\cap A_{k}$
. Observe that
$\operatorname {diam}(h_0(L_{j}))\le 2^{-j}$
for all
$j=i+1,\ldots ,k$
. Thus,
$$ \begin{align} \sum_{j=i+1}^{k}\operatorname{diam}(h_0(L_{j}))\le\sum_{j=i+1}^{k}2^{-j}<\sum_{j=i+1}^{\infty}2^{-j}=2^{-i}. \end{align} $$
Clearly,
$\bigcup _{j=i+1}^{k}L_j=ab$
. Let M be a subset of
$\{i+1,i+2,\ldots ,k\}$
minimal with respect to the property
$\bigcup _{j\in M}L_j=ab$
. Let m denote the number of elements of M. Since the intersection of an arc with a continuum, both contained in a dendrite, is either the empty set, or a point, or a non-degenerate arc, we infer that
$L_j$
is a non-degenerate arc for each
$j\in ~M$
. Since
$\bigcup _{j=j+1}^{k}L_j=ab$
is connected, there is a one-to-one function of
$\{1,\ldots ,m\}$
onto M such that
$a\in L_{\sigma (1)}$
and
$L_{\sigma (n)}\cap (\bigcup _{j=1}^{n-1}L_{\sigma (j)})\ne \emptyset $
for all
$n=2,\ldots ,m$
. It follows from the minimality of M that
$b\in L_{\sigma (m)}$
and
$L_{\sigma (j)}\cap L_{\sigma (n)}\ne \emptyset $
if and only if
$|n-j|\le 1$
for all
$j,n=1,\ldots ,m$
. Consequently,
$|h_0(a)-h_0(b)|\le \sum _{j=1}^m\operatorname {diam}(h_0(L_{\sigma (j)}))\le \sum _{j=i+1}^{k}\operatorname {diam}(h_0(L_{j}))$
. Thus, it follows from equation (*) that
$|h_0(a)-h_0(b)|<2^{-i}$
and the claim is true.
For an arbitrary point
$x\in D$
and an arbitrary non-negative integer i, let
$K_i(x)$
be the continuum defined in the claim. Observe that
$K^{\prime }_i(x)= \bigcap _{j=0}^iK_j(x)$
is a continuum containing x in its interior. So, we may replace
$K_i(x)$
in the claim by
$K^{\prime }_i(x)$
and have the additional property that
$K_{i+1}(x)\subset K_i(x)$
for each non-negative integer i.
$K_i(x)\cap \bigcup _{j=0}^\infty A_j\ne \emptyset $
because
$K_i(x)$
has non-empty interior and
$\bigcup _{j=0}^\infty A_j$
is dense in D. So,
$H_i(x)=h_0(K_i(x)\cap \bigcup _{j=0}^\infty A_j)$
is not empty. It follows from the choice of
$K_i(x)$
that
$H_{i+1}(x)\subset H_i(x)$
and
$\operatorname {diam}(H_i(x))\le 2^{-i}\kern-1.2pt$
. Consequently,
$\operatorname {cl}(H_i(x))\subset [0,1]$
is a closed non-empty set,
$\operatorname {cl}(H_{i+1}(x))\subset \operatorname {cl}(H_i(x))$
and
$\operatorname {diam}(\operatorname {cl}(H_i(x)))\le 2^{-i}$
for all non-negative i. It follows that
$ \bigcap _{j=0}^{\infty } \operatorname {cl}(H_j(x))$
is a single point. We denote this point by
$h(x)$
. Clearly,
$h(x)\in \operatorname {cl}(H_j(x))$
for all non-negative integers j.
We will show that h is continuous. Take an arbitrary point
$x\in D$
and a positive number
$\epsilon $
. We will show that there is an open neighborhood U of x in D such that
$|h(z)-h(x)|<\epsilon $
for each
$z\in U$
. Let i be a non-negative integer such that
$2^{-i}<\epsilon $
. Set
$U=\operatorname {int}(K_i(x))$
and take an arbitrary point
$z\in U$
. There is an integer n such that
$B_D(z,2^{-n})\subset U=\operatorname {int}(K_i(x))\subset K_i(x)$
. Hence,
$K_n(z)\subset K_i(x)$
. It follows that
$H_n(z)= h_0(K_n(z)\cap \bigcup _{j=0}^\infty A_j) \subset h_0(K_i(x)\cap \bigcup _{j=0}^\infty A_j)=H_i(x)$
. So,
$h(z)\in \operatorname {cl}(H_n(z)) \subset \operatorname {cl}(H_i(x))$
. Since
$\operatorname {diam}(\operatorname {cl}(H_i(x)))\le 2^{-i}$
and both
$h(z)$
and
$h(x)$
belong to
$\operatorname {cl}(H_i(x))$
, we have the result
$|h(z)-h(x)|\le 2^{-i}<\epsilon $
. Hence, h is continuous.
Finally, we must observe that h is an extension of
$h_0$
. Suppose that
$x\in \bigcup _{j=0}^\infty A_j$
. Then
$x\in K_i(x)\cap \bigcup _{j=0}^\infty A_j$
for each non-negative integer i. It follows that
$h_0(x)\in H_i(x)$
for all
$i\ge 0$
. Consequently,
$\bigcap _{i=0}^{\infty } \operatorname {cl}(H_i(x))=\{h_0(x)\}$
and, therefore,
$h(x)=h_0(x)$
. The extension is unique since it is continuous and
$\bigcup _{j=0}^\infty A_j$
is dense in D.
4 Factorization lemma and the small folds property
In this section, we introduce the notion of a small folds property for interval maps (Definition 4.4), and then show that every map with that property can be factored through an arbitrary dendrite, see Lemma 4.5.
Proposition 4.1. Let X and Y be two compact spaces, and let
$g:X\to Y$
and
$h:Y\to X$
be two continuous mappings. Then
$\varprojlim (X,h\circ g)$
and
$\varprojlim (Y,g\circ h)$
are homeomorphic. Moreover, the following statements are true.
-
(1) Suppose g is a surjection and
$h\circ g$
is transitive on X. Then
$g\circ h$
is transitive on Y. -
(2) Suppose g is a surjection and
$h\circ g$
is topologically mixing on X. Then
$g\circ h$
is topologically mixing on Y. -
(3) Suppose g is a surjection and
$h\circ g$
is topologically exact on X. Then
$g\circ h$
is topologically exact on Y.
Proof. Consider the sequence
$(Z_i)_{i=1}^\infty $
where
$Z_i=X$
for even i and
$Z_i=Y$
odd i. Let
$f_i:Z_{i+1}\to Z_i$
be h if i is even and g if i is odd. Observe that restricting all threads
$(z_i)_{i=0}^\infty \in \varprojlim (Z_i,f_i)$
to even terms results in all threads belonging to
$\varprojlim (X,h\circ g)$
. Such a restriction is a homeomorphism between the corresponding inverse limits. This follows from a more general result [Reference Engelking20, Corollary 2.5.11], but it can also be easily seen as follows. Suppose for
$(z_i)_{i=0}^\infty $
and
$(z^{\prime }_i)_{i=0}^\infty $
, we have that
$z_{2i}=z^{\prime }_{2i}$
for all
$i\in \mathbb {N}$
. Then
$z_{2i-1}=g(z_{2i})=g(z^{\prime }_{2i})=z^{\prime }_{2i-1}$
for all i, and consequently
$z_{i}=z^{\prime }_{i}$
for all
$i\in \mathbb {N}$
. It follows that the restriction is one-to-one, and since it is also clearly a surjection onto a compact space, it is a homeomorphism. Therefore,
$\varprojlim (X,h\circ g)$
and
$\varprojlim (Z_i,f_i)$
are homeomorphic. Similarly,
$\varprojlim (Y,g\circ h)$
and
$\varprojlim (Z_i,f_i)$
are homeomorphic, since restricting
$(z_i)_{i=0}^\infty $
to odd terms results in all threads belonging to
$\varprojlim (Y,g\circ h)$
. Hence,
$\varprojlim (X,h\circ g)$
and
$\varprojlim (Y,g\circ h)$
are homeomorphic.
Suppose that assumptions of the statement (1) are satisfied. Then there is
$x\in X$
such that
$((h\circ g)^i(x))_{i=1}^\infty $
is dense in X. Observe that
$g((h\circ g)^i(x))=(g\circ h)^i(g(x))$
for each positive integer i. Since g is a surjection, the image of a dense set in X is dense in Y. Consequently,
$(g((h\circ g)^i(x)))_{i=1}^\infty =((g\circ h)^i(g(x)))_{i=1}^\infty $
is dense in Y. So, the orbit of
$g(x)$
under
$g\circ h$
is dense in Y. Thus,
$g\circ h$
is transitive on Y and the statement (1) is true.
Now, suppose that assumptions of the statement (2) are satisfied. Let U and V be arbitrary open non-empty subsets of Y. Clearly,
$g{}^{-1}(U)$
and
$g{}^{-1}(V)$
are open non-empty subsets of X. Also,
$g(g{}^{-1}(U))=U$
and
$g(g{}^{-1}(V))=V$
. Since
$h\circ g$
is topologically mixing, there exists a number N such that
$(h\circ g)^i(g{}^{-1}(U))\cap g{}^{-1}(V)\ne \emptyset $
for all
$i>N$
. So,
$$ \begin{align*} g((h\circ g)^i(g{}^{-1}(U))\cap g{}^{-1}(V)) \ne\emptyset \quad \text{for all }i>N. \end{align*} $$
Since
$g(A\cap B)\subset g(A)\cap g(B)$
for all
$A,B\subset X$
, we infer that
$$ \begin{align*} g((h\circ g)^i(g{}^{-1}(U)))\cap g(g{}^{-1}(V)) \ne\emptyset \quad \text{for all }i>N. \end{align*} $$
Since
$g((h\circ g)^i(g{}^{-1}(U)))=(g\circ h)^i(g(g{}^{-1}(U)))=(g\circ h)^i(U)$
and
$g(g{}^{-1}(V)) = V$
, we get the result that
$(g\circ h)^i(U)\cap V \ne \emptyset $
for all
$i>N$
. Hence, the statement (2) is true.
Finally, suppose that assumptions of the statement (3) are satisfied. Let U be an arbitrary non-empty open subset of Y. Then
$V=g{}^{-1}(U)$
is a non-empty open subset of X such that
$g(V)=U$
. Since
$h\circ g$
is topologically exact on X, there is a positive integer i such that
$(h\circ g)^i(V)=X$
. It follows that
$g\circ (h\circ g)^i(V)=g(X)=Y$
since g is a surjection. Since
$g\circ (h\circ g)^i(V)=(g\circ h)^i\circ g(V)$
and
$g(V)=U$
, we infer that
$(g\circ h)^i(U)=Y$
. Consequently,
$g\circ h$
is topologically exact on Y.
Note that
$\sigma _{g \circ h}$
and
$\sigma _{h \circ g}$
are conjugate via
$H : \varprojlim (Y,g\circ h) \to \varprojlim (X,h\circ g)$
given by
$H((y_0, y_1, \ldots , y_k, y_{k+1}, \ldots )) = (h(y_1), \ldots , h(y_k), h(y_{k+1}), \ldots )$
,
$(y_i)_{i=0}^\infty \in \varprojlim (Y,g\circ ~h)$
.
Proposition 4.2. Let f be a continuous real function defined on an interval I. Suppose
$a,b\in f(I)$
and
$a\ne b$
. Then there are points
$c,d\in I$
such that
$f(c)=a$
,
$f(d)=b$
and
$f(t)\in (a,b)$
for each
$t\in (c,d)$
.
Proof. Let
$c_o,d_0\in I$
be such that
$f(c_0)=a$
and
$f(d_0)=b$
. Let d be the first point in the oriented interval
$[c_0,d_0]$
such that
$f(d)=b$
. Finally, let c be the last point in the oriented interval
$[c_0,d]$
such that
$f(c)=a$
.
Definition 4.3. (See [Reference Minc and Transue33, p. 1166])
Let
$f:[0, 1]\to [0, 1]$
be a continuous function. Let a and b be two points of the interval
$[0, 1]$
, and let
$\delta $
be a positive number. We say that f is
$\delta $
-crooked between a and b if for every two points
$c,d\in [0, 1]$
such that
$f(c) = a$
and
$f(d) = b$
, there is a point
$c^{\prime }$
between c and d and there is a point
$d^{\prime }$
between
$c^{\prime }$
and d such that
$|b - f(c^{\prime })| \le \delta $
and
$|a - f(d^{\prime })| \le \delta $
. We say that f is
$\delta $
-crooked if it is
$\delta $
-crooked between every pair of points.
Definition 4.4. Let
$f:[0, 1]\to [0, 1]$
be a continuous function. We say that f has the small folds property if for every positive number
$\unicode{x3bb} <1$
, there exist positive numbers
$\beta <\unicode{x3bb} $
and
$\xi <\beta /4$
satisfying the following condition:
$$ \begin{align*} \text{for every }a \text{ and }b \text{ such that } |a - b| < \beta, f \text{ is } \xi\text{-crooked between }a \text{ and } b. \end{align*} $$
Lemma 4.5. (Factorization lemma)
Let
$f:[0, 1]\to [0, 1]$
be a continuous surjection with the small folds property and let D be a dendrite. Then there are continuous surjections
$g:[0,1]\to D$
and
$h:D\to [0,1]$
such that
$h\circ g=f$
and
$\operatorname {int}_{[0,1]}(h(U))\ne \emptyset $
for each non-empty open set
$U\subset D$
.
Proof. We will assume here that D is not a tree. The proof in the case where D is a tree is similar, but much simpler. We include a short sketch of the proof in this case at the end of our argument.
Let
$A_0=p_0q_0, A_1=p_1q_1, A_2=p_2q_2,\ldots $
,
$l(i)$
,
$\mu (n,i)$
, and
$\prec $
be as in §3.
Let
$r_0=0$
,
$s_0=1$
, and let
$\tau _0$
be a homeomorphism of
$[r_0,s_0]$
onto
$A_0$
such that
$\tau _0(r_0)=p_0$
and
$\tau _0(s_0)=q_0$
. Additionally, let
$u_0,v_0\in [0,1]$
be such that
$u_0<v_0$
and the interval
$[u_0,v_0]$
is minimal with respect to the property
$f([u_0,v_0])=[0,1]=[r_0,s_0]$
.
We will construct sequences
$(r_i)_{i=1}^\infty $
,
$(s_i)_{i=1}^\infty $
,
$(\tau _i)_{i=1}^\infty $
,
$(u_i)_{i=1}^\infty $
, and
$(v_i)_{i=1}^\infty $
satisfying the following conditions for all positive integers i.
-
(1) i
$0\le r_i<s_i\le r_i+2^{-i}$
. -
(2) i
$\tau _i$
is a homeomorphism of
$[r_i,s_i]$
onto
$A_i$
such that
$\tau _i(r_i)=p_i$
and
$\tau _i(s_i)=q_i$
. -
(3) i
$r_i=\tau _{l(i)}{}^{-1}(p_i)$
. -
(4) i
$u_i<v_i$
. -
(5) i
$f(u_i)=f(v_i)=r_i$
. -
(5) i
$f(t)> r_i$
for
$t\in (u_i,v_i)$
. -
(7) i
$s_i=\max (f[u_i,v_i])$
. -
(8) i
$\operatorname {diam}(\tau _{l(i)}(f([u_i,v_i])))<2^{-i}$
, where
$\operatorname {diam}(*)$
is the diameter in D. -
(9) i Suppose n is integer such that
$0\le n< i$
. Then the following three statements are equivalent: -
•
$[u_i,v_i]\cap [u_n,v_n]\ne \emptyset $
; -
•
$[u_i,v_i]\subset (u_n,v_n)$
; -
•
$n\prec i$
.
-
-
(10) i Suppose n is an integer such that
$0\le n\le i$
. Suppose also
$x\in (r_n,s_n)$
. Then there is an interval
$I\subset (u_n,v_n)\setminus \bigcup _{j\in \mu (n,i)}[u_j,v_j]$
such that
$x\in \operatorname {int}(f(I))$
.
Observe that
$(10)_0$
is satisfied.
Let i be a positive integer. Suppose
$(r_j)_{j=0}^{i-1}$
,
$(s_j)_{j=0}^{i-1}$
,
$(\tau _j)_{j=0}^{i-1}$
,
$(u_j)_{j=1}^{i-1}$
, and
$(v_j)_{j=1}^{i-1}$
satisfying the above conditions have been constructed. We will now construct
$r_i$
,
$s_i$
,
$\tau _i$
,
$u_i$
, and
$v_i$
.
Set
$r_i=\tau _{l(i)}{}^{-1}(p_i)$
. Using
$(10)_{i-1}$
with
$n=l(i)$
and
$x=r_i$
, we get an interval
$I\subset (u_{l(i)},v_{l(i)})\setminus \bigcup _{j\in \mu (l(i),i-1)}[u_j,v_j]$
such that
$r_i\in \operatorname {int}(f(I))$
. Let
$\unicode{x3bb} $
be a positive number satisfying the following conditions:
-
(
$\unicode{x3bb} $
-1)
$\unicode{x3bb} < 2^{-i}$
; -
(
$\unicode{x3bb} $
-2)
$\operatorname {diam}(\tau _{l(i)}([r_i-\unicode{x3bb} ,r_i+\unicode{x3bb} ]))<2^{-i}$
; and -
(
$\unicode{x3bb} $
-3)
$[r_i-\unicode{x3bb} ,r_i+\unicode{x3bb} ]\subset f(I)$
.
Let
$\beta <\unicode{x3bb} $
and
$\xi <\beta /4$
be positive numbers as in Definition 4.4. Set
$a=r_i-2\xi $
and
$b=r_i+2\xi $
. Clearly,
$[a,b]\subset (r_i-\unicode{x3bb} ,r_i+\unicode{x3bb} )\subset f(I)$
. Using Proposition 4.2, we get points
$c,d\in I$
such that
$f(c)=a$
,
$f(d)=b$
, and
$f(t)\in (a,b)$
for each t between c and d. Since
$b-a=4\xi <\beta $
and f is
$\xi $
-crooked between a and b, there is a point
$c^{\prime }$
between c and d, and there is a point
$d^{\prime }$
between
$c^{\prime }$
and d such that
$|b - f(c^{\prime })| \le \xi $
and
$|a - f(d^{\prime })| \le \xi $
. It follows that
$$ \begin{align*} r_i+\xi\le f(c^{\prime})<r_i+2\xi=b \quad\text{and}\quad a=r_i-2\xi<f(d^{\prime})\le r_i-\xi. \end{align*} $$
We will now consider the cases
$c<d$
and
$d<c$
to define
$u_i$
,
$v_i$
, and an interval
$J\subset (u_{l(i)},v_{l(i)})\setminus \bigcup _{j\in \mu (l(i),i)}[u_j,v_j]$
such that
$$ \begin{align} f([u_i,v_i])\subset\operatorname{int}(f(J)). \end{align} $$
Case
$c<d$
. In this case,
$c<c^{\prime }<d^{\prime }<d$
. Let
$u_i$
be the greatest number in the interval
$[c,c^{\prime }]$
such that
$f(u_i)=r_i$
, and let
$v_i$
be the least number in the interval
$[c^{\prime },d^{\prime }]$
such that
$f(v_i)=r_i$
. Also, set
$J=[d^{\prime },d]$
.
Case
$d<c$
. In this case,
$d<d^{\prime }<c^{\prime }<c$
. Let
$u_i$
be the greatest number in the interval
$[d^{\prime },c^{\prime }]$
such that
$f(u_i)=r_i$
, and let
$v_i$
be the least number in the interval
$[c^{\prime },c]$
such that
$f(v_i)=r_i$
. Also, set
$J=[d,d^{\prime }]$
.
Observe that (*) is satisfied in both cases. To conclude the construction, we set
$s_i=\max (f[u_i,v_i])$
as required in condition
$(7)_i$
. It is easy to check that conditions
$(1)_i$
–
$(9)_i$
are true.
Proof of
$(10)_i$
. If
$n=i$
, then
$\mu (n,i)=\emptyset $
. So,
$(u_n,v_n)\setminus \bigcup _{j\in \mu (n,i)}[u_j,v_j]=(u_n,v_n)$
and
$(10)_i$
follows from
$(5)_i$
and
$(7)_i$
. So we may assume that
$n<i$
. Using
$(10)_{i-1}$
for
$x\in (u_n,v_n)$
, we infer that there is an interval
$I_{i-1}\subset (u_n,v_n)\setminus \bigcup _{j\in \mu (n,i-1)}[u_j,v_j]$
such that
$x\in \operatorname {int}(f(I_{i-1}))$
. If
$n\ne l(i)$
, then
$i\notin \mu (n,i)$
,
$\mu (n,i)=\mu (n,i-1)$
, and
$(10)_i$
is satisfied by letting
$I=I_{i-1}$
. So, we may assume that
$n=l(i)$
. To finish the proof of
$(10)_i$
, we will consider the following two cases
$x\notin f([u_i,v_i])$
and
$x\in f([u_i,v_i])$
.
Case
$x\notin f([u_i,v_i])$
. In this case, there is an interval
$L\subset f(I_{i-1})$
such that
$x\in \operatorname {int}(L)$
and
$L\cap f([u_i,v_i])=\emptyset $
. It follows from Proposition 4.2 that there is an interval
$I\subset I_{i-1}$
such that
$f(I)=L$
. Observe that this choice of I satisfies condition
$(10)_i$
.
Case
$x\in f([u_i,v_i])$
. In this case, set
$I=J$
and observe that
$(10)_i$
follows from (*).
The construction of
$(r_i)_{i=1}^\infty $
,
$(s_i)_{i=1}^\infty $
,
$(\tau _i)_{i=1}^\infty $
,
$(u_i)_{i=1}^\infty $
, and
$(v_i)_{i=1}^\infty $
satisfying
$(1)_i$
–
$(10)_i$
is now complete.
Let
$h_0$
be a real function of
$\bigcup _{j=0}^{\infty }A_j$
defined by
$h_0(x)=\tau _i{}^{-1}(x)$
for
$x\in A_i$
for every non-negative integer i. Observe that conditions
$(1)_i$
–
$(7)_i$
guarantee that
$h_0$
is a well-defined function onto
$[0,1]$
satisfying the assumptions of Proposition 3.11. Thus, there is a unique extension of
$h_0$
to a continuous mapping
$h:D\to [0,1]$
.
Since
$\tau _i{}^{-1}$
is an embedding of
$A_i$
into
$[0,1]$
for each non-negative integer i, it follows from Corollary 3.6 that
$\operatorname {int}_{[0,1]}(h(U))\ne \emptyset $
for each non-empty open set
$U\subset D$
.
For each non-negative integer i, we will define a function
$g_i:[0,1]\to \bigcup _{j=0}^{i}A_j$
by a recursive formula. Set
$g_0=\tau _0\circ f$
and, for each positive integer i, let
$g_i$
be defined by
$$ \begin{align*}g_i(t)= \begin{cases} g_{i-1}(t) & \mbox{if }t\in[0,1]\setminus(u_i,v_i), \\ \tau_i\circ f(t) & \mbox{if }t\in(u_i,v_i). \end{cases} \end{align*} $$
The following claim is an easy consequence of the above definition.
Claim 4.5.1. Suppose n and i are integers such that
$0\le n<i$
. Then,
$g_i(t)=g_n(t)$
for each
$t\in [0,1]\setminus \bigcup _{j=n+1}^i(u_j,v_j)$
.
Claim 4.5.2. Let i be a non-negative integer. Then the following properties are true.
-
(P-1) i
$g_i$
is a continuous surjection onto
$\bigcup _{j=0}^iA_j$
. -
(P-2) i
$h\circ g_i=f$
. -
(P-3) i Suppose n is an integer such that
$0\le n\le i$
, then:-
(i) n
$g_i(t)=g_n(t)=\tau _n\circ f(t)$
for
$t\in [u_n,v_n]\setminus \bigcup _{j\in \mu (n,i)}(u_j,v_j)$
; -
(ii) n
$g_i([u_n,v_n]\setminus \bigcup _{j\in \mu (n,i)}(u_j,v_j))=A_n$
; and -
(iii) n
$g_i((u_n,v_n))\subset C_n$
.
-
Proof of Claim 4.5.2
We will prove the claim by induction with respect to i. Observe that
$(\mathrm {P-1})_0$
–
$(\mathrm {P-3})_0$
are true. Suppose that i is a positive integer such that
$(\mathrm {P-1})_{\mathrm {i-1}}$
–
$(\mathrm {P-3})_{\mathrm {i-1}}$
are satisfied. We will prove
$(\mathrm {P-1})_{\mathrm {i}}$
–
$(\mathrm {P-3})_{\mathrm {i}}$
.
Clearly,
$l(i)<i$
. If
$j\in \mu (l(i),i-1)$
, then
$j\not \prec i$
by Proposition 3.8. So, it follows from
$(9)_i$
used with
$n=j$
that
$[u_i,v_i]\cap \bigcup _{j\in \mu (l(i),i-1)}[u_j,v_j]=\emptyset $
. Using
$(9)_i$
again, this time with
$n=l(i)$
, we get the result that
$[u_i,v_i]\subset (u_{l(i)},v_{l(i)})$
. It follows from
$(2)_{l(i)}$
,
$(3)_i$
,
$(5)_i$
, and
$(\mathrm {P-3})_{\mathrm {i-1}}\ (\mathrm {i})_{\mathrm {l(i)}}$
that
$g_{i-1}(u_i)=g_{i-1}(v_i)=p_i$
. So,
$g_{i-1}$
restricted to
$[0,1]\setminus (u_i,v_i)$
and
$\tau _i\circ f$
defined on
$[u_i,v_i]$
are two continuous functions agreeing on the intersection of their (compact) domains. Consequently,
$g_i$
, which is the union of these two functions, is continuous on the interval
$[0,1]$
. Also, observe that this definition of
$g_i$
guarantees
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {i})_{\mathrm {i}}$
. If
$0\le n<i$
, then
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {i})_{\mathrm {n}}$
follows automatically from
$(\mathrm {P-3})_{\mathrm {i-1}}\ (\mathrm {i})_{\mathrm {n}}$
because
$\mu (n,i-1)\subset \mu (n,i)$
. So,
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {i})_{\mathrm {n}}$
is true for all integers n such that
$0\le n\le i$
. The property
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {ii})_{\mathrm {n}}$
follows from continuity of
$g_i$
,
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {i})_{\mathrm {n}}$
and
$(10)_i$
.
Proof of
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {iii})_{\mathrm {n}}$
. Observe that
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {iii})_{\mathrm {i}}$
is true since
$g_i((u_i,v_i))\subset A_i\setminus \{p_i\}\subset C_i$
. Hence, it is enough to prove
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {iii})_{\mathrm {n}}$
for each non-negative integer
$n<i$
. In this case, we may use
$(\mathrm {P-}3)_{\mathrm {i-1}}\ (\mathrm {iii})_{\mathrm {n}}$
to infer that
$g_{i-1}((u_n,v_n))\subset C_n$
. Suppose
$n\not \prec i$
. Then
$[u_i,v_i]\cap [u_n,v_n]=\emptyset $
by
$(9)_i$
, and
$g_i\mid [u_n,v_n]=g_{i-1}\mid [u_n,v_n]$
. So
$g_{i}((u_n,v_n))=g_{i-1}((u_n,v_n))\subset C_n$
. Hence, we may assume that
$n\prec i$
. In such a case,
$[u_i,v_i]\subset (u_n,v_n)$
by
$(9)_i$
. Consequently,
$g_i(u_i)=g_{i-1}(u_i)=\tau _n\circ f(u_i)=p_i$
belongs to
$C_i$
. Thus,
$A_i\subset C_i$
since
$p_n\notin A_i$
. This implies that
$g_i([u_i,v_i])\subset A_i\subset C_n$
. It follows that
$g_i([u_n,v_n])\subset C_n$
since
$g_{i}([u_n,v_n]\setminus (u_i,v_i))=g_{i-1}([u_n,v_n]\setminus (u_i,v_i))$
. This completes the proof of
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {iii})_{\mathrm {n}}$
and the proof of
$(\mathrm {P-}3)_{\mathrm {i}}$
in general.
It follows from
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {ii})_{\mathrm {n}}$
that
$g_i([0,1])=\bigcup _{j=0}^iA_j$
. So,
$(\mathrm {P-1})_{\mathrm {i}}$
is true since we have already proven that
$g_i$
is continuous.
To show
$(\mathrm {P-2})_{\mathrm {i}}$
, recall that
$h\mid \bigcup _{j=0}^\infty A_j=h_0$
and
$h_0(x)=\tau _i{}^{-1}(x)$
for all
$x\in A_i$
. It follows from the definition of
$g_i$
that
$g_i(t)=\tau _i\circ f(t)\in A_i$
for all
$t\in (u_i,v_i)$
. So,
$h\circ g_i(t)=\tau _i{}^{-1}\circ \tau _i\circ f(t)=f(t)$
for all
$t\in (u_i,v_i)$
. Now,
$(\mathrm {P-2})_{\mathrm {i}}$
follows from
$(\mathrm {P-2})_{\mathrm {i-1}}$
. Hence, the claim is true.
Claim 4.5.3.
$(g_i)$
is a Cauchy sequence.
Proof of Claim 4.5.3
Let
$\epsilon $
be an arbitrary positive number. It follows from Theorem 3.10 that there is an integer m such that
$2^{-m}<\epsilon $
and
$\operatorname {diam}(C_j)<\epsilon /2$
for each
$j\ge m$
. Let i be an arbitrary integer greater than m and let t be an arbitrary element of
$[0,1]$
. To complete the proof of the claim, we will show that
$$\begin{align} d(g_i(t),g_m(t))<\epsilon. \end{align} $$
If
$t\notin \bigcup _{j=m+1}^i(u_j,v_j)$
, then
$g_i(t)=g_m(t)$
by Claim 4.5.1, and the equation (*0) is true. So, we may assume that
$t\in \bigcup _{j=m+1}^i(u_j,v_j)$
. Let n be the least integer such that
$m<n\le i$
and
$t\in (u_n,v_n)$
. It follows from
$(\mathrm {P-3})_{\mathrm {i}}\ (\mathrm {iii})_{\mathrm {n}}$
that
$g_i(t)\in C_n$
. Since
$p_n\in \operatorname {cl}(C_n)$
by Proposition 3.9(2), we infer that
$$\begin{align} d(g_i(t),p_n)\le \operatorname{diam}(C_n)<\epsilon/2. \end{align} $$
Clearly,
$l(n)<n\le i$
. Since
$t\in (u_n,v_n)\subset (u_{l(n)},v_{l(n)})$
by
$(9)_n$
, the choice of n implies that
$l(n)\le m$
.
Suppose there exists an integer j such that
$l(n)\le m$
and
$t\in (u_j,v_j)$
. Then, since
$m<n$
and
$t\in (u_n,v_n)\cap (u_j,v_j)\cap (u_{l(n)},v_{l(n)})$
,
$(9)_j$
and
$(9)_n$
imply that
$l(n)\prec j\prec n$
, which contradicts Proposition 3.8. So,
$t\notin \bigcup _{j=l(n)+1}^m(u_j,v_j)$
and Claim 4.5.1 implies
$$\begin{align} g_{l(n)}(t)=g_m(t). \end{align} $$
Using
$(2)_n$
,
$(3)_n$
, and
$(5)_n$
, we infer that
$\tau _{l(n)}(f(u_n))=p_n$
. It follows from
$(\mathrm {P-}3)_{\mathrm {l(n)}}\ (\mathrm {i})_{\mathrm {l(n)}}$
that
$g_{l(n)}(u_n)=\tau _{l(n)}(f(u_n))=p_n$
and
$g_{l(n)}(t)=\tau _{l(n)}(f(t))$
. We now apply
$(8)_n$
to estimate the distance between
$g_{l(n)}(t)$
and
$p_n$
in the following way:
$d(p_n,g_{l(n)}(t))\ {=}\ d(\tau _{l(n)}(f(u_n)),\ \tau _{l(n)}(f(t)))\ {\le}\ \operatorname {diam}(\tau _{l(n)}(f[u_n,v_n]))\ {<}\ 2^{-n}$
. Since
$2^{-n}\le 2^{-m-1}<\epsilon $
, we get the result
$$\begin{align} d(p_n,g_{l(n)}(t))<\epsilon/2. \end{align} $$
Combining equations (*1), (*3), and (*2), we infer that
$$ \begin{align*} d(g_i(t),g_m(t))\le d(g_i(t),p_n)+d(p_n,g_{l(n)}(t))+d(g_{l(n)}(t),g_m(t))<\epsilon/2+\epsilon/2+0. \end{align*} $$
Hence, Claim 4.5.3 is true and the proof of the claim is complete.
Let
$g=\lim _{i\to \infty }g_i$
. Clearly, g is continuous as the limit of a uniformly convergent sequence of continuous functions into a compact space D. Observe that
$g([0,1])=D$
since
$\bigcup _{j=0}^\infty A_j$
is dense in D and
$g_i$
is a surjection onto
$\bigcup _{j=0}^iA_j$
by
$(\mathrm {P-}1)_{\mathrm {i}}$
. Finally, observe that the sequence
$(h\circ g_i)$
converges uniformly to
$h\circ g$
since the sequence
$(g_i)$
converges uniformly to g and h is continuous. However,
$h\circ g_i=f$
for all i. Consequently,
$h\circ g=f$
. This completes the proof of the lemma in the case for when D is not a tree.
Sketch of Proof in the case when D is a tree. In this case, D may be represented as a finite union
$\bigcup _{i=0}^kA_i$
, see Proposition 3.1. Set
$r_0$
,
$s_0$
,
$\tau _0$
,
$u_0$
, and
$v_0$
the same way as before and then construct
$(r_i)_{i=1}^k$
,
$(s_i)_{i=1}^k$
,
$(\tau _i)_{i=1}^k$
,
$(u_i)_{i=1}^k$
, and
$(v_i)_{i=1}^k$
satisfying conditions
$(1)_{i}$
–
$(10)_{i}$
for all positive integers
$i\le k$
. Note that
$(8)_{i}$
and other estimates of distance by
$2^{-i}$
are irrelevant in this finite case and may be omitted. After the kth step of the construction, define
$h:D\to [0,1]$
by
$h(x)=\tau _i{}^{-1}(x)$
for
$x\in A_i$
for every non-negative integer
$i\le k$
. Then construct
$g_0, g_1,\ldots ,g_k$
using the same recursive formula as above. Finally, set
$g=g_k$
and observe that h and g defined this way satisfy the lemma.
5 A transitive map on
$[0,1]$
with the small folds property
W. R. R. Transue and the second author of the present paper constructed, in [Reference Minc and Transue33], a transitive map f of
$[0,1]$
onto itself such that
$\varprojlim ([0,1],f)$
is homeomorphic to the pseudo-arc. It is possible, but not entirely clear, that the map on
$[0,1]$
constructed in [Reference Minc and Transue33] has the small folds property. In this section, we will tweak the original construction very slightly to be able to show that the small folds property is satisfied. For the reader’s convenience, and to make this paper self-contained, we include Appendix A, where we cite three results from [Reference Minc and Transue33] needed in this section, Proposition 5 on p. 1166, Lemma on p. 1167, and Theorem on p. 1169.
5.1 Summary of the original construction in [Reference Minc and Transue33]
The two key elements of that construction are [Reference Minc and Transue33, Proposition 5, p. 1166] and [Reference Minc and Transue33, Lemma, p. 1167], which are stated in this paper as Proposition A.1 and Lemma A.2, respectively. The lemma is used repeatedly by the inductive construction in the proof of the main result in [Reference Minc and Transue33] (Theorem on p. 1169), stated in this paper as Theorem A.3. In turn, the lemma uses Proposition 5 in each pass. We will summarize the proposition by briefly describing arguments passed to the routines and the output produced by them.
-
• [Reference Minc and Transue33, Proposition 5, p. 1166]. Input: positive numbers
$\epsilon <1$
and
$\gamma <\epsilon /4$
. Output: A piecewise linear continuous function g mapping
$[0,1]$
onto itself such that the distance between g and the identity is estimated by
$\epsilon $
, and g is
$\gamma $
-crooked between all
$a,b\in [0,1]$
such that
$|a-b|<\epsilon $
. (See the original statement of the proposition in [Reference Minc and Transue33] for more essential properties of g.)A continuous and piecewise linear function f of
$[0,1]$
onto itself is called admissible if
$|f^{\prime }(t)|\ge 4$
for every t such that
$f^{\prime }(t)$
exists and for every
$0 \le a < b \le 1$
, there is a positive integer m such that
$f^m([a,b])=[0,1]$
. For example, the second iteration of the full tent map is admissible. -
• [Reference Minc and Transue33, Lemma, p. 1167]. Input: an admissible map f and positive numbers
$\eta $
and
$\delta $
. Output: A positive integer n and an admissible map F such that f and F are
$\eta $
close,
$F^n$
is
$\delta $
-crooked. Moreover, if
$0\le a < b \le 1$
and
$b - a\ge \eta $
, then
$f([a,b])\subset F([a,b])$
and
$F^n([a,b])=[0,1]$
.In the proof of the lemma, properties of the input are used to select a positive number
$\epsilon $
, a positive integer n, and a positive number
$\gamma $
. (The order of this choice is important. The choice of n depends on that of
$\epsilon $
. The choice of
$\gamma $
depends on
$\epsilon n$
.) Then [Reference Minc and Transue33, Proposition 5, p. 1166] is used to obtain g. The function
$F=f\circ g$
satisfies the lemma.
Since f is piecewise linear, there is a positive number
$\alpha $
such that if
$0 \le a < b \le 1$
and
$b - a < \alpha $
, then between a and b, there is a point c such that f is linear on both intervals
$[a, c]$
and
$[c, b]$
. Since
$|f'(t)| \ge 4$
for
$t \in (a, c) \cup (c, b)$
, it follows that
$$\begin{align} \operatorname{diam} (f([a,b])) \ge 2(b - a) \quad\mbox{for every } a, b \mbox{ with } 0 \le a < b \le 1, \ b - a < \alpha. \end{align}$$
Also, there is a number s such that
$|f'(t)| < s$
for every t such that
$f'(t)$
exists. In the proof of [Reference Minc and Transue33, Lemma, p. 1167],
$\epsilon $
is selected to be exactly
$\eta /s$
. Since f is admissible, there is a positive integer n such that if
$0 \le a < b \le 1$
and
$b - a> \epsilon /4$
, then
$f^n([a, b]) = [0, 1]$
. Again, in the proof of [Reference Minc and Transue33, Lemma, p. 1167],
$\gamma $
is selected to be a positive real number less than
$\min (\alpha ,s^{-n},\epsilon /4,\delta s^{-n}/5)$
.
Observation 5.1. We may set
$\epsilon $
to be any positive number
$\le \eta /s$
and apply the same proof as it is written in [Reference Minc and Transue33] without any need for an additional change. Another degree of freedom in the proof of the lemma is the choice of
$\gamma $
. After
$\epsilon $
and n are selected,
$\gamma $
may be chosen to be any positive number less than
$\min (\alpha ,s^{-n},\epsilon /4,\delta s^{-n}/5)$
. This will allow us to strengthen the lemma by imposing an additional condition on
$\gamma $
.
In the proof of the main result in [Reference Minc and Transue33] (Theorem on p. 1169), a sequence of admissible functions
$f_1,f_2,\ldots $
and a sequence of positive integers
$n(1),n(2),\ldots $
are constructed by induction to satisfy the following three conditions:
-
(i)
$|f_{i+1}(t)-f_i(t)|<2^{-i}$
for each
$t\in [0,1]$
; -
(ii)
$f_i^{n(k)}$
is
$(2^{-k}-2^{-k-i})$
-crooked for each positive integer
$k\le i$
; and -
(iii) if
$0\le a<b\le 1$
and
$b-a\ge 2^{-k}$
, then
$f_i^{n(k)}([a,b])=[0,1]$
for each positive integer
$k\le i$
.
For each integer
$i\ge 2$
, [Reference Minc and Transue33, Lemma, p. 1167] is used with
$f=f_{i-1}$
and with a certain choice of
$\eta $
and
$\delta $
. Then
$n(i)$
and
$f_i$
are defined by setting
$n(i)=n$
and
$f_i=F$
, where n and F are output by the lemma.
The first condition in the construction guarantees that the sequence
$(f_i)$
converges uniformly. The second condition implies that the inverse limit of copies of
$[0,1]$
with
$\lim _{i\to \infty }f_i$
, as the bonding map is the pseudo-arc. Finally,
$\lim _{i\to \infty }f_i$
is transitive by condition (iii) and Theorem 6 of [Reference Barge and Martin6].
5.2 Adjustments to the construction
We will use Observation 5.1 to obtain the following lemma.
Lemma 5.2. (Replacement for [Reference Minc and Transue33, Lemma, p. 1167])
Let
$f:[0,1]\to [0,1]$
be an admissible map. Let
$\eta $
,
$\delta $
, and
$\unicode{x3bb} $
be three positive numbers. Then there is an integer n and there are continuous maps g and F of
$[0,1]$
onto itself satisfying the following conditions:
-
(1)
$F=f\circ g$
; -
(2)
$|F(t)-f(t)|<\eta $
and
$|g(t)-t|<\eta $
for each
$t\in [0,1]$
; -
(3)
$F^n$
is
$\delta $
-crooked; -
(4) if
$0\le a<b\le 1$
and
$b-a\ge \eta $
, then
$f^j([a,b])\subset F^j([a,b])$
for each positive integer j; -
(5) if
$0\le a<b\le 1$
and
$b-a\ge \eta $
, then
$F^n([a,b])=[0,1]$
; -
(6) F is admissible; and
-
(7) there exist positive numbers
$\beta <\unicode{x3bb} $
and
$\xi <\beta /4$
satisfying the following condition: for every a and b such that
$|a - b| < \beta $
, F is
$\xi $
-crooked between a and b.
Proof. Let
$\alpha $
and s be defined as above Observation 5.1. Let
$\epsilon $
be a positive number less than
$\min (\eta /s,\alpha )$
. From (**), the following observation can be made.
Observation 5.2.1. Suppose that
$a,b,a^{\prime },b^{\prime }\in [0,1]$
are such that
$|a-b|<2\epsilon $
and
$[a^{\prime },b^{\prime }]\subset f{}^{-1}([a,b])$
. Then
$|a^{\prime }-b^{\prime }|<\epsilon $
.
Let n be defined in the same way as above Observation 5.1, that is, if
$0\le a<b\le 1$
and
$b-a>\epsilon /4$
, then
$f^n([a,b])=[0,1]$
. Let
$\beta $
be a positive number less than
$\min (2\epsilon ,\unicode{x3bb} )$
, let
$\xi $
be a positive number less than
$\beta /4$
, and let
$\gamma $
be a positive number less than
$\min (\alpha ,s^{-n},\epsilon /4,\delta s^{-n}/5,\xi /s)$
. As it was done in the original proof, we now use [Reference Minc and Transue33, Proposition 5] to get the map g and define
$F=f\circ g$
. (Notice that
$|g(t)-t|$
could be estimated in condition (2) by
$\eta /s$
instead of just by
$\eta $
, as it is stated in that condition.) The proof of all conditions except for conditions (4) and (7) was given in [Reference Minc and Transue33] and will be omitted here. We will only prove conditions (4) and (7).
Proof of condition (4)
Recall that the number s was defined in [Reference Minc and Transue33] such that
$|f^{\prime }(t)|<s$
for all t such that
$f^{\prime }(t)$
is defined. Observe that
$s>4$
because f is admissible. It was observed in [Reference Minc and Transue33] that
$\operatorname {diam}(f(C))\le s\operatorname {diam}(C)$
for every
$C\subset [0,1]$
; see item (2) on p. 1167 in [Reference Minc and Transue33].
Let a and b be such that
$0\le a<b\le 1$
and
$b-a\ge \eta $
. Since
$\epsilon <\eta /s<\eta /4$
,
$b-a\ge 4\epsilon>\epsilon /4$
. It follows from the choice of n that
$f^n([a,b])=[0,1]$
. Observe that
$$ \begin{align} \operatorname{diam}(f^j([a,b]))\ge \gamma \quad \text{for each non-negative integer }j. \end{align} $$
Otherwise,
$\operatorname {diam}(f^{j+n}([a,b]))\le s^n\operatorname {diam}(f^{j}([a,b]))<s^n\gamma $
, which is a contradiction because
$f^{j+n}([a,b])=[0,1]$
and
$s^n\gamma <s^ns^{-n}=1$
.
[Reference Minc and Transue33, Proposition 5(v)] states that
$A\subset g(A)$
for each interval
$A\subset [0,1]$
such that
$\operatorname {diam}(A)\ge \gamma $
. Applying f to both sides of the inclusion
$A\subset g(A)$
, we get
$f(A)\subset f\circ g(A)=F(A)$
. Hence,
$$\begin{align} f(A)\subset F(A) \quad \text{for each interval }A\subset[0,1] \text{ such that } \operatorname{diam}(A)\ge\gamma. \end{align} $$
We will prove the inclusion
$$\begin{align} f^{j}([a,b])\subset F^{j}([a,b]) \end{align} $$
by induction with respect to j. It follows from equation (*) for
$j=0$
that
$b-a\ge \gamma $
. So we may use equation (**) with
$A=[a,b]$
to get (I
$_1$
). Now, suppose
$j\ge 2$
and (I
$_{j-1}$
) is true. We need to show (I
$_{j}$
). Applying f to both sides of the inequality (I
$_{j-1}$
), we infer that
$f^{j}([a,b])\subset f(F^{j-1}([a,b]))$
. Since it follows from equation (*) for
$j-1$
and (I
$_{j-1}$
) that
$\operatorname {diam}(F^{j-1}([a,b]))\ge \gamma $
, we may use equation (**) with
$A=F^{j-1}([a,b])$
to get
$f(F^{j-1}([a,b]))\subset F(F^{j-1}([a,b]))=F^{j}([a,b])$
. Hence,
$$ \begin{align*}f^{j}([a,b])\subset f(F^{j-1}([a,b]))\subset F^{j}([a,b]).\end{align*} $$
So, (I
$_{j}$
) is true and the proof of condition (4) is complete.
Proof of (7)
Take any a and b such that
$|a - b| < \beta $
. We need to show that
$F=f\circ g$
is
$\xi $
-crooked between a and b. Take
$c,d\in [0,1]$
such that
$f\circ g(c)=a$
and
$f\circ g(d)=b$
. Let
$c_0$
be the last point in
$[c,d]$
such that
$f\circ g(c_0)=a$
. Clearly,
$c_0\in [c,d)$
. Let
$d_0$
be the first point in
$[c_0,d]$
such that
$f\circ g(d_0)=b$
. Clearly,
$f\circ g([c_0,d_0])=[a,b]$
and
$f\circ g((c_0,d_0))=(a,b)$
. Consequently,
$g([c_0,d_0])=[g(c_0),g(d_0)]$
and
$g((c_0,d_0))=(g(c_0),g(d_0))$
. Since
$|a - b| < \beta <2\epsilon $
, it follows from Observation 5.2.1 that
$|g(c_0)-g(d_0)|<\epsilon $
. By [Reference Minc and Transue33, Proposition 5(ii)], g is
$\gamma $
-crooked between
$g(c_0)$
and
$g(d_0)$
. So, there exists
$c^{\prime }$
between
$c_0$
and
$d_0$
, and there exists
$d^{\prime }$
between
$c^{\prime }$
and
$d_0$
such that
$|g(d_0)-g(c^{\prime })|<\gamma $
and
$|g(c_0)-g(d^{\prime })|<\gamma $
. It follows from the choice of
$c_0$
and
$d_0$
that
$c^{\prime }$
is between c and d, and
$d^{\prime }$
is between
$c^{\prime }$
and d. Since
$\operatorname {diam}(f(C))<s\operatorname {diam}(C)$
for every non-empty set
$C\subset [0,1]$
by [Reference Minc and Transue33, Equation (2), p. 1167],
$\gamma <\xi /s$
,
$f\circ g(d_0)=b$
, and
$f\circ g(c_0)=a$
, we infer that
$|b-f\circ g(c^{\prime })|<\xi $
and
$|a-f\circ g(d^{\prime })|<\xi $
. Thus,
$F=f\circ g$
is
$\xi $
-crooked between a and b.
Proposition 5.3. Let f and g be continuous functions of
$[0,1]$
into
$[0,1]$
. Suppose that f is
$\xi $
-crooked between a and b for some
$a,b\in [0,1]$
and a positive number
$\xi $
. Then
$f\circ g$
is also
$\xi $
-crooked between a and b.
Proof. Suppose there are
$c,d\in [0,1]$
such that
$f\circ g(c)=a$
and
$f\circ g(d)=b$
. Since f is
$\xi $
-crooked between a and b for some
$a,b\in [0,1]$
, there is a point
$c_1$
between
$g(c)$
and
$g(d)$
, and there is a point
$d_1$
between
$c_1$
and
$g(d)$
such that
$|b-f(c_1)|\le \xi $
and
$|a-f(d_1)|\le \xi $
. Since g is continuous, there is a point
$c^{\prime }$
between c and d, and there is a point
$d^{\prime }$
between
$c^{\prime }$
and d such that
$g(c^{\prime })=c_1$
and
$g(d^{\prime })=d_1$
. Observe that
$|b-f\circ g(c^{\prime })|=|b-f(c_1)|\le \xi $
and
$|a-f\circ g(d^{\prime })|=|a-f(d_1)|\le \xi $
.
Proposition 5.4. Let
$(g_i)_{j=1}^\infty $
be a sequence of continuous functions of
$[0,1]$
into
$[0,1]$
. For all integers i and j such that
$1\le i< j$
, let
$g_{i,j}$
denote the composition
$g_i\circ g_{i+1}\circ \ldots g_j$
. Additionally, set
$g_{i,i}=g_i$
. Suppose that for each non-negative integer i, the sequence
$(g_{i,j})_{j=i}^\infty $
uniformly converges. Let
$g_{i,\infty }=\lim _{j\to \infty }g_{i,j}$
. Then
$g_{i,j}\circ g_{j+1,\infty }=g_{i,\infty }$
for all positive integers i and j such that
$i\le j$
.
In the next proposition, we will use the same notation as in the previous one.
Proposition 5.5. Let
$(g_i)_{j=1}^\infty $
be a sequence with the same properties as in Proposition 5.4. Suppose also that for each
$\unicode{x3bb}>0$
, there is a positive integer j, and there exist positive numbers
$\beta <\unicode{x3bb} $
and
$\xi <\beta /4$
satisfying the following condition:
$$\begin{align} \text{for every }a \text{ and }b \text{ such that } |a - b| < \beta ,\ g_{1,j} \text{ is }\xi\text{-crooked between } a \text{ and } b. \end{align} $$
Then,
$g_{1,\infty }$
has the small folds property.
Proof. To prove the proposition, it is enough to show (
$*_{1,\infty }$
) that is equation (*1,j
) with
$g_{1,j}$
replaced by
$g_{1,\infty }$
. For that purpose, observe that
$g_{1,\infty }=g_{1,j}\circ g_{j+1,\infty }$
by Proposition 5.4. Now, use Proposition 5.3 with
$f=g_{1,j}$
and
$g=g_{1,\infty }$
.
The following proposition is well known. We state it here for convenience. Note that F in this proposition does not have to be continuous. Also, a similar proposition with
$[0,1]$
replaced by an arbitrary compact metric space is true.
Proposition 5.6. Suppose n is a positive integer and
$f:[0,1]\to [0,1]$
is a continuous function. Then, for each
$\epsilon>0$
, there exists
$\eta>0$
with the property
$|f^n(t)-F^n(t)|<\epsilon $
for all
$t\in [0,1]$
and each function
$F:[0,1]\to [0,1]$
such that
$|f(t)-F(t)|<\eta $
for all
$t\in [0,1]$
.
Proof. The proposition is trivial if
$n=1$
. Suppose
$n>1$
and the proposition is true for
$n-1$
. We will prove that it is also true for n.
Take an arbitrary
$\epsilon>0$
. Since f is continuous, there is
$\delta>0$
such that
$|f(a)-f(b)|<\epsilon /2$
for all
$a,b\in [0,1]$
such that
$|a-b|<\delta $
. Using the proposition with
$n-1$
and
$\epsilon $
replaced by
$\delta $
, we infer that there is a positive number
$\eta \le \epsilon /2$
with the property
$|f^{n-1}(t)-F^{n-1}(t)|<\delta $
for all
$t\in [0,1]$
and each function
$F:[0,1]\to [0,1]$
such that
$|f(t)-F(t)|<\eta $
for all
$t\in [0,1]$
. Suppose F is a specific function such that
$|f(t)-F(t)|<\eta $
for all
$t\in [0,1]$
. In particular,
$|f(F^{n-1}(t))-F(F^{n-1}(t))|<\eta \le \epsilon /2$
for all
$t\in [0,1]$
. It follows from the choices of
$\eta $
and
$\delta $
that
$|f(f^{n-1}(t))-f(F^{n-1}(t))|<\epsilon /2$
for all
$t\in [0,1]$
. Consequently,
$|f^{n}(t)-F^{n}(t)|=|f^{n}(t)-f(F^{n-1}(t))+f(F^{n-1}(t))-F^{n}(t)|\ {\le}\ |f(f^{n-1}(t))-f(F^{n-1}(t))|\ {+}\ |f(F^{n-1}(t))\ {-}\ F(F^{n-1}(t))|\ {<}\ \epsilon /2\ {+}\ \epsilon /2\ {=}\ \epsilon $
for all
$t\in [0,1]$
.
Theorem 5.7. There is a map
$f:[0,1]\to [0,1]$
such that:
-
(1) the inverse limit of copies of
$[0,1]$
with f as the bonding map is a pseudo-arc; -
(2) f is topologically exact; and
-
(3) f has the small folds property.
Proof. The proof of this theorem is very similar to that of [Reference Minc and Transue33, Theorem, p. 1169]. As it was done in [Reference Minc and Transue33], we construct a sequence of positive integers
$n(1), n(2), \ldots $
and a sequence of admissible functions
$f_1, f_2, \ldots $
of
$[0,1]$
onto itself. In [Reference Minc and Transue33], the lemma was used with
$f=f_{i-1}$
to define
$f_i$
as
$F=f\circ g$
for
$i\ge 2$
. We will use here Lemma 5.2 instead and remember g as
$g_i$
for future use. So, we will also construct another sequence of continuous functions
$g_2,g_3,\ldots $
of
$[0,1]$
onto itself. Additionally, we set
$g_1=f_1$
. This allows us to use the notation from Proposition 5.4. In particular,
$f_i=g_{1,i}$
for each integer i.
Our construction will have the following properties for each positive integer i:
-
(i) if
$i>1$
, then
$|g_{k,i-1}(t)-g_{k,i}(t)|<2^{-i}$
for each
$t\in [0,1]$
and each positive integer
$k\le i-1$
; -
(ii)
$f_i^{n(k)}$
is
$(2^{-k}-2^{-k-i})$
-crooked for each positive integer
$k\le i$
; -
(iii) if
$0\le a<b\le 1$
and
$b-a\ge 2^{-k}$
, then
$f_i^{n(k)}([a,b])=[0,1]$
for each positive integer
$k\le i$
; and -
(iv) there are positive numbers
$\beta <2^{-i}$
and
$\xi <\beta /4$
satisfying the condition: for every a and b such that
$|a - b| < \beta $
,
$g_1^i=f_i$
is
$\xi $
-crooked between a and b.
To construct
$n(1)$
and
$f_1$
, we use Lemma 5.2 with any admissible map f,
$\eta =1/2$
,
$\delta =1/4$
, and
$\unicode{x3bb} =1/2$
. Then we set
$n(1)=n$
,
$f_1=F$
, and
$g_1=F$
, where n and F are from the lemma. We assume that
$n(1),\ldots ,n(i-1)$
,
$f_1,\ldots ,f_{i-1}$
, and
$g_1,\ldots ,g_{i-1}$
have already been constructed for some integer
$i\ge 2$
. We will construct
$n(i)$
,
$f_i$
, and
$g_i$
.
Since each of the functions
$g_1,\ldots ,g_{i-1}$
is continuous, there is a positive number
$\eta ^{\prime }$
with the property that if
$g:[0,1]\to [0,1]$
is a function such that
$|g(t)-t|<\eta ^{\prime }$
for all
$t\in [0,1]$
, then
$|g_{k,i-1}(t)-g_{k,i-1}\circ g(t)|<2^{-i}$
for each positive integer
$k\le i-1$
and all
$t\in [0,1]$
.
For each positive integer
$k\le i-1$
, use Proposition 5.6 with
$n=n(k)$
,
$f=F_{i-1}$
, and
$\epsilon =2^{-k-i-1}$
to get a positive number
$\eta _k$
with the property
$$ \begin{align} |f_{i-1}^{n(k)}(t)-F^{n(k)}(t)|<2^{-k-i-1} \quad \text{for all }t\in[0,1] \end{align} $$
and each function
$F:[0,1]\to [0,1]$
such that
$|f_{i-1}(t)-F(t)|<\eta _k$
for all
$t\in [0,1]$
. Observe that it follows from condition (ii) for
$i-1$
, equation (*), and [Reference Minc and Transue33, Proposition 2] that
$$\begin{align} F^{n(k)} \text{ is }(2^{-k}-2^{-k-i})\text{-crooked}. \end{align} $$
Let
$\eta $
be a positive number less than
$\min (2^{-i},\eta ^{\prime },\eta _1,\eta _2,\ldots ,\eta _{i-1})$
. Now we use Lemma 5.2 with
$\eta $
we defined,
$f=f_{i-1}$
,
$\delta =2^{-i}-2^{-i-i}$
, and
$\unicode{x3bb} =2^{-i}$
. Then we set
$n(i)=n$
,
$f_i=F$
, and
$g_i=g$
, where n, F and g are obtained from the lemma. Clearly,
$f_i=f_{i-1}\circ g_i$
and
$f_i=g_{1,i}$
. Observe that condition (i) is satisfied since
$\eta <\eta ^{\prime }$
. Condition (ii) follows from equation (**) since
$\eta <\eta _k$
for each positive integer
$k\le i-1$
. To prove condition (iii), it is enough to observe that if
$b-a\ge 2^{-i}>\eta $
, then
$f_{i-1}^j([a,b])\subset f_i^j([a,b])$
for each positive integer j, see Lemma 5.2(4). Finally, condition (iv) follows from Lemma 5.2(7) since
$\unicode{x3bb} =2^{-i}$
.
By condition (i), the sequence
$(g_{i,j})_{j=i}^\infty $
converges uniformly for each positive integer i. In particular,
$(g_{1,j})_{j=1}^\infty =(f_j)_{j=1}^\infty $
converges uniformly. Denote its limit by f. Our proof of Theorems 5.7(1) and 5.7(2) exactly follows [Reference Minc and Transue33]. Applying Propositions 1 and 3 in [Reference Minc and Transue33], we infer that
$f^{n(k)}$
is
$(2^{-k})$
-crooked for each positive integer k. Applying Propositions 1 and 4 in [Reference Minc and Transue33], we get the result that the inverse limit of copies of
$[0,1]$
with f as the bonding map is a pseudo-arc. Condition (iii) of the construction implies that if
$0\le a<b\le 1$
and
$b-a\ge 2^{-k}$
, then
$f^{n(k)}([a,b])=[0,1]$
. It follows that f is topologically exact. Since the sequence
$(g_{i,j})_{j=i}^\infty $
converges uniformly for each positive integer i, condition (iv) of the construction allows us to use Proposition 5.5 and get the result that f has the small folds property.
Theorem 5.8. There exists a topologically mixing map f of
$[0,1]$
onto itself such that the inverse limit space
$\varprojlim ([0,1],f)$
is the pseudo-arc, and for any non-degenerate dendrite D, there exist onto maps
$g:[0,1]\to D$
and
$h:D\to [0,1]$
such that
$h\circ g=f$
. Moreover, the map
$F=g\circ h$
of D onto itself is topologically mixing, the natural extensions of f and F are conjugate, and the inverse limit space
$\varprojlim (D,F)$
is the pseudo-arc.
Our construction gives, in fact, the following stronger result.
Theorem 5.9. There exists a topologically mixing map f of
$[0,1]$
onto itself such that the inverse limit space
$\varprojlim ([0,1],f)$
is the pseudo-arc, and for any
$k\in \mathbb {N}$
and any non-degenerate dendrites
$D_1,\ldots ,D_k$
, there exist onto maps
$g_i:[0,1]\to D_i$
and
$h_i:D_i\to [0,1]$
for
$i=1,\ldots ,k$
, such that
$h_i\circ g_i=f$
. Moreover, the map
${F_i = g_i \circ \cdots \circ h_i}$
of
$D_i$
onto itself is topologically mixing, the natural extensions of f and
$F_i$
are conjugate, and the inverse limit space
$\varprojlim (D_i,F_i)$
is the pseudo-arc for
$i=1,\ldots ,k$
.
6 Final remarks
After the initial submission of the present paper, the first and third named authors proved that the inverse limit models in [Reference Boroński and Štimac10] are optimal indeed; that is, the Lozi and Hénon maps considered therein are not conjugate to natural extensions of maps on dendrites whose sets of branch points are not dense (see appendix in [Reference Boroński and Štimac10]).
The following questions appear naturally.
Question 6.1. Is there an analogue of Theorem 5.8 with interval map f such that:
-
(a)
$\varprojlim ([0,1],f)$
is not a pseudo-arc?; -
(b) f has finite topological entropy?;
-
(c) f has zero topological entropy?
Question 6.2. Suppose that
$M_1$
and
$M_2$
are two non-homeomorphic n-manifolds (or branched n-manifolds) with
$n\geq 2$
. Do there exist surjective maps
$\{f_i:M_i\to M_i\}_{i=1,2}$
whose natural extensions
$\sigma _{f_1}$
, and
$\sigma _{f_1}$
are conjugate?
Acknowledgements
J.B. was supported by the National Science Centre, Poland (NCN), grant no. 2019/34/E/ST1/00237: ‘Topological and Dynamical Properties in Parameterized Families of Non-Hyperbolic Attractors: the inverse limit approach’.
S.Š. was supported, in part, by the Croatian Science Foundation grant IP-2018-01-7491.
A. Appendix
For a positive number r and
$A \subset [0, 1]$
, let
${\mathcal B} (A,r) = \{ x \in [0, 1] : \text {there exists } y~\in ~A \ \textrm {with} |x - y| \le r \}$
.
Proposition A.1. [Reference Minc and Transue33, Proposition 5, p. 1166]
Let
$\epsilon < 1$
and
$\gamma < \epsilon /4$
be two positive numbers. Then there is a piecewise linear and continuous map
$g : [0, 1] \to [0, 1]$
such that
-
(i)
$|t - g(t)| < \epsilon /2 + \gamma $
for each
$t \in [0, 1]$
, -
(ii) for every a and b such that
$|a - b| < \epsilon $
, g is
$\gamma $
-crooked between a and b, and for each subinterval A of
$[0,1]$
we have -
(iii)
$\operatorname {diam} (g(A)) \ge \operatorname {diam} (A)$
, and if, additionally,
$\operatorname {diam} (A) \ge \gamma $
, then -
(iv)
$\operatorname {diam} (g(A))> \epsilon /2$
, -
(v)
$A \subset g(A)$
, and -
(vi)
$g(B) \subset {\mathcal B} (g(A), r + \gamma )$
for each real number r and each set
$B \subset {\mathcal B} (A, r)$
.
Lemma A.2. [Reference Minc and Transue33, Lemma, p. 1167]
Let
$f : [0, 1] \to [0, 1]$
be an admissible map. Let
$\eta $
and
$\delta $
be two positive numbers. Then there is an admissible map
$F : [0, 1] \to [0, 1]$
and there is a positive integer n such that
$F^n$
is
$\delta $
-crooked and
$|F(t) - f(t)| < \eta $
for every
$t \in [0, 1]$
. Moreover, if
$0 \le a < b \le 1$
and
$b - a \ge \eta $
, then
$f([a, b]) \subset F([a, b])$
and
$F^n([a, b]) = [0, 1]$
.
Theorem A.3. [Reference Minc and Transue33, Theorem, p. 1169]
There is a transitive map
$f : [0, 1] \to [0, 1]$
such that the inverse limit of copies of
$[0, 1]$
with f as the bonding map is a pseudoarc.
