1 INTRODUCTION
The existence of planets in orbit about solar-type stars is now a well-established observational result. Obviously, the ultimate quest of this type of study is to discover Earth-type planets and moons located in the habitable zones (HZs) of their host stars. Despite a lack of discoveries,Footnote 1 the existence of Earth-mass planets, including those hosted by solar-type stars, is strongly implied by various observational findings, including the occurrence and mass distribution of close-in super-Earths, Neptunes, and Jupiters (Howard et al. Reference Howard2010). Measurements by Howard et al. (Reference Howard2010) indicate an increasing planet occurrence with decreasing planetary mass mp akin to m −0.48 p , implying that 23% of stars harbor a close-in Earth-mass planet (ranging from 0.5 to 2.0 M⊕); see also Marcy & Butler (Reference Marcy and Butler2000) for earlier results. More recent results were given by Wittenmyer et al. (Reference Wittenmyer, Tinney, Butler, O'Toole, Jones, Carter, Bailey and Horner2011); they indicate that based on the analysis of 67 solar-type stars, nearly 20% of stars are expected to host planets with a minimum mass of less than 10 M⊕.
There is also a range of studies focusing on exosolar moons, especially moons possibly located in stellar HZs. Previous studies on exosolar moons include work by Williams, Kasting, & Wade (Reference Williams, Kasting and Wade1997), Barnes & O'Brien (Reference Barnes and O'Brien2002), and more recently by, e.g., Kipping, Fossey, & Campanella (Reference Kipping, Fossey and Campanella2009), Kaltenegger (Reference Kaltenegger2010), and Weidner & Horne (Reference Weidner and Horne2010). Williams et al. (Reference Williams, Kasting and Wade1997) investigated appropriate orbital parameters of possible moons and argued that the moons need to be large enough (i.e. > 0.12 M⊕) to retain a substantial and long-lived atmosphere and would also need to possess a significant magnetic field to be continuously habitable. The work by Kipping et al. (Reference Kipping, Fossey and Campanella2009), Kaltenegger (Reference Kaltenegger2010), and Weidner & Horne (Reference Weidner and Horne2010) focused on the properties and detectability of moons of transiting planets, particularly those which can be detected as part of the Kepler mission. Kipping et al. (Reference Kipping, Fossey and Campanella2009) pointed out that HZ exomoons down to 0.2 M⊕ may be detected and approximately 25 000 stars could be surveyed for HZ exomoons with Kepler’s field of view. Kaltenegger (Reference Kaltenegger2010) conveyed that transmission spectroscopy of moons detected as part of the Kepler mission has a unique potential to screen them for habitability in the near future. In addition, Weidner & Horne (Reference Weidner and Horne2010) explored the limits on the orbits and masses of moons around currently known transiting exoplanets, particularly those discovered by the COROT mission. Recently, Kipping et al. (Reference Kipping, Hartman, Buchhave, Schmitt, Bakos and Nesvorný2013) showed seven possible candidates for transiting exomoons using observations from the Kepler mission.
Additional recent studies with implications on the possibility of habitable exomoons were carried out by Tinney et al. (Reference Tinney, Wittenmyer, Butler, Jones, O'Toole, Bailey and Horner2011), Robertson et al. (Reference Robertson2012), and Heller & Barnes (Reference Heller and Barnes2013). Tinney et al. (Reference Tinney, Wittenmyer, Butler, Jones, O'Toole, Bailey and Horner2011) focused on the detection of a gas-giant exoplanet around HD 38283, a G0/G1 V star, in an eccentric orbit with a period of almost exactly one year; a detailed discussion about the potential existence of exomoons and exo-Trojans (see later) is given by the authors. Another interesting study about gaseous planets about solar-type stars permitting the principal possibility of habitable exomoons was done by Robertson et al. (Reference Robertson2012). Heller & Barnes (Reference Heller and Barnes2013) provide a thorough analysis of exomoon habitability constrained by stellar illumination and tidal heating.
Moon formation scenarios based on a Solar System-like nebula have shown that a mass scaling ratio, which is ~10−4, exists, thereby preventing gaseous planets using core accretion to gain enough material for forming Earth-mass moons (Canup & Ward Reference Canup and Ward2006). However, this has not dissuaded the possibility of gaseous planets from acquiring large Earth-mass moons. Previous studies have indicated that there can be large stability zones for irregular or captured satellites. In the Solar System, Kuiper belt objects (see e.g. Luu et al. Reference Luu, Marsden, Jewitt, Trujillo, Hergenrother, Chen and Offutt1997) have demonstrated retrograde motion resulting from formation scenarios with proper conditions (Schlichting & Sari Reference Schlichting and Sari2008). Moreover, many irregular moons have been discovered where collisions have accreted to substantial sizes (Nesvorný et al. Reference Nesvorný, Alvarellos, Dones and Levison2003). Currently, the Hunt for Exomoons with Kepler (HEK; Kipping et al. Reference Kipping, Bakos, Buchhave, Nesvorný and Schmitt2012) project has utilised the hypothesis of acquiring Earth-mass exomoons via capture which would most likely be identified as orbiting in retrograde direction.
Long-term orbital stability in stellar HZs is a necessary condition for the evolution of any form of life, particularly intelligent life. Examples of previous studies on the orbital stability of hypothetical Earth-mass planets in stellar HZs include the works by Gehman, Adams, & Laughlin (Reference Gehman, Adams and Laughlin1996), Noble, Musielak, & Cuntz (Reference Noble, Musielak and Cuntz2002), Menou & Tabachnik (Reference Menou and Tabachnik2003), Cuntz et al. (Reference Cuntz, von Bloh, Bounama and Franck2003), Asghari et al. (Reference Asghari2004), Jones, Underwood, & Sleep (Reference Jones, Underwood and Sleep2005), Jones, Sleep, & Underwood (Reference Jones, Sleep and Underwood2006), Jones & Sleep (Reference Jones and Sleep2010), Kopparapu & Barnes (Reference Kopparapu and Barnes2010), and Eberle et al. (Reference Eberle, Cuntz, Quarles and Musielak2011). These studies explore the dynamics of multi-body systems noting that many extrasolar planetary systems contain more than one extrasolar giant planet (EGP), which is of pivotal importance for the orbital stability of possible Earth-mass objects in those systems.
For example, in the HD 23079 system, a Jupiter-mass planet is found to orbit the star in the HZ, therefore jeopardising the existence of habitable terrestrial planets. This system has previously been studied by Dvorak et al. (Reference Dvorak, Pilat-Lohinger, Schwarz and Freistetter2004), Schwarz et al. (Reference Schwarz, Dvorak, Süli and Érdi2007), and Eberle et al. (Reference Eberle, Cuntz, Quarles and Musielak2011). The study of HD 23079 is of particular interest because (1) the mass and spectral type of the center star is fairly similar to the Sun, (2) the Jupiter-mass planet is found to orbit the star in a nearly circular orbit, and (3) any exomoon of that planet, if such a moon exists, would therefore exhibit a relatively stable climate.
In systems such as HD 23079, there is the general possibility of habitable Trojan planets as well as habitable exomoons. A Trojan planet is one that librates around one of the Lagrangian points L4 and L5 of the giant planet. These points lie on the giant planets orbit, ahead (L4) and behind (L5) the planet, each forming an equilateral triangle with the planet and its star. Dvorak et al. (Reference Dvorak, Pilat-Lohinger, Schwarz and Freistetter2004) investigated the stability regions of hypothetical terrestrial Trojans librating around L4 and L5 in specific systems, including HD 23079, and obtained relationships between the size of the stability regions and the orbital parameters of the giant planets, particularly its eccentricity. Schwarz et al. (Reference Schwarz, Dvorak, Süli and Érdi2007) thereafter identified numerous exoplanetary systems that can harbor Trojan planets in stable orbits. All these systems also provide the opportunity for hosting exomoons around Jupiter-type planets, including exomoons located in stellar HZs. Updated results for HD 23079 given by Eberle et al. (Reference Eberle, Cuntz, Quarles and Musielak2011) showed that this system is also well suited for the existence of habitable Earth-type Trojans, especially if a generalised stellar HZ is assumed, which in the Solar System corresponds to 0.84–1.67 AU from the Sun (Kasting, Whitmire, & Reynolds Reference Kasting, Whitmire and Reynolds1993); see Section 2.2 for details.
A more recent example of a system with the potential of hosting both exomoons and exo-Trojans in the ‘habitability phase space’ is HD 38283, as described by Tinney et al. (Reference Tinney, Wittenmyer, Butler, Jones, O'Toole, Bailey and Horner2011). This system is known to possess an EGP around its host star largely or entirely located in the stellar HZ, considering that HD 38283b's orbit is highly eccentric (i.e. ep ≃ 0.41), a notable difference to HD 23079b considered in the present study. Exomoons and exo-Trojans as companions of gas-giant exoplanets in 0.5–2 AU orbits (somewhat depending on the stellar spectral type) thus offer the possibility of providing circumstellar habitability. Exomoons and/or exo-Trojans may be able to form in situ or be captured; examples of the latter include the outer satellites of Jupiter and Saturn (e.g. Jewitt & Haghighipour Reference Jewitt and Haghighipour2007).
In the present study, we focus on the system of HD 23079 with concentration on the principal possibility of habitable exomoons. Our paper is structured as follows. First, we discuss the stellar and planetary parameters of the HD 23079 system. Next, we comment on the circumstellar habitability of HD 23079. Thereafter, we present our results and discussion, including a detailed statistical analysis of the exomoon orbital stability limits as well as a comparison of our results with the formulae of Domingos et al. (Reference Domingos, Winter and Yokoyama2006). Finally, we present summary and conclusions.
2 THEORETICAL APPROACH
2.1 Stellar and planetary parameters
HD 23079 has been monitored as part of the Anglo-Australian Planet Search (AAPS) program (Tinney et al. Reference Tinney, Butler, Marcy, Jones, Penny, McCarthy and Carter2002), which is able to perform extrasolar planet detection and measurements with a long-term, systematic radial velocity precision of 3 m s−1 or better. HD 23079 was identified to host a Jupiter-mass planet in a relatively large and nearly circular orbit. HD 23079 is an inactive main-sequence star. Gray et al. (Reference Gray, Corbally, Garrison, McFadden, Bubar, McGahee, O'Donoghue and Knox2006) classified HD 23079 as F9.5 V (see Table 1; all parameters have their usual meaning), an updated result compared with Houk & Cowley (Reference Houk and Cowley1975), who found that HD 23079 is intermediate between an F8 and a G0 star. Its stellar spectral type corresponds to a mass of M = 1.10 ± 0.15 M⊙. The stellar effective temperature and radius are given as T eff = 6030 ± 52 K and R = 1.106 ± 0.022 R⊙, respectively (Ribas et al. Reference Ribas, Solano, Masana and Giménez2003). Thus, HD 23079 is fairly similar to the Sun, though slightly hotter and slightly more massive. The detected planet (HD 23079b) has a minimum mass of mp sin i = 2.45 ± 0.21 M J . Furthermore, it has a semimajor axis of ap = 1.596 ± 0.093 AU and an eccentricity of ep = 0.102 ± 0.031 (Butler et al. Reference Butler2006), corresponding to an orbital period of P = 730.6 ± 5.7 days. The original results by Tinney et al. (Reference Tinney, Butler, Marcy, Jones, Penny, McCarthy and Carter2002) indicated very similar planetary parameters.
Table 1. Stellar and planetary parameters.

a Data from SIMBAD, see http://simbad.u-strasbg.fr.
b Adopted from the Hipparcos catalogue.
c Based on spectral type.
d Based on parallax 28.90 ± 0.56 mas.
The orbital parameters of HD 23079b are relatively similar to those of Mars, implying that HD 23079b is orbiting its host star in or near the outskirts of the stellar HZ (see the discussion later). The existence of HD 23079b, a planet about two and a half times more massive than Jupiter, makes it difficult for a terrestrial planet to orbit HD 23079 at a similar distance without being heavily affected by the giant planet; see results from previous case studies by Noble et al. (Reference Noble, Musielak and Cuntz2002) and Yeager, Eberle, & Cuntz (Reference Yeager, Eberle and Cuntz2011), who focused on the dynamics of HD 20782, HD 188015, and HD 210277, which are systems of similar dynamical settings. Concerning HD 23079, previous investigations pertaining to habitable terrestrial Trojan planets were carried out by Dvorak et al. (Reference Dvorak, Pilat-Lohinger, Schwarz and Freistetter2004) and Eberle et al. (Reference Eberle, Cuntz, Quarles and Musielak2011).
2.2 Stellar habitable zone
The extent of the HZ of HD 23079 can be calculated following the formalism of Underwood, Jones, & Sleep (Reference Underwood, Jones and Sleep2003) based on the work of Kasting et al. (Reference Kasting, Whitmire and Reynolds1993), while also adopting an appropriate correction for the solar effective temperature used in the definition of solar luminosity, L ⊙. Underwood et al. (Reference Underwood, Jones and Sleep2003) supplied a polynomial fit that allows the computation of the extent of the conservative and the generalised HZ based on prescribed values of the stellar luminosity and the stellar effective temperature (see Table 2). Noting that HD 23079 is considerably more luminous than the Sun, it is expected that its HZ is more extended than the solar HZ, for which the inner and outer limits of the generalised HZ were obtained as 0.84 and 1.67 AU, respectively (Kasting et al. Reference Kasting, Whitmire and Reynolds1993).
Table 2. Orbit of the EGP and HZ.
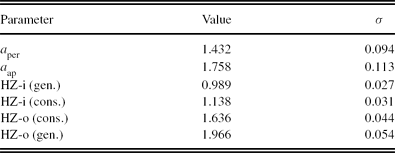
Note. All data are given in units of AU.
The generalised HZ is defined as bordered by the runaway greenhouse effect (inner limit), where water vapor enhances the greenhouse effect, thus leading to runaway surface warming, and by the maximum greenhouse effect (outer limit), where a surface temperature of 273 K can still be maintained by a cloud-free CO2 atmosphere. The inner limit of the conservative HZ is defined by the onset of water loss, i.e. the atmosphere is warm enough to allow for a wet stratosphere from where water is gradually lost by photodissociation and subsequent hydrogen loss to space. Furthermore, the outer limit of the conservative HZ is defined by the first CO2 condensation attained by the onset of the formation of CO2 clouds at a temperature of 273 K.
For HD 23079, the limits of the conservative HZ are given as 1.138 and 1.636 AU, whereas the limits of the generalised HZ are given as 0.989 and 1.966 AU (see Figure 1). The limits of the generalised HZ are those employed in our numerical planetary studies.Footnote 2 The underlying definition of habitability is based on the assumption that liquid surface water is a prerequisite for life, a key concept that is also the basis of ongoing and future searches for extrasolar habitable planets (e.g. Catanzarite et al. Reference Catanzarite, Shao, Tanner, Unwin and Yu2006; Cockell et al. Reference Cockell2009). The numerical evaluation of these limits is based on an Earth-type planet with a CO2/H2O/N2 atmosphere; see the work by Kasting et al. (Reference Kasting, Whitmire and Reynolds1993) and subsequent studies.

Figure 1. Extent of the HZ for HD 23079, defined by its conservative limits (dark gray) and generalised limits (medium gray). In addition, we depict the outer limit of an extreme version of the generalised HZ (light gray) following the work of Mischna et al. (Reference Mischna, Kasting, Pavlov and Freedman2000), although this limit may still be controversial. The orbit of HD 23079b is depicted by a thick solid line.
We point out that concerning the outer edge of habitability, even less conservative limits have been proposed in the meantime (e.g. Forget & Pierrehumbert Reference Forget and Pierrehumbert1997; Mischna et al. Reference Mischna, Kasting, Pavlov and Freedman2000). They are based on the assumption of relatively thick planetary CO2 atmospheres and invoke strong backwarming that may further be enhanced by the presence of CO2 crystals and clouds. However, as these limits, which can be as large as 2.4 AU in case of the Sun, depend on distinct properties of the planetary atmosphere, they are not relevant for our study. Nevertheless, we present this type of limit for the sake of curiosity (see Figure 1), noting that it has properly been adjusted to 2.75 AU considering the radiative conditions of the planetary host star, HD 23079. Moreover, the significance of this extreme limit has meanwhile been challenged based on detailed radiative transfer simulations (Halevy, Pierrehumbert, & Schrag Reference Halevy, Pierrehumbert and Schrag2009).
A more thorough investigation of exoplanet and exomoon habitability points to the consideration of additional factors that might influence the facilitation of an habitable environment. Detailed reviews by, e.g., Lammer et al. (Reference Lammer2009) and Horner & Jones (Reference Horner and Jones2010) indicate the importance of magnetic fields and plate tectonics as well as the prospects for the object of being hydrated as potentially decisive. Exomoons of HD 23079b are expected to be in a fortunate situation from that point of view as one would expect that tidal effects of the EGP on the moon might result in a hot interior, and hence make plate tectonics and a magnetic field more likely. Moreover, if the giant planet had migrated in from beyond the snow line (e.g. Armitage Reference Armitage2007), it could help hydrate the moon.
As part of our evaluation of habitability around HD 23079, we explored whether or not the orbit of HD 23079b is indeed fully located in the HZ of HD 23079. Thus, we calculated the limits of the generalised HZ by also considering the uncertainties in the stellar luminosity and effective temperature while employing the formalism of Underwood et al. (Reference Underwood, Jones and Sleep2003) based on second-order polynomials. The stellar luminosity and effective temperature were assumed as 1.45 ± 0.08 L⊙ and 6030 ± 52 K, respectively. Therefore, the outer limit of the generalised HZ, denoted as HZ-o (gen.), see Table 2, is obtained as 1.966 ± 0.054 AU.
In addition, we calculated the periastron and apastron of HD 23079b, denoted as a per and a ap, respectively, while also considering the statistical uncertainties in the planetary orbital parameters, i.e. the semimajor axis and eccentricity, given as 1.596 ± 0.093 AU and 0.102 ± 0.031, respectively (see Table 1). Hence, the values for the periastron and apastron are identified as 1.432 ± 0.094 AU and 1.758 ± 0.113, respectively (see Table 2). Our analysis shows that the orbit of the EGP is almost certainly completely positioned in HD 23079’s HZ; the probability for HD 23079b's orbit to be partially outside the generalised HZ is only 5%. It should also be noted that following the study by Williams & Pollard (Reference Williams and Pollard2002), brief excursions from the stellar HZ do not necessarily nullify planetary habitability because the latter is expected to depend mainly on the average stellar flux received over an entire orbit.
3 RESULTS AND DISCUSSION
3.1 Orbital stability simulations
For our simulations of the HD 23079 system, we consider both the observed giant planet HD 23079b and an object of one Earth mass, i.e. 3.005 × 10−6 M⊙, which, based on our choice of initial conditions, is expected to constitute a moon in regard to the giant planet. Consequently, we execute a grid of model simulations by considering different starting conditions for the moon candidate. The method of integration assumes a fourth-order Runge–Kutta integration scheme (Garcia Reference Garcia2000) and an eighth-order Gragg–Bulirsch–Stoer (GBS) integration scheme (Grazier et al. Reference Grazier, Newman, Varadi, Goldstein and Kaula1996). The code has been extensively tested against known analytical solutions, including the two-body and restricted three-body problem (see Noble et al. Reference Noble, Musielak and Cuntz2002; Cuntz, Eberle, & Musielak Reference Cuntz, Eberle and Musielak2007; Eberle, Cuntz, & Musielak Reference Eberle, Cuntz and Musielak2008, for detailed results).
We limit our computations to a simulation time of 106 years and apply a time step of 10−4 years for the integration scheme; the latter is found to be fully appropriate. In conjunction with previous investigations of habitable Trojan planets in the HD 23079 system (Eberle et al. Reference Eberle, Cuntz, Quarles and Musielak2011), we pursued test simulations comparing the planetary orbits based on three different integration time steps, i.e. 10−3, 10−4, and 10−5 years. In particular, we evaluated ΔRij , i.e. the magnitude of the difference between the position of the planet when different step sizes of 10−i and 10−j were used. We found no discernible differences in the outcome between models with time steps of 10−4 and 10−5 years, thus justifying the usage of 10−4 as time step for such simulations.
The giant planet always starts out at the 3 o'clock position relative to the star placed at the origin, which is assumed to coincide with its periastron position. The initial condition (i.e. starting velocity) for the orbit of the terrestrial moon is chosen such that it is assumed to be coplanar regarding the motions of the star and the EGP, as well as in a circular orbit about the EGP, although it is evident that it will be significantly affected immediately by the gravitational pull of the star, which is expected to prevent the moon from continuing its circular motion. Furthermore, the moon always starts at the 9 o'clock position relative to the giant planet. Our set of models is defined by five values for the semimajor axis ap and five values for the eccentricity ep of the giant planet, which range from 1.503 to 1.689 AU in increments of 0.0465 and from 0.071 to 0.133 in increments of 0.0155, respectively. For the EGP, we assume its minimum mass value of 2.45 M J as default. However, for models with ap = 1.596 AU and ep = 0.102, the mass of the EGP is increased by factors of 1.5 and 2.0.
3.2 Derivation of orbital stability limits
In our model simulations, we consider both prograde and retrograde orbits of the moon candidate. In the selected coordinate system, the giant planet orbits the star in a counterclockwise sense, which means that for prograde orbits, the moon orbits the giant planet in a counterclockwise sense as well. Hence, for retrograde orbits, the moon orbits the giant planet in a clockwise sense. The overwhelming majority of our simulations assumes a minimum mass for the giant planet; these models will be the focus of the following methodology.
The identification of model-dependent orbital stability limits for the moon requires a large number of simulations since the stability limits (i.e. maximum radii of possible orbits) can only be determined through trial and error. For the selected approach, both for prograde and retrograde orbits, a two-step process is adopted. First, we consider a preliminary 3 × 3 grid for the targeted array of values for the semimajor axis ap and eccentricity ep of the EGP; for ap , these are given as 1.503, 1.596, and 1.689 AU, whereas for ep , they are 0.071, 0.102, and 0.133.
For each grid value, a simulation time of 5 × 104 years is used to obtain estimates for the stability limit of each (ap , ep ) combination. For each prograde model, we perform a total of 201 simulations, based on intervals for the moon's starting distance, with 0.0520 and 0.0720 AU as lower and upper limits, respectively. Thus, the simulations are advanced in increments of 1 × 10−4 AU regarding the moon's starting distance. For each retrograde model, we simulate 201 initial conditions as well; here the limits of the intervals for the moon's starting distance are given as 0.1050 and 0.1250 AU. This approach amounts to nearly 3 600 simulations for the prograde and retrograde models combined.
To refine our search for orbital stability limits, a second step is implemented involving two aspects, that is, augmenting the preliminary coarse 3 × 3 grid to the full 5 × 5 grid, while also considering substantially longer simulation times for each model, i.e. target time spans of 106 years. For each (ap , ep ) combination, these long-term simulations again utilise intervals for setting the moon's starting distance. For each grid combination, we execute 16 simulations centered at the expected value for the model-dependent orbital stability limit.
For models already part of the preliminary 3 × 3 grid, the expected values for the orbital stability limits are obviously given by the results of the previous short-term computations. For models beyond the preliminary 3 × 3 grid, the expected values for models with intermediate values of the semimajor axis (i.e. 1.5495 and 1.6425 AU) are generated through applying a polynomial fitting assuming constant values for ap (i.e. 1.503, 1.596, and 1.689 AU). The polynomial fitting process also assisted us in estimating where stability limits should occur for intermediate values of eccentricity (i.e. 0.0865 and 0.1175).
Our results are given in Tables 3–5; for convenience, the data of Table 3 and 4 are also depicted in Figures 2 and 3. Based on the total number of simulations, it is found that, if the EGP is assumed to possess minimum mass, the stability limit for habitable moons varies between 0.05236 and 0.06955 AU (prograde orbits) and between 0.1023 and 0.1190 AU (retrograde orbits) depending on the orbital parameters of the giant planet. By keeping the EGP's mass and the semimajor axis fixed, expressions are encountered structurally similar to those of Holman & Wiegert (Reference Holman and Wiegert1999); however, with different coefficients naturally related to our particular study.
Table 3. Stability limits of habitable moons in prograde orbits.

Note. All data are given in units of AU. The stability limits represent maximum radii for the orbits.
Table 4. Stability limits of habitable moons in retrograde orbits.

Note. All data are given in units of AU. The stability limits represent maximum radii for the orbits.
Table 5. Stability limits of habitable moons for different EGP masses.
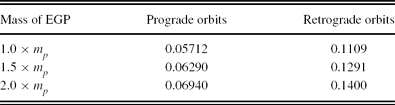
Note. The simulations are given for ap = 1.596 AU and ep = 0.102. All data are given in units of AU. The stability limits represent maximum radii for the orbits.

Figure 2. Depiction of orbital stability limits of habitable moons for prograde orbits; see Table 3 for data information. The data are grouped in regard to the EGP's eccentricity ep .

Figure 3. Depiction of orbital stability limits of habitable moons for retrograde orbits; see Table 4 for data information. The data are grouped in regard to the EGP's eccentricity ep .
Somewhat larger stability limits of the candidate moon are obtained if an increased value for the mass of the EGP is considered. Specifically, if the mass of the giant planet is increased by factors of 1.5 and 2.0, the stability limit for prograde orbits increases from 0.05712 to 0.06290 and 0.06940 AU, respectively. Furthermore, for retrograde orbits, the stability limit of habitable moons is found to increase from 0.1109 to 0.1291 and 0.1400 AU, respectively.
3.3 Examples
Examples of orbital stability and instability of exomoons around HD 23079b are given in Figures 4–8. The orbital parameters of the giant planet considered in these case studies are ap = 1.596 AU and ep = 0.102; additionally, the EGP is assumed to be of minimum mass. Figures 4 and 5 indicate that for prograde orbits, short-term (≃104 years) stability is found for a separation distance of 0.0574 AU, and instability is found for a separation distance of 0.0576 AU. The escape occurs after only 4 442 years. Furthermore, as indicated in Figures 6 and 7, short-term stability is found for retrograde orbits for a separation distance of 0.1112 AU, whereas instability is found for a separation distance of 0.1113 AU. Here the escape occurs after 3 145 years. Figure 8 shows an example of a long-term (≃106 years) instability transition for an exomoon in a retrograde orbit. Here we chose two nearby starting positions, i.e. 0.1107 and 0.1111 AU, to determine if the choice of initial conditions in this region will largely determine the long-term stability.

Figure 4. Orbital stability simulations for the moon assumed to orbit HD 23079b (red line) for an elapsed simulation time of 104 years. The orbital parameters of the planet are given as ap = 1.596 AU and ep = 0.102. The moon has been placed in a prograde orbit about the planet with its starting distance given as 0.0574 AU (top) and 0.0576 AU (bottom).

Figure 5. Separation distance of the moon from HD 23079b for the orbital stability study depicted in Fig. 4. Note that the moon has been placed in a prograde orbit about the planet with its starting distance given as 0.0574 AU (top) and 0.0576 AU (bottom).

Figure 6. Orbital stability simulations for the moon assumed to orbit HD 23079b (red line) for an elapsed simulation time of 104 years. The orbital parameters of the planet are given as ap = 1.596 AU and ep = 0.102. The moon has been placed in a retrograde orbit about the planet with its starting distance given as 0.1112 AU (top) and 0.1113 AU (bottom).

Figure 7. Separation distance of the moon from HD 23079b for the orbital stability studies depicted in Figure 6. Note that the moon has been placed in a retrograde orbit about the planet with its starting distance given as 0.1112 AU (top) and 0.1113 AU (bottom).

Figure 8. Orbital stability simulations for the moon assumed to orbit HD 23079b (small five-side star). The orbital parameters of the EGP are given as ap = 1.596 AU and ep = 0.102. The moon has been placed in a retrograde orbit within a rotating reference frame about the planet with its starting distance given as 0.1111 AU (top). Time series of the semimajor axis (middle) and eccentricity (bottom) are shown with respect to the designated starting distance in a retrograde orbit.
Figure 8 (top panel) depicts the orbit, within a rotating reference frame, of an exomoon in a retrograde orbit using the 0.1111 AU starting position; the exomoon escapes from the system after 4 000 years. Furthermore, we investigated how the semimajor axis (middle panel) and eccentricity (bottom panel) evolve over time considering these two nearby initial positions. Figure 8 (middle panel) shows that the semimajor axis for am = 0.1107 AU (depicted as dots) remains relatively constant with minor fluctuations in time for at least 105 years, whereas the alternative am (depicted as plus symbols) experiences an increase. The subsequent decrease in the semimajor axis indicates the loss of the moon due to ejection as also seen in the evolution of eccentricity.
Figure 8 (bottom panel) demonstrates more clearly for a 104-year time span the instability transition occurring at 4 000 years for the am = 0.1111 AU case, exhibiting a similar trend in the value of eccentricity. These simulations were performed with the thoroughly tested GBS integration scheme. Incidentally, in our previous study aimed at habitable Trojan planets (Eberle et al. Reference Eberle, Cuntz, Quarles and Musielak2011), we already encountered a by-chance scenario with a habitable moon in a retrograde orbit about the giant planet; it occurred due to a particular set-up of the initial conditions. In this case, the semimajor axis of the exomoon was identified as 0.051 AU, which is consistent with the stability limit attained in our present, more detailed study.
Technically speaking, the results on limits of orbital stability described so far should be referred to as outer orbital stability limits. The inner orbital stability limits of exomoons in the HD 23079 system are given by the Roche limit of the giant planet; see discussion by Williams (Reference Williams2003) and references therein. The evaluation of the Roche limit typically yields a distance of about 2.45 radii from the central object (here the EGP) as stability limit; its assessment requires an approach distinctly separate from the main focus of this paper. The Roche limit is known to depend on, e.g., the radius, oblateness, and density of the primary, and structural and rotational properties of the satellite. In the absence of a more detailed discussion, the inner stability limit for exomoons around HD 23079b can be estimated as about 0.0015 AU; note that this estimate is weakly dependent on the mass of the giant planet.
3.4 Statistical assessments
Another aspect of our investigation concerns the statistical assessment of the orbital stability limits obtained through numerical simulations. Previously, this has been done by applying the criterion of the Hill stability (e.g. Hamilton & Burns Reference Hamilton and Burns1992; Donnison Reference Donnison2010), which often serves as a customary approximation utilised in conjunction with time-dependent simulations to gauge the onset of orbital instability of planets in multi-body systems (e.g. Menou & Tabachnik Reference Menou and Tabachnik2003; Jones et al. Reference Jones, Underwood and Sleep2005; von Bloh, Bounama, & Franck Reference Bloh, Bounama and Franck2007), although the Hill stability concept has previously been identified as largely defunct in particular applications (Cuntz & Yeager Reference Cuntz and Yeager2009).
For the parameter space as studied (see Tables 3 and 4), we find that the stability limit for exomoons varies between 0.05236 and 0.06955 AU (prograde orbits) and between 0.1023 and 0.1190 AU (retrograde orbits), depending on the orbital parameters of the Jupiter-type planet if a minimum mass is assumed. In general, we find that the larger the semimajor axis ap , the larger is the stability limit. Moreover, we also find that the larger the eccentricity ep , the smaller is the stability limit.
Guided by the definition of the Hill radius (see Section 3.5), we assume that the exomoon's orbital stability limit z lim follows a relationship akin to
First, we focus on the case where the EGP is assumed to have minimum mass, mp ; this allows us to constrain all parameters but γ (see Table 6). In this case, there are 25 models of prograde orbits and 25 models of retrograde orbits available. Fitting the data yields A 0 = 0.296, α = 1.02, and β = 0.68 for the prograde models, and A 0 = 0.572, α = 0.99, and β = 0.52 for the retrograde models. As quality checks we assessed the mean and maximum errors obtained for the two data sets as well as the errors for the master models (MMod) given as ap = 1.596 AU and ep = 0.102.
Table 6. Functional parameters of z lim, error analysis.

We find that the attained fits for the prograde and retrograde cases are fully acceptable; the errors are typically ≲10% while noting that in the retrograde case the errors are considerably smaller as some stability limits in the prograde case are adversely affected by resonance phenomena (see later). In order to simplify the fits, we pursued tests with α = 1.0 and β = 0.5 as well as β = 1.0 for the prograde and retrograde cases. Even though these choices were found to be largely inconsequential for the quality of the fits, we elected α = 1.0 and β = 1.0 (adjusted fit 2) as our preferred choice for both the prograde and retrograde cases, as this choice also reflects the functional form of the Hill stability radius (see Section 3.5). Additionally, it is found that the preferred fit renders the lowest maximum and MMod errors compared with the best fit and the adjusted fit 1. Moreover, the differences regarding the mean errors between adjusted fit 2 (our preferred choice) and the best fit are also found to be relatively minor.
Some values in Table 3 do not perfectly fit the expected progression of stability limit regarding the surrounding (ap , ep ) results. Specifically, we find that for the cases where ap = 1.6425, the predicted stability limits would reside near an 11:2 mean motion resonance. Recent studies with the circumbinary planet, Kepler-16b, have shown that the Saturnian planet routinely clears the surrounding stability pockets near the same resonance (Popova & Shevchenko Reference Popova and Shevchenko2012; Quarles, Cuntz, & Musielak Reference Quarles, Cuntz and Musielak2012). Thus, our estimations of the stability limit for this region would be truncated due to this type of behavior. Fortunately, our overall statistics is not considerably impacted by this phenomenon.
As part of our study, the mass of the EGP was increased by factors of 1.5 and 2.0 relative to its minimum mass (see Table 5). This also allows us to deduce the parameter γ (see Equation (1)), which we identified as γ = 0.309 ± 0.061 (1σ) with σM = 0.031, the standard error of the mean. Note that the value of γ as determined does not significantly deviate from the theoretical value of γ = 1/3; it obviously agrees with the model-dependent value by less than 1σM.
Another quantity of interest concerning our stability studies is the ratio of orbital stability limits between models of moons in retrograde and prograde orbits, i.e.
3.5 Comparison with previous work
Finally, we compared the stability limits obtained through our numerical simulations with the results of the fitting formulae given by Domingos et al. (Reference Domingos, Winter and Yokoyama2006, hereafter D06). With R H denoting the well-established Hill radius (e.g. Hamilton & Burns Reference Hamilton and Burns1992) given as
A simple test of using the D06 formulae for the limiting case of ep →0 and em →0 reveals a promising result: the value of η (D06) is identified as 0.9309/0.4895 = 1.902, which is in perfect agreement with the η value identified for our simulations (see Section 3.4).
However, a more appropriate evaluation of the D06 formulation requires the checking of its applicability to the z lim values for prograde and retrograde orbits in a separate manner. Thus, we introduce
Therefore, for prograde orbits, if em = 0.95 is used, we find q = 1.027 with σM = 9.11 × 10−3. Moreover, if em = 0.99 is used, we find q = 1.005 with σM = 9.06 × 10−3. Hence, for prograde orbits, the D06 formula is identified as fully applicable to represent the z lim values of orbital stability for exomoons in the HD 23079 system. However, similar tests for retrograde orbits show that the D06 formula is off by about an order of magnitude. Thus, we conclude that the D06 formulation has not been well tested for parameter sets of the latter kind.
4 SUMMARY AND CONCLUSIONS
The aim of our study was to explore the general possibility of habitable moons in the HD 23079 star–planet system. This system consists of a main-sequence star slightly hotter than the Sun. It also contains a Jupiter-mass planet, HD 23079b, with a minimum mass of 2.45 M J in a slightly elliptical orbit that is almost certainly completely positioned in the HZ of HD 23079. We studied if Earth-mass habitable moons can potentially exist in this system. Thus, we deduced the orbital stability limits of moons orbiting HD 23079b by considering both prograde and retrograde orbits.
The set of models of our study also took into account the observational uncertainties of ap and ep for HD 23079b, which for the minimum mass case of the EGP resulted in the establishment of a 5 × 5 grid of stability limits for both prograde and retrograde orbits; clearly, a much larger number of models was pursued for the derivation of the stability limits due to the required test simulations given by different exomoon starting distances from the EGP. Moreover, the semimajor axis ap of the EGP was varied from 1.503 to 1.689 AU in 0.0465 increments, whereas its eccentricity ep was varied from 0.071 to 0.133 in 0.0155 increments. Furthermore, for the master model with ap = 1.596 AU and ep = 0.102, the mass of the EGP, mp , was increased by factors of 1.5 and 2.0.
For the minimum mass case of the EGP, the orbital stability limits were found to vary between 0.05236 and 0.06955 AU (prograde orbits) and 0.1023 and 0.1190 AU (retrograde orbits), corresponding 0.306 and 0.345 (prograde orbits) and 0.583 and 0.611 (retrograde orbits) of the EGP's Hill radius. Somewhat larger stability limits for the exomoons were obtained if an increased value for the mass of the Jupiter-type planet was adopted, as expected. Generally, it was found that the larger the semimajor axis ap , the larger is the stability limit. It was also found that the larger the eccentricity ep , the smaller is the stability limit. A small number of exceptions were identified when the orbital motion of the exomoon was affected by resonances. Also note that the limits as deduced constitute, technically speaking, outer orbital stability limits; the inner limits of orbital stability are given by the EGP Roche limit.
Another element of our study was the derivation of the functional dependencies of the orbital stability limits on the EGP parameters based on z lim∝a α p m γ p (1−ep )β guided by the customary notion of the Hill stability. Based on our simulations, we inferred α = 1, β = 1, and γ = 1/3 for both prograde and retrograde orbits, which is in agreement with the functional dependencies of the Hill stability radius. In addition, we also found that the stability limits for prograde orbits were in perfect agreement with the analytical formula of D06. However, no such agreement was identified for retrograde orbits, which is most likely attributable to the fact that the formula for retrograde satellite motion of D06 may be inapplicable for ep →0 and em →1.
A further quantity considered in our study concerns the ratio of orbital stability limits between models of moons in retrograde and prograde orbits η (see Equation (2)). According to our model simulations, we found that η is given as 1.902 with σM = 0.019. Thus, on average, the stability limit for retrograde orbits is increased by 90% compared with the limit of stability for prograde orbits. This result is, in principle, consistent with the previous study of Jefferys (Reference Jefferys1974), who explored the orbital stability of the restricted three-body problem based on the usage of Henon stability maps. He identified considerably broader stability regions for the massless particle-type object if a retrograde instead of a prograde orbit about the primary object was assumed.
Another example for significantly increased stability limits for retrograde orbits has been given by Eberle & Cuntz (Reference Eberle and Cuntz2010b). They pursued a theoretical investigation of a previous observational finding about the ν Octantis binary system (Ramm et al. Reference Ramm, Pourbaix, Hearnshaw and Komonjinda2009) that indicates the possible existence of a Jupiter-mass planet, although the planet appears to be located outside the zone of orbital stability. Based on detailed numerical studies, Eberle & Cuntz (Reference Eberle and Cuntz2010b) argued that the Jupiter-mass may be in a retrograde orbit relative to the motion of the binary components, which would allow the planet to be orbitally stable. Additional results in line with this reasoning have recently been given by Quarles et al. (Reference Quarles, Cuntz and Musielak2012) and Goździewski et al. (Reference Goździewski, Słonina, Migaszewski and Rozenkiewicz2013).
The study of exomoons is currently receiving heightened attention because of the ongoing Kepler mission. For example, the recent work by Kipping et al. (Reference Kipping, Fossey and Campanella2009) addressed the detectability of moons of transiting planets, including those that are expected to be detected by Kepler or photometry of approximately equal quality. These studies conveyed both the predicted transit timing signal amplitudes and the estimated uncertainties on such measurements to provide realistic confidence levels for the detection of such bodies for a broad spectrum of orbital arrangements. They concluded that HZ exomoons down to 0.2 M⊕ may be detectable and approximately 25 000 stars could be surveyed for HZ exomoons with Kepler’s field of view. Moreover, Kipping et al. (Reference Kipping, Hartman, Buchhave, Schmitt, Bakos and Nesvorný2013) recently presented seven possible candidates for transiting exomoons using observations from the Kepler mission. Previously, Kaltenegger (Reference Kaltenegger2010) discussed the possibility of screening the atmospheres of exomoons for habitability based on the concept of biomarkers. These investigations will potentially allow the identification of the existence of habitable exomoons around different types of stars, which will allow contesting results and predictions from earlier studies by Williams et al. (Reference Williams, Kasting and Wade1997), Barnes & O'Brien (Reference Barnes and O'Brien2002), and more recently by Kipping et al. (Reference Kipping, Fossey and Campanella2009), Kaltenegger (Reference Kaltenegger2010), Weidner & Horne (Reference Weidner and Horne2010), Robertson et al. (Reference Robertson2012), Heller & Barnes (Reference Heller and Barnes2013), and others.
Our study complements a previous investigation by our research group, given by Eberle et al. (Reference Eberle, Cuntz, Quarles and Musielak2011), that showed that the HD 23079 star–planet system is also a suitable candidate for hosting habitable Trojan planets.
ACKNOWLEDGMENTS
This work has been supported by the SETI institute (M.C.), the U.S. Department of Education under GAANN grant no. P200A090284 (B.Q. and J.E.), and by the University of Texas at Arlington through its Research Enhancement Program (M.C. and A.S.).

















