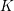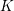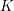Introduction
One of the main achievements in the algebraic
$K$
-theory of rings is the solution of the excision problem, first rationally by Suslin and Wodzicki [Reference Suslin and WodzickiSW92] and later integrally by Suslin [Reference SuslinSus95]: for a two-sided ideal
$I$
in a unital ring
$A$
one defines the relative
$K$
-theory spectrum
$K(A,I)$
as the homotopy fibre of the map of
$K$
-theory spectra
$K(A)\rightarrow K(A/I)$
, so that its homotopy groups
$K_{\ast }(A,I)$
fit in a long exact sequence
$$\begin{eqnarray}\cdots \rightarrow K_{i}(A,I)\rightarrow K_{i}(A)\rightarrow K_{i}(A/I)\rightarrow K_{i-1}(A,I)\rightarrow \cdots \,.\end{eqnarray}$$
If
$I$
is a not necessarily unital ring, one defines
$K_{\ast }(I):=K_{\ast }(\mathbf{Z}\ltimes I,I)$
where
$\mathbf{Z}\ltimes I$
is the unitalization of
$I$
. For every unital ring
$A$
containing
$I$
as a two-sided ideal there is a canonical map
$\mathbf{Z}\ltimes I\rightarrow A$
. It induces a map
$K_{\ast }(I)\rightarrow K_{\ast }(A,I)$
and one says that
$I$
satisfies excision in algebraic
$K$
-theory if this map is an isomorphism for all such
$A$
.
Equivalently,
$I$
satisfies excision in algebraic
$K$
-theory if, for every ring
$A$
containing
$I$
as a two-sided ideal and any ring homomorphism
$A\rightarrow B$
sending
$I$
isomorphically onto an ideal of
$B$
, the pullback square of rings
where
$A^{\prime }=A/I$
,
$B^{\prime }=B/I$
induces a homotopy cartesian square of non-connective
$K$
-theory spectra.
A ring
$I$
is called Tor-unital if
$\operatorname{Tor}_{i}^{\mathbf{Z}\ltimes I}(\mathbf{Z},\mathbf{Z})=0$
for all
$i>0$
. Every unital ring is Tor-unital, since if
$I$
is unital, then
$\mathbf{Z}\ltimes I\cong \mathbf{Z}\times I$
and the projection to
$\mathbf{Z}$
is flat.
Theorem 1 (Suslin).
If
$I$
is Tor-unital, then
$I$
satisfies excision in algebraic
$K$
-theory.
In fact, both statements are equivalent [Reference SuslinSus95, Theorem A]. For
$\mathbf{Q}$
-algebras, this was proven before by Suslin and Wodzicki [Reference Suslin and WodzickiSW92, Theorem A]. Wodzicki [Reference WodzickiWod89] gives many examples of Tor-unital
$\mathbf{Q}$
-algebras, for instance all
$C^{\ast }$
-algebras. These results are the main ingredients in the proof of Karoubi’s conjecture about algebraic and topological
$K$
-theory of stable
$C^{\ast }$
-algebras in [Reference Suslin and WodzickiSW92, Theorem 10.9]. On the other hand, by work of Morrow [Reference MorrowMor18] ideals
$I$
in commutative noetherian rings are pro-Tor-unital in the sense that the pro-groups
$\{\operatorname{Tor}_{i}^{\mathbf{Z}\ltimes I^{n}}(\mathbf{Z},\mathbf{Z})\}_{n}$
vanish for all
$i>0$
.
Suslin’s proof of Theorem 1 uses the description of algebraic
$K$
-theory in terms of Quillen’s plus-construction and relies on a careful study of the homology of affine groups. By completely different methods we prove the following generalization of Theorem 1.
Theorem 2. Assume that (1) is a homotopy pullback square of ring spectra such that the multiplication map
$A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime }$
is an equivalence. Then the square (2) of non-connective
$K$
-theory spectra is homotopy cartesian.
Here the tensor denotes the derived tensor product, and
$K$
-theory is the non-connective
$K$
-theory of perfect modules.
Example 3. Assume that (1) is a diagram of discrete rings. When viewed as a diagram of ring spectra, this is a homotopy pullback square if and only if the induced sequence of abelian groups
$$\begin{eqnarray}0\rightarrow A\rightarrow A^{\prime }\oplus B\rightarrow B^{\prime }\rightarrow 0\end{eqnarray}$$
is exact. The multiplication map
$A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime }$
is an equivalence if and only if
$\operatorname{Tor}_{i}^{A}(A^{\prime },A^{\prime })=0$
for all
$i>0$
and the ordinary tensor product of
$A^{\prime }$
with itself over
$A$
is isomorphic to
$A^{\prime }$
via the multiplication.
There are two basic cases where both conditions are satisfied: the first one is that
$A^{\prime }=A/I$
for a Tor-unital two-sided ideal
$I$
in
$A$
(see Example 24). This gives Suslin’s result. The second one is that (1) is an elementary affine Nisnevich square, i.e. all rings are commutative,
$A^{\prime }=A[f^{-1}]$
is a localization of
$A$
,
$A\rightarrow B$
is an étale map inducing an isomorphism
$A/(f)\cong B/(f)$
, and
$B^{\prime }=B[f^{-1}]$
(see Example 25). Note that by [Reference Asok, Hoyois and WendtAHW17, Proposition 2.3.2] the family of coverings of the form
$\{\operatorname{Spec}(A[f^{-1}])\rightarrow \operatorname{Spec}(A),\operatorname{Spec}(B)\rightarrow \operatorname{Spec}(A)\}$
generate the Nisnevich topology on the category of affine schemes (of finite presentation over some base). Thus Theorem 2 also implies Nisnevich descent for the algebraic
$K$
-theory of affine schemes.
In general, the condition that
$A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime }$
be an equivalence is equivalent to
$\operatorname{LMod}(A)\rightarrow \operatorname{LMod}(A^{\prime })$
being a localization, where
$\operatorname{LMod}$
denotes the
$\infty$
-category of left modules in spectra. In particular, under this condition
$\operatorname{LMod}(A^{\prime })$
is a Verdier quotient of
$\operatorname{LMod}(A)$
. The usual method that is used, for example, to produce localization sequences in
$K$
-theory (see [Reference SchlichtingSch11, § 3] for an overview, [Reference Neeman and RanickiNR04, Theorem 0.5] for the case of a non-commutative localization where a similar condition on Tor-groups appears), would be to apply Neeman’s generalization of Thomason’s localization theorem [Reference NeemanNee92, Theorem 2.1] in order to deduce that also the induced functor on the subcategories of compact objects, which are precisely the perfect modules,
$\operatorname{Perf}(A)\rightarrow \operatorname{Perf}(A^{\prime })$
is a Verdier quotient. However, Neeman’s theorem does not apply here, since the kernel of
$\operatorname{LMod}(A)\rightarrow \operatorname{LMod}(A^{\prime })$
need not be compactly generated. Indeed, there is an example by Keller [Reference KellerKel94, § 2] of a ring map
$A\rightarrow A^{\prime }$
satisfying the hypotheses of Theorem 2, where this kernel has no non-zero compact objects at all and
$\operatorname{Perf}(A^{\prime })$
is not a Verdier quotient of
$\operatorname{Perf}(A)$
.
Instead, under the conditions of Theorem 2 we prove a derived version of Milnor patching (Theorem 26) saying that (1) induces a pullback diagram of
$\infty$
-categories of left modules, i.e.
$$\begin{eqnarray}\operatorname{LMod}(A)\simeq \operatorname{LMod}(A^{\prime })\times _{\operatorname{ LMod}(B^{\prime })}\operatorname{LMod}(B).\end{eqnarray}$$
Its proof is inspired by a similar patching result for connective modules over connective ring spectra due to Lurie [Reference LurieLur17b, Theorem 16.2.0.2]. We use this to show that
$\operatorname{LMod}(A)$
can be embedded as a full subcategory in the lax pullback
$\operatorname{LMod}(A^{\prime })\,\overrightarrow{\times }_{\operatorname{LMod}(B^{\prime })}\operatorname{LMod}(B)$
(see § 1) and to identify the Verdier quotient with
$\operatorname{LMod}(B^{\prime })$
. Now the Thomason–Neeman theorem applies and gives an exact sequence of small stable
$\infty$
-categories
$$\begin{eqnarray}\operatorname{Perf}(A)\xrightarrow[{}]{i}\operatorname{Perf}(A^{\prime })\,\overrightarrow{\times }_{\operatorname{ Perf}(B^{\prime })}\operatorname{Perf}(B)\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Perf}(B^{\prime }),\end{eqnarray}$$
i.e. the composite
$\unicode[STIX]{x1D70B}\circ i$
is zero and the induced functor from the Verdier quotient of the middle term by
$\operatorname{Perf}(A)$
to
$\operatorname{Perf}(B^{\prime })$
is an equivalence up to idempotent completion. This implies the assertion of Theorem 2 not only for algebraic
$K$
-theory, but for any invariant which can be defined for small stable
$\infty$
-categories and which sends exact sequences of such to fibre sequences. In fact, in § 1 we prove the existence of the analog of the exact sequence (3) for any so-called excisive square of small stable
$\infty$
-categories (Theorem 15). In § 2 we then prove that any square of ring spectra satisfying the hypotheses of Theorem 2 yields an excisive square of
$\infty$
-categories of perfect modules (see Theorem 28). These are the two main results of the paper.
Remark 4. The failure of excision in
$K$
-theory is measured in (topological) cyclic homology: Cortiñas [Reference CortiñasCor06] proved that the fibre of the rational Goodwillie–Jones Chern character from rational algebraic
$K$
-theory to negative cyclic homology satisfies excision, i.e. sends the pullback square of rings (1) with
$B\rightarrow B^{\prime }$
surjective to a homotopy pullback square of spectra without any further condition. Geisser and Hesselholt [Reference Geisser and HesselholtGH06] proved the analogous result with finite coefficients, replacing the Goodwillie–Jones Chern character by the cyclotomic trace map from
$K$
-theory to topological cyclic homology. Both use pro versions of the results of Suslin and Wodzicki. Building on these results, Dundas and Kittang [Reference Dundas and KittangDK08, Reference Dundas and KittangDK13] prove that the fibre of the cyclotomic trace satisfies excision also for connective ring spectra, and with integral coefficients (under the technical assumption that both,
$\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{0}(B^{\prime })$
and
$\unicode[STIX]{x1D70B}_{0}(A^{\prime })\rightarrow \unicode[STIX]{x1D70B}_{0}(B^{\prime })$
are surjective).
In this general situation, i.e. without assuming any Tor-unitality condition, one still has the sequence (3), but the induced functor
$f$
from the Verdier quotient to
$\operatorname{Perf}(B^{\prime })$
need not be an equivalence up to idempotent completion. It would therefore be interesting to find conditions on an invariant
$E$
that guarantee that
$E(f)$
is still an equivalence. From the results mentioned above we know that
$E(f)$
is an equivalence for
$E$
the fibre of the cyclotomic trace.
We use
$\infty$
-categorical language. More concretely, we use the model of quasi-categories, which are the fibrant objects for the Joyal model structure on simplicial sets, as developed by Joyal [Reference JoyalJoy08] and Lurie in his books [Reference LurieLur09, Reference LurieLur17a, Reference LurieLur17b].
1 Pullbacks and exact sequences of stable
$\infty$
-categories
In this section, we discuss the pullback and the lax pullback of a diagram
$A\rightarrow C\leftarrow B$
of
$\infty$
-categories. In the stable case, we relate these by exact sequences. We further prove our first main result (Theorem 18) saying that any excisive square of small stable
$\infty$
-categories (see Definition 14) yields a pullback square upon applying any localizing invariant.
Let
$I=\unicode[STIX]{x1D6E5}[1]\in \text{sSet}$
be the standard simplicial 1-simplex. For any
$\infty$
-category
$C$
, we denote by
$C^{I}=\text{Fun}(I,C)$
the arrow category of
$C$
. The inclusion
$\{0,1\}\subseteq I$
induces the source and target maps
$s,t:C^{I}\rightarrow C$
.
Consider a diagram of
$\infty$
-categories as follows.
Definition 5. The lax pullback
$A\,\overrightarrow{\times }_{C}\,B$
of (4) is defined via the pullback diagram
in simplicial sets.
By [Reference JoyalJoy08, ch. 5, Theorem A] the map
$C^{I}\xrightarrow[{}]{(s,t)}C\,\times \,C$
is a categorical fibration, i.e. a fibration in the Joyal model structure. Since the lower and upper right corners in (5) are
$\infty$
-categories, this implies that
$A\,\overrightarrow{\times }_{C}\,B$
is indeed an
$\infty$
-category, and that (5) is homotopy cartesian with respect to the Joyal model structure.
Remark 6. The objects of
$A\,\overrightarrow{\times }_{C}\,B$
are triples of the form
$(a,b,g:p(a)\rightarrow q(b))$
, where
$a$
,
$b$
are objects of
$A$
,
$B$
respectively and
$g$
is a morphism
$p(a)\rightarrow q(b)$
in
$C$
. If
$(a,b,g)$
and
$(a^{\prime },b^{\prime },g^{\prime })$
are two objects of
$A\,\overrightarrow{\times }_{C}\,B$
, the mapping space between these sits in a homotopy cartesian diagram of spaces.
Indeed, using Lurie’s
$\operatorname{Hom}^{\text{R}}$
-model for the mapping spaces [Reference LurieLur09, § 1.2.2] gives a cartesian diagram of simplicial sets in which the right vertical map is a Kan fibration by [Reference LurieLur09, Lemma 2.4.4.1].
Remark 7. Denote by
$C^{(I)}\subseteq C^{I}$
the full subcategory spanned by the equivalences in
$C$
. It follows from [Reference JoyalJoy08, Proposition 5.17] that the pullback of the diagram
in simplicial sets models the homotopy pullback of
$\infty$
-categories
$A\times _{C}B$
. In particular, we can identify
$A\times _{C}B$
with the full subcategory of
$A\,\overrightarrow{\times }_{C}\,B$
spanned by those objects
$(a,b,g)$
where
$g$
is an equivalence in
$C$
.
Lemma 8. (i) Let
$K$
be a simplicial set and
$\unicode[STIX]{x1D6FF}:K\rightarrow A\,\overrightarrow{\times }_{C}\,B$
a diagram. If the compositions of
$\unicode[STIX]{x1D6FF}$
with the projections to
$A$
and
$B$
admit colimits and these colimits are preserved by
$p$
and
$q$
respectively, then
$\unicode[STIX]{x1D6FF}$
admits a colimit, which is preserved by the projections to
$A$
and
$B$
. The same statement holds for diagrams in
$A\times _{C}B$
.
(ii) If
$A$
and
$B$
are idempotent complete, then
$A\,\overrightarrow{\times }_{C}\,B$
and
$A\times _{C}B$
are idempotent complete.
(iii) If
$A$
,
$B$
, and
$C$
are presentable and
$p$
and
$q$
commute with colimits, then both
$\infty$
-categories
$A\,\overrightarrow{\times }_{C}\,B$
and
$A\times _{C}B$
are presentable. Moreover, a functor from a presentable
$\infty$
-category
$D$
to
$A\times _{C}B$
or
$A\,\overrightarrow{\times }_{C}\,B$
preserves colimits if and only if the compositions with the projections to
$A$
and
$B$
do.
(iv) If
$A$
,
$B$
, and
$C$
are stable, and
$p$
and
$q$
are exact, then both
$\infty$
-categories
$A\,\overrightarrow{\times }_{C}\,B$
and
$A\times _{C}B$
are stable.
For the definition of a presentable
$\infty$
-category see [Reference LurieLur09, Definition 5.5.0.1], for that of an idempotent complete
$\infty$
-category [Reference LurieLur09, § 4.4.5], and for that of a stable
$\infty$
-category [Reference LurieLur17a, Definition 1.1.1.9].
Proof. (i) The assumptions and [Reference LurieLur09, Proposition 5.1.2.2] (applied to the projection
$C\times I\rightarrow I$
) imply that the composition of
$\unicode[STIX]{x1D6FF}$
with the projection to
$C^{I}$
also admits a colimit. Now the claim follows from [Reference LurieLur09, Lemmas 5.4.5.4, 5.4.5.2].
(ii) Let
$\operatorname{Idem}$
be the nerve of the 1-category with a single object
$X$
and
$\operatorname{Hom}(X,X)=\{\text{id}_{X},e\}$
, where
$e\circ e=e$
. An
$\infty$
-category
$D$
is idempotent complete if and only if any diagram
$\operatorname{Idem}\rightarrow D$
admits a colimit.Footnote
1
It follows from [Reference LurieLur09, Proposition 4.4.5.12, Lemma 4.3.2.13] that every functor between
$\infty$
-categories
$D\rightarrow D^{\prime }$
preserves colimits of diagrams indexed by
$\operatorname{Idem}$
. Hence the claim follows from part (i).
By construction of the lax pullback, it suffices to check the remaining assertions for pullbacks and functor categories.
(iii) For the functor category see [Reference LurieLur09, Proposition 5.5.3.6, Corollary 5.1.2.3] and for the pullback [Reference LurieLur09, Proposition 5.5.3.12].
(iv) See [Reference LurieLur17a, Proposition 1.1.3.1] for the functor category, [Reference LurieLur17a, Proposition 1.1.4.2] for the pullback. ◻
From now on, we will mainly be concerned with stable
$\infty$
-categories. Recall that by [Reference LurieLur17a, Theorem 1.1.2.14] the homotopy category
$\operatorname{Ho}(A)$
of a stable
$\infty$
-category
$A$
is a triangulated category.
Recollection 9. We recall the
$\infty$
-categorical version of Verdier quotients. For a detailed discussion see [Reference Blumberg, Gepner and TabuadaBGT13, § 5]. Let
$\Pr _{\text{st}}^{\text{L}}$
denote the
$\infty$
-category of presentable stable
$\infty$
-categories and left adjoint (equivalently, colimit preserving) functors, and let
$\text{Cat}_{\infty }^{\text{ex}}$
be the
$\infty$
-category of small stable
$\infty$
-categories and exact functors. Both admit small colimits. Given a fully faithful functor
$A\rightarrow B$
in either of these,
$B/A$
denotes its cofibre. By [Reference Blumberg, Gepner and TabuadaBGT13, Proposition 5.9, 5.14] the functor
$B\rightarrow B/A$
induces an equivalence of the Verdier quotient
$\operatorname{Ho}(B)/\operatorname{Ho}(A)$
with
$\operatorname{Ho}(B/A)$
.
A sequence
$A\rightarrow B\rightarrow C$
in
$\Pr _{\text{st}}^{\text{L}}$
or
$\text{Cat}_{\infty }^{\text{ex}}$
is called exact if the composite is zero,
$A\rightarrow B$
is fully faithful, and the induced map
$B/A\rightarrow C$
is an equivalence after idempotent completion. It follows from [Reference Blumberg, Gepner and TabuadaBGT13, Proposition 5.10] and the above that
$A\rightarrow B\rightarrow C$
is exact if and only
$\operatorname{Ho}(A)\rightarrow \operatorname{Ho}(B)\rightarrow \operatorname{Ho}(C)$
is exact (up to factors) in the sense of triangulated categories (see e.g. [Reference SchlichtingSch11, Definition 3.1.10]).
If
$C$
is a localization of
$B$
, i.e. the functor
$B\rightarrow C$
has a fully faithful right adjoint, and
$A\rightarrow B$
induces an equivalence of
$A$
with the kernel of
$B\rightarrow C$
, i.e. the full subcategory of objects of
$B$
that map to a zero object in
$C$
, then
$A\rightarrow B\rightarrow C$
is exact.
For the remainder of this section, we assume that (4) is a diagram of stable
$\infty$
-categories and exact functors.
The pair of functors
$B\rightarrow A\times B$
,
$b\mapsto (0,b)$
, and
$B\rightarrow C^{I}$
,
$b\mapsto (0\rightarrow q(b))$
, induces a functor
$r:B\rightarrow A\,\overrightarrow{\times }_{C}\,B$
. Similarly, the functors
$A\rightarrow A\times B$
,
$a\mapsto (a,0)$
, and
$A\rightarrow C^{I}$
,
$a\mapsto (p(a)\rightarrow 0)$
, induce a functor
$s:A\rightarrow A\,\overrightarrow{\times }_{C}\,B$
.
Proposition 10. Assume that (4) is a diagram of stable
$\infty$
-categories and exact functors. We have a split exact sequence
i.e. the sequence is exact,
$\text{pr}_{2}$
and
$s$
are right adjoints of
$r$
,
$\text{pr}_{1}$
, respectively, and
$\text{id}_{B}\simeq \text{pr}_{2}\circ r$
,
$\text{pr}_{1}\circ s\simeq \text{id}_{A}$
via unit and counit, respectively.
Proof. By construction, we have
$\text{id}_{B}=\text{pr}_{2}\circ r$
and we claim that this is a unit transformation for the desired adjunction (see [Reference LurieLur09, Proposition 5.2.2.8]). That is, we have to show that for any object
$b$
in
$B$
and
$(a^{\prime },b^{\prime },g^{\prime })$
in
$A\,\overrightarrow{\times }_{C}\,B$
the map
$\operatorname{Map}(r(b),(a^{\prime },b^{\prime },g^{\prime }))\rightarrow \operatorname{Map}(b,b^{\prime })$
induced by
$\text{pr}_{2}$
is an equivalence. This map is the second component of the left vertical map in the following diagram.
By Remark 6 this diagram is homotopy cartesian. Since the functor
$C\rightarrow C^{I}$
,
$c\mapsto (0\rightarrow c)$
, is a left adjoint of
$t:C^{I}\rightarrow C$
, the right vertical map is an equivalence. Hence the left vertical map is an equivalence (use that
$\operatorname{Map}(0,a^{\prime })$
and
$\operatorname{Map}(0,p(a^{\prime }))$
are contractible).
Similarly, one shows that
$s$
is a right adjoint of
$\text{pr}_{1}$
. Since the counit
$\text{pr}_{1}\circ s\rightarrow \text{id}_{A}$
is an equivalence,
$s$
is fully faithful. Since moreover
$r$
induces an equivalence of
$B$
with the kernel of
$\text{pr}_{1}$
, the sequence in the statement of the lemma is exact by Recollection 9.◻
We let
$\unicode[STIX]{x1D70B}$
be the composition of functors
$A\,\overrightarrow{\times }_{C}\,B\xrightarrow[{}]{\text{pr}_{3}}C^{I}\xrightarrow[{}]{\text{Cone}}C$
, where
$\text{Cone}:C^{I}\rightarrow C$
sends a morphism in
$C$
to its cofibre.
Proposition 11. Assume that (4) is a diagram of stable
$\infty$
-categories and exact functors. Assume furthermore that
$q:B\rightarrow C$
admits a fully faithful right adjoint
$v:C\rightarrow B$
. Then the composite
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:C\xrightarrow[{}]{v}B\xrightarrow[{}]{r}A\,\overrightarrow{\times }_{C}\,B\end{eqnarray}$$
is a fully faithful right adjoint of
$\unicode[STIX]{x1D70B}$
.
Proof. Since
$v$
is fully faithful by assumption, and
$r$
is fully faithful by Proposition 10, the functor
$\unicode[STIX]{x1D70C}$
is fully faithful. The functor
$\text{Cone}:C^{I}\rightarrow C$
has the right adjoint
$\unicode[STIX]{x1D6FD}$
mapping
$c$
to
$(0\rightarrow c)$
[Reference LurieLur17a, Remark 1.1.1.8]. By the construction of
$r$
we have a canonical equivalence
$\text{pr}_{3}\circ r\simeq \unicode[STIX]{x1D6FD}\circ q$
. Hence the counit of the adjoint pair
$(\text{Cone},\unicode[STIX]{x1D6FD})$
induces a natural transformation
$\unicode[STIX]{x1D70B}\circ r=\text{Cone}\circ \text{pr}_{3}\circ r\simeq \text{Cone}\circ \unicode[STIX]{x1D6FD}\circ q\rightarrow q$
and hence
$\unicode[STIX]{x1D70B}\circ r\circ v\rightarrow q\circ v$
. Composing with the counit of the adjoint pair
$(q,v)$
we get a natural transformation
$\unicode[STIX]{x1D702}:\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70B}\circ r\circ v\rightarrow \text{id}_{C}$
. We claim that
$\unicode[STIX]{x1D702}$
is a counit transformation for the desired adjunction. This will imply the claim by [Reference LurieLur09, Proposition 5.2.2.8]. We thus have to show that the composition
$$\begin{eqnarray}\operatorname{Map}((a,b,g),\unicode[STIX]{x1D70C}(c))\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Map}(\unicode[STIX]{x1D70B}((a,b,g)),\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D70C}(c)))\xrightarrow[{}]{\unicode[STIX]{x1D702}}\operatorname{Map}(\unicode[STIX]{x1D70B}((a,b,g)),c)\end{eqnarray}$$
is an equivalence for every object
$(a,b,g)$
in
$A\,\overrightarrow{\times }_{C}\,B$
and any object
$c$
in
$C$
.
From Remark 6 we have the following homotopy pullback square of spaces.
Since
$v$
is fully faithful,
$q(v(c))\simeq c$
and the lower horizontal map is an equivalence by adjunction. Hence the upper horizontal map
$\text{pr}_{3}$
is an equivalence, too. The
$(\text{Cone},\unicode[STIX]{x1D6FD})$
-adjunction yields an equivalence
$$\begin{eqnarray}\operatorname{Map}(g,(0\rightarrow q(v(c))))\xrightarrow[{}]{\simeq }\operatorname{Map}(\text{Cone}(g),q(v(c))).\end{eqnarray}$$
By construction, (6) is the composition of the equivalences
$\text{pr}_{3}$
in (7) and (8) and the map induced by the counit
$q(v(c))\rightarrow c$
, which is an equivalence by fully faithfulness of
$v$
. Hence (6) is an equivalence, as desired.◻
Corollary 12. Assume that (4) is a diagram in
$\Pr _{\text{st}}^{\text{L}}$
. If the right adjoint of
$B\rightarrow C$
is fully faithful, then the sequence
$$\begin{eqnarray}A\times _{C}B\rightarrow A\,\overrightarrow{\times }_{C}\,B\xrightarrow[{}]{\unicode[STIX]{x1D70B}}C\end{eqnarray}$$
is exact.
Proof. An object
$(a,b,g)$
of
$A\,\overrightarrow{\times }_{C}\,B$
belongs to
$A\times _{C}B$
if and only if
$g$
is an equivalence, if and only if
$\text{Cone}(g)\simeq 0$
. This shows that the composite is trivial and that
$A\times _{C}B$
is precisely the kernel of
$\unicode[STIX]{x1D70B}$
. The claim now follows, since
$\unicode[STIX]{x1D70B}$
admits a fully faithful right adjoint by Proposition 11.◻
Let
$A^{\prime }$
be a small stable
$\infty$
-category. Then the
$\infty$
-category
$\operatorname{Ind}(A^{\prime })$
of Ind-objects of
$A^{\prime }$
[Reference LurieLur09, Definition 5.3.5.1] is presentable [Reference LurieLur09, Theorem 5.5.1.1] and stable [Reference LurieLur17a, Proposition 1.1.3.6]. A stable
$\infty$
-category
$A$
is called compactly generated if there exists a small stable
$\infty$
-category
$A^{\prime }$
and an equivalence
$\operatorname{Ind}(A^{\prime })\simeq A$
(see [Reference LurieLur09, Definition 5.5.7.1] and the text following it). If this is the case, then
$A^{\prime }\rightarrow A$
induces an equivalence of the idempotent completion of
$A^{\prime }$
[Reference LurieLur09, § 5.1.4] with the full stable subcategory
$A^{\unicode[STIX]{x1D714}}$
of the compact objects in
$A$
[Reference LurieLur09, Lemma 5.4.2.4]. In particular, if
$A$
is compactly generated,
$A^{\unicode[STIX]{x1D714}}$
is (essentially) small and
$\operatorname{Ind}(A^{\unicode[STIX]{x1D714}})\simeq A$
. Whether a stable
$\infty$
-category is idempotent complete or compactly generated only depends on its homotopy category [Reference LurieLur17a, Lemma 1.2.4.6, Remark 1.4.4.3].
Proposition 13. Assume that (4) is a diagram in
$\Pr _{\text{st}}^{\text{L}}$
in which
$A$
and
$B$
are compactly generated and the functors
$p:A\rightarrow C$
and
$q:B\rightarrow C$
map compact objects to compact objects. Then
$A\,\overrightarrow{\times }_{C}\,B$
is compactly generated as well and
$(A\,\overrightarrow{\times }_{C}\,B)^{\unicode[STIX]{x1D714}}\simeq A^{\unicode[STIX]{x1D714}}\overrightarrow{\times }_{C^{\unicode[STIX]{x1D714}}}B^{\unicode[STIX]{x1D714}}$
.
Proof. By Lemma 8(iii) the
$\infty$
-category
$A\,\overrightarrow{\times }_{C}\,B$
is presentable and hence admits all small colimits. Let
$D^{\prime }:=A^{\unicode[STIX]{x1D714}}\overrightarrow{\times }_{C^{\unicode[STIX]{x1D714}}}B^{\unicode[STIX]{x1D714}}$
. This is an (essentially) small full stable subcategory of
$A\,\overrightarrow{\times }_{C}\,B$
. It follows from [Reference LurieLur09, Lemmas 5.4.5.7, 5.3.4.9] that
$D^{\prime }$
consists of compact objects in
$A\,\overrightarrow{\times }_{C}\,B$
. Hence the induced functor
$\operatorname{Ind}(D^{\prime })\rightarrow A\,\overrightarrow{\times }_{C}\,B$
is fully faithful. Since the functors
$r:B\rightarrow A\,\overrightarrow{\times }_{C}\,B$
and
$s:A\rightarrow A\,\overrightarrow{\times }_{C}\,B$
preserve colimits by Lemma 8(iii) and since
$A$
and
$B$
are compactly generated, it follows that the essential image of
$\operatorname{Ind}(D^{\prime })$
in
$A\,\overrightarrow{\times }_{C}\,B$
contains
$A$
and
$B$
. Proposition 10 implies that every object
$X$
of
$A\,\overrightarrow{\times }_{C}\,B$
sits in a fibre sequence
$X^{\prime }\rightarrow X\rightarrow X^{\prime \prime }$
with
$X^{\prime }\in B$
and
$X^{\prime \prime }\in A$
. Hence the essential image of
$\operatorname{Ind}(D^{\prime })$
must be all of
$A\,\overrightarrow{\times }_{C}\,B$
, and hence the latter is compactly generated. Since
$A^{\unicode[STIX]{x1D714}}$
and
$B^{\unicode[STIX]{x1D714}}$
are idempotent complete, so is
$D^{\prime }$
by Lemma 8(ii). Hence
$D^{\prime }\simeq (A\,\overrightarrow{\times }_{C}\,B)^{\unicode[STIX]{x1D714}}$
.◻
Definition 14. An excisive square of small stable
$\infty$
-categories is a commutative square
in
$\text{Cat}_{\infty }^{\text{ex}}$
such that the induced square
in
$\Pr _{\text{st}}^{\text{L}}$
is a pullback square and
$\operatorname{Ind}(B)\rightarrow \operatorname{Ind}(C)$
is a localization, i.e. its right adjoint is fully faithful.
The following is the categorical version of our first main result.
Theorem 15. Assume that (9) is an excisive square of small stable
$\infty$
-categories. Then there is an exact sequence
$$\begin{eqnarray}D\xrightarrow[{}]{i}A\,\overrightarrow{\times }_{C}\,B\xrightarrow[{}]{\unicode[STIX]{x1D70B}}C.\end{eqnarray}$$
Proof. If we apply Corollary 12 to the pullback diagram (10), we get the exact sequence
$$\begin{eqnarray}\operatorname{Ind}(D)\rightarrow \operatorname{Ind}(A)\overrightarrow{\times }_{\operatorname{Ind}(C)}\operatorname{Ind}(B)\rightarrow \operatorname{Ind}(C)\end{eqnarray}$$
in
$\Pr _{\text{st}}^{\text{L}}$
. Clearly, the first and the third term in this sequence are compactly generated. Proposition 13 implies that also the middle term is compactly generated, and that the functors preserve compact objects. Recall from Recollection 9 that we can test exactness on the level of homotopy categories. Thus we may apply the Thomason–Neeman localization theorem [Reference NeemanNee92, Theorem 2.1] to conclude that the induced sequence of compact objects is exact. But up to idempotent completion this is exactly (11). ◻
We now apply this to localizing invariants.
Definition 16. A weakly localizing invariant is a functor
$$\begin{eqnarray}E:\text{Cat}_{\infty }^{\text{ex}}\rightarrow T\end{eqnarray}$$
from
$\text{Cat}_{\infty }^{\text{ex}}$
to some stable
$\infty$
-category
$T$
which sends exact sequences in
$\text{Cat}_{\infty }^{\text{ex}}$
to fibre sequences in
$T$
.
Example 17. Any localizing invariant in the sense of [Reference Blumberg, Gepner and TabuadaBGT13] is weakly localizing. Concrete examples are non-connective algebraic
$K$
-theory à la Bass and Thomason [Reference Blumberg, Gepner and TabuadaBGT13, § 9.1], topological Hochschild homology
$THH$
[Reference Blumberg, Gepner and TabuadaBGT13, § 10.1], or
$p$
-typical topological cyclic homology
$TC$
for some prime
$p$
[Reference Blumberg, Gepner and TabuadaBGT13, § 10.3], [Reference Blumberg and MandellBM12]. In all these examples
$T$
is the
$\infty$
-category of spectra.
Theorem 18. Assume that (9) is an excisive square of small stable
$\infty$
-categories, and let
$E:\text{Cat}_{\infty }^{\text{ex}}\rightarrow T$
be a weakly localizing invariant. Then the induced square in
$T$
is cartesian.
Proof. Applying
$E$
to the exact sequence (11) provided by Theorem 15 yields the fibre sequence
$$\begin{eqnarray}E(D)\xrightarrow[{}]{E(i)}E(A\,\overrightarrow{\times }_{C}\,B)\xrightarrow[{}]{E(\unicode[STIX]{x1D70B})}E(C)\end{eqnarray}$$
in
$T$
. On the other hand, applying
$E$
to the split exact sequence of Proposition 10 gives an equivalence
$$\begin{eqnarray}E(s)\oplus E(r):E(A)\oplus E(B)\xrightarrow[{}]{\simeq }E(A\,\overrightarrow{\times }_{C}\,B)\end{eqnarray}$$
with inverse induced by the projections
$\text{pr}_{1}$
,
$\text{pr}_{2}$
. Combining (13) and (14), we get a fibre sequence
$$\begin{eqnarray}E(D)\rightarrow E(A)\oplus E(B)\rightarrow E(C),\end{eqnarray}$$
where the first map is induced by the given functors
$D\rightarrow A$
and
$D\rightarrow B$
. The map
$E(A)\rightarrow E(C)$
is induced by the functor
$a\mapsto \text{Cone}(p(a)\rightarrow 0)\simeq \unicode[STIX]{x1D6F4}p(a)$
. Since the endofunctor
$\unicode[STIX]{x1D6F4}:C\rightarrow C$
induces
$-\text{id}$
on
$E(C)$
, the map
$E(A)\rightarrow E(C)$
in (15) is the negative of the map induced by the functor
$p:A\rightarrow C$
. Finally, the map
$E(B)\rightarrow E(C)$
in (15) is induced by the functor
$b\mapsto \text{Cone}(0\rightarrow q(b))\simeq q(b)$
. Thus (15) being a fibre sequence in
$T$
implies that (12) is cartesian.◻
Remark 19. This theorem can also be used to prove the Mayer–Vietoris property of algebraic
$K$
-theory for the Zariski topology [Reference Thomason and TrobaughTT90, Theorem 8.1] for quasi-compact quasi-separated schemes without using Thomason’s localization theorem [Reference Thomason and TrobaughTT90, Theorem 7.4]. Together with Example 3 one may then deduce Nisnevich descent for noetherian schemes in general.
2 Application to ring spectra
In this section, we apply the constructions of § 1 to the
$\infty$
-categories of (perfect) modules over an
$E_{1}$
-ring spectrum, discuss Tor-unitality, and we prove our second main result (Theorem 28) saying that a pullback square of ring spectra where one map is Tor-unital (Definition 21) yields an excisive square upon applying
$\operatorname{Perf}(-)$
. From this we finally deduce Theorems 1 and 2 of the Introduction.
The
$\infty$
-categories of
$E_{1}$
-ring spectra and their modules are discussed in [Reference LurieLur17a, ch. 7]. For an
$E_{1}$
-ring spectrum
$A$
, we write
$\operatorname{LMod}(A)$
for the stable
$\infty$
-category of left
$A$
-module spectra, which we will simply call left
$A$
-modules henceforth. A left
$A$
-module is called perfect if it belongs to the smallest stable subcategory
$\operatorname{Perf}(A)$
of
$\operatorname{LMod}(A)$
which contains
$A$
and is closed under retracts. By [Reference LurieLur17a, Proposition 7.2.4.2],
$\operatorname{LMod}(A)$
is compactly generated and the compact objects are precisely the perfect
$A$
-modules.
Example 20. Any discrete ring
$A$
can be considered as an
$E_{1}$
-ring spectrum. Then
$\operatorname{Ho}(\operatorname{LMod}(A))$
is equivalent to the unbounded derived category of
$A$
in the classical sense [Reference LurieLur17a, Remark 7.1.1.16].
Definition 21. A map
$f:A\rightarrow A^{\prime }$
of
$E_{1}$
-ring spectra is called Tor-unital if the following equivalent conditions are satisfied.
(i) The map
$A^{\prime }\otimes _{A}A^{\prime }\rightarrow A^{\prime }$
given by multiplication is an equivalence.(ii) The map
$A^{\prime }\rightarrow A^{\prime }\otimes _{A}A^{\prime }$
induced from
$A\rightarrow A^{\prime }$
by
$A^{\prime }\otimes _{A}(-)$
is an equivalence.(iii) If
$I$
is the fibre of
$A\rightarrow A^{\prime }$
in
$\operatorname{LMod}(A)$
, we have
$A^{\prime }\otimes _{A}I\simeq 0$
.
We have the following easy but important further characterization of Tor-unitality.
Lemma 22. A morphism
$A\rightarrow A^{\prime }$
of
$E_{1}$
-ring spectra is Tor-unital if and only if the forgetful functor
$\operatorname{LMod}(A^{\prime })\rightarrow \operatorname{LMod}(A)$
is fully faithful.
Proof. By [Reference LurieLur17a, Proposition 4.6.2.17] the forgetful functor
$v$
is right adjoint to
$A^{\prime }\,\otimes _{A}\,-:\operatorname{LMod}(A)\rightarrow \operatorname{LMod}(A^{\prime })$
. It is fully faithful if and only if the counit
$A^{\prime }\otimes _{A}M\rightarrow M$
is an equivalence for every
$A^{\prime }$
-module
$M$
. Taking
$M=A^{\prime }$
, we see that fully faithfulness of
$v$
implies Tor-unitality of
$A\rightarrow A^{\prime }$
. The converse follows, since
$\operatorname{LMod}(A^{\prime })$
is generated by
$A^{\prime }$
under small colimits and finite limits, and the tensor product preserves both.◻
Now consider a pullback square of
$E_{1}$
-ring spectra as follows.
Lemma 23. Assume that (16) is a pullback square of
$E_{1}$
-ring spectra in which
$A\rightarrow A^{\prime }$
is Tor-unital. Then also
$B\rightarrow B^{\prime }$
is Tor-unital. Moreover, the canonical map
$A^{\prime }\otimes _{A}B\rightarrow A^{\prime }\otimes _{A}B^{\prime }$
induced from
$B\rightarrow B^{\prime }$
is an equivalence.
See Remark 27 for a partial converse.
Proof. Write
$I$
for the fibre of
$A\rightarrow A^{\prime }$
. Since
$A\rightarrow A^{\prime }$
is Tor-unital,
$A^{\prime }\otimes _{A}I\simeq 0$
. As by assumption (16) is a pullback square, the fibre of
$B\rightarrow B^{\prime }$
is equivalent (as left
$A$
-module) to
$I$
, hence
$A^{\prime }\otimes _{A}B\rightarrow A^{\prime }\otimes _{A}B^{\prime }$
is an equivalence, too. By Lemma 22 the counit
$A^{\prime }\otimes _{A}M\rightarrow M$
is an equivalence for every
$A^{\prime }$
-module
$M$
. In particular,
$A^{\prime }\otimes _{A}B^{\prime }\rightarrow B^{\prime }$
is an equivalence. Summing up, the canonical map
$A^{\prime }\otimes _{A}B\rightarrow B^{\prime }$
is an equivalence. Thus
$$\begin{eqnarray}B^{\prime }\otimes _{B}B^{\prime }\simeq (A^{\prime }\otimes _{A}B)\otimes _{B}B^{\prime }\simeq A^{\prime }\otimes _{A}B^{\prime }\simeq B^{\prime }\end{eqnarray}$$
and
$B\rightarrow B^{\prime }$
is Tor-unital.◻
Example 24. Let
$A\rightarrow B$
be a morphism of discrete unital rings sending a two-sided ideal
$I$
of
$A$
isomorphically onto an ideal of
$B$
. Then the Milnor square
is a pullback diagram in rings. Since
$B\rightarrow B/I$
is surjective, this diagram is also a pullback when considered as a diagram of
$E_{1}$
-ring spectra. The map
$A\rightarrow A/I$
is Tor-unital if and only if
$\operatorname{Tor}_{i}^{A}(A/I,A/I)=0$
for all
$i>0$
.
In particular, if the discrete, not necessarily unital ring
$I$
is Tor-unital in the classical sense that
$\operatorname{Tor}_{i}^{\mathbf{Z}\ltimes I}(\mathbf{Z},\mathbf{Z})=0$
for all
$i>0$
, then Lemma 23 applied to the Milnor square
implies that
$A\rightarrow A/I$
is Tor-unital for any ring
$A$
containing
$I$
as a two-sided ideal.
Example 25. Assume that
$A$
is a commutative, unital discrete ring, and let
$f\in A$
. Then
$A\rightarrow A[f^{-1}]$
is Tor-unital. Assume further that
$A\rightarrow B$
is an étale ring map which induces an isomorphism
$A/(f)\xrightarrow[{}]{{\sim}}B/(f)$
. Then the diagram
viewed as a diagram of
$E_{1}$
-ring spectra, is a pullback square. Indeed, this is equivalent to the exactness of the sequence
$$\begin{eqnarray}0\rightarrow A\rightarrow A[f^{-1}]\oplus B\rightarrow B[f^{-1}]\rightarrow 0,\end{eqnarray}$$
which may be checked directly. Alternatively, one may use the Mayer–Vietoris exact sequence of étale cohomology groups
$$\begin{eqnarray}0\rightarrow A\rightarrow A[f^{-1}]\oplus B\rightarrow B[f^{-1}]\rightarrow H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{Spec}(A),{\mathcal{O}}_{\operatorname{ Spec}(A)}),\end{eqnarray}$$
which may be deduced from [Reference MilneMil80, Proposition III.1.27], together with the vanishing of the higher étale cohomology of quasi-coherent sheaves on affine schemes.
The following is a derived version of Milnor patching.
Theorem 26. Assume that (16) is a pullback square of
$E_{1}$
-ring spectra where the morphism
$A\rightarrow A^{\prime }$
is Tor-unital. Then extension of scalars induces an equivalence
$$\begin{eqnarray}\operatorname{LMod}(A)\simeq \operatorname{LMod}(A^{\prime })\times _{\operatorname{ LMod}(B^{\prime })}\operatorname{LMod}(B).\end{eqnarray}$$
Proof. Let
$F$
be the functor
$\operatorname{LMod}(A)\rightarrow \operatorname{LMod}(A^{\prime })\times _{\operatorname{LMod}(B^{\prime })}\operatorname{LMod}(B)$
induced by extension of scalars. Since both
$\infty$
-categories are presentable and
$F$
preserves colimits by Lemma 8(iii),
$F$
admits a right adjoint
$G$
. Explicitly, if
$(M,N,g)$
is an object of
$\operatorname{LMod}(A^{\prime })\times _{\operatorname{LMod}(B^{\prime })}\operatorname{LMod}(B)$
, then
$G(M,N,g)$
is the pullback in left
$A$
-modules
$$\begin{eqnarray}G(M,N,g)\simeq M\times _{B^{\prime }\otimes _{B}N}N,\end{eqnarray}$$
where the map
$M\rightarrow B^{\prime }\otimes _{B}N$
is the composition
$M\rightarrow B^{\prime }\otimes _{A^{\prime }}M\xrightarrow[{}]{g}B^{\prime }\otimes _{B}N$
. We claim that the unit
$$\begin{eqnarray}P\rightarrow (A^{\prime }\otimes _{A}P)\times _{B^{\prime }\otimes _{B}(B\otimes _{A}P)}(B\otimes _{A}P)\end{eqnarray}$$
of the adjunction is an equivalence for any
$A$
-module
$P$
. Since also
$G$
commutes with colimits, it suffices to check this for
$P=A$
. In that case the claim follows from the assumption that (16) is a pullback square. Hence
$F$
is fully faithful.
It now suffices to show that the right adjoint
$G$
of
$F$
is conservative. For this it is enough to show that
$G$
detects zero objects. So let
$(M,N,g)$
be an object of the pullback and assume that
$G(M,N,g)\simeq 0$
. There is a fibre sequence of left
$A$
-modules
$$\begin{eqnarray}G(M,N,g)\rightarrow M\oplus N\rightarrow B^{\prime }\otimes _{B}N\end{eqnarray}$$
and hence the map
$$\begin{eqnarray}M\oplus N\xrightarrow[{}]{\simeq }B^{\prime }\otimes _{B}N\end{eqnarray}$$
is an equivalence. Extending scalars from
$A$
to
$A^{\prime }$
we get an equivalence
$$\begin{eqnarray}A^{\prime }\otimes _{A}M\oplus A^{\prime }\otimes _{A}N\xrightarrow[{}]{\simeq }A^{\prime }\otimes _{A}B^{\prime }\otimes _{B}N.\end{eqnarray}$$
From Lemma 23 we know that
$A^{\prime }\otimes _{A}B\rightarrow A^{\prime }\otimes _{A}B^{\prime }$
is an equivalence. Since
$\operatorname{LMod}(B)$
is generated by
$B$
under colimits and finite limits, we conclude that
$A^{\prime }\otimes _{A}P\rightarrow A^{\prime }\otimes _{A}B^{\prime }\otimes _{B}P$
is an equivalence for every left
$B$
-module
$P$
. Applying this with
$P=N$
, we see that the restriction of (18) to the second summand is an equivalence. Hence
$A^{\prime }\otimes _{A}M\simeq 0$
. Since
$M$
is an
$A^{\prime }$
-module, Lemma 22 implies that the counit is an equivalence
$A^{\prime }\otimes _{A}M\simeq M$
, i.e.
$M\simeq 0$
. But then also
$B^{\prime }\otimes _{B}N\simeq B^{\prime }\otimes _{A^{\prime }}M\simeq 0$
, and hence
$N\simeq 0$
by (17).◻
Remark 27. Without the Tor-unitality assumption Theorem 26 does not hold, see [Reference LurieLur17b, Warning 16.2.0.3] for a counter example.
However, if one assumes instead that (16) is a pullback square of connective ring spectra with
$\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{0}(B^{\prime })$
surjective, then [Reference LurieLur17b, Proposition 16.2.2.1] implies that restricting the functors
$F$
and
$G$
from the proof of Theorem 26 to the subcategories of connective modules gives inverse equivalences
$$\begin{eqnarray}\operatorname{LMod}(A)_{{\geqslant}0}\leftrightarrows \operatorname{LMod}(A^{\prime })_{{\geqslant}0}\times _{\operatorname{LMod}(B^{\prime })_{{\geqslant}0}}\operatorname{LMod}(B)_{{\geqslant}0}.\end{eqnarray}$$
One can use this to show that in this situation, Tor-unitality of
$B\rightarrow B^{\prime }$
implies Tor-unitality of
$A\rightarrow A^{\prime }$
as follows. Let
$I$
be the fibre of
$B\rightarrow B^{\prime }$
. Since
$\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{0}(B^{\prime })$
is surjective,
$I$
is connective. Since
$B\rightarrow B^{\prime }$
is Tor-unital,
$B^{\prime }\otimes _{B}I\simeq 0$
. Hence we may view
$(0,I,0)$
as an object of the pullback
$\operatorname{LMod}(A^{\prime })_{{\geqslant}0}\times _{\operatorname{LMod}(B^{\prime })_{{\geqslant}0}}\operatorname{LMod}(B)_{{\geqslant}0}$
. The functor
$G$
sends
$(0,I,0)$
to the
$A$
-module
$0\times _{0}I\simeq I$
. By the above the counit
$F(I)\simeq F(G(0,I,0))\rightarrow (0,I,0)$
is an equivalence. Looking at the first component we deduce that
$A^{\prime }\otimes _{A}I\rightarrow 0$
is an equivalence, i.e.
$A\rightarrow A^{\prime }$
is Tor-unital.
Theorem 28. Assume that (16) is a pullback square of
$E_{1}$
-ring spectra where the morphism
$A\rightarrow A^{\prime }$
is Tor-unital. Then the square
is excisive. In particular, if
$E:\text{Cat}_{\infty }^{\text{ex}}\rightarrow T$
is a weakly localizing invariant, then the induced square
in
$T$
is cartesian.
Proof. Applying
$\operatorname{Ind}$
to diagram (19) yields the following diagram.
This is a pullback diagram by Theorem 26. As
$A\rightarrow A^{\prime }$
is Tor-unital, so is
$B\rightarrow B^{\prime }$
by Lemma 23. Hence the right adjoint of
$\operatorname{LMod}(B)\rightarrow \operatorname{LMod}(B^{\prime })$
, which is the forgetful functor, is fully faithful by Lemma 22. So the square (19) is excisive. Now the second assertion follows by applying Theorem 18.◻
Proof of Theorems 1 and 2.
If we apply Theorem 28 with
$E=K$
, we immediately get Theorem 2.
Now let
$I$
be a ring which is Tor-unital in the classical sense, and let
$A$
be any unital ring containing
$I$
as a two-sided ideal. Then the Milnor square
(viewed as square of
$E_{1}$
-ring spectra) is a pullback square (see Example 24). By assumption, the top horizontal map is Tor-unital in our sense. Hence we may apply Theorem 2 to deduce that the map on relative
$K$
-groups
$K_{\ast }(I)=K_{\ast }(\mathbf{Z}\ltimes I,I)\rightarrow K_{\ast }(A,I)$
is an isomorphism.◻
Acknowledgements
I would like to express my sincere gratitude to the referee for the efforts taken to improve both the exposition and the results of this paper. The referee gave a hint which led to a simplification of the proof of the main result of the first version of this paper, and also suggested to formulate the general categorical Theorem 18 in terms of excisive squares and to deduce the excision result via Theorem 28. I would also like to thank Justin Noel and Daniel Schäppi for discussions about (lax) pullbacks of
$\infty$
-categories.
