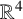1 Introduction
The purpose of this note is to prove a Reidemeister theorem for solid ribbon torus links, which are close cousins of welded links.
Welded links are tori embedded in
$\mathbb {R}^4$
which are fillable to solid tori with only ribbon singularities (see details below). In the 1960s, Yajima and Yanagawa [Reference Yajima13–Reference Yanagawa16] studied ribbon 2-knots (which are spheres, rather than tori, embedded in
$\mathbb {R}^4$
). Welded knot theory in its current form emerged from the work of Fenn et al. [Reference Fenn, Rimányi and Rourke9] on welded braids. In this context, a Reidemeister theorem, or Artin presentation, exists [Reference Brendle and Hatcher8, Reference Goldsmith10, Reference Satoh11]. The braid approach can be applied to prove a Reidemeister theorem for welded homotopy string links, where self-crossings of the same component are transparent (virtualisable) [Reference Audoux, Bellingeri, Meilhan and Wagner4, Reference Audoux, Bellingeri, Meilhan and Wagner5]. However, a full Reidemeister description of welded links remains elusive.
A welded torus link is a ribbon embedding of finitely many disjoint tori in
$\mathbb {R}^4$
, as in Figure 1. A ribbon embedding is one which admits a filling to immersed solid tori, where singularities are ribbon singularities. A ribbon singularity is a transverse singular disc with two preimages:
-
• one preimage is a contractible disc in the interior of a solid torus; and
-
• the other preimage’s circle boundary is essential in the boundary of a solid torus.
Welded torus links are considered up to ambient isotopy via generalised ribbon embeddings (Definition 2.3).
Figure 1 On the left, the welded trefoil knot. On the right, the building block corresponding to a positive crossing. Both are shown as broken surface diagrams: the broken parts of the surface are lower in the 4th coordinate.
A welded link diagram (Definition 2.6) is a finite set of immersed circles in
$\mathbb {R}^2$
, with two types of transverse double points called crossings. Crossings can be classical (endowed with over/under information) or virtual (without over/under information). Welded link diagrams are considered up to a set of welded Reidemeister moves (see Figure 3).
To each welded link diagram, the tube map [Reference Bar-Natan and Dancso7, Reference Satoh11, Reference Yajima13] associates a welded link, mapping equivalent diagrams to isotopic links. Informally, to each classical crossing, the tube map associates a ‘building block’ consisting of a tube braided through another as in the right of Figure 1; or equivalently, obtained by spinning a classical crossing around a regular projection plane embedded in
$\mathbb {R}^4$
. The building blocks are then connected by gluing in annuli according to the diagram. Virtual crossings are ignored: they are only important in their capacity to allow nonplanar connections between the ends of crossings.
It is easy to see that the welded Reidemeister moves are in the kernel of the tube map. It is known that the kernel is at least slightly larger than this, by a global symmetry [Reference Satoh11, Reference Winter12]. It remains an open question to fully determine the kernel; the key ingredient missing is a combinatorial understanding of filling changes.
In this note, we circumvent the filling change issue by including the filling information in the data of a link: that is, by studying solid ribbon torus links. Using Satoh’s [Reference Satoh11] generalisation of Yajima’s tube map, Audoux ([Reference Audoux3, Proposition 3.7], see also [Reference Audoux2]) gave a sketch of a proof for a Reidemeister theorem for solid ribbon string links up to strict ambient isotopy (no Reidemeister moves). Our goal is to prove the following welded Reidemeister theorem (stated without proof in [Reference Audoux and Meilhan6]) which gives a full combinatorial description for solid ribbon torus links up to generalised ribbon isotopies, showing that these always correspond to welded Reidemeister moves.
Theorem 1.1. Welded link diagrams modulo welded moves are in bijection with solid ribbon torus links up to generalised ribbon isotopy.
The proof expands on Audoux’s idea [Reference Audoux3, Proposition 3.7] to define and study the inverse map to Satoh’s tube map, called the connection map.
2 Solid ribbon torus links and welded link diagrams
In this section, we describe solid ribbon torus links and welded link diagrams.
2.1 Solid ribbon torus links
Throughout, we denote by
$\mathbb {T}$
an oriented solid torus
$B^2 \times S^1$
.
Definition 2.1. For an immersion
$\bigcup _{i\in \{1,\ldots ,n\}}\mathbb {T}_{i}\rightarrow \mathbb {R}^{4}$
, a ribbon singularity is a flatly transverse disc in the image. The preimage is a disjoint union of two discs: of these, one disc is in the interior of one of the tori
$\mathbb {T}_{i}$
; the other has its interior in the interior of one of the tori
$\mathbb {T}_{j}$
and its boundary is essentially embedded in
$\partial \mathbb {T}_{j}$
. (Possibly
$i=j$
.) If an immersion has only ribbon singularities, it is called a ribbon immersion.
Definition 2.2. For
$n\geq 1$
, an oriented solid ribbon torus link with n components is a ribbon immersion of n oriented solid tori
$\sqcup _{i\in \{1,\ldots ,n\}}\mathbb {T}_i$
in
$\mathbb {R}^4$
. Each solid torus
${\mathbb {T}=B^2\times S^1}$
is equipped with a directed core
$\{0\}\times S^1 \subseteq \mathbb {T}$
(an oriented circle).
Next, we define equivalence of solid ribbon torus links. Ambient isotopy is a very fine notion of equivalence, which diagrammatically corresponds to welded diagrams but no Reidemeister moves [Reference Audoux3, Proposition 3.7]. In other words, Reidemeister moves relate solid ribbon torus links which belong to distinct ambient isotopy classes. To achieve a notion of equivalence more in line with intuition (diagrammatically corresponding to welded diagrams up to welded moves), one needs to introduce generalised ribbon isotopies, which are allowed to move through finitely many moments of immersions with generalised ribbon singularities [Reference Audoux and Meilhan6, Section 3].
Definition 2.3. Given an immersion
$\bigcup _{i\in \{1,\ldots ,n\}}\mathbb {T}_{i}\rightarrow \mathbb {R}^{4}$
, we say that a connected component D of the singular set, contained in an open four-ball
$B\subseteq \mathbb {R}^4$
, is a generalised ribbon singularity (see Figure 2) if it belongs to one of the following types, given in terms of a local system of coordinates
$\varphi $
for
$B\cong \mathbb {R}^4$
.
-
(0) Type 0 (strict ribbon singularity, as in Definition 2.1), where there is a local system of coordinates
$\varphi $
for
$B\cong \mathbb {R}^4$
such that
$\varphi ^{-1}(B)$
is a disjoint union
$B_{1}\sqcup B_{2}$
of two 3-balls and
$$ \begin{align*}\quad\begin{cases} \varphi(B_1)=\{(t,r\cos(s),r\sin(s),0)\} & t,s\in \mathbb{R}, r\in[0,2], \\ \varphi(B_2)=\{(0,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in [0,1]. \end{cases}\end{align*} $$
-
(2) Type 2 (tangential, see bottom left of Figure 2), where there is a local system of coordinates
$\varphi $
for
$B\cong \mathbb {R}^4$
such that
$\varphi ^{-1}(B)$
is the disjoint union
$B_{1}\sqcup B_{2}$
of two 3-balls and
$$ \begin{align*}\quad\begin{cases} \varphi(B_1)=\{(0,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in[0,2], \\ \varphi(B_2)=\{(-t^2,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in [0,1]. \end{cases}\end{align*} $$
-
(3) Type 3 (nested, see bottom right of Figure 2), where there is a local system of coordinates
$\varphi $
for
$B\cong \mathbb {R}^4$
such that
$\varphi ^{-1}(B)$
is the disjoint union
$B_{1}\sqcup B_{2}\sqcup B_{3}$
of three 3-balls and
$$ \begin{align*}\quad\begin{cases} \varphi(B_1)=\{(0,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in [0,3], \\ \varphi(B_2)=\{(t,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in [0,2], \\ \varphi(B_3)=\{(2t,r\cos(s),r\sin(s),t)\} & t,s\in \mathbb{R}, r\in [0,1]. \end{cases}\end{align*} $$
Figure 2 Type 2 and Type 3 generalised ribbon singularities in the preimage.
Remark 2.4. We will see later that the Type 2 and 3 singularities correspond to Reidemeister 2 and 3 moves. There is no ‘Type 1’ singularity, since a Reidemeister 1 move merely creates a cusp, not a new type of singularity.
Definition 2.5. A generalised ribbon isotopy of solid ribbon torus links is a regular homotopy via ribbon immersions which may pass through finitely many moments of generalised ribbon immersions.
2.2 Welded diagrams and the tube map
This note proves that solid ribbon torus links modulo generalised ribbon isotopy are represented by welded diagrams modulo welded Reidemeister moves. We now define welded diagrams, and the enhanced tube map which relates them to solid ribbon torus links.
Definition 2.6. An oriented welded link diagram (or welded diagram for short) is an immersion of a disjoint union of oriented circles in
$\mathbb {R}^{2}$
, with only transverse double points, each of which belongs to one of two types: classical crossings – which may be positive 
or negative 
– and virtual crossings 
. Welded diagrams are considered modulo planar isotopy as four-valent graphs, by the welded Reidemeister moves shown in Figure 3, and the convention that a purely virtual path (a path which goes through only virtual crossings) can be equivalently re-routed in any other purely virtual way (see Figure 4).
Figure 3 The Reidemeister moves for welded diagrams. Orientations are suppressed: the relations are imposed in all consistent orientations of the strands.
Figure 4 An example of the re-routing move for a purely virtual strand.
Remark 2.7. The re-routing convention can be replaced with a set of three virtual Reidemeister moves and one mixed move. We prefer the re-routing convention, which is a step closer to Gauss codes. Gauss codes encode welded diagrams as a list of classical crossings, and the list of connections between their endpoints, ignoring the planar embedding (and virtual crossings) of the strands which create these connections.
There are three maps which clarify the relationship between solid ribbon torus links and welded diagrams. The enhanced spun and tube maps [Reference Satoh11] construct solid ribbon torus links from diagrams: the enhanced spun map from classical diagrams (with no virtual crossings), and the enhanced tube map from all welded link diagrams. The connection map [Reference Audoux3] constructs a welded diagram from a solid ribbon torus link. We will prove that for solid ribbon torus links up to generalised ribbon isotopy, the enhanced tube map and the connection map are mutual inverses.
The most intuitive of the three maps is the enhanced spun map for link diagrams with only classical crossings. Such a diagram represents a link in
$\mathbb {R}^3$
: that is, an embedding
$\bigcup _{i\in \{1,\ldots ,n\}}S^1 \hookrightarrow \mathbb {R}^3$
. The enhanced spun map, denoted
$\mathit {Spun}^\bullet $
, associates to this classical link a solid ribbon torus link, by including
$\mathbb {R}^3$
in
$\mathbb {R}^4$
and spinning the link in
$\mathbb {R}^4$
around a regular projection plane. The output is the surface ‘drawn’ by the spun link, filled by the union of projection rays: this indeed is a solid ribbon torus link with one ribbon singularity for each crossing in the link diagram.
The enhanced tube map generalises this construction to all welded diagrams:
$$ \begin{align*}\text{Tube}^{\bullet}:\{\text{welded link diagrams}\}\rightarrow \{\text{solid ribbon torus links}\}.\end{align*} $$
Applying
$\text {Spun}^{\bullet }$
to only a disc neighbourhood of a classical crossing results in two cylinders
$B^2\times I$
, one of which is threaded through the other in
$\mathbb {R}^4$
: call this a spun crossing. Given a welded diagram with r classical crossings, for each classical crossing
$\text {Tube}^{\bullet }$
embeds a spun crossing in disjoint 4-balls
$B^4$
in
$\mathbb {R}^4$
, in which the two bottom and two top discs
$B^2\times \{0\}$
and
$B^2\times \{1\}$
of the spun crossing are on the boundaries
$\partial B^4$
: call these boundary discs. Denote by Y the complement of the r 4-balls which contain the spun crossings. In the diagram, there are strands (plane-immersed intervals) connecting the ‘ends’ of the crossings. For each such embedded interval, glue in a regularly embedded
$D^{2}\times I$
in Y to the appropriate boundary discs in
$\partial Y$
.
Proposition 2.8. Up to strict ribbon isotopy,
$\text {Tube}^{\bullet }$
is well defined.
Proof. The proof we present is a slightly extended version of the corresponding part of [Reference Audoux3, proof of Proposition 3.7].
In the
$\text {Tube}^{\bullet }$
construction, choices of specific embeddings are made when gluing in the connecting solid tubes
$D^2 \times I$
. We need to show that such embeddings always exist and are equivalent up to isotopy.
Indeed, since each
$D^2\times I$
is embedded in Y, it can be retracted to a path connecting
$D^2 \times \{0\}$
to
$D^2 \times \{1\}$
. The embedding of
$D^2\times I$
specifies a framing for this path (a framing for a path is a section of the normal bundle, that is, a continuous choice of normal vectors along the path). Namely, choose the positive normal vector to
$D^2\times I$
in
$\mathbb {R}^4$
at each point. Call this path a framed core for the embedded cylinder
$D^2 \times I$
.
However, a framed path
$\gamma $
between the boundary 2-balls can be ‘inflated’ to a regularly embedded 3-ball
$D^2 \times I$
connecting these 2-balls. To do so, for each point
$x\in \gamma $
, consider a two-dimensional neighbourhood of x which is orthogonal to both the derivative of
$\gamma $
and the framing, and take the union of a continuous choice of such neighbourhoods.
These retractions and inflations are mutual inverses up to isotopy of, on one hand, the embedded 3-balls fixing
$D^2 \times \{0\}$
and
$D^2 \times \{1\}$
; and on the other hand, the framed paths, fixing the endpoints. Thus, two embeddings of
$D^2\times I$
between the same boundary 2-balls are isotopic if and only if their framed cores are. The framing along a path
$\gamma $
is always orthogonal to
$\gamma $
, so it can be seen as a path on
$S^2$
, and since
$\pi _1(S^2)=1$
, all framings are equivalent up to isotopy. Thus, it is enough to consider isotopy of unframed paths. Finally, since the paths are one-dimensional, all embeddings in the punctured 4-ball Y (with the given starting and ending points) are isotopic.
Proposition 2.9. Under the
$\mathit {Tube}^\bullet $
map, the two sides of each welded Reidemeister move are equivalent under generalised ribbon isotopy.
Proof. The Reidemeister 1, 2 and 3 moves of welded link diagrams are local equivalences between locally classical string link diagrams. Thus,
$\mathrm {Tube}^\bullet $
and
$\mathrm {Spun}^\bullet $
coincide for these moves, and applying
$\mathrm {Spun}^\bullet $
to the corresponding classical link isotopies gives generalised ribbon isotopies of solid ribbon torus links. In fact, R1 gives a strict isotopy, R2 a generalised ribbon isotopy with a single type 2 singularity and R3 a generalised ribbon isotopy with a single type 3 singularity.
Figure 5 The
$\mathrm {Tube}^\bullet $
image of the OC move, represented as a homotopy of movies of flying discs.
The OC move involves a virtual crossing, so it does not follow from classical isotopies. We represent the
$\mathrm {Tube}^\bullet $
image of both sides as movies of flying discs, as shown in Figure 5. On the left, disc one (blue) flies through disc two (orange), and then disc three (red) flies through disc two (orange). On the right, disc three (red) flies through disc two (orange) first, then disc one (blue) flies through disc two. These movies are isotopic via the middle movie of discs one and three flying through disc two side by side at the same time. This is a strict ribbon isotopy of solid ribbon torus links.
Corollary 2.10. The enhanced tube map descends to a well-defined map on generalised welded link diagrams modulo welded Reidemeister moves.
The goal of this section is to prove Theorem 1.1, namely, to show that there exists a bijection between solid ribbon torus links (up to generalised ribbon isotopy), and welded link diagrams up to welded equivalence. To do so, we introduce the Connection (
$\operatorname {Conn}$
) map inspired by [Reference Audoux3, Section 3.2], and show that it is inverse to
$\mathrm {Tube}^\bullet $
. In particular, the
$\operatorname {Conn}$
map assigns a welded diagram to a solid ribbon torus link: crossings are associated to ribbon singularities and connected based on the sequence of preimages of singularities within each torus. The following theorem is a more precise version of Theorem 1.1.
Theorem 2.11. The connection map is a set bijection
$$ \begin{align*}\operatorname{Conn:} \frac{\{\text{solid ribbon torus links}\}}{\text{generalised ribbon isotopy}}\rightarrow \frac{\{\text{welded diagrams}\}}{\text{welded equivalence}}.\end{align*} $$
We define the Connection map for solid ribbon torus links (ignoring isotopies) first, in two separate parts:
-
(1)
$\sigma _{\operatorname {Conn}}(R)$
describes the sign of each crossing using the orientation of the tori around each singularity; -
(2)
$t_{\operatorname {Conn}}(R)$
prescribes how to connect the crossings in the welded diagrams from the combinatorial structure of the singularities of the solid ribbon torus links.
For a ribbon immersion
$R:\bigcup _{i\in \{1,\ldots ,n\}} \mathbb {T}_i \to \mathbb {R}^4$
, let
$\Delta =\{\delta _1, \delta _2, \ldots , \delta _k\}$
denote the set of ribbon singularities. These correspond to the set of (classical) crossings in the welded diagram.
To each ribbon singularity
$\delta $
, we associate a sign. Let
$\gamma \subseteq \mathbb {T}_k$
and
$\varepsilon \subseteq \mathbb {T}_l$
denote respectively the contractible and essential preimages of
$\delta $
. Let x be a point in the interior of
$\delta $
, and let
$x_c\in \gamma $
and
$x_e\in \varepsilon $
denote the preimages of x. Choose a positive basis in
$T_{x_c} \mathbb {T}_k$
and denote by
$\{u_1, u_2, u_3\}$
its push-forward in
$T_x (\mathbb {R}^4)$
. Let
$v \in T_x(\mathbb {R}^4)$
be a push-forward of a normal vector to
$T_{x_e}(\varepsilon ) \subseteq T_{x_e} \mathbb {T} _l$
, pointing ahead of
$\varepsilon $
in the direction of the core. Then, the sign of
$\delta $
is defined to be the sign of the basis
$u_1, u_2,\ldots , u_3, v$
for
$T_x(\mathbb {R}^4)$
.
Definition 2.12 (
$\sigma _{\operatorname {Conn}(R)}$
).
The map
$\sigma _{\operatorname {Conn}(R)}:\Delta \rightarrow \{-1,1\} $
assigns to each ribbon singularity its sign.
Thus, from a solid ribbon torus link, we have produced a list of oriented crossings. Place these oriented crossings arbitrarily in disjoint discs in the plane (see the red, green and blue discs in Figure 6). Here, arbitrarily means that the location, direction (strands pointing up, down, left or right) and size of the crossings are all chosen arbitrarily, as long as the crossings occupy disjoint discs, are numbered and are of the correct sign. What remains is to describe how to connect these crossings to produce a welded diagram.
Figure 6 On the left are the preimages of the ribbon singularities. On the right is the welded diagram: the output of the Connection map.
Denote the set of essential preimages of ribbon singularities by
$E=\{\varepsilon _1,\ldots ,\varepsilon _n\}$
and the contractible preimages by
$\Gamma =\{\gamma _1,\ldots ,\gamma _k\}$
. The set
$E \cup \Gamma $
is partitioned into n subsets, according to in which of the n tori each preimage falls:
$$ \begin{align*}E\cup \Gamma = \sqcup_{i=1}^n S_i.\end{align*} $$
For example, in Figure 6,
$S_1=\{\gamma _1, \gamma _2, \varepsilon _3\}, S_2=\{\varepsilon _1, \gamma _3\}$
and
$S_3=\{\varepsilon _2\}$
.
Definition 2.13 (
$t_{\operatorname {Conn}(R)}$
).
The component
$t_{\operatorname {Conn}(R)}$
is a partial cyclic ordering on each of the partition sets
$S_i$
. Each essential preimage intersects the core of its component
$\mathbb {T}_i$
at least once. Since the core is oriented, the order of first intersections is a complete cyclic order on the essential singularities in
$S_i$
. Furthermore, the essential singularities in
$\mathbb {T}_i$
partition
$\mathbb {T}_i$
into chambers. Each contractible singularity in
$\mathbb {T}_i$
belongs to a unique chamber, and thus is cyclically comparable to the essential singularities in
$\mathbb {T}_i$
and to the contractible singularities in other chambers. Contractible singularities in the same chamber are not comparable to each other.
This partial cyclic order on the
$\{S_i\}_{i=1}^n$
determines the welded diagram, as follows. Each essential singularity
$\varepsilon _r \in S_i$
corresponds to the under-strand of the crossing r. Identify the next essential singularity
$\varepsilon _s \in S_i$
in the partial cyclic order
$t_{\operatorname {Conn}(R)}$
on
$S_i$
, noting that possibly
$r=s$
. There is possibly a set of contractible singularities
$\{\gamma _{p_1},\ldots ,\gamma _{p_m}\}$
between
$\varepsilon _r$
and
$\varepsilon _s$
in the partial order of
$S_i$
. Connect the outgoing under-strand of crossing r to the incoming under-strand of crossing s via the over-strands of crossings
$p_1, \ldots ,p_m$
, introducing virtual crossings if necessary. Note that different orderings of going over the crossings
$p_1, \ldots ,p_m$
are all OC-equivalent (as in the middle tube of Figure 7). Continue this process until all crossings have been connected. A special case is when a torus contains only contractible singularities, corresponding to over-strands only. In this case, connect those over-strands in a loop, in any order, introducing virtual crossings as needed.
Figure 7 Differently ordered connections of over-strands corresponding to contractible singularities within a chamber are OC-equivalent.
Example 2.14. The left-hand side of Figure 6 shows the preimages of ribbon singularities for a solid ribbon torus link: for
$i=1,2,3$
, the contractible preimage of
$\delta _i$
is labelled
$\gamma _i$
and the essential preimage is labelled
$\varepsilon _i$
.
The
$\operatorname {Conn}$
map provides the information for constructing the welded diagram shown on the right of Figure 6. We know that there are three singularities, corresponding to three crossings, and
$\sigma _{\operatorname {Conn}(R)}(\delta _i)$
specifies their signs. We place the three crossings on the right (in any position), highlighted red, blue and green.
Based on the first torus, we need to connect the outgoing under-strand of
$\delta _3$
(red) to the incoming under-strand of the same crossing, and on the way cross over
$\delta _1$
and
$\delta _2$
in any order. Then, based on the second torus, we connect the outgoing under-strand of
$\delta _1$
(blue) to the incoming under-strand of the same crossing, on the way crossing over
$\delta _3$
(green). This loop introduces a virtual crossing. Finally, based on the third torus, we connect the outgoing under-strand of
$\delta _2$
(green) to the incoming under-strand of the same crossing, introducing some virtual crossings along the way.
Working towards the proof of Theorem 2.11, we first prove that the
$\operatorname {Conn}$
map, which a priori maps solid ribbon immersions to welded diagrams modulo the OC move, descends to a well-defined map of solid ribbon torus links up to generalised ribbon isotopy, to welded diagrams modulo welded Reidemeister moves.
Theorem 2.15. If
$R_0$
and
$R_1$
are solid ribbon torus links related by generalised ribbon isotopy, then
$\operatorname {Conn}(R_0)$
and
$\operatorname {Conn}(R_1)$
are related by Reidemeister moves of welded link diagrams.
Proof. The image of the
$\operatorname {Conn}$
map depends only on the combinatorial structure of the preimages of singularities and the orientations around the ribbon singularities of a solid ribbon torus link. Hence, we need to analyse how this combinatorial structure changes throughout a generalised ribbon isotopy.
Let
$\eta : (\bigcup _i (B^2\times I)_i)\times I \to B^3\times I$
be a generalised ribbon isotopy of ribbon torus links and let
$\eta _t$
denote the immersion
$\eta _t: (\bigcup _i (B^2\times I)_i)\times \{t\} \to B^3\times I$
. Assume that
$\eta _0 \equiv R_0$
and
$\eta _1 \equiv R_1$
. Recall that, at finitely many discrete values of t,
$\eta _t$
may include generalised ribbon singularities, as in Definition 2.3.
In the preimage,
$\eta $
manifests as a movie of the essential and contractible preimages of the singularities moving around within the tori, and appearing or disappearing at discrete times. With the exception of finitely many discrete values of t, this does not change the combinatorial structure (partial ordering of essential singularities or signs) and hence it does not affect the value of the
$\operatorname {Conn}$
map. The goal is to analyse the discrete values of t where the value of the
$\operatorname {Conn}$
map does change. We base the case analysis on whether a generalised singularity occurs at t and which kind.
Case 1: No generalised singularities. In the preimage of a solid ribbon torus link, the preimages of the singularities do not intersect. Therefore, an isotopy which does not involve generalised singularities cannot change the cyclic ordering of the essential preimages of existing essential singularities, and the signs of the singularities are also rigid. However, the value of the Connection map may change, as singularities may appear or disappear. Since there are no tangential intersections, each appearing/disappearing singularity involves only one tube, and the preimages must be adjacent. By local deformation one may arrange for such appearances/disappearances to occur one at a time. A single instance of this is shown in Figure 8. Observe that the effect of this local isotopy on the value of the Conn map is an R1 move.
Figure 8 An isotopy creating a single ribbon singularity via a cusp.
Case 2: Type 2 generalised ribbon singularities. A type 2 (tangential) generalised ribbon singularity can be eliminated by a small local perturbation in two ways: one resulting in no singularity, the other in two (transverse) ribbon singularities. In the image of the Connection map, this amounts to a Reidemeister 2 move (see Figure 9).
Figure 9 Two possible resolutions of a Type 2 (tangential) generalised ribbon singularity.
Case 3: Type 3 generalised ribbon singularities. The preimage of a nested singularity is shown in Figure 10, along with the two possible ways of resolving it. Each of the resolutions results in three ribbon singularities. The difference between the two resolutions in the image of the Connection map is a Reidemeister 3 move.
Figure 10 Two possible resolutions of a Type 3 (nested) generalised ribbon singularity.
Hence, isotopies of solid ribbon torus links manifest as Reidemeister moves in the image of the Connection map.
Corollary 2.16. The map
$\operatorname {Conn}$
on solid ribbon torus links descends to a well-defined map on solid ribbon torus links up to generalised ribbon isotopies
$$ \begin{align*}\operatorname{Conn:} \frac{\{solid \ ribbon \ torus\ links\}}{generalised \ ribbon \ isotopy}\rightarrow \frac{\{welded \ diagrams\}}{welded \ equivalence}.\end{align*} $$
With Theorem 2.15 and Corollary 2.16 in place, the rest of the proof of the main theorem uses the ideas of [Reference Audoux3, Proposition 3.7].
Proof of Theorem 2.11.
We need to show that the
$\operatorname {Conn}$
map is surjective and injective. Surjectivity is immediate from Proposition 2.8, as
$\operatorname {Tube}^\bullet $
is a right-sided inverse to
$\operatorname {Conn}$
: given a welded diagram D, apply the
$\operatorname {Tube}^\bullet $
map to produce a solid ribbon torus link
$\operatorname {Tube}^\bullet (D)$
. Then, by definition,
$\operatorname {Conn}(\operatorname {Tube}^\bullet (D))=D$
.
Figure 11 Deforming the interior of an essential singularity.
For injectivity, consider two solid ribbon torus links
$R_1$
and
$R_2$
such that
$\operatorname {Conn}(R_1)\sim \operatorname {Conn}(R_2)$
; we need to show that
$R_1$
is generalised ribbon isotopic to
$R_2$
. By Proposition 2.9, Reidemeister moves represent local generalised ribbon isotopies under the
$\operatorname {Tube}^\bullet $
map, and hence we may assume that
$\operatorname {Conn}(R_1)= \operatorname {Conn}(R_2)$
.
The equality
$\operatorname {Conn}(R_1)=\operatorname {Conn}(R_2)$
induces a one-to-one correspondence between the ribbon singularities:
Number the crossings of
$\operatorname {Conn}(R_1)$
and use the bijection
$\xi $
to number the crossings of
$\operatorname {Conn}(R_2)$
in the same order.
By local isotopy, the essential singularities can be deformed to essential horizontal discs as follows. The boundary of an essential singularity is an embedded
${S}^1$
along the boundary of the tube and thus can be transformed by local isotopy to a horizontal circle. Then, we use the standard argument to deform the interior of the disc to a horizontal disc. Take a tubular neighbourhood of the singularity.
-
(1) If the essential preimage does not intersect the horizontal disc filling its boundary, then their union is a 2-sphere, which admits a filling and hence an isotopy of the essential preimage to the flat disc.
-
(2) If the interior of the essential preimage intersects the interior of the flat disc filling the boundary
${S}^1$
, first ensure by local isotopy that all intersections are transverse double points, as on the left of Figure 11. Thus, the intersections form a disjoint union of finitely many nested closed loops, as on the right of Figure 11. Select a loop innermost in the nesting; this loop can be removed by filling the sphere formed by its interior disc and the flat disc it bounds. Thus, all intersections can be recursively removed to reduce to the previous case.
By a further re-parametrisation, obtain
$\tilde {R}_1$
and
$\tilde {R}_2$
with the properties:
-
(1) each contractible preimage of a ribbon singularity
$\delta $
belongs to the interior of a slice
$(B^2 \times \{t_{\delta }\} )_{i_{\delta }}$
of
$\tilde {R}_{1}$
or
$\tilde {R}_{2}$
for some
$i_{\delta }\in \{1,2,\ldots ,n\}$
and
$t_{\delta }\in I$
; -
(2) for every ribbon singularity
$\delta $
of
$\tilde {R}_1$
,
$(i_{\xi (\delta )}, t_{\xi (\delta )} )=(i_{\delta },t_{\delta })$
.
The first point is achieved by Alexander’s trick [Reference Alexander1]. The second point is achievable by re-parametrising because the partial ordering of the essential singularities are the same.
For each ribbon singularity
$\delta _i$
of
$\tilde {R}_1$
, fix a small tubular neighbourhood
$U_i$
of its image: a 4-ball, which intersects
$\tilde {R}_1$
in exactly four 2-balls. Then, since the signs and ordering of the singularities agree,
$\tilde {R}_2$
can be isotoped such that
$\tilde {R}_1 \cap U_i = \tilde {R}_2 \cap U_i$
, that is, the singularities in the two links happen at exactly the same place in exactly the same way. The rest of the proof then amounts to isotoping the solid tubes which connect the singularities to match, which is the same as the proof of the well definedness of the
$\operatorname {Tube}^\bullet $
map (Proposition 2.8).
Acknowledgements
The authors are grateful to Benjamin Audoux, Dror Bar-Natan and Hans Boden for several insightful conversations. We thank the Knot at Lunch Student Group, Alec Elhindi, Grace Garden, Tamara Hogan, Damian Lin, James Morgan, Tilda Wilkinson-Finch and Grace Yuan, for their insights and support. We also thank Brigitte Podrasky for her contribution of many illustrations.
