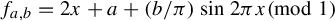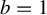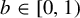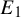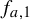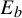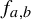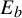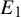1 Introduction
In one-dimensional dynamics, a lot is known about the families of smooth maps with a critical point, such as quadratic maps, and about the maps that have no critical points (local diffeomorphisms of the circle). Here we start to investigate what happens at the interface of those two cases.
Consider the family of double standard maps of the circle onto itself, given by
where the parameters
![]() $a,b$
are real,
$a,b$
are real,
![]() $a \in [0,1)$
and
$a \in [0,1)$
and
![]() $b\in [0,1]$
. In fact, we consider a from the circle
$b\in [0,1]$
. In fact, we consider a from the circle
![]() $\mathbb {R}/\mathbb {Z}$
, but since we are mostly working locally (and far from
$\mathbb {R}/\mathbb {Z}$
, but since we are mostly working locally (and far from
![]() $a=0$
), considering a real is simpler. This family of maps was introduced in [Reference Misiurewicz and Rodrigues19].
$a=0$
), considering a real is simpler. This family of maps was introduced in [Reference Misiurewicz and Rodrigues19].
For
![]() $b=1$
, maps of the family (1.1) have a unique cubic critical point (at
$b=1$
, maps of the family (1.1) have a unique cubic critical point (at
![]() $c=1/2$
) and negative Schwarzian derivative. Thus, they behave similarly to quadratic maps. In particular, there is a set of parameters a for which there is an invariant probability measure, absolutely continuous with respect to the Lebesgue measure. For
$c=1/2$
) and negative Schwarzian derivative. Thus, they behave similarly to quadratic maps. In particular, there is a set of parameters a for which there is an invariant probability measure, absolutely continuous with respect to the Lebesgue measure. For
![]() $b<1$
, there is no critical point, so the maps are local diffeomorphisms. Complexification of the maps, obtained by conjugacy via
$b<1$
, there is no critical point, so the maps are local diffeomorphisms. Complexification of the maps, obtained by conjugacy via
![]() $e^{2\pi ix}$
, gives the family
$e^{2\pi ix}$
, gives the family
Those maps are symmetric with respect to the unit circle, and factored by this symmetry, they have only one critical point and no asymptotic values in
![]() $\mathbb {C}\setminus \{0\}$
. Therefore a map
$\mathbb {C}\setminus \{0\}$
. Therefore a map
![]() $f_{a,b}$
has at most one attracting or neutral periodic orbit (see [Reference Dezotti9, Reference Fagella and Garijo10, Reference Misiurewicz and Rodrigues19]).
$f_{a,b}$
has at most one attracting or neutral periodic orbit (see [Reference Dezotti9, Reference Fagella and Garijo10, Reference Misiurewicz and Rodrigues19]).
One can also look at the family of double standard maps as a hybrid between the family of standard maps, studied by Arnold (see [Reference Arnold1]) and important in the creation of the Kolmogorov–Arnold–Moser theory, and expanding maps of the circle (see [Reference Shub and Sullivan23]). Of course instead of maps of degree 2 one can take maps of higher degrees and the results will be practically the same (but we would introduce one more parameter and lose the nice name of the family).
Some recent work has been done for classes of families that include double standard maps. Misiurewicz and Rodrigues studied them in [Reference Misiurewicz and Rodrigues19, Reference Misiurewicz and Rodrigues20]. Benedicks and Rodrigues [Reference Benedicks and Rodrigues4] investigated symbolic dynamics for this family. Universality for critical circle covers was studied by Levin and Świątek [Reference Levin and Świątek14]. Levin and van Strien [Reference Levin and van Strien15] proved complex bounds, quasisymmetric rigidity and density of hyperbolicity for a class of real analytic maps which includes the double standard maps. Fagella and Garijo [Reference Fagella and Garijo10] studied a class of complex maps containing the maps
![]() $g_{a,b}$
. Dezotti [Reference Dezotti9] also considered maps
$g_{a,b}$
. Dezotti [Reference Dezotti9] also considered maps
![]() $g_{a,b}$
and, using complex methods, obtained important results on the real case.
$g_{a,b}$
and, using complex methods, obtained important results on the real case.
As for the Arnold family, for the double standard family we call the sets for which there is an attracting periodic orbit of a given type (period plus combinatorics) tongues. Dezotti [Reference Dezotti9] proved that tongues are connected. The lowest tongue tip is at
![]() $b=1/2$
, for the period-1 tongue. If
$b=1/2$
, for the period-1 tongue. If
![]() $0<b<1/2$
, the map
$0<b<1/2$
, the map
![]() $f_{a,b}$
is expanding. At higher b-levels there may be finitely or infinitely many tongues (see [Reference Misiurewicz and Rodrigues19]). In particular, at the critical level
$f_{a,b}$
is expanding. At higher b-levels there may be finitely or infinitely many tongues (see [Reference Misiurewicz and Rodrigues19]). In particular, at the critical level
![]() $b=1$
all tongues are present, and it is easy to prove that they are dense at this level (see [Reference Levin and van Strien15]). We show (in Theorem A) that at the lower levels
$b=1$
all tongues are present, and it is easy to prove that they are dense at this level (see [Reference Levin and van Strien15]). We show (in Theorem A) that at the lower levels
![]() $f_{a,b}$
can have an attracting or neutral periodic orbit, and otherwise it is expanding. Moreover, the set of expanding maps is dense in the complement of the tongues.
$f_{a,b}$
can have an attracting or neutral periodic orbit, and otherwise it is expanding. Moreover, the set of expanding maps is dense in the complement of the tongues.
For simplicity, we will be using the notation
![]() $f_a$
for
$f_a$
for
![]() $f_{a,1}$
. A parameter
$f_{a,1}$
. A parameter
![]() $a_0$
will be called an MT parameter (for Misiurewicz--Thurston) if the trajectory of the critical point
$a_0$
will be called an MT parameter (for Misiurewicz--Thurston) if the trajectory of the critical point
![]() $c=1/2$
is preperiodic (but not periodic).
$c=1/2$
is preperiodic (but not periodic).
In this case
![]() $f_{a_0}$
has an absolutely continuous invariant measure [Reference Misiurewicz17], and it is also true that the critical value
$f_{a_0}$
has an absolutely continuous invariant measure [Reference Misiurewicz17], and it is also true that the critical value
![]() $f_{a_0}(\tfrac 12)$
satisfies the Collet–Eckmann condition, that is, that there exist
$f_{a_0}(\tfrac 12)$
satisfies the Collet–Eckmann condition, that is, that there exist
![]() $C_{\mathrm {CE}}>0$
and
$C_{\mathrm {CE}}>0$
and
![]() such that for
such that for
![]() $a=a_0$
,
$a=a_0$
,
which implies the existence of an absolutely continuous invariant measure [Reference Nowicki and van Strien22, Reference van Strien25].
Using the methods of [Reference Benedicks and Carleson2] it is possible to prove the following proposition.
Proposition 1.1. There is a set of positive Lebesgue measure
![]() $\tilde {E}_1$
so that for all
$\tilde {E}_1$
so that for all
![]() $a\in \tilde {E}_1$
there is
$a\in \tilde {E}_1$
there is
![]() $n_0(a)$
such that
$n_0(a)$
such that
Here
![]() $\tfrac 23$
can be replaced by any constant
$\tfrac 23$
can be replaced by any constant
![]() $\sigma <1$
.
$\sigma <1$
.
A parameter exclusion requiring
will be sufficient to prove (1.3) and then Jacobson’s theorem also follows.
Using the methods of Large deviations of [Reference Benedicks and Carleson3] it is possible to prove the following result.
Proposition 1.2. There is a set of positive Lebesgue measure
![]() $E_1$
and some
$E_1$
and some
![]() $\kappa>0$
such that for all
$\kappa>0$
such that for all
![]() $a\in E_1$
,
$a\in E_1$
,
For a similar result, see [Reference Thieullen, Tresser and Young24].
In the present paper we will consider the non-critical case
![]() $0<b<1$
and use more elementary methods based on [Reference Benedicks and Carleson2], which give stretched exponential growth of the type
$0<b<1$
and use more elementary methods based on [Reference Benedicks and Carleson2], which give stretched exponential growth of the type
for all
![]() $a\in \tilde {E}_b$
for a set
$a\in \tilde {E}_b$
for a set
![]() $\tilde {E}_b$
, which is a finite union of intervals. To obtain this it is sufficient to carry out parameter exclusions of the type
$\tilde {E}_b$
, which is a finite union of intervals. To obtain this it is sufficient to carry out parameter exclusions of the type
and then prove exponential expansion in §8. The proof is discussed further at the end of this section.
We will outline the proof of Proposition 1.1 after the proof of Theorem A.
By the results of [Reference Bruin, Luzzatto and van Strien5, Reference Bruin, Rivera-Letelier, van Strien and Shen6], if
![]() $f_a(c)$
satisfies the Collet–Eckmann condition, then
$f_a(c)$
satisfies the Collet–Eckmann condition, then
![]() $f_a$
has an absolutely continuous invariant measure. This is the analogue of Jakobson’s theorem [Reference Jakobson11] in this case.
$f_a$
has an absolutely continuous invariant measure. This is the analogue of Jakobson’s theorem [Reference Jakobson11] in this case.
It is also possible to prove (1.2) for a in a set
![]() $E_1$
of positive Lebesgue measure, but with the present setup this would require the method of large deviations of [Reference Benedicks and Carleson3], and this is not required when
$E_1$
of positive Lebesgue measure, but with the present setup this would require the method of large deviations of [Reference Benedicks and Carleson3], and this is not required when
![]() $0<b<1$
.
$0<b<1$
.
Let us introduce some notation. For a fixed b, let us denote the sets of those parameters a for which
![]() $f_{a,b}$
has an attracting (respectively, neutral) orbit
$f_{a,b}$
has an attracting (respectively, neutral) orbit
![]() $T_b$
(respectively,
$T_b$
(respectively,
![]() $TN_b$
). Moreover, let
$TN_b$
). Moreover, let
![]() $E_b$
be the set of those parameters a for which
$E_b$
be the set of those parameters a for which
![]() $f_{a,b}$
is expanding, that is, there exist
$f_{a,b}$
is expanding, that is, there exist
![]() $C>0$
and
$C>0$
and
![]() $\kappa>0$
such that
$\kappa>0$
such that
By the result of Mañé [Reference Mañé16], if a does not belong to
![]() $T_b$
or
$T_b$
or
![]() $TN_b$
, then it belongs to
$TN_b$
, then it belongs to
![]() $E_b$
. Observe that by the definition, a small perturbation of an expanding map is also expanding, so
$E_b$
. Observe that by the definition, a small perturbation of an expanding map is also expanding, so
![]() $E_b$
is open. In fact, the set
$E_b$
is open. In fact, the set
![]() $E=\{(a,b):a\in E_b, 0\le b<1\}$
is open in
$E=\{(a,b):a\in E_b, 0\le b<1\}$
is open in
![]() $[0,1)\times [0,1)$
.
$[0,1)\times [0,1)$
.
Note that our definition of
![]() $E_1$
or
$E_1$
or
![]() $\tilde {E}_1$
is quite different from the non-critical case, that is, the case of
$\tilde {E}_1$
is quite different from the non-critical case, that is, the case of
![]() $E_b$
for
$E_b$
for
![]() $b<1$
. Nevertheless, there are some common features of the non-critical case, because if
$b<1$
. Nevertheless, there are some common features of the non-critical case, because if
![]() $f_{a,b}$
is expanding, then by the results of Krzy
$f_{a,b}$
is expanding, then by the results of Krzy
![]() $\dot{\textrm{z}}$
ewski and Szlenk [Reference Krzyżewski and Szlenk12], or by the Lasota–Yorke theorem [Reference Lasota and Yorke13], there exists an absolutely continuous invariant measure.
$\dot{\textrm{z}}$
ewski and Szlenk [Reference Krzyżewski and Szlenk12], or by the Lasota–Yorke theorem [Reference Lasota and Yorke13], there exists an absolutely continuous invariant measure.
Extending the methods of the proof of (1.3), we prove the following theorem.
Theorem A. Let
![]() $a_0$
be an MT parameter for the family
$a_0$
be an MT parameter for the family
![]() $\{f_a\}$
. Denote
$\{f_a\}$
. Denote
![]() $\omega (\varepsilon )=(a_0-\varepsilon, a_0+\varepsilon )$
. Then for some
$\omega (\varepsilon )=(a_0-\varepsilon, a_0+\varepsilon )$
. Then for some
![]() $\varepsilon _0>0$
there is a function
$\varepsilon _0>0$
there is a function
![]() $b_0:(0,\varepsilon _0) \to (0,1)$
such that
$b_0:(0,\varepsilon _0) \to (0,1)$
such that
Here
![]() $|A|$
denotes the Lebesgue measure of the set A.
$|A|$
denotes the Lebesgue measure of the set A.
This can be considered as the main result of the paper. It gives a quantitative relation between the behavior of the system for
![]() $b<1$
, where the maps are local diffeomorphisms, and for
$b<1$
, where the maps are local diffeomorphisms, and for
![]() $b=1$
, the critical case.
$b=1$
, the critical case.
Finally, we prove a topological result, using very different methods.
Theorem B. For each
![]() $b<1$
, the set
$b<1$
, the set
![]() $E_b$
is dense in the complement of
$E_b$
is dense in the complement of
![]() $T_b$
. In particular, every interval of the parameters a either is contained in a closure of one tongue or intersects
$T_b$
. In particular, every interval of the parameters a either is contained in a closure of one tongue or intersects
![]() $E_b$
.
$E_b$
.
The above theorem in some sense complements Theorem A. Locally it says less about the set
![]() $E_b$
, but it applies to all
$E_b$
, but it applies to all
![]() $b<1$
, not only to b sufficiently close to
$b<1$
, not only to b sufficiently close to
![]() $1$
(moreover, this closeness in Theorem A depends on
$1$
(moreover, this closeness in Theorem A depends on
![]() $a_0$
).
$a_0$
).
This paper is organized as follows. In §2 we introduce notation and some definitions that we will use throughout the paper. In §3 we prove the transversality condition for maps of the family (1.1). In §4 we prove that we have exponential growth of the derivative for an orbit of a map
![]() $f_{a,b}$
that moves outside an open interval containing the critical point when
$f_{a,b}$
that moves outside an open interval containing the critical point when
![]() $(a,b)$
is a small perturbation of an MT parameter
$(a,b)$
is a small perturbation of an MT parameter
![]() $(a_0,1)$
. In §5 we describe the induction including its startup and prove that the conditions on the induction statement are satisfied for the first free return time. Furthermore, we define the bound period and prove some results concerning the derivative growth during the bound period. In §6 we prove the global distortion lemma and in §7 we start the proof of Theorem A. In §8 we finish this proof. Finally, in §9 we prove Theorem B.
$(a_0,1)$
. In §5 we describe the induction including its startup and prove that the conditions on the induction statement are satisfied for the first free return time. Furthermore, we define the bound period and prove some results concerning the derivative growth during the bound period. In §6 we prove the global distortion lemma and in §7 we start the proof of Theorem A. In §8 we finish this proof. Finally, in §9 we prove Theorem B.
Let us indicate what is technically new in this paper compared to previous work. The proof of Theorem A is based on techniques in [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3].
The main strategy of the proof of Theorem A is the inductive proof of
up to a certain time
![]() $\hat {N}$
.
$\hat {N}$
.
The set
![]() $\tilde {E}_1$
in the critical case
$\tilde {E}_1$
in the critical case
![]() $b=1$
is a Cantor set of positive measure represented as
$b=1$
is a Cantor set of positive measure represented as
 $$ \begin{align*} E_1=\bigcap_{n=0}^\infty A_n, \end{align*} $$
$$ \begin{align*} E_1=\bigcap_{n=0}^\infty A_n, \end{align*} $$
where each
![]() $A_n$
is a disjoint union of intervals
$A_n$
is a disjoint union of intervals
![]() $\{I_n^j\}$
. Here
$\{I_n^j\}$
. Here
![]() $A_{n+1}\subset A_n$
and the set
$A_{n+1}\subset A_n$
and the set
![]() $A_{n+1}$
are defined by removing subintervals of each
$A_{n+1}$
are defined by removing subintervals of each
![]() $I_{n}^j$
according to two rules. First those subintervals that do not satisfy an approach rate condition (1.4) for the critical point (or inflexion point)
$I_{n}^j$
according to two rules. First those subintervals that do not satisfy an approach rate condition (1.4) for the critical point (or inflexion point)
![]() $c=\tfrac 12$
are deleted. This replaces the basic assumption (BA) in [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3]. In the non-critical case
$c=\tfrac 12$
are deleted. This replaces the basic assumption (BA) in [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3]. In the non-critical case
![]() $0<b<1$
this condition corresponds to (1.7).
$0<b<1$
this condition corresponds to (1.7).
The proof of Theorem A is different from that of Proposition 1.1 in the critical case due to the fact that the behavior at the inflexion point
![]() $c=\tfrac 12$
is given by the Taylor series
$c=\tfrac 12$
is given by the Taylor series
 $$ \begin{align*} f_{a,b}(x)&=a+(2-2b)\bigg(x-\frac12\bigg)+\sum_{k=1}^\infty a_{2k+1}\bigg(x-\frac{1}{2}\bigg)^{2k+1}\\ &=a+(2-2b)\bigg(x-\frac12\bigg)+g(x). \end{align*} $$
$$ \begin{align*} f_{a,b}(x)&=a+(2-2b)\bigg(x-\frac12\bigg)+\sum_{k=1}^\infty a_{2k+1}\bigg(x-\frac{1}{2}\bigg)^{2k+1}\\ &=a+(2-2b)\bigg(x-\frac12\bigg)+g(x). \end{align*} $$
Here
![]() $g(x)/(x-\tfrac 12)^3$
is bounded above and below by strictly numerical positive constants, depending only on the MT map
$g(x)/(x-\tfrac 12)^3$
is bounded above and below by strictly numerical positive constants, depending only on the MT map
![]() $f_{a_0}$
. Furthermore,
$f_{a_0}$
. Furthermore,
![]() $g'(x)/(x-\tfrac 12)^2$
has similar bounds from above and below.
$g'(x)/(x-\tfrac 12)^2$
has similar bounds from above and below.
This means that when a point
![]() $y=f_{a,b}^n(x)$
is close to
$y=f_{a,b}^n(x)$
is close to
![]() $c=\tfrac 12$
, the derivative
$c=\tfrac 12$
, the derivative
![]() $f_{a,b}'(y)$
will be dominated either by
$f_{a,b}'(y)$
will be dominated either by
![]() $2-2b$
or by the quadratic term
$2-2b$
or by the quadratic term
![]() $g'(y)$
and these two cases will be treated differently.
$g'(y)$
and these two cases will be treated differently.
The induction in the non-critical case
![]() $b<1$
can actually be terminated at the time
$b<1$
can actually be terminated at the time
![]() $\hat {N}$
defined by the condition that the constant term in the derivative
$\hat {N}$
defined by the condition that the constant term in the derivative
![]() $2-2b$
can be of size comparable to
$2-2b$
can be of size comparable to
![]() $g'(x)$
, which is quadratic, that is,
$g'(x)$
, which is quadratic, that is,
where
![]() $\sim $
means that the two sides are comparable within fixed constants, which depend only on
$\sim $
means that the two sides are comparable within fixed constants, which depend only on
![]() $f_{a_0}$
. Defining
$f_{a_0}$
. Defining
![]() $\hat {N}$
this way, we can stop the induction at time
$\hat {N}$
this way, we can stop the induction at time
![]() $\hat {N}$
and the remaining set
$\hat {N}$
and the remaining set
![]() $E_b=\bigcap _{n=0}^{\hat {N}} A_n(b)$
is a finite union of intervals.
$E_b=\bigcap _{n=0}^{\hat {N}} A_n(b)$
is a finite union of intervals.
Another new aspect of the present paper is that for
![]() $b<1$
the condition of Collet–Eckmann type (again with
$b<1$
the condition of Collet–Eckmann type (again with
![]() $c=\tfrac 12$
)
$c=\tfrac 12$
)
is no longer sufficient for the existence of absolutely continuous invariant measures for
![]() $f_{a,b}$
. There is, however, another argument given in §8 which uses (1.11) together with bound period estimates (see §4) which prove uniform hyperbolicity (1.8). As general references for the theory of one-dimensional maps we mention [Reference Collet and Eckmann7, Reference de Melo and van Strien8, Reference Misiurewicz, Iooss, Helleman and Stora18, Reference Misiurewicz and Rodrigues21].
$f_{a,b}$
. There is, however, another argument given in §8 which uses (1.11) together with bound period estimates (see §4) which prove uniform hyperbolicity (1.8). As general references for the theory of one-dimensional maps we mention [Reference Collet and Eckmann7, Reference de Melo and van Strien8, Reference Misiurewicz, Iooss, Helleman and Stora18, Reference Misiurewicz and Rodrigues21].
2 Notation
Throughout this paper, C is a general numeric constant. For a set
![]() $A\subset \mathbb {R}$
we will denote by
$A\subset \mathbb {R}$
we will denote by
![]() $|A|$
its Lebesgue measure.
$|A|$
its Lebesgue measure.
Consider the family of double standard maps given by (1.1) with
![]() $b=1$
. Throughout this paper we write
$b=1$
. Throughout this paper we write
![]() $f_a(x)=f_{a,1}(x)$
and denote by
$f_a(x)=f_{a,1}(x)$
and denote by
![]() $\xi _j(a)$
the orbit of the critical point:
$\xi _j(a)$
the orbit of the critical point:
![]() $\xi _j(a)=f_a^j(c)$
.
$\xi _j(a)=f_a^j(c)$
.
For a general
![]() $b\leq 1$
, we also use the notation
$b\leq 1$
, we also use the notation
![]() $\xi _j(a,b)=f_{a,b}^j(c)$
. It is clear that when
$\xi _j(a,b)=f_{a,b}^j(c)$
. It is clear that when
![]() $b<1$
, the point
$b<1$
, the point
![]() $c=\tfrac 12$
is an inflexion point. Sometimes we also use the notation
$c=\tfrac 12$
is an inflexion point. Sometimes we also use the notation
![]() $f(x,a,b)$
for
$f(x,a,b)$
for
![]() $f_{a,b}(x)$
and
$f_{a,b}(x)$
and
![]() $f(x,a)$
for
$f(x,a)$
for
![]() $f_a(x)$
.
$f_a(x)$
.
By
![]() $\partial _a f_{a,b}^j(x)$
we denote the partial derivative of
$\partial _a f_{a,b}^j(x)$
we denote the partial derivative of
![]() $f_{a,b}^j(x)$
with respect to a and by
$f_{a,b}^j(x)$
with respect to a and by
![]() $\partial _a f_a^j(x)$
the partial derivative of
$\partial _a f_a^j(x)$
the partial derivative of
![]() $f_a^j(x)$
with respect to a.
$f_a^j(x)$
with respect to a.
Definition 2.1. A parameter
![]() $a=a_0$
will be called an MT parameter (for Misiurewicz--Thurston), if there exist an integer m and a period length
$a=a_0$
will be called an MT parameter (for Misiurewicz--Thurston), if there exist an integer m and a period length
![]() $\ell $
such that
$\ell $
such that
![]() $\xi _m(a_0)$
is a periodic point of
$\xi _m(a_0)$
is a periodic point of
![]() $f_{a_0}$
of period
$f_{a_0}$
of period
![]() $\ell $
and the multiplier
$\ell $
and the multiplier
![]() $\Lambda :=(f_{a_0}^\ell )'(\xi _m(a_0))$
is greater than
$\Lambda :=(f_{a_0}^\ell )'(\xi _m(a_0))$
is greater than
![]() $1$
.
$1$
.
As in [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3], we define a partition
![]() ${\mathcal Q}=\{ I_{r,l} \}$
of the return interval
${\mathcal Q}=\{ I_{r,l} \}$
of the return interval
![]() $I^{*}=(c-\delta ,c+\delta )$
, where
$I^{*}=(c-\delta ,c+\delta )$
, where
![]() $\delta =e^{-r_\delta }$
. We first divide
$\delta =e^{-r_\delta }$
. We first divide
![]() $I^{*}$
,
$I^{*}$
,
 $$ \begin{align*} I^{*}=\bigcup_{r=r_\delta}^\infty I_r\cup\bigcup_{r=r_\delta}^\infty I_{-r}, \end{align*} $$
$$ \begin{align*} I^{*}=\bigcup_{r=r_\delta}^\infty I_r\cup\bigcup_{r=r_\delta}^\infty I_{-r}, \end{align*} $$
where
![]() $I_r$
is the interval
$I_r$
is the interval
![]() $(c+e^{-r-1},c+e^{-r})$
for
$(c+e^{-r-1},c+e^{-r})$
for
![]() $r_\delta \leq r <\infty $
, and
$r_\delta \leq r <\infty $
, and
![]() $I_{-r}$
is the interval
$I_{-r}$
is the interval
![]() $(c-e^{-r},c-e^{-r-1})$
.
$(c-e^{-r},c-e^{-r-1})$
.
We then subdivide
![]() $I_r$
into
$I_r$
into
![]() $r^2$
intervals of equal length with disjoint interiors as follows:
$r^2$
intervals of equal length with disjoint interiors as follows:
 $$ \begin{align*} I_r=\bigcup_{\ell=0}^{r^2-1}I_{r,\ell}. \end{align*} $$
$$ \begin{align*} I_r=\bigcup_{\ell=0}^{r^2-1}I_{r,\ell}. \end{align*} $$
For convenience we also use the convention that
![]() $I_{r,r^2}=I_{r-1,0}$
,
$I_{r,r^2}=I_{r-1,0}$
,
![]() $r>0$
, and the analogous convention for
$r>0$
, and the analogous convention for
![]() $r<0$
.
$r<0$
.
Note that we have
![]() $| I_{r,l}|={e^{-r}}/{r^2}(1-e^{-1})$
and
$| I_{r,l}|={e^{-r}}/{r^2}(1-e^{-1})$
and
![]() $|I_{r}|= e^{-r}(1-e^{-1})$
. We will also need the extended interval
$|I_{r}|= e^{-r}(1-e^{-1})$
. We will also need the extended interval
For technical reasons we will also need a partition
![]() ${\mathcal Q}'=\{ I_{r,l} \}$
,
${\mathcal Q}'=\{ I_{r,l} \}$
,
![]() $|r|\geq r_\delta ^1$
, of an interval
$|r|\geq r_\delta ^1$
, of an interval
![]() $I^{**}=(c-\delta _1,c+\delta _1)$
, where
$I^{**}=(c-\delta _1,c+\delta _1)$
, where
![]() $|r|\geq r_\delta ^1$
, for some
$|r|\geq r_\delta ^1$
, for some
![]() $r_\delta ^1<r_\delta $
, that is,
$r_\delta ^1<r_\delta $
, that is,
![]() $\delta _1=e^{-r_\delta ^1}>\delta $
.
$\delta _1=e^{-r_\delta ^1}>\delta $
.
An important tool in this paper is a sequence of partitions
![]() ${\mathcal P}_n$
,
${\mathcal P}_n$
,
![]() $n=0,1,2,\ldots ,$
of the parameter space which is induced by the phase space partition. We define
$n=0,1,2,\ldots ,$
of the parameter space which is induced by the phase space partition. We define
We call a time n a free return if there is a parameter interval
![]() $\omega $
belonging to a partition
$\omega $
belonging to a partition
![]() $\mathcal {P}_n$
such that
$\mathcal {P}_n$
such that
Similarly, if we fix
![]() $b<1$
, we will have
$b<1$
, we will have
(In some cases, for technical reasons, these two conditions will have to be replaced by
![]() $I_{r,\ell }\subset \xi _n(\omega )\subset I_{r,\ell }^+$
or
$I_{r,\ell }\subset \xi _n(\omega )\subset I_{r,\ell }^+$
or
![]() $I_{r,\ell }\subset \xi _n(\omega ,b)\subset I_{r,\ell }^+$
.)
$I_{r,\ell }\subset \xi _n(\omega ,b)\subset I_{r,\ell }^+$
.)
3 Transversality
In this section we prove the transversality condition for maps belonging to the family (1.1).
Lemma 3.1. The following formula holds:
 $$ \begin{align} \partial_a f^n_{a,b}(x)=\sum_{k=0}^{n-1}(f^k_{a,b})'(f^{n-k}_{a,b}(x)) =(f^{n-1}_{a,b})'(f_{a,b}(x))\sum_{k=0}^{n-1} \frac1{(f^k_{a,b})'(f_{a,b}(x))}. \end{align} $$
$$ \begin{align} \partial_a f^n_{a,b}(x)=\sum_{k=0}^{n-1}(f^k_{a,b})'(f^{n-k}_{a,b}(x)) =(f^{n-1}_{a,b})'(f_{a,b}(x))\sum_{k=0}^{n-1} \frac1{(f^k_{a,b})'(f_{a,b}(x))}. \end{align} $$
Proof. We have
(note that
![]() $\partial _a f^0_{a,b}(x)=0$
and
$\partial _a f^0_{a,b}(x)=0$
and
![]() $\partial _a f^1_{a,b}(x)=1$
). Using this formula, we prove by induction that
$\partial _a f^1_{a,b}(x)=1$
). Using this formula, we prove by induction that
 $$ \begin{align} \partial_a f^n_{a,b}(x)=\sum_{k=0}^{n-1}(f^k_{a,b})'(f^{n-k}_{a,b}(x)). \end{align} $$
$$ \begin{align} \partial_a f^n_{a,b}(x)=\sum_{k=0}^{n-1}(f^k_{a,b})'(f^{n-k}_{a,b}(x)). \end{align} $$
If
![]() $n=0$
, then both sides of (3.3) are 0. Assume now that (3.3) holds for some n and prove it for
$n=0$
, then both sides of (3.3) are 0. Assume now that (3.3) holds for some n and prove it for
![]() $n+1$
instead:
$n+1$
instead:
 $$ \begin{align*} \partial_a f^{n+1}_{a,b}(x)&=1+f_{a,b}'(f^n_{a,b}(x))\cdot\sum_{k=0}^{n-1} (f^k_{a,b})'(f^{n-k}_{a,b}(x)) =1+\sum_{k=0}^{n-1}(f^{k+1}_{a,b})'(f^{n-k}_{a,b}(x))\\ &=1+\sum_{k=1}^n(f^k_{a,b})'(f^{n-(k-1)}_{a,b}(x))=\sum_{k=0}^n (f^k_{a,b})'(f^{(n+1)-k}_{a,b}(x)). \end{align*} $$
$$ \begin{align*} \partial_a f^{n+1}_{a,b}(x)&=1+f_{a,b}'(f^n_{a,b}(x))\cdot\sum_{k=0}^{n-1} (f^k_{a,b})'(f^{n-k}_{a,b}(x)) =1+\sum_{k=0}^{n-1}(f^{k+1}_{a,b})'(f^{n-k}_{a,b}(x))\\ &=1+\sum_{k=1}^n(f^k_{a,b})'(f^{n-(k-1)}_{a,b}(x))=\sum_{k=0}^n (f^k_{a,b})'(f^{(n+1)-k}_{a,b}(x)). \end{align*} $$
Thus, by induction, (3.3) holds for every n.
Now we have
From this and (3.3) we get
 $$ \begin{align*} \partial_a f^n_{a,b}(x)&=(f^{n-1}_{a,b})'(f_{a,b}(x))\sum_{k=0}^{n-1} \frac1{(f^{n-k-1}_{a,b})'(f_{a,b}(x))}\\ &=(f^{n-1}_{a,b})'(f_{a,b}(x)) \sum_{k=0}^{n-1}\frac1{(f^k_{a,b})'(f_{a,b}(x))}.\\[-3.7pc] \end{align*} $$
$$ \begin{align*} \partial_a f^n_{a,b}(x)&=(f^{n-1}_{a,b})'(f_{a,b}(x))\sum_{k=0}^{n-1} \frac1{(f^{n-k-1}_{a,b})'(f_{a,b}(x))}\\ &=(f^{n-1}_{a,b})'(f_{a,b}(x)) \sum_{k=0}^{n-1}\frac1{(f^k_{a,b})'(f_{a,b}(x))}.\\[-3.7pc] \end{align*} $$
We get the following immediate corollary.
Corollary 3.2. We have
![]() $\partial _a f_{a,b}(x)\equiv 1$
and if
$\partial _a f_{a,b}(x)\equiv 1$
and if
![]() $n>0$
then
$n>0$
then
![]() $\partial _a f^n_{a,b}(x)\ge 1$
. Moreover,
$\partial _a f^n_{a,b}(x)\ge 1$
. Moreover,
 $$ \begin{align} \frac{\partial_a\xi_n(a,b)}{(f_{a,b}^{n-1})'(f_{a,b}(c))} =\sum_{k=0}^{n-1}\frac1{(f^k_{a,b})'(f_{a,b}(c))}, \end{align} $$
$$ \begin{align} \frac{\partial_a\xi_n(a,b)}{(f_{a,b}^{n-1})'(f_{a,b}(c))} =\sum_{k=0}^{n-1}\frac1{(f^k_{a,b})'(f_{a,b}(c))}, \end{align} $$
so, in particular,
In a special case, when there is a constant
such that
then for all
![]() $\nu \leq n$
we obtain, by combining the inequality with the lower bound (3.5),
$\nu \leq n$
we obtain, by combining the inequality with the lower bound (3.5),
 $$ \begin{align} 1\leq\frac{\partial_a\xi_n(a,b)}{(f_{a,b}^{n-1})'(f_{a,b}(c))}\le q_*, \end{align} $$
$$ \begin{align} 1\leq\frac{\partial_a\xi_n(a,b)}{(f_{a,b}^{n-1})'(f_{a,b}(c))}\le q_*, \end{align} $$
where

Remark 3.3. We would like to emphasize the central role that Corollary 3.2 plays in this paper. We prove the estimate (3.6) successively by induction on
![]() $\nu $
. We can then conclude that (3.7) holds with n replaced by
$\nu $
. We can then conclude that (3.7) holds with n replaced by
![]() $\nu $
for a given
$\nu $
for a given
![]() $\nu $
. From this estimate we conclude that the x- and a-derivative are comparable at a given time
$\nu $
. From this estimate we conclude that the x- and a-derivative are comparable at a given time
![]() $\nu $
. It is important that we prove the x-expansion first and then verify the comparison. The constant
$\nu $
. It is important that we prove the x-expansion first and then verify the comparison. The constant
![]() $q_*$
will be fixed, that is, it only depends on
$q_*$
will be fixed, that is, it only depends on
![]() $f_{a_0}$
.
$f_{a_0}$
.
We will also need the following lemma which can be viewed as a lower bound for the Radon–Nikodym derivative of
![]() $\xi _\nu (a,b)\mapsto \xi _\mu (a,b)$
,
$\xi _\nu (a,b)\mapsto \xi _\mu (a,b)$
,
![]() $\nu <\mu $
(with respect to
$\nu <\mu $
(with respect to
![]() $a\in \omega $
).
$a\in \omega $
).
Lemma 3.4. Suppose that
![]() $\omega $
is a parameter interval and
$\omega $
is a parameter interval and
![]() $\nu <\mu $
. Assume further that there is a constant
$\nu <\mu $
. Assume further that there is a constant
![]() $q'$
such that for all
$q'$
such that for all
![]() $t\in \omega $
,
$t\in \omega $
,
Then
Proof. By Corollary 3.2,
However, by (3.8) we have
 $$ \begin{align*} (f_{t,b}^{\mu-1})'(f_{t,b}(c))&=(f_{t,b}^{\mu-\nu})'(f_{t,b}^\nu(c)) \cdot (f_{t,b}^{\nu-1})'(f_{t,b}(c))\\ &\ge\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot \frac1{q'}\partial_a\xi_\nu(t,b). \end{align*} $$
$$ \begin{align*} (f_{t,b}^{\mu-1})'(f_{t,b}(c))&=(f_{t,b}^{\mu-\nu})'(f_{t,b}^\nu(c)) \cdot (f_{t,b}^{\nu-1})'(f_{t,b}(c))\\ &\ge\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot \frac1{q'}\partial_a\xi_\nu(t,b). \end{align*} $$
Together with (3.9), we get
 $$ \begin{align*} |\xi_{\mu}(\omega,b)|&\ge \frac1{q'}\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot \int_\omega\partial_a\xi_\nu(t,b)\,dt\\&= \frac1{q'}\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot|\xi_\nu(\omega,b)|.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} |\xi_{\mu}(\omega,b)|&\ge \frac1{q'}\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot \int_\omega\partial_a\xi_\nu(t,b)\,dt\\&= \frac1{q'}\inf_{a\in\omega} (f_{a,b}^{\mu-\nu})'(f_{a,b}^\nu(c))\cdot|\xi_\nu(\omega,b)|.\\[-3.5pc] \end{align*} $$
4 The outside expansion
The aim of this section is to prove that we have exponential growth of the derivative for an orbit of a map
![]() $f_{a,b}$
that moves outside an open interval I containing c, when
$f_{a,b}$
that moves outside an open interval I containing c, when
![]() $(a,b)$
is a small perturbation of an MT parameter
$(a,b)$
is a small perturbation of an MT parameter
![]() $(a_0,1)$
. We consider the parameter space
$(a_0,1)$
. We consider the parameter space
![]() $\mathbb {R}/\mathbb {Z}\times (0,1]$
, and when we speak of a neighborhood of
$\mathbb {R}/\mathbb {Z}\times (0,1]$
, and when we speak of a neighborhood of
![]() $(a_0,1)$
, we mean its neighborhood in this space.
$(a_0,1)$
, we mean its neighborhood in this space.
By
![]() $|x-y|$
we denote the distance between x and y on the circle. Since the points x and y will be usually close to each other, this makes perfect sense. Denote
$|x-y|$
we denote the distance between x and y on the circle. Since the points x and y will be usually close to each other, this makes perfect sense. Denote
By the definition of an MT parameter, we have
![]() $\overline {d}>0$
.
$\overline {d}>0$
.
Since
![]() $f_{a_0}$
has negative Schwarzian derivative, the following lemma follows immediately from Theorem 1.3 of [Reference Misiurewicz17] (in a general case one could use also the result of Mañé (see [Reference Mañé16])).
$f_{a_0}$
has negative Schwarzian derivative, the following lemma follows immediately from Theorem 1.3 of [Reference Misiurewicz17] (in a general case one could use also the result of Mañé (see [Reference Mañé16])).
Lemma 4.1. Let I be an open interval containing c. Then there exist a neighborhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $(a_0,1)$
, positive constants
$(a_0,1)$
, positive constants
![]() , and an integer
, and an integer
![]() $M_1$
such that if
$M_1$
such that if
![]() $(a,b)\in \mathcal {N}$
then:
$(a,b)\in \mathcal {N}$
then:
-
(i) if
 $x, f_{a,b} (x),\ldots , f_{a,b}^{n-1}(x) \notin I$
, then
$x, f_{a,b} (x),\ldots , f_{a,b}^{n-1}(x) \notin I$
, then 
-
(ii) if
 $x,f_{a,b}(x) \ldots ,\ f_{a,b}^{n-1}(x) \notin I$
and
$x,f_{a,b}(x) \ldots ,\ f_{a,b}^{n-1}(x) \notin I$
and
 $n\ge M_1$
, then
$n\ge M_1$
, then 
Proof. By Theorem 1.3 of [Reference Misiurewicz17] (or a result of Mañé [Reference Mañé16]), there exist
![]() $L>0$
and
$L>0$
and
such that if
![]() $x, f_{a_0} (x),\ldots , f_{a_0}^{L-1}(x) \notin I$
, then
$x, f_{a_0} (x),\ldots , f_{a_0}^{L-1}(x) \notin I$
, then
. Therefore, if
![]() $\mathcal {N}$
is a sufficiently small neighborhood of
$\mathcal {N}$
is a sufficiently small neighborhood of
![]() $(a_0,1)$
, then for all
$(a_0,1)$
, then for all
![]() $(a,b)\in \mathcal {N}$
and x such that
$(a,b)\in \mathcal {N}$
and x such that
![]() $x, f_{a,b} (x),\ldots , f_{a,b}^{L-1}(x) \notin I$
, we have
$x, f_{a,b} (x),\ldots , f_{a,b}^{L-1}(x) \notin I$
, we have
. Since the infimum of
![]() $(f_{a,b}^i)'(x)$
over
$(f_{a,b}^i)'(x)$
over
![]() $(a,b)\in \mathcal {N}$
,
$(a,b)\in \mathcal {N}$
,
![]() $x\notin I$
and
$x\notin I$
and
![]() $i=0,1,\ldots ,L-1$
is positive, there exists a positive constant
$i=0,1,\ldots ,L-1$
is positive, there exists a positive constant
such that (i) holds with
. Thus it also holds with
, and then (ii) holds with any
Now we fix a positive constant
![]() $\beta>0$
. It will depend only on the unperturbed map
$\beta>0$
. It will depend only on the unperturbed map
![]() $f_{a_0}$
and can be chosen as, say
$f_{a_0}$
and can be chosen as, say
![]() . Here
. Here
![]() $\tilde {\kappa }=(1/\ell )\log \Lambda $
, where
$\tilde {\kappa }=(1/\ell )\log \Lambda $
, where
![]() $\Lambda $
is the multiplier of the repelling periodic point of the MT point, and
$\Lambda $
is the multiplier of the repelling periodic point of the MT point, and
![]() is the Lyapunov exponent in Lemma 4.6.
is the Lyapunov exponent in Lemma 4.6.
Definition 4.2. Let
![]() $x \in I^{**}=(c-\delta _1,c+\delta _1)$
. We say that x is
$x \in I^{**}=(c-\delta _1,c+\delta _1)$
. We say that x is
![]() $\beta $
-bound to the critical point c up to time p for
$\beta $
-bound to the critical point c up to time p for
![]() $f_{a,b}$
if p is the maximal integer such that
$f_{a,b}$
if p is the maximal integer such that
Observe that for every
![]() $a,b$
(where
$a,b$
(where
![]() $b\le 1$
) and every x we have
$b\le 1$
) and every x we have
Let us state a version of the bound distortion lemma (see [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3]).
Lemma 4.3. If
![]() $\delta _1$
is sufficiently small, then there is a constant
$\delta _1$
is sufficiently small, then there is a constant
![]() , which converges to
, which converges to
![]() $1$
as
$1$
as
![]() $\delta _1\to 0$
, such that for every
$\delta _1\to 0$
, such that for every
![]() $x \in I^{**}=(c-\delta _1,c+\delta _1)$
if x is
$x \in I^{**}=(c-\delta _1,c+\delta _1)$
if x is
![]() $\beta $
-bound to c up to time p for
$\beta $
-bound to c up to time p for
![]() $f_{a_0}$
, then
$f_{a_0}$
, then

for all
![]() $k \leq p$
. Moreover, there is a constant
$k \leq p$
. Moreover, there is a constant
![]() , which converges to
, which converges to
![]() $0$
as
$0$
as
![]() $\delta _1\to 0$
, such that
$\delta _1\to 0$
, such that
for all
![]() $k \leq p$
.
$k \leq p$
.
Proof. Assume that x is bound to c up to time p. Now choose
![]() $p_1=\frac {1}{10}\log (1/\delta _1)$
. Then by (4.3) we can estimate
$p_1=\frac {1}{10}\log (1/\delta _1)$
. Then by (4.3) we can estimate
if
![]() $j\le p_1$
and
$j\le p_1$
and
if
![]() $p_1<j\le p$
. Thus, if
$p_1<j\le p$
. Thus, if
![]() $\delta _1$
is sufficiently small then
$\delta _1$
is sufficiently small then
![]() $|f_{a_0}^j(x)-f_{a_0}^j(c)|\le {\overline d}/2$
and therefore
$|f_{a_0}^j(x)-f_{a_0}^j(c)|\le {\overline d}/2$
and therefore
for all
![]() $j\le p$
.
$j\le p$
.
This also proves the last statement of the lemma.
We have

The last sum in the exponential may be empty.
Similarly, using (4.6), we get

The sums in (4.7) and (4.8) are bounded by a constant, which only depends on
![]() $\delta _1$
, so we get (4.4). Moreover, by (4.7) and (4.8),
$\delta _1$
, so we get (4.4). Moreover, by (4.7) and (4.8),
![]() converges to
converges to
![]() $1$
as
$1$
as
![]() $\delta _1\to 0$
.
$\delta _1\to 0$
.
Set
![]() $\tilde {\kappa }=(1/\ell )\log \Lambda $
. Then there is a constant
$\tilde {\kappa }=(1/\ell )\log \Lambda $
. Then there is a constant
![]() $C_6=C_6(a_0)$
such that
$C_6=C_6(a_0)$
such that
for all
![]() $j\ge 1$
.
$j\ge 1$
.
At c, the first two derivatives of
![]() $f_a$
vanish, but the third one does not. Therefore, there are positive constants
$f_a$
vanish, but the third one does not. Therefore, there are positive constants
![]() such that for all a sufficiently close to
such that for all a sufficiently close to
![]() $a_0$
,
$a_0$
,
whenever
![]() $x\in I^{**}$
. If
$x\in I^{**}$
. If
![]() $\delta _1$
is small, the constants
$\delta _1$
is small, the constants
![]() and
and
![]() can be made close to each other. Similarly, for some positive constants
can be made close to each other. Similarly, for some positive constants
![]() and
and
![]() ,
,
whenever
![]() $x\in I^{**}$
. If instead of
$x\in I^{**}$
. If instead of
![]() $f_a$
we consider
$f_a$
we consider
![]() $f_{a,b}$
with b sufficiently close to 1, we similarly obtain
$f_{a,b}$
with b sufficiently close to 1, we similarly obtain
and
and we chose
![]() and
and
![]() so that these estimates are valid for all
so that these estimates are valid for all
![]() $b\leq 1$
. Moreover, we have
$b\leq 1$
. Moreover, we have
In the following lemma we estimate the length of the bound period.
Lemma 4.4. If
![]() $\delta _1$
is sufficiently small, x is
$\delta _1$
is sufficiently small, x is
![]() $\beta $
-bound to c up to time p for
$\beta $
-bound to c up to time p for
![]() $f_{a_0}$
, and
$f_{a_0}$
, and
![]() $x\in I^{**}\setminus \{c\}$
, then
$x\in I^{**}\setminus \{c\}$
, then
In the particular case when
![]() $x\in I_{\pm r}$
we obtain
$x\in I_{\pm r}$
we obtain
Proof. By Lemma 4.3, we have

Taking into account (4.9) and (4.10), we get
If
![]() $\delta _1$
is small, then
$\delta _1$
is small, then
, so taking logarithms gives us
If
![]() $\delta _1$
is small, then
$\delta _1$
is small, then
![]() $-\log |x-c|$
is large, so we get
$-\log |x-c|$
is large, so we get
, and therefore
![]() $\tilde {\kappa}\hspace{-1pt}p<-4\log |x-c|$
.
$\tilde {\kappa}\hspace{-1pt}p<-4\log |x-c|$
.
We need a derivative estimate for an orbit of
![]() $f_{a_0}$
that moves completely outside
$f_{a_0}$
that moves completely outside
![]() $I^*=(c-\delta ,c+\delta )$
or
$I^*=(c-\delta ,c+\delta )$
or
![]() $I^{**}=(c-\delta _1,c+\delta _1)$
but returns to one of these intervals at time n.
$I^{**}=(c-\delta _1,c+\delta _1)$
but returns to one of these intervals at time n.
In the proof of the next lemma we will use the fact that
![]() $f_a$
has negative Schwarzian derivative. This result can be generalized to the
$f_a$
has negative Schwarzian derivative. This result can be generalized to the
![]() $C^2$
case (see van Strien [Reference van Strien25]).
$C^2$
case (see van Strien [Reference van Strien25]).
Lemma 4.5. Let
![]() $\overline {d}$
be as in (4.1). For every
$\overline {d}$
be as in (4.1). For every
![]() $\delta _1 \in (0, \overline {d}/2)$
and for every
$\delta _1 \in (0, \overline {d}/2)$
and for every
![]() $n \geq 1$
, if x is such that
$n \geq 1$
, if x is such that
![]() $f^j_{a_{0}}(x) \notin I^{**}$
for
$f^j_{a_{0}}(x) \notin I^{**}$
for
![]() $j=0,\ldots ,n-1$
, and
$j=0,\ldots ,n-1$
, and
![]() $ f^n_{a_0}(x)\in I^{**}$
, then
$ f^n_{a_0}(x)\in I^{**}$
, then
![]() $(f^n_{a_0})'(x)> \overline {d} /2.$
$(f^n_{a_0})'(x)> \overline {d} /2.$
Proof. On each side of x there are the two closest preimages of c of order less than n:
![]() $\eta _1<x$
and
$\eta _1<x$
and
![]() $\eta _2>x$
. Then
$\eta _2>x$
. Then
![]() $f_{a_0}^n$
has positive derivative on
$f_{a_0}^n$
has positive derivative on
![]() $(\eta _1,\eta _2)$
and has negative Schwarzian derivative on that interval. Therefore on one of the intervals
$(\eta _1,\eta _2)$
and has negative Schwarzian derivative on that interval. Therefore on one of the intervals
![]() $[\eta _1,x]$
and
$[\eta _1,x]$
and
![]() $[x,\eta _2]$
the maximum of the derivative
$[x,\eta _2]$
the maximum of the derivative
![]() $(f_{a_0}^n)'$
is attained at x. We may assume that this is the interval
$(f_{a_0}^n)'$
is attained at x. We may assume that this is the interval
![]() $[\eta _1,x]$
. Then
$[\eta _1,x]$
. Then
![]() $f_{a_0}^n(\eta _1)=f_{a_0}^k(c)$
for some
$f_{a_0}^n(\eta _1)=f_{a_0}^k(c)$
for some
![]() $k>0$
, so
$k>0$
, so
By the mean value theorem,
for some
![]() $t\in (\eta _1,x)$
, and thus,
$t\in (\eta _1,x)$
, and thus,
In the following lemma we consider what we call a free period.
Lemma 4.6. Given
![]() $\delta _1$
sufficiently small, there exist a neighborhood
$\delta _1$
sufficiently small, there exist a neighborhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $(a_0,1)$
in the parameter space and positive constants
$(a_0,1)$
in the parameter space and positive constants
![]() $C^*$
and
$C^*$
and
![]() , such that if
, such that if
![]() $(a,b)\in {\mathcal N}$
, then if
$(a,b)\in {\mathcal N}$
, then if
![]() $x,f_{a,b}(x),\ldots , f_{a,b}^{q-1}(x)\not \in I^{**}$
and
$x,f_{a,b}(x),\ldots , f_{a,b}^{q-1}(x)\not \in I^{**}$
and
![]() $f_{a,b}^q(x)\in I^{**}$
then
$f_{a,b}^q(x)\in I^{**}$
then
Here the constant
![]() $C^*$
depends only on the unperturbed map
$C^*$
depends only on the unperturbed map
![]() $f_{a_0}$
, while
$f_{a_0}$
, while
![]() depends on
depends on
![]() $\delta _1$
.
$\delta _1$
.
Proof. By Lemma 4.1,
![]() . For a general q write
. For a general q write
![]() $q=kM_1+\ell $
,
$q=kM_1+\ell $
,
![]() $0\leq \ell <M_1$
. Choose
$0\leq \ell <M_1$
. Choose
![]() so that
so that
![]() .
.
Since
![]() $\ell <M_1$
, we have
$\ell <M_1$
, we have
![]() $(f_{a,b}^{\ell })'(f_{a,b}^{kM_1}(x))> \overline {d}/4$
by Lemma 4.5 (here we can extend the estimate to a neighborhood of
$(f_{a,b}^{\ell })'(f_{a,b}^{kM_1}(x))> \overline {d}/4$
by Lemma 4.5 (here we can extend the estimate to a neighborhood of
![]() ${\mathcal N}_2$
of
${\mathcal N}_2$
of
![]() $(a_0,1)$
because we consider only finitely many iterates of the map). Then for
$(a_0,1)$
because we consider only finitely many iterates of the map). Then for
![]() $(a,b)\in {\mathcal N}= {\mathcal N}_1\cap {\mathcal N}_2$
,
$(a,b)\in {\mathcal N}= {\mathcal N}_1\cap {\mathcal N}_2$
,

so (4.17) follows with
![]() $C^*=\overline {d}/8$
and
$C^*=\overline {d}/8$
and
. Note that, as required,
![]() $C^*$
only depends on the unperturbed map
$C^*$
only depends on the unperturbed map
![]() $f_{a_0}$
, while
$f_{a_0}$
, while
depends on
![]() $\delta _1$
.
$\delta _1$
.
We will also need an estimate of the derivative during the bound period.
Lemma 4.7. Assume that
![]() $9\beta \le \tilde {\kappa }$
. Let
$9\beta \le \tilde {\kappa }$
. Let
![]() $C^*$
be the constant from Lemma 4.6. Then there is an arbitrarily small
$C^*$
be the constant from Lemma 4.6. Then there is an arbitrarily small
![]() $\delta _1$
such that if x is
$\delta _1$
such that if x is
![]() $\beta $
-bound to c up to time p for
$\beta $
-bound to c up to time p for
![]() $f_{a_0}$
and
$f_{a_0}$
and
![]() $x\in I^{**}=(c-\delta _1,c+\delta _1)$
then
$x\in I^{**}=(c-\delta _1,c+\delta _1)$
then
Proof. By the mean value theorem, there is a y between
![]() $f_{a_0}(x)$
and
$f_{a_0}(x)$
and
![]() $f_{a_0}(c)$
such that
$f_{a_0}(c)$
such that
By this, Lemma 4.3 and (4.10), there exists a constant
such that if
![]() $\delta _1$
is sufficiently small then
$\delta _1$
is sufficiently small then
Similarly, since
![]() $(f_{a_0}^p)'(x)=f_{a_0}'(x)\cdot (f_{a_0}^{p-1})' (f_{a_0}(x))$
, we get by Lemma 4.3 and (4.11) that there exists a constant
$(f_{a_0}^p)'(x)=f_{a_0}'(x)\cdot (f_{a_0}^{p-1})' (f_{a_0}(x))$
, we get by Lemma 4.3 and (4.11) that there exists a constant
such that if
![]() $\delta _1$
is sufficiently small then
$\delta _1$
is sufficiently small then
By the definition of p we have
and therefore for some constant
,
Thus,
so
Together with an earlier estimate, this gives us
Since
![]() $9\beta \le \tilde {\kappa }$
, we have
$9\beta \le \tilde {\kappa }$
, we have
and therefore (4.18) holds if
where
![]() $p(\delta _1)$
is the bound period associated with
$p(\delta _1)$
is the bound period associated with
![]() $\delta _1$
. Since
$\delta _1$
. Since
![]() $p(\delta _1)\to \infty $
as
$p(\delta _1)\to \infty $
as
![]() $\delta _1\to 0$
, and
$\delta _1\to 0$
, and
![]() $C^*$
is independent of
$C^*$
is independent of
![]() $\delta _1$
, the above inequality holds if
$\delta _1$
, the above inequality holds if
![]() $\delta _1$
is sufficiently small.
$\delta _1$
is sufficiently small.
Remark 4.8. If in (4.18) we replace (on both sides of the inequality) p by
![]() $p-1$
or
$p-1$
or
![]() $p+1$
, then at the right-hand side of in (4.19) there will be one more multiplicative constant. Since it was irrelevant in the proof what constant is there, Lemma 4.7 still holds with a suitably modified inequality (4.18).
$p+1$
, then at the right-hand side of in (4.19) there will be one more multiplicative constant. Since it was irrelevant in the proof what constant is there, Lemma 4.7 still holds with a suitably modified inequality (4.18).
The following lemma is very similar to Lemma 4.1, but the exponent in the estimate does not depend on the size of the neighborhood of c that we consider. In this lemma we assume that
![]() $\delta _1$
is sufficiently small (so that the lemmas that we use in the proof hold) but fixed.
$\delta _1$
is sufficiently small (so that the lemmas that we use in the proof hold) but fixed.
Lemma 4.9. Let I be an open symmetric interval around c, whose closure is contained in
![]() $I^{**}$
. Fix a sufficiently small neighborhood
$I^{**}$
. Fix a sufficiently small neighborhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $(a_0,1)$
(depending on I). Then there are constants
$(a_0,1)$
(depending on I). Then there are constants
![]() and
and
![]() , (independent of I) and an integer M (depending on I) such that for
, (independent of I) and an integer M (depending on I) such that for
![]() $(a,b)\in \mathcal {N}$
:
$(a,b)\in \mathcal {N}$
:
-
(i) if
 $x,f_{a,b}(x),\ldots , f_{a,b}^{n-1}(x) \notin I$
and
$x,f_{a,b}(x),\ldots , f_{a,b}^{n-1}(x) \notin I$
and
 $f_{a,b}^n(x) \in I^{**}$
, then
$f_{a,b}^n(x) \in I^{**}$
, then 
-
(ii) if
 $x,f_{a,b}(x),\ldots , f_{a,b}^{n-1}(x) \notin I$
and
$x,f_{a,b}(x),\ldots , f_{a,b}^{n-1}(x) \notin I$
and
 $n\geq M$
, then
$n\geq M$
, then 
Remark. Note that we state (i) with the weaker assumption
![]() $f_{a,b}^n(x) \in I^{**}$
instead of the more natural
$f_{a,b}^n(x) \in I^{**}$
instead of the more natural
![]() $f_{a,b}^n(x) \in I$
. This slightly stronger statement will be used in the proof of (ii).
$f_{a,b}^n(x) \in I$
. This slightly stronger statement will be used in the proof of (ii).
Proof. Let
![]() $0=t_0<t_1<t_2<\cdots <t_S<t_{S+1}=n$
, where
$0=t_0<t_1<t_2<\cdots <t_S<t_{S+1}=n$
, where
![]() $t_i$
for
$t_i$
for
![]() $i\in \{1,2,\ldots ,S\}$
are the times when
$i\in \{1,2,\ldots ,S\}$
are the times when
![]() $f_{a,b}^{t_i}(x)\in I^{**}\setminus I$
. We want to estimate
$f_{a,b}^{t_i}(x)\in I^{**}\setminus I$
. We want to estimate
 $$ \begin{align*} (f_{a,b}^n)'(x)=\prod_{j=0}^S (f_{a,b}^{t_{j+1}-t_j})'(f_{a,b}^{t_j}(x)). \end{align*} $$
$$ \begin{align*} (f_{a,b}^n)'(x)=\prod_{j=0}^S (f_{a,b}^{t_{j+1}-t_j})'(f_{a,b}^{t_j}(x)). \end{align*} $$
The times from
![]() $[t_0,t_1)$
form a free period; let
$[t_0,t_1)$
form a free period; let
![]() $t_1-t_0=q_0$
. Hence, by Lemma 4.6,
$t_1-t_0=q_0$
. Hence, by Lemma 4.6,
Consider now times from
![]() $[t_j,t_{j+1})$
, where
$[t_j,t_{j+1})$
, where
![]() $j>0$
. We can write this interval as a union of a bound period
$j>0$
. We can write this interval as a union of a bound period
![]() $[t_j,t_j+p_j)$
and a free period
$[t_j,t_j+p_j)$
and a free period
![]() $[t_j+p_j,t_{j+1})$
, and we write its length as
$[t_j+p_j,t_{j+1})$
, and we write its length as
![]() $t_{j+1}-t_j=p_j+q_j$
. For the bound periods
$t_{j+1}-t_j=p_j+q_j$
. For the bound periods
![]() $[t_j,t_j+p_j)$
we can use the estimate from Lemma 4.7 if
$[t_j,t_j+p_j)$
we can use the estimate from Lemma 4.7 if
![]() $\mathcal {N}$
is sufficiently small, because by Lemma 4.4 we work only with the finite number of iterates (for I fixed; this is why
$\mathcal {N}$
is sufficiently small, because by Lemma 4.4 we work only with the finite number of iterates (for I fixed; this is why
![]() $\mathcal {N}$
depends on I). Although p may depend on the map that we are using, if
$\mathcal {N}$
depends on I). Although p may depend on the map that we are using, if
![]() $\mathcal {N}$
is sufficiently small, it may only change to
$\mathcal {N}$
is sufficiently small, it may only change to
![]() $p\pm 1$
, and then by Remark 4.8 we can still use Lemma 4.7.
$p\pm 1$
, and then by Remark 4.8 we can still use Lemma 4.7.
Thus, for the bound periods
![]() $[t_j,t_j+p_j)$
we get
$[t_j,t_j+p_j)$
we get
and for the free period, as before, the estimate from Lemma 4.6 gives us
Combining these estimates, we get

with
. This completes the proof of (i).
Under the assumptions of (ii) instead of (i) we make the same construction and estimates. The only difference is that we do not know that
![]() $f_{a,b}^n(x)\in I^{**}$
, so we lose information about the last period. There are two cases.
$f_{a,b}^n(x)\in I^{**}$
, so we lose information about the last period. There are two cases.
Case 1.
![]() $f_{a,b}^n(x)$
is still in bound state to the last return to
$f_{a,b}^n(x)$
is still in bound state to the last return to
![]() $I^{**}$
at time
$I^{**}$
at time
![]() $t_S$
. At time
$t_S$
. At time
![]() $t_S$
we can use the estimate of (i),
$t_S$
we can use the estimate of (i),
The derivative contribution at time
![]() $t_S$
is
$t_S$
is
Then there is a derivative contribution from the time
![]() $[t_{S}+1,t_S+j]$
,
$[t_{S}+1,t_S+j]$
,
![]() $j=n-t_S$
. Since
$j=n-t_S$
. Since
![]() $1\leq j\leq p_S$
we can use the Collet–Eckmann condition (1.2) and the distortion estimate Lemma 4.3, combined with continuity in a for
$1\leq j\leq p_S$
we can use the Collet–Eckmann condition (1.2) and the distortion estimate Lemma 4.3, combined with continuity in a for
![]() $a\in {\mathcal A}$
, and the fact that
$a\in {\mathcal A}$
, and the fact that
![]() $p_S$
is bounded to conclude that, say
$p_S$
is bounded to conclude that, say
Combining these estimates and using the chain rule, we get that
and since
![]() $n\geq M$
, where M is allowed to depend on
$n\geq M$
, where M is allowed to depend on
![]() $\delta $
, this gives estimate (ii) with a suitable
$\delta $
, this gives estimate (ii) with a suitable
.
Case 2.
![]() $n\geq t_S+p_S$
. In this case we can use (4.20) with
$n\geq t_S+p_S$
. In this case we can use (4.20) with
![]() $j=S$
to obtain
$j=S$
to obtain
Then
where
![]() $q_S=n-(t_S+p_S)$
. Using Lemma 4.1 and the simple estimate
$q_S=n-(t_S+p_S)$
. Using Lemma 4.1 and the simple estimate
for
![]() $|x-c|\geq \delta _1$
, we get that
$|x-c|\geq \delta _1$
, we get that

Using that the constants
![]() $\delta _1$
,
$\delta _1$
,
,
and
![]() $M_1$
only depend on
$M_1$
only depend on
![]() $f_{a_0}$
, we conclude that (ii) holds with
$f_{a_0}$
, we conclude that (ii) holds with
for
![]() $n\geq M$
, if M is sufficiently large. The final
$n\geq M$
, if M is sufficiently large. The final
is then chosen as
.
Remark 4.10. Note that we in this setting will have an analogue of Lemma 4.4 and the estimate
holds.
Remark 4.11. We will on several occasions need a distortion estimate in the situation of Lemma 4.9, that is, for orbits located outside of I. We need the estimate for parameter dynamics, that is, we have a parameter interval
![]() $\omega $
in the space of a-parameters, and we consider
$\omega $
in the space of a-parameters, and we consider
![]() $\xi _j(\omega ,b)$
for j satisfying
$\xi _j(\omega ,b)$
for j satisfying
![]() $\nu \leq j<\mu =n$
, where
$\nu \leq j<\mu =n$
, where
![]() $\xi _j(\omega ,b)\cap I=\emptyset $
for
$\xi _j(\omega ,b)\cap I=\emptyset $
for
![]() $j=\nu ,\ldots ,n-1$
and
$j=\nu ,\ldots ,n-1$
and
![]() $\xi _n(\omega ,b)\cap I\neq \emptyset $
. Let
$\xi _n(\omega ,b)\cap I\neq \emptyset $
. Let
![]() $\omega '\subset \omega $
be the interval that is mapped onto I. Then Lemma 4.9(i) implies that
$\omega '\subset \omega $
be the interval that is mapped onto I. Then Lemma 4.9(i) implies that
We also assume that (3.6) holds at time
![]() $\nu $
, that is, for
$\nu $
, that is, for
![]() $a\in \omega $
,
$a\in \omega $
,
Then by Corollary 3.2,
 $$ \begin{align} 1\leq\frac{\partial_a\xi_\nu(a,b)}{(f_{a,b}^{\nu-1})'(f_{a,b}(c))}\le q_*. \end{align} $$
$$ \begin{align} 1\leq\frac{\partial_a\xi_\nu(a,b)}{(f_{a,b}^{\nu-1})'(f_{a,b}(c))}\le q_*. \end{align} $$
Then we conclude from Lemma 3.4 that
Lemma 4.12. There exists a constant
![]() such that in the situation of Remark 4.11, if
such that in the situation of Remark 4.11, if
![]() $a',a^{\prime \prime }\in \omega '$
then
$a',a^{\prime \prime }\in \omega '$
then

Proof. Set
![]() $x_k=f^{\nu +k}_{a',b}(c)$
and
$x_k=f^{\nu +k}_{a',b}(c)$
and
![]() $y_k=f^{\nu +k}_{a^{\prime \prime },b}(c)$
. Note that
$y_k=f^{\nu +k}_{a^{\prime \prime },b}(c)$
. Note that
![]() $f_{a,b}'(x)$
is independent of a. Therefore,
$f_{a,b}'(x)$
is independent of a. Therefore,
 $$ \begin{align*} \log\frac{(f_{a',b}^{n-\nu})'(x_0)}{(f_{a^{\prime\prime},b}^{n-\nu})'(y_0)} & = \sum_{k=0}^{n-\nu-1}(\log f^{\prime}_{a',b}(x_k)- \log f^{\prime}_{a',b}(y_k))\\& \leq \sum_{k=0}^{n-\nu-1}\bigg(\frac{|f_{a',b}^{\prime\prime}(\eta_k)|} {f_{a',b}'(\eta_k)}\cdot |x_k-y_k| \bigg) \end{align*} $$
$$ \begin{align*} \log\frac{(f_{a',b}^{n-\nu})'(x_0)}{(f_{a^{\prime\prime},b}^{n-\nu})'(y_0)} & = \sum_{k=0}^{n-\nu-1}(\log f^{\prime}_{a',b}(x_k)- \log f^{\prime}_{a',b}(y_k))\\& \leq \sum_{k=0}^{n-\nu-1}\bigg(\frac{|f_{a',b}^{\prime\prime}(\eta_k)|} {f_{a',b}'(\eta_k)}\cdot |x_k-y_k| \bigg) \end{align*} $$
for some
![]() $\eta _k$
between
$\eta _k$
between
![]() $x_k$
and
$x_k$
and
![]() $y_k$
. Since
$y_k$
. Since
![]() $\eta _k\notin I^*$
for
$\eta _k\notin I^*$
for
![]() $k=0,\ldots ,n-\nu -1$
, we get, by (4.13) and (4.14),
$k=0,\ldots ,n-\nu -1$
, we get, by (4.13) and (4.14),

Therefore,

We have
![]() $x_k=\xi _{\nu +k}(a',b)$
and
$x_k=\xi _{\nu +k}(a',b)$
and
![]() $y_k=\xi _{\nu +k}(a^{\prime \prime },b)$
. Therefore, by Remark 4.11,
$y_k=\xi _{\nu +k}(a^{\prime \prime },b)$
. Therefore, by Remark 4.11,
Thus,

Together with (4.29), we get

and we have proved (4.27) with
Remark 4.13. We note that the distortion in Lemma 4.12 is uniformly bounded since
![]() $|f^{n}_{a,b}(c)-f^{n}_{a',b}(c)|\leq 2\delta $
.
$|f^{n}_{a,b}(c)-f^{n}_{a',b}(c)|\leq 2\delta $
.
We will need a distortion estimate of the same type as Lemma 4.12 in the situation when we only assume estimates such as (4.23) for all
![]() $\nu <n$
and with another Lyapunov exponent
$\nu <n$
and with another Lyapunov exponent
![]() , together with (4.24). This is the case of hyperbolic times in the sense of Alves.
, together with (4.24). This is the case of hyperbolic times in the sense of Alves.
Lemma 4.14. Assume that
![]() $\xi _j(\omega ,b)$
,
$\xi _j(\omega ,b)$
,
![]() $j=\nu ,\ldots ,n$
, is located in
$j=\nu ,\ldots ,n$
, is located in
![]() $U=S^1\setminus I^{**}$
, and
$U=S^1\setminus I^{**}$
, and
Furthermore, assume that (4.24) is satisfied. Then

Here the constant
![]() can be chosen as
can be chosen as
![]() , where
, where
![]() $N(f_{\mathcal N},U)$
is the maximal nonlinearity
$N(f_{\mathcal N},U)$
is the maximal nonlinearity
 $$ \begin{align*} N(f_{\mathcal N},U)=\sup_{(a,b)\in{\mathcal N}} \max_{x\in U} \frac{|f_{a,b}^{\prime\prime}(x)|}{f^{\prime}_{a,b}(x)}. \end{align*} $$
$$ \begin{align*} N(f_{\mathcal N},U)=\sup_{(a,b)\in{\mathcal N}} \max_{x\in U} \frac{|f_{a,b}^{\prime\prime}(x)|}{f^{\prime}_{a,b}(x)}. \end{align*} $$
![]() $N(f_{\mathcal N},U)$
depends only on
$N(f_{\mathcal N},U)$
depends only on
![]() $f_{a_0}$
and hence not on
$f_{a_0}$
and hence not on
![]() $\delta $
, and
$\delta $
, and
![]() is a constant that only depends on
is a constant that only depends on
![]() $f_{a_0}$
.
$f_{a_0}$
.
5 Induction
Recall that the partition of the return interval
![]() $I^*=(c-\delta ,c+\delta )$
was introduced in §2.
$I^*=(c-\delta ,c+\delta )$
was introduced in §2.
Recall also that we defined
![]() $\xi _n(a,b)=f^n_{a,b}(c)$
.
$\xi _n(a,b)=f^n_{a,b}(c)$
.
The next lemma will be used to start the induction.
Lemma 5.1. Assume that
![]() $\delta _1$
is sufficiently small and the neighborhood
$\delta _1$
is sufficiently small and the neighborhood
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $(a_0,1)$
is sufficiently small. Then there are constants
$(a_0,1)$
is sufficiently small. Then there are constants
![]() ,
,
![]() ,
,
![]() such that for every
such that for every
![]() $\varepsilon =2^{-J_0}$
sufficiently small, there is a function
$\varepsilon =2^{-J_0}$
sufficiently small, there is a function
![]() $b_0(\varepsilon )$
such that for every
$b_0(\varepsilon )$
such that for every
![]() $b_0(\varepsilon ) \leq b<1$
one can partition
$b_0(\varepsilon ) \leq b<1$
one can partition
![]() $(a_0-\varepsilon ,a_0-\varepsilon ^2)$
into a partition
$(a_0-\varepsilon ,a_0-\varepsilon ^2)$
into a partition
![]() ${\mathcal Q}$
of countable number of parameter intervals
${\mathcal Q}$
of countable number of parameter intervals
![]() $\omega $
and an exceptional set
$\omega $
and an exceptional set
![]() ${\mathcal E}$
of measure
${\mathcal E}$
of measure
![]() $o(\epsilon )$
, such that for all
$o(\epsilon )$
, such that for all
![]() $\omega \in {\mathcal Q}$
there is an
$\omega \in {\mathcal Q}$
there is an
![]() $n_0=n_0(\omega )$
such that for some
$n_0=n_0(\omega )$
such that for some
![]() $(r,\ell )$
, with
$(r,\ell )$
, with
![]() $r\leq \sqrt {n_0}$
(or equivalently
$r\leq \sqrt {n_0}$
(or equivalently
![]() $e^{-r}\geq e^{-\sqrt {n_0}}$
),
$e^{-r}\geq e^{-\sqrt {n_0}}$
),
and such that for every
![]() $a\in \omega $
:
$a\in \omega $
:
-
(a)
 for
for
 $0\leq j \leq n_0-1$
;
$0\leq j \leq n_0-1$
; -
(b)
 for
for
 $1\leq j \leq n_0$
;
$1\leq j \leq n_0$
; -
(c)
 for
for
 $1 \leq j < n_0$
;
$1 \leq j < n_0$
; -
(d)
 $(f^{n_0-1}_{a,b})'(f_{a,b}(c))\geq e^{2(n_0-1)^{2/3}}$
;
$(f^{n_0-1}_{a,b})'(f_{a,b}(c))\geq e^{2(n_0-1)^{2/3}}$
; -
(e)
 $|\xi _{n_0}(a,b)-c|\geq e^{-\sqrt {n_0}}$
.
$|\xi _{n_0}(a,b)-c|\geq e^{-\sqrt {n_0}}$
.
The corresponding statement holds also for the interval
![]() $(a_0+\varepsilon ^2,a_0+\varepsilon )$
.
$(a_0+\varepsilon ^2,a_0+\varepsilon )$
.
Proof. We partition
![]() $(a_0-\varepsilon ,a_0-\varepsilon ^2)$
into subintervals
$(a_0-\varepsilon ,a_0-\varepsilon ^2)$
into subintervals
![]() $\eta _j=(a_0-2^{-j},a_0-2^{-j-1})=(a_j',a_j^{\prime \prime })$
,
$\eta _j=(a_0-2^{-j},a_0-2^{-j-1})=(a_j',a_j^{\prime \prime })$
,
![]() $j=J_0,\ldots ,2J_0-1$
. The critical point c of unperturbed map
$j=J_0,\ldots ,2J_0-1$
. The critical point c of unperturbed map
![]() $f_{a_0}$
is mapped to a repelling periodic point P in m iterates. Let
$f_{a_0}$
is mapped to a repelling periodic point P in m iterates. Let
![]() $U_0$
be a symmetric interval contained in the linearization domain of P such that
$U_0$
be a symmetric interval contained in the linearization domain of P such that
Let
![]() $\tilde {\eta }_j=(a_0-2^{-j},a_0)$
. Then there is a constant
$\tilde {\eta }_j=(a_0-2^{-j},a_0)$
. Then there is a constant
so that
as long as
![]() $\xi _{m+i}(\tilde {\eta }_j,b)\subset U_0$
. We now state a version of Lemma 4.12 which will be used in the startup construction.
$\xi _{m+i}(\tilde {\eta }_j,b)\subset U_0$
. We now state a version of Lemma 4.12 which will be used in the startup construction.
Lemma 5.2. Suppose that for
![]() $a\in \omega $
there is a constant
$a\in \omega $
there is a constant
![]() $\tilde {C}=\tfrac 12$
, say, such that
$\tilde {C}=\tfrac 12$
, say, such that
and
Then there is a constant
![]() such that
such that

We will not give the proof of this lemma since it is identical to that of Lemma 4.12. We conclude that
and
![]() $q_*$
has a uniform control by Corollary 3.2.
$q_*$
has a uniform control by Corollary 3.2.
We also get a uniform distortion control of
![]() $\partial _af_{a,b}^\nu (\xi _j(a,b))$
, that is, there is a constant
$\partial _af_{a,b}^\nu (\xi _j(a,b))$
, that is, there is a constant
![]() $\tilde {C}$
depending only on
$\tilde {C}$
depending only on
![]() $a_0$
such that for all a,
$a_0$
such that for all a,
![]() $a'$
in
$a'$
in
![]() $\tilde {\eta }_j$
,
$\tilde {\eta }_j$
,
 $$ \begin{align} \frac{1}{\tilde{C}}\leq \frac{\partial_af_{a,b}^\nu(\xi_j(a,b))}{\partial_af_{a',b}^\nu(\xi_j(a',b))}\leq \tilde{C},\quad \nu=1,2,\ldots, \end{align} $$
$$ \begin{align} \frac{1}{\tilde{C}}\leq \frac{\partial_af_{a,b}^\nu(\xi_j(a,b))}{\partial_af_{a',b}^\nu(\xi_j(a',b))}\leq \tilde{C},\quad \nu=1,2,\ldots, \end{align} $$
as long as
![]() $\xi _{m+\nu }(\tilde {\eta }_j,b)\subset U_0$
.
$\xi _{m+\nu }(\tilde {\eta }_j,b)\subset U_0$
.
It follows that there is a first time L such that
![]() $\xi _{m+L+1}(\tilde {\eta }_j,b)\not \subset U_0$
. We write
$\xi _{m+L+1}(\tilde {\eta }_j,b)\not \subset U_0$
. We write
![]() $\tilde {\eta }_j$
as the disjoint union (except for an endpoint)
$\tilde {\eta }_j$
as the disjoint union (except for an endpoint)
By (5.4) it follows that
![]() $\xi _{m+L }(\eta _j,b)$
and
$\xi _{m+L }(\eta _j,b)$
and
![]() $\xi _{m+L }(\eta _j',b)$
are comparable within a fixed constant
$\xi _{m+L }(\eta _j',b)$
are comparable within a fixed constant
![]() , which only depends on
, which only depends on
![]() $f_{a_0}$
.
$f_{a_0}$
.
We continue to iterate
![]() $\xi _{m+L+i}(\eta _j,b)$
for
$\xi _{m+L+i}(\eta _j,b)$
for
![]() $i=1,2,\ldots .$
By Lemmas 4.9, 3.4 and the control of the constant
$i=1,2,\ldots .$
By Lemmas 4.9, 3.4 and the control of the constant
![]() $q_*$
it follows that at the first time J such that
$q_*$
it follows that at the first time J such that
![]() $\xi _{m+L+J}(\eta _j,b)\cap I^*\neq \emptyset $
,
$\xi _{m+L+J}(\eta _j,b)\cap I^*\neq \emptyset $
,
Then
is the required Lyapunov exponent in (a). It follows by Lemmas 4.9(ii), 3.4 and the control of
![]() $q_*$
that the time J will be finite. At time
$q_*$
that the time J will be finite. At time
![]() $N_0=m+L+J$
, we partition
$N_0=m+L+J$
, we partition
into preimages
![]() $\{\omega \}$
under the map
$\{\omega \}$
under the map
![]() $a\mapsto \xi _{N_0}(a,b)$
of the partition
$a\mapsto \xi _{N_0}(a,b)$
of the partition
![]() ${\mathcal Q}=\{I_{r,l}\}$
and define
${\mathcal Q}=\{I_{r,l}\}$
and define
![]() $n_0=N_0$
for these
$n_0=N_0$
for these
![]() $\omega $
s. In the special case when
$\omega $
s. In the special case when
![]() $\xi _{N_0}(\eta _j,b)$
only intersects partially an end interval of
$\xi _{N_0}(\eta _j,b)$
only intersects partially an end interval of
![]() ${\mathcal Q}=\{I_{r,l}\}$
, we just keep iterating until we cover complete intervals of
${\mathcal Q}=\{I_{r,l}\}$
, we just keep iterating until we cover complete intervals of
![]() ${\mathcal Q}$
. In other special case when
${\mathcal Q}$
. In other special case when
![]() $\xi _{N_0}(\eta _j,b)$
only partially covers an
$\xi _{N_0}(\eta _j,b)$
only partially covers an
![]() $I_{r,l}$
interval we adjoin the corresponding preimage to the adjacent interval. Simultaneously we delete the part of
$I_{r,l}$
interval we adjoin the corresponding preimage to the adjacent interval. Simultaneously we delete the part of
![]() $ \eta _j$
that is mapped to
$ \eta _j$
that is mapped to
![]() $(c-e^{-\sqrt {n_0}},c+e^{-\sqrt {n_0}})$
. By the uniform distortion of both the x-derivative and a-derivative which follows from Lemmas 4.9, 4.12 and Corollary 3.2 a proportion of at most
$(c-e^{-\sqrt {n_0}},c+e^{-\sqrt {n_0}})$
. By the uniform distortion of both the x-derivative and a-derivative which follows from Lemmas 4.9, 4.12 and Corollary 3.2 a proportion of at most
of the piece of
![]() $\eta _j$
is mapped into
$\eta _j$
is mapped into
![]() $(c-e^{-\sqrt {n_0}},c+e^{-\sqrt {n_0}})$
. Here
$(c-e^{-\sqrt {n_0}},c+e^{-\sqrt {n_0}})$
. Here
is a constant only depending on
![]() $f_{a_0}$
. We continue to iterate
$f_{a_0}$
. We continue to iterate
![]() $\xi _{N_0}(\eta _j,b)\setminus (c-\delta ,c+\delta ) $
, still using Lemmas 4.9, 4.12 and Corollary 3.2. For the new returning interval
$\xi _{N_0}(\eta _j,b)\setminus (c-\delta ,c+\delta ) $
, still using Lemmas 4.9, 4.12 and Corollary 3.2. For the new returning interval
![]() $\omega $
formed in this way
$\omega $
formed in this way
![]() $n_0(\omega )>N_0$
and still only a quantity proportional to
$n_0(\omega )>N_0$
and still only a quantity proportional to
![]() $e^{-\sqrt {n_0}}/\delta $
is deleted. Conclusions (a)–(e) of Lemma 5.1 are immediately verified.
$e^{-\sqrt {n_0}}/\delta $
is deleted. Conclusions (a)–(e) of Lemma 5.1 are immediately verified.
Remark 5.3. The startup argument is essentially the same as the free period argument in the main induction and the argument in Lemma 4.9 in §4. See the main induction below in this section for a more thorough discussion. The only difference is the initial period that is spent close to the repelling periodic point which in some sense replaces the bound period. The expansive behavior close to the repelling periodic point allows us to avoid inessential free returns and gives the initial exclusion ratio of at most
![]() .
.
Let us now fix b,
![]() $0< b_0(\varepsilon )\leq b <1$
. Note that for every positive integer n we have a family
$0< b_0(\varepsilon )\leq b <1$
. Note that for every positive integer n we have a family
![]() $\mathcal {P}_n$
of subintervals of
$\mathcal {P}_n$
of subintervals of
![]() $(a_0-\varepsilon , a_0+\varepsilon )$
(as in Lemma 5.1) with pairwise disjoint interiors, such that each element of
$(a_0-\varepsilon , a_0+\varepsilon )$
(as in Lemma 5.1) with pairwise disjoint interiors, such that each element of
![]() $\mathcal {P}_{n+1}$
is contained in some element of
$\mathcal {P}_{n+1}$
is contained in some element of
![]() $\mathcal {P}_n$
. In the set of pairs
$\mathcal {P}_n$
. In the set of pairs
![]() $(n,\omega )$
such that
$(n,\omega )$
such that
![]() $\omega \in \mathcal {P}_n$
there is a natural structure of a combinatorial tree that goes down with its branches. Pairs
$\omega \in \mathcal {P}_n$
there is a natural structure of a combinatorial tree that goes down with its branches. Pairs
![]() $(n,\omega )$
are vertices of this tree; n is the level on which the vertex lies; there is an edge from
$(n,\omega )$
are vertices of this tree; n is the level on which the vertex lies; there is an edge from
![]() $(n,\omega )$
to
$(n,\omega )$
to
![]() $(n+1,\omega ')$
if and only if
$(n+1,\omega ')$
if and only if
![]() $\omega '\subset \omega $
.
$\omega '\subset \omega $
.
Certain pairs with the property
![]() $\xi _n(\omega ,b) \subset I^*$
will be called free return pairs.
$\xi _n(\omega ,b) \subset I^*$
will be called free return pairs.
The induction will be separate on every branch of the tree. Fixing the branch results in considering a descending sequence of intervals
![]() $\omega _n\in \mathcal {P}_n$
. If
$\omega _n\in \mathcal {P}_n$
. If
![]() $(n,\omega _n)$
is a free return pair, then we will call n a free return time. An important feature of the construction is that if n is not a free return time then
$(n,\omega _n)$
is a free return pair, then we will call n a free return time. An important feature of the construction is that if n is not a free return time then
![]() $\omega _n=\omega _{n-1}$
. The main induction step will be from a free return time to the next free return time. The constants
$\omega _n=\omega _{n-1}$
. The main induction step will be from a free return time to the next free return time. The constants
![]() and
and
![]() are as in Lemma 5.1. Throughout the entire induction they will stay the same.
are as in Lemma 5.1. Throughout the entire induction they will stay the same.
Our induction statement is as follows. If n is a free return time and
![]() $a\in \omega $
, then:
$a\in \omega $
, then:
-
(i) we have
(5.5) $$ \begin{align} (f_{a,b}^{n-1})'(f_{a,b}(c))\geq e^{2(n-1)^{2/3}}; \end{align} $$
$$ \begin{align} (f_{a,b}^{n-1})'(f_{a,b}(c))\geq e^{2(n-1)^{2/3}}; \end{align} $$
-
(ii) for every
 $\nu \in [n_0,n)$
, (5.6)
$\nu \in [n_0,n)$
, (5.6) $$ \begin{align} (f_{a,b}^\nu)'(f_{a,b}(c))\geq e^{\nu^{2/3}}; \end{align} $$
$$ \begin{align} (f_{a,b}^\nu)'(f_{a,b}(c))\geq e^{\nu^{2/3}}; \end{align} $$
-
(iii) for every
 $\nu \in [1,n)$
, (5.7)
$\nu \in [1,n)$
, (5.7)
-
(iv) if
 $\nu <n$
is also a free return time, then (5.8)
$\nu <n$
is also a free return time, then (5.8) $$ \begin{align} (f^{n-\nu}_{a,b})'(f^{\nu}_{a,b}(c))\geq C(\delta)\gg 1; \end{align} $$
$$ \begin{align} (f^{n-\nu}_{a,b})'(f^{\nu}_{a,b}(c))\geq C(\delta)\gg 1; \end{align} $$
-
(v) for every
 $\nu \in [n_0,n]$
, (5.9)
$\nu \in [n_0,n]$
, (5.9) $$ \begin{align} |\xi_\nu(a,b)-c|\geq e^{- \sqrt{\nu}}; \end{align} $$
$$ \begin{align} |\xi_\nu(a,b)-c|\geq e^{- \sqrt{\nu}}; \end{align} $$
-
(vi) for every
 $\nu \in [0,n]$
, (5.10)
$\nu \in [0,n]$
, (5.10)
In [Reference Benedicks and Carleson2, Reference Benedicks and Carleson3] statements (v) and (vi) are called the basic assumption (BA).
Remember that b sufficiently close to
![]() $1$
is fixed. We set
$1$
is fixed. We set
![]() $\mathcal {P}_n=\{\omega _b\}$
for
$\mathcal {P}_n=\{\omega _b\}$
for
![]() $n=1,2,\ldots ,N_0$
. Thus, this is the beginning of every branch. Then we declare
$n=1,2,\ldots ,N_0$
. Thus, this is the beginning of every branch. Then we declare
![]() $n_0=n_0(\omega )$
to be the first free return time according to the startup construction. Thus, for every branch we have to start induction by checking that the above conditions are satisfied for
$n_0=n_0(\omega )$
to be the first free return time according to the startup construction. Thus, for every branch we have to start induction by checking that the above conditions are satisfied for
![]() $n=n_0(\omega )$
.
$n=n_0(\omega )$
.
Lemma 5.4. The induction statement conditions (i)–(vi) are satisfied for
![]() $n=n_0$
.
$n=n_0$
.
This is a consequence of the startup construction, Lemma 5.1.
Now we make a small modification to Definition 4.2.
Definition 5.5. Let
![]() $a'$
be the midpoint of the interval
$a'$
be the midpoint of the interval
![]() $\omega $
such that
$\omega $
such that
for some
![]() $n,r,l$
. We define the bound period as the maximal integer p such that for all
$n,r,l$
. We define the bound period as the maximal integer p such that for all
![]() $j \leq p$
,
$j \leq p$
,
![]() $a\in \omega $
, and
$a\in \omega $
, and
![]() $x \in \xi _n(\omega ,b)$
,
$x \in \xi _n(\omega ,b)$
,
By (4.3) and Lemma 3.1, we get for every
![]() $n,a,b,x$
,
$n,a,b,x$
,
 $$ \begin{align} \partial_a f_{a,b}^n(x)\le\sum_{k=0}^{n-1}4^k=\frac{4^n-1}3<4^n. \end{align} $$
$$ \begin{align} \partial_a f_{a,b}^n(x)\le\sum_{k=0}^{n-1}4^k=\frac{4^n-1}3<4^n. \end{align} $$
In the next several lemmas we will be using the same set of assumptions. We formalize these in the following definition.
Definition 5.6. We say that condition (*) is satisfied if:
-
•
 $\omega $
,
$\omega $
,
 $n,r,l,p$
and
$n,r,l,p$
and
 $a'$
are as in Definition 5.5,
$a'$
are as in Definition 5.5, -
• conditions (iii), (v) and (vi) of the induction statement hold.
Next we formulate another version of the bound distortion lemma.
Lemma 5.7. There is a constant
![]() such that if condition (*) holds, then
such that if condition (*) holds, then

and

for every
![]() $x\in I_{r,l}$
, y between x and c,
$x\in I_{r,l}$
, y between x and c,
![]() $a\in \omega $
, and
$a\in \omega $
, and
![]() $k\le \max (p,n)$
. By making
$k\le \max (p,n)$
. By making
![]() $\delta $
sufficiently small, the constant
$\delta $
sufficiently small, the constant
![]() can be chosen arbitrarily close to
can be chosen arbitrarily close to
![]() $1$
.
$1$
.
Proof. The proof will proceed by induction on k. Using (4.3), we get, in the same way as in the proof of Lemma 4.3,
 $$ \begin{align} \frac{(f_{a,b}^k)'(f_{a,b}(y))}{(f_{a,b}^k)'(f_{a,b}(c))} \leq \exp \bigg( \sum_{j=1}^{k} \dfrac{13 |f_{a,b}^j(y)-f_{a,b}^j(c)|} {f_{a,b}'(f_{a,b}^j(c))} \bigg). \end{align} $$
$$ \begin{align} \frac{(f_{a,b}^k)'(f_{a,b}(y))}{(f_{a,b}^k)'(f_{a,b}(c))} \leq \exp \bigg( \sum_{j=1}^{k} \dfrac{13 |f_{a,b}^j(y)-f_{a,b}^j(c)|} {f_{a,b}'(f_{a,b}^j(c))} \bigg). \end{align} $$
Furthermore,
and by (5.11) we have
Thus, we need to estimate
![]() $|f_{a',b}^j(c)-f_{a,b}^j(c)|$
. Note that by the mean value theorem there is
$|f_{a',b}^j(c)-f_{a,b}^j(c)|$
. Note that by the mean value theorem there is
![]() $a^{\prime \prime }$
between a and
$a^{\prime \prime }$
between a and
![]() $a'$
such that
$a'$
such that
Note that
![]() $|a-a'|$
can be interpreted as
$|a-a'|$
can be interpreted as
![]() $|\xi _1(a,b)-\xi _1(a',b)|$
. By Lemma 3.4,
$|\xi _1(a,b)-\xi _1(a',b)|$
. By Lemma 3.4,
By induction statement (iii),
![]() . We may therefore conclude that
. We may therefore conclude that
![]() . But by the mean value theorem,
. But by the mean value theorem,
 $$ \begin{align} |f_{a,b}^j(x)-f_{a',b}^j(c)|&=|f_{a,b}^{j-1}(f_{a,b}(x))-f_{a,b}^{j-1}(f_{a,b}(c))|\nonumber\\ &=(f^{j-1}_{a,b})'(f_{a,b}(y))\cdot |f_{a,b}(c)-f_{a,b}(x)|. \end{align} $$
$$ \begin{align} |f_{a,b}^j(x)-f_{a',b}^j(c)|&=|f_{a,b}^{j-1}(f_{a,b}(x))-f_{a,b}^{j-1}(f_{a,b}(c))|\nonumber\\ &=(f^{j-1}_{a,b})'(f_{a,b}(y))\cdot |f_{a,b}(c)-f_{a,b}(x)|. \end{align} $$
However, since
![]() $|\xi _n(a,b)-\xi _n(a',b)|\leq e^{-r}$
, we have
$|\xi _n(a,b)-\xi _n(a',b)|\leq e^{-r}$
, we have
By the basic assumption
![]() . Note also that by Corollary 3.2,
. Note also that by Corollary 3.2,
![]() $\partial _af^j_{a^{\prime \prime },b}(c)$
is comparable within the multiplicative constant
$\partial _af^j_{a^{\prime \prime },b}(c)$
is comparable within the multiplicative constant
![]() $q_*$
to
$q_*$
to
![]() $(f^{j-1}_{a^{\prime \prime },b})'(f_{a^{\prime \prime },b}(c))$
. But this quantity is in itself by induction comparable within a multiplicative constant
$(f^{j-1}_{a^{\prime \prime },b})'(f_{a^{\prime \prime },b}(c))$
. But this quantity is in itself by induction comparable within a multiplicative constant
![]() to
to
![]() $\inf _{\tilde {a}\in [a,a']}(f_{\tilde {a},b}^{n-1})'(f_{\tilde {a},b}(c))$
. We use the statement of our result for
$\inf _{\tilde {a}\in [a,a']}(f_{\tilde {a},b}^{n-1})'(f_{\tilde {a},b}(c))$
. We use the statement of our result for
![]() $k=j-1$
.
$k=j-1$
.
We use (5.18) and note that
![]() $|a-a'|$
can also be written as
$|a-a'|$
can also be written as
![]() $|\xi (a,b)-\xi _1(a',b)|$
. By Lemma 3.4,
$|\xi (a,b)-\xi _1(a',b)|$
. By Lemma 3.4,
By combining (5.19), (5.20) and (5.21), we obtain
 $$ \begin{align*} &|f^j_{a,b}(x)-f^j_{a,b}(c)|\\&\quad=|f_{a,b}^{j-1}(f_{a,b}(x))-f_{a,b}^{j-1}(f_{a,b}(c))|\geq(f^{j-1})'(f_{a,b}(y))|f_{a,b}(x)-f_{a,b}(c)| \\ &\quad\geq\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))\,|f_{a,b}(x)-f_{a,b}(c)|\\ &\quad\geq C_7 e^{-3r}\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))\\ &\quad\geq C_7 e^{-2r}\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))|\xi_n(a,b)-\xi_n(a',b)|\\ &\quad\geq C_7e^{-2r} \inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))(\inf_{\tilde{a}\in[a,a']}\partial_af^{n}_{a^{\prime\prime},b}(c))|\xi_1(a,b)-\xi_1(a',b)|\\ &\quad\geq C_7 e^{-2r} \frac{ \inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))}{ \sup_{z\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(z))} (\inf_{\tilde{a}\in[a,a']}\partial_af^{n}_{a^{\prime\prime},b}(c))|)\,|\xi_j(a,b)-\xi_j(a',b)|. \end{align*} $$
$$ \begin{align*} &|f^j_{a,b}(x)-f^j_{a,b}(c)|\\&\quad=|f_{a,b}^{j-1}(f_{a,b}(x))-f_{a,b}^{j-1}(f_{a,b}(c))|\geq(f^{j-1})'(f_{a,b}(y))|f_{a,b}(x)-f_{a,b}(c)| \\ &\quad\geq\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))\,|f_{a,b}(x)-f_{a,b}(c)|\\ &\quad\geq C_7 e^{-3r}\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))\\ &\quad\geq C_7 e^{-2r}\inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))|\xi_n(a,b)-\xi_n(a',b)|\\ &\quad\geq C_7e^{-2r} \inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))(\inf_{\tilde{a}\in[a,a']}\partial_af^{n}_{a^{\prime\prime},b}(c))|\xi_1(a,b)-\xi_1(a',b)|\\ &\quad\geq C_7 e^{-2r} \frac{ \inf_{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))}{ \sup_{z\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(z))} (\inf_{\tilde{a}\in[a,a']}\partial_af^{n}_{a^{\prime\prime},b}(c))|)\,|\xi_j(a,b)-\xi_j(a',b)|. \end{align*} $$
Now
![]() $\sup _{z\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(z))$
and
$\sup _{z\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(z))$
and
![]() $\inf _{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))$
are comparable within constant
$\inf _{y\in I_r}(f^{j-1}_{a,b})'(f_{a,b}(y))$
are comparable within constant
![]() , by the statement of Lemma 5.7 with
, by the statement of Lemma 5.7 with
![]() $k=j-1$
. This is where the inductive step is used. Moreover, by Corollary 3.2 and induction statement (i), we have
$k=j-1$
. This is where the inductive step is used. Moreover, by Corollary 3.2 and induction statement (i), we have
![]() $\partial _af_{a,b}^n(c)\geq q_*^{-1} e^{2(n-1)^{2/3}}$
. Furthermore
$\partial _af_{a,b}^n(c)\geq q_*^{-1} e^{2(n-1)^{2/3}}$
. Furthermore
![]() $e^{-2r}\geq e^{-2\sqrt {n}}$
, by induction statement (v). Combining these estimates, we get
$e^{-2r}\geq e^{-2\sqrt {n}}$
, by induction statement (v). Combining these estimates, we get
since
![]() $n\geq n_0(a)$
and
$n\geq n_0(a)$
and
![]() $n_0(a)$
can be chosen arbitrarily large.
$n_0(a)$
can be chosen arbitrarily large.
When inserting this estimate in (5.16) we conclude that
To estimate
![]() $f_{a,b}'(f_{a,b}^j(c))$
from below, we use induction statement (vi) and (4.13). We get
$f_{a,b}'(f_{a,b}^j(c))$
from below, we use induction statement (vi) and (4.13). We get
Putting together (5.15), (5.22) and (5.23), we obtain
 $$ \begin{align} \frac{(f_{a,b}^k)'(f_{a,b}(y))}{(f_{a,b}^k)'(f_{a,b}(c))}< \exp\bigg(\frac{13\cdot 2}{C_9\cdot C_1^2}\sum_{j=1}^k \frac{e^{-4\sqrt{j}}}{e^{-2\sqrt {j}}}\bigg). \end{align} $$
$$ \begin{align} \frac{(f_{a,b}^k)'(f_{a,b}(y))}{(f_{a,b}^k)'(f_{a,b}(c))}< \exp\bigg(\frac{13\cdot 2}{C_9\cdot C_1^2}\sum_{j=1}^k \frac{e^{-4\sqrt{j}}}{e^{-2\sqrt {j}}}\bigg). \end{align} $$
For the lower bound, we obtain, in a similar way to (5.15),
 $$ \begin{align*} \frac{(f_{a,b}^k)'(f_{a,b}(c))}{(f_{a,b}^k)'(f_{a,b}(y))} \leq \exp \bigg( \sum_{j=1}^{k} \dfrac{13|f_{a,b}^j(y)-f_{a,b}^j(c)|} {(f_{a,b})'(f_{a,b}^j(y))} \bigg). \end{align*} $$
$$ \begin{align*} \frac{(f_{a,b}^k)'(f_{a,b}(c))}{(f_{a,b}^k)'(f_{a,b}(y))} \leq \exp \bigg( \sum_{j=1}^{k} \dfrac{13|f_{a,b}^j(y)-f_{a,b}^j(c)|} {(f_{a,b})'(f_{a,b}^j(y))} \bigg). \end{align*} $$
Note, however, that
and, using (5.9) and (5.22), we get
whenever
. Now
is fixed, and thus there is a positive integer
![]() $\tilde N$
such that if
$\tilde N$
such that if
![]() $j\ge \tilde N$
then
$j\ge \tilde N$
then
, and then
By making
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $I^*$
sufficiently small, we can make
$I^*$
sufficiently small, we can make
![]() $|f_{a,b}^j(c) - f_{a,b}^j(y)|$
smaller than
$|f_{a,b}^j(c) - f_{a,b}^j(y)|$
smaller than
instead of
![]() $2e^{-4\sqrt {j}}$
, and then we get
$2e^{-4\sqrt {j}}$
, and then we get
for some constant
depending only on
![]() $a_0$
. Thus, in the same way as we obtained (5.24), we get a similar estimate for the reciprocal ratio, but with a different constant. We choose the larger of those constants as
$a_0$
. Thus, in the same way as we obtained (5.24), we get a similar estimate for the reciprocal ratio, but with a different constant. We choose the larger of those constants as
and we get (5.13). The proof of (5.14) is completely analogous and will be omitted. As for the statement that
can be chosen arbitrarily close to
![]() $1$
(but larger than
$1$
(but larger than
![]() $1$
), we refer to the argument in Lemma 4.3.
$1$
), we refer to the argument in Lemma 4.3.
Lemma 5.8. Assume that condition (*) holds. Then the bound period p in the sense of Definition 5.5 satisfies
Proof. We claim that
![]() $p\leq 8r^{3/2}$
. Note that
$p\leq 8r^{3/2}$
. Note that
![]() $8 r^{3/2}\leq 8 n^{3/4} < n$
. We argue by contradiction. Assume that there is
$8 r^{3/2}\leq 8 n^{3/4} < n$
. We argue by contradiction. Assume that there is
![]() $k>8r^{3/2}$
such that
$k>8r^{3/2}$
such that
![]() $f^j_{a,b}(f_{a.b}(z)$
is still bound to
$f^j_{a,b}(f_{a.b}(z)$
is still bound to
![]() $f^j_{a,b}(f_{a.b}(c)$
for all
$f^j_{a,b}(f_{a.b}(c)$
for all
![]() $x\in I_{r,l}$
and all z between x and c. By the mean value theorem, there is a point y between x and c such that
$x\in I_{r,l}$
and all z between x and c. By the mean value theorem, there is a point y between x and c such that
By Lemma 5.7 and induction statement (iii),
Since
![]() $|x-c|\ge e^{-r-1}$
, by (4.13) we get
$|x-c|\ge e^{-r-1}$
, by (4.13) we get
Putting the last three inequalities together, we get
Taking into account (5.22) (which is valid also for
![]() $y=x$
), we get
$y=x$
), we get
Therefore,
where
is a constant only depending on
![]() $a_0$
.
$a_0$
.
If
![]() $\delta $
is sufficiently small, then
$\delta $
is sufficiently small, then
![]() , and we get
, and we get
![]() $ k^{2/3}<(k-1)^{2/3}+\tfrac 23k^{-1/3} <4r$
. We conclude that
$ k^{2/3}<(k-1)^{2/3}+\tfrac 23k^{-1/3} <4r$
. We conclude that
![]() $k\leq 8r^{3/2}$
and this gives a contradiction.
$k\leq 8r^{3/2}$
and this gives a contradiction.
Let us prove an elementary lemma about our family.
Lemma 5.9. For the family of double standard maps, if
![]() $0<|x-c|<\frac 12$
then
$0<|x-c|<\frac 12$
then
Proof. We have
![]() $c=\frac 12$
and
$c=\frac 12$
and
![]() $f_{a,b}^{\prime \prime }(t)=-4\pi b\sin (2\pi t)$
. Therefore
$f_{a,b}^{\prime \prime }(t)=-4\pi b\sin (2\pi t)$
. Therefore
![]() $f_{a,b}$
is strictly convex in
$f_{a,b}$
is strictly convex in
![]() $(c,c+\frac 12)$
, and thus for
$(c,c+\frac 12)$
, and thus for
![]() $x\in (c,c+\frac 12)$
we get (5.25). Similarly, in
$x\in (c,c+\frac 12)$
we get (5.25). Similarly, in
![]() $(c-\frac 12,c)$
the function
$(c-\frac 12,c)$
the function
![]() $f_{a,b}$
is strictly concave, and (5.25) follows.
$f_{a,b}$
is strictly concave, and (5.25) follows.
Lemma 5.10. There exists a positive constant
![]() such that if condition (*) holds, then
such that if condition (*) holds, then
Proof. By Definition 5.5, there exists
![]() $a\in \omega $
such that
$a\in \omega $
such that
We have
By the mean value theorem, there is a point y between x and c such that
Now we estimate the second summand in (5.28). As in the proof of Lemma 5.7, we can prove that
Therefore
From Lemma 5.7 we get

so

By the chain rule and Lemma 5.9 we get, from this inequality,

Since
![]() $x\in I_r$
, we have
$x\in I_r$
, we have
![]() $|x-c|\le e^{-r}$
, and we get (5.26) with a suitable choice of
$|x-c|\le e^{-r}$
, and we get (5.26) with a suitable choice of
.
Let
![]() $(n,\omega )$
be a free return pair. Consider the intervals
$(n,\omega )$
be a free return pair. Consider the intervals
![]() $\xi _{n+p+1+s}(\omega ,b)$
,
$\xi _{n+p+1+s}(\omega ,b)$
,
![]() $s=0,\ldots , s_0-1$
, where
$s=0,\ldots , s_0-1$
, where
![]() $s_0$
is the smallest non-negative integer such that
$s_0$
is the smallest non-negative integer such that
For
![]() $0 \leq s < s_0,$
we say that
$0 \leq s < s_0,$
we say that
![]() $\xi _{n+p+1+s} (\omega ,b)$
is in free orbit and the length of this orbit is
$\xi _{n+p+1+s} (\omega ,b)$
is in free orbit and the length of this orbit is
![]() $s_0$
. We also use the notation
$s_0$
. We also use the notation
![]() $n'=n+p+1+s_0$
and it is our new free return time.
$n'=n+p+1+s_0$
and it is our new free return time.
At the first free return there are different cases that can occur.
Case 1.
![]() $\Omega _{n'}=\xi _{n'}(\omega ,b)$
is completely contained in
$\Omega _{n'}=\xi _{n'}(\omega ,b)$
is completely contained in
![]() $I^*$
but does not contain a complete interval
$I^*$
but does not contain a complete interval
![]() $I_{r,\ell }$
. Then either
$I_{r,\ell }$
. Then either
![]() $\xi _{n+p+1+s_0}(\omega ,b)$
is contained in an interval
$\xi _{n+p+1+s_0}(\omega ,b)$
is contained in an interval
![]() $I_{r,l}$
or it is contained in the union of two adjacent intervals
$I_{r,l}$
or it is contained in the union of two adjacent intervals
![]() $I_{r,l} \cup I_{r,l+1}$
.
$I_{r,l} \cup I_{r,l+1}$
.
This is called an inessential free return. In this case
![]() $\omega \in {\mathcal P}_{n'}$
, and we just continue to iterate. This also applies if
$\omega \in {\mathcal P}_{n'}$
, and we just continue to iterate. This also applies if
![]() $\Omega _{n'}$
intersects the boundary of
$\Omega _{n'}$
intersects the boundary of
![]() $I^*$
but does not contain any of the end intervals.
$I^*$
but does not contain any of the end intervals.
Case 2.
![]() $\Omega _{n'}$
contains at least one of the partition intervals
$\Omega _{n'}$
contains at least one of the partition intervals
![]() $I_{r,\ell }$
. This is the case of an essential free return. We then proceed to define a new partition on a subset of
$I_{r,\ell }$
. This is the case of an essential free return. We then proceed to define a new partition on a subset of
![]() $\omega $
according to the following algorithm.
$\omega $
according to the following algorithm.
-
• We do not include the preimage of
 $(c- e^{-\sqrt { n'}},c+e^{-\sqrt { n'}})$
under
$(c- e^{-\sqrt { n'}},c+e^{-\sqrt { n'}})$
under
 $a\mapsto \xi _{n'}(a,b)$
in
$a\mapsto \xi _{n'}(a,b)$
in
 $\bigcup _{\omega '\in \mathcal {P}_{n'}}\omega '$
, in order that (BA) should be satisfied.
$\bigcup _{\omega '\in \mathcal {P}_{n'}}\omega '$
, in order that (BA) should be satisfied. -
• The intervals
 $\omega _{r,\ell }$
and
$\omega _{r,\ell }$
and
 $\omega _{r,\ell }'$
are defined as the preimages of
$\omega _{r,\ell }'$
are defined as the preimages of
 $I_{r,\ell }$
under
$I_{r,\ell }$
under
 $\omega \ni a\mapsto \xi _{n'}(a,b)$
. Because of the double covering property of
$\omega \ni a\mapsto \xi _{n'}(a,b)$
. Because of the double covering property of
 $f_{a,b}$
, there could be no, one or two such intervals. These will be new partition intervals of
$f_{a,b}$
, there could be no, one or two such intervals. These will be new partition intervals of
 ${\mathcal P}_{n'}$
. At the two ends of
${\mathcal P}_{n'}$
. At the two ends of
 $\omega $
we could have the property that some intervals only partially cover
$\omega $
we could have the property that some intervals only partially cover
 $I_{r,\ell }$
. In that case we use the special rule that we adjoin the corresponding subintervals to the adjacent intervals of
$I_{r,\ell }$
. In that case we use the special rule that we adjoin the corresponding subintervals to the adjacent intervals of
 ${\mathcal P}_{n'}$
.
${\mathcal P}_{n'}$
. -
• There may be at most three subintervals of
 $\omega $
(call them
$\omega $
(call them
 $\omega _1$
,
$\omega _1$
,
 $\omega _2$
and
$\omega _2$
and
 $\omega _3$
) that are mapped outside
$\omega _3$
) that are mapped outside
 $I^*$
by
$I^*$
by
 $\omega \ni a \mapsto \xi _{n'}(a,b)$
. At the beginning of the procedure there are at most two intervals mapped outside, but at later stages, because of the double covering property of
$\omega \ni a \mapsto \xi _{n'}(a,b)$
. At the beginning of the procedure there are at most two intervals mapped outside, but at later stages, because of the double covering property of
 $f_{a,b}$
, there can be three. In this case these intervals are long, that is, they are not contained in intervals adjacent to the end intervals in the partition of
$f_{a,b}$
, there can be three. In this case these intervals are long, that is, they are not contained in intervals adjacent to the end intervals in the partition of
 $(c-e^{-r_\delta +1},c+e^{-r_\delta +1})$
, they are considered to be still free, and the free period continues for these intervals. If one or more of the intervals
$(c-e^{-r_\delta +1},c+e^{-r_\delta +1})$
, they are considered to be still free, and the free period continues for these intervals. If one or more of the intervals
 $\omega _1$
,
$\omega _1$
,
 $\omega _2$
or
$\omega _2$
or
 $\omega _3$
are short, rather than long, they are adjoined to their adjacent neighbor.
$\omega _3$
are short, rather than long, they are adjoined to their adjacent neighbor.
Let
![]() $X_{\text {BA}}$
be the set that is mapped to
$X_{\text {BA}}$
be the set that is mapped to
![]() $(c-e^{-\sqrt {n'}},c+e^{-\sqrt {n'}})$
. Then we define the partition
$(c-e^{-\sqrt {n'}},c+e^{-\sqrt {n'}})$
. Then we define the partition
![]() ${\mathcal P}_{n'}|(\omega \setminus X_{\text {BA}})$
as the intervals
${\mathcal P}_{n'}|(\omega \setminus X_{\text {BA}})$
as the intervals
![]() $\{\omega _{r,\ell }\}$
,
$\{\omega _{r,\ell }\}$
,
![]() $\{\omega _{r,\ell }'\}$
and
$\{\omega _{r,\ell }'\}$
and
![]() $\omega _i$
,
$\omega _i$
,
![]() $i=1,2,3$
. Some of these intervals may be empty.
$i=1,2,3$
. Some of these intervals may be empty.
Later we will see that deletions because of (BA) do not happen in Case 1, because the interval
![]() $\Omega _{n'}$
is too long.
$\Omega _{n'}$
is too long.
In order to proceed, we need to verify, at least partially, the induction step from time n to time
![]() $n'$
. Here
$n'$
. Here
![]() $n'$
is interpreted as the first free return to
$n'$
is interpreted as the first free return to
![]() $I^*$
after n. There may be previous returns
$I^*$
after n. There may be previous returns
![]() $\nu $
, where another partition element of
$\nu $
, where another partition element of
![]() ${\mathcal P}_{\nu }$
has a free return, while the present parameter interval does not return.
${\mathcal P}_{\nu }$
has a free return, while the present parameter interval does not return.
Lemma 5.11. Assume induction statements (i)–(vi). Then induction statement conditions (i), (ii), (iii) and (iv) hold for any free return pair
![]() $(n',\omega ')$
, where
$(n',\omega ')$
, where
![]() $n'$
is as above.
$n'$
is as above.
Proof. Let
![]() $\eta $
be the distance from
$\eta $
be the distance from
![]() $\xi _n(\omega ,b)$
to c. Therefore, by induction statement (i) and (4.13),
$\xi _n(\omega ,b)$
to c. Therefore, by induction statement (i) and (4.13),
However, by (v),
, so we get
After time n there follows the bound period p, and by Lemma 5.7 and (iii) we get
for all
![]() $k\le p$
. Combining (5.30) and (5.31), we conclude that
$k\le p$
. Combining (5.30) and (5.31), we conclude that
For
![]() $k\leq p \leq 8r^{3/2}\leq 8 n^{3/4}$
, we conclude that
$k\leq p \leq 8r^{3/2}\leq 8 n^{3/4}$
, we conclude that
At time
![]() $n+p+1$
the bound period has expired and we have for all
$n+p+1$
the bound period has expired and we have for all
![]() $a\in \omega $
,
$a\in \omega $
,
where
![]() is a constant only depending on
is a constant only depending on
![]() $f_{a_0}$
.
$f_{a_0}$
.
For the total derivative we obtain
After raising (5.33) to the power
![]() $\tfrac 23$
we obtain
$\tfrac 23$
we obtain
Looking at the exponents, we get, using (5.7), the lower bound
Here we have used the information from Lemma 5.8,
![]() $p\leq 8n^{3/4}$
and that if
$p\leq 8n^{3/4}$
and that if
![]() $p\leq {1}/{100}n$
then
$p\leq {1}/{100}n$
then
Now, if
![]() $k=p+s$
and
$k=p+s$
and
![]() $0<s\le s_0$
, then we can use Lemma 4.9(ii). If
$0<s\le s_0$
, then we can use Lemma 4.9(ii). If
![]() $s\ge M$
then
$s\ge M$
then
If
![]() $s<M$
we use Lemma 4.5, which allows a perturbation to
$s<M$
we use Lemma 4.5, which allows a perturbation to
![]() $(a,b)\in {\mathcal N}$
with a worse constant
$(a,b)\in {\mathcal N}$
with a worse constant
![]() $\overline {d}/4$
instead of
$\overline {d}/4$
instead of
![]() $\overline {d}/2$
and we get
$\overline {d}/2$
and we get
Thus, independently of whether
![]() $s\ge M$
or
$s\ge M$
or
![]() $s<M$
, we have
$s<M$
, we have
Together with (5.32) (where we substitute
![]() $k=p+s$
), we get
$k=p+s$
), we get

Note that since the constants
![]() ,
,
![]() ,
,
![]() ,
,
![]() are absolute constants, p can be made arbitrarily large by making
are absolute constants, p can be made arbitrarily large by making
![]() $\delta $
sufficiently small. Doing this, we conclude that induction statements (ii) and (iii) hold for
$\delta $
sufficiently small. Doing this, we conclude that induction statements (ii) and (iii) hold for
![]() $\nu $
satisfying
$\nu $
satisfying
![]() $n+p<\nu < n'$
where
$n+p<\nu < n'$
where
![]() $n'$
is the next free return time.
$n'$
is the next free return time.
We now turn to verifying (i) at the next free return time
![]() $n'$
. Using the previous derivative estimates and (i) of Lemma 4.9, we get, after writing
$n'$
. Using the previous derivative estimates and (i) of Lemma 4.9, we get, after writing
![]() $n'=n+p+1+q$
, that
$n'=n+p+1+q$
, that
where
is an absolute constant only depending on
![]() $a_0$
. Arguing in different cases depending on the relative sizes of n and q, one can verify that induction statement (i) with n replaced by
$a_0$
. Arguing in different cases depending on the relative sizes of n and q, one can verify that induction statement (i) with n replaced by
![]() $n'$
holds.
$n'$
holds.
Since
and
do not depend on
![]() $\delta $
, while by making
$\delta $
, while by making
![]() $\delta $
sufficiently small we can make p as large as we want, we conclude using Lemma 5.8 that
$\delta $
sufficiently small we can make p as large as we want, we conclude using Lemma 5.8 that
This proves (iv) for
![]() $n'$
.
$n'$
.
We now delete the parameters that are mapped to
where
. We conclude that induction statements (v) and (vi) also hold. This completes the proof of the induction step.
We note that the proof also gives the information
Remark 5.12. From (5.36) it immediately follows that
which will be used later. We will also later use (5.36).
Remark 5.13. Clearly, in Lemma 3.4,
![]() $\omega $
can be replaced by any subinterval
$\omega $
can be replaced by any subinterval
![]() $\omega '\subset \omega $
. If we choose
$\omega '\subset \omega $
. If we choose
![]() $\mu =n'$
and if
$\mu =n'$
and if
![]() $\xi _{n'}(\omega ',b)\subset I^*$
, and
$\xi _{n'}(\omega ',b)\subset I^*$
, and
![]() $n+p+1\le \nu < \mu =n'$
, we can use Lemma 4.9(i) to estimate
$n+p+1\le \nu < \mu =n'$
, we can use Lemma 4.9(i) to estimate
![]() $\inf _{a\in \omega } (f_{a,b}^{n'-\nu })'(f_{a,b}^\nu (c))$
from below by
$\inf _{a\in \omega } (f_{a,b}^{n'-\nu })'(f_{a,b}^\nu (c))$
from below by
. Moreover, by Lemma 5.11 we know that induction statement (iii) holds for
![]() $\nu <n'$
. Therefore, we conclude from (3.7) that (3.8) holds with
$\nu <n'$
. Therefore, we conclude from (3.7) that (3.8) holds with
![]() $q'=q_*$
. We thus get
$q'=q_*$
. We thus get
6 The global distortion lemma
Lemma 6.1. There exists a constant
![]() , such that if a and
, such that if a and
![]() $a'$
are two parameter points, so that
$a'$
are two parameter points, so that
![]() $a,a'\in \omega \in {\mathcal P}_n$
, where n is a free return time and the induction statement for n (and all smaller free return times) holds, then
$a,a'\in \omega \in {\mathcal P}_n$
, where n is a free return time and the induction statement for n (and all smaller free return times) holds, then

for all
![]() $k \leq n-1$
.
$k \leq n-1$
.
Proof. Let us fix
![]() $k \leq n-1$
. Set
$k \leq n-1$
. Set
![]() $t_0=1$
and let
$t_0=1$
and let
![]() $\{t_j\}_{j=1}^m$
be the free return times arranged in increasing order. Here m is defined by the condition
$\{t_j\}_{j=1}^m$
be the free return times arranged in increasing order. Here m is defined by the condition
![]() $t_{m-1} < k \leq t_m-1$
, and we can assume that
$t_{m-1} < k \leq t_m-1$
, and we can assume that
![]() $t_m=n$
. Observe that for all free returns
$t_m=n$
. Observe that for all free returns
![]() $t_j$
there is
$t_j$
there is
![]() $r_j$
such that
$r_j$
such that
![]() $\xi _{t_j}(a,b), \xi _{t_j}(a',b) \in I_{r_j}$
.
$\xi _{t_j}(a,b), \xi _{t_j}(a',b) \in I_{r_j}$
.
Note that
![]() $f^{\prime }_{a,b}(x)=f^{\prime }_{a',b}(x)$
. Thus, using the mean value theorem, we can write the logarithm of the left-hand side of (6.1) as
$f^{\prime }_{a,b}(x)=f^{\prime }_{a',b}(x)$
. Thus, using the mean value theorem, we can write the logarithm of the left-hand side of (6.1) as
 $$ \begin{align*} &\log \frac{(f_{a,b}^{k})'(f_{a,b}(c))}{(f_{a',b}^{k})'(f_{a',b}(c))} = \log\frac{\prod_{j=1}^{k} f^{\prime}_{a,b}(\xi_j(a,b))} {\prod_{j=1}^{k} f^{\prime}_{a,b}(\xi_j(a',b))}\\ &\quad \leq\sum_{i=0}^{m-1}\bigg(\sum_{j=t_i}^{t_i+p_i}\bigg| \frac{f_{a,b}^{\prime\prime}(\eta_j)}{f_{a,b}'(\eta_j)}\bigg| |\xi_j(a,b)-\xi_j(a',b)| +\log\frac{(f_{a,b}^{t_{i+1}-t_i-p_i-1})'(\xi_{t_i+p_i+1}(a,b))} {(f_{a',b}^{t_{i+1}-t_i-p_i-1})'(\xi_{t_i+p_i+1}(a',b))}\bigg) \end{align*} $$
$$ \begin{align*} &\log \frac{(f_{a,b}^{k})'(f_{a,b}(c))}{(f_{a',b}^{k})'(f_{a',b}(c))} = \log\frac{\prod_{j=1}^{k} f^{\prime}_{a,b}(\xi_j(a,b))} {\prod_{j=1}^{k} f^{\prime}_{a,b}(\xi_j(a',b))}\\ &\quad \leq\sum_{i=0}^{m-1}\bigg(\sum_{j=t_i}^{t_i+p_i}\bigg| \frac{f_{a,b}^{\prime\prime}(\eta_j)}{f_{a,b}'(\eta_j)}\bigg| |\xi_j(a,b)-\xi_j(a',b)| +\log\frac{(f_{a,b}^{t_{i+1}-t_i-p_i-1})'(\xi_{t_i+p_i+1}(a,b))} {(f_{a',b}^{t_{i+1}-t_i-p_i-1})'(\xi_{t_i+p_i+1}(a',b))}\bigg) \end{align*} $$
for some
![]() $\eta _j$
between
$\eta _j$
between
![]() $\xi _j(a,b)$
and
$\xi _j(a,b)$
and
![]() $\xi _j(a',b)$
, where
$\xi _j(a',b)$
, where
![]() $p_i$
is the corresponding bound time and
$p_i$
is the corresponding bound time and
![]() $p_0=-1$
. We will denote the first sum in the parentheses above by
$p_0=-1$
. We will denote the first sum in the parentheses above by
![]() $S_i'$
and the second term in the parentheses by
$S_i'$
and the second term in the parentheses by
![]() $S_i^{\prime \prime }$
. Note that the sum
$S_i^{\prime \prime }$
. Note that the sum
![]() $S_0'$
is empty.
$S_0'$
is empty.

Set
![]() $\sigma _i=|\xi _{t_i}(a,b)-\xi _{t_i}(a',b)|$
. We claim that the sum
$\sigma _i=|\xi _{t_i}(a,b)-\xi _{t_i}(a',b)|$
. We claim that the sum
![]() $S_i'$
can be estimated from above by a constant times
$S_i'$
can be estimated from above by a constant times
![]() $\sigma _i e^{r_i}$
.
$\sigma _i e^{r_i}$
.
First we note that by (6.2), the first term of
![]() $S_i'$
can be estimated by
$S_i'$
can be estimated by
![]() .
.
For the remaining terms we introduce the reference interval
![]() $\Omega _{t_i}=I_{r_i+1}$
and intervals
$\Omega _{t_i}=I_{r_i+1}$
and intervals
![]() $\Omega _{t_i+\nu }= f_{a,b}^\nu (\Omega _{t_i})$
,
$\Omega _{t_i+\nu }= f_{a,b}^\nu (\Omega _{t_i})$
,
![]() $\nu =0,1,2,\ldots ,p_i$
. We have
$\nu =0,1,2,\ldots ,p_i$
. We have
 $$ \begin{align*} \xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)&= (f_{a,b}(\xi_{t_i}(a,b))-f_{a,b}(\xi_{t_i}(a',b))\\ &\quad+(f_{a,b}(\xi_{t_i}(a',b)-f_{a',b}(\xi_{t_i}(a',b))\\ &=f_{a,b}'(y)(\xi_{t_i}(a,b)-\xi_{t_i}(a',b))+(a-a') \end{align*} $$
$$ \begin{align*} \xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)&= (f_{a,b}(\xi_{t_i}(a,b))-f_{a,b}(\xi_{t_i}(a',b))\\ &\quad+(f_{a,b}(\xi_{t_i}(a',b)-f_{a',b}(\xi_{t_i}(a',b))\\ &=f_{a,b}'(y)(\xi_{t_i}(a,b)-\xi_{t_i}(a',b))+(a-a') \end{align*} $$
for some y between
![]() $\xi _{t_i}(a,b)$
and
$\xi _{t_i}(a,b)$
and
![]() $\xi _{t_i}(a',b)$
. Furthermore,
$\xi _{t_i}(a',b)$
. Furthermore,
![]() $|\Omega _{t_i+1}|=f_{a,b}'(y')|\Omega _{t_i}|$
for some
$|\Omega _{t_i+1}|=f_{a,b}'(y')|\Omega _{t_i}|$
for some
![]() $y'\in \Omega _{t_i}$
.
$y'\in \Omega _{t_i}$
.
We get
 $$ \begin{align} \frac{|\xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)|}{|\Omega_{t_i+1}|} =\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot\frac{\sigma_i} {|\Omega_{t_i}|}\pm\frac{|a-a'|}{f_{a,b}'(y')|\Omega_{t_i}|}. \end{align} $$
$$ \begin{align} \frac{|\xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)|}{|\Omega_{t_i+1}|} =\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot\frac{\sigma_i} {|\Omega_{t_i}|}\pm\frac{|a-a'|}{f_{a,b}'(y')|\Omega_{t_i}|}. \end{align} $$
By the mean value theorem,
 $$ \begin{align*} \frac{|a-a'|}{f_{a,b}'(y)\sigma_i}=\frac1{f_{a,b}'(y)\partial_a \xi_{t_i}(a^{\prime\prime},b)} \end{align*} $$
$$ \begin{align*} \frac{|a-a'|}{f_{a,b}'(y)\sigma_i}=\frac1{f_{a,b}'(y)\partial_a \xi_{t_i}(a^{\prime\prime},b)} \end{align*} $$
for some
![]() $a^{\prime \prime }$
between a and
$a^{\prime \prime }$
between a and
![]() $a'$
. By (3.5) and induction statement (iii),
$a'$
. By (3.5) and induction statement (iii),
By (4.13) and induction statement (v),
Therefore, we get

Since
![]() $t_i$
can be made as large as we want (because
$t_i$
can be made as large as we want (because
![]() $t_i\ge n_0$
), we get
$t_i\ge n_0$
), we get
![]() $|a-a'|<f_{a,b}'(y)\sigma _i/2$
. Therefore, from (6.3) we get
$|a-a'|<f_{a,b}'(y)\sigma _i/2$
. Therefore, from (6.3) we get
 $$ \begin{align*} \frac12\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot\frac{\sigma_i} {|\Omega_{t_i}|}<\frac{|\xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)|} {|\Omega_{t_i+1}|}<2\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot \frac{\sigma_i}{|\Omega_{t_i}|}. \end{align*} $$
$$ \begin{align*} \frac12\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot\frac{\sigma_i} {|\Omega_{t_i}|}<\frac{|\xi_{t_i+1}(a,b)-\xi_{t_i+1}(a',b)|} {|\Omega_{t_i+1}|}<2\frac{f_{a,b}'(y)}{f_{a,b}'(y')}\cdot \frac{\sigma_i}{|\Omega_{t_i}|}. \end{align*} $$
Since
![]() $y,y'\in I_{r_i}\cup I_{r_i+1}$
, we have
$y,y'\in I_{r_i}\cup I_{r_i+1}$
, we have
![]() $|y-c|\in [e^{-r_i-2},e^{-r_i}]$
, and the same holds for
$|y-c|\in [e^{-r_i-2},e^{-r_i}]$
, and the same holds for
![]() $y'$
. Therefore, by (4.13), we get
$y'$
. Therefore, by (4.13), we get

The right-hand side above is a weighted average between
![]() $(2-2b)/(2-2b)=1$
and
$(2-2b)/(2-2b)=1$
and
, so it is smaller than
. Since we can switch y and
![]() $y'$
, we get
$y'$
, we get

Thus, we get the following inequality with
:

Now we want to estimate
 $$ \begin{align*} \frac{|\xi_{t_i+{\nu}}(a,b)-\xi_{t_i+{\nu}}(a',b)|} {|\Omega_{t_i+{\nu}}|} \end{align*} $$
$$ \begin{align*} \frac{|\xi_{t_i+{\nu}}(a,b)-\xi_{t_i+{\nu}}(a',b)|} {|\Omega_{t_i+{\nu}}|} \end{align*} $$
from above. The numerator can be estimated as follows:
 $$ \begin{align} |\xi_{t_i+{\nu}}(a,b)-\xi_{t_{i+{\nu}}}(a',b)| &\leq |f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a,b}(c)) -f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a',b}(c))|\\ &+|f_{a,b}^{\nu}(f^{t_i}_{a',b}(c)) -f_{a',b}^{\nu}(f^{t_i}_{a',b}(c))|. \nonumber \end{align} $$
$$ \begin{align} |\xi_{t_i+{\nu}}(a,b)-\xi_{t_{i+{\nu}}}(a',b)| &\leq |f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a,b}(c)) -f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a',b}(c))|\\ &+|f_{a,b}^{\nu}(f^{t_i}_{a',b}(c)) -f_{a',b}^{\nu}(f^{t_i}_{a',b}(c))|. \nonumber \end{align} $$
By a similar argument to the proof of Lemma 5.8, in particular estimating
![]() $|a-a'|$
as in that lemma, we obtain that
$|a-a'|$
as in that lemma, we obtain that
Therefore, we get the estimate
 $$ \begin{align} |\xi_{t_i+{\nu}}(a,b)-\xi_{t_{i+{\nu}}}(a',b)| &\leq 2|f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a,b}(c)) -f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a',b}(c))|\\ &=2(f^{{\nu}-1}_{a,b})'(y)|\xi_{t_i+1}(a,b)- \xi_{t_i+1}(a',b)|,\nonumber \end{align} $$
$$ \begin{align} |\xi_{t_i+{\nu}}(a,b)-\xi_{t_{i+{\nu}}}(a',b)| &\leq 2|f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a,b}(c)) -f_{a,b}^{{\nu}-1}(f^{t_i+1}_{a',b}(c))|\\ &=2(f^{{\nu}-1}_{a,b})'(y)|\xi_{t_i+1}(a,b)- \xi_{t_i+1}(a',b)|,\nonumber \end{align} $$
where y is between
![]() $\xi _{t_{i+1}}(a,b)$
and
$\xi _{t_{i+1}}(a,b)$
and
![]() $\xi _{t_{i+1}}(a',b)$
(using the mean value theorem). Again by the same theorem there is
$\xi _{t_{i+1}}(a',b)$
(using the mean value theorem). Again by the same theorem there is
![]() $y^{\prime \prime }\in \Omega _{t_i+1}$
such that
$y^{\prime \prime }\in \Omega _{t_i+1}$
such that
By Lemma 5.7,
![]() , so we get
, so we get

Let us consider the interval
![]() $\omega _i\in \mathcal {P}_{t_i}$
containing
$\omega _i\in \mathcal {P}_{t_i}$
containing
![]() $\omega $
and denote its midpoint by
$\omega $
and denote its midpoint by
![]() $\hat {a}_i$
. Then by (5.11),
$\hat {a}_i$
. Then by (5.11),
for all
![]() $\tilde {a}\in \omega _i$
and
$\tilde {a}\in \omega _i$
and
![]() $\nu \le p_i$
.
$\nu \le p_i$
.
We claim that for all
![]() $\tilde {a}\in \omega _i$
and
$\tilde {a}\in \omega _i$
and
![]() $\nu \le p_i$
we have
$\nu \le p_i$
we have
There is an integer
![]() $\nu _0$
such that
$\nu _0$
such that
for all
![]() $\nu \geq \nu _0$
. Note that
$\nu \geq \nu _0$
. Note that
![]() $\nu _0$
depends only on
$\nu _0$
depends only on
![]() , which is independent of
, which is independent of
![]() $\delta $
. Therefore, we may assume that
$\delta $
. Therefore, we may assume that
![]() $\delta $
is so small that
$\delta $
is so small that
Moreover, by induction statement (v),
Consider
![]() $\nu \le p_i$
. If
$\nu \le p_i$
. If
![]() $\nu \ge \nu _0$
, then by (6.8), (6.10) and (6.12), we get
$\nu \ge \nu _0$
, then by (6.8), (6.10) and (6.12), we get
Therefore,
and (6.9) follows.
If
![]() $\nu <\nu _0$
then by (4.3) and (5.12),
$\nu <\nu _0$
then by (4.3) and (5.12),
 $$ \begin{align*} |\xi_{t_i+\nu}(\tilde{a},b)-\xi_\nu(\hat{a}_i,b)| &\le |\xi_{t_i+\nu}(\tilde{a},b)-\xi_\nu(\tilde{a},b)|+ |\xi_\nu(\tilde{a},b)-\xi_\nu(\hat{a}_i,b)|\\ &\le 4^\nu|\xi_{t_i}(\tilde{a},b)-c|+4^\nu|\tilde{a}-\hat{a}_i|\le 4^\nu(\delta+|\omega_i|). \end{align*} $$
$$ \begin{align*} |\xi_{t_i+\nu}(\tilde{a},b)-\xi_\nu(\hat{a}_i,b)| &\le |\xi_{t_i+\nu}(\tilde{a},b)-\xi_\nu(\tilde{a},b)|+ |\xi_\nu(\tilde{a},b)-\xi_\nu(\hat{a}_i,b)|\\ &\le 4^\nu|\xi_{t_i}(\tilde{a},b)-c|+4^\nu|\tilde{a}-\hat{a}_i|\le 4^\nu(\delta+|\omega_i|). \end{align*} $$
By Lemma 5.1(b) for
![]() $j=n_0$
and by making
$j=n_0$
and by making
![]() $n_0$
sufficiently large, we get
$n_0$
sufficiently large, we get
![]() $\partial _a\xi _j(a,b)\ge 1$
. Therefore,
$\partial _a\xi _j(a,b)\ge 1$
. Therefore,
Thus,
![]() $|\omega _i|\le \delta $
, and we get
$|\omega _i|\le \delta $
, and we get
Together with (6.11) and (6.12) in this case we also get (6.13), and (6.9) follows.
Now for each
![]() $\nu $
we choose
$\nu $
we choose
![]() $\tilde {a}_\nu $
between a and
$\tilde {a}_\nu $
between a and
![]() $a'$
, so that
$a'$
, so that
![]() $\xi _{t_i+\nu }(\tilde {a}_\nu ,b)=\eta _{t_i+\nu }$
. Thus, by (6.9) and (6.12),
$\xi _{t_i+\nu }(\tilde {a}_\nu ,b)=\eta _{t_i+\nu }$
. Thus, by (6.9) and (6.12),
By (6.2) we have

By the definition of bound periods and the definition of
![]() $\Omega _{t_i+\nu }$
, we have
$\Omega _{t_i+\nu }$
, we have
Moreover,
Substituting those two inequalities, (6.14), (6.7) and (6.4) into the right-hand side of (6.15), we get

for some constant
. This implies that there is a constant
such that

Together with the estimate on the first term of
![]() $S_i'$
, that we obtained long ago, we get a constant
$S_i'$
, that we obtained long ago, we get a constant
such that
Note that
depends on
, but not on
![]() $\delta $
.
$\delta $
.
To estimate
![]() $S_i^{\prime \prime }$
, we use Lemma 4.12, and immediately get
$S_i^{\prime \prime }$
, we use Lemma 4.12, and immediately get
However,
![]() $\delta>e^{-r_{i+1}}$
, so
$\delta>e^{-r_{i+1}}$
, so
This estimate also applies to
![]() $S_0^{\prime \prime }$
.
$S_0^{\prime \prime }$
.
By Lemma 3.4 applied to a subinterval
![]() $\omega '=[a,a']$
(or
$\omega '=[a,a']$
(or
![]() $[a',a]$
) of
$[a',a]$
) of
![]() $\omega $
(made possible by Remark 5.13) and (5.36) (see Remark 5.12), we get
$\omega $
(made possible by Remark 5.13) and (5.36) (see Remark 5.12), we get
As we already noticed in the proof of Lemma 5.11, by taking
![]() $\delta $
sufficiently small we can make
$\delta $
sufficiently small we can make
![]() $p_i$
as large as we need and we may assume that
$p_i$
as large as we need and we may assume that
and therefore we get
We are now ready to estimate the logarithm of the left-hand side of (6.1), which is less then or equal to
![]() $\sum _{i=0}^{m-1}(S_i'+S_i^{\prime \prime })$
. By (6.16) and (6.17), we get
$\sum _{i=0}^{m-1}(S_i'+S_i^{\prime \prime })$
. By (6.16) and (6.17), we get

Rearrange the sum
![]() $\sum _{i=0}^m\sigma _i/e^{-r_i}$
and group it according to the values of
$\sum _{i=0}^m\sigma _i/e^{-r_i}$
and group it according to the values of
![]() $r_i$
. Set
$r_i$
. Set
![]() $W_k=\{i\in [1,m]:r_i=k\}$
. Consider k such that
$W_k=\{i\in [1,m]:r_i=k\}$
. Consider k such that
![]() $W_k$
is non-empty. Then we can write
$W_k$
is non-empty. Then we can write
![]() $W_k=\{i_s<i_{s-1}<\cdots <i_0\}$
, and by (6.18) we have
$W_k=\{i_s<i_{s-1}<\cdots <i_0\}$
, and by (6.18) we have
![]() $\sigma _{i_j}\le \sigma _{i_0}/2^j$
. Thus,
$\sigma _{i_j}\le \sigma _{i_0}/2^j$
. Thus,
 $$ \begin{align*} \sum_{i\in W_k}\frac{\sigma_i}{e^{-r_i}}\le2\frac{\sigma_{\mu_k}} {e^{-k}}, \end{align*} $$
$$ \begin{align*} \sum_{i\in W_k}\frac{\sigma_i}{e^{-r_i}}\le2\frac{\sigma_{\mu_k}} {e^{-k}}, \end{align*} $$
where
![]() $\mu _k$
is the largest element of
$\mu _k$
is the largest element of
![]() $W_k$
. However,
$W_k$
. However,
![]() $\sigma _{\mu _k}$
is the length of an interval which is contained in the union of three subintervals of
$\sigma _{\mu _k}$
is the length of an interval which is contained in the union of three subintervals of
![]() $I_k$
, and the length of each of those subintervals is
$I_k$
, and the length of each of those subintervals is
![]() $|I_k|/k^2$
. Moreover,
$|I_k|/k^2$
. Moreover,
![]() $|I_k|<e^{-k}$
. Thus,
$|I_k|<e^{-k}$
. Thus,
 $$ \begin{align} \sum_{i\in W_k}\frac{\sigma_i}{e^{-r_i}}\le\frac6{k^2}. \end{align} $$
$$ \begin{align} \sum_{i\in W_k}\frac{\sigma_i}{e^{-r_i}}\le\frac6{k^2}. \end{align} $$
If
![]() $W_k$
is empty, then of course (6.19) also holds. In this way we get
$W_k$
is empty, then of course (6.19) also holds. In this way we get

The right-hand side of the above inequality is finite, so we can denote its exponential by
and then (6.1) holds.
Lemma 6.2. There exists a constant
![]() , such that if a and
, such that if a and
![]() $a'$
are two parameter points, so that
$a'$
are two parameter points, so that
![]() $a,a'\in \omega \in {\mathcal P}_n$
, where n is a free return time and the induction statement for n (and all smaller free return times) holds, then
$a,a'\in \omega \in {\mathcal P}_n$
, where n is a free return time and the induction statement for n (and all smaller free return times) holds, then

for all
![]() $k \leq n$
.
$k \leq n$
.
7 Part I of the proof of Theorem A
In this section we prove a proposition which is an essential part of the proof of Theorem A and is stated as follows.
Proposition 7.1. Let
![]() $a=a_0$
be an MT parameter for
$a=a_0$
be an MT parameter for
![]() $f_{a}$
and let
$f_{a}$
and let
![]() $\varepsilon>0$
be given. There exist a function
$\varepsilon>0$
be given. There exist a function
![]() $\eta (\varepsilon )\to 0$
and a function
$\eta (\varepsilon )\to 0$
and a function
![]() $b_0(\varepsilon )\to 1$
as
$b_0(\varepsilon )\to 1$
as
![]() $\varepsilon \to 0$
such that if
$\varepsilon \to 0$
such that if
![]() $b_0(\varepsilon )<b<1$
, if
$b_0(\varepsilon )<b<1$
, if
![]() $\omega _0$
is a parameter interval such that
$\omega _0$
is a parameter interval such that
such that
![]() $I_{r,\ell }\subset \xi _{n_0}(\omega _0,b)\subset I_{r,\ell }^+$
and such that induction assumptions (i)–(vi) are satisfied for
$I_{r,\ell }\subset \xi _{n_0}(\omega _0,b)\subset I_{r,\ell }^+$
and such that induction assumptions (i)–(vi) are satisfied for
![]() $n=n_0$
, then there is a set
$n=n_0$
, then there is a set
![]() $\tilde {E}_b\subset \omega _0$
such that
$\tilde {E}_b\subset \omega _0$
such that
![]() $|\tilde {E}_b|\geq (1-\eta (\varepsilon ))|\omega _0|$
,
$|\tilde {E}_b|\geq (1-\eta (\varepsilon ))|\omega _0|$
,
![]() $C=C(a_0)$
and
$C=C(a_0)$
and
![]() $\hat {\kappa }=\hat {\kappa }(a_0)>0$
so that
$\hat {\kappa }=\hat {\kappa }(a_0)>0$
so that
Note that the assumptions of Proposition 7.1 are satisfied by Lemma 5.1.
This, together with Proposition 8.1 in §8, immediately leads to the following corollary.
Corollary 7.2. The set E of parameters for which the double standard map is uniformly expanding accumulates on the MT points
![]() $(a_0,1)$
in the parameter space.
$(a_0,1)$
in the parameter space.
However, we will need a more general formulation of the propositions given above in order to prove Theorem A.
The proofs will be based on the induction formulated in §5. In the critical case
![]() $b=1$
, which we are not treating in detail, the remaining parameter set is of positive measure, while in the non-critical case
$b=1$
, which we are not treating in detail, the remaining parameter set is of positive measure, while in the non-critical case
![]() $b<1$
the remaining parameter set is a finite union of intervals.
$b<1$
the remaining parameter set is a finite union of intervals.
We first discuss the parameter deletion due to the (BA) assumption.
If n is a free essential return time for a partition element
![]() $\omega =(a,a')$
of a partition
$\omega =(a,a')$
of a partition
![]() ${\mathcal P}_{n^{\prime \prime }}$
, let
${\mathcal P}_{n^{\prime \prime }}$
, let
![]() $n^{\prime \prime }$
be the essential free return immediately before n.
$n^{\prime \prime }$
be the essential free return immediately before n.
At each time we may have to omit a fraction of the parameter interval because of (BA). Assume that the previous free return occurred in the interval
![]() $I_{r^{\prime \prime },\ell }$
. Its length is
$I_{r^{\prime \prime },\ell }$
. Its length is
![]() ${c}/{r^{\prime \prime 2}}|I_{r^{\prime \prime }}|$
,
${c}/{r^{\prime \prime 2}}|I_{r^{\prime \prime }}|$
,
![]() $1\leq c\leq 3$
. By the (BA) assumption applied to time
$1\leq c\leq 3$
. By the (BA) assumption applied to time
![]() $n^{\prime \prime }$
, we have
$n^{\prime \prime }$
, we have
Observe that the minimal length of
![]() $n-n^{\prime \prime }$
has a lower bound
$n-n^{\prime \prime }$
has a lower bound
![]() $n-n^{\prime \prime }\geq C\log(1/\delta )$
, where C is a constant only depending on
$n-n^{\prime \prime }\geq C\log(1/\delta )$
, where C is a constant only depending on
![]() $f_{a_0}$
. Note also that
$f_{a_0}$
. Note also that
![]() $r^{\prime \prime }\leq \sqrt {n}$
.
$r^{\prime \prime }\leq \sqrt {n}$
.
During the bound period the interval
![]() ${\mathcal K}_{r^{\prime \prime }+1}=(c,c+e^{-r^{\prime \prime }-1)})$
of size
${\mathcal K}_{r^{\prime \prime }+1}=(c,c+e^{-r^{\prime \prime }-1)})$
of size
![]() $e^{-r^{\prime \prime }-1}$
is increased to size
$e^{-r^{\prime \prime }-1}$
is increased to size
![]() $e^{-\sqrt {p^{\prime \prime }+1}}$
, where
$e^{-\sqrt {p^{\prime \prime }+1}}$
, where
![]() $p^{\prime \prime }\leq 8(r^{\prime \prime })^{3/2}$
by Lemma 5.8. Our present interval is of length
$p^{\prime \prime }\leq 8(r^{\prime \prime })^{3/2}$
by Lemma 5.8. Our present interval is of length
![]() ${c'}/{r^{\prime \prime 2}}|I_{r^{\prime \prime }}|$
,
${c'}/{r^{\prime \prime 2}}|I_{r^{\prime \prime }}|$
,
![]() $1\leq c' \leq 3$
.
$1\leq c' \leq 3$
.
For
![]() $a=a'$
the size of
$a=a'$
the size of
![]() $f_{a',b}({\mathcal K}_{r^{\prime \prime }+1})$
can be estimated by formula (4.12) as follows:
$f_{a',b}({\mathcal K}_{r^{\prime \prime }+1})$
can be estimated by formula (4.12) as follows:
By inserting
![]() $x=c+e^{-r^{\prime \prime }-1}$
we obtain an estimate for
$x=c+e^{-r^{\prime \prime }-1}$
we obtain an estimate for
![]() $|f_{a,b}({\mathcal K}_{r^{\prime \prime }+1})|$
as follows:
$|f_{a,b}({\mathcal K}_{r^{\prime \prime }+1})|$
as follows:
For the image of
![]() $\omega $
at time
$\omega $
at time
![]() $n^{\prime \prime }+1$
we obtain the estimate
$n^{\prime \prime }+1$
we obtain the estimate
Here
![]() $y\in I_r$
so it follows from (4.13) that
$y\in I_r$
so it follows from (4.13) that
![]() $|a-a'|$
can be estimated by the first term as in the estimate of (6.3) and we obtain
$|a-a'|$
can be estimated by the first term as in the estimate of (6.3) and we obtain
By the definition of a free return we also have the estimate
By Lemma 5.7 (the bound distortion lemma) and comparison with the orbit of
![]() ${\mathcal K}_{r^{\prime \prime }}$
the size of
${\mathcal K}_{r^{\prime \prime }}$
the size of
![]() $|\xi _{n^{\prime \prime }+p^{\prime \prime }+1}(a,b)-\xi _{n^{\prime \prime }+p^{\prime \prime }+1}(a',b)|$
has the lower bound
$|\xi _{n^{\prime \prime }+p^{\prime \prime }+1}(a,b)-\xi _{n^{\prime \prime }+p^{\prime \prime }+1}(a',b)|$
has the lower bound

We have again used that
![]() $\delta $
may be chosen arbitrarily small. Using (6.18) and Lemmas 4.9 and 3.4, it follows that the relative fraction to be deleted is at most
$\delta $
may be chosen arbitrarily small. Using (6.18) and Lemmas 4.9 and 3.4, it follows that the relative fraction to be deleted is at most

since
![]() $n\geq n_0$
; at each time n we may in principle to have to do such a deletion. The remaining fraction of the parameter interval can then be estimated from below as
$n\geq n_0$
; at each time n we may in principle to have to do such a deletion. The remaining fraction of the parameter interval can then be estimated from below as
 $$ \begin{align} \geq \prod_{n=N_0}^\infty(1- e^{-{1}/{2} \sqrt{n}}). \end{align} $$
$$ \begin{align} \geq \prod_{n=N_0}^\infty(1- e^{-{1}/{2} \sqrt{n}}). \end{align} $$
Note that this is arbitrarily close to 1 as
![]() $N_0(\varepsilon )\to \infty $
as
$N_0(\varepsilon )\to \infty $
as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
Outline of proof of Proposition 7.1.
The proof of Proposition 7.1 is based on induction. Note that the Cantor set construction can be stopped at a finite stage
![]() $\hat {N}$
, which is defined by the relation
$\hat {N}$
, which is defined by the relation
After this time the term
![]() $2-2b$
of equation (4.12) dominates in the derivative and we conclude that for all
$2-2b$
of equation (4.12) dominates in the derivative and we conclude that for all
![]() $a\in \tilde {E}_b$
there is a constant
$a\in \tilde {E}_b$
there is a constant
![]() $C>0$
such that
$C>0$
such that
A more general result with a more detailed proof is given in Proposition 8.1.
Outline of the proof of Proposition 1.1
. We proceed as in the proof of Theorem A. In this case the time
![]() $\hat {N}$
, after which the linear term
$\hat {N}$
, after which the linear term
![]() $2-2b$
dominates in the derivative, does not exist and the induction proceeds to infinite time. We now have to use the large deviation argument of [Reference Benedicks and Carleson3]. The main idea is that you delete parameters for which the critical orbits spend too large fractions of the time recovering the derivative loss from returns to
$2-2b$
dominates in the derivative, does not exist and the induction proceeds to infinite time. We now have to use the large deviation argument of [Reference Benedicks and Carleson3]. The main idea is that you delete parameters for which the critical orbits spend too large fractions of the time recovering the derivative loss from returns to
![]() $(c-\delta ^2,c +\delta ^2)$
. However, an estimate similar to (7.6) is still valid. We do not give the full details.
$(c-\delta ^2,c +\delta ^2)$
. However, an estimate similar to (7.6) is still valid. We do not give the full details.
8 Part II of the proof of Theorem A: the uniform expansion
In this section we consider
![]() $b<1$
, and we construct a non-empty union of open intervals
$b<1$
, and we construct a non-empty union of open intervals
![]() $\hat {E}_b \supset \tilde {E}_b$
so that for
$\hat {E}_b \supset \tilde {E}_b$
so that for
![]() $a\in \hat {E}_b$
there is an integer N such that
$a\in \hat {E}_b$
there is an integer N such that
![]() $f_{a,b}^N$
is uniformly expanding. This is formulated in Proposition 8.1. The set
$f_{a,b}^N$
is uniformly expanding. This is formulated in Proposition 8.1. The set
![]() $\hat {E}_b$
is obtained by stopping the construction of the parameter set
$\hat {E}_b$
is obtained by stopping the construction of the parameter set
![]() $\tilde {E}_b$
of Proposition 7.1 at a finite stage.
$\tilde {E}_b$
of Proposition 7.1 at a finite stage.
Let us outline the main idea of the proof of the uniform expansion. We will heavily use that the fact that
![]() $d=2-2b>0$
, that is, that the inflexion point is non-critical. In the case where the starting point x is outside the return interval
$d=2-2b>0$
, that is, that the inflexion point is non-critical. In the case where the starting point x is outside the return interval
![]() $I^*$
we can use (i) of Lemma 4.9 to conclude that if
$I^*$
we can use (i) of Lemma 4.9 to conclude that if
![]() $x, f_{a,b} (x),\ldots , f_{a,b}^{n-1}(x) \notin I^*$
, and
$x, f_{a,b} (x),\ldots , f_{a,b}^{n-1}(x) \notin I^*$
, and
![]() $f_{a,b}^n(x)\in I^*$
then
$f_{a,b}^n(x)\in I^*$
then
Here it is important that the constant
does not depend on
![]() $\delta $
.
$\delta $
.
At the return time n we have a derivative loss but this derivative loss is compensated during the bound period by Lemma 4.7. Since
![]() $p\to \infty $
as
$p\to \infty $
as
![]() $\delta \to 0$
, we can make the factor
$\delta \to 0$
, we can make the factor
![]() $e^{p^{2/3}}$
compensate
$e^{p^{2/3}}$
compensate
![]() $C_2/{C^*}$
by making
$C_2/{C^*}$
by making
![]() $\delta $
sufficiently small. We also use that the derivative of
$\delta $
sufficiently small. We also use that the derivative of
![]() $f_{a,b}$
is bounded below by
$f_{a,b}$
is bounded below by
![]() $f^{\prime }_{a,b}(\tfrac 12)=2-2b$
, and we will also denote this number by d.
$f^{\prime }_{a,b}(\tfrac 12)=2-2b$
, and we will also denote this number by d.
We state this result as follows.
Proposition 8.1. Let
![]() $a=a_0$
be an MT parameter. Then if
$a=a_0$
be an MT parameter. Then if
![]() $b_0=b_0(a_0)<1$
is sufficiently close to
$b_0=b_0(a_0)<1$
is sufficiently close to
![]() $1$
then for all
$1$
then for all
![]() $b\in (b_0,1)$
there is a set
$b\in (b_0,1)$
there is a set
![]() $\hat {E}_b$
which is a finite union of intervals
$\hat {E}_b$
which is a finite union of intervals
![]() $\{\omega _j\}_{j=0}^{J_0}$
such that, for
$\{\omega _j\}_{j=0}^{J_0}$
such that, for
![]() $a\in \omega _j$
, there is an integer
$a\in \omega _j$
, there is an integer
![]() $M_j$
such that for all
$M_j$
such that for all
![]() $x\in {\mathbb T}$
,
$x\in {\mathbb T}$
,
Proof. The proof is initially the same as the proof of Proposition 7.1 .
As before, we carry out the construction only until time
![]() $\hat {N}$
. Here
$\hat {N}$
. Here
![]() $\hat {N}$
is the smallest integer satisfying
$\hat {N}$
is the smallest integer satisfying
At time
![]() $\hat {N}$
we have a partition
$\hat {N}$
we have a partition
![]() ${\mathcal P}_{\hat {N}}$
consisting of finitely many intervals
${\mathcal P}_{\hat {N}}$
consisting of finitely many intervals
![]() $\{\omega _j\}_{j=1}^{M_{\hat {N}}}$
.
$\{\omega _j\}_{j=1}^{M_{\hat {N}}}$
.
We now aim to prove that the hyperbolicity statement (8.1) is true.
We first recall the two outside expansion statements of Lemma 4.9. Suppose that
![]() $(a,b)\in {\mathcal N}$
and chose
$(a,b)\in {\mathcal N}$
and chose
![]() $I=I^*=(c-\delta ,c+\delta )$
in that lemma. Then the following assertions hold.
$I=I^*=(c-\delta ,c+\delta )$
in that lemma. Then the following assertions hold.
-
(1) If
 $x,\ f_{a,b}x,\ldots , f_{a,b}^{n-1}x\not \in I^*$
and
$x,\ f_{a,b}x,\ldots , f_{a,b}^{n-1}x\not \in I^*$
and
 $f_{a,b}^n x\in I^*$
, then
$f_{a,b}^n x\in I^*$
, then 
-
(2) There is an integer M such that if
 $x, f_{a,b}x,\ldots ,f_{a,b}^{M-1}x\not \in I^*$
then
$x, f_{a,b}x,\ldots ,f_{a,b}^{M-1}x\not \in I^*$
then 
Let us define
![]() $R_0$
as the smallest integer satisfying
$R_0$
as the smallest integer satisfying
![]() $e^{-2R_0}\leq e^{-\sqrt {\hat {N}}}$
, that is,
$e^{-2R_0}\leq e^{-\sqrt {\hat {N}}}$
, that is,
![]() $R_0$
corresponds to the r where the square term in the expression for the derivative is of the same size as the constant term
$R_0$
corresponds to the r where the square term in the expression for the derivative is of the same size as the constant term
![]() $d=2-2b$
. The bound period
$d=2-2b$
. The bound period
![]() $p(x)$
,
$p(x)$
,
![]() $x\in (c-e^{-R_0},c+e^{-R_0})$
, is chosen to be the infimum of the bound period for
$x\in (c-e^{-R_0},c+e^{-R_0})$
, is chosen to be the infimum of the bound period for
![]() $y\in I_{\pm R_0}$
.
$y\in I_{\pm R_0}$
.
We also know by (5.6) and Lemma 5.7 that
and we also have that
Introducing
as
we can in all cases write these estimates as
The factor
![]() $\tfrac 12$
is here used to absorb the constant
$\tfrac 12$
is here used to absorb the constant
![]() .
.
Let us in the following use the notation
![]() $\hat {I}_{R_0}$
for the union of
$\hat {I}_{R_0}$
for the union of
![]() $(c-e^{-R_0-1},c+e^{-R_0-1})$
and the previously defined
$(c-e^{-R_0-1},c+e^{-R_0-1})$
and the previously defined
![]() $I_{-R_0}$
and
$I_{-R_0}$
and
![]() $I_{R_0}$
. The idea is that the derivative recovery has the same estimate for these three (original) intervals since
$I_{R_0}$
. The idea is that the derivative recovery has the same estimate for these three (original) intervals since
![]() $(f_{a,b})'(x)\sim d=2-2b$
in
$(f_{a,b})'(x)\sim d=2-2b$
in
![]() $\hat {I}_{R_0}$
and the bound period is defined in terms of
$\hat {I}_{R_0}$
and the bound period is defined in terms of
![]() ${I}_{R_0}$
.
${I}_{R_0}$
.
Divide the set
![]() ${\mathbb T}\setminus I^*$
into several pieces.
${\mathbb T}\setminus I^*$
into several pieces.
We first consider the set
For
![]() $x\in X_M$
, hyperbolicity is valid by Lemma 4.9(ii):
$x\in X_M$
, hyperbolicity is valid by Lemma 4.9(ii):
We also introduce the sets
Pick a
![]() $k\geq 1$
. Now write the set
$k\geq 1$
. Now write the set
 $$ \begin{align*} X_k=\bigcup_{r_\delta\leq |r|\leq R_0}X_{k,r}, \end{align*} $$
$$ \begin{align*} X_k=\bigcup_{r_\delta\leq |r|\leq R_0}X_{k,r}, \end{align*} $$
where
![]() $X_{k,r}=\{x\in X_k: f_{a,b}^kx\in I_r\}$
,
$X_{k,r}=\{x\in X_k: f_{a,b}^kx\in I_r\}$
,
![]() $|r_\delta |\leq |r|<R_0$
and
$|r_\delta |\leq |r|<R_0$
and
Then we know that for
![]() $x\in X_{k,r}$
,
$x\in X_{k,r}$
,
where
.
Here we have used the fact that also for the minimal possible p the factor
![]() always compensates the constant
always compensates the constant
![]() of Lemma 4.9, and this constant is independent of
of Lemma 4.9, and this constant is independent of
![]() $\delta $
.
$\delta $
.
Hence, we know that the entire set
![]() ${\mathbb T}$
can be written as a disjoint union of sets
${\mathbb T}$
can be written as a disjoint union of sets
![]() $\{Y_j\}_{j=1}^J$
so that for some
$\{Y_j\}_{j=1}^J$
so that for some
and all
![]() $x\in Y_j$
,
$x\in Y_j$
,
We start with an
![]() $x\in Y_{j_0}$
. After
$x\in Y_{j_0}$
. After
![]() $n_{j_0}$
steps we will end up in
$n_{j_0}$
steps we will end up in
![]() $Y_{j_1}$
and after another
$Y_{j_1}$
and after another
![]() $n_{j_1}$
steps we will end up in
$n_{j_1}$
steps we will end up in
![]() $Y_{j_2}$
, and so on. The total time will be
$Y_{j_2}$
, and so on. The total time will be
![]() $n_{j_0}+n_{j_1}+n_{j_2}+\cdots +n_{j_s}$
and
$n_{j_0}+n_{j_1}+n_{j_2}+\cdots +n_{j_s}$
and
where
 $$ \begin{align*} n_{j_s}+\cdots+n_{j_0}=\sum_{i=1}^{m} k_in_i. \end{align*} $$
$$ \begin{align*} n_{j_s}+\cdots+n_{j_0}=\sum_{i=1}^{m} k_in_i. \end{align*} $$
Let
![]() $n_{\max }=\max _{1\leq j \leq J}n_j$
and pick an integer N very large so that
$n_{\max }=\max _{1\leq j \leq J}n_j$
and pick an integer N very large so that
Here
![]() $d_1=1/B$
, where
$d_1=1/B$
, where
![]() $B=4\geq \max _{x\in {\mathbb T}}|f_{a,b}'(x)|$
.
$B=4\geq \max _{x\in {\mathbb T}}|f_{a,b}'(x)|$
.
For each point x there is an
![]() $n=n(x)=n_{j_0}+n_{j_1}+n_{j_2}+\cdots +n_{j_s}$
such that
$n=n(x)=n_{j_0}+n_{j_1}+n_{j_2}+\cdots +n_{j_s}$
such that
We claim that
This follows since
for a suitably
. We conclude that the statement of Proposition 8.1 holds.
![]() $\Box $
$\Box $
We now have all ingredients for the proof of Theorem A.
Let
![]() $\omega _0$
be an interval as defined in Proposition 7.1 satisfying (7.1) and let
$\omega _0$
be an interval as defined in Proposition 7.1 satisfying (7.1) and let
![]() $\tilde {E}_b$
be the set defined in this proposition. Let
$\tilde {E}_b$
be the set defined in this proposition. Let
![]() $\hat {E}_b=\hat {E}_b^{\hat {N}}\supset \tilde {E}_b$
be the set corresponding to the
$\hat {E}_b=\hat {E}_b^{\hat {N}}\supset \tilde {E}_b$
be the set corresponding to the
![]() $\hat {N}$
th-order construction of Proposition 8.1. Here
$\hat {N}$
th-order construction of Proposition 8.1. Here
![]() $\hat {N}$
is determined as the smallest integer satisfying
$\hat {N}$
is determined as the smallest integer satisfying
![]() $e^{-\hat {N}}\!\leq d$
as in the proof of Proposition 8.1. By (8.1) it then follows that the conclusion of Theorem A holds.
$e^{-\hat {N}}\!\leq d$
as in the proof of Proposition 8.1. By (8.1) it then follows that the conclusion of Theorem A holds.
9 Proof of Theorem B
In this section we prove our last result. The methods of its proof will be completely different than the ones used in the rest of the paper. We will use the term ‘countable’ in the sense of ‘at most countable’. For the definitions, see the Introduction.
Proof of Theorem B
Fix
![]() $b<1$
. Each tongue is open, so the set
$b<1$
. Each tongue is open, so the set
![]() $T_b$
is open. Therefore, it is the union of countably many components, each of them an open interval. Since the points on the boundary of a tongue belong to
$T_b$
is open. Therefore, it is the union of countably many components, each of them an open interval. Since the points on the boundary of a tongue belong to
![]() $TN$
, and the sets T and
$TN$
, and the sets T and
![]() $TN$
are disjoint, each component is contained in one tongue.
$TN$
are disjoint, each component is contained in one tongue.
We claim that the intersection of the closures of two distinct components
![]() $A_1$
and
$A_1$
and
![]() $A_2$
is empty. Suppose it is not and that a belongs to this intersection. Then
$A_2$
is empty. Suppose it is not and that a belongs to this intersection. Then
![]() $(a,b)\in TN$
, so it has its type. This type must be the same as the type of each of the tongues containing
$(a,b)\in TN$
, so it has its type. This type must be the same as the type of each of the tongues containing
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, so those types are the same, that is,
$A_2$
, so those types are the same, that is,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are contained in the same tongue. If n is the period of the neutral periodic orbit of
$A_2$
are contained in the same tongue. If n is the period of the neutral periodic orbit of
![]() $f_{a,b}$
, the map
$f_{a,b}$
, the map
![]() $f_{a,b}^n$
has an interval on which it looks like one of Cases 1, 2 or 4 of Lemma 4.1 of [Reference Misiurewicz and Rodrigues19]. By Theorem 4.1 and Lemma 2.6 of [Reference Misiurewicz and Rodrigues20], this cannot be Case 4 (a neutral periodic point repelling from both sides), and by Lemma 4.2 of [Reference Misiurewicz and Rodrigues19] it cannot be Case 1 or 2 (a neutral periodic point repelling from one side). This proves our claim.
$f_{a,b}^n$
has an interval on which it looks like one of Cases 1, 2 or 4 of Lemma 4.1 of [Reference Misiurewicz and Rodrigues19]. By Theorem 4.1 and Lemma 2.6 of [Reference Misiurewicz and Rodrigues20], this cannot be Case 4 (a neutral periodic point repelling from both sides), and by Lemma 4.2 of [Reference Misiurewicz and Rodrigues19] it cannot be Case 1 or 2 (a neutral periodic point repelling from one side). This proves our claim.
If a parameter
![]() $a\in TN_b$
does not belong to a boundary of a component of
$a\in TN_b$
does not belong to a boundary of a component of
![]() $T_b$
, then by Lemma 4.2 of [Reference Misiurewicz and Rodrigues19] the neutral periodic orbit of
$T_b$
, then by Lemma 4.2 of [Reference Misiurewicz and Rodrigues19] the neutral periodic orbit of
![]() $f_{a,b}$
is repelling from both sides (Case 4), so by Theorem 4.1 and Lemma 2.6 of [Reference Misiurewicz and Rodrigues20] a is isolated in the set of elements of
$f_{a,b}$
is repelling from both sides (Case 4), so by Theorem 4.1 and Lemma 2.6 of [Reference Misiurewicz and Rodrigues20] a is isolated in the set of elements of
![]() $T_b\cup TN_b$
which have type of the same period. This proves that there are only countably many such values of a.
$T_b\cup TN_b$
which have type of the same period. This proves that there are only countably many such values of a.
By the claim, the complement of
![]() $T_b$
is a closed set without isolated points. The set
$T_b$
is a closed set without isolated points. The set
![]() $TN_b$
is countable. Therefore
$TN_b$
is countable. Therefore
![]() $E_b$
(which is the complement of
$E_b$
(which is the complement of
![]() $T_b$
minus
$T_b$
minus
![]() $TN_b$
) is dense in the complement of
$TN_b$
) is dense in the complement of
![]() $T_b$
.
$T_b$
.
The second part of the statement follows from the first and the fact that each component of
![]() $T_b$
is contained in one tongue.
$T_b$
is contained in one tongue.
Acknowledgements
The authors would like to thank the referee for his careful reading and several valuable suggestions and corrections. The authors would like to thank the Göran Gustafsson Foundation UU/KTH for financial support. The research of Michał Misiurewicz was partially supported by grant no. 4266012 from the Simons Foundation, and the research of Michael Benedicks was partially supported by the Swedish Research Council, grant no. 2016-05482.