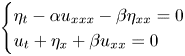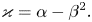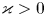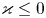1. Introduction
1.1 The model system
Given the parameters $\alpha \neq 0$![]() and $\beta \in \mathbb {R}$
and $\beta \in \mathbb {R}$![]() , we consider the system of linear partial differential equations
, we consider the system of linear partial differential equations

ruling the evolution of the variables,
subject to the boundary conditions
The system is supplemented with the initial conditions
where $\phi$![]() and $\psi$
and $\psi$![]() are assigned functions. In this presentation, the interval $[0,\,\pi ]$
are assigned functions. In this presentation, the interval $[0,\,\pi ]$![]() is clearly fungible, and could be replaced by any interval $[a,\,b]$
is clearly fungible, and could be replaced by any interval $[a,\,b]$![]() .
.
System (1.1) arises in the theoretical treatment of hydrodynamics, where it appears as the linearization of a renowned model for the propagation of shallow water waves. In this context, $\eta$![]() represents the height surface of the wave, while $u$
represents the height surface of the wave, while $u$![]() is the speed of propagation. Although the general model was first introduced by Kuperschmidt in 1985 [Reference Kupershmidt13] as a generalization of the Boussinesq system, a number of particular instances were already well known in the literature. For this reason, (1.1) is often referred to as the Whitham–Broer–Kaup (WBK) system, after the names of the ones who first derived and analysed it for specific values of $\alpha$
is the speed of propagation. Although the general model was first introduced by Kuperschmidt in 1985 [Reference Kupershmidt13] as a generalization of the Boussinesq system, a number of particular instances were already well known in the literature. For this reason, (1.1) is often referred to as the Whitham–Broer–Kaup (WBK) system, after the names of the ones who first derived and analysed it for specific values of $\alpha$![]() and $\beta$
and $\beta$![]() (see [Reference Broer7, Reference Kaup12, Reference Whitham18]).
(see [Reference Broer7, Reference Kaup12, Reference Whitham18]).
Nowadays, the topic is deserving some attention: there is a wide recent literature on both the linear and the nonlinear versions of (1.1). Great part of the studies have been devoted to the search of solitons and travelling wave solutions (see, e.g., [Reference Atangana and Baleanu4, Reference Li and Xu14, Reference Rogers and Pashaev16, Reference Xie, Yan and Zhang19–Reference Yan and Zhang21] and references therein), but some effort has also been directed towards numerical investigations [Reference Anber and Dahmani2, Reference Asgari, Dehghan and Mohebbi3, Reference Chen and Wang8, Reference Daniali and Rafei9]. In spite of this number of contributions, however, very few papers are concerned with the well-posedness of the general system, and with the decay properties (if any) of the general solution. One recent example are the works [Reference Bedjaoui, Kumar and Mammeri5, Reference Bedjaoui and Mammeri6] where, among other results, the authors show that system (1.1) is ill-posed when $\alpha \leq \beta ^2$![]() .
.
Without exception, all of these articles share the common assumption that the variables involved are defined on the whole real line $\mathbb {R}$![]() . Indeed, the analysis on unbounded domains is quite common in the theory of hydrodynamics, for it allows to investigate many interesting phenomena, ranging from the existence of solitons to the dispersive properties of the model. Notwithstanding, albeit being certainly useful for applicative purposes, the unboundedness hypothesis is a modelling simplification, that does not comply with the real (and structurally bounded) world. For this reason, it is of paramount importance to provide a solid mathematical justification of the model by thoroughly investigating the physical case of bounded domains. This is exactly the purpose of this work. Indeed, our aim is to describe the WBK system's properties in this novel setting. Which thing poses a main problem, since the Fourier transform is no longer applicable. Another issue is the correct choice of the boundary conditions. Letting aside the undeniable interest from the mathematical physics point of view, a strong theoretical background for the bounded case is also pivotal for numerical applications.
. Indeed, the analysis on unbounded domains is quite common in the theory of hydrodynamics, for it allows to investigate many interesting phenomena, ranging from the existence of solitons to the dispersive properties of the model. Notwithstanding, albeit being certainly useful for applicative purposes, the unboundedness hypothesis is a modelling simplification, that does not comply with the real (and structurally bounded) world. For this reason, it is of paramount importance to provide a solid mathematical justification of the model by thoroughly investigating the physical case of bounded domains. This is exactly the purpose of this work. Indeed, our aim is to describe the WBK system's properties in this novel setting. Which thing poses a main problem, since the Fourier transform is no longer applicable. Another issue is the correct choice of the boundary conditions. Letting aside the undeniable interest from the mathematical physics point of view, a strong theoretical background for the bounded case is also pivotal for numerical applications.
1.2 The results
We perform a complete analysis of (1.1)–(1.3), in dependence of the structural parameters $\alpha$![]() and $\beta$
and $\beta$![]() . Defining the number
. Defining the number
we show that the problem is well-posed if and only if
At first glance, this might seem surprising. While the first leading equation, when $\beta >0$![]() and in absence of the coupling, is of diffusion type, the second one resembles a backward heat equation, which is known to be ill-posed. Or the other way around if $\beta <0$
and in absence of the coupling, is of diffusion type, the second one resembles a backward heat equation, which is known to be ill-posed. Or the other way around if $\beta <0$![]() . This seeming contradiction can be resolved upon a closer look to system (1.1). Indeed, although the nature of the model looks parabolic, the system actually conceals a wave-like (hence hyperbolic) structure. To uncover it, one can simply take the time derivative of the two equations. After some simplifications, one arrives at
. This seeming contradiction can be resolved upon a closer look to system (1.1). Indeed, although the nature of the model looks parabolic, the system actually conceals a wave-like (hence hyperbolic) structure. To uncover it, one can simply take the time derivative of the two equations. After some simplifications, one arrives at

that is, two uncoupled wave equations, except with the Bilaplacian instead of the usual Laplace-Dirichlet operator [Reference Bedjaoui, Kumar and Mammeri5].
When the system is well-posed, we are actually able to compute the exact solution to (1.1)–(1.3), whose corresponding energy turns out to be constant in time, in compliance with the wave-like nature of (1.1).
Nevertheless, for the ill-posed problem corresponding to $\varkappa \leq 0$![]() , we can still prove uniqueness within the class of strong solutions, as well as exponential instability, by means of logarithmic convexity arguments. A particular situation occurs in the limit case $\varkappa =0$
, we can still prove uniqueness within the class of strong solutions, as well as exponential instability, by means of logarithmic convexity arguments. A particular situation occurs in the limit case $\varkappa =0$![]() , where, although the problem is generally ill-posed, we have existence and uniqueness of strong solutions.
, where, although the problem is generally ill-posed, we have existence and uniqueness of strong solutions.
Our approach heavily relies on the theory of linear semigroups. Specifically, having called ${\boldsymbol {u}}(t) = (\eta (t),\, u(t))$![]() , we rephrase our system as the abstract ODE
, we rephrase our system as the abstract ODE
on a suitable Hilbert space ${\mathcal {H}}$![]() . The well-posedness of the system strongly depends on the knowledge of the spectrum $\sigma ({\mathbb {A}})$
. The well-posedness of the system strongly depends on the knowledge of the spectrum $\sigma ({\mathbb {A}})$![]() of ${\mathbb {A}}$
of ${\mathbb {A}}$![]() , of which a detailed description is given, showing in particular that it is purely punctual whenever $\varkappa \neq 0$
, of which a detailed description is given, showing in particular that it is purely punctual whenever $\varkappa \neq 0$![]() . Besides, when $\varkappa >0$
. Besides, when $\varkappa >0$![]() the (normalized) eigenfunctions of ${\mathbb {A}}$
the (normalized) eigenfunctions of ${\mathbb {A}}$![]() form a complete orthonormal basis of ${\mathcal {H}}$
form a complete orthonormal basis of ${\mathcal {H}}$![]() . This fact is quite remarkable, as the operator ${\mathbb {A}}$
. This fact is quite remarkable, as the operator ${\mathbb {A}}$![]() is not selfadjoint. Incidentally, this is what allows us to write down the exact solutions to the system.
is not selfadjoint. Incidentally, this is what allows us to write down the exact solutions to the system.
2. Preliminaries
2.1 Functional setting and notation
In what follows, the symbols $\langle \cdot,\, \cdot \rangle$![]() and $\|\cdot \|$
and $\|\cdot \|$![]() stand for the inner product and norm on the real Hilbert space of square summable functions $H = L^2(0,\,\pi )$
stand for the inner product and norm on the real Hilbert space of square summable functions $H = L^2(0,\,\pi )$![]() . Besides, we denote the standard Sobolev spaces $H^j(0,\,\pi )$
. Besides, we denote the standard Sobolev spaces $H^j(0,\,\pi )$![]() and $H^1_0(0,\,\pi )$
and $H^1_0(0,\,\pi )$![]() simply by $H^j$
simply by $H^j$![]() and $H^1_0$
and $H^1_0$![]() . Finally, we define the Hilbert subspace $H_*$
. Finally, we define the Hilbert subspace $H_*$![]() of $H$
of $H$![]() of zero-mean functions, i.e.,
of zero-mean functions, i.e.,
and we set
2.2 Some operator theoretical issues
We recall some basic facts on the functional calculus of the Laplace-Dirichlet operator
that will be used in the sequel (see, e.g., [Reference Rudin17]). It is well known that the spectrum $\sigma (A)$![]() of $A$
of $A$![]() is purely punctual. Being defined on the interval $[0,\,\pi ]$
is purely punctual. Being defined on the interval $[0,\,\pi ]$![]() , the eigenvalues of $A$
, the eigenvalues of $A$![]() are given by
are given by
Besides, each $\lambda _n$![]() is simple, and the corresponding (normalized) eigenfunction is
is simple, and the corresponding (normalized) eigenfunction is
By the spectral theorem, the set $\{w_n\}_{n=1}^{\infty }$![]() forms a complete orthonormal basis of $H$
forms a complete orthonormal basis of $H$![]() . For every measurable function $F:\sigma (A)\to \mathbb {C}$
. For every measurable function $F:\sigma (A)\to \mathbb {C}$![]() , it is possible to define via the functional calculus the operator $F(A):H\to H$
, it is possible to define via the functional calculus the operator $F(A):H\to H$![]() as
as

with domain

In particular, $F(A)$![]() is a bounded operator on $H$
is a bounded operator on $H$![]() if and only if $F$
if and only if $F$![]() is a bounded function on $\sigma (A)$
is a bounded function on $\sigma (A)$![]() . Finally, given two measurable functions $G,\,F$
. Finally, given two measurable functions $G,\,F$![]() on $\sigma (A)$
on $\sigma (A)$![]() , the operator $G(A)F(A)$
, the operator $G(A)F(A)$![]() acts as
acts as

wherever is defined.
Remark 2.1 We will also consider the complexification of $A$![]() (that we keep denoting by $A$
(that we keep denoting by $A$![]() ), namely, the operator on the complex Hilbert space $H\oplus iH$
), namely, the operator on the complex Hilbert space $H\oplus iH$![]() acting as
acting as
with $u,\,v$![]() real-valued functions.
real-valued functions.
3. The problem in abstract form
We introduce the phase space of our problem, namely, the product Hilbert space
endowed with the scalar product
and norm
Remark 3.1 The norm in $H^1_*$![]() does not contain the term $\|u\|$
does not contain the term $\|u\|$![]() due to the Poincaré inequality, which holds for zero-mean functions.
due to the Poincaré inequality, which holds for zero-mean functions.
Defining the state vector
we view (1.1)–(1.2) as the ODE in ${\mathcal {H}}$![]()
Here, ${\mathbb {A}}$![]() is the linear operator on ${\mathcal {H}}$
is the linear operator on ${\mathcal {H}}$![]() acting as
acting as
with (dense) domain
As typically occurs for differential operators, it can be easily seen that ${\mathbb {A}}$![]() is a closed operator. Besides, observe that if $(\eta,\,u) \in {\mathfrak {D}}({\mathbb {A}})$
is a closed operator. Besides, observe that if $(\eta,\,u) \in {\mathfrak {D}}({\mathbb {A}})$![]() , then
, then
Remark 3.2 When $\varkappa \neq 0$![]() the domain of ${\mathbb {A}}$
the domain of ${\mathbb {A}}$![]() can be equivalently written as
can be equivalently written as

Remark 3.3 Instead, when $\varkappa =0$![]() ,
,
Accordingly, the two conditions in the definition of ${\mathfrak {D}}({\mathbb {A}})$![]() coincide, and this does not allow to recover (1.2) any longer. Indeed, although in the previous literature the boundary conditions are always given in the form (1.2), even when $\varkappa =0$
coincide, and this does not allow to recover (1.2) any longer. Indeed, although in the previous literature the boundary conditions are always given in the form (1.2), even when $\varkappa =0$![]() , we believe that more correctly they should read
, we believe that more correctly they should read
In which case, (1.2) and (3.1) are the same if and only if $\varkappa \neq 0$![]() .
.
4. The spectrum of ${\mathbb {A}}$
In this section, we provide a complete characterization of the spectrum $\sigma ({\mathbb {A}})$![]() of the (complexification of the) operator ${\mathbb {A}}$
of the (complexification of the) operator ${\mathbb {A}}$![]() . We first consider the case $\varkappa \neq 0$
. We first consider the case $\varkappa \neq 0$![]() . To this end, we define the parameter
. To this end, we define the parameter

The following theorem holds.
Theorem 4.1 Let $\varkappa \neq 0$![]() , and let $\lambda$
, and let $\lambda$![]() be a complex number such that
be a complex number such that
Then $\lambda$![]() belongs to the resolvent set $\rho ({\mathbb {A}})$
belongs to the resolvent set $\rho ({\mathbb {A}})$![]() of ${\mathbb {A}}$
of ${\mathbb {A}}$![]() .
.
Proof. Let $\lambda \in {\mathbb {C}}$![]() be fixed. For ${\boldsymbol {f}} = (f,\,g) \in {\mathcal {H}}$
be fixed. For ${\boldsymbol {f}} = (f,\,g) \in {\mathcal {H}}$![]() , we look for the unique solution to the functional equation
, we look for the unique solution to the functional equation
In components, this reads

Setting $v=u_x$![]() , and taking the derivative of the second equation, we get
, and taking the derivative of the second equation, we get

We now multiply the first equation of (4.2) by $\beta$![]() , and the second one by $\alpha$
, and the second one by $\alpha$![]() . Adding the results, we obtain
. Adding the results, we obtain
where
At this point, we introduce the new variable
and we consider the system made by (minus) the first equation of (4.2) and (4.3), to wit,

where $A$![]() is the Laplace-Dirichlet operator discussed in Subsection 2.2. Then, from the first equation above we learn that
is the Laplace-Dirichlet operator discussed in Subsection 2.2. Then, from the first equation above we learn that
Substituting (4.5) into the second equation of (4.4), we end up with
having set
and
By the functional calculus of $A$![]() , we conclude that (4.6) has a unique solution given by
, we conclude that (4.6) has a unique solution given by
where
if and only if $G$![]() is bounded on the spectrum of $A$
is bounded on the spectrum of $A$![]() . More explicitly, recalling (2.2),
. More explicitly, recalling (2.2),

Thus, we have a unique solution for every $q\in H$![]() if and only if
if and only if
that is, if and only if
In which case, since when $s\to +\infty$![]()
the solution $\eta$![]() belongs to the space $H^2\cap H_0^1$
belongs to the space $H^2\cap H_0^1$![]() . By (4.5), this implies that $\xi \in H^2\cap H_0^1$
. By (4.5), this implies that $\xi \in H^2\cap H_0^1$![]() . Finally, from the very definition of $\xi$
. Finally, from the very definition of $\xi$![]() , we read that $u_x \in H^1_0$
, we read that $u_x \in H^1_0$![]() and $u \in H^3$
and $u \in H^3$![]() . Summarizing, for every $\lambda \not = \pm \rho n^2$
. Summarizing, for every $\lambda \not = \pm \rho n^2$![]() we have found a unique solution $(\eta,\,u) \in {\mathfrak {D}}({\mathbb {A}})$
we have found a unique solution $(\eta,\,u) \in {\mathfrak {D}}({\mathbb {A}})$![]() to the resolvent equation (4.1). Hence, each of these $\lambda$
to the resolvent equation (4.1). Hence, each of these $\lambda$![]() belongs to the resolvent set $\rho ({\mathbb {A}})$
belongs to the resolvent set $\rho ({\mathbb {A}})$![]() .
.
To complete the analysis, we show that the remaining values of $\lambda$![]() are elements of the spectrum of ${\mathbb {A}}$
are elements of the spectrum of ${\mathbb {A}}$![]() .
.
Theorem 4.2 Let $\varkappa \neq 0$![]() . Then all the numbers
. Then all the numbers
are eigenvalues of ${\mathbb {A}}$![]() . Besides, they are all simple.
. Besides, they are all simple.
Proof. For every $n = 1,\,2,\,3,\,\ldots$![]() , let us define the functions
, let us define the functions
It is apparent that
and a straightforward calculation reveals that
This tells that each $\lambda ^\pm _n$![]() is an eigenvalue of ${\mathbb {A}}$
is an eigenvalue of ${\mathbb {A}}$![]() , and ${\boldsymbol {u}}^{\pm }_n$
, and ${\boldsymbol {u}}^{\pm }_n$![]() is a corresponding eigenfunction. We are left to show that any other eigenfunction of $\lambda ^\pm _n$
is a corresponding eigenfunction. We are left to show that any other eigenfunction of $\lambda ^\pm _n$![]() is a multiple of ${\boldsymbol {u}}^{\pm }_n$
is a multiple of ${\boldsymbol {u}}^{\pm }_n$![]() . To this end, let $n$
. To this end, let $n$![]() be fixed, and let ${\boldsymbol {v}}=(\eta,\,u)$
be fixed, and let ${\boldsymbol {v}}=(\eta,\,u)$![]() be an eigenfunction of $\lambda _n^+$
be an eigenfunction of $\lambda _n^+$![]() (the argument for $\lambda _n^-$
(the argument for $\lambda _n^-$![]() is the same). Hence,
is the same). Hence,
Exploiting the same change of variables of the previous proof, we arrive at the system

Then,
and substituting this expression into the second equation above, we get
Therefore, either $\eta = 0$![]() , in which case $\xi = 0$
, in which case $\xi = 0$![]() , or $\eta$
, or $\eta$![]() is an eigenfunction of the operator $A^2$
is an eigenfunction of the operator $A^2$![]() relative to the eigenvalue $n^4$
relative to the eigenvalue $n^4$![]() . In the latter case, since the eigenvalues of $A^2$
. In the latter case, since the eigenvalues of $A^2$![]() are all simple (a straightforward consequence of the functional calculus of $A$
are all simple (a straightforward consequence of the functional calculus of $A$![]() ), $\eta$
), $\eta$![]() is unique up to a multiplicative constant. More precisely, $\eta =w_n$
is unique up to a multiplicative constant. More precisely, $\eta =w_n$![]() , with $w_n$
, with $w_n$![]() given by (2.1). But then $\xi$
given by (2.1). But then $\xi$![]() is unique as well (up to the same constant), and in turn so is $u$
is unique as well (up to the same constant), and in turn so is $u$![]() . In conclusion, ${\boldsymbol {v}}={\boldsymbol {u}}_n^+$
. In conclusion, ${\boldsymbol {v}}={\boldsymbol {u}}_n^+$![]() , up to a multiplicative constant, meaning that $\lambda ^+_n$
, up to a multiplicative constant, meaning that $\lambda ^+_n$![]() is a simple eigenvalue.
is a simple eigenvalue.
Remark 4.3 The proof of the invertibility of ${\mathbb {A}}$![]() , is actually simpler. Indeed, it amounts to consider system (4.4) with $\lambda = 0$
, is actually simpler. Indeed, it amounts to consider system (4.4) with $\lambda = 0$![]() . At that point, noting that the domain of ${\mathbb {A}}$
. At that point, noting that the domain of ${\mathbb {A}}$![]() is compactly embedded into ${\mathcal {H}}$
is compactly embedded into ${\mathcal {H}}$![]() , one could conclude that the spectrum of ${\mathbb {A}}$
, one could conclude that the spectrum of ${\mathbb {A}}$![]() is made by eigenvalues only (and each with finite multiplicity). This is a direct consequence of a celebrated theorem of Kato [Reference Kato11, Th. 6.29], which states that the spectrum of a closed operator with compact inverse is purely punctual.
is made by eigenvalues only (and each with finite multiplicity). This is a direct consequence of a celebrated theorem of Kato [Reference Kato11, Th. 6.29], which states that the spectrum of a closed operator with compact inverse is purely punctual.
We finally turn to the case $\varkappa = 0$![]() . Here the picture is much different.
. Here the picture is much different.
Theorem 4.4 Let $\varkappa = 0$![]() . Then the spectrum of ${\mathbb {A}}$
. Then the spectrum of ${\mathbb {A}}$![]() is the whole complex plane $\mathbb {C}$
is the whole complex plane $\mathbb {C}$![]() . Furthermore, $0$
. Furthermore, $0$![]() is the only eigenvalue of ${\mathbb {A}}$
is the only eigenvalue of ${\mathbb {A}}$![]() .
.
Proof. Let $\lambda \in {\mathbb {C}}$![]() such that $\lambda \neq 0$
such that $\lambda \neq 0$![]() be fixed. We consider once again the resolvent equation
be fixed. We consider once again the resolvent equation
for ${\boldsymbol {f}} = (f,\,g) \in {\mathcal {H}}$![]() . We show that for some ${\boldsymbol {f}} \in {\mathcal {H}}$
. We show that for some ${\boldsymbol {f}} \in {\mathcal {H}}$![]() the equation above has no solution in ${\mathfrak {D}}({\mathbb {A}})$
the equation above has no solution in ${\mathfrak {D}}({\mathbb {A}})$![]() . By the same computations of the proof of theorem 4.2, we arrive at the system
. By the same computations of the proof of theorem 4.2, we arrive at the system

with
From (4.8) we immediately obtain
In particular, this implies that $\xi$![]() attains the same regularity of $h$
attains the same regularity of $h$![]() . Thus, taking $h$
. Thus, taking $h$![]() in $H$
in $H$![]() but not more regular (e.g., $h\not \in H^2$
but not more regular (e.g., $h\not \in H^2$![]() ), the resolvent equation will have no solution in ${\mathfrak {D}}({\mathbb {A}})$
), the resolvent equation will have no solution in ${\mathfrak {D}}({\mathbb {A}})$![]() . On the other hand, if ${\boldsymbol {f}}=(0,\,0)$
. On the other hand, if ${\boldsymbol {f}}=(0,\,0)$![]() , the unique solution is clearly the null one. Accordingly, $\lambda$
, the unique solution is clearly the null one. Accordingly, $\lambda$![]() is not an eigenvalue.
is not an eigenvalue.
Instead, when $\lambda = 0$![]() , let $u \neq 0$
, let $u \neq 0$![]() be any function such that $u \in H^3$
be any function such that $u \in H^3$![]() and $u_x \in H^1_0$
and $u_x \in H^1_0$![]() , and define
, and define
It is then apparent that $\eta \in H^2 \cap H^1_0$![]() . Besides, since $\varkappa = 0$
. Besides, since $\varkappa = 0$![]() implies $\alpha = \beta ^2$
implies $\alpha = \beta ^2$![]() , a quick check reveals that
, a quick check reveals that
so that $0$![]() is an eigenvalue, as claimed.
is an eigenvalue, as claimed.
Remark 4.5 When $\lambda \neq 0$![]() , if $f$
, if $f$![]() and $h$
and $h$![]() have enough regularity, system (4.8) has actually the unique solution
have enough regularity, system (4.8) has actually the unique solution
This tells that the resolvent equation is solvable for a dense set of functions ${\boldsymbol {f}}$![]() . In other words, the range of $({\mathbb {A}} -\lambda )$
. In other words, the range of $({\mathbb {A}} -\lambda )$![]() is dense in ${\mathcal {H}}$
is dense in ${\mathcal {H}}$![]() . Accordingly, every $\lambda \neq 0$
. Accordingly, every $\lambda \neq 0$![]() belongs to the continuous spectrum of ${\mathbb {A}}$
belongs to the continuous spectrum of ${\mathbb {A}}$![]() .
.
5. The ill-posed problem
By the Hille–Yosida theorem (see, e.g., [Reference Engel and Nagel10, Reference Pazy15]), if a closed operator ${\mathbb {A}}$![]() is the infinitesimal generator of a strongly continuous semigroup of linear operators, then it has a finite spectral bound, that is,
is the infinitesimal generator of a strongly continuous semigroup of linear operators, then it has a finite spectral bound, that is,
But we know from the previous § 4 that this is never the case when $\varkappa \leq 0$![]() . Thus, if $\varkappa \leq 0$
. Thus, if $\varkappa \leq 0$![]() we do not have a well-posedness result for (1.1)–(1.3), at least not for every possible choice of the initial data $(\phi,\,\psi )\in {\mathcal {H}}$
we do not have a well-posedness result for (1.1)–(1.3), at least not for every possible choice of the initial data $(\phi,\,\psi )\in {\mathcal {H}}$![]() . Nevertheless, for the case $\varkappa < 0$
. Nevertheless, for the case $\varkappa < 0$![]() we can prove a uniqueness result for those solutions that belong to the domain of ${\mathbb {A}}$
we can prove a uniqueness result for those solutions that belong to the domain of ${\mathbb {A}}$![]() for all times, generally called strong solutions.
for all times, generally called strong solutions.
Proposition 5.1 Let $\varkappa < 0$![]() . If $(\eta,\,u)$
. If $(\eta,\,u)$![]() is a strong solution to (1.1)–(1.3) then it is unique.
is a strong solution to (1.1)–(1.3) then it is unique.
Proof. In light of the linearity of the problem, it is sufficient to show that the only strong solution corresponding to null initial data is the trivial one. To this end, let $(\eta,\,u)$![]() be any strong solution to (1.1)–(1.3) with $(\phi,\,\psi ) = (0,\,0)$
be any strong solution to (1.1)–(1.3) with $(\phi,\,\psi ) = (0,\,0)$![]() . Defining
. Defining
and taking into account the null initial conditions, integrating (1.1) in time we get

where $\zeta _t=\eta$![]() and $v_t=u$
and $v_t=u$![]() . Taking the derivative in space of the second equation of (5.1), after some straightforward manipulations we obtain
. Taking the derivative in space of the second equation of (5.1), after some straightforward manipulations we obtain
which tells that
Let us now introduce the functional
Considering the first equation of system (1.1), written in terms of $\zeta$![]() and $v$
and $v$![]() , along with the first equation of (5.1), we end up with
, along with the first equation of (5.1), we end up with
A simple computation yields
hence
At this point, we introduce the further functional
Then we have
Moreover, by (5.2) together with the fact that $\zeta _{xx}\in H^2\cap H_0^1$![]() , and exploiting (5.3),
, and exploiting (5.3),
By the Cauchy–Schwarz inequality,
where we used the dot to denote the time derivative. This implies that ${\mathsf G}$![]() is a log-convex function of time. Accordingly, for any fixed interval $[0,\,T]$
is a log-convex function of time. Accordingly, for any fixed interval $[0,\,T]$![]() , we must have that
, we must have that
Since ${\mathsf G}(0)= 0$![]() , we conclude that ${\mathsf G}(t)$
, we conclude that ${\mathsf G}(t)$![]() is zero for every $t$
is zero for every $t$![]() , implying that $\zeta =0$
, implying that $\zeta =0$![]() . But this in turn implies that $\eta =0$
. But this in turn implies that $\eta =0$![]() . Once we know that $\eta =0$
. Once we know that $\eta =0$![]() , the first equation of (1.1) simply becomes
, the first equation of (1.1) simply becomes
which, as $u_{xxx}\in H^2\cap H_0^1$![]() , readily yields $u_x=0$
, readily yields $u_x=0$![]() . Since $u\in H^1_*$
. Since $u\in H^1_*$![]() , the latter equality implies that $u=0$
, the latter equality implies that $u=0$![]() as well.
as well.
Under certain conditions on the initial data, the unique strong solution, whenever exists, blows up exponentially fast as time goes to infinity.
Proposition 5.2 Let $\varkappa < 0$![]() and let $(\eta,\,u)$
and let $(\eta,\,u)$![]() be a strong solution to (1.1)–(1.3), for some initial data $(\phi,\,\psi )$
be a strong solution to (1.1)–(1.3), for some initial data $(\phi,\,\psi )$![]() . If either
. If either
or
then it follows that
for some $c>0$![]() and $\nu >0$
and $\nu >0$![]() , both depending on $(\phi,\,\psi )$
, both depending on $(\phi,\,\psi )$![]() .
.
Proof. Let $(\eta,\,u)$![]() be a strong solution. Once we know from proposition 5.1 that it is unique, it is standard matter to approximate it with solutions as regular as needed. Accordingly, along this proof, we can work with functions regular enough to withstand the forthcoming calculations. Let us assume (5.4). We first define the counterpart of the functional ${\mathsf F}$
be a strong solution. Once we know from proposition 5.1 that it is unique, it is standard matter to approximate it with solutions as regular as needed. Accordingly, along this proof, we can work with functions regular enough to withstand the forthcoming calculations. Let us assume (5.4). We first define the counterpart of the functional ${\mathsf F}$![]() of the previous proof, that is,
of the previous proof, that is,
Observe that ${\mathsf F}_0(t) = {\mathsf F}_0(0)$![]() for every $t$
for every $t$![]() and
and
Besides, let
where $\omega$![]() and $t_0$
and $t_0$![]() are two strictly positive constants to be chosen later. By the same computations of the previous proof, just replacing $(\zeta,\,v)$
are two strictly positive constants to be chosen later. By the same computations of the previous proof, just replacing $(\zeta,\,v)$![]() with $(\eta,\,u)$
with $(\eta,\,u)$![]() , we arrive at
, we arrive at
Hence, taking $\omega = - {\mathsf F}_0(0)$![]() , we get
, we get
and a simple calculations yields (see, e.g., [Reference Ames and Straughan1])
Choosing $t_0$![]() such that $\dot {\mathsf G}_0(0) > 0$
such that $\dot {\mathsf G}_0(0) > 0$![]() we have obtained that the norm of $\eta$
we have obtained that the norm of $\eta$![]() (hence the norm of the solution) blows up exponentially fast. If instead (5.5) holds, in a completely similar way we can prove the exponential blow up of $\|u_x\|$
(hence the norm of the solution) blows up exponentially fast. If instead (5.5) holds, in a completely similar way we can prove the exponential blow up of $\|u_x\|$![]() .
.
Remark 5.3 The norm of the solution blows up exponentially even in the case ${\mathsf F}_0(0) = 0$![]() , provided that
, provided that
Indeed, recasting the proof of the proposition above with $\omega = 0$![]() , we still end up with the final exponential estimate, and the condition above is precisely equivalent to $\dot {\mathsf G}_0(0) > 0$
, we still end up with the final exponential estimate, and the condition above is precisely equivalent to $\dot {\mathsf G}_0(0) > 0$![]() .
.
Our analysis is much more precise in the case $\varkappa = 0$![]() , where we do have existence and uniqueness of strong solutions.
, where we do have existence and uniqueness of strong solutions.
Proposition 5.4 Let $\varkappa = 0$![]() . Then, system (1.1)–(1.3) has a unique solution for any $(\phi,\,\psi ) \in {\mathfrak {D}}({\mathbb {A}})$
. Then, system (1.1)–(1.3) has a unique solution for any $(\phi,\,\psi ) \in {\mathfrak {D}}({\mathbb {A}})$![]() . Besides, such a solution is a strong one.
. Besides, such a solution is a strong one.
Proof. Since $\alpha = \beta ^2$![]() , system (1.1) becomes
, system (1.1) becomes

Let $(\phi,\,\psi ) \in {\mathfrak {D}}({\mathbb {A}})$![]() . Then it is straightforward to check that the functions
. Then it is straightforward to check that the functions
are (strong) solutions to (5.6) with initial conditions (1.3). To prove the uniqueness, let $(\eta,\,u)$![]() be a solution to (5.6) with initial conditions (1.3). Then, adding the first equation to the spatial derivative of the second equation multiplied by $\beta$
be a solution to (5.6) with initial conditions (1.3). Then, adding the first equation to the spatial derivative of the second equation multiplied by $\beta$![]() , we see at once that
, we see at once that
This gives
where $p: [0,\,\pi ] \to \mathbb {R}$![]() is the time-independent function
is the time-independent function
Substituting $\eta$![]() into the second equation, we get
into the second equation, we get
implying that
In turn, this yields
which establishes the desired uniqueness.
6. The well-posed problem
We now turn to the case $\varkappa > 0$![]() . In this situation, we show that problem (1.1)–(1.2) is well-posed. Specifically, we have the following result.
. In this situation, we show that problem (1.1)–(1.2) is well-posed. Specifically, we have the following result.
Theorem 6.1 Let $\varkappa > 0$![]() . Then the operator ${\mathbb {A}}$
. Then the operator ${\mathbb {A}}$![]() is the infinitesimal generator of a strongly continuous bounded semigroup
is the infinitesimal generator of a strongly continuous bounded semigroup
Accordingly, for every initial datum $\boldsymbol {\phi } = (\phi,\,\psi )\in {\mathcal {H}}$![]() , there exists a unique solution
, there exists a unique solution
to (1.1)-(1.3). Moreover, there exists an equivalent norm on ${\mathcal {H}}$![]() for which $S(t)$
for which $S(t)$![]() is a actually a contraction semigroup.
is a actually a contraction semigroup.
In order to prove the theorem, the first step is to devise the correct norm. To this end, let us introduce the functional $\boldsymbol {|} \cdot \boldsymbol {|}_{{\mathcal {H}}}$![]() on ${\mathcal {H}}$
on ${\mathcal {H}}$![]() , acting as
, acting as
This object turns out to be an equivalent norm on ${\mathcal {H}}$![]() . This is a consequence of the following lemma.
. This is a consequence of the following lemma.
Lemma 6.2 Let $\varkappa >0$![]() . Then there exist a constant $c>1$
. Then there exist a constant $c>1$![]() such that
such that
Proof. The second inequality is straightforward. Concerning the first one, notice that by the Young inequality we have
Therefore,
Exploiting the fact that $\varkappa > 0$![]() , we can choose $\varepsilon$
, we can choose $\varepsilon$![]() close to 1 so that
close to 1 so that
and the proof is finished.
Remark 6.3 For ${\boldsymbol {u}} = (\eta,\,u)$![]() and ${\boldsymbol {u}}' = (\eta ',\,u')$
and ${\boldsymbol {u}}' = (\eta ',\,u')$![]() , the norm $\boldsymbol {|} \cdot \boldsymbol {|}_{{\mathcal {H}}}$
, the norm $\boldsymbol {|} \cdot \boldsymbol {|}_{{\mathcal {H}}}$![]() defined in (6.1) is induced by the scalar product
defined in (6.1) is induced by the scalar product
We are ready to prove theorem 6.1.
Proof Proof of Theorem 6.1
Consider the space ${\mathcal {H}}$![]() endowed with the equivalent norm $\boldsymbol {|} \cdot \boldsymbol {|}_{{\mathcal {H}}}$
endowed with the equivalent norm $\boldsymbol {|} \cdot \boldsymbol {|}_{{\mathcal {H}}}$![]() . The result then follows from an application of the classical Lumer–Phillips theorem (see [Reference Engel and Nagel10, Reference Pazy15]), which states that a densely defined linear operator ${\mathbb {A}}$
. The result then follows from an application of the classical Lumer–Phillips theorem (see [Reference Engel and Nagel10, Reference Pazy15]), which states that a densely defined linear operator ${\mathbb {A}}$![]() is the infinitesimal generator of a contraction semigroup $S(t) = e^{t{\mathbb {A}}}$
is the infinitesimal generator of a contraction semigroup $S(t) = e^{t{\mathbb {A}}}$![]() if and only if
if and only if
(i) ${\mathbb {A}}$
 is dissipative, that is,
\[ \boldsymbol{(} {\mathbb{A}} {\boldsymbol{u}}, {\boldsymbol{u}} \boldsymbol{)}_{{\mathcal{H}}} \leq 0, \quad \forall\ {\boldsymbol{u}} \in {\mathfrak{D}}({\mathbb{A}}). \]
is dissipative, that is,
\[ \boldsymbol{(} {\mathbb{A}} {\boldsymbol{u}}, {\boldsymbol{u}} \boldsymbol{)}_{{\mathcal{H}}} \leq 0, \quad \forall\ {\boldsymbol{u}} \in {\mathfrak{D}}({\mathbb{A}}). \]
(ii) The operator ${\mathbb {A}} - {\mathbb {I}}$
 is onto, where ${\mathbb {I}}$
is onto, where ${\mathbb {I}}$ is the identity operator on ${\mathcal {H}}$
is the identity operator on ${\mathcal {H}}$ .
.
Indeed, after theorem 4.1, we know that $1\in \rho ({\mathbb {A}})$![]() , which implies (ii). We are left to prove (i). A direct computation yields
, which implies (ii). We are left to prove (i). A direct computation yields
Accordingly, by an integration by parts, along with the fact that $\eta,\,u_x \in H^1_0$![]() ,
,
for every choice of $(\eta,\,u)\in {\mathfrak {D}}({\mathbb {A}})$![]() .
.
Remark 6.4 It is apparent from the proof that the operator $-{\mathbb {A}}$![]() fulfils the hypotheses of the Lumer–Phillips Theorem as well. Consequently, $S(t)$
fulfils the hypotheses of the Lumer–Phillips Theorem as well. Consequently, $S(t)$![]() is actually a strongly continuous group of bounded operators (see, e.g., [Reference Pazy15]).
is actually a strongly continuous group of bounded operators (see, e.g., [Reference Pazy15]).
The energy corresponding to the solution (1.1)–(1.2) with initial datum $\boldsymbol {\phi } = (\phi,\,\psi )$![]() is classically defined by
is classically defined by
Such an energy turns out to be conserved.
Corollary 6.5 For every initial datum $\boldsymbol {\phi }\in {\mathcal {H}}$![]() , the corresponding energy ${\mathsf E}(t)$
, the corresponding energy ${\mathsf E}(t)$![]() is constant.
is constant.
Proof. Assume first $\boldsymbol {\phi } \in {\mathfrak {D}}({\mathbb {A}})$![]() . Since ${\mathbb {A}}$
. Since ${\mathbb {A}}$![]() is the infinitesimal generator of $S(t)$
is the infinitesimal generator of $S(t)$![]() , we know that ${\boldsymbol {u}}(t) \in {\mathfrak {D}}({\mathbb {A}})$
, we know that ${\boldsymbol {u}}(t) \in {\mathfrak {D}}({\mathbb {A}})$![]() for every $t \geq 0$
for every $t \geq 0$![]() , and
, and
Therefore, exploiting (6.3),
Accordingly, the equality
holds for every $t\geq 0$![]() . By density, and due to the continuity properties of the semigroup, this equality remains valid for every $\boldsymbol {\phi } \in {\mathcal {H}}$
. By density, and due to the continuity properties of the semigroup, this equality remains valid for every $\boldsymbol {\phi } \in {\mathcal {H}}$![]() .
.
7. The explicit representation of the solutions
When the problem is well-posed, it is actually possible to provide an explicit representation for the solution to (1.1)–(1.3).
Theorem 7.1 Let $\varkappa =\alpha -\beta ^2>0$![]() . For any $(\phi,\, \psi )\in {\mathcal {H}}$
. For any $(\phi,\, \psi )\in {\mathcal {H}}$![]() and any $n = 1,\,2,\,3,\,\ldots$
and any $n = 1,\,2,\,3,\,\ldots$![]() , define the sequences
, define the sequences
Then the solution $(\eta,\,u)$![]() to problem (1.1)–(1.2) with initial data (1.3) has the explicit representation
to problem (1.1)–(1.2) with initial data (1.3) has the explicit representation

and

where
and
In order to prove the theorem, we work in the complexification of the Hilbert space ${\mathcal {H}}$![]() , endowed with the (complex) scalar product $\boldsymbol {(} \cdot,\, \cdot \boldsymbol{)} _{{\mathcal {H}}}$
, endowed with the (complex) scalar product $\boldsymbol {(} \cdot,\, \cdot \boldsymbol{)} _{{\mathcal {H}}}$![]() given by (6.2). Hence, the norm of ${\boldsymbol {u}} = (\eta,\,u)$
given by (6.2). Hence, the norm of ${\boldsymbol {u}} = (\eta,\,u)$![]() now reads
now reads
Let us consider suitable multiples of the eigenfunctions ${\boldsymbol {u}}^{\pm }_n$![]() given by (4.7), corresponding to the eigenvalues $\lambda _n^\pm =\pm i\sqrt {\varkappa }\,n^2$
given by (4.7), corresponding to the eigenvalues $\lambda _n^\pm =\pm i\sqrt {\varkappa }\,n^2$![]() of ${\mathbb {A}}$
of ${\mathbb {A}}$![]() , namely,
, namely,
The following holds.
Proposition 7.2 For $n = 1,\,2,\,3,\,\ldots$![]() , the functions ${\boldsymbol {w}}^{\pm }_n$
, the functions ${\boldsymbol {w}}^{\pm }_n$![]() form an orthonormal basis of (the complexification of) ${\mathcal {H}}$
form an orthonormal basis of (the complexification of) ${\mathcal {H}}$![]() , with respect to the scalar product $\boldsymbol {(} \cdot,\, \cdot \boldsymbol{)} _{{\mathcal {H}}}$
, with respect to the scalar product $\boldsymbol {(} \cdot,\, \cdot \boldsymbol{)} _{{\mathcal {H}}}$![]() .
.
Proof. By direct calculations, one can check the relations
and
We are left to show that the system is complete. Let ${\boldsymbol {f}} = (f,\,g) \in {\mathcal {H}}$![]() . The two components of ${\boldsymbol {f}}$
. The two components of ${\boldsymbol {f}}$![]() can be decomposed as
can be decomposed as

It is then sufficient to verify that each vector
can be expressed as a linear combination of ${\boldsymbol {w}}^+_n$![]() and ${\boldsymbol {w}}^-_n$
and ${\boldsymbol {w}}^-_n$![]() . That is, we are looking for constants $c_n$
. That is, we are looking for constants $c_n$![]() and $d_n$
and $d_n$![]() such that
such that
which is equivalent to solve

But for every $n$![]() , this system has a unique solution, due to the fact that $\varkappa \neq 0$
, this system has a unique solution, due to the fact that $\varkappa \neq 0$![]() .
.
Proof Proof of Theorem 7.1
On account of proposition 7.2, we look for a solution ${\boldsymbol {u}}(t)=(\eta (t),\,u(t))$![]() to (the complexification of) (1.1)–(1.3) of the form
to (the complexification of) (1.1)–(1.3) of the form

Then, it is readily seen that

where the initial values $a_n^\pm (0)$![]() are deduced from the initial conditions (1.3) via the formula
are deduced from the initial conditions (1.3) via the formula
More explicitly,
At this point, assuming $\phi$![]() and $\psi$
and $\psi$![]() to be real functions, we find the explicit form of the (real) solution $\eta (t)$
to be real functions, we find the explicit form of the (real) solution $\eta (t)$![]() and $u(t)$
and $u(t)$![]() as in the statement of the theorem.
as in the statement of the theorem.
The explicit representation of the solution allows us to recover the conservation of the energy predicted by corollary 6.5. Indeed, the energy ${\mathsf E}(t)$![]() corresponding to the initial datum $(\phi,\,\psi )$
corresponding to the initial datum $(\phi,\,\psi )$![]() reads
reads

Observe that for every fixed $n$![]() , the equality
, the equality
holds for every $t\geq 0$![]() . This means that
. This means that

that is, the energy is constant in time, as expected.
Remark 7.3 In fact, the representation above for $(\eta,\,u)$![]() is valid for all times $t \in \mathbb {R}$
is valid for all times $t \in \mathbb {R}$![]() .
.
8. Analysis of the case $\alpha = 0$
Although in the whole paper we have assumed $\alpha \neq 0$![]() , for the sake of completeness we finally discuss the degenerate case $\alpha =0$
, for the sake of completeness we finally discuss the degenerate case $\alpha =0$![]() . We shall distinguish two cases.
. We shall distinguish two cases.
8.1 The case $\boldsymbol {\beta \neq 0}$
System (1.1) becomes

Since $\varkappa = - \beta ^2 < 0$![]() , in light of theorem 6.1 well-posedness is not expected. This is exactly what happens. Clearly, the first equation can only have a solution if $\beta > 0$
, in light of theorem 6.1 well-posedness is not expected. This is exactly what happens. Clearly, the first equation can only have a solution if $\beta > 0$![]() , for otherwise it is a backward heat equation, which is known to be ill-posed. However, if $\beta >0$
, for otherwise it is a backward heat equation, which is known to be ill-posed. However, if $\beta >0$![]() , once $\eta$
, once $\eta$![]() is deduced from the first equation, we end up with a nonhomogeneous backward heat equation for $u$
is deduced from the first equation, we end up with a nonhomogeneous backward heat equation for $u$![]() , once again ill-posed.
, once again ill-posed.
8.2 The case $\boldsymbol {\beta = 0}$
We have the even simpler system

If there exists a solution in some weak sense, with initial data $(\phi,\,\psi )$![]() , it must be of the form
, it must be of the form
Then it is readily seen that it is not possible to find a solution for all initial data in ${\mathcal {H}}$![]() . Just choose $\phi \in H$
. Just choose $\phi \in H$![]() but not more regular. Nevertheless, the problem turns out to be well-posed if we change the underlying phase space. For instance, considering the space
but not more regular. Nevertheless, the problem turns out to be well-posed if we change the underlying phase space. For instance, considering the space
we see that for every initial datum $(\phi,\,\psi ) \in {\mathcal {V}}$![]() , the pair $(\eta,\,u)$
, the pair $(\eta,\,u)$![]() defined above is indeed the unique solution of the system in ${\mathcal {V}}$
defined above is indeed the unique solution of the system in ${\mathcal {V}}$![]() .
.
Acknowledgements
This paper is partially supported by the Italian MIUR-PRIN Grant 2020F3NCPX ‘Mathematics for industry 4.0 (Math4I4)’, and it is part of the project PID2019-105118GB-I00, funded by the Spanish Ministry of Science, Innovation and Universities and FEDER ‘A way to make Europe’.