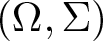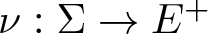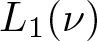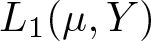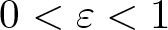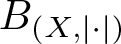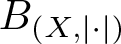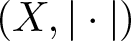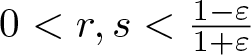1. Introduction
Let ![]() $(X,\|\cdot\|)$ be a Banach space. The (closed) unit ball and the unit sphere of X are denoted by
$(X,\|\cdot\|)$ be a Banach space. The (closed) unit ball and the unit sphere of X are denoted by ![]() $B_{(X,\|\cdot\|)}$ and
$B_{(X,\|\cdot\|)}$ and ![]() $S_{(X,\|\cdot\|)}$, respectively. If the norm does not need to be explicitly mentioned, we just write BX and SX instead. Given a bounded set
$S_{(X,\|\cdot\|)}$, respectively. If the norm does not need to be explicitly mentioned, we just write BX and SX instead. Given a bounded set ![]() $C \subseteq X$, a slice of C is a set of the form
$C \subseteq X$, a slice of C is a set of the form
for some ![]() $x^*\in X^*$ (the topological dual of X) and α > 0. Notice that
$x^*\in X^*$ (the topological dual of X) and α > 0. Notice that ![]() $S(C,x^*,\alpha)$ is non-empty and relatively weakly open in C. A Banach space is said to have the slice diameter two property (slice-D2P) (respectively, diameter two property – D2P, strong diameter two property – SD2P) if every slice (respectively, non-empty relatively weakly open subset, convex combination of slices) of the unit ball has diameter 2. D2Ps have attracted the attention of many researchers in the last 20 years (see, e.g., [Reference Abrahamsen, Hájek, Nygaard, Talponen and Troyanski1, Reference Abrahamsen, Lima and Nygaard3, Reference Guerrero, López-Pérez and Zoca19, Reference Guerrero, López-Pérez and Zoca20, Reference Haller, Langemets and Põldvere25]) and have motivated the appearance of new properties of Banach spaces (almost squareness [Reference Abrahamsen, Langemets and Lima2], symmetric strong D2Ps [Reference Haller, Langemets, Lima and Nadel24, Reference Langemets and Zoca34], or diametral D2Ps [Reference Guerrero, López-Pérez and Zoca23]).
$S(C,x^*,\alpha)$ is non-empty and relatively weakly open in C. A Banach space is said to have the slice diameter two property (slice-D2P) (respectively, diameter two property – D2P, strong diameter two property – SD2P) if every slice (respectively, non-empty relatively weakly open subset, convex combination of slices) of the unit ball has diameter 2. D2Ps have attracted the attention of many researchers in the last 20 years (see, e.g., [Reference Abrahamsen, Hájek, Nygaard, Talponen and Troyanski1, Reference Abrahamsen, Lima and Nygaard3, Reference Guerrero, López-Pérez and Zoca19, Reference Guerrero, López-Pérez and Zoca20, Reference Haller, Langemets and Põldvere25]) and have motivated the appearance of new properties of Banach spaces (almost squareness [Reference Abrahamsen, Langemets and Lima2], symmetric strong D2Ps [Reference Haller, Langemets, Lima and Nadel24, Reference Langemets and Zoca34], or diametral D2Ps [Reference Guerrero, López-Pérez and Zoca23]).
According to Abrahamsen et al. [Reference Abrahamsen, Langemets and Lima2], a Banach space ![]() $(X,\|\cdot\|)$ is said to be
$(X,\|\cdot\|)$ is said to be
(i) locally almost square (LASQ) if for every
 $x\in S_{(X,\|\cdot\|)}$, there exists a sequence
$x\in S_{(X,\|\cdot\|)}$, there exists a sequence  $(y_n)_{n\in \mathbb{N}}$ in
$(y_n)_{n\in \mathbb{N}}$ in  $B_{(X,\|\cdot\|)}$ such that
$B_{(X,\|\cdot\|)}$ such that  $\Vert x\pm y_n\Vert\rightarrow 1$ and
$\Vert x\pm y_n\Vert\rightarrow 1$ and  $\Vert y_n\Vert\rightarrow 1$;
$\Vert y_n\Vert\rightarrow 1$;(ii) weakly almost square (WASQ) if for every
 $x\in S_{(X,\|\cdot\|)}$, there exists a weakly null sequence
$x\in S_{(X,\|\cdot\|)}$, there exists a weakly null sequence  $(y_n)_{n\in \mathbb{N}}$ in
$(y_n)_{n\in \mathbb{N}}$ in  $B_{(X,\|\cdot\|)}$ such that
$B_{(X,\|\cdot\|)}$ such that  $\Vert x\pm y_n\Vert\rightarrow 1$ and
$\Vert x\pm y_n\Vert\rightarrow 1$ and  $\Vert y_n\Vert\rightarrow 1$;
$\Vert y_n\Vert\rightarrow 1$;(iii) almost square (ASQ) if for every finite set
 $\{x_1,\ldots, x_k\} \subseteq S_{(X,\|\cdot\|)}$, there exists a sequence
$\{x_1,\ldots, x_k\} \subseteq S_{(X,\|\cdot\|)}$, there exists a sequence  $(y_n)_{n\in \mathbb{N}}$ in
$(y_n)_{n\in \mathbb{N}}$ in  $B_{(X,\|\cdot\|)}$ such that
$B_{(X,\|\cdot\|)}$ such that  $\Vert x_i\pm y_n\Vert\rightarrow 1$ for every
$\Vert x_i\pm y_n\Vert\rightarrow 1$ for every  $i\in\{1,\ldots, k\}$ and
$i\in\{1,\ldots, k\}$ and  $\Vert y_n\Vert\rightarrow 1$.
$\Vert y_n\Vert\rightarrow 1$.
All these properties are isometric in nature, that is, they depend on the norm considered. For instance, the basic example of an ASQ space is c 0 with its usual norm, while every Banach space admits an equivalent norm failing the slice-D2P and so it cannot be LASQ (see, e.g., [Reference Guerrero, López-Pérez and Zoca22, Lemma 2.1]).
Even though the previous properties were introduced in [Reference Abrahamsen, Langemets and Lima2], LASQ and WASQ spaces were implicitly used by Kubiak [Reference Kubiak31] to study the D2P in some Cesàro function spaces. Apart from being interesting by themselves, almost squareness properties have shown to be a powerful tool in order to study D2Ps in certain Banach spaces where there is no good description of the dual space. In this direction, let us mention, for instance, that in [Reference Hardtke27, Section 4], it is proved that if X is LASQ (respectively, ASQ), then any ultrapower ![]() $X_\mathcal U$ of X is LASQ (respectively, ASQ), and, in particular,
$X_\mathcal U$ of X is LASQ (respectively, ASQ), and, in particular, ![]() $X_\mathcal U$ has the slice-D2P (respectively, SD2P). Observe that it is unclear whether
$X_\mathcal U$ has the slice-D2P (respectively, SD2P). Observe that it is unclear whether ![]() $X_\mathcal U$ has the slice-D2P (respectively, SD2P) if X has the slice-D2P (respectively, SD2P). Another context in which these properties are useful are the projective symmetric tensor products. It is known that if X is WASQ and has the Dunford-Pettis property (respectively, X is ASQ), then all the projective symmetric tensor products
$X_\mathcal U$ has the slice-D2P (respectively, SD2P) if X has the slice-D2P (respectively, SD2P). Another context in which these properties are useful are the projective symmetric tensor products. It is known that if X is WASQ and has the Dunford-Pettis property (respectively, X is ASQ), then all the projective symmetric tensor products  $\widehat{\otimes}_{\pi, s, N}X$ have the slice-D2P [Reference Langemets, Lima and Zoca33, Proposition 3.6] (respectively, SD2P [Reference Guerrero, López-Pérez and Zoca21, Theorem 3.3]). Notice that it is unknown whether any of the D2Ps is stable by taking projective symmetric tensor products.
$\widehat{\otimes}_{\pi, s, N}X$ have the slice-D2P [Reference Langemets, Lima and Zoca33, Proposition 3.6] (respectively, SD2P [Reference Guerrero, López-Pérez and Zoca21, Theorem 3.3]). Notice that it is unknown whether any of the D2Ps is stable by taking projective symmetric tensor products.
Among all the almost squareness properties introduced in [Reference Abrahamsen, Langemets and Lima2], it is clear that ASQ has been studied in a more intensive way because it turns out to characterize the containment of c 0. More precisely, a Banach space admits an ASQ equivalent renorming if and only if it contains an isomorphic copy of c 0 (see [Reference Abrahamsen, Langemets and Lima2, Lemma 2.6] and [Reference Guerrero, López-Pérez and Zoca21, Theorem 2.3]). The contribution to examples of LASQ and WASQ spaces has been more modest. In spite of that, we find several results in the literature about these properties in the context of function spaces. On the one hand, Kubiak proved in [Reference Kubiak31, Lemma 3.3] that the weighted Cesàro function spaces on an interval are WASQ. In particular, ![]() $L_1[0,1]$ is WASQ. On the other hand, Hardtke proved in [Reference Hardtke28, Theorem 3.1] that the Köthe–Bochner space E(X) is LASQ whenever the Banach space X is LASQ, for any Banach function space E.
$L_1[0,1]$ is WASQ. On the other hand, Hardtke proved in [Reference Hardtke28, Theorem 3.1] that the Köthe–Bochner space E(X) is LASQ whenever the Banach space X is LASQ, for any Banach function space E.
The aim of this note is to deepen the understanding of WASQ and LASQ Banach spaces. The paper is organized as follows.
In § 2, we focus on certain Banach function spaces, which play an important role in Banach lattice and operator theory. Namely, we consider the space ![]() $L_1(\nu)$ of all real-valued functions that are integrable with respect to a countably additive vector measure ν (defined on a σ-algebra and taking values in a Banach space). Up to Banach lattice isometries, these spaces represent all order continuous Banach lattices having a weak order unit (see, e.g., [Reference Curbera12, Theorem 8]). Therefore, there are reflexive (hence, having the Radon–Nikodým property and so failing the slice-D2P) Banach lattices within this class, like
$L_1(\nu)$ of all real-valued functions that are integrable with respect to a countably additive vector measure ν (defined on a σ-algebra and taking values in a Banach space). Up to Banach lattice isometries, these spaces represent all order continuous Banach lattices having a weak order unit (see, e.g., [Reference Curbera12, Theorem 8]). Therefore, there are reflexive (hence, having the Radon–Nikodým property and so failing the slice-D2P) Banach lattices within this class, like ![]() $\ell_p$ and
$\ell_p$ and ![]() $L_p[0,1]$ for
$L_p[0,1]$ for ![]() $1 \lt p \lt \infty$. For detailed information on the L 1 space of a vector measure, see [Reference Okada, Ricker and Sánchez Pérez38]. More recent references on this topic are [Reference Calabuig, Lajara, Rodríguez and Sánchez-Pérez10, Reference Curbera and Ricker14, Reference Curbera and Ricker15, Reference Nygaard and Rodríguez37, Reference Rodríguez39]. Our main result in this section is the following:
$1 \lt p \lt \infty$. For detailed information on the L 1 space of a vector measure, see [Reference Okada, Ricker and Sánchez Pérez38]. More recent references on this topic are [Reference Calabuig, Lajara, Rodríguez and Sánchez-Pérez10, Reference Curbera and Ricker14, Reference Curbera and Ricker15, Reference Nygaard and Rodríguez37, Reference Rodríguez39]. Our main result in this section is the following:
Theorem 1.1. Let ![]() $(\Omega,\Sigma)$ be a measurable space, let E be a Banach lattice and let
$(\Omega,\Sigma)$ be a measurable space, let E be a Banach lattice and let ![]() $\nu:\Sigma \to E$ be a countably additive measure. If ν is non-atomic and the set
$\nu:\Sigma \to E$ be a countably additive measure. If ν is non-atomic and the set
(the range of ν) is a relatively norm compact subset of ![]() $E^+:=\{x\in E: x\geq 0\}$, then
$E^+:=\{x\in E: x\geq 0\}$, then ![]() $L_1(\nu)$ is WASQ.
$L_1(\nu)$ is WASQ.
Clearly, Theorem 1.1 generalizes the fact that the classical space ![]() $L_1(\mu)$ of a non-atomic finite measure µ is WASQ. As an application of Theorem 1.1 and some results of Curbera and Ricker [Reference Curbera and Ricker13], it follows that if E is an order continuous rearrangement invariant Banach function space on
$L_1(\mu)$ of a non-atomic finite measure µ is WASQ. As an application of Theorem 1.1 and some results of Curbera and Ricker [Reference Curbera and Ricker13], it follows that if E is an order continuous rearrangement invariant Banach function space on ![]() $[0,1]$, then the abstract Cesàro function space
$[0,1]$, then the abstract Cesàro function space ![]() $[\mathcal C,E]$ is WASQ (Corollary 2.3). This generalizes the aforementioned result by Kubiak in the case of the interval
$[\mathcal C,E]$ is WASQ (Corollary 2.3). This generalizes the aforementioned result by Kubiak in the case of the interval ![]() $[0,1]$. Abstract Cesàro function spaces have been widely studied in the literature (see, e.g., [Reference Astashkin and Maligranda6, Reference Astashkin, Lesnik and Maligranda7, Reference Curbera and Ricker13]).
$[0,1]$. Abstract Cesàro function spaces have been widely studied in the literature (see, e.g., [Reference Astashkin and Maligranda6, Reference Astashkin, Lesnik and Maligranda7, Reference Curbera and Ricker13]).
The techniques of Theorem 1.1 allow us to show the Lebesgue–Bochner space ![]() $L_1(\mu,Y)$ is WASQ for any Banach space Y whenever µ is a non-atomic finite measure (Corollary 2.5). This result should be compared with the above mentioned result of [Reference Hardtke28] that the property of being LASQ passes from a Banach space Y to the Köthe–Bochner space E(Y), for any Banach function space E. We finish § 2 with an example of a WASQ Banach space of the form
$L_1(\mu,Y)$ is WASQ for any Banach space Y whenever µ is a non-atomic finite measure (Corollary 2.5). This result should be compared with the above mentioned result of [Reference Hardtke28] that the property of being LASQ passes from a Banach space Y to the Köthe–Bochner space E(Y), for any Banach function space E. We finish § 2 with an example of a WASQ Banach space of the form ![]() $L_1(\nu)$ as in Theorem 1.1, which is not an
$L_1(\nu)$ as in Theorem 1.1, which is not an ![]() $\mathcal L_1$-space (§ 2.3).
$\mathcal L_1$-space (§ 2.3).
In § 3, we go a bit further in the analysis of the link between almost squareness and D2Ps. One of the main questions raised in [Reference Abrahamsen, Langemets and Lima2] is whether there exists an LASQ Banach space that is not WASQ. Very recently, Kaasik and Veeorg proved in [Reference Kaasik and Veeorg29, Section 2] that the answer is negative and that an example can be found in the class of Lipschitz-free spaces over complete metric spaces. For such spaces, the properties SD2P, D2P, slice-D2P and LASQ are equivalent (combine [Reference Avilés and Martínez-Cervantes8, Theorem 1.5] and [Reference Haller, Kaasik and Ostrak26, Theorem 3.1]), so the above mentioned example satisfies the SD2P. Since the slice-D2P and the D2P are different properties [Reference Guerrero, López-Pérez and Zoca19], it is a natural question whether there exists an LASQ Banach space that fails the D2P. Within the framework of Banach lattices, a stronger version of the LASQ property that implies the D2P has been considered in [Reference Ciaci11]. Even though we do not know the answer to the previous question, we make some progress in this direction. Our main result in § 3 is the following:
Theorem 1.2. Let X be a Banach space containing a complemented isomorphic copy of c 0. Then for any ![]() $0 \lt \varepsilon \lt 1$, there exists an equivalent norm
$0 \lt \varepsilon \lt 1$, there exists an equivalent norm ![]() $|\cdot|$ on X such that:
$|\cdot|$ on X such that:
(i)
 $(X,|\cdot|)$ has the slice-D2P, that is, every slice of
$(X,|\cdot|)$ has the slice-D2P, that is, every slice of  $B_{(X,|\cdot|)}$ has a diameter 2.
$B_{(X,|\cdot|)}$ has a diameter 2.(ii) There are non-empty relatively weakly open subsets of
 $B_{(X,|\cdot|)}$ of arbitrarily small diameter.
$B_{(X,|\cdot|)}$ of arbitrarily small diameter.(iii)
 $(X,|\cdot|)$ is (r, s)-SQ for all
$(X,|\cdot|)$ is (r, s)-SQ for all  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ in the sense of [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Section 6], that is, for every finite set
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ in the sense of [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Section 6], that is, for every finite set  $\{x_1,\ldots, x_n\}\subseteq S_X$, there exists
$\{x_1,\ldots, x_n\}\subseteq S_X$, there exists  $y\in S_X$ satisfying
$y\in S_X$ satisfying
 \begin{equation*}
|rx_i \pm sy|\le1\ \text{for every}\ i\in \{1,\dots,n\}.
\end{equation*}
\begin{equation*}
|rx_i \pm sy|\le1\ \text{for every}\ i\in \{1,\dots,n\}.
\end{equation*}
Condition (iii) measures somehow how far is the norm from being ASQ. Notice that a Banach space is ASQ if and only if it is (r, s)-SQ for all ![]() $0 \lt r,s \lt 1$.
$0 \lt r,s \lt 1$.
Theorem 1.2 applies to any separable Banach space containing an isomorphic copy of c 0, thanks to Sobczyk’s theorem. The proof of Theorem 1.2 is inspired by the renorming technique developed by Becerra Guerrero et al. in [Reference Guerrero, López-Pérez and Zoca19, Theorem 2.4], which in turn uses ideas of the example of Argyros et al. [Reference Argyros, Odell and Rosenthal5] of a closed bounded convex subset of c 0 having the convex point of continuity property but failing the point of continuity property.
Terminology
We follow standard notation as can be found in [Reference Albiac and Kalton4, Reference Diestel and Uhl17]. We will consider real Banach spaces only. By an operator we mean a continuous linear map between Banach spaces. By a subspace of a Banach space we mean a norm closed linear subspace. Let ![]() $(X,\|\cdot\|)$ be a Banach space. Given a set
$(X,\|\cdot\|)$ be a Banach space. Given a set ![]() $C \subseteq X$, we denote by
$C \subseteq X$, we denote by ![]() ${\rm conv}(C)$ (respectively,
${\rm conv}(C)$ (respectively, ![]() $\overline{{\rm conv}}(C)$) its convex hull (respectively, closed convex hull). The diameter of C is defined by
$\overline{{\rm conv}}(C)$) its convex hull (respectively, closed convex hull). The diameter of C is defined by ![]() ${\rm diam}_{\|\cdot\|}(C):=\sup\{\|x-x^{\prime}\|:x,x^{\prime}\in C\}$ and will be also denoted by
${\rm diam}_{\|\cdot\|}(C):=\sup\{\|x-x^{\prime}\|:x,x^{\prime}\in C\}$ and will be also denoted by ![]() ${\rm diam}(C)$ if no confusion arises.
${\rm diam}(C)$ if no confusion arises.
Let ![]() $(\Omega,\Sigma,\mu)$ be a finite measure space. A Banach space
$(\Omega,\Sigma,\mu)$ be a finite measure space. A Banach space ![]() $(E,\|\cdot\|)$ is said to be a Banach function space on
$(E,\|\cdot\|)$ is said to be a Banach function space on ![]() $(\Omega,\Sigma,\mu)$ (or just over µ) if the following conditions hold:
$(\Omega,\Sigma,\mu)$ (or just over µ) if the following conditions hold:
(i) E is a (not necessarily closed) linear subspace of
 $L_1(\mu)$;
$L_1(\mu)$;(ii) if
 $f\in L_0(\mu)$ and
$f\in L_0(\mu)$ and  $|f| \leq |g|$ µ-a.e. for some
$|f| \leq |g|$ µ-a.e. for some  $g \in E$, then
$g \in E$, then  $f \in E$ and
$f \in E$ and  $\|f\| \leq \|g\|$;
$\|f\| \leq \|g\|$;(iii) the characteristic function χA of each
 $A \in \Sigma$ belongs to E.
$A \in \Sigma$ belongs to E.
In this case, E is a Banach lattice when endowed with the µ-a.e. order, and the inclusion map from E to ![]() $L_1(\mu)$ is an operator. A set
$L_1(\mu)$ is an operator. A set ![]() $H \subseteq E$ is called uniformly µ-integrable if for each ɛ > 0 there is δ > 0 such that
$H \subseteq E$ is called uniformly µ-integrable if for each ɛ > 0 there is δ > 0 such that ![]() $\|f \chi_A\| \leq \varepsilon$ for every
$\|f \chi_A\| \leq \varepsilon$ for every ![]() $f\in H$ and for every
$f\in H$ and for every ![]() $A\in \Sigma$ with
$A\in \Sigma$ with ![]() $\mu(A)\leq \delta$. Suppose now that E is order continuous. Then every bounded uniformly µ-integrable subset of E is relatively weakly compact (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Proposition 2.39]), but the converse might fail, in contrast to the case of the classical L 1 space of a finite measure (for which the Dunford–Pettis theorem ensures the equivalence). Moreover, given
$\mu(A)\leq \delta$. Suppose now that E is order continuous. Then every bounded uniformly µ-integrable subset of E is relatively weakly compact (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Proposition 2.39]), but the converse might fail, in contrast to the case of the classical L 1 space of a finite measure (for which the Dunford–Pettis theorem ensures the equivalence). Moreover, given ![]() $f,g\in E$ with
$f,g\in E$ with ![]() $f\leq g$, the order interval
$f\leq g$, the order interval ![]() $[f,g] \subseteq E$ is uniformly µ-integrable (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Lemma 2.37]) and weakly compact.
$[f,g] \subseteq E$ is uniformly µ-integrable (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Lemma 2.37]) and weakly compact.
2. WASQ Banach function spaces
We begin this section with some preliminaries on the L 1 space of a vector measure (see [Reference Okada, Ricker and Sánchez Pérez38, Chapter 3] for the basics on this topic). Let ![]() $(\Omega,\Sigma)$ be a measurable space, let X be a Banach space and let
$(\Omega,\Sigma)$ be a measurable space, let X be a Banach space and let ![]() $\nu:\Sigma\to X$ be a countably additive measure. A set
$\nu:\Sigma\to X$ be a countably additive measure. A set ![]() $A\in \Sigma$ is said to be ν-null if
$A\in \Sigma$ is said to be ν-null if ![]() $\nu(B)=0$ for every
$\nu(B)=0$ for every ![]() $B\in \Sigma$ with
$B\in \Sigma$ with ![]() $B\subseteq A$. The family of all ν-null sets is denoted by
$B\subseteq A$. The family of all ν-null sets is denoted by ![]() $\mathcal{N}(\nu)$. We say that a property holds ν-a.e. if it holds on some
$\mathcal{N}(\nu)$. We say that a property holds ν-a.e. if it holds on some ![]() $A\in \Sigma$ such that
$A\in \Sigma$ such that ![]() $\Omega \setminus A\in \mathcal{N}(\nu)$. We say that a set
$\Omega \setminus A\in \mathcal{N}(\nu)$. We say that a set ![]() $A\in \Sigma \setminus \mathcal{N}(\nu)$ is an atom of ν if for every
$A\in \Sigma \setminus \mathcal{N}(\nu)$ is an atom of ν if for every ![]() $B \in \Sigma$ with
$B \in \Sigma$ with ![]() $B \subseteq A$, we have either
$B \subseteq A$, we have either ![]() $B\in \mathcal{N}(\nu)$ or
$B\in \mathcal{N}(\nu)$ or ![]() $A\setminus B\in \mathcal{N}(\nu)$. We say that ν is non-atomic if it has no atoms. By a Rybakov control measure of ν, we mean a finite measure of the form
$A\setminus B\in \mathcal{N}(\nu)$. We say that ν is non-atomic if it has no atoms. By a Rybakov control measure of ν, we mean a finite measure of the form ![]() $\mu=|x_0^*\circ \nu|$ (the variation of the signed measure
$\mu=|x_0^*\circ \nu|$ (the variation of the signed measure ![]() $x_0^*\circ \nu:\Sigma\to \mathbb R$) for some
$x_0^*\circ \nu:\Sigma\to \mathbb R$) for some ![]() $x_0^*\in X^*$ such that
$x_0^*\in X^*$ such that ![]() $\mathcal{N}(\mu) = \mathcal{N}(\nu)$ (see, e.g., [Reference Diestel and Uhl17, p. 268, Theorem 2] for a proof of the existence of Rybakov control measures).
$\mathcal{N}(\mu) = \mathcal{N}(\nu)$ (see, e.g., [Reference Diestel and Uhl17, p. 268, Theorem 2] for a proof of the existence of Rybakov control measures).
A Σ-measurable function ![]() $f:\Omega \to \mathbb{R}$ is called ν-integrable if
$f:\Omega \to \mathbb{R}$ is called ν-integrable if ![]() $f\in L_1(|x^*\circ \nu|)$ for all
$f\in L_1(|x^*\circ \nu|)$ for all ![]() $x^*\in X^*$ and, for each
$x^*\in X^*$ and, for each ![]() $A\in \Sigma$, there is
$A\in \Sigma$, there is  $\int_A f \, {\rm d}\nu\in X$ such that
$\int_A f \, {\rm d}\nu\in X$ such that
 \begin{equation*}
x^*\left ( \int_A f \, {\rm d}\nu \right)=\int_A f\,{\rm d}(x^*\circ \nu) \quad\text{for all}\ x^*\in X^*.
\end{equation*}
\begin{equation*}
x^*\left ( \int_A f \, {\rm d}\nu \right)=\int_A f\,{\rm d}(x^*\circ \nu) \quad\text{for all}\ x^*\in X^*.
\end{equation*} Identifying functions that coincide ν-a.e., the set ![]() $L_1(\nu)$ of all (equivalence classes of) ν-integrable functions is a Banach lattice with the ν-a.e. order and the norm
$L_1(\nu)$ of all (equivalence classes of) ν-integrable functions is a Banach lattice with the ν-a.e. order and the norm
 \begin{equation*}
\|f\|_{L_1(\nu)}:=\sup_{x^*\in B_{X^*}}\int_\Omega |f|\,{\rm d}|x^*\circ \nu|.
\end{equation*}
\begin{equation*}
\|f\|_{L_1(\nu)}:=\sup_{x^*\in B_{X^*}}\int_\Omega |f|\,{\rm d}|x^*\circ \nu|.
\end{equation*} ![]() $L_1(\nu)$ is an order continuous Banach function space over any Rybakov control measure of ν. The (norm 1) operator
$L_1(\nu)$ is an order continuous Banach function space over any Rybakov control measure of ν. The (norm 1) operator ![]() $I_\nu: L_1(\nu)\to X$ defined by
$I_\nu: L_1(\nu)\to X$ defined by
 \begin{equation*}
I_\nu(f):=\int_\Omega f\, {\rm d}\nu
\quad\text{for all}\ f\in L_1(\nu)
\end{equation*}
\begin{equation*}
I_\nu(f):=\int_\Omega f\, {\rm d}\nu
\quad\text{for all}\ f\in L_1(\nu)
\end{equation*}is called the integration operator of ν.
To provide a proof of Theorem 1.1, we need a couple of lemmata. The first one belongs to the folklore (cf. [Reference Albiac and Kalton4, Lemma 6.3.2] for the case of the unit interval):
Lemma 2.1. Let ![]() $(\Omega,\Sigma,\mu)$ be a non-atomic finite measure space. Then there is a sequence
$(\Omega,\Sigma,\mu)$ be a non-atomic finite measure space. Then there is a sequence ![]() $(r_n)_{n\in \mathbb{N}}$ in
$(r_n)_{n\in \mathbb{N}}$ in ![]() $L_\infty(\mu)$ such that:
$L_\infty(\mu)$ such that:
(i)
 $|r_n|=1$ for all
$|r_n|=1$ for all  $n\in \mathbb{N}$; and
$n\in \mathbb{N}$; and(ii) for each
 $f\in L_1(\mu)$, the sequence
$f\in L_1(\mu)$, the sequence  $(fr_n)_{n\in \mathbb{N}}$ is weakly null in
$(fr_n)_{n\in \mathbb{N}}$ is weakly null in  $L_1(\mu)$.
$L_1(\mu)$.
A sequence as in the previous lemma will be called a Rademacher-type sequence on ![]() $(\Omega,\Sigma,\mu)$.
$(\Omega,\Sigma,\mu)$.
Lemma 2.2. Let ![]() $(\Omega,\Sigma)$ be a measurable space, let X be a Banach space and let
$(\Omega,\Sigma)$ be a measurable space, let X be a Banach space and let ![]() $\nu:\Sigma \to X$ be a non-atomic countably additive measure. Let µ be a Rybakov control measure of ν and let
$\nu:\Sigma \to X$ be a non-atomic countably additive measure. Let µ be a Rybakov control measure of ν and let ![]() $(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on
$(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on ![]() $(\Omega,\Sigma,\mu)$. Then for each
$(\Omega,\Sigma,\mu)$. Then for each ![]() $f\in L_1(\nu)$, the sequence
$f\in L_1(\nu)$, the sequence ![]() $(fr_n)_{n\in \mathbb{N}}$ is weakly null in
$(fr_n)_{n\in \mathbb{N}}$ is weakly null in ![]() $L_1(\nu)$.
$L_1(\nu)$.
Proof. Fix ![]() $f\in L_1(\nu)$ and take any
$f\in L_1(\nu)$ and take any ![]() $\varphi \in L_1(\nu)^*$. Since
$\varphi \in L_1(\nu)^*$. Since ![]() $L_1(\nu)$ is an order continuous Banach function space over µ, there is
$L_1(\nu)$ is an order continuous Banach function space over µ, there is ![]() $g\in L_1(\mu)$ such that for each
$g\in L_1(\mu)$ such that for each ![]() $h\in L_1(\nu)$, we have
$h\in L_1(\nu)$, we have ![]() $hg\in L_1(\mu)$ and
$hg\in L_1(\mu)$ and
 \begin{equation*}
\varphi(h)=\int_\Omega hg \, {\rm d}\mu
\end{equation*}
\begin{equation*}
\varphi(h)=\int_\Omega hg \, {\rm d}\mu
\end{equation*} (see, e.g., [Reference Lindenstrauss and Tzafriri36, p. 29]). In particular, we have ![]() $fg\in L_1(\mu)$ and so
$fg\in L_1(\mu)$ and so ![]() $(fgr_n)_{n\in\mathbb{N}}$ is weakly null in
$(fgr_n)_{n\in\mathbb{N}}$ is weakly null in ![]() $L_1(\mu)$. Hence,
$L_1(\mu)$. Hence,  $\varphi(f r_n)=\int_\Omega fg r_n \, {\rm d}\mu \to 0$ as
$\varphi(f r_n)=\int_\Omega fg r_n \, {\rm d}\mu \to 0$ as ![]() $n\to \infty$.
$n\to \infty$.
Proof of Theorem 1.1
The fact that ![]() $\mathcal{R}(\nu)=\{\nu(A): A\in \Sigma\} \subseteq E^+$ ensures that
$\mathcal{R}(\nu)=\{\nu(A): A\in \Sigma\} \subseteq E^+$ ensures that
 \begin{equation}
\|h\|_{L_1(\nu)}=\left\|\int_\Omega |h| \, {\rm d}\nu\right\|_E
\quad\text{for all}\ h\in L_1(\nu)
\end{equation}
\begin{equation}
\|h\|_{L_1(\nu)}=\left\|\int_\Omega |h| \, {\rm d}\nu\right\|_E
\quad\text{for all}\ h\in L_1(\nu)
\end{equation} (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Lemma 3.13]), where ![]() $\|\cdot\|_E$ denotes the norm of E. Let µ be a Rybakov control measure of ν and let
$\|\cdot\|_E$ denotes the norm of E. Let µ be a Rybakov control measure of ν and let ![]() $(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on
$(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on ![]() $(\Omega,\Sigma,\mu)$.
$(\Omega,\Sigma,\mu)$.
Fix ![]() $f\in S_{L_1(\nu)}$. For each
$f\in S_{L_1(\nu)}$. For each ![]() $n\in \mathbb{N}$, we have
$n\in \mathbb{N}$, we have ![]() $fr_n\in L_1(\nu)$ and
$fr_n\in L_1(\nu)$ and
 \begin{equation*}
\|fr_n\|_{L_1(\nu)}\stackrel{\stackrel{(2.1)}{}}{=} \left\|\int_{\Omega} |fr_n| \, {\rm d}\nu \right\|_E=\left\|\int_{\Omega} |f| \, {\rm d}\nu \right\|_E
\stackrel{\stackrel{(2.1)}{}}{=} \|f\|_{L_1(\nu)}=1.
\end{equation*}
\begin{equation*}
\|fr_n\|_{L_1(\nu)}\stackrel{\stackrel{(2.1)}{}}{=} \left\|\int_{\Omega} |fr_n| \, {\rm d}\nu \right\|_E=\left\|\int_{\Omega} |f| \, {\rm d}\nu \right\|_E
\stackrel{\stackrel{(2.1)}{}}{=} \|f\|_{L_1(\nu)}=1.
\end{equation*} Moreover, the sequence ![]() $(fr_n)_{n\in \mathbb{N}}$ is weakly null in
$(fr_n)_{n\in \mathbb{N}}$ is weakly null in ![]() $L_1(\nu)$ (by Lemma 2.2).
$L_1(\nu)$ (by Lemma 2.2).
We claim that ![]() $\|f\pm fr_n\|_{L_1(\nu)}\to 1$ as
$\|f\pm fr_n\|_{L_1(\nu)}\to 1$ as ![]() $n\to \infty$. Indeed, for each
$n\to \infty$. Indeed, for each ![]() $n\in \mathbb{N}$, we have
$n\in \mathbb{N}$, we have ![]() $1\pm r_n\geq 0$ and so
$1\pm r_n\geq 0$ and so
Therefore, both sequences ![]() $(g_n^+)_{n\in \mathbb{N}}$ and
$(g_n^+)_{n\in \mathbb{N}}$ and ![]() $(g_n^-)_{n\in \mathbb{N}}$ converge weakly to
$(g_n^-)_{n\in \mathbb{N}}$ converge weakly to ![]() $|f|$ in
$|f|$ in ![]() $L_1(\nu)$ (by Lemma 2.2 applied to
$L_1(\nu)$ (by Lemma 2.2 applied to ![]() $|f|$). Hence,
$|f|$). Hence, ![]() $(I_\nu(g_n^+))_{n\in \mathbb{N}}$ and
$(I_\nu(g_n^+))_{n\in \mathbb{N}}$ and ![]() $(I_\nu(g_n^-))_{n\in \mathbb{N}}$ converge weakly to
$(I_\nu(g_n^-))_{n\in \mathbb{N}}$ converge weakly to ![]() $I_\nu(|f|)$ in E, where
$I_\nu(|f|)$ in E, where ![]() $I_\nu:L_1(\nu)\to E$ denotes the integration operator of ν. Observe that each
$I_\nu:L_1(\nu)\to E$ denotes the integration operator of ν. Observe that each ![]() $g_n^{\pm}$ belongs to the order interval
$g_n^{\pm}$ belongs to the order interval ![]() $K:=[0,2|f|] \subseteq L_1(\nu)$, which is uniformly µ-integrable and weakly compact.
$K:=[0,2|f|] \subseteq L_1(\nu)$, which is uniformly µ-integrable and weakly compact.
Since ![]() $\mathcal{R}(\nu)$ is relatively norm compact, Iν maps every bounded, uniformly µ-integrable subset of
$\mathcal{R}(\nu)$ is relatively norm compact, Iν maps every bounded, uniformly µ-integrable subset of ![]() $L_1(\nu)$ to a relatively norm compact subset of E (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Proposition 3.56(I)]). Therefore,
$L_1(\nu)$ to a relatively norm compact subset of E (see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Proposition 3.56(I)]). Therefore, ![]() $I_\nu(K)$ is norm compact. It follows that both sequences
$I_\nu(K)$ is norm compact. It follows that both sequences ![]() $(I_\nu(g_n^+))_{n\in \mathbb{N}}$ and
$(I_\nu(g_n^+))_{n\in \mathbb{N}}$ and ![]() $(I_\nu(g_n^-))_{n\in \mathbb{N}}$ are norm convergent to
$(I_\nu(g_n^-))_{n\in \mathbb{N}}$ are norm convergent to ![]() $I_\nu(|f|)$, so
$I_\nu(|f|)$, so
 \begin{equation*}
\|f\pm fr_n\|_{L_1(\nu)}\stackrel{\stackrel{(2.1)}{}}{=}
\left\|I_\nu(g_n^{\pm}) \right\|_E \to \left\|I_\nu(|f|) \right\|_E \stackrel{\stackrel{(2.1)}{}}{=} \|f\|_{L_1(\nu)}=1
\end{equation*}
\begin{equation*}
\|f\pm fr_n\|_{L_1(\nu)}\stackrel{\stackrel{(2.1)}{}}{=}
\left\|I_\nu(g_n^{\pm}) \right\|_E \to \left\|I_\nu(|f|) \right\|_E \stackrel{\stackrel{(2.1)}{}}{=} \|f\|_{L_1(\nu)}=1
\end{equation*}as ![]() $n\to \infty$. The proof is completed.
$n\to \infty$. The proof is completed.
The rest of this section is devoted to providing applications of Theorem 1.1.
2.1. Cesàro function spaces
The Cesàro “operator” is the map ![]() $f \mapsto \mathcal{C}(f)$ defined pointwise by
$f \mapsto \mathcal{C}(f)$ defined pointwise by  $\mathcal{C}(f)(x):=\frac{1}{x}\int_0^x f(t) \, {\rm d}t$ for any
$\mathcal{C}(f)(x):=\frac{1}{x}\int_0^x f(t) \, {\rm d}t$ for any ![]() $f\in L_1[0,1]$. Given a rearrangement invariant Banach function space
$f\in L_1[0,1]$. Given a rearrangement invariant Banach function space ![]() $(E,\|\cdot\|_E)$ on
$(E,\|\cdot\|_E)$ on ![]() $[0,1]$, the Cesàro function space
$[0,1]$, the Cesàro function space ![]() $[\mathcal{C},E]$ is the Banach function space on
$[\mathcal{C},E]$ is the Banach function space on ![]() $[0,1]$ consisting of all
$[0,1]$ consisting of all ![]() $f\in L_1[0,1]$ for which
$f\in L_1[0,1]$ for which ![]() $\mathcal{C}(|f|)\in E$, equipped with the norm
$\mathcal{C}(|f|)\in E$, equipped with the norm ![]() $\|f\|_{[\mathcal{C},E]}:=\|\mathcal{C}(|f|)\|_{E}$.
$\|f\|_{[\mathcal{C},E]}:=\|\mathcal{C}(|f|)\|_{E}$.
Corollary 2.3. Let E be an order continuous rearrangement invariant Banach function space on ![]() $[0,1]$. Then the Cesàro function space
$[0,1]$. Then the Cesàro function space ![]() $[\mathcal{C},E]$ is WASQ.
$[\mathcal{C},E]$ is WASQ.
Proof. By [Reference Curbera and Ricker13, Theorem 2.1], the formula ![]() $\nu(A):=\mathcal{C}(\chi_A)$ defines an
$\nu(A):=\mathcal{C}(\chi_A)$ defines an ![]() $E^+$-valued countably additive measure on the Lebesgue σ-algebra of
$E^+$-valued countably additive measure on the Lebesgue σ-algebra of ![]() $[0,1]$ such that ν has the same null sets as the Lebesgue measure (hence, it is non-atomic) and the range of ν is relatively norm compact. Since E is order continuous, we have
$[0,1]$ such that ν has the same null sets as the Lebesgue measure (hence, it is non-atomic) and the range of ν is relatively norm compact. Since E is order continuous, we have ![]() $[\mathcal{C},E]=L_1(\nu)$ (see [Reference Curbera and Ricker13, Proposition 3.1]). The conclusion now follows from Theorem 1.1.
$[\mathcal{C},E]=L_1(\nu)$ (see [Reference Curbera and Ricker13, Proposition 3.1]). The conclusion now follows from Theorem 1.1.
We stress that the weighed Cesàro function space ![]() $C_{p,w}$ on
$C_{p,w}$ on ![]() $[0,1]$ considered in [Reference Kubiak31], for
$[0,1]$ considered in [Reference Kubiak31], for ![]() $1\leq p \lt \infty$ and a measurable positive function w, is equal to
$1\leq p \lt \infty$ and a measurable positive function w, is equal to ![]() $[\mathcal{C},E]$ for
$[\mathcal{C},E]$ for ![]() $E=L_p((xw(x))^p \, {\rm d}x)$. Thus, the previous corollary generalizes [Reference Kubiak31, Lemma 3.3] in the case of
$E=L_p((xw(x))^p \, {\rm d}x)$. Thus, the previous corollary generalizes [Reference Kubiak31, Lemma 3.3] in the case of ![]() $[0,1]$.
$[0,1]$.
2.2. Köthe–Bochner spaces
Let ![]() $(E,\|\cdot\|_E)$ be a Banach function space on a finite measure space
$(E,\|\cdot\|_E)$ be a Banach function space on a finite measure space ![]() $(\Omega,\Sigma,\mu)$ and let
$(\Omega,\Sigma,\mu)$ and let ![]() $(Y,\|\cdot\|)$ be a Banach space. The Köthe–Bochner space E(Y) is the Banach space of all (equivalence classes of) strongly µ-measurable functions
$(Y,\|\cdot\|)$ be a Banach space. The Köthe–Bochner space E(Y) is the Banach space of all (equivalence classes of) strongly µ-measurable functions ![]() $f:\Omega \to Y$ such that
$f:\Omega \to Y$ such that ![]() $\|f(\cdot)\|\in E$, with the norm
$\|f(\cdot)\|\in E$, with the norm ![]() $\|f\|_{E(Y)}:=\|\|f(\cdot)\|\|_E$. Here
$\|f\|_{E(Y)}:=\|\|f(\cdot)\|\|_E$. Here ![]() $\|f(\cdot)\|:\Omega \to \mathbb{R}$ is the µ-measurable function given by
$\|f(\cdot)\|:\Omega \to \mathbb{R}$ is the µ-measurable function given by ![]() $t \mapsto \|f(t)\|$.
$t \mapsto \|f(t)\|$.
The following result should be compared with [Reference Hardtke28, Theorem 3.1], where it is proved that E(Y) is LASQ if Y is LASQ.
Theorem 2.4. Let ![]() $(\Omega,\Sigma)$ be a measurable space, let X be a Banach lattice and let
$(\Omega,\Sigma)$ be a measurable space, let X be a Banach lattice and let ![]() $\nu:\Sigma \to X$ be a non-atomic countably additive measure such that
$\nu:\Sigma \to X$ be a non-atomic countably additive measure such that ![]() $\mathcal{R}(\nu)$ is a relatively norm compact subset of
$\mathcal{R}(\nu)$ is a relatively norm compact subset of ![]() $X^+$. Let µ be a Rybakov control measure of ν and consider
$X^+$. Let µ be a Rybakov control measure of ν and consider ![]() $E:=L_1(\nu)$ as a Banach function space on
$E:=L_1(\nu)$ as a Banach function space on ![]() $(\Omega,\Sigma,\mu)$. Let Y be a Banach space. Then the Köthe–Bochner space E(Y) is WASQ.
$(\Omega,\Sigma,\mu)$. Let Y be a Banach space. Then the Köthe–Bochner space E(Y) is WASQ.
Proof. Let ![]() $(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on
$(r_n)_{n\in \mathbb{N}}$ be a Rademacher-type sequence on ![]() $(\Omega,\Sigma,\mu)$ (see Lemma 2.1).
$(\Omega,\Sigma,\mu)$ (see Lemma 2.1).
Fix ![]() $f\in S_{E(Y)}$. Then
$f\in S_{E(Y)}$. Then ![]() $fr_n\in S_{E(Y)}$ for every
$fr_n\in S_{E(Y)}$ for every ![]() $n\in \mathbb{N}$, and we claim that
$n\in \mathbb{N}$, and we claim that ![]() $(fr_n)_{n\in \mathbb{N}}$ is weakly null in E(Y). Indeed, given any
$(fr_n)_{n\in \mathbb{N}}$ is weakly null in E(Y). Indeed, given any ![]() $\varphi \in E(Y)^*$, the order continuity of E allows us to represent φ as a
$\varphi \in E(Y)^*$, the order continuity of E allows us to represent φ as a ![]() $w^*$-scalarly µ-measurable function
$w^*$-scalarly µ-measurable function ![]() $\varphi:\Omega \to Y^*$ such that
$\varphi:\Omega \to Y^*$ such that ![]() $\|\varphi(\cdot)\| \in E^*$, the duality being given by
$\|\varphi(\cdot)\| \in E^*$, the duality being given by
 \begin{equation*}
\varphi(h)=\int_\Omega \langle \varphi,h\rangle \, {\rm d}\mu
\quad\text{for every}\ h\in E(Y)
\end{equation*}
\begin{equation*}
\varphi(h)=\int_\Omega \langle \varphi,h\rangle \, {\rm d}\mu
\quad\text{for every}\ h\in E(Y)
\end{equation*} (see, e.g., [Reference Lin35, Theorem 3.2.4]). Here we denote by ![]() $\|\cdot\|$ the norm of both Y and
$\|\cdot\|$ the norm of both Y and ![]() $Y^*$, while
$Y^*$, while ![]() $\langle \varphi,h \rangle \in L_1(\mu)$ is defined by
$\langle \varphi,h \rangle \in L_1(\mu)$ is defined by ![]() $t \mapsto \langle \varphi(t),h(t) \rangle$. Therefore, we have
$t \mapsto \langle \varphi(t),h(t) \rangle$. Therefore, we have  $\varphi(fr_n)=\int_\Omega \langle \varphi, f \rangle r_n \, {\rm d}\mu \to 0$ as
$\varphi(fr_n)=\int_\Omega \langle \varphi, f \rangle r_n \, {\rm d}\mu \to 0$ as ![]() $n\to \infty$. This shows that
$n\to \infty$. This shows that ![]() $(fr_n)_{n\in \mathbb{N}}$ is weakly null in E(Y), as claimed.
$(fr_n)_{n\in \mathbb{N}}$ is weakly null in E(Y), as claimed.
Moreover, we have ![]() $\|f(\cdot)\| \in S_E$ and so
$\|f(\cdot)\| \in S_E$ and so
 \begin{equation*}
\|f\pm fr_n\|_{E(Y)}=
\left\|\|f(\cdot )\| (1\pm r_n)\right\|_{L_1(\nu)} \to 1
\end{equation*}
\begin{equation*}
\|f\pm fr_n\|_{E(Y)}=
\left\|\|f(\cdot )\| (1\pm r_n)\right\|_{L_1(\nu)} \to 1
\end{equation*}as ![]() $n\to \infty$, by the proof of Theorem 1.1.
$n\to \infty$, by the proof of Theorem 1.1.
To the best of our knowledge, the following corollary seems to be new:
Corollary 2.5. Let ![]() $(\Omega,\Sigma,\mu)$ be a non-atomic finite measure space and let Y be a Banach space. Then the Lebesgue–Bochner space
$(\Omega,\Sigma,\mu)$ be a non-atomic finite measure space and let Y be a Banach space. Then the Lebesgue–Bochner space ![]() $L_1(\mu,Y)$ is WASQ.
$L_1(\mu,Y)$ is WASQ.
Remark 2.6. The previous result is also interesting from the point of view of the identification of the space ![]() $L_1(\mu,Y)$ as the projective tensor product
$L_1(\mu,Y)$ as the projective tensor product ![]() $L_1(\mu){\widehat{\otimes}_\pi} Y$ (see, e.g., [Reference Diestel and Uhl17, p. 228, Example 10]). In general, given two Banach spaces X and Y, it is not known whether
$L_1(\mu){\widehat{\otimes}_\pi} Y$ (see, e.g., [Reference Diestel and Uhl17, p. 228, Example 10]). In general, given two Banach spaces X and Y, it is not known whether ![]() $X{\widehat{\otimes}_\pi} Y$ is WASQ if X is WASQ. It is even open if
$X{\widehat{\otimes}_\pi} Y$ is WASQ if X is WASQ. It is even open if ![]() $X{\widehat{\otimes}_\pi} Y$ has the D2P if X has the D2P (see [Reference Langemets, Lima and Zoca33, Question 4.2]).
$X{\widehat{\otimes}_\pi} Y$ has the D2P if X has the D2P (see [Reference Langemets, Lima and Zoca33, Question 4.2]).
2.3. An example
The aim of this subsection is to give an example of a WASQ Banach function space as in Theorem 1.1, which is not an ![]() $\mathcal L_1$-space. To do so, we need to introduce some terminology first. Throughout this subsection,
$\mathcal L_1$-space. To do so, we need to introduce some terminology first. Throughout this subsection, ![]() $(p_n)_{n\in \mathbb{N}}$ is a sequence in
$(p_n)_{n\in \mathbb{N}}$ is a sequence in ![]() $(1,\infty)$.
$(1,\infty)$.
The Nakano sequence space ![]() $\ell_{(p_n)}$ is the Banach lattice consisting of all sequences
$\ell_{(p_n)}$ is the Banach lattice consisting of all sequences ![]() $(a_n)_{n\in \mathbb{N}}\in \mathbb{R}^{\mathbb{N}}$ such that
$(a_n)_{n\in \mathbb{N}}\in \mathbb{R}^{\mathbb{N}}$ such that ![]() $\sum_{n\in \mathbb{N}}|s a_n|^{p_n} \lt \infty$ for some s > 0, equipped with the coordinate-wise ordering and the norm
$\sum_{n\in \mathbb{N}}|s a_n|^{p_n} \lt \infty$ for some s > 0, equipped with the coordinate-wise ordering and the norm
 \begin{equation*}
\left\|(a_n)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}:=\inf\left\{t \gt 0: \sum_{n\in \mathbb{N}}\left|\frac{a_n}{t}\right|^{p_n} \leq 1 \right\}.
\end{equation*}
\begin{equation*}
\left\|(a_n)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}:=\inf\left\{t \gt 0: \sum_{n\in \mathbb{N}}\left|\frac{a_n}{t}\right|^{p_n} \leq 1 \right\}.
\end{equation*} Given a sequence of Banach spaces ![]() $(X_n,\|\cdot\|_{X_n})_{n\in \mathbb{N}}$, its
$(X_n,\|\cdot\|_{X_n})_{n\in \mathbb{N}}$, its ![]() $\ell_{(p_n)}$-sum is the Banach space
$\ell_{(p_n)}$-sum is the Banach space ![]() $\ell_{(p_n)}(X_n)$ consisting of all sequences
$\ell_{(p_n)}(X_n)$ consisting of all sequences ![]() $(x_n)_{n\in \mathbb{N}}\in \prod_{n\in \mathbb{N}}X_n$, such that
$(x_n)_{n\in \mathbb{N}}\in \prod_{n\in \mathbb{N}}X_n$, such that ![]() $(\|x_n\|_{X_n})_{n\in \mathbb{N}}\in \ell_{(p_n)}$, with the norm
$(\|x_n\|_{X_n})_{n\in \mathbb{N}}\in \ell_{(p_n)}$, with the norm
 \begin{equation*}
\left\|(x_n)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}(X_n)}:=\left\|\left(\|x_n\|_{X_n}\right)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}.
\end{equation*}
\begin{equation*}
\left\|(x_n)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}(X_n)}:=\left\|\left(\|x_n\|_{X_n}\right)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}.
\end{equation*} If ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded, then the unit vectors form an unconditional basis of
$(p_n)_{n\in \mathbb{N}}$ is bounded, then the unit vectors form an unconditional basis of ![]() $\ell_{(p_n)}$ (see, e.g., [Reference Woo41, Theorem 3.5]) and so [Reference Abrahamsen, Langemets and Lima2, Proposition 5.2] applies to get:
$\ell_{(p_n)}$ (see, e.g., [Reference Woo41, Theorem 3.5]) and so [Reference Abrahamsen, Langemets and Lima2, Proposition 5.2] applies to get:
Corollary 2.7. Suppose that ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded and let
$(p_n)_{n\in \mathbb{N}}$ is bounded and let ![]() $(X_n)_{n\in \mathbb{N}}$ be a sequence of Banach spaces which are WASQ. Then
$(X_n)_{n\in \mathbb{N}}$ be a sequence of Banach spaces which are WASQ. Then ![]() $\ell_{(p_n)}(X_n)$ is WASQ.
$\ell_{(p_n)}(X_n)$ is WASQ.
We denote by λ the Lebesgue measure on the Lebesgue σ-algebra Σ of ![]() $[0,1]$.
$[0,1]$.
Proposition 2.8. Let ![]() $(A_n)_{n\in \mathbb{N}}$ be a partition of
$(A_n)_{n\in \mathbb{N}}$ be a partition of ![]() $[0,1]$ such that
$[0,1]$ such that ![]() $A_n\in \Sigma \setminus \mathcal{N}(\lambda)$ for all
$A_n\in \Sigma \setminus \mathcal{N}(\lambda)$ for all ![]() $n\in \mathbb{N}$. Then the map
$n\in \mathbb{N}$. Then the map ![]() $\nu:\Sigma \to \ell_{(p_n)}$ given by
$\nu:\Sigma \to \ell_{(p_n)}$ given by
 \begin{equation*}
\nu(A):=\big(\lambda(A\cap A_n)\big)_{n\in \mathbb{N}}
\quad
\text{for all}\ A\in \Sigma
\end{equation*}
\begin{equation*}
\nu(A):=\big(\lambda(A\cap A_n)\big)_{n\in \mathbb{N}}
\quad
\text{for all}\ A\in \Sigma
\end{equation*}is a well-defined countably additive measure. Moreover,
(i) ν is non-atomic and
 $\mathcal{R}(\nu)$ is relatively norm compact.
$\mathcal{R}(\nu)$ is relatively norm compact.(ii)
 $L_1(\nu)$ is WASQ.
$L_1(\nu)$ is WASQ.(iii) For each
 $n\in\mathbb{N}$, let λn be the restriction of λ to the σ-algebra on An given by
$n\in\mathbb{N}$, let λn be the restriction of λ to the σ-algebra on An given by  $\Sigma_n:=\{A\cap A_n:A\in \Sigma\}$. If
$\Sigma_n:=\{A\cap A_n:A\in \Sigma\}$. If  $(p_n)_{n\in \mathbb{N}}$ is bounded, then the map
given by
$(p_n)_{n\in \mathbb{N}}$ is bounded, then the map
given by \begin{equation*}
\Phi: L_1(\nu) \to \ell_{(p_n)}(L_1(\lambda_n))
\end{equation*}is a well-defined lattice isometry.
\begin{equation*}
\Phi: L_1(\nu) \to \ell_{(p_n)}(L_1(\lambda_n))
\end{equation*}is a well-defined lattice isometry. \begin{equation*}
\Phi(f):=\big(f|_{A_n}\big)_{n\in \mathbb{N}}
\quad\text{for all}\ f\in L_1(\nu)
\end{equation*}
\begin{equation*}
\Phi(f):=\big(f|_{A_n}\big)_{n\in \mathbb{N}}
\quad\text{for all}\ f\in L_1(\nu)
\end{equation*}
Proof. Define ![]() $\tilde{\nu}:\Sigma \to \ell_1$ by
$\tilde{\nu}:\Sigma \to \ell_1$ by
 \begin{equation*}
\tilde{\nu}(A):=\big(\lambda(A\cap A_n)\big)_{n\in \mathbb{N}}
\quad
\text{for all}\ A\in \Sigma.
\end{equation*}
\begin{equation*}
\tilde{\nu}(A):=\big(\lambda(A\cap A_n)\big)_{n\in \mathbb{N}}
\quad
\text{for all}\ A\in \Sigma.
\end{equation*} Note that ![]() $\tilde{\nu}$ is finitely additive and satisfies
$\tilde{\nu}$ is finitely additive and satisfies ![]() $\|\tilde{\nu}(A)\|_{\ell_1}=\lambda(A)$ for all
$\|\tilde{\nu}(A)\|_{\ell_1}=\lambda(A)$ for all ![]() $A\in \Sigma$; hence,
$A\in \Sigma$; hence, ![]() $\tilde{\nu}$ is countably additive. Since the inclusion
$\tilde{\nu}$ is countably additive. Since the inclusion ![]() $\iota:\ell_1\hookrightarrow \ell_{(p_n)}$ is a well-defined operator, the composition
$\iota:\ell_1\hookrightarrow \ell_{(p_n)}$ is a well-defined operator, the composition ![]() $\nu=\iota\circ \tilde{\nu}:\Sigma \to \ell_{(p_n)}$ is a countably additive measure.
$\nu=\iota\circ \tilde{\nu}:\Sigma \to \ell_{(p_n)}$ is a countably additive measure.
(i) Clearly, we have
 $\mathcal{N}(\lambda)=\mathcal{N}(\nu)$, so ν is non-atomic. The range of any countably additive Banach space-valued measure is relatively weakly compact (see, e.g., [Reference Diestel and Uhl17, p. 14, Corollary 7]). Hence, by the Schur property of
$\mathcal{N}(\lambda)=\mathcal{N}(\nu)$, so ν is non-atomic. The range of any countably additive Banach space-valued measure is relatively weakly compact (see, e.g., [Reference Diestel and Uhl17, p. 14, Corollary 7]). Hence, by the Schur property of  $\ell_1$, the set
$\ell_1$, the set  $\mathcal{R}(\tilde{\nu})$ is relatively norm compact. Alternatively, this can also be deduced from the usual criterion of relative norm compactness in
$\mathcal{R}(\tilde{\nu})$ is relatively norm compact. Alternatively, this can also be deduced from the usual criterion of relative norm compactness in  $\ell_1$ (see, e.g., [Reference Diestel16, p. 6, Exercise 6]). Therefore,
$\ell_1$ (see, e.g., [Reference Diestel16, p. 6, Exercise 6]). Therefore,  $\mathcal{R}(\nu)=\iota(\mathcal{R}(\tilde{\nu}))$ is relatively norm compact as well.
$\mathcal{R}(\nu)=\iota(\mathcal{R}(\tilde{\nu}))$ is relatively norm compact as well.(ii) Follows from (i) and Theorem 1.1 (note that ν takes values in
 $\ell_{(p_n)}^+$).
$\ell_{(p_n)}^+$).(iii) Fix
 $f\in L_1(\nu)$. For each
$f\in L_1(\nu)$. For each  $n\in \mathbb{N}$, let
$n\in \mathbb{N}$, let  $\pi_n\in \ell_{(p_n)}^*$ be the nth-coordinate functional. Since
$\pi_n\in \ell_{(p_n)}^*$ be the nth-coordinate functional. Since  $(\pi_n\circ \nu)(A)=\lambda(A\cap A_n)$ for all
$(\pi_n\circ \nu)(A)=\lambda(A\cap A_n)$ for all  $A\in \Sigma$ and
$A\in \Sigma$ and  $f\in L_1(\pi_n\circ \nu)$, we have
$f\in L_1(\pi_n\circ \nu)$, we have  $f|_{A_n} \in L_1(\lambda_n)$ and
$f|_{A_n} \in L_1(\lambda_n)$ and
 \begin{equation*}
\pi_n\left( I_\nu(|f|) \right)=
\int_{[0,1]} |f| \,{\rm d}(\pi_n\circ \nu)=\left\|f|_{A_n}\right\|_{L_1(\lambda_n)}.
\end{equation*}
\begin{equation*}
\pi_n\left( I_\nu(|f|) \right)=
\int_{[0,1]} |f| \,{\rm d}(\pi_n\circ \nu)=\left\|f|_{A_n}\right\|_{L_1(\lambda_n)}.
\end{equation*}
Hence,  $(\left\|f|_{A_n}\right\|_{L_1(\lambda_n)})_{n\in \mathbb{N}}=I_\nu(|f|)\in \ell_{(p_n)}$. Moreover, the fact that ν takes values in
$(\left\|f|_{A_n}\right\|_{L_1(\lambda_n)})_{n\in \mathbb{N}}=I_\nu(|f|)\in \ell_{(p_n)}$. Moreover, the fact that ν takes values in  $\ell_{(p_n)}^+$ ensures that
$\ell_{(p_n)}^+$ ensures that
 \begin{equation*}
\|f\|_{L_1(\nu)}=\big\|I_\nu(|f|)\big\|_{\ell_{(p_n)}}=
\left\|\left(\left\|f|_{A_n}\right\|_{L_1(\lambda_n)}\right)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}
\end{equation*}
\begin{equation*}
\|f\|_{L_1(\nu)}=\big\|I_\nu(|f|)\big\|_{\ell_{(p_n)}}=
\left\|\left(\left\|f|_{A_n}\right\|_{L_1(\lambda_n)}\right)_{n\in \mathbb{N}}\right\|_{\ell_{(p_n)}}
\end{equation*}(see, e.g., [Reference Okada, Ricker and Sánchez Pérez38, Lemma 3.13]). Thus, Φ is a well-defined isometric embedding. Clearly, Φ is a lattice homomorphism. It remains to check that Φ is surjective.
Let ![]() $(f_n)_{n\in \mathbb{N}}\in \ell_{(p_n)}(L_1(\lambda_n))$. Define
$(f_n)_{n\in \mathbb{N}}\in \ell_{(p_n)}(L_1(\lambda_n))$. Define ![]() $f\in L_0[0,1]$ by declaring
$f\in L_0[0,1]$ by declaring ![]() $f|_{A_n}:=f_n$ for all
$f|_{A_n}:=f_n$ for all ![]() $n\in \mathbb{N}$. Since
$n\in \mathbb{N}$. Since ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded, the space
$(p_n)_{n\in \mathbb{N}}$ is bounded, the space ![]() $\ell_{(p_n)}$ contains no isomorphic copy of c 0 (see, e.g., [Reference Woo41, Theorem 3.5]). Therefore, in order to prove that
$\ell_{(p_n)}$ contains no isomorphic copy of c 0 (see, e.g., [Reference Woo41, Theorem 3.5]). Therefore, in order to prove that ![]() $f\in L_1(\nu)$, it suffices to show that
$f\in L_1(\nu)$, it suffices to show that ![]() $f\in L_1(|\varphi \circ \nu|)$ for every
$f\in L_1(|\varphi \circ \nu|)$ for every  $\varphi\in \ell_{(p_n)}^*$ (see, e.g., [Reference Kluvánek and Knowles30, p. 31, Theorem 1]). It is known that
$\varphi\in \ell_{(p_n)}^*$ (see, e.g., [Reference Kluvánek and Knowles30, p. 31, Theorem 1]). It is known that  $\ell_{(p_n)}^*=\ell_{(q_n)}$, where
$\ell_{(p_n)}^*=\ell_{(q_n)}$, where ![]() $(q_n)_{n\in \mathbb{N}}$ is the sequence in
$(q_n)_{n\in \mathbb{N}}$ is the sequence in ![]() $(1,\infty)$ defined by
$(1,\infty)$ defined by ![]() $1/p_n+1/q_n=1$ for all
$1/p_n+1/q_n=1$ for all ![]() $n\in \mathbb{N}$, the duality being
$n\in \mathbb{N}$, the duality being
 \begin{equation*}
\big\langle (a_n)_{n\in \mathbb{N}},(b_n)_{n\in \mathbb{N}}\big\rangle=\sum_{n\in \mathbb{N}}a_nb_n
\quad\text{for all}\ (a_n)_{n\in \mathbb{N}}\in \ell_{(p_n)}\ \text{and}\ (b_n)_{n\in \mathbb{N}}\in \ell_{(q_n)}
\end{equation*}
\begin{equation*}
\big\langle (a_n)_{n\in \mathbb{N}},(b_n)_{n\in \mathbb{N}}\big\rangle=\sum_{n\in \mathbb{N}}a_nb_n
\quad\text{for all}\ (a_n)_{n\in \mathbb{N}}\in \ell_{(p_n)}\ \text{and}\ (b_n)_{n\in \mathbb{N}}\in \ell_{(q_n)}
\end{equation*} (see, e.g., [Reference Woo41, Theorem 4.2]). Take any ![]() $\varphi=(b_n)_{n\in \mathbb{N}} \in \ell_{(q_n)}$. Then
$\varphi=(b_n)_{n\in \mathbb{N}} \in \ell_{(q_n)}$. Then
 \begin{equation*}
(\varphi \circ \nu)(A)=\sum_{n\in \mathbb{N}}b_n \lambda(A\cap A_n)
\quad
\text{for all}\ A\in \Sigma
\end{equation*}
\begin{equation*}
(\varphi \circ \nu)(A)=\sum_{n\in \mathbb{N}}b_n \lambda(A\cap A_n)
\quad
\text{for all}\ A\in \Sigma
\end{equation*}and so the variation of ![]() $\varphi \circ \nu$ is given by
$\varphi \circ \nu$ is given by
 \begin{equation*}
|\varphi \circ \nu|(A)=\sum_{n\in \mathbb{N}}|b_n| \lambda(A\cap A_n)
\quad
\text{for all}\ A\in \Sigma.
\end{equation*}
\begin{equation*}
|\varphi \circ \nu|(A)=\sum_{n\in \mathbb{N}}|b_n| \lambda(A\cap A_n)
\quad
\text{for all}\ A\in \Sigma.
\end{equation*}Then
 \begin{align*}
\int_{[0,1]} |f| \, {\rm d}|\varphi \circ \nu| = \sum_{n\in \mathbb{N}} \int_{A_n} |f|& \, {\rm d}|\varphi \circ \nu| \\ & =
\sum_{n\in \mathbb{N}}|b_n|\int_{A_n}|f| \, {\rm d}\lambda=
\sum_{n\in \mathbb{N}}|b_n| \|f_n\|_{L_1(\lambda_n)} \lt \infty,
\end{align*}
\begin{align*}
\int_{[0,1]} |f| \, {\rm d}|\varphi \circ \nu| = \sum_{n\in \mathbb{N}} \int_{A_n} |f|& \, {\rm d}|\varphi \circ \nu| \\ & =
\sum_{n\in \mathbb{N}}|b_n|\int_{A_n}|f| \, {\rm d}\lambda=
\sum_{n\in \mathbb{N}}|b_n| \|f_n\|_{L_1(\lambda_n)} \lt \infty,
\end{align*}because  $\left(\|f_n\big\|_{L_1(\lambda_n)}\right)_{n\in \mathbb{N}} \in \ell_{(p_n)}$ and
$\left(\|f_n\big\|_{L_1(\lambda_n)}\right)_{n\in \mathbb{N}} \in \ell_{(p_n)}$ and ![]() $\varphi\in \ell_{(q_n)}$. Thus,
$\varphi\in \ell_{(q_n)}$. Thus, ![]() $f\in L_1(\nu)$, and we have
$f\in L_1(\nu)$, and we have ![]() $\Phi(f)=(f_n)_{n\in \mathbb{N}}$. The proof is completed.
$\Phi(f)=(f_n)_{n\in \mathbb{N}}$. The proof is completed.
Remark 2.9. Note that each ![]() $L_1(\lambda_n)$ is WASQ (in fact, it is isometrically isomorphic to
$L_1(\lambda_n)$ is WASQ (in fact, it is isometrically isomorphic to ![]() $L_1[0,1]$). Hence, when
$L_1[0,1]$). Hence, when ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded, the fact that
$(p_n)_{n\in \mathbb{N}}$ is bounded, the fact that ![]() $L_1(\nu)$ is WASQ can also be deduced from Corollary 2.7 and Proposition 2.8(iii).
$L_1(\nu)$ is WASQ can also be deduced from Corollary 2.7 and Proposition 2.8(iii).
Proposition 2.10. Let ν be as in Proposition 2.8. If ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded and
$(p_n)_{n\in \mathbb{N}}$ is bounded and  $\frac{p_n}{(p_n-1)\log n}\to 0$ as
$\frac{p_n}{(p_n-1)\log n}\to 0$ as ![]() $n\to \infty$, then
$n\to \infty$, then ![]() $L_1(\nu)$ is not an
$L_1(\nu)$ is not an ![]() $\mathcal{L}_1$-space.
$\mathcal{L}_1$-space.
Proof. Since ![]() $(p_n)_{n\in \mathbb{N}}$ is bounded, the space
$(p_n)_{n\in \mathbb{N}}$ is bounded, the space ![]() $\ell_{(p_n)}$ has an unconditional basis (see, e.g., [Reference Woo41, Theorem 3.5]). The additional condition on
$\ell_{(p_n)}$ has an unconditional basis (see, e.g., [Reference Woo41, Theorem 3.5]). The additional condition on ![]() $(p_n)_{n\in \mathbb{N}}$ implies that
$(p_n)_{n\in \mathbb{N}}$ implies that ![]() $\ell_{(p_n)}$ is not isomorphic to
$\ell_{(p_n)}$ is not isomorphic to ![]() $\ell_1$, see [Reference Wnuk40, Lemma 4]. Therefore,
$\ell_1$, see [Reference Wnuk40, Lemma 4]. Therefore, ![]() $\ell_{(p_n)}$ cannot be isomorphic to a complemented subspace of an
$\ell_{(p_n)}$ cannot be isomorphic to a complemented subspace of an ![]() $\mathcal{L}_1$-space (see, e.g., [Reference Diestel, Jarchow and Tonge18, Theorem 3.13]).
$\mathcal{L}_1$-space (see, e.g., [Reference Diestel, Jarchow and Tonge18, Theorem 3.13]).
Since ![]() $L_1(\nu)$ contains a complemented subspace isomorphic to
$L_1(\nu)$ contains a complemented subspace isomorphic to ![]() $\ell_{(p_n)}$ (this can be deduced from Proposition 2.8(iii)), it follows that
$\ell_{(p_n)}$ (this can be deduced from Proposition 2.8(iii)), it follows that ![]() $L_1(\nu)$ is not an
$L_1(\nu)$ is not an ![]() $\mathcal{L}_1$-space.
$\mathcal{L}_1$-space.
For instance, the sequence ![]() $p_n:=1+(\log (n+1))^{-1/2}$ satisfies the conditions of Proposition 2.10.
$p_n:=1+(\log (n+1))^{-1/2}$ satisfies the conditions of Proposition 2.10.
3. Proof of Theorem 1.2
The aim of this section is to provide a proof of Theorem 1.2. The first step is to prove the result for the space c 0, see Theorem 3.5 below. The proof of this particular case is based on the renorming technique of [Reference Guerrero, López-Pérez and Zoca19, Theorem 2.4], where it was shown that every Banach space containing an isomorphic copy of c 0 admits an equivalent norm so that its unit ball contains non-empty relatively weakly open subsets with arbitrarily small diameter, but every slice has a diameter 2.
The symbol ![]() $\mathbb N^{ \lt \omega}$ stands for the Baire tree, i.e., the set of all finite sequences of positive integers. The empty sequence is included in
$\mathbb N^{ \lt \omega}$ stands for the Baire tree, i.e., the set of all finite sequences of positive integers. The empty sequence is included in ![]() $\mathbb N^{ \lt \omega}$ as the root of the tree. The order on
$\mathbb N^{ \lt \omega}$ as the root of the tree. The order on ![]() $\mathbb N^{ \lt \omega}$ is defined by declaring that
$\mathbb N^{ \lt \omega}$ is defined by declaring that ![]() $\alpha \preceq \beta$ if and only if β extends α. Given
$\alpha \preceq \beta$ if and only if β extends α. Given ![]() $\alpha\in \mathbb{N}^{ \lt \omega}$ and
$\alpha\in \mathbb{N}^{ \lt \omega}$ and ![]() $p\in \mathbb{N}$, we denote by
$p\in \mathbb{N}$, we denote by ![]() $\alpha\smallfrown p \in \mathbb{N}^{ \lt \omega}$ the sequence defined by
$\alpha\smallfrown p \in \mathbb{N}^{ \lt \omega}$ the sequence defined by ![]() $\alpha\smallfrown p:=(\alpha_1,\dots,\alpha_n,p)$ if
$\alpha\smallfrown p:=(\alpha_1,\dots,\alpha_n,p)$ if ![]() $\alpha=(\alpha_1,\dots,\alpha_n)$ or
$\alpha=(\alpha_1,\dots,\alpha_n)$ or ![]() $\alpha\smallfrown p:=(p)$ (a sequence with just one element) if
$\alpha\smallfrown p:=(p)$ (a sequence with just one element) if ![]() $\alpha=\emptyset$. The following is standard (see, e.g., [Reference Guerrero, López-Pérez and Zoca19, p. 857]):
$\alpha=\emptyset$. The following is standard (see, e.g., [Reference Guerrero, López-Pérez and Zoca19, p. 857]):
Lemma 3.1. There exists a bijection ![]() $\phi:\mathbb N^{ \lt \omega}\rightarrow \mathbb N$ such that:
$\phi:\mathbb N^{ \lt \omega}\rightarrow \mathbb N$ such that:
(i)
 $\phi (\emptyset)=1$.
$\phi (\emptyset)=1$.(ii)
 $\phi(\alpha)\leq\phi(\beta)$ for all
$\phi(\alpha)\leq\phi(\beta)$ for all  $\alpha,\beta \in \mathbb N^{ \lt \omega}$ with
$\alpha,\beta \in \mathbb N^{ \lt \omega}$ with  $\alpha\preceq \beta$.
$\alpha\preceq \beta$.(iii)
 $\phi(\alpha\smallfrown j) \lt \phi(\alpha \smallfrown k)$ for every
$\phi(\alpha\smallfrown j) \lt \phi(\alpha \smallfrown k)$ for every  $\alpha\in \mathbb N^{ \lt \omega}$ and for all
$\alpha\in \mathbb N^{ \lt \omega}$ and for all  $j, k\in\mathbb N$ with j < k.
$j, k\in\mathbb N$ with j < k.
Let c be the subspace of ![]() $\ell_\infty$ consisting of all convergent sequences and let
$\ell_\infty$ consisting of all convergent sequences and let ![]() $c(\mathbb N^{ \lt \omega})$ be the subspace of
$c(\mathbb N^{ \lt \omega})$ be the subspace of ![]() $\ell_\infty(\mathbb N^{ \lt \omega})$ defined by
$\ell_\infty(\mathbb N^{ \lt \omega})$ defined by
Clearly, ![]() $c(\mathbb N^{ \lt \omega})$ and c are isometric; hence,
$c(\mathbb N^{ \lt \omega})$ and c are isometric; hence, ![]() $c(\mathbb N^{ \lt \omega})$ is isomorphic to c 0. We denote by
$c(\mathbb N^{ \lt \omega})$ is isomorphic to c 0. We denote by ![]() $\lim \in c(\mathbb N^{ \lt \omega})^*$ the functional defined by
$\lim \in c(\mathbb N^{ \lt \omega})^*$ the functional defined by
 \begin{equation*}
\lim x:=\lim_{n\to \infty} x(\phi^{-1}(n))
\quad
\text{for all}\ x\in c(\mathbb N^{ \lt \omega}).
\end{equation*}
\begin{equation*}
\lim x:=\lim_{n\to \infty} x(\phi^{-1}(n))
\quad
\text{for all}\ x\in c(\mathbb N^{ \lt \omega}).
\end{equation*} For each ![]() $\alpha\in \mathbb N^{ \lt \omega}$, we denote by
$\alpha\in \mathbb N^{ \lt \omega}$, we denote by ![]() $e_\alpha^*\in c(\mathbb N^{ \lt \omega})^*$ the functional defined by
$e_\alpha^*\in c(\mathbb N^{ \lt \omega})^*$ the functional defined by
Given ![]() $\alpha\in \mathbb N^{ \lt \omega}$, we define
$\alpha\in \mathbb N^{ \lt \omega}$, we define ![]() $x_\alpha\in \ell_\infty(\mathbb N^{ \lt \omega})$ by the formula
$x_\alpha\in \ell_\infty(\mathbb N^{ \lt \omega})$ by the formula
 \begin{equation*}
x_\alpha(\beta):=\left\{
\begin{array}{cc}
1 & \text{if}\ \beta\preceq \alpha\\
-1 & \text{otherwise}
\end{array} \right.
\end{equation*}
\begin{equation*}
x_\alpha(\beta):=\left\{
\begin{array}{cc}
1 & \text{if}\ \beta\preceq \alpha\\
-1 & \text{otherwise}
\end{array} \right.
\end{equation*}so that ![]() $x_\alpha\in S_{c(\mathbb N^{ \lt \omega})}$ and
$x_\alpha\in S_{c(\mathbb N^{ \lt \omega})}$ and ![]() $\lim x_\alpha=-1$. Define
$\lim x_\alpha=-1$. Define
 \begin{equation*}
A:=\{x_\alpha: \alpha\in\mathbb N^{ \lt \omega}\} \subseteq S_{c(\mathbb{N}^{ \lt \omega})}
\quad\text{and} \quad
K:=\overline{\operatorname{conv}}(A\cup -A) \subseteq B_{c(\mathbb{N}^{ \lt \omega})}.
\end{equation*}
\begin{equation*}
A:=\{x_\alpha: \alpha\in\mathbb N^{ \lt \omega}\} \subseteq S_{c(\mathbb{N}^{ \lt \omega})}
\quad\text{and} \quad
K:=\overline{\operatorname{conv}}(A\cup -A) \subseteq B_{c(\mathbb{N}^{ \lt \omega})}.
\end{equation*}We will need the following result (see [Reference Guerrero, López-Pérez and Zoca19, Proposition 2.2]):
Lemma 3.2. Let ![]() $n\in\mathbb N$ and ρ > 0. Define
$n\in\mathbb N$ and ρ > 0. Define
 \begin{align*}
W_{n,\rho}:=\left\{x\in K: e_{\emptyset\smallfrown i}^*(x) \gt \frac{2}{n}-1-2\rho \quad \text{for all}\ i\in \{1,\dots,n\} \right. \\ \left. \vphantom{\frac{2}{n}}\text{and}\ \lim x \lt -1+\rho\right\}.
\end{align*}
\begin{align*}
W_{n,\rho}:=\left\{x\in K: e_{\emptyset\smallfrown i}^*(x) \gt \frac{2}{n}-1-2\rho \quad \text{for all}\ i\in \{1,\dots,n\} \right. \\ \left. \vphantom{\frac{2}{n}}\text{and}\ \lim x \lt -1+\rho\right\}.
\end{align*} Then ![]() $W_{n,\rho}$ is a non-empty relatively weakly open subset of K and
$W_{n,\rho}$ is a non-empty relatively weakly open subset of K and ![]() ${\rm diam}(W_{n,\rho})\to 0$ as
${\rm diam}(W_{n,\rho})\to 0$ as ![]() $n\to \infty$ and ρ → 0.
$n\to \infty$ and ρ → 0.
The following lemma is elementary and its proof will be omitted:
Lemma 3.3. Let V be a linear space, let ![]() $A_1,\dots,A_m$ be subsets of V and let
$A_1,\dots,A_m$ be subsets of V and let ![]() $v\in {\rm conv}(A_1\cup \cdots\cup A_m)$. Then there exist
$v\in {\rm conv}(A_1\cup \cdots\cup A_m)$. Then there exist ![]() $v_i\in {\rm conv}(A_i)$ and
$v_i\in {\rm conv}(A_i)$ and ![]() $c_i \in [0,\infty)$ for
$c_i \in [0,\infty)$ for ![]() $i\in \{1,\dots,m\}$ such that
$i\in \{1,\dots,m\}$ such that ![]() $\sum_{i=1}^m c_i v_i=v$ and
$\sum_{i=1}^m c_i v_i=v$ and ![]() $\sum_{i=1}^m c_i=1$.
$\sum_{i=1}^m c_i=1$.
Lemma 3.4. Let ![]() $(X,\|\cdot\|)$ be a Banach space, let
$(X,\|\cdot\|)$ be a Banach space, let ![]() $S \subseteq S_{(X,\|\cdot\|)}$ be a dense set and let
$S \subseteq S_{(X,\|\cdot\|)}$ be a dense set and let ![]() $0 \lt \delta \lt 1$. Suppose that for all
$0 \lt \delta \lt 1$. Suppose that for all ![]() $0 \lt r,s \lt \delta$ and for every finite set
$0 \lt r,s \lt \delta$ and for every finite set ![]() $\{x_1,\ldots, x_n\}\subseteq S$, there exists
$\{x_1,\ldots, x_n\}\subseteq S$, there exists ![]() $y\in S_{(X,\|\cdot\|)}$ satisfying
$y\in S_{(X,\|\cdot\|)}$ satisfying
Then ![]() $(X,\|\cdot\|)$ is (r, s)-SQ for all
$(X,\|\cdot\|)$ is (r, s)-SQ for all ![]() $0 \lt r,s \lt \delta$.
$0 \lt r,s \lt \delta$.
Proof. Fix ![]() $0 \lt r,s \lt \delta$. Choose
$0 \lt r,s \lt \delta$. Choose ![]() $r \lt r^{\prime} \lt \delta$ such that
$r \lt r^{\prime} \lt \delta$ such that  $s^{\prime}:=s\frac{r^{\prime}}{r} \lt \delta$ and then choose θ > 0 such that
$s^{\prime}:=s\frac{r^{\prime}}{r} \lt \delta$ and then choose θ > 0 such that ![]() $r\theta+\frac{r}{r^{\prime}}\leq 1$. Take any finite set
$r\theta+\frac{r}{r^{\prime}}\leq 1$. Take any finite set ![]() $\{x_1,\ldots, x_n\}\subseteq S_{(X,\|\cdot\|)}$. Since S is dense in
$\{x_1,\ldots, x_n\}\subseteq S_{(X,\|\cdot\|)}$. Since S is dense in ![]() $S_{(X,\|\cdot\|)}$, there exist
$S_{(X,\|\cdot\|)}$, there exist ![]() $x^{\prime}_1,\ldots,x^{\prime}_n\in S$ such that
$x^{\prime}_1,\ldots,x^{\prime}_n\in S$ such that ![]() $\|x_i-x^{\prime}_i\|\leq \theta$ for every
$\|x_i-x^{\prime}_i\|\leq \theta$ for every ![]() $i\in \{1,\ldots,n\}$. By the assumption, we can find
$i\in \{1,\ldots,n\}$. By the assumption, we can find ![]() $y\in S_{(X,\|\cdot\|)}$ in such a way that
$y\in S_{(X,\|\cdot\|)}$ in such a way that ![]() $\|r^{\prime}x^{\prime}_i \pm s^{\prime}y\|\le1$ for every
$\|r^{\prime}x^{\prime}_i \pm s^{\prime}y\|\le1$ for every ![]() $i\in \{1,\dots,n\}$. Then
$i\in \{1,\dots,n\}$. Then
 \begin{equation*}
\|rx_i \pm sy\|\leq
r\|x_i-x^{\prime}_i\|+\frac{r}{r^{\prime}}\|r^{\prime}x^{\prime}_i \pm s^{\prime}y\| \leq r\theta + \frac{r}{r^{\prime}} \leq 1
\end{equation*}
\begin{equation*}
\|rx_i \pm sy\|\leq
r\|x_i-x^{\prime}_i\|+\frac{r}{r^{\prime}}\|r^{\prime}x^{\prime}_i \pm s^{\prime}y\| \leq r\theta + \frac{r}{r^{\prime}} \leq 1
\end{equation*}for every ![]() $i\in \{1,\dots,n\}$. This shows that
$i\in \{1,\dots,n\}$. This shows that ![]() $(X,\|\cdot\|)$ is (r, s)-SQ.
$(X,\|\cdot\|)$ is (r, s)-SQ.
Theorem 3.5. Let ![]() $0 \lt \varepsilon \lt 1$. Then there exists an equivalent norm
$0 \lt \varepsilon \lt 1$. Then there exists an equivalent norm ![]() $|\cdot|$ on c 0 such that:
$|\cdot|$ on c 0 such that:
(i)
 $(c_0,|\cdot|)$ has the slice-D2P.
$(c_0,|\cdot|)$ has the slice-D2P.(ii) There are non-empty relatively weakly open subsets of
 $B_{(c_0,|\cdot|)}$ of arbitrarily small diameter.
$B_{(c_0,|\cdot|)}$ of arbitrarily small diameter.(iii)
 $(c_0,|\cdot|)$ is (r, s)-SQ for all
$(c_0,|\cdot|)$ is (r, s)-SQ for all  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$.
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$.
Proof. Let us denote by ![]() $\|\cdot\|_Z$ the norm of the Banach space
$\|\cdot\|_Z$ the norm of the Banach space ![]() $Z:=c(\mathbb N^{ \lt \omega})\oplus_\infty c_0$. Since c 0 and Z are isomorphic, it suffices to prove the statement of the theorem for the space
$Z:=c(\mathbb N^{ \lt \omega})\oplus_\infty c_0$. Since c 0 and Z are isomorphic, it suffices to prove the statement of the theorem for the space ![]() $(Z,\|\cdot\|_Z)$. Let
$(Z,\|\cdot\|_Z)$. Let ![]() $c_0(\mathbb N^{ \lt \omega}) \subseteq c(\mathbb N^{ \lt \omega})$ be the subspace of all
$c_0(\mathbb N^{ \lt \omega}) \subseteq c(\mathbb N^{ \lt \omega})$ be the subspace of all ![]() $x\in c(\mathbb N^{ \lt \omega})$ such that
$x\in c(\mathbb N^{ \lt \omega})$ such that ![]() $\lim x=0$. For each
$\lim x=0$. For each ![]() $\alpha\in \mathbb N^{ \lt \omega}$, we write eα to denote the element of
$\alpha\in \mathbb N^{ \lt \omega}$, we write eα to denote the element of ![]() $S_{c_0(\mathbb N^{ \lt \omega})}$ defined by
$S_{c_0(\mathbb N^{ \lt \omega})}$ defined by ![]() $e_\alpha(\alpha)=1$ and
$e_\alpha(\alpha)=1$ and ![]() $e_\alpha(\beta)=0$ for every
$e_\alpha(\beta)=0$ for every ![]() $\beta \in \mathbb N^{ \lt \omega}\setminus \{\alpha\}$.
$\beta \in \mathbb N^{ \lt \omega}\setminus \{\alpha\}$.
Let ![]() $|\cdot|$ be the Minkowski functional of the closed convex symmetric set
$|\cdot|$ be the Minkowski functional of the closed convex symmetric set
 \begin{equation*}
B:=\overline{\operatorname{conv}}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right) \subseteq Z,
\end{equation*}
\begin{equation*}
B:=\overline{\operatorname{conv}}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right) \subseteq Z,
\end{equation*}that is, ![]() $|z|:=\inf\{t \gt 0: z\in tB\}$ for all
$|z|:=\inf\{t \gt 0: z\in tB\}$ for all ![]() $z\in Z$. Since
$z\in Z$. Since ![]() $(1-\varepsilon)B_Z\subseteq B\subseteq B_Z$, it follows that
$(1-\varepsilon)B_Z\subseteq B\subseteq B_Z$, it follows that ![]() $|\cdot|$ is an equivalent norm on Z with unit ball
$|\cdot|$ is an equivalent norm on Z with unit ball ![]() $B_{(Z,|\cdot|)}=B$. We have
$B_{(Z,|\cdot|)}=B$. We have
 \begin{equation}
\|z\|_Z \leq |z|\leq \frac{1}{1-\varepsilon}\|z\|_Z\quad\text{for all}\ z\in Z
\end{equation}
\begin{equation}
\|z\|_Z \leq |z|\leq \frac{1}{1-\varepsilon}\|z\|_Z\quad\text{for all}\ z\in Z
\end{equation}and
because  $B_{c_0(\mathbb N^{ \lt \omega})}\times \{0\}\subseteq B$. We denote by
$B_{c_0(\mathbb N^{ \lt \omega})}\times \{0\}\subseteq B$. We denote by ![]() $\|\cdot\|_{Z^*}$ and
$\|\cdot\|_{Z^*}$ and ![]() $|\cdot|_{Z^*}$ the equivalent norms on
$|\cdot|_{Z^*}$ the equivalent norms on ![]() $Z^*$ induced by
$Z^*$ induced by ![]() $\|\cdot\|_Z$ and
$\|\cdot\|_Z$ and ![]() $|\cdot|$, respectively. We will check that
$|\cdot|$, respectively. We will check that ![]() $|\cdot|$ satisfies the required properties.
$|\cdot|$ satisfies the required properties.
Proof of (i). Let ![]() $S \subseteq B$ be a slice of B. Since
$S \subseteq B$ be a slice of B. Since ![]() $B \setminus S$ is convex and closed, we have
$B \setminus S$ is convex and closed, we have
 \begin{equation*}
S\cap \left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right)\neq\emptyset.
\end{equation*}
\begin{equation*}
S\cap \left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right)\neq\emptyset.
\end{equation*}We now distinguish several cases.
Case (a): ![]() $S\cap (A\times \{0\})\neq \emptyset$. Then
$S\cap (A\times \{0\})\neq \emptyset$. Then ![]() $(x_\alpha,0)\in S$ for some
$(x_\alpha,0)\in S$ for some ![]() $\alpha\in \mathbb N^{ \lt \omega}$. Observe that the sequence
$\alpha\in \mathbb N^{ \lt \omega}$. Observe that the sequence ![]() $((x_{\alpha\smallfrown n},0))_{n\in \mathbb{N}}=((x_\alpha+2e_{\alpha\smallfrown n},0))_{n\in \mathbb{N}}$ converges weakly to
$((x_{\alpha\smallfrown n},0))_{n\in \mathbb{N}}=((x_\alpha+2e_{\alpha\smallfrown n},0))_{n\in \mathbb{N}}$ converges weakly to ![]() $(x_\alpha,0)$ in Z (because
$(x_\alpha,0)$ in Z (because ![]() $(e_{\alpha\smallfrown n})_{n\in \mathbb{N}}$ is weakly null in
$(e_{\alpha\smallfrown n})_{n\in \mathbb{N}}$ is weakly null in ![]() $c_0(\mathbb N^{ \lt \omega})$). Since S is relatively weakly open in B and
$c_0(\mathbb N^{ \lt \omega})$). Since S is relatively weakly open in B and ![]() $(x_{\alpha\smallfrown n},0)\in B$ for every
$(x_{\alpha\smallfrown n},0)\in B$ for every ![]() $n\in\mathbb N$, we have
$n\in\mathbb N$, we have ![]() $(x_{\alpha\smallfrown n_0},0)\in S$ for large enough
$(x_{\alpha\smallfrown n_0},0)\in S$ for large enough ![]() $n_0\in \mathbb{N}$. Hence,
$n_0\in \mathbb{N}$. Hence,
 \begin{equation*}
\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)\geq \vert (x_{\alpha\smallfrown n_0},0)-(x_{\alpha},0)\vert=2\vert (e_{\alpha\smallfrown n_0},0)\vert
\stackrel{\stackrel{(3.2)}{}}{=}2\Vert (e_{\alpha\smallfrown n_0},0)\Vert_Z=2
\end{equation*}
\begin{equation*}
\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)\geq \vert (x_{\alpha\smallfrown n_0},0)-(x_{\alpha},0)\vert=2\vert (e_{\alpha\smallfrown n_0},0)\vert
\stackrel{\stackrel{(3.2)}{}}{=}2\Vert (e_{\alpha\smallfrown n_0},0)\Vert_Z=2
\end{equation*}and, therefore, ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$.
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$.
Case (b): ![]() $S\cap (-A\times \{0\})\neq \emptyset$. The proof that
$S\cap (-A\times \{0\})\neq \emptyset$. The proof that ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$ runs similarly as in (a).
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$ runs similarly as in (a).
Case (c):  $S\cap ((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times \{0\})\neq \emptyset$. Then we can pick
$S\cap ((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times \{0\})\neq \emptyset$. Then we can pick ![]() $(x,y)\in B_Z$ and
$(x,y)\in B_Z$ and  $x^{\prime}\in B_{c_0(\mathbb N^{ \lt \omega})}$ in such a way that
$x^{\prime}\in B_{c_0(\mathbb N^{ \lt \omega})}$ in such a way that
We can assume without loss of generality that x ʹ has finite support because the set of all finitely supported functions from ![]() $\mathbb N^{ \lt \omega}$ to
$\mathbb N^{ \lt \omega}$ to ![]() $[-1,1]$ is a norm dense subset of
$[-1,1]$ is a norm dense subset of ![]() $B_{c_0(\mathbb N^{ \lt \omega})}$. Choose
$B_{c_0(\mathbb N^{ \lt \omega})}$. Choose ![]() $\alpha\in \mathbb N^{ \lt \omega}$ such that
$\alpha\in \mathbb N^{ \lt \omega}$ such that ![]() $x^{\prime}(\alpha\smallfrown n)=0$ for every
$x^{\prime}(\alpha\smallfrown n)=0$ for every ![]() $n\in\mathbb N$. Observe that
$n\in\mathbb N$. Observe that
 \begin{equation*}
x-x(\alpha\smallfrown n)e_{\alpha\smallfrown n}\pm e_{\alpha\smallfrown n}\in B_{c(\mathbb N^{ \lt \omega})}
\quad
\text{and}
\quad
x^{\prime}\pm e_{\alpha\smallfrown n}\in B_{c_0(\mathbb N^{ \lt \omega})}
\end{equation*}
\begin{equation*}
x-x(\alpha\smallfrown n)e_{\alpha\smallfrown n}\pm e_{\alpha\smallfrown n}\in B_{c(\mathbb N^{ \lt \omega})}
\quad
\text{and}
\quad
x^{\prime}\pm e_{\alpha\smallfrown n}\in B_{c_0(\mathbb N^{ \lt \omega})}
\end{equation*}and so
 \begin{align*}
z_n^{\pm}:=(1-\varepsilon)\big(x&-x(\alpha\smallfrown n)e_{\alpha\smallfrown n},y\big)+\varepsilon (x^{\prime},0)\pm (e_{\alpha\smallfrown n},0) \\
&= (1-\varepsilon)\big(x-x(\alpha\smallfrown n)e_{\alpha\smallfrown n}\pm e_{\alpha\smallfrown n},y\big)+
\varepsilon (x^{\prime}\pm e_{\alpha\smallfrown n},0)\in B
\end{align*}
\begin{align*}
z_n^{\pm}:=(1-\varepsilon)\big(x&-x(\alpha\smallfrown n)e_{\alpha\smallfrown n},y\big)+\varepsilon (x^{\prime},0)\pm (e_{\alpha\smallfrown n},0) \\
&= (1-\varepsilon)\big(x-x(\alpha\smallfrown n)e_{\alpha\smallfrown n}\pm e_{\alpha\smallfrown n},y\big)+
\varepsilon (x^{\prime}\pm e_{\alpha\smallfrown n},0)\in B
\end{align*}for every ![]() $n\in\mathbb N$. Since S is relatively weakly open in B and both sequences
$n\in\mathbb N$. Since S is relatively weakly open in B and both sequences ![]() $(z_n^{+})_{n\in \mathbb{N}}$ and
$(z_n^{+})_{n\in \mathbb{N}}$ and ![]() $(z_n^{-})_{n\in \mathbb{N}}$ converge weakly to z in Z, we can find
$(z_n^{-})_{n\in \mathbb{N}}$ converge weakly to z in Z, we can find ![]() $n_0\in\mathbb N$ large enough so that both
$n_0\in\mathbb N$ large enough so that both  $z_{n_0}^{+}$ and
$z_{n_0}^{+}$ and ![]() $z_{n_0}^{-}$ belong to S. Hence,
$z_{n_0}^{-}$ belong to S. Hence,
 \begin{equation*}
\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)\geq |z_{n_0}^{+} - z_{n_0}^{-}| =2\vert (e_{\alpha\smallfrown n_0},0)\vert \stackrel{\stackrel{(3.2)}{}}{=}
2\Vert (e_{\alpha\smallfrown n_0},0)\Vert_Z=2
\end{equation*}
\begin{equation*}
\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)\geq |z_{n_0}^{+} - z_{n_0}^{-}| =2\vert (e_{\alpha\smallfrown n_0},0)\vert \stackrel{\stackrel{(3.2)}{}}{=}
2\Vert (e_{\alpha\smallfrown n_0},0)\Vert_Z=2
\end{equation*}and so ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$. This completes the proof of (i).
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(S)=2$. This completes the proof of (i).
Proof of (ii). Fix θ > 0. By Lemma 3.2, we can take ![]() $n\in \mathbb{N}$ and ρ > 0 such that
$n\in \mathbb{N}$ and ρ > 0 such that
 \begin{equation}
\mathop{\mathrm{diam}}\nolimits(W_{n,\rho})\leq \frac{(1-\varepsilon)\theta}{2}
\quad\text{and}\quad
\eta:=\frac{2\rho}{5} \leq \frac{\theta}{16}.
\end{equation}
\begin{equation}
\mathop{\mathrm{diam}}\nolimits(W_{n,\rho})\leq \frac{(1-\varepsilon)\theta}{2}
\quad\text{and}\quad
\eta:=\frac{2\rho}{5} \leq \frac{\theta}{16}.
\end{equation}Define
 \begin{align*}
U:=\Big\{z\in B: (e_{\emptyset\smallfrown i}^*,0)(z) \gt \frac{2}{n}-1-\eta \quad \text{for all}\ i\in& \{1,\ldots,n\} \\
&\text{and}\ (\lim,0)(z) \lt -1+\varepsilon\eta\Big\}.
\end{align*}
\begin{align*}
U:=\Big\{z\in B: (e_{\emptyset\smallfrown i}^*,0)(z) \gt \frac{2}{n}-1-\eta \quad \text{for all}\ i\in& \{1,\ldots,n\} \\
&\text{and}\ (\lim,0)(z) \lt -1+\varepsilon\eta\Big\}.
\end{align*} It is clear that U is a relatively weakly open subset of B. To prove that ![]() $U\neq \emptyset$, we will check that the vector
$U\neq \emptyset$, we will check that the vector  $z_0:=(\frac{1}{n}\sum_{j=1}^n x_{\emptyset\smallfrown j},0)\in B$ belongs to U. Indeed, for each
$z_0:=(\frac{1}{n}\sum_{j=1}^n x_{\emptyset\smallfrown j},0)\in B$ belongs to U. Indeed, for each ![]() $i\in \{1,\ldots,n\}$, we have
$i\in \{1,\ldots,n\}$, we have
 \begin{equation*}
(e_{\emptyset\smallfrown i}^*,0)(z_0)=\frac{1}{n}
\sum_{j=1}^n e_{\emptyset\smallfrown i}^*(x_{\emptyset\smallfrown j})=\frac{1}{n}\big(1-(n-1)\big)=\frac{2}{n}-1 \gt \frac{2}{n}-1-\eta,
\end{equation*}
\begin{equation*}
(e_{\emptyset\smallfrown i}^*,0)(z_0)=\frac{1}{n}
\sum_{j=1}^n e_{\emptyset\smallfrown i}^*(x_{\emptyset\smallfrown j})=\frac{1}{n}\big(1-(n-1)\big)=\frac{2}{n}-1 \gt \frac{2}{n}-1-\eta,
\end{equation*}and we also have
 \begin{equation*}
(\lim,0)(z_0)=\frac{1}{n}\sum_{j=1}^n \lim x_{\emptyset\smallfrown j}=-1 \lt -1+\varepsilon\eta.
\end{equation*}
\begin{equation*}
(\lim,0)(z_0)=\frac{1}{n}\sum_{j=1}^n \lim x_{\emptyset\smallfrown j}=-1 \lt -1+\varepsilon\eta.
\end{equation*} Hence, ![]() $z_0\in U$ and so
$z_0\in U$ and so ![]() $U\neq \emptyset$.
$U\neq \emptyset$.
We will show that ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(U)\leq \theta$. The key point is the following:
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(U)\leq \theta$. The key point is the following:
Claim. For every
 \begin{equation*}
z\in V:=U \cap {\rm conv}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right),
\end{equation*}
\begin{equation*}
z\in V:=U \cap {\rm conv}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \left((1-\varepsilon)B_Z+\varepsilon B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}\right)\right),
\end{equation*} there is ![]() $z^{\prime}\in W_{n,\rho}\times \{0\}$ such that
$z^{\prime}\in W_{n,\rho}\times \{0\}$ such that ![]() $|z-z^{\prime}| \lt 4\eta$.
$|z-z^{\prime}| \lt 4\eta$.
Indeed, by Lemma 3.3, we can write
for some ![]() $a,b,c\geq 0$ with
$a,b,c\geq 0$ with ![]() $a+b+c=1$ and
$a+b+c=1$ and
 \begin{equation*}
z_1,z_2\in {\rm conv}(A\times \{0\}), \quad
u\in B_{Z}\ \text{and} \
v\in B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}.
\end{equation*}
\begin{equation*}
z_1,z_2\in {\rm conv}(A\times \{0\}), \quad
u\in B_{Z}\ \text{and} \
v\in B_{c_0(\mathbb N^{ \lt \omega})}\times\{0\}.
\end{equation*}Observe that
because ![]() $\lim x_\alpha=-1$ for all
$\lim x_\alpha=-1$ for all ![]() $\alpha \in \mathbb N^{ \lt \omega}$. We also have
$\alpha \in \mathbb N^{ \lt \omega}$. We also have
Thus,
 \begin{align*}
-1+\varepsilon\eta \gt (\lim,0)& (z) \stackrel{\stackrel{(3.4)}{}}{=} -a+b+c(1-\varepsilon)(\lim ,0)(u) \\ &\geq -a+b-c(1-\varepsilon) =-a-b-c+2b+\varepsilon c=
-1+2b+\varepsilon c,
\end{align*}
\begin{align*}
-1+\varepsilon\eta \gt (\lim,0)& (z) \stackrel{\stackrel{(3.4)}{}}{=} -a+b+c(1-\varepsilon)(\lim ,0)(u) \\ &\geq -a+b-c(1-\varepsilon) =-a-b-c+2b+\varepsilon c=
-1+2b+\varepsilon c,
\end{align*}and so ![]() $2b+\varepsilon c \lt \varepsilon\eta$. This inequality implies that
$2b+\varepsilon c \lt \varepsilon\eta$. This inequality implies that ![]() $b \lt \eta$ (bear in mind that ɛ < 1) and that
$b \lt \eta$ (bear in mind that ɛ < 1) and that ![]() $c \lt \eta$. Consequently,
$c \lt \eta$. Consequently,
 \begin{eqnarray*}
\vert z-z_1\vert &\stackrel{\stackrel{(3.4)}{}}{=}& \left| (a-1) z_1-b z_2+c((1-\varepsilon)u+\varepsilon v) \right| \\
& = & \left| -b(z_1+z_2)+c((1-\varepsilon)u+\varepsilon v-z_1) \right| \\
& \leq & b |z_1|+b|z_2|+c\big|(1-\varepsilon)u+\varepsilon v\big|+c|z_1| \\
& \stackrel{(\star)}{\leq} & 2b+2c \lt 4\eta,
\end{eqnarray*}
\begin{eqnarray*}
\vert z-z_1\vert &\stackrel{\stackrel{(3.4)}{}}{=}& \left| (a-1) z_1-b z_2+c((1-\varepsilon)u+\varepsilon v) \right| \\
& = & \left| -b(z_1+z_2)+c((1-\varepsilon)u+\varepsilon v-z_1) \right| \\
& \leq & b |z_1|+b|z_2|+c\big|(1-\varepsilon)u+\varepsilon v\big|+c|z_1| \\
& \stackrel{(\star)}{\leq} & 2b+2c \lt 4\eta,
\end{eqnarray*}where inequality ![]() $(\star)$ follows from the fact that z 1, z 2 and
$(\star)$ follows from the fact that z 1, z 2 and ![]() $(1-\varepsilon)u+\varepsilon v$ belong to
$(1-\varepsilon)u+\varepsilon v$ belong to ![]() $B=B_{(Z,|\cdot|)}$. Hence,
$B=B_{(Z,|\cdot|)}$. Hence, ![]() $|z-z_1| \lt 4\eta$.
$|z-z_1| \lt 4\eta$.
We can write ![]() $z_1=(x,0)$ for some
$z_1=(x,0)$ for some ![]() $x\in {\rm conv}(A)$. Then
$x\in {\rm conv}(A)$. Then ![]() $\lim x=-1$ and for each
$\lim x=-1$ and for each ![]() $i\in \{1,\dots,n\}$, we have
$i\in \{1,\dots,n\}$, we have
 \begin{equation*}
e_{\emptyset\smallfrown i}^*(x)=
(e_{\emptyset\smallfrown i}^*,0)(z_1)\geq (e_{\emptyset\smallfrown i}^*,0)(z)-\vert (e_{\emptyset\smallfrown i}^*,0)\vert_{Z^*} \vert z-z_1\vert \gt \frac{2}{n}-1-5\eta
\end{equation*}
\begin{equation*}
e_{\emptyset\smallfrown i}^*(x)=
(e_{\emptyset\smallfrown i}^*,0)(z_1)\geq (e_{\emptyset\smallfrown i}^*,0)(z)-\vert (e_{\emptyset\smallfrown i}^*,0)\vert_{Z^*} \vert z-z_1\vert \gt \frac{2}{n}-1-5\eta
\end{equation*}because ![]() $z\in U$ and
$z\in U$ and ![]() $\vert (e_{\emptyset\smallfrown i}^*,0)\vert_{Z^*} \leq \|(e_{\emptyset\smallfrown i}^*,0)\|_{Z^*}=1$ (by Equation (3.1)). This implies, with the notation of Lemma 3.2, that
$\vert (e_{\emptyset\smallfrown i}^*,0)\vert_{Z^*} \leq \|(e_{\emptyset\smallfrown i}^*,0)\|_{Z^*}=1$ (by Equation (3.1)). This implies, with the notation of Lemma 3.2, that ![]() $x\in W_{n,\rho}$ (recall that
$x\in W_{n,\rho}$ (recall that  $\eta=\frac{2}{5}\rho$). Therefore, the conclusion of the Claim holds taking
$\eta=\frac{2}{5}\rho$). Therefore, the conclusion of the Claim holds taking ![]() $z^{\prime}=z_1$.
$z^{\prime}=z_1$.
Finally, let ![]() $w_1,w_2\in U$ and fix s > 0. Since U is relatively open in B, we can find
$w_1,w_2\in U$ and fix s > 0. Since U is relatively open in B, we can find ![]() $v_1,v_2\in V$ such that
$v_1,v_2\in V$ such that ![]() $|w_1-v_1|\leq s$ and
$|w_1-v_1|\leq s$ and ![]() $|w_2-v_2|\leq s$. By the Claim above, there exist
$|w_2-v_2|\leq s$. By the Claim above, there exist ![]() $v^{\prime}_1,v^{\prime}_2\in W_{n,\rho}\times \{0\}$ such that
$v^{\prime}_1,v^{\prime}_2\in W_{n,\rho}\times \{0\}$ such that ![]() $|v_1-v^{\prime}_1| \lt 4\eta$ and
$|v_1-v^{\prime}_1| \lt 4\eta$ and ![]() $|v_2-v^{\prime}_2| \lt 4\eta$. Then
$|v_2-v^{\prime}_2| \lt 4\eta$. Then
 \begin{equation*}
|v^{\prime}_1-v^{\prime}_2| \stackrel{\stackrel{(3.1)}{}}{\leq}
\frac{1}{1-\varepsilon}\|v^{\prime}_1-v^{\prime}_2\|_Z \stackrel{\stackrel{(3.2)}{}}{\leq}
\frac{1}{1-\varepsilon}\mathop{\mathrm{diam}}\nolimits(W_{n,\rho}) \stackrel{\stackrel{(3.3)}{}}{\leq} \frac{\theta}{2}
\end{equation*}
\begin{equation*}
|v^{\prime}_1-v^{\prime}_2| \stackrel{\stackrel{(3.1)}{}}{\leq}
\frac{1}{1-\varepsilon}\|v^{\prime}_1-v^{\prime}_2\|_Z \stackrel{\stackrel{(3.2)}{}}{\leq}
\frac{1}{1-\varepsilon}\mathop{\mathrm{diam}}\nolimits(W_{n,\rho}) \stackrel{\stackrel{(3.3)}{}}{\leq} \frac{\theta}{2}
\end{equation*}and so
 \begin{equation*}
|w_1-w_2| \lt 2s+8\eta + \frac{\theta}{2}\stackrel{\stackrel{(3.3)}{}}{\leq} 2s+\theta.
\end{equation*}
\begin{equation*}
|w_1-w_2| \lt 2s+8\eta + \frac{\theta}{2}\stackrel{\stackrel{(3.3)}{}}{\leq} 2s+\theta.
\end{equation*} As ![]() $w_1,w_2\in U$ and s > 0 are arbitrary, we conclude that
$w_1,w_2\in U$ and s > 0 are arbitrary, we conclude that ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(U)\leq \theta$.
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(U)\leq \theta$.
Proof of (iii). We will show that ![]() $(Z,|\cdot|)$ is (r, s)-SQ for any
$(Z,|\cdot|)$ is (r, s)-SQ for any  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ with the help of Lemma 3.4. Let H be the norm dense subset of
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ with the help of Lemma 3.4. Let H be the norm dense subset of ![]() $B_{c_{0}}$ consisting of all finitely supported functions from
$B_{c_{0}}$ consisting of all finitely supported functions from ![]() $\mathbb{N}$ to
$\mathbb{N}$ to ![]() $[-1,1]$. Then the set
$[-1,1]$. Then the set
 \begin{equation*}
S:=S_{(Z,|\cdot|)} \cap {\rm conv}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \big((1-\varepsilon)(B_{c(\mathbb{N}^{\omega})} \times H)+
\varepsilon B_{c_0(\mathbb{N}^{\omega})} \times\{0\}\big)\right)
\end{equation*}
\begin{equation*}
S:=S_{(Z,|\cdot|)} \cap {\rm conv}\left((A\times\{0\})\cup ({-A}\times \{0\})\cup \big((1-\varepsilon)(B_{c(\mathbb{N}^{\omega})} \times H)+
\varepsilon B_{c_0(\mathbb{N}^{\omega})} \times\{0\}\big)\right)
\end{equation*}is norm dense in ![]() $S_{(Z,|\cdot|)}$. Fix
$S_{(Z,|\cdot|)}$. Fix  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ and take finitely many
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ and take finitely many ![]() $z_1,\ldots, z_m\in S$. By Lemma 3.3, each zi can be written as
$z_1,\ldots, z_m\in S$. By Lemma 3.3, each zi can be written as
 \begin{equation*}
z_i=a_i (x^1_i,0)+b_i (-x^2_i,0)+c_i\big((1-\varepsilon)(x_i,y_i)+\varepsilon (x^3_i,0)\big)
\end{equation*}
\begin{equation*}
z_i=a_i (x^1_i,0)+b_i (-x^2_i,0)+c_i\big((1-\varepsilon)(x_i,y_i)+\varepsilon (x^3_i,0)\big)
\end{equation*}for some ![]() $a_i,b_i,c_i\geq 0$ with
$a_i,b_i,c_i\geq 0$ with ![]() $a_i+b_i+c_i=1$ and
$a_i+b_i+c_i=1$ and
 \begin{equation*}
x^1_i,x^2_i\in {\rm conv}(A), \
x_i \in B_{c(\mathbb{N}^{\omega})},\ y_i\in H \ \text{and} \
x_i^3 \in B_{c_0(\mathbb N^{ \lt \omega})}.
\end{equation*}
\begin{equation*}
x^1_i,x^2_i\in {\rm conv}(A), \
x_i \in B_{c(\mathbb{N}^{\omega})},\ y_i\in H \ \text{and} \
x_i^3 \in B_{c_0(\mathbb N^{ \lt \omega})}.
\end{equation*} Let ![]() $(e_n)_{n\in \mathbb{N}}$ be the usual basis of c 0 and choose
$(e_n)_{n\in \mathbb{N}}$ be the usual basis of c 0 and choose ![]() $n\in\mathbb N$ large enough such that
$n\in\mathbb N$ large enough such that ![]() $\Vert y_i\pm e_n\Vert_{\infty}\leq 1$ for all
$\Vert y_i\pm e_n\Vert_{\infty}\leq 1$ for all ![]() $i\in \{1,\dots,m\}$.
$i\in \{1,\dots,m\}$.
Observe that for each ![]() $i\in \{1,\dots,m\}$, we have
$i\in \{1,\dots,m\}$, we have
 \begin{equation*}
z_i\pm (0,e_n)=a_i (x^1_i,\pm e_n)+b_i (-x^2_i, \pm e_n)+c_i\big((1-\varepsilon)(x_i,y_i\pm e_n)+\varepsilon (x^3_i,\pm e_n)\big),
\end{equation*}
\begin{equation*}
z_i\pm (0,e_n)=a_i (x^1_i,\pm e_n)+b_i (-x^2_i, \pm e_n)+c_i\big((1-\varepsilon)(x_i,y_i\pm e_n)+\varepsilon (x^3_i,\pm e_n)\big),
\end{equation*}thus
 \begin{align*}
\| z_i\pm (0,e_n)\|_Z \leq a_i\|(x^1_i,\pm e_n)\|_Z+b_i \|&(x^2_i,\pm e_n)\|_Z+c_i\big((1-\varepsilon)\|(x_i,y_i\pm e_n)\|_Z+\varepsilon \| \\ &(x^3_i,\pm e_n)\|_Z\big)
\leq a_i+b_i+c_i((1-\varepsilon)+\varepsilon)) = 1,
\end{align*}
\begin{align*}
\| z_i\pm (0,e_n)\|_Z \leq a_i\|(x^1_i,\pm e_n)\|_Z+b_i \|&(x^2_i,\pm e_n)\|_Z+c_i\big((1-\varepsilon)\|(x_i,y_i\pm e_n)\|_Z+\varepsilon \| \\ &(x^3_i,\pm e_n)\|_Z\big)
\leq a_i+b_i+c_i((1-\varepsilon)+\varepsilon)) = 1,
\end{align*}which combined with Equation (3.1) yields
 \begin{equation}
\vert z_i\pm (0,e_n)\vert\leq \frac{1}{1-\varepsilon}.
\end{equation}
\begin{equation}
\vert z_i\pm (0,e_n)\vert\leq \frac{1}{1-\varepsilon}.
\end{equation} Another appeal to Equation (3.1) gives  $1 =\|(0,e_n)\|_Z\leq |(0,e_n)|\leq \frac{1}{1-\varepsilon}$ and, therefore, the vector
$1 =\|(0,e_n)\|_Z\leq |(0,e_n)|\leq \frac{1}{1-\varepsilon}$ and, therefore, the vector  $z:=\frac{1}{|(0,e_n)|}(0,e_n)\in S_{(Z,|\cdot|)}$ satisfies
$z:=\frac{1}{|(0,e_n)|}(0,e_n)\in S_{(Z,|\cdot|)}$ satisfies
 \begin{equation*}
|(0,e_n)-z|=\left|\left(1-\frac{1}{|(0,e_n)|}\right)(0,e_n) \right|=
|(0,e_n)|-1 \leq \frac{1}{1-\varepsilon}-1 =\frac{\varepsilon}{1-\varepsilon}.
\end{equation*}
\begin{equation*}
|(0,e_n)-z|=\left|\left(1-\frac{1}{|(0,e_n)|}\right)(0,e_n) \right|=
|(0,e_n)|-1 \leq \frac{1}{1-\varepsilon}-1 =\frac{\varepsilon}{1-\varepsilon}.
\end{equation*}This inequality and Equation (3.5) give
 \begin{equation*}
\vert z_i\pm z\vert \leq \frac{1}{1-\varepsilon}+\frac{\varepsilon}{1-\varepsilon}=\frac{1+\varepsilon}{1-\varepsilon}
\quad\text{for every}\ i\in \{1,\ldots,m\}.
\end{equation*}
\begin{equation*}
\vert z_i\pm z\vert \leq \frac{1}{1-\varepsilon}+\frac{\varepsilon}{1-\varepsilon}=\frac{1+\varepsilon}{1-\varepsilon}
\quad\text{for every}\ i\in \{1,\ldots,m\}.
\end{equation*} Since  $r,s \leq \frac{1-\varepsilon}{1+\varepsilon}$, we can apply [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Lemma 6.3] to conclude that
$r,s \leq \frac{1-\varepsilon}{1+\varepsilon}$, we can apply [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Lemma 6.3] to conclude that
From Lemma 3.4, it follows that ![]() $(Z,|\cdot|)$ is (r, s)-SQ for all
$(Z,|\cdot|)$ is (r, s)-SQ for all  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$. The proof is completed.
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$. The proof is completed.
We can now prove Theorem 1.2 in full generality.
Proof of Theorem 1.2
Let Z and W be subspaces of X such that Z is isomorphic to c 0 and ![]() $X=Z\oplus W$. Fix
$X=Z\oplus W$. Fix ![]() $0 \lt \varepsilon \lt 1$ and let
$0 \lt \varepsilon \lt 1$ and let ![]() $|\cdot|_Z$ be an equivalent norm on Z like in Theorem 3.5. Since any Banach space admits an equivalent norm for which the unit ball has slices of arbitrarily small diameter (see, e.g., [Reference Guerrero, López-Pérez and Zoca22, Lemma 2.1]), we can take an equivalent norm
$|\cdot|_Z$ be an equivalent norm on Z like in Theorem 3.5. Since any Banach space admits an equivalent norm for which the unit ball has slices of arbitrarily small diameter (see, e.g., [Reference Guerrero, López-Pérez and Zoca22, Lemma 2.1]), we can take an equivalent norm ![]() $|\cdot|_W$ on W satisfying that property. Let
$|\cdot|_W$ on W satisfying that property. Let ![]() $|\cdot|$ be the equivalent norm on X defined by
$|\cdot|$ be the equivalent norm on X defined by ![]() $|z+w|:=\max\{|z|_Z,|w|_W\}$ for every
$|z+w|:=\max\{|z|_Z,|w|_W\}$ for every ![]() $z\in Z$ and for every
$z\in Z$ and for every ![]() $w\in W$. We claim that
$w\in W$. We claim that ![]() $(X,|\cdot|)$ satisfies all the requirements.
$(X,|\cdot|)$ satisfies all the requirements.
(i) The ![]() $\ell_\infty$-sum of two Banach spaces has the slice-D2P whenever one of the factors has the slice-D2P (see, e.g., [Reference Langemets32, Theorem 2.29]). Since
$\ell_\infty$-sum of two Banach spaces has the slice-D2P whenever one of the factors has the slice-D2P (see, e.g., [Reference Langemets32, Theorem 2.29]). Since ![]() $(Z,|\cdot|_Z)$ has the slice-D2P, we conclude that the same holds for
$(Z,|\cdot|_Z)$ has the slice-D2P, we conclude that the same holds for ![]() $(X,|\cdot|)$.
$(X,|\cdot|)$.
(ii) Let us prove that ![]() $B_{(X,|\cdot|)}$ contains non-empty relatively weakly open subsets of arbitrarily small diameter. Fix η > 0. Then there exists a non-empty relatively weakly open set
$B_{(X,|\cdot|)}$ contains non-empty relatively weakly open subsets of arbitrarily small diameter. Fix η > 0. Then there exists a non-empty relatively weakly open set ![]() $U \subseteq B_{(Z,|\cdot|_Z)}$ with
$U \subseteq B_{(Z,|\cdot|_Z)}$ with ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|_Z}(U) \lt \eta$. Now, take a slice S of
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|_Z}(U) \lt \eta$. Now, take a slice S of ![]() $B_{(W,|\cdot|_W)}$ with
$B_{(W,|\cdot|_W)}$ with ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|_W}(S) \lt \eta$. Since the map
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|_W}(S) \lt \eta$. Since the map ![]() $\varphi:B_{(Z,|\cdot|_Z)}\times B_{(W,|\cdot|_W)} \to B_{(X,|\cdot|)}$ given by
$\varphi:B_{(Z,|\cdot|_Z)}\times B_{(W,|\cdot|_W)} \to B_{(X,|\cdot|)}$ given by
is a homeomorphism when each of the balls is equipped with the restriction of the weak topology, it follows that ![]() $V:=\varphi(U\times S)$ is a relatively weakly open subset of
$V:=\varphi(U\times S)$ is a relatively weakly open subset of ![]() $B_{(X,|\cdot|)}$. Clearly,
$B_{(X,|\cdot|)}$. Clearly, ![]() $V\neq \emptyset$ and
$V\neq \emptyset$ and ![]() $\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(V) \lt \eta$, as desired.
$\mathop{\mathrm{diam}}\nolimits_{|\cdot|}(V) \lt \eta$, as desired.
(iii) The space ![]() $(X,|\cdot|)$ is (r, s)-SQ for arbitrary
$(X,|\cdot|)$ is (r, s)-SQ for arbitrary  $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ because so is
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$ because so is ![]() $(Z,|\cdot|_Z)$, and the
$(Z,|\cdot|_Z)$, and the ![]() $\ell_\infty$-sum of two Banach spaces is (r, s)-SQ whenever one of the factors is (r, s)-SQ (see [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Proposition 6.6]).
$\ell_\infty$-sum of two Banach spaces is (r, s)-SQ whenever one of the factors is (r, s)-SQ (see [Reference Avilés, Ciaci, Langemets, Lissitsin and Zoca9, Proposition 6.6]).
Acknowledgements
We thank Antonio Avilés for valuable discussions on the results of this paper.
Funding Statement
The research was supported by grants PID2021-122126NB-C32 (J. Rodríguez) and PID2021-122126NB-C31 (A. Rueda Zoca) funded by MCIN/AEI/10.13039/501100011033 and “ERDF: A way of making Europe” and also by grant 21955/PI/22 funded by Fundación Séneca - ACyT Región de Murcia. The research of A. Rueda Zoca was also supported by grants FQM-0185 and PY20_00255 funded by Junta de Andalucía and by the Generalitat Valenciana project CIGE/2022/97.