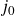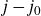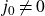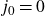1. Introduction
This paper is devoted to the study of some diophantine properties of j-invariants of elliptic curves with complex multiplication defined over
![]() $\mathbb{C}$
. These numbers, which are classically known by the name of singular moduli, have been studied since the time of Kronecker and Weber, who were interested in explicit generation of class fields relative to imaginary quadratic fields [
Reference Frei16
]. In this respect, singular moduli prove to be a useful tool, since they are indeed algebraic integers which can be used to generate ring class fields of imaginary quadratic fields [
Reference Cox11
, Theorem 11.1].
$\mathbb{C}$
. These numbers, which are classically known by the name of singular moduli, have been studied since the time of Kronecker and Weber, who were interested in explicit generation of class fields relative to imaginary quadratic fields [
Reference Frei16
]. In this respect, singular moduli prove to be a useful tool, since they are indeed algebraic integers which can be used to generate ring class fields of imaginary quadratic fields [
Reference Cox11
, Theorem 11.1].
During the last decade, there has been an increasing interest in understanding more diophantine properties of these invariants. One of the questions that, for instance, has been addressed is the following: given a set S of rational primes, is the set of singular moduli that are S-units (singular S-units) finite? In case of an affirmative answer, is it possible to provide an effective method to explicitly compute this set? This question, which has been originally motivated by the proof of some effective results of André–Oort type (see [ 3] and [ Reference Kühne29 ]), does not have at present a complete answer. Several partial results have nonetheless been achieved.
In [
Reference Bilu, Habegger and Kuhne2
] it is proved, building on the previous ineffective result of Habegger [
Reference Habegger23
], that no singular modulus can be a unit in the ring of algebraic integers. This settles the case
![]() $S=\emptyset$
of the question. With different techniques, Li generalises this theorem and proves in [
Reference Li34
] that for every pair
$S=\emptyset$
of the question. With different techniques, Li generalises this theorem and proves in [
Reference Li34
] that for every pair
![]() $j_1,j_2 \in \overline{\mathbb{Q}}$
of singular moduli, the algebraic integer
$j_1,j_2 \in \overline{\mathbb{Q}}$
of singular moduli, the algebraic integer
![]() $\Phi_N(\,j_1,j_2)$
can never be a unit. Here
$\Phi_N(\,j_1,j_2)$
can never be a unit. Here
![]() $\Phi_N(X,Y) \in \mathbb{Z}[X,Y]$
denotes the classical modular polynomial of level N, so we recover the main result of [
Reference Bilu, Habegger and Kuhne2
] by setting
$\Phi_N(X,Y) \in \mathbb{Z}[X,Y]$
denotes the classical modular polynomial of level N, so we recover the main result of [
Reference Bilu, Habegger and Kuhne2
] by setting
![]() $j_2=0$
and
$j_2=0$
and
![]() $N=1$
. In a different direction, the fact that no singular modulus is a unit has been used by the author of this manuscript to prove that, if
$N=1$
. In a different direction, the fact that no singular modulus is a unit has been used by the author of this manuscript to prove that, if
![]() $S_0$
is the infinite set of primes congruent to 1 mod 3, then the set of singular moduli that are
$S_0$
is the infinite set of primes congruent to 1 mod 3, then the set of singular moduli that are
![]() $S_0$
-units is empty [
Reference Campagna8
]. Moreover, very recently Herrero, Menares and Rivera–Letelier gave an ineffective proof of the fact that for every fixed singular modulus
$S_0$
-units is empty [
Reference Campagna8
]. Moreover, very recently Herrero, Menares and Rivera–Letelier gave an ineffective proof of the fact that for every fixed singular modulus
![]() $j_0 \in \overline{\mathbb{Q}}$
and for every finite set of primes S, the set of singular moduli j such that
$j_0 \in \overline{\mathbb{Q}}$
and for every finite set of primes S, the set of singular moduli j such that
![]() $j-j_0$
is an S-unit is finite, see [
Reference Herrero, Menares and Rivera–Letelier25
] [
Reference Herrero, Menares and Rivera–Letelier26
] and [
Reference Herrero, Menares and Rivera–Letelier27
].
$j-j_0$
is an S-unit is finite, see [
Reference Herrero, Menares and Rivera–Letelier25
] [
Reference Herrero, Menares and Rivera–Letelier26
] and [
Reference Herrero, Menares and Rivera–Letelier27
].
In this paper we explore the possibility of providing, for a given singular modulus
![]() $j_0$
and for specific sets of primes S, an effective procedure to determine the set of all singular moduli j such that
$j_0$
and for specific sets of primes S, an effective procedure to determine the set of all singular moduli j such that
![]() $j-j_0$
is an S-unit. In order to better state our main results, we introduce some notation. First of all, we say that a singular modulus has discriminant
$j-j_0$
is an S-unit. In order to better state our main results, we introduce some notation. First of all, we say that a singular modulus has discriminant
![]() $\Delta \in \mathbb{Z}$
if it is the j-invariant of an elliptic curve
$\Delta \in \mathbb{Z}$
if it is the j-invariant of an elliptic curve
![]() $E_{/\mathbb{C}}$
with complex multiplication by an order of discriminant
$E_{/\mathbb{C}}$
with complex multiplication by an order of discriminant
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
$j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
![]() $\Delta$
and let
$\Delta$
and let
![]() $S \subseteq \mathbb{N}$
be a finite set of prime numbers. We call the pair (j,S) a nice
$S \subseteq \mathbb{N}$
be a finite set of prime numbers. We call the pair (j,S) a nice
![]() $\Delta$
-pair if the following two conditions hold:
$\Delta$
-pair if the following two conditions hold:
-
(1) every prime
 $\ell \in S$
splits completely in
$\ell \in S$
splits completely in
 $\mathbb{Q}(\,j)$
;
$\mathbb{Q}(\,j)$
; -
(2) we have
 $\ell \nmid N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j) N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j-1728) \Delta$
for all
$\ell \nmid N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j) N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j-1728) \Delta$
for all
 $\ell \in S$
, where
$\ell \in S$
, where
 $N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\!\cdot\!)$
denotes the norm map from
$N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\!\cdot\!)$
denotes the norm map from
 $\mathbb{Q}(\,j)$
to
$\mathbb{Q}(\,j)$
to
 $\mathbb{Q}$
.
$\mathbb{Q}$
.
The first main result of the paper is the following.
Theorem 1·1. Let
![]() $(\,j_0,S)$
be a nice
$(\,j_0,S)$
be a nice
![]() $\Delta_0$
-pair with
$\Delta_0$
-pair with
![]() $\Delta_0 < -4$
and
$\Delta_0 < -4$
and
![]() $\#S \leq 2$
. Then there exists an effectively computable bound
$\#S \leq 2$
. Then there exists an effectively computable bound
![]() $B=B(\,j_0,S) \in \mathbb{R}_{\geq 0}$
such that the discriminant
$B=B(\,j_0,S) \in \mathbb{R}_{\geq 0}$
such that the discriminant
![]() $\Delta$
of every singular modulus
$\Delta$
of every singular modulus
![]() $j \in \overline{\mathbb{Q}}$
for which
$j \in \overline{\mathbb{Q}}$
for which
![]() $j-j_0$
is an S-unit satisfies
$j-j_0$
is an S-unit satisfies
![]() $|\Delta| \leq B$
. Moreover, if the extension
$|\Delta| \leq B$
. Moreover, if the extension
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
is not Galois, then the discriminant
$\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
is not Galois, then the discriminant
![]() $\Delta$
of any singular modulus j such that
$\Delta$
of any singular modulus j such that
![]() $j-j_0$
is an S-unit is of the form
$j-j_0$
is an S-unit is of the form
![]() $\Delta=p^{2n} \Delta_0$
for some prime
$\Delta=p^{2n} \Delta_0$
for some prime
![]() $p \in S$
and some non-negative integer n.
$p \in S$
and some non-negative integer n.
The bound
![]() $B(\,j_0,S)$
in the statement of Theorem 1·1 can be made explicit from its proof. To give an idea of what kind of bounds one can get, we take
$B(\,j_0,S)$
in the statement of Theorem 1·1 can be made explicit from its proof. To give an idea of what kind of bounds one can get, we take
![]() $j_0=-3375$
, the j-invariant of any elliptic curve with complex multiplication by
$j_0=-3375$
, the j-invariant of any elliptic curve with complex multiplication by
![]() $\mathbb{Z}[(1+\sqrt{-7})/2]$
, and choose S to be any subset of at most two elements in
$\mathbb{Z}[(1+\sqrt{-7})/2]$
, and choose S to be any subset of at most two elements in
![]() $\{13,17,19\}$
. We get the following result.
$\{13,17,19\}$
. We get the following result.
Theorem 1·2. Let
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
$j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
![]() $\Delta$
, and let
$\Delta$
, and let
![]() $S\;:\!=\;\{13,17\}$
. If
$S\;:\!=\;\{13,17\}$
. If
![]() $j+3375$
is an S-unit, then
$j+3375$
is an S-unit, then
![]() $|\Delta| \leq 10^{81}$
. The same holds with
$|\Delta| \leq 10^{81}$
. The same holds with
![]() $S'=\{13,19 \}$
and
$S'=\{13,19 \}$
and
![]() $S''=\{17,19 \}$
.
$S''=\{17,19 \}$
.
In general, in order to construct nice
![]() $\Delta$
-pairs it suffices to fix a singular modulus j of discriminant
$\Delta$
-pairs it suffices to fix a singular modulus j of discriminant
![]() $\Delta$
and to choose, among the set of primes splitting completely in
$\Delta$
and to choose, among the set of primes splitting completely in
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
, a finite subset S satisfying condition (2) above. Since the set of rational primes that are totally split in
$\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
, a finite subset S satisfying condition (2) above. Since the set of rational primes that are totally split in
![]() $\mathbb{Q}(\,j)$
is infinite by the Chebotarëv’s density theorem, this gives rise to infinitely many nice
$\mathbb{Q}(\,j)$
is infinite by the Chebotarëv’s density theorem, this gives rise to infinitely many nice
![]() $\Delta$
-pairs for a fixed discriminant
$\Delta$
-pairs for a fixed discriminant
![]() $\Delta$
. We remark that if
$\Delta$
. We remark that if
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is not Galois, then every prime splitting completely in this extension will be also totally split in
$\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is not Galois, then every prime splitting completely in this extension will be also totally split in
![]() $\mathbb{Q}(\sqrt{\Delta})$
(see the end of the proof of Theorem 1·1). Hence, in some cases one could use [
Reference Campagna7
, Theorem 2.2.1] to show that, for appropriate nice
$\mathbb{Q}(\sqrt{\Delta})$
(see the end of the proof of Theorem 1·1). Hence, in some cases one could use [
Reference Campagna7
, Theorem 2.2.1] to show that, for appropriate nice
![]() $\Delta_0$
-pair
$\Delta_0$
-pair
![]() $(\,j_0,S)$
with
$(\,j_0,S)$
with
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
non-Galois, the set of singular moduli
$\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
non-Galois, the set of singular moduli
![]() $j \in \overline{\mathbb{Q}}$
for which
$j \in \overline{\mathbb{Q}}$
for which
![]() $j-j_0$
is an S-unit is in fact empty. We point out that the set of singular moduli j that generate a Galois extension of
$j-j_0$
is an S-unit is in fact empty. We point out that the set of singular moduli j that generate a Galois extension of
![]() $\mathbb{Q}$
is finite, see Proposition 4·2.
$\mathbb{Q}$
is finite, see Proposition 4·2.
The reason why Theorem 1·1 only deals with sets S containing at most two primes will be apparent from its proof, which we now sketch. Our strategy follows the same idea used in [
Reference Bilu, Habegger and Kuhne2
]: given a singular modulus
![]() $j \in \overline{\mathbb{Q}}$
such that
$j \in \overline{\mathbb{Q}}$
such that
![]() $j-j_0$
is an S-unit, we compute the (logarithmic) Weil height
$j-j_0$
is an S-unit, we compute the (logarithmic) Weil height
![]() $h(\,j-j_0)$
. This is defined, for every
$h(\,j-j_0)$
. This is defined, for every
![]() $x \in \overline{\mathbb{Q}}$
, as
$x \in \overline{\mathbb{Q}}$
, as
where
![]() $K\;:\!=\;\mathbb{Q}(x)$
is the field generated by x over the rationals,
$K\;:\!=\;\mathbb{Q}(x)$
is the field generated by x over the rationals,
![]() $\mathcal{M}_K$
is the set of all places of K, the integer
$\mathcal{M}_K$
is the set of all places of K, the integer
![]() $[K_v\;:\;\mathbb{Q}_v]$
is the local degree at the place v and
$[K_v\;:\;\mathbb{Q}_v]$
is the local degree at the place v and
![]() $\log^+|x|_v\;:\!=\;\log \max \{1,|x|_v\}$
. Here, for every non-archimedean place v corresponding to the prime ideal
$\log^+|x|_v\;:\!=\;\log \max \{1,|x|_v\}$
. Here, for every non-archimedean place v corresponding to the prime ideal
![]() $\mathfrak{p}_v$
lying above the rational prime
$\mathfrak{p}_v$
lying above the rational prime
![]() $p_v$
, the absolute value
$p_v$
, the absolute value
![]() $|\!\cdot\!|_v$
is normalised in such a way that
$|\!\cdot\!|_v$
is normalised in such a way that
where
![]() $e_v$
is the ramification index of
$e_v$
is the ramification index of
![]() $\mathfrak{p}_v$
over
$\mathfrak{p}_v$
over
![]() $p_v$
and
$p_v$
and
![]() $v_{\mathfrak{p}_v}(x)$
is the exponent with which
$v_{\mathfrak{p}_v}(x)$
is the exponent with which
![]() $\mathfrak{p}_v$
appears in the prime ideal factorisation of the
$\mathfrak{p}_v$
appears in the prime ideal factorisation of the
![]() $\mathcal{O}_K$
-fractional ideal generated by x. Hence the logarithmic Weil height naturally decomposes into an “archimedean” and “non-archimedean” part.
$\mathcal{O}_K$
-fractional ideal generated by x. Hence the logarithmic Weil height naturally decomposes into an “archimedean” and “non-archimedean” part.
Since
![]() $j-j_0$
is an algebraic integer, the non-archimedean part of its Weil height vanishes. In order to exploit the fact that the above difference is an S-unit, we rather compute the height of
$j-j_0$
is an algebraic integer, the non-archimedean part of its Weil height vanishes. In order to exploit the fact that the above difference is an S-unit, we rather compute the height of
![]() $(\,j-j_0)^{-1}$
. Using standard properties of the Weil height, we obtain
$(\,j-j_0)^{-1}$
. Using standard properties of the Weil height, we obtain
with
where the sum is taken over the prime ideals of
![]() $\mathbb{Q}(\,j-j_0)$
lying above the rational primes contained in S and, for every such prime
$\mathbb{Q}(\,j-j_0)$
lying above the rational primes contained in S and, for every such prime
![]() $\mathfrak{p}$
, we denote by
$\mathfrak{p}$
, we denote by
![]() $f_\mathfrak{p}$
and
$f_\mathfrak{p}$
and
![]() $\ell_\mathfrak{p}$
respectively the inertia degree and the residue characteristic of
$\ell_\mathfrak{p}$
respectively the inertia degree and the residue characteristic of
![]() $\mathfrak{p}$
. Our goal is to effectively bound this height from above and from below in such a way that the two bounds contradict each other when the absolute value of the discriminant of the singular modulus j becomes large. This will give the desired effective bound.
$\mathfrak{p}$
. Our goal is to effectively bound this height from above and from below in such a way that the two bounds contradict each other when the absolute value of the discriminant of the singular modulus j becomes large. This will give the desired effective bound.
An upper bound for the archimedean part has been already studied in [
Reference Bilu, Habegger and Kuhne2
] and [
Reference Cai6
]. In order to estimate from above the non-archimedean part, we have to understand the valuation of
![]() $j-j_0$
at primes above S. This requires the use of some deformation-theoretic arguments involving quaternion algebras, and constitutes the technical core of the paper. We detail this discussion in Section 3, which culminates in the proof of Theorem 3·1, where we obtain the seeked estimates. Concerning the lower bound for the Weil height, we compare it to the stable Faltings height of the elliptic curve with complex multiplication having j as singular invariant. Using work of Colmez [
Reference Colmez9
] and Nakkajima–Taguchi [
Reference Nakkajima and Taguchi36
] it is possible to relate this Faltings height to the logarithmic derivative of the L-function corresponding to the CM field evaluated in 1. The known lower bounds on this logarithmic derivative become strong enough for our purposes only if we restrict to sets S containing no more than two primes.
$j-j_0$
at primes above S. This requires the use of some deformation-theoretic arguments involving quaternion algebras, and constitutes the technical core of the paper. We detail this discussion in Section 3, which culminates in the proof of Theorem 3·1, where we obtain the seeked estimates. Concerning the lower bound for the Weil height, we compare it to the stable Faltings height of the elliptic curve with complex multiplication having j as singular invariant. Using work of Colmez [
Reference Colmez9
] and Nakkajima–Taguchi [
Reference Nakkajima and Taguchi36
] it is possible to relate this Faltings height to the logarithmic derivative of the L-function corresponding to the CM field evaluated in 1. The known lower bounds on this logarithmic derivative become strong enough for our purposes only if we restrict to sets S containing no more than two primes.
When
![]() $\Delta_0 \in \{-3,-4\}$
, i.e. when
$\Delta_0 \in \{-3,-4\}$
, i.e. when
![]() $j_0 \in \{0,1728\}$
, the same techniques also lead to similar finiteness results, but one has to be more careful in theses cases since the complex elliptic curves having
$j_0 \in \{0,1728\}$
, the same techniques also lead to similar finiteness results, but one has to be more careful in theses cases since the complex elliptic curves having
![]() $j_0$
as singular invariant possess non-trivial automorphisms. This is indeed a problem, and will force us to resort to the Generalised Riemann Hypothesis (GRH) in the case
$j_0$
as singular invariant possess non-trivial automorphisms. This is indeed a problem, and will force us to resort to the Generalised Riemann Hypothesis (GRH) in the case
![]() $j_0=0$
. Here are the results that we obtain in these two cases.
$j_0=0$
. Here are the results that we obtain in these two cases.
Theorem 1·3. Let
![]() $S_0$
be the set of rational primes congruent to 1 modulo 4, let
$S_0$
be the set of rational primes congruent to 1 modulo 4, let
![]() $\ell \geq 5$
be an arbitrary prime and set
$\ell \geq 5$
be an arbitrary prime and set
![]() $S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. Then there exists an effectively computable bound
$S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. Then there exists an effectively computable bound
![]() $B=B(\ell) \in \mathbb{R}_{\geq 0}$
such that the discriminant
$B=B(\ell) \in \mathbb{R}_{\geq 0}$
such that the discriminant
![]() $\Delta$
of every singular modulus
$\Delta$
of every singular modulus
![]() $j \in \overline{\mathbb{Q}}$
for which
$j \in \overline{\mathbb{Q}}$
for which
![]() $j-1728$
is an
$j-1728$
is an
![]() $S_\ell$
-unit satisfies
$S_\ell$
-unit satisfies
![]() $|\Delta| \leq B$
.
$|\Delta| \leq B$
.
Theorem 1·4. Let
![]() $S_0$
be the set of rational primes congruent to 1 modulo 3, let
$S_0$
be the set of rational primes congruent to 1 modulo 3, let
![]() $\ell \geq 5$
be an arbitrary prime and set
$\ell \geq 5$
be an arbitrary prime and set
![]() $S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. If the Generalised Riemann Hypothesis holds for the Dirichlet L-functions attached to imaginary quadratic number fields, then there exists an effectively computable bound
$S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. If the Generalised Riemann Hypothesis holds for the Dirichlet L-functions attached to imaginary quadratic number fields, then there exists an effectively computable bound
![]() $B=B(\ell) \in \mathbb{R}_{\geq 0}$
such that the discriminant
$B=B(\ell) \in \mathbb{R}_{\geq 0}$
such that the discriminant
![]() $\Delta$
of every singular
$\Delta$
of every singular
![]() $S_\ell$
-unit
$S_\ell$
-unit
![]() $j \in \overline{\mathbb{Q}}$
satisfies
$j \in \overline{\mathbb{Q}}$
satisfies
![]() $|\Delta| \leq B$
.
$|\Delta| \leq B$
.
The statement of Theorem 1·4 has been simplified for the sake of exposition in this introduction. Indeed, one does not need the full strength of GRH to carry out the proof, but only a weaker, more technical assumption on the logarithmic derivative at
![]() $s=1$
of the Dirichlet L-functions of imaginary quadratic fields. We refer the reader to Theorem 5·5 for the stronger result that we are actually going to prove.
$s=1$
of the Dirichlet L-functions of imaginary quadratic fields. We refer the reader to Theorem 5·5 for the stronger result that we are actually going to prove.
After performing some numerical computations, one soon realizes that, given a singular modulus
![]() $j_0$
and a finite set of primes S, the upper bound for the number of singular moduli j such that
$j_0$
and a finite set of primes S, the upper bound for the number of singular moduli j such that
![]() $j-j_0$
is an S-unit seems not to depend on the primes contained in S but only on the size of the set S itself. Since being an S-unit is a Galois-invariant property, this would entail a bound, depending only on
$j-j_0$
is an S-unit seems not to depend on the primes contained in S but only on the size of the set S itself. Since being an S-unit is a Galois-invariant property, this would entail a bound, depending only on
![]() $\#S$
, on the size of the Galois orbits of such j’s and, by the Brauer–Siegel theorem [
Reference Lang32
, Chapter XIII, Theorem 4], an analogous bound on their discriminants. Choosing
$\#S$
, on the size of the Galois orbits of such j’s and, by the Brauer–Siegel theorem [
Reference Lang32
, Chapter XIII, Theorem 4], an analogous bound on their discriminants. Choosing
![]() $j_0=0$
, this observation leads to the formulation of the following conjecture for singular S-units.
$j_0=0$
, this observation leads to the formulation of the following conjecture for singular S-units.
Conjecture 1·5. For every
![]() $s \in \mathbb{N}$
, the number of singular moduli that are S-units for some set of rational primes S with
$s \in \mathbb{N}$
, the number of singular moduli that are S-units for some set of rational primes S with
![]() $\#S=s$
is finite.
$\#S=s$
is finite.
This conjecture, which we will call “uniformity conjecture for singular S-units”, will be discussed in Section 7, where we also provide some numerical data to support it.
The paper is structured as follows. In Section 2 we recall known facts from the theory of complex multiplication and quaternion algebras, and we fix the terminology which will be used in the paper. In Section 3 we prove Theorem 3·1, which allows to bound the
![]() $\ell$
-adic absolute value of differences of singular moduli for certain primes
$\ell$
-adic absolute value of differences of singular moduli for certain primes
![]() $\ell$
. In Section 4 we provide a proof of Theorems 1·1 and 1·2 while in Section 5 we give a proof of Theorems 1·3 and 1·4. Section 6 discusses the optimality of the bounds found in Theorem 3·1 in the case
$\ell$
. In Section 4 we provide a proof of Theorems 1·1 and 1·2 while in Section 5 we give a proof of Theorems 1·3 and 1·4. Section 6 discusses the optimality of the bounds found in Theorem 3·1 in the case
![]() $j_0=0$
. Finally in Section 7 we provide numerical evidence for some uniformity conjectures concerning differences of singular moduli that are S-units.
$j_0=0$
. Finally in Section 7 we provide numerical evidence for some uniformity conjectures concerning differences of singular moduli that are S-units.
2. Prelude: CM elliptic curves, quaternion algebras and optimal embeddings
We recall in this section some of the main definitions and results that will be used in the rest of the paper. We fix once and for all an algebraic closure
![]() $\overline{\mathbb{Q}} \supseteq \mathbb{Q}$
of the rationals.
$\overline{\mathbb{Q}} \supseteq \mathbb{Q}$
of the rationals.
A singular modulus is the j-invariant of an elliptic curve defined over
![]() $\overline{\mathbb{Q}}$
with complex multiplication. For every imaginary quadratic order
$\overline{\mathbb{Q}}$
with complex multiplication. For every imaginary quadratic order
![]() $\mathcal{O}$
of discriminant
$\mathcal{O}$
of discriminant
![]() $\Delta \in \mathbb{Z}_{<0}$
there are exactly
$\Delta \in \mathbb{Z}_{<0}$
there are exactly
![]() $C_{\Delta}$
isomorphism classes of elliptic curves over
$C_{\Delta}$
isomorphism classes of elliptic curves over
![]() $\overline{\mathbb{Q}}$
with complex multiplication by
$\overline{\mathbb{Q}}$
with complex multiplication by
![]() $\mathcal{O}$
, where
$\mathcal{O}$
, where
![]() $C_{\Delta} \in \mathbb{N}$
denotes the class number of the order
$C_{\Delta} \in \mathbb{N}$
denotes the class number of the order
![]() $\mathcal{O}$
. Hence, there are
$\mathcal{O}$
. Hence, there are
![]() $C_{\Delta}$
corresponding singular moduli, which are all algebraic integers and form a full Galois orbit over
$C_{\Delta}$
corresponding singular moduli, which are all algebraic integers and form a full Galois orbit over
![]() $\mathbb{Q}$
(see [
Reference Cox11
, Corollary 10.20], [
Reference Cox11
, Theorem 11.1] and [
Reference Cox11
, Proposition 13.2]). We call them singular moduli of discriminant
$\mathbb{Q}$
(see [
Reference Cox11
, Corollary 10.20], [
Reference Cox11
, Theorem 11.1] and [
Reference Cox11
, Proposition 13.2]). We call them singular moduli of discriminant
![]() $\Delta$
or singular moduli relative to the order
$\Delta$
or singular moduli relative to the order
![]() $\mathcal{O}$
. Reversing subject and complements, we will sometimes also speak of discriminant, CM order, CM field, etc… associated to a singular modulus j.
$\mathcal{O}$
. Reversing subject and complements, we will sometimes also speak of discriminant, CM order, CM field, etc… associated to a singular modulus j.
Recall that, given a number field
![]() $K \subseteq \overline{\mathbb{Q}}$
and a set
$K \subseteq \overline{\mathbb{Q}}$
and a set
![]() $S\subseteq \mathbb{N}$
of rational primes, an element
$S\subseteq \mathbb{N}$
of rational primes, an element
![]() $x \in K$
is called an S-unit if for every prime
$x \in K$
is called an S-unit if for every prime
![]() $\mathfrak{p} \subseteq K$
not lying above any prime
$\mathfrak{p} \subseteq K$
not lying above any prime
![]() $p \in S$
, we have
$p \in S$
, we have
![]() $x \in \mathcal{O}_{K_\mathfrak{p}}^{\times}$
, where
$x \in \mathcal{O}_{K_\mathfrak{p}}^{\times}$
, where
![]() $\mathcal{O}_{K_\mathfrak{p}} \subseteq K_\mathfrak{p}$
denotes the ring of integers in the completion
$\mathcal{O}_{K_\mathfrak{p}} \subseteq K_\mathfrak{p}$
denotes the ring of integers in the completion
![]() $K_\mathfrak{p}$
of the number field K at the prime
$K_\mathfrak{p}$
of the number field K at the prime
![]() $\mathfrak{p}$
. Note that this definition does not depend on the particular number field K containing x. Moreover, if x is actually an algebraic integer, then x is an S-unit if and only if its absolute norm
$\mathfrak{p}$
. Note that this definition does not depend on the particular number field K containing x. Moreover, if x is actually an algebraic integer, then x is an S-unit if and only if its absolute norm
![]() $N_{K/\mathbb{Q}}(x)$
is divided only by primes in S. In this paper we are interested in the study of S-units of the form
$N_{K/\mathbb{Q}}(x)$
is divided only by primes in S. In this paper we are interested in the study of S-units of the form
![]() $j-j_0$
with
$j-j_0$
with
![]() $j,j_0 \in \overline{\mathbb{Q}}$
singular moduli. If
$j,j_0 \in \overline{\mathbb{Q}}$
singular moduli. If
![]() $j_0=0$
is the unique singular modulus of discriminant
$j_0=0$
is the unique singular modulus of discriminant
![]() $\Delta_0=-3$
, we speak of singular S-units. As we will see, the study of these singular differences is intimately related to the theory of supersingular elliptic curves and quaternion algebras. We summarize some relevant results from this theory.
$\Delta_0=-3$
, we speak of singular S-units. As we will see, the study of these singular differences is intimately related to the theory of supersingular elliptic curves and quaternion algebras. We summarize some relevant results from this theory.
Let k be a field of characteristic
![]() $\textrm{char}(k)=\ell >0$
with algebraic closure
$\textrm{char}(k)=\ell >0$
with algebraic closure
![]() $\overline{k} \supseteq k$
and let
$\overline{k} \supseteq k$
and let
![]() $E/k$
be an elliptic curve. We say that E is supersingular if
$E/k$
be an elliptic curve. We say that E is supersingular if
![]() $E[\ell](\overline{k})=\{O\}$
i.e. if the unique
$E[\ell](\overline{k})=\{O\}$
i.e. if the unique
![]() $\ell$
-torsion point of E defined over
$\ell$
-torsion point of E defined over
![]() $\overline{k}$
is the identity
$\overline{k}$
is the identity
![]() $O \in E(\overline{k})$
. If this is the case, then the endomorphism ring
$O \in E(\overline{k})$
. If this is the case, then the endomorphism ring
![]() $\textrm{End}_{\overline{k}}(E)$
is isomorphic to a maximal order in the unique (up to isomorphism) quaternion algebra over
$\textrm{End}_{\overline{k}}(E)$
is isomorphic to a maximal order in the unique (up to isomorphism) quaternion algebra over
![]() $\mathbb{Q}$
ramified only at
$\mathbb{Q}$
ramified only at
![]() $\ell$
and
$\ell$
and
![]() $\infty$
(see [
Reference Deuring13
] or [
Reference Voight44
, Proposition 42.1.7 and Theorem 42.1.9] for a modern exposition). If k is a finite field, then by Deuring’s lifting theorem [
Reference Lang31
, Chapter 13, Theorem 14] every supersingular elliptic curve over
$\infty$
(see [
Reference Deuring13
] or [
Reference Voight44
, Proposition 42.1.7 and Theorem 42.1.9] for a modern exposition). If k is a finite field, then by Deuring’s lifting theorem [
Reference Lang31
, Chapter 13, Theorem 14] every supersingular elliptic curve over
![]() $\overline{k}$
arises as the reduction of some elliptic curve with complex multiplication defined over a number field. Finding such a CM elliptic curve is difficult in general. In contrast, it is very easy to see for which primes a CM elliptic curve defined over a number field has good supersingular reduction. Namely, let F be a number field with ring of integers
$\overline{k}$
arises as the reduction of some elliptic curve with complex multiplication defined over a number field. Finding such a CM elliptic curve is difficult in general. In contrast, it is very easy to see for which primes a CM elliptic curve defined over a number field has good supersingular reduction. Namely, let F be a number field with ring of integers
![]() $\mathcal{O}_F$
and let
$\mathcal{O}_F$
and let
![]() $E_{/F}$
be an elliptic curve with CM by an order in an imaginary quadratic field K. Fix a prime ideal
$E_{/F}$
be an elliptic curve with CM by an order in an imaginary quadratic field K. Fix a prime ideal
![]() $\mu \subseteq \mathcal{O}_F$
lying above a rational prime
$\mu \subseteq \mathcal{O}_F$
lying above a rational prime
![]() $\ell \in \mathbb{Z}$
that does not split in K. Since CM elliptic curves have potential good reduction everywhere (see [
Reference Silverman43
, VII, Proposition 5.5]) we can assume, possibly after enlarging the field of definition F, that E has good reduction at
$\ell \in \mathbb{Z}$
that does not split in K. Since CM elliptic curves have potential good reduction everywhere (see [
Reference Silverman43
, VII, Proposition 5.5]) we can assume, possibly after enlarging the field of definition F, that E has good reduction at
![]() $\mu$
and that all the geometric endomorphisms of E are defined over F. Then the reduced elliptic curve
$\mu$
and that all the geometric endomorphisms of E are defined over F. Then the reduced elliptic curve
![]() $\widetilde{E}\;:\!=\; E \text{ mod } \mu$
is supersingular by [
Reference Lang31
, Chapter 13, Theorem 12]. Moreover, the natural reduction map modulo
$\widetilde{E}\;:\!=\; E \text{ mod } \mu$
is supersingular by [
Reference Lang31
, Chapter 13, Theorem 12]. Moreover, the natural reduction map modulo
![]() $\mu$
induces an injective ring homomorphism
$\mu$
induces an injective ring homomorphism
between the corresponding endomorphism rings (see [
Reference Silverman42
, II, Proposition 4.4]). As we will see in Theorem 2·4, in many cases (depending on the prime
![]() $\ell$
and on the CM order of E) the above embedding will be optimal, in the following sense.
$\ell$
and on the CM order of E) the above embedding will be optimal, in the following sense.
Let
![]() $\mathbb{B}$
be a quaternion algebra over
$\mathbb{B}$
be a quaternion algebra over
![]() $\mathbb{Q}$
and let
$\mathbb{Q}$
and let
![]() $R \subseteq \mathbb{B}$
be an order, i.e. a full
$R \subseteq \mathbb{B}$
be an order, i.e. a full
![]() $\mathbb{Z}$
-lattice which is also a subring of
$\mathbb{Z}$
-lattice which is also a subring of
![]() $\mathbb{B}$
. Let
$\mathbb{B}$
. Let
![]() $\mathbb{Q} \subseteq K$
be a quadratic field extension and let
$\mathbb{Q} \subseteq K$
be a quadratic field extension and let
![]() $\mathcal{O} \subseteq K$
also be an order. Any ring homomorphism
$\mathcal{O} \subseteq K$
also be an order. Any ring homomorphism
![]() $\varphi\;:\;\mathcal{O} \to R$
can be naturally extended, after tensoring with
$\varphi\;:\;\mathcal{O} \to R$
can be naturally extended, after tensoring with
![]() $\mathbb{Q}$
, to a ring homomorphism
$\mathbb{Q}$
, to a ring homomorphism
![]() $K \to \mathbb{B}$
that we still denote by
$K \to \mathbb{B}$
that we still denote by
![]() $\varphi$
, with abuse of notation. We say that an injective ring homomorphism
$\varphi$
, with abuse of notation. We say that an injective ring homomorphism
![]() $\iota\;:\;\mathcal{O} \hookrightarrow R$
is an optimal embedding if
$\iota\;:\;\mathcal{O} \hookrightarrow R$
is an optimal embedding if
where the above intersection takes place in
![]() $\mathbb{B}$
. There is a simple criterion which allows to determine whether a given imaginary quadratic order optimally embeds into a quaternionic order. In order to state it, let us denote by
$\mathbb{B}$
. There is a simple criterion which allows to determine whether a given imaginary quadratic order optimally embeds into a quaternionic order. In order to state it, let us denote by
![]() $\textrm{trd}, \textrm{nrd}\;:\;\mathbb{B} \to \mathbb{Q}$
respectively the reduced trace and the reduced norm in the quaternion algebra
$\textrm{trd}, \textrm{nrd}\;:\;\mathbb{B} \to \mathbb{Q}$
respectively the reduced trace and the reduced norm in the quaternion algebra
![]() $\mathbb{B}$
, see [
Reference Voight44
, Section 3.3]. This notation will be in force for the rest of the paper.
$\mathbb{B}$
, see [
Reference Voight44
, Section 3.3]. This notation will be in force for the rest of the paper.
Lemma 2·1. Let R be an order in a quaternion algebra
![]() $\mathbb{B}$
and
$\mathbb{B}$
and
![]() $\mathcal{O}$
an order of discriminant
$\mathcal{O}$
an order of discriminant
![]() $\Delta$
in an imaginary quadratic field K. Let
$\Delta$
in an imaginary quadratic field K. Let
![]() $V\subseteq \mathbb{B}$
be the subspace of pure quaternions
$V\subseteq \mathbb{B}$
be the subspace of pure quaternions
Then
![]() $\mathcal{O}$
embeds (resp. optimally embeds) in R if and only if
$\mathcal{O}$
embeds (resp. optimally embeds) in R if and only if
![]() $|\Delta|$
is represented (resp. primitively represented) by the ternary quadratic lattice
$|\Delta|$
is represented (resp. primitively represented) by the ternary quadratic lattice
endowed with the natural scalar product induced by the reduced norm on
![]() $\mathbb{B}$
.
$\mathbb{B}$
.
Remark 2·2. This lemma has been proved for non-optimal embeddings and for maximal orders R in [
Reference Gross19
, Proposition 12.9]. Probably for this reason, the lattice
![]() $R_0$
is sometimes called the Gross lattice associated to R. The argument in loc. cit. easily generalises to our situation. We provide a full proof for completeness.
$R_0$
is sometimes called the Gross lattice associated to R. The argument in loc. cit. easily generalises to our situation. We provide a full proof for completeness.
Proof. We first prove that
![]() $\mathcal{O}$
embeds in R if and only if
$\mathcal{O}$
embeds in R if and only if
![]() $|\Delta|$
is represented by
$|\Delta|$
is represented by
![]() $R_0$
, and we discuss conditions on the optimality of this embedding at a second stage.
$R_0$
, and we discuss conditions on the optimality of this embedding at a second stage.
Write
![]() $\mathcal{O}=\mathbb{Z}[ ({\Delta+\sqrt{\Delta}})/{2} ]$
and suppose first that
$\mathcal{O}=\mathbb{Z}[ ({\Delta+\sqrt{\Delta}})/{2} ]$
and suppose first that
![]() $f\;:\;\mathcal{O} \hookrightarrow R$
is an embedding. Let
$f\;:\;\mathcal{O} \hookrightarrow R$
is an embedding. Let
![]() $b\;:\!=\;f(\sqrt{\Delta})$
so that
$b\;:\!=\;f(\sqrt{\Delta})$
so that
![]() $\textrm{trd}(b)=0$
and
$\textrm{trd}(b)=0$
and
![]() $\textrm{nrd}(b)=|\Delta|$
. Since
$\textrm{nrd}(b)=|\Delta|$
. Since
 \begin{equation*}f\left( \frac{\Delta+\sqrt{\Delta}}{2} \right)=\frac{\Delta+b}{2} \in R\end{equation*}
\begin{equation*}f\left( \frac{\Delta+\sqrt{\Delta}}{2} \right)=\frac{\Delta+b}{2} \in R\end{equation*}
we see that
![]() $b\in R_0$
so that
$b\in R_0$
so that
![]() $|\Delta|$
is represented by this lattice. Suppose conversely that there exists
$|\Delta|$
is represented by this lattice. Suppose conversely that there exists
![]() $b \in R_0$
such that
$b \in R_0$
such that
![]() $\textrm{nrd}(b)=|\Delta|$
. Since
$\textrm{nrd}(b)=|\Delta|$
. Since
![]() $\textrm{trd}(b)=0$
, we see that
$\textrm{trd}(b)=0$
, we see that
![]() $b^2=\Delta$
. By writing
$b^2=\Delta$
. By writing
![]() $b=a+2r$
with
$b=a+2r$
with
![]() $a\in \mathbb{Z}$
and
$a\in \mathbb{Z}$
and
![]() $r\in R$
, one has
$r\in R$
, one has
and this immediately implies that
![]() $a\equiv \Delta \text{ mod } 2$
, so that
$a\equiv \Delta \text{ mod } 2$
, so that
![]() $\Delta+b \in 2R$
. Hence we have
$\Delta+b \in 2R$
. Hence we have
![]() $(\Delta+b)/2 \in R$
and we obtain an embedding
$(\Delta+b)/2 \in R$
and we obtain an embedding
![]() $f\;:\;\mathcal{O}\hookrightarrow R$
by setting
$f\;:\;\mathcal{O}\hookrightarrow R$
by setting
 \begin{equation} f\left( \frac{\Delta+\sqrt{\Delta}}{2} \right)=\frac{\Delta+b}{2}.\end{equation}
\begin{equation} f\left( \frac{\Delta+\sqrt{\Delta}}{2} \right)=\frac{\Delta+b}{2}.\end{equation}
We now discuss optimality. Fix
![]() $\{\alpha_1,\alpha_2, \alpha_3 \}$
to be a basis of
$\{\alpha_1,\alpha_2, \alpha_3 \}$
to be a basis of
![]() $R_0$
as a
$R_0$
as a
![]() $\mathbb{Z}$
-module and let Q(X, Y, Z) be the ternary quadratic form induced by the reduced norm with respect to this basis.
$\mathbb{Z}$
-module and let Q(X, Y, Z) be the ternary quadratic form induced by the reduced norm with respect to this basis.
Assume that
![]() $f\;:\;\mathcal{O} \hookrightarrow R$
is an optimal embedding. By the proof above, we know that
$f\;:\;\mathcal{O} \hookrightarrow R$
is an optimal embedding. By the proof above, we know that
![]() $b\;:\!=\;f(\sqrt{\Delta}) \in R_0$
is such that
$b\;:\!=\;f(\sqrt{\Delta}) \in R_0$
is such that
![]() $\textrm{nrd}(b)=|\Delta|$
. Suppose by contradiction that
$\textrm{nrd}(b)=|\Delta|$
. Suppose by contradiction that
![]() $b=a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3$
with
$b=a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3$
with
![]() $a_1,a_2,a_3 \in \mathbb{Z}$
not coprime, so that
$a_1,a_2,a_3 \in \mathbb{Z}$
not coprime, so that
![]() $c\;:\!=\; \gcd(a_1,a_2,a_3)>1$
(we adopt the convention that the greatest common divisor is always positive). Then
$c\;:\!=\; \gcd(a_1,a_2,a_3)>1$
(we adopt the convention that the greatest common divisor is always positive). Then
![]() $\widetilde{b}\;:\!=\;b/c \in R_0$
satisfies
$\widetilde{b}\;:\!=\;b/c \in R_0$
satisfies
in the same way as above. Thus
![]() $\frac{1}{2} \left( ({\Delta}/{c^2})+({\sqrt{\Delta}}/{c})\right) \in K$
is an algebraic integer and the order
$\frac{1}{2} \left( ({\Delta}/{c^2})+({\sqrt{\Delta}}/{c})\right) \in K$
is an algebraic integer and the order
![]() $\widetilde{\mathcal{O}}\;:\!=\;\mathbb{Z} \left[ \frac{1}{2} \left(({\Delta}/{c^2})+({\sqrt{\Delta}}/{c})\right) \right]$
, which strictly contains
$\widetilde{\mathcal{O}}\;:\!=\;\mathbb{Z} \left[ \frac{1}{2} \left(({\Delta}/{c^2})+({\sqrt{\Delta}}/{c})\right) \right]$
, which strictly contains
![]() $\mathcal{O}$
, also embeds in R through the extension
$\mathcal{O}$
, also embeds in R through the extension
![]() $f\;:\;K \hookrightarrow \mathbb{B}$
. This contradicts the optimality of
$f\;:\;K \hookrightarrow \mathbb{B}$
. This contradicts the optimality of
![]() $f\;:\;\mathcal{O} \hookrightarrow R$
.
$f\;:\;\mathcal{O} \hookrightarrow R$
.
Suppose now that
![]() $|\Delta|$
is primitively represented by
$|\Delta|$
is primitively represented by
![]() $R_0$
i.e. that there exist
$R_0$
i.e. that there exist
![]() $a_1,a_2,a_3 \in \mathbb{Z}$
coprime such that
$a_1,a_2,a_3 \in \mathbb{Z}$
coprime such that
![]() $\textrm{nrd}(a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3)=|\Delta|$
. We want to show that, setting
$\textrm{nrd}(a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3)=|\Delta|$
. We want to show that, setting
![]() $b\;:\!=\;a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3$
, the embedding f defined by (1) is optimal. We will equivalently prove that, if
$b\;:\!=\;a_1 \alpha_1+a_2 \alpha_2+a_3 \alpha_3$
, the embedding f defined by (1) is optimal. We will equivalently prove that, if
![]() $c\in \mathbb{Z}_{>0}$
is such that
$c\in \mathbb{Z}_{>0}$
is such that
![]() $\widetilde{\mathcal{O}}\;:\!=\;\mathbb{Z} \left[ \frac{1}{2} \left(({\sqrt{\Delta}}/{c})+({\Delta}/{c^2})\right) \right]$
is an order, then
$\widetilde{\mathcal{O}}\;:\!=\;\mathbb{Z} \left[ \frac{1}{2} \left(({\sqrt{\Delta}}/{c})+({\Delta}/{c^2})\right) \right]$
is an order, then
implies
![]() $\widetilde{\mathcal{O}}=\mathcal{O}$
. Since
$\widetilde{\mathcal{O}}=\mathcal{O}$
. Since
![]() $b=f(\sqrt{\Delta})$
, equality (2) entails
$b=f(\sqrt{\Delta})$
, equality (2) entails
![]() $\frac{1}{2} \left(({b}/{c})+({\Delta}/{c^2})\right) \in R$
so that
$\frac{1}{2} \left(({b}/{c})+({\Delta}/{c^2})\right) \in R$
so that
![]() $b/c \in R_0$
. But now
$b/c \in R_0$
. But now
and all the coefficients
![]() $a_i/c$
must be integral since
$a_i/c$
must be integral since
![]() $\{\alpha_1, \alpha_2, \alpha_3 \}$
is a basis of
$\{\alpha_1, \alpha_2, \alpha_3 \}$
is a basis of
![]() $R_0$
as a
$R_0$
as a
![]() $\mathbb{Z}$
-module. By assumption, the
$\mathbb{Z}$
-module. By assumption, the
![]() $a_i$
’s are coprime, so we must have
$a_i$
’s are coprime, so we must have
![]() $c=1$
. Hence
$c=1$
. Hence
![]() $\widetilde{\mathcal{O}}=\mathcal{O}$
and this concludes the proof.
$\widetilde{\mathcal{O}}=\mathcal{O}$
and this concludes the proof.
Remark 2·3. The proof of Lemma 2·1 actually establishes a bijection between the set of embeddings
![]() $f\;:\;\mathcal{O} \hookrightarrow R$
and the set of elements
$f\;:\;\mathcal{O} \hookrightarrow R$
and the set of elements
![]() $b \in R_0$
such that
$b \in R_0$
such that
![]() $\textrm{nrd}(b)=|\Delta|$
. Under this bijection, the embedding f corresponds to the element
$\textrm{nrd}(b)=|\Delta|$
. Under this bijection, the embedding f corresponds to the element
![]() $f(\sqrt{\Delta}) \in R_0$
.
$f(\sqrt{\Delta}) \in R_0$
.
In order to carry out our study of singular differences that are S-units, it is fundamental to understand what is the biggest exponent with which a prime ideal can appear in the factorisation of such a difference. Roughly speaking, saying that a difference of singular moduli
![]() $j-j_0$
has a certain
$j-j_0$
has a certain
![]() $\mu$
-adic valuation
$\mu$
-adic valuation
![]() $n=v_{\mu}(\,j-j_0)$
for some prime ideal
$n=v_{\mu}(\,j-j_0)$
for some prime ideal
![]() $\mu \subseteq \mathbb{Q}(\,j-j_0)$
is equivalent to saying that the CM elliptic curve
$\mu \subseteq \mathbb{Q}(\,j-j_0)$
is equivalent to saying that the CM elliptic curve
![]() $E_j$
with
$E_j$
with
![]() $j(E_j)=j$
is isomorphic to the elliptic curve
$j(E_j)=j$
is isomorphic to the elliptic curve
![]() $E_{j_0}$
with
$E_{j_0}$
with
![]() $j(E_0)=j_0$
when reduced modulo
$j(E_0)=j_0$
when reduced modulo
![]() $\mu^n$
. Therefore, in order to understand the exponents appearing in the prime ideal factorisation of a singular difference, it is crucial to determine when such isomorphisms can occur. With this goal in mind, we conclude this section by outlining some aspects of the reduction theory of CM elliptic curves defined over number fields. We refer the reader to [
Reference Conrad10
,
Reference Gross20
,
Reference Gross and Zagier21
] and [
Reference Lauter and Viray33
] for further discussions on the topic.
$\mu^n$
. Therefore, in order to understand the exponents appearing in the prime ideal factorisation of a singular difference, it is crucial to determine when such isomorphisms can occur. With this goal in mind, we conclude this section by outlining some aspects of the reduction theory of CM elliptic curves defined over number fields. We refer the reader to [
Reference Conrad10
,
Reference Gross20
,
Reference Gross and Zagier21
] and [
Reference Lauter and Viray33
] for further discussions on the topic.
Let
![]() $\mathcal{O}$
be an order of discriminant
$\mathcal{O}$
be an order of discriminant
![]() $\Delta$
in an imaginary quadratic field K and let
$\Delta$
in an imaginary quadratic field K and let
![]() $\ell \nmid \Delta$
be a prime inert in K. Consider an elliptic curve E
′ with complex multiplication by the order
$\ell \nmid \Delta$
be a prime inert in K. Consider an elliptic curve E
′ with complex multiplication by the order
![]() $\mathcal{O}$
and defined over the ring class field
$\mathcal{O}$
and defined over the ring class field
![]() $H_\mathcal{O}\;:\!=\;K(\,j(E'))$
. After completing with respect to any prime above
$H_\mathcal{O}\;:\!=\;K(\,j(E'))$
. After completing with respect to any prime above
![]() $\ell$
, we can consider
$\ell$
, we can consider
![]() $H_\mathcal{O}$
as a subfield of the maximal unramified extension
$H_\mathcal{O}$
as a subfield of the maximal unramified extension
![]() $\mathbb{Q}_{\ell}^{\text{unr}}$
of
$\mathbb{Q}_{\ell}^{\text{unr}}$
of
![]() $\mathbb{Q}_\ell$
. This is because the extension
$\mathbb{Q}_\ell$
. This is because the extension
![]() $\mathbb{Q} \subseteq H_\mathcal{O}$
is unramified at
$\mathbb{Q} \subseteq H_\mathcal{O}$
is unramified at
![]() $\ell$
by the assumption
$\ell$
by the assumption
![]() $\ell \nmid \Delta$
, see [
Reference Cox11
, Chapter 9, Section A]. Let
$\ell \nmid \Delta$
, see [
Reference Cox11
, Chapter 9, Section A]. Let
![]() $L\;:\!=\;\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
be the completion of
$L\;:\!=\;\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
be the completion of
![]() $\mathbb{Q}_{\ell}^{\text{unr}}$
with ring of integers W and uniformiser
$\mathbb{Q}_{\ell}^{\text{unr}}$
with ring of integers W and uniformiser
![]() $\pi$
. Then by [
Reference Serre and Tate40
, Theorems 8 and 9] and [
Reference Lang31
, Chapter 13, Theorem 12] there exists an elliptic scheme
$\pi$
. Then by [
Reference Serre and Tate40
, Theorems 8 and 9] and [
Reference Lang31
, Chapter 13, Theorem 12] there exists an elliptic scheme
![]() $\mathcal{E} \to \textrm{Spec}\ W$
such that:
$\mathcal{E} \to \textrm{Spec}\ W$
such that:
-
(i) the generic fiber
 $E\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ L$
is isomorphic to
$E\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ L$
is isomorphic to
 $E^{\prime} $
over the algebraic closure of L. Since the CM order
$E^{\prime} $
over the algebraic closure of L. Since the CM order
 $\mathcal{O}$
is contained in W, all the geometric endomorphisms of E are defined over L, see [
Reference Shimura41
, Chapter II, Proposition 30];
$\mathcal{O}$
is contained in W, all the geometric endomorphisms of E are defined over L, see [
Reference Shimura41
, Chapter II, Proposition 30]; -
(ii) the special fiber
 $E_0\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ W/\pi$
is a supersingular elliptic curve since, by assumption,
$E_0\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ W/\pi$
is a supersingular elliptic curve since, by assumption,
 $\ell$
does not split in K. Note that
$\ell$
does not split in K. Note that
 $W/\pi \cong \overline{\mathbb{F}}_\ell$
, the algebraic closure of the finite field with
$W/\pi \cong \overline{\mathbb{F}}_\ell$
, the algebraic closure of the finite field with
 $\ell$
elements.
$\ell$
elements.
For all
![]() $n\in \mathbb{N}$
, set
$n\in \mathbb{N}$
, set
![]() $E_n\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ W/ \pi^{n+1}$
. We are interested in understanding the endomorphism rings
$E_n\;:\!=\;\mathcal{E} \times_W \textrm{Spec}\ W/ \pi^{n+1}$
. We are interested in understanding the endomorphism rings
![]() $A_{\ell,n}\;:\!=\;\textrm{End}_{W/\pi^{n+1}}(E_n)$
. When
$A_{\ell,n}\;:\!=\;\textrm{End}_{W/\pi^{n+1}}(E_n)$
. When
![]() $n=0$
, we have already seen that the ring
$n=0$
, we have already seen that the ring
![]() $A_{\ell,0}$
is isomorphic to a maximal order in
$A_{\ell,0}$
is isomorphic to a maximal order in
![]() $\mathbb{B}_{\ell, \infty}$
, the unique (up to isomorphism) definite quaternion algebra over the rationals which ramifies only at
$\mathbb{B}_{\ell, \infty}$
, the unique (up to isomorphism) definite quaternion algebra over the rationals which ramifies only at
![]() $\ell$
and
$\ell$
and
![]() $\infty$
. All the other rings
$\infty$
. All the other rings
![]() $A_{\ell,n}$
can be recovered from
$A_{\ell,n}$
can be recovered from
![]() $A_{\ell,0}$
, as explained in the following theorem.
$A_{\ell,0}$
, as explained in the following theorem.
Theorem 2·4. Let
![]() $\mathcal{O}$
be an order of discriminant
$\mathcal{O}$
be an order of discriminant
![]() $\Delta$
in an imaginary quadratic field K and let
$\Delta$
in an imaginary quadratic field K and let
![]() $\ell \nmid \Delta$
be a prime inert in K. Set
$\ell \nmid \Delta$
be a prime inert in K. Set
![]() $L\;:\!=\;\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
to be the completion of the maximal unramified extension of
$L\;:\!=\;\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
to be the completion of the maximal unramified extension of
![]() $\mathbb{Q}_\ell$
, with ring of integers W and uniformiser
$\mathbb{Q}_\ell$
, with ring of integers W and uniformiser
![]() $\pi$
. Let
$\pi$
. Let
![]() $\mathcal{E} \to \textrm{Spec} (W)$
be an elliptic scheme whose generic fiber
$\mathcal{E} \to \textrm{Spec} (W)$
be an elliptic scheme whose generic fiber
![]() $E\;:\!=\; \mathcal{E} \times_W \textrm{Spec}\ L$
has complex multiplication by
$E\;:\!=\; \mathcal{E} \times_W \textrm{Spec}\ L$
has complex multiplication by
![]() $\mathcal{O}$
. For every
$\mathcal{O}$
. For every
![]() $n \in \mathbb{N}$
, denote by
$n \in \mathbb{N}$
, denote by
respectively the reduction of
![]() $\mathcal{E}$
modulo
$\mathcal{E}$
modulo
![]() $\pi^{n+1}$
and its endomorphism ring. Then:
$\pi^{n+1}$
and its endomorphism ring. Then:
-
(a) for every
 $n \in \mathbb{N}$
we have where the sum takes place in
$n \in \mathbb{N}$
we have where the sum takes place in \begin{equation*} A_{\ell,n} \cong \mathcal{O} + \ell^n A_{\ell,0}, \end{equation*}
\begin{equation*} A_{\ell,n} \cong \mathcal{O} + \ell^n A_{\ell,0}, \end{equation*}
 $A_{\ell,0}$
in which
$A_{\ell,0}$
in which
 $\mathcal{O}$
is embedded via the reduction modulo
$\mathcal{O}$
is embedded via the reduction modulo
 $\pi$
;
$\pi$
;
-
(b) for every
 $n \in \mathbb{N}$
the ring
$n \in \mathbb{N}$
the ring
 $\textrm{End}_{W/\pi^{n+1}}(E_n)$
is isomorphic to a quaternion order in
$\textrm{End}_{W/\pi^{n+1}}(E_n)$
is isomorphic to a quaternion order in
 $\mathbb{B}_{\ell, \infty}$
and the natural reduction map induced by the reduction modulo
$\mathbb{B}_{\ell, \infty}$
and the natural reduction map induced by the reduction modulo \begin{equation*} \mathcal{O} \cong \textrm{End}_W (\mathcal{E}) \longrightarrow \textrm{End}_{W/\pi^{n+1}}(E_n) \end{equation*}
\begin{equation*} \mathcal{O} \cong \textrm{End}_W (\mathcal{E}) \longrightarrow \textrm{End}_{W/\pi^{n+1}}(E_n) \end{equation*}
 $\pi^{n+1}$
is an optimal embedding.
$\pi^{n+1}$
is an optimal embedding.
The above theorem is a combination and a reformulation of various results already appearing in the literature. We give a brief overview of the proof and point out the relevant references.
Proof of Theorem
2·4. Part (a) of the theorem is a special case of [
Reference Lauter and Viray33
, Formula 6.6]. As for part (b): the first statement follows from the fact that
![]() $\ell$
is a prime of supersingular reduction for E and from part (a). For the second statement, note first of all that there is a natural isomorphism between
$\ell$
is a prime of supersingular reduction for E and from part (a). For the second statement, note first of all that there is a natural isomorphism between
![]() $\textrm{End}_L(E) \cong \mathcal{O}$
and
$\textrm{End}_L(E) \cong \mathcal{O}$
and
![]() $\textrm{End}_W(\mathcal{E})$
, since by assumption
$\textrm{End}_W(\mathcal{E})$
, since by assumption
![]() $\mathcal{E}$
is a Néron model for E over W (see [
Reference Bosch, Lutkebohmert and Raynaud5
, Propositions 1.2/8 and 1.4/4]). Reductions modulo
$\mathcal{E}$
is a Néron model for E over W (see [
Reference Bosch, Lutkebohmert and Raynaud5
, Propositions 1.2/8 and 1.4/4]). Reductions modulo
![]() $\pi$
and
$\pi$
and
![]() $\pi^n$
give the following commutative diagram
$\pi^n$
give the following commutative diagram

in which all the arrows are injective by [
Reference Conrad10
, Theorem 2.1 (2)]. Since
![]() $\ell$
does not divide the conductor of the order
$\ell$
does not divide the conductor of the order
![]() $\mathcal{O}$
, the embedding
$\mathcal{O}$
, the embedding
![]() $\varphi_0$
is optimal by [
Reference Lauter and Viray33
, Proposition 2.2]. It follows from the commutativity of the diagram above that also the embedding
$\varphi_0$
is optimal by [
Reference Lauter and Viray33
, Proposition 2.2]. It follows from the commutativity of the diagram above that also the embedding
![]() $\varphi_{n-1}$
is optimal, and the theorem is proved.
$\varphi_{n-1}$
is optimal, and the theorem is proved.
3. The
 $\ell$
-adic valuation of differences of singular moduli
$\ell$
-adic valuation of differences of singular moduli
In order to bound from above the Weil height of a difference of singular moduli, it is of crucial importance to understand the exponents appearing in the prime factorisation of such a difference. The goal of this section is to prove, under certain conditions, an upper bound for these exponents. In what follows, we will always use
![]() $\mathbb{F}_\ell$
to denote the finite field with
$\mathbb{F}_\ell$
to denote the finite field with
![]() $\ell$
elements, where
$\ell$
elements, where
![]() $\ell \in \mathbb{N}$
is a prime number, and denote by
$\ell \in \mathbb{N}$
is a prime number, and denote by
![]() $\overline{\mathbb{F}}_\ell$
an algebraic closure of this field. Recall also that given an order
$\overline{\mathbb{F}}_\ell$
an algebraic closure of this field. Recall also that given an order
![]() $\mathcal{O}$
in an imaginary quadratic field K, the ring class field of K relative to the order
$\mathcal{O}$
in an imaginary quadratic field K, the ring class field of K relative to the order
![]() $\mathcal{O}$
is the field generated over K by any singular modulus relative to
$\mathcal{O}$
is the field generated over K by any singular modulus relative to
![]() $\mathcal{O}$
.
$\mathcal{O}$
.
Theorem 3·1. Let
![]() $j_0 \in \overline{\mathbb{Q}}$
be a singular modulus relative to an order
$j_0 \in \overline{\mathbb{Q}}$
be a singular modulus relative to an order
![]() $\mathcal{O}_{j_0}$
of discriminant
$\mathcal{O}_{j_0}$
of discriminant
![]() $\Delta_0$
and let
$\Delta_0$
and let
![]() $\ell \in \mathbb{Z}$
be a prime not dividing
$\ell \in \mathbb{Z}$
be a prime not dividing
![]() $\Delta_0$
. For any singular modulus
$\Delta_0$
. For any singular modulus
![]() $j \in \overline{\mathbb{Q}}$
relative to an order
$j \in \overline{\mathbb{Q}}$
relative to an order
![]() $\mathcal{O}_j$
of discriminant
$\mathcal{O}_j$
of discriminant
![]() $\Delta \neq \Delta_0$
, denote by H the compositum of the ring class fields relative to
$\Delta \neq \Delta_0$
, denote by H the compositum of the ring class fields relative to
![]() $\mathcal{O}_{j_0}$
and
$\mathcal{O}_{j_0}$
and
![]() $\mathcal{O}_j$
. Let
$\mathcal{O}_j$
. Let
![]() $\mu \subseteq H$
be a prime ideal lying above
$\mu \subseteq H$
be a prime ideal lying above
![]() $\ell$
and assume that:
$\ell$
and assume that:
-
(i) the prime
 $\mu \cap \mathbb{Q}(\,j_0)$
has residue degree 1 over
$\mu \cap \mathbb{Q}(\,j_0)$
has residue degree 1 over
 $\ell$
;
$\ell$
; -
(ii) there exists an elliptic curve
 ${E_0}_{/\mathbb{Q}(\,j_0)}$
with
${E_0}_{/\mathbb{Q}(\,j_0)}$
with
 $j(E_0)=j_0$
and having good reduction at
$j(E_0)=j_0$
and having good reduction at
 $\mu \cap \mathbb{Q}(\,j_0)$
.
$\mu \cap \mathbb{Q}(\,j_0)$
.
Then, if
![]() $v_\mu(\!\cdot\!)$
denotes the normalised valuation associated to
$v_\mu(\!\cdot\!)$
denotes the normalised valuation associated to
![]() $\mu$
, we have
$\mu$
, we have
 \begin{equation} v_\mu(\,j-j_0) \leq\begin{cases}\frac{d_0}{2} \left( \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell}+ \frac{1}{2} \right) &\text{ if } \ell \nmid \Delta \text{ and } \mathcal{O}_{j_0} \not \subseteq \mathcal{O}_j, \\\frac{d_0}{2} &\text{ if } \ell \mid \Delta,\end{cases}\end{equation}
\begin{equation} v_\mu(\,j-j_0) \leq\begin{cases}\frac{d_0}{2} \left( \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell}+ \frac{1}{2} \right) &\text{ if } \ell \nmid \Delta \text{ and } \mathcal{O}_{j_0} \not \subseteq \mathcal{O}_j, \\\frac{d_0}{2} &\text{ if } \ell \mid \Delta,\end{cases}\end{equation}
where
![]() $d_0$
is the number of automorphisms of any elliptic curve
$d_0$
is the number of automorphisms of any elliptic curve
![]() $E_{/\overline{\mathbb{F}}_\ell}$
with
$E_{/\overline{\mathbb{F}}_\ell}$
with
![]() $j(E) = j_0 \text{ mod } \mu$
.
$j(E) = j_0 \text{ mod } \mu$
.
Remark 3·2. Note that we have
![]() $d_0=2$
in all cases except if
$d_0=2$
in all cases except if
![]() $j_0 \equiv 0$
or
$j_0 \equiv 0$
or
![]() $j_0 \equiv 1728$
mod
$j_0 \equiv 1728$
mod
![]() $\mu$
. In these two cases, the value of
$\mu$
. In these two cases, the value of
![]() $d_0$
also depends on
$d_0$
also depends on
![]() $\ell$
, see [
Reference Silverman43
, III, Theorem 10.1].
$\ell$
, see [
Reference Silverman43
, III, Theorem 10.1].
The dichotomy in the conclusion of Theorem 3·1 is reflected by its proof, which we divide according to the conditions displayed in (3). In all cases, everything boils down to the study of optimal embeddings of the order
![]() $\mathcal{O}_j$
in a family of nested orders contained in the endomorphism ring of a certain supersingular elliptic curve defined over
$\mathcal{O}_j$
in a family of nested orders contained in the endomorphism ring of a certain supersingular elliptic curve defined over
![]() $\overline{\mathbb{F}}_\ell$
. One of the main issues is that for a supersingular elliptic curve
$\overline{\mathbb{F}}_\ell$
. One of the main issues is that for a supersingular elliptic curve
![]() $E_{/\overline{\mathbb{F}}_\ell}$
, explicitely computing its endomorphism ring is a difficult problem in general. An explicit parametrisation of the endomorphism rings of supersingular elliptic curves over
$E_{/\overline{\mathbb{F}}_\ell}$
, explicitely computing its endomorphism ring is a difficult problem in general. An explicit parametrisation of the endomorphism rings of supersingular elliptic curves over
![]() $\overline{\mathbb{F}}_\ell$
has been achieved by Lauter and Viray in [
Reference Lauter and Viray33
, Section 6]. However, the author found these parametrizations somehow difficult to use for explicit estimates. Therefore, in order to achieve our results, we adopted a different strategy. The idea is that, since we are only interested in providing estimates for the
$\overline{\mathbb{F}}_\ell$
has been achieved by Lauter and Viray in [
Reference Lauter and Viray33
, Section 6]. However, the author found these parametrizations somehow difficult to use for explicit estimates. Therefore, in order to achieve our results, we adopted a different strategy. The idea is that, since we are only interested in providing estimates for the
![]() $\mu$
-adic valuation of singular differences and not in precisely determining their prime ideal factorisation, we do not need the full knowledge of the supersingular endomorphism rings of the elliptic curves involved. We instead “approximate”, when possible, the unknown quaternion orders with quaternion orders whose properties are less mysterious. The next proposition is the cornerstone of this strategy.
$\mu$
-adic valuation of singular differences and not in precisely determining their prime ideal factorisation, we do not need the full knowledge of the supersingular endomorphism rings of the elliptic curves involved. We instead “approximate”, when possible, the unknown quaternion orders with quaternion orders whose properties are less mysterious. The next proposition is the cornerstone of this strategy.
Proposition 3·3. Let
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
$j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
![]() $\Delta$
and let
$\Delta$
and let
![]() $E_{/\mathbb{Q}(\,j)}$
be an elliptic curve with
$E_{/\mathbb{Q}(\,j)}$
be an elliptic curve with
![]() $j(E)=j$
. Choose a degree 1 prime
$j(E)=j$
. Choose a degree 1 prime
![]() $\mathfrak{p} \subseteq \mathbb{Q}(\,j)$
lying above a rational prime
$\mathfrak{p} \subseteq \mathbb{Q}(\,j)$
lying above a rational prime
![]() $p \in \mathbb{Z}$
not dividing
$p \in \mathbb{Z}$
not dividing
![]() $\Delta$
and suppose that E has good supersingular reduction
$\Delta$
and suppose that E has good supersingular reduction
![]() $\widetilde{E}$
modulo
$\widetilde{E}$
modulo
![]() $\mathfrak{p}$
. Denote by
$\mathfrak{p}$
. Denote by
![]() $\varphi \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
the Frobenius endomorphism
$\varphi \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
the Frobenius endomorphism
![]() $(x,y) \mapsto (x^{\,p},y^{\,p})$
, where the coordinates x,y come from the choice of a Weierstrass model for E. Then there exists a morphism
$(x,y) \mapsto (x^{\,p},y^{\,p})$
, where the coordinates x,y come from the choice of a Weierstrass model for E. Then there exists a morphism
![]() $\psi \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
such that
$\psi \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
such that
where
![]() $\overline{\cdot}\;:\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q} \to \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
denotes the standard involution. In fact, the morphism
$\overline{\cdot}\;:\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q} \to \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
denotes the standard involution. In fact, the morphism
![]() $\psi$
can be taken inside the image of the reduction map
$\psi$
can be taken inside the image of the reduction map
![]() $\textrm{End}_{\overline{\mathbb{Q}}}(E) \to \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
modulo any prime in
$\textrm{End}_{\overline{\mathbb{Q}}}(E) \to \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
modulo any prime in
![]() $\overline{\mathbb{Q}}$
lying above
$\overline{\mathbb{Q}}$
lying above
![]() $\mathfrak{p}$
.
$\mathfrak{p}$
.
Remark 3·4. Recall that the standard involution on the quaternion algebra
![]() $\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
corresponds to taking the dual isogeny when restricted to
$\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
corresponds to taking the dual isogeny when restricted to
![]() $\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. This essentially follows from the uniqueness of the standard involution on quaternion algebras, see [
Reference Voight44
, Corollary 3.4.4].
$\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. This essentially follows from the uniqueness of the standard involution on quaternion algebras, see [
Reference Voight44
, Corollary 3.4.4].
Proof. In this proof, we fix for convenience an embedding
![]() $\overline{\mathbb{Q}} \hookrightarrow \mathbb{C}$
. Let
$\overline{\mathbb{Q}} \hookrightarrow \mathbb{C}$
. Let
![]() $\mathcal{O}$
be the order of discriminant
$\mathcal{O}$
be the order of discriminant
![]() $\Delta$
and
$\Delta$
and
![]() $K \subseteq \overline{\mathbb{Q}}$
be its field of fractions. For an element
$K \subseteq \overline{\mathbb{Q}}$
be its field of fractions. For an element
![]() $\beta \in K$
, we denote by
$\beta \in K$
, we denote by
![]() $\overline{\beta}$
its conjugate through the unique non-trivial automorphism of
$\overline{\beta}$
its conjugate through the unique non-trivial automorphism of
![]() $K/\mathbb{Q}$
. This will not cause confusion with the standard involution on
$K/\mathbb{Q}$
. This will not cause confusion with the standard involution on
![]() $\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
, as we explain below.
$\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
, as we explain below.
By assumption, there exists an elliptic scheme
![]() $\mathcal{E}$
over the localisation at
$\mathcal{E}$
over the localisation at
![]() $\mathfrak{p}$
of the ring of integers in
$\mathfrak{p}$
of the ring of integers in
![]() $\mathbb{Q}(\,j)$
such that the generic fiber of
$\mathbb{Q}(\,j)$
such that the generic fiber of
![]() $\mathcal{E}$
is isomorphic to E while its special fiber is a supersingular elliptic curve
$\mathcal{E}$
is isomorphic to E while its special fiber is a supersingular elliptic curve
![]() $\widetilde{E}$
defined over
$\widetilde{E}$
defined over
![]() $\mathbb{F}_p$
. Set
$\mathbb{F}_p$
. Set
![]() $H_\mathcal{O}\;:\!=\;K(\,j)$
, which is a degree 2 extension of
$H_\mathcal{O}\;:\!=\;K(\,j)$
, which is a degree 2 extension of
![]() $\mathbb{Q}(\,j)$
, and fix a prime
$\mathbb{Q}(\,j)$
, and fix a prime
![]() $\mathcal{P} \subseteq H_\mathcal{O}$
lying above
$\mathcal{P} \subseteq H_\mathcal{O}$
lying above
![]() $\mathfrak{p}$
. Since E has supersingular reduction modulo
$\mathfrak{p}$
. Since E has supersingular reduction modulo
![]() $\mathfrak{p}$
, the latter has degree 1 and p is unramified in K, by [
Reference Lang31
, Chapter 13, Theorem 12] we must have
$\mathfrak{p}$
, the latter has degree 1 and p is unramified in K, by [
Reference Lang31
, Chapter 13, Theorem 12] we must have
![]() $f(\mathcal{P}/\mathfrak{p})=2$
, where
$f(\mathcal{P}/\mathfrak{p})=2$
, where
![]() $f(\mathcal{P}/\mathfrak{p})$
denotes the inertia degree of
$f(\mathcal{P}/\mathfrak{p})$
denotes the inertia degree of
![]() $\mathcal{P}$
over
$\mathcal{P}$
over
![]() $\mathfrak{p}$
. In particular, we see that the decomposition group of
$\mathfrak{p}$
. In particular, we see that the decomposition group of
![]() $\mathcal{P}$
over
$\mathcal{P}$
over
![]() $\mathfrak{p}$
is precisely
$\mathfrak{p}$
is precisely
![]() $\textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
. We fix
$\textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
. We fix
![]() $\sigma \in \textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
to be the unique non-trivial element. Then
$\sigma \in \textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
to be the unique non-trivial element. Then
![]() $\sigma$
restricts to an automorphism of
$\sigma$
restricts to an automorphism of
![]() $R_\mathcal{P}$
, the localization at
$R_\mathcal{P}$
, the localization at
![]() $\mathcal{P}$
of the ring of integers of
$\mathcal{P}$
of the ring of integers of
![]() $H_\mathcal{O}$
, inducing the Frobenius endomorphism
$H_\mathcal{O}$
, inducing the Frobenius endomorphism
![]() $\tau\;:\;x \mapsto x^p$
on the residue field.
$\tau\;:\;x \mapsto x^p$
on the residue field.
With abuse of notation, we denote again by
![]() $\mathcal{E}$
the base-change
$\mathcal{E}$
the base-change
![]() $\mathcal{E}_{R_\mathcal{P}}$
and by
$\mathcal{E}_{R_\mathcal{P}}$
and by
![]() $\widetilde{E}$
the special fiber of
$\widetilde{E}$
the special fiber of
![]() $\mathcal{E}_{R_\mathcal{P}}$
(which is isomorphic to the base-change of the special fiber of
$\mathcal{E}_{R_\mathcal{P}}$
(which is isomorphic to the base-change of the special fiber of
![]() $\mathcal{E}$
to the residue field of
$\mathcal{E}$
to the residue field of
![]() $R_\mathcal{P}$
). It follows from the Néron mapping property [
Reference Bosch, Lutkebohmert and Raynaud5
, Proposition 1.4/4] that every endomorphism
$R_\mathcal{P}$
). It follows from the Néron mapping property [
Reference Bosch, Lutkebohmert and Raynaud5
, Proposition 1.4/4] that every endomorphism
![]() $\lambda \in \textrm{End}_{H_\mathcal{O}}(E)$
induces an endomorphism
$\lambda \in \textrm{End}_{H_\mathcal{O}}(E)$
induces an endomorphism
![]() $\lambda_\mathcal{E}$
of
$\lambda_\mathcal{E}$
of
![]() $\mathcal{E}$
. Define
$\mathcal{E}$
. Define
![]() $\lambda \text{ mod } \mathcal{P}$
to be the restriction of
$\lambda \text{ mod } \mathcal{P}$
to be the restriction of
![]() $\lambda_\mathcal{E}$
to
$\lambda_\mathcal{E}$
to
![]() $\widetilde{E}$
. The Galois group
$\widetilde{E}$
. The Galois group
![]() $\textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
acts on
$\textrm{Gal}(H_\mathcal{O}/\mathbb{Q}(\,j))$
acts on
![]() $R_\mathcal{P}$
and this in turn induces a Galois action on
$R_\mathcal{P}$
and this in turn induces a Galois action on
![]() $\textrm{End}_{R_\mathcal{P}}(\mathcal{E})$
. In the same way, there is an action of
$\textrm{End}_{R_\mathcal{P}}(\mathcal{E})$
. In the same way, there is an action of
![]() $\textrm{Gal}(\overline{\mathbb{F}}_p/\mathbb{F}_p)$
on
$\textrm{Gal}(\overline{\mathbb{F}}_p/\mathbb{F}_p)$
on
![]() $\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. These two actions are compatible, in the sense that for every
$\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. These two actions are compatible, in the sense that for every
![]() $\lambda \in \textrm{End}_{H_\mathcal{O}}(E)$
we have
$\lambda \in \textrm{End}_{H_\mathcal{O}}(E)$
we have
as one can see using the various functorial properties of fibered products. In what follows, we will often omit the subscript
![]() $\mathcal{E}$
when dealing with endomorphism of
$\mathcal{E}$
when dealing with endomorphism of
![]() $\mathcal{E}$
induced by elements in
$\mathcal{E}$
induced by elements in
![]() $\textrm{End}_{H_\mathcal{O}}(E)$
. This allows us to ease a bit the notation, since usually elements of
$\textrm{End}_{H_\mathcal{O}}(E)$
. This allows us to ease a bit the notation, since usually elements of
![]() $\textrm{End}_{H_\mathcal{O}}(E)$
will already come equipped with their own subscript.
$\textrm{End}_{H_\mathcal{O}}(E)$
will already come equipped with their own subscript.
We now fix a normalised isomorphism
following [
Reference Silverman42
, II, Proposition 1.1]. Let
![]() $\alpha\;:\!=\; ({\Delta+\sqrt{\Delta}})/{2} \in \mathcal{O}$
and note that
$\alpha\;:\!=\; ({\Delta+\sqrt{\Delta}})/{2} \in \mathcal{O}$
and note that
![]() $[\alpha]_E \in \textrm{End}_{H_\mathcal{O}}(E)$
because, by [
Reference Shimura41
, Chapter II, Proposition 30], all the endomorphisms of E are defined over
$[\alpha]_E \in \textrm{End}_{H_\mathcal{O}}(E)$
because, by [
Reference Shimura41
, Chapter II, Proposition 30], all the endomorphisms of E are defined over
![]() $H_\mathcal{O}$
. Since
$H_\mathcal{O}$
. Since
![]() $\alpha^2+|\Delta| \alpha+ ({\Delta^2 + |\Delta|})/{4}=0$
, also
$\alpha^2+|\Delta| \alpha+ ({\Delta^2 + |\Delta|})/{4}=0$
, also
![]() $[\alpha]_E$
satisfies the same relation. One also has
$[\alpha]_E$
satisfies the same relation. One also has
where the first equality follows from [
Reference Silverman42
, II, Theorem 2.2 (a)] and in the second equality we are using the fact that E is defined over
![]() $\mathbb{Q}(\,j)$
and
$\mathbb{Q}(\,j)$
and
![]() $\sigma$
is non-trivial.
$\sigma$
is non-trivial.
Let now
![]() $\psi\;:\!=\;\left( [\alpha]_E \text{ mod } \mathcal{P} \right) \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. For
$\psi\;:\!=\;\left( [\alpha]_E \text{ mod } \mathcal{P} \right) \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
. For
![]() $\beta \in \mathcal{O}$
, the association
$\beta \in \mathcal{O}$
, the association
![]() $[\beta]_E \mapsto [\overline{\beta}]_E$
defines a standard involution on
$[\beta]_E \mapsto [\overline{\beta}]_E$
defines a standard involution on
![]() $\textrm{End}_{H_\mathcal{O}}(E)$
, in the sense of [
Reference Voight44
, Definition 3.2.4]. Since reduction mod
$\textrm{End}_{H_\mathcal{O}}(E)$
, in the sense of [
Reference Voight44
, Definition 3.2.4]. Since reduction mod
![]() $\mathcal{P}$
defines an embedding of
$\mathcal{P}$
defines an embedding of
![]() $\textrm{End}_{H_\mathcal{O}}(E) \hookrightarrow \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
, by the uniqueness of the standard involution on quadratic
$\textrm{End}_{H_\mathcal{O}}(E) \hookrightarrow \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
, by the uniqueness of the standard involution on quadratic
![]() $\mathbb{Q}$
-algebras (see [
Reference Voight44
, Lemma 3.4.2]) we have
$\mathbb{Q}$
-algebras (see [
Reference Voight44
, Lemma 3.4.2]) we have
![]() $[\overline{\alpha}]_E \text{ mod } \mathcal{P}= \overline{\psi}$
, where now the conjugation above
$[\overline{\alpha}]_E \text{ mod } \mathcal{P}= \overline{\psi}$
, where now the conjugation above
![]() $\psi$
denotes the usual standard involution on the quaternion algebra
$\psi$
denotes the usual standard involution on the quaternion algebra
![]() $\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
. We have
$\textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E}) \otimes_\mathbb{Z} \mathbb{Q}$
. We have
where we have applied equalities (4) and (5). This yields
and here we have used the facts that for every
![]() $\lambda \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
one has
$\lambda \in \textrm{End}_{\overline{\mathbb{F}}_p}(\widetilde{E})$
one has
![]() $\varphi \circ \lambda = \tau(\lambda) \circ \varphi$
, as can be checked using local coordinates for
$\varphi \circ \lambda = \tau(\lambda) \circ \varphi$
, as can be checked using local coordinates for
![]() $\widetilde{E}$
, and that
$\widetilde{E}$
, and that
![]() $\tau(\tau(\psi))=\psi$
because
$\tau(\tau(\psi))=\psi$
because
![]() $\psi$
is defined over a quadratic extension of
$\psi$
is defined over a quadratic extension of
![]() $\mathbb{F}_p$
. The proof is concluded.
$\mathbb{F}_p$
. The proof is concluded.
We are now ready to begin the proof of Theorem 3·1. Let us fix the notation that will be in force during the entire argument. Given the orders
![]() $\mathcal{O}_j=\mathbb{Z} \left[ ({\Delta+\sqrt{\Delta}})/{2} \right]$
and
$\mathcal{O}_j=\mathbb{Z} \left[ ({\Delta+\sqrt{\Delta}})/{2} \right]$
and
![]() $\mathcal{O}_{j_0}=\mathbb{Z} \left[ ({\Delta_0+\sqrt{\Delta_0}})/{2} \right]$
as in the statement of Theorem 3·1, we denote by
$\mathcal{O}_{j_0}=\mathbb{Z} \left[ ({\Delta_0+\sqrt{\Delta_0}})/{2} \right]$
as in the statement of Theorem 3·1, we denote by
![]() $K_j$
and
$K_j$
and
![]() $K_{j_0}$
the corresponding imaginary quadratic fields containing them. We then set
$K_{j_0}$
the corresponding imaginary quadratic fields containing them. We then set
![]() $H_j$
and
$H_j$
and
![]() $H_{j_0}$
to be the ring class fields of
$H_{j_0}$
to be the ring class fields of
![]() $K_j$
and
$K_j$
and
![]() $K_{j_0}$
relative to the orders
$K_{j_0}$
relative to the orders
![]() $\mathcal{O}_j$
and
$\mathcal{O}_j$
and
![]() $\mathcal{O}_{j_0}$
respectively. Using this notation, the field H in the statement of Theorem 3·1 is the compositum in
$\mathcal{O}_{j_0}$
respectively. Using this notation, the field H in the statement of Theorem 3·1 is the compositum in
![]() $\overline{\mathbb{Q}}$
of
$\overline{\mathbb{Q}}$
of
![]() $H_j$
and
$H_j$
and
![]() $H_{j_0}$
.
$H_{j_0}$
.
3·1. First case:
 $\ell$
does not divide
$\ell$
does not divide
 $\Delta$
and
$\Delta$
and
 $\mathcal{O}_{j_0} \not \subseteq \mathcal{O}_j$
$\mathcal{O}_{j_0} \not \subseteq \mathcal{O}_j$
Assume that
![]() $E_0$
in the statement of the theorem is given by an integral model over the ring of integers of
$E_0$
in the statement of the theorem is given by an integral model over the ring of integers of
![]() $\mathbb{Q}(\,j_0)$
with good reduction at
$\mathbb{Q}(\,j_0)$
with good reduction at
![]() $\mu \cap \mathbb{Q}(\,j_0)$
. Let
$\mu \cap \mathbb{Q}(\,j_0)$
. Let
![]() $(E_0)_{/H}$
be the base-change to H of the elliptic curve
$(E_0)_{/H}$
be the base-change to H of the elliptic curve
![]() $(E_0)_{/\mathbb{Q}(\,j_0)}$
, and let
$(E_0)_{/\mathbb{Q}(\,j_0)}$
, and let
![]() $(E_j)_{/H}$
be an elliptic curve with
$(E_j)_{/H}$
be an elliptic curve with
![]() $j(E_j)=j$
and with good reduction at all prime ideals above
$j(E_j)=j$
and with good reduction at all prime ideals above
![]() $\ell$
. Such an elliptic curve
$\ell$
. Such an elliptic curve
![]() $E_j$
exists by [
Reference Serre and Tate40
, Theorems 8 and 9], which we can apply since
$E_j$
exists by [
Reference Serre and Tate40
, Theorems 8 and 9], which we can apply since
![]() $\ell \nmid \Delta$
by assumption. In particular,
$\ell \nmid \Delta$
by assumption. In particular,
![]() $E_j$
will have good reduction at the prime
$E_j$
will have good reduction at the prime
![]() $\mu$
. We will always identify
$\mu$
. We will always identify
![]() $\mathcal{O}_j$
and
$\mathcal{O}_j$
and
![]() $\mathcal{O}_{j_0}$
with the endomorphism rings of
$\mathcal{O}_{j_0}$
with the endomorphism rings of
![]() $E_j$
and
$E_j$
and
![]() $E_0$
respectively.
$E_0$
respectively.
Let
![]() $H_\mu$
be the completion of H at the prime
$H_\mu$
be the completion of H at the prime
![]() $\mu$
. The extension
$\mu$
. The extension
![]() $\mathbb{Q} \subseteq H$
is unramified at
$\mathbb{Q} \subseteq H$
is unramified at
![]() $\ell$
because
$\ell$
because
![]() $\ell \nmid \Delta \Delta_0$
(see [
Reference Cox11
, Chapter 9, Section A]), hence
$\ell \nmid \Delta \Delta_0$
(see [
Reference Cox11
, Chapter 9, Section A]), hence
![]() $H_\mu$
is contained in
$H_\mu$
is contained in
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
, the completion of the maximal unramified extension of
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
, the completion of the maximal unramified extension of
![]() $\mathbb{Q}_\ell$
. Denote by W the ring of integers in
$\mathbb{Q}_\ell$
. Denote by W the ring of integers in
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
and let
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
and let
![]() $\pi \in W$
be a uniformizer. By abuse of notation, we also use
$\pi \in W$
be a uniformizer. By abuse of notation, we also use
![]() $E_0, E_j$
to denote the elliptic schemes over W with generic fibers isomorphic to the base-changes of
$E_0, E_j$
to denote the elliptic schemes over W with generic fibers isomorphic to the base-changes of
![]() $E_0, E_j$
to
$E_0, E_j$
to
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
respectively. Note that, by our choices,
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
respectively. Note that, by our choices,
![]() $E_0 \text{ mod } \pi$
is defined over
$E_0 \text{ mod } \pi$
is defined over
![]() $\mathbb{F}_\ell$
.
$\mathbb{F}_\ell$
.
Lemma 3·5. In the notation above, we have
where, for every
![]() $n \in \mathbb{Z}_{\geq 1}$
, we denote by
$n \in \mathbb{Z}_{\geq 1}$
, we denote by
![]() ${Iso}_{W/\pi^n} (E_j, E_0)$
the set of isomorphisms between
${Iso}_{W/\pi^n} (E_j, E_0)$
the set of isomorphisms between
![]() $E_j \text{ mod } \pi^n$
and
$E_j \text{ mod } \pi^n$
and
![]() $E_0\ \textrm{mod}\ \pi^n$
.
$E_0\ \textrm{mod}\ \pi^n$
.
Proof. Notice first of all that the normalised valuation on
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
, i.e the valuation v satisfying
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
, i.e the valuation v satisfying
![]() $v(\pi)=1$
, extends the
$v(\pi)=1$
, extends the
![]() $\mu$
-adic valuation
$\mu$
-adic valuation
![]() $v_\mu$
on H because
$v_\mu$
on H because
![]() $v_\mu(\ell)=1$
. Since W is a complete discrete valuation ring whose quotient field has characteristic 0 and whose residue field
$v_\mu(\ell)=1$
. Since W is a complete discrete valuation ring whose quotient field has characteristic 0 and whose residue field
![]() $\overline{\mathbb{F}}_\ell$
is algebraically closed of characteristic
$\overline{\mathbb{F}}_\ell$
is algebraically closed of characteristic
![]() $\ell >0$
, we can apply [
Reference Gross and Zagier21
, Proposition 2.3] which gives
$\ell >0$
, we can apply [
Reference Gross and Zagier21
, Proposition 2.3] which gives
 \begin{equation*}v_\mu(\,j-j_0)= \frac{1}{2} \sum_{n=1}^{\infty} \# \textrm{Iso}_{W/\pi^n} (E_j, E_0).\end{equation*}
\begin{equation*}v_\mu(\,j-j_0)= \frac{1}{2} \sum_{n=1}^{\infty} \# \textrm{Iso}_{W/\pi^n} (E_j, E_0).\end{equation*}
Now, certainly
![]() $\textrm{Iso}_{W/\pi^{n+1}} (E_j, E_0) \neq \emptyset$
implies
$\textrm{Iso}_{W/\pi^{n+1}} (E_j, E_0) \neq \emptyset$
implies
![]() $\textrm{Iso}_{W/\pi^{n}} (E_j, E_0) \neq \emptyset$
for every
$\textrm{Iso}_{W/\pi^{n}} (E_j, E_0) \neq \emptyset$
for every
![]() $n \in \mathbb{N}_{>0}$
, since reductions of isomorphisms are isomorphisms. Moreover, whenever the set
$n \in \mathbb{N}_{>0}$
, since reductions of isomorphisms are isomorphisms. Moreover, whenever the set
![]() $\textrm{Iso}_{W/\pi^n} (E_j, E_0)$
is non-empty, its cardinality equals the order of the automorphism group
$\textrm{Iso}_{W/\pi^n} (E_j, E_0)$
is non-empty, its cardinality equals the order of the automorphism group
![]() $\textrm{Aut}_{W/\pi^n}(E_0)$
of
$\textrm{Aut}_{W/\pi^n}(E_0)$
of
![]() $E_0 \text{ mod } \pi^n$
. By [
Reference Conrad10
, Theorem 2.1 (2)], we always have the inclusions
$E_0 \text{ mod } \pi^n$
. By [
Reference Conrad10
, Theorem 2.1 (2)], we always have the inclusions
induced respectively by the reduction modulo
![]() $\pi^n$
and modulo
$\pi^n$
and modulo
![]() $\pi$
. This means that
$\pi$
. This means that
so, setting
![]() $M\;:\!=\;\max \{n \in \mathbb{N}_{\geq 1}\;:\;\textrm{Iso}_{W/\pi^n} (E_j, E_0) \neq \emptyset \}$
, we obtain
$M\;:\!=\;\max \{n \in \mathbb{N}_{\geq 1}\;:\;\textrm{Iso}_{W/\pi^n} (E_j, E_0) \neq \emptyset \}$
, we obtain
 \begin{equation*}v_\mu(\,j-j_0)= \frac{1}{2} \sum_{n=1}^{\infty} \# \textrm{Iso}_{W/\pi^n} (E_j, E_0)=\frac{1}{2} \sum_{n=1}^{M} \# \textrm{Aut}_{W/\pi^n}(E_0) \leq \frac{d_0}{2}\cdot M\end{equation*}
\begin{equation*}v_\mu(\,j-j_0)= \frac{1}{2} \sum_{n=1}^{\infty} \# \textrm{Iso}_{W/\pi^n} (E_j, E_0)=\frac{1}{2} \sum_{n=1}^{M} \# \textrm{Aut}_{W/\pi^n}(E_0) \leq \frac{d_0}{2}\cdot M\end{equation*}
which proves the lemma.
By Lemma 3·5, in order to estimate the valuation at
![]() $\mu$
of the difference
$\mu$
of the difference
![]() $j-j_0$
, we need to bound the biggest index n such that the reductions modulo
$j-j_0$
, we need to bound the biggest index n such that the reductions modulo
![]() $\pi^n$
of the elliptic curves
$\pi^n$
of the elliptic curves
![]() $E_j$
and
$E_j$
and
![]() $E_0$
are isomorphic. If this maximum is 0, then the two elliptic curves are not even isomorphic over
$E_0$
are isomorphic. If this maximum is 0, then the two elliptic curves are not even isomorphic over
![]() $\overline{\mathbb{F}}_\ell \cong W/\pi$
, so the prime
$\overline{\mathbb{F}}_\ell \cong W/\pi$
, so the prime
![]() $\mu$
cannot divide
$\mu$
cannot divide
![]() $j-j_0$
and there is nothing to prove. Hence, from now on we suppose that
$j-j_0$
and there is nothing to prove. Hence, from now on we suppose that
![]() $\mu$
divides
$\mu$
divides
![]() $j-j_0$
so that
$j-j_0$
so that
![]() $E_0 \text{ mod } \pi \cong E_j \text{ mod } \pi$
over
$E_0 \text{ mod } \pi \cong E_j \text{ mod } \pi$
over
![]() $\overline{\mathbb{F}}_\ell$
. Since
$\overline{\mathbb{F}}_\ell$
. Since
![]() $\ell$
does not divide the conductors of the orders
$\ell$
does not divide the conductors of the orders
![]() $\mathcal{O}_j$
and
$\mathcal{O}_j$
and
![]() $\mathcal{O}_{j_0}$
by assumption, and the two orders are different, [
Reference Lang31
, Chapter 13, Theorem 12] ensures that
$\mathcal{O}_{j_0}$
by assumption, and the two orders are different, [
Reference Lang31
, Chapter 13, Theorem 12] ensures that
![]() $\ell$
is a prime of supersingular reduction for both
$\ell$
is a prime of supersingular reduction for both
![]() $E_j$
and
$E_j$
and
![]() $E_{0}$
. In particular, the ring
$E_{0}$
. In particular, the ring
![]() $R\;:\!=\;\textrm{End}_{W/\pi}(E_0)$
is isomorphic to a maximal order in
$R\;:\!=\;\textrm{End}_{W/\pi}(E_0)$
is isomorphic to a maximal order in
![]() $\mathbb{B}_{\ell, \infty}\cong R \otimes_\mathbb{Z} \mathbb{Q}$
.
$\mathbb{B}_{\ell, \infty}\cong R \otimes_\mathbb{Z} \mathbb{Q}$
.
Suppose now that
![]() $\textrm{Iso}_{W/\pi^{n+1}}(E_j,E_0)$
is non-empty. Our goal is to find a bound on the exponent
$\textrm{Iso}_{W/\pi^{n+1}}(E_j,E_0)$
is non-empty. Our goal is to find a bound on the exponent
![]() $n+1$
. A choice of
$n+1$
. A choice of
![]() $f \in \textrm{Iso}_{W/\pi^{n+1}}(E_j,E_0)$
induces an isomorphism
$f \in \textrm{Iso}_{W/\pi^{n+1}}(E_j,E_0)$
induces an isomorphism
which, precomposed with the reduction map
![]() $\mathcal{O}_j \hookrightarrow \textrm{End}_{W/\pi^{n+1}}(E_j)$
, gives rise to an optimal embedding
$\mathcal{O}_j \hookrightarrow \textrm{End}_{W/\pi^{n+1}}(E_j)$
, gives rise to an optimal embedding
by Theorem 2·4 (b). For growing n, Theorem 2·4 (a) shows that the endomorphism ring of
![]() $E_0 \text{ mod } \pi^{n+1}$
becomes more and more “
$E_0 \text{ mod } \pi^{n+1}$
becomes more and more “
![]() $\ell$
-adically close” to the order
$\ell$
-adically close” to the order
![]() $\mathcal{O}_{j_0}$
. Intuitively, this must imply that having an embedding as in (7) should not be possible for n large enough, yielding the desired bound on
$\mathcal{O}_{j_0}$
. Intuitively, this must imply that having an embedding as in (7) should not be possible for n large enough, yielding the desired bound on
![]() $n+1$
. This intuition is correct, as we show below. The main obstacle to making this idea precise is that, as we already said, it is not easy to explicitly compute the endomorphism rings
$n+1$
. This intuition is correct, as we show below. The main obstacle to making this idea precise is that, as we already said, it is not easy to explicitly compute the endomorphism rings
![]() $\textrm{End}_{W/\pi^{n+1}}(E_0)$
for a generic elliptic curve
$\textrm{End}_{W/\pi^{n+1}}(E_0)$
for a generic elliptic curve
![]() ${E_0}_{/W}$
. To circumvent this problem, we “approximate” the rings
${E_0}_{/W}$
. To circumvent this problem, we “approximate” the rings
![]() $\textrm{End}_{W/\pi^{n+1}}(E_0)$
with smaller orders where we are able to perform the relevant computations. The hypotheses on the prime
$\textrm{End}_{W/\pi^{n+1}}(E_0)$
with smaller orders where we are able to perform the relevant computations. The hypotheses on the prime
![]() $\mu$
and on the elliptic curve
$\mu$
and on the elliptic curve
![]() $E_0$
will make this strategy successful.
$E_0$
will make this strategy successful.
Recall that
![]() $\mathcal{O}_{j_0}=\mathbb{Z} \left[ ({\Delta_0 + \sqrt{\Delta_0}})/{2} \right]$
and let
$\mathcal{O}_{j_0}=\mathbb{Z} \left[ ({\Delta_0 + \sqrt{\Delta_0}})/{2} \right]$
and let
![]() $\psi \in R$
be the image of
$\psi \in R$
be the image of
![]() $({\Delta_0 + \sqrt{\Delta_0}})/{2}$
via the reduction map modulo
$({\Delta_0 + \sqrt{\Delta_0}})/{2}$
via the reduction map modulo
![]() $\pi$
. Denote also by
$\pi$
. Denote also by
![]() $\varphi \in \textrm{End}_{W/\pi}(E_0)$
the Frobenius endomorphism
$\varphi \in \textrm{End}_{W/\pi}(E_0)$
the Frobenius endomorphism
![]() $(x,y) \mapsto (x^\ell, y^\ell)$
. By Proposition 3·3 and using the fact that
$(x,y) \mapsto (x^\ell, y^\ell)$
. By Proposition 3·3 and using the fact that
![]() $E_0 \text{ mod } \pi$
is a supersingular elliptic curve defined over
$E_0 \text{ mod } \pi$
is a supersingular elliptic curve defined over
![]() $\mathbb{F}_\ell$
, we have
$\mathbb{F}_\ell$
, we have
where
![]() $\overline{\cdot}$
denotes the standard involution on
$\overline{\cdot}$
denotes the standard involution on
![]() $\textrm{End}_{W/\pi}(E_0) \otimes_\mathbb{Z} \mathbb{Q}$
. Hence, the ring
$\textrm{End}_{W/\pi}(E_0) \otimes_\mathbb{Z} \mathbb{Q}$
. Hence, the ring
![]() $\widetilde{R}\;:\!=\;\mathbb{Z}[ \psi, \varphi] \subseteq R$
is a rank-4 order inside
$\widetilde{R}\;:\!=\;\mathbb{Z}[ \psi, \varphi] \subseteq R$
is a rank-4 order inside
![]() $\mathbb{B}_{\ell, \infty}$
with basis
$\mathbb{B}_{\ell, \infty}$
with basis
![]() $\mathcal{B}=\{1, \psi, \varphi, \psi \varphi \}$
satisfying the relations (8). Notice that the reduction map
$\mathcal{B}=\{1, \psi, \varphi, \psi \varphi \}$
satisfying the relations (8). Notice that the reduction map
![]() $\mathcal{O}_{j_0} \hookrightarrow R$
identifies
$\mathcal{O}_{j_0} \hookrightarrow R$
identifies
![]() $\mathcal{O}_{j_0}$
with the subring
$\mathcal{O}_{j_0}$
with the subring
![]() $\mathbb{Z}[\psi] \subseteq \mathbb{Z}[\psi, \varphi]$
. The matrix of the bilinear pairing
$\mathbb{Z}[\psi] \subseteq \mathbb{Z}[\psi, \varphi]$
. The matrix of the bilinear pairing
![]() $\langle \alpha, \beta \rangle=\textrm{trd}(\alpha \overline{\beta})$
computed on the basis
$\langle \alpha, \beta \rangle=\textrm{trd}(\alpha \overline{\beta})$
computed on the basis
![]() $\mathcal{B}$
is given by
$\mathcal{B}$
is given by
 \begin{equation*}A=\begin{pmatrix}2\;\;\;\;\;\; & \Delta_0\;\;\;\;\;\; & 0\;\;\;\;\;\; & 0 \\\Delta_0\;\;\;\;\;\; & \frac{\Delta_0^2 + |\Delta_0|}{2}\;\;\;\;\;\; & 0\;\;\;\;\;\; & 0 \\0\;\;\;\;\;\; & 0\;\;\;\;\;\; & 2\ell\;\;\;\;\;\; & \Delta_0 \ell \\0\;\;\;\;\;\; & 0\;\;\;\;\;\; & \Delta_0 \ell \;\;\;\;\;\; & \frac{\Delta_0^2 + |\Delta_0|}{2} \ell \end{pmatrix}\end{equation*}
\begin{equation*}A=\begin{pmatrix}2\;\;\;\;\;\; & \Delta_0\;\;\;\;\;\; & 0\;\;\;\;\;\; & 0 \\\Delta_0\;\;\;\;\;\; & \frac{\Delta_0^2 + |\Delta_0|}{2}\;\;\;\;\;\; & 0\;\;\;\;\;\; & 0 \\0\;\;\;\;\;\; & 0\;\;\;\;\;\; & 2\ell\;\;\;\;\;\; & \Delta_0 \ell \\0\;\;\;\;\;\; & 0\;\;\;\;\;\; & \Delta_0 \ell \;\;\;\;\;\; & \frac{\Delta_0^2 + |\Delta_0|}{2} \ell \end{pmatrix}\end{equation*}
so the discriminant of the order
![]() $\widetilde{R}$
equals
$\widetilde{R}$
equals
![]() $\det A=\Delta_0^2 \ell^2$
(see [
Reference Voight44
, Definition 15.2.2 and Exercise 13 in Chapter 15]). Hence, by [
Reference Voight44
, Lemma 15.2.15, Lemma 15.4.7 and Theorem 15.5.5]
$\det A=\Delta_0^2 \ell^2$
(see [
Reference Voight44
, Definition 15.2.2 and Exercise 13 in Chapter 15]). Hence, by [
Reference Voight44
, Lemma 15.2.15, Lemma 15.4.7 and Theorem 15.5.5]
![]() $\widetilde{R}$
has index
$\widetilde{R}$
has index
![]() $|\Delta_0|$
inside any maximal order containing it, so in particular
$|\Delta_0|$
inside any maximal order containing it, so in particular
![]() $|R\;:\;\widetilde{R}|=|\Delta_0|$
. Now, since we are in the hypotheses of Theorem 2·4 (a), we have
$|R\;:\;\widetilde{R}|=|\Delta_0|$
. Now, since we are in the hypotheses of Theorem 2·4 (a), we have
and we shall show that the index of the latter inclusion is also bounded by
![]() $|\Delta_0|$
.
$|\Delta_0|$
.
Lemma 3·6. For all
![]() $n\in \mathbb{N}$
the index
$n\in \mathbb{N}$
the index
![]() $\left| (\mathbb{Z}[\psi] + \ell^n R) \;:\;(\mathbb{Z}[\psi] + \ell^n \widetilde{R}) \right|$
divides
$\left| (\mathbb{Z}[\psi] + \ell^n R) \;:\;(\mathbb{Z}[\psi] + \ell^n \widetilde{R}) \right|$
divides
![]() $|\Delta_0|$
.
$|\Delta_0|$
.
Proof. Since
![]() $\widetilde{R} \subseteq R$
, we have
$\widetilde{R} \subseteq R$
, we have
![]() $\mathbb{Z}[\psi] + \ell^n R = \mathbb{Z}[\psi] + \ell^n R + \ell^n \widetilde{R}$
. Hence
$\mathbb{Z}[\psi] + \ell^n R = \mathbb{Z}[\psi] + \ell^n R + \ell^n \widetilde{R}$
. Hence
 \begin{equation*} \frac{\mathbb{Z}[\psi] + \ell^n R}{\mathbb{Z}[\psi] + \ell^n\vphantom{\hat{\widetilde{R}}} \widetilde{R}} = \frac{\mathbb{Z}[\psi] + \ell^n R + \ell^n \widetilde{R}}{\mathbb{Z}[\psi] + \ell^n \vphantom{\hat{\widetilde{R}}}\widetilde{R}} \cong \frac{\ell^n R}{(\mathbb{Z}[\psi] + \ell^n \vphantom{\hat{\widetilde{R}}}\widetilde{R}) \cap \ell^n R} \end{equation*}
\begin{equation*} \frac{\mathbb{Z}[\psi] + \ell^n R}{\mathbb{Z}[\psi] + \ell^n\vphantom{\hat{\widetilde{R}}} \widetilde{R}} = \frac{\mathbb{Z}[\psi] + \ell^n R + \ell^n \widetilde{R}}{\mathbb{Z}[\psi] + \ell^n \vphantom{\hat{\widetilde{R}}}\widetilde{R}} \cong \frac{\ell^n R}{(\mathbb{Z}[\psi] + \ell^n \vphantom{\hat{\widetilde{R}}}\widetilde{R}) \cap \ell^n R} \end{equation*}
as abelian groups. Now, the containment
![]() $\ell^n \widetilde{R} \subseteq (\mathbb{Z}[\psi] + \ell^n \widetilde{R}) \cap \ell^n R$
gives an epimorphism
$\ell^n \widetilde{R} \subseteq (\mathbb{Z}[\psi] + \ell^n \widetilde{R}) \cap \ell^n R$
gives an epimorphism
and, since R is non-torsion, we have
![]() $\ell^n R / \ell^n \widetilde{R} \cong R/\widetilde{R}$
. Since the latter has cardinality
$\ell^n R / \ell^n \widetilde{R} \cong R/\widetilde{R}$
. Since the latter has cardinality
![]() $|\Delta_0|$
, the lemma is proved.
$|\Delta_0|$
, the lemma is proved.
Corollary 3·7. The embedding (7) induces an injection
 \begin{equation} \mathcal{O}_{j,|\Delta_0|}\;:\!=\;\mathbb{Z} \left[ \frac{\Delta_0^2 \Delta+\sqrt{\Delta_0^2 \Delta}}{2} \right] \hookrightarrow \mathbb{Z}[\psi] + \ell^n \widetilde{R}.\end{equation}
\begin{equation} \mathcal{O}_{j,|\Delta_0|}\;:\!=\;\mathbb{Z} \left[ \frac{\Delta_0^2 \Delta+\sqrt{\Delta_0^2 \Delta}}{2} \right] \hookrightarrow \mathbb{Z}[\psi] + \ell^n \widetilde{R}.\end{equation}
Proof. By Lemma 3·6, for every
![]() $x \in \mathbb{Z}[\psi] + \ell^n R$
we have
$x \in \mathbb{Z}[\psi] + \ell^n R$
we have
![]() $|\Delta_0| x \in \mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. Since
$|\Delta_0| x \in \mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. Since
![]() $\mathcal{O}_{j,|\Delta_0|}=\mathbb{Z}+|\Delta_0| \mathcal{O}_j$
, the corollary follows.
$\mathcal{O}_{j,|\Delta_0|}=\mathbb{Z}+|\Delta_0| \mathcal{O}_j$
, the corollary follows.
Combining Corollary 3·7 with Lemma 2·1, we see that
![]() $|\textrm{disc}(\mathcal{O}_{j,|\Delta_0|})|=\Delta_0^2 |\Delta|$
must be represented by the Gross lattice
$|\textrm{disc}(\mathcal{O}_{j,|\Delta_0|})|=\Delta_0^2 |\Delta|$
must be represented by the Gross lattice
![]() $\Lambda_{\ell,n}$
of the order
$\Lambda_{\ell,n}$
of the order
![]() $\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. Note that this representation is not necessarily primitive, because the embedding (9) is not necessarily optimal. A computation shows that
$\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. Note that this representation is not necessarily primitive, because the embedding (9) is not necessarily optimal. A computation shows that
i.e.
![]() $\mathcal{B}'=\{|\Delta_0| + 2\psi, 2\ell^n \varphi, 2 \ell^n \psi \varphi \}$
is a
$\mathcal{B}'=\{|\Delta_0| + 2\psi, 2\ell^n \varphi, 2 \ell^n \psi \varphi \}$
is a
![]() $\mathbb{Z}$
-basis for the Gross lattice of
$\mathbb{Z}$
-basis for the Gross lattice of
![]() $\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. The reduced norm restricted to the lattice
$\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. The reduced norm restricted to the lattice
![]() $\Lambda_{\ell,n}$
induces the ternary quadratic form
$\Lambda_{\ell,n}$
induces the ternary quadratic form
written with respect to the basis
![]() $\mathcal{B}'$
.
$\mathcal{B}'$
.
After setting
we get the diagonal quadratic form
Suppose now that
![]() $Q_{\ell,n}(X,Y,Z)=\Delta_0^2|\Delta|$
has an integral solution
$Q_{\ell,n}(X,Y,Z)=\Delta_0^2|\Delta|$
has an integral solution
![]() $(x,y,z) \in \mathbb{Z}^3$
corresponding to the embedding (9). We first claim that at least one among y and z is non-zero. This follows from our assumptions on
$(x,y,z) \in \mathbb{Z}^3$
corresponding to the embedding (9). We first claim that at least one among y and z is non-zero. This follows from our assumptions on
![]() $\mathcal{O}_j$
and from the following proposition.
$\mathcal{O}_j$
and from the following proposition.
Proposition 3·8. If
![]() $y=z=0$
then
$y=z=0$
then
![]() $\mathcal{O}_{j_0} \subseteq \mathcal{O}_j$
.
$\mathcal{O}_{j_0} \subseteq \mathcal{O}_j$
.
Proof. Let
![]() $x \in \mathbb{Z}_{>0}$
be such that
$x \in \mathbb{Z}_{>0}$
be such that
![]() $Q_{\ell,n}(x,0,0)=\Delta_0^2|\Delta|$
. By Remark 2·3, this equality corresponds to the embedding
$Q_{\ell,n}(x,0,0)=\Delta_0^2|\Delta|$
. By Remark 2·3, this equality corresponds to the embedding

of the order
![]() $\mathcal{O}_{j,|\Delta_0|}\subseteq K\;:\!=\;\mathbb{Q}(\sqrt{\Delta})$
into
$\mathcal{O}_{j,|\Delta_0|}\subseteq K\;:\!=\;\mathbb{Q}(\sqrt{\Delta})$
into
![]() $\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. The injection (11) is not optimal if
$\mathbb{Z}[\psi] + \ell^n \widetilde{R}$
. The injection (11) is not optimal if
![]() $x \neq \pm 1$
. Indeed, using the proof of Lemma 2·1 we get the optimal embedding
$x \neq \pm 1$
. Indeed, using the proof of Lemma 2·1 we get the optimal embedding

determined by the equality
![]() $Q_{\ell,n}(1,0,0)=(\Delta_0^2|\Delta|)/x^2$
. Since
$Q_{\ell,n}(1,0,0)=(\Delta_0^2|\Delta|)/x^2$
. Since
![]() $Q_{\ell,n}(1,0,0)=|\Delta_0|$
, we see that the above injection is actually the same as
$Q_{\ell,n}(1,0,0)=|\Delta_0|$
, we see that the above injection is actually the same as
Recall that we also have embedding (7), which can be rewritten as

We remind the reader that the above injection (13) is again optimal, and that (11) is originally induced by (13). It is then clear that the injections (11), (12) and (13) are all compatible between each other, meaning that, after tensoring with
![]() $\mathbb{Q}$
, one gets the same map
$\mathbb{Q}$
, one gets the same map
![]() $\iota\;:\;K \hookrightarrow \mathbb{B}_{\ell, \infty}$
. In particular,
$\iota\;:\;K \hookrightarrow \mathbb{B}_{\ell, \infty}$
. In particular,
![]() $\mathcal{O}_j$
and
$\mathcal{O}_j$
and
![]() $\mathcal{O}_{j_0}$
are contained inside the same imaginary quadratic field
$\mathcal{O}_{j_0}$
are contained inside the same imaginary quadratic field
![]() $K=\mathbb{Q}(\sqrt{\Delta})=\mathbb{Q}(\sqrt{\Delta_0})$
.
$K=\mathbb{Q}(\sqrt{\Delta})=\mathbb{Q}(\sqrt{\Delta_0})$
.
Consider now the order
![]() $\mathcal{O}\;:\!=\;\mathcal{O}_{j} + \mathcal{O}_{j_0} \subseteq K$
. We have that
$\mathcal{O}\;:\!=\;\mathcal{O}_{j} + \mathcal{O}_{j_0} \subseteq K$
. We have that
![]() $\iota(\mathcal{O}) \subseteq \mathbb{Z}[\psi] + \ell^n R$
, and from the optimality of (13) it follows that
$\iota(\mathcal{O}) \subseteq \mathbb{Z}[\psi] + \ell^n R$
, and from the optimality of (13) it follows that
![]() $\mathcal{O}=\mathcal{O}_j$
. Hence
$\mathcal{O}=\mathcal{O}_j$
. Hence
![]() $\mathcal{O}_{j_0} \subseteq \mathcal{O}_j$
, and this concludes the proof.
$\mathcal{O}_{j_0} \subseteq \mathcal{O}_j$
, and this concludes the proof.
Since at least one among y and z is non-zero, we also have that at least one among
![]() $\widetilde{y}\;:\!=\;y+ (\Delta_0 z)/2$
and
$\widetilde{y}\;:\!=\;y+ (\Delta_0 z)/2$
and
![]() $\widetilde{z}=z$
is non-zero. Note that
$\widetilde{z}=z$
is non-zero. Note that
![]() $\widetilde{y} \in \frac{1}{2}\mathbb{Z}$
and
$\widetilde{y} \in \frac{1}{2}\mathbb{Z}$
and
![]() $\widetilde{z} \in \mathbb{Z}$
. Then we have
$\widetilde{z} \in \mathbb{Z}$
. Then we have
which implies
Combining now (14) with Lemma 3·5 concludes the first case of the proof of Theorem 3·1.
3·2. Second case:
 $\ell$
divides
$\ell$
divides
 $\Delta$
$\Delta$
For this part of the proof, we are going to heavily rely on [
Reference Lauter and Viray33
], of which we have kept the notation. We again assume that the elliptic curve
![]() $E_0$
is given by an integral model over the ring of integers of
$E_0$
is given by an integral model over the ring of integers of
![]() $\mathbb{Q}(\,j_0)$
that has good reduction at
$\mathbb{Q}(\,j_0)$
that has good reduction at
![]() $\mu \cap \mathbb{Q}(\,j_0)$
.
$\mu \cap \mathbb{Q}(\,j_0)$
.
Suppose initially that
![]() $\ell$
divides the conductor of the order
$\ell$
divides the conductor of the order
![]() $\mathcal{O}_j$
. Let
$\mathcal{O}_j$
. Let
![]() $H_{j} \subseteq F$
be a minimal extension of the ring class field
$H_{j} \subseteq F$
be a minimal extension of the ring class field
![]() $H_{j}$
such that there exists an elliptic curve
$H_{j}$
such that there exists an elliptic curve
![]() $(E_j)_{/F}$
with
$(E_j)_{/F}$
with
![]() $j(E_j)=j$
and having good reduction at all primes of F lying above
$j(E_j)=j$
and having good reduction at all primes of F lying above
![]() $\ell$
. Fix such an elliptic curve
$\ell$
. Fix such an elliptic curve
![]() $E_j$
and base-change it to the compositum
$E_j$
and base-change it to the compositum
![]() $L=F\cdot H_{j_0}$
. Consider also a prime
$L=F\cdot H_{j_0}$
. Consider also a prime
![]() $\mu_L \subseteq L$
lying above
$\mu_L \subseteq L$
lying above
![]() $\mu \subseteq H$
and denote by A the ring of integers in the completion of the maximal unramified extension of
$\mu \subseteq H$
and denote by A the ring of integers in the completion of the maximal unramified extension of
![]() $L_{\mu_L}$
, with maximal ideal
$L_{\mu_L}$
, with maximal ideal
![]() $\mu_L A \subseteq A$
. By abuse of notation, we denote by
$\mu_L A \subseteq A$
. By abuse of notation, we denote by
![]() $E_0, E_j$
the elliptic schemes over A with generic fibers isomorphic to the base-changes of
$E_0, E_j$
the elliptic schemes over A with generic fibers isomorphic to the base-changes of
![]() $E_0, E_j$
to the completion of the maximal unramified extension of
$E_0, E_j$
to the completion of the maximal unramified extension of
![]() $L_{\mu_L}$
. The elliptic schemes
$L_{\mu_L}$
. The elliptic schemes
![]() ${E_j}$
and
${E_j}$
and
![]() $E_0$
have good reduction over A and, since A is a complete discrete valuation ring of characteristic 0 with algebraically closed residue field of characteristic
$E_0$
have good reduction over A and, since A is a complete discrete valuation ring of characteristic 0 with algebraically closed residue field of characteristic
![]() $\ell>0$
, we can use the same proof of Lemma 3·5 to see that
$\ell>0$
, we can use the same proof of Lemma 3·5 to see that
Since
![]() $\ell \nmid \Delta_0$
, we can now apply [33, Proposition 4.1] with
$\ell \nmid \Delta_0$
, we can now apply [33, Proposition 4.1] with
![]() $E=E_0$
,
$E=E_0$
,
![]() $\mathcal{O}_{d_1}=\mathcal{O}_{j_0}$
and
$\mathcal{O}_{d_1}=\mathcal{O}_{j_0}$
and
![]() $\mathcal{O}_{d_2}= \mathcal{O}_j$
. This proposition, used together with the fact that
$\mathcal{O}_{d_2}= \mathcal{O}_j$
. This proposition, used together with the fact that
![]() $\ell$
divides the conductor of
$\ell$
divides the conductor of
![]() $\mathcal{O}_j$
, implies that
$\mathcal{O}_j$
, implies that
![]() $\textrm{Iso}_{A/\mu_L^n A} (E_j, E_0)=\emptyset$
if
$\textrm{Iso}_{A/\mu_L^n A} (E_j, E_0)=\emptyset$
if
![]() $n>1$
. Combined with (15), this gives
$n>1$
. Combined with (15), this gives
as desired. This yields the theorem in the case that
![]() $\ell$
divides the conductor of
$\ell$
divides the conductor of
![]() $\mathcal{O}_j$
.
$\mathcal{O}_j$
.
Assume now that
![]() $\ell$
divides
$\ell$
divides
![]() $\Delta$
but does not divide the conductor of the order
$\Delta$
but does not divide the conductor of the order
![]() $\mathcal{O}_j$
. Then, if again
$\mathcal{O}_j$
. Then, if again
![]() $E_j$
is an elliptic curve with
$E_j$
is an elliptic curve with
![]() $j(E_j)=j$
, we can choose
$j(E_j)=j$
, we can choose
![]() $F=H_j$
as a field where
$F=H_j$
as a field where
![]() $E_j$
has a model with good reduction at all primes dividing
$E_j$
has a model with good reduction at all primes dividing
![]() $\ell$
. This follows from [
Reference Serre and Tate40
, Theorem 9]. If we complete H at
$\ell$
. This follows from [
Reference Serre and Tate40
, Theorem 9]. If we complete H at
![]() $\mu$
, and we take A to be the ring of integers in the completion of the maximal unramified extension of
$\mu$
, and we take A to be the ring of integers in the completion of the maximal unramified extension of
![]() $H_{\mu}$
and W to be the ring of integers in the completion of the maximal unramified extension of
$H_{\mu}$
and W to be the ring of integers in the completion of the maximal unramified extension of
![]() $\mathbb{Q}_\ell$
, then
$\mathbb{Q}_\ell$
, then
![]() $\text{Frac}(W) \subseteq \textrm{Frac}(A)$
is a ramified degree 2 field extension because the ramification index
$\text{Frac}(W) \subseteq \textrm{Frac}(A)$
is a ramified degree 2 field extension because the ramification index
![]() $e(\mu/\ell) = 2$
by our assumptions. Again by [
Reference Lauter and Viray33
, Proposition 4.1], since we are assuming that
$e(\mu/\ell) = 2$
by our assumptions. Again by [
Reference Lauter and Viray33
, Proposition 4.1], since we are assuming that
![]() $\ell$
does not divide the conductor of
$\ell$
does not divide the conductor of
![]() $\mathcal{O}_j$
, for every
$\mathcal{O}_j$
, for every
![]() $n\in \mathbb{N}_{>0}$
we have
$n\in \mathbb{N}_{>0}$
we have
where
![]() $C=C(\,j) \leq 6$
is a positive constant depending on j and
$C=C(\,j) \leq 6$
is a positive constant depending on j and
![]() $S_n^{\text{Lie}}(E_0/A)$
is the set of all endomorphisms
$S_n^{\text{Lie}}(E_0/A)$
is the set of all endomorphisms
![]() $\varphi \in \textrm{End}_{A/\mu^n A}(E_0)$
satisfying the following three conditions (cfr. [
Reference Lauter and Viray33
, pag. 9218]):
$\varphi \in \textrm{End}_{A/\mu^n A}(E_0)$
satisfying the following three conditions (cfr. [
Reference Lauter and Viray33
, pag. 9218]):
-
(1)
 $\varphi^2-\Delta \varphi+\frac{1}{4}(\Delta^2-\Delta)=0$
;
$\varphi^2-\Delta \varphi+\frac{1}{4}(\Delta^2-\Delta)=0$
; -
(2) the inclusion
 $\mathbb{Z}[\varphi] \hookrightarrow \textrm{End}_{A/\mu A}(E_0)$
is optimal at all primes
$\mathbb{Z}[\varphi] \hookrightarrow \textrm{End}_{A/\mu A}(E_0)$
is optimal at all primes
 $p\neq \ell$
. We recall that an embedding of
$p\neq \ell$
. We recall that an embedding of
 $\mathbb{Z}$
-modules
$\mathbb{Z}$
-modules
 $\mathcal{O} \hookrightarrow R$
is optimal at a prime p if the equality holds (note that the corresponding [ Reference Lauter and Viray33 , Definition 2.1] contains a misprint);
$\mathcal{O} \hookrightarrow R$
is optimal at a prime p if the equality holds (note that the corresponding [ Reference Lauter and Viray33 , Definition 2.1] contains a misprint); \begin{equation*} (\iota (\mathcal{O}) \otimes_\mathbb{Z} \mathbb{Q}_p) \cap (R \otimes_\mathbb{Z} \mathbb{Z}_p) = \iota (\mathcal{O}) \otimes_\mathbb{Z} \mathbb{Z}_p \end{equation*}
\begin{equation*} (\iota (\mathcal{O}) \otimes_\mathbb{Z} \mathbb{Q}_p) \cap (R \otimes_\mathbb{Z} \mathbb{Z}_p) = \iota (\mathcal{O}) \otimes_\mathbb{Z} \mathbb{Z}_p \end{equation*}
-
(3) as endomorphism of
 $\text{Lie}(E_0 \text{ mod } \mu^n A)$
we have
$\text{Lie}(E_0 \text{ mod } \mu^n A)$
we have
 $\varphi \equiv \delta \text{ mod } \mu^n$
, where
$\varphi \equiv \delta \text{ mod } \mu^n$
, where
 $\delta \in A$
is a fixed root of the polynomial
$\delta \in A$
is a fixed root of the polynomial
 $x^2-\Delta x+\frac{1}{4}(\Delta^2-\Delta)$
.
$x^2-\Delta x+\frac{1}{4}(\Delta^2-\Delta)$
.
The set
![]() $S_n^{\text{Lie}}(E_0/A)$
can be partitioned as
$S_n^{\text{Lie}}(E_0/A)$
can be partitioned as
where
![]() $S_{n,m}^{\text{Lie}}(E_0/A)$
consists of all the endomorphisms
$S_{n,m}^{\text{Lie}}(E_0/A)$
consists of all the endomorphisms
![]() $\varphi \in S_n^{\text{Lie}}(E_0/A)$
such that
$\varphi \in S_n^{\text{Lie}}(E_0/A)$
such that
We first claim that, under our assumptions, the sets
![]() $S_{n,0}^{\text{Lie}}(E_0/A)$
are empty for all
$S_{n,0}^{\text{Lie}}(E_0/A)$
are empty for all
![]() $n \in \mathbb{N}_{>0}$
. Indeed, let
$n \in \mathbb{N}_{>0}$
. Indeed, let
![]() $\varphi \in S_{n,0}^{\text{Lie}}(E_0/A)$
so that
$\varphi \in S_{n,0}^{\text{Lie}}(E_0/A)$
so that
![]() $\textrm{disc} \left(\mathcal{O}_{j_0}[\varphi]\right)=0$
. Since a division quaternion algebra does not contain suborders of rank 3, this in particular implies that
$\textrm{disc} \left(\mathcal{O}_{j_0}[\varphi]\right)=0$
. Since a division quaternion algebra does not contain suborders of rank 3, this in particular implies that
![]() $\mathcal{O}_{j_0}[\varphi]$
has rank 2 as
$\mathcal{O}_{j_0}[\varphi]$
has rank 2 as
![]() $\mathbb{Z}$
-module, so that
$\mathbb{Z}$
-module, so that
![]() $\mathbb{Z}[\varphi]$
is isomorphic to an order in
$\mathbb{Z}[\varphi]$
is isomorphic to an order in
![]() $K_{j_0}$
, not necessarily contained in
$K_{j_0}$
, not necessarily contained in
![]() $\mathcal{O}_{j_0}$
. By the definition of
$\mathcal{O}_{j_0}$
. By the definition of
![]() $S_n^{\text{Lie}}(E_0/A)$
, the order
$S_n^{\text{Lie}}(E_0/A)$
, the order
![]() $\mathbb{Z}[\varphi]$
has discriminant
$\mathbb{Z}[\varphi]$
has discriminant
![]() $\Delta$
, and we deduce that
$\Delta$
, and we deduce that
![]() $\mathbb{Z}[\varphi] \cong \mathcal{O}_j \subseteq K_{j_0}$
. However, by assumption
$\mathbb{Z}[\varphi] \cong \mathcal{O}_j \subseteq K_{j_0}$
. However, by assumption
![]() $\ell$
divides
$\ell$
divides
![]() $\Delta$
but does not divide the conductor of
$\Delta$
but does not divide the conductor of
![]() $\mathcal{O}_j$
. Hence
$\mathcal{O}_j$
. Hence
![]() $\ell$
must divide the discriminant of
$\ell$
must divide the discriminant of
![]() $K_{j_0}$
which in turn implies
$K_{j_0}$
which in turn implies
![]() $\ell \mid \Delta_0$
, contradicting our hypotheses. This proves the claim.
$\ell \mid \Delta_0$
, contradicting our hypotheses. This proves the claim.
On the other hand, in the second paragraph of [
Reference Lauter and Viray33
, pag. 9247] it is proved that, when
![]() $\ell$
divides
$\ell$
divides
![]() $\Delta$
but does not divide the conductor of
$\Delta$
but does not divide the conductor of
![]() $\mathcal{O}_{j}$
, and
$\mathcal{O}_{j}$
, and
![]() $\ell \nmid \Delta_0$
, then for every
$\ell \nmid \Delta_0$
, then for every
![]() $m>0$
and
$m>0$
and
![]() $n>1$
, the set
$n>1$
, the set
![]() $S_{n,m}^{\text{Lie}}(E/A)$
is empty. We deduce that
$S_{n,m}^{\text{Lie}}(E/A)$
is empty. We deduce that
![]() $S_n^{\text{Lie}}(E/A)=\emptyset$
for all
$S_n^{\text{Lie}}(E/A)=\emptyset$
for all
![]() $n>1$
, and combining this with inequality (16) we obtain
$n>1$
, and combining this with inequality (16) we obtain
![]() $\textrm{Iso}_{A/\mu^n A}(E_0,E_j)=\emptyset$
for all
$\textrm{Iso}_{A/\mu^n A}(E_0,E_j)=\emptyset$
for all
![]() $n>1$
. Finally, using [
Reference Gross and Zagier21
, Proposition 2.3] we obtain
$n>1$
. Finally, using [
Reference Gross and Zagier21
, Proposition 2.3] we obtain
and this concludes the proof of Theorem 3·1.
4. Proof of Theorem 1·1
The main scope of this section is to present the proof of Theorem 1·1. At the end of this proof, we will point at the precise estimates that can be used to prove Theorem 1·2 and similar results, and we will provide a proof of the fact (stated in the introduction) that the extension
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
can be Galois for at most a finite number of singular moduli
$\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
can be Galois for at most a finite number of singular moduli
![]() $j_0$
. Before starting, let us recall some notation already used in the introduction. For a number field K we denote by
$j_0$
. Before starting, let us recall some notation already used in the introduction. For a number field K we denote by
![]() $\mathcal{M}_K$
the set of all places of K and by
$\mathcal{M}_K$
the set of all places of K and by
![]() $\mathcal{M}^{\infty}_K \subseteq \mathcal{M}_K$
the subset of all the infinite ones. For every
$\mathcal{M}^{\infty}_K \subseteq \mathcal{M}_K$
the subset of all the infinite ones. For every
![]() $w \in \mathcal{M}_K \setminus \mathcal{M}^{\infty}_K$
we indicate by
$w \in \mathcal{M}_K \setminus \mathcal{M}^{\infty}_K$
we indicate by
![]() $|\!\cdot\!|_w$
the absolute value in the class of w normalised as follows: if
$|\!\cdot\!|_w$
the absolute value in the class of w normalised as follows: if
![]() $\mathfrak{p}_w$
denotes the prime ideal corresponding to w and
$\mathfrak{p}_w$
denotes the prime ideal corresponding to w and
![]() $p_w$
is the rational prime lying below
$p_w$
is the rational prime lying below
![]() $\mathfrak{p}_w$
, then
$\mathfrak{p}_w$
, then
for all
![]() $x \in K\setminus \{ 0 \}$
, where
$x \in K\setminus \{ 0 \}$
, where
![]() $v_{\mathfrak{p}_w}(x)$
is the exponent with which the prime
$v_{\mathfrak{p}_w}(x)$
is the exponent with which the prime
![]() $\mathfrak{p}_w$
appears in the factorisation of x, and
$\mathfrak{p}_w$
appears in the factorisation of x, and
![]() $e_w$
is the ramification index of
$e_w$
is the ramification index of
![]() $\mathfrak{p}_w$
over
$\mathfrak{p}_w$
over
![]() $p_w$
.
$p_w$
.
Proof of Theorem
1·1. Let
![]() $(\,j_0,S)$
be a nice
$(\,j_0,S)$
be a nice
![]() $\Delta_0$
-pair with
$\Delta_0$
-pair with
![]() $\Delta_0 < -4$
and
$\Delta_0 < -4$
and
![]() $\#S \leq 2$
. We can assume without loss of generality that
$\#S \leq 2$
. We can assume without loss of generality that
![]() $\#S=2$
, since if S contains fewer than two elements the statement of the theorem becomes weaker. Hence we can write
$\#S=2$
, since if S contains fewer than two elements the statement of the theorem becomes weaker. Hence we can write
![]() $S=\{\ell_1, \ell_2 \}$
with
$S=\{\ell_1, \ell_2 \}$
with
![]() $\ell_1, \ell_2 \in \mathbb{N}$
two distinct primes.
$\ell_1, \ell_2 \in \mathbb{N}$
two distinct primes.
In order to prove Theorem 1·1, we follow the strategy used in [
Reference Bilu, Habegger and Kuhne2
] to prove the emptiness of the set of singular units. Let j be a singular modulus of discriminant
![]() $\Delta$
such that
$\Delta$
such that
![]() $j-j_0$
is an S-unit, and let
$j-j_0$
is an S-unit, and let
![]() $h(\!\cdot\!)$
denote the logarithmic Weil height on algebraic numbers. By the usual properties of height functions [
Reference Bombieri and Gubler4
, Lemma 1.5.18], we have
$h(\!\cdot\!)$
denote the logarithmic Weil height on algebraic numbers. By the usual properties of height functions [
Reference Bombieri and Gubler4
, Lemma 1.5.18], we have
 \begin{equation} h(\,j-j_0)=h((\,j-j_0)^{-1})=\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}_{\mathbb{Q}(\,j-j_0)}} d_v \log^+ |(\,j-j_0)^{-1}|_v = A + N,\end{equation}
\begin{equation} h(\,j-j_0)=h((\,j-j_0)^{-1})=\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}_{\mathbb{Q}(\,j-j_0)}} d_v \log^+ |(\,j-j_0)^{-1}|_v = A + N,\end{equation}
where
![]() $d_v\;:\!=\;[\mathbb{Q}(\,j-j_0)_v\;:\;\mathbb{Q}_v]$
is the local degree of the field
$d_v\;:\!=\;[\mathbb{Q}(\,j-j_0)_v\;:\;\mathbb{Q}_v]$
is the local degree of the field
![]() $\mathbb{Q}(\,j-j_0)$
at the place v and
$\mathbb{Q}(\,j-j_0)$
at the place v and
 \begin{align*} &A\;:\!=\;\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}^{\infty}_{\mathbb{Q}(\,j-j_0)}} d_v \log^+ |(\,j-j_0)^{-1}|_v, \\ &N\;:\!=\;\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \mid \ell_1 \ell_2 } d_v \log |(\,j-j_0)^{-1}|_v\end{align*}
\begin{align*} &A\;:\!=\;\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}^{\infty}_{\mathbb{Q}(\,j-j_0)}} d_v \log^+ |(\,j-j_0)^{-1}|_v, \\ &N\;:\!=\;\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \mid \ell_1 \ell_2 } d_v \log |(\,j-j_0)^{-1}|_v\end{align*}
are, respectively, the archimedean and non-archimedean components of the height. Notice that the expression for N follows from our assumption on
![]() $j-j_0$
being an S-unit and from the fact that
$j-j_0$
being an S-unit and from the fact that
![]() $j-j_0$
is an algebraic integer. We study these two components separately, starting with the archimedean one. From now on, we assume
$j-j_0$
is an algebraic integer. We study these two components separately, starting with the archimedean one. From now on, we assume
![]() $|\Delta| > \max \{|\Delta_0|, 10^{15} \}$
.
$|\Delta| > \max \{|\Delta_0|, 10^{15} \}$
.
Denote by
![]() $C_0$
and
$C_0$
and
![]() $C_\Delta$
the class numbers of the orders associated to
$C_\Delta$
the class numbers of the orders associated to
![]() $j_0$
and to j respectively. Then by [
Reference Cai6
, Corollary 4.2 (1)] we have
$j_0$
and to j respectively. Then by [
Reference Cai6
, Corollary 4.2 (1)] we have
where
![]() $F\;:\!=\; \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
and
$F\;:\!=\; \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
and
![]() $\omega(n)$
denotes the number of prime divisors of an integer
$\omega(n)$
denotes the number of prime divisors of an integer
![]() $n\in \mathbb{N}$
. Using [
Reference Faye and Riffaut15
, Theorem 4.1] we have
$n\in \mathbb{N}$
. Using [
Reference Faye and Riffaut15
, Theorem 4.1] we have
which, combined with (18), gives
As far as the non-archimedean part is concerned, we have
 \begin{align} N&=\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \mid \ell_1 \ell_2 } d_v \log |(\,j-j_0)^{-1}|_v= \frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{i\in \{1,2\}} \sum_{\mathfrak{p} \mid \ell_i} v_{\mathfrak{p}}(\,j-j_0) \log \ell_i^{f_{\mathfrak{p}}} \nonumber\\ \, \, \, \, \, \, \, \, \, \, &=\frac{\log \ell_1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_1} v_{\mathfrak{p}}(\,j-j_0) f_{\mathfrak{p}} + \frac{\log \ell_2}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_2} v_{\mathfrak{p}}(\,j-j_0) f_{\mathfrak{p}}, \end{align}
\begin{align} N&=\frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{v \mid \ell_1 \ell_2 } d_v \log |(\,j-j_0)^{-1}|_v= \frac{1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{i\in \{1,2\}} \sum_{\mathfrak{p} \mid \ell_i} v_{\mathfrak{p}}(\,j-j_0) \log \ell_i^{f_{\mathfrak{p}}} \nonumber\\ \, \, \, \, \, \, \, \, \, \, &=\frac{\log \ell_1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_1} v_{\mathfrak{p}}(\,j-j_0) f_{\mathfrak{p}} + \frac{\log \ell_2}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_2} v_{\mathfrak{p}}(\,j-j_0) f_{\mathfrak{p}}, \end{align}
where
![]() $f_{\mathfrak{p}}$
denotes the residue degree of the prime
$f_{\mathfrak{p}}$
denotes the residue degree of the prime
![]() $\mathfrak{p} \subseteq \mathbb{Q}(\,j-j_0)$
lying over
$\mathfrak{p} \subseteq \mathbb{Q}(\,j-j_0)$
lying over
![]() $\mathfrak{p}\cap \mathbb{Q}$
. For every
$\mathfrak{p}\cap \mathbb{Q}$
. For every
![]() $\mathfrak{p}\mid \ell_1 \ell_2$
, we choose a prime ideal
$\mathfrak{p}\mid \ell_1 \ell_2$
, we choose a prime ideal
![]() $\mu \subseteq H$
that divides
$\mu \subseteq H$
that divides
![]() $\mathfrak{p}$
, where H denotes the compositum inside
$\mathfrak{p}$
, where H denotes the compositum inside
![]() $\overline{\mathbb{Q}}$
of the ring class fields relative to j and
$\overline{\mathbb{Q}}$
of the ring class fields relative to j and
![]() $j_0$
. Note that this makes sense, since we have
$j_0$
. Note that this makes sense, since we have
![]() $\mathbb{Q}(\,j-j_0)\subseteq \mathbb{Q}(\,j,j_0) \subseteq H$
(the first inclusion is actually an equality by [
Reference Faye and Riffaut15
, Theorem 4.1]). We wish now to use Theorem 3·1 to bound
$\mathbb{Q}(\,j-j_0)\subseteq \mathbb{Q}(\,j,j_0) \subseteq H$
(the first inclusion is actually an equality by [
Reference Faye and Riffaut15
, Theorem 4.1]). We wish now to use Theorem 3·1 to bound
![]() $v_\mu(\,j-j_0)$
for all these primes
$v_\mu(\,j-j_0)$
for all these primes
![]() $\mu$
. Let’s check that the hypotheses of the theorem are verified in our context:
$\mu$
. Let’s check that the hypotheses of the theorem are verified in our context:
-
(1) since we are assuming
 $|\Delta_0| < |\Delta|$
, certainly we have
$|\Delta_0| < |\Delta|$
, certainly we have
 $\Delta \neq \Delta_0$
;
$\Delta \neq \Delta_0$
; -
(2) since
 $(\,j_0,S)$
is a nice
$(\,j_0,S)$
is a nice
 $\Delta_0$
-pair, for
$\Delta_0$
-pair, for
 $i \in \{1,2\}$
the prime
$i \in \{1,2\}$
the prime
 $\ell_i$
splits completely in
$\ell_i$
splits completely in
 $\mathbb{Q}(\,j_0)$
. In particular,
$\mathbb{Q}(\,j_0)$
. In particular,
 $\mu \cap \mathbb{Q}(\,j_0)$
has residue degree 1, as required;
$\mu \cap \mathbb{Q}(\,j_0)$
has residue degree 1, as required; -
(3) since
 $(\,j_0,S)$
is a nice
$(\,j_0,S)$
is a nice
 $\Delta_0$
-pair, for
$\Delta_0$
-pair, for
 $i \in \{1,2\}$
the prime
$i \in \{1,2\}$
the prime
 $\ell_i$
does not divide either
$\ell_i$
does not divide either
 $\Delta_0$
or
$\Delta_0$
or
 $N_{\mathbb{Q}(\,j_0)/\mathbb{Q}}(\,j_0(\,j_0-1728))$
. In particular, this last condition implies that the elliptic curvewith
$N_{\mathbb{Q}(\,j_0)/\mathbb{Q}}(\,j_0(\,j_0-1728))$
. In particular, this last condition implies that the elliptic curvewith \begin{equation*} {E_0}_{/\mathbb{Q}(\,j_0)}\;:\;y^2+xy=x^3-\frac{36}{j_0-1728} x - \frac{1}{j_0-1728} \end{equation*}
\begin{equation*} {E_0}_{/\mathbb{Q}(\,j_0)}\;:\;y^2+xy=x^3-\frac{36}{j_0-1728} x - \frac{1}{j_0-1728} \end{equation*}
 $j(E_0)=j_0$
, has good reduction at
$j(E_0)=j_0$
, has good reduction at
 $\mu$
.
$\mu$
.
This discussion shows that we can apply Theorem 3·1 to bound
![]() $v_\mu(\,j-j_0)$
. Notice that under our assumptions we have, in the notation of the theorem, that
$v_\mu(\,j-j_0)$
. Notice that under our assumptions we have, in the notation of the theorem, that
![]() $d_0=2$
since
$d_0=2$
since
![]() $\ell_i \nmid N_{\mathbb{Q}(\,j_0)/\mathbb{Q}}(\,j_0(\,j_0-1728))$
for
$\ell_i \nmid N_{\mathbb{Q}(\,j_0)/\mathbb{Q}}(\,j_0(\,j_0-1728))$
for
![]() $i \in \{1,2\}$
. Moreover, the imaginary quadratic order associated to j cannot contain the order associated to
$i \in \{1,2\}$
. Moreover, the imaginary quadratic order associated to j cannot contain the order associated to
![]() $j_0$
because
$j_0$
because
![]() $|\Delta| >|\Delta_0|$
. Thus we obtain
$|\Delta| >|\Delta_0|$
. Thus we obtain
 \begin{equation*} v_{\mathfrak{p}}(\,j-j_0) \leq v_{\mu}(\,j-j_0) \leq \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_i}+ \frac{1}{2}, 1 \right \}\end{equation*}
\begin{equation*} v_{\mathfrak{p}}(\,j-j_0) \leq v_{\mu}(\,j-j_0) \leq \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_i}+ \frac{1}{2}, 1 \right \}\end{equation*}
for all primes
![]() $\mathfrak{p} \mid \ell_i$
. Combining this with (20) and setting
$\mathfrak{p} \mid \ell_i$
. Combining this with (20) and setting
![]() $L\;:\!=\;\max \{ \ell_1, \ell_2 \}$
we obtain
$L\;:\!=\;\max \{ \ell_1, \ell_2 \}$
we obtain
 \begin{align} N &\leq \frac{\log \ell_1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_1} \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_1}+ \frac{1}{2}, 1 \right \} f_{\mathfrak{p}} + \frac{\log \ell_2}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \end{align}
\begin{align} N &\leq \frac{\log \ell_1}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell_1} \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_1}+ \frac{1}{2}, 1 \right \} f_{\mathfrak{p}} + \frac{\log \ell_2}{[\mathbb{Q}(\,j-j_0)\;:\;\mathbb{Q}]} \end{align}
 \begin{align} &\times \sum_{\mathfrak{p} \mid \ell_2} \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_2}+ \frac{1}{2}, 1 \right \} f_{\mathfrak{p}}\nonumber \\ &\leq (\log \ell_1) \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_1}+ \frac{1}{2}, 1 \right \} + (\log \ell_2) \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_2}+ \frac{1}{2}, 1 \right \} \nonumber \\ &= \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log \ell_1}{2}, \log \ell_1 \right \} + \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log \ell_2}{2}, \log \ell_2 \right \} \nonumber \\ &\leq 2 \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log L}{2}, \log L \right \} = \max \{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \}, \nonumber\end{align}
\begin{align} &\times \sum_{\mathfrak{p} \mid \ell_2} \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_2}+ \frac{1}{2}, 1 \right \} f_{\mathfrak{p}}\nonumber \\ &\leq (\log \ell_1) \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_1}+ \frac{1}{2}, 1 \right \} + (\log \ell_2) \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2 \log \ell_2}+ \frac{1}{2}, 1 \right \} \nonumber \\ &= \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log \ell_1}{2}, \log \ell_1 \right \} + \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log \ell_2}{2}, \log \ell_2 \right \} \nonumber \\ &\leq 2 \max \left \{ \frac{\log(\Delta_0^2|\Delta|)}{2}+ \frac{\log L}{2}, \log L \right \} = \max \{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \}, \nonumber\end{align}
where in the second inequality we have used the fact that, for every number field K and any prime
![]() $q \in \mathbb{N}$
, we always have
$q \in \mathbb{N}$
, we always have
![]() $\sum_{\mathfrak{q}\mid q} f_{\mathfrak{q}} \leq [K\;:\;\mathbb{Q}]$
(here the sum is taken over the prime ideals of K lying above q). Using now together (17), (19) and (21) we obtain the following upper bound
$\sum_{\mathfrak{q}\mid q} f_{\mathfrak{q}} \leq [K\;:\;\mathbb{Q}]$
(here the sum is taken over the prime ideals of K lying above q). Using now together (17), (19) and (21) we obtain the following upper bound
for the Weil height of
![]() $j-j_0$
. We now look into lower bounds.
$j-j_0$
. We now look into lower bounds.
In order to find a lower bound for
![]() $h(\,j-j_0)$
, we first reduce to the problem of finding a lower bound for h(j) by means of the elementary inequality
$h(\,j-j_0)$
, we first reduce to the problem of finding a lower bound for h(j) by means of the elementary inequality
see [ Reference Bombieri and Gubler4 , Proposition 1.5.15]. As for bounding h(j), we use the lower bound [ Reference Bilu, Habegger and Kuhne2 , Proposition 4.3]
together with [ Reference Bilu, Habegger and Kuhne2 , Proposition 4.1]
which generally holds for
![]() $|\Delta| \geq 16$
. Combining (23) with (24) and (25), and adding 1 on both sides, we obtain
$|\Delta| \geq 16$
. Combining (23) with (24) and (25), and adding 1 on both sides, we obtain
Concatenating now (26) with (22), and dividing both sides by
![]() $Y(\Delta)$
, yields the inequality
$Y(\Delta)$
, yields the inequality
where
 \begin{align*} &A(\Delta)= \frac{8 F \log |\Delta| \cdot C_0}{Y(\Delta) C_\Delta},\\[5pt] &B(\Delta)= \frac{\log \left( F \log |\Delta| \right) + \log C_0 + 4\log |\Delta_0| + h(\,j_0) + 1.33 + \log 2}{Y(\Delta)}, \\[5pt] &C(\Delta)= \frac{1}{Y(\Delta)} \log \left( \frac{|\Delta|^{1/2}}{C_\Delta} \right), \\[5pt] &D(\Delta)= \frac{1}{Y(\Delta)} \cdot \max \{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \}.\end{align*}
\begin{align*} &A(\Delta)= \frac{8 F \log |\Delta| \cdot C_0}{Y(\Delta) C_\Delta},\\[5pt] &B(\Delta)= \frac{\log \left( F \log |\Delta| \right) + \log C_0 + 4\log |\Delta_0| + h(\,j_0) + 1.33 + \log 2}{Y(\Delta)}, \\[5pt] &C(\Delta)= \frac{1}{Y(\Delta)} \log \left( \frac{|\Delta|^{1/2}}{C_\Delta} \right), \\[5pt] &D(\Delta)= \frac{1}{Y(\Delta)} \cdot \max \{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \}.\end{align*}
We want to show that (27) cannot hold if
![]() $|\Delta|$
is sufficiently large. As far as estimating the first three terms of (27) is concerned, we find ourselves in the same situation as Cai in [
Reference Cai6
, Sections 6.1–6.4], and we can directly use the bounds therein obtained. More precisely from [
Reference Cai6
, Section 6.2] we have, since
$|\Delta|$
is sufficiently large. As far as estimating the first three terms of (27) is concerned, we find ourselves in the same situation as Cai in [
Reference Cai6
, Sections 6.1–6.4], and we can directly use the bounds therein obtained. More precisely from [
Reference Cai6
, Section 6.2] we have, since
![]() $|\Delta| > 10^{15}$
, that
$|\Delta| > 10^{15}$
, that
so for every
![]() $\varepsilon_A>0$
,
$\varepsilon_A>0$
,
holds for
![]() $|\Delta|$
sufficiently large. Moreover, using
$|\Delta|$
sufficiently large. Moreover, using
which is [
Reference Bilu, Habegger and Kuhne2
, Inequality (5.8)] (here
![]() $c_1 \in \mathbb{R}$
is an effectively computable absolute constant defined in [
Reference Bilu, Habegger and Kuhne2
, Section 5.2]), we have that, for every
$c_1 \in \mathbb{R}$
is an effectively computable absolute constant defined in [
Reference Bilu, Habegger and Kuhne2
, Section 5.2]), we have that, for every
![]() $\varepsilon_B>0$
, the inequality
$\varepsilon_B>0$
, the inequality
where
![]() $K\;:\!=\;\log C_0 + 4\log |\Delta_0| + h(\,j_0) + 1.33 + \log 2$
, holds for
$K\;:\!=\;\log C_0 + 4\log |\Delta_0| + h(\,j_0) + 1.33 + \log 2$
, holds for
![]() $|\Delta|$
sufficiently large. Finally, using the fact that
$|\Delta|$
sufficiently large. Finally, using the fact that
![]() $x \mapsto \log(x)/x$
is a decreasing function when
$x \mapsto \log(x)/x$
is a decreasing function when
![]() $x\geq 4$
, for every
$x\geq 4$
, for every
![]() $\varepsilon_C>0$
one has
$\varepsilon_C>0$
one has
 \begin{align} C(\Delta) & \leq \frac{1}{Y(\Delta)} \log \left( \pi^{-1} Y(\Delta)\right) \nonumber \\ & \leq \frac{1}{(3/\sqrt{5})\log |\Delta| -8.79} \log \left(\pi^{-1} \left(\frac{3}{\sqrt{5}}\log |\Delta| -8.79 \right) \right) < \varepsilon_C\end{align}
\begin{align} C(\Delta) & \leq \frac{1}{Y(\Delta)} \log \left( \pi^{-1} Y(\Delta)\right) \nonumber \\ & \leq \frac{1}{(3/\sqrt{5})\log |\Delta| -8.79} \log \left(\pi^{-1} \left(\frac{3}{\sqrt{5}}\log |\Delta| -8.79 \right) \right) < \varepsilon_C\end{align}
for
![]() $|\Delta|$
sufficiently large. We are then left with bounding
$|\Delta|$
sufficiently large. We are then left with bounding
![]() $D(\Delta)$
from above. For
$D(\Delta)$
from above. For
![]() $|\Delta| \geq L/|\Delta_0|^2$
we have
$|\Delta| \geq L/|\Delta_0|^2$
we have
 \begin{align*} D(\Delta)&= \frac{1}{Y(\Delta)} \cdot \max \left\{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \right\} \\ &\leq \frac{1}{\frac{3}{\sqrt{5}}\log |\Delta| -8.79} \cdot \left(\log |\Delta|+\log L \left( \frac{\log \Delta_0^2}{\log L}+1 \right) \right) \\ &= \frac{\sqrt{5}}{3} + \frac{1}{\frac{3}{\sqrt{5}}\log |\Delta| -8.79} \cdot \left(\frac{\sqrt{5}}{3}\cdot 8.79 + \log L \left( \frac{\log \Delta_0^2}{\log L}+1 \right) \right)\end{align*}
\begin{align*} D(\Delta)&= \frac{1}{Y(\Delta)} \cdot \max \left\{\log(\Delta_0^2|\Delta|) + \log L, 2 \log L \right\} \\ &\leq \frac{1}{\frac{3}{\sqrt{5}}\log |\Delta| -8.79} \cdot \left(\log |\Delta|+\log L \left( \frac{\log \Delta_0^2}{\log L}+1 \right) \right) \\ &= \frac{\sqrt{5}}{3} + \frac{1}{\frac{3}{\sqrt{5}}\log |\Delta| -8.79} \cdot \left(\frac{\sqrt{5}}{3}\cdot 8.79 + \log L \left( \frac{\log \Delta_0^2}{\log L}+1 \right) \right)\end{align*}
so for every
![]() $\varepsilon_D>0$
we obtain
$\varepsilon_D>0$
we obtain
for
![]() $|\Delta|$
sufficiently large (depending on
$|\Delta|$
sufficiently large (depending on
![]() $\Delta_0$
and
$\Delta_0$
and
![]() $\ell_1, \ell_2$
). We can now combine (28), (29), (30), (31) with (27) to obtain
$\ell_1, \ell_2$
). We can now combine (28), (29), (30), (31) with (27) to obtain
which holds for
![]() $|\Delta| \gg_{\ell_1, \ell_2, \Delta_0, \varepsilon_A, \varepsilon_B, \varepsilon_C, \varepsilon_D} 0$
. Choosing
$|\Delta| \gg_{\ell_1, \ell_2, \Delta_0, \varepsilon_A, \varepsilon_B, \varepsilon_C, \varepsilon_D} 0$
. Choosing
![]() $\varepsilon_A, \varepsilon_B, \varepsilon_C, \varepsilon_D$
small enough, the inequality cannot be verified for sufficiently large
$\varepsilon_A, \varepsilon_B, \varepsilon_C, \varepsilon_D$
small enough, the inequality cannot be verified for sufficiently large
![]() $|\Delta|$
. This proves that there are at most finitely many singular moduli j such that
$|\Delta|$
. This proves that there are at most finitely many singular moduli j such that
![]() $j-j_0$
is an S-unit, and concludes the proof of the first part of Theorem 1·1.
$j-j_0$
is an S-unit, and concludes the proof of the first part of Theorem 1·1.
We now begin the proof of the second part of Theorem 1·1. Suppose
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
is not Galois. We first claim that every prime in S must be split in
$\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
is not Galois. We first claim that every prime in S must be split in
![]() $\mathbb{Q}(\sqrt{\Delta_0})$
. Indeed, assume by contradiction that a prime
$\mathbb{Q}(\sqrt{\Delta_0})$
. Indeed, assume by contradiction that a prime
![]() $\ell \in S$
is inert in
$\ell \in S$
is inert in
![]() $\mathbb{Q}(\sqrt{\Delta_0})$
(it cannot ramify by definition of a nice
$\mathbb{Q}(\sqrt{\Delta_0})$
(it cannot ramify by definition of a nice
![]() $\Delta_0$
-pair). Let
$\Delta_0$
-pair). Let
![]() $H_\mathcal{O}\;:\!=\; \mathbb{Q}(\,j_0, \sqrt{\Delta_0})$
which is a semidihedral Galois extension of
$H_\mathcal{O}\;:\!=\; \mathbb{Q}(\,j_0, \sqrt{\Delta_0})$
which is a semidihedral Galois extension of
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
with generator
![]() $\sigma \in H$
. Since
$\sigma \in H$
. Since
![]() $\ell$
splits completely in
$\ell$
splits completely in
![]() $\mathbb{Q}(\,j_0)$
and is inert in
$\mathbb{Q}(\,j_0)$
and is inert in
![]() $\mathbb{Q}(\sqrt{\Delta_0})$
, the decomposition group of any prime of
$\mathbb{Q}(\sqrt{\Delta_0})$
, the decomposition group of any prime of
![]() $H_\mathcal{O}$
above
$H_\mathcal{O}$
above
![]() $\ell$
has order 2 and certainly contains H, since all the primes in
$\ell$
has order 2 and certainly contains H, since all the primes in
![]() $\mathbb{Q}(\,j_0)$
lying above
$\mathbb{Q}(\,j_0)$
lying above
![]() $\ell$
are inert in
$\ell$
are inert in
![]() $\mathbb{Q}(\,j_0) \subseteq H_\mathcal{O}$
. Hence, every such decomposition group must be equal to H and this means in particular that
$\mathbb{Q}(\,j_0) \subseteq H_\mathcal{O}$
. Hence, every such decomposition group must be equal to H and this means in particular that
![]() $\tau H \tau^{-1} = H$
for all
$\tau H \tau^{-1} = H$
for all
![]() $\tau \in G$
. We deduce that
$\tau \in G$
. We deduce that
![]() $\sigma$
commutes with every element of G, so G must be abelian and we reach the desired contradiction.
$\sigma$
commutes with every element of G, so G must be abelian and we reach the desired contradiction.
Let now
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
$j \in \overline{\mathbb{Q}}$
be a singular modulus of discriminant
![]() $\Delta$
such that
$\Delta$
such that
![]() $j-j_0$
is an S-unit. Since
$j-j_0$
is an S-unit. Since
![]() $j-j_0$
cannot be a unit by [
Reference Li34
, Corollary 1.3], there exists a prime
$j-j_0$
cannot be a unit by [
Reference Li34
, Corollary 1.3], there exists a prime
![]() $\ell \in S$
dividing the norm of
$\ell \in S$
dividing the norm of
![]() $j-j_0$
. This implies that there exists a number field K, a prime
$j-j_0$
. This implies that there exists a number field K, a prime
![]() $\mu \subseteq K$
lying above
$\mu \subseteq K$
lying above
![]() $\ell$
and two elliptic curves
$\ell$
and two elliptic curves
![]() $E_0,E_j$
defined over K with good reduction at
$E_0,E_j$
defined over K with good reduction at
![]() $\mu$
such that
$\mu$
such that
![]() $j(E_j)=j$
,
$j(E_j)=j$
,
![]() $j(E_0)=j_0$
and
$j(E_0)=j_0$
and
![]() $E_0 \text{ mod } \mu \cong_{\overline{\mathbb{F}}_\ell} E_j \text{ mod } \mu$
. Moreover, since
$E_0 \text{ mod } \mu \cong_{\overline{\mathbb{F}}_\ell} E_j \text{ mod } \mu$
. Moreover, since
![]() $\ell$
splits in
$\ell$
splits in
![]() $\mathbb{Q}(\sqrt{\Delta_0})$
by the discussion above, both
$\mathbb{Q}(\sqrt{\Delta_0})$
by the discussion above, both
![]() $E_0$
and
$E_0$
and
![]() $E_j$
have ordinary reduction modulo
$E_j$
have ordinary reduction modulo
![]() $\mu$
by [
Reference Lang31
, Chapter 13, Theorem 12]. From the reduction theory of CM orders (see again [
Reference Lang31
, Chapter 13, Theorem 12]) and the fact that
$\mu$
by [
Reference Lang31
, Chapter 13, Theorem 12]. From the reduction theory of CM orders (see again [
Reference Lang31
, Chapter 13, Theorem 12]) and the fact that
![]() $\ell \nmid \Delta_0$
, we deduce that
$\ell \nmid \Delta_0$
, we deduce that
![]() $\Delta=\ell^{2n} \Delta_0$
for some non-negative integer n, as wanted.
$\Delta=\ell^{2n} \Delta_0$
for some non-negative integer n, as wanted.
Remark 4·1. The proof of Theorem 1·1 can now be specialised to different situations to obtain explicit results on singular differences that are S-units. Indeed, for a given nice
![]() $\Delta_0$
-pair
$\Delta_0$
-pair
![]() $(\,j_0,S)$
, it suffices to find a discriminant
$(\,j_0,S)$
, it suffices to find a discriminant
![]() $\Delta$
whose absolute value is sufficiently large to violate inequality (32), which in turn is a combination of the explicit inequalities (28), (29), (30) and (31). For instance, in the case of Theorem 1·2, with the choice of the nice
$\Delta$
whose absolute value is sufficiently large to violate inequality (32), which in turn is a combination of the explicit inequalities (28), (29), (30) and (31). For instance, in the case of Theorem 1·2, with the choice of the nice
![]() $(\!-\!7)$
-pair
$(\!-\!7)$
-pair
![]() $(\!-\!3375,\{13,17\})$
and
$(\!-\!3375,\{13,17\})$
and
![]() $|\Delta|>10^{81}$
one gets
$|\Delta|>10^{81}$
one gets
and similarly with the other choices of primes in the theorem.
We conclude this section by proving that the hypothesis on the extension
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
being Galois, which appears in the statement of Theorem 1·1, is verified only for finitely many singular moduli
$\mathbb{Q} \subseteq \mathbb{Q}(\,j_0)$
being Galois, which appears in the statement of Theorem 1·1, is verified only for finitely many singular moduli
![]() $j_0$
.
$j_0$
.
Proposition 4·2. There are at most finitely many singular moduli
![]() $j \in \overline{\mathbb{Q}}$
such that the extension
$j \in \overline{\mathbb{Q}}$
such that the extension
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is Galois.
$\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is Galois.
Proof. Let
![]() $\mathcal{O}$
be the imaginary quadratic order relative to j, and denote by K its fraction field, with ring of integers
$\mathcal{O}$
be the imaginary quadratic order relative to j, and denote by K its fraction field, with ring of integers
![]() $\mathcal{O}_K$
and discriminant
$\mathcal{O}_K$
and discriminant
![]() $\Delta_K$
. By [
Reference Allombert, Bilu and Pizarro-Madariaga1
, Corollary 3.3] the extension
$\Delta_K$
. By [
Reference Allombert, Bilu and Pizarro-Madariaga1
, Corollary 3.3] the extension
![]() $\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is Galois if and only if the class group
$\mathbb{Q} \subseteq \mathbb{Q}(\,j)$
is Galois if and only if the class group
![]() $\textrm{Pic}(\mathcal{O})$
of the order
$\textrm{Pic}(\mathcal{O})$
of the order
![]() $\mathcal{O}$
is elementary 2-abelian. Since the natural homomorphism
$\mathcal{O}$
is elementary 2-abelian. Since the natural homomorphism
![]() $\textrm{Pic}(\mathcal{O}) \to \textrm{Pic}(\mathcal{O}_K)$
is surjective (see [
Reference Neukirch37
, Proposition I.12.9]), we deduce that also the class group of
$\textrm{Pic}(\mathcal{O}) \to \textrm{Pic}(\mathcal{O}_K)$
is surjective (see [
Reference Neukirch37
, Proposition I.12.9]), we deduce that also the class group of
![]() $\mathcal{O}_K$
has exponent 2. Hence, by [
Reference Weinberger45
, Theorem 1], there exists a negative fundamental discriminant D such that either
$\mathcal{O}_K$
has exponent 2. Hence, by [
Reference Weinberger45
, Theorem 1], there exists a negative fundamental discriminant D such that either
![]() $|\Delta_K| \leq 5460$
or
$|\Delta_K| \leq 5460$
or
![]() $\Delta_K=D$
. In particular, we have only a finite number of possibilities for the imaginary quadratic field K.
$\Delta_K=D$
. In particular, we have only a finite number of possibilities for the imaginary quadratic field K.
In order to show that there is also a finite number of possibilities for the order
![]() $\mathcal{O}$
, we need to bound the possible conductors
$\mathcal{O}$
, we need to bound the possible conductors
![]() $f\;:\!=\;|\mathcal{O}_K \;:\;\mathcal{O}|$
. To do so, consider the genus field
$f\;:\!=\;|\mathcal{O}_K \;:\;\mathcal{O}|$
. To do so, consider the genus field
![]() $G_\mathcal{O}$
relative to the order
$G_\mathcal{O}$
relative to the order
![]() $\mathcal{O}$
: it is the maximal subextension of the ring class field
$\mathcal{O}$
: it is the maximal subextension of the ring class field
![]() $H_\mathcal{O}$
that contains K and is abelian over
$H_\mathcal{O}$
that contains K and is abelian over
![]() $\mathbb{Q}$
. It can also be described as the fixed field by
$\mathbb{Q}$
. It can also be described as the fixed field by
![]() $\textrm{Pic}(\mathcal{O})^2$
under the Artin isomorphism
$\textrm{Pic}(\mathcal{O})^2$
under the Artin isomorphism
![]() $\textrm{Gal}(H_\mathcal{O}/K) \cong \textrm{Pic}(\mathcal{O})$
, see [
Reference Halter-Koch24
] and [
Reference Kühne30
, Section 2.2] (note also that the first part of the proof of [
Reference Cox11
, Theorem 6.1] carries over to non-maximal orders after making appropriate modifications). Since
$\textrm{Gal}(H_\mathcal{O}/K) \cong \textrm{Pic}(\mathcal{O})$
, see [
Reference Halter-Koch24
] and [
Reference Kühne30
, Section 2.2] (note also that the first part of the proof of [
Reference Cox11
, Theorem 6.1] carries over to non-maximal orders after making appropriate modifications). Since
![]() $\textrm{Pic}(\mathcal{O})$
is elementary 2-abelian by hypothesis, we deduce that
$\textrm{Pic}(\mathcal{O})$
is elementary 2-abelian by hypothesis, we deduce that
![]() $G_\mathcal{O}=H_\mathcal{O}$
and then [
Reference Kühne30
, Equation (2.3)] implies that
$G_\mathcal{O}=H_\mathcal{O}$
and then [
Reference Kühne30
, Equation (2.3)] implies that
where
![]() $\omega (f^2 \Delta_K)$
denotes the number of distinct prime divisors of
$\omega (f^2 \Delta_K)$
denotes the number of distinct prime divisors of
![]() $f^2 \Delta_K$
. On the other hand, by [
Reference Cox11
, Theorem 7.24] we can write
$f^2 \Delta_K$
. On the other hand, by [
Reference Cox11
, Theorem 7.24] we can write
 \begin{equation} f \prod_{p\mid f} \left( 1-\left(\frac{\Delta_K}{p} \right) \frac{1}{p} \right) = \frac{|\mathcal{O}_K^\times \;:\;\mathcal{O}^\times|}{\# \textrm{Pic}(\mathcal{O}_K)} \# \textrm{Pic}(\mathcal{O}).\end{equation}
\begin{equation} f \prod_{p\mid f} \left( 1-\left(\frac{\Delta_K}{p} \right) \frac{1}{p} \right) = \frac{|\mathcal{O}_K^\times \;:\;\mathcal{O}^\times|}{\# \textrm{Pic}(\mathcal{O}_K)} \# \textrm{Pic}(\mathcal{O}).\end{equation}
Combining (33) with (34), and using the fact that K ranges among a finite set of imaginary quadratic fields, it is not difficult to see that f must be in fact bounded. This concludes the proof.
5. Theorems 1·3 and 1·4
The proofs of Theorems 1·3 and 1·4, after a preliminary reduction step, become analogous to the proof of Theorem 1·1. The reader may then wonder why we decided to not write one single argument for all these results. The reason is double: first, for clarity of exposition, since already the proof of Theorem 1·1 contains quite involved computations. Second, because differences of the form
![]() $j-j_0$
with
$j-j_0$
with
![]() $j_0 \in \{0,1728\}$
require some extra attention due to the fact that the corresponding elliptic curves
$j_0 \in \{0,1728\}$
require some extra attention due to the fact that the corresponding elliptic curves
![]() $(E_0)_{/\mathbb{Q}}$
with
$(E_0)_{/\mathbb{Q}}$
with
![]() $j(E_0)=j_0$
have more geometric automorphisms than in the other cases. After pondering all these aspects, we chose to only sketch the proofs of the two aforementioned theorems, outlining with all the details only the parts in which they differ from the proof of Theorem 1·1. We begin with Theorem 1·3.
$j(E_0)=j_0$
have more geometric automorphisms than in the other cases. After pondering all these aspects, we chose to only sketch the proofs of the two aforementioned theorems, outlining with all the details only the parts in which they differ from the proof of Theorem 1·1. We begin with Theorem 1·3.
Proof of Theorem
1·3. First of all, we show that it is sufficient to prove that, under the assumptions of the theorem, the set of singular moduli j such that
![]() $j-1728$
is an
$j-1728$
is an
![]() $\{\ell \}$
-unit is finite and the discriminants of its elements can be effectively bounded. Indeed, suppose that
$\{\ell \}$
-unit is finite and the discriminants of its elements can be effectively bounded. Indeed, suppose that
![]() $j-1728$
is a singular
$j-1728$
is a singular
![]() $S_\ell$
-unit and assume that
$S_\ell$
-unit and assume that
![]() $p \in S_0$
is a prime dividing its norm
$p \in S_0$
is a prime dividing its norm
![]() $N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j-1728)$
. Then for every prime
$N_{\mathbb{Q}(\,j)/\mathbb{Q}}(\,j-1728)$
. Then for every prime
![]() $\mathfrak{p} \subseteq \overline{\mathbb{Q}}$
lying above p we have
$\mathfrak{p} \subseteq \overline{\mathbb{Q}}$
lying above p we have
![]() $j\equiv 1728 \text{ mod } \mathfrak{p}$
and
$j\equiv 1728 \text{ mod } \mathfrak{p}$
and
![]() $\mathfrak{p}$
is a prime of ordinary reduction for every elliptic curve over
$\mathfrak{p}$
is a prime of ordinary reduction for every elliptic curve over
![]() $\overline{\mathbb{Q}}$
with j-invariant 1728 or j. In particular, 1728 and j must be associated with the same imaginary quadratic field
$\overline{\mathbb{Q}}$
with j-invariant 1728 or j. In particular, 1728 and j must be associated with the same imaginary quadratic field
![]() $\mathbb{Q}(\sqrt{-1})$
. It has then been proved in [
Reference Campagna8
, Claim 6.1] that in this case, there are at least other 3 primes not congruent to 1 modulo 4 dividing this norm. In particular,
$\mathbb{Q}(\sqrt{-1})$
. It has then been proved in [
Reference Campagna8
, Claim 6.1] that in this case, there are at least other 3 primes not congruent to 1 modulo 4 dividing this norm. In particular,
![]() $j-1728$
cannot be a singular
$j-1728$
cannot be a singular
![]() $S_\ell$
-unit (the existence of this argument is also remarked in [
Reference Herrero, Menares and Rivera–Letelier27
, Section 1.1]).
$S_\ell$
-unit (the existence of this argument is also remarked in [
Reference Herrero, Menares and Rivera–Letelier27
, Section 1.1]).
Hence we are reduced to bounding the discriminants of the singular moduli j such that
![]() $j-1728$
is an
$j-1728$
is an
![]() $\{\ell\}$
-unit for
$\{\ell\}$
-unit for
![]() $\ell \geq 5$
a prime congruent to 3 modulo 4. Let then
$\ell \geq 5$
a prime congruent to 3 modulo 4. Let then
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus such that
$j \in \overline{\mathbb{Q}}$
be a singular modulus such that
![]() $j-1728$
is an
$j-1728$
is an
![]() $\{\ell\}$
-unit. In the same way as in the previous section, we compute the Weil height
$\{\ell\}$
-unit. In the same way as in the previous section, we compute the Weil height
 \begin{equation} h(\,j-1728)=h((\,j-1728)^{-1})=\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}_{\mathbb{Q}(\,j)}} d_v \log^+ |(\,j-1728)^{-1}|_v = A + N, \end{equation}
\begin{equation} h(\,j-1728)=h((\,j-1728)^{-1})=\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}_{\mathbb{Q}(\,j)}} d_v \log^+ |(\,j-1728)^{-1}|_v = A + N, \end{equation}
where, again,
![]() $d_v\;:\!=\;[\mathbb{Q}(\,j)_v\;:\;\mathbb{Q}_v]$
is the local degree at the place v and
$d_v\;:\!=\;[\mathbb{Q}(\,j)_v\;:\;\mathbb{Q}_v]$
is the local degree at the place v and
 \begin{align*}A&\;:\!=\;\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}^{\infty}_{\mathbb{Q}(\,j)}} d_v \log^+ |(\,j-1728)^{-1}|_v \quad \text{and} \quad \\ N & \;:\!=\;\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \mid \ell } d_v \log^+ |(\,j-1728)^{-1}|_v\end{align*}
\begin{align*}A&\;:\!=\;\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \in \mathcal{M}^{\infty}_{\mathbb{Q}(\,j)}} d_v \log^+ |(\,j-1728)^{-1}|_v \quad \text{and} \quad \\ N & \;:\!=\;\frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{v \mid \ell } d_v \log^+ |(\,j-1728)^{-1}|_v\end{align*}
are, respectively, the archimedean and non-archimedean components of the height. For
![]() $|\Delta|$
big enough, we can bound the archimedean component using another time the work of Cai [
Reference Cai6
]. More precisely, [
Reference Cai6
, Corollary 4.2] gives for
$|\Delta|$
big enough, we can bound the archimedean component using another time the work of Cai [
Reference Cai6
]. More precisely, [
Reference Cai6
, Corollary 4.2] gives for
![]() $|\Delta| \geq 10^{14}$
$|\Delta| \geq 10^{14}$
where
![]() $C_{\Delta}$
is the class number of the order of discriminant
$C_{\Delta}$
is the class number of the order of discriminant
![]() $\Delta$
and
$\Delta$
and
![]() $F= \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
as in the previous section. The non-archimedean component can be rewritten as
$F= \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
as in the previous section. The non-archimedean component can be rewritten as
 \begin{align} N= \frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j-1728) \log \ell^{f_{\mathfrak{p}}}=\frac{\log \ell}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j-1728) f_{\mathfrak{p}},\end{align}
\begin{align} N= \frac{1}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j-1728) \log \ell^{f_{\mathfrak{p}}}=\frac{\log \ell}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j-1728) f_{\mathfrak{p}},\end{align}
where the sum runs over primes
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $\mathbb{Q}(\,j)$
lying above
$\mathbb{Q}(\,j)$
lying above
![]() $\ell$
, and
$\ell$
, and
![]() $f_\mathfrak{p}$
denotes the residue degree of
$f_\mathfrak{p}$
denotes the residue degree of
![]() $\mathfrak{p}$
over
$\mathfrak{p}$
over
![]() $\ell$
. To estimate the valuation from above, we can apply Theorem 3·1 since all the hypotheses are met also in this case:
$\ell$
. To estimate the valuation from above, we can apply Theorem 3·1 since all the hypotheses are met also in this case:
![]() $\ell$
has certainly degree 1 in
$\ell$
has certainly degree 1 in
![]() $\mathbb{Q}(1728)=\mathbb{Q}$
and is coprime with
$\mathbb{Q}(1728)=\mathbb{Q}$
and is coprime with
![]() $-4=\textrm{disc}\ \mathbb{Q}(i)$
. Moreover, the elliptic curve
$-4=\textrm{disc}\ \mathbb{Q}(i)$
. Moreover, the elliptic curve
![]() ${E_{1728}}_{/\mathbb{Q}}\;:\;y^2=x^3+x$
has
${E_{1728}}_{/\mathbb{Q}}\;:\;y^2=x^3+x$
has
![]() $j(E_{1728})=1728$
and good reduction at all primes
$j(E_{1728})=1728$
and good reduction at all primes
![]() $\ell \neq 2$
. We deduce that for all
$\ell \neq 2$
. We deduce that for all
![]() $\mathfrak{p} \mid \ell$
we have
$\mathfrak{p} \mid \ell$
we have
where in the application of Theorem 3·1 one has
![]() $d_0=4$
since
$d_0=4$
since
![]() $\ell \geq 5$
(see [
Reference Silverman43
, III, Theorem 10.1]). Combining the above estimate with (37) we obtain
$\ell \geq 5$
(see [
Reference Silverman43
, III, Theorem 10.1]). Combining the above estimate with (37) we obtain
so putting together (35), (36) and (38) we get
 \begin{align} h(\,j-1728) & \leq \frac{4 F \log |\Delta|}{C_{\Delta}}+2 \log \frac{F |\Delta|^{1/2} \log |\Delta|}{C_{\Delta}}-2.68 \nonumber \\ & + \max \{\log (16 |\Delta|) + \log \ell, 2\log \ell \}\end{align}
\begin{align} h(\,j-1728) & \leq \frac{4 F \log |\Delta|}{C_{\Delta}}+2 \log \frac{F |\Delta|^{1/2} \log |\Delta|}{C_{\Delta}}-2.68 \nonumber \\ & + \max \{\log (16 |\Delta|) + \log \ell, 2\log \ell \}\end{align}
for
![]() $|\Delta| \geq 10^{14}$
. Now the lower bound (26) allows to conclude exactly in the same way as in the proof of Theorem 1·1.
$|\Delta| \geq 10^{14}$
. Now the lower bound (26) allows to conclude exactly in the same way as in the proof of Theorem 1·1.
As the reader may have noticed, the intimate reason why the proofs of Theorems 1·1 and 1·3 work out is that the lower bound (26) is sufficiently good to prevail on the estimates (21) and (38) for the non-archimedean parts of the relevant Weil heights. This will not be the case for
![]() $j_0=0$
, since in this case one has to take
$j_0=0$
, since in this case one has to take
![]() $d_0 \geq 6$
in the inequalities of Theorem 3·1. This is the reason why the proof of Theorem 1·4 is conditional under GRH. However, as already mentioned in the introduction, Theorem 1·4 does not need the full strength of the Generalised Riemann Hypothesis to be proved, but only that a weaker condition on the Dirichlet L-functions associated to imaginary quadratic fields holds. The aim of the subsequent discussion is to introduce this condition, and to deduce from its assumption a lower bound for the Weil height of a singular modulus that is sharp enough to prove Theorem 1·4 with our methods.
$d_0 \geq 6$
in the inequalities of Theorem 3·1. This is the reason why the proof of Theorem 1·4 is conditional under GRH. However, as already mentioned in the introduction, Theorem 1·4 does not need the full strength of the Generalised Riemann Hypothesis to be proved, but only that a weaker condition on the Dirichlet L-functions associated to imaginary quadratic fields holds. The aim of the subsequent discussion is to introduce this condition, and to deduce from its assumption a lower bound for the Weil height of a singular modulus that is sharp enough to prove Theorem 1·4 with our methods.
Recall that non-principal real primitive Dirichlet characters are precisely the Kronecker symbols attached to quadratic field extensions of
![]() $\mathbb{Q}$
. We say that such a Dirichlet character has discriminant
$\mathbb{Q}$
. We say that such a Dirichlet character has discriminant
![]() $D \in \mathbb{Z}$
if it is the Kronecker symbol attached to a quadratic field of discriminant D.
$D \in \mathbb{Z}$
if it is the Kronecker symbol attached to a quadratic field of discriminant D.
Definition 5·1. Let
![]() $k \in \mathbb{R}$
be a non-negative real number. A non-principal real primitive Dirichlet character
$k \in \mathbb{R}$
be a non-negative real number. A non-principal real primitive Dirichlet character
![]() $\chi$
of discriminant D is said to satisfy property P(k) if
$\chi$
of discriminant D is said to satisfy property P(k) if
where the left-hand side of the inequality is the logarithmic derivative of the Dirichlet L-function
![]() $L(\chi,s)$
associated to
$L(\chi,s)$
associated to
![]() $\chi$
.
$\chi$
.
Remark 5·2. The inequality appearing in Definition 5·1 may seem a bit arbitrary, and indeed it is. Actually for our purposes, we could take any inequality of the form
with
![]() $c<0.25$
as a definition for the property
$c<0.25$
as a definition for the property
![]() $P(k)$
, and all the following proofs would work in the same way.
$P(k)$
, and all the following proofs would work in the same way.
Remark 5·3. It is proved in [ Reference Mourtada and Kumar Murty35 ] that the logarithmic derivative of Dirichlet L-functions attached to Kronecker symbols of imaginary quadratic fields is actually positive for infinitely many negative fundamental discriminants. In particular, property P(0) holds for infinitely many real primitive Dirichlet characters of negative discriminant.
Let now
![]() $j \in \overline{\mathbb{Q}}$
be a singular modulus relative to an order in the imaginary quadratic field K. Under the assumption that the Kronecker symbol associated to K satisfies property
$j \in \overline{\mathbb{Q}}$
be a singular modulus relative to an order in the imaginary quadratic field K. Under the assumption that the Kronecker symbol associated to K satisfies property
![]() $P(k)$
for some non-negative
$P(k)$
for some non-negative
![]() $k \in \mathbb{R}$
, we are able to provide a lower bound for the Weil height of j in terms of its discriminant
$k \in \mathbb{R}$
, we are able to provide a lower bound for the Weil height of j in terms of its discriminant
![]() $\Delta$
. In order to make this assertion precise, we introduce some notation. For an elliptic curve E defined over a number field L, denote by
$\Delta$
. In order to make this assertion precise, we introduce some notation. For an elliptic curve E defined over a number field L, denote by
![]() $h_F(E)$
its stable Faltings height [
Reference Faltings14
, pag. 354] with Deligne’s normalisation [
Reference Deligne12
]. We continue writing
$h_F(E)$
its stable Faltings height [
Reference Faltings14
, pag. 354] with Deligne’s normalisation [
Reference Deligne12
]. We continue writing
![]() $h\;:\;\overline{\mathbb{Q}} \to \mathbb{R}$
for the logarithmic Weil height of an algebraic number.
$h\;:\;\overline{\mathbb{Q}} \to \mathbb{R}$
for the logarithmic Weil height of an algebraic number.
Proposition 5·4. Let j be a singular modulus of discriminant
![]() $\Delta=f^2 \Delta_K$
, where
$\Delta=f^2 \Delta_K$
, where
![]() $\Delta_K$
is the discriminant of the imaginary quadratic field K relative to j. If for some
$\Delta_K$
is the discriminant of the imaginary quadratic field K relative to j. If for some
![]() $k\in \mathbb{R}_{\geq 0}$
property P(k) holds for the non-principal real primitive Dirichlet character
$k\in \mathbb{R}_{\geq 0}$
property P(k) holds for the non-principal real primitive Dirichlet character
![]() $\chi$
of discriminant
$\chi$
of discriminant
![]() $\Delta_K$
, then
$\Delta_K$
, then
for some effective constant
![]() $C=C(k) \in \mathbb{R}$
.
$C=C(k) \in \mathbb{R}$
.
Proof. Let
![]() $E_{/ \mathbb{Q}(\,j)}$
be an elliptic curve with
$E_{/ \mathbb{Q}(\,j)}$
be an elliptic curve with
![]() $j(E)=j$
. Using [
Reference Gaudron and Remond17
, Lemma 7.9], the logarithmic Weil height of j can be bounded from below by the stable Faltings height of E as follows
$j(E)=j$
. Using [
Reference Gaudron and Remond17
, Lemma 7.9], the logarithmic Weil height of j can be bounded from below by the stable Faltings height of E as follows
We can explicitly compute the stable Faltings height of E using the well-known results of Colmez [ Reference Colmez9 ] and Nakkajima–Taguchi [ Reference Nakkajima and Taguchi36 ], as done for instance in [ Reference Habegger22 , Lemma 4.1]. One has
 \begin{equation*}h_F(E)=\frac{1}{4} \log(|\Delta|) + \frac{1}{2}\frac{L'(\chi,1)}{L(\chi,1)} - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi))\end{equation*}
\begin{equation*}h_F(E)=\frac{1}{4} \log(|\Delta|) + \frac{1}{2}\frac{L'(\chi,1)}{L(\chi,1)} - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi))\end{equation*}
where
![]() $\gamma$
is the Euler–Mascheroni constant, f is the conductor of the CM order and for a prime p we define
$\gamma$
is the Euler–Mascheroni constant, f is the conductor of the CM order and for a prime p we define
Using property
![]() $P(k)$
we then get
$P(k)$
we then get
 \begin{align*} h_F(E) &\geq \frac{1}{4} \log(|\Delta|) + \frac{1}{2} \left(-0.2485 \log |\Delta_K| - k \right) - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi)) \\ &= \frac{1}{4} \log(|\Delta|) + \frac{1}{2}(-0.2485 \log |\Delta| - 0.2485 \log f^{-2}-k) \nonumber \\ & \quad - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi)) \\ &=0.12575 \log |\Delta| + 0.2485 \log f - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi) + k).\end{align*}
\begin{align*} h_F(E) &\geq \frac{1}{4} \log(|\Delta|) + \frac{1}{2} \left(-0.2485 \log |\Delta_K| - k \right) - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi)) \\ &= \frac{1}{4} \log(|\Delta|) + \frac{1}{2}(-0.2485 \log |\Delta| - 0.2485 \log f^{-2}-k) \nonumber \\ & \quad - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi)) \\ &=0.12575 \log |\Delta| + 0.2485 \log f - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right) -\frac{1}{2} (\gamma+\log(2\pi) + k).\end{align*}
We want to bound from below the quantity
 \begin{equation*}A(\,f)\;:\!=\;0.2485 \log f - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right).\end{equation*}
\begin{equation*}A(\,f)\;:\!=\;0.2485 \log f - \frac{1}{2} \left(\sum_{p\mid f} e_f(p) \log p \right).\end{equation*}
To do this, one can proceed exactly as in [ Reference Bilu, Habegger and Kuhne2 , Section 4]. First, one notices that
by considering all the possible values of the Dirichlet character
![]() $\chi(p)$
. Setting now for all
$\chi(p)$
. Setting now for all
![]() $n\in \mathbb{N}_{>0}$
$n\in \mathbb{N}_{>0}$
 \begin{equation*}\delta(n)\;:\!=\;0.2485 \log n - \left(\sum_{p\mid n} \frac{\log p}{p+1} \cdot \frac{1-p^{-v_p(n)}}{1-p^{-1}} \right),\end{equation*}
\begin{equation*}\delta(n)\;:\!=\;0.2485 \log n - \left(\sum_{p\mid n} \frac{\log p}{p+1} \cdot \frac{1-p^{-v_p(n)}}{1-p^{-1}} \right),\end{equation*}
one notices that
![]() $\delta(n)$
is an additive function and satisfies
$\delta(n)$
is an additive function and satisfies
![]() $\delta(p^{r+1}) \geq \delta(p^r)$
for all primes
$\delta(p^{r+1}) \geq \delta(p^r)$
for all primes
![]() $p \in \mathbb{N}$
and integers
$p \in \mathbb{N}$
and integers
![]() $r>0$
. Since one has
$r>0$
. Since one has
![]() $\delta(2), \delta(3) < 0$
and
$\delta(2), \delta(3) < 0$
and
![]() $\delta(p)>0$
for all primes
$\delta(p)>0$
for all primes
![]() $p\geq 5$
, we deduce that
$p\geq 5$
, we deduce that
![]() $\delta(n) \geq \delta(2) + \delta(3)$
for all
$\delta(n) \geq \delta(2) + \delta(3)$
for all
![]() $n \in \mathbb{N}_{>0}$
. We then have
$n \in \mathbb{N}_{>0}$
. We then have
In conclusion, we obtain
where we set
Combining now (40) with (41) we obtain
and this concludes the proof.
We now state and prove a stronger version of Theorem 1·4, whose proof relies on the use of property
![]() $P(k)$
rather than on the use of GRH. We then show how Theorem 1·4 follows from this stronger statement.
$P(k)$
rather than on the use of GRH. We then show how Theorem 1·4 follows from this stronger statement.
Theorem 5·5. Let
![]() $S_0$
be the set of rational primes congruent to 1 modulo 3, let
$S_0$
be the set of rational primes congruent to 1 modulo 3, let
![]() $\ell \geq 5$
be an arbitrary prime and set
$\ell \geq 5$
be an arbitrary prime and set
![]() $S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. Assume that all the Kronecker symbols attached to imaginary quadratic fields satisfy property P(k) for some fixed
$S_\ell\;:\!=\;S_0 \cup \{\ell \}$
. Assume that all the Kronecker symbols attached to imaginary quadratic fields satisfy property P(k) for some fixed
![]() $k \in \mathbb{R}_{\geq 0}$
. Then there exists an effectively computable bound
$k \in \mathbb{R}_{\geq 0}$
. Then there exists an effectively computable bound
![]() $B=B(\ell,k) \in \mathbb{R}_{\geq 0}$
such that the discriminant
$B=B(\ell,k) \in \mathbb{R}_{\geq 0}$
such that the discriminant
![]() $\Delta_j$
of every singular
$\Delta_j$
of every singular
![]() $S_\ell$
-unit
$S_\ell$
-unit
![]() $j \in \overline{\mathbb{Q}}$
satisfies
$j \in \overline{\mathbb{Q}}$
satisfies
![]() $|\Delta_j| \leq B$
. In particular, the set of singular moduli that are
$|\Delta_j| \leq B$
. In particular, the set of singular moduli that are
![]() $S_\ell$
-units is finite and its cardinality can be effectively bounded.
$S_\ell$
-units is finite and its cardinality can be effectively bounded.
Proof. The proof is essentially identical to the proof of Theorem 1·3, and we only sketch the argument. First of all, it is again sufficient to prove that, under the assumptions of the theorem, the set of singular
![]() $\{\ell\}$
-units is finite and the discriminants of its elements can be effectively bounded. This follows in the same way as done at the beginning of the proof of Theorem 1·3, but this time appealing to the proofs of [
Reference Campagna8
, Theorem 1.2 and Claim 3.1]. Hence we are reduced to bounding the discriminants of singular
$\{\ell\}$
-units is finite and the discriminants of its elements can be effectively bounded. This follows in the same way as done at the beginning of the proof of Theorem 1·3, but this time appealing to the proofs of [
Reference Campagna8
, Theorem 1.2 and Claim 3.1]. Hence we are reduced to bounding the discriminants of singular
![]() $\{\ell\}$
-units for
$\{\ell\}$
-units for
![]() $\ell \geq 5$
a prime congruent to 2 modulo 3. Let j be a singular
$\ell \geq 5$
a prime congruent to 2 modulo 3. Let j be a singular
![]() $\{\ell\}$
-unit relative to the order
$\{\ell\}$
-unit relative to the order
![]() $\mathcal{O}$
of discriminant
$\mathcal{O}$
of discriminant
![]() $\Delta$
. Again, one decomposes its logarithmic Weil height h(j) into a sum
$\Delta$
. Again, one decomposes its logarithmic Weil height h(j) into a sum
![]() $h(\,j)=A+N$
of an archimedean and a non-archimedean component.
$h(\,j)=A+N$
of an archimedean and a non-archimedean component.
The archimedean component A has been studied in [
Reference Bilu, Habegger and Kuhne2
, Corollary 3.2]. Here it is proved that, for
![]() $|\Delta| \geq 10^{14}$
, we have
$|\Delta| \geq 10^{14}$
, we have
where
![]() $C_{\Delta}$
is the usual class number of the order of discriminant
$C_{\Delta}$
is the usual class number of the order of discriminant
![]() $\Delta$
and
$\Delta$
and
![]() $F= \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
. Note that, although [
Reference Bilu, Habegger and Kuhne2
, Corollary 3.2] is only formulated for singular units, it also holds for general singular moduli (with the same proof) if one restricts to considering the archimedean component of their height. The non-archimedean part can be written as
$F= \max \{2^{\omega(a)}\;:\;a\leq |\Delta|^{1/2} \}$
. Note that, although [
Reference Bilu, Habegger and Kuhne2
, Corollary 3.2] is only formulated for singular units, it also holds for general singular moduli (with the same proof) if one restricts to considering the archimedean component of their height. The non-archimedean part can be written as
 \begin{align} N=\frac{\log \ell}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j) f_{\mathfrak{p}},\end{align}
\begin{align} N=\frac{\log \ell}{[\mathbb{Q}(\,j)\;:\;\mathbb{Q}]} \sum_{\mathfrak{p} \mid \ell} v_{\mathfrak{p}}(\,j) f_{\mathfrak{p}},\end{align}
where
![]() $f_{\mathfrak{p}}$
denotes the residue degree of the prime
$f_{\mathfrak{p}}$
denotes the residue degree of the prime
![]() $\mathfrak{p} \subseteq \mathbb{Q}(\,j)$
lying above
$\mathfrak{p} \subseteq \mathbb{Q}(\,j)$
lying above
![]() $\ell$
. Using Theorem 3·1 with the elliptic curve
$\ell$
. Using Theorem 3·1 with the elliptic curve
![]() ${E_0}_{/\mathbb{Q}}\;:\;y^2=x^3+1$
with
${E_0}_{/\mathbb{Q}}\;:\;y^2=x^3+1$
with
![]() $j(E_0)=0$
and noticing that
$j(E_0)=0$
and noticing that
![]() $d_0=6$
because
$d_0=6$
because
![]() $\ell \geq 5$
we have
$\ell \geq 5$
we have
and, combining this estimate with equality (43), we get
A lower bound for the height h(j) can be obtained by combining the conditional Proposition 5·4 with (25). The conclusion of the proof can be then carried out in the same way as the proof of Theorem 1·1.
Proof of Theorem
1·4. The fact that the Dirichlet L-functions attached to imaginary quadratic fields satisfy GRH implies in particular that for every non-principal real primitive Dirichlet character
![]() $\chi$
of negative discriminant D we have
$\chi$
of negative discriminant D we have
where the implied constant is absolute, see for instance [
Reference Granville and Stark18
, Section 3.1] or [
Reference Ihara28
, Theorems 1 and 3] for the explicitness of the implied constant in the case
![]() $|D|>8$
(in the remaining cases, one can find an explicit bound for the absolute value of the logarithmic derivative for instance by first relating it to the Faltings height as done in [
Reference Habegger22
, Lemma 4.1] and then by using some bounds on the difference between the Faltings height and the j-height [
Reference Pazuki38
, Lemmas 2.6 and 3.2]). In particular, there exists
$|D|>8$
(in the remaining cases, one can find an explicit bound for the absolute value of the logarithmic derivative for instance by first relating it to the Faltings height as done in [
Reference Habegger22
, Lemma 4.1] and then by using some bounds on the difference between the Faltings height and the j-height [
Reference Pazuki38
, Lemmas 2.6 and 3.2]). In particular, there exists
![]() $k \in \mathbb{R}_{\geq 0}$
such that property
$k \in \mathbb{R}_{\geq 0}$
such that property
![]() $P(k)$
holds for all Kronecker symbols attached to imaginary quadratic fields. Now one concludes by applying Theorem 5·5.
$P(k)$
holds for all Kronecker symbols attached to imaginary quadratic fields. Now one concludes by applying Theorem 5·5.
6. An unsuccessful attempt at making Theorem 1·4 unconditional
The aim of this section is to show that the naive attempt at making Theorem 1·4 unconditional by improving the bounds obtained in Theorem 3·1 is fruitless. Namely, we will prove that the order of magnitude of the bounds appearing in Theorem 3·1 cannot be improved in general, at least in the case
![]() $j_0=0$
. Under the condition that the considered prime
$j_0=0$
. Under the condition that the considered prime
![]() $\ell$
divides the discriminant of the order
$\ell$
divides the discriminant of the order
![]() $\mathcal{O}_j$
corresponding to the singular modulus j, it is easy to provide examples in which the second upper-bound of (3) is reached. For instance, each of the singular moduli j of discriminant
$\mathcal{O}_j$
corresponding to the singular modulus j, it is easy to provide examples in which the second upper-bound of (3) is reached. For instance, each of the singular moduli j of discriminant
![]() $\Delta=-7\cdot 5^2$
is divided by the unique prime
$\Delta=-7\cdot 5^2$
is divided by the unique prime
![]() $\mathfrak{p}_5 \subseteq \mathbb{Q}(\,j)$
above 5 and we have
$\mathfrak{p}_5 \subseteq \mathbb{Q}(\,j)$
above 5 and we have
![]() $v_{\mathfrak{p}_5}(\,j)=3$
(note that
$v_{\mathfrak{p}_5}(\,j)=3$
(note that
![]() $d_0=6$
in this case). On the other hand, if
$d_0=6$
in this case). On the other hand, if
![]() $\ell$
does not divide the discriminant of
$\ell$
does not divide the discriminant of
![]() $\mathcal{O}_j$
the claimed optimality follows from the following theorem.
$\mathcal{O}_j$
the claimed optimality follows from the following theorem.
Theorem 6·1. Let
![]() $\ell \geq 5$
be a prime with
$\ell \geq 5$
be a prime with
![]() $\ell \equiv 2 \text{ mod } 3$
. There exists an infinite family of singular moduli j whose corresponding discriminant
$\ell \equiv 2 \text{ mod } 3$
. There exists an infinite family of singular moduli j whose corresponding discriminant
![]() $\Delta_j$
is coprime with
$\Delta_j$
is coprime with
![]() $\ell$
and which satisfy
$\ell$
and which satisfy
for some prime ideal
![]() $\mu \subseteq H_\mathcal{O}$
lying above
$\mu \subseteq H_\mathcal{O}$
lying above
![]() $\ell$
. Here
$\ell$
. Here
![]() $H_\mathcal{O}$
denotes the ring class field relative to the order
$H_\mathcal{O}$
denotes the ring class field relative to the order
![]() $\mathcal{O}$
associated to j.
$\mathcal{O}$
associated to j.
To prove the theorem, we need two preliminary results.
Proposition 6·2. Let
![]() $\ell \geq 5$
be a prime with
$\ell \geq 5$
be a prime with
![]() $\ell \equiv 2 \text{ mod } 3$
and consider the elliptic curve
$\ell \equiv 2 \text{ mod } 3$
and consider the elliptic curve
![]() $E_0\;:\;y^2=x^3+1$
defined over
$E_0\;:\;y^2=x^3+1$
defined over
![]() $\mathbb{F}_\ell$
. Then we have that
$\mathbb{F}_\ell$
. Then we have that
is isomorphic to a maximal order in the quaternion algebra
![]() $\mathbb{B}_{\ell, \infty}$
. Here, if
$\mathbb{B}_{\ell, \infty}$
. Here, if
![]() $\zeta \in \overline{\mathbb{F}}_\ell$
denotes a fixed primitive 3-rd root of unity, the endomorphisms
$\zeta \in \overline{\mathbb{F}}_\ell$
denotes a fixed primitive 3-rd root of unity, the endomorphisms
![]() $\zeta_3, \varphi, \xi, \eta \in \textrm{End}_{\overline{\mathbb{F}}_\ell}(E_0)$
are such that
$\zeta_3, \varphi, \xi, \eta \in \textrm{End}_{\overline{\mathbb{F}}_\ell}(E_0)$
are such that
![]() $\zeta_3\;:\;(x,y) \mapsto (\zeta x,y)$
,
$\zeta_3\;:\;(x,y) \mapsto (\zeta x,y)$
,
![]() $\varphi\;:\;(x,y) \mapsto (x^\ell, y^\ell)$
,
$\varphi\;:\;(x,y) \mapsto (x^\ell, y^\ell)$
,
![]() $3\xi= 2 + \zeta_3 + 2\varphi +\zeta_3 \varphi$
and
$3\xi= 2 + \zeta_3 + 2\varphi +\zeta_3 \varphi$
and
![]() $3\eta = -1+\zeta_3-\varphi-2\zeta_3 \varphi$
.
$3\eta = -1+\zeta_3-\varphi-2\zeta_3 \varphi$
.
Proof. This proposition is certainly well known, but the author has not been able to find a suitable reference. One could directly verify that the given order is a maximal order in
![]() $\mathbb{B}_{\ell, \infty}$
whose elements represent endomorphisms of the elliptic curve
$\mathbb{B}_{\ell, \infty}$
whose elements represent endomorphisms of the elliptic curve
![]() $E_0$
. We outline a possible strategy leading to the computation of this endomorphism ring, kindly suggested to the author by John Voight.
$E_0$
. We outline a possible strategy leading to the computation of this endomorphism ring, kindly suggested to the author by John Voight.
Since
![]() $\ell \equiv 2 \text{ mod } 3$
, the elliptic curve
$\ell \equiv 2 \text{ mod } 3$
, the elliptic curve
![]() $E_0$
is supersingular and
$E_0$
is supersingular and
![]() $\mathcal{O}_{E_0}\;:\!=\;\textrm{End}_{\overline{\mathbb{F}}_\ell} (E_0)$
is a maximal order in the quaternion algebra
$\mathcal{O}_{E_0}\;:\!=\;\textrm{End}_{\overline{\mathbb{F}}_\ell} (E_0)$
is a maximal order in the quaternion algebra
![]() $\mathbb{B}_{\ell,\infty}$
. Throughout this proof, we will always identify
$\mathbb{B}_{\ell,\infty}$
. Throughout this proof, we will always identify
![]() $\mathcal{O}_{E_0}$
with its image in
$\mathcal{O}_{E_0}$
with its image in
![]() $\mathbb{B}_{\ell,\infty}$
under some fixed embedding. Notice that
$\mathbb{B}_{\ell,\infty}$
under some fixed embedding. Notice that
![]() $\mathcal{O}_{E_0}$
contains the subring
$\mathcal{O}_{E_0}$
contains the subring
![]() $\mathcal{O}\;:\!=\; \mathbb{Z}[\zeta_3,\varphi]$
. As we have
$\mathcal{O}\;:\!=\; \mathbb{Z}[\zeta_3,\varphi]$
. As we have
![]() $\varphi^2=-\ell$
, the ring
$\varphi^2=-\ell$
, the ring
![]() $\mathcal{O}$
is actually a rank 4 suborder of
$\mathcal{O}$
is actually a rank 4 suborder of
![]() $\mathcal{O}_{E_0}$
having
$\mathcal{O}_{E_0}$
having
![]() $\mathbb{Z}$
-basis
$\mathbb{Z}$
-basis
![]() $\{1,\zeta_3, \varphi, \zeta_3 \varphi \}$
, and a discriminant computation shows that
$\{1,\zeta_3, \varphi, \zeta_3 \varphi \}$
, and a discriminant computation shows that
![]() $|\mathcal{O}_{E_0} \;:\;\mathcal{O}|=3$
. Hence,
$|\mathcal{O}_{E_0} \;:\;\mathcal{O}|=3$
. Hence,
![]() $\mathcal{O}_{E_0}$
contains an element of the form
$\mathcal{O}_{E_0}$
contains an element of the form
with
![]() $3 \nmid \gcd(A,B,C,D)$
. Since
$3 \nmid \gcd(A,B,C,D)$
. Since
![]() $\alpha$
is an element of a quaternion order, it is in particular integral. This implies that its reduced trace and norm must both be integers. One has
$\alpha$
is an element of a quaternion order, it is in particular integral. This implies that its reduced trace and norm must both be integers. One has
 \begin{align*}&\textrm{trd}(\alpha)=\frac{2A-B}{3} \\[5pt] &\textrm{nrd}(\alpha)= \frac{-\ell CD-AB+A^2+B^2+\ell (C^2+D^2)}{9},\end{align*}
\begin{align*}&\textrm{trd}(\alpha)=\frac{2A-B}{3} \\[5pt] &\textrm{nrd}(\alpha)= \frac{-\ell CD-AB+A^2+B^2+\ell (C^2+D^2)}{9},\end{align*}
where
![]() $\textrm{trd}(\!\cdot\!)$
and
$\textrm{trd}(\!\cdot\!)$
and
![]() $\textrm{nrd}(\!\cdot\!)$
denote respectively the reduced trace and the reduced norm in the quaternion algebra
$\textrm{nrd}(\!\cdot\!)$
denote respectively the reduced trace and the reduced norm in the quaternion algebra
![]() $\mathbb{B}_{\ell, \infty}$
. Note now that, since
$\mathbb{B}_{\ell, \infty}$
. Note now that, since
![]() $\mathcal{O} \subseteq \mathcal{O}_{E_0}$
, the integers A, B, C, D can be chosen to lie in
$\mathcal{O} \subseteq \mathcal{O}_{E_0}$
, the integers A, B, C, D can be chosen to lie in
![]() $\{0,1,2\}$
. Hence there is just a finite number of possibilities to check. A computation shows that the possible options for the tuple (A,B,C,D) are the following four:
$\{0,1,2\}$
. Hence there is just a finite number of possibilities to check. A computation shows that the possible options for the tuple (A,B,C,D) are the following four:
By adding the corresponding
![]() $\alpha$
’s to the order
$\alpha$
’s to the order
![]() $\mathcal{O}$
we get the following possibilities:
$\mathcal{O}$
we get the following possibilities:
 \begin{align*}&(1,2,1,2),\;\;\;\; \mathcal{O}_1\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{1}{3}-\frac{1}{3} \zeta_3 + \frac{1}{3}\varphi+\frac{2}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{2}{3}-\frac{1}{3} \zeta_3 - \frac{2}{3}\varphi-\frac{1}{3}\zeta_3 \varphi\!\right) \\&(1,2,2,1),\;\;\;\; \mathcal{O}_2\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{1}{3}-\frac{1}{3} \zeta_3 + \frac{2}{3}\varphi+\frac{1}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{2}{3}-\frac{1}{3} \zeta_3 - \frac{1}{3}\varphi-\frac{2}{3}\zeta_3 \varphi\!\right) \\&(2,1,1,2),\;\;\;\; \mathcal{O}_3\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{2}{3}+\frac{1}{3} \zeta_3 + \frac{1}{3}\varphi+\frac{2}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{1}{3}+\frac{1}{3} \zeta_3 - \frac{2}{3}\varphi-\frac{1}{3}\zeta_3 \varphi\!\right) \\&(2,1,2,1),\;\;\;\; \mathcal{O}_4\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{2}{3}+\frac{1}{3} \zeta_3 + \frac{2}{3}\varphi+\frac{1}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{1}{3}+\frac{1}{3} \zeta_3 - \frac{1}{3}\varphi-\frac{2}{3}\zeta_3 \varphi\!\right)\!. \\\end{align*}
\begin{align*}&(1,2,1,2),\;\;\;\; \mathcal{O}_1\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{1}{3}-\frac{1}{3} \zeta_3 + \frac{1}{3}\varphi+\frac{2}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{2}{3}-\frac{1}{3} \zeta_3 - \frac{2}{3}\varphi-\frac{1}{3}\zeta_3 \varphi\!\right) \\&(1,2,2,1),\;\;\;\; \mathcal{O}_2\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{1}{3}-\frac{1}{3} \zeta_3 + \frac{2}{3}\varphi+\frac{1}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{2}{3}-\frac{1}{3} \zeta_3 - \frac{1}{3}\varphi-\frac{2}{3}\zeta_3 \varphi\!\right) \\&(2,1,1,2),\;\;\;\; \mathcal{O}_3\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{2}{3}+\frac{1}{3} \zeta_3 + \frac{1}{3}\varphi+\frac{2}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{1}{3}+\frac{1}{3} \zeta_3 - \frac{2}{3}\varphi-\frac{1}{3}\zeta_3 \varphi\!\right) \\&(2,1,2,1),\;\;\;\; \mathcal{O}_4\;:\;\mathbb{Z}+\mathbb{Z} \zeta_3+\mathbb{Z}\left(\frac{2}{3}+\frac{1}{3} \zeta_3 + \frac{2}{3}\varphi+\frac{1}{3}\zeta_3 \varphi\!\right) + \mathbb{Z} \left(-\frac{1}{3}+\frac{1}{3} \zeta_3 - \frac{1}{3}\varphi-\frac{2}{3}\zeta_3 \varphi\!\right)\!. \\\end{align*}
Looking at the generators of these orders, we see that
![]() $\mathcal{O}_1=\mathcal{O}_4$
and
$\mathcal{O}_1=\mathcal{O}_4$
and
![]() $\mathcal{O}_2=\mathcal{O}_3$
, so we discard the first two and we only consider
$\mathcal{O}_2=\mathcal{O}_3$
, so we discard the first two and we only consider
![]() $\mathcal{O}_3$
and
$\mathcal{O}_3$
and
![]() $\mathcal{O}_4$
. We need to decide which of these two rings is the “correct one”. Indeed, the desired order must be identified with the endomorphism ring of the elliptic curve
$\mathcal{O}_4$
. We need to decide which of these two rings is the “correct one”. Indeed, the desired order must be identified with the endomorphism ring of the elliptic curve
![]() $E_0$
. An element of the form
$E_0$
. An element of the form
![]() $\frac{1}{3} \beta$
, with
$\frac{1}{3} \beta$
, with
![]() $\beta \in \textrm{End}_{\overline{\mathbb{F}}_\ell}(E_0)$
, is an endomorphism of
$\beta \in \textrm{End}_{\overline{\mathbb{F}}_\ell}(E_0)$
, is an endomorphism of
![]() $E_0$
if and only if the endomorphism
$E_0$
if and only if the endomorphism
![]() $\beta$
factors through the multiplication-by-3 morphism. This happens if and only if the 3-torsion points of
$\beta$
factors through the multiplication-by-3 morphism. This happens if and only if the 3-torsion points of
![]() $E_0$
are in the kernel of
$E_0$
are in the kernel of
![]() $\beta$
. The idea is then to compute the generators of the group of 3-torsion points of
$\beta$
. The idea is then to compute the generators of the group of 3-torsion points of
![]() $E_0$
and to test which order contains the “right” elements. The 3-division polynomial of
$E_0$
and to test which order contains the “right” elements. The 3-division polynomial of
![]() $E_0$
is
$E_0$
is
so we can choose as generators of the full 3-torsion subgroup
![]() $E_0[3](\overline{\mathbb{F}}_\ell)$
the points
$E_0[3](\overline{\mathbb{F}}_\ell)$
the points
for fixed choices of
![]() $\sqrt[3]{4}, \sqrt{-3} \in \overline{\mathbb{F}}_\ell$
as follows. Observe that for a prime
$\sqrt[3]{4}, \sqrt{-3} \in \overline{\mathbb{F}}_\ell$
as follows. Observe that for a prime
![]() $\ell \geq 5$
and
$\ell \geq 5$
and
![]() $\ell \equiv 2 \text{ mod } 3$
, all elements in
$\ell \equiv 2 \text{ mod } 3$
, all elements in
![]() $\mathbb{F}_\ell$
are cubes and
$\mathbb{F}_\ell$
are cubes and
![]() $-3$
is not a square modulo
$-3$
is not a square modulo
![]() $\ell$
. In view of this remark, we choose Q in such a way that the first coordinate lies in
$\ell$
. In view of this remark, we choose Q in such a way that the first coordinate lies in
![]() $\mathbb{F}_\ell$
. The second coordinate of Q defines in any case a quadratic extension of
$\mathbb{F}_\ell$
. The second coordinate of Q defines in any case a quadratic extension of
![]() $\mathbb{F}_\ell$
, so that
$\mathbb{F}_\ell$
, so that
We are ready to verify that
![]() $\mathcal{O}_4$
is the correct order. Let
$\mathcal{O}_4$
is the correct order. Let
Then, using the fact that
![]() $2P=-P$
and
$2P=-P$
and
![]() $2Q=-Q$
we get that
$2Q=-Q$
we get that
![]() $\Phi=\Psi$
on the 3-torsion points, so
$\Phi=\Psi$
on the 3-torsion points, so
 \begin{align*}&\Phi (P)=[2](0,1)+(0,1)+[2](0,1)+(0,1)=0 \\[5pt] \Phi (Q)&=(-\sqrt[3]{4},-\sqrt{-3})+(-\zeta \sqrt[3]{4}, \sqrt{-3})+[2]((-\sqrt[3]{4})^\ell, (\sqrt{-3})^\ell)\\[5pt] &\quad +(\zeta (-\sqrt[3]{4})^\ell,(\sqrt{-3})^\ell)=0\end{align*}
\begin{align*}&\Phi (P)=[2](0,1)+(0,1)+[2](0,1)+(0,1)=0 \\[5pt] \Phi (Q)&=(-\sqrt[3]{4},-\sqrt{-3})+(-\zeta \sqrt[3]{4}, \sqrt{-3})+[2]((-\sqrt[3]{4})^\ell, (\sqrt{-3})^\ell)\\[5pt] &\quad +(\zeta (-\sqrt[3]{4})^\ell,(\sqrt{-3})^\ell)=0\end{align*}
which shows that
![]() $E_0[3] \subseteq \ker \Phi$
and
$E_0[3] \subseteq \ker \Phi$
and
![]() $E_0[3] \subseteq \ker \Psi$
. One can also verify that
$E_0[3] \subseteq \ker \Psi$
. One can also verify that
This proves the proposition.
Proposition 6·3. Let
![]() $\mathcal{O}$
be an order in an imaginary quadratic field K and
$\mathcal{O}$
be an order in an imaginary quadratic field K and
![]() $\ell \in \mathbb{N}$
be a prime inert in K that does not divide the conductor of
$\ell \in \mathbb{N}$
be a prime inert in K that does not divide the conductor of
![]() $\mathcal{O}$
. Let W be the ring of integers in the completion
$\mathcal{O}$
. Let W be the ring of integers in the completion
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
of the maximal unramified extension of
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
of the maximal unramified extension of
![]() $\mathbb{Q}_\ell$
, with uniformizer
$\mathbb{Q}_\ell$
, with uniformizer
![]() $\pi \in W$
. Fix
$\pi \in W$
. Fix
![]() $n \in \mathbb{Z}_{>0}$
and let
$n \in \mathbb{Z}_{>0}$
and let
![]() $E_0 \to \textrm{Spec} (W/\pi^n)$
be an elliptic scheme such that the reduction modulo
$E_0 \to \textrm{Spec} (W/\pi^n)$
be an elliptic scheme such that the reduction modulo
![]() $\pi$
is supersingular. If
$\pi$
is supersingular. If
![]() $f\;:\;\mathcal{O} \hookrightarrow \textrm{End}_{W/\pi^n}(E_0)$
is an optimal embedding, then there exists an elliptic curve
$f\;:\;\mathcal{O} \hookrightarrow \textrm{End}_{W/\pi^n}(E_0)$
is an optimal embedding, then there exists an elliptic curve
![]() $E_{/W}$
such that:
$E_{/W}$
such that:
-
(i)
 $E \text{ mod } \pi^n \cong E_0$
;
$E \text{ mod } \pi^n \cong E_0$
; -
(ii)
 $\textrm{End}_W(E) \cong \mathcal{O}$
.
$\textrm{End}_W(E) \cong \mathcal{O}$
.
Proof. This is an application of Gross and Zagier’s generalisation [
Reference Gross and Zagier21
, Proposition 2.7] of the Deuring lifting Theorem [
Reference Lang31
, Theorem 13.14]. Note that the proof of Gross and Zagier’s result in the supersingular case does not require, in their notation, the ring
![]() $\mathbb{Z}[\alpha_0]$
to be integrally closed but only
$\mathbb{Z}[\alpha_0]$
to be integrally closed but only
![]() $\ell$
not dividing its conductor.
$\ell$
not dividing its conductor.
Write
![]() $\mathcal{O}=\mathbb{Z}[\tau]$
for some imaginary quadratic
$\mathcal{O}=\mathbb{Z}[\tau]$
for some imaginary quadratic
![]() $\tau \in K$
and let
$\tau \in K$
and let
![]() $\alpha_0\;:\!=\;f(\tau)$
. The endomorphism
$\alpha_0\;:\!=\;f(\tau)$
. The endomorphism
![]() $\alpha_0$
induces on the tangent space
$\alpha_0$
induces on the tangent space
![]() $\text{Lie}(E_0)$
the multiplication by an element
$\text{Lie}(E_0)$
the multiplication by an element
![]() $w_0 \in W/\pi^n$
which is a root of the minimal polynomial
$w_0 \in W/\pi^n$
which is a root of the minimal polynomial
![]() $g(x)=x^2+Ax+B \in \mathbb{Z}[x]$
of
$g(x)=x^2+Ax+B \in \mathbb{Z}[x]$
of
![]() $\tau$
over
$\tau$
over
![]() $\mathbb{Q}$
. In order to apply [
Reference Gross and Zagier21
, Proposition 2.7], we need to show that there exists
$\mathbb{Q}$
. In order to apply [
Reference Gross and Zagier21
, Proposition 2.7], we need to show that there exists
![]() $w \in W$
such that
$w \in W$
such that
![]() $g(w)=0$
and
$g(w)=0$
and
![]() $w\ \textrm{mod}\ \pi^n=w_0$
. Let
$w\ \textrm{mod}\ \pi^n=w_0$
. Let
![]() $\beta\;:\!=\; w_0 \text{ mod } \pi \in \overline{\mathbb{F}}_\ell$
. Then
$\beta\;:\!=\; w_0 \text{ mod } \pi \in \overline{\mathbb{F}}_\ell$
. Then
![]() $\beta$
is a root of
$\beta$
is a root of
![]() $g(x) \text{ mod } \pi$
lying in
$g(x) \text{ mod } \pi$
lying in
![]() $\overline{\mathbb{F}}_\ell$
. If
$\overline{\mathbb{F}}_\ell$
. If
![]() $g^{\prime}(\beta)=0$
, then
$g^{\prime}(\beta)=0$
, then
![]() $\beta$
would actually lie in
$\beta$
would actually lie in
![]() $\mathbb{F}_\ell$
. However, since
$\mathbb{F}_\ell$
. However, since
![]() $\ell$
is inert in K and does not divide the conductor of
$\ell$
is inert in K and does not divide the conductor of
![]() $\mathcal{O}$
, the polynomial g(x) is irreducible over
$\mathcal{O}$
, the polynomial g(x) is irreducible over
![]() $\mathbb{F}_\ell$
by the Kummer–Dedekind Theorem [
Reference Neukirch37
, Proposition I.8.3], and this implies that the derivative of g(x) does not vanish on
$\mathbb{F}_\ell$
by the Kummer–Dedekind Theorem [
Reference Neukirch37
, Proposition I.8.3], and this implies that the derivative of g(x) does not vanish on
![]() $\beta$
(an irreducible polynomial over a finite field has never a common zero with its derivative). Then by Hensel’s lemma there exists a unique
$\beta$
(an irreducible polynomial over a finite field has never a common zero with its derivative). Then by Hensel’s lemma there exists a unique
![]() $w \in W$
lifting
$w \in W$
lifting
![]() $\beta$
. This w satisfies
$\beta$
. This w satisfies
![]() $g(w)=0$
and
$g(w)=0$
and
![]() $w \text{ mod } \pi^n = w_0$
by construction.
$w \text{ mod } \pi^n = w_0$
by construction.
We now apply [
Reference Gross and Zagier21
, Proposition 2.7] to deduce that there exists an elliptic curve
![]() $E_{/W}$
and an endomorphism
$E_{/W}$
and an endomorphism
![]() $\alpha \in \textrm{End}_W(E)$
such that
$\alpha \in \textrm{End}_W(E)$
such that
![]() $E \text{ mod } \pi^n \cong E_0$
and
$E \text{ mod } \pi^n \cong E_0$
and
![]() $\alpha \text{ mod } \pi^n = \alpha_0$
. In principle, the ring
$\alpha \text{ mod } \pi^n = \alpha_0$
. In principle, the ring
![]() $\textrm{End}_W(E)$
could strictly contain the order
$\textrm{End}_W(E)$
could strictly contain the order
![]() $\mathbb{Z}[\alpha]$
. However, the reduction map identifies
$\mathbb{Z}[\alpha]$
. However, the reduction map identifies
![]() $\mathbb{Z}[\alpha]$
with
$\mathbb{Z}[\alpha]$
with
![]() $\mathcal{O}$
, and the latter optimally embeds in
$\mathcal{O}$
, and the latter optimally embeds in
![]() $\textrm{End}_{W/\pi^n}(E_0)$
. Since the reduction map also embeds
$\textrm{End}_{W/\pi^n}(E_0)$
. Since the reduction map also embeds
![]() $\textrm{End}_W(E) \hookrightarrow \textrm{End}_{W/\pi^n}(E_0)$
, we deduce that
$\textrm{End}_W(E) \hookrightarrow \textrm{End}_{W/\pi^n}(E_0)$
, we deduce that
![]() $\textrm{End}_W(E)= \mathbb{Z}[\alpha] \cong \mathcal{O}$
, as wanted.
$\textrm{End}_W(E)= \mathbb{Z}[\alpha] \cong \mathcal{O}$
, as wanted.
Proof of Theorem
6·1. Let W be the ring of integers in the completion
![]() $\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
of the maximal unramified extension of
$\widehat{\mathbb{Q}^{\text{unr}}_\ell}$
of the maximal unramified extension of
![]() $\mathbb{Q}_\ell$
, with uniformizer
$\mathbb{Q}_\ell$
, with uniformizer
![]() $\pi \in W$
. For every
$\pi \in W$
. For every
![]() $n \in \mathbb{N}$
let
$n \in \mathbb{N}$
let
![]() $R_n\;:\!=\;\textrm{End}_{W/\pi^{n+1}}(E_0)$
be the endomorphism ring of the reduction of
$R_n\;:\!=\;\textrm{End}_{W/\pi^{n+1}}(E_0)$
be the endomorphism ring of the reduction of
![]() $E_0:\ y^2=x^3+1$
modulo
$E_0:\ y^2=x^3+1$
modulo
![]() $\pi^{n+1}$
. By Theorem 2·4 (a) we know that
$\pi^{n+1}$
. By Theorem 2·4 (a) we know that
![]() $R_n \cong \mathbb{Z}[\zeta_3]+\ell^n R_0$
, where
$R_n \cong \mathbb{Z}[\zeta_3]+\ell^n R_0$
, where
![]() $R_0$
is the order appearing in the statement of Proposition 6·2. A computation similar to the one carried out during the proof of Theorem 3·1 shows that the ternary quadratic form induced by the reduced norm on the Gross lattice of
$R_0$
is the order appearing in the statement of Proposition 6·2. A computation similar to the one carried out during the proof of Theorem 3·1 shows that the ternary quadratic form induced by the reduced norm on the Gross lattice of
![]() $R_n$
with basis
$R_n$
with basis
![]() $\{1+2\zeta_3, \ell^n(2\xi -1), 2\ell^n (\varphi + \zeta_3 \varphi) \}$
is given by
$\{1+2\zeta_3, \ell^n(2\xi -1), 2\ell^n (\varphi + \zeta_3 \varphi) \}$
is given by
for all
![]() $n \in \mathbb{N}$
. Proposition 6·3 combined with Lemma 2·1 implies in particular that, for any primitive triple of integers
$n \in \mathbb{N}$
. Proposition 6·3 combined with Lemma 2·1 implies in particular that, for any primitive triple of integers
![]() $(x,y,z) \in \mathbb{Z}^3$
such that
$(x,y,z) \in \mathbb{Z}^3$
such that
![]() $-D\;:\!=\;Q_{\ell,n}(x,y,z)$
is not divisible by
$-D\;:\!=\;Q_{\ell,n}(x,y,z)$
is not divisible by
![]() $\ell$
, there exists an elliptic curve
$\ell$
, there exists an elliptic curve
![]() $E_{/W}$
with complex multiplication by the order of discriminant D and which is isomorphic to
$E_{/W}$
with complex multiplication by the order of discriminant D and which is isomorphic to
![]() $E_0\;:\;y^2=x^3+1$
modulo
$E_0\;:\;y^2=x^3+1$
modulo
![]() $\pi^{n+1}$
. The primitive triple (1, 0, 1) gives
$\pi^{n+1}$
. The primitive triple (1, 0, 1) gives
which is not divisible by
![]() $\ell$
. The j-invariant of the corresponding elliptic curve E with CM by the order of discriminant D will satisfy, by [
Reference Gross and Zagier21
, Proposition 2.3], the inequality
$\ell$
. The j-invariant of the corresponding elliptic curve E with CM by the order of discriminant D will satisfy, by [
Reference Gross and Zagier21
, Proposition 2.3], the inequality
for some prime
![]() $\mu \subseteq H_\mathcal{O}$
lying above
$\mu \subseteq H_\mathcal{O}$
lying above
![]() $\ell$
. This concludes the proof of the theorem.
$\ell$
. This concludes the proof of the theorem.
7. A uniformity conjecture for singular moduli
In this final section we make some speculations, based on computer-assisted numerical calculations, concerning differences of singular moduli that are S-units. The starting point of our discussion is the following observation, which was already made in a previous version of this manuscript (compare also with [
Reference Herrero, Menares and Rivera–Letelier27
, Question 1.2]): numerical computations seem to show that
![]() $j_{-11}=-2^{15}$
, which is the unique singular modulus relative to the order of discriminant
$j_{-11}=-2^{15}$
, which is the unique singular modulus relative to the order of discriminant
![]() $\Delta=-11$
, may also be the only singular modulus that is an
$\Delta=-11$
, may also be the only singular modulus that is an
![]() $\{\ell\}$
-unit for some prime
$\{\ell\}$
-unit for some prime
![]() $\ell$
. In other words, it seems that the set
$\ell$
. In other words, it seems that the set
![]() $\mathcal{J}_1$
of singular moduli that are S-units for some set of primes S of cardinality 1 contains only one element, namely
$\mathcal{J}_1$
of singular moduli that are S-units for some set of primes S of cardinality 1 contains only one element, namely
![]() $j_{-11}$
. It appears then natural to ask what happens if we increase the cardinality of the set S. Motivated by this question, we have performed some computations, whose results are displayed in Table 1. Let us describe the notation and the content of this table.
$j_{-11}$
. It appears then natural to ask what happens if we increase the cardinality of the set S. Motivated by this question, we have performed some computations, whose results are displayed in Table 1. Let us describe the notation and the content of this table.
Table 1. The table displays for
![]() $s\in \{1,...,7\}$
the number of imaginary quadratic discriminants up to
$s\in \{1,...,7\}$
the number of imaginary quadratic discriminants up to
![]() $-5\cdot 10^4$
for which the corresponding singular moduli are S-units with
$-5\cdot 10^4$
for which the corresponding singular moduli are S-units with
![]() $\#S=s$
(second column). The third column shows the biggest among the found discriminants and the fourth column shows all the primes appearing in the factorisations of the norms of the corresponding singular moduli.
$\#S=s$
(second column). The third column shows the biggest among the found discriminants and the fourth column shows all the primes appearing in the factorisations of the norms of the corresponding singular moduli.

If a singular modulus of discriminant
![]() $\Delta$
is an S-unit for some set S of rational primes, then actually all singular moduli of discriminant
$\Delta$
is an S-unit for some set S of rational primes, then actually all singular moduli of discriminant
![]() $\Delta$
are singular S-units since, as we discussed in Section 2, the set of singular moduli relative to the same discriminant form a full Galois orbit over
$\Delta$
are singular S-units since, as we discussed in Section 2, the set of singular moduli relative to the same discriminant form a full Galois orbit over
![]() $\mathbb{Q}$
. For every
$\mathbb{Q}$
. For every
![]() $s,A \in \mathbb{N}$
denote then by
$s,A \in \mathbb{N}$
denote then by
![]() $\mathcal{J}_s$
the set of Galois orbits of singular moduli that are S-units for some set S of rational primes satisfying
$\mathcal{J}_s$
the set of Galois orbits of singular moduli that are S-units for some set S of rational primes satisfying
![]() $\#S=s$
and by
$\#S=s$
and by
![]() $\mathcal{J}_{s}(A)$
the subset of
$\mathcal{J}_{s}(A)$
the subset of
![]() $\mathcal{J}_s$
consisting of those orbits whose corresponding singular moduli have discriminant
$\mathcal{J}_s$
consisting of those orbits whose corresponding singular moduli have discriminant
![]() $\Delta$
satisfying
$\Delta$
satisfying
![]() $|\Delta| \leq A$
. Similarly, denote by
$|\Delta| \leq A$
. Similarly, denote by
![]() $\Delta_{\text{max},s}$
(resp.
$\Delta_{\text{max},s}$
(resp.
![]() $\Delta_{\text{max},s}(A)$
) the biggest (in absolute value) imaginary quadratic discriminant such that there exists a singular modulus of discriminant
$\Delta_{\text{max},s}(A)$
) the biggest (in absolute value) imaginary quadratic discriminant such that there exists a singular modulus of discriminant
![]() $\Delta_{\text{max},s}$
whose Galois orbit belongs to
$\Delta_{\text{max},s}$
whose Galois orbit belongs to
![]() $\mathcal{J}_s$
(resp. to
$\mathcal{J}_s$
(resp. to
![]() $\mathcal{J}_{s}(A)$
). If
$\mathcal{J}_{s}(A)$
). If
![]() $\mathcal{J}_s$
is an infinite set, we put
$\mathcal{J}_s$
is an infinite set, we put
![]() $\Delta_{\text{max},s}=-\infty$
. Clearly, for every pair of natural numbers
$\Delta_{\text{max},s}=-\infty$
. Clearly, for every pair of natural numbers
![]() $A_1 \leq A_2$
we have
$A_1 \leq A_2$
we have
In Table 1 we have computed, with the help of SAGE [
39
], the cardinality of
![]() $\mathcal{J}_{s}(50000)$
for
$\mathcal{J}_{s}(50000)$
for
![]() $s \in \{1,...,7\}$
, and the corresponding
$s \in \{1,...,7\}$
, and the corresponding
![]() $\Delta_{\text{max},s}(50000)$
. Moreover, in the last column we have collected all the primes appearing in the norm factorisations of
$\Delta_{\text{max},s}(50000)$
. Moreover, in the last column we have collected all the primes appearing in the norm factorisations of
![]() $j \in \mathcal{J}_{s}(50000)$
.
$j \in \mathcal{J}_{s}(50000)$
.
The results displayed in Table 1 show, for small values of
![]() $s \in \mathbb{N}$
, that
$s \in \mathbb{N}$
, that
![]() $\Delta_{\text{max},s}(50000)$
is much smaller compared to the bound
$\Delta_{\text{max},s}(50000)$
is much smaller compared to the bound
![]() $|\Delta| \leq 50000$
up to which we have performed our computations. For instance, we see that among all the Galois orbits of singular moduli with discriminant
$|\Delta| \leq 50000$
up to which we have performed our computations. For instance, we see that among all the Galois orbits of singular moduli with discriminant
![]() $|\Delta| \leq 50000$
, only 9 orbits contain singular S-units for some set S with
$|\Delta| \leq 50000$
, only 9 orbits contain singular S-units for some set S with
![]() $\#S \leq 2$
. Moreover, the biggest discriminant associated to a singular modulus belonging to one of these 9 orbits is
$\#S \leq 2$
. Moreover, the biggest discriminant associated to a singular modulus belonging to one of these 9 orbits is
![]() $\Delta=-83$
. All this seems to suggest that
$\Delta=-83$
. All this seems to suggest that
![]() $\Delta_{\text{max},s}(A)$
will remain constant for all
$\Delta_{\text{max},s}(A)$
will remain constant for all
![]() $A \geq 50000$
i.e. that
$A \geq 50000$
i.e. that
![]() $\Delta_{\text{max},s}(50000)=\Delta_{\text{max},s}$
for
$\Delta_{\text{max},s}(50000)=\Delta_{\text{max},s}$
for
![]() $s \in \{1,...,7\}$
, which would mean that the number of primes dividing the norm of a singular modulus must increase as the absolute value of its discriminant gets bigger. If this were actually true, then the last column of Table 1 would show which primes a set S of cardinality s must contain in order for the set of singular S-units whose norm has exactly s prime factors to be non-empty (but for some of the resulting s-tuples the corresponding set of singular S-units is empty). For example, it seems from these computations that the set of singular
$s \in \{1,...,7\}$
, which would mean that the number of primes dividing the norm of a singular modulus must increase as the absolute value of its discriminant gets bigger. If this were actually true, then the last column of Table 1 would show which primes a set S of cardinality s must contain in order for the set of singular S-units whose norm has exactly s prime factors to be non-empty (but for some of the resulting s-tuples the corresponding set of singular S-units is empty). For example, it seems from these computations that the set of singular
![]() $\{17,23\}$
-units does not contain any singular modulus. All this discussion leads to the formulation of the following conjecture.
$\{17,23\}$
-units does not contain any singular modulus. All this discussion leads to the formulation of the following conjecture.
Table 2. The table displays for
![]() $s\in \{1,...,7\}$
the number of imaginary quadratic discriminants up to
$s\in \{1,...,7\}$
the number of imaginary quadratic discriminants up to
![]() $-5\cdot 10^4$
for which the corresponding singular moduli j are such that
$-5\cdot 10^4$
for which the corresponding singular moduli j are such that
![]() $j-1728$
is an S-unit for some S with
$j-1728$
is an S-unit for some S with
![]() $\#S=s$
(second column). The third column shows the biggest among the found discriminants and the fourth column shows all the primes appearing in the factorisations of the corresponding norms of
$\#S=s$
(second column). The third column shows the biggest among the found discriminants and the fourth column shows all the primes appearing in the factorisations of the corresponding norms of
![]() $j-1728$
.
$j-1728$
.

Conjecture 7·1 (Uniformity conjecture for singular units). For every
![]() $s \in \mathbb{N}$
, the set
$s \in \mathbb{N}$
, the set
![]() $\mathcal{J}_s$
is finite.
$\mathcal{J}_s$
is finite.
We could have equivalently formulated the above conjecture by saying that for every finite set S of rational primes, the set of singular S-units is finite and its cardinality can be bounded only in terms of the cardinality of S, regardless from the primes contained in the latter set. The fact that this statement is equivalent to Conjecture 7·1 can be seen as follows: suppose that for every
![]() $s \in \mathbb{N}$
there exists a constant
$s \in \mathbb{N}$
there exists a constant
![]() $C(s) \geq 0$
such that the set of singular S-units has cardinality bounded by C(s) whenever S is a set of rational primes satisfying
$C(s) \geq 0$
such that the set of singular S-units has cardinality bounded by C(s) whenever S is a set of rational primes satisfying
![]() $\#S=s$
. Since being an S-unit is Galois invariant, this implies that C(s) also bounds the size of the Galois orbit of any such singular S-unit, hence the class number of the corresponding imaginary quadratic order. By the Brauer–Siegel Theorem [
Reference Lang32
, Chapter XIII, Theorem 4] this entails a bound on the discriminant of any singular S-unit with
$\#S=s$
. Since being an S-unit is Galois invariant, this implies that C(s) also bounds the size of the Galois orbit of any such singular S-unit, hence the class number of the corresponding imaginary quadratic order. By the Brauer–Siegel Theorem [
Reference Lang32
, Chapter XIII, Theorem 4] this entails a bound on the discriminant of any singular S-unit with
![]() $\#S=s$
. Hence any such singular modulus must lie in a finite set that depends only on s, but not on S and Conjecture 7·1 follows.
$\#S=s$
. Hence any such singular modulus must lie in a finite set that depends only on s, but not on S and Conjecture 7·1 follows.
Inspecting the computations displayed in Table 1, one could also try to be more precise on the cardinality of the sets
![]() $\mathcal{J}_s$
. For instance, we may ask the following
$\mathcal{J}_s$
. For instance, we may ask the following
Question 7.2. Is it true that there exists only 1 singular modulus which is an S-unit for
![]() $\#S=1$
, and 9 Galois orbits of singular moduli that are S-units for
$\#S=1$
, and 9 Galois orbits of singular moduli that are S-units for
![]() $\#S=2$
?
$\#S=2$
?
The author finds it more difficult to formulate precise conjectures on how the number of primes dividing the norm of a singular modulus increases with respect to its discriminant.
Of course, there is no reason to restrict our attention to singular S-units. One can make similar conjectures for differences of the form
![]() $j-j_0$
with
$j-j_0$
with
![]() $j_0$
a fixed singular modulus. For instance, Table 2 shows how the above considerations seem to hold true also for differences of the form
$j_0$
a fixed singular modulus. For instance, Table 2 shows how the above considerations seem to hold true also for differences of the form
![]() $j-1728$
. The notation is the same used for Table 1, but with the necessary modifications:
$j-1728$
. The notation is the same used for Table 1, but with the necessary modifications:
![]() $\mathcal{J}_s$
is the set of Galois orbits of singular moduli j such that
$\mathcal{J}_s$
is the set of Galois orbits of singular moduli j such that
![]() $j-1728$
is an S-unit for some set S of rational primes satisfying
$j-1728$
is an S-unit for some set S of rational primes satisfying
![]() $\#S=s$
, etc. Further computations with other differences
$\#S=s$
, etc. Further computations with other differences
![]() $j-j_0$
would probably shed more light on whether it is possible that for every
$j-j_0$
would probably shed more light on whether it is possible that for every
![]() $s\in \mathbb{N}$
, there is only a finite number of singular differences
$s\in \mathbb{N}$
, there is only a finite number of singular differences
![]() $j_1-j_2$
that are S-units for some sets S of cardinality s. But we do not want to enter this territory here.
$j_1-j_2$
that are S-units for some sets S of cardinality s. But we do not want to enter this territory here.
Acknowledgments
The author would like to thank Fabien Pazuki for his constant support and for the comments on previous versions of this manuscript. He would also like to thank Philipp Habegger and the University of Basel for their hospitality, and Jared Asuncion, Yuri Bilu, Gabriel Dill, Florent Jouve, Riccardo Pengo and Emanuele Tron for the useful discussions. Finally, he would like to thank the anonymous referee for their careful review and the great number of suggestions that have very much improved the manuscript.
The author is grateful to Max Planck Institute for Mathematics in Bonn for its hospitality and financial support. The author is also supported by ANR-20-CE40-0003 Jinvariant.
This project has received funding from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 801199.