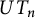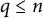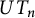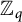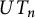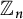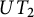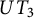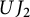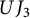1 Introduction
Let
![]() $\mathcal {A}$
be an associative algebra over a field F, and let
$\mathcal {A}$
be an associative algebra over a field F, and let
![]() $f\in F\langle X\rangle $
be a multilinear polynomial from the free associative algebra
$f\in F\langle X\rangle $
be a multilinear polynomial from the free associative algebra
![]() $F\langle X\rangle $
. Lvov posed the question to determine whether the image of a multilinear f when evaluated on
$F\langle X\rangle $
. Lvov posed the question to determine whether the image of a multilinear f when evaluated on
![]() $\mathcal {A}=M_n(F)$
, is always a vector subspace of
$\mathcal {A}=M_n(F)$
, is always a vector subspace of
![]() $M_n(F)$
(see [Reference Filippov, Kharchenko and Shestakov17, Problem 1.93]). The original question is attributed to Kaplansky and asks the determination of the image of a polynomial f on
$M_n(F)$
(see [Reference Filippov, Kharchenko and Shestakov17, Problem 1.93]). The original question is attributed to Kaplansky and asks the determination of the image of a polynomial f on
![]() $\mathcal {A}$
. It is well known that the above question is equivalent to that of determining whether the image of a multilinear f on
$\mathcal {A}$
. It is well known that the above question is equivalent to that of determining whether the image of a multilinear f on
![]() $M_n(F)$
is 0, the scalar matrices,
$M_n(F)$
is 0, the scalar matrices,
![]() $sl_n(F)$
, or
$sl_n(F)$
, or
![]() $M_n(F)$
. Clearly, the first possibility corresponds to f being a polynomial identity on
$M_n(F)$
. Clearly, the first possibility corresponds to f being a polynomial identity on
![]() $M_n(F)$
, and the second gives the central polynomials.
$M_n(F)$
, and the second gives the central polynomials.
Recall here that the description of all polynomial identities on
![]() $M_n(F)$
is known only for
$M_n(F)$
is known only for
![]() $n\le 2$
(see [Reference Drensky12, Reference Razmyslov36] for the case when F is of characteristic 0 and [Reference Koshlukov28] for the case of F infinite of characteristic
$n\le 2$
(see [Reference Drensky12, Reference Razmyslov36] for the case when F is of characteristic 0 and [Reference Koshlukov28] for the case of F infinite of characteristic
![]() $p>2$
). The same holds for the central polynomials [Reference Colombo and Koshlukov9, Reference Okhitin35]. The theorem of Amitsur and Levitzki gives the least degree polynomial identity for
$p>2$
). The same holds for the central polynomials [Reference Colombo and Koshlukov9, Reference Okhitin35]. The theorem of Amitsur and Levitzki gives the least degree polynomial identity for
![]() $M_n(F)$
, the standard polynomial
$M_n(F)$
, the standard polynomial
![]() $s_{2n}$
(see [Reference Amitsur and Levitzki2]). Recall also that one of the major breakthroughs in polynomial identities (PI) theory was achieved by Formanek and by Razmyslov [Reference Formanek18, Reference Razmyslov37], who proved the existence of nontrivial (that is not identities) central polynomials for the matrix algebras. As for
$s_{2n}$
(see [Reference Amitsur and Levitzki2]). Recall also that one of the major breakthroughs in polynomial identities (PI) theory was achieved by Formanek and by Razmyslov [Reference Formanek18, Reference Razmyslov37], who proved the existence of nontrivial (that is not identities) central polynomials for the matrix algebras. As for
![]() $sl_n(F)$
, a theorem of Shoda [Reference Shoda38] gives that every
$sl_n(F)$
, a theorem of Shoda [Reference Shoda38] gives that every
![]() $n\times n$
matrix over a field of zero characteristic is the commutator of two matrices; later on, Albert and Muckenhoupt [Reference Albert and Muckenhoupt1] generalized this to arbitrary fields. Hence, all four conjectured possibilities for the image of a multilinear polynomial on
$n\times n$
matrix over a field of zero characteristic is the commutator of two matrices; later on, Albert and Muckenhoupt [Reference Albert and Muckenhoupt1] generalized this to arbitrary fields. Hence, all four conjectured possibilities for the image of a multilinear polynomial on
![]() $M_n(F)$
can be achieved.
$M_n(F)$
can be achieved.
The study of images of polynomials on the full matrix algebra is of considerable interest for obvious reasons, among these the relation to polynomial identities. In [Reference Kanel-Belov, Malev and Rowen24], the authors settled the conjecture due to Lvov in the case of
![]() $2\times 2$
matrices over a quadratically closed field F (that is, if f is a given polynomial in several variables, then every polynomial in one variable of degree
$2\times 2$
matrices over a quadratically closed field F (that is, if f is a given polynomial in several variables, then every polynomial in one variable of degree
![]() $\le 2\deg f$
over F has a root in F). They proved that for every multilinear polynomial f and for every field F that is quadratically closed with respect to f, the image of f on
$\le 2\deg f$
over F has a root in F). They proved that for every multilinear polynomial f and for every field F that is quadratically closed with respect to f, the image of f on
![]() $M_2(F)$
is 0, F,
$M_2(F)$
is 0, F,
![]() $sl_2(F)$
, or
$sl_2(F)$
, or
![]() $M_2(F)$
. It should be noted that the authors in [Reference Kanel-Belov, Malev and Rowen24] proved a stronger result. Namely, they considered a so-called semi-homogeneous polynomial f: a polynomial in m variables
$M_2(F)$
. It should be noted that the authors in [Reference Kanel-Belov, Malev and Rowen24] proved a stronger result. Namely, they considered a so-called semi-homogeneous polynomial f: a polynomial in m variables
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_m$
of weights
$x_m$
of weights
![]() $d_1$
, …,
$d_1$
, …,
![]() $d_m$
, respectively, such that every monomial of f is of (weighted) degree d for a fixed d. They proved that the image of such a polynomial on
$d_m$
, respectively, such that every monomial of f is of (weighted) degree d for a fixed d. They proved that the image of such a polynomial on
![]() $M_2(F)$
must be 0, F,
$M_2(F)$
must be 0, F,
![]() $sl_2(F)$
, the set of all non-nilpotent traceless matrices, or a dense subset of
$sl_2(F)$
, the set of all non-nilpotent traceless matrices, or a dense subset of
![]() $M_2(F)$
. Here, the density is according to the Zariski topology. Later on, in [Reference Malev33], the author gave the solution to the problem for
$M_2(F)$
. Here, the density is according to the Zariski topology. Later on, in [Reference Malev33], the author gave the solution to the problem for
![]() $2\times 2$
matrices for the case when F is the field of the real numbers. In the case of
$2\times 2$
matrices for the case when F is the field of the real numbers. In the case of
![]() $3\times 3$
matrices, the known results can be found in [Reference Kanel-Belov, Malev and Rowen25]. The images of polynomials on
$3\times 3$
matrices, the known results can be found in [Reference Kanel-Belov, Malev and Rowen25]. The images of polynomials on
![]() $n\times n$
matrices for
$n\times n$
matrices for
![]() $n>3$
are hard to describe, and there are only partial results (see, for example, [Reference Kanel-Belov, Malev and Rowen26]). Hence, in the case of
$n>3$
are hard to describe, and there are only partial results (see, for example, [Reference Kanel-Belov, Malev and Rowen26]). Hence, in the case of
![]() $n\times n$
matrices, one is led to study images of polynomials of low degree. Interesting results in this direction are due to Špenko [Reference Špenko40], who proved the conjecture raised by Lvov in case F is an algebraically closed field of characteristic 0, and f is a multilinear Lie polynomial of degree at most 4. Further advances in the field were made in [Reference Brešar5–Reference Brešar and Klep7]. In [Reference Brešar5], the author proved that if A is an algebra over an infinite field F and
$n\times n$
matrices, one is led to study images of polynomials of low degree. Interesting results in this direction are due to Špenko [Reference Špenko40], who proved the conjecture raised by Lvov in case F is an algebraically closed field of characteristic 0, and f is a multilinear Lie polynomial of degree at most 4. Further advances in the field were made in [Reference Brešar5–Reference Brešar and Klep7]. In [Reference Brešar5], the author proved that if A is an algebra over an infinite field F and
![]() $A=[A,A]$
, then the image of an arbitrary polynomial which is neither an identity nor a central polynomial equals A. Recently, Malev [Reference Malev34] described completely the images of multilinear polynomials on the real quaternion algebra; he also described the images of semi-homogeneous polynomials on the same algebra.
$A=[A,A]$
, then the image of an arbitrary polynomial which is neither an identity nor a central polynomial equals A. Recently, Malev [Reference Malev34] described completely the images of multilinear polynomials on the real quaternion algebra; he also described the images of semi-homogeneous polynomials on the same algebra.
If the base field F is finite, a theorem of Chuang [Reference Chuang8] states that the image of a polynomial without constant term can be every subset of
![]() $M_n(F)$
that contains
$M_n(F)$
that contains
![]() $0$
and is closed under conjugation by invertible matrices. In the same paper, it was also shown that such a statement fails when F is infinite.
$0$
and is closed under conjugation by invertible matrices. In the same paper, it was also shown that such a statement fails when F is infinite.
Therefore, it seems likely it should be very difficult to describe satisfactorily the images of multilinear polynomials on
![]() $M_n(F)$
. That is why people started studying images of polynomials on “easier” algebras, and also on algebras with an additional structure. The upper triangular matrix algebras are quite important in Linear Algebra because of their applications to different branches of Mathematics and Physics. They are also very important in PI theory: they describe, in a sense, the subvarieties of the variety of algebras generated by
$M_n(F)$
. That is why people started studying images of polynomials on “easier” algebras, and also on algebras with an additional structure. The upper triangular matrix algebras are quite important in Linear Algebra because of their applications to different branches of Mathematics and Physics. They are also very important in PI theory: they describe, in a sense, the subvarieties of the variety of algebras generated by
![]() $M_2(F)$
in characteristic 0. Block-triangular matrices appear in the description of the so-called minimal varieties of algebras. The images of polynomials on the upper triangular matrices have been studied rather extensively. In [Reference Wang43], the author described the images of multilinear polynomials on
$M_2(F)$
in characteristic 0. Block-triangular matrices appear in the description of the so-called minimal varieties of algebras. The images of polynomials on the upper triangular matrices have been studied rather extensively. In [Reference Wang43], the author described the images of multilinear polynomials on
![]() $UT_2(F)$
, the
$UT_2(F)$
, the
![]() $2\times 2$
upper triangular matrices over a field F. The images of multilinear polynomials of degree up to 4 on
$2\times 2$
upper triangular matrices over a field F. The images of multilinear polynomials of degree up to 4 on
![]() $UT_n=UT_n(F)$
for every n were classified in [Reference Fagundes and de Mello16], and in [Reference Fagundes15] the first-named author of the present paper described the images of arbitrary multilinear polynomials on the strictly upper triangular matrices. It turned out that if f is a multilinear polynomial of degree m, then its image on the strictly upper triangular matrix algebra J is either 0 or
$UT_n=UT_n(F)$
for every n were classified in [Reference Fagundes and de Mello16], and in [Reference Fagundes15] the first-named author of the present paper described the images of arbitrary multilinear polynomials on the strictly upper triangular matrices. It turned out that if f is a multilinear polynomial of degree m, then its image on the strictly upper triangular matrix algebra J is either 0 or
![]() $J^{m}$
. The following conjecture was raised in [Reference Fagundes and de Mello16]: Is the image of a multilinear polynomial on
$J^{m}$
. The following conjecture was raised in [Reference Fagundes and de Mello16]: Is the image of a multilinear polynomial on
![]() $UT_n(F)$
always a vector subspace of
$UT_n(F)$
always a vector subspace of
![]() $UT_n(F)$
? This conjecture was solved independently in [Reference Luo and Wang32], for infinite fields (or finite fields with sufficiently many elements), and in [Reference Gargate and de Mello19]. Further results concerning images of polynomials on the upper triangular matrix algebra can be found in [Reference de Mello10, Reference Wang, Zhou and Luo44, Reference Zhou and Wang45].
$UT_n(F)$
? This conjecture was solved independently in [Reference Luo and Wang32], for infinite fields (or finite fields with sufficiently many elements), and in [Reference Gargate and de Mello19]. Further results concerning images of polynomials on the upper triangular matrix algebra can be found in [Reference de Mello10, Reference Wang, Zhou and Luo44, Reference Zhou and Wang45].
Gradings on algebras appeared long ago; the polynomial ring in one or several variables is naturally graded by the infinite cyclic group
![]() $\mathbb {Z}$
by the degree. Gradings on algebras by finite groups are important in Linear Algebra and also in Theoretical Physics: the Grassmann (or exterior) algebra is naturally graded by the cyclic group of order 2,
$\mathbb {Z}$
by the degree. Gradings on algebras by finite groups are important in Linear Algebra and also in Theoretical Physics: the Grassmann (or exterior) algebra is naturally graded by the cyclic group of order 2,
![]() $\mathbb {Z}_2$
. In fact, the Grassmann algebra is the most well-known example of a superalgebra. It should be noted that while in the associative case, the term “superalgebra” is synonymous to “
$\mathbb {Z}_2$
. In fact, the Grassmann algebra is the most well-known example of a superalgebra. It should be noted that while in the associative case, the term “superalgebra” is synonymous to “
![]() $\mathbb {Z}_2$
-graded algebra,” if one considers nonassociative algebras, these notions are very different: a Lie or a Jordan superalgebra seldom is a Lie or a Jordan algebra. We are not going to discuss further such topics because these are not relevant for our exposition.
$\mathbb {Z}_2$
-graded algebra,” if one considers nonassociative algebras, these notions are very different: a Lie or a Jordan superalgebra seldom is a Lie or a Jordan algebra. We are not going to discuss further such topics because these are not relevant for our exposition.
In [Reference Wall42], Wall classified the finite-dimensional
![]() $\mathbb {Z}_2$
-graded algebras that are graded simple. Later on, the description of all gradings on matrix algebras was obtained as well as on simple Lie and Jordan algebras. We refer the readers to the monograph [Reference Elduque and Kochetov14] for the state-of-the-art and for further references. In PI theory, gradings appeared in the works of Kemer (see [Reference Kemer27]), and constituted one of the main tools in the classification of the ideals of identities of associative algebras, which in turn led him to the positive solution of the long-standing Specht Problem. It turns out that the graded identities are easier to describe than the ordinary ones; still they provide a lot of information on the latter. It is somewhat surprising that the images of polynomials have not been studied extensively in the graded setting. In [Reference Kulyamin31], Kulyamin described the images of graded polynomials on matrix algebras over the group algebra of a finite group over a finite field.
$\mathbb {Z}_2$
-graded algebras that are graded simple. Later on, the description of all gradings on matrix algebras was obtained as well as on simple Lie and Jordan algebras. We refer the readers to the monograph [Reference Elduque and Kochetov14] for the state-of-the-art and for further references. In PI theory, gradings appeared in the works of Kemer (see [Reference Kemer27]), and constituted one of the main tools in the classification of the ideals of identities of associative algebras, which in turn led him to the positive solution of the long-standing Specht Problem. It turns out that the graded identities are easier to describe than the ordinary ones; still they provide a lot of information on the latter. It is somewhat surprising that the images of polynomials have not been studied extensively in the graded setting. In [Reference Kulyamin31], Kulyamin described the images of graded polynomials on matrix algebras over the group algebra of a finite group over a finite field.
The upper triangular matrix algebra admits various gradings, and these were shown to be isomorphic to elementary ones (see [Reference Valenti and Zaicev41]). A grading on a subalgebra A of
![]() $M_n(F)$
is elementary if all matrix units
$M_n(F)$
is elementary if all matrix units
![]() $e_{ij}\in A$
are homogeneous in the grading. All elementary gradings on
$e_{ij}\in A$
are homogeneous in the grading. All elementary gradings on
![]() $UT_n$
were classified in [Reference Di Vincenzo, Koshlukov and Valenti11]; in the same paper, the authors described the graded identities for all these gradings. In this paper, we fix an arbitrary field F and the upper triangular matrix algebra
$UT_n$
were classified in [Reference Di Vincenzo, Koshlukov and Valenti11]; in the same paper, the authors described the graded identities for all these gradings. In this paper, we fix an arbitrary field F and the upper triangular matrix algebra
![]() $UT_n$
.
$UT_n$
.
In Section 3, we prove that for an arbitrary group grading on
![]() $UT_n$
,
$UT_n$
,
![]() $n>1$
, there are no nontrivial graded central polynomials. (Hence, the image of a graded polynomial on
$n>1$
, there are no nontrivial graded central polynomials. (Hence, the image of a graded polynomial on
![]() $UT_n$
cannot be equal to the scalar matrices whenever
$UT_n$
cannot be equal to the scalar matrices whenever
![]() $n>1$
.) In Section 4, we consider a specific grading on
$n>1$
.) In Section 4, we consider a specific grading on
![]() $UT_n$
, and describe all possible images of multilinear graded polynomials for that grading. It turns out that the images are always homogeneous vector subspaces. We impose a mild restriction on the cardinality of the base field. As a by-product of the proof, we obtain a precise description of the graded identities for this grading.
$UT_n$
, and describe all possible images of multilinear graded polynomials for that grading. It turns out that the images are always homogeneous vector subspaces. We impose a mild restriction on the cardinality of the base field. As a by-product of the proof, we obtain a precise description of the graded identities for this grading.
In Section 5, we give a sufficient condition for the traceless matrices to be contained in the image of a multilinear graded polynomial. Once again, we require a mild condition on the cardinality of the field. Section 6 studies the graded algebras
![]() $UT_2$
and
$UT_2$
and
![]() $UT_3$
. We prove that the image of a multilinear graded polynomial on
$UT_3$
. We prove that the image of a multilinear graded polynomial on
![]() $UT_2$
, for every group grading, is a homogeneous subspace. In the case of
$UT_2$
, for every group grading, is a homogeneous subspace. In the case of
![]() $UT_3$
, the image of such a polynomial is also a homogeneous subspace provided that the grading is nontrivial. In the case of the trivial grading, if the field contains at least three elements, then the image of every multilinear polynomial is a vector subspace. Then we proceed with the Jordan algebra structure
$UT_3$
, the image of such a polynomial is also a homogeneous subspace provided that the grading is nontrivial. In the case of the trivial grading, if the field contains at least three elements, then the image of every multilinear polynomial is a vector subspace. Then we proceed with the Jordan algebra structure
![]() $UJ_n$
obtained from
$UJ_n$
obtained from
![]() $UT_n$
by the Jordan (symmetric) product
$UT_n$
by the Jordan (symmetric) product
![]() $a\circ b= ab+ba$
provided that the characteristic of the base field is different from 2. The description of all group gradings on
$a\circ b= ab+ba$
provided that the characteristic of the base field is different from 2. The description of all group gradings on
![]() $UJ_n$
is more complicated than that on
$UJ_n$
is more complicated than that on
![]() $UT_n$
(see [Reference Koshlukov and Yasumura30]), there appear gradings that are not isomorphic to elementary ones. The gradings on
$UT_n$
(see [Reference Koshlukov and Yasumura30]), there appear gradings that are not isomorphic to elementary ones. The gradings on
![]() $UJ_2$
were described in [Reference Koshlukov and Martino29]. We consider each one of these gradings, and prove that the image of a multilinear graded polynomial is always a homogeneous subspace. No restrictions on the base field are imposed (apart from the characteristic being different from 2). An analogous result is deduced for the Lie algebra
$UJ_2$
were described in [Reference Koshlukov and Martino29]. We consider each one of these gradings, and prove that the image of a multilinear graded polynomial is always a homogeneous subspace. No restrictions on the base field are imposed (apart from the characteristic being different from 2). An analogous result is deduced for the Lie algebra
![]() $UT_2^{(-)}$
obtained from
$UT_2^{(-)}$
obtained from
![]() $UT_n$
by substituting the associative product by the Lie bracket
$UT_n$
by substituting the associative product by the Lie bracket
![]() $[a,b]=ab-ba$
. Finally, we consider
$[a,b]=ab-ba$
. Finally, we consider
![]() $UJ_3$
equipped with the natural
$UJ_3$
equipped with the natural
![]() $\mathbb {Z}_3$
-grading:
$\mathbb {Z}_3$
-grading:
![]() $\deg e_{ij} = j-i\pmod {3}$
for every
$\deg e_{ij} = j-i\pmod {3}$
for every
![]() $i\le j$
, assuming the base field infinite and of characteristic different from 2. We prove that the image of a multilinear graded polynomial is always a homogeneous subspace.
$i\le j$
, assuming the base field infinite and of characteristic different from 2. We prove that the image of a multilinear graded polynomial is always a homogeneous subspace.
We hope that this paper will initiate a more detailed study of images of polynomials on algebras with additional structures.
2 Preliminaries
Unless otherwise stated, we denote by F an arbitrary field and
![]() $\mathcal {A}$
an associative algebra over F. Given a group G, a G-grading on
$\mathcal {A}$
an associative algebra over F. Given a group G, a G-grading on
![]() $\mathcal {A}$
is a decomposition of
$\mathcal {A}$
is a decomposition of
![]() $\mathcal {A}$
in a direct sum of subspaces
$\mathcal {A}$
in a direct sum of subspaces
![]() $\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
such that
$\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
such that
![]() $\mathcal {A}_{g}\mathcal {A}_{h}\subset \mathcal {A}_{gh}$
, for all g,
$\mathcal {A}_{g}\mathcal {A}_{h}\subset \mathcal {A}_{gh}$
, for all g,
![]() $h \in G$
. We define the support of a G-grading on
$h \in G$
. We define the support of a G-grading on
![]() $\mathcal {A}$
as the subset
$\mathcal {A}$
as the subset
![]() $\mathrm{supp}(\mathcal {A})=\{g\in G\mid \mathcal {A}_{g}\neq 0\}$
. A subspace U of
$\mathrm{supp}(\mathcal {A})=\{g\in G\mid \mathcal {A}_{g}\neq 0\}$
. A subspace U of
![]() $\mathcal {A}$
is called homogeneous if
$\mathcal {A}$
is called homogeneous if
![]() $U=\bigoplus _{g\in G}(U\cap \mathcal {A}_{g})$
. A graded homomorphism between two graded algebras
$U=\bigoplus _{g\in G}(U\cap \mathcal {A}_{g})$
. A graded homomorphism between two graded algebras
![]() $\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
and
$\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
and
![]() $\mathcal {B}=\bigoplus _{g\in G}\mathcal {B}_{g}$
is defined as an algebra homomorphism
$\mathcal {B}=\bigoplus _{g\in G}\mathcal {B}_{g}$
is defined as an algebra homomorphism
![]() $\varphi \colon \mathcal {A}\rightarrow \mathcal {B}$
such that
$\varphi \colon \mathcal {A}\rightarrow \mathcal {B}$
such that
![]() $\varphi (\mathcal {A}_{g})\subset \mathcal {B}_{g}$
for every
$\varphi (\mathcal {A}_{g})\subset \mathcal {B}_{g}$
for every
![]() $g\in G$
. We denote by
$g\in G$
. We denote by
![]() $F\langle X \rangle ^{gr}$
the free G-graded associative algebra generated by a set of noncommuting variables
$F\langle X \rangle ^{gr}$
the free G-graded associative algebra generated by a set of noncommuting variables
![]() $X=\{x_{i}^{(g)}\mid i\in \mathbb {N},g\in G\}$
. We also denote the neutral (that is of degree
$X=\{x_{i}^{(g)}\mid i\in \mathbb {N},g\in G\}$
. We also denote the neutral (that is of degree
![]() $1\in G$
) variables by y and call them even variables, and the nonneutral ones by z, and we call them odd variables. We draw the reader’s attention that odd variables may have different degrees in the G-grading.
$1\in G$
) variables by y and call them even variables, and the nonneutral ones by z, and we call them odd variables. We draw the reader’s attention that odd variables may have different degrees in the G-grading.
We define the image of a graded polynomial on an algebra as in [Reference Kulyamin31].
Definition 2.1 Let
![]() $f\in F\langle X \rangle ^{gr}$
be a G-graded polynomial. The image of f on the G-graded algebra
$f\in F\langle X \rangle ^{gr}$
be a G-graded polynomial. The image of f on the G-graded algebra
![]() $\mathcal {A}$
is the set
$\mathcal {A}$
is the set
Equivalently, if
![]() $f(x_{1}^{(g_{1})},\dots ,x_{n}^{(g_{n})})\in F\langle X \rangle ^{gr}$
, then the image of f on the algebra
$f(x_{1}^{(g_{1})},\dots ,x_{n}^{(g_{n})})\in F\langle X \rangle ^{gr}$
, then the image of f on the algebra
![]() $\mathcal {A}$
is the set
$\mathcal {A}$
is the set
![]() $\mathrm{Im}(f)=\{f(a_{1}^{(g_{1})},\dots ,a_{n}^{(g_{n})})\mid a_{i}^{(g_{i})}\in \mathcal {A}_{g_{i}}\}$
. We will also denote the image of f on
$\mathrm{Im}(f)=\{f(a_{1}^{(g_{1})},\dots ,a_{n}^{(g_{n})})\mid a_{i}^{(g_{i})}\in \mathcal {A}_{g_{i}}\}$
. We will also denote the image of f on
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $f(\mathcal {A})$
.
$f(\mathcal {A})$
.
We now recall some basic properties of images of graded polynomials on algebras that will be used throughout the paper.
Proposition 2.2 Let
![]() $f\in F\langle X \rangle ^{gr}$
be a polynomial, and let
$f\in F\langle X \rangle ^{gr}$
be a polynomial, and let
![]() $\mathcal {A}$
be a G-graded algebra.
$\mathcal {A}$
be a G-graded algebra.
-
(1) Let U be one-dimensional subspace of
 $\mathcal {A}$
such that
$\mathcal {A}$
such that
 $\mathrm{Im}(f)\subset U$
and assume that
$\mathrm{Im}(f)\subset U$
and assume that
 $\lambda \mathrm{Im}(f)\subset \mathrm{Im}(f)$
for every
$\lambda \mathrm{Im}(f)\subset \mathrm{Im}(f)$
for every
 $\lambda \in F$
. Then either
$\lambda \in F$
. Then either
 $\mathrm{Im}(f)=\{0\}$
or
$\mathrm{Im}(f)=\{0\}$
or
 $\mathrm{Im}(f)=U$
.
$\mathrm{Im}(f)=U$
. -
(2) If
 $1\in \mathcal {A}$
and
$1\in \mathcal {A}$
and
 $f\in F\langle X \rangle ^{gr}$
is a multilinear polynomial in neutral variables such that the sum of its coefficients is nonzero, then
$f\in F\langle X \rangle ^{gr}$
is a multilinear polynomial in neutral variables such that the sum of its coefficients is nonzero, then
 $\mathrm{Im}(f)=\mathcal {A}_{1}$
.
$\mathrm{Im}(f)=\mathcal {A}_{1}$
. -
(3)
 $\mathrm{Im}(f)$
is invariant under graded endomorphisms of
$\mathrm{Im}(f)$
is invariant under graded endomorphisms of
 $F\langle X \rangle ^{gr}$
.
$F\langle X \rangle ^{gr}$
. -
(4) If
 $\mathrm{supp}(\mathcal {A})$
is abelian and
$\mathrm{supp}(\mathcal {A})$
is abelian and
 $f\in F\langle X \rangle ^{gr}$
is multilinear, then
$f\in F\langle X \rangle ^{gr}$
is multilinear, then
 $\mathrm{Im}(f)$
is a homogeneous subset.
$\mathrm{Im}(f)$
is a homogeneous subset.
Proof The proofs of the first and third items are straightforward. For the second item, it is enough to recall that if
![]() $\mathcal {A}$
is a graded algebra with
$\mathcal {A}$
is a graded algebra with
![]() $1$
, then
$1$
, then
![]() $1\in \mathcal {A}_{1}$
. Hence, given
$1\in \mathcal {A}_{1}$
. Hence, given
![]() $a\in \mathcal {A}_{1}$
, we have
$a\in \mathcal {A}_{1}$
, we have
![]() $a=f(\alpha ^{-1} a,1,\dots ,1)$
, where
$a=f(\alpha ^{-1} a,1,\dots ,1)$
, where
![]() $\alpha \neq 0$
is the sum of the coefficients of f, and then
$\alpha \neq 0$
is the sum of the coefficients of f, and then
![]() $\mathrm{Im}(f)=\mathcal {A}_{1}$
. For the last item, let
$\mathrm{Im}(f)=\mathcal {A}_{1}$
. For the last item, let
![]() $g_{1}$
, …,
$g_{1}$
, …,
![]() $g_{m}$
be the homogeneous degree of the variables that occur in f. If some
$g_{m}$
be the homogeneous degree of the variables that occur in f. If some
![]() $g_{i}\notin \mathrm{supp}(\mathcal {A})$
, then
$g_{i}\notin \mathrm{supp}(\mathcal {A})$
, then
![]() $\mathrm{Im}(f)=\{0\}$
is a homogeneous subspace. Otherwise, since
$\mathrm{Im}(f)=\{0\}$
is a homogeneous subspace. Otherwise, since
![]() $\mathrm{supp}(\mathcal {A})$
is abelian, we have that each monomial of f is of homogeneous degree
$\mathrm{supp}(\mathcal {A})$
is abelian, we have that each monomial of f is of homogeneous degree
![]() $g_{1}\cdots g_{m}$
, and hence the same holds for f.
$g_{1}\cdots g_{m}$
, and hence the same holds for f.
We say that a nonzero polynomial
![]() $f\in F\langle X \rangle ^{gr}$
is a graded polynomial identity for a G-graded algebra
$f\in F\langle X \rangle ^{gr}$
is a graded polynomial identity for a G-graded algebra
![]() $\mathcal {A}$
if its image on
$\mathcal {A}$
if its image on
![]() $\mathcal {A}$
is zero. The set of all graded polynomial identities of
$\mathcal {A}$
is zero. The set of all graded polynomial identities of
![]() $\mathcal {A}$
will be denoted by
$\mathcal {A}$
will be denoted by
![]() $\mathrm{Id}^{gr}(\mathcal {A})$
. It is easy to check that
$\mathrm{Id}^{gr}(\mathcal {A})$
. It is easy to check that
![]() $\mathrm{Id}^{gr}(\mathcal {A})$
is actually an ideal of
$\mathrm{Id}^{gr}(\mathcal {A})$
is actually an ideal of
![]() $F\langle X \rangle ^{gr}$
invariant under graded endomorphisms of
$F\langle X \rangle ^{gr}$
invariant under graded endomorphisms of
![]() $F\langle X \rangle ^{gr}$
. It is called the
$F\langle X \rangle ^{gr}$
. It is called the
![]() $T_{G}$
-ideal of
$T_{G}$
-ideal of
![]() $\mathcal {A}$
. Given a nonempty subset S of
$\mathcal {A}$
. Given a nonempty subset S of
![]() $F\langle X \rangle ^{gr}$
, we denote by
$F\langle X \rangle ^{gr}$
, we denote by
![]() $\langle S \rangle ^{T_{G}}$
the
$\langle S \rangle ^{T_{G}}$
the
![]() $T_{G}$
-ideal generated by S, that is the least
$T_{G}$
-ideal generated by S, that is the least
![]() $T_{G}$
-ideal that contains the set S. The linearization process also holds for graded polynomials, and as in the ordinary case, we have the following statement.
$T_{G}$
-ideal that contains the set S. The linearization process also holds for graded polynomials, and as in the ordinary case, we have the following statement.
Proposition 2.3 If
![]() $\mathcal {A}$
satisfies a graded polynomial identity, then
$\mathcal {A}$
satisfies a graded polynomial identity, then
![]() $\mathcal {A}$
also satisfies a multilinear one. Moreover, if
$\mathcal {A}$
also satisfies a multilinear one. Moreover, if
![]() $\mathrm{char}(F)=0$
, then
$\mathrm{char}(F)=0$
, then
![]() $\mathrm{Id}^{gr}(\mathcal {A})$
is generated by its multilinear polynomials.
$\mathrm{Id}^{gr}(\mathcal {A})$
is generated by its multilinear polynomials.
Let now
![]() $\mathcal {A}=UT_{n}$
be the algebra of
$\mathcal {A}=UT_{n}$
be the algebra of
![]() $n\times n$
upper triangular matrices over the field F. A G-grading on
$n\times n$
upper triangular matrices over the field F. A G-grading on
![]() $\mathcal {A}$
is said to be elementary if all elementary matrices are homogeneous in this grading, or equivalently, if there exists an n-tuple
$\mathcal {A}$
is said to be elementary if all elementary matrices are homogeneous in this grading, or equivalently, if there exists an n-tuple
![]() $(g_{1},\dots ,g_{n})\in G^{n}$
such that
$(g_{1},\dots ,g_{n})\in G^{n}$
such that
![]() $\deg (e_{ij})=g_{i}^{-1}g_{j}$
. A theorem of Valenti and Zaicev states that every grading on
$\deg (e_{ij})=g_{i}^{-1}g_{j}$
. A theorem of Valenti and Zaicev states that every grading on
![]() $UT_{n}$
is essentially elementary.
$UT_{n}$
is essentially elementary.
Theorem 2.4 [Reference Valenti and Zaicev41]
Let G be a group, and let F be a field. Assume that
![]() $UT_{n}=\mathcal {A}=\bigoplus _{g\in G} \mathcal {A}_{g}$
is G-graded. Then
$UT_{n}=\mathcal {A}=\bigoplus _{g\in G} \mathcal {A}_{g}$
is G-graded. Then
![]() $\mathcal {A}$
is G-graded isomorphic to
$\mathcal {A}$
is G-graded isomorphic to
![]() $UT_{n}$
endowed with some elementary G-grading.
$UT_{n}$
endowed with some elementary G-grading.
By Proposition 1.6 of [Reference Di Vincenzo, Koshlukov and Valenti11], we have that an elementary grading on
![]() $UT_{n}$
is completely determined by the sequence
$UT_{n}$
is completely determined by the sequence
![]() $(\deg (e_{12}),\deg (e_{23}),\ldots ,\deg (e_{n-1,n}))\in G^{n-1}$
.
$(\deg (e_{12}),\deg (e_{23}),\ldots ,\deg (e_{n-1,n}))\in G^{n-1}$
.
We recall now some recent results about the description of images of multilinear polynomials on the algebra of upper triangular matrices. We start with the definition of the so-called commutator degree of an associative polynomial.
Definition 2.5 Let
![]() $f\in F\langle X \rangle $
be a polynomial. We say that f has commutator degree r if
$f\in F\langle X \rangle $
be a polynomial. We say that f has commutator degree r if
In [Reference Gargate and de Mello19], Gargate and de Mello used the above definition to give a complete description of images of multilinear polynomials on
![]() $UT_{n}$
over infinite fields. Denoting by J the Jacobson radical of
$UT_{n}$
over infinite fields. Denoting by J the Jacobson radical of
![]() $UT_{n}$
and
$UT_{n}$
and
![]() $J^{0}=UT_{n}$
, they proved the following theorem.
$J^{0}=UT_{n}$
, they proved the following theorem.
Theorem 2.6 Let F be an infinite field, and let
![]() $f\in F\langle X \rangle $
be a multilinear polynomial. Then
$f\in F\langle X \rangle $
be a multilinear polynomial. Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}$
is
$UT_{n}$
is
![]() $J^{r}$
if and only if f has commutator degree r.
$J^{r}$
if and only if f has commutator degree r.
One of the main steps in the proof of Theorem 2.6 was the characterization of the polynomials of commutator degree r in terms of their coefficients. An instance of such characterization has already been known (see [Reference Gargate and de Mello19, Lemma 3.3(2)]).
Lemma 2.7 [Reference Gargate and de Mello19]
Let F be an arbitrary field, and let
![]() $f\in F\langle X \rangle $
be a multilinear polynomial. Then
$f\in F\langle X \rangle $
be a multilinear polynomial. Then
![]() $f\in \langle [x_{1},x_{2}]\rangle ^{T}$
if and only if the sum of its coefficients is zero.
$f\in \langle [x_{1},x_{2}]\rangle ^{T}$
if and only if the sum of its coefficients is zero.
It is worth mentioning that the above theorem has been extended for a larger class of fields by Luo and Wang in [Reference Luo and Wang32].
Theorem 2.8 [Reference Luo and Wang32]
Let
![]() $n\geq 2 $
be an integer, let F be a field with at least
$n\geq 2 $
be an integer, let F be a field with at least
![]() $n(n-1)/2$
elements, and let
$n(n-1)/2$
elements, and let
![]() $f\in F\langle X \rangle $
be a multilinear polynomial. If f has commutator degree r, then
$f\in F\langle X \rangle $
be a multilinear polynomial. If f has commutator degree r, then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}$
is
$UT_{n}$
is
![]() $J^{r}$
.
$J^{r}$
.
In the next corollary, we denote by
![]() $UT_{n}^{(-)}$
the Lie algebra defined on
$UT_{n}^{(-)}$
the Lie algebra defined on
![]() $UT_{n}$
by means of the Lie bracket
$UT_{n}$
by means of the Lie bracket
![]() $[a,b]=ab-ba$
.
$[a,b]=ab-ba$
.
Corollary 2.9 Let F be a field with at least
![]() $n(n-1)/2$
elements, and let
$n(n-1)/2$
elements, and let
![]() $f\in L(X)$
be a multilinear Lie polynomial. Then
$f\in L(X)$
be a multilinear Lie polynomial. Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}^{(-)}$
is
$UT_{n}^{(-)}$
is
![]() $J^{r}$
, for some
$J^{r}$
, for some
![]() $0\leq r \leq n$
.
$0\leq r \leq n$
.
Proof We use the Poincaré–Birkhoff-Witt theorem (and more precisely the Witt theorem) to consider the free Lie algebra
![]() $L(X)$
as the subalgebra of
$L(X)$
as the subalgebra of
![]() $F\langle X \rangle ^{(-)}$
generated by the set X. Since
$F\langle X \rangle ^{(-)}$
generated by the set X. Since
![]() $F\langle X\rangle $
is the universal enveloping algebra of
$F\langle X\rangle $
is the universal enveloping algebra of
![]() $L(X)$
, given a multilinear Lie polynomial
$L(X)$
, given a multilinear Lie polynomial
![]() $f\in L(X)$
, there exists an associative polynomial
$f\in L(X)$
, there exists an associative polynomial
![]() $\tilde {f}\in F\langle X \rangle $
such that
$\tilde {f}\in F\langle X \rangle $
such that
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}^{(-)}$
is equal to
$UT_{n}^{(-)}$
is equal to
![]() $\mathrm{Im}(\tilde {f})$
on
$\mathrm{Im}(\tilde {f})$
on
![]() $UT_{n}$
. Now, it is enough to apply Theorem 2.8.
$UT_{n}$
. Now, it is enough to apply Theorem 2.8.
Let
![]() $UT_{n}(d_{1},\ldots ,d_{k})$
be the upper block-triangular matrix algebra, that is, the subalgebra of
$UT_{n}(d_{1},\ldots ,d_{k})$
be the upper block-triangular matrix algebra, that is, the subalgebra of
![]() $M_{n}(F)$
consisting of all block-triangular matrices of the form
$M_{n}(F)$
consisting of all block-triangular matrices of the form
 $$\begin{align*}\begin{pmatrix} A_{1}& & * \\ & \ddots & \\ 0 & & A_{k} \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} A_{1}& & * \\ & \ddots & \\ 0 & & A_{k} \end{pmatrix}, \end{align*}$$
where
![]() $n=d_{1}+\cdots +d_{k}$
and
$n=d_{1}+\cdots +d_{k}$
and
![]() $A_{i}$
is a
$A_{i}$
is a
![]() $d_{i}\times d_{i}$
matrix. We will denote by T the subalgebra of
$d_{i}\times d_{i}$
matrix. We will denote by T the subalgebra of
![]() $UT_{n}(d_{1},\ldots ,d_{k})$
, which consists of only triangular blocks of sizes
$UT_{n}(d_{1},\ldots ,d_{k})$
, which consists of only triangular blocks of sizes
![]() $d_{i}$
on the main diagonal and zero elsewhere. That is,
$d_{i}$
on the main diagonal and zero elsewhere. That is,
 $$\begin{align*}T=\begin{pmatrix} UT_{d_{1}} & &0 \\ & \ddots & \\ 0& & UT_{d_{k}} \end{pmatrix}. \end{align*}$$
$$\begin{align*}T=\begin{pmatrix} UT_{d_{1}} & &0 \\ & \ddots & \\ 0& & UT_{d_{k}} \end{pmatrix}. \end{align*}$$
As a consequence of the above theorem, we obtain the following lemma.
Lemma 2.10 Let F be a field with at least
![]() $n(n-1)/2$
elements, and let
$n(n-1)/2$
elements, and let
![]() $f\in F\langle X \rangle $
be a multilinear polynomial of commutator degree r. Then the image
$f\in F\langle X \rangle $
be a multilinear polynomial of commutator degree r. Then the image
![]() $\mathrm{Im}(f)$
on T is
$\mathrm{Im}(f)$
on T is
![]() $J^{r}$
, where
$J^{r}$
, where
![]() $J=\mathrm{Jac}(T)$
is the Jacobson radical of T.
$J=\mathrm{Jac}(T)$
is the Jacobson radical of T.
Proof We note that
![]() $T\cong UT_{d_{1}}\times \cdots \times UT_{d_{k}}$
. Hence, by [Reference Brešar4, Proposition 5.60],
$T\cong UT_{d_{1}}\times \cdots \times UT_{d_{k}}$
. Hence, by [Reference Brešar4, Proposition 5.60],
 $$\begin{align*}J=\begin{pmatrix} J_{d_{1}} & & \\ & \ddots & \\ & & J_{d_{k}} \end{pmatrix}, \end{align*}$$
$$\begin{align*}J=\begin{pmatrix} J_{d_{1}} & & \\ & \ddots & \\ & & J_{d_{k}} \end{pmatrix}, \end{align*}$$
where
![]() $J_{d_{i}}=\mathrm{Jac}(UT_{d_{i}})$
. Therefore, by Theorem 2.8, we have
$J_{d_{i}}=\mathrm{Jac}(UT_{d_{i}})$
. Therefore, by Theorem 2.8, we have
 $$\begin{align*}f(T)=\begin{pmatrix} f(UT_{d_{1}}) & & \\ &\ddots &\\ & & f(UT_{d_{k}}) \end{pmatrix} =\begin{pmatrix} J_{d_{1}}^{r} & & \\ &\ddots &\\ & & J_{d_{k}}^{r} \end{pmatrix}=J^{r}. \end{align*}$$
$$\begin{align*}f(T)=\begin{pmatrix} f(UT_{d_{1}}) & & \\ &\ddots &\\ & & f(UT_{d_{k}}) \end{pmatrix} =\begin{pmatrix} J_{d_{1}}^{r} & & \\ &\ddots &\\ & & J_{d_{k}}^{r} \end{pmatrix}=J^{r}. \end{align*}$$
Throughout this paper, we use the letters
![]() $w_{i}$
and
$w_{i}$
and
![]() $w_{i}^{(j)}$
to denote commuting variables. We recall the following well-known result about commutative polynomials.
$w_{i}^{(j)}$
to denote commuting variables. We recall the following well-known result about commutative polynomials.
Lemma 2.11 Let F be an infinite field, and let
![]() $f_{1}(w_{1},\dots ,w_{m})$
, …,
$f_{1}(w_{1},\dots ,w_{m})$
, …,
![]() $f_{n}(w_{1},\dots ,w_{m})$
be nonzero commutative polynomials. Then there exist
$f_{n}(w_{1},\dots ,w_{m})$
be nonzero commutative polynomials. Then there exist
![]() $a_{1}$
, …,
$a_{1}$
, …,
![]() $a_{m}\in F$
such that
$a_{m}\in F$
such that
A similar result also holds for finite fields, as long as some boundedness on the degrees of the variables is given (see [Reference Drensky13, Proposition 4.2.3]).
Lemma 2.12 Let F be a finite field with n elements, and let
![]() $f_{1}(w_{1}\dots ,w_{m})$
, …,
$f_{1}(w_{1}\dots ,w_{m})$
, …,
![]() $f_{n-1}(w_{1},\dots ,w_{m})$
be nonzero polynomials in commuting variables. If
$f_{n-1}(w_{1},\dots ,w_{m})$
be nonzero polynomials in commuting variables. If
![]() $\deg _{w_{i}}(f_{j})\leq 1$
for all i and j, then there exist
$\deg _{w_{i}}(f_{j})\leq 1$
for all i and j, then there exist
![]() $a_{1}$
, …,
$a_{1}$
, …,
![]() $a_{m}\in F$
such that
$a_{m}\in F$
such that
3 Graded central polynomials for
 $UT_{n}$
$UT_{n}$
Our goal in this section is to prove the nonexistence of graded central polynomials for the graded algebra of upper triangular matrices with entries in an arbitrary field. It is well known that the algebra of upper block triangular matrices has no central polynomials (see [Reference Giambruno and Zaicev20, Lemma 1]).
We will denote by
![]() $Z(\mathcal {A})$
the center of the algebra
$Z(\mathcal {A})$
the center of the algebra
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Definition 3.1 Let
![]() $f\in F\langle X \rangle ^{gr}$
. We say that f is a graded central polynomial for the algebra
$f\in F\langle X \rangle ^{gr}$
. We say that f is a graded central polynomial for the algebra
![]() $\mathcal {A}$
if
$\mathcal {A}$
if
![]() $\mathrm{Im}(f)\subset Z(\mathcal {A})$
and
$\mathrm{Im}(f)\subset Z(\mathcal {A})$
and
![]() $f\notin \mathrm{Id}^{gr}(\mathcal {A})$
.
$f\notin \mathrm{Id}^{gr}(\mathcal {A})$
.
We recall the following fact from [Reference Di Vincenzo, Koshlukov and Valenti11, Lemma 1.4].
Lemma 3.2 Let
![]() $UT_{n}$
be endowed with some elementary grading. Then the subspace of all diagonal matrices is homogeneous of neutral degree.
$UT_{n}$
be endowed with some elementary grading. Then the subspace of all diagonal matrices is homogeneous of neutral degree.
Theorem 3.3 Let
![]() $UT_{n}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be a G-grading on the algebra of upper triangular matrices over an arbitrary field. If
$UT_{n}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be a G-grading on the algebra of upper triangular matrices over an arbitrary field. If
![]() $n>1$
, then there exist no graded central polynomials for
$n>1$
, then there exist no graded central polynomials for
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof By Theorem 2.4, we have that
![]() $\mathcal {A}$
is graded isomorphic to some elementary grading on
$\mathcal {A}$
is graded isomorphic to some elementary grading on
![]() $UT_{n}$
. Hence, we may reduce our problem to elementary gradings. Now, we assume that
$UT_{n}$
. Hence, we may reduce our problem to elementary gradings. Now, we assume that
![]() $f\in F\langle X \rangle ^{gr}$
is a polynomial with zero constant term, such that
$f\in F\langle X \rangle ^{gr}$
is a polynomial with zero constant term, such that
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $\mathcal {A}$
is contained in
$\mathcal {A}$
is contained in
![]() $F=Z(\mathcal {A})$
. We write f as
$F=Z(\mathcal {A})$
. We write f as
![]() $f=f_{1}+f_{2}$
where
$f=f_{1}+f_{2}$
where
![]() $f_{1}$
contains neutral variables only and
$f_{1}$
contains neutral variables only and
![]() $f_{2}$
has at least one nonneutral variable in each of its monomials. Consider
$f_{2}$
has at least one nonneutral variable in each of its monomials. Consider
![]() $a_{1}$
, …,
$a_{1}$
, …,
![]() $a_{m}\in \mathcal {A}_{1}$
, and
$a_{m}\in \mathcal {A}_{1}$
, and
![]() $b_{1}$
, …,
$b_{1}$
, …,
![]() $b_{l}$
are nonneutral variables (of homogeneous degree
$b_{l}$
are nonneutral variables (of homogeneous degree
![]() $\ne \ 1$
) that occur in f. Hence,
$\ne \ 1$
) that occur in f. Hence,
![]() $f(a_{1},\dots ,a_{m},b_{1},\dots ,b_{l})=f_{1}(\overline {a}_{1},\dots ,\overline {a}_{m})+j$
, where
$f(a_{1},\dots ,a_{m},b_{1},\dots ,b_{l})=f_{1}(\overline {a}_{1},\dots ,\overline {a}_{m})+j$
, where
![]() $j\in J$
, the Jacobson radical of
$j\in J$
, the Jacobson radical of
![]() $\mathcal {A}$
, and
$\mathcal {A}$
, and
![]() $\overline {a}_{i}$
is the diagonal part of
$\overline {a}_{i}$
is the diagonal part of
![]() $a_{i}$
. Since
$a_{i}$
. Since
![]() $\mathrm{Im}(f)\subset F$
, then
$\mathrm{Im}(f)\subset F$
, then
![]() $j=0$
and hence
$j=0$
and hence
![]() $\mathrm{Im}(f)=\mathrm{Im}(f_{1})$
, where the image of
$\mathrm{Im}(f)=\mathrm{Im}(f_{1})$
, where the image of
![]() $f_{1}$
is taken on diagonal matrices only. Now, note that if
$f_{1}$
is taken on diagonal matrices only. Now, note that if
![]() $\lambda _{1}$
, …,
$\lambda _{1}$
, …,
![]() $\lambda _{m}\in F$
are arbitrary, then
$\lambda _{m}\in F$
are arbitrary, then
Since
![]() $\mathrm{Im}(f_{1})\subset F$
, we must have
$\mathrm{Im}(f_{1})\subset F$
, we must have
![]() $f_{1}(\lambda _{1},\dots ,\lambda _{m})=0$
. Hence, for diagonal matrices
$f_{1}(\lambda _{1},\dots ,\lambda _{m})=0$
. Hence, for diagonal matrices
 $D_{i}=\displaystyle \sum _{k=1}^{n}\lambda _{k}^{(i)}e_{kk}$
, we have
$D_{i}=\displaystyle \sum _{k=1}^{n}\lambda _{k}^{(i)}e_{kk}$
, we have
 $$\begin{align*}f_{1}(D_{1},\dots,D_{m})=\sum_{k=1}^{n}f_{1}(\lambda_{1}^{(k)},\dots,\lambda_{k}^{(m)})e_{kk}=0, \end{align*}$$
$$\begin{align*}f_{1}(D_{1},\dots,D_{m})=\sum_{k=1}^{n}f_{1}(\lambda_{1}^{(k)},\dots,\lambda_{k}^{(m)})e_{kk}=0, \end{align*}$$
and thus
![]() $\mathrm{Im}(f)=\{0\}$
. We conclude the nonexistence of graded central polynomials for
$\mathrm{Im}(f)=\{0\}$
. We conclude the nonexistence of graded central polynomials for
![]() $UT_{n}$
.
$UT_{n}$
.
4 Certain
 ${\mathbb {Z}}_{q}$
-gradings on
${\mathbb {Z}}_{q}$
-gradings on
 $UT_{n}$
$UT_{n}$
Throughout this section, we denote
![]() $UT_{n}=\mathcal {A}$
, endowed with the elementary
$UT_{n}=\mathcal {A}$
, endowed with the elementary
![]() $\mathbb {Z}_{q}$
-grading given by the following sequence in
$\mathbb {Z}_{q}$
-grading given by the following sequence in
![]() $\mathbb {Z}_{q}^{n}$
:
$\mathbb {Z}_{q}^{n}$
:
 $$\begin{align*}(\overline{0},\overline{1},\dots,\overline{q-2},\underbrace{\overline{q-1},\overline{q-1}, \dots,\overline{q-1}}_{n-q+1 \text{ times}}). \end{align*}$$
$$\begin{align*}(\overline{0},\overline{1},\dots,\overline{q-2},\underbrace{\overline{q-1},\overline{q-1}, \dots,\overline{q-1}}_{n-q+1 \text{ times}}). \end{align*}$$
Given
![]() $q\leq n$
an integer, we study the images of multilinear graded polynomials on
$q\leq n$
an integer, we study the images of multilinear graded polynomials on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
One can see that, for
![]() $q=n$
, we have the natural
$q=n$
, we have the natural
![]() ${\mathbb {Z}}_{n}$
-grading on
${\mathbb {Z}}_{n}$
-grading on
![]() $UT_{n}$
given by
$UT_{n}$
given by
![]() $\deg e_{ij}=j-i\pmod {n}$
for every
$\deg e_{ij}=j-i\pmod {n}$
for every
![]() $i\le j$
.
$i\le j$
.
We note that the neutral component of
![]() $UT_{n}$
is given by a block triangular matrix with
$UT_{n}$
is given by a block triangular matrix with
![]() $q-1$
triangular blocks of size one each and a triangular block of size
$q-1$
triangular blocks of size one each and a triangular block of size
![]() $n-q+1$
in the bottom right corner:
$n-q+1$
in the bottom right corner:
 $$\begin{align*}\mathcal{A}_{0}=\begin{pmatrix} * & & & 0 \\ & \ddots & & \\ & & * & \\ 0& & & UT_{n-q+1} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{A}_{0}=\begin{pmatrix} * & & & 0 \\ & \ddots & & \\ & & * & \\ 0& & & UT_{n-q+1} \end{pmatrix}. \end{align*}$$
For
![]() $l\in \{1,\dots ,q-1\}$
, we have that the homogeneous component of degree
$l\in \{1,\dots ,q-1\}$
, we have that the homogeneous component of degree
![]() $\overline {l}$
is given by
$\overline {l}$
is given by
For
![]() $1\leq r \leq n-q$
, we also define the following homogeneous subspaces of
$1\leq r \leq n-q$
, we also define the following homogeneous subspaces of
![]() $A_{\overline {l}}$
:
$A_{\overline {l}}$
:
An immediate computation shows that the following are graded identities for
![]() $\mathcal {A}$
:
$\mathcal {A}$
:
where the variables
![]() $y_i$
are neutral ones, z,
$y_i$
are neutral ones, z,
![]() $z_{1}$
,
$z_{1}$
,
![]() $z_{2}$
are nonneutral variables, and
$z_{2}$
are nonneutral variables, and
![]() $\deg (z_{1})+\deg (z_{2})=\overline {0}$
. A complete description of the graded polynomial identities for elementary gradings on
$\deg (z_{1})+\deg (z_{2})=\overline {0}$
. A complete description of the graded polynomial identities for elementary gradings on
![]() $UT_{n}$
was given in [Reference Di Vincenzo, Koshlukov and Valenti11] for infinite fields and in [Reference Gonçalves and Riva21] for finite fields.
$UT_{n}$
was given in [Reference Di Vincenzo, Koshlukov and Valenti11] for infinite fields and in [Reference Gonçalves and Riva21] for finite fields.
We state several lemmas concerning the description of some graded polynomials on
![]() $\mathcal {A}$
. In the upcoming lemmas, unless otherwise stated, we assume that the field F has at least
$\mathcal {A}$
. In the upcoming lemmas, unless otherwise stated, we assume that the field F has at least
![]() $n(n-1)/2$
elements and
$n(n-1)/2$
elements and
![]() $f\in F\langle X \rangle ^{gr}$
is a multilinear polynomial.
$f\in F\langle X \rangle ^{gr}$
is a multilinear polynomial.
Lemma 4.1 If
![]() $f=f(y_{1},\dots ,y_{m})$
, then
$f=f(y_{1},\dots ,y_{m})$
, then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $\mathcal {A}$
is a homogeneous vector subspace.
$\mathcal {A}$
is a homogeneous vector subspace.
Proof It is enough to apply Lemma 2.10.
In the next two lemmas, we will assume that
![]() $f=f(z_{1},\dots ,z_{l},y_{l+1},\dots ,y_{m})$
, where
$f=f(z_{1},\dots ,z_{l},y_{l+1},\dots ,y_{m})$
, where
![]() $\deg (z_{i})=\overline {1}$
,
$\deg (z_{i})=\overline {1}$
,
![]() $1\leq i \leq l$
. It is obvious that, in this case, one must have
$1\leq i \leq l$
. It is obvious that, in this case, one must have
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $\mathcal {A}$
as a subset of
$\mathcal {A}$
as a subset of
![]() $\mathcal {A}_{\overline {l}}$
. Modulo the identity
$\mathcal {A}_{\overline {l}}$
. Modulo the identity
![]() $(1)$
, we rewrite the polynomial f as
$(1)$
, we rewrite the polynomial f as
where
![]() $y_{\boldsymbol {i_{j}}}=y_{i_{j_{1}}}\cdots y_{i_{j_{k_{j}}}}$
is such that
$y_{\boldsymbol {i_{j}}}=y_{i_{j_{1}}}\cdots y_{i_{j_{k_{j}}}}$
is such that
![]() $i_{j_{1}}<\cdots <i_{j_{k_{j}}}$
. Moreover
$i_{j_{1}}<\cdots <i_{j_{k_{j}}}$
. Moreover
![]() $g_{\boldsymbol {i_{1}},\dots ,\boldsymbol {i_{l}}}$
is the polynomial obtained by permuting the neutral variables whose indices are different from either of
$g_{\boldsymbol {i_{1}},\dots ,\boldsymbol {i_{l}}}$
is the polynomial obtained by permuting the neutral variables whose indices are different from either of
![]() $\boldsymbol {i_{1}}$
, …,
$\boldsymbol {i_{1}}$
, …,
![]() $\boldsymbol {i_{l}}$
, and forming a linear combination of such monomials. Furthermore, h is the sum of polynomial that differ from the first summand of f by nontrivial permutations of the odd variables.
$\boldsymbol {i_{l}}$
, and forming a linear combination of such monomials. Furthermore, h is the sum of polynomial that differ from the first summand of f by nontrivial permutations of the odd variables.
Among all polynomials
![]() $g_{\boldsymbol {i_{1}},\dots ,\boldsymbol {i_{l}}}$
(including those in h), we choose one of least commutator degree, say g, of commutator degree r. Up to permuting the odd variables, we can assume that the polynomial g occurs in the first summand of f.
$g_{\boldsymbol {i_{1}},\dots ,\boldsymbol {i_{l}}}$
(including those in h), we choose one of least commutator degree, say g, of commutator degree r. Up to permuting the odd variables, we can assume that the polynomial g occurs in the first summand of f.
Hence, in case
![]() $1\leq r \leq n-q$
, we can improve the inclusion
$1\leq r \leq n-q$
, we can improve the inclusion
![]() $\mathrm{Im}(f)\subset \mathcal {A}_{\overline {l}}$
to
$\mathrm{Im}(f)\subset \mathcal {A}_{\overline {l}}$
to
![]() $\mathrm{Im}(f)\subset \mathcal {B}_{\overline {l},r}$
. Our goal is to prove that
$\mathrm{Im}(f)\subset \mathcal {B}_{\overline {l},r}$
. Our goal is to prove that
![]() $\mathrm{Im}(f)=\mathcal {A}_{\overline {l}}$
in case
$\mathrm{Im}(f)=\mathcal {A}_{\overline {l}}$
in case
![]() $r=0$
and
$r=0$
and
![]() $\mathrm{Im}(f)=\mathcal {B}_{\overline {l},r}$
otherwise.
$\mathrm{Im}(f)=\mathcal {B}_{\overline {l},r}$
otherwise.
Lemma 4.2 If
![]() $1\leq r \leq n-q$
, then
$1\leq r \leq n-q$
, then
![]() $\mathrm{Im}(f)=\mathcal {B}_{\overline {l},r}$
.
$\mathrm{Im}(f)=\mathcal {B}_{\overline {l},r}$
.
Proof Let
![]() $\overline {g}=y_{\boldsymbol {i_{1}}}z_{1}y_{\boldsymbol {i_{2}}}z_{2}\cdots y_{\boldsymbol {i_{l}}}z_{l}g$
be a nonzero summand of f written as above, where the commutator degree of g is r. We consider the following evaluations: the variables in
$\overline {g}=y_{\boldsymbol {i_{1}}}z_{1}y_{\boldsymbol {i_{2}}}z_{2}\cdots y_{\boldsymbol {i_{l}}}z_{l}g$
be a nonzero summand of f written as above, where the commutator degree of g is r. We consider the following evaluations: the variables in
![]() $y_{\boldsymbol {i_{1}}}$
by
$y_{\boldsymbol {i_{1}}}$
by
![]() $e_{q-l,q-l}$
, the ones in
$e_{q-l,q-l}$
, the ones in
![]() $y_{\boldsymbol {i_{2}}}$
by
$y_{\boldsymbol {i_{2}}}$
by
![]() $e_{q-l+1,q-l+1}$
,…, and all variables in
$e_{q-l+1,q-l+1}$
,…, and all variables in
![]() $y_{\boldsymbol {i_{l}}}$
by
$y_{\boldsymbol {i_{l}}}$
by
![]() $e_{q-1,q-1}$
. We also put
$e_{q-1,q-1}$
. We also put
![]() $z_{1}=e_{q-l,q-l+1}$
,
$z_{1}=e_{q-l,q-l+1}$
,
![]() $z_{2}=e_{q-l+1,q-l+2}$
, …,
$z_{2}=e_{q-l+1,q-l+2}$
, …,
![]() $z_{l-1}=e_{q-2,q-1}$
, and
$z_{l-1}=e_{q-2,q-1}$
, and
![]() $z_{l}=\sum _{k=q}^{n}w_{k}e_{q-1,k}$
. Since g is of commutator degree r, Theorem 2.8 enables us to evaluate the even variables in g by matrices from
$z_{l}=\sum _{k=q}^{n}w_{k}e_{q-1,k}$
. Since g is of commutator degree r, Theorem 2.8 enables us to evaluate the even variables in g by matrices from
 $$\begin{align*}\begin{pmatrix} 0&0\\ 0&UT_{n-q+1} \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&0\\ 0&UT_{n-q+1} \end{pmatrix} \end{align*}$$
in order to obtain the matrix
![]() $e_{q,q+r}+e_{q+1,q+r+1}+\cdots + e_{n-r,n}$
.
$e_{q,q+r}+e_{q+1,q+r+1}+\cdots + e_{n-r,n}$
.
Note that the evaluations that we have considered allow us to reduce the study of the image of f to the polynomial
![]() $\overline {g}$
. Under these evaluations, we have
$\overline {g}$
. Under these evaluations, we have
 $$ \begin{align*} \overline{g}&=(w_{q}e_{q-l,q}+w_{q+1}e_{q-l,q+1}+\cdots+w_{n}e_{q-l,n})(e_{q,q+r}+e_{q+1,q+r+1}+\cdots+e_{n-r,n})\\ &=w_{q}e_{q-l,q+r}+w_{q+1}e_{q-l,q+r+1}+\cdots+w_{n-r}e_{q-l,n}. \end{align*} $$
$$ \begin{align*} \overline{g}&=(w_{q}e_{q-l,q}+w_{q+1}e_{q-l,q+1}+\cdots+w_{n}e_{q-l,n})(e_{q,q+r}+e_{q+1,q+r+1}+\cdots+e_{n-r,n})\\ &=w_{q}e_{q-l,q+r}+w_{q+1}e_{q-l,q+r+1}+\cdots+w_{n-r}e_{q-l,n}. \end{align*} $$
Taking a matrix
![]() $B\in \mathcal {B}_{\overline {l},r}$
, say
$B\in \mathcal {B}_{\overline {l},r}$
, say
![]() $B=b_{q}e_{q-l,q+r}+\cdots +b_{n-r}e_{q-l,n}$
, we can easily realize B as image of
$B=b_{q}e_{q-l,q+r}+\cdots +b_{n-r}e_{q-l,n}$
, we can easily realize B as image of
![]() $\overline {g}$
by choosing
$\overline {g}$
by choosing
![]() $w_{j}=b_{j}$
,
$w_{j}=b_{j}$
,
![]() $j=q$
, …,
$j=q$
, …,
![]() $n-r$
.
$n-r$
.
Hence,
![]() $f(\mathcal {A})=\mathcal {B}_{\overline {l},r}$
.
$f(\mathcal {A})=\mathcal {B}_{\overline {l},r}$
.
Lemma 4.3 If F is a field with at least n elements and
![]() $r=0$
, then
$r=0$
, then
![]() $\mathrm{Im}(f)=\mathcal {A}_{\overline {l}}$
.
$\mathrm{Im}(f)=\mathcal {A}_{\overline {l}}$
.
Proof Denoting by
![]() $\mathcal {D}$
the homogeneous subspace of diagonal matrices of
$\mathcal {D}$
the homogeneous subspace of diagonal matrices of
![]() $\mathcal {A}$
, we consider the following homogeneous subalgebra of
$\mathcal {A}$
, we consider the following homogeneous subalgebra of
![]() $\mathcal {A}$
:
$\mathcal {A}$
:
We will show that
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $\mathcal {S}$
is
$\mathcal {S}$
is
![]() $\mathcal {A}_{\overline {l}}$
, which is enough to conclude the lemma. Note that
$\mathcal {A}_{\overline {l}}$
, which is enough to conclude the lemma. Note that
![]() $\mathcal {S}$
still satisfies the identity (2) and it also satisfies
$\mathcal {S}$
still satisfies the identity (2) and it also satisfies
![]() $[y_{1},y_{2}]\equiv 0$
.
$[y_{1},y_{2}]\equiv 0$
.
By the identity
![]() $[y_{1},y_{2}]\equiv 0$
, we may write the polynomial
$[y_{1},y_{2}]\equiv 0$
, we may write the polynomial
![]() $\overline {g}$
as
$\overline {g}$
as
where
![]() $\beta $
is the sum of all coefficients of the polynomial g and
$\beta $
is the sum of all coefficients of the polynomial g and
![]() $y_{\boldsymbol {i_{l+1}}}$
is the product of the variables of g in increasing order of the indices. Since
$y_{\boldsymbol {i_{l+1}}}$
is the product of the variables of g in increasing order of the indices. Since
![]() $r=0$
, we get from Definition 2.5 that
$r=0$
, we get from Definition 2.5 that
![]() $\beta \neq 0$
.
$\beta \neq 0$
.
Now, we write
![]() $f=f(z_{1},\dots ,z_{l},y_{l+1},\dots ,y_{m})$
as
$f=f(z_{1},\dots ,z_{l},y_{l+1},\dots ,y_{m})$
as
 $$\begin{align*}f=\sum_{j=1}^{l}f_{j}, \end{align*}$$
$$\begin{align*}f=\sum_{j=1}^{l}f_{j}, \end{align*}$$
where
![]() $f_{j}$
is the sum of all monomials of f such that the variable
$f_{j}$
is the sum of all monomials of f such that the variable
![]() $z_{l}$
is in the jth position in relation to the odd variables.
$z_{l}$
is in the jth position in relation to the odd variables.
For each
![]() $j=1$
, …, l, we write
$j=1$
, …, l, we write
where
![]() $S_{l}^{(j)}=\{\sigma \in S_{l}|\sigma (l)=j\}$
, and
$S_{l}^{(j)}=\{\sigma \in S_{l}|\sigma (l)=j\}$
, and
![]() $f_{j,\sigma }$
is the sum of all monomials of
$f_{j,\sigma }$
is the sum of all monomials of
![]() $f_{j}$
where the order of the odd variables is given by the permutation
$f_{j}$
where the order of the odd variables is given by the permutation
![]() $\sigma $
.
$\sigma $
.
Taking
 $\displaystyle z_{i}=\sum _{k=1}^{q-1}w_{k}^{(i)}e_{k,k+1}+w_{q}^{(i)}e_{q-1,q+1}+\cdots +w_{n-1}^{(i)}e_{q-1,n}$
and
$\displaystyle z_{i}=\sum _{k=1}^{q-1}w_{k}^{(i)}e_{k,k+1}+w_{q}^{(i)}e_{q-1,q+1}+\cdots +w_{n-1}^{(i)}e_{q-1,n}$
and
 $\displaystyle y_{j}=\sum _{k=1}^{n}w_{k}^{(j)}e_{kk}$
, we have
$\displaystyle y_{j}=\sum _{k=1}^{n}w_{k}^{(j)}e_{kk}$
, we have
 $$ \begin{align*} &f_{l,id}(z_{1},\dots,z_{l},y_{l+1},\dots,y_{m})=\sum_{k=1}^{q-l}p_{k}w_{k}^{(1)}w_{k+1}^{(2)}\cdots w_{k+l-1}^{(l)}e_{k,k+l}\\ &+ p_{q-l+1}w_{q-l}^{(1)}\cdots w_{q-2}^{(l-1)}w_{q}^{(l)}e_{q-l,q+1}+\cdots+ p_{n-l}w_{q-l}^{(1)}\cdots w_{q-2}^{(l-1)}w_{n-1}^{(l)}e_{q-l,n}, \end{align*} $$
$$ \begin{align*} &f_{l,id}(z_{1},\dots,z_{l},y_{l+1},\dots,y_{m})=\sum_{k=1}^{q-l}p_{k}w_{k}^{(1)}w_{k+1}^{(2)}\cdots w_{k+l-1}^{(l)}e_{k,k+l}\\ &+ p_{q-l+1}w_{q-l}^{(1)}\cdots w_{q-2}^{(l-1)}w_{q}^{(l)}e_{q-l,q+1}+\cdots+ p_{n-l}w_{q-l}^{(1)}\cdots w_{q-2}^{(l-1)}w_{n-1}^{(l)}e_{q-l,n}, \end{align*} $$
where
![]() $p_{k}$
,
$p_{k}$
,
![]() $k=1$
, …,
$k=1$
, …,
![]() $n-l$
, are polynomials in the variables
$n-l$
, are polynomials in the variables
![]() $w^{(l+1)}$
, …,
$w^{(l+1)}$
, …,
![]() $w^{(m)}$
. We note that all polynomials
$w^{(m)}$
. We note that all polynomials
![]() $p_{k}$
,
$p_{k}$
,
![]() $k=1$
, …,
$k=1$
, …,
![]() $n-l$
, are nonzero ones. Indeed, we just have to check that different monomials in
$n-l$
, are nonzero ones. Indeed, we just have to check that different monomials in
![]() $f_{l,id}$
give different monomials in
$f_{l,id}$
give different monomials in
![]() $p_{k}$
. To this end, note that if
$p_{k}$
. To this end, note that if
![]() $m_{1}$
and
$m_{1}$
and
![]() $m_{2}$
are different monomials in
$m_{2}$
are different monomials in
![]() $f_{l,id}$
, then there exists some even variable
$f_{l,id}$
, then there exists some even variable
![]() $y_{j}$
such that the quantity of preceding odd variables in relation to
$y_{j}$
such that the quantity of preceding odd variables in relation to
![]() $y_{j}$
is distinct in
$y_{j}$
is distinct in
![]() $m_{1}$
and
$m_{1}$
and
![]() $m_{2}$
. This gives us variables
$m_{2}$
. This gives us variables
![]() $w^{(j)}$
with different lower indices in the two monomials in
$w^{(j)}$
with different lower indices in the two monomials in
![]() $p_{k}$
given by
$p_{k}$
given by
![]() $m_{1}$
and
$m_{1}$
and
![]() $m_{2}$
, which proves our claim. Moreover, we note that every variable in each monomial of the polynomial
$m_{2}$
, which proves our claim. Moreover, we note that every variable in each monomial of the polynomial
![]() $p_{k}$
appears exactly once.
$p_{k}$
appears exactly once.
Since we have at most
![]() $n-1$
polynomials
$n-1$
polynomials
![]() $p_{k}$
, by Lemma 2.12, there exist evaluations of the even variables
$p_{k}$
, by Lemma 2.12, there exist evaluations of the even variables
![]() $y_{j}$
by diagonal matrices
$y_{j}$
by diagonal matrices
![]() $D_{j}$
such that
$D_{j}$
such that
![]() $p_{k}$
take nonzero values simultaneously for all k. In case F is infinite, the same conclusion holds by applying Lemma 2.11. Hence,
$p_{k}$
take nonzero values simultaneously for all k. In case F is infinite, the same conclusion holds by applying Lemma 2.11. Hence,
 $$ \begin{align*} f_{l}&=\sum_{k=1}^{q-l}\bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{k}^{(\sigma(1))}\cdots w_{k+l-2}^{(\sigma(l-1))}\bigg)w_{k+l-1}^{(l)}e_{k,k+l}\\& \quad + \bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{q-l}^{(\sigma(1))}\cdots w_{q-2}^{(\sigma(l-1))}\bigg)w_{q}^{(l)}e_{q-l,q+1}\\& \quad +\cdots+ \bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{q-l}^{(\sigma(1))}\cdots w_{q-2}^{(\sigma(l-1))}\bigg)w_{n-1}^{(l)}e_{q-l,n}, \end{align*} $$
$$ \begin{align*} f_{l}&=\sum_{k=1}^{q-l}\bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{k}^{(\sigma(1))}\cdots w_{k+l-2}^{(\sigma(l-1))}\bigg)w_{k+l-1}^{(l)}e_{k,k+l}\\& \quad + \bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{q-l}^{(\sigma(1))}\cdots w_{q-2}^{(\sigma(l-1))}\bigg)w_{q}^{(l)}e_{q-l,q+1}\\& \quad +\cdots+ \bigg(\sum_{\sigma\in S_{l}^{(l)}}\alpha_{\sigma}w_{q-l}^{(\sigma(1))}\cdots w_{q-2}^{(\sigma(l-1))}\bigg)w_{n-1}^{(l)}e_{q-l,n}, \end{align*} $$
with
![]() $\alpha _{id}\neq 0$
. So the polynomials inside the brackets above are nonzero ones, and each of their monomials has variables of degree one. Applying Lemma 2.12 once again, we may evaluate the variables
$\alpha _{id}\neq 0$
. So the polynomials inside the brackets above are nonzero ones, and each of their monomials has variables of degree one. Applying Lemma 2.12 once again, we may evaluate the variables
![]() $z_{1}$
, …,
$z_{1}$
, …,
![]() $z_{l-1}$
by matrices in
$z_{l-1}$
by matrices in
![]() $C_{1}$
, …,
$C_{1}$
, …,
![]() $C_{l-1}\in A_{\overline {1}}$
such that all these polynomials take nonzero values on F (in case F is infinite, we apply Lemma 2.11). Denote by
$C_{l-1}\in A_{\overline {1}}$
such that all these polynomials take nonzero values on F (in case F is infinite, we apply Lemma 2.11). Denote by
![]() $\alpha _{l,k}\in F\setminus \{0\}$
,
$\alpha _{l,k}\in F\setminus \{0\}$
,
![]() $k =1$
, …,
$k =1$
, …,
![]() $q-l$
, the values of the polynomials inside the brackets after such evaluations.
$q-l$
, the values of the polynomials inside the brackets after such evaluations.
Therefore,
 $$ \begin{align*} &f(C_{1},\dots,C_{l-1},z_{l},D_{l+1},\dots,D_{m})\\&=\sum_{k=1}^{q-l}\bigg(\alpha_{1,k}w_{k}^{(l)}+\cdots +\alpha_{l-1,k}w_{k+l-2}^{(l)} +\alpha_{l,k}w_{k+l-1}^{(l)}\bigg)e_{k,k+l}\\& \quad +\bigg(\alpha_{1,q}w_{q-l}^{(l)}+\cdots + \alpha_{l-1,q}w_{q-2}^{(l)}+\alpha_{l,q-l}w_{q}^{(l)}\bigg)e_{q-l,q+1}\\& \quad +\cdots+ \bigg(\alpha_{1,n-1}w_{q-l}^{(l)}+\cdots + \alpha_{l-1,n-1}w_{q-2}^{(l)}+\alpha_{l,q-l}w_{n-1}^{(l)}\bigg)e_{q-l,n}, \end{align*} $$
$$ \begin{align*} &f(C_{1},\dots,C_{l-1},z_{l},D_{l+1},\dots,D_{m})\\&=\sum_{k=1}^{q-l}\bigg(\alpha_{1,k}w_{k}^{(l)}+\cdots +\alpha_{l-1,k}w_{k+l-2}^{(l)} +\alpha_{l,k}w_{k+l-1}^{(l)}\bigg)e_{k,k+l}\\& \quad +\bigg(\alpha_{1,q}w_{q-l}^{(l)}+\cdots + \alpha_{l-1,q}w_{q-2}^{(l)}+\alpha_{l,q-l}w_{q}^{(l)}\bigg)e_{q-l,q+1}\\& \quad +\cdots+ \bigg(\alpha_{1,n-1}w_{q-l}^{(l)}+\cdots + \alpha_{l-1,n-1}w_{q-2}^{(l)}+\alpha_{l,q-l}w_{n-1}^{(l)}\bigg)e_{q-l,n}, \end{align*} $$
where
![]() $\alpha _{l,k}\neq 0$
for every
$\alpha _{l,k}\neq 0$
for every
![]() $k=1$
, …,
$k=1$
, …,
![]() $q-l$
.
$q-l$
.
Then, given a matrix
 $B=\displaystyle \sum _{k=1}^{q-l}b_{k}e_{k,k+l}+b_{q-l+1}e_{q-l,q+1}+\cdots + b_{n-l}e_{q-l,n}\in \mathcal {A}_{\overline {l}}$
, we take
$B=\displaystyle \sum _{k=1}^{q-l}b_{k}e_{k,k+l}+b_{q-l+1}e_{q-l,q+1}+\cdots + b_{n-l}e_{q-l,n}\in \mathcal {A}_{\overline {l}}$
, we take
and we obtain a linear system in the variables
![]() $w^{(l)}$
whose solution (not necessarily unique) can be found recursively.
$w^{(l)}$
whose solution (not necessarily unique) can be found recursively.
Theorem 4.4 Let F be a field with at least
![]() $n(n-1)/2$
elements, let
$n(n-1)/2$
elements, let
![]() $UT_{n}=\bigoplus _{k\in \mathbb {Z}_{q}}\mathcal {A}_{k}$
be endowed with the elementary
$UT_{n}=\bigoplus _{k\in \mathbb {Z}_{q}}\mathcal {A}_{k}$
be endowed with the elementary
![]() $\mathbb {Z}_{q}$
-grading given by the sequence
$\mathbb {Z}_{q}$
-grading given by the sequence
![]() $(\overline {0},\overline {1},\dots ,\overline {q-2}, \overline {q-1},\dots ,\overline {q-1})$
, and let
$(\overline {0},\overline {1},\dots ,\overline {q-2}, \overline {q-1},\dots ,\overline {q-1})$
, and let
![]() $f\in F\langle X \rangle ^{gr}$
be a multilinear polynomial. Then
$f\in F\langle X \rangle ^{gr}$
be a multilinear polynomial. Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}$
is
$UT_{n}$
is
![]() $\{0\}$
,
$\{0\}$
,
![]() $J^{r}$
,
$J^{r}$
,
![]() $\mathcal {B}_{\overline {l},r}$
, or
$\mathcal {B}_{\overline {l},r}$
, or
![]() $\mathcal {A}_{\overline {l}}$
, where
$\mathcal {A}_{\overline {l}}$
, where
![]() $J=\mathrm{Jac}(\mathcal {A}_{0})$
. In particular, the image is always a homogeneous vector subspace.
$J=\mathrm{Jac}(\mathcal {A}_{0})$
. In particular, the image is always a homogeneous vector subspace.
Proof By Lemmas 4.1–4.3, we only need to analyze the case where f is a polynomial in neutral variables and nonneutral ones (that is of degree different from
![]() $\overline {1}$
). However, we can reduce this case to the aforementioned lemmas. Indeed, modulo the graded identities (1)–(3), let f and g be as in the comments before Lemma 4.2 and let r be the commutator degree of g. Hence,
$\overline {1}$
). However, we can reduce this case to the aforementioned lemmas. Indeed, modulo the graded identities (1)–(3), let f and g be as in the comments before Lemma 4.2 and let r be the commutator degree of g. Hence,
![]() $\mathrm{Im}(f)\subset \mathcal {B}_{\overline {l},r}$
if
$\mathrm{Im}(f)\subset \mathcal {B}_{\overline {l},r}$
if
![]() $r\neq 0$
and
$r\neq 0$
and
![]() $\mathrm{Im}(f)\subset \mathcal {A}_{\overline {l}}$
otherwise. By Proposition 2.2(3), the image of the polynomial
$\mathrm{Im}(f)\subset \mathcal {A}_{\overline {l}}$
otherwise. By Proposition 2.2(3), the image of the polynomial
![]() $\tilde {f}$
obtained from f by evaluating every nonneutral variable
$\tilde {f}$
obtained from f by evaluating every nonneutral variable
![]() $z_{i}$
of homogeneous degree
$z_{i}$
of homogeneous degree
![]() $\overline {k}$
by a product of k variables of homogeneous degree
$\overline {k}$
by a product of k variables of homogeneous degree
![]() $\overline {1}$
, is contained in
$\overline {1}$
, is contained in
![]() $\mathrm{Im}(f)$
. However, the polynomial g defined for f (see the comments before Lemma 4.2) is the same as the one defined for
$\mathrm{Im}(f)$
. However, the polynomial g defined for f (see the comments before Lemma 4.2) is the same as the one defined for
![]() $\tilde {f}$
. This allows us to get
$\tilde {f}$
. This allows us to get
![]() $\mathcal {B}_{\overline {l},r}\subseteq \mathrm{Im}(\tilde {f})$
in case
$\mathcal {B}_{\overline {l},r}\subseteq \mathrm{Im}(\tilde {f})$
in case
![]() $r\neq 0$
and
$r\neq 0$
and
![]() $\mathcal {A}_{\overline {l}}\subseteq \mathrm{Im}(\tilde {f})$
otherwise.
$\mathcal {A}_{\overline {l}}\subseteq \mathrm{Im}(\tilde {f})$
otherwise.
Remark 4.5 Considering similar computations, one can easily see that the result is also valid for the elementary grading defined by the identities
![]() $z[y_{1},y_{2}]\equiv 0$
, (2), and (3).
$z[y_{1},y_{2}]\equiv 0$
, (2), and (3).
In the next corollary, we are assuming that F is a field of characteristic zero and
![]() $\mathcal {A}=UT_{n}$
is endowed with the elementary
$\mathcal {A}=UT_{n}$
is endowed with the elementary
![]() ${\mathbb {Z}}_{q}$
-grading given by the sequence
${\mathbb {Z}}_{q}$
-grading given by the sequence
![]() $(\overline {0},\overline {1},\dots ,\overline {q-2},\overline {q-1},\dots ,\overline {q-1})$
.
$(\overline {0},\overline {1},\dots ,\overline {q-2},\overline {q-1},\dots ,\overline {q-1})$
.
Corollary 4.6 The
![]() $T_{G}$
-ideal
$T_{G}$
-ideal
![]() $\mathrm{Id}^{gr}(\mathcal {A})$
is generated by the graded identities (1)–(3).
$\mathrm{Id}^{gr}(\mathcal {A})$
is generated by the graded identities (1)–(3).
Proof Let
![]() $f\in \mathrm{Id}^{gr}(\mathcal {A})$
. By Proposition 2.3, we may assume that f is multilinear. Note that in the proof of Theorem 4.4 and in the lemmas that precede it, we have shown that if f is not a consequence of the identities (1)–(3), then
$f\in \mathrm{Id}^{gr}(\mathcal {A})$
. By Proposition 2.3, we may assume that f is multilinear. Note that in the proof of Theorem 4.4 and in the lemmas that precede it, we have shown that if f is not a consequence of the identities (1)–(3), then
![]() $\mathrm{Im}(f)\neq \{0\}$
. In other words, if
$\mathrm{Im}(f)\neq \{0\}$
. In other words, if
![]() $f\in \mathrm{Id}^{gr}(\mathcal {A})$
, then f is a consequence of the aforementioned identities.
$f\in \mathrm{Id}^{gr}(\mathcal {A})$
, then f is a consequence of the aforementioned identities.
We recall that in case
![]() $q=n$
, we have the natural
$q=n$
, we have the natural
![]() ${\mathbb {Z}}_{n}$
-grading on
${\mathbb {Z}}_{n}$
-grading on
![]() $UT_{n}$
.
$UT_{n}$
.
Corollary 4.7 Let F be a field with at least n elements, let
![]() $UT_{n}$
be endowed with the natural
$UT_{n}$
be endowed with the natural
![]() $\mathbb {Z}_{n}$
-grading, and let
$\mathbb {Z}_{n}$
-grading, and let
![]() $f\in F\langle X \rangle ^{gr}$
be a multilinear polynomial. Then the image of f on
$f\in F\langle X \rangle ^{gr}$
be a multilinear polynomial. Then the image of f on
![]() $UT_{n}$
is either zero or some homogeneous component.
$UT_{n}$
is either zero or some homogeneous component.
Remark 4.8 Note that the same result also holds if we consider the natural
![]() ${\mathbb {Z}}$
-grading on
${\mathbb {Z}}$
-grading on
![]() $UT_{n}$
. Analogous results hold for the lower triangular matrix algebra
$UT_{n}$
. Analogous results hold for the lower triangular matrix algebra
![]() $LT_{n}$
as well (we will use this remark in the next section).
$LT_{n}$
as well (we will use this remark in the next section).
5 Graded identities and traceless matrices
In this section, we give a sufficient condition for the subspace of the traceless matrices to be contained in the image of a multilinear polynomial on the full matrix algebra.
We start by recalling the following result from [Reference Amitsur and Rowen3].
Theorem 5.1 [Reference Amitsur and Rowen3]
Let D be a division ring,
![]() $n \geq 2$
an integer, and
$n \geq 2$
an integer, and
![]() $A \in M_n(D)$
a noncentral matrix. Then A is similar (conjugate) to a matrix in
$A \in M_n(D)$
a noncentral matrix. Then A is similar (conjugate) to a matrix in
![]() $M_n(D)$
with at most one nonzero entry on the main diagonal. In particular, if A has trace zero, then it is similar to a matrix in
$M_n(D)$
with at most one nonzero entry on the main diagonal. In particular, if A has trace zero, then it is similar to a matrix in
![]() $M_n(D)$
with only zeros on the main diagonal.
$M_n(D)$
with only zeros on the main diagonal.
Consider the natural
![]() $\mathbb {Z}$
-grading on
$\mathbb {Z}$
-grading on
![]() $M_{n}(F)=\bigoplus _{r\in \mathbb {Z}}(M_{n}(F))_{r}$
given by
$M_{n}(F)=\bigoplus _{r\in \mathbb {Z}}(M_{n}(F))_{r}$
given by
 $$\begin{align*}(M_{n}(F))_{r}=\left\{\begin{array}{cl} \mathrm{span}\{e_{k,k+r}\mid k=1,\dots,n-r\}, & \mbox{if} \ 0\leq r \leq n-1, \\ \mathrm{span}\{e_{k-r,k}\mid k=1,\dots,n+r\}, & \mbox{if} \ -n+1\leq r\leq -1, \\ \{0\}, & \mbox{elsewhere.} \end{array} \right. \end{align*}$$
$$\begin{align*}(M_{n}(F))_{r}=\left\{\begin{array}{cl} \mathrm{span}\{e_{k,k+r}\mid k=1,\dots,n-r\}, & \mbox{if} \ 0\leq r \leq n-1, \\ \mathrm{span}\{e_{k-r,k}\mid k=1,\dots,n+r\}, & \mbox{if} \ -n+1\leq r\leq -1, \\ \{0\}, & \mbox{elsewhere.} \end{array} \right. \end{align*}$$
In this section, we denote
![]() $F\langle X \rangle ^{gr}$
the free
$F\langle X \rangle ^{gr}$
the free
![]() $\mathbb {Z}$
-graded algebra. We also keep the notation of using variables y’s for neutral variables and z’s for nonneutral ones.
$\mathbb {Z}$
-graded algebra. We also keep the notation of using variables y’s for neutral variables and z’s for nonneutral ones.
Theorem 5.2 Let
![]() $n\geq 2$
be an integer, let F be a field with at least
$n\geq 2$
be an integer, let F be a field with at least
![]() $(n-1)n+1$
elements where
$(n-1)n+1$
elements where
![]() $\mathrm{char}(F)$
does not divide n, and let
$\mathrm{char}(F)$
does not divide n, and let
![]() $f\in F\langle X \rangle $
be a multilinear polynomial. If
$f\in F\langle X \rangle $
be a multilinear polynomial. If
![]() $f(y_{1},\dots ,y_{m-1},z)\notin \langle [y_{1},y_{2}] \rangle ^{T_{\mathbb {Z}}}$
for every nonneutral variable z, then
$f(y_{1},\dots ,y_{m-1},z)\notin \langle [y_{1},y_{2}] \rangle ^{T_{\mathbb {Z}}}$
for every nonneutral variable z, then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $M_{n}(F)$
contains
$M_{n}(F)$
contains
![]() $sl_{n}(F)$
.
$sl_{n}(F)$
.
Proof Since
![]() $\mathrm{char}(F)$
does not divide n, then we have that any nonzero traceless matrix is noncentral. Using further that
$\mathrm{char}(F)$
does not divide n, then we have that any nonzero traceless matrix is noncentral. Using further that
![]() $\mathrm{Im}(f)$
is invariant under automorphisms, by Theorem 5.1, it is enough to show that
$\mathrm{Im}(f)$
is invariant under automorphisms, by Theorem 5.1, it is enough to show that
![]() $\mathrm{Im}(f)$
contains all matrices with zero diagonal. Let A be a zero diagonal matrix, and write A as the sum of its homogeneous components
$\mathrm{Im}(f)$
contains all matrices with zero diagonal. Let A be a zero diagonal matrix, and write A as the sum of its homogeneous components
 $$\begin{align*}A=\sum_{i=-n+1}^{-1}A_{i}+\sum_{i=1}^{n-1}A_{i}, \end{align*}$$
$$\begin{align*}A=\sum_{i=-n+1}^{-1}A_{i}+\sum_{i=1}^{n-1}A_{i}, \end{align*}$$
where
 $A_{i}=\displaystyle \sum _{k=1}^{n+i}a_{k-i,k}e_{k-i,k}$
, for
$A_{i}=\displaystyle \sum _{k=1}^{n+i}a_{k-i,k}e_{k-i,k}$
, for
![]() $i=-n+1$
, …,
$i=-n+1$
, …,
![]() $-1$
, and
$-1$
, and
 $A_{i}=\displaystyle \sum _{k=1}^{n-i}a_{k,k+i}e_{k,k+i}$
, for
$A_{i}=\displaystyle \sum _{k=1}^{n-i}a_{k,k+i}e_{k,k+i}$
, for
![]() $i=1$
, …,
$i=1$
, …,
![]() $n-1$
.
$n-1$
.
By hypothesis,
![]() $f(y_{1},\dots ,y_{m-1},z^{(i)})$
is not a graded polynomial identity for
$f(y_{1},\dots ,y_{m-1},z^{(i)})$
is not a graded polynomial identity for
![]() $UT_{n}$
with the natural
$UT_{n}$
with the natural
![]() $\mathbb {Z}$
-grading, for every variable
$\mathbb {Z}$
-grading, for every variable
![]() $z^{(i)}$
of homogeneous degree i where
$z^{(i)}$
of homogeneous degree i where
![]() $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
We now consider the following evaluations on generic matrices:
 $y_{j}=\displaystyle \sum _{k=1}^{n}w_{k}^{(j)}e_{kk}$
, for all
$y_{j}=\displaystyle \sum _{k=1}^{n}w_{k}^{(j)}e_{kk}$
, for all
![]() $j=1$
, …,
$j=1$
, …,
![]() $m-1$
, and
$m-1$
, and
 $z^{(i)}=\displaystyle \sum _{k=1}^{n-i}w_{k}^{(m,i)}e_{k,k+i}$
.
$z^{(i)}=\displaystyle \sum _{k=1}^{n-i}w_{k}^{(m,i)}e_{k,k+i}$
.
Hence,
 $$\begin{align*}f(y_{1},\dots,y_{m-1},z^{(i)})=\sum_{k=1}^{n-i}p_{k,i}w_{k}^{(m,i)}e_{k,k+i}, \end{align*}$$
$$\begin{align*}f(y_{1},\dots,y_{m-1},z^{(i)})=\sum_{k=1}^{n-i}p_{k,i}w_{k}^{(m,i)}e_{k,k+i}, \end{align*}$$
where
![]() $p_{k,i}$
is a polynomial in the variables
$p_{k,i}$
is a polynomial in the variables
![]() $w_{k}^{(j)}$
. Since
$w_{k}^{(j)}$
. Since
![]() $f\notin \mathrm{Id}^{gr}(UT_{n})$
, Corollary 4.7 gives us that the image of
$f\notin \mathrm{Id}^{gr}(UT_{n})$
, Corollary 4.7 gives us that the image of
![]() $f(y_{1},\dots ,y_{m-1},z^{(i)})$
on
$f(y_{1},\dots ,y_{m-1},z^{(i)})$
on
![]() $UT_{n}$
is exactly
$UT_{n}$
is exactly
![]() $(UT_{n})_{i}$
. Hence, all
$(UT_{n})_{i}$
. Hence, all
![]() $p_{k,i}$
are nonzero polynomials. Moreover, note that
$p_{k,i}$
are nonzero polynomials. Moreover, note that
![]() $p_{k,i}$
is such that all its monomials are multilinear ones.
$p_{k,i}$
is such that all its monomials are multilinear ones.
Analogously, we also have that
![]() $f(y_{1},\dots ,y_{m-1},z^{(i)})$
is not a graded polynomial identity for the lower triangular matrix algebra
$f(y_{1},\dots ,y_{m-1},z^{(i)})$
is not a graded polynomial identity for the lower triangular matrix algebra
![]() $LT_{n}$
endowed with the natural
$LT_{n}$
endowed with the natural
![]() $\mathbb {Z}$
-grading, for
$\mathbb {Z}$
-grading, for
![]() $i=-n+1$
, …,
$i=-n+1$
, …,
![]() $-1$
. Therefore,
$-1$
. Therefore,
 $$\begin{align*}f(y_{1},\dots,y_{m-1},z^{(i)})=\sum_{k=1}^{n-i}q_{k,i}w_{k}^{(m,-i)}e_{k+i,k}, \end{align*}$$
$$\begin{align*}f(y_{1},\dots,y_{m-1},z^{(i)})=\sum_{k=1}^{n-i}q_{k,i}w_{k}^{(m,-i)}e_{k+i,k}, \end{align*}$$
where
 $z^{(i)}=\displaystyle \sum _{k=1}^{n+i}w_{k}^{(m,-i)}e_{k-i,k}$
and
$z^{(i)}=\displaystyle \sum _{k=1}^{n+i}w_{k}^{(m,-i)}e_{k-i,k}$
and
![]() $q_{k,i}$
are nonzero commutative polynomials with multilinear monomials.
$q_{k,i}$
are nonzero commutative polynomials with multilinear monomials.
The number of polynomials
![]() $p_{k,i}$
and
$p_{k,i}$
and
![]() $q_{k,i}$
is exactly
$q_{k,i}$
is exactly
![]() $(n-1)n$
. We now apply Lemma 2.12 to get an evaluation of all variables
$(n-1)n$
. We now apply Lemma 2.12 to get an evaluation of all variables
![]() $w_{k}^{(j)}$
such that the polynomials
$w_{k}^{(j)}$
such that the polynomials
![]() $p_{k,i}$
and
$p_{k,i}$
and
![]() $q_{k,i}$
assume simultaneously nonzero values in F. Such evaluations give us diagonal matrices
$q_{k,i}$
assume simultaneously nonzero values in F. Such evaluations give us diagonal matrices
![]() $D_{1}$
, …,
$D_{1}$
, …,
![]() $D_{m-1}$
such that
$D_{m-1}$
such that
 $$\begin{align*}f(D_{1},\dots,D_{m-1},z^{(i)})=\sum_{k=1}^{n-i}\alpha_{i,k}w_{k}^{(m,i)}e_{k,k+i}, \end{align*}$$
$$\begin{align*}f(D_{1},\dots,D_{m-1},z^{(i)})=\sum_{k=1}^{n-i}\alpha_{i,k}w_{k}^{(m,i)}e_{k,k+i}, \end{align*}$$
where
![]() $\alpha _{i,k}$
are nonzero scalars. Therefore, each matrix
$\alpha _{i,k}$
are nonzero scalars. Therefore, each matrix
![]() $A_{i}$
can be realized as
$A_{i}$
can be realized as
![]() $f(D_{1},\dots ,D_{m-1},B_{i})$
for a suitable matrix
$f(D_{1},\dots ,D_{m-1},B_{i})$
for a suitable matrix
![]() $B_{i}\in (UT_{n})_{i}$
, for every
$B_{i}\in (UT_{n})_{i}$
, for every
![]() $i=1$
, …,
$i=1$
, …,
![]() $n-1$
. Similarly, we also have that each matrix
$n-1$
. Similarly, we also have that each matrix
![]() $A_{i}$
can be realized as
$A_{i}$
can be realized as
![]() $f(D_{1},\dots ,D_{m-1},C_{i})$
for a suitable matrix
$f(D_{1},\dots ,D_{m-1},C_{i})$
for a suitable matrix
![]() $C_{i}\in (LT_{n})_{i}$
, for all
$C_{i}\in (LT_{n})_{i}$
, for all
![]() $i=-n+1$
, …,
$i=-n+1$
, …,
![]() $-1$
. Hence,
$-1$
. Hence,
 $$\begin{align*}A=\sum_{i=-n+1}^{-1}A_{i}+\sum_{i=1}^{n-1}A_{i}=\sum_{i=-n+1}^{-1}f(D_{1},\ldots,D_{m-1},C_{i})+\sum_{i=1}^{n-1}f(D_{1},\ldots,D_{m-1},B_{i}), \end{align*}$$
$$\begin{align*}A=\sum_{i=-n+1}^{-1}A_{i}+\sum_{i=1}^{n-1}A_{i}=\sum_{i=-n+1}^{-1}f(D_{1},\ldots,D_{m-1},C_{i})+\sum_{i=1}^{n-1}f(D_{1},\ldots,D_{m-1},B_{i}), \end{align*}$$
and it is enough to use the linearity of f in one variable to get
![]() $A\in \mathrm{Im}(f)$
.
$A\in \mathrm{Im}(f)$
.
6 The low-dimension cases
6.1 Arbitrary gradings on
 $UT_{2}$
and
$UT_{2}$
and
 $UT_{3}$
$UT_{3}$
We start this section with the following proposition.
Proposition 6.1 Let G be a group, and let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be two G-graded algebras such that
$\mathcal {B}$
be two G-graded algebras such that
![]() $\mathcal {B}$
is a graded homomorphic image of
$\mathcal {B}$
is a graded homomorphic image of
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $f\in F\langle X \rangle ^{gr}$
be a graded polynomial and assume that
$f\in F\langle X \rangle ^{gr}$
be a graded polynomial and assume that
![]() $f(\mathcal {A})$
is a homogeneous subspace of
$f(\mathcal {A})$
is a homogeneous subspace of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $f(\mathcal {B})$
is also a homogeneous subspace of
$f(\mathcal {B})$
is also a homogeneous subspace of
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Proof Let
![]() $\phi \colon \mathcal {A}\rightarrow \mathcal {B}$
be a graded epimorphism. We start by noting that
$\phi \colon \mathcal {A}\rightarrow \mathcal {B}$
be a graded epimorphism. We start by noting that
![]() $\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
. Then taking
$\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
. Then taking
![]() $b_{i}^{(1)}$
,
$b_{i}^{(1)}$
,
![]() $b_{i}^{(2)}\in \mathcal {B}_{g_{i}}$
,
$b_{i}^{(2)}\in \mathcal {B}_{g_{i}}$
,
![]() $i=1$
, …, m, we have
$i=1$
, …, m, we have
![]() $b_{i}^{(j)}=\phi (a_{i}^{(j)})$
for some
$b_{i}^{(j)}=\phi (a_{i}^{(j)})$
for some
![]() $a_{i}^{(j)}\in \mathcal {A}_{g_{i}}$
, since
$a_{i}^{(j)}\in \mathcal {A}_{g_{i}}$
, since
![]() $\phi $
is surjective. This leads us to
$\phi $
is surjective. This leads us to
 $$ \begin{align*} &\alpha f(b_{1}^{(1)},\dots,b_{m}^{(1)})+f(b_{1}^{(2)},\dots,b_{m}^{(2)})\\ & \quad =\alpha f(\phi(a_{1}^{(1)}),\dots,\phi(a_{m}^{(1)}))+f(\phi(a_{1}^{(2)}),\dots,\phi(a_{m}^{(2)}))\\ &\quad =\phi(\alpha f(a_{1}^{(1)},\dots,a_{m}^{(1)})+f(a_{1}^{(2)},\dots,a_{m}^{(2)})), \end{align*} $$
$$ \begin{align*} &\alpha f(b_{1}^{(1)},\dots,b_{m}^{(1)})+f(b_{1}^{(2)},\dots,b_{m}^{(2)})\\ & \quad =\alpha f(\phi(a_{1}^{(1)}),\dots,\phi(a_{m}^{(1)}))+f(\phi(a_{1}^{(2)}),\dots,\phi(a_{m}^{(2)}))\\ &\quad =\phi(\alpha f(a_{1}^{(1)},\dots,a_{m}^{(1)})+f(a_{1}^{(2)},\dots,a_{m}^{(2)})), \end{align*} $$
which is an element from
![]() $\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
since we are assuming that
$\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
since we are assuming that
![]() $f(\mathcal {A})$
is a subspace. Then
$f(\mathcal {A})$
is a subspace. Then
![]() $f(\mathcal {B})$
is also a subspace.
$f(\mathcal {B})$
is also a subspace.
Now, we assume that
![]() $f(\mathcal {A})$
is a homogeneous subspace and let
$f(\mathcal {A})$
is a homogeneous subspace and let
![]() $b=b_{h_{1}}+\cdots + b_{h_{k}}$
be an element in
$b=b_{h_{1}}+\cdots + b_{h_{k}}$
be an element in
![]() $f(\mathcal {B})$
written as the sum of its homogeneous components. Since
$f(\mathcal {B})$
written as the sum of its homogeneous components. Since
![]() $b\in f(\mathcal {B})$
, let
$b\in f(\mathcal {B})$
, let
for some
![]() $b_{i}=\phi (a_{i})$
, and let
$b_{i}=\phi (a_{i})$
, and let
be the sum of its homogeneous components. It follows that
and that since
![]() $\phi $
is a graded homomorphism, we must have
$\phi $
is a graded homomorphism, we must have
![]() $k=l$
and every
$k=l$
and every
![]() $g_{t}$
must be equal to some
$g_{t}$
must be equal to some
![]() $h_{s}$
. Without loss of generality, we assume that
$h_{s}$
. Without loss of generality, we assume that
![]() $b_{g_{t}}=\phi (a_{g_{t}})$
. Now, it is enough to use that
$b_{g_{t}}=\phi (a_{g_{t}})$
. Now, it is enough to use that
![]() $f(\mathcal {A})$
is homogeneous and
$f(\mathcal {A})$
is homogeneous and
![]() $\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
.
$\phi (f(\mathcal {A}))=f(\phi (\mathcal {A}))$
.
Remark 6.2 In the proof of Proposition 6.1, we have not used the associativity of
![]() $\mathcal {A}$
. Therefore, it also holds for arbitrary algebras, in particular an analogous proposition holds for graded Jordan algebras.
$\mathcal {A}$
. Therefore, it also holds for arbitrary algebras, in particular an analogous proposition holds for graded Jordan algebras.
As a consequence of Proposition 6.1, we have the following theorem.
Theorem 6.3 Let
![]() $UT_{2}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be some grading on
$UT_{2}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be some grading on
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $f\in F\langle X \rangle ^{gr}$
be a multilinear graded polynomial. Then
$f\in F\langle X \rangle ^{gr}$
be a multilinear graded polynomial. Then
![]() $f(\mathcal {A})$
is a homogeneous subspace of
$f(\mathcal {A})$
is a homogeneous subspace of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof By Theorem 2.4 and Proposition 6.1, it is enough to consider images of multilinear graded polynomials on elementary gradings only. We note that just two elementary G-gradings can be defined on
![]() $\mathcal {A}=UT_{2}$
. Indeed, an elementary grading on
$\mathcal {A}=UT_{2}$
. Indeed, an elementary grading on
![]() $UT_{2}$
is completely determined by the homogeneous degree of
$UT_{2}$
is completely determined by the homogeneous degree of
![]() $e_{12}$
. If
$e_{12}$
. If
![]() $\deg (e_{12})=1$
, then we have the trivial grading, and we apply Theorem 2.8. Hence, we assume that
$\deg (e_{12})=1$
, then we have the trivial grading, and we apply Theorem 2.8. Hence, we assume that
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22}\}$
and
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22}\}$
and
![]() $\mathcal {A}_{g}=\mathrm{span}\{e_{12}\}$
, where
$\mathcal {A}_{g}=\mathrm{span}\{e_{12}\}$
, where
![]() $g\neq 1$
. In this grading, the images of multilinear polynomials in neutral variables are handled by Lemma 2.7 and Proposition 2.2(2). Since
$g\neq 1$
. In this grading, the images of multilinear polynomials in neutral variables are handled by Lemma 2.7 and Proposition 2.2(2). Since
![]() $\mathcal {A}_{g}^{2}=\{0\}$
, it is enough to consider multilinear polynomials in one variable of homogeneous degree g and all remaining variables of neutral degree. In this case, the image is contained in
$\mathcal {A}_{g}^{2}=\{0\}$
, it is enough to consider multilinear polynomials in one variable of homogeneous degree g and all remaining variables of neutral degree. In this case, the image is contained in
![]() $\mathcal {A}_{g}$
, and by Proposition 2.2(1), we are done.
$\mathcal {A}_{g}$
, and by Proposition 2.2(1), we are done.
Now, we prove an analogous fact to Theorem 6.3 with
![]() $\mathcal {A}=UT_{3}$
instead of
$\mathcal {A}=UT_{3}$
instead of
![]() $UT_{2}$
. From now on, in this subsection, we assume that
$UT_{2}$
. From now on, in this subsection, we assume that
![]() $\mathcal {A}$
is endowed with some elementary G-grading given by a tuple
$\mathcal {A}$
is endowed with some elementary G-grading given by a tuple
![]() $(g_{1},g_{2})\in G^{2}$
. Hence,
$(g_{1},g_{2})\in G^{2}$
. Hence,
![]() $g_{1}=\deg (e_{12})$
,
$g_{1}=\deg (e_{12})$
,
![]() $g_{2}=\deg (e_{23})$
, and
$g_{2}=\deg (e_{23})$
, and
![]() $g_{3}:=g_{1}g_{2}=\deg (e_{13})$
.
$g_{3}:=g_{1}g_{2}=\deg (e_{13})$
.
Hence, the elementary gradings on
![]() $UT_{3}$
are exactly the ones given by following relations.
$UT_{3}$
are exactly the ones given by following relations.
-
(I)
 $\{1\}\cap \{g_{1},g_{2},g_{3}\}\neq \emptyset $
.
$\{1\}\cap \{g_{1},g_{2},g_{3}\}\neq \emptyset $
.-
(a)
 $g_{1}=g_{2}=1$
, which implies
$g_{1}=g_{2}=1$
, which implies
 $g_{3}=1$
;
$g_{3}=1$
; -
(b)
 $g_{1}=1$
, which implies
$g_{1}=1$
, which implies
 $g_{2}=g_{3}$
;
$g_{2}=g_{3}$
; -
(c)
 $g_{2}=1$
, which implies
$g_{2}=1$
, which implies
 $g_{1}=g_{3}$
;
$g_{1}=g_{3}$
; -
(d)
 $g_{3}=1$
and
$g_{3}=1$
and
 $g_{1}=g_{2}$
;
$g_{1}=g_{2}$
; -
(e)
 $g_{3}=1$
and
$g_{3}=1$
and
 $g_{1}\neq g_{2}$
.
$g_{1}\neq g_{2}$
.
-
-
(II)
 $\{1\}\cap \{g_{1},g_{2},g_{3}\}=\emptyset $
.
$\{1\}\cap \{g_{1},g_{2},g_{3}\}=\emptyset $
.-
(a)
 $1,g_{1},g_{2},g_{3}$
are pairwise distinct elements;
$1,g_{1},g_{2},g_{3}$
are pairwise distinct elements; -
(b)
 $g_{1}=g_{2}\neq g_{3}$
.
$g_{1}=g_{2}\neq g_{3}$
.
-
In the following lemmas, we discuss the grading on
![]() $UT_{3}$
determined by each relation above and the respective image of a multilinear graded polynomial on such a graded algebra.
$UT_{3}$
determined by each relation above and the respective image of a multilinear graded polynomial on such a graded algebra.
Lemma 6.4 Let
![]() $UT_{3}$
be endowed with the grading (I)(b). Then
$UT_{3}$
be endowed with the grading (I)(b). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof We denote
![]() $g_{2}=g$
, then we have
$g_{2}=g$
, then we have
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{12}\}$
and
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{12}\}$
and
![]() $\mathcal {A}_{g}=\mathrm{span}\{e_{13},e_{23}\}$
. Note that
$\mathcal {A}_{g}=\mathrm{span}\{e_{13},e_{23}\}$
. Note that
![]() $\mathcal {A}_{g}^{2}=\{0\}$
and hence we only need to analyze multilinear polynomials in at most one variable of homogeneous degree g.
$\mathcal {A}_{g}^{2}=\{0\}$
and hence we only need to analyze multilinear polynomials in at most one variable of homogeneous degree g.
The case when f is a multilinear polynomial in neutral variables is settled by Lemma 2.7 and Proposition 2.2(2).
Now, we consider f as a multilinear polynomial in one nonneutral variable and
![]() $m-1$
neutral ones. Since
$m-1$
neutral ones. Since
![]() $\mathcal {A}$
satisfies the graded identity
$\mathcal {A}$
satisfies the graded identity
![]() $z[y_{1},y_{2}]\equiv 0$
, then modulo this identity, we write f as
$z[y_{1},y_{2}]\equiv 0$
, then modulo this identity, we write f as
If all polynomials
![]() $h_{i_{1}, \dots , i_{k}}$
have commutator degree different from
$h_{i_{1}, \dots , i_{k}}$
have commutator degree different from
![]() $0$
, then
$0$
, then
![]() $\mathrm{Im}(f)\subset \mathrm{span}\{e_{13}\}$
and then we apply Proposition 2.2(1). Otherwise, we may assume, without loss of generality, that
$\mathrm{Im}(f)\subset \mathrm{span}\{e_{13}\}$
and then we apply Proposition 2.2(1). Otherwise, we may assume, without loss of generality, that
![]() $h_{1,\dots ,k}$
has commutator degree
$h_{1,\dots ,k}$
has commutator degree
![]() $0$
. Then we perform the following evaluations:
$0$
. Then we perform the following evaluations:
![]() $y_{1}=\cdots =y_{k}=e_{33}$
,
$y_{1}=\cdots =y_{k}=e_{33}$
,
![]() $y_{j}=e_{11}+e_{22}$
for every
$y_{j}=e_{11}+e_{22}$
for every
![]() $j\notin \{1,\dots ,k\}$
, and
$j\notin \{1,\dots ,k\}$
, and
![]() $z_{m}=\alpha ^{-1}(a_{1}e_{13}+a_{2}e_{23})$
, where
$z_{m}=\alpha ^{-1}(a_{1}e_{13}+a_{2}e_{23})$
, where
![]() $\alpha $
is the sum of the coefficients of
$\alpha $
is the sum of the coefficients of
![]() $h_{1,\dots ,k}$
. Note that, under such an evaluation, we have
$h_{1,\dots ,k}$
. Note that, under such an evaluation, we have
![]() $a_{1}e_{13}+a_{2}e_{23}\in \mathrm{Im}(f)$
, which proves that
$a_{1}e_{13}+a_{2}e_{23}\in \mathrm{Im}(f)$
, which proves that
![]() $\mathrm{Im}(f)=\mathcal {A}_{g}$
.
$\mathrm{Im}(f)=\mathcal {A}_{g}$
.
Lemma 6.5 Let
![]() $UT_{3}$
be endowed with the grading (I)(c). Then
$UT_{3}$
be endowed with the grading (I)(c). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof Note that
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{23}\}$
,
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{23}\}$
,
![]() $\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12},e_{13}\}$
, and
$\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12},e_{13}\}$
, and
![]() $\mathcal {A}$
satisfies the identities
$\mathcal {A}$
satisfies the identities
![]() $[y_{1},y_{2}]z\equiv 0$
and
$[y_{1},y_{2}]z\equiv 0$
and
![]() $z_{1}z_{2}\equiv 0$
. Thus, the proof is similar to the one for (I)(b).
$z_{1}z_{2}\equiv 0$
. Thus, the proof is similar to the one for (I)(b).
Lemma 6.6 Let
![]() $UT_{3}$
be endowed with the grading (I)(e). Then
$UT_{3}$
be endowed with the grading (I)(e). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof Here, we must have
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{13}\}$
,
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{13}\}$
,
![]() $\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12}\}$
, and
$\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12}\}$
, and
![]() $\mathcal {A}_{g_{2}}=\mathrm{span}\{e_{23}\}$
. Note that
$\mathcal {A}_{g_{2}}=\mathrm{span}\{e_{23}\}$
. Note that
![]() $\mathcal {A}_{g_{1}}^{2}=\mathcal {A}_{g_{2}}^{2}=\{0\}$
,
$\mathcal {A}_{g_{1}}^{2}=\mathcal {A}_{g_{2}}^{2}=\{0\}$
,
![]() $\mathcal {A}_{g_{2}}\mathcal {A}_{g_{1}}=\{0\}$
, and
$\mathcal {A}_{g_{2}}\mathcal {A}_{g_{1}}=\{0\}$
, and
![]() $\mathcal {A}_{g_{1}}\mathcal {A}_{g_{2}}\subset \mathrm{span}\{e_{13}\}$
.
$\mathcal {A}_{g_{1}}\mathcal {A}_{g_{2}}\subset \mathrm{span}\{e_{13}\}$
.
The case when f is a multilinear polynomial in neutral variables can be treated as in the grading (I)(b). Hence, we may consider f is a multilinear polynomial in one variable of degree
![]() $g_{1}$
(resp.
$g_{1}$
(resp.
![]() $g_{2}$
) and
$g_{2}$
) and
![]() $m-1$
neutral variables, or in one variable of degree
$m-1$
neutral variables, or in one variable of degree
![]() $g_{1}$
, one of degree
$g_{1}$
, one of degree
![]() $g_{2}$
, and
$g_{2}$
, and
![]() $m-2$
neutral ones. In each of these situations, we have that
$m-2$
neutral ones. In each of these situations, we have that
![]() $\mathrm{Im}(f)$
is contained in a one-dimensional space and we apply Proposition 2.2(1).
$\mathrm{Im}(f)$
is contained in a one-dimensional space and we apply Proposition 2.2(1).
Lemma 6.7 Let
![]() $UT_{3}$
be endowed with the grading (II)(a). Then
$UT_{3}$
be endowed with the grading (II)(a). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof We have
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
![]() $\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12}\}$
,
$\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12}\}$
,
![]() $\mathcal {A}_{g_{2}}=\mathrm{span}\{e_{23}\}$
, and
$\mathcal {A}_{g_{2}}=\mathrm{span}\{e_{23}\}$
, and
![]() $\mathcal {A}_{g_{3}}=\mathrm{span}\{e_{13}\}$
. The only nontrivial relation among the nonneutral homogeneous components is given by
$\mathcal {A}_{g_{3}}=\mathrm{span}\{e_{13}\}$
. The only nontrivial relation among the nonneutral homogeneous components is given by
![]() $\mathcal {A}_{g_{1}}\mathcal {A}_{g_{3}}=\mathcal {A}_{g_{2}}$
.
$\mathcal {A}_{g_{1}}\mathcal {A}_{g_{3}}=\mathcal {A}_{g_{2}}$
.
The case of f in neutral variables is the same as for the grading (I)(b).
Since the nonneutral components are one-dimensional, then the image of a multilinear polynomial in one nonneutral variable and
![]() $m-1$
neutral ones is always zero or the respective homogeneous component.
$m-1$
neutral ones is always zero or the respective homogeneous component.
In case f has one variable of homogeneous degree
![]() $g_{1}$
, one of degree
$g_{1}$
, one of degree
![]() $g_{3}$
, and
$g_{3}$
, and
![]() $m-2$
neutral ones, then the image is contained in
$m-2$
neutral ones, then the image is contained in
![]() $\mathcal {A}_{g_{2}}$
, and we are done.
$\mathcal {A}_{g_{2}}$
, and we are done.
Lemma 6.8 Let
![]() $UT_{3}$
be endowed with the grading (II)(b). Then
$UT_{3}$
be endowed with the grading (II)(b). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof Note that
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
![]() $\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12},e_{23}\}$
, and
$\mathcal {A}_{g_{1}}=\mathrm{span}\{e_{12},e_{23}\}$
, and
![]() $\mathcal {A}_{g_{3}}=\mathrm{span}\{e_{13}\}$
. We only need to consider the case when f is a multilinear polynomial in
$\mathcal {A}_{g_{3}}=\mathrm{span}\{e_{13}\}$
. We only need to consider the case when f is a multilinear polynomial in
![]() $m-1$
neutral variables and one of homogeneous degree
$m-1$
neutral variables and one of homogeneous degree
![]() $g_{1}$
, since the remaining cases can be treated as above. We write
$g_{1}$
, since the remaining cases can be treated as above. We write
 $f=\displaystyle \sum _{j=1}^{m}f_{j}$
where
$f=\displaystyle \sum _{j=1}^{m}f_{j}$
where
![]() $f_{j}$
is the sum of all monomials from f which contain the variable
$f_{j}$
is the sum of all monomials from f which contain the variable
![]() $z_{m}$
in the jth position. Hence, modulo
$z_{m}$
in the jth position. Hence, modulo
![]() $[y_{1},y_{2}]\equiv 0$
, we have
$[y_{1},y_{2}]\equiv 0$
, we have
where
![]() $k_{1}<\cdots <k_{m-j}$
. We evaluate
$k_{1}<\cdots <k_{m-j}$
. We evaluate
![]() $y_{i}=w_{1}^{(i)}e_{11}+e_{22}+w_{3}^{(i)}e_{33}$
and
$y_{i}=w_{1}^{(i)}e_{11}+e_{22}+w_{3}^{(i)}e_{33}$
and
![]() $z_{m}=w_{1}^{(m)}e_{12}+w_{2}^{(m)}e_{23}$
. Thus,
$z_{m}=w_{1}^{(m)}e_{12}+w_{2}^{(m)}e_{23}$
. Thus,
![]() $f(y_{1},\dots ,y_{m-1},z_{m})$
is given by
$f(y_{1},\dots ,y_{m-1},z_{m})$
is given by
 $$\begin{align*}\begin{pmatrix} 0&p_{1}(w_{1}^{(1)},\dots,w_{1}^{(m-1)})w_{1}^{(m)} & 0\\ &0 &p_{2}(w_{3}^{(1)},\dots,w_{3}^{(m-1)})w_{2}^{(m)} \\ & &0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0&p_{1}(w_{1}^{(1)},\dots,w_{1}^{(m-1)})w_{1}^{(m)} & 0\\ &0 &p_{2}(w_{3}^{(1)},\dots,w_{3}^{(m-1)})w_{2}^{(m)} \\ & &0 \end{pmatrix}, \end{align*}$$
where
 $p_{1}(w_{1}^{(1)},\dots ,w_{1}^{(m-1)})=\displaystyle \sum _{j=1}^{m}\sum _{1\leq i_{1}<\cdots <i_{j-1}\leq m-1}\alpha _{i_{1},\dots ,i_{j-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{j-1})}$
and
$p_{1}(w_{1}^{(1)},\dots ,w_{1}^{(m-1)})=\displaystyle \sum _{j=1}^{m}\sum _{1\leq i_{1}<\cdots <i_{j-1}\leq m-1}\alpha _{i_{1},\dots ,i_{j-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{j-1})}$
and
![]() $p_{2}$
is given analogously.
$p_{2}$
is given analogously.
We claim that
![]() $p_{1}$
takes nonzero values on F. Indeed, assume that
$p_{1}$
takes nonzero values on F. Indeed, assume that
![]() $p_{1}$
is a polynomial identity for F and denote
$p_{1}$
is a polynomial identity for F and denote
![]() $e_{j}=\displaystyle \sum _{1\leq i_{1}<\cdots < i_{j-1}\leq m-1}\alpha _{i_{1},\dots ,i_{j-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{j-1})}$
. Note that
$e_{j}=\displaystyle \sum _{1\leq i_{1}<\cdots < i_{j-1}\leq m-1}\alpha _{i_{1},\dots ,i_{j-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{j-1})}$
. Note that
![]() $e_{1}\in F$
and taking
$e_{1}\in F$
and taking
![]() $w_{1}^{(1)}=\cdots =w_{1}^{(m-1)}=0$
we have
$w_{1}^{(1)}=\cdots =w_{1}^{(m-1)}=0$
we have
![]() $e_{1}=0$
. Taking
$e_{1}=0$
. Taking
![]() $w_{1}^{(l)}=1$
and zero for the remaining values of
$w_{1}^{(l)}=1$
and zero for the remaining values of
![]() $w_{1}$
, we have
$w_{1}$
, we have
![]() $\alpha _{l}=0$
for all
$\alpha _{l}=0$
for all
![]() $l\in \{1,\dots ,m-1\}$
and hence
$l\in \{1,\dots ,m-1\}$
and hence
![]() $e_{2}=0$
. Now, assume
$e_{2}=0$
. Now, assume
![]() $e_{l}=0$
for all
$e_{l}=0$
for all
![]() $l<k$
, and we shall prove that
$l<k$
, and we shall prove that
![]() $e_{k}=0$
. For each chosen
$e_{k}=0$
. For each chosen
![]() $i_{1}$
, …,
$i_{1}$
, …,
![]() $i_{k-1}$
, we take
$i_{k-1}$
, we take
![]() $w_{1}^{(r)}=0$
for all
$w_{1}^{(r)}=0$
for all
![]() $r\notin \{i_{1},\dots ,i_{k-1}\}$
, then
$r\notin \{i_{1},\dots ,i_{k-1}\}$
, then
![]() $e_{l}=0$
for all
$e_{l}=0$
for all
![]() $l>k$
and
$l>k$
and
![]() $e_{k}=\alpha _{i_{1},\dots ,i_{k-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{k-1})}$
. Then we take
$e_{k}=\alpha _{i_{1},\dots ,i_{k-1}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{k-1})}$
. Then we take
![]() $w_{1}^{(i_{1})}=\cdots =w_{1}^{(i_{k-1})}=1$
, and we conclude that
$w_{1}^{(i_{1})}=\cdots =w_{1}^{(i_{k-1})}=1$
, and we conclude that
![]() $\alpha _{i_{1},\dots ,i_{k-1}}=0$
. Hence,
$\alpha _{i_{1},\dots ,i_{k-1}}=0$
. Hence,
![]() $p_{1}=0$
, which is a contradiction. Analogous claim holds for
$p_{1}=0$
, which is a contradiction. Analogous claim holds for
![]() $p_{2}$
. Therefore, it is enough to use the variables
$p_{2}$
. Therefore, it is enough to use the variables
![]() $w_{1}^{(m)}$
and
$w_{1}^{(m)}$
and
![]() $w_{2}^{(m)}$
to realize any matrix in
$w_{2}^{(m)}$
to realize any matrix in
![]() $\mathcal {A}_{g_{1}}$
in the image of f.
$\mathcal {A}_{g_{1}}$
in the image of f.
Lemma 6.9 Let
![]() $UT_{3}$
be endowed with the grading (I)(d). Then
$UT_{3}$
be endowed with the grading (I)(d). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{3}$
is a homogeneous subspace.
$UT_{3}$
is a homogeneous subspace.
Proof We denote
![]() $g=g_{1}$
and note that
$g=g_{1}$
and note that
![]() $\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{13}\}$
and
$\mathcal {A}_{1}=\mathrm{span}\{e_{11},e_{22},e_{33},e_{13}\}$
and
![]() $\mathcal {A}_{g}=\mathrm{span}\{e_{12},e_{23}\}$
. Then
$\mathcal {A}_{g}=\mathrm{span}\{e_{12},e_{23}\}$
. Then
![]() $\mathcal {A}_{g}^{2}\subset \mathrm{span}\{e_{13}\}$
and
$\mathcal {A}_{g}^{2}\subset \mathrm{span}\{e_{13}\}$
and
![]() $\mathcal {A}$
satisfies the identities
$\mathcal {A}$
satisfies the identities
![]() $z[y_{1},y_{2}]\equiv 0$
and
$z[y_{1},y_{2}]\equiv 0$
and
![]() $[y_{1},y_{2}]z\equiv 0$
. The case when f has one variable of homogeneous degree g and
$[y_{1},y_{2}]z\equiv 0$
. The case when f has one variable of homogeneous degree g and
![]() $m-1$
neutral variables can be treated as in the previous lemma. The remaining cases are considered as above.
$m-1$
neutral variables can be treated as in the previous lemma. The remaining cases are considered as above.
Hence, we have the following theorem.
Theorem 6.10 Let F be an arbitrary field, let
![]() $UT_{3}=\mathcal {A}=\bigoplus _{g\in G}A_{g}$
be some nontrivial grading on
$UT_{3}=\mathcal {A}=\bigoplus _{g\in G}A_{g}$
be some nontrivial grading on
![]() $\mathcal {A}$
, and let
$\mathcal {A}$
, and let
![]() $f\in F\langle X \rangle ^{gr}$
be a multilinear graded polynomial. Then
$f\in F\langle X \rangle ^{gr}$
be a multilinear graded polynomial. Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $\mathcal {A}$
is a homogeneous subspace of
$\mathcal {A}$
is a homogeneous subspace of
![]() $\mathcal {A}$
. If
$\mathcal {A}$
. If
![]() $|F|\geq 3$
and
$|F|\geq 3$
and
![]() $\mathcal {A}$
is equipped with the trivial grading, then the image is also a subspace.
$\mathcal {A}$
is equipped with the trivial grading, then the image is also a subspace.
Proof The proof is clear from the previous lemmas and Proposition 6.1.
6.2 The graded Jordan algebra
 $UJ_{2}$
$UJ_{2}$
Throughout this subsection, we assume that F is a field of characteristic different from
![]() $2$
and we denote by
$2$
and we denote by
![]() $UJ_{n}$
the Jordan algebra of the upper triangular matrices with product
$UJ_{n}$
the Jordan algebra of the upper triangular matrices with product
![]() $a\circ b=ab+ba$
. Unlike the associative setting, gradings on
$a\circ b=ab+ba$
. Unlike the associative setting, gradings on
![]() $UJ_{n}$
are not only elementary ones. Actually, a second kind of grading also occurs on
$UJ_{n}$
are not only elementary ones. Actually, a second kind of grading also occurs on
![]() $UJ_{n}$
, the so-called mirror-type gradings, and we define these below. First of all, let us introduce the following notation.
$UJ_{n}$
, the so-called mirror-type gradings, and we define these below. First of all, let us introduce the following notation.
Let i, m be nonnegative integers and set
Definition 6.11 A G-grading on
![]() $UJ_{n}$
is called of mirror type if the matrices
$UJ_{n}$
is called of mirror type if the matrices
![]() $E_{i:m}^{+}$
and
$E_{i:m}^{+}$
and
![]() $E_{i:m}^{-}$
are homogeneous, and
$E_{i:m}^{-}$
are homogeneous, and
![]() $\deg (E_{i:m}^{+})\neq \deg (E_{i:m}^{-})$
.
$\deg (E_{i:m}^{+})\neq \deg (E_{i:m}^{-})$
.
We recall the following theorem from [Reference Koshlukov and Yasumura30].
Theorem 6.12 [Reference Koshlukov and Yasumura30]
The G-gradings on the Jordan algebra
![]() $UJ_{n}$
are, up to a graded isomorphism, elementary or of mirror type.
$UJ_{n}$
are, up to a graded isomorphism, elementary or of mirror type.
In particular, we have the following classification of the gradings on
![]() $UJ_{2}$
.
$UJ_{2}$
.
Proposition 6.13 Up to a graded isomorphism, the gradings on
![]() $UJ_{2}$
are given by
$UJ_{2}$
are given by
![]() $UJ_{2}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
where:
$UJ_{2}=\mathcal {A}=\bigoplus _{g\in G}\mathcal {A}_{g}$
where:
-
(I) elementary ones;
-
(a) trivial grading;
-
(b)
 $\mathcal {A}_{1}=Fe_{11}+Fe_{22}$
,
$\mathcal {A}_{1}=Fe_{11}+Fe_{22}$
,
 $\mathcal {A}_{g}=Fe_{12}$
;
$\mathcal {A}_{g}=Fe_{12}$
;
-
-
(II) mirror type ones;
-
(a)
 $\mathcal {A}_{1}=F(e_{11}+e_{22})$
,
$\mathcal {A}_{1}=F(e_{11}+e_{22})$
,
 $\mathcal {A}_{g}=F(e_{11}-e_{22})+Fe_{12}$
;
$\mathcal {A}_{g}=F(e_{11}-e_{22})+Fe_{12}$
; -
(b)
 $\mathcal {A}_{1}=F(e_{11}+e_{22})+Fe_{12}$
,
$\mathcal {A}_{1}=F(e_{11}+e_{22})+Fe_{12}$
,
 $\mathcal {A}_{g}=F(e_{11}-e_{22})$
;
$\mathcal {A}_{g}=F(e_{11}-e_{22})$
; -
(c)
 $\mathcal {A}_{1}=F(e_{11}+e_{22})$
,
$\mathcal {A}_{1}=F(e_{11}+e_{22})$
,
 $\mathcal {A}_{g}=F(e_{11}-e_{22})$
,
$\mathcal {A}_{g}=F(e_{11}-e_{22})$
,
 $\mathcal {A}_{h}=Fe_{12}$
;
$\mathcal {A}_{h}=Fe_{12}$
;
-
where g,
![]() $h\in G$
are elements of order
$h\in G$
are elements of order
![]() $2$
.
$2$
.
In [Reference Koshlukov and Yasumura30], it was also proved that the support of a grading on
![]() $UJ_{n}$
is always abelian (see [Reference Koshlukov and Yasumura30, Theorem 24]). Hence, by Proposition 2.2(4), we have that
$UJ_{n}$
is always abelian (see [Reference Koshlukov and Yasumura30, Theorem 24]). Hence, by Proposition 2.2(4), we have that
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{n}$
is a homogeneous subset for any multilinear graded polynomial
$UJ_{n}$
is a homogeneous subset for any multilinear graded polynomial
![]() $f\in J(X)$
.
$f\in J(X)$
.
Next, we analyze the images of a multilinear graded Jordan polynomial f on the gradings considered above.
Lemma 6.14 Let
![]() $UJ_{2}$
be endowed with the grading (I)(b). Then
$UJ_{2}$
be endowed with the grading (I)(b). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is a homogeneous subspace.
$UJ_{2}$
is a homogeneous subspace.
Proof We start with a multilinear polynomial f in m neutral variables. We evaluate each variable
![]() $y_{i}$
to an arbitrary diagonal matrix
$y_{i}$
to an arbitrary diagonal matrix
![]() $D_{i}$
. Therefore, each monomial
$D_{i}$
. Therefore, each monomial
![]() $\mathbf {m}$
in f is evaluated to
$\mathbf {m}$
in f is evaluated to
![]() $2^{m-1}\beta D_{1}\cdots D_{m}$
, where
$2^{m-1}\beta D_{1}\cdots D_{m}$
, where
![]() $\beta \in F$
is the coefficient of
$\beta \in F$
is the coefficient of
![]() $\mathbf {m}$
. Hence,
$\mathbf {m}$
. Hence,
where
![]() $\alpha \in F$
is the sum of all coefficients of f. In case
$\alpha \in F$
is the sum of all coefficients of f. In case
![]() $\alpha =0$
, then
$\alpha =0$
, then
![]() $f=0$
is a graded polynomial identity for
$f=0$
is a graded polynomial identity for
![]() $UJ_{2}$
; otherwise, we can take
$UJ_{2}$
; otherwise, we can take
![]() $D_{2}=\cdots =D_{m}=I_{2}$
and use
$D_{2}=\cdots =D_{m}=I_{2}$
and use
![]() $D_{1}$
in order to obtain every diagonal matrix in the image of f.
$D_{1}$
in order to obtain every diagonal matrix in the image of f.
Since
![]() $UJ_{2}$
satisfies the graded identity
$UJ_{2}$
satisfies the graded identity
![]() $z_{1}\circ z_{2}=0$
such that
$z_{1}\circ z_{2}=0$
such that
![]() $\deg (z_{1})=\deg (z_{2})=g$
, then we only need to analyze the case where f is a multilinear polynomial in
$\deg (z_{1})=\deg (z_{2})=g$
, then we only need to analyze the case where f is a multilinear polynomial in
![]() $m-1$
neutral variables and one of homogeneous degree g. Obviously, we must have
$m-1$
neutral variables and one of homogeneous degree g. Obviously, we must have
![]() $\mathrm{Im}(f)\subset \mathcal {A}_{g}$
and this homogeneous component is one-dimensional, then we are done.
$\mathrm{Im}(f)\subset \mathcal {A}_{g}$
and this homogeneous component is one-dimensional, then we are done.
For the grading (II)(a), we recall a lemma from [Reference Gonçalves and Salomão22] applied to multilinear polynomials. In order to make the notation more compact, we omit the symbol
![]() $\circ $
for the Jordan product, and we write
$\circ $
for the Jordan product, and we write
![]() $ab$
instead of
$ab$
instead of
![]() $a\circ b$
. If no brackets are given in a product, we assume that these are left-normed, that is,
$a\circ b$
. If no brackets are given in a product, we assume that these are left-normed, that is,
![]() $abc=(ab)c$
.
$abc=(ab)c$
.
Lemma 6.15 [Reference Gonçalves and Salomão22]
Let
![]() $UJ_{2}$
be endowed with the grading (II)(a), and let
$UJ_{2}$
be endowed with the grading (II)(a), and let
![]() $f\in J(X)_{g}$
be a multilinear
$f\in J(X)_{g}$
be a multilinear
![]() $\mathbb {Z}_{2}$
-graded polynomial. Then, modulo the graded identities of
$\mathbb {Z}_{2}$
-graded polynomial. Then, modulo the graded identities of
![]() $UJ_{2}$
, we can write f as a linear combination of monomials of the type
$UJ_{2}$
, we can write f as a linear combination of monomials of the type
Lemma 6.16 Let
![]() $UJ_{2}$
be endowed with the grading (II)(a). Then
$UJ_{2}$
be endowed with the grading (II)(a). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is a homogeneous subspace.
$UJ_{2}$
is a homogeneous subspace.
Proof Since
![]() $\dim \mathcal {A}_{1}=1$
, it follows that if the image of a multilinear polynomial on
$\dim \mathcal {A}_{1}=1$
, it follows that if the image of a multilinear polynomial on
![]() $UJ_{2}$
is contained in
$UJ_{2}$
is contained in
![]() $\mathcal {A}_{1}$
, then it must be either
$\mathcal {A}_{1}$
, then it must be either
![]() $\{0\}$
or
$\{0\}$
or
![]() $\mathcal {A}_{1}$
.
$\mathcal {A}_{1}$
.
Now, we consider a multilinear polynomial f in homogeneous variables of degree
![]() $1$
and g such that
$1$
and g such that
![]() $\deg f=g$
. Let
$\deg f=g$
. Let
![]() $\mathbf {m}=y_{1}\cdots y_{l}z_{i_{0}}(z_{i_{1}}z_{i_{2}})\cdots (z_{i_{2m-1}}z_{i_{2m}})$
be a monomial as in Lemma 6.15. We note that the main diagonal of a matrix in
$\mathbf {m}=y_{1}\cdots y_{l}z_{i_{0}}(z_{i_{1}}z_{i_{2}})\cdots (z_{i_{2m-1}}z_{i_{2m}})$
be a monomial as in Lemma 6.15. We note that the main diagonal of a matrix in
![]() $m(UJ_{2})$
is such that the entry
$m(UJ_{2})$
is such that the entry
![]() $(k,k)$
is given by
$(k,k)$
is given by
![]() $(-1)^{k+1}2^{m+l+1}a$
where a is the product of the entries at position
$(-1)^{k+1}2^{m+l+1}a$
where a is the product of the entries at position
![]() $(1,1)$
of all matrices y and z. Hence, every matrix in
$(1,1)$
of all matrices y and z. Hence, every matrix in
![]() $\mathrm{Im}(f)$
is of the form
$\mathrm{Im}(f)$
is of the form
 $$\begin{align*}\begin{pmatrix} 2^{m+l+1}\alpha\cdot a & * \\ & -2^{m+l+1}\alpha\cdot a \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 2^{m+l+1}\alpha\cdot a & * \\ & -2^{m+l+1}\alpha\cdot a \end{pmatrix}, \end{align*}$$
where
![]() $\alpha $
is the sum of all coefficients of f.
$\alpha $
is the sum of all coefficients of f.
In case
![]() $\alpha =0$
, then
$\alpha =0$
, then
![]() $\mathrm{Im}(f)\subset \mathrm{span}\{e_{12}\}$
and then the image is completely determined.
$\mathrm{Im}(f)\subset \mathrm{span}\{e_{12}\}$
and then the image is completely determined.
We consider now
![]() $\alpha \neq 0$
. Without loss of generality, we assume that the nonzero scalar occurs in the monomial
$\alpha \neq 0$
. Without loss of generality, we assume that the nonzero scalar occurs in the monomial
![]() $y_{1}\cdots y_{l}z_{0}(z_{1}z_{2})\cdots (z_{2m-1}z_{2m})$
. Then we make the following evaluation:
$y_{1}\cdots y_{l}z_{0}(z_{1}z_{2})\cdots (z_{2m-1}z_{2m})$
. Then we make the following evaluation:
![]() $y_{1}=\cdots =y_{l}=I_{2}$
,
$y_{1}=\cdots =y_{l}=I_{2}$
,
![]() $z_{0}=w_{1}(e_{11}-e_{22})+w_{2}e_{12}$
, and
$z_{0}=w_{1}(e_{11}-e_{22})+w_{2}e_{12}$
, and
![]() $z_{i}=e_{11}-e_{22}$
, for every
$z_{i}=e_{11}-e_{22}$
, for every
![]() $i=1$
, …,
$i=1$
, …,
![]() $2m$
, where
$2m$
, where
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
are commutative variables. Therefore,
$w_{2}$
are commutative variables. Therefore,
 $$\begin{align*}f(y_{1},\dots,y_{l},z_{0},\dots,z_{2m})=\begin{pmatrix} 2^{m+l+1}\alpha w_{1} & 2^{m+l+1}w_{2} \\ & -2^{m+l+1}\alpha w_{1} \end{pmatrix}. \end{align*}$$
$$\begin{align*}f(y_{1},\dots,y_{l},z_{0},\dots,z_{2m})=\begin{pmatrix} 2^{m+l+1}\alpha w_{1} & 2^{m+l+1}w_{2} \\ & -2^{m+l+1}\alpha w_{1} \end{pmatrix}. \end{align*}$$
Since
![]() $\mathrm{char}(F)\neq 2$
and
$\mathrm{char}(F)\neq 2$
and
![]() $\alpha \neq 0$
, it follows that
$\alpha \neq 0$
, it follows that
![]() $\mathrm{Im}(f)=\mathcal {A}_{g}$
.
$\mathrm{Im}(f)=\mathcal {A}_{g}$
.
Now, we consider the grading (II)(b) and we recall another lemma from [Reference Gonçalves and Salomão22].
Lemma 6.17 [Reference Gonçalves and Salomão22]
Let
![]() $f\in J(X)_{1}$
be a multilinear polynomial. Then, modulo the graded identities of
$f\in J(X)_{1}$
be a multilinear polynomial. Then, modulo the graded identities of
![]() $UJ_{2}$
, f can be written as a linear combination of monomials of the form:
$UJ_{2}$
, f can be written as a linear combination of monomials of the form:
-
(1)
 $(y_{i_{1}}\cdots y_{i_{r}})(z_{j_{1}}\cdots z_{j_{l}})$
;
$(y_{i_{1}}\cdots y_{i_{r}})(z_{j_{1}}\cdots z_{j_{l}})$
; -
(2)
 $(((y_{i}z_{j_{1}})z_{j_{2}})y_{i_{1}}\cdots y_{i_{r}})z_{j_{3}}\cdots z_{j_{l}}$
,
$(((y_{i}z_{j_{1}})z_{j_{2}})y_{i_{1}}\cdots y_{i_{r}})z_{j_{3}}\cdots z_{j_{l}}$
,
where
![]() $l\geq 0$
is even,
$l\geq 0$
is even,
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $i_{1}<\cdots <i_{r}$
, and
$i_{1}<\cdots <i_{r}$
, and
![]() $z_{j_{1}}<z_{j_{2}}<z_{j_{3}}<\cdots <z_{j_{l}}$
.
$z_{j_{1}}<z_{j_{2}}<z_{j_{3}}<\cdots <z_{j_{l}}$
.
Lemma 6.18 Let
![]() $UJ_{2}$
be endowed with the grading (II)(b). Then
$UJ_{2}$
be endowed with the grading (II)(b). Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is a homogeneous subspace.
$UJ_{2}$
is a homogeneous subspace.
Proof We start with a multilinear polynomial f in m neutral variables. Note that a multilinear monomial of degree m evaluated on
![]() $\mathcal {A}_{1}$
is a matrix whose main diagonal is given by
$\mathcal {A}_{1}$
is a matrix whose main diagonal is given by
![]() $2^{m-1}aI_{2}$
where a is the product of the entries on the main diagonal of the matrices used in the evaluation. Hence, a matrix in
$2^{m-1}aI_{2}$
where a is the product of the entries on the main diagonal of the matrices used in the evaluation. Hence, a matrix in
![]() $\mathrm{Im}(f)$
must be of the form
$\mathrm{Im}(f)$
must be of the form
 $$\begin{align*}\begin{pmatrix} 2^{m-1}\alpha\cdot a & * \\ & 2^{m-1}\alpha\cdot a \end{pmatrix}, \end{align*}$$
$$\begin{align*}\begin{pmatrix} 2^{m-1}\alpha\cdot a & * \\ & 2^{m-1}\alpha\cdot a \end{pmatrix}, \end{align*}$$
where
![]() $\alpha $
is the sum of all coefficients of f. In case
$\alpha $
is the sum of all coefficients of f. In case
![]() $\alpha =0$
, we have
$\alpha =0$
, we have
![]() $\mathrm{Im}(f)\subset \mathrm{span}\{e_{12}\}$
and the image is completely determined. From now on, we assume
$\mathrm{Im}(f)\subset \mathrm{span}\{e_{12}\}$
and the image is completely determined. From now on, we assume
![]() $\alpha \neq 0$
, and we evaluate
$\alpha \neq 0$
, and we evaluate
![]() $m-1$
matrices by
$m-1$
matrices by
![]() $I_{2}$
and one matrix, say
$I_{2}$
and one matrix, say
![]() $y_{1}$
, by
$y_{1}$
, by
![]() $w_{1}(e_{11}+e_{22})+w_{2}e_{12}$
, where
$w_{1}(e_{11}+e_{22})+w_{2}e_{12}$
, where
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
are commuting variables. Therefore,
$w_{2}$
are commuting variables. Therefore,
 $$\begin{align*}f(y_{1},\dots,y_{m})=\begin{pmatrix} 2^{m-1}\alpha w_{1} & 2^{m-1}\alpha w_{2} \\ & 2^{m-1}\alpha w_{1} \end{pmatrix}, \end{align*}$$
$$\begin{align*}f(y_{1},\dots,y_{m})=\begin{pmatrix} 2^{m-1}\alpha w_{1} & 2^{m-1}\alpha w_{2} \\ & 2^{m-1}\alpha w_{1} \end{pmatrix}, \end{align*}$$
and since
![]() $\mathrm{char}(F)\neq 2$
and
$\mathrm{char}(F)\neq 2$
and
![]() $\alpha \neq 0$
, we have that
$\alpha \neq 0$
, we have that
![]() $\mathrm{Im}(f)=\mathcal {A}_{1}$
.
$\mathrm{Im}(f)=\mathcal {A}_{1}$
.
Now, we consider a multilinear polynomial f which has at least one variable of homogeneous degree g. In case
![]() $\deg f=g$
, the image
$\deg f=g$
, the image
![]() $\mathrm{Im}(f)$
is completely determined, since
$\mathrm{Im}(f)$
is completely determined, since
![]() $\dim \mathcal {A}_{g}=1$
. So we assume
$\dim \mathcal {A}_{g}=1$
. So we assume
![]() $\deg f=1$
. In case f is a multilinear polynomial in variables of homogeneous degree g, then
$\deg f=1$
. In case f is a multilinear polynomial in variables of homogeneous degree g, then
![]() $\mathrm{Im}(f)$
is contained in the vector space of the scalars matrices, and therefore the image is completely determined. Hence, we assume further that f has at least one variable of neutral degree and let f be a multilinear polynomial in l neutral variables
$\mathrm{Im}(f)$
is contained in the vector space of the scalars matrices, and therefore the image is completely determined. Hence, we assume further that f has at least one variable of neutral degree and let f be a multilinear polynomial in l neutral variables
![]() $y_{1}$
, …,
$y_{1}$
, …,
![]() $y_{l}$
, and
$y_{l}$
, and
![]() $m-l$
variables
$m-l$
variables
![]() $z_{l+1}$
, …,
$z_{l+1}$
, …,
![]() $z_{m}$
of homogeneous degree g. Then, by Lemma 6.17, we write f as
$z_{m}$
of homogeneous degree g. Then, by Lemma 6.17, we write f as
 $$\begin{align*}f=\alpha_{1}(y_{1}\cdots y_{l})(z_{l+1}\cdots z_{m})+\sum_{i=1}^{l}\alpha_{i+1}(((y_{i}z_{l+1})z_{l+2})y_{1}\cdots \widehat{y}_{i}\cdots y_{l})z_{l+3}\cdots z_{m}. \end{align*}$$
$$\begin{align*}f=\alpha_{1}(y_{1}\cdots y_{l})(z_{l+1}\cdots z_{m})+\sum_{i=1}^{l}\alpha_{i+1}(((y_{i}z_{l+1})z_{l+2})y_{1}\cdots \widehat{y}_{i}\cdots y_{l})z_{l+3}\cdots z_{m}. \end{align*}$$
Here,
![]() $\widehat {y}_{i}$
means that the variable
$\widehat {y}_{i}$
means that the variable
![]() $y_{i}$
does not appear in the product
$y_{i}$
does not appear in the product
![]() $y_{1}\cdots \widehat {y}_{i}\cdots y_{l}$
.
$y_{1}\cdots \widehat {y}_{i}\cdots y_{l}$
.
We replace
![]() $y_{i}=w_{1}^{(i)}(e_{11}+e_{22})+w_{2}^{(i)}e_{12}$
and
$y_{i}=w_{1}^{(i)}(e_{11}+e_{22})+w_{2}^{(i)}e_{12}$
and
![]() $z_{j}=w_{1}^{(j)}(e_{11}-e_{22})$
, where the w’s are commuting variables. Note that the Jordan product of two matrices
$z_{j}=w_{1}^{(j)}(e_{11}-e_{22})$
, where the w’s are commuting variables. Note that the Jordan product of two matrices
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
is given by
$y_{2}$
is given by
![]() $2y_{1}\cdot y_{2}$
where the dot
$2y_{1}\cdot y_{2}$
where the dot
![]() $\cdot $
stands for the usual product of matrices. On the other hand, the usual product of n matrices
$\cdot $
stands for the usual product of matrices. On the other hand, the usual product of n matrices
![]() $y_{1}$
, …,
$y_{1}$
, …,
![]() $y_{n}$
is given by
$y_{n}$
is given by
 $$\begin{align*}\begin{pmatrix} w_{1}^{(1)}\cdots w_{n}^{(n)} & w \\ & w_{1}^{(1)}\cdots w_{n}^{(n)} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} w_{1}^{(1)}\cdots w_{n}^{(n)} & w \\ & w_{1}^{(1)}\cdots w_{n}^{(n)} \end{pmatrix}. \end{align*}$$
Here,
 $w=\displaystyle \sum _{\substack {1\leq i_{1}<\cdots <i_{n-1}\leq n \\ i_{n}\in \{1,\dots ,n\}\setminus \{i_{1},\dots ,i_{n-1}\}}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{n-1})}w_{2}^{(i_{n})}$
, as one can see by induction on n. Hence, the image of the monomial
$w=\displaystyle \sum _{\substack {1\leq i_{1}<\cdots <i_{n-1}\leq n \\ i_{n}\in \{1,\dots ,n\}\setminus \{i_{1},\dots ,i_{n-1}\}}}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{n-1})}w_{2}^{(i_{n})}$
, as one can see by induction on n. Hence, the image of the monomial
![]() $\alpha _{i+1}(((y_{i}z_{l+1})z_{l+2})y_{1}\cdots \widehat {y}_{i}\cdots y_{l})z_{l+3}\cdots z_{m}$
is equal to
$\alpha _{i+1}(((y_{i}z_{l+1})z_{l+2})y_{1}\cdots \widehat {y}_{i}\cdots y_{l})z_{l+3}\cdots z_{m}$
is equal to
 $$\begin{align*}2^{m-1}\alpha_{i+1}\begin{pmatrix} w_{1}^{(l)}\cdots w_{1}^{(l)}w_{1}^{(l+1)}\cdots w_{1}^{(m)} & w_{i}w_{1}^{(l+1)}\cdots w_{1}^{(m)} \\ & w_{1}^{(l)}\cdots w_{1}^{(l)}w_{1}^{(l+1)}\cdots w_{1}^{(m)} \end{pmatrix}, \end{align*}$$
$$\begin{align*}2^{m-1}\alpha_{i+1}\begin{pmatrix} w_{1}^{(l)}\cdots w_{1}^{(l)}w_{1}^{(l+1)}\cdots w_{1}^{(m)} & w_{i}w_{1}^{(l+1)}\cdots w_{1}^{(m)} \\ & w_{1}^{(l)}\cdots w_{1}^{(l)}w_{1}^{(l+1)}\cdots w_{1}^{(m)} \end{pmatrix}, \end{align*}$$
where
![]() $w_{i}$
is given as w above but
$w_{i}$
is given as w above but
![]() $i_{n}\neq i$
.
$i_{n}\neq i$
.
Therefore, the main diagonal of
![]() $f(y_{1},\dots ,y_{l},z_{l+1},\dots ,z_{m})$
is given by
$f(y_{1},\dots ,y_{l},z_{l+1},\dots ,z_{m})$
is given by
where
![]() $\alpha $
is the sum of all coefficients in f. The entry at position
$\alpha $
is the sum of all coefficients in f. The entry at position
![]() $(1,2)$
is
$(1,2)$
is
 $$\begin{align*}\displaystyle\sum_{\substack{1\leq i_{1}<\cdots<i_{l-1}\leq l \\ k\in\{1,\dots,l\}\setminus\{i_{1},\dots,i_{l-1}\}}}\beta_{k}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{l-1})}w_{2}^{(k)}w_{1}^{(l+1)}\cdots w_{1}^{(m)}, \end{align*}$$
$$\begin{align*}\displaystyle\sum_{\substack{1\leq i_{1}<\cdots<i_{l-1}\leq l \\ k\in\{1,\dots,l\}\setminus\{i_{1},\dots,i_{l-1}\}}}\beta_{k}w_{1}^{(i_{1})}\cdots w_{1}^{(i_{l-1})}w_{2}^{(k)}w_{1}^{(l+1)}\cdots w_{1}^{(m)}, \end{align*}$$
where
 $\beta _{k}=\alpha _{1}+\displaystyle \sum _{\substack {j=1 \\ j\neq k}}^{l}\alpha _{j+1}$
.
$\beta _{k}=\alpha _{1}+\displaystyle \sum _{\substack {j=1 \\ j\neq k}}^{l}\alpha _{j+1}$
.
If all
![]() $\beta _{k}$
are equal to zero, then
$\beta _{k}$
are equal to zero, then
![]() $\mathrm{Im}(f)$
is contained in the space of the scalar matrices and we are done. So we may assume that some of the
$\mathrm{Im}(f)$
is contained in the space of the scalar matrices and we are done. So we may assume that some of the
![]() $\beta _{k}$
is nonzero, and without loss of generality, we suppose
$\beta _{k}$
is nonzero, and without loss of generality, we suppose
![]() $\beta _{l}\neq 0$
. In this case, we claim that the image will be the whole neutral component. Indeed, take
$\beta _{l}\neq 0$
. In this case, we claim that the image will be the whole neutral component. Indeed, take
![]() $A=a_{1}(e_{11}+e_{22})+a_{2}e_{12}\in \mathcal {A}_{1}$
. We evaluate the matrices of degree g by
$A=a_{1}(e_{11}+e_{22})+a_{2}e_{12}\in \mathcal {A}_{1}$
. We evaluate the matrices of degree g by
![]() $e_{11}-e_{22}$
, that is, we take
$e_{11}-e_{22}$
, that is, we take
![]() $w_{1}^{(l+1)}=\cdots =w_{1}^{(m)}=1$
. We also evaluate the neutral matrices
$w_{1}^{(l+1)}=\cdots =w_{1}^{(m)}=1$
. We also evaluate the neutral matrices
![]() $y_{1}$
, …,
$y_{1}$
, …,
![]() $y_{l-1}$
by the identity matrix, that is, we take
$y_{l-1}$
by the identity matrix, that is, we take
![]() $w_{1}^{(1)}=\cdots = w_{1}^{(l-1)}=1$
and
$w_{1}^{(1)}=\cdots = w_{1}^{(l-1)}=1$
and
![]() $w_{2}^{(1)}=\cdots =w_{2}^{(l-1)}=0$
. Hence, the equality
$w_{2}^{(1)}=\cdots =w_{2}^{(l-1)}=0$
. Hence, the equality
leads us to the following linear system:
 $$\begin{align*}\left\{\begin{array}{c} 2^{m-1}\alpha w_{1}^{(l)}=a_{1}, \\ 2^{m-1}\beta_{l}w_{2}^{(l)}=a_{2}, \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{\begin{array}{c} 2^{m-1}\alpha w_{1}^{(l)}=a_{1}, \\ 2^{m-1}\beta_{l}w_{2}^{(l)}=a_{2}, \end{array} \right. \end{align*}$$
which has
![]() $w_{1}^{(1)}=(2^{m-1}\alpha )^{-1}a_{1}$
and
$w_{1}^{(1)}=(2^{m-1}\alpha )^{-1}a_{1}$
and
![]() $w_{2}^{(2)}=(2^{m-1}\beta _{1})^{-1}a_{2}$
as the solution.
$w_{2}^{(2)}=(2^{m-1}\beta _{1})^{-1}a_{2}$
as the solution.
Theorem 6.19 Let
![]() $UJ_{2}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be a nontrivial G-grading, and let
$UJ_{2}=\bigoplus _{g\in G}\mathcal {A}_{g}$
be a nontrivial G-grading, and let
![]() $f\in J(X)$
be a multilinear graded Jordan polynomial. Then
$f\in J(X)$
be a multilinear graded Jordan polynomial. Then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is a homogeneous subspace. The same conclusion also holds for the trivial grading on
$UJ_{2}$
is a homogeneous subspace. The same conclusion also holds for the trivial grading on
![]() $UJ_{2}$
for arbitrary fields.
$UJ_{2}$
for arbitrary fields.
Proof We first consider a nontrivial grading on
![]() $UJ_{2}$
. By Remark 6.2, we may reduce the defined grading on
$UJ_{2}$
. By Remark 6.2, we may reduce the defined grading on
![]() $UJ_{2}$
to one of those described above. We note that the case of the grading (II)(c) follows from the fact that
$UJ_{2}$
to one of those described above. We note that the case of the grading (II)(c) follows from the fact that
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is a homogeneous subset and all homogeneous components in this grading are one-dimensional. We use Lemmas 6.14, 6.16, and 6.18 for the remaining nontrivial gradings. Now, we consider the trivial grading on
$UJ_{2}$
is a homogeneous subset and all homogeneous components in this grading are one-dimensional. We use Lemmas 6.14, 6.16, and 6.18 for the remaining nontrivial gradings. Now, we consider the trivial grading on
![]() $UJ_{2}$
. Let
$UJ_{2}$
. Let
![]() $f\in J(X)$
be a multilinear polynomial. We may assume that
$f\in J(X)$
be a multilinear polynomial. We may assume that
![]() $f\notin \mathrm{Id}(UJ_{2})$
. By [Reference Slinko39], the algebra
$f\notin \mathrm{Id}(UJ_{2})$
. By [Reference Slinko39], the algebra
![]() $J(X)/\mathrm{Id}(UJ_{2})$
is a special Jordan algebra, and hence we may assume that f is an element in the free special Jordan algebra. Therefore, the image
$J(X)/\mathrm{Id}(UJ_{2})$
is a special Jordan algebra, and hence we may assume that f is an element in the free special Jordan algebra. Therefore, the image
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UJ_{2}$
is equal to the image of some associative polynomial on
$UJ_{2}$
is equal to the image of some associative polynomial on
![]() $UT_{2}$
. Hence,
$UT_{2}$
. Hence,
![]() $\mathrm{Im}(f)\in \{J,UJ_{2}\}$
.
$\mathrm{Im}(f)\in \{J,UJ_{2}\}$
.
Remark 6.20 Consider the Lie algebra
![]() $UT_{n}^{(-)}$
with product given by the Lie bracket. Given a grading on
$UT_{n}^{(-)}$
with product given by the Lie bracket. Given a grading on
![]() $UT_{n}^{(-)}$
, note that
$UT_{n}^{(-)}$
, note that
![]() $J=[UT_{n}^{(-)},UT_{n}^{(-)}]$
is always a homogeneous ideal. We also note that if
$J=[UT_{n}^{(-)},UT_{n}^{(-)}]$
is always a homogeneous ideal. We also note that if
![]() $f\in L(X)^{gr}$
is a multilinear polynomial of degree
$f\in L(X)^{gr}$
is a multilinear polynomial of degree
![]() $\ge 2$
, then
$\ge 2$
, then
![]() $\mathrm{Im}(f)$
on
$\mathrm{Im}(f)$
on
![]() $UT_{n}^{(-)}$
is contained in J. In particular, for
$UT_{n}^{(-)}$
is contained in J. In particular, for
![]() $n=2$
, we must have that
$n=2$
, we must have that
![]() $\mathrm{Im}(f)$
is contained in
$\mathrm{Im}(f)$
is contained in
![]() $\mathrm{span}\{e_{12}\}$
which is a homogeneous subspace. Since the image of multilinear polynomials of degree
$\mathrm{span}\{e_{12}\}$
which is a homogeneous subspace. Since the image of multilinear polynomials of degree
![]() $1$
is trivial, we have that
$1$
is trivial, we have that
![]() $\mathrm{Im}(f)$
on the graded algebra
$\mathrm{Im}(f)$
on the graded algebra
![]() $UT_{2}^{(-)}$
is always a homogeneous subspace, regardless of the grading defined on
$UT_{2}^{(-)}$
is always a homogeneous subspace, regardless of the grading defined on
![]() $UT_{2}^{(-)}$
.
$UT_{2}^{(-)}$
.
6.3 The natural elementary
 ${\mathbb {Z}}_{3}$
-grading in the Jordan algebra
${\mathbb {Z}}_{3}$
-grading in the Jordan algebra
 $UJ_{3}$
$UJ_{3}$
In this subsection, we study images of multilinear polynomials on the Jordan algebra
![]() $\mathcal {A}=UJ_{3}$
endowed with the elementary
$\mathcal {A}=UJ_{3}$
endowed with the elementary
![]() ${\mathbb {Z}}_{3}$
-grading given by the sequence
${\mathbb {Z}}_{3}$
-grading given by the sequence
![]() $(\overline {0},\overline {1},\overline {2})$
, that is,
$(\overline {0},\overline {1},\overline {2})$
, that is,
![]() $\mathcal {A}_{\overline {0}}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
$\mathcal {A}_{\overline {0}}=\mathrm{span}\{e_{11},e_{22},e_{33}\}$
,
![]() $\mathcal {A}_{\overline {1}}=\mathrm{span}\{e_{12},e_{23}\}$
, and
$\mathcal {A}_{\overline {1}}=\mathrm{span}\{e_{12},e_{23}\}$
, and
![]() $\mathcal {A}_{\overline {2}}=\mathrm{span}\{e_{13}\}$
.
$\mathcal {A}_{\overline {2}}=\mathrm{span}\{e_{13}\}$
.
We denote by
![]() $(x_{1},x_{2},x_{3})=(x_{1}x_{2})x_{3}-x_{1}(x_{2}x_{3})$
the associator of the elements
$(x_{1},x_{2},x_{3})=(x_{1}x_{2})x_{3}-x_{1}(x_{2}x_{3})$
the associator of the elements
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}$
,
$x_{2}$
,
![]() $x_{3}$
.
$x_{3}$
.
We recall the following identity which holds in any Jordan algebra.
Lemma 6.21 Let
![]() $\mathcal {J}$
be a Jordan algebra. Then
$\mathcal {J}$
be a Jordan algebra. Then
for all a, b, c,
![]() $d\in \mathcal {J}$
.
$d\in \mathcal {J}$
.
Proof See, for example, [Reference Jacobson23, p. 34].
As an easy consequence of Lemma 6.21, we have
for every a, b, c,
![]() $d\in \mathcal {J}$
.
$d\in \mathcal {J}$
.
The next lemma points out some graded identities for the algebra
![]() $UJ_{3}$
.
$UJ_{3}$
.
Lemma 6.22 The identities
hold for
![]() $UJ_{3}$
, where z is an odd variable and
$UJ_{3}$
, where z is an odd variable and
![]() $\deg (z_{1})+\deg (z_{2})=\overline {0}$
.
$\deg (z_{1})+\deg (z_{2})=\overline {0}$
.
Proof A straightforward computation, hence omitted.
The next lemma has the same proof as [Reference Gonçalves and Salomão22, Lemma 5.3]. However, we will consider its proof here for the sake of completeness.
Lemma 6.23 The polynomial
 $$\begin{align*}g=y_{1}(y_{2}(y_{3}z))-\frac{1}{2}\bigg(y_{1}(z(y_{2}y_{3})) +y_{2}(z(y_{1}y_{3}))+y_{3}(z(y_{1}y_{2}))-z(y_{1}(y_{2}y_{3}))\bigg) \end{align*}$$
$$\begin{align*}g=y_{1}(y_{2}(y_{3}z))-\frac{1}{2}\bigg(y_{1}(z(y_{2}y_{3})) +y_{2}(z(y_{1}y_{3}))+y_{3}(z(y_{1}y_{2}))-z(y_{1}(y_{2}y_{3}))\bigg) \end{align*}$$
is a consequence of
![]() $(y_{1},z,y_{2})$
, where
$(y_{1},z,y_{2})$
, where
![]() $\deg (z)\in \{\overline {1},\overline {2}\}$
.
$\deg (z)\in \{\overline {1},\overline {2}\}$
.
Proof By identity (4), we have
Hence, we can write
![]() $h=2g$
as
$h=2g$
as
 $$ \begin{align*} h= & \ 2(y_{1}(y_{2}(y_{3}z))-((y_{2}z)y_{1})y_{3}-((y_{3}z)y_{1})y_{2}\\ = & \ (y_{3},z,y_{2})y_{1}+(y_{2},zy_{3},y_{1})+(y_{3},zy_{2},y_{1}), \end{align*} $$
$$ \begin{align*} h= & \ 2(y_{1}(y_{2}(y_{3}z))-((y_{2}z)y_{1})y_{3}-((y_{3}z)y_{1})y_{2}\\ = & \ (y_{3},z,y_{2})y_{1}+(y_{2},zy_{3},y_{1})+(y_{3},zy_{2},y_{1}), \end{align*} $$
which implies that g is a consequence of
![]() $(y_{1},z,y_{2})$
.
$(y_{1},z,y_{2})$
.
Given two even variables
![]() $y_{i}$
and
$y_{i}$
and
![]() $y_{j}$
, we set
$y_{j}$
, we set
![]() $y_{i}<y_{j}$
if
$y_{i}<y_{j}$
if
![]() $i<j$
. Hence, we define an order on words in even variables
$i<j$
. Hence, we define an order on words in even variables
![]() $Y_{1}<Y_{2}$
considering the left lexicographic order in case
$Y_{1}<Y_{2}$
considering the left lexicographic order in case
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
have the same length, and
$Y_{2}$
have the same length, and
![]() $Y_{1}<Y_{2}$
in case
$Y_{1}<Y_{2}$
in case
![]() $Y_{2}$
is longer than
$Y_{2}$
is longer than
![]() $Y_1$
. For the next lemma, we use ideas from [Reference Gonçalves and Salomão22, Lemma 5.6]. We denote by T the T-ideal generated by the identities from Lemma 6.22.
$Y_1$
. For the next lemma, we use ideas from [Reference Gonçalves and Salomão22, Lemma 5.6]. We denote by T the T-ideal generated by the identities from Lemma 6.22.
Lemma 6.24 Let
![]() $f=f(y_{1},\dots ,y_{m-1},z_{m})\in J(X)$
be a multilinear polynomial, where
$f=f(y_{1},\dots ,y_{m-1},z_{m})\in J(X)$
be a multilinear polynomial, where
![]() $\deg (z_{m})\in \{\overline {1},\overline {2}\}$
. Then, modulo T, f is a linear combination of monomials of the form
$\deg (z_{m})\in \{\overline {1},\overline {2}\}$
. Then, modulo T, f is a linear combination of monomials of the form
![]() $Y_{1}(zY_{2})$
, where each
$Y_{1}(zY_{2})$
, where each
![]() $Y_{i}$
is an increasingly ordered product of even variables and
$Y_{i}$
is an increasingly ordered product of even variables and
![]() $Y_{1}<Y_{2}$
.
$Y_{1}<Y_{2}$
.
Proof It is enough to consider
![]() $f=f(y_{1},\dots ,y_{m-1},z_{m})$
as a monomial. We apply induction on m. If
$f=f(y_{1},\dots ,y_{m-1},z_{m})$
as a monomial. We apply induction on m. If
![]() $m=1$
or
$m=1$
or
![]() $m=2$
, then the conclusion is obvious. So we assume
$m=2$
, then the conclusion is obvious. So we assume
![]() $m\geq 3$
and we write
$m\geq 3$
and we write
![]() $f=gh$
where g,
$f=gh$
where g,
![]() $h\in J(X)$
. Without loss of generality, we may assume that the odd variable
$h\in J(X)$
. Without loss of generality, we may assume that the odd variable
![]() $z_{m}$
occurs in g. Hence,
$z_{m}$
occurs in g. Hence,
![]() $h=Y_{1}$
, and by the induction hypothesis, we must have g as a linear combination of monomials of the form
$h=Y_{1}$
, and by the induction hypothesis, we must have g as a linear combination of monomials of the form
![]() $Y_{2}(zY_{3})$
. On the other hand, we have
$Y_{2}(zY_{3})$
. On the other hand, we have
 $$\begin{align*}(Y_{2}(zY_{3}))Y_{1}=\frac{1}{2}\bigg(Y_{1}(z(Y_{2}Y_{3}))+Y_{2}(z(Y_{1}Y_{3})+Y_{3}(z(Y_{1}Y_{2}))-z(Y_{1}(Y_{2}Y_{3}))\bigg). \end{align*}$$
$$\begin{align*}(Y_{2}(zY_{3}))Y_{1}=\frac{1}{2}\bigg(Y_{1}(z(Y_{2}Y_{3}))+Y_{2}(z(Y_{1}Y_{3})+Y_{3}(z(Y_{1}Y_{2}))-z(Y_{1}(Y_{2}Y_{3}))\bigg). \end{align*}$$
Now, it is enough to use the identities
![]() $(y_{1},y_{2},y_{3})\equiv 0$
,
$(y_{1},y_{2},y_{3})\equiv 0$
,
![]() $(y_{1},z,y_{2})\equiv 0$
, and the commutativity of the Jordan product to get the desired conclusion.
$(y_{1},z,y_{2})\equiv 0$
, and the commutativity of the Jordan product to get the desired conclusion.
Now, we are ready to prove the main theorem of this subsection.
Theorem 6.25 Let F be an infinite field of characteristic different from 2, and let
![]() $f\in J(X)$
be a multilinear graded polynomial. Then the image of f on the graded Jordan algebra
$f\in J(X)$
be a multilinear graded polynomial. Then the image of f on the graded Jordan algebra
![]() $UJ_{3}$
endowed with the natural elementary
$UJ_{3}$
endowed with the natural elementary
![]() ${\mathbb {Z}}_{3}$
-grading is either
${\mathbb {Z}}_{3}$
-grading is either
![]() $\{0\}$
or some homogeneous component.
$\{0\}$
or some homogeneous component.
Proof Since f is a homogeneous polynomial in the graded algebra
![]() $J(X)$
and
$J(X)$
and
![]() $z_{1}z_{2}\equiv 0$
holds on
$z_{1}z_{2}\equiv 0$
holds on
![]() $UJ_{3}$
, for
$UJ_{3}$
, for
![]() $\deg z_{1}+\deg z_{2}=\overline {0}$
, we will consider the following three cases in our proof.
$\deg z_{1}+\deg z_{2}=\overline {0}$
, we will consider the following three cases in our proof.
Case 1:
![]() $\deg f=\overline {0}$
. Here, we must have
$\deg f=\overline {0}$
. Here, we must have
![]() $f=f(y_{1},\dots ,y_{m})$
and the proof is the same as the first paragraph of the proof of Lemma 6.14.
$f=f(y_{1},\dots ,y_{m})$
and the proof is the same as the first paragraph of the proof of Lemma 6.14.
Case 2:
![]() $\deg f=\overline {1}$
. Let
$\deg f=\overline {1}$
. Let
![]() $f=f(y_{1},\dots ,y_{m-1},z_{m})$
be such that
$f=f(y_{1},\dots ,y_{m-1},z_{m})$
be such that
![]() $\deg z_{m}=\overline {1}$
. By Lemma 6.24, modulo T, we may write f as a linear combination of monomials of the form
$\deg z_{m}=\overline {1}$
. By Lemma 6.24, modulo T, we may write f as a linear combination of monomials of the form
![]() $Y_{1}(z_{m}Y_{2})$
, where
$Y_{1}(z_{m}Y_{2})$
, where
![]() $Y_{1}<Y_{2}$
. On the other hand, given
$Y_{1}<Y_{2}$
. On the other hand, given
 $$ \begin{align} y_{i}=\sum_{k=1}^{3}w_{k}^{(i)}e_{kk} \ \mbox{and} \ z_{m}=w_{1}^{(m)}e_{12}+w_{2}^{(m)}e_{23}, \end{align} $$
$$ \begin{align} y_{i}=\sum_{k=1}^{3}w_{k}^{(i)}e_{kk} \ \mbox{and} \ z_{m}=w_{1}^{(m)}e_{12}+w_{2}^{(m)}e_{23}, \end{align} $$
note that
 $y_{i}z_{m}=\begin {pmatrix} 0&(w_{1}^{(i)}+w_{2}^{(i)})w_{1}^{(m)} &0 \\ &0 &(w_{2}^{(i)}+w_{3}^{(i)})w_{2}^{(m)} \\ & &0 \end {pmatrix}$
and then
$y_{i}z_{m}=\begin {pmatrix} 0&(w_{1}^{(i)}+w_{2}^{(i)})w_{1}^{(m)} &0 \\ &0 &(w_{2}^{(i)}+w_{3}^{(i)})w_{2}^{(m)} \\ & &0 \end {pmatrix}$
and then
 $$\begin{align*}f(y_{1},\dots,y_{m-1},z_{m})=\begin{pmatrix} 0&p_{1}w_{1}^{(m)} &0 \\ &0 &p_{2}w_{2}^{(m)} \\ & &0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}f(y_{1},\dots,y_{m-1},z_{m})=\begin{pmatrix} 0&p_{1}w_{1}^{(m)} &0 \\ &0 &p_{2}w_{2}^{(m)} \\ & &0 \end{pmatrix}, \end{align*}$$
where
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are polynomials in the variables
$p_{2}$
are polynomials in the variables
![]() $w^{(i)}$
,
$w^{(i)}$
,
![]() $i=1$
, …,
$i=1$
, …,
![]() $m-1$
. We claim that if
$m-1$
. We claim that if
![]() $f\neq 0$
modulo T, then
$f\neq 0$
modulo T, then
![]() $p_{1}\neq 0$
and
$p_{1}\neq 0$
and
![]() $p_{2}\neq 0$
. Indeed, consider the monomial
$p_{2}\neq 0$
. Indeed, consider the monomial
![]() $\mathbf {m}=\alpha Y_{1}(z_{m}Y_{2})$
, where
$\mathbf {m}=\alpha Y_{1}(z_{m}Y_{2})$
, where
![]() $Y_{1}=y_{j_{1}}\cdots y_{j_{r}}$
,
$Y_{1}=y_{j_{1}}\cdots y_{j_{r}}$
,
![]() $Y_{2}= y_{l_{1}}\cdots y_{l_{s}}$
, and
$Y_{2}= y_{l_{1}}\cdots y_{l_{s}}$
, and
![]() $Y_{1}<Y_{2}$
. Note that the
$Y_{1}<Y_{2}$
. Note that the
![]() $(1,2)$
entry of the image of
$(1,2)$
entry of the image of
![]() $\mathbf {m}$
under the evaluation (5) is given by
$\mathbf {m}$
under the evaluation (5) is given by
for some power of
![]() $2$
. Hence,
$2$
. Hence,
![]() $p_{1}$
contains the following monomials:
$p_{1}$
contains the following monomials:
Since
![]() $Y_{1}<Y_{2}$
, the two monomials above can only be obtained from the monomial
$Y_{1}<Y_{2}$
, the two monomials above can only be obtained from the monomial
![]() $\mathbf {m}$
. Hence, if
$\mathbf {m}$
. Hence, if
![]() $f\neq 0$
modulo T, then f contains some monomial
$f\neq 0$
modulo T, then f contains some monomial
![]() $\mathbf {m}$
as above for some nonzero
$\mathbf {m}$
as above for some nonzero
![]() $\alpha $
, which will imply in nonzero monomials in
$\alpha $
, which will imply in nonzero monomials in
![]() $p_{1}$
that are not multiple of any other one that comes from the remaining monomials of f. The same ideas also prove that
$p_{1}$
that are not multiple of any other one that comes from the remaining monomials of f. The same ideas also prove that
![]() $p_{2}\neq 0$
.
$p_{2}\neq 0$
.
Now, we use the fact that F is infinite to get evaluations of the even variables for diagonal matrices such that
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
assume nonzero values on F, simultaneously. We finally use the variables
$p_{2}$
assume nonzero values on F, simultaneously. We finally use the variables
![]() $w_{1}^{(m)}$
and
$w_{1}^{(m)}$
and
![]() $w_{2}^{(m)}$
to get arbitrary odd matrices in
$w_{2}^{(m)}$
to get arbitrary odd matrices in
![]() $\mathrm{Im}(f)$
, that is,
$\mathrm{Im}(f)$
, that is,
![]() $\mathrm{Im}(f)=(UJ_{3})_{\overline {1}}$
.
$\mathrm{Im}(f)=(UJ_{3})_{\overline {1}}$
.
Case 3:
![]() $\deg f=\overline {2}$
. This last case follows from the fact that the homogeneous component of degree
$\deg f=\overline {2}$
. This last case follows from the fact that the homogeneous component of degree
![]() $\overline {2}$
is one-dimensional.
$\overline {2}$
is one-dimensional.
Acknowledgment
Thanks are due to the Referee whose careful reading and suggestions, accepted with gratitude, helped us improve the exposition of the results in our paper.