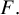1 Introduction
Let
$F: U \to V$
be a biholomorphism where U and V are open sets of
${\mathbb C}^{n}$
that contain the origin
$0$
and
$F(0) = 0$
. For fixed
$p\in U,$
we define
$F^0(p)=p$
and, if
$F^0(p),\ldots , F^{j-1}(p)\in ~U$
for
$ j>0,$
we define
$F^{j}(p)=F(F^{j-1}(p)).$
Given
$A\subset U\cap V$
, we define
${\mathcal I}_{F,A}^{+} (p)$
as the set of non-negative integers j such that
$F^{k} (p) \in A$
for any
$0 \leq k \leq j$
. We define the positive orbit of p by F in A as
$$ \begin{align*}O_{F, A}^{+}(p) = \{ F^{j}(p); j \in {\mathcal I}_{F,A}^{+} (p) \}. \end{align*} $$
Note that the positive F-orbit of p in A is infinite if and only if
$F^{j} (p) \in A$
for any
$j \geq 0$
and the set
$\{ F^{j} (p) : j \geq 0 \}$
is infinite. We define the negative F-orbit of p in A as
$$ \begin{align*} O_{F, A}^{-}(p) = O_{F^{-1}, A}^{+}(p), \end{align*} $$
where
$F^{-1}$
denotes the inverse of F. Analogously as above, the negative F-orbit of p in A is infinite if and only if
$F^{-j} (p) \in A$
for any
$j \geq 0$
and
$\{ F^{-j} (p) : j \geq 0 \}$
is infinite where
$F^{-j}=(F^{-1})^{j}$
. We define the F-orbit of p in A as
$$ \begin{align*} O_{F, A}(p)= O_{F, A}^{+}(p) \cup O_{F, A}^{-}(p). \end{align*} $$
There are two types of finite orbits
$O_{F, A}(p)$
, namely either
${\mathcal I}_{F,A}^{+} (p)$
and
${\mathcal I}_{F^{-1},A}^{+} (p)$
are finite or
$$ \begin{align*} {\mathcal I}_{F,A}^{+} (p) = {\mathcal I}_{F^{-1},A}^{+} (p) = {\mathbb N} \cup \{0\} \end{align*} $$
and p is a periodic point, that is, there exists
$k \in {\mathbb N}$
such that
$F^{k}(p)=p$
.
We say that F has finite orbits in A if
$O_{F,A}(p)$
is a finite set for all
$p\in A.$
In this case, F has finite orbits in B for any subset B of A since
$O_{F,B}(p)\subset O_{F,A}(p)$
for all
$p \in B$
. As a consequence, the finite-orbits property can be defined for
$F \in \mathrm {Diff}(\mathbb {C}^n,0)$
, where
$\mathrm {Diff}(\mathbb {C}^n,0)$
is the group of germs of biholomorphism fixing the origin
$0\in \mathbb {C}^n$
.
Definition 1. Let
$F\in \mathrm {Diff}(\mathbb {C}^n,0)$
be a local biholomorphism. We say that F is a finite-orbits germ or that it has finite orbits (and then we write
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}{}^{n},0)$
) if there exist a representative
$F:U\to V$
and a neighborhood
$ A\subset U\cap V$
of
$0$
such that F has finite orbits in
$A.$
Finite-orbits local biholomorphisms appear in the study of foliations with closed leaves. In [Reference Mattei and MoussuMM80] Mattei and Moussu proved one of the most important theorems in the theory of holomorphic foliations, namely the topological characterization of the existence of a non-constant holomorphic first integral for germs of codimension-1 holomorphic foliations. More precisely, they show that a singular holomorphic foliation
$\mathcal F$
on
$({\mathbb C}^{n},0)$
of codimension 1 has a first integral if and only if the leaves of
$\mathcal F$
are closed subsets of the complement of the singular set and only finitely many of them accumulate at 0. A fundamental ingredient of the proof is that, in dimension 1, the finite-orbits property is equivalent to periodicity. More precisely, they show that a biholomorphism
$F\in \mathrm {Diff}({\mathbb C},0)$
has finite orbits if and only if F is a finite order element of the group
$\mathrm {Diff}({\mathbb C},0)$
. For dimension
$n\geq 2,$
the equivalence does not hold. For example, the local biholomorphism
$F(x,y) = (x, y+ x^{2})$
has finite orbits but is of infinite order.
It is possible to recover the equivalence periodicity
$\leftrightarrow $
finite orbits by replacing the finite order property with stronger conditions and so to obtain, in dimension greater than
$1,$
analogues of the topological criterion of Mattei and Moussu [Reference Câmara and ScárduaCS09, Reference Câmara and ScárduaCS17, Reference Rebelo and ReisRR15]. In spite of this, the following elementary problems, related to the finite-orbits property, have hitherto been open:
-
(1) the description of the properties of the differential
$D_0 F$
at the origin of a finite-orbits germ F; -
(2) the description of the set of periodic points of
$F \in \mathrm {Diff}{}_{<\infty }({\mathbb C}{}^{n},0)$
.
We answer these questions in dimension
$2$
and provide partial answers for higher dimension. A natural question (hitherto open) is whether the finite-orbits property for
$F \in \mathrm {Diff}(\mathbb {C}^n,0)$
implies the analogue for the linear part
$D_0 F$
of F at the origin. The next result provides the first counterexamples.
Theorem 1. Suppose that
$\unicode{x3bb} \in \mathbb {C}$
satisfies the Cremer condition and
$n \geq 1$
. Then there exists a global biholomorphism
$F\in \mathrm {Diff}(\mathbb {C}^{n+1})$
such that
$\mathrm {Spec}(D_0 F)=\{\unicode{x3bb} ,1\}$
, the algebraic multiplicity of the eigenvalue
$1$
of
$D_0 F$
is equal to
$1$
, and F has finite orbits in every set of the form
${\mathbb C^{n}} \times U,$
where
$U\subset \mathbb {C}$
is a bounded open set.
Let us stress that F is a counterexample because, in the linear case, F has finite orbits if and only if the spectrum of
$D_0 F$
consists of roots of unity (cf. Proposition 2). It is already known that finite-orbits local biholomorphisms F satisfy that the eigenvalues of
$D_0 F$
have modulus
$1$
by the stable manifold theorem (cf. Corollary 5).
The next result gives an indication of why the examples of
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}{}^{n},0)$
such that
$\mathrm {spec} (D_0 F)$
is not contained in the group of roots of unity have been missing in the literature: there are no ‘continuous’ examples, that is, where F belongs to a one-parameter group. Let
${\mathfrak X}(\mathbb {C}^n,0)$
denote the Lie algebra of singular local holomorphic vector fields at the origin.
Theorem 2. Let
$X\in {\mathfrak X}(\mathbb {C}^n,0)$
and let F be the time-1 map of
$X.$
Suppose that F has finite orbits. Then it satisfies
$$ \begin{align*}\mathrm{Spec} (D_0F)\subset e^{2\pi i \mathbb{Q}}.\end{align*} $$
The existence of the examples provided by Theorem 1 has consequences in the problem of geometrical realization of formal invariant curves. Indeed, it was proved in [Reference López-Hernanz, Raissy, Ribón and Sanz-SánchezLHRRSS21] that if the multiplier of the restriction
$F_{|\Gamma }$
of
$F\in \mathrm {Diff}({\mathbb C}^{2},0)$
to a formal invariant curve
$\Gamma $
is not an element of
$e^{2 \pi i({\mathbb R} \setminus {\mathbb Q})}$
and F is non-periodic then either the curve
$\Gamma $
is convergent or there are invariant analytic sets asymptotic to
$\Gamma $
and consisting of stable orbits, that is, orbits of points p such that
$\lim _{k \to \infty } F^{k} (p) =0$
. Our examples show that in general there is no systematic approach to the geometrical realization of
$\Gamma $
as a stable set if the multiplier of
$F_{|\Gamma }$
is irrationally neutral, that is, if it belongs to
$e^{2 \pi i ({\mathbb R} \setminus {\mathbb Q})}$
. This completes the realization program in [Reference López-Hernanz, Raissy, Ribón and Sanz-SánchezLHRRSS21, Reference López-Hernanz, Ribón, Sanz-Sánchez and VivasLHRSSV]. More precisely, the examples provided by Theorem 1 for dimension
$2$
have a formal curve
$\Gamma $
invariant by
$F,$
such that the multiplier
$\unicode{x3bb} $
of
$F|_\Gamma $
belongs to
$e^{2 \pi i ({\mathbb R} \setminus {\mathbb Q})},$
but F has no stable sets, since it has finite orbits.
Theorem 1 suggests that the finite-orbits property is related to small divisors. Note that the multiplier
$\unicode{x3bb} $
in Theorem 1 is very well approached by roots of unity since it is a Cremer number. Such a circumstance is not accidental; indeed, we show, by applying a theorem of Pöschel [Reference PöschelPös86], that there is no
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}{}^{2},0)$
such that
$\mathrm {Spec} (D_0F)$
contains a Bruno number (Proposition 5). In particular, we show that if the multiplier of
$F_{|\Gamma }$
is a Bruno number, for
$F\in \mathrm {Diff}({\mathbb C}^{2},0)$
and a formal invariant curve
$\Gamma $
of F, then F is not a finite-orbits germ (Corollary 7).
The natural follow-up question to Theorem 1 is to understand whether
$D_{0} F$
shares some properties with finite-orbits linear biholomorphisms if
$F \in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
. In particular, are there
$F \in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
such that
$\mathrm {Spec} (D_0F) \cap e^{2\pi i \mathbb {Q}} = \emptyset $
? The answer is negative for dimension 2.
Theorem 3. Let
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
. Then at least one eigenvalue of
$D_0F$
is a root of unity (and all of them belong to the unit circle).
As a consequence, the examples of Theorem 1 have the minimal number of roots-of-unity eigenvalues and hence Theorem 3 is sharp. Moreover, we classify the finite-orbits local biholomorphisms
$F\in \mathrm {Diff}({\mathbb C}^{2},0)$
such that
$\mathrm {Spec} (D_0F)$
contains a non-root-of-unity eigenvalue: essentially they are the examples provided by Theorem 1 (Proposition 5). Theorem 3 is a consequence of the fixed-point curve theorem that we discuss next. A classical result about vector fields in dimension
$n=2$
is the Camacho–Sad theorem [Reference Camacho and SadCS82], which states that every vector field
$X\in {\mathfrak X}(\mathbb {C}^2,0)$
admits a germ of invariant curve at the origin. The existence of invariant objects for local biholomorphisms tangent to the identity
$F\in \mathrm {Diff}{}_{1}({\mathbb C}^{2},0)$
is also well known (see [Reference AbateAba01, Reference Brochero Martínez, Cano and López-HernanzBMCLH08, Reference López-Hernanz and SánchezLS18], for example). In [Reference AbateAba01] Abate generalizes to
$\mathbb {C}^2$
the classical Leau–Fatou flower theorem proving that if
$F\in \mathrm {Diff}{}_{1}({\mathbb C}^{2},0)$
has an isolated fixed point at
$0$
then F has at least one parabolic curve, that is, a F-invariant holomorphic curve, with the origin in their boundary, and whose orbits tend to
$0$
; in particular, it is not a finite-orbits germ. Thus, if
$F\in \mathrm {Diff}{}_{1}({\mathbb C}^{2},0)\cap \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
then F has a non-isolated fixed point at the origin. Later on, López-Hernanz and Sánchez [Reference López-Hernanz and SánchezLS18] showed that if F has a formal invariant curve
$\Gamma $
that is not contained in the fixed-point set of F then F or
$F^{-1}$
has a parabolic curve asymptotic to
$\Gamma $
. In particular, if
$F\in \mathrm {Diff}{}_{1}({\mathbb C}^{2},0)\cap \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
then every formal invariant curve is a fixed-point curve.
In contrast to the previous approach, the second author showed that existence of germs of analytic invariant curves does not hold for biholomorphisms
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
in general [Reference RibónRib05]. Moreover, the counterexamples can be chosen to be tangent to the identity or formally linearizable.
In this work we prove the following theorem. It is a version of the Camacho–Sad theorem for finite-orbits local biholomorphisms.
Fixed point curve theorem. Let
$F\in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
be a finite-orbits diffeomorphism. Then there exists
$m\in \mathbb {N}$
such that
$F^m$
has a germ
$\Gamma $
of complex analytic curve consisting of fixed points.
We can apply the fixed-point curve theorem to obtain a generalization of a Rebelo–Reis theorem in the context of cyclic subgroups of
$\mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
. More precisely, a consequence of Theorem A in [Reference Rebelo and ReisRR15] is that if, for all
$m\in \mathbb {N},$
every point
$p \in \mathrm {Fix}(F^{m})$
in a neighborhood of
$0$
satisfies that either p is an isolated fixed point of
$F^{m}$
or the germ of
$F^{m}$
at p is equal to the identity map, then F is periodic. We provide a stronger version of this result in dimension 2, namely, it suffices to check the condition at the origin. Thus, we obtain a negative criterion for the finite-orbits property.
Corollary 1. Let
$F \in \mathrm {Diff} ({\mathbb C}^{2},0)$
such that
$0$
is an isolated fixed point of
$F^{m}$
for every
$m \in {\mathbb N}$
. Then F is not a finite-orbits germ.
Our approach to showing the fixed-point curve theorem relies on describing the connected components of the set of periodic points of
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
.
Theorem 4. Let
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
. Let B be an open or closed ball centered at the origin such that F and
$F^{-1}$
are defined in a neighborhood U of
$\overline {B}$
and F has finite orbits in U. Consider the sets
for
$k \in {\mathbb N}$
. Let C be a connected component of
$\mathrm {Per} (F):=\bigcup _{k=1}^{\infty } \mathrm {Per}_{k} (F)$
. Then C is semianalytic and there exists
$m=m(C)$
such that C is a connected component of the semianalytic set
$\mathrm {Per}_{m} (F)$
. Moreover, if B is an open ball then C is complex analytic in B and the irreducible components of C have positive dimension.
Suppose that B is a closed ball since it is simpler to work in compact sets. Let
${\mathcal B}$
be the set of points
$p \in B$
such that the map
$q \mapsto \sharp O_{F,B} (q)$
is an unbounded function in every neighborhood of p. Such a set is the analogue for diffeomorphisms of the so-called bad set associated to smooth foliations by compact leaves of compact manifolds; it consists of the leaves where the volume function (defined in the space of leaves) is not locally bounded. The properties of the bad set are one of the ingredients used by Edwards, Millet and Sullivan to show that, under a suitable homological condition, the volume function associated to a smooth foliation by compact leaves is uniformly bounded [Reference Edwards, Millett and SullivanEMS77]. In the finite-orbits case for
$n=2$
, the bad set
${\mathcal B}$
is contained in
$\mathrm {Per} (F)$
and moreover, the connected components of
${\mathcal B}$
are also connected components of
$\mathrm {Per} (F)$
. In general, the structure of the bad set can be very complicated. However, the finite-orbits property constrains the connected components of the bad set
${\mathcal B}$
to be simple for
$n=2$
. Indeed, they are semianalytic by Theorem 4.
Our results can be used to study holomorphic foliations of codimension
$2$
defined in a neighborhood of a compact leaf and whose leaves are closed. Such a problem will be contemplated in future work.
Section 2 introduces the setting of the paper along with some elementary results. Theorem 2 is proved in §3. We show Theorems 4, 3 and the fixed-point curve theorem in §4. Finally, we provide examples satisfying the thesis of Theorem 1 in §5.
2 Notation and first results
As above, we denote by
$\mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
the group of germs of biholomorphisms fixing
$0\in \mathbb {C}^n$
and by
$\mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
the subset of
$\mathrm { Diff}{}_{}({\mathbb C}^{n},0)$
consisting of those having finite orbits. In this section we include some elementary results about the finite-orbits property for the sake of completeness.
Proposition 1.
Let
$F\in \mathrm {Diff}(\mathbb {C}^n,0).$
-
(i) (Invariance by analytic conjugation) If
$F=HGH^{-1}$
for some
$H\in \mathrm { Diff}{}_{}({\mathbb C}^{n},0)$
, then
$$ \begin{align*} F\in \mathrm{Diff}{}_{<\infty}({\mathbb C}^{n},0) \Leftrightarrow G\in \mathrm{Diff}{}_{<\infty}({\mathbb C}^{n},0). \end{align*} $$
-
(ii) (Invariance by iteration) The following assertions are equivalent.
-
(a)
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
. -
(b)
$F^m\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0) \text { for all } m\in \mathbb {N}.$
-
(c)
$F^m \in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
for some
$m\in \mathbb {N}.$
-
Proof. (i) Assume
$H\circ G=F\circ H$
and let U be a connected open neighborhood of
$0$
in which all germs involved have injective representatives. There exists a neighborhood
$0\in A\subset U$
such that
$G(A),H(A),H(G(A))\subset U.$
By using
$H\circ G=F\circ H$
, we can show by induction that, if
$x,G^{\pm }(x),\ldots ,G^{\pm k}(x)\in A,$
then
$F^l(H(x))=H(G^l(x))$
for
$l=\pm 1,\ldots ,\pm k.$
Therefore,
$$ \begin{align*}H (O_{G,A}(x))= O_{F, H(A)}(H(x))\quad \mbox{for any }x\in A.\end{align*} $$
In particular, G has finite orbits in A if and only if F has finite orbits in
$H(A).$
This shows (i).
(ii) To show that (a)
$\Rightarrow $
(b), suppose
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
and let U be a connected open neighborhood of
$0$
in which F e
$F^{-1}$
are defined and have finite orbits. Given
$m\in \mathbb {N},$
there exists a connected open neighborhood V of
$0$
such that
$F^{\pm j}(p)\in U$
for all
$ p\in V$
and
$0\leq j\leq m.$
As a consequence, we obtain
$$ \begin{align*}O_{F^m,V}(p)\subset O_{F,U}(p)\quad \text{for all } p\in V,\end{align*} $$
and hence
$F^m\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
for any
$m\in \mathbb {N}.$
It is obvious that (b)
$\Rightarrow $
(c). Let us show that (c)
$\Rightarrow $
(a). Let
$m\in \mathbb {N}$
such that
$F^m\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
. As before, let V be a connected open neighborhood of
$0$
in which
$F^m$
has finite orbits. Up to considering a smaller V, we can assume that
are defined in V. Since, for each
$p\in V,$
the set
$O_{F^m,V}(p)$
is finite and
$$ \begin{align*} O_{F,V}(p) \subset \bigcup_{j=-(m-1)}^{m-1} F^{j} (O_{F^m,V}(p)) , \end{align*} $$
we deduce that
$O_{F,V}(p)$
is finite; that is,
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
. This concludes the proof.
We say that a biholomorphism
$F\in \mathrm {Diff}(\mathbb {C}^n,0)$
is periodic if it is a finite order element of the group
$\mathrm {Diff}({\mathbb C}^{n},0),$
that is, if there exists
$m\in \mathbb {N}$
such that
$F^m=\mathrm {id}.$
In dimension
$n=1,$
Mattei and Moussu proved in [Reference Mattei and MoussuMM80] that the finite-orbits property is equivalent to periodicity. For dimension
$n>1,$
the equivalence is far from true. For example, the biholomorphism
$F(x,y)=(x,x+y)$
is non-periodic, but has finite orbits in each bounded neighborhood of
$0\in \mathbb {C}^2:$
the line
$\{x=0\}$
is the set of fixed points of F and F is a non-trivial translation on
$\{x=c\}$
with
$c \neq 0.$
Remark 1. The subset
$\mathrm {Diff}{}_{<\infty }({\mathbb C}^{},0)$
of
$ \mathrm {Diff}{}_{}({\mathbb C}^{},0)$
is not a subgroup. For example, the biholomorphisms
$F(x)=-x$
and
$G(x)=-{x}/({1-x})$
are periodic of period 2 and, hence, belong to
$\mathrm {Diff}{}_{<\infty }({\mathbb C}^{},0)$
. However, the composition
$$ \begin{align*}H(x)=(F\circ G)(x)=\frac{x}{1-x}\end{align*} $$
is not periodic, since
$H^n(x)={x}/({1-nx}), n\in \mathbb {N}.$
On the other hand, it is easy to check that the subset of
$\mathrm {Diff}{}_{}({\mathbb C}^{},0)$
formed by the linear isomorphisms with finite orbits is a subgroup of
$\mathrm {Diff}{}_{}({\mathbb C}^{},0)$
, isomorphic to the group of roots of unity. Nevertheless, this does not hold for dimension greater than
$1$
(cf. Corollary 2).
Proposition 2. (Linear case)
Let
$F\in \mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
be analytically linearizable. Then F has finite orbits if and only if its eigenvalues are roots of unity. Furthermore, if m is the least positive integer such that
$F^m$
is unipotent then every periodic point of F is a fixed point of
$F^m$
.
Proof. Applying Proposition 1(i), we can assume
$F(x)=Ax,$
where
$A\in \mathrm {GL}(n,\mathbb {C}).$
Let
$\unicode{x3bb} \in \mathrm {Spec}(A)$
and let B be an arbitrary ball centered at
$0.$
If
$v\in B$
is an eigenvector of F associated with
$\unicode{x3bb} ,$
then
$F^m(v)=\unicode{x3bb} ^mv$
for all
$m\in \mathbb {Z}.$
In particular,
$O_{F,B}(v)$
is finite if and only if
$\unicode{x3bb} $
is a root of unity. Hence, the finite orbits property implies that all eigenvalues of F are roots of unity.
Conversely, suppose that the eigenvalues of F are roots of unity. It suffices to show that
$\mathbb {C} ^n$
admits a decomposition
$\mathbb {C}^n=V_1\oplus \cdots \oplus V_r$
as F-invariant subspaces such that, for each
$x_j \in V_j,$
the orbit
${\mathcal O}_{F,U}(x_j)$
is finite for any bounded set U and any
$x_j\in U\cap V_j.$
Thus, it suffices to consider the case where A is a Jordan block
$$ \begin{align*} A = \left[ \begin{array}{ccccc} \unicode{x3bb} & & & &\\ 1 & \unicode{x3bb} & & &\\ & 1 & \ddots & &\\ & & \ddots & \unicode{x3bb}& \\ & & &1& \unicode{x3bb}\\ \end{array} \right], \end{align*} $$
where
$\unicode{x3bb} $
is a root of unity. We can assume
$n>1$
since the remaining case is trivial. Let
$x=(x_1,\ldots ,x_n)\in \mathbb {C}^n.$
By using induction on m it is easy to see that
$$ \begin{align*}F^m(x)=(\unicode{x3bb}^mx_1,m\unicode{x3bb} ^{m-1}x_1+\unicode{x3bb}^m x_2, \ldots,\quad P_{n,m}(x_1,\ldots,x_{n-2})+m\unicode{x3bb} ^{m-1}x_{n-1}+\unicode{x3bb}^mx_n),\end{align*} $$
with
$P_{j,m}$
linear for all
$j,m\in \mathbb {N}.$
In other words, if
$\pi _j$
is the jth projection on
$\mathbb {C}^n,$
then
$$ \begin{align*}\begin{array}{cclcc} \pi_1(F^m(x)) & = & \unicode{x3bb}^m x_1, &\\ \pi_2(F^m(x)) & = & m\unicode{x3bb} ^{m-1}x_1+\unicode{x3bb}^m x_2, & &\\ \pi_3(F^m(x)) & = & P_{3,m}(x_1)+m\unicode{x3bb}^{m-1}x_{2}+\unicode{x3bb} ^mx_3, & \\ & \vdots & & \\ \pi_n(F^m(x)) & = & P_{n,m}(x_1,\ldots,x_{n-2})+m\unicode{x3bb} ^{m-1}x_{n-1}+\unicode{x3bb}^mx_n. &\\ \end{array} \end{align*} $$
Consider
$x \neq 0.$
Let
$j_0$
be the first index such that
$x_{j_0} \neq 0$
. If
$j_0 = n$
then x is periodic; so it has a finite orbit. Consider
$j_0 < n.$
Then
$$ \begin{align*}|\pi_{j_0+1}(F^m (x))|=|m\unicode{x3bb}^{m-1}x_{j_0}+\unicode{x3bb} ^mx_{j_0+1}|\to \infty\quad \mbox{when }\ m\to \infty.\end{align*} $$
In any case, we see that x has finite positive orbit in any bounded neighborhood of
$0.$
Since the eigenvalues of
$A^{-1}$
are the inverses of the eigenvalues of
$A,$
we show analogously that every negative orbit of x is finite. This shows that F has finite orbits. Moreover, if m is the least positive integer such that
$F^m$
is unipotent, the discussion above shows that for a Jordan block the set of periodic points coincide with
$\mathrm {Fix}(F^m).$
Therefore,
$\mathrm {Fix}(F^m)$
is the set of periodic points of F.
Corollary 2. Suppose
$n \geq 2$
. Then the subset of
$\mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
consisting of finite-orbits linear biholomorphisms is not a subgroup of
$\mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
.
Proof. Let
$$ \begin{align*} F(x_1,\ldots,x_n)&=(x_1,x_1+x_2,x_3,\ldots,x_n),\\ G(x_1,\ldots,x_n)&=(x_1+x_2,x_2,x_3,\ldots,x_n). \end{align*} $$
Then F and G are linear and have finite orbits, since they are unipotent. However,
$F\circ G=(x_1+x_2,x_1+2x_2,x_3,\ldots ,x_n)\notin \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
, since
$({3 + \sqrt {5}})/{2}$
and
$({3 - \sqrt {5}})/{2}$
are eigenvalues of
$F \circ G$
.
2.1 Formal diffeomorphisms
We denote by
${\mathcal O}_{n,0}$
(respectively,
$\hat {\mathcal O}_{n,0}$
) the local ring of convergent (respectively, formal) power series with complex coefficients in n variables centered at the origin of
${\mathbb C}^{n}$
. Let
${\mathfrak m}$
be the maximal ideal of
$\hat {\mathcal O}_{n,0}$
.
Definition 2. The group
$\widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{n},0)}$
of formal diffeomorphisms consists of the elements
of
${\mathfrak m} \times \cdots \times {\mathfrak m}$
such that its first jet
$D_0 F$
belongs to
$\mathrm {GL}(n, {\mathbb C})$
.
Remark 2. As a consequence of the inverse function theorem, we can identify
$\mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
with the subset of
$\widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{n},0)}$
of formal diffeomorphisms
such that
$F_j \in {\mathfrak m} \cap {\mathcal O}_{n,0}$
for every
$1 \leq j \leq n$
.
Definition 3. We denote by
$\widehat {\mathrm {Diff}}{{\,}_{u}({\mathbb C}^{n},0)}$
the set of unipotent formal biholomorphisms, that is, the elements
$F\in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{n},0)}$
such that
$\mathrm {Spec}(D_0F)=\{1\}$
. Its subset
$\widehat {\mathrm {Diff}}{{\,}_{1}({\mathbb C}^{n},0)} := \{ F \in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{n},0)} : D_0 F = \mathrm {id} \}$
is called the group of tangent-to-the-identity formal diffeomorphisms in n variables.
2.2 Vector fields and flows
Let
${\mathfrak X}(\mathbb {C}^n,0)$
denote the Lie algebra of singular local holomorphic vector fields at
$0\in \mathbb {C}^n.$
Let
$X\in {\mathfrak X}(\mathbb {C}^n,0)$
and denote by
$\phi ^{t}(z)$
its local flow, defined in a neighborhood of
$\mathbb{C} \times \{0\}$
in
${\mathbb C}^{n+1}$
. Then, for each
$t\in {\mathbb C}$
, the map
$z\mapsto \phi ^t(z)$
is defined in a neighborhood
$U_t$
of
$0$
in
${\mathbb C}^{n}$
and hence defines a biholomorphism
$\phi ^t\in \mathrm {Diff}(\mathbb {C}^n,0),$
the so-called time-t map of
$X,$
also denoted by
$\exp (tX).$
We also use
$\exp (1X)=\exp (X)$
to denote the time-
$1$
map of
$X.$
It turns out that if
$f\in {\mathcal O}_{n,0}$
then
$$ \begin{align*}f\circ\exp(tX)(z)=f(z)+\sum_{j=1}^{\infty}\frac{t^j}{j!}X^j(f)\end{align*} $$
by Taylor’s formula, where X is now understood as a derivation in the ring
${\mathcal O}_{n,0}$
and
$X^j=X\circ X^{j-1}.$
By considering
$f=z_j, j=1,\ldots ,n,$
we obtain
$$ \begin{align*}\exp(tX)(z_1,\ldots,z_n)=\bigg(z_1+\sum_{j=1}^{\infty}\frac{t^j}{j!}X^j(z_1), \ldots ,z_n+\sum_{j=1}^{\infty}\frac{t^j}{j!}X^j(z_n)\bigg).\end{align*} $$
This last identity allows us to extend the definition of flow associated to a germ of holomorphic singular vector field to a formal singular vector field
$X\in \widehat {{\mathfrak X}}(\mathbb {C}^n,0),$
that is, a derivation of the ring of formal power series that preserves the maximal ideal. Indeed,
$\exp (t X) \in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{n},0)}$
for all
$X \in \widehat {{\mathfrak X}}(\mathbb {C}^n,0)$
and
$t \in {\mathbb C}$
. We say that two vector fields
$X,Y\in {\mathfrak X}{\,}_{}({\mathbb C}^{n},0)$
are analytically equivalent if there exists
$H\in \mathrm {Diff}(\mathbb {C}^n,0)$
such that
$H_*X=Y,$
that is,
$$ \begin{align*}D_xH \cdot X(x)=Y(H (x))\end{align*} $$
for any x in a neighborhood of the origin. The map H is called a conjugacy between X and
$Y$
. In this case, one could show that H is also a conjugacy between their time-t maps for any
$t \in {\mathbb C}.$
Definition 4. We say that a singular vector field
$X\in {\mathfrak X}{\,}_{}({\mathbb C}^{n},0)$
has finite orbits (writing
$X\in {\mathfrak X}{\,}_{<\infty }({\mathbb C}^{n},0)$
) if
$\exp (X)\in \mathrm { Diff}{}_{<\infty }({\mathbb C}^{n},0)$
.
We now derive some properties of finite-orbits vector fields.
Corollary 3. Let
$X\in {\mathfrak X}{\,}_{}({\mathbb C}^{n},0)$
be a singular vector field.
-
(i) If
$Y\in {\mathfrak X}{\,}_{}({\mathbb C}^{n},0)$
is singular and analytically conjugated to X then
$$ \begin{align*} X \in {\mathfrak X}{\,}_{<\infty}({\mathbb C}^{n},0) \Leftrightarrow Y\in {\mathfrak X}{\,}_{<\infty}({\mathbb C}^{n},0).\end{align*} $$
-
(ii) The following statements are equivalent.
-
(a) X has finite orbits.
-
(b)
$mX$
has finite orbits for all
$ m\in \mathbb {N}.$
-
(c)
$mX$
has finite orbits for some
$m\in \mathbb {N}.$
-
Proof. (i) As
$\exp (X)$
is conjugated to
$\exp (Y)$
, we can apply Proposition 1(i).
(ii) Set
$F=\exp (X)\in \mathrm {Diff}(\mathbb {C}^n,0).$
Then
$$ \begin{align*}F^m=\exp(mX)\quad \mbox{for all } m\in \mathbb{Z}.\end{align*} $$
Then we can apply Proposition 1(ii).
Remark 3. The last corollary implies that the
$\mathbb {Z}$
-multiples of X have finite orbits. However, in general such a property is not satisfied for
$\mathbb {R}$
- or
$\mathbb {C}$
-multiples of X. In fact, the time-
$1$
map of the one-dimensional field
$X=\unicode{x3bb} x({\partial }/{\partial x})$
is
$f=e^\unicode{x3bb} x, \unicode{x3bb} \in \mathbb {C}.$
Since in dimension one finite orbits are equivalent to finite order, it follows that
$$ \begin{align*}X\in {\mathfrak X}{\,}_{<\infty}({\mathbb C}^{},0)\Leftrightarrow f \mbox{ has finite order} \Leftrightarrow \unicode{x3bb}\in2\pi i\mathbb{Q}.\end{align*} $$
Corollary 4. Let
$X\in {\mathfrak X}(\mathbb {C}^n,0)$
be an analytically linearizable vector field. Then
$$ \begin{align*}X \in {\mathfrak X}{\,}_{<\infty}({\mathbb C}^{n},0)\Leftrightarrow \mathrm{Spec}(D_0X)\subset 2\pi i \mathbb{Q}.\end{align*} $$
Proof. The time-1 map
$F:=\exp (X)$
is linearizable and its eigenvalues have the form
$e^\unicode{x3bb} $
with
$\unicode{x3bb} \in \mathrm {Spec}(D_0X).$
The proof now is a consequence of Proposition 2.
Example 1. Consider the vector field
$\displaystyle X=x(2\pi i+y){\partial }/{\partial x}.$
Then we have
$$ \begin{align*}\exp(X)=(e^{2\pi i+y}x,y)=(e^yx,y). \end{align*} $$
Moreover, at each level
$\{y=c\}$
with
$c\notin 2\pi i \mathbb {Q}$
every point
$x\neq 0$
has an infinite orbit. Since the linear part
$X_0=2\pi i x({\partial }/{\partial x})$
has finite orbits, it follows that X is not analytically linearizable.
2.3 Semisimple/nilpotent decomposition of vector fields
We say that a singular vector field
$X\in {\hat {\mathfrak X}}{\,}_{}({\mathbb C}^{n},0)$
is semisimple if it is formally conjugated to a vector field of the form
$\sum _{j=1}^{n}\unicode{x3bb} _jx_j({\partial }/{\partial x_j}).$
We say that X is nilpotent if the linear part of X is nilpotent. Finally, we say that
$$ \begin{align*}X=X_S+X_N\end{align*} $$
is the semisimple/nilpotent decomposition of X if
$X_S$
is semisimple,
$X_N$
is nilpotent and
$[X_N,X_S]=0.$
Every singular formal vector field X admits a unique semisimple/nilpotent decomposition (cf. [Reference MartinetMar81]). We denote by
$\hat {{\mathfrak X}}_N(\mathbb {C}^n,0)$
the subset of
$ {\hat {\mathfrak X}}{\,}_{}({\mathbb C}^{n},0)$
consisting of the formal nilpotent vector fields.
Proposition 3. (Cf. [Reference ÉcalleÉca75, Reference Martinet and RamisMR83])
The image of
$\hat {{\mathfrak X}}_N(\mathbb {C}^n,0)$
by the exponential application is
$\widehat {\mathrm {Diff}}_{u}(\mathbb {C}^n,0)$
and the map
$\exp :\hat {{\mathfrak X}}_N(\mathbb {C}^n,0)\to \widehat {\mathrm {Diff}}_{u}(\mathbb {C}^n,0)$
is a bijection.
2.4 Poincaré–Dulac normal form
First, let us recall that a point
$\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n)$
of
$\mathbb {C}^n$
is said to be resonant if there exist
$m\in \mathbb {N}_0^n$
with
$|m|\geq 2$
and some
$1\leq k\leq n$
such that
$$ \begin{align*}\langle\unicode{x3bb},m\rangle=\unicode{x3bb}_1m_1+\cdots +\unicode{x3bb}_nm_n=\unicode{x3bb}_k.\end{align*} $$
This equation is called a resonance and its resonant monomial is the vector field
$$ \begin{align*}F_{k,m}~=x^m e_k=(0,\ldots,x_1^{m_1}\cdots x_n^{m_n},\ldots0).\end{align*} $$
Note that
$\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n)$
is resonant if and only if
$(\unicode{x3bb} _{\sigma (1)},\ldots ,\unicode{x3bb} _{\sigma (n)})$
is resonant for every permutation of the set of indexes
$\{1,2,\ldots ,n\}.$
Keeping this in mind, we say that a singular vector field
$X\in {\mathfrak X}{\,}_{}({\mathbb C}^{n},0)$
is resonant if the n-tuple formed by the eigenvalues of the linearization matrix
$D_0X$
of X is resonant. Finally, we say that a singular vector field
$X\in {\mathfrak X}(\mathbb {C}^n,0)$
is in the Poincaré domain if
$0$
does not belong to the convex hull of
$\mathrm {Spec}(D_0X)=\{\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n\},$
that is, there is no choice of
$t_j \in [0,1]$
for
$1 \leq j \leq n$
such that
$$ \begin{align*}t_1+\cdots +t_n=1\quad \mbox{and}\quad t_1\unicode{x3bb}_1+\cdots+t_n\unicode{x3bb}_n=0.\end{align*} $$
Poincaré–Dulac normal form. (Cf. [Reference Ilyashenko and YakovenkoIY08])
Let
$X\in {\mathfrak X}(\mathbb {C}^n,0)$
be a singular vector field in the Poincaré domain. Then X has only finitely many resonances and it is analytically conjugate to
$$ \begin{align*}Ax+\sum c_{k,m}F_{k,m},\end{align*} $$
where A is in Jordan normal form,
$c_{k,m}\in \mathbb {C}$
and the
$F_{k,m}$
are the resonant monomials of
$X.$
In particular, if X is in the Poincaré domain and it has no resonances, then X is analytically linearizable.
2.5 Stable manifold theorem
We denote by
$(W,p)$
the germ of an analytic variety at a point p. A germ of analytic variety
$W\subset (\mathbb {C}^n,0)$
is said to be invariant by
$F\in \mathrm { Diff}{}_{}({\mathbb C}^{n},0)$
if the germs of W and
$F(W)$
coincide at the origin. Additionally, we say that W is stable if there exists a neighborhood U of
$0$
where F and W are defined and satisfy
-
(1)
$F(U\cap W)\subset U\cap W$
and -
(2) for each
$x\in U\cap W,$
the positive orbit
$(F^m(x))_{m\in \mathbb {N}}$
converges to
$0$
.
Analogously, a variety
$W\subset (\mathbb {C}^n,0)$
is invariant by
$X \in {\mathfrak X} (\mathbb {C}^n,0)$
if
$X(x)$
is tangent to W at
$x,$
for every regular point
$x\in (W,0).$
In particular, W is invariant by
$\exp (X).$
We say that W is stable by X if is stable for its real flow, that is, for any
$x \in U \cap W$
, we have
$\mathrm {exp}(t X)(x) \in U \cap W$
for any
$t \in {\mathbb R}^{+}$
, and
$\lim _{t \to \infty } \mathrm {exp} (t X)(x) =0$
.
Holomorphic stable manifold theorem for diffeomorphisms. (Cf. [Reference RuelleRue89, p. 26], [Reference Ilyashenko and YakovenkoIY08, p. 107])
Let
$F\in \mathrm {Diff}{}_{}({\mathbb C}^{n},0)$
and
$\rho \in (0,1].$
Let
$$ \begin{align*} L^{-} =\oplus_{\unicode{x3bb} \in A_{\rho}^{-}} \ker (D_0 F - \unicode{x3bb} \mathrm{id})^{n} \end{align*} $$
be the sum of the generalized eigenspaces associated to the eigenvalues of
$D_0F$
in
$$ \begin{align*} A_\rho^-=\{\unicode{x3bb}\in \mathrm{Spec} (D_0F); |\unicode{x3bb}| < \rho\}. \end{align*} $$
Then there exists a unique F-stable manifold
$W^{-}$
whose tangent space at
$0$
is
$L^{-}$
.
Corollary 5. Let
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{n},0)$
. Then
$|\unicode{x3bb} |=1$
for any
$\unicode{x3bb} \in \mathrm {Spec}(D_0F).$
Proof. Suppose F has an eigenvalue
$\unicode{x3bb} $
such that
$|\unicode{x3bb} |\neq 1.$
So, up to change F by
$F^{-1},$
we can suppose
$|\unicode{x3bb} |<1.$
Thus F admits a stable manifold
$W^{-} \neq \{0\}$
invariant by F and associated to
$A_1^-.$
Hence, the points of
$W^{-}$
close to
$0$
have infinite orbits.
Holomorphic stable manifold theorem for vector fields. (Cf. [Reference Carrillo and SanzCS14])
Let
$X\in {\mathfrak X} (\mathbb {C}^n,0)$
be a singular vector field and
$\theta \in {\mathbb R}_{<0}$
. Suppose
$$ \begin{align*} S_{\theta}^{-}:=\{\unicode{x3bb}\in \mathrm{Spec}(D_0X); \mathrm{Re}(\unicode{x3bb}) \leq \theta\}\neq \emptyset \end{align*} $$
and denote by
$L_{\theta }^{-} =\oplus _{\unicode{x3bb} \in S_{\theta }^{-}(X)} \ker (D_0 X - \unicode{x3bb} \mathrm {id})^{n}$
the direct sum of the generalized eigenspaces associated to the eigenvalues in
$S_{\theta }^{-} (X).$
Then X admits a unique germ of stable manifold
$W_{\theta }^{-}$
whose tangent space at
$0$
is
$L_{\theta }^{-}$
.
3 Finite orbits and one-parameter groups
In this section we show Theorem 2.
Proof. Suppose that X has finite orbits. Applying the stable manifold theorem for X, we conclude that
$\mathrm {Spec} (D_0X)\subset i\mathbb {R}.$
The proof now follows by induction on
$n.$
If
$n=1,$
then the finite-orbits property is equivalent to periodicity and hence
$\mathrm {Spec} (D_0X)=\{\unicode{x3bb} \}\subset 2\pi i\mathbb {Q}.$
Now, suppose
$n\geq 2$
and assume the theorem holds in dimension less than
$n.$
Set
$$ \begin{align*}A_{>0}=\{\unicode{x3bb}\in \mathrm{Spec}(D_0X); \unicode{x3bb}\in i\mathbb{R}_{>0}\}\quad \mbox{and}\quad A_{<0}=\{\unicode{x3bb}\in \mathrm{Spec}(D_0X); \unicode{x3bb}\in i\mathbb{R}_{<0}\}. \end{align*} $$
Suppose
$A_{>0}\neq \emptyset $
. Let us prove that
$A_{>0}\subset 2\pi i \mathbb {Q}.$
Setting
$\tilde {X}=iX,$
we obtain a vector field whose complex trajectories coincide with those of
$X,$
both interpreted as sets. The subset of
$D_0 \tilde {X}$
consisting of eigenvalues with negative real part is
$i A_{>0}$
. Therefore,
$\tilde {X}$
admits a stable manifold
$V_0$
, which is invariant by X, such that
$\mathrm {Spec} (D_0 X_0)= A_{>0},$
where
$X_0= X_{|V_0}$
. Since X has finite orbits, so does
$X_0.$
If
$A_{>0}\neq \mathrm {Spec}(D_0X),$
then
$\dim V_0<n$
and so by the induction hypothesis we have
$A_{>0}\subset 2\pi i \mathbb {Q}.$
Therefore, we can suppose
$A_{>0}=\mathrm {Spec}(D_0X)$
and
$V_0$
is an open subset of
$\mathbb {C}^n$
. Hence,
$X=X_0$
is in the Poincaré domain. If X has no resonances then X is analytically linearizable and we have
$A_{>0}\subset 2\pi i\mathbb {Q}$
by Corollary 4. Suppose, then, that X admits resonances. It follows that
$k:= \sharp (\mathrm {Spec}(D_0 X))$
is greater than
$1$
. Set
$\mathrm {Spec}( D_0 X)=\{\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _k\}$
with
$\mbox { Im }(\unicode{x3bb} _1)>\cdots >\mbox { Im }(\unicode{x3bb} _k).$
By applying the stable manifold theorem to
$i X$
and
$\theta = i \unicode{x3bb} _1$
,
, we find invariant manifolds
such that
where
$X_j : = X|_{V_j}$
for all
$1\leq j\leq k.$
Consequently,
$X_1$
has no resonances and so is analytically linearizable. It follows from Corollary 4 that
$\unicode{x3bb} _1\in 2\pi i\mathbb {Q}.$
Suppose that
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _l\in 2\pi i \mathbb {Q}, l<k.$
We will show that
$\unicode{x3bb} _{l+1}\in 2\pi i \mathbb {Q}$
. Since
$\mbox { Im }(\unicode{x3bb} _1)>\cdots >\mbox { Im }(\unicode{x3bb} _k),$
it follows that
$X_{l+1}$
is linearizable (in which case
$\unicode{x3bb} _1,\ldots , \unicode{x3bb} _{l+1}\in 2\pi i \mathbb {Q}$
) or the possible resonances of
$X_{l+1}$
have the form
$$ \begin{align*}\unicode{x3bb}_j=|M_{j+1}|\unicode{x3bb}_{j+1}+\cdots+|M_{l+1}|\unicode{x3bb}_{l+1},\quad \sum_{k=j+1}^{l+1}|M_k|\geq 2,\end{align*} $$
where
$M_j\in \mathbb {Z}_{\geq 0}^{n_j}$
, and
$n_j$
is the algebraic multiplicity of
$\unicode{x3bb} _j$
for
$j=1,\ldots ,l.$
By using the Poincaré–Dulac normal form, we have coordinates
$x=(x_1,\ldots ,x_{l+1})\in \mathbb {C}^{n_1}\times \cdots \times \mathbb {C}^{n_{l+1}}=\mathbb {C}^m$
such that
$X_{l+1}\sim Ax+(*,*,\ldots ,*,0),$
where the first spot corresponds to the
$n_1$
first coordinates, the second spot to the next
$n_2$
coordinates and so on. If there exists some resonance with
$M_{l+1}\neq 0,$
then we can write
$\unicode{x3bb} _{l+1}$
as a combination of
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _l$
with rational coefficients, that is,
$\unicode{x3bb} _{l+1}\in 2\pi i\mathbb {Q}.$
If all resonances satisfy
$M_{l+1}=0,$
then
$X_{l+1} \sim Ax+(*,*,\ldots *,0,0)$
and we see that the manifold
$W=\{x_l=0\}\subset \mathbb {C}^m$
has dimension
$n_1+n_2+\cdots +n_{l-1}+n_{l+1},$
is invariant by
$X_{l+1}$
and the restriction
$X|_W$
has eigenvalues
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _{l-1},\unicode{x3bb} _{l+1}.$
By the induction hypothesis, we see that
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _{l-1},\unicode{x3bb} _{l+1}\in 2\pi i\mathbb {Q}.$
This shows that
$A_{>0}\subset 2\pi i \mathbb {Q}.$
Analogously,
$A_{<0}$
is contained in
$2\pi i \mathbb {Q}$
and hence
$\mathrm {Spec}(D_0X)\subset 2\pi i \mathbb {Q}$
.
The converse proposition of the above theorem is not true, even in dimension
$1$
, as we can see in the next example.
Example 2. The vector field
$X(z)=z^2 ({\partial }/{\partial z})$
has spectrum
$\mathrm {Spec}(D_0X)=\{0\},$
but it is not a finite-orbits germ, since
$\exp (X)=z+z^2+O(z^3)$
is clearly non-periodic.
4 Fixed-point curve theorem
In this section we prove that if
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
then some iterate
$F^m$
admits a curve of fixed points at
$0.$
First, we use constructions and ideas featuring in Mattei and Moussu [Reference Mattei and MoussuMM80], Rebelo and Reis [Reference Rebelo and ReisRR15] and Pérez-Marco [Reference Pérez-MarcoPM97] to show that there is a non-trivial continuum K containing the origin and satisfying
$F(K)=K$
. The set K consists of periodic points of F and can be obtained as a limit of compact sets where we consider the Hausdorff topology on the compact subsets of
$\overline {B}$
. Finally, we will use the theory of semianalytic sets (see [Reference Bierstone and MilmanBM88, Reference LojasiewiczLoj64]) to show that the continuum K is contained in an analytic curve which is invariant by some iterate of
$F$
.
4.1 Continua
For the sake of simplicity, we recall in this section the Sierpiński theorem and the Hausdorff topology on compact sets.
A topological space X is called a continuum if X is both connected and compact. The next result will be a key ingredient in the description of the connected components of the set of periodic points of a finite-orbits local biholomorphism.
Sierpiński theorem. (See [Reference EngelkingEng89, p. 358])
Let X be a continuum that has a countable cover
$\{X_j\}_{j=1}^{\infty }$
by pairwise disjoint closed subsets. Then at most one of the sets
$X_j$
is non-empty.
We now define the Hausdorff topology. Let
$(M,d)$
be a metric space and denote by
$H(M)$
the space of bounded, non-empty closed subsets of
$M.$
Note that
$H(M)$
is the set of compact subsets of M if M is compact. We define the Hausdorff metric
$\rho :H(M)\times H(M)\to [0,\infty )$
by
$$ \begin{align*}\rho(A,B)=\max\{\sup_{x\in A}d(x,B), \sup_{y\in B}d(A,y)\}.\end{align*} $$
Consider
$A\subset M$
and
$\varepsilon>0$
. We define the
$\varepsilon $
-neighborhood of A by
$$ \begin{align*}V_\varepsilon(A)=\bigcup_{x\in A}B_\varepsilon(x), \end{align*} $$
where
$B_{\epsilon } (x)= \{y \in M; d(y,x) < \epsilon \}$
. The Hausdorff metric satisfies
$$ \begin{align*}\rho(A,B)=\inf\{\varepsilon>0;\ V_\varepsilon(A)\supset B\ \mbox{and}\ V_\varepsilon(B)\supset A\}\end{align*} $$
for all
$A,B \in H(M)$
. Moreover, the metric space
$(H(M),\rho )$
is compact if M is compact [Reference NadlerNad92, Theorem 4.13, p. 59]. We assume from now on that M is compact. Given a sequence
$(A_n)_{n \geq 1}$
of subsets of M, let
$\liminf A_n$
be the set of points
$x \in M$
such that any neighborhood of x intersects
$A_n$
for all but finitely many n. We define
$\limsup A_n$
as the set of points
$x \in M$
such that any neighborhood of x intersects infinitely many of the sets in the sequence
$(A_n)_{n \geq 1}$
. Both sets are compact and
$\liminf A_n \subset \limsup A_n$
. Given a sequence
$(K_n)_{n \geq 1}$
of compact subsets of M, the sequence converges in the Hausdorff topology to K if and only if
$$ \begin{align*} \liminf K_n = \limsup K_n = K \end{align*} $$
(see [Reference NadlerNad92, Theorem 4.11, p. 57]). Moreover, the subset of
$H(M)$
consisting of continua is compact if M is compact (cf. [Reference NadlerNad92, Theorem 4.17, p. 61]).
4.2 Invariant curves
A formal curve at
$0\in \mathbb {C}^2$
is a proper radical ideal
$\Gamma =(f)$
of
$\mathbb {C}[[x, y]].$
Such a condition is equivalent to f being reduced, that is, f having no multiple irreducible factors.
-
(i) We say that
$\Gamma $
is invariant by
$F\in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{2},0)}$
if
$\Gamma \circ F=\Gamma $
, that is, f divides
$f\circ F.$
-
(ii) We say that
$\Gamma $
is a fixed-point curve of
$F\in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{2},0)}$
if f divides
$x\circ (F-\mathrm {id})$
and
$y\circ (F-\mathrm {id})$
. -
(iii) We say that
$\Gamma $
is invariant by
$X\in {\hat {\mathfrak X}}{\,}_{}({\mathbb C}^{2},0)$
if
$X(\Gamma )\subset \Gamma ,$
that is, f divides
$X(f).$
-
(iv) We say that
$\Gamma $
is a singular curve of X if f divides X.
In the case where the curve
$\Gamma =(f)$
is a radical ideal of
$\mathbb {C} \{ x, y \}$
, we identify it with the germ of analytic set
$V_\Gamma =(f=0)$
and the conditions above coincide with the natural ones for
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
and
$X \in {\mathfrak X}{\,}_{}({\mathbb C}^{2},0)$
:
-
(i) We have the equality
$F(V_\Gamma )=V_\Gamma $
of germs of analytic sets at
$0.$
-
(ii)
$F|_{V_\Gamma }=\mathrm {id}.$
-
(iii) X is tangent to
$V_\Gamma $
at any of its regular points. -
(iv)
$X|_{V_\Gamma }=0.$
Lemma 1. (Cf. [Reference RibónRib05])
Let
$X\in {\hat {\mathfrak X}}{\,}_{N}({\mathbb C}^{2},0)$
and let
$\Gamma $
be a formal curve at
$0.$
-
(a)
$\Gamma $
is invariant by X if and only if
$\Gamma $
is invariant by
$\exp (X).$
-
(b)
$\Gamma $
is singular curve of X if and only if
$\Gamma $
is a fixed-point curve of
$\exp (X)$
.
Lemma 2. Let
$V,W\subset (\mathbb {C}^2,0)$
be different germs of non-trivial analytic sets. Consider
$\psi \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
such that
$V,W\subset \mathrm {Fix}(\psi )$
. Then
$\psi $
is tangent to the identity.
Proof. We have
$V\neq \{0\}\neq W$
and
$V \neq W$
by hypothesis. If
$V=(\mathbb {C}^2,0)$
or
$W=(\mathbb {C}^2,0)$
then
$\psi =id.$
Therefore, we can suppose that V and W are analytic curves with reduced equation
$f=0$
and
$g=0,$
respectively, at
$0$
. So both f and g divide
$x\circ \psi -x$
and
$y\circ \psi -y.$
If
$\mathrm {ord}(f)\geq 2$
or
$\mathrm {ord}(g)\geq 2,$
then the first jet
$J^1\psi $
of
$\psi $
is equal to
$Id.$
So we can assume
$\mathrm {ord}(f)=\mathrm {ord}(g)=1$
. Since
$V \neq W$
, we deduce
$fg|x\circ \psi -x$
and
$fg|y\circ \psi -y.$
Again, we obtain
$J^1\psi =Id.$
This concludes the proof.
4.3 Connected components of the set of periodic points
Let us assume that
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0), U$
is a neighborhood of
$0$
in which F is defined and injective, and fix a closed ball
$\overline {B}_{\rho } (0)$
such that
$ \overline {B}_{\rho } (0) \subset U.$
Let us also set
$$ \begin{align} \mathrm{Per}_k (F) :=\{p\in {B}_{\rho} (0);\ F(p),\ldots,F^{k-1}(p)\in {B}_{\rho} (0) \ \mbox{and}\ F^{k}(p)=p\} \end{align} $$
and
$$ \begin{align*} \overline{\mathrm{Per}}_k (F) :=\{p\in \overline{B}_{\rho} (0);\ F(p),\ldots,F^{k-1}(p)\in \overline{B}_{\rho} (0) \ \mbox{and}\ F^{k}(p)=p\} \end{align*} $$
for
$k \in {\mathbb N}$
and
$$ \begin{align} \mathrm{Per} (F)=~\bigcup_{k\in \mathbb{N}} \mathrm{Per}_k (F), \ \ \overline{\mathrm{Per}} (F)=~\bigcup_{k\in \mathbb{N}} \overline{\mathrm{Per}}_k (F). \end{align} $$
Lemma 3. There is a subset
$K \subset \overline {\mathrm {Per}} (F)$
with the following properties.
-
(1) K is a continuum,
-
(2)
$0\in K$
and
$K\cap \partial {B}_{\rho } (0) \neq \emptyset $
. -
(3)
$F(K)=K$
.
Proof. We have
$\mathrm {Spec} (D_0F)\subset S^1$
as a consequence of the stable manifold theorem. For each
$n\in \mathbb {N},$
set
$F_n=e^{-1/n}F.$
Thus,
$F_n$
is a biholomorphism with
$\mathrm {Spec} (D_0F_n)\subset \{\unicode{x3bb} \in ~\mathbb {C};\ |\unicode{x3bb} |<1\}.$
Claim. We denote
$B_r = B_r (0)$
and
$\overline {B}_r = \overline {B}_r (0)$
for
$r \in \mathbb {R}^{+}$
and
$B= B_{\rho }$
,
$\overline {B}= \overline {B}_{\rho }$
. There are sequences
$(k_n)$
of positive integer numbers and
$(r_n)$
of positive real numbers such that:
-
(1)
$\lim _{n \to \infty } r_n=0$
and the closed ball
$\overline {B}_{r_n}$
satisfies
$$ \begin{align*}\bigcup_{j=1}^{\infty} F_{n}^{j}(\overline{B}_{r_n}) \subset \overline{B};\end{align*} $$
-
(2)
$\overline {B}_{r_n},F_n^{-1}(\overline {B}_{r_n}),\ldots ,\ F_n^{-k_n}(\overline {B}_{r_n})\subset \overline {B}$
and
$F_n^{-k_n}(\overline {B}_{r_n})\cap \partial B \neq \emptyset .$
Let us assume this for a moment to prove the lemma. We define
$$ \begin{align*}V_n = \overline{\bigcup_{j \geq -k_n} F_{n}^{j}(\overline{B}_{r_n})}.\end{align*} $$
Then
$V_n$
is connected since it is the closure of a union of connected sets that have the origin as a common point. Thus,
$V_n$
is a continuum contained in
$\overline {B}$
such that
$F_{n}^{j} (V_n) \subset V_n$
for all
$j \geq 0$
and there exists
$p_n\in V_n\cap \partial B.$
Passing to a subsequence if necessary, we can assume that
$V_n\to K,$
in the Hausdorff topology of compact subsets of
$\overline {B},$
and also
$p_n\to p\in K\cap \partial B.$
Since
$\{ 0, p \} \subset \limsup V_n$
, K is a continuum containing the origin such that
$K\cap \partial B\neq \emptyset $
. Since
$(F_n)_{n \geq 1}$
converges to F uniformly in
$\overline {B}$
, it is easy to check that
$$ \begin{align*} F(\liminf V_n) \subset \liminf F_n (V_n) \quad \mathrm{and} \quad F(\limsup V_n)= \limsup F_n (V_n). \end{align*} $$
Since
$F_{n}(V_n) \subset V_n$
for every
$n \in {\mathbb N}$
and
$V_n \to K,$
we deduce that
$$ \begin{align*} F(K) = F(\limsup V_n) = \limsup F_n (V_n) \subset \limsup V_n = K. \end{align*} $$
Therefore, since F has finite orbits, we obtain
$K \subset \overline {\mathrm {Per}} (F)$
. In particular, K is contained in the image of
$F|_K$
and hence
$F(K)=K$
.
Proof of the claim
Let us construct
$0 < r_n < 1/n$
and
$k_n$
. Since the origin is an attractor for
$F_n$
, there exists
$R \in (0, 1/n)$
such that the closed ball
$\overline {B}_{R}$
is contained in the basin of attraction of
$0$
and satisfies
$\bigcup _{j=1}^{\infty } F_n^{j}(\overline {B}_{R}) \subset \overline {B}$
. We claim that there exists
$k_n \in {\mathbb N}$
such that
$$ \begin{align*} F_n^{-1} (\overline{B}_{R}) \cup \cdots \cup F_n^{- (k_{n}-1)} (\overline{B}_{R}) \subset \overline{B} \quad\mathrm{and}\quad F_n^{-k_n} (\overline{B}_{R}) \setminus \overline{B} \neq \emptyset. \end{align*} $$
Assume, towards a contradiction, that no such
$k_n$
exists. Denote
$A = D_0 F_n^{-1}$
and
$A^{k} = (a_{ij;k})_{1 \leq i,j \leq 2}$
for
$k \in {\mathbb Z}$
. We have
$$ \begin{align*} a_{11;k} = \frac{1}{(2 \pi i)^{2}} \int_{|x| = |y| = {R}/{2}} \frac{x \circ F_{n}^{-k}}{x^2 y} dx dy \!\implies\! |a_{11;k}| \leq \frac{1}{(2 \pi)^{2}} (\pi R)^{2} \rho {\bigg(\frac{2}{R} \bigg)}^{3} = \frac{2 \rho}{R} \end{align*} $$
for any
$k \in {\mathbb N}$
. Analogously, we obtain
$ |a_{12;k}| \leq 2 \rho / R$
,
$ |a_{21;k}| \leq 2 \rho / R$
and
$ |a_{22;k}| \leq 2 \rho / R$
for any
$k \in {\mathbb N}$
. We have proved that the sequence
$(A^{k})_{k \geq 1}$
is bounded, contradicting
$\mathrm {spec} (A) \subset \{ z \in {\mathbb C}; |z|>1 \}$
.
By defining
$$ \begin{align*} r_n = \inf \{ s \in (0, R); F_n^{-k_n} (\overline{B}_s) \setminus \overline{B} \neq \emptyset \}, \end{align*} $$
we obtain
$k_n$
and
$r_n$
satisfying the desired properties.
Definition 5. Let M be a real analytic manifold. A subset X of M is semianalytic if each
$p\in M$
has a neighborhood V such that
$X\cap V$
has the form
$$ \begin{align*}X\cap V=\bigcup_{i=1}^{m}\bigcap_{j=1}^nX_{ij},\end{align*} $$
where
$X_{ij}=\{f_{ij}=0\}$
or
$X_{ij}=\{f_{ij}>0\}$
with
$f_{ij}$
real analytic on
$V.$
Remark 4. Notice that every (real or complex) analytic set X is semianalytic with
$m=1$
and
$X_{ij}=\{f_{ij}=0\}.$
Moreover, since
$\{f_{ij}<0\}=\{-f_{ij}>0\}, \{f_{ij}\geq 0\}=\{f_{ij}=0\}\cup \{f_{ij}>0\}$
and
$\{f_{ij}\leq 0\}=\{f_{ij}=0\}\cup \{f_{ij}<0\},$
we can add these types of sets to the possible options for
$X_{ij}$
to obtain an alternative definition.
Example 3. For each
$r>0$
the closed ball
$ \overline {B}_r(0) $
is semianalytic in
$\mathbb {C}^n,$
since it can be written as
$ \overline {B}_r(0) =\{f\geq 0\},$
where
$f(x)~=~r^2-|x_1|^2-\cdots -|x_n|^2.$
Lemma 4. Under the hypotheses above, each set
$\overline {\mathrm {Per}}_k (F)$
is semianalytic in U, has finitely many connected components, and each of its connected components is semianalytic and path connected.
Proof. We denote
${\mathcal P}_k = \overline {\mathrm {Per}}_k (F)$
. Let
$p\in {\mathcal P}_k $
. The local biholomorphism
$F^k$
is well defined in some neighborhood V of
$p.$
Moreover, we have
$$ \begin{align*} {\mathcal P}_k \cap V =\bigg(\bigcap_{j=1}^4\{f_j=0\}\bigg)\cap\bigg(\bigcap_{l=0}^{k-1}\{f\circ F^l\geq 0\}\bigg),\end{align*} $$
where
$f_1=\mbox {Re}(x\circ F^k-x), f_2=\mbox {Im }(x\circ F^k-x), f_3=\mbox { Re}(y\circ F^k-y), f_4=\mbox {Im }(y\circ F^k-y),$
and
$f(x,y)~=~r^2-|x|^2-|y|^2.$
Therefore,
${\mathcal P}_k$
is semianalytic. Now, by Corollary 2.7 in [Reference Bierstone and MilmanBM88], we know that each connected component of
${\mathcal P}_k$
is also semianalytic and the family of connected components of
${\mathcal P}_k$
is locally finite. Since
${\mathcal P}_k$
is compact, it has finitely many connected components. Finally, by using Theorem 1 in [Reference LojasiewiczLoj64], we know that
${\mathcal P}_k$
is triangulable and so is locally path connected. Thus, each connected component of
${\mathcal P}_k$
is path connected.
Lemma 5. Let C be a connected component of
$\overline {\mathrm {Per}_{kl}} (F)$
for some
$l \in {\mathbb N}$
and suppose that
$$ \begin{align*}E=\{p\in C; F^k(p)=p \mbox{ and the germ }F^k_p \mbox{ of } F^{k} \mbox{ at } p \mbox{ is unipotent} \}\end{align*} $$
is non-empty. Then C is a subset of
$\overline {\mathrm {Per}_{k}} (F)$
and
$D_{p} F^{k}$
is unipotent for all
$p \in C$
.
Proof. Denote
$\psi = F^{k}.$
We know that if
$\psi (p)=p$
then the characteristic polynomial of
$D_p\psi $
is
$$ \begin{align*}P_{D_p\psi}(x)=x^2-\mathrm{tr}(D_p\psi)x+\det D_p\psi=x^2-Sx+P,\end{align*} $$
where S is the sum and P is the product of the eigenvalues of
$D_p\psi .$
Therefore,
$$ \begin{align*}E= \{ p \in C ; \psi(p)=p, \mathrm{tr}(D_p \psi)=2 \ \mathrm{ and }\det(D_ p \psi) = 1 \}.\end{align*} $$
In order to prove the lemma it suffices to show that
$E=C.$
Since
$E\neq \emptyset ,$
the set C is connected, and E is closed in
$C,$
it suffices to show that E is open in
$C.$
Consider
$p\in E .$
Let us first prove that the germ
$(C,p)$
of C at p is contained in
$\overline {\mathrm {Per}_{k}} (F)$
. Set
$$ \begin{align*}A = \{ q \in U; \psi (q) = q \}\quad\mathrm{and}\quad B=\{q\in U;\ \psi^{l}(q)=q\}.\end{align*} $$
It is obvious that A and B are analytic and
$(C,p)\subset (B,p)$
. Now since
$\psi (p)=p$
and
$D_p\psi $
is unipotent, we can consider the infinitesimal generator
$X_p$
of the germ
$\psi _p,$
that is, the nilpotent formal vector field
$X_p$
such that
$\exp (X_p)=\psi _p.$
Consequently,
$lX_p$
is the infinitesimal generator of
$\psi ^l_p=F^{kl}_p.$
Since
$(\psi _p^l)|_{B}=\mathrm {id},$
Lemma 1, applied to the germ of B at p, implies that
$(B,p)\subset \mathrm {Sing}(lX_p)=\mathrm {Sing}(X_p)$
and therefore
$\psi _{p}|_{B}=\mathrm {id}$
. In particular, we obtain
$ (C,p)\subset \overline {\mathrm {Per}_{k}} (F) $
.
Now let us prove that
$(C,p)\subset (E,p).$
Define
$f: A \to {\mathbb C}$
by setting
$f(q)= \det (D_q \psi )$
. The restrictions of f to the irreducible components of the germ of A at p are holomorphic functions. As F has finite orbits, it follows by the stable manifold theorem that the eigenvalues of
$D_q \psi $
have modulus
$1$
and then the image of f is contained in the circle
$S^1$
, since
$\det (D_q \psi )$
is the product of the eigenvalues of
$D_q \psi .$
In particular, the image of f does not contain any open set. We obtain that f is locally constant in a neighborhood of
$C \cap A$
in A by the open mapping theorem. Since
$f(p)=1$
and
$ (C,p)\subset A$
, we deduce that
$(C,p) \subset \{ f = 1 \}$
. Now we consider a function
$g: A \to {\mathbb C},$
defined by
$g(q)= \mathrm {tr} (D_q \psi ).$
For each q in some neighborhood of p in A, the eigenvalues
$\unicode{x3bb} $
and
$\mu $
of
$D_q \psi $
satisfy
$|\unicode{x3bb} |=|\mu |=1$
and
$\unicode{x3bb} \mu =1$
since
$\mathrm {Spec} (D_p \psi ) \subset S^1$
and
$(C,p) \subset \{ f = 1 \}$
. Therefore, we obtain
$ \mathrm {tr} (D_q \psi ) = \unicode{x3bb} + \overline {\unicode{x3bb} } = 2 \mathrm {Re}(\unicode{x3bb} ) \in [-2,2]$
. Again, the restriction of g to the irreducible components of
$(A,p)$
defines holomorphic functions whose images do not contain any open set. Hence,
$g \equiv g(p)=2$
is constant in a neighborhood of p in A. It follows that
$(C,p)\subset (E,p).$
This concludes the proof.
We have already seen in Lemma 4 that each
$\overline {\mathrm {Per}}_k (F)$
has finitely many connected components (say,
$C^{k}_1,\ldots ,C^{k}_l$
). Let us now consider the family of all components of F in
$D,$
namely,
$$ \begin{align*}{\mathcal A}:=\{C_j^k;\ k\in \mathbb{N}\ \mathrm{ and }\ C_j^k \mbox{ is a connected component of } \overline{\mathrm{Per}}_k (F) \}.\end{align*} $$
We say that two components
$C,D\in \mathcal A$
are equivalent (and we write
$C\sim D$
) if there are
$$ \begin{align*}C_{\alpha_1}^{k_1},\ldots,C_{\alpha_r}^{k_r}\in\mathcal A\end{align*} $$
such that
$C=C_{\alpha _1}^{k_1},\ D=C_{\alpha _r}^{k_r}$
and
$C_{\alpha _s}^{k_s}\cap C_{\alpha _{s+1}}^{k_{s+1}}\neq \emptyset $
for all
$1\leq s<r.$
Notice that
$\sim $
is an equivalence relation in
$\mathcal A.$
Remark 5. If
$C_{\alpha _1}^{k_1},\ldots ,C_{\alpha _r}^{k_r}$
are components in
$\mathcal {A}$
such that
$C_{\alpha _s}^{k_s}\cap C_{\alpha _{s+1}}^{k_{s+1}}\neq \emptyset $
for all
$1\leq s<r,$
then there are
$j,k\in \mathbb {N}$
such that
$\bigcup _{s} C_{\alpha _s}^{k_s}\subset C_{j}^{k}.$
If fact, since the union is connected and is contained in
, it is contained in
$C^{k_1\ldots k_r}_{j}$
for some
$j.$
Lemma 6. (stability of classes)
If
$[C]$
is an equivalence class (possibly infinite) in
${\mathcal A}/\sim ,$
then
$$ \begin{align*}\bigcup_{C_j\in [C]}C_j= C^{k_0}_{j_0}\end{align*} $$
for some
$j_0,k_0.$
Proof. The result is obvious if there is at most one non-unitary component in
$[C]$
, that is, a component
$C_{j}^{k}$
of
$[C]$
such that
$\sharp C_{j}^{k}>1$
. Thus, we can assume that there are two distinct non-unitary components
$C_a$
and
$C_b$
of
$[C]$
such that
$C_a \cap C_b \neq \emptyset $
. Suppose that
$C_a$
is a connected component of
${\mathcal P}_a$
and
$C_b$
is a connected component of
${\mathcal P}_b$
, where we denote
${\mathcal P}_j =\overline {\mathrm {Per}}_j (F)$
.
Let us show that there is
$p\in C_a\cap C_b$
such that
$D_pF^{ab}$
is unipotent. First of all, there is
$p \in C_a \cap C_b$
such that
$(C_a,p) \neq (C_b,p)$
in
$\overline {B}$
since
$C_a$
and
$C_b$
are connected. Let
$(V_a,p)$
and
$(V_b,p)$
be the germs of the analytic set of equations
$F^a = Id$
and
$F^b=Id,$
respectively, defined in some neighborhood of p in
$U.$
Since
$C_a$
and
$C_b$
are non-unitary, we have
$\dim (V_a,p) \geq 1$
and
$\dim (V_b,p) \geq 1.$
We claim that
$(V_a , p) \neq (V_b , p)$
. Otherwise, we have
$(C_a\cup C_b,p)\subset {\mathcal P}_a \cap {\mathcal P}_b $
and hence
$$ \begin{align*} (C_a,p)=(C_a\cup C_b,p)=(C_b,p),\end{align*} $$
contradicting the choice of p. Therefore we obtain
$D_pF^{ab}=\mbox {id}$
by Lemma 2.
Consider the connected component
$C_{\ell }^{ab}$
of
${\mathcal P}_{ab}$
containing p. Let A be a connected union of finitely many components of
$[C]$
that contains p. Then
$A \subset C_{\ell }^{ab}$
by Lemma 4.5. By varying A, we deduce
$\bigcup _{C_j \in [C]} C_j = C_{\ell }^{ab}$
.
4.4 Structure of the set of periodic points
Now, we combine the previous results to show Theorem 4 and the fixed point curve theorem.
Proof of Theorem 4 and the fixed-point curve theorem.
Let B an open ball such that F and
$F^{-1}$
are defined in a neighborhood of
$\overline {B}$
. Let
${\mathcal P}$
be a connected component of
$\overline {\mathrm {Per}} (F)$
. It is a countable union of elements of the family
$\mathcal A$
of components of F in
$\overline {B}$
. Up to considering only maximal components of F in
$\overline {B}$
, we can suppose that such a union is disjoint by Lemma 6. Therefore, we obtain
${\mathcal P} = C$
for some
$C\in \mathcal A$
by Sierpiński’s theorem. Hence,
${\mathcal P}$
is a connected component of some
$\overline {\mathrm {Per}}_k (F)$
. Both C and
$\overline {\mathrm {Per}}_k (F)$
are semianalytic by Lemma 4.
Let
${\mathcal Q}$
be a connected component of
$\mathrm {Per} (F)$
. It is contained in a connected component
${\mathcal Q}'$
of
$\overline {\mathrm {Per}} (F)$
. Then
${\mathcal Q}'$
is a semianalytic subset of
$\overline {\mathrm {Per}}_k (F)$
for some
$k \in \mathbb {N}$
by the first part of the proof. We obtain
${\mathcal Q} \subset {\mathrm {Per}}_k (F)$
and hence the set
${\mathcal Q}$
is given locally by the equation
$F^{k} = \mathrm {id}$
. It follows that
${\mathcal Q}$
is a complex analytic subset of the open ball. Since the set
${\mathrm {Per}}_k (F) \cap {\mathcal Q}'$
is semianalytic and relatively compact, it follows that it has finitely many connected components [Reference Bierstone and MilmanBM88, Corollary 2.7] and they are all semianalytic. We deduce that
${\mathcal Q}$
is a semianalytic subset of
${\mathbb C}^{2}$
.
We claim that
$\dim ({\mathcal Q},p) \geq 1$
for any
$p \in {\mathcal Q}$
. This is equivalent to the property
$\sharp {\mathcal Q}>1$
since
${\mathcal Q}$
is a connected component of
$\mathrm {Per}_{k}(F)$
. First, suppose
$0 \in {\mathcal Q}$
. Since
${\mathcal Q}' \subset \overline {\mathrm {Per}}_k (F)$
, there exists a neighborhood W of the origin such that
$$ \begin{align*} W \cap {\mathcal Q} = W \cap {\mathcal Q}' = W \cap \mathrm{Fix}(F^{k}). \end{align*} $$
Note that
${\mathcal Q}'$
is a continuum that contains the non-trivial subcontinuum K obtained in Lemma 3. Since
${\mathcal Q}'$
is a non-trivial continuum, we deduce that the germ of
$\mathrm {Fix}(F^{k})$
and that of
${\mathcal Q}$
at the origin have positive dimension and thus contain an analytic curve
$\Gamma $
passing through
$0$
. Finally, consider a general connected component
${\mathcal Q}$
of
$\mathrm {Per} (F)$
. Given
$p \in {\mathcal Q}$
, there exists a germ of analytic curve
$\Gamma '$
at p contained in
$\mathrm {Per}_{l}(F)$
for some
$l \in \mathbb {N}$
by the previous discussion. Since
$(\Gamma ', p) \subset {\mathcal Q}$
, we obtain
$\dim ({\mathcal Q},p) \geq 1$
.
Proof of Theorem 3
The eigenvalues of
$D_0 F$
belong to the unit circle by Corollary 5. By the fixed-point curve theorem, there exists an analytic curve
$\Gamma \subset \mathrm {Fix}(F^k)$
through the origin for some
$k \geq 1$
. Suppose
$1 \not \in \mathrm {spec} (D_0 F^k).$
Then
$D_0 (F^k - \mathrm {Id})$
is a regular matrix, therefore
$F^{k}-\mathrm {Id}$
is a local diffeomorphism at
$0.$
But this contradicts
$\Gamma \subset (F^k - \mathrm {Id})^{-1} (0)$
. Therefore, we obtain
$1 \in \mathrm {spec} (D_0 F^{k})$
. Since the eigenvalues of
$D_0 F^k$
are kth powers of eigenvalues of
$D_0 F,$
it follows that there exists
$\unicode{x3bb} \in \mathrm {spec}(D_0 F)$
such that
$\unicode{x3bb} ^{k}=1.$
Remark 6. Corollary 1 provides negative algebraic criteria for the finite-orbits property. For instance, let
$F(x,y)= (x+ f_1(x,y), y+ f_2 (x,y)) \in \mathrm {Diff}_{1} ({\mathbb C}^{2},0)$
where
$f_j (x,y) = \sum _{k=m}^{\infty } P_{k,j}(x,y)$
is the expansion of
$f_j \in {\mathbb C} \{x,y\}$
as a sum of homogeneous polynomials for
$j \in \{1,2\}$
, where
$m \geq 2$
. Assume that
$P_{m,1}$
and
$P_{m,2}$
are relatively prime. Since
$$ \begin{align*} x \circ F^{k} - x = k P_{m,1} + h.o.t. \quad\mathrm{and}\quad y \circ F^{k} - y = k P_{m,2} + h.o.t., \end{align*} $$
where
$h.o.t.$
denotes higher order terms, we deduce that the fixed point
$(0,0)$
of
$F^{k}$
is isolated for any
$k \in {\mathbb N}$
and hence F is not a finite-orbits germ.
Later on, we will see that there exists
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
with finite orbits but that
$D_0 F$
has no finite orbits (see Theorem 1). It makes sense to study whether the finite-orbits property for other actions naturally associated to F implies
$\mathrm {spec} (D_0 F) \subset e^{2 \pi i {\mathbb Q}}$
. We will consider the blow-up
$\pi : \tilde {\mathbb C}^{2} \to {\mathbb C}^{2}$
of the origin and the diffeomorphism
$\tilde {F}$
induced by F in a neighborhood of the divisor
$D:= \pi ^{-1}(0)$
(see [Reference RibónRib05]).
Corollary 6. Let
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
. Assume that the germ of
$\tilde {F}$
defined in the neighborhood of D in
$\tilde {\mathbb C}^{2}$
has finite orbits. Then
$\mathrm {spec} (D_0 F)$
consists of roots of unity.
Proof. The diffeomorphism
$\tilde {F}_{|D}$
has finite orbits and hence
$D_0 F$
induces an element of finite order of
$\mathrm {PGL} (2, {\mathbb C})$
. Thus
$D_0 F$
is diagonalizable and has eigenvalues
$\unicode{x3bb} , \mu \in \mathbb {C}^{*}$
such that
$\unicode{x3bb} / \mu $
is a root of unity. Since at least one eigenvalue of
$D_0 F$
is a root of unity by Theorem 3, we deduce
$\mathrm {spec} (D_0 F) \subset e^{2 \pi i {\mathbb Q}}$
.
Remark 7. In general, a germ of biholomorphism H does not admit germs of fixed-point curves, even when
$F\in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
. For example,
$F(x,y)=(-x,-x-y)$
is a finite-orbits germ, because it is linear and
$\mathrm {Spec}(D_0F)=\{-1\},$
but the only fixed point of F is the origin. Note, however, that
$F^2(x,y)=(x,2x+y)$
and
$\{x=0\}$
is a fixed-point curve of
$F^2.$
Moreover, the curve
$\{x=0\}$
is an irreducible curve invariant by F.
We conclude this section by providing an example of
$F \in \mathrm {Diff} ({\mathbb C}^{2},0)$
that has finite orbits but no irreducible germ of invariant curve. The diffeomorphism F is of the form
$F= S \circ T$
where
$S(x,y)= (iy, ix)$
,
$T = \mathrm {exp} (X)$
and
$$ \begin{align*} X = xy \bigg( x \frac{\partial}{\partial x} - y \frac{\partial}{\partial y} \bigg) + i x^{2} y^{2} \bigg( x \frac{\partial}{\partial x} + y \frac{\partial}{\partial y} \bigg) .\end{align*} $$
Note that
$S^{*} X = X$
and hence S and T commute. Moreover, S has order
$4$
. Any germ of irreducible curve
$\gamma $
that is invariant by F is also invariant by
$F^4$
and hence by
$\mathrm {exp} (4 X)$
. Since X is the infinitesimal generator of a tangent to the identity local biholomorphism, we deduce that
$\gamma $
is invariant by X by Lemma 1. Note that the singularity of
$X/(xy)$
at the origin is reduced and hence
$X/(xy)$
has only two irreducible invariant curves by the Briot–Bouquet theorem, namely the x- and y-axes. As a consequence, the axes are the unique irreducible germs of X-invariant curves. Since S permutes the axes, it follows that F has no irreducible germ of invariant curve.
Let us show that F has finite orbits. It suffices to prove that
$F^{4} = T^{4}$
has finite orbits by Proposition 1. Indeed, it suffices to show that T has finite orbits by the same result. Next, we study the action induced by X on the leaves of the foliation
$d(xy)=0$
. Such a foliation is preserved by X since
$X (xy) = 2 i (x y)^{3} $
. We can relate the properties of X with those of
$Z = 2 i z^{3} \partial / \partial z$
and its time-
$1$
map
$G= \mathrm {exp} (Z)$
. Indeed, we have
$$ \begin{align*} (xy) \circ T^{k} (x, y) = G^{k} (x y) \end{align*} $$
for
$k \in {\mathbb Z}$
.
Fix a small bounded neighborhood
$V'$
of
$0$
in
${\mathbb C}$
and a small bounded neighborhood V of
$(0,0)$
in
${\mathbb C}^{2}$
such that
$(xy) (V) \subset V'$
. Consider
$(x_0, y_0) \in V$
and denote
$z_0 = x_0 y_0$
. Since the axes consist of fixed points of T, we can suppose
$x_0 y_0 \neq 0$
. Assume, towards a contradiction, that the positive T-orbit of
$(x_0, y_0)$
in V is infinite. Therefore,
$G^{k} (z_0)$
is well defined and belongs to
$V'$
for any
$k \geq 0$
. Since G has a dynamics of flower type, we deduce
$$ \begin{align*} \lim_{k \to \infty} G^{k} (z_0) =0 \quad\mathrm{and}\quad \lim_{k \to \infty} \frac{G^{k} (z_0)}{|G^{k} (z_0)|} \in \{ e^{{i \pi}/{4}}, - e^{{i \pi}/{4}} \}. \end{align*} $$
Assume that the latter limit is equal to
$e^{{i \pi }/{4}}$
. Let us study the variation of the monomials
$x^{a} y^{b}$
by iteration; we have
$$ \begin{align*} x^{a} y^{b} \circ T = x^{a} y^{b} (1 + (a -b) xy + O(x^{2} y^{2})) \end{align*} $$
for any
$(a,b) \in {\mathbb Z}_{\geq 0} \times {\mathbb Z}_{\geq 0}$
. As a consequence, we get
$$ \begin{align*} |x \circ T^{k+1} (x_0,y_0)|> |x \circ T^{k} (x_0,y_0)|, \quad |(x^{2} y) \circ T^{k+1} (x_0,y_0)| > |(x^{2} y) \circ T^{k} (x_0,y_0)| \end{align*} $$
for any non-negative integer number k. Since
$|x|$
increases along the positive T-orbit of
$(x_0,y_0)$
and
$\lim _{k \to \infty } (xy)(T^{k}(x_0,y_0)) =0$
, we get
$\lim _{k \to \infty } y (T^{k}(x_0,y_0)) =0$
. Moreover, since
$|x^{2} y|$
increases along the positive T-orbit of
$(x_0, y_0)$
. it follows that
$\lim _{k \to \infty } |x| (T^{k}(x_0,y_0)) =\infty $
. This property contradicts V being bounded. The case
$\lim _{k \to \infty } {G^{k} (z_0)}/{|G^{k} (z_0)|} = - e^{{i \pi }/{4}}$
is treated in a similar way. Analogously, we can show that the negative T-orbit of
$(x_0,y_0)$
is finite.
5 Non-virtually unipotent biholomorphisms with finite orbits
So far, all the examples in the literature of finite-orbits local diffeomorphisms have been virtually unipotent, that is, the eigenvalues of their linear parts have been roots of unity. The likely reason is revealed in Theorem 2: time-1 maps with finite orbits have roots-of-unity eigenvalues. In this section we construct a family of finite-orbits local diffeomorphisms that are non-virtually unipotent.
Definition 6. We say that
$\unicode{x3bb} \in \mathbb {C}$
is a Cremer number if
$\unicode{x3bb} $
is not a root of unity, but
$$ \begin{align*} |\unicode{x3bb}|=1\quad \mbox{and} \quad \liminf_{m \to \infty} \sqrt[m]{|\unicode{x3bb}^{m}-1|} =0. \end{align*} $$
This equation is called Cremer’s condition.
Fix
$n\geq 1$
and consider coordinates
$x=(x_1,\ldots ,x_n)\in \mathbb {C}^n$
and
$y\in \mathbb {C}.$
Given
$j \in {\mathbb N}$
, we denote by
$[j]$
the unique natural number
such that
$j-j'$
is a multiple of n. The proof of Theorem 1 involves building a convergent power series
$$ \begin{align} a(x_1,\ldots,x_n) = \sum_{j=1}^{\infty} \frac{(2 j x_{[j]})^{m_{j}}}{M_{j}^{m_{j}}} = \sum_{j=1}^{\infty} \bigg(\frac{2j}{M_j}\bigg)^{m_j}x_{[j]}^{m_j}, \end{align} $$
where
$(m_j)_{j \geq 1}$
is an increasing sequence of natural numbers and
$(M_j)_{j \geq 1}$
is a sequence of positive numbers that will be chosen to ensure that
$$ \begin{align} F(x,y) = (\unicode{x3bb} x_1, \unicode{x3bb} x_2, \ldots, \unicode{x3bb} x_n, y + a(x_1, \ldots, x_n)) \end{align} $$
has finite orbits. We need auxiliary sequences
$(k_j)_{j \geq 1}$
and
$(r_j)_{j \geq 1}$
of natural numbers. These satisfy certain conditions that are provided by the following lemma.
Lemma 7. Let
$\unicode{x3bb} $
be a Cremer number. There exist a sequence
$(M_j)_{j \geq 1}$
in
${\mathbb R}_{+}$
and sequences
$(m_j)_{j \geq 1}$
,
$(k_j)_{j \geq 1}$
and
$(r_j)_{j \geq 1}$
in
${\mathbb N}$
such that, for any
$j \in {\mathbb N}$
:
-
(C1)
$M_j := {1}/{\sqrt [{m_j\ \,}]{|\unicode{x3bb} ^{m_j}-1|}}$
satisfies
$M_j \geq 4j^{2}$
; -
(C2)
$2^{m_j} \geq 1 + j + \sum _{\ell =1}^{j-1} 2 (2\ell )^{m_\ell } j^{m_\ell }\ (2^{m_1}\geq 2)$
; -
(C3)
$\min (m_j, r_j)> \max (m_{j-1}, r_{j-1})$
if
$j \geq 2$
; -
(C4)
$|\unicode{x3bb} ^{k_j m_j} - 1| \geq 1$
; -
(C5)
$k_j \sum _{\ell = r_j}^{\infty } {1}/{2^{\ell }} < 1$
.
Proof. Since
$\unicode{x3bb} $
satisfies the Cremer condition, we can choose
$m_1$
and
$M_1$
such that the first three conditions hold, where (C3) is an empty condition. As
$\unicode{x3bb} ^{m_1}$
is not a root of unity, the sequence
$(\unicode{x3bb} ^{k m_1})_{k \geq 1}$
is dense on the unit circle; hence, there exists
$k_1 \in {\mathbb N}$
such that the fourth condition holds for
$j=1.$
Now we can define
$r_1$
in such a way that the last condition holds for
$j=1.$
Analogously, we can define
$(M_2, m_2)$
,
$k_2$
and
$r_2$
such that (C1)–(C5) hold for
$j=2.$
Indeed, we define the sequences
$(M_j)_{j \geq 1}$
,
$(m_j)_{j \geq 1}$
,
$(k_j)_{j \geq 1}$
and
$(r_j)_{j \geq 1}$
recursively for
$j \in {\mathbb N}$
.
Remark 8. Notice that conditions (C1)–(C5) still hold if we replace
$\unicode{x3bb} $
by
$\unicode{x3bb} ^{-1},$
since
$\overline {\unicode{x3bb} } = \unicode{x3bb} ^{-1}$
implies
$$ \begin{align*} |\unicode{x3bb}^{-n} -1| = |\overline{\unicode{x3bb}^{n}-1}| = | \unicode{x3bb}^{n} -1| \end{align*} $$
for any
$n \in {\mathbb Z}$
.
Lemma 8. Consider the setting provided by Lemma 7. Then
$a(x)$
(see equation (3)) is an entire function of
${\mathbb C}^{n}$
. Moreover, the map
$F(x,y)=(\unicode{x3bb} x, y+ a(x))$
is a holomorphic automorphism of
$\mathbb {C}^{n+1}$
whose inverse is
$$ \begin{align*} F^{-1}(x_1, \ldots, x_n,y)=(\unicode{x3bb}^{-1} x_1, \ldots, \unicode{x3bb}^{-1} x_n , y - a(\unicode{x3bb}^{-1} x_1, \ldots, \unicode{x3bb}^{-1} x_n)). \end{align*} $$
Proof. Since
$M_j \geq 4 j^{2}$
for any
$j \geq 1$
, it follows that
$$ \begin{align*} \lim_{j \to \infty} \sqrt[m_j\,]{{\bigg( \frac{2j}{M_j} \bigg)}^{m_j}} = \lim_{j \to \infty} \frac{2j}{M_j} = 0 \end{align*} $$
and hence
$a(x_1, \ldots , x_n)$
is an entire function. We can verify directly that
$F^{-1}(x,y)= (\unicode{x3bb} ^{-1} x, y - a(\unicode{x3bb} ^{-1} x))$
is the inverse of F.
Now note that if
is a power series and
then we can show that
for any
$k \in {\mathbb N}$
by induction, where
$L_k$
is the linear operator of the ring of convergent power series defined by
where
$|j|=j_1 + j_2 + \cdots + j_n$
.
Lemma 9. Consider
$j \geq 1$
and
$x\in \mathbb {C}$
with
$\max _{1 \leq k \leq n} |x_k| \leq j$
and
$|x_{[j]}| \geq 1/j$
. Then we have
$$ \begin{align*}j\leq|(L_{k_j} a)(x)|\leq 2(2j^2)^{m_j}+2^{m_j}-j.\end{align*} $$
Proof. First, let us study
$| L_{k_j} {(2j x_{[j]})^{m_j}}/{M_j^{m_j}} |.$
By (5) we have
$$ \begin{align*} \bigg| L_{k_j} \frac{(2j x_{[j]})^{m_j}}{M_j^{m_j}} \bigg| = \bigg| \frac{\unicode{x3bb}^{k_j m_j} -1}{\unicode{x3bb}^{m_j}-1} \frac{(2j x_{[j]})^{m_j}}{M_j^{m_j}} \bigg| = | (\unicode{x3bb}^{k_j m_j} -1) (2j x_{[j]})^{m_j}|,\end{align*} $$
where the second equality follows from the definition of
$M_j.$
Thus, the choice of
$k_j$
allows us to conclude that
$$ \begin{align*}2^{m_j}\leq\bigg| L_{k_j} \frac{(2j x_{[j]})^{m_j}}{M_j^{m_j}} \bigg|\leq 2(2j^2)^{m_j}\end{align*} $$
since
${1}/{j} \leq |x_{[j]}| \leq j$
. Now, let us study
$$ \begin{align*} L_{k_j} \left( \sum_{l=1}^{j-1} \frac{(2l x_{[l]})^{m_l}}{M_{l}^{m_l}} \right). \end{align*} $$
We obtain
$$ \begin{align} \bigg| L_{k_j} \bigg( \sum_{l=1}^{j-1} \frac{(2l x_{[l]})^{m_l}}{M_{l}^{m_l}} \bigg) \bigg| &= \bigg| \sum_{l=1}^{j-1} \frac{\unicode{x3bb}^{k_j m_l} -1}{\unicode{x3bb}^{m_l}-1} \frac{(2l x_{[l]})^{m_l}}{M_{l}^{m_l}} \bigg| \\ &=\bigg| \sum_{l=1}^{j-1} (\unicode{x3bb}^{k_j m_l} -1) (2l)^{m_l} x_{[l]}^{m_l} \bigg|\nonumber\\ &\leq \sum_{l=1}^{j-1} 2 (2l)^{m_l} j^{m_l} \nonumber\\ &\leq 2^{m_j} - (j+1)\nonumber \end{align} $$
if
, where the final inequality follows from condition (C2). Finally, let us consider
$$ \begin{align*} L_{k_j} \bigg( \sum_{l=j+1}^{\infty} \frac{(2l x_{[l]})^{m_l}}{M_{l}^{m_l}} \bigg). \end{align*} $$
Condition (C1) implies
${2l}/{M_l}<{1}/{ 2j}$
for any
$l>j.$
Therefore,
implies
$$ \begin{align} \bigg| L_{k_j} \bigg( \sum_{l=j+1}^{\infty} \bigg(\frac{2l}{M_l}\bigg)^{m_l}x_{[l]}^{m_l}\bigg) \bigg| &\leq\sum_{l=j+1}^{\infty} |1 + \unicode{x3bb}^{m_l} + \unicode{x3bb}^{2 m_l} + \cdots + \unicode{x3bb}^{(k_j-1) m_l}| \frac{1}{2^{m_l}} \\ &\leq k_j \sum_{l=j+1}^{\infty} \frac{1}{2^{m_l}}\nonumber\\ &\leq k_j \sum_{l=r_j}^{\infty} \frac{1}{2^l} \nonumber \\ &< 1\nonumber \end{align} $$
by conditions (C3) and (C5). In particular, by combining the previous estimates, we get
$$ \begin{align*}j= 2^{m_j} - ( 2^{m_j} - (j+1) ) -1 <|(L_{k_j} a)(x)| < 2(2j^2)^{m_j}+2^{m_j}-j \end{align*} $$
if
and
$|x_{[j]}| \geq 1/j$
.
The next lemma concludes the proof of Theorem 1.
Lemma 10. Let
$\unicode{x3bb} \in {\mathbb C}$
be a Cremer number and
$n \geq 1$
. Consider the function
$a(x)$
in equation (3) where
$(M_j)_{j \geq 1}$
and
$(m_j)_{j \geq 1}$
are provided by Lemma 7. Then the biholomorphism
$F(x,y)= (\unicode{x3bb} x, y+a(x))$
has finite orbits in any set of the form
$\mathbb {C}^{n} \times U,$
where U is a bounded open set in
$\mathbb {C}$
.
Proof. Let d be the diameter of
$U.$
Fix
Then there exists
$j \in {\mathbb N}$
such that
,
$x_{[j],0} \geq 1/j$
and
$j>d$
. Lemma 9 implies that
$F^{k_j} (x_0, y_0)$
does not belong to
${\mathbb C}^{n} \times U$
. Notice that by Remark 8 conditions (C1)–(C5) still hold if we replace
$\unicode{x3bb} $
by
$\unicode{x3bb} ^{-1}$
. Since
$F^{-1} (x,y) = (\unicode{x3bb} ^{-1} x, y - a(\unicode{x3bb} ^{-1} x))$
, we have
that is, the monomials of
$- a(\unicode{x3bb} ^{-1} x)$
are obtained by multiplying those of
$a(x)$
by complex numbers of modulus
$1.$
In particular, the proof of Lemma 9 is still valid for
$F^{-1}.$
One concludes that
$F^{-k_j}(x_0, y_0) \not \in {\mathbb C}^{n} \times U.$
Therefore, F has finite orbits in
$({\mathbb C}^{n} \setminus \{0\}) \times U$
. On the other hand, as
$x=0$
is a fixed-point curve of
$F,$
it is clear that F has finite orbits in
${\mathbb C}^{n} \times U.$
Theorem 5. Consider the hypotheses in Lemma 10. Then the local diffeomorphism
$F(x,y)=(\unicode{x3bb} x,y+a(x))$
is formally linearizable. In particular, F has a first integral of the form
$y + b(x),$
where
$b(x)$
is a divergent power series with
$b(0)=0.$
Specifically,
$y-y_0 + b(x)=0$
defines a (divergent) formal invariant hypersurface through the point
$(0,y_0)$
for every
$y_0\in \mathbb {C}$
.
Proof. The conjugacy equation
$$ \begin{align*} (x, y + b(x)) \circ (\unicode{x3bb} x, y +a (x)) \circ (x, y-b(x)) = (\unicode{x3bb} x, y) \end{align*} $$
is equivalent to
$$ \begin{align*} b(x) - b(\unicode{x3bb} x)= a(x).\end{align*} $$
Setting
$b(x)=\sum _{j\in \mathbb {N}^n} b_jx^j\ \mbox { and }\ a(x)=\sum _{j\in \mathbb {N}^n} a_jx^j,$
we see that
$b(x) - b(\unicode{x3bb} x)= a(x)$
can be expressed as
$$ \begin{align*}\sum_{j\in \mathbb{N}^n} (b_j -\unicode{x3bb}^{|j|} b_j-a_j)x^j=0.\end{align*} $$
Hence, the conjugacy equation has a solution
$$ \begin{align*}b(x)=\sum_{j\in \mathbb{N}^n} \frac{a_j}{1-\unicode{x3bb}^{|j|}} x^{j}.\end{align*} $$
Since y is a first integral of
$(x,y) \mapsto (\unicode{x3bb} x,y),$
the series
$y + b(x)$
is a first integral of
$F.$
Note that the series
$b(x)$
is divergent, otherwise F and
$(x,y) \mapsto (\unicode{x3bb} x,y)$
would be analytically conjugated, which is impossible, because F has finite orbits whereas
$(x,y) \mapsto (\unicode{x3bb} x,y)$
does not.
We want to understand the non-virtually unipotent diffeomorphisms
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
with finite orbits. First, we focus on the arithmetic properties of the non-root of unity eigenvalue. It is no coincidence that in our examples such an eigenvalue is well approximated by roots of unity.
Definition 7. A number
$\unicode{x3bb} \in \mathbb {C}$
is called a Bruno number if there is a sequence
$1<q_1<q_2<\ldots $
of integers such that
$$ \begin{align} |\unicode{x3bb}| =1\quad\mbox{and}\quad\sum_{k=1}^{\infty}\frac{1}{q_k}\log\frac{1}{\Omega_\unicode{x3bb}(q_{k+1})}<+\infty, \end{align} $$
where
$\Omega _\unicode{x3bb} (m) = \min _{2 \leq k \leq m} |\unicode{x3bb} ^{k} - \unicode{x3bb} | $
for all
$m\geq 2.$
Condition 8 is called the Bruno condition and it is equivalent to the following (see [Reference BryunoBry73]):
$$ \begin{align*} \sum_{k=1}^{\infty}\frac{1}{2^k}\log\frac{1}{\Omega_\unicode{x3bb}(2^{k+1})}<+\infty. \end{align*} $$
Given
$\unicode{x3bb} \in {\mathbb S}^1$
and
$l \in {\mathbb N}$
, we see that
$\Omega _{\unicode{x3bb} ^l}(m)\geq \Omega _{\unicode{x3bb} } ((m-1)l+1)$
for all
$m\geq 2.$
Thus we can adjust (8) to conclude that if
$\unicode{x3bb} $
is a Bruno number then so is
$\unicode{x3bb} ^{l}.$
Proposition 4. Consider
$F \in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
with
$D_0 F \not \in \mathrm { Diff}{}_{<\infty }({\mathbb C}^{2},0)$
. Let
$\unicode{x3bb} $
be the eigenvalue of
$D_0 F$
that is not a root of unity. Then
$\unicode{x3bb} $
is not a Bruno number.
Proof. Suppose, aiming a contradiction, that one of the eigenvalues of
$D_0 F$
is a Bruno number. By Theorem 3, up to replacing F with a non-trivial iterate
$F^k$
, we can suppose that
$\mathrm {spec} (D_0 F) = \{1, \unicode{x3bb} \}$
, where
$\unicode{x3bb} $
is a Bruno number.
Up to a linear change of coordinates, we can suppose
$(D_0 F)(x,y)=(\unicode{x3bb} x, y)$
. Note that the line
$y=0$
is invariant by
$D_0 F$
. Now, we apply a theorem of Pöschel that relates the invariant manifolds of
$D_0 F$
and F [Reference PöschelPös86]. In our context, it determines a sufficient condition for the existence of a smooth analytic curve
$\gamma $
, invariant by F, tangent to
$y=0$
at
$0$
and such that
$F_{|\gamma }$
is analytically conjugated to the rotation
$x \mapsto \unicode{x3bb} x$
. The Pöschel condition is
$$ \begin{align} \sum_{\nu \geq 0} 2^{-\nu} \log \omega^{-1} (2^{\nu +1}) < \infty, \end{align} $$
where we define
$$ \begin{align*} \omega (m) = \min_{2 \leq k \leq m} (|\unicode{x3bb}^{k} - \unicode{x3bb}|, |\unicode{x3bb}^{k}-1|).\end{align*} $$
Since
$\omega (m) \geq \Omega _\unicode{x3bb} (m+1)$
for
$m \geq 2$
, it follows that property (9) is a consequence of the Bruno condition. Thus, the intended
$\gamma $
exists and
$F_{|\gamma }$
is an irrational rotation, contradicting F being a finite-orbits germ.
Corollary 7. Let
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
. Consider a formal invariant curve
$\Gamma $
such that the multiplier of
$F_{|\Gamma }$
is a Bruno number. Then F is not a finite-orbits germ.
Proof. Assume, towards a contradiction, that F has finite orbits. Let
$\gamma (t)$
be a Puiseux parametrization of
$\Gamma $
. Since
$\Gamma $
is invariant, we have
$F (\gamma (t)) = (\gamma \circ h)(t)$
for some
$h \in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{},0)}$
. We denote the multiplier of
$F_{|\Gamma }$
by
$\mu $
; it satisfies
$\mu = h' (0)$
. We can suppose that
$1 \in \mathrm {spec}(D_0 F)$
up to replacing F with some non-trivial iterate
$F^{k}$
by Theorem 3. Note that the multiplier of
$F_{|\Gamma }^{k}$
is equal to
$\mu ^{k}$
. Since
$\mu ^{k}$
is a Bruno number, the hypothesis still holds for
$F^{k}$
and
$\Gamma $
. The tangent cone of
$\Gamma $
is a subspace of eigenvectors of
$D_0 F$
, associated to an eigenvalue that we denote by
$\unicode{x3bb} $
. Moreover, we have
$\mu ^{m} = \unicode{x3bb} $
, where m is the multiplicity of
$\Gamma $
. Since
$\mu $
is a Bruno number, so is
$\unicode{x3bb} $
. Proposition 4 implies that
$\unicode{x3bb} $
is not a Bruno number, providing a contradiction.
Next, we see that the diffeomorphisms provided by Theorem 1 are archetypic examples of finite-orbits diffeomorphisms
$F \in \mathrm {Diff}{}_{}({\mathbb C}^{2},0)$
such that
$D_0 F$
has no finite orbits. Indeed, the next result classifies the properties of such diffeomorphisms.
Proposition 5. Let
$F \in \mathrm {Diff}{}_{<\infty }({\mathbb C}^{2},0)$
with
$\mathrm {spec}(D_0 F)=\{1, \unicode{x3bb} \}$
where
$\unicode{x3bb} $
is not a root of unity. Then F satisfies the following properties:
-
•
$\unicode{x3bb} $
is not a Bruno number; -
•
$\mathrm {Fix} (F)$
is a smooth curve through the origin; -
• F is formally conjugated to
$(x,y) \mapsto (\unicode{x3bb} x, y)$
by a formal diffeomorphism that is transversally formal along
$\mathrm {Fix}(F)$
; -
• there exists a divergent smooth invariant curve through any point
$p \in \mathrm {Fix}(F)$
.
Proof. The eigenvalue
$\unicode{x3bb} $
is a non-Bruno number by Proposition 4. Fix a sufficiently small domain of definition
$B_{\rho } (0)$
. Let C be the connected component of the origin of
$\mathrm {Per}(F)$
(cf. equation (1)). It is complex analytic, has positive dimension and is contained in
$\mathrm {Fix}(F^{m})$
for some
$m \in {\mathbb N}$
by Theorem 4. The dimension of the germ of C at the origin is less than
$2$
, since otherwise the germ of
$F^{m}$
at
$0$
is the identity map, contradicting
$\unicode{x3bb} \not \in e^{2 \pi i {\mathbb Q}}$
. Therefore, the germ of C at
$0$
is an analytic curve
$\gamma $
. Moreover,
$\gamma $
is irreducible and smooth, since otherwise
$F^{m}$
is tangent to the identity by Lemma 2. Since
$F_{|\gamma }$
is a local biholomorphism in one variable with finite orbits, it has finite order. Therefore, its multiplier at
$0$
is a root of unity and thus necessarily equal to
$1$
. Since the unique periodic tangent to the identity local diffeomorphism is the identity map, we deduce
$\gamma \subset \mathrm {Fix}(F)$
. It is clear that the germ of
$\mathrm {Fix}(F)$
at
$0$
is contained in C and hence the germs of
$\mathrm {Fix}(F)$
and
$\gamma $
at
$0$
coincide.
Up to a change of coordinates in a neighborhood of the origin, we can assume
$\mathrm {Fix}(F)= \{x=0\}$
. As a consequence
$1 \in \mathrm {spec} (D_{(0,y)} F)$
for any y in a neighborhood of
$0$
. We denote
$\mathrm {spec} (D_{(0,y)} F) = \{ 1, \unicode{x3bb} (y) \}$
. The function
$\unicode{x3bb} (y)$
is constant equal to
$\unicode{x3bb} $
by the proof of Lemma 5. We obtain that F is of the form
$$ \begin{align*} F(x,y) = \bigg( \unicode{x3bb} x + \sum_{j=2}^{\infty} a_{j}(y) x^{j}, y + \sum_{j=1}^{\infty} b_{j}(y) x^{j} \bigg), \end{align*} $$
where
$a_{j+1}, b_{j}$
are defined in a common open neighborhood U of
$0$
in
${\mathbb C}$
for any
$j \in {\mathbb N}$
. We want to conjugate F with
$D_0 F$
. In order to do so, we consider sequences
$(G_{2,j})_{j \geq 1}, (G_{1,j+1})_{j \geq 1}$
of diffeomorphisms of the form
$$ \begin{align*} G_{1,j+1}(x,y)= (x + c_{j+1}(y) x^{j+1}, y) \quad\mathrm{and}\quad G_{2,j}(x,y)= (x, y + d_{j} (y) x^{j}), \end{align*} $$
where
$d_{j}, c_{j+1} \in {\mathcal O}(U)$
for any
$j \in {\mathbb N}$
. We define
$F_{1,1} =F$
,
$F_{2,j} = G_{2,j}^{-1} \circ F_{1,j} \circ G_{2,j}$
and
$F_{1,j+1} = G_{1,j+1}^{-1} \circ F_{2,j} \circ G_{1,j+1}$
for
$j \in {\mathbb N}$
. We want
$F_{2,j}$
and
$F_{1,j+1}$
to be of the form
$$ \begin{align*} F_{2,j} (x,y)&= (\unicode{x3bb} x + O(x^{j+1}), y + O(x^{j+1})),\\ F_{1,j+1} (x,y) &= (\unicode{x3bb} x + O(x^{j+2}), y + O(x^{j+1})) \end{align*} $$
for any
$j \in {\mathbb N}$
. Indeed, if
$\alpha _{j+1} (y)$
is the coefficient of
$x^{j+1}$
in
$x \circ F_{2,j}$
, it suffices to define
$c_{j+1}(y)= \alpha _{j+1}(y)/(\unicode{x3bb} ^{j+1} - \unicode{x3bb} )$
for
$j \in {\mathbb N}$
. Analogously, if
$\beta _{j}(y)$
is the coefficient of
$x^{j}$
in
$y \circ F_{1,j}$
, we have
$d_{j}(y) = \beta _{j}(y)/(\unicode{x3bb} ^{j}-1)$
for
$j \in {\mathbb N}$
. The diffeomorphism
$$ \begin{align*} H_{j} : = G_{2,1} \circ G_{1,2} \circ G_{2,2} \circ G_{1,3} \circ \cdots \circ G_{2,j-1} \circ G_{1,j} \end{align*} $$
conjugates F with
$F_{1,j}$
for
$j \geq 2$
. By construction, it converges in the
$(x)$
-adic topology to some
$H \in \widehat {\mathrm {Diff}}{{\,}_{}({\mathbb C}^{2},0)}$
that is transversally formal along
$x=0$
and satisfies
$H^{-1} \circ F \circ H = D_0 F$
.
Note that
$y \circ D_0 F \equiv y$
implies
$(y \circ H^{-1}) \circ F \equiv y \circ H^{-1}$
. Since
$y \circ H^{-1}$
is transversally formal along
$x=0$
, there exists a formal invariant curve
$\gamma _{y}$
through
$(0,y)$
that is transverse to
$\mathrm {Fix}(F)$
, for any
$y \in U$
. We claim that
$\gamma _{y}$
is divergent for any
$y \in U$
. Otherwise, there exists
$y_0 \in U$
such that
$\gamma _{y_0}$
is an analytic curve, and since the multiplier of
$F_{|\gamma _{y_0}}$
at
$(0,y_0)$
is equal to
$\unicode{x3bb} $
, the diffeomorphism
$F_{|\gamma _{y_0}}$
is non-periodic. This contradicts the one-dimensional diffeomorphism
$F_{|\gamma _{y_0}}$
having finite orbits.
