1. Introduction
For aerodynamic flows, a passive flow control device (flap) inspired by self-actuating covert feathers of birds has been shown to improve lift at post-stall angles of attack (Bramesfeld & Maughmer Reference Bramesfeld and Maughmer2002; Duan & Wissa Reference Duan and Wissa2021). In particular, when the flap is mounted via a torsional spring, further aerodynamic benefits can be obtained compared with a free (zero hinge stiffness) or static configuration (Rosti, Omidyeganeh & Pinelli Reference Rosti, Omidyeganeh and Pinelli2018). These added benefits arise from rich fluid–structure interaction (FSI) between the flap and vortex dynamics (Nair & Goza Reference Nair and Goza2022a). This outcome teases a question: Could additional lift enhancement be achieved if the flap motion was controlled to yield more favourable flapping amplitudes and phase relative to key flow processes?
To address this question, we propose a hybrid active–passive flow control method to adaptively tune the flap stiffness. That is, the flap dynamics are passively induced by the FSI, according to the actively modulated hinge stiffness. This hybrid approach could incur less expense as compared to a fully active control method where the flap deflection is controlled using a rotary actuator. Our focus is on the design of a control algorithm that can actuate the hinge stiffness to provide aerodynamic benefits without accounting for how these stiffness changes are implemented, and on explaining the physical mechanisms that drive these benefits. We note, however, that there are various ways of achieving stiffness modulation in practice via continuous variable-stiffness actuators (VSAs) (Wolf et al. Reference Wolf2015), used extensively in robotics (Ham et al. Reference Ham, Sugar, Vanderborght, Hollander and Lefeber2009), wing morphing (Sun et al. Reference Sun, Guan, Liu and Leng2016), etc. A discrete VSA restricts the stiffness to vary discretely across fixed stiffness levels, but it weighs less and requires lower power (Diller, Majidi & Collins Reference Diller, Majidi and Collins2016).
Historically, linear approximations of fundamentally nonlinear systems are used to design optimal controllers (Kim & Bewley Reference Kim and Bewley2007). While these linear techniques have been effective in stabilizing separated flows at low Reynolds number, ![]() $Re\sim O(10^2)$, where the base state has a large basin of attraction, its effectiveness is compromised at larger
$Re\sim O(10^2)$, where the base state has a large basin of attraction, its effectiveness is compromised at larger ![]() $Re$ (Ahuja & Rowley Reference Ahuja and Rowley2010). These challenges are exacerbated by the nonlinear FSI coupling between the flap and vortex shedding of interest here. Model predictive control (MPC) uses nonlinear models to make real-time predictions of the future states to guide the control actuations. The need for fast real-time predictions necessitates the use of reduced-order models where the control optimization problem is solved using a reduced system of equations (Peitz, Otto & Rowley Reference Peitz, Otto and Rowley2020). Machine learning in fluid mechanics has provided further avenues of deriving more robust reduced nonlinear models to be used with MPC (Baumeister, Brunton & Kutz Reference Baumeister, Brunton and Kutz2018; Mohan & Gaitonde Reference Mohan and Gaitonde2018; Bieker et al. Reference Bieker, Peitz, Brunton, Kutz and Dellnitz2020). However, these reduced-order modelling efforts remain an area of open investigation, and would be challenging for the strongly coupled flow–airfoil–flap FSI system. We therefore utilize a model-free, reinforcement learning (RL) framework to develop our controller. RL has recently gained attention in fluid mechanics (Garnier et al. Reference Garnier, Viquerat, Rabault, Larcher, Kuhnle and Hachem2021), and is used to learn an effective control strategy by trial and error via stochastic agent–environment interactions (Sutton & Barto Reference Sutton and Barto2018). Unlike MPC, the control optimization problem is completely solved offline, thereby not requiring real-time predictions. RL has been successfully applied to attain drag reduction (Rabault et al. Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019; Fan et al. Reference Fan, Yang, Wang, Triantafyllou and Karniadakis2020; Paris, Beneddine & Dandois Reference Paris, Beneddine and Dandois2021; Li & Zhang Reference Li and Zhang2022), for shape optimization (Viquerat et al. Reference Viquerat, Rabault, Kuhnle, Ghraieb, Larcher and Hachem2021) and understanding swimming patterns (Verma, Novati & Koumoutsakos Reference Verma, Novati and Koumoutsakos2018; Zhu et al. Reference Zhu, Tian, Young, Liao and Lai2021).
$Re$ (Ahuja & Rowley Reference Ahuja and Rowley2010). These challenges are exacerbated by the nonlinear FSI coupling between the flap and vortex shedding of interest here. Model predictive control (MPC) uses nonlinear models to make real-time predictions of the future states to guide the control actuations. The need for fast real-time predictions necessitates the use of reduced-order models where the control optimization problem is solved using a reduced system of equations (Peitz, Otto & Rowley Reference Peitz, Otto and Rowley2020). Machine learning in fluid mechanics has provided further avenues of deriving more robust reduced nonlinear models to be used with MPC (Baumeister, Brunton & Kutz Reference Baumeister, Brunton and Kutz2018; Mohan & Gaitonde Reference Mohan and Gaitonde2018; Bieker et al. Reference Bieker, Peitz, Brunton, Kutz and Dellnitz2020). However, these reduced-order modelling efforts remain an area of open investigation, and would be challenging for the strongly coupled flow–airfoil–flap FSI system. We therefore utilize a model-free, reinforcement learning (RL) framework to develop our controller. RL has recently gained attention in fluid mechanics (Garnier et al. Reference Garnier, Viquerat, Rabault, Larcher, Kuhnle and Hachem2021), and is used to learn an effective control strategy by trial and error via stochastic agent–environment interactions (Sutton & Barto Reference Sutton and Barto2018). Unlike MPC, the control optimization problem is completely solved offline, thereby not requiring real-time predictions. RL has been successfully applied to attain drag reduction (Rabault et al. Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019; Fan et al. Reference Fan, Yang, Wang, Triantafyllou and Karniadakis2020; Paris, Beneddine & Dandois Reference Paris, Beneddine and Dandois2021; Li & Zhang Reference Li and Zhang2022), for shape optimization (Viquerat et al. Reference Viquerat, Rabault, Kuhnle, Ghraieb, Larcher and Hachem2021) and understanding swimming patterns (Verma, Novati & Koumoutsakos Reference Verma, Novati and Koumoutsakos2018; Zhu et al. Reference Zhu, Tian, Young, Liao and Lai2021).
In this work, we develop a closed-loop feedback controller using deep RL for our proposed hybrid control approach consisting of a tunable-stiffness covert-inspired flap. We train and test this controller using high-fidelity fully coupled simulations of the airfoil–flap–flow dynamics, and demonstrate the effectiveness of the variable-stiffness control paradigm compared with the highest-performing passive (single-stiffness) case. We explain the lift-enhancement mechanisms by relating the large-amplitude flap dynamics to those of the vortex formation and shedding processes around the airfoil.
2. Methodology
2.1. Hybrid active–passive control
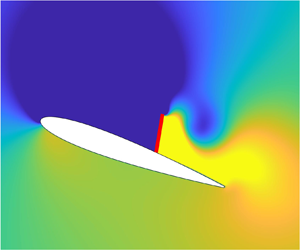
The problem set-up is shown in figure 1, which consists of a NACA0012 airfoil of chord ![]() $c$ at an angle of attack of
$c$ at an angle of attack of ![]() $20^\circ$ and
$20^\circ$ and ![]() ${Re} = 1000$, where significant flow separation and vortex shedding occur. A flap of length
${Re} = 1000$, where significant flow separation and vortex shedding occur. A flap of length ![]() $0.2c$ is hinged on the upper surface of the airfoil via a torsional spring with stiffness
$0.2c$ is hinged on the upper surface of the airfoil via a torsional spring with stiffness ![]() ${k_{{\beta }}}$, where
${k_{{\beta }}}$, where ![]() ${\beta }$ denotes the deflection of the flap from the airfoil surface. The FSI problem considered here is two-dimensional (2-D), similar to most studies on covert-inspired flaps (Bramesfeld & Maughmer Reference Bramesfeld and Maughmer2002; Duan & Wissa Reference Duan and Wissa2021) and applicable to high-aspect-ratio, bio-inspired flows largely dominated by 2-D effects (Taira & Colonius Reference Taira and Colonius2009; Zhang et al. Reference Zhang, Hayostek, Amitay, He, Theofilis and Taira2020). In the passive control approach (Nair & Goza Reference Nair and Goza2022a),
${\beta }$ denotes the deflection of the flap from the airfoil surface. The FSI problem considered here is two-dimensional (2-D), similar to most studies on covert-inspired flaps (Bramesfeld & Maughmer Reference Bramesfeld and Maughmer2002; Duan & Wissa Reference Duan and Wissa2021) and applicable to high-aspect-ratio, bio-inspired flows largely dominated by 2-D effects (Taira & Colonius Reference Taira and Colonius2009; Zhang et al. Reference Zhang, Hayostek, Amitay, He, Theofilis and Taira2020). In the passive control approach (Nair & Goza Reference Nair and Goza2022a), ![]() ${k_{{\beta }}}$ was fixed and maximum lift was attained at
${k_{{\beta }}}$ was fixed and maximum lift was attained at ![]() ${k_{{\beta }}}=0.015$. In our hybrid active–passive control, the stiffness is a function of time,
${k_{{\beta }}}=0.015$. In our hybrid active–passive control, the stiffness is a function of time, ![]() ${k_{{\beta }}}(t)$, determined by an RL-trained closed-loop feedback controller described in § 2.2. While the stiffness variation is allowed to take any functional form, it is restricted to vary in
${k_{{\beta }}}(t)$, determined by an RL-trained closed-loop feedback controller described in § 2.2. While the stiffness variation is allowed to take any functional form, it is restricted to vary in ![]() ${k_{{\beta }}}(t) \in [10^{-4}, 10^{-1}]$, similar to the range of stiffness values considered in the passive control study. The mass and location of the flap are fixed at
${k_{{\beta }}}(t) \in [10^{-4}, 10^{-1}]$, similar to the range of stiffness values considered in the passive control study. The mass and location of the flap are fixed at ![]() ${m_{{\beta }}}=0.01875$ and
${m_{{\beta }}}=0.01875$ and ![]() ${60\,\%}$ of the chord length from the leading edge, chosen here since they induced the maximal lift benefits in the passive (single-stiffness) configuration (cf. figure 5(e–h) for vorticity contours at four time instants in one periodic lift cycle for this highest-lift single-stiffness case).
${60\,\%}$ of the chord length from the leading edge, chosen here since they induced the maximal lift benefits in the passive (single-stiffness) configuration (cf. figure 5(e–h) for vorticity contours at four time instants in one periodic lift cycle for this highest-lift single-stiffness case).

Figure 1. Schematic of the problem set-up and RL framework.
2.2. Reinforcement learning (RL)
A schematic of the RL framework is shown in figure 1, where an agent (with a controller) interacts with an environment. At each time step, ![]() ${m}$, the agent observes the current state of the environment,
${m}$, the agent observes the current state of the environment, ![]() ${\boldsymbol {s}_{{m}}} \in {\mathbb {R}}^{{N_{s}}}$ (where
${\boldsymbol {s}_{{m}}} \in {\mathbb {R}}^{{N_{s}}}$ (where ![]() ${N_{s}}$ is the number of states), implements an action,
${N_{s}}$ is the number of states), implements an action, ![]() ${a_{{m}}} \in {\mathbb {R}}$, and receives a reward,
${a_{{m}}} \in {\mathbb {R}}$, and receives a reward, ![]() ${r_{{m}}} \in {\mathbb {R}}$. The environment then advances to a new state,
${r_{{m}}} \in {\mathbb {R}}$. The environment then advances to a new state, ![]() ${\boldsymbol {s}_{{m}+1}}$. This process is continued for
${\boldsymbol {s}_{{m}+1}}$. This process is continued for ![]() ${M_{\tau }}$ time steps and the resulting sequence forms a trajectory,
${M_{\tau }}$ time steps and the resulting sequence forms a trajectory, ![]() ${\tau }= \{{\boldsymbol {s}_{0}},{a_{0}},{r_{0}},\ldots,{\boldsymbol {s}_{{M_{\tau }}}}, {a_{{M_{\tau }}}},{r_{{M_{\tau }}}}\}$. The actions chosen by the agent to generate this trajectory are determined by the stochastic policy of the controller,
${\tau }= \{{\boldsymbol {s}_{0}},{a_{0}},{r_{0}},\ldots,{\boldsymbol {s}_{{M_{\tau }}}}, {a_{{M_{\tau }}}},{r_{{M_{\tau }}}}\}$. The actions chosen by the agent to generate this trajectory are determined by the stochastic policy of the controller, ![]() ${{\rm \pi} _{{\boldsymbol {\theta }}}}({a_{{m}}}|{\boldsymbol {s}_{{m}}})$, parametrized by weights
${{\rm \pi} _{{\boldsymbol {\theta }}}}({a_{{m}}}|{\boldsymbol {s}_{{m}}})$, parametrized by weights ![]() ${\boldsymbol {\theta }}$. This policy outputs a probability distribution of actions, from which
${\boldsymbol {\theta }}$. This policy outputs a probability distribution of actions, from which ![]() ${a_{{m}}}$ is sampled,
${a_{{m}}}$ is sampled, ![]() ${a_{{m}}} \sim {{\rm \pi} _{{\boldsymbol {\theta }}}}({a_{{m}}}|{\boldsymbol {s}_{{m}}})$, as shown in figure 1.
${a_{{m}}} \sim {{\rm \pi} _{{\boldsymbol {\theta }}}}({a_{{m}}}|{\boldsymbol {s}_{{m}}})$, as shown in figure 1.
In policy-based deep RL methods, a neural network is used as a nonlinear function approximator for the policy, as shown in figure 1. Accordingly, ![]() ${\boldsymbol {\theta }}$ corresponds to the weights of the neural network. The goal in RL is to learn an optimal control policy that maximizes an objective function
${\boldsymbol {\theta }}$ corresponds to the weights of the neural network. The goal in RL is to learn an optimal control policy that maximizes an objective function ![]() ${J}(\,{\cdot }\,)$, defined as the expected sum of rewards as
${J}(\,{\cdot }\,)$, defined as the expected sum of rewards as
 \begin{equation} {J}({\boldsymbol{\theta}}) = {\mathbb{E}}_{{\tau} \sim {{\rm \pi}_{{\boldsymbol{\theta}}}}} \left[\sum_{m=0}^{{M_{\tau}}} {r_{{m}}}\right]. \end{equation}
\begin{equation} {J}({\boldsymbol{\theta}}) = {\mathbb{E}}_{{\tau} \sim {{\rm \pi}_{{\boldsymbol{\theta}}}}} \left[\sum_{m=0}^{{M_{\tau}}} {r_{{m}}}\right]. \end{equation}
Here, the expectation is performed over ![]() ${N_{\tau }}$ different trajectories sampled using the policy,
${N_{\tau }}$ different trajectories sampled using the policy, ![]() ${\tau } \sim {{\rm \pi} _{{\boldsymbol {\theta }}}}$. The maximization problem is then solved by gradient ascent, where an approximate gradient of the objective function,
${\tau } \sim {{\rm \pi} _{{\boldsymbol {\theta }}}}$. The maximization problem is then solved by gradient ascent, where an approximate gradient of the objective function, ![]() $\nabla _{{\boldsymbol {\theta }}} {J}({\boldsymbol {\theta }})$, is obtained from the policy gradient theorem (Nota & Thomas Reference Nota and Thomas2019).
$\nabla _{{\boldsymbol {\theta }}} {J}({\boldsymbol {\theta }})$, is obtained from the policy gradient theorem (Nota & Thomas Reference Nota and Thomas2019).
In this work, we use the PPO algorithm (Schulman et al. Reference Schulman, Wolski, Dhariwal, Radford and Klimov2017) for computing the gradient, which is a policy-based RL method suitable for continuous control problems, as opposed to ![]() $Q$-learning methods for discrete problems (Sutton & Barto Reference Sutton and Barto2018). PPO has been used successfully to develop RL controllers for fluid flows (Rabault et al. Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019), and is chosen here among other policy-based methods due to its relative simplicity in implementation, better sample efficiency and ease of hyperparameter tuning.
$Q$-learning methods for discrete problems (Sutton & Barto Reference Sutton and Barto2018). PPO has been used successfully to develop RL controllers for fluid flows (Rabault et al. Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019), and is chosen here among other policy-based methods due to its relative simplicity in implementation, better sample efficiency and ease of hyperparameter tuning.
In our hybrid control problem, the environment is the strongly coupled FSI solver of Nair & Goza (Reference Nair and Goza2022b), where the incompressible Navier–Stokes equation for the fluid coupled with Newton's equation of motion for the flap are solved numerically. The state provided as input to the controller are sensor measurements consisting of flow vorticity in the wake, ![]() ${\boldsymbol {\omega }}_{m}$, and flap deflection,
${\boldsymbol {\omega }}_{m}$, and flap deflection, ![]() ${\beta }_{m}$. The action is the time-varying stiffness,
${\beta }_{m}$. The action is the time-varying stiffness, ![]() ${a_{{m}}} = {{k_{{\beta }}}}_{{m}} \in {\mathbb {R}}^+$. Similar to Rabault et al. (Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019), when advancing a single control time step from
${a_{{m}}} = {{k_{{\beta }}}}_{{m}} \in {\mathbb {R}}^+$. Similar to Rabault et al. (Reference Rabault, Kuchta, Jensen, Réglade and Cerardi2019), when advancing a single control time step from ![]() ${m}$ to
${m}$ to ![]() ${m}+1$, the flow–airfoil–flap system is simulated for
${m}+1$, the flow–airfoil–flap system is simulated for ![]() ${N_{t}}$ numerical time steps of the FSI solver. In this duration, the chosen value of the stiffness is kept constant. The reason for introducing these two time scales – control and numerical – is to allow the FSI system to meaningfully respond to the applied stiffness and achieve faster learning.
${N_{t}}$ numerical time steps of the FSI solver. In this duration, the chosen value of the stiffness is kept constant. The reason for introducing these two time scales – control and numerical – is to allow the FSI system to meaningfully respond to the applied stiffness and achieve faster learning.
The reward for the lift maximization problem of our hybrid control approach is
The first term is the mean lift coefficient of the airfoil, ![]() ${{\bar{C}_l}}_m$, evaluated over the
${{\bar{C}_l}}_m$, evaluated over the ![]() ${N_{t}}$ numerical time steps. The second term, where
${N_{t}}$ numerical time steps. The second term, where ![]() ${p_1}>0$ and
${p_1}>0$ and ![]() ${p_2} \gg 1$ are constants whose values are given in § 3, is a physics-based penalty term that provides an exponentially growing negative contribution to the reward if the flap remains undeployed for several consecutive control time steps (intuitively, one wishes to avoid periods of prolonged zero deployment angle). Accordingly,
${p_2} \gg 1$ are constants whose values are given in § 3, is a physics-based penalty term that provides an exponentially growing negative contribution to the reward if the flap remains undeployed for several consecutive control time steps (intuitively, one wishes to avoid periods of prolonged zero deployment angle). Accordingly, ![]() ${u}$ denotes the current count of consecutive control time steps that the flap has remained undeployed and
${u}$ denotes the current count of consecutive control time steps that the flap has remained undeployed and ![]() ${u_{max}}$ is the maximum number of consecutive time steps that the flap may remain undeployed. The flap is deemed undeployed if
${u_{max}}$ is the maximum number of consecutive time steps that the flap may remain undeployed. The flap is deemed undeployed if ![]() ${\beta}_{{m}} < {\beta}_{min}$.
${\beta}_{{m}} < {\beta}_{min}$.
The reward (2.2) can be augmented with additional penalty terms to achieve goals of fluctuation minimization, drag reduction or improving aerodynamic efficiency. For minimizing lift fluctuations about the mean, the penalty term could take the form of the time derivative of lift, ![]() $-\text {d}{\bar{C}_{l}}_m/\text {d}t^2$, the difference between the instantaneous lift and target lift,
$-\text {d}{\bar{C}_{l}}_m/\text {d}t^2$, the difference between the instantaneous lift and target lift, ![]() $-({\bar{C}_{l}}_m -{C_{l}}_{target})^2$, or the running average of lift evaluated at previous time steps,
$-({\bar{C}_{l}}_m -{C_{l}}_{target})^2$, or the running average of lift evaluated at previous time steps, ![]() $-({\bar{C}_{l}}_m - {\bar{C}_{l}}_{run})^2$. For drag minimization or improving aerodynamic efficiency, the airfoil drag,
$-({\bar{C}_{l}}_m - {\bar{C}_{l}}_{run})^2$. For drag minimization or improving aerodynamic efficiency, the airfoil drag, ![]() $-{\bar{C}_{d}}_m^2$, could be incorporated into the reward. In this work, we do not consider these additional penalty terms because the hybrid control approach is inspired from covert feathers in birds, which are used as high-lift devices in stalled large-angle-of-attack scenarios. The primary aerodynamic aim in this setting is to attain increased lift, at the potential cost of drag, efficiency or fluctuations (Rosti et al. Reference Rosti, Omidyeganeh and Pinelli2018; Nair & Goza Reference Nair and Goza2022a).
$-{\bar{C}_{d}}_m^2$, could be incorporated into the reward. In this work, we do not consider these additional penalty terms because the hybrid control approach is inspired from covert feathers in birds, which are used as high-lift devices in stalled large-angle-of-attack scenarios. The primary aerodynamic aim in this setting is to attain increased lift, at the potential cost of drag, efficiency or fluctuations (Rosti et al. Reference Rosti, Omidyeganeh and Pinelli2018; Nair & Goza Reference Nair and Goza2022a).
The RL algorithm is proceeded iteratively as shown in . Each iteration consists of sampling trajectories spanning a total of ![]() ${M_i}$ control time steps (lines 4 and 5) and using the collected data to optimize
${M_i}$ control time steps (lines 4 and 5) and using the collected data to optimize ![]() ${\boldsymbol {\theta }}$ (line 19). We also define an episode as either the full set of
${\boldsymbol {\theta }}$ (line 19). We also define an episode as either the full set of ![]() ${M_i}$ time steps or, in the case where the parameters yield an undeployed flap, the time steps until
${M_i}$ time steps or, in the case where the parameters yield an undeployed flap, the time steps until ![]() ${u}={u_{max}}$. Note that an episode and iteration coincide only if an episode is not terminated early. The state is only reset after an episode terminates (line 14), which could occur within an iteration if the episode terminates early (line 13).
${u}={u_{max}}$. Note that an episode and iteration coincide only if an episode is not terminated early. The state is only reset after an episode terminates (line 14), which could occur within an iteration if the episode terminates early (line 13).
Algorithm 1 The PPO RL algorithm applied to hybrid control

We also use a modified strategy to update ![]() ${\boldsymbol {\theta }}$ in a given iteration. In policy-based methods, the weights update step is performed after trajectory sampling. Generally, in one iteration, trajectories are collected only once. This implies that (a) typically the weights are updated once in one training iteration and (b) the length of the trajectory is equal to the iteration length,
${\boldsymbol {\theta }}$ in a given iteration. In policy-based methods, the weights update step is performed after trajectory sampling. Generally, in one iteration, trajectories are collected only once. This implies that (a) typically the weights are updated once in one training iteration and (b) the length of the trajectory is equal to the iteration length, ![]() ${M_{\tau }} = {M_i}$. However, in our work, we perform
${M_{\tau }} = {M_i}$. However, in our work, we perform ![]() ${k}>1$ number of weight updates in a single iteration by sampling
${k}>1$ number of weight updates in a single iteration by sampling ![]() ${k}$ trajectories each of length
${k}$ trajectories each of length ![]() ${M_{\tau }} = {M_i}/ {k}$. This procedure is found to exhibit faster learning since the frequent weight updates sequentially cater to optimizing shorter temporal windows of the long-time horizon. We therefore refer to this procedure as the long–short-term training strategy and demonstrate its effectiveness in § 3. As shown in Algorithm 1, each iteration is divided into
${M_{\tau }} = {M_i}/ {k}$. This procedure is found to exhibit faster learning since the frequent weight updates sequentially cater to optimizing shorter temporal windows of the long-time horizon. We therefore refer to this procedure as the long–short-term training strategy and demonstrate its effectiveness in § 3. As shown in Algorithm 1, each iteration is divided into ![]() ${k}$ optimization windows (line 4) and
${k}$ optimization windows (line 4) and ![]() ${\boldsymbol {\theta }}$ is updated at the end of each window (line 19). Finally, for computing more accurate estimates of the expected values used in (2.1) and for evaluating gradients, the
${\boldsymbol {\theta }}$ is updated at the end of each window (line 19). Finally, for computing more accurate estimates of the expected values used in (2.1) and for evaluating gradients, the ![]() ${m}$th time advancement (line 5) is performed
${m}$th time advancement (line 5) is performed ![]() ${N_{\tau }}$ times independently (line 6) (Schulman et al. Reference Schulman, Wolski, Dhariwal, Radford and Klimov2017). For accelerated training, this set of
${N_{\tau }}$ times independently (line 6) (Schulman et al. Reference Schulman, Wolski, Dhariwal, Radford and Klimov2017). For accelerated training, this set of ![]() ${N_{\tau }}$ trajectories is sampled in parallel (Rabault & Kuhnle Reference Rabault and Kuhnle2019; Pawar & Maulik Reference Pawar and Maulik2021).
${N_{\tau }}$ trajectories is sampled in parallel (Rabault & Kuhnle Reference Rabault and Kuhnle2019; Pawar & Maulik Reference Pawar and Maulik2021).
3. Results
3.1. RL and FSI parameters
The parameters of the FSI environment are the same as in Nair & Goza (Reference Nair and Goza2022b), which contains the numerical convergence details. The spatial grid and time-step sizes are ![]() ${\rm \Delta} x/{c}=0.00349$ and
${\rm \Delta} x/{c}=0.00349$ and ![]() ${\rm \Delta} t/({c}/{U_{\infty }}) = 0.0004375$, respectively. For the multi-domain approach for far-field boundary conditions, five grids of increasing coarseness are used, where the finest and coarsest grids are
${\rm \Delta} t/({c}/{U_{\infty }}) = 0.0004375$, respectively. For the multi-domain approach for far-field boundary conditions, five grids of increasing coarseness are used, where the finest and coarsest grids are ![]() $[-0.5,2.5]{c} \times [-1.5, 1.5]{c}$ and
$[-0.5,2.5]{c} \times [-1.5, 1.5]{c}$ and ![]() $[-23,25]{c} \times [-24, 24]{c}$, respectively. The airfoil leading edge is located at the origin. For the subdomain approach, a rectangular subdomain that bounds the physical limits of flap displacements,
$[-23,25]{c} \times [-24, 24]{c}$, respectively. The airfoil leading edge is located at the origin. For the subdomain approach, a rectangular subdomain that bounds the physical limits of flap displacements, ![]() $[0.23,0.7] c\times [-0.24,0.1] c$, is utilized. The FSI solver is parallelized and simulated across six processors.
$[0.23,0.7] c\times [-0.24,0.1] c$, is utilized. The FSI solver is parallelized and simulated across six processors.
For the states, ![]() ${N_{s}} = 65$ sensor measurements are used, which measure vorticity at
${N_{s}} = 65$ sensor measurements are used, which measure vorticity at ![]() $64$ locations distributed evenly across
$64$ locations distributed evenly across ![]() $[1,2.4] c\times [-0.6,0.1] c$ and flap deflection as denoted by the red markers in figure 1. To ensure unbiased stiffness sampling across
$[1,2.4] c\times [-0.6,0.1] c$ and flap deflection as denoted by the red markers in figure 1. To ensure unbiased stiffness sampling across ![]() $[10^{-4}, 10^{-1}]$, a transformation between stiffness and action is introduced:
$[10^{-4}, 10^{-1}]$, a transformation between stiffness and action is introduced: ![]() ${{k_{{\beta }}}}_{{m}} = 10^{{a_{{m}}}}$. Accordingly,
${{k_{{\beta }}}}_{{m}} = 10^{{a_{{m}}}}$. Accordingly, ![]() ${a_{{m}}}$ is sampled from a normal distribution,
${a_{{m}}}$ is sampled from a normal distribution, ![]() $\mathcal {N}({a_{{m}}},{\sigma })$ in the range
$\mathcal {N}({a_{{m}}},{\sigma })$ in the range ![]() $[-4, -1]$, so that
$[-4, -1]$, so that ![]() ${{k_{{\beta }}}}_{{m}}$ is sampled from a log-normal distribution. The neural network consists of fully connected layers with two hidden layers. The size of each hidden layer is
${{k_{{\beta }}}}_{{m}}$ is sampled from a log-normal distribution. The neural network consists of fully connected layers with two hidden layers. The size of each hidden layer is ![]() $64$ and the hyperbolic tangent (tanh) function is used for nonlinear activations. The parameters in the reward function (2.2) are
$64$ and the hyperbolic tangent (tanh) function is used for nonlinear activations. The parameters in the reward function (2.2) are ![]() ${p_1}=0.845$,
${p_1}=0.845$, ![]() ${p_2}=10\ 000$,
${p_2}=10\ 000$, ![]() ${u_{max}}=20$ and
${u_{max}}=20$ and ![]() ${\beta }_{min}=5^\circ$.
${\beta }_{min}=5^\circ$.
The initial state for initializing every episode corresponds to the limit cycle oscillation solution obtained at the end of a simulation with a constant ![]() ${k_{{\beta }}}=0.015$ spanning
${k_{{\beta }}}=0.015$ spanning ![]() $40$ convective time units (
$40$ convective time units (![]() ${t}=0$ in this work denotes the instant at the end of this simulation). In advancing one control time step,
${t}=0$ in this work denotes the instant at the end of this simulation). In advancing one control time step, ![]() ${N_{t}}=195$ numerical time steps of the FSI solver are performed, or approximately
${N_{t}}=195$ numerical time steps of the FSI solver are performed, or approximately ![]() $0.085$ convective time units. That is, the control actuation is provided every
$0.085$ convective time units. That is, the control actuation is provided every ![]() $5\,\%$ of the vortex-shedding cycle. The various PPO-related parameters are the discount factor
$5\,\%$ of the vortex-shedding cycle. The various PPO-related parameters are the discount factor ![]() ${\gamma }=0.9$, learning rate
${\gamma }=0.9$, learning rate ![]() $\alpha =0.0003$,
$\alpha =0.0003$, ![]() ${n_{e}}=10$ epochs and clipping fraction
${n_{e}}=10$ epochs and clipping fraction ![]() ${\epsilon }=0.2$. Refer to Schulman et al. (Reference Schulman, Wolski, Dhariwal, Radford and Klimov2017) for the details of these parameters. The
${\epsilon }=0.2$. Refer to Schulman et al. (Reference Schulman, Wolski, Dhariwal, Radford and Klimov2017) for the details of these parameters. The ![]() ${N_{\tau }}=3$ trajectories are sampled in parallel. The PPO RL algorithm is implemented by using the Stable-Baselines3 library (Raffin et al. Reference Raffin, Hill, Gleave, Kanervisto, Ernestus and Dormann2021) in Python.
${N_{\tau }}=3$ trajectories are sampled in parallel. The PPO RL algorithm is implemented by using the Stable-Baselines3 library (Raffin et al. Reference Raffin, Hill, Gleave, Kanervisto, Ernestus and Dormann2021) in Python.
We test the utility of our long–short-term strategy described in § 2.2 against the traditional long-term strategy. In the latter, the controller is optimized for a long-time horizon of 10 convective time units (![]() ${M_i}=120$) spanning approximately six vortex-shedding cycles, and weights are updated traditionally, i.e. only once in an iteration (
${M_i}=120$) spanning approximately six vortex-shedding cycles, and weights are updated traditionally, i.e. only once in an iteration (![]() ${M_{\tau }}=120, {k}=1$ window). On the other hand, in the long–short-term strategy, while the long-time horizon is kept the same (
${M_{\tau }}=120, {k}=1$ window). On the other hand, in the long–short-term strategy, while the long-time horizon is kept the same (![]() ${M_i}=120$), the optimization is performed on two shorter optimization windows (
${M_i}=120$), the optimization is performed on two shorter optimization windows (![]() ${M_{\tau }}=60,\ {k}=2$). For all cases, a single iteration comprising
${M_{\tau }}=60,\ {k}=2$). For all cases, a single iteration comprising ![]() $M_i=120$ control time steps, and
$M_i=120$ control time steps, and ![]() $N_\tau =3$ simultaneously running FSI simulations, each parallelized across six processors, takes approximately 2.7 hours to run on a Illinois Campus Cluster node consisting of 20 cores and 128 GB memory.
$N_\tau =3$ simultaneously running FSI simulations, each parallelized across six processors, takes approximately 2.7 hours to run on a Illinois Campus Cluster node consisting of 20 cores and 128 GB memory.
3.2. Implementation, results and mechanisms
To demonstrate the effectiveness of the long–short-term strategy, the evolution of the mean reward (sum of rewards divided by episode length) versus iterations for the two learning strategies as well as the passive case of ![]() ${k_{{\beta }}}=0.015$ (for reference) are shown in figure 2. Firstly, we note that the evolution is oscillatory because of the stochasticity in stiffness sampling during training. Next, it can be seen that, with increasing iterations, for both cases, the controller gradually learns an effective policy as the mean reward increases beyond the passive reference case. However, the long–short-term strategy is found to exhibit faster learning as well as attain a larger reward at the end of 90 iterations as compared to the long-term one. This is because splitting the long-time horizon into two shorter windows and sequentially updating the weights for each window alleviates the burden of learning an effective policy for the entire long horizon as compared to learning via a single weight update in the long-term strategy. The remainder of the results focus on the performance of the control policy obtained after the 90th iteration of the long–short strategy. A deterministic policy is used for evaluating the true performance of the controller, where the actuation provided by the neural network is directly used as the stiffness instead of stochastically sampling a suboptimal stiffness in training.
${k_{{\beta }}}=0.015$ (for reference) are shown in figure 2. Firstly, we note that the evolution is oscillatory because of the stochasticity in stiffness sampling during training. Next, it can be seen that, with increasing iterations, for both cases, the controller gradually learns an effective policy as the mean reward increases beyond the passive reference case. However, the long–short-term strategy is found to exhibit faster learning as well as attain a larger reward at the end of 90 iterations as compared to the long-term one. This is because splitting the long-time horizon into two shorter windows and sequentially updating the weights for each window alleviates the burden of learning an effective policy for the entire long horizon as compared to learning via a single weight update in the long-term strategy. The remainder of the results focus on the performance of the control policy obtained after the 90th iteration of the long–short strategy. A deterministic policy is used for evaluating the true performance of the controller, where the actuation provided by the neural network is directly used as the stiffness instead of stochastically sampling a suboptimal stiffness in training.

Figure 2. Evolution of mean rewards with iterations for different training strategies.
The airfoil lift of the flapless, maximal passive control and hybrid control cases are plotted in figure 3(a). For hybrid control, the lift is plotted not only for ![]() ${t} \in [0, 10]$, for which the controller has been trained, but also for
${t} \in [0, 10]$, for which the controller has been trained, but also for ![]() ${t} \in [10, 20]$. It can be seen that the hybrid controller trained using the long–short-term strategy is able to significantly increase the lift in the training duration and beyond. Overall, in
${t} \in [10, 20]$. It can be seen that the hybrid controller trained using the long–short-term strategy is able to significantly increase the lift in the training duration and beyond. Overall, in ![]() ${t} \in [0, 20]$, a significant lift improvement of
${t} \in [0, 20]$, a significant lift improvement of ![]() $136.43\,\%$ is achieved as compared to the flapless case. For comparison, the corresponding lift improvement of the best passive case is
$136.43\,\%$ is achieved as compared to the flapless case. For comparison, the corresponding lift improvement of the best passive case is ![]() $27\,\%$ (Nair & Goza Reference Nair and Goza2022a). We note that this large lift improvement is, however, attained at the cost of increased lift fluctuations, the cause for which will be discussed at the end of this section. We emphasize that, while the maximum peak-to-trough fluctuation in a vortex-shedding cycle for the hybrid case has increased by 376 % as compared to the baseline flapless case, the standard deviation of lift in the pseudo-steady regime,
$27\,\%$ (Nair & Goza Reference Nair and Goza2022a). We note that this large lift improvement is, however, attained at the cost of increased lift fluctuations, the cause for which will be discussed at the end of this section. We emphasize that, while the maximum peak-to-trough fluctuation in a vortex-shedding cycle for the hybrid case has increased by 376 % as compared to the baseline flapless case, the standard deviation of lift in the pseudo-steady regime, ![]() $t > 10$, has increased by a relatively smaller amount of 104 %. For reference, the corresponding maximum lift fluctuations and standard deviation for the passive case are
$t > 10$, has increased by a relatively smaller amount of 104 %. For reference, the corresponding maximum lift fluctuations and standard deviation for the passive case are ![]() $43.8\,\%$ and
$43.8\,\%$ and ![]() $44.2\,\%$, respectively. The standard deviation provides a more representative measure of the magnitude of fluctuations since the spikes occur in a smaller time scale. When lift fluctuation minimization is of importance, additional penalty terms can be incorporated into the reward, as described in § 2.2.
$44.2\,\%$, respectively. The standard deviation provides a more representative measure of the magnitude of fluctuations since the spikes occur in a smaller time scale. When lift fluctuation minimization is of importance, additional penalty terms can be incorporated into the reward, as described in § 2.2.

Figure 3. Temporal plots for flapless (no control), passive and hybrid flow control cases: (a) airfoil lift coefficient, (b) hinge stiffness and (c) flap deflection.
We also show the lift of the hybrid controller trained using the long-term strategy. While it is able to provide similar large lift improvements as compared to the long–short-term strategy in the training duration, the lift drops considerably in the duration beyond training, implying that more training iterations are required for robustness. Hereafter, we discuss the results obtained from the long–short-term strategy only. The stiffness actuations outputted by the controller and the resulting flap deflection are plotted in figure 3(b) and 3(c), respectively. It can be observed for hybrid control that the stiffness varies across four orders of magnitude (as compared to fixed ![]() ${k_{{\beta }}}=0.015$ in passive control) and often reaching its bounding values of
${k_{{\beta }}}=0.015$ in passive control) and often reaching its bounding values of ![]() ${k_{{\beta }}}=10^{-4}$ and
${k_{{\beta }}}=10^{-4}$ and ![]() $10^{-1}$. Owing to these large stiffness variations, the flap oscillates with an amplitude that is more than twice that in passive control, indicating that larger-amplitude flap oscillations can yield larger lift benefits when timed appropriately with key flow processes.
$10^{-1}$. Owing to these large stiffness variations, the flap oscillates with an amplitude that is more than twice that in passive control, indicating that larger-amplitude flap oscillations can yield larger lift benefits when timed appropriately with key flow processes.
To understand the physical mechanisms driving lift benefits for the hybrid case, we show various quantities during the first and sixth vortex-shedding cycles (cf. figure 3a). These distinct cycles allow for a comparison of the transient and quasi-periodic regimes. The perfectly periodic dynamics of the passive ![]() ${k_{{\beta }}}=0.015$ case are also shown for reference. Firstly, from figure 4(c), we can see that initially, in
${k_{{\beta }}}=0.015$ case are also shown for reference. Firstly, from figure 4(c), we can see that initially, in ![]() ${t/T}\in [0,0.16]$, the controller actuation is lower (
${t/T}\in [0,0.16]$, the controller actuation is lower (![]() ${k_{{\beta }}}= 10^{-4}$) than the constant passive actuation (
${k_{{\beta }}}= 10^{-4}$) than the constant passive actuation (![]() ${k_{{\beta }}}=0.015$). This low stiffness prompts the hybrid flap in the first cycle to undergo a slightly larger deflection until
${k_{{\beta }}}=0.015$). This low stiffness prompts the hybrid flap in the first cycle to undergo a slightly larger deflection until ![]() ${\beta }\approx 50^\circ$ in figure 4(b). The decisive actuation occurs at
${\beta }\approx 50^\circ$ in figure 4(b). The decisive actuation occurs at ![]() ${t/T}\approx 0.21$ when the largest
${t/T}\approx 0.21$ when the largest ![]() ${k_{{\beta }}}=10^{-1}$ is prescribed (cf. figure 4c), which forces the flap to oscillate downwards within a short time span until
${k_{{\beta }}}=10^{-1}$ is prescribed (cf. figure 4c), which forces the flap to oscillate downwards within a short time span until ![]() ${t/T}=0.4$ (cf. figure 4b). The flap then begins to rise only after the actuation is reduced back to
${t/T}=0.4$ (cf. figure 4b). The flap then begins to rise only after the actuation is reduced back to ![]() ${k_{{\beta }}}=10^{-4}$ by
${k_{{\beta }}}=10^{-4}$ by ![]() ${t/T}=0.5$ (cf. figure 4c). For comparison, the rising and falling of the single-stiffness flap in the same duration of
${t/T}=0.5$ (cf. figure 4c). For comparison, the rising and falling of the single-stiffness flap in the same duration of ![]() ${t/T}\in [0,0.5]$ occurs gradually (cf. figure 4b).
${t/T}\in [0,0.5]$ occurs gradually (cf. figure 4b).

Figure 4. Time variation in various quantities during the lone periodic cycle for the passive case, and the first and sixth cycles of the hybrid case (highlighted in figure 3a): (a) lift coefficient, (b) flap deflection, (c) stiffness, (d) TEV strength and (e) LEV strength (magnitude).
To understand the effect of such an aggressive flapping mechanism on airfoil lift, we plot the circulation strengths of the trailing- and leading-edge vortices (TEV and LEV, respectively) in figures 4(d) and 4(e), respectively. Here, ![]() ${\varGamma _{TEV}}$ and
${\varGamma _{TEV}}$ and ![]() ${\varGamma _{LEV}}$ are the magnitudes of positive and negative circulation strengths evaluated in bounding boxes,
${\varGamma _{LEV}}$ are the magnitudes of positive and negative circulation strengths evaluated in bounding boxes, ![]() $[0.85, 1.1]c \times [-0.35, -0.1]c$ and
$[0.85, 1.1]c \times [-0.35, -0.1]c$ and ![]() $[0, 1.1]c \times [-0.35, 0.2]c$, respectively. It can be observed that, after
$[0, 1.1]c \times [-0.35, 0.2]c$, respectively. It can be observed that, after ![]() ${t/T}\approx 0.18$ when the flap strongly oscillates downwards in the first cycle,
${t/T}\approx 0.18$ when the flap strongly oscillates downwards in the first cycle, ![]() ${\varGamma _{TEV}}$ and
${\varGamma _{TEV}}$ and ![]() ${\varGamma _{LEV}}$ for the hybrid case are decreased and increased, respectively, as compared to the passive case. The overall effect on performance is that the lift of the hybrid case in the first cycle begins to increase at
${\varGamma _{LEV}}$ for the hybrid case are decreased and increased, respectively, as compared to the passive case. The overall effect on performance is that the lift of the hybrid case in the first cycle begins to increase at ![]() ${t/T}\approx 0.4$ after an initial dip, as seen in figure 4(a).
${t/T}\approx 0.4$ after an initial dip, as seen in figure 4(a).
Now, as time progresses, this aggressive flapping mechanism continues, but with increasing amplitude, as observed in figure 3(c). Eventually, by the sixth cycle, the switching in stiffness occurs at delayed time instants of ![]() ${t/T}\approx 0.53$ and
${t/T}\approx 0.53$ and ![]() $0.7$ (cf. figure 4c). As a consequence, the flap oscillates upwards until
$0.7$ (cf. figure 4c). As a consequence, the flap oscillates upwards until ![]() ${t/T}=0.5$ and attains a large deflection of
${t/T}=0.5$ and attains a large deflection of ![]() ${\beta }\approx 100^\circ$ (cf. figure 4b). Then, as the stiffness switches to high
${\beta }\approx 100^\circ$ (cf. figure 4b). Then, as the stiffness switches to high ![]() ${k_{{\beta }}}=10^{-1}$, the flap deflection suddenly drops to
${k_{{\beta }}}=10^{-1}$, the flap deflection suddenly drops to ![]() ${\beta }\approx 5 ^\circ$ within a short time span. Similar to the first cycle, this strong downward motion mitigates the TEV and enhances the LEV, as seen in figures 4(d) and 4(e), respectively, but now to a much stronger degree.
${\beta }\approx 5 ^\circ$ within a short time span. Similar to the first cycle, this strong downward motion mitigates the TEV and enhances the LEV, as seen in figures 4(d) and 4(e), respectively, but now to a much stronger degree.
To visualize these effects, vorticity contours at four time instants in the sixth cycle are plotted in figures 5(a)–5(d) and compared to passive control in figures 5(e)–5(h). The TEV, which is clearly decipherable for the passive case in figure 5(g), is now limited to a much smaller size in the hybrid case in figure 5(c). This is because the strong angular velocity of the downward-oscillating flap sheds away the TEV quickly and restricts its growth. This downward motion further contributes to a reduced width of the separated recirculation region in the airfoil-normal direction in figure 5(a) as compared to passive control in figure 5(e). Owing to the TEV mitigating, LEV enhancing and separation width reducing mechanisms of hybrid flow control, the airfoil attains a much higher lift by the sixth cycle as compared to the passive case (cf. figure 4a).

Figure 5. Vorticity contours for hybrid control during the sixth cycle and passive single-stiffness control at four instants indicated by the markers in figure 4(a). Hybrid: (a) ![]() $t=0 T$, (b)
$t=0 T$, (b) ![]() $t=0.27 T$, (c)
$t=0.27 T$, (c) ![]() $t=0.55 T$ and (d)
$t=0.55 T$ and (d) ![]() $t=0.82 T$. Passive: (e)
$t=0.82 T$. Passive: (e) ![]() $t=0 T$, (f)
$t=0 T$, (f) ![]() $t=0.27 T$, (g)
$t=0.27 T$, (g) ![]() $t=0.55 T$ and (h)
$t=0.55 T$ and (h) ![]() $t=0.82 T$.
$t=0.82 T$.
Now, we briefly discuss the occurrence of the spikes observed in the lift signal in figure 3(a) by focusing on the spike in the sixth cycle in figure 4(a), visualized via ![]() $C_p$ contours at four time instants surrounding the occurrence of the spike in figures 6(a)–6(d). We note that the spike initiates at
$C_p$ contours at four time instants surrounding the occurrence of the spike in figures 6(a)–6(d). We note that the spike initiates at ![]() ${t/T}\approx 0.53$ when the flap attains its highest deflection (cf. figures 4a and 4b). Preceding this instant, as the flap oscillates upwards, it induces the fluid in the vicinity to move upstream due to its no-slip condition. When the flap comes to a sudden stop, as the stiffness switches from
${t/T}\approx 0.53$ when the flap attains its highest deflection (cf. figures 4a and 4b). Preceding this instant, as the flap oscillates upwards, it induces the fluid in the vicinity to move upstream due to its no-slip condition. When the flap comes to a sudden stop, as the stiffness switches from ![]() $10^{-4}$ to
$10^{-4}$ to ![]() $10^{-1}$ at
$10^{-1}$ at ![]() ${t/T}\approx 0.53$ (cf. figure 4c), the moving fluid in the region post-flap abruptly loses its momentum. This momentum loss is manifested as a strong rise in post-flap pressure (cf. figure 6b). The fluid in the pre-flap region, however, does not experience a barrier in its upstream motion, and instead continues to roll up and builds up the suction pressure. The flap dividing the high-pressure post-flap and low-pressure pre-flap regions can be clearly seen in figures 6(a) and 6(c), respectively. This large pressure difference across the flap contributes to the large spikes in the airfoil lift.
${t/T}\approx 0.53$ (cf. figure 4c), the moving fluid in the region post-flap abruptly loses its momentum. This momentum loss is manifested as a strong rise in post-flap pressure (cf. figure 6b). The fluid in the pre-flap region, however, does not experience a barrier in its upstream motion, and instead continues to roll up and builds up the suction pressure. The flap dividing the high-pressure post-flap and low-pressure pre-flap regions can be clearly seen in figures 6(a) and 6(c), respectively. This large pressure difference across the flap contributes to the large spikes in the airfoil lift.

Figure 6. The ![]() ${C_p}$ contours at four time instants in the sixth cycle of hybrid control. Hybrid: (a)
${C_p}$ contours at four time instants in the sixth cycle of hybrid control. Hybrid: (a) ![]() $t=0.45 T$, (b)
$t=0.45 T$, (b)![]() $\ t=0.55 T$, (c)
$\ t=0.55 T$, (c) ![]() $t=0.64 T$ and (d)
$t=0.64 T$ and (d) ![]() $t=0.73 T$.
$t=0.73 T$.
Finally, we remark on the effectiveness of the control strategy learned in 2-D conditions on three-dimensional (3-D) flows past a wing. At similar Reynolds numbers, for sufficiently high aspect ratio (![]() $AR\ge 3$) and a large angle of attack of
$AR\ge 3$) and a large angle of attack of ![]() $20^\circ$, the separation process is similar to that in 2-D, where vortex shedding from the leading and trailing edges is more dominant than the wing-tip vortices (Taira & Colonius Reference Taira and Colonius2009; Zhang et al. Reference Zhang, Hayostek, Amitay, He, Theofilis and Taira2020). In this regime, it is plausible that the actuation strategy learnt in 2-D would provide lift benefits in the 3-D flow, though these would presumably be alleviated by tip-vortex effects. For smaller aspect ratios (
$20^\circ$, the separation process is similar to that in 2-D, where vortex shedding from the leading and trailing edges is more dominant than the wing-tip vortices (Taira & Colonius Reference Taira and Colonius2009; Zhang et al. Reference Zhang, Hayostek, Amitay, He, Theofilis and Taira2020). In this regime, it is plausible that the actuation strategy learnt in 2-D would provide lift benefits in the 3-D flow, though these would presumably be alleviated by tip-vortex effects. For smaller aspect ratios (![]() $AR=1$), the tip vortex dominates and qualitatively changes the separated flow behaviour. In this case, the 2-D-trained controller is unlikely to yield lift benefits. However, such aspect ratios are significantly smaller than the bio-inspired flows of interest. Moreover, actuation with flaps has the potential to be a useful paradigm in this regime as well (Arivoli & Singh Reference Arivoli and Singh2016), due to similar length scales of flow separation, vortex formation and interaction processes between 2-D and 3-D. We also emphasize that the RL framework is agnostic to the environment, and provided that a 3-D solver were developed to simulate the dynamics, the same training procedure could be performed without modification.
$AR=1$), the tip vortex dominates and qualitatively changes the separated flow behaviour. In this case, the 2-D-trained controller is unlikely to yield lift benefits. However, such aspect ratios are significantly smaller than the bio-inspired flows of interest. Moreover, actuation with flaps has the potential to be a useful paradigm in this regime as well (Arivoli & Singh Reference Arivoli and Singh2016), due to similar length scales of flow separation, vortex formation and interaction processes between 2-D and 3-D. We also emphasize that the RL framework is agnostic to the environment, and provided that a 3-D solver were developed to simulate the dynamics, the same training procedure could be performed without modification.
4. Conclusions
A hybrid active–passive flow control method was introduced as an extension of the covert-inspired passive flow control method, consisting of a torsionally mounted flap on an airfoil at post-stall conditions involving vortex shedding. This hybrid strategy consisted of actively actuating the hinge stiffness to passively control the dynamics of the flap. A closed-loop feedback controller trained using deep RL was used to provide effective stiffness actuations to maximize lift. The RL framework was described, including modifications to the traditional RL methodology that enabled faster training for our hybrid control problem. The hybrid controller provided lift improvements as high as ![]() $136\,\%$ and
$136\,\%$ and ![]() $85\,\%$ with respect to the flapless airfoil and the maximal passive control (single-stiffness) cases, respectively. These lift improvements were attributed to large flap oscillations due to stiffness variations occurring over four orders of magnitude. Detailed flow analysis revealed an aggressive flapping mechanism that led to significant TEV mitigation, LEV enhancement and reduction of separation region width. We remark that, since the stiffness changes can be well approximated by a small number of finite jumps, a discrete VSA could be a pathway to realizing this actuation strategy.
$85\,\%$ with respect to the flapless airfoil and the maximal passive control (single-stiffness) cases, respectively. These lift improvements were attributed to large flap oscillations due to stiffness variations occurring over four orders of magnitude. Detailed flow analysis revealed an aggressive flapping mechanism that led to significant TEV mitigation, LEV enhancement and reduction of separation region width. We remark that, since the stiffness changes can be well approximated by a small number of finite jumps, a discrete VSA could be a pathway to realizing this actuation strategy.
Declaration of interests
The authors report no conflict of interest.