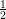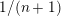1 Introduction
The notion of birational superrigidity was introduced as a generalization of Iskovskih and Manin’s work [Reference Iskovskih and ManinIM71] on the non-rationality of quartic threefolds; on the other hand, the concept of K-stability emerges in the study of Kähler–Einstein metrics on Fano manifolds. While the two notions have different nature of origin, they seem to resemble each other in the following sense: it is well known that a Fano variety
![]() $X$
of Picard number one is birationally superrigid if and only if
$X$
of Picard number one is birationally superrigid if and only if
![]() $(X,M)$
has canonical singularities for every movable boundary
$(X,M)$
has canonical singularities for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
; on the other hand, by the recent work of [Reference Fujita and OdakaFO18, Reference Blum and JonssonBJ17], the K-(semi)stability of
$M{\sim}_{\mathbb{Q}}-K_{X}$
; on the other hand, by the recent work of [Reference Fujita and OdakaFO18, Reference Blum and JonssonBJ17], the K-(semi)stability of
![]() $X$
is (roughly speaking) characterized by the log canonicity of basis type divisors, which is the average of a basis of some pluri-anticanonical system. In other words, both notions are tied to the singularities of certain anticanonical
$X$
is (roughly speaking) characterized by the log canonicity of basis type divisors, which is the average of a basis of some pluri-anticanonical system. In other words, both notions are tied to the singularities of certain anticanonical
![]() $\mathbb{Q}$
-divisors and so it is very natural to expect some relation between them. Indeed, the slope stability (a weaker notion of K-stability) of birationally superrigid Fano manifolds has been established by [Reference Odaka and OkadaOO13] under some mild assumptions, and it is conjectured [Reference Odaka and OkadaOO13, Reference Kim, Okada and WonKOW18] that birationally rigid Fano varieties are always K-stable.
$\mathbb{Q}$
-divisors and so it is very natural to expect some relation between them. Indeed, the slope stability (a weaker notion of K-stability) of birationally superrigid Fano manifolds has been established by [Reference Odaka and OkadaOO13] under some mild assumptions, and it is conjectured [Reference Odaka and OkadaOO13, Reference Kim, Okada and WonKOW18] that birationally rigid Fano varieties are always K-stable.
In this note, we give a partial solution to this conjecture. Here is our main result.
Definition 1.1. The alpha invariant
![]() $\unicode[STIX]{x1D6FC}(X)$
of a
$\unicode[STIX]{x1D6FC}(X)$
of a
![]() $\mathbb{Q}$
-Fano variety
$\mathbb{Q}$
-Fano variety
![]() $X$
(i.e.
$X$
(i.e.
![]() $X$
has Kawamata log terminal (klt) singularities and
$X$
has Kawamata log terminal (klt) singularities and
![]() $-K_{X}$
is ample) is defined as the supremum of all
$-K_{X}$
is ample) is defined as the supremum of all
![]() $t>0$
such that
$t>0$
such that
![]() $(X,tD)$
is log canonical (lc) for every effective
$(X,tD)$
is log canonical (lc) for every effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D{\sim}_{\mathbb{Q}}-K_{X}$
.
$D{\sim}_{\mathbb{Q}}-K_{X}$
.
Theorem 1.2. Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of Picard number one. If
$\mathbb{Q}$
-Fano variety of Picard number one. If
![]() $X$
is birationally superrigid (or, more generally,
$X$
is birationally superrigid (or, more generally,
![]() $(X,M)$
is log canonical for every movable boundary
$(X,M)$
is log canonical for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
) and
$M{\sim}_{\mathbb{Q}}-K_{X}$
) and
![]() $\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
(respectively
$\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
(respectively
![]() ${>}\frac{1}{2}$
), then
${>}\frac{1}{2}$
), then
![]() $X$
is K-semistable (respectively K-stable).
$X$
is K-semistable (respectively K-stable).
It is well known that smooth Fano hypersurfaces of index one and dimension
![]() $n\geqslant 3$
are birationally superrigid [Reference Iskovskih and ManinIM71, Reference de Fernex, Ein and MustaţădFEM03, Reference de FernexdF16] and their alpha invariants are at least
$n\geqslant 3$
are birationally superrigid [Reference Iskovskih and ManinIM71, Reference de Fernex, Ein and MustaţădFEM03, Reference de FernexdF16] and their alpha invariants are at least
![]() $n/(n+1)$
[Reference CheltsovChe01]; hence, we have the following immediate corollary, reproving the K-stability of Fano hypersurfaces of index one.
$n/(n+1)$
[Reference CheltsovChe01]; hence, we have the following immediate corollary, reproving the K-stability of Fano hypersurfaces of index one.
Corollary 1.3 [Reference FujitaFuj19b].
Let
![]() $X\subseteq \mathbb{P}^{n}$
be a smooth hypersurface of degree
$X\subseteq \mathbb{P}^{n}$
be a smooth hypersurface of degree
![]() $n\geqslant 4$
; then
$n\geqslant 4$
; then
![]() $X$
is K-stable.
$X$
is K-stable.
Another application is to the K-stability of general index-two hypersurfaces. By [Reference CheltsovChe01] and [Reference PukhlikovPuk16], such hypersurfaces have alpha invariant
![]() $\frac{1}{2}$
and
$\frac{1}{2}$
and
![]() $(X,M)$
is lc for every movable boundary
$(X,M)$
is lc for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
. Hence, by analyzing the equality case in Theorem 1.2, we prove the following result.
$M{\sim}_{\mathbb{Q}}-K_{X}$
. Hence, by analyzing the equality case in Theorem 1.2, we prove the following result.
Corollary 1.4. Let
![]() $n\geqslant 16$
and let
$n\geqslant 16$
and let
![]() $U\subseteq \mathbb{P}H^{0}(\mathbb{P}^{n+1},{\mathcal{O}}_{\mathbb{P}^{n+1}}(n))$
be the parameter space of smooth index-two hypersurfaces. Let
$U\subseteq \mathbb{P}H^{0}(\mathbb{P}^{n+1},{\mathcal{O}}_{\mathbb{P}^{n+1}}(n))$
be the parameter space of smooth index-two hypersurfaces. Let
![]() $T\subseteq U$
be the set of hypersurfaces that are not K-stable. Then
$T\subseteq U$
be the set of hypersurfaces that are not K-stable. Then
![]() $\text{codim}_{U}T\geqslant \frac{1}{2}(n-11)(n-10)-10$
.
$\text{codim}_{U}T\geqslant \frac{1}{2}(n-11)(n-10)-10$
.
Although alpha invariants are in general hard to estimate, the known examples seem to suggest that birationally (super)rigid varieties have large alpha invariants. In view of Theorem 1.2, it is therefore natural to ask the following question.
Question 1.5. Let
![]() $X$
be a birationally superrigid Fano variety. Is it true that
$X$
be a birationally superrigid Fano variety. Is it true that
![]() $\unicode[STIX]{x1D6FC}(X)>\frac{1}{2}$
?
$\unicode[STIX]{x1D6FC}(X)>\frac{1}{2}$
?
Obviously, a positive answer to this question will confirm the K-stability of all birationally superrigid Fano varieties. At this point, we only have a weaker estimate.
Theorem 1.6. Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of Picard number one and dimension
$\mathbb{Q}$
-Fano variety of Picard number one and dimension
![]() $n\geqslant 3$
. Assume that
$n\geqslant 3$
. Assume that
![]() $X$
is birationally superrigid (or, more generally,
$X$
is birationally superrigid (or, more generally,
![]() $(X,M)$
is log canonical for every movable boundary
$(X,M)$
is log canonical for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
),
$M{\sim}_{\mathbb{Q}}-K_{X}$
),
![]() $-K_{X}$
generates the class group
$-K_{X}$
generates the class group
![]() $\text{Cl}(X)$
of
$\text{Cl}(X)$
of
![]() $X$
and
$X$
and
![]() $|-K_{X}|$
is base-point-free, then
$|-K_{X}|$
is base-point-free, then
![]() $\unicode[STIX]{x1D6FC}(X)\geqslant 1/(n+1)$
.
$\unicode[STIX]{x1D6FC}(X)\geqslant 1/(n+1)$
.
Note that this is in line with the conjectural K-stability of such varieties, since, by [Reference Fujita and OdakaFO18, Theorem 3.5], the alpha invariant of a K-semistable Fano variety is always
![]() ${\geqslant}1/(n+1)$
. We also remark that the assumptions about the index and base-point freeness in the above theorem seem to be mild and they are satisfied by most known examples of birationally superrigid varieties.
${\geqslant}1/(n+1)$
. We also remark that the assumptions about the index and base-point freeness in the above theorem seem to be mild and they are satisfied by most known examples of birationally superrigid varieties.
As other evidence towards a positive answer of Question 1.5 and K-stability of birationally superrigid Fano varieties, we prove the following result.
Theorem 1.7. Let
![]() $f:X\rightarrow C$
,
$f:X\rightarrow C$
,
![]() $g:Y\rightarrow C$
be two flat families of
$g:Y\rightarrow C$
be two flat families of
![]() $\mathbb{Q}$
-Fano varieties (i.e. all geometric fibers are integral, normal and
$\mathbb{Q}$
-Fano varieties (i.e. all geometric fibers are integral, normal and
![]() $\mathbb{Q}$
-Fano) over a smooth pointed curve
$\mathbb{Q}$
-Fano) over a smooth pointed curve
![]() $0\in C$
. Assume that the central fibers
$0\in C$
. Assume that the central fibers
![]() $X_{0}=f^{-1}(0)$
and
$X_{0}=f^{-1}(0)$
and
![]() $Y_{0}=g^{-1}(0)$
are birationally superrigid and there exists an isomorphism
$Y_{0}=g^{-1}(0)$
are birationally superrigid and there exists an isomorphism
![]() $\unicode[STIX]{x1D70C}:X\backslash X_{0}\cong Y\backslash Y_{0}$
over the punctured curve
$\unicode[STIX]{x1D70C}:X\backslash X_{0}\cong Y\backslash Y_{0}$
over the punctured curve
![]() $C\backslash 0$
. Then
$C\backslash 0$
. Then
![]() $\unicode[STIX]{x1D70C}$
induces an isomorphism
$\unicode[STIX]{x1D70C}$
induces an isomorphism
![]() $X\cong Y$
over
$X\cong Y$
over
![]() $C$
.
$C$
.
In other words, the moduli space (if it exists) of birationally superrigid Fano varieties is separated. A similar statement is also conjectured for families of K-stable Fano varieties (postscript note: this has now been proved by Blum and Xu) and our proof of Theorem 1.7 is indeed inspired by the recent work [Reference Blum and XuBX18] in the uniformly K-stable case. One should also note that if the answer to Question 1.5 is positive, then Theorem 1.7 follows immediately from [Reference CheltsovChe09, Theorem 1.5].
2 Preliminary
2.1 Notation and conventions
We work over the field
![]() $\mathbb{C}$
of complex numbers. Unless otherwise specified, all varieties are assumed to be projective and normal and divisors are understood as
$\mathbb{C}$
of complex numbers. Unless otherwise specified, all varieties are assumed to be projective and normal and divisors are understood as
![]() $\mathbb{Q}$
-divisors. The notions of canonical, klt and lc singularities are defined in the sense of [Reference KollárKol97, Definition 3.5]. A movable boundary is defined as an expression of the form
$\mathbb{Q}$
-divisors. The notions of canonical, klt and lc singularities are defined in the sense of [Reference KollárKol97, Definition 3.5]. A movable boundary is defined as an expression of the form
![]() $a{\mathcal{M}}$
, where
$a{\mathcal{M}}$
, where
![]() $a\in \mathbb{Q}$
and
$a\in \mathbb{Q}$
and
![]() ${\mathcal{M}}$
is a movable linear system. Its
${\mathcal{M}}$
is a movable linear system. Its
![]() $\mathbb{Q}$
-linear equivalence class is defined in an evident way. If
$\mathbb{Q}$
-linear equivalence class is defined in an evident way. If
![]() $M=a{\mathcal{M}}$
is a movable boundary on
$M=a{\mathcal{M}}$
is a movable boundary on
![]() $X$
, we say that
$X$
, we say that
![]() $(X,M)$
is klt (respectively canonical, lc) if for
$(X,M)$
is klt (respectively canonical, lc) if for
![]() $k\gg 0$
and for general members
$k\gg 0$
and for general members
![]() $D_{1},\ldots ,D_{k}$
of the linear system
$D_{1},\ldots ,D_{k}$
of the linear system
![]() ${\mathcal{M}}$
, the pair
${\mathcal{M}}$
, the pair
![]() $(X,M_{k})$
(where
$(X,M_{k})$
(where
![]() $M_{k}=(a/k)\sum _{i=1}^{k}D_{i}$
) is klt (respectively canonical, lc) in the usual sense. The lc threshold [Reference KollárKol97, Definition 8.1] of a divisor
$M_{k}=(a/k)\sum _{i=1}^{k}D_{i}$
) is klt (respectively canonical, lc) in the usual sense. The lc threshold [Reference KollárKol97, Definition 8.1] of a divisor
![]() $D$
on
$D$
on
![]() $X$
is denoted by
$X$
is denoted by
![]() $\text{lct}(X;D)$
.
$\text{lct}(X;D)$
.
2.2 K-stability
We refer to [Reference TianTia97, Reference DonaldsonDon02] for the original definition of K-stability using test configurations. In this paper we use the following equivalent valuative criterion.
Definition 2.1 [Reference FujitaFuj19a, Definition 1.1].
Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $F$
be a prime divisor over
$F$
be a prime divisor over
![]() $X$
, i.e. there exists a projective birational morphism
$X$
, i.e. there exists a projective birational morphism
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
![]() $Y$
normal such that
$Y$
normal such that
![]() $F$
is a prime divisor on
$F$
is a prime divisor on
![]() $Y$
.
$Y$
.
(i) For any
 $x\geqslant 0$
, we define
$x\geqslant 0$
, we define
 $\text{vol}_{X}(-K_{X}-xF):=\text{vol}_{Y}(-\unicode[STIX]{x1D70B}^{\ast }K_{X}-xF)$
.
$\text{vol}_{X}(-K_{X}-xF):=\text{vol}_{Y}(-\unicode[STIX]{x1D70B}^{\ast }K_{X}-xF)$
.(ii) The pseudo-effective threshold
 $\unicode[STIX]{x1D70F}(F)$
of
$\unicode[STIX]{x1D70F}(F)$
of
 $F$
with respect to
$F$
with respect to
 $-K_{X}$
is defined as
$-K_{X}$
is defined as  $$\begin{eqnarray}\unicode[STIX]{x1D70F}(F):=\sup \{\unicode[STIX]{x1D70F}>0\mid \text{vol}_{X}(-K_{X}-\unicode[STIX]{x1D70F}F)>0\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(F):=\sup \{\unicode[STIX]{x1D70F}>0\mid \text{vol}_{X}(-K_{X}-\unicode[STIX]{x1D70F}F)>0\}.\end{eqnarray}$$
(iii) Let
 $A_{X}(F)$
be the log discrepancy of
$A_{X}(F)$
be the log discrepancy of
 $F$
with respect to
$F$
with respect to
 $X$
. We set
$X$
. We set  $$\begin{eqnarray}\unicode[STIX]{x1D6FD}(F):=A_{X}(F)\cdot ((-K_{X})^{n})-\int _{0}^{\infty }\text{vol}_{X}(-K_{X}-xF)\,dx.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(F):=A_{X}(F)\cdot ((-K_{X})^{n})-\int _{0}^{\infty }\text{vol}_{X}(-K_{X}-xF)\,dx.\end{eqnarray}$$
(iv)
 $F$
is said to be dreamy if the graded algebra is finitely generated for some (hence, for any)
$F$
is said to be dreamy if the graded algebra is finitely generated for some (hence, for any) $$\begin{eqnarray}\bigoplus _{k,j\in \mathbb{Z}_{{\geqslant}0}}H^{0}(Y,-kr\unicode[STIX]{x1D70B}^{\ast }K_{X}-jF)\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{k,j\in \mathbb{Z}_{{\geqslant}0}}H^{0}(Y,-kr\unicode[STIX]{x1D70B}^{\ast }K_{X}-jF)\end{eqnarray}$$
 $r\in \mathbb{Z}>0$
with
$r\in \mathbb{Z}>0$
with
 $rK_{X}$
Cartier.
$rK_{X}$
Cartier.
Theorem 2.2 [Reference FujitaFuj19a, Theorems 1.3 and 1.4] and [Reference LiLi17, Theorem 3.7].
Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety. Then
$\mathbb{Q}$
-Fano variety. Then
![]() $X$
is K-stable (respectively K-semistable) if and only if
$X$
is K-stable (respectively K-semistable) if and only if
![]() $\unicode[STIX]{x1D6FD}(F)>0$
(respectively
$\unicode[STIX]{x1D6FD}(F)>0$
(respectively
![]() $\unicode[STIX]{x1D6FD}(F)\geqslant 0$
) holds for any dreamy prime divisor
$\unicode[STIX]{x1D6FD}(F)\geqslant 0$
) holds for any dreamy prime divisor
![]() $F$
over
$F$
over
![]() $X$
.
$X$
.
2.3 Birational superrigidity
A Fano variety
![]() $X$
is said to be birationally superrigid if it has terminal singularities, is
$X$
is said to be birationally superrigid if it has terminal singularities, is
![]() $\mathbb{Q}$
-factorial of Picard number one and every birational map
$\mathbb{Q}$
-factorial of Picard number one and every birational map
![]() $f:X{\dashrightarrow}Y$
from
$f:X{\dashrightarrow}Y$
from
![]() $X$
to a Mori fiber space is an isomorphism (see e.g. [Reference Cheltsov and ShramovCS08, Definition 1.25]). We have the following equivalent characterization of birational superrigidity.
$X$
to a Mori fiber space is an isomorphism (see e.g. [Reference Cheltsov and ShramovCS08, Definition 1.25]). We have the following equivalent characterization of birational superrigidity.
Theorem 2.3 [Reference Cheltsov and ShramovCS08, Theorem 1.26].
Let
![]() $X$
be a Fano variety. Then it is birationally superrigid if and only if it has
$X$
be a Fano variety. Then it is birationally superrigid if and only if it has
![]() $\mathbb{Q}$
-factorial terminal singularities, Picard number one and, for every movable boundary
$\mathbb{Q}$
-factorial terminal singularities, Picard number one and, for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
on
$M{\sim}_{\mathbb{Q}}-K_{X}$
on
![]() $X$
, the pair
$X$
, the pair
![]() $(X,M)$
has canonical singularities.
$(X,M)$
has canonical singularities.
3 Proofs
In this section we prove the results stated in the introduction.
Proof of Theorem 1.2.
The proof strategy is similar to those of [Reference FujitaFuj19c, Proposition 2.1]. By assumption, we have
![]() $\text{lct}(X;D)\geqslant \frac{1}{2}$
(respectively
$\text{lct}(X;D)\geqslant \frac{1}{2}$
(respectively
![]() ${>}\frac{1}{2}$
) for every effective divisor
${>}\frac{1}{2}$
) for every effective divisor
![]() $D{\sim}_{\mathbb{Q}}-K_{X}$
. For simplicity we only prove the K-semistability, since the K-stability part is almost identical. As such, we assume that
$D{\sim}_{\mathbb{Q}}-K_{X}$
. For simplicity we only prove the K-semistability, since the K-stability part is almost identical. As such, we assume that
![]() $\text{lct}(X;D)\geqslant \frac{1}{2}$
in the rest of the proof. Let
$\text{lct}(X;D)\geqslant \frac{1}{2}$
in the rest of the proof. Let
![]() $F$
be a dreamy divisor over
$F$
be a dreamy divisor over
![]() $X$
and let
$X$
and let
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}(F)$
. Let
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}(F)$
. Let
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a projective birational morphism such that
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a projective birational morphism such that
![]() $F$
is a prime divisor on
$F$
is a prime divisor on
![]() $Y$
and let
$Y$
and let
By Theorem 2.2, it suffices to show that
![]() $b\leqslant A=A_{X}(F)$
.
$b\leqslant A=A_{X}(F)$
.
Suppose that this is not the case, i.e.
![]() $b>A$
. As in the proof of [Reference FujitaFuj19c, Proposition 2.1], we have
$b>A$
. As in the proof of [Reference FujitaFuj19c, Proposition 2.1], we have
where
![]() $\text{vol}_{Y|F}$
denotes the restricted volume of a divisor to
$\text{vol}_{Y|F}$
denotes the restricted volume of a divisor to
![]() $F$
(see [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and PopaELM09]). Since
$F$
(see [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and PopaELM09]). Since
![]() $X$
has Picard number one, every divisor on
$X$
has Picard number one, every divisor on
![]() $X$
is linearly equivalent to a multiple of
$X$
is linearly equivalent to a multiple of
![]() $-K_{X}$
and hence by our assumption that
$-K_{X}$
and hence by our assumption that
![]() $(X,M)$
is lc for every movable boundary
$(X,M)$
is lc for every movable boundary
![]() $M$
, we see that there exists at most one irreducible divisor
$M$
, we see that there exists at most one irreducible divisor
![]() $D{\sim}_{\mathbb{Q}}-K_{X}$
such that
$D{\sim}_{\mathbb{Q}}-K_{X}$
such that
![]() $\text{ord}_{F}(D)>A$
. It follows that
$\text{ord}_{F}(D)>A$
. It follows that
![]() $\text{ord}_{F}(D)=\unicode[STIX]{x1D70F}$
by the definition of
$\text{ord}_{F}(D)=\unicode[STIX]{x1D70F}$
by the definition of
![]() $\unicode[STIX]{x1D70F}(F)$
. Moreover if
$\unicode[STIX]{x1D70F}(F)$
. Moreover if
![]() $x\geqslant A$
and
$x\geqslant A$
and
![]() $D^{\prime }{\sim}_{\mathbb{Q}}-K_{X}$
is an effective divisor for which
$D^{\prime }{\sim}_{\mathbb{Q}}-K_{X}$
is an effective divisor for which
![]() $\text{ord}_{F}(D^{\prime })\geqslant x$
and we write
$\text{ord}_{F}(D^{\prime })\geqslant x$
and we write
![]() $D^{\prime }=aD+\unicode[STIX]{x1D6E4}$
, where
$D^{\prime }=aD+\unicode[STIX]{x1D6E4}$
, where
![]() $D\not \subseteq \text{Supp}~(\unicode[STIX]{x1D6E4})$
, then
$D\not \subseteq \text{Supp}~(\unicode[STIX]{x1D6E4})$
, then
![]() $\text{ord}_{F}(\unicode[STIX]{x1D6E4})\leqslant A$
. As
$\text{ord}_{F}(\unicode[STIX]{x1D6E4})\leqslant A$
. As
we see that
![]() $a\geqslant (x-A)/(\unicode[STIX]{x1D70F}-A)$
and, therefore, if in addition
$a\geqslant (x-A)/(\unicode[STIX]{x1D70F}-A)$
and, therefore, if in addition
![]() $x\in \mathbb{Q}$
and
$x\in \mathbb{Q}$
and
![]() $m$
is sufficiently divisible, then the natural inclusion
$m$
is sufficiently divisible, then the natural inclusion
given by the multiplication of
![]() $m\cdot ((x-A)/(\unicode[STIX]{x1D70F}-A))(\unicode[STIX]{x1D70B}^{\ast }D-\unicode[STIX]{x1D70F}F)$
is an isomorphism. By the definition and the continuity of restricted volume, this implies (note that
$m\cdot ((x-A)/(\unicode[STIX]{x1D70F}-A))(\unicode[STIX]{x1D70B}^{\ast }D-\unicode[STIX]{x1D70F}F)$
is an isomorphism. By the definition and the continuity of restricted volume, this implies (note that
![]() $F$
is not in the support of
$F$
is not in the support of
![]() $\unicode[STIX]{x1D70B}^{\ast }D-\unicode[STIX]{x1D70F}F$
) that
$\unicode[STIX]{x1D70B}^{\ast }D-\unicode[STIX]{x1D70F}F$
) that
when
![]() $A\leqslant x\leqslant \unicode[STIX]{x1D70F}$
. On the other hand, by the log-concavity of restricted volume [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and PopaELM09, Theorem A], we have
$A\leqslant x\leqslant \unicode[STIX]{x1D70F}$
. On the other hand, by the log-concavity of restricted volume [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and PopaELM09, Theorem A], we have
whenever
![]() $x\in [0,A]$
. Since
$x\in [0,A]$
. Since
![]() $b>A$
, combining (1), (2) and (3), we get the inequality
$b>A$
, combining (1), (2) and (3), we get the inequality
which is equivalent to
As
![]() $b>A$
, we have
$b>A$
, we have
![]() $\text{ord}_{F}(D)=\unicode[STIX]{x1D70F}>2A$
, which implies that
$\text{ord}_{F}(D)=\unicode[STIX]{x1D70F}>2A$
, which implies that
![]() $\text{lct}(X;D)<\frac{1}{2}$
, contradicting our assumption.◻
$\text{lct}(X;D)<\frac{1}{2}$
, contradicting our assumption.◻
Remark 3.1. Let us also give a somewhat conceptual summary of the proof (for K-semistability). In terms of the equation (1), it suffices to check that the center of mass of the interval
![]() $[0,\unicode[STIX]{x1D70F}]$
with density function
$[0,\unicode[STIX]{x1D70F}]$
with density function
![]() $f(x)=(1/(-K_{X})^{n})\text{vol}_{Y|F}(-\unicode[STIX]{x1D70B}^{\ast }K_{X}-xF)$
is at most
$f(x)=(1/(-K_{X})^{n})\text{vol}_{Y|F}(-\unicode[STIX]{x1D70B}^{\ast }K_{X}-xF)$
is at most
![]() $A$
. The assumption that
$A$
. The assumption that
![]() $(X,M)$
is lc for every movable boundary
$(X,M)$
is lc for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
implies that
$M{\sim}_{\mathbb{Q}}-K_{X}$
implies that
![]() $g(x)=f(x)^{1/(n-1)}$
is linear when
$g(x)=f(x)^{1/(n-1)}$
is linear when
![]() $x\geqslant A$
and
$x\geqslant A$
and
![]() $g(\unicode[STIX]{x1D70F})=0$
if
$g(\unicode[STIX]{x1D70F})=0$
if
![]() $\unicode[STIX]{x1D70F}>A$
, while
$\unicode[STIX]{x1D70F}>A$
, while
![]() $\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
implies that the length of the interval is at most
$\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
implies that the length of the interval is at most
![]() $2A$
. Since
$2A$
. Since
![]() $g(x)$
is also concave, it is clear (by looking at the graph of
$g(x)$
is also concave, it is clear (by looking at the graph of
![]() $g(x)$
) that the center of mass is at most
$g(x)$
) that the center of mass is at most
![]() $A$
.
$A$
.
It is not hard to characterize the equality case from the above proof.
Corollary 3.2. Let
![]() $X$
be a
$X$
be a
![]() $\mathbb{Q}$
-Fano variety of Picard number one. Assume that
$\mathbb{Q}$
-Fano variety of Picard number one. Assume that
![]() $(X,M)$
is lc for every movable boundary
$(X,M)$
is lc for every movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
,
$M{\sim}_{\mathbb{Q}}-K_{X}$
,
![]() $\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
but
$\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
but
![]() $X$
is not K-stable; then there exist a dreamy prime divisor
$X$
is not K-stable; then there exist a dreamy prime divisor
![]() $F$
over
$F$
over
![]() $X$
, a movable boundary
$X$
, a movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
and an effective divisor
$M{\sim}_{\mathbb{Q}}-K_{X}$
and an effective divisor
![]() $D{\sim}_{\mathbb{Q}}-K_{X}$
such that
$D{\sim}_{\mathbb{Q}}-K_{X}$
such that
![]() $F$
is a log canonical place of
$F$
is a log canonical place of
![]() $(X,M)$
and
$(X,M)$
and
![]() $(X,\frac{1}{2}D)$
. In particular, if
$(X,\frac{1}{2}D)$
. In particular, if
![]() $X$
is birationally superrigid and
$X$
is birationally superrigid and
![]() $\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
, then
$\unicode[STIX]{x1D6FC}(X)\geqslant \frac{1}{2}$
, then
![]() $X$
is K-stable.
$X$
is K-stable.
Proof. We keep the notation from the above proof. Let
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(F)$
be the movable threshold of
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(F)$
be the movable threshold of
![]() $-K_{X}$
with respect to
$-K_{X}$
with respect to
![]() $F$
, i.e. the supremum of
$F$
, i.e. the supremum of
![]() $c\geqslant 0$
such that there exists an effective divisor
$c\geqslant 0$
such that there exists an effective divisor
![]() $D_{0}{\sim}_{\mathbb{Q}}-K_{X}$
with
$D_{0}{\sim}_{\mathbb{Q}}-K_{X}$
with
![]() $\text{ord}_{F}(D_{0})=c$
whose support does not contain
$\text{ord}_{F}(D_{0})=c$
whose support does not contain
![]() $D$
(see e.g. [Reference ZhuangZhu18, Definition 4.1]). Since
$D$
(see e.g. [Reference ZhuangZhu18, Definition 4.1]). Since
![]() $F$
is dreamy, this is indeed a maximum and there exists
$F$
is dreamy, this is indeed a maximum and there exists
![]() $D_{1}{\sim}_{\mathbb{Q}}-K_{X}$
such that
$D_{1}{\sim}_{\mathbb{Q}}-K_{X}$
such that
![]() $\text{ord}_{F}(D_{1})=\unicode[STIX]{x1D702}$
(one can simply take
$\text{ord}_{F}(D_{1})=\unicode[STIX]{x1D702}$
(one can simply take
![]() $D_{1}$
to be the divisor corresponding to a generator of
$D_{1}$
to be the divisor corresponding to a generator of
![]() $\bigoplus _{k,j\in \mathbb{Z}_{{\geqslant}0}}H^{0}(Y,-kr\unicode[STIX]{x1D70B}^{\ast }K_{X}-jF)$
with largest slope
$\bigoplus _{k,j\in \mathbb{Z}_{{\geqslant}0}}H^{0}(Y,-kr\unicode[STIX]{x1D70B}^{\ast }K_{X}-jF)$
with largest slope
![]() $j/kr$
among those that do not vanish on
$j/kr$
among those that do not vanish on
![]() $D$
).
$D$
).
Suppose that
![]() $X$
is not K-stable and choose
$X$
is not K-stable and choose
![]() $F$
to be a dreamy divisor over
$F$
to be a dreamy divisor over
![]() $X$
such that
$X$
such that
![]() $\unicode[STIX]{x1D6FD}(F)=0$
; then we have
$\unicode[STIX]{x1D6FD}(F)=0$
; then we have
![]() $b=A\geqslant \unicode[STIX]{x1D702}$
. In this case by the same proof as above the (in)equalities (2), (3), (4) and (5) hold true with
$b=A\geqslant \unicode[STIX]{x1D702}$
. In this case by the same proof as above the (in)equalities (2), (3), (4) and (5) hold true with
![]() $\unicode[STIX]{x1D702}$
in place of
$\unicode[STIX]{x1D702}$
in place of
![]() $A$
and we have
$A$
and we have
or
![]() $(\unicode[STIX]{x1D70F}-2A)+(n-1)(\unicode[STIX]{x1D702}-A)\geqslant 0$
(note that
$(\unicode[STIX]{x1D70F}-2A)+(n-1)(\unicode[STIX]{x1D702}-A)\geqslant 0$
(note that
![]() $b=A$
). But by assumption we have
$b=A$
). But by assumption we have
![]() $\unicode[STIX]{x1D70F}\leqslant 2A$
and
$\unicode[STIX]{x1D70F}\leqslant 2A$
and
![]() $\unicode[STIX]{x1D702}\leqslant A$
and hence this is only possible when
$\unicode[STIX]{x1D702}\leqslant A$
and hence this is only possible when
![]() $\unicode[STIX]{x1D702}=A$
and
$\unicode[STIX]{x1D702}=A$
and
![]() $\unicode[STIX]{x1D70F}=2A$
. Taking
$\unicode[STIX]{x1D70F}=2A$
. Taking
![]() $M$
to be the linear system generated by a sufficiently divisible multiple of
$M$
to be the linear system generated by a sufficiently divisible multiple of
![]() $D$
and
$D$
and
![]() $D_{1}$
(and then rescale so that
$D_{1}$
(and then rescale so that
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
) finishes the proof.◻
$M{\sim}_{\mathbb{Q}}-K_{X}$
) finishes the proof.◻
Proof of Corollary 1.4.
Let
![]() $S\subseteq U$
be the set of regular hypersurfaces as defined in [Reference PukhlikovPuk17, §0.2]. By [Reference PukhlikovPuk17, Theorem 2],
$S\subseteq U$
be the set of regular hypersurfaces as defined in [Reference PukhlikovPuk17, §0.2]. By [Reference PukhlikovPuk17, Theorem 2],
![]() $S$
is non-empty and the complement of
$S$
is non-empty and the complement of
![]() $S$
has codimension at least
$S$
has codimension at least
![]() $\frac{1}{2}(n-11)(n-10)-10$
. Therefore, it suffices to show that every hypersurface in the set
$\frac{1}{2}(n-11)(n-10)-10$
. Therefore, it suffices to show that every hypersurface in the set
![]() $S$
is K-stable. Let
$S$
is K-stable. Let
![]() $X$
be such a hypersurface.
$X$
be such a hypersurface.
Let
![]() $H$
be the hyperplane class and let
$H$
be the hyperplane class and let
![]() $D{\sim}_{\mathbb{Q}}H{\sim}_{\mathbb{Q}}-\frac{1}{2}K_{X}$
be an effective divisor. By [Reference CheltsovChe01, Lemma 3.1],
$D{\sim}_{\mathbb{Q}}H{\sim}_{\mathbb{Q}}-\frac{1}{2}K_{X}$
be an effective divisor. By [Reference CheltsovChe01, Lemma 3.1],
![]() $(X,D)$
is lc and indeed by [Reference PukhlikovPuk02, Proposition 5] we have
$(X,D)$
is lc and indeed by [Reference PukhlikovPuk02, Proposition 5] we have
![]() $\text{mult}_{x}D\leqslant 1$
for all but finitely many
$\text{mult}_{x}D\leqslant 1$
for all but finitely many
![]() $x\in X$
; hence, by [Reference KollárKol97, (3.14.1)],
$x\in X$
; hence, by [Reference KollárKol97, (3.14.1)],
![]() $(X,D)$
has canonical singularities outside a finite number of points. It follows that every lc center of
$(X,D)$
has canonical singularities outside a finite number of points. It follows that every lc center of
![]() $(X,D)$
is either a divisor on
$(X,D)$
is either a divisor on
![]() $X$
or an isolated point.
$X$
or an isolated point.
On the other hand, let
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
be a movable boundary; then, by the main result of [Reference PukhlikovPuk17], the only possible center of maximal singularities of
$M{\sim}_{\mathbb{Q}}-K_{X}$
be a movable boundary; then, by the main result of [Reference PukhlikovPuk17], the only possible center of maximal singularities of
![]() $(X,M)$
is a linear section of
$(X,M)$
is a linear section of
![]() $X$
of codimension two. It follows that
$X$
of codimension two. It follows that
![]() $(X,M)$
is lc and every lc center of
$(X,M)$
is lc and every lc center of
![]() $(X,M)$
is a linear section of codimension two.
$(X,M)$
is a linear section of codimension two.
Hence,
![]() $X$
is K-semistable by Theorem 1.2. Suppose that it is not K-stable; then by Corollary 3.2 there exist a movable boundary
$X$
is K-semistable by Theorem 1.2. Suppose that it is not K-stable; then by Corollary 3.2 there exist a movable boundary
![]() $M{\sim}_{\mathbb{Q}}-K_{X}$
and an effective divisor
$M{\sim}_{\mathbb{Q}}-K_{X}$
and an effective divisor
![]() $D{\sim}_{\mathbb{Q}}H$
such that
$D{\sim}_{\mathbb{Q}}H$
such that
![]() $(X,M)$
and
$(X,M)$
and
![]() $(X,D)$
have a common lc center. But, by the previous analysis, this is impossible as the lc centers of
$(X,D)$
have a common lc center. But, by the previous analysis, this is impossible as the lc centers of
![]() $(X,M)$
and
$(X,M)$
and
![]() $(X,D)$
always have different dimension. Therefore,
$(X,D)$
always have different dimension. Therefore,
![]() $X$
is K-stable and the proof is complete.◻
$X$
is K-stable and the proof is complete.◻
Proof of Theorem 1.6.
It suffices to show that
![]() $\text{lct}(X;D)\geqslant 1/(n+1)$
for every
$\text{lct}(X;D)\geqslant 1/(n+1)$
for every
![]() $D{\sim}_{\mathbb{Q}}-K_{X}$
. We may assume that
$D{\sim}_{\mathbb{Q}}-K_{X}$
. We may assume that
![]() $D$
is irreducible. Since
$D$
is irreducible. Since
![]() $\text{Cl}(X)$
is generated by
$\text{Cl}(X)$
is generated by
![]() $-K_{X}$
, we have
$-K_{X}$
, we have
![]() $\text{mult}_{\unicode[STIX]{x1D702}}D\leqslant 1$
, where
$\text{mult}_{\unicode[STIX]{x1D702}}D\leqslant 1$
, where
![]() $\unicode[STIX]{x1D702}$
is the generic point of
$\unicode[STIX]{x1D702}$
is the generic point of
![]() $D$
. It follows that
$D$
. It follows that
![]() $(X,D)$
is lc in codimension one [Reference KollárKol97, (3.14.1)] and hence the multiplier ideal
$(X,D)$
is lc in codimension one [Reference KollárKol97, (3.14.1)] and hence the multiplier ideal
![]() ${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)$
(where
${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)$
(where
![]() $0<\unicode[STIX]{x1D716}\ll 1$
) defines a subscheme of codimension at least two. By Nadel vanishing,
$0<\unicode[STIX]{x1D716}\ll 1$
) defines a subscheme of codimension at least two. By Nadel vanishing,
for every
![]() $i>0$
and
$i>0$
and
![]() $r\geqslant 0$
; therefore, by Castelnuovo–Mumford regularity (see e.g. [Reference LazarsfeldLaz04, §1.8]), the sheaf
$r\geqslant 0$
; therefore, by Castelnuovo–Mumford regularity (see e.g. [Reference LazarsfeldLaz04, §1.8]), the sheaf
![]() ${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)\otimes {\mathcal{O}}_{X}(-nK_{X})$
is generated by its global sections and we get a movable linear system
${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)\otimes {\mathcal{O}}_{X}(-nK_{X})$
is generated by its global sections and we get a movable linear system
Suppose that
![]() $\text{lct}(X;D)<1/(n+1)$
, let
$\text{lct}(X;D)<1/(n+1)$
, let
![]() $E$
be an exceptional divisor over
$E$
be an exceptional divisor over
![]() $X$
that computes it, let
$X$
that computes it, let
![]() $A=A_{X}(E)$
and let
$A=A_{X}(E)$
and let
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a projective birational morphism such that the center of
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a projective birational morphism such that the center of
![]() $E$
on
$E$
on
![]() $Y$
is a divisor; then
$Y$
is a divisor; then
![]() $A\in \mathbb{Z}$
(since
$A\in \mathbb{Z}$
(since
![]() $-K_{X}$
is Cartier by assumption) and we have
$-K_{X}$
is Cartier by assumption) and we have
![]() $d=\text{ord}_{E}(D)>(n+1)A$
and
$d=\text{ord}_{E}(D)>(n+1)A$
and
![]() ${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)\subseteq \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}((A-1-\lfloor (1-\unicode[STIX]{x1D716})d\rfloor )E)\subseteq \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}(-(nA+1)E)$
. It follows that
${\mathcal{J}}(X,(1-\unicode[STIX]{x1D716})D)\subseteq \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}((A-1-\lfloor (1-\unicode[STIX]{x1D716})d\rfloor )E)\subseteq \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}(-(nA+1)E)$
. It follows that
![]() $\text{ord}_{E}({\mathcal{M}})\geqslant nA+1$
and hence for the movable boundary
$\text{ord}_{E}({\mathcal{M}})\geqslant nA+1$
and hence for the movable boundary
![]() $M=(1/n){\mathcal{M}}{\sim}_{\mathbb{Q}}-K_{X}$
we have
$M=(1/n){\mathcal{M}}{\sim}_{\mathbb{Q}}-K_{X}$
we have
![]() $\text{ord}_{E}(M)>A$
and
$\text{ord}_{E}(M)>A$
and
![]() $(X,M)$
is not lc, violating our assumption. Thus,
$(X,M)$
is not lc, violating our assumption. Thus,
![]() $\text{lct}(X;D)\geqslant 1/(n+1)$
and we are done.◻
$\text{lct}(X;D)\geqslant 1/(n+1)$
and we are done.◻
Finally we prove the separatedness statement (Theorem 1.7). For this we recall the following criterion.
Lemma 3.3. Let
![]() $f:X\rightarrow C$
,
$f:X\rightarrow C$
,
![]() $g:Y\rightarrow C$
be flat families of
$g:Y\rightarrow C$
be flat families of
![]() $\mathbb{Q}$
-Fano varieties over a smooth pointed curve
$\mathbb{Q}$
-Fano varieties over a smooth pointed curve
![]() $0\in C$
with central fibers
$0\in C$
with central fibers
![]() $X_{0}$
and
$X_{0}$
and
![]() $Y_{0}$
. Assume that
$Y_{0}$
. Assume that
![]() $K_{X}$
and
$K_{X}$
and
![]() $K_{Y}$
are
$K_{Y}$
are
![]() $\mathbb{Q}$
-Cartier and let
$\mathbb{Q}$
-Cartier and let
![]() $D_{X}{\sim}_{\mathbb{Q}}-K_{X}$
,
$D_{X}{\sim}_{\mathbb{Q}}-K_{X}$
,
![]() $D_{Y}{\sim}_{\mathbb{Q}}-K_{Y}$
be effective divisors not containing
$D_{Y}{\sim}_{\mathbb{Q}}-K_{Y}$
be effective divisors not containing
![]() $X_{0}$
or
$X_{0}$
or
![]() $Y_{0}$
. Assume that there exists an isomorphism
$Y_{0}$
. Assume that there exists an isomorphism
over
![]() $C^{\circ }=C\backslash 0$
, that
$C^{\circ }=C\backslash 0$
, that
![]() $(X_{0},D_{X}|_{X_{0}})$
is klt and that
$(X_{0},D_{X}|_{X_{0}})$
is klt and that
![]() $(Y_{0},D_{Y}|_{Y_{0}})$
is lc. Then
$(Y_{0},D_{Y}|_{Y_{0}})$
is lc. Then
![]() $\unicode[STIX]{x1D70C}$
extends to an isomorphism
$\unicode[STIX]{x1D70C}$
extends to an isomorphism
![]() $(X,D_{X})\cong (Y,D_{Y})$
.
$(X,D_{X})\cong (Y,D_{Y})$
.
Proof. This follows from the exact same proof of [Reference Li, Wang and XuLWX19, Theorem 5.2] (see also [Reference Blum and XuBX18, Proposition 3.2]).◻
Proof of Theorem 1.7.
Since birationally superrigid Fano varieties have terminal singularities,
![]() $K_{X}$
and
$K_{X}$
and
![]() $K_{Y}$
are
$K_{Y}$
are
![]() $\mathbb{Q}$
-Cartier by [Reference de Fernex and HacondFH11, Proposition 3.5]. Hence, the result follows from Theorem 2.3 and the following more general statement.◻
$\mathbb{Q}$
-Cartier by [Reference de Fernex and HacondFH11, Proposition 3.5]. Hence, the result follows from Theorem 2.3 and the following more general statement.◻
Lemma 3.4. Let
![]() $f:X\rightarrow C$
,
$f:X\rightarrow C$
,
![]() $g:Y\rightarrow C$
be flat families of
$g:Y\rightarrow C$
be flat families of
![]() $\mathbb{Q}$
-Fano varieties over a smooth pointed curve
$\mathbb{Q}$
-Fano varieties over a smooth pointed curve
![]() $0\in C$
that are isomorphic over
$0\in C$
that are isomorphic over
![]() $C^{\circ }=C\backslash 0$
. Let
$C^{\circ }=C\backslash 0$
. Let
![]() $X_{0}$
and
$X_{0}$
and
![]() $Y_{0}$
be their central fibers. Assume that:
$Y_{0}$
be their central fibers. Assume that:
(i)
 $K_{X}$
and
$K_{X}$
and
 $K_{Y}$
are
$K_{Y}$
are
 $\mathbb{Q}$
-Cartier;
$\mathbb{Q}$
-Cartier;(ii) for every movable boundary
 $M_{X}{\sim}_{\mathbb{Q}}-K_{X_{0}}$
,
$M_{X}{\sim}_{\mathbb{Q}}-K_{X_{0}}$
,
 $(X_{0},M_{X})$
is klt;
$(X_{0},M_{X})$
is klt;(iii) for every movable boundary
 $M_{Y}{\sim}_{\mathbb{Q}}-K_{Y_{0}}$
,
$M_{Y}{\sim}_{\mathbb{Q}}-K_{Y_{0}}$
,
 $(Y_{0},M_{Y})$
is lc.
$(Y_{0},M_{Y})$
is lc.
Then
![]() $X\cong Y$
over
$X\cong Y$
over
![]() $C$
.
$C$
.
Proof. By assumption,
![]() $X$
is birational to
$X$
is birational to
![]() $Y$
over
$Y$
over
![]() $C$
. Let
$C$
. Let
![]() $m$
be a sufficiently large and divisible integer and let
$m$
be a sufficiently large and divisible integer and let
![]() $D_{1}\in |-mK_{X_{0}}|$
,
$D_{1}\in |-mK_{X_{0}}|$
,
![]() $D_{2}\in |-mK_{Y_{0}}|$
be general divisors in the corresponding linear system. Choose effective divisors
$D_{2}\in |-mK_{Y_{0}}|$
be general divisors in the corresponding linear system. Choose effective divisors
![]() $D_{X,1}\sim -mK_{X}$
,
$D_{X,1}\sim -mK_{X}$
,
![]() $D_{Y,2}\sim -mK_{Y}$
not containing
$D_{Y,2}\sim -mK_{Y}$
not containing
![]() $X_{0}$
or
$X_{0}$
or
![]() $Y_{0}$
such that
$Y_{0}$
such that
![]() $D_{X,1}|_{X_{0}}=D_{1}$
and
$D_{X,1}|_{X_{0}}=D_{1}$
and
![]() $D_{Y,2}|_{Y_{0}}=D_{2}$
. Let
$D_{Y,2}|_{Y_{0}}=D_{2}$
. Let
![]() $D_{Y,1}$
and
$D_{Y,1}$
and
![]() $D_{X,2}$
be their strict transforms to the other family. Since
$D_{X,2}$
be their strict transforms to the other family. Since
![]() $X$
and
$X$
and
![]() $Y$
are isomorphic over
$Y$
are isomorphic over
![]() $C^{\circ }$
, we have
$C^{\circ }$
, we have
![]() $D_{Y,1}\sim -mK_{Y}+W$
, where
$D_{Y,1}\sim -mK_{Y}+W$
, where
![]() $W$
is supported on
$W$
is supported on
![]() $Y_{0}$
; but, as
$Y_{0}$
; but, as
![]() $Y_{0}$
is irreducible, we have
$Y_{0}$
is irreducible, we have
![]() $W=\ell Y_{0}=\ell g^{\ast }(0)$
for some integer
$W=\ell Y_{0}=\ell g^{\ast }(0)$
for some integer
![]() $\ell$
. Since the question is local around
$\ell$
. Since the question is local around
![]() $0\in C$
, we may shrink
$0\in C$
, we may shrink
![]() $C$
so that
$C$
so that
![]() $Y_{0}\sim 0$
and thus
$Y_{0}\sim 0$
and thus
![]() $D_{Y,1}\sim -mK_{Y}$
. Similarly, we also have
$D_{Y,1}\sim -mK_{Y}$
. Similarly, we also have
![]() $D_{X,2}\sim -mK_{X}$
. Let
$D_{X,2}\sim -mK_{X}$
. Let
![]() $D_{1}^{\prime }=D_{Y,1}|_{Y_{0}}$
and
$D_{1}^{\prime }=D_{Y,1}|_{Y_{0}}$
and
![]() $D_{2}^{\prime }=D_{X,2}|_{X_{0}}$
. Let
$D_{2}^{\prime }=D_{X,2}|_{X_{0}}$
. Let
![]() ${\mathcal{M}}_{X}$
be the linear system spanned by
${\mathcal{M}}_{X}$
be the linear system spanned by
![]() $D_{X,1}$
and
$D_{X,1}$
and
![]() $D_{X,2}$
and let
$D_{X,2}$
and let
![]() $M_{X}=(1/m){\mathcal{M}}_{X}{\sim}_{\mathbb{Q}}-K_{X}$
. Similarly, we have
$M_{X}=(1/m){\mathcal{M}}_{X}{\sim}_{\mathbb{Q}}-K_{X}$
. Similarly, we have
![]() ${\mathcal{M}}_{Y}$
and
${\mathcal{M}}_{Y}$
and
![]() $M_{Y}{\sim}_{\mathbb{Q}}-K_{Y}$
. As
$M_{Y}{\sim}_{\mathbb{Q}}-K_{Y}$
. As
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
are general,
$D_{2}$
are general,
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}^{\prime }$
have no common components; hence, the restriction of
$D_{2}^{\prime }$
have no common components; hence, the restriction of
![]() $M_{X}$
to
$M_{X}$
to
![]() $X_{0}$
is still a movable boundary and, therefore, by our second assumption,
$X_{0}$
is still a movable boundary and, therefore, by our second assumption,
![]() $(X_{0},M_{X}|_{X_{0}})$
is klt. Similarly,
$(X_{0},M_{X}|_{X_{0}})$
is klt. Similarly,
![]() $(Y_{0},M_{Y}|_{Y_{0}})$
is lc and we conclude by Lemma 3.3.◻
$(Y_{0},M_{Y}|_{Y_{0}})$
is lc and we conclude by Lemma 3.3.◻
Acknowledgements
The authors would like to thank their advisor János Kollár for constant support, encouragement and numerous inspiring conversations. The first author wishes to thank Harold Blum for a useful discussion as well. Both authors also wish to thank Yuchen Liu for helpful discussions.