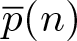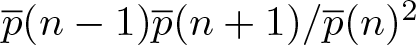1. Introduction
Partition of a positive integer n is a non-increasing sequence of positive integers whose sum is n. Let p(n) denote the number of partitions of n. Recall that a sequence ![]() $\{a_n\}_{n\geq0}$ is called log-concave if
$\{a_n\}_{n\geq0}$ is called log-concave if
Moreover, this sequence is said to be asymptotically r-log-concave if there exists N such that
 \begin{align*}
{\hat{\mathscr{L}}}\{a_n\}_{n\geq N},\ {\hat{\mathscr{L}}}^2\{a_n\}_{n\geq N}, \ldots, {\hat{\mathscr{L}}}^r\{a_n\}_{n\geq N}
\end{align*}
\begin{align*}
{\hat{\mathscr{L}}}\{a_n\}_{n\geq N},\ {\hat{\mathscr{L}}}^2\{a_n\}_{n\geq N}, \ldots, {\hat{\mathscr{L}}}^r\{a_n\}_{n\geq N}
\end{align*}are all non-negative sequences, where
 \begin{equation*}{\hat{\mathscr{L}}}\{a_n\}_{n\geq 0}=\{a_{n+1}^2-a_na_{n+2}\}_{n\geq0}\quad\text{and}
\quad
{\hat{\mathscr{L}}}^k\{a_n\}_{n\geq 0}={\hat{\mathscr{L}}}\left({\hat{\mathscr{L}}}^{k-1}\{a_n\}_{n\geq 0}\right).\end{equation*}
\begin{equation*}{\hat{\mathscr{L}}}\{a_n\}_{n\geq 0}=\{a_{n+1}^2-a_na_{n+2}\}_{n\geq0}\quad\text{and}
\quad
{\hat{\mathscr{L}}}^k\{a_n\}_{n\geq 0}={\hat{\mathscr{L}}}\left({\hat{\mathscr{L}}}^{k-1}\{a_n\}_{n\geq 0}\right).\end{equation*}Based on the Hardy–Ramanujan–Rademacher formula [Reference Andrews1, Reference Hardy8, Reference Hardy and Ramanujan9, Reference Rademacher18] and the error estimation given by Lehmer [Reference Lehmer14, Reference Lehmer15], DeSalvo and Pak [Reference DeSalvo and Pak6] showed that the partition function p(n) is log-concave for all n > 25, which was conjectured by Chen [Reference Chen2]. Consequently, Chen, Wang and Xie proved the DeSalvo–Pak conjecture that states
Theorem 1.1 (Conjecture 1.3, [Reference Chen, Wang and Xie4])
For ![]() $n \geq 45$, we have
$n \geq 45$, we have
 \begin{equation*}
\dfrac{p(n-1)}{p(n)}\left(1+\dfrac{\pi}{\sqrt{24}n^{3/2}}\right)\gt\dfrac{p(n)}{p(n+1)}.
\end{equation*}
\begin{equation*}
\dfrac{p(n-1)}{p(n)}\left(1+\dfrac{\pi}{\sqrt{24}n^{3/2}}\right)\gt\dfrac{p(n)}{p(n+1)}.
\end{equation*} Recently, Chen et al. [Reference Chen, Jia and Wang3] proceeded further to show that ![]() $\{p(n)\}_{n \geq 95}$ satisfies the higher order Turán inequality and to formulate a conjecture [Reference Chen, Jia and Wang3, Conjecture 1.2] in a somewhat similar spirit to Theorem 1.1, which was settled by Larson and Wagner [Reference Larson and Wagner13, Theorem 1.2]. Hou and Zhang [Reference Hou and Zhang11] proved the asymptotic r-log-concavity of p(n), and as a consequence, they showed that
$\{p(n)\}_{n \geq 95}$ satisfies the higher order Turán inequality and to formulate a conjecture [Reference Chen, Jia and Wang3, Conjecture 1.2] in a somewhat similar spirit to Theorem 1.1, which was settled by Larson and Wagner [Reference Larson and Wagner13, Theorem 1.2]. Hou and Zhang [Reference Hou and Zhang11] proved the asymptotic r-log-concavity of p(n), and as a consequence, they showed that ![]() $\{p(n)\}_{n \geq 221}$ is 2-log-concave, whereas an alternative approach through studying determinant of certain class of matrix can be found in [Reference Jia and Wang12].
$\{p(n)\}_{n \geq 221}$ is 2-log-concave, whereas an alternative approach through studying determinant of certain class of matrix can be found in [Reference Jia and Wang12].
The overpartition function also reflects similar log-behavior. Recall an overpartition [Reference Corteel and Lovejoy5] of a non-negative integer n is a partition of n where the first occurrence of each distinct part may be overlined. Let ![]() ${\overline{p}}(n)$ denote the number of overpartitions of n. Zuckerman [Reference Zuckerman20] gave a formula for the overpartition function, which was considered by Sills [Reference Sills19] as a Rademacher-type convergent series
${\overline{p}}(n)$ denote the number of overpartitions of n. Zuckerman [Reference Zuckerman20] gave a formula for the overpartition function, which was considered by Sills [Reference Sills19] as a Rademacher-type convergent series
 \begin{align}
{\overline{p}}(n)=\frac{1}{2\pi}\sum_{k=1\atop 2\nmid k}^\infty\sqrt{k}\sum_{h=0\atop (h,k)=1}^k
\frac{\omega(h,k)^2}{\omega(2h,k)}\,{\rm e}^{-\frac{2\pi inh}{k}}\,\frac{\mathrm{d}}{\mathrm{d}n}
\left(\frac{\sinh\frac{\pi\sqrt{n}}{k}}{\sqrt{n}}\right),
\end{align}
\begin{align}
{\overline{p}}(n)=\frac{1}{2\pi}\sum_{k=1\atop 2\nmid k}^\infty\sqrt{k}\sum_{h=0\atop (h,k)=1}^k
\frac{\omega(h,k)^2}{\omega(2h,k)}\,{\rm e}^{-\frac{2\pi inh}{k}}\,\frac{\mathrm{d}}{\mathrm{d}n}
\left(\frac{\sinh\frac{\pi\sqrt{n}}{k}}{\sqrt{n}}\right),
\end{align}where
 \begin{equation*}\omega(h,k):=\exp\left(\pi i\sum_{r=1}^{k-1}\frac{r}{k}\left(\frac{hr}{k}
-\left\lfloor\frac{hr}{k}\right\rfloor-\frac{1}{2}\right)\right)\end{equation*}
\begin{equation*}\omega(h,k):=\exp\left(\pi i\sum_{r=1}^{k-1}\frac{r}{k}\left(\frac{hr}{k}
-\left\lfloor\frac{hr}{k}\right\rfloor-\frac{1}{2}\right)\right)\end{equation*}for positive integers h and k.
Let ![]() ${\widehat{\mu}}(n):=\pi\sqrt{n}$. From this Rademacher-type series (1.1), Engel [Reference Engel7] provided an error term for the overpartition function
${\widehat{\mu}}(n):=\pi\sqrt{n}$. From this Rademacher-type series (1.1), Engel [Reference Engel7] provided an error term for the overpartition function
 \begin{align*}
{\overline{p}}(n)=\frac{1}{2\pi}\sum_{k=1\atop 2\nmid k}^N\sqrt{k}\sum_{h=0\atop (h,k)=1}^k
\frac{\omega(h,k)^2}{\omega(2h,k)}\,{\rm e}^{-\frac{2\pi inh}{k}}\,\frac{\mathrm{d}}{\mathrm{d}n}
\left(\frac{\sinh\frac{{\widehat{\mu}}(n)}{k}}{\sqrt{n}}\right)+R_2(n,N),
\end{align*}
\begin{align*}
{\overline{p}}(n)=\frac{1}{2\pi}\sum_{k=1\atop 2\nmid k}^N\sqrt{k}\sum_{h=0\atop (h,k)=1}^k
\frac{\omega(h,k)^2}{\omega(2h,k)}\,{\rm e}^{-\frac{2\pi inh}{k}}\,\frac{\mathrm{d}}{\mathrm{d}n}
\left(\frac{\sinh\frac{{\widehat{\mu}}(n)}{k}}{\sqrt{n}}\right)+R_2(n,N),
\end{align*}where ![]() $R_2(n,N)$ satisfies
$R_2(n,N)$ satisfies
 \begin{align*}
\left|R_2(n,N)\right|\leq \frac{N^{\frac{5}{2}}}{n{\widehat{\mu}}(n)}\,
\sinh\left(\frac{{\widehat{\mu}}(n)}{N}\right).
\end{align*}
\begin{align*}
\left|R_2(n,N)\right|\leq \frac{N^{\frac{5}{2}}}{n{\widehat{\mu}}(n)}\,
\sinh\left(\frac{{\widehat{\mu}}(n)}{N}\right).
\end{align*}In particular, when N = 3, we have
 \begin{align}
{\overline{p}}(n)=\frac{1}{8n}\left[\left(1+\frac{1}{{\widehat{\mu}}(n)}\right){\rm e}^{-{\widehat{\mu}}(n)}+\left(1-\frac{1}{{\widehat{\mu}}(n)}\right){\rm e}^{{\widehat{\mu}}(n)}\right]
+R_2(n,3),
\end{align}
\begin{align}
{\overline{p}}(n)=\frac{1}{8n}\left[\left(1+\frac{1}{{\widehat{\mu}}(n)}\right){\rm e}^{-{\widehat{\mu}}(n)}+\left(1-\frac{1}{{\widehat{\mu}}(n)}\right){\rm e}^{{\widehat{\mu}}(n)}\right]
+R_2(n,3),
\end{align}where
 \begin{align}
\left|R_2(n,3)\right|\leq \frac{3^{\frac{5}{2}}}{n{\widehat{\mu}}(n)}\,
\sinh\left(\frac{{\widehat{\mu}}(n)}{3}\right)\leq \frac{3^{\frac{5}{2}}\,{\rm e}^{\frac{{\widehat{\mu}}(n)}{3}}}{2n{\widehat{\mu}}(n)}.
\end{align}
\begin{align}
\left|R_2(n,3)\right|\leq \frac{3^{\frac{5}{2}}}{n{\widehat{\mu}}(n)}\,
\sinh\left(\frac{{\widehat{\mu}}(n)}{3}\right)\leq \frac{3^{\frac{5}{2}}\,{\rm e}^{\frac{{\widehat{\mu}}(n)}{3}}}{2n{\widehat{\mu}}(n)}.
\end{align} Similar to the work done in the world of partitions, Engel initiated the study of log-concavity property of the overpartition function in his work [Reference Engel7]. The second author and Liu established the analog of Theorem 1.1 in context of overpartitions in [Reference Liu and Zhang16, Equation (1.6)]. They also proved the higher-order Turán property of ![]() ${\overline{p}}(n)$ for
${\overline{p}}(n)$ for ![]() $n \geq 16$ (see [Reference Liu and Zhang16, Theorem 1.2]). Following the treatment in [Reference Jia and Wang12], the first author [Reference Mukherjee17, Theorem 1.7] laid out a proof that
$n \geq 16$ (see [Reference Liu and Zhang16, Theorem 1.2]). Following the treatment in [Reference Jia and Wang12], the first author [Reference Mukherjee17, Theorem 1.7] laid out a proof that ![]() $\{{\overline{p}}(n)\}_{n \geq 42}$ is 2-log-concave.
$\{{\overline{p}}(n)\}_{n \geq 42}$ is 2-log-concave.
In this paper, our main goal is to prove the asymptotic r-log-concavity for the overpartition function, stated in Theorem 1.2. In the proof of Theorem 1.2, we give a bound for ![]() ${\overline{p}}(n+1)/{\overline{p}}(n)$ and an asymptotic expression of
${\overline{p}}(n+1)/{\overline{p}}(n)$ and an asymptotic expression of ![]() ${\overline{p}}(n-1){\overline{p}}(n+1)/{\overline{p}}(n)^2$. More precisely, we shall study the asymptotic growth of the quotient
${\overline{p}}(n-1){\overline{p}}(n+1)/{\overline{p}}(n)^2$. More precisely, we shall study the asymptotic growth of the quotient ![]() ${\overline{p}}(n-1){\overline{p}}(n+1)/{\overline{p}}(n)^2$ up to n −4, stated in Theorem 1.3. This in turn helps for a further study of certain quotients stated in Theorems 1.6 and 1.9. A host of inequalities for overpartition function, see Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11, appear as a special case of the theorems and are analogs of results in the case of p(n). The primary objective of this paper is to exploit the proof of Theorem 1.2, so that one can bring in all the proofs of Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11 under a unique structure, unlike the different array of structure of proofs for inequalities in the context of the partition function.
${\overline{p}}(n-1){\overline{p}}(n+1)/{\overline{p}}(n)^2$ up to n −4, stated in Theorem 1.3. This in turn helps for a further study of certain quotients stated in Theorems 1.6 and 1.9. A host of inequalities for overpartition function, see Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11, appear as a special case of the theorems and are analogs of results in the case of p(n). The primary objective of this paper is to exploit the proof of Theorem 1.2, so that one can bring in all the proofs of Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11 under a unique structure, unlike the different array of structure of proofs for inequalities in the context of the partition function.
Theorem 1.2. The sequence ![]() $\{{\overline{p}}(n)\}_{n\geq1}$ is asymptotically r-log-concave for any positive integer r.
$\{{\overline{p}}(n)\}_{n\geq1}$ is asymptotically r-log-concave for any positive integer r.
We need some notation to state our next result. Define the sequence ![]() ${\overline{u}}_n$ by
${\overline{u}}_n$ by
 \begin{equation*}{\overline{u}}_n:=\dfrac{{\overline{p}}(n-1){\overline{p}}(n+1)}{{\overline{p}}(n)^2}.\end{equation*}
\begin{equation*}{\overline{u}}_n:=\dfrac{{\overline{p}}(n-1){\overline{p}}(n+1)}{{\overline{p}}(n)^2}.\end{equation*} Theorem 1.2 is entangled with Theorem 1.3 by its proof methodology. Precisely, Theorem 1.2 requires the full asymptotic expansion of ![]() ${\overline{u}}_n$, and by error bound computation for the asymptotic expansion after partial sums of the first seven terms, we get Theorem 1.3.
${\overline{u}}_n$, and by error bound computation for the asymptotic expansion after partial sums of the first seven terms, we get Theorem 1.3.
Theorem 1.3. For all ![]() $n \geq 37$, we have
$n \geq 37$, we have
 \begin{equation}
s_n-\dfrac{15}{n^4}\lt{\overline{u}}_n \lt s_n+\dfrac{20}{n^4},
\end{equation}
\begin{equation}
s_n-\dfrac{15}{n^4}\lt{\overline{u}}_n \lt s_n+\dfrac{20}{n^4},
\end{equation}where
 \begin{equation*}
s_n:=1-\dfrac{\pi}{4n^{3/2}}+\dfrac{1}{n^2}-\dfrac{3}{4\pi n^{5/2}}+\dfrac{-32+\pi^4}{32\pi^2}\dfrac{1}{n^3}-\left(\dfrac{5}{4\pi^3}+\dfrac{21\pi}{64}\right)\dfrac{1}{n^{7/2}}.
\end{equation*}
\begin{equation*}
s_n:=1-\dfrac{\pi}{4n^{3/2}}+\dfrac{1}{n^2}-\dfrac{3}{4\pi n^{5/2}}+\dfrac{-32+\pi^4}{32\pi^2}\dfrac{1}{n^3}-\left(\dfrac{5}{4\pi^3}+\dfrac{21\pi}{64}\right)\dfrac{1}{n^{7/2}}.
\end{equation*} Theorem 1.3. has manifold applications to various types of inequalities for ![]() ${\overline{p}}(n)$ arising from different contexts. Log-concavity and its companion inequality for
${\overline{p}}(n)$ arising from different contexts. Log-concavity and its companion inequality for ![]() ${\overline{p}}(n)$, given in Corollaries 1.4 and 1.5, are direct consequences of Theorem 1.3.
${\overline{p}}(n)$, given in Corollaries 1.4 and 1.5, are direct consequences of Theorem 1.3.
Corollary 1.4. ([Reference Engel7, Theorem 1.2])
![]() $\{{\overline{p}}(n)\}_{n \geq 4}$ is log-concave.
$\{{\overline{p}}(n)\}_{n \geq 4}$ is log-concave.
Corollary 1.5. ([Reference Liu and Zhang16, Equation (1.6)])
For ![]() $n \geq 2$,
$n \geq 2$,
 \begin{equation}
\dfrac{{\overline{p}}(n-1)}{{\overline{p}}(n)}\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt\dfrac{{\overline{p}}(n)}{{\overline{p}}(n+1)}.
\end{equation}
\begin{equation}
\dfrac{{\overline{p}}(n-1)}{{\overline{p}}(n)}\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt\dfrac{{\overline{p}}(n)}{{\overline{p}}(n+1)}.
\end{equation} Applying Theorem 1.3, we obtain an inequality for the quotient  $\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})}$ in Theorem 1.6 so as to prove 2-log-concavity and its companion inequality for
$\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})}$ in Theorem 1.6 so as to prove 2-log-concavity and its companion inequality for ![]() ${\overline{p}}(n)$, given in Corollaries 1.7 and 1.8.
${\overline{p}}(n)$, given in Corollaries 1.7 and 1.8.
Theorem 1.6 For all ![]() $n \geq 31$,
$n \geq 31$,
 \begin{equation}
t_n-\dfrac{120}{n^{5/2}}\lt \dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})} \lt t_n+\dfrac{120}{n^{5/2}},
\end{equation}
\begin{equation}
t_n-\dfrac{120}{n^{5/2}}\lt \dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})} \lt t_n+\dfrac{120}{n^{5/2}},
\end{equation}where
 \begin{equation*}
t_n:=1+\dfrac{\pi}{2n^{3/2}}-\dfrac{7}{2n^2}.
\end{equation*}
\begin{equation*}
t_n:=1+\dfrac{\pi}{2n^{3/2}}-\dfrac{7}{2n^2}.
\end{equation*}Corollary 1.7. ([Reference Mukherjee17, Theorem 1.7])
![]() $\{{\overline{p}}(n)\}_{n \geq 42}$ is 2-log-concave.
$\{{\overline{p}}(n)\}_{n \geq 42}$ is 2-log-concave.
Corollary 1.8. For ![]() $n \geq 52$,
$n \geq 52$,
 \begin{equation}
{\overline{u}}^2_n (1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1}) \Bigl(1+\dfrac{\pi}{2n^{3/2}}\Bigr)\gt(1-{\overline{u}}_n)^2.
\end{equation}
\begin{equation}
{\overline{u}}^2_n (1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1}) \Bigl(1+\dfrac{\pi}{2n^{3/2}}\Bigr)\gt(1-{\overline{u}}_n)^2.
\end{equation} As a final application of Theorem 1.3, we get Theorem 1.9 which helps us to retrieve the higher-order Turán inequality along with its companion inequality for ![]() ${\overline{p}}(n)$, stated in Corollaries 1.10 and 1.11.
${\overline{p}}(n)$, stated in Corollaries 1.10 and 1.11.
Theorem 1.9 For all ![]() $n \geq 2$,
$n \geq 2$,
 \begin{equation}
v_n-\dfrac{120}{n^{5/2}}\lt \dfrac{4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1})}{(1-{\overline{u}}_n{\overline{u}}_{n+1})^2} \lt v_n+\dfrac{101}{n^{5/2}},
\end{equation}
\begin{equation}
v_n-\dfrac{120}{n^{5/2}}\lt \dfrac{4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1})}{(1-{\overline{u}}_n{\overline{u}}_{n+1})^2} \lt v_n+\dfrac{101}{n^{5/2}},
\end{equation}where
 \begin{equation*}
v_n:=1+\dfrac{\pi}{4n^{3/2}}-\dfrac{25}{16n^2}.
\end{equation*}
\begin{equation*}
v_n:=1+\dfrac{\pi}{4n^{3/2}}-\dfrac{25}{16n^2}.
\end{equation*}Corollary 1.10. ([Reference Liu and Zhang16, Theorem 1.2])
![]() $\{{\overline{p}}(n)\}_{n \geq 16}$ satisfies the higher-order Turán inequalities.
$\{{\overline{p}}(n)\}_{n \geq 16}$ satisfies the higher-order Turán inequalities.
Corollary 1.11. For ![]() $n \geq 2$,
$n \geq 2$,
 \begin{equation}
(1-{\overline{u}}_n{\overline{u}}_{n+1})^2 \left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1}).
\end{equation}
\begin{equation}
(1-{\overline{u}}_n{\overline{u}}_{n+1})^2 \left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1}).
\end{equation} The paper is organized as follows. The proof of Theorem 1.2 is given in ![]() $\S$ 2. First we obtain an error estimation of
$\S$ 2. First we obtain an error estimation of ![]() ${\overline{p}}(n)$ in
${\overline{p}}(n)$ in ![]() $\S$ 2.1. We then compute the asymptotic expression of
$\S$ 2.1. We then compute the asymptotic expression of ![]() ${\overline{u}}_n$ by studying the bounds for the ratio
${\overline{u}}_n$ by studying the bounds for the ratio ![]() ${\overline{p}}(n+1)/{\overline{p}}(n)$ in
${\overline{p}}(n+1)/{\overline{p}}(n)$ in ![]() $\S$ 2.2. The proof of Theorems 1.3, 1.6 and 1.9 and Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11 are given in
$\S$ 2.2. The proof of Theorems 1.3, 1.6 and 1.9 and Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11 are given in ![]() $\S$ 3.
$\S$ 3.
2. Proof of Theorem 1.2
In this section, we utilize the Rademacher-type convergent series and the error estimation given by Engel to derive an estimation for ![]() ${\overline{p}}(n)$. In view of Equation (1.2),
${\overline{p}}(n)$. In view of Equation (1.2), ![]() ${\overline{p}}(n)$ can be written as
${\overline{p}}(n)$ can be written as
 \begin{align}
{\overline{p}}(n)={\widehat{T}}(n)+{\widehat{R}}(n),
\end{align}
\begin{align}
{\overline{p}}(n)={\widehat{T}}(n)+{\widehat{R}}(n),
\end{align}where
 \begin{align}
{\widehat{T}}(n)&:=\frac{1}{8n}\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)\,{\rm e}^{{\widehat{\mu}}(n)},
\end{align}
\begin{align}
{\widehat{T}}(n)&:=\frac{1}{8n}\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)\,{\rm e}^{{\widehat{\mu}}(n)},
\end{align} \begin{align}
{\widehat{R}}(n)&:=\frac{1}{8n}\left(1+\frac{1}{{\widehat{\mu}}(n)}\right)\,{\rm e}^{-{\widehat{\mu}}(n)}+R_2(n,3).
\end{align}
\begin{align}
{\widehat{R}}(n)&:=\frac{1}{8n}\left(1+\frac{1}{{\widehat{\mu}}(n)}\right)\,{\rm e}^{-{\widehat{\mu}}(n)}+R_2(n,3).
\end{align}2.1. Estimation of the error term for  ${\overline{p}}(n)$
${\overline{p}}(n)$
In this section, our goal is to get an upper bound for the absolute value of the error term  $\widehat{R}(n)/\widehat{T}(n)$ which in turn helps to get an estimation for the error term of
$\widehat{R}(n)/\widehat{T}(n)$ which in turn helps to get an estimation for the error term of ![]() $\overline{p}(n)$. To obtain the error estimation of
$\overline{p}(n)$. To obtain the error estimation of ![]() ${\overline{p}}(n)$, we need to introduce the following lemma.
${\overline{p}}(n)$, we need to introduce the following lemma.
Lemma 2.1. For any integer ![]() $m\geq1$, there exists a real number
$m\geq1$, there exists a real number
 \begin{equation*}
N_0(m) :=
\begin{cases}
1, &\quad \text{if}\ m=1,\\
2m\, \log m-m\, \log\, \log m, & \quad \text{if}\ m \geq 2,
\end{cases}
\end{equation*}
\begin{equation*}
N_0(m) :=
\begin{cases}
1, &\quad \text{if}\ m=1,\\
2m\, \log m-m\, \log\, \log m, & \quad \text{if}\ m \geq 2,
\end{cases}
\end{equation*}such that
Proof. For m = 1, it is immediate that ![]() $N_0(m)=1$. For
$N_0(m)=1$. For ![]() $m \geq 2$, rewrite the inequality
$m \geq 2$, rewrite the inequality ![]() $x^m\,{\rm e}^{-x}\lt1$ as
$x^m\,{\rm e}^{-x}\lt1$ as ![]() $f(x):=x-m\,\log x\gt0$. Now f(x) is strictly increasing for x > m. In order to show
$f(x):=x-m\,\log x\gt0$. Now f(x) is strictly increasing for x > m. In order to show ![]() $f(x)\gt0$ for
$f(x)\gt0$ for ![]() $x\geq N_0(m)$, first we show that
$x\geq N_0(m)$, first we show that ![]() $N_0(m)\gt m$ and then it is enough to show
$N_0(m)\gt m$ and then it is enough to show ![]() $f(N_0(m))\gt0$. To prove
$f(N_0(m))\gt0$. To prove ![]() $N_0(m)\gt m$, it is equivalent to show
$N_0(m)\gt m$, it is equivalent to show ![]() $m^2\gt{\rm e}\,\log m$, which holds for
$m^2\gt{\rm e}\,\log m$, which holds for ![]() $m \geq 2$. Next, we observe that
$m \geq 2$. Next, we observe that
 \begin{equation}
f(N_0(m))\gt0 \Leftrightarrow\log m \gt \log 2+2 \log\, \log m+\log \left(1-\dfrac{\log\, \log m}{2\log m}\right)\nonumber\\.
\end{equation}
\begin{equation}
f(N_0(m))\gt0 \Leftrightarrow\log m \gt \log 2+2 \log\, \log m+\log \left(1-\dfrac{\log\, \log m}{2\log m}\right)\nonumber\\.
\end{equation} For ![]() $m \geq 3$, we have
$m \geq 3$, we have  $\log \left(1-\dfrac{\log \,\log m}{2\,\log m}\right) \lt0$, and hence, it is sufficient to prove
$\log \left(1-\dfrac{\log \,\log m}{2\,\log m}\right) \lt0$, and hence, it is sufficient to prove
which holds for ![]() $m \geq 14$. Therefore,
$m \geq 14$. Therefore, ![]() $f(N_0(m))\gt0$ for all
$f(N_0(m))\gt0$ for all ![]() $m \geq 14$, and we conclude the proof by checking numerically that
$m \geq 14$, and we conclude the proof by checking numerically that ![]() $f(N_0(m))\gt0$ for
$f(N_0(m))\gt0$ for ![]() $2\leq m \leq 13$.
$2\leq m \leq 13$.
With the aid of Lemma 2.1, we obtain the following result.
Theorem 2.2. For any integer ![]() $m\geq2$, there exists an integer
$m\geq2$, there exists an integer ![]() $N_1(m)$ with
$N_1(m)$ with
 \begin{align*}
N_1(m):=\max\left\{184,\left\lceil\dfrac{9}{4\pi^2} N^2_0(m)\right\rceil\right\},
\end{align*}
\begin{align*}
N_1(m):=\max\left\{184,\left\lceil\dfrac{9}{4\pi^2} N^2_0(m)\right\rceil\right\},
\end{align*}such that for all ![]() $n \geq N_1(m)$,
$n \geq N_1(m)$,
 \begin{align*}
\left|{\widehat{y}}_n\right|\lt\left(\frac{3}{2}\right)^{m+1}{\widehat{\mu}}(n)^{-m},
\end{align*}
\begin{align*}
\left|{\widehat{y}}_n\right|\lt\left(\frac{3}{2}\right)^{m+1}{\widehat{\mu}}(n)^{-m},
\end{align*}where  ${\widehat{y}}_n:={\widehat{R}}(n)/{\widehat{T}}(n)$.
${\widehat{y}}_n:={\widehat{R}}(n)/{\widehat{T}}(n)$.
Proof. Using Equation (1.3) in addition to Equations (2.2) and (2.3), we have
 \begin{align}
{\widehat{y}}_{n}\leq {\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}}\left({\widehat{T}}_1(n)+{\widehat{R}}_1(n)\right),
\end{align}
\begin{align}
{\widehat{y}}_{n}\leq {\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}}\left({\widehat{T}}_1(n)+{\widehat{R}}_1(n)\right),
\end{align}where
 \begin{align*}
{\widehat{T}}_1(n):=\frac{{\widehat{\mu}}(n)+1}{{\widehat{\mu}}(n)-1}\,{\rm e}^{-\frac{4{\widehat{\mu}}(n)}{3}},
\qquad
{\widehat{R}}_1(n):=4\cdot3^{\frac{5}{2}}\frac{1}{{\widehat{\mu}}(n)-1}.
\end{align*}
\begin{align*}
{\widehat{T}}_1(n):=\frac{{\widehat{\mu}}(n)+1}{{\widehat{\mu}}(n)-1}\,{\rm e}^{-\frac{4{\widehat{\mu}}(n)}{3}},
\qquad
{\widehat{R}}_1(n):=4\cdot3^{\frac{5}{2}}\frac{1}{{\widehat{\mu}}(n)-1}.
\end{align*} From the fact that  ${\widehat{T}}_1(n)$ and
${\widehat{T}}_1(n)$ and  ${\widehat{R}}_1(n)$ are decreasing functions of n for
${\widehat{R}}_1(n)$ are decreasing functions of n for ![]() $n\geq 184$, it follows that
$n\geq 184$, it follows that
 \begin{align*}
{\widehat{T}}_1(n)+{\widehat{R}}_1(n)\leq{\widehat{T}}_1(184)+{\widehat{R}}_1(184)\lt\frac{3}{2}.
\end{align*}
\begin{align*}
{\widehat{T}}_1(n)+{\widehat{R}}_1(n)\leq{\widehat{T}}_1(184)+{\widehat{R}}_1(184)\lt\frac{3}{2}.
\end{align*}Therefore,
 \begin{align*}
\left|{\widehat{y}}_n\right|&\lt\frac{3}{2}\,{\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}},\qquad\text{for}\ n\geq 184.
\end{align*}
\begin{align*}
\left|{\widehat{y}}_n\right|&\lt\frac{3}{2}\,{\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}},\qquad\text{for}\ n\geq 184.
\end{align*} According to Lemma 2.1, there exists a real number ![]() $N_0(m)$, such that for
$N_0(m)$, such that for  $\frac{2}{3}{\widehat{\mu}}(n)\geq N_0(m),$
$\frac{2}{3}{\widehat{\mu}}(n)\geq N_0(m),$
 \begin{align*}
{\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}}\lt\left(\frac{3}{2}\right)^m{\widehat{\mu}}(n)^{-m}.
\end{align*}
\begin{align*}
{\rm e}^{-\frac{2{\widehat{\mu}}(n)}{3}}\lt\left(\frac{3}{2}\right)^m{\widehat{\mu}}(n)^{-m}.
\end{align*}On the other side,
 \begin{align*}
n^{\frac{1}{2}}=\frac{{\widehat{\mu}}(n)}{\pi}.
\end{align*}
\begin{align*}
n^{\frac{1}{2}}=\frac{{\widehat{\mu}}(n)}{\pi}.
\end{align*}Therefore, when
 \begin{align*}
n\geq\max\left\{184, \Biggl\lceil\dfrac{9}{4\pi^2} N^2_0(m)\Biggr\rceil\right\}= N_1(m),
\end{align*}
\begin{align*}
n\geq\max\left\{184, \Biggl\lceil\dfrac{9}{4\pi^2} N^2_0(m)\Biggr\rceil\right\}= N_1(m),
\end{align*}we have
 \begin{align*}
{\widehat{\mu}}(n)\gt\dfrac{3}{2}N_0(m),
\end{align*}
\begin{align*}
{\widehat{\mu}}(n)\gt\dfrac{3}{2}N_0(m),
\end{align*}which completes the proof.
2.2. Bounds for the ratio  ${\overline{p}}(n+1)/{\overline{p}}(n)$
${\overline{p}}(n+1)/{\overline{p}}(n)$
In order to obtain an estimation of ![]() ${\overline{p}}(n+1)/{\overline{p}}(n)$, we need the following lower and upper bounds for
${\overline{p}}(n+1)/{\overline{p}}(n)$, we need the following lower and upper bounds for  ${\widehat{T}}(n+1)/{\widehat{T}}(n)$.
${\widehat{T}}(n+1)/{\widehat{T}}(n)$.
Lemma 2.3. For any integer m, let ![]() $m^\prime:=\lfloor\frac{m}{2}\rfloor$,
$m^\prime:=\lfloor\frac{m}{2}\rfloor$, ![]() ${\widehat{\nu}}(n):={\widehat{\mu}}(n)({\widehat{\mu}}_1(n)-1)$ and
${\widehat{\nu}}(n):={\widehat{\mu}}(n)({\widehat{\mu}}_1(n)-1)$ and
 \begin{align*}
{\widehat{\mu}}_1(n)&:=\sum_{k=0}^{m^\prime}{1/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k},\qquad
{\widehat{\varepsilon}}_1(n):=\left|{1/2\choose m^\prime+1}\right|\pi^{2(m^\prime+1)}{\widehat{\mu}}(n)^{-2(m^\prime+1)},
\\[3pt]
{\widehat{\mu}}_2(n)&:=\sum_{k=0}^{m^\prime}{-3/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}, \qquad
{\widehat{\varepsilon}}_2(n):=\left|{-3/2\choose m^\prime+1}\right|\pi^{2(m^\prime+1)}{\widehat{\mu}}(n)^{-2(m^\prime+1)},
\\[3pt]
{\widehat{\nu}}_1(n)&:=\left({\widehat{\mu}}_1(n)-{\widehat{\varepsilon}}_1(n)-\frac{1}{{\widehat{\mu}}(n)}\right)\sum_{k=0}^m{\widehat{\mu}}(n)^{-k},
\\[3pt]
{\widehat{\nu}}_2(n)&:=\left({\widehat{\mu}}_1(n)+{\widehat{\varepsilon}}_1(n)-\frac{1}{{\widehat{\mu}}(n)}\right)
\left(\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}+2{\widehat{\mu}}(n)^{-m-1}\right),
\end{align*}
\begin{align*}
{\widehat{\mu}}_1(n)&:=\sum_{k=0}^{m^\prime}{1/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k},\qquad
{\widehat{\varepsilon}}_1(n):=\left|{1/2\choose m^\prime+1}\right|\pi^{2(m^\prime+1)}{\widehat{\mu}}(n)^{-2(m^\prime+1)},
\\[3pt]
{\widehat{\mu}}_2(n)&:=\sum_{k=0}^{m^\prime}{-3/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}, \qquad
{\widehat{\varepsilon}}_2(n):=\left|{-3/2\choose m^\prime+1}\right|\pi^{2(m^\prime+1)}{\widehat{\mu}}(n)^{-2(m^\prime+1)},
\\[3pt]
{\widehat{\nu}}_1(n)&:=\left({\widehat{\mu}}_1(n)-{\widehat{\varepsilon}}_1(n)-\frac{1}{{\widehat{\mu}}(n)}\right)\sum_{k=0}^m{\widehat{\mu}}(n)^{-k},
\\[3pt]
{\widehat{\nu}}_2(n)&:=\left({\widehat{\mu}}_1(n)+{\widehat{\varepsilon}}_1(n)-\frac{1}{{\widehat{\mu}}(n)}\right)
\left(\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}+2{\widehat{\mu}}(n)^{-m-1}\right),
\end{align*}then
 \begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}&\gt{\widehat{\nu}}_1(n)\left({\widehat{\mu}}_2(n)-{\widehat{\varepsilon}}_2(n)\right)
(1-{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n))\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
\end{align}
\begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}&\gt{\widehat{\nu}}_1(n)\left({\widehat{\mu}}_2(n)-{\widehat{\varepsilon}}_2(n)\right)
(1-{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n))\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
\end{align}and
 \begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}&\lt{\widehat{\nu}}_2(n)({\widehat{\mu}}_2(n)+{\widehat{\varepsilon}}_2(n))
(1+2{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n))\left(\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
+{\rm e}^{{\widehat{\nu}}(n)}\frac{{\widehat{\nu}}(n)^{m+1}}{(m+1)!}\right),
\end{align}
\begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}&\lt{\widehat{\nu}}_2(n)({\widehat{\mu}}_2(n)+{\widehat{\varepsilon}}_2(n))
(1+2{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n))\left(\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
+{\rm e}^{{\widehat{\nu}}(n)}\frac{{\widehat{\nu}}(n)^{m+1}}{(m+1)!}\right),
\end{align}where  ${\widehat{T}}(n)$ is defined as in Equation (2.2).
${\widehat{T}}(n)$ is defined as in Equation (2.2).
Proof. By Equation (2.2), we have
 \begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}=\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\cdot\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\cdot {\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}.
\end{align}
\begin{align}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}=\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\cdot\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\cdot {\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}.
\end{align}Now we consider the above ratio term by term. For the first factor, we have
 \begin{align*}
\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}=\frac{\frac{{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}-\frac{1}{{\widehat{\mu}}(n)}}{1-\frac{1}{{\widehat{\mu}}(n)}}.
\end{align*}
\begin{align*}
\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}=\frac{\frac{{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}-\frac{1}{{\widehat{\mu}}(n)}}{1-\frac{1}{{\widehat{\mu}}(n)}}.
\end{align*}By Taylor’s Theorem, we have since
 \begin{align*}
\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)^{-1}
=\sum_{k=0}^\infty {\widehat{\mu}}(n)^{-k}
\end{align*}
\begin{align*}
\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)^{-1}
=\sum_{k=0}^\infty {\widehat{\mu}}(n)^{-k}
\end{align*}that
 \begin{align}
\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}\lt\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)^{-1}
\lt\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}+2{\widehat{\mu}}(n)^{-m-1}.
\end{align}
\begin{align}
\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}\lt\left(1-\frac{1}{{\widehat{\mu}}(n)}\right)^{-1}
\lt\sum_{k=0}^m{\widehat{\mu}}(n)^{-k}+2{\widehat{\mu}}(n)^{-m-1}.
\end{align}Note that
 \begin{align*}
{\widehat{\mu}}(n+1)={\widehat{\mu}}(n)\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{\frac{1}{2}}.
\end{align*}
\begin{align*}
{\widehat{\mu}}(n+1)={\widehat{\mu}}(n)\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{\frac{1}{2}}.
\end{align*}Since
 \begin{align*}
\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{\frac{1}{2}}=\sum_{k=0}^{m^\prime}{1/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}
+{1/2\choose m^\prime+1}\left(\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{m^\prime+1}\left(1+\xi\right)^{\frac{1}{2}-m^\prime-1},
\end{align*}
\begin{align*}
\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{\frac{1}{2}}=\sum_{k=0}^{m^\prime}{1/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}
+{1/2\choose m^\prime+1}\left(\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{m^\prime+1}\left(1+\xi\right)^{\frac{1}{2}-m^\prime-1},
\end{align*}where ξ is some number in the interval  $\left(0,\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)$, we have
$\left(0,\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)$, we have
 \begin{align}
{\widehat{\mu}}_1(n)-{\widehat{\varepsilon}}_1(n)\lt\frac{{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\lt{\widehat{\mu}}_1(n)+{\widehat{\varepsilon}}_1(n).
\end{align}
\begin{align}
{\widehat{\mu}}_1(n)-{\widehat{\varepsilon}}_1(n)\lt\frac{{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\lt{\widehat{\mu}}_1(n)+{\widehat{\varepsilon}}_1(n).
\end{align}Combining Equations (2.8) and (2.9), we deduce that
 \begin{align}
{\widehat{\nu}}_1(n)\lt\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\lt{\widehat{\nu}}_2(n).
\end{align}
\begin{align}
{\widehat{\nu}}_1(n)\lt\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\lt{\widehat{\nu}}_2(n).
\end{align}For the second factor, we have
 \begin{align*}
\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}=\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-3/2}.
\end{align*}
\begin{align*}
\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}=\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-3/2}.
\end{align*}Since
 \begin{align*}
\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-\frac{3}{2}}=\sum_{k=0}^{m^\prime}{-3/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}
+{-3/2\choose m^\prime+1}\left(\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{m^\prime+1}\left(1+\xi\right)^{-\frac{3}{2}-m^\prime-1},
\end{align*}
\begin{align*}
\left(1+\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-\frac{3}{2}}=\sum_{k=0}^{m^\prime}{-3/2\choose k}\pi^{2k}{\widehat{\mu}}(n)^{-2k}
+{-3/2\choose m^\prime+1}\left(\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)^{m^\prime+1}\left(1+\xi\right)^{-\frac{3}{2}-m^\prime-1},
\end{align*} where ξ is some number in the interval  $\left(0,\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)$, we have
$\left(0,\frac{\pi^2}{{\widehat{\mu}}(n)^2}\right)$, we have
 \begin{align}
{\widehat{\mu}}_2(n)-{\widehat{\varepsilon}}_2(n)\lt\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\lt{\widehat{\mu}}_2(n)+{\widehat{\varepsilon}}_2(n).
\end{align}
\begin{align}
{\widehat{\mu}}_2(n)-{\widehat{\varepsilon}}_2(n)\lt\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\lt{\widehat{\mu}}_2(n)+{\widehat{\varepsilon}}_2(n).
\end{align}For the last factor, using Equation (2.9), we have
Evidently, for  $0\lt x\lt\frac{1}{2}$,
$0\lt x\lt\frac{1}{2}$,
and for x > 0,
 \begin{equation*}\sum_{k=0}^m\frac{x^k}{k!}\lt{\rm e}^x\lt\sum_{k=0}^m\frac{x^k}{k!}+{\rm e}^x\frac{x^{m+1}}{(m+1)!},\end{equation*}
\begin{equation*}\sum_{k=0}^m\frac{x^k}{k!}\lt{\rm e}^x\lt\sum_{k=0}^m\frac{x^k}{k!}+{\rm e}^x\frac{x^{m+1}}{(m+1)!},\end{equation*}so that
 \begin{align}
{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\gt\left(1-{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n)\right)\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
\end{align}
\begin{align}
{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\gt\left(1-{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n)\right)\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
\end{align}and
 \begin{align}
{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\lt\left(1+2{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n)\right)\left(\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
+{\rm e}^{{\widehat{\nu}}(n)}\frac{{\widehat{\nu}}(n)^{m+1}}{(m+1)!}\right).
\end{align}
\begin{align}
{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\lt\left(1+2{\widehat{\mu}}(n){\widehat{\varepsilon}}_1(n)\right)\left(\sum_{k=0}^m\frac{{\widehat{\nu}}(n)^k}{k!}
+{\rm e}^{{\widehat{\nu}}(n)}\frac{{\widehat{\nu}}(n)^{m+1}}{(m+1)!}\right).
\end{align}Applying the estimates (2.10)–(2.13) to (2.7), we reach Equations (2.5) and (2.6). This completes the proof.
Theorem 2.4. For any positive integer m, there exists an integer ![]() $N_1(m)$, real numbers a k and
$N_1(m)$, real numbers a k and ![]() $C_1, C_2\gt0$ such that for
$C_1, C_2\gt0$ such that for ![]() $n\geq N_1(m)$, we have
$n\geq N_1(m)$, we have
 \begin{align}
\sum_{k=0}^ma_k{\widehat{\mu}}(n)^{-k}-C_1{\widehat{\mu}}(n)^{-m-1}\lt\frac{{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\sum_{k=0}^ma_k{\widehat{\mu}}(n)^{-k}+C_2{\widehat{\mu}}(n)^{-m-1}.
\end{align}
\begin{align}
\sum_{k=0}^ma_k{\widehat{\mu}}(n)^{-k}-C_1{\widehat{\mu}}(n)^{-m-1}\lt\frac{{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\sum_{k=0}^ma_k{\widehat{\mu}}(n)^{-k}+C_2{\widehat{\mu}}(n)^{-m-1}.
\end{align}Proof. By Equation (2.1) and Theorem 2.2, for any ![]() $m\geq2$, there exists an integer
$m\geq2$, there exists an integer ![]() $N_1(m)$ such that
$N_1(m)$ such that
 \begin{equation*}
\left|{\overline{p}}(n)/{\widehat{T}}(n)-1\right|\lt\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m},\qquad \text{for all}\ n\geq N_1(m).
\end{equation*}
\begin{equation*}
\left|{\overline{p}}(n)/{\widehat{T}}(n)-1\right|\lt\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m},\qquad \text{for all}\ n\geq N_1(m).
\end{equation*}Therefore, we have
 \begin{equation*}
{\widehat{T}}(n)\left(1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}\right)\lt{\overline{p}}(n)\lt{\widehat{T}}(n)\left(1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}\right).
\end{equation*}
\begin{equation*}
{\widehat{T}}(n)\left(1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}\right)\lt{\overline{p}}(n)\lt{\widehat{T}}(n)\left(1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}\right).
\end{equation*} Since ![]() ${\widehat{\mu}}(n)$ is an increasing function of n, we derive that
${\widehat{\mu}}(n)$ is an increasing function of n, we derive that
 \begin{equation*}
\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)} \frac {1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}{1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}\lt\frac {{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)} \frac {1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}{1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}.
\end{equation*}
\begin{equation*}
\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)} \frac {1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}{1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}\lt\frac {{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)} \frac {1+\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}{1-\left(\frac 32\right)^{m+1}{\widehat{\mu}}(n)^{-m}}.
\end{equation*} We find that for ![]() $0\lt\lambda\lt1/3$,
$0\lt\lambda\lt1/3$,
 \begin{equation*}
\frac {1+\lambda}{1-\lambda}\lt1+3\lambda\quad \text{and}\quad \frac {1-\lambda}{1+\lambda}\gt1-2\lambda.
\end{equation*}
\begin{equation*}
\frac {1+\lambda}{1-\lambda}\lt1+3\lambda\quad \text{and}\quad \frac {1-\lambda}{1+\lambda}\gt1-2\lambda.
\end{equation*}By
 \begin{equation*}0\lt\frac {\left(\frac 32\right)^{m+1}}{{\widehat{\mu}}(n)^m}\lt\frac 13,\end{equation*}
\begin{equation*}0\lt\frac {\left(\frac 32\right)^{m+1}}{{\widehat{\mu}}(n)^m}\lt\frac 13,\end{equation*}we have for all ![]() $n\geq N_1(m)$ that
$n\geq N_1(m)$ that
 \begin{equation}
\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)}\left(1-4\cdot 2^m{\widehat{\mu}}(n)^{-m}\right)\lt\frac {{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)}\left(1+6\cdot2^m{\widehat{\mu}}(n)^{-m}\right).
\end{equation}
\begin{equation}
\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)}\left(1-4\cdot 2^m{\widehat{\mu}}(n)^{-m}\right)\lt\frac {{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\frac {{\widehat{T}}(n+1)}{{\widehat{T}}(n)}\left(1+6\cdot2^m{\widehat{\mu}}(n)^{-m}\right).
\end{equation} By Lemma 2.3, we can see that  ${\widehat{T}}(n+1)/{\widehat{T}}(n)$ is bounded by a pair of polynomials in
${\widehat{T}}(n+1)/{\widehat{T}}(n)$ is bounded by a pair of polynomials in ![]() ${\widehat{\mu}}(n)^{-1}$ whose difference is a polynomial in
${\widehat{\mu}}(n)^{-1}$ whose difference is a polynomial in ![]() ${\widehat{\mu}}(n)^{-1}$ of degree at least m + 1. Combining Equation (2.15) and
${\widehat{\mu}}(n)^{-1}$ of degree at least m + 1. Combining Equation (2.15) and ![]() $\lim_{n\rightarrow+\infty}{\widehat{\mu}}(n)=+\infty$, we have Equation (2.14). This completes the proof.
$\lim_{n\rightarrow+\infty}{\widehat{\mu}}(n)=+\infty$, we have Equation (2.14). This completes the proof.
For any positive integer m, we can explicitly determine the parameters a k, C 1, C 2 in the above result. To do so, we follow the Mathematica package of Hou and Zhang [Reference Hou and Zhang11] to compute these parameters. For example, we compute that for ![]() $n\geq 184$, we have
$n\geq 184$, we have
 \begin{equation*}
\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}-\frac {146}{{\widehat{\mu}}(n)^5}\lt\frac{{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}+\frac {756}{{\widehat{\mu}}(n)^5},
\end{equation*}
\begin{equation*}
\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}-\frac {146}{{\widehat{\mu}}(n)^5}\lt\frac{{\overline{p}}(n+1)}{{\overline{p}}(n)}\lt\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}+\frac {756}{{\widehat{\mu}}(n)^5},
\end{equation*}where
 \begin{equation*}
\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}=1 +\frac {\pi^2}{2{\widehat{\mu}}(n)} +\frac {-\pi^2 +\frac {\pi^4}8}{{\widehat{\mu}}(n)^2} +\frac {\frac {\pi^2}2 - \frac {5 \pi^4}8 +\frac {\pi^6}{48}}{{\widehat{\mu}}(n)^3} +\frac {\frac {\pi^2}2 +\frac {5 \pi^4}4 -\frac {3 \pi^6}{16} +\frac {\pi^8}{384}}{{\widehat{\mu}}(n)^4}.
\end{equation*}
\begin{equation*}
\sum_{k=0}^4a_k{\widehat{\mu}}(n)^{-k}=1 +\frac {\pi^2}{2{\widehat{\mu}}(n)} +\frac {-\pi^2 +\frac {\pi^4}8}{{\widehat{\mu}}(n)^2} +\frac {\frac {\pi^2}2 - \frac {5 \pi^4}8 +\frac {\pi^6}{48}}{{\widehat{\mu}}(n)^3} +\frac {\frac {\pi^2}2 +\frac {5 \pi^4}4 -\frac {3 \pi^6}{16} +\frac {\pi^8}{384}}{{\widehat{\mu}}(n)^4}.
\end{equation*} We give a specific example to present the calculating process in ![]() $\S$ 3.
$\S$ 3.
The following lemma given by Hou and Zhang [Reference Hou and Zhang10] plays an important role in the proof of Theorem 1.2.
Lemma 2.5. Let ![]() $\{a_n\}_{n\geq0}$ be a positive sequence such that
$\{a_n\}_{n\geq0}$ be a positive sequence such that ![]() $\mathscr{R}^2a_n=a_na_{n+2}/a_{n+1}^2$ has the following asymptotic expression
$\mathscr{R}^2a_n=a_na_{n+2}/a_{n+1}^2$ has the following asymptotic expression
 \begin{equation*}
\mathscr{R}^2a_n=1+\frac c{n^\alpha}+\cdots+o\left(\frac 1{n^\beta}\right),\qquad n\rightarrow \infty,
\end{equation*}
\begin{equation*}
\mathscr{R}^2a_n=1+\frac c{n^\alpha}+\cdots+o\left(\frac 1{n^\beta}\right),\qquad n\rightarrow \infty,
\end{equation*}where ![]() $0\lt\alpha\leq\beta$. If c < 0 and α < 2, then
$0\lt\alpha\leq\beta$. If c < 0 and α < 2, then ![]() $\{a_n\}_{n\geq0}$ is asymptotically
$\{a_n\}_{n\geq0}$ is asymptotically ![]() $\lfloor\beta /\alpha\rfloor$-log-concave.
$\lfloor\beta /\alpha\rfloor$-log-concave.
Now we are in a position to prove Theorem 1.2.
Proof of Theorem 1.2
Based on Equation (2.14), we consider the bound of ![]() ${\widehat{\mu}}(n+1)^{-r}$ and
${\widehat{\mu}}(n+1)^{-r}$ and ![]() $1/h({\widehat{\mu}}(n)^{-1})$, where
$1/h({\widehat{\mu}}(n)^{-1})$, where ![]() $h({\widehat{\mu}}(n)^{-1})$ is a polynomial in
$h({\widehat{\mu}}(n)^{-1})$ is a polynomial in ![]() ${\widehat{\mu}}(n)^{-1}$ with constant term 1.
${\widehat{\mu}}(n)^{-1}$ with constant term 1.
Let c denote the coefficient of the term with the highest power of ![]() $h({\widehat{\mu}}(n)^{-1})-1$. If c > 0, there exists a positive integer N such that
$h({\widehat{\mu}}(n)^{-1})-1$. If c > 0, there exists a positive integer N such that
By Taylor’s Theorem, we have
 \begin{align*}
1-\lambda+\lambda^2-\cdots +(-1)^m\lambda^m-\lambda^{m+1}\lt\frac 1{h({\widehat{\mu}}(n)^{-1})}&=\frac 1{1+\left(h({\widehat{\mu}}(n)^{-1})-1\right)}\\[3pt]
&\!\!\!\!\!\lt1-\lambda+\lambda^2-\cdots +(-1)^m\lambda^m+\lambda^{m+1},
\end{align*}
\begin{align*}
1-\lambda+\lambda^2-\cdots +(-1)^m\lambda^m-\lambda^{m+1}\lt\frac 1{h({\widehat{\mu}}(n)^{-1})}&=\frac 1{1+\left(h({\widehat{\mu}}(n)^{-1})-1\right)}\\[3pt]
&\!\!\!\!\!\lt1-\lambda+\lambda^2-\cdots +(-1)^m\lambda^m+\lambda^{m+1},
\end{align*}where ![]() $\lambda=h({\widehat{\mu}}(n)^{-1})-1$. If c < 0, there exists a positive integer N such that
$\lambda=h({\widehat{\mu}}(n)^{-1})-1$. If c < 0, there exists a positive integer N such that
 \begin{equation*}
0\lt1-h({\widehat{\mu}}(n)^{-1})\lt\frac 12,\qquad\text{for all}\ n\geq N.
\end{equation*}
\begin{equation*}
0\lt1-h({\widehat{\mu}}(n)^{-1})\lt\frac 12,\qquad\text{for all}\ n\geq N.
\end{equation*}So
 \begin{align*}
1+\lambda+\lambda^2+\cdots +\lambda^m+\lambda^{m+1}\lt\frac 1{h({\widehat{\mu}}(n)^{-1})}&=\frac 1{1-\left(1-h({\widehat{\mu}}(n)^{-1})\right)}\\[3pt]
&\lt1+\lambda+\lambda^2+\cdots+\lambda^m+2\lambda^{m+1},
\end{align*}
\begin{align*}
1+\lambda+\lambda^2+\cdots +\lambda^m+\lambda^{m+1}\lt\frac 1{h({\widehat{\mu}}(n)^{-1})}&=\frac 1{1-\left(1-h({\widehat{\mu}}(n)^{-1})\right)}\\[3pt]
&\lt1+\lambda+\lambda^2+\cdots+\lambda^m+2\lambda^{m+1},
\end{align*}where ![]() $\lambda=1-h({\widehat{\mu}}(n)^{-1})$.
$\lambda=1-h({\widehat{\mu}}(n)^{-1})$.
We now consider the bound of ![]() ${\widehat{\mu}}(n+1)^{-r}$. It is easy to see that
${\widehat{\mu}}(n+1)^{-r}$. It is easy to see that
 \begin{equation*}
\left(\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\right)^{-r}=\left(1+\frac {\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-r/2}.
\end{equation*}
\begin{equation*}
\left(\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\right)^{-r}=\left(1+\frac {\pi^2}{{\widehat{\mu}}(n)^2}\right)^{-r/2}.
\end{equation*} Then we can derive the bounds of  $\left(\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\right)^{-r}$ in a way similar to the estimation of
$\left(\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}\right)^{-r}$ in a way similar to the estimation of  $\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}$, thus get an estimation of
$\frac {{\widehat{\mu}}(n+1)}{{\widehat{\mu}}(n)}$, thus get an estimation of ![]() ${\widehat{\mu}}(n+1)^{-r}$.
${\widehat{\mu}}(n+1)^{-r}$.
Based on the above estimations, we compute an asymptotic expression of ![]() ${\overline{u}}_n$ by Mathematica. In particular, for any positive integer m, we have
${\overline{u}}_n$ by Mathematica. In particular, for any positive integer m, we have
 \begin{equation*}
{\overline{u}}_n=1-\frac {\pi}{4n^{3/2}}+\cdots+o\left(\frac 1{n^m}\right).
\end{equation*}
\begin{equation*}
{\overline{u}}_n=1-\frac {\pi}{4n^{3/2}}+\cdots+o\left(\frac 1{n^m}\right).
\end{equation*}By Lemma 2.5, the proof is complete.
3. Proof of Theorems 1.3, 1.6 and 1.9 and Corollaries 1.4, 1.5, 1.7, 1.8, 1.10 and 1.11
In ![]() $\S$ 2, we prove the asymptotic r-log-concavity for the overpartition function. In this section, we study the 2-log-concavity as an example, stated in Corollary 1.7. It is worth noting that we can derive 3-log-concavity (or more generally r-log-concavity) in the same way. But it could be more difficult as r becomes larger.
$\S$ 2, we prove the asymptotic r-log-concavity for the overpartition function. In this section, we study the 2-log-concavity as an example, stated in Corollary 1.7. It is worth noting that we can derive 3-log-concavity (or more generally r-log-concavity) in the same way. But it could be more difficult as r becomes larger.
The key idea behind the proof of Theorem 1.3 lies in a detailed analysis of the proof of Theorem 2.4, in particular exploiting Equations (2.7) and (2.15). More specifically, we shall proceed with a detailed inquiry of the exact asymptotics for each of the factor present in  ${\widehat{T}}(n+1)/{\widehat{T}}(n)$ explicitly by studying the Taylor expansion of the form
${\widehat{T}}(n+1)/{\widehat{T}}(n)$ explicitly by studying the Taylor expansion of the form  $\sum_{m \geq 0}a_m(\sqrt{n})^{-m}$ upto order 7 and bounding the error term. This will set the stage for the proof of Theorems 1.6 and 1.9.
$\sum_{m \geq 0}a_m(\sqrt{n})^{-m}$ upto order 7 and bounding the error term. This will set the stage for the proof of Theorems 1.6 and 1.9.
Proof of Theorem 1.3
We recall Equation (2.7):
 \begin{equation*}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}=\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\cdot\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\cdot {\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}.
\end{equation*}
\begin{equation*}
\frac{{\widehat{T}}(n+1)}{{\widehat{T}}(n)}=\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}\cdot\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3}\cdot {\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}.
\end{equation*}By Taylor’s theorem, we have
 \begin{equation*}
\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}=s^{(1)}_+(n)+O\left(\dfrac{1}{n^4}\right),
\end{equation*}
\begin{equation*}
\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1}=s^{(1)}_+(n)+O\left(\dfrac{1}{n^4}\right),
\end{equation*}where
 \begin{equation*}
\begin{split}
s^{(1)}_+(n): &= 1+\dfrac{1}{2n}+\dfrac{1}{2\pi n^{3/2}}+\left(\dfrac{1}{2\pi^2}-\dfrac{1}{8}\right)\dfrac{1}{n^2}+\left(\dfrac{1}{2\pi^3}-\dfrac{1}{8\pi}\right)\dfrac{1}{n^{5/2}}
\\
& \quad+\left(\dfrac{1}{16}+\dfrac{1}{2\pi^4}-\dfrac{1}{8\pi^2}\right)\dfrac{1}{n^3} + \left(\dfrac{1}{2\pi^5}-\dfrac{1}{8\pi^3}+\dfrac{1}{16\pi}\right)\dfrac{1}{n^{7/2}}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
s^{(1)}_+(n): &= 1+\dfrac{1}{2n}+\dfrac{1}{2\pi n^{3/2}}+\left(\dfrac{1}{2\pi^2}-\dfrac{1}{8}\right)\dfrac{1}{n^2}+\left(\dfrac{1}{2\pi^3}-\dfrac{1}{8\pi}\right)\dfrac{1}{n^{5/2}}
\\
& \quad+\left(\dfrac{1}{16}+\dfrac{1}{2\pi^4}-\dfrac{1}{8\pi^2}\right)\dfrac{1}{n^3} + \left(\dfrac{1}{2\pi^5}-\dfrac{1}{8\pi^3}+\dfrac{1}{16\pi}\right)\dfrac{1}{n^{7/2}}.
\end{split}
\end{equation*} It is easy to observe that for ![]() $n \geq 1$, we have
$n \geq 1$, we have
 \begin{equation}
s^{(1)}_+(n)-\dfrac{2}{n^4}\lt\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1} \lt s^{(1)}_+(n)+\dfrac{2}{n^4}.
\end{equation}
\begin{equation}
s^{(1)}_+(n)-\dfrac{2}{n^4}\lt\frac{{\widehat{\mu}}(n+1)-1}{{\widehat{\mu}}(n)-1} \lt s^{(1)}_+(n)+\dfrac{2}{n^4}.
\end{equation} Similarly, for ![]() $n \geq 1$, we obtain
$n \geq 1$, we obtain
 \begin{equation}
s^{(2)}_+(n)-\dfrac{3}{n^4}\lt\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3} \lt s^{(2)}_+(n)+\dfrac{3}{n^4},
\end{equation}
\begin{equation}
s^{(2)}_+(n)-\dfrac{3}{n^4}\lt\frac{{\widehat{\mu}}(n)^3}{{\widehat{\mu}}(n+1)^3} \lt s^{(2)}_+(n)+\dfrac{3}{n^4},
\end{equation}where
 \begin{equation*}s^{(2)}_+(n):=1-\dfrac{3}{2n}+\dfrac{15}{8n^2}-\dfrac{35}{16n^3}.\end{equation*}
\begin{equation*}s^{(2)}_+(n):=1-\dfrac{3}{2n}+\dfrac{15}{8n^2}-\dfrac{35}{16n^3}.\end{equation*} For the factor ![]() ${\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}$, we first estimate
${\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}$, we first estimate ![]() ${\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)$ as follows. For
${\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)$ as follows. For ![]() $n \geq 1$, we have
$n \geq 1$, we have
 \begin{equation}
s^{(3,0)}_+(n)\lt{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n) \lt s^{(3,0)}_+(n)+\dfrac{3}{n^4},
\end{equation}
\begin{equation}
s^{(3,0)}_+(n)\lt{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n) \lt s^{(3,0)}_+(n)+\dfrac{3}{n^4},
\end{equation}where
 \begin{equation*}s^{(3,0)}_+(n):=\dfrac{\pi}{2\sqrt{n}}-\dfrac{\pi}{8n^{3/2}}+\dfrac{\pi}{16n^{5/2}}-\dfrac{5\pi}{128n^{7/2}}.\end{equation*}
\begin{equation*}s^{(3,0)}_+(n):=\dfrac{\pi}{2\sqrt{n}}-\dfrac{\pi}{8n^{3/2}}+\dfrac{\pi}{16n^{5/2}}-\dfrac{5\pi}{128n^{7/2}}.\end{equation*} Truncating the Taylor series of  ${\rm e}^{s^{(3,0)}_+(n)}$ at the order
${\rm e}^{s^{(3,0)}_+(n)}$ at the order  $\dfrac{1}{n^{7/2}}$ and bounding the error term, we obtain for
$\dfrac{1}{n^{7/2}}$ and bounding the error term, we obtain for ![]() $n \geq 2$,
$n \geq 2$,
 \begin{equation}
\ {\rm e}^{3/n^4}\lt1+\dfrac{4}{n^4}\quad \text{and}\quad s^{(3)}_+(n)-\dfrac{1}{n^4}\lt{\rm e}^{s^{(3,0)}_+(n)} \lt s^{(3)}_+(n)+\dfrac{1}{n^4},
\end{equation}
\begin{equation}
\ {\rm e}^{3/n^4}\lt1+\dfrac{4}{n^4}\quad \text{and}\quad s^{(3)}_+(n)-\dfrac{1}{n^4}\lt{\rm e}^{s^{(3,0)}_+(n)} \lt s^{(3)}_+(n)+\dfrac{1}{n^4},
\end{equation}where
 \begin{equation*}s^{(3)}_+(n):=\sum_{m=0}^{7}s^{(3)}_{+,m}\left(\dfrac{1}{\sqrt{n}}\right)^m.\end{equation*}
\begin{equation*}s^{(3)}_+(n):=\sum_{m=0}^{7}s^{(3)}_{+,m}\left(\dfrac{1}{\sqrt{n}}\right)^m.\end{equation*} The coefficients  $\{s^{(3)}_{+,m}\}_{0\leq m\leq7}$ are as follows:
$\{s^{(3)}_{+,m}\}_{0\leq m\leq7}$ are as follows:
 \begin{align*}
&s^{(3)}_{+,0}:=1, \quad
s^{(3)}_{+,1}:=\dfrac{\pi}{2}, \quad
s^{(3)}_{+,2}:=\dfrac{\pi^2}{8}, \quad
s^{(3)}_{+,3}:=\dfrac{\pi (\pi^2-6)}{48},
\quad
s^{(3)}_{+,4}:=\dfrac{\pi^2 (\pi^2-24)}{384},
\\[3pt]
&s^{(3)}_{+,5}:=\dfrac{\pi (\pi^4-60\pi^2+240)}{3840},
\quad
s^{(3)}_{+,6}:=\dfrac{\pi^2 (\pi^4-120\pi^2+1800)}{46080},
\\[3pt]
&s^{(3)}_{+,7}:=\dfrac{\pi (\pi^6-210\pi^4+7560\pi^2-25200)}{645120}.
\end{align*}
\begin{align*}
&s^{(3)}_{+,0}:=1, \quad
s^{(3)}_{+,1}:=\dfrac{\pi}{2}, \quad
s^{(3)}_{+,2}:=\dfrac{\pi^2}{8}, \quad
s^{(3)}_{+,3}:=\dfrac{\pi (\pi^2-6)}{48},
\quad
s^{(3)}_{+,4}:=\dfrac{\pi^2 (\pi^2-24)}{384},
\\[3pt]
&s^{(3)}_{+,5}:=\dfrac{\pi (\pi^4-60\pi^2+240)}{3840},
\quad
s^{(3)}_{+,6}:=\dfrac{\pi^2 (\pi^4-120\pi^2+1800)}{46080},
\\[3pt]
&s^{(3)}_{+,7}:=\dfrac{\pi (\pi^6-210\pi^4+7560\pi^2-25200)}{645120}.
\end{align*}From Equations (3.3) and (3.4), we obtain
 \begin{equation}
\left(s^{(3)}_+(n)-\dfrac{1}{n^4}\right)\lt{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\lt\left(s^{(3)}_+(n)+\dfrac{1}{n^4}\right)\left(1+\dfrac{4}{n^4}\right).
\end{equation}
\begin{equation}
\left(s^{(3)}_+(n)-\dfrac{1}{n^4}\right)\lt{\rm e}^{{\widehat{\mu}}(n+1)-{\widehat{\mu}}(n)}\lt\left(s^{(3)}_+(n)+\dfrac{1}{n^4}\right)\left(1+\dfrac{4}{n^4}\right).
\end{equation} It can be easily checked that for ![]() $n \geq 1$, we have
$n \geq 1$, we have
 \begin{equation}
1-\dfrac{4\cdot2^8} {{\widehat{\mu}}(n)^{8}}\gt1-\dfrac{1}{n^4}\quad \text{and}\quad 1+\dfrac{6\cdot2^8} {{\widehat{\mu}}(n)^{8}}\lt1+\dfrac{1}{n^4}.
\end{equation}
\begin{equation}
1-\dfrac{4\cdot2^8} {{\widehat{\mu}}(n)^{8}}\gt1-\dfrac{1}{n^4}\quad \text{and}\quad 1+\dfrac{6\cdot2^8} {{\widehat{\mu}}(n)^{8}}\lt1+\dfrac{1}{n^4}.
\end{equation} Hence, by Equations (3.1), (3.2), (3.5) and (3.6) and using Equation (2.15) with m = 8, we obtain for all ![]() $n \geq 184$ that
$n \geq 184$ that
 \begin{equation}
L_{+}(n)\lt\dfrac{{\overline{p}}(n+1)}{{\overline{p}}(n)} \lt U_{+}(n),
\end{equation}
\begin{equation}
L_{+}(n)\lt\dfrac{{\overline{p}}(n+1)}{{\overline{p}}(n)} \lt U_{+}(n),
\end{equation}where
 \begin{align*}
U_{+}(n)&:= \left(s^{(1)}_+(n)+\dfrac{2}{n^4}\right)\left(s^{(2)}_+(n)
+\dfrac{3}{n^4}\right)\left(s^{(3)}_+(n)+\dfrac{1}{n^4}\right)
\left(1+\dfrac{4}{n^4}\right)\left(1+\dfrac{1}{n^4}\right),
\\[3pt]
L_{+}(n)&:=\left(s^{(1)}_+(n)-\dfrac{2}{n^4}\right)
\left(s^{(2)}_+(n)-\dfrac{3}{n^4}\right)\left(s^{(3)}_+(n)
-\dfrac{1}{n^4}\right)\left(1-\dfrac{1}{n^4}\right).
\end{align*}
\begin{align*}
U_{+}(n)&:= \left(s^{(1)}_+(n)+\dfrac{2}{n^4}\right)\left(s^{(2)}_+(n)
+\dfrac{3}{n^4}\right)\left(s^{(3)}_+(n)+\dfrac{1}{n^4}\right)
\left(1+\dfrac{4}{n^4}\right)\left(1+\dfrac{1}{n^4}\right),
\\[3pt]
L_{+}(n)&:=\left(s^{(1)}_+(n)-\dfrac{2}{n^4}\right)
\left(s^{(2)}_+(n)-\dfrac{3}{n^4}\right)\left(s^{(3)}_+(n)
-\dfrac{1}{n^4}\right)\left(1-\dfrac{1}{n^4}\right).
\end{align*} In the similar way stated before, we obtain for all ![]() $n \geq 184$ that
$n \geq 184$ that
 \begin{equation}
L_{-}(n)\lt\dfrac{{\overline{p}}(n-1)}{{\overline{p}}(n)} \lt U_{-}(n),
\end{equation}
\begin{equation}
L_{-}(n)\lt\dfrac{{\overline{p}}(n-1)}{{\overline{p}}(n)} \lt U_{-}(n),
\end{equation}where
 \begin{align*}
U_{-}(n)&:= \left(s^{(1)}_-(n)+\dfrac{1}{n^4}\right)\left(s^{(2)}_-(n)+\dfrac{3}{n^4}\right)
\left(s^{(3)}_-(n)+\dfrac{1}{n^4}\right)\left(1+\dfrac{1}{n^4}\right),\\ L_{-}(n)&:=\left(s^{(1)}_-(n)-\dfrac{1}{n^4}\right)\left(s^{(2)}_-(n)\right)\left(s^{(3)}_-(n)\right)\left(1-\dfrac{1}{n^4}\right)^2.
\end{align*}
\begin{align*}
U_{-}(n)&:= \left(s^{(1)}_-(n)+\dfrac{1}{n^4}\right)\left(s^{(2)}_-(n)+\dfrac{3}{n^4}\right)
\left(s^{(3)}_-(n)+\dfrac{1}{n^4}\right)\left(1+\dfrac{1}{n^4}\right),\\ L_{-}(n)&:=\left(s^{(1)}_-(n)-\dfrac{1}{n^4}\right)\left(s^{(2)}_-(n)\right)\left(s^{(3)}_-(n)\right)\left(1-\dfrac{1}{n^4}\right)^2.
\end{align*} The sequences  $\{s^{(i)}_-(n)\}_{1\leq i\leq 3}$ is defined as follows:
$\{s^{(i)}_-(n)\}_{1\leq i\leq 3}$ is defined as follows:
 \begin{align*}
s^{(1)}_-(n)&:=1-\dfrac{1}{2n}-\dfrac{1}{2\pi n^{3/2}}-\left(\dfrac{1}{2\pi^2}+\dfrac{1}{8}\right)\dfrac{1}{n^2}
-\left(\dfrac{1}{2\pi^3}+\dfrac{1}{8\pi}\right)\dfrac{1}{n^{5/2}}
\\[3pt]
&\quad-\left(\dfrac{1}{16}+\dfrac{1}{2\pi^4}+\dfrac{1}{8\pi^2}\right)\dfrac{1}{n^3}
-\left(\dfrac{1}{2\pi^5}+\dfrac{1}{8\pi^3}+\dfrac{1}{16\pi}\right)\dfrac{1}{n^{7/2}},
\\[3pt]
s^{(2)}_-(n)&:=1+\dfrac{3}{2n}+\dfrac{15}{8n^2}+\dfrac{35}{16n^3},
\\[3pt]
s^{(3)}_-(n)&:=\sum_{m=0}^{7}s^{(3)}_{-,m}\left(\dfrac{1}{\sqrt{n}}\right)^m,
\end{align*}
\begin{align*}
s^{(1)}_-(n)&:=1-\dfrac{1}{2n}-\dfrac{1}{2\pi n^{3/2}}-\left(\dfrac{1}{2\pi^2}+\dfrac{1}{8}\right)\dfrac{1}{n^2}
-\left(\dfrac{1}{2\pi^3}+\dfrac{1}{8\pi}\right)\dfrac{1}{n^{5/2}}
\\[3pt]
&\quad-\left(\dfrac{1}{16}+\dfrac{1}{2\pi^4}+\dfrac{1}{8\pi^2}\right)\dfrac{1}{n^3}
-\left(\dfrac{1}{2\pi^5}+\dfrac{1}{8\pi^3}+\dfrac{1}{16\pi}\right)\dfrac{1}{n^{7/2}},
\\[3pt]
s^{(2)}_-(n)&:=1+\dfrac{3}{2n}+\dfrac{15}{8n^2}+\dfrac{35}{16n^3},
\\[3pt]
s^{(3)}_-(n)&:=\sum_{m=0}^{7}s^{(3)}_{-,m}\left(\dfrac{1}{\sqrt{n}}\right)^m,
\end{align*}with
 \begin{align*}
&s^{(3)}_{-,0}:=1,\quad
s^{(3)}_{-,1}:=-\dfrac{\pi}{2},\quad
s^{(3)}_{-,2}:=\dfrac{\pi^2}{8},\quad
s^{(3)}_{-,3}:=-\dfrac{\pi (\pi^2+6)}{48},\quad
s^{(3)}_{-,4}:=\dfrac{\pi^2 (\pi^2+24)}{384},
\\[3pt]
&s^{(3)}_{-,5}:=-\dfrac{\pi (\pi^4+60\pi^2+240)}{3840}, \quad
s^{(3)}_{-,6}:=\dfrac{\pi^2 (\pi^4+120\pi^2+1800)}{46080},
\\[3pt]
&s^{(3)}_{-,7}:=-\dfrac{\pi (\pi^6+210\pi^4+7560\pi^2+25200)}{645120}.
\end{align*}
\begin{align*}
&s^{(3)}_{-,0}:=1,\quad
s^{(3)}_{-,1}:=-\dfrac{\pi}{2},\quad
s^{(3)}_{-,2}:=\dfrac{\pi^2}{8},\quad
s^{(3)}_{-,3}:=-\dfrac{\pi (\pi^2+6)}{48},\quad
s^{(3)}_{-,4}:=\dfrac{\pi^2 (\pi^2+24)}{384},
\\[3pt]
&s^{(3)}_{-,5}:=-\dfrac{\pi (\pi^4+60\pi^2+240)}{3840}, \quad
s^{(3)}_{-,6}:=\dfrac{\pi^2 (\pi^4+120\pi^2+1800)}{46080},
\\[3pt]
&s^{(3)}_{-,7}:=-\dfrac{\pi (\pi^6+210\pi^4+7560\pi^2+25200)}{645120}.
\end{align*} Now by Equations (3.7) and (3.8), it follows that for ![]() $n \geq 184$, we have
$n \geq 184$, we have
It can be readily checked that for ![]() $n \geq 2$, we have
$n \geq 2$, we have
 \begin{equation*}
U_{+}(n)\cdot U_{-}(n) \lt s(n)+\dfrac{20}{n^4}\quad \text{and}\quad L_{+}(n)\cdot L_{-}(n) \gt s(n)-\dfrac{15}{n^4}.
\end{equation*}
\begin{equation*}
U_{+}(n)\cdot U_{-}(n) \lt s(n)+\dfrac{20}{n^4}\quad \text{and}\quad L_{+}(n)\cdot L_{-}(n) \gt s(n)-\dfrac{15}{n^4}.
\end{equation*} This finishes the proof of Equation (1.4) for ![]() $n \geq 184$. For the values
$n \geq 184$. For the values ![]() $37 \leq n \leq 183$, one can check numerically in Mathematica.
$37 \leq n \leq 183$, one can check numerically in Mathematica.
Proof of Corollary 1.4
It is easy to check that  $s_n+\frac{20}{n^4}\lt1$ for
$s_n+\frac{20}{n^4}\lt1$ for ![]() $n \geq 5$ and therefore from Equation (1.4), we can conclude that
$n \geq 5$ and therefore from Equation (1.4), we can conclude that ![]() ${\overline{u}}_n\lt1$ for
${\overline{u}}_n\lt1$ for ![]() $n \geq 37$, which is equivalent to saying that
$n \geq 37$, which is equivalent to saying that ![]() $\{{\overline{p}}(n)\}_{n \geq 37}$ is log-concave. For the values
$\{{\overline{p}}(n)\}_{n \geq 37}$ is log-concave. For the values ![]() $4 \leq n \leq 37$, one can check numerically in Mathematica.
$4 \leq n \leq 37$, one can check numerically in Mathematica.
Proof of Corollary 1.5
Note that for ![]() $n \geq 5$, we have
$n \geq 5$, we have
 \begin{equation*}\left(s_n-\frac{15}{n^4}\right)\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt1,\end{equation*}
\begin{equation*}\left(s_n-\frac{15}{n^4}\right)\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt1,\end{equation*}and therefore from Equation (1.4), it follows that for ![]() $n \geq 37$, we have
$n \geq 37$, we have
 \begin{equation*}{\overline{u}}_n\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt1,\end{equation*}
\begin{equation*}{\overline{u}}_n\left(1+\dfrac{\pi}{4n^{3/2}}\right)\gt1,\end{equation*}which is equivalent to Equation (1.5). For the values ![]() $2 \leq n \leq 37$, one can check numerically in Mathematica.
$2 \leq n \leq 37$, one can check numerically in Mathematica.
Define
 \begin{equation*}
U_n:= s_n+\dfrac{20}{n^4}\quad \text{and}\quad L_n:=s_n-\dfrac{15}{n^4}.
\end{equation*}
\begin{equation*}
U_n:= s_n+\dfrac{20}{n^4}\quad \text{and}\quad L_n:=s_n-\dfrac{15}{n^4}.
\end{equation*}Proof of Theorem 1.6
Using Equation (1.4) from Theorem 1.3, it follows that for ![]() $n \geq 37$, we have
$n \geq 37$, we have
 \begin{equation*}
\dfrac{(1-U_n)^2}{U^2_n(1-L_{n-1})(1-L_{n+1})}\lt\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})} \lt \dfrac{(1-L_n)^2}{L^2_n(1-U_{n-1})(1-U_{n+1})}.
\end{equation*}
\begin{equation*}
\dfrac{(1-U_n)^2}{U^2_n(1-L_{n-1})(1-L_{n+1})}\lt\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})} \lt \dfrac{(1-L_n)^2}{L^2_n(1-U_{n-1})(1-U_{n+1})}.
\end{equation*} Moreover, it can be readily checked that for ![]() $n \geq 29$, we have
$n \geq 29$, we have
 \begin{equation*}
\dfrac{(1-L_n)^2}{L^2_n(1-U_{n-1})(1-U_{n+1})} \lt t_n+\dfrac{120}{n^{5/2}}
\end{equation*}
\begin{equation*}
\dfrac{(1-L_n)^2}{L^2_n(1-U_{n-1})(1-U_{n+1})} \lt t_n+\dfrac{120}{n^{5/2}}
\end{equation*}and
 \begin{equation*}
\dfrac{(1-U_n)^2}{U^2_n(1-L_{n-1})(1-L_{n+1})}\gt t_n-\dfrac{120}{n^{5/2}}.
\end{equation*}
\begin{equation*}
\dfrac{(1-U_n)^2}{U^2_n(1-L_{n-1})(1-L_{n+1})}\gt t_n-\dfrac{120}{n^{5/2}}.
\end{equation*} We conclude the proof of Equation (1.6) by checking numerically for the values ![]() $31 \leq n \leq 36$ in Mathematica.
$31 \leq n \leq 36$ in Mathematica.
Proof of Corollary 1.7
It is equivalent to show that for ![]() $n \geq 42$, we have
$n \geq 42$, we have
 \begin{equation*}\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})}\gt1.\end{equation*}
\begin{equation*}\dfrac{(1-{\overline{u}}_n)^2}{{\overline{u}}^2_n(1-{\overline{u}}_{n-1})(1-{\overline{u}}_{n+1})}\gt1.\end{equation*} From the fact that for all ![]() $n \geq 99$, we have
$n \geq 99$, we have
 \begin{equation*}t_n-\dfrac{120}{n^{5/2}}\gt1,\end{equation*}
\begin{equation*}t_n-\dfrac{120}{n^{5/2}}\gt1,\end{equation*}and by Equation (1.6), the proof is finished after the numerical verification for the values ![]() $42 \leq n \leq 98$ in Mathematica.
$42 \leq n \leq 98$ in Mathematica.
Proof of Corollary 1.8
For all ![]() $n \geq 1176$, we have
$n \geq 1176$, we have
 \begin{equation*}t_n+\dfrac{120}{n^{5/2}}\lt1+\dfrac{\pi}{2n^{3/2}}.\end{equation*}
\begin{equation*}t_n+\dfrac{120}{n^{5/2}}\lt1+\dfrac{\pi}{2n^{3/2}}.\end{equation*} By Equation (1.6), we complete the proof for ![]() $n \geq 1176$. We can check Equation (1.7) numerically for the values
$n \geq 1176$. We can check Equation (1.7) numerically for the values ![]() $52 \leq n \leq 1175$ in Mathematica.
$52 \leq n \leq 1175$ in Mathematica.
Proof of Theorem 1.9
Following the definition given before and by Equation (1.4) of Theorem 1.3, it follows that for ![]() $n \geq 37$, we have
$n \geq 37$, we have
 \begin{equation*}
\dfrac{4(1-U_n)(1-U_{n+1})}{(1-L_{n}L_{n+1})^2}\lt \dfrac{4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1})}{(1-{\overline{u}}_n{\overline{u}}_{n+1})^2}\lt \dfrac{4(1-L_n)(1-L_{n+1})}{(1-U_{n}U_{n+1})^2}.
\end{equation*}
\begin{equation*}
\dfrac{4(1-U_n)(1-U_{n+1})}{(1-L_{n}L_{n+1})^2}\lt \dfrac{4(1-{\overline{u}}_n)(1-{\overline{u}}_{n+1})}{(1-{\overline{u}}_n{\overline{u}}_{n+1})^2}\lt \dfrac{4(1-L_n)(1-L_{n+1})}{(1-U_{n}U_{n+1})^2}.
\end{equation*} It is easy to observe that for ![]() $n \geq 99$, we have
$n \geq 99$, we have
 \begin{equation*}
\dfrac{4(1-L_n)(1-L_{n+1})}{(1-U_{n}U_{n+1})^2} \lt v_n+\dfrac{101}{n^{5/2}}
\end{equation*}
\begin{equation*}
\dfrac{4(1-L_n)(1-L_{n+1})}{(1-U_{n}U_{n+1})^2} \lt v_n+\dfrac{101}{n^{5/2}}
\end{equation*}and
 \begin{equation*}
\dfrac{4(1-U_n)(1-U_{n+1})}{(1-L_{n}L_{n+1})^2}\gt v_n-\dfrac{120}{n^{5/2}}.
\end{equation*}
\begin{equation*}
\dfrac{4(1-U_n)(1-U_{n+1})}{(1-L_{n}L_{n+1})^2}\gt v_n-\dfrac{120}{n^{5/2}}.
\end{equation*} We conclude the proof of Equation (1.8) by checking numerically for the values ![]() $2 \leq n \leq 98$ in Mathematica.
$2 \leq n \leq 98$ in Mathematica.
Proof of Corollary 1.10
We observe that  $v_n-\dfrac{120}{n^{5/2}}\gt1$ for all
$v_n-\dfrac{120}{n^{5/2}}\gt1$ for all ![]() $n \geq 180$ and hence by Equation (1.8), it follows immediately that
$n \geq 180$ and hence by Equation (1.8), it follows immediately that ![]() $\{{\overline{p}}(n)\}_{n \geq 180}$ satisfies higher-order Turán inequality and for the values
$\{{\overline{p}}(n)\}_{n \geq 180}$ satisfies higher-order Turán inequality and for the values ![]() $16 \leq n \leq 179$, we verified numerically in Mathematica.
$16 \leq n \leq 179$, we verified numerically in Mathematica.
Proof of Corollary 1.11
It is straightforward to check that  $v_n+\dfrac{101}{n^{5/2}}\lt 1+\dfrac{\pi}{4n^{3/2}}$ for all
$v_n+\dfrac{101}{n^{5/2}}\lt 1+\dfrac{\pi}{4n^{3/2}}$ for all ![]() $n \geq 4179$ in Equation (1.8). To finish the proof of Equation (1.9), it remains to verify for the values
$n \geq 4179$ in Equation (1.8). To finish the proof of Equation (1.9), it remains to verify for the values ![]() $2 \leq n \leq 4178$, which was done by numerical verification in Mathematica.
$2 \leq n \leq 4178$, which was done by numerical verification in Mathematica.
Funding Statement
The first author would like to acknowledge that the research was funded by the Austrian Science Fund (FWF): W1214-N15, project DK13. The second author would like to acknowledge that the research was supported by the National Natural Science Foundation of China (grant nos. 12001182 and 12171487), the Fundamental Research Funds for the Central Universities (grant no. 531118010411) and Hunan Provincial Natural Science Foundation of China (grant no. 2021JJ40037).
Competing interests
The authors declare none.