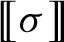1 Introduction
Often in geometric group theory, one considers a growth function
$F_{\Gamma }$
, which describes some part of the asymptotic structure of a finitely generated group
$\Gamma $
. Examples include subgroup growth, word growth, conjugacy growth, the Dehn function, the Følner function and residual finiteness growth. Having introduced
$F_{\Gamma }$
, it is always natural to attempt to estimate
$F_{\Gamma }$
for some group
$\Gamma $
of interest, to relate the behaviour of
$F_{\Gamma }$
to structural features of
$\Gamma $
or its actions, and to explore the types of functions which can arise as
$F_{\Gamma }$
for some
$\Gamma $
. In this paper we make contributions to all three of these themes for the LEF growth function, by examining some groups arising in Cantor dynamics.
1.1 Statement of results
A group
$\Gamma $
is locally embeddable into finite groups (LEF) if every finite subset of
$\Gamma $
admits an injective partial homomorphism (a local embedding) into a finite group. In other words, every finite subset of the multiplication table of
$\Gamma $
occurs in the multiplication table of some finite group. If
$\Gamma $
is finitely generated by S, the prototypical finite subsets are the balls
$B_S(n)$
in the associated word metric. The LEF growth function
$\mathcal {L}_{\Gamma } ^S$
sends
$n\in \mathbb {N}$
to the minimal order of a finite group into which
$B_S(n)$
locally embeds. The dependence of the function on S is slight, so we suppress S from our notation for the rest of this introduction.
That the topological full group
of a Cantor minimal system
$(X,\varphi )$
is an LEF group was proved by Grigorchuk and Medynets [Reference Grigorchuk and Medynets8]. We prove an effective version of their result, in the case of a two-sided minimal subshift
$(X,\sigma )$
over a finite alphabet. Let
$R_X : \mathbb {N} \rightarrow \mathbb {N}$
be the recurrence function of
$(X,\sigma )$
(see Definition 2.12 below).
Theorem 1.1. Let
$\Gamma $
be a finitely generated subgroup of
. Then
$$ \begin{align} \mathcal{L}_{\Gamma} (n) \preceq ( 2 R_X(n))!{.} \end{align} $$
In particular, this inequality holds for
.
For non-decreasing unbounded functions
$F_1$
and
$F_2$
we write
$F_1 \preceq F_2$
if, up to constant rescaling of the argument,
$F_2$
bounds
$F_1$
from above (see Definition 2.4 below). Note that the Cantor minimal system
$(X,\varphi )$
being isomorphic to a minimal subshift is a necessary and sufficient condition for
to be finitely generated [Reference Matui13]. In the other direction, we have the following lower bound on the LEF growth of
. Let
$p_X : \mathbb {N} \rightarrow \mathbb {N}$
be the complexity function of the minimal subshift
$(X,\sigma )$
(see Definition 2.10 below).
Theorem 1.2. There exists
$c>0$
such that
.
Our proof yields
$c=\log (60)/9 \approx 0.455$
, but small modifications to the argument would enable us to make c arbitrarily large. The group
always has exponential word growth, which immediately implies that
grows at least exponentially. One consequence of Theorem 1.1 is that when the subshift X is extremely ‘orderly’, this exponential lower bound is close to best possible.
Example 1.3. Let X be a linearly recurrent subshift. Then
On the other hand, if X is highly non-deterministic, then Theorem 1.2 gives a novel lower bound for the LEF growth of
.
Example 1.4. Let X be a subshift of positive entropy. Then
See §2.2 for definitions of linear recurrence and entropy. Although the upper and lower bounds proved in Theorems 1.1 and 1.2 are some distance apart, they are powerful enough to allow us to observe new phenomena in the kinds of functions which can arise as the LEF growth functions of groups. To achieve this, we adapt a construction of Jung, Lee and Park [Reference Jung, Lee and Park10] to obtain a sufficient diversity of subshifts.
Theorem 1.5. For every
$r \in [ 2,\infty )$
, there are a minimal subshift
$(X_r , \sigma )$
, constants
$C_r , c_r>0$
, and an increasing sequence
$(n_i ^{(r)})$
of integers such that:
-
(i) for all
$n\geq 2$
,
$R_{X_r} (n) \leq \exp ( C_r (\log n)^r )$
; -
(ii) for all
$i \in \mathbb {N}$
,
$p_{X_r} (n_i ^{(r)}) \geq \exp ( c_r (\log n_i ^{(r)} )^r )$
.
Applying Theorems 1.1 and 1.2 to the groups
arising from the subshifts
$(X_r , \sigma )$
of Theorem 1.5 yields that uncountably many inequivalent LEF growth functions occur among finitely generated LEF groups, answering a question posed in [Reference Bradford5].
Theorem 1.6. For any
$r \in [ 2,\infty )$
, there exists a finitely generated LEF group
$\Gamma ^{(r)}$
such that:
-
(i) there exists
$C_r> 0$
such that
$\mathcal {L}_{\Gamma ^{(r)}} (n) \preceq \exp ( \exp (C_r (\log n)^r ) )$
; -
(ii) for any
$2 \leq r^{\prime } < r$
, and for all
$C>0$
,
$\mathcal {L}_{\Gamma ^{(r)}} (n) \npreceq \exp ( \exp ( C(\log n)^{r^{\prime }} ) )$
.
Consequently, there is an uncountable family
$\mathcal {F}$
of pairwise non-isomorphic finitely generated LEF groups such that, for
$\Gamma _1 , \Gamma _2 \in \mathcal {F}$
, if
$\Gamma _1 \neq \Gamma _2$
then
.
We write
$F_1 \approx F_2$
if
$F_1 \preceq F_2$
and
$F_2 \preceq F_1$
(see Definition 2.4 below). Conclusions (i) and (ii) of Theorem 1.6 for the group
follow from Theorem 1.5(i) and (ii), by Theorems 1.1 and 1.2, respectively. Further examples of subshifts of ‘intermediate’ complexity could be a rich source of examples of new exotic behaviours in the LEF growth of groups, and this should be investigated further.
1.2 Background
The concept of an LEF group first appears in the work of Mal’cev, but was developed and popularized by Vershik and Gordon [Reference Vershik and Gordon16]. All residually finite groups are LEF, including all finitely generated nilpotent or linear groups, but local embeddability into finite groups enjoys some closure properties that residual finiteness does not: for instance, the (regular restricted) wreath product of LEF groups is LEF. Among finitely presented groups, the classes of LEF and residually finite groups coincide, and this observation provides a useful tool for proving that certain groups are not finitely presentable (see [Reference Grigorchuk and Medynets8] for a proof along these lines for derived subgroups of topological full groups). LEF groups have also been studied in connection with weaker approximation properties of groups, such as soficity and hyperlinearity, since they provide a source of examples beyond those arising from residual finiteness or amenability. For instance, Elek and Szabó [Reference Elek and Szabó7] used the LEF property to construct the first examples of sofic groups which are not residually amenable.
The LEF growth function was introduced independently in [Reference Arzhantseva and Cherix1, Reference Bou-Rabee and Studenmund4] (in the latter under the name geometric full residual finiteness growth), and fits into the extensive literature on quantifying finite approximations of infinite groups which has developed over the last decade. This program started with the work of Bou-Rabee and collaborators on quantitative residual finiteness (see [Reference Bou-Rabee, Chen and Timashova3] and the references therein). Using results on quantitative residual finiteness, word growth, and finite presentability, the LEF growth function has been estimated for several natural classes of groups (see [Reference Bradford5, §2.4]).
Example 1.7. Let
$\Gamma $
be a finitely generated group.
-
(i) If
$\Gamma $
is virtually
$\mathbb {Z}^d$
, then
$\mathcal {L}_{\Gamma } (n) \approx n^d$
. -
(ii)
$\mathcal {L}_{\Gamma }$
is bounded above by a polynomial function if and only if
$\Gamma $
is virtually nilpotent. -
(iii) If
$\Gamma \leq \operatorname {\mathrm {GL}}_d (\mathbb {Z})$
is finitely generated, not virtually nilpotent, then
$\mathcal {L}_{\Gamma } (n) \approx \exp (n)$
.
Groups of larger LEF growth can be explicitly constructed using wreath products.
Theorem 1.8. [Reference Bradford5, Theorem 1.8]
If
$\Gamma $
is a finitely generated LEF group with word growth function
$\gamma _{\Gamma }$
, and
$\Delta $
is a finite non-trivial centreless group, then
$\exp ( \gamma _{\Gamma } (n) ) \preceq \mathcal {L}_{\Delta \wr \Gamma } (n) \preceq \exp ( \mathcal {L}_{\Gamma } (n) )$
.
In particular, using Example 1.7, Theorem 1.8 allows us to construct groups of LEF growth
$\approx \exp (\exp (n))$
and
$\approx \exp (n^d)$
(for any
$d \in \mathbb {N}$
). The only other functions which have been observed to arise as LEF growth functions of groups are inexplicit and very large (see [Reference Bradford5, §5]). Our Theorem 1.6 therefore greatly extends the spectrum of known growth types.
The derived subgroup of the topological full group
of a minimal subshift
$(X,\sigma )$
is a remarkable object in group theory. It is a finitely generated infinite simple group, which, as well as being LEF, is amenable [Reference Juschenko and Monod12] (and indeed was the first group discovered with this combination of properties). It is also a natural invariant from the point of view of topological dynamics. As shown in [Reference Bezuglyi and Medynets2], for any Cantor minimal system
$(X,\varphi )$
,
retains perfect information about the dynamics of
$(X,\varphi )$
.
Theorem 1.9. (Bezuglyi and Medynets)
Let
$(X,\varphi )$
and
$(Y,\psi )$
be Cantor minimal systems. Then
if and only if
$(X,\varphi )$
and
$(Y,\psi )$
are flip-conjugate.
It is therefore reasonable to expect that group-theoretic asymptotic invariants of
should reflect asymptotic features of the dynamical system
$(X,\varphi )$
. Our Theorems 1.1 and 1.2 are in this spirit: knowing the LEF growth function of
allows one to deduce some bounds on the recurrence or complexity functions of X.
1.3 Methods and structure of the paper
Our proof of Theorem 1.1 is based on Elek’s streamlined proof of LEF for topological full groups [Reference Elek6]. Given
, finitely generated by S, and a two-sided sequence
$\mathbf {x} \in X$
, the
$\sigma $
-orbit
$\mathcal {O}$
of
$\mathbf {x}$
is dense in X, so
$\Gamma $
acts faithfully on
$\mathcal {O}$
. Further, any short word in S moves some cylinder set
$C \subseteq X$
, defined by a short string in
$\mathbf {x}$
. Since only finitely many such cylinder sets C arise, each of which intersects
$\mathcal {O}$
, there exists
$M \in \mathbb {N}$
such that no non-identity element of
$B_S (n)$
fixes
$\lbrace \sigma ^i \mathbf {x} : 1 \leq i \leq M \rbrace $
pointwise; moreover, we can take
$M \leq R_X (Cn)$
for some
$C>0$
. Carefully choosing the exact value of M to ensure consistency, we use this to construct a local embedding
$B_S(n) \rightarrow \operatorname {\mathrm {Sym}}(M)$
.
For our lower bound, we observe that
contains many copies of the alternating group
$\operatorname {\mathrm {Alt}}(5)$
, acting on disjoint subsets of X (hence generating their direct product). It follows that any finite group admitting a local embedding of a large ball in
also contains a direct product of many copies of
$\operatorname {\mathrm {Alt}}(5)$
as a subgroup, and so has large order. The supply of disjoint subsets on which to act, in this construction, is limited by the complexity function
$p_X$
, hence the appearance of
$p_X$
in Theorem 1.2.
This paper is structured as follows. In §§2.1–2.3 we collect necessary background results about LEF growth of groups, symbolic dynamics, and topological full groups, respectively. In §3 we construct the local embeddings required to prove Theorem 1.1. In §4 we prove Theorem 1.2. In §5 we describe the construction of the minimal subshifts arising in Theorem 1.5, and deduce Theorems 1.6.
2 Preliminaries
2.1 LEF groups and Schreier graphs
Definition 2.1. For
$\Gamma ,\Delta $
groups and
$F \subseteq \Gamma $
, a partial homomorphism of F into
$\Delta $
is a function
$\phi : F \rightarrow \Delta $
such that, for all
$g,h \in F$
, if
$gh \in F$
, then
$\phi (gh)=\phi (g)\phi (h)$
. A partial homomorphism
$\phi $
is called a local embedding if it is injective.
$\Gamma $
is locally embeddable into finite groups if, for all finite
$F \subseteq \Gamma $
, there exist a finite group Q and a local embedding of F into Q.
Henceforth suppose that
$\Gamma $
is LEF and generated by the finite set S. Let
$B_S(n) \subseteq \Gamma $
denote those elements of length at most n, with respect to the word metric induced on
$\Gamma $
by S.
Definition 2.2. The LEF growth of
$\Gamma $
(with respect to S) is
$$ \begin{align*} \mathcal{L}_{\Gamma} ^S (n) = \min \lbrace \lvert Q \rvert : \text{ there exists }\phi :B_S(n)\rightarrow Q\text{ a local embedding} \rbrace, \end{align*} $$
and the LEF action growth is
$$ \begin{align*} \mathcal{LA}_{\Gamma} ^S (n) = \min \lbrace d : \text{ there exists }\phi :B_S(n)\rightarrow \operatorname{\mathrm{Sym}}(d)\text{ a local embedding} \rbrace. \end{align*} $$
Remark 2.3. It is clear that
$\mathcal {LA}_{\Gamma } ^S (n) \leq \mathcal {L}_{\Gamma } ^S (n) \leq \mathcal {LA}_{\Gamma } ^S (n)!$
, though of course typically neither inequality will be sharp. Theorem 1.1 will be obtained from combining the second of these inequalities with an upper bound on the LEF action growth (see Theorem 3.7). We comment below (Remark 3.8) on whether our bound in Theorem 1.1 could be improved by avoiding the use of LEF action growth. Meanwhile the proof of Theorem 1.2 also yields a bound on
$\mathcal {LA}$
which is slightly stronger than that which could be obtained by using the above inequalities and treating the conclusion of Theorem 1.2 as a black box (see Remark 4.9). In summary, for
as in Theorems 1.1 and 1.2, we have
$$ \begin{align*} p_X (n^{1/2}) \preceq \mathcal{LA}_{\Gamma} (n) \preceq 2 R_X (n). \end{align*} $$
Definition 2.4. For
$F_1 , F_2 : \mathbb {N} \rightarrow \mathbb {N}$
non-decreasing functions, write
$F_1 \preceq F_2$
if there exists
$C>0$
such that
$F_1 (n) \leq F_2 (Cn)$
for all n. Write
$F_1 \approx F_2$
if
$F_1 \preceq F_2$
and
$F_2 \preceq F_1$
.
Lemma 2.5. Let
$\mathcal {F} = \mathcal {L}$
or
$\mathcal {LA}$
. Let
$\Delta \leq \Gamma $
be finitely generated by T. Then there exists
$C>0$
such that, for all n,
$$ \begin{align*} \mathcal{F}_{\Delta} ^T (n) \leq \mathcal{F}_{\Gamma} ^S (Cn) \end{align*} $$
In particular, for T a second finite generating set for
$\Gamma $
,
$\mathcal {F}_{\Gamma } ^S \approx \mathcal {F}_{\Gamma } ^T$
.
Proof. This is proved for
$\mathcal {F}=\mathcal {L}$
as Corollary 2.7 in [Reference Bradford5]; the proof for
$\mathcal {F} = \mathcal {LA}$
is identical.
The next proposition is key to the proof of Theorem 1.2. It uses an idea already exploited in [Reference Bradford5, Theorem 3.4] to control the LEF growth of wreath products.
Proposition 2.6. Let
$n \in \mathbb {N}$
and
$m \geq 2$
. Suppose
$\Delta _1 , \ldots , \Delta _m \leq \Gamma $
are finite centreless subgroups, generating their direct product, and that
$\Delta _i \subseteq B_S (n)$
. Suppose that Q is a finite group and that
$\phi : B_S (2n) \rightarrow Q$
is a local embedding. Then the
$\phi (\Delta _i) \leq Q$
generate their direct product, and
$\lvert Q \rvert \geq \prod _i \lvert \Delta _i \rvert $
.
Proof. Since
$\phi $
restricts to an injective homomorphism on each
$\Delta _i$
,
$\phi (\Delta _i)$
is a subgroup of Q, isomorphic to
$\Delta _i$
. Certainly, for
$i \neq j$
and
$g_i \in \Delta _i$
,
$g_j \in \Delta _j$
,
$$ \begin{align*} \phi(g_i)\phi(g_j) = \phi(g_i g_j) = \phi(g_j g_i) = \phi(g_j)\phi(g_i). \end{align*} $$
Therefore, if the
$\phi (\Delta _i)$
fail to generate their direct product, there exist
$1 \leq i \leq m$
and
$1 \neq g \in \Delta _i$
such that
$\phi (g) \in P$
, where
$P = \langle \phi (\Delta _j):i\neq j \rangle \leq Q$
. P centralizes
$\phi (\Delta _i)$
, since the
$\phi (\Delta _j)$
do, so for
$h \in \Delta _i$
,
$\phi (gh) = \phi (g)\phi (h) = \phi (h)\phi (g) = \phi (hg)$
. By injectivity of
$\phi $
restricted to
$\Delta _j$
, g is central in
$\Delta _i$
, a contradiction.
A based graph is a pair
$(G,v)$
, where G is a directed graph and
$v \in V(G)$
. A morphism of based graphs
$(G_1,v_1)\rightarrow (G_2,v_2)$
is a graph morphism
$\phi : G_1 \rightarrow G_2$
with
$\phi (v_1)=v_2$
. For C a set, an edge colouring of the graph G in C is a function
$c:E(G)\rightarrow C$
. A morphism
$(G_1,v_1,c_1)\rightarrow (G_2,v_2,c_2)$
of based graphs with edge colourings in C is a morphism
$\phi :(G_1,v_1)\rightarrow (G_2,v_2)$
of based graphs such that, for all
$e \in E(G_1)$
,
$c_1 (e) = c_2 (\phi (e))$
.
Definition 2.7. Let
$\Gamma $
be a group,
$\Omega $
be a
$\Gamma $
-set, and
$S \subseteq \Gamma $
. The associated Schreier graph
$\operatorname {\mathrm {Schr}}(\Gamma ,\Omega ,\mathbf {S})$
is the graph with vertex set
$\Omega $
and edge set
$\Omega \times S$
, with the edge
$(\omega ,s)$
running from
$\omega $
to
$s \omega $
. Impose an ordering on the elements of S, to obtain an ordered
$\lvert S \rvert $
-tuple
$\mathbf {S} \in \Gamma ^{\lvert S \rvert }$
(equivalently, fix a bijection
$c:S\rightarrow \lbrace 1,\ldots ,\lvert S \rvert \rbrace $
). Then
$\operatorname {\mathrm {Schr}}(\Gamma ,\Omega ,\mathbf {S})$
is naturally an edge-coloured graph with colours in
$\lbrace 1,\ldots ,\lvert S \rvert \rbrace $
, via
$c ( (\omega , s) ) = c(s)$
.
Definition 2.8. Let
$G_1 , G_2$
be directed edge-coloured graphs (with colours in C) and let
$r \in \mathbb {N}$
. We say that
$G_1$
is locally embedded in
$G_2$
at radius r if, for every
$v \in V(G_1)$
, there exists
$w \in V(G_2)$
and an isomorphism of based coloured graphs
$(B_v (r),v) \cong (B_w (r),w)$
(here
$B_v (r) \subseteq G_1$
is the induced subgraph on the closed ball of radius r around v in the path metric on
$G_1$
, and likewise for
$B_w (r)\subseteq G_2$
). We say that
$G_1$
and
$G_2$
are locally colour isomorphic at radius r if each is locally embedded in the other at radius r, that is,
$G_1$
and
$G_2$
have the same set of isomorphism types of balls of radius r.
The next observation is our key tool for constructing the local embeddings needed in Theorem 1.1; it is proved as Lemma 4.2 in [Reference Bradford5].
Lemma 2.9. For
$i=1,2$
, let
$\Gamma _i$
be a group acting faithfully on a set
$\Omega _i$
, and let
$\mathbf {S}_i$
be an ordered generating d-tuple in
$\Gamma _i$
. Suppose that the Schreier graphs
$\operatorname {\mathrm {Schr}} (\Gamma _i,\Omega _i,\mathbf {S}_i)$
are locally colour-isomorphic at some radius at least
$\lceil 3r/2 \rceil $
. Then there is a local embedding
$B_{\mathbf {S}_1} (r) \rightarrow \Gamma _2$
extending
$(\mathbf {S}_1)_j \mapsto (\mathbf {S}_2)_j$
.
2.2 Words
Throughout, the alphabet A will be a finite discrete set with
$\lvert A \rvert \geq 2$
. Let
$A^{\ast } = \bigsqcup _n A^n$
be the set of finite words over A. An infinite word shall be an element of either
$A^{\mathbb {Z}}$
or
$A^{\mathbb {N}}$
. We equip the latter sets with the product topology; note that both are thereby homeomorphic to the Cantor space.
Definition 2.10. Let
$w \in A^{\mathbb {Z}}$
. For
$k \in \mathbb {Z}$
and
$n \in \mathbb {N}$
, the kth n-factor of w is
$w_k w_{k+1} \cdots w_{k+n-1} \in A^n$
.
$v \in A^n$
is an n-factor of w if it is the kth n-factor for some k. n-factors of words in
$A^{\mathbb {N}}$
and
$A^{\ast }$
are defined similarly, with the requirement that
$k \in \mathbb {N}$
and, for
$w \in A^{\ast }$
, that
$k \leq \lvert w \rvert -n+1$
.
In any case, the set of all n-factors of w is denoted by
$F_n (w)$
. For w an infinite word, the complexity function
$p_w :\mathbb {N}\rightarrow \mathbb {N}$
of w is given by
$p_w (n) = \lvert F_n (w) \rvert $
.
It is immediate from the definitions that
$p_w (n+m) \leq p_w(n)p_w(m)$
and
$p_{w}(n) \leq \lvert A \rvert ^n$
for all
$n,m \in \mathbb {N}$
.
Definition 2.11. The entropy of
$w \in A^{\mathbb {Z}}$
is
$$ \begin{align*} h(w) = \lim_{n \rightarrow \infty} \frac{\log p_w(n)}{n} \end{align*} $$
(the limit is well defined, by the preceding remarks).
Definition 2.12.
$\mathbf {x} \in A^{\mathbb {Z}}$
is uniformly recurrent if, for every
$n \in \mathbb {N}$
, there exists
$M_n \in \mathbb {N}$
such that, for every
$w \in F_n (\mathbf {x})$
and
$v \in F_{M_n} (\mathbf {x})$
,
$w \in F_n (v)$
. The smallest such
$M_n$
is denoted by
$R_{\mathbf {x}} (n)$
, and
$R_{\mathbf {x}} : \mathbb {N} \rightarrow \mathbb {N}$
is the recurrence function of
$\mathbf {x}$
.
Henceforth assume
$\mathbf {x} \in A^{\mathbb {Z}}$
to be uniformly recurrent non-periodic.
Theorem 2.13. [Reference Morse and Hedlund14, Theorem 7.5]
$R_{\mathbf {x}} (n) \geq p_{\mathbf {x}}(n)+n \geq 2n+1$
for all
$n \in \mathbb {N}$
.
In particular,
$R_{\mathbf {x}}$
grows at least linearly in n.
Definition 2.14.
$\mathbf {x}$
is linearly recurrent if there exists
$C> 0$
such that
$R_{\mathbf {x}} (n) \leq Cn$
for all
$n \in \mathbb {N}$
.
Example 2.15. [Reference Morse and Hedlund15, Theorem 11.4]
The Fibonacci word is linearly recurrent.
Definition 2.16. A cylinder set of
$A^{\mathbb {Z}}$
is a set of the form
$$ \begin{align*} \ll u_{k},\ldots,u_{-1},\underline{u}_0,u_1,\ldots,u_l\gg \, =\, \lbrace \mathbf{y} \in A^{\mathbb{Z}} : y_i = u_i \text{ for } k \leq i \leq l \rbrace, \end{align*} $$
where
$k,l \in \mathbb {Z}$
with
$k \leq 0 \leq l$
and
$u_i \in A$
for
$k \leq i \leq l$
. For
$u \in A^n$
and
$1 \leq i \leq n$
, we write
$\ll u \gg _i$
for the cylinder set
$\ll u_1,\ldots ,u_{i-1},\underline {u}_i,u_{i+1},\ldots ,u_n\gg $
. Note that
$$ \begin{align*} \ll u_1,\ldots,u_{i-1},\underline{u}_i,u_{i+1},\ldots,u_n\gg \, =\, \ll v_k,\ldots,v_{-1},\underline{v}_0,v_1,\ldots,v_l\gg \end{align*} $$
where
$k=1-i$
,
$l=n-i$
and
$v_j=u_{j+i}$
for
$k\leq j\leq l$
.
For
$X \subseteq A^{\mathbb {Z}}$
clopen and
$m \in \mathbb {N}$
, an m-cylinder of X is a non-empty set of the form
$$ \begin{align*} X \cap \ll u_{-m},\ldots,u_{-1},\underline{u}_0,u_1,\ldots,u_m\gg. \end{align*} $$
The set of m-cylinders of X will be denoted by
$\operatorname {\mathrm {Cyl}}_X (m)$
.
Remark 2.17. Let
$u \in A^n$
and
$1 \leq i \leq n$
.
-
(i) For any
$k,l\in \mathbb {N}$
, In particular, for any
$$ \begin{align*} \bigsqcup_{v \in A^k} \ll vu \gg_{k+i} \,{=}\, \ll u \gg_i = \bigsqcup_{w \in A^l} \ll uw \gg_{i} \end{align*} $$
$m \in \mathbb {N}$
, the set of all m-cylinders of X forms a clopen partition of X, and for
$1 \leq k \leq m$
, any k-cylinder of X is the disjoint union of the m-cylinders of X which intersect it.
-
(ii) The cylinder sets form a basis for the topology on
$A^{\mathbb {Z}}$
. Hence, for any clopen subset Y of
$A^{\mathbb {Z}}$
, Y is the union of cylinder sets. By compactness, and by (i), there exists
$C=C(Y)>0$
such that, for all
$m \geq C$
, Y is the disjoint union of m-cylinders of
$A^{\mathbb {Z}}$
. -
(iii) Since
$\mathcal {O}(\mathbf {x})=\lbrace \sigma ^i(\mathbf {x}):i\in \mathbb {Z}\rbrace $
is dense in X, for
$u_i \in A$
,
$U =\, \ll u_{-m},\ldots ,u_{-1},\underline {u}_0, u_1,\ldots ,u_m\gg $
intersects X if and only if for some
$i \in \mathbb {Z}$
,
$\sigma ^i (\mathbf {x}) \in U$
, which occurs if and only if
$u_j = x_{i+j}$
for
$-m \leq j \leq m$
. That is, U intersects X if and only if
$u_{-m} \cdots u_m$
is a factor of
$\mathbf {x}$
. Thus the map sending
$u_{-m} \cdots u_m$
to
$U \cap X$
is a bijection from
$F_{2m+1} (\mathbf {x})$
to
$\operatorname {\mathrm {Cyl}}_X (m)$
, hence
$\lvert \operatorname {\mathrm {Cyl}}_X (m) \rvert = p_X (2m+1)$
.
2.3 Topological full groups and minimal subshifts
Let
$\mathbf {C}$
be the Cantor space. A Cantor dynamical system is a pair
$(X,\varphi )$
, where X is a space homeomorphic to
$\mathbf {C}$
, and
$\varphi \in \operatorname {\mathrm {Homeo}}(X)$
(we specify the space X, rather than always taking
$X=\mathbf {C}$
, in case the homeomorphism
$\varphi $
is described in terms of a particular model X of Cantor space; in particular, this will be the case when the system is a subshift). The system
$(X,\varphi )$
is called minimal if every orbit in X under the action of
$\langle \varphi \rangle $
is dense in X.
Example 2.18. Let A be a finite discrete space with
$\lvert A \rvert \geq 2$
. Then
$A^{\mathbb {Z}} \cong \mathbf {C}$
. The shift over A is
$\sigma \in \operatorname {\mathrm {Homeo}} (A^{\mathbb {Z}})$
given, for
$\mathbf {a} = (a_i)_{i\in \mathbb {Z}}$
, by
$\sigma (\mathbf {a})_i = a_{i+1}$
. The Cantor dynamical system
$(A^{\mathbb {Z}},\sigma )$
is never minimal.
Definition 2.19. The topological full group
of the system
$(X,\varphi )$
is the set of all homeomorphisms g of X such that there exists a continuous function
$f_g : X \rightarrow \mathbb {Z}$
(called the orbit cocycle of g) such that for all
$x \in X$
,
$g (x) = \varphi ^{f_g (x)} (x)$
(here we assume
$\mathbb {Z}$
equipped with the discrete topology).
Equivalently,
$g \in \operatorname {\mathrm {Homeo}} (X)$
lies in
if there exist a finite clopen partition
$C_1 , \ldots , C_d$
of X and integers
$a_1 , \ldots , a_d$
such that for
$1 \leq i \leq d$
,
$g|_{C_i} = \varphi ^{a_i} |_{C_i}$
(taking
$\lbrace a_1,\ldots ,a_d\rbrace = \operatorname {\mathrm {im}}(f_g)$
,
$C_i = f_g ^{-1}(a_i)$
). It is straightforward to check that
is a subgroup of
$\operatorname {\mathrm {Homeo}}(X)$
.
Remark 2.20. If
$(X,\varphi )$
is a minimal system, then the orbit cocycle
$f_g$
is uniquely determined by
, since
$\varphi $
has no periodic points.
The next result gives the key source of minimal systems for our purposes.
Proposition 2.21. Suppose
$\mathbf {x} \in A^{\mathbb {Z}}$
is uniformly recurrent non-periodic. Then
$\overline {\mathcal {O}(\mathbf {x})} \cong \mathbf {C}$
, and the system
$(\overline {\mathcal {O}(\mathbf {x})},\sigma )$
is minimal.
Proof. For minimality, see [Reference Juschenko11, Theorem 1.0.1]. To prove
$\overline {\mathcal {O}(\mathbf {x})} \cong \mathbf {C}$
, note that the only property not automatically inherited by subspaces of
$\mathbf {C}$
is being perfect. Then, if
$Y=\overline {\mathcal {O}(\mathbf {x})}$
, a non-periodic
$\mathbf {x}$
must have
$\lvert Y\rvert =\infty $
, which implies that Y has an accumulation point in
$\mathbf {C}$
. But Y contains its set of accumulation points
$\mathrm {Acc}(Y)$
in
$\mathbf {C}$
(by compactness), and
$\mathrm {Acc}(Y)$
is closed and
$\sigma $
-invariant, so by minimality
$Y=\mathrm {Acc}(Y)$
.
Definition 2.22. A subspace
$X = \overline {\mathcal {O}(\mathbf {x})} \subseteq A^{\mathbb {Z}}$
constructed as in the statement of Proposition 2.21 is called a minimal subshift.
Remark 2.23. Suppose
$\mathbf {x} \in A^{\mathbb {Z}}$
is uniformly recurrent non-periodic. For any
$\mathbf {y}\in \overline {\mathcal {O}(\mathbf {x})}$
and
$n\in \mathbb {N}$
,
$F_n (\mathbf {x}) = F_n (\mathbf {y})$
. In particular,
$p_{\mathbf {x}}$
and
$R_{\mathbf {x}}$
depend only on X, and we may henceforth write
$p_X$
or
$R_X$
instead.
Let
denote the derived subgroup of
. The reason for our focus on minimal subshifts, among all minimal systems, is made clear by the next result.
Theorem 2.24. [Reference Matui13, Theorem 5.4]
For
$(X,\varphi )$
a Cantor minimal system,
is a finitely generated group if and only if
$(X,\varphi )$
is isomorphic to a minimal subshift.
Theorem 2.25. [Reference Grigorchuk and Medynets8, Proposition 2.4]
Let
$(X,\sigma )$
be a minimal subshift, and let S be a finite generating set for
. Then
$\lvert B_S(n) \rvert \succeq \exp (n)$
.
Corollary 2.26. We have
.
Proof. This is immediate from the preceding theorem: if
$\phi : B_S (n) \rightarrow Q$
is a local embedding, then
$\phi $
is injective, so
$\lvert Q \rvert \geq \lvert B_S(n) \rvert $
.
Thus our Theorem 1.2 is only new in the case
$p_X (n) \npreceq n^2$
.
3 Construction of local embeddings
In this section we prove Theorem 1.1. Let
$(X,\sigma )$
be a minimal subshift over the alphabet A.
Proposition 3.1. Let
be finite. Then there exists an integer
$C_1 = C_1(S) \geq 1$
such that, for all
$r \in \mathbb {N}$
and all
$g \in B_S (r)$
:
-
(i)
$\max \lbrace \lvert f_g (x)\rvert : x\in X\rbrace \leq C_1 r$
; -
(ii) for all
$m \geq C_1 r$
,
$f_g$
is constant on every m-cylinder of X.
Proof. For (i), for
write
$\unicode{x3bb} (g) = \max \lbrace \lvert f_g (x)\rvert : x\in X\rbrace $
. Since S is finite, we may choose
$C_1 \geq \max \lbrace \unicode{x3bb} (s):s\in S \rbrace $
. For
,
$\unicode{x3bb} (gh) \leq \unicode{x3bb} (g)+\unicode{x3bb} (h)$
, so by induction
$\unicode{x3bb} (g) \leq C_1 r$
for all
$g \in B_S (r)$
.
For (ii), for every
$s \in S \cup S^{-1}$
there is a finite clopen partition
$\mathcal {C}_s$
of X, such that
$f_s$
is constant on the parts of
$\mathcal {C}_s$
. By Remark 2.17(ii), we may choose
$C_1$
sufficiently large that, for all
$s \in S \cup S^{-1}$
and
$m \geq C_1$
,
$f_s$
is constant on every m-cylinder of X. Let
$r \geq 2$
and suppose by induction that the claim holds for smaller r. Let
$m \geq C_1 r$
, let U be an m-cylinder of X, and let
$g \in B_S (r)$
. Then there exist
$h\in B_S (r-1)$
and
$s\in S\cup S^{-1}\cup \lbrace e\rbrace $
such that
$g=sh$
. By inductive hypothesis,
$f_h$
is constant on U, say with value i. Observe that, for any
$k,l \in \mathbb {N}$
, if
$x,y \in X$
lie in the same
$(k+l)$
-cylinder of X, then
$\sigma ^{\pm l} x , \sigma ^{\pm l} y$
lie in the same k-cylinder of X. Thus, there is a unique
$(m-\lvert i\rvert )$
-cylinder containing
$h(U)$
. By (i),
$i \in [-C_1 (r-1) , C_1 (r-1)]$
, so
$m-\lvert i\rvert \geq C_{1}$
. This implies that
$f_s$
is constant on
$h(U)$
, hence
$f_g$
is constant on U.
Remark 3.2. By Proposition 3.1(i), for
$k\in \mathbb {N}$
and
$m \geq C_1 r$
, if
$x,y \in X$
lie in the same
$(k+m)$
-cylinder of X, then
$g(x),g(y)$
lie in the same k-cylinder of X for any
$g \in B_S (r)$
.
Lemma 3.3. Let
$C_1$
be as in Proposition 3.1. For all
$r \in \mathbb {N}$
, there exists
$M = M(r) \in \mathbb {N}$
satisfying:
-
(i)
$\lbrace \sigma ^i \mathbf {x} : 1\leq i\leq M \rbrace $
intersects every
$C_1(r+1)$
-cylinder of X; -
(ii)
$\mathbf {x}$
and
$\sigma ^M \mathbf {x}$
lie in the same
$C_1(2r+1)$
-cylinder of X; -
(iii)
$10 C_1 r \leq M \leq 2 R_X (10 C_1 r)$
.
Proof. Let
$u \in A^{2C_1(r + 1)+1}$
. Then
$\ll u \gg _{C_1(r + 1)+1}\cap X$
is a
$C_1(r + 1)$
-cylinder of X if and only if
$u \in F_{2C_1(r + 1)+1} (\mathbf {x})$
. Therefore (i) holds for any
$M \geq R_X (2C_1(r + 1)+1)$
. For the same reason, a value of M satisfying (ii) occurs at least once in every interval of length
$R_X (2 C_1(2r+1)+1)$
. Therefore we can choose
$M \leq R_X (2 C_1(2r+1)+1) + 10 C_1 r$
satisfying (i), (ii) and the first inequality of (iii). Since
$10 C_1 r \leq R_X (5 C_1 r)$
by Theorem 2.13, and since
$R_X$
is non-decreasing, the second inequality of (iii) also holds.
Corollary 3.4. Let M be as in Lemma 3.3. For any
$\lvert i \rvert \leq C_1 r$
,
$\sigma ^i \mathbf {x}$
and
$\sigma ^{M+i} \mathbf {x}$
lie in the same
$C_1(r+1)$
-cylinder of X.
Fix
$\mathbf {x} \in X$
and let
$\mathcal {O}=\mathcal {O}(\mathbf {x})$
be the orbit of
$\mathbf {x}$
under
$\sigma $
. Then
acts on
$\mathcal {O}$
. Since X has no periodic points, this action induces a well-defined homomorphism
by
$$ \begin{align} g (\sigma^n \mathbf{x})=\sigma^{\phi(g)[n]} ( \mathbf{x}){.} \end{align} $$
In other words,
$\phi (g) [n] = n + f_{g}(\sigma ^n \mathbf {x})$
. Since
$\mathcal {O}$
is dense in X,
$\phi $
is injective.
Let
be finitely generated, and let
$\mathbf {S} = (s_1,\ldots ,s_d)$
be an ordered generating d-tuple of elements of
$\Gamma $
. Then
$\Gamma $
acts faithfully on
$\mathbb {Z}$
via
$\phi $
. Let
$G = \operatorname {\mathrm {Schr}}(\Gamma ,\mathbb {Z},\mathbf {S})$
be the associated Schreier graph of the action of
$\Gamma $
on
$\mathbb {Z}$
with respect to
$\mathbf {S}$
. Let
$C_1 = C_1 (\lbrace s_1 , \ldots ,s_d \rbrace )\geq 1$
be as in Proposition 3.1.
Lemma 3.5. For
$n \in \mathbb {Z}$
and
$r \in \mathbb {N}$
, the isomorphism type of
$B_G(n,r) \subseteq G$
(as a based, edge-coloured graph) depends only on the
$C_1 (r + 1)$
-cylinder of X in which
$\sigma ^n \mathbf {x}$
lies.
Proof. By Proposition 3.1(i),
$B_G(n,r) \subseteq [n-C_1 r , n+C_1 r] \cap \mathbb {Z}$
. For
$\lvert i\rvert \leq C_1 r $
,
$n+i \in B_G(n,r)$
if and only if, for some
$g \in B_{\mathbf {S}} (r)$
,
$f_g(\sigma ^n \mathbf {x}) = i$
, and by Proposition 3.1(ii), this condition depends only on the
$C_1 r$
-cylinder of X containing
$\sigma ^n \mathbf {x}$
.
For
$n+i,n+j \in B_G(n,r)$
, and
$1 \leq c \leq d$
,
$(n+i,n+j)$
is a c-coloured edge in G if and only if
$f_{s_c} (\sigma ^{n+i} \mathbf {x}) = j-i$
. This depends only on the
$C_1$
-cylinder of X containing
$\sigma ^{n+i} \mathbf {x}$
, which in turn depends only on the
$C_1 (r+1)$
-cylinder of X containing
$\sigma ^n \mathbf {x}$
.
Let
$r \geq 1$
and let
$M = M(r)$
be as in Lemma 3.3. For
$1\leq c \leq d$
define
$\overline {s}_c :\mathbb {Z}/M\mathbb {Z} \rightarrow \mathbb {Z}/M\mathbb {Z}$
by
$$ \begin{align*} \overline{s}_c (n + M \mathbb{Z}) = \phi(s_c)[n] + M \mathbb{Z}\quad\text{for }1 \leq n \leq M. \end{align*} $$
Proposition 3.6. The function
$\overline {s}_c$
lies in
$\operatorname {\mathrm {Sym}}(\mathbb {Z}/M\mathbb {Z})$
.
Proof. We check that
$\overline {s}_c$
is injective, and therefore is indeed a well-defined permutation. If
$1 \leq m<n \leq M$
with
$\phi (s_c)[n] \equiv \phi (s_c)[m]\ \mathrm {mod}\ {M}$
, then
$$ \begin{align*} n-m\equiv f_{s_c}(\sigma^m \mathbf{x})-f_{s_c}(\sigma^n\mathbf{x})\ \mathrm{mod}\ {M}, \end{align*} $$
but by Proposition 3.1(i),
$$ \begin{align*} \lvert f_{s_c}(\sigma^m \mathbf{x}) - f_{s_c}(\sigma^n\mathbf{x}) \rvert \leq 2 C_1 \end{align*} $$
while
$1 \leq n-m \leq M-1$
, so either
$1 \leq n-m \leq 2C_1$
or
$M-2C_1 \leq n-m \leq M-1$
. In the former case,
$$ \begin{align*} \phi(s_c)[n] \equiv \phi(s_c)[m]\ \mathrm{mod}\ {M} \quad\text{but}\quad \lvert \phi(s_c)[n] - \phi(s_c)[m] \rvert \leq 4 C_1, \end{align*} $$
and since
$M \geq 10 C_1$
by Lemma 3.3(iii),
$\phi (s_c)[n]=\phi (s_c)[m]$
, contradicting the injectivity of
$\phi (s_c)$
. The latter case is similar; we have
$$ \begin{align*} 1 \leq m \leq 2C_1\quad\text{and}\quad 1 \leq m+M - n \leq 2C_1. \end{align*} $$
By Corollary 3.4,
$\sigma ^{m+M} \mathbf {x}$
and
$\sigma ^m \mathbf {x}$
lie in the same
$C_1 (r+1)$
-cylinder of X, so by Proposition 3.1,
$f_{s_c} (\sigma ^{m+M} \mathbf {x}) = f_{s_c} (\sigma ^m \mathbf {x})$
. We may therefore argue as in the former case, with
$m+M$
replacing m.
Theorem 1.1 is now immediate, by Remark 2.3, from the next result.
Theorem 3.7. We have
$\mathcal {LA}_{\Gamma }^S (\lfloor 2r/3 \rfloor ) \leq 2 R_X (10 C_1 r)$
.
Proof. Let M be as in Lemma 3.3. By the upper bound on M from Lemma 3.3(iii), it suffices to show that there is a local embedding
$B_{\mathbf {S}}(\lfloor 2r/3 \rfloor ) \rightarrow \operatorname {\mathrm {Sym}} (\mathbb {Z}/M\mathbb {Z})$
sending
$s_c$
to
$\overline {s}_c$
for
$1 \leq c \leq d$
. Let
$\overline {\mathbf {S}}=\lbrace \overline {s}_1 ,\ldots ,\overline {s}_d\rbrace $
; let
$\overline {\Gamma } = \langle \overline {\mathbf {S}} \rangle \leq \operatorname {\mathrm {Sym}} (\mathbb {Z}/M\mathbb {Z})$
, and let
$\overline {G} = \operatorname {\mathrm {Schr}} (\overline {\Gamma },\mathbb {Z}/M\mathbb {Z},\overline {\mathbf {S}})$
. By Lemma 2.9, it suffices to show that G and
$\overline {G}$
are locally colour-isomorphic at radius r.
By Lemmas 3.5 and 3.3(i), for every
$m \in \mathbb {Z}$
,
$B_G(m , r) \subseteq G$
is isomorphic (as a based, edge-coloured graph) to
$B_G(n , r)$
, for some
$1 \leq n \leq M$
. Let
$\pi _M:\mathbb {Z}\rightarrow \mathbb {Z}/M\mathbb {Z}$
be reduction modulo M. It suffices to check that for every
$1 \leq n \leq M$
the restriction of
$\pi _M$
to
$V( B_G(n , r) ) \subseteq \mathbb {Z}$
induces an isomorphism of based edge-coloured graphs
$B_G(n,r) \rightarrow B_{\overline {G}}(\pi _M (n),r)$
.
Consider
$I_n = [n-C_1 r,n+C_1 r] \cap \mathbb {Z}$
. Since
$2 C_1 r < M$
(by Lemma 3.3), the restriction of
$\pi _M$
to
$I_n$
is injective. By Proposition 3.1(i),
$V( B_G(n , r) ) \subseteq I_{n}$
, so the restriction of
$\pi _M$
to
$V( B_G(n , r) )$
is a bijection onto its image. Then it suffices to show that
$\pi _{M}(\phi (s_{c})[k])=\overline {s}_{c}(\pi _{M}(k))$
for all
$k\in I_{n}$
and all c.
Since
$-C_1 r \leq k \leq M + C_1 r$
, there exists
$\epsilon \in \{0,\pm 1\}$
such that
$k'=k+\epsilon M$
is the representative of
$k+M\mathbb {Z}$
in
$[1,M]$
. By Corollary 3.4 and Proposition 3.1(ii) (or by
$k=k'$
) we have
$f_{s_{c}}(\sigma ^{k}\mathbf {x})=f_{s_{c}}(\sigma ^{k'}\mathbf {x})$
, which means
$\phi (s_{c})[k]=\phi (s_{c})[k']+\epsilon M$
. Then
$$ \begin{align*} \pi_{M}(\phi(s_{c})[k])=\pi_{M}(\phi(s_{c})[k']+\epsilon M)=\pi_{M}(\phi(s_{c})[k']) = \overline{s}_{c}(k'+M\mathbb{Z})=\overline{s}_{c}(\pi_{M}(k)) \end{align*} $$
as claimed.
By the preceding paragraph, the restriction of
$\pi _M$
to
$V( B_G(n , r) )$
preserves edges and colours. In particular, the vertices of
$B_{\overline {G}}(\pi _M (n),r)$
, which are precisely the endpoints of (undirected) edge-paths of length no greater than r in
$\overline {G}$
starting at
$\pi _M (n)$
, are exactly the image under
$\pi _M$
of the endpoints of edge paths of length no greater than r in G starting at n, namely the vertices of
$B_G(n , r)$
. Hence
$\pi _M$
does indeed induce the desired isomorphism of based edge-coloured graphs.
Remark 3.8. In the proof of Theorem 3.7, it is unclear what can be said in general about the subgroup
$\overline {\Gamma }$
of
$\operatorname {\mathrm {Sym}}(\mathbb {Z}/M\mathbb {Z})$
generated by
$\overline {s}_1 , \ldots , \overline {s}_d$
. If
$\overline {\Gamma }$
were to be much smaller than
$\operatorname {\mathrm {Sym}}(\mathbb {Z}/M\mathbb {Z})$
, then we might deduce a better upper bound in Theorem 1.1 than that obtained by combining Theorem 1.1 with Remark 2.3. That said, it is known that a ‘generic’ subset of
$\operatorname {\mathrm {Sym}}(\mathbb {Z}/M\mathbb {Z})$
(in various senses) generates a subgroup containing
$\operatorname {\mathrm {Alt}}(\mathbb {Z}/M\mathbb {Z})$
, so absent a specific reason for expecting the contrary, it is reasonable to suspect the index of
$\overline {\Gamma }$
in
$\operatorname {\mathrm {Sym}}(\mathbb {Z}/M\mathbb {Z})$
to be small.
4 Obstructions to small local embeddings
Let
$(X,\sigma )$
be a minimal subshift over A, and fix
$\mathbf {x} \in A^{\mathbb {Z}}$
with
$X = \overline {\mathcal {O}(\mathbf {x})}$
. Let
be a finite generating set (such exists by Theorem 2.24), and let
$\lvert \cdot \rvert _S$
be the word length function induced on
by S. Recall that
$p_X = p_{\mathbf {x}} : \mathbb {N} \rightarrow \mathbb {N}$
is the complexity function of
$\mathbf {x}$
;
$R_X = R_{\mathbf {x}} : \mathbb {N} \rightarrow \mathbb {N}$
is the recurrence function of
$\mathbf {x}$
, and
$\operatorname {\mathrm {Cyl}}_X(m)$
denotes the set of m-cylinders of X.
Lemma 4.1. Suppose that
$m \geq (R_{\mathbf {x}}(4)-1)/2$
, and let
$U \in \operatorname {\mathrm {Cyl}}_X(m)$
. Then the sets
$\sigma ^{i}(U)$
, for
$-2\leq i\leq 2$
, are pairwise disjoint.
Proof. Suppose to the contrary that
$\mathbf {y} \in \sigma ^{i}(U) \cap \sigma ^{j}(U)$
, for some
$-2 \leq i < j \leq 2$
. Writing
$k =j-i$
, we have
$y_l = y_{l+k}$
for
$-m \leq l \leq m-k$
. Letting
$w = y_{-m} y_{-m+1}\cdots y_m \in F_{2m+1} (\mathbf {x})$
, we have
$\lvert F_k(w)\rvert \leq k$
. On the other hand,
$2m+1 \geq R_{\mathbf {x}}(k)$
, so by the definition of
$R_{\mathbf {x}}$
,
$\lvert F_k(w) \rvert = \lvert F_k(\mathbf {x}) \rvert =p_{\mathbf {x}}(k)\geq k+1$
(the last inequality holding by Theorem 2.13), a contradiction.
Lemma 4.2. Let
$m \geq \max \lbrace (R_{\mathbf {x}}(4)-1)/2 , 5 \rbrace $
. There exists a set
$\operatorname {\mathrm {DCyl}}_X(m) \subseteq \operatorname {\mathrm {Cyl}}_X(m)$
such that the sets
$\sigma ^i (U)$
, for
$ U \in \operatorname {\mathrm {DCyl}}_X(m)$
and
$-2 \leq i \leq 2$
, are pairwise disjoint, and
$$ \begin{align} \lvert \operatorname{\mathrm{DCyl}}_X(m) \rvert \geq p_{\mathbf{x}} (2m-7)/9{.} \end{align} $$
Proof. We construct
$\operatorname {\mathrm {DCyl}}_X(m)$
via an iterative process as follows. At step
$0$
, let
$U_0$
be any m-cylinder. Then the
$\sigma ^i (U_0)$
, for
$-2 \leq i \leq 2$
, are pairwise disjoint, by Lemma 4.1. Let
$A_0$
be the set of
$(m-4)$
-cylinders containing one of the
$\sigma ^j (U_0)$
, for
$-4 \leq j \leq 4$
, so that
$\lvert A_0 \rvert \leq 9$
, and let
$B_0 = \lbrace U_0 \rbrace $
.
At each subsequent step
$k+1$
, we start with
$B_k$
a family of m-cylinders and
$A_k$
a family of
$(m-4)$
-cylinders such that, for any
$U \in B_k$
and
$-4 \leq j \leq 4$
, there exists
$V \in A_k$
such that
$\sigma ^j (U) \subseteq V$
. If
$A_k$
is a cover of X, then set
$\operatorname {\mathrm {DCyl}}_X(m) = B_k$
and stop. Otherwise, choose
$\mathbf {y}_k \in X \setminus (\bigcup _{V \in A_k} V)$
and let
$U_{k+1}$
be the m-cylinder of X containing
$\mathbf {y}_k$
. Then
$\sigma ^i (U_{k+1})$
(
$-2 \leq i \leq 2$
) are pairwise disjoint (by Lemma 4.1). If there exist
$0 \leq l \leq k$
and
$-2 \leq i,j \leq 2$
such that
$\sigma ^i (U_{k+1}) \cap \sigma ^j (U_l) \neq \emptyset $
, then, letting
$V \in A_k$
be such that
$\sigma ^{j-i} (U_l) \subseteq V$
,
$U_{k+1} \subseteq V$
(by Remark 2.17), contradicting the choice of
$\mathbf {y}_k$
.
We may therefore let
$B_{k+1} = B_k \cup \lbrace U_{k+1} \rbrace $
and produce
$A_{k+1}$
by adding to
$A_k$
all
$(m-4)$
-cylinders containing one of the
$\sigma ^j (U_{k+1})$
,
$-4 \leq j \leq 4$
. At every stage
$\lvert A_{k+1} \rvert \leq \lvert A_k \rvert +9$
,
$\lvert B_{k+1} \rvert \geq \lvert B_k \rvert + 1$
, and by Remark 2.17(iii), the process terminates only when
$\lvert A_k \rvert = p_{\mathbf {x}} (2m-7)$
.
Notation 4.3. Let
$U \subseteq X$
be a non-empty clopen set, such that
$\sigma ^{-1}(U)$
, U and
$\sigma (U)$
are pairwise disjoint. We denote by
$f_U$
the element of
given by
$$ \begin{align*} f_U (\mathbf{y}) =\begin{cases} \sigma(\mathbf{y}), & \mathbf{y} \in U \cup \sigma^{-1} (U), \\ \sigma^{-2}(\mathbf{y}), & \mathbf{y} \in \sigma (U), \\ \mathbf{y} & \text{otherwise.} \end{cases} \end{align*} $$
Lemma 4.4. All
$f_U$
lie in
.
Proof. Define
by
$$ \begin{align*} h_U (\mathbf{y}) =\begin{cases} \sigma(\mathbf{y}), & \mathbf{y} \in \sigma^{-1} (U), \\ \sigma^{-1}(\mathbf{y}), & \mathbf{y} \in U, \\ \mathbf{y} & \text{otherwise.} \end{cases} \end{align*} $$
Then
$f_U = f_U ^{-1} h_U ^{-1} f_U h_U$
.
The following identities appear as [Reference Matui13, Lemma 5.3]; they are proved by direct calculation, some of which is explained in [Reference Juschenko11, Lemma 3.0.11].
Lemma 4.5. Let
$U , V \subseteq X$
be non-empty clopen subsets.
-
(i) If
$\sigma ^i (V)$
are pairwise disjoint for
$-2 \leq i \leq 2$
, and
$U \subseteq V$
, then where
$$ \begin{align*} \tau_V f_U \tau_V ^{-1} & = f_{\sigma(U)}, \\ \tau_V ^{-1} f_U \tau_V & = f_{\sigma^{-1}(U)}, \end{align*} $$
$\tau _V = f_{\sigma ^{-1}(V)} f_{\sigma (V)}$
.
-
(ii) If
$\sigma ^{-1} (U)$
, U,
$\sigma (U) \cup \sigma ^{-1} (V)$
, V,
$\sigma (V)$
are pairwise disjoint, then
$$ \begin{align*} f_{\sigma (U) \cap \sigma^{-1}(V)} = f_V f_U ^{-1} f_V ^{-1} f_U{.} \end{align*} $$
Proposition 4.6. There exists
$C_2 = C_2 (X,S)> 0$
such that, for all
$m \geq (R_{\mathbf {x}}(4)-1)/2$
, if
$W \subseteq X$
is an m-cylinder of X, then
$f_{\sigma ^{-1}(W)},f_W,f_{\sigma (W)} \in B_S (C_2 m^2)$
.
Proof. Write
$C_0 = \lceil (R_{\mathbf {x}}(4)-1)/2 \rceil +1$
, and define
$m_n = C_0 (2^n + 1)$
, so that
$m_{n+1} = 2 m_n - C_0$
. We inductively construct a non-decreasing sequence
$(l_n)$
of positive integers, such that, if
$W \subseteq X$
is an m-cylinder of X, with
$C_0 \leq m \leq m_n$
, then
$f_{\sigma ^{-1}(W)} , f_W , f_{\sigma (W)} \in B_S (l_n)$
. We then analyse the growth of
$l_n$
. Since there are finitely many m-cylinders W of X with
$C_0 \leq m \leq m_0 = 2C_0$
, and, for each,
by Lemma 4.4, there is a constant
$l_0$
such that
$f_{\sigma ^{-1}(W)} , f_W , f_{\sigma (W)} \in B_S (l_0)$
for all such W. For
$n \geq 1$
, suppose
$m_{n-1} < m \leq m_n$
and let
$$ \begin{align*} W = \ll w_{-m},\ldots,w_{-1},\underline{w_0},w_1,\ldots,w_m \gg \cap X \end{align*} $$
be an m-cylinder of X. Set
$C = C_0$
or
$C_0-1$
, such that
$m + C$
is even, and let
$$ \begin{align*} U & = \ll w_{-m},\ldots,w_{-2},\underline{w_{-1}},w_0,\ldots,w_{C} \gg, \\ V & = \ll w_{-C},\ldots,w_0,\underline{w_1},w_2,\ldots,w_m \gg \end{align*} $$
so that
$\sigma (U) \cap \sigma ^{-1} (V) = W$
, and
$$ \begin{align*} \sigma (U) \cup \sigma^{-1} (V) \subseteq \ll w_{-C},\ldots,w_{-1},\underline{w_0},w_1,\ldots,w_C \gg, \end{align*} $$
so by Lemma 4.1, U and V satisfy the conditions of Lemma 4.5(ii), and
$$ \begin{align} \lvert f_W \rvert_S \leq 2 (\lvert f_U \rvert_S + \lvert f_V \rvert_S){.} \end{align} $$
Now,
$\sigma ^{-(m-C-2)/2}(U)$
and
$\sigma ^{(m-C-2)/2}(V)$
are
$(m+C)/2$
-cylinders of X, and
$(m+C)/2 \leq m_{n-1}$
, so by induction,
$$ \begin{align} \lvert f_{\sigma^{-(m-C-2)/2}(U)}\rvert_S, \lvert f_{\sigma^{(m-C-2)/2}(V)}\rvert_S \leq l_{n-1}{.} \end{align} $$
Let
$U_i ^{\prime }$
be the
$C_0$
-cylinder of X containing
$\sigma ^{-i} (U)$
, for
$1 \leq i \leq (m-C-2)/2$
. Then by Lemma 4.5(i),
$f_U$
can be obtained from
$f_{\sigma ^{-(m-C-2)/2}(U)}$
by conjugating by
$\tau _{U_{(m-C-2)/2} ^{\prime }} , \ldots , \tau _{U_1 ^{\prime }}$
in sequence. By our base case,
$\lvert \tau _{U_i ^{\prime }} \rvert _S \leq 2 l_0$
for all i, so
$$ \begin{align*} \lvert f_U\rvert_S \leq \lvert f_{\sigma^{-(m-C-2)/2}(U)}\rvert_S + 2l_0 (m-C-2), \end{align*} $$
and arguing similarly for V,
$$ \begin{align*} \lvert f_V \rvert_S \leq \lvert f_{\sigma^{(m-C-2)/2}(V)}\rvert_S + 2l_0 (m-C-2){.} \end{align*} $$
Combining with (4.2), (4.3), and our bound on
$m_n$
, we have
$$ \begin{align} \lvert f_W \rvert_S \leq 4 l_{n-1} + C^{\prime} 2^n + C^{\prime\prime} \end{align} $$
for some constants
$C^{\prime },C^{\prime \prime }> 0$
. Finally, applying Lemma 4.5(i) a final time, we conjugate
$f_W$
by
$\tau _{W^{\prime }}$
or
$\tau _{W^{\prime }} ^{-1}$
where
$W^{\prime }$
is the
$C_0$
-cylinder of X containing W, and
$\lvert f_{\sigma (W)} \rvert _S , \lvert f_{\sigma ^{-1}(W)} \rvert _S$
also satisfy a bound as in (4.4) (for some larger
$C^{\prime \prime }$
). We may therefore take
$l_n = 4 l_{n-1} + C^{\prime } 2^n + C^{\prime \prime }$
, so that
$f_{\sigma ^{-1}(W)} , f_W , f_{\sigma (W)} \in B_S (l_n)$
. Solving the recurrence for
$l_n$
, we obtain
$l_n \leq C_2 ^{\prime } 4^n \leq (4 C_2 ^{\prime } / C_0 ^2) m_{n-1} ^2 \leq (4 C_2 ^{\prime } / C_0 ^2) m^2$
for some
$C_2 ^{\prime }> 0$
.
Recall that for
$g \in \operatorname {\mathrm {Homeo}} (X)$
, the support of g is
$$ \begin{align*} \operatorname{\mathrm{supp}}(g) = \lbrace x \in X : g(x)\neq x \rbrace. \end{align*} $$
Proposition 4.7. Let m and
$\operatorname {\mathrm {DCyl}}_X(m)$
be as in Lemma 4.2. There exists
$C_3 = C_3(X,S)>0$
such that, for all
$U \in \operatorname {\mathrm {DCyl}}_X(m)$
, there is a subgroup
satisfying:
-
(i)
$\Delta _U \cong \operatorname {\mathrm {Alt}}(5)$
; -
(ii)
$\Delta _U \subseteq B_S (C_3 m^2)$
; -
(iii) for all
$g \in \Delta _U$
, (4.5)
$$ \begin{align} \operatorname{\mathrm{supp}}(g) \subseteq \bigcup_{i=-2} ^2 \sigma^i (U){.} \end{align} $$
Proof. For
$U \in \operatorname {\mathrm {DCyl}}_X (m)$
, let
$\Delta _U = \langle f_{\sigma ^{-1}(U)},f_U,f_{\sigma (U)} \rangle $
. Then (iii) holds, since it holds for
$g \in \lbrace f_{\sigma ^{-1}(U)},f_U,f_{\sigma (U)} \rbrace $
. Now
$\Delta _U$
acts, faithfully, on
$\lbrace \sigma ^i(U):\lvert i\rvert \leq 2\rbrace $
. Identifying this set in the obvious way with
$\lbrace -2,-1,0,1,2 \rbrace $
,
$f_{\sigma ^{-1}(U)}$
,
$f_U$
and
$f_{\sigma (U)}$
act, respectively, as the
$3$
-cycles
$(-2 \: -1 \: 0)$
,
$(-1 \: 0 \: 1)$
and
$(0 \: 1 \: 2)$
. As such,
$\Delta _U$
acts as the alternating group on
$\lbrace -2,-1,0,1,2\rbrace $
, and we have (i).
By Proposition 4.6,
$f_{\sigma ^{-1}(U)},f_U,f_{\sigma (U)} \in B_S (C_2 m^2)$
, and since
$\lvert \Delta _U \rvert = 60$
,
$\Delta _U \subseteq B_S (60 C_2 m^2)$
, whence (ii).
Proof of Theorem 1.2
Let Q be a finite group and
$\pi : B_S (r) \rightarrow Q$
be a local embedding. For any
$m \leq (r/2C_3)^{1/2}$
, we have
$\Delta _U \leq B_S(r/2)$
, where
$C_3> 0$
and
$\Delta _U$
are as in Proposition 4.7. We apply Proposition 2.6 to the family
$\lbrace \Delta _U : U \in \operatorname {\mathrm {DCyl}}(m) \rbrace $
for
$m \geq c' r^{1/2}$
(
$c'>0$
sufficiently small), and r larger than a constant such that
$m \geq (R_{\mathbf {x}}(4)-1)/2$
. Since the
$\Delta _U$
are disjointly supported (by Lemma 4.2 and (4.5)), they do indeed generate their direct product. From Proposition 2.6 we conclude that
$$ \begin{align*} \begin{aligned} \lvert Q \rvert & \geq \prod_{U \in \operatorname{\mathrm{DCyl}}_X(m)} \lvert \Delta_U \rvert & \\[3pt] & \geq \exp (c p_{\mathbf{x}} (2m-7))& \text{(by (4.1))} \\[3pt] & \geq \exp (c p_{\mathbf{x}} (2c' r^{1/2}-7))& \end{aligned} \end{align*} $$
for
$c = \log (60)/9$
.
Remark 4.8. We can improve the constant c by modifying the construction so as to take
$\Delta _U \cong \operatorname {\mathrm {Alt}}(2d+1)$
for large d, instead of
$\operatorname {\mathrm {Alt}}(5)$
. To do this we would need to take
$\operatorname {\mathrm {DCyl}}_X (m)$
to be a family of m-cylinders U such that all sets
$\sigma ^i (U)$
are pairwise disjoint for
$-d \leq i \leq d$
, so that our construction in Lemma 4.2 would lead to a bound
$\lvert \operatorname {\mathrm {DCyl}}_X (m) \rvert \geq p_X (2m-C)/(2d-1)$
. We could nevertheless take
$c = \log (d!/2)/ (2d-1)$
, which grows in d.
Remark 4.9. The same argument also gives a lower bound on the LEF action growth of
, which is a little stronger than that obtained by applying Remark 2.3 to the conclusion of Theorem 1.2. Suppose
$\pi : B_S(r) \rightarrow \operatorname {\mathrm {Sym}} (d)$
is a local embedding. Then by Propositions 2.6 and 4.7,
$\operatorname {\mathrm {im}}(\pi )$
contains a subgroup isomorphic to the direct product of
$P = p_{\mathbf {x}} (2c r^{1/2}-7)$
copies of
$\operatorname {\mathrm {Alt}}(5)$
, which in turn contains the direct product of P copies of
$C_5$
. By [Reference Johnson9, Theorem 2], the minimal degree of a faithful permutation representation of the latter is
$5 P$
. Hence
.
5 Systems of intermediate growth
In this section we prove Theorem 1.5, and deduce Theorem 1.6. The following example is modelled on the construction in [Reference Jung, Lee and Park10, §3]. In this section, ‘large’ means larger than a certain absolute constant (which we do not compute), so as to make true some needed inequalities. We start with a general observation, the utility of which is that it allows us to obtain an infinite word whose asymptotic features (such as the behaviour of the complexity or recurrence functions) can be controlled in terms of the sets of factors of a sequence of finite words
$u^{(n)}$
.
Lemma 5.1. Let
$(L_j)$
be an increasing sequence of positive integers; let
$x^{(j)} \in A^{L_j}$
. For each
$j \in \mathbb {N}$
, let
$K_j \in \mathbb {N}$
with
$2 \leq K_j \leq L_{j+1} - L_j$
and suppose that
$x^{(j)}$
is the
$K_j$
th
$L_j$
-factor of
$x^{(j+1)}$
. Choose
$M_0 \in \mathbb {N}$
with
$1 \leq M_0 \leq L_0$
, and define
$(M_j)$
recursively via
$M_{j+1} = M_j + K_j - 1$
. Then there is a unique point
$\mathbf {x} \in A^{\mathbb {Z}}$
lying in the intersection of the cylinder sets
$\ll x^{(j)} \gg _{M_j}$
. Moreover, for all n,
$F_n (\mathbf {x}) = \bigcup _j F_n (x^{(j)})$
.
Proof. By construction the
$\ll x^{(j)} \gg _{M_n}$
form a nested descending sequence of non-empty closed sets in the compact space
$A^{\mathbb {Z}}$
, hence their intersection is non-empty. Let
$\mathbf {x}$
lie in this intersection.
In
$x^{(j)}$
, there are
$M_j - 1 = M_{j-1} + K_{j-1} - 2$
letters strictly to the left of the
$M_j$
th letter, and
$L_j - M_j \geq (L_{j-1} - M_{j-1})+1$
strictly to the right. Since both these quantities tend to
$\infty $
, for every
$i \in \mathbb {Z}$
, the ith letter of
$\mathbf {x}$
is uniquely determined by
$\mathbf {x} \in \ll x^{(j)} \gg _{M_j}$
, provided j is sufficiently large. Similarly, for any i and n, the ith n-factor of
$\mathbf {x}$
lies in
$x^{(j)}$
for j sufficiently large, so
$F_n (\mathbf {x}) \subseteq \bigcup _j F_n (x^{(j)})$
. Conversely,
$\mathbf {x} \in \ll x^{(j)} \gg _{M_j}$
implies
$x^{(j)}$
(and hence every n-factor of
$x^{(j)}$
) is a factor of
$\mathbf {x}$
.
Choose a real number
$r\geq 2$
. First, fix a large x divisible by
$3$
. We work over the alphabet
$A = \lbrace a,b\rbrace $
. Fix two words
$w^{(0)},w^{\prime (0)} \in A^{\ast }$
of length
$x/3$
. Among all words
$w^{(0)}vw^{\prime (0)}$
for
$\lvert v\rvert =x/3$
, take a subset
$\mathcal {C}_{0}$
with
$\lvert \mathcal {C}_{0}\rvert =x$
and such that no factor of any element of
$\mathcal {C}_{0}$
is equal to
$w^{(0)},w^{\prime (0)}$
except for the prefixes and suffixes themselves. This is easily achieved: for instance, taking
$w^{(0)} = a^{x/3}$
,
$w^{\prime (0)} = b^{x/3}$
, we can form
$\mathcal {C}_{0}$
by choosing v from among those words starting in b and ending in a (of which there are
$2^{(x/3)-2} \geq x$
for x large).
Assuming that we have already defined
$\mathcal {C}_{j}$
, we will define
$\mathcal {C}_{j+1}$
; for all i, we set
$N_{i}=\lvert \mathcal {C}_{i}\rvert $
and
$l_{i}$
the length of any element of
$\mathcal {C}_{i}$
, so that
$N_{0}=l_{0}=x$
. We prove the following statements for all
$j\geq 0$
.
-
(i)
$N_{j},l_{j}$
are large and increasing in j;
$3 | N_{j}$
,
$3 | l_{j}$
; all words in
$\mathcal {C}_{j}$
have the same prefix of length
$l_j / 3$
, and the same suffix of length
$l_j / 3$
. -
(ii)
$N_{j+2}\leq \exp (2^{r}(\log N_{j})^{r})$
,
$N_{j+1}\geq N_{j}^{2}$
, and, for j even,
$N_{j+1}\geq \exp (\tfrac 12(\log N_{j})^{r})$
. -
(iii)
$N_{j}<l_{j+1}\leq N_{j}^{2}$
.
We prove (i) and (iii) by induction with base case
$j=0$
, for which all claims are true (for
$l_{1}$
see below), and (ii) directly.
Fix an ordering of
$\mathcal {C}_{j}$
, arbitrarily: the elements of
$\mathcal {C}_{j}$
are words
$u^{(j)}_{i}$
, where the index i follows the ordering. Define the word
$$ \begin{align*} u^{(j+1)}=u^{(j)}_{1}u^{(j)}_{2}u^{(j)}_{3}\cdots u^{(j)}_{N_{j}-1}u^{(j)}_{N_{j}}=w^{(j+1)}u^{(j)}_{{1}/{3} N_{j}+1}u^{(j)}_{{1}/{3} N_{j}+2}\cdots u^{(j)}_{{2}/{3} N_{j}}w^{\prime(j+1)}, \end{align*} $$
where
$w^{(j+1)}$
and
$w^{\prime (j+1)}$
collect the first and last third of the
$u^{(j)}_{i}$
, respectively: this is possible since
$3 | N_{j}$
by induction, and it implies
$3 | l_{j+1}$
where
$l_{j+1}=\lvert u^{(j+1)}\rvert = l_{j}N_{j}$
is large. Take a collection
$P_{j} \subset \mathrm {Sym}(N_{j}/3)$
: if j is even, choose
$\lvert P_{j}\rvert = 3\lfloor \exp ((\log N_{j})^{r})/3\rfloor $
, otherwise choose
$\lvert P_{j}\rvert =N_{j}^{2}$
(note that this is possible for x large). Then define
$\mathcal {C}_{j+1}$
to be the set of all words
$\lbrace w^{(j+1)}v_{\pi } ^{(j+1)}w^{\prime (j+1)} : \pi \in P_j \rbrace $
where, for
$\pi \in P_j$
,
$v_{\pi } ^{(j+1)}$
is obtained by permuting the factors
$u^{(j)}_{i}$
of
$u^{(j+1)}$
with
$i\in (N_{j} / 3,2N_{j} / 3]$
according to
$\pi $
; that is,
$$ \begin{align*} v_{\pi} ^{(j+1)} = u^{(j)}_{{1}/{3} N_{j}+\pi(1)}u^{(j)}_{{1}/{3} N_{j}+\pi(2)}\cdots u^{(j)}_{{1}/{3} N_{j} + \pi ({1}/{3} N_{j})}. \end{align*} $$
By definition we have
$3 | N_{j+1}$
and
$N_{j+1}$
large;
$l_{j+1}> l_j$
,
$N_{j+1}> N_j$
, and for all
$j\geq 0$
,
$$ \begin{align*} & N_{j+2}\leq\begin{cases} \exp (2(\log N_{j})^{r}) & (2\mid j) \\[3pt] \exp ((\log N_{j}^{2})^{r}) & (2\nmid j) \end{cases} \leq \exp (2^{r}(\log N_{j})^{r}); \\[3pt] & N_{j+1}\geq\min \{N_{j}^{2},\exp((\log N_{j})^{r})-3\} =N_{j}^{2}; \\[3pt] 2 | j \ \Rightarrow \ & N_{j+1} \geq \exp((\log N_{j})^{r})-3 \geq \exp((\log N_{j})^{r} / 2); \\[3pt] & l_{1}=x^{2}=N_{0}^{2}>N_{0}; \\[3pt] j\geq 1 \ \Rightarrow \ & N_{j}<l_{j+1}=l_{j}N_{j}\leq N_{j-1}^{2}N_{j}\leq N_{j}^{2}, \end{align*} $$
so (i)–(iii) do indeed hold. Two key features of this construction are that, for all j:
-
(a) all words in
$\mathcal {C}_j$
have the same prefix
$w^{(j)}$
and suffix
$w^{\prime (j)}$
of length
$\tfrac 13 l_{j}$
; -
(b) every word in
$\mathcal {C}_{j+1}$
is the product of all the words from
$\mathcal {C}_j$
(in some order).
We now construct a uniformly recurrent non-periodic word
$\mathbf {x} = \mathbf {x}(r)$
, such that the subshift
$X_r = \overline {\mathcal {O}(\mathbf {x})}$
satisfies the conditions of Theorem 1.5. Consider the words
$x^{(j)} = u_{N_j / 3} ^{(j)}$
. Then
$x^{(j)}$
is the
$K_j = (l_j (N_j / 3 - 1) + 1)$
th
$l_j$
-factor of
$x^{(j+1)}$
, for all j, and
$2 \leq K_j \leq l_{j+1} - l_j$
. For any
$1 \leq M_0 \leq l_0$
, apply Lemma 5.1 to the sequence
$x^{(j)}$
(with
$L_j = l_j$
) to obtain
$\mathbf {x}$
.
Proposition 5.2. The complexity function
$p_{\mathbf {x}}$
of
$\mathbf {x}$
satisfies
$p_{\mathbf {x}}(l_j) \geq \exp ( (\log l_j)^{r}/2^{r+1})$
, for all
$j \in \mathbb {N}$
odd.
Proof. Since
$u_{N_j / 3} ^{(j+1)} \in \mathcal {C}_{j+1}$
is a factor of
$\mathbf {x}$
, we have by (b) above that all elements of
$\mathcal {C}_j$
are distinct factors of
$\mathbf {x}$
of length
$l_j$
, so
$p_{\mathbf {x}}(l_j)\geq N_{j}$
for all
$j \in \mathbb {N}$
. For j odd, it follows that
$$ \begin{align*} p_{\mathbf{x}}(l_j) & \geq N_{j}\geq \exp((\log N_{j-1})^{r} / 2)\geq \exp((\log\sqrt{l_{j}})^{r} / 2)= \exp( (\log l_j)^{r}/2^{r+1}) \end{align*} $$
by (ii) and (iii) above.
Proposition 5.3. The recurrence function
$R_{\mathbf {x}}$
of
$\mathbf {x}$
satisfies
$$ \begin{align*} R_{\mathbf{x}}(n)\leq C \exp ( 4^{r+1}(\log n)^{r}) \end{align*} $$
for some
$C>0$
and all
$n \in \mathbb {N}$
.
Proof. Fix any factor w of
$\mathbf {x}$
of length n, and suppose that j is such that
$n< 2 l_{j} / 3$
. w is a factor of some
$x^{(k)} = u_{N_k / 3} ^{(k)}$
, for
$k> j$
, and applying (b) above repeatedly,
$x^{(k)}$
is expressible as a product of words
$u_i ^{(j)}$
. Therefore, there are indices
$i_1$
and
$i_2$
such that w is a factor of some
$u^{(j)}_{i_1}u^{(j)}_{i_2}$
; moreover, it intersects the middle third of at most one of
$u^{(j)}_{i_1}$
or
$u^{(j)}_{i_2}$
, so by (a) above, it sits entirely inside either
$u^{(j)}_{i_1}w^{(j)}$
or
$w^{\prime (j)}u^{(j)}_{i_2}$
.
Now let v be any factor
$\mathbf {x}$
of length
$3 l_{j+1}$
. As before, v is a factor of some
$x^{(k')}=u_{N_{k'} / 3} ^{(k')}$
, for
$k'> j+1$
, and applying (b) above repeatedly,
$x^{(k')}$
is expressible as a product of words
$u_i ^{(j+1)}$
. Therefore, there are indices
$i^{\prime } _1$
and
$i^{\prime } _2$
such that
$u_{i^{\prime } _1} ^{(j+1)} u_{i^{\prime } _2} ^{(j+1)}$
is a factor of v. By (b) above, and the fact that every
$u_i ^{(j)}$
has
$w^{(j)}$
as a prefix and
$w^{\prime (j)}$
as a suffix, it follows that
$u^{(j)}_{i_1}w^{(j)}$
and
$w^{\prime (j)}u^{(j)}_{i_2}$
are factors of
$u_{i^{\prime } _1} ^{(j+1)} u_{i^{\prime } _2} ^{(j+1)}$
, hence w is a factor of v. That is,
$R_{\mathbf {x}}(n)\leq 3 l_{j+1}$
.
Partitioning the integers, we have
$R_{\mathbf {x}}(n)\leq 3l_{j+1}$
for any
$n\in [2l_{j-1} /3,2l_{j}/3 )$
. For
$j\geq 2$
, we have
$$ \begin{align*} \log R_{\mathbf{x}}(n) - \log 3 & \leq \log l_{j+1} \leq 2 \log N_j \leq 2^{r+1}(\log N_{j-2})^{r} \\ & < 2^{r+1}(\log l_{j-1})^{r} \leq 2^{r+1}(\log (3n/2))^{r} \leq 4^{r+1} (\log n)^r \end{align*} $$
by (ii) and (iii), and our bounds on n, as required.
Proof of Theorem 1.5
Let
$\mathbf {x} = \mathbf {x}(r)$
be as above. Set
$X_r = \overline {\mathcal {O}(\mathbf {x})}$
. By Remark 2.23, items (i) and (ii) follow from Propositions 5.3 and 5.2, respectively, with
$n_i ^{(r)} = l_{2i+1}$
.
Proof of Theorem 1.6
Recall that
$N! \leq \exp (N \log N)$
for all N. Applying Theorem 1.1 to
, where
$(X_r,\sigma )$
is as in Theorem 1.5, we have
$$ \begin{align} \mathcal{L}_{\Gamma^{(r)}} ^S (n) \leq \exp ( 2 R_X(Cn)\log ( 2R_X(Cn)) ), \end{align} $$
for all n and for some
$C>0$
, where
$X=X_r$
, so that
$R_X (n) \leq \exp ( C_r (\log n)^r )$
. Hence, for
$n\geq 2$
,
$$ \begin{align*} \log ( 2R_X(Cn) )\leq C_r (\log n + \log C)^r + \log 2 \leq C_r ' (\log n)^r \end{align*} $$
for a possibly larger constant
$C_r '$
, so that
$$ \begin{align*} \log ( 2R_X(Cn)) + \log \log ( 2R_X(Cn)) & \leq C_r ^{\prime} (\log n)^r + r \log \log n + \log C_r ' \\ & \leq C_r '' (\log n)^r \end{align*} $$
again, for
$C_r ''$
a possibly larger constant. Thus, by (5.1),
$\mathcal {L}_{\Gamma ^{(r)}} ^S (n) \leq \exp (\exp (C_r '' (\log n)^r))$
, and we have (i).
For (ii), suppose for a contradiction that
$2 \leq r' < r$
and that
$C , C'> 0$
are such that, for all n sufficiently large,
$$ \begin{align} \mathcal{L}_{\Gamma^{(r)}} ^S (n)\leq \exp ( \exp ( C(\log C'n)^{r^{\prime}} ) ). \end{align} $$
By Theorems 1.2 and 1.5(ii), we have
$$ \begin{align*} \mathcal{L}_{\Gamma^{(r)}}^S (\lceil n_i ^{(r)}/c\rceil^2) \geq \exp ( c p_X ( n_i ^{(r)}) ) \geq \exp ( c \exp ( c_r ( \log n_i ^{(r)})^r ) ) \end{align*} $$
for some
$c>0$
and all
$i \in \mathbb {N}$
. Hence by (5.2),
$$ \begin{align*} C(2\log n_i ^{(r)} + \log C' -2\log c+1)^{r^{\prime}} \geq c_r ( \log n_i ^{(r)} )^r + \log c \end{align*} $$
for all i sufficiently large, a contradiction.
For the final statement, let
$\mathcal {F} = \lbrace \Gamma ^{(r)} : r \geq 2 \rbrace $
. Let
$2 \leq r^{\prime } < r$
, and suppose for a contradiction that
$\mathcal {L}_{\Gamma ^{(r)}} \preceq \mathcal {L}_{\Gamma ^{(r^{\prime })}}$
. By (i),
$$ \begin{align*} \mathcal{L}_{\Gamma^{(r)}} (n)\preceq \exp ( \exp ( C_{r^{\prime}}(\log n)^{r^{\prime}} ) ), \end{align*} $$
contradicting (ii).
Acknowledgements
Both authors were supported by ERC grant no. 648329 ‘GRANT’, during their permanence at Georg-August-Universität Göttingen. The second author was supported by the Emily Erskine Endowment Fund and Israel Science Foundation Grant No. 686/17 of Aner Shalev, during his permanence at the Hebrew University of Jerusalem.
