1. Introduction
In this paper, we consider the classical compound Poisson risk model perturbed by diffusion, so that the insurer's surplus level at time ![]() $t$ is given by
$t$ is given by
 \begin{equation} U(t)=u+ct-\sum_{k=1}^{N(t)}Y_k+\sigma B(t),\quad t\ge 0, \end{equation}
\begin{equation} U(t)=u+ct-\sum_{k=1}^{N(t)}Y_k+\sigma B(t),\quad t\ge 0, \end{equation}where ![]() $u=U(0)\ge 0$ is the initial surplus level,
$u=U(0)\ge 0$ is the initial surplus level, ![]() $c>0$ is the incoming premium rate per unit time,
$c>0$ is the incoming premium rate per unit time, ![]() $Y_k$ is the size of the
$Y_k$ is the size of the ![]() $k$th insurance claim,
$k$th insurance claim, ![]() $\{N(t)\}_{t\ge 0}$ is a Poisson process with rate
$\{N(t)\}_{t\ge 0}$ is a Poisson process with rate ![]() $\lambda >0$,
$\lambda >0$, ![]() $\{B(t)\}_{t\ge 0}$ is a standard Brownian motion, and
$\{B(t)\}_{t\ge 0}$ is a standard Brownian motion, and ![]() $\sigma >0$ is the volatility parameter. It is further assumed that
$\sigma >0$ is the volatility parameter. It is further assumed that ![]() $\{Y_k\}_{k=1}^{\infty }$ is a sequence of independent and identically distributed (i.i.d.) positive random variables with common probability density
$\{Y_k\}_{k=1}^{\infty }$ is a sequence of independent and identically distributed (i.i.d.) positive random variables with common probability density ![]() $p(\cdot )$ and Laplace transform
$p(\cdot )$ and Laplace transform ![]() $\tilde {p}(\cdot )$, and moreover
$\tilde {p}(\cdot )$, and moreover ![]() $\{Y_k\}_{k=1}^{\infty }$,
$\{Y_k\}_{k=1}^{\infty }$, ![]() $\{N(t)\}_{t\ge 0}$, and
$\{N(t)\}_{t\ge 0}$, and ![]() $\{B(t)\}_{t\ge 0}$ are mutually independent. The time of ruin of the surplus process
$\{B(t)\}_{t\ge 0}$ are mutually independent. The time of ruin of the surplus process ![]() $\{U(t)\}_{t\ge 0}$ is defined by
$\{U(t)\}_{t\ge 0}$ is defined by ![]() $\tau =\inf \{t\ge 0:U(t)<0\}$. We assume that the positive security loading condition, which ensures the ruin probability
$\tau =\inf \{t\ge 0:U(t)<0\}$. We assume that the positive security loading condition, which ensures the ruin probability ![]() $\psi (u)=\Pr \{\tau <\infty \,|\,U(0)=u\}$ is less than one for
$\psi (u)=\Pr \{\tau <\infty \,|\,U(0)=u\}$ is less than one for ![]() $u>0$, is satisfied. Such a condition is given by
$u>0$, is satisfied. Such a condition is given by ![]() $\theta >0$, where
$\theta >0$, where ![]() $\theta$ is defined via
$\theta$ is defined via ![]() $c=(1+\theta )\lambda E[Y_1]$. Note that ruin occurs immediately by diffusion if the process starts with zero initial surplus.
$c=(1+\theta )\lambda E[Y_1]$. Note that ruin occurs immediately by diffusion if the process starts with zero initial surplus.
The ruin probability of the model (1.1) was first obtained by Dufresne and Gerber [Reference Dufresne and Gerber17], who also decomposed the probability into two components, namely ruin by oscillation (i.e. ![]() $U(\tau )=0$) and ruin by a claim (i.e.
$U(\tau )=0$) and ruin by a claim (i.e. ![]() $U(\tau )<0$). These results were generalized by Gerber and Landry [Reference Gerber and Landry22] and Tsai and Willmot [Reference Tsai and Willmot34] who looked into the Gerber-Shiu expected discounted penalty function (see [Reference Gerber and Shiu23] and Eq. (1.2) below with
$U(\tau )<0$). These results were generalized by Gerber and Landry [Reference Gerber and Landry22] and Tsai and Willmot [Reference Tsai and Willmot34] who looked into the Gerber-Shiu expected discounted penalty function (see [Reference Gerber and Shiu23] and Eq. (1.2) below with ![]() $n=m=0$), which takes into account not only the ruin time
$n=m=0$), which takes into account not only the ruin time ![]() $\tau$ but also the surplus immediately prior to ruin
$\tau$ but also the surplus immediately prior to ruin ![]() $U(\tau ^{-})$ and the deficit at ruin
$U(\tau ^{-})$ and the deficit at ruin ![]() $|U(\tau )|$. See also, for example, Tsai [Reference Tsai32,Reference Tsai33] and Tsai and Willmot [Reference Tsai and Willmot35] for the application of Gerber-Shiu function in the present model to find related ruin functions such as the (joint) moments of the afore-mentioned variables. Extension to a perturbed renewal risk process was subsequently considered by Li and Garrido [Reference Li and Garrido27]. In the absence of the Brownian motion, various generalizations of the Gerber-Shiu function have been proposed to incorporate additional information of the surplus process before ruin occurrence. For example, Cheung et al. [Reference Cheung, Landriault, Willmot and Woo12] and Woo [Reference Woo37] included the surplus immediately after the second last claim before ruin and the minimum surplus before ruin into the penalty function whereas Cheung and Landriault [Reference Cheung and Landriault9] and Woo et al. [Reference Woo, Xu and Yang38] considered the maximum surplus before ruin. In addition, Cai et al. [Reference Cai, Feng and Willmot7] studied the total discounted operating costs defined via an integral of the sample path until ruin (see also [Reference Feng18,Reference Feng19]). Analysis of the Gerber-Shiu function in more general Lévy risk models has been performed by, for example, Garrido and Morales [Reference Garrido and Morales21], Asmussen and Albrecher [Reference Asmussen and Albrecher1, Chaps. XI and XII], and Kyprianou [Reference Kyprianou25], and extensions to path-dependent penalties can be found in, for example, Biffis and Morales [Reference Biffis and Morales2] and Feng and Shimizu [Reference Feng and Shimizu20]. On the other hand, Cheung [Reference Cheung8] and Cheung and Woo [Reference Cheung and Woo11] proposed to include in the Gerber-Shiu function a moment-based component pertaining to the total discounted claim cost until ruin, which is defined by
$|U(\tau )|$. See also, for example, Tsai [Reference Tsai32,Reference Tsai33] and Tsai and Willmot [Reference Tsai and Willmot35] for the application of Gerber-Shiu function in the present model to find related ruin functions such as the (joint) moments of the afore-mentioned variables. Extension to a perturbed renewal risk process was subsequently considered by Li and Garrido [Reference Li and Garrido27]. In the absence of the Brownian motion, various generalizations of the Gerber-Shiu function have been proposed to incorporate additional information of the surplus process before ruin occurrence. For example, Cheung et al. [Reference Cheung, Landriault, Willmot and Woo12] and Woo [Reference Woo37] included the surplus immediately after the second last claim before ruin and the minimum surplus before ruin into the penalty function whereas Cheung and Landriault [Reference Cheung and Landriault9] and Woo et al. [Reference Woo, Xu and Yang38] considered the maximum surplus before ruin. In addition, Cai et al. [Reference Cai, Feng and Willmot7] studied the total discounted operating costs defined via an integral of the sample path until ruin (see also [Reference Feng18,Reference Feng19]). Analysis of the Gerber-Shiu function in more general Lévy risk models has been performed by, for example, Garrido and Morales [Reference Garrido and Morales21], Asmussen and Albrecher [Reference Asmussen and Albrecher1, Chaps. XI and XII], and Kyprianou [Reference Kyprianou25], and extensions to path-dependent penalties can be found in, for example, Biffis and Morales [Reference Biffis and Morales2] and Feng and Shimizu [Reference Feng and Shimizu20]. On the other hand, Cheung [Reference Cheung8] and Cheung and Woo [Reference Cheung and Woo11] proposed to include in the Gerber-Shiu function a moment-based component pertaining to the total discounted claim cost until ruin, which is defined by ![]() $Z_\delta (\tau )$ where
$Z_\delta (\tau )$ where ![]() $Z_\delta (t)=\sum _{k=1}^{N(t)}e^{-\delta T_k}f(Y_k)$ for
$Z_\delta (t)=\sum _{k=1}^{N(t)}e^{-\delta T_k}f(Y_k)$ for ![]() $t\ge 0$. Here,
$t\ge 0$. Here, ![]() $\{T_k\}_{k=1}^{\infty }$ are the arrival times of the claims (which are the arrival epochs of the Poisson process
$\{T_k\}_{k=1}^{\infty }$ are the arrival times of the claims (which are the arrival epochs of the Poisson process ![]() $\{N(t)\}_{t\ge 0}$ in our model),
$\{N(t)\}_{t\ge 0}$ in our model), ![]() $f(\cdot )$ is a non-negative “cost function” defined on
$f(\cdot )$ is a non-negative “cost function” defined on ![]() $(0,\infty )$ that assigns a cost to each claim amount, and
$(0,\infty )$ that assigns a cost to each claim amount, and ![]() $\delta \ge 0$ is the force of interest for discounting the costs. Higher moments of the present value of dividends until ruin were further added to the analysis under different dividend strategies by Cheung et al. [Reference Cheung, Liu and Woo13] and Cheung and Liu [Reference Cheung and Liu10].
$\delta \ge 0$ is the force of interest for discounting the costs. Higher moments of the present value of dividends until ruin were further added to the analysis under different dividend strategies by Cheung et al. [Reference Cheung, Liu and Woo13] and Cheung and Liu [Reference Cheung and Liu10].
While the Brownian motion ![]() $\{B(t)\}_{t\ge 0}$ in the dynamics (1.1) is typically interpreted as small perturbations of the surplus process due to the uncertainties in day-to-day insurance operation not explained by insurance claims, in financial mathematics it is important to take into account the time value of money. This suggests that one may look into ruin quantities in relation to the stochastic integral
$\{B(t)\}_{t\ge 0}$ in the dynamics (1.1) is typically interpreted as small perturbations of the surplus process due to the uncertainties in day-to-day insurance operation not explained by insurance claims, in financial mathematics it is important to take into account the time value of money. This suggests that one may look into ruin quantities in relation to the stochastic integral ![]() $B_\delta (t)=\int _0^{t} e^{-\delta s}\,dB(s)$ for
$B_\delta (t)=\int _0^{t} e^{-\delta s}\,dB(s)$ for ![]() $t\ge 0$. Inspired by the above latest developments in the study of discounted claim costs until ruin, we shall consider the total discounted perturbation until ruin, namely
$t\ge 0$. Inspired by the above latest developments in the study of discounted claim costs until ruin, we shall consider the total discounted perturbation until ruin, namely ![]() $B_\delta (\tau )$. To the best of our knowledge, the quantity
$B_\delta (\tau )$. To the best of our knowledge, the quantity ![]() $B_\delta (\tau )=\int _0^{\tau } e^{-\delta s}\,dB(s)$ has never been analyzed in the context of Gerber-Shiu functions. Note that although
$B_\delta (\tau )=\int _0^{\tau } e^{-\delta s}\,dB(s)$ has never been analyzed in the context of Gerber-Shiu functions. Note that although ![]() $E[B_\delta (t)]=0$ for fixed time
$E[B_\delta (t)]=0$ for fixed time ![]() $t\ge 0$, in general
$t\ge 0$, in general ![]() $B_\delta (\tau )$ does not necessarily have zero mean because the ruin time
$B_\delta (\tau )$ does not necessarily have zero mean because the ruin time ![]() $\tau$ is a random variable that depends on the sample path of
$\tau$ is a random variable that depends on the sample path of ![]() $\{U(t)\}_{t\ge 0}$ which, in turn, involves
$\{U(t)\}_{t\ge 0}$ which, in turn, involves ![]() $\{B(t)\}_{t\ge 0}$. Indeed, one expects that sample paths of
$\{B(t)\}_{t\ge 0}$. Indeed, one expects that sample paths of ![]() $\{U(t)\}_{t\ge 0}$ leading to ruin are more likely to have faced unfavorable business conditions, and therefore,
$\{U(t)\}_{t\ge 0}$ leading to ruin are more likely to have faced unfavorable business conditions, and therefore, ![]() $B_\delta (\tau )$ is expected to have negative mean (see numerical illustrations in Section 4). Hence,
$B_\delta (\tau )$ is expected to have negative mean (see numerical illustrations in Section 4). Hence, ![]() $-B_\delta (\tau )$ may be regarded as part of the discounted costs (in addition to discounted claims), which can be important for risk management purposes as far as the event of ruin is concerned. For
$-B_\delta (\tau )$ may be regarded as part of the discounted costs (in addition to discounted claims), which can be important for risk management purposes as far as the event of ruin is concerned. For ![]() $n,m\in \mathbb {N}$ (with
$n,m\in \mathbb {N}$ (with ![]() $\mathbb {N}$ the set of non-negative integers), we propose to study the generalized Gerber-Shiu function
$\mathbb {N}$ the set of non-negative integers), we propose to study the generalized Gerber-Shiu function
where
is contributed by ruin occurrence due to a claim, and
is the contribution from ruin by oscillation. In addition, ![]() $w(\cdot,\cdot )$ appearing in (1.3) is a non-negative “penalty” defined on
$w(\cdot,\cdot )$ appearing in (1.3) is a non-negative “penalty” defined on ![]() $[0,\infty )\times (0,\infty )$ as a function of the surplus prior to ruin and the deficit, and
$[0,\infty )\times (0,\infty )$ as a function of the surplus prior to ruin and the deficit, and ![]() $w_0\ge 0$ in (1.2) is the constant “penalty” due at ruin if ruin occurs by oscillation. The notation “
$w_0\ge 0$ in (1.2) is the constant “penalty” due at ruin if ruin occurs by oscillation. The notation “![]() $\delta _{123}$” above can be regarded as an abbreviation that contains information about
$\delta _{123}$” above can be regarded as an abbreviation that contains information about ![]() $\delta _1$,
$\delta _1$, ![]() $\delta _2$, and
$\delta _2$, and ![]() $\delta _3$, which are possibly of different values and assumed non-negative. When the orders of moments
$\delta _3$, which are possibly of different values and assumed non-negative. When the orders of moments ![]() $n$ and
$n$ and ![]() $m$ are both equal to zero,
$m$ are both equal to zero, ![]() $\phi _{\delta _{123},n,m}(u)$ reduces to the traditional Gerber-Shiu function. For convenience, the powers of
$\phi _{\delta _{123},n,m}(u)$ reduces to the traditional Gerber-Shiu function. For convenience, the powers of ![]() $B_{\delta _2}(\tau )$ and
$B_{\delta _2}(\tau )$ and ![]() $Z_{\delta _3}(\tau )$ are written as
$Z_{\delta _3}(\tau )$ are written as ![]() $B_{\delta _2}^{n}(\tau )=\{B_{\delta _2}(\tau )\}^{n}$ and
$B_{\delta _2}^{n}(\tau )=\{B_{\delta _2}(\tau )\}^{n}$ and ![]() $Z_{\delta _3}^{m}(\tau )=\{Z_{\delta _3}(\tau )\}^{m}$, respectively, and we shall also denote the power of cost function as
$Z_{\delta _3}^{m}(\tau )=\{Z_{\delta _3}(\tau )\}^{m}$, respectively, and we shall also denote the power of cost function as ![]() $f^{m}(y)=\{f(y)\}^{m}$. We remark that the special case of
$f^{m}(y)=\{f(y)\}^{m}$. We remark that the special case of ![]() $\phi _{\delta _{123},n,m}(u)$ where
$\phi _{\delta _{123},n,m}(u)$ where ![]() $n=0$ and the penalty function only depends on the deficit was analyzed by Liu and Zhang [Reference Liu and Zhang28]. Our general version
$n=0$ and the penalty function only depends on the deficit was analyzed by Liu and Zhang [Reference Liu and Zhang28]. Our general version ![]() $\phi _{\delta _{123},n,m}(u)$ allows us to obtain not only the moments of
$\phi _{\delta _{123},n,m}(u)$ allows us to obtain not only the moments of ![]() $B_{\delta _2}(\tau )$ but also the joint moments of
$B_{\delta _2}(\tau )$ but also the joint moments of ![]() $B_{\delta _2}(\tau )$ and
$B_{\delta _2}(\tau )$ and ![]() $Z_{\delta _3}(\tau )$. In particular, the covariance between
$Z_{\delta _3}(\tau )$. In particular, the covariance between ![]() $B_{\delta _2}(\tau )$ and
$B_{\delta _2}(\tau )$ and ![]() $Z_{\delta _3}(\tau )$ (conditional on ruin) represents an interesting quantity that indicates whether the discounted small fluctuations and the discounted claims tend to move in the same or opposite direction when ruin occurs (see numerical analysis in Section 4). Moreover, (joint) moments involving the time of ruin
$Z_{\delta _3}(\tau )$ (conditional on ruin) represents an interesting quantity that indicates whether the discounted small fluctuations and the discounted claims tend to move in the same or opposite direction when ruin occurs (see numerical analysis in Section 4). Moreover, (joint) moments involving the time of ruin ![]() $\tau$ can also be obtained from our Gerber-Shiu functions by differentiation with respect to
$\tau$ can also be obtained from our Gerber-Shiu functions by differentiation with respect to ![]() $\delta _1$ (see (4.2)). It is worthwhile to point out that the technique of using potential measures in Liu and Zhang [Reference Liu and Zhang28] is no longer applicable in our case due to the presence of the stochastic integral
$\delta _1$ (see (4.2)). It is worthwhile to point out that the technique of using potential measures in Liu and Zhang [Reference Liu and Zhang28] is no longer applicable in our case due to the presence of the stochastic integral ![]() $B_{\delta _2}(\tau )$ in our Gerber-Shiu function, and we must resort to the use of Itô's lemma.
$B_{\delta _2}(\tau )$ in our Gerber-Shiu function, and we must resort to the use of Itô's lemma.
This paper is organized as follows. In Section 2, with the help of Itô's lemma, recursive integro-differential equations (in ![]() $n$ and
$n$ and ![]() $m$) satisfied by
$m$) satisfied by ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ are derived. These are then transformed to defective renewal equations where the components are specified (and hence, general solutions are available). Section 3 derives the explicit solutions under the special case where the claim amounts are distributed as a combination of exponentials and the penalty function
$\phi _{d,\delta _{123},n,m}(\cdot )$ are derived. These are then transformed to defective renewal equations where the components are specified (and hence, general solutions are available). Section 3 derives the explicit solutions under the special case where the claim amounts are distributed as a combination of exponentials and the penalty function ![]() $w(\cdot,\cdot )$ depends on the deficit only but not on the surplus prior to ruin. Section 4 ends the paper with numerical illustrations, which include the computation of the covariance between discounted claims and discounted perturbation until ruin along with some intuitive explanations.
$w(\cdot,\cdot )$ depends on the deficit only but not on the surplus prior to ruin. Section 4 ends the paper with numerical illustrations, which include the computation of the covariance between discounted claims and discounted perturbation until ruin along with some intuitive explanations.
2. General results on the joint moments
Before studying ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ defined by (1.3) and (1.4) for
$\phi _{d,\delta _{123},n,m}(u)$ defined by (1.3) and (1.4) for ![]() $n,m\in \mathbb {N}$, we would like to collect the assumptions/conditions that will be used in the upcoming analysis. It will be seen from Theorem 1 that the integro-differential equation (2.2) satisfied by
$n,m\in \mathbb {N}$, we would like to collect the assumptions/conditions that will be used in the upcoming analysis. It will be seen from Theorem 1 that the integro-differential equation (2.2) satisfied by ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ is recursive in
$\phi _{w,\delta _{123},n,m}(\cdot )$ is recursive in ![]() $n$ and
$n$ and ![]() $m$. In particular, the nonhomogeneous term (2.4) in such equation contains the “lower-order” Gerber-Shiu functions
$m$. In particular, the nonhomogeneous term (2.4) in such equation contains the “lower-order” Gerber-Shiu functions ![]() $\phi _{w,\delta _{123},n-1,m}(\cdot )$,
$\phi _{w,\delta _{123},n-1,m}(\cdot )$, ![]() $\phi _{w,\delta _{123},n-2,m}(\cdot )$, and
$\phi _{w,\delta _{123},n-2,m}(\cdot )$, and ![]() $\{\phi _{w,\delta _{123},n,j}(\cdot )\}_{j=0}^{m-1}$. As a result, its general solution in Theorem 2 depends on these lower-order Gerber-Shiu functions which, in turn, depend on Gerber-Shiu functions that are of even lower order. Inductively, the solution for
$\{\phi _{w,\delta _{123},n,j}(\cdot )\}_{j=0}^{m-1}$. As a result, its general solution in Theorem 2 depends on these lower-order Gerber-Shiu functions which, in turn, depend on Gerber-Shiu functions that are of even lower order. Inductively, the solution for ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ (for given
$\phi _{w,\delta _{123},n,m}(\cdot )$ (for given ![]() $n,m\in \mathbb {N}$) relies on and requires the existence of solutions for
$n,m\in \mathbb {N}$) relies on and requires the existence of solutions for ![]() $\phi _{w,\delta _{123},i,j}(\cdot )$'s with
$\phi _{w,\delta _{123},i,j}(\cdot )$'s with ![]() $(i,j)\in \Upsilon (n,m)$, where
$(i,j)\in \Upsilon (n,m)$, where ![]() $\Upsilon (n,m)=\{(i,j): 0\leq i\leq n; 0\leq j \leq m\}\setminus \{(n,m)\}$. Therefore, the following assumptions/conditions concerning the analysis of
$\Upsilon (n,m)=\{(i,j): 0\leq i\leq n; 0\leq j \leq m\}\setminus \{(n,m)\}$. Therefore, the following assumptions/conditions concerning the analysis of ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ for given
$\phi _{w,\delta _{123},n,m}(\cdot )$ for given ![]() $n,m\in \mathbb {N}$ are also a result of the inductive procedure. The same comments apply to
$n,m\in \mathbb {N}$ are also a result of the inductive procedure. The same comments apply to ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$.
$\phi _{d,\delta _{123},n,m}(\cdot )$.
• Assumption 1. For
 $i=0,1,2,\ldots,n$ and
$i=0,1,2,\ldots,n$ and  $j=0,1,2,\ldots,m$, the functions
$j=0,1,2,\ldots,m$, the functions  $\phi _{w,\delta _{123},i,j}(\cdot )$ and
$\phi _{w,\delta _{123},i,j}(\cdot )$ and  $\phi _{d,\delta _{123},i,j}(\cdot )$ are twice continuously differentiable on
$\phi _{d,\delta _{123},i,j}(\cdot )$ are twice continuously differentiable on  $[0,\infty )$.
$[0,\infty )$.• Assumption 2. For
 $i=0,1,2,\ldots,n$ and
$i=0,1,2,\ldots,n$ and  $j=0,1,2,\ldots,m$, the functions
$j=0,1,2,\ldots,m$, the functions  $\phi _{w,\delta _{123},i,j}(\cdot )$ and
$\phi _{w,\delta _{123},i,j}(\cdot )$ and  $\phi _{d,\delta _{123},i,j}(\cdot )$ are bounded on
$\phi _{d,\delta _{123},i,j}(\cdot )$ are bounded on  $[0,\infty )$, and their first and second derivatives are bounded on
$[0,\infty )$, and their first and second derivatives are bounded on  $[0,\infty )$ as well.
$[0,\infty )$ as well.
Assumptions 1 and 2 concerning continuous differentiability and bounded derivatives are rather common in ruin theory involving diffusion (e.g. [Reference Paulsen and Gjessing30, Thm. 2.1], [Reference Cai and Yang6, Thms. 3.2 and 3.3], and [Reference Cai and Xu5, Thms. 2.1–2.3]) and they are not easy to verify or prove in general. Interested readers are referred to, for example, Wang and Wu [Reference Wang and Wu36], Cai [Reference Cai4, Thm. 3.2], Cai and Yang [Reference Cai and Yang6, Thm. 2.1], Loisel [Reference Loisel29], and Zhu and Yang [Reference Zhu and Yang39] for detailed treatment of differentiability of ruin functions.
• Assumption 3. For
 $i=0,1,2,\ldots,n$ and
$i=0,1,2,\ldots,n$ and  $j=0,1,2,\ldots,m$, the limits
$j=0,1,2,\ldots,m$, the limits  $\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{w,\delta _{123},i,j}(u)=\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{w,\delta _{123},i,j}'(u)=0$ and
$\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{w,\delta _{123},i,j}(u)=\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{w,\delta _{123},i,j}'(u)=0$ and  $\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{d,\delta _{123},i,j}(u)=\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{d,\delta _{123},i,j}'(u)=0$ are valid, where
$\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{d,\delta _{123},i,j}(u)=\lim _{u \to \infty } e^{-\rho _{i,j}u}\phi _{d,\delta _{123},i,j}'(u)=0$ are valid, where  $\rho _{i,j}$ is the unique non-negative root of the Lundberg's equation (in
$\rho _{i,j}$ is the unique non-negative root of the Lundberg's equation (in  $\xi$)
(2.1)
$\xi$)
(2.1) \begin{equation} \frac{\sigma^{2}}{2}\xi^{2}+c\xi-(\lambda +\delta_1+i\delta_2+j\delta_3)+\lambda \tilde{p}(\xi)=0. \end{equation}
\begin{equation} \frac{\sigma^{2}}{2}\xi^{2}+c\xi-(\lambda +\delta_1+i\delta_2+j\delta_3)+\lambda \tilde{p}(\xi)=0. \end{equation}
Except for ![]() $\rho _{i,j}$, all other roots of the Lundberg's equation (2.1) have negative real parts. In particular,
$\rho _{i,j}$, all other roots of the Lundberg's equation (2.1) have negative real parts. In particular, ![]() $\rho _{i,j}=0$ when
$\rho _{i,j}=0$ when ![]() $\delta _1+i\delta _2+j\delta _3=0$ and
$\delta _1+i\delta _2+j\delta _3=0$ and ![]() $\rho _{i,j}>0$ when
$\rho _{i,j}>0$ when ![]() $\delta _1+i\delta _2+j\delta _3>0$ (see, e.g., [Reference Gerber and Landry22]). The Lundberg's equation (2.1) typically arises when taking Laplace transforms on both sides of the integro-differential equation satisfied by a Gerber-Shiu type function to convert it to a defective renewal equation (see, e.g., [Reference Tsai and Willmot34]). In such a transformation concerning
$\delta _1+i\delta _2+j\delta _3>0$ (see, e.g., [Reference Gerber and Landry22]). The Lundberg's equation (2.1) typically arises when taking Laplace transforms on both sides of the integro-differential equation satisfied by a Gerber-Shiu type function to convert it to a defective renewal equation (see, e.g., [Reference Tsai and Willmot34]). In such a transformation concerning ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$, Assumption 3 will be needed.
$\phi _{d,\delta _{123},n,m}(\cdot )$, Assumption 3 will be needed.
• Condition 1. For
 $k=0,1,2,\ldots,m$, the integral
$k=0,1,2,\ldots,m$, the integral  $\int _0^{\infty } f^{k}(y)p(y)\,dy$ is finite.
$\int _0^{\infty } f^{k}(y)p(y)\,dy$ is finite.• Condition 2. For
 $k=0,1,2,\ldots,m$, the integral
$k=0,1,2,\ldots,m$, the integral  $\int _{u}^{\infty } f^{k}(y)w(u,y-u)p(y)\,dy$ (as a function of
$\int _{u}^{\infty } f^{k}(y)w(u,y-u)p(y)\,dy$ (as a function of  $u\ge 0$) is bounded.
$u\ge 0$) is bounded.
Condition 2 above involves the penalty function and is only required for the analysis of ![]() $\phi _{w,\delta _{123},n,m}(u)$ but not
$\phi _{w,\delta _{123},n,m}(u)$ but not ![]() $\phi _{d,\delta _{123},n,m}(u)$. Note that, upon specifying the claim density
$\phi _{d,\delta _{123},n,m}(u)$. Note that, upon specifying the claim density ![]() $p(\cdot )$, cost function
$p(\cdot )$, cost function ![]() $f(\cdot )$, and penalty function
$f(\cdot )$, and penalty function ![]() $w(\cdot,\cdot )$, Conditions 1 and 2 can be checked on a case-by-case basis via direct integration.
$w(\cdot,\cdot )$, Conditions 1 and 2 can be checked on a case-by-case basis via direct integration.
For ease of reference, some notation that will be used repeatedly is summarized in Table 1.
TABLE 1. Definition of some important notation.

2.1. Integro-differential equations
We have the following theorem regarding the integro-differential equations satisfied by ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$.
$\phi _{d,\delta _{123},n,m}(\cdot )$.
Theorem 1 (Integro-differential equations for  $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and  $\phi _{d,\delta _{123},n,m}(\cdot )$)
$\phi _{d,\delta _{123},n,m}(\cdot )$)
Under Assumptions 1–2 and Conditions 1–2, ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ satisfy the recursive integro-differential equations (for
$\phi _{d,\delta _{123},n,m}(\cdot )$ satisfy the recursive integro-differential equations (for ![]() $n,m\in \mathbb {N}$ and
$n,m\in \mathbb {N}$ and ![]() $u>0$)
$u>0$)
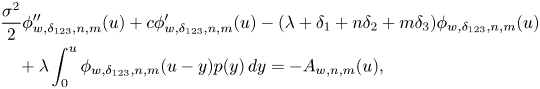 \begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},n,m}''(u)+c\phi_{w,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad +\lambda \int_0^{u} \phi_{w,\delta_{123},n,m}(u-y)p(y)\,dy={-}A_{w,n,m}(u), \end{align}
\begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},n,m}''(u)+c\phi_{w,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad +\lambda \int_0^{u} \phi_{w,\delta_{123},n,m}(u-y)p(y)\,dy={-}A_{w,n,m}(u), \end{align}and
 \begin{align} & \frac{\sigma^{2}}{2} \phi_{d,\delta_{123},n,m}''(u)+c\phi_{d,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{d,\delta_{123},n,m}(u)\nonumber\\ & \quad +\lambda \int_0^{u} \phi_{d,\delta_{123},n,m}(u-y)p(y)\,dy={-}A_{d,n,m}(u), \end{align}
\begin{align} & \frac{\sigma^{2}}{2} \phi_{d,\delta_{123},n,m}''(u)+c\phi_{d,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{d,\delta_{123},n,m}(u)\nonumber\\ & \quad +\lambda \int_0^{u} \phi_{d,\delta_{123},n,m}(u-y)p(y)\,dy={-}A_{d,n,m}(u), \end{align}respectively. The nonhomogeneous terms above are given by
 \begin{align} A_{w,n,m}(u)& =n\sigma 1_{\{n \geq 1\}} \phi_{w,\delta_{123},n-1,m}'(u)+\frac{n(n-1)}{2}1_{\{n \geq 2\}}\phi_{w,\delta_{123},n-2,m}(u)\nonumber\\ & \quad +\lambda \sum_{j=0}^{m-1} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy \nonumber\\ & \quad +\lambda 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy, \end{align}
\begin{align} A_{w,n,m}(u)& =n\sigma 1_{\{n \geq 1\}} \phi_{w,\delta_{123},n-1,m}'(u)+\frac{n(n-1)}{2}1_{\{n \geq 2\}}\phi_{w,\delta_{123},n-2,m}(u)\nonumber\\ & \quad +\lambda \sum_{j=0}^{m-1} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy \nonumber\\ & \quad +\lambda 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy, \end{align}and
 \begin{align} A_{d,n,m}(u)& =n\sigma 1_{\{n \geq 1\}} \phi_{d,\delta_{123},n-1,m}'(u)+\frac{n(n-1)}{2}1_{\{n \geq 2\}}\phi_{d,\delta_{123},n-2,m}(u)\nonumber\\ & \quad +\lambda \sum_{j=0}^{m-1} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{d,\delta_{123},n,j}(u-y)p(y)\,dy, \end{align}
\begin{align} A_{d,n,m}(u)& =n\sigma 1_{\{n \geq 1\}} \phi_{d,\delta_{123},n-1,m}'(u)+\frac{n(n-1)}{2}1_{\{n \geq 2\}}\phi_{d,\delta_{123},n-2,m}(u)\nonumber\\ & \quad +\lambda \sum_{j=0}^{m-1} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{d,\delta_{123},n,j}(u-y)p(y)\,dy, \end{align}which are expressed in terms of the respective lower-order Gerber-Shiu functions.
Proof. For notational brevity, the initial condition ![]() $U(0)=u>0$ will be suppressed throughout the proof. We first consider the Gerber-Shiu function
$U(0)=u>0$ will be suppressed throughout the proof. We first consider the Gerber-Shiu function ![]() $\phi _{w,\delta _{123},n,m}(u)$ defined in (1.3). By conditioning on whether the first claim occurs by time
$\phi _{w,\delta _{123},n,m}(u)$ defined in (1.3). By conditioning on whether the first claim occurs by time ![]() $t$ (for some
$t$ (for some ![]() $t>0$ where we will let
$t>0$ where we will let ![]() $t\to 0^{+}$ later on), we arrive at
$t\to 0^{+}$ later on), we arrive at
 \begin{align} \phi_{w,\delta_{123},n,m}(u) & =e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} | T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \big| T_1=s]\,ds. \end{align}
\begin{align} \phi_{w,\delta_{123},n,m}(u) & =e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} | T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \big| T_1=s]\,ds. \end{align} For any ![]() $s\ge 0$, let
$s\ge 0$, let ![]() $\mathcal {G}_s$ be the sigma-field generated by
$\mathcal {G}_s$ be the sigma-field generated by ![]() $\{B(v)\}_{0 \leq v \leq s}$. For any
$\{B(v)\}_{0 \leq v \leq s}$. For any ![]() $t>0$, let
$t>0$, let ![]() $\hat {B}_t(s)=B(s+t)-B(t)$ for
$\hat {B}_t(s)=B(s+t)-B(t)$ for ![]() $s \geq 0$. Since
$s \geq 0$. Since ![]() $\{Y_k\}_{k=1}^{\infty },$
$\{Y_k\}_{k=1}^{\infty },$ ![]() $\{N(s)\}_{s\ge 0}$, and
$\{N(s)\}_{s\ge 0}$, and ![]() $\{B(s)\}_{s \geq 0}$ are mutually independent and a Brownian motion has stationary and independent increments, it is clear that
$\{B(s)\}_{s \geq 0}$ are mutually independent and a Brownian motion has stationary and independent increments, it is clear that ![]() $\{\hat {B}_t(s)\}_{s \geq 0}$ is a standard Brownian motion independent of
$\{\hat {B}_t(s)\}_{s \geq 0}$ is a standard Brownian motion independent of ![]() $\{B(s)\}_{0 \leq s \leq t}$,
$\{B(s)\}_{0 \leq s \leq t}$, ![]() $\{Y_k\}_{k=1}^{\infty }$, and
$\{Y_k\}_{k=1}^{\infty }$, and ![]() $\{N(s)\}_{s\ge 0}$. Also, let
$\{N(s)\}_{s\ge 0}$. Also, let ![]() $\hat {\tau }_0=\inf \{s\ge 0: u+cs+\sigma B(s)<0\}$ be the first time when the drifted Brownian motion
$\hat {\tau }_0=\inf \{s\ge 0: u+cs+\sigma B(s)<0\}$ be the first time when the drifted Brownian motion ![]() $\{u+cs+\sigma B(s)\}_{s\ge 0}$ falls below zero, and this stopping time will repeatedly appear in our analysis. Because ruin occurs by a claim on the set
$\{u+cs+\sigma B(s)\}_{s\ge 0}$ falls below zero, and this stopping time will repeatedly appear in our analysis. Because ruin occurs by a claim on the set ![]() $\{\tau <\infty,U(\tau )<0\}$, given that the first claim occurs after time
$\{\tau <\infty,U(\tau )<0\}$, given that the first claim occurs after time ![]() $t$ one must have
$t$ one must have ![]() $\hat {\tau }_0>t$ (otherwise ruin would have occurred by oscillation). Therefore, the first expectation term in (2.6) is
$\hat {\tau }_0>t$ (otherwise ruin would have occurred by oscillation). Therefore, the first expectation term in (2.6) is
 \begin{align} & E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}}\,|\, T_1>t]\nonumber\\ & \quad = E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t]\nonumber\\ & \quad = E\left[e^{-\delta_1 \tau}\left(B_{\delta_2}(t)+\int_t^{\tau} e^{-\delta_2 s}\,dB(s) \right)^{n} \left(e^{-\delta_3 t} \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} \right.\nonumber\\ & \qquad \left.\times w(U(\tau^{-}),|U(\tau)|) 1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+m\delta_3) t}E\left[e^{-\delta_1 (\tau-t)}B_{\delta_2}^{i} (t)\left(\int_t^{\tau} e^{-\delta_2 s}\,dB(s) \right)^{n-i} \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m}\right.\nonumber\\ & \qquad \left.\times w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)e^{-\delta_1 (\tau-t)}\left(\int_0^{\tau-t} e^{-\delta_2 s}\,dB(s+t) \right)^{n-i}\right.\nonumber\\ & \qquad \left.\times \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}}E\left[e^{-\delta_1 (\tau-t)}\left(\int_0^{\tau-t} e^{-\delta_2 s}\,d\hat{B}_t(s)\right)^{n-i}\right.\right.\nonumber\\ & \qquad \left.\left.\left.\times \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \,|\, \mathcal{G}_t \vee \{T_1>t\}\right]\right|\, T_1>t\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\,|\,T_1>t]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))]. \end{align}
\begin{align} & E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}}\,|\, T_1>t]\nonumber\\ & \quad = E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t]\nonumber\\ & \quad = E\left[e^{-\delta_1 \tau}\left(B_{\delta_2}(t)+\int_t^{\tau} e^{-\delta_2 s}\,dB(s) \right)^{n} \left(e^{-\delta_3 t} \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} \right.\nonumber\\ & \qquad \left.\times w(U(\tau^{-}),|U(\tau)|) 1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+m\delta_3) t}E\left[e^{-\delta_1 (\tau-t)}B_{\delta_2}^{i} (t)\left(\int_t^{\tau} e^{-\delta_2 s}\,dB(s) \right)^{n-i} \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m}\right.\nonumber\\ & \qquad \left.\times w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)e^{-\delta_1 (\tau-t)}\left(\int_0^{\tau-t} e^{-\delta_2 s}\,dB(s+t) \right)^{n-i}\right.\nonumber\\ & \qquad \left.\times \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} 1_{\{\hat{\tau}_0>t\}}\,|\, T_1>t\vphantom{\sum_{k=1}^{N(\tau)}}\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}}E\left[e^{-\delta_1 (\tau-t)}\left(\int_0^{\tau-t} e^{-\delta_2 s}\,d\hat{B}_t(s)\right)^{n-i}\right.\right.\nonumber\\ & \qquad \left.\left.\left.\times \left( \sum_{k=1}^{N(\tau)} e^{-\delta_3 (T_k-t)} f(Y_k)\right)^{m} w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \,|\, \mathcal{G}_t \vee \{T_1>t\}\right]\right|\, T_1>t\right]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\,|\,T_1>t]\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))]. \end{align} In the third last step above, we have applied the tower property of conditional expectation and the fact that both ![]() $B_{\delta _2}(t)$ and
$B_{\delta _2}(t)$ and ![]() $1_{\{\hat {\tau }_0>t\}}$ are
$1_{\{\hat {\tau }_0>t\}}$ are ![]() $\mathcal {G}_t$-measurable. Moreover, in the second last step, conditional on
$\mathcal {G}_t$-measurable. Moreover, in the second last step, conditional on ![]() $\mathcal {G}_t \vee \{T_1>t\}$ and based on the memoryless property of the exponential arrival time
$\mathcal {G}_t \vee \{T_1>t\}$ and based on the memoryless property of the exponential arrival time ![]() $T_1$, the surplus process at time
$T_1$, the surplus process at time ![]() $t$ is “renewed” at level
$t$ is “renewed” at level ![]() $u+ct+\sigma B(t)$ which is positive (almost surely) on the set
$u+ct+\sigma B(t)$ which is positive (almost surely) on the set ![]() $\{\hat {\tau }_0>t\}$.
$\{\hat {\tau }_0>t\}$.
Next, we look at the integral term in (2.6). Again, given that ![]() $T_1=s$, one must have
$T_1=s$, one must have ![]() $\hat {\tau }_0>s$ on the set
$\hat {\tau }_0>s$ on the set ![]() $\{\tau <\infty,U(\tau )<0\}$. Further distinguishing whether the first claim at time
$\{\tau <\infty,U(\tau )<0\}$. Further distinguishing whether the first claim at time ![]() $s$ causes ruin leads to
$s$ causes ruin leads to
 \begin{align} & \int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \,|\, T_1=s]\,ds\nonumber\\ & \quad= \int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s]\,ds\nonumber\\ & \qquad +\int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}\,|\, T_1=s]\,ds. \end{align}
\begin{align} & \int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}} \,|\, T_1=s]\,ds\nonumber\\ & \quad= \int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s]\,ds\nonumber\\ & \qquad +\int_0^{t}\lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}\,|\, T_1=s]\,ds. \end{align} Defining ![]() $\mathcal {H}(Y_1)$ to be the sigma-field generated by the random variable
$\mathcal {H}(Y_1)$ to be the sigma-field generated by the random variable ![]() $Y_1$, the expectation in the integrand of the first integral above can be obtained as
$Y_1$, the expectation in the integrand of the first integral above can be obtained as
 \begin{align} & E\left[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|) 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s\right]\nonumber\\ & \quad = E[ E[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} ] \,|\, T_1=s]\nonumber\\ & \quad =E\left[ E\left[ e^{-\delta_1 \tau}\left(B_{\delta_2} (s)+\int_s^{\tau} e^{-\delta_2 v}\,dB(v)\right)^{n} \left( e^{-\delta_3 s} f(Y_1) + \sum_{k=2}^{N(\tau)} e^{-\delta_3 T_k}f(Y_k) \right)^{m} w(U(\tau^{-}),|U(\tau)|)\right.\right.\nonumber\\ & \qquad \left.\left.\left.\times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} \vphantom{\sum_{k=2}^{N(\tau)}}\right] \,\right| T_1=s\right]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\vphantom{\sum_{k=2}^{N(\tau)}}\right.\nonumber\\ & \qquad \times E\left[ e^{-\delta_1 (\tau-s)}\left(\int_0^{\tau-s} e^{-\delta_2 v}\,d\hat{B}_s(v)\right)^{i} \left( \sum_{k=2}^{N(\tau)}e^{-\delta_3 (T_k-s)} f(Y_k) \right)^{j} w(U(\tau^{-}),|U(\tau)|)\right.\nonumber\\ & \qquad \left.\left.\left.\times 1_{\{\tau<\infty,U(\tau)<0\}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} \vphantom{\sum_{k=2}^{N(\tau)}}\right] \right|\,T_1=s\right]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) \,|\, T_1=s]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) ]. \end{align}
\begin{align} & E\left[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|) 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s\right]\nonumber\\ & \quad = E[ E[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)\nonumber\\ & \qquad \times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} ] \,|\, T_1=s]\nonumber\\ & \quad =E\left[ E\left[ e^{-\delta_1 \tau}\left(B_{\delta_2} (s)+\int_s^{\tau} e^{-\delta_2 v}\,dB(v)\right)^{n} \left( e^{-\delta_3 s} f(Y_1) + \sum_{k=2}^{N(\tau)} e^{-\delta_3 T_k}f(Y_k) \right)^{m} w(U(\tau^{-}),|U(\tau)|)\right.\right.\nonumber\\ & \qquad \left.\left.\left.\times 1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} \vphantom{\sum_{k=2}^{N(\tau)}}\right] \,\right| T_1=s\right]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\vphantom{\sum_{k=2}^{N(\tau)}}\right.\nonumber\\ & \qquad \times E\left[ e^{-\delta_1 (\tau-s)}\left(\int_0^{\tau-s} e^{-\delta_2 v}\,d\hat{B}_s(v)\right)^{i} \left( \sum_{k=2}^{N(\tau)}e^{-\delta_3 (T_k-s)} f(Y_k) \right)^{j} w(U(\tau^{-}),|U(\tau)|)\right.\nonumber\\ & \qquad \left.\left.\left.\times 1_{\{\tau<\infty,U(\tau)<0\}}\,|\,\mathcal{G}_s \vee \mathcal{H}(Y_1) \vee \{T_1=s\} \vphantom{\sum_{k=2}^{N(\tau)}}\right] \right|\,T_1=s\right]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) \,|\, T_1=s]\nonumber\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) ]. \end{align} For now, we focus on the expectation term above. By conditioning on ![]() $Y_1$ and using the independence between
$Y_1$ and using the independence between ![]() $\mathcal {H}(Y_1)$ and
$\mathcal {H}(Y_1)$ and ![]() $\mathcal {G}_s$, we get
$\mathcal {G}_s$, we get
 \begin{align} & E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) \right]\nonumber\\ & \quad= \int_0^{\infty} E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y)\right]p(y)\,dy\nonumber\\ & \quad= E\left[\int_0^{\infty} B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]\nonumber\\ & \quad= E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]. \end{align}
\begin{align} & E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) \right]\nonumber\\ & \quad= \int_0^{\infty} E\left[B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y)\right]p(y)\,dy\nonumber\\ & \quad= E\left[\int_0^{\infty} B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]\nonumber\\ & \quad= E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]. \end{align} Note that the interchange of integration and expectation in the second last equality is due to Fubini's theorem as follows. Recall that the Gerber-Shiu functions ![]() $\phi _{w,\delta _{123},i,j}(\cdot )$'s are assumed bounded (see Assumption 2) and integrals in the form of
$\phi _{w,\delta _{123},i,j}(\cdot )$'s are assumed bounded (see Assumption 2) and integrals in the form of ![]() $\int _0^{\infty } f^{m-j}(y)p(y)\,dy$ are assumed finite (see Condition 1). Therefore, there exists
$\int _0^{\infty } f^{m-j}(y)p(y)\,dy$ are assumed finite (see Condition 1). Therefore, there exists ![]() $L>0$ such that
$L>0$ such that
 \begin{align} & \int_0^{\infty} |B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)|\,dy \nonumber\\ & \quad \leq L |B_{\delta_2}(s)|^{n-i} \end{align}
\begin{align} & \int_0^{\infty} |B_{\delta_2}^{n-i} (s)f^{m-j}(y) 1_{\{\hat{\tau}_0>s\}} 1_{\{y\le u+cs+\sigma B(s) \}} \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)|\,dy \nonumber\\ & \quad \leq L |B_{\delta_2}(s)|^{n-i} \end{align}for ![]() $0\leq s \leq t$. Because
$0\leq s \leq t$. Because ![]() $B_{\delta _2}(s)=\int _0^{s} e^{-\delta _2 v}\,dB(v)$ follows a normal distribution (with mean
$B_{\delta _2}(s)=\int _0^{s} e^{-\delta _2 v}\,dB(v)$ follows a normal distribution (with mean ![]() $0$ and variance
$0$ and variance ![]() $\int _0^{s} e^{-2\delta _2 v}\,dv$), the random variable
$\int _0^{s} e^{-2\delta _2 v}\,dv$), the random variable ![]() $|B_{\delta _2}(s)|$ follows a half-normal distribution. For
$|B_{\delta _2}(s)|$ follows a half-normal distribution. For ![]() $k\in \mathbb {N}^{+}$ (where
$k\in \mathbb {N}^{+}$ (where ![]() $\mathbb {N}^{+}$ is the set of positive integers), its
$\mathbb {N}^{+}$ is the set of positive integers), its ![]() $k$th moment is known to be bounded because
$k$th moment is known to be bounded because
 \begin{equation} E[|B_{\delta_2}(s)|^{k}]= L^{*}_k \left(\int_0^{s} e^{{-}2\delta_2 v}\,dv\right)^{\frac{k}{2}} \end{equation}
\begin{equation} E[|B_{\delta_2}(s)|^{k}]= L^{*}_k \left(\int_0^{s} e^{{-}2\delta_2 v}\,dv\right)^{\frac{k}{2}} \end{equation}for some constant ![]() $L^{*}_k$. Therefore, the expectation on the right-hand side of (2.11) is bounded for
$L^{*}_k$. Therefore, the expectation on the right-hand side of (2.11) is bounded for ![]() $0\leq s \leq t$ and
$0\leq s \leq t$ and ![]() $i=0,1,\ldots,n$, justifying the use of Fubini's theorem.
$i=0,1,\ldots,n$, justifying the use of Fubini's theorem.
Similarly, we omit the repetitive details and state that the expectation in the integrand of the second integral in (2.8) is given by
 \begin{align} & E\left[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}\,|\, T_1=s\right]\nonumber\\ & \quad = E[ e^{-\delta_1 s}B_{\delta_2}^{n} (s)(e^{-\delta_3 s}f(Y_1))^{m} w(u+cs+\sigma B(s),Y_1-u-cs-\sigma B(s))1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}]\nonumber\\ & \quad=e^{-(\delta_1+m\delta_3) s}E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right], \end{align}
\begin{align} & E\left[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)w(U(\tau^{-}),|U(\tau)|)1_{\{\tau<\infty,U(\tau)<0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}\,|\, T_1=s\right]\nonumber\\ & \quad = E[ e^{-\delta_1 s}B_{\delta_2}^{n} (s)(e^{-\delta_3 s}f(Y_1))^{m} w(u+cs+\sigma B(s),Y_1-u-cs-\sigma B(s))1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1>u+cs+\sigma B(s) \}}]\nonumber\\ & \quad=e^{-(\delta_1+m\delta_3) s}E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right], \end{align}where Condition 2 has been used.
Using (2.7)–(2.10) and (2.13), it can be seen that (2.6) becomes
 \begin{align} & \phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\lambda+\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\right]\nonumber\\ & \qquad +\lambda \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} \int_0^{t} e^{-(\lambda+\delta_1+i\delta_2+m\delta_3 )s} \nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]ds\nonumber\\ & \qquad +\lambda \int_0^{t} e^{-(\lambda+\delta_1+m\delta_3) s}\nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right]ds. \end{align}
\begin{align} & \phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\lambda+\delta_1+(n-i)\delta_2+m\delta_3) t}E\left[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\right]\nonumber\\ & \qquad +\lambda \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} \int_0^{t} e^{-(\lambda+\delta_1+i\delta_2+m\delta_3 )s} \nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]ds\nonumber\\ & \qquad +\lambda \int_0^{t} e^{-(\lambda+\delta_1+m\delta_3) s}\nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right]ds. \end{align}With the help of the L'Hôpital's rule, we would like to consider the limits
 \begin{align} & \lim_{t \to 0^{+}} \frac{1}{t}\int_0^{t} e^{-(\lambda+\delta_1+i\delta_2+m\delta_3 )s} \nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]ds \nonumber\\ & \quad = \lim_{t \to 0^{+}} E\left[B_{\delta_2}^{n-i} (t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y) p(y)\,dy\right] \end{align}
\begin{align} & \lim_{t \to 0^{+}} \frac{1}{t}\int_0^{t} e^{-(\lambda+\delta_1+i\delta_2+m\delta_3 )s} \nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n-i} (s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y) p(y)\,dy\right]ds \nonumber\\ & \quad = \lim_{t \to 0^{+}} E\left[B_{\delta_2}^{n-i} (t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)} f^{m-j}(y) \phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y) p(y)\,dy\right] \end{align}and
 \begin{align} & \lim_{t \to 0^{+}} \frac{1}{t} \int_0^{t} e^{-(\lambda+\delta_1+m\delta_3) s}\nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right]ds\nonumber\\ & \quad = \lim_{t \to 0^{+}} E\left[B_{\delta_2}^{n} (t) 1_{\{\hat{\tau}_0>t\}} \int_{u+ct+\sigma B(t) }^{\infty} f^{m}(y) w(u+ct+\sigma B(t),y-u-ct-\sigma B(t)) p(y)\,dy\right]. \end{align}
\begin{align} & \lim_{t \to 0^{+}} \frac{1}{t} \int_0^{t} e^{-(\lambda+\delta_1+m\delta_3) s}\nonumber\\ & \qquad \times E\left[B_{\delta_2}^{n} (s) 1_{\{\hat{\tau}_0>s\}} \int_{u+cs+\sigma B(s) }^{\infty} f^{m}(y) w(u+cs+\sigma B(s),y-u-cs-\sigma B(s)) p(y)\,dy\right]ds\nonumber\\ & \quad = \lim_{t \to 0^{+}} E\left[B_{\delta_2}^{n} (t) 1_{\{\hat{\tau}_0>t\}} \int_{u+ct+\sigma B(t) }^{\infty} f^{m}(y) w(u+ct+\sigma B(t),y-u-ct-\sigma B(t)) p(y)\,dy\right]. \end{align}To evaluate (2.15), we can follow the discussions subsequent to (2.10) and note also that (2.11) implies
 \begin{equation} \left| B_{\delta_2}^{n-i}(s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y)p(y)\,dy \right| \leq L |B_{\delta_2}(s)|^{n-i} \end{equation}
\begin{equation} \left| B_{\delta_2}^{n-i}(s) 1_{\{\hat{\tau}_0>s\}} \int_0^{u+cs+\sigma B(s)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+cs+\sigma B(s)-y)p(y)\,dy \right| \leq L |B_{\delta_2}(s)|^{n-i} \end{equation}for ![]() $0\leq s \leq t$. Utilizing (2.12) for
$0\leq s \leq t$. Utilizing (2.12) for ![]() $k\in \mathbb {N}^{+}$, one has
$k\in \mathbb {N}^{+}$, one has
for ![]() $i< n$ where we have used the fact that
$i< n$ where we have used the fact that ![]() $B_{\delta _2}(t)$ is continuous in
$B_{\delta _2}(t)$ is continuous in ![]() $t\ge 0$ and
$t\ge 0$ and ![]() $B_{\delta _2}(0)=0$ in the last equality. When
$B_{\delta _2}(0)=0$ in the last equality. When ![]() $i=n$, the right-hand side of (2.17) is equal to the constant
$i=n$, the right-hand side of (2.17) is equal to the constant ![]() $L$. Consolidating these results for
$L$. Consolidating these results for ![]() $i\le n$, noting that
$i\le n$, noting that ![]() $\hat {\tau }_0>0$ almost surely given
$\hat {\tau }_0>0$ almost surely given ![]() $u>0$ and utilizing the generalized dominated convergence theorem (see, e.g., [Reference Billingsley3, Prob. 16.4]), we find that
$u>0$ and utilizing the generalized dominated convergence theorem (see, e.g., [Reference Billingsley3, Prob. 16.4]), we find that
 \begin{align} & \lim_{t \to 0^{+}}E\left[B_{\delta_2}^{n-i}(t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y)p(y)\,dy\right] \nonumber\\ & \quad =E\left[\lim_{t \to 0^{+}}B_{\delta_2}^{n-i}(t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y)p(y)\,dy\right]\nonumber\\ & \quad =1_{\{i=n\}}\int_0^{u}f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy. \end{align}
\begin{align} & \lim_{t \to 0^{+}}E\left[B_{\delta_2}^{n-i}(t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y)p(y)\,dy\right] \nonumber\\ & \quad =E\left[\lim_{t \to 0^{+}}B_{\delta_2}^{n-i}(t) 1_{\{\hat{\tau}_0>t\}} \int_0^{u+ct+\sigma B(t)}f^{m-j}(y)\phi_{w,\delta_{123},i,j}(u+ct+\sigma B(t)-y)p(y)\,dy\right]\nonumber\\ & \quad =1_{\{i=n\}}\int_0^{u}f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy. \end{align}Moreover, under Condition 2, it can be shown that (2.16) is given by
 \begin{align} & \lim_{t \to 0^{+}}E\left[B_{\delta_2}^{n}(t) 1_{\{\hat{\tau}_0>t\}} \int_{u+ct+\sigma B(t)}^{\infty} f^{m}(y)w(u+ct+\sigma B(t),y-u-ct-\sigma B(t))p(y)\,dy\right]\nonumber\\ & \quad = 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy. \end{align}
\begin{align} & \lim_{t \to 0^{+}}E\left[B_{\delta_2}^{n}(t) 1_{\{\hat{\tau}_0>t\}} \int_{u+ct+\sigma B(t)}^{\infty} f^{m}(y)w(u+ct+\sigma B(t),y-u-ct-\sigma B(t))p(y)\,dy\right]\nonumber\\ & \quad = 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy. \end{align}In light of the first term in (2.14), we also apply similar arguments to obtain
 \begin{align} & \lim_{t \to 0^{+}}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))]\nonumber\\ & \quad =E\left[\lim_{t \to 0^{+}}B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\right]\nonumber\\ & \quad =1_{\{i=0\}} \phi_{w,\delta_{123},n,m}(u). \end{align}
\begin{align} & \lim_{t \to 0^{+}}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))]\nonumber\\ & \quad =E\left[\lim_{t \to 0^{+}}B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))\right]\nonumber\\ & \quad =1_{\{i=0\}} \phi_{w,\delta_{123},n,m}(u). \end{align} Now, we proceed by rearranging the terms in (2.14), dividing both sides by ![]() $t$ and taking the limit
$t$ and taking the limit ![]() $t \to 0^{+}$. Applying (2.18)–(2.20) and further noting that
$t \to 0^{+}$. Applying (2.18)–(2.20) and further noting that ![]() $e^{-(\lambda +\delta _1+(n-i)\delta _2+m\delta _3)t}=1-(\lambda +\delta _1+(n-i)\delta _2+m\delta _3)t+o(t)$, we arrive at
$e^{-(\lambda +\delta _1+(n-i)\delta _2+m\delta _3)t}=1-(\lambda +\delta _1+(n-i)\delta _2+m\delta _3)t+o(t)$, we arrive at
 \begin{align} & \lim_{t \to 0^{+}}\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t))]-\phi_{w,\delta_{123},n,m}(u)}{t}\nonumber\\ & \quad -\lim_{t \to 0^{+}}\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat{\tau}_0>t\}})]}{t}\nonumber\\ & \quad +\sum_{i=1}^{n} {n \choose i} \lim_{t \to 0^{+}} \frac{E[B_{\delta_2}^{i}(t)\phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & \quad-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad+\lambda \sum_{j=0}^{m} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy\nonumber\\ & \quad +\lambda 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy =0. \end{align}
\begin{align} & \lim_{t \to 0^{+}}\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t))]-\phi_{w,\delta_{123},n,m}(u)}{t}\nonumber\\ & \quad -\lim_{t \to 0^{+}}\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat{\tau}_0>t\}})]}{t}\nonumber\\ & \quad +\sum_{i=1}^{n} {n \choose i} \lim_{t \to 0^{+}} \frac{E[B_{\delta_2}^{i}(t)\phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & \quad-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u)\nonumber\\ & \quad+\lambda \sum_{j=0}^{m} {m \choose j}\int_0^{u} f^{m-j}(y)\phi_{w,\delta_{123},n,j}(u-y)p(y)\,dy\nonumber\\ & \quad +\lambda 1_{\{n=0\}} \int_u^{\infty} f^{m}(y)w(u,y-u)p(y)\,dy =0. \end{align} The three limits in the above equation will be evaluated as follows. First, as ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ is assumed twice continuously differentiable as in Assumption 1, it follows from, for example, Tsai and Willmot [Reference Tsai and Willmot34, Sect. 2] that the first limit in the above equation is given by
$\phi _{w,\delta _{123},n,m}(\cdot )$ is assumed twice continuously differentiable as in Assumption 1, it follows from, for example, Tsai and Willmot [Reference Tsai and Willmot34, Sect. 2] that the first limit in the above equation is given by
To derive the second limit in (2.21), the boundedness of ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ on
$\phi _{w,\delta _{123},n,m}(\cdot )$ on ![]() $[0,\infty )$ in Assumption 2 (together with the convention that
$[0,\infty )$ in Assumption 2 (together with the convention that ![]() $\phi _{w,\delta _{123},n,m}(\cdot )=0$ on
$\phi _{w,\delta _{123},n,m}(\cdot )=0$ on ![]() $(-\infty,0)$ in connection to the trivial boundary condition (2.40)) assures that there exists some
$(-\infty,0)$ in connection to the trivial boundary condition (2.40)) assures that there exists some ![]() $L^{\ast }>0$ such that
$L^{\ast }>0$ such that ![]() $|\phi _{w,\delta _{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat {\tau }_0>t\}})|\le L^{\ast } (1-1_{\{\hat {\tau }_0>t\}})$. Thus, we have
$|\phi _{w,\delta _{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat {\tau }_0>t\}})|\le L^{\ast } (1-1_{\{\hat {\tau }_0>t\}})$. Thus, we have
 \begin{align} \lim_{t \to 0^{+}}\left|\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat{\tau}_0>t\}}) ]}{t}\right| & \leq L^{{\ast}} \lim_{t \to 0^{+}} \frac{E[1-1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & = L^{{\ast}} \lim_{t \to 0^{+}} \frac{\Pr\{\hat{\tau}_0 \leq t\}}{t}\nonumber\\ & = L^{{\ast}} \lim_{t \to 0^{+}} \frac{\Pr\{\inf_{0 \leq s \leq t} (cs+\sigma B(s))\leq{-}u\}}{t}\nonumber\\ & = 0, \end{align}
\begin{align} \lim_{t \to 0^{+}}\left|\frac{E[\phi_{w,\delta_{123},n,m}(u+ct+\sigma B(t)) (1-1_{\{\hat{\tau}_0>t\}}) ]}{t}\right| & \leq L^{{\ast}} \lim_{t \to 0^{+}} \frac{E[1-1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & = L^{{\ast}} \lim_{t \to 0^{+}} \frac{\Pr\{\hat{\tau}_0 \leq t\}}{t}\nonumber\\ & = L^{{\ast}} \lim_{t \to 0^{+}} \frac{\Pr\{\inf_{0 \leq s \leq t} (cs+\sigma B(s))\leq{-}u\}}{t}\nonumber\\ & = 0, \end{align}where the last step follows from the last equality on p. 147 of Jeanblanc et al. [Reference Jeanblanc, Yor and Chesney24] concerning an explicit expression for ![]() $\Pr \{\inf _{0 \leq s \leq t} (cs+\sigma B(s))\leq -u\}$. The above implies
$\Pr \{\inf _{0 \leq s \leq t} (cs+\sigma B(s))\leq -u\}$. The above implies
It requires much more efforts to determine the third limit in (2.21). Since ![]() $B_{\delta _2}(t)=\int _0^{t} e^{-\delta _2s}\,dB(s)$, it is immediate that
$B_{\delta _2}(t)=\int _0^{t} e^{-\delta _2s}\,dB(s)$, it is immediate that ![]() $dB_{\delta _2}(s)=e^{-\delta _2 s}\,dB(s)$ and hence
$dB_{\delta _2}(s)=e^{-\delta _2 s}\,dB(s)$ and hence ![]() $dB_{\delta _2}(s)\,dB_{\delta _2}(s)=e^{-2\delta _2 s}\,ds$. For
$dB_{\delta _2}(s)\,dB_{\delta _2}(s)=e^{-2\delta _2 s}\,ds$. For ![]() $i \geq 2$, use of Itô's lemma gives rise to
$i \geq 2$, use of Itô's lemma gives rise to
 \begin{align*} dB_{\delta_2}^{i}(s)& =i B_{\delta_2}^{i-1}(s)\,dB_{\delta_2}(s)+\tfrac{1}{2}i(i-1)B_{\delta_2}^{i-2}(s)\,dB_{\delta_2}(s)\,dB_{\delta_2}(s)\\ & =ie^{-\delta_2 s} B_{\delta_2}^{i-1}(s)\,dB(s)+\tfrac{1}{2}i(i-1)e^{{-}2\delta_2 s}B_{\delta_2}^{i-2}(s)\,ds. \end{align*}
\begin{align*} dB_{\delta_2}^{i}(s)& =i B_{\delta_2}^{i-1}(s)\,dB_{\delta_2}(s)+\tfrac{1}{2}i(i-1)B_{\delta_2}^{i-2}(s)\,dB_{\delta_2}(s)\,dB_{\delta_2}(s)\\ & =ie^{-\delta_2 s} B_{\delta_2}^{i-1}(s)\,dB(s)+\tfrac{1}{2}i(i-1)e^{{-}2\delta_2 s}B_{\delta_2}^{i-2}(s)\,ds. \end{align*} Applying Itô's lemma to the term ![]() $\phi _{w,\delta _{123},n-i,m}(u+cs+\sigma B(s))$ on the set
$\phi _{w,\delta _{123},n-i,m}(u+cs+\sigma B(s))$ on the set ![]() $\{\hat {\tau }_0>t\}$ (because of twice continuous differentiability of
$\{\hat {\tau }_0>t\}$ (because of twice continuous differentiability of ![]() $\phi _{w,\delta _{123},n-i,m}(\cdot )$ on
$\phi _{w,\delta _{123},n-i,m}(\cdot )$ on ![]() $[0,\infty )$ as in Assumption 1 and the fact that
$[0,\infty )$ as in Assumption 1 and the fact that ![]() $\inf _{0 \leq s \leq t}(u+cs+\sigma B(s))>0$ on
$\inf _{0 \leq s \leq t}(u+cs+\sigma B(s))>0$ on ![]() $\{\hat {\tau }_0>t\}$) yields
$\{\hat {\tau }_0>t\}$) yields
 \begin{align*} & d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\\ & \quad =\left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds\\ & \qquad +\sigma \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s). \end{align*}
\begin{align*} & d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\\ & \quad =\left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds\\ & \qquad +\sigma \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s). \end{align*} With these two results, for ![]() $i=1,2,\ldots,n$ we have by Itô's product rule that
$i=1,2,\ldots,n$ we have by Itô's product rule that
 \begin{align*} & d\left(B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\right)\\ & \quad =B_{\delta_2}^{i}(s)\,d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) +\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\,dB_{\delta_2}^{i}(s) \\ & \qquad +d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\,dB_{\delta_2}^{i}(s)\\ & \quad = B_{\delta_2}^{i}(s) \left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds \\ & \qquad + \sigma B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s)\\ & \qquad +\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) \left(ie^{-\delta_2 s} B_{\delta_2}^{i-1}(s)\,dB(s)+\frac{1}{2}i(i-1)1_{\{i \geq 2\}}e^{{-}2\delta_2 s}B_{\delta_2}^{i-2}(s)\,ds\right)\\ & \qquad +i \sigma e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\,ds. \end{align*}
\begin{align*} & d\left(B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\right)\\ & \quad =B_{\delta_2}^{i}(s)\,d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) +\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\,dB_{\delta_2}^{i}(s) \\ & \qquad +d\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))\,dB_{\delta_2}^{i}(s)\\ & \quad = B_{\delta_2}^{i}(s) \left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds \\ & \qquad + \sigma B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s)\\ & \qquad +\phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) \left(ie^{-\delta_2 s} B_{\delta_2}^{i-1}(s)\,dB(s)+\frac{1}{2}i(i-1)1_{\{i \geq 2\}}e^{{-}2\delta_2 s}B_{\delta_2}^{i-2}(s)\,ds\right)\\ & \qquad +i \sigma e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\,ds. \end{align*} By rewriting this in integral form, multiplying by ![]() $1_{\{\hat {\tau }_0>t\}}$ and taking expectation, we obtain
$1_{\{\hat {\tau }_0>t\}}$ and taking expectation, we obtain
 \begin{align} & E[B_{\delta_2}^{i}(t) \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]\nonumber\\ & \quad =E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\right.\right.\nonumber\\ & \qquad \left.\left.+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds\right]\nonumber\\ & \qquad +\sigma E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\nonumber\\ & \qquad +iE\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \,dB(s) \right]\nonumber\\ & \qquad +\frac{1}{2}i(i-1)1_{\{i \geq 2\}} E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))e^{{-}2\delta_2s}B_{\delta_2}^{i-2}(s)\,ds\right]\nonumber\\ & \qquad +i \sigma E\left[1_{\{\hat{\tau}_0>t\}} \int_0^{t} e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\,ds\right]. \end{align}
\begin{align} & E[B_{\delta_2}^{i}(t) \phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]\nonumber\\ & \quad =E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \left(c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\right.\right.\nonumber\\ & \qquad \left.\left.+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s))\right)\,ds\right]\nonumber\\ & \qquad +\sigma E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\nonumber\\ & \qquad +iE\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s)) e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \,dB(s) \right]\nonumber\\ & \qquad +\frac{1}{2}i(i-1)1_{\{i \geq 2\}} E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-i,m}(u+cs+\sigma B(s))e^{{-}2\delta_2s}B_{\delta_2}^{i-2}(s)\,ds\right]\nonumber\\ & \qquad +i \sigma E\left[1_{\{\hat{\tau}_0>t\}} \int_0^{t} e^{-\delta_2 s} B_{\delta_2}^{i-1}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))\,ds\right]. \end{align} As we will be dividing the above expression by ![]() $t$ and letting
$t$ and letting ![]() $t \to 0^{+}$ according to (2.21), we first deal with the first expectation on the right-hand side. Noting that
$t \to 0^{+}$ according to (2.21), we first deal with the first expectation on the right-hand side. Noting that ![]() $\phi _{w,\delta _{123},n-i,m}'(\cdot )$ and
$\phi _{w,\delta _{123},n-i,m}'(\cdot )$ and ![]() $\phi _{w,\delta _{123},n-i,m}''(\cdot )$ are bounded according to Assumption 2 and the moments of
$\phi _{w,\delta _{123},n-i,m}''(\cdot )$ are bounded according to Assumption 2 and the moments of ![]() $|B_{\delta _2}(s)|$ (and hence,
$|B_{\delta _2}(s)|$ (and hence, ![]() $\int _0^{t} E[|B_{\delta _2}^{i}(s)|]\,ds$) are finite, we apply Fubini's theorem to arrive at
$\int _0^{t} E[|B_{\delta _2}^{i}(s)|]\,ds$) are finite, we apply Fubini's theorem to arrive at
 \begin{align*} & \lim_{t \to 0^{+}} \left|\frac{E[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) (c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s)))\,ds ]}{t}\right|\\ & \quad \leq \lim_{t \to 0^{+}} \frac{\int_0^{t} E[|B_{\delta_2}^{i}(s) (c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s)))|]\,ds}{t}\\ & \quad =\lim_{t \to 0^{+}} E\left[\left|B_{\delta_2}^{i}(t) \left(c\phi_{w,\delta_{123},n-i,m}'(u+ct+\sigma B(t))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+ct+\sigma B(t))\right)\right|\right]\\ & \quad=0. \end{align*}
\begin{align*} & \lim_{t \to 0^{+}} \left|\frac{E[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) (c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s)))\,ds ]}{t}\right|\\ & \quad \leq \lim_{t \to 0^{+}} \frac{\int_0^{t} E[|B_{\delta_2}^{i}(s) (c\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+cs+\sigma B(s)))|]\,ds}{t}\\ & \quad =\lim_{t \to 0^{+}} E\left[\left|B_{\delta_2}^{i}(t) \left(c\phi_{w,\delta_{123},n-i,m}'(u+ct+\sigma B(t))+\frac{\sigma^{2}}{2}\phi_{w,\delta_{123},n-i,m}''(u+ct+\sigma B(t))\right)\right|\right]\\ & \quad=0. \end{align*} Note that we have also used generalized dominated convergence theorem (similar to the proof of (2.18)) and the fact that ![]() $B_{\delta _2}^{i}(0)=0$ (as
$B_{\delta _2}^{i}(0)=0$ (as ![]() $i$ starts from 1). The inequality above implies
$i$ starts from 1). The inequality above implies
Similarly, for the fourth expectation in (2.25), one has for ![]() $i>2$ that
$i>2$ that
with the understanding that ![]() $\phi _{w,\delta _{123},n-i,m}(\cdot )\equiv 0$ for
$\phi _{w,\delta _{123},n-i,m}(\cdot )\equiv 0$ for ![]() $i>n$. Next, we shall find the above limit but for
$i>n$. Next, we shall find the above limit but for ![]() $i=2$ and begin by writing
$i=2$ and begin by writing
 \begin{align*} & \lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\\ & \quad = \lim_{t \to 0^{+}} \frac{E[\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\\ & \qquad -\lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t} \\ & \quad =\phi_{w,\delta_{123},n-2,m}(u)-\lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}, \end{align*}
\begin{align*} & \lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0>t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\\ & \quad = \lim_{t \to 0^{+}} \frac{E[\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\\ & \qquad -\lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t} \\ & \quad =\phi_{w,\delta_{123},n-2,m}(u)-\lim_{t \to 0^{+}} \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}, \end{align*}where the last equality follows from Fubini's theorem, L'Hôpital's rule and dominated convergence theorem. The limiting term in the last line is indeed equal to zero, which can be shown by noting that the boundedness of ![]() $\phi _{w,\delta _{123},n-2,m}(\cdot )$ in Assumption 2 implies there exists
$\phi _{w,\delta _{123},n-2,m}(\cdot )$ in Assumption 2 implies there exists ![]() $L^{**}>0$ such that
$L^{**}>0$ such that
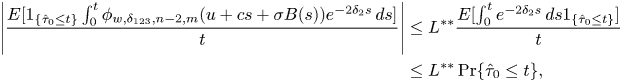 \begin{align*} \left| \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\right| & \leq L^{**} \frac{E[\int_0^{t} e^{{-}2\delta_2 s}\,ds1_{\{\hat{\tau}_0\leq t\}}]}{t}\\ & \le L^{**}\Pr\{\hat{\tau}_0\leq t\}, \end{align*}
\begin{align*} \left| \frac{E[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} \phi_{w,\delta_{123},n-2,m}(u+cs+\sigma B(s))e^{{-}2\delta_2 s}\,ds]}{t}\right| & \leq L^{**} \frac{E[\int_0^{t} e^{{-}2\delta_2 s}\,ds1_{\{\hat{\tau}_0\leq t\}}]}{t}\\ & \le L^{**}\Pr\{\hat{\tau}_0\leq t\}, \end{align*}and taking limit as ![]() $t \to 0^{+}$ yields zero following the steps in (2.23). Combining this case of
$t \to 0^{+}$ yields zero following the steps in (2.23). Combining this case of ![]() $i=2$ with (2.27) for the case
$i=2$ with (2.27) for the case ![]() $i>2$ results in
$i>2$ results in
Similarly, for the fifth expectation in (2.25), we get
Next, the second expectation in (2.25) involving a stochastic integral can be expressed as
 \begin{align*} & E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right ]\\ & \quad = E\left[\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\\ & \qquad -E\left[(1-1_{\{\hat{\tau}_0>t\}})\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\\ & \quad ={-}E\left[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]. \end{align*}
\begin{align*} & E\left[1_{\{\hat{\tau}_0>t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right ]\\ & \quad = E\left[\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\\ & \qquad -E\left[(1-1_{\{\hat{\tau}_0>t\}})\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]\\ & \quad ={-}E\left[1_{\{\hat{\tau}_0\leq t\}}\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) \right]. \end{align*}With the help of the Hölder's inequality, it is found that
 \begin{align} & \left| \frac{E[1_{\{\hat{\tau}_0\leq t\}} \int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) ]}{t} \right| \nonumber\\ & \quad \leq \frac{E[1_{\{\hat{\tau}_0\leq t\}} |\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s)| ]}{t} \nonumber\\ & \quad \leq \frac{\sqrt{\Pr\{\hat{\tau}_0\leq t\}}\sqrt{E[ (\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s))^{2} ]} }{t} \nonumber\\ & \quad =\frac{\sqrt{\Pr\{\hat{\tau}_0\leq t\}}\sqrt{E[ \int_0^{t} B_{\delta_2}^{2i}(s) (\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)))^{2} \,ds ]} }{t} \nonumber\\ & \quad \leq L^{***} \sqrt{\frac{\Pr\{\hat{\tau}_0\leq t\}}{t}} \sqrt{\frac{E[ \int_0^{t} B_{\delta_2}^{2i}(s)\,ds ]}{t}}, \end{align}
\begin{align} & \left| \frac{E[1_{\{\hat{\tau}_0\leq t\}} \int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s) ]}{t} \right| \nonumber\\ & \quad \leq \frac{E[1_{\{\hat{\tau}_0\leq t\}} |\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s)| ]}{t} \nonumber\\ & \quad \leq \frac{\sqrt{\Pr\{\hat{\tau}_0\leq t\}}\sqrt{E[ (\int_0^{t} B_{\delta_2}^{i}(s) \phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)) \,dB(s))^{2} ]} }{t} \nonumber\\ & \quad =\frac{\sqrt{\Pr\{\hat{\tau}_0\leq t\}}\sqrt{E[ \int_0^{t} B_{\delta_2}^{2i}(s) (\phi_{w,\delta_{123},n-i,m}'(u+cs+\sigma B(s)))^{2} \,ds ]} }{t} \nonumber\\ & \quad \leq L^{***} \sqrt{\frac{\Pr\{\hat{\tau}_0\leq t\}}{t}} \sqrt{\frac{E[ \int_0^{t} B_{\delta_2}^{2i}(s)\,ds ]}{t}}, \end{align}for some ![]() $L^{***}>0$ because of the boundedness of
$L^{***}>0$ because of the boundedness of ![]() $\phi _{w,\delta _{123},n-i,m}(\cdot )$ in Assumption 2. Using Fubini's theorem followed by L'Hôpital's rule, we have
$\phi _{w,\delta _{123},n-i,m}(\cdot )$ in Assumption 2. Using Fubini's theorem followed by L'Hôpital's rule, we have
where the last equality follows from (2.12) as ![]() $i$ starts from 1 regarding the third limit in (2.21). Since it is known from the steps leading to (2.23) that
$i$ starts from 1 regarding the third limit in (2.21). Since it is known from the steps leading to (2.23) that ![]() $\lim _{t \to 0^{+}}\Pr \{\hat {\tau }_0\leq t\}/t =0$, one asserts from (2.30) that the second expectation in (2.25) satisfies
$\lim _{t \to 0^{+}}\Pr \{\hat {\tau }_0\leq t\}/t =0$, one asserts from (2.30) that the second expectation in (2.25) satisfies
Similarly, the same arguments can be applied to show the limiting result
concerning the third expectation in (2.25). Utilizing the five limiting results (2.26), (2.28), (2.29), (2.31), and (2.32) together with (2.25), the third limit in (2.21) reduces to
 \begin{align} & \sum_{i=1}^{n} {n \choose i} \lim_{t \to 0^{+}} \frac{E[B_{\delta_2}^{i}(t)\phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & \quad = \sum_{i=1}^{n} {n \choose i} \left(\frac{1}{2}i(i-1)1_{\{i = 2\}} \phi_{w,\delta_{123},n-i,m}(u)+i \sigma 1_{\{i = 1\}}\phi_{w,\delta_{123},n-i,m}'(u)\right)\nonumber\\ & \quad =\frac{n(n-1)}{2}\phi_{w,\delta_{123},n-2,m}(u)1_{\{n \geq 2\}}+n\sigma \phi_{w,\delta_{123},n-1,m}'(u)1_{\{n \geq 1\}}. \end{align}
\begin{align} & \sum_{i=1}^{n} {n \choose i} \lim_{t \to 0^{+}} \frac{E[B_{\delta_2}^{i}(t)\phi_{w,\delta_{123},n-i,m}(u+ct+\sigma B(t))1_{\{\hat{\tau}_0>t\}}]}{t}\nonumber\\ & \quad = \sum_{i=1}^{n} {n \choose i} \left(\frac{1}{2}i(i-1)1_{\{i = 2\}} \phi_{w,\delta_{123},n-i,m}(u)+i \sigma 1_{\{i = 1\}}\phi_{w,\delta_{123},n-i,m}'(u)\right)\nonumber\\ & \quad =\frac{n(n-1)}{2}\phi_{w,\delta_{123},n-2,m}(u)1_{\{n \geq 2\}}+n\sigma \phi_{w,\delta_{123},n-1,m}'(u)1_{\{n \geq 1\}}. \end{align} Then, upon substitution of (2.22), (2.24), and (2.33) into (2.21), we obtain the integro-differential equation (2.2) satisfied by ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$, where
$\phi _{w,\delta _{123},n,m}(\cdot )$, where ![]() $A_{w,n,m}(\cdot )$ is given in (2.4).
$A_{w,n,m}(\cdot )$ is given in (2.4).
The proof that ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ satisfies the integro-differential equation (2.3) with
$\phi _{d,\delta _{123},n,m}(\cdot )$ satisfies the integro-differential equation (2.3) with ![]() $A_{d,n,m}(\cdot )$ defined in (2.5) can be proved in a similar manner, and we focus on highlighting the key steps and discussing the similarities and differences compared to the proof for
$A_{d,n,m}(\cdot )$ defined in (2.5) can be proved in a similar manner, and we focus on highlighting the key steps and discussing the similarities and differences compared to the proof for ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$. Similar to (2.6), by conditioning on the time of the first claim we have
$\phi _{w,\delta _{123},n,m}(\cdot )$. Similar to (2.6), by conditioning on the time of the first claim we have
 \begin{align} \phi_{d,\delta_{123},n,m}(u) & =e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0\leq t\}} \,|\, T_1>t]\nonumber\\ & \quad +e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0\leq s\}} \,|\, T_1=s]\,ds\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\,ds\nonumber\\ & =e^{-\lambda t} 1_{\{m=0\}} E[ e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0)1_{\{\hat{\tau}_0\leq t\}} ]\nonumber\\ & \quad +e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq s\}} ]\,ds\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\,ds, \end{align}
\begin{align} \phi_{d,\delta_{123},n,m}(u) & =e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0\leq t\}} \,|\, T_1>t]\nonumber\\ & \quad +e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0\leq s\}} \,|\, T_1=s]\,ds\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\,ds\nonumber\\ & =e^{-\lambda t} 1_{\{m=0\}} E[ e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0)1_{\{\hat{\tau}_0\leq t\}} ]\nonumber\\ & \quad +e^{-\lambda t} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq s\}} ]\,ds\nonumber\\ & \quad +\int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\,ds, \end{align}where the independence between ![]() $\hat {\tau }_0$ and
$\hat {\tau }_0$ and ![]() $T_1$ has been used. Because sample paths for which ruin occurs (by oscillation) before the first claim contribute to
$T_1$ has been used. Because sample paths for which ruin occurs (by oscillation) before the first claim contribute to ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ but not
$\phi _{d,\delta _{123},n,m}(\cdot )$ but not ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$, the first and the third terms above are new compared to (2.6). As we will divide (2.34) by
$\phi _{w,\delta _{123},n,m}(\cdot )$, the first and the third terms above are new compared to (2.6). As we will divide (2.34) by ![]() $t$ and let
$t$ and let ![]() $t \to 0^{+}$, in light of the first term we apply the Hölder's inequality and consider
$t \to 0^{+}$, in light of the first term we apply the Hölder's inequality and consider
 \begin{equation} \left|\frac{E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0)1_{\{\hat{\tau}_0\leq t\}}]}{t}\right| \leq \frac{E[(|B_{\delta_2}^{n} (\hat{\tau}_0)| 1_{\{\hat{\tau}_0\leq t\}})1_{\{\hat{\tau}_0\leq t\}}]}{t} \leq \sqrt{E[B_{\delta_2}^{2n} ({\tau}_0)1_{\{\hat{\tau}_0\leq t\}}]} \sqrt{\frac{ \Pr\{\hat{\tau}_0\leq t\}}{t^{2}}}. \end{equation}
\begin{equation} \left|\frac{E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0)1_{\{\hat{\tau}_0\leq t\}}]}{t}\right| \leq \frac{E[(|B_{\delta_2}^{n} (\hat{\tau}_0)| 1_{\{\hat{\tau}_0\leq t\}})1_{\{\hat{\tau}_0\leq t\}}]}{t} \leq \sqrt{E[B_{\delta_2}^{2n} ({\tau}_0)1_{\{\hat{\tau}_0\leq t\}}]} \sqrt{\frac{ \Pr\{\hat{\tau}_0\leq t\}}{t^{2}}}. \end{equation} We would like to show that the limit of the final expression as ![]() $t \to 0^{+}$ equals zero. To this end, the exact formula for
$t \to 0^{+}$ equals zero. To this end, the exact formula for ![]() $\Pr \{\hat {\tau }_0\leq t\}$ on p. 147 of Jeanblanc et al. [Reference Jeanblanc, Yor and Chesney24] can be used to show that
$\Pr \{\hat {\tau }_0\leq t\}$ on p. 147 of Jeanblanc et al. [Reference Jeanblanc, Yor and Chesney24] can be used to show that ![]() $\lim _{t \to 0^{+}}\Pr \{\hat {\tau }_0\leq t\}/t^{2} = 0$. It remains to show that
$\lim _{t \to 0^{+}}\Pr \{\hat {\tau }_0\leq t\}/t^{2} = 0$. It remains to show that ![]() $\lim _{t \to 0^{+}} E[B_{\delta _2}^{2n} (\hat {\tau }_0)1_{\{\hat {\tau }_0\leq t\}}]$ is finite. The case
$\lim _{t \to 0^{+}} E[B_{\delta _2}^{2n} (\hat {\tau }_0)1_{\{\hat {\tau }_0\leq t\}}]$ is finite. The case ![]() $n=0$ is trivial because this equals
$n=0$ is trivial because this equals ![]() $\lim _{t \to 0^{+}} \Pr \{\hat {\tau }_0\leq t\}=0$, and therefore, we consider
$\lim _{t \to 0^{+}} \Pr \{\hat {\tau }_0\leq t\}=0$, and therefore, we consider ![]() $n\ge 1$. It is first noted that
$n\ge 1$. It is first noted that
Since ![]() $\{B_{\delta _2}(s)\}_{s \ge 0}$ is a martingale, by Doob's martingale inequality and (2.12) one has
$\{B_{\delta _2}(s)\}_{s \ge 0}$ is a martingale, by Doob's martingale inequality and (2.12) one has
 $$E\left[\left(\sup_{0 \leq s \leq t} |B_{\delta_2}(s)|\right)^{2n}\right] \leq \left(\frac{2n}{2n-1}\right)^{2n}E[|B_{\delta_2}(s)|^{2n}] = \left(\frac{2n}{2n-1}\right)^{2n} L^{*}_{2n} \left(\int_0^{t} e^{{-}2\delta_2 y}\,dy\right)^{n},$$
$$E\left[\left(\sup_{0 \leq s \leq t} |B_{\delta_2}(s)|\right)^{2n}\right] \leq \left(\frac{2n}{2n-1}\right)^{2n}E[|B_{\delta_2}(s)|^{2n}] = \left(\frac{2n}{2n-1}\right)^{2n} L^{*}_{2n} \left(\int_0^{t} e^{{-}2\delta_2 y}\,dy\right)^{n},$$which tends to zero as ![]() $t \to 0^{+}$. Therefore, taking expectation in (2.36) followed by letting
$t \to 0^{+}$. Therefore, taking expectation in (2.36) followed by letting ![]() $t \to 0^{+}$, we get
$t \to 0^{+}$, we get
With the above results, getting back to ![]() $n\in \mathbb {N}$ one confirms from (2.35) that
$n\in \mathbb {N}$ one confirms from (2.35) that
Concerning the third term in (2.34), we have
 \begin{align} & \lim_{t \to 0^{+}}\frac{\int_0^{t} \lambda e^{-\lambda s} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq s\}} ]\,ds}{t} \nonumber\\ & \quad = \lim_{t \to 0^{+}}\lambda e^{-\lambda t} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq t\}} ] =0, \end{align}
\begin{align} & \lim_{t \to 0^{+}}\frac{\int_0^{t} \lambda e^{-\lambda s} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq s\}} ]\,ds}{t} \nonumber\\ & \quad = \lim_{t \to 0^{+}}\lambda e^{-\lambda t} 1_{\{m=0\}} E[e^{-\delta_1 \hat{\tau}_0}B_{\delta_2}^{n} (\hat{\tau}_0) 1_{\{\hat{\tau}_0\leq t\}} ] =0, \end{align}where the last equality follows because ![]() $E[e^{-\delta _1 \hat {\tau }_0}B_{\delta _2}^{n} (\hat {\tau }_0) 1_{\{\hat {\tau }_0\leq t\}}]=o(t)$ according to (2.37).
$E[e^{-\delta _1 \hat {\tau }_0}B_{\delta _2}^{n} (\hat {\tau }_0) 1_{\{\hat {\tau }_0\leq t\}}]=o(t)$ according to (2.37).
The results in (2.37) and (2.38) imply that the contributions of the first and the third terms in (2.34), being ![]() $o(t)$, are negligible. The analysis of the second term in (2.34) is almost identical to that for the first term in (2.6), and analogous to (2.7) one has
$o(t)$, are negligible. The analysis of the second term in (2.34) is almost identical to that for the first term in (2.6), and analogous to (2.7) one has
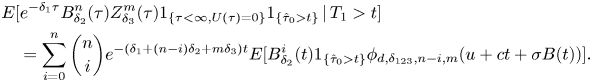 \begin{align*} & E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{d,\delta_{123},n-i,m}(u+ct+\sigma B(t)) ]. \end{align*}
\begin{align*} & E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>t\}} \,|\, T_1>t]\\ & \quad = \sum_{i=0}^{n} {n \choose i} e^{-(\delta_1+(n-i)\delta_2+m\delta_3) t}E[B_{\delta_2}^{i} (t)1_{\{\hat{\tau}_0>t\}} \phi_{d,\delta_{123},n-i,m}(u+ct+\sigma B(t)) ]. \end{align*}For the fourth term in (2.34), it is important to note that the amount of the first claim should not be large enough to cause immediate ruin, and therefore, it is clear that
 \begin{align} & \int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\nonumber\\ & \quad = \int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\, T_1=s]\,ds. \end{align}
\begin{align} & \int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} \,|\, T_1=s]\nonumber\\ & \quad = \int_0^{t} \lambda e^{-\lambda s} E[e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau)1_{\{\tau<\infty,U(\tau)=0\}} 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\,|\, T_1=s]\,ds. \end{align}Similar to (2.9), the expectation in the above integrand is
 \begin{align*} & E\left[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau) 1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s\right]\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{d,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) ]. \end{align*}
\begin{align*} & E\left[ e^{-\delta_1 \tau}B_{\delta_2}^{n} (\tau)Z_{\delta_3}^{m}(\tau) 1_{\{\tau<\infty,U(\tau)=0\}}1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}} \,|\, T_1=s\right]\\ & \quad = \sum_{i=0}^{n} \sum_{j=0}^{m} {n \choose i} {m \choose j} e^{-(\delta_1+i\delta_2+m\delta_3 )s} E[B_{\delta_2}^{n-i} (s)f^{m-j}(Y_1) 1_{\{\hat{\tau}_0>s\}} 1_{\{Y_1\le u+cs+\sigma B(s) \}}\nonumber\\ & \qquad \times \phi_{d,\delta_{123},i,j}(u+cs+\sigma B(s)-Y_1) ]. \end{align*} The rest of the proof is essentially the same as the proof for ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$. It is worthwhile to mention that, compared to (2.8), the term involving
$\phi _{w,\delta _{123},n,m}(\cdot )$. It is worthwhile to mention that, compared to (2.8), the term involving ![]() $1_{\{Y_1> u+cs+\sigma B(s) \}}$ no longer appears in (2.39). Consequently,
$1_{\{Y_1> u+cs+\sigma B(s) \}}$ no longer appears in (2.39). Consequently, ![]() $A_{w,n,m}(u)$ in (2.4) and
$A_{w,n,m}(u)$ in (2.4) and ![]() $A_{d,n,m}(u)$ in (2.5) are almost identical except that
$A_{d,n,m}(u)$ in (2.5) are almost identical except that ![]() $A_{d,n,m}(u)$ does not contain the term involving the penalty function which is for ruin due to a claim.
$A_{d,n,m}(u)$ does not contain the term involving the penalty function which is for ruin due to a claim.
Note that, since ruin occurs immediately by diffusion with ![]() $B_{\delta _2}(\tau )=Z_{\delta _3}(\tau )=0$ when the initial surplus is zero, the trivial boundary conditions at zero are given by
$B_{\delta _2}(\tau )=Z_{\delta _3}(\tau )=0$ when the initial surplus is zero, the trivial boundary conditions at zero are given by
2.2. Defective renewal equations
With the boundary conditions (2.40)–(2.42), the integro-differential equations (2.2) and (2.3) can be transformed to defective renewal equations. These are stated in the following theorem.
Theorem 2 (Defective renewal equations for  $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and  $\phi _{d,\delta _{123},n,m}(\cdot )$)
$\phi _{d,\delta _{123},n,m}(\cdot )$)
Under Assumptions 1–3 and Conditions 1–2, ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ satisfies the recursive defective renewal equation
$\phi _{w,\delta _{123},n,m}(\cdot )$ satisfies the recursive defective renewal equation
for ![]() $n,m\in \mathbb {N}$, whereas
$n,m\in \mathbb {N}$, whereas ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ satisfies the recursive defective renewal equation
$\phi _{d,\delta _{123},n,m}(\cdot )$ satisfies the recursive defective renewal equation
for ![]() $n\in \mathbb {N}^{+}$ or
$n\in \mathbb {N}^{+}$ or ![]() $m\in \mathbb {N}^{+}$, with the starting point
$m\in \mathbb {N}^{+}$, with the starting point
In the above equations,
is a defective density such that
 \begin{equation} \int_0^{\infty} g_{n,m}(y)\,dy =\begin{cases} \dfrac{1}{1+\theta}<1, & \delta_1 +n\delta_2+m\delta_3=0,\\[6pt] \dfrac{\frac{\sigma^{2}}{2}\rho_{n,m}^{2}+c\rho_{n,m}-(\delta_1+n\delta_2+m\delta_3)}{\frac{\sigma^{2}}{2}\rho_{n,m}^{2}+c\rho_{n,m}}<1, & \delta_1 +n\delta_2+m\delta_3>0, \end{cases} \end{equation}
\begin{equation} \int_0^{\infty} g_{n,m}(y)\,dy =\begin{cases} \dfrac{1}{1+\theta}<1, & \delta_1 +n\delta_2+m\delta_3=0,\\[6pt] \dfrac{\frac{\sigma^{2}}{2}\rho_{n,m}^{2}+c\rho_{n,m}-(\delta_1+n\delta_2+m\delta_3)}{\frac{\sigma^{2}}{2}\rho_{n,m}^{2}+c\rho_{n,m}}<1, & \delta_1 +n\delta_2+m\delta_3>0, \end{cases} \end{equation}while
and
depend on the lower-order Gerber-Shiu functions via ![]() $A_{w,n,m}(\cdot )$ and
$A_{w,n,m}(\cdot )$ and ![]() $A_{d,n,m}(\cdot )$ defined in (2.4) and (2.5), respectively, with
$A_{d,n,m}(\cdot )$ defined in (2.4) and (2.5), respectively, with ![]() $b_{n,m}=2c/\sigma ^{2}+\rho _{n,m}$ being a constant.
$b_{n,m}=2c/\sigma ^{2}+\rho _{n,m}$ being a constant.
Proof. Here, we provide the necessary arguments in connection to the existing literature to see why the results are valid. First, we note that the integro-differential equation (2.2) is structurally identical to the one in Tsai and Willmot [Reference Tsai and Willmot34, Sect. 2]. Along with the boundary condition (2.40) and Assumption 3, one can readily follow the proof of their Theorem 1 to arrive at the defective renewal equation (2.43) for ![]() $n,m\in \mathbb {N}$. Due to the resemblance of (2.3) and (2.42) to (2.2) and (2.40), the defective renewal equation (2.44) also follows for
$n,m\in \mathbb {N}$. Due to the resemblance of (2.3) and (2.42) to (2.2) and (2.40), the defective renewal equation (2.44) also follows for ![]() $n\in \mathbb {N}^{+}$ or
$n\in \mathbb {N}^{+}$ or ![]() $m\in \mathbb {N}^{+}$. When
$m\in \mathbb {N}^{+}$. When ![]() $n=m=0$, the defective renewal equation for
$n=m=0$, the defective renewal equation for ![]() $\phi _{d,\delta _{123},0,0}(\cdot )$ is different from (2.44) because (2.3) is a homogeneous integro-differential equation in this case (as
$\phi _{d,\delta _{123},0,0}(\cdot )$ is different from (2.44) because (2.3) is a homogeneous integro-differential equation in this case (as ![]() $A_{d,0,0}(u)=0$ according to (2.5)) and the boundary condition (2.41) is different from (2.42). Indeed,
$A_{d,0,0}(u)=0$ according to (2.5)) and the boundary condition (2.41) is different from (2.42). Indeed, ![]() $\phi _{d,\delta _{123},0,0}(u)$ is the Laplace transform of the ruin time due to diffusion and (2.45) was given by Gerber and Landry [Reference Gerber and Landry22, Eq. (17)]. The defectiveness of the density (2.46) stated in (2.47) follows from, for example, Dufresne and Gerber [Reference Dufresne and Gerber17, Eq. (2.9)] and Gerber and Landry [Reference Gerber and Landry22, Eq. (16)]. Finally, we remark that general solutions to defective renewal equations are standard can be found in, for example, Resnick [Reference Resnick31, Sect. 3.5], and are thus omitted here for brevity.
$\phi _{d,\delta _{123},0,0}(u)$ is the Laplace transform of the ruin time due to diffusion and (2.45) was given by Gerber and Landry [Reference Gerber and Landry22, Eq. (17)]. The defectiveness of the density (2.46) stated in (2.47) follows from, for example, Dufresne and Gerber [Reference Dufresne and Gerber17, Eq. (2.9)] and Gerber and Landry [Reference Gerber and Landry22, Eq. (16)]. Finally, we remark that general solutions to defective renewal equations are standard can be found in, for example, Resnick [Reference Resnick31, Sect. 3.5], and are thus omitted here for brevity.
3. Claim amounts distributed as combination of exponentials
Although general solutions for ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ are in principle obtainable recursively as solutions to defective renewal equations, these involve integrals and convolution terms which can be challenging to compute. To obtain explicit expressions that are computationally more attractive, in this section it is assumed that the claim amounts are distributed as a combination of exponentials with density
$\phi _{d,\delta _{123},n,m}(u)$ are in principle obtainable recursively as solutions to defective renewal equations, these involve integrals and convolution terms which can be challenging to compute. To obtain explicit expressions that are computationally more attractive, in this section it is assumed that the claim amounts are distributed as a combination of exponentials with density
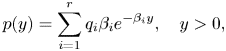 \begin{equation} p(y)=\sum_{i=1}^{r} q_i \beta_i e^{-\beta_i y}, \quad y > 0, \end{equation}
\begin{equation} p(y)=\sum_{i=1}^{r} q_i \beta_i e^{-\beta_i y}, \quad y > 0, \end{equation}where ![]() $\beta _i$'s are distinct positive parameters, and
$\beta _i$'s are distinct positive parameters, and ![]() $q_i$'s are nonzero such that
$q_i$'s are nonzero such that ![]() $\sum _{i=1}^{r} q_i=1$ and
$\sum _{i=1}^{r} q_i=1$ and ![]() $p(y) \geq 0$ for all
$p(y) \geq 0$ for all ![]() $y>0$. It is well known that the class of combinations of exponentials is dense in the set of distributions on
$y>0$. It is well known that the class of combinations of exponentials is dense in the set of distributions on ![]() $[0,\infty )$ (see, e.g., [Reference Dufresne16]). Motivated by Cheung et al. [Reference Cheung, Liu and Woo13] and Cheung and Woo [Reference Cheung and Woo11], among others, we let the cost function be
$[0,\infty )$ (see, e.g., [Reference Dufresne16]). Motivated by Cheung et al. [Reference Cheung, Liu and Woo13] and Cheung and Woo [Reference Cheung and Woo11], among others, we let the cost function be ![]() $f(x)=x$ so that
$f(x)=x$ so that ![]() $Z_{\delta _3}(\tau )=\sum _{k=1}^{N(\tau )}e^{-\delta _3 T_k}Y_k$ represents the total discounted claims until ruin. Furthermore, the penalty function is assumed to only depend on the deficit such that
$Z_{\delta _3}(\tau )=\sum _{k=1}^{N(\tau )}e^{-\delta _3 T_k}Y_k$ represents the total discounted claims until ruin. Furthermore, the penalty function is assumed to only depend on the deficit such that ![]() $w(x,y)=w(y)$, and the forces of interest used for discounting the Brownian motion and the claim amounts are assumed positive, that is,
$w(x,y)=w(y)$, and the forces of interest used for discounting the Brownian motion and the claim amounts are assumed positive, that is, ![]() $\delta _2$,
$\delta _2$, ![]() $\delta _3>0$.
$\delta _3>0$.
Note that Condition 1, which requires the existence of first ![]() $m$ moments of the claim distribution with the current choice of
$m$ moments of the claim distribution with the current choice of ![]() $f(x)=x$, is automatically satisfied by (3.1). Regarding Condition 2, for
$f(x)=x$, is automatically satisfied by (3.1). Regarding Condition 2, for ![]() $k=0,1,2,\ldots,m$, we would like to ensure the finiteness of the integral
$k=0,1,2,\ldots,m$, we would like to ensure the finiteness of the integral
 \begin{align} \int_u^{\infty} y^{k} w(y-u)p(y)\,dy & =\int_0^{\infty} (u+y)^{k} w(y) \sum_{i=1}^{r} q_i \beta_i e^{-\beta_i(u+y)}\,dy \nonumber\\ & =k! \sum_{i=1}^{r}\sum_{j=0}^{k} q_i\beta_i \mathcal{T}_{\beta_i}^{k-j+1} w(0) \frac{u^{j} e^{-\beta_i u}}{j!}, \end{align}
\begin{align} \int_u^{\infty} y^{k} w(y-u)p(y)\,dy & =\int_0^{\infty} (u+y)^{k} w(y) \sum_{i=1}^{r} q_i \beta_i e^{-\beta_i(u+y)}\,dy \nonumber\\ & =k! \sum_{i=1}^{r}\sum_{j=0}^{k} q_i\beta_i \mathcal{T}_{\beta_i}^{k-j+1} w(0) \frac{u^{j} e^{-\beta_i u}}{j!}, \end{align}where we have applied a binomial expansion and utilized (a special case of) multiple Dickson-Hipp operators (see, e.g., [Reference Dickson and Hipp15,Reference Li and Garrido26]) under the notation
for ![]() $a\in \mathbb {N}^{+}$, complex number
$a\in \mathbb {N}^{+}$, complex number ![]() $s$ with
$s$ with ![]() $\Re (s)\ge 0$ and any integrable function
$\Re (s)\ge 0$ and any integrable function ![]() $b(\cdot )$ on
$b(\cdot )$ on ![]() $(0,\infty )$. Therefore, Condition 2 is satisfied if
$(0,\infty )$. Therefore, Condition 2 is satisfied if ![]() $\mathcal {T}_{\beta _i}^{a} w(0)$ is finite for
$\mathcal {T}_{\beta _i}^{a} w(0)$ is finite for ![]() $i=1,2,\ldots,r$ and
$i=1,2,\ldots,r$ and ![]() $a=1,2,\ldots,m+1$, which clearly depends on the choice the penalty function
$a=1,2,\ldots,m+1$, which clearly depends on the choice the penalty function ![]() $w(\cdot )$. Note that the Laplace transform of
$w(\cdot )$. Note that the Laplace transform of ![]() $b(\cdot )$, namely
$b(\cdot )$, namely ![]() $\tilde {b}(s) = \int _0^{\infty } e^{-sy}b(y)\,dy$, is a special case of the above notion with
$\tilde {b}(s) = \int _0^{\infty } e^{-sy}b(y)\,dy$, is a special case of the above notion with ![]() $\tilde {b}(s) = \mathcal {T}_s^{1}b(0)$.
$\tilde {b}(s) = \mathcal {T}_s^{1}b(0)$.
The starting point of the analysis of ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ relies on finding the form of the solutions (apart from some unknown constants to be determined). Under the distributional assumption (3.1) on the claim amounts, a trick will be to apply the operator
$\phi _{d,\delta _{123},n,m}(u)$ relies on finding the form of the solutions (apart from some unknown constants to be determined). Under the distributional assumption (3.1) on the claim amounts, a trick will be to apply the operator ![]() $\prod _{l=1}^{r}(d/du+\beta _l)$ to the integro-differential equations (2.2) and (2.3) to translate them to ordinary differential equations (see Remark 1). In particular, using the fact that
$\prod _{l=1}^{r}(d/du+\beta _l)$ to the integro-differential equations (2.2) and (2.3) to translate them to ordinary differential equations (see Remark 1). In particular, using the fact that
it can be seen that
 $$\left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]\int_0^{u} \phi_{w,\delta_{123},n,m}(u-y)p(y)\,dy = \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}\left(\frac{d}{du}+\beta_l\right) \right] \phi_{w,\delta_{123},n,m}(u).$$
$$\left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]\int_0^{u} \phi_{w,\delta_{123},n,m}(u-y)p(y)\,dy = \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}\left(\frac{d}{du}+\beta_l\right) \right] \phi_{w,\delta_{123},n,m}(u).$$ Consequently, application of ![]() $\prod _{l=1}^{r}(d/du+\beta _l)$ to both sides of (2.2) leads us to
$\prod _{l=1}^{r}(d/du+\beta _l)$ to both sides of (2.2) leads us to
 \begin{align} & \left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]\left(\frac{\sigma^{2}}{2} \phi_{w,\delta_{123},n,m}''(u)+c\phi_{w,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u) \right)\nonumber\\ & \quad +\lambda \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}\left(\frac{d}{du}+\beta_l\right) \right] \phi_{w,\delta_{123},n,m}(u) ={-}\left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]A_{w,n,m}(u). \end{align}
\begin{align} & \left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]\left(\frac{\sigma^{2}}{2} \phi_{w,\delta_{123},n,m}''(u)+c\phi_{w,\delta_{123},n,m}'(u)-(\lambda+\delta_1 +n\delta_2+m\delta_3)\phi_{w,\delta_{123},n,m}(u) \right)\nonumber\\ & \quad +\lambda \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}\left(\frac{d}{du}+\beta_l\right) \right] \phi_{w,\delta_{123},n,m}(u) ={-}\left[\prod_{l=1}^{r}\left(\frac{d}{du}+\beta_l\right) \right]A_{w,n,m}(u). \end{align} The characteristic equation (in ![]() $\xi$) of the associated homogeneous differential equation is thus
$\xi$) of the associated homogeneous differential equation is thus
 $$\left[\prod_{l=1}^{r}(\xi+\beta_l) \right] \left(\frac{\sigma^{2}}{2} \xi^{2} + c\xi - (\lambda+\delta_1 +n\delta_2+m\delta_3) \right) +\lambda \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}(\xi+\beta_l) \right] = 0,$$
$$\left[\prod_{l=1}^{r}(\xi+\beta_l) \right] \left(\frac{\sigma^{2}}{2} \xi^{2} + c\xi - (\lambda+\delta_1 +n\delta_2+m\delta_3) \right) +\lambda \sum_{i=1}^{r} q_i \beta_i \left[\prod_{l=1,l\ne i}^{r}(\xi+\beta_l) \right] = 0,$$which can be rewritten as
 \begin{equation} \frac{\sigma^{2}}{2}\xi^{2}+c\xi-(\lambda +\delta_1+n\delta_2+m\delta_3)+\lambda \sum_{i=1}^{r} \frac{q_i \beta_i}{\beta_i+\xi}=0. \end{equation}
\begin{equation} \frac{\sigma^{2}}{2}\xi^{2}+c\xi-(\lambda +\delta_1+n\delta_2+m\delta_3)+\lambda \sum_{i=1}^{r} \frac{q_i \beta_i}{\beta_i+\xi}=0. \end{equation} This is, in turn, equivalent to (2.1) (with ![]() $i=n$ and
$i=n$ and ![]() $j=m$) under the assumption (3.1), and therefore it has a unique non-negative root
$j=m$) under the assumption (3.1), and therefore it has a unique non-negative root ![]() $\rho _{n,m}$ and all other roots, namely
$\rho _{n,m}$ and all other roots, namely ![]() $\{-R_{n,m,k}\}_{k=1}^{r+1}$, have negative real parts and are assumed to be distinct. From the theory of differential equations, the general solution of (3.3) consists of linear sum of
$\{-R_{n,m,k}\}_{k=1}^{r+1}$, have negative real parts and are assumed to be distinct. From the theory of differential equations, the general solution of (3.3) consists of linear sum of ![]() $e^{\rho _{n,m}u}$ and
$e^{\rho _{n,m}u}$ and ![]() $\{e^{-R_{n,m,k}u}\}_{k=1}^{r+1}$ plus other terms to be determined in relation to the right-hand side of (3.3). However, the coefficient of
$\{e^{-R_{n,m,k}u}\}_{k=1}^{r+1}$ plus other terms to be determined in relation to the right-hand side of (3.3). However, the coefficient of ![]() $e^{\rho _{n,m}u}$ must equal zero because
$e^{\rho _{n,m}u}$ must equal zero because ![]() $\lim _{u \to \infty }e^{-\rho _{n,m}u}\phi _{w,\delta _{123},n,m}(u)=\lim _{u \to \infty }e^{-\rho _{n,m}u}\phi _{w,\delta _{123},n,m}'(u)=0$ in Assumption 3. The same comments apply to
$\lim _{u \to \infty }e^{-\rho _{n,m}u}\phi _{w,\delta _{123},n,m}(u)=\lim _{u \to \infty }e^{-\rho _{n,m}u}\phi _{w,\delta _{123},n,m}'(u)=0$ in Assumption 3. The same comments apply to ![]() $\phi _{d,\delta _{123},n,m}(u)$ as well. The following lemma provides the general solution of
$\phi _{d,\delta _{123},n,m}(u)$ as well. The following lemma provides the general solution of ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$.
$\phi _{d,\delta _{123},n,m}(u)$.
Lemma 1 (Solution form of  $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and  $\phi _{d,\delta _{123},n,m}(\cdot )$)
$\phi _{d,\delta _{123},n,m}(\cdot )$)
Suppose that the claim amounts have density (3.1), the forces of interest ![]() $\delta _2$ and
$\delta _2$ and ![]() $\delta _3$ are positive, the cost function is
$\delta _3$ are positive, the cost function is ![]() $f(x)=x$, and the penalty function
$f(x)=x$, and the penalty function ![]() $w(x,y)=w(y)$ depends on the deficit only and is such that
$w(x,y)=w(y)$ depends on the deficit only and is such that ![]() $\mathcal {T}_{\beta _i}^{a} w(0)$ is finite for
$\mathcal {T}_{\beta _i}^{a} w(0)$ is finite for ![]() $i=1,2,\ldots,r$ and
$i=1,2,\ldots,r$ and ![]() $a=1,2,\ldots,m+1$. Further assume that, for each fixed pair of
$a=1,2,\ldots,m+1$. Further assume that, for each fixed pair of ![]() $i=0,1,\ldots,n$ and
$i=0,1,\ldots,n$ and ![]() $j=0,1,\ldots,m$, the roots
$j=0,1,\ldots,m$, the roots ![]() $\{-R_{i,j,k}\}_{k=1}^{r+1}$ (those with negative real parts) of (2.1) are distinct. Then, under Assumptions 1–3,
$\{-R_{i,j,k}\}_{k=1}^{r+1}$ (those with negative real parts) of (2.1) are distinct. Then, under Assumptions 1–3, ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ admit the solution form (for
$\phi _{d,\delta _{123},n,m}(u)$ admit the solution form (for ![]() $n,m\in \mathbb {N}$ and
$n,m\in \mathbb {N}$ and ![]() $u\ge 0$)
$u\ge 0$)
 \begin{equation} \phi_{w,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k} e^{{-}R_{i,j,k}u} +\sum_{j=0}^{m-1}\sum_{l=1}^{r} C_{w,n,m,j,l}u^{j} e^{-\beta_l u}, \end{equation}
\begin{equation} \phi_{w,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k} e^{{-}R_{i,j,k}u} +\sum_{j=0}^{m-1}\sum_{l=1}^{r} C_{w,n,m,j,l}u^{j} e^{-\beta_l u}, \end{equation}and
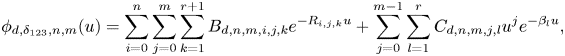 \begin{equation} \phi_{d,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k} e^{{-}R_{i,j,k}u} +\sum_{j=0}^{m-1}\sum_{l=1}^{r} C_{d,n,m,j,l}u^{j} e^{-\beta_l u}, \end{equation}
\begin{equation} \phi_{d,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k} e^{{-}R_{i,j,k}u} +\sum_{j=0}^{m-1}\sum_{l=1}^{r} C_{d,n,m,j,l}u^{j} e^{-\beta_l u}, \end{equation}for some constants ![]() $B_{w,n,m,i,j,k}$'s,
$B_{w,n,m,i,j,k}$'s, ![]() $B_{d,n,m,i,j,k}$'s,
$B_{d,n,m,i,j,k}$'s, ![]() $C_{w,n,m,j,l}$'s, and
$C_{w,n,m,j,l}$'s, and ![]() $C_{d,n,m,j,l}$'s.
$C_{d,n,m,j,l}$'s.
Proof. We only show (3.5) since the proof of (3.6) can be done in an identical manner. The result can be deduced inductively, and the proof can be divided into two steps.
Step 1. We start by considering ![]() $n=m=0$. Indeed, (3.5) was shown to hold true in such simplest case by Liu and Zhang [Reference Liu and Zhang28, Eq. (3.14)] using a different technique. Nevertheless, we can quickly see why (3.5) is valid as follows. Since
$n=m=0$. Indeed, (3.5) was shown to hold true in such simplest case by Liu and Zhang [Reference Liu and Zhang28, Eq. (3.14)] using a different technique. Nevertheless, we can quickly see why (3.5) is valid as follows. Since ![]() $A_{w,0,0}(u)$ in (2.4) is simply proportional to
$A_{w,0,0}(u)$ in (2.4) is simply proportional to ![]() $\int _u^{\infty } w(y-u)p(y)\,dy$ which is given by (3.2) at
$\int _u^{\infty } w(y-u)p(y)\,dy$ which is given by (3.2) at ![]() $k=0$, the right-hand side of (3.3) is zero, and therefore, the general solution of (3.3) is a linear sum of
$k=0$, the right-hand side of (3.3) is zero, and therefore, the general solution of (3.3) is a linear sum of ![]() $\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$.
$\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$.
Step 2(i). The case where ![]() $n,m\in \mathbb {N}$ can be shown to hold true by induction. Instead of considering such most general case, to see how this works we first fix
$n,m\in \mathbb {N}$ can be shown to hold true by induction. Instead of considering such most general case, to see how this works we first fix ![]() $m=0$ and consider
$m=0$ and consider ![]() $n\in \mathbb {N}^{+}$. Then, the summation term and the integral term in (2.4) vanish. Starting with
$n\in \mathbb {N}^{+}$. Then, the summation term and the integral term in (2.4) vanish. Starting with ![]() $n=1$ one sees that
$n=1$ one sees that ![]() $A_{w,1,0}(u)=\sigma \phi _{w,\delta _{123},0,0}'(u)$, and hence the right-hand side of (3.3) is a linear sum of
$A_{w,1,0}(u)=\sigma \phi _{w,\delta _{123},0,0}'(u)$, and hence the right-hand side of (3.3) is a linear sum of ![]() $\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$. Together with the solution of the homogeneous version of (3.3) which contains
$\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$. Together with the solution of the homogeneous version of (3.3) which contains ![]() $\{e^{-R_{1,0,k}u}\}_{k=1}^{r+1}$, we observe that (3.5) is valid when
$\{e^{-R_{1,0,k}u}\}_{k=1}^{r+1}$, we observe that (3.5) is valid when ![]() $n=1$. Recursively, for
$n=1$. Recursively, for ![]() $n\in \mathbb {N}^{+}$ (and fixed
$n\in \mathbb {N}^{+}$ (and fixed ![]() $m=0$), we note that the right-hand side of (3.3) consists of
$m=0$), we note that the right-hand side of (3.3) consists of ![]() $\{e^{-R_{i,0,k}u}: 0\le i\le n-1; 1\le k\le r+1\}$, and along with the homogeneous solution one deduces that (3.5) is correct in this case as well.
$\{e^{-R_{i,0,k}u}: 0\le i\le n-1; 1\le k\le r+1\}$, and along with the homogeneous solution one deduces that (3.5) is correct in this case as well.
Step 2(ii). To see how things change when ![]() $m$ increases, next we fix
$m$ increases, next we fix ![]() $n=0$ and consider
$n=0$ and consider ![]() $m\in \mathbb {N}^{+}$ instead. Then, the first two terms in (2.4) vanish. In particular, when
$m\in \mathbb {N}^{+}$ instead. Then, the first two terms in (2.4) vanish. In particular, when ![]() $m=1$, the summation term in
$m=1$, the summation term in ![]() $A_{w,0,1}(u)$ only consists of
$A_{w,0,1}(u)$ only consists of ![]() $\lambda \int _0^{u} y \phi _{w,\delta _{123},0,0}(u-y)p(y)\,dy$. Using (3.1) and the solution form of
$\lambda \int _0^{u} y \phi _{w,\delta _{123},0,0}(u-y)p(y)\,dy$. Using (3.1) and the solution form of ![]() $\phi _{w,\delta _{123},0,0}(u)$ from Step 1 above, it is found that this integral involves terms in the form of
$\phi _{w,\delta _{123},0,0}(u)$ from Step 1 above, it is found that this integral involves terms in the form of ![]() $\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$,
$\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$, ![]() $\{e^{-\beta _l u}\}_{l=1}^{r}$, and
$\{e^{-\beta _l u}\}_{l=1}^{r}$, and ![]() $\{ue^{-\beta _l u}\}_{l=1}^{r}$. The final term in (2.4) is proportional to (3.2) at
$\{ue^{-\beta _l u}\}_{l=1}^{r}$. The final term in (2.4) is proportional to (3.2) at ![]() $k=1$ which contains
$k=1$ which contains ![]() $\{e^{-\beta _l u}\}_{l=1}^{r}$ and
$\{e^{-\beta _l u}\}_{l=1}^{r}$ and ![]() $\{ue^{-\beta _l u}\}_{l=1}^{r}$. As a result, the right-hand side of (3.3) involves
$\{ue^{-\beta _l u}\}_{l=1}^{r}$. As a result, the right-hand side of (3.3) involves ![]() $\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$ and
$\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$ and ![]() $\{e^{-\beta _l u}\}_{l=1}^{r}$, and the solution form (3.5) is valid taking into account the homogeneous solution. When
$\{e^{-\beta _l u}\}_{l=1}^{r}$, and the solution form (3.5) is valid taking into account the homogeneous solution. When ![]() $m=2$, using the obtained solution form of
$m=2$, using the obtained solution form of ![]() $\phi _{w,\delta _{123},0,0}(u)$ and
$\phi _{w,\delta _{123},0,0}(u)$ and ![]() $\phi _{w,\delta _{123},0,1}(u)$, the same procedure reveals that the right-hand side of (3.3) consists of
$\phi _{w,\delta _{123},0,1}(u)$, the same procedure reveals that the right-hand side of (3.3) consists of ![]() $\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$,
$\{e^{-R_{0,0,k}u}\}_{k=1}^{r+1}$, ![]() $\{e^{-R_{0,1,k}u}\}_{k=1}^{r+1}$,
$\{e^{-R_{0,1,k}u}\}_{k=1}^{r+1}$, ![]() $\{e^{-\beta _l u}\}_{l=1}^{r}$, and
$\{e^{-\beta _l u}\}_{l=1}^{r}$, and ![]() $\{ue^{-\beta _l u}\}_{l=1}^{r}$, and then, the solution for
$\{ue^{-\beta _l u}\}_{l=1}^{r}$, and then, the solution for ![]() $\phi _{w,\delta _{123},0,2}(u)$ follows. Inductively, (3.5) is valid for
$\phi _{w,\delta _{123},0,2}(u)$ follows. Inductively, (3.5) is valid for ![]() $n=0$ and
$n=0$ and ![]() $m\in \mathbb {N}^{+}$.
$m\in \mathbb {N}^{+}$.
Step 2(iii). Returning to the case where ![]() $n,m\in \mathbb {N}$, the induction assumption supposes that for some
$n,m\in \mathbb {N}$, the induction assumption supposes that for some ![]() $N,M\in \mathbb {N}$, (3.5) is true for all
$N,M\in \mathbb {N}$, (3.5) is true for all ![]() $(n,m)\in \Upsilon (N,M)$. One can proceed in the same manner as in Steps 2(i) and 2(ii) such that (2.4) can be used to determine (the form of)
$(n,m)\in \Upsilon (N,M)$. One can proceed in the same manner as in Steps 2(i) and 2(ii) such that (2.4) can be used to determine (the form of) ![]() $A_{w,M,N}(u)$ and hence
$A_{w,M,N}(u)$ and hence ![]() $[\prod _{l=1}^{r}(d/du+\beta _l)]A_{w,M,N}(u)$, so that (3.5) is valid for
$[\prod _{l=1}^{r}(d/du+\beta _l)]A_{w,M,N}(u)$, so that (3.5) is valid for ![]() $(n,m)=(N,M)$ and the induction is completed.
$(n,m)=(N,M)$ and the induction is completed.
Remark 1 At a first glance, one may require the higher-order derivatives of ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ to exist (in addition to the first two derivatives as in Assumption 1) in order to justify the application of the operator
$\phi _{d,\delta _{123},n,m}(\cdot )$ to exist (in addition to the first two derivatives as in Assumption 1) in order to justify the application of the operator ![]() $\prod _{l=1}^{r}(d/du+\beta _l)$ to (2.2) and (2.3). Indeed, the results of Lemma 1 can also be proved by taking Laplace transforms of the defective renewal equations (2.43) and (2.44), isolating
$\prod _{l=1}^{r}(d/du+\beta _l)$ to (2.2) and (2.3). Indeed, the results of Lemma 1 can also be proved by taking Laplace transforms of the defective renewal equations (2.43) and (2.44), isolating ![]() $\tilde {\phi }_{w,\delta _{123},n,m}(s)$ and
$\tilde {\phi }_{w,\delta _{123},n,m}(s)$ and ![]() $\tilde {\phi }_{d,\delta _{123},n,m}(s)$, resolving them into partial fractions (recursive in
$\tilde {\phi }_{d,\delta _{123},n,m}(s)$, resolving them into partial fractions (recursive in ![]() $n$ and
$n$ and ![]() $m$) and then inverting the Laplace transforms. Under such a procedure, the existence of the higher-order differentiability of
$m$) and then inverting the Laplace transforms. Under such a procedure, the existence of the higher-order differentiability of ![]() $\phi _{w,\delta _{123},n,m}(\cdot )$ and
$\phi _{w,\delta _{123},n,m}(\cdot )$ and ![]() $\phi _{d,\delta _{123},n,m}(\cdot )$ is not needed as an assumption but is implied from the solution form. However, the proof will require the introduction of various properties of Dickson-Hipp operators and is more tedious, and therefore, we opt to present the operator approach which is more direct.
$\phi _{d,\delta _{123},n,m}(\cdot )$ is not needed as an assumption but is implied from the solution form. However, the proof will require the introduction of various properties of Dickson-Hipp operators and is more tedious, and therefore, we opt to present the operator approach which is more direct.
The next theorem shows how the constants ![]() $B_{w,n,m,i,j,k}$'s and
$B_{w,n,m,i,j,k}$'s and ![]() $C_{w,n,m,j,l}$'s in (3.5) can be determined. Specifically, (3.5) can be further simplified such that the coefficients
$C_{w,n,m,j,l}$'s in (3.5) can be determined. Specifically, (3.5) can be further simplified such that the coefficients ![]() $C_{w,n,m,j,l}$'s are all zero.
$C_{w,n,m,j,l}$'s are all zero.
Theorem 3 (Full solution of  $\phi _{w,\delta _{123},n,m}(\cdot )$)
$\phi _{w,\delta _{123},n,m}(\cdot )$)
Under the same assumptions as in Lemma 1, the Gerber-Shiu function ![]() $\phi _{w,\delta _{123},n,m}(u)$ defined in (1.3) is given by (for
$\phi _{w,\delta _{123},n,m}(u)$ defined in (1.3) is given by (for ![]() $n,m\in \mathbb {N}$ and
$n,m\in \mathbb {N}$ and ![]() $u\ge 0$)
$u\ge 0$)
 \begin{equation} \phi_{w,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k} e^{{-}R_{i,j,k}u}. \end{equation}
\begin{equation} \phi_{w,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k} e^{{-}R_{i,j,k}u}. \end{equation} The coefficients ![]() $\{B_{w,n,m,i,j,k}: (i,j) \in \Upsilon (n,m);k=1,2,\ldots, r+1 \}$ can be first obtained directly in terms of those of the lower-order Gerber-Shiu functions as
$\{B_{w,n,m,i,j,k}: (i,j) \in \Upsilon (n,m);k=1,2,\ldots, r+1 \}$ can be first obtained directly in terms of those of the lower-order Gerber-Shiu functions as
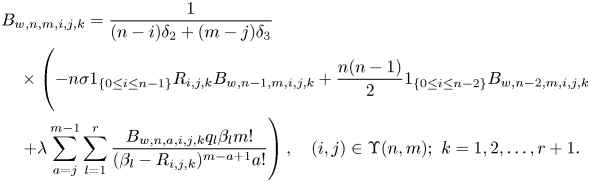 \begin{align} & B_{w,n,m,i,j,k} = \frac{1}{(n-i)\delta_2+(m-j)\delta_3}\nonumber\\ & \quad \times \left({-}n\sigma 1_{\{0\le i\le n-1\}} R_{i,j,k} B_{w,n-1,m,i,j,k} + \frac{n(n-1)}{2} 1_{\{0\le i\le n-2\}} B_{w,n-2,m,i,j,k}\vphantom{\sum_{a=j}^{m-1}}\right. \nonumber\\ & \quad \left.+\lambda\sum_{a=j}^{m-1} \sum_{l=1}^{r}\frac{B_{w,n,a,i,j,k}q_l \beta_lm!}{(\beta_l-R_{i,j,k})^{m-a+1}a!}\right),\quad (i,j) \in \Upsilon(n,m);\ k=1,2,\ldots, r+1. \end{align}
\begin{align} & B_{w,n,m,i,j,k} = \frac{1}{(n-i)\delta_2+(m-j)\delta_3}\nonumber\\ & \quad \times \left({-}n\sigma 1_{\{0\le i\le n-1\}} R_{i,j,k} B_{w,n-1,m,i,j,k} + \frac{n(n-1)}{2} 1_{\{0\le i\le n-2\}} B_{w,n-2,m,i,j,k}\vphantom{\sum_{a=j}^{m-1}}\right. \nonumber\\ & \quad \left.+\lambda\sum_{a=j}^{m-1} \sum_{l=1}^{r}\frac{B_{w,n,a,i,j,k}q_l \beta_lm!}{(\beta_l-R_{i,j,k})^{m-a+1}a!}\right),\quad (i,j) \in \Upsilon(n,m);\ k=1,2,\ldots, r+1. \end{align} Then, ![]() $\{B_{w,n,m,n,m,k}\}_{k=1}^{r+1}$ can be solved from the system of
$\{B_{w,n,m,n,m,k}\}_{k=1}^{r+1}$ can be solved from the system of ![]() $r+1$ linear equations consisting of
$r+1$ linear equations consisting of
 \begin{equation} \sum_{a=0}^{m}\sum_{i=0}^{n}\sum_{j=0}^{a}\sum_{k=1}^{r+1} \frac{B_{w,n,a,i,j,k}}{(\beta_l-R_{i,j,k})^{m-a+1}a!}=1_{\{n=0\}}\mathcal{T}_{\beta_l}^{m+1}w(0), \quad l=1,2,\ldots,r, \end{equation}
\begin{equation} \sum_{a=0}^{m}\sum_{i=0}^{n}\sum_{j=0}^{a}\sum_{k=1}^{r+1} \frac{B_{w,n,a,i,j,k}}{(\beta_l-R_{i,j,k})^{m-a+1}a!}=1_{\{n=0\}}\mathcal{T}_{\beta_l}^{m+1}w(0), \quad l=1,2,\ldots,r, \end{equation}and
 \begin{equation} \sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k}=0. \end{equation}
\begin{equation} \sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{w,n,m,i,j,k}=0. \end{equation}Proof. The proof consists of the two steps that are similar to those in Lemma 1. But instead of working with the ordinary differential equation (3.3), we shall substitute the known solution form (3.5) into the integro-differential equation (2.2) to get information on the unknwon coefficients ![]() $B_{w,n,m,i,j,k}$'s and
$B_{w,n,m,i,j,k}$'s and ![]() $C_{w,n,m,j,l}$'s. We shall start with Step 1 concerning the starting point
$C_{w,n,m,j,l}$'s. We shall start with Step 1 concerning the starting point ![]() $n=m=0$. Note that (3.8) is nonexistent (because
$n=m=0$. Note that (3.8) is nonexistent (because ![]() $\Upsilon (0,0)$ is an empty set) in this case. Moreover, with
$\Upsilon (0,0)$ is an empty set) in this case. Moreover, with ![]() $m=0$, the second summation in (3.5) is an empty sum and therefore (3.5) is already in the form of (3.7). Upon substitution of (3.5), the claim density (3.1) and the penalty
$m=0$, the second summation in (3.5) is an empty sum and therefore (3.5) is already in the form of (3.7). Upon substitution of (3.5), the claim density (3.1) and the penalty ![]() $w(x,y)=w(y)$ into (2.2) followed by the use of (2.4) and (3.2), it is found after some simple calculations that
$w(x,y)=w(y)$ into (2.2) followed by the use of (2.4) and (3.2), it is found after some simple calculations that
 \begin{align*} & \frac{\sigma^{2}}{2}\sum_{k=1}^{r+1} B_{w,0,0,0,0,k}R_{0,0,k}^{2} e^{{-}R_{0,0,k}u} -c\sum_{k=1}^{r+1} B_{w,0,0,0,0,k}R_{0,0,k} e^{{-}R_{0,0,k}u}\\ & \quad -(\lambda+\delta_1)\sum_{k=1}^{r+1} B_{w,0,0,0,0,k} e^{{-}R_{0,0,k}u} +\lambda \sum_{i=1}^{r} \sum_{k=1}^{r+1} \frac{q_i \beta_i B_{w,0,0,0,0,k} }{\beta_i - R_{0,0,k}}(e^{{-}R_{0,0,k} u}-e^{-\beta_i u})\\ & \quad +\lambda \sum_{i=1}^{r} q_i \beta_i \mathcal{T}_{\beta_i}^{1} w(0)e^{-\beta_i u}=0. \end{align*}
\begin{align*} & \frac{\sigma^{2}}{2}\sum_{k=1}^{r+1} B_{w,0,0,0,0,k}R_{0,0,k}^{2} e^{{-}R_{0,0,k}u} -c\sum_{k=1}^{r+1} B_{w,0,0,0,0,k}R_{0,0,k} e^{{-}R_{0,0,k}u}\\ & \quad -(\lambda+\delta_1)\sum_{k=1}^{r+1} B_{w,0,0,0,0,k} e^{{-}R_{0,0,k}u} +\lambda \sum_{i=1}^{r} \sum_{k=1}^{r+1} \frac{q_i \beta_i B_{w,0,0,0,0,k} }{\beta_i - R_{0,0,k}}(e^{{-}R_{0,0,k} u}-e^{-\beta_i u})\\ & \quad +\lambda \sum_{i=1}^{r} q_i \beta_i \mathcal{T}_{\beta_i}^{1} w(0)e^{-\beta_i u}=0. \end{align*} Note that, for each ![]() $k=1,2,\ldots,r+1$, the sum of the coefficients of
$k=1,2,\ldots,r+1$, the sum of the coefficients of ![]() $e^{-R_{0,0,k} u}$ is zero because
$e^{-R_{0,0,k} u}$ is zero because ![]() $-R_{0,0,k}$ satisfies the Lundberg's equation (3.4) with
$-R_{0,0,k}$ satisfies the Lundberg's equation (3.4) with ![]() $n=m=0$. Meanwhile, (3.9) at
$n=m=0$. Meanwhile, (3.9) at ![]() $n=m=0$ can be obtained by equating the coefficients of
$n=m=0$ can be obtained by equating the coefficients of ![]() $e^{-\beta _i u}$ for each
$e^{-\beta _i u}$ for each ![]() $i=1,2,\ldots,r$. Lastly, with
$i=1,2,\ldots,r$. Lastly, with ![]() $n=m=0$, (3.10) directly follows from the solution form (3.5) and the boundary condition (2.40). Thus, Theorem 3 is true for
$n=m=0$, (3.10) directly follows from the solution form (3.5) and the boundary condition (2.40). Thus, Theorem 3 is true for ![]() $n=m=0$.
$n=m=0$.
In the inductive step, it is assumed that, for some ![]() $N,M\in \mathbb {N}$, Theorem 3 is true for all
$N,M\in \mathbb {N}$, Theorem 3 is true for all ![]() $(n,m)\in \Upsilon (N,M)$. Our goal is to show that Theorem 3 is valid for
$(n,m)\in \Upsilon (N,M)$. Our goal is to show that Theorem 3 is valid for ![]() $(n,m)=(N,M)$. With (2.4),
$(n,m)=(N,M)$. With (2.4), ![]() $f(x)=x$ and
$f(x)=x$ and ![]() $w(x,y)=w(y)$, we begin by writing the integro-differential equation (2.2) at
$w(x,y)=w(y)$, we begin by writing the integro-differential equation (2.2) at ![]() $(n,m)=(N,M)$ explicitly as
$(n,m)=(N,M)$ explicitly as
 \begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},N,M}''(u)+c\phi_{w,\delta_{123},N,M}'(u)-(\lambda+\delta_1 +N\delta_2+M\delta_3)\phi_{w,\delta_{123},N,M}(u)\nonumber\\ & \quad+\lambda \int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy+N\sigma 1_{\{N \geq 1\}} \phi_{w,\delta_{123},N-1,M}'(u)\nonumber\\ & \quad+\frac{N(N-1)}{2}1_{\{N \geq 2\}}\phi_{w,\delta_{123},N-2,M}(u) +\lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy \nonumber\\ & \quad+\lambda 1_{\{N=0\}} \int_u^{\infty} y^{M}w(y-u)p(y)\,dy =0. \end{align}
\begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},N,M}''(u)+c\phi_{w,\delta_{123},N,M}'(u)-(\lambda+\delta_1 +N\delta_2+M\delta_3)\phi_{w,\delta_{123},N,M}(u)\nonumber\\ & \quad+\lambda \int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy+N\sigma 1_{\{N \geq 1\}} \phi_{w,\delta_{123},N-1,M}'(u)\nonumber\\ & \quad+\frac{N(N-1)}{2}1_{\{N \geq 2\}}\phi_{w,\delta_{123},N-2,M}(u) +\lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy \nonumber\\ & \quad+\lambda 1_{\{N=0\}} \int_u^{\infty} y^{M}w(y-u)p(y)\,dy =0. \end{align} Using the solution form (3.5) from Lemma 1 at ![]() $(n,m)=(N,M)$, we evaluate the first integral term as
$(n,m)=(N,M)$, we evaluate the first integral term as
 \begin{align} & \lambda\int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy\nonumber\\ & \quad =\lambda\sum_{i=0}^{N}\sum_{j=0}^{M} \sum_{k=1}^{r+1} \sum_{l=1}^{r} B_{w,N,M,i,j,k}q_l \beta_l \int_0^{u} e^{{-}R_{i,j,k}(u-y)} e^{-\beta_l y}\,dy\nonumber\\ & \qquad + \lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1}^{r} C_{w,N,M,j,k} q_l \beta_l \int_0^{u} (u-y)^{j} e^{-\beta_k (u-y)}e^{-\beta_l y}\,dy \nonumber\\ & \quad = \lambda\sum_{i=0}^{N}\sum_{j=0}^{M} \sum_{k=1}^{r+1} \sum_{l=1}^{r} \frac{B_{w,N,M,i,j,k}q_l \beta_l }{\beta_l-R_{i,j,k}} (e^{{-}R_{i,j,k}u}-e^{-\beta_l u}) \nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1, l\neq k}^{r} \frac{C_{w,N,M,j,k} q_l \beta_l j!}{(\beta_k-\beta_l)^{j+1}} \left(e^{-\beta_l u} -\sum_{b=0}^{j} \frac{(\beta_k-\beta_l)^{b} u^{b} e^{-\beta_k u}}{b!}\right) \nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \frac{C_{w,N,M,j,k} q_k \beta_k}{j+1} u^{j+1} e^{-\beta_k u}. \end{align}
\begin{align} & \lambda\int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy\nonumber\\ & \quad =\lambda\sum_{i=0}^{N}\sum_{j=0}^{M} \sum_{k=1}^{r+1} \sum_{l=1}^{r} B_{w,N,M,i,j,k}q_l \beta_l \int_0^{u} e^{{-}R_{i,j,k}(u-y)} e^{-\beta_l y}\,dy\nonumber\\ & \qquad + \lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1}^{r} C_{w,N,M,j,k} q_l \beta_l \int_0^{u} (u-y)^{j} e^{-\beta_k (u-y)}e^{-\beta_l y}\,dy \nonumber\\ & \quad = \lambda\sum_{i=0}^{N}\sum_{j=0}^{M} \sum_{k=1}^{r+1} \sum_{l=1}^{r} \frac{B_{w,N,M,i,j,k}q_l \beta_l }{\beta_l-R_{i,j,k}} (e^{{-}R_{i,j,k}u}-e^{-\beta_l u}) \nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1, l\neq k}^{r} \frac{C_{w,N,M,j,k} q_l \beta_l j!}{(\beta_k-\beta_l)^{j+1}} \left(e^{-\beta_l u} -\sum_{b=0}^{j} \frac{(\beta_k-\beta_l)^{b} u^{b} e^{-\beta_k u}}{b!}\right) \nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \frac{C_{w,N,M,j,k} q_k \beta_k}{j+1} u^{j+1} e^{-\beta_k u}. \end{align} Next, inserting the claim density (3.1) and the induction assumption concerning the form of ![]() $\phi _{w,\delta _{123},N,a}(\cdot )$ for
$\phi _{w,\delta _{123},N,a}(\cdot )$ for ![]() $a=0,1,\ldots,M-1$, the summation involving
$a=0,1,\ldots,M-1$, the summation involving ![]() $M-1$ integrals in (3.11) is found to be
$M-1$ integrals in (3.11) is found to be
 \begin{align} & \lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy\nonumber\\ & \quad = \lambda \sum_{a=0}^{M-1} {M \choose a}\sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r} B_{w,N,a,i,j,k} q_l \beta_l \int_0^{u} y^{M-a} e^{{-}R_{i,j,k}(u-y)}e^{-\beta_l y}\,dy\nonumber\\ & \quad = \lambda \sum_{a=0}^{M-1} {M \choose a}\sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_l(M-a)!}{(\beta_l-R_{i,j,k})^{M-a+1}}\nonumber\\ & \qquad \times \left(e^{{-}R_{i,j,k}u}-\sum_{b=0}^{M-a}\frac{(\beta_l-R_{i,j,k})^{b} u^{b} e^{-\beta_l u}}{b!}\right). \end{align}
\begin{align} & \lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy\nonumber\\ & \quad = \lambda \sum_{a=0}^{M-1} {M \choose a}\sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r} B_{w,N,a,i,j,k} q_l \beta_l \int_0^{u} y^{M-a} e^{{-}R_{i,j,k}(u-y)}e^{-\beta_l y}\,dy\nonumber\\ & \quad = \lambda \sum_{a=0}^{M-1} {M \choose a}\sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_l(M-a)!}{(\beta_l-R_{i,j,k})^{M-a+1}}\nonumber\\ & \qquad \times \left(e^{{-}R_{i,j,k}u}-\sum_{b=0}^{M-a}\frac{(\beta_l-R_{i,j,k})^{b} u^{b} e^{-\beta_l u}}{b!}\right). \end{align} Note that the summation terms involving ![]() $B_{w,N,M,i,j,k}$'s in the above two equations can be combined to form a single summation. Therefore, summing (3.12) and (3.13) followed by a change of order of summation yields
$B_{w,N,M,i,j,k}$'s in the above two equations can be combined to form a single summation. Therefore, summing (3.12) and (3.13) followed by a change of order of summation yields
 \begin{align} & \lambda\int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy + \lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy\nonumber\\ & \quad = \lambda \sum_{j=0}^{M} \sum_{a=j}^{M} \sum_{i=0}^{N} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} e^{{-}R_{i,j,k}u} \nonumber\\ & \qquad - \lambda \sum_{b=0}^{M} \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} u^{b} e^{-\beta_l u}\nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1, l\neq k}^{r} \frac{C_{w,N,M,j,k} q_l \beta_l j!}{(\beta_k-\beta_l)^{j+1}} e^{-\beta_l u} \nonumber\\ & \qquad -\lambda \sum_{b=0}^{M-1}\sum_{j=b}^{M-1}\sum_{l=1}^{r} \sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} u^{b} e^{-\beta_l u} \nonumber\\ & \qquad +\lambda\sum_{b=1}^{M} \sum_{l=1}^{r} \frac{C_{w,N,M,b-1,l}q_l \beta_l}{b} u^{b} e^{-\beta_l u}. \end{align}
\begin{align} & \lambda\int_0^{u} \phi_{w,\delta_{123},N,M}(u-y)p(y)\,dy + \lambda \sum_{a=0}^{M-1} {M \choose a}\int_0^{u} y^{M-a}\phi_{w,\delta_{123},N,a}(u-y)p(y)\,dy\nonumber\\ & \quad = \lambda \sum_{j=0}^{M} \sum_{a=j}^{M} \sum_{i=0}^{N} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} e^{{-}R_{i,j,k}u} \nonumber\\ & \qquad - \lambda \sum_{b=0}^{M} \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} u^{b} e^{-\beta_l u}\nonumber\\ & \qquad +\lambda\sum_{j=0}^{M-1}\sum_{k=1}^{r} \sum_{l=1, l\neq k}^{r} \frac{C_{w,N,M,j,k} q_l \beta_l j!}{(\beta_k-\beta_l)^{j+1}} e^{-\beta_l u} \nonumber\\ & \qquad -\lambda \sum_{b=0}^{M-1}\sum_{j=b}^{M-1}\sum_{l=1}^{r} \sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} u^{b} e^{-\beta_l u} \nonumber\\ & \qquad +\lambda\sum_{b=1}^{M} \sum_{l=1}^{r} \frac{C_{w,N,M,b-1,l}q_l \beta_l}{b} u^{b} e^{-\beta_l u}. \end{align}Moreover, using (3.2), we see that
 \begin{equation} \lambda 1_{\{N =0\}}\int_u^{\infty} y^{M} w(y-u)p(y)\,dy =\lambda 1_{\{N =0\}} M! \sum_{l=1}^{r}\sum_{b=0}^{M} \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!} u^{b} e^{-\beta_l u}. \end{equation}
\begin{equation} \lambda 1_{\{N =0\}}\int_u^{\infty} y^{M} w(y-u)p(y)\,dy =\lambda 1_{\{N =0\}} M! \sum_{l=1}^{r}\sum_{b=0}^{M} \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!} u^{b} e^{-\beta_l u}. \end{equation} With the integrals in (3.11) obtained, we now further evaluate the derivatives of ![]() $\phi _{w,\delta _{123},N,M}(u)$ (using (3.5)) and
$\phi _{w,\delta _{123},N,M}(u)$ (using (3.5)) and ![]() $\phi _{w,\delta _{123},N-1,M}(u)$ (using the induction hypothesis) so that the remaining terms in (3.11) become
$\phi _{w,\delta _{123},N-1,M}(u)$ (using the induction hypothesis) so that the remaining terms in (3.11) become
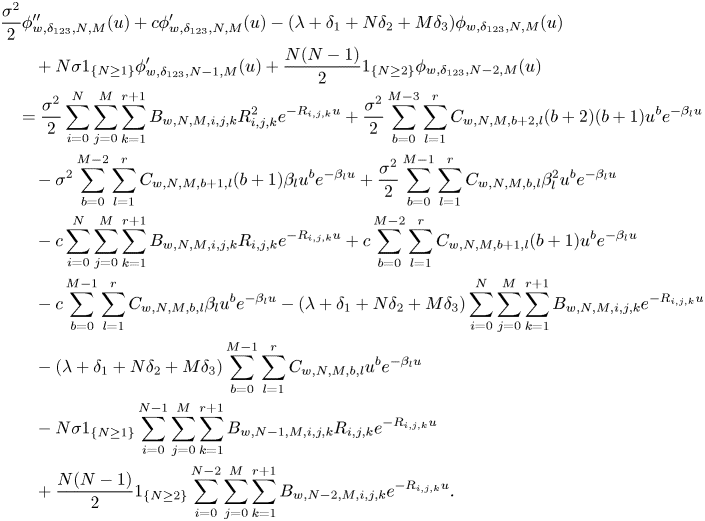 \begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},N,M}''(u)+c\phi_{w,\delta_{123},N,M}'(u)-(\lambda+\delta_1 +N\delta_2+M\delta_3)\phi_{w,\delta_{123},N,M}(u) \nonumber\\ & \qquad +N\sigma 1_{\{N \geq 1\}} \phi_{w,\delta_{123},N-1,M}'(u)+\frac{N(N-1)}{2}1_{\{N \geq 2\}}\phi_{w,\delta_{123},N-2,M}(u)\nonumber\\ & \quad = \frac{\sigma^{2}}{2}\sum_{i=0}^{N} \sum_{j=0}^{M}\sum_{k=1}^{r+1} B_{w,N,M,i,j,k} R_{i,j,k}^{2} e^{{-}R_{i,j,k}u} + \frac{\sigma^{2}}{2}\sum_{b=0}^{M-3}\sum_{l=1}^{r} C_{w,N,M,b+2,l}(b+2)(b+1)u^{b}e^{-\beta_l u}\nonumber\\ & \qquad -\sigma^{2} \sum_{b=0}^{M-2}\sum_{l=1}^{r} C_{w,N,M,b+1,l}(b+1)\beta_l u^{b}e^{-\beta_l u} + \frac{\sigma^{2}}{2}\sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}\beta_l^{2} u^{b} e^{-\beta_l u}\nonumber\\ & \qquad -c\sum_{i=0}^{N} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N,M,i,j,k} R_{i,j,k} e^{{-}R_{i,j,k}u} +c \sum_{b=0}^{M-2}\sum_{l=1}^{r} C_{w,N,M,b+1,l}(b+1) u^{b} e^{-\beta_l u} \nonumber\\ & \qquad -c \sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}\beta_l u^{b} e^{-\beta_l u}-(\lambda+\delta_1 +N\delta_2+M\delta_3) \sum_{i=0}^{N} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N,M,i,j,k} e^{{-}R_{i,j,k}u}\nonumber\\ & \qquad -(\lambda+\delta_1 +N\delta_2+M\delta_3)\sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}u^{b} e^{-\beta_l u} \nonumber\\ & \qquad -N\sigma 1_{\{N \geq 1\}} \sum_{i=0}^{N-1} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N-1,M,i,j,k} R_{i,j,k} e^{{-}R_{i,j,k}u}\nonumber\\ & \qquad +\frac{N(N-1)}{2} 1_{\{N \geq 2\}} \sum_{i=0}^{N-2} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N-2,M,i,j,k} e^{{-}R_{i,j,k}u}. \end{align}
\begin{align} & \frac{\sigma^{2}}{2} \phi_{w,\delta_{123},N,M}''(u)+c\phi_{w,\delta_{123},N,M}'(u)-(\lambda+\delta_1 +N\delta_2+M\delta_3)\phi_{w,\delta_{123},N,M}(u) \nonumber\\ & \qquad +N\sigma 1_{\{N \geq 1\}} \phi_{w,\delta_{123},N-1,M}'(u)+\frac{N(N-1)}{2}1_{\{N \geq 2\}}\phi_{w,\delta_{123},N-2,M}(u)\nonumber\\ & \quad = \frac{\sigma^{2}}{2}\sum_{i=0}^{N} \sum_{j=0}^{M}\sum_{k=1}^{r+1} B_{w,N,M,i,j,k} R_{i,j,k}^{2} e^{{-}R_{i,j,k}u} + \frac{\sigma^{2}}{2}\sum_{b=0}^{M-3}\sum_{l=1}^{r} C_{w,N,M,b+2,l}(b+2)(b+1)u^{b}e^{-\beta_l u}\nonumber\\ & \qquad -\sigma^{2} \sum_{b=0}^{M-2}\sum_{l=1}^{r} C_{w,N,M,b+1,l}(b+1)\beta_l u^{b}e^{-\beta_l u} + \frac{\sigma^{2}}{2}\sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}\beta_l^{2} u^{b} e^{-\beta_l u}\nonumber\\ & \qquad -c\sum_{i=0}^{N} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N,M,i,j,k} R_{i,j,k} e^{{-}R_{i,j,k}u} +c \sum_{b=0}^{M-2}\sum_{l=1}^{r} C_{w,N,M,b+1,l}(b+1) u^{b} e^{-\beta_l u} \nonumber\\ & \qquad -c \sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}\beta_l u^{b} e^{-\beta_l u}-(\lambda+\delta_1 +N\delta_2+M\delta_3) \sum_{i=0}^{N} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N,M,i,j,k} e^{{-}R_{i,j,k}u}\nonumber\\ & \qquad -(\lambda+\delta_1 +N\delta_2+M\delta_3)\sum_{b=0}^{M-1}\sum_{l=1}^{r} C_{w,N,M,b,l}u^{b} e^{-\beta_l u} \nonumber\\ & \qquad -N\sigma 1_{\{N \geq 1\}} \sum_{i=0}^{N-1} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N-1,M,i,j,k} R_{i,j,k} e^{{-}R_{i,j,k}u}\nonumber\\ & \qquad +\frac{N(N-1)}{2} 1_{\{N \geq 2\}} \sum_{i=0}^{N-2} \sum_{j=0}^{M} \sum_{k=1}^{r+1} B_{w,N-2,M,i,j,k} e^{{-}R_{i,j,k}u}. \end{align} Due to (3.11), the sum of (3.14)–(3.16) is zero for all ![]() $u\geq 0$. First, equating the coefficients of
$u\geq 0$. First, equating the coefficients of ![]() $e^{-R_{i,j,k}u}$ for each
$e^{-R_{i,j,k}u}$ for each ![]() $i=0,1,\ldots,N$;
$i=0,1,\ldots,N$; ![]() $j=0,1,\ldots,M$; and
$j=0,1,\ldots,M$; and ![]() $k=1,2,\ldots, r+1$ gives rise to
$k=1,2,\ldots, r+1$ gives rise to
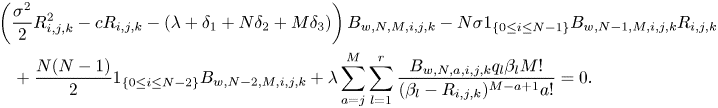 \begin{align*} & \left(\frac{\sigma^{2}}{2} R_{i,j,k}^{2} -c R_{i,j,k} -(\lambda+\delta_1 +N\delta_2+M\delta_3) \right) B_{w,N,M,i,j,k} -N\sigma 1_{\{0\le i\le N-1\}} B_{w,N-1,M,i,j,k} R_{i,j,k}\\ & \quad +\frac{N(N-1)}{2} 1_{\{0\le i\le N-2\}} B_{w,N-2,M,i,j,k} + \lambda \sum_{a=j}^{M} \sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} =0. \end{align*}
\begin{align*} & \left(\frac{\sigma^{2}}{2} R_{i,j,k}^{2} -c R_{i,j,k} -(\lambda+\delta_1 +N\delta_2+M\delta_3) \right) B_{w,N,M,i,j,k} -N\sigma 1_{\{0\le i\le N-1\}} B_{w,N-1,M,i,j,k} R_{i,j,k}\\ & \quad +\frac{N(N-1)}{2} 1_{\{0\le i\le N-2\}} B_{w,N-2,M,i,j,k} + \lambda \sum_{a=j}^{M} \sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} =0. \end{align*} Separating the term ![]() $a=M$ of the summation and using the fact that
$a=M$ of the summation and using the fact that ![]() $\{-R_{i,j,k}\}_{k=1}^{r+1}$ satisfy the Lundberg's equation (2.1), this can be simplified to yield
$\{-R_{i,j,k}\}_{k=1}^{r+1}$ satisfy the Lundberg's equation (2.1), this can be simplified to yield
 \begin{align*} & -[(N-i)\delta_2+(M-j)\delta_3]B_{w,N,M,i,j,k} -N\sigma 1_{\{0\le i\le N-1\}} B_{w,N-1,M,i,j,k} R_{i,j,k}\\ & \quad +\frac{N(N-1)}{2} 1_{\{0\le i\le N-2\}} B_{w,N-2,M,i,j,k} + \lambda \sum_{a=j}^{M-1} \sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} =0. \end{align*}
\begin{align*} & -[(N-i)\delta_2+(M-j)\delta_3]B_{w,N,M,i,j,k} -N\sigma 1_{\{0\le i\le N-1\}} B_{w,N-1,M,i,j,k} R_{i,j,k}\\ & \quad +\frac{N(N-1)}{2} 1_{\{0\le i\le N-2\}} B_{w,N-2,M,i,j,k} + \lambda \sum_{a=j}^{M-1} \sum_{l=1}^{r}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} =0. \end{align*} When ![]() $(i,j)=(N,M)$, the above equation does not yield any useful information on the coefficients because the left-hand side is simply zero. For
$(i,j)=(N,M)$, the above equation does not yield any useful information on the coefficients because the left-hand side is simply zero. For ![]() $(i,j)\in \Upsilon (N,M)$, by rearrangements one can confirm that (3.8) holds true for
$(i,j)\in \Upsilon (N,M)$, by rearrangements one can confirm that (3.8) holds true for ![]() $(n,m)=(N,M)$.
$(n,m)=(N,M)$.
Second, we look at terms in the form of ![]() $u^{b} e^{-\beta _l u}$ and distinguish between three cases, namely (i)
$u^{b} e^{-\beta _l u}$ and distinguish between three cases, namely (i) ![]() $b=M$; (ii)
$b=M$; (ii) ![]() $b=1,2,\ldots,M-1$; and (iii)
$b=1,2,\ldots,M-1$; and (iii) ![]() $b=0$. (Note that if
$b=0$. (Note that if ![]() $M=0$, then we will only use Case (iii) whereas if
$M=0$, then we will only use Case (iii) whereas if ![]() $M=1$ there will only be Cases (i) and (iii).) Beginning with Case (i), the coefficients of
$M=1$ there will only be Cases (i) and (iii).) Beginning with Case (i), the coefficients of ![]() $u^{M} e^{-\beta _l u}$ for
$u^{M} e^{-\beta _l u}$ for ![]() $l=1,2,\ldots,r$ imply
$l=1,2,\ldots,r$ imply
 $$- \lambda \sum_{i=0}^{N} \sum_{k=1}^{r+1}\frac{B_{w,N,0,i,0,k}q_l \beta_l}{\beta_l-R_{i,0,k}} +\lambda \frac{C_{w,N,M,M-1,l}q_l \beta_l}{M} +\lambda 1_{\{N =0\}} q_l\beta_l \mathcal{T}_{\beta_l}^{1} w(0) = 0.$$
$$- \lambda \sum_{i=0}^{N} \sum_{k=1}^{r+1}\frac{B_{w,N,0,i,0,k}q_l \beta_l}{\beta_l-R_{i,0,k}} +\lambda \frac{C_{w,N,M,M-1,l}q_l \beta_l}{M} +\lambda 1_{\{N =0\}} q_l\beta_l \mathcal{T}_{\beta_l}^{1} w(0) = 0.$$ Under the induction assumption, (3.9) holds true for ![]() $(n,m)=(N,0)$, and therefore, one observes from the above equation that
$(n,m)=(N,0)$, and therefore, one observes from the above equation that ![]() $C_{w,N,M,M-1,l}=0$ for
$C_{w,N,M,M-1,l}=0$ for ![]() $l=1,2,\ldots,r$. Concerning Case (ii), for
$l=1,2,\ldots,r$. Concerning Case (ii), for ![]() $b=1,2,\ldots,M-1$ and
$b=1,2,\ldots,M-1$ and ![]() $l=1,2,\ldots,r$, we get from the terms involving
$l=1,2,\ldots,r$, we get from the terms involving ![]() $u^{b} e^{-\beta _l u}$ that
$u^{b} e^{-\beta _l u}$ that
 \begin{align} & \frac{\sigma^{2}}{2}1_{\{1\le b\le M-3\}}C_{w,N,M,b+2,l}(b+2)(b+1) -\sigma^{2} 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\beta_l + \frac{\sigma^{2}}{2}C_{w,N,M,b,l}\beta_l^{2}\nonumber\\ & \quad +c 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1) -c C_{w,N,M,b,l}\beta_l -(\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,b,l}\nonumber\\ & \quad- \lambda \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} -\lambda \sum_{j=b}^{M-1}\sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} \nonumber\\ & \quad +\lambda\frac{C_{w,N,M,b-1,l}q_l \beta_l}{b}+\lambda 1_{\{N =0\}} M! \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!}=0. \end{align}
\begin{align} & \frac{\sigma^{2}}{2}1_{\{1\le b\le M-3\}}C_{w,N,M,b+2,l}(b+2)(b+1) -\sigma^{2} 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\beta_l + \frac{\sigma^{2}}{2}C_{w,N,M,b,l}\beta_l^{2}\nonumber\\ & \quad +c 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1) -c C_{w,N,M,b,l}\beta_l -(\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,b,l}\nonumber\\ & \quad- \lambda \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} -\lambda \sum_{j=b}^{M-1}\sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} \nonumber\\ & \quad +\lambda\frac{C_{w,N,M,b-1,l}q_l \beta_l}{b}+\lambda 1_{\{N =0\}} M! \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!}=0. \end{align}Focusing on the quadruple summation term and the final term on the left-hand side, we note that
 $$- \lambda \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} +\lambda 1_{\{N =0\}} M! \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!}=0$$
$$- \lambda \sum_{a=0}^{M-b} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1}\frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a-b+1}a!b!} +\lambda 1_{\{N =0\}} M! \frac{q_l\beta_l \mathcal{T}_{\beta_l}^{M-b+1} w(0)}{b!}=0$$because (3.9) is valid for ![]() $n=N$ and
$n=N$ and ![]() $m=M-b$ (where
$m=M-b$ (where ![]() $b$ varies from 1 to
$b$ varies from 1 to ![]() $M-1$) as part of the induction assumption. As a result, (3.17) becomes
$M-1$) as part of the induction assumption. As a result, (3.17) becomes
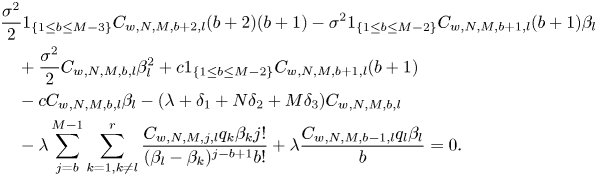 \begin{align} & \frac{\sigma^{2}}{2}1_{\{1\le b\le M-3\}}C_{w,N,M,b+2,l}(b+2)(b+1) -\sigma^{2} 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\beta_l \nonumber\\ & \quad + \frac{\sigma^{2}}{2}C_{w,N,M,b,l}\beta_l^{2}+c 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\nonumber\\ & \quad -c C_{w,N,M,b,l}\beta_l -(\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,b,l}\nonumber\\ & \quad -\lambda \sum_{j=b}^{M-1}\sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} +\lambda\frac{C_{w,N,M,b-1,l}q_l \beta_l}{b}=0. \end{align}
\begin{align} & \frac{\sigma^{2}}{2}1_{\{1\le b\le M-3\}}C_{w,N,M,b+2,l}(b+2)(b+1) -\sigma^{2} 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\beta_l \nonumber\\ & \quad + \frac{\sigma^{2}}{2}C_{w,N,M,b,l}\beta_l^{2}+c 1_{\{1\le b\le M-2\}} C_{w,N,M,b+1,l}(b+1)\nonumber\\ & \quad -c C_{w,N,M,b,l}\beta_l -(\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,b,l}\nonumber\\ & \quad -\lambda \sum_{j=b}^{M-1}\sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,j,l} q_k \beta_k j!}{(\beta_l-\beta_k)^{j-b+1}b!} +\lambda\frac{C_{w,N,M,b-1,l}q_l \beta_l}{b}=0. \end{align} Recall that Case (ii) only exists when ![]() $M\ge 2$, and without loss of generality we assume
$M\ge 2$, and without loss of generality we assume ![]() $M\ge 2$ in this case. We proceed by substituting
$M\ge 2$ in this case. We proceed by substituting ![]() $b=M-1$ into (3.18) to arrive at
$b=M-1$ into (3.18) to arrive at
 \begin{align*} & \frac{\sigma^{2}}{2}C_{w,N,M,M-1,l}\beta_l^{2} -c C_{w,N,M,M-1,l}\beta_l - (\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,M-1,l}\\ & \quad -\lambda \sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,M-1,l} q_k \beta_k }{\beta_l-\beta_k}+\lambda\frac{C_{w,N,M,M-2,l}q_l \beta_l}{M-1} =0. \end{align*}
\begin{align*} & \frac{\sigma^{2}}{2}C_{w,N,M,M-1,l}\beta_l^{2} -c C_{w,N,M,M-1,l}\beta_l - (\lambda+\delta_1 +N\delta_2+M\delta_3) C_{w,N,M,M-1,l}\\ & \quad -\lambda \sum_{k=1, k\neq l}^{r} \frac{C_{w,N,M,M-1,l} q_k \beta_k }{\beta_l-\beta_k}+\lambda\frac{C_{w,N,M,M-2,l}q_l \beta_l}{M-1} =0. \end{align*} Since ![]() $\{C_{w,N,M,M-1,l}\}_{l=1}^{r}$ are already known to be zero from the conclusion of Case (i), it is clear from the above equation that
$\{C_{w,N,M,M-1,l}\}_{l=1}^{r}$ are already known to be zero from the conclusion of Case (i), it is clear from the above equation that ![]() $\{C_{w,N,M,M-2,l}\}_{l=1}^{r}$ are all zero as well. If
$\{C_{w,N,M,M-2,l}\}_{l=1}^{r}$ are all zero as well. If ![]() $M\ge 3$, then we further put
$M\ge 3$, then we further put ![]() $b=M-2$ into (3.18) and use the fact that
$b=M-2$ into (3.18) and use the fact that ![]() $\{C_{w,N,M,M-1,l}\}_{l=1}^{r}$ and
$\{C_{w,N,M,M-1,l}\}_{l=1}^{r}$ and ![]() $\{C_{w,N,M,M-2,l}\}_{l=1}^{r}$ are zero to see that
$\{C_{w,N,M,M-2,l}\}_{l=1}^{r}$ are zero to see that ![]() $\{C_{w,N,M,M-3,l}\}_{l=1}^{r}$ are zero. Repeating this procedure until we reach
$\{C_{w,N,M,M-3,l}\}_{l=1}^{r}$ are zero. Repeating this procedure until we reach ![]() $b=1$, we can conclude that
$b=1$, we can conclude that ![]() $C_{w,N,M,j,l}=0$ for all
$C_{w,N,M,j,l}=0$ for all ![]() $j=0,1,\ldots,M-1$ and
$j=0,1,\ldots,M-1$ and ![]() $l=1,2,\ldots,r$, confirming that the solution form (3.5) reduces to (3.7) when
$l=1,2,\ldots,r$, confirming that the solution form (3.5) reduces to (3.7) when ![]() $(n,m)=(N,M)$. Moving to Case (iii) where
$(n,m)=(N,M)$. Moving to Case (iii) where ![]() $b=0$, because
$b=0$, because ![]() $C_{w,N,M,j,l}=0$ in (3.14)–(3.16), equating the coefficients of
$C_{w,N,M,j,l}=0$ in (3.14)–(3.16), equating the coefficients of ![]() $e^{-\beta _l u}$ in (3.11) with zero leads to
$e^{-\beta _l u}$ in (3.11) with zero leads to
 $$- \lambda \sum_{a=0}^{M} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1} \frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} + \lambda 1_{\{N =0\}} M! q_l\beta_l \mathcal{T}_{\beta_l}^{M+1} w(0) =0.$$
$$- \lambda \sum_{a=0}^{M} \sum_{i=0}^{N} \sum_{j=0}^{a} \sum_{k=1}^{r+1} \frac{B_{w,N,a,i,j,k}q_l \beta_lM!}{(\beta_l-R_{i,j,k})^{M-a+1}a!} + \lambda 1_{\{N =0\}} M! q_l\beta_l \mathcal{T}_{\beta_l}^{M+1} w(0) =0.$$ In other words, (3.9) holds true for ![]() $(n,m)=(N,M)$.
$(n,m)=(N,M)$.
Finally, when ![]() $(n,m)=(N,M)$, the formula (3.10) clearly holds true because of the boundary condition (2.40) and the solution form (3.7). Combining all the above results, we see that Theorem 3 is true for
$(n,m)=(N,M)$, the formula (3.10) clearly holds true because of the boundary condition (2.40) and the solution form (3.7). Combining all the above results, we see that Theorem 3 is true for ![]() $(n,m)=(N,M)$, and the induction is completed.
$(n,m)=(N,M)$, and the induction is completed.
The determination of the full solution for ![]() $\phi _{d,\delta _{123},n,m}(u)$ can be proved in an almost identical manner to Theorem 3, and the results are stated without proof in the following theorem.
$\phi _{d,\delta _{123},n,m}(u)$ can be proved in an almost identical manner to Theorem 3, and the results are stated without proof in the following theorem.
Theorem 4 (Full solution of  $\phi _{d,\delta _{123},n,m}(\cdot )$)
$\phi _{d,\delta _{123},n,m}(\cdot )$)
Under the same assumptions as in Lemma 1, the Gerber-Shiu function ![]() $\phi _{d,\delta _{123},n,m}(u)$ defined in (1.4) is given by (for
$\phi _{d,\delta _{123},n,m}(u)$ defined in (1.4) is given by (for ![]() $n,m\in \mathbb {N}$ and
$n,m\in \mathbb {N}$ and ![]() $u\ge 0$)
$u\ge 0$)
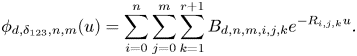 \begin{equation} \phi_{d,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k} e^{{-}R_{i,j,k}u}. \end{equation}
\begin{equation} \phi_{d,\delta_{123},n,m}(u)=\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k} e^{{-}R_{i,j,k}u}. \end{equation} The coefficients ![]() $\{B_{d,n,m,i,j,k}: (i,j) \in \Upsilon (n,m);k=1,2,\ldots, r+1 \}$ can be first obtained directly in terms of those of the lower-order Gerber-Shiu functions as
$\{B_{d,n,m,i,j,k}: (i,j) \in \Upsilon (n,m);k=1,2,\ldots, r+1 \}$ can be first obtained directly in terms of those of the lower-order Gerber-Shiu functions as
 \begin{align} & B_{d,n,m,i,j,k}= \frac{1}{(n-i)\delta_2+(m-j)\delta_3}\nonumber\\ & \quad \times \left({-}n\sigma 1_{\{0\le i\le n-1\}} R_{i,j,k} B_{d,n-1,m,i,j,k} + \frac{n(n-1)}{2} 1_{\{0\le i\le n-2\}} B_{d,n-2,m,i,j,k}\right.\nonumber\\ & \quad \left.+\lambda \sum_{a=j}^{m-1} \sum_{l=1}^{r}\frac{B_{d,n,a,i,j,k}q_l \beta_lm!}{(\beta_l-R_{i,j,k})^{m-a+1}a!}\right),\quad (i,j) \in \Upsilon(n,m);\ k=1,2,\ldots, r+1. \end{align}
\begin{align} & B_{d,n,m,i,j,k}= \frac{1}{(n-i)\delta_2+(m-j)\delta_3}\nonumber\\ & \quad \times \left({-}n\sigma 1_{\{0\le i\le n-1\}} R_{i,j,k} B_{d,n-1,m,i,j,k} + \frac{n(n-1)}{2} 1_{\{0\le i\le n-2\}} B_{d,n-2,m,i,j,k}\right.\nonumber\\ & \quad \left.+\lambda \sum_{a=j}^{m-1} \sum_{l=1}^{r}\frac{B_{d,n,a,i,j,k}q_l \beta_lm!}{(\beta_l-R_{i,j,k})^{m-a+1}a!}\right),\quad (i,j) \in \Upsilon(n,m);\ k=1,2,\ldots, r+1. \end{align} Then, ![]() $\{B_{d,n,m,n,m,k}\}_{k=1}^{r+1}$ can be solved from the system of
$\{B_{d,n,m,n,m,k}\}_{k=1}^{r+1}$ can be solved from the system of ![]() $r+1$ linear equations consisting of
$r+1$ linear equations consisting of
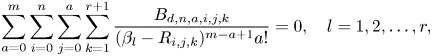 $$\sum_{a=0}^{m}\sum_{i=0}^{n}\sum_{j=0}^{a}\sum_{k=1}^{r+1}\frac{B_{d,n,a,i,j,k}}{(\beta_l-R_{i,j,k})^{m-a+1}a!}=0, \quad l=1,2,\ldots,r,$$
$$\sum_{a=0}^{m}\sum_{i=0}^{n}\sum_{j=0}^{a}\sum_{k=1}^{r+1}\frac{B_{d,n,a,i,j,k}}{(\beta_l-R_{i,j,k})^{m-a+1}a!}=0, \quad l=1,2,\ldots,r,$$and
 $$\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k}=1_{\{n=m=0\}}.$$
$$\sum_{i=0}^{n} \sum_{j=0}^{m} \sum_{k=1}^{r+1} B_{d,n,m,i,j,k}=1_{\{n=m=0\}}.$$4. Numerical illustrations
In this section, we shall demonstrate the applicability of the exact and explicit formulas developed in the previous section to study moment-based quantities (including correlation) in relation to the total discounted perturbation until ruin ![]() $B_{\delta _2}(\tau )=\int _0^{\tau } e^{-\delta _2 s}\,dB(s)$, the total discounted claims until ruin
$B_{\delta _2}(\tau )=\int _0^{\tau } e^{-\delta _2 s}\,dB(s)$, the total discounted claims until ruin ![]() $Z_{\delta _3}(\tau )=\sum _{k=1}^{N(\tau )}e^{-\delta _3 T_k}Y_k$ (i.e. the cost function
$Z_{\delta _3}(\tau )=\sum _{k=1}^{N(\tau )}e^{-\delta _3 T_k}Y_k$ (i.e. the cost function ![]() $f(x)=x$ is assumed), and the ruin time
$f(x)=x$ is assumed), and the ruin time ![]() $\tau$. For our purposes, it is sufficient to let the penalty function be
$\tau$. For our purposes, it is sufficient to let the penalty function be ![]() $w\equiv 1$ throughout the section. The afore-mentioned quantities will be calculated conditional on ruin occurrence. To simplify notation, the expectation of a random variable
$w\equiv 1$ throughout the section. The afore-mentioned quantities will be calculated conditional on ruin occurrence. To simplify notation, the expectation of a random variable ![]() $X$ conditional on
$X$ conditional on ![]() $\tau <\infty$ under an initial surplus of
$\tau <\infty$ under an initial surplus of ![]() $u\ge 0$ is denoted by
$u\ge 0$ is denoted by ![]() $E_{\text {ruin}}[X\,|\,u]=E[X1_{\{\tau <\infty \}}\,|\,U(0)=u]/\psi (u)$, where
$E_{\text {ruin}}[X\,|\,u]=E[X1_{\{\tau <\infty \}}\,|\,U(0)=u]/\psi (u)$, where ![]() $\psi (u)=\Pr \{\tau <\infty \,|\,U(0)=u\}=\phi _{w,\delta _{123},0,0}(u)|_{\delta _1=0}+\phi _{d,\delta _{123},0,0}(u)|_{\delta _1=0}$. Clearly, for
$\psi (u)=\Pr \{\tau <\infty \,|\,U(0)=u\}=\phi _{w,\delta _{123},0,0}(u)|_{\delta _1=0}+\phi _{d,\delta _{123},0,0}(u)|_{\delta _1=0}$. Clearly, for ![]() $n,m\in \mathbb {N}$, the (joint) moments of
$n,m\in \mathbb {N}$, the (joint) moments of ![]() $B_{\delta _2}(\tau )$ and
$B_{\delta _2}(\tau )$ and ![]() $Z_{\delta _3}(\tau )$ are given by
$Z_{\delta _3}(\tau )$ are given by
More generally, for ![]() $\ell, n,m\in \mathbb {N}$, the (joint) moments involving
$\ell, n,m\in \mathbb {N}$, the (joint) moments involving ![]() $\tau$ are obtainable via
$\tau$ are obtainable via
 \begin{equation} E_{\text{ruin}}[\tau^{\ell} B_{\delta_2}^{n}(\tau)Z_{\delta_3}^{m}(\tau)\,|\,u] = \left.\frac{({-}1)^{\ell} \frac{\partial^{\ell}}{\partial \delta_1^{\ell}} [\phi_{w,\delta_{123},n,m}(u)+\phi_{d,\delta_{123},n,m}(u)]}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right|_{\delta_1=0}. \end{equation}
\begin{equation} E_{\text{ruin}}[\tau^{\ell} B_{\delta_2}^{n}(\tau)Z_{\delta_3}^{m}(\tau)\,|\,u] = \left.\frac{({-}1)^{\ell} \frac{\partial^{\ell}}{\partial \delta_1^{\ell}} [\phi_{w,\delta_{123},n,m}(u)+\phi_{d,\delta_{123},n,m}(u)]}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right|_{\delta_1=0}. \end{equation} We remark that, in view of the computation of the derivatives in (4.2), it is important to specify the relevant quantities as a function of ![]() $\delta _1$ in the programming task for
$\delta _1$ in the programming task for ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ when using (3.7) and (3.19) for claims distributed as a combination of exponentials. Note that the roots
$\phi _{d,\delta _{123},n,m}(u)$ when using (3.7) and (3.19) for claims distributed as a combination of exponentials. Note that the roots ![]() $\{-R_{i,j,k}\}_{k=1}^{r+1}$ depend on
$\{-R_{i,j,k}\}_{k=1}^{r+1}$ depend on ![]() $\delta _1$ in an implicit manner as they are solved from the Lundberg's equation (2.1) (or (3.4) with
$\delta _1$ in an implicit manner as they are solved from the Lundberg's equation (2.1) (or (3.4) with ![]() $i$ and
$i$ and ![]() $j$ in place of
$j$ in place of ![]() $n$ and
$n$ and ![]() $m$) that involves
$m$) that involves ![]() $\delta _1$. This can be handled by Mathematica using the function “Solve” or “NSolve”. Then,
$\delta _1$. This can be handled by Mathematica using the function “Solve” or “NSolve”. Then, ![]() $B_{w,n,m,i,j,k}$'s in (3.7) (resp.
$B_{w,n,m,i,j,k}$'s in (3.7) (resp. ![]() $B_{d,n,m,i,j,k}$'s in (3.19)) depend on
$B_{d,n,m,i,j,k}$'s in (3.19)) depend on ![]() $\delta _1$ via the recursive procedure in Theorem 3 (resp. Theorem 4). The derivatives of
$\delta _1$ via the recursive procedure in Theorem 3 (resp. Theorem 4). The derivatives of ![]() $\phi _{w,\delta _{123},n,m}(u)$ and
$\phi _{w,\delta _{123},n,m}(u)$ and ![]() $\phi _{d,\delta _{123},n,m}(u)$ with respective to
$\phi _{d,\delta _{123},n,m}(u)$ with respective to ![]() $\delta _1$ can be calculated with Mathematica using the function “D”. Clearly, the moments in (4.1) and (4.2) can be used to compute (conditional) variance, covariance, and correlation. In general, the variance of
$\delta _1$ can be calculated with Mathematica using the function “D”. Clearly, the moments in (4.1) and (4.2) can be used to compute (conditional) variance, covariance, and correlation. In general, the variance of ![]() $X$ will be denoted by
$X$ will be denoted by ![]() $\text {Var}_{\text {ruin}}(X\,|\,u)= E_{\text {ruin}}[X^{2}\,|\,u]-(E_{\text {ruin}}[X\,|\,u])^{2}$, and the covariance between two random variables
$\text {Var}_{\text {ruin}}(X\,|\,u)= E_{\text {ruin}}[X^{2}\,|\,u]-(E_{\text {ruin}}[X\,|\,u])^{2}$, and the covariance between two random variables ![]() $X_1$ and
$X_1$ and ![]() $X_2$ is
$X_2$ is ![]() $\text {Cov}_{\text {ruin}}(X_1,X_2\,|\,u) =E_{\text {ruin}}[X_1X_2\,|\,u]-E_{\text {ruin}}[X_1\,|\,u]E_{\text {ruin}}[X_2\,|\,u]$. Consequently, the correlation is
$\text {Cov}_{\text {ruin}}(X_1,X_2\,|\,u) =E_{\text {ruin}}[X_1X_2\,|\,u]-E_{\text {ruin}}[X_1\,|\,u]E_{\text {ruin}}[X_2\,|\,u]$. Consequently, the correlation is ![]() $\text {Corr}_{\text {ruin}}(X_1,X_2\,|\,u) =\text {Cov}_{\text {ruin}}(X_1,X_2\,|\,u)/\sqrt {\text {Var}_{\text {ruin}}(X_1\,|\,u)\,\text {Var}_{\text {ruin}}(X_2\,|\,u)}$.
$\text {Corr}_{\text {ruin}}(X_1,X_2\,|\,u) =\text {Cov}_{\text {ruin}}(X_1,X_2\,|\,u)/\sqrt {\text {Var}_{\text {ruin}}(X_1\,|\,u)\,\text {Var}_{\text {ruin}}(X_2\,|\,u)}$.
For all numerical illustrations, we assume that the Poisson claim arrival rate is ![]() $\lambda =1$ and the volatility parameter associated with the Brownian motion is
$\lambda =1$ and the volatility parameter associated with the Brownian motion is ![]() $\sigma =1/\sqrt {2}=0.707$. We consider three different distributions for the claim amounts: (i) a sum of two independent exponentials (with means
$\sigma =1/\sqrt {2}=0.707$. We consider three different distributions for the claim amounts: (i) a sum of two independent exponentials (with means ![]() $2/3$ and
$2/3$ and ![]() $1/3$) with
$1/3$) with ![]() $p(y)=2(\frac {3}{2}e^{-\frac {3}{2}y})+(-1)(3e^{-3x})$; (ii) an exponential distribution with
$p(y)=2(\frac {3}{2}e^{-\frac {3}{2}y})+(-1)(3e^{-3x})$; (ii) an exponential distribution with ![]() $p(y)=e^{-y}$; and (iii) a mixture of two exponentials with
$p(y)=e^{-y}$; and (iii) a mixture of two exponentials with ![]() $p(y)=\frac {1}{3} (\frac {1}{2}e^{-\frac {1}{2}y})+\frac {2}{3}(2e^{-2y})$. These are labeled as “Sum Exp”, “Exp”, and “Mixed Exp”, respectively, in subsequent figures. All these distributions have the same mean of 1 but have different respective variances of 0.56, 1, and 2, and they all belong to the class of combinations of exponentials with density in the form of (3.1). Assuming a premium rate of
$p(y)=\frac {1}{3} (\frac {1}{2}e^{-\frac {1}{2}y})+\frac {2}{3}(2e^{-2y})$. These are labeled as “Sum Exp”, “Exp”, and “Mixed Exp”, respectively, in subsequent figures. All these distributions have the same mean of 1 but have different respective variances of 0.56, 1, and 2, and they all belong to the class of combinations of exponentials with density in the form of (3.1). Assuming a premium rate of ![]() $c=1.2$, the loading factor is
$c=1.2$, the loading factor is ![]() $\theta =20\%$.
$\theta =20\%$.
We begin with the total discounted claim amount ![]() $Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$, and its mean and variance (conditional on ruin) are given in Figure 1. First, for each claim distribution, Figure 1(a) shows that when
$Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$, and its mean and variance (conditional on ruin) are given in Figure 1. First, for each claim distribution, Figure 1(a) shows that when ![]() $u$ increases the mean
$u$ increases the mean ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ increases and then converges to some finite value. On the other hand, the variance
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ increases and then converges to some finite value. On the other hand, the variance ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ in Figure 1(b) is not monotone in
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ in Figure 1(b) is not monotone in ![]() $u$ but it still converges as
$u$ but it still converges as ![]() $u$ increases (see Remark 2). Indeed, in the absence of the diffusion component in the risk process, plots of very similar shape were also reported in Cheung [Reference Cheung8, Figs. 5–8] and Cheung et al. [Reference Cheung, Liu and Willmot14, Fig. 4(a) and (b)], although these works focused on renewal insurance risk models without and with upward jumps, respectively. Nevertheless, some probabilistic interpretation therein is also applicable. In particular, when the insurer starts with a higher initial capital
$u$ increases (see Remark 2). Indeed, in the absence of the diffusion component in the risk process, plots of very similar shape were also reported in Cheung [Reference Cheung8, Figs. 5–8] and Cheung et al. [Reference Cheung, Liu and Willmot14, Fig. 4(a) and (b)], although these works focused on renewal insurance risk models without and with upward jumps, respectively. Nevertheless, some probabilistic interpretation therein is also applicable. In particular, when the insurer starts with a higher initial capital ![]() $u$, the mean
$u$, the mean ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ would increase because a larger total nominal (i.e. before discounting) claim amount is required to ruin the surplus process. However, when
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ would increase because a larger total nominal (i.e. before discounting) claim amount is required to ruin the surplus process. However, when ![]() $u$ increases further, ruin of the surplus process occurs later but claims that occur late become insignificant when discounted. This explains why the curve levels off as
$u$ increases further, ruin of the surplus process occurs later but claims that occur late become insignificant when discounted. This explains why the curve levels off as ![]() $u$ gets large. Comparing across the three claim distributions, we note that while the resulting curves of
$u$ gets large. Comparing across the three claim distributions, we note that while the resulting curves of ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ are very close, the variance
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ are very close, the variance ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ appears to be ordered according to the variance of the claim amounts. The latter finding complements the results in Cheung [Reference Cheung8] and Cheung et al. [Reference Cheung, Liu and Willmot14], which suggested that
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ appears to be ordered according to the variance of the claim amounts. The latter finding complements the results in Cheung [Reference Cheung8] and Cheung et al. [Reference Cheung, Liu and Willmot14], which suggested that ![]() $Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$ is more likely to take on extreme values if the summand
$Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$ is more likely to take on extreme values if the summand ![]() $e^{-0.01 T_k}Y_k$ has a higher variability (due to an increase in variance of
$e^{-0.01 T_k}Y_k$ has a higher variability (due to an increase in variance of ![]() $Y_k$ in our case but due to an increase in variance of
$Y_k$ in our case but due to an increase in variance of ![]() $e^{-0.01 T_k}$ in Cheung [Reference Cheung8] and Cheung et al. [Reference Cheung, Liu and Willmot14]).
$e^{-0.01 T_k}$ in Cheung [Reference Cheung8] and Cheung et al. [Reference Cheung, Liu and Willmot14]).
Remark 2 For exponential claims, ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ and
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ and ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ have also been studied by Liu and Zhang [Reference Liu and Zhang28] under the same parameter setting. While our plot of
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ have also been studied by Liu and Zhang [Reference Liu and Zhang28] under the same parameter setting. While our plot of ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ in Figure 1(a) agrees their Figure 4(a), our
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ in Figure 1(a) agrees their Figure 4(a), our ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ in Figure 1(b) does not agree with their Figure 4(b). It is noted that Liu and Zhang [Reference Liu and Zhang28] have also plotted
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ in Figure 1(b) does not agree with their Figure 4(b). It is noted that Liu and Zhang [Reference Liu and Zhang28] have also plotted ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )<0\}}\,|\,u)$ and
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )<0\}}\,|\,u)$ and ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )=0\}}\,|\,u)$ against
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )=0\}}\,|\,u)$ against ![]() $u$. We have looked into this further and found that although their values of
$u$. We have looked into this further and found that although their values of ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )<0\}}\,|\,u)$ and
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )<0\}}\,|\,u)$ and ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )=0\}}\,|\,u)$ are correct (and can be reproduced using our results), they have mistakenly calculated
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )1_{\{U(\tau )=0\}}\,|\,u)$ are correct (and can be reproduced using our results), they have mistakenly calculated ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ as the sum of these two quantities. Our Figure 1(b) shows the correct plot of
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$ as the sum of these two quantities. Our Figure 1(b) shows the correct plot of ![]() $\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$.
$\text {Var}_{\text {ruin}}(Z_{0.01}(\tau )\,|\,u)$.

FIGURE 1. (a) Expectation and (b) variance of total discounted claims until ruin.
Next, we investigate the total discounted perturbation until ruin ![]() $B_{0.01}(\tau )=\int _0^{\tau } e^{-0.01 s}\,dB(s)$ which is a novel quantity that represents the present value of the small fluctuations arising from the uncertainties of the insurance business not explained by claims. Unlike the total discounted claim amount
$B_{0.01}(\tau )=\int _0^{\tau } e^{-0.01 s}\,dB(s)$ which is a novel quantity that represents the present value of the small fluctuations arising from the uncertainties of the insurance business not explained by claims. Unlike the total discounted claim amount ![]() $Z_{0.01}(\tau )$ which must be non-negative, the random variable
$Z_{0.01}(\tau )$ which must be non-negative, the random variable ![]() $B_{0.01}(\tau )$ may take on any values on the real line. As explained in Section 1, one expects
$B_{0.01}(\tau )$ may take on any values on the real line. As explained in Section 1, one expects ![]() $B_{0.01}(\tau )$ to be negative on average. In the definition (1.1), the total claims are subtracted from the surplus while the Brownian motion is added to the process (which is the usual convention). Therefore, for a fair comparison between the discounted claims and the discounted perturbation, it makes more sense to look at
$B_{0.01}(\tau )$ to be negative on average. In the definition (1.1), the total claims are subtracted from the surplus while the Brownian motion is added to the process (which is the usual convention). Therefore, for a fair comparison between the discounted claims and the discounted perturbation, it makes more sense to look at ![]() $-B_{0.01}(\tau )$ instead of
$-B_{0.01}(\tau )$ instead of ![]() $B_{0.01}(\tau )$ so that both
$B_{0.01}(\tau )$ so that both ![]() $Z_{0.01}(\tau )$ and
$Z_{0.01}(\tau )$ and ![]() $-B_{0.01}(\tau )$ correspond to discounted costs to the insurer (apart from a multiplicative factor of
$-B_{0.01}(\tau )$ correspond to discounted costs to the insurer (apart from a multiplicative factor of ![]() $\sigma =1/\sqrt {2}$ in the latter quantity). As expected, Figure 2(a) shows that the mean of
$\sigma =1/\sqrt {2}$ in the latter quantity). As expected, Figure 2(a) shows that the mean of ![]() $-B_{0.01}(\tau )$ is non-negative (see Remark 3). Under the current parameter setting,
$-B_{0.01}(\tau )$ is non-negative (see Remark 3). Under the current parameter setting, ![]() $E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is of smaller magnitude than
$E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is of smaller magnitude than ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$, meaning that the usual claims result in a higher discounted cost to the insurer until ruin. Moreover, for each claim distribution,
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$, meaning that the usual claims result in a higher discounted cost to the insurer until ruin. Moreover, for each claim distribution, ![]() $E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is increasing in
$E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is increasing in ![]() $u$ and converges as
$u$ and converges as ![]() $u$ gets large, and similar explanations to those for
$u$ gets large, and similar explanations to those for ![]() $E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ are applicable. For a given initial surplus
$E_{\text {ruin}}[Z_{0.01}(\tau )\,|\,u]$ are applicable. For a given initial surplus ![]() $u$, it is interesting to note that
$u$, it is interesting to note that ![]() $E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is larger when the claim amount has a smaller variance. This may be explained as follows. A separate plot (which is omitted here for brevity) reveals that the ruin probability
$E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$ is larger when the claim amount has a smaller variance. This may be explained as follows. A separate plot (which is omitted here for brevity) reveals that the ruin probability ![]() $\psi (u)$ is ordered according to the variance of the claim distribution. In other words, when the claim variance is smaller, the ruin set
$\psi (u)$ is ordered according to the variance of the claim distribution. In other words, when the claim variance is smaller, the ruin set ![]() $\{\tau <\infty \}$ (for the same fixed
$\{\tau <\infty \}$ (for the same fixed ![]() $u$) becomes smaller because it is more difficult for the surplus process to get ruined with the claims less likely to be large. Consequently, sample paths where the perturbation has been favorable to the insurance business are excluded from the ruin set, resulting in a higher value of
$u$) becomes smaller because it is more difficult for the surplus process to get ruined with the claims less likely to be large. Consequently, sample paths where the perturbation has been favorable to the insurance business are excluded from the ruin set, resulting in a higher value of ![]() $E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$. Turning to Figure 2(b), the variance
$E_{\text {ruin}}[-B_{0.01}(\tau )\,|\,u]$. Turning to Figure 2(b), the variance ![]() $\text {Var}_{\text {ruin}}(-B_{0.01}(\tau )\,|\,u)$ increases with
$\text {Var}_{\text {ruin}}(-B_{0.01}(\tau )\,|\,u)$ increases with ![]() $u$ but does not seem to be sensitive to the choice of the claim distribution.
$u$ but does not seem to be sensitive to the choice of the claim distribution.
Remark 3 We have also plotted the conditional mean of ![]() $-B_{0.01}(\tau )$ separately for ruin occurrence due to a claim (given by (
$-B_{0.01}(\tau )$ separately for ruin occurrence due to a claim (given by (![]() $-\phi _{w,\delta _{123},1,0}(u)/\phi _{w,\delta _{123},0,0}(u))|_{\delta _1=0}$) and for ruin occurrence due to oscillation (given by
$-\phi _{w,\delta _{123},1,0}(u)/\phi _{w,\delta _{123},0,0}(u))|_{\delta _1=0}$) and for ruin occurrence due to oscillation (given by ![]() $(-\phi _{d,\delta _{123},1,0}(u)/\phi _{d,\delta _{123},0,0}(u))|_{\delta _1=0}$). While the plots are not reproduced here, it is remarked that they both look almost the same as Figure 2(a). This suggests that the conditional mean of
$(-\phi _{d,\delta _{123},1,0}(u)/\phi _{d,\delta _{123},0,0}(u))|_{\delta _1=0}$). While the plots are not reproduced here, it is remarked that they both look almost the same as Figure 2(a). This suggests that the conditional mean of ![]() $-B_{0.01}(\tau )$ is insensitive to the cause of ruin. Similar comments also apply to
$-B_{0.01}(\tau )$ is insensitive to the cause of ruin. Similar comments also apply to ![]() $Z_{0.01}(\tau )$, and in particular it is found that the conditional mean of
$Z_{0.01}(\tau )$, and in particular it is found that the conditional mean of ![]() $Z_{0.01}(\tau )$ for either cause of ruin is almost identical to Figure 1(a). Intuitively, when ruin occurs by diffusion (resp. a claim), it simply means that the diffusion (resp. a claim) drags down the surplus process at the ruin time, but taking into account the time value of money such contribution to
$Z_{0.01}(\tau )$ for either cause of ruin is almost identical to Figure 1(a). Intuitively, when ruin occurs by diffusion (resp. a claim), it simply means that the diffusion (resp. a claim) drags down the surplus process at the ruin time, but taking into account the time value of money such contribution to ![]() $-B_{0.01}(\tau )$ (resp.
$-B_{0.01}(\tau )$ (resp. ![]() $Z_{0.01}(\tau )$) is rather minimal.
$Z_{0.01}(\tau )$) is rather minimal.

FIGURE 2. (a) Expectation and (b) variance of total discounted perturbation until ruin.
We now focus on the covariance between ![]() $Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$ and
$Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$ and ![]() $\tau$. For each claim distribution, it is observed from Figure 3(a) that as
$\tau$. For each claim distribution, it is observed from Figure 3(a) that as ![]() $u$ increases, the covariance first increases from zero until it reaches a maximum and then it decreases and turns negative. A similar pattern is also evident in Cheung and Woo [Reference Cheung and Woo11] who analyzed a dependent renewal risk model without diffusion, and the change in sign of the covariance may be interpreted in a similar way as follows. For a given initial surplus level
$u$ increases, the covariance first increases from zero until it reaches a maximum and then it decreases and turns negative. A similar pattern is also evident in Cheung and Woo [Reference Cheung and Woo11] who analyzed a dependent renewal risk model without diffusion, and the change in sign of the covariance may be interpreted in a similar way as follows. For a given initial surplus level ![]() $u$, if
$u$, if ![]() $\tau$ is on the higher end (above its mean), then there are possibly two opposing effects to the total discounted claim amount
$\tau$ is on the higher end (above its mean), then there are possibly two opposing effects to the total discounted claim amount ![]() $Z_{0.01}(\tau )$. On the one hand, the amount of premium collected before ruin, namely
$Z_{0.01}(\tau )$. On the one hand, the amount of premium collected before ruin, namely ![]() $c\tau$, is higher and hence the total claim amount
$c\tau$, is higher and hence the total claim amount ![]() $\sum _{k=1}^{N(\tau )} Y_k$ (without discounting) is likely to be higher in order to cause ruin. On the other hand, when ruin happens at a later time, the afore-mentioned claims occur throughout a longer period (and large claims would not have occurred early otherwise these would have caused early ruin), and therefore discounting will have a negative effect on
$\sum _{k=1}^{N(\tau )} Y_k$ (without discounting) is likely to be higher in order to cause ruin. On the other hand, when ruin happens at a later time, the afore-mentioned claims occur throughout a longer period (and large claims would not have occurred early otherwise these would have caused early ruin), and therefore discounting will have a negative effect on ![]() $Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$. Our numerical results suggest that the latter effect is dominant as
$Z_{0.01}(\tau )=\sum _{k=1}^{N(\tau )}e^{-0.01 T_k}Y_k$. Our numerical results suggest that the latter effect is dominant as ![]() $u$ is over a certain threshold (around 70 in our example), which is not surprising because the effect of discounting is getting more significant as
$u$ is over a certain threshold (around 70 in our example), which is not surprising because the effect of discounting is getting more significant as ![]() $e^{-0.01 T_k}$ decreases exponentially in the
$e^{-0.01 T_k}$ decreases exponentially in the ![]() $k$th claim arrival time. While the absolute value of
$k$th claim arrival time. While the absolute value of ![]() $\text {Cov}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ appears to increase with the claim variance for most values of
$\text {Cov}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ appears to increase with the claim variance for most values of ![]() $u$, the corresponding correlation depicted in Figure 3(b) is rather insensitive to the claim distribution. Interestingly,
$u$, the corresponding correlation depicted in Figure 3(b) is rather insensitive to the claim distribution. Interestingly, ![]() $\text {Corr}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ can be as high as 0.9 for small values of
$\text {Corr}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ can be as high as 0.9 for small values of ![]() $u$, indicating strong positive dependence (and almost linear relationship) in such cases.
$u$, indicating strong positive dependence (and almost linear relationship) in such cases.

FIGURE 3. (a) Covariance and (b) correlation between discounted claims and ruin time.
Turning our attention to the covariance between ![]() $-B_{0.01}(\tau )$ and
$-B_{0.01}(\tau )$ and ![]() $\tau$, we see from Figure 4(a) that
$\tau$, we see from Figure 4(a) that ![]() $\text {Cov}_{\text {ruin}}(-B_{0.01}(\tau ),\tau \,|\,u)$ changes from positive to negative as
$\text {Cov}_{\text {ruin}}(-B_{0.01}(\tau ),\tau \,|\,u)$ changes from positive to negative as ![]() $u$ reaches around 20. It is noted that the magnitude of
$u$ reaches around 20. It is noted that the magnitude of ![]() $\text {Corr}_{\text {ruin}}(-B_{0.01}(\tau ),\tau \,|\,u)$ in Figure 4(b) is smaller than that of
$\text {Corr}_{\text {ruin}}(-B_{0.01}(\tau ),\tau \,|\,u)$ in Figure 4(b) is smaller than that of ![]() $\text {Corr}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ in Figure 3(b) for most values of
$\text {Corr}_{\text {ruin}}(Z_{0.01}(\tau ),\tau \,|\,u)$ in Figure 3(b) for most values of ![]() $u$, indicating that the ruin time has a stronger relationship with the discounted claim amount than with the discounted perturbation. Finally, the covariance and the correlation between
$u$, indicating that the ruin time has a stronger relationship with the discounted claim amount than with the discounted perturbation. Finally, the covariance and the correlation between ![]() $-B_{0.01}(\tau )$ and
$-B_{0.01}(\tau )$ and ![]() $Z_{0.01}(\tau )$ are given in Figure 5, and these values are mostly negative (except for small values of
$Z_{0.01}(\tau )$ are given in Figure 5, and these values are mostly negative (except for small values of ![]() $u$). A possible explanation for such negative correlation is as follows. For a given initial surplus
$u$). A possible explanation for such negative correlation is as follows. For a given initial surplus ![]() $u$, we consider sample paths where ruin occurs and it is clear from (1.1) that one has the relationship
$u$, we consider sample paths where ruin occurs and it is clear from (1.1) that one has the relationship
 $$u+c\tau+|U(\tau)|=\sum_{k=1}^{N(\tau)}Y_k+\sigma({-}B(\tau))\text{ on the set } \{\tau<\infty\}$$
$$u+c\tau+|U(\tau)|=\sum_{k=1}^{N(\tau)}Y_k+\sigma({-}B(\tau))\text{ on the set } \{\tau<\infty\}$$among the random variables ![]() $\sum _{k=1}^{N(\tau )}Y_k$ and
$\sum _{k=1}^{N(\tau )}Y_k$ and ![]() $-B(\tau )$ (which are the counterparts of
$-B(\tau )$ (which are the counterparts of ![]() $Z_{0.01}(\tau )$ and
$Z_{0.01}(\tau )$ and ![]() $-B_{0.01}(\tau )$ without discounting). While the deficit at ruin
$-B_{0.01}(\tau )$ without discounting). While the deficit at ruin ![]() $|U(\tau )|$ (if positive) is part of the total claim amount
$|U(\tau )|$ (if positive) is part of the total claim amount ![]() $\sum _{k=1}^{N(\tau )}Y_k$, the amount
$\sum _{k=1}^{N(\tau )}Y_k$, the amount ![]() $u+c\tau$ on the left-hand side is split between
$u+c\tau$ on the left-hand side is split between ![]() $\sum _{k=1}^{N(\tau )}Y_k$ and
$\sum _{k=1}^{N(\tau )}Y_k$ and ![]() $\sigma (-B(\tau ))$. Conditional on the value of
$\sigma (-B(\tau ))$. Conditional on the value of ![]() $\tau$, this constraint somehow limits how large (or how small) both
$\tau$, this constraint somehow limits how large (or how small) both ![]() $\sum _{k=1}^{N(\tau )}Y_k$ and
$\sum _{k=1}^{N(\tau )}Y_k$ and ![]() $-B(\tau )$ can be and may have a tendency to lead these quantities to opposite direction. Such tendency is also translated to the discounted versions
$-B(\tau )$ can be and may have a tendency to lead these quantities to opposite direction. Such tendency is also translated to the discounted versions ![]() $Z_{0.01}(\tau )$ and
$Z_{0.01}(\tau )$ and ![]() $-B_{0.01}(\tau )$. It is interesting to note that the covariance and the correlation between
$-B_{0.01}(\tau )$. It is interesting to note that the covariance and the correlation between ![]() $Z_{0.01}(\tau )$ and
$Z_{0.01}(\tau )$ and ![]() $-B_{0.01}(\tau )$ converge to zero as the initial surplus level
$-B_{0.01}(\tau )$ converge to zero as the initial surplus level ![]() $u$ tends to infinity. When claims follow a combination of exponentials, this can be proved analytically as follows. First we recall that
$u$ tends to infinity. When claims follow a combination of exponentials, this can be proved analytically as follows. First we recall that
 \begin{align} \text{Cov}_{\text{ruin}}({-}B_{\delta_2}(\tau),Z_{\delta_3}(\tau)\,|\,u)& = \left\{\left(\frac{\phi_{w,\delta_{123},1,0}(u)+\phi_{d,\delta_{123},1,0}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right) \left(\frac{\phi_{w,\delta_{123},0,1}(u)+\phi_{d,\delta_{123},0,1}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right)\right.\nonumber\\ & \quad \left.\left.- \frac{\phi_{w,\delta_{123},1,1}(u)+\phi_{d,\delta_{123},1,1}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right\}\right|_{\delta_1=0}. \end{align}
\begin{align} \text{Cov}_{\text{ruin}}({-}B_{\delta_2}(\tau),Z_{\delta_3}(\tau)\,|\,u)& = \left\{\left(\frac{\phi_{w,\delta_{123},1,0}(u)+\phi_{d,\delta_{123},1,0}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right) \left(\frac{\phi_{w,\delta_{123},0,1}(u)+\phi_{d,\delta_{123},0,1}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right)\right.\nonumber\\ & \quad \left.\left.- \frac{\phi_{w,\delta_{123},1,1}(u)+\phi_{d,\delta_{123},1,1}(u)}{\phi_{w,\delta_{123},0,0}(u)+\phi_{d,\delta_{123},0,0}(u)}\right\}\right|_{\delta_1=0}. \end{align}In the upcoming discussion, it is sufficient to assume ![]() $\delta _1=0$ (while
$\delta _1=0$ (while ![]() $\delta _2,\delta _3>0$). For each
$\delta _2,\delta _3>0$). For each ![]() $i,j\in \mathbb {N}$, we denote
$i,j\in \mathbb {N}$, we denote ![]() $-R_{i,j,1}$ to be the root of the Lundberg's equation (2.1) with the least negative real part (among the roots
$-R_{i,j,1}$ to be the root of the Lundberg's equation (2.1) with the least negative real part (among the roots ![]() $\{-R_{i,j,k}\}_{k=1}^{r+1}$). The quantity
$\{-R_{i,j,k}\}_{k=1}^{r+1}$). The quantity ![]() $R_{i,j,1}$ is called the adjustment coefficient and is known to be real (e.g. [Reference Gerber and Landry22,Reference Tsai and Willmot34]). In particular, it can be shown that
$R_{i,j,1}$ is called the adjustment coefficient and is known to be real (e.g. [Reference Gerber and Landry22,Reference Tsai and Willmot34]). In particular, it can be shown that ![]() $R_{i,j,1}$ is increasing in
$R_{i,j,1}$ is increasing in ![]() $i\delta _2+j\delta _3$. Therefore, one has
$i\delta _2+j\delta _3$. Therefore, one has ![]() $R_{0,0,1}< R_{i,j,1}$ for
$R_{0,0,1}< R_{i,j,1}$ for ![]() $(i,j)\in \mathbb {N}\times \mathbb {N}\setminus \{(0,0)\}$. Consequently, the dominant term in (3.7) (resp. (3.19)) must be the exponential term
$(i,j)\in \mathbb {N}\times \mathbb {N}\setminus \{(0,0)\}$. Consequently, the dominant term in (3.7) (resp. (3.19)) must be the exponential term ![]() $B_{w,n,m,0,0,1} e^{-R_{0,0,1}u}$ (resp.
$B_{w,n,m,0,0,1} e^{-R_{0,0,1}u}$ (resp. ![]() $B_{d,n,m,0,0,1} e^{-R_{0,0,1}u}$) and thus taking limit in (4.3) yields
$B_{d,n,m,0,0,1} e^{-R_{0,0,1}u}$) and thus taking limit in (4.3) yields
 \begin{align} & \lim_{u\to\infty}\text{Cov}_{\text{ruin}}({-}B_{\delta_2}(\tau),Z_{\delta_3}(\tau)\,|\,u)\nonumber\\ & \quad =\left(\frac{B_{w,1,0,0,0,1}+B_{d,1,0,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\right) \left(\frac{B_{w,0,1,0,0,1}+B_{d,0,1,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\right) -\frac{B_{w,1,1,0,0,1}+B_{d,1,1,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\nonumber\\ & \quad=\left(\frac{B^{*}_{1,0,0,0,1}}{B^{*}_{0,0,0,0,1}}\right) \left(\frac{B^{*}_{0,1,0,0,1}}{B^{*}_{0,0,0,0,1}}\right) - \frac{B^{*}_{1,1,0,0,1}}{B^{*}_{0,0,0,0,1}}, \end{align}
\begin{align} & \lim_{u\to\infty}\text{Cov}_{\text{ruin}}({-}B_{\delta_2}(\tau),Z_{\delta_3}(\tau)\,|\,u)\nonumber\\ & \quad =\left(\frac{B_{w,1,0,0,0,1}+B_{d,1,0,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\right) \left(\frac{B_{w,0,1,0,0,1}+B_{d,0,1,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\right) -\frac{B_{w,1,1,0,0,1}+B_{d,1,1,0,0,1}}{B_{w,0,0,0,0,1}+B_{d,0,0,0,0,1}}\nonumber\\ & \quad=\left(\frac{B^{*}_{1,0,0,0,1}}{B^{*}_{0,0,0,0,1}}\right) \left(\frac{B^{*}_{0,1,0,0,1}}{B^{*}_{0,0,0,0,1}}\right) - \frac{B^{*}_{1,1,0,0,1}}{B^{*}_{0,0,0,0,1}}, \end{align}where for convenience we have defined ![]() $B^{*}_{n,m,0,0,1}=B_{w,n,m,0,0,1}+B_{d,n,m,0,0,1}$ for
$B^{*}_{n,m,0,0,1}=B_{w,n,m,0,0,1}+B_{d,n,m,0,0,1}$ for ![]() $n,m\in \mathbb {N}$. Note that the recursive formulas (3.8) and (3.20) satisfied by
$n,m\in \mathbb {N}$. Note that the recursive formulas (3.8) and (3.20) satisfied by ![]() $B_{w,n,m,0,0,1}$ and
$B_{w,n,m,0,0,1}$ and ![]() $B_{d,n,m,0,0,1}$ are of identical form (albeit different initial conditions). This implies
$B_{d,n,m,0,0,1}$ are of identical form (albeit different initial conditions). This implies ![]() $B^{*}_{n,m,0,0,1}$ also satisfies the same recursive formula and this results in
$B^{*}_{n,m,0,0,1}$ also satisfies the same recursive formula and this results in
 \begin{align*} B^{*}_{1,1,0,0,1} & = \frac{1}{\delta_2+\delta_3}\left(-\sigma R_{0,0,1} B^{*}_{0,1,0,0,1} +\lambda \sum_{l=1}^{r}\frac{B^{*}_{1,0,0,0,1}q_l \beta_l}{(\beta_l-R_{0,0,1})^{2}}\right),\\ B^{*}_{1,0,0,0,1} & = \frac{1}{\delta_2}\left(-\sigma R_{0,0,1} B^{*}_{0,0,0,0,1} \right), \end{align*}
\begin{align*} B^{*}_{1,1,0,0,1} & = \frac{1}{\delta_2+\delta_3}\left(-\sigma R_{0,0,1} B^{*}_{0,1,0,0,1} +\lambda \sum_{l=1}^{r}\frac{B^{*}_{1,0,0,0,1}q_l \beta_l}{(\beta_l-R_{0,0,1})^{2}}\right),\\ B^{*}_{1,0,0,0,1} & = \frac{1}{\delta_2}\left(-\sigma R_{0,0,1} B^{*}_{0,0,0,0,1} \right), \end{align*}and
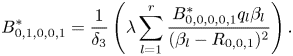 $$B^{*}_{0,1,0,0,1} = \frac{1}{\delta_3}\left(\lambda \sum_{l=1}^{r}\frac{B^{*}_{0,0,0,0,1}q_l \beta_l}{(\beta_l-R_{0,0,1})^{2}}\right).$$
$$B^{*}_{0,1,0,0,1} = \frac{1}{\delta_3}\left(\lambda \sum_{l=1}^{r}\frac{B^{*}_{0,0,0,0,1}q_l \beta_l}{(\beta_l-R_{0,0,1})^{2}}\right).$$Using the above three equations, it is straightforward to show that the right-hand side of (4.4) equals zero.
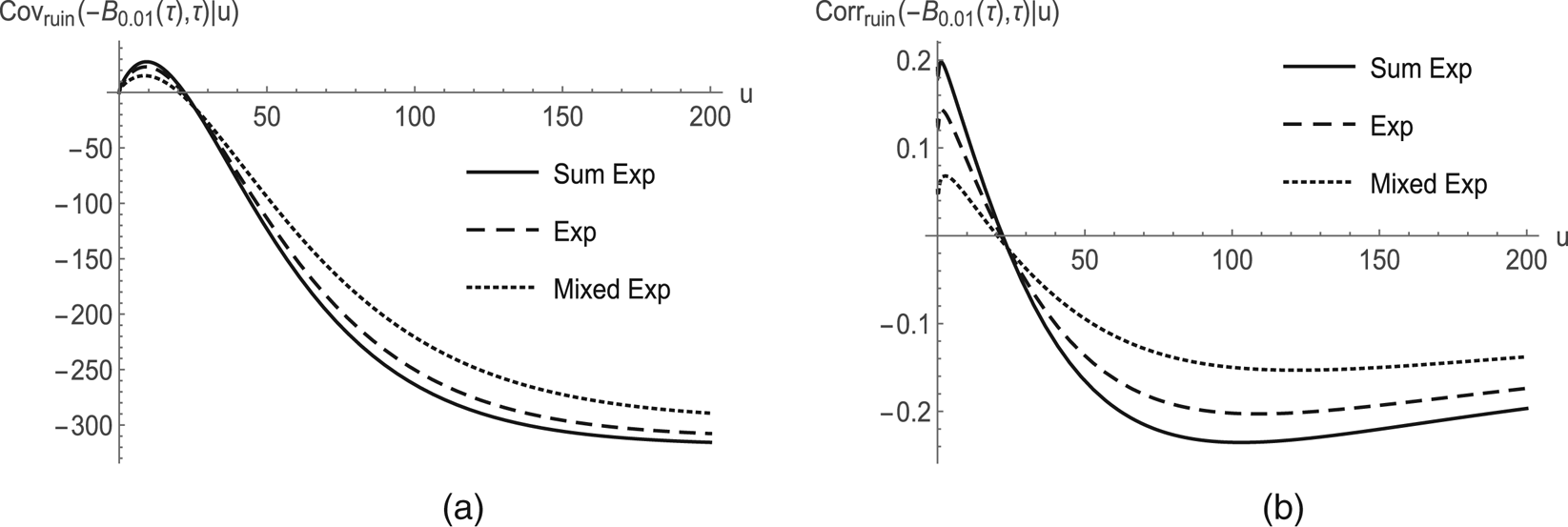
FIGURE 4. (a) Covariance and (b) correlation between discounted perturbation and ruin time.

FIGURE 5. (a) Covariance and (b) correlation between discounted perturbation and discounted claims.
Acknowledgments
The authors would like to thank the anonymous reviewers for helpful comments and suggestions which improved an earlier version of the manuscript. Eric Cheung gratefully acknowledges the support from the Australian Research Council's Discovery Project (DP200100615). The views expressed herein are those of the authors and are not necessarily those of the Australian Research Council.
Competing interest
The authors declare no conflict of interest.








