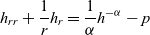1. Introduction
The equation
has been used to model the dynamics of long-wave unstable thin films of viscous fluids. Here h is the thickness of the thin film and the nonlinear mobility is given by
with
![]() $\lambda\geq0,$
$\lambda\geq0,$
![]() $n>0$
, and
$n>0$
, and
![]() $b\in\left( 0,3\right) $
where
$b\in\left( 0,3\right) $
where
![]() $\lambda=0$
corresponds to the no-slip boundary condition. And we assume the pressure
$\lambda=0$
corresponds to the no-slip boundary condition. And we assume the pressure
where
![]() $\alpha>1$
is a sum of contributions from disjointing pressure due to an attractive van der Waals force and a linearised curvature term corresponding to surface tension effects.
$\alpha>1$
is a sum of contributions from disjointing pressure due to an attractive van der Waals force and a linearised curvature term corresponding to surface tension effects.
With different formulations of coefficient M(h) and pressure p, equation (1.1) could model thin film under various practical physical forces and boundary conditions between fluid and the solid surface. For
![]() $M(h) = h$
and
$M(h) = h$
and
![]() $\alpha= -1$
, it models the thin film in a gravity-driven Hele-Shaw cell [Reference Almgren, Bertozzi and Brenner1, Reference Constantin, Dupont, Goldstein, Kadanoff, Shelley and Zhou9, Reference Dupont, Goldstein, Kadanoff and Zhou10, Reference Goldstein, Pesci and Shelley12]. For
$\alpha= -1$
, it models the thin film in a gravity-driven Hele-Shaw cell [Reference Almgren, Bertozzi and Brenner1, Reference Constantin, Dupont, Goldstein, Kadanoff, Shelley and Zhou9, Reference Dupont, Goldstein, Kadanoff and Zhou10, Reference Goldstein, Pesci and Shelley12]. For
![]() $M(h) = h^{3}$
and
$M(h) = h^{3}$
and
![]() $\alpha= -3$
, it models the fluid droplet hanging from a ceiling [Reference Ehrhard11]. The existence and evolution of solutions to thin-film equations have been studied by a lot of authors [Reference Barenblatt, Beretta and Bertsch2, Reference Beretta3, Reference Bertozzi, Grün and Witelski4, Reference Bertozzi and Pugh5, Reference Bertozzi6, Reference Bertsch, Dal Passo, Garcke and Grün7, Reference Chen and Jiang8, Reference Jiang14, Reference Jiang and Lin15, 24, Reference Witelski and Bernoff25, Reference Witelski and Bernoff26]. Also, extensive mathematical analysis has been made for the steady states on the above thin-film equation in one-dimensional space [Reference Laugesen and Pugh18, Reference Laugesen and Pugh19, Reference Laugesen and Pugh20, Reference Laugesen and Pugh21].
$\alpha= -3$
, it models the fluid droplet hanging from a ceiling [Reference Ehrhard11]. The existence and evolution of solutions to thin-film equations have been studied by a lot of authors [Reference Barenblatt, Beretta and Bertsch2, Reference Beretta3, Reference Bertozzi, Grün and Witelski4, Reference Bertozzi and Pugh5, Reference Bertozzi6, Reference Bertsch, Dal Passo, Garcke and Grün7, Reference Chen and Jiang8, Reference Jiang14, Reference Jiang and Lin15, 24, Reference Witelski and Bernoff25, Reference Witelski and Bernoff26]. Also, extensive mathematical analysis has been made for the steady states on the above thin-film equation in one-dimensional space [Reference Laugesen and Pugh18, Reference Laugesen and Pugh19, Reference Laugesen and Pugh20, Reference Laugesen and Pugh21].
Back to thin-film equation driven by van der Waals force, we consider viscous fluids in a cylindrical container whose bottom is represented by
![]() $\Omega$
, a bounded smooth domain in
$\Omega$
, a bounded smooth domain in
![]() $\mathbb{R}^{2}$
. Since there is no flux across the boundary, we have the Neumann boundary condition
$\mathbb{R}^{2}$
. Since there is no flux across the boundary, we have the Neumann boundary condition
We also ignore the wetting or non-wetting effect and assume that the fluid surface is orthogonal to the boundary of the container, i.e.
Let
be the associated energy functional to (1.1). Formally, using (1.1) and the boundary conditions (1.3) (1.4), we have
 \begin{align*}\frac{d}{dt}E(h) & =\int_{\Omega}\nabla h\nabla h_{t}+\frac{1}{\alpha}h^{-\alpha}h_{t}\\[3pt]
& =\int_{\Omega}\left( -\Delta h+\frac{1}{\alpha}h^{-\alpha}\right) h_{t}\\[3pt]
& =\int_{\Omega}p \nabla\cdot\left( M(h) \nabla p\right) \\[3pt]
& =-\int_{\Omega}M(h) \left\vert \nabla p\right\vert ^{2}\leq0.\end{align*}
\begin{align*}\frac{d}{dt}E(h) & =\int_{\Omega}\nabla h\nabla h_{t}+\frac{1}{\alpha}h^{-\alpha}h_{t}\\[3pt]
& =\int_{\Omega}\left( -\Delta h+\frac{1}{\alpha}h^{-\alpha}\right) h_{t}\\[3pt]
& =\int_{\Omega}p \nabla\cdot\left( M(h) \nabla p\right) \\[3pt]
& =-\int_{\Omega}M(h) \left\vert \nabla p\right\vert ^{2}\leq0.\end{align*}
Hence, for a thin-film fluid at rest, the pressure p has to be a constant, and h satisfies the elliptic equation (1.2) with the Neumann boundary condition (1.4).
In physical experiments, usually the total volume of the fluid is a known parameter, i.e.
is given. Therefore for any given
![]() $\bar{h}>0$
, we need to find a function h and an unknown constant p satisfying
$\bar{h}>0$
, we need to find a function h and an unknown constant p satisfying
 \begin{equation}\left\{\begin{array}{c}\Delta h=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ \Omega,\\ \\[-7pt]
\dfrac{1}{\left\vert \Omega\right\vert }\int_{\Omega}h(x)dx=\bar{h},\\ \\[-7pt]
\dfrac{\partial h}{\partial\nu}=0\ \ \ \ \ \ \ \ \ \text{on}\ \ \partial\Omega.\end{array}\right. \end{equation}
\begin{equation}\left\{\begin{array}{c}\Delta h=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ \Omega,\\ \\[-7pt]
\dfrac{1}{\left\vert \Omega\right\vert }\int_{\Omega}h(x)dx=\bar{h},\\ \\[-7pt]
\dfrac{\partial h}{\partial\nu}=0\ \ \ \ \ \ \ \ \ \text{on}\ \ \partial\Omega.\end{array}\right. \end{equation}
Obviously,
![]() $h\equiv\bar{h}$
with
$h\equiv\bar{h}$
with
![]() $p=\frac{1}{\alpha}\bar{h}^{-\alpha}$
is always a solution. However, the solutions are not unique even if we restrict to radially symmetric thin-film distributions.
$p=\frac{1}{\alpha}\bar{h}^{-\alpha}$
is always a solution. However, the solutions are not unique even if we restrict to radially symmetric thin-film distributions.
For equation (1.6) without the volume constraint, Jiang and Ni [Reference Jiang and Ni17] have provided a complete description to the radial solution with
![]() $h(0)=\eta$
. The existence of radial rupture solution in our physical dimension space
$h(0)=\eta$
. The existence of radial rupture solution in our physical dimension space
![]() $\mathbb{R}^{2}$
has been extended to a larger class of equations in [Reference Jiang and Miloua16]. Guo et al. [Reference Guo, Ye and Zhou13] have obtained a singular solution in
$\mathbb{R}^{2}$
has been extended to a larger class of equations in [Reference Jiang and Miloua16]. Guo et al. [Reference Guo, Ye and Zhou13] have obtained a singular solution in
![]() $\mathbb{R}^{N}$
with
$\mathbb{R}^{N}$
with
![]() $N\geq3$
.
$N\geq3$
.
Let
![]() $\left\{ r_{k}^{\ast}\right\} $
be the increasing divergent sequence of all positive critical points of
$\left\{ r_{k}^{\ast}\right\} $
be the increasing divergent sequence of all positive critical points of
which is known as the Bessel’s function of the first kind with order 0.
Theorem 1. Let
![]() $\Omega=B_{1}(0)$
be the unit disk in
$\Omega=B_{1}(0)$
be the unit disk in
![]() $\mathbb{R}^{2}$
. Given
$\mathbb{R}^{2}$
. Given
![]() $\bar{h}>0$
. Let
$\bar{h}>0$
. Let
Then for any
![]() $k\geq K$
, (1.6) admits a radially symmetric solution
$k\geq K$
, (1.6) admits a radially symmetric solution
![]() $\left( h_{k},p_{k}\right) $
such that
$\left( h_{k},p_{k}\right) $
such that
![]() $h_{k}$
has exactly k critical points for
$h_{k}$
has exactly k critical points for
![]() $r\in\left( 0,1\right] $
. In particular, there are infinitely many radially symmetric solutions to (1.6) for any given
$r\in\left( 0,1\right] $
. In particular, there are infinitely many radially symmetric solutions to (1.6) for any given
![]() $\bar{h}>0$
.
$\bar{h}>0$
.
We remark here that K is finite since
![]() $\lim_{k\rightarrow\infty}(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}=0$
.
$\lim_{k\rightarrow\infty}(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}=0$
.
An early version of the result is also presented in the third author’s thesis [Reference Liu22].
This result provides an answer to the question raised in [Reference Jiang and Ni17] by the second author and W. Ni on the number of solutions with given mass constraint. Our result is interesting since it seems rare to have a mass constraint elliptic problem to have infinitely many symmetric solutions.
We also want to compare our result with an interesting uniqueness result by M. del Pino and G. Hernandez which implies
Proposition 1. [Reference Pino and Hernandez23] There exists a constant
![]() $p_{0}$
, such that for any
$p_{0}$
, such that for any
![]() $0< p\leq p_{0}$
, constant solution
$0< p\leq p_{0}$
, constant solution
![]() $h\equiv( \alpha p )^{-\frac{1}{\alpha}}$
is the only radial solution of the Neumann boundary value problem
$h\equiv( \alpha p )^{-\frac{1}{\alpha}}$
is the only radial solution of the Neumann boundary value problem
 \begin{align*}\Delta h & =\frac{1}{\alpha}h^{-\alpha}-p\ \text{in}\ B_{1}(0) ,\\[3pt]
\frac{\partial h}{\partial\nu} & =0\text{ on }\partial B_{1}(0) .\end{align*}
\begin{align*}\Delta h & =\frac{1}{\alpha}h^{-\alpha}-p\ \text{in}\ B_{1}(0) ,\\[3pt]
\frac{\partial h}{\partial\nu} & =0\text{ on }\partial B_{1}(0) .\end{align*}
Hence, any nontrivial radial solutions to (1.6) must satisfy
![]() $p>p_{0}$
. Since
$p>p_{0}$
. Since
naively, large p implies small h. We may ask about the existence of a critical average film thickness
![]() $\bar{h}_{0}$
so that there is no nontrivial solutions to (1.6) whenever
$\bar{h}_{0}$
so that there is no nontrivial solutions to (1.6) whenever
![]() $h>\bar{h}_{0}$
. Our result shows such
$h>\bar{h}_{0}$
. Our result shows such
![]() $\bar{h}_{0}$
does not exist. Physically, when the film is thick enough, we do expect that it will be evenly distributed. Our result suggests that either the equation we are using could not accurately describe the thin film which is not too thin or the nontrivial solutions we constructed are highly unstable. We will investigate the linear and nonlinear stability of the steady states in future researches.
$\bar{h}_{0}$
does not exist. Physically, when the film is thick enough, we do expect that it will be evenly distributed. Our result suggests that either the equation we are using could not accurately describe the thin film which is not too thin or the nontrivial solutions we constructed are highly unstable. We will investigate the linear and nonlinear stability of the steady states in future researches.
The paper is organised in the following manner: we will first discuss the scaling property of global radial solutions following the framework of [Reference Jiang and Ni17]. It was shown that all non-constant radial solutions to (1.6) with assumption
![]() $p=\frac{1}{\alpha}$
and without volume constraint form a two parameter family
$p=\frac{1}{\alpha}$
and without volume constraint form a two parameter family
![]() $h^{\eta,k}$
where
$h^{\eta,k}$
where
![]() $\eta:=h(0)\in\left[ 0,1\right) \cup\left( 1,\infty\right) $
and
$\eta:=h(0)\in\left[ 0,1\right) \cup\left( 1,\infty\right) $
and
![]() $k\in\mathbb{N}$
is the number of critical points. We remark here that the case
$k\in\mathbb{N}$
is the number of critical points. We remark here that the case
![]() $\eta=1$
is special since it corresponds to the constant solution. We will prove Theorem 1 while postponing the analysis of asymptotic behaviour of
$\eta=1$
is special since it corresponds to the constant solution. We will prove Theorem 1 while postponing the analysis of asymptotic behaviour of
![]() $h^{\eta,k}$
to later sections: We consider the limit behaviours of
$h^{\eta,k}$
to later sections: We consider the limit behaviours of
![]() $h^{\eta,k}$
as
$h^{\eta,k}$
as
![]() $\eta\rightarrow1$
in Section 3 and as
$\eta\rightarrow1$
in Section 3 and as
![]() $\eta\rightarrow\infty$
in Sections 4 and 5 to obtain the dependency of average thickness
$\eta\rightarrow\infty$
in Sections 4 and 5 to obtain the dependency of average thickness
![]() $\bar{h}=\bar{h}^{\eta,k}$
on initial value
$\bar{h}=\bar{h}^{\eta,k}$
on initial value
![]() $\eta$
. In Section 6, we discuss some properties of blowing down limit profile of
$\eta$
. In Section 6, we discuss some properties of blowing down limit profile of
![]() $h^{\eta,k}$
as
$h^{\eta,k}$
as
![]() $\eta\rightarrow\infty$
by performing the inductive calculations of the local minimum to the limiting problem.
$\eta\rightarrow\infty$
by performing the inductive calculations of the local minimum to the limiting problem.
2. Scaling property of global radial solutions
Given
![]() $\bar{h}>0$
and let
$\bar{h}>0$
and let
![]() $h=h\left( \left\vert x\right\vert \right) $
be a radial solution to (1.6) in
$h=h\left( \left\vert x\right\vert \right) $
be a radial solution to (1.6) in
![]() $\Omega=B_{1}(0) $
, we have
$\Omega=B_{1}(0) $
, we have
 \begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ B_{1}(0),\\ \\[-7pt]
2\int_{0}^{1}rh(r)dr=\bar{h},\\ \\[-7pt]
h^{\prime}(1) =0.\end{array}\right. \end{equation}
\begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ B_{1}(0),\\ \\[-7pt]
2\int_{0}^{1}rh(r)dr=\bar{h},\\ \\[-7pt]
h^{\prime}(1) =0.\end{array}\right. \end{equation}
From the elliptic theory, h is smooth whenever it is positive; hence, we also require that
![]() $h^{\prime}(0) =0$
if
$h^{\prime}(0) =0$
if
![]() $h(0) >0$
.
$h(0) >0$
.
We follow the construction of radial solutions in [Reference Jiang and Ni17]. Fixing
![]() $p=\frac{1}{\alpha}$
, we consider the ordinary differential equation
$p=\frac{1}{\alpha}$
, we consider the ordinary differential equation
defined on
![]() $\left[ 0,\infty\right) $
. It has been shown in [Reference Jiang and Ni17] that for any
$\left[ 0,\infty\right) $
. It has been shown in [Reference Jiang and Ni17] that for any
![]() $\eta>0$
,
$\eta>0$
,
 \begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-\dfrac{1}{\alpha},\\ \\[-9pt]
h(0) = \eta,\\ \\[-9pt]
h^{\prime}(0) = 0\end{array}\right. \end{equation}
\begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-\dfrac{1}{\alpha},\\ \\[-9pt]
h(0) = \eta,\\ \\[-9pt]
h^{\prime}(0) = 0\end{array}\right. \end{equation}
has a unique positive solution
![]() $h^{\eta}$
defined on
$h^{\eta}$
defined on
![]() $\left[ 0,\infty\right)$
. And when
$\left[ 0,\infty\right)$
. And when
![]() $\eta=0$
, there exists a unique rupture solution
$\eta=0$
, there exists a unique rupture solution
![]() $h^{0}$
which is continuous on
$h^{0}$
which is continuous on
![]() $\left[ 0,\infty\right) $
such that
$\left[ 0,\infty\right) $
such that
![]() $h\left( 0\right) =0$
and h is positive and satisfies (2.2) on
$h\left( 0\right) =0$
and h is positive and satisfies (2.2) on
![]() $\left( 0,\infty\right) $
. We remark here that
$\left( 0,\infty\right) $
. We remark here that
![]() $h^{0}$
is a weak solution to (2.2) in the sense of distribution even though
$h^{0}$
is a weak solution to (2.2) in the sense of distribution even though
![]() $\left( h^{0}\right)_{r}(0) =\infty$
. Please see Remark 4.3 in [Reference Jiang and Ni17] for the definition of weak solutions which have higher integrability.
$\left( h^{0}\right)_{r}(0) =\infty$
. Please see Remark 4.3 in [Reference Jiang and Ni17] for the definition of weak solutions which have higher integrability.
Obviously
![]() $h\equiv1$
if
$h\equiv1$
if
![]() $\eta=1$
. When
$\eta=1$
. When
![]() $\eta\geq0$
,
$\eta\geq0$
,
![]() $\eta\not =1$
,
$\eta\not =1$
,
![]() $h^{\eta}$
oscillates around 1 and there exists an increasing sequence of positive critical radii
$h^{\eta}$
oscillates around 1 and there exists an increasing sequence of positive critical radii
![]() $\left\{ r_{k}^{\eta}\right\} _{k=1}^{\infty}$
satisfying
$\left\{ r_{k}^{\eta}\right\} _{k=1}^{\infty}$
satisfying
such that
![]() $\left( h^{\eta} \right) ^{\prime}( r_{k}^{\eta} )=0$
.
$\left( h^{\eta} \right) ^{\prime}( r_{k}^{\eta} )=0$
.
Remark 1. The local maximum and minimum values of
![]() $h^{\eta}$
at
$h^{\eta}$
at
![]() $r_{k}^{\eta}$
form two monotone sequences converging to 1. [Reference Jiang and Ni17]
$r_{k}^{\eta}$
form two monotone sequences converging to 1. [Reference Jiang and Ni17]
Given
![]() $\eta\geq0$
,
$\eta\geq0$
,
![]() $\eta\not =1$
and a positive integer k,
$\eta\not =1$
and a positive integer k,
![]() $h^{\eta}(r)$
satisfies the Neumann boundary condition at
$h^{\eta}(r)$
satisfies the Neumann boundary condition at
![]() $r=r_{k}^{\eta}$
. We now define a scaled function
$r=r_{k}^{\eta}$
. We now define a scaled function
and a constant
One can easily verify that
![]() $h^{\eta,k}\left( x\right) =h^{\eta,k}(\left\vert x\right\vert ) $
satisfies the elliptic equation
$h^{\eta,k}\left( x\right) =h^{\eta,k}(\left\vert x\right\vert ) $
satisfies the elliptic equation
with Neumann boundary condition
We can also calculate the average thickness for
![]() $h^{\eta,k}$
,
$h^{\eta,k}$
,
 \begin{align*}\bar{h}^{\eta,k} & = \frac{1}{|B_{1}(0)|}\int_{B_{1}(0)}h^{\eta,k}(x)dx=\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr\\[3pt]
& =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr.\end{align*}
\begin{align*}\bar{h}^{\eta,k} & = \frac{1}{|B_{1}(0)|}\int_{B_{1}(0)}h^{\eta,k}(x)dx=\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr\\[3pt]
& =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr.\end{align*}
So far we constructed a solution
![]() $h^{\eta,k}$
to (2.1) with
$h^{\eta,k}$
to (2.1) with
Actually, all non-constant radial solutions to (2.1) could be obtained in this fashion. Hence, solving (2.1) for given
![]() $\bar{h}$
is reduced to find
$\bar{h}$
is reduced to find
![]() $\eta,k$
so that
$\eta,k$
so that
![]() $\bar{h}=\bar{h}^{\eta,k}$
. So we will analyse the dependence of
$\bar{h}=\bar{h}^{\eta,k}$
. So we will analyse the dependence of
![]() $\bar{h}^{\eta,k}$
on
$\bar{h}^{\eta,k}$
on
![]() $\eta$
and k.
$\eta$
and k.
Denote
![]() $\bar{h}( \eta,k ) =\bar{h}^{\eta,k}$
as a function of
$\bar{h}( \eta,k ) =\bar{h}^{\eta,k}$
as a function of
![]() $\eta$
and k for averaging thickness. Fixing a positive integer k, from the continuous dependence of ordinary differential equations on the initial data,
$\eta$
and k for averaging thickness. Fixing a positive integer k, from the continuous dependence of ordinary differential equations on the initial data,
![]() $\bar{h}(\eta,k ) $
is continuous for
$\bar{h}(\eta,k ) $
is continuous for
![]() $\eta$
in
$\eta$
in
![]() $\left( 0,1 \right) \cup\left(1,\infty\right) $
. As
$\left( 0,1 \right) \cup\left(1,\infty\right) $
. As
![]() $\eta\rightarrow0^{+}$
,
$\eta\rightarrow0^{+}$
,
![]() $h^{\eta}$
converges uniformly to the rupture solution
$h^{\eta}$
converges uniformly to the rupture solution
![]() $h^{0}$
on
$h^{0}$
on
![]() $\left[ 0,\infty\right) $
as proved in [Reference Jiang and Miloua16]. Hence,
$\left[ 0,\infty\right) $
as proved in [Reference Jiang and Miloua16]. Hence,
![]() $\bar{h}( \eta,k ) $
is continuous at
$\bar{h}( \eta,k ) $
is continuous at
![]() $\eta=0$
. Moreover, we have
$\eta=0$
. Moreover, we have
Please refer to Theorem 1.6 of [Reference Jiang and Ni17].
Function
![]() $\bar{h}( \eta,k ) $
is not well defined when
$\bar{h}( \eta,k ) $
is not well defined when
![]() $\eta=1$
. We will discuss the behaviour of
$\eta=1$
. We will discuss the behaviour of
![]() $\bar{h}( \eta,k ) $
when
$\bar{h}( \eta,k ) $
when
![]() $\eta\rightarrow1$
and
$\eta\rightarrow1$
and
![]() $\eta\rightarrow\infty$
, respectively, in the next sections. We will first show that
$\eta\rightarrow\infty$
, respectively, in the next sections. We will first show that
where
![]() $\left\{ r_{k}^{\ast} \right\} $
is the increasing divergent sequence of the positive critical points of
$\left\{ r_{k}^{\ast} \right\} $
is the increasing divergent sequence of the positive critical points of
![]() $J_{0}$
, the Bessel’s function of the first kind with order 0 given by (1.7). Hence,
$J_{0}$
, the Bessel’s function of the first kind with order 0 given by (1.7). Hence,
![]() $\bar{h}( \eta,k ) $
is a continuous positive function for
$\bar{h}( \eta,k ) $
is a continuous positive function for
![]() $\eta\in\left[ 0,\infty\right) $
if we define
$\eta\in\left[ 0,\infty\right) $
if we define
![]() $\bar{h}( 1,k )=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}$
. When
$\bar{h}( 1,k )=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}$
. When
![]() $\eta\rightarrow\infty$
, we will show in Section 4 that
$\eta\rightarrow\infty$
, we will show in Section 4 that
for some
![]() $A_{k}\in\left( 0,\infty\right) $
. That is,
$A_{k}\in\left( 0,\infty\right) $
. That is,
Now we are ready to prove our main theorem.
Proof of Theorem 1. Given any
![]() $\bar{h}\in\left(0,\infty\right) $
. Define
$\bar{h}\in\left(0,\infty\right) $
. Define
Then we have
for any
![]() $k\geq K$
. Now
$k\geq K$
. Now
![]() $\bar{h}( \eta,k ) $
is a continuous positive function of
$\bar{h}( \eta,k ) $
is a continuous positive function of
![]() $\eta$
on
$\eta$
on
![]() $\left( 1,\infty\right) $
with
$\left( 1,\infty\right) $
with
and
Intermediate value theorem implies the existence of
![]() $\eta^{k}>1$
, such that
$\eta^{k}>1$
, such that
Hence, (1.6) admits a radially symmetric solution
![]() $\left( h_{k},p_{k}\right) $
where
$\left( h_{k},p_{k}\right) $
where
and the pressure
Moreover,
![]() $h_{k}$
has exactly k critical points for
$h_{k}$
has exactly k critical points for
![]() $r = |x| \in\left( 0,1\right]$
.
$r = |x| \in\left( 0,1\right]$
.
3. Behaviour of
 $\bar{h}( \eta,k ) $
when
$\bar{h}( \eta,k ) $
when
 $\eta\rightarrow1$
$\eta\rightarrow1$
To understand the behaviour of
![]() $\bar{h}( \eta,k )$
as
$\bar{h}( \eta,k )$
as
![]() $\eta\rightarrow1$
, we need to understand the behaviour of
$\eta\rightarrow1$
, we need to understand the behaviour of
![]() $h^{\eta}(r)$
as
$h^{\eta}(r)$
as
![]() $\eta\rightarrow1$
. Recall that
$\eta\rightarrow1$
. Recall that
![]() $h^{\eta}$
is a solution to (2.2) with
$h^{\eta}$
is a solution to (2.2) with
![]() $h^{\eta}(0) =\eta$
and
$h^{\eta}(0) =\eta$
and
![]() $\left( h^{\eta}\right) _{r}(0) =0$
. Let
$\left( h^{\eta}\right) _{r}(0) =0$
. Let
![]() $\varepsilon=\eta-1$
and
$\varepsilon=\eta-1$
and
Then
![]() $w^{\eta}$
is a solution to the differential equation
$w^{\eta}$
is a solution to the differential equation
with initial condition
As
![]() $\eta\rightarrow1$
,
$\eta\rightarrow1$
,
![]() $\varepsilon\rightarrow0$
, formally, (3.1) converges to the Bessel’s differential equation with order 0,
$\varepsilon\rightarrow0$
, formally, (3.1) converges to the Bessel’s differential equation with order 0,
with the initial condition
![]() $w^{\ast}( 0 ) =1,\,w^{\ast\prime}( 0 ) = 0$
. Such limiting initial value problem has a unique solution
$w^{\ast}( 0 ) =1,\,w^{\ast\prime}( 0 ) = 0$
. Such limiting initial value problem has a unique solution
![]() $J_{0}$
given by (1.7).
$J_{0}$
given by (1.7).
We remark here that
![]() $J_{0}$
is oscillating around 0. Denote
$J_{0}$
is oscillating around 0. Denote
![]() $r_{k}$
to be the increasing sequence of the critical points of w and
$r_{k}$
to be the increasing sequence of the critical points of w and
![]() $r_{k}^{\ast}$
to be the increasing sequence of the critical points of
$r_{k}^{\ast}$
to be the increasing sequence of the critical points of
![]() $J_{0}$
, we have
$J_{0}$
, we have
Proposition 2. As
![]() $\eta\rightarrow1$
, the solution
$\eta\rightarrow1$
, the solution
![]() $w^{\eta}$
to (3.1) with initial data (3.2) converges uniformly to
$w^{\eta}$
to (3.1) with initial data (3.2) converges uniformly to
![]() $J_{0}$
in
$J_{0}$
in
![]() $\left[ 0,\infty\right) $
. Furthermore, for any positive integer k,
$\left[ 0,\infty\right) $
. Furthermore, for any positive integer k,
Proof. We first show that
![]() $w^{\eta}$
is uniformly bounded as
$w^{\eta}$
is uniformly bounded as
![]() $\eta\rightarrow1$
. For simplicity, we will suppress
$\eta\rightarrow1$
. For simplicity, we will suppress
![]() $\eta$
here. Since h is the solution to (2.3), we define energy function
$\eta$
here. Since h is the solution to (2.3), we define energy function
F(h) attains its minimum
![]() $\frac{1}{\alpha-1}$
in
$\frac{1}{\alpha-1}$
in
![]() $\left( 0,\infty\right) $
at
$\left( 0,\infty\right) $
at
![]() $h=1.$
We have
$h=1.$
We have
It yields that
![]() $F(h(r))\leq e(r)\leq e(0)=F(\eta)$
. Note that as
$F(h(r))\leq e(r)\leq e(0)=F(\eta)$
. Note that as
![]() $\eta\rightarrow1$
,
$\eta\rightarrow1$
,
 \begin{align*}& F(1+2(1-\eta))-F(\eta)\\& =[F(1)+\frac{1}{2}F^{\prime\prime}(1)\left[ 2(1-\eta)\right]^{2}]-[F(1)+\frac{1}{2}F^{\prime\prime}(1)(\eta-1)^{2}]+O((\eta-1)^{3})\\& =\frac{3}{2}(1-\eta)^{2}+O((\eta-1)^{3}),\end{align*}
\begin{align*}& F(1+2(1-\eta))-F(\eta)\\& =[F(1)+\frac{1}{2}F^{\prime\prime}(1)\left[ 2(1-\eta)\right]^{2}]-[F(1)+\frac{1}{2}F^{\prime\prime}(1)(\eta-1)^{2}]+O((\eta-1)^{3})\\& =\frac{3}{2}(1-\eta)^{2}+O((\eta-1)^{3}),\end{align*}
hence for some constant
![]() $\delta>0$
,
$\delta>0$
,
![]() $F(1+2(1-\eta))\geq F(\eta)$
holds whenever
$F(1+2(1-\eta))\geq F(\eta)$
holds whenever
![]() $\left\vert \eta-1\right\vert <\delta$
. If
$\left\vert \eta-1\right\vert <\delta$
. If
![]() $1<\eta<1+\delta$
, then
$1<\eta<1+\delta$
, then
![]() $F(h(r))\leq F( \eta) $
implies
$F(h(r))\leq F( \eta) $
implies
![]() $1+2(1-\eta)\leq h(r)\leq\eta$
and if
$1+2(1-\eta)\leq h(r)\leq\eta$
and if
![]() $1-\delta<\eta<1$
, then
$1-\delta<\eta<1$
, then
![]() $\eta\leq h(r)\leq1+2(1-\eta)$
, in both cases
$\eta\leq h(r)\leq1+2(1-\eta)$
, in both cases
Thus,
![]() $|w\left( r\right) |\leq2$
for any
$|w\left( r\right) |\leq2$
for any
![]() $r>0$
whenever
$r>0$
whenever
![]() $\left\vert\eta-1\right\vert <\delta$
.
$\left\vert\eta-1\right\vert <\delta$
.
The uniform boundedness of w, as
![]() $\eta\rightarrow1$
, implies
$\eta\rightarrow1$
, implies
hence w(x) and
![]() $w^{\prime}(x)$
converge uniformly to
$w^{\prime}(x)$
converge uniformly to
![]() $J_{0}(x)$
and
$J_{0}(x)$
and
![]() $J_{0}^{\prime}(x)$
on any bounded interval which implies the convergence of critical points as
$J_{0}^{\prime}(x)$
on any bounded interval which implies the convergence of critical points as
![]() $\eta\rightarrow1$
since both w and
$\eta\rightarrow1$
since both w and
![]() $J_{0}$
are oscillating around 0. From Remark 1, the local maximum and minimum values of
$J_{0}$
are oscillating around 0. From Remark 1, the local maximum and minimum values of
![]() $\omega$
at
$\omega$
at
![]() $r_{k}^{\eta}$
form two monotone sequences converging to zero; hence, the local convergence of w(x) to
$r_{k}^{\eta}$
form two monotone sequences converging to zero; hence, the local convergence of w(x) to
![]() $J_{0}( x ) $
implies the uniform convergence on
$J_{0}( x ) $
implies the uniform convergence on
![]() $\left[ 0,\infty\right) $
.
$\left[ 0,\infty\right) $
.
Since
![]() $h^{\eta}=1+\varepsilon w^{\eta}\rightarrow1$
uniformly as
$h^{\eta}=1+\varepsilon w^{\eta}\rightarrow1$
uniformly as
![]() $\eta\rightarrow1$
, we have
$\eta\rightarrow1$
, we have
 \begin{equation*}\lim_{\eta\rightarrow1}\bar{h}^{\eta,k}=\lim_{\eta\rightarrow1}\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}.\end{equation*}
\begin{equation*}\lim_{\eta\rightarrow1}\bar{h}^{\eta,k}=\lim_{\eta\rightarrow1}\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}.\end{equation*}
Hence,
![]() $\bar{h}^{\eta,k}$
is a continuous function in
$\bar{h}^{\eta,k}$
is a continuous function in
![]() $\eta$
on
$\eta$
on
![]() $\left[0,\infty\right) $
if we define
$\left[0,\infty\right) $
if we define
4. Limiting profile when
 $\eta\rightarrow\infty$
$\eta\rightarrow\infty$
In this section, we will analyse the behaviour of
![]() $\bar{h}(\eta,k)=\bar{h}^{\eta,k}$
as
$\bar{h}(\eta,k)=\bar{h}^{\eta,k}$
as
![]() $\eta\rightarrow\infty$
.
$\eta\rightarrow\infty$
.
Let
![]() $\eta>1$
and
$\eta>1$
and
![]() $h^{\eta}$
be the solution to (2.3). We define the blow-down solution z by
$h^{\eta}$
be the solution to (2.3). We define the blow-down solution z by
![]() $z\left( x\right) =\frac{1}{\eta}h^{\eta}(r)$
with
$z\left( x\right) =\frac{1}{\eta}h^{\eta}(r)$
with
![]() $r=\sqrt{\alpha\eta}x$
. Then we have
$r=\sqrt{\alpha\eta}x$
. Then we have
Denoting
![]() $\varepsilon=\frac{1}{\eta}$
, we have
$\varepsilon=\frac{1}{\eta}$
, we have
![]() $\varepsilon\rightarrow0^{+}$
as
$\varepsilon\rightarrow0^{+}$
as
![]() $\eta\rightarrow\infty$
. The blow-down function z is a solution to the initial value problem
$\eta\rightarrow\infty$
. The blow-down function z is a solution to the initial value problem
 \begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=\dfrac{\varepsilon^{\alpha}}{z^{\alpha}}-1\text{ for }x\in\left( 0,\infty\right) ,\\ \\[-9pt]
z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right. \end{equation}
\begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=\dfrac{\varepsilon^{\alpha}}{z^{\alpha}}-1\text{ for }x\in\left( 0,\infty\right) ,\\ \\[-9pt]
z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right. \end{equation}
Formally, as
![]() $\varepsilon\rightarrow0^{+}$
, (4.1) converges to the limiting equation
$\varepsilon\rightarrow0^{+}$
, (4.1) converges to the limiting equation
 \begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=-1,\\ \\[-9pt]
z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right.\end{equation}
\begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=-1,\\ \\[-9pt]
z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right.\end{equation}
which has a unique global solution
However, we cannot expect
since the function
![]() $1-\frac{1}{4}x^{2}$
becomes negative when
$1-\frac{1}{4}x^{2}$
becomes negative when
![]() $x>2$
.
$x>2$
.
Nonetheless, we can establish the following theorem:
Theorem 2. For every
![]() $\varepsilon>0$
, let
$\varepsilon>0$
, let
![]() $z^{\varepsilon}(x) $
be the unique solution of the initial value problem (4.1). Then as
$z^{\varepsilon}(x) $
be the unique solution of the initial value problem (4.1). Then as
![]() $\varepsilon\rightarrow0^{+}$
,
$\varepsilon\rightarrow0^{+}$
,
![]() $z^{\varepsilon}(x) $
converges uniformly to
$z^{\varepsilon}(x) $
converges uniformly to
![]() $z_{\ast}(x)$
, the solution of the limiting initial value problem
$z_{\ast}(x)$
, the solution of the limiting initial value problem
 \begin{equation}\left\{\begin{array}{c}z_{\ast}^{\prime\prime}+\frac{1}{x}z_{\ast}^{\prime}=-1,\ \ z_{\ast}>0\ \text{in }\bigcup_{j=0}^{\infty}(a_{j},a_{j+1}).\\ \\[-9pt]
z_{\ast}(0) =1,\ \ \text{and}\ \ z_{\ast}^{\prime}(0) =0,\\ \\[-9pt]
z_{\ast}( a_{j} ) =0,\ \ z_{\ast}^{\prime}( a_{j}^{+} ) =-z_{\ast}^{\prime}(a_{j}^{-} ),\end{array}\right. \end{equation}
\begin{equation}\left\{\begin{array}{c}z_{\ast}^{\prime\prime}+\frac{1}{x}z_{\ast}^{\prime}=-1,\ \ z_{\ast}>0\ \text{in }\bigcup_{j=0}^{\infty}(a_{j},a_{j+1}).\\ \\[-9pt]
z_{\ast}(0) =1,\ \ \text{and}\ \ z_{\ast}^{\prime}(0) =0,\\ \\[-9pt]
z_{\ast}( a_{j} ) =0,\ \ z_{\ast}^{\prime}( a_{j}^{+} ) =-z_{\ast}^{\prime}(a_{j}^{-} ),\end{array}\right. \end{equation}
where
![]() $a_{0}=0$
,
$a_{0}=0$
,
![]() $2=a_{1}<a_{2}<\cdots$
could be inductively computed by solving the initial value problem (4.3).
$2=a_{1}<a_{2}<\cdots$
could be inductively computed by solving the initial value problem (4.3).
We will prove Theorem 2 in Section 5 and perform the inductive calculations in Section 6 to obtain the asymptotic behaviour of
![]() $a_{k}$
.
$a_{k}$
.
The above theorem implies that
![]() $z^{\varepsilon}( x ) \ $
converges uniformly to
$z^{\varepsilon}( x ) \ $
converges uniformly to
![]() $1-\frac{1}{4}x^{2}$
on
$1-\frac{1}{4}x^{2}$
on
![]() $\left[ 0,2\right] $
as
$\left[ 0,2\right] $
as
![]() $\varepsilon\rightarrow0$
and
$\varepsilon\rightarrow0$
and
![]() $\frac{r_{1}^{\eta}}{\sqrt{\alpha\eta}}$
converges to
$\frac{r_{1}^{\eta}}{\sqrt{\alpha\eta}}$
converges to
![]() $a_{1}=2$
as
$a_{1}=2$
as
![]() $\eta\rightarrow\infty$
. More generally, we have for
$\eta\rightarrow\infty$
. More generally, we have for
![]() $k=1,2,3,\cdots$
,
$k=1,2,3,\cdots$
,
where
![]() $b_{k}$
is the maximum point of
$b_{k}$
is the maximum point of
![]() $z_{\ast}$
in
$z_{\ast}$
in
![]() $\left( a_{k},a_{k+1}\right) $
.
$\left( a_{k},a_{k+1}\right) $
.
Given a positive integer k and given
![]() $\eta>1$
, we have
$\eta>1$
, we have
 \begin{align*}\bar{h}^{\eta,k} & =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr\\& =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\alpha\eta^{2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds\\& =2\alpha^{-\frac{1}{1+\alpha}}\eta^{\frac{\alpha}{1+\alpha}}\left(\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}\right) ^{-\frac{2}{1+\alpha}-2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds.\end{align*}
\begin{align*}\bar{h}^{\eta,k} & =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr\\& =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\alpha\eta^{2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds\\& =2\alpha^{-\frac{1}{1+\alpha}}\eta^{\frac{\alpha}{1+\alpha}}\left(\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}\right) ^{-\frac{2}{1+\alpha}-2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds.\end{align*}
Hence, we have for
![]() $k=1,2,3,\cdots$
,
$k=1,2,3,\cdots$
,
and
We remark here that for each positive integer k,
![]() $\bar{h}^{\eta,k}\rightarrow\infty$
as
$\bar{h}^{\eta,k}\rightarrow\infty$
as
![]() $\eta\rightarrow\infty$
.
$\eta\rightarrow\infty$
.
5. Convergence to the limiting profile
In this section, our goal here is to prove Theorem 2.
Let
![]() $\varepsilon\in(0,1) $
, and recall z(x),
$\varepsilon\in(0,1) $
, and recall z(x),
![]() $x\geq0$
, be the unique solution to (4.1). We need to show that z converges uniformly to
$x\geq0$
, be the unique solution to (4.1). We need to show that z converges uniformly to
![]() $z_{\ast}$
in
$z_{\ast}$
in
![]() $\left[0,\infty\right) $
as
$\left[0,\infty\right) $
as
![]() $\varepsilon\rightarrow0^{+}$
where
$\varepsilon\rightarrow0^{+}$
where
![]() $z_{\ast}$
is defined by (4.3).
$z_{\ast}$
is defined by (4.3).
We define an energy function
where
It is easy to check that G, defined for
![]() $z\in\left( 0,\infty\right) $
, has the following properties:
$z\in\left( 0,\infty\right) $
, has the following properties:
 \begin{equation*}\left\{\begin{array}[c]{l}G( \varepsilon) =\min_{z\in\left( 0,\infty\right) } G(z) =\frac{\alpha}{\alpha-1}\varepsilon,\\ \\[-9pt]
G^{\prime}(z) >0\text{ for }z>\varepsilon\text{ and }G^{\prime}(z) <0\text{for }0<z<\varepsilon,\\ \\[-9pt]
G^{\prime\prime}(z) >0\text{ for any }z\in\left( 0,\infty\right) ,\\ \\[-9pt]
\lim_{z\rightarrow0}G\left( z\right) =\lim_{z\rightarrow\infty}G(z) =\infty.\end{array}\right.\end{equation*}
\begin{equation*}\left\{\begin{array}[c]{l}G( \varepsilon) =\min_{z\in\left( 0,\infty\right) } G(z) =\frac{\alpha}{\alpha-1}\varepsilon,\\ \\[-9pt]
G^{\prime}(z) >0\text{ for }z>\varepsilon\text{ and }G^{\prime}(z) <0\text{for }0<z<\varepsilon,\\ \\[-9pt]
G^{\prime\prime}(z) >0\text{ for any }z\in\left( 0,\infty\right) ,\\ \\[-9pt]
\lim_{z\rightarrow0}G\left( z\right) =\lim_{z\rightarrow\infty}G(z) =\infty.\end{array}\right.\end{equation*}
Since
e(x) is monotone decreasing. Hence, for any
![]() $x\in\left[ 0,\infty\right)$
,
$x\in\left[ 0,\infty\right)$
,
which implies the bounds
 \begin{equation*}0<z(x) \leq1\text{, }\left\vert z^{\prime}(x) \right\vert \leq\sqrt{2\left(\frac{\varepsilon^{\alpha}}{\alpha-1}+1\right) }\text{ for any }x\in\left[0,\infty\right) .\end{equation*}
\begin{equation*}0<z(x) \leq1\text{, }\left\vert z^{\prime}(x) \right\vert \leq\sqrt{2\left(\frac{\varepsilon^{\alpha}}{\alpha-1}+1\right) }\text{ for any }x\in\left[0,\infty\right) .\end{equation*}
A direct calculation also yields the following simple but useful formulas:
Lemma 1.
Applying the convexity property of G, we have
Lemma 2. Suppose
![]() $m<\varepsilon$
, for any
$m<\varepsilon$
, for any
![]() $z\in\left( m,\varepsilon\right] $
, we have
$z\in\left( m,\varepsilon\right] $
, we have
Suppose
![]() $M>\varepsilon$
, for any
$M>\varepsilon$
, for any
![]() $z\in\left[ \varepsilon,M\right) $
, we have
$z\in\left[ \varepsilon,M\right) $
, we have
Proof.
G(z) is a convex function with minimum at
![]() $z=\varepsilon$
. The estimates follow from the geometry of convex functions.
$z=\varepsilon$
. The estimates follow from the geometry of convex functions.
For any
![]() $\varepsilon\in\left( 0,1\right) $
, z(x) is oscillating around
$\varepsilon\in\left( 0,1\right) $
, z(x) is oscillating around
![]() $\varepsilon$
and the roots to
$\varepsilon$
and the roots to
![]() $z(x)=\varepsilon$
could be listed in order as
$z(x)=\varepsilon$
could be listed in order as
such that
We refer the readers to [Reference Jiang and Ni17] for more details.
Our first step is to show the convergence of z to
![]() $z_{\ast}$
on
$z_{\ast}$
on
![]() $\left[0,x_{1} \right) $
as
$\left[0,x_{1} \right) $
as
![]() $\varepsilon\rightarrow0^{+}$
:
$\varepsilon\rightarrow0^{+}$
:
Proposition 3.
 \begin{align*}\lim_{\varepsilon\rightarrow0^{+}}x_{1} & =a_{1}=2,\\[3pt]
\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{1} ) & = z_{\ast}^{\prime}(a_{1}^{-} ) =-1.\end{align*}
\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}x_{1} & =a_{1}=2,\\[3pt]
\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{1} ) & = z_{\ast}^{\prime}(a_{1}^{-} ) =-1.\end{align*}
Moreover,
Proof. Integrating (5.3) from 0 to x, we have
hence
![]() $z^{\prime}(x)\geq-\frac{x}{2}$
. Integrating again, we obtain
$z^{\prime}(x)\geq-\frac{x}{2}$
. Integrating again, we obtain
Plugging the lower bound for z back into (5.6), we have for any
![]() $x\in\left( 0,2\right) $
,
$x\in\left( 0,2\right) $
,
 \begin{equation*}xz^{\prime}(x) =\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx-\frac{x^{2}}{2}\leq\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left(1-\frac{y^{2}}{4}\right) ^{\alpha}}dy-\frac{x^{2}}{2}\end{equation*}
\begin{equation*}xz^{\prime}(x) =\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx-\frac{x^{2}}{2}\leq\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left(1-\frac{y^{2}}{4}\right) ^{\alpha}}dy-\frac{x^{2}}{2}\end{equation*}
hence
 \begin{equation*}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left( 1-\frac{y^{2}}{4}\right) ^{\alpha}}dy\leq\frac{x\varepsilon^{\alpha}}{2\left( 1-\frac{x^{2}}{4}\right) ^{\alpha}}.\end{equation*}
\begin{equation*}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left( 1-\frac{y^{2}}{4}\right) ^{\alpha}}dy\leq\frac{x\varepsilon^{\alpha}}{2\left( 1-\frac{x^{2}}{4}\right) ^{\alpha}}.\end{equation*}
Fix any
![]() $a\in\left( 0,2\right) $
, we have
$a\in\left( 0,2\right) $
, we have
 \begin{equation}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{a\varepsilon^{\alpha}}{2\left(1-\frac{a^{2}}{4}\right) ^{\alpha}} \end{equation}
\begin{equation}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{a\varepsilon^{\alpha}}{2\left(1-\frac{a^{2}}{4}\right) ^{\alpha}} \end{equation}
holds for any
![]() $x\in\left[ 0,a\right] $
. Hence, for any
$x\in\left[ 0,a\right] $
. Hence, for any
![]() $x\in\left[0,a\right] $
$x\in\left[0,a\right] $
 \begin{equation*}1-\frac{x^{2}}{4}\leq z(x) \leq1-\frac{x^{2}}{4}+\frac{a^{2}\varepsilon^{\alpha}}{2\left( 1-\frac{a^{2}}{4}\right) ^{\alpha}}.\end{equation*}
\begin{equation*}1-\frac{x^{2}}{4}\leq z(x) \leq1-\frac{x^{2}}{4}+\frac{a^{2}\varepsilon^{\alpha}}{2\left( 1-\frac{a^{2}}{4}\right) ^{\alpha}}.\end{equation*}
In particular, z converges to
![]() $1-\frac{x^{2}}{4}$
uniformly on
$1-\frac{x^{2}}{4}$
uniformly on
![]() $\left[ 0,a\right] $
as
$\left[ 0,a\right] $
as
![]() $\varepsilon\rightarrow0^{+}$
, such fact actually follows directly from the continuously dependence of ordinary differential equations since singularity can be avoided on
$\varepsilon\rightarrow0^{+}$
, such fact actually follows directly from the continuously dependence of ordinary differential equations since singularity can be avoided on
![]() $\left[ 0,a\right] $
with fixed
$\left[ 0,a\right] $
with fixed
![]() $a<2$
.
$a<2$
.
Such convergence implies
![]() $x_{1}>1$
for sufficiently small
$x_{1}>1$
for sufficiently small
![]() $\varepsilon$
. (5.3) implies
$\varepsilon$
. (5.3) implies
![]() $xz^{\prime}(x) $
is decreasing on
$xz^{\prime}(x) $
is decreasing on
![]() $\left( 0,x_{1}\right) $
, hence for any
$\left( 0,x_{1}\right) $
, hence for any
![]() $x\in\left[1,x_{1}\right] $
,
$x\in\left[1,x_{1}\right] $
,
![]() $xz^{\prime}(x) \leq z^{\prime}(1) <0$
and
$xz^{\prime}(x) \leq z^{\prime}(1) <0$
and
Since
the above estimate implies that
![]() $x_{1}\leq C$
for some constant C independent of
$x_{1}\leq C$
for some constant C independent of
![]() $\varepsilon\in\left( 0,1\right) $
.
$\varepsilon\in\left( 0,1\right) $
.
For any
![]() $x\in\left[ 1,x_{1}\right] $
, we have
$x\in\left[ 1,x_{1}\right] $
, we have
 \begin{align*}0 & \leq z^{\prime}(x)+\frac{x}{2}=\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\leq\int_{0}^{1}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy+\int_{1}^{x_{1}}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\\[3pt]
& \leq\frac{1}{2}\left( z\left( 1\right) \right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z(1)}\frac{y\varepsilon^{\alpha}}{z^{\alpha}\left\vert \frac{dz}{dy}\right\vert }dz\\[3pt]
& \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z\left( 1\right) }\frac{y^{2}\varepsilon^{\alpha}}{z^{\alpha}\left\vert z^{\prime}(1)\right\vert }dz\\[3pt]
& \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}}{\left\vert z^{\prime}(1)\right\vert }\int_{\varepsilon}^{\infty}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dz\\[3pt]
& =\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}\varepsilon}{\left\vert z^{\prime}(1)\right\vert \left(\alpha-1\right) }\leq C\varepsilon\end{align*}
\begin{align*}0 & \leq z^{\prime}(x)+\frac{x}{2}=\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\leq\int_{0}^{1}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy+\int_{1}^{x_{1}}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\\[3pt]
& \leq\frac{1}{2}\left( z\left( 1\right) \right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z(1)}\frac{y\varepsilon^{\alpha}}{z^{\alpha}\left\vert \frac{dz}{dy}\right\vert }dz\\[3pt]
& \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z\left( 1\right) }\frac{y^{2}\varepsilon^{\alpha}}{z^{\alpha}\left\vert z^{\prime}(1)\right\vert }dz\\[3pt]
& \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}}{\left\vert z^{\prime}(1)\right\vert }\int_{\varepsilon}^{\infty}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dz\\[3pt]
& =\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}\varepsilon}{\left\vert z^{\prime}(1)\right\vert \left(\alpha-1\right) }\leq C\varepsilon\end{align*}
for some constant C independent of
![]() $\varepsilon\in\left( 0,1\right) $
. Combining the estimate (5.7) with
$\varepsilon\in\left( 0,1\right) $
. Combining the estimate (5.7) with
![]() $a=1$
, we conclude for any
$a=1$
, we conclude for any
![]() $x\in\left( 0,x_{1}\right] $
$x\in\left( 0,x_{1}\right] $
where C is some constant independent of
![]() $\varepsilon\in\left( 0,1\right)$
. Integrating from 0 to x, we have for any
$\varepsilon\in\left( 0,1\right)$
. Integrating from 0 to x, we have for any
![]() $x\in\left[ 0,x_{1}\right]$
,
$x\in\left[ 0,x_{1}\right]$
,
In particular, evaluating at
![]() $x=x_{1}$
,
$x=x_{1}$
,
we deduce
And (5.8) implies
Next, we work on intervals
![]() $\left( x_{k},y_{k}\right) $
,
$\left( x_{k},y_{k}\right) $
,
![]() $k=1,2,3,\cdots$
.
$k=1,2,3,\cdots$
.
Proposition 4. Let
![]() $1<a<b$
and z(x),
$1<a<b$
and z(x),
![]() $x\in\left[ a,b\right] $
be the solution to
$x\in\left[ a,b\right] $
be the solution to
 \begin{equation}\left\{\begin{array}{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt]
z(a)=z(b)=\varepsilon.\end{array}\right.\end{equation}
\begin{equation}\left\{\begin{array}{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt]
z(a)=z(b)=\varepsilon.\end{array}\right.\end{equation}
Assume that:
-
(1)
 $z<\varepsilon\ in\ (a,b).$
$z<\varepsilon\ in\ (a,b).$
-
(2)
 $\textit{z}\ attains\ its\ unique\ minimum\ \textit{m}\ at\ x_{\min}\in(a,b).$
$\textit{z}\ attains\ its\ unique\ minimum\ \textit{m}\ at\ x_{\min}\in(a,b).$
-
(3)
 $z^{\prime}<0\ in\ \left[ a,x_{\min}\right)\ and\ z^{\prime}>0\ in\ \left( x_{\min},b\right] .$
$z^{\prime}<0\ in\ \left[ a,x_{\min}\right)\ and\ z^{\prime}>0\ in\ \left( x_{\min},b\right] .$
Then there exists
![]() $\varepsilon_{0}>0$
such that for any
$\varepsilon_{0}>0$
such that for any
![]() $\varepsilon\in\left(0,\varepsilon_{0}\right] $
,
$\varepsilon\in\left(0,\varepsilon_{0}\right] $
,
![]() $b-a\leq C_{1}\varepsilon$
and
$b-a\leq C_{1}\varepsilon$
and
where
![]() $\varepsilon_{0}$
,
$\varepsilon_{0}$
,
![]() $C_{1}$
,
$C_{1}$
,
![]() $C_{2}$
are positive constants only depending on
$C_{2}$
are positive constants only depending on
![]() $A,B,\alpha$
if
$A,B,\alpha$
if
![]() $a<A$
,
$a<A$
,
![]() $e(a)<A$
and
$e(a)<A$
and
![]() $\left\vert z^{\prime}(a)\right\vert >B>0$
.
$\left\vert z^{\prime}(a)\right\vert >B>0$
.
Proof. Integrating (5.2) from
![]() $x_{\min}$
to x yields
$x_{\min}$
to x yields
Suppose
![]() $x\in\left[ a, x_{\min} \right] $
, we deduce
$x\in\left[ a, x_{\min} \right] $
, we deduce
Evaluating at
![]() $x=a$
, we have
$x=a$
, we have
Next, applying (5.4),
Hence,
 \begin{align*}a^{2}\left( z^{\prime}(a) \right) ^{2} & \leq2x_{\min}^{2}\left[G(m)-G(\varepsilon) \right] \\[3pt]
& \leq2\left( a+\frac{\sqrt{2} \varepsilon}{\sqrt{G(m) -G(\varepsilon) }}\right) ^{2}\left[ G(m) -G(\varepsilon) \right] \\[3pt]
& \leq2\left( a\sqrt{G(m) }+\sqrt{2}\varepsilon\right) ^{2}.\end{align*}
\begin{align*}a^{2}\left( z^{\prime}(a) \right) ^{2} & \leq2x_{\min}^{2}\left[G(m)-G(\varepsilon) \right] \\[3pt]
& \leq2\left( a+\frac{\sqrt{2} \varepsilon}{\sqrt{G(m) -G(\varepsilon) }}\right) ^{2}\left[ G(m) -G(\varepsilon) \right] \\[3pt]
& \leq2\left( a\sqrt{G(m) }+\sqrt{2}\varepsilon\right) ^{2}.\end{align*}
So if
we have for any
![]() $\varepsilon\leq\varepsilon_{0}$
,
$\varepsilon\leq\varepsilon_{0}$
,
 \begin{equation*}G(m) \geq\left( \frac{\left\vert z^{\prime}(a) \right\vert }{\sqrt{2}}-\frac{\sqrt{2}\varepsilon}{a}\right) ^{2}\geq\frac{\left\vert z^{\prime}(a)\right\vert ^{2}}{8}\geq\frac{B^{2}}{8}.\end{equation*}
\begin{equation*}G(m) \geq\left( \frac{\left\vert z^{\prime}(a) \right\vert }{\sqrt{2}}-\frac{\sqrt{2}\varepsilon}{a}\right) ^{2}\geq\frac{\left\vert z^{\prime}(a)\right\vert ^{2}}{8}\geq\frac{B^{2}}{8}.\end{equation*}
Hence from the structure of function G, we have
![]() $m\leq C\varepsilon^{\frac{\alpha}{\alpha-1}}$
. Now with
$m\leq C\varepsilon^{\frac{\alpha}{\alpha-1}}$
. Now with
![]() $\varepsilon_{0}$
sufficiently small, we have for any
$\varepsilon_{0}$
sufficiently small, we have for any
![]() $\varepsilon\leq\varepsilon_{0}$
,
$\varepsilon\leq\varepsilon_{0}$
,
![]() $m\leq\frac{\varepsilon}{2}$
. Hence,
$m\leq\frac{\varepsilon}{2}$
. Hence,
since
And
 \begin{align*}\int_{a}^{x_{\min}}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & =\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{x_{\min}\left( \sqrt{2\left[ G(m)-G(z) \right]}\right) }{x^{2}}dz\\[3pt]
& \leq\frac{x_{\min}\sqrt{2G(m)}}{a^{2}}\varepsilon\leq\frac{\left(a+C_{1}\varepsilon\right) \sqrt{2e(a) }}{a^{2}}\varepsilon.\end{align*}
\begin{align*}\int_{a}^{x_{\min}}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & =\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{x_{\min}\left( \sqrt{2\left[ G(m)-G(z) \right]}\right) }{x^{2}}dz\\[3pt]
& \leq\frac{x_{\min}\sqrt{2G(m)}}{a^{2}}\varepsilon\leq\frac{\left(a+C_{1}\varepsilon\right) \sqrt{2e(a) }}{a^{2}}\varepsilon.\end{align*}
Suppose
![]() $x\in\left[ x_{\min},b\right] $
, we have
$x\in\left[ x_{\min},b\right] $
, we have
Applying (5.4) again,
so we have
 \begin{align*}\frac{x_{\min}}{b}\left( b-x_{\min}\right) & \leq\int_{x_{\min}}^{b}\frac{x_{\min}}{x}dx\leq\int_{m}^{\varepsilon}\frac{dz}{\sqrt{\frac{2 ( G(m)-G(\varepsilon) ) }{\varepsilon-m}}\sqrt{z-m}}\\& =\frac{\sqrt{2}\left( \varepsilon-m\right) }{\sqrt{G(m)-G(\varepsilon) }}\leq C_{1}\varepsilon.\end{align*}
\begin{align*}\frac{x_{\min}}{b}\left( b-x_{\min}\right) & \leq\int_{x_{\min}}^{b}\frac{x_{\min}}{x}dx\leq\int_{m}^{\varepsilon}\frac{dz}{\sqrt{\frac{2 ( G(m)-G(\varepsilon) ) }{\varepsilon-m}}\sqrt{z-m}}\\& =\frac{\sqrt{2}\left( \varepsilon-m\right) }{\sqrt{G(m)-G(\varepsilon) }}\leq C_{1}\varepsilon.\end{align*}
Hence for sufficient small
![]() $\varepsilon$
,
$\varepsilon$
,
And
 \begin{align*}\int_{x_{\min}}^{b}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & \leq\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{\sqrt{2\left[ G(m)-G(z) \right] }}{x}dz\\[3pt]
& \leq\frac{\sqrt{ 2G(m) }}{ x_{\min} }\varepsilon\leq\frac{\sqrt{2e(a)}}{a}\varepsilon.\\[-30pt] \end{align*}
\begin{align*}\int_{x_{\min}}^{b}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & \leq\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{\sqrt{2\left[ G(m)-G(z) \right] }}{x}dz\\[3pt]
& \leq\frac{\sqrt{ 2G(m) }}{ x_{\min} }\varepsilon\leq\frac{\sqrt{2e(a)}}{a}\varepsilon.\\[-30pt] \end{align*}
Corollary 1. Suppose
Then
Moreover
Proof. Since
we have
![]() $\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$
. Now
$\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$
. Now
hence
Since
![]() $z^{\prime}( y_{k} ) >0$
, we conclude
$z^{\prime}( y_{k} ) >0$
, we conclude
The convergence
follows from the fact that both z and
![]() $z_{\ast}$
converge to 0 in the shrinking to a point interval
$z_{\ast}$
converge to 0 in the shrinking to a point interval
![]() $\left[ x_{k},y_{k}\right] $
.
$\left[ x_{k},y_{k}\right] $
.
Finally, we deal with intervals
![]() $\left( y_{k},x_{k+1}\right) $
,
$\left( y_{k},x_{k+1}\right) $
,
![]() $k=1,2,3,\cdots$
.
$k=1,2,3,\cdots$
.
Proposition 5. Let
![]() $1<a<b$
and z(x),
$1<a<b$
and z(x),
![]() $x\in\left[ a,b\right] $
be the solution to
$x\in\left[ a,b\right] $
be the solution to
 \begin{equation}\left\{\begin{array}[c]{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt]
z(a) = z(b) = \varepsilon.\end{array}\right.\end{equation}
\begin{equation}\left\{\begin{array}[c]{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt]
z(a) = z(b) = \varepsilon.\end{array}\right.\end{equation}
Assume that:
-
(1)
 $z>\varepsilon\ in\ (a,b).$
$z>\varepsilon\ in\ (a,b).$
-
(2)
 $\textit{z}\ attains\ its\ unique\ maximum\ M<1\ at\ x_{\max}\ \in(a,b).$
$\textit{z}\ attains\ its\ unique\ maximum\ M<1\ at\ x_{\max}\ \in(a,b).$
-
(3)
 $z^{\prime}>0\ in\ \left[a,x_{\max}\right)\ and\ z^{\prime}<0\ in\ \left( x_{\max},b\right] .$
$z^{\prime}>0\ in\ \left[a,x_{\max}\right)\ and\ z^{\prime}<0\ in\ \left( x_{\max},b\right] .$
Then for any
![]() $0<\varepsilon\leq\varepsilon_{0}$
,
$0<\varepsilon\leq\varepsilon_{0}$
,
![]() $C_{1}\leq b-a\leq C_{2}$
and
$C_{1}\leq b-a\leq C_{2}$
and
where
![]() $\varepsilon_{0}$
,
$\varepsilon_{0}$
,
![]() $C_{i}$
are constants depending only on
$C_{i}$
are constants depending only on
![]() $\alpha$
, the upper bound of a and the positive lower bound of
$\alpha$
, the upper bound of a and the positive lower bound of
![]() $z^{\prime}\left(a\right) $
.
$z^{\prime}\left(a\right) $
.
Proof. Integrating (5.3) from a to x, we have
So
whenever
Hence,
and
 \begin{align*}M & \geq z\left( \sqrt{a^{2}+2az^{\prime}(a) }\right) \\ \\[-9pt]
& \geq\int_{a}^{\sqrt{a^{2}+2az^{\prime}(a) }}\frac{1} {x}\left[ az^{\prime}(a) -\frac{1}{2}\left( x^{2} - a^{2}\right) \right] dx =\frac{a^{2}}{4}u(\frac{2z^{\prime}(a)}{a}) \geq C,\end{align*}
\begin{align*}M & \geq z\left( \sqrt{a^{2}+2az^{\prime}(a) }\right) \\ \\[-9pt]
& \geq\int_{a}^{\sqrt{a^{2}+2az^{\prime}(a) }}\frac{1} {x}\left[ az^{\prime}(a) -\frac{1}{2}\left( x^{2} - a^{2}\right) \right] dx =\frac{a^{2}}{4}u(\frac{2z^{\prime}(a)}{a}) \geq C,\end{align*}
where
![]() $u(x)=\left( 1+x\right) \ln(1+x) -x$
is positive and increasing for
$u(x)=\left( 1+x\right) \ln(1+x) -x$
is positive and increasing for
![]() $x>0$
and C is some constant independent of
$x>0$
and C is some constant independent of
![]() $\varepsilon$
. We could see that M is uniformly bounded in
$\varepsilon$
. We could see that M is uniformly bounded in
![]() $\left[ C,1 \right] $
and then we could assume for any
$\left[ C,1 \right] $
and then we could assume for any
![]() $\varepsilon\leq\varepsilon_{0}$
by taking
$\varepsilon\leq\varepsilon_{0}$
by taking
![]() $\varepsilon_{0}$
sufficiently small and any
$\varepsilon_{0}$
sufficiently small and any
![]() $z\in\left[ \varepsilon,M\right] $
$z\in\left[ \varepsilon,M\right] $
Next, integrating (5.2) from
![]() $x_{\max}$
to x yields
$x_{\max}$
to x yields
Suppose
![]() $x \in\left[ a,x_{\max} \right] $
, we have
$x \in\left[ a,x_{\max} \right] $
, we have
hence
 \begin{align*}x_{\max}-a & = \int_{a}^{x_{\max}}dx\leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\[3pt]
& \leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{M-z}} \leq2\sqrt{M}.\end{align*}
\begin{align*}x_{\max}-a & = \int_{a}^{x_{\max}}dx\leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\[3pt]
& \leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{M-z}} \leq2\sqrt{M}.\end{align*}
Now we estimate
 \begin{align*}\int_{a}^{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\ \\[-9pt]
& \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} = \int_{\varepsilon}^{M/2}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}+\int_{M/2}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}\\ \\[-9pt]
& \leq\frac{\varepsilon}{\left( \alpha-1\right) \sqrt{M/2}}+\frac{2^{\alpha}\varepsilon^{\alpha}}{M^{\alpha}}2\sqrt{M} \leq C_{2}\varepsilon.\end{align*}
\begin{align*}\int_{a}^{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\ \\[-9pt]
& \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} = \int_{\varepsilon}^{M/2}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}+\int_{M/2}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}\\ \\[-9pt]
& \leq\frac{\varepsilon}{\left( \alpha-1\right) \sqrt{M/2}}+\frac{2^{\alpha}\varepsilon^{\alpha}}{M^{\alpha}}2\sqrt{M} \leq C_{2}\varepsilon.\end{align*}
On the other hand, suppose
![]() $x\in\left[ x_{\max},b\right] $
, we have
$x\in\left[ x_{\max},b\right] $
, we have
hence
which yields
We also have
and
 \begin{align*}\int_{x_{\max}}^{b}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{x}{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M) -G(z) \right) }}\\& \leq\frac{b}{x_{\max}}\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} \leq\frac{b}{x_{\max}}C_{2}\varepsilon\leq C_{3}\varepsilon.\\[-40pt]\end{align*}
\begin{align*}\int_{x_{\max}}^{b}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{x}{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M) -G(z) \right) }}\\& \leq\frac{b}{x_{\max}}\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} \leq\frac{b}{x_{\max}}C_{2}\varepsilon\leq C_{3}\varepsilon.\\[-40pt]\end{align*}
Corollary 2. Suppose that
Then
Moreover,
Proof. We define
![]() $\tilde{z}$
on
$\tilde{z}$
on
![]() $\left[ y_{k},x_{k+1}\right] $
as a solution to
$\left[ y_{k},x_{k+1}\right] $
as a solution to
satisfying
![]() $\tilde{z}(y_{k}) = z(y_{k}) $
and
$\tilde{z}(y_{k}) = z(y_{k}) $
and
![]() $\tilde{z}^{\prime}( y_{k} ) =z^{\prime}( y_{k} )$
. Integrating
$\tilde{z}^{\prime}( y_{k} ) =z^{\prime}( y_{k} )$
. Integrating
from
![]() $y_{k}$
, we have
$y_{k}$
, we have
Integrating again, we obtain
In particular, at
![]() $x_{k+1}$
, we have
$x_{k+1}$
, we have
Let
![]() $\tilde{z}^{\ast}$
, defined for
$\tilde{z}^{\ast}$
, defined for
![]() $x\geq\min\left( y_{k},a_{k}\right) $
be the solution to
$x\geq\min\left( y_{k},a_{k}\right) $
be the solution to
satisfying
Since
![]() $x_{k+1}-y_{k}\geq C$
and
$x_{k+1}-y_{k}\geq C$
and
![]() $\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$
, we have
$\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$
, we have
![]() $x_{k+1}-a_{k}\geq C$
. The continuously dependence of differential equations with initial data implies
$x_{k+1}-a_{k}\geq C$
. The continuously dependence of differential equations with initial data implies
Since
has a unique root
![]() $a_{k+1}$
in
$a_{k+1}$
in
![]() $\left( a_{k},\infty\right) $
, we conclude
$\left( a_{k},\infty\right) $
, we conclude
And
Since
and all the functions are uniformly small near
![]() $a_{k}$
and
$a_{k}$
and
![]() $a_{k+1}$
, it is easy to check
$a_{k+1}$
, it is easy to check
Now we are ready to prove Theorem 2 using the asymptotic behaviour of limit solution
![]() $z_{\ast}$
which we will prove in the next section.
$z_{\ast}$
which we will prove in the next section.
Proof of Theorem 2. Note that energy function e(x) defined by (5.1) is bounded by e(0). Combining Proposition 3, Corollary 1 and 2 hold, we conclude z(x) converges to
![]() $z_{\ast}(x)$
locally uniformly on
$z_{\ast}(x)$
locally uniformly on
![]() $\left[ 0,\infty\right) $
as
$\left[ 0,\infty\right) $
as
![]() $\varepsilon\rightarrow0^{+}$
. From Remark 1, the local maximum and the local minimum of z(x) form two monotone sequences converging to
$\varepsilon\rightarrow0^{+}$
. From Remark 1, the local maximum and the local minimum of z(x) form two monotone sequences converging to
![]() $\varepsilon$
. Since
$\varepsilon$
. Since
![]() $\lim_{x\rightarrow\infty}z_{\ast}(x)=0$
, the local uniform convergence of z to
$\lim_{x\rightarrow\infty}z_{\ast}(x)=0$
, the local uniform convergence of z to
![]() $z_{\ast}$
implies the global uniform convergence on
$z_{\ast}$
implies the global uniform convergence on
![]() $\left[0,\infty\right) $
as
$\left[0,\infty\right) $
as
![]() $\varepsilon\rightarrow0^{+}$
.
$\varepsilon\rightarrow0^{+}$
.
6. Asymptotic behaviour of limit solution
From Theorem 2, we have as
![]() $\varepsilon\rightarrow0^{+}$
, z(x) converges uniformly on
$\varepsilon\rightarrow0^{+}$
, z(x) converges uniformly on
![]() $\left[0,\infty\right) $
to the limit
$\left[0,\infty\right) $
to the limit
![]() $z_{\ast}(x)$
satisfying (4.3). Now we are going to apply inductive calculations to compute
$z_{\ast}(x)$
satisfying (4.3). Now we are going to apply inductive calculations to compute
![]() $a_{j}$
and analyse the asymptotic behaviours in the following manner. Similarly as previous, we define the energy function
$a_{j}$
and analyse the asymptotic behaviours in the following manner. Similarly as previous, we define the energy function
and
![]() $e_{j} = e(a_{j})$
. It is easy to check that e(x) is decreasing in x and
$e_{j} = e(a_{j})$
. It is easy to check that e(x) is decreasing in x and
![]() $e_{j}$
is decreasing in j.
$e_{j}$
is decreasing in j.
(i) In
![]() $\left[0,a_{1}\right] $
, we have
$\left[0,a_{1}\right] $
, we have
Hence,
(ii) In
![]() $[a_{1},a_{2}],$
$[a_{1},a_{2}],$
Then
Note that
![]() $z_{\ast}^{\prime\prime}(x)=-\frac{4}{x^{2}}-\frac{1}{2}<0,$
$z_{\ast}^{\prime\prime}(x)=-\frac{4}{x^{2}}-\frac{1}{2}<0,$
![]() $z_{\ast}(x)$
is concave down. Therefore, there exists a unique solution
$z_{\ast}(x)$
is concave down. Therefore, there exists a unique solution
![]() $a_{2}\in(2,\infty)$
to
$a_{2}\in(2,\infty)$
to
That is,
(iii) In
![]() $[a_{j},a_{j+1}]$
,
$[a_{j},a_{j+1}]$
,
![]() $j\geq2$
,
$j\geq2$
,
![]() $z_{\ast}$
is defined by the initial value problem
$z_{\ast}$
is defined by the initial value problem
For any
![]() $x\geq a_{j}$
, integrating twice from
$x\geq a_{j}$
, integrating twice from
![]() $a_{j}$
to x, we obtain
$a_{j}$
to x, we obtain
 \begin{equation*}z_{\ast}(x) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right) \ln\frac{x}{a_{j}}-\frac{x^{2}-a_{j}^{2}}{4}.\end{equation*}
\begin{equation*}z_{\ast}(x) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right) \ln\frac{x}{a_{j}}-\frac{x^{2}-a_{j}^{2}}{4}.\end{equation*}
Since
on
![]() $\left( a_{j},\infty\right) $
, there is a unique root
$\left( a_{j},\infty\right) $
, there is a unique root
![]() $a_{j+1}\in(a_{j},\infty)$
such that
$a_{j+1}\in(a_{j},\infty)$
such that
 \begin{equation}z_{\ast} ( a_{j+1} ) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right)\ln\frac{a_{j+1}}{a_{j}}-\frac{a_{j+1}^{2}-a_{j}^{2}}{4}=0.\end{equation}
\begin{equation}z_{\ast} ( a_{j+1} ) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right)\ln\frac{a_{j+1}}{a_{j}}-\frac{a_{j+1}^{2}-a_{j}^{2}}{4}=0.\end{equation}
And
![]() $\sqrt{e_{j+1}}$
is given by
$\sqrt{e_{j+1}}$
is given by
Next, we consider the asymptotic behaviour of
![]() $a_{j}$
and
$a_{j}$
and
![]() $e_{j}$
as
$e_{j}$
as
![]() $j\rightarrow\infty$
.
$j\rightarrow\infty$
.
Theorem 3. There exists positive constant A such that as
![]() $j\rightarrow\infty$
,
$j\rightarrow\infty$
,
Proof. Let
![]() $b_{j}=\frac{\sqrt{e_{j}}}{a_{j}}$
, (6.2) implies
$b_{j}=\frac{\sqrt{e_{j}}}{a_{j}}$
, (6.2) implies
Since
![]() $\sqrt{e_{j}}$
is decreasing and
$\sqrt{e_{j}}$
is decreasing and
![]() $a_{j}$
is increasing in j,
$a_{j}$
is increasing in j,
![]() $b_{j}$
is decreasing. If
$b_{j}$
is decreasing. If
![]() $\lim_{j\rightarrow\infty}b_{j}\not =0$
, then
$\lim_{j\rightarrow\infty}b_{j}\not =0$
, then
![]() $a_{j}=\frac{\sqrt{e_{j}}}{b_{j}}$
is bounded and hence
$a_{j}=\frac{\sqrt{e_{j}}}{b_{j}}$
is bounded and hence
![]() $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
. If
$\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
. If
![]() $\lim_{j\rightarrow\infty}b_{j}=0$
, then (6.3) implies
$\lim_{j\rightarrow\infty}b_{j}=0$
, then (6.3) implies
![]() $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
. Hence, in any case,
$\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
. Hence, in any case,
![]() $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
which also implies
$\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$
which also implies
![]() $\lim_{j\rightarrow\infty}b_{j}=0$
. Denote
$\lim_{j\rightarrow\infty}b_{j}=0$
. Denote
![]() $t_j=(\frac{a_{j+1}}{a_{j}})^{2}-1$
, we have
$t_j=(\frac{a_{j+1}}{a_{j}})^{2}-1$
, we have
![]() $\lim_{j\rightarrow\infty}t_j=0$
. Now (6.1) could be rewritten into
$\lim_{j\rightarrow\infty}t_j=0$
. Now (6.1) could be rewritten into
By Taylor expansion, we have
which yields
Therefore,
 \begin{align*}\frac{a_{j}}{a_{j+1}} & =\left( 1+t_j\right)^{-\frac{1}{2}}=1-\frac{1}{2}t_j+\frac{3t_j^{2}}{8}+O\left(t_j^{3}\right) \\& =1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3}).\end{align*}
\begin{align*}\frac{a_{j}}{a_{j+1}} & =\left( 1+t_j\right)^{-\frac{1}{2}}=1-\frac{1}{2}t_j+\frac{3t_j^{2}}{8}+O\left(t_j^{3}\right) \\& =1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3}).\end{align*}
Plug the above expansion into (6.3), we have
 \begin{align*}b_{j+1} & =\frac{1}{2}-\frac{1}{2}\left( 1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3})\right) ^{2}\left( 1+2b_{j}\right) \\& =b_{j}-\frac{8}{3}b_{j}^{2}+O(b_{j}^{3})\end{align*}
\begin{align*}b_{j+1} & =\frac{1}{2}-\frac{1}{2}\left( 1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3})\right) ^{2}\left( 1+2b_{j}\right) \\& =b_{j}-\frac{8}{3}b_{j}^{2}+O(b_{j}^{3})\end{align*}
which implies
As
![]() $b_{j}$
is decreasing and converges to 0, we conclude
$b_{j}$
is decreasing and converges to 0, we conclude
Next, since
 \begin{align*}\frac{b_{j+1}a_{j+1}^{\frac{4}{3}}}{b_{j}a_{j}^{\frac{4}{3}}} &=\frac{b_{j+1}}{b_{j}}\left( \frac{a_{j+1}}{a_{j}}\right) ^{\frac{4}{3}}=\frac{\left( 1-\frac{8}{3}b_{j}+O(b_{j}^{2})\right) }{\left[1-2b_{j}+O(b_{j}^{2})\right] ^{4/3}}\\& =1+O(b_{j}^{2}),\end{align*}
\begin{align*}\frac{b_{j+1}a_{j+1}^{\frac{4}{3}}}{b_{j}a_{j}^{\frac{4}{3}}} &=\frac{b_{j+1}}{b_{j}}\left( \frac{a_{j+1}}{a_{j}}\right) ^{\frac{4}{3}}=\frac{\left( 1-\frac{8}{3}b_{j}+O(b_{j}^{2})\right) }{\left[1-2b_{j}+O(b_{j}^{2})\right] ^{4/3}}\\& =1+O(b_{j}^{2}),\end{align*}
the order of
![]() $b_{j}$
implies the limit
$b_{j}$
implies the limit
![]() $\gamma=\lim_{j\rightarrow\infty}b_{j}a_{j}^{\frac{4}{3}}>0$
exists. Hence,
$\gamma=\lim_{j\rightarrow\infty}b_{j}a_{j}^{\frac{4}{3}}>0$
exists. Hence,
 \begin{equation*}\lim_{j\rightarrow\infty}\frac{a_{j}}{j^{\frac{3}{4}}}=\lim_{j\rightarrow\infty}\left( \frac{b_{j}a_{j}^{\frac{4}{3}}}{jb_{j}}\right) ^{\frac{3}{4}}=\left( \frac{8\gamma}{3}\right) ^{\frac{3}{4}}=A\end{equation*}
\begin{equation*}\lim_{j\rightarrow\infty}\frac{a_{j}}{j^{\frac{3}{4}}}=\lim_{j\rightarrow\infty}\left( \frac{b_{j}a_{j}^{\frac{4}{3}}}{jb_{j}}\right) ^{\frac{3}{4}}=\left( \frac{8\gamma}{3}\right) ^{\frac{3}{4}}=A\end{equation*}
and finally
Acknowledgments
The authors would like to thank the anonymous referees for providing insightful comments and valuable suggestions.