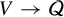1 Introduction
The mapping class group
${\mathrm{Mod}}(S)$
of a closed surface S of genus
$g\geq 0$
with
$m\geq 0$
punctures and
$3g-3+m\geq 2$
acts by precomposition of marking on the Teichmüller space
${\cal T}(S)$
of marked complex structures on S. The action is properly discontinuous, with quotient the moduli space
${\cal M}$
of complex structures on S.
If
$m=0$
, then the Hodge bundle
${\cal H}\to {\cal M}$
over moduli space is the bundle whose fibre over a Riemann surface x equals the vector space of holomorphic one-forms on x. This is a holomorphic vector bundle (in the orbifold sense) of complex dimension g which decomposes into strata of differentials with zeros of given number and multiplicities. Strata need not be connected, but their components are classified [Reference Kontsevich and ZorichKZ03]. The sphere subbundle for the natural norm obtained by integration of a holomorphic one-form over the base surface is the moduli space of area-one abelian differentials on S. There is a natural
$SL(2,\mathbb {R})$
-action on this sphere bundle preserving every component
${\cal Q}$
of a stratum. The action of the diagonal subgroup is called the Teichmüller flow
$\Phi ^t$
.
Similarly, for arbitrary
$(g,m)$
, the sphere bundle in the cotangent bundle of
${\cal M}$
can be identified with the (orbifold) bundle of area-one quadratic differentials over
${\cal M}$
. It decomposes into strata of differentials with fixed number and multiplicities of zeros and simple poles. Strata need not be connected, but connected components are classified [Reference LanneauL08]. Each connected component of such a stratum is invariant under a natural
$SL(2,\mathbb {R})$
-action whose diagonal subgroup acts as the Teichmüller flow
$\Phi ^t$
.
Let now
${\cal Q}$
be such a component of area-one abelian or quadratic differentials. Let
$k\geq 1$
be the total number of zeros and poles of the differentials in
${\cal Q}$
and let
$h=2g-1+k$
in case
${\cal Q}$
is a component of abelian differentials, and
$h=2g-2+k$
otherwise. Let
$\Gamma $
be the set of all periodic orbits for
$\Phi ^t$
in
${\cal Q}$
. The length of a periodic orbit
$\gamma \in \Gamma $
is denoted by
$\ell (\gamma )$
.
As an application of [Reference Eskin, Mirzakhani and RafiEMR19] (see also [Reference Eskin and MirzakhaniEM11]), we showed in [Reference HamenstädtH13] that
$$ \begin{align*}\sharp\{\gamma\in \Gamma\mid \ell(\gamma)\leq R\}\frac{hR}{e^{hR}}\to 1\quad (R\to \infty).\end{align*} $$
Call a subset
${\cal A}$
of
$\Gamma $
typical if
$$ \begin{align*}\sharp \{\gamma\in {\cal A}\mid \ell(\gamma)\leq R\}\frac{hR}{e^{hR}}\to 1\quad (R\to \infty).\end{align*} $$
Thus, a subset of
$\Gamma $
is typical if its growth rate is maximal. The intersection of two typical subsets of
$\Gamma $
is typical.
Now let us assume that we are given a finite-dimensional real or complex vector space V and a representation
$\Psi :{\mathrm{Mod}}(S)\to {\mathrm{GL}}(V)$
. Using this representation, we can form the flat vector bundle
${\cal N}_0={\cal T}(S)\times _{\mathrm{Mod(S)}} V\to {\cal M}$
, where
${\mathrm{Mod}}(S)$
acts on V via the representation
$\Psi $
. This bundle is equipped with a natural flat connection. For each component
${\cal Q}$
of a stratum of area-one abelian or quadratic differentials, we can consider the pullback
$P^*{\cal N}_0={\cal N}$
of
${\cal N}_0$
to
${\cal Q}$
, where
$P:{\cal Q}\to {\cal M}$
is the natural projection. The pullback bundle is equipped with the flat pullback connection.
An important example for
$m=0$
arises from the representation
$$ \begin{align*}\Psi:{\textrm{Mod}}(S)\to {\textrm{Sp}}(2g,\mathbb{Z})\end{align*} $$
defined by the action of
${\mathrm{Mod}}(S)$
on the first real cohomology group
$H^1(S,\mathbb {R})$
of S which preserves the intersection form
$\iota $
on
$H^1(S,\mathbb {Z})$
. The corresponding flat bundle over moduli space is just the Hodge bundle, and the flat connection obtained in this way is called the Gauss–Manin connection.
Given a flat vector bundle
${\cal N}\to {\cal Q}$
, we can parallel transport the fibres of
${\cal N}$
along the flow lines of the Teichmüller flow
$\Phi ^t$
. This defines a continuous cocycle over
$\Phi ^t$
.
A periodic orbit
$\gamma \in \Gamma $
for
$\Phi ^t$
determines a holonomy map for
${\cal N}$
, which is the first return map of the parallel transport along
$\gamma $
for a fixed choice of a base point in
$\gamma $
. Different base points give rise to conjugate maps. Thus, a periodic orbit
$\gamma \in \Gamma $
determines the conjugacy class
$[A(\gamma )]$
of a matrix
$A(\gamma )\in {\mathrm{GL}}(V)$
, which is just the image under the representation
$\Psi $
of the conjugacy class of a pseudo-Anosov mapping class
$\phi $
which defines the periodic orbit
$\gamma $
.
The
$SL(2,\mathbb {R})$
-action on
${\cal Q}$
preserves a Borel probability measure
$\unicode{x3bb} $
in the Lebesgue measure class, the so-called Masur–Veech measure [Reference MasurM82, Reference VeechV86]. If the cocycle defined by the flat bundle
${\cal N}$
is integrable for the action of the Teichmüller flow with respect to this measure, then we can apply the Oseledets multiplicative ergodic theorem [Reference OseledetsO68] to obtain Lyapunov exponents of the cocycle with respect to
$\unicode{x3bb} $
. These Lyapunov exponents
$$ \begin{align*}\kappa_1\geq \cdots \geq \kappa_n\end{align*} $$
listed in descending order describe the asymptotic growth rate of vectors in subcones determined by the Lyapunov filtration of
${\cal N}$
as described by Oseledec’s theorem. As an example, the flat bundle defined by the standard representation
${\mathrm{Mod}}(S)\to {\mathrm{Sp}}(2g,\mathbb {Z})$
is integrable in this sense.
For
$\gamma \in \Gamma $
, let
$\hat \alpha _i(\gamma )$
be the logarithm of the absolute value of the ith eigenvalue of the matrix
$A(\gamma )$
, ordered in decreasing order, and write
$\alpha _i(\gamma )=\hat \alpha _i(\gamma )/\ell (\gamma )$
. Since eigenvalues of matrices are invariant under conjugation, this does not depend on the choice of a representative in the class
$[A(\gamma )]$
and, for
$ i\leq n$
, we obtain in this way a function
$\alpha _i:\Gamma \to \mathbb {R}$
.
We show the following result.
Theorem 1 For each
$\epsilon>0$
, the set
$\{\gamma \in \Gamma \mid \vert \alpha _i(\gamma )-\kappa _i\vert <\epsilon \} (1\leq i\leq n)$
is typical.
The main technical tool towards this result is a hyperbolicity property for the action of the Teichmüller flow on a component
${\cal Q}$
of a stratum of abelian or quadratic differentials. For its formulation, recall [Reference MasurM82, Reference VeechV86] that for every
$q\in {\cal Q}$
, the set of differentials in
${\cal Q}$
with the same vertical (or horizontal) measured foliation as q is a local suborbifold
$W^{ss}_{\cal Q}(q)$
(or
$W^{su}_{\cal Q}(q)$
) of
${\cal Q}$
. These local suborbifolds can be equipped with a natural distance function
$d_H$
obtained from the modified Hodge norm [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12]. For
$r>0$
, we denote by
$B^i_{\cal Q}(q,r)\subset W_{\cal Q}^i(q) (i=ss,su)$
the ball of radius r about q for the distance function
$d_H$
.
Denote the set of manifold points in
${\cal Q}$
by
${\cal Q}_{\mathrm{good}}$
. Then
${\cal Q}_{\mathrm{good}}$
is an open dense
$\Phi ^t$
-invariant subset of
${\cal Q}$
(see the discussion in §3 for more details). Call a point
$q\in {\cal Q}$
recurrent if it is contained in its own
$\alpha $
- and
$\omega $
-limit set for the action of
$\Phi ^t$
. This means that there are sequences
$s_i,t_i\to \infty $
so that
$\Phi ^{t_i}q\to q$
and
$\Phi ^{-s_i}q\to q (i\to \infty )$
. We show in §4 the following strengthening of contraction results, which can be found in [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12, Reference HamenstädtH13].
Theorem 2 Let
$q\in {\cal Q}_{\mathrm{good}}$
be a recurrent point. Then there is a number
$r_0=r_0(q)>0$
and there is a neighborhood U of q in
${\cal Q}_{\mathrm{good}}$
with the following property. Let
$z\in U$
be recurrent; then, for every
$a>0$
, there is a number
$T(z,a)>0$
so that for all
$T>T(z,a)$
, we have
$\Phi ^TB_{\cal Q}^{ss}(z,r_0)\subset B_{\cal Q}^{ss}(\Phi ^T(z),a)$
and
$\Phi ^{T}B_{\cal Q}^{su}(z,a)\supset B_{\cal Q}^{su}(\Phi ^T(z),r_0)$
.
Theorem 2 states in a precise and quantitative way that the Teichmüller flow is non-uniformly hyperbolic, that is, it contracts and expands balls of locally uniform size on the strong stable and strong unstable manifolds along any recurrent orbit. Thus, it applies to any orbit which is typical for any finite invariant Borel probability measure, and it does not rely on assumptions like the percentage of time the orbit spends in the thick part of moduli space used in [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12]. This is particularly valuable as there are periodic orbits and hence invariant measures for the Teichmüller flow which are entirely contained in any prescribed neighborhood of the cusp of moduli space [Reference HamenstädtH16].
The proof of Theorem 2 rests on two facts. First, although Teichmüller space equipped with the Teichmüller metric is far from being hyperbolic or even resembling in the large a
${\mathrm{CAT}}(0)$
metric space, convex subsets of its thick part are hyperbolic in the sense of Gromov in a way which can be made quantitative [Reference HamenstädtH10]. Second, Teichmüller space is acylindrically hyperbolic in the sense that it admits a coarsely well defined coarsely Lipschitz
${\mathrm{Mod}}(S)$
-equivariant map onto the curve graph of S, a Gromov hyperbolic
${\mathrm{Mod}}(S)$
-graph. This curve graph records hyperbolic behavior in Teichmüller space and hence of its geodesic flow, the Teichmüller flow. In spite of being a locally infinite graph, it can effectively be used as a witness of hyperbolicity. As far as we know, quantitative results on non-uniform hyperbolicity of the Teichmüller flow as strong as Theorem 2 are out of reach using more standard methods. What is more, such ideas are most likely applicable to other non-uniformly hyperbolic geometric flows, like geodesic flows on closed rank-one manifolds of non-positive curvature with acylindrically hyperbolic fundamental group.
The structure of this article is as follows. In §2 we recall some properties of flat bundles needed later on. Section 3 introduces the curve graph, geodesic laminations and some additional basic tools used in the proofs and explains some technical results from [Reference HamenstädtH13]. This section was included to make the article essentially self-contained. Section 4 is devoted to a study of some specific properties of the Teichmüller flow which resemble properties of a hyperbolic flow, extending the results of [Reference HamenstädtH13]. We also prove Theorem 2, which is the main technical tool for the proof of Theorem 1. In §5 we establish a local criterion for a property to be typical, which is applied in §6 to show Theorem 1.
2 Flat bundles
Let S be an oriented surface of finite type, that is, S is a closed surface of genus
$g\geq 0$
from which
$m\geq 0$
points, so-called punctures, have been deleted. We assume that
$3g-3+m\geq 2$
, which means that S is not a sphere with at most four punctures or a torus with at most one puncture.
The Teichmüller space
${\cal T}(S)$
of S is the quotient of the space of all complete finite-volume hyperbolic metrics on S under the action of the group of diffeomorphisms of S which are isotopic to the identity. The fibre bundle
$\tilde {\cal Q}(S)$
over
${\cal T}(S)$
of all marked holomorphic quadratic differentials of area one can be viewed as the unit cotangent bundle of
${\cal T}(S)$
for the Teichmüller metric
$d_{\cal T}$
. Each such differential is holomorphic on the complement of the punctures and has at most a simple pole at each puncture. The Teichmüller flow
$\Phi ^t$
on
$\tilde {\cal Q}(S)$
commutes with the action of the mapping class group
${\mathrm{Mod}}(S)$
of all isotopy classes of orientation-preserving self-homeomorphisms of S. Therefore, this flow descends to a flow on the quotient orbifold
${\cal Q}(S)= \tilde {\cal Q}(S)/{\mathrm{Mod}}(S)$
, again denoted by
$\Phi ^t$
. This orbifold is a fibre bundle in the orbifold sense over the moduli space of curves
${\cal M}= {\cal T}(S)/{\mathrm{Mod}}(S)$
.
Let V be a finite-dimensional real or complex vector space and let
$\Psi :{\mathrm{Mod}}(S)\to {\mathrm{GL}}(V)$
be an irreducible representation. Then we obtain a flat bundle
$$ \begin{align*}{\cal N}_0={\cal T}(S)\times_{{\textrm{Mod}}(S)} V\to {\cal M},\end{align*} $$
where
${\mathrm{Mod}}(S)$
acts on
${\cal T}(S)\times V$
from the right by
$(x,Z)\phi = (x\phi ,\Psi (\phi ^{-1})(Z))$
. The pullback of
${\cal N}_0$
to a component
${\cal Q}$
of a stratum of abelian or quadratic differentials is again a flat vector bundle
${\cal N}\to {\cal Q}$
, equipped with the pullback connection.
The Teichmüller flow
$\Phi ^t$
acts on
${\cal N}$
as a one-parameter group of bundle automorphisms. It associates to
$(t,v,Z)$
the image of Z under parallel transport along the subsegment of the flow line of the Teichmüller flow through v of oriented length t.
The holonomy group of the bundle
${\cal N}_0={\cal T}(S)\times _{{\mathrm{Mod}}(S)}V\to {\cal M}$
is the image of
${\mathrm{Mod}}(S)$
under the homomorphism
$\Psi $
. As the action of the mapping class group on
${\cal T}(S)$
is not free, we have to be slightly careful when computing the holonomy about a closed loop in
${\cal M}$
. The following discussion is geared at circumventing this difficulty.
Let
${\mathrm{Sing}}\subset {\cal T}(S)$
be the
${\mathrm{Mod}}(S)$
-invariant subvariety of surfaces with non-trivial automorphisms. The complex codimension of
${\mathrm{Sing}}$
is at least two. We will not need this fact in the following; all we need is that this set is closed and nowhere dense. Let
$\tilde \alpha :[0,1]\to {\cal T}(S)$
be any smooth path with
$\tilde \alpha (0),\tilde \alpha (1)\in {\cal T}(S)-{\mathrm{Sing}}$
. Assume that there is an element
$\phi \in {\mathrm{Mod}}(S)$
so that
$\phi (\tilde \alpha (0))=\tilde \alpha (1)$
. Then
$\phi $
is unique. Furthermore,
$\tilde \alpha $
projects to a closed path
$\alpha $
in
${\cal M}$
. Up to conjugation, the holonomy along
$\alpha $
for the flat connection on
${\cal N}_0$
equals the map
$\Psi \circ \phi ^{-1}$
which maps the fibre of
${\cal N}_0$
over
$\tilde \alpha (1)$
to the fibre of
${\cal N}_0$
over
$\tilde \alpha (0)$
. It depends only on the end points of
$\tilde \alpha $
. In particular, it is well defined even if the path
$\tilde \alpha $
is not entirely contained in
${\cal T}(S)-{\mathrm{Sing}}$
.
As
${\mathrm{Sing}}\subset {\cal T}(S)$
is closed and nowhere dense, there exists a contractible neighborhood U of
$\tilde \alpha (0)$
which is entirely contained in
${\cal T}(S)-{\mathrm{Sing}}$
and such that
$\eta (U)\cap U=\emptyset $
for all
${\mathrm{Id}}\not =\eta \in {\mathrm{Mod}}(S)$
. Let
$\gamma :[0,1]\to {\cal T}(S)-{\mathrm{Sing}}$
be any smooth path which connects a point
$\gamma (0)\in U$
to a point
$\gamma (1)=\phi (\gamma (0))$
in
$\phi (U)$
. The discussion in the previous paragraph shows that the holonomy of the parallel transport of
${\cal N}$
along the projection of
$\gamma $
to
${\cal M}$
is conjugate to the holonomy of the parallel transport along
$\alpha $
. In particular, the absolute values of the eigenvalues of these holonomy maps coincide. The same consideration is also valid for the holonomy of the pullback bundle
${\cal N}\to {\cal Q}$
with respect to the flat pullback connection.
We use this fact as follows. Define the good subset
${\cal Q}_{{\mathrm{good}}}$
of
${\cal Q}$
to be the set of all points
$q\in {\cal Q}$
with the following property. Let
$\tilde {\cal Q}$
be a component of the preimage of
${\cal Q}$
in the Teichmüller space of marked abelian or quadratic differentials and let
$\tilde q\in \tilde {\cal Q}$
be a lift of q; then an element of
${\mathrm{Mod}}(S)$
which fixes
$\tilde q$
acts as the identity on
$\tilde {\cal Q}$
(compare [Reference HamenstädtH13] for more information on this technical condition) and hence it centralizes the stabilizer of
$\tilde {\cal Q}$
in
${\mathrm{Mod}}(S)$
and fixes every point in the projection of
$\tilde {\cal Q}$
to
${\cal T}(S)$
. Due to the existence of hyperelliptic components of strata, this group may be non-trivial.
To avoid technical issues related to this fact, we always assume in the following that the restriction of the representation to the stabilizer of
$\tilde {\cal Q}$
in
${\mathrm{Mod}}(S)$
factors through the quotient by the finite subgroup which acts trivially on
$\tilde {\cal Q}$
. We then always pass to this quotient whenever the component
${\cal Q}$
has this property. This is consistent with the fact that the orbifold fundamental group of
${\cal Q}$
equals this quotient. Note that
${\cal Q}_{{\mathrm{good}}}$
is precisely the subset of
${\cal Q}$
of manifold points. Lemma 4.4 of [Reference HamenstädtH13] shows that the good subset
${\cal Q}_{{\mathrm{good}}}$
of
${\cal Q}$
is open, dense and
$\Phi ^t$
-invariant.
Definition 2.1 A closed curve
$\eta :[0,a]\to {\cal Q}_{{\mathrm{good}}}$
defines the conjugacy class of a pseudo-Anosov mapping class
$\phi \in {\mathrm{Mod}}(S)$
if the following holds true. Let
$\tilde \eta $
be a lift of
$\eta $
to an arc in the Teichmüller space of abelian differentials. Then
$\psi \tilde \eta (0)=\tilde \eta (a)$
for some
$\psi \in {\mathrm{Mod}}(S)$
and we require that
$\psi $
is conjugate to
$\phi $
.
In the above definition, we associate a conjugacy class in
${\mathrm{Mod}}(S)$
to a parameterized curve
$\eta $
. That is, we think of the curve as defining an element in the (orbifold) fundamental group of
${\cal M}$
by projecting it to a loop in
${\cal M}$
. As the loop
$\eta $
is contained in
${\cal Q}_{\mathrm{good}}$
, its lifts to the Teichmüller space of abelian differentials consist of a countable collection of arcs whose end points are not fixed by any element in
${\mathrm{Mod}}(S)$
(unless the element fixes a component
$\tilde {\cal Q}$
of the preimage of
$\tilde {\cal Q}$
pointwise and hence is contained in the center of the stabilizer of
$\tilde {\cal Q}$
and, in this case, by the above convention, the definition still makes sense).
Since
$\eta $
is a closed curve, its projection to
${\cal M}$
is closed as well and hence the end points of such a lift (which are points in the cotangent space of
${\cal T}(S)$
) are paired by an element in
${\mathrm{Mod}}(S)$
, which moreover is unique. A different choice of lift defines an element of
${\mathrm{Mod}}(S)$
in the same conjugacy class. Moreover, changing the parameterization preserves the conjugacy class as well. Note also that a closed curve in
${\cal Q}_{\mathrm{good}}$
may define the conjugacy class of an element of
${\mathrm{Mod}}(S)$
which is not pseudo-Anosov. As we will see later, those curves play no role for us.
Consider a smooth closed parameterized curve
$\alpha :[0,1]\to {\cal Q}_{{\mathrm{good}}}$
. As before, the parallel transport along
$\alpha $
of the bundle
${\cal N}=P^*{\cal N}_0\to {\cal Q}$
with respect to the flat pullback connection is defined.
Using Definition 2.1, the following is now immediate from the above discussion.
Lemma 2.2 Let
$\eta \subset {\cal Q}_{{\mathrm{good}}}$
be a closed curve which defines the conjugacy class of a pseudo-Anosov mapping class
$\phi \in {\mathrm{Mod}}(S)$
. Then the eigenvalues of the holonomy map obtained by parallel transport of the bundle
${\cal N}$
along
$\eta $
coincide with the eigenvalues of the map
$\Psi \circ \phi ^{-1}$
.
Proof. As discussed above, if
$\eta :[0,a]\to {\cal Q}_{{\mathrm{good}}}$
is a closed curve and if
$\tilde \eta $
is a lift of
$\eta $
to the Teichmüller space of marked abelian differentials, then there is a unique element
$\psi \in {\mathrm{Mod}}(S)$
with
$\psi (\tilde \eta (0))= \tilde \eta (a)$
. This element pairs the end points of the projection of
$\tilde \eta $
to
${\cal T}(S)$
. The conjugacy class of the element
$\Psi \circ \psi ^{-1}\in {\mathrm{GL}}(V)$
does not depend on choices. Since
${\cal N}$
is the pullback of a bundle on
${\cal M}$
, the absolute values of the eigenvalues of
$\Psi \circ \psi ^{-1}$
are precisely the absolute values of the eigenvalues of the holonomy map for parallel transport of
${\cal N}$
along
$\eta $
. The lemma now follows from the definition of a curve which defines the conjugacy class of
$\phi $
.
3 Laminations and the curve graph
The goal of this section is to summarize some results from [Reference HamenstädtH13] used later on. It was included here to make the article self-contained. An introduction to the complex of curves can be found in [Reference SchleimerS06]. Geodesic laminations are introduced and discussed in detail in [Reference Canary, Epstein and GreenCEG06, Reference MartelliMar16]. The surveys [Reference WrightWr16, Reference ZorichZ99] give an accessible introduction to flat surfaces and dynamics on the moduli space of abelian and quadratic differentials.
3.1 Geodesic laminations
A geodesic lamination for a complete hyperbolic structure on S of finite volume is a compact subset of S which is foliated into simple geodesics. A geodesic lamination
$\nu $
is called minimal if each of its half-leaves is dense in
$\nu $
. Thus, a simple closed geodesic is a minimal geodesic lamination. A minimal geodesic lamination with more than one leaf has uncountably many leaves and is called minimal arational.
Every geodesic lamination
$\nu $
consists of a disjoint union of finitely many minimal components and a finite number of isolated leaves. Each of the isolated leaves of
$\nu $
either is an isolated closed geodesic and hence a minimal component, or it spirals about one or two minimal components. A geodesic lamination
$\nu $
tightly fills S if its complementary components are topological discs or once-punctured monogons, that is, once-punctured discs bounded by a single leaf of
$\nu $
. Note that this definition deviates from the standard definition of filling, which only requires that a geodesic lamination decomposes S into discs and once-punctured discs. A geodesic lamination which tightly fills a surface with punctures is not orientable.
The set
${\cal L}$
of all geodesic laminations on S can be equipped with the restriction of the Hausdorff topology for compact subsets of S. With respect to this topology, the space
${\cal L}$
is compact.
A measured geodesic lamination is a geodesic lamination
$\nu $
equipped with a translation-invariant transverse measure
$\xi $
such that the
$\xi $
-weight of every compact arc in S with end points in
$S-\nu $
which intersects
$\nu $
non-trivially and transversely is positive. We say that
$\nu $
is the support of the measured geodesic lamination. The geodesic lamination
$\nu $
is uniquely ergodic if, up to scale,
$\xi $
is the only transverse measure with support
$\nu $
.
The space
${\cal M\cal L}$
of measured geodesic laminations equipped with the weak
$^*$
-topology admits a natural continuous action of the multiplicative group
$(0,\infty )$
. The quotient under this action is the space
${\cal P\cal M\cal L}$
of projective measured geodesic laminations which is homeomorphic to the sphere
$S^{6g-7+2m}$
.
Every simple closed geodesic c on S defines a measured geodesic lamination. The geometric intersection number between simple closed curves on S extends to a continuous function
$\iota $
on
${\cal M\cal L}\times {\cal M\cal L}$
, the intersection form. We say that a pair
$(\xi ,\mu )\in {\cal M\cal L}\times {\cal M\cal L}$
of measured geodesic laminations binds S if, for every measured geodesic lamination
$\eta \in {\cal M\cal L}$
, we have
$\iota (\eta ,\xi )+\iota (\eta ,\mu )>0$
. This is equivalent to stating that every complete simple (possibly infinite) geodesic on S intersects either the support of
$\xi $
or the support of
$\mu $
transversely.
3.2 The curve graph
The curve graph
${\cal C}(S)$
of S is the locally infinite metric graph whose vertices are the free homotopy classes of essential simple closed curves on S, that is, curves which are neither contractible nor freely homotopic into a puncture. Two such curves are connected by an edge of length one if and only if they can be realized disjointly. The mapping class group
${\mathrm{Mod}}(S)$
of S acts on
${\cal C}(S)$
as a group of simplicial isometries.
The curve graph
${\cal C}(S)$
is a hyperbolic geodesic metric space [Reference Masur and MinksyMM99] and hence it admits a Gromov boundary
$\partial {\cal C}(S)$
. For
$c\in {\cal C}(S)$
, there is a complete distance function
$\delta _c$
on
$\partial {\cal C}(S)$
of uniformly bounded diameter and there is a number
$\rho>0$
such that
$$ \begin{align*}\delta_c\leq e^{\rho d(c,a)}\delta_a\quad\text{for all }c,a\in {\cal C}(S).\end{align*} $$
The group
${\mathrm{Mod}}(S)$
acts on
$\partial {\cal C}(S)$
as a group of homeomorphisms.
Let
$\kappa _0>0$
be a Bers constant for S, that is,
$\kappa _0$
is such that for every complete hyperbolic metric on S of finite volume, there is a pants decomposition of S consisting of pants curves of length at most
$\kappa _0$
. Define a map
$$ \begin{align} \Upsilon_{\cal T}:{\cal T}(S)\to {\cal C}(S)\end{align} $$
by associating to
$x\in {\cal T}(S)$
a simple closed curve of x-length at most
$\kappa _0$
. Then there is a number
$c>0$
such that
$$ \begin{align} d_{\cal T}(x,y)\geq d(\Upsilon_{\cal T}(x),\Upsilon_{\cal T}(y))/c-c \end{align} $$
for all
$x,y\in {\cal T}(S)$
[Reference Masur and MinksyMM99] (see also the discussion in [Reference HamenstädtH10]).
For a number
$L>1$
, a map
$\gamma :[0,s)\to {\cal C}(S) (s\in (0,\infty ])$
is an L-quasi-geodesic if, for all
$t_1,t_2\in [0,s)$
, we have
$$ \begin{align*}\vert t_1-t_2\vert/L-L\leq d(\gamma(t_1),\gamma(t_2))\leq L\vert t_1-t_2\vert +L.\end{align*} $$
A map
$\gamma :[0,\infty )\to {\cal C}(S)$
is called an unparameterized L-quasi-geodesic if there is an increasing homeomorphism
$\phi :[0,s)\to [0,\infty ) (s\in (0,\infty ])$
such that
$\gamma \circ \phi $
is an L-quasi-geodesic. We say that an unparameterized quasi-geodesic is infinite if its image set has infinite diameter. The following important result was established in [Reference Masur and MinksyMM99].
Theorem 3.1 There is a number
$p>1$
such that the image under
$\Upsilon _{\cal T}$
of every Teichmüller geodesic is an unparameterized p-quasi-geodesic.
Choose a smooth function
$\sigma :[0,\infty )\to [0,1]$
with
$\sigma [0,\kappa _0]\equiv 1$
and
$\sigma [2\kappa _0,\infty )\equiv 0$
. For each
$x\in {\cal T}(S)$
, the number of essential simple closed curves c on S whose x-length
$\ell _x(c)$
(that is, the length of a geodesic representative in its free homotopy class) does not exceed
$2\kappa _0$
is bounded from above by a constant not depending on x, and the diameter of the subset of
${\cal C}(S)$
containing these curves is uniformly bounded as well. Thus, we obtain for every
$x\in {\cal T}(S)$
a finite Borel measure
$\mu _x$
on
${\cal C}(S)$
by defining
$$ \begin{align*} \mu_x=\sum_{c\in {\cal C}(S)} \sigma(\ell_x(c))\Delta_c, \end{align*} $$
where
$\Delta _c$
denotes the Dirac mass at c. The total mass of
$\mu _x$
is bounded from above and below by a universal positive constant, and the diameter of the support of
$\mu _x$
in
${\cal C}(S)$
is uniformly bounded as well. Moreover, the measures
$\mu _x$
depend continuously on
$x\in {\cal T}(S)$
in the weak
$^*$
-topology. This means that for every bounded function
$f:{\cal C}(S)\to \mathbb {R}$
, the function
$x\to \int f\, d\mu _x$
is continuous.
For
$x\in {\cal T}(S)$
, define a distance
$\delta _x$
on
$\partial {\cal C}(S)$
by
$$ \begin{align} \delta_x(\xi,\zeta)=\int \delta_c(\xi,\zeta) \,d\mu_x(c)/\mu_x({\cal C}(S)).\end{align} $$
The distances
$\delta _x$
are equivariant with respect to the action of
${\mathrm{Mod}}(S)$
on
${\cal T}(S)$
and
$\partial {\cal C}(S)$
. Moreover, there is a constant
$\kappa>0$
such that
$$ \begin{align} \delta_x\leq e^{\kappa d_{\cal T}(x,y)}\delta_y\quad\text{and}\quad\kappa^{-1}\delta_y\leq \delta_{\Upsilon_{\cal T}(y)}\leq \kappa \delta_y\end{align} $$
for all
$x,y\in {\cal T}(S)$
(see [Reference HamenstädtH09, pp. 230 and 231]).
3.3 Quadratic differentials
An area-one quadratic differential
$z\in \tilde {\cal Q}(S)$
is determined by a pair
$(\mu ,\nu )$
of measured geodesic laminations which bind S and such that
$\iota (\mu ,\nu )=1$
. The laminations
$\mu ,\nu $
are called vertical and horizontal, respectively. Namely, Levitt [Reference LevittL83] constructed from a measured foliation on S a measured geodesic lamination, and the measured geodesic lamination determines the measured foliation up to Whitehead moves. On the other hand, a pair
$(\hat \mu ,\hat \nu )$
of measured foliations is the pair consisting of the horizontal and the vertical measured foliations for a quadratic differential z on S if and only if the corresponding measured geodesic laminations bind S.
For
$z\in \tilde {\cal Q}(S)$
, let
$W^{u}(z)\subset \tilde {\cal Q}(S)$
be the set of all quadratic differentials whose horizontal projective measured geodesic laminations coincide with the horizontal projective measured geodesic lamination of z. The space
$W^u(z)$
is called the unstable manifold of z and these unstable manifolds define the unstable foliation
$W^u$
of
$\tilde {\cal Q}(S)$
. The strong unstable manifold
$W^{su}(z)\subset W^u(z)$
is the set of all quadratic differentials whose horizontal measured geodesic laminations coincide with the horizontal measured geodesic lamination of z. These sets define the strong unstable foliation
$W^{su}$
of
$\tilde {\cal Q}(S)$
. The flip
${\cal F}:z\to {\cal F}(z)=-z$
exchanges the vertical and the horizontal measured geodesic laminations of a quadratic differential z. The image of the unstable (or the strong unstable) foliation of
$\tilde {\cal Q}(S)$
under the flip
${\cal F}$
is the stable foliation
$W^s$
(or the strong stable foliation
$W^{ss}$
).
By the Hubbard–Masur theorem [Reference Hubbard and MasurHM79], for each
$z\in \tilde {\cal Q}(S)$
, the restriction to
$W^{u}(z)$
of the canonical projection
$$ \begin{align*}P:\tilde {\cal Q}(S)\to {\cal T}(S)\end{align*} $$
is a homeomorphism. Thus, the Teichmüller metric lifts to a complete path metric
$d^u$
on
$W^u(z)$
(that is, a complete distance function so that any two points can be connected by a minimal geodesic). Denote by
$d^{su}$
the restriction of this distance function to
$W^{su}(z)$
. Then
$d^s=d^u\circ {\cal F},d^{ss}=d^{su}\circ {\cal F}$
are distance functions on the leaves of the stable and strong stable foliations, respectively. For
$z\in \tilde {\cal Q}(S)$
and
$r>0$
, let
$B^i(z,r)\subset W^i(z)$
be the closed ball of radius r about z with respect to
$d^i (i=u,su,s,ss)$
.
Let
$$ \begin{align} \tilde {\cal A}\subset \tilde {\cal Q}(S)\end{align} $$
be the set of all marked quadratic differentials z such that the unparameterized quasi-geodesic
$t\to \Upsilon _{\cal T}(P\Phi ^tz) (t\in [0,\infty ))$
is infinite. Then
$\tilde {\cal A}$
is the set of all quadratic differentials whose vertical measured geodesic lamination fills up S (that is, its support decomposes S into ideal polygons and once-punctured polygons; see [Reference Hamenstädt, Minsky, Sakuma and SeriesH06] for a comprehensive discussion of this result of Klarreich [Reference KlarreichKl99]). There is a natural surjective map
$$ \begin{align*}F:\tilde {\cal A}\to \partial {\cal C}(S)\end{align*} $$
which associates to a point
$z\in \tilde {\cal A}$
the end point of the infinite unparameterized quasi-geodesic
$t\to \Upsilon _{\cal T}(P\Phi ^tz) (t\in [0,\infty ))$
. This map is equivariant with respect to the action of the mapping class group on
$\tilde {\cal A}\subset \tilde {\cal Q}(S)$
and on
$\partial {\cal C}(S)$
.
Call a marked quadratic differential
$z\in \tilde {\cal Q}(S)$
uniquely ergodic if the support of its vertical measured geodesic lamination is uniquely ergodic and fills up S. A uniquely ergodic quadratic differential is contained in the set
$\tilde {\cal A}$
. The following is Lemma 2.3 of [Reference HamenstädtH13].
Lemma 3.2
-
(1) The map
$F:\tilde {\cal A}\to \partial {\cal C}(S)$
is continuous and closed. -
(2) If
$z\in \tilde {\cal Q}(S)$
is uniquely ergodic, then the sets
$F(B^{su}(z,r)\cap \tilde {\cal A}) (r>0)$
form a neighborhood basis for
$F(z)$
in
$\partial {\cal C}(S)$
.
For
$z\in \tilde {\cal A}$
and
$r>0$
, let
$$ \begin{align*}D(z,r)\end{align*} $$
be the closed ball of radius r about
$F(z)$
with respect to the distance function
$\delta _{Pz}$
. As a consequence of Lemma 3.2, if
$z\in \tilde {\cal Q}(S)$
is uniquely ergodic, then, for every
$r>0$
, there are numbers
$r_0<r$
and
$\beta>0$
such that
$$ \begin{align}F(B^{su}(z,r_0)\cap \tilde {\cal A}) \subset D(z,\beta) \subset F(B^{su}(z,r)\cap\tilde {\cal A}).\end{align} $$
3.4 Strata
A tuple
$(m_1,\ldots ,m_\ell ;-m)$
of positive integers
$1\leq m_1\leq \cdots \leq m_\ell $
with
$\sum _im_i=4g-4+m$
defines a stratum
$\tilde {\cal Q}(m_1,\ldots ,m_\ell ;-m)$
in
$\tilde {\cal Q}(S)$
. This stratum consists of all marked area-one quadratic differentials with m simple poles and
$\ell $
zeros of order
$m_1,\ldots ,m_\ell $
which are not squares of holomorphic one-forms. The stratum is a real hypersurface in a complex manifold of dimension
$2g-2+m+\ell $
.
The closure in
$\tilde {\cal Q}(S)$
of a stratum is a union of components of strata. Strata are invariant under the action of the mapping class group
${\mathrm{Mod}}(S)$
of S and hence they project to strata in the moduli space
${\cal Q}(S)=\tilde {\cal Q}(S)/{\mathrm{Mod}}(S)$
of quadratic differentials on S with at most simple poles at the punctures. We denote the projection of the stratum
$\tilde {\cal Q}(m_1,\ldots ,m_\ell ;-m)$
by
${\cal Q}(m_1,\ldots ,m_\ell ;-m)$
.
The strata in moduli space need not be connected, but their connected components have been identified by Lanneau [Reference LanneauL08]. A stratum in
${\cal Q}(S)$
has at most three connected components. The entropy h of the invariant Lebesgue measure on a component
${\cal Q}$
of a stratum
${\cal Q}(m_1,\ldots ,m_\ell ;-m)$
just equals the dimension
$2g-2+m+\ell $
[Reference MasurM82, Reference VeechV86], that is, we have
$$ \begin{align} h=2g-2+m+\ell.\end{align} $$
Similarly, if
$m=0$
, then we let
$\tilde {\cal H}(S)$
be the bundle of marked area-one holomorphic one-forms over Teichmüller space
${\cal T}(S)$
of S. For a tuple
$k_1\leq \cdots \leq k_\ell $
of positive integers with
$\sum _ik_i=2g-2$
, the stratum
$\tilde {\cal H}(k_1,\ldots ,k_\ell )$
of marked area-one holomorphic one-forms on S with
$\ell $
zeros of order
$k_i (i=1,\ldots ,\ell )$
is a real hypersurface in a complex manifold of dimension
$2g-1+\ell $
. It projects to a stratum
${\cal H}(k_1,\ldots ,k_\ell )$
in the moduli space
${\cal H}(S)$
of area-one holomorphic one-forms on S. Strata of holomorphic one-forms in moduli space need not be connected, but the number of connected components of a stratum is at most three [Reference Kontsevich and ZorichKZ03]. Moreover, as before, the entropy of the invariant Lebesgue measure on a component of a stratum
${\cal H}(k_1,\ldots ,k_\ell )$
coincides with the dimension
$2g-1+\ell $
, that is, we have
$$ \begin{align} h=2g-1+\ell.\end{align} $$
Let
$\tilde {\cal Q}$
be a component of a stratum
$\tilde {\cal Q}(m_1,\ldots ,m_\ell ;-m)$
of marked quadratic differentials or of a stratum
$\tilde {\cal H}(k_1,\ldots ,k_\ell )$
of marked abelian differentials. Using period coordinates, one sees that every
$q\in \tilde {\cal Q}$
has a connected neighborhood U in
$\tilde {\cal Q}$
with the following properties [Reference HamenstädtH13]. For
$u\in U$
, let
$[u^v]$
(or
$[u^h]$
) be the vertical (or the horizontal) projective measured geodesic lamination of u. Then
$\{[u^v]\mid u\in U\}$
is homeomorphic to an open ball in
$\mathbb {R}^{h-1}$
(where
$h>0$
is as in equations (7) and (8)). Moreover, for
$q\in U$
, the set
$$ \begin{align*}\{u\in U\mid [u^v]=[q^v]\}=W^s_{\tilde{\cal Q},{\textrm{loc}}}(q)\subset W^s(q)\end{align*} $$
is a smooth connected local submanifold of U of (real) dimension h, which is called the local stable manifold of q in
$\tilde {\cal Q}$
. Similarly, we define the local unstable manifold
$W^u_{\tilde {\cal Q},{\mathrm{loc}}}(q)$
of q in
$\tilde {\cal Q}$
. If two such local stable (or unstable) manifolds intersect, then their union is again a local stable (or unstable) manifold. The maximal connected set containing q which is a union of intersecting local stable (or unstable) manifolds is the stable manifold
$W^s_{\tilde {\cal Q}} (q)$
(or the unstable manifold
$W^u_{\tilde {\cal Q}}(q)$
) of q in
$\tilde {\cal Q}$
. Note that
$W^i_{\tilde {\cal Q}}(q)\subset W^i(q) (i=s,u)$
. A stable (or unstable) manifold is invariant under the action of the Teichmüller flow
$\Phi ^t$
.
The stable and unstable manifolds define smooth foliations
$W_{\tilde {\cal Q}}^s,W_{\tilde {\cal Q}}^u$
of
$\tilde {\cal Q}$
, which are called the stable and unstable foliations of
$\tilde {\cal Q}$
, respectively. Define the strong stable foliation
$W^{ss}_{\tilde {\cal Q}}$
(or the strong unstable foliation
$W^{su}_{\tilde {\cal Q}}$
) of
$\tilde {\cal Q}$
by requiring that the leaf
$W^{ss}_{\tilde {\cal Q}}(q)$
(or
$W^{su}_{\tilde {\cal Q}}(q)$
) through q is the subset of
$W^s_{\tilde {\cal Q}}(q)$
(or of
$W^u_{\tilde {\cal Q}}(q)$
) of all marked quadratic differentials whose vertical (or horizontal) measured geodesic lamination equals the vertical (or horizontal) measured geodesic lamination of q. The strong stable foliation of
$\tilde {\cal Q}$
is transverse to the unstable foliation of
$\tilde {\cal Q}$
.
The foliations
$W^i_{\tilde {\cal Q}} (i=ss,s,su,u)$
are invariant under the action of the stabilizer
${\mathrm{Stab}}(\tilde {\cal Q})$
of
$\tilde {\cal Q}$
in
${\mathrm{Mod}}(S)$
and they project to
$\Phi ^t$
-invariant singular foliations
$W^i_{\cal Q}$
of
${\cal Q}=\tilde {\cal Q}/{\mathrm{Stab}}(\tilde {\cal Q})$
.
As in §2, let
$\tilde {\cal Q}_{\mathrm{good}}$
be the subset of
$\tilde {\cal Q}$
of all points
$\tilde q$
so that the stabilizer of
$\tilde q$
in
${\mathrm{Mod}}(S)$
is contained in the subgroup of all elements which stabilize the component
$\tilde {\cal Q}$
pointwise. For
$\tilde q\in \tilde {\cal Q}_{\mathrm{good}}$
and
$z\in W^{s}_{\tilde {\cal Q}}(\tilde q)$
, there is a neighborhood V of
$\tilde q$
in
$W_{\tilde {\cal Q}}^{su}(\tilde q)$
, and there is a homeomorphism
$$ \begin{align} \Xi_z:V\to \Xi_z(V)\subset W_{\tilde {\cal Q}}^{su}(z)\end{align} $$
with
$\Xi _z(\tilde q)=z$
which is determined by the requirement that
$\Xi _z(u)\in W_{\tilde {\cal Q}}^s(u)$
for all
${u\in V}$
. We call
$\Xi _z$
a holonomy map for the strong unstable foliation along the stable foliation.
To be more precise, since
$z\in W_{\tilde {\cal Q}}^s(\tilde q)$
, the vertical measured geodesic lamination
$\tilde q^v$
of
$\tilde q$
and the horizontal measured lamination
$z^h$
of z bind S. Since binding S is an open condition for pairs of measured laminations, there is a neighborhood Z of
$[\tilde q^v]$
in
${\cal P\cal M\cal L}$
such that for every
$[\nu ]\in Z$
and every representative
$\nu $
of the projective class
$[\nu ]$
, the laminations
$\nu $
and
$z^h$
bind S. But this just means that there is a point in
$W^{su}_{\tilde {\cal Q}}(z)$
whose projective vertical measured lamination equals
$[\nu ]$
.
Similarly, for
$\tilde q\in \tilde {\cal Q}_{\mathrm{good}}$
and
$z\in W_{\tilde {\cal Q}}^{u}(\tilde q)$
, there is a neighborhood Y of
$\tilde q$
in
$W^{ss}_{\tilde {\cal Q}}(\tilde q)$
, and there is a homeomorphism
$$ \begin{align} \Theta_z:Y\to \Theta_z(Y)\subset W^{ss}_{\tilde {\cal Q}}(z)\end{align} $$
with
$\Theta _z(\tilde q)=z$
which is determined by the requirement that
$\Theta _z(u)\in W^u_{\tilde {\cal Q}}(u)$
for all
$u\in Y$
. We call
$\Theta _z$
a holonomy map for the strong stable foliation along the unstable foliation. The holonomy maps are equivariant under the action of the mapping class group and hence they project to locally defined holonomy maps in the projection
${\cal Q}$
of
$\tilde {\cal Q}$
to the moduli space of area-one quadratic or abelian differentials, which are denoted by the same symbols.
The tangent bundle of the strong stable and strong unstable foliations of the component
${\cal Q}$
can be equipped with the so-called modified Hodge norm, which induces a Hodge distance
$d_H$
on the leaves of the foliation. This distance is locally uniformly equivalent to any other distance defined by a continuous norm on that tangent bundle.
Let
$$ \begin{align*}\Pi:\tilde {\cal Q}(S)\to {\cal Q}(S)\end{align*} $$
be the canonical projection. For
$q\in {\cal Q}_{\mathrm{good}}$
and
$r>0$
, let
$$ \begin{align*}B_{\cal Q}^i(q,r)\end{align*} $$
be the closed ball of radius r about q in
$W_{\cal Q}^i(q) (i=ss,su)$
with respect to the metric
$d_H$
. Call such a ball
$B_{\cal Q}^{i}(q,r)$
admissible if the following holds true. Let
$\tilde q\in \tilde {\cal Q}$
be a preimage of q; then the restriction of
$\Pi $
to the component
$B_{\tilde {\cal Q}}^i(\tilde q,r)$
containing
$\tilde q$
of the preimage of
$B_{\cal Q}^i(q,r)$
is a diffeomorphism.
For every point
$q\in {\cal Q}_{\mathrm{good}}$
, there is a number
$$ \begin{align*}a_{\cal Q}(q)>0\end{align*} $$
such that the balls
$B_{\cal Q}^i(q,a_{\cal Q}(q))$
are admissible
$(i=ss,su)$
and that for any preimage
$\tilde q$
of q in
$\tilde {\cal Q}$
and any
$z\in B_{\cal Q}^{ss}(\tilde q,a_{\cal Q}(q))$
(or
$z\in B_{\cal Q}^{su}(\tilde q,a_{\cal Q}(q))$
), the holonomy map
$\Xi _z$
(or
$\Theta _z$
) is defined on
$B_{\tilde {\cal Q}}^{su}(\tilde q,a_{\cal Q}(q))$
(or on
$B_{\tilde {\cal Q}}^{ss}(\tilde q,a_{\cal Q}(q))$
).
Now let
$$ \begin{align*}W_1\subset B_{\cal Q}^{ss}(q,a_{\cal Q}(q)),\quad W_2\subset B_{\cal Q}^{su}(q,a_{\cal Q}(q))\end{align*} $$
be Borel sets and let
$\tilde W_1\subset B_{\tilde {\cal Q}}^{ss}(\tilde q,a_{\cal Q}(q))$
,
$\tilde W_2\subset B_{\tilde {\cal Q}}^{su}(\tilde q,a_{\cal Q}(q))$
be the preimages of
$W_1,W_2$
in
$B_{\tilde {\cal Q}}^{ss}(\tilde q,a_{\cal Q}(q)), B_{\tilde {\cal Q}}^{su}(\tilde q,a_{\cal Q}(q))$
. Define
$$ \begin{align*}V(\tilde W_1,\tilde W_2) = \bigcup_{z\in \tilde W_1}\Xi_z\tilde W_2\quad \text{and}\quad V(W_1,W_2) =\Pi V(\tilde W_1,\tilde W_2). \end{align*} $$
Note that the map
$\Omega :\tilde W_1\times \tilde W_2\to V(\tilde W_1,\tilde W_2)$
defined by
$\Omega (z,u)=\Xi _z(u)$
is a homeomorphism. If
$W_1,W_2$
are path connected and contain the point q, then the set
$V(\tilde W_1,\tilde W_2)$
is path connected and
$V(W_1,W_2)$
is path connected as well.
Similarly, define
$$ \begin{align*}Y(\tilde W_1,\tilde W_2)=\bigcup_{u\in \tilde W_2} \Theta_u \tilde W_1\quad\text{and}\quad Y(W_1,W_2)=\Pi Y(\tilde W_1,\tilde W_2).\end{align*} $$
Then there is a continuous function
$$ \begin{align} \sigma:V(B_{\tilde {\cal Q}}^{ss}(\tilde q,a_{\cal Q}(q)), B_{\tilde {\cal Q}}^{su}(\tilde q,a_{\cal Q}(q)))\to \mathbb{R}\end{align} $$
which vanishes on
$B_{\tilde {\cal Q}}^{ss}(\tilde q,a_{\cal Q}(q))\cup B_{\tilde {\cal Q}}^{su}(\tilde q,a_{\cal Q}(q))$
and such that
$$ \begin{align*}Y(\tilde W_1,\tilde W_2)= \{\Phi^{\sigma(z)}z\mid z\in V(\tilde W_1,\tilde W_2)\}.\end{align*} $$
In particular, for every number
$\kappa>0$
, there is a number
$r(q,\kappa )>0$
such that the restriction of the function
$\sigma $
to
$V(B_{\tilde {\cal Q}}^{ss}(\tilde q,r(q,\kappa )), B_{\tilde {\cal Q}}^{su}(\tilde q,r(q,\kappa )))$
assumes values in
$[-\kappa ,\kappa ]$
.
For
$t_0>0$
, define
$$ \begin{align} V(\tilde W_1,\tilde W_2,t_0)= &\bigcup_{-t_0\leq s\leq t_0} \Phi^sV(\tilde W_1,\tilde W_2)\\ \text{and}\quad V(W_1,W_2,t_0)=& \,\Pi V(\tilde W_1,\tilde W_2,t_0). \notag \end{align} $$
Then, for sufficiently small
$t_0$
, say for all
$t_0\leq t_{\cal Q}(q)$
, the following properties are satisfied.
-
(a)
$V(W_1,W_2,t_0)$
is homeomorphic to
$V(\tilde W_1,\tilde W_2)\times [-t_0,t_0]$
. -
(b) Every connected component of the intersection of an orbit of
$\Phi ^t$
with
$V(W_1,W_2,t_0)$
is an arc of length
$2t_0$
.
We call a set
$V(W_1,W_2,t_0)$
as in (12) which satisfies the assumptions (a) and (b) a set with a local product structure. Note that every point
$q\in {\cal Q}_{\mathrm{good}}$
has a neighborhood in
${\cal Q}$
with a local product structure, e.g. the set
$V(B^{ss}_{\cal Q}(q,r),B^{su}_{\cal Q}(q,r),t)$
for
$r\in (0,a_{\cal Q}(q))$
and
$t\in (0,t_{\cal Q}(q))$
. Moreover, the neighborhoods of q with a local product structure form a basis of neighborhoods of q in
${\cal Q}$
.
Period coordinates can be used to pull the standard Lebesgue measure on
$\mathbb {C}^k$
back to a
$\Phi ^t$
-invariant Borel probability measure
$\unicode{x3bb} $
on
${\cal Q}$
in the Lebesgue measure class (see [Reference MasurM82, Reference VeechV86]—the point here is that this measure is finite). The measure
$\unicode{x3bb} $
admits a natural family of conditional measures
$\unicode{x3bb} ^{ss},\unicode{x3bb} ^{su}$
on strong stable and strong unstable manifolds. The conditional measures
$\unicode{x3bb} ^i$
are well defined up to a universal constant, and they transform under the Teichmüller geodesic flow
$\Phi ^t$
via
$$ \begin{align*}d\unicode{x3bb}^{ss}\circ \Phi^t=e^{-ht}d\unicode{x3bb}^{ss}\quad\text{and}\quad d\unicode{x3bb}^{su}\circ \Phi^t=e^{ht}d\unicode{x3bb}^{su}.\end{align*} $$
Let
${\cal F}:{\cal Q}(S)\to {\cal Q}(S)$
be the flip
$q\to {\cal F}(q)=-q$
and let
$dt$
be the Lebesgue measure on the flow lines of the Teichmüller flow. Any given choice of conditional measures
$\unicode{x3bb} ^{su}$
on the strong unstable manifolds determines a choice of conditional measures
$\unicode{x3bb} ^{ss}$
on the strong stable manifolds by the requirement that
${\cal F}_*\unicode{x3bb} ^{su}=\unicode{x3bb} ^{ss}$
. The measure which can be written with respect to a local product structure in the form
$$ \begin{align*}d\unicode{x3bb}^{ss}\times d\unicode{x3bb}^{su}\times dt\end{align*} $$
is invariant under the Teichmüller flow and contained in the Lebesgue measure class. This implies that there is a unique choice of conditionals
$\unicode{x3bb} ^{su}$
such that
$$ \begin{align*}d\unicode{x3bb}=d\unicode{x3bb}^{ss}\times d\unicode{x3bb}^{su}\times dt,\end{align*} $$
that is, so that the measure on the right-hand side of the equation is a probability measure. The measures
$\unicode{x3bb} ^u$
on unstable manifolds defined by
$d\unicode{x3bb} ^u=d\unicode{x3bb} ^{su}\times dt$
are invariant under holonomy along strong stable manifolds.
The following is Lemma 3.2 of [Reference HamenstädtH13].
Lemma 3.3 Let
$q\in {\cal Q}_{\mathrm{good}}$
be a smooth point. Then, for every
$\epsilon>0$
, there is a number
$a(q,\epsilon )\in (0,a_{\cal Q}(q))$
with the following property. For every
$a\leq a(q,\epsilon )$
, the holonomy maps define a homeomorphism
$$ \begin{align*}\Psi:B_{{\cal Q}}^{ss}(q,a) \times B^{su}_{{\cal Q}}(q,a)\times [-t_{\cal Q}(q),t_{\cal Q}(q)]\to V(B^{ss}_{\cal Q}(q,a),B^{su}_{\cal Q}(q,a),t_{\cal Q}(q))\end{align*} $$
whose Jacobian with respect to the measure
$\unicode{x3bb} ^{ss}\times \unicode{x3bb} ^{su}\times dt$
and the measure
$\unicode{x3bb} $
is contained in the interval
$[(1+\epsilon )^{-1},1+\epsilon ]$
.
4 Contraction and recurrence control
In this section we establish a contraction property for the modified Hodge distances
$d_H$
and use this to obtain some quantitative recurrence properties for the Teichmüller flow using the tools from the previous sections.
The following is the first part of Theorem 3.15 of [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12].
Theorem 4.1 There exists a number
$c_H>0$
not depending on choices such that for any
$q\in {\cal Q}$
, any
$q^\prime \in W^{ss}_{{\cal Q},{\mathrm{loc}}}(q)$
and all
$t>0$
, we have
$$ \begin{align*} d_H(\Phi^tq,\Phi^tq^\prime)\leq c_Hd_H(q,q^\prime).\notag\end{align*} $$
Theorem 4.1 is in general not sufficient to obtain contraction of distances on strong stable manifolds. We aim at a contraction result which is more general than what can be extracted from [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12].
A point
$q\in {\cal Q}$
is called forward recurrent (or backward recurrent) if it is contained in its own
$\omega $
-limit set (or in its own
$\alpha $
-limit set) under the action of
$\Phi ^t$
. A point
$q\in {\cal Q}$
is recurrent if it is forward and backward recurrent. The set
${\cal R}\subset {\cal Q}$
of recurrent points is a
$\Phi ^t$
-invariant Borel subset of
${\cal Q}$
. It follows from the work of Masur [Reference MasurM82] that a recurrent point
$q\in {\cal R}$
has uniquely ergodic vertical and horizontal measured geodesic laminations whose supports fill up S. As a consequence, the preimage
$\tilde {\cal R}$
of
${\cal R}$
in
$\tilde {\cal Q}(S)$
is contained in the set
$\tilde {\cal A}$
defined in (5) of §3.
Using the notation from §3, by Theorem 3.1, there is a number
$p>1$
such that for every
$q\in \tilde {\cal Q}(S)$
, the map
$t\to \Upsilon _{\cal T}(P\Phi ^tq)$
is an unparameterized p-quasi-geodesic in the curve graph
${\cal C}(S)$
. If q is a lift of a recurrent point in
${\cal Q}(S)$
, then this unparameterized quasi-geodesic is of infinite diameter (see [Reference HamenstädtH13] for more and references).
Recall from (3) of §3 the definitions of the distances
$\delta _x (x\in {\cal T}(S))$
on
$\partial {\cal C}(S)$
and of the sets
$D(q,r)\subset \partial {\cal C}(S)$
$(q\in \tilde {\cal A},r>0)$
. The following lemma is Lemma 4.2 of [Reference HamenstädtH13], which is going to be used as a substitute for hyperbolicity.
Lemma 4.2 There are numbers
$c_0>0,\ell >0,b>0$
with the following property. Let
$q\in \tilde {\cal R}$
and, for
$s>0$
, write
$\sigma (s)=d(\Upsilon _{\cal T}(Pq), \Upsilon _{\cal T}(P\Phi ^sq))$
; then
$$ \begin{align*}\ell e^{-b\sigma(s)}\delta_{P\Phi^sq} \leq \delta_{Pq}\leq \ell^{-1}e^{-b\sigma(s)}\delta_{P\Phi^sq}\quad\text{on } D(\Phi^sq,c_0).\end{align*} $$
Let
$\tilde {\cal Q}\subset \tilde {\cal Q}(S)$
be a component of the preimage of
${\cal Q}$
and let
${\mathrm{Stab}}(\tilde {\cal Q})<{\mathrm{Mod}}(S)$
be the stabilizer of
$\tilde {\cal Q}$
in
${\mathrm{Mod}}(S)$
. The
$\Phi ^t$
-invariant Borel probability measure
$\unicode{x3bb} $
on
${\cal Q}$
in the Lebesgue measure class (that is, the normalized Masur–Veech measure) lifts to a
${\mathrm{Stab}}(\tilde {\cal Q})$
-invariant locally finite measure on
$\tilde {\cal Q}$
, which we again denote by
$\unicode{x3bb} $
. The conditional measures
$\unicode{x3bb} ^{ss}, \unicode{x3bb} ^{su}$
of
$\unicode{x3bb} $
on the leaves of the strong stable and strong unstable foliations of
${\cal Q}$
lift to a family of locally finite Borel measures on the leaves of the strong stable and strong unstable foliations
$W_{\tilde {\cal Q}}^{ss},W_{\tilde {\cal Q}}^{su}$
of
$\tilde {\cal Q}$
, respectively, which we again denote by
$\unicode{x3bb} ^{ss},\unicode{x3bb} ^{su}$
(see the discussion in §3.3).
The following observation is Lemma 4.3 of [Reference HamenstädtH13]. In its formulation, the number
$c_0>0$
is the constant from Lemma 4.2.
Lemma 4.3 There exists
$c_0>0$
and, for every
$\epsilon>0$
, for every
$\tilde q\in \tilde {\cal Q}_{\mathrm{good}}\cap \tilde {\cal R}$
and for all compact neighborhoods
$W_1\subset W_2$
of
$\tilde q$
in
$W^{su}_{\tilde {\cal Q}}(\tilde q)$
, there are compact neighborhoods
$K\subset C\subset W_1$
of
$\tilde q$
in
$W_{\tilde {\cal Q}}^{su}(\tilde q)$
with the following properties.
-
(1) There are numbers
$0<r_1<r_2<c_0/2$
such that
$$ \begin{align*}K=\overline{W_1\cap F^{-1}D(\tilde q,r_1)},\, C=\overline{W_1\cap F^{-1}D(\tilde q,r_2)}.\end{align*} $$
-
(2)
$\unicode{x3bb} ^{su}(K)(1+\epsilon )\geq \unicode{x3bb} ^{su}(C)$
. -
(3) If
$z\in K\cap \tilde {\cal A}$
, then
$\overline {F^{-1}D(z,(r_2-r_1)/2)\cap W_2}\subset C$
.
We next show Theorem 2 from the introduction. It translates some structural results on non-uniform hyperbolicity of the Teichmüller flow which are described in [Reference HamenstädtH13] using the curve graph into a property for the modified Hodge distance
$d_H$
. To this end, denote as before by
$B_{\cal Q}^i(q,r)$
the
$d_H$
-ball of radius r about q in
$W^i_{\cal Q}(q)$
.
The main point of the theorem is that the local strong stable and strong unstable manifolds which appear in the statement do not depend on the constant
$a>0$
.
Theorem 4.4 Let
$q\in {\cal Q}_{\mathrm{good}}$
be a recurrent point. Then there is a number
$r_0=r_0(q)>0$
, and there is a neighborhood U of q in
${\cal Q}_{\mathrm{good}}$
with the following property. Let
$z\in U$
be recurrent; then, for every
$a>0$
, there is a number
$T(z,a)>0$
so that for all
$T>T(z,a)$
, we have
$\Phi ^TB_{\cal Q}^{ss}(z,r_0)\subset B_{\cal Q}^{ss}(\Phi ^T(z),a)$
and
$\Phi ^{T}B_{\cal Q}^{su}(z,a)\supset B_{\cal Q}^{su}(\Phi ^T(z),r_0)$
.
Proof. We only show the statement for strong unstable manifolds, that is, the containment
$\Phi ^{T}B_{\cal Q}^{su}(z,a)\supset B_{\cal Q}^{su}(\Phi ^{T}(z),r_0)$
. The statement for strong stable manifolds is completely analogous and will be left to the reader.
Let
$q\in {\cal Q}$
be recurrent and let
$\tilde q\in \tilde {\cal Q}$
be a lift of q. By the second part of Lemma 3.2, there is a number
$r_0>0$
such that
$$ \begin{align*}B_{\tilde {\cal Q}}^{su}(\tilde q,2c_Hr_0)\subset \overline{F^{-1}D(\tilde q,c_0/2)},\end{align*} $$
where
$c_0>0$
is as in Lemma 4.2. Namely,
$\tilde q$
is uniquely ergodic and the balls
$D(\tilde q, \epsilon ) (\epsilon>0)$
form a neighborhood basis of
$F(\tilde q)$
in the Gromov boundary of the curve graph of S. We may also assume that the balls
$B_{\tilde {\cal Q}}^{su}(\tilde w,r)$
are contractible for all
$r\leq 2c_Hr_0$
and all points
$\tilde w$
in a neighborhood
$\tilde W$
of
$\tilde z$
in
$\tilde {\cal Q}$
.
By continuity of the Hodge distance on the leaves of the strong stable foliation and by continuity of the dependence of the distances
$\delta _{P\tilde z}$
on
$\tilde z\in \tilde {\cal Q}$
as made precise in inequality (4), there is a neighborhood
$\tilde U\subset \tilde W$
of
$\tilde q$
in
$\tilde {\cal Q}$
such that the following holds true. Let
$\tilde z\in \tilde U$
be a lift of a recurrent point
$z\in {\cal Q}$
; then
$$ \begin{align} B_{\tilde {\cal Q}}^{su}(\tilde z,c_Hr_0)\subset \overline{F^{-1}D(\tilde z,c_0)}.\end{align} $$
Denote by U the projection of
$\tilde U$
to
${\cal Q}$
. Let
$z\in U$
be recurrent and let
$a\in (0,c_Hr_0)$
. Consider the preimage
$\tilde z$
of z in
$\tilde U$
. Since
$B_{\tilde {\cal Q}}^{su}(\tilde z,a/2)$
is a neighborhood of
$\tilde z$
in
$W^{su}_{\tilde {\cal Q}}(\tilde z)$
, by Lemma 4.3 there exists a number
$c_1=c_1(z,a)>0$
such that
$$ \begin{align*}B_{\tilde {\cal Q}}^{su}(\tilde z,a/2) \supset \overline{F^{-1}D(\tilde z,2c_1)}\cap B^{su}_{\tilde {\cal Q}}(\tilde z,2c_Hr_0).\end{align*} $$
Using once more continuity as in the beginning of this proof, we then can find a neighborhood
$\tilde V\subset \tilde U$
of
$\tilde z$
so that
$$ \begin{align} B_{\tilde {\cal Q}}^{su}(\tilde u,a)\supset \overline{F^{-1}D(\tilde u, c_1)}\cap B_{\tilde {\cal Q}}^{su}(\tilde u,c_Hr_0)\end{align} $$
for all
$\tilde u\in \tilde V$
which project to recurrent points in U.
Let
$V\subset U$
be the projection of
$\tilde V$
. Lemma 4.2 shows that there exists a number
$R(z,a)>0$
so that for all
$R>R(z,a)$
, we have
$$ \begin{align} D(\Phi^R\tilde z,c_0)\subset D(\tilde z,c_1),\end{align} $$
where
$c_1>0$
is as in (14). As z is recurrent, there exists furthermore a number
$T>R(z,a)$
so that
$\Phi ^{T}z\in V$
.
By equivariance under the action of the mapping class group, the assumption that
$\Phi ^Tz\in V$
and the estimate (13), we have
$B_{\tilde {\cal Q}}^{su}(\Phi ^T\tilde z,c_Hr_0)\subset \overline {F^{-1}D(\Phi ^T\tilde z,c_0)}$
and together with (15) we conclude that
$$ \begin{align} \Phi^{-T}B_{\tilde {\cal Q}}^{su}(\Phi^T\tilde z,c_Hr_0)\subset \overline{F^{-1}D(\tilde z,c_1)}.\end{align} $$
On the other hand, as
$\tilde z\in \tilde V$
, the estimate (14) holds true. But
$a<c_Hr_0$
and consequently (14) and (16) together with the assumption that for
$u\in V$
the ball
$B_{\tilde {\cal Q}}^{su}(u,c_Hr_0)$
is contractible yield
$$ \begin{align*}\Phi^{-T} B_{\cal Q}^{su}(\Phi^T z,c_Hr_0)\subset B_{\cal Q}^{su}(z,a)\end{align*} $$
or, equivalently,
$$ \begin{align*}B_{\cal Q}^{su}(\Phi^T z,c_Hr_0)\subset \Phi^T B_{\cal Q}^{su}(z,a).\end{align*} $$
By Theorem 4.1, this implies that
$\Phi ^{R}B_{\cal Q}^{su}(z,a)\supset B^{su}_{\cal Q}(\Phi ^Rz,r_0)$
for all
$R>T=T(z,a)$
. As
$z\in U$
and
$a\in (0,c_Hr_0)$
were arbitrary, this is what we wanted to show.
Definition 4.5 A flow
$\Phi ^t$
on an orbifold X admits a uniformly hyperbolic localization near a point
$p\in X$
if there exists a neighborhood U of p in X with the properties stated in Theorem 4.4.
To summarize, Theorem 4.4 shows that the Teichmüller flow on a component of a stratum of abelian or quadratic differentials admits a uniformly hyperbolic localization near every recurrent point.
Let as before
$\unicode{x3bb} $
be the normalized Masur–Veech measure on
${\cal Q}$
. A version of the following technical result was established in [Reference HamenstädtH13]. As it is not explicitly formulated in [Reference HamenstädtH13] in the form we need, we provide a proof. Its proof is a variation of the arguments of Margulis [Reference MargulisMa04], adapted to our situation.
Before we can proceed, we introduce the notion of a characteristic curve. To this end, let
$U\subset {\cal Q}_{\mathrm{good}}$
be an open contractible set, let
$u\in U$
and let
$T>>0$
be such that
$\Phi ^Tu\in U$
. Connect
$\Phi ^Tu$
to u by a path in U and let
$\zeta $
be the resulting closed curve. We call
$\zeta $
a characteristic curve of the pseudo-orbit
$(u,\Phi ^Tu)$
with end points in U.
As
$U\subset {\cal Q}_{\mathrm{good}}$
is contractible, there exists an open subset
$\tilde U$
of
$\tilde {\cal Q}_{\mathrm{good}}$
so that the canonical projection
$\Pi :\tilde {\cal Q}\to {\cal Q}$
maps
$\tilde U$
diffeomorphically onto U. Furthermore, there exists a unique mapping class
$\phi \in {\mathrm{Mod}}(S)$
so that for the lift
$\tilde u\in \tilde U$
of u, we have
$\Phi ^T\tilde u\in \phi (\tilde U)$
. The curve
$\zeta $
then lifts to a curve in
$\tilde {\cal Q}$
which connects
$\tilde u$
to
$\phi (\tilde u)$
; in particular, the conjugacy class of the element
$\phi $
depends only on u and T and not on the particular choice of the curve
$\zeta $
. In other words, a characteristic curve of a pseudo-orbit with end points in U determines uniquely the conjugacy class of an element in
${\mathrm{Mod}}(S)$
.
Lemma 5.1 of [Reference HamenstädtH13] shows that even more is true. By perhaps decreasing U and increasing T, the conjugacy class of the element
$\phi \in {\mathrm{Mod}}(S)$
is pseudo-Anosov, and it defines a periodic orbit
$\gamma $
contained in
${\cal Q}$
which passes through a neighborhood of U of controlled size. We use these facts for the following strengthening of the main technical result in [Reference HamenstädtH13].
In its statement, there appear two a priori chosen constants
$\delta>0,\eta >0$
. The number
$\delta $
is used to control volume ratios. As we are interested in properties which are true almost surely, we can think of
$\delta $
as the total measure of points which fail to have a sufficiently controlled recurrence behavior. The number
$\eta>0$
controls the lengths of connected orbit segments which are contained in a suitably chosen set with a product structure. It will only be used in §6. What matters later on is that
$\eta $
can be chosen as small as we wish, independent of
$\delta $
. The result translates uniformly hyperbolic localization into measure control.
Proposition 4.6 Let
${\cal Q}$
be a component of a stratum and let
$q\in {\cal Q}_{\mathrm{good}}$
be a good recurrent point. Then, for every neighborhood U of q and for all
$\delta>0,\eta >0$
, there are contractible closed neighborhoods
$Z_1\subset Z_2\subset U$
of q with local product structures, there are a Borel set
$Z_0\subset Z_1$
and a number
$R_0>0$
with the following properties.
-
(1)
$\unicode{x3bb} (Z_2)\leq (1-\delta )^{-1}\unicode{x3bb} (Z_0)$
. -
(2) For some integer
$m>1/\delta $
, a
$\Phi ^t$
-orbit intersects
$Z_1,Z_2$
in arcs of length
$2t_0<\eta /m$
. -
(3) The set
has a product structure and the same holds true for
$$ \begin{align*}Z_4=\bigcup_{-t_0m\leq t\leq t_0m}\Phi^tZ_2\subset U\end{align*} $$
Furthermore,
$$ \begin{align*}Z_3=\bigcup_{-t_0(m-2)\leq t\leq t_0(m-2)}\Phi^tZ_1\subset Z_4.\end{align*} $$
$Z_3$
is contained in the interior of
$Z_4$
.
-
(4) Let
$z\in Z_0$
and let
$T>R_0$
be such that
$\Phi ^Tz\in Z_3$
. Then there exists a path-connected set
$B(z)\subset Z_2$
containing z, with There is a periodic orbit
$$ \begin{align*}\quad \quad\Phi^TB(z)\subset Z_4\quad\text{and}\quad \unicode{x3bb}(B(z))\in [(1-\delta)e^{-hT}\unicode{x3bb}(Z_1), (1-\delta)^{-1}e^{-hT}\unicode{x3bb}(Z_1)].\end{align*} $$
$\gamma $
for
$\Phi ^t$
of length contained in
$[T-mt_0,T+mt_0]$
such that for each
$u\in B(z)$
, the characteristic curve of the pseudo-orbit
$(u,\Phi ^Tu)$
with end points in
$Z_4$
determines the same component
$\gamma (z,T)$
of
$\gamma \cap Z_4$
. If
$u\in Z_0-B(z)$
and if
$\Phi ^Tu\in Z_3$
, then the arc
$\gamma (u,T)$
is disjoint from
$\gamma (z,T)$
.
Proof. The basic idea goes back to Margulis, who proved a similar but somewhat stronger result for Anosov flows on closed manifolds, using uniform expansion (or contraction) of strong unstable (or strong stable) manifolds. The book [Reference MargulisMa04] contains a very detailed account on these by now classical arguments.
The Teichmüller flow is not hyperbolic, but we shall show that uniformly hyperbolic localization as established in Theorem 4.4 and non-uniform recurrence suffice to establish the proposition. The price we pay is that the set
$Z_0$
which appears in its statement and which can be chosen to be open in the setting of Anosov flows is now only a Borel set. As counting results rely on mixing properties, this is not a problem for our main goal.
We start with obtaining some volume control using absolute continuity of the strong stable and strong unstable foliations. Namely, recall [Reference MasurM82, Reference VeechV86] that there is a family of conditional measures
$\unicode{x3bb} ^{ss},\unicode{x3bb} ^{su}$
for the Masur–Veech measure
$\unicode{x3bb} $
on strong stable and strong unstable manifolds in the Lebesgue measure class, uniquely determined by
$\unicode{x3bb} $
and equivariance under the flip
$z\to -z$
. We have
$$ \begin{align*}d\unicode{x3bb}=d\unicode{x3bb}^{su}\times d\unicode{x3bb}^{ss}\times dt\quad \text{and}\quad \frac{d\Phi^t\circ \unicode{x3bb}^{su}}{d\unicode{x3bb}^{su}}=e^{ht},\, \frac{d\Phi^t\circ \unicode{x3bb}^{ss}}{d\unicode{x3bb}^{ss}}=e^{-ht}.\end{align*} $$
Let
$q\in {\cal Q}_{\mathrm{good}}$
be a recurrent point and let
$U\subset {\cal Q}_{\mathrm{good}}$
be an open neighborhood of q. By perhaps making U smaller, we may assume that U satisfies the assumptions in Theorem 4.4. By making U even smaller, we may moreover assume that U has a product structure. More precisely, for the number
$r_0=r_0(q)$
as in Theorem 4.4, we may assume that there are some
$r_1<r_0$
and some
$s_0>0$
so that
$$ \begin{align*}U= V(B_{\cal Q}^{ss}(q,r_1),B_{\cal Q}^{su}(q,r_1),s_0).\end{align*} $$
Let
$\delta>0$
, let
$\eta>0$
and let
$\kappa <1$
be sufficiently small that
$(1+\kappa )^7<(1-\delta )^{-1}$
. Recall from §3 the definition of the holonomy maps
$\Xi _u, \Theta _z$
. By the equation (11) and invariance of the construction in §3 under the action of the mapping class group, for
$u\in B^{ss}_{\cal Q}(q,r_1)$
and
$z\in B^{su}_{\cal Q}(q,r_1)$
, we have
$$ \begin{align} \Theta_z(u)=\Phi^{\sigma(u,z)} \Xi_u(z),\end{align} $$
for a number
$\sigma (u,z)$
which depends continuously on
$u,z$
, and
$\sigma (q,q)=0$
.
Let
$m>1/\delta $
be an integer. As the Hodge distance is defined by a continuous norm on the tangent bundle of strong stable and strong unstable manifolds of the component
${\cal Q}$
and as holonomy maps are smooth, we can find numbers
$\epsilon <\min \{\kappa ,s_0,1/4\}$
,
$r_2<r_1(1-2\epsilon )/4$
and
$s_1<\min \{s_0,\eta \}$
with the following properties.
-
(a) If
$r\leq r_2$
, then
$\unicode{x3bb} ^iB^i_{\cal Q}(q,r)\leq (1+\kappa ) \unicode{x3bb} ^iB^i_{\cal Q}(q,r(1-2\epsilon ))$
(
$i=ss,su$
). -
(b) If
$u\in B_{\cal Q}^{ss}(q,r_2)$
and
$t\in [-s_1,s_1]$
, then the restriction of the map
$\Phi ^t\circ \Xi _u$
to
$B_{\cal Q}^{su}(q,r_2)$
is a
$(1+\epsilon )$
-bilipschitz diffeomorphism of
$B_{\cal Q}^{su}(q,r_2)$
into
$B_{\cal Q}^{su}(\Phi ^t u,r_1)$
. Its Jacobian for the measures
$\unicode{x3bb} ^{su}$
is contained in the interval
$[(1+\kappa )^{-1},1+\kappa ]$
. Furthermore, if
$z\in B_{\cal Q}^{su}(q,r_2)$
and
$t\in [-2s_1,2s_1]$
, then the restriction of the map
$\Phi ^t\circ \Theta _z$
to
$B_{\cal Q}^{ss}(q,r_2)$
is a
$(1+\epsilon )$
-bilipschitz diffeomorphism of
$B_{\cal Q}^{ss}(q,r_2)$
into
$B_{\cal Q}^{ss}(\Phi ^tz,r_1)$
. -
(c) The map
$\Lambda :B_{\cal Q}^{ss}(q,r_2)\times B_{\cal Q}^{su}(q,r_2)\times (-s_1,s_1)\to U$
defined by
$\Lambda (u,z,t)=\Phi ^t\Xi _u(z)$
is a diffeomorphism onto its image, and its Jacobian with respect to the product measure
$\unicode{x3bb} ^{ss}\times \unicode{x3bb} ^{su}\times dt$
on
$B_{\cal Q}^{ss}(q,r_2)\times B_{\cal Q}^{su}(q,r_2)\times (-s_1,s_1)$
and the Masur–Veech measure
$\unicode{x3bb} $
on U is contained in the interval
$[(1+\kappa )^{-1},1+\kappa ]$
. Furthermore, the analogous statement also holds true for the map
$\Psi :B_{\cal Q}^{ss}(q,r_2)\times B_{\cal Q}^{su}(q,r_2)\times (-s_1,s_1)\to U$
defined by
$\Psi (u,z,t)=\Phi ^t\Theta _z(u)$
. -
(d)
$\vert \sigma (u,z)\vert \leq s_1/m$
for all
$(u,z)\in B^{ss}_{\cal Q}(q,r_2)\times B^{su}_{\cal Q}(q,r_2)$
.
Constants with these properties can be determined as follows.
The constants
$s_0,r_1$
are invariants of the set U, and the number
$\kappa $
depends only on an a priori chosen number
$\delta>0$
.
Given
$s_0,r_1,\kappa $
, we next determine a number
$\epsilon $
as specified in (a) above. Namely, as the measures
$\unicode{x3bb} ^{i}$
can be defined by a smooth volume form on a local strong stable or strong unstable manifold in
${\cal Q}$
, and as the Hodge distance is defined by a smooth norm, near the point q the volumes of balls of sufficiently small radius are uniformly equivalent to the volumes of euclidean balls. This implies that for the given number
$\kappa>0$
, we can find a number
$\epsilon \in (0,\min \{\kappa , s_0,1/4\})$
such that property (a) holds true for this
$\epsilon $
and for all sufficiently small numbers
$r>0$
, say for all
$r\leq \hat r_2$
for some
$\hat r_2<r_1$
.
Once the numbers
$s_0,r_1,\kappa ,\epsilon $
are fixed, we have to find
$r_2,s_1$
. This is done in two steps. First we determine a number
$\tilde r_2<\min \{r_1(1-2\epsilon )/4,\hat r_2\}$
such that property (b) holds true for
$r_2=\tilde r_2$
and for
$t=0$
, and where the number
$1+\epsilon $
in the statement is replaced by
$\sqrt {1+\epsilon }$
and the number
$1+\kappa $
is replaced by
$\sqrt {1+\kappa }$
. This is possible because the map
$(u,z)\in B_{\cal Q}^{ss}(q,r_1)\times B_{\cal Q}^{su}(q,r_1)\to \Xi _u(z)$
(or
$(u,z)\in B_{\cal Q}^{ss}(q,r_1)\times B_{\cal Q}^{su}(q,r_1)\to \Theta _z(u)$
) is smooth, its restriction to
$\{q\}\times B_{\cal Q}^{su}(q,r_1)$
(or to
$B_{\cal Q}^{ss}(q,r_1)\times \{q\}$
) is just the second (or the first) factor projection and since the Hodge norm is smooth.
By possibly decreasing
$\tilde r_2$
, we may also assume that property (c) holds true for the restriction of the diffeomorphism
$\Lambda $
(or the restriction of the diffeomorphism
$\Psi $
) to the set
$B_{\cal Q}^{ss}(q,\tilde r_2)\times B_{\cal Q}^{su}(q,\tilde r_2)\times \{0\}$
, with
$1+\kappa $
replaced by
$\sqrt {1+\kappa }$
. Namely,
$\Lambda $
(or
$\Psi $
) is a diffeomorphism onto its image and its Jacobian equals one at the point
$(q,q,0)$
.
Given such a number
$\tilde r_2$
, and for an a priori chosen constant
$\eta>0$
which is independent of any other constraint, we determine a number
$s_1<\min \{s_0,\eta \}$
such that property (b) holds true for
$\tilde r_2$
,
$t\in [-s_1,s_1]$
and the constants
$1+\epsilon , 1+\kappa $
, and that property (c) holds true for
$\tilde r_2$
, the constant
$1+\kappa $
and this number
$s_1$
. By the choice of
$\tilde r_2$
, such a number
$s_1$
can be found by continuity.
For the numbers
$\kappa ,\epsilon ,\tilde r_2,s_1$
, properties (a)–(c) hold true as required, but this may not be the case for (d). However, as
$\sigma (q,q)=0$
, we can find a number
$r_2<\tilde r_2$
such that property (d) holds true if we replace
$\tilde r_2$
by
$r_2$
. As this does not affect the validity of statements (a)–(c) for the fixed number
$s_1$
, we have found numbers
$\epsilon ,s_1,r_2$
for which properties (a)–(d) above hold true.
For this number
$r_2<r_1(1-2\epsilon )/4$
and for any
$\rho \in (0,s_1)$
, define
$$ \begin{align*}Z_1(\rho)&=V(B_{\cal Q}^{ss}(q,r_2(1-2\epsilon)), B_{\cal Q}^{su}(q,r_2(1-2\epsilon)),\rho) \quad\text{and}\\ Z_2(\rho) &= V(B_{\cal Q}^{ss}(q,r_2), B_{\cal Q}^{su}(q,r_2),\rho). \end{align*} $$
It follows from properties (a) and (c) that
$$ \begin{align} \unicode{x3bb}(Z_2(\rho))\leq (1+\kappa)^4\unicode{x3bb}(Z_1(\rho))\end{align} $$
for all
$\rho \in (0,s_1)$
. Namely, by property (c), we know that
$$ \begin{align*} \unicode{x3bb}(Z_1(\rho))\geq 2\rho (1+\kappa)^{-1} \unicode{x3bb}^{ss}B^{ss}_{\cal Q}(q,r_2(1-2\epsilon)) \unicode{x3bb}^{su} B^{su}_{\cal Q}(q,r_2(1-2\epsilon));\notag\end{align*} $$
on the other hand, also
$$ \begin{align*}\unicode{x3bb}(Z_2(\rho))\leq 2\rho (1+\kappa)\unicode{x3bb}^{ss}B^{ss}_{\cal Q}(q,r_2) \unicode{x3bb}^{su}B_{\cal Q}^{su}(q,r_2).\end{align*} $$
Together with property (a), this yields the estimate (18).
Furthermore, by property (b), if
$u\in Z_2(s_1)$
, then the local strong unstable manifold
$W^{su}_{Z_2(s_1),{\mathrm{loc}}}(u)$
of u in
$Z_2(s_1)$
(that is, the intersection of
$Z_2(s_1)$
with the local strong unstable manifold of u in
${\cal Q}$
) is contained in the ball
$B_{\cal Q}^{su}(u,r_1)$
and, if
$u\in Z_1(s_1)$
, then
$$ \begin{align} B_{\cal Q}^{su}(u,\epsilon r_2)\subset W^{su}_{Z_2(s_1),{\textrm{loc}}}(u). \end{align} $$
Namely, as the distance between a point
$u\in B_{\cal Q}^{su}(q,r_2(1-2\epsilon ))$
and the boundary of
$B_{\cal Q}^{su}(q,r_2)$
is not smaller than
$2\epsilon r_2$
, the distance between the image of u and the image of the boundary of
$B_{\cal Q}^{su}(q,r_2)$
under a
$1+\epsilon <2$
bilipschitz diffeomorphism is at least
$2\epsilon r_2/2=\epsilon r_2$
. Thus, the estimate (19) follows from the requirement (b) and the definitions.
By equation (17) and property (d) above, if
$u\in Z_2(s_1(1-1/m))$
, then the intersection of
$Z_2(s_1)$
with the local strong stable manifold through u just equals the image of
$B_{\cal Q}^{ss}(q,r_2)$
under the map
$\Phi ^t\Theta _z$
for some
$z\in B_{\cal Q}^{su}(q,r_2)$
and some
$t\in (-s_1,s_1)$
which is determined by u (this is in general not true for points in
$Z_2(s_1)-Z_2(s_1(1-1/m)$
). As a consequence, the discussion in the previous paragraph shows that for all
$u\in Z_1(s_1(1-1/m))$
, we have
$$ \begin{align} B^{ss}_{\cal Q}(u,\epsilon r_2)\subset W^{ss}_{Z_2(s_1),{\textrm{loc}}}(u), \end{align} $$
where
$m>1/\delta $
is as above.
Recall that the number
$r_1>0$
was chosen so that Theorem 4.4 is valid for the set U and the number
$r_1$
. Since the Borel subset of
${\cal Q}$
of recurrent points has full measure, there are a number
$R_0>0$
and a Borel subset
$E\subset B^{ss}_{\cal Q}(q,r_2(1-2\epsilon ))\times B^{su}_{\cal Q}(q,r_2(1-2\epsilon ))$
with the following property. For
$\rho \in (0, s_1)$
, write
$$ \begin{align} Z_0(\rho)=\Lambda(E\times (-\rho,\rho))\subset Z_1(\rho). \end{align} $$
If
$z\in Z_0(\rho )$
and if
$T>R_0$
, then the
$d_H$
-diameter of
$\Phi ^{-T}B_{\cal Q}^{su}(\Phi ^Tz,r_1)$
is at most
$\epsilon r_2/2$
and the
$d_H$
-diameter of
$\Phi ^{T}B_{\cal Q}^{ss}(u,r_1)$
is at most
$\epsilon r_2/2$
. Furthermore, we have
$$ \begin{align} \unicode{x3bb}(Z_0(\rho))>(1+\kappa)^{-5}\unicode{x3bb}(Z_2(\rho))>(1-\delta) \unicode{x3bb}(Z_2(\rho)).\end{align} $$
Note that this estimate relies on the estimate (18).
By equation (19), we know that if
$u\in Z_1(s_1)$
, then
$B_{\cal Q}^{su}(u,\epsilon r_2)\subset W^{su}_{Z_2(s_1),{\mathrm{loc}}}(u)$
. Furthermore, as for any
$\rho <s_1$
and any
$v\in Z_2(\rho )$
the set
$W^{su}_{Z_2(\rho ),{\mathrm{loc}}}(v)$
is the image of
$B^{su}(q,r_2)$
under a
$(1+\epsilon )$
-bilipschitz diffeomorphism, the
$d_H$
-diameter of
$W^{su}_{Z_2(\rho ),{\mathrm{loc}}}(v)$
is at most
$2r_2(1+\epsilon )<r_1$
.
Let
$\rho <s_1$
and let
$z\in Z_0(\rho )\subset Z_1(\rho )$
and
$T>R_0$
be such that
$\Phi ^Tz\in Z_1(s_1)$
. The estimate in the previous paragraph shows that
$W^{su}_{Z_2(s_1),{\mathrm{loc}}}(\Phi ^Tz)\subset B^{su}_{\cal Q}(\Phi ^Tz,r_1)$
. Thus, by the choice of the set
$Z_0(\rho )$
and the assumption on T, the
$d_H$
-diameter of
$\Phi ^{-T}W^{su}_{Z_2(s_1),{\mathrm{loc}}}(\Phi ^Tz)$
is at most
$\epsilon r_2/2$
. But
$z\in \Phi ^{-T}W^{su}_{Z_2(s_1),{\mathrm{loc}}}(\Phi ^Tz)\cap Z_1(\rho )$
and therefore the estimate (19) shows that
$$ \begin{align} \Phi^{-T}W^{su}_{Z_2(s_1),{\textrm{loc}}}(\Phi^Tz)\subset W^{su}_{Z_2(\rho),{\textrm{loc}}}(z).\end{align} $$
Note that by invariance of strong unstable manifolds under the Teichmüller flow and by the definition of the holonomy maps and the definition of the sets
$Z_i(\rho )$
, although in the above discussion we may choose
$\rho <s_1$
to be different from
$s_1$
, it still holds true that
$\Phi ^{-T}W^{su}_{Z_2(s_1),{\mathrm{loc}}}(\Phi ^Tz)\subset W^{su}_{Z_2(\rho ),{\mathrm{loc}}}(z)$
since, by assumption, the point z is contained in
$Z_2(\rho )$
and, for
$z\in Z_2(\rho )\subset Z_2(s_1)$
, we have
$$ \begin{align*}W^{su}_{Z_2(s_1),{\textrm{loc}}}(z)=W^{su}_{Z_2(\rho),{\textrm{loc}}}(z).\end{align*} $$
Now let us assume in addition that
$\Phi ^Tz\in Z_1(\rho (1-1/m))\subset Z_1(\rho )$
. The above argument, with the roles of
$\Phi ^{-T}$
and
$\Phi ^{T}$
exchanged and replacing (19) by the estimate (20), which accommodates the time shift in the relation between the holonomy maps
$\Xi _z$
and
$\Theta _u$
, yields that
$$ \begin{align} \Phi^TW^{ss}_{Z_2(\rho),{\textrm{loc}}}(z)\subset W^{ss}_{Z_2(\rho),{\textrm{loc}}}(\Phi^Tz).\end{align} $$
For
$t_0=s_1/2m$
, define
$$ \begin{align*}Z_0=Z_0(t_0),\quad Z_1=Z_1(t_0),\quad Z_2=Z_2(t_0),\notag\\ Z_3=Z_1(s_1(1-2/m)),\quad Z_4=Z_2(s_1).\notag \end{align*} $$
We claim that these sets have the properties (1)–(4) stated in the proposition.
Note that
$2t_0m<\eta $
follows from the assumption
$s_1<\eta $
. Property (1) coincides with the estimate (22) for
$\rho =t_0$
, and Property (2) holds true by the definition of the sets
$Z_1,Z_2$
. Property (3) is an immediate consequence of the definitions as well.
To show property (4), assume that
$z\in Z_0$
and
$T>R_0$
are such that
$\Phi ^Tz\in Z_3$
. We first identify the connected component
$B(z)$
of z in
$Z_2\cap \Phi ^{-T}Z_4$
.
To this end, recall that
$W^{su}_{Z_3,{\mathrm{loc}}}(\Phi ^Tz)= W^{su}_{Z_4,{\mathrm{loc}}}(\Phi ^Tz)$
and note that
$$ \begin{align*}\Phi^{-T}W^{su}_{Z_4,{\textrm{loc}}}(\Phi^Tz)\subset Z_2\end{align*} $$
by the estimate (23). Since
$W^{su}_{Z_4,{\mathrm{loc}}}(\Phi ^Tz)$
is diffeomorphic to a ball and holonomy maps are diffeomorphisms, there exist a ball
$A\subset B^{su}_{\cal Q}(q,r_2)$
, a point
$y\in B^{ss}_{\cal Q}(q,r_2)$
and a number
$s\in [-t_0,t_0]$
such that
$$ \begin{align*}\Phi^{-T}W^{su}_{Z_4,{\textrm{loc}}}(\Phi^Tz)=\Phi^s\Xi_yA.\end{align*} $$
Here
$y\in B^{ss}_{\cal Q}(q,r_2)$
and
$s\in [-t_0,t_0]$
are such that
$z\in \Phi ^s\Xi _yB^{su}_{\cal Q}(q,r_2)$
. It then follows from two applications of property (b) and the fact that
$$ \begin{align*}\unicode{x3bb}^{su}(\Phi^{-T}W^{su}_{Z_4,{\textrm{loc}}}(\Phi^Tz))= e^{-hT}\unicode{x3bb}^{su}(W^{su}_{Z_4,{\textrm{loc}}}(\Phi^Tz))\end{align*} $$
that
$$ \begin{align*}\unicode{x3bb}^{su}(A)\in [(1+\kappa)^{-2}e^{-hT} \unicode{x3bb}^{su}(B^{su}_{\cal Q}(q,r_2)),(1+\kappa)^2e^{-hT} \unicode{x3bb}^{su}(B^{su}_{\cal Q}(q,r_2))].\end{align*} $$
In particular, if we define
$$ \begin{align*}\hat B(z)=\bigcup_{-t_0\leq t\leq t_0} \bigcup_{u\in B^{ss}_{{\cal Q}}(q,r_2)} \Phi^t\Xi_u(A),\end{align*} $$
then property (c) above shows that
$$ \begin{align*}\unicode{x3bb}(\hat B(z))\in [(1+\kappa)^{-3}e^{-hT}\unicode{x3bb}(Z_2), (1+\kappa)^3 e^{-hT}\unicode{x3bb}(Z_2)].\end{align*} $$
We now claim that in fact
$B(z)=\hat B(z)$
. Since
$(1+\kappa )^7<(1-\delta )^{-1}$
and since
$\unicode{x3bb} (Z_2)<(1+\kappa )^4\unicode{x3bb} (Z_1)$
by inequality (18), this then yields the measure control for
$B(z)$
stated in part (4) of the proposition.
To show that
$\hat B(z)\subset B(z)$
, we have to show that
$\Phi ^T\hat B(z)\subset Z_4$
. For this, let
$u\in A\subset B^{su}_{\cal Q}(q,r_2)$
and
$s\in [-t_0,t_0]$
be such that
$\Phi ^s\Xi _y(u)=z$
. By property (b) above, the image of
$B^{ss}_{\cal Q}(q,r_2)$
under the map
$\Phi ^s\Theta _y$
is contained in the ball
$B^{ss}_{\cal Q}(z,r_1)$
. Hence, by the choice of
$Z_0$
and by property (20), we have
$$ \begin{align*}\Phi^TB^{ss}_{\cal Q}(z,r_1)\subset B^{ss}_{\cal Q}(\Phi^Tz,\epsilon r_2/2)\subset W^{ss}_{Z_4,{\textrm{loc}}}(\Phi^Tz).\end{align*} $$
More precisely, the
$d_H$
-diameter of
$\Phi ^TB_{\cal Q}^{ss}(z,r_1)$
is at most
$\epsilon r_2/2$
.
Now the Teichmüller flow commutes with holonomy maps, and holonomy maps for
$Z_4$
are
$(1+\epsilon )$
- bilipschitz by property (b) above. From
$(1+\epsilon )^2<2$
and by the choice of
$t_0$
and the definition of
$Z_3\subset Z_4$
, we conclude that the diameter of
$\Phi ^T\Phi ^s \Theta _v B^{ss}_{\cal Q}(q,r_2)\subset W^{ss}_{Z_4,{\mathrm{loc}}}(\Phi ^T\Phi ^s v)$
is at most
$\epsilon r_2$
for all
$v\in A\subset B^{su}_{\cal Q}(q,r_2)$
. Taking into account the control on the time shift between the holonomy maps
$\Theta _z,\Xi _y$
and the fact that
$\Phi ^{T+\tau }(z)\in Z_4$
for all
$\tau \in [-4t_0,4t_0]$
, this yields that, indeed,
$\Phi ^T\hat B(z)\subset Z_4$
.
Since A is a ball, the set
$\hat B(z)$
is connected and hence to show that
$\hat B(z)=B(z)$
it suffices to show the following. Let
$y\in B^{ss}_{\cal Q}(q,r_2)$
; then there exists an open neighborhood W of A in
$B^{su}_{\cal Q}(q,r_1)$
such that
$\Phi ^T(\Xi _y(W-A))\cap Z_4=\emptyset $
. However, this holds true by equivariance under holonomy, the fact that for every
$u\in A$
we have
$\Phi ^T(\Xi _y(A))= W^{su}_{Z_4,{\mathrm{loc}}}(\Phi ^T(\Xi _y u))$
and the fact that
$\Phi ^T$
preserves the strong unstable foliation.
Finally, we show that
$B(z)$
defines a periodic orbit for the Teichmüller flow. Namely, connect
$\Phi ^Tz$
to z by an arc contained in
$Z_3$
and let
$\zeta $
be the resulting based loop. Note that
$\zeta \subset {\cal Q}_{\mathrm{good}}$
by construction. In particular,
$\zeta $
determines the conjugacy class of an element
$\phi \in {\mathrm{Mod}}(S)$
as explained in §2.
By [Reference HamenstädtH13],
$\phi $
is pseudo-Anosov. Furthermore, [Reference HamenstädtH13] shows that the periodic orbit for
$\Phi ^t$
determined by the conjugacy class of
$\phi $
passes through
$Z_4$
. The period of
$\gamma $
is contained in the interval
$[T-mt_0,T+mt_0]$
. The choice of the base point
$z\in Z_0$
for the loop
$\zeta $
determines a component
$\gamma (z,T)$
of the intersection of
$\gamma $
with
$Z_4$
. This means the following. The periodic orbit
$\gamma $
may intersect
$Z_4$
in many different components. As
$\zeta $
fellow travels
$\gamma $
[Reference RafiR14], the choice of the base point z for
$\zeta $
determines a base point for
$\gamma $
which is contained in
$Z_4$
, unique up to a small time shift along a subarc of
$\gamma $
entirely contained in
$Z_4$
. Thus, it determines an intersection component of
$\gamma $
with
$Z_4$
.
As the orbit segment
$\gamma (z,T)$
is contained in
$B(z)$
and the set
$B(z)$
is a component of
$Z_2\cap \Phi ^{-T}Z_4$
, we conclude that if
$u\in Z_0-B(z)$
and if
$\Phi ^Tu\in Z_3$
, then the orbit segment
$\gamma (u,T)$
is disjoint from
$\gamma (z,T)$
(see [Reference HamenstädtH13] for more details). This completes the proof of the proposition.
Remark 4.7 The only information about the Teichmüller flow
$\Phi ^t$
on components
${\cal Q}$
of strata of quadratic or abelian differentials used in Proposition 4.6 is local uniform hyperbolicity as established in Theorem 4.4 and the existence of a
$\Phi ^t$
-invariant Borel probability measure which is absolutely continuous with respect to the strong unstable and strong stable foliations, with uniformly expanding (or contracting) conditional measures. Using these hypotheses, the proof of Proposition 4.6 is an adaptation of Margulis’ argument as laid out in [Reference MargulisMa04].
As a consequence, the proposition holds true for all locally uniformly hyperbolic flows on a smooth manifold which admits such a measure. We believe that this class includes geodesic flows on compact rank-one manifolds of non-positive curvature, equipped with the unique measure of maximal entropy.
5 Counting periodic orbits
This section is devoted to a discussion of counting results for periodic orbits of the Teichmüller flow in a component
${\cal Q}$
of a stratum of area-one abelian or quadratic differentials on S. Recall from the introduction that the Teichmüller flow
$\Phi ^t$
acts on
${\cal Q}$
preserving a Borel probability measure
$\unicode{x3bb} $
in the Lebesgue measure class, the normalized Masur–Veech measure. Let
$k\geq 1$
be the number of zeros of a differential in
${\cal Q}$
and let
$h=2g-2+k$
be the entropy of
$\Phi ^t$
with respect to the measure
$\unicode{x3bb} $
.
The only properties we use from the Teichmüller flow
$\Phi ^t$
on
${\cal Q}$
are as follows. The Masur–Veech measure
$\unicode{x3bb} $
is ergodic and it is obtained from Bowen’s construction as formulated in Theorem 5.1 below.
Let
$$ \begin{align*}\Gamma\subset {\cal Q}\end{align*} $$
be the countable collection of all periodic orbits for
$\Phi ^t$
contained in
${\cal Q}$
. Denote by
$\ell (\gamma )$
the period of
$\gamma \in \Gamma $
and let
$\delta _\gamma $
be the standard
$\Phi ^t$
-invariant Lebesgue measure on
$\gamma $
of total mass
$\ell (\gamma )$
.
Using an approach by Margulis [Reference MargulisMa04], the asymptotic growth rate of the number of these periodic orbits can explicitly be determined. In fact, these orbits determine the Lebesgue measure
$\unicode{x3bb} $
on
${\cal Q}$
via a construction due to Bowen [Reference BowenBw73]. The following is the main result of [Reference HamenstädtH13].
Theorem 5.1 The measures
$$ \begin{align*}\mu_R=h e^{-hR}\sum_{\gamma\in \Gamma, \ell(\gamma)\leq R} \delta_\gamma\end{align*} $$
converge as
$R\to \infty $
weakly to the Masur–Veech measure on
${\cal Q}$
.
Note that in the formula in [Reference HamenstädtH13], the factor h is erroneously missing.
As
${\cal Q}$
is not compact, this does not immediately imply that
$\lim _{R\to \infty }\mu _R(Q)=1$
, nor does it determine the asymptotic growth rate of the number of periodic orbits on
${\cal Q}$
. However, a formula for this asymptotic growth rate follows from Theorem 5.1 and the main result of [Reference Eskin, Mirzakhani and RafiEMR19] (which rules out escape of mass) as formulated in the corollary in the introduction of [Reference HamenstädtH13].
Theorem 5.2
$\sharp \{\gamma \in \Gamma \mid \ell (\gamma )\leq R\}hRe^{-hR}\to 1$
as
$R\to \infty .$
Corollary 5.3
$\lim _{R\to \infty }\mu _R({\cal Q})=1$
.
Proof. That the statement in the corollary follows from Theorem 5.2 (and, under the assumption of Theorem 5.1, is in fact equivalent to Theorem 5.2) has been used many times in the literature; see e.g. [Reference Eskin and MirzakhaniEM11, Reference Eskin, Mirzakhani and RafiEMR19, Reference MargulisMa04]. Differentiate the function
$f(t)= ({e^{ht}}/{ht})$
to find
$f^\prime (t)=({e^{ht}}/{t})-({e^{ht}}/{ht^2})$
. Then note that under the assumption that the asymptotic formula in Theorem 5.2 holds true, as
$R\to \infty $
the value
$\mu _R({\cal Q})$
is close to
$$ \begin{align*}he^{-hR}\int_1^Rf^\prime(t)t\, dt=he^{-hR}\int_1^Re^{ht}(1-1/ht)\,dt,\end{align*} $$
which converges to one as
$R\to \infty $
.
For
$R_1<R_2$
, let
$\Gamma (R_1,R_2)\subset \Gamma $
be the set of all periodic orbits for
$\Phi ^t$
of prime period contained in the interval
$(R_1,R_2]$
(asking for prime period means that we do not consider multiply covered orbits). For
$R>0,0<\sigma <R$
, define a measure
$$ \begin{align*}\nu_{R,\sigma}=he^{-hR}(1-e^{-h\sigma})^{-1}\sum_{\gamma\in \Gamma(R-\sigma,R)}\delta_\gamma.\end{align*} $$
As an immediate consequence of Corollary 5.3, we observe the following result.
Corollary 5.4 For every
$\sigma>0$
, the measures
$\nu _{R,\sigma }$
converge as
$R\to \infty $
weakly to the Masur–Veech measure on
${\cal Q}$
, and
$\lim _{R\to \infty } \nu _{R,\sigma }({\cal Q})=1$
.
Proof. By definition, we have (as signed measures)
$$ \begin{align*}(1-e^{-h\sigma})\nu_{R,\sigma}=\mu_R-e^{-h\sigma}\mu_{R-\sigma}.\end{align*} $$
Thus, the corollary follows from Theorem 5.1 and Corollary 5.3.
Let
${\cal P}$
be a property for periodic orbits
$\gamma \in \Gamma $
. For a periodic orbit
$\gamma \in \Gamma $
, write
$\chi _{\cal P}(\gamma )=1$
if
$\gamma \in {\cal P}$
and write
$\chi _{\cal P}(\gamma )=0$
otherwise. We call
${\cal P}$
typical if as
$R\to \infty $
, the number of all
$\gamma \in \Gamma $
with
$\ell (\gamma )\leq R$
and
$\chi _{\cal P}(\gamma )=1$
is asymptotic to
$e^{hR}/hR$
.
For two finite Borel measures
$\nu _1,\nu _2$
on
${\cal Q}$
, write
$\nu _1\leq \nu _2$
if
$\nu _1(A)\leq \nu _2(A)$
for all Borel subsets A of
${\cal Q}$
. For
$R>0,0<\sigma <R$
, let
$$ \begin{align*}\nu_{R,\sigma,{\cal P}}=he^{-hR}(1-e^{-h\sigma})^{-1} \sum_{\gamma\in \Gamma(R-\sigma,R)}\chi_{\cal P}(\gamma)\delta_\gamma.\end{align*} $$
Clearly,
$\nu _{R,\sigma ,{\cal P}}\leq \nu _{R,\sigma }$
for all
$R,\sigma $
.
The next proposition is our main tool for showing that a property
${\cal P}$
for periodic orbits in
${\cal Q}$
is typical.
Proposition 5.5 A property
${\cal P}$
for
$\Gamma $
is typical if, for all
$\delta>0$
, there exists a number
$\sigma>0$
such that
$$ \begin{align*}\lim\inf_{R\to \infty} \nu_{R,\sigma,{\cal P}}({\cal Q})\geq 1-\delta.\end{align*} $$
Proof. Assume that the condition in the proposition is fulfilled. It suffices to show that for every
$\alpha>0$
, there exists a number
$R=R(\alpha )>0$
such that for all
$R\geq R(\alpha )$
, the number of periodic orbits
$\gamma \in {\cal P}$
with
$\ell (\gamma )\leq R$
is at least
$(1-\alpha )e^{hR}/hR$
.
To this end, let
$\delta>0$
be sufficiently small such that
$(1-\delta )^5\geq 1-\alpha $
. For this number
$\delta $
, let
$\sigma>0$
be such that the condition in the proposition holds true. By Corollary 5.4, there exists a number
$R_0=R_0(\sigma ,\delta )>0$
such that
$\nu _{R,\sigma }({\cal Q})\leq (1-\delta )^{-1}$
for all
$R\geq R_0$
. By perhaps increasing
$R_0$
, we may assume that
$\sigma /R\leq \delta $
for all
$R\geq R_0$
.
Since
$\lim \inf _{R\to \infty }\nu _{R,\sigma ,{\cal P}}({\cal Q})\geq 1-\delta $
, for sufficiently large R, say for all
$R\geq R_1\geq R_0$
, we have
$\nu _{R,\sigma ,{\cal P}}({\cal Q})\geq (1-\delta )^2$
. Let
$R\geq R_1$
. As each orbit
$\gamma \in {\cal P}$
with
$R-\sigma < \ell (\gamma )\leq R$
contributes to the total mass of
$\nu _{R,\sigma ,{\cal P}}$
with a weight contained in the interval
$$ \begin{align*}[he^{-hR}(1-e^{-h\sigma})^{-1}(R-\sigma),he^{-hR}(1-e^{-h\sigma})^{-1}R],\end{align*} $$
there are at least
$(1-\delta )^2e^{hR}(1-e^{-h\sigma })/hR$
periodic orbits
$\gamma \in {\cal P}$
of period in
$(R-\sigma ,R]$
.
Similarly, each orbit
$\gamma \in \Gamma (R-\sigma ,R)$
contributes at least
$he^{-hR}(1-e^{-h\sigma })^{-1}(R-\sigma )$
to the total mass of
$\nu _{R,\sigma }$
. Now
$\nu _{R,\sigma }({\cal Q})\leq (1-\delta )^{-1}$
and therefore there are at most
$(1-\delta )^{-1}e^{hR}(1-e^{-h\sigma })/h(R-\sigma )$
periodic orbits
$\gamma \in \Gamma (R-\sigma ,R)$
. Since
$(R-\sigma )/ R\geq 1-\delta $
by assumption, we conclude that the proportion of the number of periodic orbits in
$\Gamma (R-\sigma ,R)$
which are contained in
${\cal P}$
is at least
$(1-\delta )^4$
.
As the number of periodic orbits in
$\Gamma $
of length R growths exponentially with R, we can choose
$m_0>0$
sufficiently large that the number of periodic orbits in
$\Gamma $
of length at most
$R_1$
is smaller than
$\delta $
times the number of periodic orbits in
$\Gamma (R_1,R_1+m_0\sigma )$
. For
$m\geq m_0$
, summing the above estimate for the cardinalities of
${\cal P}\cap \Gamma (R_1+(j-1)\sigma ,R_1+j\sigma ) (j=1,\ldots ,m)$
and for
$\Gamma (R_1+(j-1)\sigma ,R_1+j\sigma ) (j=1,\ldots ,m)$
yields that the proportion of periodic orbits in
${\cal P}$
of period at most
$R_1+m\sigma $
among all periodic orbits of period at most
$R_1+m\sigma $
is at least
$(1-\delta )^5\geq 1-\alpha $
. As
$m\geq m_0$
was arbitrary, this shows the required estimate.
Remark 5.6 Although we did not check this, we believe that the condition in Proposition 5.5 is not necessary for a property
${\cal P}$
to be typical.
Corollary 5.7 Suppose that for every
$\delta>0$
, there exist an open relative compact subset U of
${\cal Q}$
with
$\unicode{x3bb} (\partial U)=0$
and a number
$\sigma>0$
such that
$$ \begin{align*}\lim\inf_{R\to \infty}\nu_{R,\sigma,{\cal P}}(U)\geq (1-\delta)\unicode{x3bb}(U).\end{align*} $$
Then
${\cal P}$
is typical.
Proof. By Proposition 5.5, it suffices to show that under the assumption of the corollary, for every
$\delta>0$
there exists some
$\sigma>0$
such that
$$ \begin{align*}\lim\inf_{R\to \infty}\nu_{R,\sigma,{\cal P}}({\cal Q})\geq 1-\delta.\end{align*} $$
To this end, choose an open set
$U\subset {\cal Q}$
and a number
$\sigma>0$
with the properties stated in the proposition, that is, such that
$\unicode{x3bb} (\partial U)=0$
and
$\lim \inf _{R\to \infty } \nu _{R,\sigma ,{\cal P}}(U)\geq (1-\delta )\unicode{x3bb} (U)$
.
Note that for all
$R>0$
, the measure
$\nu _{R,\sigma ,{\cal P}}$
is invariant under the Teichmüller flow
$\Phi ^t$
and we have
$\nu _{R,\sigma ,{\cal P}}\leq \nu _{R,\sigma }$
. As
$\nu _{R,\sigma }\to \unicode{x3bb} $
weakly as
$R\to \infty $
, we conclude that any weak limit
$\nu $
of a sequence of measures
$\nu _{R_i,\sigma ,{\cal P}}$
with
$R_i\to \infty $
$(i\to \infty )$
is
$\Phi ^t$
-invariant and satisfies
$\nu \leq \unicode{x3bb} $
. Then
$\nu =f \unicode{x3bb} $
for a
$\Phi ^t$
-invariant Borel function
$f:{\cal Q}\to [0,1]$
. As
$\unicode{x3bb} $
is ergodic [Reference MasurM82, Reference VeechV86], the function f is constant almost everywhere and
$\nu =c\unicode{x3bb} $
for a number
$c\in [0,1]$
. But
$\nu (U)\geq (1-\delta )\unicode{x3bb} (U)$
by assumption, and
$\unicode{x3bb} (U)>0$
as
$\unicode{x3bb} $
is of full support. This shows that
$c\geq 1-\delta $
and hence
$\lim \inf _{R\to \infty }\nu _{R,\sigma ,{\cal P}}({\cal Q})\geq 1-\delta $
. The corollary follows.
6 Lyapunov exponents
In this section we apply the criterion established in Corollary 5.7 to prove the main theorem from the introduction. The only tools we are going to use are Proposition 4.6, Corollary 5.7 and mixing of the Teichmüller flow. As these tools are available for Anosov flows on compact manifolds and the unique measure of maximal entropy, the main result (Theorem 6.1) is valid for cocycles over such flows as well.
Let as before
${\cal Q}$
be a component of a stratum of abelian or quadratic differentials. Consider a flat rank
$n\geq 1$
vector bundle
${\cal N}\to {\cal Q}$
(here flat is taken in the orbifold sense). Note that this implies that the restriction of
${\cal N}$
to
${\cal Q}_{\mathrm{good}}$
is a smooth vector bundle in the usual sense. Parallel transport for the flat connection then defines a cocycle
$\Theta ^t$
over the Teichmüller flow
$\Phi ^t$
. We assume that the bundle
${\cal N}$
is equipped with a continuous norm
$\Vert \,\Vert $
and that with respect to this norm, this cocycle is integrable with respect to the Masur–Veech measure
$\unicode{x3bb} $
on
${\cal Q}$
. Then its Lyapunov exponents are defined. These exponents measure the asymptotic growth rate of vectors along orbits of
$\Phi ^t$
which are generic for
$\unicode{x3bb} $
. Let
$$ \begin{align} \kappa_1\geq \cdots \geq \kappa_n\end{align} $$
be the n Lyapunov exponents.
Let
$\gamma \in \Gamma $
be a periodic orbit for
$\Phi ^t$
contained in
${\cal Q}_{\mathrm{good}}$
. Then parallel transport of
${\cal N}$
along
$\gamma $
determines a holonomy transformation whose conjugacy class does not depend on choices. If we define
$$ \begin{align*}\alpha_1(\gamma)\geq \cdots\geq \alpha_n(\gamma)\geq 0\end{align*} $$
to be the quotients by the length
$\ell (\gamma )$
of
$\gamma $
of the logarithms of the n absolute values of the eigenvalues of the holonomy transformation along
$\gamma $
, ordered in decreasing order and counted with multiplicities, then the numbers
$\alpha _i(\gamma )$
depend only on
$\gamma $
and not on any choices made.
Let
$\epsilon>0$
. For
$\gamma \in \Gamma $
, define
$\chi _\epsilon (\gamma )=1$
if
$\vert \alpha _i(\gamma )-\kappa _i\vert <\epsilon $
for every
$i\in \{1,\ldots ,n\}$
and define
$\chi _\epsilon (\gamma )=0$
otherwise. Thus, for a periodic orbit
$\gamma $
with
$\chi _\epsilon (\gamma )=1$
, the vector of absolute values of the normalized eigenvalues for the return map
$A(\gamma )$
of the holonomy along
$\gamma $
at any choice of a point
$p\in \gamma $
, ordered in descending order, is
$\epsilon $
-close to the vector given by the Lyapunov exponents for the cocycle. Recall that this property is independent of the choice of the point p on
$\gamma $
. We refer to §2 for more details.
Our goal is to show that periodic orbits
$\gamma \in \Gamma $
with
$\chi _\epsilon (\gamma )=1$
are typical in the sense described in the introduction. The strategy is to find for every
$\delta>0$
an open relatively compact subset U of
${\cal Q}$
and a number
$\sigma>0$
with the property stated in Corollary 5.7, where
${\cal P}=\{\gamma \in \Gamma \mid \chi _\epsilon (\gamma )=1\}$
.
Theorem 6.1 For every
$\epsilon>0$
, the set
$$ \begin{align*}\{\gamma\in \Gamma\mid \vert \alpha_i(\gamma)-\kappa_i\vert \leq \epsilon\}\end{align*} $$
is typical.
Proof. Let
$V\subset {\cal Q}_{\mathrm{good}}$
be an open relatively compact contractible neighborhood of a recurrent point
$q\in {\cal Q}_{\mathrm{good}}$
.
Let
$\Vert \cdot \Vert $
be a continuous riemannian norm on the vector bundle
${\cal N}\to {\cal Q}$
so that the cocycle defined by parallel transport is integrable for this norm and the Masur–Veech measure
$\unicode{x3bb} $
on
${\cal Q}$
. Let
$\epsilon>0$
.
Adjust the riemannian norm
$\Vert \cdot \Vert $
on V so that it is invariant under parallel transport along curves in V and it is unchanged outside a small contractible compact neighborhood
$V^\prime $
of V. As
$V^\prime $
is compact and since every orbit which intersects
$V^\prime $
also exits
$V^\prime $
, this does not change Lyapunov exponents.
Let
$\Theta ^t$
be the lift of the Teichmüller flow on
${\cal Q}_{\mathrm{good}}$
to a flow on
${\cal N}$
defined by parallel transport for the flat connection. For
$z\in {\cal Q}_{\mathrm{good}}$
, let
${\cal N}_z$
be the fibre of
${\cal N}$
at z. For
$1\leq i\leq n$
and for
$t>0$
, let
$$ \begin{align*}\zeta_i(t,z)\end{align*} $$
be the infimum of the operator norms for
$\Vert \cdot \Vert $
of the restriction of
$\Theta ^t (z)$
to a subspace of
${\cal N}_z$
of codimension
$i-1$
. Define
$$ \begin{align*}\kappa_i(t,z)=\frac{1}{t}\log \zeta_i(t,z).\end{align*} $$
As the Teichmüller flow is ergodic for the Masur–Veech measure
$\unicode{x3bb} $
[Reference MasurM82, Reference VeechV86], the Oseledets multiplicative ergodic theorem [Reference OseledetsO68] states that for
$\unicode{x3bb} $
-almost every point
$z\in {\cal Q}$
, the numbers
$\kappa _i(R,z)$
converge as
$R\to \infty $
to the ith Lyapunov exponent
$\kappa _i$
of the cocycle defined by the flow
$\Theta ^t$
.
Let
$\delta>0$
. As
$\lim _{\sigma \searrow 0} h\sigma (1-e^{-h\sigma })^{-1}\to 1$
, for sufficiently small
$\sigma>0$
, say for all
$\sigma <\sigma _0$
, we have
$h(1-e^{-h\sigma })^{-1}\in [\sigma ^{-1}(1-\delta ),\sigma ^{-1}(1-\delta )^{-1}]$
; furthermore, we may assume that
$e^{h\sigma }\leq (1-\delta )^{-1}$
. Using the notation from §5, for
${\cal P}= \{\gamma \mid \chi _\epsilon (\gamma )=1\}$
and a number
$\sigma <\sigma _0/2$
to be determined below, define
$\nu _{R,\sigma ,\epsilon }=\nu _{R,\sigma ,{\cal P}}$
. Our goal is to find an open set
$U\subset V$
in
${\cal Q}_{\mathrm{good}}$
such that
$$ \begin{align*}\lim\inf_{R\to \infty}\nu_{R,\sigma,\epsilon}(U)\geq \unicode{x3bb}(U)(1-\delta)^7.\end{align*} $$
By Corollary 5.7, this is sufficient for the proof of the theorem.
To this end, let
$m>1/\delta $
be sufficiently large such that
$(({m-2})/{m})>1-\delta $
. Assume that this holds true for all
$m> ({1}/{\delta ^\prime })$
, where
$\delta ^\prime <\delta $
. Consider neighborhoods
$Z_1\subset Z_2$
and
$Z_3\subset Z_4\subset V$
as in Proposition 4.6, constructed from V, the volume control constant
$\delta ^\prime $
and the length control constant
$\eta =\sigma _0/2$
. As we require
$m>1/\delta ^\prime $
, we have
$(({m-2})/{m})>1-\delta $
.
Let
$\sigma =s_1\in (0,\sigma _0/2)$
be as in property (b) in the proof of Proposition 4.6 and put
$t_0=\sigma /2m$
. Let
$Z_0\subset Z_1$
and
$R_0>0$
be as in Proposition 4.6. Then there are a number
$R(\epsilon )>R_0$
and a Borel subset
$E\subset Z_0$
of measure
$$ \begin{align*}\unicode{x3bb}(E)>\unicode{x3bb}(Z_0)(1-\delta) \geq (1-\delta)^2\unicode{x3bb}(Z_2)\geq (1-\delta)^2\unicode{x3bb}(Z_1)\end{align*} $$
with the following property. Let
$u\in E$
and let
$R>R(\epsilon )$
; then
$\vert \kappa _i(R,u)-\kappa _i\vert \leq \epsilon /2$
.
Let
$R\geq R(\epsilon )$
and let
$z\in E$
be such that
$\Phi ^Rz\in Z_3$
. By Proposition 4.6, the pseudo-orbit
$(z,T)$
with end points in
$Z_3$
determines a subarc
$\gamma (z,R)$
of a periodic orbit
$\gamma $
for
$\Phi ^t$
passing through
$Z_4$
. The period of
$\gamma $
is contained in
$[R-\sigma ,R+\sigma ]$
. Moreover, there exists a set
$B(z)\subset Z_2$
with
$\Phi ^RB(z)\subset Z_4$
and
$$ \begin{align} \unicode{x3bb}(B(z))\in [e^{-hR}\unicode{x3bb}(Z_1)(1-\delta)^2, e^{-hR}\unicode{x3bb}(Z_1)(1-\delta)^{-2}]\end{align} $$
consisting of points with the same characteristic curve as the pseudo-orbit
$(z,R)$
.
There may however be a small shift in length, that is, the period of
$\gamma $
may differ from the return time R by an additive constant of absolute value up to
$\sigma $
. Now, as the Lyapunov exponents are uniformly bounded, there exists a number
$R_1>R(\epsilon )$
such that for all
$t\geq R_1$
, all i, all
$\vert s\vert \leq \sigma $
and all
$z\in E$
, we have
$$ \begin{align*}\bigg\vert \frac{1}{t+s}\log \zeta_i(t,z)-\frac{1}{t}\log \zeta_i(t,z)\bigg\vert <\epsilon/2.\end{align*} $$
By the assumption that the norm is invariant under parallel transport along curves in the set V, we conclude that for
$R>R_1$
and all i, we have
$$ \begin{align*}\bigg\vert \frac{1}{\ell(\gamma)}\log \zeta_i(\ell(\gamma),\gamma(0))-\kappa_i\bigg\vert <\epsilon,\end{align*} $$
where, as before,
$\ell (\gamma )$
is the length of the periodic orbit
$\gamma $
. This shows that
$\chi _\epsilon (\gamma )=1$
. Recall that furthermore if
$u\in E-B(z)$
and if
$\Phi ^Ru\in Z_3$
, then the set
$B(u)$
is disjoint from
$B(z)$
, and the intersection arc
$\eta (u,R)$
with
$Z_4$
of the corresponding periodic orbit
$\eta $
is distinct from
$\gamma (z,R)$
.
Now the Teichmüller flow is mixing for
$\unicode{x3bb} $
[Reference MasurM82, Reference VeechV86] and consequently there is a number
$R_2>R_1$
such that
$$ \begin{align} \unicode{x3bb}(\Phi^R E\cap Z_3)\geq \unicode{x3bb}(E)\unicode{x3bb}(Z_3)(1-\delta) \end{align} $$
for all
$R\geq R_2$
.
By (27) and the estimate (26), for large enough
$R>R_2$
, the number of components of the intersection of the set
$Z_4$
with periodic orbits of period in the interval
$[R-\sigma ,R+\sigma ]$
which are induced by the characteristic curve of a point
$z\in E$
recurring to
$Z_3$
after time R is at least
$$ \begin{align*}\unicode{x3bb}(E)\unicode{x3bb}(Z_3)(1-\delta)e^{hR}\unicode{x3bb}(Z_1)^{-1}(1-\delta)^2 \geq e^{hR}(1-\delta)^5\unicode{x3bb}(Z_3)\geq e^{hR}(1-\delta)^6\unicode{x3bb}(Z_4).\end{align*} $$
Each of these intersection components is an arc of length
$2\sigma $
and hence it deposits the mass
$2\sigma $
on
$Z_4$
.
Now
$h(1-e^{-h2\sigma })^{-1}\in [(2\sigma )^{-1}(1-\delta ),(2\sigma )^{-1}(1-\delta )^{-1}]$
and therefore multiplying the above estimate with
$h(1-e^{-h2\sigma })^{-1}$
yields that for
$R>R_2+mt_0$
, we have
$$ \begin{align*}\nu_{R+\sigma,2\sigma,\epsilon}(Z_4)\geq (1-\delta)^7\unicode{x3bb}(Z_4).\end{align*} $$
In other words, the set
$Z_4$
fulfills the estimate in Corollary 5.7 for the constant
$(1-\delta )^7$
. Since
$\delta>0$
was arbitrary, the theorem follows.
Acknowledgements
I am grateful to the anonymous referee for careful reading and several suggestions which improved the exposition. The research is supported by ERC grant ‘Moduli’.
