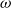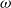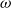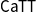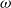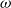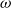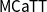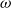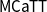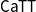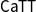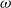1. Introduction
Weak
![]() $\omega$
-categories are algebraic structures occurring naturally in modern algebraic topology and type theory. They consist of collections of cells in every dimension, which can be composed in various ways. The main difficulty in properly establishing a definition for those is due to the fact that the usual coherence axioms imposed on composition, such as associativity, are here relaxed and only supposed up to invertible higher cells, that we call witnesses for these axioms. Moreover, these witnesses themselves admit compositions, which satisfy axioms up to new witnesses, and so on, making the compositions and their coherence axioms intricate. There have been different approaches to propose a definition of weak
$\omega$
-categories are algebraic structures occurring naturally in modern algebraic topology and type theory. They consist of collections of cells in every dimension, which can be composed in various ways. The main difficulty in properly establishing a definition for those is due to the fact that the usual coherence axioms imposed on composition, such as associativity, are here relaxed and only supposed up to invertible higher cells, that we call witnesses for these axioms. Moreover, these witnesses themselves admit compositions, which satisfy axioms up to new witnesses, and so on, making the compositions and their coherence axioms intricate. There have been different approaches to propose a definition of weak
![]() $\omega$
-categories, which are summed up in a couple of surveys (Cheng and Lauda Reference Cheng and Lauda2004; Leinster Reference Leinster2002). These approaches are based on various shapes, such as simplicial sets or opetopic sets. In this article, we are interested in approaches based on globular sets. Examples of such approaches can be found in the work of Batanin (Reference Batanin1998) and Leinster (Reference Leinster2004), relying on the structure of globular operad. Independently Maltsioniotis proposed an alternative approach (Maltsiniotis Reference Maltsiniotis2010), inspired by a definition of weak
$\omega$
-categories, which are summed up in a couple of surveys (Cheng and Lauda Reference Cheng and Lauda2004; Leinster Reference Leinster2002). These approaches are based on various shapes, such as simplicial sets or opetopic sets. In this article, we are interested in approaches based on globular sets. Examples of such approaches can be found in the work of Batanin (Reference Batanin1998) and Leinster (Reference Leinster2004), relying on the structure of globular operad. Independently Maltsioniotis proposed an alternative approach (Maltsiniotis Reference Maltsiniotis2010), inspired by a definition of weak
![]() $\omega$
-groupoid (i.e., weak
$\omega$
-groupoid (i.e., weak
![]() $\omega$
-categories whose all cells are invertible) proposed by Grothendieck (Reference Grothendieck1983), and which is based on presheaves preserving some structure on a well-chosen category. The two approaches have been proved equivalent by Ara (Reference Ara2010).
$\omega$
-categories whose all cells are invertible) proposed by Grothendieck (Reference Grothendieck1983), and which is based on presheaves preserving some structure on a well-chosen category. The two approaches have been proved equivalent by Ara (Reference Ara2010).
Type theoretical approach. An important observation which came along with the development of homotopy type theory (The Univalent Foundations Program 2013) is the fact that the types in Martin–Löf type theory, and in homotopy type theory carry a structure of weak
![]() $\omega$
-groupoid, where the higher cells are given by identity types (Altenkirch and Rypacek Reference Altenkirch and Rypacek2012; Lumsdaine Reference Lumsdaine2009; Van Den Berg and Garner Reference Van Den Berg and Garner2011). This allowed Brunerie to extract a minimal set of rules from homotopy type theory for generating the weak
$\omega$
-groupoid, where the higher cells are given by identity types (Altenkirch and Rypacek Reference Altenkirch and Rypacek2012; Lumsdaine Reference Lumsdaine2009; Van Den Berg and Garner Reference Van Den Berg and Garner2011). This allowed Brunerie to extract a minimal set of rules from homotopy type theory for generating the weak
![]() $\omega$
-categories (Brunerie Reference Brunerie2016), that he could prove to be equivalent to the definition of Grothendieck. Recently, Finster and Mimram proposed a generalization of Brunerie’s type theory to weak
$\omega$
-categories (Brunerie Reference Brunerie2016), that he could prove to be equivalent to the definition of Grothendieck. Recently, Finster and Mimram proposed a generalization of Brunerie’s type theory to weak
![]() $\omega$
-categories (Finster and Mimram Reference Finster and Mimram2017), parallel to the generalization Maltsiniotis proposed from Grothendieck definition. The type theory they introduced is called
$\omega$
-categories (Finster and Mimram Reference Finster and Mimram2017), parallel to the generalization Maltsiniotis proposed from Grothendieck definition. The type theory they introduced is called
![]() $\mathsf{CaTT}$
, and has been proved to be equivalent to the definition of Maltsiniotis (Benjamin et al. Reference Benjamin, Finster and Mimram2021).
$\mathsf{CaTT}$
, and has been proved to be equivalent to the definition of Maltsiniotis (Benjamin et al. Reference Benjamin, Finster and Mimram2021).
Monoidal categories. In this article, we are interested in monoidal weak
![]() $\omega$
-categories. These are categories equipped with a tensor product allowing new ways to compose cells of every dimension. In particular, one cannot compose the cells of dimension 0 in weak
$\omega$
-categories. These are categories equipped with a tensor product allowing new ways to compose cells of every dimension. In particular, one cannot compose the cells of dimension 0 in weak
![]() $\omega$
-categories, but one can compose them in monoidal weak
$\omega$
-categories, but one can compose them in monoidal weak
![]() $\omega$
-categories. Moreover these new compositions are required to satisfy axioms like associativity, but since it happens in a weak setup, these axioms are again relaxed versions with witnesses in higher dimensions. This can be seen as a categorification of the notion of monoid. Our goal here is to provide a variant of the
$\omega$
-categories. Moreover these new compositions are required to satisfy axioms like associativity, but since it happens in a weak setup, these axioms are again relaxed versions with witnesses in higher dimensions. This can be seen as a categorification of the notion of monoid. Our goal here is to provide a variant of the
![]() $\mathsf{CaTT}$
type theory in order to describe monoidal weak
$\mathsf{CaTT}$
type theory in order to describe monoidal weak
![]() $\omega$
-categories.
$\omega$
-categories.
As noticed by Baez and Dolan (Reference Baez and Dolan1995), Baez (Reference Baez2006), monoidal weak
![]() $\omega$
-categories should be equivalent to weak
$\omega$
-categories should be equivalent to weak
![]() $\omega$
-categories with only one 0-cell. In this correspondence, there is a shift in dimension: the 0-cells of the monoidal
$\omega$
-categories with only one 0-cell. In this correspondence, there is a shift in dimension: the 0-cells of the monoidal
![]() $\omega$
-category are the 1-cells of the
$\omega$
-category are the 1-cells of the
![]() $\omega$
-category with one 0-cell, and so on. The monoidal tensor product becomes the composition of arrows of the
$\omega$
-category with one 0-cell, and so on. The monoidal tensor product becomes the composition of arrows of the
![]() $\omega$
-category, and all its coherences are exactly those satisfied by these arrows in the
$\omega$
-category, and all its coherences are exactly those satisfied by these arrows in the
![]() $\omega$
-category.
$\omega$
-category.
Taking this correspondence as a starting point, we work out an explicit type theory
![]() $\mathsf{MCaTT}$
whose models are monoidal categories, by describing
$\mathsf{MCaTT}$
whose models are monoidal categories, by describing
![]() $\mathsf{CaTT}$
with the extra restriction that there should be only one 0-cell. To achieve this, we rely on the type theory
$\mathsf{CaTT}$
with the extra restriction that there should be only one 0-cell. To achieve this, we rely on the type theory
![]() $\mathsf{CaTT}$
and use its constituent to express the rules of the theory
$\mathsf{CaTT}$
and use its constituent to express the rules of the theory
![]() $\mathsf{MCaTT}$
. We then define a pair of translations back and forth between
$\mathsf{MCaTT}$
. We then define a pair of translations back and forth between
![]() $\mathsf{CaTT}$
and
$\mathsf{CaTT}$
and
![]() $\mathsf{MCaTT}$
, and use the interaction of these translations with the structure of the type theory to show that our proposed definition satisfies the correspondence we started with.
$\mathsf{MCaTT}$
, and use the interaction of these translations with the structure of the type theory to show that our proposed definition satisfies the correspondence we started with.
Plan of the paper. In Section 2, we introduce the type theory
![]() $\mathsf{CaTT}$
along with the general tools we use to study type theories and their models. Then in Section 3 we define the type theory
$\mathsf{CaTT}$
along with the general tools we use to study type theories and their models. Then in Section 3 we define the type theory
![]() $\mathsf{MCaTT}$
along with a pair of translations between the theories
$\mathsf{MCaTT}$
along with a pair of translations between the theories
![]() $\mathsf{CaTT}$
and
$\mathsf{CaTT}$
and
![]() $\mathsf{MCaTT}$
. We show that these translation exhibit a coreflective adjunction between the syntactic categories associated to the theory that lifts as an equivalence between a localization of the models of
$\mathsf{MCaTT}$
. We show that these translation exhibit a coreflective adjunction between the syntactic categories associated to the theory that lifts as an equivalence between a localization of the models of
![]() $\mathsf{CaTT}$
and the models of
$\mathsf{CaTT}$
and the models of
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.
The author would like to thank Samuel Mimram and Eric Finster for their valuable discussions regarding the work presented in this article, as well as the reviewers for their helpful comments.
2. Type Theory for Weak
 $\omega$
-Categories
$\omega$
-Categories
This section is dedicated to the type theory
![]() $\mathsf{CaTT}$
introduced by Finster and Mimram (Reference Finster and Mimram2017) to describe weak
$\mathsf{CaTT}$
introduced by Finster and Mimram (Reference Finster and Mimram2017) to describe weak
![]() $\omega$
-categories. The account we provide is introductory, and we refer the reader to Benjamin et al. (Reference Benjamin, Finster and Mimram2021) for a more in-depth presentation. We first define our setting for type theory, and introduce a type theory that describes globular sets. Then we extend this theory with extra term constructors, to obtain the theory
$\omega$
-categories. The account we provide is introductory, and we refer the reader to Benjamin et al. (Reference Benjamin, Finster and Mimram2021) for a more in-depth presentation. We first define our setting for type theory, and introduce a type theory that describes globular sets. Then we extend this theory with extra term constructors, to obtain the theory
![]() $\mathsf{CaTT}$
.
$\mathsf{CaTT}$
.
2.1 Type theories: notations and categorical semantics
We establish the terminology and conventions that are used throughout this article to manipulate type theories. Note that our method consists in formulating a type theory to describe a structure, as opposed to developing said structure internally to Martin–Löf type theory.
Expressions. A type theory manipulates various kind of objects, that we present here along with the convention we use for naming them.
-
variables are elements of a given infinite countable set of variables, we denote them
 $x,y,z,\ldots$
,
$x,y,z,\ldots$
, -
terms, which are built out of variables and constructors, we denote them
 $t,u,\ldots$
,
$t,u,\ldots$
, -
types, which are built out of terms and constructors, we denote them
 $A,B,\ldots$
,
$A,B,\ldots$
, -
contexts are supported by association lists of the form
 $x:A$
, they are denoted
$x:A$
, they are denoted
 $\Gamma,\Delta,\ldots$
,
$\Gamma,\Delta,\ldots$
, -
substitutions are supported by lists of mappings of the form
 $x\mapsto t$
where x is a variable and t a term, we denote them
$x\mapsto t$
where x is a variable and t a term, we denote them
 $\gamma,\delta,\ldots$
.
$\gamma,\delta,\ldots$
.
The constructors for terms and type depend on the theory we consider, and we introduce them individually. These all come with associated set of variables,
![]() $\operatorname{Var}$
and that is the set of variables needed to build it out. We denote
$\operatorname{Var}$
and that is the set of variables needed to build it out. We denote
![]() $\operatorname{Var}({t:A})$
for the union of
$\operatorname{Var}({t:A})$
for the union of
![]() $\operatorname{Var}(t)$
and
$\operatorname{Var}(t)$
and
![]() $\operatorname{Var}(A)$
. For contexts and substitutions, we always have the following formulas
$\operatorname{Var}(A)$
. For contexts and substitutions, we always have the following formulas
Action of substitutions. We define the action of a substitution
![]() $\gamma$
on a type A (resp. on a term t) denoted
$\gamma$
on a type A (resp. on a term t) denoted
![]() $A[\gamma]$
(resp.
$A[\gamma]$
(resp.
![]() $t[\gamma]$
). These are defined separately on each theory, but share the variable case in common:
$t[\gamma]$
). These are defined separately on each theory, but share the variable case in common:
 \begin{equation*} x[\langle{}\rangle] = x \qquad\qquad x[\langle{\gamma,y\mapsto t}\rangle] = \left\{ \begin{array}{ll} t & \text{If $x = y$} \\ x[\gamma] & \text{Otherwise} \end{array} \right.\end{equation*}
\begin{equation*} x[\langle{}\rangle] = x \qquad\qquad x[\langle{\gamma,y\mapsto t}\rangle] = \left\{ \begin{array}{ll} t & \text{If $x = y$} \\ x[\gamma] & \text{Otherwise} \end{array} \right.\end{equation*}
This action provides a composition of substitutions given inductively by
Judgments. There are four kinds of judgments that are commons to all of our type theories, they express the well-definedness of the previously introduced objects:
 \begin{equation*} \begin{array}{l@{\quad \rightsquigarrow \quad}l@{\qquad\quad}l@{\quad \rightsquigarrow \quad}l} \Gamma\vdash & \text{$\Gamma$ is a valid context} & \Gamma\vdash t:A & t \, \text{is a valid term of type} \, A \, \text{in} \, \Gamma\\ \Gamma\vdash A & A \, \text{is a valid type in} \, \Gamma & \Delta\vdash \gamma:\Gamma & \gamma \, \text{is a valid substitution from $\Delta$ to $\Gamma$} \end{array}\end{equation*}
\begin{equation*} \begin{array}{l@{\quad \rightsquigarrow \quad}l@{\qquad\quad}l@{\quad \rightsquigarrow \quad}l} \Gamma\vdash & \text{$\Gamma$ is a valid context} & \Gamma\vdash t:A & t \, \text{is a valid term of type} \, A \, \text{in} \, \Gamma\\ \Gamma\vdash A & A \, \text{is a valid type in} \, \Gamma & \Delta\vdash \gamma:\Gamma & \gamma \, \text{is a valid substitution from $\Delta$ to $\Gamma$} \end{array}\end{equation*}
In order to distinguish, we sometimes refer to the raw syntax, or to expressions for a syntactic entity which is not assumed to satisfy any of the above judgment.
Basic rules. The following rules are common to all the type theories that we consider

Where in the rules ce and se we assume that
![]() $x\notin\operatorname{Var}(\Gamma)$
.
$x\notin\operatorname{Var}(\Gamma)$
.
Syntactic category. We admit that for all the theories that we consider, the action of substitution makes the following rules admissible

and that the action of substitutions is compatible with the composition, thus making the composition associative
Moreover, we can define an identity substitution, defined on a context
![]() $\Gamma = (x_i:A_i)_{i\in I}$
by
$\Gamma = (x_i:A_i)_{i\in I}$
by
![]() $\operatorname{id}_{\Gamma} = \langle{x_i\mapsto x_i}\rangle_{i\in I}$
. One can show that whenever
$\operatorname{id}_{\Gamma} = \langle{x_i\mapsto x_i}\rangle_{i\in I}$
. One can show that whenever
![]() $\Gamma\vdash$
is derivable, then so is
$\Gamma\vdash$
is derivable, then so is
![]() $\Gamma\vdash \operatorname{id}_{\Gamma}: \Gamma$
and that whenever
$\Gamma\vdash \operatorname{id}_{\Gamma}: \Gamma$
and that whenever
![]() $\Delta\vdash\gamma:\Gamma$
,
$\Delta\vdash\gamma:\Gamma$
,
![]() $\Gamma\vdash A$
and
$\Gamma\vdash A$
and
![]() $\Gamma\vdash t:A$
hold, the following equalities are satisfied.
$\Gamma\vdash t:A$
hold, the following equalities are satisfied.
Hence one can construct a syntactic category
![]() $\operatorname{\mathcal{S}}_{\mathfrak{T}}$
associated to a type theory
$\operatorname{\mathcal{S}}_{\mathfrak{T}}$
associated to a type theory
![]() $\mathfrak{T}$
, whose objects are the contexts of the type theory
$\mathfrak{T}$
, whose objects are the contexts of the type theory
![]() $\mathfrak{T}$
, and whose morphisms are the substitutions.
$\mathfrak{T}$
, and whose morphisms are the substitutions.
Properties. We admit that all our type theories also satisfy the following properties, that one can prove by induction on the derivation trees. We refer the reader to a formalization in Agda Footnote 1 where we define prove these properties for some of the theories.
Proposition 1. In all the theories we consider, the following rules are admissible

Moreover, for every derivable judgment
![]() $\Gamma\vdash A$
(resp.
$\Gamma\vdash A$
(resp.
![]() $\Gamma\vdash t:A$
), we have
$\Gamma\vdash t:A$
), we have
![]() $\operatorname{Var}(A) \subset \operatorname{Var}(\Gamma)$
(resp.
$\operatorname{Var}(A) \subset \operatorname{Var}(\Gamma)$
(resp.
![]() $\operatorname{Var}(t) \subset \operatorname{Var}(\Gamma)$
). For every derivable judgment
$\operatorname{Var}(t) \subset \operatorname{Var}(\Gamma)$
). For every derivable judgment
![]() $\Delta\vdash \gamma:\Gamma$
, we have
$\Delta\vdash \gamma:\Gamma$
, we have
![]() $\operatorname{Var}(\gamma) \subset\operatorname{Var}(\Delta)$
, and writing
$\operatorname{Var}(\gamma) \subset\operatorname{Var}(\Delta)$
, and writing
![]() $\gamma = \langle{x_i\mapsto t_i}\rangle_{0\leq i\leq n}$
and
$\gamma = \langle{x_i\mapsto t_i}\rangle_{0\leq i\leq n}$
and
![]() $\Gamma= (y_i : A_i)_{0\leq i\leq m}$
, we have
$\Gamma= (y_i : A_i)_{0\leq i\leq m}$
, we have
![]() $n = m$
and for all i,
$n = m$
and for all i,
![]() $x_i = y_i$
.
$x_i = y_i$
.
Category with families. We use the formalism of categories with families, introduced by Dybjer (Reference Dybjer1996) as our categorical axiomatization of dependent type theories. Denote Fam the category of families, where objects are families of sets
![]() $(A_i)_{i\in I}$
, and morphisms
$(A_i)_{i\in I}$
, and morphisms
![]() $f:(A_i)_{i\in I}\to (B_j)_{j\in J}$
are pairs consisting of a function
$f:(A_i)_{i\in I}\to (B_j)_{j\in J}$
are pairs consisting of a function
![]() $f:I\to J$
and a family of functions
$f:I\to J$
and a family of functions
![]() $(f_i:A_i\to B_{f(i)})_{i\in I}$
. Given a category C equipped with a functor T : C op → Fam. Given an object
$(f_i:A_i\to B_{f(i)})_{i\in I}$
. Given a category C equipped with a functor T : C op → Fam. Given an object
![]() $\Gamma$
of C, its image will be denoted
$\Gamma$
of C, its image will be denoted
i.e.,
![]() $\operatorname{Ty}^\Gamma$
is the index set and
$\operatorname{Ty}^\Gamma$
is the index set and
![]() $\operatorname{Tm}^\Gamma_A$
is an element of the family. By analogy with a type theory, for a morphism
$\operatorname{Tm}^\Gamma_A$
is an element of the family. By analogy with a type theory, for a morphism
![]() $\gamma : \Delta \to \Gamma$
an element
$\gamma : \Delta \to \Gamma$
an element
![]() $A\in\operatorname{Ty}^\Gamma$
and an element
$A\in\operatorname{Ty}^\Gamma$
and an element
![]() $t\in\operatorname{Tm}^\Gamma_A$
, we write
$t\in\operatorname{Tm}^\Gamma_A$
, we write
![]() $A[\gamma] = T\gamma(A)$
the image of A in
$A[\gamma] = T\gamma(A)$
the image of A in
![]() $\operatorname{Ty}^\Delta$
, and
$\operatorname{Ty}^\Delta$
, and
![]() $t[\gamma] = T_A\gamma(t)$
the image of t in
$t[\gamma] = T_A\gamma(t)$
the image of t in
![]() $\operatorname{Tm}^\Delta_{A[\gamma]}$
. With those notations, the functoriality of T can be written as, for all composable morphisms
$\operatorname{Tm}^\Delta_{A[\gamma]}$
. With those notations, the functoriality of T can be written as, for all composable morphisms
![]() $\gamma$
,
$\gamma$
,
![]() $\delta$
in C,
$\delta$
in C,
A category with families (or CwF) consists of a category C equipped with a functor as above T : C op → Fam, such that C has a terminal object, denoted
![]() $\varnothing$
, and that there is a context comprehension operation: given a context
$\varnothing$
, and that there is a context comprehension operation: given a context
![]() $\Gamma$
and type
$\Gamma$
and type
![]() $A\in\operatorname{Ty}^\Gamma$
, there is a context
$A\in\operatorname{Ty}^\Gamma$
, there is a context
![]() $\left({\Gamma,A}\right)$
, together with a projection morphism
$\left({\Gamma,A}\right)$
, together with a projection morphism
![]() $\pi:\left({\Gamma,A}\right) \to \Gamma$
and a term
$\pi:\left({\Gamma,A}\right) \to \Gamma$
and a term
![]() $p\in\operatorname{Tm}^{\left({\Gamma,A}\right)}_{A[\pi]}$
, such that for every morphism
$p\in\operatorname{Tm}^{\left({\Gamma,A}\right)}_{A[\pi]}$
, such that for every morphism
![]() $\sigma : \Delta\to\Gamma$
in C together with a term
$\sigma : \Delta\to\Gamma$
in C together with a term
![]() $t \in\operatorname{Tm}^{\Delta}_{A[\sigma]}$
, there exists a unique morphism
$t \in\operatorname{Tm}^{\Delta}_{A[\sigma]}$
, there exists a unique morphism
![]() $\langle{\sigma,t}\rangle : \Delta\to\left({\Gamma,A}\right)$
such that
$\langle{\sigma,t}\rangle : \Delta\to\left({\Gamma,A}\right)$
such that
![]() $p[\langle{\sigma,t}\rangle] = t$
:
$p[\langle{\sigma,t}\rangle] = t$
:

We call an arrow of the form
![]() $\pi:(\Gamma,A)\to\Gamma$
a display map. The following result is well-known and allow for giving structure to the syntactic category of a type theory.
$\pi:(\Gamma,A)\to\Gamma$
a display map. The following result is well-known and allow for giving structure to the syntactic category of a type theory.
Proposition 2. The syntactic category of a type theory is endowed with a structure of category with families. For every context
![]() $\Gamma$
,
$\Gamma$
,
![]() $\operatorname{Ty}^\Gamma$
is the set of derivable types in
$\operatorname{Ty}^\Gamma$
is the set of derivable types in
![]() $\Gamma$
and
$\Gamma$
and
![]() $\operatorname{Tm}^\Gamma_A$
is the set of derivable terms of type A in
$\operatorname{Tm}^\Gamma_A$
is the set of derivable terms of type A in
![]() $\Gamma$
.
$\Gamma$
.
Models of a category with families. The structure of category with families enforces some compatibility between context comprehension and the action of morphisms on the type.
Lemma 3. In a category with families C, for every morphism
![]() $f:\Delta\to\Gamma$
in C and
$f:\Delta\to\Gamma$
in C and
![]() $A\in\operatorname{Ty}^\Gamma$
, the following square is a pullback
$A\in\operatorname{Ty}^\Gamma$
, the following square is a pullback

where
![]() $\pi':(\Delta,A[f])\to\Delta$
and
$\pi':(\Delta,A[f])\to\Delta$
and
![]() $p'\in\operatorname{Tm}^{(\Delta,A[f])}_{A[f][\pi']}$
are obtained by context comprehension.
$p'\in\operatorname{Tm}^{(\Delta,A[f])}_{A[f][\pi']}$
are obtained by context comprehension.
This is essentially a reformulation of the universal property of the context comprehension and was observed by Dybjer (Reference Dybjer1996). The entire formalism of categories with families can be seen as an axiomatization of a category with a split choice of pullbacks along the display maps.
Definition 4 (Models of a category with families). Consider a category with families C, we say that a functor F : C → Set is a (set-theoretic) model of C if it sends all the pullbacks along display maps in C onto pullbacks in Set.
Morphisms of category with families. We call a morphism of categories with families a functor that preserves the terminal object and the context comprehension on the nose. Since the pullbacks are computed from this structure, the morphisms of categories with families preserve the pullbacks along display maps.
2.2 Globular sets
Globular weak
![]() $\omega$
-categories are supported by globular sets, which are presheaves over the category of globes G, generated by
$\omega$
-categories are supported by globular sets, which are presheaves over the category of globes G, generated by ![]() (with
(with
![]() $ts = ss$
and
$ts = ss$
and
![]() $st = tt$
). We denote
$st = tt$
). We denote
![]() $\operatorname{GSet} = \widehat{\operatorname{G}}$
the category of globular sets, and in this category, we call the n-dimensional disk the representable object represented by n and denote it
$\operatorname{GSet} = \widehat{\operatorname{G}}$
the category of globular sets, and in this category, we call the n-dimensional disk the representable object represented by n and denote it
![]() $D^n$
.
$D^n$
.
Type theory for globular sets. Following Finster and Mimram (Reference Finster and Mimram2017), we first give a type theoretic description of the theory
![]() $\mathfrak{G}$
describing globular sets. This theory has two type constructors
$\mathfrak{G}$
describing globular sets. This theory has two type constructors
![]() $\star$
and
$\star$
and
![]() $\to$
and no term constructor. Intuitively,
$\to$
and no term constructor. Intuitively,
![]() $\star$
is the types of the objects of the set, and given a type A and two terms t, u, the type
$\star$
is the types of the objects of the set, and given a type A and two terms t, u, the type
![]() ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
is the type of higher cells from t to u. Define the variables of a type, as well as the action of substitutions as follows
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
is the type of higher cells from t to u. Define the variables of a type, as well as the action of substitutions as follows
These constructors are subject to the following introduction rules

Since there are no term constructors, the only terms in the theory
![]() $\mathfrak{G}$
are variables. A self-contained description of this theory is provided in Appendix A.1.
$\mathfrak{G}$
are variables. A self-contained description of this theory is provided in Appendix A.1.
Semantics of the theory
![]() $\mathfrak{G}$
. Here, we present results about the theory
$\mathfrak{G}$
. Here, we present results about the theory
![]() $\mathfrak{G}$
without proofs; a detailed presentation can be found in Finster and Mimram (Reference Finster and Mimram2017), Benjamin et al. (Reference Benjamin, Finster and Mimram2021). The following result characterizes the syntactic category of
$\mathfrak{G}$
without proofs; a detailed presentation can be found in Finster and Mimram (Reference Finster and Mimram2017), Benjamin et al. (Reference Benjamin, Finster and Mimram2021). The following result characterizes the syntactic category of
![]() $\mathfrak{G}$
and is illustrated in Figure 1.
$\mathfrak{G}$
and is illustrated in Figure 1.

Figure 1. A context and its corresponding globular set.
Proposition 5 (Finster and Mimram 2017, Prop. 11, Benjamin et al. 2021, Th. 16) The syntactic category of the theory
![]() $\mathfrak{G}$
is equivalent to the opposite of the category of finite globular sets.
$\mathfrak{G}$
is equivalent to the opposite of the category of finite globular sets.
Proposition 6 (Finster and Mimram 2017, Prop. 13, Benjamin et al. 2021, Th. 22). The category of models of
![]() $\mathfrak{G}$
is equivalent to the category of globular sets.
$\mathfrak{G}$
is equivalent to the category of globular sets.
Disk contexts. The category of finite globular sets contains in particular the representable objects
![]() $D^n$
, we also denote
$D^n$
, we also denote
![]() $D^n$
, and call disk contexts, the corresponding contexts in
$D^n$
, and call disk contexts, the corresponding contexts in
![]() $\mathfrak{G}$
given by Proposition 5. In low dimensions, they are given (up to renaming of their variables), by
$\mathfrak{G}$
given by Proposition 5. In low dimensions, they are given (up to renaming of their variables), by
2.3 The type theory
 $\mathsf{CaTT}$
$\mathsf{CaTT}$
In order to axiomatize the weak
![]() $\omega$
-category structure, we add new terms, that we call operations and coherences. This can be done by adding term constructors to the theory
$\omega$
-category structure, we add new terms, that we call operations and coherences. This can be done by adding term constructors to the theory
![]() $\mathfrak{G}$
. To express the rules for these constructors, we introduce the ps-contexts, which are a particular class of ps-contexts.
$\mathfrak{G}$
. To express the rules for these constructors, we introduce the ps-contexts, which are a particular class of ps-contexts.
Ps-contexts. We define ps-contexts to be a particular class of contexts in the theory
![]() $\mathfrak{G}$
that we describe using rules of a type-theoretic flavor. We thus introduce two new judgment kinds
$\mathfrak{G}$
that we describe using rules of a type-theoretic flavor. We thus introduce two new judgment kinds

The second judgment is just a convenient auxiliary, where the dangling variable indicates the unique variable on which one is allowed to glue a cell at the next step. These two judgments are subject to the following rules

A ps-context
![]() $\Gamma$
comes equipped with notion of i-source
$\Gamma$
comes equipped with notion of i-source
![]() $\partial^-(i) \Gamma$
and i-target
$\partial^-(i) \Gamma$
and i-target
![]() $\partial^+(i) \Gamma$
for every number
$\partial^+(i) \Gamma$
for every number
![]() $i\in\mathbb{N}$
, defined inductively on its structure:
$i\in\mathbb{N}$
, defined inductively on its structure:
 \begin{equation*} \partial^-(i) {(x:\star)} = (x:\star) \qquad\qquad\partial^-_i(\Gamma,y:A,f:x\to y) = \left\{ \begin{array}{l@{\quad}l} \partial^-_i\Gamma & \text{if $\dim A \geq i$}\\ \partial^-_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right.\end{equation*}
\begin{equation*} \partial^-(i) {(x:\star)} = (x:\star) \qquad\qquad\partial^-_i(\Gamma,y:A,f:x\to y) = \left\{ \begin{array}{l@{\quad}l} \partial^-_i\Gamma & \text{if $\dim A \geq i$}\\ \partial^-_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right.\end{equation*}
 \begin{equation*} \partial^+(i) {(x:\star)} = (x:\star) \qquad\qquad \partial^+_i(\Gamma,y:A,f:x\to y) = \left\{ \begin{array}{l@{\quad}l} \partial^+_i\Gamma & \text{if $\dim A > i$}\\ \operatorname{drop}(\partial^+_i\Gamma),y:A & \text{if $\dim A = i$}\\ \partial^+_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right.\end{equation*}
\begin{equation*} \partial^+(i) {(x:\star)} = (x:\star) \qquad\qquad \partial^+_i(\Gamma,y:A,f:x\to y) = \left\{ \begin{array}{l@{\quad}l} \partial^+_i\Gamma & \text{if $\dim A > i$}\\ \operatorname{drop}(\partial^+_i\Gamma),y:A & \text{if $\dim A = i$}\\ \partial^+_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right.\end{equation*}
where
![]() $\operatorname{drop}(\Gamma)$
is the context
$\operatorname{drop}(\Gamma)$
is the context
![]() $\Gamma$
with its last variable removed, i.e.,
$\Gamma$
with its last variable removed, i.e.,
![]() $\operatorname{drop}(\Gamma,x:A)=\Gamma$
. We write
$\operatorname{drop}(\Gamma,x:A)=\Gamma$
. We write
![]() $\partial^{\pm} \Gamma = \partial^{\pm}_{\dim\Gamma - 1}$
. With these conventions,
$\partial^{\pm} \Gamma = \partial^{\pm}_{\dim\Gamma - 1}$
. With these conventions,
![]() $\partial^-(x:\star)$
and
$\partial^-(x:\star)$
and
![]() $\partial^+(x:\star)$
are not defined.
$\partial^+(x:\star)$
are not defined.
Remark 7. Under the correspondence of Proposition 5, the ps-contexts correspond to a class of finite globular sets called pasting schemes, which can be described in several different way and play a significant role in weak
![]() $\omega$
-category theory (Batanin 1998; Leinster 2004; Maltsiniotis 2010). Intuitively they are the globular sets that can be completely composed in an essentially unique way, and they are used to index all the operations. More details about their relation to ps-contexts can be found in Benjamin et al. (2021), Th.73.
$\omega$
-category theory (Batanin 1998; Leinster 2004; Maltsiniotis 2010). Intuitively they are the globular sets that can be completely composed in an essentially unique way, and they are used to index all the operations. More details about their relation to ps-contexts can be found in Benjamin et al. (2021), Th.73.
Syntax of the theory CaTT. The syntax is obtained by adding two term constructors
![]() $\mathsf{op}$
and
$\mathsf{op}$
and
![]() $\mathsf{coh}$
, do the theory
$\mathsf{coh}$
, do the theory
![]() $\mathfrak{G}$
. A term expression in this theory is thus defined to be either a variable or of the form
$\mathfrak{G}$
. A term expression in this theory is thus defined to be either a variable or of the form
![]() $\mathsf{op}_{\Delta,A}[\delta]$
or
$\mathsf{op}_{\Delta,A}[\delta]$
or
![]() $\mathsf{coh}_{\Delta,A}[\delta]$
, where in both the latter cases
$\mathsf{coh}_{\Delta,A}[\delta]$
, where in both the latter cases
![]() $\Delta$
is a context, A is a type and
$\Delta$
is a context, A is a type and
![]() $\delta$
is a substitution. To simplify the notations, we denote
$\delta$
is a substitution. To simplify the notations, we denote
![]() $\mathsf{constr}$
to be either
$\mathsf{constr}$
to be either
![]() $\mathsf{op}$
or
$\mathsf{op}$
or
![]() $\mathsf{coh}$
.The set of variables and the application of substitutions are defined by the formulas
$\mathsf{coh}$
.The set of variables and the application of substitutions are defined by the formulas
Side conditions. The introduction rules for the term constructors
![]() $\mathsf{op}$
and
$\mathsf{op}$
and
![]() $\mathsf{coh}$
have to verify some side conditions regarding the variables that are used in the type that we derive. Intuitively the introduction rule for the constructor
$\mathsf{coh}$
have to verify some side conditions regarding the variables that are used in the type that we derive. Intuitively the introduction rule for the constructor
![]() $\mathsf{op}$
creates witnesses for operations, for instance the composition, or whiskering, which a priori have no reason to be invertible, whereas the introduction rule for the constructor
$\mathsf{op}$
creates witnesses for operations, for instance the composition, or whiskering, which a priori have no reason to be invertible, whereas the introduction rule for the constructor
![]() $\mathsf{coh}$
creates witnesses for coherences, as for instance the associators, which are always weakly invertible. In order to simplify the notations, we encapsulate the requirements for these rules along with their side conditions in new judgments
$\mathsf{coh}$
creates witnesses for coherences, as for instance the associators, which are always weakly invertible. In order to simplify the notations, we encapsulate the requirements for these rules along with their side conditions in new judgments
![]() $\Gamma\vdash_{\mathsf{op}} A$
and
$\Gamma\vdash_{\mathsf{op}} A$
and
![]() $\Gamma\vdash_{\mathsf{coh}} A$
that we interpret as stating that A defines a valid operation (resp. coherence) in the context
$\Gamma\vdash_{\mathsf{coh}} A$
that we interpret as stating that A defines a valid operation (resp. coherence) in the context
![]() $\Gamma$
. These two judgments are subject to the following derivation rules, which express all the requirements for the introduction rules of the constructors
$\Gamma$
. These two judgments are subject to the following derivation rules, which express all the requirements for the introduction rules of the constructors
![]() $\mathsf{op}$
and
$\mathsf{op}$
and
![]() $\mathsf{coh}$
$\mathsf{coh}$

Note that whenever
![]() $\Gamma\vdash_{\mathsf{op}} A$
is derivable, then a top-dimensional variable of
$\Gamma\vdash_{\mathsf{op}} A$
is derivable, then a top-dimensional variable of
![]() $\Gamma$
cannot appear in A, whereas whenever
$\Gamma$
cannot appear in A, whereas whenever
![]() $\Gamma\vdash_{\mathsf{coh}} A$
is derivable, a top-dimensional variable of
$\Gamma\vdash_{\mathsf{coh}} A$
is derivable, a top-dimensional variable of
![]() $\Gamma$
has to appear in A, hence these two rules are mutually exclusive.
$\Gamma$
has to appear in A, hence these two rules are mutually exclusive.
Operations and coherences. We can now give the introduction rules for the new term constructors
![]() $\mathsf{coh}$
and
$\mathsf{coh}$
and
![]() $\mathsf{op}$
.
$\mathsf{op}$
.

The resulting type theory obtained by adding these rules is called
![]() $\mathsf{CaTT}$
. We present all the rules of the type theory
$\mathsf{CaTT}$
. We present all the rules of the type theory
![]() $\mathsf{CaTT}$
together in Appendix A.2.
$\mathsf{CaTT}$
together in Appendix A.2.
Interpretation. The ps-contexts intuitively represent all the context in which there ought to be an essentially unique definition (in a weak situation, they have a contractible set worth of composition). The rule (
![]() $\mathsf{op}-$
intro) enforces a composition to exist for every ps-context, while the rule (
$\mathsf{op}-$
intro) enforces a composition to exist for every ps-context, while the rule (
![]() $\mathsf{coh}-$
intro) enforces that any two composition of a ps-context are related, together, they provide a directed formulation of the idea of contractibility. Note that our formulation of the rule (
$\mathsf{coh}-$
intro) enforces that any two composition of a ps-context are related, together, they provide a directed formulation of the idea of contractibility. Note that our formulation of the rule (
![]() $\mathsf{coh}-$
intro) is slightly different than the one introduced by Finster and Mimram (Reference Finster and Mimram2017). Actually the two can be proven equivalent, but the proof is surprisingly involved Benjamin (Reference Benjamin2020), Coro. 103.
$\mathsf{coh}-$
intro) is slightly different than the one introduced by Finster and Mimram (Reference Finster and Mimram2017). Actually the two can be proven equivalent, but the proof is surprisingly involved Benjamin (Reference Benjamin2020), Coro. 103.
Examples. We give a few examples of derivations in this system illustrating how it describes weak
![]() $\omega$
-categories. This shows the introduction of a new operation and a new coherence and emphasizes the role of the substitutions taken as their arguments.
$\omega$
-categories. This shows the introduction of a new operation and a new coherence and emphasizes the role of the substitutions taken as their arguments.
-
Composition: In
 $\mathsf{CaTT}$
one can use an operation to derive a witness for composition of 1-cells. Start by considering the context
$\mathsf{CaTT}$
one can use an operation to derive a witness for composition of 1-cells. Start by considering the context
 $\Gamma_ {\texttt{comp}} = (x:\star,y:\star,f:x\to y,z:\star,g:y\to z)$
. One can check that
$\Gamma_ {\texttt{comp}} = (x:\star,y:\star,f:x\to y,z:\star,g:y\to z)$
. One can check that
 $\Gamma_{\texttt{comp}}\vdash_{\mathsf{ps}}$
, and compute its source
$\Gamma_{\texttt{comp}}\vdash_{\mathsf{ps}}$
, and compute its source
 $\partial^-({\Gamma_{\texttt{comp}}}) = (x:\star)$
and target
$\partial^-({\Gamma_{\texttt{comp}}}) = (x:\star)$
and target
 $\partial^+({\Gamma_{\texttt{comp}}}) = (z:\star)$
. Thus, the judgment
$\partial^+({\Gamma_{\texttt{comp}}}) = (z:\star)$
. Thus, the judgment
 $\Gamma_{\texttt{comp}}\vdash_{\mathsf{op}} x\to z$
is derivable. Now considering with two terms v,w in a context
$\Gamma_{\texttt{comp}}\vdash_{\mathsf{op}} x\to z$
is derivable. Now considering with two terms v,w in a context
 $\Gamma$
such that
$\Gamma$
such that
 $\Gamma\vdash v:u\to u'$
and
$\Gamma\vdash v:u\to u'$
and
 $\Gamma\vdash w:u'\to u''$
(i.e., two composable 1-cells u and v), we define the substitution
$\Gamma\vdash w:u'\to u''$
(i.e., two composable 1-cells u and v), we define the substitution
 $\gamma = \langle{x\mapsto u,y\mapsto u',f\mapsto v,z\mapsto u'',g\mapsto w}\rangle$
. The judgment
$\gamma = \langle{x\mapsto u,y\mapsto u',f\mapsto v,z\mapsto u'',g\mapsto w}\rangle$
. The judgment
 $\Gamma\vdash \gamma:\Gamma_{\texttt{comp}}$
is then derivable, thus so it
$\Gamma\vdash \gamma:\Gamma_{\texttt{comp}}$
is then derivable, thus so it
 $\Gamma\vdash\mathsf{op}_{\Gamma_{\texttt{comp},x\to z}}[\gamma] : u\to u''$
. We denote this term with the simpler and more usual notation
$\Gamma\vdash\mathsf{op}_{\Gamma_{\texttt{comp},x\to z}}[\gamma] : u\to u''$
. We denote this term with the simpler and more usual notation
 $\Gamma\vdash \texttt{comp}\ v\ w : u\to u''$
.
$\Gamma\vdash \texttt{comp}\ v\ w : u\to u''$
. -
Associativity: Similarly, one can define the context
and check that \begin{equation*} \Gamma_ {\texttt{assoc}} = (x:\star,y:\star,f:x\to y,z:\star,g:y\to z,w:\star,h:z\to w) \end{equation*}
\begin{equation*} \Gamma_ {\texttt{assoc}} = (x:\star,y:\star,f:x\to y,z:\star,g:y\to z,w:\star,h:z\to w) \end{equation*}
 $\Gamma_{\texttt{assoc}}\vdash_{\mathsf{ps}}$
, and
$\Gamma_{\texttt{assoc}}\vdash_{\mathsf{ps}}$
, and
 $\Gamma_{\texttt{assoc}} \vdash_{\mathsf{coh}} {\texttt{comp}\ (\texttt{comp}\ f\ g)\ h} \to {\texttt{comp}\ f\ (\texttt{comp}\ g\ h)} $
are both derivable. Whenever a context
$\Gamma_{\texttt{assoc}} \vdash_{\mathsf{coh}} {\texttt{comp}\ (\texttt{comp}\ f\ g)\ h} \to {\texttt{comp}\ f\ (\texttt{comp}\ g\ h)} $
are both derivable. Whenever a context
 $\Gamma$
defines three terms u,v,w that are composable 1-cells, the rule
$\Gamma$
defines three terms u,v,w that are composable 1-cells, the rule
 $\mathsf{coh}$
-intro provides a witness for the associativity of their compositions, denoted
$\mathsf{coh}$
-intro provides a witness for the associativity of their compositions, denoted  \begin{equation*} \Gamma\vdash\texttt{assoc}\ u\ v\ w : {\texttt{comp}\ (\texttt{comp}\ u\ v)\ w} \to {\texttt{comp}\ u\ (\texttt{comp}\ v\ w)} \end{equation*}
\begin{equation*} \Gamma\vdash\texttt{assoc}\ u\ v\ w : {\texttt{comp}\ (\texttt{comp}\ u\ v)\ w} \to {\texttt{comp}\ u\ (\texttt{comp}\ v\ w)} \end{equation*}
Models. For the purpose of this article, we define the category of weak
![]() $\omega$
-categories to be the category of models of
$\omega$
-categories to be the category of models of
![]() $\mathsf{CaTT}$
, and we refer the reader to Benjamin et al. (Reference Benjamin, Finster and Mimram2021) for a formal exploration of how they relate to other known definitions of weak
$\mathsf{CaTT}$
, and we refer the reader to Benjamin et al. (Reference Benjamin, Finster and Mimram2021) for a formal exploration of how they relate to other known definitions of weak
![]() $\omega$
-categories. We can however explain informally why this definition is sensible: Considering a model
$\omega$
-categories. We can however explain informally why this definition is sensible: Considering a model
![]() $F:\operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to{\operatorname{Set}}$
, we define its set of objects to be
$F:\operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to{\operatorname{Set}}$
, we define its set of objects to be
![]() $F(D^0)$
, and given two objects
$F(D^0)$
, and given two objects
![]() $x,y\in F(D^0)$
, the set of 1-cells between x and y in F to be
$x,y\in F(D^0)$
, the set of 1-cells between x and y in F to be
![]() $\operatorname{Hom}_F(x,y) = \left\{{f\in F(D^1), F(s)(f)=x, F(t)(f)=y}\right\}$
where
$\operatorname{Hom}_F(x,y) = \left\{{f\in F(D^1), F(s)(f)=x, F(t)(f)=y}\right\}$
where
![]() $D^1\vdash s:D^0$
is the source substitution and
$D^1\vdash s:D^0$
is the source substitution and
![]() $D^1\vdash t:D^0$
is the target substitution. Two 1-cells
$D^1\vdash t:D^0$
is the target substitution. Two 1-cells
![]() $f\in\operatorname{Hom}_F(x,y)$
and
$f\in\operatorname{Hom}_F(x,y)$
and
![]() $g\in\operatorname{Hom}_F(y,z)$
define a unique element of
$g\in\operatorname{Hom}_F(y,z)$
define a unique element of
![]() $F(\Gamma_{\texttt{comp}})$
. Then, the constructor comp defines a substitution
$F(\Gamma_{\texttt{comp}})$
. Then, the constructor comp defines a substitution
![]() $\Gamma_{\texttt{comp}}\to D^1$
, which induces the element of
$\Gamma_{\texttt{comp}}\to D^1$
, which induces the element of
![]() $F(D^1)$
corresponding to the composition of f and g. This observation can be generalized, so that all derivable terms correspond to additional algebraic structure on the globular set induced by F.
$F(D^1)$
corresponding to the composition of f and g. This observation can be generalized, so that all derivable terms correspond to additional algebraic structure on the globular set induced by F.
Syntactic category. We have seen that the category
![]() ${\operatorname{\mathcal{S}}_{\mathfrak{G}}}^{\text{op}}$
consists in the finite globular sets, which are also the finitely generated ones since the representable are finite. Similarly the category
${\operatorname{\mathcal{S}}_{\mathfrak{G}}}^{\text{op}}$
consists in the finite globular sets, which are also the finitely generated ones since the representable are finite. Similarly the category
![]() ${\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}^{\text{op}}$
can be conceived as the full subcategory of
${\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}^{\text{op}}$
can be conceived as the full subcategory of
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
whose objects are the computads with finitely many generators for the weak
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
whose objects are the computads with finitely many generators for the weak
![]() $\omega$
-category monad. Making this statement precise requires adapting the notion of computad (Burroni Reference Burroni1993; Street Reference Street1976) to this case, or working with a monadic formulation of the theory such as Leinster’s (2004). This formulation is equivalent to the Grothendieck–Maltsiniotis definition, pas proved by Ara (Reference Ara2010). We leave the details about these computads for further work, but still mention it here in order to draw the connection with the Gabriel–Ulmer duality (Gabriel and Ulmer Reference Gabriel and Ulmer2006).
$\omega$
-category monad. Making this statement precise requires adapting the notion of computad (Burroni Reference Burroni1993; Street Reference Street1976) to this case, or working with a monadic formulation of the theory such as Leinster’s (2004). This formulation is equivalent to the Grothendieck–Maltsiniotis definition, pas proved by Ara (Reference Ara2010). We leave the details about these computads for further work, but still mention it here in order to draw the connection with the Gabriel–Ulmer duality (Gabriel and Ulmer Reference Gabriel and Ulmer2006).
3. The Type Theory
 $\mathsf{MCaTT}$
for Monoidal Weak ω-Category
$\mathsf{MCaTT}$
for Monoidal Weak ω-Category
We now present a new type theory
![]() $\mathsf{MCaTT}$
, which is an original contribution of this article, and which aims at describing monoidal weak
$\mathsf{MCaTT}$
, which is an original contribution of this article, and which aims at describing monoidal weak
![]() $\omega$
-categories. The main intuition behind this definition is to start from the idea that a monoidal weak
$\omega$
-categories. The main intuition behind this definition is to start from the idea that a monoidal weak
![]() $\omega$
-category is a weak
$\omega$
-category is a weak
![]() $\omega$
-category with a single object, and enforce this constraint on the theory
$\omega$
-category with a single object, and enforce this constraint on the theory
![]() $\mathsf{CaTT}$
. This induces a shift in dimension, so we refer to this new unique object as being of “dimension
$\mathsf{CaTT}$
. This induces a shift in dimension, so we refer to this new unique object as being of “dimension
![]() $-1$
”, in such a way that the cells of dimension 0 of the monoidal categories really are the objects.
$-1$
”, in such a way that the cells of dimension 0 of the monoidal categories really are the objects.
The subcategory of context with one object. A natural candidate for the syntactic category of the theory of weak
![]() $\omega$
-categories with one object is the full subcategory of
$\omega$
-categories with one object is the full subcategory of
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
whose objects are the contexts containing exactly one cell of type
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
whose objects are the contexts containing exactly one cell of type
![]() $\star$
. We denote this category
$\star$
. We denote this category
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. It is not clear however that this category can be equipped with a structure of category with families. We introduce the theory
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. It is not clear however that this category can be equipped with a structure of category with families. We introduce the theory
![]() $\mathsf{MCaTT}$
, and prove later that its syntactic category is equivalent to
$\mathsf{MCaTT}$
, and prove later that its syntactic category is equivalent to
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. This answers the above question, by constructing an actual theory presenting
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. This answers the above question, by constructing an actual theory presenting
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
.
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
.
3.1 Globular sets with a unit type
We first define a variant of the type theory
![]() $\mathfrak{G}$
, that we call
$\mathfrak{G}$
, that we call
![]() $\mathfrak{G}_{{1}}$
, in order to handle the dimension shift that happens.
$\mathfrak{G}_{{1}}$
, in order to handle the dimension shift that happens.
Unit type. The type theory
![]() $\mathfrak{G}_{{1}}$
is obtained from the theory
$\mathfrak{G}_{{1}}$
is obtained from the theory
![]() $\mathfrak{G}$
by formally replacing the type
$\mathfrak{G}$
by formally replacing the type
![]() $\star$
by a unit type that we denote 1, together with a constant that we denote (), which represent a term of this unit type. We keep the constructor
$\star$
by a unit type that we denote 1, together with a constant that we denote (), which represent a term of this unit type. We keep the constructor
![]() $\to$
. These new constructors have the following set of variables and action under substitutions
$\to$
. These new constructors have the following set of variables and action under substitutions
The type introduction rules for the theory
![]() $\mathfrak{G}_{1}$
are the following:
$\mathfrak{G}_{1}$
are the following:

We also add a computation rule to this theory, that postulates a new definitional equality. We use the symbol
![]() $\equiv$
to denote such definitional equalities. We require the two following rules, so that typing respects definitional equality and that 1 is a unit type.
$\equiv$
to denote such definitional equalities. We require the two following rules, so that typing respects definitional equality and that 1 is a unit type.

We refer the reader to Appendix A.3 for a summary of all the rules of the theory
Theories with definitional equalities The addition of definitional equality complicates the theory quite substantially in general. A slight technical problem is that the rule (
![]() $\eta_{1}$
) makes the set of variables of a term not invariant. This is easily solved since we do not use this set in the presence of the unit type. A more profound issue is that one needs to account for this equality in the definition of the syntactic category. This is why we now take the set of objects to be the contexts up to definitional equality, and the morphisms to be substitutions up to definitional equality. We also consider the set of terms and types associated to a context to be up to definitional equality. The last difficulty is that adding definitional equality may break the decidability of type checking. We admit that in our case, we can actually define a normal form by rewriting any term
$\eta_{1}$
) makes the set of variables of a term not invariant. This is easily solved since we do not use this set in the presence of the unit type. A more profound issue is that one needs to account for this equality in the definition of the syntactic category. This is why we now take the set of objects to be the contexts up to definitional equality, and the morphisms to be substitutions up to definitional equality. We also consider the set of terms and types associated to a context to be up to definitional equality. The last difficulty is that adding definitional equality may break the decidability of type checking. We admit that in our case, we can actually define a normal form by rewriting any term
![]() $\Gamma\vdash t:{1}$
into the term (). This ensures that the type checking is decidable. From now on, we always implicitly normalize all the expression we consider and thus eliminate all the difficulties due to definitional equality.
$\Gamma\vdash t:{1}$
into the term (). This ensures that the type checking is decidable. From now on, we always implicitly normalize all the expression we consider and thus eliminate all the difficulties due to definitional equality.
Notations for mixing theories. When it is ambiguous, we write
![]() $\vdash_{\mathcal{T}}$
for judgments that are derivable in the type theory
$\vdash_{\mathcal{T}}$
for judgments that are derivable in the type theory
![]() $\mathcal{T}$
. In order to simplify the formulation, we allow for rules that combine judgments coming from different theory, in particular, we may say for example that any of the following rule is admissible to express the fact that we can construct a derivation of the lower judgment in the theory
$\mathcal{T}$
. In order to simplify the formulation, we allow for rules that combine judgments coming from different theory, in particular, we may say for example that any of the following rule is admissible to express the fact that we can construct a derivation of the lower judgment in the theory
![]() $\mathcal{T}'$
from a derivation of the upper judgment in the theory
$\mathcal{T}'$
from a derivation of the upper judgment in the theory
![]() $\mathcal{T}$
.
$\mathcal{T}$
.

Dimension and type of terms. We define the dimension of a type in the theory
![]() $\mathfrak{G}_{1}$
by induction: dim 1 = −2 and
$\mathfrak{G}_{1}$
by induction: dim 1 = −2 and
![]() $\dim{{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}} = \dim A + 1$
. The dimension of a term
$\dim{{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}} = \dim A + 1$
. The dimension of a term
![]() $\Gamma\vdash t:A$
is
$\Gamma\vdash t:A$
is
![]() $\dim t = 1 + \dim A$
. Note that for every context
$\dim t = 1 + \dim A$
. Note that for every context
![]() $\Gamma$
, there is only ever one type of dimension
$\Gamma$
, there is only ever one type of dimension
![]() $-1$
that is in normal form, the type
$-1$
that is in normal form, the type
![]() $\Gamma\vdash{()}\underset{{1}}{\xrightarrow{\phantom{{1}}}}{()}$
, we denote this type
$\Gamma\vdash{()}\underset{{1}}{\xrightarrow{\phantom{{1}}}}{()}$
, we denote this type
![]() $\star$
by analogy with the theory
$\star$
by analogy with the theory
![]() $\mathfrak{G}$
. When we define operations acting on
$\mathfrak{G}$
. When we define operations acting on
![]() $\mathfrak{G}_{{1}}$
, we always ensure that they respect the definitional equality by defining them only in normal form. That means that in practice, we may treat
$\mathfrak{G}_{{1}}$
, we always ensure that they respect the definitional equality by defining them only in normal form. That means that in practice, we may treat
![]() $\star$
as a separate case if needed, keeping in mind that it is simply a short form for
$\star$
as a separate case if needed, keeping in mind that it is simply a short form for
![]() ${()}\underset{{1}}{\xrightarrow{\phantom{{1}}}}{()}$
.
${()}\underset{{1}}{\xrightarrow{\phantom{{1}}}}{()}$
.
Semantics. We now show that the semantics of the theory
![]() $\mathfrak{G}_{{1}}$
is the same as the semantics of the theory
$\mathfrak{G}_{{1}}$
is the same as the semantics of the theory
![]() $\mathfrak{G}$
.
$\mathfrak{G}$
.
Lemma 8. The context
![]() $(x:{1})$
is terminal in the category
$(x:{1})$
is terminal in the category
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
$\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
Proof. For any context
![]() $\Gamma$
, we always have the substitution
$\Gamma$
, we always have the substitution
![]() $\Gamma\vdash\langle{x\mapsto ()}\rangle:(x:{1})$
. Moreover, consider a substitution
$\Gamma\vdash\langle{x\mapsto ()}\rangle:(x:{1})$
. Moreover, consider a substitution
![]() $\Gamma\vdash\gamma:(x:{1})$
. Then by construction of substitutions,
$\Gamma\vdash\gamma:(x:{1})$
. Then by construction of substitutions,
![]() $\gamma$
is necessarily of the form
$\gamma$
is necessarily of the form
![]() $\gamma=\langle{x\mapsto t}\rangle$
with a derivation for the judgment
$\gamma=\langle{x\mapsto t}\rangle$
with a derivation for the judgment
![]() $\Gamma\vdash t:{1}$
. The conversion rule
$\Gamma\vdash t:{1}$
. The conversion rule
![]() $(\eta_{{1}})$
applies and gives a definitional equality
$(\eta_{{1}})$
applies and gives a definitional equality
![]() $\Gamma\vdash t\equiv
():{1}$
. Hence, we have a definitional equality between the substitutions
$\Gamma\vdash t\equiv
():{1}$
. Hence, we have a definitional equality between the substitutions
![]() $\Gamma\vdash\gamma\equiv\langle{x\mapsto()}\rangle:(x:{1})$
. This proves that there is a unique morphism
$\Gamma\vdash\gamma\equiv\langle{x\mapsto()}\rangle:(x:{1})$
. This proves that there is a unique morphism
![]() $\Gamma\to(x:{1})$
in the syntactic category
$\Gamma\to(x:{1})$
in the syntactic category
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}}$
.
$\operatorname{\mathcal{S}}_{\mathfrak{G}}$
.
Lemma 9. The syntactic categories
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}}$
and
$\operatorname{\mathcal{S}}_{\mathfrak{G}}$
and
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
are equivalent.
$\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
are equivalent.
Proof. Since the theory
![]() $\mathfrak{G}_{{1}}$
contains all the rules of the theory
$\mathfrak{G}_{{1}}$
contains all the rules of the theory
![]() $\mathfrak{G}$
, any valid context
$\mathfrak{G}$
, any valid context
![]() $\Gamma\vdash$
(resp. any valid substitution
$\Gamma\vdash$
(resp. any valid substitution
![]() $\Delta\vdash \gamma:\Gamma$
) in the theory
$\Delta\vdash \gamma:\Gamma$
) in the theory
![]() $\mathfrak{G}$
also defines a valid context
$\mathfrak{G}$
also defines a valid context
![]() $\Gamma\vdash$
(resp. a valid substitution
$\Gamma\vdash$
(resp. a valid substitution
![]() $\Delta\vdash \gamma : \Gamma$
) in the theory
$\Delta\vdash \gamma : \Gamma$
) in the theory
![]() $\mathfrak{G}_{{1}}$
. Hence, there is an inclusion functor
$\mathfrak{G}_{{1}}$
. Hence, there is an inclusion functor
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}} \to \operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
. We show that this functor is an equivalence, by showing that it is fully faithful and essentially surjective. First we show that it is faithful by induction on the length of the target context: If the target context is empty, then it is terminal, so the statement is vacuous, consider two distinct substitutions
$\operatorname{\mathcal{S}}_{\mathfrak{G}} \to \operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
. We show that this functor is an equivalence, by showing that it is fully faithful and essentially surjective. First we show that it is faithful by induction on the length of the target context: If the target context is empty, then it is terminal, so the statement is vacuous, consider two distinct substitutions
![]() $\Delta\vdash \langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
and
$\Delta\vdash \langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
and
![]() $\Delta\vdash\langle{\gamma',x\mapsto t'}\rangle:(\Gamma,x:A)$
in the theory
$\Delta\vdash\langle{\gamma',x\mapsto t'}\rangle:(\Gamma,x:A)$
in the theory
![]() $\mathfrak{G}$
. Then either the two substitutions
$\mathfrak{G}$
. Then either the two substitutions
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma'$
are distinct in
$\gamma'$
are distinct in
![]() $\mathfrak{G}$
, in which case the induction hypothesis shows that they are distinct in
$\mathfrak{G}$
, in which case the induction hypothesis shows that they are distinct in
![]() $\mathfrak{G}_{{1}}$
, or necessarily the terms t and t’ are distinct in
$\mathfrak{G}_{{1}}$
, or necessarily the terms t and t’ are distinct in
![]() $\mathfrak{G}$
. Since these terms are in
$\mathfrak{G}$
. Since these terms are in
![]() $\mathfrak{G}$
, they are not of type 1, so there cannot be a definitional equality between them in
$\mathfrak{G}$
, they are not of type 1, so there cannot be a definitional equality between them in
![]() $\mathfrak{G}_{{1}}$
. This proves that
$\mathfrak{G}_{{1}}$
. This proves that
![]() $\langle{\gamma,x\mapsto t}\rangle$
and
$\langle{\gamma,x\mapsto t}\rangle$
and
![]() $\langle{\gamma',x\mapsto t'}\rangle$
define distinct arrows in
$\langle{\gamma',x\mapsto t'}\rangle$
define distinct arrows in
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
, hence the functor is faithful. We show that it is full by considering two contexts
$\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
, hence the functor is faithful. We show that it is full by considering two contexts
![]() $\Delta$
and
$\Delta$
and
![]() $\Gamma$
of
$\Gamma$
of
![]() $\mathfrak{G}$
together with a substitution
$\mathfrak{G}$
together with a substitution
![]() $\Delta\vdash \gamma:\Gamma$
in
$\Delta\vdash \gamma:\Gamma$
in
![]() $\mathfrak{G}_{{1}}$
. Then the substitution is built out of terms of the context
$\mathfrak{G}_{{1}}$
. Then the substitution is built out of terms of the context
![]() $\Delta$
, and since none of the variables in
$\Delta$
, and since none of the variables in
![]() $\Gamma$
has type 1, none of those terms have type 1, so they are all variables, of
$\Gamma$
has type 1, none of those terms have type 1, so they are all variables, of
![]() $\Delta$
, and hence the substitution
$\Delta$
, and hence the substitution
![]() $\gamma$
is in fact definable in
$\gamma$
is in fact definable in
![]() $\mathfrak{G}$
. Finally, we prove that this functor is essentially surjective. Indeed, first note that for all context
$\mathfrak{G}$
. Finally, we prove that this functor is essentially surjective. Indeed, first note that for all context
![]() $\Gamma$
, we have the pullback in
$\Gamma$
, we have the pullback in
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
:
$\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
:

Since both
![]() $(x:{1})$
and
$(x:{1})$
and
![]() $\varnothing$
are terminal objects in
$\varnothing$
are terminal objects in
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
, the display map
$\operatorname{\mathcal{S}}_{\mathfrak{G}_{{1}}}$
, the display map
![]() $(\Gamma,x:{1})\to\Gamma$
is an isomorphism. Using this fact we can recursively eliminate all the variables of type 1 in a context and show that every context is isomorphic to one without any variable of type 1, that is, it is isomorphic to a context of
$(\Gamma,x:{1})\to\Gamma$
is an isomorphism. Using this fact we can recursively eliminate all the variables of type 1 in a context and show that every context is isomorphic to one without any variable of type 1, that is, it is isomorphic to a context of
![]() $\mathfrak{G}$
.
$\mathfrak{G}$
.
Proposition 10. There is an equivalence between the models of the theory
![]() $\mathfrak{G}$
and the models of the theory
$\mathfrak{G}$
and the models of the theory
![]() $\mathfrak{G}_{{1}}$
.
$\mathfrak{G}_{{1}}$
.
Proof. First note that the equivalence functor
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}}\to\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}$
induces an equivalence of categories by pre-composition
$\operatorname{\mathcal{S}}_{\mathfrak{G}}\to\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}$
induces an equivalence of categories by pre-composition
![]() $\operatorname{Set}^{\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}}\to \operatorname{Set}^{\operatorname{\mathcal{S}}_{\mathfrak{G}}}$
. Since any type (resp. any term) in the theory
$\operatorname{Set}^{\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}}\to \operatorname{Set}^{\operatorname{\mathcal{S}}_{\mathfrak{G}}}$
. Since any type (resp. any term) in the theory
![]() $\mathfrak{G}$
also defines a type (resp. a term) in the theory
$\mathfrak{G}$
also defines a type (resp. a term) in the theory
![]() $\mathfrak{G}_{{1}}$
, the functor
$\mathfrak{G}_{{1}}$
, the functor
![]() $\operatorname{\mathcal{S}}_{\mathfrak{G}}\to \operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}$
can be seen as a functor above the category
$\operatorname{\mathcal{S}}_{\mathfrak{G}}\to \operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}$
can be seen as a functor above the category
![]() $\operatorname{Fam}$
. Moreover, it is straightforward from the syntactic definition of this functor that it preserves the terminal object and the context extension on the nose, hence this functor defines morphism of category with families.This shows that the pre-composition restricts to the models to provide a functor
$\operatorname{Fam}$
. Moreover, it is straightforward from the syntactic definition of this functor that it preserves the terminal object and the context extension on the nose, hence this functor defines morphism of category with families.This shows that the pre-composition restricts to the models to provide a functor
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}}})$
. Consider the functor
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}}})$
. Consider the functor
![]() $f : \operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}\to \operatorname{\mathcal{S}}_{\mathfrak{G}}$
which is the adjoint inverse of the inclusion. Remark that the functor f cannot be made into a functor of categories with families, since for instance it sends the context
$f : \operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}\to \operatorname{\mathcal{S}}_{\mathfrak{G}}$
which is the adjoint inverse of the inclusion. Remark that the functor f cannot be made into a functor of categories with families, since for instance it sends the context
![]() $(\varnothing,x:{1})$
onto the context
$(\varnothing,x:{1})$
onto the context
![]() $\varnothing$
, so it cannot preserve the context extension on the nose. However, by definition f preserves all limits, so in particular it preserves the terminal objects and the pullbacks along display maps. Considering a model
$\varnothing$
, so it cannot preserve the context extension on the nose. However, by definition f preserves all limits, so in particular it preserves the terminal objects and the pullbacks along display maps. Considering a model
![]() $F : \operatorname{\mathcal{S}}_{\mathfrak{G}} \to \operatorname{Set}$
, this implies that
$F : \operatorname{\mathcal{S}}_{\mathfrak{G}} \to \operatorname{Set}$
, this implies that
![]() $f^\star F$
also preserves the terminal object and the pullbacks along the display maps, so it is a model and hence
$f^\star F$
also preserves the terminal object and the pullbacks along the display maps, so it is a model and hence
![]() $f^\star$
restricts as a functor on the models
$f^\star$
restricts as a functor on the models
![]() $f^\star : \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}})$
, defining an inverse to the previous functor, hence the equivalence of categories.
$f^\star : \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathfrak{G}_{1}}})$
, defining an inverse to the previous functor, hence the equivalence of categories.
The desuspension operation. In order to express the theory
![]() $\mathsf{MCaTT}$
, we need an operation that we call the desuspension, that we first describe as associating, to every context
$\mathsf{MCaTT}$
, we need an operation that we call the desuspension, that we first describe as associating, to every context
![]() $\Gamma$
of
$\Gamma$
of
![]() $\mathfrak{G}$
, the context
$\mathfrak{G}$
, the context
![]() $\big\downarrow{\Gamma}$
in
$\big\downarrow{\Gamma}$
in
![]() $\mathfrak{G}_{{1}}$
. It is defined by induction on the raw syntax of the theory
$\mathfrak{G}_{{1}}$
. It is defined by induction on the raw syntax of the theory
![]() $\mathfrak{G}$
, together with the corresponding operation on types of
$\mathfrak{G}$
, together with the corresponding operation on types of
![]() $\mathfrak{G}$
$\mathfrak{G}$
![]()
Proposition 11. The desuspension respects the judgments, the following rules are derivable

Proof. We prove this result by mutual induction on the derivation tree of valid judgments.
Induction case for contexts:
-
A derivable context obtained by the rule ec is necessarily the context
 $\varnothing\vdash_{\mathfrak{G}}$
. The rule ec gives a derivation of
$\varnothing\vdash_{\mathfrak{G}}$
. The rule ec gives a derivation of
 $\big\downarrow{\varnothing} \vdash_{\mathfrak{G}_{1}}$
$\big\downarrow{\varnothing} \vdash_{\mathfrak{G}_{1}}$
-
A derivable context obtained by the rule ce is of the form
 $(\Gamma,x:A)\vdash_{\mathfrak{G}}$
, by the induction case on types we have
$(\Gamma,x:A)\vdash_{\mathfrak{G}}$
, by the induction case on types we have
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} \big\downarrow{A}$
. The rule ce yields a derivation for
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} \big\downarrow{A}$
. The rule ce yields a derivation for
 $\big\downarrow{\Gamma},x:\big\downarrow{A}\vdash_{\mathfrak{G}_{1}}$
.
$\big\downarrow{\Gamma},x:\big\downarrow{A}\vdash_{\mathfrak{G}_{1}}$
.
Induction for types:
-
A derivable type obtained by the rule
 $\star$
-intro is of the form
$\star$
-intro is of the form
 $\Gamma\vdash_{\mathfrak{G}} \star$
, we necessarily have
$\Gamma\vdash_{\mathfrak{G}} \star$
, we necessarily have
 $\Gamma\vdash_{\mathfrak{G}}$
. The induction case for contexts implies
$\Gamma\vdash_{\mathfrak{G}}$
. The induction case for contexts implies
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}$
. The rule 1-intro then provides a derivation for
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}$
. The rule 1-intro then provides a derivation for
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}{1}$
.
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}{1}$
. -
A derivable type obtained by the rule
 $\to$
-intro is of the form
$\to$
-intro is of the form
 $\Gamma\vdash_{\mathfrak{G}} {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
. The induction cases for types and variables provide derivations for
$\Gamma\vdash_{\mathfrak{G}} {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
. The induction cases for types and variables provide derivations for
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} A$
,
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} A$
,
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} t:\big\downarrow{A}$
and
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} t:\big\downarrow{A}$
and
 $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} u:\big\downarrow{A}$
. The rule
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} u:\big\downarrow{A}$
. The rule
 $\to$
-intro then gives a derivation for
$\to$
-intro then gives a derivation for
 $\big\downarrow{\Gamma}\vdash {t}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{u}$
.
$\big\downarrow{\Gamma}\vdash {t}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{u}$
.
Induction for variables: A term obtained by the rule Var is a variable
![]() $\Gamma\vdash_{\mathfrak{G}} x:A$
, and we have
$\Gamma\vdash_{\mathfrak{G}} x:A$
, and we have
![]() $\Gamma\vdash_{\mathfrak{G}}$
. The induction for contexts implies
$\Gamma\vdash_{\mathfrak{G}}$
. The induction for contexts implies
![]() $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}$
. Moreover,
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}}$
. Moreover,
![]() $(x:A)\in\Gamma$
implies
$(x:A)\in\Gamma$
implies
![]() $(x:\big\downarrow{A})\in\big\downarrow{\Gamma}$
. The rule var lets us construct a derivation for
$(x:\big\downarrow{A})\in\big\downarrow{\Gamma}$
. The rule var lets us construct a derivation for
![]() $\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} x:\big\downarrow{A}$
.
$\big\downarrow{\Gamma}\vdash_{\mathfrak{G}_{1}} x:\big\downarrow{A}$
.
From now on, when we perform proofs by induction on the derivation tree, we rely on the form of the judgment, for instance, we may write: “For the context
![]() $\varnothing\vdash$
” to mean that we discriminate on the rule ec and that in this case the context is necessarily
$\varnothing\vdash$
” to mean that we discriminate on the rule ec and that in this case the context is necessarily
![]() $\varnothing$
. This is justified since the rule ec is the only one that allows to derive
$\varnothing$
. This is justified since the rule ec is the only one that allows to derive
![]() $\varnothing\vdash$
, and more generally each syntactic constructor corresponds to exactly one introduction rule.
$\varnothing\vdash$
, and more generally each syntactic constructor corresponds to exactly one introduction rule.
Examples. We illustrate the desuspension with a few examples. Intuitively merely consists in rewriting the type
![]() $\star$
into the type 1. For each of the context in
$\star$
into the type 1. For each of the context in
![]() $\mathfrak{G}_{{1}}$
, we also give a simpler context to which it is isomorphic.
$\mathfrak{G}_{{1}}$
, we also give a simpler context to which it is isomorphic.

3.2 The theory
 $\mathsf{MCaTT}$
$\mathsf{MCaTT}$
The type theory
![]() $\mathsf{MCaTT}$
relies on the theory
$\mathsf{MCaTT}$
relies on the theory
![]() $\mathsf{CaTT}$
on a fundamental level. Its inference rules use the derivability of judgments in
$\mathsf{CaTT}$
on a fundamental level. Its inference rules use the derivability of judgments in
![]() $\mathsf{CaTT}$
. To express these rules, we need to generalize the desuspension as an operation from the raw syntax of
$\mathsf{CaTT}$
. To express these rules, we need to generalize the desuspension as an operation from the raw syntax of
![]() $\mathsf{CaTT}$
to the raw syntax of
$\mathsf{CaTT}$
to the raw syntax of
![]() $\mathsf{MCaTT}$
. The raw syntax of
$\mathsf{MCaTT}$
. The raw syntax of
![]() $\mathsf{MCaTT}$
is obtained from the one of
$\mathsf{MCaTT}$
is obtained from the one of
![]() $\mathfrak{G}_{{1}}$
by adding two term constructors
$\mathfrak{G}_{{1}}$
by adding two term constructors
![]() $\mathsf{mop}$
and
$\mathsf{mop}$
and
![]() $\mathsf{mcoh}$
. A term expression is either a variable, or of the form
$\mathsf{mcoh}$
. A term expression is either a variable, or of the form
![]() $\mathsf{mop}_{\Gamma,A}[\gamma]$
or
$\mathsf{mop}_{\Gamma,A}[\gamma]$
or
![]() $\mathsf{mcoh}_{\Gamma,A}[\Gamma]$
with
$\mathsf{mcoh}_{\Gamma,A}[\Gamma]$
with
![]() $\Gamma$
a ps-context and A a type and
$\Gamma$
a ps-context and A a type and
![]() $\delta$
a substitution. We sometimes unite these two cases under the notation
$\delta$
a substitution. We sometimes unite these two cases under the notation
![]() $\mathsf{mconstr}$
which means either one of
$\mathsf{mconstr}$
which means either one of
![]() $\mathsf{mop}$
or
$\mathsf{mop}$
or
![]() $\mathsf{mcoh}$
. The variable set of these terms is not well defined (since not invariant under definitional equality), but the action of substitution is, and it is defined by
$\mathsf{mcoh}$
. The variable set of these terms is not well defined (since not invariant under definitional equality), but the action of substitution is, and it is defined by
![]() $\mathsf{mconstr}_{\Gamma,A}[\gamma][\delta] = \mathsf{mconstr}_{\Gamma,A}[\gamma\circ\delta]$
. By convention, whenever we use
$\mathsf{mconstr}_{\Gamma,A}[\gamma][\delta] = \mathsf{mconstr}_{\Gamma,A}[\gamma\circ\delta]$
. By convention, whenever we use
![]() $\mathsf{constr}$
and
$\mathsf{constr}$
and
![]() $\mathsf{mconstr}$
in the same equality, they are corresponding constructors, so either
$\mathsf{mconstr}$
in the same equality, they are corresponding constructors, so either
![]() $\mathsf{op}$
and
$\mathsf{op}$
and
![]() $\mathsf{mop}$
or
$\mathsf{mop}$
or
![]() $\mathsf{coh}$
and
$\mathsf{coh}$
and
![]() $\mathsf{mcoh}$
.
$\mathsf{mcoh}$
.
The general desuspension operation. We generalize the desuspension operation to contexts, types, terms and substitutions expressions of the theory
![]() $\mathsf{CaTT}$
as follows:
$\mathsf{CaTT}$
as follows:
 \begin{align*} \big\downarrow{\varnothing} &= \varnothing & \big\downarrow{(\Gamma,x:A)} &= \big\downarrow{\Gamma} , x:\big\downarrow{A}\\ \big\downarrow{\star} &= {1} & \big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})} &= {\big\downarrow{t}}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{\big\downarrow{u}} \\ \big\downarrow{x} &= x & \big\downarrow{\mathsf{constr}_{\Gamma,A}[\gamma]} &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\gamma}]\\ \big\downarrow{\langle{}\rangle} &= \langle{}\rangle & \big\downarrow{\langle{\gamma,x\mapsto t}\rangle} &= \langle{\big\downarrow{\gamma}, x\mapsto \big\downarrow{t}}\rangle\end{align*}
\begin{align*} \big\downarrow{\varnothing} &= \varnothing & \big\downarrow{(\Gamma,x:A)} &= \big\downarrow{\Gamma} , x:\big\downarrow{A}\\ \big\downarrow{\star} &= {1} & \big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})} &= {\big\downarrow{t}}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{\big\downarrow{u}} \\ \big\downarrow{x} &= x & \big\downarrow{\mathsf{constr}_{\Gamma,A}[\gamma]} &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\gamma}]\\ \big\downarrow{\langle{}\rangle} &= \langle{}\rangle & \big\downarrow{\langle{\gamma,x\mapsto t}\rangle} &= \langle{\big\downarrow{\gamma}, x\mapsto \big\downarrow{t}}\rangle\end{align*}
The theory
![]() $\mathsf{MCaTT}$
. The introduction rules for the constructors
$\mathsf{MCaTT}$
. The introduction rules for the constructors
![]() $\mathsf{mop}$
and
$\mathsf{mop}$
and
![]() $\mathsf{mcoh}$
reuse a lot of the machinery that we have developed for the theory
$\mathsf{mcoh}$
reuse a lot of the machinery that we have developed for the theory
![]() $\mathsf{CaTT}$
. We use the desuspension operation to transfer this machinery to the theory
$\mathsf{CaTT}$
. We use the desuspension operation to transfer this machinery to the theory
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.

In the above rules, the judgments
![]() $\Gamma\vdash_{\mathsf{ps}}$
,
$\Gamma\vdash_{\mathsf{ps}}$
,
![]() $\Gamma\vdash_{\mathsf{op}} A$
and
$\Gamma\vdash_{\mathsf{op}} A$
and
![]() $\Gamma\vdash_{\mathsf{coh}} A$
are the judgments defined for the theory
$\Gamma\vdash_{\mathsf{coh}} A$
are the judgments defined for the theory
![]() $\mathsf{CaTT}$
. In particular, although A is used as an index for the terms of the theory
$\mathsf{CaTT}$
. In particular, although A is used as an index for the terms of the theory
![]() $\mathsf{MCaTT}$
, it may not be a valid type in this theory, but it has to be a valid type in the theory
$\mathsf{MCaTT}$
, it may not be a valid type in this theory, but it has to be a valid type in the theory
![]() $\mathsf{CaTT}$
. For instance in the second of our following example, the type A uses the expression
$\mathsf{CaTT}$
. For instance in the second of our following example, the type A uses the expression
![]() $\texttt{comp}$
that we have defined as a constructor of
$\texttt{comp}$
that we have defined as a constructor of
![]() $\mathsf{CaTT}$
and not of
$\mathsf{CaTT}$
and not of
![]() $\mathsf{MCaTT}$
. All the rules of the theory
$\mathsf{MCaTT}$
. All the rules of the theory
![]() $\mathsf{MCaTT}$
are summarized in Appendix A.4 to provide a self-contained overview.
$\mathsf{MCaTT}$
are summarized in Appendix A.4 to provide a self-contained overview.
Examples. We do not provide an implementation for this theory, but we can check by hand a few examples of derivations as a sanity check for our definition of monoidal weak
![]() $\omega$
-categories.
$\omega$
-categories.
-
Monoidal product: First consider the ps-context
 $\Gamma_{\texttt{comp}}$
, that we have defined in Section 2.3. We have
$\Gamma_{\texttt{comp}}$
, that we have defined in Section 2.3. We have
 $\big\downarrow{\Gamma_{\texttt{comp}}} \simeq (f:\star,g:\star)$
, thus for any context
$\big\downarrow{\Gamma_{\texttt{comp}}} \simeq (f:\star,g:\star)$
, thus for any context
 $\Delta$
, a pair of terms t,u of type
$\Delta$
, a pair of terms t,u of type
 $\star$
in
$\star$
in
 $\Delta$
define a unique substitution
$\Delta$
define a unique substitution
 $\Delta\vdash \gamma : \big\downarrow{\Gamma}_{\texttt{comp}}$
. The rule
$\Delta\vdash \gamma : \big\downarrow{\Gamma}_{\texttt{comp}}$
. The rule
 $\mathsf{mop}$
-intro gives a derivation of the product of t and u as
$\mathsf{mop}$
-intro gives a derivation of the product of t and u as
 $\Delta\vdash \mathsf{mop}_{\Gamma_{\texttt{comp},x\to\ z}} [\gamma]: \star$
. We simplify this notation as
$\Delta\vdash \mathsf{mop}_{\Gamma_{\texttt{comp},x\to\ z}} [\gamma]: \star$
. We simplify this notation as
 $\Delta\vdash\texttt{prod}\ t\ u : \star$
.
$\Delta\vdash\texttt{prod}\ t\ u : \star$
. -
Associativity of monoidal product: Similarly, consider the context
 $\Gamma_{\texttt{assoc}}$
defined in Section 2.3. A context
$\Gamma_{\texttt{assoc}}$
defined in Section 2.3. A context
 $\Delta$
in
$\Delta$
in
 $\mathsf{MCaTT}$
equipped with three terms t,u,v of type
$\mathsf{MCaTT}$
equipped with three terms t,u,v of type
 $\star$
define a unique substitution
$\star$
define a unique substitution
 $\Delta\vdash \gamma:\big\downarrow{\Gamma}_{\texttt{assoc}}$
. Hence, the rule
$\Delta\vdash \gamma:\big\downarrow{\Gamma}_{\texttt{assoc}}$
. Hence, the rule
 $\mathsf{mcoh}$
-intro provides an associator for the monoidal product
$\mathsf{mcoh}$
-intro provides an associator for the monoidal product
 $\Delta\vdash \mathsf{mop}_{\Gamma_{\texttt{assoc}},{\texttt{comp}\ (\texttt{comp}\ f\ g)\ h \to }{\texttt{comp}\ f (\texttt{comp}\ g\ h)}} : {\texttt{prod}\ (\texttt{prod}\ t\ u )\ v} \to {\texttt{prod}\ t\ (\texttt{prod}\ u\ v)}$
. We simplify this notation as
$\Delta\vdash \mathsf{mop}_{\Gamma_{\texttt{assoc}},{\texttt{comp}\ (\texttt{comp}\ f\ g)\ h \to }{\texttt{comp}\ f (\texttt{comp}\ g\ h)}} : {\texttt{prod}\ (\texttt{prod}\ t\ u )\ v} \to {\texttt{prod}\ t\ (\texttt{prod}\ u\ v)}$
. We simplify this notation as
 $\Delta\vdash \texttt{passoc}\ t\ u\ v: {\texttt{prod}\ (\texttt{prod}\ t\ u )\ v} \to {\texttt{prod}\ t\ (\texttt{prod}\ u\ v)}$
.
$\Delta\vdash \texttt{passoc}\ t\ u\ v: {\texttt{prod}\ (\texttt{prod}\ t\ u )\ v} \to {\texttt{prod}\ t\ (\texttt{prod}\ u\ v)}$
. -
Neutral element: Consider the ps-context
 $\Gamma_{\texttt{neutral}}=(x:\star)$
. Then
$\Gamma_{\texttt{neutral}}=(x:\star)$
. Then
 $\big\downarrow{\Gamma_{\texttt{neutral}}}$
is terminal. The rule (
$\big\downarrow{\Gamma_{\texttt{neutral}}}$
is terminal. The rule (
 $\mathsf{mcoh}$
-intro) allows to derive the unit in any context
$\mathsf{mcoh}$
-intro) allows to derive the unit in any context
 $\Delta$
as
$\Delta$
as
 $\Delta\vdash \mathsf{mcoh}_{\Gamma_{\texttt{neutral}},x\to\ x} : \star$
.
$\Delta\vdash \mathsf{mcoh}_{\Gamma_{\texttt{neutral}},x\to\ x} : \star$
.
4. Syntactic Categories of
 $\mathsf{CaTT}$
and
$\mathsf{CaTT}$
and
 $\mathsf{MCaTT}$
$\mathsf{MCaTT}$
We now relate the two theories
![]() $\mathsf{CaTT}$
and
$\mathsf{CaTT}$
and
![]() $\mathsf{MCaTT}$
to each other via a pair of functorial translations. We have already seen one of these translations: the desuspension, the other one is called the reduced suspension. Our approach for defining these translations follows the same plan: first define them on a raw syntactic level, and then lift them to the syntactic categories by showing that they preserve the judgments. We then prove that these two translations are closely related, as they define a coreflective adjunction between the syntactic categories.
$\mathsf{MCaTT}$
to each other via a pair of functorial translations. We have already seen one of these translations: the desuspension, the other one is called the reduced suspension. Our approach for defining these translations follows the same plan: first define them on a raw syntactic level, and then lift them to the syntactic categories by showing that they preserve the judgments. We then prove that these two translations are closely related, as they define a coreflective adjunction between the syntactic categories.
4.1 The desuspension functor
We have already defined the desuspension operation, that we have used freely on the raw syntax of the theory. We now lift this operation to the syntactic categories by showing that it respects the derivability of judgments. We first prove following result about the interaction of the desuspension with the application of substitutions on a raw syntax level.
Lemma 12. Given a substitution
![]() $\Delta\vdash \gamma:\Gamma$
, for any type
$\Delta\vdash \gamma:\Gamma$
, for any type
![]() $\Gamma\vdash A$
, we have
$\Gamma\vdash A$
, we have
![]() $\big\downarrow{(A[\gamma])} = \big\downarrow{A}[\big\downarrow{\gamma}]$
, for any term
$\big\downarrow{(A[\gamma])} = \big\downarrow{A}[\big\downarrow{\gamma}]$
, for any term
![]() $\Gamma\vdash t:A$
, we have
$\Gamma\vdash t:A$
, we have
![]() $\big\downarrow{(t[\gamma])} = \big\downarrow{t}[\big\downarrow{\gamma}]$
and for any substitution
$\big\downarrow{(t[\gamma])} = \big\downarrow{t}[\big\downarrow{\gamma}]$
and for any substitution
![]() $\Gamma\vdash\theta : \Theta$
, we have
$\Gamma\vdash\theta : \Theta$
, we have
![]() $\big\downarrow{(\theta\circ \gamma)} = \big\downarrow{\theta}\circ \big\downarrow{\gamma}$
.
$\big\downarrow{(\theta\circ \gamma)} = \big\downarrow{\theta}\circ \big\downarrow{\gamma}$
.
Proof. We prove this by mutual induction
Induction for types:
-
In the case of the type
 $\star$
, we have
$\star$
, we have
 $\big\downarrow{(\star[\gamma])} = {1}$
and
$\big\downarrow{(\star[\gamma])} = {1}$
and
 $\big\downarrow{\star}[\big\downarrow{\gamma}] = {1}$
.
$\big\downarrow{\star}[\big\downarrow{\gamma}] = {1}$
. -
In the case of a type of the form
 ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the following equalities and we conclude by induction on types and terms.
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the following equalities and we conclude by induction on types and terms. \begin{align*} \big\downarrow{(({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\gamma])} &= {\big\downarrow{(t[\gamma])}}\underset{{\big\downarrow{(A[\gamma])}}}{\xrightarrow{\phantom{{\big\downarrow{(A[\gamma])}}}}}{\big\downarrow{(u[\gamma])}} & \big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})}[\big\downarrow{\gamma}] &= {\big\downarrow{t}[\big\downarrow{\gamma}]}\underset{{\big\downarrow{A}[\big\downarrow{\gamma}]}}{\xrightarrow{\phantom{\big\downarrow{A}[\big\downarrow{\gamma}]}}} {\big\downarrow{u} [\big\downarrow{\gamma}]} \end{align*}
\begin{align*} \big\downarrow{(({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\gamma])} &= {\big\downarrow{(t[\gamma])}}\underset{{\big\downarrow{(A[\gamma])}}}{\xrightarrow{\phantom{{\big\downarrow{(A[\gamma])}}}}}{\big\downarrow{(u[\gamma])}} & \big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})}[\big\downarrow{\gamma}] &= {\big\downarrow{t}[\big\downarrow{\gamma}]}\underset{{\big\downarrow{A}[\big\downarrow{\gamma}]}}{\xrightarrow{\phantom{\big\downarrow{A}[\big\downarrow{\gamma}]}}} {\big\downarrow{u} [\big\downarrow{\gamma}]} \end{align*}
Induction for terms:
-
In the case of a variable
 $\Gamma\vdash x:A$
, denote
$\Gamma\vdash x:A$
, denote
 $t = x[\gamma]$
. Then the association
$t = x[\gamma]$
. Then the association
 $x\mapsto \big\downarrow{t}$
appears in
$x\mapsto \big\downarrow{t}$
appears in
 $\big\downarrow{\gamma}$
. Hence,
$\big\downarrow{\gamma}$
. Hence,
 $x[\big\downarrow{\gamma}] = \big\downarrow{(x[\gamma])}$
.
$x[\big\downarrow{\gamma}] = \big\downarrow{(x[\gamma])}$
. -
In the case of a term of the form
 $\mathsf{constr}_{\Gamma,A}[\delta]$
, the following equalities hold The induction case for substitution then provides the equality between these two expressions.
$\mathsf{constr}_{\Gamma,A}[\delta]$
, the following equalities hold The induction case for substitution then provides the equality between these two expressions. \begin{align*} \big\downarrow{(\mathsf{constr}_{\Gamma,A}[\delta][\gamma])} &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{(\delta\circ\gamma)}] & \big\downarrow{(\mathsf{constr}_{\Gamma,A}[\delta])}[\big\downarrow{\gamma}] &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\delta}\circ\big\downarrow{\gamma}] \end{align*}
\begin{align*} \big\downarrow{(\mathsf{constr}_{\Gamma,A}[\delta][\gamma])} &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{(\delta\circ\gamma)}] & \big\downarrow{(\mathsf{constr}_{\Gamma,A}[\delta])}[\big\downarrow{\gamma}] &= \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\delta}\circ\big\downarrow{\gamma}] \end{align*}
Induction for substitutions:
-
In the case of the empty substitution
 $\langle{}\rangle$
, we have
$\langle{}\rangle$
, we have
 $\langle{}\rangle\circ\gamma = \langle{}\rangle$
, and hence
$\langle{}\rangle\circ\gamma = \langle{}\rangle$
, and hence
 $\big\downarrow{\left({\langle{}\rangle\circ \gamma}\right)} = \langle{}\rangle$
. But we also have
$\big\downarrow{\left({\langle{}\rangle\circ \gamma}\right)} = \langle{}\rangle$
. But we also have
 $\big\downarrow{\langle{}\rangle}\circ \gamma = \langle{}\rangle$
.
$\big\downarrow{\langle{}\rangle}\circ \gamma = \langle{}\rangle$
. -
In the case of a substitution of the form
 $\langle{\theta,x\mapsto t}\rangle$
, we have the following equalities Then the induction case for substitutions proves that
$\langle{\theta,x\mapsto t}\rangle$
, we have the following equalities Then the induction case for substitutions proves that \begin{align*} \big\downarrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\downarrow{(\theta\circ\gamma)},x\mapsto \big\downarrow{(t[\gamma])}}\rangle & \big\downarrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\downarrow{\gamma} &= \langle{\big\downarrow{\theta}\circ\big\downarrow{\gamma},x\mapsto\big\downarrow{t} [\big\downarrow{\gamma}]}\rangle \end{align*}
\begin{align*} \big\downarrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\downarrow{(\theta\circ\gamma)},x\mapsto \big\downarrow{(t[\gamma])}}\rangle & \big\downarrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\downarrow{\gamma} &= \langle{\big\downarrow{\theta}\circ\big\downarrow{\gamma},x\mapsto\big\downarrow{t} [\big\downarrow{\gamma}]}\rangle \end{align*}
 $\big\downarrow{(\theta\circ\gamma)} = \big\downarrow{\theta}\circ\big\downarrow{\gamma}$
, and the induction case for terms applies and shows that
$\big\downarrow{(\theta\circ\gamma)} = \big\downarrow{\theta}\circ\big\downarrow{\gamma}$
, and the induction case for terms applies and shows that
 $\big\downarrow{(t[\gamma])} = \big\downarrow{t}[\big\downarrow{\gamma}]$
. This proves the equality between the two above expressions.
$\big\downarrow{(t[\gamma])} = \big\downarrow{t}[\big\downarrow{\gamma}]$
. This proves the equality between the two above expressions.
Proposition 13. The rules are admissible

Proof. We prove this result by mutual induction on the derivation of the judgements. Induction for contexts:
-
For the empty context
 $\varnothing\vdash_{\mathsf{CaTT}}$
, we have
$\varnothing\vdash_{\mathsf{CaTT}}$
, we have
 $\big\downarrow{\varnothing} = \varnothing$
and the rule ec gives a derivation of
$\big\downarrow{\varnothing} = \varnothing$
and the rule ec gives a derivation of
 $\big\downarrow{\varnothing}\vdash_{\mathsf{MCaTT}}$
.
$\big\downarrow{\varnothing}\vdash_{\mathsf{MCaTT}}$
. -
For the context
 $(\Gamma,x:A)\vdash_{\mathsf{CaTT}}$
, we necessarily have
$(\Gamma,x:A)\vdash_{\mathsf{CaTT}}$
, we necessarily have
 $\Gamma\vdash_{\mathsf{CaTT}}$
and
$\Gamma\vdash_{\mathsf{CaTT}}$
and
 $\Gamma\vdash_{\mathsf{CaTT}} A$
. By induction, we have
$\Gamma\vdash_{\mathsf{CaTT}} A$
. By induction, we have
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
and
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
and
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}} \big\downarrow{A}$
. Hence, the rule ce gives a derivation for
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}} \big\downarrow{A}$
. Hence, the rule ce gives a derivation for
 $(\big\downarrow{\Gamma},x:\big\downarrow{A})\vdash$
. We conclude by noticing that
$(\big\downarrow{\Gamma},x:\big\downarrow{A})\vdash$
. We conclude by noticing that
 $\big\downarrow{(\Gamma,x:A)} = (\big\downarrow{\Gamma},x:\big\downarrow{A})$
.
$\big\downarrow{(\Gamma,x:A)} = (\big\downarrow{\Gamma},x:\big\downarrow{A})$
.
Induction for types:
-
For the type
 $\Gamma\vdash_{\mathsf{CaTT}}\star$
, we necessarily have
$\Gamma\vdash_{\mathsf{CaTT}}\star$
, we necessarily have
 $\Gamma\vdash_{\mathsf{CaTT}}$
. By induction, this implies
$\Gamma\vdash_{\mathsf{CaTT}}$
. By induction, this implies
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
. The rule 1-intro gives a derivation for
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
. The rule 1-intro gives a derivation for
 $\big\downarrow{\Gamma}\vdash\big\downarrow{\star}$
.
$\big\downarrow{\Gamma}\vdash\big\downarrow{\star}$
. -
For the type
 $\Gamma\vdash_{\mathsf{CaTT}} {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have a derivation of
$\Gamma\vdash_{\mathsf{CaTT}} {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have a derivation of
 $\Gamma\vdash_{\mathsf{CaTT}} A$
,
$\Gamma\vdash_{\mathsf{CaTT}} A$
,
 $\Gamma\vdash_{\mathsf{CaTT}}t:A$
and
$\Gamma\vdash_{\mathsf{CaTT}}t:A$
and
 $\Gamma\vdash_{\mathsf{CaTT}}u:A$
. By induction, we get a derivation of
$\Gamma\vdash_{\mathsf{CaTT}}u:A$
. By induction, we get a derivation of
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}\big\downarrow{A}$
,
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}\big\downarrow{A}$
,
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}} \big\downarrow{t}: \big\downarrow{A}$
and
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}} \big\downarrow{t}: \big\downarrow{A}$
and
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}\big\downarrow{u} : \big\downarrow{A}$
. The rule
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}\big\downarrow{u} : \big\downarrow{A}$
. The rule
 $\to$
-intro then provides a derivation of
$\to$
-intro then provides a derivation of
 $\big\downarrow{\Gamma}\vdash{\big\downarrow{t}}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{\big\downarrow{u}}$
.
$\big\downarrow{\Gamma}\vdash{\big\downarrow{t}}\underset{\big\downarrow{A}}{\xrightarrow{\phantom{\big\downarrow{A}}}}{\big\downarrow{u}}$
.
Induction for terms:
-
For a variable
 $\Gamma\vdash_{\mathsf{CaTT}} x:A$
, we necessarily have
$\Gamma\vdash_{\mathsf{CaTT}} x:A$
, we necessarily have
 $\Gamma\vdash_{\mathsf{CaTT}}$
. By induction, it provides a derivation of
$\Gamma\vdash_{\mathsf{CaTT}}$
. By induction, it provides a derivation of
 $\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
. Moreover, we have the condition
$\big\downarrow{\Gamma}\vdash_{\mathsf{MCaTT}}$
. Moreover, we have the condition
 $(x:A)\in\Gamma$
, hence
$(x:A)\in\Gamma$
, hence
 $(x:\big\downarrow{A})\in\big\downarrow{\Gamma}$
. The rule var then proves
$(x:\big\downarrow{A})\in\big\downarrow{\Gamma}$
. The rule var then proves
 $\big\downarrow{\Gamma}\vdash x:\big\downarrow{A}$
.
$\big\downarrow{\Gamma}\vdash x:\big\downarrow{A}$
. -
For a term of the form
 $\Delta\vdash_{\mathsf{CaTT}}\mathsf{constr}_{\Gamma,A}[\gamma]:A[\gamma]$
, we have a derivation of
$\Delta\vdash_{\mathsf{CaTT}}\mathsf{constr}_{\Gamma,A}[\gamma]:A[\gamma]$
, we have a derivation of
 $\Delta\vdash_{\mathsf{CaTT}}\gamma:\Gamma$
. By induction, provides a derivation for
$\Delta\vdash_{\mathsf{CaTT}}\gamma:\Gamma$
. By induction, provides a derivation for
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{\gamma}:\big\downarrow{\Gamma}$
. The rule
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{\gamma}:\big\downarrow{\Gamma}$
. The rule
 $\mathsf{mop}$
-intro or (
$\mathsf{mop}$
-intro or (
 $\mathsf{mcoh}$
-intro) then gives a derivation of
$\mathsf{mcoh}$
-intro) then gives a derivation of
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\gamma}]:\big\downarrow{A}[\big\downarrow{\gamma}]$
.
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \mathsf{mconstr}_{\Gamma,A}[\big\downarrow{\gamma}]:\big\downarrow{A}[\big\downarrow{\gamma}]$
.
Induction for substitutions:
-
For the empty substitution
 $\Delta\vdash_{\mathsf{CaTT}}\langle{}\rangle:\varnothing$
, we have a derivation of
$\Delta\vdash_{\mathsf{CaTT}}\langle{}\rangle:\varnothing$
, we have a derivation of
 $\Delta\vdash_{\mathsf{CaTT}}$
. By induction, it provides a derivation of
$\Delta\vdash_{\mathsf{CaTT}}$
. By induction, it provides a derivation of
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}$
. The rule es then proves
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}$
. The rule es then proves
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}\langle{}\rangle:\varnothing$
.
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}\langle{}\rangle:\varnothing$
. -
For the substitution
 $\Delta\vdash_{\mathsf{CaTT}}\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have derivations of
$\Delta\vdash_{\mathsf{CaTT}}\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have derivations of
 $\Delta\vdash_{\mathsf{CaTT}}\gamma:\Gamma$
,
$\Delta\vdash_{\mathsf{CaTT}}\gamma:\Gamma$
,
 $\Gamma,x:A\vdash_{\mathsf{CaTT}}$
and
$\Gamma,x:A\vdash_{\mathsf{CaTT}}$
and
 $\Delta\vdash_{\mathsf{CaTT}}t:A[\gamma]$
. By induction those provide derivations of
$\Delta\vdash_{\mathsf{CaTT}}t:A[\gamma]$
. By induction those provide derivations of
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{\gamma}:\big\downarrow{\Gamma}$
,
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{\gamma}:\big\downarrow{\Gamma}$
,
 $\big\downarrow{\Gamma},x:\big\downarrow{A} \vdash_{\mathsf{MCaTT}}$
and
$\big\downarrow{\Gamma},x:\big\downarrow{A} \vdash_{\mathsf{MCaTT}}$
and
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{t} : \big\downarrow{(A[\gamma])}$
. Moreover, by Lemma 12, the last judgment rewrites as
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}} \big\downarrow{t} : \big\downarrow{(A[\gamma])}$
. Moreover, by Lemma 12, the last judgment rewrites as
 $\big\downarrow{\Delta} \vdash \big\downarrow{t}: \big\downarrow{A}[\big\downarrow{\gamma}]$
. Hence, the rule es provides a derivation of the judgment
$\big\downarrow{\Delta} \vdash \big\downarrow{t}: \big\downarrow{A}[\big\downarrow{\gamma}]$
. Hence, the rule es provides a derivation of the judgment
 $\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}\langle{\big\downarrow{\gamma}, x\mapsto \big\downarrow{t}}\rangle : (\big\downarrow{\Gamma},x:\big\downarrow{A})$
.
$\big\downarrow{\Delta}\vdash_{\mathsf{MCaTT}}\langle{\big\downarrow{\gamma}, x\mapsto \big\downarrow{t}}\rangle : (\big\downarrow{\Gamma},x:\big\downarrow{A})$
.
Categorical reformulation. We reformulate Lemma 12 and Proposition 13 in a categorical fashion, taking advantage of the formalism of categories with families.
Corollary 14. The desuspension defines a morphism of categories with families
![]() $\big\downarrow{}:\operatorname{\mathcal{S}}_{\mathsf{CaTT}} \to \operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
.
$\big\downarrow{}:\operatorname{\mathcal{S}}_{\mathsf{CaTT}} \to \operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
.
Proof. We have proved in Proposition 13 that the desuspension sends contexts (resp. substitutions) in
![]() $\mathsf{CaTT}$
onto contexts (resp. substitutions) in
$\mathsf{CaTT}$
onto contexts (resp. substitutions) in
![]() $\mathsf{MCaTT}$
, and Lemma 12 shows that it respects composition. Hence, to prove that it is a functor, it suffices to show that it preserves identity, which we do by induction.
$\mathsf{MCaTT}$
, and Lemma 12 shows that it respects composition. Hence, to prove that it is a functor, it suffices to show that it preserves identity, which we do by induction.
-
For the empty context
 $\varnothing$
, the identity is the empty substitution
$\varnothing$
, the identity is the empty substitution
 $\operatorname{id}_{\varnothing} = \langle{}\rangle$
, and we have
$\operatorname{id}_{\varnothing} = \langle{}\rangle$
, and we have
 $\big\downarrow{\langle{}\rangle} = \langle{}\rangle$
.
$\big\downarrow{\langle{}\rangle} = \langle{}\rangle$
. -
For the context
 $(\Gamma,x:A)$
, the identity is
$(\Gamma,x:A)$
, the identity is
 $\langle{\operatorname{id}_{\Gamma},x\mapsto x}\rangle$
, whose image is
$\langle{\operatorname{id}_{\Gamma},x\mapsto x}\rangle$
, whose image is
 $\langle{\big\downarrow{\operatorname{id}_{\Gamma}},x\mapsto x}\rangle$
. By induction, we have
$\langle{\big\downarrow{\operatorname{id}_{\Gamma}},x\mapsto x}\rangle$
. By induction, we have
 $\big\downarrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
, which gives the equality
$\big\downarrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
, which gives the equality
 $\big\downarrow{\operatorname{id}_{(\Gamma,x:A)}} = \operatorname{id}_{\big\downarrow{(\Gamma,x:A)}}$
.
$\big\downarrow{\operatorname{id}_{(\Gamma,x:A)}} = \operatorname{id}_{\big\downarrow{(\Gamma,x:A)}}$
.
We now show that this functor is a morphism of categories with families, be defining the image of a type
![]() $\Gamma\vdash A$
to be
$\Gamma\vdash A$
to be
![]() $\big\downarrow{A}$
and the image of a term
$\big\downarrow{A}$
and the image of a term
![]() $\Gamma\vdash t:A$
to be
$\Gamma\vdash t:A$
to be
![]() $\big\downarrow{t} $
. Proposition 13 shows that these elements live in the adequate set, and Lemma 12 moreover ensures that this association is functorial, so
$\big\downarrow{t} $
. Proposition 13 shows that these elements live in the adequate set, and Lemma 12 moreover ensures that this association is functorial, so
![]() $\big\downarrow{}$
defines a morphism in the slice category
$\big\downarrow{}$
defines a morphism in the slice category
![]() $\operatorname{Cat}/\operatorname{Fam}$
. Since moreover the operation
$\operatorname{Cat}/\operatorname{Fam}$
. Since moreover the operation
![]() $\big\downarrow{}$
is defined to preserve the terminal context and the context comprehension (by definition, we have
$\big\downarrow{}$
is defined to preserve the terminal context and the context comprehension (by definition, we have
![]() $\big\downarrow{\varnothing} = \varnothing$
and
$\big\downarrow{\varnothing} = \varnothing$
and
![]() $\big\downarrow{(\Gamma,x:A)} = (\big\downarrow{\Gamma},x:\big\downarrow{A})$
and
$\big\downarrow{(\Gamma,x:A)} = (\big\downarrow{\Gamma},x:\big\downarrow{A})$
and
![]() $\big\downarrow{\langle{\gamma,x\mapsto t}\rangle} = \langle{\big\downarrow{\gamma},x\mapsto \big\downarrow{t}}\rangle$
), it is a morphism of categories with families.
$\big\downarrow{\langle{\gamma,x\mapsto t}\rangle} = \langle{\big\downarrow{\gamma},x\mapsto \big\downarrow{t}}\rangle$
), it is a morphism of categories with families.
4.2 The reduced suspension functor
We define another translation going in the opposite direction called the reduced suspension. It is an operation associating an expression of the theory
![]() $\mathsf{CaTT}$
to every expression of the theory
$\mathsf{CaTT}$
to every expression of the theory
![]() $\mathsf{MCaTT}$
. This operation is not however purely syntactic, and even though it outputs a raw expression of
$\mathsf{MCaTT}$
. This operation is not however purely syntactic, and even though it outputs a raw expression of
![]() $\mathsf{CaTT}$
, it is only properly defined on the derivable expression of
$\mathsf{CaTT}$
, it is only properly defined on the derivable expression of
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.
The reduced suspension operation. In order to define the reduced suspension, we assume the existence of a variable name that is completely fresh and call it
![]() $\bullet_{}$
. This could be achieved by extending the set of variables that we use with the variable
$\bullet_{}$
. This could be achieved by extending the set of variables that we use with the variable
![]() $\bullet_{}$
.
$\bullet_{}$
.

In the case of a variable
![]() $\Gamma\vdash x:A$
, we have to assume that A ≠ 1 to ensure that the term is in normal form so that definitional equality is respected.
$\Gamma\vdash x:A$
, we have to assume that A ≠ 1 to ensure that the term is in normal form so that definitional equality is respected.
Remark 15. We do not define the reduced suspension as a function on the raw syntax of
![]() $\mathsf{MCaTT}$
because we rely on the normal form in the theory
$\mathsf{MCaTT}$
because we rely on the normal form in the theory
![]() $\mathsf{MCaTT}$
, which is not defined on the raw syntax. To define the reduced suspension of a variable term x, we need to know whether
$\mathsf{MCaTT}$
, which is not defined on the raw syntax. To define the reduced suspension of a variable term x, we need to know whether
![]() $\Gamma\vdash x:{1}$
is derivable, in which case the term is sent onto
$\Gamma\vdash x:{1}$
is derivable, in which case the term is sent onto
![]() $\bullet$
.
$\bullet$
.
Syntactic properties of the reduced suspension. We show a few technical results, that are useful to prove that the reduced suspension preserves the judgments.
Lemma 16. For all substitution
![]() $\Delta\vdash_{\mathsf{MCaTT}}\gamma:\Gamma$
, we have
$\Delta\vdash_{\mathsf{MCaTT}}\gamma:\Gamma$
, we have
![]() $\bullet {}[\big\uparrow{\gamma}] = \bullet {}$
.
$\bullet {}[\big\uparrow{\gamma}] = \bullet {}$
.
Proof. By definition of
![]() $\big\uparrow{\gamma}$
, the only mapping
$\big\uparrow{\gamma}$
, the only mapping
![]() $\bullet_{}\mapsto t$
in
$\bullet_{}\mapsto t$
in
![]() $\big\uparrow{\gamma}$
is
$\big\uparrow{\gamma}$
is
![]() $\bullet {}\mapsto\bullet {}$
.
$\bullet {}\mapsto\bullet {}$
.
Lemma 17. Given a substitution
![]() $\Delta\vdash_{\mathsf{MCaTT}}\gamma:\Gamma$
, the following hold
$\Delta\vdash_{\mathsf{MCaTT}}\gamma:\Gamma$
, the following hold
-
for any type
 $\Gamma\vdash_{\mathsf{MCaTT}} A$
we have the equality
$\Gamma\vdash_{\mathsf{MCaTT}} A$
we have the equality
 $\big\uparrow{(A[\gamma])}=\big\uparrow{A}[\big\uparrow{\gamma}]$
$\big\uparrow{(A[\gamma])}=\big\uparrow{A}[\big\uparrow{\gamma}]$
-
for any term
 $\Gamma\vdash_{\mathsf{MCaTT}} t:A$
, we have the equality
$\Gamma\vdash_{\mathsf{MCaTT}} t:A$
, we have the equality
 $\big\uparrow{(t[\gamma])} = \big\uparrow{t}[\big\uparrow{\gamma}]$
$\big\uparrow{(t[\gamma])} = \big\uparrow{t}[\big\uparrow{\gamma}]$
-
for any substitution
 $\Gamma\vdash_{\mathsf{MCaTT}}\delta:\Delta$
, we have the equality
$\Gamma\vdash_{\mathsf{MCaTT}}\delta:\Delta$
, we have the equality
 $\big\uparrow{\delta\circ \gamma} = \big\uparrow{\delta}\circ\big\uparrow{\gamma}$
.
$\big\uparrow{\delta\circ \gamma} = \big\uparrow{\delta}\circ\big\uparrow{\gamma}$
.
Proof. We suppose given the substitution
![]() $\gamma$
and prove these three results by mutual induction
$\gamma$
and prove these three results by mutual induction
Induction for types:
-
For the type 1, we have
 ${1}[\gamma] = {1}$
, hence
${1}[\gamma] = {1}$
, hence
 $\big\uparrow{\left({{1}[\gamma]}\right)} = \big\uparrow{1} = \star$
. But we also have
$\big\uparrow{\left({{1}[\gamma]}\right)} = \big\uparrow{1} = \star$
. But we also have
 $\big\uparrow{1}[\big\uparrow{\gamma}] = \star[\big\uparrow{\gamma}]=\star$
.
$\big\uparrow{1}[\big\uparrow{\gamma}] = \star[\big\uparrow{\gamma}]=\star$
. -
For the type
 ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the two following equalities and by induction, we have
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the two following equalities and by induction, we have \begin{align*} \big\uparrow{(({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\gamma])} &= {\big\uparrow{(t[\gamma])}}\underset{\big\uparrow{(A[\gamma])}}{\xrightarrow{\phantom{\big\uparrow{(A[\gamma])}}}}{\big\uparrow{(u[\gamma])}} & (\big\uparrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})})[\big\uparrow{\gamma}] &={(\big\uparrow{t})[\big\uparrow{\gamma}]}\underset{(\big\uparrow{A})[\big\uparrow{\gamma}]}{\xrightarrow{\phantom{(\big\uparrow{A})[\big\uparrow{\gamma}]}}}{(\big\uparrow{u})[\big\uparrow{\gamma}]} \end{align*}
\begin{align*} \big\uparrow{(({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\gamma])} &= {\big\uparrow{(t[\gamma])}}\underset{\big\uparrow{(A[\gamma])}}{\xrightarrow{\phantom{\big\uparrow{(A[\gamma])}}}}{\big\uparrow{(u[\gamma])}} & (\big\uparrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})})[\big\uparrow{\gamma}] &={(\big\uparrow{t})[\big\uparrow{\gamma}]}\underset{(\big\uparrow{A})[\big\uparrow{\gamma}]}{\xrightarrow{\phantom{(\big\uparrow{A})[\big\uparrow{\gamma}]}}}{(\big\uparrow{u})[\big\uparrow{\gamma}]} \end{align*}
 $\big\uparrow{(A[\gamma])} = (\big\uparrow{A})[\big\uparrow{\gamma}]$
,
$\big\uparrow{(A[\gamma])} = (\big\uparrow{A})[\big\uparrow{\gamma}]$
,
 $\big\uparrow{(t[\gamma])} = (\big\uparrow{t})[\big\uparrow{\gamma}]$
and
$\big\uparrow{(t[\gamma])} = (\big\uparrow{t})[\big\uparrow{\gamma}]$
and
 $\big\uparrow{(u[\gamma])} = (\big\uparrow{u})[\big\uparrow{\gamma}]$
.
$\big\uparrow{(u[\gamma])} = (\big\uparrow{u})[\big\uparrow{\gamma}]$
.
Induction for terms:
-
For the term
 $\texttt{()}$
, we have
$\texttt{()}$
, we have
 $\big\uparrow{\left({\texttt{()}[\gamma]}\right)} = \bullet_{}$
. and also
$\big\uparrow{\left({\texttt{()}[\gamma]}\right)} = \bullet_{}$
. and also
 $\big\uparrow{\texttt{()}}[\big\uparrow{\gamma}] = \bullet_{}[\big\uparrow{\gamma}]$
. Lemma 16 shows
$\big\uparrow{\texttt{()}}[\big\uparrow{\gamma}] = \bullet_{}[\big\uparrow{\gamma}]$
. Lemma 16 shows
 $\big\uparrow{\texttt{()}}[\big\uparrow{\gamma}] = \bullet_{}$
.
$\big\uparrow{\texttt{()}}[\big\uparrow{\gamma}] = \bullet_{}$
. -
For the term
 $\Gamma\vdash x:A$
(
$\Gamma\vdash x:A$
(
 $\neq {1}$
), by definition,
$\neq {1}$
), by definition,
 $\big\uparrow{\gamma}$
defines the mapping
$\big\uparrow{\gamma}$
defines the mapping
 $x\mapsto \big\uparrow{(x[\gamma])}$
, so
$x\mapsto \big\uparrow{(x[\gamma])}$
, so
 $x[\big\uparrow{\gamma}] = \big\uparrow{(x[\gamma])}$
.
$x[\big\uparrow{\gamma}] = \big\uparrow{(x[\gamma])}$
. -
For a term of the form
 $\mathsf{mop}_{\Gamma,A}[\delta]$
, we have the following equalities By induction and associativity of composition, these two terms are equal.
$\mathsf{mop}_{\Gamma,A}[\delta]$
, we have the following equalities By induction and associativity of composition, these two terms are equal. \begin{align*} \big\uparrow{(\mathsf{mconstr}_{\Gamma,A}[\delta][\gamma])} &= \mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{(\delta\circ\gamma)}}] \\ (\big\uparrow{\mathsf{mconstr}_{\Gamma,A}[\delta]})[\big\uparrow{\gamma}] &= \mathsf{constr}_{\Gamma,A}[(\bullet_{\Gamma\circ\big\uparrow{\delta})\circ\big\uparrow{\gamma}}] \end{align*}
\begin{align*} \big\uparrow{(\mathsf{mconstr}_{\Gamma,A}[\delta][\gamma])} &= \mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{(\delta\circ\gamma)}}] \\ (\big\uparrow{\mathsf{mconstr}_{\Gamma,A}[\delta]})[\big\uparrow{\gamma}] &= \mathsf{constr}_{\Gamma,A}[(\bullet_{\Gamma\circ\big\uparrow{\delta})\circ\big\uparrow{\gamma}}] \end{align*}
Induction for substitutions:
-
For the substitution
 $\langle{}\rangle$
, we have
$\langle{}\rangle$
, we have
 $\big\uparrow{(\langle{}\rangle\circ\gamma)} = \langle{\bullet {}\mapsto\bullet {}}\rangle$
and
$\big\uparrow{(\langle{}\rangle\circ\gamma)} = \langle{\bullet {}\mapsto\bullet {}}\rangle$
and
 $\big\uparrow{\langle{}\rangle}\circ\big\uparrow{\gamma} = \langle{\bullet {}\mapsto\bullet {}[\big\uparrow{\gamma}]}\rangle$
. Lemma 16 this shows that
$\big\uparrow{\langle{}\rangle}\circ\big\uparrow{\gamma} = \langle{\bullet {}\mapsto\bullet {}[\big\uparrow{\gamma}]}\rangle$
. Lemma 16 this shows that
 $\big\uparrow{\langle{}\rangle}\circ\big\uparrow{\gamma} = \langle{\bullet {}\mapsto\bullet {}}\rangle$
.
$\big\uparrow{\langle{}\rangle}\circ\big\uparrow{\gamma} = \langle{\bullet {}\mapsto\bullet {}}\rangle$
. -
For the substitution
 $\Gamma\vdash\langle{\theta,x\mapsto t}\rangle:(\Theta,x:{1})$
, we have the following equalities and we conclude by the induction case for substitutions.
$\Gamma\vdash\langle{\theta,x\mapsto t}\rangle:(\Theta,x:{1})$
, we have the following equalities and we conclude by the induction case for substitutions. \begin{align*} \big\uparrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\uparrow{(\theta\circ\gamma)}}\rangle & \big\uparrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\uparrow{\gamma} &= \langle{\big\uparrow{\theta}\circ\big\uparrow{\gamma}}\rangle \end{align*}
\begin{align*} \big\uparrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\uparrow{(\theta\circ\gamma)}}\rangle & \big\uparrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\uparrow{\gamma} &= \langle{\big\uparrow{\theta}\circ\big\uparrow{\gamma}}\rangle \end{align*}
-
For a substitution of the form
 $\Gamma\vdash\langle{\theta,x\mapsto t}\rangle:(\Theta,x:A)$
with
$\Gamma\vdash\langle{\theta,x\mapsto t}\rangle:(\Theta,x:A)$
with
 $$A \ne 1$$
, we have the equalities and by conclude by the induction cases for substitutions and terms.
$$A \ne 1$$
, we have the equalities and by conclude by the induction cases for substitutions and terms. \begin{align*} \big\uparrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\uparrow{(\theta\circ\gamma)},x\mapsto\big\uparrow{(t[\gamma])}}\rangle &\big\uparrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\uparrow{\gamma} &= \langle{\big\uparrow{\theta}\circ\big\uparrow{\gamma},x\mapsto(\big\uparrow{t})[\big\uparrow{\gamma}]}\rangle \end{align*}
\begin{align*} \big\uparrow{(\langle{\theta,x\mapsto t}\rangle\circ\gamma)} &= \langle{\big\uparrow{(\theta\circ\gamma)},x\mapsto\big\uparrow{(t[\gamma])}}\rangle &\big\uparrow{\langle{\theta,x\mapsto t}\rangle}\circ\big\uparrow{\gamma} &= \langle{\big\uparrow{\theta}\circ\big\uparrow{\gamma},x\mapsto(\big\uparrow{t})[\big\uparrow{\gamma}]}\rangle \end{align*}
Reduced suspension on the theory
![]() $\mathfrak{G}$
. Note that the theory
$\mathfrak{G}$
. Note that the theory
![]() $\mathfrak{G}$
can be included in the theory
$\mathfrak{G}$
can be included in the theory
![]() $\mathsf{MCaTT}$
, by sending any expression in the theory
$\mathsf{MCaTT}$
, by sending any expression in the theory
![]() $\mathfrak{G}$
to the same expression, seen as an expression of
$\mathfrak{G}$
to the same expression, seen as an expression of
![]() $\mathsf{MCaTT}$
. The only difference is that the type
$\mathsf{MCaTT}$
. The only difference is that the type
![]() $\star$
is primitive in
$\star$
is primitive in
![]() $\mathfrak{G}$
while it is interpreted as
$\mathfrak{G}$
while it is interpreted as
![]() ${\texttt{()}}\to{\texttt{()}}$
in
${\texttt{()}}\to{\texttt{()}}$
in
![]() $\mathsf{MCaTT}$
. We first focus on the restriction of the reduced suspension to the theory
$\mathsf{MCaTT}$
. We first focus on the restriction of the reduced suspension to the theory
![]() $\mathfrak{G}$
. Since the reduced suspension sends variables on variables, it preserves the expressions of
$\mathfrak{G}$
. Since the reduced suspension sends variables on variables, it preserves the expressions of
![]() $\mathfrak{G}$
. We show that this transformation respects the derivation. This is a technical intermediate for generalizing the reduced suspension as a transformation from
$\mathfrak{G}$
. We show that this transformation respects the derivation. This is a technical intermediate for generalizing the reduced suspension as a transformation from
![]() $\mathsf{MCaTT}$
to
$\mathsf{MCaTT}$
to
![]() $\mathsf{CaTT}$
.
$\mathsf{CaTT}$
.
Lemma 18. In the theory
![]() $\mathfrak{G}$
, the following rules are admissible
$\mathfrak{G}$
, the following rules are admissible

Proof. We prove this result by mutual induction on contexts, types, terms, and substitutions Induction for contexts:
-
For the empty context
 $\varnothing$
, we have
$\varnothing$
, we have
 $\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and we can construct a derivation of
$\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and we can construct a derivation of
 $\big\uparrow{\varnothing}\vdash$
by applying successively the rules ec,
$\big\uparrow{\varnothing}\vdash$
by applying successively the rules ec,
 $\star$
-intro and ce.
$\star$
-intro and ce. -
For the context
 $(\Gamma,x:A)\vdash$
(
$(\Gamma,x:A)\vdash$
(
 $$A \ne 1$$
since we are in the theory
$$A \ne 1$$
since we are in the theory
 $\mathfrak{G}$
), we have
$\mathfrak{G}$
), we have
 $\Gamma\vdash A$
. By induction this gives a derivation for
$\Gamma\vdash A$
. By induction this gives a derivation for
 $\big\uparrow{\Gamma}\vdash \big\uparrow{A}$
. The rule ce provides a derivation for
$\big\uparrow{\Gamma}\vdash \big\uparrow{A}$
. The rule ce provides a derivation for
 $(\big\uparrow{\Gamma},x:\big\uparrow{A})\vdash$
$(\big\uparrow{\Gamma},x:\big\uparrow{A})\vdash$
Induction for types:
-
For the type
 $\Gamma\vdash \star$
, we have a derivation of
$\Gamma\vdash \star$
, we have a derivation of
 $\Gamma\vdash$
. By the induction, this shows
$\Gamma\vdash$
. By the induction, this shows
 $\big\uparrow{\Gamma}\vdash$
. Since
$\big\uparrow{\Gamma}\vdash$
. Since
 $(\bullet {}:\star)\in\big\uparrow{\Gamma}$
, we can construct a derivation of
$(\bullet {}:\star)\in\big\uparrow{\Gamma}$
, we can construct a derivation of
 $\big\uparrow{\Gamma}\vdash\big\uparrow{\star}$
as follows
$\big\uparrow{\Gamma}\vdash\big\uparrow{\star}$
as follows

-
For the type
 $\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have derivations of
$\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have derivations of
 $\Gamma\vdash A$
,
$\Gamma\vdash A$
,
 $\Gamma\vdash t:A$
and
$\Gamma\vdash t:A$
and
 $\Gamma\vdash u:A$
. By induction, those give derivations of
$\Gamma\vdash u:A$
. By induction, those give derivations of
 $\big\uparrow{\Gamma}\vdash\big\uparrow{A}$
,
$\big\uparrow{\Gamma}\vdash\big\uparrow{A}$
,
 $\big\uparrow{\Gamma}\vdash \big\uparrow{t} : \big\uparrow{A}$
and
$\big\uparrow{\Gamma}\vdash \big\uparrow{t} : \big\uparrow{A}$
and
 $\big\uparrow{\Gamma}\vdash \big\uparrow{u} : \big\uparrow{A}$
. The rule
$\big\uparrow{\Gamma}\vdash \big\uparrow{u} : \big\uparrow{A}$
. The rule
 $\to$
-intro then provides a derivation of
$\to$
-intro then provides a derivation of
 $\big\uparrow{\Gamma}\vdash {\big\uparrow{t}}\underset{\big\uparrow{A}}{\xrightarrow{\phantom{\big\uparrow{A}}}}{\big\uparrow{u}}$
.
$\big\uparrow{\Gamma}\vdash {\big\uparrow{t}}\underset{\big\uparrow{A}}{\xrightarrow{\phantom{\big\uparrow{A}}}}{\big\uparrow{u}}$
.
Induction for terms: A term in
![]() $\mathfrak{G}$
is a variable
$\mathfrak{G}$
is a variable
![]() $\Gamma\vdash x:A$
. For such a variable, we have a derivation of
$\Gamma\vdash x:A$
. For such a variable, we have a derivation of
![]() $\Gamma\vdash$
, and by induction it gives a derivation of
$\Gamma\vdash$
, and by induction it gives a derivation of
![]() $\big\uparrow{\Gamma}\vdash$
. Moreover, the condition
$\big\uparrow{\Gamma}\vdash$
. Moreover, the condition
![]() $(x:A)\in\Gamma$
is satisfied, and since we are the in the theory
$(x:A)\in\Gamma$
is satisfied, and since we are the in the theory
![]() $\mathfrak{G}$
,
$\mathfrak{G}$
,
![]() $A \neq {1}$
. So we have
$A \neq {1}$
. So we have
![]() $(x:\big\uparrow{A})\in\big\uparrow{\Gamma}$
. The rule var then yields a derivation of
$(x:\big\uparrow{A})\in\big\uparrow{\Gamma}$
. The rule var then yields a derivation of
![]() $\big\uparrow{\Gamma}\vdash x:\big\uparrow{A}$
.
$\big\uparrow{\Gamma}\vdash x:\big\uparrow{A}$
.
Induction for substitutions:
-
For the substitution
 $\Delta\vdash\langle{}\rangle:\varnothing$
, we have a derivation of
$\Delta\vdash\langle{}\rangle:\varnothing$
, we have a derivation of
 $\Delta\vdash$
. By induction, this gives a derivation of
$\Delta\vdash$
. By induction, this gives a derivation of
 $\big\uparrow{\Delta}\vdash$
. Moreover, we also have by definition that
$\big\uparrow{\Delta}\vdash$
. Moreover, we also have by definition that
 $(\bullet {}:\star)\in\big\uparrow{\Delta}$
, and we have already constructed a derivation of
$(\bullet {}:\star)\in\big\uparrow{\Delta}$
, and we have already constructed a derivation of
 $(\bullet_{}:\star)\vdash$
. This lets us construct a derivation for
$(\bullet_{}:\star)\vdash$
. This lets us construct a derivation for
 $\big\uparrow{\Delta} \vdash \big\uparrow{\langle{}\rangle}:\big\uparrow{\varnothing}$
as follows
$\big\uparrow{\Delta} \vdash \big\uparrow{\langle{}\rangle}:\big\uparrow{\varnothing}$
as follows

-
For the substitution
 $\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have
$\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have
 $$A \ne 1$$
since we are in
$$A \ne 1$$
since we are in
 $\mathfrak{G}$
. Then we necessarily have derivations of
$\mathfrak{G}$
. Then we necessarily have derivations of
 $\Delta\vdash \gamma:\Gamma$
,
$\Delta\vdash \gamma:\Gamma$
,
 $(\Gamma,x:A)\vdash$
and
$(\Gamma,x:A)\vdash$
and
 $\Delta\vdash t:A[\gamma]$
. By induction, those give derivations of the judgments
$\Delta\vdash t:A[\gamma]$
. By induction, those give derivations of the judgments
 $\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
,
$\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
,
 $\big\uparrow{\Gamma},x:\big\uparrow{A}\vdash$
and
$\big\uparrow{\Gamma},x:\big\uparrow{A}\vdash$
and
 $\big\uparrow{\Delta}\vdash \big\uparrow{t}: \big\uparrow{A[\gamma]}$
. Lemma 17 allows to rewrite the last of these judgments as
$\big\uparrow{\Delta}\vdash \big\uparrow{t}: \big\uparrow{A[\gamma]}$
. Lemma 17 allows to rewrite the last of these judgments as
 $\big\uparrow{\Delta}\vdash \big\uparrow{t}:\big\uparrow{A}[\big\uparrow{\gamma}]$
. The rule se then provides a derivation of
$\big\uparrow{\Delta}\vdash \big\uparrow{t}:\big\uparrow{A}[\big\uparrow{\gamma}]$
. The rule se then provides a derivation of
 $\big\uparrow{\Delta}\vdash\big\uparrow{\langle{\gamma,x\mapsto t}\rangle}:\big\uparrow{(\Gamma,x:A)}$
.
$\big\uparrow{\Delta}\vdash\big\uparrow{\langle{\gamma,x\mapsto t}\rangle}:\big\uparrow{(\Gamma,x:A)}$
.
Properties of the substitution
![]() $\bullet_{\Delta}$
. The definition of the reduced suspension relies on the substitution
$\bullet_{\Delta}$
. The definition of the reduced suspension relies on the substitution
![]() $\bullet_{\Delta}$
. We prove syntactic properties about this substitution.
$\bullet_{\Delta}$
. We prove syntactic properties about this substitution.
Lemma 19. We have the following result for the action of the substitution
![]() $\bullet_{\Delta}$
on terms, types and substitutions.
$\bullet_{\Delta}$
on terms, types and substitutions.
-
For any type
 $\Delta\vdash_{\mathsf{CaTT}} A$
, we have
$\Delta\vdash_{\mathsf{CaTT}} A$
, we have
 $A[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{A}}$
$A[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{A}}$
-
For any term
 $\Delta\vdash_{\mathsf{CaTT}} t:A$
, we have
$\Delta\vdash_{\mathsf{CaTT}} t:A$
, we have
 $t[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{t}}$
.
$t[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{t}}$
. -
For any substitution
 $\Delta\vdash_{\mathsf{CaTT}} \gamma:\Gamma$
, we have
$\Delta\vdash_{\mathsf{CaTT}} \gamma:\Gamma$
, we have
 $\gamma\circ\bullet_{\Delta} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
.
$\gamma\circ\bullet_{\Delta} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
.
Proof. We prove these equalities by mutual induction
Induction on types:
-
For the type
 $\Delta\vdash_{\mathsf{CaTT}}\star$
, we have
$\Delta\vdash_{\mathsf{CaTT}}\star$
, we have
 $\big\uparrow{\big\downarrow{\star}} = \star$
and by definition,
$\big\uparrow{\big\downarrow{\star}} = \star$
and by definition,
 $\star[\bullet_{\Delta}] = \star$
.
$\star[\bullet_{\Delta}] = \star$
. -
For the type
 $\Delta\vdash_{\mathsf{CaTT}}{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the equalities and by induction
$\Delta\vdash_{\mathsf{CaTT}}{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have the equalities and by induction \begin{align*} ({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\bullet_\Delta] &= {t[\bullet_\Delta]}\underset{A[\bullet_\Delta]}{\xrightarrow{\phantom{A[\bullet_\Delta]}}} {u[\bullet_\Delta]} & \big\uparrow{\big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})}} &= {\big\uparrow{\big\downarrow{t}}}\underset{\big\uparrow{\big\downarrow{A}}}{\xrightarrow{\phantom{\big\uparrow{\big\downarrow{A}}}}} {\big\uparrow{\big\downarrow{u} }} \end{align*}
\begin{align*} ({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})[\bullet_\Delta] &= {t[\bullet_\Delta]}\underset{A[\bullet_\Delta]}{\xrightarrow{\phantom{A[\bullet_\Delta]}}} {u[\bullet_\Delta]} & \big\uparrow{\big\downarrow{({t}\underset{A}{\xrightarrow{\phantom{A}}}{u})}} &= {\big\uparrow{\big\downarrow{t}}}\underset{\big\uparrow{\big\downarrow{A}}}{\xrightarrow{\phantom{\big\uparrow{\big\downarrow{A}}}}} {\big\uparrow{\big\downarrow{u} }} \end{align*}
 $A[\bullet_\Delta] = \big\uparrow{\big\downarrow{A}}$
,
$A[\bullet_\Delta] = \big\uparrow{\big\downarrow{A}}$
,
 $t[\bullet_\Delta]=\big\uparrow{\big\downarrow{t}}$
and
$t[\bullet_\Delta]=\big\uparrow{\big\downarrow{t}}$
and
 $u[\bullet_\Delta] = \big\uparrow{\big\downarrow{u}}$
.
$u[\bullet_\Delta] = \big\uparrow{\big\downarrow{u}}$
.
Induction on terms:
-
For a variable
 $\Delta\vdash x:A$
, by definition the mapping
$\Delta\vdash x:A$
, by definition the mapping
 $x\mapsto \big\uparrow{\big\downarrow{x}}$
is the only mapping for x in
$x\mapsto \big\uparrow{\big\downarrow{x}}$
is the only mapping for x in
 $\bullet_{\Delta}$
, hence
$\bullet_{\Delta}$
, hence
 $x[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{x}}$
.
$x[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{x}}$
. -
For a term of the form
 $\Delta\vdash\mathsf{constr}_{\Gamma,A}[\gamma]:A[\gamma]$
, we have the following equations and the induction case for substitutions then gives the equality.
$\Delta\vdash\mathsf{constr}_{\Gamma,A}[\gamma]:A[\gamma]$
, we have the following equations and the induction case for substitutions then gives the equality. \begin{align*} \mathsf{constr}_{\Gamma,A}[\gamma][\bullet_{\Delta}] &= \mathsf{constr}_{\Gamma,A}[\gamma\circ\bullet_{\Delta}] & \big\uparrow{\big\downarrow{\mathsf{constr}}_{\Gamma,A}[\gamma]} &= \mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}] \end{align*}
\begin{align*} \mathsf{constr}_{\Gamma,A}[\gamma][\bullet_{\Delta}] &= \mathsf{constr}_{\Gamma,A}[\gamma\circ\bullet_{\Delta}] & \big\uparrow{\big\downarrow{\mathsf{constr}}_{\Gamma,A}[\gamma]} &= \mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}] \end{align*}
Induction case for substitutions:
-
For the empty substitution
 $\Delta\vdash\langle{}\rangle:\varnothing$
, since
$\Delta\vdash\langle{}\rangle:\varnothing$
, since
 $\bullet_{\varnothing} = \langle{}\rangle$
, we have the equalities
$\bullet_{\varnothing} = \langle{}\rangle$
, we have the equalities  \begin{align*} \langle{}\rangle\circ\bullet_{\Delta} &= \langle{}\rangle & \bullet_{\varnothing\circ \big\uparrow{\big\downarrow{\langle{}\rangle}}} &= \langle{}\rangle \end{align*}
\begin{align*} \langle{}\rangle\circ\bullet_{\Delta} &= \langle{}\rangle & \bullet_{\varnothing\circ \big\uparrow{\big\downarrow{\langle{}\rangle}}} &= \langle{}\rangle \end{align*}
-
For of the substitution
 $\Delta\vdash\langle{\gamma,x\mapsto t}\rangle : (\Gamma,x:A)$
, since the substitution
$\Delta\vdash\langle{\gamma,x\mapsto t}\rangle : (\Gamma,x:A)$
, since the substitution
 $\bullet_{\Gamma}$
has source
$\bullet_{\Gamma}$
has source
 $\big\uparrow{\big\downarrow{\Gamma}}$
that do not use the variable x, we have
$\big\uparrow{\big\downarrow{\Gamma}}$
that do not use the variable x, we have
 $\bullet_{\Gamma\circ\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t}}}\rangle} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
. Moreover, if x is of type
$\bullet_{\Gamma\circ\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t}}}\rangle} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
. Moreover, if x is of type
 $\star$
we have
$\star$
we have
 $\big\uparrow{\big\downarrow{x}}[\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t} }}\rangle] = \bullet_{} = \big\uparrow{\big\downarrow{t}}$
, and if x is not of type
$\big\uparrow{\big\downarrow{x}}[\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t} }}\rangle] = \bullet_{} = \big\uparrow{\big\downarrow{t}}$
, and if x is not of type
 $\star$
, the expression
$\star$
, the expression
 $x[\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t} }}\rangle]=\big\uparrow{\big\downarrow{t}}$
. Using the two previously shown equalities to simplify the expressions yields By induction we have
$x[\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto\big\uparrow{\big\downarrow{t} }}\rangle]=\big\uparrow{\big\downarrow{t}}$
. Using the two previously shown equalities to simplify the expressions yields By induction we have \begin{align*} \langle{\gamma,x\mapsto t}\rangle\circ\bullet_{\Delta} &= \langle{\gamma\circ\bullet_{\Delta},x\mapsto t[\bullet_{\Delta}]}\rangle& \bullet_{(\Gamma,x:A)}\circ\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto \big\uparrow{\big\downarrow{t}}}\rangle &= \langle{\bullet_{\Gamma\circ \big\uparrow{\big\downarrow{\gamma}},x\mapsto \big\uparrow{\big\downarrow{t}}}}\rangle \end{align*}
\begin{align*} \langle{\gamma,x\mapsto t}\rangle\circ\bullet_{\Delta} &= \langle{\gamma\circ\bullet_{\Delta},x\mapsto t[\bullet_{\Delta}]}\rangle& \bullet_{(\Gamma,x:A)}\circ\langle{\big\uparrow{\big\downarrow{\gamma}},x\mapsto \big\uparrow{\big\downarrow{t}}}\rangle &= \langle{\bullet_{\Gamma\circ \big\uparrow{\big\downarrow{\gamma}},x\mapsto \big\uparrow{\big\downarrow{t}}}}\rangle \end{align*}
 $\gamma\circ\bullet_{\Delta} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
and
$\gamma\circ\bullet_{\Delta} = \bullet_{\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}}$
and
 $t[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{t}}$
$t[\bullet_{\Delta}] = \big\uparrow{\big\downarrow{t}}$
Lemma 20. The following rule is admissible

Proof. This result is proved by induction on the context
![]() $\Gamma$
.
$\Gamma$
.
-
For the context
 $\varnothing$
, we have already proven that
$\varnothing$
, we have already proven that
 $\big\uparrow{\big\downarrow{\varnothing}}\vdash$
. The rule es proves that
$\big\uparrow{\big\downarrow{\varnothing}}\vdash$
. The rule es proves that
 $\big\uparrow{\big\downarrow{\varnothing}}\vdash \langle{}\rangle:\varnothing$
.
$\big\uparrow{\big\downarrow{\varnothing}}\vdash \langle{}\rangle:\varnothing$
. -
For the context
 $(\Gamma,x:A)\vdash$
, we have by induction
$(\Gamma,x:A)\vdash$
, we have by induction
 $\big\uparrow{\big\downarrow{\Gamma}}\vdash \bullet_{\Gamma} : \Gamma$
. By Proposition 1, this gives a derivation of
$\big\uparrow{\big\downarrow{\Gamma}}\vdash \bullet_{\Gamma} : \Gamma$
. By Proposition 1, this gives a derivation of
 $\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash \bullet_{\Gamma:\Gamma}$
. Moreover, by Lemma 18, we have that
$\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash \bullet_{\Gamma:\Gamma}$
. Moreover, by Lemma 18, we have that
 $\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash x:\big\uparrow{\big\downarrow{A}}$
, and Lemma 19 then shows that we have
$\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash x:\big\uparrow{\big\downarrow{A}}$
, and Lemma 19 then shows that we have
 $\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash x:A[\bullet_\Gamma]$
. The rule se then gives a derivation of
$\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash x:A[\bullet_\Gamma]$
. The rule se then gives a derivation of
 $\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash\bullet_{(\Gamma,x:A)}:(\Gamma,x:A)$
.
$\big\uparrow{\big\downarrow{(\Gamma,x:A)}}\vdash\bullet_{(\Gamma,x:A)}:(\Gamma,x:A)$
.
Correctness of the reduced suspension. We are now equipped to generalize the reduced suspension as an operation from the theory
![]() $\mathsf{MCaTT}$
to the theory
$\mathsf{MCaTT}$
to the theory
![]() $\mathsf{CaTT}$
. We prove the following correctness result showing that this operation is a well-defined translation between these two theories.
$\mathsf{CaTT}$
. We prove the following correctness result showing that this operation is a well-defined translation between these two theories.
Proposition 21. The reduced suspension operation preserves derivability, the following rules are admissible

Proof. The proof of this result is essentially the same as the proof of Lemma 18, but still needs some adaptations. For the sake of completeness and to avoid the reader to constantly refer to the previous proof, we give the complete proof here. We perform mutual induction on the derivation trees and keep all the cases in normal form.
Induction for contexts:
-
For the empty context
 $\varnothing$
, we have
$\varnothing$
, we have
 $\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and we can construct a derivation of
$\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and we can construct a derivation of
 $\big\uparrow{\varnothing}\vdash$
by applying successively the rules ec,
$\big\uparrow{\varnothing}\vdash$
by applying successively the rules ec,
 $\star$
-intro and ce.
$\star$
-intro and ce. -
For the context
 $(\Gamma,x:{1})\vdash$
, we have
$(\Gamma,x:{1})\vdash$
, we have
 $\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
and by induction
$\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
and by induction
 $\big\uparrow{\Gamma}\vdash$
.
$\big\uparrow{\Gamma}\vdash$
. -
For the context
 $(\Gamma,x:A)\vdash$
with
$(\Gamma,x:A)\vdash$
with
 $$A \ne 1$$
, we have
$$A \ne 1$$
, we have
 $\Gamma\vdash A$
. By induction this gives a derivation for
$\Gamma\vdash A$
. By induction this gives a derivation for
 $\big\uparrow{\Gamma}\vdash \big\uparrow{A}$
. The rule ce, provides a derivation for
$\big\uparrow{\Gamma}\vdash \big\uparrow{A}$
. The rule ce, provides a derivation for
 $(\big\uparrow{\Gamma},x:\big\uparrow{A})\vdash$
$(\big\uparrow{\Gamma},x:\big\uparrow{A})\vdash$
Induction for types:
-
For the type
 $\Gamma\vdash{1}$
, we have a derivation of
$\Gamma\vdash{1}$
, we have a derivation of
 $\Gamma\vdash$
. By induction, we have a derivation of
$\Gamma\vdash$
. By induction, we have a derivation of
 $\big\uparrow{\Gamma}\vdash$
. The rule
$\big\uparrow{\Gamma}\vdash$
. The rule
 $\star$
-intro then applies to provide a derivation of
$\star$
-intro then applies to provide a derivation of
 $\big\uparrow{\Gamma}\vdash\star$
.
$\big\uparrow{\Gamma}\vdash\star$
. -
For the type
 $\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have derivations of
$\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
, we have derivations of
 $\Gamma\vdash A$
,
$\Gamma\vdash A$
,
 $\Gamma\vdash t:A$
and
$\Gamma\vdash t:A$
and
 $\Gamma\vdash u:A$
. By induction, those give derivations of
$\Gamma\vdash u:A$
. By induction, those give derivations of
 $\big\uparrow{\Gamma}\vdash\big\uparrow{A}$
,
$\big\uparrow{\Gamma}\vdash\big\uparrow{A}$
,
 $\big\uparrow{\Gamma}\vdash \big\uparrow{t} : \big\uparrow{A}$
and
$\big\uparrow{\Gamma}\vdash \big\uparrow{t} : \big\uparrow{A}$
and
 $\big\uparrow{\Gamma}\vdash \big\uparrow{u} : \big\uparrow{A}$
. The rule
$\big\uparrow{\Gamma}\vdash \big\uparrow{u} : \big\uparrow{A}$
. The rule
 $\to$
-intro then provides a derivation of
$\to$
-intro then provides a derivation of
 $\big\uparrow{\Gamma}\vdash{\big\uparrow{t}}\underset{\big\uparrow{A}}{\xrightarrow{\phantom{\big\uparrow{A}}}}{\big\uparrow{u}}$
.
$\big\uparrow{\Gamma}\vdash{\big\uparrow{t}}\underset{\big\uparrow{A}}{\xrightarrow{\phantom{\big\uparrow{A}}}}{\big\uparrow{u}}$
.
Induction for terms:
-
For the term
 $\Gamma\vdash \texttt{()}:{1}$
, we have
$\Gamma\vdash \texttt{()}:{1}$
, we have
 $\big\uparrow{\texttt{()}} = \bullet_{}$
. By induction, we have
$\big\uparrow{\texttt{()}} = \bullet_{}$
. By induction, we have
 $\big\uparrow{\Gamma}\vdash$
. Since moreover
$\big\uparrow{\Gamma}\vdash$
. Since moreover
 $(\bullet_{}:\star)\in\big\uparrow{\Gamma}$
, the rule var gives a derivation of
$(\bullet_{}:\star)\in\big\uparrow{\Gamma}$
, the rule var gives a derivation of
 $\big\uparrow{\Gamma}\vdash \bullet_{} : \star$
.
$\big\uparrow{\Gamma}\vdash \bullet_{} : \star$
. -
For a variable
 $\Gamma\vdash x:A$
, since we consider normal forms,
$\Gamma\vdash x:A$
, since we consider normal forms,
 $$A \ne 1$$
. We have a derivation of
$$A \ne 1$$
. We have a derivation of
 $\Gamma\vdash$
, and by induction it gives a derivation of
$\Gamma\vdash$
, and by induction it gives a derivation of
 $\big\uparrow{\Gamma}\vdash$
. Moreover, the condition
$\big\uparrow{\Gamma}\vdash$
. Moreover, the condition
 $(x:A)\in\Gamma$
is satisfied, hence so is
$(x:A)\in\Gamma$
is satisfied, hence so is
 $(x:\big\uparrow{A})\in\big\uparrow{\Gamma}$
. The rule var then yields a derivation of
$(x:\big\uparrow{A})\in\big\uparrow{\Gamma}$
. The rule var then yields a derivation of
 $\big\uparrow{\Gamma}\vdash x:\big\uparrow{A}$
.
$\big\uparrow{\Gamma}\vdash x:\big\uparrow{A}$
. -
For a term of the form
 $\mathsf{mconstr}_{\Gamma,A}[\gamma]$
, we have a derivation of
$\mathsf{mconstr}_{\Gamma,A}[\gamma]$
, we have a derivation of
 $\Delta\vdash \gamma:\big\downarrow{\Gamma}$
. By induction, this gives a derivation for
$\Delta\vdash \gamma:\big\downarrow{\Gamma}$
. By induction, this gives a derivation for
 $\big\uparrow{\Delta}\vdash \big\uparrow{\gamma}:\big\uparrow{\big\downarrow{\Gamma}}$
. Moreover, Lemma 20 ensures that we have
$\big\uparrow{\Delta}\vdash \big\uparrow{\gamma}:\big\uparrow{\big\downarrow{\Gamma}}$
. Moreover, Lemma 20 ensures that we have
 $\big\uparrow{\big\downarrow{\Gamma}}\vdash \bullet_{\Gamma : \Gamma}$
, hence we have a substitution
$\big\uparrow{\big\downarrow{\Gamma}}\vdash \bullet_{\Gamma : \Gamma}$
, hence we have a substitution
 $\big\uparrow{\Delta}\vdash \bullet_{\Gamma\circ\big\uparrow{\gamma} : \Gamma}$
. By applying the rule
$\big\uparrow{\Delta}\vdash \bullet_{\Gamma\circ\big\uparrow{\gamma} : \Gamma}$
. By applying the rule
 $\mathsf{op}$
-intro or
$\mathsf{op}$
-intro or
 $\mathsf{coh}$
-intro, this provides a derivation for the judgment
$\mathsf{coh}$
-intro, this provides a derivation for the judgment
 $\big\uparrow{\Delta}\vdash\mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\gamma}}] : A[\bullet_{\Gamma\circ\big\uparrow{\gamma}}]$
. The following equalities then prove that the type is the one we expect
$\big\uparrow{\Delta}\vdash\mathsf{constr}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\gamma}}] : A[\bullet_{\Gamma\circ\big\uparrow{\gamma}}]$
. The following equalities then prove that the type is the one we expect  \begin{align*} A[\bullet_{\Gamma\circ \big\uparrow{\gamma}}] &= \big\uparrow{\big\downarrow{A}}[\big\uparrow{\gamma}] & \text{By Lemma 19} \\ &= \big\uparrow{((\big\downarrow{A})[\gamma])} & \text{By Lemma 17} \end{align*}
\begin{align*} A[\bullet_{\Gamma\circ \big\uparrow{\gamma}}] &= \big\uparrow{\big\downarrow{A}}[\big\uparrow{\gamma}] & \text{By Lemma 19} \\ &= \big\uparrow{((\big\downarrow{A})[\gamma])} & \text{By Lemma 17} \end{align*}
Induction for substitutions:
-
For the substitution
 $\Delta\vdash\langle{}\rangle:\varnothing$
, we have a derivation of
$\Delta\vdash\langle{}\rangle:\varnothing$
, we have a derivation of
 $\Delta\vdash$
. By induction, this gives a derivation of
$\Delta\vdash$
. By induction, this gives a derivation of
 $\big\uparrow{\Delta}\vdash$
. Moreover, we also have by definition that
$\big\uparrow{\Delta}\vdash$
. Moreover, we also have by definition that
 $(\bullet {}:\star)\in\big\uparrow{\Delta}$
, and we have already constructed a derivation of
$(\bullet {}:\star)\in\big\uparrow{\Delta}$
, and we have already constructed a derivation of
 $(\bullet_{}:\star)\vdash$
. This lets us construct a derivation for
$(\bullet_{}:\star)\vdash$
. This lets us construct a derivation for
 $\big\uparrow{\Delta} \vdash \big\uparrow{\langle{}\rangle}:\big\uparrow{\varnothing}$
as follows
$\big\uparrow{\Delta} \vdash \big\uparrow{\langle{}\rangle}:\big\uparrow{\varnothing}$
as follows

-
For the substitution
 $\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:{1})$
, we have the equalities Since we have
$\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:{1})$
, we have the equalities Since we have \begin{align*} \big\uparrow{(\Gamma,x:{1})} &= \big\uparrow{\Gamma} & \big\uparrow{\langle{\gamma,x\mapsto t}\rangle} &= \big\uparrow{\gamma} \end{align*}
\begin{align*} \big\uparrow{(\Gamma,x:{1})} &= \big\uparrow{\Gamma} & \big\uparrow{\langle{\gamma,x\mapsto t}\rangle} &= \big\uparrow{\gamma} \end{align*}
 $\Delta\vdash \gamma:\Gamma$
, by induction we deduce
$\Delta\vdash \gamma:\Gamma$
, by induction we deduce
 $\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
.
$\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
.
-
For the substitution
 $\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have
$\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
, we have
 $$A \ne 1$$
since we are in
$$A \ne 1$$
since we are in
 $\mathfrak{G}$
. Then we necessarily have derivations of
$\mathfrak{G}$
. Then we necessarily have derivations of
 $\Delta\vdash \gamma:\Gamma$
,
$\Delta\vdash \gamma:\Gamma$
,
 $(\Gamma,x:A)\vdash$
and
$(\Gamma,x:A)\vdash$
and
 $\Delta\vdash t:A[\gamma]$
. By induction, those give derivations of the judgments
$\Delta\vdash t:A[\gamma]$
. By induction, those give derivations of the judgments
 $\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
,
$\big\uparrow{\Delta}\vdash\big\uparrow{\gamma}:\big\uparrow{\Gamma}$
,
 $\big\uparrow{\Gamma},x:\big\uparrow{A}\vdash$
and
$\big\uparrow{\Gamma},x:\big\uparrow{A}\vdash$
and
 $\big\uparrow{\Delta}\vdash \big\uparrow{t}: \big\uparrow{A[\gamma]}$
. Lemma allows to rewrite the last of these judgments as
$\big\uparrow{\Delta}\vdash \big\uparrow{t}: \big\uparrow{A[\gamma]}$
. Lemma allows to rewrite the last of these judgments as
 $\big\uparrow{\Delta}\vdash \big\uparrow{t}:\big\uparrow{A}[\big\uparrow{\gamma}]$
. The rule se then provides a derivation of
$\big\uparrow{\Delta}\vdash \big\uparrow{t}:\big\uparrow{A}[\big\uparrow{\gamma}]$
. The rule se then provides a derivation of
 $\big\uparrow{\Delta}\vdash\big\uparrow{\langle{\gamma,x\mapsto t}\rangle}:\big\uparrow{(\Gamma,x:A)}$
.
$\big\uparrow{\Delta}\vdash\big\uparrow{\langle{\gamma,x\mapsto t}\rangle}:\big\uparrow{(\Gamma,x:A)}$
.
Examples. We give a few examples of contexts in
![]() $\mathsf{MCaTT}$
along with their translations in
$\mathsf{MCaTT}$
along with their translations in
![]() $\mathsf{CaTT}$
to build intuition on this translation:
$\mathsf{CaTT}$
to build intuition on this translation:
 \begin{align*} \Gamma &= (x:\star) & \big\uparrow{\Gamma} &= (\bullet_{}:\star, x:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}} {\bullet_{}})\\ \Gamma &= (x:\star,f:{x}\underset{\star}{\xrightarrow{\phantom{\star}}}{x}, a:{1}) & \big\uparrow{\Gamma} &= (\bullet_{}:\star,x:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},f:{x}\underset{{\bullet_{}} \to {\bullet_{}}}{\xrightarrow{\phantom{{\bullet_{}} \to {\bullet_{}}}}}{x})\\ \Gamma &= (x:\star,y:\star;f:{x}\underset{\star}{\xrightarrow{\phantom{\star}}}{y}) & \big\uparrow{\Gamma} &= (\bullet_{}:\star,x: {\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},y:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},f: {x}\underset{{\bullet_{}} \to {\bullet_{}}}{\xrightarrow{\phantom{{\bullet_{}}\to{\bullet_{}}}}}{y})\end{align*}
\begin{align*} \Gamma &= (x:\star) & \big\uparrow{\Gamma} &= (\bullet_{}:\star, x:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}} {\bullet_{}})\\ \Gamma &= (x:\star,f:{x}\underset{\star}{\xrightarrow{\phantom{\star}}}{x}, a:{1}) & \big\uparrow{\Gamma} &= (\bullet_{}:\star,x:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},f:{x}\underset{{\bullet_{}} \to {\bullet_{}}}{\xrightarrow{\phantom{{\bullet_{}} \to {\bullet_{}}}}}{x})\\ \Gamma &= (x:\star,y:\star;f:{x}\underset{\star}{\xrightarrow{\phantom{\star}}}{y}) & \big\uparrow{\Gamma} &= (\bullet_{}:\star,x: {\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},y:{\bullet_{}}\underset{\star}{\xrightarrow{\phantom{\star}}}{\bullet_{}},f: {x}\underset{{\bullet_{}} \to {\bullet_{}}}{\xrightarrow{\phantom{{\bullet_{}}\to{\bullet_{}}}}}{y})\end{align*}
These examples help understand why it is important to require that the translation is defined on normal forms. Indeed, in the second example, we have a derivation
![]() $\Gamma\vdash a:{1}$
but the term is not in normal form. Putting it in normal form before applying the reduced suspension yields to the term
$\Gamma\vdash a:{1}$
but the term is not in normal form. Putting it in normal form before applying the reduced suspension yields to the term
![]() $\Gamma\vdash\bullet_{}:{1}$
which is indeed derivable. However, had we simply defined the reduced suspension of any variable to be itself, without consideration of whether it is in normal form, we would have gotten the judgment
$\Gamma\vdash\bullet_{}:{1}$
which is indeed derivable. However, had we simply defined the reduced suspension of any variable to be itself, without consideration of whether it is in normal form, we would have gotten the judgment
![]() $\big\uparrow{\Gamma}\vdash a:\star$
which is not derivable.
$\big\uparrow{\Gamma}\vdash a:\star$
which is not derivable.
Reduced suspension as a functor. Like for the desuspension, we can reformulate this result in a more categorical flavor. However the result that we prove here is weaker.
Corollary 22. The reduced suspension operation defines a functor
![]() $\big\uparrow{} : \operatorname{\mathcal{S}}_{\mathsf{MCaTT}} \to \operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
.
$\big\uparrow{} : \operatorname{\mathcal{S}}_{\mathsf{MCaTT}} \to \operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
.
Proof. We have proved in Lemma 17 and Proposition 13 that this operation is well defined, and that it preserves the composition of substitutions, so it suffices to prove that it preserves the identity. We proceed by induction on the length of the context
-
For the empty context
 $\varnothing$
, we have
$\varnothing$
, we have
 $\operatorname{id}_{\varnothing} = \langle{}\rangle$
along with
$\operatorname{id}_{\varnothing} = \langle{}\rangle$
along with
 $\big\uparrow{\varnothing} = (\bullet_{}:\star)$
and
$\big\uparrow{\varnothing} = (\bullet_{}:\star)$
and
 $\big\uparrow{\langle{}\rangle}=\langle{\bullet_{}\mapsto \bullet_{}}\rangle$
, which is the identity of
$\big\uparrow{\langle{}\rangle}=\langle{\bullet_{}\mapsto \bullet_{}}\rangle$
, which is the identity of
 $\big\uparrow{\varnothing}$
.
$\big\uparrow{\varnothing}$
. -
For a context of the form
 $(\Gamma, x:{1})$
, we have
$(\Gamma, x:{1})$
, we have
 $\operatorname{id}_{(\Gamma,x:{1})} = \langle{\operatorname{id}_{\Gamma},\bullet_{}\mapsto\bullet_{}}\rangle$
. Hence
$\operatorname{id}_{(\Gamma,x:{1})} = \langle{\operatorname{id}_{\Gamma},\bullet_{}\mapsto\bullet_{}}\rangle$
. Hence
 $\big\uparrow{\operatorname{id}_{(\Gamma,x:{1})}} = \big\uparrow{\operatorname{id}_{\Gamma}}$
, and by induction
$\big\uparrow{\operatorname{id}_{(\Gamma,x:{1})}} = \big\uparrow{\operatorname{id}_{\Gamma}}$
, and by induction
 $\big\uparrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}}$
. We conclude using the fact that
$\big\uparrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}}$
. We conclude using the fact that
 $\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
.
$\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
. -
For a context of the form
 $(\Gamma,x:A)$
with
$(\Gamma,x:A)$
with
 $$A \ne 1$$
, we have
$$A \ne 1$$
, we have
 $\big\uparrow{\operatorname{id}_{(\Gamma,x:A)}} = \langle{\big\uparrow{\operatorname{id}_{\Gamma}},x\mapsto x}\rangle$
, and by induction, we have
$\big\uparrow{\operatorname{id}_{(\Gamma,x:A)}} = \langle{\big\uparrow{\operatorname{id}_{\Gamma}},x\mapsto x}\rangle$
, and by induction, we have
 $\big\uparrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}}$
, which lets us conclude that
$\big\uparrow{\operatorname{id}_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}}$
, which lets us conclude that
 $\big\uparrow{\operatorname{id}_{(\Gamma,x:A)}} = \operatorname{id}_{\big\uparrow{(\Gamma,x:A)}}$
.
$\big\uparrow{\operatorname{id}_{(\Gamma,x:A)}} = \operatorname{id}_{\big\uparrow{(\Gamma,x:A)}}$
.
Note that in fact Lemma 17 and Proposition 13 provide more structure than this. They show that this functor is almost a morphism of category with families. In fact it defines a morphism in
![]() $\operatorname{Cat}/\operatorname{Fam}$
, which respects the structures of categories with families of
$\operatorname{Cat}/\operatorname{Fam}$
, which respects the structures of categories with families of
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
and
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
and
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
. This functor however fails to be a morphism of categories with families as it does not preserve the terminal object, since the context
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
. This functor however fails to be a morphism of categories with families as it does not preserve the terminal object, since the context
![]() $\varnothing$
is sent onto
$\varnothing$
is sent onto
![]() $(\bullet_{}:\star)$
which is not terminal. This result however is complicated to formulate cleanly in a categorical way.
$(\bullet_{}:\star)$
which is not terminal. This result however is complicated to formulate cleanly in a categorical way.
4.3 Interaction between desuspension and reduced suspension
We have defined the theory
![]() $\mathsf{MCaTT}$
together with two translations, the desuspension and the reduced suspension, that define functors between their syntactic categories. We now study how these translations relate to each other syntactically and translate this result categorically as a relation between the two functors. In order to understand the interaction between the desuspension and the reduced suspension, we first show the following result, analogous to Lemma 8 for the theory
$\mathsf{MCaTT}$
together with two translations, the desuspension and the reduced suspension, that define functors between their syntactic categories. We now study how these translations relate to each other syntactically and translate this result categorically as a relation between the two functors. In order to understand the interaction between the desuspension and the reduced suspension, we first show the following result, analogous to Lemma 8 for the theory
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.
Lemma 23. The context
![]() $(x:{1})$
is terminal in the category
$(x:{1})$
is terminal in the category
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
, and more generally the family of substitutions
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
, and more generally the family of substitutions
![]() $\Gamma\vdash \langle{\operatorname{id}_{\Gamma},x\mapsto ()}\rangle : (\Gamma,x:{1})$
defines a natural isomorphism.
$\Gamma\vdash \langle{\operatorname{id}_{\Gamma},x\mapsto ()}\rangle : (\Gamma,x:{1})$
defines a natural isomorphism.
Proof. The proof of the initiality of the context
![]() $(x:{1})$
is the exact same that the one of Lemma 8. The generalization of this statement is obtained by noticing that we have the following pullback square
$(x:{1})$
is the exact same that the one of Lemma 8. The generalization of this statement is obtained by noticing that we have the following pullback square

Since the map
![]() $(x : {1}) \to \varnothing$
is an isomorphism whose inverse is given by the substitution
$(x : {1}) \to \varnothing$
is an isomorphism whose inverse is given by the substitution
![]() $\varnothing \vdash \langle{x\mapsto ()}\rangle : (x:{1})$
in this pullback implies that the left most vertical arrow is an isomorphism. Moreover, the structure of category with families implies that the inverse of this map is given by the substitution
$\varnothing \vdash \langle{x\mapsto ()}\rangle : (x:{1})$
in this pullback implies that the left most vertical arrow is an isomorphism. Moreover, the structure of category with families implies that the inverse of this map is given by the substitution
![]() $\langle{\operatorname{id}_{\Gamma},x\mapsto ()}\rangle$
. The family of morphisms defined this way is natural since the substitution is functorial, as it is defined by a universal property.
$\langle{\operatorname{id}_{\Gamma},x\mapsto ()}\rangle$
. The family of morphisms defined this way is natural since the substitution is functorial, as it is defined by a universal property.
Desuspension of the reduced suspension. We can now express one of the relations that link the desuspension and the reduced suspension. We first express these relations on the type theory before leveraging the expressive power of the categorical semantics to provide a much more compact reformulation.
Proposition 24. There exists a natural transformation
![]() $\eta : \operatorname{id}_{\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}} \to \big\downarrow{}\circ\big\uparrow{}$
which is natural isomorphism.
$\eta : \operatorname{id}_{\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}} \to \big\downarrow{}\circ\big\uparrow{}$
which is natural isomorphism.
Proof. We define a family of maps
![]() $\eta_\Gamma : \Gamma \to \big\downarrow{\big\uparrow{\Gamma}}$
for every context
$\eta_\Gamma : \Gamma \to \big\downarrow{\big\uparrow{\Gamma}}$
for every context
![]() $\Gamma$
of the theory
$\Gamma$
of the theory
![]() $\mathsf{MCaTT}$
, and show that these maps are isomorphisms and that they are natural in
$\mathsf{MCaTT}$
, and show that these maps are isomorphisms and that they are natural in
![]() $\Gamma$
. We proceed by mutual induction on the theory
$\Gamma$
. We proceed by mutual induction on the theory
![]() $\mathsf{MCaTT}$
and prove
$\mathsf{MCaTT}$
and prove
-
For all context
 $\Gamma\vdash$
, there is an isomorphism
$\Gamma\vdash$
, there is an isomorphism
 $\eta_\Gamma : \Gamma \to \big\downarrow{\big\uparrow{\Gamma}}$
.
$\eta_\Gamma : \Gamma \to \big\downarrow{\big\uparrow{\Gamma}}$
. -
For all type
 $\Gamma\vdash A$
, we have the equality
$\Gamma\vdash A$
, we have the equality
 $\Gamma\vdash A \equiv \big\downarrow{\big\uparrow{\Gamma}}[\eta_\Gamma]$
.
$\Gamma\vdash A \equiv \big\downarrow{\big\uparrow{\Gamma}}[\eta_\Gamma]$
. -
For all term
 $\Gamma\vdash t:A$
, we have
$\Gamma\vdash t:A$
, we have
 $\Gamma\vdash t \equiv \big\downarrow{\big\uparrow{t}}[\eta_\Gamma]:A$
.
$\Gamma\vdash t \equiv \big\downarrow{\big\uparrow{t}}[\eta_\Gamma]:A$
. -
For all substitution
 $\Delta\vdash \gamma:\Gamma$
, the following square commutes
$\Delta\vdash \gamma:\Gamma$
, the following square commutes

-
(auxiliary induction case) for all context
 $\Gamma$
in the theory
$\Gamma$
in the theory
 $\mathsf{CaTT}$
, we have
$\mathsf{CaTT}$
, we have
 $\big\downarrow{\bullet_{\Gamma}}\circ\eta_{\big\downarrow{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
.
$\big\downarrow{\bullet_{\Gamma}}\circ\eta_{\big\downarrow{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
.
Induction for contexts:
-
For the empty context
 $\varnothing\vdash$
, we have
$\varnothing\vdash$
, we have
 $\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and thus
$\big\uparrow{\varnothing} = (\bullet {}:\star)$
, and thus
 $\big\downarrow{\big\uparrow{\varnothing}} = (\bullet_{}:{1})$
. Lemma 23 then provides the desired isomorphism
$\big\downarrow{\big\uparrow{\varnothing}} = (\bullet_{}:{1})$
. Lemma 23 then provides the desired isomorphism
 $\eta_\varnothing=\langle{\bullet_{}\mapsto ()}\rangle : \varnothing \to \big\downarrow{\big\uparrow{\varnothing}}$
.
$\eta_\varnothing=\langle{\bullet_{}\mapsto ()}\rangle : \varnothing \to \big\downarrow{\big\uparrow{\varnothing}}$
. -
For a context of the form
 $(\Gamma,x:{1})\vdash$
, we have
$(\Gamma,x:{1})\vdash$
, we have
 $\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
, hence
$\big\uparrow{(\Gamma,x:{1})} = \big\uparrow{\Gamma}$
, hence
 $\big\downarrow{\big\uparrow{(\Gamma,x:{1})}} = \big\downarrow{\big\uparrow{\Gamma}}$
. By Lemma 23, the following weakening is an isomorphism
$\big\downarrow{\big\uparrow{(\Gamma,x:{1})}} = \big\downarrow{\big\uparrow{\Gamma}}$
. By Lemma 23, the following weakening is an isomorphism
 $\pi : (\Gamma,x:{1})\overset{\sim}\to \Gamma$
, and the induction hypothesis on contexts provides the isomorphism
$\pi : (\Gamma,x:{1})\overset{\sim}\to \Gamma$
, and the induction hypothesis on contexts provides the isomorphism
 $\eta_\Gamma : \Gamma \overset{\sim}\to \big\downarrow{\big\uparrow{\gamma}}$
. By composition, this provides the isomoprhism following (writing the weakening implicitly)
$\eta_\Gamma : \Gamma \overset{\sim}\to \big\downarrow{\big\uparrow{\gamma}}$
. By composition, this provides the isomoprhism following (writing the weakening implicitly)
 $\eta_{(\Gamma,x:{1})} = \eta_\Gamma : (\Gamma,x:{1}) \to \big\downarrow{\big\uparrow{(\Gamma,x:{1})}}$
.
$\eta_{(\Gamma,x:{1})} = \eta_\Gamma : (\Gamma,x:{1}) \to \big\downarrow{\big\uparrow{(\Gamma,x:{1})}}$
. -
For a context of the form
 $(\Gamma,x:A)\vdash$
with
$(\Gamma,x:A)\vdash$
with
 $$A \ne 1$$
, we have
$$A \ne 1$$
, we have
 $\big\uparrow{(\Gamma,x:A)} = (\big\uparrow{\Gamma},x:\big\uparrow{A})$
. Since
$\big\uparrow{(\Gamma,x:A)} = (\big\uparrow{\Gamma},x:\big\uparrow{A})$
. Since
 $\big\uparrow{A}$
is necessarily distinct from
$\big\uparrow{A}$
is necessarily distinct from
 $\star$
, we have
$\star$
, we have
 $\big\downarrow{\big\uparrow{(\Gamma,x:A)}} = (\big\downarrow{\big\uparrow {\Gamma}},x:\big\downarrow{\big\uparrow{A}})$
, and the induction case for contexts provides the isomoprhism
$\big\downarrow{\big\uparrow{(\Gamma,x:A)}} = (\big\downarrow{\big\uparrow {\Gamma}},x:\big\downarrow{\big\uparrow{A}})$
, and the induction case for contexts provides the isomoprhism
 $\eta_\Gamma : \Gamma\overset{\sim}\to\big\downarrow{\big\uparrow{\Gamma}}$
. Moreover, the induction case for types shows that
$\eta_\Gamma : \Gamma\overset{\sim}\to\big\downarrow{\big\uparrow{\Gamma}}$
. Moreover, the induction case for types shows that
 $\Gamma\vdash A\equiv \big\downarrow{\big\uparrow{A}}[\eta_\Gamma]$
. Hence we define the isomoprhism
$\Gamma\vdash A\equiv \big\downarrow{\big\uparrow{A}}[\eta_\Gamma]$
. Hence we define the isomoprhism
 $\eta_{(\Gamma,x:A)} = \langle{\eta_\Gamma,x\mapsto x}\rangle : (\Gamma,x:A)\overset\sim\to \big\downarrow{\big\uparrow{(\Gamma,x:A)}}$
, whose inverse is given by
$\eta_{(\Gamma,x:A)} = \langle{\eta_\Gamma,x\mapsto x}\rangle : (\Gamma,x:A)\overset\sim\to \big\downarrow{\big\uparrow{(\Gamma,x:A)}}$
, whose inverse is given by
 $\langle{\eta_\Gamma^{-1} , x\mapsto x}\rangle$
.
$\langle{\eta_\Gamma^{-1} , x\mapsto x}\rangle$
.
Induction for types:
-
For the type
 $\Gamma\vdash {1}$
, we have
$\Gamma\vdash {1}$
, we have
 $\big\downarrow{\big\uparrow{1}}[\eta_\Gamma] = {1}[\eta_\Gamma]$
. Since we have also by definition
$\big\downarrow{\big\uparrow{1}}[\eta_\Gamma] = {1}[\eta_\Gamma]$
. Since we have also by definition
 ${1}[\eta_\Gamma] = {1}$
, this shows that
${1}[\eta_\Gamma] = {1}$
, this shows that
 ${1} = \big\downarrow{\big\uparrow{1}}[\eta_\Gamma]$
.
${1} = \big\downarrow{\big\uparrow{1}}[\eta_\Gamma]$
. -
For the type
 $\star ={()}\underset{1}{\xrightarrow{\phantom{1}}}{()}$
, we have
$\star ={()}\underset{1}{\xrightarrow{\phantom{1}}}{()}$
, we have
 $\big\downarrow{\big\uparrow{\star}}[\eta_\Gamma] = {\bullet_{}[\eta_\Gamma]}\underset{1}{\xrightarrow{\phantom{1}}}{\bullet_{}[\eta_\Gamma]}$
. Note that by Proposition 21 along with the induction case for contexts, we have a derivation of
$\big\downarrow{\big\uparrow{\star}}[\eta_\Gamma] = {\bullet_{}[\eta_\Gamma]}\underset{1}{\xrightarrow{\phantom{1}}}{\bullet_{}[\eta_\Gamma]}$
. Note that by Proposition 21 along with the induction case for contexts, we have a derivation of
 $\Gamma\vdash \bullet_{}[\eta_\Gamma]:{1}$
. Hence, the rule
$\Gamma\vdash \bullet_{}[\eta_\Gamma]:{1}$
. Hence, the rule
 $\eta_{1}$
applies and provides the equality
$\eta_{1}$
applies and provides the equality
 $\Gamma\vdash \star\equiv \big\downarrow{\big\uparrow{\star}}[\eta_\Gamma]$
.
$\Gamma\vdash \star\equiv \big\downarrow{\big\uparrow{\star}}[\eta_\Gamma]$
. -
For a type of the form
 $\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with
$\Gamma\vdash {t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with
 $$A \ne 1$$
,
$$A \ne 1$$
,
 $\big\downarrow{\big\uparrow{{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}}} ={\big\downarrow{\big\uparrow{t}}}\underset{\big\downarrow{\big\uparrow{A}}}{\xrightarrow{\phantom{\big\downarrow{\big\uparrow {A}}}}}{\big\downarrow{\big\uparrow{u}}}$
. The induction case for types then shows that
$\big\downarrow{\big\uparrow{{t}\underset{A}{\xrightarrow{\phantom{A}}}{u}}} ={\big\downarrow{\big\uparrow{t}}}\underset{\big\downarrow{\big\uparrow{A}}}{\xrightarrow{\phantom{\big\downarrow{\big\uparrow {A}}}}}{\big\downarrow{\big\uparrow{u}}}$
. The induction case for types then shows that
 $\Gamma\vdash A\equiv\big\downarrow{\big\uparrow{A}}[\eta_\Gamma]$
, and the induction case for terms shows
$\Gamma\vdash A\equiv\big\downarrow{\big\uparrow{A}}[\eta_\Gamma]$
, and the induction case for terms shows
 $\Gamma\vdash t:A\equiv \big\downarrow{\big\uparrow{t}}[\eta_\Gamma]$
similarly for u, which lets us conclude.
$\Gamma\vdash t:A\equiv \big\downarrow{\big\uparrow{t}}[\eta_\Gamma]$
similarly for u, which lets us conclude.
Induction for terms:
-
For the term
 $\Gamma\vdash ():{1}$
, we have
$\Gamma\vdash ():{1}$
, we have
 $\Gamma\vdash \big\downarrow{\big\uparrow{()}}[\eta_\Gamma] : {1}$
, and the rule
$\Gamma\vdash \big\downarrow{\big\uparrow{()}}[\eta_\Gamma] : {1}$
, and the rule
 $\eta_{1}$
gives the desired definitional equality.
$\eta_{1}$
gives the desired definitional equality. -
For a variable
 $\Gamma\vdash x:A$
, we need to have
$\Gamma\vdash x:A$
, we need to have
 $$A \ne 1$$
for the term to be in normal form, we have
$$A \ne 1$$
for the term to be in normal form, we have
 $\big\uparrow{x} = x$
and thus
$\big\uparrow{x} = x$
and thus
 $\big\downarrow{\big\uparrow{x}} = x$
. Moreover, since the pair
$\big\downarrow{\big\uparrow{x}} = x$
. Moreover, since the pair
 $x:A$
appears in
$x:A$
appears in
 $\Gamma$
with
$\Gamma$
with
 $$A \ne 1$$
, by definition of
$$A \ne 1$$
, by definition of
 $\eta_\Gamma$
(induction case for contexts), the association
$\eta_\Gamma$
(induction case for contexts), the association
 $x\mapsto x$
appears in
$x\mapsto x$
appears in
 $\eta_\Gamma$
, and hence
$\eta_\Gamma$
, and hence
 $\big\downarrow{\big\uparrow{x}}[\eta_\Gamma] = x$
.
$\big\downarrow{\big\uparrow{x}}[\eta_\Gamma] = x$
. -
For a term of the form
 $\mathsf{mop}_{\Gamma,A}[\gamma]$
, we have
$\mathsf{mop}_{\Gamma,A}[\gamma]$
, we have
 $\big\uparrow{\mathsf{mop}_{\Gamma,A}[\gamma]} = \mathsf{op}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\gamma}}]$
, and thus we have the following equalities Note that in the third step, the substitution
$\big\uparrow{\mathsf{mop}_{\Gamma,A}[\gamma]} = \mathsf{op}_{\Gamma,A}[\bullet_{\Gamma\circ\big\uparrow{\gamma}}]$
, and thus we have the following equalities Note that in the third step, the substitution \begin{align*} (\big\downarrow{\big\uparrow{\mathsf{mop}_{\Gamma,A}[\gamma]}})[\eta_\Delta] &= \mathsf{mop}_{\Gamma,A}[\big\downarrow{(\bullet_{\Gamma\circ\big\uparrow{\gamma})}\circ \eta_\Delta}] \\ &= \mathsf{mop}_{\Gamma,A}[\big\downarrow{\bullet_{\Gamma}}\circ(\big\downarrow{\big\uparrow{\gamma}}\circ \eta_\Delta)] & \text{by Lemma} \, 12\\ &\equiv \mathsf{mop}_{\Gamma,A}[(\big\downarrow{\bullet_\Gamma}\circ \eta_{\big\downarrow{\Gamma}}) \circ \gamma] & \text{by the induction case for substitutions} \\ &\equiv \mathsf{mop}_{\Gamma,A}[\gamma] & \text{by the auxiliary induction case}\end{align*}
\begin{align*} (\big\downarrow{\big\uparrow{\mathsf{mop}_{\Gamma,A}[\gamma]}})[\eta_\Delta] &= \mathsf{mop}_{\Gamma,A}[\big\downarrow{(\bullet_{\Gamma\circ\big\uparrow{\gamma})}\circ \eta_\Delta}] \\ &= \mathsf{mop}_{\Gamma,A}[\big\downarrow{\bullet_{\Gamma}}\circ(\big\downarrow{\big\uparrow{\gamma}}\circ \eta_\Delta)] & \text{by Lemma} \, 12\\ &\equiv \mathsf{mop}_{\Gamma,A}[(\big\downarrow{\bullet_\Gamma}\circ \eta_{\big\downarrow{\Gamma}}) \circ \gamma] & \text{by the induction case for substitutions} \\ &\equiv \mathsf{mop}_{\Gamma,A}[\gamma] & \text{by the auxiliary induction case}\end{align*}
 $\eta_{\big\downarrow{\Gamma}}$
appears since we started with a definition
$\eta_{\big\downarrow{\Gamma}}$
appears since we started with a definition
 $\Gamma$
whose target is
$\Gamma$
whose target is
 $\big\downarrow{\Gamma}$
.
$\big\downarrow{\Gamma}$
.
-
The case for a term of the form
 $\mathsf{mcoh}_{\Gamma,A}[\gamma]$
follows the exact same steps.
$\mathsf{mcoh}_{\Gamma,A}[\gamma]$
follows the exact same steps.
Induction for substitutions:
-
For the empty substitution
 $\Delta\vdash \langle{}\rangle:\varnothing$
, by the induction case for contexts, we have the following square of maps
$\Delta\vdash \langle{}\rangle:\varnothing$
, by the induction case for contexts, we have the following square of maps

Since by Lemma 23 both
![]() $\varnothing$
and
$\varnothing$
and
![]() $(x:{1})$
are terminal objects, this square has to commute.
$(x:{1})$
are terminal objects, this square has to commute.
-
For a substitution of the form
 $\Delta\vdash \langle{\Gamma,x\mapsto t}\rangle:(\Gamma,x:{1})$
, after applying the induction case for contexts and computing the expressions, we are left with the following square.
$\Delta\vdash \langle{\Gamma,x\mapsto t}\rangle:(\Gamma,x:{1})$
, after applying the induction case for contexts and computing the expressions, we are left with the following square.

Note that by definition, the map
![]() $\eta_{(\Gamma,x:{1})} = (\Gamma,x:{1}) \to \big\downarrow{\big\uparrow{\Gamma}}$
is the map
$\eta_{(\Gamma,x:{1})} = (\Gamma,x:{1}) \to \big\downarrow{\big\uparrow{\Gamma}}$
is the map
![]() $\eta_\Gamma$
weakened with respect to the variable x, hence we have
$\eta_\Gamma$
weakened with respect to the variable x, hence we have
![]() $\eta_{(\Gamma,x:{1})} \circ \langle{\gamma,x\mapsto t}\rangle = \eta_\Gamma \circ \gamma$
. By the induction case for substitutions, this expression is equal to
$\eta_{(\Gamma,x:{1})} \circ \langle{\gamma,x\mapsto t}\rangle = \eta_\Gamma \circ \gamma$
. By the induction case for substitutions, this expression is equal to
![]() $\big\downarrow{\big\uparrow{\gamma}} \circ\eta_\Delta$
, which exactly provides the commutation of the above square.
$\big\downarrow{\big\uparrow{\gamma}} \circ\eta_\Delta$
, which exactly provides the commutation of the above square.
-
For a substitution of the form
 $\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
with
$\Delta\vdash\langle{\gamma,x\mapsto t}\rangle:(\Gamma,x:A)$
with
 $$A \ne 1$$
, we have the following equalities which give exactly the commutation of desired naturality square.
$$A \ne 1$$
, we have the following equalities which give exactly the commutation of desired naturality square. \begin{align*} \langle{\big\downarrow{\big\uparrow{\gamma}},x\mapsto \big\downarrow{\big\uparrow{t}}}\rangle\circ \eta_\Delta &= \langle{\big\downarrow{\big\uparrow{\gamma}}\circ\eta_\Delta, x\mapsto \big\downarrow{\big\uparrow{t}}[\eta_\Delta]}\rangle\\ &= \langle{\eta_\Gamma\circ \gamma, x\mapsto t}\rangle &\text{By induction on terms and substitutions}\\ &=\langle{\eta_\Gamma,x\mapsto x}\rangle \circ \langle{\gamma,x\mapsto t}\rangle &\text{Since $\eta_\Gamma$ is weakened with respect to} \, x \end{align*}
\begin{align*} \langle{\big\downarrow{\big\uparrow{\gamma}},x\mapsto \big\downarrow{\big\uparrow{t}}}\rangle\circ \eta_\Delta &= \langle{\big\downarrow{\big\uparrow{\gamma}}\circ\eta_\Delta, x\mapsto \big\downarrow{\big\uparrow{t}}[\eta_\Delta]}\rangle\\ &= \langle{\eta_\Gamma\circ \gamma, x\mapsto t}\rangle &\text{By induction on terms and substitutions}\\ &=\langle{\eta_\Gamma,x\mapsto x}\rangle \circ \langle{\gamma,x\mapsto t}\rangle &\text{Since $\eta_\Gamma$ is weakened with respect to} \, x \end{align*}
Auxiliary induction case: We prove by induction on contexts that
![]() $\big\downarrow{\bullet_\Gamma}\circ\eta_{\big\downarrow{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
$\big\downarrow{\bullet_\Gamma}\circ\eta_{\big\downarrow{\Gamma}} = \operatorname{id}_{\big\downarrow{\Gamma}}$
-
For the context
 $\varnothing$
in
$\varnothing$
in
 $\mathsf{CaTT}$
, the map
$\mathsf{CaTT}$
, the map
 $\big\downarrow{\bullet_\varnothing}\circ\eta_{\big\downarrow{\varnothing}}$
defines a map
$\big\downarrow{\bullet_\varnothing}\circ\eta_{\big\downarrow{\varnothing}}$
defines a map
 $\big\downarrow{\varnothing}\to\big\downarrow{\varnothing}$
. By definition,
$\big\downarrow{\varnothing}\to\big\downarrow{\varnothing}$
. By definition,
 $\big\downarrow{\varnothing}$
is the terminal object in the category
$\big\downarrow{\varnothing}$
is the terminal object in the category
 $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
, the aforementioned map is thus necessarily the identity.
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
, the aforementioned map is thus necessarily the identity. -
For the context
 $(\Gamma,x:A)$
in
$(\Gamma,x:A)$
in
 $\mathsf{CaTT}$
, we have the following equalities
$\mathsf{CaTT}$
, we have the following equalities
 \begin{align*} \big\downarrow{\bullet_{(\Gamma,x:A)}}\circ\eta_{\big\downarrow{(\Gamma,x:A)}} &= \langle{\big\downarrow{\bullet_\Gamma},\big\downarrow{\big\uparrow{\big\downarrow{x}}}}\rangle \circ \eta_{\big\downarrow{\Gamma}} \\ &= \langle{\big\downarrow{\bullet_\Gamma}\circ\eta_\Gamma, \big\downarrow{\big\uparrow{x}}[\eta_{\big\downarrow{\Gamma}}]}\rangle &\text{Since $\big\downarrow{x} = x$}\\ &= \langle{\operatorname{id}_{\Gamma},x\mapsto x}\rangle &\text{By induction on terms} \end{align*}
\begin{align*} \big\downarrow{\bullet_{(\Gamma,x:A)}}\circ\eta_{\big\downarrow{(\Gamma,x:A)}} &= \langle{\big\downarrow{\bullet_\Gamma},\big\downarrow{\big\uparrow{\big\downarrow{x}}}}\rangle \circ \eta_{\big\downarrow{\Gamma}} \\ &= \langle{\big\downarrow{\bullet_\Gamma}\circ\eta_\Gamma, \big\downarrow{\big\uparrow{x}}[\eta_{\big\downarrow{\Gamma}}]}\rangle &\text{Since $\big\downarrow{x} = x$}\\ &= \langle{\operatorname{id}_{\Gamma},x\mapsto x}\rangle &\text{By induction on terms} \end{align*}
A natural transformation. In order to study the reduced suspension, we have introduced the family of substitutions
![]() $\bullet_\Gamma$
for all contexts
$\bullet_\Gamma$
for all contexts
![]() $\Gamma$
, and we have proved in Lemma 20, that it defines a family of morphisms
$\Gamma$
, and we have proved in Lemma 20, that it defines a family of morphisms
![]() $\bullet_\Gamma:\big\uparrow{\big\downarrow{\Gamma}}\to\Gamma$
. Moreover, the equality
$\bullet_\Gamma:\big\uparrow{\big\downarrow{\Gamma}}\to\Gamma$
. Moreover, the equality
![]() $\gamma\circ\bullet_\Delta =\bullet_\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}$
that we proved in Lemma 19 for all substitution
$\gamma\circ\bullet_\Delta =\bullet_\Gamma\circ\big\uparrow{\big\downarrow{\gamma}}$
that we proved in Lemma 19 for all substitution
![]() $\gamma$
can be expressed by the commutation of the following diagram
$\gamma$
can be expressed by the commutation of the following diagram

So we have in fact already proven the following proposition, which is simply a categorical reformulation of our previous fact
Proposition 25. The family of morphisms
![]() $\bullet_{\Gamma} : \big\uparrow{\big\downarrow{\Gamma}}\to \Gamma$
defines a natural transformation
$\bullet_{\Gamma} : \big\uparrow{\big\downarrow{\Gamma}}\to \Gamma$
defines a natural transformation
![]() $\big\uparrow{}\circ\big\downarrow{} \Rightarrow \operatorname{id}_{\operatorname{\mathcal{S}}_\mathsf{CaTT}}$
.
$\big\uparrow{}\circ\big\downarrow{} \Rightarrow \operatorname{id}_{\operatorname{\mathcal{S}}_\mathsf{CaTT}}$
.
Adjunction between desuspension and reduced suspension. Combining Propositions 24 and 25, we have in fact proved the following categorical result about the functors induced by desuspension and the reduced suspension.
Theorem The functor
![]() $\big\uparrow{}$
is left adjoint to
$\big\uparrow{}$
is left adjoint to
![]() $\big\downarrow{}$
, the counit is given by the family
$\big\downarrow{}$
, the counit is given by the family
![]() $\bullet_\Gamma$
and the unit is the natural family of isomorphisms
$\bullet_\Gamma$
and the unit is the natural family of isomorphisms
![]() $\eta_\Gamma$
. This adjunction is thus coreflective.
$\eta_\Gamma$
. This adjunction is thus coreflective.
Proof. We have already proved that these two natural transformations
![]() $\bullet_\Gamma$
and
$\bullet_\Gamma$
and
![]() $\eta_\Gamma$
are well defined, and that
$\eta_\Gamma$
are well defined, and that
![]() $\eta_\Gamma$
is an isomorphism. So it suffices to prove that they satisfy the zigzag identities. In fact we have also already proved one of these, as the auxiliary induction case while proving Proposition 24. So we are left to check the other identity, namely that for all context
$\eta_\Gamma$
is an isomorphism. So it suffices to prove that they satisfy the zigzag identities. In fact we have also already proved one of these, as the auxiliary induction case while proving Proposition 24. So we are left to check the other identity, namely that for all context
![]() $\Gamma$
in the theory
$\Gamma$
in the theory
![]() $\mathsf{MCaTT}$
, we have
$\mathsf{MCaTT}$
, we have
![]() $\bullet_{\big\uparrow{\Gamma}}\circ \big\uparrow{\eta_\Gamma} = \big\uparrow{\Gamma}$
. We prove this statement by induction on contexts.
$\bullet_{\big\uparrow{\Gamma}}\circ \big\uparrow{\eta_\Gamma} = \big\uparrow{\Gamma}$
. We prove this statement by induction on contexts.
-
For the empty context
 $\varnothing$
, since
$\varnothing$
, since
 $\bullet_{}$
is a variable, we have
$\bullet_{}$
is a variable, we have
 $\big\uparrow{\big\downarrow{\bullet_{}}} = \bullet_{}$
, and hence
$\big\uparrow{\big\downarrow{\bullet_{}}} = \bullet_{}$
, and hence  \begin{equation*} \bullet_{\big\uparrow{\varnothing}}\circ\big\uparrow{\eta_\varnothing} = \bullet_{(\bullet_{},\star)}\circ\big\uparrow{\langle{\bullet_{}\mapsto ()}\rangle} = \langle{\bullet_{}\mapsto \big\uparrow{\big\downarrow{\bullet_{}}}}\rangle\circ\langle{\bullet_{}\mapsto\bullet_{}}\rangle = \langle{\bullet_{}\mapsto\bullet_{}}\rangle = \operatorname{id}_{\big\uparrow{\varnothing}} \end{equation*}
\begin{equation*} \bullet_{\big\uparrow{\varnothing}}\circ\big\uparrow{\eta_\varnothing} = \bullet_{(\bullet_{},\star)}\circ\big\uparrow{\langle{\bullet_{}\mapsto ()}\rangle} = \langle{\bullet_{}\mapsto \big\uparrow{\big\downarrow{\bullet_{}}}}\rangle\circ\langle{\bullet_{}\mapsto\bullet_{}}\rangle = \langle{\bullet_{}\mapsto\bullet_{}}\rangle = \operatorname{id}_{\big\uparrow{\varnothing}} \end{equation*}
-
For the context
 $(\Gamma,x:{1})$
, we have by induction
$(\Gamma,x:{1})$
, we have by induction  \begin{equation*} \bullet_{\big\uparrow{\Gamma,x:{1}}}\circ\big\uparrow{\eta_{(\Gamma,x:{1})}} = \bullet_{\big\uparrow{\Gamma}}\circ\big\uparrow{\eta_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma,x:{1}}} \end{equation*}
\begin{equation*} \bullet_{\big\uparrow{\Gamma,x:{1}}}\circ\big\uparrow{\eta_{(\Gamma,x:{1})}} = \bullet_{\big\uparrow{\Gamma}}\circ\big\uparrow{\eta_{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma}} = \operatorname{id}_{\big\uparrow{\Gamma,x:{1}}} \end{equation*}
-
For the context
 $(\Gamma,x:A)$
with
$(\Gamma,x:A)$
with
 $$A \ne 1$$
, we have Using the induction hypothesis, and the fact that since x is a variable, we have
$$A \ne 1$$
, we have Using the induction hypothesis, and the fact that since x is a variable, we have \begin{align*} \bullet_{\big\uparrow{\Gamma,x:A}}\circ\big\uparrow{\eta_{(\Gamma,x:A)}} &= \bullet_{(\big\uparrow{\Gamma},x:\big\uparrow{A})}\circ\langle{\big\uparrow{\eta_{\Gamma}},x\mapsto x}\rangle \\ &=\langle{\bullet_{\big\uparrow{\Gamma}},x\mapsto \big\uparrow{\big\downarrow{x}}}\rangle \circ \langle{\big\uparrow{\eta_{\Gamma}},x\mapsto \big\uparrow{x}}\rangle\\ & = \langle{\bullet_{\big\uparrow{\Gamma}} \circ \big\uparrow{\eta_\Gamma}, x\mapsto \big\uparrow{\big\downarrow{x}} [\langle{\eta_\Gamma,x\mapsto \big\uparrow{x}}\rangle]}\rangle \end{align*}
\begin{align*} \bullet_{\big\uparrow{\Gamma,x:A}}\circ\big\uparrow{\eta_{(\Gamma,x:A)}} &= \bullet_{(\big\uparrow{\Gamma},x:\big\uparrow{A})}\circ\langle{\big\uparrow{\eta_{\Gamma}},x\mapsto x}\rangle \\ &=\langle{\bullet_{\big\uparrow{\Gamma}},x\mapsto \big\uparrow{\big\downarrow{x}}}\rangle \circ \langle{\big\uparrow{\eta_{\Gamma}},x\mapsto \big\uparrow{x}}\rangle\\ & = \langle{\bullet_{\big\uparrow{\Gamma}} \circ \big\uparrow{\eta_\Gamma}, x\mapsto \big\uparrow{\big\downarrow{x}} [\langle{\eta_\Gamma,x\mapsto \big\uparrow{x}}\rangle]}\rangle \end{align*}
 $x = \big\downarrow{x} = \big\uparrow{\big\downarrow{x}}$
, it follows that
$x = \big\downarrow{x} = \big\uparrow{\big\downarrow{x}}$
, it follows that
 $\bullet_{\big\uparrow{(\Gamma,x:A)}}\circ\big\uparrow{\eta_{(\Gamma,x:A)}} = \operatorname{id}_{(\big\uparrow{\Gamma},x:\big\uparrow{A})}$
.
$\bullet_{\big\uparrow{(\Gamma,x:A)}}\circ\big\uparrow{\eta_{(\Gamma,x:A)}} = \operatorname{id}_{(\big\uparrow{\Gamma},x:\big\uparrow{A})}$
.
This adjunction is to be understood as an analogue in the world of categories of the topological adjunction between the reduced suspension and the loop space. In our terminology, the desuspension corresponds to the loop space, and the reduced suspension corresponds to the reduced suspension.
Remark 26. The coreflective adjunction exhibits
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
as isomorphic to a coreflective subcategory of
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
as isomorphic to a coreflective subcategory of
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
. Moreover, the essential image of
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
. Moreover, the essential image of
![]() $\big\uparrow{}$
is exactly the category
$\big\uparrow{}$
is exactly the category
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. So a way to understand our type theory
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
. So a way to understand our type theory
![]() $\mathsf{MCaTT}$
is that it achieves a structure of category with families on a category which is equivalent to
$\mathsf{MCaTT}$
is that it achieves a structure of category with families on a category which is equivalent to
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
, in such a way that that this structure coincide with the structure on
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
, in such a way that that this structure coincide with the structure on
![]() $\mathsf{CaTT}$
under the equivalence between
$\mathsf{CaTT}$
under the equivalence between
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
and
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
and
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
.
$\operatorname{\mathcal{S}}_{\mathsf{CaTT},\bullet}$
.
5. Models of the Type Theory
 $\mathsf{MCaTT}$
$\mathsf{MCaTT}$
Thanks to the desuspension and to the reduced suspension functors that we have defined and establish a strong relation between the models of the theory
![]() $\mathsf{CaTT}$
and those of the theory
$\mathsf{CaTT}$
and those of the theory
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.
5.1 Action of reduced suspension and desuspension on the models
Desuspension acting on the models of
![]() $\mathsf{MCaTT}$
. Consider a model
$\mathsf{MCaTT}$
. Consider a model
![]() $F : \operatorname{\mathcal{S}}_{\mathsf{MCaTT}}\to\operatorname{Set}$
and define the functor
$F : \operatorname{\mathcal{S}}_{\mathsf{MCaTT}}\to\operatorname{Set}$
and define the functor
![]() $\big\downarrow^*{F} : \operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to\operatorname{Set}$
by precomposing with the functor
$\big\downarrow^*{F} : \operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to\operatorname{Set}$
by precomposing with the functor
![]() $\big\downarrow{}$
, so we have
$\big\downarrow{}$
, so we have
![]() $\big\downarrow^*{F}(\Gamma) = F(\big\downarrow{\Gamma})$
and
$\big\downarrow^*{F}(\Gamma) = F(\big\downarrow{\Gamma})$
and
![]() $\big\downarrow^*{F} (\gamma) = F(\big\downarrow{\gamma})$
. By Corollary 14,
$\big\downarrow^*{F} (\gamma) = F(\big\downarrow{\gamma})$
. By Corollary 14,
![]() $\big\downarrow{}$
is a morphism of categories with families, and those preserve display maps, the terminal object and pullbacks along display maps. Since F is a model, it also preserves the terminal and the pullback along display maps, hence so does the composite
$\big\downarrow{}$
is a morphism of categories with families, and those preserve display maps, the terminal object and pullbacks along display maps. Since F is a model, it also preserves the terminal and the pullback along display maps, hence so does the composite
![]() $\big\downarrow^*{F}$
. Thus
$\big\downarrow^*{F}$
. Thus
![]() $\big\downarrow^*{F}$
is a model of the theory
$\big\downarrow^*{F}$
is a model of the theory
![]() $\mathsf{CaTT}$
, and the desuspension induces a functor
$\mathsf{CaTT}$
, and the desuspension induces a functor
![]() $\big\downarrow^*{}:\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})\to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. Moreover, we have
$\big\downarrow^*{}:\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})\to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. Moreover, we have
![]() $\big\downarrow^*{F}(x:\star) = F(x:{1})$
and by Lemma 23, the context
$\big\downarrow^*{F}(x:\star) = F(x:{1})$
and by Lemma 23, the context
![]() $(x:{1})$
is terminal and by definition, F preserves the terminal object, it follows that
$(x:{1})$
is terminal and by definition, F preserves the terminal object, it follows that
![]() $\big\downarrow^*{F}(x:\star)$
is terminal in
$\big\downarrow^*{F}(x:\star)$
is terminal in
![]() $\operatorname{Set}$
, hence
$\operatorname{Set}$
, hence
![]() $\big\downarrow^*{F}$
is an object of
$\big\downarrow^*{F}$
is an object of
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. This shows that the desuspension induces a functor
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. This shows that the desuspension induces a functor
![]() $\big\downarrow^*{}:\mathrm{Mod}({\mathsf{MCaTT}}) \to \mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
.
$\big\downarrow^*{}:\mathrm{Mod}({\mathsf{MCaTT}}) \to \mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
.
Reduced suspension acting on the models of
![]() $\mathsf{CaTT}$
. We define a similar construction for the reduced suspension. However, since the reduced suspension does not define an image for every term and does not preserve the terminal object, the construction is slightly more involved. We first consider start by showing the following result.
$\mathsf{CaTT}$
. We define a similar construction for the reduced suspension. However, since the reduced suspension does not define an image for every term and does not preserve the terminal object, the construction is slightly more involved. We first consider start by showing the following result.
Lemma 27. Given a model
![]() $F:\mathsf{CaTT}\to\operatorname{Set}$
of the type theory
$F:\mathsf{CaTT}\to\operatorname{Set}$
of the type theory
![]() $\mathsf{CaTT}$
, the functor
$\mathsf{CaTT}$
, the functor
![]() $\big\uparrow^*{F}$
preserves the pullbacks along display maps of
$\big\uparrow^*{F}$
preserves the pullbacks along display maps of
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
.
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
.
Proof. We consider a pullback along a display map, which is of the form

We first consider the case
![]() $A={1}$
. In this case, the image by
$A={1}$
. In this case, the image by
![]() $\big\uparrow^*{F}$
of the above square writes as
$\big\uparrow^*{F}$
of the above square writes as

which is a pullback. We now consider the case
![]() $$A \ne 1$$
, then the equality
$$A \ne 1$$
, then the equality
![]() $\big\uparrow{(A[\gamma])} = \big\uparrow{A}[\big\uparrow{\gamma}]$
given by Lemma 17 along with Lemma 3 shows that we have the following pullback square in
$\big\uparrow{(A[\gamma])} = \big\uparrow{A}[\big\uparrow{\gamma}]$
given by Lemma 17 along with Lemma 3 shows that we have the following pullback square in
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$

Since F preserves pullbacks along display maps, this shows that the image of the initial square by
![]() $\big\uparrow^*{F}$
is a pullback
$\big\uparrow^*{F}$
is a pullback

This shows that
![]() $\big\uparrow^*{F}$
is a model exactly when it preserves the initial object. Since we have by definition
$\big\uparrow^*{F}$
is a model exactly when it preserves the initial object. Since we have by definition
![]() $\big\uparrow^*{F} (\varnothing) = F(\bullet_{}:\star)$
, this condition translates to
$\big\uparrow^*{F} (\varnothing) = F(\bullet_{}:\star)$
, this condition translates to
![]() $F (\bullet_{},\varnothing)$
being a singleton. Hence
$F (\bullet_{},\varnothing)$
being a singleton. Hence
![]() $\big\uparrow^*{F}$
is a model if and only if F is an object of
$\big\uparrow^*{F}$
is a model if and only if F is an object of
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. This shows that
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. This shows that
![]() $\big\uparrow^*{}$
defines a functor
$\big\uparrow^*{}$
defines a functor
![]() $ \big\uparrow^*{}:\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
.
$ \big\uparrow^*{}:\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}) \to \mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
.
5.2 Models of the category
 $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
Using the desuspension and the reduced suspension, we have defined a pair of functors
![]() $\big\downarrow^*{}$
and
$\big\downarrow^*{}$
and
![]() $\big\uparrow^*{}$
between the categories
$\big\uparrow^*{}$
between the categories
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
and
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
and
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
.
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
.
Theorem The functors
![]() $\big\downarrow^*{}$
and
$\big\downarrow^*{}$
and
![]() $\big\uparrow^*{}$
define an equivalence of categories between
$\big\uparrow^*{}$
define an equivalence of categories between
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
and
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
and
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
Proof. First, Proposition 24 implies
![]() $\big\uparrow^*{}\circ\big\downarrow^*{} = \left({\big\downarrow{}\circ\big\uparrow{}}\right)^* \simeq \operatorname{id}_{\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}}$
and Proposition 25 shows that there is a natural transformation, obtained by whiskering
$\big\uparrow^*{}\circ\big\downarrow^*{} = \left({\big\downarrow{}\circ\big\uparrow{}}\right)^* \simeq \operatorname{id}_{\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}}$
and Proposition 25 shows that there is a natural transformation, obtained by whiskering
![]() $\big\downarrow^*{}\circ\big\uparrow^*{} = \left({\big\uparrow{}\circ\big\downarrow{}}\right)^* \Rightarrow \operatorname{id}_{\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})}$
So it suffices to show that this natural transformation is a natural isomorphism, that is for any
$\big\downarrow^*{}\circ\big\uparrow^*{} = \left({\big\uparrow{}\circ\big\downarrow{}}\right)^* \Rightarrow \operatorname{id}_{\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})}$
So it suffices to show that this natural transformation is a natural isomorphism, that is for any
![]() $F\in\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
and all context
$F\in\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
and all context
![]() $\Gamma$
in
$\Gamma$
in
![]() $\mathsf{CaTT}$
, the map
$\mathsf{CaTT}$
, the map
![]() $F(\bullet_\Gamma) : F(\big\uparrow{\big\downarrow{\Gamma}}) \to F(\Gamma)$
is an isomorphism. We prove this property by induction on the context
$F(\bullet_\Gamma) : F(\big\uparrow{\big\downarrow{\Gamma}}) \to F(\Gamma)$
is an isomorphism. We prove this property by induction on the context
![]() $\Gamma$
.
$\Gamma$
.
-
For the empty context
 $\varnothing$
, we necessarily have that
$\varnothing$
, we necessarily have that
 $F(\varnothing) = \left\{{\bullet}\right\}$
, and since
$F(\varnothing) = \left\{{\bullet}\right\}$
, and since
 $\big\uparrow{\big\downarrow{\varnothing}} = D^0$
and
$\big\uparrow{\big\downarrow{\varnothing}} = D^0$
and
 $F\in\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, we also have that
$F\in\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, we also have that
 $F(\big\uparrow{\big\downarrow{\varnothing}}) = \left\{{\bullet}\right\}$
. Hence,
$F(\big\uparrow{\big\downarrow{\varnothing}}) = \left\{{\bullet}\right\}$
. Hence,
 $F(\bullet_\varnothing)$
is the unique map between the singleton to itself, which is an isomorphism.
$F(\bullet_\varnothing)$
is the unique map between the singleton to itself, which is an isomorphism. -
For a context of the form
 $(\Gamma,x:\star)$
, it is obtained as a (trivial) pullback, and the map
$(\Gamma,x:\star)$
, it is obtained as a (trivial) pullback, and the map
 $\bullet_{(\Gamma,x:\star)}$
is obtained by universal property of the pullback, as follows
$\bullet_{(\Gamma,x:\star)}$
is obtained by universal property of the pullback, as follows

Taking the image by F on this pullback yields another pullback in
![]() $\operatorname{Set}$
(since F is a model of
$\operatorname{Set}$
(since F is a model of
![]() $\mathsf{CaTT}$
), as follows
$\mathsf{CaTT}$
), as follows

Since the square is a pullback,
![]() $F\pi$
is an isomorphism, and since by induction
$F\pi$
is an isomorphism, and since by induction
![]() $F\bullet_\Gamma$
is also an isomorphism, necessarily
$F\bullet_\Gamma$
is also an isomorphism, necessarily
![]() $F\bullet_{\Gamma,x:\star}$
is an isomorphism.
$F\bullet_{\Gamma,x:\star}$
is an isomorphism.
-
For a context of the form
 $(\Gamma,x:A)$
where A is a type distinct from
$(\Gamma,x:A)$
where A is a type distinct from
 $\star$
, the context is obtained as a pullback, the context
$\star$
, the context is obtained as a pullback, the context
 $\big\uparrow{\big\downarrow{(\Gamma,x:A)}}$
is also a pullback and the substitution
$\big\uparrow{\big\downarrow{(\Gamma,x:A)}}$
is also a pullback and the substitution
 $\bullet_{(\Gamma,x:A)}$
is obtained by universal property as described in the following diagram which has the shape of a cube whose faces are commutative and whose front and back face are pullbacks
$\bullet_{(\Gamma,x:A)}$
is obtained by universal property as described in the following diagram which has the shape of a cube whose faces are commutative and whose front and back face are pullbacks

Taking the image by F of this diagram yields another cube whose faces are all commutative square, and whose front and back square are again pullback squares, since as a model, F preserves the pullbacks along the display maps (in the following figure, we have left implicit most of the arrows, they are simply the image by F of the ones of the previous figure).

By induction, the map
![]() $F(\bullet_\Gamma)$
is an isomorphism, making the span defining
$F(\bullet_\Gamma)$
is an isomorphism, making the span defining
![]() $F(\Gamma,x:A)$
and the span defining
$F(\Gamma,x:A)$
and the span defining
![]() $F(\big\uparrow{\big\downarrow{(\Gamma,x:A)}})$
isomorphic. This proves that the map
$F(\big\uparrow{\big\downarrow{(\Gamma,x:A)}})$
isomorphic. This proves that the map
![]() $F(\bullet_{(\Gamma,x:A)})$
is also an isomorphism, by uniqueness of the pullback up to isomorphism.
$F(\bullet_{(\Gamma,x:A)})$
is also an isomorphism, by uniqueness of the pullback up to isomorphism.
Reflective localization. We now give a reformulation of the construction we have presented. First note that the opposite of a category with families C embeds inside its category of models via a Yoneda embedding
Indeed, the functor
![]() $C(\Gamma,\_)$
preserves the pullbacks along display maps (and in fact all limits) by continuity of the Hom-functor. This lets us see the objects
$C(\Gamma,\_)$
preserves the pullbacks along display maps (and in fact all limits) by continuity of the Hom-functor. This lets us see the objects
![]() $\varnothing$
and
$\varnothing$
and
![]() $D^0$
as particular objects of
$D^0$
as particular objects of
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, with
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, with
![]() $\varnothing$
being the initial object. We then consider the unique map
$\varnothing$
being the initial object. We then consider the unique map
![]() $s:\varnothing \to D^0$
in the category
$s:\varnothing \to D^0$
in the category
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. Then the category
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
. Then the category
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
is the category of all the s-local objects, i.e., all objects F such that the map
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
is the category of all the s-local objects, i.e., all objects F such that the map
is a natural isomorphism. Indeed, since
![]() $\varnothing$
is an initial objects, s-local objects are exactly those such that
$\varnothing$
is an initial objects, s-local objects are exactly those such that
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})(D^0,F)$
is a singleton, which reformulates as
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})(D^0,F)$
is a singleton, which reformulates as
![]() $F(D^0)$
being a singleton by the Yoneda lemma. This exhibits
$F(D^0)$
being a singleton by the Yoneda lemma. This exhibits
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
as a reflective localization of the category
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
as a reflective localization of the category
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
at s. Theorem 5.2 then shows that
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
at s. Theorem 5.2 then shows that
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
is equivalent to
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
is equivalent to
![]() $\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, and thus is also a reflective localization of
$\mathrm{Mod}[_\bullet]({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
, and thus is also a reflective localization of
![]() $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
at s. This localization lifts the coreflective adjunction between
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
at s. This localization lifts the coreflective adjunction between
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
and
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
and
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
realized by the desuspension and the reduced suspension, that we have stated in Theorem 4.3.
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
realized by the desuspension and the reduced suspension, that we have stated in Theorem 4.3.
5.3 Interpretation
As we have proved independently (Benjamin et al. Reference Benjamin, Finster and Mimram2021), the models of the theory
![]() $\mathsf{CaTT}$
are equivalent to the Grothendieck–Maltsiniotis definition of weak
$\mathsf{CaTT}$
are equivalent to the Grothendieck–Maltsiniotis definition of weak
![]() $\omega$
-categories with the Batanin–Leinster coherator. In light of this fact, Theorem 5.2 can be reformulated as stating that the models of
$\omega$
-categories with the Batanin–Leinster coherator. In light of this fact, Theorem 5.2 can be reformulated as stating that the models of
![]() $\mathsf{MCaTT}$
are the weak
$\mathsf{MCaTT}$
are the weak
![]() $\omega$
-categories (in the sense of Grothendieck–Malstiniotis with the Batanin–Leinster coherator) with a single object. It is expected from higher category theory that such a result holds (Baez Reference Baez2006). Recall our interpretation of
$\omega$
-categories (in the sense of Grothendieck–Malstiniotis with the Batanin–Leinster coherator) with a single object. It is expected from higher category theory that such a result holds (Baez Reference Baez2006). Recall our interpretation of
![]() ${\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}^{\text{op}}$
as finitely generated computads, and assume that similarly
${\operatorname{\mathcal{S}}_{\mathsf{CaTT}}}^{\text{op}}$
as finitely generated computads, and assume that similarly
![]() ${\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}}^{\text{op}}$
is the category of finitely generated computads for an appropriate notion of computads for monoidal weak
${\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}}^{\text{op}}$
is the category of finitely generated computads for an appropriate notion of computads for monoidal weak
![]() $\omega$
-categories. We can always view a computad for monoidal weak
$\omega$
-categories. We can always view a computad for monoidal weak
![]() $\omega$
-category as a weak
$\omega$
-category as a weak
![]() $\omega$
-category with a single object. In this case, it turns out that when adopting this view, the weak
$\omega$
-category with a single object. In this case, it turns out that when adopting this view, the weak
![]() $\omega$
-category that we retrieve is again a freely generated computad, and this is why we were able to formulate the theory of monoidal weak
$\omega$
-category that we retrieve is again a freely generated computad, and this is why we were able to formulate the theory of monoidal weak
![]() $\omega$
-categories in terms of the theory of weak
$\omega$
-categories in terms of the theory of weak
![]() $\omega$
-category.
$\omega$
-category.
However, this fails for k-monoidal weak
![]() $\omega$
-categories, for
$\omega$
-categories, for
![]() $k>1$
. We illustrate this with
$k>1$
. We illustrate this with
![]() $k=2$
, defining 2-monoidal
$k=2$
, defining 2-monoidal
![]() $\omega$
-categories as 1-monoidal
$\omega$
-categories as 1-monoidal
![]() $\omega$
-categories with a single object, and we assume a suitable notion of computad for those. Then a computad for 2-monoidal
$\omega$
-categories with a single object, and we assume a suitable notion of computad for those. Then a computad for 2-monoidal
![]() $\omega$
-categories is naturally a 1-monoidal category with a single object. However, viewed as a 1-monoidal
$\omega$
-categories is naturally a 1-monoidal category with a single object. However, viewed as a 1-monoidal
![]() $\omega$
-category, it is not a computad. Indeed, any computad must contain at least the monoidal unit object e as well as all its iterated products
$\omega$
-category, it is not a computad. Indeed, any computad must contain at least the monoidal unit object e as well as all its iterated products
![]() $(e^{\otimes n})_{n \in\mathbb{N}}$
, so no computad may have a single object. As a result, it is impossible to transcribe the same ideas for 2-monoidal
$(e^{\otimes n})_{n \in\mathbb{N}}$
, so no computad may have a single object. As a result, it is impossible to transcribe the same ideas for 2-monoidal
![]() $\omega$
-categories literally. Still, we conjecture that there exists a dependent type theory for 2-monoidal weak
$\omega$
-categories literally. Still, we conjecture that there exists a dependent type theory for 2-monoidal weak
![]() $\omega$
-categories, along with a pair of translations back and forth to the theory
$\omega$
-categories, along with a pair of translations back and forth to the theory
![]() $\mathsf{MCaTT}$
, and that those translation compensate the aforementioned obstruction by relying on a strictification procedure for 1-monoidal weak
$\mathsf{MCaTT}$
, and that those translation compensate the aforementioned obstruction by relying on a strictification procedure for 1-monoidal weak
![]() $\omega$
-categories, that strictifies the unit law of the monoidal product. We think that this construction should be related to the work of Finster et al. (Reference Finster, Reutter and Vicary2020) on strictly unital weak
$\omega$
-categories, that strictifies the unit law of the monoidal product. We think that this construction should be related to the work of Finster et al. (Reference Finster, Reutter and Vicary2020) on strictly unital weak
![]() $\omega$
-categories, but we leave this conjecture and the connection between these theories for future work
$\omega$
-categories, but we leave this conjecture and the connection between these theories for future work
We also speculate that weak
![]() $\omega$
-categories should be compared with an appropriate notion of weak equivalence, that can be described by a structure akin to a model structure, and similarly for the monoidal weak
$\omega$
-categories should be compared with an appropriate notion of weak equivalence, that can be described by a structure akin to a model structure, and similarly for the monoidal weak
![]() $\omega$
-categories. We have presented an equivalence between the categories with strict functors, but we expect this equivalence to lift and provide an equivalence between weak categories with weak functors. We conjecture that the relevant property in this weakened world is not having a single object (which is not expected to be invariant under weak equivalences), but having a 0-connected groupoidal core. Investigation in this direction to straighten and prove those claims are left for further work.
$\omega$
-categories. We have presented an equivalence between the categories with strict functors, but we expect this equivalence to lift and provide an equivalence between weak categories with weak functors. We conjecture that the relevant property in this weakened world is not having a single object (which is not expected to be invariant under weak equivalences), but having a 0-connected groupoidal core. Investigation in this direction to straighten and prove those claims are left for further work.
6. Conclusion
We have developed the type theory
![]() $\mathsf{MCaTT}$
whose models are monoidal weak
$\mathsf{MCaTT}$
whose models are monoidal weak
![]() $\omega$
-categories. To this end, we rely on an existing type theory describing weak
$\omega$
-categories. To this end, we rely on an existing type theory describing weak
![]() $\omega$
-categories and index the rule of our theory with the rule of the existing theory. We were then able to prove correctness results, using syntactic translations between the two theories and lifting the results as a correspondence between their models.
$\omega$
-categories and index the rule of our theory with the rule of the existing theory. We were then able to prove correctness results, using syntactic translations between the two theories and lifting the results as a correspondence between their models.
A forgetful functor. There is another translation from
![]() $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
to
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
to
![]() $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
that we have not presented here. Given a ps-context
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
that we have not presented here. Given a ps-context
![]() $\Gamma$
, we can produce its suspension
$\Gamma$
, we can produce its suspension
![]() $\Sigma \Gamma$
, obtained by formally adding two objects and lifting all the dimensions by 1, in such a way that an object in
$\Sigma \Gamma$
, obtained by formally adding two objects and lifting all the dimensions by 1, in such a way that an object in
![]() $\Gamma$
becomes a 1-cell between the two new objects in
$\Gamma$
becomes a 1-cell between the two new objects in
![]() $\Sigma\Gamma$
. We can then leverage this operation to define a translation, which gives a morphism of categories with families
$\Sigma\Gamma$
. We can then leverage this operation to define a translation, which gives a morphism of categories with families
![]() $u:\operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
. The induced functor on the categories of models
$u:\operatorname{\mathcal{S}}_{\mathsf{CaTT}}\to\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
. The induced functor on the categories of models
is the forgetful functor, which, given a monoidal weak
![]() $\omega$
-category, forgets the monoidal product and gives the underlying weak
$\omega$
-category, forgets the monoidal product and gives the underlying weak
![]() $\omega$
-category. Importantly, in this case there is no shift of dimension; the objects of the
$\omega$
-category. Importantly, in this case there is no shift of dimension; the objects of the
![]() $\omega$
-category are the objects of the monoidal
$\omega$
-category are the objects of the monoidal
![]() $\omega$
-category, but without the ability to be composed. The existence of this functor is closely related to the well-definedness of an operation of suspension in the theory
$\omega$
-category, but without the ability to be composed. The existence of this functor is closely related to the well-definedness of an operation of suspension in the theory
![]() $\mathsf{CaTT}$
(Benjamin and Mimram Reference Benjamin and Mimram2019).
$\mathsf{CaTT}$
(Benjamin and Mimram Reference Benjamin and Mimram2019).
Alternate presentations of
![]() $\mathsf{MCaTT}$
. We have worked out different presentations for the theory
$\mathsf{MCaTT}$
. We have worked out different presentations for the theory
![]() $\mathsf{MCaTT}$
, all of them being centered around the idea of enforcing the constraint of having a unique object of dimension
$\mathsf{MCaTT}$
, all of them being centered around the idea of enforcing the constraint of having a unique object of dimension
![]() $-1$
. We give in Benjamin (Reference Benjamin2020) two other presentations. The first one is very similar to the one that we have given here, but the difference is that we do not introduce a type 1 in
$-1$
. We give in Benjamin (Reference Benjamin2020) two other presentations. The first one is very similar to the one that we have given here, but the difference is that we do not introduce a type 1 in
![]() $\mathsf{MCaTT}$
. The price to pay is that the desuspension becomes a partial operation, since there is no type to send the type
$\mathsf{MCaTT}$
. The price to pay is that the desuspension becomes a partial operation, since there is no type to send the type
![]() $\star$
to, but this gets compensated by the fact that the theory can be expressed without definitional equalities and thus there is no need to carefully work with terms in normal forms. Both these presentation are relatively close, and none of them really surpasses the other. The second presentation that we give in Benjamin (Reference Benjamin2020) encodes all the properties with lists of contexts. This presentation is more involved and significantly harder to study, however it gives a syntax that is a bit more concise. It also provides a framework which is more independent of
$\star$
to, but this gets compensated by the fact that the theory can be expressed without definitional equalities and thus there is no need to carefully work with terms in normal forms. Both these presentation are relatively close, and none of them really surpasses the other. The second presentation that we give in Benjamin (Reference Benjamin2020) encodes all the properties with lists of contexts. This presentation is more involved and significantly harder to study, however it gives a syntax that is a bit more concise. It also provides a framework which is more independent of
![]() $\mathsf{CaTT}$
, and for which the conditions for constructing the derivation trees are more straightforwardly verified. For these reasons, we believe that the latter presentation is to be preferred for a potential future implementation of the theory
$\mathsf{CaTT}$
, and for which the conditions for constructing the derivation trees are more straightforwardly verified. For these reasons, we believe that the latter presentation is to be preferred for a potential future implementation of the theory
![]() $\mathsf{MCaTT}$
.
$\mathsf{MCaTT}$
.
Monoidal closed higher categories. It would be valuable to connect the result we have presented with recent work of Finster for integrating the theory of monoidal higher categories in the tool Opetopic (Finster Reference Finster2020), although it necessitates to establish a connection between globular and opetopic shapes.
A. Summary of the type theories
A.1 The type theory
 $\mathfrak{G}$
$\mathfrak{G}$
A.1.1 Syntax
Contexts: lists
![]() $(x_0:A_0,\ldots,x_n:A_n)$
with
$(x_0:A_0,\ldots,x_n:A_n)$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $A_i$
types
$A_i$
types
Types: either
![]() $\star$
or of the form
$\star$
or of the form
![]() ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms
Terms: variables
Substitutions: lists
![]() $\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
$\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $t_i$
terms
$t_i$
terms
A.1.2 Inference rules


A.1.3 Semantics
A.2 The type theory
 $\mathsf{CaTT}$
$\mathsf{CaTT}$
A.2.1 Syntax
Contexts: lists
![]() $(x_0:A_0,\ldots,x_n:A_n)$
with
$(x_0:A_0,\ldots,x_n:A_n)$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $A_i$
types Types: either
$A_i$
types Types: either
![]() $\star$
or of the form
$\star$
or of the form
![]() ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: either variables or of the form
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: either variables or of the form
![]() $\mathsf{op}_{\Gamma,A}[\gamma]$
or
$\mathsf{op}_{\Gamma,A}[\gamma]$
or
![]() $\mathsf{coh}_{\Gamma,A}[\gamma]$
with
$\mathsf{coh}_{\Gamma,A}[\gamma]$
with
![]() $\Gamma$
a ps-context, A a type and
$\Gamma$
a ps-context, A a type and
![]() $\gamma$
a substitution Substitutions: lists
$\gamma$
a substitution Substitutions: lists
![]() $\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
$\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $t_i$
terms
$t_i$
terms
A.2.2 Rules for ps-contexts

A.2.3 Source and target of a ps-context
 \begin{align*} \partial^-_i(x:\star) &= (x:\star) & \partial^-_i(\Gamma,y:A,f:x\to y) &= \left\{ \begin{array}{l@{\quad}l} \partial^-_i\Gamma & \text{if $\dim A~\geq i-1$} \\ (\partial^-_i\Gamma,y:A,f:x\to y) & \text{otherwise} \end{array} \right. \\[2em] \partial_i^+(x:\star) &= (x:\star) & \partial^+_i(\Gamma,y:A,f:x\to y) &= \left\{ \begin{array}{l@{\quad}l} \partial^+_i\Gamma & \text{if $\dim A~\geq i$} \\ \mathrm{drop}(\partial^+_i\Gamma),y:A~& \text{if $\dim A~= i-1$}\\ \partial^+_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right. \\[2em] \partial^-(\Gamma) &= \partial_{\dim \Gamma-1}^- \Gamma & \partial^+(\Gamma) &= \partial_{\dim\Gamma-1}^+\Gamma\end{align*}
\begin{align*} \partial^-_i(x:\star) &= (x:\star) & \partial^-_i(\Gamma,y:A,f:x\to y) &= \left\{ \begin{array}{l@{\quad}l} \partial^-_i\Gamma & \text{if $\dim A~\geq i-1$} \\ (\partial^-_i\Gamma,y:A,f:x\to y) & \text{otherwise} \end{array} \right. \\[2em] \partial_i^+(x:\star) &= (x:\star) & \partial^+_i(\Gamma,y:A,f:x\to y) &= \left\{ \begin{array}{l@{\quad}l} \partial^+_i\Gamma & \text{if $\dim A~\geq i$} \\ \mathrm{drop}(\partial^+_i\Gamma),y:A~& \text{if $\dim A~= i-1$}\\ \partial^+_i\Gamma,y:A,f:x\to y & \text{otherwise} \end{array} \right. \\[2em] \partial^-(\Gamma) &= \partial_{\dim \Gamma-1}^- \Gamma & \partial^+(\Gamma) &= \partial_{\dim\Gamma-1}^+\Gamma\end{align*}
where
![]() $\mathrm{drop}(\Gamma)$
is the context
$\mathrm{drop}(\Gamma)$
is the context
![]() $\Gamma$
with its last variable removed.
$\Gamma$
with its last variable removed.
A.2.4 Side conditions

A.2.5 Inference rules


A.2.6 Semantics
A.3 The theory
 $\mathfrak{G}_{{1}}$
$\mathfrak{G}_{{1}}$
Contexts: lists
![]() $(x_0:A_0,\ldots,x_n:A_n)$
with
$(x_0:A_0,\ldots,x_n:A_n)$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $A_i$
types Types: either 1 or of the form
$A_i$
types Types: either 1 or of the form
![]() ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: variables Substitutions: lists
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: variables Substitutions: lists
![]() $\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
$\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $t_i$
terms
$t_i$
terms
A.3.1 Inference rules


A.3.2 Semantics
A.4 The theory
 $\mathsf{MCaTT}$
$\mathsf{MCaTT}$
A.4.1 Syntax
Contexts: lists
![]() $(x_0:A_0,\ldots,x_n:A_n)$
with
$(x_0:A_0,\ldots,x_n:A_n)$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $A_i$
types Types: either 1 or of the form
$A_i$
types Types: either 1 or of the form
![]() ${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: either variables or of the form
${t}\underset{A}{\xrightarrow{\phantom{A}}}{u}$
with A type and t and u terms Terms: either variables or of the form
![]() $\mathsf{mop}_{\Gamma,A}[\gamma]$
or
$\mathsf{mop}_{\Gamma,A}[\gamma]$
or
![]() $\mathsf{mcoh}_{\Gamma,A}[\gamma]$
with
$\mathsf{mcoh}_{\Gamma,A}[\gamma]$
with
![]() $\Gamma$
a ps-context, A a type and
$\Gamma$
a ps-context, A a type and
![]() $\gamma$
a substitution Substitutions: lists
$\gamma$
a substitution Substitutions: lists
![]() $\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
$\langle{x_0\mapsto t_0,\ldots,x_n\mapsto t_n}\rangle$
with
![]() $x_i$
variables and
$x_i$
variables and
![]() $t_i$
terms
$t_i$
terms
A.4.2 Desuspension

A.4.3 Inference rules

A.4.4 Semantics
-
 $\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
is equivalent to the full subcategory of
$\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}$
is equivalent to the full subcategory of
 $\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
whose objects are the contexts with a unique variable of type
$\operatorname{\mathcal{S}}_{\mathsf{CaTT}}$
whose objects are the contexts with a unique variable of type
 $\star$
.
$\star$
. -
 $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
is equivalent to the full subcategory of
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{MCaTT}}})$
is equivalent to the full subcategory of
 $\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
that define a single 0-cell
$\mathrm{Mod}({\operatorname{\mathcal{S}}_{\mathsf{CaTT}}})$
that define a single 0-cell