1. Introduction
1.1. Hodge groups
Fix a period domain
![]() $ \mathcal{D}={\mathcal{D}}_{\mathrm{h}}={\mathcal{G}}_{\mathrm{\mathbb{R}}}/{\mathcal{G}}_{\mathrm{\mathbb{R}}}^0 $
parameterizing Q–polarized Hodge structures on a rational vector space V with Hodge numbers
$ \mathcal{D}={\mathcal{D}}_{\mathrm{h}}={\mathcal{G}}_{\mathrm{\mathbb{R}}}/{\mathcal{G}}_{\mathrm{\mathbb{R}}}^0 $
parameterizing Q–polarized Hodge structures on a rational vector space V with Hodge numbers
![]() $ \mathrm{h}=\left({h}^{n,0},\dots, {h}^{0,n}\right) $
. Here
$ \mathrm{h}=\left({h}^{n,0},\dots, {h}^{0,n}\right) $
. Here
is either an orthogonal group
![]() $ \mathrm{O}\left(a, 2b\right) $
(if
$ \mathrm{O}\left(a, 2b\right) $
(if
![]() $ n $
is even) or a symplectic group Sp
$ n $
is even) or a symplectic group Sp
![]() $ \left(2r, \mathrm{\mathbb{R}}\right) $
(if
$ \left(2r, \mathrm{\mathbb{R}}\right) $
(if
![]() $ n $
is odd), and
$ n $
is odd), and
![]() $ {\mathcal{G}}_{\mathrm{\mathbb{R}}}^0 $
is the compact stabilizer of a fixed
$ {\mathcal{G}}_{\mathrm{\mathbb{R}}}^0 $
is the compact stabilizer of a fixed
![]() $ \varphi \in \mathcal{D} $
. To each Hodge structure
$ \varphi \in \mathcal{D} $
. To each Hodge structure
![]() $ \varphi \in \mathcal{D} $
is associated
$ \varphi \in \mathcal{D} $
is associated
![]() $ \mathrm{a} $
(
$ \mathrm{a} $
(
![]() $ \mathrm{\mathbb{Q}} $
–algebraic) Hodge group
$ \mathrm{\mathbb{Q}} $
–algebraic) Hodge group
![]() $ {\mathbf{G}}_{\varphi} \subset \mathrm{Aut}\left(V, Q\right) $
, and a Mumford–Tate domain
$ {\mathbf{G}}_{\varphi} \subset \mathrm{Aut}\left(V, Q\right) $
, and a Mumford–Tate domain
![]() $ D={D}_{\varphi }={G}_{\varphi}\cdot \varphi \subset \mathcal{D} $
, where
$ D={D}_{\varphi }={G}_{\varphi}\cdot \varphi \subset \mathcal{D} $
, where
![]() $ {G}_{\varphi }={\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{R}}\right) $
. Briefly, the Hodge structure
$ {G}_{\varphi }={\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{R}}\right) $
. Briefly, the Hodge structure
![]() $ \varphi \in \mathcal{D} $
determines a homomorphism of
$ \varphi \in \mathcal{D} $
determines a homomorphism of
![]() $ \mathrm{\mathbb{R}} $
–algebraic groups
$ \mathrm{\mathbb{R}} $
–algebraic groups
![]() $ \varphi :{S}^1\to \mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
, and the Hodge group
$ \varphi :{S}^1\to \mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
, and the Hodge group
![]() $ {\mathbf{G}}_{\varphi } $
is the
$ {\mathbf{G}}_{\varphi } $
is the
![]() $ \mathrm{\mathbb{Q}} $
–algebraic closure of
$ \mathrm{\mathbb{Q}} $
–algebraic closure of
![]() $ \varphi \left({S}^1\right) $
. The Hodge group
$ \varphi \left({S}^1\right) $
. The Hodge group
![]() $ {\mathbf{G}}_{\varphi } $
may be equivalently defined as the stabilizer of the Hodge tensors of
$ {\mathbf{G}}_{\varphi } $
may be equivalently defined as the stabilizer of the Hodge tensors of
![]() $ \varphi $
.
$ \varphi $
.
1.2. Motivations
The geometric considerations motivating a classification of the Hodge groups for a given period domain
![]() $ \mathcal{D} $
include the following. For generic choice of
$ \mathcal{D} $
include the following. For generic choice of
![]() $ \varphi \in D $
, the Hodge group
$ \varphi \in D $
, the Hodge group
![]() $ {\mathbf{G}}_{\varphi } $
is the full automorphism group
$ {\mathbf{G}}_{\varphi } $
is the full automorphism group
![]() $ \mathrm{Aut}\left(V, Q\right) $
. So when containment
$ \mathrm{Aut}\left(V, Q\right) $
. So when containment
![]() $ {\mathbf{G}}_{\varphi} \subsetneq \mathrm{Aut}\left(V, Q\right) $
is strict, the Hodge structure has nongeneric Hodge tensors. (And, because
$ {\mathbf{G}}_{\varphi} \subsetneq \mathrm{Aut}\left(V, Q\right) $
is strict, the Hodge structure has nongeneric Hodge tensors. (And, because
![]() $ {\mathbf{G}}_{\varphi^{\prime }} \subset {\mathbf{G}}_{\varphi } $
for all
$ {\mathbf{G}}_{\varphi^{\prime }} \subset {\mathbf{G}}_{\varphi } $
for all
![]() $ {\varphi}^{\prime}\in {D}_{\varphi } $
, the Mumford–Tate domain
$ {\varphi}^{\prime}\in {D}_{\varphi } $
, the Mumford–Tate domain
![]() $ {D}_{\varphi } $
will parameterize Hodge structures with nongeneric Hodge tensors.) An extreme example here is the case that
$ {D}_{\varphi } $
will parameterize Hodge structures with nongeneric Hodge tensors.) An extreme example here is the case that
![]() $ {D}_{\varphi } $
is a point
$ {D}_{\varphi } $
is a point
![]() $ \left\{\varphi \right\} $
; this is the case if and only if
$ \left\{\varphi \right\} $
; this is the case if and only if
![]() $ {\mathbf{G}}_{\varphi } $
is a torus; equivalently, End
$ {\mathbf{G}}_{\varphi } $
is a torus; equivalently, End
![]() $ \left(V, \varphi \right) $
is a CM field. When containment
$ \left(V, \varphi \right) $
is a CM field. When containment
![]() $ {\mathbf{G}}_{\varphi}\subsetneq \mathrm{Aut}\left(V, Q\right) $
is strict and the Hodge structure is realized by the cohomology of an algebraic variety, the variety and its self-products “should” admit nongeneric arithmetic properties (such as extra Hodge classes, or automorphisms, et cetera). In general, the Hodge group can have significant geometric consequences; for example, it plays a key role in Ribet’s study (Ribet, Reference Ribet1983) of the Hodge conjecture for principally polarized abelian varieties (expanding upon earlier work of Tanke’ev’s, Reference Tankeev1981; Reference Tankeev1982).
$ {\mathbf{G}}_{\varphi}\subsetneq \mathrm{Aut}\left(V, Q\right) $
is strict and the Hodge structure is realized by the cohomology of an algebraic variety, the variety and its self-products “should” admit nongeneric arithmetic properties (such as extra Hodge classes, or automorphisms, et cetera). In general, the Hodge group can have significant geometric consequences; for example, it plays a key role in Ribet’s study (Ribet, Reference Ribet1983) of the Hodge conjecture for principally polarized abelian varieties (expanding upon earlier work of Tanke’ev’s, Reference Tankeev1981; Reference Tankeev1982).
Likewise much geometric motivation for the classification of the Mumford–Tate domains comes from the moduli of algebraic varieties. In general, the period domain is not Hermitian. Two significant exceptions are the period domains arising when considering moduli spaces of principally polarized abelian varieties and K3 surfaces. The Hermitian symmetric structure of
![]() $ \mathcal{D} $
in these two cases, along with global Torelli theorems, is the underlying structure that has made Hodge theory such a powerful tool in the study of these moduli spaces and their compactifications (Laza, Reference Laza2016). Even when the period domain
$ \mathcal{D} $
in these two cases, along with global Torelli theorems, is the underlying structure that has made Hodge theory such a powerful tool in the study of these moduli spaces and their compactifications (Laza, Reference Laza2016). Even when the period domain
![]() $ \mathcal{D} $
is not Hermitian, it may contain Hermitian symmetric Mumford–Tate subdomains D. (For example, every horizontal subdomain is Hermitian symmetric.) If a moduli space
$ \mathcal{D} $
is not Hermitian, it may contain Hermitian symmetric Mumford–Tate subdomains D. (For example, every horizontal subdomain is Hermitian symmetric.) If a moduli space
![]() $ \mathrm{\mathcal{M}} $
has an injective period map
$ \mathrm{\mathcal{M}} $
has an injective period map
![]() $ \Phi :\mathrm{\mathcal{M}}\to \Gamma \backslash \mathcal{D} $
(a Torelli-type theorem) and the image is a Zariski open subset of the locally Hermitian symmetric
$ \Phi :\mathrm{\mathcal{M}}\to \Gamma \backslash \mathcal{D} $
(a Torelli-type theorem) and the image is a Zariski open subset of the locally Hermitian symmetric
![]() $ \pi (D) \subset \Gamma \backslash \mathcal{D}, $
with
$ \pi (D) \subset \Gamma \backslash \mathcal{D}, $
with
![]() $ \pi :\mathcal{D}\to \Gamma \backslash \mathcal{D} $
the quotient, then Hodge theory is again a significant tool in the study of
$ \pi :\mathcal{D}\to \Gamma \backslash \mathcal{D} $
the quotient, then Hodge theory is again a significant tool in the study of
![]() $ \mathrm{\mathcal{M}} $
and its compactifications, cf. Allcock et al. (Reference Allcock, Carlson and Toledo2002, Reference Allcock, Carlson and Toledo2011), Borcea (Reference Borcea1997), Garbagnati and van Geeme, (Reference Garbagnati and van
Geemen2010), Kondo (Reference Kondo2000), Laza et al. (Reference Laza, Pearlstein and Zhang2018), Pearlstein and Zhang (Reference Pearlstein and Zhang2019), Rohde (Reference Rohde2009), and Voisin (Reference Voisin1983). Reciprocally, given a Hermitian symmetric Mumford–Tate domain
$ \mathrm{\mathcal{M}} $
and its compactifications, cf. Allcock et al. (Reference Allcock, Carlson and Toledo2002, Reference Allcock, Carlson and Toledo2011), Borcea (Reference Borcea1997), Garbagnati and van Geeme, (Reference Garbagnati and van
Geemen2010), Kondo (Reference Kondo2000), Laza et al. (Reference Laza, Pearlstein and Zhang2018), Pearlstein and Zhang (Reference Pearlstein and Zhang2019), Rohde (Reference Rohde2009), and Voisin (Reference Voisin1983). Reciprocally, given a Hermitian symmetric Mumford–Tate domain
![]() $ D \subset \mathcal{D} $
it is a very interesting problem to find geometric (or motivic) realizations of the domain; work in this direction includes Kerr and Pearlstein (Reference Kerr and Pearlstein2016), Pearlstein and Zhang (Reference Pearlstein and Zhang2019), and Zhang (Reference Zhang2014, Reference Zhang2016).
$ D \subset \mathcal{D} $
it is a very interesting problem to find geometric (or motivic) realizations of the domain; work in this direction includes Kerr and Pearlstein (Reference Kerr and Pearlstein2016), Pearlstein and Zhang (Reference Pearlstein and Zhang2019), and Zhang (Reference Zhang2014, Reference Zhang2016).
1.3. Objective and approach
The principal goal of this paper is to present an expository discussion of the Green–Griffiths–Kerr (Green et al., Reference Green, Griffiths and Kerr2012) prescription to identify the real algebraic groups
![]() $ {G}_{\varphi }={\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{R}}\right) $
that may arise. More precisely, Green–Griffiths–Kerr identify the underlying real Lie algebra
$ {G}_{\varphi }={\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{R}}\right) $
that may arise. More precisely, Green–Griffiths–Kerr identify the underlying real Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
. This determines
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
. This determines
![]() $ {G}_{\varphi } $
to finite data, and suffices to identify the domains
$ {G}_{\varphi } $
to finite data, and suffices to identify the domains
![]() $ {D}_{\varphi } $
as intrinsic
$ {D}_{\varphi } $
as intrinsic
![]() $ {G}_{\varphi}^{\mathrm{ad}} $
–homogeneous spaces. (See Patrikis, Reference Patrikis2016 for the classification of general
$ {G}_{\varphi}^{\mathrm{ad}} $
–homogeneous spaces. (See Patrikis, Reference Patrikis2016 for the classification of general
![]() $ {\mathbf{G}}_{\varphi }. $
)
$ {\mathbf{G}}_{\varphi }. $
)
Example 1.1. The case of weight one Hodge representations is classical (Deligne, Reference Deligne1979; Milne, Reference Milne2005): The real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
is one of
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
is one of
![]() $ {\mathfrak{sp}}_{2r}\mathrm{\mathbb{R}}, \mathfrak{u}\left(a, b\right) $
,
$ {\mathfrak{sp}}_{2r}\mathrm{\mathbb{R}}, \mathfrak{u}\left(a, b\right) $
,
![]() $ \mathfrak{su}\left(a, a\right) $
,
$ \mathfrak{su}\left(a, a\right) $
,
![]() $ \mathfrak{so}\left(2, m\right) $
and
$ \mathfrak{so}\left(2, m\right) $
and
![]() $ {\mathfrak{so}}^{\ast }(2r) $
. See Example 3.3 for the corresponding Hodge representations.
$ {\mathfrak{so}}^{\ast }(2r) $
. See Example 3.3 for the corresponding Hodge representations.
Remark 1.2. We are aware of only a few cases in which the classification of the
![]() $ {\mathbf{G}}_{\varphi } $
as
$ {\mathbf{G}}_{\varphi } $
as
![]() $ \mathrm{\mathbb{Q}} $
–algebraic groups has been completely worked out. These include Zarhin’s classification (Zarhin, Reference Zarhin1983) of the Hodge groups of K3 surfaces (see Example 5.3 for the corresponding Hodge representations), and Green–Griffiths–Kerr classification (Green et al., Reference Green, Griffiths and Kerr2012,
$ \mathrm{\mathbb{Q}} $
–algebraic groups has been completely worked out. These include Zarhin’s classification (Zarhin, Reference Zarhin1983) of the Hodge groups of K3 surfaces (see Example 5.3 for the corresponding Hodge representations), and Green–Griffiths–Kerr classification (Green et al., Reference Green, Griffiths and Kerr2012,
![]() $ \S $
7) for period domains
$ \S $
7) for period domains
![]() $ \mathcal{D} $
with Hodge numbers
$ \mathcal{D} $
with Hodge numbers
![]() $ \mathbf{h}=\left(2,2\right) $
and
$ \mathbf{h}=\left(2,2\right) $
and
![]() $ \mathbf{h}=\left(\mathrm{1,1,1,1}\right) $
.
$ \mathbf{h}=\left(\mathrm{1,1,1,1}\right) $
.
Green–Griffiths–Kerr (Green et al., Reference Green, Griffiths and Kerr2012) showed that the Hodge groups
![]() $ \mathbf{G}={\mathbf{G}}_{\varphi } $
and Mumford–Tate domains
$ \mathbf{G}={\mathbf{G}}_{\varphi } $
and Mumford–Tate domains
![]() $ D={D}_{\varphi} \subset {\mathcal{D}}_{\mathrm{h}} $
are in bijection with Hodge representations.
$ D={D}_{\varphi} \subset {\mathcal{D}}_{\mathrm{h}} $
are in bijection with Hodge representations.
![]() $ {S}^1\ \overset{\phi }{\to }\ \boldsymbol{G}(\mathrm{\mathbb{R}}), \mathbf{G} $
↪
$ {S}^1\ \overset{\phi }{\to }\ \boldsymbol{G}(\mathrm{\mathbb{R}}), \mathbf{G} $
↪
![]() $ \mathrm{Aut}\left(V, Q\right), $
.
$ \mathrm{Aut}\left(V, Q\right), $
.
with Hodge numbers
![]() $ {\mathbf{h}}_{\phi} \le \mathbf{h} $
. (Given
$ {\mathbf{h}}_{\phi} \le \mathbf{h} $
. (Given
![]() $ {\mathbf{h}}_1=\left({h}_1^{n,0},, {h}_1^{0,n}\right) $
and
$ {\mathbf{h}}_1=\left({h}_1^{n,0},, {h}_1^{0,n}\right) $
and
![]() $ {\mathbf{h}}_2=\left({h}_2^{n,0},, {h}_2^{0,n}\right) $
, we write
$ {\mathbf{h}}_2=\left({h}_2^{n,0},, {h}_2^{0,n}\right) $
, we write
![]() $ {\mathbf{h}}_1 \le {\mathbf{h}}_2 $
if
$ {\mathbf{h}}_1 \le {\mathbf{h}}_2 $
if
![]() $ {h}_1^{p,q} \le {h}_2^{p,q} $
for all
$ {h}_1^{p,q} \le {h}_2^{p,q} $
for all
![]() $ p, q. $
) Effectively one may say that the Hodge groups and Mumford–Tate domains are classified by the Hodge representations: given a fixed
$ p, q. $
) Effectively one may say that the Hodge groups and Mumford–Tate domains are classified by the Hodge representations: given a fixed
![]() $ \mathcal{D}={\mathcal{D}}_{\mathrm{h}} $
(with specified Hodge numbers
$ \mathcal{D}={\mathcal{D}}_{\mathrm{h}} $
(with specified Hodge numbers
![]() $ \mathbf{h} $
), one identifies all possible Hodge domains
$ \mathbf{h} $
), one identifies all possible Hodge domains
![]() $ D \subset \mathcal{D} $
by enumerating the Hodge representations with
$ D \subset \mathcal{D} $
by enumerating the Hodge representations with
![]() $ {\mathbf{h}}_{\phi} \le \mathbf{h} $
.
$ {\mathbf{h}}_{\phi} \le \mathbf{h} $
.
Remark 1.3. There are some obvious subdomains that can be identified without Hodge representations: (products of) period subdomains. If
![]() $ {\mathcal{D}}_i $
is the period domain for Hodge numbers
$ {\mathcal{D}}_i $
is the period domain for Hodge numbers
![]() $ {\mathbf{h}}_i $
and
$ {\mathbf{h}}_i $
and
![]() $ {\mathbf{h}}_1+\cdots +{\mathbf{h}}_{\mathrm{\ell}} \le \mathbf{h} $
, then
$ {\mathbf{h}}_1+\cdots +{\mathbf{h}}_{\mathrm{\ell}} \le \mathbf{h} $
, then
![]() $ {\mathcal{D}}_1\times \cdots \times {\mathcal{D}}_{\mathrm{\ell}} $
is a Mumford–Tate subdomain of
$ {\mathcal{D}}_1\times \cdots \times {\mathcal{D}}_{\mathrm{\ell}} $
is a Mumford–Tate subdomain of
![]() $ \mathcal{D} $
.
$ \mathcal{D} $
.
Green–Griffiths–Kerr’s characterization of the Hodge representations is formulated as Theorem 3.1, which asserts that the induced (real Lie algebra) Hodge representations
are enumerated by tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}^{\mathrm{ss}}, \mu, c\right) $
consisting of:
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}^{\mathrm{ss}}, \mu, c\right) $
consisting of:
-
(i) a semisimple complex Lie algebra
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}=\left[{\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}}\right] $
,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}=\left[{\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}}\right] $
, -
(ii) an element
 $ {\mathtt{E}}^{\mathrm{ss}}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
with the property that ad
$ {\mathtt{E}}^{\mathrm{ss}}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
with the property that ad
 $ {\mathtt{E}}^{\mathrm{ss}} $
acts on
$ {\mathtt{E}}^{\mathrm{ss}} $
acts on
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
diagonalizably with integer eigenvalues,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
diagonalizably with integer eigenvalues, -
(iii) a highest weight
 $ \mu $
of
$ \mu $
of
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
, and
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
, and -
(iv) a constant
 $ c\in \mathrm{\mathbb{Q}} $
satisfying
$ c\in \mathrm{\mathbb{Q}} $
satisfying
 $ \mu \left({\mathtt{E}}^{\mathrm{SS}}\right)+c\in \frac{1}{2}\mathrm{\mathbb{Z}} $
.
$ \mu \left({\mathtt{E}}^{\mathrm{SS}}\right)+c\in \frac{1}{2}\mathrm{\mathbb{Z}} $
.
The real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}}^{\mathrm{ss}} $
is the Lie algebra of the image
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}}^{\mathrm{ss}} $
is the Lie algebra of the image
![]() $ {G}_{\varphi}^{\mathrm{ad}} $
of
$ {G}_{\varphi}^{\mathrm{ad}} $
of
![]() $ \mathrm{Ad}:{G}_{\varphi}\to \mathrm{Aut}\left({\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right) $
. We have
$ \mathrm{Ad}:{G}_{\varphi}\to \mathrm{Aut}\left({\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right) $
. We have
![]() $ {D}_{\varphi }={G}_{\varphi}^{\mathrm{ad}}\cdot \varphi $
, and
$ {D}_{\varphi }={G}_{\varphi}^{\mathrm{ad}}\cdot \varphi $
, and
![]() $ {\mathtt{E}}^{\mathrm{ss}} $
is essentially equivalent to the isotropy group
$ {\mathtt{E}}^{\mathrm{ss}} $
is essentially equivalent to the isotropy group
![]() $ {\mathrm{Stab}}_{G_{\varphi}^{\mathrm{ad}}}\left(\varphi \right) $
.
$ {\mathrm{Stab}}_{G_{\varphi}^{\mathrm{ad}}}\left(\varphi \right) $
.
1.4. Examples and special cases
1.4.1. Horizontal Hodge domains
As discussed above (
![]() $ \S $
1.2) the identification of the horizontal subdomains is of particular interest. These are the domains that satisfy the infinitesimal period relation (IPR, a.k.a. Griffiths’ transversality). It is well-known that horizontal subdomains are necessarily Hermitian, and as such their structure as intrinsic homogeneous complex manifolds is classical and well-understood. These results are reviewed in
$ \S $
1.2) the identification of the horizontal subdomains is of particular interest. These are the domains that satisfy the infinitesimal period relation (IPR, a.k.a. Griffiths’ transversality). It is well-known that horizontal subdomains are necessarily Hermitian, and as such their structure as intrinsic homogeneous complex manifolds is classical and well-understood. These results are reviewed in
![]() $ \S $
3.2. The Hodge representations with horizontal
$ \S $
3.2. The Hodge representations with horizontal
![]() $ {D}_{\phi } $
are characterized in Proposition 3.7.
$ {D}_{\phi } $
are characterized in Proposition 3.7.
1.4.2. Weight two Hodge representations
In
![]() $ \S $
4 we apply the prescription of Theorem 3.1 to identify all Hodge representations and Mumford–Tate subdomains
$ \S $
4 we apply the prescription of Theorem 3.1 to identify all Hodge representations and Mumford–Tate subdomains
![]() $ D $
of the period domain
$ D $
of the period domain
![]() $ \mathcal{D} $
parameterizing
$ \mathcal{D} $
parameterizing
![]() $ Q $
–polarized, (effective) weight
$ Q $
–polarized, (effective) weight
![]() $ n=2 $
Hodge structures with
$ n=2 $
Hodge structures with
![]() $ {p}_g={h}^{2,0}=2 $
(Theorems 4.1, 4.3, 4.4 and Theorem 4.6). This period domain is chosen as our primary example for two reasons. First, it is in a certain sense the simplest example of a period domain that is not Hermitian symmetric. (The infinitesimal period relation is a contact subbundle of
$ {p}_g={h}^{2,0}=2 $
(Theorems 4.1, 4.3, 4.4 and Theorem 4.6). This period domain is chosen as our primary example for two reasons. First, it is in a certain sense the simplest example of a period domain that is not Hermitian symmetric. (The infinitesimal period relation is a contact subbundle of
![]() $ T\mathcal{D}. $
) Second, it is the period domain arising when considering families of Horikawa surfaces (Horikawa, Reference Horikawa1978; Reference Horikawa1978/79), in which there has been much interest recently (Franciosi et al., Reference Franciosi, Pardini and Rollenske2015; Reference Franciosi, Pardini and Rollenske2017; Pearlstein & Zhang, Reference Pearlstein and Zhang2019).
$ T\mathcal{D}. $
) Second, it is the period domain arising when considering families of Horikawa surfaces (Horikawa, Reference Horikawa1978; Reference Horikawa1978/79), in which there has been much interest recently (Franciosi et al., Reference Franciosi, Pardini and Rollenske2015; Reference Franciosi, Pardini and Rollenske2017; Pearlstein & Zhang, Reference Pearlstein and Zhang2019).
1.4.3. Hodge representations of Calabi–Yau type
Hodge representations of CY-type (those with first Hodge number
![]() $ {h}^{n,0}=1 $
) are of considerable interest and have been studied by several authors, including Friedman and Laza (Reference Friedman and Laza2013, Reference Friedman and Laza2014), Gross (Reference Gross1994), and Sheng and Zuo (Reference Sheng and Zuo2010). Much of this work is over
$ {h}^{n,0}=1 $
) are of considerable interest and have been studied by several authors, including Friedman and Laza (Reference Friedman and Laza2013, Reference Friedman and Laza2014), Gross (Reference Gross1994), and Sheng and Zuo (Reference Sheng and Zuo2010). Much of this work is over
![]() $ \mathrm{\mathbb{R}} $
, but Friedman and Laza (Reference Friedman and Laza2014) have identified some rational forms
$ \mathrm{\mathbb{R}} $
, but Friedman and Laza (Reference Friedman and Laza2014) have identified some rational forms
![]() $ {\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{Q}}\right) $
admitting Hodge representations of CY 3-fold type. In
$ {\mathbf{G}}_{\varphi}\left(\mathrm{\mathbb{Q}}\right) $
admitting Hodge representations of CY 3-fold type. In
![]() $ \S $
5 we classify the (Lie algebra) Hodge representations of CY-type (Theorem 5.2). The CY-Hodge representations with
$ \S $
5 we classify the (Lie algebra) Hodge representations of CY-type (Theorem 5.2). The CY-Hodge representations with
![]() $ D $
Hermitian are well- known, and those with
$ D $
Hermitian are well- known, and those with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
semisimple have been classified (Robles, Reference Robles2014, Proposition 6.1); so the content of Theorem 5.2 is to drop the hypothesis that
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
semisimple have been classified (Robles, Reference Robles2014, Proposition 6.1); so the content of Theorem 5.2 is to drop the hypothesis that
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
be semisimple from the classification. This result is used in Han (Reference Han2021) to enumerate the set of all Hodge representations of CY 3-fold type. Those with horizontal (and therefore Hermitian) domain
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
be semisimple from the classification. This result is used in Han (Reference Han2021) to enumerate the set of all Hodge representations of CY 3-fold type. Those with horizontal (and therefore Hermitian) domain
![]() $ D \subset \mathcal{D} $
are listed in Example 5.4, completing the classification begun in Friedman and Laza (Reference Friedman and Laza2013,
$ D \subset \mathcal{D} $
are listed in Example 5.4, completing the classification begun in Friedman and Laza (Reference Friedman and Laza2013,
![]() $ \S $
2.3).
$ \S $
2.3).
1.5. Acknowledgements
We thank the referees for their thoughtful comments and corrections.
2. Hodge representations
What follows is a laconic review of the necessary background material on Hodge representations. References for more detailed discussion include Green et al. (Reference Green, Griffiths and Kerr2012), Robles (Reference Robles2014,
![]() $ \S \S $
2–3) and Robles (Reference Robles2016,
$ \S \S $
2–3) and Robles (Reference Robles2016,
![]() $ \S \S $
2–3).
$ \S \S $
2–3).
2.1. Basics
Let
be the data of a (real) Hodge representation (Green et al., Reference Green, Griffiths and Kerr2012). Without loss of generality, we may suppose that the induced Lie algebra representation
is faithful. The associated Hodge decomposition
is the
![]() $ \phi $
–eigenspace decomposition; that is,
$ \phi $
–eigenspace decomposition; that is,
The associated grading element
![]() $ {\mathtt{E}}_{\phi}\in {\mathfrak{ig}}_{\mathrm{\mathbb{R}}} $
(or infinitesimal Hodge structure) (Robles, Reference Robles2014) is defined by
$ {\mathtt{E}}_{\phi}\in {\mathfrak{ig}}_{\mathrm{\mathbb{R}}} $
(or infinitesimal Hodge structure) (Robles, Reference Robles2014) is defined by
![]() $ {\mathtt{E}}_{\phi }(v)=\frac{1}{2}\left(p-q\right)v $
for all
$ {\mathtt{E}}_{\phi }(v)=\frac{1}{2}\left(p-q\right)v $
for all
![]() $ v\in {V}_{\phi}^{p,q} $
; that is,
$ v\in {V}_{\phi}^{p,q} $
; that is,
![]() $ {\mathtt{E}}_{\phi}\in \mathrm{End}\left({V}_{\mathrm{\mathbb{C}}}\right) $
is defined so that
$ {\mathtt{E}}_{\phi}\in \mathrm{End}\left({V}_{\mathrm{\mathbb{C}}}\right) $
is defined so that
![]() $ {V}_{\phi}^{p,q} $
is the
$ {V}_{\phi}^{p,q} $
is the
![]() $ {\mathtt{E}}_{\phi } $
–eigenspace with eigenvalue
$ {\mathtt{E}}_{\phi } $
–eigenspace with eigenvalue
![]() $ \frac{1}{2}\left(p-q\right) $
; for this reason it is sometimes convenient to write
$ \frac{1}{2}\left(p-q\right) $
; for this reason it is sometimes convenient to write
Remark 2.3. Together the grading element
![]() $ E $
and Lie algebra representation (2.2) determine the group representation (2.1) up to finite data.
$ E $
and Lie algebra representation (2.2) determine the group representation (2.1) up to finite data.
Definition 2.4. We call the pair
![]() $ \Big({\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
↪
$ \Big({\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
↪
![]() $ \mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right),\mathtt{E}\Big) $
the data of a real, Lie algebra Hodge representation (
$ \mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right),\mathtt{E}\Big) $
the data of a real, Lie algebra Hodge representation (
![]() $ \mathrm{\mathbb{R}} $
-LAHR).
$ \mathrm{\mathbb{R}} $
-LAHR).
Remark 2.5. A key point here is that a Hodge representation (2.1) determines a grading element
![]() $ {\mathtt{E}}_{\phi}\in {\mathfrak{ig}}_{\mathrm{\mathbb{R}}} $
. Conversely a complex reductive Lie algebra
$ {\mathtt{E}}_{\phi}\in {\mathfrak{ig}}_{\mathrm{\mathbb{R}}} $
. Conversely a complex reductive Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, a grading element
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, a grading element
![]() $ \mathtt{E}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
determines both a real form
$ \mathtt{E}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
determines both a real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
(
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
(
![]() $ \S $
2.3.2) and a Hodge representation (
$ \S $
2.3.2) and a Hodge representation (
![]() $ \S $
2.3.3).
$ \S $
2.3.3).
Notice that
![]() $ \phi $
is a level
$ \phi $
is a level
![]() $ n $
Hodge structure on
$ n $
Hodge structure on
![]() $ {V}_{\mathrm{\mathbb{R}}} $
if and only if the
$ {V}_{\mathrm{\mathbb{R}}} $
if and only if the
![]() $ {\mathtt{E}}_{\phi } $
–eigenspace decomposition is
$ {\mathtt{E}}_{\phi } $
–eigenspace decomposition is
Remark 2.7. The Hodge structure is of level zero (equivalently,
![]() $ {V}_{\mathrm{\mathbb{C}}}={V}_{\phi}^{0,0}\Big) $
if and only if
$ {V}_{\mathrm{\mathbb{C}}}={V}_{\phi}^{0,0}\Big) $
if and only if
![]() $ \phi $
is trivial. We assume this is not the case.
$ \phi $
is trivial. We assume this is not the case.
Remark 2.8 (Period domains). The Hodge domain
![]() $ D $
determined by (2.1) is a period domain if and only if
$ D $
determined by (2.1) is a period domain if and only if
![]() $ {G}_{\mathrm{\mathbb{R}}}=\mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
.
$ {G}_{\mathrm{\mathbb{R}}}=\mathrm{Aut}\left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
.
2.2. Induced Hodge representation
There is an induced Hodge representation on the Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
. Define
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
. Define
Then
is a weight zero Hodge structure on
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
that is polarized by
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
that is polarized by
![]() $ -\kappa $
, with
$ -\kappa $
, with
![]() $ \kappa $
the Killing form.
$ \kappa $
the Killing form.
The Jacobi identity implies
The subalgebra
is the complexification
![]() $ {\mathfrak{k}}_{\phi }{\otimes}_{\mathrm{\mathbb{R}}}\mathrm{\mathbb{C}} $
of the (unique) maximal compact subalgebra
$ {\mathfrak{k}}_{\phi }{\otimes}_{\mathrm{\mathbb{R}}}\mathrm{\mathbb{C}} $
of the (unique) maximal compact subalgebra
![]() $ {\mathfrak{k}}_{\phi} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
containing the Lie algebra
$ {\mathfrak{k}}_{\phi} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
containing the Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}}^0={\mathfrak{g}}_{\mathrm{\mathbb{R}}} \cap {\mathfrak{g}}_{\phi}^{0,0} $
of the stabilizer/centralizer
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}}^0={\mathfrak{g}}_{\mathrm{\mathbb{R}}} \cap {\mathfrak{g}}_{\phi}^{0,0} $
of the stabilizer/centralizer
![]() $ {G}_{\mathrm{\mathbb{R}}}^0 $
of
$ {G}_{\mathrm{\mathbb{R}}}^0 $
of
![]() $ \phi $
.
$ \phi $
.
2.3. Grading elements
Hodge structures are closely related to grading elements. This relationship is briefly reviewed here; see Robles (Reference Robles2014,
![]() $ \S \S $
2–3) and Robles (Reference Robles2016,
$ \S \S $
2–3) and Robles (Reference Robles2016,
![]() $ \S \S $
2–3) for details.
$ \S \S $
2–3) for details.
Remark 2.10. Here grading elements are essentially linearizations of the circle
![]() $ \phi :{S}^1 $
↪
$ \phi :{S}^1 $
↪
![]() $ {G}_{\mathrm{\mathbb{R}}} $
in the Hodge representation (2.1). The essential observation of this section is that the data
$ {G}_{\mathrm{\mathbb{R}}} $
in the Hodge representation (2.1). The essential observation of this section is that the data
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
determines the real form
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
determines the real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
, and the Hodge domain and compact dual
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
, and the Hodge domain and compact dual
![]() $ D \subset \check{D} $
(as intrinsic homogeneous spaces. They are not represented as subdomains of a period domain
$ D \subset \check{D} $
(as intrinsic homogeneous spaces. They are not represented as subdomains of a period domain
![]() $ \mathcal{D} $
until we select the second half
$ \mathcal{D} $
until we select the second half
![]() $ {G}_{\mathrm{\mathbb{R}}} $
↪ Aut
$ {G}_{\mathrm{\mathbb{R}}} $
↪ Aut
![]() $ \left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
of the Hodge representation (2.1)).
$ \left({V}_{\mathrm{\mathbb{R}}}, Q\right) $
of the Hodge representation (2.1)).
2.3.1. Definition
Fix a complex reductive Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. A grading element is any element
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. A grading element is any element
![]() $ \mathtt{E}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with the property that ad(E)
$ \mathtt{E}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with the property that ad(E)
![]() $ \in $
End
$ \in $
End
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}\right) $
acts diagonalizably on
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}\right) $
acts diagonalizably on
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with integer eigenvalues; that is,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with integer eigenvalues; that is,
Remark 2.12. The notation
![]() $ {\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
is meant to be suggestive. The grading element
$ {\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
is meant to be suggestive. The grading element
![]() $ \mathtt{E} $
determines a weight zero (real) Hodge decomposition that is polarized by
$ \mathtt{E} $
determines a weight zero (real) Hodge decomposition that is polarized by
![]() $ -\kappa $
, with
$ -\kappa $
, with
![]() $ \kappa $
the Killing form
$ \kappa $
the Killing form
![]() $ \left(\S \mathrm{2.3.3}\right) $
.
$ \left(\S \mathrm{2.3.3}\right) $
.
Remark 2.13. The data
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
determines a parabolic subgroup
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
determines a parabolic subgroup
![]() $ {P}_{\mathtt{E}} \subset {G}_{\mathrm{\mathbb{C}}} $
with Lie algebra
$ {P}_{\mathtt{E}} \subset {G}_{\mathrm{\mathbb{C}}} $
with Lie algebra
![]() $ {\mathfrak{p}}_{\mathtt{E}}={\oplus}_{\mathrm{\ell}\ge 0}{\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
. The resulting generalized grassmannian
$ {\mathfrak{p}}_{\mathtt{E}}={\oplus}_{\mathrm{\ell}\ge 0}{\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
. The resulting generalized grassmannian
![]() $ \check{D}={G}_{\mathrm{\mathbb{C}}}/{P}_{\mathtt{E}} $
(or rational homogeneous variety) is the compact dual of the Hodge domain (as an intrinsic homogeneous space).
$ \check{D}={G}_{\mathrm{\mathbb{C}}}/{P}_{\mathtt{E}} $
(or rational homogeneous variety) is the compact dual of the Hodge domain (as an intrinsic homogeneous space).
2.3.2. Grading elements versus real forms
Fix a complex reductive Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. Given
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. Given
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and
![]() $ \mathtt{E} $
, there is a unique real form
$ \mathtt{E} $
, there is a unique real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
of
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
of
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
such that (2.11) is a weight zero Hodge structure on
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
such that (2.11) is a weight zero Hodge structure on
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
that is polarized by
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
that is polarized by
![]() $ -\kappa $
(Robles, Reference Robles2016,
$ -\kappa $
(Robles, Reference Robles2016,
![]() $ \S $
3.1.2). The real form
$ \S $
3.1.2). The real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
is determined by the condition that
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
is determined by the condition that
![]() $ {\oplus}_{\mathrm{\ell}}{\mathfrak{g}}^{2\mathrm{\ell},-2\mathrm{\ell}} $
is the complexification
$ {\oplus}_{\mathrm{\ell}}{\mathfrak{g}}^{2\mathrm{\ell},-2\mathrm{\ell}} $
is the complexification
![]() $ {\mathfrak{k}}_{\mathrm{\mathbb{C}}} $
of a maximal compact subalgebra
$ {\mathfrak{k}}_{\mathrm{\mathbb{C}}} $
of a maximal compact subalgebra
![]() $ \mathfrak{k} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
.
$ \mathfrak{k} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
.
See
![]() $ \S $
3.2 for a discussion of the examples that are of the most interest here.
$ \S $
3.2 for a discussion of the examples that are of the most interest here.
2.3.3. Grading elements versus Hodge representations
Given the data of
![]() $ \S $
2.3.2, the grading element
$ \S $
2.3.2, the grading element
![]() $ \mathtt{E} $
acts on any representation
$ \mathtt{E} $
acts on any representation
![]() $ {G}_{\mathrm{\mathbb{R}}}\to $
Aut
$ {G}_{\mathrm{\mathbb{R}}}\to $
Aut
![]() $ \left({V}_{\mathrm{\mathbb{R}}}\right) $
by rational eigenvalues. The
$ \left({V}_{\mathrm{\mathbb{R}}}\right) $
by rational eigenvalues. The
![]() $ \mathtt{E} $
–eigenspace decomposition
$ \mathtt{E} $
–eigenspace decomposition
![]() $ {V}_{\mathrm{\mathbb{C}}}={\oplus}_{k\in \mathrm{\mathbb{Q}}}{V}_k $
is a Hodge decomposition (polarized by some
$ {V}_{\mathrm{\mathbb{C}}}={\oplus}_{k\in \mathrm{\mathbb{Q}}}{V}_k $
is a Hodge decomposition (polarized by some
![]() $ Q $
), with
$ Q $
), with
![]() $ {V}^{p,q}={V}_{\left(p-q\right)/2} $
as in
$ {V}^{p,q}={V}_{\left(p-q\right)/2} $
as in
![]() $ \S $
2.1, if and only if those eigenvalues lie in
$ \S $
2.1, if and only if those eigenvalues lie in
![]() $ \frac{1}{2}\mathrm{\mathbb{Z}} $
(Green et al., Reference Green, Griffiths and Kerr2012). The corresponding Hodge representation is given by the circle
$ \frac{1}{2}\mathrm{\mathbb{Z}} $
(Green et al., Reference Green, Griffiths and Kerr2012). The corresponding Hodge representation is given by the circle
![]() $ \phi :{S}^1\to {G}_{\mathrm{\mathbb{R}}} $
defined by
$ \phi :{S}^1\to {G}_{\mathrm{\mathbb{R}}} $
defined by
Note that
![]() $ \mathtt{E}={\mathtt{E}}_{\phi } $
.
$ \mathtt{E}={\mathtt{E}}_{\phi } $
.
2.3.4. Normalization of grading element
The Lie algebra
![]() $ \mathfrak{g} $
of
$ \mathfrak{g} $
of
![]() $ G $
is reductive. Let
$ G $
is reductive. Let
denote the decomposition of
![]() $ \mathfrak{g} $
into its center
$ \mathfrak{g} $
into its center
![]() $ \mathfrak{z} $
and semisimple factor
$ \mathfrak{z} $
and semisimple factor
![]() $ {\mathfrak{g}}^{\mathrm{SS}}=\left[\mathfrak{g}, \mathfrak{g}\right] $
. Let
$ {\mathfrak{g}}^{\mathrm{SS}}=\left[\mathfrak{g}, \mathfrak{g}\right] $
. Let
![]() $ \mathtt{E}={\mathtt{E}}^{\prime }+{\mathtt{E}}^{\mathrm{SS}} $
be the decomposition given by (2.14). The Hodge domain
$ \mathtt{E}={\mathtt{E}}^{\prime }+{\mathtt{E}}^{\mathrm{SS}} $
be the decomposition given by (2.14). The Hodge domain
![]() $ D $
is determined by
$ D $
is determined by
![]() $ {\mathfrak{g}}^{\mathrm{SS}} $
and
$ {\mathfrak{g}}^{\mathrm{SS}} $
and
![]() $ {\mathtt{E}}^{\mathrm{SS}} $
.
$ {\mathtt{E}}^{\mathrm{SS}} $
.
Fix a Cartan subalgebra
![]() $ \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
that contains
$ \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
that contains
![]() $ {\mathtt{E}}_{\phi } $
, is contained in
$ {\mathtt{E}}_{\phi } $
, is contained in
![]() $ {\mathfrak{g}}_{\phi}^{0,0} $
and that is defined over
$ {\mathfrak{g}}_{\phi}^{0,0} $
and that is defined over
![]() $ \mathrm{\mathbb{R}} $
. Then
$ \mathrm{\mathbb{R}} $
. Then
where
![]() $ {\mathfrak{h}}^{\mathrm{SS}}=\mathfrak{h}\cap {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
is a Cartan subalgebra of
$ {\mathfrak{h}}^{\mathrm{SS}}=\mathfrak{h}\cap {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
is a Cartan subalgebra of
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
. Choose simple roots
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
. Choose simple roots
![]() $ \left\{{\alpha}_1,,,,, , {\alpha}_r\right\}\in {\left({\mathfrak{h}}^{\mathrm{SS}}\right)}^{\ast } $
of
$ \left\{{\alpha}_1,,,,, , {\alpha}_r\right\}\in {\left({\mathfrak{h}}^{\mathrm{SS}}\right)}^{\ast } $
of
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
so that
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{SS}} $
so that
![]() $ {\alpha}_j\left({\mathtt{E}}^{\mathrm{ss}}\right) \ge 0 $
, for all
$ {\alpha}_j\left({\mathtt{E}}^{\mathrm{ss}}\right) \ge 0 $
, for all
![]() $ j $
. Without loss of generality, we may assume that
$ j $
. Without loss of generality, we may assume that
![]() $ {\alpha}_j\left(\mathtt{E}\right)\in \left\{0,1\right\} $
(Robles, Reference Robles2014, §3.3).Footnote
1 This is equivalent to the condition that the infinitesimal period relation
$ {\alpha}_j\left(\mathtt{E}\right)\in \left\{0,1\right\} $
(Robles, Reference Robles2014, §3.3).Footnote
1 This is equivalent to the condition that the infinitesimal period relation
![]() $ {T}^hD \subset TD $
is bracket–generating; equivalently,
$ {T}^hD \subset TD $
is bracket–generating; equivalently,
![]() $ {\mathfrak{g}}^{1,-1} $
generates
$ {\mathfrak{g}}^{1,-1} $
generates
![]() $ {\mathfrak{g}}^{+,-}={\oplus}_{\mathrm{\ell}>0}{\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
as a Lie algebra.
$ {\mathfrak{g}}^{+,-}={\oplus}_{\mathrm{\ell}>0}{\mathfrak{g}}^{\mathrm{\ell},-\mathrm{\ell}} $
as a Lie algebra.
2.4. Reduction to irreducible
![]() $ V $
. If
$ V $
. If
![]() $ {V}_{\mathrm{\mathbb{R}}}={V}_1\oplus {V}_2 $
is reducible as a real representation, then the associated domain
$ {V}_{\mathrm{\mathbb{R}}}={V}_1\oplus {V}_2 $
is reducible as a real representation, then the associated domain
![]() $ D $
factors
$ D $
factors
![]() $ D={D}_1\times {D}_2 $
into the product of the domains
$ D={D}_1\times {D}_2 $
into the product of the domains
![]() $ {D}_i $
for the
$ {D}_i $
for the
![]() $ {V}_i $
. So without loss of generality we may assume that
$ {V}_i $
. So without loss of generality we may assume that
![]() $ {V}_{\mathrm{\mathbb{R}}} $
is irreducible.Footnote
2 The Schur lemma (and our hypothesis that (2.2) is faithful) implies
$ {V}_{\mathrm{\mathbb{R}}} $
is irreducible.Footnote
2 The Schur lemma (and our hypothesis that (2.2) is faithful) implies
Remark 2.16. Note that
![]() $ \mathfrak{z}= $
span
$ \mathfrak{z}= $
span
![]() $ \left\{{\mathtt{E}}^{\prime}\right\} $
, so that
$ \left\{{\mathtt{E}}^{\prime}\right\} $
, so that
![]() $ \mathfrak{g}={\mathfrak{g}}^{\mathrm{SS}} $
if and only if
$ \mathfrak{g}={\mathfrak{g}}^{\mathrm{SS}} $
if and only if
![]() $ {\mathtt{E}}^{\prime }=0 $
.
$ {\mathtt{E}}^{\prime }=0 $
.
Given an irreducible real representation
![]() $ {V}_{\mathrm{\mathbb{R}}} $
there exists a (unique) irreducible representation
$ {V}_{\mathrm{\mathbb{R}}} $
there exists a (unique) irreducible representation
![]() $ U $
of
$ U $
of
![]() $ {G}_{\mathrm{\mathbb{C}}} $
such that one of the following holds:
$ {G}_{\mathrm{\mathbb{C}}} $
such that one of the following holds:
 $$ {V}_{\mathrm{\mathbb{R}}}\otimes \mathrm{\mathbb{C}}=\left\{\begin{array}{ll}U \mathrm{and} U={U}^{\ast }& \left(U \mathrm{is} real \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right),\\ {}U\oplus {U}^{\ast} \mathrm{and} U\ne {U}^{\ast }& \left(U \mathrm{is} complex \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right),\\ {}U\oplus {U}^{\ast} \mathrm{and} U={U}^{\ast }& \left(U \mathrm{is} quaternionic \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right).\end{array}\right. $$
$$ {V}_{\mathrm{\mathbb{R}}}\otimes \mathrm{\mathbb{C}}=\left\{\begin{array}{ll}U \mathrm{and} U={U}^{\ast }& \left(U \mathrm{is} real \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right),\\ {}U\oplus {U}^{\ast} \mathrm{and} U\ne {U}^{\ast }& \left(U \mathrm{is} complex \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right),\\ {}U\oplus {U}^{\ast} \mathrm{and} U={U}^{\ast }& \left(U \mathrm{is} quaternionic \mathrm{w}.\mathrm{r}. \mathrm{t}. {\mathfrak{g}}_{\mathrm{\mathbb{R}}}\right).\end{array}\right. $$
Let
![]() $ \mu, {\mu}^{\ast}\in {\mathfrak{h}}^{\ast } $
denote the highest weights of
$ \mu, {\mu}^{\ast}\in {\mathfrak{h}}^{\ast } $
denote the highest weights of
![]() $ U $
and
$ U $
and
![]() $ {U}^{\ast } $
respectively. When we wish to emphasize the highest weight of
$ {U}^{\ast } $
respectively. When we wish to emphasize the highest weight of
![]() $ U $
, we will write
$ U $
, we will write
![]() $ U={U}_{\mu } $
.
$ U={U}_{\mu } $
.
Remark 2.18 (Period domains). In this case of Remark 2.8, we have
![]() $ {V}_{\mathrm{\mathbb{C}}}={U}_{\omega_1} $
, with
$ {V}_{\mathrm{\mathbb{C}}}={U}_{\omega_1} $
, with
![]() $ \mu ={\omega}_1 $
the first fundamental weight.
$ \mu ={\omega}_1 $
the first fundamental weight.
Remark 2.19. It follows from Remark 2.16 that action of the center
![]() $ \mathfrak{z} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
on
$ \mathfrak{z} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
on
![]() $ {V}_{\mathrm{\mathbb{R}}} $
is determined by the action of
$ {V}_{\mathrm{\mathbb{R}}} $
is determined by the action of
![]() $ {\mathtt{E}}^{\prime } $
The latter acts on
$ {\mathtt{E}}^{\prime } $
The latter acts on
![]() $ U $
by scalar multiplication by
$ U $
by scalar multiplication by
![]() $ c=\mu \left({\mathtt{E}}^{\prime}\right)\in \mathrm{\mathbb{Q}} $
. In particular,
$ c=\mu \left({\mathtt{E}}^{\prime}\right)\in \mathrm{\mathbb{Q}} $
. In particular,
![]() $ \mathfrak{z}\ne 0 $
if and only if
$ \mathfrak{z}\ne 0 $
if and only if
![]() $ c\ne 0 $
. Moreover,
$ c\ne 0 $
. Moreover,
![]() $ {\mathtt{E}}^{\prime } $
necessarily acts on the dual by
$ {\mathtt{E}}^{\prime } $
necessarily acts on the dual by
![]() $ -c={\mu}^{\ast}\left({\mathtt{E}}^{\prime}\right) $
. So
$ -c={\mu}^{\ast}\left({\mathtt{E}}^{\prime}\right) $
. So
![]() $ \mu \ne {\mu}^{\ast }, $
and
$ \mu \ne {\mu}^{\ast }, $
and
![]() $ U $
is complex with respect to
$ U $
is complex with respect to
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
whenever
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
whenever
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
has a nontrivial center
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
has a nontrivial center
![]() $ \left(\mathfrak{z}\ne 0\right) $
.
$ \left(\mathfrak{z}\ne 0\right) $
.
2.5. Real, complex and quaternionic representations
Note that
![]() $ U $
is complex if and only if
$ U $
is complex if and only if
![]() $ \mu \ne {\mu}^{\ast } $
By Remark 2.19, this is always the case when
$ \mu \ne {\mu}^{\ast } $
By Remark 2.19, this is always the case when
![]() $ \mathfrak{z}\ne 0 $
; equivalently,
$ \mathfrak{z}\ne 0 $
; equivalently,
![]() $ \mathfrak{g}\ne {\mathfrak{g}}^{\mathrm{SS}} $
. When
$ \mathfrak{g}\ne {\mathfrak{g}}^{\mathrm{SS}} $
. When
![]() $ \mathfrak{z}=0 \left(\mathrm{equivalently}, \mathfrak{g} ={\mathfrak{g}}^{\mathrm{SS}} \mathrm{is} \mathrm{semisimple}\right) $
the real and quaternionic representations may be distinguished as follows. Recall the conventions of
$ \mathfrak{z}=0 \left(\mathrm{equivalently}, \mathfrak{g} ={\mathfrak{g}}^{\mathrm{SS}} \mathrm{is} \mathrm{semisimple}\right) $
the real and quaternionic representations may be distinguished as follows. Recall the conventions of
![]() $ \S $
2.3.4, and let
$ \S $
2.3.4, and let
![]() $ \left\{{\mathrm{A}}^1,, {\mathrm{A}}^r\right\} \subset {\mathfrak{h}}^{\mathrm{ss}} $
be the basis dual to the simple roots
$ \left\{{\mathrm{A}}^1,, {\mathrm{A}}^r\right\} \subset {\mathfrak{h}}^{\mathrm{ss}} $
be the basis dual to the simple roots
![]() $ \left\{{\alpha}_1,,{\alpha}_r\right\} $
. Then
$ \left\{{\alpha}_1,,{\alpha}_r\right\} $
. Then
Define
 $$ {\mathtt{T}}_{\phi}:= 2\sum \limits_{\alpha_i\left({\mathtt{E}}_{\phi}^{\mathrm{ss}}\right)=0}{\mathrm{A}}^i. $$
$$ {\mathtt{T}}_{\phi}:= 2\sum \limits_{\alpha_i\left({\mathtt{E}}_{\phi}^{\mathrm{ss}}\right)=0}{\mathrm{A}}^i. $$
If
![]() $ \mu ={\mu}^{\ast } $
, then
$ \mu ={\mu}^{\ast } $
, then
![]() $ U $
is real if and only if
$ U $
is real if and only if
![]() $ \mu \left({\mathtt{T}}_{\phi}\right) $
is even, and is quaternionic if and only if
$ \mu \left({\mathtt{T}}_{\phi}\right) $
is even, and is quaternionic if and only if
![]() $ \mu \left({\mathtt{T}}_{\phi}\right) $
is odd (Green et al., Reference Green, Griffiths and Kerr2012).
$ \mu \left({\mathtt{T}}_{\phi}\right) $
is odd (Green et al., Reference Green, Griffiths and Kerr2012).
2.6. Eigenvalues and level of the Hodge structure
Set
Then the nontrivial eigenvalues of
![]() $ {\mathtt{E}}_{\phi } $
on
$ {\mathtt{E}}_{\phi } $
on
![]() $ U $
are
$ U $
are
Equation (2.6) implies
The Hodge structure
![]() $ \phi $
on
$ \phi $
on
![]() $ {V}_{\mathrm{\mathbb{R}}} $
is of level
$ {V}_{\mathrm{\mathbb{R}}} $
is of level
2.7. Reductive versus semisimple
Let
![]() $ \left({\mathrm{g}}_{\mathrm{\mathbb{C}}}, {\mathrm{E}}_{\phi }, \mu \right) $
be a triple underlying a Hodge representation;
$ \left({\mathrm{g}}_{\mathrm{\mathbb{C}}}, {\mathrm{E}}_{\phi }, \mu \right) $
be a triple underlying a Hodge representation;
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is a complex reductive Lie algebra,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is a complex reductive Lie algebra,
![]() $ {\mathtt{E}}_{\phi}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is a grading element (determining a real form
$ {\mathtt{E}}_{\phi}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is a grading element (determining a real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
,
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
,
![]() $ \S $
2.3.2), and
$ \S $
2.3.2), and
![]() $ \mu $
is the highest weight of an irreducible
$ \mu $
is the highest weight of an irreducible
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
–module
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
–module
![]() $ U={U}_{\mu } $
. The purpose of this section is to observe that such triples are equivalent to tuples
$ U={U}_{\mu } $
. The purpose of this section is to observe that such triples are equivalent to tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}_{\phi}^{\mathrm{ss}}, {\mu}^{\mathrm{ss}}, c\right) $
with
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}_{\phi}^{\mathrm{ss}}, {\mu}^{\mathrm{ss}}, c\right) $
with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
a complex semisimple Lie algebra,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
a complex semisimple Lie algebra,
![]() $ {\mathtt{E}}_{\phi}^{\mathrm{ss}}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
a grading element,
$ {\mathtt{E}}_{\phi}^{\mathrm{ss}}\in {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
a grading element,
![]() $ {\mu}^{\mathrm{ss}} $
the highest weight of an irreducible
$ {\mu}^{\mathrm{ss}} $
the highest weight of an irreducible
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
–module, and
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
–module, and
![]() $ c\in \mathrm{\mathbb{Q}} $
.
$ c\in \mathrm{\mathbb{Q}} $
.
Recall the notations of
![]() $ \S $
2.3.4. As discussed in Remark 2.19, the central factor
$ \S $
2.3.4. As discussed in Remark 2.19, the central factor
![]() $ {\mathtt{E}}_{\phi}^{\prime } $
acts on the irreducible
$ {\mathtt{E}}_{\phi}^{\prime } $
acts on the irreducible
![]() $ U $
by a scalar
$ U $
by a scalar
and on
![]() $ {U}^{\ast } $
by
$ {U}^{\ast } $
by
![]() $ -c $
. It follows that
$ -c $
. It follows that
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathtt{E}}_{\phi }, \mu \right) $
and
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathtt{E}}_{\phi }, \mu \right) $
and
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}_{\phi}^{\mathrm{ss}}, {\mu}^{\mathrm{ss}}, c\right) $
carry the same data. (Here
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}}, {\mathtt{E}}_{\phi}^{\mathrm{ss}}, {\mu}^{\mathrm{ss}}, c\right) $
carry the same data. (Here
![]() $ {\left.{\mu}^{\mathrm{ss}}=\mu \right|}_{{\mathfrak{h}}^{\mathrm{ss}}} $
is the highest weight of
$ {\left.{\mu}^{\mathrm{ss}}=\mu \right|}_{{\mathfrak{h}}^{\mathrm{ss}}} $
is the highest weight of
![]() $ U $
as a
$ U $
as a
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
–module.)
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
–module.)
As noted in Remark 2.19,
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
is semisimple if and only if
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
is semisimple if and only if
![]() $ c=0 $
.
$ c=0 $
.
The remainder of this section is devoted to discussing the relationship between the
![]() $ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
$ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
![]() $ U $
and the Hodge decomposition (
$ U $
and the Hodge decomposition (
![]() $ \S $
2.1) of
$ \S $
2.1) of
![]() $ {V}_{\mathrm{\mathbb{R}}} $
.
$ {V}_{\mathrm{\mathbb{R}}} $
.
Let
be the
![]() $ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
$ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
![]() $ U $
. We have
$ U $
. We have
Likewise, the
![]() $ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
$ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenspace decomposition of
![]() $ {U}^{\ast } $
is
$ {U}^{\ast } $
is
It is a general fact from representation theory that
![]() $ \mu \left({\mathtt{E}}_{\phi}^{\mathrm{SS}}\right) $
and
$ \mu \left({\mathtt{E}}_{\phi}^{\mathrm{SS}}\right) $
and
![]() $ -{\mu}^{\ast}\left({\mathtt{E}}_{\phi}^{\mathrm{SS}}\right) $
are both elements of
$ -{\mu}^{\ast}\left({\mathtt{E}}_{\phi}^{\mathrm{SS}}\right) $
are both elements of
![]() $ \mathrm{\mathbb{Q}}, $
and any two nontrivial
$ \mathrm{\mathbb{Q}}, $
and any two nontrivial
![]() $ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenvalues of
$ {\mathtt{E}}_{\phi}^{\mathrm{ss}} $
–eigenvalues of
![]() $ U $
differ by an integer.
$ U $
differ by an integer.
-
(a) If
 $ {U}_{\mu } $
is real, then
$ {U}_{\mu } $
is real, then
 $ \mu ={\mu}^{\ast } $
and
$ \mu ={\mu}^{\ast } $
and
 $ {V}_{\mathrm{\mathbb{C}}}={U}_{\mu } $
imply that
$ {V}_{\mathrm{\mathbb{C}}}={U}_{\mu } $
imply that
 $ c=0 $
and
$ c=0 $
and $$ {V}^{p,q}={U}_{\left(p-q\right)/2}. $$
$$ {V}^{p,q}={U}_{\left(p-q\right)/2}. $$
(In this case, we have
 $ \mathfrak{z}=0 $
.)
$ \mathfrak{z}=0 $
.) -
(b) If
 $ U $
is complex or quaternionic, then
$ U $
is complex or quaternionic, then $$ {V}^{p,q}={U}_{\left(p-q\right)/2-c}\oplus {U}_{\left(p-q\right)/2+c}^{\ast }. $$
$$ {V}^{p,q}={U}_{\left(p-q\right)/2-c}\oplus {U}_{\left(p-q\right)/2+c}^{\ast }. $$
Remark 2.21. From (2.20), we see that the number of nontrivial
![]() $ \mathtt{E} $
–eigenvalues for
$ \mathtt{E} $
–eigenvalues for
![]() $ {U}_{\mu } $
is precisely
$ {U}_{\mu } $
is precisely
![]() $ e\left(\mu, \mathtt{E}\right)=\left(\mu +{\mu}^{\ast}\right)\left(\mathtt{E}\right)+1 $
. By (2.6) and (2.17), we have
$ e\left(\mu, \mathtt{E}\right)=\left(\mu +{\mu}^{\ast}\right)\left(\mathtt{E}\right)+1 $
. By (2.6) and (2.17), we have
![]() $ e\left(\mu, \mathtt{E}\right) \le n+1 $
. And by Remark 2.7,
$ e\left(\mu, \mathtt{E}\right) \le n+1 $
. And by Remark 2.7,
![]() $ e\left(\mu, \mathtt{E}\right) \ge 2 $
. Thus
$ e\left(\mu, \mathtt{E}\right) \ge 2 $
. Thus
3. Identification of Hodge domains: general strategy
3.1. Main result
Given a complex semisimple Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with Cartan subalgebra
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
with Cartan subalgebra
![]() $ \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, and irreducible
$ \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, and irreducible
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
–representation
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
–representation
![]() $ U $
and a rational number
$ U $
and a rational number
![]() $ c\in \mathrm{\mathbb{Q}} $
, let
$ c\in \mathrm{\mathbb{Q}} $
, let
![]() $ {\mathtt{E}}^{\prime }= c $
Id
$ {\mathtt{E}}^{\prime }= c $
Id
![]() $ \in $
End
$ \in $
End
![]() $ (U) $
be the operator acting on
$ (U) $
be the operator acting on
![]() $ U $
by scalar multiplication. We specify that
$ U $
by scalar multiplication. We specify that
![]() $ {\mathtt{E}}^{\prime }=-c $
Id
$ {\mathtt{E}}^{\prime }=-c $
Id
![]() $ \in $
End
$ \in $
End
![]() $ \left({U}^{\ast}\right) $
act by
$ \left({U}^{\ast}\right) $
act by
![]() $ -c $
on the dual representation. Then
$ -c $
on the dual representation. Then
is a reductive Lie algebra (semisimple if
![]() $ c=0 $
), with semisimple factor
$ c=0 $
), with semisimple factor
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and center
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and center
![]() $ \mathfrak{z} $
spanned by
$ \mathfrak{z} $
spanned by
![]() $ {\mathtt{E}}^{\prime } $
(We are essentially making a change of notation here, replacing the reductive/semisimple pair
$ {\mathtt{E}}^{\prime } $
(We are essentially making a change of notation here, replacing the reductive/semisimple pair
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
of the previous sections with (possibly) reductive/semisimple pair
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\mathrm{ss}} $
of the previous sections with (possibly) reductive/semisimple pair
![]() $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. This is done for notational simplicity: it is cleaner to drop the
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{C}}}, {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
. This is done for notational simplicity: it is cleaner to drop the
![]() $ {}^{\mathrm{ss}} $
superscript.)
$ {}^{\mathrm{ss}} $
superscript.)
The upshot of the discussions in
![]() $ \S \S $
2.3–2.7 is.
$ \S \S $
2.3–2.7 is.
Theorem 3.1 (Green–Griffiths–Kerr [Green et al., Reference Green, Griffiths and Kerr2012]). In order to identify the Hodge representations (2.1) with specified Hodge numbers
![]() $ \mathbf{h}=\left({h}^{n,0},\dots, {h}^{0,n}\right) $
, it suffices to identify tuples
$ \mathbf{h}=\left({h}^{n,0},\dots, {h}^{0,n}\right) $
, it suffices to identify tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
consisting of a complex semisimple Lie algebra
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
consisting of a complex semisimple Lie algebra
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, a grading element
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
, a grading element
![]() $ \mathtt{E}\in \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
(as in
$ \mathtt{E}\in \mathfrak{h} \subset {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
(as in
![]() $ \S $
2.3.2 and
$ \S $
2.3.2 and
![]() $ \S $
2.3.4), the highest weight
$ \S $
2.3.4), the highest weight
![]() $ \mu \in {\mathfrak{h}}^{\ast } $
of an a irreducible
$ \mu \in {\mathfrak{h}}^{\ast } $
of an a irreducible
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
– module
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
– module
![]() $ U $
, and
$ U $
, and
![]() $ c\in \mathrm{\mathbb{Q}} $
that satisfy the following conditions:
$ c\in \mathrm{\mathbb{Q}} $
that satisfy the following conditions:
![]() $ m;=\mu \left(\mathtt{E}\right)+c\in \frac{1}{2}\mathrm{\mathbb{Z}} $
, and the irreducible representation
$ m;=\mu \left(\mathtt{E}\right)+c\in \frac{1}{2}\mathrm{\mathbb{Z}} $
, and the irreducible representation
![]() $ {V}_{\mathrm{\mathbb{R}}} $
$ {V}_{\mathrm{\mathbb{R}}} $
![]() $ \left(\S 2.4\right) $
of the real form
$ \left(\S 2.4\right) $
of the real form
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
determined by
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
determined by
![]() $ \mathtt{E} $
(
$ \mathtt{E} $
(
![]() $ \S $
2.3.2) has
$ \S $
2.3.2) has
![]() $ \left(\mathtt{E}+{\mathtt{E}}^{\prime}\right) $
–eigenspace decomposition of the form (2.6) with
$ \left(\mathtt{E}+{\mathtt{E}}^{\prime}\right) $
–eigenspace decomposition of the form (2.6) with
![]() $ \dim {V}_{\left(p-q\right)/2}={h}^{p,q} $
.
$ \dim {V}_{\left(p-q\right)/2}={h}^{p,q} $
.
Example 3.2 (Period domains). The domain
![]() $ {D}_{\phi } $
is a period domain if and only if the tuple
$ {D}_{\phi } $
is a period domain if and only if the tuple
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
is of one of the following two forms:
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
is of one of the following two forms:
-
(i)
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sp}}_{2r}\mathrm{\mathbb{C}};\mu ={\omega}_1 $
, so that
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sp}}_{2r}\mathrm{\mathbb{C}};\mu ={\omega}_1 $
, so that
 $ U={\mathrm{\mathbb{C}}}^{2r} $
is the standard representation;
$ U={\mathrm{\mathbb{C}}}^{2r} $
is the standard representation;
 $ {\alpha}_r\left(\mathtt{E}\right)=1 $
and
$ {\alpha}_r\left(\mathtt{E}\right)=1 $
and
 $ c=0. $
$ c=0. $
-
(ii)
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{so}}_m\mathrm{\mathbb{C}};\mu ={\omega}_1 $
, so that
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{so}}_m\mathrm{\mathbb{C}};\mu ={\omega}_1 $
, so that
 $ U={\mathrm{\mathbb{C}}}^m $
is the standard representation; and
$ U={\mathrm{\mathbb{C}}}^m $
is the standard representation; and
 $ c=0 $
. If
$ c=0 $
. If
 $ m=2r $
is even, then we also have
$ m=2r $
is even, then we also have
 $ \left({\alpha}_{r-1}+{\alpha}_r\right)\left(\mathtt{E}\right)\in \left\{0,2\right\} $
.
$ \left({\alpha}_{r-1}+{\alpha}_r\right)\left(\mathtt{E}\right)\in \left\{0,2\right\} $
.
Example 3.3 (Weight
![]() $ n=1 $
). The weight
$ n=1 $
). The weight
![]() $ n=1 $
Hodge representations are well understood (Deligne, Reference Deligne1979; Milne, Reference Milne2005). The corresponding tuples
$ n=1 $
Hodge representations are well understood (Deligne, Reference Deligne1979; Milne, Reference Milne2005). The corresponding tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
are.
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
are.
-
(i)
 $ \left({\mathfrak{sp}}_{2r}\mathrm{\mathbb{C}}, {\mathrm{A}}^r, {\omega}_1,0\right) $
, with
$ \left({\mathfrak{sp}}_{2r}\mathrm{\mathbb{C}}, {\mathrm{A}}^r, {\omega}_1,0\right) $
, with
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}={\mathfrak{sp}}_{2r}\mathrm{\mathbb{R}} $
. The corresponding Hodge domain
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}={\mathfrak{sp}}_{2r}\mathrm{\mathbb{R}} $
. The corresponding Hodge domain
 $ D $
is the period domain
$ D $
is the period domain
 $ \mathcal{D} $
parameterizing polarized Hodge structures with
$ \mathcal{D} $
parameterizing polarized Hodge structures with
 $ \mathbf{h}=\left(r, r\right) $
.
$ \mathbf{h}=\left(r, r\right) $
. -
(ii)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_i, \frac{i}{r+1}-\frac{1}{2}\right) $
, with
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_i, \frac{i}{r+1}-\frac{1}{2}\right) $
, with
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{su}\left(1, r\right) $
if
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{su}\left(1, r\right) $
if
 $ 2i=r+1 $
, and
$ 2i=r+1 $
, and
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}=\mathrm{u}\left(1, r\right) $
otherwise.
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}=\mathrm{u}\left(1, r\right) $
otherwise. -
(iii)
 $ \left({\mathfrak{sl}}_{a+b}\mathrm{\mathbb{C}}, {\mathrm{A}}^a, {\omega}_1, \frac{1}{2}-\frac{b}{a+b}\right) $
, with
$ \left({\mathfrak{sl}}_{a+b}\mathrm{\mathbb{C}}, {\mathrm{A}}^a, {\omega}_1, \frac{1}{2}-\frac{b}{a+b}\right) $
, with
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{su}\left(a, a\right) $
if
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{su}\left(a, a\right) $
if
 $ a=b $
, and
$ a=b $
, and
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}=\mathfrak{u}\left(a, b\right) $
otherwise.
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}=\mathfrak{u}\left(a, b\right) $
otherwise. -
(iv)
 $ \left({\mathfrak{so}}_{m+2}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_r, 0\right) $
, with
$ \left({\mathfrak{so}}_{m+2}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_r, 0\right) $
, with
 $ m+2\in \left\{2r, 2r+1\right\} $
and
$ m+2\in \left\{2r, 2r+1\right\} $
and
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{so}\left(2, m\right) $
.
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{g}}_{\mathrm{\mathbb{R}}}=\mathfrak{so}\left(2, m\right) $
. -
(v)
 $ \left({\mathfrak{so}}_{2r}\mathrm{\mathbb{C}}, {\mathrm{A}}^r, {\omega}_1,0\right) $
, with
$ \left({\mathfrak{so}}_{2r}\mathrm{\mathbb{C}}, {\mathrm{A}}^r, {\omega}_1,0\right) $
, with
 $ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{so}}^{\ast }(2r) $
.
$ {\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\tilde{\mathfrak{g}}}_{\mathrm{\mathbb{R}}}={\mathfrak{so}}^{\ast }(2r) $
.
Remark 3.4. Note that the two tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
and
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
and
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, {\mu}^{\ast }, -c\right) $
determine the same Hodge representation (
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, {\mu}^{\ast }, -c\right) $
determine the same Hodge representation (
![]() $ \S \S $
2.4 & 2.7).
$ \S \S $
2.4 & 2.7).
Remark 3.5. One consequence of Remark 1.3 is that in any particular example – that is, the case of a fixed period domain
![]() $ \mathcal{D} $
with specified Hodge numbers
$ \mathcal{D} $
with specified Hodge numbers
![]() $ \mathbf{h} $
– it suffices to identify the irreducible Hodge domains
$ \mathbf{h} $
– it suffices to identify the irreducible Hodge domains
![]() $ D $
with Hodge numbers
$ D $
with Hodge numbers
![]() $ {\mathbf{h}}^{\prime} \le \mathbf{h} $
. For example, in
$ {\mathbf{h}}^{\prime} \le \mathbf{h} $
. For example, in
![]() $ \S $
4, where we consider the case that
$ \S $
4, where we consider the case that
![]() $ \mathbf{h}=\left(2, {h}^{1,1},2\right) $
, it will suffice to consider the two cases that
$ \mathbf{h}=\left(2, {h}^{1,1},2\right) $
, it will suffice to consider the two cases that
![]() $ {h}^{\prime }=\left(1, h, 1\right) $
and
$ {h}^{\prime }=\left(1, h, 1\right) $
and
![]() $ {h}^{\prime }=\left(2, h, 2\right) $
with
$ {h}^{\prime }=\left(2, h, 2\right) $
with
![]() $ h \le {h}^{1,1} $
.
$ h \le {h}^{1,1} $
.
3.2. Horizontal Hodge domains
Theorem 3.1 identifies all the Hodge subdomains
![]() $ D $
of the period domain
$ D $
of the period domain
![]() $ {\mathcal{D}}_{\mathrm{h}} $
. We are especially interested in the horizontal subdomains, which are necessarily Hermitian. These are the domains that satisfy the infinitesimal period relation (IPR, a.k.a. Griffiths’ transversality). These distinguished subdomains may be identified as follows.
$ {\mathcal{D}}_{\mathrm{h}} $
. We are especially interested in the horizontal subdomains, which are necessarily Hermitian. These are the domains that satisfy the infinitesimal period relation (IPR, a.k.a. Griffiths’ transversality). These distinguished subdomains may be identified as follows.
It is a consequence of the normalization in
![]() $ \S $
2.3.4 that the Hodge subdomain
$ \S $
2.3.4 that the Hodge subdomain
![]() $ D \subset \mathcal{D} $
is horizontal if and only if the induced Hodge decomposition (2.9) is of the form
$ D \subset \mathcal{D} $
is horizontal if and only if the induced Hodge decomposition (2.9) is of the form
that is,
![]() $ {\mathfrak{g}}_{\phi}^{\mathrm{\ell},-\mathrm{\ell}}=0 $
for all
$ {\mathfrak{g}}_{\phi}^{\mathrm{\ell},-\mathrm{\ell}}=0 $
for all
![]() $ \mid \mathrm{\ell}\mid \ge 2 $
, cf. Čap and Slovák (Reference Čap and Slovák2009) and Robles (Reference Robles2014,
$ \mid \mathrm{\ell}\mid \ge 2 $
, cf. Čap and Slovák (Reference Čap and Slovák2009) and Robles (Reference Robles2014,
![]() $ \S \S $
2–3). This is a condition on the grading element:
$ \S \S $
2–3). This is a condition on the grading element:
where
![]() $ \tilde{\alpha} $
is the highest root. All such domains are necessarily Hermitian symmetric.
$ \tilde{\alpha} $
is the highest root. All such domains are necessarily Hermitian symmetric.
For the simple, complex Lie groups
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
the set of all such grading elements (see
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
the set of all such grading elements (see
![]() $ \S $
2.5 for notation), the corresponding compact duals Ď, the real forms
$ \S $
2.5 for notation), the corresponding compact duals Ď, the real forms
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
, and the maximal compact subalgebra
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
, and the maximal compact subalgebra
![]() $ \mathfrak{k} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
are listed in Table 3.1. Here Gr
$ \mathfrak{k} \subset {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
are listed in Table 3.1. Here Gr
![]() $ \left(a, {\mathrm{\mathbb{C}}}^{a+b}\right) $
is the grassmannian of
$ \left(a, {\mathrm{\mathbb{C}}}^{a+b}\right) $
is the grassmannian of
![]() $ a $
–plane in
$ a $
–plane in
![]() $ {\mathrm{\mathbb{C}}}^{a+b}, {\mathcal{Q}}^d \subset {\mathrm{\mathbb{P}}}^{d+1} $
is the quadric hypersurface, and
$ {\mathrm{\mathbb{C}}}^{a+b}, {\mathcal{Q}}^d \subset {\mathrm{\mathbb{P}}}^{d+1} $
is the quadric hypersurface, and
![]() $ {\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right) $
is the Lagrangian grassmannian of
$ {\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right) $
is the Lagrangian grassmannian of
![]() $ Q $
–isotropic
$ Q $
–isotropic
![]() $ r $
plane in
$ r $
plane in
![]() $ {\mathrm{\mathbb{C}}}^{2r} $
. The following proposition is immediate and well-known.
$ {\mathrm{\mathbb{C}}}^{2r} $
. The following proposition is immediate and well-known.
Proposition 3.7.
If
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
is a tuple indexing a Hodge representation (2.1) (cf. Theorem 3.1), then the resulting Hodge domain
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
is a tuple indexing a Hodge representation (2.1) (cf. Theorem 3.1), then the resulting Hodge domain
![]() $ {D}_{\phi } $
is horizontal if and only if
$ {D}_{\phi } $
is horizontal if and only if
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
is a sum of those pairs listed in Table 3.1.
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}\right) $
is a sum of those pairs listed in Table 3.1.
In general the Hodge domains
![]() $ D \subset $
Ď are cut out by positivity conditions defined by a Hermitian form
$ D \subset $
Ď are cut out by positivity conditions defined by a Hermitian form
![]() $ \mathrm{\mathscr{H}} $
. For example, in the case of period domains, the compact dual essentially encodes the first Hodge–Riemann bilinear relation, and the second Hodge–Riemann bilinear relation is the positivity condition cutting out
$ \mathrm{\mathscr{H}} $
. For example, in the case of period domains, the compact dual essentially encodes the first Hodge–Riemann bilinear relation, and the second Hodge–Riemann bilinear relation is the positivity condition cutting out
![]() $ D $
. To illustrate this, we describe the Hodge domains for the first three rows of Table 3.1.
$ D $
. To illustrate this, we describe the Hodge domains for the first three rows of Table 3.1.
-
(1) In the case of Ď
 $ = $
Gr
$ = $
Gr
 $ \left(a, {\mathrm{\mathbb{C}}}^{a+b}\right) $
, we note that
$ \left(a, {\mathrm{\mathbb{C}}}^{a+b}\right) $
, we note that
 $ {\mathrm{\mathbb{C}}}^{a+b} $
has an underlying real structure, and we fix a nondegenerate Hermitian form
$ {\mathrm{\mathbb{C}}}^{a+b} $
has an underlying real structure, and we fix a nondegenerate Hermitian form
 $ \mathrm{\mathscr{H}} $
on
$ \mathrm{\mathscr{H}} $
on
 $ {\mathrm{\mathbb{C}}}^{a+b} $
of signature
$ {\mathrm{\mathbb{C}}}^{a+b} $
of signature
 $ \left(a, b\right) $
. Then
$ \left(a, b\right) $
. Then $$ D=\left\{E\in \mathrm{Gr}\left(a, {\mathrm{\mathbb{C}}}^{a+b}\right){\left|\mathrm{\mathscr{H}}\right|}_E\mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
$$ D=\left\{E\in \mathrm{Gr}\left(a, {\mathrm{\mathbb{C}}}^{a+b}\right){\left|\mathrm{\mathscr{H}}\right|}_E\mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
-
(2) In the case that Ď
 $ ={\mathcal{Q}}^d={\mathrm{Gr}}^Q\left(1, {\mathrm{\mathbb{C}}}^{d+2}\right) $
we define a Hermitian form
$ ={\mathcal{Q}}^d={\mathrm{Gr}}^Q\left(1, {\mathrm{\mathbb{C}}}^{d+2}\right) $
we define a Hermitian form
 $ \mathrm{\mathscr{H}} $
on
$ \mathrm{\mathscr{H}} $
on
 $ {\mathrm{\mathbb{C}}}^{d+2} $
by
$ {\mathrm{\mathbb{C}}}^{d+2} $
by
 $ \mathrm{\mathscr{H}}\left(u, v\right)=-Q\left(u,\overline{v}\right) $
. Then
$ \mathrm{\mathscr{H}}\left(u, v\right)=-Q\left(u,\overline{v}\right) $
. Then $$ D=\left\{E\in {\mathrm{Gr}}^Q\left(1, {\mathrm{\mathbb{C}}}^{d+2}\right){\left|\mathrm{\mathscr{H}}\right|}_E \mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
$$ D=\left\{E\in {\mathrm{Gr}}^Q\left(1, {\mathrm{\mathbb{C}}}^{d+2}\right){\left|\mathrm{\mathscr{H}}\right|}_E \mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
-
(3) In the case that Ď
 $ ={\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right) $
we define a Hermitian form
$ ={\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right) $
we define a Hermitian form
 $ \mathrm{\mathscr{H}} $
on
$ \mathrm{\mathscr{H}} $
on
 $ {\mathrm{\mathbb{C}}}^{2r} $
by
$ {\mathrm{\mathbb{C}}}^{2r} $
by
 $ \mathrm{\mathscr{H}}\left(u, v\right)=\mathbf{i}Q\left(u,\overline{v}\right) $
. Then
$ \mathrm{\mathscr{H}}\left(u, v\right)=\mathbf{i}Q\left(u,\overline{v}\right) $
. Then $$ D=\left\{E\in {\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right){\left|\mathrm{\mathscr{H}}\right|}_E\mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
$$ D=\left\{E\in {\mathrm{Gr}}^Q\left(r, {\mathrm{\mathbb{C}}}^{2r}\right){\left|\mathrm{\mathscr{H}}\right|}_E\mathrm{is} \mathrm{pos} \mathrm{def}\right\}. $$
Table 3.1 Data underlying irreducible Hermitian symmetric Hodge domains

4. Example: Hodge domains for level 2 Hodge structures
The purpose of this section is to illustrate the application of the strategy outlined in
![]() $ \S $
3 in the case that
$ \S $
3 in the case that
![]() $ \mathcal{D}={\mathcal{D}}_{\mathrm{h}} $
is the period domain parameterizing
$ \mathcal{D}={\mathcal{D}}_{\mathrm{h}} $
is the period domain parameterizing
![]() $ Q $
–polarized, (effective) weight two Hodge structures on
$ Q $
–polarized, (effective) weight two Hodge structures on
![]() $ {V}_{\mathrm{\mathbb{R}}} $
with Hodge numbers
$ {V}_{\mathrm{\mathbb{R}}} $
with Hodge numbers
Equivalently,
![]() $ \varphi \in \mathcal{D} $
parameterizes Hodge decompositions
$ \varphi \in \mathcal{D} $
parameterizes Hodge decompositions
with
(We assume throughout that
![]() $ {h}^{1,1}={\dim}_{\mathrm{\mathbb{C}}} {V}^{1,1}\ne 0. $
) Geometrically such Hodge structures arise when studying smooth projective surfaces with
$ {h}^{1,1}={\dim}_{\mathrm{\mathbb{C}}} {V}^{1,1}\ne 0. $
) Geometrically such Hodge structures arise when studying smooth projective surfaces with
![]() $ {p}_g=2 $
.
$ {p}_g=2 $
.
We have
As discussed in
![]() $ \S $
1.3 it suffices to identify the irreducible Hodge representations (2.1) with either
$ \S $
1.3 it suffices to identify the irreducible Hodge representations (2.1) with either
![]() $ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
or
$ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
or
![]() $ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
, and
$ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
, and
![]() $ h \le {h}^{1,1} $
. (Each such Hodge representation corresponds to a Hodge subdomain
$ h \le {h}^{1,1} $
. (Each such Hodge representation corresponds to a Hodge subdomain
![]() $ D={G}_{\mathrm{\mathbb{R}}}\cdot \phi $
of the period domain
$ D={G}_{\mathrm{\mathbb{R}}}\cdot \phi $
of the period domain
![]() $ \mathcal{D}={\mathcal{D}}_{{\mathrm{h}}_{\phi }} $
parameterizing
$ \mathcal{D}={\mathcal{D}}_{{\mathrm{h}}_{\phi }} $
parameterizing
![]() $ Q $
–polarized Hodge structures on
$ Q $
–polarized Hodge structures on
![]() $ {V}_{\mathrm{\mathbb{R}}} $
with Hodge numbers
$ {V}_{\mathrm{\mathbb{R}}} $
with Hodge numbers
![]() $ {\mathbf{h}}_{\phi }. $
) The analysis decomposes into three parts:
$ {\mathbf{h}}_{\phi }. $
) The analysis decomposes into three parts:
-
(A) We begin with the simplifying assumptions that
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is simple and that
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is simple and that
 $ D $
is horizontal. This has the strong computational advantage that we may take the grading element
$ D $
is horizontal. This has the strong computational advantage that we may take the grading element
 $ \mathtt{E} $
to be as listed in Table 3.1. The resulting domains are enumerated in Theorems 4.1 and 4.3.
$ \mathtt{E} $
to be as listed in Table 3.1. The resulting domains are enumerated in Theorems 4.1 and 4.3. -
(B) Continuing to assume that
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is simple, we turn to the case that horizontality fails; the domains are enumerated in Theorem 4.4.
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is simple, we turn to the case that horizontality fails; the domains are enumerated in Theorem 4.4. -
(C) Finally we consider in Theorem 4.6 the case that
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is semisimple (but not simple).
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
is semisimple (but not simple).
Together Theorems 4.1, 4.3, 4.4 and 4.6 give a complete list of the irreducible Hodge representations (2.1) with
![]() $ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
.
$ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
.
Theorem 4.1.
The irreducible Hodge representations (2.1) with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple,
![]() $ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
and horizontal Hodge domain
$ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
and horizontal Hodge domain
![]() $ D \subset {\mathcal{D}}_{\left(1,h,1\right)} $
are given by the following tuples
$ D \subset {\mathcal{D}}_{\left(1,h,1\right)} $
are given by the following tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
:
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
:
-
(i) Period domains:
 $ \left(\mathfrak{so} \left(h+2, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_1,0\right) $
, with
$ \left(\mathfrak{so} \left(h+2, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_1,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
.
$ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
. -
(ii) Complex balls: both tuples
 $$ \left(\mathfrak{sl}\left(1+r, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_r, -1/\left(r+1\right)\right) and \left(\mathfrak{sl}\left(1+r, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^r, {\omega}_1, -1/\left(r+1\right)\right) $$
$$ \left(\mathfrak{sl}\left(1+r, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_r, -1/\left(r+1\right)\right) and \left(\mathfrak{sl}\left(1+r, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^r, {\omega}_1, -1/\left(r+1\right)\right) $$
yield Hodge representations with
![]() $ {\mathbf{h}}_{\phi }=\left(1,2r, 1\right) $
.
$ {\mathbf{h}}_{\phi }=\left(1,2r, 1\right) $
.
Remark 4.2 (Geometric realizations). Pearlstein and Zhang (Reference Pearlstein and Zhang2019) have exhibited geometric realizations of
![]() $ {G}_{\varphi }={G}_1\times {G}_2 $
with
$ {G}_{\varphi }={G}_1\times {G}_2 $
with
![]() $ {G}_i $
one of
$ {G}_i $
one of
![]() $ \mathrm{SO}\left(2, {h}_i\right) $
or
$ \mathrm{SO}\left(2, {h}_i\right) $
or
![]() $ \mathrm{U}\left(1, {r}_i\right) $
, corresponding to the two cases/factors of Theorem 4.1.
$ \mathrm{U}\left(1, {r}_i\right) $
, corresponding to the two cases/factors of Theorem 4.1.
Theorem 4.3.
The irreducible Hodge representations (2.1) with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple,
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple,
![]() $ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
and horizontal Hodge domain
$ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
and horizontal Hodge domain
![]() $ D \subset {\mathcal{D}}_{\left(2,h,2\right)} $
are all grassmannian Hodge domains (corresponding to the first row of Table 3.1), and are given by the following tuples
$ D \subset {\mathcal{D}}_{\left(2,h,2\right)} $
are all grassmannian Hodge domains (corresponding to the first row of Table 3.1), and are given by the following tuples
![]() $ \Big(\mathfrak{sl}\left(a+b, \mathrm{\mathbb{C}}\right) $
,
$ \Big(\mathfrak{sl}\left(a+b, \mathrm{\mathbb{C}}\right) $
,
![]() $ {\mathrm{A}}^a, \mu, c\Big) $
:
$ {\mathrm{A}}^a, \mu, c\Big) $
:
-
(i) The tuples
yield Hodge representations with $$ \left(\mathfrak{sl}\left(3, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_2,2/3\right) and \left(\mathfrak{sl}\left(3, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_1, -2/3\right) $$
$$ \left(\mathfrak{sl}\left(3, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_2,2/3\right) and \left(\mathfrak{sl}\left(3, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^1, {\omega}_1, -2/3\right) $$
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{2,2,2}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{2,2,2}\right) $
.
-
(ii) The tuple
 $ \left(\mathfrak{sl}\left(r+1, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^2, {\omega}_1,2/\left(r+1\right)\right) $
yields a Hodge representation with
$ \left(\mathfrak{sl}\left(r+1, \mathrm{\mathbb{C}}\right), {\mathbf{A}}^2, {\omega}_1,2/\left(r+1\right)\right) $
yields a Hodge representation with
 $ {\mathbf{h}}_{\phi }=\left(2,2r-2,2\right) $
.
$ {\mathbf{h}}_{\phi }=\left(2,2r-2,2\right) $
.
Theorem 4.4.
The irreducible Hodge representations (2.1) with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple and
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
simple and
![]() $ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
, for which the Hodge domain
$ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
, for which the Hodge domain
![]() $ D \subset {\mathcal{D}}_{\mathbf{h}} $
is not horizontal are given by the following tuples
$ D \subset {\mathcal{D}}_{\mathbf{h}} $
is not horizontal are given by the following tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
:
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
:
-
(i) Period domains:
 $ \left(\mathfrak{so} \left(h+4, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_1,0\right) $
, with
$ \left(\mathfrak{so} \left(h+4, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_1,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
.
$ {\mathbf{h}}_{\phi }=\left(2, h, 2\right) $
. -
(ii) Special Linear contact domains:
 $ \left(\mathfrak{sl}\left(r+1, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1+{\mathrm{A}}^r, {\omega}_1,0\right) $
, with
$ \left(\mathfrak{sl}\left(r+1, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1+{\mathrm{A}}^r, {\omega}_1,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(2,2r-2,2\right) $
.
$ {\mathbf{h}}_{\phi }=\left(2,2r-2,2\right) $
. -
(iii) Special Linear contact domains:
 $ \left(\mathfrak{sl}\left(4, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1+{\mathrm{A}}^3, {\omega}_2,0\right) $
, with
$ \left(\mathfrak{sl}\left(4, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1+{\mathrm{A}}^3, {\omega}_2,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{2,2,2}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{2,2,2}\right) $
. -
(iv) Spinor contact domains:
 $ \left(\mathfrak{so}\left(5, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_2,0\right) $
and
$ \left(\mathfrak{so}\left(5, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_2,0\right) $
and
 $ \left(\mathfrak{so} \left(7, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_3,0\right) $
, both with
$ \left(\mathfrak{so} \left(7, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_3,0\right) $
, both with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{2,4,2}\right) $
. (The first is quaternionic, the second is real.)
$ {\mathbf{h}}_{\phi }=\left(\mathrm{2,4,2}\right) $
. (The first is quaternionic, the second is real.) -
(v) Symplectic contact domains:
 $ \left(\mathfrak{sp}\left(2\mathrm{r}, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1, {\omega}_1,0\right) $
, with
$ \left(\mathfrak{sp}\left(2\mathrm{r}, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^1, {\omega}_1,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(2,4\left(r-1\right), 2\right) $
.
$ {\mathbf{h}}_{\phi }=\left(2,4\left(r-1\right), 2\right) $
. -
(vi) Exceptional contact domains:
 $ \left({\mathfrak{g}}_2, {\mathrm{A}}^2, {\omega}_1,0\right) $
with
$ \left({\mathfrak{g}}_2, {\mathrm{A}}^2, {\omega}_1,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{2,3,2}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{2,3,2}\right) $
.
See Han and Robles (Reference Han and Robles2020,
![]() $ \S $
A.8) for further discussion of the domains
$ \S $
A.8) for further discussion of the domains
![]() $ D $
appearing in Theorem 4.4 as homogeneous spaces.
$ D $
appearing in Theorem 4.4 as homogeneous spaces.
Remark 4.5. The Spinor contact domain given by the tuple
![]() $ \left(\mathfrak{so} \left(5, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_2,0\right) $
in Theorem 4.3(iv) is a special case of Theorem 4.3(v) under the isomorphism
$ \left(\mathfrak{so} \left(5, \mathrm{\mathbb{C}}\right), {\mathrm{A}}^2, {\omega}_2,0\right) $
in Theorem 4.3(iv) is a special case of Theorem 4.3(v) under the isomorphism
![]() $ \mathfrak{so}\left(5, \mathrm{\mathbb{C}}\right)\simeq \mathfrak{sp}\left(4, \mathrm{\mathbb{C}}\right) $
.
$ \mathfrak{so}\left(5, \mathrm{\mathbb{C}}\right)\simeq \mathfrak{sp}\left(4, \mathrm{\mathbb{C}}\right) $
.
Theorem 4.6.
The irreducible Hodge representations (2.1) with
![]() $ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
and
$ {\mathbf{h}}_{\phi} \le \mathbf{h}=\left(2, {h}^{1,1},2\right) $
and
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
semisimple (but not simple) are given by:
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
semisimple (but not simple) are given by:
-
(i)
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_2\mathrm{\mathbb{C}} $
acting on
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_2\mathrm{\mathbb{C}} $
acting on
 $ U={\mathrm{\mathbb{C}}}^2\otimes {\mathrm{\mathbb{C}}}^2 $
with
$ U={\mathrm{\mathbb{C}}}^2\otimes {\mathrm{\mathbb{C}}}^2 $
with
 $ \mathtt{E}={\mathrm{A}}^1+{\mathrm{A}}^2 $
; and
$ \mathtt{E}={\mathrm{A}}^1+{\mathrm{A}}^2 $
; and -
(ii)
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_4\mathrm{\mathbb{C}} $
acting on
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}}={\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_4\mathrm{\mathbb{C}} $
acting on
 $ U={\mathrm{\mathbb{C}}}^2\otimes {\mathrm{\mathbb{C}}}^4 $
with
$ U={\mathrm{\mathbb{C}}}^2\otimes {\mathrm{\mathbb{C}}}^4 $
with
 $ \mathtt{E}={\mathrm{A}}^1+{\mathrm{A}}^3 $
.
$ \mathtt{E}={\mathrm{A}}^1+{\mathrm{A}}^3 $
.Each of these Hodge representations is real (implying ). The Hodge numbers are and
 $ \mathbf{h}=\left(\mathrm{1,2,1}\right) $
and
$ \mathbf{h}=\left(\mathrm{1,2,1}\right) $
and
 $ \mathbf{h}=\left(\mathrm{2,4,2}\right) $
$ \mathbf{h}=\left(\mathrm{2,4,2}\right) $
 $ c=0 $
respectively.
$ c=0 $
respectively.
The theorems are proved in the Appendix (Han & Robles, Reference Han and Robles2020,
![]() $ \S $
A).
$ \S $
A).
5. Hodge representations of Calabi–Yau type
We say that a Hodge representation (2.1) is of Calabi–Yau type (or CY-type if the first Hodge number
![]() $ {h}_{\phi}^{n,0}=1 $
. The irreducible CY-Hodge representations with
$ {h}_{\phi}^{n,0}=1 $
. The irreducible CY-Hodge representations with
![]() $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
semisimple are classified in (Robles, Reference Robles2014, Proposition 6.1). They are precisely the tuples
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
semisimple are classified in (Robles, Reference Robles2014, Proposition 6.1). They are precisely the tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 with
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 with
![]() $ c=0 $
(
$ c=0 $
(
![]() $ \S $
2.7), and such that:
$ \S $
2.7), and such that:
-
(a)
 $ {\mu}^i=0 $
whenever
$ {\mu}^i=0 $
whenever
 $ {\alpha}_i\left(\mathtt{E}\right)=0 $
, where
$ {\alpha}_i\left(\mathtt{E}\right)=0 $
, where
 $ {\alpha}_i $
are the simple roots of (the semisimple)
$ {\alpha}_i $
are the simple roots of (the semisimple)
 $ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and the
$ {\mathfrak{g}}_{\mathrm{\mathbb{C}}} $
and the
 $ 0 \le {\mu}^i\in \mathrm{\mathbb{Z}} $
are the coefficients of
$ 0 \le {\mu}^i\in \mathrm{\mathbb{Z}} $
are the coefficients of
 $ \mu ={\mu}^i{\omega}_i $
as a linear combination of the fundamental weights
$ \mu ={\mu}^i{\omega}_i $
as a linear combination of the fundamental weights
 $ {\omega}_i $
;
$ {\omega}_i $
; -
(b) either the representation is real
 $ \Big(\mathrm{equivalently}, U={U}^{\ast} \mathrm{and} \mu \left({\mathrm{T}}_{\phi}\right) $
is an even integer), or
$ \Big(\mathrm{equivalently}, U={U}^{\ast} \mathrm{and} \mu \left({\mathrm{T}}_{\phi}\right) $
is an even integer), or -
(c)
 $ \mu \left({\mathtt{E}}_{\phi}\right)\ne {\mu}^{\ast}\left({\mathtt{E}}_{\phi}\right) $
, and
$ \mu \left({\mathtt{E}}_{\phi}\right)\ne {\mu}^{\ast}\left({\mathtt{E}}_{\phi}\right) $
, and
 $ U $
is necessarily complex.
$ U $
is necessarily complex.
Remark 5.1. The condition (a) above is equivalent to the statement that
![]() $ \dim {U}_{\mu \left(\mathtt{E}\right)}=1 $
; equivalently,
$ \dim {U}_{\mu \left(\mathtt{E}\right)}=1 $
; equivalently,
![]() $ {U}_{\mu \left(\mathtt{E}\right)} $
is a highest weight line.
$ {U}_{\mu \left(\mathtt{E}\right)} $
is a highest weight line.
Theorem 5.2.
An irreducible Hodge representation (2.1) is of
![]() $ CY $
-type if and only if the corresponding tuple
$ CY $
-type if and only if the corresponding tuple
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 has the properties:
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 has the properties:
-
(i) The condition (a) above holds.
-
(ii) If
 $ {U}_{\mu } $
is not real (with respect to the semisimple
$ {U}_{\mu } $
is not real (with respect to the semisimple
 $ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
), then
$ {\mathfrak{g}}_{\mathrm{\mathbb{R}}} $
), then
 $ \mu \left(\mathtt{E}\right)+c>{\mu}^{\ast}\left(\mathtt{E}\right)-c $
.
$ \mu \left(\mathtt{E}\right)+c>{\mu}^{\ast}\left(\mathtt{E}\right)-c $
.
Proof. It is straightforward to deduce the theorem from the proof of Robles (Reference Robles2014, Proposition 6.1) and the discussion of
![]() $ \S $
2.7. Details are left to the reader.
$ \S $
2.7. Details are left to the reader.
![]() $ \square $
$ \square $
Example 5.3. The (rational) Hodge groups of K3 type (CY 2-fold type) were determined by Zarhin (Reference Zarhin1983). The corresponding (real) Hodge representations (2.1) are those with Hodge numbers
![]() $ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
. The list of all associated tuples (Theorem 3.1) is.
$ {\mathbf{h}}_{\phi }=\left(1, h, 1\right) $
. The list of all associated tuples (Theorem 3.1) is.
-
(i)
 $ \left({\mathfrak{so}}_{h+2}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right) $
, with
$ \left({\mathfrak{so}}_{h+2}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right) $
, with
 $ {\mathrm{h}}_{\phi }=\left(1, h, 1\right) $
and
$ {\mathrm{h}}_{\phi }=\left(1, h, 1\right) $
and
 $ h \ge 3 $
.Footnote
3
$ h \ge 3 $
.Footnote
3 -
(ii)
 $ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1+{\mathrm{A}}^2, {\omega}_1+{\omega}_2,0\right) $
, with
$ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}\oplus {\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1+{\mathrm{A}}^2, {\omega}_1+{\omega}_2,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,2,1}\right) $
.Footnote
4
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,2,1}\right) $
.Footnote
4 -
(iii)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1, \frac{1}{r+1}\right) $
with
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1, \frac{1}{r+1}\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1,2r, 1\right) $
and
$ {\mathbf{h}}_{\phi }=\left(1,2r, 1\right) $
and
 $ r \ge 2 $
.
$ r \ge 2 $
. -
(iv)
 $ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1,2{\omega}_1,0\right) $
with
$ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1,2{\omega}_1,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,1,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,1,1}\right) $
. -
(v)
 $ \left({\mathfrak{sl}}_4\mathrm{\mathbb{C}}, {\mathrm{A}}^2, {\omega}_2,0\right) $
, with
$ \left({\mathfrak{sl}}_4\mathrm{\mathbb{C}}, {\mathrm{A}}^2, {\omega}_2,0\right) $
, with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,4,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,4,1}\right) $
.
Example 5.4. The set of all Hodge representations (2.1) of CY 3-fold type (Hodge numbers
![]() $ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right)\Big) $
is enumerated in Han (Reference Han2021). In the case that
$ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right)\Big) $
is enumerated in Han (Reference Han2021). In the case that
![]() $ {D}_{\phi } $
is horizontal (and therefore Hermitian) these are of particular interest (Friedman & Laza, Reference Friedman and Laza2013; Reference Friedman and Laza2014; Gross, Reference Gross1994). In fact, this completes the classification begun in Friedman and Laza (Reference Friedman and Laza2013,
$ {D}_{\phi } $
is horizontal (and therefore Hermitian) these are of particular interest (Friedman & Laza, Reference Friedman and Laza2013; Reference Friedman and Laza2014; Gross, Reference Gross1994). In fact, this completes the classification begun in Friedman and Laza (Reference Friedman and Laza2013,
![]() $ \S $
2.3); our (v), (vii) and (x) are omitted from Friedman and Laza (Reference Friedman and Laza2013, Corollary 2.29). The corresponding (horizontal) tuples
$ \S $
2.3); our (v), (vii) and (x) are omitted from Friedman and Laza (Reference Friedman and Laza2013, Corollary 2.29). The corresponding (horizontal) tuples
![]() $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 are.
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}, \mathtt{E}, \mu, c\right) $
of Theorem 3.1 are.
-
(i)
 $ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1,3{\omega}_1,0\right) $
with
$ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1,3{\omega}_1,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1,1,1,1\right) $
.
$ {\mathbf{h}}_{\phi }=\left(1,1,1,1\right) $
. -
(ii)
 $ {\left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right)}^{\oplus 3} $
with
$ {\left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right)}^{\oplus 3} $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,3,3,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,3,3,1}\right) $
. -
(iii)
 $ \left({\mathfrak{sl}}_6\mathrm{\mathbb{C}}, {\mathrm{A}}^3, {\omega}_3,0\right) $
with
$ \left({\mathfrak{sl}}_6\mathrm{\mathbb{C}}, {\mathrm{A}}^3, {\omega}_3,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,9,9,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,9,9,1}\right) $
. -
(iv)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1, \frac{3}{2}-\frac{r}{r+1}\right) $
with
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1, \frac{3}{2}-\frac{r}{r+1}\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1, r, r, 1\right) $
.
$ {\mathbf{h}}_{\phi }=\left(1, r, r, 1\right) $
. -
(v)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1,2{\omega}_1, \frac{3}{2}-\frac{2r}{r+1}\right) $
with
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1,2{\omega}_1, \frac{3}{2}-\frac{2r}{r+1}\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
$ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
 $ h+1=\frac{1}{2}\left(r+1\right)\left(r+2\right) $
.
$ h+1=\frac{1}{2}\left(r+1\right)\left(r+2\right) $
. -
(vi)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^2, {\omega}_2, \frac{3}{2}-\frac{2\left(r-1\right)}{r+1}\right) $
with
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^2, {\omega}_2, \frac{3}{2}-\frac{2\left(r-1\right)}{r+1}\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
$ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
 $ h+1=\frac{1}{2}r\left(r+1\right) $
.
$ h+1=\frac{1}{2}r\left(r+1\right) $
. -
(vii)
 $ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1\right)\oplus \left({\mathfrak{sl}}_{r^{\prime }+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1\right) $
and
$ \left({\mathfrak{sl}}_{r+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1\right)\oplus \left({\mathfrak{sl}}_{r^{\prime }+1}\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1\right) $
and
 $ c=\frac{3}{2}-\frac{r}{r+1}-\frac{r^{\prime }}{r+1} $
, with
$ c=\frac{3}{2}-\frac{r}{r+1}-\frac{r^{\prime }}{r+1} $
, with
 $ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
$ {\mathbf{h}}_{\phi }=\left(1, h, h, 1\right) $
and
 $ h=r+{r}^{\prime }+r{r}^{\prime } $
.
$ h=r+{r}^{\prime }+r{r}^{\prime } $
. -
(viii)
 $ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right)\oplus \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\prime }, {\mathtt{E}}^{\prime }, {\mu}^{\prime }, {c}^{\prime}\right) $
with
$ \left({\mathfrak{sl}}_2\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,0\right)\oplus \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\prime }, {\mathtt{E}}^{\prime }, {\mu}^{\prime }, {c}^{\prime}\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1, {h}^{\prime }+1, {h}^{\prime }+1,1\right) $
, where
$ {\mathbf{h}}_{\phi }=\left(1, {h}^{\prime }+1, {h}^{\prime }+1,1\right) $
, where
 $ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\prime }, {\mathtt{E}}^{\prime }, {\mu}^{\prime }, {c}^{\prime}\right) $
is any tuple of Example 5.3 with Hodge numbers
$ \left({\mathfrak{g}}_{\mathrm{\mathbb{C}}}^{\prime }, {\mathtt{E}}^{\prime }, {\mu}^{\prime }, {c}^{\prime}\right) $
is any tuple of Example 5.3 with Hodge numbers
 $ {\mathbf{h}}^{\prime }=\left(1, {h}^{\prime }, 1\right) $
.
$ {\mathbf{h}}^{\prime }=\left(1, {h}^{\prime }, 1\right) $
. -
(ix)
 $ \left({\mathfrak{sp}}_6\mathrm{\mathbb{C}}, {\mathrm{A}}^3, {\omega}_3,0\right) $
with
$ \left({\mathfrak{sp}}_6\mathrm{\mathbb{C}}, {\mathrm{A}}^3, {\omega}_3,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,6,6,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,6,6,1}\right) $
. -
(x)
 $ \left({\mathfrak{so}}_m\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,1/2\right) $
with
$ \left({\mathfrak{so}}_m\mathrm{\mathbb{C}}, {\mathrm{A}}^1, {\omega}_1,1/2\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(1, m-1, m-1,1\right) $
.
$ {\mathbf{h}}_{\phi }=\left(1, m-1, m-1,1\right) $
. -
(xi)
 $ \left({\mathfrak{so}}_{10}\mathrm{\mathbb{C}}, {\mathrm{A}}^5, {\omega}_5,1/4\right) $
with
$ \left({\mathfrak{so}}_{10}\mathrm{\mathbb{C}}, {\mathrm{A}}^5, {\omega}_5,1/4\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,15,15,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,15,15,1}\right) $
. -
(xii)
 $ \left({\mathfrak{so}}_{12}\mathrm{\mathbb{C}}, {\mathrm{A}}^6, {\omega}_6,0\right) $
with
$ \left({\mathfrak{so}}_{12}\mathrm{\mathbb{C}}, {\mathrm{A}}^6, {\omega}_6,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,15,15,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,15,15,1}\right) $
. -
(xiii)
 $ \left({\mathfrak{e}}_6, {\mathrm{A}}^6, {\omega}_6,1/6\right) $
with
$ \left({\mathfrak{e}}_6, {\mathrm{A}}^6, {\omega}_6,1/6\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,26,26,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,26,26,1}\right) $
. -
(xiv)
 $ \left({\mathfrak{e}}_7, {\mathrm{A}}^7, {\omega}_7,0\right) $
with
$ \left({\mathfrak{e}}_7, {\mathrm{A}}^7, {\omega}_7,0\right) $
with
 $ {\mathbf{h}}_{\phi }=\left(\mathrm{1,27,27,1}\right) $
.
$ {\mathbf{h}}_{\phi }=\left(\mathrm{1,27,27,1}\right) $
.
Author Contributions
Results proved by XH and CR. Article written by CR.
Funding Information
This work was supported by the National Science Foundation, Division of Mathematical Sciences, CR grant numbers 1611939 and 1906352.
Data Availability Statement
Data available within the article or its supplementary materials.
Conflicts of Interest
XH and CR declare none.
Supplementary Materials
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/exp.2020.55.

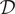
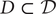
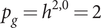


Comments
Comments to the Author: Given a classifying space for polarized Hodge structures with given Hodge numbers h, its Mumford-Tate subdomains are the loci on which the Hodge (or Mumford-Tate) group drops. From the standpoint of algebraic geometry, having a classification in hand is valuable given the control exerted by the Hodge group on monodromy, algebraic cycles, degenerations, and arithmetic. In particular, the horizontal subdomains and the compactifications of their quotients have played a central role in recent studies of completions of period maps, and of families of algebraic varieties parametrized by automorphic data. The classification of all real M-T subdomain types provided herein for h=(2,n,2), and the authors' completion of the Friedman-Laza classification of (real types of) horizontal subdomains for Hodge numbers h=(1,n,n,1), are thus an important addition to the literature: we may think of each of the Hodge representations they enumerate (more precisely, each of its Q-forms) as an algebro-geometric realization problem.